Люди: работа, энергия, мощность. Энергия работа мощность физика

Работа. Мощность. Закон сохранения механической энергии [wiki.eduVdom.com]

Пространственной характеристикой действия силы является работа силы - произведение проекции силы на ось Х и перемещения тела вдоль этой оси: $$ A=\left ( Fcos \alpha \right )\Delta x $$ где F - модуль силы, $ \Delta x $ - модуль перемещения, $ \alpha $ - угол между силой и перемещением. Единица работы - джоуль $ 1Дж=1кг\cdot м^{2}/с^{2} $

В механике силы делят на две группы: потенциальные и непотенциальные.

Потенциальная сила - сила, работа которой при перемещении материальной точки зависит только от начального и конечного положений точки в пространстве.

Для непотенциальной силы работа зависит от траектории движения материальной точки между начальным и конечным положениями точки.

Потенциальная энергия тела в данной точке - скалярная физическая величина, равная работе, совершаемой потенциальной силой при перемещении тела из этой точки в точку, принятую за нуль отсчёта потенциальной энергии.

Потенциальная энергия тела на высоте Н над поверхностью Земли $$ E_{p}=mgH $$ нуль отсчёта потенциальной энергии выбран на поверхности Земли.

Потенциальная энергия тела, находящегося в поле тяжести Земли на расстоянии г от её центра. $$ E_{p}\left ( r \right )=-G\frac{mM_{З}}{r} $$

где $ M_{З} $- масса Земли. Нулевой уровень потенциальной энергии в бесконечно удаленной точке. Потенциальная энергия упруго деформированной пружины жёстко- стью k, растянугой на величину х, $$ E_{p}=\frac{kx^{2}}{2} $$ нулевой уровень потенциальной энергии - в положении равновесия.

Принцип минимума потенциальной энергии: любая замкнутая система стремится перейти а такое состояние, в котором её потенциальная энергия минимальна.

Кинетическая энергия тела скалярная физическая величина, численно равная половине произведения массы тела на квадрат его скорости: $$ E_{k}=\frac{mV^{2}}{2} $$ Соответственно $$ E_{k0}=\frac{mV_{0}^{2}}{2} $$ где $ V_{0} $ - скорость тела в начальныймомент времени.

Теорема о кинетической энергии: изменение кинетической энергии материальной точки равно работе всех сил, действующих на эту точку

$$ E_{k}-E_{k0}=A $$

Средняя мощность - скалярная физическая величина, равная отношению работы к промежутку времени, за который она совершена: $$ P_{ср}=\frac{A}{t} $$

Мпювенная мощность силы, действующей на тело, равна произведению модуля скорости тела на проекцию силы на направление мгновенной скорости тела: $$ P=F_{x}V_{x} $$ Полная механическая энергия системы - сумма её кинетической и потенциальной энергий: $$ E=E_{k}+E_{p} $$

Консервативная система - механическая система, в которой действуют только потенциальные силы.

Закон сохранения механической энергии: в консервативной системе полная механическая энергия сохраняется (не изменяется со временем): $$ E_{k}+E_{p}=E_{k0}+E_{p0} $$ Кинетическая энергия может переходить в потенциальную и обратно в равных количествах.

Абсолютно неупругий удар столкновение тел, в результате которого тела движутся как единое целое. При таком ударе кинетическая энергия системы не сохраняется.

Абсолютно упругий удар - столкновение, при котором деформация тел оказывается обратимой, т. е. исчезает после прекращения взаимодействия. При абсолютно упругом ударе кинетическая энергия системы сохраняется.

wiki.eduvdom.com

Механическая работа, энергия, мощность | Физика для студентов | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать это изменение, в механике вводится понятие работы силы. Если F=const, то:

A=Fs•S=F•S•cosα (2.14), где Fs – проекция вектора силы на направление перемещения. «Работа – это скалярная величина». В общем случае сила может изменяться как по модулю, так и по направлению, поэтому:

A=Fs•dS (2.15) [A]=1Дж=1Н•м

Энергия – универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В механике рассматривается кинетическая и потенциальная энергии механической системы.

Кинетическая энергия – это энергия механического движения системы. Сила F, действуя на тело, вызывает его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы.

dA=dT (2.16)

mυdυ=dT; T=mυdυ=mυ2/2 (2.17)

Таким образом, тело массой m, движущееся со скоростью υ, обладает кинетической энергией: T=mυ2/2 (2.18)

Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Если взаимодействие тел осуществляется посредством силовых полей, характеризующимся тем, что работа сил при перемещении тела не зависит от формы траектории, а зависит только от начального и конечного положений, то такие поля называются потенциальными, а силы, действующие в них, - консервативными. Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа в потенциальном поле сил совершается за счет убыли потенциальной энергии:

dA=-dП (2.19)

Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:

N=dA/dt=F•dr/dt=Fυ (2.20)

N – скалярная величина. Единица измерения мощности – 1Ватт (Вт), 1Вт=1Дж/с

testent.ru

Люди: работа, энергия, мощность

Физика > Люди: работа, энергия, мощность

 

Человеческое тело трансформирует энергию, накопленную в пище, в работу, тепловую энергию и химическую, сохраняющуюся в жировой ткани.

Задача обучения

• Вычислить факторы, влияющие на Базальную скорость метаболизма (БСМ).

Основные пункты

• Скорость метаболизма – скорость, с которой организм использует энергию пищи для поддержания жизни и выполнения различной работы, а Базальная скорость метаболизма – та же скорость, но в состоянии покоя.
• Энергия в БСМ делится между системами в организме, причем большая часть идет в селезенку и печень, а потом уже в мозг и дальше.
• Примерно 75% калорий используется для поддержания главных функций организма.
• Выполняемую человеком работу иногда называют полезной (работа с внешней средой).
• Количество усвоенной человеком энергии можно вычислить через измерение потребленного кислорода.

Термин

• Базальная скорость метаболизма (БСМ) – количество энергии, расходуемой в период покоя в нейтрально-умеренной среде.

Люди: работа, энергия и сила

Как и прочие организмы, человеческое тело выступает своеобразной машиной по энергетической трансформации. Когда мы говорим о сохранении, то подразумеваем, что химическая энергия в пище переходит в работу, тепловую энергию или остается как химическая энергия в жировой ткани. Большая часть передается в тепловую энергию, хотя точный процент зависит от типа физической активности. Общая часть передачи зависит от количества съеденного и уровня физической активности. Если мы употребляем еды больше, чем нужно для выполнения работы, то остаток переходит в жир.

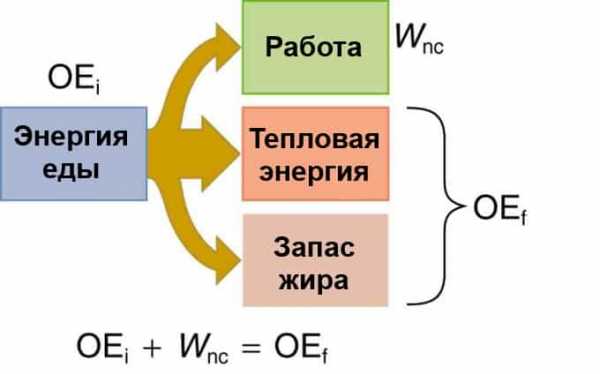
Употребляемая нами энергия трансформируется в работу, тепловую энергию и накопленный жир. Наибольшая часть отдается теплу, хотя все зависит от физической активности

Нуждающиеся в энергии функции

Энергия расходуется на все физические функции: от формирования мысли до поднятия тяжести. И это без учета биения сердца, пищеварительного тракта и многих других процессов, которые мы не осознаем. К примеру, дрожь выступает ответной реакцией на низкий показатель температуры тела. Большую часть энергии требуют почки и печень. Примерно 25% энергии уходит на то, чтобы поддержать энергетический потенциал во всех живых клетках.

Базальная скорость метаболизма

Скорость метаболизма – скорость, с которой организм использует энергию пищи для поддержания жизни и выполнения различной работы, а БСМ – полная скорость трансформации энергии в состоянии покоя. Наибольшая часть отходит печени и селезенке, а дальше уже идет в мозг и т.д. Во время энергичных упражнений скелетные мышцы и сердце заметно увеличивают потребность в энергии. БСМ – индивидуальная черта каждого человека, зависящая от пола, возраста, массы и рода деятельности (поэтому у спортсменов БСМ больше).

Полезная работа

Иногда выполняемую человеком работу называют полезной. Она нуждается в мощности, действующей на расстоянии во внешнем мире, поэтому исключается внутренняя работа (качание крови сердцем). Полезная работа появляется, когда вы поднимаетесь по лестнице или бежите. Силы выступают неконсервативными, поэтому могут менять механическую энергию (KE + PE).

Например, какая мощность у 60-кг женщины, поднимающейся по лестнице высотою в 3 м за 3.50 с, если стартовая точка отдыха составляла 2 м/с?

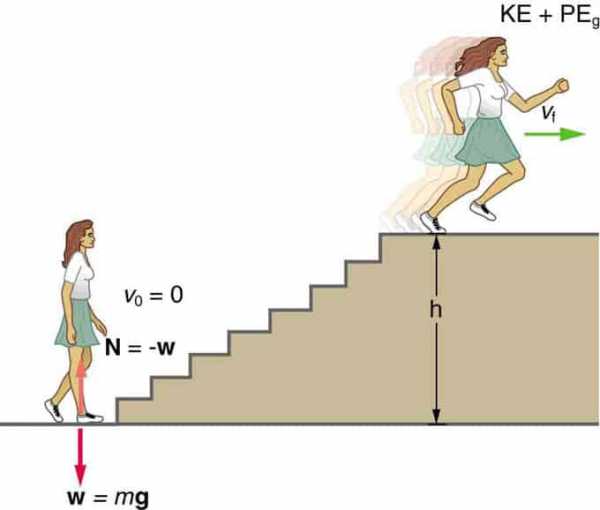
Когда женщина поднимается, начиная с момента отдыха, то трансформирует химическую энергию из пищи в кинетическую и потенциальную гравитации. Мощность зависит от скорости выполнения этого процесса

Мощность зависит от скорости выполнения процесса. Работа в механической энергии выглядит как W = KE + PE. Внизу мы возьмем эти значения как нулевые, поэтому:

Здесь h – вертикальная высота лестницы. Мы можем определить W, а потом поделить его на время, чтобы добыть мощность. Получаем:

Женщина выполняет 1764 Дж работы, чтобы подняться по лестнице, и всего 120 Дж на увеличение кинетической энергии. Поэтому большая часть мощности нужна для восхождения, а не ускорения.

При помощи замера потребляемого кислорода можно вычислить, сколько энергии было использовано при конкретном виде деятельности. Независимо от типа пищи, примерно 20 кДж энергии создается для каждого литра используемого кислорода.

Люди: работа, энергия, мощность

Оцените нашу статью

v-kosmose.com

Глава 3 Работа и энергия §11. Энергия, работа, мощность

Энергия — универсальная мера различных форм движения и взаимодействия. С раз­личными формами движения материи связывают различные формы энергии: механи­ческую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движе­ния материи не изменяется (например, горячее тело нагревает холодное), в дру­гих — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом.

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.

Если тело движется прямолинейнои на него действует постоянная сила F, которая составляет некоторый уголс направлением перемещения, то работа этой силы равна произведению проекции силыFsна направление перемещения (Fs=Fcos), умноженной на перемещение точки приложения силы:

(11.1)

В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементар­ное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным.Элементарной работойсилы F на перемещении dr называетсяскалярнаявеличина

где — угол между векторами F и dr;ds= |dr| — элементарный путь;Fs —проекция вектора F на вектор dr (рис. 13).

Работа силы на участке траектории от точки 1до точки2равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу

(11.2)

Для вычисления этого интеграла надо знать зависимость силы Fs,от путиsвдоль траектории1—2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работаАопределяется на графике площадью заштрихованной фигуры. Если, например, тело движется прямолинейно, силаF=constи=const, то получим

где s— пройденный телом путь (см. также формулу (11.1)).

Из формулы (11.1) следует, что при </2 работа силы положительна, в этом случае составляющаяFsсовпадает по направлению с вектором скорости движе­нияv (см. рис. 13). Если>/2, то работа силы отрицательна. При=/2 (сила направлена перпендикулярно перемещению) работа силы равна нулю.

Единица работы — джоуль(Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Нм).

Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:

(11.3)

За время dt сила Fсовершает работуFdr, и мощность, развиваемая этой силой, в данный момент времени

т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N —величинаскалярная.

Единица мощности — ватт(Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).

§ 12. Кинетическая и потенциальная энергии

Кинетическая энергиямеханической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dAсилы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергииdTтела, т. е.

Используя второй закон Ньютона и умножая на перемещениеdrполучаем

Так как тоdA =mvdv=mvdv=dT, откуда

Таким образом, тело массой т, движущееся со скоростью v,обладает кинетической энергией

(12.1)

Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.

При выводе формулы (12.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньюто­на. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.

Потенциальная энергия— механическая энергия системы тел, определяемая их вза­имным расположением и характером сил взаимодействия между ними.

Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, —консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называетсядиссипатнвной; ее примером является сила трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении кон­фигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

(12.2)

Работа dAвыражается как скалярное произведение силыFна перемещениеdrи выражение (12.2) можно записать в виде

(12.3)

Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению.

Потенциальная энергия может быть определена исходя из (12.3) как

где С— постоянная интегрирования, т. е. потенциальная энергия определяется с точ­ностью до некоторой произвольной постоянной. Это, однако, не отражается на физи­ческих законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энер­гию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают от­носительно нулевого уровня. Для консервативных сил

или в векторном виде

(12.4)

где

(12.5)

(i,j,k— единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называетсяградиентом скаляраП.

Для него наряду с обозначением gradП применяется также обозначениеП.(«набла») означает символический вектор, называемый оператором Гамильтона* или набла-оператором:

(12.6)

* У. Гамильтон (1805—1865) — ирландский математик и физик.

Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т,поднятого на высотуhнад поверхностью Земли, равна

(12.7)

где высота hотсчитывается от нулевого уровня, для которого П0=0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высотыhна поверхность Земли.

Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!).Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубинаh' ), П=—mgh'.

Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:

где Fx упp —проекция силы упругости на осьх; k —коэффициент упругости(для пружины —жесткость), а знак минус указывает, чтоFx упp направлена в сторону, противоположную деформацииx.

По третьему закону Ньютона, деформирующая сила равна по модулю силе уп­ругости и противоположно ей направлена, т. е.

Элементарная работа dA,совершаемая силойFxпри бесконечно малой деформацииdx, равна

а полная работа

идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела

Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.

Полная механическая энергия системы— энергия механического движения и вза­имодействия:

т. е. равна сумме кинетической и потенциальной энергий.

studfiles.net

---

• 
  Подсветка приусадебного участка
• 
  Техническое обслуживание ктп перечень работ
• 
  Обозначение сопротивлений
• 
  Точечные светильники как подключить
• 
  Мощность холостого хода трансформатора
• 
  Мособлгаз заявка на технологическое присоединение
• 
  Класс влагозащиты ipx4 что это
• 
  Типы движителей
• 
  Диммирование что такое
• 
  Бесплатное электричество в частном доме
• 
  Какой кабель нужен для подключения электроплиты