3.7. Энергия, запасенная в конденсаторе. Энергия запасенная в конденсаторе

Энергия запасенная в конденсаторе « Учи физику!

Конденсаторы изготовляют для разных целей. В некоторых электрических цепях применение конденсаторов позволяет пропускать быстрые изменения потенциалов, но задерживать их медленные изменения. (Иначе говоря, как будет видно ниже, переменный ток может проходить через конденсаторы, в то время как постоянный — нет.) В других устройствах конденсаторы используются для того, чтобы накапливать на короткое время заряд, или электрическую энергию. На рисунке показан высоковольтный конденсатор, предназначенный для накопления энергии. Он имеет емкость в 1 микрофараду и рассчитан на разность потенциалов в 2000 вольт. В качестве диэлектрика в нем используется масло, что обеспечивает более высокую диэлектрическую проницаемость, чем воздух, и позволяет предотвратить проскакивание искр между пластинами.

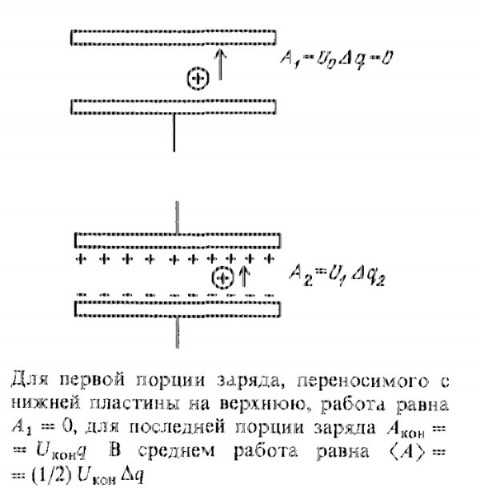
Работа, совершаемая при переносе очередной небольшой порции заряда от нижней пластины к верхней, равна произведению имеющейся разности потенциалов на переносимый заряд: A2=U1Δq2,

Когда переносится последняя порция заряда от нижней пластины к верхней, совершаемая работа равна произведению этого заряда на полную разность потенциалов в конденсаторе. Среднее значение разности потенциалов, через которую переносились заряды, равна половине окончательной разности потенциалов. Поэтому работа, совершаемая при зарядке конденсатора, равна qU/2, где U — разность потенциалов между пластинами, часто называемая «электрическое напряжение». Эта работа равна энергии W запасенной в конденсаторе.

Автор Кл. Э. Суорц “Необыкновенная физика обыкновенных явлений”

Интересные научные игрушки

uchifiziku.ru

Энергия конденсатора

Господа, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться!

В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически. Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно.

Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.

Полагаю, что механику вы изучали когда-то и это знаете . Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:

Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:

То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле.

Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля. Это позволяет использовать формулу работы без векторов:

Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил.

Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать

Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.

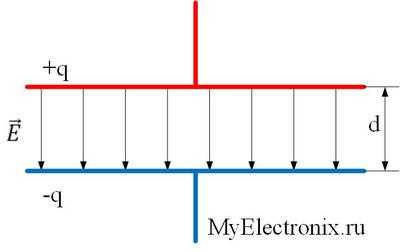
Рисунок 1 – Плоский конденсатор

Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно. Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q. Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за . Однако мы будем сразу работать по упрощенной схеме. Хотелось бы только отметить, что это верно для случая, когда поле у нас однородно и заряды по всем пластинам распределены равномерно. В действительности это не всегда так, однако такое упрощение позволяет существенно облегчить все расчеты и избежать всяких градиентов и интегралов без существенного вреда для практики.

Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке. Таким образом (отбрасывая вектора), можно записать

Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем

Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:

Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить. Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра.

Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:

Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем

Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:

Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем

Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле. Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости.

Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии

Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя.

Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор

Рисунок 2 – Конденсатор

И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:

Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт. Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций.

Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть . Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!

Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

myelectronix.ru

Энергия конденсатора, теория и примеры

Определение и общие сведения о энергии конденсатора

В том случае, если обкладки заряженного конденсатора замыкают при помощи проводника, то в проводнике появляется электрический ток, и через некоторое время конденсатор разряжается. При прохождении тока по проводнику выделяется некоторое количество теплоты, следовательно, конденсатор, обладающий зарядом, имеет энергию.

Определим энергию заряженного конденсатора. Будем считать, что конденсатор заряжают и этот процесс происходит очень медленно. Мгновенное значение напряжения между его обкладками обозначим как u. Так как процесс зарядки считаем квазистатическим, между обкладками увеличивается бесконечно медленно. Тогда потенциал каждой обкладки в каждый момент времени можно считать одинаковым в любом месте обкладки. При увеличении заряда обкладки на величину dq, совершается внешняя работа (работа источника) равная :

Используем формулу, которая связывает заряд, емкость и напряжение, получим:

В том случае, если емкость не зависит от напряжения электрического поля, то работа идет на увеличение энергии конденсатора (dW). Проинтегрируем выражение (2), учитывая, что напряжение изменяется от 0 до величины U, имеем:

Применяя формулу:

выражение для энергии поля конденсатора можно преобразовать к виду:

Именно благодаря своей способности запасать энергию, конденсаторы имеют большое значение в радиотехнике и электронике.

Энергия поля плоского конденсатора

Напряжение между обкладками плоского конденсатора может быть найдено как:

где d — расстояние между пластинами конденсатора. Учитывая, что для плоского конденсатора емкость определена выражением:

имеем:

где – объем конденсатора; E – напряженность электрического поля в конденсаторе. Объемная плотность энергии (w) может быть найдена как:

Примеры решения задач

ru.solverbook.com

Формула расчета энергии конденсаторов, как зарядить плоский конденсатор

Конденсаторы являются неотъемлемой частью электрических схем. В большинстве случаев оперируют такими понятиями, как емкость и рабочее напряжение. Эти параметры являются основополагающими.

Конденсаторы различных типов

В некоторых случаях для более полного понимания работы упомянутого элемента необходимо иметь представление, что означает энергия заряженного конденсатора, как она вычисляется и от чего зависит.

Определение понятия энергии

Наиболее просто вести рассуждения применительно к плоскому конденсатору. В основе его конструкции лежат две металлических обкладки, разделенные тонким слоем диэлектрика.

Плоский конденсатор

Если подключить емкость к источнику напряжения, то нужно обратить внимание на следующее:

На разделение зарядов по обкладкам электрическим полем затрачивается определенная работа. В соответствии с законом сохранения энергии, эта работа равняется энергии заряженного конденсатора;
Разноименно заряженные обкладки притягиваются друг к другу. Энергия заряженного конденсатора в этом случае равняется работе, затраченной на сближение пластин друг к другу вплотную.

Данные соображения позволяют сделать вывод, что формулу энергии заряженного конденсатора можно получить несколькими способами.

Вывод формулы

Энергия заряженного плоского конденсатора наиболее просто определяется, исходя из работы по сближению обкладок.

Рассмотрим силу притяжения единичного заряда одной из обкладок к противоположной:

F=q0E.

В данном выражении q0 – величина заряда, E – напряженность поля обкладки.

Поскольку напряженность электрического поля определяется из выражения:

E=q/(2ε0S), где:

q – величина заряда,
ε0 – электрическая постоянная,
S – площадь обкладок,

формулу силы притяжения можно записать как:

F=q0 q/(2ε0S).

Для всех зарядов сила взаимодействия между обкладками, соответственно, составляет:

F=q2/(2ε0S).

Работа по сближению пластин равняется произведению силы взаимодействия на пройденное расстояние. Таким образом, энергия заряженного конденсатора определяется выражением:

W=A=Fd.

Важно! В приведенном выражении должна быть разница в положениях пластин. Записывая только одну величину d, подразумеваем, что конечным результатом будет полное сближение, то есть d2=0.

С учетом предыдущих выражений можно записать:

W=d q2/(2ε0S).

Известно, что емкость плоского конденсатора определяется из такого выражения:

C=d/(ε0S).

В результате энергия определяется как:

W=q2/(2С).

Полученное выражение неудобно тем, что вызывает определенные затруднения определения заряда на обкладках. К счастью, заряд, емкость и напряжение имеют строгую взаимосвязь:

q = С U.

Теперь выражение принимает полностью понятный вид:

W=CU2/2.

Полученное выражение справедливо для конденсаторов любых типов, не только плоских, и позволяет без затруднений в любой момент времени определять накопленную энергию. Емкость обозначается на корпусе и является величиной постоянной. В крайнем случае ее несложно измерять, используя специальные приборы. Напряжение измеряется вольтметром с необходимой точностью. К тому же очень просто зарядить конденсатор не полностью (меньшим напряжением), снизив, таким образом, запасенную энергию.

Для чего необходимо знать энергию

В большинстве случаев применения емкостей в электрических цепях понятие энергии не употребляется. Особенно это относится к время,- и частотозадающим цепям, фильтрам. Но есть области, где необходимо использовать накопители энергии. Наиболее яркий пример –фотографические вспышки. В накопительном конденсаторе энергия источника питания накапливается сравнительно медленно – несколько секунд, но разряд происходит практически мгновенно через электроды импульсной лампы.

Конденсатор, подобно аккумулятору, служит для накопления электрического заряда, но между этими элементами есть много различий. Емкость аккумулятора несравненно выше, чем у конденсатора, но последний способен отдать ее практически мгновенно. Лишь недавно, с появлением ионисторов, это различие несколько сгладилось.

Ионистор

Какова же ориентировочная величина энергии? Можно для примера вычислить ее для уже упомянутой фотовспышки. Пускай, напряжение питания составляет 300 В, а емкость накопительного конденсатора – 1000 мкФ. При полном заряде величина энергии составит 45 Дж. Это довольно большая величина. Прикосновение к выводам заряженного элемента может привести к несчастному случаю.

Конденсатор фотовспышки

Важно! Принудительный разряд путем закорачивания выводов металлическими предметами чреват выходом устройства из строя. Накопленная энергия конденсатора способна за долю секунды расплавить выводы внутри элемента и вывести его из строя.

Видео

Оцените статью:

elquanta.ru

Энергия поля конденсатора - Основы электроники

Вся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накопленную в конденсаторе, можно определить следующим образом. Представим себе, что мы заряжаем конденсатор не сразу, а постепенно, перенося электрические заряды с одной его пластины на другую.

При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последующий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое количество электричества, которое мы обозначим буквой Q.

Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U.

Как мы уже заметили, разность потенциалов в процессе заряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U.

Для упрощения вычисления энергии допустим, что мы перенесли весь электрический заряд Q с одной пластины конденсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пластинами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запасенная в электрическом поле конденсатора, будет равна половине напряжения U, умноженной на общее количество перенесенного электричества Q.

Полученный результат мы можем записать в виде следующей математической формулы:

W = UQ/2 (1)

Если напряжение в этой формуле будет выражено в вольтах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накопленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде:

W = CU2/2 (2)

Выражение (2) говорит нам о том, что энергия, сосредоточенная в поле конденсатора, равна половине произведения емкости конденсатора на квадрат напряжения между его пластинами.

Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

3.7. Энергия, запасенная в конденсаторе : Электричество и магнетизм : Юридическая библиотека

Рассмотрим конденсатор емкостью С, с разностью потенциалов ф12между пластинами. Зарядфравен Сф13. На одной пластине имеется заряд Q, а на другой — Q. У в е л и ч и м заряд от Q до Q rdQ, перенеся положительный заряд dQ с отрицательно заряженной пластины на положительную, т. е. произведя работу против разности потенциалов ф12. Затраченная работа равна dW=(fi2dQ=QdQ;C. Следовательно, для того чтобы зарядить незаряженный конденсатор некоторым конечным зарядом QK, требуется затратить работу

W = (20)

Q = 0

Это и есть энергия, «запасенная» в конденсаторе. Ее можно также выразить уравнением

U = Сф12/2. (21)

Емкость плоского конденсатора с площадью пластин А и зазором s равна C=A!4ns, а электрическое поле E=(p12/s. Следовательно, уравнение (21) эквивалентно также выражению

и= Т Ш W = ША5 = Ш- объем- (22)

Это выражение согласуется с общей формулой (2.36) для энергии, запасенной в электрическом поле *).

*) Все вышесказанное относится к «воздушным конденсаторам», выполненным из проводников, между которыми находится воздух. Как вам известно из лабораторных работ, большинство конденсаторов, применяемых в электрических контурах, заполнено изоляторами или «диэлектриками». Мы будем изучать свойства таких конденсаторов в гл. 9.

3.8. Различные методы решения задачи с граничными условиями

Было бы ошибочным создать впечатление, что не существует общих методов решения граничной задачи для уравнения Лапласа. Не имея возможности подробно рассмотреть этот вопрос, мы укажем на три полезные и интересные метода, с которыми вы встретитесь при дальнейшем изучении физики или прикладной математики. Первый метод — это элегантный метод анализа, называемый конформным отображением; он основан на теории функций комплексного переменного. К сожалению, его можно применять только к двумерной системе. Существуют системы, в которых ср зависит только от х и у, например, случай, когда все поверхности проводников расположены параллельно оси 2. Тогда уравнение Лапласа принимает вид

О-ф

дх"

ду-

(23)

с граничными условиями, заданными на некоторых линиях или кривых в плоскости ху. В практике встречается много таких систем, или подобных им, поэтому метод, помимо математического интереса, является практически полезным. Например, точное решение для потенциала вблизи двух длинных параллельных полос легко получить методом конформного отображения. Силовые линии и эквипотенциальные поверхности изображены в поперечном сечении па рис. 3.16. Рисунок дает нам представление о краевом эффекте поля плоских конденсаторов, длина которых велика по сравнению с расстоянием между пластинами. Поле, изображенное на рис. 3.11, б, было построено на основании такого решения. Вы сможете пользоваться этим методом после того, как более глубоко изучите функции комплексного переменного.

Вторым методом является численное определение приближенных решений задачи об электростатическом потенциале при заданных граничных

условиях. Этот очень простой и почти универсальный метод основан на свойстве гармонических функций, с которым вы уже знакомы: значение функции в точке равно ее среднему значению по окрестности этой точки. В этом методе потенциальная функция <р представлена только значениями ряда дискретных точек, включая дискретные точки на границах. Значения функции в точках, не лежащих на границах, подбираются до тех пор, пока каждое из них

Рис. 3.16. Силовые линии и эквипотенциальные поверхности для двух бесконечно длинных проводящих полос.

не будет равно среднему из соседних значений. В принципе это можно сделать, решая одновременно большое количество уравнений, равное числу внутренних точек. Но приближенное решение можно получить гораздо проще, систематически изменяя каждое значение, чтобы приблизить его к среднему из соседних значений, и повторяя этот процесс до тех пор, пока изменения не станут пренебрежимо малыми. Этот метод носит название метода релаксации. Единственным препятствием к применению этого метода является трудоемкость процесса вычисления, но теперь это препятствие устранено, так как расчет производится быстродействующими вычислительными машинами, которые идеально подходят для этого метода. Если вам это интересно, обратитесь к задачам 3.29 и 3.30.

Третьим методом приближенного решения краевой задачи является вариационный метод. Он основан на принципе, который встречается во многих разделах физики, от ньютоновской динамики до оптики и квантовой механики. В электростатике этот принцип выражается в следующей форме: нам уже известно, что полная энергия электростатического поля дается выражением

и = (24)

Если вы решили задачу 2.19, то знаете, что в этом очень простом случае заряд на проводящей поверхности с постоянным потенциалом (состоящей из двух сфер, связанных проводом) распределен таким образом, чтобы энергия, запасенная во всем поле,была минимальной. Это общее правило. В любой системе проводников, при различных фиксированных значениях потенциалов, заряд распределяется по каждому проводнику таким образом, чтобы значение энергии, запасенной в поле, стало минимальным. Это становится почти очевидным, если указать, что любое уменьшение полной энергии поля связано с совершением работы перераспределения заряда *). Плоская поверхность воды в сосуде имеет то же объяснение.

Рассмотрим теперь потенциальную функцию q>(x, у, г) в некоторой области, заключающей в себе несколько граничных поверхностей с заданными потенциалами. Точное значение функции ф(х, у,г), т. е. решение уравнения У2ф = 0, удовлетворяющее заданным потенциалам на границах, отличается от всех других функций, удовлетворяющих граничным условиям, но не удовлетворяющих уравнению Лапласа, например от 1|з(лг, у, z), так как запасенная энергия для ф меньше, чем для г|э. Выразим энергию через ф, как в уравнении (2.38):

= - (25)

*) Рассуждая таким образом, мы считаем, что течение заряда сопровождается некоторым рассеянием энергии. Это так обычно и бывает. В противном случае система, не находящаяся вначале в состоянии равновесия, не могла бы придти в это состояние, избавившись от лишней энергии. Как вы думаете, что произошло бы в этом случае?

Теперь мы можем поставить граничную задачу по-новому, не упоминая о лапласиане. Потенциальная функция — это та функция, которая минимизирует интеграл уравнения (25) по сравнению со всеми другими функциями, удовлетворяющими тем же граничным условиям. Следовательно, возможным методом получения приближенного решения данной краевой задачи является испытание большого количества функций, имеющих заданные граничные значения, и последующий выбор той функции, которая обеспечивает минимальное значение U. Можно также взять функцию с одним или двумя переменными параметрами и использовать эти математические «кнопки» для минимизации U. Этот метод особенно удобен для определения самой энергии, часто наиболее важной неизвестной величины. Поскольку энергия U минимальна для точного значения ф, то она мало чувствительна к отклонениям от этого значения. Задача 3.32 иллюстрирует простоту и точность вариационного метода.

Вариационный принцип представляет собой альтернативную формулировку основного закона электростатического поля, и это для нас более существенно, чем польза, которую он приносит при вычислениях. Известно, что формулировка физических законов в виде вариационных принципов часто весьма плодотворна. Профессор Р. П. Фейнман, известный своими блестящими работами в этой области, дал живое и элементарное изложение вариационных идей в книге «Фейнмановские лекции по физике» (см. т. 6, гл. 19).

bookzie.com

3.7. Энергия, запасенная в конденсаторе : Электричество и магнетизм : Юридическая библиотека

W = (20)

Q = 0

Это и есть энергия, «запасенная» в конденсаторе. Ее можно также выразить уравнением

U = Сф12/2. (21)

и= Т Ш W = ША5 = Ш- объем- (22)

Это выражение согласуется с общей формулой (2.36) для энергии, запасенной в электрическом поле *).

3.8. Различные методы решения задачи с граничными условиями

О-ф

дх"

ду-

(23)

Рис. 3.16. Силовые линии и эквипотенциальные поверхности для двух бесконечно длинных проводящих полос.

и = (24)

= - (25)

bookzie.com

3.7. Энергия, запасенная в конденсаторе. Энергия запасенная в конденсаторе

Энергия запасенная в конденсаторе « Учи физику!

Энергия конденсатора

Энергия конденсатора, теория и примеры

Определение и общие сведения о энергии конденсатора

Энергия поля плоского конденсатора

Примеры решения задач

Формула расчета энергии конденсаторов, как зарядить плоский конденсатор

Определение понятия энергии

Вывод формулы

Для чего необходимо знать энергию

Видео

Энергия поля конденсатора - Основы электроники

Похожие материалы:

Добавить комментарий

3.7. Энергия, запасенная в конденсаторе : Электричество и магнетизм : Юридическая библиотека

3.7. Энергия, запасенная в конденсаторе : Электричество и магнетизм : Юридическая библиотека

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30