Логические выражения и ветвление. C логическое и

Логические выражения и ветвление [Амперка / Вики]

Для работы с целыми числами в C/C++ существует тип переменных int. Но операции над целыми числами — не единственный инструмент в арсенале разработчика. Одними из важнейших элементов в программировании являются логические операции, выражения и типы данных.

В то время как переменные типа int могут хранить произвольные целые числа, а операции над ними подчиняются законам целочисленной арифметики; логические переменные могут хранить лишь одно из двух значений: истину или ложь, а операции над ними подчиняются законам алгебры логики.

Алгебра логики — умное название для интуитивно понятных вещей: операций «и», «или», «не» над высказываниями, которые либо справедливы, либо нет. Например, рассмотрим такое логическое выражение: «в коридоре темно и по коридору идёт человек». Оно состоит из двух логических значений (утверждения про темноту и человека) и одного оператора (союз «и»). Его итоговым значением также будет логическое значение, которое можно использовать, скажем, как сигнал для включения света в коридоре гостиницы.

В программировании переменные, которые хранят логические значения называются булевыми переменными, а операторы, которые производят над ними действия называют булевыми операторами или просто логическими операторами.

Логические операции в C++

В C++ для булевых переменных существует тип bool. Для обозначения истины в C++ используется слово true, а для обозначения лжи — слово false. Таким образом, если для объявления целочисленных переменных мы используем:

int myValue = 42;

Для логических переменных, используется:

bool tooDark = false; bool humanDetected = true;

Поскольку C++ для Arduino — это некоторая надстройка над голым C++, для обозначения логического типа наряду с bool существует ещё слово boolean. Это абсолютные синонимы. Можете использовать и то и другое. Просто из соображений единого стиля и повышения читаемости кода выберите один из терминов и используйте его всюду. Мы в статье будем использовать bool, просто потому что в нём меньше букв и он входит в стандарт языка.

Применение на практике: экологичный отель

Давайте разовьём тему с энергосберегающим освещением и сделаем на Arduino устройство, которое включает свет в коридоре только тогда, когда это действительно необходимо.

Допустим, к Arduino подключён аналоговый датчик уровня освещённости, пироэлектрический цифровой датчик движения тёплых объектов и экологичная светодиодная лампа.

Тогда скетч будет выглядеть следующим образом:

#define LIGHT_SENSOR_PIN A0 #define MOTION_SENSOR_PIN 2 #define LED_LAMP_PIN 5   #define LIGHT_LEVEL_THRESHOLD 600   void setup() { pinMode(LIGHT_SENSOR_PIN, INPUT); pinMode(MOTION_SENSOR_PIN, INPUT); pinMode(LED_LAMP_PIN, OUTPUT); }   void loop() { int lightLevel = analogRead(LIGHT_SENSOR_PIN); bool motionDetected = digitalRead(MOTION_SENSOR_PIN); bool tooDark = lightLevel < LIGHT_LEVEL_THRESHOLD; bool lightningRequired = tooDark && motionDetected; digitalWrite(LED_LAMP_PIN, lightningRequired ? HIGH : LOW); }

Взглянем на loop и поймём что здесь происходит. С первой строкой всё понятно: мы считываем значение освещённости с аналогового сенсора с помощью встроенной функции analogRead и присваиваем его переменной с именем lightLevel.

Далее мы объявляем логическую переменную motionDetected в качестве значения которой присваиваем результат вызова встроенной функции digitalRead. Функция digitalRead похожа по своей сути на analogRead, но может возвращать лишь одно из двух значений: либо истину (true), либо ложь (false). То есть это функция, которая возвращает логическое значение. Она подходит для считывания показаний разнообразных бинарных цифровых датчиков. В нашем примере мы как раз использовали такой: пироэлектрический сенсор, который выдаёт 0 вольт, пока движения в его радиусе видимости нет и 5 вольт, когда замечено перемещение тёплого объекта: человека, кошки или кого-то ещё. Нулю вольт микроконтроллер ставит в соответствие значение false, а пяти вольтам — true.

Итак, по итогам исполнения второй строки, в переменной motionDetected будет храниться либо истина, либо ложь в зависимости от того замечено ли движение в коридоре.

Далее мы видим определение булевой переменной tooDark, которой в качестве значения присваивается значение выражения lightLevel < LIGHT_LEVEL_THRESHOLD. Символ <, как можно догадаться, в C++ означает оператор «меньше, чем». Из двух численных операндов, этот оператор делает один логический результат. Значение всего выражения считается истинным, если то, что записано слева от знака (lightLevel в нашем случае) меньше, чем то, что записано справа от знака (LIGHT_LEVEL_THRESHOLD). Довольно логично и интуитивно понятно, не правда ли?!

Таким образом в переменной tooDark окажется значение true, только если значение уровня освещённости lightLevel, полученное ранее, окажется меньше 600. В противном случае, в переменной окажется false.

Конкретное значение, вроде 600 в нашем случае, в подобных случаях часто получают экспериментально: в зависимости от используемого сенсора и конфигурации помещения, где стоит устройство.

Идём дальше. Мы видим объявление булевой переменной lightningRequired, в качестве значения которой присваивается значение выражения tooDark && motionDetected. Символ && в C++ означает оператор логического «и». Как можно догадаться, всё выражение считается истинным тогда и только тогда, когда и то, что справа, и то что слева от оператора истинно. Таким образом, переменная lightningRequired примет значение true, если в коридоре одновременно: и слишком темно, и замечено движение человека. Если не выполнено хоть одно из условий, результатом будет false. Как раз то, что нужно.

И наконец, последним выражением идёт вызов функции digitalWrite для пина Arduino, к которому подключена лампа. Нам нужно включить лампу, если переменная lightningRequired содержит истинное значение и выключить, если в ней хранится ложь. Чтобы сделать это, мы используем тернарный условный оператор ? :. Где в качестве условия используем просто значение переменной lightningRequired. Помните? В тернарном операторе условие считается выполненным, если его значение — не ноль; и не выполненным если его значение — ноль.

На самом деле для процессора не существует понятия логических значений. Всё что он умеет — оперировать над целыми числами. Поэтому в C++ существует автоматическое преобразование типов. Там, где ожидается int, а мы используем bool, за кадром происходит автоматическое преобразование: true превращается в целое число 1, а false — в целое число 0.

Так что, булевы выражения и переменные — ни что иное, как удобство для программистов, синтаксический сахар, который позволяет писать программы более понятно и выразительно.

Возвращаясь к нашему примеру, в выражении:

digitalWrite(LED_LAMP_PIN, lightningRequired ? HIGH : LOW);

второй аргумент примет значение HIGH, если lightningRequired — это true; и LOW, если lightningRequired — это false. Таким образом, мы добились чего хотели: включения света, если он нужен и выключения, если он не уместен.

О краткости записи

Если вспомнить об автоматическом преобразовании переменных разных типов, а ещё о том, что HIGH — это ничто иное, как макроопределение числа 1, а LOW — макроопределение числа 0, последнюю строку в нашем примере можно сократить до лаконичного выражения:

digitalWrite(LED_LAMP_PIN, lightningRequired);

Мы обошлись без тернарного оператора: ведь всё равно функция digitalWrite получит:

• единицу: то же самое, что и HIGH, если lightningRequired будет true

• ноль: то же самое, что и LOW, если lightningRequired будет false

Кроме того, логические выражения — это самые обычные выражения в C++, к которым применяются общие правила встраивания. Поэтому весь код loop в примере с экологичным освещением на самом деле мог бы быть записан в одну строку:

void loop() { digitalWrite(LED_LAMP_PIN, analogRead(LIGHT_SENSOR_PIN) < LIGHT_LEVEL_THRESHOLD && digitalRead(MOTION_SENSOR_PIN)); }

Да, код теперь находится на грани читаемости, но это всего лишь демонстрация возможностей. В реальной жизни лучше использовать пару промежуточных переменных:

void loop() { bool tooDark = analogRead(LIGHT_SENSOR_PIN) < LIGHT_LEVEL_THRESHOLD; bool motionDetected = digitalRead(MOTION_SENSOR_PIN); digitalWrite(LED_LAMP_PIN, tooDark && motionDetected); }

Или хотя бы использовать перенос строк для наглядности:

void loop() { digitalWrite(LED_LAMP_PIN, analogRead(LIGHT_SENSOR_PIN) < LIGHT_LEVEL_THRESHOLD && digitalRead(MOTION_SENSOR_PIN) ); }

А если свет таки нужен: условное выражение if

Внимательный читатель мог заметить, что приведённый скетч едва ли может работать в реальных условиях. Если мы включим свет, когда слишком темно и зафиксировано движение, при следующем же прогоне loop датчик «увидит» свет от нашей же лампы, программа посчитает, что и так достаточно светло и выключит лампу. Процесс постоянного выключения и включения так и будет продолжаться пока пироэлектрический датчик будет фиксировать движение. В лучшем случае мы получим свечение лампы в пол силы, в худшем — раздражающее мерцание. Как быть?

Можно после включения лампы усыплять программу на, скажем, 30 секунд. Вполне достаточно, чтобы дать постояльцу отеля пройти коридор и не так уж расточительно с точки зрения экономии электроэнергии.

Как сделать так, чтобы задержка на 30 секунд производилась только после включения лампы, но не после выключения? Для этого в C++ существует условное выражение «if». Используя его, скетч может выглядеть следующим образом:

#define LIGHT_SENSOR_PIN A0 #define MOTION_SENSOR_PIN 2 #define LED_LAMP_PIN 5   #define LIGHT_LEVEL_THRESHOLD 600   void setup() { pinMode(LIGHT_SENSOR_PIN, INPUT); pinMode(MOTION_SENSOR_PIN, INPUT); pinMode(LED_LAMP_PIN, OUTPUT); }   void loop() { bool tooDark = analogRead(LIGHT_SENSOR_PIN) < LIGHT_LEVEL_THRESHOLD; bool motionDetected = digitalRead(MOTION_SENSOR_PIN);   if (tooDark && motionDetected) { digitalWrite(LED_LAMP_PIN, HIGH); delay(30000); // спать 30 секунд } else { digitalWrite(LED_LAMP_PIN, LOW); } }

Начало программы прежнее, но в loop появляется новое составное выражение, обозначаемое словами if, else и фигурными скобками. Давайте поймём в чём его суть.

Сразу после слова if компилятор C++ ожидает в круглых скобках увидеть логическое выражение, которое в этом случае называется условием. Оно имеет тот же смысл, что и для тернарного оператора. Если его значение — не ноль или истинно, выполняется блок кода, который следует сразу после условия в фигурных скобках. В нашем случае, если tooDark и motionDetected истины, будет выполнен блок кода из двух строк:

digitalWrite(LED_LAMP_PIN, HIGH); delay(30000); // спать 30 секунд

Если же условие было нулём, или что то же самое — ложно, блок кода следующий за условием пропускается и не выполняется вовсе. Зато, если после после этого пропущенного блока следует слово else, выполняется блок кода в фигурных скобках, следующий после этого слова. В нашем случае, если либо tooDark, либо motionDetected были false, выполнится блок кода из одной строки:

digitalWrite(LED_LAMP_PIN, LOW);

Стоит отметить, что в случае выполнения условия, блок кода следующий после else не выполняется, а пропускается. То есть, на самом деле, выражение if — это отображение в языке программирования простого и понятного утверждения: «если что-то, делай то-то, а иначе делай сё-то».

Возвращаясь к нашему примеру, код можно интерпретировать так: «если требуется освещение, включить свет и уснуть на 30 секунд, а если свет не нужен — выключить его». Довольно просто и логично.

Использование выражений, которые меняют ход программы в зависимости от каких-то условий называется ветвлением программы, а блоки кода после if и else называются ветками.

Краткая версия if

При использовании выражения if совершенно не обязательно использовать ветку else. Если что-то должно произойти при выполнении условия, а при невыполнении не должно происходить ничего, ветку else можно просто опустить. Например, мы можем изменить loop нашей программы следующим образом:

void loop() { bool tooDark = analogRead(LIGHT_SENSOR_PIN) < LIGHT_LEVEL_THRESHOLD; bool motionDetected = digitalRead(MOTION_SENSOR_PIN); bool lightningRequired = tooDark && motionDetected;   digitalWrite(LED_LAMP_PIN, lightningRequired);   if (lightningRequired) { delay(30000); // спать 30 секунд } }

Эта вариация кода делает абсолютно то же, что и раньше. Просто теперь код организован иначе. Мы в любом случае делаем указание лампе на включение или выключение, вызывая digitalWrite с булевым значением lightningRequired, но засыпаем на 30 секунд только если мы включаем свет, т.е. если переменная lightningRequired истинна. Если мы только что выключали свет, спать не нужно: нужно пропустить delay и сразу оказаться в конце функции loop. Поэтому мы не писали ветку else вовсе.

Более того, если в блоке кода после if или else содержится всего одно выражение, фигурные скобки можно не писать:

if (lightningRequired) delay(30000); // спать 30 секунд

Вложенные выражения if

Блоки кода, используемые в условных выражениях — это самые обычные блоки, которые следуют общим правилам C++. Поэтому в ветку одного if можно запросто вкладывать другой if.

Для примера рассмотрим скетч устройства, которое контролирует открывание двери холодильника, автомобиля или чего-то такого. Мы хотим, чтобы при открытии двери включалась подсветка, а если дверь остаётся открытой более 20 секунд, раздавался бы предупреждающий писк. При этом, хочется, чтобы писк можно было отключить переключателем, на случай когда производится длительная загрузка/разгрузка: так он не будет нервировать.

Допустим на дверце установлен постоянный магнит, а на раме бинарный цифровой датчик магнитного поля. Если магнитное поле фиксируется — дверца закрыта; иначе магнит отходит от датчика слишком далеко, магнитного поля нет — можно понять, что дверца открыта. Также мы подключим к Arduino лампу подсветки, пьезо-пищалку (buzzer) и рокерный выключатель.

В этом случае код работающего устройства может выглядеть так:

#define DOOR_SENSOR_PIN 2 #define BUZZER_PIN 3 #define SWITCH_PIN 4 #define LAMP_PIN 5   #define BUZZ_TIMEOUT 20 #define BUZZ_FREQUENCY 4000   void setup() { pinMode(DOOR_SENSOR_PIN, INPUT); pinMode(SWITCH_PIN, INPUT); pinMode(BUZZER_PIN, OUTPUT); pinMode(LAMP_PIN, OUTPUT); }   void loop() { bool doorOpened = !digitalRead(DOOR_SENSOR_PIN);   if (doorOpened) { digitalWrite(LAMP_PIN, HIGH); delay(BUZZ_TIMEOUT * 1000); bool buzzEnabled = digitalRead(SWITCH_PIN); if (buzzEnabled) { tone(BUZZER_PIN, BUZZ_FREQUENCY); } } else { digitalWrite(LAMP_PIN, LOW); noTone(BUZZER_PIN); } }

Давайте разберём происходящее в loop. Первым делом мы определяем переменную doorOpened и присваиваем ей значение выражения !digitalRead(DOOR_SENSOR_PIN). Как уже говорилось, дверь стоит считать открытой, если магнитного поля нет, т.е. digitalRead для нашего сенсора возвращает false. Символ ! перед логическим выражением в C++ означает оператор логического «не» или просто оператор отрицания. Он действует на значение, записанное после него, и из true делает false, а из false делает true. Как раз то, что нам нужно в этом случае.

Далее следует выражение if, проверяющее открыта ли дверь. Если да, начинается исполнение блока кода, следующего непосредственно за условием. В нём мы первым делом включаем подсветку. Затем засыпаем на 20 секунд (20×1000 мс).

Далее мы должны включить пищалку если только она не была умышленно выключена. Для этого мы проверяем состояние переключателя, который за это отвечает. Мы объявляем переменную buzzEnabled, которой присваиваем логическое значение, считанное с выключателя.

Обратите внимание, переменная buzzEnabled объявлена прямо внутри блока кода, следующего за if. Так делать можно и нужно: хорошей практикой является объявление переменных как можно ближе к тому месту, где они впервые используются.

Напомним о понятии области видимости переменных: переменные доступны для использования только внутри того блока, где они объявлены. В нашем случае buzzEnabled может быть использована в выражениях внутри блока кода, следующего за if (doorOpened), но попытка обращения к ней откуда-то ещё: например, из блока кода ветки else или непосредственно в loop вне ветки if, приведёт к ошибке на этапе компиляции программы. И это хорошо: нам не стоит впутывать переменную, которая нужна сию секунду в другие происходящие процессы; это делает программу чище и нагляднее.

Вслед за чтением переключателя следует вложенное условное выражение. Его суть абсолютно та же, что и ранее: в зависимости от условия выполнить или не выполнить код. Одно лишь отличие: оно расположено прямо в блоке кода ветки другого if. Это распространённая практика, которая встречается в программировании довольно часто. На самом деле, во вложенный if можно вкладывать другие if, в них ещё одни и т.д. до бесконечности: язык C++ вас в этом не ограничивает.

Возвращаясь к примеру, если переключатель находится в положении «включён», т.е. buzzEnabled содержит true, мы включаем писк. Это делается с помощью встроенной функции tone. Она принимает 2 аргумента: номер пина Arduino, куда подключён пьезоизлучатель и частоту писка. В данном случае, мы выбрали частоту 4000 Гц, т.е. 4 КГц.

Наконец, если дверь была закрыта, т.е. doorOpened содержит ложь, мы убеждаемся, что подсветка и пищалка выключены. Это делается в ветке else первого условия if. Как выключить лампу вы понимаете, а функция noTone, как можно догадаться, отключает писк на указанном пине.

Вспоминая о правилах короткой записи и встраивании выражений, мы можем чуть упростить код loop. Он может выглядеть так:

void loop() { if (!digitalRead(DOOR_SENSOR_PIN)) { digitalWrite(LAMP_PIN, HIGH); delay(BUZZ_TIMEOUT * 1000); if (digitalRead(SWITCH_PIN)) tone(BUZZER_PIN, BUZZ_FREQUENCY); } else { digitalWrite(LAMP_PIN, LOW); noTone(BUZZER_PIN); } }

Мы убрали фигурные скобки для внутреннего if и встроили вызовы digitalRead прямо в условные выражения.

Обратите внимание, как правильное использование отступов в блоках кода, помогает легко понять к какому if относится else и что за чем и при каких условиях следует. Никогда не пишите без отступов несмотря на то, что компилятору всё равно. Это делает код не читаемым и для других людей, и для вас самих:

void loop() { if (!digitalRead(DOOR_SENSOR_PIN)) { digitalWrite(LAMP_PIN, HIGH); delay(BUZZ_TIMEOUT * 1000); if (digitalRead(SWITCH_PIN)) tone(BUZZER_PIN, BUZZ_FREQUENCY); } else { digitalWrite(LAMP_PIN, LOW); noTone(BUZZER_PIN); } }

Клики кнопок

Одной из типичных задач при создании устройств на микроконтроллерах является определение момента клика тактовой кнопки, чтобы на это можно было как-то отреагировать. Проблема в том, что кнопка, как сенсор, может лишь сообщить зажата ли она сейчас или отпущена. Она не может сообщить, что была «нажата только что».

Но эта проблема легко решается с помощью небольшого приёма в программной части проекта. Давайте сделаем примитивное устройство с лампой и кнопкой, которое бы включало и выключало лампу, поочерёдно, при нажатии кнопки: клик — включили, клик — выключили:

#define BUTTON_PIN 2 #define LAMP_PIN 5   bool lampState = false; bool wasButtonDown = false;   void setup() { pinMode(BUTTON_PIN, INPUT); pinMode(LAMP_PIN, OUTPUT); }   void loop() { bool isButtonDown = digitalRead(BUTTON_PIN); if (isButtonDown && !wasButtonDown) { lampState = !lampState; delay(10); }   wasButtonDown = isButtonDown; digitalWrite(LAMP_PIN, lampState); }

В скетче мы можем видеть 2 булевы переменные:

• lampState содержит true, если лампа должна быть сейчас включена и false в противном случае

• wasButtonDown хранит состояние кнопки на момент последнего прогона loop: если кнопка была зажата, значением будет true

Теперь взглянем на сам loop. Первым делом мы считываем состояние кнопки в логическую переменную isButtonDown. Если кнопка зажата isButtonDown будет содержать true.

Далее следует условное выражение if с проверкой условия, суть которого в том, чтобы понять была ли нажата кнопка только что, или она зажата уже давно. Для этого и используется значение wasButtonDown.

Таким образом, условие стоит воспринимать как «кнопка зажата сейчас и не была зажата ранее». Это и есть условие сиемоментного «клика» кнопкой.

Если условие клика выполнено — действуем. Переворачиваем значение lampState с ног на голову:

lampState = !lampState;

Далее, в ветке if следует delay(10). Вызов delay здесь сделан исключительно из-за несовершенства механических кнопок. При нажатии, за микросекунды, когда соприкасаются пластины, кнопка может зафиксировать замыкание и размыкание десятки раз. Добавив delay(10) мы просто пережидаем шторм. Десять миллисекунд — более чем достаточно для успокоения кнопки, но достаточно мало, чтобы человек заметил это.

Далее мы присваиваем переменной wasButtonDown недавно считанное значение isButtonDown, говорящее о том нажата ли кнопка сейчас. Если кнопка была зажата только что, произойдёт переключение состояния лампы lampState, а переменная wasButtonDown в итоге примет значение true и будет оставаться с ним пока кнопку не отпустят. Таким образом, при следующем вызове loop состояние не будет изменено снова.

Если бы мы не прибегали к этому трюку, а использовали только текущее состояние кнопки без оглядки на предысторию, состояния бы менялись пока кнопка зажата, десятки тысяч раз в секунду. С точки зрения человека это выглядело бы как явная, назойливая проблема с устройством.

Цепочки if

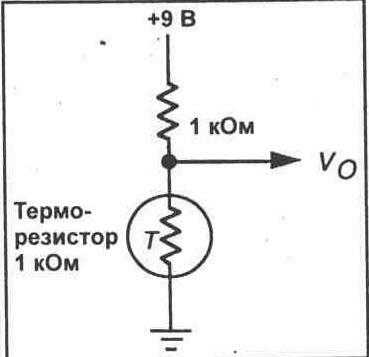
Напоследок давайте запрограммируем устройство, которое является простым климат-контролем для, например, террариума. Допустим к Arduino подключён термистор, кондиционер, обогреватель и зелёный светодиод. Если получаемая температура слишком высокая, мы должны включать кондиционер, если слишком низкая — обогреватель, а если в пределах нормы — включать светодиод.

Тогда программа может выглядеть так:

#define CONDITIONER_PIN 4 #define HEATER_PIN 5 #define OK_LED_PIN 6 #define THERMISTOR_PIN A0   #define TEMP_MIN 400 #define TEMP_MAX 500   void setup() { pinMode(CONDITIONER_PIN, OUTPUT); pinMode(HEATER_PIN, OUTPUT); pinMode(OK_LED_PIN, OUTPUT); }   void loop() { int temp = analogRead(THERMISTOR_PIN);   if (temp < TEMP_MIN) { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, HIGH); digitalWrite(OK_LED_PIN, LOW); } else if (temp > TEMP_MAX) { digitalWrite(CONDITIONER_PIN, HIGH); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, LOW); } else { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, HIGH); } }

В этой программе всё должно быть знакомым. Вопрос может вызвать лишь использование else и if рядом, на одной строке. На самом деле — это всего лишь иной способ записать несколько вложенных условных выражений. Мы могли бы написать то же самое таким образом:

if (temp < TEMP_MIN) { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, HIGH); digitalWrite(OK_LED_PIN, LOW); } else { if (temp > TEMP_MAX) { digitalWrite(CONDITIONER_PIN, HIGH); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, LOW); } else { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, HIGH); } }

Но вспомним, что условное выражение — это полноправное выражение в C++. В внешней ветке else оно одно, поэтому фигурные скобки можно опустить:

if (temp < TEMP_MIN) { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, HIGH); digitalWrite(OK_LED_PIN, LOW); } else if (temp > TEMP_MAX) { digitalWrite(CONDITIONER_PIN, HIGH); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, LOW); } else { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, HIGH); }

А вспомнив о том, что пустое пространство для компилятора ничего не значит, можем убрать несколько отступов и перенос строки, чтобы получить:

if (temp < TEMP_MIN) { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, HIGH); digitalWrite(OK_LED_PIN, LOW); } else if (temp > TEMP_MAX) { digitalWrite(CONDITIONER_PIN, HIGH); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, LOW); } else { digitalWrite(CONDITIONER_PIN, LOW); digitalWrite(HEATER_PIN, LOW); digitalWrite(OK_LED_PIN, HIGH); }

Подобные цепочки из выражений if — довольно частое явление. Если бы вариантов было больше трёх, вложенные if смотрелись бы громоздко и уродливо, в то время как такая цепочка выглядела бы всё равно понятно и хорошо.

На самом деле, программу климат-контроля можно написать компактнее. В этом виде она приведена просто для демонстрации if - else if - else цепочки. Для полноты картины приведём краткую версию:

#define CONDITIONER_PIN 4 #define HEATER_PIN 5 #define OK_LED_PIN 6 #define THERMISTOR_PIN A0   #define TEMP_MIN 400 #define TEMP_MAX 500   void setup() { pinMode(CONDITIONER_PIN, OUTPUT); pinMode(HEATER_PIN, OUTPUT); pinMode(OK_LED_PIN, OUTPUT); }   void loop() { int temp = analogRead(THERMISTOR_PIN); bool tooCold = temp < TEMP_MIN; bool tooHot = temp > TEMP_MAX;   digitalWrite(CONDITIONER_PIN, tooHot); digitalWrite(HEATER_PIN, tooCold); digitalWrite(OK_LED_PIN, !(tooCold || tooHot)); }

Опять же, всё знакомо за исключением, быть может значения выражения !(tooCold || tooHot). Символ || в C++ — это оператор логического «или». Значение выражения истинно если хотя бы одно из значений: слева или справа от оператора истинны.

Логические выражения — ни что иное, как арифметические выражения. Здесь действуют всё те же правила: в одном выражении может быть сколько угодно операторов, а очерёдность их применения можно обозначить скобками. В данном случае, мы сначала вычисляем логическое значение tooCold || tooHot, а затем оператором логического «не» (!) инвертируем полученное значение.

Итак, вы познакомились с логическими переменными, выражениями и сопутствующими операторами. Это уже позволяет делать устройства, которые выглядят умными. Включайте фантазию, дерзайте!

wiki.amperka.ru

Логическое И Вики

Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И»[1].

Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).

Обозначения[ | код]

Наиболее часто встречаются следующие обозначения для операции конъюнкции:

a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}

(в случае использования точки как знака логического умножения этот знак — как и при обычном умножении в алгебре — может быть опущен: ab{\displaystyle ab}[1]).

При этом обозначение a∧b{\displaystyle a\land b} наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &[1]; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия)[2][3]. Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение[4]. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930)[5].

Обозначение ⋀ для конъюнкции было использовано и в раннем языке программирования Алгол 60[6]. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения .AND. и & (с возможностью замены последнего на ключевое слово AND)[7]; в языках Паскаль и Ада используется зарезервированное слово and[8][9]; в языках C и C++ применяются обозначения & для побитовой конъюнкции и && для логической конъюнкции[10]).

Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что 0<1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(mod⁡k){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {0,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел)[11][12].

Булева алгебра[ | код]

Определение.Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).

Правило: результат равен наименьшему операнду.

Описание.В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, true>false{\displaystyle true>false}, при цифровом обозначении старшинство естественно 1>0{\displaystyle 1>0}. Правило: результат равен 1{\displaystyle 1}, если все операнды равны 1{\displaystyle 1}; во всех остальных случаях результат равен 0{\displaystyle 0}.

Таблицы истинности:для бинарной конъюнкции

для тернарной конъюнкции

a{\displaystyle a} b{\displaystyle b} c{\displaystyle c} a∧b∧c{\displaystyle a\land b\land c}

0	0	0	0
1	0	0	0
0	1	0	0
1	1	0	0
0	0	1	0
1	0	1	0
0	1	1	0
1	1	1	1

Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции[13].

Многозначная логика[ | код]

Операции, называемой в двоичной логике конъюнкция, в многозначных логиках обычно сопоставляется операция минимум: min(a,b){\displaystyle min(a,b)}, где a,b∈{0,…,k−1},{\displaystyle a,b\in \{0,\dots ,k-1\},} а k{\displaystyle k} — значность логики; впрочем, возможны и другие варианты обобщения обычной конъюнкции на многозначный случай. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 0{\displaystyle 0} и k−1{\displaystyle k-1}.

Следует отметить, что название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.

Классическая логика[ | код]

В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции: a∧b→a{\displaystyle a\land b\to a} a∧b→b{\displaystyle a\land b\to b} a→(b→(a∧b)){\displaystyle a\to (b\to (a\land b))}

С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

Схемотехника[ | код]

Логический элемент «И»

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения[13]. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах есть «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе есть «0»

Теория множеств[ | код]

С точки зрения теории множеств, конъюнкция аналогична операции пересечения.

Программирование[ | код]

В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.

Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата false{\displaystyle false} или true{\displaystyle true}. Например:

if (a & b & c) { /* какие-то действия */ };

Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:

a = false; b = true; c = true; if (a && b && c) { /* какие-то действия */ };

Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.

Результат будет равен true{\displaystyle true}, если оба операнда равны true{\displaystyle true} (для числовых типов не равны 0{\displaystyle 0}). В любом другом случае результат будет равен false{\displaystyle false}.

При этом применяется стандартное соглашение: если значение левого операнда равно false{\displaystyle false}, то значение правого операнда не вычисляется (вместо b{\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую

или выключающую

подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:

if (a != 0 && b / a > 3) { /* какие-то действия */ };

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.

Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =	011001012{\displaystyle 01100101_{2}}
b =	001010012{\displaystyle 00101001_{2}}
то
a И b =	001000012{\displaystyle 00100001_{2}}

Связь с естественным языком[ | код]

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как 0{\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».

Примечания[ | код]

1. ↑ 1 2 3 Кондаков, 1975, с. 264—266, 534—536.
2. ↑ Ampersand. // Website Online Etymology Dictionary. Проверено 7 февраля 2016.
3. ↑ Кондаков, 1975, с. 67.
4. ↑ Стяжкин Н. И.  Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
5. ↑ Earliest Uses of Symbols of Set Theory and Logic. // Website Jeff Miller Web Pages. Проверено 7 февраля 2016.
6. ↑ Кондаков, 1975, с. 30.
7. ↑ Пратт Т.  Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
8. ↑ Грогоно П.  Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
9. ↑ Вегнер П.  Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
10. ↑ Эллис М., Строуструп Б.  Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
11. ↑ Яблонский С. В.  Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
12. ↑ Рвачёв В. Л.  Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
13. ↑ 1 2 Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.

Литература[ | код]

ru.wikibedia.ru

Логические схемы и таблицы истинности

В цифровой схемотехнике цифровой сигнал - это сигнал, который может принимать два значения, рассматриваемые как логическая "1" и логический "0".

Логические схемы реализуются на логических элементах: "НЕ", "И", "ИЛИ", "И-НЕ", "ИЛИ-НЕ", "Исключающее ИЛИ" и "Эквивалентность". Первые три логических элемента позволяют реализовать любую, сколь угодно сложную логическую функцию в булевом базисе. Мы будем решать задачи на логические схемы, реализованные именно в булевом базисе.

Для обозначения логических элементов используется несколько стандартов. Наиболее распространёнными являются американский (ANSI), европейский (DIN), международный (IEC) и российский (ГОСТ). На рисунке ниже приведены обозначения логических элементов в этих стандартах (для увеличения можно нажать на рисунок левой кнопкой мыши).

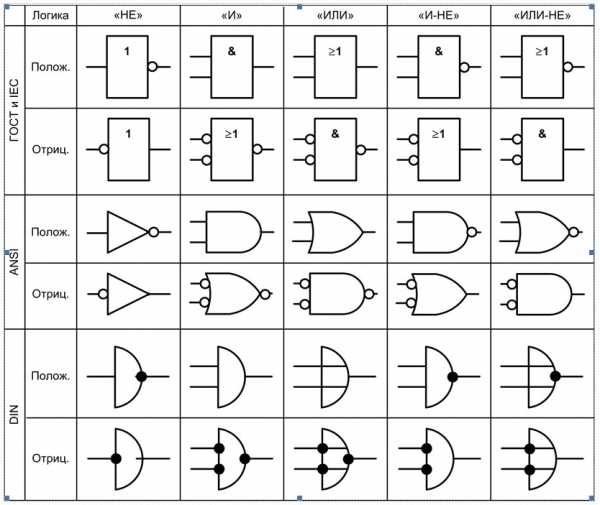
На этом уроке будем решать задачи на логические схемы, на которых логические элементы обозначены в стандарте ГОСТ.

Задачи на логические схемы бывают двух видов: задача синтеза логических схемы и задачи анализа логических схем. Мы начнём с задачи второго типа, так как в таком порядке удаётся быстрее научиться читать логические схемы.

Задача анализа заключается в определении функции f, реализуемой заданной логической схемой. При решении такой задачи удобно придерживаться следующей последовательности действий.

1. Логическая схема разбивается на ярусы. Ярусам присваиваются последовательные номера.
2. Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра - номер яруса, а остальные цифры - порядковый номер элемента в ярусе.
3. Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
4. Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.

Пример 1. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

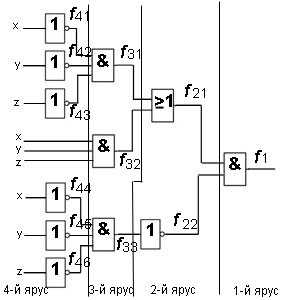
Решение. Разбиваем логическую схему на ярусы, что уже показано на рисунке. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

.

Таблица истинности для данной логической схемы:

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

Пример 4. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

.

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	0	1	1
1	1	0	0	1	1
1	0	1	1	0	1
1	0	0	0	0	0
0	1	1	0	1	1
0	1	0	0	1	1
0	0	1	0	1	1
0	0	0	0	1	1

Пример 5. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Структура данной логической схемы, в отличие от предыдущих примеров, имеет 5 ярусов, а не 4. Но одна входная переменная - самая нижняя - пробегает все ярусы и напрямую входит в логический элемент в первом ярусе. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

.

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	1	1	1
1	1	0	1	1	1
1	0	1	1	0	1
1	0	0	1	0	1
0	1	1	1	1	1
0	1	0	1	1	1
0	0	1	1	0	1
0	0	0	1	0	1

Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы.

Каждой дизъюнкции (логической сумме) соответствует элемент "ИЛИ", число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент "И", число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент "НЕ".

Часто разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схемы. В этом случае дана только таблица истинности логической схемы. Мы разберём именно такой пример, то есть, решим задачу, полностью обратную рассмотренной выше задаче анализа логических схем.

Пример 6. Построить логическую схему, реализующую функцию с данной таблицей истинности:

Решение. Разбираем таблицу истинности для логической схемы. Определяем функцию, которая получится на выходе схемы и промежуточные функции, которые на входе принимают аргументы x и y. В первой строке результатом реализации выходной функции при том, что значения входных переменных равны единицам, должен быть логический "0", во второй строке - при разных значениях входных переменных на выходе тоже должен быть логический "0". Поэтому нужно, чтобы выходная функция была конъюнкцией (логическим произведением).

Теперь подбираем промежуточные функции. Получаем следующую таблицу для промежуточных функций и выходной функции - конъюнкции промежуточных функций:

Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Из выражения видно, что понадобятся 3 схемы "НЕ", две двухвходовых схемы "И" и одна двухвходовая схема "ИЛИ". В соответствии с выходной функцией получаем следующую логическую схему:

function-x.ru

---

• 
  Измерительный трансформатор
• 
  Нет горячей воды что делать
• 
  Терморезистор с отрицательным температурным коэффициентом сопротивления
• 
  Фото сварка полуавтоматом
• 
  Во сколько дадут горячую воду
• 
  Прожекторное освещение
• 
  Сопротивление проводника формулы
• 
  Изолированная нейтраль для чего нужна
• 
  Моэск 13 район
• 
  Сечения проводов таблица
• 
  Онлайн расчет солнечной электростанции для дома