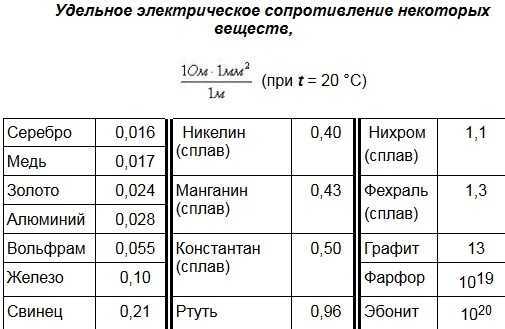
Чему равно полное сопротивление

Полное сопротивление Википедия

Электри́ческий импеда́нс (комплексное сопротивление, полное сопротивление) (англ. impedance от лат. impedio «препятствовать»)  — комплексное сопротивление двухполюсника для гармонического сигнала. Это понятие ввёл физик и математик О. Хевисайд в 1886 году.[1][2]

Резистор — пассивный элемент, обладающий чисто активным сопротивлением (реактивная составляющая сопротивления отсутствует, так как поведение резистора не зависит от частоты тока/напряжения; пассивный элемент, поскольку не содержит внутренних источников энергии). Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):

R=UI.{\displaystyle R={\frac {U}{I}}.}

Попытка применения понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что:

• сопротивление идеальной катушки индуктивности стремится к нулю:

если пропустить через катушку некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым U=0;{\displaystyle U=0;} R=UI=0I=0;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым I=0;{\displaystyle I=0;} R=UI=U0=∞.{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}

Но это справедливо лишь для постоянного тока и напряжения. В случае же переменного тока и напряжения свойства реактивных элементов существенно иные:

• разность напряжений на концах катушки индуктивности не равна нулю;
• ток, протекающий через конденсатор, не равен нулю.

Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.

Было бы удобно иметь некоторую характеристику и для реактивных элементов, которая бы при любых условиях связывала ток и напряжение на них подобно сопротивлению. Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно оно позволяет одновременно учитывать и амплитудные, и фазовые характеристики сигналов и систем.

Определение

Импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.

z^(jω)=u^(jω,t)i^(jω,t)=U(ω)ej(ωt+ϕu(ω))I(ω)ej(ωt+ϕi(ω))=U(ω)ejϕu(ω)I(ω)ejϕi(ω)=U^(jω)I^(jω){\displaystyle {\hat {z}}(j\omega )\;={\frac {{\hat {u}}(j\omega ,t)\;}{{\hat {i}}(j\omega ,t)\;}}={\frac {U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}{I(\omega )e^{j(\omega t+\phi _{i}(\omega ))}}}={\frac {U(\omega )e^{j\phi _{u}(\omega )}}{I(\omega )e^{j\phi _{i}(\omega )}}}={\frac {{\hat {U}}(j\omega )\;}{{\hat {I}}(j\omega )\;}}}

(1)

Здесь

Исторически сложилось, что обозначение импеданса, комплексных амплитуд и других комплекснозначных функций частоты записывают как f(jω){\displaystyle f(j\omega )}, а не f(ω){\displaystyle f(\omega )}. Такое обозначение показывает, что мы имеем дело с комплексными представлениями гармонических функций вида ejωt{\displaystyle e^{j\omega t}}. Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: U˙(jω){\displaystyle {\dot {U}}(j\omega )\;} чтобы отличать от соответствующих действительных (некомплексных) величин.

Физический смысл

Алгебраическая форма

Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} можно рассматривать как последовательно соединенные резистор с сопротивлением ℜ(z^(jω)){\displaystyle \Re ({\hat {z}}(j\omega ))} и чисто реактивный элемент с импедансом ℑ(z^(jω)){\displaystyle \Im ({\hat {z}}(j\omega ))}

Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.

Тригонометрическая форма

Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько фаза тока отстаёт от фазы напряжения или опережает.

Ограничения

Понятие импеданса применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его свойства не менялись со временем. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель ejωt{\displaystyle e^{j\omega t}} в (1) не сокращается.

• Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).

Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.

Вычисление импеданса

Идеальные элементы

Резистор

Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:

zR=R{\displaystyle z_{R}=R}

(2)

Конденсатор

Ток и напряжение для конденсатора связаны соотношением:

i(t)=CdUdt.{\displaystyle i(t)=C{\frac {dU}{dt}}.}

(3)

Отсюда следует, что при напряжении

u^(jω,t)=U(ω)ej(ωt+ϕu(ω)){\displaystyle {\hat {u}}(j\omega ,t)=U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}

(4)

ток, текущий через конденсатор, будет равен:

i^(jω,t)=Cddt(U(ω)ej(ωt+ϕu(ω)))=jωCU(ω)ej(ωt+ϕu(ω)).{\displaystyle {\hat {i}}(j\omega ,t)=C{\frac {d}{dt}}\left(U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}\right)=j\omega CU(\omega )e^{j(\omega t+\phi _{u}(\omega ))}.}

(5)

После подстановки (4) и (5) в (1) получаем:

z^C(jω)=1jωC=−jωC.{\displaystyle {\hat {z}}_{C}(j\omega )={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}.}

(6)

Катушка индуктивности

Аналогичное рассмотрение для катушки индуктивности приводит к результату:

z^L(jω)=jωL{\displaystyle {\hat {z}}_{L}(j\omega )\;=j\omega L}

(7)

Общий случай

Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:

z^(jω)=R+1jωC+jωL{\displaystyle {\hat {z}}(j\omega )\;=R+{\frac {1}{j\omega C}}+j\omega L}

(8)

Экспериментальное измерение импеданса

Импеданс реальных элементов может быть измерен специальными приборами: измерителем RLC или анализатором импеданса. Эти приборы позволяют производить измерения в широком диапазоне частот и при различных напряжениях смещения.

Применение импеданса

Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал.

См. также

Примечания

1. ↑ Science, p. 18, 1888
2. ↑ Oliver Heaviside. The Electrician. P. 212; 23 July 1886 reprinted as Electrical Papers, p64, AMS Bookstore, ISBN 0-8218-3465-7
3. ↑ В электротехнике и электронике принято мнимую единицу обозначать символом j, во избежание путаницы с символом i, применяемом для обозначения силы тока.

Литература

• Бессонов Л. А. Теоретические основы электротехники. — 9-е изд. — М.: Высшая школа, 1996.
• Графов Б. М., Укше Е. А. Электрохимические цепи переменного тока. — М.: Наука, 1983.

wikiredia.ru

Ответы@Mail.Ru: Чему равно сопротивление резистора?

Что-то не так в условиях. Характеристика "ЭДС" больше подходит к источнику напряжения. И если допустить, что Вы ошиблись в терминах, Тогда по закону Ома для полной цепи (R + r внутр. ) = ЭДС / (ток цепи) ; Или 10 / 2 = 5 Ом Из этих 5 Ом вычитаем внутреннее сопротивление источника и у нас остаётся 4 Ома на резистор подключенный к источнику напряжения с ЭДС равной 10 В.

хм, заучи: А=в/ом а значит 10/5

Общее сопротивление цепи 10:2=5 ом, у резистора 4 Ом

Из формулы I=E/(R+r) получим R=(E-Ir)/I=(10-2*1)/2=4 Ом

touch.otvet.mail.ru

Два проводника сопротивлением R1 = 100 Ом и R2 = 100 Ом соединены параллельно. Чему равно их общее сопротивление?

По закону Ома же. 13.

Закон Ома для параллельно соедениненных провдников. 1/R*2 = 1/R1 +1/R2 Итого: 2/200 = х/2 х = 150 ом

Закон ома для параллельных проводников. 13 Ом.

ответ 50 ом, Р= Р/н, где эн - колво проводников с одинаковым сопротивлением

два проводника с сопротивлением r1=2 ом и r2=3 ом соединены последовательно и присоединены к источнику тока с напряжением 12 В. Как изменяется сила тока в цепи, если сила второго проводника увеличится в двое ?

touch.otvet.mail.ru

Привет всем, а как понимать "сопротивление равно бесконечности"?

Сопротивление - величина, обратная проводимости. Если проводимость - ноль, ни единого электрона не проходит, то единица делить на ноль, равно бесконечность.

ет зчь хрен када сдвинешь

не пропускает электроток полностью <a href="/" rel="nofollow" title="3546815:##:http://www.elektrobezopasnost.narod.ru" target="_blank" >[ссылка заблокирована по решению администрации проекта]</a>

это например розетка. вобщем обрыв цепи

обычно оно бывает только у идеального источника тока. Означает, что какое сопротивление ни поставь в параллель такому источнику - ток всегда будет одним и тем же, а падение напряжения будет зависеть от подключенного сопротивления.

Проводник имеет сопротивление близкое к бесконечности, если при приложении к концам такова проводника напряжения сколь угодно большого по величине, ток через проводник всегда равен нулю. Соотвественно данное понятие является теоретическим, на практике есть материалы - проводники и диэлектрики. Диэлектрики не проводят ток, но для каждого диэлектрика существует реальное напряжение, при котором он пробивается, т. е. теряет свои свойства и становиться проводником. В электротехники бесконечно большое сопротивление используется в схемах идеальных источников питания. Идеальный источник питания (напряжения или тока) отличается от реального тем, что его внутреннее сопротивление принимается равным бесконечному сопротивлению (ид. ист. тока) или его проводимость считается бесконечной (ид. ист. напряжения) , т. е. такой источник всегда создает ток в цепи (ид. ист. тока) или напряжение (ид. ист. напряжения) на своих зажимах неизменными, независимо от того к какой нагрузке или внешней цепи он подключен.

Это разрыв цепи. Какое напряжение ни прикладывай, ток равен нулю.

touch.otvet.mail.ru

---

• 
  Сайт вл
• 
  Розетки в плацкарте
• 
  Какие документы нужны для замены счетчика воды
• 
  Когда должны включать отопление по закону в московской области
• 
  Может ли ук переносить платежи
• 
  Показания за электроэнергию нижегородская область
• 
  Какую группу по электробезопасности должен иметь производитель работ
• 
  Рпн это
• 
  Проводит алюминий электричество
• 
  Управляемые выпрямители принцип действия
• 
  Оптрон диодный