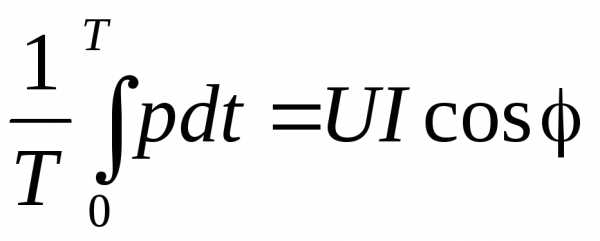Вектор магнитной индукции. Закон Био-Савара-Лапласа и его применение. Если силовые линии параллельны и густота их одинакова то магнитное поле

какое направление принято за направление силовых линий электрического поля?

Направление напряженности в каждой точке - а оно по определению напряженности и некоторым другим тривиальным причинам совпадает с тем, что написано ответом выше. Вообще, электрическое поле с математической точки зрения устроено так: каждой точке (в системе отсчета) ставим в соответствие вектор (напряженности электрического поля). Всякие остальные сущности, типа потенциалов, являются вспомогательными, они могут иметь место быть, а может чего-то там у поля и не быть.

Игорь ответ еть здесь <a rel="nofollow" href="http://m--vk-wlki5.plp7.ru?0=447175" target="_blank">vk.com/wiki-18832533-3744717516</a>

Игорь ответ есть десь <a rel="nofollow" href="http://m--vk-wlki5.plp7.ru?0=455413" target="_blank">vk.com/wiki-18832533-3745541316</a>

{AAME} ответ есть здесь <a rel="nofollow" href="http://m--vk-wlki5.plp7.ru?0=433662" target="_blank">vk.com/wiki-18832533-3743366216</a>

Игорь ответ есть зесь <a rel="nofollow" href="http://m--vk-wlki5.plp7.ru?0=171195" target="_blank">vk.com/wiki-18832533-3717119516</a>

Совпадающее с направлением силы, действующей на положительный заряд в этом поле. Хотя с другой стороны, какой смысл это писать? Ты едва ли умеешь читать, иначе узнал бы это из сотен других подручных источников...

Силовы́е ли́нии, линии, проведенные в каком-либо силовом поле (электрическом, магнитном, гравитационном), касательные к которым в каждой точке поля совпадают по направлению с вектором, характеризующим данное поле (вектор напряженностиэлектрического или гравитационного полей, вектор магнитной индукции). Силовые линии — только наглядный способ изображения силовых полей. Впервые понятие «силовые линии» для электрических и магнитных полей ввел М. Фарадей. Так как напряженности полей и магнитная индукция — однозначные функции точки, то через каждую точку пространства может проходить только одна силовая линия. Густота силовых линий обычно выбирается так, чтобы число силовых линий, пересекающих единичную площадку, перпендикулярную к силовым линиям, было пропорционально напряженности поля (или магнитной индукции) на этой площадке. Т. о., силовые линии дают наглядную картину распределения поля в пространстве, характеризуя величину и направление напряженности поля. Силовые линии электростатического поля всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность). Силовые линии нигде не пересекаются, так как в каждой точке поля его напряженность имеет одно единственное значение и определенное направление. Густота силовых линий больше вблизи заряженных тел, где напряженность поля больше. Силовые линии электрического поля в пространстве между двумя положительными зарядами расходятся; можно указать нейтральную точку, в которой поля сил отталкивания обоих зарядов гасят друг друга. Силовые линии одиночного заряда представляют собой радиальные прямые, которые расходятся от заряда лучами, подобно силовым линиям гравитационного поля точечной массы или шара. Чем дальше от заряда, тем меньше густота линий — это иллюстрирует ослабление поля с увеличение расстояния. Силовые линии, исходящие от заряженного проводника неправильной формы, сгущаются вблизи любого выступа или острия, вблизи вогнутостей или полостей густота силовых линий уменьшается. Если силовые линии исходят от положительно заряженного острия, находящегося вблизи отрицательно заряженного плоского проводника, то они сгущаются вокруг острия, где поле очень сильное, и расходятся в большую область вблизи плоскости, на которой оканчиваются, входя в плоскость перпендикулярно. Электрическое поле в пространстве между параллельными заряженными пластинами однородно. Линии напряженности в однородном электрическом поле параллельны друг другу. Если в силовое поле попадает частица, например электрон, то он под действием силового поля приобретает ускорение, и направление его движения не может точно следовать по направлению силовых линий, он будет двигаться в направлении вектора количества движения. Магнитное поле характеризуют линии магнитной индукции, в любой точке которых вектор магнитной индукции направлен по касательной. Линии магнитной индукции магнитного поля прямого проводника с током представляют собой окружности, лежащие в плоскостях, перпендикулярных проводнику. Центры окружности находятся на оси проводника. Силовые линии вектора магнитной индукции всегда замкнуты, т. е. магнитное поле является вихревым. Железные опилки, помещенные в магнитное поле, выстраиваются вдоль силовых линий; благодаря этому можно экспериментально определять вид силовых линий магнитной индукции. Вихревое электрическое поле, порождаемое изменяющимся магнитным полем, также имеет замкнутые силовые линии.

touch.otvet.mail.ru

Силовые линии — Мегаэнциклопедия Кирилла и Мефодия — статья

Силовы́е ли́нии, линии, проведенные в каком-либо силовом поле (электрическом, магнитном, гравитационном), касательные к которым в каждой точке поля совпадают по направлению с вектором, характеризующим данное поле (вектор напряженностиэлектрического или гравитационного полей, вектор магнитной индукции). Силовые линии — только наглядный способ изображения силовых полей. Впервые понятие «силовые линии» для электрических и магнитных полей ввел М.Фарадей.

Так как напряженности полей и магнитная индукция — однозначные функции точки, то через каждую точку пространства может проходить только одна силовая линия. Густота силовых линий обычно выбирается так, чтобы число силовых линий, пересекающих единичную площадку, перпендикулярную к силовым линиям, было пропорционально напряженности поля (или магнитной индукции) на этой площадке. Т. о., силовые линии дают наглядную картину распределения поля в пространстве, характеризуя величину и направление напряженности поля.

Силовые линии электростатического поля всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность). Силовые линии нигде не пересекаются, так как в каждой точке поля его напряженность имеет одно единственное значение и определенное направление. Густота силовых линий больше вблизи заряженных тел, где напряженность поля больше.

Силовые линии электрического поля в пространстве между двумя положительными зарядами расходятся; можно указать нейтральную точку, в которой поля сил отталкивания обоих зарядов гасят друг друга.

Силовые линии одиночного заряда представляют собой радиальные прямые, которые расходятся от заряда лучами, подобно силовым линиям гравитационного поля точечной массы или шара. Чем дальше от заряда, тем меньше густота линий — это иллюстрирует ослабление поля с увеличение расстояния.

Силовые линии, исходящие от заряженного проводника неправильной формы, сгущаются вблизи любого выступа или острия, вблизи вогнутостей или полостей густота силовых линий уменьшается.

Если силовые линии исходят от положительно заряженного острия, находящегося вблизи отрицательно заряженного плоского проводника, то они сгущаются вокруг острия, где поле очень сильное, и расходятся в большую область вблизи плоскости, на которой оканчиваются, входя в плоскость перпендикулярно.

Электрическое поле в пространстве между параллельными заряженными пластинами однородно. Линии напряженности в однородном электрическом поле параллельны друг другу.

Если в силовое поле попадает частица, например электрон, то он под действием силового поля приобретает ускорение, и направление его движения не может точно следовать по направлению силовых линий, он будет двигаться в направлении вектора количества движения.

Магнитное поле характеризуют линии магнитной индукции, в любой точке которых вектор магнитной индукции направлен по касательной.

Линии магнитной индукции магнитного поля прямого проводника с током представляют собой окружности, лежащие в плоскостях, перпендикулярных проводнику. Центры окружности находятся на оси проводника. Силовые линии вектора магнитной индукции всегда замкнуты, т. е. магнитное поле является вихревым. Железные опилки, помещенные в магнитное поле, выстраиваются вдоль силовых линий; благодаря этому можно экспериментально определять вид силовых линий магнитной индукции. Вихревое электрическое поле, порождаемое изменяющимся магнитным полем, также имеет замкнутые силовые линии.

megabook.ru

Однородное и неоднородное магнитные поля

Если линии располагаются параллельно друг другу, их густота одинакова, то в этом случае говорят, что магнитное поле однородно. Если, наоборот, этого не выполняется, т.е. густота разная, линии искривлены, то такое поле будет называться неоднородным. В заключение урока хотелось бы обратить ваше внимание на следующие рисунки.

Рис. 6. Неоднородное магнитное поле

 

 

Во-первых, теперь мы уже знаем, чтомагнитные линии можно изображать стрелками. И рисунок представляет именно неоднородное магнитное поле. Густота в разных местах разная, значит, силовое воздействие этого поля на магнитную стрелку будет разным.

На следующем рисунке представлено уже однородное поле. Линии направлены в одну сторону, и их густота одинакова.

Рис. 7. Однородное магнитное поле

 

 

Однородное магнитное поле – это поле, которое встречается внутри катушки с большим числом витков или внутри прямолинейного, полосового магнита. Магнитное поле вне полосового магнита или то, что мы сегодня наблюдали на уроке, это поле неоднородное. Чтобы все это до конца усвоить, давайте посмотрим на таблицу.

	Неоднородное магнитное поле	Однородное Магнитное поле
Сила, действующая в разных точках	Различна	Одинакова (как по модулю, так и по направлению)
Линии магнитного поля	Искривлены, их густота различна	Параллельны, их густота одинакова
Примеры	Поле магнита вне его Поле прямолинейного проводника с током	Поле внутри длинной катушки с большим числом витков. Поле внутри магнита

Список дополнительной литературы:

Белкин И.К. Электрическое и магнитное поля // Квант. — 1984. — № 3. — С. 28-31. Кикоин А.К. Откуда берется магнетизм? // Квант. — 1992. — № 3. — С. 37-39,42 Леенсон И. Загадки магнитной стрелки // Квант. — 2009. — № 3. — С. 39-40. Элементарный учебник физики. Под ред. Г.С. Ландсберга. Т. 2. – М., 1974

Тема: Электромагнитные явления

Урок 40. Направление тока и направление линий его магнитного поля

Ерюткин Евгений Сергеевич

 

Опыт Эрстеда

В ходе урока мы определим взаимосвязь электрического тока и направления его магнитных линий. Для поиска закономерностей необходимо обратиться к опыту, который впервые был проведен в 1820 году датским ученым Эрстедом.

Рис. 1. Схема опыта Эрстеда

 

 

Обратимся к схеме опыта. В двух штативах был укреплен прямой проводник, подключенный к источнику тока. Под проводником располагалась магнитная стрелка, когда протекал электрический ток, магнитная стрелка располагалась перпендикулярно проводнику с током. Следующий эксперимент с изменением полярности. Электрический ток протекает в противоположную сторону. В результате направление тока в проводнике изменилось. Что произошло с магнитной стрелкой? Магнитная стрелка развернулась на 180 °. Обратите внимание, теперь южный полюс стрелки указывал туда, куда указывал северный, а северный – в противоположном направлении.

О чем этот эксперимент говорит? О том, что, когда изменяется направление электрического тока, изменяется направление магнитных линий.



infopedia.su

Вектор магнитной индукции. Закон Био-Савара-Лапласа и его применение

Глава 15. Магнитное поле

Все электрические и магнитные явления взаимосвязаны и взаимоза­висимы, так как являются различными формами проявления единого электромагнитного поля.

Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).

Магнитным полем называется вид материи, через которую передаётся силовое воздействие на движущиеся электрические заряды и тела, обладающие магнитным моментом.

Пробным элементом для изучения магнитного поля является бесконечно маленькая магнитная стрелка или контур с током, которые своим магнитным полем не искажают исследованное поле. Основным свойством неизменного во вре­мени магнитного поля служит силовое воздейст­вие его как на движущиеся в нем заряженные тела, так и на проводники с электрическим током (неподвижный электрический заряд, находящий­ся в магнитном поле, не испытывает никакого воздействия с его стороны).

Силовой характеристикой магнитного поля является вектор магнитной индукции .

❖ Единица магнитной индукции — тесла (Тл).

Магнитное поле может быть описано полностью, если в каждой его точке найдены модуль и направление магнитной индукции .

Подобно тому, как электрические поля графически изображают с помощью линий напряжённости (силовых линий), магнитные поля изображают с помощью линий магнитной индукции (силовых линий).

Линии магнитной индукции – линии, касательные к которым в данной точке совпадают по направлению с вектором в этой точке. Направление линий магнитной индукции связано с направлением тока в проводнике.

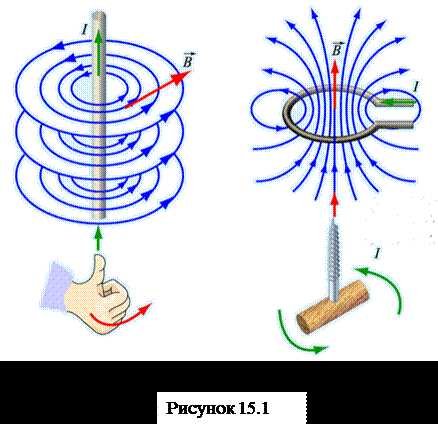
Направление В можно определить по правилу буравчика (рис.15.1): если буравчик с правой резьбой ввинчивать по направлению тока в проводнике, то направление вращения рукоятки буравчика совпадает с направлением вектора магнитной индукции магнитного поля, создаваемого этим током.

Есть и другое правило для определения направления – правило обхвата правой рукой: если обхватить проводник правой рукой, направив отставленный большой палец вдоль тока, то остальные пальцы этой руки укажут направление вектора магнитной индукции магнитного поля данного тока.

Силовые линии магнитного поля прямолинейного провода с током представляют собой концентрические окружности, охватывающие проводник и лежащие в плоскости перпендикулярной току. Центр этих окружностей находится на оси проводника.

Силовые линии магнитного поля не имеют ни начала, ни конца, они либо замкнуты, либо выходят из бесконечности и уходят снова в бесконечность. Это отличает их от линий напряжённости электрического поля. Замкнутость силовых линий магнитной индукции говорит о том, что в магнитном поле не существует источников и стоков, или в природе не существует магнитных зарядов, на которых они начинались или кончались. Такие поля называют вихревыми.

Магнитное поле является вихревым.

Циркуляция вектора магнитной индукции по любому замкнутому контуру не равна нулю:

(15.1)

В отличии от потенциального, каким является электростатическое поле

Магнитное поле называют однородным, если векторы магнитной индукции во всех его точках одинаковы:

(15.2)

Линии магнитной индукции однородного поля параллельны, и их густота везде одинакова. Плотностью линий магнитной индукции можно характеризовать магнитную индукцию .

Обобщая экспериментальные данные французских физиков Био и Савара, Лаплас (французский математик) предложил формулу, по которой можно вычислить индукцию магнитного поля, создаваемого элементом тока в точке М, расположенной от этого элемента на расстоянии r (рис. 15.2)

или

(15.3)

По формуле (15.3) определяем индукцию поля, создаваемого участком проводника, по которому течёт ток I. Чтобы найти индукцию магнитного поля, создаваемого всем проводником, нужно применить принцип суперпозиции, или наложения полей.

Ø Магнитное поле прямолинейного бесконечно длинного проводника с током

Определим напряжённость поля, создаваемого прямолинейным бесконечно длинным проводником с током в точке М, находящейся на расстоянии r0 от проводника. Выделим на проводнике элемент тока Idℓ (рис. 15.2) и проведем радиус-вектор г в точ­ку М. Магнитная индукция поля, создаваемо­го в точке М элементом тока Idℓ, опре­деляется по формуле (15.3). Из рис. 15.2 видно, что

(15.4)

(15.5)

Подставляя эти выражения в (15.3), находим, что магнитная индукция поля, соз­даваемая элементом тока dℓ, равна

(15.6)

Чтобы определить магнитную индукцию, создаваемого бесконечно длинным прямолинейным проводником с током, нужно про­интегрировать выражение (15.6) в пределах от α1 до α2

(15.7)

Используя формулу (15.7) можно определить магнитную индукцию поля, создаваемого проводником конечной длины (рис.15.3).

Для бесконечно длинного проводника: α1→0; cos 0=1.

α1→π; cos π =-1

Подставим в (15.7), получим

(15.8)

Магнитная индукция поля, создаваемого бесконечно длинным проводником, равна

(15.9)

 

Ø Магнитное поле в центре кругового тока

Пусть ток протекает по окружности (рис. 15.4). В этом случае все элементы проводника перпендикулярны радиус-вектору r и sinα=1. Расстояние всех элементов проводника до центра одинаково и равно r.

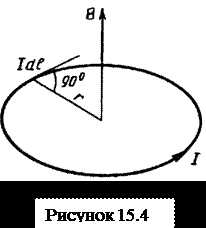
Магнитная индукция в центре кругового тока равна

(15.10)

Принцип суперпозиции позволяет описать поле, создаваемое любой системой проводников. В общем случае принцип суперпозициидля магнитных полей формулируется так: магнитная индукция поля, создаваемого несколькими проводниками с током, равна векторной сумме магнитных индукций, создаваемых каждым из проводников в отдельности.

или (15.11)

Из принципа суперпозиции полей следует, что при наложении полей они не оказывают никакого влияния друг на друга.

Магнитное поле в вакууме принято характеризовать не индукцией В, а напряжённостью Н магнитного поля. Эти величины связаны между собой:

(15.12)

Векторы и совпадают по направлению.

 

studopedya.ru

Магнитное поле. Линии - материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: взаимодействие магнитов, магнитное поле проводника с током.

Магнитные свойства вещества известны людям давно. Магниты получили своё название от античного города Магнесия: в его окрестностях был распространён минерал (названный впоследствии магнитным железняком или магнетитом), куски которого притягивали железные предметы.

Взаимодействие магнитов

На двух сторонах каждого магнита расположены северный полюс и южный полюс. Два магнита притягиваются друг к другу разноимёнными полюсами и отталкиваются одноимёнными. Магниты могут действовать друг на друга даже сквозь вакуум! Всё это напоминает взаимодействие электрических зарядов, однако взаимодействие магнитов не является электрическим. Об этом свидетельствуют следующие опытные факты.

• Магнитная сила ослабевает при нагревании магнита. Сила же взаимодействия точечных зарядов не зависит от их температуры.

• Магнитная сила ослабевает, если трясти магнит. Ничего подобного с электрически заряженными телами не происходит.

• Положительные электрические заряды можно отделить от отрицательных (например, при электризации тел). А вот разделить полюса магнита не получается: если разрезать магнит на две части, то в месте разреза также возникают полюса, и магнит распадается на два магнита с разноимёнными полюсами на концах (ориентированных точно так же, как и полюса исходного магнита).

Таким образом, магниты всегда двухполюсные, они существуют только в виде диполей. Изолированных магнитных полюсов (так называемых магнитных монополей — аналогов электрического заряда)в при роде не существует (во всяком случае, экспериментально они пока не обнаружены). Это, пожалуй, самая впечатляющая асимметрия между электричеством и магнетизмом.

• Как и электрически заряженные тела, магниты действуют на электрические заряды. Однако магнит действует только на движущийся заряд; если заряд покоится относительно магнита, то действия магнитной силы на заряд не наблюдается. Напротив, наэлектризованное тело действует на любой заряд ,вне зависимости от того, покоится он или движется.

По современным представлениям теории близкодействия, взаимодействие магнитов осуществляется посредством магнитного поля.А именно, магнит создаёт в окружающем пространстве магнитное поле, которое действует на другой магнит и вызывает видимое притяжение или отталкивание этих магнитов.

Примером магнита служит магнитная стрелка компаса. С помощью магнитной стрелки можно судить о наличии магнитного поля в данной области пространства, а также о направлении поля.

Наша планета Земля является гигантским магнитом. Неподалёку от северного географического полюса Земли расположен южный магнитный полюс. Поэтому северный конец стрелки компаса, поворачиваясь к южному магнитному полюсу Земли, указывает на географический север. Отсюда, собственно, и возникло название «северный полюс» магнита.

Линии магнитного поля

Электрическое поле, напомним, исследуется с помощью маленьких пробных зарядов, по действию на которые можно судить о величине и направлении поля. Аналогом пробного заряда в случае магнитного поля является маленькая магнитная стрелка.

Например, можно получить некоторое геометрическое представление о магнитном поле, если разместить в разных точках пространства очень маленькие стрелки компаса. Опыт показывает, что стрелки выстроятся вдоль определённых линий —так называемых линий магнитного поля . Дадим определение этого понятия в виде следующих трёх пунктов.

1. Линии магнитного поля, или магнитные силовые линии — это направленные линии в пространстве, обладающие следующим свойством: маленькая стрелка компаса, помещённая в каждой точке такой линии, ориентируется по касательной к этой линии.

2. Направлением линии магнитного поля считается направление северных концов стрелок компаса, расположенных в точках данной линии.

3. Чем гуще идут линии, тем сильнее магнитное поле в данной области пространства.

Роль стрелок компаса с успехом могут выполнять железные опилки: в магнитном поле маленькие опилки намагничиваются и ведут себя в точности как магнитные стрелки.

Так, насыпав железных опилок вокруг постоянного магнита, мы увидим примерно следующую картину линий магнитного поля (рис. 1).

Рис. 1. Поле постоянного магнита

Северный полюс магнита обозначается синим цветом и буквой ; южный полюс — красным цветом и буквой . Обратите внимание, что линии поля выходят из северного полюса магнита и входят в южный полюс: ведь именно к южному полюсу магнита будет направлен северный конец стрелки компаса.

Опыт Эрстеда

Несмотря на то, что электрические и магнитные явления были известны людям ещё с античности, никакой взаимосвязи между ними долгое время не наблюдалось. В течение нескольких столетий исследования электричества и магнетизма шли параллельно и независимо друг от друга.

Тот замечательный факт, что электрические и магнитные явления на самом деле связаны друг с другом, был впервые обнаружен в 1820 году — в знаменитом опыте Эрстеда.

Схема опыта Эрстеда показана на рис. 2 (изображение с сайта rt.mipt.ru). Над магнитной стрелкой ( и — северный и южный полюсы стрелки) расположен металлический проводник, подключённый к источнику тока. Если замкнуть цепь, то стрелка поворачивается перпендикулярно проводнику!Этот простой опыт прямо указал на взаимосвязь электричества и магнетизма. Эксперименты последовавшие за опытом Эрстеда, твёрдо установили следующую закономерность: магнитное поле порождается электрическими токами и действует на токи.

Рис. 2. Опыт Эрстеда

Картина линий магнитного поля, порождённого проводником с током, зависит от формы проводника.

Магнитное поле прямого провода с током

Линии магнитного поля прямолинейного провода с током являются концентрическими окружностями. Центры этих окружностей лежат на проводе, а их плоскости перпендикулярны проводу (рис. 3).

Рис. 3. Поле прямого провода с током

Для определения направления линий магнитного поля прямого тока существуют два альтернативных правила.

Правило часовой стрелки . Линии поля идут против часовой стрелки, если смотреть так, чтобы ток тёк на нас.

Правило винта (или правило буравчика, или правило штопора — это уж кому что ближе ;-)). Линии поля идут туда, куда надо вращать винт (с обычной правой резьбой), чтобы он двигался по резьбе в направлении тока.

Пользуйтесь тем правилом, которое вам больше по душе. Лучше привыкнуть к правилу часовой стрелки — вы сами впоследствии убедитесь, что оно более универсально и им проще пользоваться (а потом с благодарностью вспомните его на первом курсе, когда будете изучать аналитическую геометрию).

На рис. 3 появилось и кое-что новое: это вектор , который называется индукцией магнитного поля, или магнитной индукцией. Вектор магнитной индукции является аналогом вектора напряжённости электрического поля: он служит силовой характеристикой магнитного поля, определяя силу, с которой магнитное поле действует на движущиеся заряды.

О силах в магнитном поле мы поговорим позже, а пока отметим лишь, что величина и направление магнитного поля определяется вектором магнитной индукции . В каждой точке пространства вектор направлен туда же,куда и северный конец стрелки компаса, помещённой в данную точку, а именно по касательной к линии поля в направлении этой линии. Измеряется магнитная индукция в теслах (Тл).

Как и в случае электрического поля, для индукции магнитного поля справедлив принцип суперпозиции. Он заключается в том, что индукции магнитных полей , создаваемых в данной точке различными токами, складываются векторно и дают результирующий вектор магнитной индукции: .

Магнитное поле витка с током

Рассмотрим круговой виток, по которому циркулирует постоянный ток . Источник,создающий ток, мы на рисунке не показываем.

Картина линий поля нашего витка будет иметь приблизительно следующий вид (рис. 4).

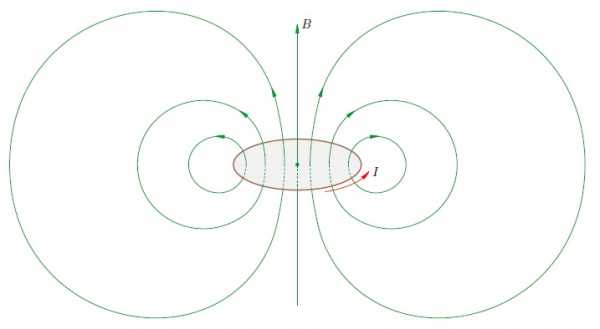
Рис. 4. Поле витка с током

Нам будет важно уметь определять, в какое полупространство (относительно плоскости витка) направлено магнитное поле. Снова имеем два альтернативных правила.

Правило часовой стрелки. Линии поля идут туда, глядя откуда ток кажется циркулирующим против часовой стрелки.

Правило винта. Линии поля идут туда, куда будет перемещаться винт (с обычной правой резьбой), если вращать его в направлении тока.

Как видите, ток и поле меняются ролями — по сравнению с формулировками этих правил для случая прямого тока.

Магнитное поле катушки с током

Катушка получится, если плотно, виток к витку, намотать провод в достаточно длинную спираль (рис. 5 - изображение с сайта en.wikipedia.org). В катушке может быть несколько десятков, сотен или даже тысяч витков. Катушка называется ещё соленоидом.

Рис. 5. Катушка (соленоид)

Магнитное поле одного витка, как мы знаем, выглядит не очень-то просто. Поля? отдельных витков катушки накладываются друг на друга, и, казалось бы, в результате должна получиться совсем уж запутанная картина. Однако это не так: поле длинной катушки имеет неожиданно простую структуру (рис. 6).

Рис. 6. поле катушки с током

На этом рисунке ток в катушке идёт против часовой стрелки, если смотреть слева (так будет, если на рис. 5 правый конец катушки подключить к «плюсу» источника тока, а левый конец — к «минусу»). Мы видим, что магнитное поле катушки обладает двумя характерными свойствами.

1. Внутри катушки вдали от её краёв магнитное поле является однородным : в каждой точке вектор магнитной индукции одинаков по величине и направлению. Линии поля — параллельные прямые; они искривляются лишь вблизи краёв катушки, когда выходят наружу.

2. Вне катушки поле близко к нулю. Чем больше витков в катушке — тем слабее поле снаружи неё.

Заметим, что бесконечно длинная катушка вообще не выпускает поле наружу: вне катушки магнитное поле отсутствует. Внутри такой катушки поле всюду является однородным.

Ничего не напоминает? Катушка является «магнитным» аналогом конденсатора. Вы же помните, что конденсатор создаёт внутри себя однородное электрическое поле, линии которого искривляются лишь вблизи краёв пластин, а вне конденсатора поле близко к нулю; конденсатор с бесконечными обкладками вообще не выпускает поле наружу, а всюду внутри него поле однородно.

А теперь — главное наблюдение. Сопоставьте, пожалуйста, картину линий магнитного поля вне катушки (рис. 6) с линиями поля магнита на рис. 1. Одно и то же, не правда ли? И вот мы подходим к вопросу, который, вероятно, у вас уже давно возник: если магнитное поле порождается токами и действует на токи, то какова причина возникновения магнитного поля вблизи постоянного магнита? Ведь этот магнит вроде бы не является проводником с током!

Гипотеза Ампера. Элементарные токи

Поначалу думали, что взаимодействие магнитов объясняется особыми магнитными зарядами, сосредоточенными на полюсах. Но, в отличие от электричества, никто не мог изолировать магнитный заряд; ведь, как мы уже говорили, не удавалось получить по отдельности северный и южный полюс магнита — полюса всегда присутствуют в магните парами.

Сомнения насчёт магнитных зарядов усугубил опыт Эрстеда, когда выяснилось, что магнитное поле порождается электрическим током. Более того, оказалось, что для всякого магнита можно подобрать проводник с током соответствующей конфигурации, такой, что поле этого проводника совпадает с полем магнита.

Ампер выдвинул смелую гипотезу. Нет никаких магнитных зарядов. Действие магнита объясняется замкнутыми электрическими токами внутри него.

Что это за токи? Эти элементарные токи циркулируют внутри атомов и молекул; они связаны с движением электронов по атомным орбитам. Магнитное поле любого тела складывается из магнитных полей этих элементарных токов.

Элементарные токи могут быть беспорядочным образом расположены друг относительно друга. Тогда их поля взаимно погашаются, и тело не проявляет магнитных свойств.

Но если элементарные токи расположены согласованно,то их поля,складываясь,усиливают друг друга. Тело становится магнитом (рис. 7; магнитое поле будет направлено на нас; также на нас будет направлен и северный полюс магнита).

Рис. 7. Элементарные токи магнита

Гипотеза Ампера об элементарных токах прояснила свойства магнитов.Нагревание и тряска магнита разрушают порядок расположения его элементарных токов, и магнитные свойства ослабевают. Неразделимость полюсов магнита стала очевидной: в месте разреза магнита мы получаем те же элементарные токи на торцах. Способность тела намагничиваться в магнитном поле объясняется согласованным выстраиванием элементарных токов, «поворачивающихся» должным образом (о повороте кругового тока в магнитном поле читайте в следующем листке).

Гипотеза Ампера оказалась справедливой — это показало дальнейшее развитие физики. Представления об элементарных токах стали неотъемлемой частью теории атома, разработанной уже в ХХ веке — почти через сто лет после гениальной догадки Ампера.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

1.5. Графическое изображение электрических полей. Силовые линии и эквипотенциальные поверхности

Для большей наглядности электрическое поле часто изображается при помощи силовых линий и эквипотенциальных поверхностей.

Силовые линии – это непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности электрического поля (рис. 1.5). Густота силовых линий (число силовых линий, проходящих через единицу площади) пропор­ци­о­нальна напряженности электрического поля.

Эквипотенциальные поверхности (экви­по­тенциали) – поверхности равного потен­циала. Это поверхности (линии), при движении по которым потенциал не меняется. Иначе, разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю. Силовые линии перпендикулярны эквипотенциальным поверхностям и направлены в сторону наиболее резкого убывания потенциала. Этот факт следует из уравнения (1.10) и доказывается в курсе математического анализа разделе «Скалярные и векторные поля».

Рассмотрим в качестве примера электрическое поле, создаваемое на расстоянии 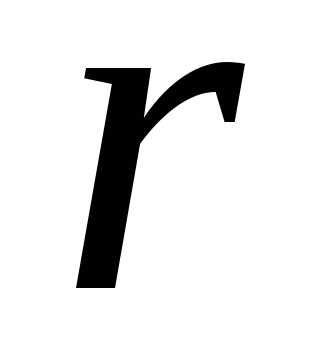от точечного заряда. Согласно (1.11,б) вектор напряженности совпадает с направлением вектора, если заряд положительный, и противоположен ему, если заряд отрицательный. Следовательно, силовые линии расходятся радиально от заряда (рис. 1.6, а, б). Густота силовых линий, как и напряженность, обратно пропорциональна квадрату расстояния () до заряда. Эквипотенциальные поверхности электрического поля точечного заряда представляют собой сферы с центром в месте расположения заряда.

На рис. 1.7 показано электрическое поле системы двух равных по модулю, но противоположных по знаку точечных зарядов. Мы предоставляем разобрать этот пример читателям самостоятельно. Отметим лишь, что силовые линии всегда начинаются на положительных зарядах и заканчиваются на отрицательных. В случае электрического поля одного точечного заряда (рис. 1.6, а, б) предполагается, что силовые линии обрываются на очень удаленных зарядах противоположного знака. Считается, что Вселенная в целом нейтральна. Поэтому, если имеется заряд одного знака, то где-то обязательно найдется равный ему по модулю заряд другого знака.

1.6. Теорема Гаусса для электрического поля в вакууме

Основной задачей электростатики является задача о нахождении напряженности и потенциала электрического поля в каждой точке пространства. В п. 1.4 мы решили задачу о поле точечного заряда, а также рассмотрели поле системы точечных зарядов. В этом параграфе речь пойдет о теореме, позволяющей рассчитывать электрическое поле более сложных заряженных объектов. Например, заряженной длинной нити (прямой), заряженной плоскости, заряженной сферы и других. Рассчитав напряженность электрического поля в каждой точке пространства, используя уравнения (1.12) и (1.13), можно вычислить потенциал в каждой точке или разность потенциалов между двумя любыми точками, т.е. решить основную задачу электростатики.

Для математического описания введем понятие потока вектора напряженности или потока электрического поля. Потоком (Ф) вектора электрического поля через плоскую поверхность площадиназывается величина:

, (1.16)

где – напряженность электрического поля, которая предполагается постоянной в пределах площадки;– угол между направлением вектораи единичного вектора нормали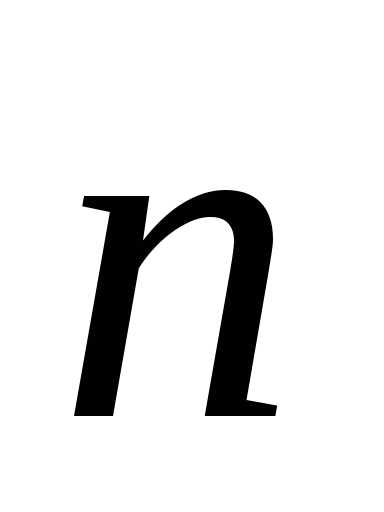к площадке(рис. 1.8). Формулу (1.16) можно записать, используя понятие скалярного произведения векторов:

. (1.15,а)

В случае, когда поверхность не плоская, для вычисления потока ее необходимо разделить на малые части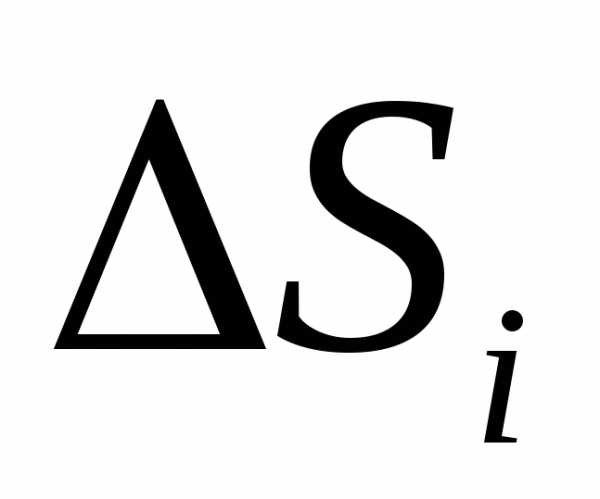, которые можно приблизительно считать плоскими, а затем записать выражение (1.16) или (1.16,а) для каждого куска поверхности и сложить их. В пределе, когда поверхностьSi очень мала (), такую сумму называют поверхностным интегралом и обозначают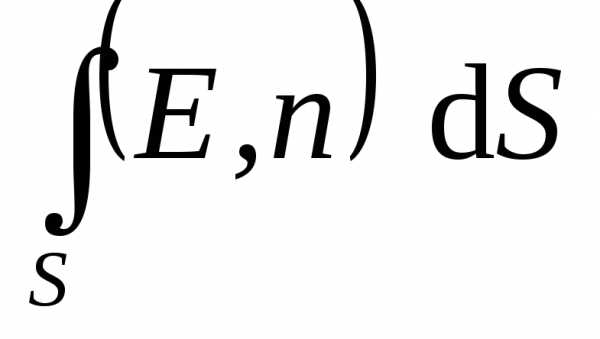. Таким образом, поток вектора напряженности электрического поля через произвольную поверхностьопределяется выражением:

. (1.17)

В качестве примера рассмотрим сферу радиуса , центром которой служит положительный точечный заряд , и определим поток электрического поля через поверхность этой сферы. Силовые линии (см., например, рис.1.6, а) выходящие из заряда, перпендикулярны поверхности сферы, и в каждой точке сферы модуль напряженности поля один и тот же

.

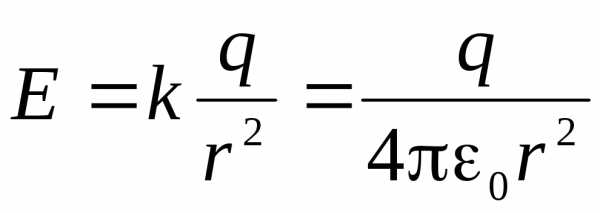Площадь сферы ,

тогда .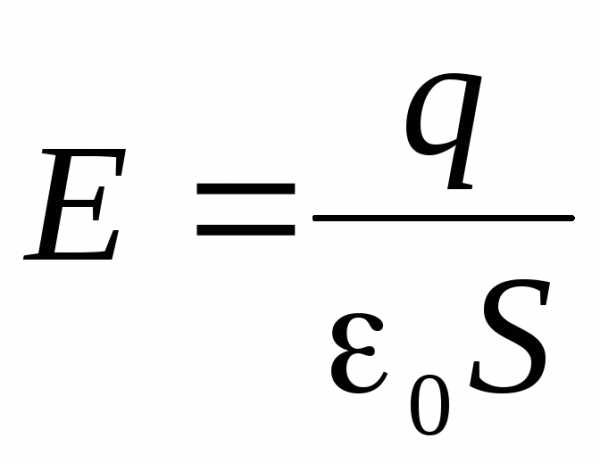

Величина и представляет собой поток электрического поля через поверхность сферы. Таким образом, получаем. Видно, что поток через поверхность сферы электрического поля не зависит от радиуса сферы, а зависит только от самого заряда. Поэтому, если провести ряд концентрических сфер, то поток электрического поля через все эти сферы будет одинаковым. Очевидно, что число силовых линий, пересекающих эти сферы, тоже будет одинаковым. Условились число силовых линий, выходящих из заряда, принимать равным потоку электрического поля:.

Если сферу заменить любой другой замкнутой поверхностью, то поток электрического поля и число силовых линий, пересекающих ее, не изменятся. Кроме того, поток электрического поля через замкнутую поверхность, а значит и число силовых линий, пронизывающих эту поверхность, равняется не только для поля точечного заряда, но и для поля, создаваемого любой совокупностью точечных зарядов, в частности – заряженным телом. Тогда величинуследует считать как алгебраическую сумму всей совокупности зарядов, находящихся внутри замкнутой поверхности. В этом и состоит суть теоремы Гаусса, которая формулируется так:

Поток вектора напряженности электрического поля через произвольную замкнутую поверхность равняется , где  алгебраическая сумма зарядов, заключенных внутри этой поверхности.

Математически теорему можно записать в виде

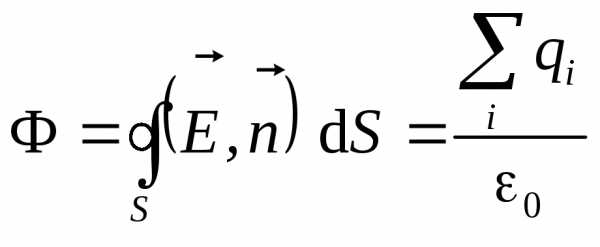. (1.18)

Отметим, что если на некоторой поверхности S вектор постоянен и параллелен вектору, то поток через такую поверхность. Преобразуя первый интеграл, мы сначала воспользовались тем, что векторыипараллельны, а значит. Затем вынесли величинуза знак интеграла в силу того, что она постоянна в любой точке сферы. Применяя теорему Гаусса для решения конкретных задач, специально в качестве произвольной замкнутой поверхности стараются выбирать поверхность, для которой выполняются описанные выше условия.

Приведем несколько примеров на применение теоремы Гаусса.

Пример 1.2. Рассчитать напряженность электрического поля равномерно заряженной бесконечной нити. Определить разность потенциалов между двумя точками в таком поле.

Решение. Предположим для определенности, что нить заряжена положительно. В силу симметрии задачи можно утверждать, что силовые линии будут радиально расходящимися от оси нити прямыми (рис.1.9), густота которых по мере удаления от нити уменьшается по какому-то закону. По этому же закону будет уменьшаться и величина электрического поля . Эквипотенци­аль­ны­ми поверхностями будут цилиндрические поверхности с осью, совпадающей с нитью.

Пусть заряд единицы длины нити равен . Эта величина называется линейной плотностью заряда и измеряется в СИ в единицах [Кл/м]. Для расчета напряженности поля применим теорему Гаусса. Для этого в качестве произвольной замкнутой поверхностивыберем цилиндр радиусаи длины, ось которого совпадает с нитью (рис.1.9). Вычислим поток электрического поля через площадь поверхности цилиндра. Полный поток складывается из потока через боковую поверхность цилиндра и потока через основания

.

Однако, , поскольку в любой точке на основаниях цилиндра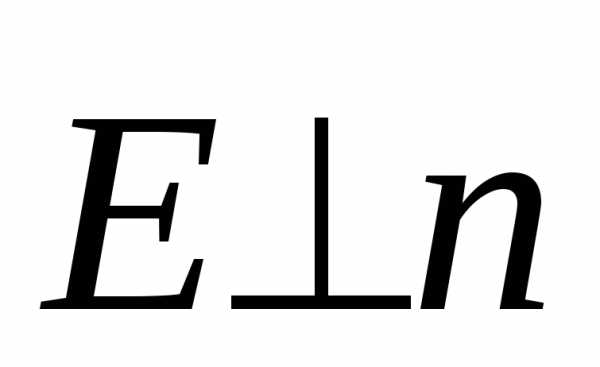. Это значит, чтов этих точках. Поток через боковую поверхность. По теореме Гаусса этот полный поток равен. Таким образом, получили

.

Сумма зарядов, находящихся внутри цилиндра, выразим через линейную плотность заряда :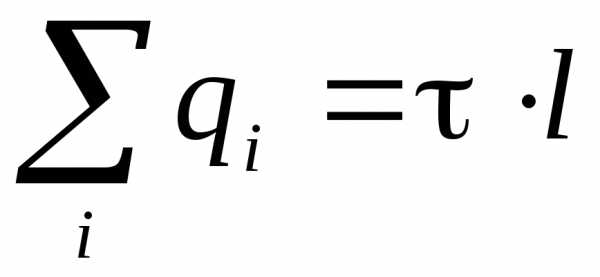. Учитывая, что, получим

,

откуда:

, (1.19)

т.е. напряженность и густота силовых линий электрического поля равномерно заряженной бесконечной нити убывает обратно пропорционально расстоянию ().

Найдем разность потенциалов между точками, находящимися на расстояниях и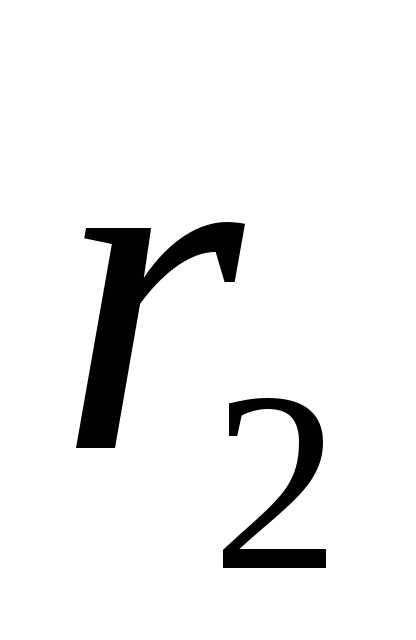от нити (принадлежащими эквипотенциальным цилиндрическим поверхностям с радиусамии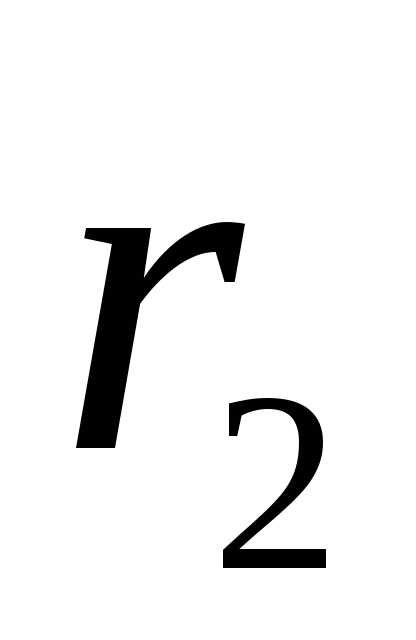). Для этого воспользуемся связью напряженности электрического поля с потенциалом в виде (1.9,в):. Учитывая выражение (1.19), получим дифференциальное уравнение с разделяющимися переменными:

.

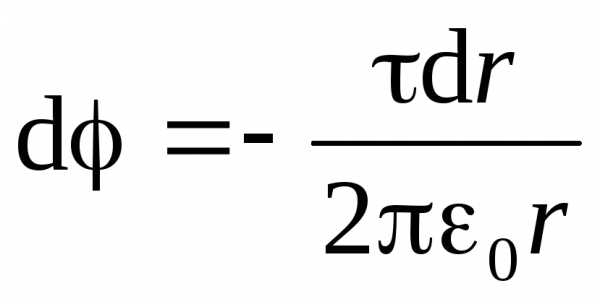
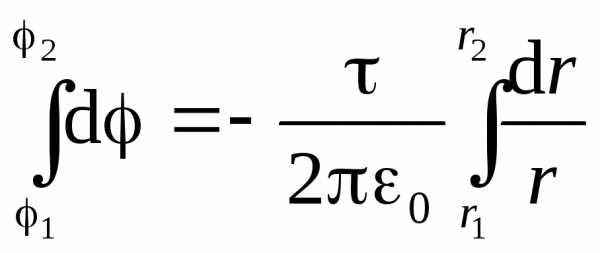
Пример 1.3. Рассчитать напряжен­ность электрического поля равномерно заряженной плоскости. Определить раз­ность потенциалов между двумя точками в таком поле.

Решение. Электрическое поле равно­мер­но заряженной плоскости показано на рис. 1.10. В силу симметрии силовые линии должны быть перпендикулярны плоскости. Поэтому сразу можно сделать вывод о том, что густота линий, а, сле­до­вательно, и напряженность электри­ческого поля при удалении от плоскости меняться не будут. Эквипотенциальные поверхности пред­став­ляют собой плоскости, параллельные данной заряженной плоскости. Пусть заряд единицы площади плоскости равен . Эта величина называется поверхностной плотностью заряда и измеряется в СИ в единицах [Кл/м2].

Применим теорему Гаусса. Для этого в качестве произвольной замкнутой поверхности выберем цилиндр длиной, ось которого перпендикулярна плоскости, а основания равноудалены от нее (рис.1.10). Общий поток электрического поля. Поток через боковую поверхность равен нулю. Поток через каждое из оснований равен, поэтому. По теореме Гаусса получим:

.

Сумму зарядов, находящихся внутри цилиндра , найдем через поверхностную плотность заряда:. Тогда, откуда:

. (1.20)

Из полученной формулы видно, что напряженность поля равномерно заряженной плоскости не зависит от расстояния до заряженной плоскости, т.е. в любой точке пространства (в одной полуплоскости) одинакова и по модулю, и по направлению. Такое поле называется однородным. Силовые линии однородного поля параллельны, их густота не меняется.

Найдем разность потенциалов между двумя точками однородного поля (принадлежащим эквипотенциальным плоскостям и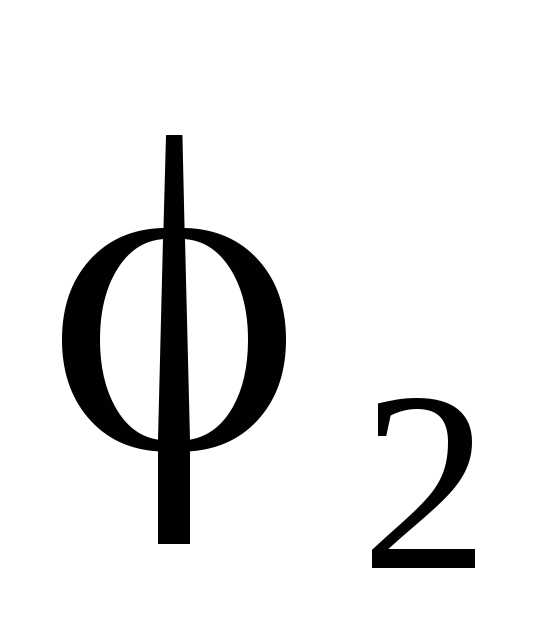, лежащим в одной полуплоскости относительно заряженной плоскости (рис.1.10)). Направим осьвертикально вверх, тогда проекция вектора напряженности на эту ось равна модулю вектора напряженности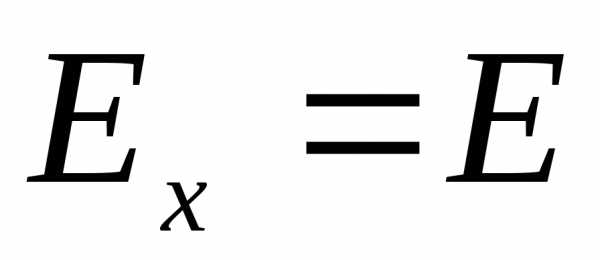. Воспользуемся уравнением (1.9):

.

Постоянную величину (поле однородно) можно вынести из под знака интеграла: . Интегрируя, получаем: . Итак, потенциал однородного поля линейно зависит от координаты.

Разность потенциалов между двумя точками электрического поля – есть напряжение между этими точками (). Обозначим расстояние между эквипотенциальными плоскостями. Тогда можно записать, что в однородном электрическом поле:

. (1.21)

Еще раз подчеркнем, что при использовании формулы (1.21) нужно помнить, что величина  не расстояние между точками 1 и 2, а расстояние между эквипотен­ци­альными плоскостями, которым эти точки принадлежат.

Пример 1.4. Рассчитать напря­жен­ность электрического поля двух параллельных плоскостей, однородно заряженных с поверхностными плотностями зарядов и.

Решение. Воспользуемся резуль­та­том примера 1.3 и принципом суперпо­зи­ции. Согласно этому принципу резуль­тиру­ющее электрическое поле в любой точке пространства , гдеи- напряженности электрических полей первой и второй плоскости. В пространстве между плоскостями вектораинаправлены в одну сторону, поэтому модуль напряженности результирующего поля. Во внешнем пространстве вектораинаправлены в разные стороны, поэтому(рис. 1.11). Таким образом, электрическое поле есть только в пространстве между плоскостями. Оно однородно, так как является суммой двух однородных полей.

Пример 1.5. Найти напряженность и потенциал электрического поля равномерно заряженной сферы. Суммарный заряд сферы равен , а радиус сферы –.

Решение. В силу симметрии распределения заряда силовые линии должны быть направлены вдоль радиусов сферы.

Рассмотрим область внутри сферы. В качестве произвольной поверхности выберем сферу радиуса, центр которой совпадает с центром заряженной сферы. Тогда поток электрического поля через сферуS: . Сумма зарядов внутри сферырадиусаравна нулю, поскольку все заряды располагаются на поверхности сферы радиуса . Тогда по теореме Гаусса: . Поскольку, то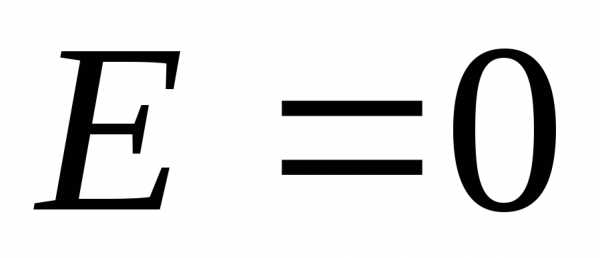. Таким образом внутри равномерно заряженной сферы поля нет.

Рассмотрим область вне сферы. В качестве произвольной поверхности выберем сферу радиуса, центр которой совпадает с центром заряженной сферы. Поток электрического поля через сферу:. Сумма зарядов внутри сферы равна полному зарядузаряженной сферы радиуса. Тогда по теореме Гаусса:. Учитывая, что, получим:

.

Рассчитаем потенциал электрического поля. Удобнее начать с внешней области , поскольку мы знаем, что на бесконечном расстоянии от центра сферы потенциал принимается равным нулю. Используя уравнение (1.11,а) получаем дифференциальное уравнение с разделяющимися переменными:

.

Константа , посколькупри. Таким образом, во внешнем пространстве ():.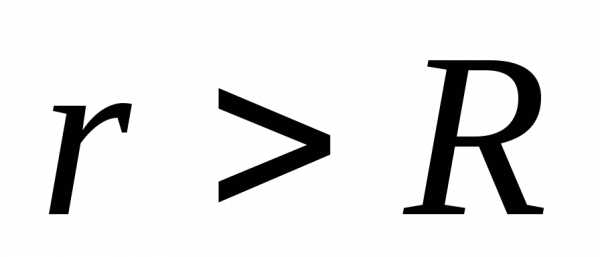

Точки на поверхности заряженной сферы () будут иметь потенциал.

Рассмотрим область 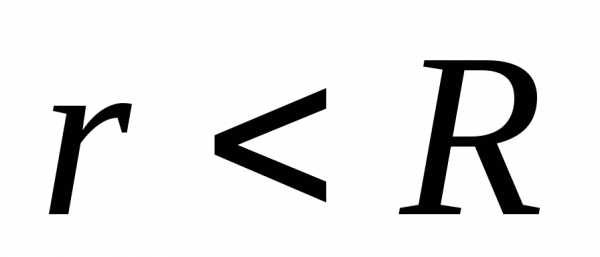. В этой области, поэтому из уравнения (1.11,а) получаем:. В силу непрерывности функцииконстантадолжна быть равна значению потенциала на поверхности заряженной сферы:. Таким образом, потенциал во всех точках внутри сферы:.

Итак, мы получили, что напряженность и потенциал электрического поля, создаваемого равномерно заряженной сферой, вне сферы равны напряженности и потенциалу поля, создаваемого точечным зарядом той же величины , что и заряд сферы, помещенным в центр сферы. Во внутреннем пространстве поле отсут­ствует, а потенциал во всех точках одинаков. Электрическое поле (силовые линии и эквипотенциальные поверхности) заряженной сферы изображены на рис. 1.12. Предполагается, что сфера заряжена положительно. Вне сферы силовые линии и распределены в пространстве точно так же, как и силовые линии точечного заряда.

На рис. 1.13 изображены графики зависимости и. Функциянепрерывна, а функция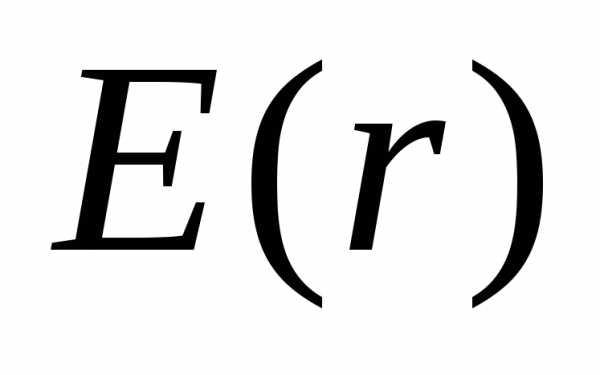скачкообразно меняется при переходе через границу заряженной сферы. Величина скачка равна. Действительно, вблизи заряженной сферы (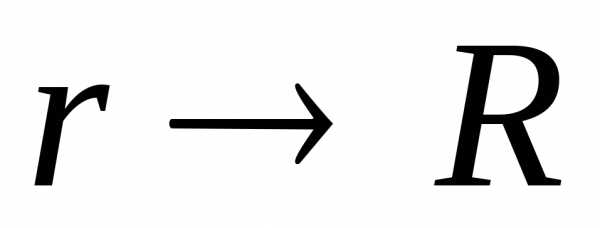) напряженность поля во внешнем пространстве, а внутри равна нулю.

Величину скачка можно выразить через поверхностную плотность заряда на сфере:

.

Заметим, что это общее свойство электростатического поля: на заряженной поверхности проекция напряженности на направление нормали всегда испытывает скачок независимо от формы поверхности. Рекомендуем проверить этот принцип для поля равномерно заряженной плоскости и поля двух параллельных заряженных плоскостей (примеры 1.3, 1.4).

С точки зрения математики непрерывность потенциала в точках заряженной поверхности означает, что. С точки зрения физики непрерывность функцииможно объяснить следующим образом. Если бы потенциал на границе некоторой области имел бы скачок (разрыв), то при бесконечно малом перемещении некоторого зарядаиз точки 1, лежащей с одной стороны границы, в точку 2, лежащую на другой ее стороне, совершалась бы конечная работа, гдеи потенциалы точек 1 и 2 соответственно, а величина 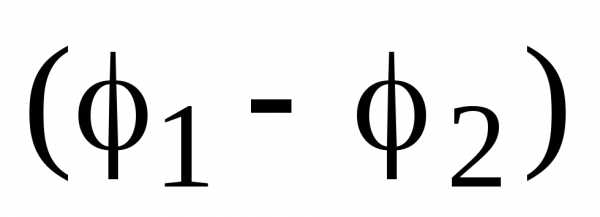равна величине скачка потенциала на границе области. Конечная работа, совершенная на бесконечно малом перемещении, означает, что на границе раздела бы действовали бесконечно большие силы, что невозможно.

Напряженность электрического поля, в отличие от потенциала, на границе области может меняться очень резко (скачкообразно).

Пример 1.6.Две концентрические сферы радиусови() равномерно заряжены равными по модулю, но противоположными по знаку зарядамии(сферический конденсатор). Определить напряженность и потенциал электрического поля во всем пространстве.

Решение. Решение этой задачи можно было бы также начать с применения теоремы Гаусса. Однако, используя результаты предыдущего примера и принцип суперпозиции (1.13, 1.14), ответ можно получить быстрее.

Во внешних точках пространства () электрическое поле создается зарядами обеих сфер. Величина напряженности поля первой сферыи направлена от сфер вдоль радиусов. Величина напряженности поля второй сферы такая же, но направлена противоположно. Следовательно, согласно принципу суперпозиции, во всех внешних точках пространства электрическое поле будет отсутствовать.

Рассмотрим точки пространства между сферами (). Эти точки являются внутренними для отрицательно заряженной сферы, поэтому в этой области(см. пример 1.5). Для положительно заряженной сферы эти точки являются внешними, поэтому. Таким образом, величина напряженности поля в этой области. Здесь поле создают только заряды меньшей сферы.

Наконец, во внутренних точках пространства ()и, поэтому электрического поля в этих точках нет.

Аналогично можно применить принцип суперпозиции и для потенциалов. Получаются следующие результаты:

: ;

: ;

: .

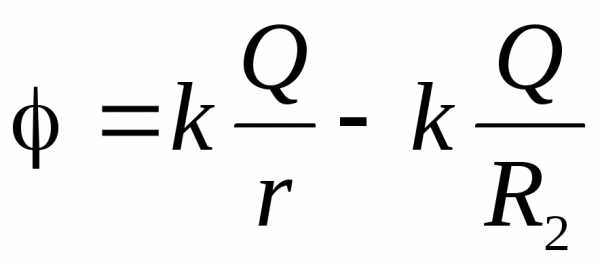Рекомендуем самостоятельно получить эти результаты, а также схематически изобразить электрическое поле и построить графики и.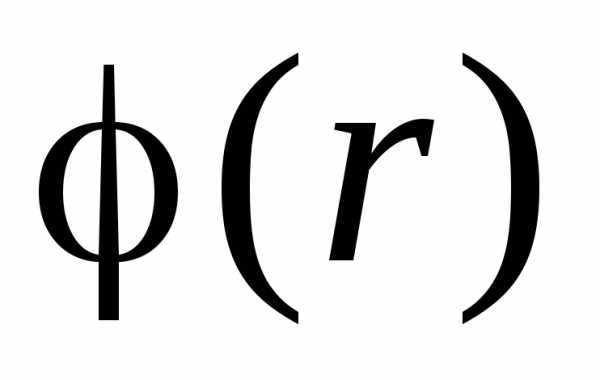

studfiles.net

Магнитное поле. Магнитные линии. Однородное и неоднородное магнитное поле :: Класс!ная физика

МАГНИТНОЕ ПОЛЕ

Магнитное поле, что это? - особый вид материи;Где существует? - вокруг движущихся электрических зарядов (в том числе вокруг проводника с током)Как обнаружить? - с помощью магнитной стрелки (или железных опилок) или по его действию на проводник с током.

Опыт Эрстеда:

Магнитная стрелка поворачивается, если по проводнику начинает протекать эл. ток, т.к. вокруг проводника с током образуется магнитное поле.

Взаимодействие двух проводников с током:

Каждый проводник с током имеет вокруг себя собственное магнитное поле, которое с некоторой силой действует на соседний проводник. В зависимости от направления токов проводники могут притягиваться или отталкиваться друг от друга.

Вспомни прошлый учебный год:магнитное поле

МАГНИТНЫЕ ЛИНИИ

(или иначе линии магнитной индукции)

Как изобразить магнитное поле? - с помощью магнитных линий;Магнитные линии, что это?

- это воображаемые линии , вдоль которых располагаются магнитные стрелки, помещенные в магнитное поле. Магнитные линии можно провести через любую точку магнитного поля, они имеют направление и всегда замкнуты.

 

Вспомни прошлый учебный год:

магнитное поле прямого проводника с током;магнитные линии.

НЕОДНОРОДНОЕ МАГНИТНОЕ ПОЛЕ

Характеристика неоднородного магнитного поля: магнитные линии искривлены;густота магнитных линий различна;сила, с которой магнитное поле действует на магнитную стрелку, различна в разных точках этого поля по величине и направлению.

Где существует неоднородное магнитное поле ?

- вокруг прямого проводника с током;

- вокруг полосового магнита;

- вокруг соленоида (катушки с током).

ОДНОРОДНОЕ МАГНИТНОЕ ПОЛЕ

Характеристика однородного магнитного поля: магнитные линии параллельные прямые;густота магнитных линий везде одинакова; сила, с которой магнитное поле действует на магнитную стрелку, одинакова во всех точках этого поля по величине и направлению.

Где существует однородное магнитное поле?

- внутри полосового магнита и внутри соленоида , если его длина много больше, чем диаметр.

КНИЖНАЯ ПОЛКА

Тайны магнита.

ИНТЕРЕСНО ?

Способность железа и его сплавов сильно намагничиваться исчезает при нагревании до высокой температуры. Чистое железо теряет такую способность при нагревании до 767 °С.

___

Мощные магниты, используемые во многих современных товарах, способны влиять на работу электронных стимуляторов сердца и вживленных сердечных устройств у кардиологических пациентов. Обычные железные или ферритовые магниты, которые легко отличить по тускло-серой окраске, обладают небольшой силой и практически не вызывают беспокойств. Однако недавно появились очень сильные магниты - блестяще-серебристые по цвету и представляющие собой сплав неодима, железа и бора. Создаваемое ими магнитное поле очень сильно, благодаря чему они широко применяются в компьютерных дисках, наушниках и динамиках, а также в игрушках, украшениях и даже одежде.

Однажды на рейде главного города Майорки, появилось французское военное судно "Ля-Ролейн". Состояние его было настолько жалким, что корабль едва дошел своим ходом до причала.. Когда на борт судна взошли французские ученые, в том числе двадцати двухлетний Араго, выяснилось, что корабль был разрушен молнией. Пока комиссия осматривала судно, покачивая головами при виде обгоревших мачт и надстроек, Араго поспешил к компасам и увидел то, что ожидал: стрелки компасов указывали в разные стороны...

___

Через год, копаясь в останках разбившегося вблизи Алжира генуэзского судна, Араго обнаружил, что стрелки компасов были размагничены. В кромешной тьме туманной ночи капитан, направив по компасу судно к северу, подальше от опасных мест, на самом деле неудержимо двигался к тому, чего так старался избежать. Корабль шел к югу, прямо к скалам, обманутый пораженным молнией магнитным компасом.

В. Карцев. Магнит за три тысячелетия.

КОМПАС

Магнитный компас был изобретен в Китае. Уже 4000 лет тому назад караванщики брали с собой глиняный горшок и "берегли его в пути пуще всех своих дорогих грузов". В нем на поверхности жидкости на деревянном поплавке лежал камень, любящий железо. Он мог поворачиваться и , все время указывал путникам в сторону юга, что при отсутствии Солнца помогало им выходить к колодцам.В начале нашей эры китайцы научились изготавливать искусственные магниты, намагничивая железную иглу.И только через тысячу лет намагниченную иглу для компаса стали применять европейцы.

МАГНИТНОЕ ПОЛЕ ЗЕМЛИ

Земля - это большой постоянный магнит.Южный магнитный полюс, хоть и расположен, по земным меркам, вблизи Северного географического полюса, их, тем не менее, разделяют около 2000 км.На поверхности Земли имеются территории, где ее собственное магнитное поле сильно искажено магнитным полем железных руд, залегающих на небольшой глубине. Одна из таких территорий – Курская магнитная аномалия, расположенная в Курской области.

___

Магнитная индукция магнитного поля Земли составляет всего около 0,0004Теслы.___

На магнитное поле Земли оказывает влияние повышенная солнечная активность. Примерно один раз в каждые 11.5 лет она возрастает настолько, что нарушается радиосвязь, ухудшается самочувствие людей и животных, а стрелки компасов начинают непредсказуемо "плясать" из стороны в сторону. В таком случае говорят, что наступает магнитная буря. Обычно она длится от нескольких часов до нескольких суток.

___

Магнитное поле Земли время от времени изменяет свою ориентацию, совершая и вековые колебания (длительностью 5–10 тыс. лет), и полностью переориентируясь, т.е. меняя местами магнитные полюсы (2–3 раза за миллион лет). На это указывают «вмороженное» в осадочные и вулканические породы магнитное поле отдаленных эпох. Поведение геомагнитного поля нельзя назвать хаотичным, оно подчиняется своеобразному «расписанию».

___

Направление и величина геомагнитного поля задаются процессами, происходящими в ядре Земли. Характерное время переполюсовки, определяемое внутренним твердым ядром, составляет от 3 до 5 тыс. лет, а определяемое внешним жидким ядром – около 500 лет. Этими временами и может обьясняться наблюдаемая динамика геомагнитного поля. Компьютерное моделирование с учетом различных внутриземных процессов ьпоказало возможность переполюсовки магнитного поля примерно за 5 тыс. лет.

ФОКУСЫ С МАГНИТАМИ

"Храм очарований, или механический, оптический и физический кабинет г. Гамулецкого де Колла" известного русского иллюзиониста Гамулецкого, просуществовавший до 1842 года, прославился помимо всего прочего тем, что посетители, поднимавшиеся по украшенной канделябрами и устланной коврами лестнице, еще издали могли заметить на верхней площадке лестницы золоченую фигуру ангела, выполненную в натуральный человеческий рост, которая парила в горизонтальном положении над дверью кабинета не будучи подвешена, ни оперта. В том, что фигура не имела никаких подпорок, мог убедиться каждый желающий. Когда посетители вступали на площадку, ангел поднимал руку, подносил ко рту валторну и играл на ней, шевеля пальцами самым естественным образом. Десять лет - говорил Гамулецкий, - я трудился, чтобы найти точку и вес магнита и железа, дабы удержать ангела в воздухе. Помимо трудов немало и средств употребил я на это чудо".

___

В средние века весьма распространенным иллюзионным номером были так называемые "послушные рыбы", изготовлявшиеся из дерева. Они плавали в бассейне и повиновались малейшему мановению руки фокусника, который заставлял их двигаться во всевозможных направлениях. Секрет фокуса был чрезвычайно прост: в рукаве у фокусника был спрятан магнит, а в головы рыб вставлены кусочки железа. Более близкими к нам по времени были манипуляции англичанина Джонаса. Его коронный номер: Джонас предлагал некоторым зрителям положить часы на стол, после чего он, не прикасаясь к часам, произвольно менял положение стрелок. Современным воплощением такой идеи является хорошо известные электрикам электромагнитные муфты, с помощью которых можно вращать устройства, отделенные от двигателя какой-нибудь преградой, например, стеной.

___

В середине 80-х годов 19 века пронеслась молва об ученом слоне, который умел не только складывать и вычитать, но даже умножать, делить и извлекать корни. Делалось это следующим образом. Дрессировщик, например, спрашивал слона: "Сколько будет семью восемь?" Перед слоном стояла доска с цифрами. После вопроса слон брал указку и уверенно показывал цифру 56. Точно так же производилось деление и извлечение квадратного корня. Фокус был достаточно прост: под каждой цифрой на доске был спрятан небольшой электромагнит. Когда слону задавался вопрос, в обмотку магнита, расположенного означающей правильный ответ, подавался ток. Железная указка в хоботе слона сама притягивалась к правильной цифре. Ответ получался автоматически. Несмотря на всю простоту этой дрессировки, секрет фокуса долгое время не могли разгадать, и "ученый слон" пользовался громадным успехом.

Источник: Вл. Карцев "Магнит за три тысячелетия".

___

Самое мощное постоянное поле величиной 35,3 ± 0,3 Тесла было получено в Национальной магнитной лаборатории им. Фрэнсиса Биттера в Массачусетском технологическом институте, США, 26 мая 1988 г. Для его получения использовался гибридный магнит с гольмиевыми полюсами. Под его воздействием усиливалось магнитное поле, создаваемое сердцем и мозгом.

Самое слабое магнитное поле было измерено в экранированном помещении той же лаборатории. Его величина составила 8·10–15 Тесла. Оно использовалось д-ром Дэвидом Коэном для изучения чрезвычайно слабых магнитных полей, создаваемых сердцем и мозгом.

Вспомни тему «Электромагнитные явления» за 8 класс:

Магнитное поле.Магнитное поле прямого проводника. Магнитные линии.Магнитное поле катушки с током. Электромагнит.Постоянные магниты.Магнитное поле Земли. Действие магнитного поля на проводник с током. Электродвигатель. Смотри другие страницы по теме «Всё о магнитах»:Магнитное полеПостоянные магнитыОрганические магнитыМагнитные жидкости ЭлектромагнитыЭлектромагниты Дж. ГенриТелеграф С. Морзе"Ювелирные" соленоиды"Шаттл" на электромагнитной тягеОпыты с магнитными иголкамиОпыт: влияние температуры на свойства магнитаМагнитное поле ЗемлиМожно ли намагнитить шар?Намагничивание в магнитном поле ЗемлиЧасы и магнетизм"Поющие" магнитыРазмагничиваниеДрейф магнитных полюсов Земли"Магометов гроб"Проект магнитного транспорта Лечение магнитами Магнитная летательная машинаСражение марсиан с земножителямиМагнитный вечный двигатель Магнитные фокусыОружие 21 векаКак влияет электросмог на всё живое?Как работает микроволновка?Загадки Николы ТеслаО полярных сиянияхНаучные игрушки с элементами "антигравитации"Применение электромагнитаБури, которые не видит глазМожет ли бритва самозатачиваться?

class-fizika.narod.ru

---

• 
  Реактивная и активная мощность определение
• 
  Как соединить две лампочки на один выключатель
• 
  Башенные градирни
• 
  Гэс тэс
• 
  Напряжение между фазами в трехфазной сети 380v
• 
  Датчик индуктивный сенсор
• 
  Векторная диаграмма напряжений и токов онлайн
• 
  Напряжение работа на заряд
• 
  Ае 206
• 
  Состав углекислотного огнетушителя
• 
  Сколько стоит куб сжиженного газа