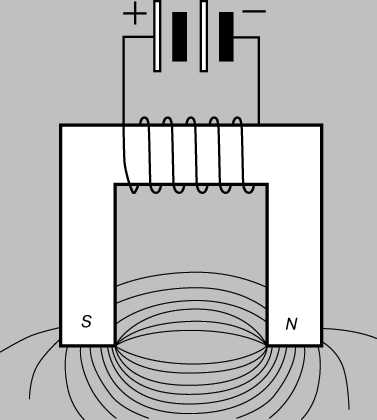
Индуктивность катушки. Какими способами можно увеличить индуктивность катушки

Ответы@Mail.Ru: вопрос по катушке индуктивности

А учебник лень почитать?

напрашивается вопрос... зачем тебе - убогому интернет?)))))

1. Реактивное сопротивление 2. Железо увеличивает индуктивность катушки, следовательно увеличивается реактивное сопротивление (на высоких частотах только портит добротность :) ) 3 ЭДС самоиндукции. 4. Увеличится.

При подаче питания постоянного тока к катушке происходит преобразование тока в магнитное поле. По этой причине ток запаздывает на 90° от напряжения. Достигнув возможно-полного преобразования тока в магнитное поле (насыщения) сопротивление катушки становится постоянным. При отключении питания, происходит обратный процесс, а именно магнитное поле преобразуется в ток и стекает по проводнику. При переменном токе происходит тоже самое преобразование только лишь в такт с частотой подаваемого питания. В момент смены полярности питания, ток стремящийся к катушке встречается с (реактивной энергией) током стекающим с неё от предыдущего такта, поэтому происходит преодоление стоящего препятствия и последующий ход в катушку и так 50 раз в секунду. Отсюда и высокое сопротивление. Если в катушку вставить стержёнь, то мы увеличиваем ёмкость поля и время задершки тока на его преобразование в магнитное поле. По причине прямой зависимости магнитного поля от приложенной частоты, можно обобщить, чем выше частота тем сильнее его преобразование в магнитное поле и соответственно меньше проходимость для высоких частот.

touch.otvet.mail.ru

Общие сведения о катушках индуктивности

Применяемые в низкочастотных усилителях трансформаторы могут подразделяться на две основные категории: силовые или сетевые трансформаторы и сигнальные трансформаторы, используемые в качестве согласующих, выходных, либо повышающих, например, для картриджей звукоснимателей с подвижной катушкой. Совершенно аналогично катушки индуктивности могут предназначаться для работы в цепях прохождения сигнала, например в различных фильтрах, либо же они могут быть мощными дросселями, используемыми в высоковольтных источниках питания. Основной особенностью этих компонентов схем является применение в них магнитных материалов. Они представляют последнюю группу идеальных пассивных компонентов схем (резисторы, конденсаторы и катушки индуктивности, включая трансформаторы). В отличие от резисторов и конденсаторов, катушки индуктивности и трансформаторы, как правило, не являются промышленными изделиями, а изготавливаются вручную. Именно по этой причине многие разработчики стараются всячески избегать их применения. Такой подход нельзя признать разумным, так как он серьезно ограничивает возможности проектирования схем.

Катушка индуктивности запасает энергию магнитного поля. Прохождение тока любой величины по проводнику всегда сопровождается возникновением магнитного поля вокруг проводника. Поэтому проводник обладает индуктивностью. Можно увеличить индуктивность, свернув провод в спираль, или намотав его в виде катушки, а если внутрь такой катушки поместить железный сердечник (магнитопровод), то индуктивность возрастет многократно. Эта зависимость может быть приближенно выражена следующим соотношением:

в котором L — индуктивность,

μ0 — магнитная проницаемость вакуума, в системе СИ равна 4π·10-7 Гн/м,

μr— относительная магнитная проницаемость магнитного материала

сердечника,

А — площадь поперечного сечения магнитопровода,

I — длина магнитопровода,

N — количество витков катушки.

Относительная магнитная проницаемость, μr, является характеристикой магнитных свойств материала, и можно провести некоторую аналогию с ранее уже упоминавшейся относительной диэлектрической проницаемостью, характеризующей диэлектрические свойства диэлектриков. Относительная магнитная проницаемость имеет различные значения и может меняться от 1 для воздуха до примерно 5500 для железа. Длина магнитопровода отсчитывается по замкнутому контура от какой-то начальной точки, а площадь поперечного сечения магнитопровода просто принимается равной площади сечения магнитного сердечника. Поэтому, может показаться, что вышеприведенное уравнение без особых трудностей может быть использовано для расчета индуктивности.

К сожалению, параметр μr сильно зависит от плотности магнитного потока, на длину магнитопровода могут сильно повлиять воздушные зазоры, а часть магнитного потока рассеивается в окружающей среде. Каждая из этих проблем будет проанализирована по отдельности несколько позже, а сейчас надо просто признать, что очень часто оказывается просто невозможным точно рассчитать значение индуктивности катушки. Поэтому на практике зачастую приходится строить всевозможные предположения, добавлять лишние витки, измерять индуктивность в условиях, максимально близким к условиям реальной работы, а затем удалять витки катушки, пока не будет получена требуемая величина индуктивности.

При каждом обсуждении свойств магнитных материалов, обычно используется зависимость, которая называется кривой (начальной) намагниченности. Данная кривая выражает зависимость результирующей магнитной индукции поля, В, от изменения величины напряженности магнитного поля, Н, иногда для простоты называемой зависимостью В-Н (рис. 5.10). В целях дальнейшего изложения следует прежде всего отметить, что относительная магнитная проницаемость m пропорциональна градиенту (или углу наклона) данной кривой, а так как градиент изменяется при изменении напряженности магнитного поля, то это означает, что будет изменяться и μ.

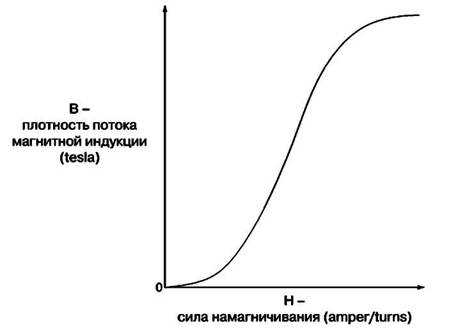
Рис. 5.10 Кривая намагничивания: непостоянство угла наклона ведет к изменению магнитной проницаемости материала

Катушка индуктивности без магнитного сердечника

Можно полностью исключить проблему, связанную с изменением параметра m при изменении напряженности магнитного поля, если использовать катушку, в которой отсутствует сердечник, изготовленный из магнитного материала. Катушка индуктивности без магнитного сердечника (воздушная катушка индуктивности) характеризуется постоянным значением индуктивности при изменении величины сигнала, следовательно, такие катушки не вызывают искажений, что делает их особо популярными для использования в схемах кроссоверов высококачественных громкоговорителей. Определить площадь, через которую проходит магнитный поток, для данного случая достаточно сложно, так как теоретически магнитный поток распространяется в бесконечность, точно также невозможно точно определить и длину «магнитопровода». Тем ни менее, для катушек с различной геометрией были предложены приближенные соотношения, из которых ниже приводится формула для наиболее интересного, с практической точки зрения, случая оптимального (то есть наименьшего) значения сопротивления воздушной катушки, обмотка которой выполнена из медного провода. Формулы для приближенного расчета были предложены А. Н. Тайлом (A.N.Thiele):

в которых (рис. 5.11), R — сопротивление обмотки, Ом,

L — Индуктивность, мкГн,

d — диаметр провода, мм,

N — количество витков,

с — обобщенный параметр каркаса, связывающий его внешний и внутренний диаметры, а также длину слоя намотки,

l — длина провода, м.

Рис. 5.11 Относительные размеры бобины, используемой для намотки воздушной катушки индуктивности (в соответствии с приведенной формулой Таила)

Формула приводится с числовыми коэффициентами для частного случая, так как провод для катушки имеет стандартизованные значения диаметра, а величина сопротивления катушки не оказывает большого влияния на получаемый результат.

Если сопротивление будет отличаться от необходимого значения, следует использовать провод с другим поперечным сечением.

Естественно было бы выполнять все расчеты с использованием персонального компьютера, поэтому ниже приводится программа, написанная на языке QBASIC (хотя основное уравнение может быть с не меньшим успехом решено с использованием широкоформатных таблиц).

CLS

L = 1

PRINT "This program designs air-cored copper"

PRINT "wire coils according to the Thiele"

PRINT "formulae. L is in micro henries, d (wire"

PRINT "diameter) is in mm"

PRINT

PRINT "To quit, input L = 0."

PRINT

DO WHILE L > 0

INPUT "Lf; L

IF L = 0 THEN END

INPUT "L’; L

R = ((8.01*10^(-3)*(L*3/d*8)^(l/5))100)\l)/100

N = (((10.2 *(L^2/d^2)^(1/5)) *100)\D/100

с = ((d * N^(l/2)/0.841)*100\l)/100

Q = (((0.188*(L *с)^(1/2))*100\1)/100

PRINT

PRINT "You need"; N; "turns on a core of"; 2*c; "ram in diameter,"; c; "mm thick."

PRINT "It will use"; Q; "meters of wire, and"

PRINT "will have a resistance of"; R; "Ohms."

PRINT

LOOP

Эксперименты вскоре показали, что катушки индуктивности без магнитного сердечника имеют высокое сопротивление, и что они очень большие по своим размерам. Проблема сопротивления остается общей для всех катушек индуктивности и является основной причиной, определяющей неидельность их характеристик. Применение воздушных катушек индуктивности не ограничивается только кроссоверами громкоговорителей, но они также широко применяются в выходных фильтрах цифро-аналоговых преобразователей (ЦАП), в которых сопротивление обмотки не является определяющим фактором. Также катушки без сердечников получили широкое применение в радиочастотной технике.

Следует отметить, что в связи с используемыми упрощающими допущениями (не учитывается эффективность намотки, изменения диаметра провода и т. д.), использование данной формулы не позволяет получить точные результаты. В силу этого, рекомендуется при расчетах предусмотреть 5% увеличение параметров, а затем удалять витки с катушки, измеряя значение индуктивности с использованием измерительного моста.

В большом количестве измерительных мостов используется генератор, имеющий собственную частоту 1 кГц. При измерении индуктивности воздушных катушек относительно высокое значение сопротивления может подавить влияние индуктивной составляющей, в силу чего при измерениях с использованием мостовой схемы можно получить неверный результат. Если возможно для питания схемы моста использовать внешний источник переменного тока, то рекомендуется применять максимальное значение частоты, которое допускается использовать производителями измерительных мостов (как правило, частота составляет 20 кГц), что позволит более точно выполнить необходимые измерения.

Броневые сердечники с зазором

Одним из путей уменьшения сопротивления без внесения заметных искажений является использование катушки, в которой имеется магнитный сердечник с зазором. Магнитный сердечник с зазором значительно увеличивает индуктивность по сравнению с воздушной катушкой индуктивности. Однако так как воздушный зазор образует сравнительно высокое сопротивление для распространения магнитного потока, то он приглушает изменения в относительной магнитной проницаемости магнитного сердечника, имеющего низкое значение сопротивления магнитному потоку, в силу чего индуктивность катушки становится более стабильной. При увеличении величины зазора величина индуктивности снижается, и при увеличении зазора до бесконечно большого значения опять будет наблюдаться предельный случай катушки индуктивности без магнитного сердечника. Подобная конструкция была много лет назад использована отделом исследований Британской радиовещательной корпорации (Би-би-си) в катушках индуктивности кроссоверов пассивных громкоговорителей.

Катушка индуктивности с магнитным сердечником, имеющим зазор, может получиться совершенно непреднамеренно. Большое количество ферритовых сердечников, используемых для небольших катушек индуктивностей, изготавливаются в виде двух половинок, которые устанавливаются снаружи катушки и сопрягаются друг с дружкой наворачиванием половинок. Наличие пыли на сопрягаемых поверхностях приводит к увеличению зазора, и если половинки сердечника во время измерений индуктивности катушки плотно прижать одну к другой, то можно будет получить значительное увеличение индуктивности.

Если по индуктивности будет протекать постоянный ток, то очень важно, чтобы постоянный ток не вызвал переход материала сердечника в область насыщения, так как в этом случае значение индуктивности резко уменьшится, а сердечник будет сильно разогреваться. Катушки индуктивности, в которых сердечники изготовлены из железа и по катушкам которых протекают постоянная составляющая тока, обязательно имеют воздушные зазоры, для того, чтобы обеспечить максимальное значение индуктивности при максимальном значении переменного тока. При этом следует учитывать, что так как в области воздушного зазора происходит рассеяние магнитного потока, вызванного протеканием переменной составляющей, такие катушки индуктивности могут сильно влиять на соседние цепи схемы, вызывая в них паразитные наводки.

Собственная емкость катушек индуктивности

Если обмотка катушки индуктивности содержит большое количество витков, и существует разность потенциалов между отдельными витками и слоями витков, то следует ожидать, что катушка тесла будет иметь некоторую емкость, которая будет включена параллельно индуктивности самой катушки (рис. 5.12).

Рис. 5.12 Эквивалентная схема замещения реальной катушки индуктивности

Таким образом, возникает хорошо знакомая цепь с параллельным резонансом а это означает, что как только частота превысит резонансную, катушка индуктивности перестанет вести себя как индуктивность, а начнет проявлять свойства конденсатора. Самый простой способ определить величину такой паразитной емкости, это собрать тестовую схему (рис. 5.13).

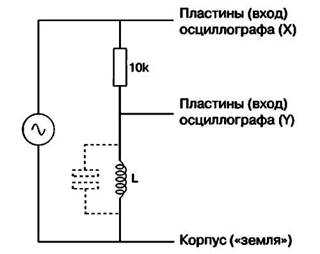
Рис. 5.13 Использование фигур Лиссажу для определения частоты собственного резонанса катушки индуктивности

В осциллографе необходимо произвести переключение в режим работы с использованием и вертикального, и горизонтального входов «XY». При изменении частоты генератора получаемые на экране осциллографа фигуры Лиссажу будут изменяться от эллипса до прямой линии. Как раз та частота, при которой будет наблюдаться прямая линия, и будет соответствовать резонансной частоте катушке индуктивности.

 

Если необходимо, то можно будет рассчитать значение шунтирующей емкости, используя нижеприведенное выражение:

Мощные дроссели (катушки фильтров выпрямителей и т. п.), предназначенные для небольших ламповых усилителей, имеют, как правило, индуктивность 10—15 Гн и рассчитаны на токи 100—250 мкА. Для таких дросселей резонансная частота составляет от 3 до 12 кГц. На частотах, превышающих значение резонансной, дроссели не могут обеспечить эффективный барьер для шумов, генерируемых при выпрямлении переменного тока, или для ВЧ шумов, поступающих по сети питания.

Вопросы применения мощных дросселей будут рассмотрены позже.

 

tubeamplifier.narod.ru

Персональный сайт - Катушки индуктивности: разновидности, применение, намотка катушек индуктивности, трансформаторов, дросселей

Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Как следствие, при протекании через катушку переменного электрического тока, наблюдается её значительная инерционность.

Устройство обычно представляет собой винтовую, спиральную или винтоспиральную катушку из одножильного или многожильного изолированного провода, намотанного на цилиндрический, тороидальный или прямоугольный каркас из диэлектрика или плоскую спираль, волну или полоску печатного или другого проводника. Также бывают и бескаркасные катушки. Намотка может быть как однослойной (рядовая и с шагом), так и многослойная (рядовая, внавал, «универсал»). Намотка «универсал» имеет меньшую паразитную ёмкость.

Для увеличения индуктивности применяют сердечники из ферромагнитных материалов: электротехнической стали, пермаллоя, флюкстрола, карбонильного железа, ферритов. Также сердечники используют для изменения индуктивности катушек в небольших пределах.

Существуют также катушки, проводники которых реализованы на печатной плате.

Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.

Основным параметром катушки индуктивности является её индуктивность, которая определяет, какой поток магнитного поля создаст катушка при протекании через неё тока силой 1 ампер. Типичные значения индуктивностей катушек от десятых долей мкГн до десятков Гн.

 

В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля наблюдаются паразитные эффекты, вследствие которых сопротивление катушки не является чисто реактивным. Наличие паразитных эффектов ведёт к появлению потерь в катушке.

 

Потери в проводах вызваны тремя причинами:

• · Провода обмотки обладают омическим (активным) сопротивлением.
• · Сопротивление провода обмотки возрастает с ростом частоты, что обусловлено скин-эффектом. Суть эффекта состоит в вытеснении тока в поверхностные слои провода. Как следствие уменьшается полезное сечение проводника и растет сопротивление.
• · В проводах обмотки, свитой в спираль, проявляется эффект близости, суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к периферии намотки. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведёт к дополнительному возрастанию сопротивления провода.

 

Потери в диэлектрике (изоляции проводов и каркасе катушки) можно отнести к двум категориям:

• · Потери от диэлектрика межвиткового конденсатора (межвитковые утечки и прочие потери характерные для диэлектриков конденсаторов).
• · Потери от магнитных свойств диэлектрика (эти потери аналогичны потерям в сердечнике).

 

В общем случае можно заметить что для современных катушек общего применения потери в диэлектрике чаще всего пренебрежимо малы.

 

Потери в сердечнике складываются из потерь на вихревые токи, потерь на гистерезис и начальных потерь.

 

Потери на вихревые токи. Ток, протекающий по проводнику, индуцирует ЭДС в окружающих проводниках, например в сердечнике, экране и в проводах соседних витков. Возникающие при этом вихревые токи становятся источником потерь из-за сопротивления проводников.

 

Разновидности катушек индуктивности

 

Контурные катушки индуктивности. Эти катушки используются совместно с конденсаторами для получения резонансных контуров. Они должны иметь высокую стабильность, точность и добротность.

 

Катушки связи. Такие катушки применяются для обеспечения индуктивной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току цепи базы и коллектора и т. д. К таким катушкам не предъявляются жёсткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи.

 

Вариометры. Это катушки, индуктивность которых можно изменять в процессе эксплуатации для перестройки колебательных контуров. Они состоят из двух катушек, соединённых последовательно. Одна из катушек неподвижная (статор), другая располагается внутри первой и вращается (ротор). При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра. Такая система позволяет изменять индуктивность в 4 − 5 раз. В ферровариометрах индуктивность изменяется перемещением ферромагнитного сердечника.

 

Дроссели. Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному. Применяются в цепях питания радиотехнических устройств в качестве фильтрующего элемента. Для сетей питания с частотами 50-60 Гц выполняются на сердечниках из трансформаторной стали. На более высоких частотах также применяются сердечники из пермаллоя или феррита. Особая разновидность дросселей — помехоподавляющие ферритовые бочонки (бусины) на проводах.

 

Сдвоенные дроссели две намотанных встречно катушки индуктивности, используются в фильтрах питания. За счёт встречной намотки и взаимной индукции более эффективны для фильтрации синфазных помех при тех же габаритах. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания; в дифференциальных сигнальных фильтрах цифровых линий, а также в звуковой технике. Т.е. предназначены как для защиты источников питания от попадания в них наведённых высокочастотных сигналов, так и во избежание засорения питающей сети электромагнитными помехами. На низких частотах используется в фильтрах цепей питания и обычно имеет ферромагнитный (из трансформаторной стали) или ферритовый сердечник.

namotkasander.narod.ru

Как наматывают катушки индуктивности?

Как наматывают катушки индуктивности?

Катушка индуктивности является одной из схем в цепочке радиотехнических устройств. Она применяется в изготовлении СВЧ-печей, трансформаторов для автономных подстанций, приемно-передающей аппаратуре и других видах электрической техники.

Принцип работы катушки индуктивности

При подаче на катушку индуктивности электричества сила тока будет постепенно возрастать. Когда энергия перестанет поступать, напряжение в катушке резко возрастет, а потом начнет постепенно ослабевать. Сила тока в цепи мгновенно измениться не может. На этом основан первый закон коммутации.

Различаются катушки индуктивности с магнитным сердечником: обычно это пластины из феррита или железа или сердечники в виде кольца, которые считаются наиболее эффективными проводниками тока. Катушки с немагнитным сердечником - это конструкции, полые внутри, то есть без какой-либо сердцевины.

Материалы для создания катушки

1. Медные изолированные провода нескольких разных сечений;
2. Пластмассовый цилиндр;
3. Небольшая стальная пластина;
4. Микрометр;
5. Линейка;
6. Картон или органическое стекло;
7. Специальный станок для намотки про

elhow.ru

Индуктивность катушки

Способность катушки индуктировать на себе э. д. с. самоиндукции называется индуктивностью катушки.

Единицей измерения индуктивности является Генри (Гн)

Индуктивностью в 1 Гн обладает такая катушка, изменения тока в которой на 1 А в секунду  создает э. д. с. самоиндукции равной 1 В.

10-3 Гн миллигенри мГн

10-6 Гн микрогенри мкГн 

  Величина индуктивности прямо пропорциональна размерам катушки и числу витков. Кроме того, индуктивность  зависит также от материала введенного в  катушку сердечника и наличия экрана. Качество работы катушки индуктивности в цепях  переменного тока характеризуется добротностью. Добротность Q катушки определяют как отношение ее индуктивного сопротивления ХL= ωL=2пfL к активному R, при рабочей  частоте f:Q=ωL/R=2пfL/R.  Активное сопротивление включает сопротивление провода обмотки катушки и сопротивление,  обусловленное потерями электрической энергии в каркасе, сердечнике,  экране и изоляции.  Чем меньше активное сопротивление, тем выше добротность катушки и ее  качество. Витки катушки, разделенные слоем изоляции, образуют элементарный конденсатор.  В многослойных катушках емкость возникает между  отделными слоями. Таким образом, катушка обладает не только индуктивными, но и  емкостными  свойствами. В большинстве  случаев  собственная емкость катушки является вредной, и ее стремятся уменьшить. Для этого применяются специальные формы каркаса катушки и способы намотки провода.  

Назначение сердечников в катушках индуктивности

  Сердечник увеличивает индуктивность катушки. Действительно катушка с сердечником обладает большим магнитным полем а значит на ней будет индуктироваться большая э. д. с. самоиндукции.

Если положение сердечника в катушке можно изменять, значит можно изменять индуктивность катушки.

Изображение сердечников на схемах

 

 

 

 

 

 

 

                           

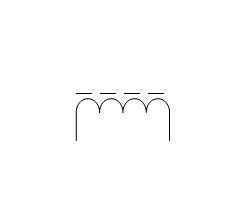
Взаимоиндукция

Явление взаимоиндукции наблюдается между близко расположенными катушками. Сущность взаимоиндукции заключается в переносе электрической энергии из одной цепи в другую посредством общего магнитного поля: в одном из контуров электрическая энергия преобразуется в энергию магнитного поля, в другом контуре происходит обратный переход энергии магнитного поля в электрическую энергию. Из сказанного следует, что магнитное поле является переносчиком электрической энергии из одной цепи в другую.

Взаимная индуктивность между двумя катушками зависит от их размеров, числа витков, взаимного расположения и магнитной проницаемости среды. 

N18

Электромагнитные колебания — это периодические изменения со временем электрических и магнитных величин (заряда, силы тока, напряжения, напряженности, магнитной индукции и др.) в электрической цепи.

Для возбуждения и поддержания электромагнитных колебаний требуются определенные системы, простейшей из которых является колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (это может быть сопротивление провода катушки и проводов, соединяющих катушку с конденсатором) (рис. 1). Идеальный контур Томсона — колебательный контур без активного сопротивления (R = 0).

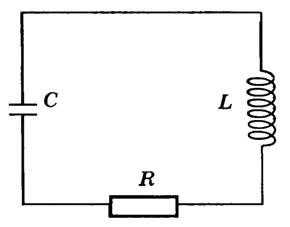
Рис. 1

Рассмотрим свободные электромагнитные колебания — колебания, происходящие в идеальном колебательном контуре за счет расходования сообщенной этому контуру энергии, которая в дальнейшем не пополняется. Рисунок 2 иллюстрирует характерные стадии колебаний в контуре за один период.

Отсчет времени t мы начинаем с момента подключения к контуру заряженного конденсатора. В этот момент (рис. 2, а) напряженность электрического поля  E⃗  в конденсаторе (направленная сверху вниз), а также напряжение U на обкладках конденсатора максимальны, а тока в контуре еще нет, следовательно, отсутствует и магнитное поле.

При этом вся энергия W колебательного контура заключена в электрическом поле конденсатора, т.е.

 W=We0=CU202=q202C.

В промежутке времени от 0 до  T4 (рис. 2, б) конденсатор, разряжаясь, создает через контур ток I, идущий по часовой стрелке. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая нарастанию этого тока. При разряде конденсатора уменьшаются напряженность электрического поля  E⃗  (сохраняя прежнее направление) и напряжение U между его обкладками, следовательно, уменьшается энергия электрического поля в конденсаторе. Сила тока I и индукция  B⃗  магнитного поля, создаваемого этим током, увеличиваются, т.е. возрастает энергия магнитного поля в катушке индуктивности. Следовательно, энергия электростатического поля конденсатора превращается в энергию магнитного поля катушки.

К моменту времени  t=T4 (рис. 2, в) конденсатор полностью разряжается, напряжение U между его обкладками становится равным нулю, и электрическое поле в нем отсутствует  E⃗ =0. К этому времени ток 1 в контуре и индукция  B⃗  магнитного поля этого тока достигают максимальных значений. Следовательно, вся энергия контура заключена в этот момент в его магнитном поле, т.е.

 W=WM0=LI202.

При этом вся энергия W колебательного контура заключена в электрическом поле конденсатора, т.е.

W=We0=CU202=q202C.

В промежутке времени от 0 до T4 (рис. 2, б) конденсатор, разряжаясь, создает через контур ток I, идущий по часовой стрелке. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая нарастанию этого тока. При разряде конденсатора уменьшаются напряженность электрического поля E⃗ (сохраняя прежнее направление) и напряжение U между его обкладками, следовательно, уменьшается энергия электрического поля в конденсаторе. Сила тока I и индукция B⃗ магнитного поля, создаваемого этим током, увеличиваются, т.е. возрастает энергия магнитного поля в катушке индуктивности. Следовательно, энергия электростатического поля конденсатора превращается в энергию магнитного поля катушки.

К моменту времени t=T4 (рис. 2, в) конденсатор полностью разряжается, напряжение U между его обкладками становится равным нулю, и электрическое поле в нем отсутствует E⃗ =0. К этому времени ток 1 в контуре и индукция B⃗ магнитного поля этого тока достигают максимальных значений. Следовательно, вся энергия контура заключена в этот момент в его магнитном поле, т.е.

W=WM0=LI202.

studfiles.net

---

• 
  Показания счетчиков воды портал госуслуг москвы
• 
  Лампа лед для аквариума
• 
  Сип 3 технические характеристики
• 
  Гарантирующий поставщик тепловой энергии это
• 
  Частота в сети 220 в россии
• 
  Индукционный трансформатор
• 
  Магнитное свойство
• 
  Тепловое действие тока закон джоуля ленца
• 
  Узо в трехфазной сети принцип работы
• 
  Устройство защитного заземления электроустановок
• 
  Что такое градильня