Магнитодвижущая сила и магнитное напряжение. Магнитное напряжение

Магнитное напряжение определение. Магнитное напряжение формула.

Магнитное напряжение

Что такое магнитное напряжение?

Магнитное напряжение определение

Определение магнитного напряжения:

Магнитное напряжение на прямолинейном участке контура есть произведение длины участка и проекции вектора магнитной напряженности на этот прямолинейный участок.

Всё это относится к однородному магнитному полю. Если поле не однородно или участок контура не прямой, то выбирают малую часть контура, которую можно считать прямолинейной, а магнитное поле в месте расположения этого участка однородным.

Магнитное напряжение формула

На картинке выше показано однородное магнитное поле с вектором напряженности H и криволинейный контур L. Контур криволинейный, поэтому определить магнитное напряжение сразу на всём контуре невозможно. Выделим на контуре отрезок ΔL (показан жирной линией), который можно считать прямолинейным, и будем находить магнитное напряжение только на этом участке. Проекция вектора напряженности магнитного поля H на направление отрезка ΔL равна:

HL = H * cos α

где α – угол между вектором H и отрезком ΔL.

Магнитное напряжение на отрезке ΔL (формула магнитного напряжения):

Um = (H * cos α) * ΔL = HL * ΔL

Выделив прямолинейные участки на остальных частях контура L, найдём магнитные напряжения на них. Тогда полное магнитное напряжение на всём контуре L будет равно сумме магнитных напряжений участков:

UL = Σ HL * ΔL

Измеряется магнитное напряжение в амперах: А.

Магнитное напряжение вдоль контура L зависит от формы этого контура.

Задача про магнитное напряжение

Теперь решим простую задачу: как будут соотноситься магнитные напряжения на отрезках ΔL, ΔL1 , ΔL2 (см. рисунок), т.е. где они больше, а где меньше? Длины всех участков одинаковы, магнитное поле всюду однородно.

Решение. При этих условиях магнитные напряжения на означенных отрезках будут отличаться только величинами проекций вектора напряженности магнитного поля на направления этих отрезков. Отрезок ΔL1 расположен под меньшим углом к направлению вектора Η по сравнению с отрезками ΔL и ΔL2, значит cos α ближе к единице и магнитное напряжение там будет больше. Отрезок ΔL2 расположен под прямым углом к направлению вектора напряженности, значит проекция вектора напряженности Η на направление отрезка ΔL2 будет равна нулю.

А теперь внимание, правильный ответ: наибольшее магнитное напряжение получим на отрезке ΔL1, а наименьшее - на отрезке ΔL2.

www.sbp-program.ru

Магнитодвижущая сила и магнитное напряжение

Магнитодвижущая сила (МДС).

Несмотря на то что электрический ток в проводе и его магнитное поле представляют собой неотделимые друг от друга стороны единого электромагнитного процесса, принято говорить, что электрический ток обладает свойством возбуждать магнитное поле. Это свойство тока называют магнитодвижущей силой (МДС) и обозначают ее буквой F.

Формально МДС F вызывает или возбуждает магнитное поле подобно тому, как ЭДС вызывает электрический ток в электрической цепи.

В Международной системе единиц МДС принимается численно равной току в проводе или витке, вызывающему магнитное поле, так что МДС F=l. Если ток проходит по катушке с числом витков w, то МДС равна произведению тока и числа витков, т. е.Естественно, что МДС, так же как и ток, измеряется в амперах, т. е.Для определения направления МДС катушки или витке с током удобно пользоваться правилом правой руки: если охватить катушку (виток) правой рукой так, чтобы четыре пальца ее расположились по направлению тока в витках катушки, то отогнутый большой палец руки укажет направление МДС. На рис. 1 показаны несколько катушек с током и направления их МДС.

Рис.1 Определении направления МДС в катушке с током.

 

 

 

 

Рис. 2 Магнитное напряжение между двумя точками

Магнитное напряжение.

По аналогии с электрическим напряжением при расчете магнитных полей пользуются понятием магнитного напряжения Uм. Магнитное напряжение между двумя точками a и b однородного магнитного поля, расположенными на одной магнитной линии (рис. 2,а), выражается произведением напряженности поля и расстояния между этими точками:В более общем случае, если в однородном поле две точки а и b находятся на расстоянии L не на одной магнитной линии (рис. 2,б), сначала вычисляется напряженность H, затем продольная слагающая вектора напряженности вдоль отрезка ab, т. е. HL = H cosa, где a—угол между векторами Н и HL. Магнитное напряжениеВ неоднородном магнитном поле магнитное напряжение между двумя точками a и b равно сумме элементарных напряжении HLdL на элементарных участках dL вдоль выбранного пути между этими точками (рис. 2,в):

Магнитное напряжение Uм может зависеть от выбранного пути между начальной и конечной точками.Магнитное напряжение в системе СИ измеряется в амперах:

Магнитное напряжение вдоль произвольного замкнутого пути (контура) представляет собой МДС вдоль этого контура. Таким образом, МДС можно определить как сумму элементарных магнитных напряжении HLdL вдоль, замкнутого контура: где знак обозначает суммирование (интегрирование) позамкнутому контуру элементарных напряжений HLdL.

electrikam.com

6.2.Магнитное напряжение на участке магнитной цепи.

М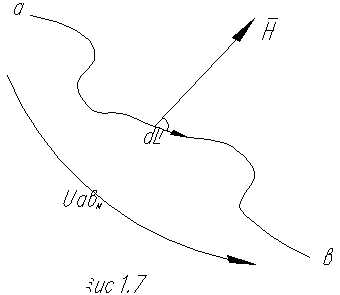агнитным напряжением между точкамиа и b магнитной цепи называют линейный интеграл от вектора напряженности магнитного поля между этими

точками (рис.1.7): 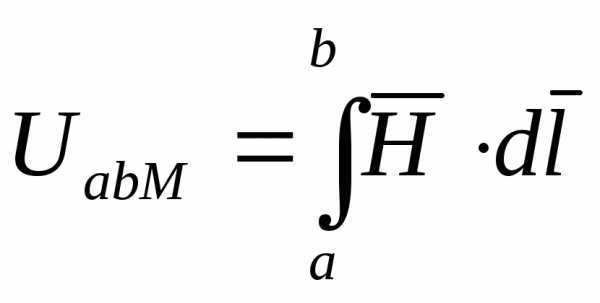1.4.

Если на участке магнитной цепи =const и совпадает по направлению с элементом пути обхода 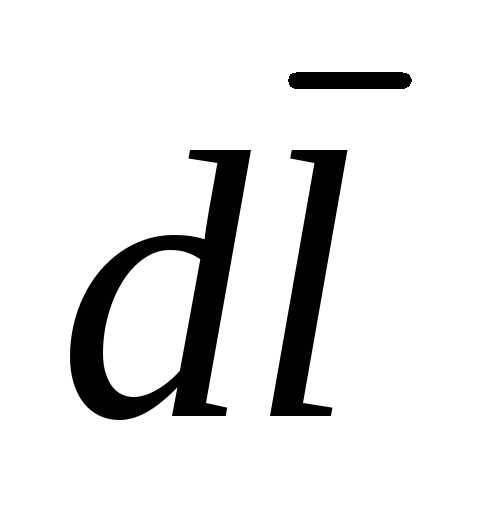, то

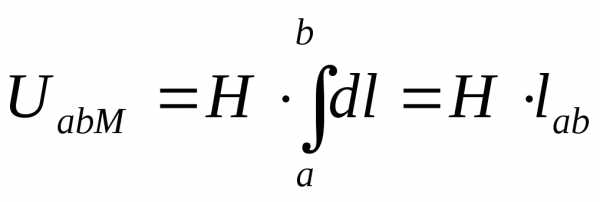1.5.

Если принять в внимание, что Н=В/mа, где mа – абсолютная магнитная проницаемость, а В=Ф/S, то формулу 1.5 магнитного напряжения UabM можно представить в виде

UabM=Ф×RM , 1.6.

где 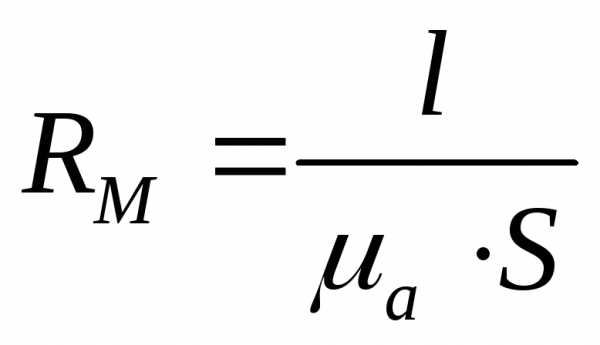– магнитное сопротивление.

Выражение 1.6 называют законом Ома для магнитной цепи по аналогии с электрической цепью (поток Ф – аналог тока I, RM – аналог электрического сопротивления R). Так же, по аналогии с электрической цепью и закон полного тока, представленный в виде

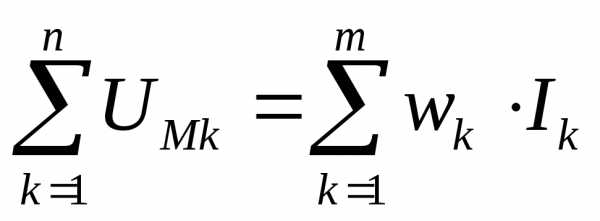, 1.7

называют вторым законом Кирхгофа для магнитной цепи (алгебраическая сумма магнитных напряжений вдоль любого замкнутого контура равна алгебраической сумме МДС).

6.3.Задачи расчета магнитных цепей.

Существует два типа задач, а именно:

1. прямая задача – по заданному значению потока Ф определяют МДС w×I обмотки;

2. обратная задача - задается значение МДС w×I и требуется определить поток Ф.

В обоих случаях должны быть известны геометрические размеры магнитопровода (длины l и площади поперечных сечений S всех участков магнитопровода), материалы участков и кривые намагничивания.

Для упрощения расчета пренебрегают магнитными потоками рассеяния Фр (рис. 1.8) и не учитывают выпучивание магнитного поля в воздушных зазорах, считая площадь сечения воздушного зазора S0 (рис. 1.8) равной площади поперечного сечения ферромагнитного магнитопровода.

1.Решение прямой задачи.

1.1Неразветвленная магнитная цепь.

Пример подобной цепи представлен на рис. 1.8.

Эту цепь можно разбить на четыре участка, три из которых выполнены из ферромагнитного материала ( например: электротехническая сталь Э2 ), кривая намагничивания которого известна рис 1.9. Четвёртый участок – воздушный зазор.

Характерный признак неразветвлённой магнитной цепи – магнитный поток Ф на всех участках один и тот же (рис. 1.8). Его значение задано в условии задачи. Магнитный поток Ф называется основным. Этот поток замыкается по магнитопроводу в отличие от потока рассеяния Фр, силовые линии которого замыкаются вокруг витков катушки по воздуху. Обычно Ф значительно больше Фр.

Рис. 1.8

Магнитная проницаемость воздуха m0=4p×10-7 Гн/м ничтожно мала по с равнению с проницаемостью ферромагнитного магнитопровода и магнитное сопротивление потокуФр несравненно выше, чем для потока Ф (Фр<<Ф).

Чтобы использовать при расчете закон полного тока, выберем контур интегрирования, проходящий внутри катушки с числом витков w и совпадающий со средней линией магнитной индукции. Разобьем магнитную цепь на отдельные участки: участок da – длина средней линии магнитной индукции l1, площадь поперечного сечения S1, на участке ab длина l2, площадь поперечного сечения S2 , на участке cd длина l3 , площадь поперечного сечения S3 , на участке воздушного зазора длина l0 , площадь S0=S2.

Пусть S1> S0=S2> S3 , тогда магнитная индукция по участкам:

studfiles.net

4.3. Магнитное напряжение зубцовых зон

При расчете магнитных напряжений зубцовых зон принимается попущение, что линии равного магнитного потенциала в попереч­ном сечении машины представляют собой окружности с центром на оси вращения ротора. При этом допущении магнитное напряжение зубцовой зоны статора Fz1 или ротора Fz2 определяется разностью магнитных потенциалов между эквипотенциальными поверхностя­ми (на поперечном сечении — окружностями), проходящими по дну пазов и по поверхности головок зубцов.

Обычно рассматривают поле в одном элементе зубцовой зоны — зубцовом (пазовом) делении tz = πD/ Z. Магнитные со­противления паза и зубца в магнитной цепи машины соединены параллельно, поэтому поток в зубцовом делении распределяется между ними пропорционально проводимостям магнитных сило­вых трубок, проходящих через зубец и паз. Пазы в электрической машине заполнены проводниками и их изоляцией, т. е. средой с магнитной проницаемостью, во много раз меньшей, чем проница­емость стали зубца. Поэтому поток в пазу составляет лишь небо­льшую часть общего потока зубцового деления. Эта часть потока как бы «вытесняется» из зубца в паз. При малом насыщении зуб­цов она очень мала и в расчетах ее не учитывают. При увеличе­нии насыщения зубцов доля потока в пазу возрастает и ее влия­ние начинает сказываться на магнитном напряжении зубцовой зоны Fz.

Рассмотрим вначале расчет магнитного напряжения зубцовой зоны без учета вытеснения части потока в паз. При принятом допу­щении о конфигурации эквипотенциальных линий и в силу симмет­рии зубцовой зоны магнитные силовые линии, проходящие через се­редины оснований зубцов, совпадают с отрезками радиусов (см. рис. 4.1, а и б), поэтому

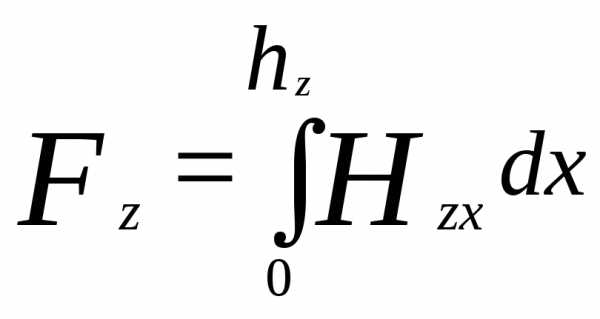(4.21)

где Hzx — напряженность магнитного поля в сечении зубца, соответ­ствующем расстоянию hzx от его узкой части; hz — высота зубца (рис. 4.5, а).

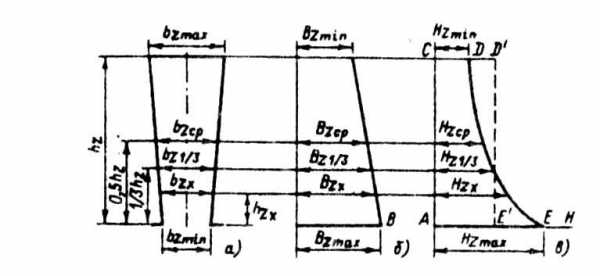
Рис. 4.5. К расчету магнитного напряжения зубцовой зоны

При постоянном сечении зубца считают, что напряженность поля в нем Hz постоянна, тогда

Fz = Hzhz (4.21 а)

При переменном сечении зубца Fz можно определить, разделив зубец по высоте на n достаточно малых участков с высотой Δh, в пределах которых изменением Hz пренебрегают. Определив для каждого участка индукцию, напряженность магнитного поля, магнитное напряже­ние и просуммировав последние, находят магнитное напряжение зубца.

Поток, приходящийся на одно зубцовое деление,

Фtz = Bδ tz lδ. (4.22)

Если через bzx обозначить ширину зубца на высоте hzx, то соот­ветствующее активное сечение зубца

Szx = kc lст b zx,

где kc — коэффициент заполнения сердечника сталью; lст — длина магнитопровода без вентиляционных каналов.

Индукция в рассматриваемом сечении зубца (рис. 4.5, б)

(4.23)

Напряженность поля определяется для соответствующей индук­ции по кривым намагничивания для выбранной марки стали.

Проведя несколько таких расчетов для различных сечений зуб­ца, можно для потока ФtZ построить кривую распределения напря­женности поля по высоте зубца (рис. 4.5, в). Площадь, ограничен­ная этой кривой, SACDE определяется в масштабе магнитного напряжения зубца:

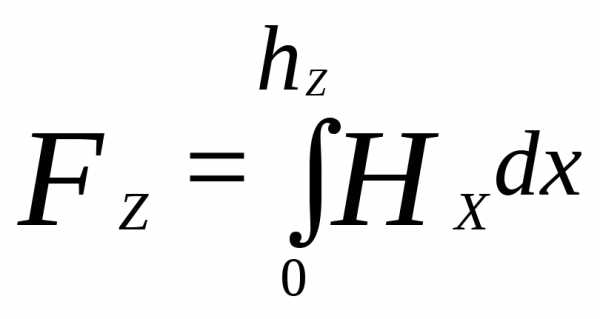
Зубцы в электрических машинах могут иметь сложную конфигу­рацию, поэтому такие расчеты выполняют лишь на ЭВМ при необ­ходимости получения уточненных данных, при этом программы расчетов должны учитывать особенности размерных соотношений данной зубцовой зоны.

В практических расчетах оказывается достаточным приближен­ное решение, когда Fz находится по (4.21) для некоторой средней расчетной напряженности Hz и расчетной высоты зубца hz, для которых справедливо .

При плавно изменяющихся сечениях зубцов расчетная напря­женность Hz достаточно точно находится по формуле

Hz = 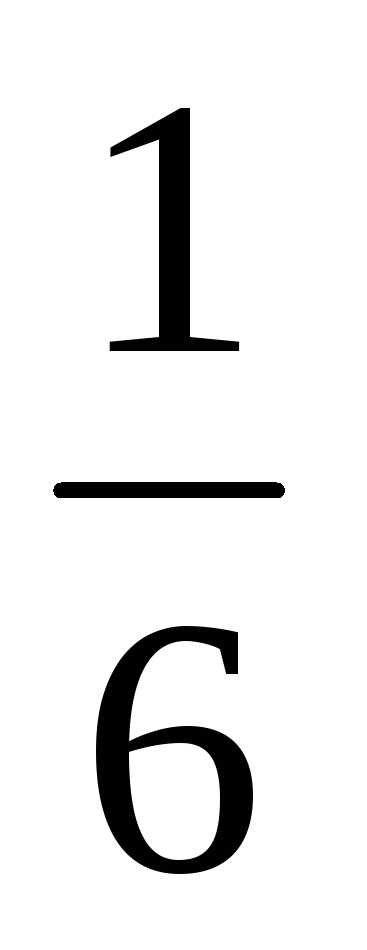( Hzmax + 4Hzср + Hzmin). (4.24)

Здесь Hzmax, Hzmin и Hzcp — напряженности поля в поперечных сечениях зубца, которые определяются по индукциям в наиболее уз­ком Szmin, наиболее широком Szmax и среднем по высоте Szcp сечениях зубца, по следующим формулам:

(4.25)

где bzmin, bzmax - наибольшая и наименьшая ширина зубца (см. рис. 4.5, б)

При прямоугольных пазах при Bzmax ≤ 2,0 Тл используется рас­пространенный метод расчета Fz по напряженности Нz1/3, определенной по индукции в сечении на 1/3 высоты зубца от его узкой час­ти (см. рис. 4.5):

Fz = Hz1/3 hz, (4.26)

дающий хорошее совпадение с уточненными расчетами при неболь­шой разнице наибольшего и наименьшего сечений зубцов. При этом площадь прямоугольника ACD'E' со сторонами Hz1/3 и hz равновели­ка площади фигуры ACDE (см. рис. 4.5, в).

В отдельных случаях при большей разнице bzmax и bzmin и боль­ших насыщениях расчет проводится более детально. Зубец делится по высоте на две части, и для каждой из них определяется средняя напряженность поля указанным методом. В этом случае расчетные сечения берутся на высоте

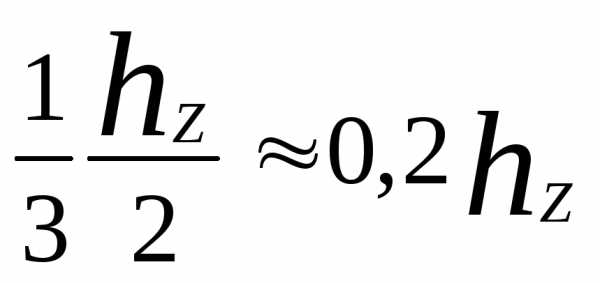и

от наиболее узкого сечения зубца.

При расчете магнитного напряжения зубцов с резко изменяю­щимся по высоте сечением, например зубцов двухклеточного рото­ра асинхронного двигателя и короткозамкнутого ротора с фигурны­ми пазами, зубцы также делятся по высоте на два участка с плавно изменяющимся сечением, при этом магнитное напряжение зубцов равно сумме магнитных напряжений участков.

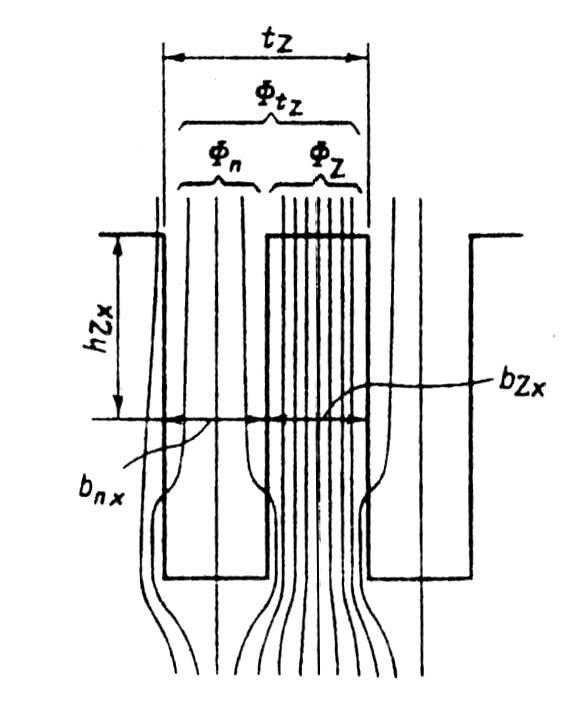
Рис. 4.6. Магнитный поток в зубцовом делении

при насы­щении стали зубцов

Влияние местных изменений сечения зубца на изменение магнитного напряже­ния, не распространяющихся на большие, участки по его высоте (углубления в стенках пазов для крепления пазовых клинь­ев, расширения в коронках зубцов и т. п.), в практических расчетах обычно не учи­тывают.

В насыщенной зубцовой зоне доля по­тока в пазу возрастает. Ее можно оценить, не прибегая к полному расчету поля на зубцовом делении, следующим образом.

Обозначим поток в зубце ФZ и поток в пазу Фп (рис. 4.6), тогда поток на зубцо­вом делении на высоте зубца hzx будет ра­вен:

Фtz = Фzx + Фпх (4.27)

Разделив (4.27) на Szx и умножив и разделив второе слагаемое правой части на Sпх = bnx lδ , получим

(4.28)

или

B'zx = Bzx + Bпх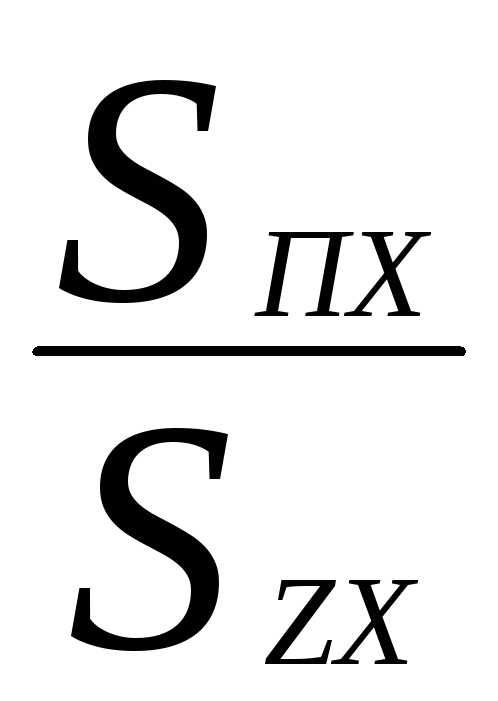 (4.29)

где В'zх — расчетная индукция, определимая полным потоком в сече­нии зубца Szx в предположении, что поток в пазу отсутствует; bzx — действительная индукция в сечении зубца Szx, т.е. индукция, опреде­ленная с учетом того, что часть потока вытесняется из зубца в паз; Впх — индукция в сечении паза Sпх, создаваемая вытесненной в паз ча­стью потока.

Так как паз заполнен средой с магнитной проницаемостью μ0 (магнитной постоянной), то

Впх = μ0 Нпх. (4.30)

На основании принятого допущения о конфигурации эквипотен­циальных линий в зубцовой зоне напряженность поля в зубце и в пазу на одной и той же высоте hzx будет одинакова, т. е.

Нпх = Hzx.

Тогда из (4.29) и (4.30) имеем

В'zх = Вzх + μ0 Нzх 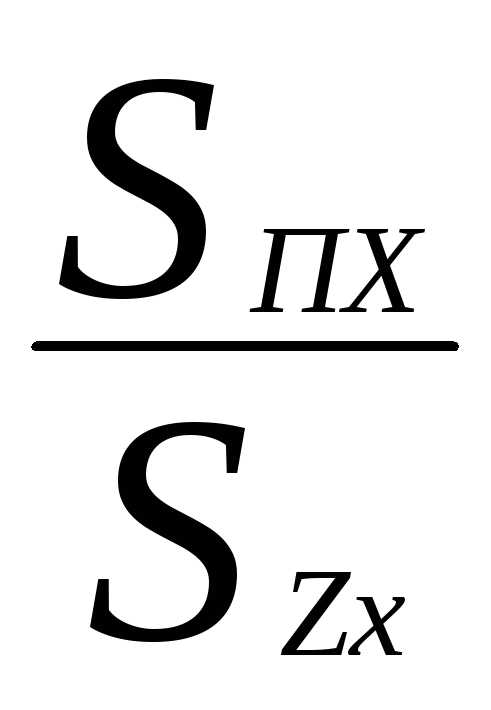(4.31)

нли

B'zx = Bzx + μ0 Hzx kпx, (4.32)

где kпx — коэффициент, определяющий отношение площадей попе­речных сечений паза и зубца на высоте hzx:

kпх = 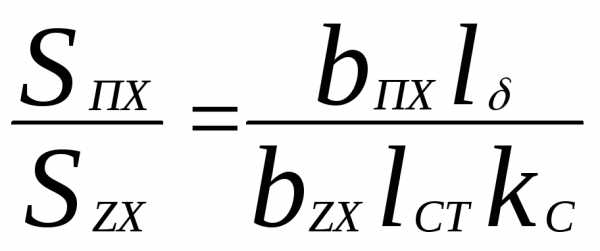(4.33)

В машинах нормального исполнения kп для различных по высоте зубца сечений обычно находится в пределах kп = 0,5 - 2,0.

Для определения действительной индукции в каждом сечении зубца первоначально находят расчетную индукцию по полному по­току зубцового деления:

В'zx= 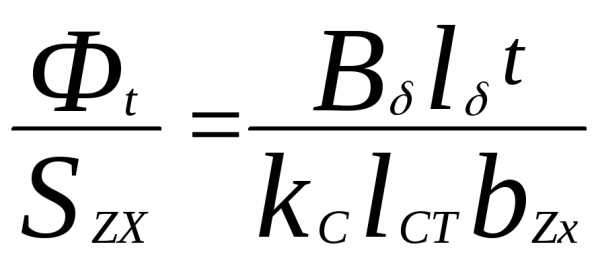(4.34)

После этого, задаваясь значениями bzx, несколько меньшими, чем B'zx, подбором находят действительную индукцию Bzx и со­ответствующее ей значение Hzx, при которых удовлетворяется ра­венство (4.32). Для облегчения расчета в приложении 2 приведе­ны кривые, позволяющие определить hzx непосредственно по расчетной индукции b'zx с учетом фиксированных значений коэф­фициента kп.

Численные значения kп и μ0 = 4π • 10-7 Гн/м в (4.32) позволя­ют судить о значениях индукции в зубцах, при которых необхо­димо учитывать ответвление потока в паз. Для большинства современных электротехнических сталей при индукции Bz ≤ 1,8 Тл напряженность поля не превышает H ≤ 16000 А/м, следователь­но, при этом уровне насыщения действительная индукция в зуб­цах будет меньше, чем расчетная, лишь на 2—3 % даже при бо­льших значениях kп, поэтому в расчетах этим изменением можно пренебречь.

При индукциях Bz ≥ 1,8 Тл расчет следует проводить с учетом ответвления потока в паз. Естественно, что вопрос о необходимости такого учета решается при определении индукции в каждом из рас­четных сечений зубца в отдельности [6].

studfiles.net

МАГНИТНОЕ НАПРЯЖЕНИЕ ЗУБЦОВЫХ ЗОН

 

При расчете магнитных напряжений зубцовых зон принимается попущение, что линии равного магнитного потенциала в попереч­ном сечении машины представляют собой окружности с центром на оси вращения ротора. При этом допущении магнитное напряжение зубцовой зоны статора FZ1 или ротора FZ2 определяется разностью магнитных потенциалов между эквипотенциальными поверхностя­ми (на поперечном сечении — окружностями), проходящими по дну пазов и по поверхности головок зубцов.

Обычно рассматривают поле в одном элементе зубцовой зоны — зубцовом (пазовом) делении tZ = πD/ Z. Магнитные со­противления паза и зубца в магнитной цепи машины соединены параллельно, поэтому поток в зубцовом делении распределяется между ними пропорционально проводимостям магнитных сило­вых трубок, проходящих через зубец и паз. Пазы в электрической машине заполнены проводниками и их изоляцией, т. е. средой с магнитной проницаемостью, во много раз меньшей, чем проница­емость стали зубца. Поэтому поток в пазу составляет лишь небо­льшую часть общего потока зубцового деления. Эта часть потока как бы «вытесняется» из зубца в паз. При малом насыщении зуб­цов она очень мала и в расчетах ее не учитывают. При увеличе­нии насыщения зубцов доля потока в пазу возрастает и ее влия­ние начинает сказываться на магнитном напряжении зубцовой зоны FZ.

Рассмотрим вначале расчет магнитного напряжения зубцовой зоны без учета вытеснения части потока в паз. При принятом допу­щении о конфигурации эквипотенциальных линий и в силу симмет­рии зубцовой зоны магнитные силовые линии, проходящие через се­редины оснований зубцов, совпадают с отрезками радиусов (см. рис. 4.1, а и б), поэтому

(4.21)

 

где HZx — напряженность магнитного поля в сечении зубца, соответ­ствующем расстоянию hZx от его узкой части; hZ — высота зубца (рис. 4.5, а).

 

Рис. 4.5. К расчету магнитного напряжения зубцовой зоны

При постоянном сечении зубца считают, что напряженность поля в нем HZ постоянна, тогда FZ = HZhZ(4.21 а) При переменном сечении зубца FZ можно определить, разделив зубец по высоте на n достаточно малых участков с высотой Δh, в пределах которых изменением HZ пренебрегают.

Определив для каждого участка индукцию, напряженность магнитного поля, магнитное напряже­ние и просуммировав последние, находят магнитное напряжение зубца.

Поток, приходящийся на одно зубцовое деление,

ФtZ = Bδ tZ lδ. (4.22)

Если через bZx обозначить ширину зубца на высоте hZx, то соот­ветствующее активное сечение зубца

SZx = kc lст bZx,

где kc — коэффициент заполнения сердечника сталью; lст — длина магнитопровода без вентиляционных каналов.

Индукция в рассматриваемом сечении зубца (рис. 4.5, б)

(4.23)

Напряженность поля определяется для соответствующей индук­ции по кривым намагничивания для выбранной марки стали.

Проведя несколько таких расчетов для различных сечений зуб­ца, можно для потока ФtZ построить кривую распределения напря­женности поля по высоте зубца (рис. 4.5, в). Площадь, ограничен­ная этой кривой, SACDE определяется в масштабе магнитного напряжения зубца:

Зубцы в электрических машинах могут иметь сложную конфигу­рацию, поэтому такие расчеты выполняют лишь на ЭВМ при необ­ходимости получения уточненных данных, при этом программы расчетов должны учитывать особенности размерных соотношений данной зубцовой зоны.

В практических расчетах оказывается достаточным приближен­ное решение, когда FZ находится по (4.21) для некоторой средней расчетной

 

напряженности HZ и расчетной высоты зубца hZ, для которых справедливо

HZ hZ = FZ

При плавно изменяющихся сечениях зубцов расчетная напря­женность HZдостаточно точно находится по формуле

HZ = ( HZmax + 4HZср + HZmin). (4.24)

Здесь HZmax, HZmin и HZcp — напряженности поля в поперечных сечениях зубца, которые определяются по индукциям в наиболее уз­ком SZmin, наиболее широком SZmax и среднем по высоте SZcp сечениях зубца, по следующим формулам:

(4.25)

где bZmin, bZmax - наибольшая и наименьшая ширина зубца (см. рис. 4.5, б)

При прямоугольных пазах при BZmax ≤ 2,0 Тл используется рас­пространенный метод расчета FZ по напряженности НZ1/3, определенной по индукции в сечении на 1/3 высоты зубца от его узкой час­ти (см. рис. 4.5):

FZ = HZ1/3 hZ, (4.26)

дающий хорошее совпадение с уточненными расчетами при неболь­шой разнице наибольшего и наименьшего сечений зубцов. При этом площадь прямоугольника ACD'E' со сторонами Hz1/3 и hZ равновели­ка площади фигуры ACDE (см. рис. 4.5, в).

В отдельных случаях при большей разнице bZmax и bZmin и боль­ших насыщениях расчет проводится более детально. Зубец делится по высоте на две части, и для каждой из них определяется средняя напряженность поля указанным методом. В этом случае расчетные сечения берутся на высоте

и

от наиболее узкого сечения зубца.

При расчете магнитного напряжения зубцов с резко изменяю­щимся по высоте сечением, например зубцов двухклеточного рото­ра асинхронного двигателя и короткозамкнутого ротора с фигурны­ми пазами, зубцы также делятся по высоте на два участка с плавно изменяющимся сечением, при том магнитное напряжение зубцов равно сумме магнитных напряжений участков.

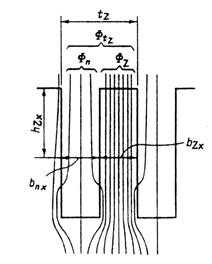Рис. 4.6. Магнитный поток в зубцовом делении при насы­щении стали зубцов

Влияние местных изменений сечения зубца на изменение магнитного напряже­ния, не распространяющихся на большие, участки по его высоте (углубления в стенках пазов для крепления пазовых клинь­ев, расширения в коронках зубцов и т. п.), в практических расчетах обычно не учи­тывают. В насыщенной зубцовой зоне доля по­тока в пазу возрастает. Ее можно оценить, не прибегая к полному расчету поля на зубцовом делении, следующим образом. Обозначим поток в зубце ФZ и поток в пазу Фп (рис. 4.6), тогда поток на зубцо­вом делении на высоте зубца hZx будет ра­вен:   ФtZ = ФZx + Фпх(4.27)

Разделив (4.27) на SZx и умножив и разделив второе слагаемое правой части на Sпх = bпxlδ , получим

(4.28)

или

B'Zx = BZx + Bпх (4.29)

где В'Zх — расчетная индукция, определимая полным потоком в сече­нии зубца SZx в предположении, что поток в пазу отсутствует; bZx — действительная индукция в сечении зубца SZx, т.е. индукция, опреде­ленная с учетом того, что часть потока вытесняется из зубца в паз; Впх — индукция в сечении паза Sпх, создаваемая вытесненной в паз ча­стью потока.

Так как паз заполнен средой с магнитной проницаемостью μ0 (магнитной постоянной), то

Впх = μ0 Нпх. (4.30)

На основании принятого допущения о конфигурации эквипотен­циальных линий в зубцовой зоне напряженность поля в зубце и в пазу на одной и той же высоте hZx будет одинакова, т. е.

Нпх = HZx.

Тогда из (4.29) и (4.30) имеем

 

В'Zх = ВZх + μ0 НZх (4.31)

или

B'Zx = BZx+ μ0 HZx kпx, (4.32)

где kпx — коэффициент, определяющий отношение площадей попе­речных сечений паза и зубца на высоте hZx:

kпх = (4.33)

В машинах нормального исполнения kп для различных по высоте зубца сечений обычно находится в пределах kп = 0,5 – 2,0.

Для определения действительной индукции в каждом сечении зубца первоначально находят расчетную индукцию по полному по­току зубцового деления:

В'Zx = (4.34)

После этого, задаваясь значениями bZx, несколько меньшими, чем B'Zx, подбором находят действительную индукцию BZx и со­ответствующее ей значение HZx, при которых удовлетворяется ра­венство (4.32). Для облегчения расчета в приложении 2 приведе­ны кривые, позволяющие определить hZx непосредственно по расчетной индукции b'Zx с учетом фиксированных значений коэф­фициента kп.

Численные значения kп и μ0 = 4π∙10-7 Гн/м в (4.32) позволя­ют судить о значениях индукции в зубцах, при которых необхо­димо учитывать ответвление потока в паз. Для большинства современных электротехнических сталей при индукции BZ ≤ 1,8 Тл напряженность поля не превышает H ≤ 16000 А/м, следователь­но, при этом уровне насыщения действительная индукция в зуб­цах будет меньше, чем расчетная, лишь на 2—3 % даже при бо­льших значениях kп, поэтому в расчетах этим изменением можно пренебречь.

При индукциях BZ ≥ 1,8 Тл расчет следует проводить с учетом ответвления потока в паз. Естественно, что вопрос о необходимости такого учета решается при определении индукции в каждом из рас­четных сечений зубца в отдельности [6].

 

Похожие статьи:

poznayka.org

16.2. Магнитное напряжение воздушного зазора

В воздушном зазоре машины большая часть главного магнитного потока сосредоточена между полюсным нако­нечником и ротором (якорем) (рис. 16.2, а). Предположим, что якорь не имеет зубцов (его поверхность гладкая) и за­зор по всей ширине полюсного наконечника постоянен. Тогда под полюсным наконечником поток в зазоре распре­деляется равномерно и индукция по всей его ширине будет иметь постоянное значение Вδ (рис. 16.2,6). В межполюс­ном промежутке вследствие увеличения длины силовой линии в воздухе, а следовательно, и увеличения магнитного сопротивления индукция падает, а в нейтрали (точке, ле­жащей в середине между полюсами) будет равна нулю (рис. 16.2, б).

В целях упрощения расчета картину поля, показанную на рис. 16.2, б, заменим более простой. Для этого действи­тельную трапецеидальную фигуру заменим прямоугольни­ком с высотой Bδ и основанием bδ. При этом площади тра­пеции и прямоугольника, пропорциональные потоку полю­са, должны быть равны. Индукция Вδ называется расчетной индукцией в воздушном зазоре, а bδ — расчетной шириной полюсного наконечника.

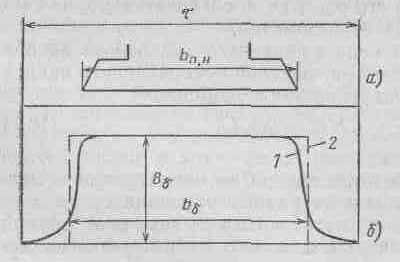
Рис. 16.2. Поле в зазоре по ширине полюсного на­конечника при гладком якоре

При практических расчетах для определения bδ не стро­ят картину распределения индукции в зазоре, а пользуются эмпирическими формулами. При равномерном зазоре меж­ду полюсным наконечником и ротором (якорем) расчетная ширина полюсного наконечника принимается равной:

где bП,Н — истинная ширина полюсного наконечника; δ — воздушный зазор.

Иногда для снижения уровня шума при работе машины полюсные наконечники выполняются со скошенными края­ми, в результате чего воздушный зазор под краями получа­ется большим, чем в середине (рис. 16.3). Расчетная шири­на полюсного наконечника в этом случае принимается равной истинной его ширине, т. е.

В последнее время для тех же целей машины выполняются со смещенными центрами радиусов дуги полюсного наконечника и якоря, вследствие чего воздушный зазор по всей ширине наконечника будет различным (рис. 16.4). Обычно δ"=3δ'. Для определения магнитного напряжения принимают эквивалентный зазор , а рас­четную ширину наконечника bδ равной bП,Н.

Отношение bδ/τ=αδ называется коэффициентом полюс­ного перекрытия. Оно показывает, какую часть полюсного деления τ охватывает полюсный наконечник. Обычно αδ=0,6…0,8.

Рассмотрим распределение магнитного поля по длине машины. Якорь в осевом направлении может состоять из одного или нескольких пакетов. Его общая длина lа или равна длине полюса lП, или принимается на 5—10 мм больше (рис. 16.5, а). При длине якоря, большей, чем длина полюса, происходит уменьшение индукции на его краях, Поток, входящий в торец якоря, уменьшается, в результа­те чего уменьшаются потери на вихревые токи в торцевых частях машины.

←Рис. 16.3. Полюс со скошенными краями наконечника

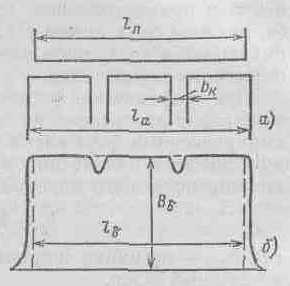
Рис. 16.4. Полюс при эксцентричном зазоре

Рис. 16.5. Распределение поля в зазоре машины по длине яко­ря

Распределение магнитной индукции по длине машины показано на рис. 16.5, б. При наличии радиальных вентиля­ционных каналов магнитное поле по длине машины пере­распределяется таким образом, что основная его часть идет по стальным пакетам. В результате этого над венти­ляционными каналами происходит снижение индукции и кривая поля приобретает зубчатый характер.

За расчетную длину якоря принимается основание пря­моугольника lδ, имеющего высоту Вδ, и площадь, равнове­ликую площади, охватываемой действительной кривой по­ля. С достаточной точностью можно считать, что

где lca=(lа—nКbК) — суммарная длина пакетов; nК — чис­ло каналов; bК — ширина вентиляционных каналов (обыч­но bК=10мм).

Исходя из заданного главного потока Ф и используя по­лученные линейные размеры lδ и bδ, находим индукцию в зазоре:

Поскольку напряженность магнитного поля в зазоре рав­на Hδ=Bδ/μ0, то

Формула (16.7) получена в предположении, что якорь гладкий. Чаще всего якорь имеет зубчатое строение, поэто­му в зазоре по ширине полюсного наконечника поле рас­пределяется неравномерно — оно сгущается под зубцами и разрежается под пазами (рис. 16.6). В результате этого кривая распределения индукции принимает зубчатый вид и будет отличаться от показанной на рис. 16.2, б. Так как силовая линия магнитного потока, вдоль которой опреде­ляем МДС, проходит через середину зубца (см. рис. 16.1), то в данном случае при определении магнитного напряжения воздушного зазора в (16,7) следует подставить индук­цию Bδm:

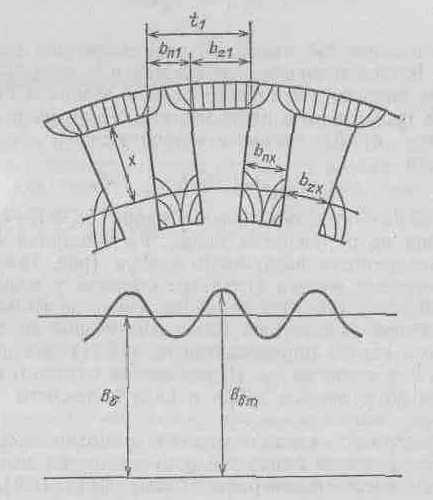
Рис. 16.6. Поле в зазоре по ширине полюсного наконечника при наличии зубцов на якоре

Отношение

носит название коэффициента воздушного зазора. Введе­нием этого коэффициента учитывается зубчатое строение якоря; коэффициент kδ, больше единицы и возрастает с уве­личением раскрытия паза. Из (16.8), (16.9) получим

Произведение kδδ называют эквивалентным воздушным зазором. Точное значение коэффициента kδδ можно получить на основе анализа магнитного поля в зазоре и пазах, что связано с громоздкими построениями. Поэтому в практике пользуются приближенными эмпирическими формулами, в частности

где t1=πDa/z — зубцовое деление якоря; bz1=t1—bП1 — ши­рина зубца по окружности якоря; bП1 — ширина открытия паза у поверхности воздушного зазора (рис. 16.6).

У некоторых машин (главным образом у машин большой мощности) зубчатое строение имеет не только якорь, но и полюсной наконечник. Для таких машин коэффициент воздушного зазора определяется по (16.11) как для якоря kδ1, так и для полюсов kδ2. В последнем случае t1 и bz1 при­нимаются по размерам зубца и паза полюсного наконеч­ника.

В тех случаях, когда крепление обмотки якоря производится с помощью бандажей, укладываемых в кольцевые канавки на внешней поверхности якоря (рис. 16.7), воздушный зазор по длине машины приобретает ступенчатую фор­му, что вызывает перераспределение магнитного поля в осе­вом направлении.

Рис. 16.7. Бандажные канавки по длине якоря

При расчете магнитного напряжения учет влияния бандажных канавок осуществляется коэффициен­том воздушного зазора kδ3. Этот коэффициент при банда­жах, выполненных из немагнитного материала, определяет­ся по формуле

где nб — число бандажных канавок

В общем случае результирующий коэффициент воздуш­ного зазора kδ, который подставляется в (16.10), будет ра­вен произведению этих трех коэффициентов:

studfiles.net

Напряжение - магнитное поле - Большая Энциклопедия Нефти и Газа, статья, страница 1

Напряжение - магнитное поле

Cтраница 1

Напряжение магнитного поля, или магнитное напряжение, в поле между двумя точками определяется работой сил магнитного поля при перемещении единичного ( пробного) магнитного потока между этими точками.  [1]

Изменяя напряжение магнитного поля, заставляют разделенный поток ионов проходить мимо щели, через которую ионы попадают в камеру, соединенную с регистрирующим устройством.  [2]

Рассмотрим теперь напряжение магнитного поля в этом случае.  [3]

Так как напряжение магнитного поля Н перпендикулярно к п и к D, то каждая из осей полученного в сечении эллипса дает также направление магнитного напряжения, соответствующее электрической индукции, направление которой совпадает с другой осью. В то же время направление напряжения электрического поля Е согласно ( 260) задается нормалью к эллипсоиду в конце той оси, которая определяет электрическую индукцию.  [4]

Таким образом, напряжение магнитного поля ( и индукция) также перпендикулярно к направлению перемещения и находится в плоскости фронта волны.  [5]

Я, v напряжения магнитного поля представляют собой косинусы трех взаимно перпендикулярных направлений.  [6]

Так как вектор напряжения магнитного поля перпендикулярен как к лучу, так и к нормали к волне, и этот вектор определяет направление поляризации, то следовательно направления поляризации являются линиями, перпендикулярными к плоскостям, заключающим нормаль к волне и лучи.  [7]

Так как вектор напряжения магнитного поля здесь перпендикулярен к лучу, он имеет две составляющие: одну перпендикулярную к плоскости падения и одну в плоскости падения. Мы можем рассмотреть отдельно волны, соответствующие этим двум составляющим.  [8]

В нервом случае постепенно изменяют напряжение магнитного поля, вследствие чего на коллектор последовательно попадают пучки ионов изучаемых участков спектра. Кривая величины тока, идущего из коллектора, записывается электронным потенциометром.  [10]

Синхронность в изменении намагниченности и напряжения магнитного поля может иметь место только при очень медленном ( квазистатическом) изменении магнитного поля. В случае переменных магнитных полей указанная синхронность отсутствует и форма динамической петли гистерезиса зависит от формы образца и от частоты переменного поля. Опыт показывает, что магнитная проницаемость существенно зависит от частоты переменного поля даже в том случае, когда исключено влияние токов Фуко.  [12]

Мы видим, что направление напряжения магнитного поля играет особую роль. Это объясняется тем, что направление его совпадает с направлением магнитной индукции, в то время как направление напряжения электрического поля, вообще говоря, не совпадает с направлением электрической индукции.  [13]

Итак, напряжение электрического поля и напряжение магнитного поля являются взаимно перпендикулярными. Любое из них может быть принято за световой вектор.  [14]

Например, течение реакций зависит также от напряжения окружающего магнитного поля, меняющегося в зависимости от времени в соответствии с характером движения Земли в космическом пространстве.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

---

• 
  Требования к монтажу электропроводки пуэ
• 
  Техническое обслуживание генераторов
• 
  Релейная защита и автоматика
• 
  Уличное светодиодное освещение
• 
  Транзисторы биполярные вах
• 
  Тн с
• 
  Как выглядит предохранитель на схеме
• 
  Ip что это такое в электрике
• 
  Когда подключат отопление
• 
  Правила правой руки физика
• 
  Начало отопительный сезон в москве