Калькулятор закона Ома. Закон ома мощность калькулятор онлайн. Онлайн расчет закон ома

Закон Ома | Мозган калькулятор онлайн

На данной странице калькулятор поможет рассчитать сопротивление, напряжение или силу тока по закону Ома онлайн.

Закон Ома - эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

Как найти сопротивление

Электрическое сопротивление определяет силу тока, текущего по цепи при заданном напряжении.

Под Электрическим сопротивлением R понимают отношение напряжения на концах проводника к силе тока, текущего по проводнику.

Формула для нахождения сопротивления по закону Ома:

U - напряжение; I - сила тока.

Как найти силу тока

Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Формула для нахождения силы тока по закону Ома:

U - напряжение; R - сопротивление.

Как найти напряжение

Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.

Формула для нахождения напряжения по закону Ома:

I - сила тока; R - сопротивление.

mozgan.ru

Закон Ома. Онлайн расчёт для постоянного и переменного тока.

- А любите ли Вы закон Ома так, как люблю его я..? - спросил учитель физики стоящего рядом с щитком и разглядывающего свой обугленный палец электрика, - Всеми силами души Вашей, со всем энтузиазмом, со всем исступлением, к которому только способна пылкая молодость - никак не угомонялся он, сверкая из-под очков пытливым взглядом. - Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным вопросом электрик и пошёл, насвистывая "Калинку-Малинку" в направлении ближайшего супермаркета - не ради пьянства окаянного, а дабы залечить свой увечный палец.

А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Формулировка закона Ома может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:

  I=U/R,

где I – сила тока в проводнике, измеряемая в амперах [А]; U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В]; R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Казалось бы, формулы настолько просты, что не стоят выеденного яйца и, уж тем более, никак не заслуживают отдельной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари! Считайте, учитывайте размерность, не стирайте из памяти, что:

1В=1000мВ=1000000мкВ; 1А=1000мА=1000000мкА; 1Ом=0.001кОм=0.000001МОм.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА. Ясен пень, что вводить нужно только два имеющихся у Вас параметра, третий посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения Rвнутр. Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + Rвнутр, после чего закон приобретает солидное название - закон Ома для полной цепи.

Теперь, что касается закона Ома для переменного тока. Если внешнее сопротивление у нас чисто активное (не содержит емкостей и индуктивностей), то формула, приведённая выше, остаётся в силе. Единственное, что надо иметь ввиду - под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока? Приведём диаграммы для нескольких различных форм сигнала.

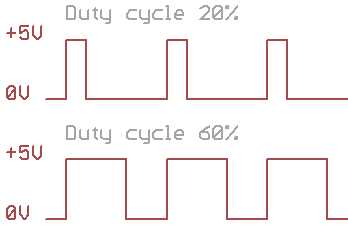
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы. Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов - это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2; для треугольника и пилы U = Uд = Uа/√3; для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока. В общем случае смотреться это будет так:

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, емкостного и индуктивного сопротивлений. Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид: Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: XC = 1/(2πƒС) , XL = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи. Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента - необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома и рассчитаем простенький бестрансформаторный источник питания.

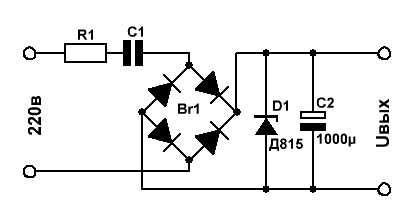
Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА. Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А. Зададимся током через стабилитрон с некоторым запасом - 200мА. С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в - 12в = 208в. Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм. Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки. Зададимся номиналами R1 - 30 Ом, С1 - 1 Мкф, частотой сети f - 50 Гц и подставим всё это хозяйство в таблицу. Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет - надо увеличивать ёмкость С1. Поигрались туда-сюда, нашли нужное значение ёмкости - 3,18 Мкф, при котором Z = 1,04кОм.

Всё - расчёт закончен. Всем спать полчаса!

 

vpayaem.ru

Калькулятор закона Ома - Arduino+

Введите любые два известных параметра схемы в приведенном ниже калькуляторе закона Ома и вычислите оставшиеся два значения в соответствии с Законом Ома.

Закон Ома - это самый фундаментальный закон, который регулирует связь между напряжением (V), током (I) и сопротивлением (R). Это определил немецкий ученый Георг Симон Ом, и, следовательно, назван в честь него. Закон гласит, что «для любой цепи электрический ток (I) прямо пропорционален напряжению (V) и обратно пропорционален сопротивлению (R)».

Это самый фундаментальный закон, из которого были получены все другие концепции; возможно, это будет первый закон, который будет представлен всем, кто интересуется электроникой. Концепция этого закона очень проста, просто означает, что напряжение на любых двух точках в цепи всегда будет равно произведению сопротивления между двумя точками и током, протекающим по цепи. Это может быть математически задано так:

V = IR

Где V = Напряжение, I = Ток и R = Сопротивление.

Эта формула также может быть переписана в следующих вариантах:

Используя эти три формулы, вы можете рассчитать значение напряжения, тока или сопротивления. Если вы знаете любой из этих двух параметров, вы также можете вычислить мощность, используя приведенные ниже формулы:

Давайте проверим наш принцип закона Ома на вышеприведенных двух схемах. Источник напряжения для схемы составляет 12 В. Но у нас есть два разных значения сопротивления для цепей, одно слева - 110 Ом, а одно справа - 220 Ом.

Вычислим ток, который должен проходить через схему для обеих цепей. Нам известна формула I = V / R.

Для левой стороны: I = V / R, I = 12/110, и это дает нам 0,109A, что составляет ~ 0,11A, если проверить его с помощью амперметра.

Для правой стороны: I = 12/220, и это дает нам 0,54A, что составляет ~ 0,5А, если проверить его с помощью амперметра.

Аналогичным образом вы можете попытаться вычислить значение сопротивления (с известным напряжением и током) или напряжение (с известным током и сопротивлением), используя калькулятор закона Ома выше. Этот калькулятор также предоставит вам номинальную мощность схемы, используя приведенные выше формулы.

arduinoplus.ru

сила тока, расчет мощности и напряжения

В сети Интернет имеется множество специальных сайтов, которые предлагают автоматизировать подсчёты различных физических величин. Для электриков, студентов и тех, кому необходимо часто решать задачи на расчёты закона Ома, созданы специальные калькуляторы онлайн, которые предназначены именно для этих целей.

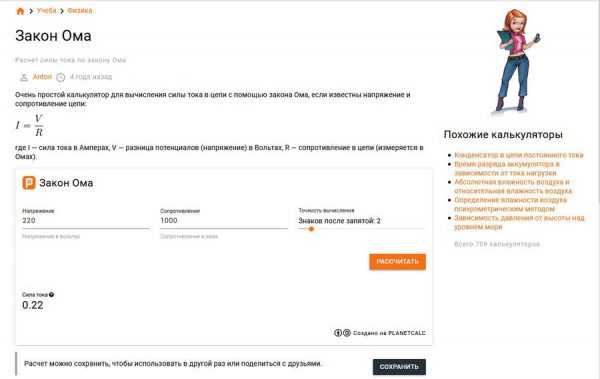
Выполнение расчёта силы тока

Закон Ома

Сформулировал его в 1827 году немецкий физик Георг Ом.

Согласно Ому, его можно записать так. Сила тока (I) на участке цепи прямо пропорциональна приложенному напряжению (U) и обратно пропорциональна сопротивлению (R).

Соответственно, формула имеет вид:

I = U/R.

Таким образом, из соотношения можно рассчитать напряжение:

U = I · R.

И сопротивление:

R = U/I.

Автоматизация расчёта участка электрической цепи

Благодаря выполнению вычислений непосредственно на сайте, можно быстро получить значение одного из параметров электрической цепи по двум другим известным характеристикам, связанным между собой законом Ома.

Обычно в таких сервисах используются все значения, представленные в единицах Си, если это не оговаривается отдельно:

• напряжение задаётся в вольтах (В),
• сопротивление вводится в омах (Ом),
• сила тока вводится в амперах (А)

Внимание! Если значения характеристик выражены в кратных или дольных единицах измерения, то для получения правильного результата нужно их привести к таким, которые приняты в Международной системе Си. Это важно выполнить в том случае, если калькулятор не позволяет осуществлять перевод автоматически.

Кратные и дольные единицы используются для более компактной записи очень больших или маленьких значений параметров. Благодаря их использованию, в записи уменьшается количество нулей. Для их обозначения применяются приставки к основным единицам измерения, например, кВ или мкА.

Для перевода можно использовать таблицу наиболее часто используемых десятичных приставок.

Таблица приставок величин

ПриставкаОбозначениеДесятичный множитель

кратные
кило	к	10^3
мега	М	10^6
гига	Г	10^9
дольные
мили	м	10^-3
микро	мк	10^+6
нано	н	10^-9

Помимо этих параметров, часто сервисы предлагают выполнить подсчёт мощности (W), которую можно определить по формулам: 

• W = U²/R,
• W = I2 · R,
• W = U · I.

Результат вычисления мощности показывается в ваттах (Вт), однако существуют программы, позволяющие получать мощность в кратных или дольных величинах (предварительно заданных на сервисе).

Вычислительные программы, размещённые онлайн, обычно имеют удобный и интуитивно понятный интерфейс. Однако на многих сайтах можно также найти инструкцию по использованию этих сервисов в своей работе.

Существует два типа размещения программ на странице.

Первый – на странице сайта размещаются три калькулятора для подсчёта каждой из величин: силы тока, сопротивления или напряжения. После выбора нужного варианта вводятся известные параметры. После нажатия на соответствующую кнопку, отображается результат подсчёта.

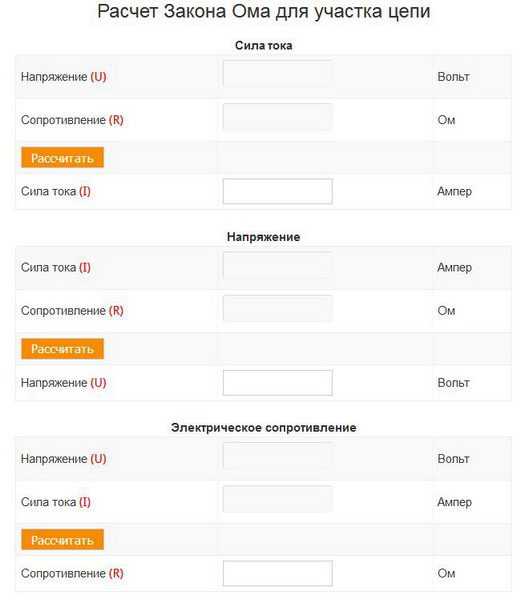
Пример интернет-сервиса для автоматизации вычислений

Второй вариант – пользователю предварительно предоставляется выбор искомой величины. Далее в соответствующие поля подставляются известные значения электрических характеристик. Для начала выполнения работы нужно нажать на соответствующую кнопку. Такой вариант представлен на рис. ниже.

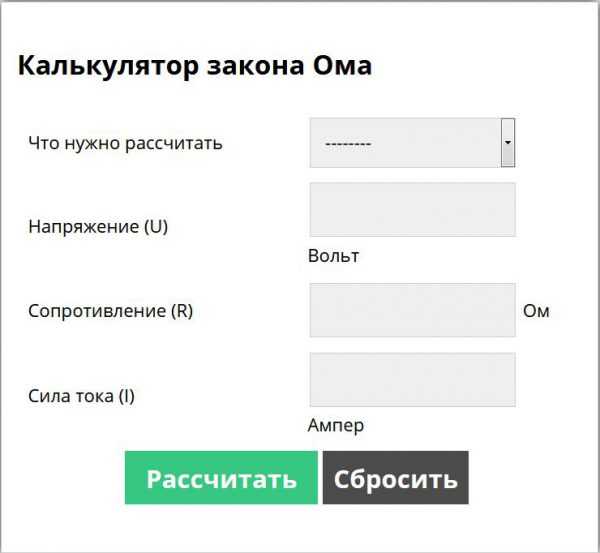
Интерфейс онлайн программы для расчёта закона Ома

Если программа позволяет вводить величины и получать результат в кратных или дольных единицах, то обязательно нужно это указать перед выполнением подсчёта.

Использование онлайн калькуляторов, предназначенных для автоматизации вычисления параметров электрических цепей, позволяет уменьшить время, затрачиваемое на решение задач такого типа.

Видео

Оцените статью:

elquanta.ru

Закон ома мощность калькулятор онлайн. Закон Ома

Закон Ома | Мозган калькулятор онлайн

На данной странице калькулятор поможет рассчитать сопротивление, напряжение или силу тока по закону Ома онлайн.

Закон Ома - эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

Как найти сопротивление

Электрическое сопротивление определяет силу тока, текущего по цепи при заданном напряжении.

Под Электрическим сопротивлением R понимают отношение напряжения на концах проводника к силе тока, текущего по проводнику.

Формула для нахождения сопротивления по закону Ома:

U - напряжение; I - сила тока.

Как найти силу тока

Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Формула для нахождения силы тока по закону Ома:

U - напряжение; R - сопротивление.

Как найти напряжение

Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.

Формула для нахождения напряжения по закону Ома:

I - сила тока; R - сопротивление.

mozgan.ru

Закон Ома. Онлайн расчёт для постоянного и переменного тока.

- А любите ли Вы закон Ома так, как люблю его я..? - спросил учитель физики стоящего рядом с щитком и разглядывающего свой обугленный палец электрика, - Всеми силами души Вашей, со всем энтузиазмом, со всем исступлением, к которому только способна пылкая молодость - никак не угомонялся он, сверкая из-под очков пытливым взглядом. - Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным вопросом электрик и пошёл, насвистывая "Калинку-Малинку" в направлении ближайшего супермаркета - не ради пьянства окаянного, а дабы залечить свой увечный палец.

А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Формулировка закона Ома может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:

  I=U/R,

где I – сила тока в проводнике, измеряемая в амперах [А]; U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В]; R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Казалось бы, формулы настолько просты, что не стоят выеденного яйца и, уж тем более, никак не заслуживают отдельной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари! Считайте, учитывайте размерность, не стирайте из памяти, что:

1В=1000мВ=1000000мкВ; 1А=1000мА=1000000мкА; 1Ом=0.001кОм=0.000001МОм.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА. Ясен пень, что вводить нужно только два имеющихся у Вас параметра, третий посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения Rвнутр. Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + Rвнутр, после чего закон приобретает солидное название - закон Ома для полной цепи.

Теперь, что касается закона Ома для переменного тока. Если внешнее сопротивление у нас чисто активное (не содержит емкостей и индуктивностей), то формула, приведённая выше, остаётся в силе. Единственное, что надо иметь ввиду - под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока? Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы. Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов - это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2; для треугольника и пилы U = Uд = Uа/√3; для меандра U = Uд = Uа.

С этим разобрались!

Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока. В общем случае смотреться это будет так:

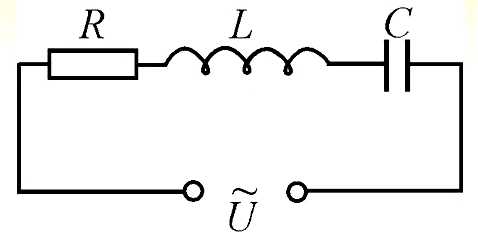
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, емкостного и индуктивного сопротивлений. Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид: Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: XC = 1/(2πƒС) , XL = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи. Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента - необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

Теперь давайте рассмотрим практический пример применения закона Ома и рассчитаем простенький бестрансформаторный источник питания.

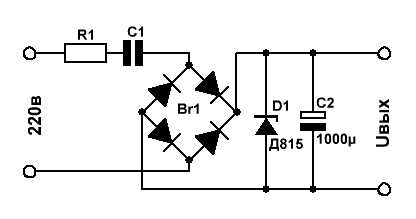
Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА. Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А. Зададимся током через стабилитрон с некоторым запасом - 200мА. С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в - 12в = 208в. Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм. Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки. Зададимся номиналами R1 - 30 Ом, С1 - 1 Мкф, частотой сети f - 50 Гц и подставим всё это хозяйство в таблицу. Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет - надо увеличивать ёмкость С1. Поигрались туда-сюда, нашли нужное значение ёмкости - 3,18 Мкф, при котором Z = 1,04кОм.

Всё - расчёт закончен. Всем спать полчаса!

 

vpayaem.ru

Калькулятор закона Ома - Arduino+

Введите любые два известных параметра схемы в приведенном ниже калькуляторе закона Ома и вычислите оставшиеся два значения в соответствии с Законом Ома.

Закон Ома - это самый фундаментальный закон, который регулирует связь между напряжением (V), током (I) и сопротивлением (R). Это определил немецкий ученый Георг Симон Ом, и, следовательно, назван в честь него. Закон гласит, что «для любой цепи электрический ток (I) прямо пропорционален напряжению (V) и обратно пропорционален сопротивлению (R)».

Это самый фундаме

xn----7sbeb3bupph.xn--p1ai

Закон ома калькулятор онлайн

Закон Ома - физический закон, определяющий зависимость между электрическими величинами - напряжением, сопротивлением и током для проводников.

Впервые открыл и описал его в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость.

Впоследствии свойства проводника, способные противостоять электрическому току на основе этой зависимости, стали называть электрическим сопротивлением (Resistance), обозначать в расчётах и на схемах буквой R и измерять в Омах в честь первооткрывателя.

Сам источник электрической энергии также обладает внутренним сопротивлением, которое принято обозначать буквой r.

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.

Отсюда следуют ещё два полезных соотношения:

Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).

Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.

Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R.

Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.

Предлагается простой Онлайн-калькулятор для практических расчётов.

После сброса ввести два любых известных параметра.

Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:

- Электродвижущая сила (ЭДС) - величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника.

r - Внутреннее сопротивление источника питания.

Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .

Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.

Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания.

С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.

По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = - I*r.

Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U.

Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.

В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U ) независимо от сопротивления внешней цепи R.

Такой источник питания называют источником напряжения.

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.

В таком случае запись Закона Ома будет иметь вид:

Здесь Z - полное (комплексное) сопротивление цепи - импеданс. В него входит активная R и реактивная X составляющие.

Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.

Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:

- комплексная амплитуда напряжения. = Uampe jφ

φ - угол сдвига фаз между током и напряжением.

e - константа, основание натурального логарифма.

Iamp , Uamp - амплитудные значения синусоидального тока и напряжения.

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников.

Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы.

Такие элементы и цепи, в которых они используются, называют нелинейными.

www.krepkoeradi.ru

4. Расчет электрической мощности | 2. Закон Ома | Часть1

4. Расчет электрической мощности

Расчет электрической мощности

В прошлой статье мы с вами вывели формулу для определения мощности в электрической цепи: умножая напряжение в "вольтах" на силу тока в "амперах", мы получаем мощность в "ваттах". Давайте применим ее к следующей схеме:  

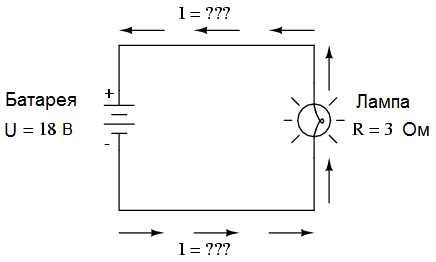
В этой схеме есть две известные нам величины: напряжение батареи составляет 18 вольт, а сопротивление лампы - 3 ома. Используя Закон Ома мы определим третью величину - силу тока:

Теперь, зная силу тока, мы можем умножить ее значение на напряжение и получить мощность:

Это означает что лампа рассеивает 108 ватт энергии в форме сета и тепла.

Давайте в этой же схеме увеличим напряжение батареи и посмотрим что произойдет. Интуиция подсказывает нам, что при увеличении напряжения и неизменном сопротивлении, сила тока в цепи также увеличится. А это значит, что увеличится и мощность:

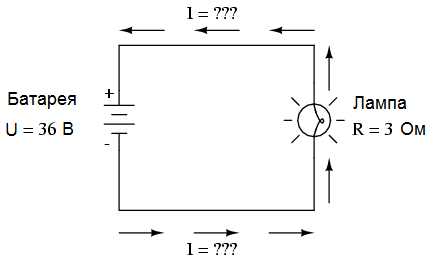
В этой схеме напряжение батареи изменено и составляет 36 вольт вместо прежних 18. Сопротивление лампы не изменилось, и равно 3 омам. Сила тока теперь будет равна:

Давайте обсудим полученное значение. Если I=U/R, и мы удваиваем значение напряжения (U), оставляя неизменным сопротивление, то по логике вещей сила тока у нас тоже должна удвоиться. Действительно, сила тока в данной схеме имеет значение 12 ампер вместо прежних 6. А сейчас давайте вычислим мощность:

Обратите внимание, что мощность у нас также увеличилась по сравнению  с предыдущим примером, и увеличилась она значительнее, чем увеличилась сила тока. Почему так получилось? Ответ на этот вопрос прост. Мощность является функцией напряжения умноженного на силу тока, а так как обе эти величины удвоились по сравнению с предыдущими значениями, то мощность увеличилась в 2х2 или в 4 раза. Вы можете проверить эту цифру разделив 432 ватта на 108 ватт и увидев, что соотношение между ними равно 4.

Используя математику мы можем преобразовать формулу мощности применительно к тем случаям, когда нам не известно значение напряжения или силы тока:

Историческая справка: первым математическую связь между рассеиваемой мощностью и силой тока через сопротивление открыл не Георг Симон Ом, а Джеймс Прескотт Джоуль. Это открытие, опубликованное в 1841 году и содержащее формулу P=I2R, стало известно как Закон Джоуля. Однако очень часто эти уравнения причисляются к Закону Ома.

Краткий обзор:

www.radiomexanik.spb.ru

---

• 
  Какой счетчик экономичнее трехфазный или однофазный
• 
  Маркировка твердотельные конденсаторы
• 
  Какой заряд у нейтрона
• 
  Обозначение датчик давления на схеме
• 
  Проверка трансформаторов тока на 10 погрешность примеры
• 
  Регулирование шим
• 
  Мосэнергосбыт поверка счетчика электроэнергии
• 
  Энергосберегающее освещение
• 
  Сенсорный выключатель для зеркала
• 
  Единица си времени
• 
  Бокс для электросчетчика и автоматов уличный