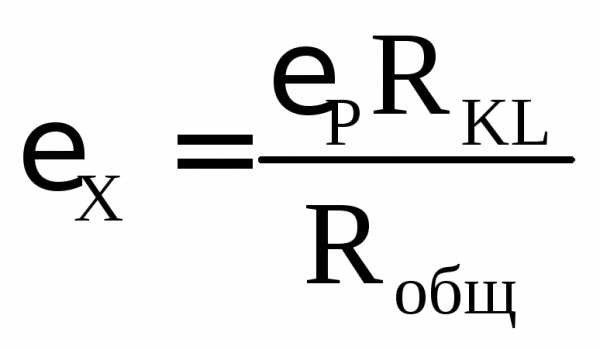6.2. Последовательное соединение резистора и конденсатора, резистора и катушки. Параллельное соединение резистора и катушки
Параллельное соединение резистора и катушки индуктивности
Цель работы: изучить свойства электрической цепи синусоидального тока с параллельным соединением резистора и катушки индуктивности, экспериментально доказать, что ток и напряжение изменяются по синусоидальному закону и существует фазовый сдвиг между напряжением и током в цепи.
Научиться измерять и производить расчет токов, напряжений и их фазовых сдвигов при параллельном соединении резистора и катушки индуктивности.
Основные теоретические сведения.
Когда к цепи (рис. 12.1) с параллельным соединением резистора и катушки подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.

Рис. 12.1
Общий ток цепи I разветвляется на ток в катушке IL(индуктивная составляющая общего тока) и ток в резисторе IR(активная составляющая).
Между токами I, IL и IR существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлением XLкатушки. Они могут быть представлены с помощью векторной диаграммы токов (рис. 12.2).
 |  |
| Рис. 12.2 | Рис. 12.3 |
Фазовый сдвиг между напряжением U цепи и током в резисторе IRотсутствует, тогда как ток в катушке IL всегда отстает от напряжения цепи (или тока в резисторе IR)на900. При этом сдвиг между полным током I и напряжением цепи Uопределяется соотношением междупроводимостями BL и G.
Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 12.3), в котором Y представляет собой так называемую полную проводимость цепи, G – активную, а BL– реактивную (индуктивную) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений токов в параллельных ветвях, как в параллельной чисто резистивной цепи, невозможно. Только в векторной форме I = IR +IL. Расчет ведется по следующим формулам:
Действующее значение полного тока цепи
,
I = U ¤ Z = UY .
Полная проводимость цепи
,
Y = 1 ¤ Z ,
где Z- полное сопротивление цепи.
Угол сдвига фаз
j = arctg (I L ¤ IR) = arctg (BL ¤ G).
Активное сопротивление цепи
G = Y × cos j\
Реактивное сопротивление цепи
B = Y × sin j.
Задание к лабораторной работе.
Задание
Для цепи с параллельным соединением резистора и катушки индуктивности измерьте действующие значения тока в резисторе IR и катушке IL, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и индуктивную реактивную проводимость BL.
student2.ru
Параллельное соединение катушки и конденсатора
Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).
На схеме рис. 14.1.1, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.
Считая известными параметры катушки G1, BL и конденсатора G2, BC, а также напряжение u = Umsinωt, определим токи в цепи и ее мощность.
Векторная диаграмма цепи. Полная проводимость цепи
Согласно первому закону Кирхгофа, мгновенная величина общего тока равна сумме мгновенных токов отдельных ветвей:
Имея в виду несовпадение по фазе активных и реактивных токов, величину общего тока найдем векторным сложением:
Для построения векторной диаграммы находим:
В зависимости от соотношения величин реактивных проводимостей ветвей с индуктивностью и емкостью можно отметить три случая.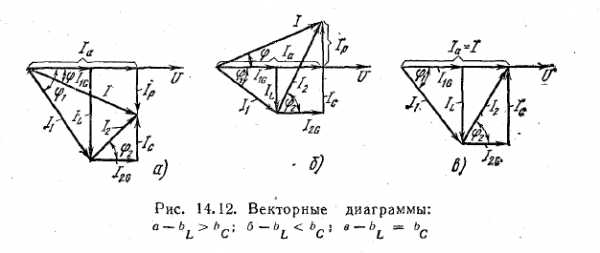
1. BL> BC. Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I1 и I2 в этих элементах:
Векторная сумма токов l1 + I2 = I дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:
Iа = I1G + I2G — активная составляющая;Ip = IL + IC — реактивная составляющая.
Векторы активных составляющих токов направлены в одну сторону, поэтому их численные значения складываются. Векторы реактивных составляющих токов направлены перпендикулярно вектору напряжения в противоположные стороны, поэтому им даются разные знаки: индуктивные токи считаются положительными, а емкостные — отрицательными. При одинаковом напряжении на всех элементах цепи IL > IC. Общий ток отстает от общего напряжения по фазе на угол ф.
Из треугольника токов следует
где G = G1 + G2 и В = BL — Bc — общие активная и реактивная проводимости цепи;
полная проводимость цепи. Эти три проводимости графически можно изобразить сторонами прямоугольного треугольника проводимостей, который получается уже известным способом’ из треугольника токов.
Полная проводимость цепи У является коэффициентом пропорциональности между действующими величинами общего тока и напряжения цепи:
Из треугольников токов и проводимостей определяют величины:
Угол сдвига по фазе между напряжением и общим током в цепи положительный(ф> 0).
2. ВL<ВC. Векторная диаграмма изображена на рис. 14.12,б. Так как IL<Iс. то напряжение отстает от общего тока на угол ф<0.
Реактивная проводимость цепи имеет емкостный характер. Расчетные формулы, полученные для случая 1, действительны и для этого случая.
3. BL = ВC. В этом случае реактивные составляющие токов катушки и конденсатора равны по величине: IL = IC. Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол ф сдвига фаз между общим током и напряжением равен нулю.
Общий ток в цепи и напряжение связаны формулой
I = UG, или U = I/G.
В случае ВL = ВC в цепи имеет место резонанс токов.
Энергетический процесс в цепи
Из векторной диаграммы токов легко получить треугольник мощностей, из которого следуют те же формулы (14.2), которые были получены для последовательного соединения катушки и конденсатора.
Реактивные мощности индуктивности и емкости входят в расчет с разными знаками: реактивная мощность индуктивности положительна, а реактивная мощность емкости отрицательна. В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует из формул (14.2).
Если ф> 0, то Q> 0; при ф< 0 Q< 0.
Активная мощность положительна при любом значении угла. Полная мощность тоже всегда положительна.
В рассматриваемой цепи активная мощность имеет определенную величину (Р ≠ 0), следовательно, имеет место преобразование электрической энергии в другой вид.
Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор (Q ≠ 0 при ф ≠ 0).
Обмен энергией совершается также между катушкой и конденсатором.
electrikam.com
ЛР 1-2 Послед. и пар. соединение 05.09
конденсаторе 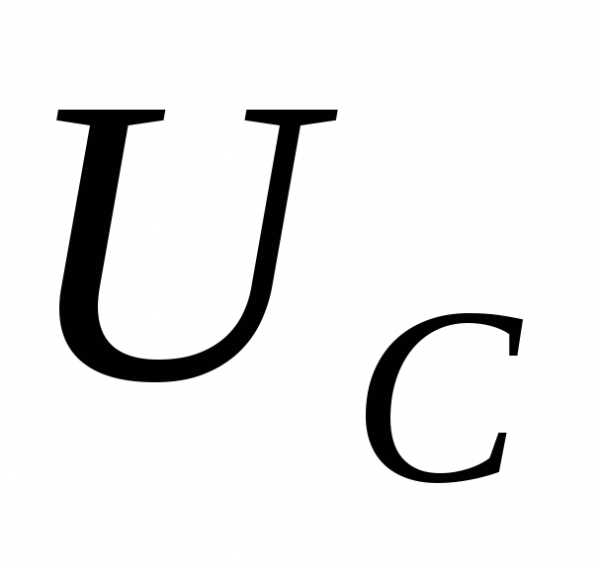 . Вольтметр должен иметь несколько пределов, чтобы в случае не совсем ясного представления об значении измеряемого напряжения можно было установить на приборе максимальный предел измерения и лишь после пробного подключения вольтметра выбрать нужный предел.
. Вольтметр должен иметь несколько пределов, чтобы в случае не совсем ясного представления об значении измеряемого напряжения можно было установить на приборе максимальный предел измерения и лишь после пробного подключения вольтметра выбрать нужный предел.
Ваттметр W фазометр φ и амперметр А измеряют соответственно активную мощность Р, угол сдвига фаз φ и ток 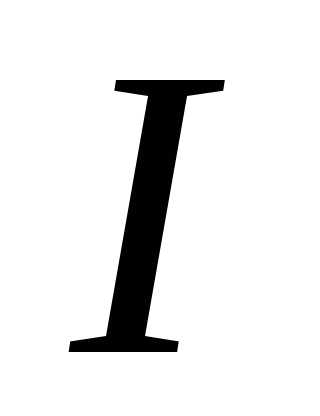 . ВаттметрW и фазометр φ необходимо включить в схему с учетом маркировки генераторных зажимов («звёздочек»).
. ВаттметрW и фазометр φ необходимо включить в схему с учетом маркировки генераторных зажимов («звёздочек»).
Порядок выполнения работы
1. Ознакомиться с приборами и оборудованием экспериментальной установки. Записать данные приборов в табл. 1. в которой в качестве примера приведены характеристики ваттметра.
Таблица 1
| Наименование прибора | Фабричный номер | Система прибора | Класс точности | Предел измерения | Цена деления |
| Ваттметр | 9615 | ЭД | 0,5 | 0–750 Вт | 5Вт/дел. |
ПРИМЕЧАНИЯ:
1. Если прибор многопредельный, записывают тот предел измерения, на который прибор был включен.
2. Предел измерения ваттметра определяется как произведение пределов измерения токовой обмотки и обмотки напряжения. Например, токовая обмотка включена на 5 А, обмотка напряжения – на 150 В, тогда предел измерения ваттметра равен: 5 А х 150 В =150 Вт. Цена деления прибора определяется как частное от деления предела измерения прибора на число делений школы. В частности, если шкала имеет 150 делении, то цена деления ваттметра равна 750 Вт: 150 дел =5 Вт/дел.
2. Собрать схему согласно рис. 12. Сборку схемы рекомендуется начать от выходных зажимов автотрансформатора. Вначале собирается последовательная часть электрической цепи. У фазометра и ваттметра сначала включаются токовые зажимы. Вольтметровые обмотки этих приборов включаются параллельно нагрузке (приемнику) после сборки последовательной цепи.
3. Перед включением установки в сеть установить ручку лабораторного автотрансформатора в положение, обеспечивающее нулевое напряжение на его выходных зажимах.
4. После включения установки в сеть плавно повышать автотрансформатором напряжение до заданного значения (порядка 100 – 120 В) и далее поддерживать постоянным.
5. В начале исследования сердечник должен быть вдвинут в катушку. Затем, плавно выдвигая сердечник из катушки, необходимо выполнить, пять измерений: два – до наступления явления резонанса напряжений, одно – при резонансе напряжений и два последних – после резонанса. Состояние резонанса точнее всего определяется по фазометру: при резонансе угол φ = 0. Переносной вольтметр V2 служит для измерения напряжений на отдельных участках цепи: на резисторе 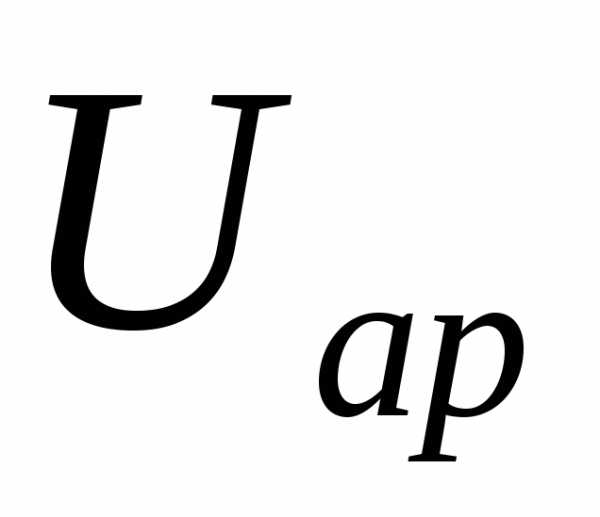 , катушке
, катушке и конденсаторе
и конденсаторе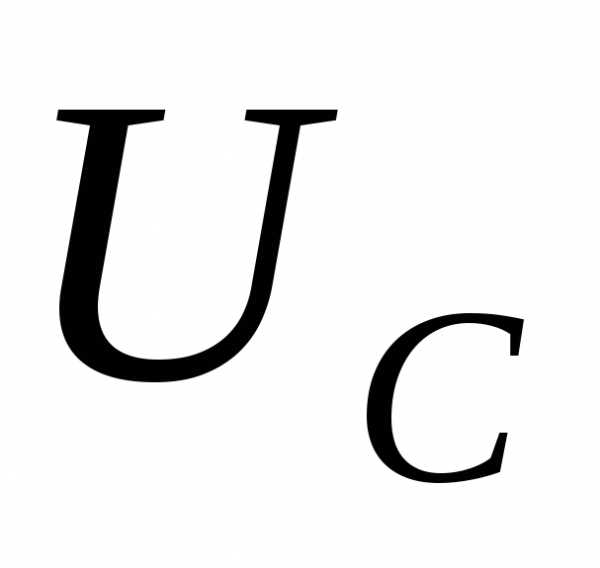 . Результаты измерений записываются в табл. 2.
. Результаты измерений записываются в табл. 2.
Содержание отчета
1. Цель работы и программа.
2. Схема соединений (рис. 12).
3. Таблица данных электроизмерительных приборов (табл. 1).
4. Таблица наблюдений и вычислений (табл. 2).
5. Примеры вычислений.
6. Три векторные диаграммы напряжений для первой, третьей и пятой строк табл. 2. Векторные диаграммы строятся на миллиметровой бумаге в одном масштабе (1 см – 10 В) для всех трех случаев.
7. Треугольники сопротивления 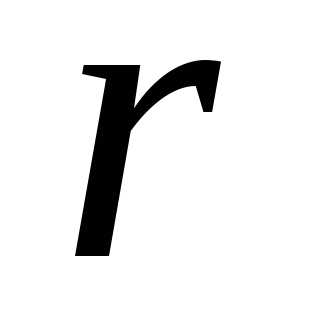 ,
, ,
, для всех трех случаев, что и в п. 6.
для всех трех случаев, что и в п. 6.
8. Кривая тока 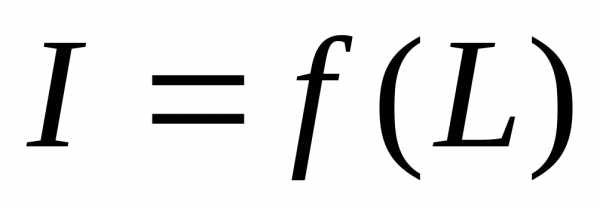 .
.
9. Выводы по работе (ответы на вопросы).
Таблица 2
| Состояние | Измеряются | Вычисляются | |||||||||||||
| U В | Uap В | Uap, В | Uap, В | φ, град | I, А | P, Вт | Z, Ом | R, Ом | x, Ом | rp, Ом | rк, Ом | L, Гн | C, мкФ | φк град | |
| 1.Сердечник полностью вдвинут | |||||||||||||||
| 2. До резонанса | |||||||||||||||
| 3. Резонанс | |||||||||||||||
| 4. После резонанса | |||||||||||||||
| 5. Сердечник полностью выдвинут | |||||||||||||||
Формулы для выполнения расчётов имеют вид
| 1. Полное сопротивление всей цепи
| 2. Активное сопротивление всей цепи
|
| 3. Реактивное сопротивление всей цепи или , где | 4. Полное сопротивление катушки
|
| 5. Активное сопротивление резистора | 6. Активное сопротивление катушки . |
| 7. Индуктивное сопротивление катушки . | 8. Ёмкостное сопротивление конденсатора
|
| 9. Индуктивность катушки
| 10. Ёмкость конденсатора
|
| 11. Угол сдвига фаз тока и напряжения катушки . |
Расчет производятся для всех пяти строк таблицы. Пример расчета приводится только для одной строки по указанию преподавателя.
основные вопросы по работе
1. Как складываются действующие значения напряжений и сопротивления в последовательной цепи переменного тока?
2. При каких условиях возникает резонанс напряжений и каковы характерные признаки резонансного состояния?
3. В чём заключается практическое использование резонанса напряжений?
4. Чем опасно явление резонанса напряжений?
Лабораторная работа №2
Параллельное соединение резистора, катушки индуктивности и конденсатора.
Резонанс токов
Цель работы – изучение основных соотношений в разветвленной цепи переменного тока, а также исследование резонанса токов.
На рис 13 изображена разветвленная цепь переменного тока, состоящая из трёх параллельно включенных приемников: резистора (лампового или проволочного реостата) с сопротивлением 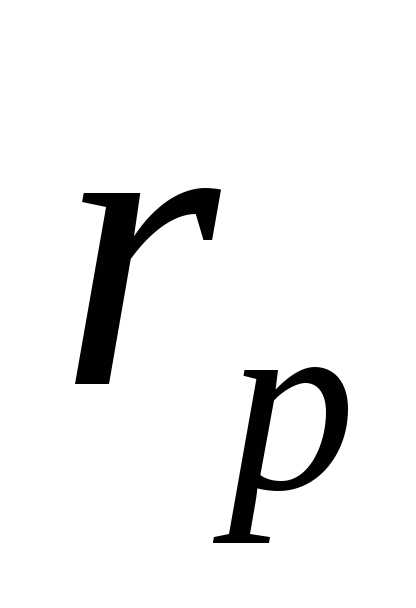 , катушки индуктивности с индуктивным сопротивлением
, катушки индуктивности с индуктивным сопротивлением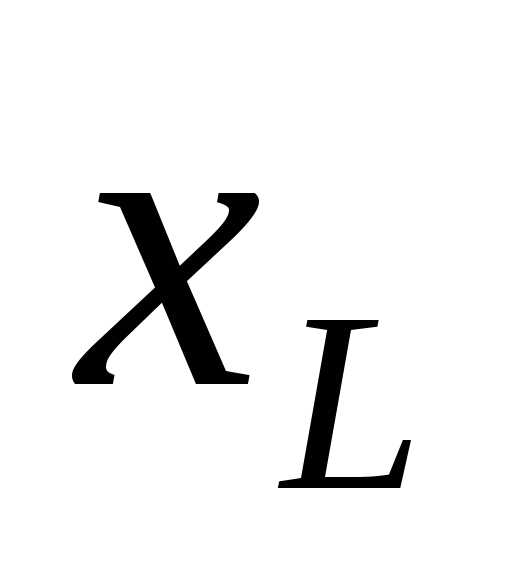 и активным сопротивлением
и активным сопротивлением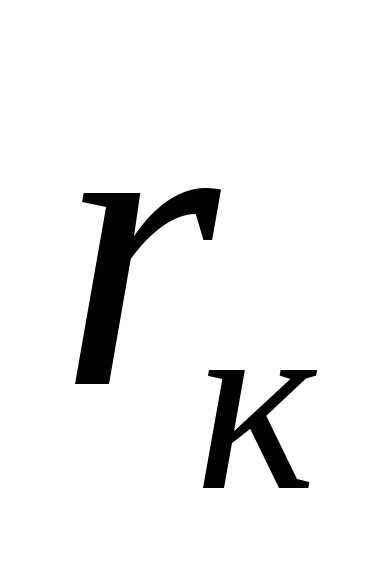 , и конденсатора с емкостным сопротивлением
, и конденсатора с емкостным сопротивлением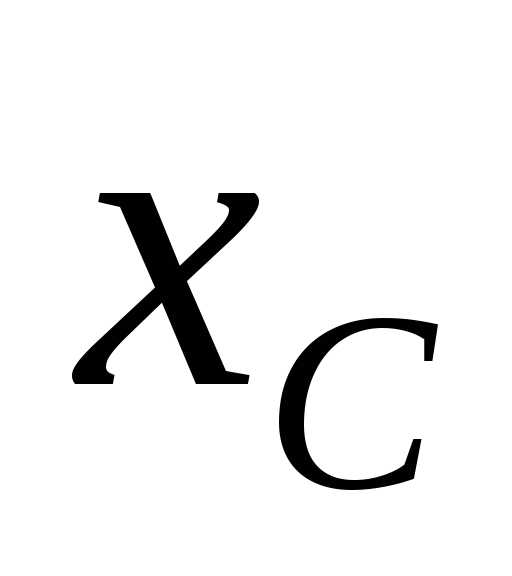 .
.
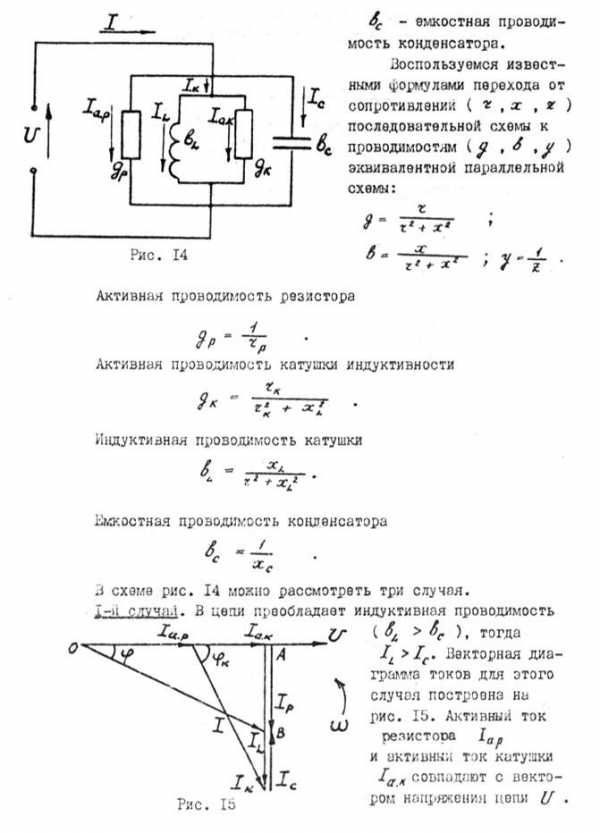
При параллельном соединении приемники электрической энергии удобнее характеризовать проводимостями, тогда от цепи, изображенной на рис. 13, можно перейти к эквивалентной ей цепи, представленной на рис. 14.
| Рис.13 | Рис.14 |
Здесь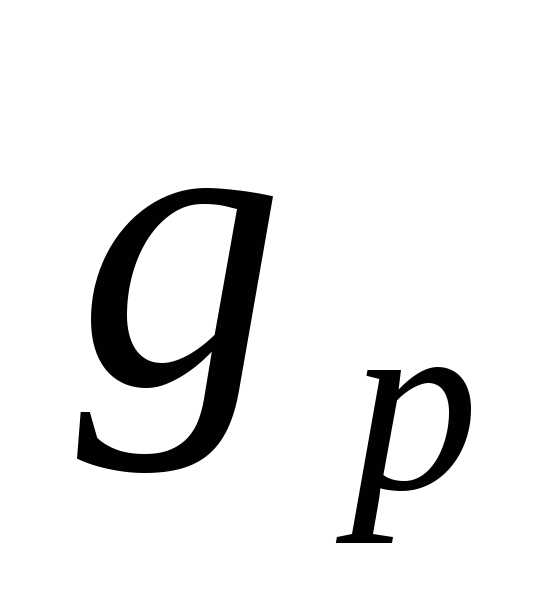 – активная проводимость резистора;
– активная проводимость резистора;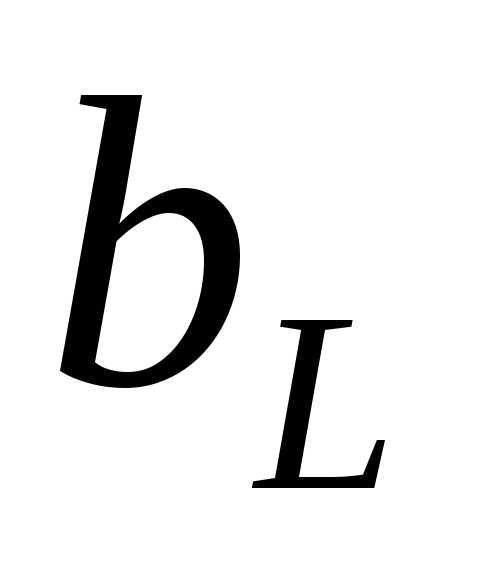 и
и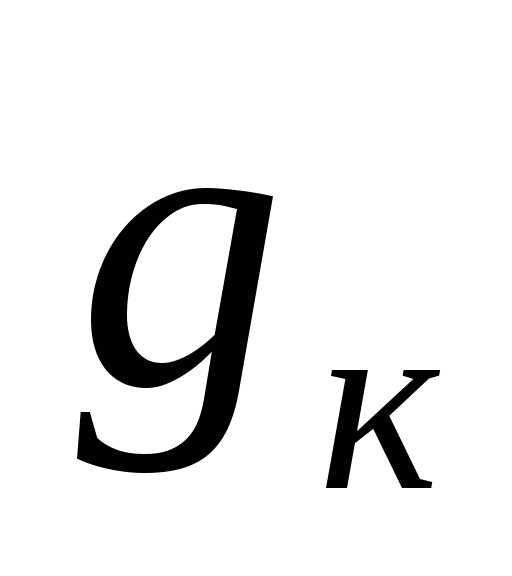 – соответственно индуктивная и активная проводимости катушки;
– соответственно индуктивная и активная проводимости катушки;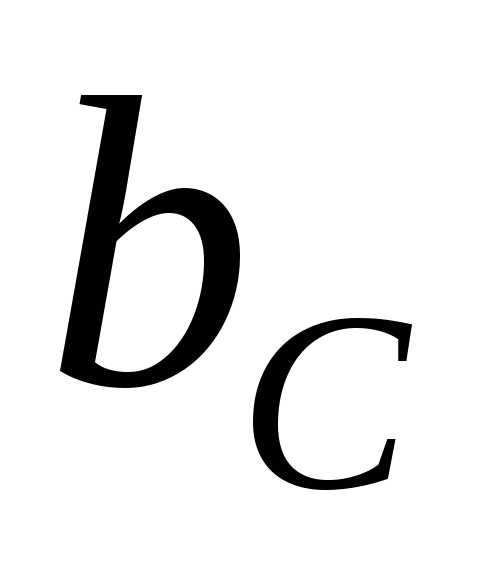 – емкостная проводимость конденсатора.
– емкостная проводимость конденсатора.
Воспользуемся известными формулами перехода от сопротивлений (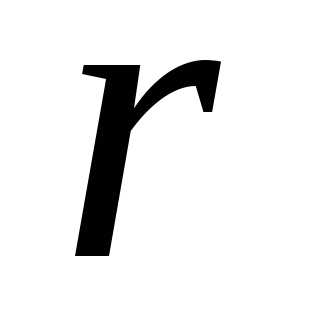 ,,
,, ) последовательной схемы к проводимостям (
) последовательной схемы к проводимостям ( ,
,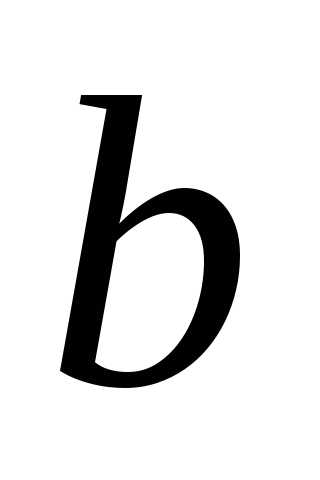 ,
, ) эквивалентной параллельной схемы:
) эквивалентной параллельной схемы:
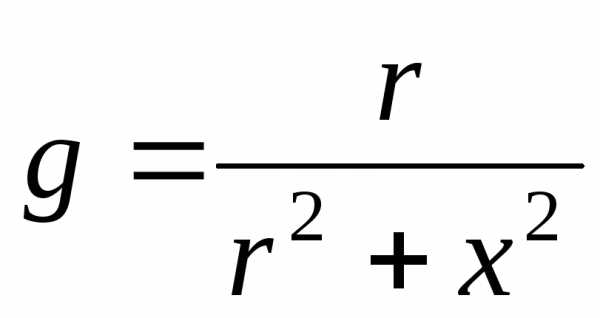 ;
;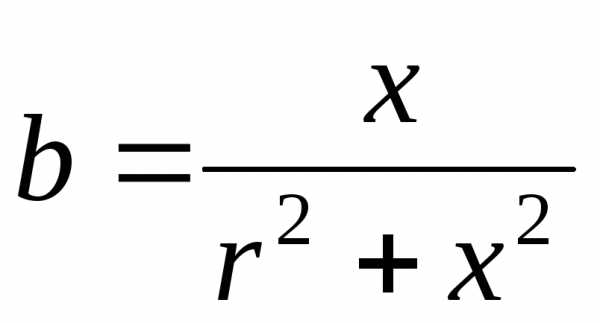 ;
;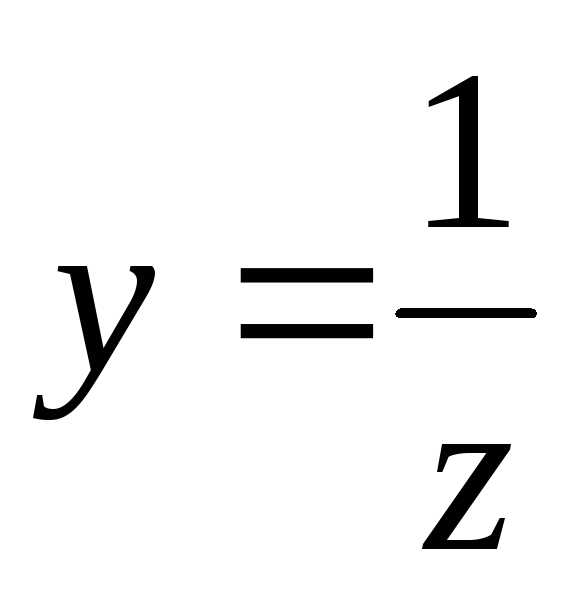 .
.
Активная проводимость резистора
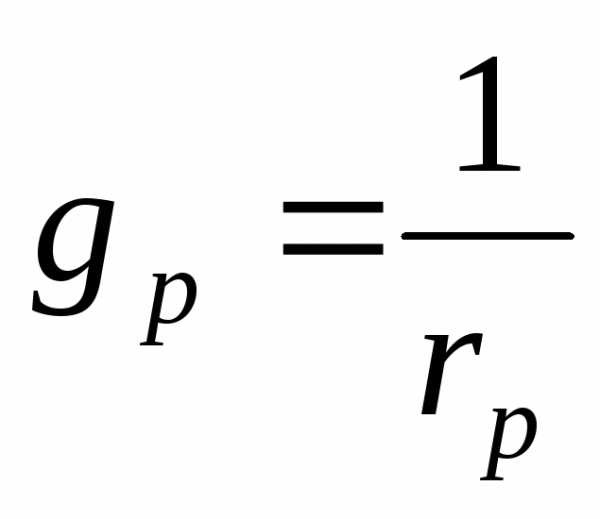 .
.
Активная проводимость катушки индуктивности
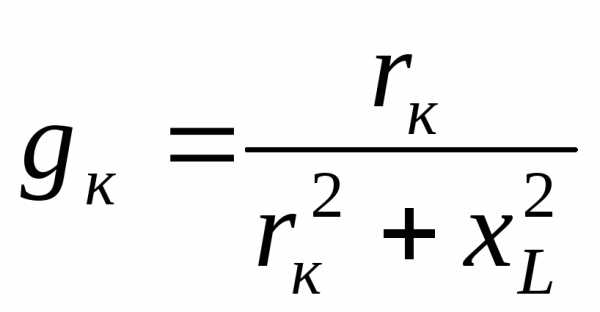 .
.
Индуктивная проводимость катушки
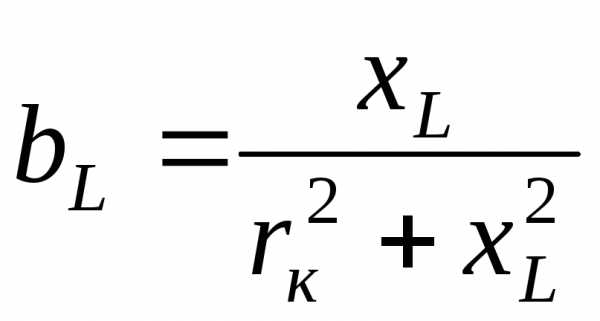 .
.
Емкостная проводимость конденсатора
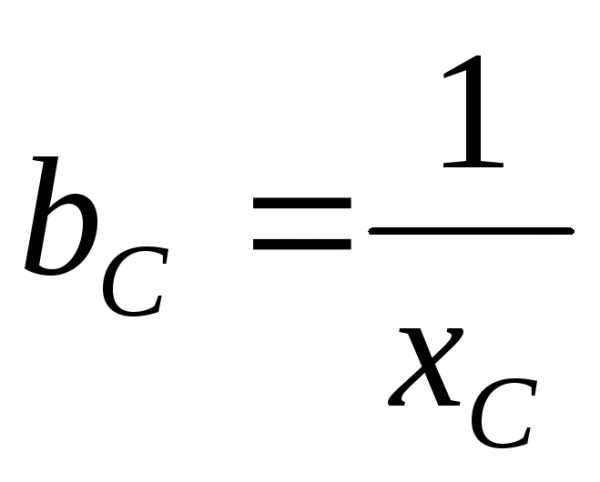 .
.
В схеме рис. 14 можно рассмотреть три случая.
1-й случай. В цепи преобладает индуктивная проводимость (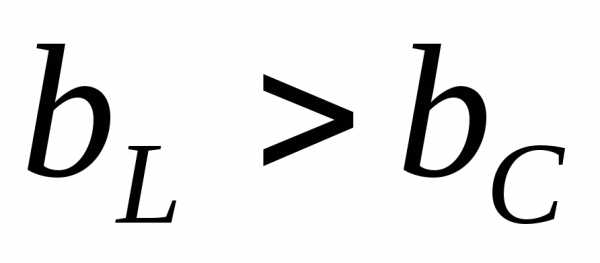 ), тогда
), тогда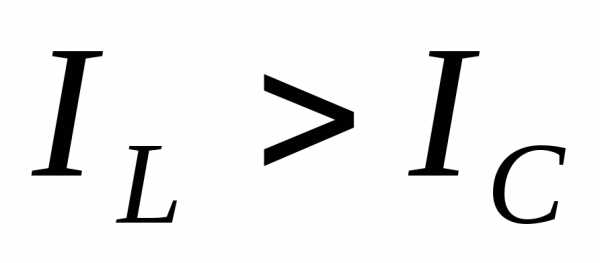 . Векторная диаграмма токов для этого случая построена на рис. 15. Активный ток резистора
. Векторная диаграмма токов для этого случая построена на рис. 15. Активный ток резистора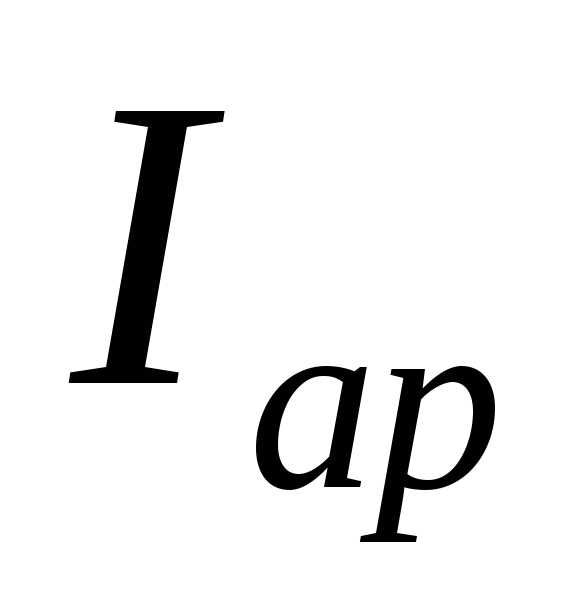 и активный ток катушки
и активный ток катушки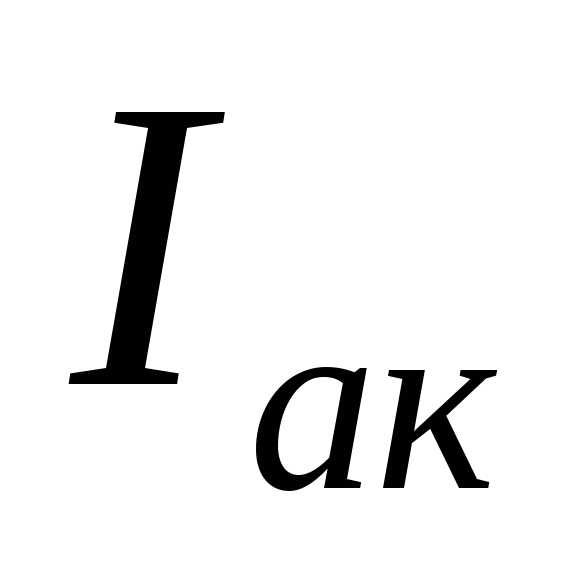 совпадают с вектором напряжения цепи
совпадают с вектором напряжения цепи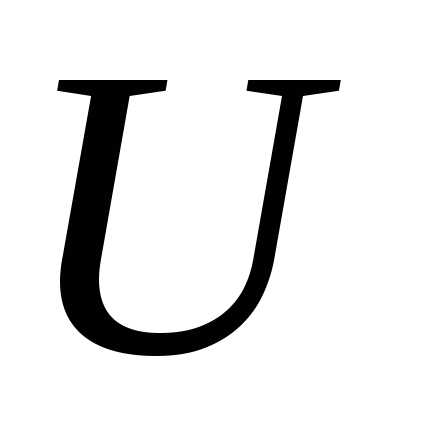 .
.
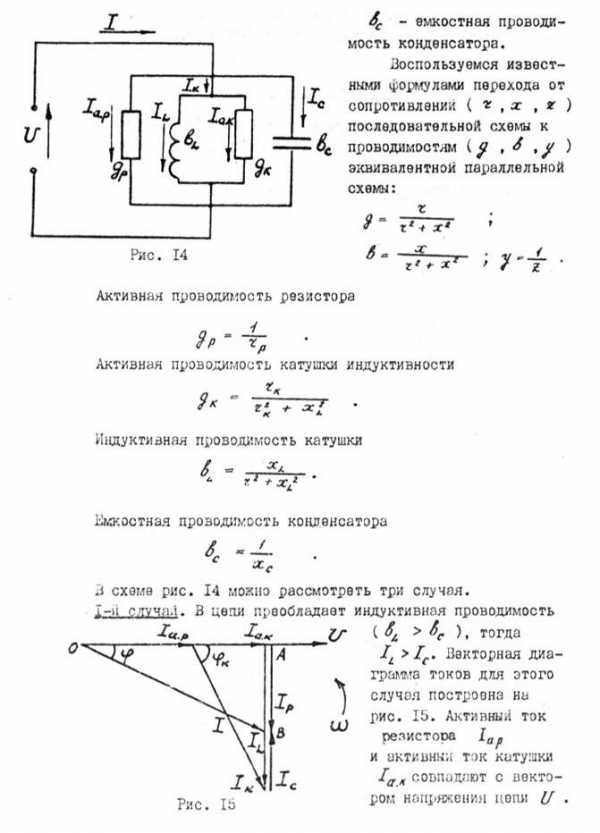
Рис.15
Индуктивный ток катушки 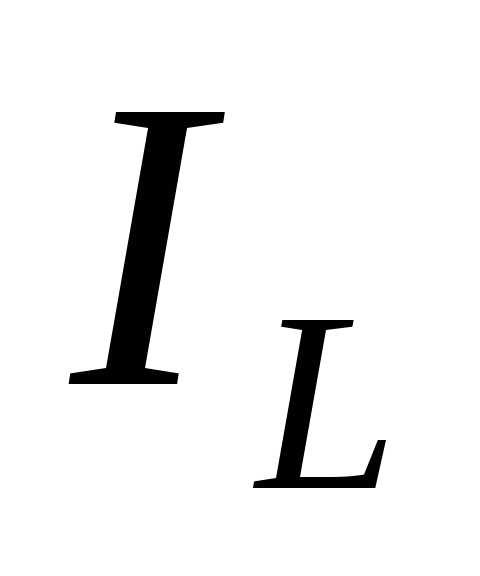 отстаёт от напряжения на угол
отстаёт от напряжения на угол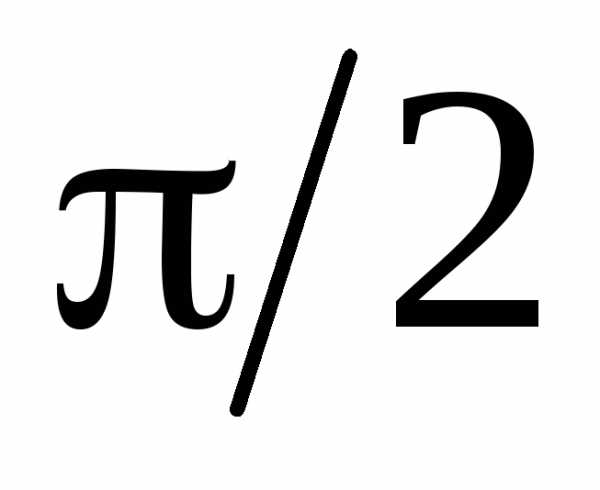 . Полный ток катушки
. Полный ток катушки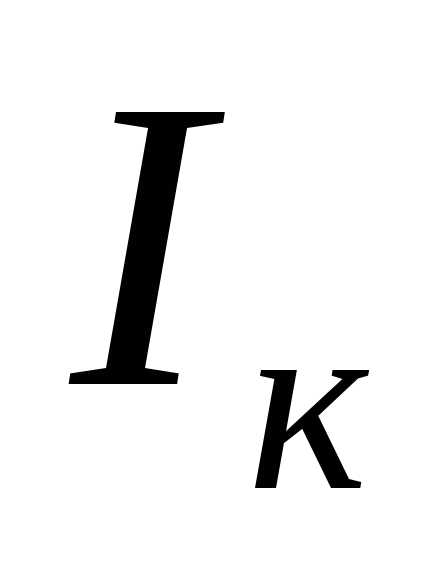 равен геометрической сумме активного и индуктивного токов катушкии отстает по фазе от напряжения на угол
равен геометрической сумме активного и индуктивного токов катушкии отстает по фазе от напряжения на угол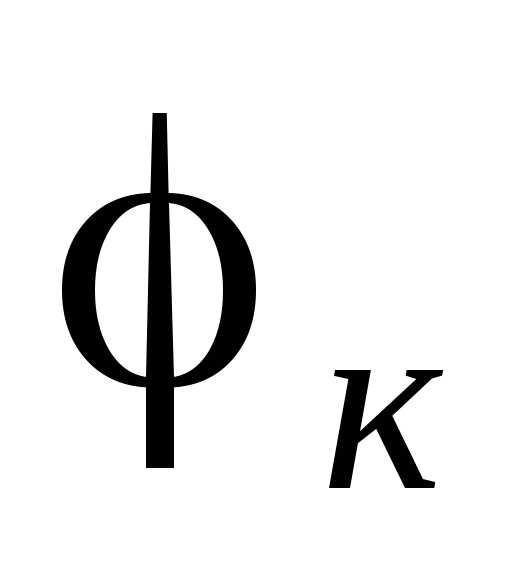 . Емкостной ток конденсатора
. Емкостной ток конденсатора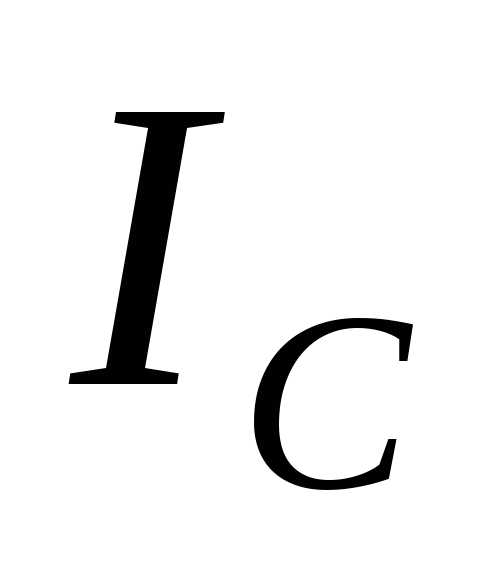 , проведенный из конца вектора
, проведенный из конца вектора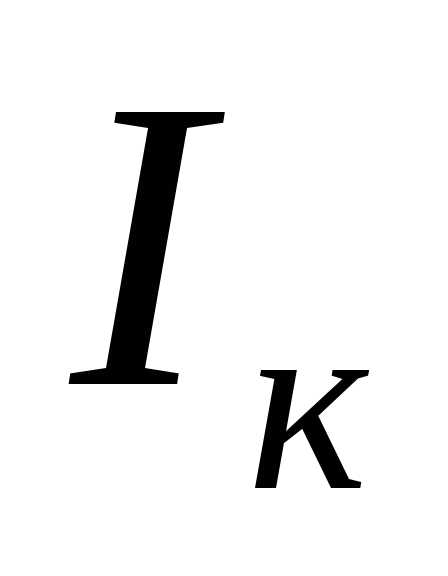 , опережает напряжение на зажимах цепи на угол
, опережает напряжение на зажимах цепи на угол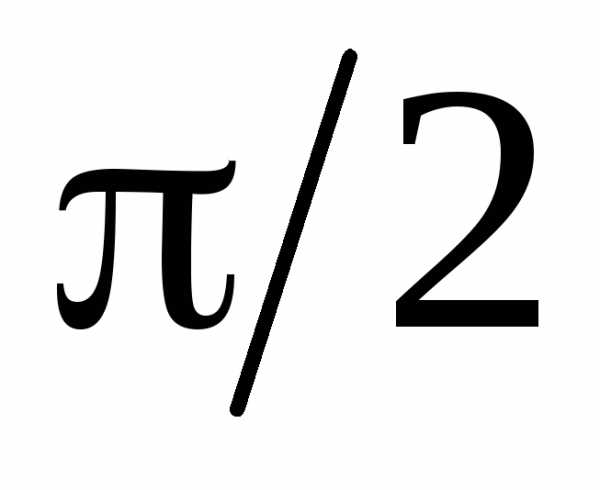 . Замыкающий вектор
. Замыкающий вектор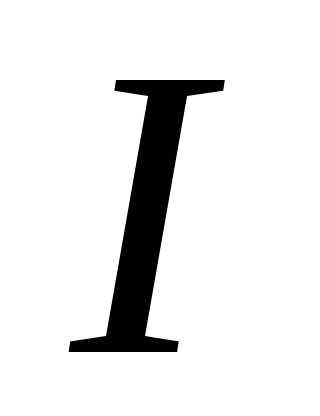 равен току в неразветвлённой части цепи.
равен току в неразветвлённой части цепи.
Из векторной диаграммы видно, что при параллельном соединении приемников активные токи складываются арифметически:
;
реактивные токи – алгебраически:
;
полные токи – геометрически :
.
Последняя формула выражает первый закон Кирхгофа для действующих значений переменного тока.
Для практических расчетов удобно пользоваться формулой
,
полученной из треугольника токов ОАB (рис. 15).
2-й случай. В цепи преобладает емкостная проводимость (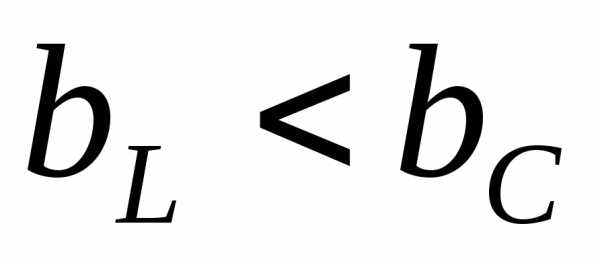 ) тогда
) тогда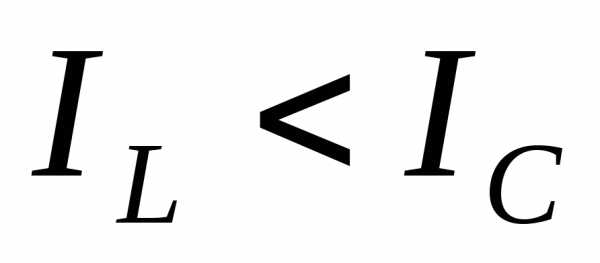 . Полный ток в цепиграфически определяется аналогично первому случаю (рис. 16). Как видно из рис. 16, ток
. Полный ток в цепиграфически определяется аналогично первому случаю (рис. 16). Как видно из рис. 16, ток 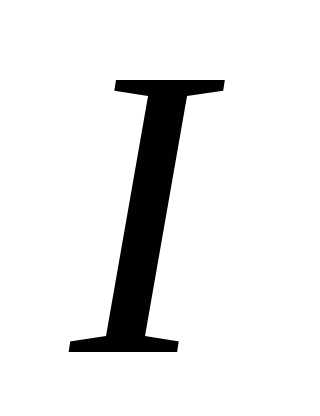 опережает напряжение
опережает напряжение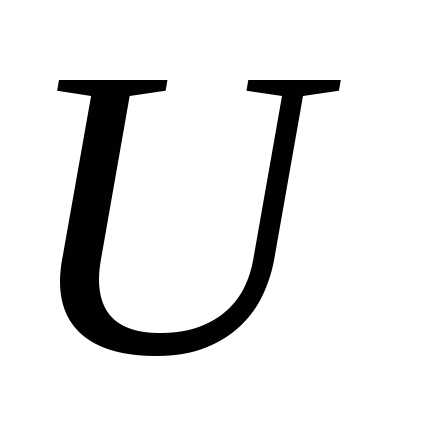 на угол
на угол .
.
З-й случай. Равенство реактивных проводимостей (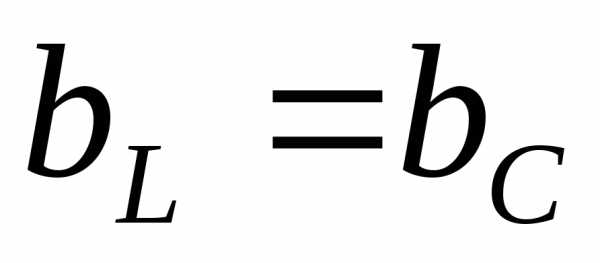 ), тогда
), тогда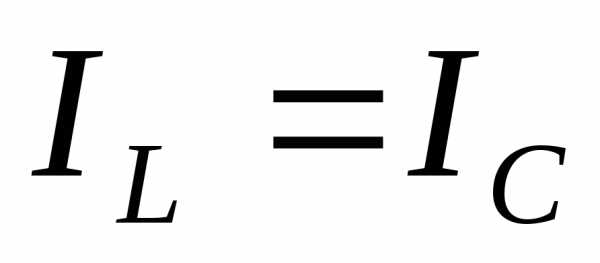 . Полный ток в этом случае (рис. 17) совпадает по фазе с напряжением (
. Полный ток в этом случае (рис. 17) совпадает по фазе с напряжением (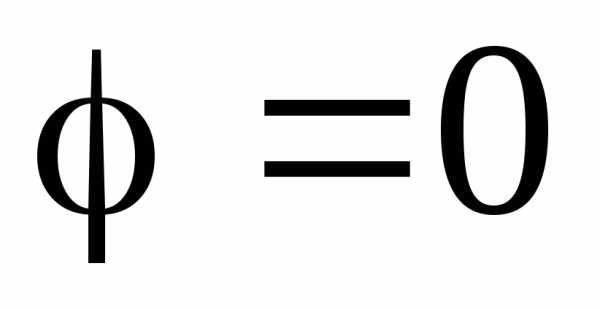 ). Этот режим называется резонансом токов, так как токи
). Этот режим называется резонансом токов, так как токи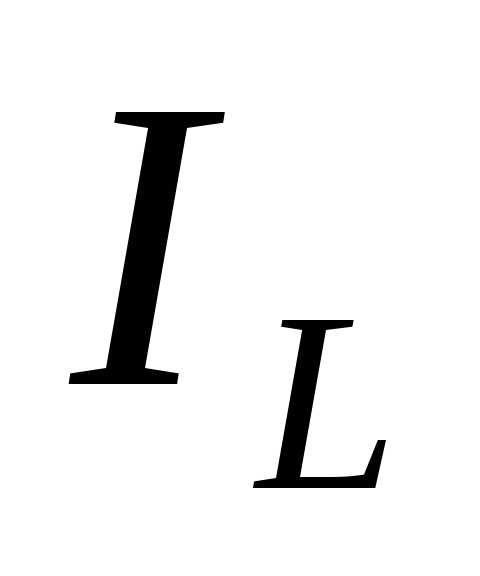 и
и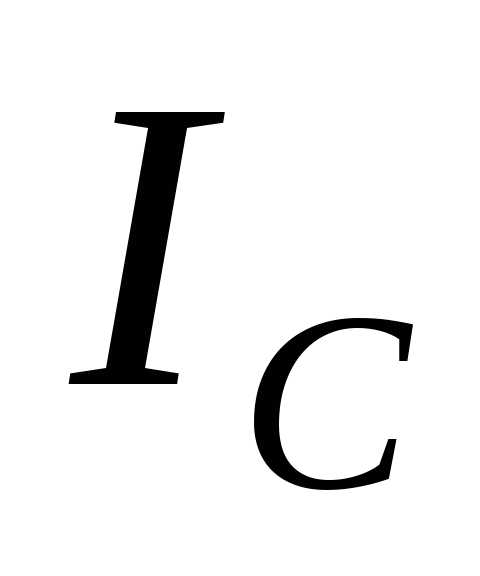 равны между собой и противоположны по фазе. Для рассматриваемой цепи (см. рис.14) условие резонанса токов может быть записано в такой форме:
равны между собой и противоположны по фазе. Для рассматриваемой цепи (см. рис.14) условие резонанса токов может быть записано в такой форме:
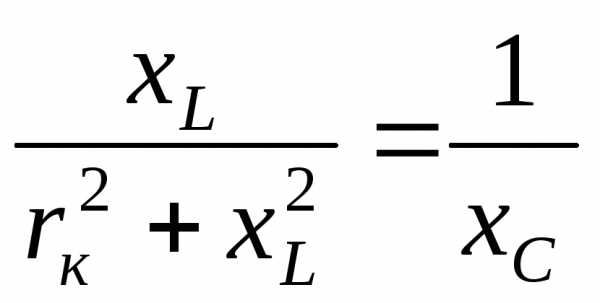 ;
;
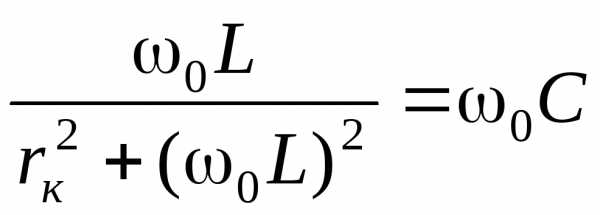 .
.
| Рис.16 | Рис.17 |
Очевидно, что резонанс токов, может быть достигнут изменением одного из параметров цепи: индуктивности 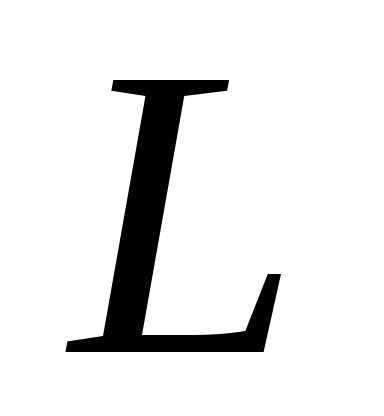 или емкости
или емкости , а также изменением частоты питающей сети
, а также изменением частоты питающей сети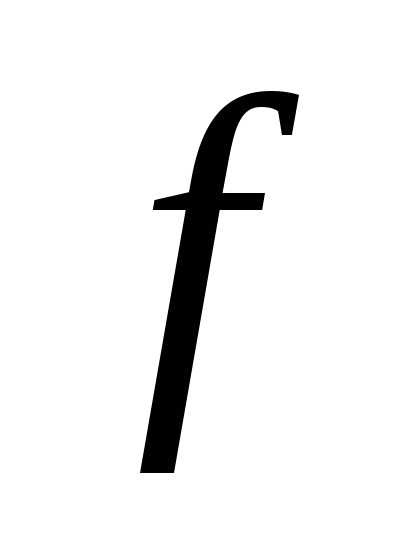 .
.
В лабораторной работе изменение режима цепи и получение резонанса токов проводится ступенчатым изменением емкости при и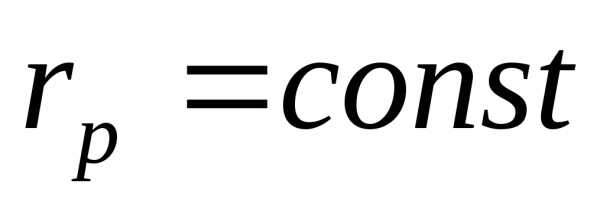 . Явление резонанса токов характеризуется следующими свойствами:
. Явление резонанса токов характеризуется следующими свойствами:
1) 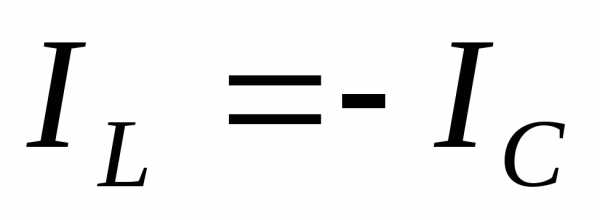 . Если катушка и конденсатор идеальные, то ток в цепи конденсатора будет равен току в цепи катушки. Практически же в момент резонанса ток в катушке
. Если катушка и конденсатор идеальные, то ток в цепи конденсатора будет равен току в цепи катушки. Практически же в момент резонанса ток в катушке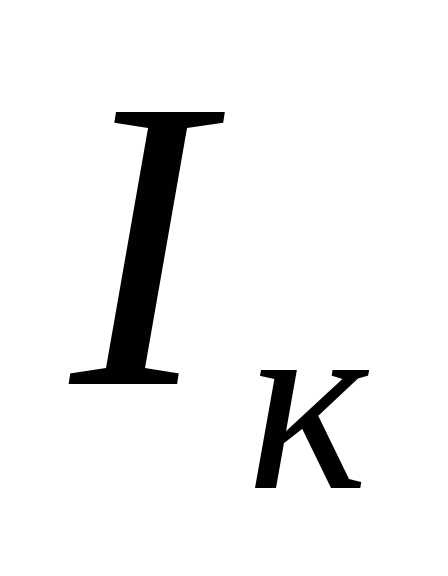 всегда больше, чем ток конденсатора
всегда больше, чем ток конденсатора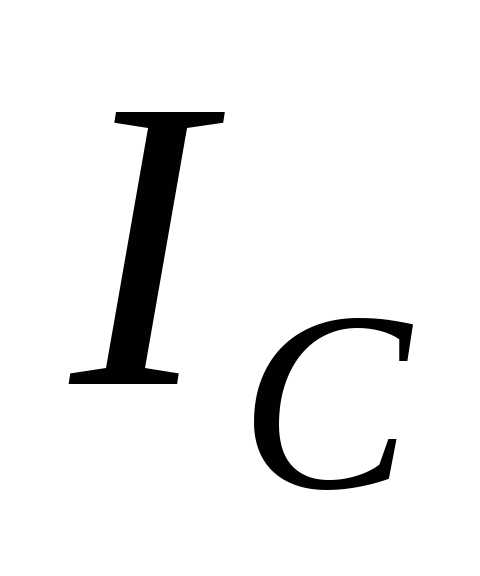 .
.
2) 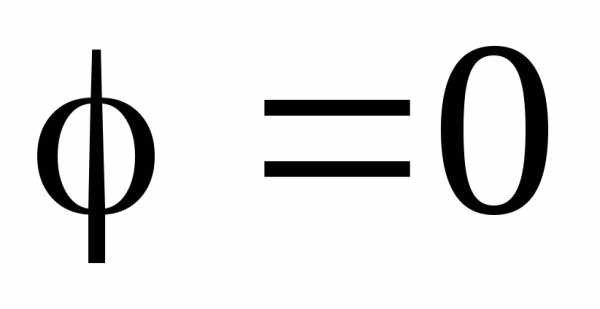 , поэтому
, поэтому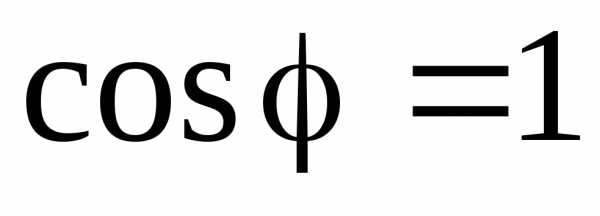 . Полная мощность всей цепи равна активной (
. Полная мощность всей цепи равна активной (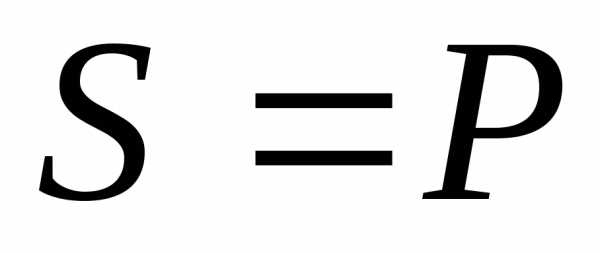 ). Следовательно, в режиме резонанса токов цепь ведет себя как активная. Причем до резонанса цепь носит активно-индуктивный характер, а после резонанса – активно-емкостной;
). Следовательно, в режиме резонанса токов цепь ведет себя как активная. Причем до резонанса цепь носит активно-индуктивный характер, а после резонанса – активно-емкостной;
3) при неизменном напряжении на зажимах цепи имеет место минимум тока в в неразветвленной части цепи (рис. 18). Действительно, ток , при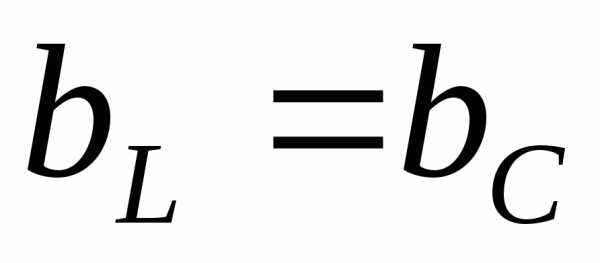 имеем;
имеем;

Рис. 18
4) при расчете резонансных контуров следует учитывать, что если 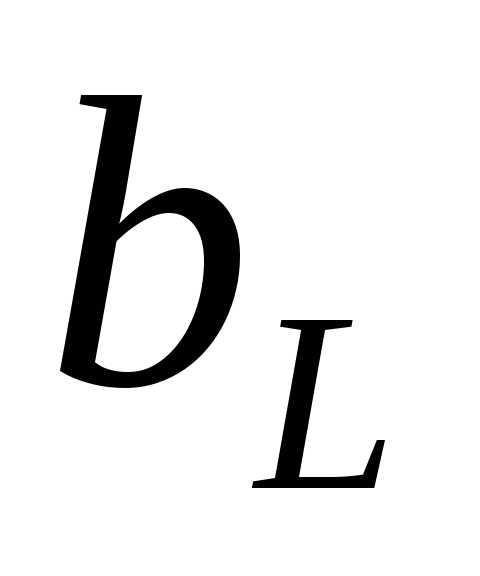 и
и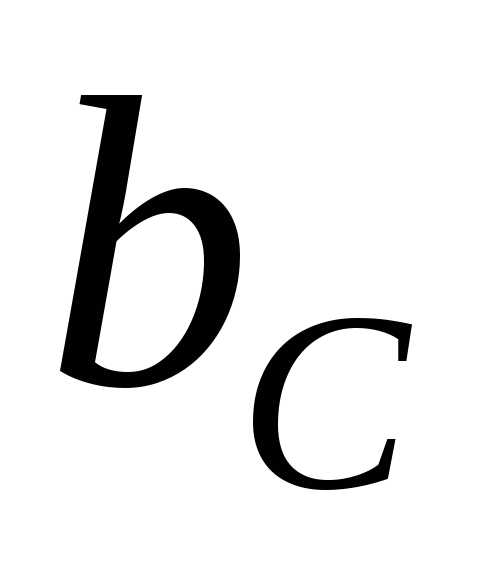 >>
>>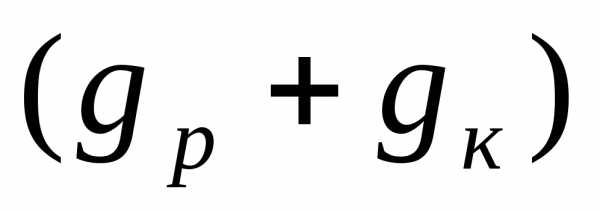 , то токи
, то токи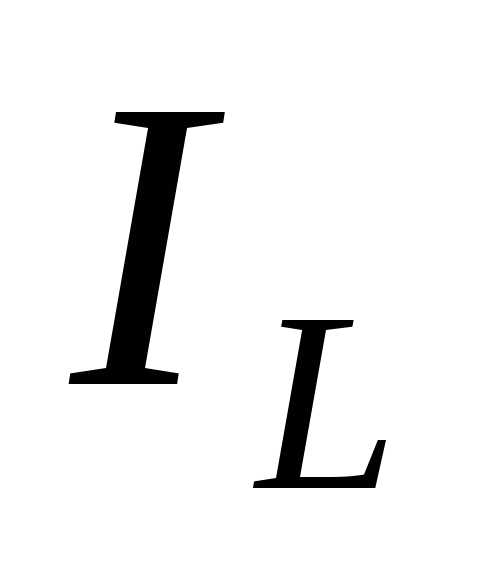 и
и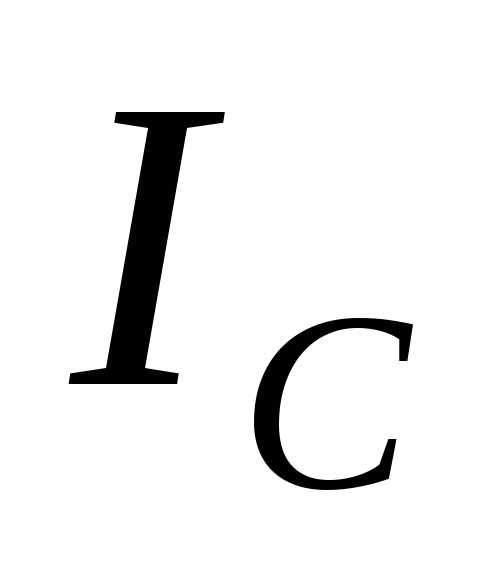 могут во много раз превышать общий ток в неразветвленной части цепи.
могут во много раз превышать общий ток в неразветвленной части цепи.
Физическая сущность резонанса токов делается ясной при рассмотрении энергетической стороны процесса. При резонансе энергия, запасенная в магнитном поле катушки, равна энергии, запасенной в электрическом поле конденсатора. При этом колебания энергии катушки и конденсатора противоположны по фазе, т.е. между катушкой и конденсатором происходит обмен энергиями. Обмена энергий между генератором, с одной стороны, и катушкой и конденсатором, с другой, – нет, и генератор передает энергию лишь в активное сопротивление. Таким образом, физическая сущность резонанса токов аналогична резонансу напряжений. Взаимный обмен реактивной энергии между катушкой индуктивности и конденсатором используется на практике, в частности для повышения коэффициента мощности на входных зажимах приемников электрической энергии.
Коэффициент мощности (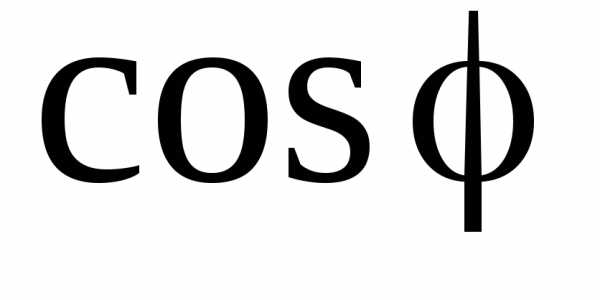 )приемников электрической энергии
)приемников электрической энергии
Обычно электрические приемники (двигатели, трансформаторы) носят активно-индуктивный характер и работают с углом сдвига фаз 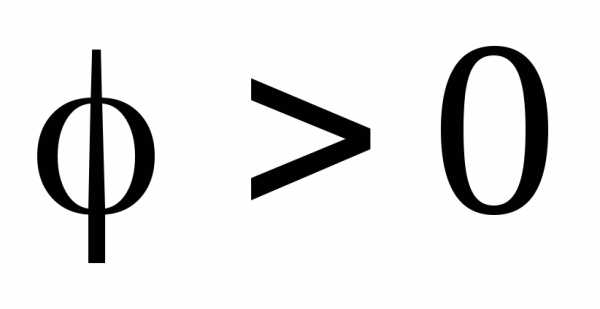 . Генератор, питающий такой приемник, линия передачи к нему и сам приемник рассчитываются на полную мощность
. Генератор, питающий такой приемник, линия передачи к нему и сам приемник рассчитываются на полную мощность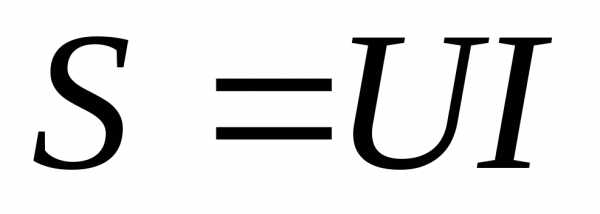 . Средняя (или активная) мощность приемника, соответствующая преобразованию электрической энергии в тепло или механическую работу, соответствует равенству. Здесь
. Средняя (или активная) мощность приемника, соответствующая преобразованию электрической энергии в тепло или механическую работу, соответствует равенству. Здесь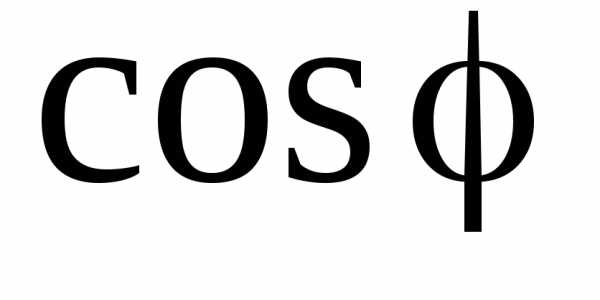 – коэффициент мощности приемника;– т.е. коэффициент мощности – это отношение активной мощности к полной. Как правило,
– коэффициент мощности приемника;– т.е. коэффициент мощности – это отношение активной мощности к полной. Как правило, , т.е. расчетная (полная) мощность генератора и линии передачи используются не с полной эффективностью. Отсюда ясна важность для народного хозяйства повышения коэффициента мощности (в предельном случае до
, т.е. расчетная (полная) мощность генератора и линии передачи используются не с полной эффективностью. Отсюда ясна важность для народного хозяйства повышения коэффициента мощности (в предельном случае до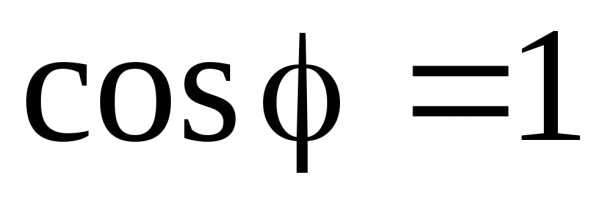 ).
).
Ток, потребляемый приемником от генератора, также зависит от коэффициента мощности, т.е.
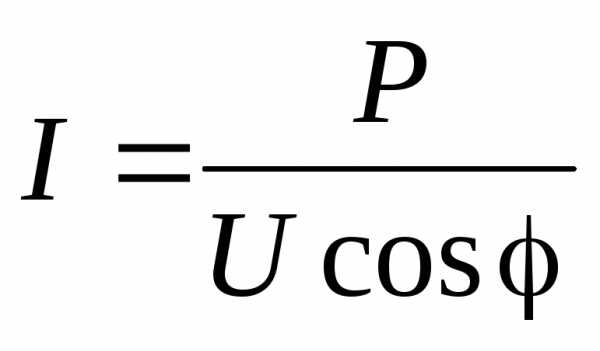 .
.
Если приемник работает при постоянной мощности  и напряжении
и напряжении , соответствующих
, соответствующих
номинальным (паспортным) данным приемника, то ток 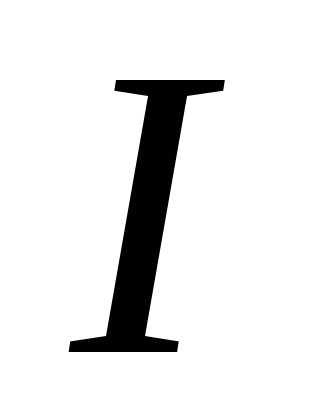 будет тем больше, чем ниже
будет тем больше, чем ниже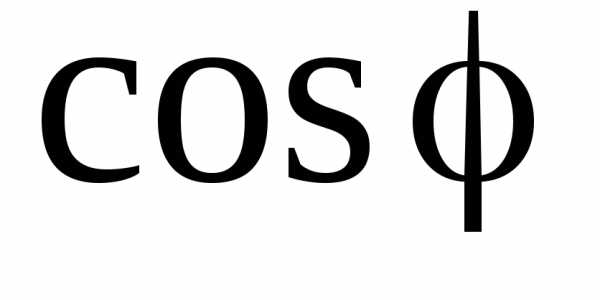 . Увеличение тока
. Увеличение тока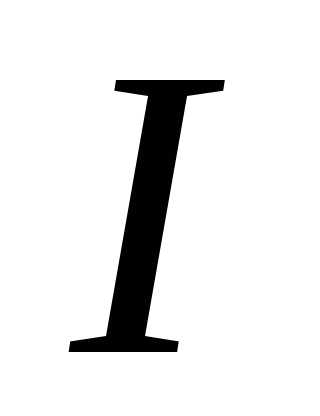 приводит к увеличению потерь энергии в генераторах, линиях передачи и приемниках. Таким образом, для полного использования расчетной мощности генераторов и уменьшения потерь энергии необходимоповышать
приводит к увеличению потерь энергии в генераторах, линиях передачи и приемниках. Таким образом, для полного использования расчетной мощности генераторов и уменьшения потерь энергии необходимоповышать 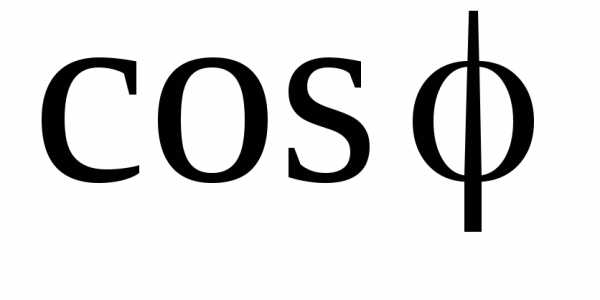 приемников. С целью повышения коэффициента мощности к приемнику подключают параллельно батарею конденсаторов.
приемников. С целью повышения коэффициента мощности к приемнику подключают параллельно батарею конденсаторов.
В этом случае , где – емкостная мощность конденсаторов;
– емкостная мощность конденсаторов;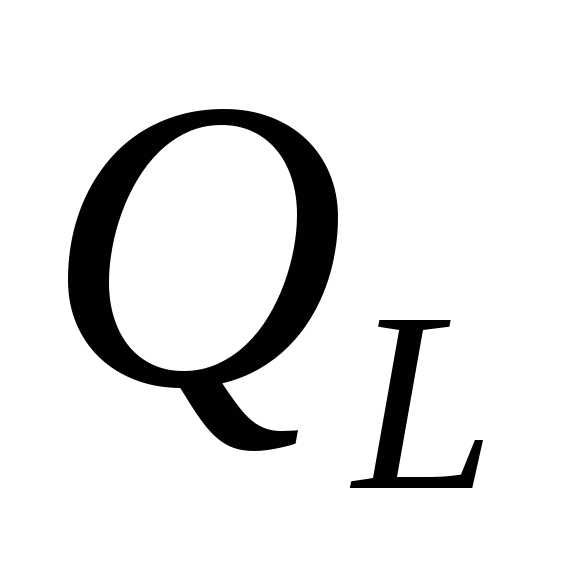 – индуктивная мощность приемника.
– индуктивная мощность приемника.
При резонансе токов ,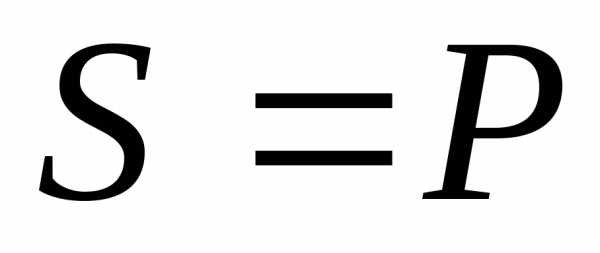 ,
,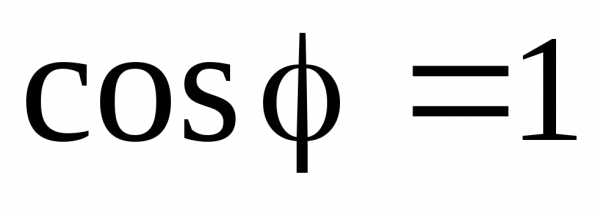 . Обычно коэффициент мощности приемников повышают до значения
. Обычно коэффициент мощности приемников повышают до значения 0,92-0,95, так как дальнейший его рост требует значительного увеличения емкости батареи конденсаторов, а следовательно, увеличения ее стоимости. Емкость конденсатора, который необходимо подключить параллельно приемнику для повышения коэффициента мощности с величины
0,92-0,95, так как дальнейший его рост требует значительного увеличения емкости батареи конденсаторов, а следовательно, увеличения ее стоимости. Емкость конденсатора, который необходимо подключить параллельно приемнику для повышения коэффициента мощности с величины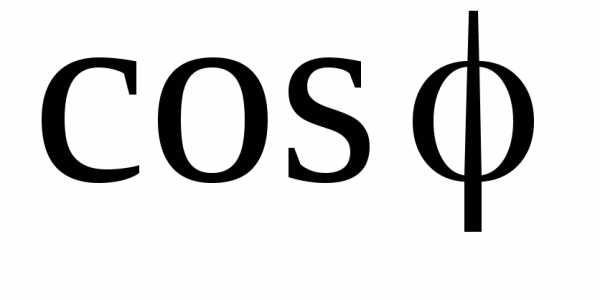 до величин!
до величин!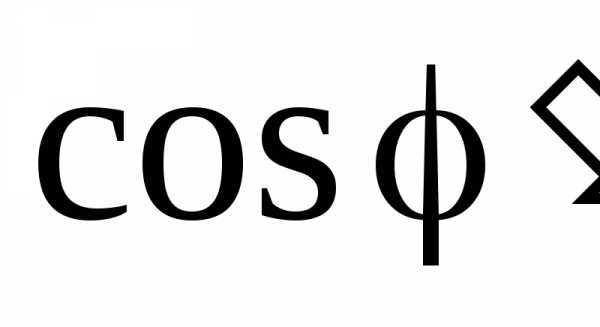 , может быть определена по формуле
, может быть определена по формуле
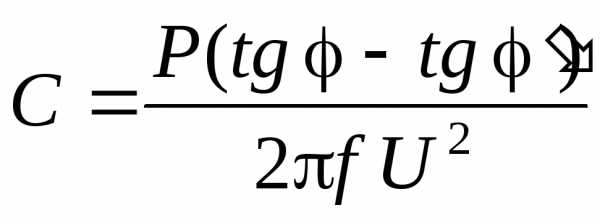 ,
,
где 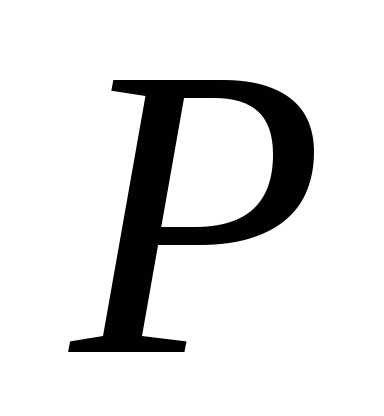 – активная мощность приемника;
– активная мощность приемника;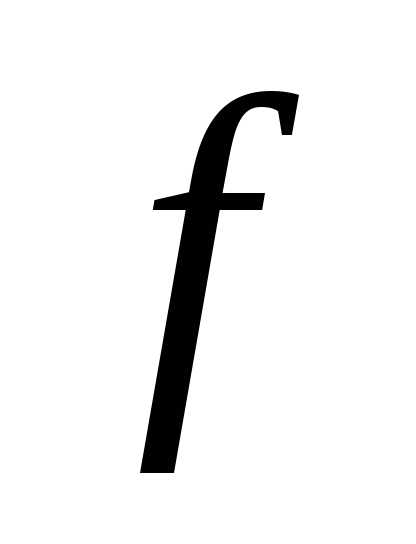 – частота сети,
– частота сети,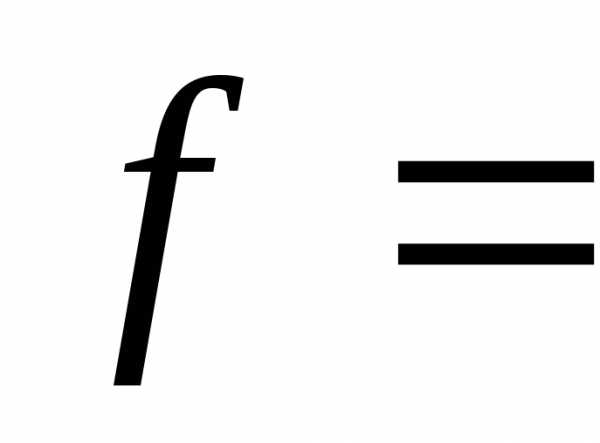 50 Гц;
50 Гц; – напряжение сети.
– напряжение сети.
Программа работы
1. Исследовать работу схемы, включая поочередно резистор, катушку и конденсатор.
2. Исследовать работу параллельно включенных резистора, катушки и конденсатора при переменной емкости до резонанса токов, при резонансе и после резонанса.
3. Рассчитать величину емкости, необходимую для повышения коэффициента мощности приемника, состоящего из параллельно включённых резистора и катушки индуктивности, до наибольшего значения  1 и сравнить с данными опыта (строка 6 в табл. 3)*.
1 и сравнить с данными опыта (строка 6 в табл. 3)*.
Порядок выполнения работы
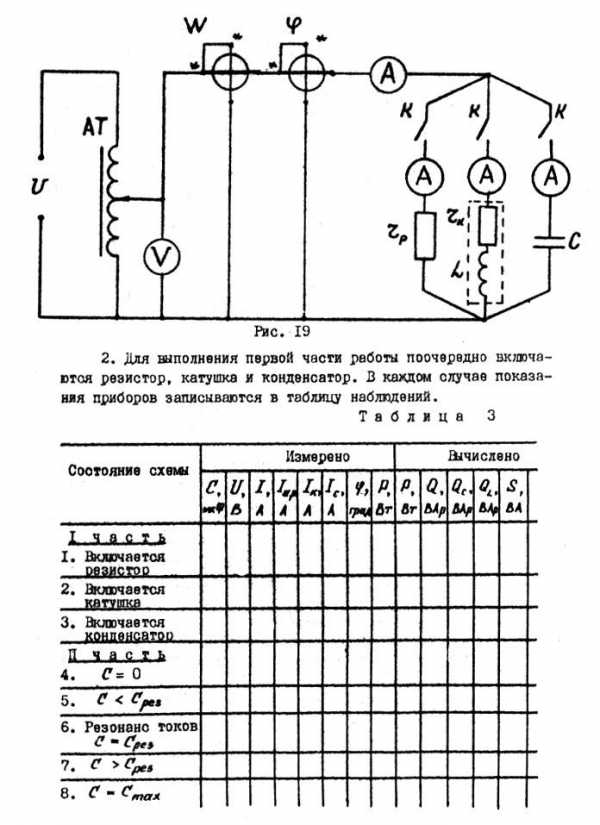
1. Собирается схема (рис. 19). Автотрансформатором AT устанавливается напряжение в пределах 90 ... 120 В, которое поддерживается постоянным при всех измерениях.
studfiles.net
Параллельное соединение резистора и катушки индуктивности
Цель работы: изучить свойства электрической цепи синусоидального тока с параллельным соединением резистора и катушки индуктивности, экспериментально доказать, что ток и напряжение изменяются по синусоидальному закону и существует фазовый сдвиг между напряжением и током в цепи.
Научиться измерять и производить расчет токов, напряжений и их фазовых сдвигов при параллельном соединении резистора и катушки индуктивности.
Основные теоретические сведения.
Когда к цепи (рис. 12.1) с параллельным соединением резистора и катушки подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.
Рис. 12.1
Общий ток цепи I разветвляется на ток в катушке IL(индуктивная составляющая общего тока) и ток в резисторе IR(активная составляющая).
Между токами I, IL и IR существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлением XLкатушки. Они могут быть представлены с помощью векторной диаграммы токов (рис. 12.2).
| Рис. 12.2 | Рис. 12.3 |
Фазовый сдвиг между напряжением U цепи и током в резисторе IRотсутствует, тогда как ток в катушке IL всегда отстает от напряжения цепи (или тока в резисторе IR)на900. При этом сдвиг между полным током I и напряжением цепи Uопределяется соотношением междупроводимостями BL и G.
Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 12.3), в котором Y представляет собой так называемую полную проводимость цепи, G – активную, а BL– реактивную (индуктивную) проводимости.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений токов в параллельных ветвях, как в параллельной чисто резистивной цепи, невозможно. Только в векторной форме I = IR +IL. Расчет ведется по следующим формулам:
Действующее значение полного тока цепи
,
I = U ¤ Z = UY .
Полная проводимость цепи
,
Y = 1 ¤ Z ,
где Z- полное сопротивление цепи.
Угол сдвига фаз
j = arctg (I L ¤ IR) = arctg (BL ¤ G).
Активное сопротивление цепи
G = Y × cos j\
Реактивное сопротивление цепи
B = Y × sin j.
Задание к лабораторной работе.
Задание
Для цепи с параллельным соединением резистора и катушки индуктивности измерьте действующие значения тока в резисторе IR и катушке IL, полный ток I и вычислите угол сдвига фаз j, полное сопротивление цепи Z и индуктивную реактивную проводимость BL.
4-i-5.ru
Параллельное соединение резистора, катушки индуктивности и конденсатора
Параллельное соединение резистора, катушки индуктивности и конденсатора.Резонанс токов
Цель работы – изучение основных соотношений в разветвленной цепи переменного тока, а также исследование резонанса токов.
На рис 13 изображена разветвленная цепь переменного тока, состоящая из трёх параллельно включенных приемников: резистора (лампового или проволочного реостата) с сопротивлением , катушки индуктивности с индуктивным сопротивлением и активным сопротивлением , и конденсатора с емкостным сопротивлением .
При параллельном соединении приемники электрической энергии удобнее характеризовать проводимостями, тогда от цепи, изображенной на рис. 13, можно перейти к эквивалентной ей цепи, представленной на рис. 14.
| Рис.13 | Рис.14 |
Воспользуемся известными формулами перехода от сопротивлений (, , ) последовательной схемы к проводимостям (,, ) эквивалентной параллельной схемы:
; ; .Активная проводимость резистора
.
Активная проводимость катушки индуктивности
.
Индуктивная проводимость катушки
.
Емкостная проводимость конденсатора
.
В схеме рис. 14 можно рассмотреть три случая.
1-й случай. В цепи преобладает индуктивная проводимость (), тогда . Векторная диаграмма токов для этого случая построена на рис. 15. Активный ток резистора и активный ток катушки совпадают с вектором напряжения цепи .
Рис.15
Индуктивный ток катушки отстаёт от напряжения на угол . Полный ток катушки равен геометрической сумме активного и индуктивного токов катушки и отстает по фазе от напряжения на угол . Емкостной ток конденсатора , проведенный из конца вектора , опережает напряжение на зажимах цепи на угол . Замыкающий вектор равен току в неразветвлённой части цепи.
Из векторной диаграммы видно, что при параллельном соединении приемников активные токи складываются арифметически:
;
реактивные токи – алгебраически:
;
полные токи – геометрически :
.
Последняя формула выражает первый закон Кирхгофа для действующих значений переменного тока.
Для практических расчетов удобно пользоваться формулой
,
полученной из треугольника токов ОАB (рис. 15).
2-й случай. В цепи преобладает емкостная проводимость () тогда . Полный ток в цепи графически определяется аналогично первому случаю (рис. 16). Как видно из рис. 16, ток опережает напряжение на угол .
З-й случай. Равенство реактивных проводимостей (), тогда . Полный ток в этом случае (рис. 17) совпадает по фазе с напряжением (). Этот режим называется резонансом токов, так как токи и равны между собой и противоположны по фазе. Для рассматриваемой цепи (см. рис.14) условие резонанса токов может быть записано в такой форме:
;
.
| Рис.16 | Рис.17 |
В лабораторной работе изменение режима цепи и получение резонанса токов проводится ступенчатым изменением емкости при и . Явление резонанса токов характеризуется следующими свойствами:
1) . Если катушка и конденсатор идеальные, то ток в цепи конденсатора будет равен току в цепи катушки. Практически же в момент резонанса ток в катушке всегда больше, чем ток конденсатора .
2) , поэтому . Полная мощность всей цепи равна активной ( ). Следовательно, в режиме резонанса токов цепь ведет себя как активная. Причем до резонанса цепь носит активно-индуктивный характер, а после резонанса – активно-емкостной;
3) при неизменном напряжении на зажимах цепи имеет место минимум тока в в неразветвленной части цепи (рис. 18). Действительно, ток , при имеем ;
Рис. 18
4) при расчете резонансных контуров следует учитывать, что если и >>, то токи и могут во много раз превышать общий ток в неразветвленной части цепи.
Физическая сущность резонанса токов делается ясной при рассмотрении энергетической стороны процесса. При резонансе энергия, запасенная в магнитном поле катушки, равна энергии, запасенной в электрическом поле конденсатора. При этом колебания энергии катушки и конденсатора противоположны по фазе, т.е. между катушкой и конденсатором происходит обмен энергиями. Обмена энергий между генератором, с одной стороны, и катушкой и конденсатором, с другой, – нет, и генератор передает энергию лишь в активное сопротивление. Таким образом, физическая сущность резонанса токов аналогична резонансу напряжений. Взаимный обмен реактивной энергии между катушкой индуктивности и конденсатором используется на практике, в частности для повышения коэффициента мощности на входных зажимах приемников электрической энергии.Коэффициент мощности () приемников электрической энергии
Обычно электрические приемники (двигатели, трансформаторы) носят активно-индуктивный характер и работают с углом сдвига фаз . Генератор, питающий такой приемник, линия передачи к нему и сам приемник рассчитываются на полную мощность . Средняя (или активная) мощность приемника, соответствующая преобразованию электрической энергии в тепло или механическую работу, соответствует равенству . Здесь – коэффициент мощности приемника; – т.е. коэффициент мощности – это отношение активной мощности к полной. Как правило, , т.е. расчетная (полная) мощность генератора и линии передачи используются не с полной эффективностью. Отсюда ясна важность для народного хозяйства повышения коэффициента мощности (в предельном случае до ).
Ток, потребляемый приемником от генератора, также зависит от коэффициента мощности, т.е.
.
Если приемник работает при постоянной мощности и напряжении , соответствующих
номинальным (паспортным) данным приемника, то ток будет тем больше, чем ниже. Увеличение тока приводит к увеличению потерь энергии в генераторах, линиях передачи и приемниках. Таким образом, для полного использования расчетной мощности генераторов и уменьшения потерь энергии необходимо повышать приемников. С целью повышения коэффициента мощности к приемнику подключают параллельно батарею конденсаторов.
В этом случае , где – емкостная мощность конденсаторов; – индуктивная мощность приемника.
При резонансе токов , , . Обычно коэффициент мощности приемников повышают до значения 0,92-0,95, так как дальнейший его рост требует значительного увеличения емкости батареи конденсаторов, а следовательно, увеличения ее стоимости. Емкость конденсатора, который необходимо подключить параллельно приемнику для повышения коэффициента мощности с величины до величин! , может быть определена по формуле
,
где – активная мощность приемника; – частота сети, 50 Гц; – напряжение сети.
Программа работы
1. Исследовать работу схемы, включая поочередно резистор, катушку и конденсатор.
2. Исследовать работу параллельно включенных резистора, катушки и конденсатора при переменной емкости до резонанса токов, при резонансе и после резонанса.
3. Рассчитать величину емкости, необходимую для повышения коэффициента мощности приемника, состоящего из параллельно включённых резистора и катушки индуктивности, до наибольшего значения 1 и сравнить с данными опыта (строка 6 в табл. 3)*.
Порядок выполнения работы
1. Собирается схема (рис. 19). Автотрансформатором AT устанавливается напряжение в пределах 90 ... 120 В, которое поддерживается постоянным при всех измерениях.
Рис.192. Для выполнения первой части работы поочередно включаются резистор, катушка и конденсатор. В каждом случае показания приборов записываются в таблицу наблюдений.
3. Вторая часть работы выполняется при одновременном включении всех трех приемников. Исследование ведется следующим образом. Изменяя емкость батареи конденсаторов, цепь настраивают по фазометру () в резонансное состояние. Некоторая доводка до резонансного состояния возможна изменением положения сердечника в катушке. После этого сердечник заклинивают, чтобы . Далее, изменяя емкость от 0 до максимально возможного значения, снимают показания приборов двух опытов до резонанса токов и двух – после резонанса. Результаты опытов заносят в табл. 3.
Таблица 3
| Состояние схемы | Измеряются | Вычисляются | |||||||||||
| С, мкФ | U В | I, А | Iap, А | Iк, А | Iс, А | φ, град | P, Вт | P, Вт | Q, ВАр | Qс, ВАр | QL, ВАр | S, ВА | |
| I.часть 1. Включается резистор | |||||||||||||
| 2. Включается катушка | |||||||||||||
| 3. Включается конденсатор | |||||||||||||
| II.часть 4. C=0 | |||||||||||||
| 5. Cрез | |||||||||||||
| 6. Резонанс токов С= Cрез | |||||||||||||
| 7. С>Cрез | |||||||||||||
| 8. С= Cmax | |||||||||||||
Содержание отчёта
1. Программа работы.
2. Схема соединений (рис. 19).
3. Таблица вычислений и наблюдений (табл. 3).
4. Векторные диаграммы токов для всех строк таблицы, кроме седьмой.
5. Треугольники мощностей для пятой, шестой и восьмом строк таблицы.
6. Кривая тока по данным строк 4...8 табл. 3.
7. Выводы по работе.
При построении векторных диаграмм токов для строк 4...8 табл. 3 рекомендуется вначале задаться вектором напряжения (см. рис. 15). С вектором напряжения совпадает по фазе ток в резисторе . Из конца вектора под углом (значение угла берется из табл. 3, строка 2) проводится вектор тока .
*Пункт 3 выполняется в порядке УИРС.
Вектор тока раскладывается графически на два вектора и . Эта часть диаграммы будет одинаковой для всех строк, начиная с четвертой. Из конца вектора проводится вектор . Замыкающий вектор представляет собой ток в неразветвленной части цепи.
Треугольник мощностей (рис. 20) строится подобно векторной диаграмме токов, причем мощности предварительно вычисляют по следующим формулам:
| Рис. 20 | полная мощность всей цепи ; активная мощность всей цепи ; реактивная мощность всей цепи емкостная мощность конденсатора ; индуктивная мощность катушки . |
Основные вопросы по работе1. Как складываются действующие значения токов, проводимости и мощности в цепи переменного тока?
2. При каких условиях возникает явление резонанс токов и какими свойствами оно характеризуется?
3. В чем заключается практическое использование резонанса токов?
4. Почему коэффициент мощности обычно не доводят до единицы?
Список литературы
1. Электротехника / Под ред. В.Г. Герасимова. – М.: Высшая школа, 1985.
2. Касаткин А.С., Немцов М.В. Электротехника, – М.: Энергоатомиздат, 1983.
Составили Л.К. ШАНГИНА, Б.В. РУДАКОВРедактор А.И.Жук
Технический редактор М.С. Савастеева
Корректор Н.А. Саруханбекян
План 1993 г., № 223Подписано в печать с оригинала – макета 18.01.94.
Формат 60 х 80 1/16. Бумага для множ. апп.
Печать офсетная. Усл. печ. л. 1,5. уч.-изд. л. 1,5. Тираж 1000.
Заказ 31 Цена 59 р.
Петербургский государственный университет путей сообщения.
190031, СПб, Московский пр., 9
Типография ПГУПС. 190031, СПб, Московский пр., 9
Отпечатано 17. 11. 08 г.
Параметры редактора формул: 13, 8, 4, 24, 9. Times New Roman.
topuch.ru
6.3. Последовательное соединение резистора и катушки индуктивности
6.3.1. Общие сведения
Когда к цепи (рис. 6.3.1) с последовательным соединением резистора и катушки индуктивности подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.
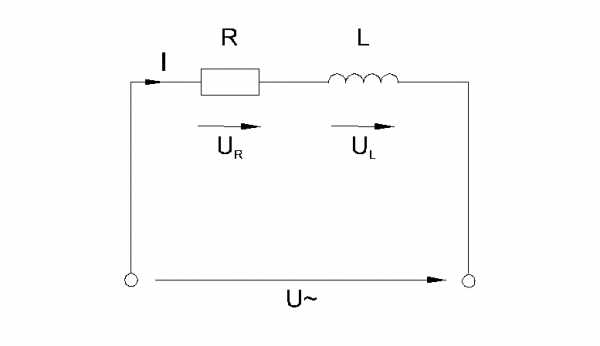
Рис. 6.3.1
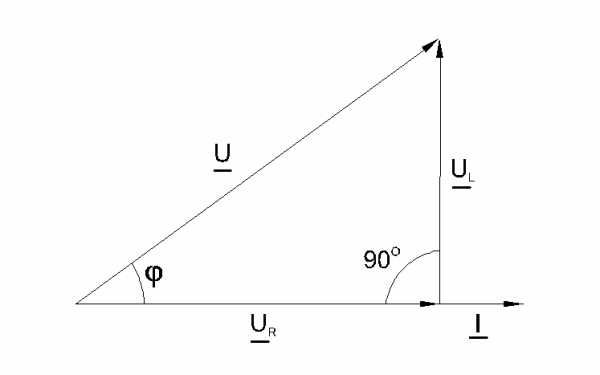
Между напряжениями UR, UL иU существуют фазовые сдвиги, обусловленные индуктивным реактивным сопротивлениемXL катушки. Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 6.3.2).
|
|
|
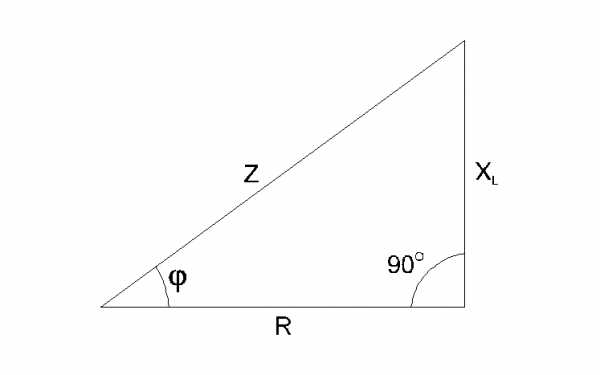
| Рис. 6.3.2 | Рис. 6.3.3 |
Фазовый сдвиг между током I и напряжением на резистореUR отсутствует, тогда как сдвиг между этим током и падением напряженияULна катушке индуктивности равен 900(ток отстает от напряжения). При этом сдвиг между полным напряжениемUцепи и током определяется соотношением между сопротивлениями XLиR. Разделив все стороны треугольника напряжений на ток, получим треугольник сопротивлений (рис. 6.3.3), в котором Zпредставляет собой так называемое полное сопротивление цепи.
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение напряжений на отдельных элементах как в последовательной чисто резистивной цепи, невозможно. Только в векторной форме U = UR +UL. Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника сопротивлений.
Действующее значение полного напряжения цепи
U = Z I
Полное сопротивление цепи
;
Z = U I
Активное сопротивление цепи
R = Z cos
Индуктивное реактивное сопротивление цепи
XL = Z sin
Угол сдвига фаз
= arctg (ХL R)
6.3.2. Экспериментальная часть Задание
Для цепи с последовательным соединением резистора и катушки индуктивности измерьте действующие значения падений напряжения на резисторе URи катушкеULи токI. Вычислите фазовый угол, полное сопротивление цепиZ, индуктивное реактивное сопротивлениеXL и фазовый сдвиг между полным напряжением цепиUи падением напряжения на катушкеUL. Активным сопротивлением катушки ввиду его малой величины можно при этом пренебречь.
Порядок выполнения работы
Соберите цепь согласно схеме (рис. 6.3.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U= 5 В,f= 200 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
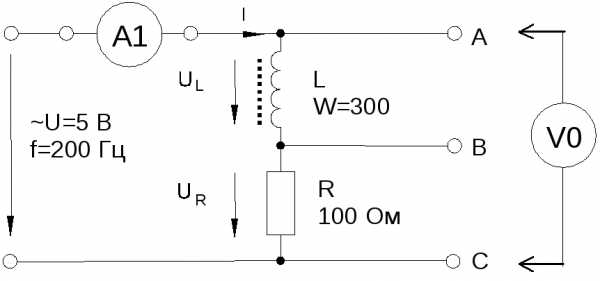
Рис. 6.3.4
Выполните измерения тока и напряжений, указанных в табл. 6.3.1. Если измерения производятся виртуальными приборами, то измерьте также R, , XL, Z.
Таблица 6.3.1.
| U,B | UL, B | UC, B | I, мА | , град | R, Ом | XL, Ом | Z, Ом | Примечание |
| Расчет | ||||||||
| Вирт. Изм |
Вычислите = arctg (UL R), Z = U I, XL = UL I, занесите результаты вычислений в табл. 6.3.1 и сравните с результатами виртуальных измерений, если они есть.
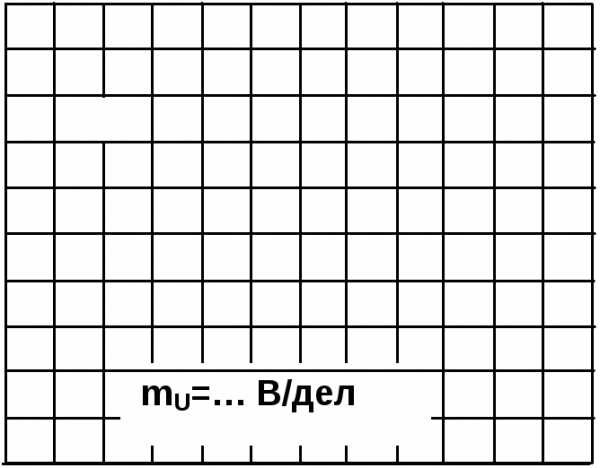
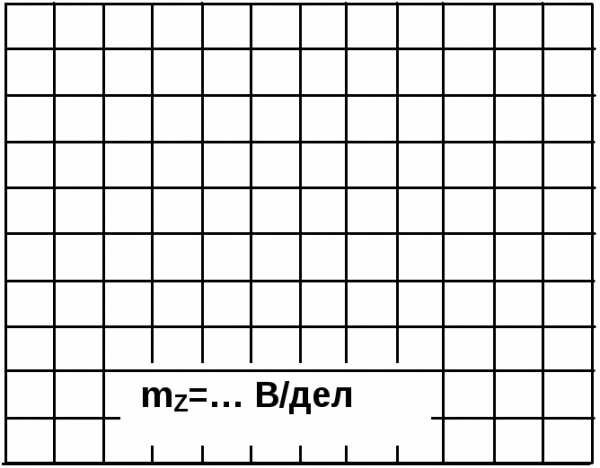
Рис. 6.3.5 Рис. 6.3.6
studfiles.net
6.2. Последовательное соединение резистора и конденсатора, резистора и катушки
индуктивности
6.2.1. Общие сведения
Когда к цепи (рис. 6.2.1) с последовательным соединением резистора и конденсатора (а) или резистора и катушки индуктивности (б) подается переменное синусоидальное напряжение, один и
тот же синусоидальный ток имеет место в обоих компонентах цепи, а напряжение на входе цепи равно сумме напряжений на двух компонентах. Поскольку эти два напряжения сдвинуты
относительно друг друга по фазе, непосредственное сложение их действующих значений или амплитуд невозможно. Необходимо либо складывать мгновенные значения этих напряжений, либо
векторы, соответствующие этим напряжениям, как показано на рис. 6.2.2а и б.
Рис. 6.2.2
Вектор напряжения на конденсаторе U отстаёт от вектора тока I на 900, а вектор напряжения на индуктивности UL опережает ток на 90°. Из векторных диаграмм следует, что в цепи с
конденсатором
U = √(UR + UC ), = -arctg(UC /UR).
Поскольку UR = R · I , a UC = XC·I, получаем
U = I"/(R + ХC ) = I·Z и =-arctg(XC/R),
где Z = √(R + ХC ) - полное сопротивление цепи, и <0, т.е. ток опережает напряжение.
Аналогично, в цепи с индуктивностью:
U = √(UR + UL ) = l√(R + XL ) = I · Z, где Z = √(R + XL ),
=
•
и
φ = arctg (XL/ R)>0, т.е. ток отстаёт от напряжения.
Если каждую сторону треугольника напряжений разделить на ток, то получим тре-
угольник сопротивлений, подобный треугольнику напряжений. (рис.6.2.3а и б). Из треугольников
сопротивлений следует, что
R = Z · cos φ, ХC = Z · sin φ и XL Z · sin φ.
6.2.2. Экспериментальная часть
Задание
Для цепи с последовательным соединением резистора и конденсатора, а также резистора и индуктивности измерьте потребляемую активную мощность, действующие значения напряжений
на резисторе UR и реактивном элементе UC, UL и ток I. Рассчитайте угол сдвига фаз , полное сопротивление цепи Z, реактивное сопротивление X и активное сопротивление R, постройте
векторную диаграмму.
Порядок выполнения работы
Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник
синусоидального
напряжения
установите
максимальную
амплитуду
синусоидального
напряжения с частотой f = 1 кГц.
•
В/дел Цепь с катушкой ти=...
Выполните измерения активной мощности, действующих значений тока и напряжений,
Вычислите: фазовый угол = arctg (Р/UI), полное сопротивление цепи Z = U/I,
Замените в схеме конденсатор на катушку индуктивности с малым активным сопро-
В
В
В
I,
φ,
R,
X,
Z,
| Р, Вт | U, | UR, | U C , U L , | мА | град | Ом | Ом | Ом | |
| Цепь с конденсатором | |||||||||
| Цепь с катушкой |
•
5
~и
т
^200
Гц
•
указанных в табл. 6.2.1. При измерениях напряжений подключайте мультиметр к различным зажимам цепи.
Таблица 6.2.1.
•
сопротивление цепи R = Z·cos и ёмкостное сопротивление ХC = Z·sin .
активное
Выберите масштаб и постройте векторную диаграмму напряжений (рис. 6.2.5).
Цепь с конденсатором тц=...
В/дел
Рис.6.2.
•
тивлением (рис.6.2.6). В качестве такой катушки используйте обмотку 300 витков
=10 в
Рис.6.2.6
разборного трансформатора. Чтобы создать немагнитный зазор в магнитопроводе, вставьте между двумя частями сердечника квадратики обычной писчей бумаги в один или два слоя.
Убавьте частоту до 200 Гц и повторите измерения, расчёт и построение векторной диаграммы.
2
2
2
2
2
2
-
-
V.
90°
^
*
• *
-
•
*
*
•
•
•
-
studfiles.net
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
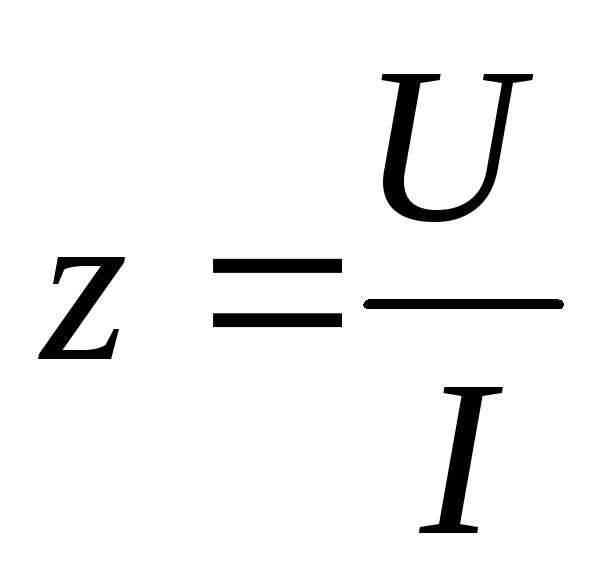 .
.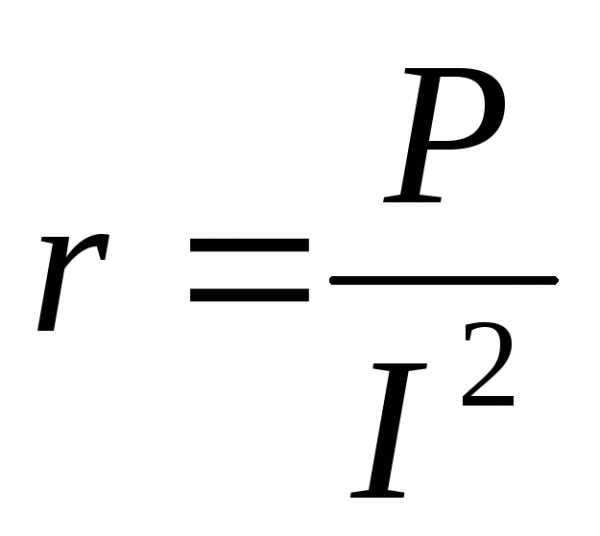 .
.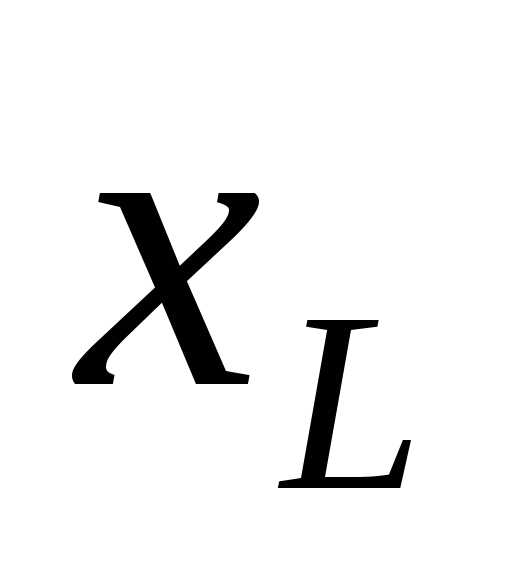 и
и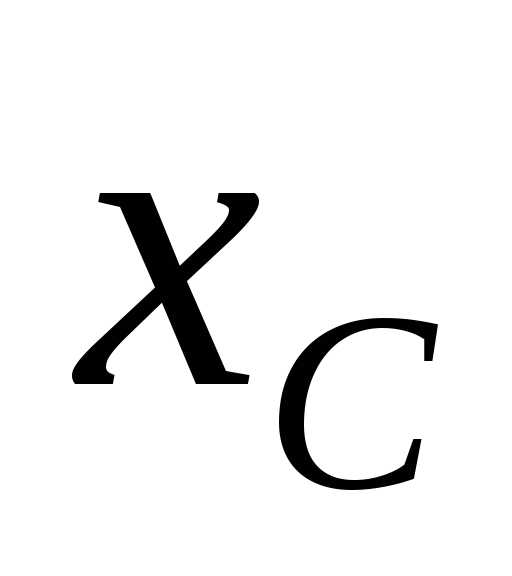 определяются соответственно по пп. 7 и 8. Эта формула позволяет определить знак у реактивного сопротивления (плюс или минус).
определяются соответственно по пп. 7 и 8. Эта формула позволяет определить знак у реактивного сопротивления (плюс или минус).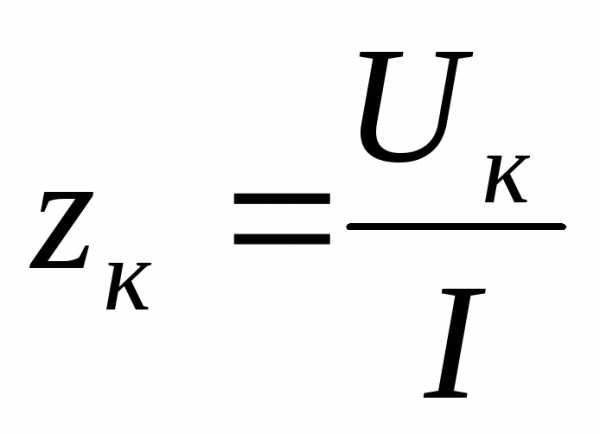 .
.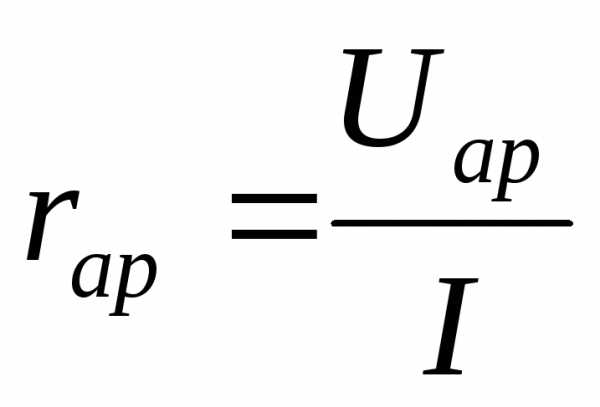 .
.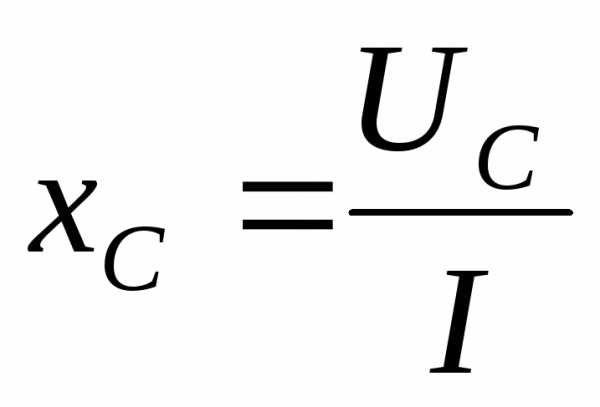 .
.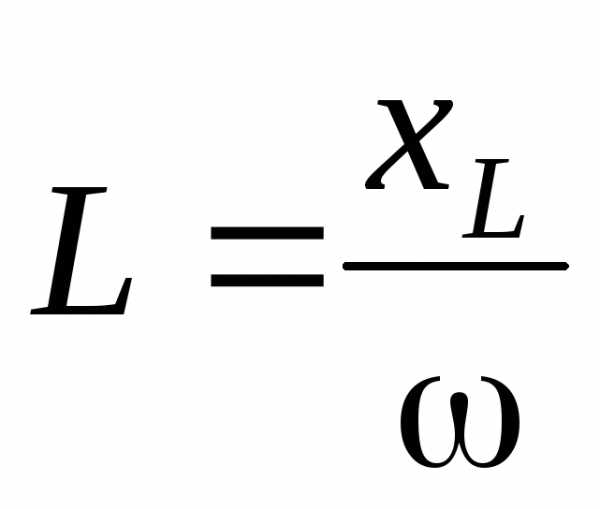 , где
, где 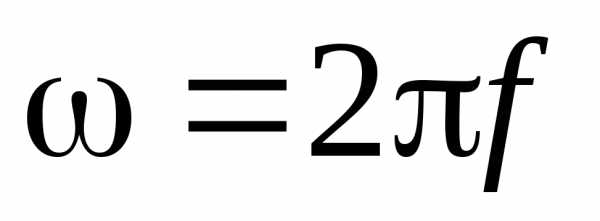 ,
,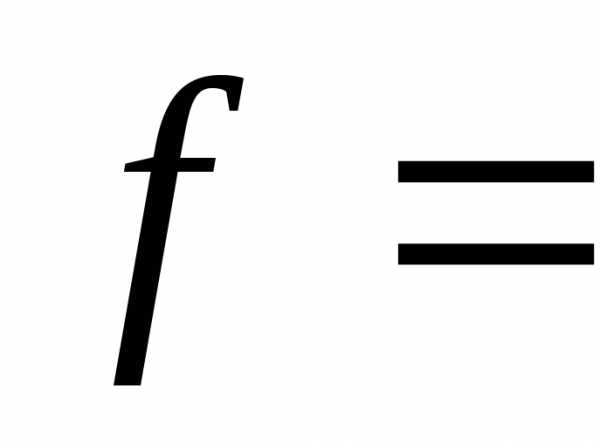 50 Гц.
50 Гц.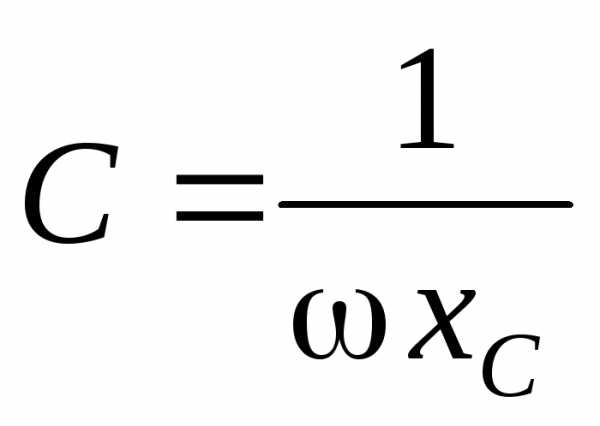 .
.