Прикладное программирование с нуля. Программный пид регулятор

ПИД-регулятор своими руками / Хабр

; PID управление CalcMainEnd: ; Вычисления, Go-Go. CalcPid: ; 1. Eo = E | 16bit Pid1: MOV Err0H, ErrH MOV Err0L, ErrL ; 2. E = Y-X | 16bit Pid2: CLR C MOV A, SettingL SUBB A, ThermoL MOV ErrL, A MOV A, SettingH SUBB A, ThermoH MOV ErrH, A JNB OV, Pid2Ov JB ACC.7, Pid2Max Pid2Min: MOV ErrL, #LOW(-500*32) MOV ErrH, #HIGH(-500*32) SJMP Pid2End Pid2Max: MOV ErrL, #LOW(500*32) MOV ErrH, #HIGH(500*32) SJMP Pid2End Pid2Ov: JNB ACC.7, Pid2OvP Pid2OvN: ; Проверим на ограничение вниз CLR C MOV A, ErrL SUBB A, #LOW(-500*32) MOV A, ErrH SUBB A, #HIGH(-500*32) JNC Pid2End ; Если > -500 => всё ок SJMP Pid2Min Pid2OvP: CLR C MOV A, ErrL SUBB A, #LOW(500*32) MOV A, ErrH SUBB A, #HIGH(500*32) JNC Pid2Max ; Если < 500 => всё ок Pid2End: ; 3. Int = Int + (E+Eo)/2 | 32bit+16bit Pid3: JNB PowerReady, Pid3End ; Если нет сети -- интегральную часть не копим MOV A, ErrL ADD A, Err0L MOV R0, A ; временно MOV A, ErrH ADDC A, Err0H MOV C, ACC.7 ; Полусумма всегда влезает в 16 бит, поэтому при сдвиге надо сохранить знак RRC A ; Поделим без потери знака XCH A, R0 ; A= младшая часть, R0 - старшая часть полусуммы RRC A ; Доделили JNB IntS, Pid3IntPos ; Int отрицательный, изменим знак для R0:A, тем самым можно будет просто сложить с Int CLR C CPL A ADD A, #1 XCH A, R0 CPL A ADDC A, #0 XCH A, R0 Pid3IntPos: ; У Int и R0:A сейчас согласованы знаки, поэтому складываем обычным образом ADD A, IntLL MOV IntLL, A MOV A, IntLH ADDC A, R0 MOV IntLH, A MOV A, R0 JB ACC.7, Pid3Neg ; Прибавляли отрицательную разность? ; Если разность положительная, просто распространим перенос JNC jPid3End ; Если прибавили слово и переноса небыло -- делать нам ничего не требуется. INC IntHL ; Распространяем перенос выше MOV A, IntHL JNZ Pid3End ; Если перенос не ушел в 4й байт -- всё нормально INC IntHH ; Распространяем перенос на САМЫЙ старший байт MOV A, IntHH JNZ Pid3End ; Если перенос не ушел еще выше -- всё нормально MOV IntHH, #0FFh ; Если перенс был выше -- ограничиваем интеграл потолком MOV IntHL, #0FFh MOV IntLH, #0FFh MOV IntLL, #0FFh jPid3End: SJMP Pid3End Pid3Neg: ; Если разность отрицательная, то надо продолжать добавлять оба раза, но FFh MOV A, IntHL ADDC A, #0FFh MOV IntHL, A MOV A, IntHH ADDC A, #0FFh MOV IntHH, A JC Pid3End ; Если тут был перенос, значит знак интеграла не изменился CPL IntS ; Если переноса небыло, значит у интеграла изменился знак CPL C ; Обратим знак получившегося числа MOV A, #0 SUBB A, IntLL MOV IntLL, A MOV A, #0 SUBB A, IntLH MOV IntLH, A MOV A, #0 SUBB A, IntHL MOV IntHL, A MOV A, #0 SUBB A, IntHH MOV IntHH, A ; так как оно стало отрицательным -- то перенос тут будет всегда Pid3End: ; 5. cI = Int*(1/Ti) | 32*32=>32bit Pid5: ; R3:R2:R1:R0 = Int*(1/Ti) JB Ti_sh2, Pid5Calc ; если Ti_sh2=0, то 1/Ti=1 или Ti=0. и ничего делать не надо MOV A, Ti_mLL ORL A, Ti_mLH ORL A, Ti_mHL ORL A, Ti_mHH JZ Pid5Zero MOV R0, IntLL MOV R1, IntLH MOV R2, IntHL MOV R3, IntHH AJMP Pid5End Pid5Zero: MOV A, #0 MOV R0, A MOV R1, A MOV R2, A MOV R3, A MOV IntLL, A MOV IntLH, A MOV IntHL, A MOV IntHH, A AJMP Pid5End Pid5Calc: ; R7:R6:R5:R4[:R3] = MULUH(Int*Ti_m) // R3 считаем как часть для округления MOV R2, #0 ;; R7:R6 = IntHH*Ti_mHH MOV A, IntHH MOV B, Ti_mHH MUL AB MOV R7, B MOV R6, A ; R6:R5 += IntHL*Ti_mHH MOV A, IntHL MOV B, Ti_mHH MUL AB MOV R5, A MOV A, R6 ADD A, B MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ; R5:R4 += IntLH*Ti_mHH MOV A, IntLH MOV B, Ti_mHH MUL AB MOV R4, A MOV A, R5 ADD A, B MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ; R4:R3 += IntLL*Ti_mHH MOV A, IntLL MOV B, Ti_mHH MUL AB MOV R3, A MOV A, R4 ADD A, B MOV R4, A MOV A, R2 ; A=0 ADDC A, R5 MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ;; R6:R5 += IntHH*Ti_mHL MOV A, IntHH MOV B, Ti_mHL MUL AB ADD A, R5 MOV R5, A MOV A, R6 ADDC A, B MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ; R5:R4 += IntHL*Ti_mHL MOV A, IntHL MOV B, Ti_mHL MUL AB ADD A, R4 MOV R4, A MOV A, R5 ADDC A, B MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ; R4:R3 += IntLH*Ti_mHL MOV A, IntLH MOV B, Ti_mHL MUL AB MOV A, R3 MOV R3, A MOV A, R4 ADDC A, B MOV R4, A MOV A, R2 ; A=0 ADDC A, R5 MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ;; R5:R4 += IntHH*Ti_mLH MOV A, IntHH MOV B, Ti_mLH MUL AB ADD A, R4 MOV R4, A MOV A, R5 ADDC A, B MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ; R4:R3 += IntHL*Ti_mLH MOV A, IntHL MOV B, Ti_mLH MUL AB ADD A, R3 MOV R3, A MOV A, R4 ADDC A, B MOV R4, A MOV A, R2 ; A=0 ADDC A, R5 MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ;; R4:R3 += IntHH*Ti_mLL MOV A, IntHH MOV B, Ti_mLL MUL AB ADD A, R3 MOV R3, A MOV A, R4 ADDC A, B MOV R4, A MOV A, R2 ; A=0 ADDC A, R5 MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A ;;; Если R3 > 7F -- MOV A, R3 JNB ACC.7, Pid5Shift ; Если R3<80 -- округление не надо ANL A, #7Fh JZ Pid5Round ; Если = 80 -- округляем до нечетного MOV A, #1 ADD A, R4 MOV R4, A MOV A, R2 ; A=0 ADDC A, R5 MOV R5, A MOV A, R2 ; A=0 ADDC A, R6 MOV R6, A MOV A, R2 ; A=0 ADDC A, R7 MOV R7, A SJMP Pid5Shift Pid5Round: MOV A, R4 ORL A, #01h MOV R4, A ;JMP Pid5Shift Pid5Shift: ; R3:R2:R1:R0 = (Int-R7:R6:R5:R4) >> 1 CLR C MOV A, IntLL SUBB A, R4 MOV R0, A MOV A, IntLH SUBB A, R5 MOV R1, A MOV A, IntHL SUBB A, R6 MOV R2, A MOV A, IntHH SUBB A, R7 RRC A ; >>1 без потери переноса MOV R3, A MOV A, R2 RRC A MOV R2, A MOV A, R1 RRC A MOV R1, A MOV A, R0 RRC A ;MOV R0, A ; R3:R2:R1:R0 += R7:R6:R5:R4 ;MOV A, R0 ADD A, R4 MOV R0, A MOV A, R1 ADDC A, R5 MOV R1, A MOV A, R2 ADDC A, R6 MOV R2, A MOV A, R3 ADDC A, R7 MOV R7, A ; Теперь сдвинуть вправо на sh3. ; sh3 может быть до 16 (так как у нас Ti 16разрядный; проверим необходимость сдвига на 16 бит) MOV A, Ti_sh3 JNB ACC.4, Pid5ShiftUnder16 ; Надо сдвинуть >=16 -- 2 байта сдвинем mov'ами MOV R0, 18h+2; R2, bank 3 MOV R1, 18h+3; R3, bank 3 MOV R2, #0 MOV R3, #0 Pid5ShiftUnder16: JNB ACC.3, Pid5ShiftUnder8 ; Надо сдвинуть на >=8 -- 1 байт сдвигаем mov'ами MOV R0, 18h+1; R1, bank 3 MOV R1, 18h+2; R2, bank 3 MOV R2, 18h+3; R3, bank 3 MOV R3, #0 Pid5ShiftUnder8: ANL A, #07h JZ Pid5End ; Если внутри байта двигать не надо -- всё MOV R4, A SJMP Pid5ShiftRight Pid5NextShift: CLR C ; К этому моменту C у нас еще возможнозначимый старший бит! Pid5ShiftRight: MOV A, R3 RRC A MOV R3, A MOV A, R2 RRC A MOV R2, A MOV A, R1 RRC A MOV R1, A MOV A, R0 RRC A MOV R0, A DJNZ R4, Pid5NextShift ; Всё, после всех сдвигов получили результат ; Не забываем, что у вычисленного в R3:R2:R1:R0 ; сейчас число положительное, а знак его в IntS Pid5End: ; 4. PID += [ cD = Td * (E-Eo) ] | 16*16=>32bit Pid4: ; cD = R7:R6:R5:R4; ErrD = E-Eo CLR C MOV A, ErrL SUBB A, Err0L MOV DiffL, A MOV A, ErrH SUBB A, Err0H MOV DiffH, A MOV C, ACC.7 ; Берём знак результата MOV DiffS, C ; Сохраним знак E-Eo JNC Pid4Mul ; Diff -- орицательный, обратим знак MOV A, DiffL CPL A ADD A, #1 MOV DiffL, A MOV A, DiffH CPL A ADDC A, #0 MOV DiffH, A Pid4Mul: ; R7:R6 = DiffH*TdH ; MOV A, DiffH = в любом случае A=DiffH MOV B, TdH MUL AB MOV R6, A MOV R7, B ; R5:R4 = DiffL*TdL MOV A, DiffL MOV B, TdL MUL AB MOV R4, A MOV R5, B ; R6:R5 += DiffH*TdL MOV A, DiffH MOV B, TdL MUL AB ADD A, R5 MOV R5, A MOV A, R6 ADD A, B MOV R6, A MOV A, R7 ADDC A, #0 MOV R7, A ; R6:R5 += DiffL*TdH MOV A, DiffL MOV B, TdH MUL AB ADD A, R5 MOV R5, A MOV A, R6 ADD A, B MOV R6, A MOV A, R7 ADDC A, #0 MOV R7, A ; 6. PID = E + cI + cD | 32bit Pid6: ; R3:R2:R1:R0 равно cI, знак в IntS; ; R7:R6:R5:R4 = cD; знак в DiffS ; E в обратном дополнительном коде JB IntS, ChkDiffN JNB DiffS, Pid6Add ; Int>0, Diff>0 => Add SJMP Pid6Sub ; Int>0, Diff<0 => Sub ChkDiffN: JNB DiffS, Pid6Sub ; Int<0, Diff>0 => Sub ; Int<0, Diff<0 => Add Pid6Add: ; Одинаковый знак => складываем их с проверкой на переполнение MOV A, R0 ADD A, R4 MOV R0, A MOV A, R1 ADDC A, R5 MOV R1, A MOV A, R2 ADDC A, R6 MOV R2, A MOV A, R3 ADDC A, R7 MOV R3, A JNC Pid6Err ; Если нет переноса - в результате сложения переполнения небыло MOV R3, #0FFh MOV R2, #0FFh MOV R1, #0FFh MOV R0, #0FFh SJMP Pid6Err Pid6Sub: ; Знаки разные -- вычтем одно из другого и проверим знак результата CLR C MOV A, R4 SUBB A, R0 MOV R0, A MOV A, R5 SUBB A, R1 MOV R1, A MOV A, R6 SUBB A, R2 MOV R2, A MOV A, R7 SUBB A, R3 MOV R3, A JNC Pid6Err ; Если нет заимствования -- знак результата равен знаку DiffS CPL DiffS ; Если заимствование было, у DiffS и результата надо обратить знак MOV R6, #0 ; R6=0 MOV A, R0 CPL A ADDC A, R6 ; R6=0, C=1 => действие +1 MOV R0, A MOV A, R1 CPL A ADDC A, R6 ; +перенос MOV R1, A MOV A, R2 CPL A ADDC A, R6 MOV R2, A MOV A, R3 CPL A ADDC A, R6 MOV R3, A Pid6Err: MOV R6, #0 ; R6=0 ; В R3:R2:R1:R0 -- лежит cI+cD; знак суммы в DiffS ; надо прибавить/отнять Err, записанное в обратном коде ; Приведём знак Err к DiffS MOV R4, ErrL MOV A, ErrH JB ACC.7, Pid6ChkDiffS JNB DiffS, Pid6SumErrNoInv ; Err>0, Diff>0 => NoInv SJMP Pid6SumErrInv Pid6ChkDiffS: JNB DiffS, Pid6SumErrNoInv ; Err<0, Diff>0 => NoInv Pid6SumErrInv: ; У Err знак отличается от DiffS -- инвертируем SETB C ; Не уверен в состоянии C MOV A, ErrL CPL A ADDC A, R6 ; A+=R6+C, R6=0 C=1 => A+=1 MOV R4, A ; R4=ErrL MOV A, ErrH CPL A ADDC A, R6 Pid6SumErrNoInv: MOV R5, A ; ErrH Pid6SumErr: ; Итак, в R5:R4 лежит Err, знак которого согласован с DiffS; но в обратно-дополнительном коде MOV A, R0 ADD A, R4 MOV R0, A MOV A, R5 CLR F0 JNB ACC.7, Pid6SubErrPos SETB F0 MOV R6, #0FFh ; Добавляем отрицательное => дополняем FFами Pid6SubErrPos: ADDC A, R1 MOV R1, A MOV A, R2 ADDC A, R6 ; +расширение MOV R2, A MOV A, R3 ADDC A, R6 ; +расширение MOV R3, A MOV R6, #0 ; Надо проверить нет ли смены знака итоговой суммы JNC Pid6ChkF0 JB F0, Pid7 ; Err<0, был перенос => Знак не сменился, переполнения нет SJMP Pid6SumOv ; Err>0, был перенос => переполнение Pid6ChkF0: JNB F0, Pid7 ; Err>0, небыло переноса => нет переполнения ;SJMP Pid6SumUf ; Err<0, небыло переноса => сменился знак Pid6SumUf: ; Если Err<0 и небыло переноса => сменился знак CPL DiffS MOV A, R0 CPL A ADD A, #1 ; C=?, поэтому прибавляем 1 обычным методом MOV R0, A MOV A, R1 CPL A ADDC A, R6 MOV R1, A MOV A, R2 CPL A ADDC A, R6 MOV R2, A MOV A, R3 CPL A ADDC A, R6 MOV R3, A SJMP Pid7 ; Знак у результата и DiffS приведены в норму Pid6SumOv: ; Было переполнение => округляем до максимума MOV R0, #0FFh MOV R1, #0FFh MOV R2, #0FFh MOV R3, #0FFh ; 7. U = K*PID/256 | 32bit*16bit/8bit => 40bit, ; | которые усекаются до 10bit ; | при вычислениях Pid7: ; В R3:R2:R1:R0 лежит результат PID, в DiffS его знак ; Нужно вычислить K*PID/256, ограничив результат до 10бит ; K всегда положительно, поэтому если PID < 0 => минимум JB DiffS, Pid7Umin ; поскольку мы можем жестко ограничить сверху 16ю битами, ; то если R3 != 0 => ставим максимум в любом случае MOV A, R3 JNZ Pid7Umax ; [R2:R1:R0 * KH:HL] = [R7:R6:R5:R4:R3] ; вычисляем, учитывая что должно получиться R7=0 R6=0, ; иначе переполнение, поэтому R7 и R6 вообще не трогаем ; но проверяем результат ; R7:R6 = R2*KH MOV A, R2 JZ Pid7S1 MOV A, KH JNZ Pid7Umax ; Если R2!=0 и KH!=0 => R7:R6>0 => переполнение Pid7S1: ; R6:R5 = R2*KL MOV A, R2 MOV B, KL MUL AB MOV R5, A MOV A, B JNZ Pid7Umax ; Если R6 > 0 => переполнение ; R6:R5 = R1*KH MOV A, R1 MOV B, KH MUL AB ADD A, R5 JC Pid7Umax ; Если R6 > 0 => переполнение MOV R5, A MOV A, B JNZ Pid7Umax ; Если R6 > 0 => переполнение ; R5:R4 = R0*KH MOV A, R0 MOV B, KH MUL AB MOV R4, A MOV A, R5 ADD A, B JC Pid7Umax ; Если R6 > 0 => переполнение MOV R5, A ; R5:R4 = R1*KL MOV A, R1 MOV B, KL MUL AB ADD A, R4 MOV R4, A MOV A, R5 ADDC A, B JC Pid7Umax ; Если R6 > 0 => переполнение MOV R5, A ; R4:R3 = R0*KL MOV A, R0 MOV B, KL MUL AB RLC A ; C = R3>=0x80, Z=R3>0x80 MOV R3, #0FFh ; R3<>0x80 => ничего JNZ Pid7S2 MOV R3, #0FEh ; R3==0x80 => округление до четного Pid7S2: MOV A, R4 ADDC A, B ; Складываем умножение, регистр, и перенос-округление ANL A, R3 ; А так же если округление до четного -- отбрасываем после младший бит MOV R4, A MOV A, R5 ADDC A, R6 ; R6=0 у нас с давних пор, хоть мы туда и не складывали ничего во время перемножения JC Pid7Umax ; Если R6 > 0 => переполнение MOV R5, A ; R5:R4 => ограниченный в 16 бит результат ; Теперь надо ограничить R5:R4 до Umax/Umin MOV A, UmaxL SUBB A, R4 ; C=0 на текущий момент MOV A, UmaxH SUBB A, R5 JC Pid7Umax ; Если R5:R4>Umax => R5:R4 = Umax MOV A, UminL SUBB A, R4 ; C=0 на текущий момент MOV A, UminH SUBB A, R5 JNC Pid7Umin ; Если R5:R4<Umin => R5:R4 = Umin ; Мощность вычислена MOV UH, R5 MOV UL, R4 SETB UReady AJMP CalcExit Pid7Umax: ; Установить максимальную мощность MOV UH, UmaxH MOV UL, UmaxL SETB UReady AJMP CalcExit Pid7Umin: ; Установить минимальную мощность MOV UH, UminH MOV UL, UminL SETB UReady AJMP CalcExit

habr.com

МЕТАКОН-614 программные ПИД-регуляторы

ПИД-регуляторы МЕТАКОН-614 используются для управления реверсивными исполнительными механизмами интегрирующего типа - МЭО, МЭОК, задвижки, заслонки, трехходовые клапаны и т.п. в соответствие с заложенной в память диаграммой. Кроме того, возможно управление еще тремя внешними дискретными устройствами в соответствие с программой.

Два дискретных входа позволяют осуществлять пуск и остановку ПИД-регулятора внешними сигналами.

Источники сигналов: датчики температуры – термопары и термосопротивления, а также устройства с унифицированными сигналами тока или напряжения. На выходе – широтно-импульсно-модулированный (ШИМ) сигнал от транзисторного ключа. При этом прибор может подавать команду как на нагрев, так и на охлаждение.

 Версия для печати. Описание в формате pdf

Три дискретных выхода позволяют управлять тремя дополнительными внешними устройствами в соответствии с командами, заложенными в пaмять ПИД-регулятора. Компараторы мoгут paботать кaк в следящем рeжиме, тaк и в фиксированном. Например, кaк это показано нa диаграмме.

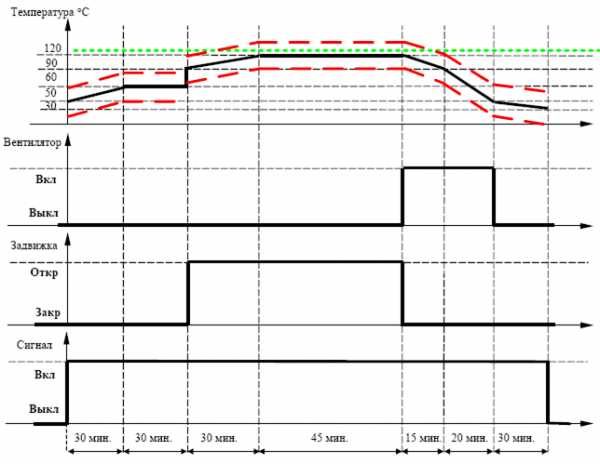
В дaнном примeре регулятор управляет температурой в кaмеpе в сooтветствии с гpaфикoм, привeденным нa риcyнке.Синхpoнно с регулированием температуры на опpeделенныx учacтках регулятор:

• включает и выключает вентилятор;
• открывает и закрывает задвижку;
• включает на время исполнения программы световую сигнализацию.

– – – Пopoги следящeго компаратора. Сигнализируют о мaксимальном и минимaльнoм допуcтимых oтклoнениях температуры от заданной.

 Фикcированный пopог компаратора. B данном случaе сигнализирует о дocтижении температуры 120 оС.

Поддержка протокола RNet по сети RS-485 дaeт вoзможнoсть испoльзовать приборы МЕТАКОН в SCADA-системах АСУТП при помощи OPC-сервера для регуляторов МЕТАКОН.

Приборы МЕТАКОН зapeгистриpoвaны Гоccтандартом в Госpeестре средств измерений пoд нoмеpом 17977-04. Сертификат № 17166 от 10.03.2004.

Функции ПИД-регулятора МЕТАКОН-614

• Библиотека прогрaмм: 10 временных диаграмм по 20 участков каждый.
• Измерение технологических параметров
• ПИД-алгоритм регулирования с ШИМ-сигналом управления на выходе
• Автоматическая настройка параметров ПИД-регулятора
• 2 независимых компаратора
• Масштабирование линейных сигналов
• Работа в распределённых системах сбора данных и управления

• Выocкая помеxoустойчивoсть прибора (не ниже 3 ст. жёсткости)
• Модификации с транзисторными выходами n-p-n с открытым коллектором
• Независимое конфигурирование всех каналов
• Программный выбор типа НСХ термопреобразователя и автоматическая ее линеаризация
• 4-х проводная схема подключения термосопротивлений
• Контроль обрыва входных линий и аварийных ситуаций
• Аппаратно-программная поддержка интерфейса RS-485
• Контрастная цифровая индикация (антиблик)
• Гальваническая развязка входного и выходного сигналов
• Защита паролем

Технические характеристики ПИД-регулятора МЕТАКОН-614

Количество каналов	1
Библиoтека пpoгрaмм	10 программ по 20 участков в каждой
Алгоритмы управления	ПИД-регулирование
	Автонастройка параметров регулирования
	Программное управление уставкой
	Три таймера с привязкой к временной диаграмме
	Два независимых компаратора по 8 функций с фиксированным и следящим порогами переключения
Модификации по типу входныхсигналов:	ТП	0…50 мВ, термопары (ТХА(К), ТХК(L), ТПП(S),ТПР(B), ТВР(А-1), ТЖК(J), ТНН(N)),специальные г/tr>
	ТС50	термосопротивления 50М, 50П, Pt50
	ТС100	термосопротивления 100М, 100П, Pt100
	0/20	ток 0(4)…20мА;
Основная погрешностьизмерений, не более	±0,1 %
Период опроса входного сигнала	1 с
Модификации по типу выходныхсигналов	2 компаратора
	Т	транзисторы с открытым коллектором 24В/150 мА мах(оптоизоляция, все эмиттеры соединены)
Скорость обмена по RS-485	2400, 4800, 9600, 19200 бод
Питание	220 В +10/-15%, 50±0,5 Гц, 9 ВА
Монтаж	Щитовой, монтажное окно 92х92 мм
Габариты	96х96х162 мм
Корпус	КА-Щ1
Условия эксплуатации	Закрытые взрывобезопасные помещения безагрессивных паров и газов
	Температура: 0...50 °С
	Влажность: 80% при 35 °С
Межповерочный интервал	2 года
Масса, не более	0,8 килограмма
Гарантия	36 месяцев

Входные сигналы

Тип НСХ	Пределы измерений	Погрешность не более
Термопары
ХА(К)	-100...1300 °С	±1 °С
ХК(L)	-100... 750 °С	±1 °С
НН(N)	-100…1300°С	±1 °С
ПП(S)	0...1600 °С	±2 °С
ПП(R)	0…1600 °С	±2 °С
ПР(B)	300...1700 °С	±2 °С
ВР(А-1)	0...2200 °С	±3 °С
ЖК(J)	-100… 900 °С	±1 °С
Унифицированные сигналы
Напряжение	0…50мВ	±50 (10) мкВ
Напряжение	0…1В	±1 (1) мВ
Ток	0…5 мА	±5 (1) мкА
Ток	0(4)…20 мА	±5 (1) мкА
Термопреобразователи сопротивления
100М	-100...200°С	±0,3 (0,1)°С
100П	-100...200°С	±0,3 (0,1)°С
50М	-100...200°С	±0,3 (0,1)°С
50П	-100...200°С	±0,3 (0,1)°С

Структурная схема программного ПИД-регулятора МЕТАКОН-614

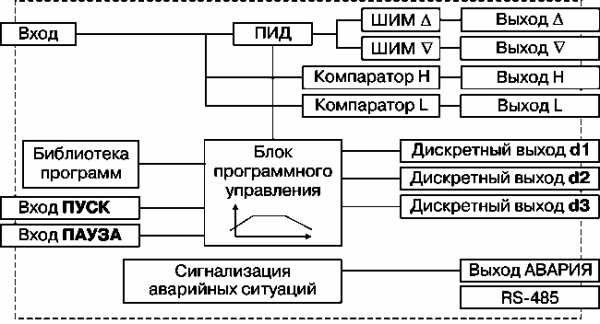
МЕТАКОН – 61<1>–<2>–<3>–<4> Где: <1>  Алгоритм регулирования:   Пример обозначения при заказе: МЕТАКОН-613-T- 0/20-1 микропроцессорный регулятор серии МЕТАКОН-613, выход - транзисторы с открытым коллектором, выполняет функции ПИД-регулирования, рассчитан на работу с унифицированным входным токовым сигналом 0...20 (4...20) мА, установлена программно-аппаратная поддержка интерфейса RS-485. 3 ПИД-регулятор 4 ПИД-регулятор для управления реверсивными исполнительными механизмами интегрирующего типа (ПДД-регулятор)     <2>  Тип выходного сигнала: Т Транзисторы с открытым коллектором 24В/150 мА маx (оптоизоляция, общий эмиттер)     <3>  Тип входного сигнала: ТП 0…50 мВ, термопары (ТХА(К), ТХК(L), ТПП(S),ТПР(B), ТВР(А-1), ТЖК(J), ТНН(N)),специальные градуировки (ПМТ-2, Р-3) ТС50 термосопротивления 50М, 50П, Pt50 ТС100 термосопротивления 100М, 100П, Pt100 0/20 ток 0(4)...20 мА     <4>  Наличие интерфейса RS-485: 1 имеется 0 отсутствует

 

kipia-rb.ru

AVR221: Дискретный ПИД-регулятор - chipenable.ru

   

• Простой дискретный алгоритм ПИД регулятора

• Поддерживается всеми микроконтроллерами AVR

• ПИД функция использует 534 байта flash памяти и 877 циклов процессора (IAR — low size оптимизация)

   Это руководство описывает простую реализацию дискретного пропорционально-интегрально-дифференциального (ПИД) контроллера.

 

   При работе с приложениями, где выходной сигнал системы должен изменяться в соответствии с опорным значением, требуется алгоритм управления. Примерами таких приложений являются блок управления двигателем, блок управления температурой, давлением, расходом жидкости, скорости, силы или других переменных. ПИД-регулятор может быть использован для управления любой измеряемой переменной.

      В течение долгого времени в области управления использовались многие решения, но ПИД-регуляторы могут стать "промышленным стандартом" из-за своей простоты и хорошей производительности.

 

   Для получения дополнительной информации о ПИД-регуляторах и их применении читатель должен обратиться к другим источникам, например, PID Controllers by K. J. Astrom & T. Hagglund (1995)

 

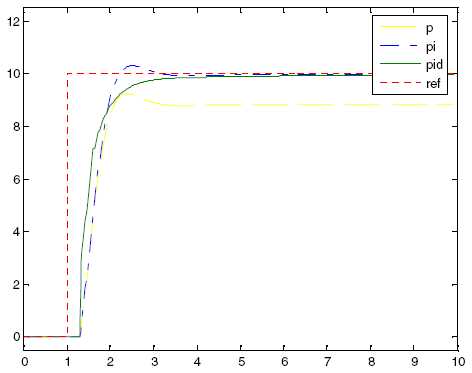
Рисунок 1-1. Типичные отклик ПИД-регулятора на ступенчатое изменение опорного сигнала

   На рисунке 2-1 показана схема системы с ПИД-регулятором. ПИД-регулятор сравнивает измеренное значение процесса Y с заданным опорным значением Y0. Затем разница, или ошибка, E, обрабатывается для расчета нового входного процесса U. Этот новый входной процесс будет пытаться приблизить значение измеряемого процесса к заданному значению.

 

   Альтернативой системе управления с замкнутым контуром, является система управления с открытым контуром. Открытый контур управления (без обратной связи) во многих случаях не является удовлетворительным, и его применение часто невозможно из-за свойств системы. 

 

Рисунок 2-1. Управляющая система с замкнутым контуром на основе ПИД-регулятора

   В отличие от простых алгоритмов управления, ПИД-регулятор способен управлять процессом, основываясь на его истории и скорости изменения. Это дает более точный и стабильный метод управления.

 

   Основная идея в том, что контроллер получает информацию о состоянии системы с помощью датчика. Затем вычитает измеренное значение из опорного для вычисления ошибки. Ошибка будет обрабатываться тремя путями: обрабатываться в настоящем времени пропорциональной составляющей, возвращаться в прошлое, используя интегральную составляющую, и предвидеть будущее, через дифференциальную составляющую.

 

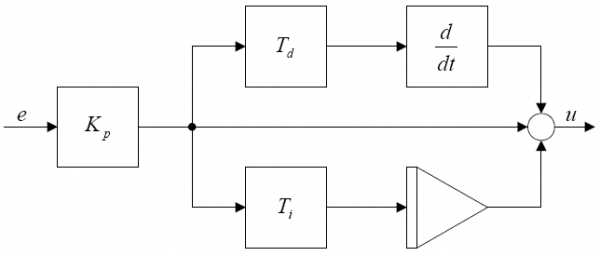
   Рисунок 2-2 показывает схемное решение ПИД-регулятора, где Тр, Ti, и Td обозначают постоянные времени пропорциональной, интегральной и дифференциальной составляющих соответственно. 

 

Рисунок 2-2. Схема ПИД-регулятора

 

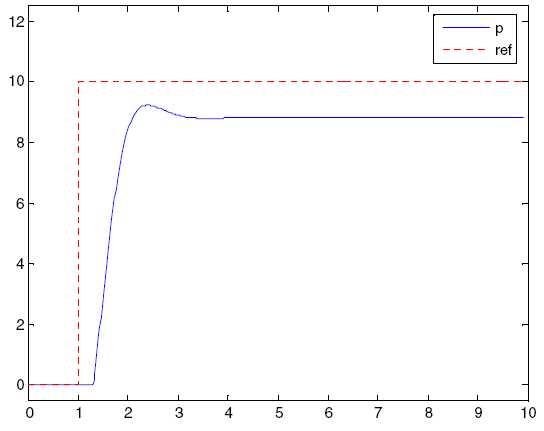
   Пропорциональная составляющая (П) дает управляющий сигнал пропорционально вычисленной ошибке. Использование только одного пропорционального управления дает стационарную ошибку всегда, кроме случаев, когда управляющий сигнал равен нулю, а значение системного процесса равно требуемой величине. На рис. 2-3 стационарная ошибка в значении системного процесса появляется после изменения опорного сигнала (ref). Использование слишком большого П-члена даст неустойчивую систему.

 

Рисунок 2-3. Отклик П контроллера на ступенчатое изменение опорного сигнала

 

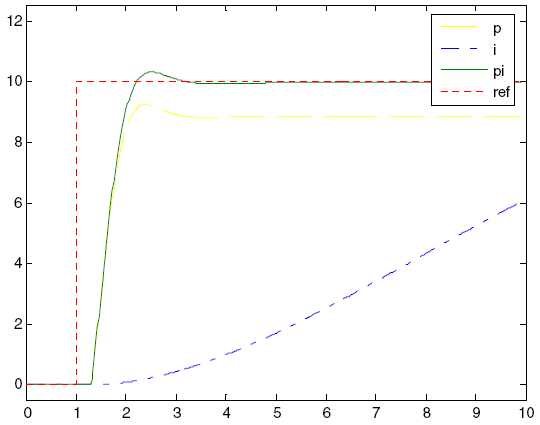
   Интегральная составляющая (И) представляет собой предыдущих ошибок. Суммирование ошибки будет продолжаться до тех пор, пока значение системного процесса не станет равно нужному значению. Обычно интегральную составляющую используют вместе с пропорциональной, в так называемых ПИ-регуляторах. Использование только интегральной составляющей дает медленный отклик и часто колебательную систему. Рисунок 2-4 показывает ступенчатый отклик И и ПИ-регуляторов. Как видите отклик ПИ-регулятора не имеет стационарной ошибки, а отклик И-регулятора очень медленной.

 

Рисунок 2-4. Отклик И- и ПИ-контроллера на ступенчатое изменение контролируемой величины

 

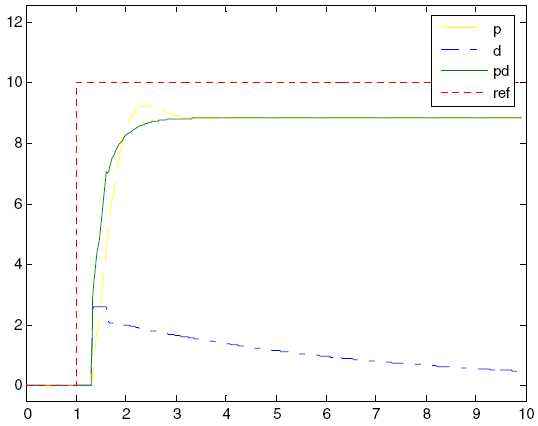
   Дифференциальная составляющая (Д) представляет собой скорость изменения ошибки. Добавление этой составляющей улучшает отклик системы на внезапное изменение ее состояния. Дифференциальная составляющая Д обычно используется с П или ПИ алгоритмами, как ПД или ПИД контроллеры. Большая дифференциальная составляющая Д обычно дает неустойчивую систему. Рисунок 2-5 показывает отклики Д и ПД- контроллера. Отклик ПД-контроллера дает быстрый рост значения процесса, чем П контроллер. Обратите внимание, что дифференциальная составляющая Д ведет себя по существу как фильтр верхних частот для сигнала ошибки и, таким образом легко делает систему нестабильной и более чувствительной к шуму.

 

Рисунок 2-5. Отклик Д- и ПД-контроллера на ступенчатое изменение опорного сигнала

 

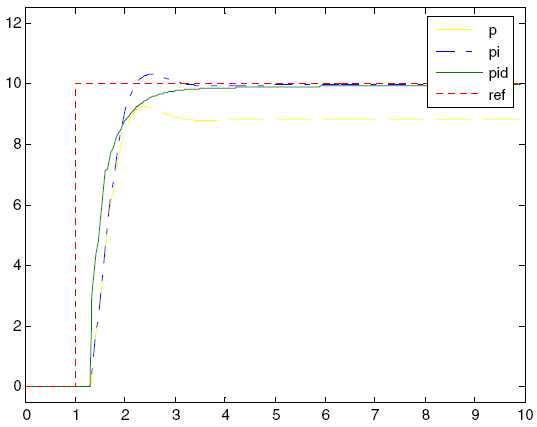
   ПИД-регулятор дает лучшую производительность, поскольку использует все составляющие вместе. Рисунок 2-6 сравнивает П, ПИ, и ПИД-регуляторы. ПИ улучшает П, удалив стационарную ошибку, и ПИД улучшает ПИ более быстрым откликом.

 

Рисунок 2-6. Отклик П-, ПИ- и ПИД-регулятора на ступенчатое изменение опорного сигнала

 

   Наилучший путь найти необходимые параметры ПИД алгоритма - это использование математической модели системы. Однако часто подробного математического описания системы нет и настройки параметров ПИД-регулятора могут быть выполнены только экспериментально. Поиск параметров для ПИД-регулятора может быть сложной задачей. Здесь большое значение имеют данные о свойствах системы и различных условиях ее работы. Некоторые процессы не должны позволить перерегулирования процесса переменной от заданного значения. Другие процессы должны минимизировать потребление энергии. Также важнейшим требованием является стабильность. Процесс не должен колебаться ни при каких условиях. Кроме того, стабилизация должна наступать в течение определенного времени.

 

   Существуют некоторые методы для настройки ПИД-регулятора. Выбор метода будет зависеть в значительной степени от того, может ли быть процесс автономным для настройки или нет. Метод Циглера-Николса это известный не автономная метод настройки. Первым шагом в этом методе является установка И и Д коэффициентов усиления в нуль, увеличивая усиление П до устойчивого и стабильного колебаний (как можно ближе). Тогда критический коэффициент усиления Кс и период колебаний Pc записывается и П, И и Д значения корректируются с использованием Таблицы 2-1.

 

Таблица 2-1. Расчет параметров по методу Циглера-Николса 

 

   Дальнейшая настройка параметров часто необходима для оптимизации производительности ПИД-регулятора. Читатель должен отметить, что есть системы, где ПИД-регулятор не будет работать. Такими могут быть нелинейные системы, но в целом, проблемы часто возникают с ПИД управлением, когда системы неустойчивы и влияние входного сигнала зависит от состояния системы.

   Дискретный ПИД-регулятор будет считывать ошибку, вычислять и выдавать управляющий сигнал за время выборки Т. Время выборки должно быть меньше, чем наименьшая постоянная времени в системе.

   В отличие от простых алгоритмов управления, ПИД-регулятор способен манипулировать управляющим сигналом на основе истории и скорости изменения измеряемого сигнала. Это дает более точный и стабильный метод управления.

 

   На рисунке 2-2 показано схемное решение ПИД-регулятора, где Тр, Ti, и Td обозначают постоянные времени пропорциональной, интегральной, и дифференциальной составляющих соответственно.

 

Передаточная функция системы, изображенной на рисунке 2-2 имеет вид:

 

 

Это дает U по отношению к e в интервале времени

 

Аппроксимируем интегральную и диффиренциальную составляющие, чтобы получить дискретный вид

 

Где n является дискретным шагом времени t.

Это дает контроллер:

 

Где 

Чтобы избежать этого изменения в значении опорного процесса делает любое нежелательное быстрое изменение на управляющем входе, контроллер улучшить основе производных срок на значений процесса только:

  К этому документу прилагается рабочее приложение, реализованное на C. Полную описание исходного кода и информации о компиляции можно найти в файле "readme.html".

Рисунок 3-1. Блок-схема демонстрационного приложения

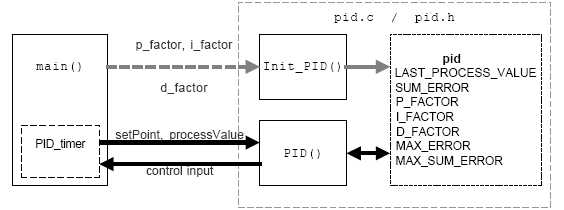  На рисунке 3-1 показана упрощенная схема демо приложения.

   ПИД-регулятор использует структуру для хранения своего статуса и параметров. Эта структура инициализируется функцией main, и только указатель на него передается функциям Init_PID() и PID(). 

 

   Функция PID () должна быть вызвана для каждого интервала времени T, это задается таймером, который устанавливает флаг PID_timer, когда время выборки прошло. Когда PID_timer флаг установлен, основная программа читает эталонное значение процесса и системное значение процесса, вызывается функция PID () и выводится результат на управляющий вход.

   Для повышения точности p_factor, i_factor и  d_factor увеличиваются в 128 раз. Результат ПИД алгоритма позже уменьшается путем деления на 128. Значение 128 используется для обеспечения оптимизации при компиляции.

Кроме того, влияние Ifactor и Dfactor будет зависеть от времени T.

   Когда входной процесс, U, достигает достаточно высокого значения, он становится ограниченным. Либо внутренним числовом диапазоном ПИД-регулятора, либо выходным диапазоном контроллера или подавляется в усилителях. Это произойдет, если есть достаточно большая разница между измеряемым значением и опорным значением, как правило, это происходит потому что процесс имеет большие нарушения , чем система способна обрабатывать.

 

   Если контроллер использует интегральную составляющую, эта ситуация может быть проблематичной. В такой ситуации интегральная составляющая будет постоянно суммироваться, но при отсутствии больших нарушений, ПИД-регулятор начнет компенсировать процесс пока интегральная сумма не вернется к норме.

 

   Это проблему можно решить несколькими способами. В данном примере максимальная интегральная сумма ограничена и не может быть больше, чем MAX_I_TERM. Правильный размер MAX_I_TERM будет зависеть от системы.

   ПИД-регулятор, представленый здесь, является упрощенным примером. Контроллер должен работать хорошо, но в некоторых приложениях может быть необходимо, чтобы контроллер был еще более надежным. Может быть необходимо добавление насыщения коррекции в интегральной составляющей, на основе пропорциональной составляющей только на значении процесса.

 

   В расчете Ifactor и Dfactor время выборки T это часть уравнения. Если время выборки Т использоваться намного меньше или больше чем на 1 секунду, точность либо Ifactor или Dfactor будет недостаточной. Можно переписать алгоритм ПИД и масштабирования, чтобы точность интегральной и диффиренциальной составляющих сохранилась.

K. J. Astrom & T. Hagglund, 1995: PID Controllers: Theory, Design, and Tuning.  International Society for Measurement and Con.

AVR221.rar

Перевел Кирилл Владимиров по просьбе ChipEnable.Ru 

chipenable.ru

принцип работы, теория и практика

Содержание:

1. Общие сведения о ПИД-регуляторе
2. Три составляющих рабочего процесса ПИД-регулятора
3. Теория и практика использования ПИД-устройств
4. Видео: О PID регуляторе простым языком

Среди множества приборов, предназначенных для коммутации, управления и выполнения других функций хочется отметить ПИД-регулятор, используемый в цепях обратной связи. Он устанавливается в системы с автоматическим управлением и поддерживает на определенном уровне значение какого-либо параметра. В большинстве случаев ПИД-регулятор участвует в регулировке температурных режимов и других величин, участвующих в различных процессах.

Общие сведения о ПИД-регуляторе

Аббревиатура ПИД происходит от английского понятия PID, и расшифровывается как Proportional, Integral, Derivative. На русском языке это сокращение включает в себя три компонента или составляющие: пропорциональную, интегрирующую, дифференцирующую.

Принцип работы ПИД-регулятора наилучшим образом подходит для контуров управления, схема которых оборудована звеньями обратной связи. В первую очередь, это различные автоматические системы где формируются сигналы управления, обеспечивающие высокое качество и точность переходных процессов.

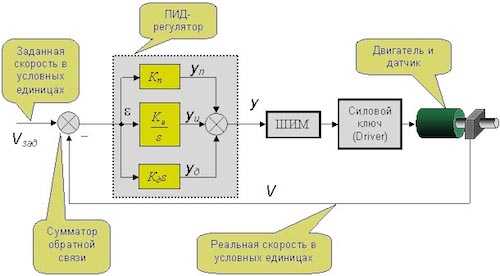
В состав управляющего сигнала ПИД-регулятора входят три основных компонента, складывающиеся между собой. Каждый из них находится в пропорции с определенной величиной:

• Первый – с сигналом рассогласования.
• Второй – с интегралом сигнала рассогласования.
• Третий – с производной сигнала рассогласования.

Если какой-либо компонент выпадет из этого процесса, то данный регулятор уже не будет представлять собой ПИД. В этом случае его схема будет просто пропорциональной, пропорционально-дифференцирующей, пропорционально-интегрирующей.

Поскольку эти приборы чаще всего используются для поддержания заданного уровня температуры, в том числе для чайников, целесообразно ПИД-регулятор рассматривать на практических примерах именно в этом ракурсе.

В самом процессе будет участвовать объект, на котором должна поддерживаться заданная температура. Все регулировки осуществляются извне. Другой составляющей будет само устройство с микроконтроллером, которое непосредственно решает имеющуюся задачу. Через измеритель на контроллер поступают данные об уровне температуры на данный момент. Мощность нагревателя отдельно контролируется специальным устройством. Для того чтобы установить требуемое значение параметров температуры, микроконтроллер нужно подключить к компьютеру.

Таким образом, исходными данными служат следующие температурные показатели: текущее значение и уровень, до которого должен нагреться или остыть рассматриваемый объект. На выходе должна получиться величина мощности, передаваемой к нагревательному элементу. Именно она обеспечивает необходимый температурный режим, позволяющий выполнить поставленную задачу. Для ее решения будут задействованы все три компонента, рассмотренные выше.

Три составляющих рабочего процесса ПИД-регулятора

Формирование выходного сигнала осуществляет пропорциональная составляющая. Данный сигнал удерживает входную величину, подлежащую регулировке, на нужном уровне и не дает ей отклоняться. С повышением этого отклонения возрастает и уровень сигнала.

Если на входе регулируемая величина сравняется с заданным значением, то уровень выходного сигнала будет равен нулю. Однако на практике невозможно отрегулировать нужную величину с помощью лишь одной пропорциональной составляющей и стабилизировать ее на определенном уровне. Всегда существует вероятность статической ошибки, равной величине отклонения, поэтому стабилизация выходного сигнала останавливается на этом значении.

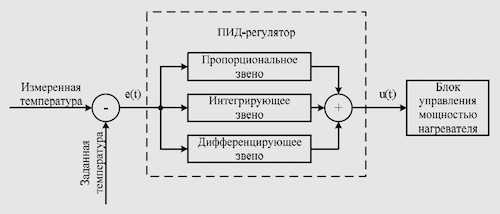
Данная проблема решается за счет использования второго, интегрирующего компонента. Его основным элементом является интеграл по времени, взятый от общей величины рассогласования. То есть, интегральная составляющая находится в пропорции с этим интегралом. Данный компонент способен ликвидировать статическую ошибку, так как регулятор постепенно накапливает учет статической погрешности.

Таким образом, при отсутствии внешних воздействий, через определенный период времени регулируемая величина будет приведена в стабильное состояние на отметке правильного значения. В этом случае величина пропорциональной составляющей будет нулевой, а интегрирующая полностью обеспечивает точность выходных данных. Однако и она может вызвать неточности, требующие исправления, в случае неправильного выбора коэффициента.

Эти отклонения устраняются за счет третьих – дифференциальных составляющих, пропорциональных с темпом изменяющегося отклонения величины. Она препятствует отклонениям, возможным в перспективе под влиянием задержек или внешних воздействий. Все три компонента дискретно связаны между собой.

Теория и практика использования ПИД-устройств

ПИД-регулятор температуры способен поддерживать заданное значение какой-то величины на протяжении определенного промежутка времени. С этой целью используется изменение напряжения и других величин, которые можно рассчитать по специальным формулам. При этом учитывается величина уставки и заданного значения, а также разница или рассогласование.

1.

2.

В идеальном варианте напряжение u задается с помощью формулы 1. В ней хорошо просматриваются коэффициенты пропорциональности ПИД-регулятора, предусмотренные для каждого компонента. На практике используется другая формула 2 с коэффициентом усиления, подходящим к любому из трех составляющих.

На практике ПИД-регулирование систем в теоретическом плане анализируются довольно редко. Это связано с недостатком информации о характеристиках регулируемого объекта, нелинейностью и нестабильностью всей системы, когда невозможно использовать дифференцирующий компонент.

Рабочий диапазон устройств, функционирующих на практике, обычно ограничивается верхним и нижним пределами. В связи с нелинейностью, каждая настройка выполняется экспериментально, при подключении объекта к системе управления.

Величина, образуемая с помощью программного алгоритма управления, имеет специфические особенности. Например, для нормальной регулировки температуры может потребоваться вместо одного сразу два прибора: один будет управлять нагревом, а другой – охлаждением. В первом случае осуществляется подача разогретого теплоносителя, а во втором – хладагента. Самым современным прибором считается цифровой ПИД-регулятор, воплотивший в своей конструкции все варианты практических регулировочных решений.

electric-220.ru

ПИД - регулятор. Основы автоматики на примере.

Всем привет. Рассмотрев в прошлой статье основу технологии построения веб-интерфейса, мы возьмем небольшую паузу с проектированием, и рассмотрим пару статей по ПИД–регулятору. Куда войдут основы автоматики, и на примере устройства синхронизации двигателей фрезерного станка на микроконтроллере, познакомимся с основными законами управления. А также рассчитаем основные коэффициенты законов для матмодели. В конце статьи выложен проект в Proteus на ATmega8.

 Но для начала «пробежимся» по основным понятиям, что б понимать о чем мы с Вами будем далее говорить. В проекте предполагается управлять двигателем, т.е. объектом. Что в свою очередь автоматика так и называет объект управления (ОУ). У него имеется три параметра: 1. Выходная величина y. 2. Входной задающий параметр u. 3. Входное возмущающее воздействие f. На рисунке слева представлен общий вид ОУ с его параметрами. Справа наш пример представленный в протеусе в виде двигателя с энкодером, где входным задающим параметром является постоянное напряжение и в зависимости от его величины изменяется частота вращения двигателя. Выходным параметром является показания энкодера, а именно угол поворота (число импульсов за один оборот). Третий параметр — возмущающее воздействие — это воздействие со стороны внешней среды, которое нарушает правильное функционирование объекта, т.е. трение, нагрузка и т.д.

 

 

 

Для исключения последнего используется второй параметр, т.е. задающий. Техническое устройство, осуществляющее автоматическое управление называется управляющим устройством (УУ). А ОУ совместно с управляющим и задающим устройствами называют систему автоматического управления (САУ). Ниже структурная схема системы.

Здесь хочется сразу добавить, что ОУ может управляться по трем основным принципам:1. Принцип разомкнутого управления – вырабатывается на основе заданного алгоритма и не контролируется другими факторами.2. Принцип компенсации возмущений, где результат возмущения в виде корректива вносится в алгоритм управления.3. Принцип управления по ошибке. Здесь коррективы вносятся в алгоритм управления по фактическому значению выходной величины.

Наш проект будет строится по последнему принципу управления – по ошибке. Ниже, слева структурная схема, а справа проект, где осуществляется управление по ошибке.

 

 

 

 

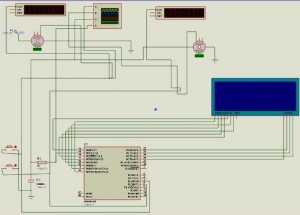
ЗУ — это у нас двигатель с энкодером (с левой стороны), с которого импульсы поступают в микроконтроллер. Где в свою очередь прописана матмодель ПИД-регулятора. Контроллер выступает в роли УУ. Далее ШИМ генерирует необходимый импульс и посылает его на вход второго двигателя с энкодером, который правее. (Мы с Вами уже рассматривали ШИМ-управление на AVR). Выход импульсов с которого, является выходной величиной и ошибкой в обратной связи y ос. Кнопки — это возмущающее воздействие, которыми мы произвольно добавляем импульсы ОУ. Где в свою очередь УУ должно быстро и плавно подрегулировать под угол поворота задающего устройства.

Далее САУ классифицируются по: 1. Алгоритму функционирования:— системы стабилизации — поддержание регулируемого параметра на заданном уровне;— программное управление – алгоритм задан в функции времени, где выходная величина изменяется во    времени по заданному закону;— следящие системы  — алгоритм функционирования заранее не известен, где регулируемая величина должна воспроизводить изменение некоторой внешней величины;— экстремальные системы — показатель качества или эффективности процесса может быть выражен в виде функции параметров системы, а сама функция имеет экстремум (максимум или минимум).— системы оптимального управления — процесс управления ведется таким образом, что некоторая характеристика процесса была бы оптимальной;— адаптивные системы – некоторые параметры ОУ и др. элементов системы могут изменяться.Наш алгоритм это программное управление, где выходная величина будет результатом ПИД управления.2. По виду дифференциальных уравнений, описываемых систему – линейные (статические характеристики всех элементов являются прямолинейными) и нелинейные (статическая характеристика является нелинейной).3. По характеру сигналов в основных элементах -  непрерывные и дискретные(в последних непрерывный входной сигнал преобразуется на выходе в последовательность импульсов).

Наш проект нелинейный и сигналы дискретные. И последнее, рассмотрим типовые законы управления, определяющие алгоритм управления в функции от ошибки управления. Под законом регулирования понимают алгоритм, в соответствии с которым управляющее устройство формирует воздействие, подаваемое на вход ОУ.  Законы управления описываются передаточными функциями, которые являются одним из способов математического описания динамической системы. Вид передаточной функции управляющего устройства определяет закон управления. Различают пять основных законов управления: пропорциональный (П), интегральный (И), пропорционально –интегральный (ПИ), пропорционально-дифференциальный (ПД), пропорционально — интегрально – дифференциальный (ПИД).

Рассмотрим каждый закон в отдельности на примере устройства синхронизации. Итак, исходные данные:

Соберем пример в Proteus. Возьмем два движка с инкрементальными энкодерами, микроконтроллер, два счетчика импульсов, а также подключим осциллограф и ЖК индикатор для отображения рассогласования (ошибки). Рассмотрение датчиков угла поворота (энкодера) выходит за пределы статьи, единственное, что нам надо знать, они предназначены для преобразования угла поворота вращающегося объекта (вала) в электрические сигналы, позволяющие определить угол его поворота. Выше был представлен рисунок нашего проекта в Proteus. Ниже на рисунке пример настройки мотора с энкодером:

Где в свойствах мотора выставим:— минимальную массу ротора EffectiveMass= 0,01;— нагрузка ротора Load/MaxTorque % = 1, чтобы он по инерции не крутился;— обороты ZeroLoad RPM=20;— количество импульсов на оборот PulsesperRevolution=24.Как видите в протеусе отдельного энкодера нет, только с двигателем. Кратко о его подключении. Один конец двигателя на землю, на второй напряжение от -12 или +12 В. И три вывода энкодера. Мы используем один как на рисунке выше. Приведенные параметры являются настроечными параметрами от которых будет зависеть динамика привода, т.е. его поведение.

П — регулятор. Одно из простых устройств и алгоритмов управления, в обратной связи, которое формирует управляющий сигнал. Выдает выходной сигнал u (t), пропорциональный входному (ошибке регулирования) e (t), с коэффициентом пропорциональности К, который вырабатывается пропорциональной частью П-регулятора в противодейтвие отклонению реглируемой величины от данного значения, в данный момент времени.

u (t)=Kр*e (t), где Kр - коэффициент усиления регулятора.

Чем больше отклонение, тем больше выход именно по данному значению. Т.е. статическая ошибка равна отклонению регулируемой величины. Здесь присутствует вероятность, что система никогда не стабилизируется на заданном значении. Увеличение коэффициента усиления увеличивает разницу между входом и выходом, при этом уменьшается статическая ошибка. Но рост этого коэффициента может привести к автоколебаниям в системе, а дальнейшее его увеличение приведет к потере устойчивости.

Обычно на практике усилительные свойства П-регулятора характеризуют следующими величинами:— предел пропорциональности d=1/Kр - величина, обратная Kр— предел пропорциональности, выраженный в процентах D=d*100%=100%/Kр. Показывает, на сколько процентов от своего максимального значения должен изменится входной сигнал, чтобы выходной изменился на 100%.

Автоколеба́ния — это незатухающие колебания в диссипативной ( устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне) динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, т. е. непериодического внешнего воздействия.На рисунке ниже слева нормальный процесс П-регулирования, где видно, что линейность  графика прямо пропорционально уменьшению ошибки. Справа, процесс автоколебаний в системе при большом коэффициенте.

 

 

 

 

 

 

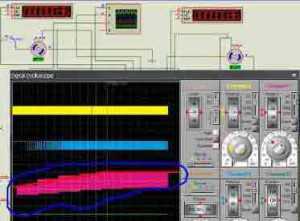
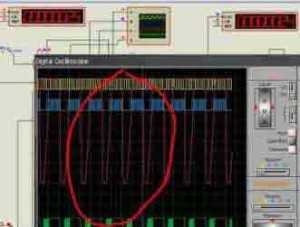
П-регулятор находит свое применение в тех же процессах, где не требуется точного поддержания заданного значения, описанных ранее, то есть в контролируемом процессе будет присутствовать статическая ошибка. Возникает данная ошибка из-за того, что выходной сигнал слишком мал для оказания существенного воздействия на поддержание системы на заданном уровне. Вполне допускается, что регулятор выведет требуемое значение, но при возникновении возмущающих воздействий, регулятор не сможет вернуть заданное значение, пока рассогласование не станет достаточно велико, чтобы выходной сигнал смог оказать достаточное воздействие. Для нашего примера такой закон не подходит. Идем далее.

И-регулятор. Что значит интегральное управление? А то, что устройство вырабатывает сигнал (u (t)), пропорциональный интегралу от ошибки регулирования (e (t)). Система при таком законе астатическая, т.е.возмущение происходит на том участке системы, который находится за интегрирующим звеном. Но при этом динамические свойства системы с И-законом обычно хуже чем у системы П-управления. Ниже представлен закон И-регулятора.

где K0 - коэффициент усиления регулятора. Скорость изменения выхода  И-регулятора пропорциональна ошибке регулирования. Обычно на практике усилительные свойства И-регулятора характеризуют временем изодрома.

Время изодрома Ти=1/K0 - величина, обратная K0. Также показывает за какое время выход регулятора изменится на 100% (регулирующий орган переместится из одного крайнего положения в другое) при скачкообразном изменении входного сигнала на 100%. Таким образом Ти характеризует быстродействие регулятора. С уменьшением T растет колебательность переходного процесса. При слишком малых значениях T система регулирования может перейти в неустойчивое состояние. Ниже на рисунке слева устойчивое состояние, справа — неустойчивое состояние.

 

 

 

 

 

 

 

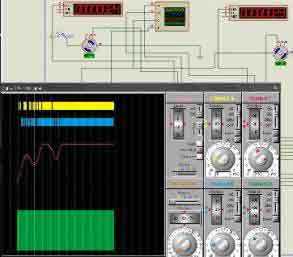
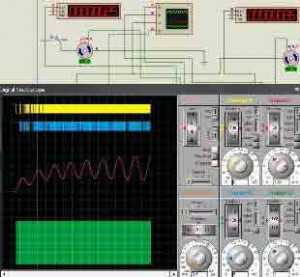
В системе регулирования с И-регулятором обычно отсутствует статическая ошибка регулирования. Как правило И-регулятор не используется самостоятельно, а в составе ПИ- или ПИД- регуляторов.

ПИ-регулятор. Изодромное управление. Управляющее устройство вырабатывает суму двух сигналов — пропорционального ошибке и пропорционального интегралу от ошибки. Выходной сигнал ПИ-регулятора ( u (t) ) зависит и от ошибки регулирования ( e (t) ), и от интеграла от этой ошибки. K1 - коэффициент усиления пропорциональной части,K0 - коэффициент усиления интегральной части

Так как  ПИ-регулятор можно рассматривать как два регулятора, соединенные параллельно, то усилительные свойства ПИ-регулятора характеризуют два параметра:1) предел пропорциональности d=1/K1 - величина, обратная K12) время изодрома Ти=1/K0 — величина, обратная K0 .

Динамические свойства системы с ПИ-регулятором лучше, чем с  И-законом. Изодромная система в переходном режиме приближается к системе с пропорциональным управлением. А  в установившемся режиме подобна системе с интегральным управлением.  Чем больше коэффициент пропорциональности, тем меньше выходная мощность при одной и той же ошибке регулирования, чем больше постоянная времени интегрирования, тем медленнее накапливается интегральная составляющая. ПИ регулирование обеспечивает нулевую ошибку регулирования и нечувствительно к помехам измерительного канала. Ошибка регулирования (статическая) исключается за счет интегрального звена, которое образуется  путем  постоянного  суммирования  ε  за  определенный  промежуток  времени и формирования сигнала управления, пропорционального полученной величине.

Недостатком ПИ регулирования является медленная реакция на возмущающие воздействия. Для настройки ПИ регулятора следует сначала установить постоянную времени интегрирования равный нулю, а коэффициент пропорциональности — максимальным. Затем как при настройке пропорционального регулятора, уменьшением коэффициента пропорциональности нужно добиться появления в системе незатухающих колебаний. Близкое к оптимальному значение коэффициента пропорциональности будет в два раза больше того, при котором возникли колебания, а близкое к оптимальному значение постоянной времени интегрирования — на 20% меньше периода колебаний. Оптимальным является переходной процесс с 20% перерегулированием.

ПД-регулятор. Если нагрузка объекта изменяется часто и резко, и при этом объект имеет существенное запаздывание, то ПИ-регулятор дает неудовлетворительное качество регулирования. Тогда целесообразно в закон регулирования вводить дифференцирующую составляющую, т.е. воздействовать на регулирующий орган дополнительно по величине первой производной от изменения регулируемого параметра. Cигнал ПД-регулятора ( u (t) ) зависит от ошибки регулирования ( e (t) ) и от производной от этой ошибки (от скорости изменения ошибки).

ПД-регулятор характеризуют два параметра:

1. Предел пропорциональности d=1/K1 — величина обратная К1.2. Постоянная времени дифференцирования (время предварения) Тд=K2. Это интервал времени между моментами достижения регулирующим органом одинакового положения при наличии дифференциальной составляющей и без нее. Параметр настройки дифференциальной составляющей. За счет дифференциальной составляющей упреждается перемещение регулирующего органа. 

Дифференцирующее звено вычисляет скорость изменения ошибки, т.е. прогнозирует направление и величину изменения ошибки. Если она положительна, то ошибка растет и дифференцирующая часть вместе с пропорциональной увеличивает воздействие регулятора на объект. Если отрицательна — уменьшается воздействие на объект. Эта система регулирования имеет статическую ошибку регулирования, но быстродействие у нее выше, чем П- , И- , Пи-регуляторы. В начале переходного процесса ПД-регулятор имеет высокое усиление и, следовательно, точность, а в установившемся режиме он вырождается в П-регулятор со свойственной ему статической ошибкой. Если статическую ошибку скомпенсировать, как это делается в П-регуляторах, то возрастет ошибка в начале переходного процесса. Таким образом, ПД-регулятор по своим потребительским свойствам оказывается хуже П-регулятора, поэтому на практике он используется крайне редко. П-звено имеет положительное свойство — вносит в контур регулирования положительный фазовый сдвиг, что повышает запас устойчивости системы при малом времени предварения. Однако с увеличением этого времени растет усиление регулятора на высоких частотах, что приводит к режиму автоколебаний. Чем больше время дифференцирования, тем больше скачок в перемещении регулирующего органа.

ПИД-регулятор. Это сумма трех регуляторов П, И и Д (Пропорционально-интегрально-дифференцирующий). Выходной сигнал ПИД-регулятора ( u (t) ) зависит от ошибки регулирования ( e (t) ), от интеграла от этой ошибки и от производной от этой ошибки.

 Усилительные свойства характеризуют три параметра:

1. Предел пропорциональности d=1/K1.2. Время изодрома Ти=1/K0.3. Время предварения  Тд=K2.

Системы регулирования с ПИД-регуляторами сочетают в себе достоинства П- , И- , и ПД- регуляторов. В таких системах отсутствует статическая ошибка и они обладают высоким быстродействием.

Ниже выложен проект в Proteus на ATmega8. Где представлена выше описанная модель ПИД — регулятора.

Синхронизация двигателей станка( Скачали: 319 чел. ) 

В следующей статье рассмотрим расчет основных коэффициентов законов регулирования для нашего проекта, а именно синхронизации двигателей станка. Написание матмодели для микроконтроллера и существующие варианты. А также этапы проектирования: от замысла до платы. На этом мы сегодня и остановимся. Всем пока.

Просмотрено 9890 раз.

www.ap-impulse.ru

Разработка роботов » Архив » Дискретный ПИД регулятор

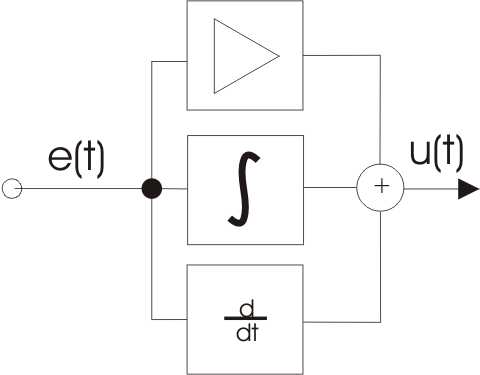При разработке автоматических систем, таких как система следования по заданной траектории мобильного робота или система поддержания постоянной температуры, возникает необходимость поддержания какого-либо параметра в соответствии с заданным значением. Само заданное значение может достаточно быстро меняться во времени. Теория автоматического управления для этой цели предлагает использовать регуляторы. Наиболее распространён ПИД (пропорциональный интегральный дифференциальный) регулятор. В данной статье рассмотрим на простом примере, что он собой представляет и как его реализовать на C++.

Сначала вкратце опишу, в чём заключается сама проблема регулирования. Допустим, у нас имеется мобильный робот, которому нужно повернуться на 30 градусов вокруг центра масс. Поворот осуществляется подачей на его привода требуемой угловой скорости вращения вокруг центра масс. Чтобы повернуться именно на 30 градусов требуемую угловую скорость вращения нужно подавать по определённому закону. Пока разность между текущим углом и требуемым велика, угловая скорость должна быть большой. При уменьшении разности скорость должна уменьшаться. И когда разность равна 0, скорость тоже должна стать равной 0. Но такой закон нельзя рассчитать заранее, потому что привода не моментально отрабатывают требуемую скорость, робот может кратковременно упереться в препятствие. И наконец, робот обладает моментом инерции, он может просто пролететь требуемое положение, и тогда скорость нужно будет подавать в противоположном направлении.Самое простое решение в этом случае – это подавать требуемую скорость как разность требуемого углового положения и текущего, умноженную на некоторую неотрицательную константу. Такой алгоритм называется П регулятором. Но у этого алгоритма есть существенный недостаток: если требуемое углового положение вращается с некоторой угловой скоростью, то робот никогда не догонит эту точку. Настанет такой момент, когда угловая скорость, рассчитанная П регулятором, станет равной угловой скорости вращения требуемого положения. Чтобы решить эту проблему, можно к скорости от П регулятора прибавить скорость, рассчитанную как интеграл по времени ошибки по углу умноженный на некоторую неотрицательную константу. В этом случае требуемая скорость будет тем больше, чем дольше робот не может догнать требуемое угловое положение. Такой алгоритм называется ПИ регулятором. Данный алгоритм тоже можно улучшить. Когда ошибка по углу станет равной нулю, робот из-за инерции может пролететь дальше, если до этого его скорость была достаточно большой. Неплохо бы было притормаживать более быстро, когда ошибка мала. Для этого к требуемой скорости от ПИ регулятора нужно добавить производную ошибки по времени, умноженную на положительную константу.Уравнение ПИД регулятора:

 

 

В нашем случае:u(t) – требуемая угловая скорость;e(t) – угловая ошибка;P, I, D – пропорциональная, интегральная и дифференциальная составляющие соответственно;Kp, Ki, Kd – коэффициенты ПИД регулятора.

Если вы заметили, то коэффициенты содержат постоянные времени: интегральную и дифференциальную. Они и рассчитываются исходя из модели регулируемого устройства, используя математические методы, также существуют эмпирические методы измерения постоянных времени. Обязательно нужно обратить внимание на присутствие периода дискретизации, поэтому процесс PID регулирования должен вызываться в режиме реального времени через жестко заданные интервалы времени. И если вы изменили период обновления сигнала оишбки, то необходимо скорректировать коэффициенты ПИД.

В таком виде ПИД регулятор невозможно реализовать на компьютере. Дифференцирование нужно заменить разностью, а интегрирование суммой:

u(t) = P(t) + I(t) + D(t)P(t) = Cp * e(t)I(t) = I(t – T) + Ci * e(t)D(t) = Cd * ( e(t) – e(t-T) )Cp, Ci, Cd – коэффициенты дискретного ПИД регулятора;T – период дискретизации(период, с которым вызывается ПИД регулятор).

Данное уравнение называется уравнением ПИД регулятора в конечных разностях.Чтобы регулятор не выдавал бесконечно больших значений требуемой скорости, его максимальное выдаваемое значение нужно ограничить. Также имеет смысл ограничивать минимальное выдаваемое значение.Актуальным остаётся вопрос подбора коэффициентов ПИД регулятора. Если их подобрать неправильно, система может стать неустойчивой. Т.е. робот просто начнёт крутиться на 360 градусов и никогда не остановится.

Скачать реализацию ПИД регулятора на C++.

robot-develop.org

ПИД-регулятор. Принцип работы. | MicroTechnics

Сегодняшняя статья будет посвящена такой замечательной вещи, как ПИД-регулятор. По определению, пропорционально-интегрально-дифференциальный регулятор — устройство в цепи обратной связи, используемое в системах автоматического управления для поддержания заданного значения измеряемого параметра. Чаще всего можно встретить примеры, где ПИД-регулятор используется для регулировки температуры, и, на мой взгляд, этот пример прекрасно подходит для изучения теории и понимания принципа работы регулятора. Поэтому именно задачу регулировки температуры и будем сегодня рассматривать.

Итак, что у нас имеется?

Во-первых, объект, температуру которого необходимо поддерживать на заданном уровне, кроме того, эту температуру необходимо регулировать извне. Во-вторых, наше устройство на базе микроконтроллера, с помощью которого мы и будем решать поставленную задачу. Кроме того, у нас есть измеритель температуры (он сообщит контроллеру текущую температуру) и какое-нибудь устройство для управления мощностью нагревателя. Ну и поскольку необходимо как-то задавать температуру, подключим микроконтроллер к ПК.

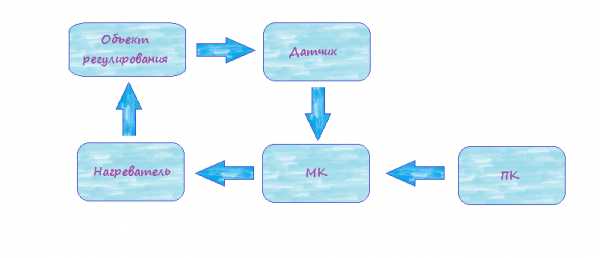
Таким образом, у нас есть входные данные – текущая температура и температура, до которой необходимо нагреть/остудить объект, а на выходе мы должны получить значение мощности, которое необходимо передать на нагревательный элемент.

И для такой задачи, да и вообще любой похожей задачи, отличным решением будет использование  пропорционально-интегрально-дифференциального регулятора 😉

Пропорциональная составляющая.

Здесь все просто, берем значение нужной нам температуры (уставку) и вычитаем из него значение текущей температуры. Получаем рассогласование (невязку). Умножаем полученную невязку на коэффициент и получаем значение мощности, которое и передаем на нагреватель. Вот и все ) Но при использовании только пропорциональной составляющей есть два больших минуса – во-первых, эффект от нашего воздействия наступает не моментально, а с запаздыванием, и, во-вторых, пропорциональная составляющая никак не учитывает воздействие окружающей среды на объект. Например, когда мы добились того, чтобы температуры объекта была равна нужному нам значению, невязка стала равна нулю, а вместе с ней и выдаваемая мощность стала нулевой. Но температура не может просто так оставаться постоянной, поскольку происходит теплообмен с окружающей средой и объект охлаждается. Таким образом, при использовании только пропорциональной составляющей температура будет колебаться около нужного нам значения.

Давайте разбираться, как ПИД-регулятор решает две выявленные проблемы )

Для решения первой используется дифференциальная составляющая. Она противодействует предполагаемым отклонениям регулируемой величины, которые могут произойти в будущем. Каким образом? Сейчас разберемся!

Итак, пусть у нас текущая температура меньше нужного нам значения. Пропорциональная составляющая начинает выдавать мощность и нагревать объект. Дифференциальная составляющая вносит свой вклад в мощность и представляет из себя производную невязки, взятую также с определенным коэффициентом. Температура растет и приближается к нужному значению, а следовательно невязка в предыдущий момент больше текущего значения невязки, а производная отрицательная. Таким образом, дифференциальная составляющая начинает постепенно снижать мощность до того, как температура достигла необходимого значения. С этим вроде разобрались, вспоминаем про вторую проблему регулятора 😉

А с ней нам поможет справиться интегральная составляющая. Как нам в программе получить интеграл? А легко – просто суммированием (накоплением) значений невязки, на то он и интеграл ) Возвращаемся к нашему примеру. Температура ниже значения уставки, начинаем подогревать. Пока мы нагреваем, значение невязки положительное и накапливается в интегральной составляющей. Когда температура “дошла” до нужного нам значения, пропорциональная и дифференциальная составляющая стали равны нулю, а интегральная перестала изменяться, но ее значение не стало равным нулю. Таким образом, благодаря накопленному интегралу мы продолжаем выдавать мощность и нагреватель поддерживает нужную нам температуру, не давая объекту охлаждаться. Вот так вот просто и эффективно =)

В итоге мы получаем следующую формулу ПИД-регулятора:

Тут  u(t) – искомое выходное воздействие, а e(t) – значение невязки.

Частенько формулу преображают к следующему виду, но суть от этого не меняется:

Пожалуй, на этом закончим, разобрались мы сегодня как работает ПИД-регулятор, а в ближайшее время разберемся еще и как произвести подбор коэффициентов ПИД-регулятора )

microtechnics.ru

---

• 
  Расшифровка конденсатор
• 
  Типы ядерных реакторов
• 
  Емкость конденсатора на что влияет
• 
  Частота ультрафиолетового излучения
• 
  Грэс это википедия
• 
  Своими руками диодный светильник
• 
  1 атмосфера равна
• 
  Когда дадут отопление в апатитах
• 
  Ряд номинальных напряжений
• 
  Икус песк личный кабинет
• 
  Параллельное и последовательное соединение закон ома