3.3. Потенциал. Разность потенциалов. Разность потенциалов в физике это

разность потенциалов в электротехнике и физике

Понятие «потенциал» широко используется в физике для характеристики различных полей и сил. Наиболее известны такие применения:

• Электромагнитный – характеристика электромагнитного поля;
• Гравитационный – характеристика полей гравитации;
• Механический – определение сил;
• Термодинамический – мера внутренней энергии тел термодинамической системы;
• Химический;
• Электродный.

Разность потенциалов

В свою очередь, электромагнитный делится на два понятия:

• Электростатический (скалярный), как характеристика электрического поля;
• Векторный, характеризующий магнитное поле.

Напряженность изменяющегося электрического поля находится через электрический потенциал, в то время как статичное поле характеризуется электростатическим.

Разность потенциалов

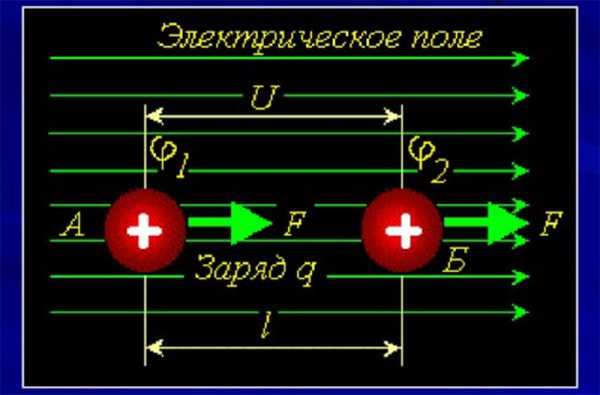
Разность потенциалов, или напряжение, – одно из основных понятий электротехники. Ее можно определить как работу электрического поля, затраченную на перенос заряда между двумя точками. Тогда на вопрос, что такое потенциал, можно ответить, что это работа по переносу единичного заряда из данной точки в бесконечность.

Как и в случае гравитационных сил, заряд, подобно телу с потенциальной энергией, имеет определенный электрический потенциал при внесении его в электрическое поле. Чем выше напряженность электрического поля, и больше величина заряда, тем выше его электрический потенциал.

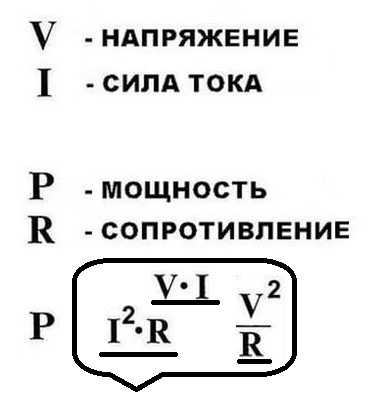
Для определения напряжения существует формула:

U=A/q,

которая связывает работу А по перемещению заряда q из одной точки в другую.

Проведя преобразование, получим:

А=Uq.

То есть чем выше напряжение, тем большую работу электрическим полем (электричеством) надо затратить по переносу зарядов.

Данное определение позволяет понять суть мощности источника питания. Чем выше его напряжение, разность потенциалов между клеммами, тем большее количество работы он может обеспечить.

Разность потенциалов измеряется в вольтах. Для измерения напряжения созданы измерительные приборы, которые именуются вольтметрами. Они основаны на принципах электродинамики. Ток, проходя по проволочной рамке вольтметра, под действием измеряемого напряжения создает электромагнитное поле. Рамка находится между полюсами магнитов.

Взаимодействие полей рамки и магнита заставляет последнюю отклониться на некоторый угол. Большая разность потенциалов создает больший ток, в результате угол отклонения увеличивается. Шкала прибора пропорциональна углу отклонения рамки, то есть разности потенциалов и проградуирована в вольтах.

Вольтметр

В руках современного электрика имеются не только стрелочные, но и цифровые измерительные приборы, которые не только измеряют электрический потенциал в определенной точке схемы, но и другие величины, характеризующие электрическую цепь. Напряжения в точках измеряются по отношению к другим, которым условно присваивают значение нуля. Тогда измеренное значение между нулевым и потенциальным выводами даст искомое напряжение.

Сказанное выше относится к напряжению как разности потенциалов между двумя зарядами. В электротехнике эта разность измеряется на участке цепи при протекании по нему тока. В случае переменного тока, то есть изменяющего во времени амплитуду и полярность, напряжение в цепи изменяется по такому же закону. Это справедливо только при наличии в схеме активных сопротивлений. Реактивные элементы в цепи переменного тока вызывают сдвиг фазы относительно протекающего тока.

Потенциометры

Напряжение источников питания, в особенности автономных, таких как аккумуляторы, химические источники, солнечные и тепловые батареи, является постоянным и не поддается регулировке. Для получения меньших значений используются, в простейшем случае, потенциометрические делители напряжения с использованием трехвыводного переменного резистора (потенциометра). Как работает потенциометр? Переменный резистор представляет собой резистивный элемент с двумя выводами, по которому может перемещаться контактный ползунок с третьим выводом.

Потенциометр-реостат

Переменный резистор может включаться двумя способами:

• Реостатным;
• Потенциометром.

В первом случае у переменного резистора используются два вывода: один – основной, другой – с ползунка. Перемещая ползунок по телу резистора, изменяют сопротивление. Включив реостат в цепь электрического тока последовательно с источником напряжения, можно регулировать ток в цепи.

Реостатное включение

Включение потенциометром требует использования всех трех выводов. Основные выводы подключаются параллельно источнику питания, а пониженное напряжение снимается с ползунка и одного из выводов.

Принцип действия потенциометра заключается в следующем. Через резистор, подключенный к источнику питания, проходит ток, который создает падение напряжения между ползунком и крайними выводами. Чем меньше сопротивление между ползунком и выводом, тем меньше напряжение. Данная схема имеет недостаток, она сильно нагружает источник питания, поскольку для корректной и точной регулировки требуется, чтобы сопротивление переменного резистора было в несколько раз меньше сопротивления нагрузки.

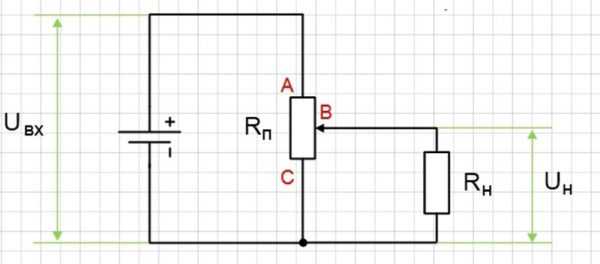
Потенциометрическое включение

Обратите внимание! Название «потенциометр» в данном случае не совсем корректно, поскольку из названия следует, что это устройство для измерения, но так как по принципу действия оно схоже с современным переменным резистором, то это название за ним прочно закрепилось, особенно в любительской среде.

Многие понятия в физике схожи и могут служить примером друг другу. Это справедливо и для такого понятия, как потенциал, который может быть как механической величиной, так и электрической. Сам по себе потенциал измерить невозможно, поэтому речь идет о разности, когда один из двух зарядов принимается за точку отсчета – нуль или заземление, как принято в электротехнике.

Видео

Оцените статью:

elquanta.ru

Потенциал электростатического поля и разность потенциалов

Потенциал электростатического поля и разность потенциалов

«Физика - 10 класс»

Обладает ли электрическое поле энергией? В чём это выражается? Как рассчитать энергию поля?

В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это силовая характеристика. Теперь введём энергетическую характеристику — потенциал.

Потенциал поля.

Работа любого электростатического поля при перемещении в нём заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля.

На замкнутой траектории работа электростатического поля всегда равна нулю.

Поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю, называют потенциальным.

Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.

Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = - (Wп2 - Wп1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой (14.14).

Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля (см. формулу (14.14)), так и для неоднородного. Следовательно, отношение потенциальной энергии к заряду не зависит от помещённого в поле заряда.

Это позволяет ввести новую количественную характеристику поля — потенциал, не зависящую от заряда, помещённого в поле.

Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень её отсчёта. При определении потенциала поля, созданного системой зарядов, как правило, предполагается, что потенциал в бесконечно удалённой точке поля равен нулю.

Потенциалом точки электростатического поля называют отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.

Согласно данному определению потенциал равен:

Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:

Напряжённость поля — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.

Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:

Разность потенциалов.

Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.

Изменение потенциала не зависит от выбора нулевого уровня отсчёта потенциала.

Так как потенциальная энергия Wn = дчр, то работа сил поля равна:

А = - (Wп2 - Wп1) = -q(φ2 - φ1) = q(φ1 - φ2) = qU.         (14.17)

Здесь

U = φ1 - φ2 —         (14.18)

разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.

Разность потенциалов называют также напряжением.

Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:

Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.

Единица разности потенциалов.

Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах.

Разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В): 1 В = 1 Дж/1 Кл.

Выразим единицу разности потенциалов через основные единицы СИ. Так как

Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электростатика - Физика, учебник для 10 класса - Класс!ная физика

Что такое электродинамика --- Электрический заряд и элементарные частицы. Закон сохранения заряд --- Закон Кулона. Единица электрического заряда --- Примеры решения задач по теме «Закон Кулона» --- Близкодействие и действие на расстоянии --- Электрическое поле --- Напряжённость электрического поля. Силовые линии --- Поле точечного заряда и заряженного шара. Принцип суперпозиции полей --- Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» --- Проводники в электростатическом поле --- Диэлектрики в электростатическом поле --- Потенциальная энергия заряженного тела в однородном электростатическом поле --- Потенциал электростатического поля и разность потенциалов --- Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности --- Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» --- Электроёмкость. Единицы электроёмкости. Конденсатор --- Энергия заряженного конденсатора. Применение конденсаторов --- Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

class-fizika.ru

Электрическое напряжение. Разность потенциалов. Напряжение тока.

 

 

 

Тема: что такое электрическое напряжение тока и разность потенциалов.

 

Пожалуй, одним из самых часто употребляемых выражений у электриков, является понятие электрическое напряжение. Его так же называют разность потенциалов и не совсем верное словосочетание, такое как напряжение тока, ну смысл у названий по сути общий. А что на самом деле обозначает это понятие? Пожалуй, для начала приведу книжную формулировку: электрическое напряжение — это отношение работы электрического поля зарядов при передачи пробного заряда из точки 1 в точку 2. Ну а простыми словами говоря, это объясняется так.

 

Напомню Вам, что заряды бывают двух видов, это положительные со знаком «+» и отрицательные со знаком «-». Большинство из нас в детстве игрались с магнитиками, которые были честно добыты из очередной сломаной машинки с электромоторчиком, где они и стояли. Так вот когда мы пытались приблизить эти самые магниты друг к другу, то в одном случае они притягивались, а если развернуть один из них наоборот, то соответственно отталкивались.

 

Это происходило, потому что у любого магнита существует два полюса, это южный и северный. В том случае, когда полюса одинаковые, то магнитики будут отталкиваться, ну а когда разноименные, притягиваться. То же самое происходит и с электрическими зарядами, причем сила взаимодействия зависит от количества и разноимённости этих заряженных частиц. Проще говоря, чем на одном предмете больше «плюса», а на другом соответственно «минуса», тем сильнее они будут притягиваться друг к другу. Либо наоборот, отталкиваться при одинаковом заряде (+ и + или - и -).

 

Теперь представим, что у нас есть два небольших железных шарика. Если мысленно заглянуть в них, можно увидеть огромное множество маленьких частичек, которые расположены друг от друга на не большом расстоянии и неспособны к свободному передвижению, это ядра нашего вещества. Вокруг этих частичек с невероятно большой скоростью вращаются более мелкие частички, под названием электроны. Они могут оторваться от одних ядер и присоединятся к другим, тем самым путешествуя по всему железному шарику. В случае, когда количество электронов соответствует количеству протонов в ядре, шарики электрически нейтральны.

 

 

А вот если каким-то образом забрать некоторое количество, такой шарик будет стремиться притянуть к себе это самое, недостающее количество электронов, тем самым образуя вокруг себя положительное поле со знаком «+». Чем больше не хватает электронов, тем сильней будет это положительное поле. В соседнем шарике сделаем на оборот и добавим лишних электронов. В итоге получим избыток и соответственно такое же электрическое поле, но со знаком «-».

 

В результате получим два потенциала, один из которых жаждет получить электроны, ну а второй от них избавится. В шаре с избытком возникает теснота и эти частицы, вокруг которых существует  поле, толкаются и выталкивают друг друга из шара. А там где их недостаток, соответственно происходит что-то наподобие вакуума, который пытается втянуть в себя эти электроны. Это наглядный пример разности потенциалов и не что иное как напряжение между ними. Но, стоит только эти железные шары соединить между собой, как произойдёт обмен и напряжение пропадёт, поскольку образуется нейтральность.

 

Грубо говоря, эта сила стремления заряженных частиц, перейти от более заряженных частей к менее заряженным между двумя точками и будет разностью потенциалов. Давайте мысленно представим провода, которые подключены к батарейке от обычного карманного фонарика. В самой батарейке происходит химическая реакция, в результате которой возникает избыток электронов («-»), внутри батареи они выталкиваются на отрицательную клемму. Эти электроны стремятся, вернутся на своё место, откуда их до этого и вытолкали.

 

Внутри батареи у них не получается, значит остаётся ждать момента, когда им сделают мостик в виде электрического проводника и по которому они быстро перебегут на плюсовую клемму батареи, куда их притягивает. А пока мостика нет, то и будет желание перейти в виде этого самого электрического напряжения или разности потенциалов (напряжение тока).

 

 

Приведу некоторый аналогичный пример на ином представлении. Имеется обычный водопроводный кран с водой. Кран закрыт и, следовательно, вода не пойдёт из него, но внутри вода всё равно есть и более того, она там находится под некоторым давлением, она из-за этого давления стремится вырваться наружу, но ей мешает закрытый кран. И как только Вы повернёте ручку краника, вода тут же побежит. Так вот это давление и можно приблизительно сравнить с напряжением, а воду с заряженными частицами. Сам поток воды будет в данном примере выступать как электрический ток в самих проводах, а закрытый краник в роли электрического выключателя. Этот пример я привел только лишь для наглядности, и он не является полной аналогией!

 

Как ни странно, но люди не тесно связанные с профессией электрика, довольно часто называют электрическое напряжение , выражением напряжение тока и это является неправильной формулировкой, поскольку напряжение, как мы выяснили это разность потенциалов электрических зарядов, а ток, это сам поток этих заряженных частиц. И получается что, произнося напряжение тока в итоге небольшое несоответствие самого понятия.

 

Напряжение, так же как и все иные величины, имеет свою единицу измерения. Она измеряется в Вольтах. Это те самые вольты, которые пишутся на устройствах и источниках питания. Например, в обычной домашней розетки 220 В, или купленная вами батарейка с напряжением 1.5 В. В общем, думаю, вы поняли в общих чертах, что же такое это самое электрическое напряжение. В этой статье я основывался лишь на простом понимании этого термина и не вдавался в глубины формулировок и формул, чтобы не усложнять понимание. На самом деле эту тему можно гораздо шире изучить, но это уже зависит от Вас и Вашего желания.

 

P.S. Будьте внимательны при работе с электричеством, высокое напряжение опасно для жизни.

electrohobby.ru

Разность потенциалов | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Определение потенциала, как и потен­циальной энергии, является в подавляющем большинстве случаев промежуточным дей­ствием. Как правило, практическое значе­ние имеет определение работы, которую выполняет электрическое поле. Связанный непосредственно с потенциальной энерги­ей, потенциал может быть определен лишь с точностью до определенной постоянной величины, значение которой зависит от выбора нулевого уровня отсчета.

Значение потенциала опреде­ляется с точностью до неко­торой постоянной величины.

Потенциал точки поля определяется по напряженности электрического поля E и расстоянию ее от нулевого уровня l.

φ = El.

Работа в электростатическом по­ле определяется однозначно.

Если выбор нулевого уровня произволь­ный, то и значение l может быть произволь­ным. Поэтому часто потенциал записывают в виде

φ = El + C,

С — константа.

Если же определять работу, которая по определению равна изменению потенциаль­ной энергии с противоположным знаком, то получается вполне определенная вели­чина:

A = qEl1 + C — qEl2 — C = qEl1 — qEl2.

Полученное выражение можно записать в виде

A = q(φ1 — φ2) = qΔφ.

Отсюда

Δφ = φ1 — φ2 = A / q.

Поскольку работа и электрический заряд измеряются однозначно, то и разность потен­циалов будет иметь вполне определенное значение. Поэтому разность потенциалов счи­тают отдельной физической величиной.

Физическая величина, характеризующая эне­ргетическое состояние поля и равная отноше­нию работы по перемещению заряженного те­ла из одной точки поля в другую к значению заряда, называется разностью потенциалов.

Разность потенциалов в элект­ростатическом поле определя­ется однозначно.

Для измерения разности потенциалов, как и потенциала, применяется единица 1 вольт и производные от него единицы: 1 мВ, 1 мкВ, 1 кВ, 1 MB. Прибор, которым измеряют разность потенциалов, называется вольтметром.

Из предыдущего известно, что разность потенциалов в однородном поле связана с напряженностью электрического поля:

φ1 — φ2 = E(l1 — l2). Материал с сайта http://worldofschool.ru

Отсюда

E = (φ1 — φ2) / (l1 — l2) = Δφ / Δl.

Последнее выражение использовано для введения единицы напряженности электри­ческого поля. При φ1 — φ2= 1 В и l1 — l2= 1 м получим Е = 1 В/м.

По разности потенциалов мож­но определить напряженность электростатического поля.

На этой странице материал по темам:

• Разность потенциалов физика величина

• Определение разность потенциалов физика

• Каким прибором измеряется разность потенциалов

• Htit,ybr yf hfpyjcnm gjntywbfkjd abpbrf

• Презентация измерения разности потенциалов

Вопросы по этому материалу:

• Почему неудобно использовать понятие потенциала для ре­шения практических задач?

• Что называется разностью потенциалов?

• Какие единицы измерения разности потенциалов?

• Каким прибором измеряется разность потенциалов?

worldofschool.ru

1.5. Потенциал. Разность потенциалов

Потенциальная энергия взаимодействия двух точечных зарядов, находящихся на расстоянии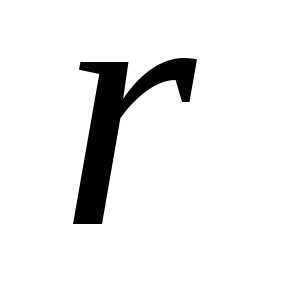

.

Потенциал электрического поля является энергетической скалярной характеристикой электрического поля и равен отношению потенциальной энергии положительного пробного точечного заряда, помещенного в данную точку поля, к величине этого заряда:

,

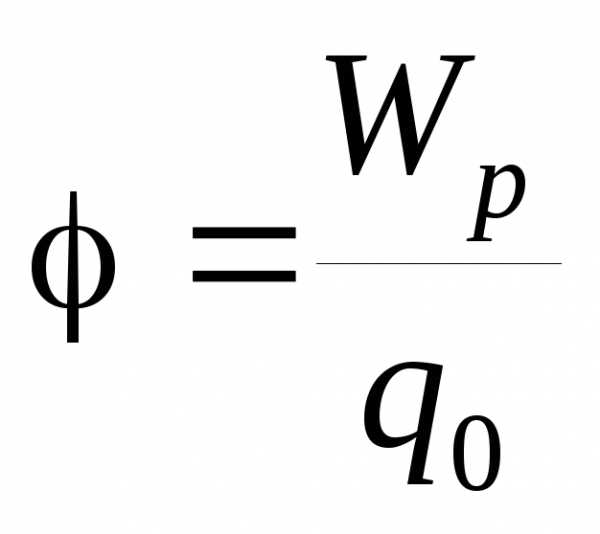где 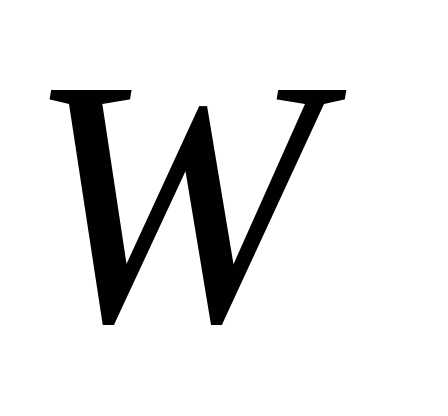– потенциальная энергия заряда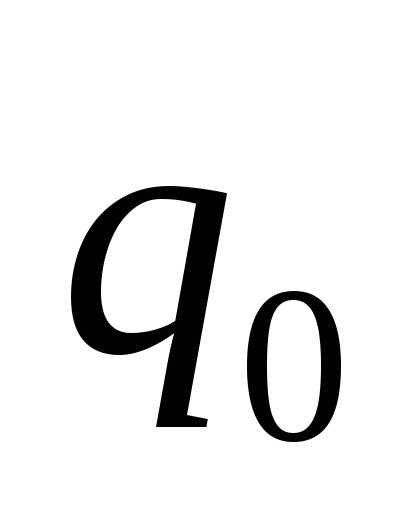, помещенного в данную точку электрического поля. Потенциальная энергия бесконечно удаленной точки принимается равной нулю. Единица потенциала – вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж.

Работа, совершенная силами поля по перемещению положительного заряда из точки 1 в точку 2:

или ,

где ‑ проекция вектора напряженностина направление; при этом интегрирование производится вдоль любой линии, соединяющей точки 1 и 2 (рис. 1.11).

Интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.

Теперь предположим, что заряд q0 перемещается из произвольной точки за пределы поля (на бесконечность), где потенциальная энергия, а значит и потенциал, равны нулю, то работа сил электростатического поля 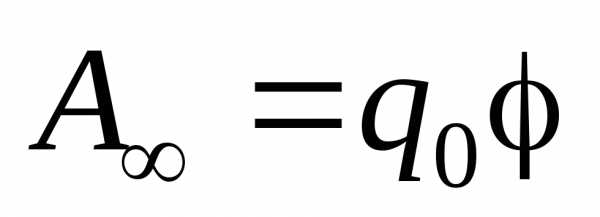, откуда получим:

.

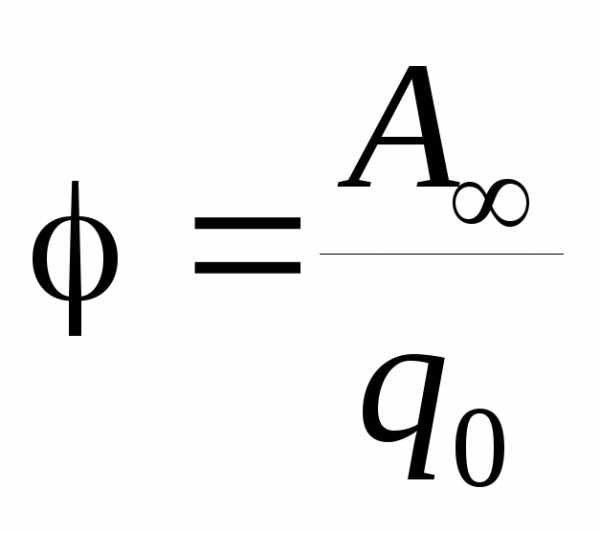Данное выражение позволяет сформулировать еще одно определение потенциала. Потенциал – это физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки пространства в бесконечность (потенциал бесконечно удаленной точки равен нулю).

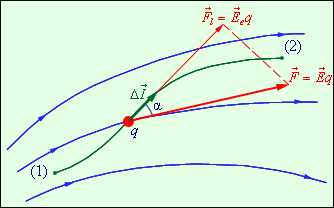
Рис. 1.11. Работа сил поля при малом перемещении заряда q

Разность потенциалов и модуль напряженности электрического поля

; ,

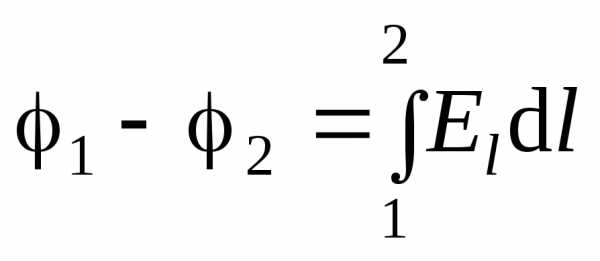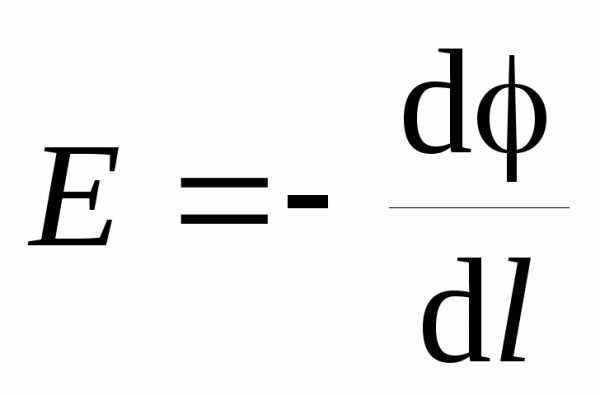где производная 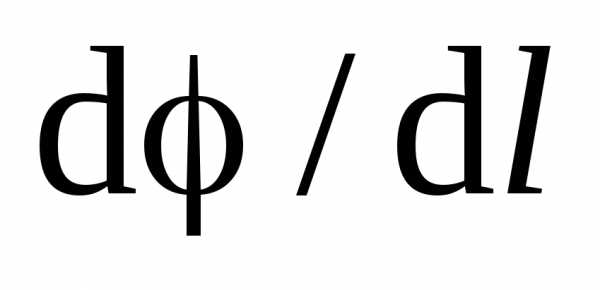берется в направлении быстрейшего изменения потенциала, т. е. вдоль силовой линии (рис. 1.12).

Для однородного поля ()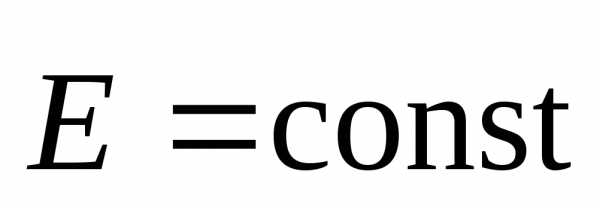

,

где ‑ расстояние между двумя точками, измеренное вдоль силовой линии.

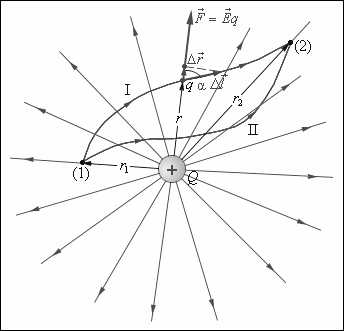
Рис. 1.12. Работа кулоновских сил при перемещении заряда q

зависит только от расстояний r1 и r2

Потенциал поля точечного заряда на расстоянииот него

.

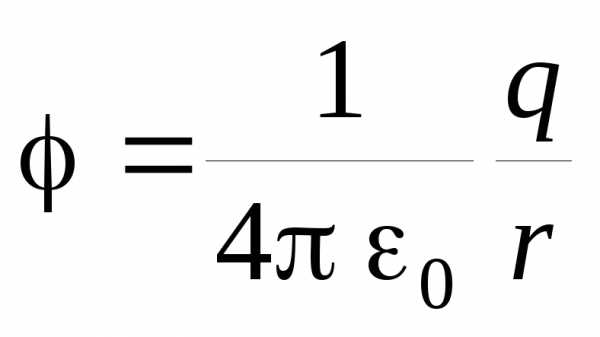Потенциал поля сферической поверхности (шара) радиуса , по которой равномерно распределен заряд:

1. 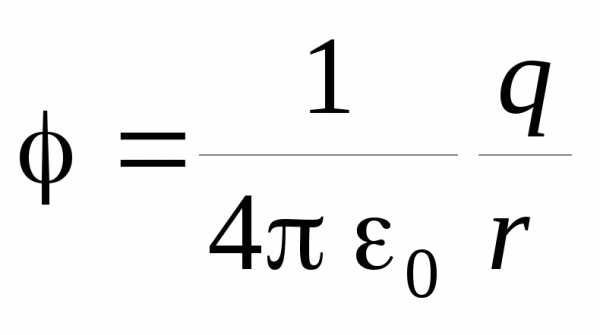 ‑ для точек, лежащих вне сферы (шара) на расстоянииот ее центра;

2.  ‑ для точек, лежащих на поверхности сферы (шара) или внутри нее.

Потенциал электрического поля внутри непроводящего шара, равномерно заряженного по объему,

,

где – диэлектрическая проницаемость материала шара;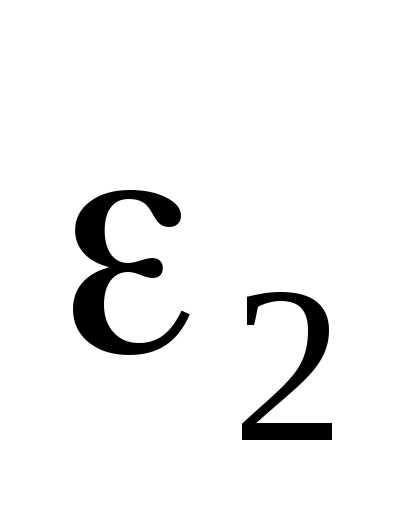– диэлектрическая проницаемость среды, в которой находится шар.

Принцип суперпозиции для потенциала электрического поля. Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности:

,

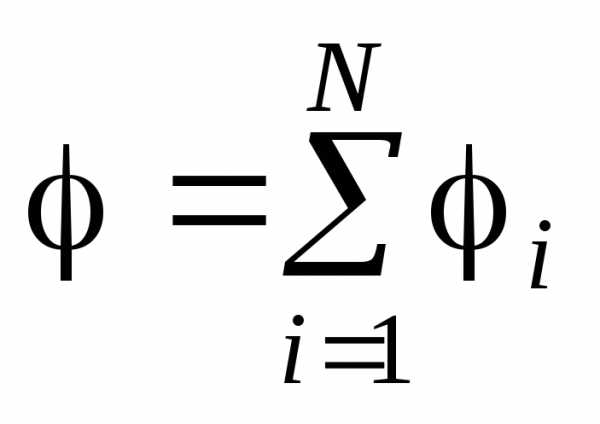где – потенциал электрического поля, созданного-м зарядом.

Для графического изображения потенциала используются эквипотенциальные поверхности– это поверхности во всех точках которых потенциал имеет одно и то же значение. Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. В любой точке эквипотенциальной поверхности силовая линия ей перпендикулярна, следовательно, перпендикулярен и вектор(рис. 1.13).

Рис. 1.13. Эквипотенциальные поверхности и силовые линии простых электрических полей: точечный заряд; электрический диполь; два равных положительных заряда

studfiles.net

3.3. Потенциал. Разность потенциалов.

Сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на заряд каждый из зарядов системы в отдельности (принцип суперпозиции).

Тогда

A = ∑Ai

Здесь каждое слагаемое не зависит от формы пути и, следовательно не зависит от формы пути и сумма.

Итак электростатическое поле потенциально.

Работу сил электростатического поля можно выразить через убыль

	потенциальной энергии – разность двух функций состояния:
	A12= Eп1– Eп2								(3.2.2)
	Тогда выражение (3.2.2) можно переписать в виде:
	A12=		qq'		−	qq'			(3.2.3)
			4πεε r			4πεε r
		0		1		0	2
	Сопоставляя формулу (3.2.2) и (3.2.3) получим выражение для потенциальной
	энергии заряда q' в поле зарядаq:	1		qq'
	En=					+const			(3.2.4)
		4πεε0			r

Потенциальную энергию определяют с точностью до постоянной интегрирования. Значение константы в выражении Eпот. выбирают таким образом, чтобы при удалении заряда на бесконечность (т. е. приr = ∞), потенциальная энергия обращалась

в нуль. Выражение (3.2.4.) – для одного заряда. Для системы зарядов
EnΣ= ∑Eni	(3.2.5)

Разные пробные заряды q',q'',… будут обладать в одной и той же точке поля разными энергиямиEn', En'' и так далее. Однако отношениеEn/q'пр. будет для всех зарядов одним и тем же.Поэтому ввели скалярную величину, являющуюся

	энергетической характеристикой собственно поля – потенциал.
	φ=	En		(3.3.1)
		q'

Из этого выражения следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

Подставив в (3.3.1.) значение потенциальной энергии (3.2.3), получим для

	потенциала точечного заряда следующее выражение:
	φ=	1	q	(3.3.2)
		4πεε0	r

Потенциал, как и потенциальная энергия, определяют с точностью до постоянной интегрирования. Договорились считать, что потенциал точки удаленной в бесконечность равен нулю. Поэтому когда говорят «потенциал такой-тоточки» – имеют в виду разность потенциалов между этой точкой и точкой, удаленной в бесконечность. Другое определение потенциала:

φ = Aq∞ или A∞ = qφ,

т.е. потенциал числено равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность

dA = Fl dl = El qdl

(наоборот – такую же работу нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.

Если поле создается системой зарядов, то, используя принцип суперпозиции, получим:

		1		N	qi q'
	En=			∑=					(3.3.3)
		4πεε			r
	0			i 1	i
	Тогда:			1				qi
	φ= ∑φi φ=					∑			(3.3.4)
				4πεε				r
					0			i

т.е. потенциал поля, создаваемый системой зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. А вот напряженности, как вы помните, складываются при наложении полей –векторно.

По этой причине потенциалы полей считать проще, чем напряженности.

Вернемся к работе сил электростатического поля над зарядом q'. Выразим работу

через разность потенциалов:
A12= En1− En2= φ1q′−φ2q′ = q′(φ1−φ2)	(3.3.5)
Т.о., работа над зарядом q' равна произведению заряда на убыль потенциала. То
есть:
A = q'(φ1 −φ2 )= q'U,
A = qU,	(3.3.6)

где U – разность потенциалов или еще называютнапряжение. Между прочим, хорошая аналогия:

A12 = mgh2 −mgh3 = m(gh2 − gh3 )

gh – имеет смысл потенциала гравитационного поля, а m – заряд.

Итак потенциал – скалярная величина, поэтому пользоваться и вычислять φ

проще, чем E . Приборы для измерения разности потенциалов широко распространены. ФормулуA∞=qφ можно использовать для установления единиц потенциала:за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из ∞ единичного положительного заряда необходимо совершить работу равную единице.

Так в СИ – единица потенциала 1В = 1Дж/1Кл, в СГСЭ 1ед.пот. = 300В.

В физике часто используется единица энергии и работы, называемой эВ – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1В, то есть:

1эВ =1,6 10−19 Кл В =1,6 10−19 Дж

3.4. Связь между напряженностью и потенциалом.

Итак электростатическое поле можно описать либо с помощью векторной

величины E , либо с помощью скалярной величиныφ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:

Изобразим перемещение заряда q по произвольному путиl.

Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl можно найти так:

(3.4.1)

El – проекцияE наdrl ;dl – произвольное направление перемещения заряда.

С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl.

	dA = −qdφ; El qdl= −qdφ			(3.4.2)
	El = −	dφ		(3.4.3)
		dl

Вот отсюда размерность напряженности поля В/м.

Для ориентации dl – (направление перемещения) в пространстве, надо знать проекцииE на оси координат:

Ex = −

∂φ

; Ey = −∂φ

; Ez = −

∂φ

;

(3.4.4)

∂x

∂y

∂z

r

∂φr

−

∂φr

∂φ r

(3.4.5)

E = −

∂x

i

∂y

j −

∂z

k

где i,j,k – орты осей – единичные вектора.

По определению градиента сумма первых производных от какой-либофункции по координатам есть градиент этой функции, то есть:

gradφ = ∂∂φx ri + ∂∂φy rj + ∂∂φz kr

Тогда коротко записывается так:
E = −gradφ	(3.4.6)
gradφ – вектор, показывающий направление наибыстрейшего	увеличения

функции. Знак минус говорит о том, что E направлен в сторону уменьшения потенциала электрического поля.

3.5. Силовые линии и эквипотенциальные поверхности.

Как мы с вами уже знаем, направление силовой линии (линии напряженности) в

каждой точке совпадает с направлением E .Отсюда следует, что напряженность E

равна разности потенциалов на единицу длины силовой линии.

Именно вдоль силовой линии происходит максимальное изменение потенциала.

Поэтому всегда можно определить E между двумя точками, измеряяU между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые

линии – прямые. Поэтому здесь определение E наиболее просто:

E =	U		В
					(3.5.1)
	l
			м

Теперь запишем определение эквипотенциальной поверхности.Воображаемая поверхность все точки, которой имеют одинаковый потенциал, называют

эквипотенциальной поверхностью. Уравнение этой поверхности
φ =φ (x,y,z) = const.	(3.5.2)

Рис. 3.4

При перемещении по этой поверхности на dl, потенциал не изменится:dφ = 0. Следовательно, проекция вектораE наdl равна0, то естьEl = 0. Отсюда

следует, что E в каждой точкенаправлена по нормали к эквипотенциальной поверхности.

Эквипотенциальных поверхностей можно провести сколько угодно много. По

густоте эквипотенциальных поверхностей можно судить о величине E , это будет при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине. На одной из лабораторных работах мы с вами будем моделировать электрическое поле и находить эквипотенциальные поверхности и силовые линии от электродов различной формы – очень наглядно вы увидите как могут располагаться эквипотенциальные поверхности.

Формула E = −gradφ – выражает связь потенциала с напряженностью и позволяет по известным значениямφ найти напряженность поля в каждой точке. Можно решить и

обратную задачу, т.е. по известным значениям E в каждой точке поля найти разностьφ между двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядомq при перемещении его из точки 1 в точку 2, может быть, вычислена как:

2 r r

A12 = ∫qEdl

1

С другой стороны работу можно представить в виде:

A12= q(φ1−φ2)

тогда

2	r r
φ1−φ2= ∫Edl		(3.5.3)
1

Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру φ1 = φ2 получим:

т.е. пришли к известной нам теореме о циркуляции вектора напряженности.

Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее этим

свойством, называется потенциальным. Из обращения в нуль циркуляции вектора E ,

следует, что линии E электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах и на отрицательных зарядах заканчиваются или уходят в бесконечность.

31

studfiles.net

Что такое потенциал в физике? Я никак не могу понять! Объясните мне пожалуйста простым языком)

Первое. Потенциал может быть не только у электрического поля, но и у гравитационного (например) . Второе. Сам по себе потенциал мало кому нужен, это величина довольно условная. И определяется как работа, которую надо совершить, чтоб удалить объект из данной точки в бесконечность (где взаимодействие этого объекта - заряда или массы - с источником поля уже можно считать нулевым) . А вот что таки да, ИМЕЕТ значение, - так это РАЗНОСТЬ потенциалов. Потому как именно разность потенциалов между двумя точками и есть та реальная работа, которую надо затратить или можнополучить, когда заряд (или тело) перемещается из одной точки в другую. Во-первых, это то, что можно измерить, потому что не надо отправляться на бесконечность. Обе точки - вот они. Во-вторых, это то, что практически и надо. Это работа, которую надо совершить, чтоб занести рояль на пятый этаж (массу рояля надо умножить на разность потенциалов гравитационного поля между первый и пятым этажами) . Это работа, которую надо совершить, чтоб пропихнуть вот этот заряд через вот эту цепь (величина заряда на разность потенциалов электрического поля на двух концах цепи) . Описание "Потенциал показывает какой потенциальной энергией будет обладать единичный положительный заряд, помещенный в данную точку электрического поля" - НЕВЕРНОЕ описание. Потому что потенциал ВСЕГДА определяется ОТНОСИТЕЛЬНО ЧЕГО-ТО. Относительно другой точки. То есть хотя бы формально (а на самом деле и практически) должно быть указано, относительно какой точки определяется или измеряется потенциал. В формальном определении за эту вторую точку принимается бесконечность. Потому что вот этот единичный положительный заряд, как и гиря в 1 кг, потенциальной энергией обладает не "вообще", а только относительно отсчётного уровня. С гирей это особенно наглядно проявляется - относительно пола у неё одна потенциальная энергия, а относительно первого этажа (напомню, мы уже добрались до пятого) - совсем другая.

Это работа, которую тело или накопленная энергия могут выполнить.. или сама энергия. Камень на высоте может упасть и разбить что-то, это тоже "работа",сжатый газ может согреть еду или машинный двигатель заставит работать.. они все обладали потенциалом в моих примерах. Да, формулировка правильная.. разность потенциалов и позволяет двигаться электрону или другой частице и обеспечить ток.. говорю примитивно чтоб мозг не вынести..

Мне кажется по простому что у этого человека есть вероятность чего то достигнуть выдающего именно в физике.

Возможность ...

Если попросту, то напор воды - потенциал, давление сжатой (ну или растянутой) пружины - тоже потенциал.

Потенциал, это работа, совершаемая силами поля, при переносе единичного заряда из данной точки поля в бесконечность.

частица энергии

потенциал - скалярная физическая величина, равная отношению потенциальной энергии, которой обладает пробный положительный заряд, помещённый в данную точку поля, к значению этого заряда

touch.otvet.mail.ru

---

• 
  Www gas nn
• 
  Мини грэс
• 
  Удельное электрическое сопротивление грунта
• 
  Счетчик электроэнергии как смотреть
• 
  Как сделать проводку в гараже своими руками видео
• 
  Ток от напряжения и мощности
• 
  Разница провод кабель
• 
  Почему не проводят газ выше 10 этажа
• 
  Комбинированная розетка для духовки и варочной панели
• 
  Охранная зона воздушной линии электропередачи
• 
  Срок эксплуатации батарей отопления в квартире