История чисел и система счисления, позиционные системы (кратко). Систему счисления

система счисления. Виды систем счисления

В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий. Основная цель - не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.

Что это значит?

Начнем с определения основного понятия. Как отмечает учебник "Информатика", система счисления - это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.

В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.

В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.

В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.

Непозиционные системы

К непозиционным системам счисления относятся:

1. Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
2. Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.
3. Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
4. Вавилонская система счисления, в которой использовалось всего два обозначения для записи – клинья и стрелочки.
5. В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.

Позиционные системы

Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:

• двоичная;
• восьмеричная;
• десятичная;
• шестнадцатеричная;
• шестидесятеричная, используемая при счете времени (к примеру, в минуте - 60 секунд, в часе - 60 минут).

Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.

Десятичная система

Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.

Двоичная система

Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.

Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.

Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Восьмеричная система

Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.

Двоично-десятичная система

Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.

Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.

Шестнадцатеричная система

В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.

При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.

Перевод чисел: из десятичной в двоичную

Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.

Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.

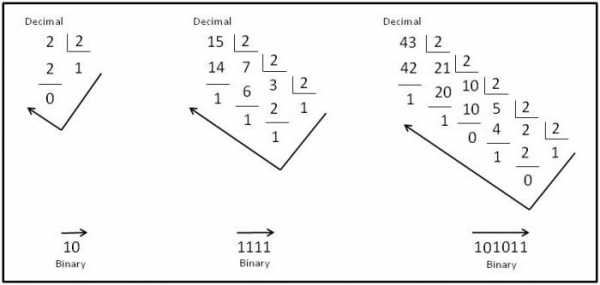
Например, переведем число 9 в двоичную систему:

Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.

После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.

Проводим ту же операцию с 2. В остатке получаем 0.

В итоге деления у нас получается 1.

Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.

Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.

Перевод чисел: из двоичной в десятичную

Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.

Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.

Для школьников этот алгоритм можно объяснить проще:

Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.

Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.

Выглядеть это будет следующим образом:

1*23 + 0*22+0*21+1*20= 8+0+0+1 =9.

При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.

Другие варианты перевода

В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».

Арифметические операции

Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.

Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.

Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.

fb.ru

Самые популярные системы счисления

Система счисления – это особый способ записи чисел с использованием определенного набора цифр - специальных знаков. Этот набор цифр представляет собой некое подобие алфавита, благодаря которому человек может прочесть записанное число.

В процессе  развития цивилизации возникало множество систем записи чисел. Сначала это были примитивные кружочки, палочки или крючки, количество которых равнялось количеству подсчитанных предметов. В качестве цифр могли выступать и буквы алфавита, и даже слоги речи. В конечном итоге все прошлые и нынешние системы счисления можно разделить на три группы: позиционные системы, непозиционные и смешанные.

В непозиционных системах вес и значимость цифры не зависит напрямую от занимаемой в числе позиции. При этом накладываются определенные ограничения на порядок цифр, их расположение по возрастанию и убыванию. Например, всем известные римские цифры – это непозиционная система счисления.

Если в системе вес цифры напрямую изменяется в зависимости от места в  последовательности, которой это число записано, то система считается позиционной. Например, число 888 записано одинаковыми цифрами, но они имеют разное количественное значение в зависимости от занимаемого места: 8 сотен, 8 десятков, 8 единиц.

Любую позиционную систему характеризует ее основание. В позиционной системе  основание – это количество разнообразных символов или знаков, которые используются для записи цифр в данной системе. В качестве основания могут выступить любые натуральные числа. Таким образом, можно построить бесконечное множество различных позиционных систем. Сейчас широко используются десятичная система, двоичная, восьмеричная и шестнадцатеричная. Давайте обсудим их подробней.

Десятичная система

Она пришла в Европу из Индии, где возникла не позднее 6 века н.э. В системе используется 10 цифр – от нуля до девяти. При этом информацию несет не только сама цифра, но и место, на котором она стоит.

Для десятичной системы число 10 и его степени являются особенно важными. Крайняя цифра в правой части числа изображает число единиц, за ней следует число десятков, сотен, тысяч и т.д.

Причина популярности и распространенности в мире десятичной системы счисления состоит в том, что первым счетным аппаратом человека явились его руки. Число пальцев и стало отправным пунктом для системы счета.

Двоичная система

В этой системе используются две цифры – один и ноль. Система строится вокруг числа два и его степеней. Крайняя правая цифра обозначает число единиц, следующая за ней – двоек, затем - четверок, восьмерок и т.д.

С помощью удобной двоичной системы любое натуральное число можно записать как последовательность нулей и единиц. Впрочем, двоичной записью можно закодировать не только числа, но и картинки, фильмы, тексты, аудиозаписи. Технически двоичное кодирование реализуется достаточно легко, поэтому оно нашло широкое применение в сфере технологий.

Восьмеричная система

В этой системе счисления восемь цифр – от нуля до семи. В младшем разряде цифра 1 обозначает просто единицу - так же , как и в десятичной системе. Но в следующем разряде единица означает 8, затем - 64 так далее. Число 100, записанное восьмеричным кодом, читается как десятичное 64.

Для перевода восьмеричного числа 611 в двоичную систему, необходимо заменить каждую цифру этого числа соответствующей двоичной триадой. А для обратного перевода числа из двоичной системы счисления в восьмеричную необходимо выделить в нем триады справа налево, затем заменить каждую тройку цифр соответствующей цифрой из восьмеричной системы.

Шестнадцатеричная система

Число, записанное в восьмеричной системе, уже выглядит достаточно компактно. Но шестнадцатеричная система позволяет сделать запись еще компактней. От 1-й до 10-й цифры в этой системе используется обычная последовательность - от нуля до девяти, а вот в качестве следующих шести цифр (от 11 до 16) используются первые шесть букв латинского алфавита.

Как и в предыдущих системах, цифра один в младшем разряде обозначает единицу. В следующем разряде она превращается в 16 (из десятичной системы), еще в следующем – в 256 (из десятичной системы). Если цифра F стоит в младшем разряде, то она обозначает десятичное число 1.

Прямой и обратный перевод из этой системы счисления в двоичную производится аналогично рассмотренному выше переводу для восьмеричной системы.

fb.ru

Системы счисления - Компьютер для новичков

В настоящее время подавляющее число людей являются грамотными и умеют считать. Тем не менее, далеко не все в курсе, что за время человеческой цивилизации было придумано большое количество самых разнообразных систем счисления. Разные народы в различные исторические периоды использовали разные системы счета, которые видоизменялись с течением времени.

Считается, что самая первая система счета у всех народов состояла всего из одного числа, единицы. Соответственно для обозначения, какого то другого числа ее следовало повторить соответствующее количество раз. В качестве обозначения могло выступать что угодно, черточки, крестики и любые другие символы. Отсутствие письменности тоже не помеха, ведь можно использовать камешки, ракушки, плоды, веточки, делать зарубки, вязать узелки и так далее.

Таким образом, для записи числа 4 требовалось собрать 4 камешка или поставить 4 черточки: ||||. Это так называемая единичная система счисления, из которой впоследствии сформировались остальные. Все предельно просто, но очень не удобно для более менее больших чисел. Через какое то время люди догадались упростить запись, объединяя какое то количество элементов в группы и обозначая их другим символом. Чаще всего встречалась группировка по 3 и 5 элементов.

Таким образом, если договориться, что черные камни обозначают единицы, а один белый камень равен 3 черным, то для обозначения допустим 8 чужаков надо показать ●●●●●●●● черных камней или ○ белый и ●●●●● черных или ○○ белых и ●● черных. Любая из этих комбинаций обозначает в нашей условной системе число 8. Такой прием, конечно, заметно упрощал счет. Впоследствии многие народы использовали в качестве обозначения чисел буквы своего алфавита.

Римская система счисления

Одной из таких систем счисления является римская, которая до сих пор находит применение, например, для обозначения веков, цифр на циферблате аналоговых часов, разделов в документе и так далее. В ее основе лежат следующие числа и соответствующие им буквы латинского алфавита.

• 1 — I
• 5 — V
• 10 — X
• 50 — L
• 100 — C
• 500 — D
• 1000 — M

Все остальные числа получаются их комбинацией в соответствии с определенными правилами, причем 0 в римской системе отсутствует. Хотя сейчас правила довольно вольные и существует множество вариантов их трактовки отличающиеся различной степенью строгости. Мы не будем их расписывать, желающие могут найти их самостоятельно. Приведем лишь несколько примеров записи чисел в римской системе счисления.

• II — 2
• IV — 4
• XVI — 16
• XXIII — 23
• XLVIII — 48

Десятичная система счисления

Однако сейчас нам привычна система счисления основанная на цифрах от 1 до 9 и 0, это так называемые арабские цифры, хотя с исторической точки зрения это не совсем так. В итоге получается 10 цифр, поэтому она называется десятичной системой счисления с основанием системы равным 10. Считается, что она обязана своему появлению количеству пальцев на руках, что сильно упрощало жизнь. Ее особенностью является то, что в зависимости от местоположения цифры в числе меняется ее значение. Например, в числе 152 цифра 5 имеет значение 50, поскольку стоит в разряде десятков, а цифра 1 имеет значение 100 так как обозначает сотни. Это так называемая позиционная система счисления.

Так же существуют непозиционные системы, где значение цифр не зависит от их места в числе, а так же смешанные системы. Примером непозиционной системы может служить единичная система счета и с некоторой оговоркой римская.

Впрочем, еще относительно недавно в историческом масштабе, вплоть до конца XVIII века на Руси применялась пятеричная система, в которой были только цифры 0, 1, 2, 3, 4 и вытесненная из обихода современной десятичной.

Помимо уже названных систем счисления имеется множество других существовавших в разное время, а так же использующих в настоящее время в разных сферах деятельности человека. Для пересчета чисел из одной системы счисления в другую, вы можете воспользоваться онлайн конвертером систем счисления в конце статьи. Дальше мы рассмотрим несколько таких систем счисления применяющихся в компьютерной технике и программном обеспечении.

Двоичная система счисления

Почти все электронные вычислительные устройства, в том числе компьютеры используют вовсе не привычную для нас десятичную, а двоичную систему счисления, где основанием системы является 2. В ее основе лежит использование всего двух чисел 0 и 1. Это очень удобно для электронных устройств в силу технических причин, поскольку соответствует всего двум состояниям включено (1) и выключено (0) или высокий и низкий сигнал или «истина» и «ложь» и так далее. Наличие всего двух состояний упрощает техническую реализацию, повышает надежность работы, уменьшает габариты и обеспечивает высокую помехоустойчивость цифровых схем, в сравнение с аналоговыми.

В итоге любые числа представлены в виде комбинаций нулей и единиц. Например, число 4 в двоичной системе счисления записывается как 100, но читается каждый символ в отдельности, то есть «один ноль ноль». Это может запутать, поскольку запись числа 4 в двоичной системе счисления внешне не отличается от числа 100 из десятичной. В некоторых ситуациях из-за этого может возникнуть путаница. В таких случаях справа от числа подстрочным шрифтом принято указывать систему счисления, к которой относится данной число в десятичном формате. Числа из нашего примера можно записать следующим образом 410 и соответственно 1002. Так же встречается вариант указания перед двоичным числом префиксов 0b или &, то есть 0b100 или &100.

Чтобы перевести десятичное число в двоичное, можно воспользоваться калькулятором расположенным ниже или применить метод Горнера. Для этого нужно десятичное число последовательно делить на основание системы, в данном случае 2. Если результат получается с остатком, то остаток отбрасываем, пишем 1 и снова делим на 2. Если результат получается без остатка, то пишем 0 и снова делим на 2. Запись нулей и единиц осуществляется справа налево, а деление продолжается пока в частном не получится ноль. Рассмотрим это на примере и преобразуем число 1110 в двоичный вид.

11/2=5 остаток 1 5/2=2 остаток 1 2/2=1 остаток 0 1/2=0 остаток 1

В частном получился ноль, осталось записать получившиеся цифры справа налево от первой к последней и в итоге получаем, что 1110=10112

Для обратной конвертации двоичных в десятичные, можно складывать последовательно цифры слева на право, умножая получившейся в предыдущем шаге результат на 2. Пересчитаем наш пример в обратную сторону.

Дано: &1011 1+0*2=1 (на первом шаге предыдущая сумма отсутствует, поэтому 0*2 ) 0+1*2=2 1+2*2=5 1+5*2=11 Результат: 1110

Чтобы окончательно вас запутать, стоит упомянуть, что для записи чисел может применяться двоичный код, а система счета при этом использоваться десятичная. Такая комбинация называется двоично-десятичное кодирование и так же находит применение в вычислительной технике.

Шестнадцатеричная система счисления

Неудобством двоичных чисел является их громоздкость и трудность визуального восприятия человеком. Поэтому для представления двоичного кода в информатике широко используется шестнадцатеричная система счисления. Как вы уже наверно догадались, в ней используется шестнадцать символов, цифры от 0 до 9 и латинские буквы A, B, C, D, E, F соответствующие числам от 10 до 15 в десятичной системе. Шестнадцатеричное число может обозначаться словом hex.

Благодаря основанию системы равному 16 для записи 1 байта требуется всего 2 цифры в этой системе, для символов юникода требуется 4 шестнадцатеричных числа (иногда больше). Может использоваться для обозначения цветов в цветовой модели RGB, в програмировании, записи адресов IPv6, представления MAC-адреса сетевого оборудования, кодов ошибок операционных систем, записи хешей,  и так далее.

Чтобы перевести десятичное число в шестнадцатеричное используйте онлайн калькулятор систем счисления в конце статьи или воспользуйтесь алгоритмом, приведенным в примере с двоичной системой. Для примера пересчитаем число 38210

382/16=23 остаток 14, пишем E 23/16=1 остаток 7, пишем 7 1/16=0 остаток 1, пишем 1 Результат: 17E16=38210

Чтобы пересчитать шестнадцатеричное число в десятичное, нужно разбить его на разряды и цифру каждого разряда умножить на 16 в степени соответствующего разряда и сложить получившиеся числа. Проще понять на примере, для этого выполним обратную операцию: 17E16=1*162+7*161+14*160=1*256+7*16+14*1=38210

Кроме рассмотренных систем существует и большое количество позиционных систем счисления с другими основаниями. Так в компьютерах одно время использовалась система с основанием 8, а такая древняя система счисления как шестидесятеричная, используется и в наше время для обозначения времени, координат и углов.

Калькулятор систем счисления

Работает только с целыми положительными числами.

beginpc.ru

Система счисления - это... Что такое Система счисления?

Системы счисления в культуре Индо-арабская система счисления Восточноазиатские системы счисления Алфавитные системы счисления Другие системы Позиционные системы счисления Смешанные системы счисления Непозиционные системы счисления

АрабскаяИндийскиеТамильскаяБирманская	КхмерскаяЛаоскаяМонгольскаяТайская
КитайскаяЯпонскаяСучжоуКорейская	ВьетнамскаяСчётные палочки
АбджадияАрмянскаяАриабхатаКириллическая	ГреческаяЭфиопскаяЕврейскаяКатапаяди
ВавилонскаяЕгипетскаяЭтрускаяРимская	АттическаяКипуМайская
Десятичная система счисления (10)
2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60
Нега-позиционная система счисления
Симметричная система счисления
Фибоначчиева система счисления
Единичная (унарная) система счисления
Список систем счисления

Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

Системы счисления подразделяются на позиционные, непозиционные и смешанные.

Позиционные системы счисления

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.

Под позиционной системой счисления обычно понимается -ричная система счисления, которая определяется целым числом , называемым основанием системы счисления. Целое число без знака в -ричной системе счисления представляется в виде конечной линейной комбинации степеней числа :

, где  — это целые числа, называемые цифрами, удовлетворяющие неравенству .

Каждая степень в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя (номером разряда). Обычно, в ненулевых числах , левые нули опускаются.

Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число записывают в виде последовательности его -ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:

Например, число сто три представляется в десятичной системе счисления в виде:

Наиболее употребляемыми в настоящее время позиционными системами являются:

В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.

Смешанные системы счисления

Смешанная система счисления является обобщением -ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел , и каждое число в ней представляется как линейная комбинация:

, где на коэффициенты , называемые как и прежде цифрами, накладываются некоторые ограничения.

Записью числа в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса , начиная с первого ненулевого.

В зависимости от вида как функции от смешанные системы счисления могут быть степенными, показательными и т. п. Когда для некоторого , смешанная система счисления совпадает с показательной -ричной системой счисления.

Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина « дней, часов, минут, секунд» соответствует значению секунд.

Факториальная система счисления

В факториальной системе счисления основаниями являются последовательность факториалов , и каждое натуральное число представляется в виде:

, где .

Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: число, на единицу меньшее номера (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i! будет обозначать число инверсий для элемента i+1 в том множестве, в котором производятся перестановки (число элементов меньших i+1, но стоящих правее его в искомой перестановке)

Пример: рассмотрим множество перестановок из 5 элементов, всего их 5! = 120 (от перестановки с номером 0 — (1,2,3,4,5) до перестановки с номером 119 — (5,4,3,2,1)), найдём 101-ую перестановку: 100 = 4!*4 + 3!*0 + 2!*2 + 1!*0 = 96 + 4; положим ti — коэффициент при числе i!, тогда t4 = 4, t3 = 0, t2 = 2, t1 = 0 , тогда: число элементов меньших 5, но стоящих правее равно 4; число элементов меньших 4, но стоящих правее равно 0; число элементов меньших 3, но стоящих правее равно 2; число элементов меньших 2, но стоящих правее равно 0 (последний элемент в перестановке «ставится» на единственное оставшееся место) — таким образом, 101-я перестановка будет иметь вид: (5,3,1,2,4) Проверка данного метода может быть осуществлена путём непосредственного подсчёта инверсий для каждого элемента перестановки.

Фибоначчиева система счисления

Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число в ней представляется в виде:

, где  — числа Фибоначчи, , при этом в коэффициентах есть конечное количество единиц и не встречаются две единицы подряд.

Непозиционные системы счисления

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

Биномиальная система счисления

Представление, использующее биномиальные коэффициенты

, где .

Система остаточных классов (СОК)

Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей с произведением так, что каждому целому числу из отрезка ставится в соответствие набор вычетов , где

…

При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка .

В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в .

Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям .

Система счисления Штерна–Броко

Система счисления Штерна–Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна–Броко.

Системы счисления разных народов

Единичная система счисления

По-видимому, хронологически первая система счисления каждого народа, овладевшего счётом. Натуральное число изображается путём повторения одного и того же знака (чёрточки или точки). Например, чтобы изобразить число 26, нужно провести 26 чёрточек (или сделать 26 засечек на кости, камне и т.д.). Впоследствии, ради удобства восприятия больших чисел, эти знаки группируются по три или по пять. Затем равнообъёмные группы знаков начинают заменяться каким-либо новым знаком - так возникают прообразы будущих цифр.

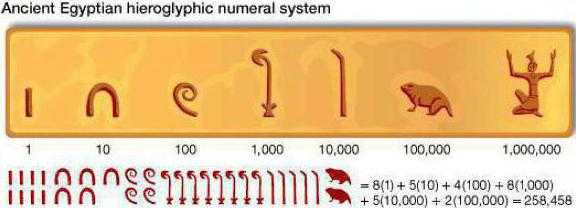
Древнеегипетская система счисления

Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия до н. э. Для обозначения чисел 0, 1, 10, 10², 10³, 104, 105, 106, 107 использовались специальные цифры. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из цифр повторялась не более девяти раз. Значение числа равно простой сумме значений цифр, участвующих в его записи.[2]

Вавилонская система счисления

Алфавитные системы счисления

Алфавитными системами счисления пользовались древние армяне, грузины, греки (ионическая система счисления), арабы (абджадия), евреи (см. гематрия) и другие народы Ближнего Востока. В славянских богослужебных книгах греческая алфавитная система была переведена на буквы кириллицы.[2]

Еврейская система счисления

Еврейская система счисления в качестве цифр использует 22 буквы еврейского алфавита. Каждая буква имеет своё числовое значение от 1 до 400 (см. т. ж. Гематрия). Ноль отсутствует. Цифры, записанные таким образом, наиболее часто можно встретить в нумерации лет по иудейскому календарю.

Греческая система счисления

Римская система счисления

Каноническим примером почти непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы:I обозначает 1,V — 5,X — 10,L — 50,C — 100,D — 500,M — 1000

Например, II = 1 + 1 = 2здесь символ I обозначает 1 независимо от места в числе.

На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:

IV = 4, в то время как:VI = 6

Система счисления майя

Майя использовали 20-ричную систему счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году.

Для записи основными знаками были точки (единицы) и отрезки (пятёрки).

Кипу инков

Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[3], так и не числовых записей в двоичной системе кодирования[4]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[5]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[6].

См. также

Примечания

Ссылки

dic.academic.ru

Перевод чисел из одной системы счисления в другую онлайн

 

 Результат уже получен!

Системы счисления

Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:

число	6	3	7	2
позиция	3	2	1	0

Тогда число 6372 можно представить в следующем виде:

6372=6000+300+70+2 =6·103+3·102+7·101+2·100.

Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.

Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:

число	1	2	8	7	.	9	2	3
позиция	3	2	1	0		-1	-2	-3

Тогда число 1287.923 можно представить в виде:

1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·103 +2·102 +8·101+7·100+9·10-1+2·10-2+3·10-3.

В общем случае формулу можно представить в следующем виде:

Цn·sn+Цn-1·sn-1+...+Ц1·s1+Ц0·s0+Д-1·s-1+Д-2·s-2+...+Д-k·s-k

(1)

где Цn-целое число в позиции n, Д-k- дробное число в позиции (-k), s - система счисления.

Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления - из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления - из множества цифр {0,1}, в шестнадцатеричной системе счисления - из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.

В таблице Таб.1 представлены числа в разных системах счисления.

Таблица 1

Система счисления
10	2	8	16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

 

Перевод чисел из одной системы счисления в другую

Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.

Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:

1·26+0·25+1·24+1·23+1·22 +0·21+1·20+0·2-1+0·2-2+1·2-3 =64+16+8+4+1+1/8=93.125

Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:

Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:

Здесь A -заменен на 10, B - на 11, C- на 12, F - на 15.

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.

Целую часть числа переводится из десятичной СС в другую систему счисления - последовательным делением целой части числа на основание системы счисления (для двоичной СС - на 2, для 8-ичной СС - на 8, для 16-ичной - на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.

Пример 4. Переведем число 159 из десятичной СС в двоичную СС:

159	2
158	79	2
1	78	39	2
	1	38	19	2
		1	18	9	2
			1	8	4	2
				1	4	2	2
					0	2	1
						0

Рис. 1

Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:

15910=100111112.

Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.

615	8
608	76	8
7	72	9	8
	4	8	1
		1

Рис. 2

При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:

61510=11478.

Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.

19673	16
19664	1229	16
9	1216	76	16
	13	64	4
		12

Рис. 3

Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 - D. Следовательно наше шестнадцатеричное число - это 4CD9.

Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.

Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).

Рассмотрим вышеизложенное на примерах.

Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.

		0.214
	x	2
0		0.428
	x	2
0		0.856
	x	2
1		0.712
	x	2
1		0.424
	x	2
0		0.848
	x	2
1		0.696
	x	2
1		0.392

Рис. 4

Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.

Следовательно можно записать:

0.21410=0.00110112.

Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.

		0.125
	x	2
0		0.25
	x	2
0		0.5
	x	2
1		0.0

Рис. 5

Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:

0.12510=0.0012.

Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.

		0.214
	x	16
3		0.424
	x	16
6		0.784
	x	16
12		0.544
	x	16
8		0.704
	x	16
11		0.264
	x	16
4		0.224

Рис. 6

Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:

0.21410=0.36C8B416.

Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.

		0.512
	x	8
4		0.096
	x	8
0		0.768
	x	8
6		0.144
	x	8
1		0.152
	x	8
1		0.216
	x	8
1		0.728

Рис. 7

Получили:

0.51210=0.4061118.

Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:

159.12510=10011111.0012.

Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:

19673.21410=4CD9.36C8B416.

matworld.ru

основание, примеры и перевод в другие системы счисления

С того момента, как человек впервые осознал себя автономным объектом в мире, огляделся вокруг, прервав замкнутый круг бездумного выживания, он начал изучать. Смотрел, сравнивал, считал, делал выводы. Именно на этих, казалось бы, элементарных действиях, которые сейчас под силу и ребенку, начали основываться современные науки.

С чем работать будем?

Для начала необходимо определиться с тем, что вообще представляет собой система счисления. Это условный принцип записи чисел, их наглядное представление, которое упрощает процесс познания. Сами по себе числа не существуют (да простит нас Пифагор, который считал число основой мироздания). Это просто абстрактный объект, что имеет физическое обоснование лишь при вычислениях, своеобразное мерило. Цифры - объекты, из которых число составляется.

Начало

Первый осознанный счет носил самый примитивный характер. Теперь его принято называть непозиционной системой счисления. На практике она представляет собой число, в которых позиция составляющих его элементов неважна. Взять, к примеру, обыкновенные черточки, каждая из которых соответствует определенному объекту: три человека эквивалентны |||. Как ни крути, три черточки - это все те же три черточки. Если брать более близкие примеры, то древние новгородцы пользовались при счете славянским алфавитом. При необходимости выделения именно числа над буквой просто проставляли знак ~. Также буквенная система счисления была в почете у древних римлян, где числа – это опять же буквы, но принадлежащие уже латинскому алфавиту.

В силу обособленности древних держав, каждая из них развивала науку самостоятельно, кто во что горазд. Примечателен тот факт, что альтернативная десятичная система счисления была выведена еще египтянами. Однако "родственницей" привычного нам понятия считать ее нельзя, так как принцип счета отличался: жители Египта использовали число десять как основание, оперируя степенями.

С развитием и усложнением процесса познания мира появилась потребность выделения разрядов. Представим, что нужно как-то зафиксировать численность армии государства, которая измеряется тысячами (в лучшем случае). Что ж теперь, бесконечно выписывать палочки? Из-за этого шумерские ученые тех лет выделили систему счисления, в которой месторасположение символа было обусловлено его разрядом. Опять же, пример: числа 789 и 987 имеют один и тот же "состав", но, в силу смены расположения цифр, второе существенно больше.

Что это такое - десятичная система счисления? Обоснование

Конечно, позиционность и закономерность были не едиными для всех методов подсчета. Например, в Вавилоне базой выступало число 60, в Греции - алфавитная система (число составляли буквы). Примечательно то, что метод подсчета жителей Вавилона жив и по сей день - он нашел свое место в астрономии.

Однако прижилась и распространилась та, у которой основание системы счисления - десятка, так как прослеживается откровенная параллель с пальцами человеческих рук. Посудите сами - поочередно сгибая пальцы, можно досчитаться чуть ли не до бесконечного множества.

Начало этой системе было положено в Индии, причем она появилась сразу на базе «10». Формирование названий чисел было двояким – например, 18 можно было прописать словом и как «восемнадцать», и как «без двух двадцать». Также именно индийские ученые вывели такое понятие, как «ноль», официально его появление зафиксировано в IX веке. Именно этот шаг стал основополагающим в формировании классических позиционных систем счисления, потому что ноль, несмотря на то, что символизирует пустоту, ничто, способен поддержать разрядность числа, дабы оно не потеряло свой смысл. Например: 100000 и 1. Первое число включает в себя 6 цифр, первая из которых – единица, а пять последних обозначают пустоту, отсутствие, а второе число – просто единица. По логике, они должны быть равны, но на практике это далеко не так. Нули в 100000 обозначают присутствие тех разрядов, которых во втором числе нет. Вот вам и «ничто».

Современность

Десятичная система счисления состоит из цифр от нуля до девяти. Числа, составленные в её рамках, строятся по следующему принципу:

крайняя справа цифра обозначает единицы, сместитесь на один шаг влево – получите десятки, еще шаг влево – сотни и так далее. Сложно? Ничего подобного! На самом деле, десятичная система примеры может предоставить весьма наглядные, взять хотя бы число 666. Состоит из трех цифр 6, каждая из которых обозначает свой разряд. Причем эта форма записи является свернутой. Если вы хотите подчеркнуть, о каком именно числе идет речь, то его можно развернуть, придав письменную форму тому, что «проговаривает» ваш внутренний голос каждый раз, когда вы видите число – «шестьсот шестьдесят шесть». Само написание включает в себя все те же единицы, десятки и сотни, то есть каждая цифра позиции умножается на определенную степень числа 10. Развернутая форма представляет собой следующее выражение:

66610 = 6х102 + 6*101 + 6*100 = 600 + 60 + 6.

Актуальные альтернативы

Второй по популярности после десятичной системы счисления является достаточно молодая разновидность - двоичная (бинарная). Появилась она благодаря вездесущему Лейбницу, который считал, что в особо сложных случаях в исследовании теории чисел бинарность будет удобнее, нежели десятизначность. Свое повсеместное распространение она получила с развитием цифровых технологий, так как имеет в основании число 2, и элементы в ней составляются из цифр 1 и 2. Кодирование информации происходит в данной системе, так как 1 - наличие сигнала, 0 - его отсутствие. На основании этого принципа можно показать несколько наглядных примеров, демонстрирующих перевод в десятичную систему счисления.

С течением времени процессы, связанные с программированием, усложнялись, поэтому ввели способы записи чисел, у которых в основании лежат 8 и 16. Почему именно они? Во-первых, количество знаков больше, а значит, само число будет короче, во-вторых - в их основе лежит степень двойки. Восьмеричная система состоит из цифр 0-7, а шестнадцатеричная - из тех же цифр, что и десятичная, плюс буквы от A до F.

Принципы и методы перевода числа

Перевести в десятичную систему счисления просто, достаточно придерживаться следующего принципа: исходное число записывается как многочлен, который состоит из сумм произведений каждого числа на основу "2", возведенную в соответствующую разрядности степень.

Основная формула для вычисления:

x2 = yk2k-1 + yk-12k-2 + yk-22k-3 + ...+ y221 + y120.

Примеры перевода

Для закрепления рассмотрим несколько выражений:

1011112 = (1x25) + (0x24) + (1x23) + (1x22) + (1x21) + (1x20) = 32 + 8 + 4 + 2 + 1 = 4710.

Усложним задачу, ибо система включает в себя перевод и дробных чисел, для этого рассмотрим отдельно целую и отдельно дробную часть - 111110,112. Итак:

111110,112 = (1x25) + (1x24) + (1x23) + (1x22) + (1x21) + (0x20) = 32 + 16 + 8 + 4 + 2 = 6210;

112 = 2-1x1 + 2-2x1 = 1/2 + 1/4 = 0,7510.

В итоге получаем, что 111110,112 = 62,7510.

Вывод

Несмотря на всю «древность», десятичная система счисления, примеры которой мы рассмотрели выше, все еще «на коне», и списывать ее со счетов не стоит. Именно она становится математической основой в школе, на ее примере познаются законы математической логики, выводится умение строить выверенные взаимосвязи. Да что уж там - практически весь мир пользуется именно этой системой, не смущаясь ее неактуальностью. Причина для этого одна: она удобная. В принципе, вывести основу счета можно любую, ею при необходимости станет даже яблоко, но зачем усложнять? Идеально выверенное количество цифр при необходимости и по пальцам пересчитать можно.

fb.ru

История чисел и система счисления, позиционные системы (кратко)

История чисел и система счисления тесно взаимосвязаны, потому что система счисления и представляет собой способ записи такого абстрактного понятия, как число. Данная тема не относится сугубо к области математики, ведь всё это является важной частью культуры народа в целом. Потому, когда разбирается история чисел и систем счисления, кратко затрагиваются и многие другие аспекты истории создавших их цивилизаций. Системы в целом делятся на позиционные, непозиционные и смешанные. Из их чередования состоят вся история чисел и систем счисления. Позиционные системы – это такие, в которых величина, обозначаемая цифрой в записи числа, зависит от ее позиции. В непозиционных системах, соответственно, такой зависимости нет. Человечеством созданы и смешанные системы.

Изучение систем счисления в школе

Сегодня урок «История чисел и систем счисления» проводится в 9 классе в рамках курса по информатике. Главное практическое его значение – научить переводить числа из одной системы счисления в другую (прежде всего из десятиричной в двоичную). Однако история чисел и систем счисления является органической частью истории в целом и вполне могла бы дополнить также и этот предмет школьной программы. Также это могло бы улучшить пропагандируемый сегодня междисциплинарный подход. В рамках общего курса истории в принципе могла бы изучаться не только история экономического развития, социально-политических движений, правлений и войн, но и в небольшой степени история чисел и систем счисления. 9 класс в курсе информатики в таком случае можно было бы в части перевода чисел из одной системы в другую снабдить значительно большим число примеров из ранее пройденного материала. А примеры эти не лишены увлекательности, что и будет показано ниже.

Возникновение систем счисления

Сложно сказать, когда, а главное, как человек научился считать (так же, как невозможно доподлинно выяснить, когда, а главное, как возник язык). Известно только, что все древние цивилизации уже имели свои системы счёта, значит, история чисел и система счисления зародились в доцивилизационное время. Камни и кости не способны рассказать нам, что происходило в человеческом сознании, а письменных источников тогда ещё не создавали. Возможно, счёт понадобился человеку при разделе добычи или много позже, уже в ходе неолитической революции, то есть при переходе к земледелию, для раздела участков поля. Любые теории на этот счёт будут в равной степени беспочвенными. Но некоторые предположения всё же можно сделать, изучая историю различных языков.

Следы древнейшей системы счисления

Самая логичная начальная система счёта – противопоставление понятий «один» – «много». Логична она для нас потому, что в современном русском языке существует только единственное и множественное число. Но во многих древних языках было также и двойственное число для обозначения двух предметов. Существовало оно и в первых индоевропейских языках, включая древнерусский. Таким образом, история чисел и система счисления начались с разделения понятий «один», «два», «много». Однако уже в самых древних известных нам цивилизациях были разработаны более детальные системы счисления.

Месопотамская запись чисел

Мы привыкли, что система счисления десятирична. Это и понятно: на руках 10 пальцев. Но тем не менее история возникновения чисел и систем счисления прошла через более сложные фазы. Месопотамская система счисления – шестидесятиричная. Потому до сих пор в часе 60 минут, а в минуте – 60 секунд. Потому год делится на число месяцев, кратное 60, а день делится на такое же число часов. Изначально это были солнечные часы, то есть каждый из них составлял 1/12 светового дня (на территории современного Ирака его длительность не сильно варьировалась). Только много позже длительность часа стали определять не по солнцу и добавили также 12 ночных часов.

Интересно то, что записывались знаки этой шестидесятиричной системы, будто она десятиричная – существовало только два знака (для обозначения единицы и десятка, не шести и не шестидесяти, а именно десятка), цифры получали, комбинируя эти знаки. Страшно себе даже вообразить, как сложно было записать сколько-нибудь большое число таким способом.

Древнеегипетская система счисления

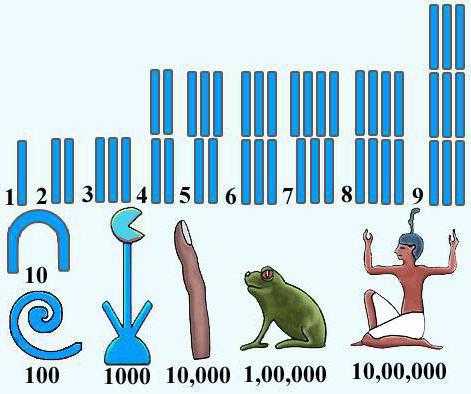И история чисел в десятиричной системе счисления, и использование многочисленных значков для обозначения чисел началось с древних египтян. Они комбинировали иероглифы, которые обозначали один, сто, тысячу, десять тысяч, сто тысяч, миллион и десять миллионов, обозначая таким образом нужное число. Такая система была гораздо удобнее, чем месопотамская, использовавшая только два знака. Но при этом она имела явное ограничение: сложно было записать число, значительно большее, чем десять миллионов. Правда, древнеегипетская цивилизация, как и большинство цивилизаций Древнего мира, с такими числами не сталкивалась.

Эллинские буквы в математических записях

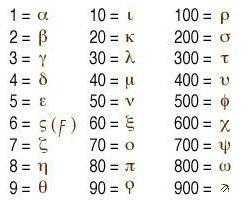История европейской философии, науки, политической мысли и многого другого во многом начинается в Древней Элладе («Эллада» – это самоназвание, оно предпочтительнее, чем придуманное римлянами «Греция»). Развиты в этой цивилизации были и математические знания. Числа эллины записывали буквами. Отдельные буквы обозначали каждое число от 1 до 9, каждый десяток от 10 до 90 и каждую сотню от 100 до 900. Только тысячу обозначали той же буквой, что и единицу, но с другим знаком рядом с буквой. Система позволяла даже большие цифры обозначать относительно короткими надписями.

Славянская система счисления как наследница эллинской

История чисел и систем счисления была бы не полной без нескольких слов о наших предках. Кириллица, как известно, основана на эллинском алфавите, потому и славянская система записи цифр также была основана на эллинской. Здесь тоже отдельными буквами обозначалось каждое число от 1 до 9, каждый десяток от 10 до 90 и каждая сотня от 100 до 900. Только использовались не эллинские буквы, а кириллица, или глаголица. Существовала также и интересная особенность: несмотря на то что и эллинские тексты в то время, и славянские с самого начала их истории записывались слева направо, славянские цифры писались как бы справа налево, то есть буквы, обозначавшие десятки ставили правее букв, обозначавших единицы, буквы, обозначавшие сотни правее букв, обозначавших десятки и т. д.

Аттическое упрощение

Эллинские учёные достигли огромных высот. Римское завоевание не прервало их изысканий. Например, судя по косвенным свидетельствам, Аристарх Самосский за 18 веков до Коперника разработал Гелиоцентрическую систему мира. Во всех этих сложных расчётах эллинским учёным помогала их система записи чисел.

Но для простых людей, например, торговцев, система зачастую оказывалась слишком сложной: чтобы её использовать, требовалось запомнить числовые значения 27 букв (вместо числовых значений 10 символов, которые учат современные школьники). Потому появилась упрощённая система, получившая название аттической (Аттика – область Эллады, одно время лидировавшая в регионе в целом и особенно в морской торговле региона, так как столицей Аттики были знаменитые Афины). В этой системе отдельными буквами стали обозначаться только числа один, пять, десять, сто, тысяча и десять тысяч. Получается всего шесть знаков – их гораздо легче запоминать, а слишком сложных вычислений торговцы всё равно не производили.

Римские цифры

И система счисления, и история чисел древних римлян, и в принципе история их науки является продолжением эллинской истории. За основу была взята аттическая система, просто эллинские буквы заменили латинскими и добавили отдельное обозначение пятидесяти и пятисот. При этом сложные расчёты в своих трактатах учёные продолжали производить эллинской системой записи в 27 букв (да и сами трактаты они обычно писали по-эллински).

Римскую систему записи чисел нельзя назвать особо совершенной. В частности, она гораздо более примитивна, чем древнерусская. Но исторически сложилось так, что она до сих пор сохраняется наравне с арабскими (так называемыми) цифрами. И забывать эту альтернативную систему, переставать её использовать не стоит. В частности, сегодня часто арабскими цифрами обозначаются количественные числительные, а римскими – порядковые.

Великое древнеиндийское изобретение

Цифры, которые сегодня используем мы, появились изначально в Индии. Точно не известно, когда история чисел и система счисления сделали этот знаменательный поворот, но, скорее всего, не позднее V века от Рождества Христова. Часто подчёркивается, что именно индийцы разработали понятие нуля. Такое понятие было известно математикам и других цивилизаций, но действительно лишь система индийцев позволила полноценно включить его в математические записи, а значит, и в вычисления.

Распространение индийской системы счисления по Земле

Предположительно в IX веке индийские цифры заимствовали арабы. В то время как европейцы пренебрежительно относились к античному наследию, а в некоторые регионах одно время даже намеренно уничтожали его как языческое, арабы бережно хранили достижения древних греков и римлян. С самого начала их завоеваний ходовым товаром стали переводы античных авторов на арабский. В основном через трактаты арабских учёных средневековые европейцы снова обрели наследие древних мыслителей. Вместе с этими трактатами пришли и индийские цифры, которые в Европе стали называть арабскими. Они не сразу были приняты, потому что для большинства людей оказались менее понятными, чем римские. Но постепенно удобство математических расчётов с помощью этих знаков победило невежественность. Лидерство европейских промышленно развитых стран привело к тому, что так называемые арабские цифры распространились по всему миру и сегодня применяются практически повсеместно.

Двоичная система счисления современных компьютеров

С появлением компьютеров постепенно совершили значительный поворот многие области знаний. Не стала исключением история чисел и систем счисления. Фото первого компьютера мало напоминает современное устройство, на мониторе которого вы читаете эту статью, но работа их обоих основана на двоичной системе счисления, коде, состоящем, только из нулей и единиц. Для обыденного сознания всё же остаётся удивительным, что с помощью комбинации из всего двух символов (фактически сигнала или его отсутствия) можно производить самые сложные вычисления и автоматически (при наличии соответствующей программы) переводить числа в десятиричной системе исчисления в числа в двоичной, шестнадцатиричной, шестидесятишестиричной и любой другой системе. И с помощью такого двоичного кода на мониторе изображается данная статья, где отражена история чисел и система счисления у разных цивилизаций в истории.

fb.ru

---

• 
  Фильтр схема
• 
  Как обозначается на схеме фаза и ноль
• 
  Коронки для подрозетников диаметр
• 
  Www vladimir esplus ru
• 
  Международная система си
• 
  Утилизация старых аккумуляторов
• 
  Www ecard dit mos ru
• 
  Материк как называется
• 
  Намагничивание стальной спицы признаки явления
• 
  Проходная розетка интернет
• 
  Допуск электробезопасности