27. Трехфазные цепи переменного тока. Соединение приемников звездой и треугольником. Основные определения. Соединение треугольником и звездой формулы
Эквивалентное преобразование треугольника в звезду
Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.
Определение соединения сопротивлений треугольником
Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.
Соединение, при котором три сопротивления, находящиеся в пассивных ветвях, соединены между собою попарно и образуют замкнутый контур - называется треугольником.
Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.
Определение соединения сопротивлений звездой
Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.
Причина преобразования треугольника в звезду
При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.
Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.
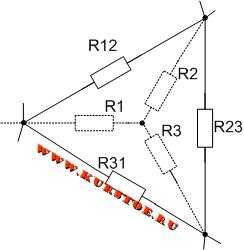
Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.
Формулы для расчета преобразования треугольника в звезду
Пример преобразования
Для электрической цепи необходимо выполнить преобразование треуголькника R12 - R23 - R31 в звезду.
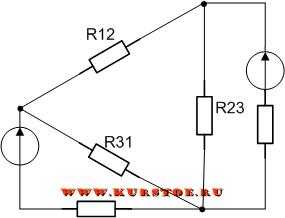
Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.
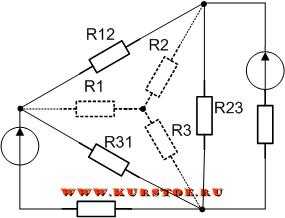
Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.
www.kurstoe.ru
Вопрос 18. Соединение резисторов треугольником и звездой. Мостовые схемы. Преобразование треугольников сопротивлений в эквивалентную звезду и наоборот.
Если имеется 3 сопротивления, образующих 3 узла, то такое сопротивление составляет пассивный треугольник, а если имеется только один узел, то сопротивления составляютпассивную звезду.
пассивный треугольник
пассивная звезда
Эти схемы можно эквивалентно заменить одна другой, если все токи в ветвях не подвергнутся преобразованию (то есть то, что за пределами штриховой линии не изменится). Из этих предпосылок получим следующие формулы преобразования:
 (преобразование треугольника в звезду):
(преобразование треугольника в звезду):
Сопротивление луча эквивалентной звезды равно произведению сопротивлений сторон треугольника, примыкающих к той же вершине, что и луч звезды, делённое на сумму всех сопротивлений сторон треугольника:
 (преобразование звезды в треугольник):
(преобразование звезды в треугольник):
Сопротивление стороны треугольника равно сумме сопротивлений лучей звезды, примыкающих к тем же вершинам, что и сторона треугольника, плюс произведение этих сопротивлений, делённое на сопротивление третьего луча звезды:
Преобразование треугольника в звезду применяется в мостовых схемах, которые представляют собой 4 резистора, соединённых четырёхугольником, в одну диагональ которого ставится источник, во вторую — измерительные приборы. Найти входное сопротивление таких схем без предварительного преобразования невозможно.
Задача
Дано:
Найти все токи и направить их.
Выполним преобразование треугольника ABC в эквивалентную звезду:
Рассчитаем входное сопротивление и ток:

Найдём напряжение на разветвлённом участке OD и токи в его ветвях:
В первоначальной схеме направим токи, ток 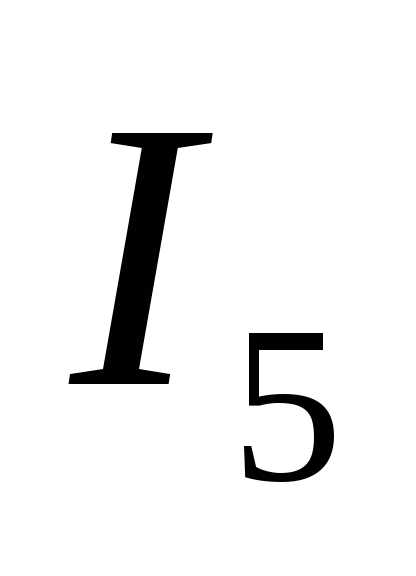 направим произвольно.
направим произвольно.
Для треугольника, который не заменяли, составляем уравнение по второму закону Кирхгофа:
Чтобы найти токи 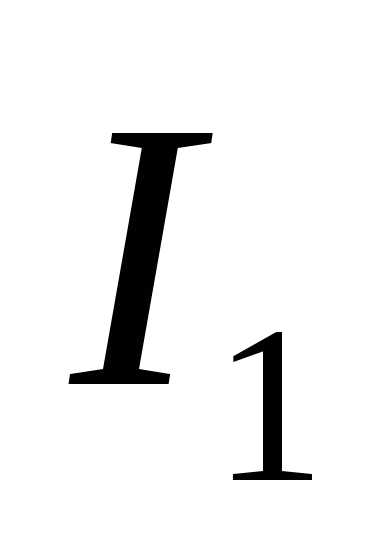 и
и 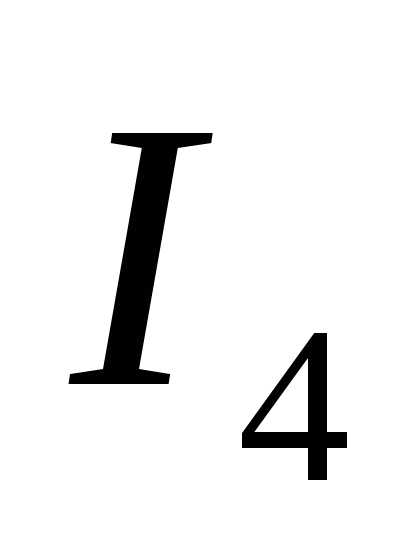 , составляем уравнения по первому закону Кирхгофа для узлов B и C:
, составляем уравнения по первому закону Кирхгофа для узлов B и C: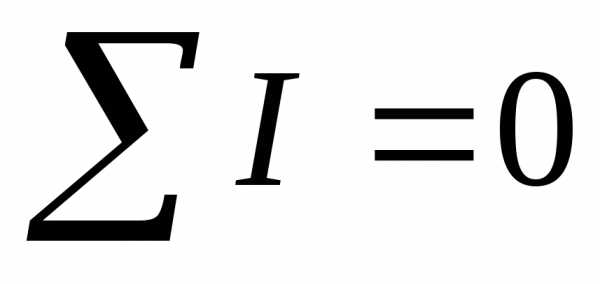
B:
С:
Вопрос 19. Первый закон Кирхгофа, узловые уравнения. Второй закон Кирхгофа, контурные уравнения.
Узел— точка, в которой сходятся не менее 3-х токов.
Ветвь— участок цепи, по которому течёт один и тот же ток.
Контур— любой замкнутый путь в схеме.
Первый закон Кирхгофа
Для любого узла сумма токов, приходящих к узлу, равна сумме токов, отходящих от узла.
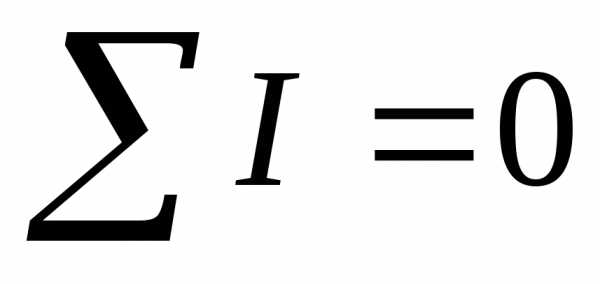
Для любого узла электрической цепи алгебраическая сумма токов равна нулю. Ток, который притекает к узлу, берётся со знаком “+”, который оттекает — со знаком “–”.
Второй закон Кирхгофа
Для любого замкнутого контура алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на участках этого контура.
Порядок составления контурных уравнений:
Выбираем произвольное направление тока ветвей.
Если в схеме n узлов, то составляем n – 1 уравнение по первому закону Кирхгофа.
Выбираем произвольное направление обхода контура.
Если направление обхода и ЭДС совпадают, то она входит в уравнение со знаком “+”, если нет — со знаком “–”.
Если ток ветви и направление обхода совпадают, то падение напряжения входит в уравнение со знаком “+”, если нет — со знаком “–”.
Если при расчёте получился отрицательный ток, значит его направление противоположно выбранному.
Задача
Составить контурные уравнения для решения сложной электрической цепи.
studfiles.net
27. Трехфазные цепи переменного тока. Соединение приемников звездой и треугольником. Основные определения
Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.
Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.
Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.
Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю.
Соответственно
На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы - последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу. Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.
2. Соединение в звезду. Схема, определения
Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.
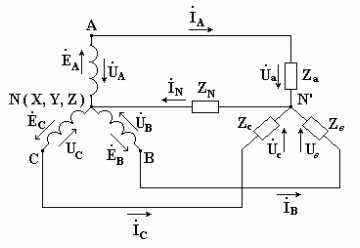 Рис. 6.1
Рис. 6.1
Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N' называют нейтральным (нулевым) проводом. Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями. Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах - линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.
Iл = Iф.
ZN - сопротивление нейтрального провода.
Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений
(7.1)
На рис. 6.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.
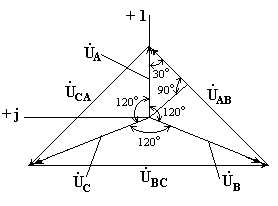 Рис. 6.2
Рис. 6.2
Из векторной диаграммы видно, что
При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз.
Uл = √3 Uф
studfiles.net
Основные сведения о трехфазном токе. Соединение звездой и треугольником.
Переменный ток, рассмотренный ранее, называется однофазным. Трехфазным называется ток, представляющий собой совокупность трех однофазных токов, сдвинутых друг относительно друга по фазе.
Простейший генератор трехфазного тока отличается от генератора однофазного тока тем, что имеет три обмотки. При вращении либо этих обмоток в поле постоянного магнита (рис.164), либо самого магнита (рис.165) в обмотках возникают переменные ЭДС одинаковой частоты, сдвинутые друг относительно друга по фазе так, что сумма трех фазных углов составляет .
Если амплитуды ЭДС равны, а сдвиг фаз между двумя любыми смежными ЭДС равен , то трехфазная система называется симметричной. В этом случае на обмотках возникают
одинаковые по величине, но сдвинутые по фазе напряжения: ,,.
Использование несвязанных между собой обмоток эквивалентно трем отдельным генераторам и требует для передачи электроэнергии потребителю три пары проводов.
Соединение обмоток между собой позволяет уменьшить количество проводов при передаче энергии и поэтому широко используется в технике.
При соединении обмоток звездой (рис.166) они имеют одну общую точку. Напряжение на каждой обмотке называется фазным. Проводник, соединенный с точкой общего потенциала, называется нулевым проводом. Проводники, соединенные со свободными концами обмоток, называются фазными проводами.
Фазные напряжения, в этом случае, это напряжения между фазными проводами и нулевым проводом. Напряжение между фазными проводами называется линейным. Ток, текущий через обмотки, называется фазным током, а ток текущий в линии, - током линии.
Из векторной диаграммы, при соединении звездой, следует, что . Кроме того при этом фазные токи равны токам в линии.
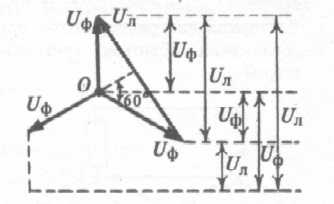
РИС.166 РИС.167 РИС.168 РИС.169 РИС.170
Если каждую обмотку замкнуть на одинаковую нагрузку R, то суммарная сила тока по нулевому проводу , так как из векторной диаграммы.
Соединение обмоток генератора звездой позволяет использовать при передаче энергии четыре провода вместо шести.
При соединении обмоток треугольником (рис.168) они образуют замкнутый контур с весьма малым сопротивлением. Линейный провод отходит от общих точек начала одной фазы и конца другой и, поэтому фазные напряжения равны линейным (рис.169).
Из векторной диаграммы токов (рис.170) следует, что
, На практике используется не только соединение обмоток генератора, но и соединение между собой нагрузок звездой или треугольником. Таких комбинаций возможного соединения генератора и нагрузок – четыре.
РИС.171 РИС.172 РИС.173 РИС.174
При соединении звезда – звезда (рис.171) на всех нагрузках разное напряжение, но если сопротивление нагрузок приблизительно равно, то ток по нулевому проводу практически равен нулю.
Тем не менее, нулевой провод нельзя убирать или ставить в него предохранители потому, что без него на каждую из пар нагрузок действует линейное напряжение, причем оно распределяется в соответствии с сопротивлением нагрузок. Получается, что напряжение, подаваемое на нагрузку, зависит от ее сопротивления, что неэффективно и опасно.
Если генератор и нагрузки соединены звезда – треугольник (рис.172), то на каждой нагрузке, независимо от ее сопротивления, одинаковое напряжение, равное линейному.
При соединении треугольник – треугольник (рис.173) на всех нагрузках фазное напряжение, независимо от их сопротивления.
Если генератор и нагрузки соединены треугольник – звезда (рис.174), то на каждой нагрузке напряжение равно .
Трехфазный ток используется для получения вращающегося магнитного поля. В этом случае трехфазный ток подводится к трем обмоткам, расположенным на неподвижной станине – статоре. Внутри статора помещен стальной барабан – ротор, вдоль образующих которого в пазах уложены провода, соединенные между собой на обоих торцах кольцами.
Обмотки статора создают магнитный поток одинаковой величины, но сдвинутый по фазе, т.е. он как бы вращается относительно ротора. В обмотках ротора возникают индукционные потоки, которые, в свою очередь, взаимодействуют с вращающимся магнитным потоком, что приводит ротор во вращение, т.е. получается электродвигатель достаточно простого устройства.
При увеличении скорости ротора уменьшается относительная скорость движения его проводников относительно магнитного поля. Если бы он достиг той же скорости вращения, что и магнитный поток статора, то индукционный ток равнялся бы нулю и, соответственно, вращающий момент стал бы равным нулю.
Следовательно, при наличии тормозного момента магнитный поток и ротор не могут вращаться с той же скоростью, что и поток статора (синхронно), - скорость вращения ротора всегда несколько меньше. Поэтому двигатели такого типа называются асихронными (несинхронными).
Трехфазная система, изобретенная русским инженером М.О.Доливо-Добровольским в XIX, применяется во всем мире для передачи и распределения энергии. Доливо-Добровольский первым получил вращающееся магнитное поле с помощью трехфазного тока и построил первый асинхронный двигатель. Трехфазная система обеспечивает наиболее экономичную передачу энергии и позволяет создать надежные в работе и простые по устройству электродвигатели, генераторы и трансформаторы.
На практике, например, электрические лампы изготавливаются на номинальные напряжения 127 и 220В. Способ их включения в цепь трехфазного тока зависит от величины линейного напряжения трехфазной сети.
Лампы с номинальным напряжением 127 В включаются звездой с нейтральным проводом при линейном напряжении сети 220 В или треугольником при линейном напряжении сети 127 В.
Лампы с номинальным напряжением 220 В соответственно включаются звездой в сеть с линейным напряжением 380 В и треугольником в сеть с напряжением 220 В.
Обмотки трехфазных двигателей изготавливаются на номинальные фазные напряжения 127, 220 и 380 В. Каждый трехфазный двигатель может быть включен или звездой в трехфазную сеть с линейным напряжением, превышающим его фазное в раз, или треугольником, если линейное напряжение сети равно фазному напряжению его обмотки. Обычно на паспорте двигателя указано, например: треугольник -220В, звезда – 380В.
Линейные цепи. Правила Кирхгофа. Методы анализа линейных цепей. Переходные процессы в цепи с конденсатором.
Элемент электрической цепи называется линейным, если его параметры не зависят от напряжения и силы тока, т.е. вольт-амперная характеристика прямая.
Электрическая цепь называется линейной если она состоит из линейных элементов.
Применение закона Ома для расчета сложных разветвленных цепей, содержащих несколько источников довольно сложно. Для расчетов таких цепей используют два правила немецкого физика Г.Кирхгофа, первое из которых вытекает из закона сохранения заряда, а второе является обобщением закона Ома на произвольное число источников сторонних ЭДС в изолированном замкнутом контуре.
Для того чтобы использовать правила Кирхгофа необходимо ввести несколько понятий.
Электрическая схема – графическое изображение электрической цепи.
Ветвь электрической цепи – один или несколько последовательно соединенных элементов цепи, по которым течет один и тот же ток.
Узел – соединение трех или большего количества ветвей. Ток, входящий в узел, считается положительным, а ток, выходящий из узла, - отрицательным.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:
Например, для узла на рис.64 I1-I2+I3-I4-I5=0
Контур – любой замкнутый путь, проходящий по нескольким ветвям. Положительное направление обхода контура выбирается произвольно, но одно и то же для всех контуров электрической цепи. Токи совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода – отрицательными. ЭДС считаются положительными, если они создают ток, направленный в сторону обхода контура.
Рассмотрим цепь, содержащую три источника (рис.65). Пусть R1, R2, R3 общие сопротивления ветвей АВ, ВС, СА соответственно. Положительное направление обхода примем по часовой стрелке. Применим к каждой ветви закон Ома для неоднородного участка цепи.
Сложив почленно эти уравнения, получим
Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:
При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1.выбрать произвольное направление токов на всех участках цепи; действительное направление токов выяснится при решении: если искомый ток получится положительным, то его направление было выбрано правильно, а если отрицательным, то его истинное направление противоположно выбранному;
2.выбрать направление обхода контуров и строго его придерживаться; записывая со соответствующими знаками токи и ЭДС;
3.составить количество уравнений равное количеству искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи).
Переходные процессы в RС и RL-цепях
Переходные процессы в электрических цепях возникают при включении или выключении э д с, а также при изменении одного или нескольких параметров цепи.
Переходные процессы в электрических линейных цепях описываются линейными дифференциальными уравнениями, составленными согласно правил Кирхгофа.
Ток заряда в RC-цепи при переходном процессе определяется
(I0 = СdUc /dt).
Iз =(U0/R) e-t/c. (8)
Напряжение на активном сопротивлении (UR =Iз R)
UR = U0 e-t/c. (9)
Анализ полученных временных зависимостей Uc(t) и Iз(t) в RC-цепи во время переходного процесса показывает, что с течением времени напряжение на конденсаторе Uc возрастает, стремясь к U0 (рис. 4), а ток убывает от значения, равного U0 /R , до нуля (рис. 5). При этом изменение напряжения на конденсаторе и тока в цепи при переходном режиме происходит тем быстрее, чем меньше постоянная времени цепи c = RC.
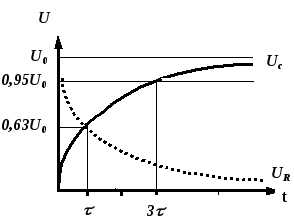
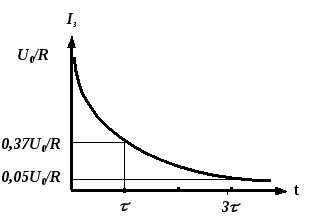
Р и с. 4 Р и с. 5
Короткое замыкание RC-цепи, т. е. разряд конденсатора С на активное сопротивление R, можно описать уравнением:
Uc + UR = 0 , (10)
где Ip = CdUc /dt; UR = IpR;
Получим однородное дифференциальное уравнение первого порядка:
Uc + RCdUc /dt = 0, (11)
Решение этого уравнения имеет вид:
Uc = U0 e-t/c, (12)
где U0 = Uc (0).
studfiles.net
Схема соединения "Треугольник"
Соединение в треугольник трехфазного генератора или вторичной обмотки трансформатора.
Соединим конец x обмотки ax с началом b обмотки by, конец y обмотки by с началом c обмотки cz, конец z обмотки cz с началом a обмотки ax так, как показано на рисунке 1. Такое соединение по виду напоминает треугольник, откуда и происходит его название. Линейные провода присоединены в вершинах треугольника.
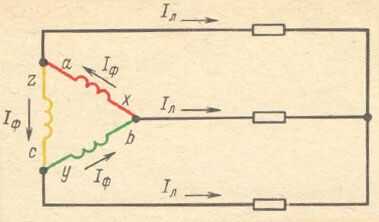
Рисунок 1. Соединение в треугольник генератора.
Основные соотношения:1. При соединении в треугольник линейные и фазные напряжения равны потому, что каждые два линейных провода (как видно из рисунка 1) присоединены к началу и концу одной из фазных обмоток, а все фазные обмотки одинаковы.2. Линейные токи Iл больше фазных Iф в √3 = 1,73 раза.
Как доказать, что Iл = 1,73 × Iф? Воспользуемся для этого векторной диаграммой рисунка 2.
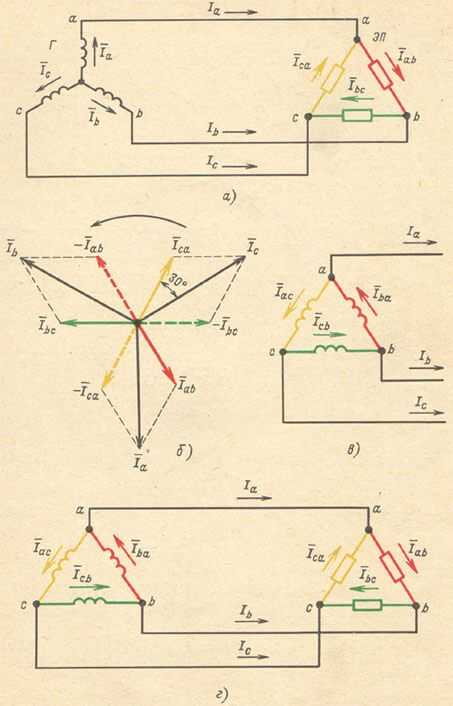
Рисунок 2. Определение линейных токов при соединении в треугольник.
Фазные токи Iab, Ibc, Ica в трех электроприемниках ЭП (рисунок 2, а) изображаются векторной диаграммой (рисунок 2, б), которая получена путем перенесения параллельно самим себе векторов с рисунка 2, а. Вершины треугольника нагрузок a, b и c являются узловыми точками. Поэтому согласно первому закону Кирхгофа справедливы равенства
Ia + Ica = Iab, откуда Ia = Iab – Ica;Ib + Iab = Ibc, откуда Ib = Ibc – Iab;Ic + Ibc = Ica, откуда Ic = Ica – Ibc.
Понятно, что эти равенства геометрические, поэтому вычитание нужно выполнять по правилам вычитания векторов, что и сделано на рисунке 2, б. Непосредственное измерение длин векторов или вычисления по правилам геометрии показывают, что линейные токи Ia, Ib и Ic больше фазных токов Iab, Ibc и Ica в √3 = 1,73 раза.
На рисунке 2, б также видно, что векторная диаграмма симметричных линейных токов Ia, Ib и Ic сдвинута на 30° в сторону, обратную вращению векторов, относительно диаграммы фазных токов Iab, Ibc и Ica. Иными словами, ток Ia отстает на 30° от тока Iab. Ток Ib отстает на 30° от тока Ibc, ток Ic отстает на 30° от тока Ica.Порядок индексов в обозначении фазных токов указывает на порядок вращения фаз. В нашем примере порядок следования (вращения) фаз: a, b, c.
На рисунке 2, в показано соединение в треугольник обмоток генератора или вторичных обмоток трансформатора. Векторы токов Iba, Iac, Icb, проходящих в обмотках генератора (вторичных обмотках трансформатора), и векторы токов в нагрузке (Iab, Ica, Ibc) соответственно параллельны, но повернуты на 180°. Причина такого расположения векторов станет ясна, если совместить рисунок 2, в с правой частью рисунка 2, а, что и выполнено на рисунке 2, г.
Обращается внимание на то, что все три обмотки внутри генератора (трансформатора) соединены последовательно и образуют замкнутую цепь. Подобное соединение в установках постоянного тока привело бы к короткому замыканию. В установках трехфазного тока в силу того, что электродвижущие силы (э. д. с.) сдвинуты по фазе на 120°, ток в этом замкнутом контуре отсутствует, так как в каждый момент сумма э. д. с. трех обмоток равна нулю 1.
Необходимо здесь же заметить, что для отсутствия тока в контуре обмоток генератора (трансформатора) необходимо, чтобы обмотки имели одинаковые числа витков, были сдвинуты на 120 электрических градусов и имели э. д. с. строго синусоидальные или во всяком случае не содержащие гармоник, кратных трем (смотрите статью "Понятие о магнитном равновесии трансформатора").
Генераторы практически никогда не соединяют в треугольник. В трансформаторах такие соединения не только распространены, но иногда выполняются с целью получения внутри трансформатора токов третьих гармоник. Зачем? Понятно не затем, чтобы создавать в трансформаторе дополнительные потери. Причины здесь гораздо сложнее, смотрите статью "Понятие о магнитном равновесии трансформатора".
Соединение в треугольник обмоток трансформаторов в двух вариантах показано на рисунке 3. Подробно вопрос о соединениях обмоток трансформаторов рассмотрен в статье "Группы соединения трансформаторов".
Рисунок 3. Соединение в треугольник трансформаторов.
Соединение в треугольник электроприемников и конденсаторных батарей.
Соединение в треугольник обмоток электродвигателей показано на рисунках 4, а – в. При этом на рисунке 4, а обмотки и соединены и расположены треугольником; на рисунке 4, б обмотки соединены треугольником, но расположены произвольно; на рисунке 4, в обмотки расположены звездой, но соединены в треугольник. На рисунке 4, г обмотки расположены треугольником, но соединены в звезду.
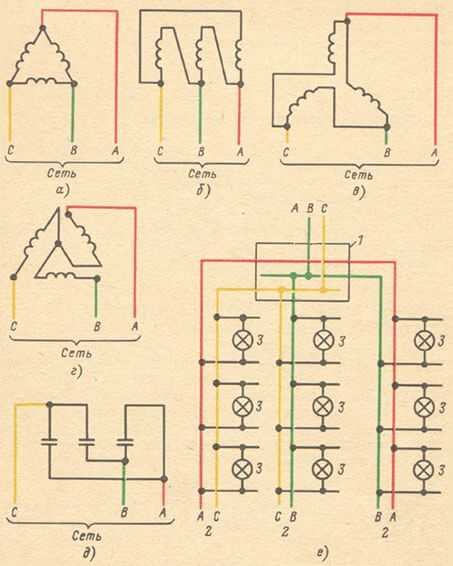
Рисунок 4. Соединение в треугольник электроприемников.
Все эти рисунки подчеркивают, что дело отнюдь не в том, как расположены изображения электроприемников на чертежах (хотя их часто удобно располагать в соответствии с видом соединения), а в том, что с чем соединено: концы (начала) всех обмоток между собой или конец одной обмотки с началом другой. В первом случае получается соединение в звезду, во втором – в треугольник.
Соединение в треугольник конденсаторных батарей показано на рисунке 4, д.
На рисунке 4, е показано соединение в треугольник ламп. Хотя лампы территориально разбросаны по разным квартирам, но они объединены сначала в группы в пределах каждой квартиры, затем в группы по стоякам 2 и, наконец, эти группы соединены в треугольник на вводном щите 1. Заметьте: до вводного щита нагрузка трехфазная, после вводного щита (в стояках и квартирах) однофазная, хотя она и включена между двумя фазами.
На каком основании нагрузка, питающаяся от двух фаз названа однофазной? На том основании, что изменения тока в обоих проводах, к которым присоединена нагрузка, происходят одинаково, то есть в каждый момент ток проходит через одни и те же фазы.
Видео 1. Соединение треугольником
1 Отсутствие тока в замкнутом контуре еще не означает, что в фазных обмотках нет тока. Токи в фазных обмотках соответствуют их нагрузкам.
Источник: Каминский Е. А., "Звезда, треугольник, зигзаг" – 4-е издание, переработанное – Москва: Энергия, 1977 – 104с.
www.electromechanics.ru
Соединение звездой и треугольником - Всё о электрике в доме
Основные сведения о трехфазном токе. Соединение звездой и треугольником
Переменный ток, рассмотренный ранее, называется однофазным. Трехфазным называется ток, представляющий собой совокупность трех однофазных токов, сдвинутых друг относительно друга по фазе.
Простейший генератор трехфазного тока отличается от генератора однофазного тока тем, что имеет три обмотки. При вращении либо этих обмоток в поле постоянного магнита (рис.164), либо самого магнита (рис.165) в обмотках возникают переменные ЭДС одинаковой частоты, сдвинутые друг относительно друга по фазе так, что сумма трех фазных углов составляет .
Если амплитуды ЭДС равны, а сдвиг фаз между двумя любыми смежными ЭДС равен . то трехфазная система называется симметричной. В этом случае на обмотках возникают
одинаковые по величине, но сдвинутые по фазе напряжения: . . .
Использование несвязанных между собой обмоток эквивалентно трем отдельным генераторам и требует для передачи электроэнергии потребителю три пары проводов.
Соединение обмоток между собой позволяет уменьшить количество проводов при передаче энергии и поэтому широко используется в технике.
При соединении обмоток звездой (рис.166) они имеют одну общую точку. Напряжение на каждой обмотке называется фазным. Проводник, соединенный с точкой общего потенциала, называется нулевым проводом. Проводники, соединенные со свободными концами обмоток, называются фазными проводами.
Фазные напряжения, в этом случае, это напряжения между фазными проводами и нулевым проводом. Напряжение между фазными проводами называется линейным. Ток, текущий через обмотки, называется фазным током, а ток текущий в линии, — током линии.
Из векторной диаграммы, при соединении звездой, следует, что . Кроме того при этом фазные токи равны токам в линии.
РИС.166 РИС.167 РИС.168 РИС.169 РИС.170
Если каждую обмотку замкнуть на одинаковую нагрузку R, то суммарная сила тока по нулевому проводу . так как из векторной диаграммы .
Соединение обмоток генератора звездой позволяет использовать при передаче энергии четыре провода вместо шести.
При соединении обмоток треугольником (рис.168) они образуют замкнутый контур с весьма малым сопротивлением. Линейный провод отходит от общих точек начала одной фазы и конца другой и, поэтому фазные напряжения равны линейным (рис.169).
Из векторной диаграммы токов (рис.170) следует, что
. На практике используется не только соединение обмоток генератора, но и соединение между собой нагрузок звездой или треугольником. Таких комбинаций возможного соединения генератора и нагрузок – четыре.
РИС.171 РИС.172 РИС.173 РИС.174
При соединении звезда – звезда (рис.171) на всех нагрузках разное напряжение, но если сопротивление нагрузок приблизительно равно, то ток по нулевому проводу практически равен нулю.
Тем не менее, нулевой провод нельзя убирать или ставить в него предохранители потому, что без него на каждую из пар нагрузок действует линейное напряжение, причем оно распределяется в соответствии с сопротивлением нагрузок. Получается, что напряжение, подаваемое на нагрузку, зависит от ее сопротивления, что неэффективно и опасно.
Если генератор и нагрузки соединены звезда – треугольник (рис.172), то на каждой нагрузке, независимо от ее сопротивления, одинаковое напряжение, равное линейному.
При соединении треугольник – треугольник (рис.173) на всех нагрузках фазное напряжение, независимо от их сопротивления.
Если генератор и нагрузки соединены треугольник – звезда (рис.174), то на каждой нагрузке напряжение равно .
Трехфазный ток используется для получения вращающегося магнитного поля. В этом случае трехфазный ток подводится к трем обмоткам, расположенным на неподвижной станине – статоре. Внутри статора помещен стальной барабан – ротор, вдоль образующих которого в пазах уложены провода, соединенные между собой на обоих торцах кольцами.
Обмотки статора создают магнитный поток одинаковой величины, но сдвинутый по фазе, т.е. он как бы вращается относительно ротора. В обмотках ротора возникают индукционные потоки, которые, в свою очередь, взаимодействуют с вращающимся магнитным потоком, что приводит ротор во вращение, т.е. получается электродвигатель достаточно простого устройства.
При увеличении скорости ротора уменьшается относительная скорость движения его проводников относительно магнитного поля. Если бы он достиг той же скорости вращения, что и магнитный поток статора, то индукционный ток равнялся бы нулю и, соответственно, вращающий момент стал бы равным нулю.
Следовательно, при наличии тормозного момента магнитный поток и ротор не могут вращаться с той же скоростью, что и поток статора (синхронно), — скорость вращения ротора всегда несколько меньше. Поэтому двигатели такого типа называются асихронными (несинхронными).
Трехфазная система, изобретенная русским инженером М.О.Доливо-Добровольским в XIX, применяется во всем мире для передачи и распределения энергии. Доливо-Добровольский первым получил вращающееся магнитное поле с помощью трехфазного тока и построил первый асинхронный двигатель. Трехфазная система обеспечивает наиболее экономичную передачу энергии и позволяет создать надежные в работе и простые по устройству электродвигатели, генераторы и трансформаторы.
На практике, например, электрические лампы изготавливаются на номинальные напряжения 127 и 220В. Способ их включения в цепь трехфазного тока зависит от величины линейного напряжения трехфазной сети.
Лампы с номинальным напряжением 127 В включаются звездой с нейтральным проводом при линейном напряжении сети 220 В или треугольником при линейном напряжении сети 127 В.
Лампы с номинальным напряжением 220 В соответственно включаются звездой в сеть с линейным напряжением 380 В и треугольником в сеть с напряжением 220 В.
Обмотки трехфазных двигателей изготавливаются на номинальные фазные напряжения 127, 220 и 380 В. Каждый трехфазный двигатель может быть включен или звездой в трехфазную сеть с линейным напряжением, превышающим его фазное в раз, или треугольником, если линейное напряжение сети равно фазному напряжению его обмотки. Обычно на паспорте двигателя указано, например: треугольник -220В, звезда – 380В.
Линейные цепи. Правила Кирхгофа. Методы анализа линейных цепей. Переходные процессы в цепи с конденсатором.
Элемент электрической цепи называется линейным, если его параметры не зависят от напряжения и силы тока, т.е. вольт-амперная характеристика прямая.
Электрическая цепь называется линейной если она состоит из линейных элементов.
Применение закона Ома для расчета сложных разветвленных цепей, содержащих несколько источников довольно сложно. Для расчетов таких цепей используют два правила немецкого физика Г.Кирхгофа, первое из которых вытекает из закона сохранения заряда, а второе является обобщением закона Ома на произвольное число источников сторонних ЭДС в изолированном замкнутом контуре.
Для того чтобы использовать правила Кирхгофа необходимо ввести несколько понятий.
Электрическая схема – графическое изображение электрической цепи.
Ветвь электрической цепи – один или несколько последовательно соединенных элементов цепи, по которым течет один и тот же ток.
Узел – соединение трех или большего количества ветвей. Ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:
Контур – любой замкнутый путь, проходящий по нескольким ветвям. Положительное направление обхода контура выбирается произвольно, но одно и то же для всех контуров электрической цепи. Токи совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода – отрицательными. ЭДС считаются положительными, если они создают ток, направленный в сторону обхода контура.
Рассмотрим цепь, содержащую три источника (рис.65). Пусть R1. R2. R3 общие сопротивления ветвей АВ, ВС, СА соответственно. Положительное направление обхода примем по часовой стрелке. Применим к каждой ветви закон Ома для неоднородного участка цепи.
Сложив почленно эти уравнения, получим
Второе правило Кирхгофа. в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:
При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1.выбрать произвольное направление токов на всех участках цепи; действительное направление токов выяснится при решении: если искомый ток получится положительным, то его направление было выбрано правильно, а если отрицательным, то его истинное направление противоположно выбранному;
2.выбрать направление обхода контуров и строго его придерживаться; записывая со соответствующими знаками токи и ЭДС;
3.составить количество уравнений равное количеству искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи).
Соединение звездой и треугольником генераторных обмоток
Автор Человек March 6, 2016
При создании любого прибора важно не только подобрать необходимые детали, но и верно их все соединить. И в рамках данной статьи будет рассказано про соединение звездой и треугольником. Где это применяется? Как схематически данное действие выглядит? На эти, а также другие вопросы и будут даны ответы в рамках статьи.
Что собой представляет трёхфазная система электроснабжения?
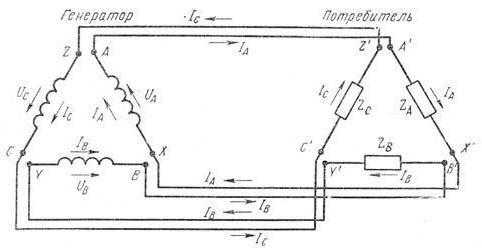 Она является частным случаем многофазных систем построения электрических цепей для переменного тока. В них действуют созданные с помощью общего источника энергии синусоидальные ЭДС, обладающие одинаковой частотой. Но при этом они сдвинуты относительно друг друга на определённую величину фазового угла. В трехфазной системе он равняется 120 градусам. Шестипроводная (часто ещё называемая многопроводной) конструкция для переменного тока была изобретена в своё время Николой Теслой. Также значительный вклад в её развитие внёс Доливо-Добровольский, который первым предложил делать трёх- и четырепроводные системы. Также он обнаружил ряд преимуществ, которые имеют трехфазные конструкции. Что же собой представляют схемы включения?
Она является частным случаем многофазных систем построения электрических цепей для переменного тока. В них действуют созданные с помощью общего источника энергии синусоидальные ЭДС, обладающие одинаковой частотой. Но при этом они сдвинуты относительно друг друга на определённую величину фазового угла. В трехфазной системе он равняется 120 градусам. Шестипроводная (часто ещё называемая многопроводной) конструкция для переменного тока была изобретена в своё время Николой Теслой. Также значительный вклад в её развитие внёс Доливо-Добровольский, который первым предложил делать трёх- и четырепроводные системы. Также он обнаружил ряд преимуществ, которые имеют трехфазные конструкции. Что же собой представляют схемы включения?
Схема звезды
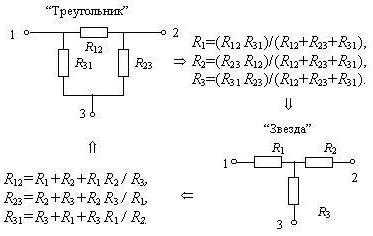 Так называют соединение, при котором концы фаз обмоток генератора соединяют в общую точку. Её называют нейтралью. Концы фаз обмоток потребителя также соединяются в одну общую точку. Теперь к проводам, которые их соединяют. Если он находится между началом фаз потребителя и генератора, его называют линейным. Провод, который соединяет нейтрали, обозначают как нейтральный. Также от него зависит название цепи. Если есть нейтральный, схема называется четырёхпроводной. В ином случае она будет трёхпроводной.
Так называют соединение, при котором концы фаз обмоток генератора соединяют в общую точку. Её называют нейтралью. Концы фаз обмоток потребителя также соединяются в одну общую точку. Теперь к проводам, которые их соединяют. Если он находится между началом фаз потребителя и генератора, его называют линейным. Провод, который соединяет нейтрали, обозначают как нейтральный. Также от него зависит название цепи. Если есть нейтральный, схема называется четырёхпроводной. В ином случае она будет трёхпроводной.
Треугольник
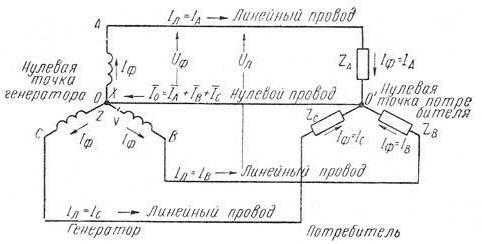 Это тип соединения, в котором начало (Н) и конец (К) схемы находятся в одной точке. Так, К первой фазы подсоединён у Н второй. Её К соединяется с Н третьей. А её конец соединён с началом первой. Такую схему можно было бы назвать кругом, если не особенность её монтирования, когда более эргономичным является размещение в виде треугольника. Чтобы узнать все особенности соединения, ознакомитесь с ниже приведёнными видами соединений. Но до этого ещё немного информации. Чем отличается соединение звездой и треугольником? Разница между ними заключается в том, что по-разному соединяются фазы. Также существуют определённые отличия в эргономичности.
Это тип соединения, в котором начало (Н) и конец (К) схемы находятся в одной точке. Так, К первой фазы подсоединён у Н второй. Её К соединяется с Н третьей. А её конец соединён с началом первой. Такую схему можно было бы назвать кругом, если не особенность её монтирования, когда более эргономичным является размещение в виде треугольника. Чтобы узнать все особенности соединения, ознакомитесь с ниже приведёнными видами соединений. Но до этого ещё немного информации. Чем отличается соединение звездой и треугольником? Разница между ними заключается в том, что по-разному соединяются фазы. Также существуют определённые отличия в эргономичности.
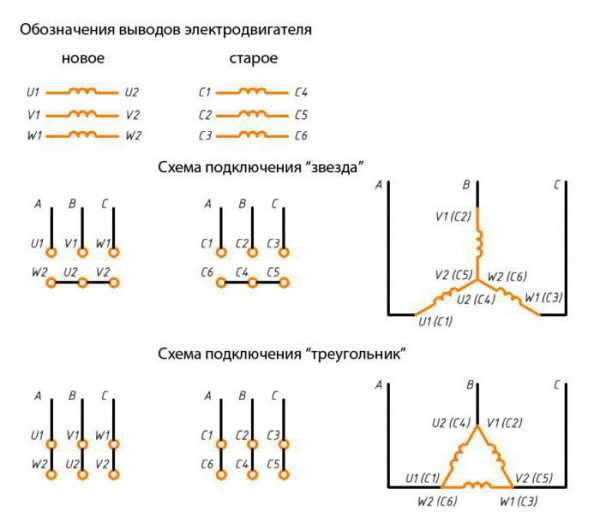 Как можно понять из рисунков, существует довольно много вариантов реализации включения деталей. Сопротивления, которые возникают в таких случаях, называют фазами нагрузки. Выделяют пять видов соединений, по которым может быть подключен генератор к нагрузке. Это:
Как можно понять из рисунков, существует довольно много вариантов реализации включения деталей. Сопротивления, которые возникают в таких случаях, называют фазами нагрузки. Выделяют пять видов соединений, по которым может быть подключен генератор к нагрузке. Это:
- Звезда–звезда. Вторая используется с нейтральным проводом.
- Звезда-звезда. Вторая используется без нейтрального провода.
- Треугольник-треугольник.
- Звезда-треугольник.
- Треугольник-звезда.
А что это за оговорки в первом и втором пунктах? Если вы уже успели задаться этим вопросом, прочитайте информацию, которая идёт к схеме звезды: там есть ответ. Но здесь хочется сделать небольшое дополнение: начала фаз генераторов обозначаются с применением заглавных букв, а нагрузки – прописными. Это относительно схематического изображения. Теперь по опыту использования: когда выбирают направление протекания тока, в линейных проводах делают так, чтобы он был направлен со стороны генератора к нагрузке. С нулевыми поступают полностью наоборот. Посмотрите, как выглядит схема соединения звезда-треугольник. Рисунки очень хорошо наглядно показывают, как и что должно быть. Схема соединения обмоток звезда/треугольник представлены в разных ракурсах, и проблем с их пониманием быть не должно.
Преимущества
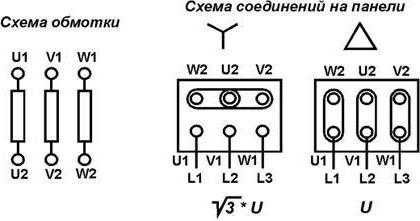 Каждая ЭДС работает в определённой фазе периодического процесса. Для обозначения проводников используют латинские буквы A, B, C, L и цифры 1, 2, 3. Говоря про трехфазные системы, обычно выделяют такие их преимущества:
Каждая ЭДС работает в определённой фазе периодического процесса. Для обозначения проводников используют латинские буквы A, B, C, L и цифры 1, 2, 3. Говоря про трехфазные системы, обычно выделяют такие их преимущества:
- Экономичность при передаче электричества на значительные расстояния, которое обеспечивает соединение звездой и треугольником.
- Малая материалоёмкость трехфазных трансформаторов.
- Уравновешенность системы. Данный пункт является одним из самых важных, поскольку позволяет избежать неравномерной механической нагрузки на электрогенерирующую установку. Из этого вытекает больший срок службы.
- Малой материалоёмкостью обладают силовые кабели. Благодаря этому при одинаковой потребляемой мощности в сравнении с однофазными цепями уменьшаются токи, которые необходимы, чтобы поддерживать соединение звездой и треугольником..
- Можно без значительных усилий получить круговое вращающееся магнитное поле, что необходимо для работоспособности электрического двигателя и целого ряда других электротехнических устройств, работающих по похожему принципу. Это достигается благодаря возможности создания более простой и одновременно эффективной конструкции, что, в свою очередь, вытекает из показателей экономичности. Это ещё один значительный плюс, который имеет соединение звездой и треугольником.
- В одной установке можно получить два рабочих напряжения – фазное и линейное. Также можно сделать два уровня мощности, когда присутствует соединение по принципу «треугольника» или «звезды».
- Можно резко уменьшать мерцание и стробоскопический эффект светильников, работающих на люминесцентных лампах, пойдя по пути размещения в нём устройств, питающихся от разных фаз.
Благодаря вышеуказанным семи преимуществам трехфазные системы сейчас являются наиболее распространёнными в современной электронике. Соединение обмоток трансформатора звезда/треугольник позволяет подобрать оптимальные возможности для каждого конкретного случая. К тому же неоценимой является возможность влиять на напряжение, передающееся по сетям к домам жителей.
Заключение
Данные системы соединения являются самыми популярными благодаря своей эффективности. Но следует помнить, что работа идёт с высоким напряжением, и необходимо соблюдать крайнюю осторожность.
Похожие статьи
Соединение звездой и треугольником обмоток электродвигателя
- Соединение обмоток звездой и треугольником
- Запуск трехфазного электродвигателя с переключением со звезды на треугольник
- Когда нужно переключаться с треугольника в звезду
- Видео
Конструкция трехфазного электродвигателя представляет собой электрическую машину, для нормальной работы которой необходимы трехфазные сети переменного тока. Основными частями такого устройства являются статор и ротор. Статор оборудован тремя обмотками, сдвинутыми между собой на 120 градусов. Когда в обмотках появляется трехфазное напряжение, на их полюсах происходит образование магнит ных потоков. За счет этих потоков, ротор двигателя начинает вращаться.
В промышленном производстве и в быту практикуется широкое применение трехфазных асинхронных двигателей. Они могут быть односкоростными, когда производится соединение звездой и треугольником обмоток электродвигателя или многоскоростными, с возможностью переключения с одной схемы на другую.
Соединение обмоток звездой и треугольником
У всех трехфазных электродвигателей обмотки соединяются по схеме звезды или треугольника.

При подключении обмоток по схема звезда, их концы соединяются в одной точке в нулевом узле. Поэтому, получается еще один дополнительный нулевой вывод. Другие концы обмоток соединяются с фазами сети 380 В.
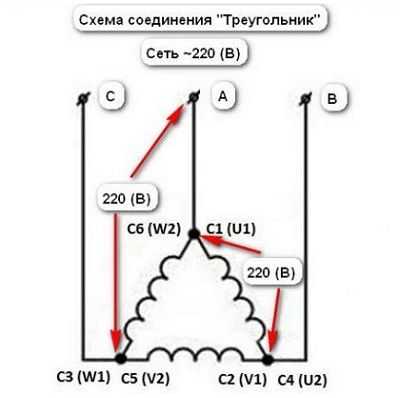
Соединение треугольником заключается в последовательном соединении обмоток. Конец первой обмотки соединяется с начальным концом второй обмотки и так далее. В конечном итоге, конец третьей обмотки, соединится с началом первой обмотки. Подача трехфазного напряжения осуществляется в каждый узел соединения. Подключение по схеме треугольник отличается отсутствием нулевого провода.
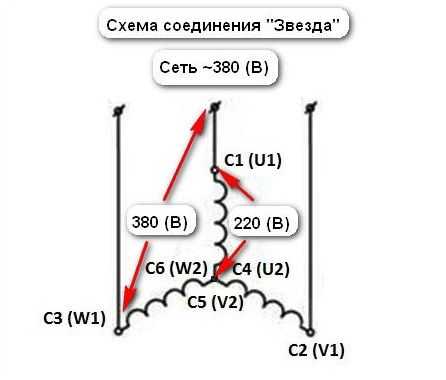
Оба вида соединений получили примерно одинаковое распространение и не имеют между собой значительных отличительных особенностей.
Существует и комбинированное подключение, когда используются оба варианта. Такой способ применяется достаточно часто, его целью является плавный запуск электродвигателя, которого не всегда можно добиться при обычных подключениях. В момент непосредственного пуска, обмотки находятся в положении звезда. Далее, используется реле, которое обеспечивает переключение в положение треугольника. За счет этого происходит уменьшение пускового тока. Комбинированная схема, чаще всего, применяется во время пуска электродвигателей, обладающих большой мощностью. Для таких двигателей требуется и значительно больший пусковой ток, превышающий номинальное значение примерно в семь раз.
Электродвигатели могут подключаться и другими способами, когда применяется двойная или тройная звезда. Такие подключения используются для двигателей с двумя и более регулируемыми скоростями.
Запуск трехфазного электродвигателя с переключением со звезды на треугольник
Данный способ применяется для того, чтобы снизить пусковой ток, который может примерно в 5-7 раз превышать номинальный ток электродвигателя. Агрегаты со слишком большой мощностью имеют такой пусковой ток, при котором легко перегорают предохранители, отключаются автоматы и, целом, значительно понижается напряжение. При таком уменьшении напряжения снижается накаливание ламп, происходит снижение вращающего момента других электродвигателей, самопроизвольно отключаются магнит ные пускатели и контакторы. Поэтому, применяются разные способы, с целью уменьшения пускового тока.
Общим для всех способов является необходимость снижения напряжения в обмотках статора на время непосредственного пуска. Чтобы уменьшить пусковой ток, цепь статора на время пуска может дополняться дросселем, реостатом или автоматическим трансформатором.
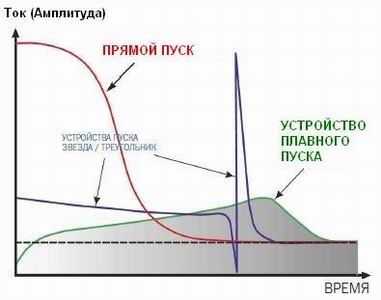
Наибольшее распространение получило переключение обмотки из звезды в положение треугольника. В положении звезды напряжение становится в 1,73 раза меньше, чем номинальное, поэтому и ток будет меньше, чем при полном напряжении. Во время пуска частота вращения электродвигателя увеличивается, происходит снижение тока и обмотки переключаются в положение треугольника.
Такое переключение допускается в электродвигателях, имеющих облегченный режим пуска, так как происходит снижение пускового момента, примерно в два раза. Данным способом переключаются те двигатели, которые конструктивно могут соединяться в треугольник. У них должны быть обмотки, способные работать при линейном напряжении сети .
Когда нужно переключаться с треугольника в звезду
Когда необходимо выполнить соединение звездой и треугольником обмоток электродвигателя, следует помнить о возможности переключения с одного вида на другой. Основным вариантом является схема переключения звезда треугольник. Однако, при необходимости, возможен и обратный вариант.
Всем известно, что у электродвигателей, загруженных не полностью, происходит снижение коэффициента мощности. Поэтому, такие двигатели желательно заменять устройствами с меньшей мощностью. Однако, при невозможности замены и большом запасе мощности, производится переключение треугольник-звезда. Ток в цепи статора не должен превышать номинала, иначе произойдет перегрев электродвигателя.
Источники: http://studopedia.ru/5_103820_osnovnie-svedeniya-o-trehfaznom-toke-soedinenie-zvezdoy-i-treugolnikom.html, http://www.syl.ru/article/234330/new_soedinenie-zvezdoy-i-treugolnikom-generatornyih-obmotok, http://electric-220.ru/news/soedinenie_zvezdoj_i_treugolnikom_obmotok_ehlektrodvigatelja/2015-02-21-837
electricremont.ru
2.5. СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ | Портал Электриков
Электрические цепи, состоящие из приемников энергии (резисторов), соединенных последовательно, параллельно или смешанно при питании их от одного источника электрической энергии (рис. 2.4—2.7), а также цепи, содержащие одни контур (рис. 1.17, 1.20), принято называть простыми цепями. При заданных ЭДС (напряжениях) источников питания и сопротивлениях токи и напряжения на всех участках простой цепи можно определить, пользуясь законом Ома и первым законом Кирхгофа (§ 2.1).
Разветвленные электрические цепн, имеющие несколько контуров с произвольным размещением потребителей и источников питания, относятся к сложным цепям, если их нельзя рассчитать, применяя только закон Ома и первый закон Кирхгофа. Методы расчета сложных цепей рассмотрены ниже.
Схему еоедииения трех ветвей, образующих замкнутый контур с тремя узлами А, Б, В (рис. 2.8, а), называют треугольником.
В некоторых случаях расчет сложной цепи значительно упрощается, если треугольник сопротивлений заменить звездой сопротивлений, т. е. тремя ветвями, имеющими дополнительный общий узел О (рис 2.8,6). В других случаях расчета цепей встречается необходимость звезду заменить треугольником. Эти взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т. е. при соответственно равных напряжениях между вершинами А, Б и В треугольника и звезды токи IA, IБ, 1В в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.
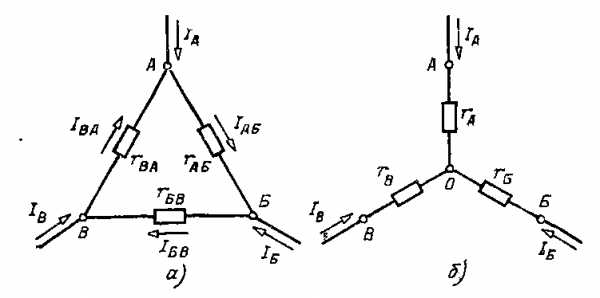
Рис 2.8 Соединение резисторов треугольником (а) и звездой (б)
Сопротивления эквивалентной звезды rа, rб, rв находятся в определенных соотношениях с сопротивлениями треугольника rаб, rбв, rва. Для выяснения этой зависимости допустим сначала, что в вершине А произошел обрыв подводящего провода и, следовательно, ток Iа=0. Сопротивления между двумя оставшимися присоединенными вершинами Б и В для обеих схем должны быть одинаковы, чтобы были соответственно равны токи IБи Iвв обеих схемах. После обрыва в вершине А сопротивления rб и rв в звезде соединены последовательно, а в треугольнике сопротивления rВА и rАБсоединенные последовательно, образуют одну ветвь с суммарным сопротивлением rВА + rАБ, параллельно которой подключено сопротивление rБв. Поэтому можно написать
(2.14)
где принята во внимание формула расчета эквивалентного сопротивления двух параллельно включенных резисторов (2.11).
Рассуждая аналогично для случая обрыва в вершине Б, при котором ток IБ = 0, а затем провода В, при котором ток Iв=0, получим аналогичные выражения:
(2 .15)
(2.16)
Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника rаб,rбв, rва, требуется определить сопротивления лучей эквивалентной звезды rа, rб, rв . Для этого составим полусумму левых и правых частей уравнений (2.15) и (2.16):
и вычтем из полученного выражения уменьшенные вдвое левую и правую части (2.14). В результате получим
(2.17)
Аналогично получим
(2.18)
(2.19)
Таким образом, сопротивление луча эквивалентной звезды равно произведению сопротивлений двух сторон треугольника, которые присоединены к той же вершине, что и луч звезды, деленному на сумму сопротивлений, всех сторон треугольника.
Если сопротивления треугольника равны друг другу: rаб = rбв=rва=rΔ, то будут равны друг другу и сопротив
ления звезды, т. е. rа = rб=rв=r λ, причем из формул (2.17)—(2.19) получается простое соотношение
(2.20)
При обратном преобразовании звезды в эквивалентный треугольник, т. е. при заданных сопротивлениях rа, rб, rв, надо решить три уравнения (2.17)—(2 19) относительно сопротивлений rаб, rбв:
(2.21)
(2.22)
(2.23)
Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды.
Пример 2.3. Определить токи в ветвях мостовой схемы (рис. 2.9), если известны параметры цепи: E=4,4 В, r1=20 Ом, r2=60 Ом, r3= 120 Ом, r4=8 Ом, r5=44 Ом.
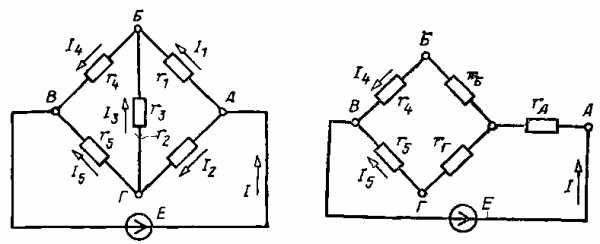
Рис 2.10. Преобразованная мос- Рис. 2.9. Мостовая схема
товая схема
Решение. Заменив один из треугольников схемы, например АБГ, образованный сопротивлениями r1, r2, r3, эквивалентной звездой, сопротивление лучей которой га, rа, rб и rв, получим простую схему смешанного соединения элементов (рис. 2.10).
Найдем сопротивления лучей звезды.
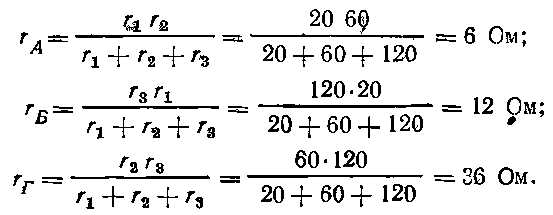
Эквивалентное сопротивление участка (рис. 2.10), состоящего из сопротивления rа и двух параллельных ветвей r4+rби r5+rГ
Ток в неразветвленной части схемы (рис. 2.10)
I=E/r=4,4/22 = 0,2 А.
Тор в ветви с сопротивлениями r4 ,rбнаходим но формулам «разброса» общего тока (2.12):
Для определения ток&в I1, I2, I3, которых нет в преобразованной схеме (рис 2.10), найдем потенциалы узлов Г и Б.
Наряжение на сопротивлении r4
Напряжение на сопротивлении r5
Полагая потенциал точки В равным нулю, получаем
Напряжение на диагонали моста ГБ
Переходя к схеме рис 2.9, найдем токи ветвей в преобразованной части моста.
www.electricsite.net
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.