Практическая работа №3 Электрический расчет кабельной линии. Таблица активное сопротивление кабеля

Активное и индуктивное сопротивление кабелей + таблица

Содержание:

Особенности активного сопротивления
Таблица и формулы для расчета
Действие индуктивного сопротивления кабельных линий
Видео

В любых электрических сетях имеет место потеря напряжения под влиянием различных факторов. В основном это такие параметры, как проводимость и сопротивление, которые следует учитывать при выполнении расчетов. Для цепей постоянного тока можно обойтись обычными характеристиками. Однако, при использовании переменного тока потребуется вычислить активное и индуктивное сопротивление кабелей, которые специальная таблица отображает с высокой точностью в разных вариантах. Для того чтобы правильно ориентироваться в этих параметрах, необходимо хорошо представлять себе особенности каждого из них.

Особенности активного сопротивления

Сопротивление в электротехнике является важнейшим параметром, с помощью которого какая-то часть электрической цепи оказывает противодействие проходящему по ней току. Образованию данной величины способствуют изменения электроэнергии и ее переход в другие виды энергетических состояний.

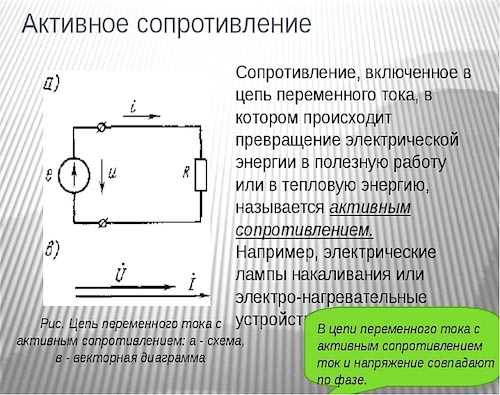
Подобное явление характерно лишь для переменного тока, под действием которого образуются активные и реактивные сопротивления кабелей. Этот процесс представляет собой необратимые изменения энергии или передачу и распределение ее между отдельными элементами цепи. Если изменения электроэнергии принимают необратимый характер, то такое сопротивление будет активным, а если имеют место обменные процессы, оно становится реактивным. Например, электрическая плита выделяет тепло, которое обратно в электрическую энергию уже не превращается.

Данное явление в полной мере затрагивает любые виды провода и кабеля. При одинаковых условиях, они будут по-разному сопротивляться прохождению постоянного и переменного тока. Подобная ситуация возникает из-за неравномерного распределения переменного тока по сечению проводника, в результате чего образуется так называемый поверхностный эффект.

Таблица и расчет по формуле

Как показывает таблица, поверхностный эффект не критично влияет на проводники, состоящие из цветных металлов и работающие при переменном напряжении с частотой 50 Гц. Поэтому для выполнения расчетов, сопротивления таких кабелей под действием постоянного и переменного тока принимаются условно равными.

Кроме таблицы, для расчетов проводников из алюминия и меди используется специальная формула r = (l * 103)/ γ3 * S = r0 * l, в которой l – длина (км), γ – удельное значение проводимости конкретного материала (м/ом * мм2), r0 – активное сопротивление 1 км кабеля (Ом/км), S – поперечное сечение (мм2).

Значение активного сопротивления кабелей зависит также от температуры окружающей среды. Для того чтобы вычислить r0 при точной температуре Θ, необходимо воспользоваться еще одной формулой r0 = r20 * [l + α * (Θ - 20)] = (l * 103)/ γ20 * S * [l + α * (Θ - 20)]. Здесь α является температурным коэффициентом сопротивления, r20 – активное сопротивление при t 200C, γ20 – удельная проводимость при этой же температуре. Эти расчеты необходимы, когда определяется точное активное и индуктивное сопротивление какого-либо проводника.

Активное сопротивление стальных проводов существенно превышает аналогичный показатель проводников из цветных металлов. Это связано с более низкой удельной проводимостью и наличием поверхностного эффекта, выраженного намного ярче по сравнению с медными и алюминиевыми проводами. Кроме того, в линиях со стальными проводами активная энергия значительно теряется на перемагничивание и вихревые токи, поэтому такие потери становятся дополнительным компонентом активного сопротивления.

У стальных проводников существует зависимость активного сопротивления от величины протекающего тока, поэтому в расчетах неприемлемо использование постоянного значения удельной проводимости.

Действие индуктивного сопротивления кабельных линий

Полное сопротивление электрической цепи разделяется на активное и индуктивное сопротивление. Из них последнее является составной частью реактивного сопротивления, возникающего во время прохождения переменного тока через элементы, относящиеся к реактивным. Индуктивность считается основной характеристикой катушек, не учитывая активное сопротивление их обмоток. Как правило, реактивное сопротивление возникает под влиянием ЭДС самоиндукции. При ее росте, в зависимости от частоты тока, происходит одновременное увеличение сопротивления.

Таким образом, активное и реактивное сопротивление кабелей образуют полное сопротивление, которое есть ни что иное, как сумма квадратов каждой составляющей. Графически это отображается в виде прямоугольного треугольника, в котором гипотенуза является полным сопротивлением, а катеты – его составными элементами.

Очень быстро вычислить активное и индуктивное сопротивление кабелей помогает таблица, в которой отражаются основные характеристики наиболее распространенных проводников. Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Х0l, где Х0 является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.

В свою очередь Х0 определяется по другой формуле X0 = 0,145lg * (2Dср/d) + 0,0157 μт, в которой 2Dср является средним расстоянием между проводниками или центрами кабельных жил, d – диаметр этих проводников или жил, μт – отражает относительную магнитную проницаемость металла проводника. Таким образом, при увеличении сечения проводника реактивное сопротивление Х0 будет незначительно уменьшаться.

electric-220.ru

Таблица активное сопротивление кабеля

Практическая работа №3 Электрический расчет кабельной линии

studfiles.net

Активные и реактивные сопротивления кабелей


Среднее геометрическое расстояние между проводами, мм	Сечение проводов, мм кв
6	10	16	25	35	50	70	95	120	150	185
Медные провода
400 600 800 1000 1250 1500 2000 2500 3000	0,371 0,397 0,415 0,429 0,443 - - - -	0,355 0,381 0,399 0,413 0,427 0,438 0,457 - -	0,333 0,358 0,377 0,391 0,405 0,416 0,435 0,449 0,460	0,319 0,345 0,363 0,377 0,391 0,402 0,421 0,435 0,446	0,308 0,336 0,352 0,366 0,380 0,391 0,410 0,424 0,435	0,297 0,325 0,341 0,355 0,369 0,380 0,398 0,413 0,423	0,283 0,309 0,327 0,341 0,355 0,366 0,385 0,399 0,410	0,274 0,300 0,318 0,332 0,346 0,357 0,376 0,390 0,401	- 0,292 0,310 0,324 0,338 0,349 0,368 0,382 0,393	- 0,287 0,305 0,319 0,333 0,344 0,363 0,377 0,388	- 0,280 0,298 0,313 0,327 0,338 0,357 0,371 0,382
Алюминиевые провода
600 800 1000 1250 1500 2000	- - - - - -	- - - - - -	0,358 0,377 0,391 0,405 - -	0,345 0,363 0,377 0,391 0,402 0,421	0,336 0,352 0,366 0,380 0,391 0,410	0,325 0,341 0,355 0,369 0,380 0,398	0,315 0,331 0,345 0,359 0,370 0,388	0,303 0,319 0,334 0,347 0,358 0,377	0,297 0,313 0,327 0,341 0,352 0,371	0,288 0,305 0,319 0,333 0,344 0,363	0,279 0,298 0,311 0,328 0,339 0,355
Сталеалюминиевые провода
2000 2500 3000	- - -	- - -	- - -	- - -	0,403 0,417 0,429	0,392 0,406 0,418	0,382 0,396 0,408	0,371 0,385 0,397	0,365 0,379 0,391	0,358 0,272 0,384	- - 0,377

Сечение жилы, мм2	Активное сопротивление при 20 °С, Ом/км, жилы	Индуктивное сопротивление, Ом/км, кабеля напряжением, кВ
	алюминиевой	медной	1	6	10	20
10	2,94	1,79	0,073	0,11	0,122
16	1,84	1,12	0,068	0,102	0,113	—
25	1,17	0,72	0,066	0,091	0,099	0,135
35	0,84	0,51	0,064	0,087	0,095	0,129
50	0,59	0,36	0,063	0,083	0,09	0,119
70	0,42	0,256	0,061	0,08	0,086	0,116
95	0,31	0,19	0,06	0,078	0,083	0,11
120	0,24	0,15	0,06	0,076	0,081	0,107
150	0,2	0,12	0,059	0,074	0,079	0,104
185	0,16	0,1	0,059	0,073	0,077	0,101
240	0,12	0,07	0,058	0,071	0,075	—

Активное сопротивление токопроводящих жил проводов марок СИП-1, СИП-2, СИП-4 при 900C

Токопроводящая жила	электрическое сопротивление токопрводящих жил на длине 1 км, Ом, не более
при номинальном сечении токопроводящих жил,мм2
16	25	35	50	70	95	120	150	185	240
из алюминиевых проволок	2.448	1.540	1.111	0.822	0.568	0.411	0.325	0.265	0.211	0.162
из проволок из алюминиевого сплава	-	1.770	1.262	0.923	0.632	0.466	0.369	0.303	0.241	0.188

Индуктивное сопротивление изолированных проводов марок СИП-1, СИП-2, СИП-4

Маркоразмер провода	Расчетное значение индуктивного сопротивления провода на длине 1 км, Ом
Основных жил	Нулевой несущей жилы
СИП-1
3x16+1x25	0.0853	0.0634
3x25+1x35	0.0816	0.0615
3x35+lx50	0.0791	0.0600
3x50+1x50	0.0782	0.0604
3x50+1x70	0.0790	0.0599
3x70+1x70	0.0774	0.0600
3x70+1x95	0.0781	0.0595
3x95+1x70	0.0746	0.0595
3x95+1x95	0.0753	6.0587
3x120+1x95	0.0735	0.0584
3z150+1x95	0.0719	0.0582
3x185+1x95	0.0711	0.0590
3x240+1x95	0.0692	0.0593
СИП-2
3x16+1x25	0.0865	0.0739
3x25+1x35	0.0827	0.0703
3x35+1x50	0.0802	0.0691
3x50+1x50	0.0794	0.0687
3x50+1x70	0.0799	0.0685
3x70+1x70	0.0785	0.0679
3x70+1x95	0,0789	0.0669
3x95+1x70	0.0758	0.0669
3x95+1x95	0.0762	0.0656
3x120+1x95	0.0745	0.0650
3x150+1x95	0.0730	0.0647
3x185+1x95	0.0723	0.0649
3x240+1x95	0.0705	0.0647
СИП 4
2x16	0.0754	-
2x25	0.0717	-
4x16	0.0821	0.0643
4x25	0.0784	0.0621

remcable.3dn.ru

Практическое пособие по определению возможной причастности токов короткого замыкания к воспламенению изоляции проводников, страница 15

Примечание. *Относится к трансформаторам старых стандартных мощностей, снятым с производства. Сопротивления трансформаторов приведены к низшему напряжению.

Таблица 2.

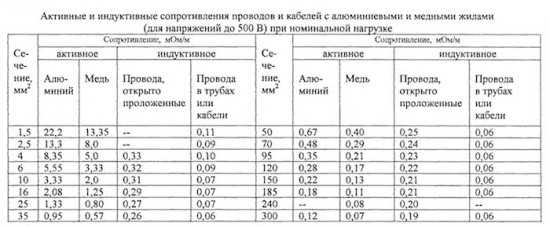
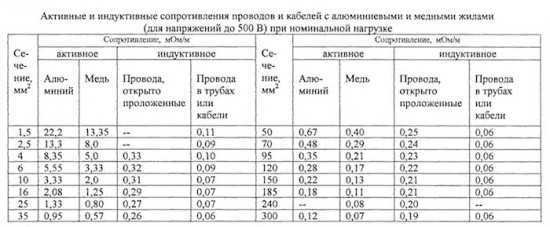
Активные и индуктивные сопротивления проводов и кабелей с алюминиевыми и медными жилами (для напряжений до 500 В) при номинальной нагрузке [10].

Сечение, мм2	Сопротивление, мОм/м	Сечение, мм2	Сопротивление, мОм/м
Активное, r	Индуктивное, x	Активное, r	Индуктивное, x
Алюминий	Медь	Провода открыто проложенные	Провода в трубках или кабели	Алюминий	Медь	Провода открыто проложенные	Провода в трубках или кабели
1,5	22,2	13,35	-	0,11	50	0,67	0,4	0,25	0,06
2,5	13,3	8	-	0,09	70	0,48	0,29	0,24	0,06
4	8,35	5	0,33	0,1	95	0,35	0,21	0,23	0,06
6	5,55	3,33	0,32	0,09	120	0,28	0,17	0,22	0,06
10	3,33	2	0,31	0,07	150	0,22	0,13	0,21	0,06
16	2,08	1,25	0,29	0,07	185	0,18	0,11	0,21	0,06
25	1,33	0,8	0,27	0,07	240	-	0,08	0,2	-
35	0,95	0,57	0,26	0,06	300	0,12	0,07	0,19	0,06

Таблица 3.

Активное и индуктивное сопротивления алюминиевых и сталеалюминиевых проводов [17].

Марка провода	Активное сопротивление, мОм/м	Индуктивное сопротивление, мОм/м, при среднем геометрическом расстоянии между проводами, мм
400	600	1000	2000	3000	4000	5000
Алюминиевые провода
А16	1,98	0,332	0,358	-	-	-	-	-
А25	1,28	0,318	0,345	-	-	-	-	-
А35	0,92	0,312	0,326	0,37	0,41	-	-	-
А50	0,64	0,297	0,325	0,36	0,4	0,42	0,44	-
А70	0,46	0,283	0,315	0,35	0,39	0,41	0,43	-
А95	0,34	0,277	0,302	0,33	0,38	0,4	0,42	-
А120	0,21	0,27	0,297	0,31	0,36	0,39	0,4	0,42
А185	0,17	-	-	0,31	0,35	0,38	0,39	0,41
А240	0,13	-	-	0,3	0,34	0,37	0,39	0,4
А300	0,11	-	-	0,29	0,34	0,36	0,37	0,39
А400	0,08	-	-	0,28	0,33	0,35	0,36	0,38
А500	0,06	-	-	0,28	0,32	0,35	0,36	0,37
А600	0,05	-	-	0,27	0,31	0,34	0,36	0,37
Сталеалюминиевые провода
АС10	3,12	0,342	0,368	-	-	-	-	-
АС16	2,06	0,318	0,354	0,33	0,43	-	-	-
АС25	1,38	0,316	0,342	0,38	0,41	0,43	-	-
АС35	0,9	0,301	0,327	0,37	0,4	0,43	0,44	-
АС 50	0,65	0,292	0,319	0,35	0,39	0,42	0,43	-
АС 70	0,46	-	-	0,34	0,38	0,41	0,42	0,44
AC 95	0,33	-	-	0,33	0,37	0,4	0,41	0,43
AC 120	0,27	-	-	0,32	0,36	0,39	0,4	0,42
AC 150	0,21	-	-	-	0,35	0,38	0,4	0,41
AC 185	0,17	-	-	-	-	0,37	0,39	0,41
AC 240	0,13	-			-	0,36	0,38	0,4
AC 300	0,11	-			-	0,35	0,37	0,39

Полный список ВУЗов

vunivere.ru

Проводимость и сопротивление воздушных и кабельных линий

Для того, чтобы произвести расчет электрической сети на потерю напряжения необходимо знать параметры линий, а именно их сопротивления и проводимости. Если производятся расчеты цепей постоянного тока, то вполне достаточно знать только омическое сопротивление линии. А вот при расчете линии переменного тока одного омического сопротивления бывает недостаточно, и помимо активных сопротивлений, необходимо знать еще индуктивные сопротивления и емкостные проводимости проводов и кабелей.

Активное сопротивление проводов и кабелей

Из электротехники известно, что полное сопротивление при равных условиях переменному и постоянному току будут отличаться. Касается это также проводов и кабелей. Это вызвано тем, что переменный ток распределяется по сечению неравномерно (поверхностный эффект). Однако для проводов из цветных металлов и с частотой переменного напряжения 50 Гц этот эффект не оказывает слишком большого влияния и им можно пренебречь. Таким образом, при расчете проводников из цветных металлов, их сопротивления переменному и постоянному току принимаются равными.

На практике активное сопротивление медных и алюминиевых проводников рассчитывают по формуле:

Где: l – длина в км, γ – удельная проводимость материала провода м/ом∙мм2, r0 – активное сопротивление 1 км провода на фазу Ом/км, s – площадь поперечного сечения, мм2.

Величина r0, как правило, берется из таблиц справочников.

На активное сопротивление провода влияет и температура окружающей среды. Величину r0 при температуре Θ можно определить по формуле:

Где: α – температурный коэффициент сопротивления; r20 – активное сопротивление при температуре 20 0С, γ20 – удельная проводимость при температуре в 20 0С.

Стальные провода обладают значительно большими активными сопротивлениями, чем аналогичные провода из цветных металлов. Его увеличение обусловлено значительно меньшей величиной удельной проводимости и поверхностным эффектом, который у стальных проводов выражен гораздо более ярко, чем у алюминиевых или медных. Более того, в стальных проводах присутствуют потери активной энергии на вихревые токи и перемагничивание, что в схемах замещения линий учитывают дополнительной составляющей активного сопротивления.

Активное сопротивление стальных проводов (в отличии от проводов из цветных металлов) сильно зависит от величины протекаемого тока, поэтому использовать постоянное значение удельной проводимости при расчетах нельзя.

Активное сопротивление стальных проводов в зависимости от протекающего тока аналитически выразить весьма трудно, поэтому для его определения используют специальные таблицы.

Индуктивное сопротивление проводов и кабелей

Для определения индуктивного сопротивления (обозначается Х) кабельной или воздушной линии определенной протяженности в километрах удобно пользоваться выражением:

Где: Х0 – индуктивное сопротивление одного километра провода или кабеля на фазу, Ом/км.

Х одного километра воздушной или кабельной линии можно определить по формуле:

Где: Dср – расстояние среднее между проводами или центрами жил кабелей, мм; d – диаметр токоведущей жилы кабеля или диаметр провода, мм; μт – относительная магнитная проницаемость материала провода;

Первый член правой части уравнения обусловлен внешним магнитным полем и называется внешним индуктивным сопротивлением Х0/. Из этого выражения видно, что Х0/ зависит только от расстояния между проводами и их диаметра, а так как расстояние между проводами выбирается исходя из номинального напряжения линии, соответственно Х0/ будет расти с ростом номинального напряжения линии. Х0/ воздушных линий больше, чем кабельных. Это связано с тем, что токоведущие жилы кабеля располагаются друг к другу значительно ближе, чем провода воздушных линий.

Для одной фазы:

Где: D1:2 расстояние между проводами.

Для одинарной трехфазной линии при расположении проводов по треугольнику:

При горизонтальном или вертикальном расположении проводов трехфазной линии в одной плоскости:

Увеличение сечения проводов линии ведет к незначительному уменьшению Х0/.

Второй член уравнения для определения X0 обусловлен магнитным полем внутри проводника. Он выражает внутреннее индуктивное сопротивление Х0//.

Таким образом выражение для Х0 можно представить в виде:

Для линий из немагнитными материалов μ = 1 внутреннее индуктивное сопротивление Х0// по сравнению с внешним Х0/ составляет ничтожную величину, поэтому им очень часто пренебрегают.

В таком случае формула для определения Х0 примет вид:

Для практических расчетов индуктивные сопротивления кабелей и проводов определяют по соответствующим таблицам.

В случае приближенных расчетов можно считать для воздушных линий напряжением 6-10 кВ Х0 = 0,3 – 0,4 Ом/км, а для кабельных Х0 = 0,08 Ом/км.

Внутренне индуктивное сопротивление стальных проводов сильно отличается от Х0// проводов из цветных металлов. Это вызвано тем, что Х0// пропорционально магнитной проницаемости μr, которая сильно зависит от величины тока в проводе. Если для проводов из цветных металлов μr = 1, то для стальных проводов μr может достигать величины в 103 и даже выше.

Х0// для линий прокладываемых стальными проводами пренебрегать нельзя. Как правило, данную величину берут из таблиц, составленных на основе экспериментальных данных.

Сопротивления r0 и Х0// при некоторых значениях тока могут достигать максимальных значений, а затем с увеличением тока уменьшатся. Это явление объясняется магнитным насыщением стали.

Емкостная проводимость линий

Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.

Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:

Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.

Емкостная проводимость одноцепной воздушной линии определяется по формуле:

Определение рабочей емкости кабельной линии по формулам, в которые входят диэлектрическая проницаемость изоляции кабеля, геометрические размеры и другие конструктивные особенности, задача не из легких, поэтому значения рабочей емкости определяют по специальным таблицам, составленным заводом изготовителем для различных марок кабелей, в зависимости от их номинального напряжения.

Емкостной ток вначале линии при холостом ходе (при отключенных электроприемниках) можно определить из формулы:

Где: U – линейное напряжение сети, В; l – длина линии, км;

Емкостные токи имеют серьезное значение в воздушных линиях с рабочим напряжением 110 кВ и выше и в кабельных линиях с напряжением выше 10 кВ. При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.

В сети с изолированной нейтралью величину емкостного тока однофазного замыкания на землю приближенно можно определить по формулам:

elenergi.ru

el-cab.ru

Удельное активное сопротивление кабеля таблица

Оцените работу специалиста!

Page 2

Технический форум

Неактивен

Консультант Технические специалисты

Re: Здравствуйте. Удельное активное и реактивное сопротивление кабелей АВВГ 4х70, 4х95, 4х120. Спасибо!

Здравствуйте! Сопротивление кабелей - активное (20ºС) / индуктивное, Ом/км:АВВГ 4х2,5-1 - 12,1 / 0,116;АВВГ 4х6-1 - 5,11 / 0,101;АВВГ 4х10-1 - 3,08 / 0,099;АВВГ 4х16-1 - 1,91 / 0,095;АВВГ 4х25-1 - 1,20 / 0,091;ВВГ 4х35-1 - 0,524 / 0,088;АВВГ 4х70-1 - 0,443 / 0,082;ВВГ 4х240-1 - 0,0754 / 0,077.

Сообщений 2

Оставить комментарий	РСС
Неактивен	Посетитель Гость Тема: Ответьте, пожалуйста на вопрос: Нормативный срок службы контрольных, силовых и в/в кабелей. Ответьте, пожалуйста на вопрос: Нормативный срок службы контрольных, силовых и в/в кабелей.	2009-01-19 04:00
Цитировать Сообщение 11
Неактивен	Консультант Moderators Re: Ответьте, пожалуйста на вопрос: Нормативный срок службы контрольных, силовых и в/в кабелей. Срок службы контрольных кабелей не менее 15 лет при прокладке в земле и не менее 25 лет при прокладке в помещениях, силовых кабелей с бумажнопропитанной, ПВХ и СПЭ изоляцией- не менее 30 лет.	2009-01-19 04:00
Цитировать Сообщение 12

cable.ru

3.5. Погонные (удельные) параметры линий

Погонное (удельное) (на единицу длины) активное сопротивление rо при частоте 50 Гц и обычно применяемых сечениях алюминиевых или медных проводов и жил кабелей можно принять равным погонному омическому сопротивлению. Явление поверхностного эффекта начинает заметно сказываться только при сечениях порядка 500 мм2.

Активное сопротивление – это сопротивление при протекании по проводнику переменного тока, омическое - это сопротивление при протекании по тому же проводнику постоянного тока. Для сталеалюминиевых проводов явление поверхностного эффекта также незначительно и может не учитываться.

Значительное влияние на активное сопротивление оказывает температура материала проводников, которая зависит от температуры окружающей среды и тока нагрузки.

Погонные (удельные) реактивные (индуктивные) сопротивления фаз линий в общем случае получаются разными. Они определяются взаимным расположением фаз и геометрическими параметрами. При расчетах симметрических рабочих режимов пользуются средними значениями (независимо от транспозиции фаз линии).

Задания для самостоятельной работы:

1. Выбор трансформаторов.

2. Методы определения параметров сети при различных конструктивных исполнениях, номинальных напряжениях и назначениях в составе ЭЭС.

3. Изучение удельных параметров проводов ЛЭП, кабельных линий, а именно воздействия на них температуры окружающей среды.

4. Составление принципиальной электрической схемы сети: генератор-двухобмоточный трансформатор-линия- двухобмоточный трансформатор-нагрузка.

Лекция 4. Схемы замещения ЛЭП. Определение параметров схемы замещения ЛЭП.

Линия электрической сети теоретически рассматривается состоящей из бесконечно большого количества равномерно распределенных вдоль нее активных и реактивных сопротивлений и проводимостей.

Точный учет влияния распределенных сопротивлений и проводимостей сложен и необходим при расчетах очень длинных линий, которые в этом курсе не рассматривается.

На практике ограничиваются упрощенными методами расчета, рассматривая линию с сосредоточенными активными и реактивными сопротивлениями и проводимостями.

Для проведения расчетов принимают упрощенные схемы замещения линии, а именно: П-образную схему замещения, состоящую из последовательно соединенных активного (rл) и реактивного (xл) сопротивлений. Активная (gл) и реактивная (емкостная) (bл) проводимости включены в начале и конце линии по 1/2.

Рис. 4.1. П-образная схема замещения характерна для воздушных ЛЭП напряжением 110-220 кВ длиной до 300-400 км.

Активное сопротивление определяется по формуле

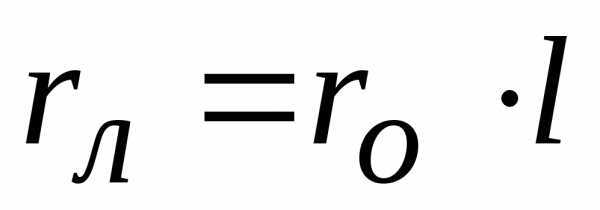где rо – удельное сопротивление Ом/км при tо провода + 20о ,

l – длина линии, км

Активное сопротивление проводов и кабелей при частоте 50 Гц обычно примерно равно омическому сопротивлению. Не учитывается явление поверхностного эффекта.

Удельное активное сопротивление rо для сталеалюминиевых и других проводов из цветных металлов определяется по таблицам в зависимости от поперечного сечения.

Для стальных проводов нельзя пренебрегать поверхностным эффектом. Для них rо зависит от сечения и протекающего тока и находится по таблицам.

При температуре провода, отличной от 20о С сопротивление линии уточняется по соответствующим формулам.

Реактивное сопротивление определяется:

где

xо - удельное реактивное сопротивление Ом/км. Удельные индуктивные сопротивления фаз ВЛ в общем случае различны (об этом уже говорилось).

При расчетах симметричных режимов используют средние значения xо :

(1),

где rпр - радиус провода, см;

Дср - среднегеометрическое расстояние между фазами, см, определяется следующим выражением:

Где Дав, Двс, Дса - расстояния между проводами соответствующих фаз А, В, С.

Например, при расположении фаз по углам равностороннего треугольника со сторонойД, среднегеометрическое расстояние равно Д.

Дав=Двс=Дас=Д

При расположении проводов ЛЭП в горизонтальном положении:

Дав=Двс=Д

Дас=2Д

При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Изменение Х0 из-за влияния второй цепи зависит от расстояния между цепями. Отличие Х0 одной цепи при учете и без учета влияния второй цепи не превышает 5-6% и не учитывается в практических расчетах.

В линиях электропередач при (иногда и при напряжении 110 и 220 кВ) провод каждой фазы расщепляется на несколько проводов.

Рис. 4.2. Пример участка ВЛ с расщеплением провода одной фазы на три провода: подвешивают одновременно несколько проводов на фазу.

Это соответствует увеличению эквивалентного радиуса. В выражении для Х0:

(1)

вместо rпр используется

где rэк - эквивалентный радиус провода, см;

аср - среднегеометрическое расстояние между проводами одной фазы, см;

nф- число проводов в одной фазе.

Для линии с расщепленными проводами последнее слагаемое в формуле 1 уменьшается в nф раз, т.е. имеет вид .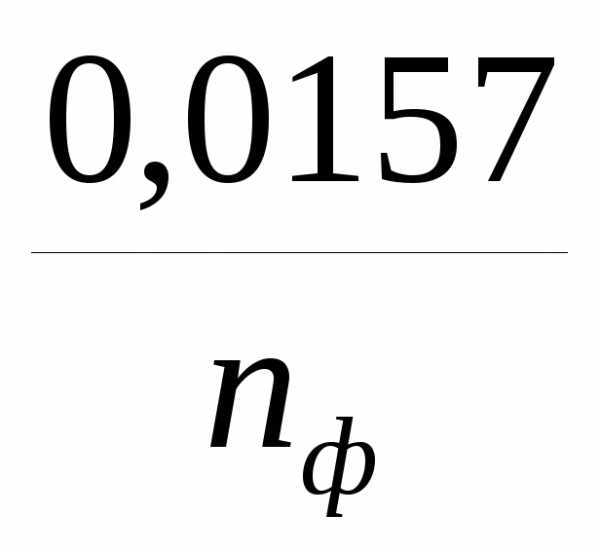

Удельное активное сопротивление фазы линии с расщепленными проводами определяются так : r0= r0пр / nф ,

Где r0пр - удельное сопротивление провода данного сечения, определенное по справочным таблицам. Для сталеалюминиевых проводов Х0 определяется по справочным таблицам, в зависимости от сечения, для стальных в зависимости от сечения и тока.

studfiles.net

Удельное индуктивное сопротивление линии. Активное сопротивление

Схемы замещения ЛЭП постоянного тока могут рассматриваться как частный случай схем замещения ЛЭП переменного тока при Х = 0 и b = 0.

Размещено 10.01.2012 (актуально до 10.04.2013)

Для проведения расчетов принимают упрощенные схемы замещения линии, а именно: П-образную схему замещения, состоящую из последовательно соединенных активного (r л) и реактивного (x л) сопротивлений. Активная (g л) и реактивная (емкостная) (b л) проводимости включены в начале и конце линии по 1/2.

П-образная схема замещения характерна для воздушных ЛЭП напряжением 110-220 кВ длиной до 300-400 км.

Активное сопротивление определяется по формуле:

r л =r о ∙l,

где r о – удельное сопротивление Ом/км при t о провода + 20 о, l – длина линии, км.

Удельное активное сопротивление r о для сталеалюминиевых и других проводов из цветных металлов определяется по таблицам в зависимости от поперечного сечения.

Для стальных проводов нельзя пренебрегать поверхностным эффектом. Для них r о зависит от сечения и протекающего тока и находится по таблицам.

При температуре провода, отличной от 20 о С сопротивление линии уточняется по соответствующим формулам.

Реактивное сопротивление определяется:

x л =x о ∙l,

где x о - удельное реактивное сопротивление Ом/км.

Удельные индуктивные сопротивления фаз ВЛ в общем случае различны. При расчетах симметричных режимов используют средние значения x о:

где r пр - радиус провода, см;

Д ср - среднегеометрическое расстояние между фазами, см, определяется следующим выражением:

Д ср =(Д АВ Д АВ Д СА) 1/3

Где Д АВ, Д АВ, Д СА - расстояния между проводами соответствующих фаз А, В, С.

Например, при расположении фаз по углам равностороннего треугольника со стороной Д, среднегеометрическое расстояние равно Д.

Д АВ =Д ВС =Д СА =Д

При расположении проводов ЛЭП в горизонтальном положении:

Д АВ =Д ВС =Д

Д СА =2Д

При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Изменение Х 0 из-за влияния второй цепи зависит от расстояния между цепями. Отличие Х 0 одной цепи при учете и без учета влияния второй цепи не превышает 5-6% и не учитывается в практических расчетах.

В линиях электропередач при U ном ≥330 кВ (иногда и при напряжении 110 и 220 кВ) провод каждой фазы расщепляется на несколько проводов. Это соответствует увеличению эквивалентного радиуса. В выражении для Х 0:

X о =0,144lg(Д ср /r пр)+0,0157 (1)

вместо r пр используется

r эк =(r пр a ср пф-1) 1/пФ,

где r эк - эквивалентный радиус провода, см;

а ср - среднегеометрическое расстояние между проводами одной фазы, см;

n ф - число проводов в одной фазе.

Для линии с расщепленными проводами последнее слагаемое в формуле 1 уменьшается в n ф раз, т.е. имеет вид 0,0157/n ф.

Удельное активное сопротивление фазы линии с расщепленными проводами определяются так:

r 0 =r 0пр /n ф,

где r 0пр - удельное сопротивление провода данного сечения, определенное по справочным таблицам.

Для сталеалюминиевых проводов Х 0 определяется по справочным таблицам, в зависимости от сечения, для стальных в зависимости от сечения и тока.

Активная проводимость (g л) линии соответствует двум видам потерь активной мощности:

1) от тока утечки через изоляторы;

2) потери на корону.

Токи утечки через изоляторы (ТФ-20) малы и потерями в изоляторах можно пренебречь. В воздушных линиях (ВЛ) напряжением 110 кВ и выше при определенных условиях напряженность электрического поля на поверхности провода возрастает и становится больше критической. Воздух вокруг провода интенсивно ионизируется, образуя свечение - корону. Короне соответствуют потери активной мощности. Наиболее радикальными средствами уменьшения потерь мощности на корону является увеличение диаметра провода, для линий высокого напряжения (330 кВ и выше) использование расщепления проводов. Иногда можно использовать так называемый системный способ уменьшения потерь мощности на корону. Диспетчер уменьшает напряжение в линии до определенной величины.

В связи с этим задаются наименьшие допустимые сечения по короне:

150 кВ - 120 мм 2 ;

220 кВ - 240 мм 2 .

Коронирование проводов приводит:

К снижению КПД,

К усиленному окислению поверхности проводов,

К появлению радиопомех.

При расчете установившихся режимов сетей до 220 кВ активная проводимость практически не учитывается.

В сетях с U ном ≥330 кВ при определении потерь мощности при расчете оптимальных режимов, необходимо учитывать потери на корону.

Емкостная проводимость (в л) линии обусловлена емкостями между проводами разных фаз и емкостью провод - земля и определяется следующим образом:

в л =в 0 l,

где в 0 - удельная емкостная проводимость См/км, которая может быть определена по справочным таблицам или по следующей формуле:

в 0 =7,58∙10- 6 /lg(Д ср /r пр) (2),

где Д ср - среднегеометрическое расстояние между проводами фаз; r пр - радиус провода.

Для большинства расчетов в сетях 110-220 кВ ЛЭП (линия электропередачи) представляется более простой схемой замещения:

Иногда в схеме замещения вместо емкостной проводимости в л /2 учитывается реактивная мощность, генерируемая емкостью линий (зарядная мощность).

Половина емкостной мощности линии, МВАр, равна:

Q C =3I c U ф =3U ф в 0 l/2=0,5V 2 в л,(*),

где U ф и U – соответственно фазное и междуфазное (линейное) напряжения, кВ;

I с - емкостный ток на землю:

Ic=U ф в л /2

Из выражения для Q C (*) следует, что мощность Q C , генерируемая линий сильно зависит от напряжения. Чем выше напряжение, тем больше емкостная мощность.

Для воздушных линий напряжением 35 кВ и ниже емкостную мощность (Q C) можно не учитывать, тогда схема замещения примет следующий вид:

Для линий с U ном ≥330 кВ при длине больше 300-400 км учитывают равномерное распределение сопротивлений и проводимостей вдоль линии.

Кабельные линии электропередачи представляют такой же П-образной схемой замещения как и ВЛ.

Удельные активные и реактивные сопротивления r 0 , х 0 определяют по справочным таблицам, так же как и для ВЛ.

Из выражения для X 0 и в 0:

X о =0,144lg(Д ср /r пр)+0,0157

в 0 =7,58∙10 -6 /lg(Д ср /r пр)

видно, что X 0 уменьшается, а в 0 растет при сближении разных проводов.

Для кабельных линий расстояние между проводами фаз значительно меньше, чем для ВЛ и Х 0 очень мало.

При расчетах режимов КЛ (кабельных линий) напряжением 10кВ и ниже можно учитывать только активное сопротивление.

Емкостный ток и Q C в кабельных линиях больше чем в ВЛ. В кабельных линиях (КЛ) высокого напряжения учитывают Q C , причем удельную емкостную мощность Q C0 кВАр/км можно определить по таблицам в справочниках.

Активную проводимость (g л)учитывают для кабелей 110 кВ и выше.

Удельные параметры кабелей X 0 , а также Q C0 приведенные в справочных таблицах ориентировочны, более точно их можно определить по заводским характеристикам кабелей.

В большинстве случаев можно полагать, что параметры линии электропередачи (активное и реактивное сопротивления, активная и емкостная проводимости) равномерно распределены по ее длине. Для линии сравнительно небольшой длины распределенность параметров можно не учитывать и использовать сосредоточенные параметры: активное и реактивное сопротивления линии Rл и Xл, активную и емкостную проводимости линии Gл и Bл.

Воздушные линии электропередачи напряжением 110 кВ и выше длиной до 300 - 400 км обычно представляются П-образной схемой замещения (рис.3.1).

Активное сопротивление линии определяется по формуле:

Rл=roL,(3.1)где

ro - удельное сопротивление, Ом/км, при температуре провода +20°С;

L - длина линии, км.

Удельное сопротивление г0 определяется по таблицам в зависимости от поперечного сечения. При температуре провода, отличной от 200С, сопротивление линии уточняется.

Реактивное сопротивление определяется следующим образом:

Xл=xoL, (3.2)

где xo - удельное реактивное сопротивление, Ом/км.

Удельные индуктивные сопротивления фаз воздушной линии в общем случае различны. При расчетах симметричных режимов используют средние значения xo:

где rпр – радиус провода, см;

Dср – среднегеометрическое расстояние между фазами, см, определяемое следующим выражением:

где Dab, Dbc, Dca – расстояния между проводами соответственно фаз a, b, c, рис.3.2.

При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Изменение xo из-за влияния второй цепи в первую очередь зависит от расстояния между цепями. Отличие xo одной цепи при учете и без учета влияния второй цепи не превышает 5-6 % и не учитывается при практических расчетах.

В линиях электропередачи при Uном ³ ЗЗ0кВ провод каждой фазы расщепляется на несколько (N) проводов. Это соответствует увеличению эквивалентного радиуса. Эквивалентный радиус расщепленной фазы:

где a – расстояние между проводами в фазе.

Для сталеалюминиевых проводов xo определяется по справочным таблицам в зависимости от сечения и числа проводов в фазе.

Активная проводимость линии Gл соответствует двум видам потерь активной мощности: от тока утечки через изоляторы и на корону.

Токи утечки через изоляторы малы, поэтому потерями мощности в изоляторах можно пренебречь. В воздушных линиях напряжением 110кВ и выше при определенных условиях напряженность электрического поля на поверхности провода возрастает и становится больше критической. Воздух вокруг провода интенсивно ионизируется, образуя свечение - корону. Короне соответствуют потери активной мощности. Наиболее радикальным средством снижения потерь мощности на корону является увеличение диаметра провода. Наименьшие допустимые сечения проводов воздушных линий нормируются по условию образования короны: 110кВ - 70 мм2; 220кВ -240 мм2; 330кВ –2х240 мм2; 500кВ – 3х300 мм2; 750кВ – 4х400 или 5х240 мм2.

При расчете установившихся режимов электрических сетей напряжением до 220кВ активная проводимость практически не учитывается. В сетях с Uном³ЗЗ0кВ при определении потерь мощности и при расчете оптимальных режимов необходимо учитывать потери на корону:

DРк = DРк0L=U2g0L,3.6)

где DРк0 - удельные потери активной мощности на корону, g0 - удельная активная проводимость.

Емкостная проводимость линии Bл обусловлена емкостями между проводами разных фаз и емкостью провод - земля и определяется следующим образом:

где bо - удельная емкостная проводимость, См/км, которая может быть определена по справочным таблицам или по следующей формуле:

Для большинства расчетов в сетях 110-220 кВ линия электропередачи обычно представляется более простой схемой замещения (рис.3.3,б). В этой схеме вместо емкостной проводимости (рис.3.3,а) учитывается реактивная мощность, генерируемая емкостью линий. Половина емкостной (зарядной) мощности линии, Мвар, равна:

UФ и U – фазное и междуфазное напряжение, кВ;

Ib – емкостный ток на землю.

Рис. 3.3. Схемы замещения линий электропередачи:

а, б - воздушная линия 110-220-330 кВ;

в - воздушная линия Uном £35 кВ;

г -кабельная линия Uном£10 кВ

Из (3.8) следует, что мощность Qb, генерируемая линией, сильно зависит от напряжения. Для воздушных линий напряжением 35 кВ и ниже емкостную мощность можно не учитывать (рис.3.3, в). Для линий Uном ³ ЗЗ0 кВ при длине более 300-400 км учитывают равномерное распределение сопротивлений и проводимостей вдоль линии. Схема замещения таких линий – четырехполюсник.

Кабельные линии электропередачи также представляют П-образной схемой замещения. Удельные активные и реактивные сопротивления ro, xo определяют по справочным таблицам, так же как и для воздушных линий. Из (3.3), (3.7) видно, что xo уменьшается, а bo растет при сближении фазных проводников. Для кабельных линий расстояния между проводниками значительно меньше, чем для воздушных, поэтому xo мало и при расчетах режимов для кабельных сетей напряжением 10 кВ и ниже можно учитывать только активное сопротивление (рис.3.3, г). Емкостный ток и зарядная мощность Qb в кабельных линиях больше, чем в воздушных. В кабельных линиях высокого напряжения учитывают Qb (рис.3.3, б). Активную проводимость Gл учитывают для кабелей 110 кВ и выше.

3.2. Потери мощности в линиях

Потери активной мощности в ЛЭП делятся на потери холостого хода DРХХ (потери на корону) и нагрузочные потери (на нагрев проводов) DРН:

В линиях потери реактивной мощности тратятся на создание магнитного потока внутри и вокруг провода

Параметры фаз линий электропередач равномерно распределены по ее длине, т.е. линия электропередачи представляет собой цепь с равномерно распределенными параметрами. Точный расчет схемы, содержащей такую цепь, приводит к сложным вычислениям. В связи с этим при расчете линий электропередач в общем случае применяют упрощенные “Т” и “П” -образные схемы замещения с сосредоточенными параметрами (рисунок №1). Погрешности электрического расчета линии при “Т” и “П”- образной схемах замещения примерно одинаковы. Они зависят от длины линии.

Допущения о сосредоточенности реального равномерно распределенных параметров по длине ЛЭП справедливо при протяженности воздушных линий (ВЛ), не превышающей 300-350 км, а для кабельных линий (КЛ) 50-60 км. Для ЛЭП большой длины применяют различные способы учеты распределенности их параметров.

Размерность схемы ЭС и, соответственно, системы моделирующих уравнений определяется числом схемы. Поэтому в практических, расчетах, в особенности с использованием ЭВМ, чаще используют “П” - образную схему замещения, имеющую одно преимущество – меньшую в 1,5 раза размерность схемы в сопоставлении с моделированием ЛЭП “Т” - образной схемой. Поэтому дальнейшее изложение будет вестись применительно к “П” - образной схеме замещения ЛЭП.

Выделим в схемах замещения продольные элементы – сопротивления ЛЭП Z=R+jX и поперечные элементы – проводимости Y=G+jB (рисунок №2). Значения указанных параметров для ЛЭП определяются по общему выражению

где П { R 0 ,X 0 ,g 0 ,b 0 } – значение продольного или поперечного параметра, отнесенного к 1 км линии протяженностью L, км. Иногда эти параметры именуются погонными.

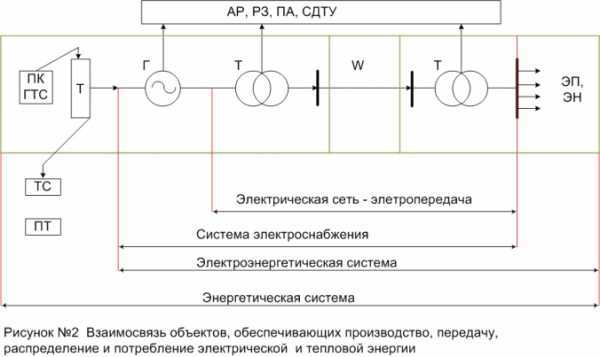
Для ЛЭП конкретного исполнения и класса напряжение используют частичные случаи этих схем в зависимости от физического проявления и величины (значения) соответствующего параметра. Рассмотрим краткую суть этих параметров.

Активное сопротивление обуславливает нагрев проводов (тепловые потери) и зависит от материала токоведущих проводников и их сечения. Для линий с проводами небольшого сечения, выполняемых цветным металлом (алюминий, медь), активное сопротивление принимают равным омическому (сопротивлению постоянному току), поскольку проявление поверхностного эффекта при промышленных частотах 50-60 Гц незаметно (около 1%). Для проводников большого сечения (500 мм 2 и более) является поверхностного эффекта при промышленных частотах значительно.

Активное сопротивление линии определяется по формуле, Ом/км,

где; – удельное активное сопротивление материала провода, Ом мм 2 /км; F- сечение фазного провода (жилы), мм 2 . Для технического алюминия в зависимости от его марки можно принять; = 29,5-31,5 Оммм 2 /км, для меди;=18-19 Оммм 2 /км.

Активное сопротивление не остается постоянным. Оно зависит от температуры провода, которая определяется температурой окружающего воздуха (среды), скорость ветра и значением проходящего по проводу тока.

Омическое сопротивление упрощенно можно трактовать как препятствие направленному движению зарядов узлов кристаллической решетки материала проводника, совершающих колебательные движения около равновесного состояния. Интенсивность колебаний и, соответственно, омическое сопротивление возрастают с ростом температуры проводника.

Зависимость активного сопротивления от температуры провода t определяется в виде

где - нормативное значение сопротивления R 0 , рассчитываются по формуле №2, при температуре проводника t= 20 0 С; α-темпиратурный коэффициент электрического сопротивления, Ом/град (для медных, алюминиевых и сталеалюминевых проводов α=0,00403, для стальных α=0,00455).

Трудность уточнения активного сопротивления линий по формуле №3 заключается в том, что температура провода, зависящая от токовой нагрузки и интенсивности охлаждения, может заметно превышать температуру окружающей среды. Необходимость такого уточнения может возникнуть при расчете сезонных электрических режимов.

При расщеплении фазы ВЛ на n одинаковых проводов в выражении №2 необходимо учитывать суммарное сечение проводов фазы:

Индуктивное сопротивление обусловлено магнитным полем, возникающим вокруг и внутри проводника при протекании по нему тока. В проводнике наводится ЭДС самоиндукции, направленная в соответствии с принципом Ленца, противоположно ЭДС источника

Противодействие которое оказывает ЭДС самоиндукции изменению ЭДС источника, и обуславливает индуктивное сопротивление проводника. Чем больше изменение потокосцепление , определяемое частотой тока;f (скоростью изменения тока di/dt), и величина индуктивности фазы L , зависящая от конструкции (разветвленности) фазы и трехфазной ЛЭП в целом, тем больше индуктивное сопротивление элемента Х=ωL. То есть для одной и той же линии (или просто электрической катушки) с ростом частоты питающего тока f индуктивное сопротивление увеличивается. Естественно, что при нулевой частоте (;f=0), например, в сетях постоянного тока, индуктивное сопротивление ЛЭП отсутствует.

На индуктивное сопротивление фаз многофазных ЛЭП оказывает влияние также взаимное расположение фазных проводов (жил). Кроме ЭДС самоиндукции, в каждой фазу наводится противодействующая ей ЭДС взаимоиндукции. Поэтому при симметричном расположении фаз, например, по вершинам равностороннего треугольника, результирующая противодействующая ЭЛС во всех фазах одинакова, а следовательно, одинаковы пропорциональные ей индуктивные сопротивления фаз. При горизонтальном расположении фазных проводов потокосцепления фаз неодинаково, поэтому индуктивные сопротивления фазных проводов отличаются друг от друга. Для достижения симметрии (одинаковости) параметров фаз на специальных опорах выполняют транспозицию (перестановку) фазных проводов.

Индуктивное сопротивление, отнесенное к 1 км линии, определяется по эмпирической формуле, Ом/км,

(5)

Если принять частоту тока 50 Гц, то при указанной частоте;f=314 рад/с для проводов из цветных металлов (μ=1) получим, Ом/км,

(6)

а при частоте 60Гц соответственно (ω=376,8 рад/с), Ом/км

(7)

При сближении фазных проводов влияние ЭДС взаимоиндукции возрастает, что приводит к уменьшению индуктивного сопротивления ЛЭП. Особенно заметно снижение индуктивного сопротивления (в 3-5 раз) в кабельных линиях. Разработаны компактные ВЛ высокого и сверхвысокого напряжения повышенной пропускной способности со сближенными на 25-20% индуктивным сопротивлением.

Величина среднегеометрического расстояния между фазными проводами (жилами), м,

(8)

зависит от расположения фазных проводов (шин). Фазы ВЛ могут располагаться горизонтально или по вершинам треугольника, фазные шины токопроводов в горизонтальной или вертикальной плоскости, жилы трехжильного кабеля – по вершинам равностороннего треугольника. Значения D ср и r пр должны иметь одинаковую размерность.

При отсутствии справочных данных фактический радиус многопроволочных проводов r пр можно определить по суммарной площади сечения токоведущей и стальной части провода, увеличив его с учетом скручивания на 15 – 20 %, т.е.

(9)

Отметим, что индуктивное сопротивление состоит из двух составляющих: внешней и внутренней. Внешнее индуктивное сопротивление определяется внешними магнитным потоком, образованным вокруг проводов, и значениями D СР и r ПР. Естественно, что с уменьшением расстояния между фазами растет влияние ЭДС взаимоиндукции и индуктивное сопротивление снижается, и наоборот. У кабельных линий с их малыми расстояниями между токоведущими жилами (на два порядка меньше, чем в ВЛ) индуктивное сопротивление значительно (в 3-5 раз) меньше, чем у воздушных. Для определения Х 0 кабельных линий формулы №5 и №6 не применяют, так как они не учитывают конструктивных особенностей кабелей.

Поэтому при расчетах пользуются заводскими данными об индуктивном сопротивлении кабелей. Внутреннее индуктивное сопротивление определяется внутренним потоком, замыкающимся в проводах.

Для стальных проводов его значение находится в зависимости от токовой нагрузки и дается в справочной литературе.

Таким образом, активное сопротивление ЛЭП зависит от материала, сечения и температуры провода. Зависимость обратно пропорциональна сечению провода, ярко выражена при малых сечениях, когда R 0 имеет большие значения, и мало заметна при больших сечениях проводов. Индуктивное сопротивление ЛЭП определяется исполнением линий, конструкцией фазы и практически не зависит от сечения проводов (значение lg(D СР /r ПР)≈const).

Емкостная проводимость обусловлена емкостями между фазами, фазными проводами (жилыми)и землей. В схеме замещения ЛЭП используется расчетная (рабочая) емкость плеча эквивалентной звезды, полученной из преобразования треугольника проводимостей в звезду (рисунок №3, в).

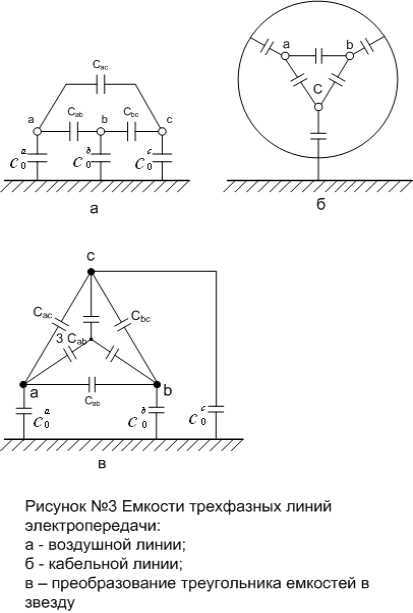
В практических расчетах рабочую емкость трехфазной ВЛ одним проводом на единицу длины (Ф/км)определяют по формуле

(10)

Рабочая емкость кабельных линий существенно выше емкости ВЛ, так как жилы очень близких друг и заземленным металлическими оболочкам. Кроме того диэлектрическая проницаемость кабельной изоляции значительно больше единицы – диэлектрической проницаемость воздуха. Большое разнообразие конструкций кабеля, отсутствие их геометрических размеров усложняет определение ее рабочей емкости, в связи с чем на практике пользуются данными эксплуатационных или заводских замеров.

Емкостная проводимость ВЛ и КЛ, См/км, определяется по общей формуле

Таблица №1 рабочая емкость С 0 (10 -6), Ф/км, трехжильных кабелей с поясной изоляцией

Напряжение, кВ	Сечение жилы, мм 2

С учетом выражения №10, (а) для воздушной линии при частоте тока 50 Гц имеем, См/км,

(11)

а для ВЛ с частотой питающего напряжения 60 Гц получим, См/км,

(12)

Емкостная проводимость зависит от конструкции кабеля и указывается заводом-изготовителем, но для ориентировочных расчетов она может быть оценена по формуле №11.

Под действием приложенного к линии напряжения через емкости линий проектируются емкостные (зарядные) токи. Тогда расчетное значение емкостного тока на единицу длины, кА/км,

(13)

и отвечающая ему зарядная мощность трехфазной ЛЭП, Мвар/км,

зависят от напряжения в каждой точке.

Значение зарядной мощности для всей ЛЭП определяется через действительные (расчетные) напряжения начала и конца линии, Мвар,

либо приближенно по номинальному напряжению линии

Для кабелей 6-35 кВ с бумажной изоляцией и вязкой пропиткой известны генерации реактивной мощности q 0 на один километр линии, с учетом которой общая генерация КЛ определится в виде

ЛЭП с поперечной емкостной проводимостью, потребляющая из сети опережающий напряжение емкостной ток, следует рассматривать как источник реактивной (индукционной) мощности, чаще называемой зарядной. Имея емкостной характер, зарядная мощность уменьшает индуктивную составляющую нагрузки, передаваемой по линии к потребителю.

В схемах замещения ВЛ, начиная с номинального напряжения 110 кВ, и в КЛ-35 кВ и более следует учитывать поперечные ветви (шунты) в виде емкостных проводимостей В с, или генерируемых мощностей Q C .

Расстояние между фазами ЛЭП в каждом классе напряжения, особенно для ВЛ, практически одинаково, что и определяет неизменность результирующего потокосцепления фаз и емкостного эффекта линий, Поэтому для ВЛ традиционного исполнения (без глубокого расщепления фаз и специальных конструкций опор) реактивные параметры мало зависят от конструктивных характеристик линии, так как отношение расстояний между фазами и сечения (радиуса) проводов практически неизменны, что в приведенных формулах отражено логарифмической функцией.

При выполнении фаз ВЛ 35-220 кВ одиночными проводами их индуктивное сопротивление в узких пределах: Х 0 =(0,40-0,44)Ом/км, а емкостная проводимости лежит в пределах b 0 =(2.6-2.8)10 -6 См/км. Влияние изменения площади сечения (радиуса) жил кабеля на Х 0 более заметно, чем в ВЛ. Поэтому для КЛ имеем более широкое изменение индуктивного сопротивления: Х 0 ≈(0,06-0,15) Ом/км. Для кабельных линий всех марок и сечений напряжением 0,38-10 кВ индуктивное сопротивление лежит в более узком интервале (0,06-0,1 Ом/км) и определяется из таблиц физико-технических данных кабелей.

Среднее значение зарядной мощности на 100 км для ВЛ 110 кВ составляет около 3,5 Мвар, для 220 кВ – 13,5 Мвар, для ВЛ 500 кВ-95 Мвар.

Учет этих показателей позволяет исключить значительные ошибки при расчете параметров линий или использовать указанные параметры в приближенных расчетах, например для оценки по реактивным параметрам ВЛ ее протяженности (км) в виде

Активная проводимость обусловлена потерями активной мощности ΔР из-за несовершенства изоляции (утечки по поверхности изоляторов, токов проводимости (смещения) в материале изолятора) и ионизации воздуха вокруг проводника вследствие коронного разряда. Удельная активная проводимость определяется по общей формуле шунта, См/км,

где U ном –номинальное напряжение ЛЭП в кВ.

Потери в изоляции ВЛ незначительны, и явление коронирования в ВЛ возникает только при превышении напряженности электрического поля у поверхности провода кВ МАКС /см:

критическая величина около 17-19 кВ/см. Такие условия для коронирования возникают в ВЛ 110 кВ и более высокого напряжения.

Коронирование и следовательно, потери активной мощности сильно зависят от напряжения ВЛ, радиуса провода, атмосферных условий и состояния поверхностности провода. Чем больше рабочее напряжение и меньше радиус проводов, тем больше напряженность электрического поля. Ухудшающие атмосферных условий (высокая влажность воздуха, мокрый снег, изморозь на поверхности проводов), заусеницы, царапины также способствуют росту напряженности электрического поля и, соответственно, потерь активной мощности на короникование. Коронный разряд вызывает помехи на радио и телевизионный прием, коррозию поверхности проводов ВЛ.

Для снижения потерь на корону до экономически приемлемого уровня правилами устройства электроустановок (ПУЭ) установлены минимальные сечения (диаметры) проводов. Например, для ВЛ 110кВ-АС 70 (11,8 мм), для ВЛ 220 кВ- АС 240 (21,6мм).

Потери мощьности на коронирование учитывают при моделировании ВЛ с номинальными напряжением 330 кВ и более.

В КЛ под влиянием наибольшей напряженности находятся слои поясной изоляции у поверхности жил кабеля. Чем больше рабочее напряжение кабеля, тем заметнее токи утечки через материалы изоляции и нарушение ее диэлектрических свойств. После характеризуются тангенсом угла диэлектрических потерь tg δ, принимаемым по данным завода-изготовителя.

Активная проводимость кабеля на единицу длинны

(20)

и соответствующий ток утечки в изоляции кабеля, А,

(21)

Тогда диэлектрические потери в материале изоляции КЛ, МВт,

Их следует учитывать для КЛ с номинальным напряжением 110 кВ и выше.

levevg.ru

Активные и реактивные сопротивления кабелей

Want create site? Find Free WordPress Themes and plugins.

Сечение жилы, мм2	Активное сопротивление при 20 °С, Ом/км, жилы	Индуктивное сопротивление, Ом/км, кабеля напряжением, кВ
алюминиевой	медной	1	6	10	20
10	2,94	1,79	0,073	0,11	0,122
16	1,84	1,12	0,068	0,102	0,113	—
25	1,17	0,72	0,066	0,091	0,099	0,135
35	0,84	0,51	0,064	0,087	0,095	0,129
50	0,59	0,36	0,063	0,083	0,09	0,119
70	0,42	0,256	0,061	0,08	0,086	0,116
95	0,31	0,19	0,06	0,078	0,083	0,110
120	0,24	0,15	0,06	0,076	0,081	0,107
150	0,2	0,12	0,059	0,074	0,079	0,104
185	0,16	0,1	0,059	0,073	0,077	0,101
240	0,12	0,07	0,058	0,071	0,075	—

Did you find apk for android? You can find new Free Android Games and apps.

Предыдущая запись

Цифровой мультиметр Mastech M838

Следующая запись

Базовые марки силовых кабелей 0,66 — 6 кВ

radioschema.ru

el-cab.ru

Практическая работа №3 Электрический расчет кабельной линии

400 600 800 1000 1250 1500 2000 2500 3000

0,371 0,397 0,415 0,429 0,443 - - - -

0,355 0,381 0,399 0,413 0,427 0,438 0,457 - -

0,333 0,358 0,377 0,391 0,405 0,416 0,435 0,449 0,460

0,319 0,345 0,363 0,377 0,391 0,402 0,421 0,435 0,446

0,308 0,336 0,352 0,366 0,380 0,391 0,410 0,424 0,435

0,297 0,325 0,341 0,355 0,369 0,380 0,398 0,413 0,423

0,283 0,309 0,327 0,341 0,355 0,366 0,385 0,399 0,410

0,274 0,300 0,318 0,332 0,346 0,357 0,376 0,390 0,401

- 0,292 0,310 0,324 0,338 0,349 0,368 0,382 0,393

- 0,287 0,305 0,319 0,333 0,344 0,363 0,377 0,388

- 0,280 0,298 0,313 0,327 0,338 0,357 0,371 0,382

600 800 1000 1250 1500 2000

- - - - - -

0,358 0,377 0,391 0,405 - -

0,345 0,363 0,377 0,391 0,402 0,421

0,336 0,352 0,366 0,380 0,391 0,410

0,325 0,341 0,355 0,369 0,380 0,398

0,315 0,331 0,345 0,359 0,370 0,388

0,303 0,319 0,334 0,347 0,358 0,377

0,297 0,313 0,327 0,341 0,352 0,371

0,288 0,305 0,319 0,333 0,344 0,363

0,279 0,298 0,311 0,328 0,339 0,355

studfiles.net

Активное и индуктивное сопротивление кабелей и проводов. Емкостная проводимость линий электропередач

Активное сопротивление проводов и кабелей

На практике активное сопротивление медных и алюминиевых проводников рассчитывают по формуле:

Величина r0, как правило, берется из таблиц справочников.

Индуктивное сопротивление проводов и кабелей

Где: Х0 – индуктивное сопротивление одного километра провода или кабеля на фазу, Ом/км.

Х одного километра воздушной или кабельной линии можно определить по формуле:

Для одной фазы:

Где: D1:2 расстояние между проводами.

Для одинарной трехфазной линии при расположении проводов по треугольнику:

При горизонтальном или вертикальном расположении проводов трехфазной линии в одной плоскости:

Увеличение сечения проводов линии ведет к незначительному уменьшению Х0/.

Таким образом выражение для Х0 можно представить в виде:

В таком случае формула для определения Х0 примет вид:

Емкостная проводимость линий

Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:

Емкостная проводимость одноцепной воздушной линии определяется по формуле:

Где: U – линейное напряжение сети, В; l – длина линии, км;

Для воздушной линии:

Для кабельной линии:

elenergi.ru

Сопротивление провода СИП больше чем у обычного, это правда? Удельное активное сопротивление кабеля таблица

Значения удельных активных сопротивлений для медных и алюминиевых проводов и кабелей

Сечение, мм	Провода и кабели, Ом/км		Сечение, мм2		Провода и кабели, Ом/км
Сечение, мм	медные	алюминиевые			медные	алюминиевые
1	18,9	-		35	0,54	0,92
1,5	12,6	—		50	0,39	0,64
2,5	7,55	12,6		70	0,28	0,46
4	4,56	7,90		95	0,2	0,34
6	3,06	5,26		120	0,158	0,27
10	1,84	3,16		150	0,123	0.21
16	1,20	1,98		185	0.103	0,17
25	0,74	1,28		240	0,17	0,132

Индуктивное сопротивление проводов и кабелей. Как уже отмечалось, при переменном токе в линии вокруг ее проводов создается переменное магнитное поле, которое обусловливает индуктивное сопротивление линии. Величина сопротивления зависит от расстояния между проводами линии, диаметра провода, относительной магнитной проницаемости, частоты переменного тока.

Значение индуктивного сопротивления 1 км трехфазной воздушной линии для любого расположения проводов, материала проводов и частоты переменного тока можно определить по формуле (Ом/км)

- угловая частота;

- среднее геометрическое расстояние между осями проводов, мм;

d - диаметр провода, мм;

- относительная магнитная проницаемость провода. Среднее геометрическое расстояние между осями трех проводов трехфазной линии, проложенных в одной плоскости, определяется выражением

При горизонтальном или вертикальном расположении проводов трехфазной линии в »лпой плоскости с расстоянием между проводами Д

Из формулы видно, что первый член представляет собой индуктивное сопро-'пвление, обусловленное внешним магнитным полем, и называется внешним индуктивным сопротивлением

Оно зависит не от материала провода и значения протекающего тока, а от расстояния между проводами и диаметра провода. Поскольку расстояние между проводами выбирают в зависимости от значения напряжения, внешнее индуктивное сопротивление тем больше, чем больше номинальное напряжение линии. Оно больше у воздушной линии, чем у калькой, так как жилы кабеля расположены значительно ближе друг к другу. Увеличение учения проводов линии ведет к незначительному уменьшению внешнего индуктивного ^противления.

Второй член формулы представляет собой индуктивное сопротивление провода, созданное переменным магнитным полем внутри проводника, и называется внутренним индуктивным сопротивлением х0". Оно зависит только от магнитной проницаемости материала провода и, следовательно, от значения тока.

Таким образом, формулу можно представить в виде суммы внешнего и ] реннего индуктивных сопротивлений:

Внутреннее индуктивное сопротивление х()" стальных проводов в отличие от прово. дов из цветных металлов имеет преобладающее значение. Это вызвано тем, что внутренне индуктивное сопротивление пропорционально магнитной проницаемости, зависящей о протекающего тока в проводе. Если для проводов из цветных металлов μ= 1, то для стопных проводов р. может достигать значения 103 и даже больше.

Для линии с проводами из цветных металлов (немагнитных), у которых μ=1, и припромышленной частоте переменного тока 50 Гц внутреннее индуктивное сопротивление по сравнению с внешним составляет ничтожно малую величину и им обычно пренебрегают: в этом случае формула примет следующий вид (Ом/км):

Для определения индуктивного сопротивления (Ом/км) воздушной или кабельтн-линии протяженностью l (км) пользуются выражением

где индуктивное сопротивление 1 км провода или кабеля на фазу; l - длина линии

Для практических расчетов индуктивные сопротивления трехфазных линий х(), Ом/км. можно определять по табл. 6.4

Таблица 4.4

studfiles.net

Сопротивление провода СИП больше чем у обычного, это правда?

Самонесущий изолированный провод "СИП" - это многожильный провод

Чтобы сравнивать сопротивление, нам понадобятся данные из нескольких нижеприведенных таблиц.

Таблица 1. Активное сопротивление токопроводящих жил изолированных проводов марок СИП-1, СИП-2, СИП-4 при 90 градусах C.

Таблица 2. Индуктивное сопротивление токопроводящих жил изолированных проводов марок СИП-1, СИП-2, СИП-4.

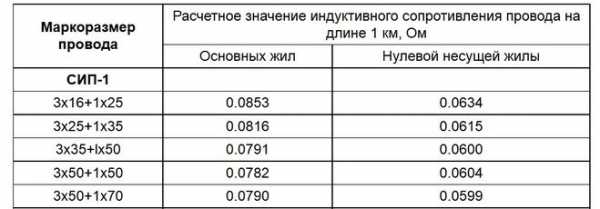
Таблица 3. Характеристики токопроводящих жил сталеалюминиевых проводов и проводов из алюминиевого сплава со стальным сердечником.

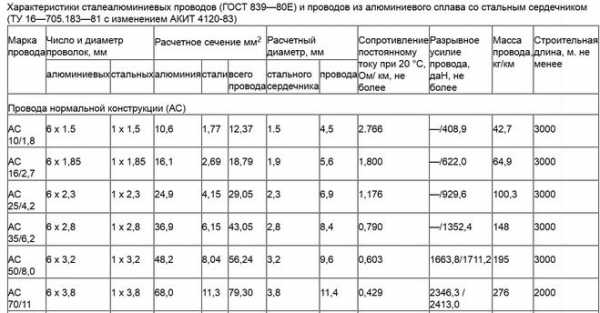
Таблица 4. Активное и реактивное сопротивление токопроводящих жил проводов, используемых в кабелях.

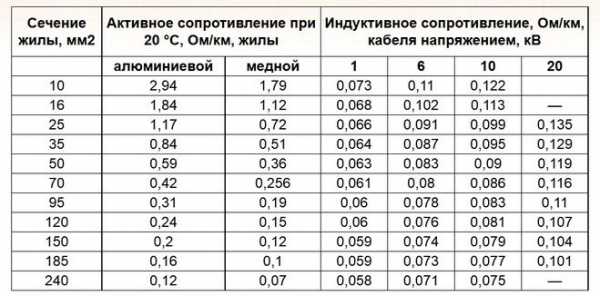
Для сравнительного анализа возьмем алюминиевые провода марок СИП4 4х16 и АС 16/2,7. Оба провода имеют одинаковое полезное сечение 16 квадратов (кв. мм.).

-Самонесущий изолированный провод марки СИП4 4х16 как правило применяется для монтажа воздушных линий силовых и осветительных электрических сетей, рассчитанных на напряжение до 1кВ. и используется для передачи и распределения электрической энергии.

-Провод для воздушных линий электропередач марки АС - это многожильный алюминиевый провод с сердечником из оцинкованных стальных проволок.

Активное сопротивление токопроводящей жилы провода СИП4 4х16 составляет 2,448 Ом на 1 км. длины провода (Таблица 1).

Активное сопротивление токопроводящей жилы провода АС 16/2,7 составляет 1,8 Ом на 1 км. длины провода (Таблица 3).

Сопротивление токопроводящих жил проводов СИП больше, чем проводов АС 16/2,7.

Сравним индуктивное сопротивление провода СИП4 4х16 (Таблица 2) - 0,0821 Ом/км.

szemp.ru

Активное и реактивное сопротивление кабелей

Активные и реактивные сопротивления кабелей - Кабели

Сечение жилы, мм2	Активное сопротивление при 20 °С, Ом/км, жилы	Индуктивное сопротивление, Ом/км, кабеля напряжением, кВ
алюминиевой	медной	1	6	10	20
10	2,94	1,79	0,073	0,11	0,122
16	1,84	1,12	0,068	0,102	0,113	—
25	1,17	0,72	0,066	0,091	0,099	0,135
35	0,84	0,51	0,064	0,087	0,095	0,129
50	0,59	0,36	0,063	0,083	0,09	0,119
70	0,42	0,256	0,061	0,08	0,086	0,116
95	0,31	0,19	0,06	0,078	0,083	0,110
120	0,24	0,15	0,06	0,076	0,081	0,107
150	0,2	0,12	0,059	0,074	0,079	0,104
185	0,16	0,1	0,059	0,073	0,077	0,101
240	0,12	0,07	0,058	0,071	0,075	—

Добавлять комментарии могут только зарегистрированные пользователи.[ Регистрация | Вход ]

Новости сайта ukrelektrik.com

Последние статьи ukrelektrik.com

Последние ответы на форуме ukrelektrik.com

Автоматика 2alpilip Артём / 24 Всё обо всём - общение kristina-asmus-3d elektro / 114 Кабели/провода Sanya puraxin / 12

ukrelektrik.com

Активные и реактивные сопротивления кабелей

АльтИнфоЮг Альтернативная энергетика и информация

Величины активных и реактивных сопротивлений кабелей различного сечения и напряжения из медных и алюминиевых жил позволяют рассчитать потери в кабеле при постоянном и переменном токе.

Активные и реактивные сопротивления кабелей Сечение жилы мм2Активное сопротивление при 200С, Ом/км, жилыИндуктивное сопротивление , Ом/км, кабеля на напряжение, кВАлюминиевойМедной161020

10	2,94	1,79	0,073	0,11	0,122	-
16	1,84	1,12	0,068	0,102	0,113	-
25	1,17	0,72	0,066	0,091	0,099	0,135
35	0,84	0,51	0,064	0,087	0,095	0,129
50	0,59	0,36	0,063	0,083	0,09	0,119
70	0,42	0,256	0,061	0,08	0,086	0,116
95	0,31	0,19	0,06	0,078	0,083	0,110
120	0,24	0,15	0,06	0,076	0,081	0,107
150	0,2	0,12	0,059	0,074	0,079	0,104
185	0,16	0,1	0,059	0,073	0,077	0,101
240	0,12	0,07	0,058	0,071	0,075	-

Литература: «Справочник энергетика» под редакцией А.Н. Чохонелидзе стр.222

altinfoyg.ru

Активное и индуктивное сопротивление кабелей - таблица

Содержание:

Особенности активного сопротивления

Таблица и расчет по формуле

Действие индуктивного сопротивления кабельных линий

electric-220.ru

Активные и реактивные сопротивления кабелей

Сечение жилы, мм2	Активное сопротивление при 20° С, Ом/км, жилы	Индуктивное сопротивление, Ом/км, кабеля напряжением, кВ
алюминиевой	медной
	2,94	1,79	0,073	0,11	0,122	-
	1,84	1,12	0,068	0,102	0,113	-
	1,7	0,72	0,066	0,091	0,099	0,135
	0,84	0,51	0,064	0,087	0,095	0,129
	0,59	0,36	0,063	0,083	0,09	0,119
	0,42	0,256	0,061	0,08	0,086	0,116
	0,31	0,19	0,06	0,078	0,083	0,110
	0,24	0,15	0,06	0,076	0,081	0,107
	0,2	0,12	0,059	0,074	0,079	0,104
	0,16	0,1	0,059	0,073	0,077	0,101
	0,12	0,07	0,058	0,071	0,075	-

ПРИЛОЖЕНИЕ VI

Векторные диаграммы токов при различных видах

Коротких замыканий для измерительной части

Дифференциальной защиты

Вид короткого замыкания	Векторные диаграммы токов при внешнем коротком замыкании за трансформатором с соединением обмоток Y/Δ-11 при	Схема упрощенных дифференциальных защит двухобмоточного трансформатора
двухрелейная	трехлинейная

Со стороны обмоток ВН, соединенных в звезду	Со стороны обмоток НН, соединенных в треугольник (ПТ=1)
Ток в реле 1 и 2	Ток в реле 3 Iр3=IВС+( Ia+Ic)
Iр1=Ica-I0	Iр2=IАВ-Iа
Трехфазное АВС
Между фазами АВ			IC=0 ICA=0
Между фазами ВС				Ia=0 IAB=0
Между фазами СА					Ia+Ic=0 Ibc=0

Таблица 14

Рис. 39. Токораспределение в цепях дифференциальной токовой защиты двух- и трехобмоточных трансформаторов: а – двойное замыкание на землю на стороне 6 – 10кВ; б – КЗ между двумя фазами на стороне «треугольник» 6 – 10кВ двухобмоточного трансформатора; в – КЗ между двумя фазами на стороне «звезды» 110-220кВ двухобмоточного трансформатора; г – КЗ между двумя фазами на стороне «звезды» 35кВ трехобмоточного трансформатора

ПРИЛОЖЕНИЕ VII

Контрольные вопросы

В целях самоконтроля и проверки остаточных знаний предлагаются тестовые вопросы. Из 22 вопросов при правильных ответах уровень знаний можно оценить:

– «удовлетворительно» – не менее 13 правильных ответов;

– «хорошо» – не менее 17 правильных ответов;

– «отлично» – не менее 20 правильных ответов.

В 1. Выбрать выдержки времени максимальной токовой защиты (МТЗ) с независимой характеристикой срабатывания реле для схемы:

1) tср1=tср2=tср3;

2) tср1>tср2>tср3;

3) tср1

lektsia.info

el-cab.ru

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

Практическая работа №3 Электрический расчет кабельной линии. Таблица активное сопротивление кабеля

Активное и индуктивное сопротивление кабелей + таблица

Особенности активного сопротивления

Таблица и расчет по формуле

Действие индуктивного сопротивления кабельных линий

Таблица активное сопротивление кабеля

Практическая работа №3 Электрический расчет кабельной линии

Активные и реактивные сопротивления кабелей

Практическое пособие по определению возможной причастности токов короткого замыкания к воспламенению изоляции проводников, страница 15

Проводимость и сопротивление воздушных и кабельных линий

Активное сопротивление проводов и кабелей

Индуктивное сопротивление проводов и кабелей

Емкостная проводимость линий

Удельное активное сопротивление кабеля таблица

Оцените работу специалиста!

Re: Здравствуйте. Удельное активное и реактивное сопротивление кабелей АВВГ 4х70, 4х95, 4х120. Спасибо!

Page 2

Технический форум

Тема: Ответьте, пожалуйста на вопрос: Нормативный срок службы контрольных, силовых и в/в кабелей.

Re: Ответьте, пожалуйста на вопрос: Нормативный срок службы контрольных, силовых и в/в кабелей.

3.5. Погонные (удельные) параметры линий

Задания для самостоятельной работы:

Удельное индуктивное сопротивление линии. Активное сопротивление

Активные и реактивные сопротивления кабелей

Практическая работа №3 Электрический расчет кабельной линии

Активное и индуктивное сопротивление кабелей и проводов. Емкостная проводимость линий электропередач

Активное сопротивление проводов и кабелей

Индуктивное сопротивление проводов и кабелей

Емкостная проводимость линий

Сопротивление провода СИП больше чем у обычного, это правда? Удельное активное сопротивление кабеля таблица

Значения удельных активных сопротивлений для медных и алюминиевых проводов и кабелей

Сопротивление провода СИП больше чем у обычного, это правда?

Активное и реактивное сопротивление кабелей

Активные и реактивные сопротивления кабелей - Кабели

Новости сайта ukrelektrik.com

Последние статьи ukrelektrik.com

Последние ответы на форуме ukrelektrik.com

Активные и реактивные сопротивления кабелей

Активное и индуктивное сопротивление кабелей - таблица

Особенности активного сопротивления

Таблица и расчет по формуле

Действие индуктивного сопротивления кабельных линий

Активные и реактивные сопротивления кабелей

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация