Вектор магнитной индукции и электромагнитная сила. Вектор магнитной индукции это физическая величина

Формула вектора магнитной индукции

Направление вектора магнитной индукции

Направлением вектора магнитной индукции считают направление, которое показывает северный полюс магнитной стрелки, которая может свободно устанавливаться в магнитном поле. Аналогичное направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре. При использовании рамки с током или магнитной стрелки можно определить направление вектора в любой точке магнитного поля.

Если магнитное поле создает прямой проводник с током, то магнитная стрелка в любой точке этого поля устанавливается по касательной к окружности, плоскость которой перпендикулярна проводнику, центр находится на оси провода. Направление вектора определяют при помощи правила правого винта (правила буравчика), которое говорит о том, что если поступательное перемещение буравчика совпадает с направлением течения тока в проводнике, то вращение головки винта совпадает с направлением вектора магнитной индукции.

Величина (модуль) вектора магнитной индукции

Магнитное поле оказывать действие на каждый участок проводника с током. Используя силу, действующую на проводник с током (силу Ампера), определяют величину вектора магнитной индукции магнитного поля. Так, модуль вектора равен частному от деления максимальной силы Ампера , с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника :

   

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. По величине ее воздействия на заряд также можно установить модуль вектора :

   

где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.

Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:

   

где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля.

Основные формулы, которые служат для вычисления вектора магнитной индукции

Закон Био-Савара-Лапласа

Данный закон предоставляет нам возможность вычислить вектор магнитной индукции () в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:

   

где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).

Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме() и в веществе (), при одинаковых условиях, связывает формула:

   

где – относительная магнитная проницаемость вещества.

Принцип суперпозиции

Магнитная индукция поля (), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей ():

   

Теорема о циркуляции

В однородном и изотропном веществе циркуляция вектора индукции магнитного поля по любому контуру L равна:

   

где – сумма токов проводимости с учетом их знака, которые охвачены рассматриваемым контуром; – магнитная проницаемость вещества. В том случае, если направление обхода контура связано с направлением течения тока при помощи правила правого винта, то ток считают положительным.

В случае непрерывного распределения тока по поверхности S силу тока вычисляют при помощи выражения:

   

где равен по модулю площади элемента поверхности – плотность тока.

Примеры частных случаев формул для нахождения вектора магнитной индукции см. раздел «Магнитная индукция формула»

Примеры решения задач по теме «Вектор магнитной индукции»

ru.solverbook.com

1. Дайте определение вектора магнитной индукции. Что такое силовая линия магнитного поля? Изобразите картину силовых линий прямого бесконечно длинного тока.

Магни́тная инду́кция —векторнаявеличина, являющаяся силовой характеристикоймагнитного поля(его действия на заряженные частицы) в данной точке пространства.

Определяет, с какой силоймагнитное поле действует назаряд, движущийся со скоростью.

Также определяется моментом

α — угол между векторами скорости и магнитной индукции – сила Лоренца.

Силовыми линиями магнитного поля называются линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции.

2. Сформулируйте закон Био-Савара-Лапласа (рисунок, указать направление вектора в). Какое направление имеет элемент тока?

Элемент тока I длины dl создает в точке Р поле с магнитной индукции dB:

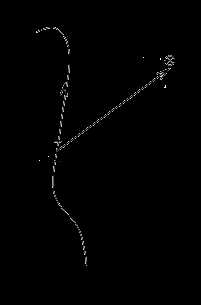
Закон Био - Савара-Лапласа устанавливает что dB:

1) 1/r2 2) I 3) dB перпендикулярно r и dl

3. Напишите формулу для магнитной индукции поля прямолинейного проводника с током конечной длины. (рисунок, указать направление вектора в). Изобразите картину прямого бесконечно длинного тока.

Два рисунка.

4. Что такое циркуляция вектора в? Сформулируйте теорему о циркуляции вектора магнитной индукции в случае магнитного поля постоянных токов( поясните все величины).

Циркуляция вектора В по замкнутому контуру называется интеграл :

где dl — вектор элементарной длины контура, направленной вдоль обхода контура, Bl=Bcosa — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), a — угол между векторами В и dl

теорема о циркуляции вектора В- циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром:

1) Циркуляция может быть по произвольному контуру

2) Сумма токов – алгебраическая ; токи положительны, если направление обхода контура совпадает с направлением силовых линий , а отрицательны, если навстречу. (рис 1)

Рассмотрим бесконечно прямой ток I

На расстоянии R*B= µ0 I/ 2piR – const

Контур L – окружность радиуса R

следует что B = Bl, так как В параллельно dl

Следует что рисунок 2

5.Что такое сила Лоренца? Когда на заряд действует сила Лоренца? Сделайте рисунок и укажите ее направление для отрицательного заряда, движущегося перпендикулярно линиям в.

Сила Лоренца – есть сила, действующая на одиночный заряд , движущийся в магнитном поле .

Одиночный заряд – электрон, протон или любой другой точечный заряд, например заряженная капля жидкости.

FЛ = q υ B sin α.

Сила Лоренца не действует на заряд в том случае, когда заряд движется вдоль линии В

Так как sin0= 0

Для отрицательного заряда сила Лоренца направлена противоположна силе, действующей на положительный заряд.

studfiles.net

Вектор магнитной индукции. Линии магнитной индукции. Однородное и неоднородное магнитное поле. Теория

Числовой характеристикой магнитного поля является вектор магнитной индукции (

). Размерность вектора магнитной индукции — Тл (Тесла), в единицах СИ: [Н/(А*м)]. Пусть источником магнитного поля будет обычный магнит (рис. 1).

Рис. 1. Магнит (линии напряжённости)

Замкнутые гладкие линии на рисунке — линии магнитной индукции. Поместим на график пару точек, в которых попытаемся нарисовать вектор магнитной индукции. Сам вектор является элементом касательной в исследуемой точке к линии магнитной индукции. В случае постоянного магнита, направление этого вектора — от северного полюса магнита (N) к южному (S) (рис. 2).

Рис. 2. Магнит (вектор магнитной индукции)

Вектора, представленные на рисунке 2, — вектора магнитной индукции, их размер диктуется набором причин: размерами магнита, удалённость точки от магнита и т.д.В случае, если значение вектора магнитной индукции постоянно во всех точках пространства, то такое поле назовём однородным магнитным полем, в обратном случае — неоднородным.

Значение модуля вектора магнитной индукции — величина расчётная и зависит от источника поля.

Поделиться ссылкой:

www.abitur.by

Вектор магнитной индукции и электромагнитная сила — Мегаобучалка

Федеральное агентство по образованию

Саратовский государственный университет им. Н.Г.Чернышевского

 

 

А.А. Князев, Н.Б. Ковылов, Ю.И. Левин, Ю.П. Шараевский

 

М А Г Н Е Т И З М

 

 

Учебно-методическое пособие к курсу «Электричество и магнетизм»

и к лабораторному практикуму по этому курсу

 

Саратов, 2011

УДК 530.10

К54 Князев А.А., Ковылов Н.Б., Левин Ю.И., Шараевский Ю.П. Магнетизм. Саратов:

Настоящее пособие содержит основные теоретические положения, лежащие в основе магнитных явлений и которые по известным причинам не рассматриваются в теоретическом курсе электромагнетизма. Эти сведения будут полезны студентам как при подготовке к практикуму, так и при работе на семинарах.

Вторая часть пособия содержит руководство по лабораторным работам, поставленным в интегрированном учебно-научном практикуме «Методика, технология и информационное обеспечение физического эксперимента». Описанные лабораторные работы отработаны на практике студентами факультета нелинейных процессов Дымовой Е.А., Цветковой Н.С. и Ахромеевым А.В. в ходе выполнения курсовых и дипломных работ.

 

Рекомендуют к печати:

кафедра нелинейной физики ФНП СГУ,

доцент кафедры общей физики СГУ А.В. Зборовский

 

 

УДК 530.10

 

ã А.А. Князев, Н.Б. Ковылов,

Ю.И. Левин, Ю.П. Шараевский,

 

Учебное издание

 

Князев Александр Александрович

Ковылов Николай Борисович

Левин Юрий Иванович

Шараевский Юрий Павлович

М А Г Н Е Т И З М

 

Учебно-методическое пособие к курсу «Электричество и магнетизм»

и к лабораторному практикуму по этому курсу

 

 

ВВЕДЕНИЕ

Наблюдение разнообразия магнитных явлений и их изучение в практикуме конструктивно распределено по нескольким модулям. Каждый из модулей дает возможность провести цикл из двух-трех опытов, используя в разных режимах одно и то же устройство, блок питания, комплект измерительной аппаратуры и (при необходимости) шину подключения к компьютеру.

Кроме чисто конструктивного удобства и экономии лабораторной площади, такое объединение работ позволяет группе студентов выполнить две-три работы за одно занятие, не прибегая к потерям времени на освоение нового экспериментального стенда.

Перед выполнением очередной работы данного цикла необходимо познакомиться с ее описанием, понять физическую схему стенда, и сопоставить содержание краткого описания с известными теоретическими сведениями о конкретном наблюдаемом явлении. Важно понять, как организована методика регистрации и измерения изучаемых характеристик. По возможности, проведите элементарные оценки значений измеряемых величин (действующие поля, токи, напряжения, частоты, времена). Обратите внимание на измерительные приборы, источники питания, генераторы, осциллографы. Их главные характеристики: тип, класс точности, пределы измерения, быстродействие. Помните, что именно так формируются профессиональные навыки исследователя – возможно и вы в скором времени окажетесь перед необходимостью самостоятельного проведения эксперимента или организации измерений.

Далее осмысливается порядок работы, производится сборка и проверка установки, проверяется работоспособность узлов и приборов.

 

 

НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

МАГНИТНЫХ ЯВЛЕНИЙ

Будем полагать, что основные сведения известны из курса школьной физики, а также из лекционного общего курса. Здесь обратим внимание на важнейшие физические величины и некоторые трудные моменты понимания в явлениях, которые рассматриваются в лабораторных работах данного практикума.

 

Вектор магнитной индукции и электромагнитная сила

Основной характеристикой магнитного поля является индукция . Эта величина, вместе с величиной напряженности электрического поля используется для описания электрического взаимодействия. Действительно, если заряды точечные электрические заряды и неподвижны, то напряженность электростатического поля характеризует электрическую силу, действующую на заряд со стороны другого заряда: . В результате получаем формулу , которая справедлива и в случае если источник поля не является точечным, а имеет более сложную форму (здесь и далее использованы стандартные обозначения).

Если заряд равномерно движется в лабораторной системе отсчета со скоростью V, а скорость равномерного движения заряда равна U, то взаимодействие зарядов ослабевает пропорционально квадрату скорости относительного движения. При этом характер его описания усложняется – из электростатического оно превращается в электродинамическое. С позиций современной физики это взаимодействие описывается уже двумя слагаемыми: электрическим и магнитным. В результате полное выражение для силы принимает вид

(сила Лоренца).

Здесь электростатическое поле заряда описывается теперь как зависящее от скорости: , здесь , – угол между направлением вектора скорости V и радиус вектора заряда q.

Дополнительно к электростатическому полю в описании возникает новое поле – магнитное – с характеристикой, получившей название магнитная индукция: .

Важно отметить, что в отличие от электрического вектора , обладающего свойством коммутативности с другими векторами, магнитный вектор является аксиальным (антикоммутативным) – т.е. выражение силовых характеристик с его участием производится в виде векторного произведения. Это означает, что полный вектор силы Лоренца уже не подчиняется коммутативному закону преобразований Галилея при переходе к другой системе координат. Электрическое взаимодействие описывается единым шестикомпонентным полем, которое и называют электромагнитным. Строго говоря, все шесть составляющих образуют величину, называемую тензором второго ранга[1], поэтому использование только векторных представлений в задачах, связанных с преобразованием систем координат, невозможно. Отметим, что с тем же математическим аппаратом имеют дело в механике при описании деформации твердого тела: отклик на силу, приложенную в произвольной точке, часто сопровождается не только сжатием или растяжением, но и скручиванием[2]. Именно в этой области науки первоначально зародилось понятие тензора (tensio – лат., упругость, натяжение). Неудивительно, поэтому, что математическое описание теории электричества было оформлено Дж.К. Максвеллом именно в терминах механики деформируемого тела (эфира), до момента предсказания (им же) явления электромагнитного излучения: возможности существования динамических полей без своих источников – зарядов и токов. Впервые на необходимость коррекции взглядов с позиции представлений о дальнодействии обратил внимание А. Эйнштейн, сумевший разрешить накопившиеся парадоксы.

 

Замечания

1. Ввиду многообразия методик изложения в различных общих курсах физики, обоснование некоторых релятивистских соотношений, используемых в данном пособии, приведено в ПРИЛОЖЕНИИ 1.

2. Для случая взаимодействия пробного заряда не с одиночным зарядом , а с целой системой зарядов или с электрическим током, величины и рассчитываются в соответствии с принципом суперпозиции. Так, если для расчета электрической напряженности поля используют приемы электростатики, то расчет величины магнитной индукции основан на формуле Био-Савара-Лапласа , указывающей алгоритм суммирования полей, порождаемых малыми элементами тока.

3. Значение силы взаимодействия, рассчитанное по вышеприведенным формулам, изменяется при переходе от одной системы отсчета к другой, поскольку другими становятся скорости всех носителей зарядов (включая и тех, что создают токи). При использовании аппарата релятивистской механики вид формулы для силы Лоренца остается прежним (инвариантным), но значения выражений для поля и соотношение между слагаемыми в формуле для силы Лоренца изменяется.

Вид формул преобразования: .

Для оценок полезно ориентироваться на инварианты преобразования, Указывающие, что для каждой пространственно-временной точки, координаты которой в разных системах связаны преобразованиями Лоренца, выполняются правила: причем, .

В общем случае, если в одной системе заряды одинакового знака неподвижны, то в подвижной системе, при V<<c, их магнитное поле . В этом случае магнитную силу можно рассматривать как релятивистскую поправку к электрической силе. Наоборот, если система неподвижных зарядов электронейтральна (заряды разного знака), то в движущейся системе при V<<c электрическое поле , так что в свою очередь электрическую силу можно рассматривать как релятивистскую поправку к магнитной. В то же время в пределе V®c в обоих случаях магнитное и электрическое действия приближаются по модулю друг к другу.

4. При ускоренном движении зарядов электрическое и магнитное поля изменяются так, что единое электромагнитное поле обнаруживает свойство независимости от порождающих его зарядов в процессе волнового распространения энергии, затраченной на ускорение источника. Теперь не только магнитная компонента поля, но и электрическая приобретают вихревой характер. В физических курсах показывается, что свободная электромагнитная волна как раз и является тем объектом, для которого и магнитное и электрическое поля совершенно равноправны.

5. Из приведенных формул видно и то, что в теории близкодействия (при ), никакого магнетизма не существовало бы (или приводило бы к парадоксам). Так, если в нештрихованной системе заряд, порождающий поле, покоится, то есть его магнитное поле ( ) равно нулю, и если , то и в любой другой системе это поле не появится, (см. последнее слагаемое в последней формуле преобразования). Релятивистская природа магнетизма связана с отсутствием магнитных зарядов и является универсальным физическим фактом. Попытки оправдания классической теории Максвелла путем введения магнитного монополя предпринимались П.А-М. Дираком (1930), но не подтверждаются в экспериментах до настоящего времени.

 

megaobuchalka.ru

Вектор индукции магнитного поля

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E  электрического поля. Такой характеристикой является вектор магнитной индукции B. Вектор магнитной индукции B определяет силы, действующие на токи или движущиеся заряды в магнитном поле. За положительное направление вектора B принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора B. Такое исследование позволяет представить пространственную структуру магнитного поля.

• Закон Био-Савара-Лапласа

физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Пусть постоянный ток течёт по контуру (проводнику), находящемуся в вакууме,— точка, в которой ищется (наблюдается) поле, тогдаиндукция магнитного поля в этой точке выражается так:

• Принцип суперпоз. Маг. Полей

магнитное поле любого тока может быть вычислено как результат векторного сложения (суперпозиции) магнитных полей, создаваемых отдельными элементами тока. Это правило получило название принципа суперпозиции магнитных полей.

№15

Теорема о циркуляции вектора индукции магнитного поля в дифференциальной и интегральной форме.

rotB=rotrotA=graddivA-∆A=μ0I;

rotB=μ0I. – дифференциальная форма теоремы о циркуляции вектора магнитной индукции.

По формуле Стокса

∫rotBdS=μ0∫IdS=μ0∑I; μ0∫IdS=∫BdL – интегральная форма теоремы о циркуляции вектора магнитной индукции.

№16

• Расчет маг. Поля соленоида и тороида.

1) Соленоид: Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора B по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен I n l. Согласно теореме о циркуляции,

откуда B = μ0 I n.

2) Тороид: — кольцевая катушка, у которой витки намотаны на сердечник, который имеет форму тора. Магнитное поле, как известно из опыта, сосредоточено внутри тороида, а вне его поле равно нулю. В данном случае линии магнитной индукции, как следует из соображений симметрии, есть окружности, у которых центры расположены по оси тороида. В качестве контура возьмем одну такую окружность радиуса r. Тогда, используя теорему о циркуляции, B•2πr=μ0NI, откуда следует, что магнитная индукция внутри тороида (в вакууме) ,где N — число витков тороида. Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует

• Намагниченность вещества

Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества: Здесь,M — вектор намагниченности; m - вектор магнитного момента; V — объём. В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как и является функцией координат.

№19

Сила действующая на эл. заряд Q движущийся в магн. поле со скоростью v называется силой Лоренца. F=Q[vB]. Направление силы Лоренца определяется по правилу левой руки. Магнитное поле не действует на покоящийся заряд. Если на движущийся заряд помимо магн. поля действует эл. поле то результирующая

сила равна векторной сумме сил. F=QE+Q[vB].

Если заряженная частица движется в магн. поле перпендикулярно вектору В, то сила Лоренца постоянна по модулю и нормальна к траектории движения частицы.

№20

studfiles.net

A. Магнитная индукция — PhysBook

Магнитная индукция

Для количественного описания магнитного поля можно воспользоваться контуром с током. Так как контур с током испытывает ориентирующее действие поля, то на него в магнитном поле действует пара сил, которая создает момент сил относительно некоторой неподвижной оси. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств контура. Для плоского контура с током I величина, равная произведению силы тока I на площадь S, ограниченную контуром, называется магнитным моментом контура pm.

Магнитный момент — векторная величина. Его направление совпадает с направлением положительной нормали к контуру.

\(~\vec p_m = IS \vec n,\)

где \(~\vec n\) — единичный вектор нормали к плоскости контура.

Опыт показывает, что вращающий момент зависит от расположения контура в магнитном поле. Вращающий момент равен О, если магнитное поле перпендикулярно плоскости контура (рис. 2, а), и максимален, если нормаль к контуру перпендикулярна магнитному полю (рис. 2, б).

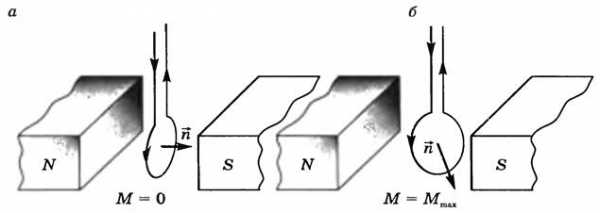
Рис. 2

Максимальный вращающий момент, как показывает опыт, пропорционален силе тока I и площади контура рамки с током, т.е.

\(~M_{max} \sim IS .\)

Если в данную точку магнитного поля помещать контуры с разными магнитными моментами, то на них будут действовать различные вращающие моменты, однако отношение \(~\frac{M_{max}}{p_m}\) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией.

Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой магнитного поля, численно равная максимальному вращающему моменту, действующему на контур с единичным магнитным моментом, и направленная вдоль положительной нормали к контуру.

Модуль магнитной индукции равен

\(~B = \frac{M_{max}}{IS} = \frac{M_{max}}{p_m}.\)

Единицей магнитной индукции в СИ является тесла (Тл).

1 Тл = Н·м/(А·м2) = Н/(А·м) .

1 Тл — магнитная индукция такого однородного поля, в котором на контур с магнитным моментом 1 А·м2 действует вращающий момент 1 Н·м.

Магнитная индукция \(~\vec B\) полностью характеризует магнитное поле. В каждой точке может быть найден ее модуль и направление.

Поле, в каждой точке которого модуль и направление магнитной индукции одинаковы (\(~\vec B = \operatorname{const}\)) , называется однородным магнитным полем.

Если магнитное поле образовано системой n проводников с токами, то, имеет место принцип суперпозиции магнитных полей: магнитная индукция поля системы токов равна геометрической сумме магнитных индукцией полей каждого из токов в отдельности:

\(~\vec B = \vec B_1 + \vec B_2 + \ldots + \vec B_n = \sum_{i=1}^n \vec B_i .\)

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 316-317.

www.physbook.ru

---

• 
  Освещение бассейнов
• 
  Ivc 34
• 
  Индукционное электрическое поле это
• 
  Строительство атомной станции в белоруссии
• 
  Паспорт на счетчики на воду
• 
  Отличие галогенных ламп от ламп накаливания
• 
  Подключение генератора к дому
• 
  Как проверить двигатель постоянного тока
• 
  Схема учета электроэнергии 10 кв
• 
  Нормы вентиляция электрощитовой
• 
  10 кв авр