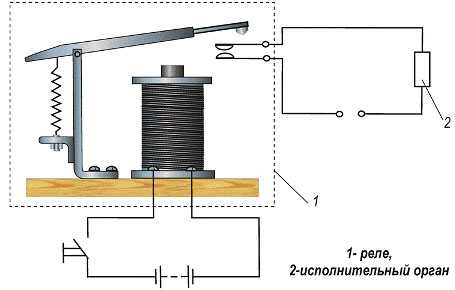
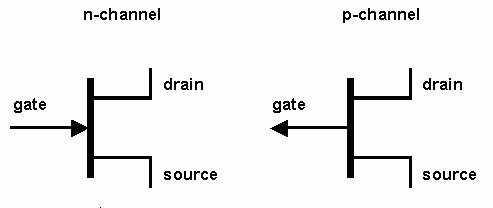
Лабораторная работа № 3 резонанс напряжений. Вследствие чего ток в цепи при резонансе напряжений имеет наибольшее значение
Резонанс напряжений и резонанс токов
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.
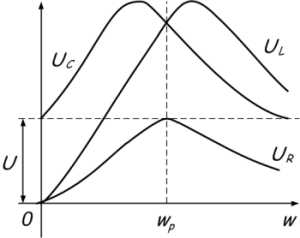
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
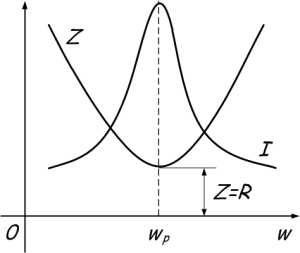
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
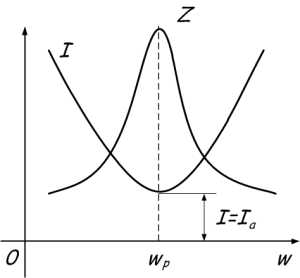
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
electroandi.ru
VI.3. Резонанс в электрических цепях
Резонансом в электрической цепи называется режим участка, содержащего индуктивный и емкостный элементы, при котором угол сдвига фаз колебаний напряжения и тока равен нулю. Резонанс характеризуется рядом особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике и других областях.
Различают несколько видов резонанса: резонанс напряжений (при последовательном соединении элементов), резонанс токов (при параллельном соединении элементов), резонанс в магнитно-связанных цепях и др.
Резонанс напряжений. Из выражения (6.10) следует, что при последовательном соединении ток в цепи приобретает максимальное значение при , то есть при Этому условию удовлетворяет частота
(6.15)
В этом случае , Z = R → min, падения напря-жения на катушке индуктивности и конденсаторе одинаковы по величине и противоположны по фазе (рис. 6.15). Таким образом, при резонансе напря-жений
,
и
(6.16)
где Q – добротность контура. Так как добротность колебательных контуров больше единицы, то напряжение, как на катушке индуктивности, так и на конденсаторе превышает напряжение U, приложенное к цепи. Из выражения (6.16) следует, что добротность контура показывает, во сколько раз при резонансе напряжение на реактивных элементах больше по величине входного напряжения.
 Явление резонанса напряжений используется в радиотехнике и электронике для усиления колебаний напряжения какой-либо определенной частоты. В электроэнергетике явление резонанса напряжений необходимо учитывать при выборе изоляции высоковольтного оборудования, так как иначе может произойти ее пробой.
Явление резонанса напряжений используется в радиотехнике и электронике для усиления колебаний напряжения какой-либо определенной частоты. В электроэнергетике явление резонанса напряжений необходимо учитывать при выборе изоляции высоковольтного оборудования, так как иначе может произойти ее пробой.
Резонанс токов возможен в цепи с параллельным соединением ветвей с параметрами и (рис. 6.16). Между током в неразветвленной части цепи и напряжением имеется некоторый сдвиг фаз . Предположим, что цепь имеет емкостный характер, то есть колебания тока опережают по фазе колебания напряжения. Тогда векторная диаграмма будет иметь вид, приведенный на рис. 6.17.
Разложим вектор тока на две составляющие: активную , находящуюся в фазе с вектором напряжения на зажимах цепи, и реактивную , перпендикулярную к . Из векторной диаграммы следует
(6.17)
Так как
и
то, подставляя эти выражения в (6.17), получим
(6.18)
(6.19)
где g и b – активная и реактивная проводимости цепи.
Найдем соотношение между активной g, реактивной b и полной Y проводимостью цепи. Из векторной диаграммы следует, что модуль действующего значения тока в неразветвленной части цепи равен
(6.20)
Так как полная проводимость Y равна обратной величине полного сопротивления, то из (6.18) и (6.19) следует
(6.21)
В режиме резонанса . Для этого реактивная составляющая тока , а, следовательно, и реактивная проводимость b цепи должны равняться нулю. Для схемы на рис. 6.16 общая реактивная проводимость цепи равна сумме реактивных проводимостей и параллельных ветвей. При резонансе
(6.22)
где
Тогда условие (6.22) примет вид
(6.23)
где – циклическая частота резонанса токов.
Из (6.23) после преобразования имеем
(6.24)
где – характеристическое сопротивление контура.
Анализ выражения (6.24) позволяет сделать ряд выводов:
1. Резонансная частота при резонансе токов зависит не только от параметров реактивных элементов, но и от активных сопротивлений и .
2. Резонанс токов возможен, если сопротивления и или больше , или меньше (в этом случае подкоренное выражение в (6.24) положительное), в противном случае – невозможен ( – мнимая величина).
3. При и , что справедливо для многих цепей, то есть резонансная частота при резонансе токов равна резонансной частоте при резонансе напряжений.
Рассмотрим контур с малыми омическими потерями в режиме резонанса токов.
1. Так как и общее сопротивление контура активное, то полная проводимость контура равна активной проводимости и минимальна:
2. Ток в неразветвленной части цепи
минимальный, что позволяет по показаниям амперметра обнаруживать резонанс токов в контуре при изменении частоты , параметров L или C.
3. Активные и реактивные составляющие токов
Так как , то реактивные составляющие токов при резонансе равны и находятся в противофазе
Векторная диаграмма цепи при резонансе токов приведена на рис. 6.18.
Ток в общей части цепи равен активной составляющей тока
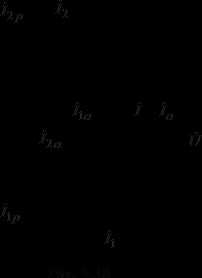 Токи в ветвях
Токи в ветвях
Если то есть и то и то есть токи в ветвях значительно превышают по величине ток в неразветвленной части цепи. Это свойство – усиление тока – является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и название этого явления.
infopedia.su
Лабораторная работа № 3 резонанс напряжений
Цель работы. Установление условий резонанса напряжений. Исследование частотных зависимостей напряжений на элементах последовательного резонансного контура.
Домашнее задание
Укажите необходимые и достаточные условия для возникновения в электрических цепях переменного синусоидального тока резонанса напряжений.
Охарактеризуйте возможные способы получения резонанса напряжений в электрической цепи? Приведите расчетные соотношения для определения значений искомых величин при резонансе напряжений?
Каким образом можно обнаружить резонанс напряжений?
Что представляет собой амплитудно-частотная характеристика (АЧХ) последовательного резонансного контура? Каким способом по АЧХ можно определить полосу пропускания (прозрачности) контура?
Что представляет собой фазочастотная характеристика (ФЧХ) последовательного резонансного контура? Почему идеальная ФЧХ в полосе пропускания должна быть линейной?
Краткие теоретические сведения
Резонансом напряжений называется режим, при котором в электрической цепи (рис. 1) с последовательным соединением индуктивного и емкостного элементов напряжение на входе цепи совпадает по фазе с током. При резонансе напряжений характерна возможность возникновения равных по модулю и противоположных по фазе действующих значений напряжений на катушке индуктивности и конденсаторе, существенно превышающих действующее значение напряжения на входе цепи. Отсюда название режима работы цепи – резонанс напряжений.
Для последовательного резонансного контура входное сопротивление контура при резонансе носит резистивный характер
.
При этом соблюдается равенство индуктивного сопротивления катушки и емкостного сопротивления конденсатора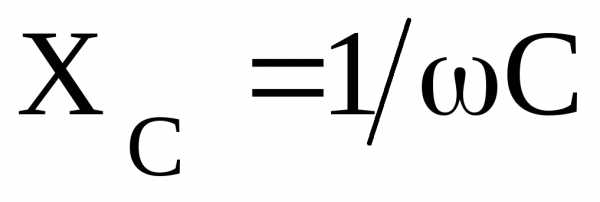 , то есть выполняется условие резонанса напряжений
, то есть выполняется условие резонанса напряжений
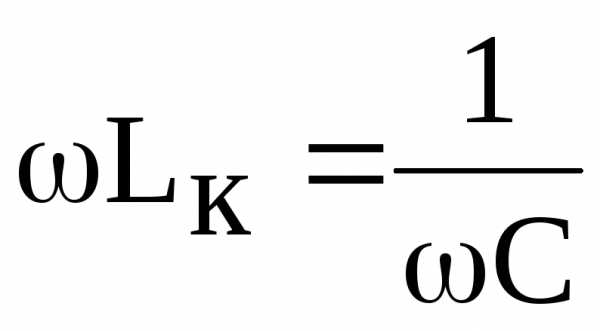 .
.
Из выражения видно, что резонанс напряжений в контуре можно получить варьированием значений одного из параметров, а именно: частоты  приложенного напряжения, индуктивности
приложенного напряжения, индуктивности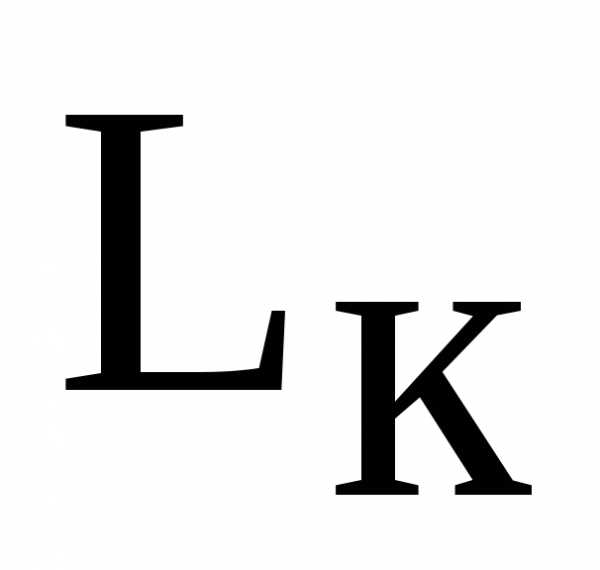 катушки, или емкостиC конденсатора. Два других параметра при этом должны быть постоянными. В частности, при фиксированных значениях параметров
катушки, или емкостиC конденсатора. Два других параметра при этом должны быть постоянными. В частности, при фиксированных значениях параметров 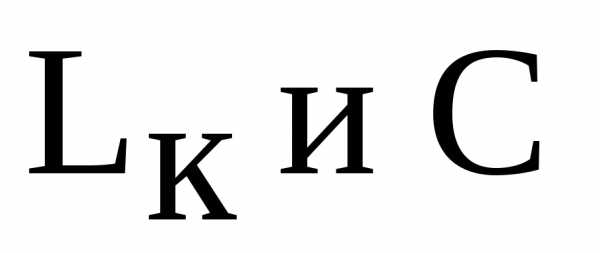 резонанс в цепи наступит при резонансной частоте
резонанс в цепи наступит при резонансной частоте
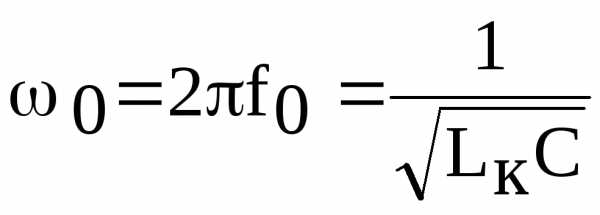 .
.
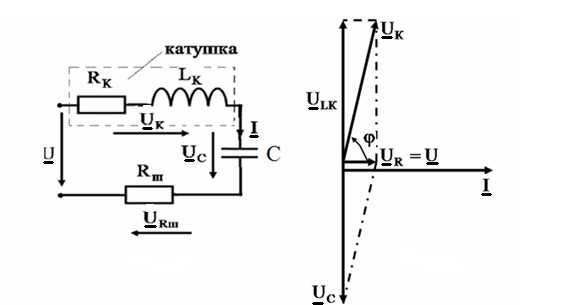
Рис. 1 Рис. 2
При резонансе ток в цепи принимает максимальное значение , если действующее значение напряжения на входе цепиU = const. При этом напряжения 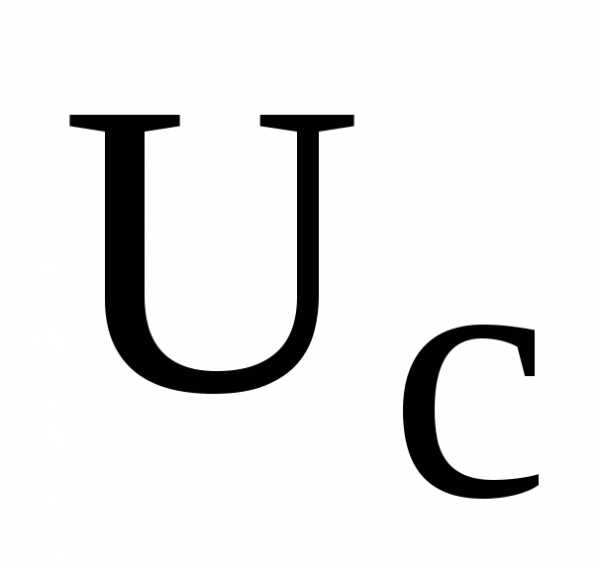 и
и могут быть много больше входного напряжения
могут быть много больше входного напряжения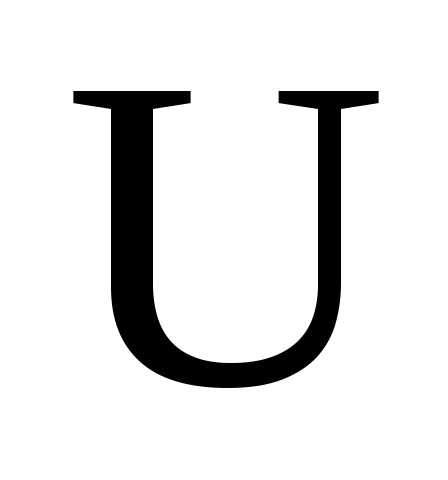 (отношение
(отношение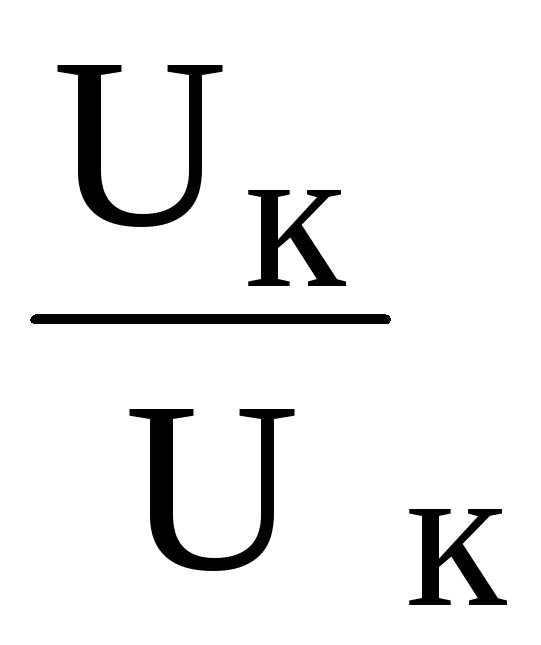 может достигать величин несколько сотен). Векторная диаграмма тока и напряжений для этого режима цепи приведена на рис. 2. Из диаграммы видно, что реактивная составляющая напряжения на катушке
может достигать величин несколько сотен). Векторная диаграмма тока и напряжений для этого режима цепи приведена на рис. 2. Из диаграммы видно, что реактивная составляющая напряжения на катушке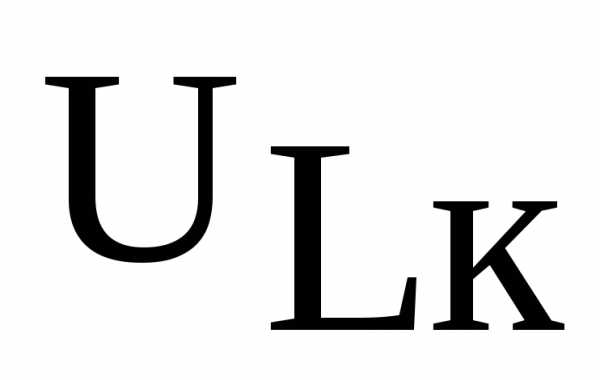 и напряжение
и напряжение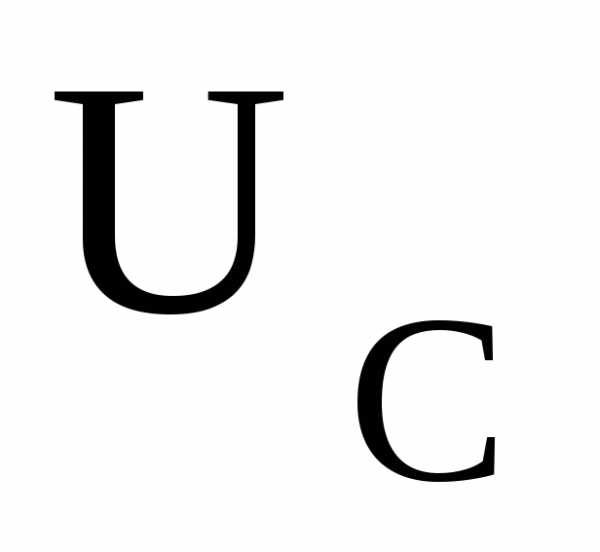 на конденсаторе при резонансе в силу равенстваравны друг другу и сдвинуты по фазе на угол почти
на конденсаторе при резонансе в силу равенстваравны друг другу и сдвинуты по фазе на угол почти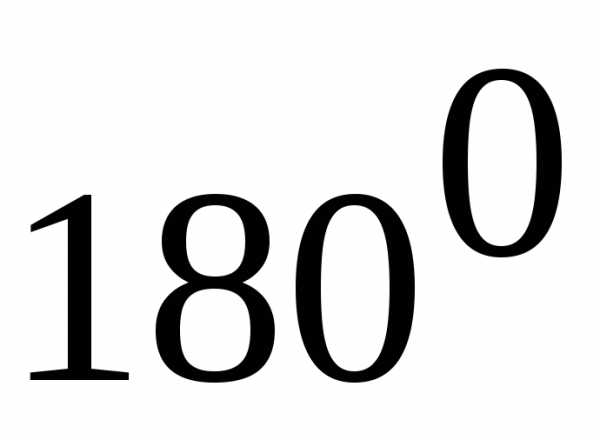 , если
, если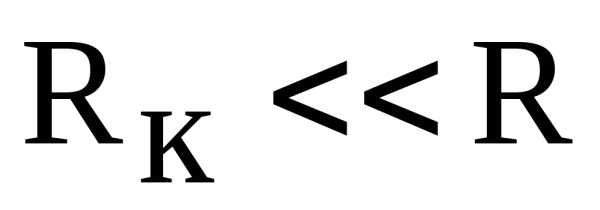 . Вследствие падения напряжения в активном сопротивлении катушки, напряжение на катушкепри резонансе оказывается больше напряжения на конденсаторе. Поэтому точка резонанса в этих условиях определяется по наибольшему значению тока в цепи.
. Вследствие падения напряжения в активном сопротивлении катушки, напряжение на катушкепри резонансе оказывается больше напряжения на конденсаторе. Поэтому точка резонанса в этих условиях определяется по наибольшему значению тока в цепи.
Частотная зависимость тока в цепи имеет вид:
.
Амплитудно- и фазочастотные характеристики тока можно записать в форме
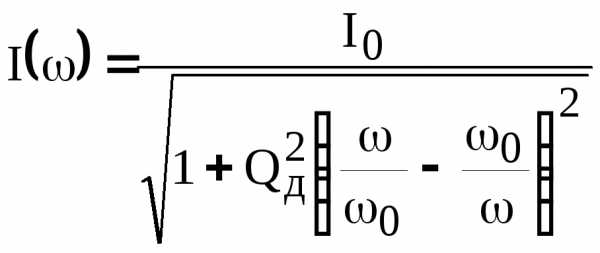 , .
, .
где - добротность контура, показывающая во сколько раз напряжения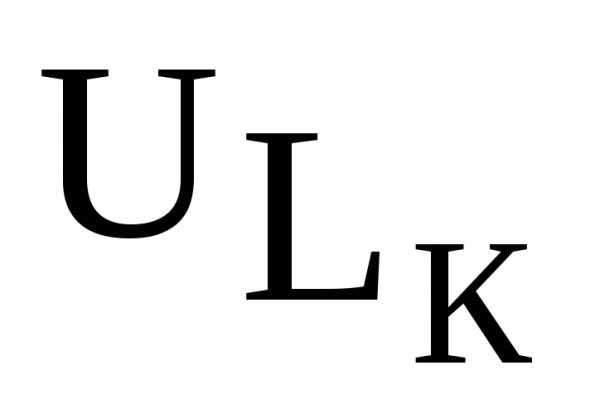 и
и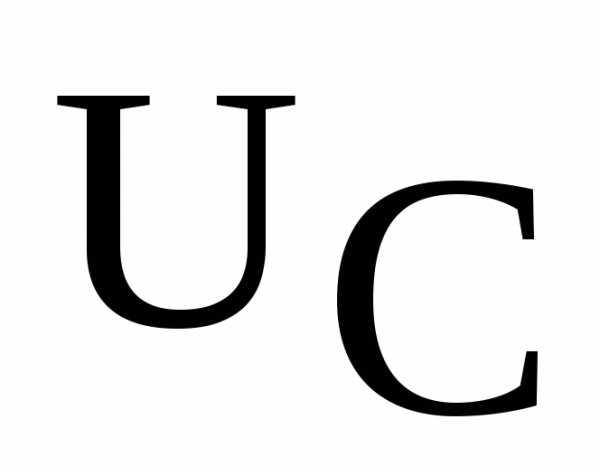 на участках контура превышают приложенное напряжениеU; d – параметр затухания;
на участках контура превышают приложенное напряжениеU; d – параметр затухания; 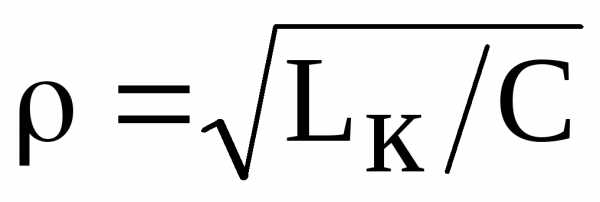 - волновое (характеристи-ческое) сопротивление резонансного контура.
- волновое (характеристи-ческое) сопротивление резонансного контура.
Частотные характеристики 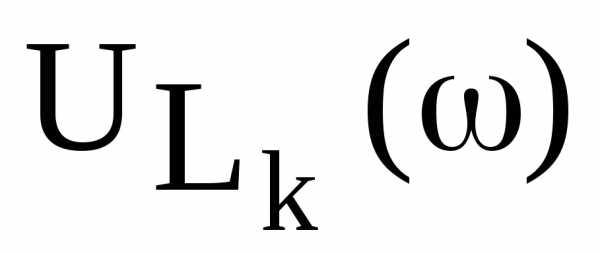 и
и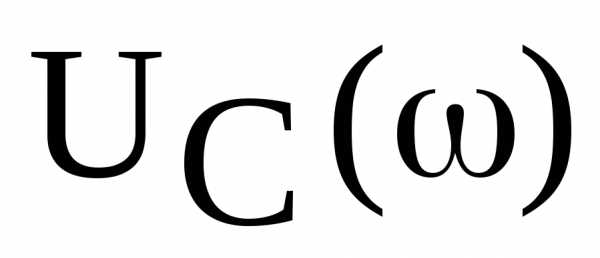 также как
также как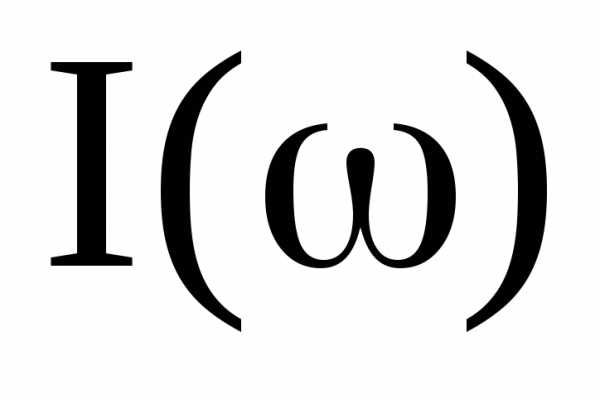 имеют максимум (рис. 3), причем максимум
имеют максимум (рис. 3), причем максимум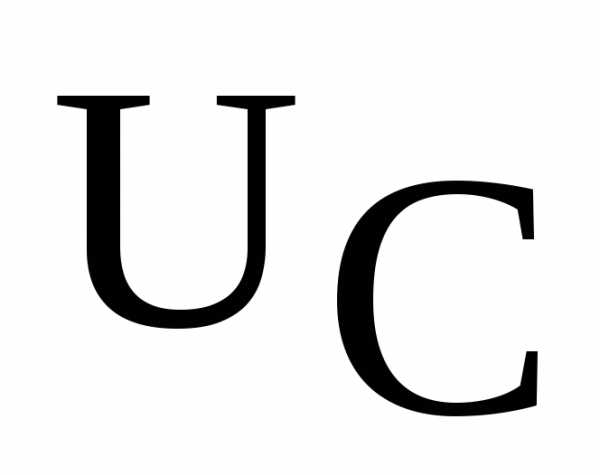 наступает при частоте
наступает при частоте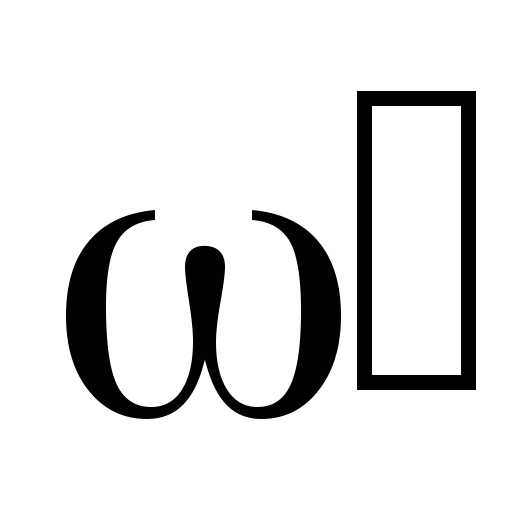 , а максимум
, а максимум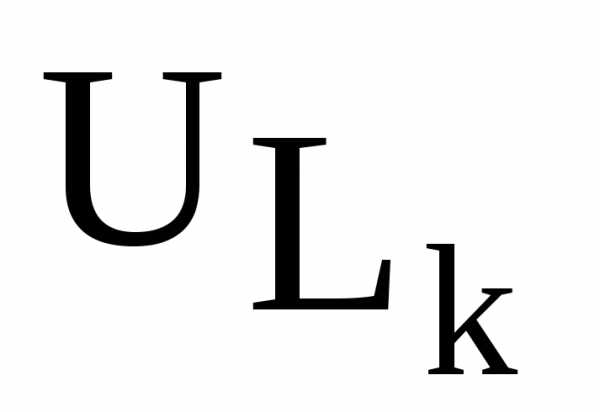 при частоте
при частоте . Частоты
. Частоты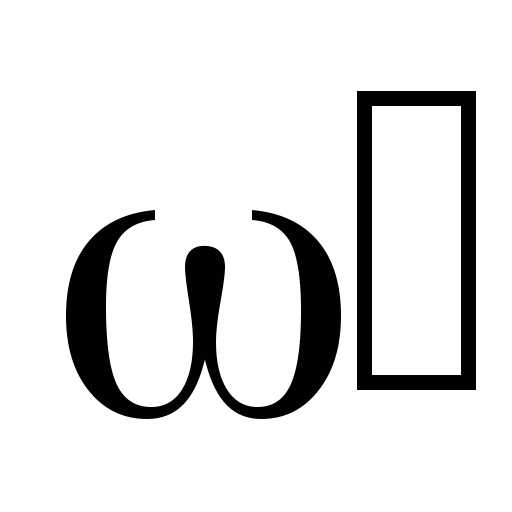 и
и находятся из соотношений:
находятся из соотношений:
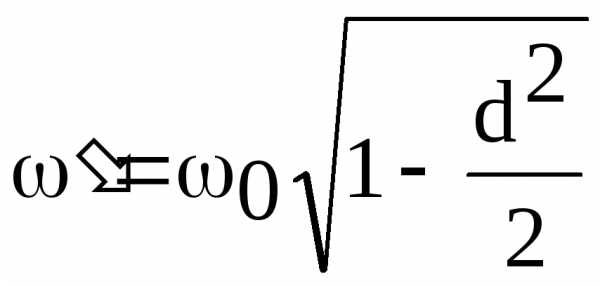 ,
, 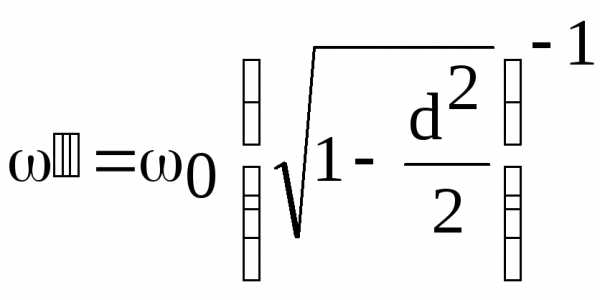 .
.
Из соотношений видно, что с уменьшением сопротивления R (коэффициента затухания d) частоты 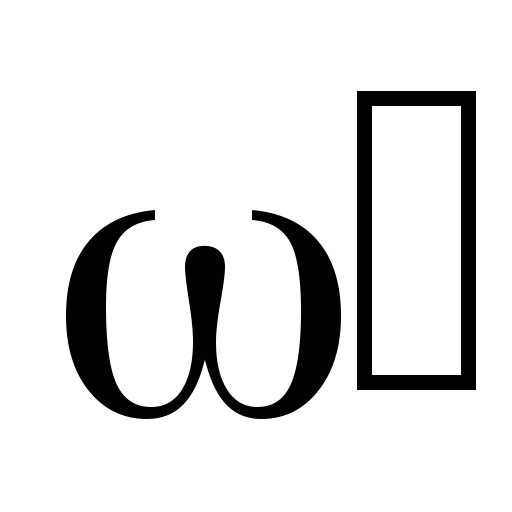 и
и стремятся к резонансной частоте
стремятся к резонансной частоте и максимумы частотных характеристик
и максимумы частотных характеристик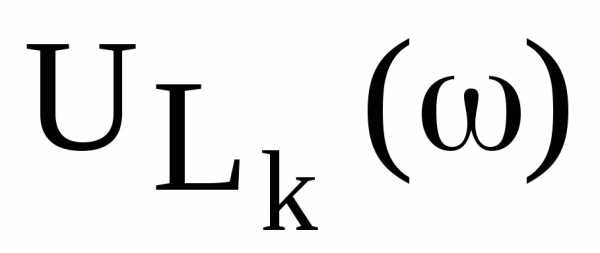 и
и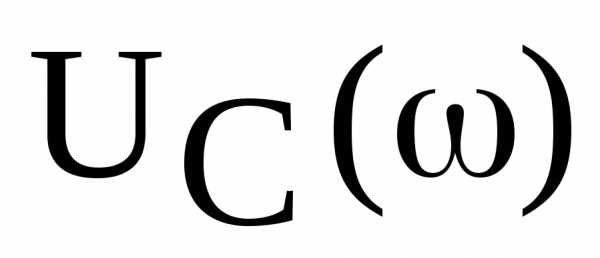 совмещаются. При возрастании сопротивленияR, наоборот, максимумы частотных характеристик расходятся.
совмещаются. При возрастании сопротивленияR, наоборот, максимумы частотных характеристик расходятся.
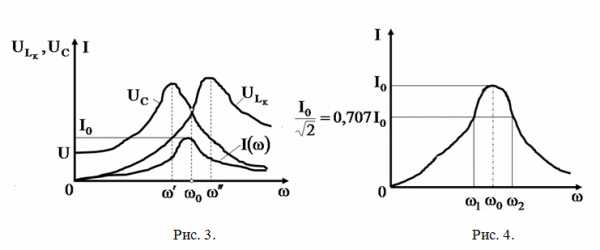
Анализ характеристики 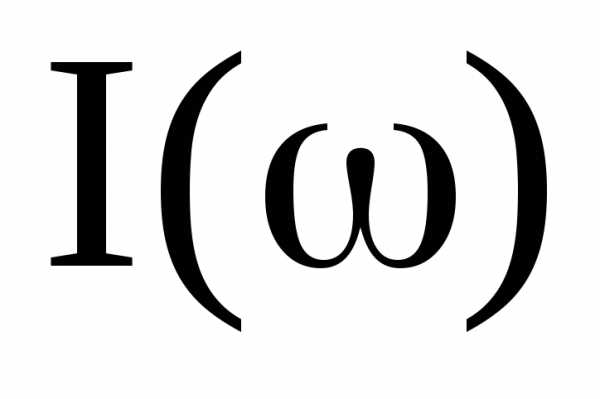 (рис. 4) показывает, что последовательный резонансный контур обладает частотной избирательностью или фильтрирую-щими свойствами. С небольшим ослаблением(не более 3 Дб) через контур можно передать сигналы в диапазоне частот. Указанную область частот называют полосой пропускания (прозрачности). Для контура формула относительной полосы пропускания частот имеет вид:
(рис. 4) показывает, что последовательный резонансный контур обладает частотной избирательностью или фильтрирую-щими свойствами. С небольшим ослаблением(не более 3 Дб) через контур можно передать сигналы в диапазоне частот. Указанную область частот называют полосой пропускания (прозрачности). Для контура формула относительной полосы пропускания частот имеет вид:
.
Активная мощность при резонансе 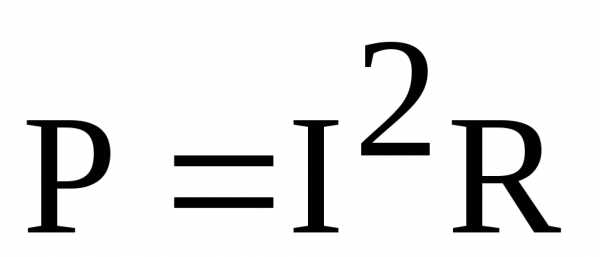 имеет наибольшее значение, равное полной мощностиS, в тоже время реактивная мощность цепи оказывается равной нулю. При этом реактивная индуктивная и реактивная емкостная составляющие полной мощности могут приобретать теоретически весьма большие значения, в зависимости от значений тока и реактивных сопротивлений.
имеет наибольшее значение, равное полной мощностиS, в тоже время реактивная мощность цепи оказывается равной нулю. При этом реактивная индуктивная и реактивная емкостная составляющие полной мощности могут приобретать теоретически весьма большие значения, в зависимости от значений тока и реактивных сопротивлений.
Рабочее задание
Собрать схему последовательного резонансного контура, используя съемную панель лабораторного стенда (рис. 5). На съемной панели размещены катушка индуктивности сопротивлением и индуктивностью, конденсаторC = 0,1 мкФ и резистор
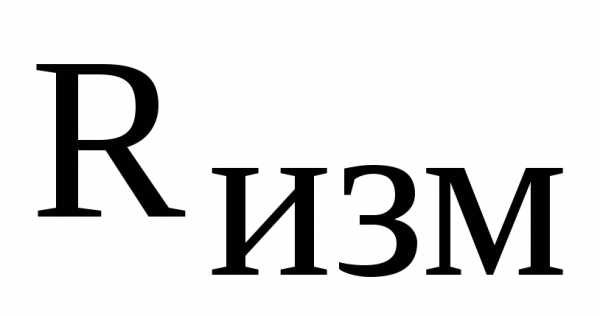 = 10 Ом. Для шунтирования сопротивленияR переключатель S перевести в положение «Вкл.».
= 10 Ом. Для шунтирования сопротивленияR переключатель S перевести в положение «Вкл.». Подключить схему последовательного резонансного контура к генера-тору низкой частоты (ГНЧ) через понижающий трансформатор (T). С помощью ГНЧ обеспечивается получение синусоидального входного напряжения, а также возможность с помощью ручек управления регулировка напряжения на выходе по амплитуде и частоте. Ручкой управления ГНЧ по уровню напряжения и показанию вольтметра PV1, подключенного к зажимам вторичной обмотки трансформатора, установить действующее значение входного напряжения на схему в диапазоне В.
Используя исходные данные пункта 1 рабочего задания рассчитать для резонансного контура:
резонансную частоту
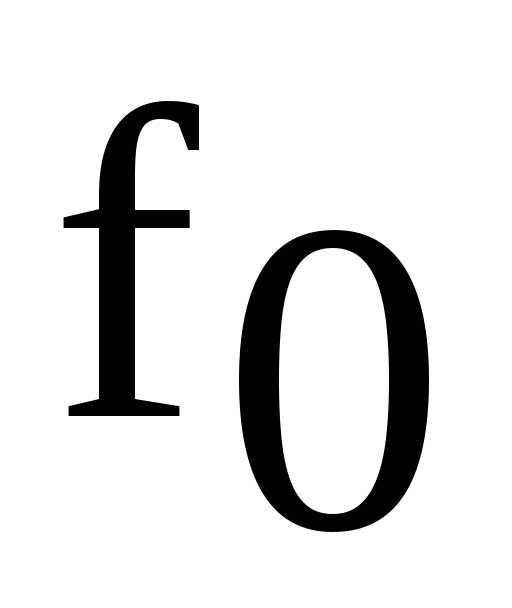 ;
; волновое сопротивление
 ;
;добротность резонансного контура
 ;
;параметр затухания d;
ток в контуре при резонансе
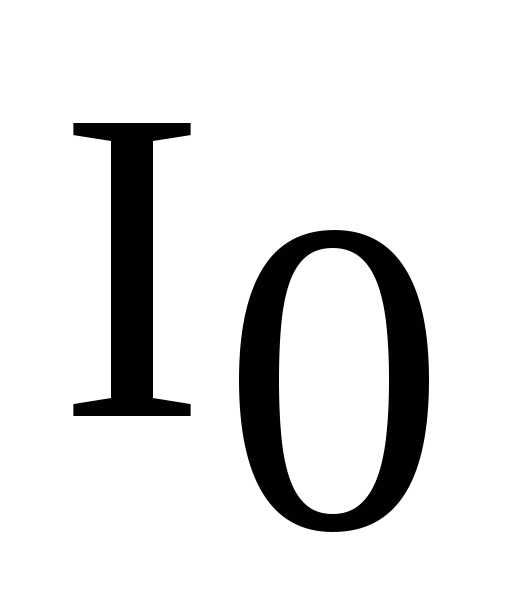 при заданном напряжении
при заданном напряжении 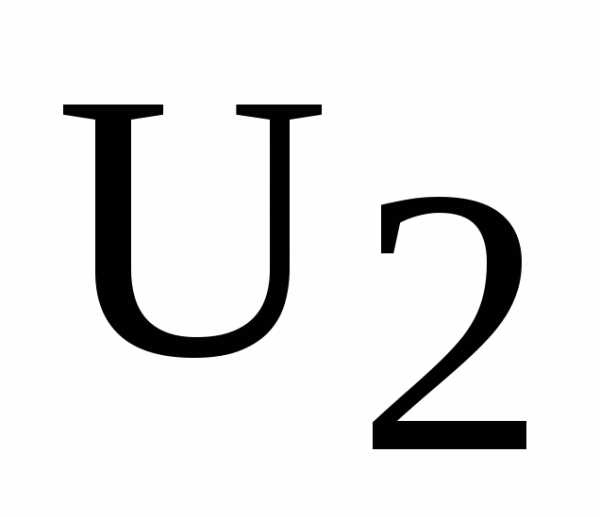 ;
; напряжение на катушке и напряжение на конденсаторе при резонансе
где .
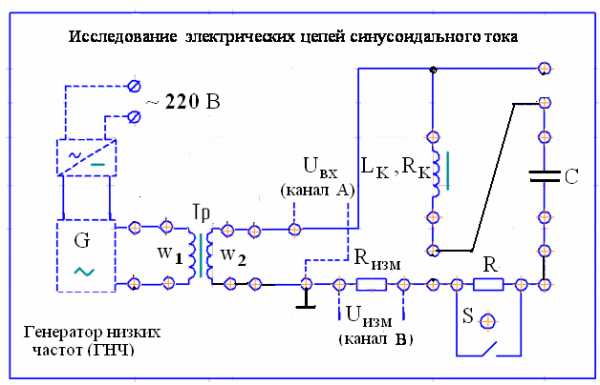
Рис. 5.
В цепи (рис. 5), находящейся под напряжением, изменяя частоту ГНЧ с помощью ручек управления «Грубо» и «Точно» в окрестности расчетного значения
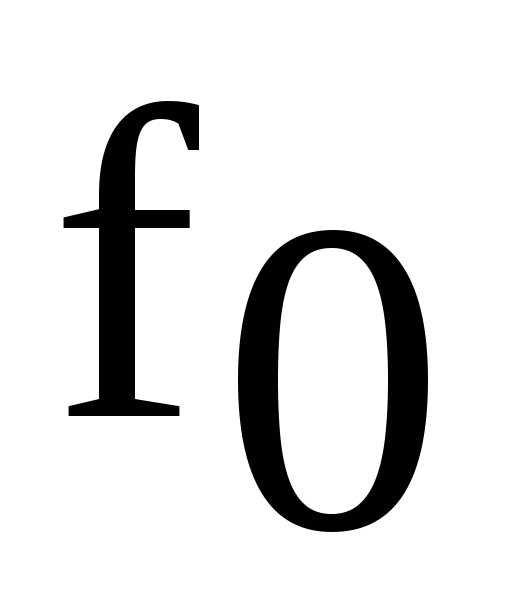 , найти резонансную частоту
, найти резонансную частоту 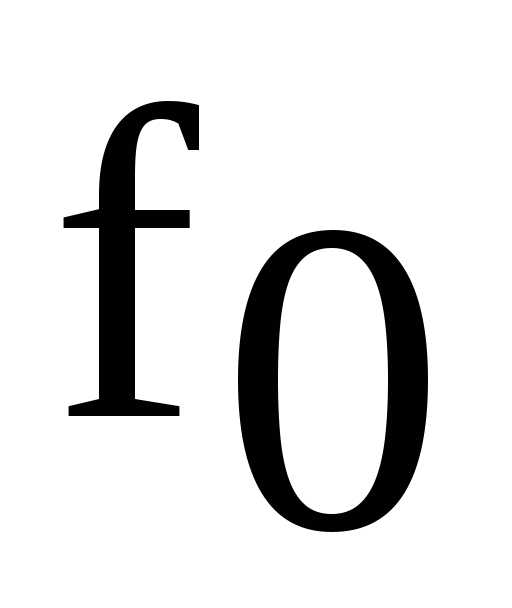 опытным путем, так чтобы на экране осциллографа угол сдвига фаз между напряжением
опытным путем, так чтобы на экране осциллографа угол сдвига фаз между напряжением 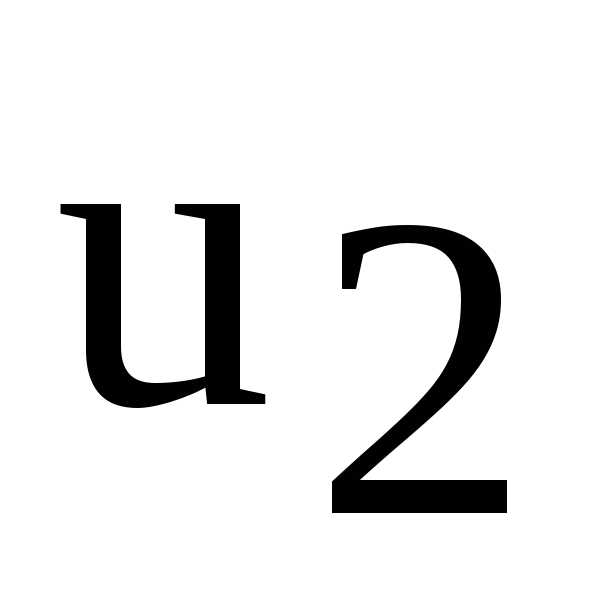 (канал B) и напряжением
(канал B) и напряжением 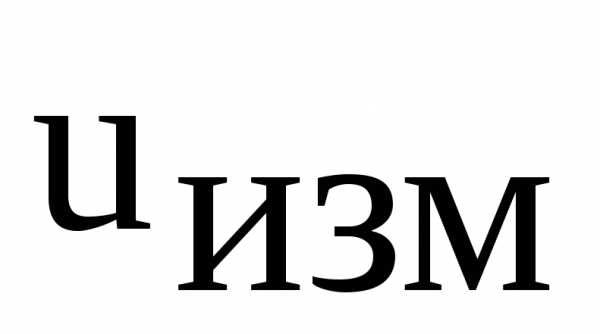 (канал A) был равен нулю.
(канал A) был равен нулю. В электрической цепи (рис. 5) измерить ток ,входное напряжение
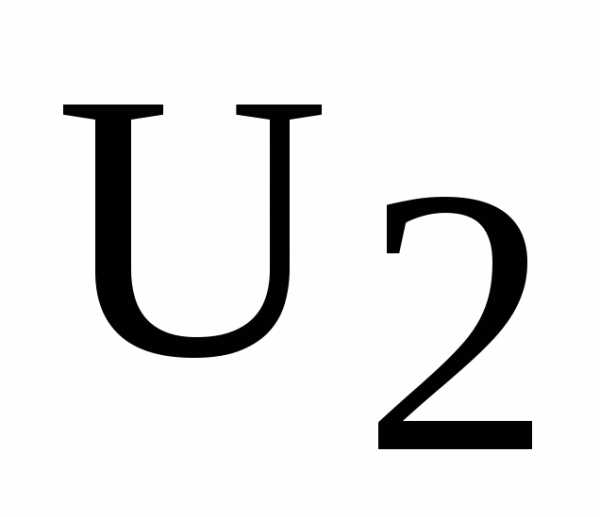 ,напряжение на катушке
,напряжение на катушке  иконденсаторе
иконденсаторе 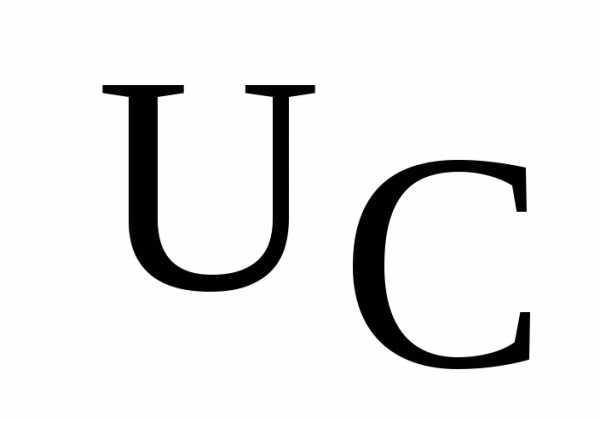 спомощью вольтметраPV1, подключая его параллельно к участкам цепи, а также угол сдвига фаз между приложенным напряжением и напряжением на сопротивлении
спомощью вольтметраPV1, подключая его параллельно к участкам цепи, а также угол сдвига фаз между приложенным напряжением и напряжением на сопротивлении 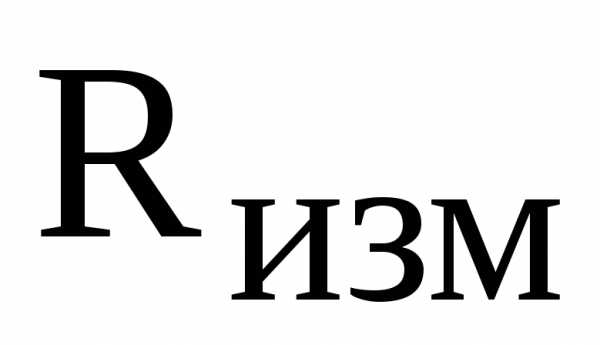 с помощью осциллографа
с помощью осциллографа
,
варьируя частоту ГНЧ (где  = 0, 1, 2) от резонансной частоты через интервалыГц с помощью ручек управления «Грубо» и «Точно». Результаты измерений занести в таблицу.
= 0, 1, 2) от резонансной частоты через интервалыГц с помощью ручек управления «Грубо» и «Точно». Результаты измерений занести в таблицу.
Таблица
| Частота, Гц. | Опыт | Расчет | |||||||||||
| В | В | В | В | град | мА | В | В | Ом | Ом | Ом | Ом | ||
Дополнить таблицу пункта 4 рабочего задания расчетными данными, определив активную
 и реактивную
и реактивную 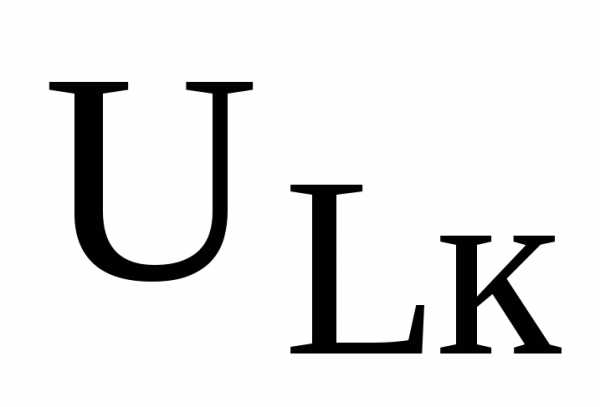 составляющие напряжения на катушке индуктивности, реактивные сопротивления катушки
составляющие напряжения на катушке индуктивности, реактивные сопротивления катушки 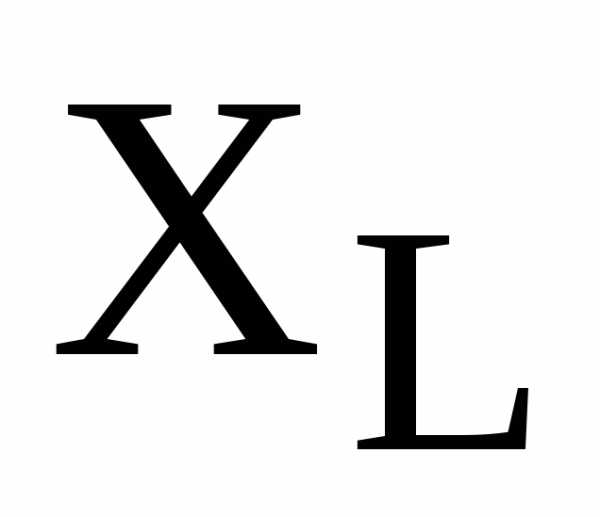 и конденсатора
и конденсатора 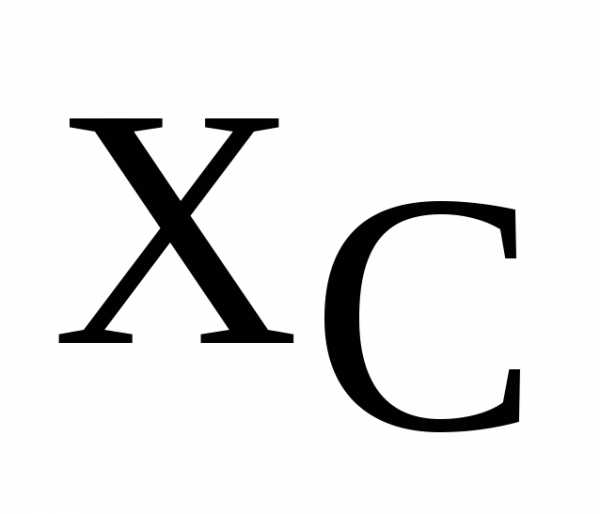 , реактивное сопротивление цепи X, а также модуль полного сопротивления контура Z.
, реактивное сопротивление цепи X, а также модуль полного сопротивления контура Z.
По данным таблицы 1 пункта 5 рабочего задания построить графики зависимости
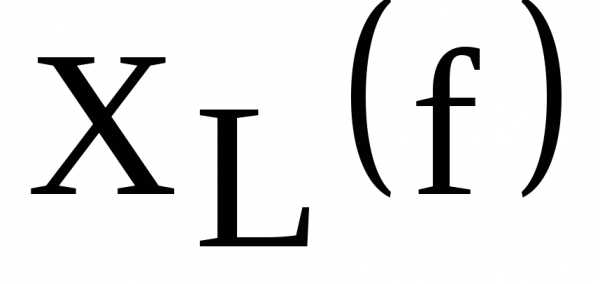 ,
,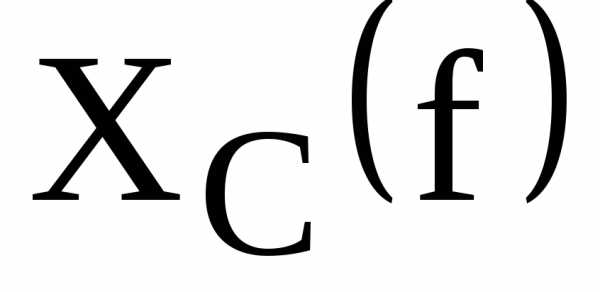 ,
,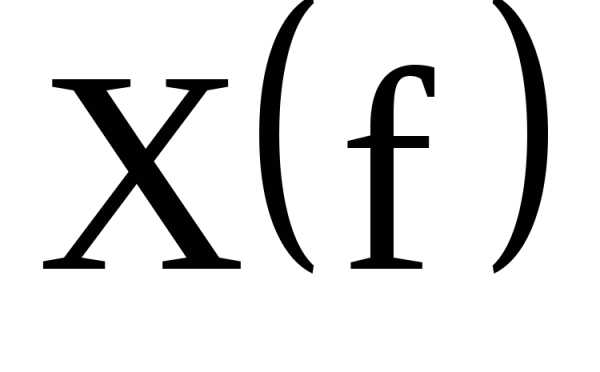 и
и 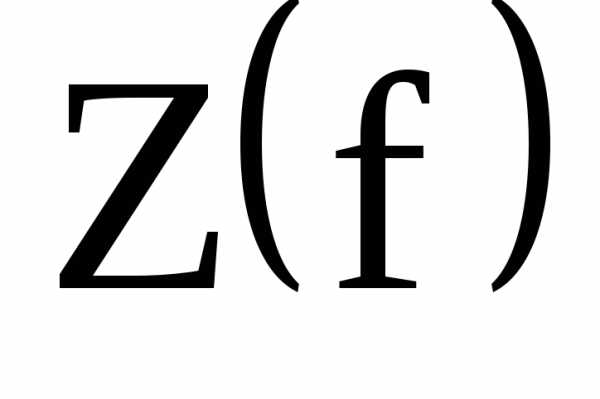 .
.
По данным таблицы 1 пункта 5 рабочего задания построить графики зависимостей
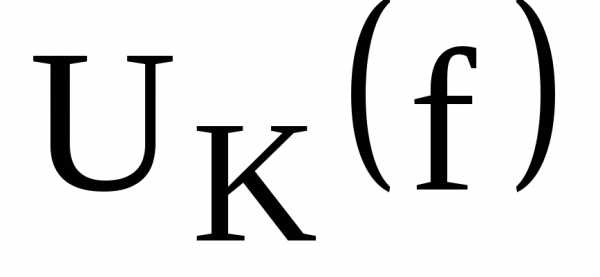 ,
,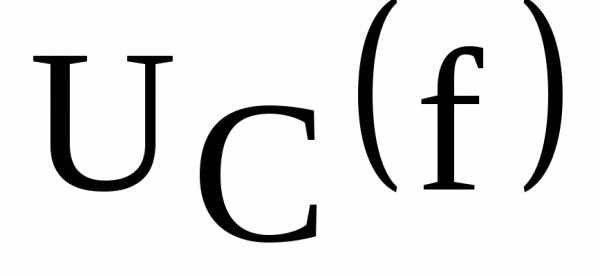 ,
,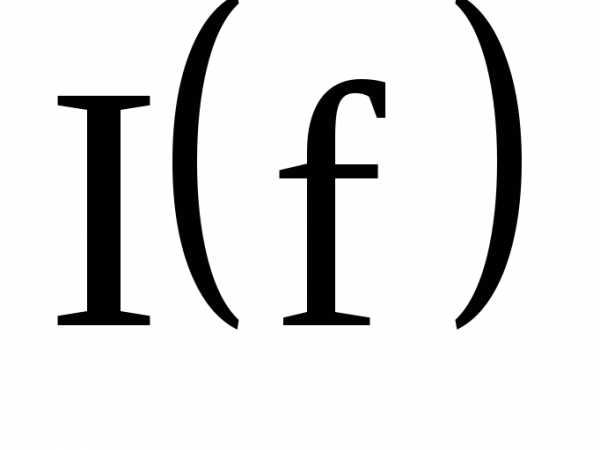 и
и 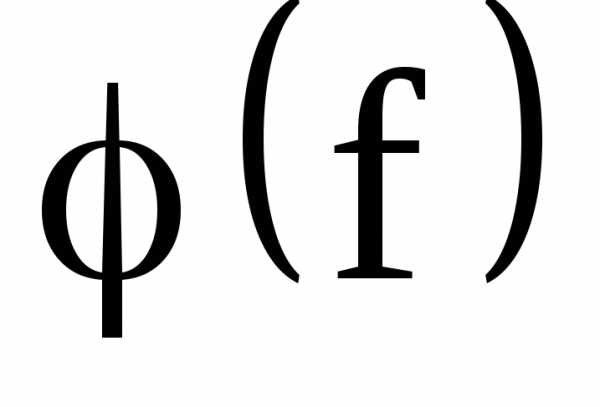 .
.
Вопросы к защите.
Как практически можно определить состояние резонанса напряжений в последовательном резонансном контуре?
Как определить частоту собственных колебаний резонансного контура?
Почему в момент резонанса не равны напряжения на катушке индуктивности
 и конденсаторе
и конденсаторе 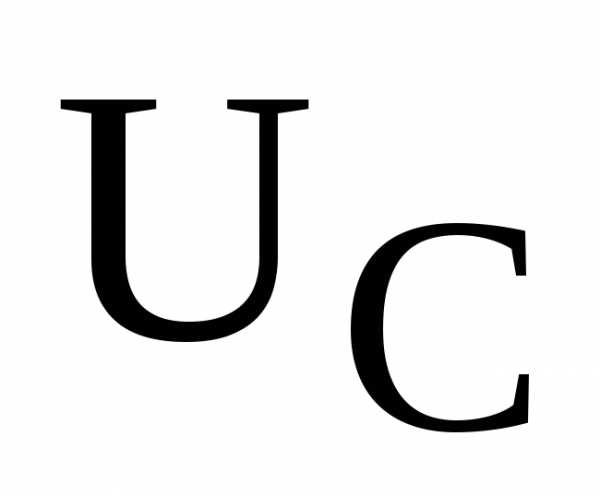 ?
?В цепи последовательного резонансного контура заданы значения R и С. Определить индуктивность катушки L, при которой в цепи возник нет резонанс, если R = 5 Ом,
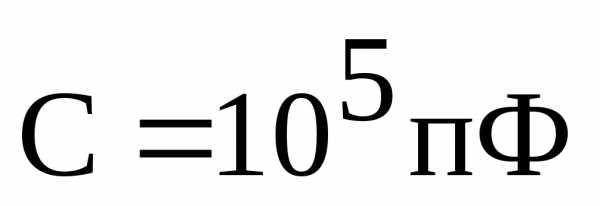 . Определите во сколько раз напряжение на емкости будет больше входного напряжения при резонансе.
. Определите во сколько раз напряжение на емкости будет больше входного напряжения при резонансе.
studfiles.net
Резонансные явления в электрических цепях — КиберПедия
Режим работы электрической цепи, при котором ток и напряжение на входе цепи совпадают по фазе, называют резонансом. При этом эквивалентное сопротивление всей цепи будет активным. В цепях, состоящих из резистивного, индуктивного и емкостного элементов, различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений может иметь место в цепи с последовательно соединенными индуктивным и емкостным элементами. Рассмотрим схему последовательного соединения резистора, индуктивности и емкости (рис. 6.1).
.
Отсюда комплексное сопротивление цепи
. (6.1)
Построим векторную диаграмму. При этом могут иметь место три случая.
1. Пусть индуктивное сопротивление больше емкостного XL> XC , тогда и индуктивное напряжение будет больше емкостного UL> UC. Векторная диаграмма будет иметь вид (рис. 6.2).
2. Пусть индуктивное сопротивление меньше емкостного XL < XC . Тогда и индуктивное напряжение станет меньше емкостного UL< UC, так как ток через элементы протекает один и тот же, а напряжение пропорционально току и сопротивлению. Векторная диаграмма будет иметь вид (рис. 6.3).
Реактивная составляющая напряжения UХ = UL – UC – отрицательна, и угол сдвига фаз между током и напряжением φ < 0. Такой характер цепи является активно- емкостным.
3. Пусть XL = XC, в этом случае индуктивное и емкостное напряжения равны по величине UL= UC. Так как они всегда противоположны по фазе, то они полностью компенсируют друг друга, следовательно, реактивная составляющая UХ = UL – UC = 0. Общее напряжение будет активным и совпадет по фазе с током φ = 0, следовательно, в цепи имеет место резонанс напряжений. Векторная диаграмма для данного случая показана на рис. 6.4.
Из вышесказанного следует, что условием, при котором наступит резонанс напряжений, является равенство индуктивного и емкостного сопротивлений.
, или .
Из выражения (6.1) следует, что при резонансе полное сопротивление цепи имеет активный характер.
Резонанс напряжений можно достигнуть подбором трех параметров:
1) изменением частоты колебательного контура , L, C = const;
2) изменением индуктивности контура , , С = const;
3) изменением емкости колебательного контура , , L = const .
При этом все три параметра связаны между собой.
Из условия получаем: , отсюда:
, , .
Частоту ω0, определяемую из такого условия, называют резонансной.
Если напряжение на зажимах цепи и активное сопротивление цепи R не изменяются, то ток при резонансе имеет максимальное значение
, так как .
Если реактивные сопротивления превосходят при резонансе активное сопротивление:
, ,
то напряжения на зажимах катушки и конденсатора могут существенно превышать напряжение на входе цепи.
Превышение напряжения на реактивных элементах над напряжением на входе принято характеризовать величиной
,
называемой волновым или характеристическим сопротивлением цепи. Волновое сопротивление численно равно индуктивному или емкостному сопротивлению на резонансной частоте.
Кратность превышения напряжения на зажимах индуктивного и емкостного сопротивлений над входным определяют отношением напряжения на реактивном элементе к напряжению на входе цепи на резонансной частоте:
.
Эта величина называется добротностью контура.
Величина, обратная добротности
,
называется затуханием контура.
 |
Избирательность контура характеризуется полосой пропускания. Полоса пропускания – это диапазон частот, для которых ток ослабляется не более чем в раз по отношению к максимальному значению
.
Ширину полосы пропускания можно определить по формуле
.
Рассмотрим резонансные кривые тока и напряжений (рис. 6.6).
При неизменных параметрах цепи и неизменном входном напряжении ток определится выражением
.
 |
Напряжение на индуктивности пропорционально частоте, следовательно, при нулевой частоте напряжение на индуктивности . При все напряжение, подаваемое от источника, приложено к индуктивности, и .
Напряжение на емкости обратно пропорционально частоте, следовательно, при все напряжение приложено к емкости . При , так как равно нулю емкостное сопротивление.
При резонансной частоте индуктивное и емкостное напряжения равны .
Напряжение на резистивном элементе пропорционально току и, следовательно, повторяет форму кривой тока при и , при .
Рассмотрим энергетические соотношения при резонансе.
Мгновенные значения мощности на зажимах катушки и конденсатора определяются выражениями:
;
.
Так как при резонансе , эти мощности в любой момент времени равны и противоположны по знаку. Это значит, что происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора, но не происходит обмена между источником и реактивными элементами, так как
и ,
то есть суммарная энергия электрического и магнитного полей остается постоянной. Энергия переходит из конденсатора в катушку в течение четверти периода, когда напряжение на конденсаторе убывает, а ток растет. В течение следующей четверти периода энергия переходит из катушки в конденсатор. Источник энергии питает только активное сопротивление.
Резонанс токов
Резонанс в идеальной цепи
Резонанс токов наступает при параллельном соединении индуктивности и емкости. Для обобщения анализов включим в цепь параллельно индуктивности и емкости активное сопротивление (рис. 6.7).
.
Запишем это выражение в комплексной форме:
,
где , , .
Вынесем напряжение за скобку, получим
.
Условием резонанса токов является равенство индуктивной и емкостной проводимостей:
.
Векторная диаграмма для режима резонанса представлена на рис. 6.8. При равенстве индуктивной и емкостной проводимостей будут равны и токи . Направленные в противофазе, эти токи компенсируют друг друга, в цепи остается только активная составляющая тока, и общий ток будет совпадать по фазе с напряжением . Поэтому резонанс называют резонансом токов.
Общий ток в цепи можно представить как ,
где – полная комплексная проводимость, модуль которой равен
.
С учетом условия резонанса, получим, что , то есть проводимость цепи минимальна, следовательно, и ток будет минимальным – это признак резонанса токов.
Из условия резонанса получим выражение для резонансной частоты
.
То есть, как и при резонансе напряжений, добиться резонанса токов можно, изменяя один из трех параметров ω, L, C.
Резонанс в реальной цепи
Реальная катушка и реальный конденсатор обладают не только реактивным, но и активным сопротивлением. Катушка – сопротивлением обмотки, конденсатор – сопротивлением токам утечки. В этом случае при большой добротности катушки или конденсатора активное сопротивление может оказаться функцией частоты.
Под добротностью катушки будем понимать отношение её индуктивного сопротивления к активному.
.
Под добротностью конденсатора – отношение его емкостного сопротивления к активному
.
Рассмотрим цепь, содержащую реальные катушку и конденсатор, представленную на рис. 6.9.
Условием резонанса токов в такой цепи является равенство нулю реактивной проводимости .
.
При резонансе b=0, то есть
. (6.1)
Из полученного выражения видно, что в отличие от идеальной цепи резонанс можно получить, регулируя не три параметра, а пять: .
Решая уравнение (6.1) относительно частоты, получим выражение для резонансной частоты
,
Рассмотрим частные случаи:
1. , тогда резонансная частота будет равна , как и в случае идеальной цепи.
2. , тогда при любом значении частоты реактивная проводимость равна нулю, то есть резонанс имеет место при любой частоте.
3. , – добротность невелика, тогда выражение под корнем отрицательно. Резонансная частота мнимая, резонанс невозможен.
При резонансе в реальной цепи, так же, как и в идеальной, ток минимален и имеет чисто активный характер.
Векторная диаграмма для режима резонанса представлена на рис. 6.10.
Контрольные вопросы и задания
1. Какой режим работы электрической цепи называют резонансом?
2. В каких цепях возможен резонанс напряжений?
3. Что является условием и признаком резонанса напряжений?
4. Поясните, какова природа резонанса напряжений.
5. Какой характер электрической цепи называют активно-индуктивным, активно-емкостным?
6. Как по векторной диаграмме определить характер электрической цепи?
7. Что называют волновым сопротивлением контура?
8. Что называют добротностью контура?
9. На какие свойства контура влияет добротность?
10. Что называется полосой пропускания?
11. В каких цепях возможен резонанс токов?
12. Что является условием и признаком резонанса токов?
13. Поясните природу резонанса токов.
14. Чем отличается резонанс токов в идеальной и реальной цепях?
15. Что называется добротностью катушки, конденсатора?
16. Какие частные случаи могут иметь место при резонансе в реальной электрической цепи?
17. Какие энергетические соотношения справедливы при резонансе?
cyberpedia.su
Резонанс напряжений | Электро
| | | | | Резонанс напряжений |Если в цепь переменного тока включены последовательно катушка индуктивности и конденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением.
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на  четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
Хобщ = XL -ХС, XL = ?L, ХС = 1 / ?С
Применив к этой цепи закон Ома, получим:
I = U / Хобщ
Формулу эту можно преобразовать следующим образом:
U = I Хобщ = I (XL -ХС) = IXL -IХС
В полученном равенстве IXL —действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХС—действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать: U = I / Z
Резонанс напряжений в цепи переменного тока
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда ?L = 1 / ?С.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R, где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = IXL так и на конденсаторе Uc = IХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений.
На рис. 1 приведены кривые напряжений, тока и мощности при резонансе напряжений в цепи.
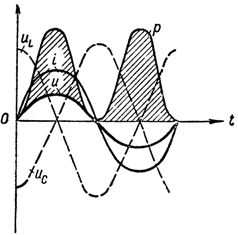
График тока напряжений и мощности при резонансе напряжений
Следует твердо помнить, что сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ?L возрастет, а ХС = = 1 / ?С уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (XL = ХС) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.
Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.
Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.
Пружина же, сообщая маятнику в нужный момент часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.
Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.
Итак, мы приходим к выводу, что цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему. Такая цепь получила название колебательного контура.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:
Lрез = 1 / ?2С, Срез = 1 / ?2L
Таким образом, изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур. 
Пример полезного применения резонанса напряжений: входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной.
Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение_ напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.
elektrolab.web-box.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
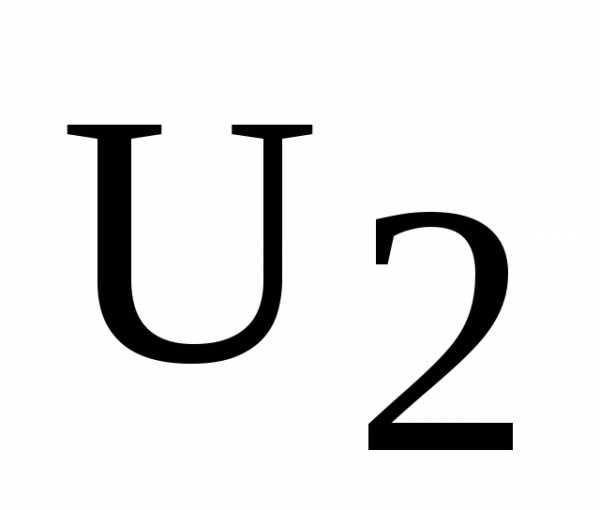 ,
, 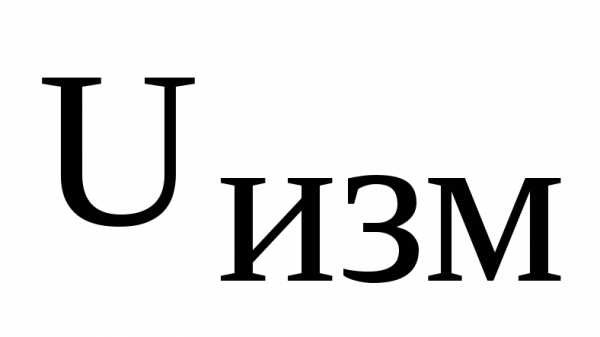 ,
, ,
,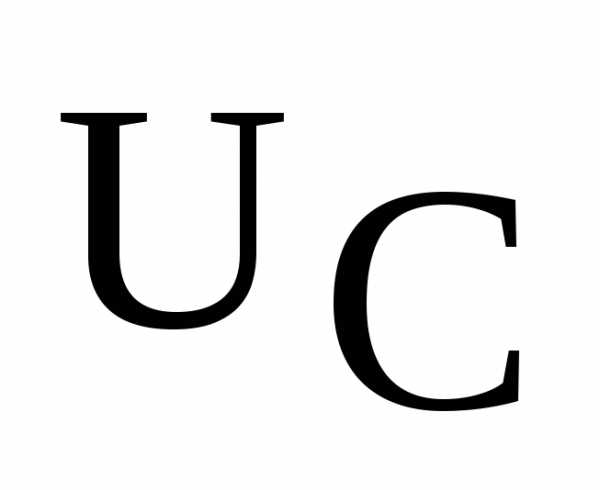 ,
,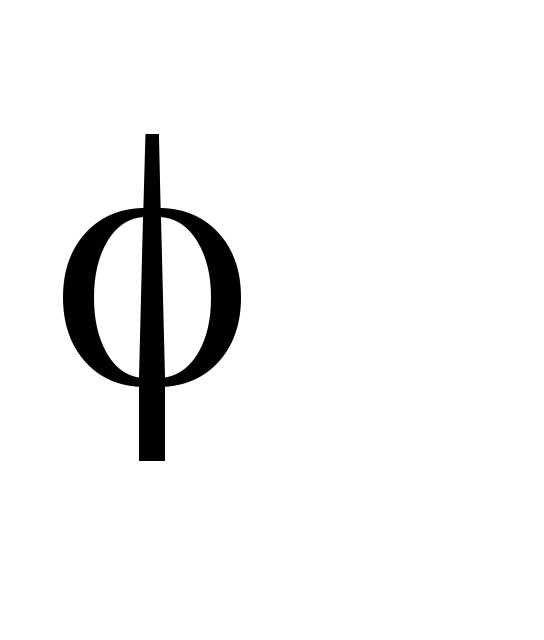 ,
,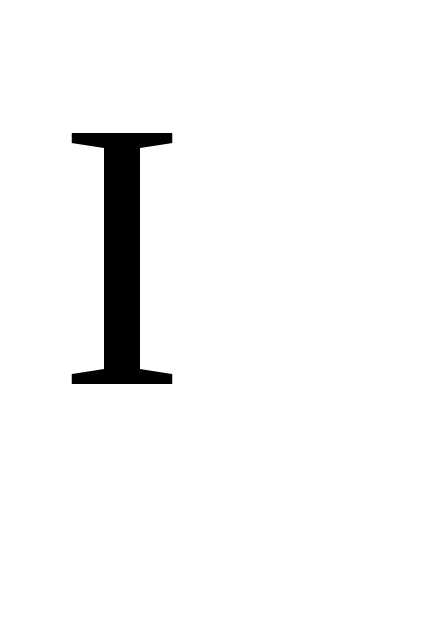 ,
,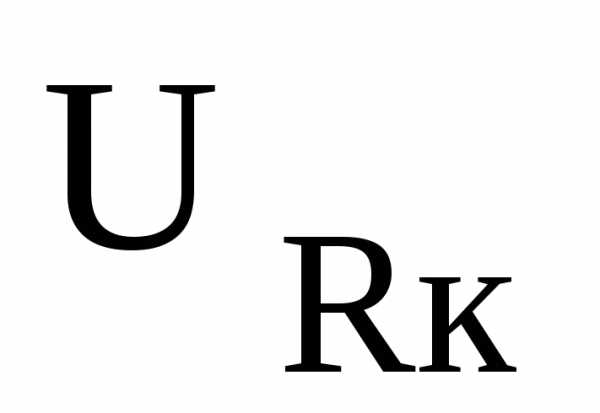 ,
,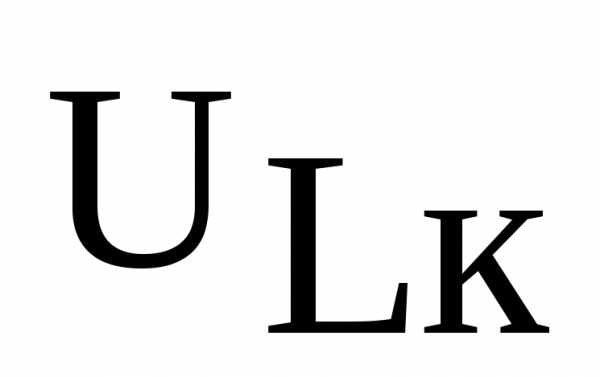 ,
,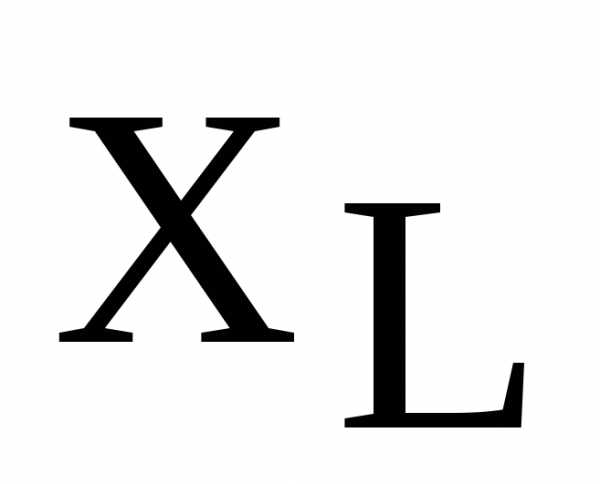 ,
,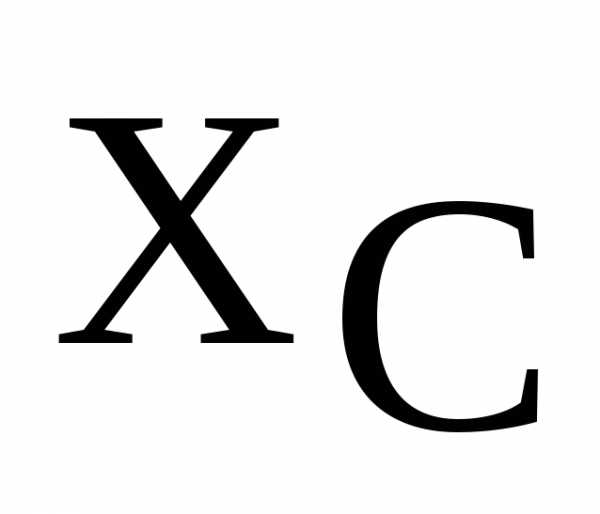 ,
, ,
, ,
,