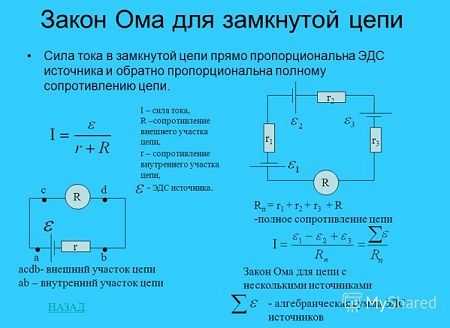
Закон Ома для участка и полной замкнутой цепи. Закон ома для замкнутой цепи

Закон Ома для замкнутой цепи

Содержание: Физические свойства закона Ома Закон Ома для выполнения расчетов Как рассчитать цепи Каждый специалист, ремонтирующий и обслуживающий электроустановки, должен хорошо знать и применять на практике закон Ома для замкнутой цепи. Это действительно так, поскольку закономерности, открытые немецким физиком Георгом Омом, лежат в основе всей электротехники. Данный закон стал весомым вкладом в дальнейшее развитие научных знаний в области электричества. Физические свойства закона Ома Прямая взаимосвязь между силой тока, напряжением, подведенным к сети, и сопротивлением проводника была обнаружена Омом в 1826 году. В дальнейшем, понятие напряжения было заменено на более точный термин – электродвижущую силу (ЭДС). После теоретического обоснования этой зависимости был выведен закон для замкнутой цепи. Его важной особенностью считается обязательное отсутствие какого-либо внешнего возмущения. Поэтому стандартные формулировки потеряют свою актуальность, если, например, поместить проводник в переменное магнитное поле. Для экспериментов по выводу закона использовалась простейшая схема, состоящая из источника питания, обладающего ЭДС и подключенных к нему двух выводов, соединенных с резистором. В проводнике начинают в определенном направлении перемещаться элементарные частицы, несущие заряд. Таким образом, сила тока представляется в виде отношения ЭДС к общему сопротивлению всей цепи: I = E/R. В представленной формуле Е – является электродвижущей силой, измеряемой в вольтах, I – сила тока в амперах, а R выступает в роли электрического сопротивления резистора, измеряемого в омах. При этом, учитываются все составляющие сопротивления и при расчетах используется их суммарное значение. Они включают сопротивление самого резистора, проводника (r) и источника питания (r0). Окончательно формула будет выглядеть так: I = E/(R+r+r0). Если значение внутреннего сопротивления источника тока r0 превышает сумму R+r, то в этом случае отсутствует зависимость силы тока от характеристик подключенной нагрузки, а источник ЭДС исполняет роль источника тока. Когда r0 ниже суммы R+r, получается обратная пропорция тока с суммарным внешним сопротивлением, а напряжение поступает за счет источника питания. Закон Ома для выполнения расчетов Точные расчеты требуют учета всех потерь напряжения, в том числе и в местах соединений. Для определения электродвижущей силы на выводах источника тока замеряется разность потенциалов при разомкнутой цепи, когда нагрузка полностью отключена. В этом случае применяется не только закон Ома для замкнутой цепи, но и закон, действующий для участка цепи. Данный участок считается однородным, поскольку здесь принимается в расчет только разность потенциалов, без учета ЭДС. Это дает возможность рассчитать каждый элемент электрической цепи по формуле I=U/R, в которой U является разностью потенциалов или напряжением, измеряемым в вольтах. Замеры выполняются с помощью вольтметра при подключении щупов к выводам нагрузки или сопротивления. Полученное значение напряжения будет всегда ниже электродвижущей силы. Это наиболее распространенная формула, позволяющая найти любую составляющую при наличии двух известных. Закон Ома для замкнутой цепи имеет много общего с законом, выведенным для магнитной цепи. В этой системе проводник выполнен в виде замкнутого магнитопровода. В качестве источника выступает обмотка катушки по виткам которой протекает электрический ток. Появляющийся магнитный поток (Ф) замыкается на магнитопровод и начинает циркулировать по контуру. Он находится в непосредственной зависимости от магнитодвижущей силы и сопротивления материала, через который проходит. Данное явление выражено формулой Ф=F/Rm, в которой F представляет собой магнитодвижущую силу, а Rm служит сопротивлением, вызывающим затухание. Как рассчитать цепи

electric-220.ru

Закон Ома для замкнутой цепи.

Замкнутая цепь содержит: источник тока, сопротивления (потреби тока), приборы для контроля характеристик тока, провода, ключ. Приме может служить цепь, приведенная на рис.5. По отношению к источнику можно выделит внешнюю цепь, содержащую элементы, находящиеся данного источника, если проследить за током от одной его клеммы другой, и внутреннюю, к которой относят проводящую среду внутри источника обозначим сопротивление внешней цепи через R, внутреннее сопротивление источника r. Тогда ток в цепи определяется по закону для замкнутой цепи, который гласит, что ток в замкнутой цепи прямо пропорционален величине ЭДС и обратно пропорционален сумме внутреннего и внешнего сопротивления цепи, т.е.

(8)

Из этого закона вытекают следующие частные случаи:

• Если R стремится к нулю (т.е. R << r), то ток I стремится к максимально

возможному значению Iк.з = , называемому током короткого

замыкания. Этот ток опасен для источников, поскольку вызывает перегрев источника и необратимые изменения проводящей среды внутри него.

• Если R стремится к бесконечно большой величине (т.е. при условии, что R >> r), ток I уменьшается, и падение напряжения внутри источника Ir становится намного меньше IR, следовательно IR. Значит, величину ЭДС источника можно практически измерить с помощью вольтметра, присоединенного к клеммам источника при условии, что сопротивление вольтметра RV >> r при разомкнутой внешней цепи.

Распределение энергии при работе источника постоянного тока

Пусть источник постоянного тока имеет ЭДС и внутреннее

сопротивление r и замкнут на сопротивление внешней нагрузки R.

Проанализируем несколько величин, характеризующих распределение энергии при работе источника постоянного тока.

а) Затраченная источником мощность Р.

Работа, совершаемая сторонними силами в замкнутой цепи по

перемещению заряда dq, равна:

dA = dq (9)

Исходя из определения, мощность, развиваемая сторонними силами в

источнике, равна:

(10)

Эта мощность расходуется источником во внешней и внутренней по отношению к источнику частях цепи. Используя закон Ома для замкнутой цепи, можно затраченную мощность представить в виде:

(11)

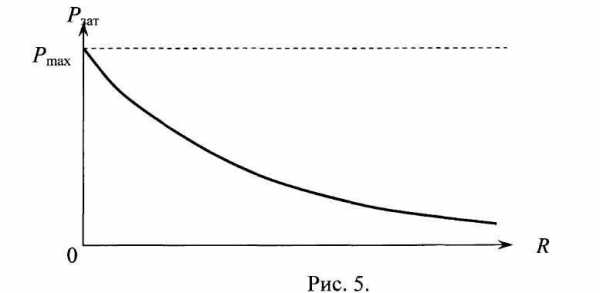
Если сопротивление нагрузки R уменьшается, стремясь к нулю, то РзатPmax = Если R увеличивается, стремясь в бесконечность, то Рзат. График зависимости затраченной сторонними силами мощности Рзат от величины внешнего сопротивления R показан на рисунке 5.

б) Полезная мощность Рпод:_

Полезной по отношению к источнику мощностью Рпод считается мощность, расходуемая источником во внешней цепи, т.е. на внешней нагрузке. Она равна:

(12)

Пользуясь законом Ома для замкнутой цепи, или заменив в последнем выражении I на /(R+r), можно представить в виде

(13)

Если числитель и знаменатель этого выражения разделить на R, то получится выражение

(13a )

наглядно демонстрирующее то, что Рпол стремится к нулю как при уменьшении R до нуля, так и при его бесконечном увеличении, т.к. в обоих случаях знаменатель этого выражения стремится к бесконечности. Это означает, что при некотором оптимальном значении R полезная мощность достигает максимального значения

Определить оптимальное значение R, а также и значение , можно, приравняв нулю первую производную функции Рпоя =f(R) пo R:

(14)

Как видно, полученное равенство соблюдается при условии

(15)

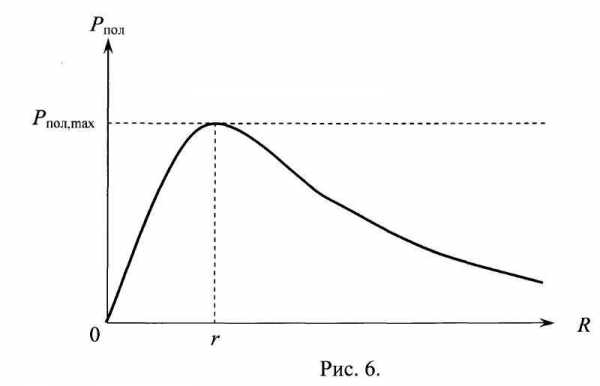
из чего следует, что R = r. Таким образом, при сопротивлении внешней цепи R, равном сопротивлению внутренней цепи г, полезная мощность источника тока имеет максимальное значение, которое может быть найдено по формуле:

(16)

График зависимости Pпол=f(R) показан на рисунке 6.

в) Коэффициент полезного действия.

Величина коэффициента полезного действия цепи г| источника тока, в соответствии с определением, составляет:

(17)

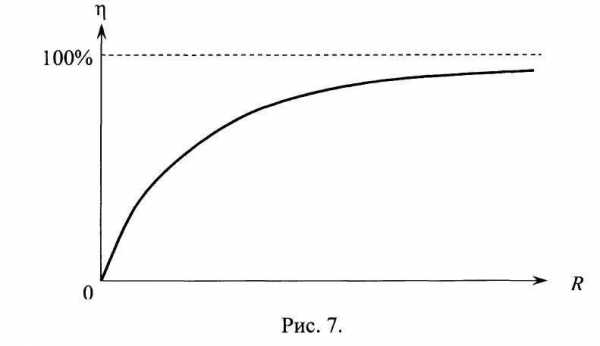
При R 0 величина 0, приR величина 100%. В последнемслучае Рпол стремится к нулю, и такие режимы работы источника не представляют практического интереса. График зависимости КПД источника тока от величины нагрузки R показан на рисунке 7.

studfiles.net

Закон Ома для замкнутой цепи

На рисунке 2 показана простейшая замкнутая цепь, состоящая из реального источника э.д.с. Е, имеющего внутреннее сопротивлениеRвти нагрузочного резистора с сопротивлениемR(сопротивление соединительных проводов включено в сопротивлениеRрезистора).

Закон Ома для замкнутой цепиформулируется следующим образом:сила тока (ток, величина тока) прямо пропорциональна электродвижущей силе (э.д.с.) источника и записывается в виде:

(4)

где 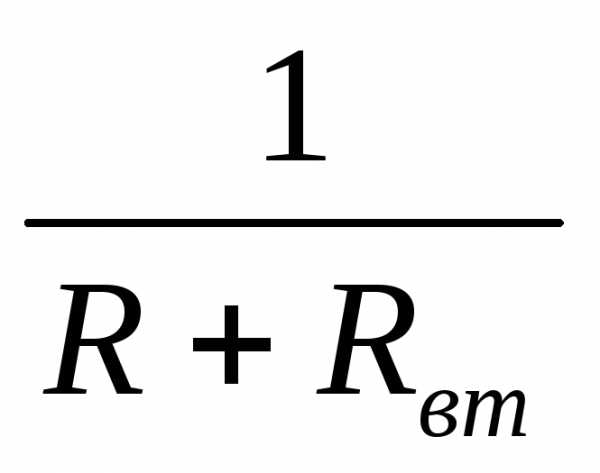– коэффициент пропорциональности.

П

(4а)

ерепишем равенство (4) в виде

и введем обозначение U=IR– напряжение на выходных зажимах источника э.д.с. (генератора), которое одновременно является падением напряжения, создаваемым токомIна внешнем сопротивленииRнагрузочного резистора.

П

(5)

одставив это обозначение в правую часть равенства (4а), можно получить следующую зависимость:

,

которая представляет собой аналитическое выражение внешней характеристики источника э.д.с. Эту зависимость можно сокращенно записать в видеU = F(I) при E = const, Rвт = const. Внешней характеристикой принято называть графическую зависимость U = F(I), показанную на рисунке 3.

Сплошной линией показана внешняя характеристика реального источника э.д.с., в котором с ростом тока I увеличивается падение напряжения на внутреннем сопротивлении IRвт, в результате чего с ростом тока выходное напряжение источника U уменьшается. Пунктирной линией на рисунке 3 показана внешняя характеристика идеального источника э.д.с., у которого отсутствует внутреннее сопротивление (Rвт = 0), а, следовательно, и внутреннее падение напряжения (IRвт = 0). В результате равенство (5) принимает вид

(5а)

,

и характеристика представляет собой горизонтальную линию. Такой идеальный источник называют источником (генератором) бесконечной мощности, поскольку он гарантирует постоянство напряжения при сколь угодно больших токах нагрузки.

Закон Ома для участка цепи, содержащего источник э.Д.С. (обобщенный закон Ома)

На рисунках 4а и 4б показаны одинаковые участки, содержащие последовательно включенные резистор R и источник э.д.с. Е, по которым протекает ток I одного и того же направления. Что касается источников, то э.д.с. в схеме на рисунке 4а совпадает с направлением тока, а на рисунке 4б – действует встречно с током.

Рис. 4

К

(6)

ак известно,под напряжением Uна участке цепипонимают разность электрических потенциаловφмежду крайними точками этого участка (аисна рисунке 4). Ток всегда течет от более высокого потенциала к более низкому потенциалу. Поскольку ток в обоих случаях (рис. 4а и 4б) направлен от точкиак точкес, то напряжение

Выразим более высокий потенциал точки ачерез потенциал точкис. При перемещении (рис. 4а) от точкиск точкеb(встречно к направлению э.д.с. Е) потенциал точкиbоказывается ниже потенциала точкисна величину э.д.с. Е, то есть. Применительно к схеме на рисунке 4б потенциал точкиbбудет выше на величину э.д.с. Е, то есть. Поскольку потенциал точкиавыше потенциала точкиbна величину падения напряженияIRна резисторе с сопротивлениемR, то.

Таким образом, для рисунка 4а: , а для рисунка 4б:.

Соответственно напряжение между границами аисучастка:

;

.

Решив равенства (6а) и (6б) относительно тока, получим обобщенный закон Ома (закон Ома для участка цепи, содержащего источник э.д.с.):

;

.

В общем случае

(7)

В частном случае, когда э.д.с. отсутствует (Е = 0) уравнение (7) превращается в закон Ома для участка цепи, не содержащего э.д.с. (1).

studfiles.net

Закон Ома для замкнутой цепи

Пример 9.8.

Д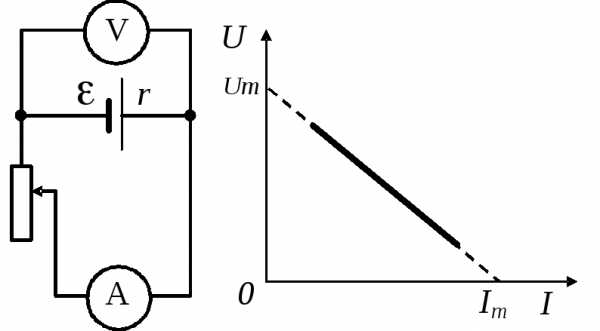ля определения ЭДС и внутреннего сопротивления r источника тока собрали цепь по схеме, приведенной на рисунке. Перемещая контакт реостата полу­чили множество пар показаний U вольтметра и I амперметра. По этим данным построили график, показанный на рисунке. Линия графика пересекает оси абс­цисс и ординат соответственно в точках 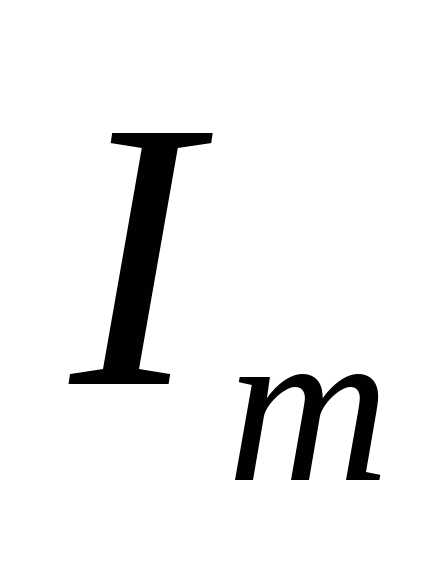и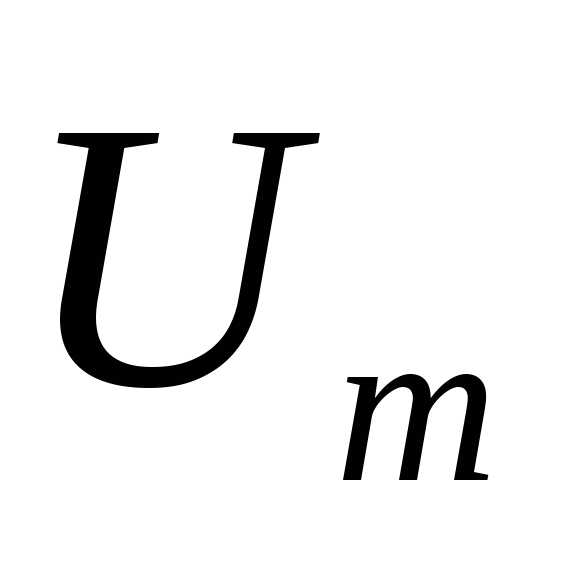.Найдите вели­чины и r. Считайте сопротивление вольтметра очень большим, а сопротивле­ние амперметра – пренебрежимо малым.

Решение

Согласно условию вольтметр и амперметр являются идеальными (т.е. не влияют на протекание тока). Вводя величины переменного сопротивления реостата , запишем закон Ома для полной цепи:. Показание вольтметра при каждом положении движка реостата равно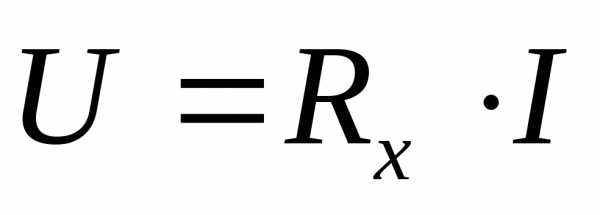. Для зависимости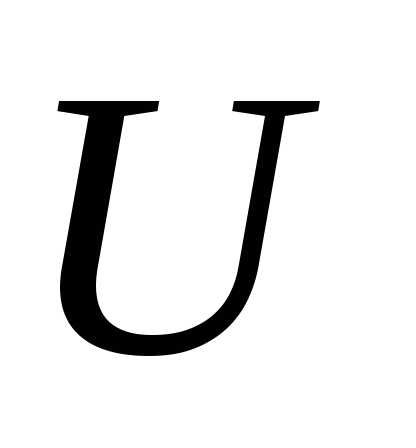от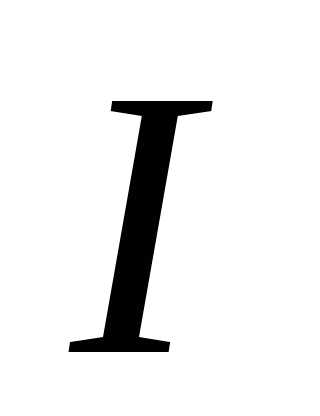получим линейное соотношение:

,

Привязка этой линейной зависимости к графику дает:

при,,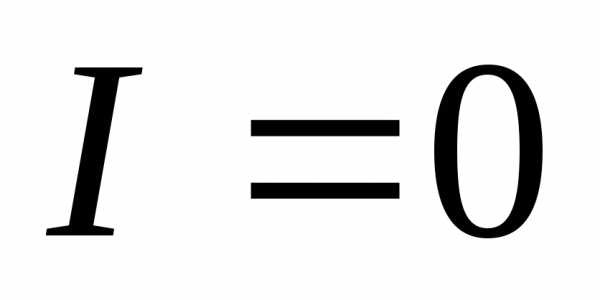

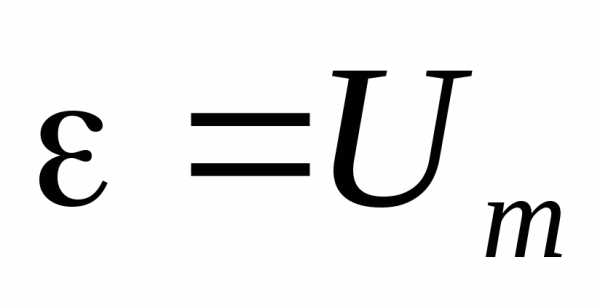при ,.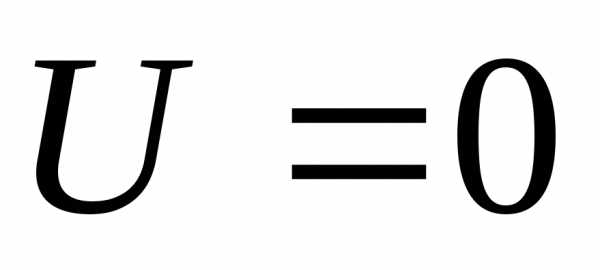

Пример 9.9.

Найдите разность потенциалов 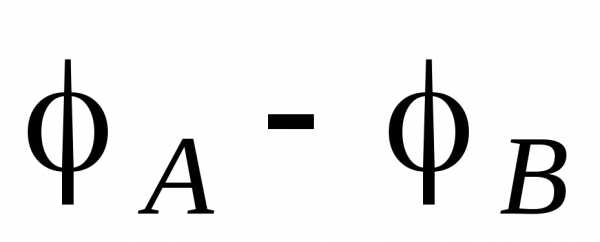в точкахА и В, если R1 =1 Ом, R2 = 3 Ом,  = 4 В (см. рис.), внутреннее сопротивление источника r = 1 Ом.

Решение.

Сопротивления двух ветвей, по которым протекают токи источника, одинаковы, поэтому:, где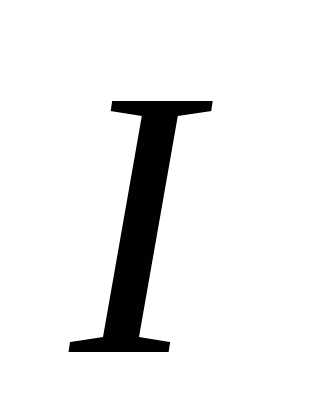- ток через источник. Для потенциалов в точках 1, А, В, из закона Ома для однородного участка цепи, следует:

.

Откуда для разности потенциалов в точках А и В получим: .Величину тока найдем, применяя закон Ома для замкнутой цепи , где- полное сопротивление участка 12. Для разности потенциалов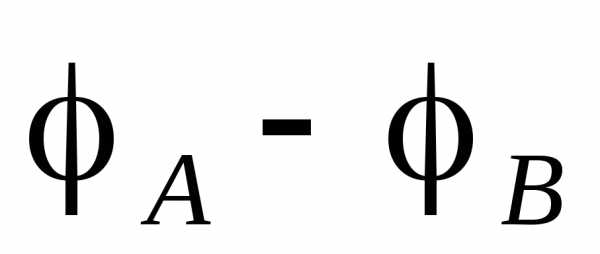получим окончательно:

В

Закон Джоуля-Ленца

Пример 9.10.

Э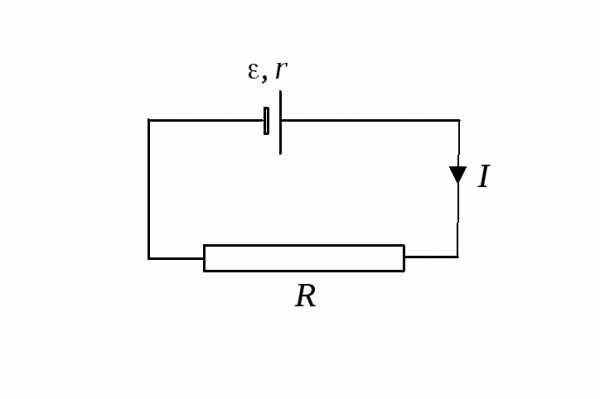лемент с ЭДС = 6 В дает максимальный ток Im= 3 А. Найдите наибольшее количество теплоты Q, которое может быть выделено во внешнем сопротивлении в единицу времени.

Решение.

Из закона Ома для замкнутой цепи , получим следующее выражение для мощности источника ЭДС:

,

где слагаемые справа представляют мощности выделения джоулева тепла на внутреннем сопротивлении источника и внешнем сопротивлении цепи соответственно. Неизвестное значение найдем, определив максимальный ток данного элемента:.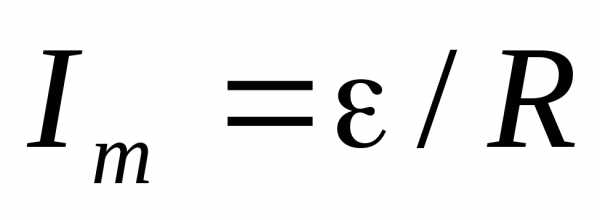

Мощность выделения тепла на внешнем сопротивлении представится соотношением:

Квадратичная зависимость мощности от тока достигает максимального значенияпри токе.

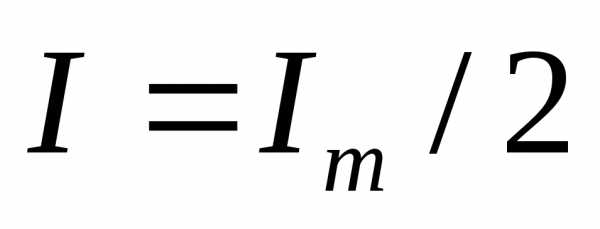Пример 9.11.

Батарея с ЭДС  = 240 В и внутренним сопротивлением r=1 Ом замкнута на внешнее сопротивление R = 23 Ом. Найдите полную мощность Р0, полезную мощность Р и КПД  батареи.

Решение.

Перепишем выделенное в рамку выражение предыдущего примера в обозначениях мощности:

,

где: 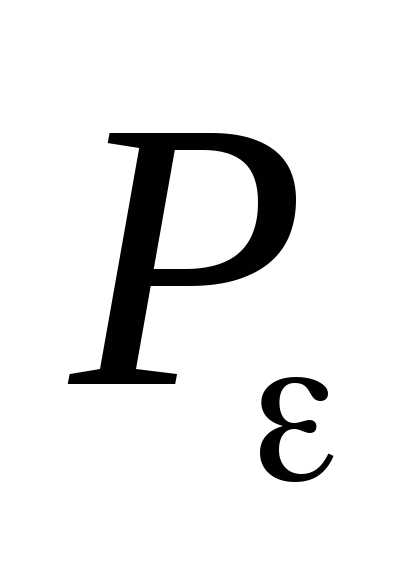- мощность источника,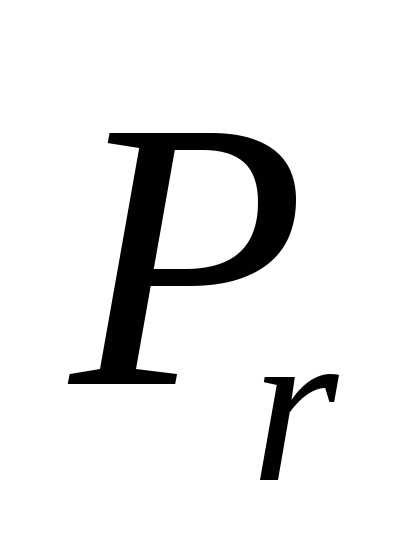- мощность выделения джоулева тепла внутри источника,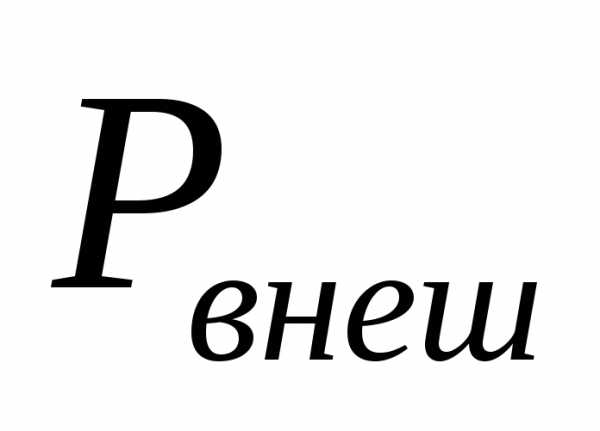- мощность выделяемая во внешней цепи. Подстановка в выражения для мощностей величины тока, дает для искомых величин:

кВт,

кВт,

/=.

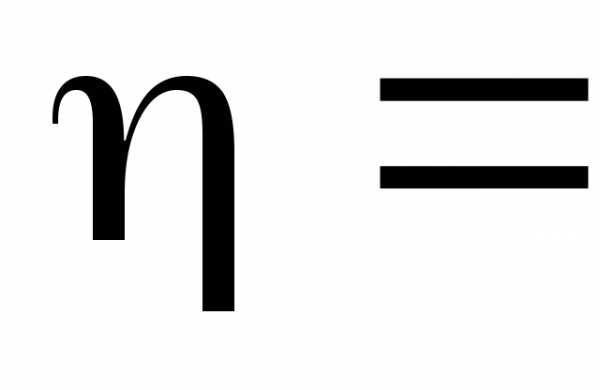
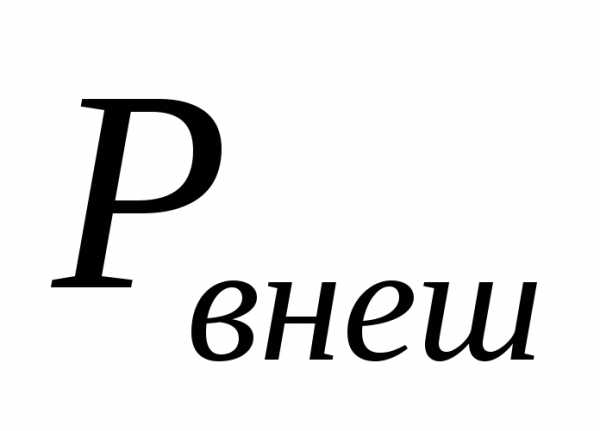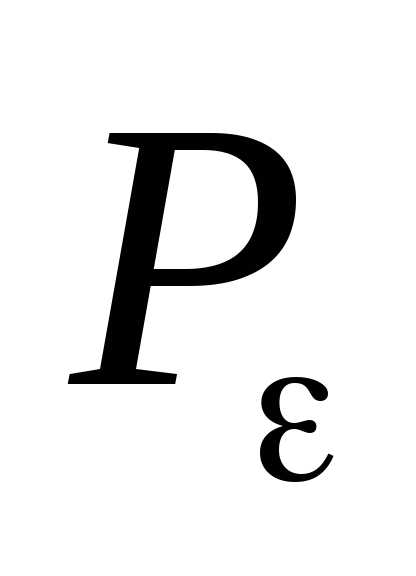Пример 9.12.

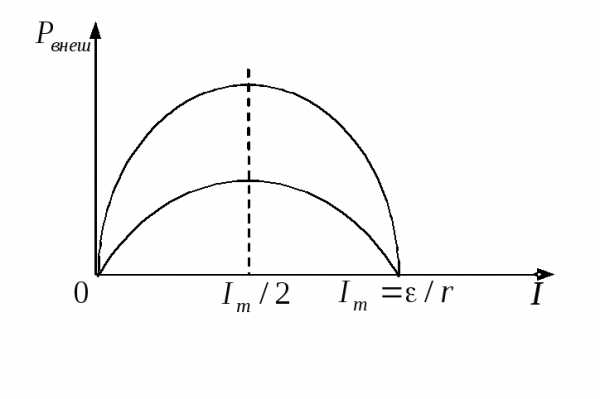В двух замкнутых электрических цепях, каждая из которых содержит источник тока и внешнее сопротивление, максимальные силы тока одинаковы, а максимальная мощность во внешней цепи в одном случае в два раза больше, чем во втором. Какими параметрами отличаются эти цепи?

Решение. Сила тока максимальна при коротком замыкании, когда внешнее сопротивление равно нулю. При этом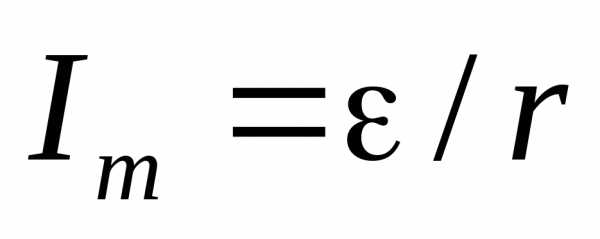и таким образом отношение величины ЭДС к внутреннему сопротивлению в обоих случаях одинаково. Максимальная полезная мощность (мощность, выделяемая во внешней цепи) достигается при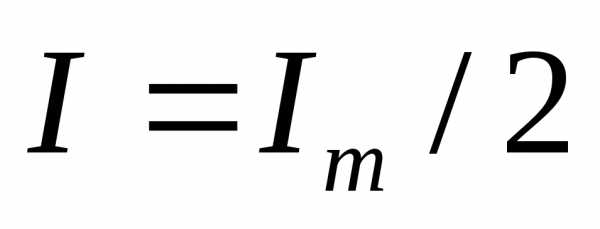, т.е. при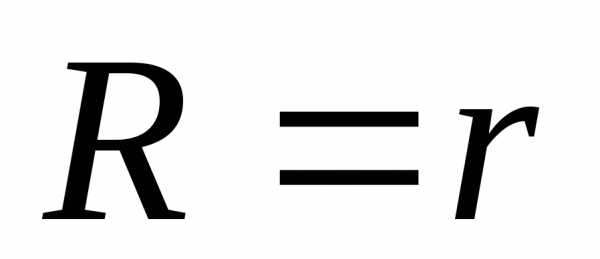

(см. пример 9.7). Эта мощность составляет . Так как отношениеодинаково в обоих случаях, то вдвое большая полезная мощность при одинаковых силах тока обеспечивается вдвое большей величиной ЭДС. При этом внутреннее сопротивление источника также вдвое больше.

studfiles.net

Закон Ома для замкнутой цепи.

Если точки 1 и 2 совпадают, то 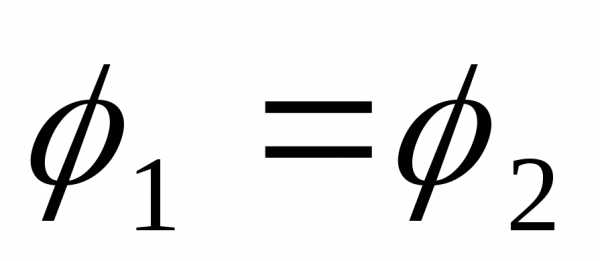и выражение закона Ома для участка приобретает более простой вид:

,

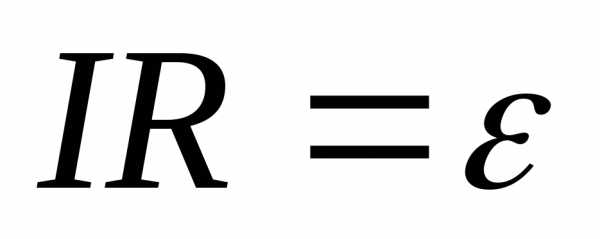где представляет собой полное сопротивление замкнутой цепи включая внутреннее сопротивление источников, а- алгебраическую сумму э.д.с. в данной цепи.

Ток, возникающий при внешнем сопротивлении равном нулю, называется током короткого замыкания.

Лекция 10.

Соединение проводников.

Используя закон Ома для участка цепи, можно показать, что сопротивление последовательного и параллельного соединения проводников равны соответственно:

Доказательство:

1. При последовательном соединении I=I1=I2= … =In. В то же время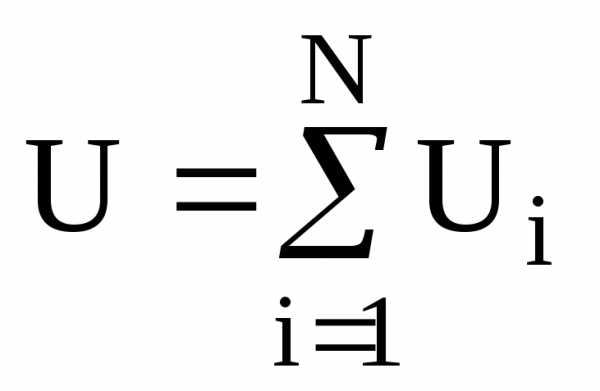. То есть.

2. При параллельном соединении U=U1=U2= … =Un. В то же время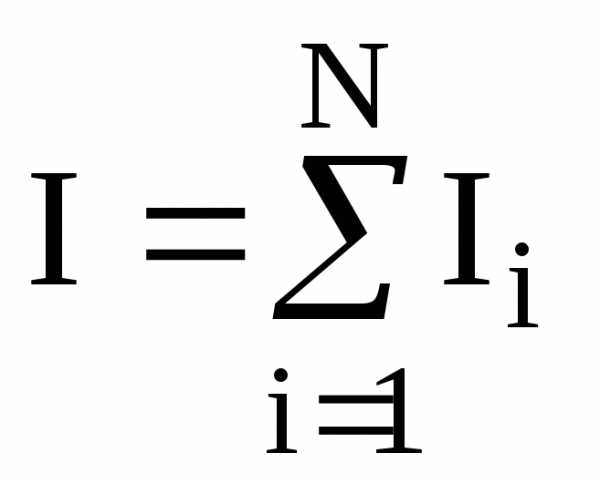. То есть.

Отметим, что при параллельном соединении проводников, общее сопротивление всегда меньше наименьшего сопротивления в параллельном соединении. Убедитесь в этом самостоятельно.

Закон Джоуля - Ленца.

При прохождении тока через проводник сопротивлением 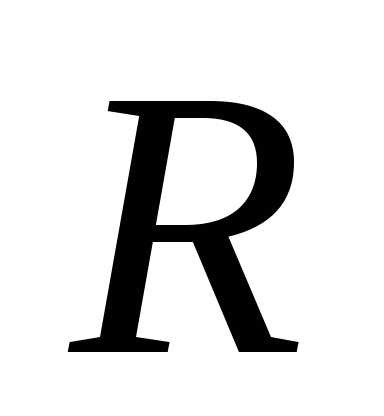выделяется теплота, которая рассеивается в окружающей среде. Найдем это количество теплоты. Воспользуемся для этого законом сохранения энергии и законом Ома.

Рассмотрим однородныйучасток цепи, на котором поддерживается постоянная разность потенциалов. Электрическое поле при этом совершает работу:

.

Если на участке отсутствует превращение в механическую, химическую или иные виды энергии кроме тепловой, то выделяющее количество теплоты равно работе электрического поля:

.

Тепловая мощность при этом равна:

Конечное количество теплоты находится интегрированием по времени:

.

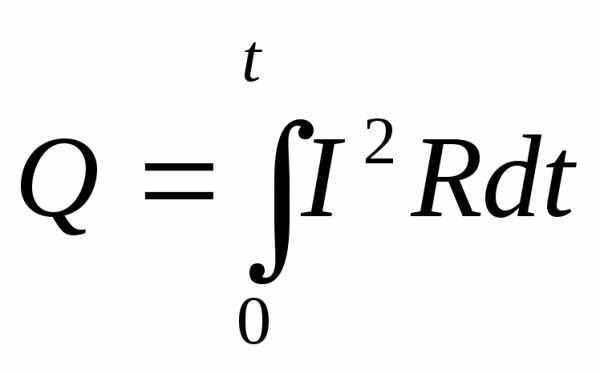Если ,

.

Это формула выражает закон Джоуля – Ленца. Механизм тепловыделения связан с превращением дополнительной кинетической энергии, которую приобретают носители тока в электрическом поле, в энергию возбуждения колебаний решетки при столкновении носителей с атомами в узлах решетки.

Найдём выражение для закона Джоуля – Ленца в локальной форме. Для этой цели выделим в проводнике элементарный объём в форме цилиндра с образующей вдоль вектора 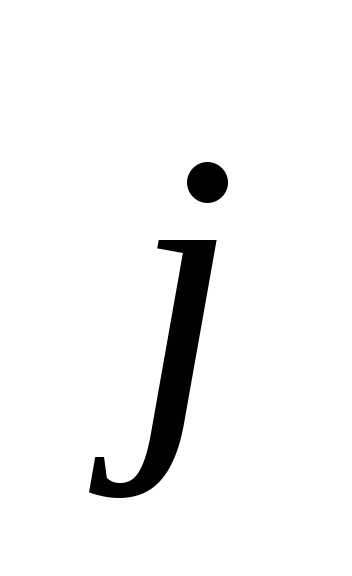. Пусть поперечное сечение цилиндра, а его длина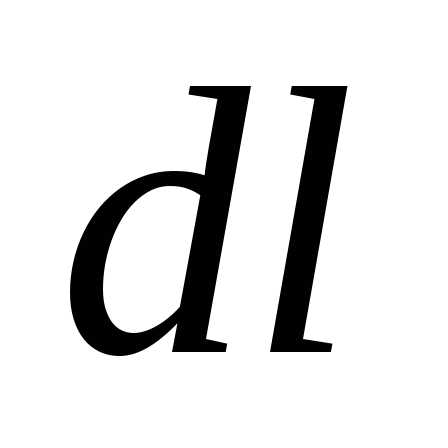. Тогда согласно закону Джоуля – Ленца в этом объеме за времявыделяется количество теплоты:

,

где - объём цилиндра. Разделив последнее соотношение на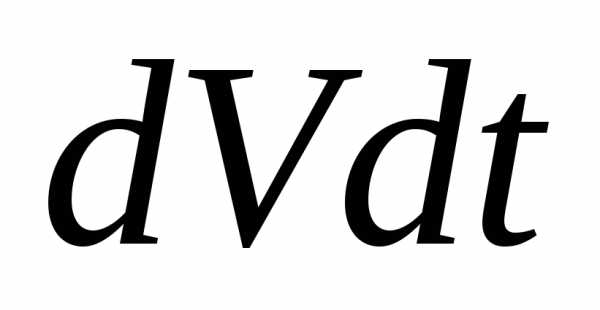получим формулу которая определяет тепловую мощность, выделяющуюся в единице объёма проводника:

- удельная тепловая мощность измеряется в.

Полученное соотношение выражает закон Джоуля – Ленца в локальной форме: удельная тепловая мощность тока пропорциональна квадрату плотности тока и удельному сопротивлению проводника в данной точке.

В такой форме закон Джоуля – Ленца применим к неоднородным проводникам любой формы, и не зависят от природы сторонних сил. Если на носители действуют только электрические силы, то на основании закона Ома :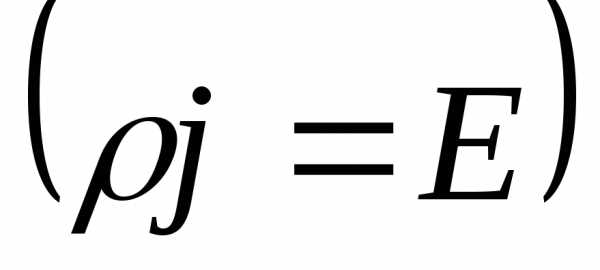

.

Если участок цепи содержит источник э.д.с., то на носители тока будут действовать не только электрические, но и сторонние силы. В этом случае тепло, которое выделяется на участке, равно алгебраической сумме работ электрических и сторонних сил.

Умножим закон Ома в интегральной форме на силу тока :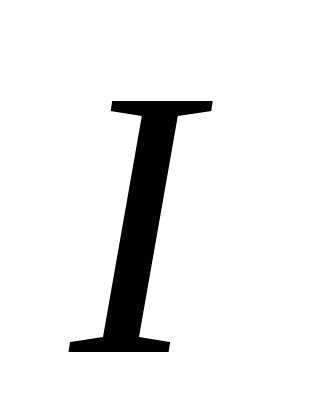

.

Здесь слева стоит (тепловая мощность), а справа алгебраическая сумма мощностей электрических и сторонних сил, которую называютмощностью тока.

В замкнутой цепи :

,

т.е. мощность тепловыделения равна мощности сторонних сил.

studfiles.net

Закон Ома для участка и полной замкнутой цепи

В 1826 г. немецкий ученый Георг Ом экспериментально установил прямую пропорциональную зависимость между силой тока I в проводнике и напряжением U на его концах: , где G - электрическая проводимость проводника. Величина, обратная проводимости называется электрическим сопротивле­ни­ем проводника R. Таким образом, закон Ома для участка цепи, не содержа­щего источника э.д.с., имеет вид . Учитывая, что в общем случае участок цепи может содержать и э.д.с., закон Ома следует представить в виде . Сопротивление проводника зависит от его размеров, формы и материала, из которого он изготовлен. Для однородного линейного проводника , где l - длина, S - площадь поперечного сечения проводника, r - удельное электриче­с­кое сопротивление, зависящее от материала, из которого изготовлен проводник. Единица сопротивления 1 Ом - это сопротивление такого проводника, в котором при напряжении 1В течет ток в 1А. Если цепь замкнута, то , , где R - общее сопротивление всей цепи, включая сопротивление источника э.д.с. Тогда закон Ома для замкнутой цепи следует записать , где e - алгебраическая сумма всех э.д.с., имеющихся в этой цепи. Принято называть сопротивление источника тока r - внутренним, а сопротив­ление всей остальной цепи R - внешним. Окончательный вид формулы закона Ома для замкнутой цепи . В системе единиц СИ напряжение и э.д.с. изме­ряются в Вольтах (В), сопротив­ление - в Омах (Ом), удельное электрическое сопротивление - в Ом-метрах (Ом×м), электрическая проводимость в Сименсах (См).   Рис.2.1. Отрезок проводни­ка. Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.2.1). Сила тока на этом участке , сопротивление , падение на­пряжения , где Е - напряженность электрического поля в проводнике. Под­ставив эти параметры в закон Ома для участка цепи, получим . Отсюда или , где - удельная электрическая проводи­мость проводникаили удельная электропроводность. В векторном виде имеем (единицей измерения g в системе СИ является сименс на метр (См/м)). Полученное выражение есть закон Ома в дифференциальной форме : плот­ность тока в любой точке внутри проводника прямо пропорциональна напря­женности поля в этой точке. 1.14 Сопротивление проводника. Явление сверхпроводимости. Способность вещества проводить ток характеризуется его удельной проводи­мостьюg, либо удельным сопротивлением r. Их величина определяется химичес­кой природой проводника и условиями, в частности температурой, при которой он находится. Для большинства металлов r растет с температурой приблизительно по линейному закону: , - удельное сопротивление при 0°С, t - температура по шкале Цельсия, a - темпе­ра­турный коэффициент сопротивления близкий к 1/273 К-1 при не очень низких темпе­ратурах. Так как R~r, то , где - сопротивление при 0°С. Преобра­зовав две последние формулы, можно записать и , где Т – температура по Кельвину. На основе температурной зависимости сопротивления метал­лов созда­ны термометры сопротивления - термисторы, позволяющие определять температуру с точно­стью до 0.003 К. При низких температурах нарушается линейность зависимости сопротивления металлов от температуры и при температуре 0 К наблюдается остаточное сопротивление Rост. Величина Rост зави­сит от чистоты материала и наличия в нем механических напряжений. Лишь у иде­ально чистого металла с идеально правильной кристаллической решеткой Rост ®0 при Т®0 (пунктирная часть кривой). Кроме этого, в 1911 г. Г.Каммерлинг-Оннес обнару­жил, что при Тк = 4.1К сопротивление ртути скачкообразно уменьшается практически до нуля. Эта температура была названа критической, а наблюдаемое яв­ление - сверхпроводимостью. Впо­следствии этот эффект был обнаружен у целого ряда дру­гих металлов (Ti, Al, Pb, Zn, V и др.) и их спла­вов в интервале температур 0.14-20 К. Вещества в сверхпроводящем состоянии обладают необычными свойствами. Однажды возбужденный в них ток может длительно существовать без источника тока. Переход в сверхпроводящее состояние сопровождается скачкообразным изме­нением теплоемкости, теплопроводности, маг­нитных свойств вещества. Выясни­лось, что внешнее магнитное поле не проникает в толщи­ну сверхпроводника, т.е. магнитная индукция внутри него всегда равна нулю. Явление сверхпроводимости объясняется на основе квантовой теории. К настоящему времени это явление обнаружено также у ряда композиционных веществ (например, соединений металлов и диэлектриков), при этом критическая температура доходит до температуры сжижения азота, что позволяет достаточно экономично использовать явление высокотемпературной сверхпроводимости в инженерной практике. Данное явление позволяет создавать: системы передачи без потерь электрического тока по проводам из таких веществ, системы для накопления электроэнергии, мощные электромагниты, магнитные подвески для различных целей. 1.15 Работа и мощность тока, закон Джоуля-Ленца. Определим работу, совершаемую постоянным током в проводнике, имеющем сопротивление R и находящемся под напряжением . Так как ток пред­ставляет собой перемещение заряда q под действием поля, то работу тока можно оп­ределить по формуле . Учитывая формулу и закон Ома, получим , или , или , где t - время протекания тока. Поделив обе части равенства на t, получим выраже­ния для мощности постоянного тока N , , . Работа тока в системе единиц СИ измеряется в доулях (Дж), а мощность - в ваттах (Вт). На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч) и киловатт-час (кВт×ч). 1Вт×ч - работа тока мощностью 1Вт в течение одного часа. 1Вт×ч=3.6×103 Дж. Опыт показывает, что ток всегда вызывает некоторое нагревание проводника. Нагревание обусловлено тем, что кинетическая энергия движущихся по проводнику электронов (т.е. энергия тока) при каждом их столкновении с ионами металличе­ской решетки переходит в теплоту Q. Если ток идет по неподвижному металличе­скому проводнику, то вся работа тока расходуется на его нагревание и, следуя за­кону сох­ранения энергии, можно записать . Данные соотношения выражают закон Джоуля-Ленца. Впервые этот закон был установлен опытным путем Д.Джоулем в 1843 г. и независимо от него Э.Ленцем в 1844 г. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А.Ладыгиным лампы накаливания. На тепловом действии тока основан целый ряд электрических приборов и ус­та­новок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы - чайники, кипятильники, утюги. В пищевой промышленности широко применяется метод электроконтактного нагрева, заключающийся в том, что электрический ток, проходя через продукт, об­ла­дающий определенным сопротивлением, вызывает его равномерное нагревание. На­пример, для производства колбасных изделий через дозатор фарш поступает в формы, торцевые стенки которых служат электродами. При такой обработке обес­пе­чивается равномерность нагрева по всему объему продукта, возможность под­держа­ния определенного температурного режима, наивысшая биологическая цен­ность из­делия, наименьшие длительность процесса и расход энергии. Определим удельную тепловую мощность токаw, т.е. количество теплоты, вы­деляющееся в единице объема за единицу времени. Выделим в проводнике элемен­тарный цилиндрический объем dV с поперечным сечением dS и длиной dl параллель­ной направлению тока, и сопротивлением , . По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота . Тогда и, используя закон Ома для плотности тока и соотно­шение , получим . Эти соотношения выражают закон Джоуля-Ленца в дифференциальной форме.   1.16. Правило Кирхгофа для разветвленных электрических цепей. До сих пор нами рассматривались простейшие электрические цепи, состоя­щие из одного замкнутого неразветвленного контура. На всех его участках силы тока оди­наковы. Расчет I, R, e в такой цепи выполняется с помощью законов Ома. Рис.2.2.Разветвленная электрическая цепь. Более сложной является разветвленная электри­ческая цепь, состоящая из нескольких замкнутых кон­ту­ров, имеющих общие участки. В каждом контуре мо­жет быть несколько источников тока. Силы тока на от­дельных участках замкнутого контура могут быть раз­личными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей. Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю: . Узел - точка цепи, в которой сходятся не менее трех про­водников. В электрической цепи на рис.2.2 имеются два узла А и В. Ток, входящий в узел, считается положительным, выходящий - отрицательным. Например, для узла А первое правило Кирх­гофа следует записать . Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать. Второе правило Кирхгофа относится к любому замкнутому контуру, выде­ленному в разветвленной цепи: алгебраическая сумма произведений токов на со­противления, включая и внутренние, на всех участках замкнутого контура равна алгебраической сумме электродвижущих сил, встречающихся в этом контуре . Контур ‑ это замкнутый участок схемы, по которому можно пройти и вернуться в исходную точку. Второе правило Кирхгофа получается из закона Ома, записанного для всех участков от узла до узла (ветвей) разветвленной схемы. В электрической цепи на рис.2.2 имеются три контура: AMNBA, CABDC, CMNDC. При этом, токи Ii в ветвях контура, совпадающие с произвольно вы­бран­ным направлением обхода контура, считаются положительными, а направлен­ные на­встречу обхода - отрицательными. Э.д.с., проходимые от «+» к «-» считаются поло­жительными и наоборот. В рассматриваемой элек­трической цепи (рис.2.2) выберем обход контуров по часовой стрелке и запишем для них уравнения по II правилу Кирхгофа: для AMNBА ; для CABDС ; для CMNDС . В данном примере внутренними сопротивлениями источников тока пренебрегаем. Первое и второе правила Кирхгофа по­зволяют составить систему линейных алгебраичес­ких уравнений, которые связывают пара­метры (I, R, ) и позволяют, зная одни, найти другие. Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как под­ключить динамики или проигрыватель к сте­реосистеме, как подсоединить сигнализацию для охраны или автомобильный кас­сетный проигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку. Большинство электрических цепей содержит комбинацию последовательно или параллельно подключенных резисторов (резистор - это элемент цепи, обла­дающий только сопротивлением). Полное сопротивление участка цепи оп­ределяется отношением падения на­пряжения на нем к величине силы тока . При последовательном соединении (рис.2.3 а) через все резисторы течет один и тот же ток. При параллельном соединении (рис.2.3 б) полный ток равен сумме токов, те­кущих в отдельных резисторах. При последовательном соединении падение на­пряже­ния на участке АВ равно , т.е. сумме падений напряжения на трех резисторах. Разделим обе части равенства на I и получим , т.е. . Таким образом, полное сопротивление участка цепи, состоящего из последо­ва­тельно соединенных резисторов, равно их алгебраической сумме . При параллельном соединении (рис..2.3 б) мы имеем . Разделим обе части равенства на U, где U - падение напряжения на участке цепи АВ, причем , и получим . Из этого равенства следует . Величина обратная полному сопротивлению параллельно соединенных резис­торов равна алгебраической сумме величин их обратных сопротивлений . В электрическую цепь может быть включено регулируемое (изменяющееся с помощью специального движка), сопротивление, которое называется реостатом. По назначению реостаты делятся на пусковые, служащие для ограничения силы тока во время пуска двигателей, и регулирующие - для регулировки силы тока в цепи (по­степенное снижение освещенности в театральных залах), регулировки скорости вращения электродвигателей и т.д. Реостат может быть использован в качестве так называемого датчика пере­мещения. В автоматических регуляторах уровня жидкос­ти в резервуарах применя­ется поплавково-реостатный датчик. Специальный поплавок крепится к движку реостата. Изменение уровня жидкости сдвигает поплавок, изменя­ет сопротивление реостата, и следовательно, силы тока в цепи, величина которого дает информацию об уровне.   Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Закон Ома для участка и полной замкнутой цепи

В 1826 г. немецкий ученый Георг Ом экспериментально установил прямую пропорциональную зависимость между силой тока I в проводнике и напряжением U на его концах: , гдеG - электрическая проводимость проводника. Величина, обратная проводимости называется электрическим сопротивле­ни­ем проводника R. Таким образом, закон Ома для участка цепи, не содержа­щего источника э.д.с., имеет вид . Учитывая, что в общем случае участок цепи может содержать и э.д.с.,закон Ома следует представить в виде .

Сопротивление проводника зависит от его размеров, формы и материала, из которого он изготовлен. Для однородного линейного проводника , гдеl - длина, S - площадь поперечного сечения проводника,  - удельное электриче­с­кое сопротивление, зависящее от материала, из которого изготовлен проводник. Единица сопротивления 1 Ом - это сопротивление такого проводника, в котором при напряжении 1В течет ток в 1А.

Если цепь замкнута, то ,, гдеR - общее сопротивление всей цепи, включая сопротивление источника э.д.с. Тогда закон Ома для замкнутой цепи следует записать , где - алгебраическая сумма всех э.д.с., имеющихся в этой цепи.

Принято называть сопротивление источника тока r - внутренним, а сопротив­ление всей остальной цепи R - внешним. Окончательный вид формулы закона Ома для замкнутой цепи . В системе единиц СИ напряжение и э.д.с. изме­ряются в Вольтах (В), сопротив­ление - в Омах (Ом), удельное электрическое сопротивление - в Ом-метрах (Омм), электрическая проводимость в Сименсах (См).

Рис.2.1. Отрезок проводни­ка.

Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.2.1). Сила тока на этом участке , сопротивление, падение на­пряжения, где Е - напряженность электрического поля в проводнике. Под­ставив эти параметры в закон Ома для участка цепи, получим. Отсюдаили, где-удельная электрическая проводи­мость проводника или удельная электропроводность. В векторном виде имеем (единицей измерения в системе СИ является сименс на метр (См/м)). Полученное выражение есть закон Ома в дифференциальной форме : плот­ность тока в любой точке внутри проводника прямо пропорциональна напря­женности поля в этой точке.

1.14 Сопротивление проводника. Явление сверхпроводимости.

Способность вещества проводить ток характеризуется его удельной проводи­мостью , либо удельным сопротивлением . Их величина определяется химичес­кой природой проводника и условиями, в частности температурой, при которой он находится. Для большинства металлов  растет с температурой приблизительно по линейному закону: ,- удельное сопротивление при 0С, t - температура по шкале Цельсия,  - темпе­ра­турный коэффициент сопротивления близкий к 1/273 К-1 при не очень низких темпе­ратурах. Так как R, то , где- сопротивление при 0С. Преобра­зовав две последние формулы, можно записать и, где Т – температура по Кельвину. На основе температурной зависимости сопротивления метал­лов созда­нытермометры сопротивления - термисторы, позволяющие определять температуру с точно­стью до 0.003 К.

При низких температурах нарушается линейность зависимости сопротивления металлов от температуры и при температуре 0 К наблюдается остаточное сопротивление Rост. Величина Rост зави­сит от чистоты материала и наличия в нем механических напряжений. Лишь у иде­ально чистого металла с идеально правильной кристаллической решеткой Rост 0 при Т0 (пунктирная часть кривой).

Кроме этого, в 1911 г. Г.Каммерлинг-Оннес обнару­жил, что при Тк = 4.1К сопротивление ртути скачкообразно уменьшается практически до нуля. Эта температура была названа критической, а наблюдаемое яв­ление - сверхпроводимостью. Впо­следствии этот эффект был обнаружен у целого ряда дру­гих металлов (Ti, Al, Pb, Zn, V и др.) и их спла­вов в интервале температур 0.14-20 К. Вещества в сверхпроводящем состоянии обладают необычными свойствами. Однажды возбужденный в них ток может длительно существовать без источника тока. Переход в сверхпроводящее состояние сопровождается скачкообразным изме­нением теплоемкости, теплопроводности, маг­нитных свойств вещества. Выясни­лось, что внешнее магнитное поле не проникает в толщи­ну сверхпроводника, т.е. магнитная индукция внутри него всегда равна нулю. Явление сверхпроводимости объясняется на основе квантовой теории. К настоящему времени это явление обнаружено также у ряда композиционных веществ (например, соединений металлов и диэлектриков), при этом критическая температура доходит до температуры сжижения азота, что позволяет достаточно экономично использовать явление высокотемпературной сверхпроводимости в инженерной практике. Данное явление позволяет создавать: системы передачи без потерь электрического тока по проводам из таких веществ, системы для накопления электроэнергии, мощные электромагниты, магнитные подвески для различных целей.

1.15 Работа и мощность тока, закон Джоуля-Ленца.

Определим работу, совершаемую постоянным током в проводнике, имеющем сопротивление R и находящемся под напряжением . Так как ток пред­ставляет собой перемещение зарядаq под действием поля, то работу тока можно оп­ределить по формуле . Учитывая формулуи закон Ома, получим, или, или, гдеt - время протекания тока. Поделив обе части равенства на t, получим выраже­ния для мощности постоянного тока N

, ,. Работа тока в системе единиц СИ измеряется в доулях (Дж), а мощность - в ваттах (Вт). На практике применяются также внесистемные единицы работы тока: ватт-час (Втч) и киловатт-час (кВтч). 1Втч - работа тока мощностью 1Вт в течение одного часа. 1Втч=3.6103 Дж.

Опыт показывает, что ток всегда вызывает некоторое нагревание проводника. Нагревание обусловлено тем, что кинетическая энергия движущихся по проводнику электронов (т.е. энергия тока) при каждом их столкновении с ионами металличе­ской решетки переходит в теплоту Q. Если ток идет по неподвижному металличе­скому проводнику, то вся работа тока расходуется на его нагревание и, следуя за­кону сох­ранения энергии, можно записать . Данные соотношения выражаютзакон Джоуля-Ленца. Впервые этот закон был установлен опытным путем Д.Джоулем в 1843 г. и независимо от него Э.Ленцем в 1844 г. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А.Ладыгиным лампы накаливания.

На тепловом действии тока основан целый ряд электрических приборов и ус­та­новок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы - чайники, кипятильники, утюги. В пищевой промышленности широко применяется метод электроконтактного нагрева, заключающийся в том, что электрический ток, проходя через продукт, об­ла­дающий определенным сопротивлением, вызывает его равномерное нагревание. На­пример, для производства колбасных изделий через дозатор фарш поступает в формы, торцевые стенки которых служат электродами. При такой обработке обес­пе­чивается равномерность нагрева по всему объему продукта, возможность под­держа­ния определенного температурного режима, наивысшая биологическая цен­ность из­делия, наименьшие длительность процесса и расход энергии.

Определим удельную тепловую мощность тока , т.е. количество теплоты, вы­деляющееся в единице объема за единицу времени. Выделим в проводнике элемен­тарный цилиндрический объем dV с поперечным сечением dS и длиной dl параллель­ной направлению тока, и сопротивлением ,. По закону Джоуля-Ленца, за времяdt в этом объеме выделится теплота . Тогдаи, используя закон Ома для плотности токаи соотно­шение, получим. Эти соотношения выражаютзакон Джоуля-Ленца в дифференциальной форме.

1.16. Правило Кирхгофа для разветвленных электрических цепей.

До сих пор нами рассматривались простейшие электрические цепи, состоя­щие из одного замкнутого неразветвленного контура. На всех его участках силы тока оди­наковы. Расчет I, R,  в такой цепи выполняется с помощью законов Ома.

Рис.2.2.Разветвленная электрическая цепь.

Более сложной является разветвленная электри­ческая цепь, состоящая из нескольких замкнутых кон­ту­ров, имеющих общие участки. В каждом контуре мо­жет быть несколько источников тока. Силы тока на от­дельных участках замкнутого контура могут быть раз­личными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей.

Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю: .Узел - точка цепи, в которой сходятся не менее трех про­водников. В электрической цепи на рис.2.2 имеются два узла А и В. Ток, входящий в узел, считается положительным, выходящий - отрицательным. Например, для узла А первое правило Кирх­гофа следует записать .

Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать.

Второе правило Кирхгофа относится к любому замкнутому контуру, выде­ленному в разветвленной цепи: алгебраическая сумма произведений токов на со­противления, включая и внутренние, на всех участках замкнутого контура равна алгебраической сумме электродвижущих сил, встречающихся в этом контуре . Контур ‑ это замкнутый участок схемы, по которому можно пройти и вернуться в исходную точку. Второе правило Кирхгофа получается из закона Ома, записанного для всех участков от узла до узла (ветвей) разветвленной схемы. В электрической цепи на рис.2.2 имеются три контура:AMNBA, CABDC, CMNDC. При этом, токи Ii в ветвях контура, совпадающие с произвольно вы­бран­ным направлением обхода контура, считаются положительными, а направлен­ные на­встречу обхода - отрицательными. Э.д.с., проходимые от «+» к «-» считаются поло­жительными и наоборот. В рассматриваемой элек­трической цепи (рис.2.2) выберем обход контуров по часовой стрелке и запишем для них уравнения по II правилу Кирхгофа: для AMNBА ; дляCABDС ; дляCMNDС . В данном примере внутренними сопротивлениями источников тока пренебрегаем. Первое и второе правила Кирхгофа по­зволяют составить систему линейных алгебраичес­ких уравнений, которые связывают пара­метры (I, R, ) и позволяют, зная одни, найти другие.

Рис.2.3. а) Последовательное соеди­нение сопротивлений; б) Параллельное соединение со­противлений.

Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как под­ключить динамики или проигрыватель к сте­реосистеме, как подсоединить сигнализацию для охраны или автомобильный кас­сетный проигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку.

Большинство электрических цепей содержит комбинацию последовательно или параллельно подключенных резисторов (резистор - это элемент цепи, обла­дающий только сопротивлением). Полное сопротивление участка цепи оп­ределяется отношением падения на­пряжения на нем к величине силы тока . При последовательном соединении (рис.2.3 а) через все резисторы течет один и тот же ток. При параллельном соединении (рис.2.3 б) полный ток равен сумме токов, те­кущих в отдельных резисторах.

При последовательном соединении падение на­пряже­ния на участке АВ равно , т.е. сумме падений напряжения на трех резисторах. Разделим обе части равенства наI и получим , т.е.. Таким образом, полное сопротивление участка цепи, состоящего из последо­ва­тельно соединенных резисторов, равно их алгебраической сумме.

При параллельном соединении (рис..2.3 б) мы имеем . Разделим обе части равенства наU, где U - падение напряжения на участке цепи АВ, причем , и получим. Из этого равенства следует. Величина обратная полному сопротивлению параллельно соединенных резис­торов равна алгебраической сумме величин их обратных сопротивлений.

В электрическую цепь может быть включено регулируемое (изменяющееся с помощью специального движка), сопротивление, которое называется реостатом. По назначению реостаты делятся на пусковые, служащие для ограничения силы тока во время пуска двигателей, и регулирующие - для регулировки силы тока в цепи (по­степенное снижение освещенности в театральных залах), регулировки скорости вращения электродвигателей и т.д. Реостат может быть использован в качестве так называемого датчика пере­мещения. В автоматических регуляторах уровня жидкос­ти в резервуарах применя­ется поплавково-реостатный датчик. Специальный поплавок крепится к движку реостата. Изменение уровня жидкости сдвигает поплавок, изменя­ет сопротивление реостата, и следовательно, силы тока в цепи, величина которого дает информацию об уровне.

studfiles.net

---

• 
  Первая помощь при поражении током
• 
  Арс smart ups арс ups 1500va
• 
  Инструктажи по электробезопасности виды и периодичность
• 
  Приемо сдаточная документация
• 
  Чем вырезать отверстие в плитке под розетку
• 
  Лампа над картиной
• 
  Природный газ фото
• 
  Мощность тепловая и мощность электрическая
• 
  Аварийная частота вернера
• 
  Подобрать сечение провода
• 
  Пусковой ток асинхронного двигателя