Заряд и разряд конденсатора. Заряд конденсатора через силу тока формула
Конденсатор
Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).
Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).
Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов. По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).
- 1nF = 0.000000001 = 10-9 F
- 1pF = 0.000000000001 = 10-12 F
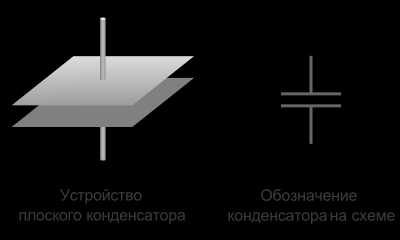
Плоский конденсатор
Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).
Заряд конденсатора. Ток
По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.
Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.
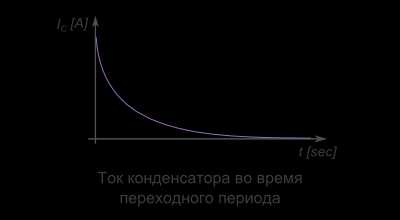
В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.
Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.
Заряд конденсатора. Напряжение
В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.
На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.
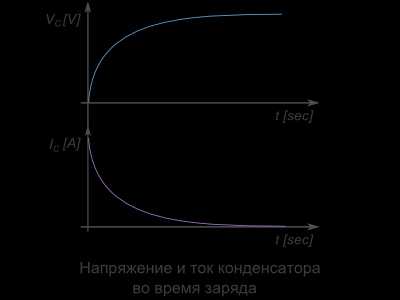
Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.
Формула для нахождения тока конденсатора во время переходного периода:
- Ic — ток конденсатора
- C — Емкость конденсатора
- ΔVc/Δt – Изменение напряжения на конденсаторе за отрезок времени
Разряд конденсатора
После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.
В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.
Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.
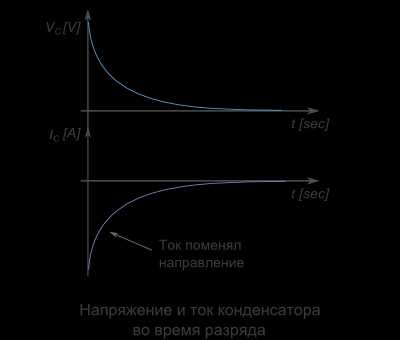
Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.
Продукт RC (сопротивление, умноженное на емкость) формирует временную константу τ (тау). За один τ конденсатор заряжается или разряжается на 63%. За пять τ конденсатор заряжается или разряжается полностью.
Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Устройство конденсатора. От чего зависит емкость?
Емкость плоского конденсатора зависит от трех основных факторов:
- Площадь пластин — A
- Расстояние между пластинами – d
- Относительная диэлектрическая проницаемость вещества между пластинами — ɛ
Площадь пластин
Чем больше площадь пластин конденсатора, тем больше заряженых частиц могут на них разместится, и тем больше емкость.
Расстояние между пластинами
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).
Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.
Относительная диэлектрическая проницаемость
Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость ɛ. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.
Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.
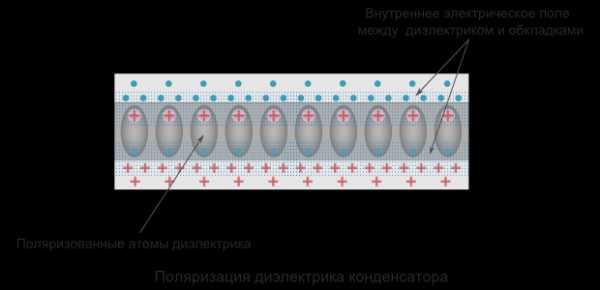
Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.
Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.
- Бумага – от 2.5 до 3.5
- Стекло – от 3 до 10
- Слюда – от 5 до 7
- Порошки оксидов металлов – от 6 до 20
Номинальное напряжение
Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).
Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.
Ток утечки
Также при работе конденсатора учитывается такой параметр как ток утечки. Поскольку в реальной жизни диэлектрик между пластинами все же пропускает маленький ток, это приводит к потере со временем начального заряда конденсатора.
hightolow.ru
Устройство конденсатора его назначение, характеристики и параметры

Конденсаторы
Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).
Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).
Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов. По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).
- 1µF = 0.000001 = 10-6 F
- 1nF = 0.000000001 = 10-9 F
- 1pF = 0.000000000001 = 10-12 F
Плоский конденсатор
Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).

Устройство конденсатора
Заряд конденсатора. Ток
По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.
Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.
Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.
Напряжение
В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.
На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.
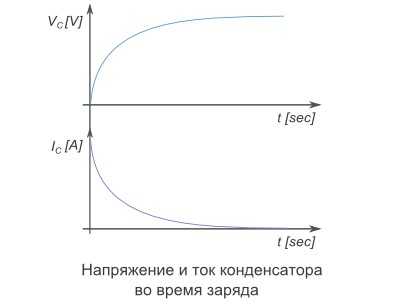
Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.
Формула для нахождения тока конденсатора во время переходного периода:
- Ic — ток конденсатора
- C — Емкость конденсатора
- ?Vc/?t – Изменение напряжения на конденсаторе за отрезок времени
Разряд конденсатора
После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.
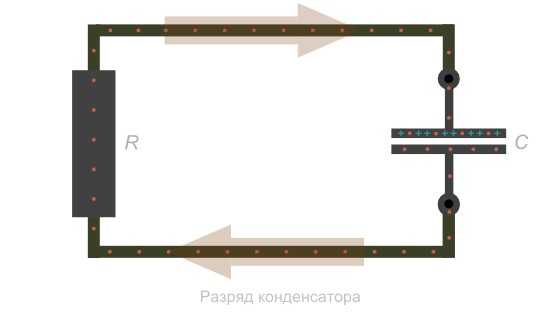
В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.
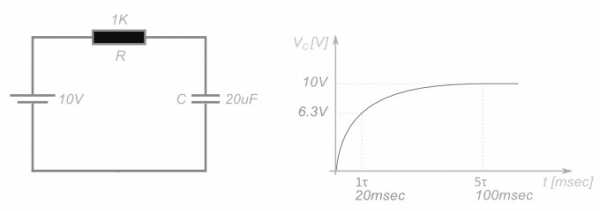
Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.
Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.
Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:
Устройство конденсатора. От чего зависит емкость?
Емкость плоского конденсатора зависит от трех основных факторов:
- Площадь пластин — A
- Расстояние между пластинами – d
- Относительная диэлектрическая проницаемость вещества между пластинами — ?
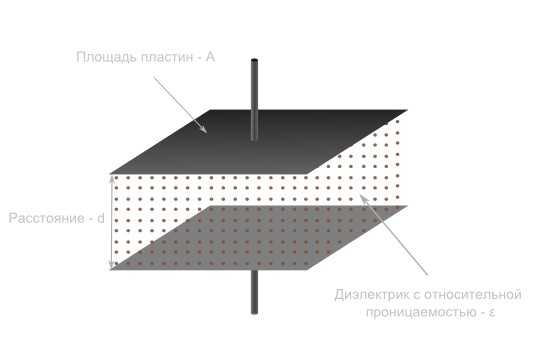
Площадь пластин
Чем больше площадь пластин конденсатора, тем больше заряженых частиц могут на них разместится, и тем больше емкость.
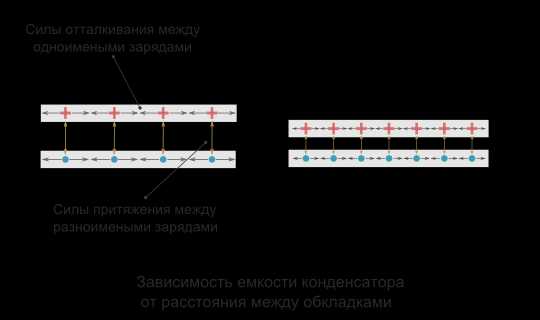
Расстояние между пластинами
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).
Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.
Относительная диэлектрическая проницаемость
Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость ?. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.
Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.
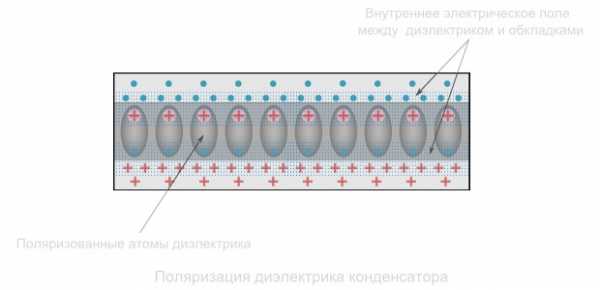
Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.
Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.
- Бумага – от 2.5 до 3.5
- Стекло – от 3 до 10
- Слюда – от 5 до 7
- Порошки оксидов металлов – от 6 до 20
Номинальное напряжение
Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).
Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.
Ток утечки
Также при работе конденсатора учитывается такой параметр как ток утечки. Поскольку в реальной жизни диэлектрик между пластинами все же пропускает маленький ток, это приводит к потере со временем начального заряда конденсатора.
Материалы с сайта http://hightolow.ru/
data-matched-content-rows-num="4,8" data-matched-content-columns-num="1,4" data-matched-content-ui-type="image_stacked" data-ad-format="autorelaxed">
xn--80aanab4adj2bicdg1q.xn--p1ai
Заряд и разряд конденсатора через сопротивление
| Полученные характеристики ЗАРЯДА конденсатора через сопротивление |
Заряд конденсатора емкостью от источника тока через наружное сопротивление происходит в соответствии с формулой
при этом мгновенный зарядный ток:
где - рассматриваемый момент времени в секундах от момента начала заряда; - напряжение на обкладках конденсатора момент времени t в Вольтах; - напряжение источника, от которого производится заряд конденсатора в Вольтах - емкость конденсатора в Фарадах - сопротивление последовательной цепи в Омах - постоянная времени в секундах ().
Разряд конденсатора емкостью , заряженного до разности потенциалов через сопротивление представляющее внешнее сопротивление разрядной цепи или внутреннее сопротивление утечки самого конденсатора происходит в соответствии с формулой
Мгновенная величина разрядного тока
где - напряжение между обкладками конденсатора через секунд после начала разряда,— ток в цепи (внешней или внутренней) конденсатора существующей через секунд после начала разряда.
| Полученные характеристики РАЗРЯДА конденсатора через сопротивление |
Процессы заряда и разряда конденсаторов рассматриваются обычно в зависимости от постоянной времени цепи . Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в раз,
от рассматриваемого напряжения. При заряде конденсатора постоянная времени указывает время (в секундах), в течение которого напряжение на обкладках повышается на 63% от разницы между имевшимся напряжением и напряжением источника тока заряда.
В связи с тем что заряд и разряд до полных значений конечных напряжений длятся неопределенно долгий срок, часто удобнее считать режим заряда законченным при доведении напряжения на обкладках до 99% от заряжающего напряжения (или до 1% от первоначальной величины напряжения при разряде).
Синтаксис
Для пользователей XMPP клиентов, используется команда
fiz ключи
где ключи это известные параметры, параметра=значение, разделенные точкой с запятой
Обязателен ключ key=razryad при расчете разаряда конденсатора
и zaryad при расчете заряда
Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.
Заметьте, чем данный калькулятор отличается от других:
Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)
Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.
Примеры использования бота
Определим время заряда конденсатора ёмкостью 1микроФарад, до 5 Вольт, если сопротивление цепи 1 килоОм.
Напряжение внешнего источника питания 12 Вольт, а на обкладках конденсатора напряжение, в момент подключения источника питания, составляло 1 Вольт.
Что бы сразу хотелось бы заметить. Как видно из задачи у нас есть остаточное напряжение на конденсаторе в размере 1 Вольт, которое надо учитывать в расчетах времени заряда.
Данные, которые мы будем вводить следующие:
U0=12-1 =11В
Ut=5-1=4В
R=1кОм
С=1мкФ
пишем запрос fiz U0=11В;Ut=4В;R=1кОм;C=1мкФ;key=zaryad
и получаем ответ
U0 = 11 Вольт
Ut = 4 Вольт
R = 1 килоОм
C = 1 микрофарад
T = 1 милисекунда
tt = 0.4519851237 милисекунда
То есть решение = 451.98 мкс
Теперь давайте проверим наши расчеты. Если бы конденсатор был бы в момент подключения источника питания полностью разряжен
То при условии зарядки его до 1 Вольта наш запрос был бы таким
fiz U0=12В;Ut=1В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 87.011377 микросекунда
а при зарядки до 5 Вольт был бы таким
fiz U0=12В;Ut=5В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 538.9965007 микросекунда
То время заряда конденсатора с 1В до 5 Вольт составило бы 538.9965007 микросекунда минус 87.011377 микросекунда = 451.98 мкс
Что несомненно говорит о правильности наших расчетов по изначальным условиям.
- Из звезды в треугольник. Эквивалентная схема. >>
5 3 51
Заряд и разряд конденсатора через сопротивление онлайн. Определение всех необходимых параметров | заряд, конденсатор, разряд, времяwww.abakbot.ru
Заряд конденсатора, теория и примеры задач
Определение и заряд конденсатора
Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).
По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.
Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.
При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.
Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Сборник формул для радиолюбителей
9. Конденсатор
Единица емкости фарада (Ф) - емкость такого конденсатора, увеличение заряда которого на 1 кулон (к) вызывает повышение разности потенциалов между обкладками конденсатора на 1 в: где C - емкость, Ф;Q - количество электричества, k;U - напряжение, в. На практике обычно пользуются значительно более мелкими единицами емкости:10-6Ф = 1 микрофарада = 1 мкф10-9Ф = 1 нанофарада = 1 нф 10-12Ф = 1 пикофарада = 1 пф1 мкф = 106 пф; 1 нф = 103 пф Напряженность поля Е между двумя пластинами (обкладками) конденсатора вычисляется по формуле где U - напряжение между обкладками, ва - расстояние между пластинами, м Так как на обеих пластинах конденсатора накапливаются заряды противоположной полярности, то эти пластины взаимно притягиваются с силой F. Она рассчитывается в ньютонах (н) следующим образом: Накопленная в конденсаторе энергия, определяемая в джоулях (дж), равна: где С - емкость, Ф;U - напряжение, в. Во время заряда или разряда конденсатора величина протекающего тока изменяется. Мгновенное значение тока выражается формулой где - изменение напряжения на обкладках конденсатора за время .Эта формула имеет важное практическое значение; она показывает, что напряжение на конденсаторе при его заряде не сразу достигает своего максимального значения. Точно так же при разряде конденсатора напряжение убывает до нуля не сразу, а постепенно. Конденсатору всегда присущи потери, которые можно представить себе в виде омического сопротивления, соединенного последовательно или параллельно с конденсатором. Если сопротивление R1 включено последовательно с конденсатором (без потерь) то при заряде его от источника, э. д. с. которого равна Е, а внутреннее сопротивление равно нулю (см рис), зарядный ток iзар и напряжение на обкладках конденсатора uс будут меняться по закону где Е - э. д. с., вt - время прошедшее с момента начала заряда, сек. Величина CR1 имеет размерность времени, так как . Её называют постоянной времени Постоянная времени характеризует скорость заряда или разряда конденсатора: где С - емкость, мкф;R1 - сопротивление, Мом. При разрядке По прошествии интервала времени величина напряжения (или тока) достигает половины максимального значения. Известно много схем, свойства которых обусловлены величиной постоянной времени. Дифференцирующая цепь где f - частота, гц.Интегрирующая цепь При расчете конденсаторов приходится учитывать абсолютную диэлектрическую проницаемость среды , которую можно представить в виде произведения двух величин: где - относительная диэлектрическая проницаемость (или просто диэлектрическая проницаемость) - величина, показывающая, во сколько раз сила взаимодействия между электрическими зарядами в данной среде меньше, чем в вакууме;= 8,86*10-12 ф/м=8,86 пф/м - электрическая постоянная, численно равная абсолютной диэлектрической проницаемости вакуума. Диэлектрическая проницаемость воздуха равна единице (=1). Значения диэлектрической проницаемости некоторых материалов приведены в табл.faza-s.narod.ru
Заряд и разряд конденсатора
Конденсатор – это элемент электрической цепи, который способен накапливать электрический заряд. Важной особенностью конденсатора является его свойство не только накапливать, но и отдавать заряд, причем практически мгновенно.
Согласно второму закону коммутации напряжение на конденсаторе не может измениться скачком. Эта особенность активно используется в различных фильтрах, стабилизаторах, интегрирующих цепях, колебательных контурах и тд.
В том, что напряжение не может измениться мгновенно, можно убедиться из формулы
Если бы напряжение в момент коммутации изменилось скачком, это означало бы, что скорость изменения du/dt = ∞, чего в природе быть не может, так как потребовался бы источник бесконечной мощности.
Процесс заряда конденсатора
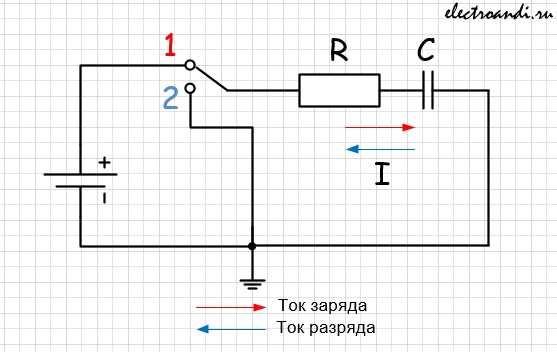
На схеме представлена RC – цепь (интегрирующая), запитанная от постоянного источника питания. При замыкании ключа в положение 1 происходит заряд конденсатора. Ток проходит по цепи: “плюс” источника – резистор – конденсатор - “минус” источника.
Напряжение на обкладках конденсатора изменяется по экспоненциальному закону. Ток, протекающий через конденсатор, также изменяется по экспоненте. Причем эти изменения взаимообратны, чем больше напряжение, тем меньше ток, протекающий через конденсатор. Когда напряжение на конденсаторе сравняется с напряжением источника, процесс заряда прекратится, и ток в цепи перестанет течь.
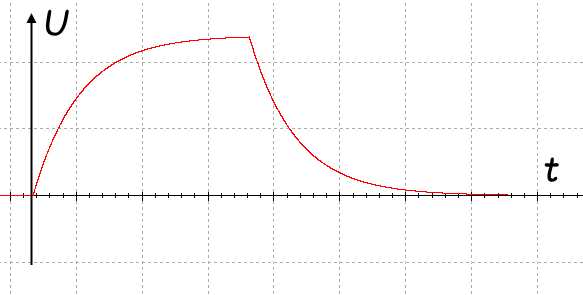
Теперь, если мы переключим ключ в положение 2, то ток потечет в обратную сторону, а именно по цепи: конденсатор – резистор – “минус” источника. Таким образом, конденсатор разрядится. Процесс будет носить также экспоненциальный характер.
Важной характеристикой данной цепи является произведение RC, которую еще называют постоянной времени τ. За время τ конденсатор заряжается или разряжается на 63%. За 5 τ конденсатор отдает или принимает заряд полностью.
От теории перейдем к практике. Возьмем конденсатор на 0,47 мкФ и резистор номиналом 10 КОм.
Рассчитаем примерное время, за которое должен зарядиться конденсатор.
Теперь соберем данную схему в multisim и попробуем промоделировать
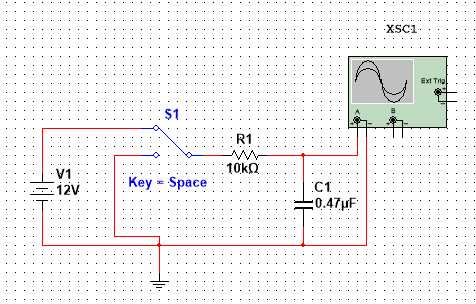
Собранная схема, запитана от батареи 12 В. Меняя положение переключателя S1, мы сначала заряжаем, а затем разряжаем конденсатор через сопротивление R = 10 КОм. Для того чтобы увидеть наглядно работу схемы посмотрите видео ниже.
electroandi.ru
Переходные процессы в цепях постоянного тока с конденсатором
ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными
РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи
IR=U,
где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что и , преобразуем закон Ома к виду
(1)
В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем
, (2)
где q0 - начальный заряд конденсатора, е - основание натурального логарифма. Произведение RC, имеющее размерность времени, называется время релаксации t . Продифференцировав выражение (2) по времени, найдём закон изменения тока:
, (3)
где I0 - сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз.
Зависимость от времени количества теплоты, выделившегося на сопротивлении R при разряде конденсатора можно найти из закона Джоуля-Ленца:
(4)
ЗАРЯДКА КОНДЕСАТОРА.
Считаем, что первоначально конденсатор не заряжен. В момент времени t = 0 ключ замкнули, и в цепи пошёл ток, заряжающий конденсатор. Увеличивающиеся заряды на обкладках конденсатора будут всё в большей степени препятствовать прохождению тока, постепенно уменьшая его. Запишем закон Ома для этой замкнутой цепи:
.
После разделения переменных уравнение примет вид:
Проинтегрировав это уравнение с учётом начального условия
q = 0 при t = 0 и с учётом того, что при изменении времени от 0 до t заряд изменяется от 0 до q, получим
, или после потенцирования
q = . (4)
Анализ этого выражения показывает, что заряд приближается к своему максимальному значению, равному С, асимптотически при t ® ?.
Подставляя в формулу (4) функцию I(t) = dq/dt, получим
. (5)
Из закона сохранения энергии следует, что при зарядке конденсатора для любого момента времени работа источника тока dАист рана сумме количества джоулевой теплоты dQ, выделившейся на резисторе R и изменению энергии конденсатора dW:
dAист= dQ + dW,
где dAист =Idt, dQ =I2Rdt, dW =d. Тогда для произвольного момента времени t имеем:
Аист(t)===С. (6)
Q(t)==С. (7)
W(t) ==. (8)
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
В реальных электрических цепях постоянного тока, содержащих конденсаторы, переходные процессы разрядки и зарядки конденсаторов проходят за время порядка 10–6 – 10-3 с. Для того,чтобы сделать доступными для наблюдения и измерения электрические параметры при переходных процессах в настоящей компьютерной модели это время значительно увеличено за счёт увеличения ёмкости конденсатора.
ЭКСПЕРИМЕНТ 1
Определение ёмкости конденсатора методом разрядки
 1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную ниже на рис.2. Для этого сначала щёлкните мышью на кнопке э.д.с.,расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашего варианта.
1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную ниже на рис.2. Для этого сначала щёлкните мышью на кнопке э.д.с.,расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашего варианта.
Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка ), Ключ К (кнопка ), вольтметр (кнопка ), амперметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рис.1 с помощью монтажных проводов (кнопка ).
2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.
3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов в таблицу 2.
4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.
5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I0. Запишите это значение в таблицу 3.
6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5, 6 ещё 4 раза.
7. Для каждого опыта рассчитайте It= I0/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.
8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.
9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к It. Запишите это значение времени t1 в таблицу 3.
10. Проделайте опыты п.п.8, 9 ещё 4 раза.
Таблица 1. Суммарное значение э.д.с. источников тока
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Э.д.с.,В |
50 |
49 |
48 |
47 |
46 |
45 |
44 |
43 |
Таблица 2. Определение сопротивления лампы.
|
№п/п |
I, А |
U, В |
R, Ом |
|
Номер опыта |
1 |
2 |
3 |
4 |
5 |
Среднее значение |
|
I0, А |
||||||
|
It, А |
||||||
|
t, с |
||||||
|
C, Ф |
Таблица 3. Результаты измерений и расчётов.
ОБРАБОТКА РЕЗУЛЬТАТОВ:
1. По закону Ома для участка цепи Л1-Л4: и результатам измерений, приведённым в таблице 2, определите сопротивление одной лампы.
2. По формуле (при разрядке конденсатора квазистационарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в таблицу 3.
3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.
ЭКСПЕРИМЕНТ 2
Изучение зависимости от времени количества тепла, выделившегося на нагрузке при разряде конденсатора
- Выполняя действия, аналогичные описанным в эксперименте 1, зарядите конденсатор до напряжения, соответствующего суммарному значению э.д.с. для вашего варианта.
- Нажмите кнопку «Стоп» и отключите ключ К.
- Проведите 5-ти секундный процесс частичного разряда конденсатора через подключённые лампы. Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора.
- Запишите показания амперметра в таблицу 4 и вновь зарядите конденсатор до первоначального напряжения.
- Последовательно увеличивая длительность процесса разрядки конденсатора на 5 с, проделайте эти опыты до времени разрядки, соответствующему полному исчезновению заряда на конденсаторе. (Напряжение на конденсаторе и ток разрядки через лампы должен быть близким к нулю). Результаты измерений тока разрядки запишите в соответствующие ячейки таблицы 4.
Таблица 4. Результаты измерений и расчетов
|
Время разрядки t, с |
5 |
10 |
15 |
20 |
… |
5n |
|
Ток разряда I через t с, А |
||||||
|
Кол-во тепла Q за t с, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- Для каждого времени разрядки вычислите по формуле (4) количество тепла, выделившегося на шести лампах и запишите эти значения в соответствующие ячейки третьей строки табл.4. Полезный совет: для расчёта Q воспользуйтесь программой MS Exсel.
- Постройте график зависимости количества выделившегося тепла Q к данному моменту времени от длительности процесса разрядки конденсатора t.
- Сравните рассчитанное количество тепла, выделившееся к моменту полного разряда конденсатора с его теоретическим значением, равным .
- Сделайте выводы по графику и ответу и проведите расчёт погрешностей измерений.
ЭКСПЕРИМЕНТ 3
Проверка закона сохранения энергии в процессе зарядки конденсатора через сопротивление
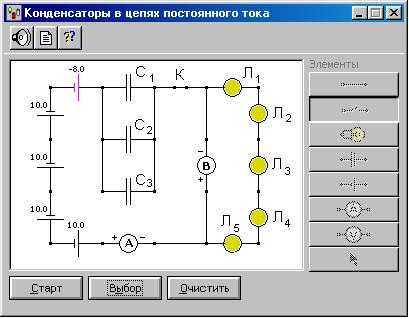 Рис.3
Рис.3
- Соберите в рабочей части экрана опыта схему, показанную на рис.3. Вольтметр, включённый параллельно 5-ти лампам, будет показывать напряжение на внешнем сопротивлении, а амперметр – силу тока через нагрузку и источники тока. Напряжение на конденсаторе определяется программой автоматически и указывается в вольтах на экране монитора над конденсатором.
- Установите суммарную э.д.с. источников тока, соответствующую значению, приведённому в табл.1 для вашего варианта.
- При разомкнутом ключе К нажмите кнопку «Старт».
- Нажатием кнопки мыши замкните ключ К и начните процесс зарядки конденсаторов. Одновременно с замыканием ключа включите секундомер.
- Через время релаксации t = RС нажатием кнопки «Стоп» остановите процесс и запишите показания электроизмерительных приборов в таблицу 5.
- Нажмите кнопку «Выбор» и обнулите показания напряжений на всех конденсаторах и на электроизмерительных приборах.
- Повторите эти измерения ещё 4 раза и заполните две верхних строки таблицы 5.
Таблица 5. Результаты измерений и расчетов
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
Среднее |
|
I, A |
||||||
|
Uc, B |
||||||
|
UR, B |
||||||
|
Аист, Дж |
||||||
|
DW, Дж |
||||||
|
Q, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- По формулам 6, 7, 8 и измеренным значениям напряжения на конденсаторе Uc рассчитайте величины работу источника тока Аист, изменение энергии конденсатора DW и выделившегося на нагрузке количества тепла Q через время заряда, равного времени релаксации.
- Проверьте выполнение закона сохранения энергии в процессе зарядки конденсатора по формуле: Аист =DW + Q.
- Сделайте выводы по итогам работы.
Вопросы и задания для самоконтроля
Вопросы и задания для самоконтроля
- Что представляет собой конденсатор и от чего зависит его ёмкость?
- Выведите формулы ёмкости плоского, цилиндрического и сферического конденсаторов.
- Как изменяется разность потенциалов на обкладках конденсатора при его зарядке и разрядке?
- Какой ток называется квазистационарным?
- Выведите формулы электроёмкости батареи последовательно и параллельно соединённых конденсаторов
- Что такое время релаксации?
- Объясните принцип работы экспериментальной установки.
- Нарисуйте графики зависимости силы тока и напряжения от времени при зарядке и разрядке конденсатора.
- Соберите на мониторе такую цепь, состоящую из источника тока, двух ламп, выключателя и соединительных проводов, чтобы с выключением лампы в одной цепи загоралась лампа в другой.
- Определите заряд, который пройдёт через гальванометр в схеме, показанной на рис. 2, при замыкании ключа.
- Конденсатор ёмкости С = 300 пФ подключается через сопротивление R =500 Ом к источнику постоянного напряжения U0. Определите: а) время, по истечению которого напряжение на конденсаторе составит 0,99 U0; в) количество тепла, которое выделится на этом сопротивлении при разрядке конденсатора за это же время.
- Имеется ключ, соединительные провода и две электрические лампочки. Составьте на мониторе электрическую схему включения в сеть этих лампочек, которая должна удовлетворять следующему условию: при замкнутом ключе горит только первая лампочка, при размыкании ключа первая гаснет, а вторая загорается.
- Конденсатору ёмкостью С сообщают заряд q, после чего обкладки конденсатора замыкают через сопротивление R. Определите: а) закон изменения силы тока, текущего через сопротивление; б) заряд, прошедший через сопротивление за время t; в) количество тепла, выделившееся в сопротивлении за это время.
- Определите количество тепла, выделившегося в цепи (рис. 4-6) при переключении ключа К из положения 1 в положение 2. Параметры цепи обозначены на рисунках.
itteach.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.