Упрощение логических выражений. 0 логики

Глава 0 логика, логическое программирование и пролог

1. Знакомство с логическим программированием Определение логического программирования

Логическое программирование — это один из подходов к информатике, при котором в качестве языка высокого уровня используется логика предикатов первого порядка в форме фраз Хорна. Начало исследованиям в области формальной логики было положено работами Аристотеля в ГУ в. до н. э. Логика предикатов первого порядка - это ветвь формальной логики, получившая развитие в основном в XX в. Это — универсальный абстрактный язык предназначенный для представления знаний и для решения задач. Его можно рассматривать как общую теорию отношений. Логическое программирование базируется на подмножестве логики предикатов первого порядка, при этом оно одинаково широко с ней по сфере охвата. Логическое программирование дает возможность программисту описывать ситуацию при помощи формул логики предикатов, а затем, для выполнения выводов из этих формул, применить автоматический решатель задач (т. е. некоторую процедуру). При использовании языка логического программирования основное внимание уделяется описанию структуры прикладной задачи, а не выработке предписаний компьютеру о том, что ему следует делать. Другие понятия информатики из таких областей, как теория реляционных баз данных, программная инженерия и представление знаний, также можно описать (и, следовательно, реализовать) с помощью логических программ. С этой позиции логическое программирование оказывает потенциально революционизирующее влияние на многие аспекты информатики.

Пролог

Обычно в языках логического программирования применяется программная технология, основывающаяся на правиле вывода путем резолюции. которое предложил Робинсон. Пролог — это наиболее известный язык логического программирования. Существуют, однако, и иные языки. Первоначальный вариант языка Пролог был разработан Алэном Кольмерором с сотрудниками в 1972 г. в Марсельском университете. В течение последнего десятилетия этот язык получил дальнейшее развитие благодаря работам, проводившимся в различных университетах Европы. Лишь начиная с 1981 г. Пролог стал привлекать внимание специалистов из США. Это произошло после того, как Министерство внешней торговли и развития Японии объявило о том, что японский проект создания ЭВМ 5-го поколения будет основываться на методах логического программирования. С этого момента интерес к Прологу непрерывно рос. Теперь Пролог применяется для решения прикладных задач многими правительственными организациями и фирмами Европы, США и Японии. Сейчас существует международное сообщество ученых и специалистов, активно работающих в области логического программирования. Японские исследователи играют важную роль в этих работах.

Язык искусственного интеллекта

Пролог часто называют языком искусственного интеллекта. Такая формулировка, однако, некорректна в двух отношениях. Лисп — это наиболее известный язык искусственного интеллекта. Если определить аналогичным образом сферу применения языка Пролог, то неизбежно начнется сопоставление этих двух языков с целью выявить, какой из них лучше. С точки зрения практики для каждого языка существует своя методология программирования. Единственно приемлемый способ сравнения языков, дающий основания заявить, что один язык "лучше" другого, заключается в учете "человеческих" факторов, т. е. в сравнении читабельности программ, легкости в пользовании языками и т. д. В настоящее время американские специалисты по искусственному интеллекту отдают предпочтение языку Лисп. Их выбор скорее обусловлен привычностью Лиспа, чем недостатками языка Пролог как такового.

Более важным моментом является то, что сфера применения Пролога не ограничивается искусственным интеллектом. Этот язык успешно использовался как для решения многих традиционных прикладных задач (программная инженерия, интерфейсы баз данных, системы помощи в принятии решений), так и для решения задач искусственного интеллекта (экспертные системы, системы обработки естественного языка).

Простота языка Пролог

Язык программирования Пролог привлекателен своей простотой (в нем насчитывается небольшое количество лексикографических символов). Пролог-программу легко читать, что является фактором, способствующим повышению производительности при программировании 'И увеличению удобств при сопровождении программ. Поскольку язык Пролог основан ни универсальных формализмах фраз Хорна, исходный текст Пролог-программ значительно менее подвержен влиянию машинно-зависимых особенностей, чем исходные тексты программ, написанных на других языках. Кроме того, в различных версиях языка Пролог проявляется тенденция к единообразию, так что программу, написанную для одной версии, легко можно преобразовать в программу для другой версии этого языка: а. В конечном счете Пролог прост в изучении.

studfiles.net

Основы логики

Логика – наука о законах и формах мышления

Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно

Утверждение – суждение, которое требуется доказать или опровергнуть

Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом

Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение

Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0)

Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.

Логические операции и таблицы истинности

A	B	F
1	1	1
1	0	0
0	1	0
0	0	0

F = A & B.

Логическое умножение  КОНЪЮНКЦИЯ  - это новое  сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

F = A + B 

Логическое сложение – ДИЗЪЮНКЦИЯ - это новое сложное выражение будет истинным тогда и только тогда, когда  истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ

Логическое отрицание : ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

Логическое следование:  ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом  "следовательно"  и  выражается словами ЕСЛИ … , ТО …

A	B	F
1	1	1
1	0	0
0	1	0
0	0	1

Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"

Порядок выполнения логических операций в сложном логическом выражении:

1. инверсия
2. конъюнкция
3. дизъюнкция
4. импликация
5. эквивалентность

 Для изменения указанного порядка выполнения операций используются скобки.

Источники:

http://informatika.sch880.ru/p25aa1.html

http://school23kovrov.ucoz.ru/EGE_IKT/-0KLQtdC80LAg-5-INCe0YHQvdC-0LLRiyDQu9C-0LPQuNC60L.pdf

ya-znau.ru

Упрощение логических выражений

Замечание 1

Логическую функцию можно записать с помощью логического выражения, а затем можно перейти к логической схеме. Упрощать логические выражения надо для того, чтобы получить как можно более простую (а значит, и более дешёвую) логическую схему. По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.

Для упрощения логических выражений используют законы алгебры логики.

Какие-то преобразования похожи на преобразования формул в классической алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), а другие преобразования основаны на свойствах, которыми операции классической алгебры не обладают (использование распределительного закона для конъюнкции, законов поглощения, склеивания, правил де Моргана и др.).

Законы алгебры логики формулируются для базовых логических операций — “НЕ” – инверсия (отрицание), “И” – конъюнкция (логическое умножение) и “ИЛИ” – дизъюнкция (логическое сложение).

Закон двойного отрицания означает, что операция “НЕ” обратима: если применить ее дважды, то в итоге логическое значение не изменится.

Закон исключенного третьего гласит, что любое логическое выражение либо истинно, либо ложно (“третьего не дано”). Поэтому если $A=1$, то $\bar{A}=0$ (и наоборот), а, значит, конъюнкция этих величин всегда равно нулю, а дизъюнкция равна единице.

Операции с константами и закон повторения легко проверяются по таблицам истинности операций “И” и “ИЛИ”.

Переместительный и сочетательный законы выглядят так же, как и в математике. Почти всегда “работает” аналогия с классической алгеброй, нужно только помнить, что в логике $1 + 1 = 1$, а не $2$.

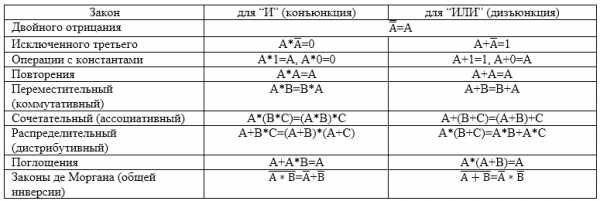
Рисунок 1.

Распределительный закон для дизъюнкции — это просто раскрытие скобок. А вот для конъюнкции выражение незнакомое, и в математике это равенство неверно. Доказательство начинаем с правой части. Раскроем скобки:

$(A+B) \cdot (A+C) = A \cdot A+A \cdot C+B \cdot A+B \cdot C$

Используем закон повторения

$A \cdot A = A$,

Далее $A \cdot A+C \cdot A = A+C \cdot A = A \cdot (1+C)=A \cdot 1 = A$

Аналогично

$A+A \cdot B = A \cdot (1+B) = A \cdot 1=A$, таким образом,

$(A+B) \cdot (A+C) = A+B \cdot C$

Равенство доказано.

Попутно был доказан закон поглощения для операции “И”.

Из распределительного закона следует полезная формула

$A+ \bar{A} \cdot B = (A+ \bar{A}) \cdot (A+B) = A+B$

Замечание 2

Правила, которые позволяют раскрывать инверсию сложных выражений, получили своё название в честь де Моргана, шотландского математика и логика. Важно следующее: “общее” отрицание не просто переходит на отдельные выражения, но и конъюнкция заменяется на дизъюнкцию (и наоборот). Доказать эти правила можно с помощью таблиц истинности.

Большинство законов и аксиом алгебры логики записаны парами. При внимательном изучении пар можно вывести принцип двойственности– если в тождестве произвести взаимные замены операций дизъюнкции и конъюнкции, а также элементы $0$ и $1$, в случае если они имеются, то получим тоже тождество. Такое свойство принято называть принципом двойственности.

Примеры упрощения логических выражений

1. $(A \cdot B) + (A \cdot \bar{B}) = A \cdot (B + B)= A \cdot 1 = A$

2. Рисунок 2.

здесь был использовано правило де Моргана для дизъюнкции и закон двойного отрицания, далее вынесли за скобку сомножитель $\bar{X}$, получили в скобках закон исключённого третьего и использовали операцию с константами.

Пример 1

Кто из учеников $A$, $B$, $C$ и $D$ играет, а кто не играет в шахматы, если известно следующее:

а) если $A$ или $B$ играет, то $C$ не играет;

б) если $B$ не играет, то играют $C$ и $D$;

в) $C$ играет

Решение. Определим следующие простые высказывания:

$A$ — «ученик $A$ играет в шахматы»;

$B$ — «ученик $B$ играет в шахматы»;

$C$ — «ученик $C$ играет в шахматы»;

$D$ — «ученик $D$ играет в шахматы».

С помощью простых высказываний запишем высказывания из условия:

а) ($A + B) → C$;

б) $B → C \cdot D$;

в) $C$.

Составим конъюнкцию записанных сложных высказываний:

$((A + B) → C) \cdot (B → C \cdot D) \cdot C.$

Упростим эту формулу:

Рисунок 3.

Отсюда следует, что $A = 0$, $B = 1$, $C = 1$, $D = 1$.

Ответ: в шахматы играют ученики $B$, $C$ и $D$, а ученик $A$ не играет.

При упрощении логических выражений можно выполнять такую последовательность действий:

1. Заменить все “небазовые” операции (эквивалентность, импликацию, исключающее ИЛИ и др.) на их выражения через базовые операции инверсию, конъюнкцию и дизъюнкцию.
2. Раскрыть инверсии сложных выражений по правилам де Моргана таким образом, чтобы операции отрицания остались только у отдельных переменных.
3. Затем упростить выражение, используя раскрытие скобок, вынесение общих множителей за скобки и другие законы алгебры логики.

Пример 2

Здесь последовательно использованы правило де Моргана, распределительный закон, закон исключенного третьего, переместительный закон, закон повторения, вновь переместительный закон и закон поглощения.

Рисунок 4.

Также можно использовать упрощение логических выражений для нахождения решений логического уравнения.

Пример 3

Требуется найти все решения уравнения

Рисунок 5.

Упрощаем выражение, заменяя импликацию по формуле $А → В = \bar{А} + В$, и получаем

Рисунок 6.

Используем правило де Моргана

$B + C + \bar{A} + \bar{A} \cdot \bar{C} + D = 0$

и закон поглощения

$B + C + \bar{A} + D = 0$

Для того чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому

$A = 1$, $B = 0$, $C = 0$, $D = 0.$

Пример 4

Выполнить преобразование логической функции

Рисунок 7.

Применим последовательно следующие законы алгебры логики: правило де Моргана для конъюнкции, правило де Моргана для дизъюнкции, закон двойного отрицания, закон исключённого третьего, вынос общего множителя за скобки и операцию с константой

Рисунок 8.

spravochnick.ru

Алгебра логики Википедия

Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики.

Определение[ | код]

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.

Высказывания строятся над множеством {B, ¬{\displaystyle \lnot }, ∧{\displaystyle \land }, ∨{\displaystyle \lor }, 0, 1}, где B — непустое множество, над элементами которого определены три операции:

¬{\displaystyle \lnot } отрицание (унарная операция), ∧{\displaystyle \land } конъюнкция (бинарная), ∨{\displaystyle \lor } дизъюнкция (бинарная),

а логический ноль 0 и логическая единица 1 — константы.

Так же используются названия

Унарная операция отрицания в тексте формул оформляется либо в виде значка перед операндом (¬x{\displaystyle \lnot x}

ru-wiki.ru

---

• 
  Услуги вц в квитанции что это
• 
  Технические характеристики ап50б 2мт
• 
  Из холодного крана течет горячая вода куда жаловаться
• 
  Правило ленца правило правой руки
• 
  Из чего состоит кабель
• 
  Реле что это такое
• 
  Общее и комбинированное освещение
• 
  Фукусима цунами
• 
  Какие документы нужны для увеличения мощности электроэнергии до 15 квт
• 
  Устройство теплового реле
• 
  Поставить пломбу на счетчик электроэнергии