Онлайн журнал электрика. 3 закона ома

3. Закон Ома

Цели

После проведения данного эксперимента Вы сможете рассчитывать и измерять ток, напряжение и сопротивление в электрической схеме для проверки закона Ома.

Необходимые принадлежности

* Цифровой мультиметр

* Макетная панель

* Источник постоянного напряжения

* Резисторы — 1/4 Вт, 5%:

один резистор 470 Ом, один резистор 680 Ом, один резистор 2, 2 кОм, один резистор 4, 7 кОм.

ВВОДНАЯ ЧАСТЬ

По-видимому, наиболее важным основным принципом в электротехнике является закон Ома. Этот закон отражает связь, которая существует между током, напряжением и сопротивлением в электрической или электронной цепи. Источник напряжения подключается к сопротивлению, что вызывает протекание через него тока. Величина тока определяется величиной приложенного напряжения и величиной сопротивления. Закон Ома утверждает, что на участке цепи ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Эта связь выражается простой формулой:

I=V/R

В данном выражении: I — ток в амперах, V — напряжение в вольтах, R — сопротивление в омах. Значение тока можно быстро вычислить использовании калькулятора. Например, какой величины ток протекает через резистор 2, 2 кОм, подключенный к источнику напряжения 6В? Ответ таков:

I = 6 В/2, 2 кОм = 6/2200 = 0, 00273 А

Это значение может быть выражено также в миллиамперах, то есть, 2, 73 мА.

Как Вы знаете, основная формула закона Ома может быть преобразована алгебраически, так что Вы сможете определять или напряжение, или сопротивление. Этими другими формулами являются:

V=IxR

R =V/I

В. Вашей работе с электроникой Вам регулярно придется использовать закон Ома; Даже в самых сложных схемах Вы будете применять это соотношение. Важно, чтобы Вы могли проделывать такие расчеты при любых условиях.

Вычисления в соответствии с законом Ома

Для выполнения расчетов в соответствии с законом Ома Вы должны знать две величины из трех. Величины тока, напряжения и сопротивления

могут быть получены различными способами. Величины сопротивлении резисторов могут определяться по их цветовому коду или фактическим измерением сопротивления резистора. Ток обычно определяется путем измерения. Величину напряжения часто бывает легко определить, поскольку напряжение подается от источника питания, выходное напряжение которого фиксированно и известно. Например, если используется батарейка для карманного фонаря, то Вы знаете, что ее напряжение составляет 1, 5 В. Все батареи элементов имеют стандартные значения выходных напряжений, как и многие источники питания. Если напряжение неизвестно, оно может быть, тем не менее, измерено.

Краткое содержание

В данном эксперименте Вы будете собирать некоторые простые электрические схемы и выполнять электрические измерения, в результате чего Вы сможете проводить расчеты в соответствии с законом Ома. Для конкретной схемы Вы научитесь делать расчет необходимых величин. Затем Вы будете конструировать различные схемы и контролировать их величины путем измерении.

ПРОЦЕДУРА

1. Обратитесь к схеме на рисунке 3-1. При известных значениях напряжения и сопротивления рассчитайте величину протекающего в схеме тока. Запишите Ваше полученное значение в предусмотренное поле.

I = ______мА (вычисленное значение)

Рис. 3-1.

2. Соберите схему, показанную на рисунке 3-1. Используйте источник питания постоянного тока, настроенный таким образом, чтобы его выходное напряжение составляло 9 В. Для измерения тока в данной схеме Вы будете использовать мультиметр. Установите предел измерения мультиметра на соответствующее значение, которое основано на Ваших расчетах в шаге 1. Вставьте красный испытательный вывод в гнездо А мультиметра.

3. После того, как Вы собрали схему, коснитесь черным пробником к отрицательному контакту батареи или источника питания, а красным пробником прикоснитесь к неприсоединенному выводу резистора. Прочитайте показание величины тока на мультиметре. Запишите полученное значение.

I = ________мА (измеренное значение)

4. Сравните Ваше расчетное и измеренное значения. Объясните причину различий, если таковые имеются.

5. Удвойте напряжение питания, указанное на рисунке 3-1. Какое теперь новое напряжение питания схемы?

Напряжение питания = ______ вольт

6. Используя величину нового напряжения питания и прежнее сопротивление резистора, рассчитайте величину нового тока.

/ = ______мА (вычисленное значение)

7. Измерьте новый ток, подсоединяя испытательные выводы мультиметра к схеме, как описано ранее.

I =______мА (измеренное значение)

8. Сравните величины токов в шагах 1 и 6 и в шагах 3 и 7. Как изменилась величина тока, когда изменилось напряжение питания? Согласуется ли такое изменение с законом Ома? Объясните.

9. Демонтируйте схему, показанную на рисунке 3-1, и соберите схему, показанную на рисунке 3-2.

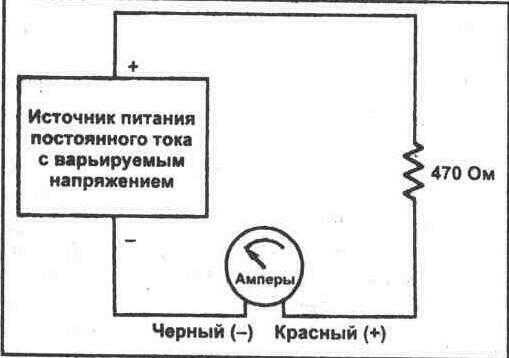
Рис. 3-2.

10. Измерьте величину тока, протекающего в схеме, используя процедуру, описанную ранее. Запишите полученное значение.

I= ________мА (измеренное значение)

1. Используя значение измеренного Вами тока, рассчитайте величину сопротивления резистора, применяя для этого закон Ома. Запишите величину сопротивления.

R = ______Ом (вычисленное значение)

12. Теперь по цветовому коду резистора определите его сопротивление и запишите найденное значение. R = _________Ом (определенное по цветовому коду)

13. Сравните значение сопротивления, вычисленное с использованием величины измеренного тока, с величиной сопротивления, определенной по цветовому коду. Объясните любой отличие.

14. Измените величину сопротивления резистора на 2, 2 кОм в схеме на рисунке 3-2.

15. Рассчитайте величину ожидаемого тока. Запишите значение.

I =_______мА (вычисленное значение)

16. Измерьте величину тока, используя процедуру, которая использовалась Вами в предыдущих шагах.

I =_______мА (измеренное значение)

17. Сравните ток, который Вы измерили в шаге 16, с током, измеренным Вами в шаге 10. Как изменился ток после изменения величины сопротивления резистора? Соответствуют л и полученные Вами результаты закону Ома? Объясните.

18. Используйте источник питания постоянного тока с варьируемым напряжением, который Вы применяли в схеме на рисунке 3-2, и резистор 2, 2 кОм. Изменяйте напряжение от 0 до 12 В шагами (дискретами) по 2 В. Измеряйте ток при каждом установленном напряжении.

19. Повторите шаг 18, используя резистор 4700м. Используя данные в шагах 18 и 19, построите графики тока в зависимости от напряжения на миллиметровой бумаге.

ОБЗОРНЫЕ ВОПРОСЫ

1. К резистору 39 кОм был подключен источник питания с неизвестным напряжением. Вы измерили ток и получили величину 0, 31 мА. Приложенное напряжение должно быть порядка:

а) 12 В,

б) 28 В,

в) 57 В,

г) 126 В.

2. Уменьшение напряжения, приложенного к резистору, приводит к:

а) увеличению тока,

б) уменьшению тока,

в) сохранению той же величины тока,

г) падению величины тока до нуля.

3. Уменьшение сопротивления резистора, соединенного с источником питания, приводит к:

а) увеличению тока,

б) уменьшению тока,

в) сохранению той же величины тока,

г) падению величины тока до нуля.

4. Смотрите Ваш график, полученный в шаге 19. Скорость изменения тока по отношению к изменению напряжения:

а) больше при меньшей величине резистора,

б) больше при большей величине резистора,

в) меньше при меньшей величине резистора,

г) та же при любой величине резистора.

5. Для измерения тока при помощи мультиметра как он должен быть подключен к схеме?

а) встречно,

б) параллельно,

в) последовательно,

г) с изменением полярности испытательных выводов.

riostat.ru

3. Закон Ома | Техническая библиотека lib.qrz.ru

ЭКСПЕРИМЕНТ 3 Закон Ома

Цели

Необходимые принадлежности

* Цифровой мультиметр

* Макетная панель

* Источник постоянного напряжения

* Резисторы — 1/4 Вт, 5%:

один резистор 470 Ом, один резистор 680 Ом, один резистор 2, 2 кОм, один резистор 4, 7 кОм.

ВВОДНАЯ ЧАСТЬ

I=V/R

I = 6 В/2, 2 кОм = 6/2200 = 0, 00273 А

Это значение может быть выражено также в миллиамперах, то есть, 2, 73 мА.

V=IxR

R =V/I

Вычисления в соответствии с законом Ома

Краткое содержание

ПРОЦЕДУРА

I = ______мА (вычисленное значение)

Рис. 3-1.

I = ________мА (измеренное значение)

4. Сравните Ваше расчетное и измеренное значения. Объясните причину различий, если таковые имеются.

5. Удвойте напряжение питания, указанное на рисунке 3-1. Какое теперь новое напряжение питания схемы?

Напряжение питания = ______ вольт

/ = ______мА (вычисленное значение)

7. Измерьте новый ток, подсоединяя испытательные выводы мультиметра к схеме, как описано ранее.

I =______мА (измеренное значение)

9. Демонтируйте схему, показанную на рисунке 3-1, и соберите схему, показанную на рисунке 3-2.

Рис. 3-2.

I= ________мА (измеренное значение)

R = ______Ом (вычисленное значение)

14. Измените величину сопротивления резистора на 2, 2 кОм в схеме на рисунке 3-2.

15. Рассчитайте величину ожидаемого тока. Запишите значение.

I =_______мА (вычисленное значение)

16. Измерьте величину тока, используя процедуру, которая использовалась Вами в предыдущих шагах.

I =_______мА (измеренное значение)

ОБЗОРНЫЕ ВОПРОСЫ

а) 12 В,

б) 28 В,

в) 57 В,

г) 126 В.

2. Уменьшение напряжения, приложенного к резистору, приводит к:

а) увеличению тока,

б) уменьшению тока,

в) сохранению той же величины тока,

г) падению величины тока до нуля.

3. Уменьшение сопротивления резистора, соединенного с источником питания, приводит к:

а) увеличению тока,

б) уменьшению тока,

в) сохранению той же величины тока,

г) падению величины тока до нуля.

4. Смотрите Ваш график, полученный в шаге 19. Скорость изменения тока по отношению к изменению напряжения:

а) больше при меньшей величине резистора,

б) больше при большей величине резистора,

в) меньше при меньшей величине резистора,

г) та же при любой величине резистора.

5. Для измерения тока при помощи мультиметра как он должен быть подключен к схеме?

а) встречно,

б) параллельно,

в) последовательно,

г) с изменением полярности испытательных выводов.

lib.qrz.ru

3. Закон Ома

ЭКСПЕРИМЕНТ 3 Закон Ома

Цели

Необходимые принадлежности

* Цифровой мультиметр

* Макетная панель

* Источник постоянного напряжения

* Резисторы — 1/4 Вт, 5%:

один резистор 470 Ом, один резистор 680 Ом, один резистор 2, 2 кОм, один резистор 4, 7 кОм.

ВВОДНАЯ ЧАСТЬ

I=V/R

I = 6 В/2, 2 кОм = 6/2200 = 0, 00273 А

Это значение может быть выражено также в миллиамперах, то есть, 2, 73 мА.

V=IxR

R =V/I

Вычисления в соответствии с законом Ома

Краткое содержание

ПРОЦЕДУРА

I = ______мА (вычисленное значение)

Рис. 3-1.

I = ________мА (измеренное значение)

4. Сравните Ваше расчетное и измеренное значения. Объясните причину различий, если таковые имеются.

5. Удвойте напряжение питания, указанное на рисунке 3-1. Какое теперь новое напряжение питания схемы?

Напряжение питания = ______ вольт

/ = ______мА (вычисленное значение)

7. Измерьте новый ток, подсоединяя испытательные выводы мультиметра к схеме, как описано ранее.

I =______мА (измеренное значение)

9. Демонтируйте схему, показанную на рисунке 3-1, и соберите схему, показанную на рисунке 3-2.

Рис. 3-2.

I= ________мА (измеренное значение)

R = ______Ом (вычисленное значение)

14. Измените величину сопротивления резистора на 2, 2 кОм в схеме на рисунке 3-2.

15. Рассчитайте величину ожидаемого тока. Запишите значение.

I =_______мА (вычисленное значение)

16. Измерьте величину тока, используя процедуру, которая использовалась Вами в предыдущих шагах.

I =_______мА (измеренное значение)

ОБЗОРНЫЕ ВОПРОСЫ

а) 12 В,

б) 28 В,

в) 57 В,

г) 126 В.

2. Уменьшение напряжения, приложенного к резистору, приводит к:

а) увеличению тока,

б) уменьшению тока,

в) сохранению той же величины тока,

г) падению величины тока до нуля.

3. Уменьшение сопротивления резистора, соединенного с источником питания, приводит к:

а) увеличению тока,

б) уменьшению тока,

в) сохранению той же величины тока,

г) падению величины тока до нуля.

4. Смотрите Ваш график, полученный в шаге 19. Скорость изменения тока по отношению к изменению напряжения:

а) больше при меньшей величине резистора,

б) больше при большей величине резистора,

в) меньше при меньшей величине резистора,

г) та же при любой величине резистора.

5. Для измерения тока при помощи мультиметра как он должен быть подключен к схеме?

а) встречно,

б) параллельно,

в) последовательно,

г) с изменением полярности испытательных выводов.

lib.qrz.ru

ЗАКОН ОМА

На рисунке показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов: источника напряжения — батареи GB, потребителя тока — нагрузки R, которой может быть, например, нить накала электрической лампы или резистор, и проводников, соединяющих источник напряжения с нагрузкой. Между прочим, если эту цепь дополнить выключателем, то получится полная схема карманного электрического фонаря.

Нагрузка R, обладающая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается следующей формулой:

I = U/R

где I — ток, выраженный в амперах, А; U — напряжение в вольтах, В; R — сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома), для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома.

Первый пример: На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи.Решение: I = U/R = 25 / 5 = 5 А.Второй пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.Третий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Следовательно, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.В связи с этим приведу еще один пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.Закон Ома и производные от него расчетные формулы, достаточно легко запомнить, если пользоваться вот этой графической схемой, т. н. треугольник закона Ома:

>Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в треугольнике означает знак деления (по аналогии дробной черты), а вертикальная линия в треугольнике означает знак умножения.

Теперь рассмотрим такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Разберем такой пример. У нас имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В? Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом, как это показано на рис..

В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, т.е. 30 Ом — сопротивление нити лампочки Н плюс 25 Ом — сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, т.е. почти такой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи. Можно включать амперметр в любую точку цепи, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.Добавочный резистор, включаемый в цепь последовательно с нагрузкой (как, например, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, Здесь U — падение напряжения, В; I — ток в цепи, A; R — сопротивление добавочного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил избыток напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где R — искомое сопротивление добавочного резистора, Ом; U-напряжение, которое необходимо погасить, В; I — ток в цепи, А. Для нашего примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, и таким образом регулировать ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом, С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть, однако, и другой способ подключения нагрузки к источнику тока с избыточным напряжением — тоже с помощью переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..

Здесь R1 — резистор, включенный потенциометром, a R2 — нагрузка, которой может быть та же лампочка накаливания или какой — то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет). По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 — лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение. Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением. Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех Случаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком — то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

Спасибо lessonradio.narod.ru

www.radioingener.ru

Закон Ома. История открытия. Различные виды закона Ома

Реферат

Закон Ома. История открытия. Различные виды закона Ома.

Содержание.

1. Общий вид закона Ома.

2. История открытия закона Ома, краткая биография ученого.

3. Виды законов Ома.

Закон Ома устанавливает зависимость между силой тока I в проводнике и разностью потенциалов (напряжением) U между двумя фиксированными точками (сечениями) этого проводника:

(1) Коэффициент пропорциональности R , зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.

Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.

Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.

В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.

В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания "Наиболее оптимальный вариант преподавания геометрии в подготовительных классах". Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием "Предварительное сообщение о законе, по которому металлы проводят контактное электричество". Статья была опубликована в 1825 году в "Журнале физики и химии", издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.

Появляется в свет его знаменитая статья "Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера", вышедшая в 1826 году в "Журнале физики и химии".

В мае 1827 года "Теоретические исследования электрических цепей" объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: "Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение".

В 1829 году появляется его статья "Экспериментальное исследование работы электромагнитного мультипликатора", в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.

В 1830 году появляется новое исследование Ома "Попытка создания приближенной теории униполярной проводимости".

Только в 1841 году работа Ома была переведена на английский язык, в 1847 году - на итальянский, в 1860 году - на французский.

16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.

Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.

В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления - 1 Ом.

В общем случае зависимость между I и U нелинейна, однако на практике всегда можно в определенном интервале напряжений считать её линейной и применять закон Ома; для металлов и их сплавов этот интервал практически неограничен.

Закон Ома в форме (1) справедлив для участков цепи, не содержащих источников ЭДС. При наличии таких источников (аккумуляторов, термопар, генераторов и т. д.) закон Ома имеет вид:

(2)

где

— ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид: (3)

где

- полное сопротивление цепи, равное сумме внешнего сопротивления r и внутреннего сопротивления источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.

Закон Ома можно записать в дифференциальной форме, связывающей в каждой точке проводника плотность тока j с полной напряжённостью электрического поля. Потенциальное. электрическое поле напряжённости Е , создаваемое в проводниках микроскопическими зарядами (электронами, ионами) самих проводников, не может поддерживать стационарное движение свободных зарядов (ток), т. к. работа этого поля на замкнутом пути равна нулю. Ток поддерживается неэлектростатическими силами различного происхождения (индукционного, химического, теплового и т.д.), которые действуют в источниках ЭДС и которые можно представить в виде некоторого эквивалентного непотенциального поля с напряженностью E СТ, называемого сторонним. Полная напряженность поля, действующего внутри проводника на заряды, в общем случае равна E + E СТ . Соответственно, дифференциальный закон Ома имеет вид:

или , (4)

где

- удельное сопротивление материала проводника, а - его удельная электропроводность.

Закон Ома в комплексной форме справедлив также для синусоидальных квазистационарных токов:

(5)

где z - полное комплексное сопротивление:

, r – активное сопротивление, а x - реактивное сопротивление цепи. При наличии индуктивности L и емкости С в цепи квазистационарного тока частоты .

Существует несколько видов закона Ома.

Закон Ома для однородного участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:

Закон Ома для замкнутой цепи: сила тока в замкнутой цепи равна отношению ЭДС источника тока к суммарному сопротивлению всей цепи:

где R - сопротивление внешней цепи, r – внутреннее сопротивление источника тока.

R - +

Закон Ома для неоднородного участка цепи (участка цепи с источником тока):

mirznanii.com

Закон Ома

Доброго дня уважаемые радиолюбители!Приветствую вас на сайте “Радиолюбитель“

Единицы измерения в электронике. Закон Ома.

Единицы измерения в электронике

Единицы измерения служат для количественного определения какой-либо физической величины. К примеру, покупая яблоки, вы измеряете их вес в килограммах. Аналогично мультиметр измеряет сопротивление элементов в омах, напряжение — в вольтах, а ток — в амперах. В табл. 1.1 показаны общепринятые единицы измерения и их аббревиатуры для физических величин, которые используются в электронике.

Физическая величина	Аббревиатура	Единицы измерения	Символ единиц измерения
Сопротивление	R	ом	Ом, ?
Емкость	С	фарад	Ф
Индуктивность	L	генри	Гн
Напряжение	U (V или Е)	вольт	В
Ток	I	ампер	А
Мощность	Р	ватт	Вт
Частота	f	герц	Гц

Таблица 1.1. Единицы измерения, используемые в электронике

Переход к большим или меньшим величинам. При измерении веса яблок очень даже можно столкнуться с малым количеством яблока (или его кусочка), а можно измерять и центнерами, не так ли? Диапазон измерения физических величин в электронике еще шире. В одной схеме вы можете иметь сопротивление в миллионы ом, тогда как в другой протекающий ток будет меньше одной тысячной ампера. Говоря о подобных величинах — как громадных, так и предельно малых, — приходится иметь дело со специальной терминологией. Чтобы показывать очень большие и очень малые числа, в электронике применяют специальные префиксы, или приставки, и экспоненциальное представление. В табл. 1.2 показаны самые широко используемые префиксы и тип записи числовых величин.

Тблица 1.2. Приставки, используемые в электронике

Число	Название	Экспоненциальное представление	Префикс	Аббревиатура
1000000000	1 миллиард	109	Гига	Г
1000000	1 миллион	106	Мега	м
1000	1 тысяча	103	кило	к
100	1 сотня	102
10	1 десяток	101
1	один	100
0,1	1 десятая	10-1
0,01	1 сотая	10-2
0,001	1 тысячная	10-3	милли	м
0,000001	1 миллионная	10-6	микро	мк
0,000000001	1 миллиардная	10-9	нано	н
0,000000000001	1триллионная	10-12	пико	п

Как же правильно прочитать число, записанное как 106 или 10-6? Экспоненциальное представление представляет собой наиболее удобный способ указания того, сколько нулей нужно добавить к числу в десятичной системе счисления, т.е. основанной на степени числа 10. Например, верхний индекс “6” в записи 106 означает, что точка, разделяющая целую и дробную части числа, должна находиться на шесть разрядов правее, а в записи 10-6 — что эту точку нужно сдвинуть на шесть разрядов левее. Таким образом, в числе 1 х 106 разделитель разрядов сдвигается на шесть мест вправо, и мы получаем в результате число 1 000 000 (1 миллион). В числе же 1 х 10-6 разделитель разрядов сдвигается на столько же мест влево, и результатом является 0,000001, или одна миллионная. 3,21 х 104 можно записать, сдвинув запятую на 4 знака вправо: 32100.

Префиксы + единицы измерения = ?

В предыдущих абзацах вы увидели как для обозначения физических величин и единиц их измерения используются аббревиатуры. В этом разделе мы научимся объединять их и использовать очень краткую запись. Например, ток 5 миллиампер можно записать в виде 5 мА, а частоту 3 мегагерца — как 3 МГц.

Кроме того, так же, как при измерении яблок удобнее всего пользоваться килограммами, а при строительстве загородного офиса большой компании вес стальных конструкций определенно будут измерять не иначе как в тоннах, в электронике тоже существуют такие физические величины, для измерения которых пользуются большими числами, и такие, которые измеряются малыми. Это значит, что чаще всего вам придется иметь дело с одним и тем же набором приставок для каждой физической величины. Ниже приведены такие комбинации величин и единиц их измерения.

> Ток: пА, нА, мкА, мА, А.

> Индуктивность: нГн, мГн, мкГн, Гн.

> Емкость: пФ, нФ, мкФ, мФ, Ф.

> Напряжение: мкВ, мВ, В, кВ.

> Сопротивление: Ом, кОм, МОм.

> Частота: Гц, кГц, МГц, ГГц.

Использование некоторых новых терминов

Хотя ранее мы уже рассматривали такие понятия, как сопротивление, напряжение и ток, есть еще некоторые термины, которые могут оказаться для вас внове.

Емкость представляет собой способность накапливать заряд под воздействием электрического поля. Такой накопленный заряд может повышать или понижать напряжение более плавно, чем в отсутствие емкости. Для применения данного свойства на практике используется такой компонент, как конденсатор.

Частотой переменного тока называется мера повторяемости сигнала. Например, напряжение в настенной розетке совершает один полный цикл изменения 50 раз в секунду.

Индуктивность – это способность запасать энергию в магнитном поле; эта накопленная энергия препятствует изменению тока точно так же, как энергия, накопленная конденсатором, препятствует резким изменениям напряжения. Для использования данного свойства на практике в электронике применяются катушки индуктивности, или дроссели.

Мощность служит мерой количества работы, которую электрический ток совершает при протекании через элементы схемы. К примеру, если приложить к электрической лампе напряжение, подведя ток при помощи проводов, то на нагрев этих проводов будет затрачивться какая-то работа. В данном случае мощность можно вычислить, перемножив приложенное к лампе напряжение на ток, протекающий по проводам.

Используя информацию, приведенную в табл. 1.1 и 1.2, вы уже можете перевести экспоненциальную запись числа или аббревиатуру физической величины на человеческий язык. Ниже дано несколько примеров:

> мА: миллиампер, или 1 тысячная ампера;

> мкВ: микровольт, или 1 миллионная вольта;

> нФ: нанофарада, или 1 миллиардная фарады;

> кВ: киловольт, или 1 тысяча вольт;

> МОм: мегаом, или 1 миллион ом;

> ГГц: гигагерц, или 1 миллиард герц.

В аббревиатурах префиксов, которые представляют числа, превышающие 1, такие как М (для приставки Мега), используют прописные буквы. Аббревиатуры приставок, которые меньше 1, пишутся со строчной буквы — как, например, в слове милли. Единственным исключением из этого правила является приставка к для обозначения префикса кило-, которая также записывается с маленькой буквы.

Иногда все же для обозначения тысяч используют и прописную литеру К — а именно при записи килоом; если вы увидите запись вида 3,3 К, то это будет значить 3,3 килоома.

Вы должны научиться преобразовывать любое число к экспоненциальному виду, чтобы затем нормально проводить расчеты. Убедиться в этом вы сможете уже в следующем разделе.

Понятие о законе Ома

Итак, давайте предположим, что вы собрали свою первую схему. Вы знаете величину тока, которую компонент схемы может выдержать, не выходя из строя, и напряжение, выдаваемое источником питания. Следовательно, вам нужно рассчитать сопротивление, которое не позволит току в цепи превысить пороговое значение.

В начале 1800-х годов Георг Ом опубликовал уравнение, названное впоследствии законом Ома, которое позволяет выполнить такой расчет. Закон Ома гласит: напряжение равняется произведению тока на сопротивление, или (в стандартной математической записи):

U = I x R

Выводы из закона Ома

Помните ли вы из школы основы алгебры? Давайте еще раз вспомним вместе: если в уравнении с тремя величинами известны две, то достаточно легко рассчитать третью неизвестную величину. Закон Ома основывается именно на таком уравнении; члены уравнения можно переставлять как угодно, но зная любые два, всегда можно вычислить третий. Например, можно сказать, что ток является частным от деления напряжения на сопротивление:

I = U / R

Наконец, можно рассчитать сопротивление при известных токе и напряжении, переставив члены того же уравнения:

R = U / I

Итак, пока вроде бы все ясно. Теперь давайте попробуем проверить наши знания на практике: пусть есть схема, питающаяся от 12-вольтовой батареи, и электрическая лампа (скажем, большой фонарик). Перед установкой лампочки в фонарик вы измерили сопротивление схемы мультиметром и нашли, что оно равно 9 Ом. Вот формула для расчета электрического тока по закону Ома:

I = U / R = 12 вольт / 9 Ом = 1,3 A

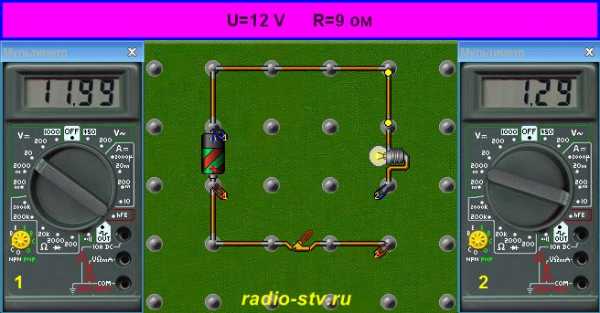
Ну, а что, если вы обнаружили, что лампочка светит чересчур уж ярко? Яркость можно изменить, уменьшив ток, т.е. просто добавив в схему резистор. Изначально мы имели сопротивление схемы 9 Ом; добавив 5-омный резистор в схему, мы повысим ее сопротивление до 14 Ом. В этом случае ток будет равен:

I = U / R = 12 вольт / 14 Ом = 0,9 А

Расчеты с применением больших и малых величин

Предположим, что у вас есть схема с небольшой сиреной, которая имеет сопротивление 2 килоома, а также 12-вольтовая батарея. Для того чтобы рассчитать ток, вам нужно выразить сопротивление цепи не в килоомах, а в базовых единицах — омах, не используя приставку “кило”. В нашем случае это значит, что нужно разделить напряжение на 2000 Ом:

I = U / R = 12 вольт / 2000 Ом = 0,006 A

В результате мы получили ток, записанный как доля 1 А. После окончания расчета будет удобнее вновь использовать префикс, чтобы дать ответ в более лаконичном виде: 0,006 А = 6 мА

Подводя итоги, можно сказать: для проведения расчетов необходимо все исходные величины преобразовать к базовым единицам счисления.

Мощность и закон Ома

Георг Ом (вот уж поистине, наш пострел везде поспел!) также нашел выражение для мощности, вычисляемое при известных напряжении и токе:

Р = U х I; или Мощность = напряжение умноженное на силу тока.

Это уравнение можно использовать для расчета мощности, потребляемой сиреной из предыдущего примера:

Р = 12 В х 0,006 А = 0,072 Вт, или 72 мВт.

Ладно, а что же делать, если напряжение на сирене нам не известно? Вы можете заняться простейшим преобразованием формулы для мощности, используя школьные знания (а вы-то думали, что зря протираете штаны на уроках физики!). Поскольку U = I х R, можно подставить это выражение в формулу для мощности, получив

Р = I2 х R; или Мощность = сила тока в квадрате умноженная на сопротивление.

Вы также можете использовать алгебраические преобразования, чтобы самостоятельно прикинуть, как можно рассчитать сопротивление, напряжение или ток, зная мощность и любой другой из этих же параметров.

radio-stv.ru

Закон Ома | Онлайн журнал электрика

Диаграмма – Закон Ома.

На рис. показана схема знакомой вам простейшей электронной цепи. Эта замкнутая цепь состоит из 3-х частей: источника напряжения – батареи GB, потребителя тока – нагрузки R, которой может быть, к примеру, нить накала электронной лампы либо резистор, и проводников, соединяющих источник напряжения с нагрузкой. Меж иным, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря.Меж иным, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря.

Простая электронная цепь неизменного тока.

Нагрузка R, владеющая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи находится в зависимости от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем огромным ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается последующей формулой: I = U/R,где I – ток, выраженный в амперах, А; U – напряжение в вольтах, В; R – сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и назад пропорционален его сопротивлению. Это основной закон электротехники, называемый законом Ома (по фамилии Г. Ома), для участка электронной цепи. Используя закон Ома, можно по двум известным электронным величинам выяснить неведомую третью. Вот несколько примеров практического внедрения закона Ома.

1-ый пример: На участке цепи, владеющем сопротивлением 5 Ом, действует напряжение 25 В. Нужно выяснить значение тока на этом участке цепи.Решение: I = U/R = 25 / 5 = 5 А.2-ой пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Сначала ток 20 мА необходимо выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.

3-ий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Тут, как и в прошлом примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Как следует, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем молвят эти сведения? О том, что лампочка будет нормально сиять при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, несложно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити существенно меньше. Закон Ома справедлив не только лишь для участка, да и для всей электронной цепи. В данном случае в значение R подставляется суммарное сопротивление всех частей цепи, в том числе и внутреннее сопротивление источника тока. Но при простых расчетах цепей обычно третируют сопротивлением соединительных проводников и внутренним сопротивлением источника тока.

В связи с этим приведу очередной пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Приблизительно таковой ток потребляет электронный паяльничек.

Всеми этими формулами, вытекающими из закона Ома, можно воспользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.

Закон Ома и производные от него расчетные формулы, довольно просто уяснить, если воспользоваться вот этой графической схемой, т. н. треугольник закона Ома:

Воспользоваться этим треугольником просто, довольно верно уяснить, что горизонтальная линия в треугольнике значит символ деления (по аналогии дробной черты), а вертикальная линия в треугольнике значит символ умножения.

Сейчас разглядим таковой вопрос: как оказывает влияние на ток резистор, включаемый в цепь поочередно с нагрузкой либо параллельно ей? Разберем таковой пример. У нас имеется лампочка от круглого электронного, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, изначальное напряжение которой 4,5 В? Несложно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежайшей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, практически в два раза превосходящий тот ток, на который она рассчитана. Таковой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все таки можно питать от батареи 336Л, если поочередно в цепь включить дополнительный резистор сопротивлением 25 Ом, как это показано на рис..

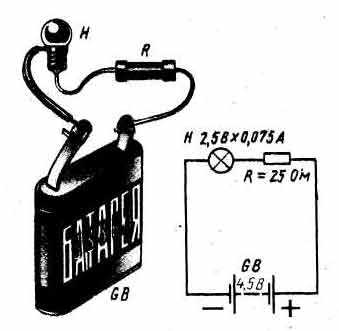Дополнительный резистор, включенный в цепь, ограничивает ток в этой цепи.

В данном случае общее сопротивление наружной цепи будет равно приблизительно 55 Ом, т.е. 30 Ом – сопротивление нити лампочки Н плюс 25 Ом – сопротивление дополнительного резистора R. В цепи, как следует, потечет ток, равный приблизительно 0,08 А, т.е. практически таковой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высочайшим напряжением и даже от электроосветительной сети, если подобрать резистор соответственного сопротивления. В этом примере дополнительный резистор ограничивает ток в цепи до подходящего нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В этом случае в цепь было включено поочередно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при поочередном соединении сопротивлений ток схож во всех точках цепи. Можно включать амперметр в всякую точку цепи, и везде он будет демонстрировать одно значение. Это явление можно сопоставить с потоком воды в реке. Русло реки на разных участках может быть широким либо узеньким, глубочайшим либо маленьким. Но за определенный просвет времени через поперечное сечение хоть какого участка русла реки всегда проходит однообразное количество воды.

Дополнительный резистор, включаемый в цепь поочередно с нагрузкой (как, к примеру, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится дополнительным резистором либо, как молвят, падает на нем, будет тем огромным, чем больше сопротивление этого резистора. Зная ток и сопротивление дополнительного резистора, падение напряжения на нем просто подсчитать все по той же знакомой вам формуле U = IR, Тут U – падение напряжения, В; I – ток в цепи, A; R – сопротивление дополнительного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил излишек напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное примерно 2,5 В, свалилось на нити лампочки. Нужное сопротивление резистора можно отыскать по другой знакомой вам формуле R = U/I, где R – разыскиваемое сопротивление дополнительного резистора, Ом; U-напряжение, которое нужно погасить, В; I – ток в цепи, А. Для нашего примера сопротивление дополнительного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать либо наращивать напряжение, которое падает на дополнительном резисторе, и таким макаром регулировать ток в цепи. Но дополнительный резистор R в таковой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

Регулирование тока в цепи при помощи переменного резистора.

В данном случае при помощи движка резистора можно плавненько изменять напряжение, подводимое к нагрузке Н, а означает, плавненько регулировать ток, протекающий через эту нагрузку. Включенный таким макаром переменный резистор именуют реостатом, При помощи реостатов регулируют токи в цепях приемников, телевизоров и усилителей. В почти всех кинозалах реостаты использовали для плавного гашения света в зрительном зале. Есть, но, и другой метод подключения нагрузки к источнику тока с лишним напряжением – тоже при помощи переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..

Регулирование напряжения на нагрузке R2 при помощи переменного резистора включенного в электронную цепь потенциометром.

Тут R1 – резистор, включенный потенциометром, a R2 – нагрузка, которой может быть та же лампочка накаливания либо какой – то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое отчасти либо стопроцентно может быть подано к нагрузке R2. Когда движок резистора находится в последнем нижнем положении, к нагрузке напряжение вообщем не подается (если это лампочка, она пылать не будет). По мере перемещения движка резистора ввысь мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в последнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 – лампочка карманного фонаря, а напряжение источника тока огромное, нить лампочки перегорит). Можно опытным методом отыскать такое положение движка переменного резистора, при котором к нагрузке будет подано нужное ей напряжение. Переменные резисторы, включаемые потенциометрами, обширно употребляют для регулирования громкости в приемниках и усилителях. Резистор может быть конкретно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет 2-мя параллельными способами: через дополнительный резистор и основную нагрузку. Больший ток будет в ветки с минимальным сопротивлением. Сумма же токов обеих веток будет равна току, используемому на питание наружной цепи. К параллельному соединению прибегают в тех cлучаях, когда нужно ограничить ток не во всей цепи, как при поочередном включении дополнительного резистора, а лишь на каком – то участке. Дополнительные резисторы подключают, к примеру, параллельно миллиамперметрам, чтоб ими можно было определять огромные токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

elektrica.info

Онлайн журнал электрика. 3 закона ома

3. Закон Ома

3. Закон Ома | Техническая библиотека lib.qrz.ru

3. Закон Ома

ЗАКОН ОМА

Закон Ома. История открытия. Различные виды закона Ома

Закон Ома

Единицы измерения в электронике. Закон Ома.

Единицы измерения в электронике

Выводы из закона Ома

Расчеты с применением больших и малых величин

Мощность и закон Ома

Закон Ома | Онлайн журнал электрика

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30