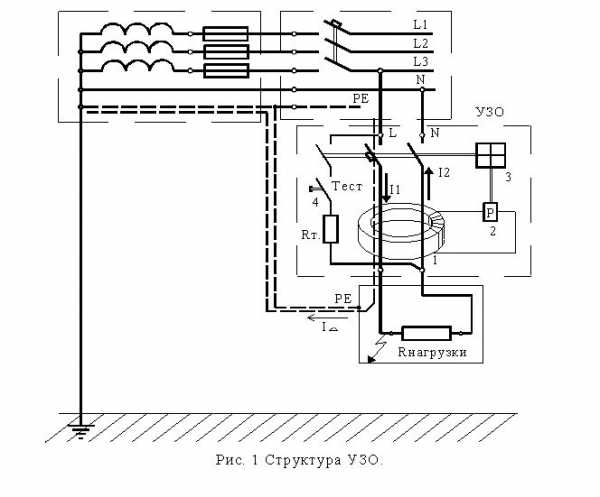
4. Баланс мощностей в цепях постоянного тока. Баланс мощностей. Баланс мощностей в цепи постоянного тока

Сложные параллельные контуры

Сложныминазываются контуры, в которых более двух реактивных элементов.

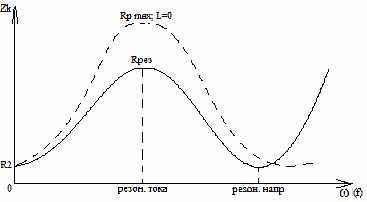
1. Контур с двумя индуктивностями – два резонанса

...

2. Контур с двумя емкостями – два резонанса

резон наприспользуется для усиления резонанса контура и лучшего подавления какой то очень мешающей помехи, соответствующей частоте минимума. Пример: Приемо-передатчик - рация ( - симплекс- попеременная работа; дуплекс – одновременная работа) - устройство приема-передачи.

fН Пер fН Пер

fН Пр fН Пр

Сигнал своего передатчика при дуплексном режиме сильно мешает своему приемнику, так как он значительно мощнее и его надо сильнее подавить.

3. Очень сложный контур - с двумя индуктивностями и двумя емкостями (три резонанса)

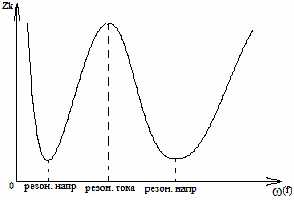
Мощность в цепи переменного тока

1. резистор

Здесь Р - это активная мощность, единица измерения которой ватт - Вт.

2. индуктивность

Pср=0=P

QL=PmL=UL·IL

3. Аналогично для емкости, но с другим знаком, так как колебания в противофазе.

QC= UC·IC

Q=QL+QC

Реактивную мощностьоценивают амплитудой обменной мощности.

[ВАр] - единица измерения реактивной мощности.

φ ( LCf)

P(t)=Im·cos(ω·t)·Um·cos(ω·t+φ)

Pср=P=U·I·cosφ

Q= U·I·sinφ

Активная мощность Pуходит из цепи в какую-то работу, а реактивная мощностьQвозвращается назад.

cosφ- это технический параметр. Для энергетиков он имеет важное значение. Для них необходимо, чтобыcosφбыл близок к 1.

Полная мощностьизмеряется в вольт-амперах - [В·А]. Она находится по формулам:S=U·Iили

, где P- активная мощность, аQ- реактивная мощность.

Расчет мощности в комплексной форме

В электротехнике вводят понятие комплексная мощность.

где P-активная мощность,Q-реактивная мощность,

S- полная мощность или математически модуль комплексной мощности,

φ – угол сдвига фаз между UиI

Баланс мощности в цепях переменного тока

В электрической цепи могут действовать несколько источников и работать несколько потребителей. В этом случае целесообразно подводить баланс мощности.

Суммарная мощность источника должна быть равна сумме мощностей потребителя.

По активной, по реактивной и по полной мощности источников ЭДС обычно рассчитываются в комплексной форме.

с +

( - → →)

Физический смысл баланса мощности

Баланс мощности- это количество энергии, выдаваемой в единицу времени источниками и потребляемое нагрузками ( скорость передачи потребления энергии.)

Баланс говорит о том, что скорость отдачи энергии источниками равна скорости потребления энергии потребителями (нагрузками).

Энергия в электрической цепи не накапливается.

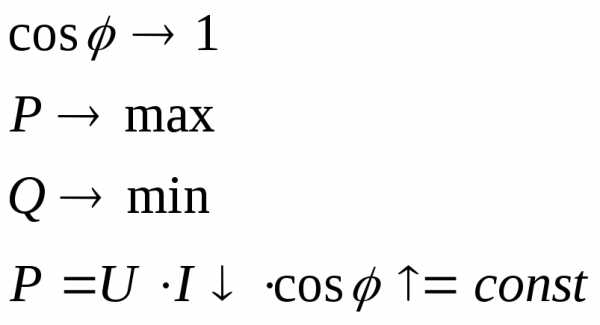
Активная энергия это энергия идущая на полезную работу, а реактивная энергия это энергия обмена между источником и потребителем обычно вредная энергия. Она излишне нагружает линии передачи энергии, что вызывает дополнительные потери в сопротивлении проводов. Поэтому стараются ее уменьшить.

studfiles.net

Тема 5. Мощность цепи постоянного тока. Баланс мощностей

1. Выражение баланса мощности для данной разветвлённой электрической цепи имеет вид

2. Мощность электрической цепи Р при U = 90 В, R = 30 Ом

равна …

1) 180 Вт

3. Мощность электрической цепи Р при I = 2A, R = 30 Ом

Равна…

1) 180 Вт

4. Мощность электрической цепи Р при I = 4A, U = 20 В равна …

1) 80 Вт

5. Мощность электрической цепи Р при I = 1A, R = 30 Ом равна …

1) 180 Вт

6. Мощность потребляемая электрической цепью при U = 100В, показании амперметра I = 1 A равна …

2) 100 Вт

7. Мощность электрической цепи при показании вольтметра V1 = 10В, сопротивлениях R =10 Ом равна …

2) 60 Вт

8. Мощность Р3, при показании вольтметра V = 20 В, сопротивлениях R1 = R2 = R3 =10 Ом равна …

1) 40 Вт

9. Мощность цепи, если Р1 = 20 Вт , Р2 = 40 Вт показания вольтметра V1 = 20 В, а сопротивление R3=10 Ом равна …

1) 100 Вт

10. Из представленных значений мощностью является…

1) 20 МВт

11. Мощность, выделяемая нагрузочным сопротивлением при протекании тока, определяется по закону…

2) Джоуля-Ленца

12. Мощность, потребляемая сопротивлением, определяется по формуле…

13. Если ток увеличить в 4 раза при неизменном сопротивлении нагрузки, то мощность ...

2) возрастёт в 16 раз

14. Сопротивление цепи при входной мощности 100 Вт и токе 2 А составит ...

1) 25 Ом

15. Сопротивление цепи при входном напряжении 10 В и мощности 100 Вт составит...

1) 1 Ом

16. Выражение баланса мощности для данной разветвлённой

электрической цепи имеет вид:

Тема 6. Расчет нелинейных цепей постоянного тока

1. Вольт-амперная характеристика принадлежит

1) диоду

2. Цепь с диодом и резистором

2) нелинейная

3. При заданной вольт-амперной характеристике статическое сопротивление нелинейного элемента в точкеА составляет ...

2) 10 Ом

4. При заданной вольт-амперной характеристике статическое сопротивление нелинейного элемента в точке А составляет…

1) 10 Ом

5. Цепь с линейным и нелинейным сопротивлением описывается уравнением

6. Сопротивление цепи при данной вольт-амперной характеристике

2) invar

7. Сопротивление цепи при заданной вольт- амперной характеристике

8. Сопротивление нелинейной цепи при токе 0,5 А равно 80 Ом, а при 1 А

1) 60 Ом

9. Сопротивление нелинейной цепи при токе 1 А 60 Ом, а при 2 А

1) 35 Ом

10. Ток нелинейной электрической цепи ВАХ-1 и внешней характеристике источника электроэнергии ВАХ- 2

1) 1 А

11. Напряжение нелинейной электрической цепи ВАХ-1 и внешней характеристике источника электроэнергии ВАХ- 2

1) 60 В

12. Сопротивление нелинейной электрической цепи ВАХ-1 и внешней характеристике источника электроэнергии ВАХ- 2

1) 60 Ом

13. Напряжения на двух последовательно соединенных нелинейных элементах соответственно U1 =20 B и U2 =40 B при заданных ВАХ-1 и ВАХ- 2 входное напряжение составит

3) 60 В

14. Ток при последовательном соединении двух нелинейных элементов ВАХ-1 и ВАХ- 2 и входном напряжении 60 В составит

4) 2 А

15. Сопротивление цепи при двух последовательно соединенных нелинейных элементах ВАХ-1 и ВАХ- 2 составит …, если входное напряжение 60 В

1) 30 Ом

16. Уравнение электрического состояния нелинейной электрической цепи имеет вид:

2) U – U2= U1

17. Сопротивление нелинейного элемента электрической цепи r1 при U2 = 10 B и U = 40 B при токе I = 2 A равно …

1) 15 Ом

18. Сопротивление нелинейного элемента электрической цепи r2 при U2= 10 B и U = 40 B при токе I = 2 A равно …

1) 5 Ом

19. Сопротивление нелинейной электрической цепи при U1 = 10 B , U2 = 30 B и токе I2 = 2 A равно…

1) 20 Ом

20. Сопротивление нелинейной электрической цепи при входном напряжении U = 60 B, U1= 20 B, U2 = 40 B и токе I = 2 A составляло 30 Ом, если изменить входное напряжение в 2 раза, то сопротивление цепи…

3) точка пересечения двух ВАХ

Дидактическая единица ГОС

«Анализ и расчет линейных цепей

переменного тока»

studfiles.net

Баланс мощностей

Математика Баланс мощностей

Количество просмотров публикации Баланс мощностей - 178

Наименование параметра	Значение
Тема статьи:	Баланс мощностей
Рубрика (тематическая категория)	Математика

, где п - число элементов схемы.

Уравнение баланса мощностей можно записать в иной форме:

Суммарная мощность, развиваемая источниками электрической энергии, равна суммарной мощности, потребляемой приемниками.

Первая обычно принято называть генерируемой мощностью, а вторая – потребляемой.

Потребляемая энергия в цепях постоянного тока связана с выделением на сопротивлениях при протекании тока теплоты и определяется в соответствии с законом Джоуля – Ленца: .

Для идеального источника напряжения генерируемая мощность определяется как , причем если направление тока совпадает с направлением ЭДС, то произведение берется со знаком ʼʼ+ʼʼ. Это означает, что источник ЭДС доставляет в цепь энергию.

В случае если направление тока встречно направлению ЭДС, то источник не поставляет энергию, а потребляет ее (к примеру, идет заряд аккумулятора). При этом произведение в уравнение энергетического баланса входит со знаком ʼʼ−ʼʼ.

В случае если источник неидеальный, то

Для источника тока

. В случае если направление тока источника совпадает с направлением напряжения, то берется со знаком ʼʼ+ʼʼ, в противном случае – со знаком ʼʼ−ʼʼ.

Баланс мощностей - понятие и виды. Классификация и особенности категории "Баланс мощностей" 2014, 2015.

Баланс мощностей

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

а) Постоянный ток

Для любой цепи постоянного тока выполняется соотношение:

(14)

Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.

Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).

8. Зависимые источники энергии

Помимо независимых в теории цепей рассматривают зависимые, или

управляемые, источники. Они представляют результат идеализации свойств

реальных электронных приборов. Управляемый источник – четырехполюс-

ный резистивный элемент, состоящий из двух ветвей и двух пар выводов:

входной и выходной. Он обладает следующими свойствами:

1) выходная величина пропорциональна входной;

2) выходная величина не влияет на входную.

Входной и выходной величинами управляемого источника могут быть

токи или напряжения. Поэтому различают четыре вида управляемых источников.

Источник ЭДС, управляемый напряжением:

Рассмотрим четырехполюсник, изображенный на рисунке. Можем сказать, что - разрыв цепи, а.

2.Источник тока, управляемый напряжением:

3.Источник ЭДС , управляемый током:

Ток в первой цепи должен протекать, тогда (кинули закоротку),.

4.Источник тока, управляемый током:

Это, как раз, наш транзисторный источник тока: .

9. Свойства наложения, взаимности и их применения для анализа электрической цепи. Принцип наложения

Принцип наложения гласит: ток в любой ветви линейной электрической цепи, находящейся под воздействием нескольких источников электрической энергии, равен алгебраической сумме частичных токов, вызываемых каждым источником в отдельности. Принцип наложения справедлив и для напряжения.

Данный метод справедлив только для линейных электрических цепей и является особенно эффективным, когда требуется вычислить токи для различных значений ЭДС и токов источников в то время, как сопротивления схемы остаются неизменными.

Данный метод основан на принципе наложения (суперпозиции), который формулируется следующим образом: ток в k – й ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников в отдельности.

Аналитически принцип наложения для цепи, содержащей n источников ЭДС и m источников тока, выражается соотношением

(1)

Здесь -комплекс входной проводимостиk – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях;

- комплекс взаимной проводимостиk – й и i– й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i– й ветви при равных нулю ЭДС в остальных ветвях.

Входные и взаимные проводимости можно определить экспериментально или аналитически, используя их указанную смысловую трактовку, при этом , что непосредственно вытекает из свойства взаимности (см. ниже).

Аналогично определяются коэффициенты передачи тока , которые в отличие от проводимостей являются величинами безразмерными.

studfiles.net

1.Ток, напряжение, энергия и мощность в электрических цепях. Баланс мощностей.

Электри́ческий ток — направленное движение электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в полупроводниках — электроны и дырки (электронно-дырочная проводимость).

Ток – постоянный(I=const действующее значение переменного тока)

– переменный (i – мгновенное значение переменного тока) i=ImSin(wt)

Напряжение – отношение затраченной энергии для перемещения заряда из одной точки в другую точку цепи. U=dW/dq; W=∫uidt

Электри́ческая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. S=P+jQ

— полная мощность, ВА (вольт-ампер)

— активная мощность, Вт (ватт)

— реактивная мощность, ВАр (вольт-ампер реактивный)

Название	Напряжение	ток	мощность
Активное сопрот.	U=Ri	i=U/R	P=I2R=U2g g=1/R
Индуктивное сопрот.	uL=Ldi/dt	iL=1/L∫uLdt	WL=Li2/2
Емкостное сопрот.	uC=1/C∫iCdt	iC=CduC/dt	WC=CU2/2

Баланс мощностей:

∑Pист=∑Pпотр

∑IiEi +∑Jk Uk=∑Ij2 Rj

2.Расчет простейших цепей с одним источником энергии (метод эквивалентных преобразований, входная и взаимная проводимости, принцип взаимности и теорема компенсации)

Входные и взаимные проводимости. Входной проводимостью gmm ветви m называется отношение тока Im ветви m к э.д.с. Em источника, помещенного в эту ветвь, при отсутствии э.д.с. в других ветвях:gmm=Im/Em

Взамной (передаточной) проводимостью gkm называется отношение тока Ik ветви k к э.д.с. Em источника ветви m. gkm=Ik/Ek

Принцип взаимности справедлив для линейных электрических цепей с одним источником э.д.с. и может быть сформулирован следующим образом: если источник э.д.с. E действует в любой ветви сколь угодно сложной цепи, не содержащей других источников э.д.с., вызывает в другой ветви ток I, то будучи перенесенным в последнюю, вызовет в первой ветви такой же ток I.

На принципе взаимности основан метод взаимности. Этот метод удобно применять для расчета цепей с одним источником э.д.с., когда его перенос упрощает расчет цепи.

Теорема компенсации. Токи в цепи не изменяются, если любое сопротивление (участок цепи) заменить источником с э.д.с., по величине равной падению напряжения на данном сопротивлении (участке цепи) и направленной навстречу току.

3.Методы расчета сложных электрических цепей. Метод непосредственного применения законов Кирхгофа (последовательность, особенности и пример расчета)

Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. Токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.

Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.

Запишем первый закон Кирхгоффа для 4 – 1 узлов:

узел 2: I5=I4+I8+J8узел 4: J2+I2=I7+I4узел 1: I7+I6=I1

Запишем второй закон Кирхгофа для трех контуров:

контур 15231: I1·R1+I8·R8+I6·(R5+R6)=E8+E6

контур 1341: I1·R1+I2·R2+I7·R7=0

контур 26432: -I4·(R8+R3)-I2·R2+I8·R8=E8

studfiles.net

4. Баланс мощностей в цепях постоянного тока. Баланс мощностей

1. /1.doc2. /10.doc3. /11.doc4. /12.doc5. /13.doc6. /14.doc7. /15.doc8. /16.doc9. /17.doc10. /18.doc11. /19.doc12. /2.doc13. /20.doc14. /3.doc15. /4.doc16. /5 не вкурил.doc17. /6.doc18. /7.doc19. /8.doc20. /9.doc

Пассивные элементы электрических цепей, основные уравненияСвойство взаимностиАмплитуда тока. Аргумент синуса называется фазой. Угол  равен фазе в начальный момент времени (t=0) и поэтому называется начальной фазойВектором, изображающим синусоидальную функцию времениЗаконом Ома в комплексной формеПусть в ветви (рис. 8), состоящей из последовательно соединенных элементовТок в сопротивлении совпадает по фазе с напряжением, ток в индуктивности отстает по фазе от напряжения на угол /2, а ток в емкости опережает напряжение по фазе на угол /2Пассивный двухполюсникУсловием наступления резонанса напряжений является равенство нулю реактивной составляющей входного сопротивления контураПараллельный r-l-c контур. Резонанс токов. Резонанс токовЗадача 88, Поливанов)§ Двухполюсные активные элементыПоложим, что за элементарный промежуток времениЗаконы Кирхгофа, использование для расчёта электрических цепей4. Баланс мощностей в цепях постоянного тока. Баланс мощностейhtml">Метод узловых потенциаловМетод контурных токовТок любой ветви схемы может быть представлен как алгебраическая сумма составляющих, обусловленных действием каждого источника в отдельностиАктивными, а двухполюсники, не содержащие источников электрической энергии, —пассивными9. Теорема об активном двухполюснике, условие передачи в нагрузку максимальной мощности

4. Баланс мощностей в цепях постоянного тока.

БАЛАНС МОЩНОСТЕЙ

Резистивные элементы всегда принимают энергию от активных элементов, их мощность всегда положительна. В резистивных элементах ток и напряжение всегда направлены в одну сторону (рис. 3.1. а)).

Источники электрической энергии могут как отдавать энергию, так и принимать ее от других источников. В первом случае их мощность положительна, во втором - отрицательна.

1. Источники э.д.с. Положительным направлением тока источника э.д.с. будем считать направление, совпадающее с направлением самой э.д.с., оно противоположно напряжению на э.д.с., тогда источник отдает энергию и его мощность положительна (рис. 3.1. б)). Отрицательное направление тока э.д.с. противоположно направлению э.д.с., тогда источник принимает энергию и его мощность отрицательна.

2. Источники тока. Направление напряжения на источнике тока, противоположное направлению его тока будем считать положительным, тогда источник отдает энергию и его мощность положительна (рис. 3.1. в)). Направление напряжения на источнике тока, совпадающее с направлением его тока будем считать отрицательным, тогда источник принимает энергию и его мощность отрицательна.

Баланс мощностей.

Алгебраическая сумма мощностей источников энергии равна сумме мощностей потребителей энергии.

E1I1+E2I2+...+EkIk+U1J1+U2J2+...+UlJl=I12R1+I22R2+...+Im2Rm. (3.1)

где: I1,I2,...,Ik - токи всех источников э.д.с.; U1,U2,...,Ul - напряжения на всех источниках тока; I1,I2,...,Im - токи всех резисторов.

Пример 1. Два источника э.д.с. включены навстречу друг другу, один отдает энергию, другой принимает (рис. 3.2.).

Ток в цепи:

I = (100 В - 1 В)/100 Ом = 0.99 А

Мощность резистора:

PП = I2R = 0.992 А2  100 Ом = 98.01 Вт.

Мощность высоковольтного источника положительна (направления э.д.с. и тока совпадают):

PА1 = 0.99 А  100 В = 99 Вт.

Мощность низковольтного источника отрицательна (направления э.д.с. и тока противоположны):

PА2 = -0.99 А  1 В = - 0.99 Вт.

Суммарная мощность источников:

PА = PА1 + PА2 = 99 Вт - 0.99 Вт = 98.01 Вт

Баланс мощностей:

PА = PП

Пример 1. Два источника тока включены навстречу друг другу, один отдает энергию, другой принимает (рис. 3.3.).

Ток в резисторе:

I = 1 А - 0.01 А = 0.99 А.

Напряжение между узлами 1 и 2, равное напряжениям на источниках:

U10 = 0.99 А  100 Ом = 99 В

Мощность резистора:

PП = I2R = 0.992 А2  100 Ом = 98.01 Вт.

Мощность высокоамперного источника положительна (направления тока и напряжения противоположны):

PА1 = 1 А  99 В = 99 Вт.

Мощность низковольтного источника отрицательна (направления э.д.с. и тока совпадают):

PА2 = 0.01 А  -99 В = - 0.99 Вт.

Суммарная мощность источников:

PА = PА1 + PА2 = 99 Вт - 0.99 Вт = 98.01 Вт

Баланс мощностей:

PА = PП

rushkolnik.ru

Баланс мощностей в цепи переменного тока

Пусть источник ЭДС 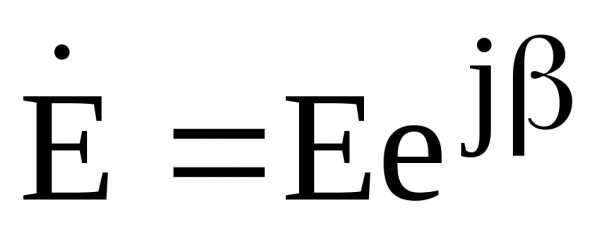нагружен на сопротивление(рис. 3.25).

Рис. 3.25

Известна величина тока в цепи . Рассмотрим так называемыйсопряженный комплекс тока, аргумент которого (начальная фаза) имеет противоположный знак по сравнению с аргументом исходного тока.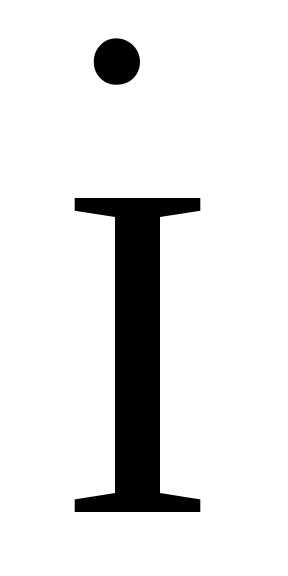

Обозначим -комплексная мощность источника. Раскроем последнее выражение:

(3.27)

Таким образом, активная мощность источника равна действительной части комплексной мощности , а реактивная мощность – мнимой части.

Активная мощность приемников может быть записана с использованием комплексных действующих значений токов и комплексных сопротивлений как , а реактивная мощность -.

Математически баланс активных и реактивных мощностей в комплексной форме можно представить одним выражением. Так, для цепи с источниками ЭДС и тока оно имеет вид

или

. (3.28)

Рис. 3.26

Составим для цепи рис. 3.26 баланс мощностей в комплексной форме:

Общее условие возникновения резонанса напряжений.

Резонанс напряжений может возникать в цепях с последовательным соединением участков, содержащих индуктивности и емкости. Примеры таких цепей приведены на рис. 6.2.

а)

б)

Рис. 6.2

Общее условие возникновения резонанса напряжений– равенство нулю входного реактивного сопротивления цепи.

Общее условие возникновения резонанса токов

Резонанс токов может возникать в цепях с параллельным соединением участков, содержащих индуктивности и емкости. Примеры таких цепей приведены на рис. 6.11.

а) б)

Рис. 6.11

Общее условие возникновения резонанса токов– равенство нулю входной реактивной проводимости цепи.

Расчет напряжения смещения нейтрали в несимметричной трехфазной цепи «Звезда-Звезда»

Несимметричный режим работы трехфазной цепи (при симметричном генераторе)обусловлен неравенством комплексных сопротивлений фаз нагрузки. В этом случае отдельные напряжения или токи трехфазной цепи не образуют симметричные системы, а в схеме “звезда – звезда без нулевого провода”, кроме того, появляется так называемоенапряжение смещения нейтрали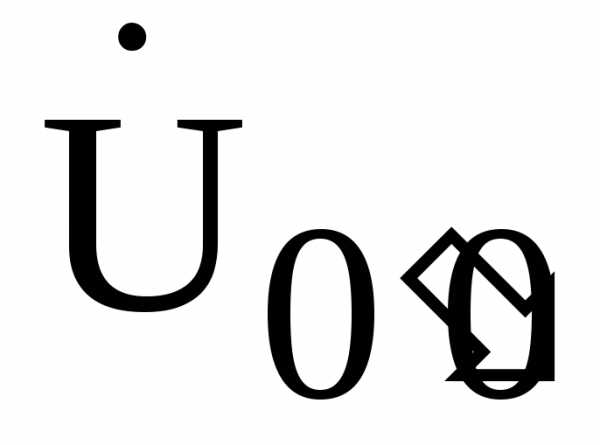(разность потенциалов между нулем генератора и нулем нагрузки).

. (7.56)

Системы прямой, обратной и нулевой последовательностей.

Любая несимметричная трехфазная система токов, напряжений, ЭДС, магнитных потоков может быть представлена в виде суммы трех симметричных систем: прямой, обратной и нулевой последовательностей фаз. Условимся обозначать величины прямой последовательности индексом “1”, обратной - “2” и нулевой - “0”.

Система прямой последовательностисостоит из трех векторов,,, равных по модулю и сдвинутых относительно друг друга на угол, причем векторотстает от векторана угол(рис. 8.3 а). Всистеме обратной последовательности(рис. 8.3 б) векторопережает вектор.Система нулевой последовательностиобразуется тремя одинаковыми векторами(рис. 8.3 в).

а) б) в)

Рис. 8.3

studfiles.net

4. Баланс мощностей в цепях постоянного тока. Баланс мощностей. Баланс мощностей в цепи постоянного тока

Сложные параллельные контуры

Мощность в цепи переменного тока

Расчет мощности в комплексной форме

Баланс мощности в цепях переменного тока

Физический смысл баланса мощности

Тема 5. Мощность цепи постоянного тока. Баланс мощностей

Тема 6. Расчет нелинейных цепей постоянного тока

Баланс мощностей

Математика Баланс мощностей

Читайте также

Баланс мощностей

8. Зависимые источники энергии

9. Свойства наложения, взаимности и их применения для анализа электрической цепи. Принцип наложения

1.Ток, напряжение, энергия и мощность в электрических цепях. Баланс мощностей.

3.Методы расчета сложных электрических цепей. Метод непосредственного применения законов Кирхгофа (последовательность, особенности и пример расчета)

4. Баланс мощностей в цепях постоянного тока. Баланс мощностей

Баланс мощностей в цепи переменного тока

Общее условие возникновения резонанса напряжений.

Общее условие возникновения резонанса токов

Расчет напряжения смещения нейтрали в несимметричной трехфазной цепи «Звезда-Звезда»

Системы прямой, обратной и нулевой последовательностей.

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30