Приведите примеры непрерывных и дискретных сигналов
Яблоки отобранные для переработки на сок, грузчики высыпал из корзины в кузов,Расписать полную, полезную и бесполезную работу
8 Файл размером 2 Мбайта передаётся через некоторое соединение за 80 секунд.Определите размер файла (в Кбайтах), который можно передать через это жесо
…
единение за 120 секунд.
(c++) надо сделать так чтобы код менял 1 число и 10 число местами с помощью for. Заготовка прикреплена.18 баллов. Использовать Массив!
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённостькоторых (в километрах) приведена в таблице. Определите длину кратчайшегопут
…
и между пунктами A и D. Передвигаться можно только по дорогам,протяжённость которых указана в таблице.Вариант 1 вопрос 2 там таблица
Як вставити фото в html, щоб на інших комп’ютерах теж відкривалося?Терміново потрібно)))
срочно помогите пожалуйста сделать программу в пайтоне буду очень сильно благодарен
Прошу, помогитее! Только правильно, пожалуйста)
Чему будет равно значение переменной N после выполнения программы:
N:=1
нц пока N > 5
N:=N-1
кц
ИНФОРМАТИКА
1. Перенесите блоки в соответствующие столбцы.
Перенесите блоки в соответствующие столбцы.
Соотнести логические переменные (пронумерованные предложения ниже) с их значениями, если из
…
вестно, чему равны логические переменные:
1) A = «Котёнок — это ребёнок кошки»
2) A = «Равенства или неравенства, которые содержат в себе переменные, относятся к высказываниям»
3) B = «5+2>7»
4) B = «Если переменные в неравенстве заменить цифрами, то оно становится высказыванием»
5) C = «Истинно или ложно то или иное высказывание, решается, исходя из тех наук, к которым оно относится»
6) C = «Числовые выражения также являются высказываниями»
Значения:
B = 1
C = 0
B = 0
C = 1
A = 1
A = 0
2. Расположить в правильном порядке действия, представленные ниже (А, Б, В), которые нужно выполнить для перевода целого десятичного числа в систему счисления с основанием q:
А) Полученные остатки, которые являются цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления.
Б) Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное 0.
В) Составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
По данным двум натуральным числам A и B (A≤B) выведите все чётные числа на отрезке от A до B. В этой задаче нельзя использовать инструкцию if.
Входные
…
данные
Вводятся два натуральных числа A и B.
Выходные данные
Выведите ответ на задачу.
питон. мне 13. пж на моём уровне
СРОЧНО !!! ПОЖАЛУЙСТА !!ПОМОГИТЕ !! Что будет записано в ячейке В1 ?
Информация и сигнал (8 класс) Информатика и ИКТ
Информация (от лат. «informatio» -осведомление, разъяснение, изложение) — очень широкое понятие, имеющее множество трактовок. Рассмотрим его с точки зрения субъективного (бытового, человеческого) подхода.
В обыденной жизни под информацией понимают всякого рода сообщения, сведения о чём-либо, которые получают и передают люди. Информация содержится в речи людей, текстах книг, колонках цифр, в звуках и видах природы, в показаниях часов, термометров и других приборов. Каждый материальный объект, с которым происходят изменения, становится источником информации либо об окружающей среде, либо о происходящих в этом объекте процессах. Эту информацию мы получаем в виде сигналов — изменений физических величин (давления, температуры, цвета и др.). Различают световые, звуковые, тепловые, механические, электрические и другие типы сигналов.
Каждый материальный объект, с которым происходят изменения, становится источником информации либо об окружающей среде, либо о происходящих в этом объекте процессах. Эту информацию мы получаем в виде сигналов — изменений физических величин (давления, температуры, цвета и др.). Различают световые, звуковые, тепловые, механические, электрические и другие типы сигналов.
Информация для человека — это содержание сигналов (сообщения), воспринимаемых человеком непосредственно или с помощью специальных устройств, расширяющее его знания об окружающем мире и протекающих в нём процессах.
Сигналы могут быть непрерывными или дискретными.
Непрерывный сигнал принимает бесконечное множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами. Сравните лестницу и наклонную плоскость. В первом случае имеется строго определённое количество фиксированных высот, равное числу ступенек. Все их можно пронумеровать. Наклонная плоскость соответствует бесконечному количеству значений высоты.
Все их можно пронумеровать. Наклонная плоскость соответствует бесконечному количеству значений высоты.
В жизни человек чаще всего имеет дело с непрерывными сигналами. Примерами непрерывных сигналов могут служить речь человека, скорость автомобиля, температура в некоторой географической точке в течение определённого периода времени и многое другое. Примером устройства, подающего дискретные сигналы, является светофор. Сигнал светофора может быть красным, жёлтым или зелёным, т. е. принимать всего три значения.
Самое главное:
- Информация для человека — это содержание сигналов ( сообщения), которые он получает из различных источников.
- Сигналы могут быть непрерывными или дискретными. Непрерывный сигнал принимает бесконечное множество значений из некоторого диапазона. Дискретный сигнал принимает конечное число значений, которые можно пронумеровать.
Вопросы и задания:
- Что такое информация для человека? Перечислите источники, из которых вы получаете информацию.

- Приведите примеры непрерывных и дискретных сигналов.
Содержание
INFOблог: Непрерывные и дискретные сигналы
В предыдущем посте мы рассматривали различные определения понятия «информация» и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация — знания, данные, сведения, характеристики, отражения и т.д. — категория нематериальная. Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.
Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации, а изменение какой-либо характеристики носителя мы будем называть сигналом.
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).
Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).
При этом сигналы могут быть двух видов: непрерывный (или аналоговый) и дискретный.
В учебнике даны следующие определения.
Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.
Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.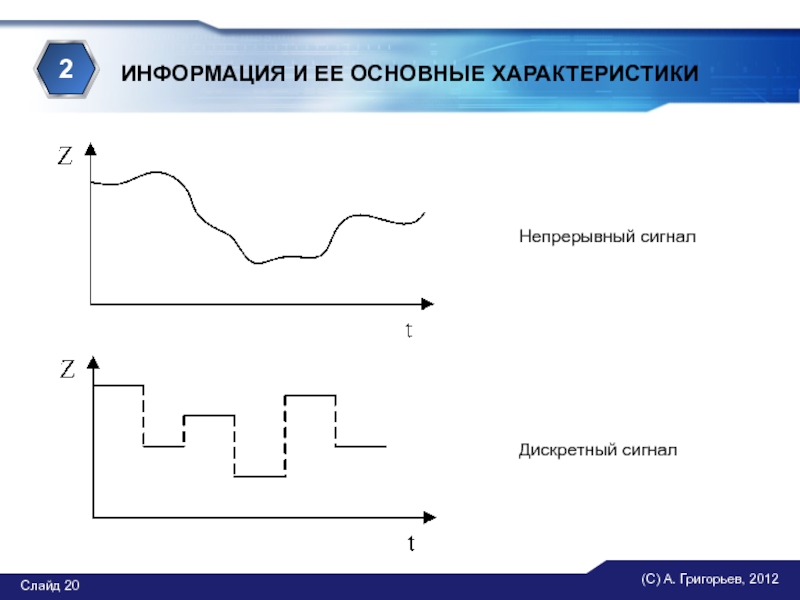
Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.
Графики этих сигналов выглядят следующим образом
Примерами непрерывных сигналов могут быть музыка, речь, изображения, показания термометра (высота столба ртути может быть любой и представляет собой ряд непрерывных значений).
Примерами дискретных сигналов могут быть показания механических или электронных часов, тексты в книгах, показания цифровых измерительных приборов и т.д.
Вернемся к примерам, рассмотренным в начале сообщения — мигающая лампочка и человеческая речь. Какой из этих сигналов является непрерывным, а какой дискретным? Ответьте в комментариях и аргументируйте свой ответ. Можно ли непрерывную информацию преобразовать в дискретную? Если да — приведите примеры.
Дискретность. Принципы и применение. Сигнал и работа.Особенности
Дискретность в переводе с латинского языка обозначает прерывистость. Данное понятие применяется в различных отраслях науки, в частности электронике, физике, биологии, математике и так далее. В электронике существует понятие дискретного сигнала, предусматривающее передачу информации в условиях изменения возможных значений передающей среды. Кроме этого прерывистость используется и в других более щепетильных сферах, к примеру, в микроэлектронике. В частности при разработке дискретных схем представляющих собой элементы линий связи.
Данное понятие применяется в различных отраслях науки, в частности электронике, физике, биологии, математике и так далее. В электронике существует понятие дискретного сигнала, предусматривающее передачу информации в условиях изменения возможных значений передающей среды. Кроме этого прерывистость используется и в других более щепетильных сферах, к примеру, в микроэлектронике. В частности при разработке дискретных схем представляющих собой элементы линий связи.
Как применяется дискретность в электронике
Существующие современные технологии связи, в том числе и разработанные для этого компьютерные программы, обеспечивают передачу голоса, являющегося звуковым потоком. При этом разработчики подобного оборудования и программного обеспечения сталкиваются с тем, что голосовой поток это непрерывная волна, передача которой возможна только на канале с высокой пропускной способностью. Его применение слишком затратно как в плане ресурсов, так и финансово. Эта проблема решается использованием принципов дискретности.
Дискретный сигнал представляет собой вместо стандартной непрерывной волны специальное цифровое выражение, способное ее описать. С установленной частотой параметры волны конвертируются в цифровую информацию и отправляются для приема. Фактически, получается обеспечить связь с минимальным применением ресурсов и энергии.
Дискретность позволяет существенно уменьшить суммарный поток данных, формируя из него пакетную передачу. При этом благодаря тому, что соблюдается выборка волны с промежутками между работой и паузами, то исключается вероятность искажения. Создается гарантия, что отправленная часть пакетных данных будет доставлена по предназначению, а за ней уже передастся следующая часть. В случае же с обыкновенными волнами, возможность помех намного выше.
Примеры простейшей дискретности
Учебники по физике для объяснения понятия дискретности при применении его к сигналу зачастую приводят аналогию с печатной книгой. Так, при ее чтении воспринимается непрерывный поток изложенной информации. При этом фактически вся изложенная в ней информация это код, состоящий из набора букв, пробелов и знаков препинания. Изначально способ общения человека – это голос, но посредством письма возможно записать звук с помощью буквенного кода. При этом, если рассматривать в плане емкости в килобайтах или мегабайтах, то объем напечатанного текста будет занимать меньше места, чем его звуковая запись.
При этом фактически вся изложенная в ней информация это код, состоящий из набора букв, пробелов и знаков препинания. Изначально способ общения человека – это голос, но посредством письма возможно записать звук с помощью буквенного кода. При этом, если рассматривать в плане емкости в килобайтах или мегабайтах, то объем напечатанного текста будет занимать меньше места, чем его звуковая запись.
Возвращаясь к примеру с книгой получается, что ее автор создает определенный дискретный сигнал, разбивая звуковой поток на блоки и излагая их определенным способом кодирования, то есть письменным языком. Сам читатель открывающий книгу посредством своих знаний в кодировании и мысли объединяет дискретные буквы в непрерывный информационный поток. Данный пример весьма удачно помогает упрощенным языком объяснить зачем нужна дискретность и почему она так тесно связана с сигналами, применяемыми в электронике.
Простым примером визуальной дискретности можно назвать старые рисованные мультфильмы.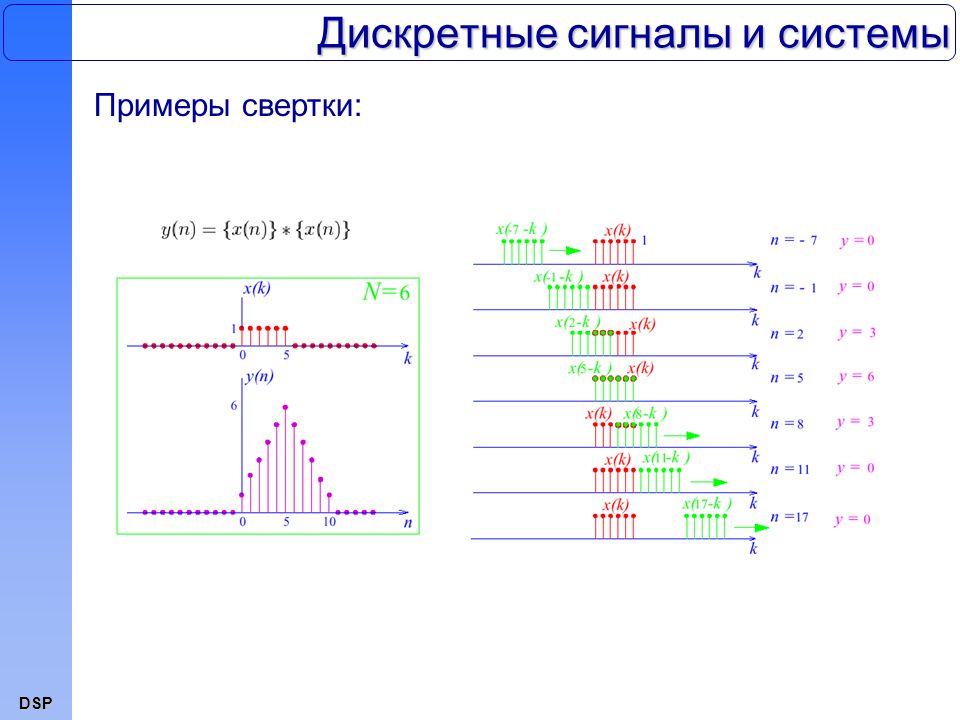 Их кадр состоял из десятков картинок, которые шли друг за другом с небольшими паузами. Каждая последующая картинка немного изменяется, поэтому глазу человека кажется, что персонажи на экране двигаются. Именно благодаря дискретности вообще возможно формировать движущееся изображение.
Их кадр состоял из десятков картинок, которые шли друг за другом с небольшими паузами. Каждая последующая картинка немного изменяется, поэтому глазу человека кажется, что персонажи на экране двигаются. Именно благодаря дискретности вообще возможно формировать движущееся изображение.
Пример с рисованными мультфильмами отображает лишь часть свойства дискретности. Аналогичная технология применяется и при создании видео. Стоит вспомнить диафильмы или старые кинопленки, когда на одной длинной ленте идет множество маленьких картинок, при изменении которых создается эффект движения на экране. Хотя современные технологии и отошли от материальных носителей кадров такого плана, но по-прежнему используется принцип дискретности, хотя и видоизмененный.
Дискретный сигнал
Данное понятие позволяет отобразить противоположное явления непрерывному сигналу. При использовании непрерывности одним из проявлений выступает звуковая волна с определенной амплитудой и частотой, которая транслируется постоянно без пауз. Хотя и существует несколько вполне эффективных способов обработки непрерывного или так называемого аналогового сигнала, позволяющих уменьшить объем информационного потока, но они не так действенны. Использование дискретной переработки позволяет делать оборудование менее объемным и отказаться от дорогостоящих коммуникаций. В электронике понятие дискретный и цифровой сигнал это практически одно и то же.
Хотя и существует несколько вполне эффективных способов обработки непрерывного или так называемого аналогового сигнала, позволяющих уменьшить объем информационного потока, но они не так действенны. Использование дискретной переработки позволяет делать оборудование менее объемным и отказаться от дорогостоящих коммуникаций. В электронике понятие дискретный и цифровой сигнал это практически одно и то же.
К неоспоримым достоинствам дискретного сигнала можно отнести:
- Возможность избежать искажения информации.
- Обеспечение высокой помехоустойчивости, что возможно в результате применения кодирования информации.
- Возможность архивирования данных для сохранения ресурсов носителей.
- Обеспечение возможности трансляции информации из различных источников по единому каналу.
- Наличие упрощенного математического описания.
Не лишена дискретность и недостатков. При ее использовании требуется применение высоких технологий, в связи с чем ответственные детали электронных механизмов теряют возможность проведения кустарного ремонта. При серьезной поломке требуется замена отдельных агрегатов. Кроме этого возможна частичная потеря информации, которая заключена в дискретном сигнале.
При серьезной поломке требуется замена отдельных агрегатов. Кроме этого возможна частичная потеря информации, которая заключена в дискретном сигнале.
Способы реализации дискретности при работе с сигналами
Как уже было выяснено, дискретный сигнал представляет собой последовательность цифровых закодированных значений. Существуют различные способы кодирования, но одним из самых популярных считаются двоичные цифровые сигналы. Они используются практически во всех электронных устройствах, поскольку легко кодируются и декодируются.
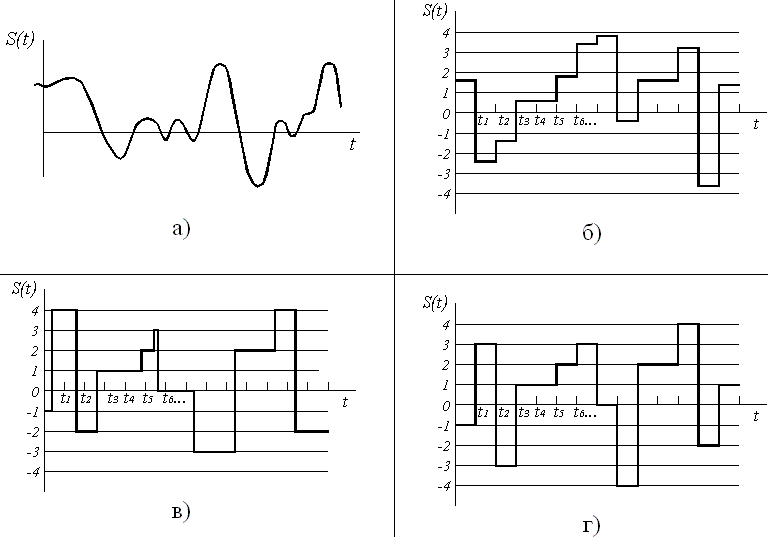
Дискретный цифровой сигнал имеет два значения «1» и «0». Для передачи данных создается импульсное напряжение. После генерации импульса принимающее его устройство воспринимает часть сигнала как «1», а последующую после этого паузу как «0». Декодирующая аппаратура оценивает частоту подаваемых импульсов и проводит их восстановление в изначальные данные. Если рассматривать график дискретного сигнала, можно увидеть, что переход между нулевым и максимальным значением происходит мгновенно.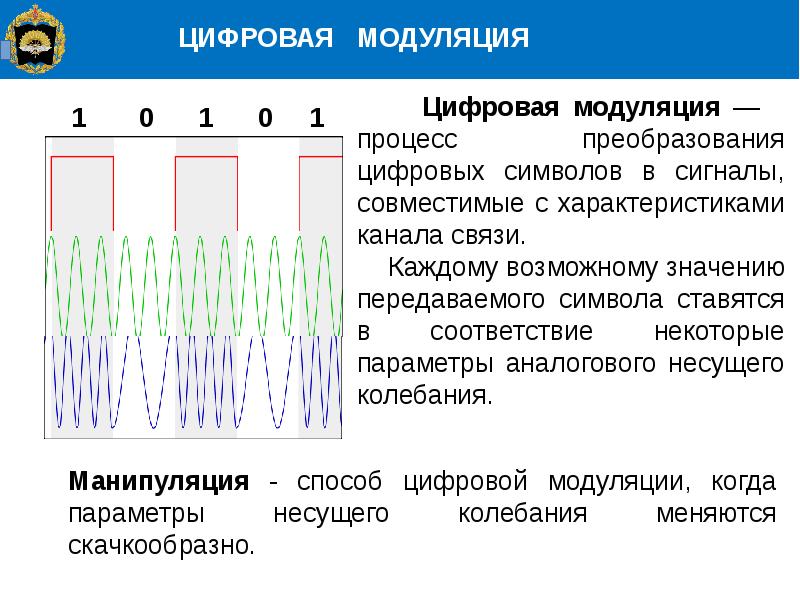 График состоит из прямоугольных углов, когда линия между верхним и нижним значением не имеет плавного перехода. Благодаря этому принимающая аппаратура считывает информацию четко, тем самым исключаются помехи, поскольку даже слабо принятый импульс будет читаться как максимум, то есть «1», а пауза как «0».
График состоит из прямоугольных углов, когда линия между верхним и нижним значением не имеет плавного перехода. Благодаря этому принимающая аппаратура считывает информацию четко, тем самым исключаются помехи, поскольку даже слабо принятый импульс будет читаться как максимум, то есть «1», а пауза как «0».
Хотя дискретность и способна значительно уменьшить образование помех, но не может исключить их полное отсутствие. Если имеется большой уровень шума цифрового потока, то восстановить данные из полученных сигналов невозможно. В случае же с непрерывными аналоговыми сигналами можно применять различные фильтры, чтобы убрать искажения и восстановить информацию. Именно поэтому принцип дискретности применяется далеко не всегда.
Техническая реализация принципов дискретности
Дискретные сигналы используются для записи на известные носители, такие как CD, DVD и так далее. Их читают цифровые проигрыватели, мобильные телефоны, модемы и практически любое техническое оборудование, которым все пользуются ежедневно. Все мультимедийные технологии состоят из устройств сжатия, кодировки и декодировки, что и позволяет работать с дискретными сигналами.
Все мультимедийные технологии состоят из устройств сжатия, кодировки и декодировки, что и позволяет работать с дискретными сигналами.
Даже те сферы, которые изначально использовали непрерывные технологии передачи данных, начинают отказываться от такого способа и внедряют дискретность. Вся современная аудиотехника работает именно по такому способу. Также происходит постепенный отказ от аналового телевещания. Отсутствие резкого перехода с одной технологии на вторую наблюдается благодаря тому, что дискретный сигнал можно обратно конвертировать в аналоговый. Это обеспечивает определенную совместимость разных систем.
Если рассматривать еще примеры оборудования, где применяются принципы дискретности, то к таким примерам можно отнести:
- Звуковые карты.
- Электронные музыкальные инструменты.
- Навигаторы.
- Цифровые фотоаппараты.
Сфера применения принципа дискретности очень обширна. В связи с этим оборудование, где он внедряется, значительно прогрессирует, при этом удобство применения такой аппаратуры многократно возрастает.
Похожие темы:
Аналоговый и цифровой сигнал. Типы сигналов и как это действует
Сигналами называют информационные коды, которые применяются людьми для того, чтобы передавать сообщения в информационной системе. Сигнал может подаваться, но его получение не обязательно. Тогда как сообщением можно считать только такой сигнал (или совокупность сигналов), который был принят и декодирован получателем (аналоговый и цифровой сигнал).
Одними из первых методов передачи информации без участия людей или других живых существ были сигнальные костры. При возникновении опасности последовательно разводились костры от одного поста к другому. Далее мы будем рассматривать способ передачи информации при помощи электромагнитных сигналов и подробно остановимся на рассмотрении темы аналоговый и цифровой сигнал.
Любой сигнал может быть представлен в виде функции, которая описывает изменения его характеристик. Такое представление удобно для изучения устройств и систем радиотехники. Помимо сигнала в радиотехнике есть еще шум, который является его альтернативой. Шум не несет полезной информации и искажает сигнал, взаимодействуя с ним.
Помимо сигнала в радиотехнике есть еще шум, который является его альтернативой. Шум не несет полезной информации и искажает сигнал, взаимодействуя с ним.
Само понятие дает возможность отвлечься от конкретных физических величин при рассмотрении явлений, связанных с кодированием и декодированием информации. Математическая модель сигнала в исследованиях позволяет опираться на параметры функции времени.
Типы сигналов
Сигналы по физической среде носителя информации делятся на электрические, оптические, акустические и электромагнитные.
По методу задания сигнал может быть регулярным и нерегулярным. Регулярный сигнал представляется детерминированной функцией времени. Нерегулярный сигнал в радиотехнике представлен хаотической функцией времени и анализируется вероятностным подходом.
Сигналы в зависимости от функции, которая описывает их параметры могут быть аналоговыми и дискретными. Дискретный сигнал, который был подвергнут квантованию называется цифровым сигналом.
Обработка сигнала
Аналоговый и цифровой сигнал обрабатывается и направлен на то, чтобы передать и получить информацию, закодированную в сигнале. После извлечения информации ее можно применять в разных целях. В частных случаях информация подвергается форматированию.
Аналоговые сигналы подвергаются усилению, фильтрации, модуляции и демодуляции. Цифровые же помимо этого еще могут подвергаться сжатию, обнаружению и др.
Аналоговый сигнал
Наши органы чувств воспринимают всю поступающую в них информацию в аналоговом виде. К примеру, если мы видим проезжающий мимо автомобиль, мы видим его движение непрерывно. Если бы наш мозг мог получать информацию о его положении раз в 10 секунд, люди бы постоянно попадали под колеса. Но мы можем оценивать расстояние куда быстрее и это расстояние в каждый момент времени четко определено.
Абсолютно то же самое происходит и с другой информацией, мы можем оценивать громкость в любой момент, чувствовать какое давление наши пальцы оказывают на предметы и т. п. Иными словами, практически вся информация, которая может возникать в природе имеет аналоговый вид. Передавать подобную информацию проще всего аналоговыми сигналами, которые являются непрерывными и определены в любой момент времени.
п. Иными словами, практически вся информация, которая может возникать в природе имеет аналоговый вид. Передавать подобную информацию проще всего аналоговыми сигналами, которые являются непрерывными и определены в любой момент времени.
Чтобы понять, как выглядит аналоговый электрический сигнал, можно представить себе график, на котором будет отображена амплитуда по вертикальной оси и время по горизонтальной оси. Если мы, к примеру, замеряем изменение температуры, то на графике появится непрерывная линия, отображающая ее значение в каждый момент времени. Чтобы передать такой сигнал с помощью электрического тока, нам надо сопоставить значение температуры со значением напряжения. Так, например, 35.342 градуса по Цельсию могут быть закодированы как напряжение 3.5342 В.
Аналоговые сигналы раньше использовались во всех видах связи. Чтобы избежать помех такой сигнал нужно усиливать. Чем выше уровень шума, то есть помех, тем сильнее надо усиливать сигнал, чтобы его можно было принять без искажения. Такой метод обработки сигнала затрачивает много энергии на выделение тепла. При этом усиленный сигнал может сам стать причиной помех для других каналов связи.
Такой метод обработки сигнала затрачивает много энергии на выделение тепла. При этом усиленный сигнал может сам стать причиной помех для других каналов связи.
Сейчас аналоговые сигналы еще применяются в телевидении и радио, для преобразования входного сигнала в микрофонах. Но, в целом, этот тип сигнала повсеместно вытеснен или вытесняется цифровыми сигналами.
Цифровой сигнал
Цифровой сигнал представлен последовательностью цифровых значений. Чаще всего сейчас применяются двоичные цифровые сигналы, так как они используются в двоичной электронике и легче кодируются.
В отличие от предыдущего типа сигнала цифровой сигнал имеет два значения «1» и «0». Если мы вспомним наш пример с измерением температуры, то тут сигнал будет сформирован иначе. Если напряжение, которое подается аналоговым сигналом соответствует значению измеряемой температуры, то в цифровом сигнале для каждого значения температуры будет подаваться определенное количество импульсов напряжения. Сам импульс напряжения тут будет равен «1», а отсутствие напряжения – «0». Приемная аппаратура будет декодировать импульсы и восстановит исходные данные.
Сам импульс напряжения тут будет равен «1», а отсутствие напряжения – «0». Приемная аппаратура будет декодировать импульсы и восстановит исходные данные.
Представив, как будет выглядеть цифровой сигнал на графике, мы увидим, что переход от нулевого значения к максимальному производится резко. Именно эта особенность позволяет принимающей аппаратуре более четко «видеть» сигнал. Если возникают какие-либо помехи, приемнику проще декодировать сигнал, нежели чем при аналоговой передаче.
Однако цифровой сигнал с очень большим уровнем шума восстановить невозможно, тогда как из аналогового типа при большом искажении еще есть возможность «выудить» информацию. Это связано с эффектом обрыва. Суть эффекта в том, что цифровые сигналы могут передаваться на определенные расстояния, а затем просто обрываются. Этот эффект возникает повсеместно и решается простой регенерацией сигнала. Там, где сигнал обрывается, нужно вставить повторитель или уменьшить длину линии связи. Повторитель не усиливает сигнал, а распознает его изначальный вид и выдает его точную копию и может использоваться сколь угодно в цепи. Такие способы повторения сигнала активно применяются в сетевых технологиях.
Такие способы повторения сигнала активно применяются в сетевых технологиях.
Помимо всего прочего аналоговый и цифровой сигнал различается и возможность кодирования и шифрования информации. Это является одной из причин перехода мобильной связи на «цифру».
Аналоговый и цифровой сигнал и цифро-аналоговое преобразования
Следует еще немного рассказать о том, как аналоговая информация передается по цифровым каналам связи. Вновь прибегнем к примерам. Как уже говорилось звук – это аналоговый сигнал.
Что происходит в мобильных телефонах, которые передают информацию по цифровым каналам
Звук, попадая в микрофон подвергается аналого-цифровому преобразованию (АЦП). Этот процесс состоит из 3 ступеней. Берутся отдельные значения сигнала через одинаковые отрезки времени, этот процесс называется дискретизация. По теореме Котельникова о пропускной способности каналов, частота взятия этих значений должна быть вдвое выше, чем самая высокая частота сигнала. То есть, если в нашем канале стоит ограничение на частоту в 4 кГц, то частота дискретизации будет составлять 8 кГц.
То есть, если в нашем канале стоит ограничение на частоту в 4 кГц, то частота дискретизации будет составлять 8 кГц.
Далее все выбранные значения сигнала округляются или, иначе говоря, квантуются. Чем больше уровней при этом будет создано, тем выше будет точность восстановленного сигнала на приемнике. Затем все значения преобразуются в двоичный код, который передается на базовую станцию и затем доходит до другого абонента, являющегося приемником. В телефоне приемника происходит процедура цифро-аналогового преобразования (ЦАП). Это обратная процедура, цель которой на выходе получить сигнал как можно более идентичный исходному. Далее уже аналоговый сигнал выходит в виде звука из динамика телефона.
Похожие темы:
Отличия аналогового и цифрового сигналов для пользователя
Простому потребителю совсем необязательно знать, какова природа сигналов. Но порой необходимо знать разницу между аналоговым и цифровым форматами, чтобы с открытыми глазами подходить к выбору того или иного варианта, ведь сегодня на слуху, что время аналоговых технологий прошло, на смену им приходят цифровые. Следует понять разницу, чтобы знать от чего уходим и чего ожидать.
Следует понять разницу, чтобы знать от чего уходим и чего ожидать.
Сигнал аналоговый — это сигнал непрерывный, имеющий бесконечное число близких по значению данных в пределах максмальных, все параметры которого описываются временной зависимой переменной.
Сигнал цифровой – это раздельный сигнал, описываемый раздельной функцией времени, соответственно в каждый момент времени, величина амплитуды сигнала имеет строго определенное значение.
Практика показала, что при аналоговых сигналах возможны помехи, устраняемые при цифровом сигнале. Кроме того, цифровой может восстановить изначальные данные. При непрерывном аналоговом сигнале проходит много информации, зачастую излишней. Вместо одного аналогового можно передать несколько цифровых.
На сегодняшний день потребителя интересует вопрос телевидения, так как именно в этом контексте чаще и произносится фраза «переход на цифровой сигнал». В этом случае аналоговый можно считать пережитком прошлого, но ведь именно его принимает существующая техника, а для приема цифрового необходима специальная.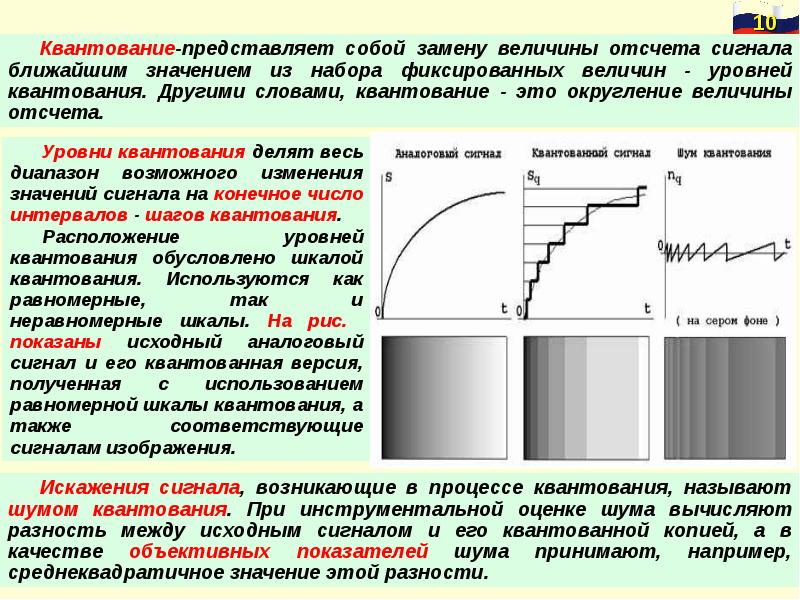 Конечно, в связи с появлением и расширением использования «цифры», аналоговые телевизоры теряют былую популярность.
Конечно, в связи с появлением и расширением использования «цифры», аналоговые телевизоры теряют былую популярность.
Преимущества и недостатки видов сигналов
Немаловажную роль в оценке параметров того или иного сигнала имеет безопасность. Различного характера влияния, посторонние вторжения делают аналоговый сигнал беззащитным. При цифровом подобное исключается, так как он кодируется из радиоимпульсов. Для больших расстояний передача цифровых сигналов усложнена, приходится использовать схемы модуляции-демодуляции.
Поводя итог, можно сказать, что отличия аналогового и цифрового сигнала состоят:
- В непрерывности аналогового и дискретности цифрового;
- В большей вероятности помех при передаче аналогового;
- В избыточности аналогового сигнала;
- В способности цифрового фильтровать помехи и восстанавливать исходую информацию;
- В передаче цифрового сигнала в закодированной форме. Один аналоговый сигнал замещается несколькими цифровыми.

Смотрите раздел «аренда проекторов».
Отличие аналоговой и цифровой связи примеры оборудования
Отличие аналоговой и цифровой связи.
Имея дело с радиосвязью, очень часто приходится сталкиваться с такими терминами, как «аналоговый сигнал» и «цифровой сигнал». Для специалистов в этих словах нет никакой тайны, но для людей несведущих разница между «цифрой» и «аналогом» может быть совсем неведомой. А между тем разница есть и весьма существенная.
Итак. Радиосвязь это всегда передача информации (речевой, СМС, телесигнализации) между двумя абонентами источником сигнала передатчиком (Радиостанцией, репитером, базовой станцией) и приемником.
Когда мы говорим о сигнале, то обычно подразумеваем электромагнитные колебания, наводящие ЭДС и вызывающие колебания тока в антенне приемника. Далее приемное устройство – переводит полученные колебания обратно в сигнал звуковой частоты и выводит на динамик.
В любом случае сигнал передатчика можно представить как в цифровой, так и в аналоговой форме. Ведь, к примеру, сам по себе звук – это аналоговый сигнал. На радиостанции звук, воспринимаемый микрофоном, преобразуется в уже упоминавшиеся электромагнитные колебания. Чем выше частота звука – тем выше частота колебаний на выходе, а чем громче говорит диктор – тем больше амплитуда.
Получившиеся электромагнитные колебания, или волны, распространяются в пространстве с помощью передаточной антенны. Чтобы эфир не забивался низкочастотными помехами, и чтобы у разных радиостанций была возможность работать параллельно, не мешая друг другу, колебания, получившиеся от воздействия звука, суммируют, то есть «накладывают» на другие колебания, имеющие постоянную частоту. Последнюю частоту принято называть «несущей», и именно на ее восприятие мы настраиваем свой радиоприемник, чтобы «поймать» аналоговый сигнал радиостанции.
В приемнике происходит обратный процесс: несущая частота отделяется, а электромагнитные колебания, полученные антенной, преобразуются в колебания звука, и из динамика слышится информация которую хотел сообщить передавший сообщение.
В процессе передачи звукового сигнала от радиостанции к приемнику могут возникнуть сторонние помехи, частота и амплитуда могут измениться, что, конечно же, отразится на звуках, издаваемых радиоприемником. Наконец, и сами передатчик и приемник во время преобразования сигнала вносят некоторую погрешность. Поэтому звук, воспроизводимый аналоговым радиоприемником, всегда имеет некоторые искажения. Голос может вполне воспроизводиться, несмотря на изменения, но фоном будет шипение или даже какие-то хрипы, вызванные помехами. Чем менее уверенным будет прием, тем громче и отчетливее будут эти посторонние шумовые эффекты.
Вдобавок эфирный аналоговый сигнал имеет очень слабую степень защиты от постороннего доступа. Для общественных радиостанций это, конечно, не имеет никакого значения. Но во время пользования первыми мобильными телефонами был один неприятный момент, связанный с тем, что почти любой посторонний радиоприемник мог быть легко настроен на нужную волну для подслушивания вашего телефонного разговора.
Для защиты от этого используют так называемое «тонирование» сигнала или по другому система CTCSS (Continuous Tone-Coded Squelch System) система шумоподавления, кодированная непрерывным тоном или система идентификации сигнала «свой/чужой», предназначенная разделять пользователей, работающих в одном частотном диапазоне, на группы. Пользователи (корреспонденты) из одной группы могут слышать друг друга благодаря идентификационному коду. Объясняя доступно, принцип действия данной системы таков. Вместе с передаваемой информацией в эфир отправляют также дополнительный сигнал (или по другому тон). Приемник, помимо несущей, распознает при соответствующей настойке этот тон и принимает сигнал. Если же в рации –приемнике тон не настроен, то приема сигнала не происходит. Стандартов шифрования существует достаточное большое количество отличающаяся для различных производителей.
Такие недостатки есть у аналогового эфирного вещания. Из-за них, к примеру, телевидение в относительно скором времени обещает стать полностью цифровым.
Цифровая связь и вещания считаются более защищенными от помех и от внешних воздействий. Все дело в том, что при использовании «цифры» аналоговый сигнал с микрофона на передающей станции зашифровывается в цифровой код. Нет, конечно, в окружающее пространство не распространяется поток цифр и чисел. Просто звуку определенной частоты и громкости присваивается код из радиоимпульсов. Продолжительность и частота импульсов задана заранее – она одна и у передатчика, и у приемника. Наличие импульса соответствует единице, отсутствие – нулю. Поэтому такая связь и получила название «цифровая».
Устройство, преобразующее аналоговый сигнал в цифровой код, называется аналого-цифровым преобразователем (АЦП). А устройство, установленное в приемнике, и преобразующее код в аналоговый сигнал, соответствующий голосу вашего знакомого в динамике сотового телефона стандарта GSM, называется цифро-аналоговый преобразователь (ЦАП).
Во время передачи цифрового сигнала ошибки и искажения практически исключены. Если импульс станет немного сильнее, продолжительнее, или наоборот, то он все равно будет распознан системой как единица. А нуль останется нулем, даже если на его месте возникнет какой-то случайный слабый сигнал. Для АЦП и ЦАП не существует других значений, как 0,2 или 0,9 – только нуль и единица. Поэтому помехи на цифровую связь и вещание почти не оказывают влияния.
Если импульс станет немного сильнее, продолжительнее, или наоборот, то он все равно будет распознан системой как единица. А нуль останется нулем, даже если на его месте возникнет какой-то случайный слабый сигнал. Для АЦП и ЦАП не существует других значений, как 0,2 или 0,9 – только нуль и единица. Поэтому помехи на цифровую связь и вещание почти не оказывают влияния.
Более того, «цифра» является и более защищенной от постороннего доступа. Ведь, чтобы ЦАП устройства смог расшифровать сигнал, необходимо, чтобы он «знал» код расшифровки. АЦП вместе с сигналом может передавать и цифровой адрес устройства, выбранного в качестве приемника. Таким образом, даже если радиосигнал и будет перехвачен, он не сможет быть распознан из-за отсутствия как минимум части кода. Это особенно актуально для связи.
Итак, отличия цифрового и аналогового сигналов:
1) Аналоговый сигнал может быть искажен помехами, а цифровой сигнал может быть или забит помехами совсем, или приходить без искажений. Цифровой сигнал или точно есть, или полностью отсутствует (или нуль, или единица).
Цифровой сигнал или точно есть, или полностью отсутствует (или нуль, или единица).
2) Аналоговый сигнал доступен для восприятия всеми устройствами, работающими по тому же принципу, что и передатчик. Цифровой сигнал надежно защищен кодом, его трудно перехватить, если вам он не предназначается.
Помимо чисто аналоговых и чисто цифровых станций, существуют и радиостанции поддерживающие как аналоговый так и цифровой режим. Они предназначены для перехода с аналоговой на цифровую связь.
Итак имея в распоряжении парк аналоговых радиостанций, вы можете постепенно перейти на цифровой стандарт связи.
Например, изначально вы строили систему связи на Радиостанциях Байкал 30.
Напомню, что это аналоговая станция с 16 каналами.
/tovar_baikal_30b5
Но идет время, и станция перестает устраивать Вас, как пользователя. Да, она надежная, да мощная, да с хорошим аккумулятором до 2600 мА/ч. Но при расширении парка радиостанций более чем на 100 человек, а особенно при работе в группах её 16 каналов начинает не хватать.
Вам совершенно не обязательно сразу бежать и покупать радиостанции цифрового стандарта. Большинство производителей, намеренно вводят модель с наличием аналогового режима передачи.
То есть вы можете поэтапно переходить на например Байкал-35 или Motorola DP-1400 сохраняя существующую систему связи в рабочем состоянии.
Плюсы такого перехода неоспоримы.
Вы получаете станцию работающую
1) дольше (в цифровом режиме меньше потребление.)
2) Имеющую большее количество функций (групповой вызов, одинокий работник)
3) 32 канала памяти.
То есть вы фактически создаете изначально 2 базы каналов. Под новые закупленные станции (цифровые каналы) и базу каналов содействия с существующими станциями (аналоговые каналы). Постепенно по мере закупки оборудования вы будете сокращать парк радиостанций второго банка и увеличивать – первого.
В конечном итоге вы достигнете поставленной задачи – перевести полностью вашу базу на цифровой стандарт связи.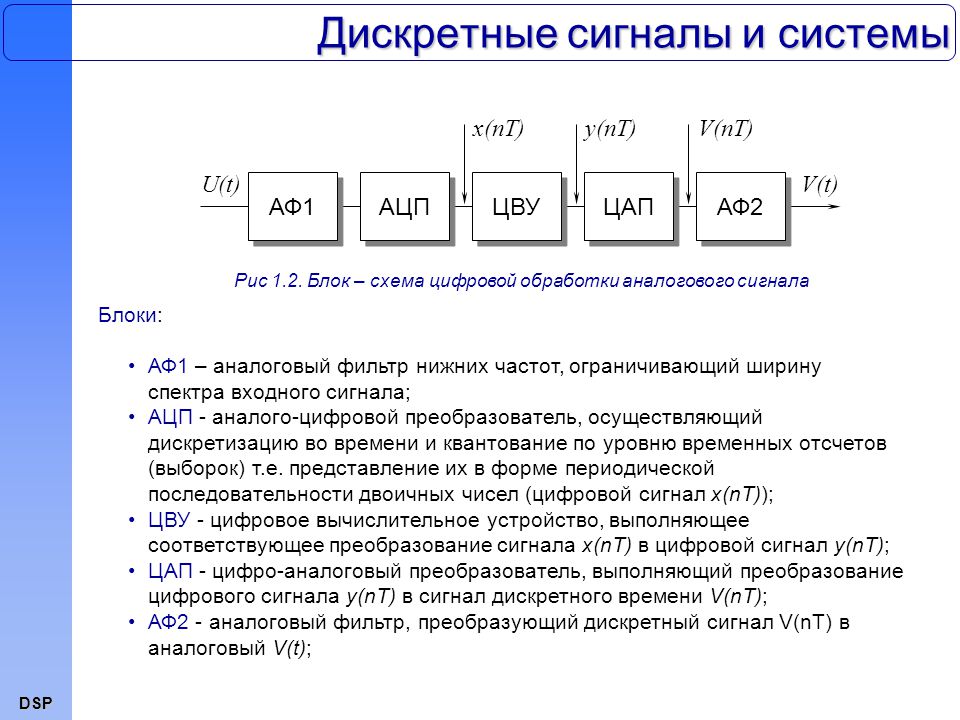
Хорошим дополнением и расширением к любой базе может послужить цифровой ретранслятор Yaesu Fusion DR-1
/tovar_dr1
Это двухдиапазонный (144/430MHz) ретранслятор, который поддерживает аналоговую FM связь, а также одновременно цифровой протокол System Fusion в пределах частотного диапазона 12.5кГц. Мы уверены, что внедрение новейшей DR-1X станет рассветом нашей новой и впечатляющей многофункциональной системы System Fusion.
Одной из ключевых возможностей System Fusion является функция AMS (автоматический выбор режима), которая мгновенно распознает принимается ли сигнал в режиме V/D, режиме голосовой связи или режиме данных FR аналоговом FM или цифровом C4FM, и автоматически переключается на соответствующий. Таким образом, благодаря нашим цифровым трансиверам FT1DR и FTM-400DRSystem Fusion, чтобы поддерживать связь с аналоговыми FM радиостанциями больше нет необходимости каждый раз вручную переключать режимы,.
На репитере DR-1X, AMS можно настроить так, чтобы входящий цифровой C4FM сигнал преобразовывался в аналоговый FM и ретранслировался, таким образом позволяя поддерживать связь между цифровым и аналоговым трансиверами. AMS также можно настроить на автоматическую ретрансляцию входящего режима на выход, позволяя цифровым и аналоговым пользователям совместно использовать один ретранслятор.
До сих пор, FM ретрансляторы использовались только для традиционной FM связи, а цифровые ретрансляторы только для цифровой. Однако, теперь просто заменив обычный аналоговый FM репитер на DR-1X, вы можете продолжать пользоваться обычной FM связью, а также использовать ретранслятор для более продвинутой цифровой радиосвязи System Fusion. Другие периферийные устройства, такие как дуплексер и усилитель и т.д. можно продолжать использоваться как обычно.
Более подробные характеристики оборудование можно увидеть на сайте www. yaesu.ru в разделе продукция
yaesu.ru в разделе продукция
Основные понятия о сигналах и системах
Сигналы и системы — это абстрактные концепции самых разных физических
переменные и процессы в различных областях техники и науки.
Большинство сигналов, представляющих интерес на практике, представляют собой записанные значения физической величины,
представлены в виде одномерных функций, таких как функция времени, или двухмерных / трехмерных
функции, такие как пространственная функция или. Примеры
сигналы включают в себя температуру во времени или пространстве, звук (речь, музыка,
и т. д.) с течением времени, изображения в пространстве и т. д.Сигнал несет информации
и содержит энергии .
- Непрерывный сигнал можно дискретизировать дискретизацией .
 Этот процесс
Этот процесс
называется непрерывно-дискретным (C / D) или аналого-цифровым преобразованием.
(АЦП, АЦП). - Дискретный сигнал можно преобразовать в непрерывный с помощью
интерполяция .Этот процесс называется дискретно-непрерывным (D / C).
или цифро-аналоговое преобразование (ЦАП, ЦАП). - Аналоговый сигнал может быть оцифрован
аналого-цифровой (A / D) преобразователь
стать цифровым сигналом (дискретным как по амплитуде, так и по времени). - Цифровой сигнал может быть преобразован обратно в аналоговый сигнал с помощью
цифро-аналоговый преобразователь.
Если не указано иное, независимая переменная сигнальной функции
считается неограниченным, т.е.грамм., ,
, или же ,
. Однако в действительности все рассматриваемые сигналы подаются
конечный усечением , определенным только внутри конечного окна, например,
или же . Сигнал не определен за окном
(не обязательно ноль).
состоит как из реальных, так и из мнимых частей:
или, что то же самое, величина и фаза:
Реальные сигналы — это частные случаи сложных сигналов.
Сигнал или может быть случайным. Если проводится эксперимент
неоднократно результаты могут не совпадать. Например, годовой
температурный профиль меняется год от года. Такая случайная функция времени есть
называется случайным процессом.
В физике квадрат переменной обычно связан с мощностью или энергией.
Например, и мощности в электрических системах,
, — кинетическая и потенциальная энергия в механических
системы.
Возводя в квадрат величину сигнала или, мы получаем
мгновенная мощность сигнала в момент или (энергия
распределение):
энергия , содержащаяся в сигнале за период времени, равна
мощность, интегрированная за период времени:
Когда
или же
, — полная энергия
содержится в сигнале. Сигналом является энергия , сигнал , если его общая энергия
Сигналом является энергия , сигнал , если его общая энергия
конечно.
Средняя мощность сигнала — это среднеквадратичное значение
или же :
и представляет собой среднеквадратичное значение сигнала (RMS) .Сигналом является сигнал мощности , если его полная энергия не конечна, но
его средняя мощность составляет. Средняя мощность энергетического сигнала равна нулю.
Большинство периодических сигналов являются сигналами мощности.
Примеры:
Система принимает сигнал или как вход (стимул, возбуждение,
и т. д.), изменяет и обрабатывает сигнал и производит сигнал или
как выход (ответ).Этот процесс можно смоделировать математически.
как оператор, применяемый к входу для получения выходных данных:
Некоторые примеры системы:
- Электрическая / электронная схема: сигнал напряжение / ток на входе
порт, напряжение / ток от выходного порта - Нейровизуальная система: обработка ввода света (фотонов) и генерации
потенциал действия (электрохимический сигнал) - Метаболизм глюкозы: преобразование глюкозы и кислорода в диоксид углерода
и вода, и производство тепловой энергии - : преобразование электромагнитного сигнала как входного и генерирующего
звук и сигнал изображения в качестве вывода.
- Механические конструкции (здания, мосты и т. Д.): Силовые воздействия,
выход движения / вибрации.
Телевизор
- Линейность: система является линейной, если она Однородная
(масштабирование):
и добавка (суперпозиция):
Комбинируя эти свойства, мы получаем: - Инвариант во времени: Система инвариантна во времени, если то, как она реагирует
к входу не изменяется со временем (где — постоянная задержка времени):Если (красный) такой же, как (синий), то система
не зависит от времени.Однако, если выход (зеленый) отличается
из ; то есть поведение системы с точки зрения того, как она реагирует на
входные данные меняются с течением времени, значит, система не является неизменной во времени. - Линейная и инвариантная во времени (LTI) система , одновременно линейная система
и не зависящий от времени.
Почему биологи заботятся о ЛТИ? Взгляни на
Системная инженерия к системной биологии .
« Отношения между входом и выходом могут быть определены и экспериментально измерены для множества биологических систем и, таким образом, могут использоваться для выявления скрытых биологических свойств.»
« Системная инженерия давно изучается, поэтому, возможно, теперь больше методов из этой зрелой области систем можно адаптировать к биологии, что позволит точно контролировать биологические входные и выходные сигналы для выявления структур, скрытых под сложными сетевыми картами ».
Знакомство с сигналами
Знакомство с сигналами
- Определение сигналов
- Типы сигналов
- Свойства сигнала
- Пример сигналов
- Различные сигналы
- Свойство периодичности
- Разница между системами CT и DT
- Дельта функция
- разворот времени
- смена времени
- замедление / сокращение времени
- Разница между CT и DT
Почему цифровая обработка сигналов?
Если вы работаете на компьютере или используете компьютер для манипулирования данными, вы почти наверняка работаете с цифровыми сигналами. Все манипуляции с данными являются примерами цифровой обработки сигналов (для нашей цели обработка сигналов с дискретным временем как экземпляры цифровой обработки сигналов).
Все манипуляции с данными являются примерами цифровой обработки сигналов (для нашей цели обработка сигналов с дискретным временем как экземпляры цифровой обработки сигналов).
Примеры использования DSP:
- Фильтрация: устранение шума из сигналов, таких как речевые сигналы и другие аудиоданные, астрономические данные, сейсмические данные, изображения.
- Синтез и манипуляции: например, синтез речи, синтез музыки, графика.
- Анализ: сейсмические данные, атмосферные данные, анализ фондового рынка.
- Голосовая связь: обработка, кодирование и декодирование для хранения и пересылки.
- Кодирование голоса, звука и изображений для сжатия.
- Активное шумоподавление: наушники, глушители в автомобилях
- Обработка изображений, компьютерное зрение
- Компьютерная графика
- Промышленное применение: анализ вибрации, химический анализ
- Biomed: МРТ, сканирование кошек, визуализация, анализы, ЭКГ, ЭМГ и т.
 Д.
Д. - Радар, Эхолот
- Сейсмология.
Определение сигналов
Что такое сигнал?
Сигнал — это способ передачи информации. Жесты, семафоры, изображения, звук — все может быть сигналами.
Технически — функция времени, пространства или другой переменной наблюдения, которая передает информацию
Распишем 3 форм сигналов:
- Непрерывный / аналоговый сигнал
- Сигнал дискретного времени
- Цифровой сигнал
Непрерывный (CT) / аналоговый сигнал
конечная , действительная , гладкая функция $ s (t) $ переменной t , которая обычно представляет время.И s , и t в $ s (t) $ являются непрерывными
Почему с реальной стоимостью ?
Обычно явления реального мира имеют реальную ценность.
Почему конечный ?
Реальные сигналы обычно имеют ограниченную энергию просто потому, что нам не доступен бесконечный источник энергии.
В качестве альтернативы, особенно когда они характеризуют долговременные явления (например, солнечное излучение), они будут ограничены по мощности.
Реальные сигналы также будут ограничены по амплитуде — их значения ни в коем случае не будут бесконечными.
Чтобы утверждать, что сигнал «конечен», нам нужна некоторая характеристика его «размера». Утверждать, что сигнал конечен, значит утверждать, что размер сигнала ограничен — он никогда не стремится к бесконечности.2 (\ тау), д \ тау. $
Почему гладкий ?
Реальные сигналы никогда не меняются резко / мгновенно. Если быть более техническим, у них конечная пропускная способность .
Обратите внимание, что хотя мы сделали предположения о сигналах (конечность, реальные, гладкие), при фактическом анализе и разработке методов обработки сигналов эти соображения обычно игнорируются.
Дискретный сигнал (DT)
Сигнал с дискретным временем — это ограниченная последовательность с непрерывными значениями $ s [n] $. С другой стороны, его можно рассматривать как непрерывную функцию от дискретного индекса $ n $. 2 [n].$ 90 291
Гладкость не применяется.
Цифровой сигнал
Мы будем работать с цифровыми сигналами, но будем развивать теорию в основном вокруг сигналов с дискретным временем .
Цифровые компьютеры имеют дело с цифровыми сигналами , а не с сигналами дискретного времени.Цифровой сигнал
представляет собой последовательность $ s [n] $, где index значения $ s [n] $ не только конечны, но могут принимать только конечный набор значений. Например,
в цифровом сигнале, где отдельные числа $ s [n] $ хранятся с использованием 16-битных целых чисел, $ s [n] $ может принимать одно из 2 16 значений.
В числовом ряду $ s [n] $ значения s могут принимать только фиксированный набор значений.
Цифровые сигналы — это сигналы с дискретным временем, полученные после «оцифровки». Цифровые сигналы также обычно получают путем измерения от
явления реального мира. Однако, в отличие от принятой нормы для аналоговых сигналов, цифровые сигналы могут принимать комплексные значения.
Выше представлены некоторые критерии для реальных сигналов. Теоретические сигналы не ограничены
реальный — это часто нарушается; работаем с комплексными числами
конечное / ограниченное
энергия — ВСЕГДА нарушается
. Сигналы, которые имеют бесконечную временную протяженность, , т.е. , которые простираются от $ — \ infty $ до $ \ infty $, могут иметь бесконечную энергию.
мощность — почти никогда: почти все сигналы, с которыми мы столкнемся, имеют ограниченную мощность
гладкость — это часто нарушается многими из рассматриваемых нами сигналов непрерывного времени.
Примеры «стандартных» сигналов
Мы перечисляем некоторые основные типы сигналов, которые часто встречаются в DSP. Мы перечисляем их версии для непрерывного и дискретного времени.
Обратите внимание, что аналоговые версии с непрерывным временем некоторых из этих сигналов являются искусственными конструкциями — они нарушают некоторые из условий, которые мы
указано выше для сигналов реального мира и фактически не может быть реализовано.
Типы сигналов
Мы можем классифицировать сигналы по их свойствам, и все это повлияет на наш анализ этих сигналов позже.
Периодические сигналы
Сигнал является периодическим, если он повторяется ровно через некоторый промежуток времени. Однако значение периодичности различается для сигналов с непрерывным и дискретным временем.Мы рассмотрим каждый из них по очереди.
Сигналы непрерывного времени
Таким образом, в непрерывном времени сигнал, если он называется периодическим, если существует какое-либо значение $ T $ такое, что
\ [
s (t) = s (t + MT), ~~~~~ — \ infty \ leq M \ leq \ infty, ~~ \ text {integer} ~ M
\]
Наименьшее значение $ T $, для которого указанное выше соотношение удерживает период сигнала.
Дискретные сигналы времени
Определение периодичности для сигналов с дискретным временем аналогично определению для сигналов с непрерывным временем с одним ключевым отличием: период должен быть целым числом .Как мы увидим, это приводит к некоторым неинтуитивным выводам.
Дискретный сигнал времени $ x [n] $ называется периодическим, если существует положительное целое значение $ N $ такое, что
\ [
x [n] = x [n + MN]
\]
для всех целых $ M $. Наименьшее значение $ N $, для которого справедливо указанное выше, является периодом сигнала.
Четные и нечетные сигналы
Симметический сигнал и даже — это сигнал, который зеркально отражается в момент времени $ t = 0 $.Сигнал считается, даже если он обладает следующим свойством:
\ [
\ text {Непрерывное время:} ~ s (t) = s (-t) \\
\ text {Дискретное время:} ~ s [n] = s [-n]
\]
Сигнал является нечетным симметическим сигналом , если он имеет следующее свойство:
\ [
\ text {Непрерывное время:} ~ s (t) = -s (-t) \\
\ text {Дискретное время:} ~ s [n] = -s [-n]
\]
На рисунке ниже показаны примеры четных и нечетных симметричных сигналов.Например, косинус даже симметричен, поскольку $ \ cos (\ theta) = \ cos (- \ theta) $, что приводит к $ \ cos (\ omega t) = \ cos (\ omega (-t)) $ . С другой стороны, синус нечетно симметричен, поскольку $ \ sin (\ theta) = — \ sin (- \ theta) $, что приводит к $ \ sin (\ omega t) = — \ sin (\ omega (-t) ) $.
Разложение сигнала на четные и нечетные составляющие
Любой сигнал $ x [n] $ может быть выражен как сумма четного и нечетного сигналов следующим образом.
\ [
x [n] = x_ {четное} [n] + x_ {нечетное} [n]
\]
где
\ [
x_ {даже} [n] = 0.5 (х [п] + х [-n]) \\
x_ {odd} [n] = 0,5 (x [n] — x [-n])
\]
Управляющие сигналы
Сигналы могут быть составлены путем манипулирования и комбинирования других сигналов. Кратко рассмотрим эти манипуляции.
Масштабирование
Простое масштабирование сигнала вверх или вниз по коэффициенту усиления.
Непрерывное время: $ y (t) = a x (t) $
Дискретное время: $ y [n] = a x [n] $
$ a $ может быть реальным / мнимым, положительным / отрицательным. Когда $ a отрицательно, сигнал переворачивается по оси y.
Обратное время
Переворот сигнала слева направо.
Непрерывное время: $ y (t) = x (-t) $
Дискретное время: $ y [n] = x [-n] $
Сдвиг по времени
Сигнал смещен вдоль оси индента на $ \ tau $ (или N для дискретного времени). Если $ \ tau $ положительно, сигнал задерживается, а если $ \ tau $
отрицательный сигнал продвигается.
Непрерывное время: $ y (t) = x (t- \ tau) $
Дискретное время: $ y [n] = x [n — N] $
Расширение
Саму временную ось можно масштабировать на $ \ alpha $.
Непрерывное время: $ y (t) = x (\ alpha t) $
Дискретное время: $ y [n] = x [/ alpha n] $
Расширение DT отличается от расширения CT, потому что $ x [n] $ определяется ТОЛЬКО для целого числа n, поэтому для существования $ y [n] = x [\ alpha n] $ «an» должно быть целым числом.
Однако $ x [\ alpha n] $ для $ a \ neq 1 $ проигрывает некоторым семплам. Вы никогда не сможете полностью восстановить x [n] из него. Этот процесс часто называют дециминкацией .
Для сигналов DT
$ y [n] = x [\ alpha n] $ для $ \ alpha интерполировать нули для неопределенных значений, если $ an $ не является целым числом.
Составление сигналов
Сигналы могут быть составлены путем манипулирования и комбинирования других сигналов.
Есть несколько способов комбинирования сигналов, и мы рассматриваем следующие два:
ДОПОЛНЕНИЕ
Непрерывное время: $ y (t) = x_1 (t) + x_2 (t) $
Дискретное время: $ y [n] = x_1 [n] + x_2 [n] $
УМНОЖЕНИЕ
Непрерывное время: $ y (t) = x_1 (t) x_2 (t) $
Дискретное время: $ y [n] = y_1 [n] y_2 [n] $
$ x_1 [n] $ и $ x_2 [n] $ сами могут быть получены путем манипулирования другими сигналами.{\ alpha t} u (t) $ для $ \ alpha
На самом деле односторонние сигналы могут быть получены умножением на u [n] (или сдвинутые / обращенные во времени версии u [n] или u (t)).
Получение основных сигналов друг от друга
Можно получить один сигнал из другого просто с помощью математических манипуляций.{\ infty} u [k] \ delta [n-k] $
На этом завершается введение в сигналы. В обзоре мы обсудили важность DSP, типы сигналов и их свойства, манипуляции с сигналами,
и состав сигнала. Далее мы обсудим системы.
Сигналы, системы и связь | Электротехника и информатика
Достижения в области технологий улучшают возможности анализа различных источников информации, таких как аудио (речь, акустика, музыка), изображения (видео, мультимедиа, медицинские сканы), медицинские сигналы (частота сердечных сокращений, артериальное давление, активность мозга) и данные дистанционного зондирования ( геофизические, радиолокационные, гидроакустические).Примерами систем, которые манипулируют сигналами, являются распознавание речи, потоковое видео, сотовые сети и медицинские сканеры, такие как МРТ. Дисциплины обработки сигналов и изображений связаны с анализом и синтезом сигналов и их взаимодействием с системами. В связи цель состоит в том, чтобы передавать информацию (сигналы) от одного или нескольких источников к одному или нескольким адресатам, что требует разработки схем передачи (например, модуляции и кодирования), приемников и фильтров.Область «Сигнальные системы и связь» охватывает основы аналоговых и цифровых сигналов и систем, математические инструменты для анализа детерминированных и случайных сигналов, а также приложения для обработки цифровых сигналов, обработки цифровых изображений и цифровой / аналоговой связи. Факультет сигналов и связи штата Орегон специализируется в таких областях, как проводная и беспроводная связь, экологические и медицинские исследования, сотовая связь, обмен данными и информацией.
Возможности трудоустройства варьируются в самых разных областях, таких как промышленность мобильных телефонов, волоконно-оптическая связь, ADSL и широкополосная кабельная связь, звуковая и аудиотехника, распознавание речи, медицинские системы визуализации (рентгеновские снимки, КТ, МРТ, ПЭТ), DSP. проектирование аппаратного и программного обеспечения, полиграфическая промышленность, цифровые дисплеи (ЭЛТ, ЖК-дисплеи, плазменные панели), цифровые камеры и видеокамеры, стандарты сжатия изображений (JPEG, MPEG).
Возможные вакансии
Инженер по обработке сигналов : разработка программного и аппаратного обеспечения для обработки сигналов в таких областях, как аудио, изображения, медицина и дистанционное зондирование для таких компаний, как Texas Instruments, HP, Intel, Google, Samsung, LT, MATLAB
Инженер по коммуникациям : проектирование, разработка и обслуживание систем связи для таких компаний, как Broadcom и Cisco, или национальных лабораторий, таких как Национальная лаборатория Лоуренса Ливермора, MIT Lincoln Labs или MITER.
Факультет
Курсы
Ядро
- ECE 461 и 462 (Связь)
- ECE 464 (цифровая обработка сигналов)
- ECE 468 (цифровая обработка изображений)
Факультативы
- ECE 463 (сеть беспроводной связи)
- CS 325 (Анализ алгоритмов)
- CS 331 (Введение в искусственный интеллект)
- CS 434 (Машинное обучение и интеллектуальный анализ данных)
- CS 450 (Введение в компьютерную графику)
- ECE 390 (электрические и магнитные поля)
- ECE 413 (датчики)
- ECE 422 и 423 (интегральные схемы CMOS)
- ECE 473 (Конструкция микропроцессорной системы)
- ECE 482 (Оптические электронные системы)
- ECE 451 / ME 430 (Системная динамика и управление)
- ECE 474 (Система СБИС)
- ECE 483 (Волноводная оптика)
Сигналы и системы
Сигнал — это описание того, как один параметр изменяется с другим параметром.Например, изменение напряжения в электронной схеме со временем или яркость
меняется в зависимости от расстояния на изображении. Система — это любой процесс, производящий
Выходной сигнал в ответ на входной сигнал . Это иллюстрируется блоком
диаграмму на рис. 5-1. Системы непрерывного ввода и вывода непрерывных сигналов,
например, в аналоговой электронике. Дискретные системы ввода и вывода дискретные
сигналы, такие как компьютерные программы, которые манипулируют значениями, хранящимися в массивах.
Для присвоения имен сигналам используется несколько правил. Это не всегда выполняется в DSP,
но они очень распространены, и вы должны их запомнить. Математика
достаточно сложно без четких обозначений. Во-первых, непрерывных сигналов используют
круглые скобки, например: x (t) и y (t) , а для дискретных сигналов используются скобки, например: x [n] и y [n] . Во-вторых, в сигналах используются строчные буквы. Буквы верхнего регистра
зарезервирован для частотной области, обсуждаемой в следующих главах.В-третьих, имя
передаваемый сигналу обычно описывает параметры, которые он представляет. Для
Например, напряжение в зависимости от времени может называться : v (t) или фондовый рынок
цена измеряется каждые дня может быть: p [d] .
Сигналы и системы часто обсуждаются, не зная точного
представляемые параметры. Это то же самое, что использовать x и y в алгебре,
без присвоения физического смысла переменным.Это приносит четвертый
правило именования сигналов. Если более информативное имя недоступно, ввод
сигнал дискретной системы обычно называется: x [n] , а выходной сигнал: y [n] .
Для непрерывных систем используются сигналы: x (t) и y (t) .
Есть много причин для понимания системы . Например, вы
может захотеть спроектировать систему для удаления шума на электрокардиограмме, повышения резкости
изображение не в фокусе или удаление эха в аудиозаписи.В остальных случаях
система может иметь искажение или мешающий эффект, который вам необходимо
охарактеризовать или измерить. Например, когда вы говорите по телефону, вы
ожидайте, что другой человек услышит что-то похожее на ваш голос.
К сожалению, входной сигнал линии передачи редко бывает идентичным
выходной сигнал. Если вы понимаете, как устроена линия передачи (система)
изменяя сигнал, возможно, вы сможете компенсировать его влияние. В еще других
случаях система может представлять собой некоторый физический процесс, который вы хотите изучить
или проанализировать.Радар и гидролокатор — хорошие тому примеры. Эти методы работают
сравнивая передаваемые и отраженные сигналы, чтобы найти характеристики
удаленный объект. С точки зрения теории систем проблема состоит в том, чтобы найти систему
который преобразует переданный сигнал в принятый.
На первый взгляд может показаться непосильной задачей понять все
возможные системы в мире. К счастью, большинство полезных систем попадают в
категория называется линейными системами.Этот факт чрезвычайно важен. Без
концепция линейной системы, мы были бы вынуждены исследовать отдельные
характеристики многих несвязанных систем. При таком подходе мы можем сосредоточиться на
черты линейной системы категории в целом. Наша первая задача — выявить
какие свойства делают систему линейной и как они вписываются в повседневное понятие
электроники, программного обеспечения и других систем обработки сигналов.
Периодический сигнал — обзор
Пример 5.1-15
Рассмотрим T -периодических сигналов, x (t) ↔Xm и w (t) ↔Wm, где w (t) равно окну Хеннинга, определенному в примере 5.1-13. Используйте свойство 7, чтобы вычислить коэффициент ряда Фурье y (t) = w (t) x (t). Объединение (5.1-74) и (5.1-75) в примере 5.1-13 дает коэффициенты ряда Фурье, Wm,
(5.1-102) Wm = {12m = 014m = ± 10 | m |> 1
Умножение свойство приводит к
(5.1-103) Ym = ∑n = −∞∞Wm − nXn = 14Xm − 1 + 12Xm + 14Xm + 1
Следовательно, умножение x (t) на окно Хэннинга эквивалентно 3- pt средневзвешенное значение коэффициента ряда Фурье.
Свойство 8 является следствием свойств умножения и сопряжения. Поскольку y¯ (t) ↔Y¯ − m, из свойства 7 следует
(5.1-104) 1T∫ − T / 2T / 2x (t) y¯ (t) e − im ω0tdt = ∑n = −∞∞XnY ¯n − m
Установка m = 0 приводит к теореме Парсеваля, которая устанавливает эквивалентность внутреннего произведения во временной области и внутреннего произведения коэффициентов Фурье. Если y (t) = x (t), мы получаем аналог теоремы Планшерала, известный как тождество Парсеваля ,
(5.1-105) 1T∫ − T / 2T / 2 | x (t) | 2dt = ∑m = −∞∞ | Xm | 2
Это приравнивает средний квадрат x (t) к сумме квадратов его коэффициентов Фурье.Мы будем называть периодические сигналы интегрируемыми с квадратом, если их средний квадрат за период конечен.
Подводя итог, интеграл ряда Фурье, уравнение. (5.1-66) связывает периодический сигнал x (t) с уникальной последовательностью его коэффициентов Фурье. Тождество Парсеваля подразумевает, что каждый квадратично интегрируемый периодический сигнал имеет коэффициенты Фурье, суммируемые с квадратом. И наоборот, уравнения. Из (5.1-105) и (5.1-65) следует, что любая суммируемая с квадратом последовательность {Xn} связана с уникальным интегрируемым с квадратом периодическим сигналом.Устанавливая эквивалентность скалярных произведений интегрируемых с квадратом периодических сигналов и суммируемых с квадратом последовательностей, теорема Парсеваля утверждает, что геометрия этих двух пространств одинакова, т. Е. Они равны изометрии .
Набор всех квадратично интегрируемых периодических сигналов с периодом T образует линейное векторное пространство, известное как гильбертово пространство . Гильбертовые пространства — это бесконечномерные обобщения конечномерных векторных пространств со скалярными произведениями, которые определяют их геометрию.Гильбертово пространство H имеет бесконечный ортонормированный базис, {um} m = 1∞, такой, что каждый вектор x∈H может быть представлен суммой базисных векторов
(5.1-106) x = ∑m = 1∞ξmunandξm = 〈x, um〉
Скаляры, ξm, являются координатами x относительно базиса. Ортонормированность базисных векторов означает, что попарные скалярные произведения удовлетворяют
(5.1-107) 〈um, un〉 = {1m = n0m ≠ n
. Рассмотрим векторы x и y с координатами ξm и ηm соответственно. Тогда ортонормированность означает, что
(5.1-108) 〈x, y〉 = ∑m = 1∞ξmη¯m
Следовательно, если x = y, получаем
(5.1-109) ‖x‖2 = 〈x, x〉 = ∑m = 1∞ | ξm | 2
В контексте периодических сигналов, интегрируемых с квадратом, и рядов Фурье, ортонормированный базис равен {eim ω0t} m = −∞∞, а скалярное произведение двух сигналов x (t) и y (t), определяется как
(5.1-110) 〈x, y〉 = 1T∫ − T / 2T / 2x (t) y¯ (t) dt
Следовательно, коэффициенты ряда Фурье — это просто координаты периодического сигнала относительно орторнормального базиса, а ряд Фурье является представлением сигнала относительно этого базиса.Также обратите внимание, что в условиях гильбертова пространства теорема и тождество Парсеваля являются непосредственными следствиями (5.1-108) и (5.1-109) соответственно. Дополнительные сведения о гильбертовых пространствах см. В Reed and Simon, 1980; Рудин, 1973.
Пусть x (t) периодический сигнал с периодом, равным T. Мы исследуем связь между коэффициентом ряда Фурье x (t) и его преобразованием Фурье. Прежде всего отметим, что периодическая функция не является абсолютно интегрируемой, следовательно, ее преобразование Фурье определяется в смысле распределения, как мы обсуждали в предыдущем разделе.Начнем с представления x (t) как репликации периода T (Briggs and Henson, 1995) базового сигнала , x0 (t),
(5.1-111) x (t) = ℜT {x0 (t)} = ∑n = −∞∞x0 (t + nT)
Мы часто будем называть ℜ {x0 (t)} T -репликацией x0 (t). Обратите внимание, что операция репликации T производит сигнал, который является периодическим с периодом, равным T. Мы будем предполагать, что x0 (t) достаточно уменьшается при t → ± ∞, так что бесконечная сумма сходится. Обратите внимание, что x0 (t) не уникален.Например, рассмотрим функции y (t) и z (t),
(5.1-112) y (t) = {x (t) 0 Тогда мы могли бы определить x0 (t) как T -репликацию либо y (t), либо z (t). Затем мы устанавливаем связь между коэффициентом ряда Фурье x (t) и преобразованием Фурье x0 (t), т. Е. (5.1-113) Xm = 1T∫ − T / 2T / 2x (t) e − im ω0tdt, ω0 = 2πT = 1T∫ − T / 2T / 2 (∑n = −∞∞x0 (t + nT)) e − im ω0tdt = 1T∑n = −∞∞∫ − T / 2T / 2×0 (t + nT) e − im ω0tdt = 1T∑n = −∞∞eim ω0 (nT) ∫nT − T / 2nT + T / 2×0 (τ) e − im ω0τdτ = 1T∑n = −∞∞∫nT− T / 2nT + T / 2×0 (τ) e − im ω0τdτ = 1T∫ − ∞∞x0 (τ) e − im ω0τdτ = X0 (mω0) T Это замечательный результат, учитывая, что базовых сигналов бесконечно много. что может дать такую же репликацию T .Предположим, что x0 (t) и y0 (t) — два разных базовых сигнала с равными T -повторениями, (5.1-114) x (t) = ∑n = −∞∞x0 (t + nT) = ∑n = −∞∞y0 (t + nT) Поскольку x0 (t) ≠ y0 (t), их преобразования Фурье также не равны, т. Е. X0 (ω) ≠ Y0 (ω). Уравнение Из (5.1-113) следует, что, поскольку x0 (t) и y0 (t) имеют одинаковую репликацию T , их преобразования Фурье, хотя и разные, должны быть одинаковыми на дискретных частотах, ωm = mω0. Ур. (5.1-113) и разложение x (t) в ряд Фурье приводят нас к следующей интересной теореме: Теорема 5.7 (обратная формула суммирования Пуассона) Предположим, что для непрерывного сигнала времени x0 (t), ℜT {x0 (t)} сходится и является конечным. Пусть ω0 = 2π / T, тогда (5.1-115) ℜT {x0 (t)} = 1T∑m = −∞∞X0 (mω0) eim ω0t Приведенная выше теорема утверждает, что дискретное обратное преобразование Фурье X0 (ω) дает T -репликацию x0 (t). Мы обсудим двойную версию теоремы 5.7 в следующем разделе, посвященном дискретизации во временной области. Из пары преобразований Фурье eim ω0t↔2π δ (ω − mω0) и (5.1-115) следует, что x (t) имеет преобразование Фурье, (5.1-116) ℜT {x0 (t)} = 1T∑m = −∞∞X0 (mω0) eim ω0t↔ω0∑m = −∞∞X0 (mω0) δ (ω − mω0) Следовательно, уравнения. (5.1-115) и (5.1-116) приводят к (5.1-117) ℜT {x0 (t)} = ∑n = −∞∞x0 (t + nT) ↔ω0∑m = −∞∞X0 ( mω0) δ (ω − mω0) То есть репликация во временной области эквивалентна дискретизации преобразования Фурье в частотной области, где X0 (mω0) — значения выборки X0 (ω). Весь мир сигналов можно сгруппировать в классы, каждый из которых имеет важные свойства.Кроме того, у этих классов есть противоположные классы. Например, противоположностью непрерывного сигнала является дискретный сигнал. Сигнал может быть определен с использованием нескольких классов, если не используются два противоположных класса. Непрерывные и дискретные сигналы Непрерывные сигналы — это сигналы, для которых значение сигнала определяется в каждом временном интервале. Это очень похоже на сигналы, описанные в предыдущем разделе. Дискретные сигналы — это сигналы, для которых значение сигнала определяется только в дискретные моменты времени, например, может быть каждую секунду.График дискретного сигнала времени выглядит так: Дискретный сигнал времени (красные стрелки) и непрерывный сигнал времени (серая линия) [2] Существует важная математика, связанная с преобразованием между непрерывными и дискретными сигналами. Часто дискретизация используется для преобразования непрерывных сигналов, встречающихся в реальном мире, в дискретные сигналы, используемые при анализе сигналов. Изменение домена вашего сигнала, как и в случае преобразования из непрерывного в дискретный, часто используется при обработке сигналов. Детерминированные и недетерминированные сигналы Детерминированные сигналы — это сигналы, в которых нет неопределенности в их значении в любой момент времени. Любой сигнал, который можно определить с помощью математической формулы, такой как функция единичного шага, является детерминированным. Недетерминированные сигналы имеют элемент случайности в их значении и поэтому не могут быть определены с помощью какой-либо четко определенной математической формулы. Вместо этого они моделируются с использованием вероятностных формул. Четные и нечетные сигналы Сигнал считается даже если он удовлетворяет уравнению f (t) = f (−t) f (t) = f (-t) f (t) = f (−t). Другими словами, четные функции симметричны относительно оси yyy. Сигнал считается нечетным, если он удовлетворяет уравнению f (t) = — f (−t) f (t) = -f (-t) f (t) = — f (−t). Другими словами, относительно оси yyy сигнал отражается относительно оси xxx. Например, cos (t) \ cos (t) cos (t) — четный сигнал, а sin (t) \ sin (t) sin (t) — нечетный сигнал. Сигнал может быть четным или нечетным; или это не может быть ни то, ни другое, как большинство из них. Четный сигнал [3] Нечетный сигнал [3] Периодические и апериодические сигналы Сигнал является периодическим, если он удовлетворяет уравнению f (t) = f (t + T) f (t) = f (t + T) f (t) = f (t + T), где TTT — основное время период. На самом деле это означает, что если сигнал f (t) f (t) f (t) повторяется каждый раз в TTT, он является периодическим. Апериодическая функция не повторяется.Примером сигнала периода является любой синусоидальный сигнал, такой как cos (x) \ cos (x) cos (x). Примером апериодического сигнала является единичный импульсный сигнал. Он сигнализирует об импульсе на f (0) f (0) f (0), но потом ничего. Реальные и мнимые сигналы Сигнал является реальным, если в каждый момент времени его значение на 100% реально, а мнимая часть равна нулю. И наоборот, сигнал является мнимым, если его значение является мнимым в каждый момент времени. Если независимая переменная ( t ) является непрерывной, то соответствующий сигнал является непрерывным сигналом времени. Если независимая переменная ( t ) принимает только дискретные значения, например t = ± 1, ± 2, ± 3, … Если преобразованный сигнал такой же, как x (t), то сигнал периодический. где T — основной период (наименьший период) сигнала x (t) В дискретном времени периодический сигнал; Каждый компонентный сигнал не имеет отношения к другим. Одной из характеристик сигнала является симметрия, которая может быть полезна для анализа сигнала. Четные сигналы симметричны относительно вертикальной оси, а нечетные сигналы симметричны относительно начала координат. Четный сигнал: Нечетный сигнал: Используя определение четного и нечетного сигнала, любой сигнал может быть разложен на сумму его четной части x e (t) и нечетной части x o (t) следующим образом: Это важный факт, потому что это относительное понятие ряда Фурье. В рядах Фурье периодический сигнал можно разбить на сумму синусоидальных и косинусных сигналов. Обратите внимание, что функция синуса является нечетным сигналом, а функция косинуса — четным сигналом. В физике энергия составляет работы , а мощность — работы за раз ; Для кинетической энергии определяется выражением В электрическом сигнале определяется мгновенная мощность для напряжения на сопротивлении R и его энергия; При обработке сигналов полная энергия сигнала x (t) определяется аналогичным образом; И он также возведен в квадрат из-за общего соглашения об использовании аналогичной терминологии для любого сигнала ( см. Определения кинетической и электрической энергии сигнала ). Следовательно, энергия сигнала определяется как сумма квадратов величины. Средняя мощность сигнала определяется величиной; Сигнал может быть разделен на сигнал энергии или сигнал мощности: сигнал энергии имеет конечную энергию, 0 Напротив, сигнал мощности не ограничен по времени. Он всегда существует от начала до конца и никогда не заканчивается. Например, синусоидальная волна бесконечной длины является сигналом мощности.Поскольку энергия сигнала мощности бесконечна, он не имеет для нас значения. Таким образом, мы используем мощность (энергию в данное время) для сигнала мощности, потому что мощность сигнала мощности конечна, 0 1) 2) . Сигналы и системы | Блестящая вики по математике и науке
сигналов
Непрерывный сигнал времени
Дискретный сигнал времени
Периодический сигнал
Ортогональный сигнал
Ортогональный сигнал обозначается как φ (t). Четный и нечетный сигнал
Сигнал называется сигналом, даже если он идентичен своим обратным во времени аналогам; х (т) = х (-t).
Сигнал является нечетным, если x (t) = -x (-t).
Нечетный сигнал должен быть равен 0 при t = 0, другими словами, нечетный сигнал проходит источник. Пример
Сигнал энергии и сигнал мощности
Работа = Сила × Смещение
Мощность = Работа / Время
(Обратите внимание, что это квадрат абсолютного значения.)
,
где | x (т) | обозначает величину x (t). Для комплексного сигнала необходимо получить скалярную величину, поскольку величина комплексного числа определяется как. Примеры
E = 1, и, Энергетический сигнал.
E = ∞, и, ∴ Сигнал мощности.



 Этот процесс
Этот процесс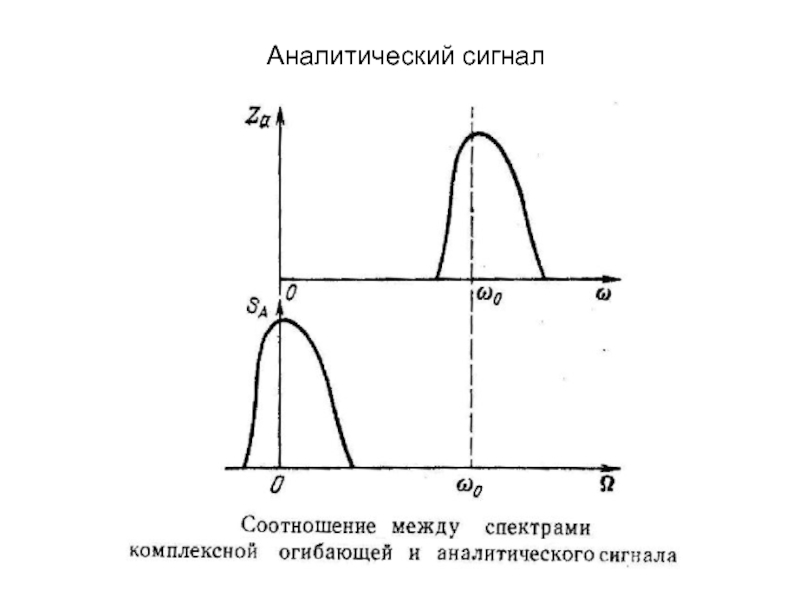

 Д.
Д.