Таблица КОСИНУСОВ для углов от 0° до 360° градусов
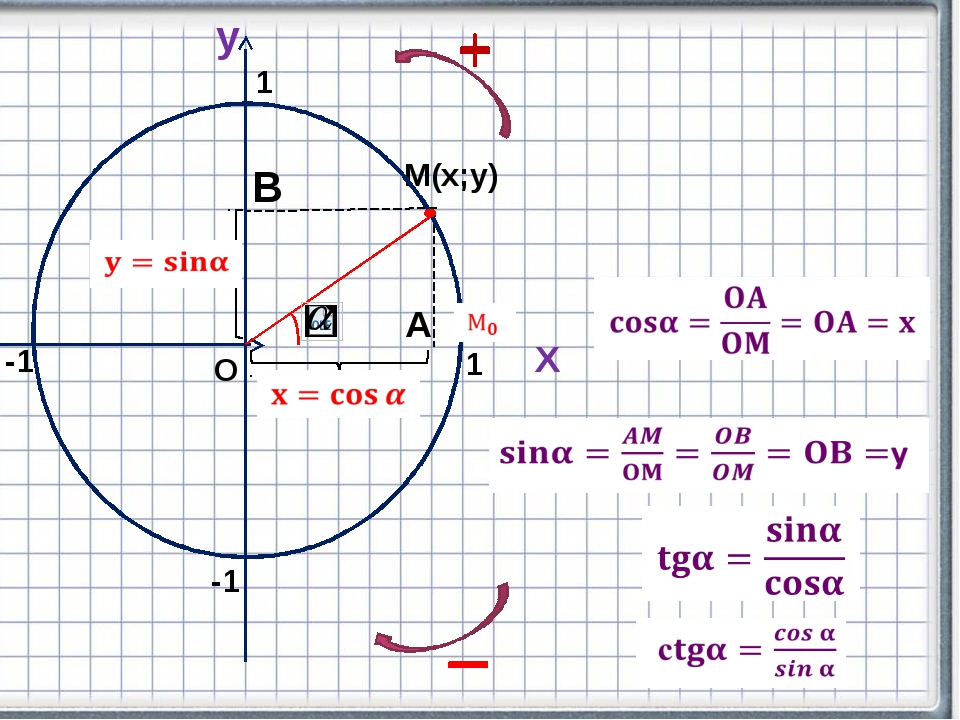
КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…
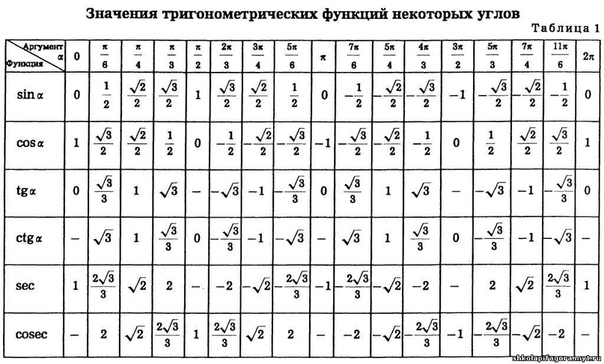
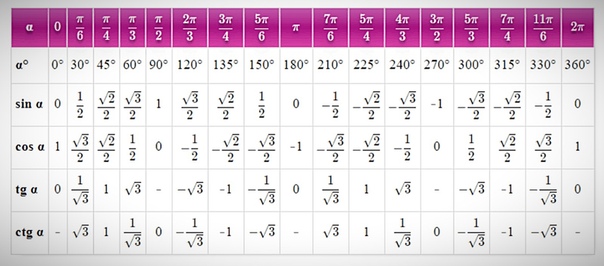
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos α (Косинус) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
…
| Угол в градусах | Cos (Косинус) |
|---|---|
| 0° | 1 |
| 1° | 0.9998 |
| 2° | 0.9994 |
| 3° | 0.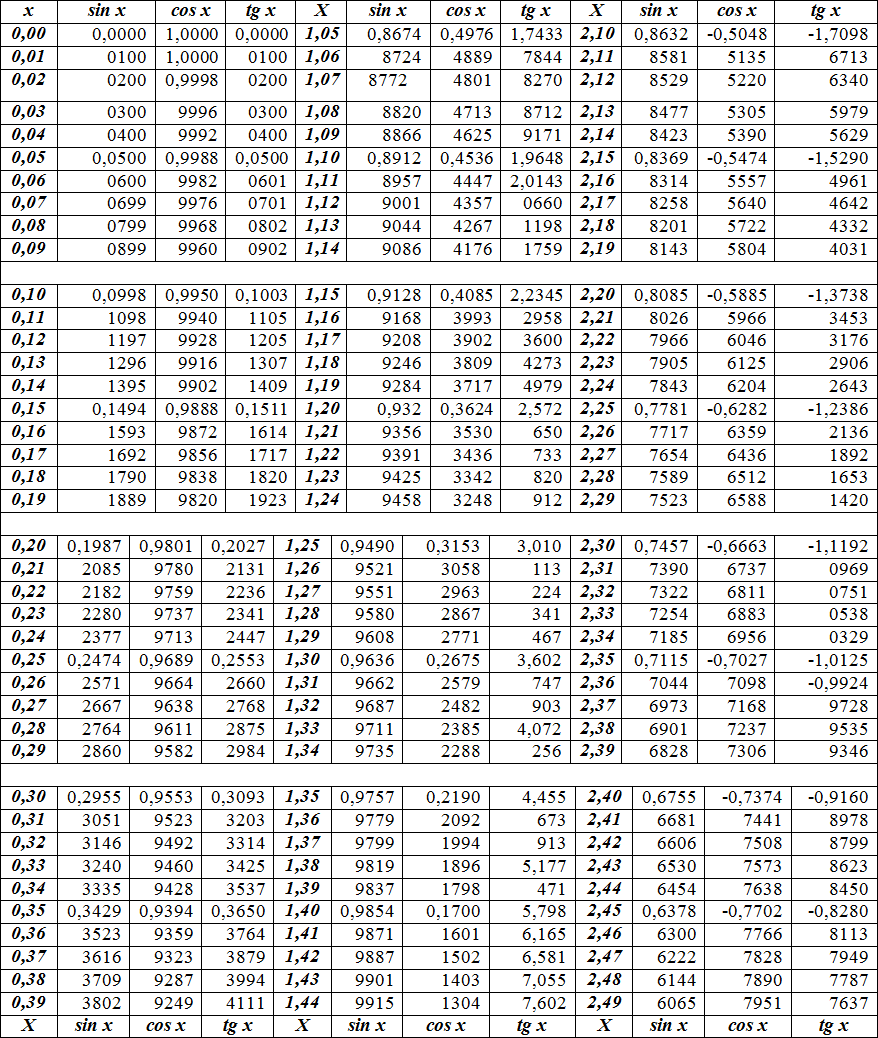 9986 9986 |
| 4° | 0.9976 |
| 5° | 0.9962 |
| 6° | 0.9945 |
| 7° | 0.9925 |
| 8° | 0.9903 |
| 9° | 0.9877 |
| 10° | 0.9848 |
| 11° | 0.9816 |
| 12° | 0.9781 |
| 13° | 0.9744 |
| 14° | 0.9703 |
| 15° | 0.9659 |
| 16° | 0.9613 |
| 17° | 0.9563 |
| 18° | 0.9511 |
| 19° | 0.9455 |
| 20° | 0.9397 |
| 21° | 0.9336 |
| 22° | 0.9272 |
| 23° | 0.9205 |
| 24° | 0.9135 |
| 25° | 0.9063 |
| 26° | 0.8988 |
| 27° | 0.891 |
| 28° | 0.8829 |
| 29° | 0.8746 |
| 30° | 0. 866 866 |
| 31° | 0.8572 |
| 32° | 0.848 |
| 33° | 0.8387 |
| 34° | 0.829 |
| 35° | 0.8192 |
| 36° | 0.809 |
| 37° | 0.7986 |
| 38° | 0.788 |
| 39° | 0.7771 |
| 40° | 0.766 |
| 41° | 0.7547 |
| 42° | 0.7431 |
| 43° | 0.7314 |
| 44° | 0.7193 |
| 45° | 0.7071 |
| 46° | 0.6947 |
| 47° | 0.682 |
| 48° | 0.6691 |
| 49° | 0.6561 |
| 50° | 0.6428 |
| 51° | 0.6293 |
| 52° | 0.6157 |
| 53° | 0.6018 |
| 54° | 0.5878 |
| 55° | 0.5736 |
| 56° | 0.5592 |
| 57° | 0.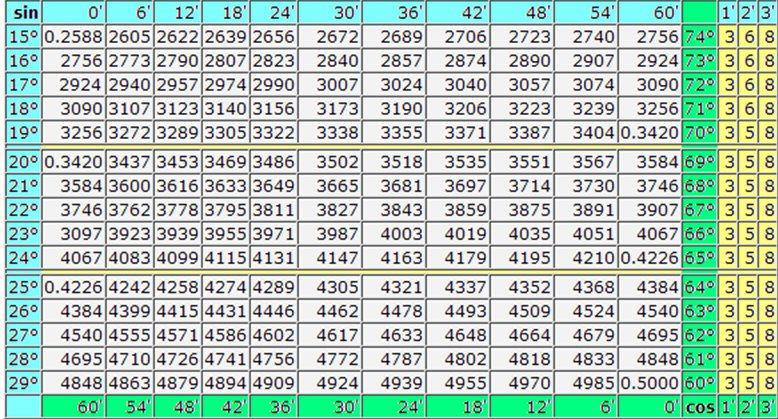 5446 5446 |
| 58° | 0.5299 |
| 59° | 0.515 |
| 60° | 0.5 |
| 61° | 0.4848 |
| 62° | 0.4695 |
| 63° | 0.454 |
| 64° | 0.4384 |
| 65° | 0.4226 |
| 66° | 0.4067 |
| 67° | 0.3907 |
| 68° | 0.3746 |
| 69° | 0.3584 |
| 70° | 0.342 |
| 71° | 0.3256 |
| 72° | 0.309 |
| 73° | 0.2924 |
| 74° | 0.2756 |
| 75° | 0.2588 |
| 76° | 0.2419 |
| 77° | 0.225 |
| 78° | 0.2079 |
| 79° | 0.1908 |
| 80° | 0.1736 |
| 81° | 0.1564 |
| 82° | 0.1392 |
| 83° | 0.1219 |
| 84° | 0.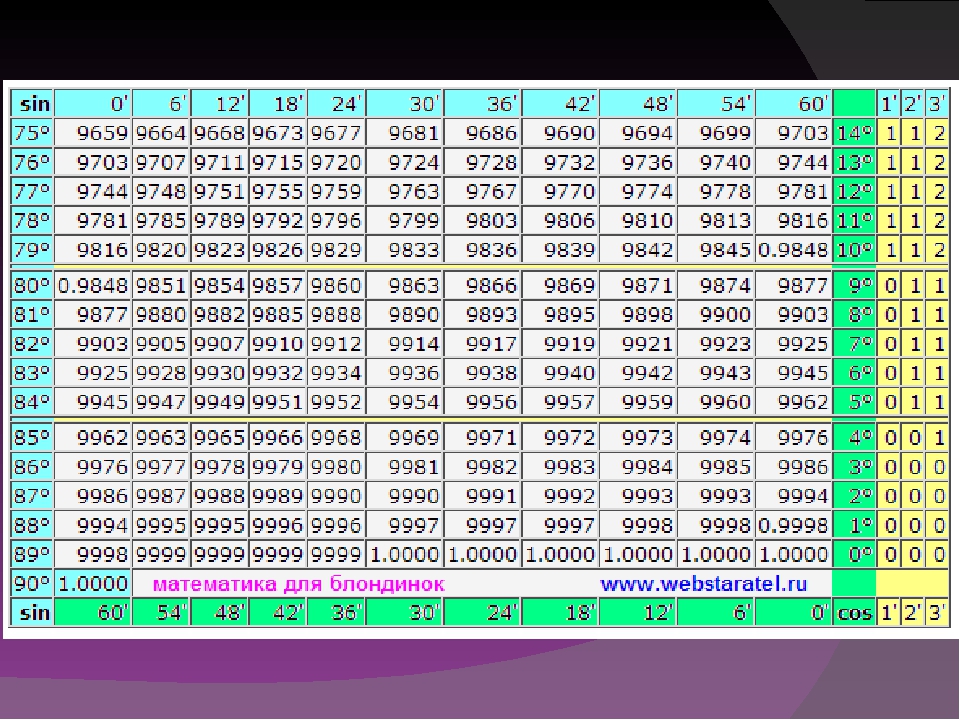 1045 1045 |
| 85° | 0.0872 |
| 86° | 0.0698 |
| 87° | 0.0523 |
| 88° | 0.0349 |
| 89° | 0.0175 |
| 90° | 0 |
…
| Угол | cos (Косинус) |
|---|---|
| 91° | -0.0175 |
| 92° | -0.0349 |
| 93° | -0.0523 |
| 94° | -0.0698 |
| 95° | -0.0872 |
| 96° | -0.1045 |
| 97° | -0.1219 |
| 98° | -0.1392 |
| 99° | -0.1564 |
| 100° | -0.1736 |
| 101° | -0.1908 |
| 102° | -0.2079 |
| 103° | -0.225 |
| 104° | -0.2419 |
| 105° | -0.2588 |
| 106° | -0.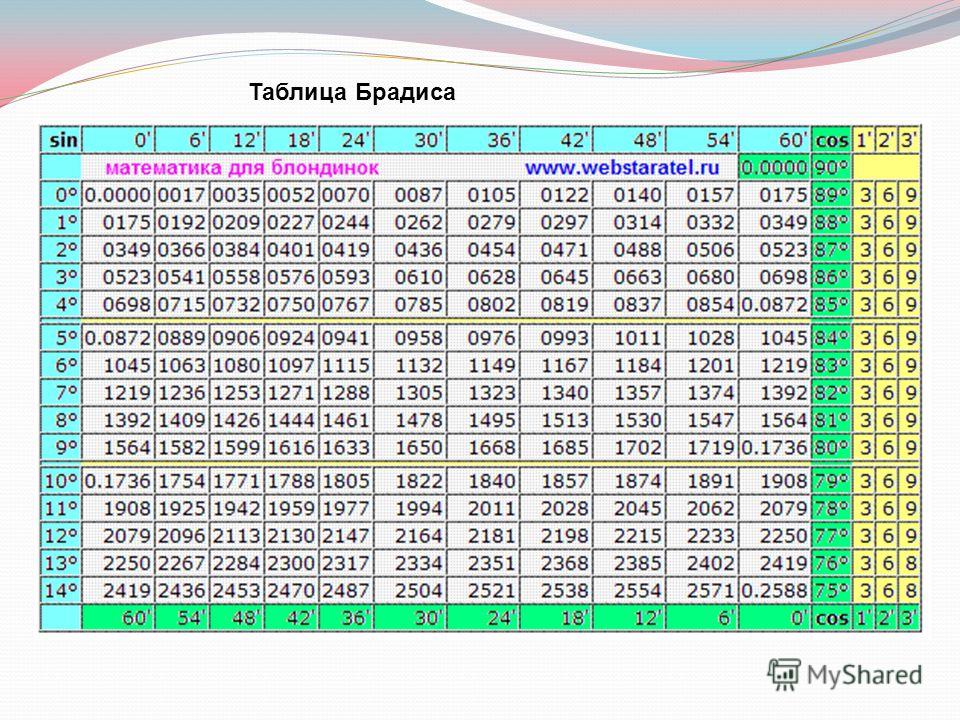 2756 2756 |
| 107° | -0.2924 |
| 108° | -0.309 |
| 109° | -0.3256 |
| 110° | -0.342 |
| 111° | -0.3584 |
| 112° | -0.3746 |
| 113° | -0.3907 |
| 114° | -0.4067 |
| 115° | -0.4226 |
| 116° | -0.4384 |
| 117° | -0.454 |
| 118° | -0.4695 |
| 119° | -0.4848 |
| 120° | -0.5 |
| 121° | -0.515 |
| 122° | -0.5299 |
| 123° | -0.5446 |
| 124° | -0.5592 |
| 125° | -0.5736 |
| 126° | -0.5878 |
| 127° | -0.6018 |
| 128° | -0.6157 |
| 129° | -0.6293 |
| 130° | -0.6428 |
| 131° | -0.6561 |
| 132° | -0.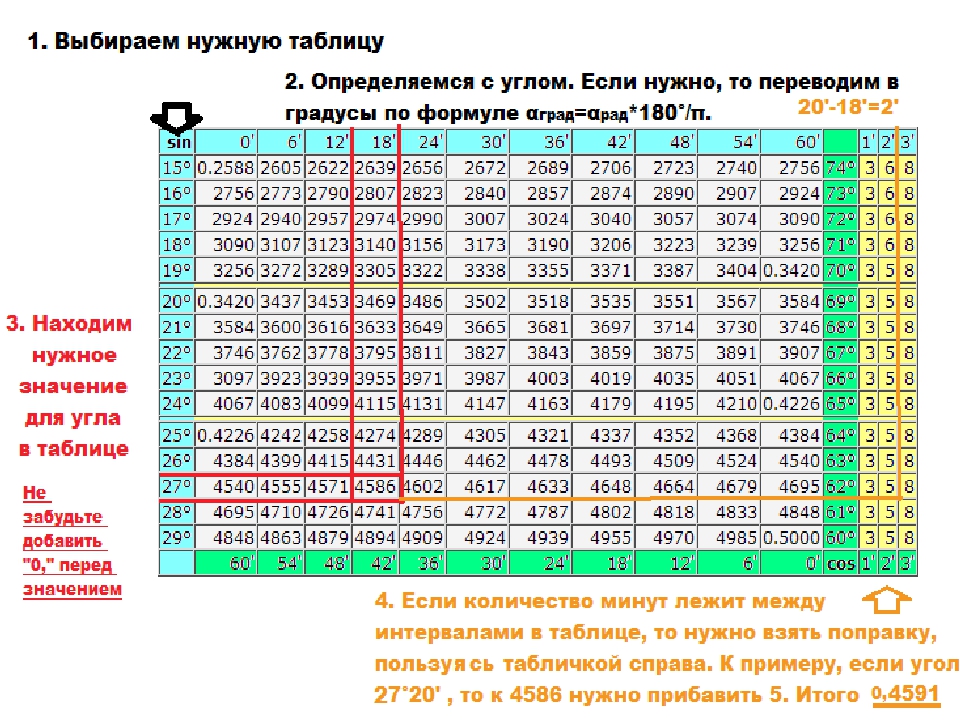 6691 6691 |
| 133° | -0.682 |
| 134° | -0.6947 |
| 135° | -0.7071 |
| 136° | -0.7193 |
| 137° | -0.7314 |
| 138° | -0.7431 |
| 139° | -0.7547 |
| 140° | -0.766 |
| 141° | -0.7771 |
| 142° | -0.788 |
| 143° | -0.7986 |
| 144° | -0.809 |
| 145° | -0.8192 |
| 146° | -0.829 |
| 147° | -0.8387 |
| 148° | -0.848 |
| 149° | -0.8572 |
| 150° | -0.866 |
| 151° | -0.8746 |
| 152° | -0.8829 |
| 153° | -0.891 |
| 154° | -0.8988 |
| 155° | -0.9063 |
| 156° | -0.9135 |
| 157° | -0.9205 |
| 158° | -0.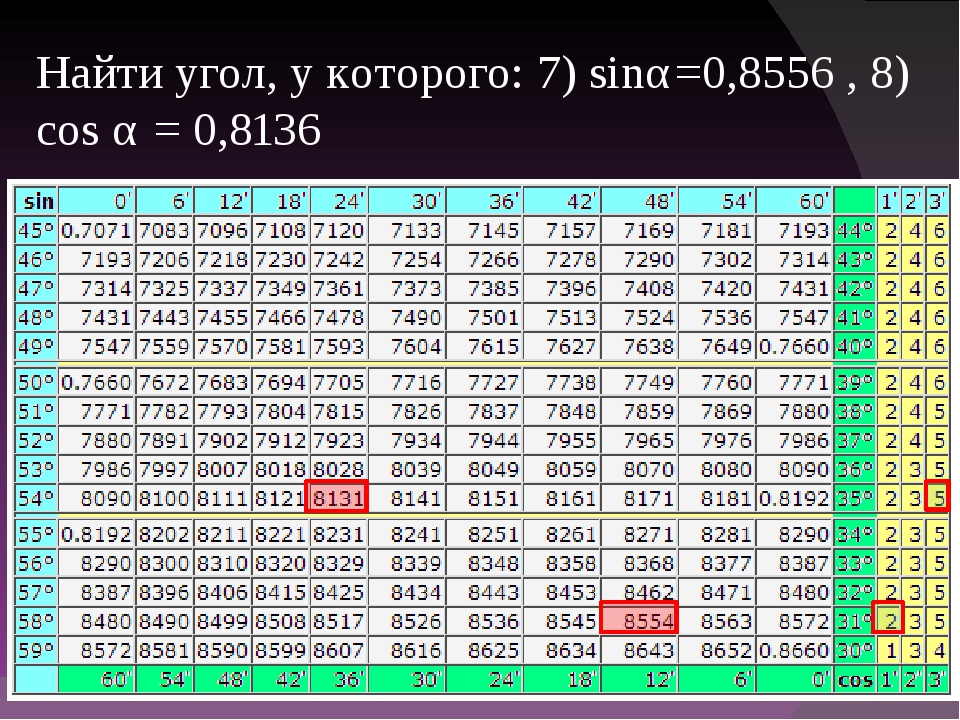 9272 9272 |
| 159° | -0.9336 |
| 160° | -0.9397 |
| 161° | -0.9455 |
| 162° | -0.9511 |
| 163° | -0.9563 |
| 164° | -0.9613 |
| 165° | -0.9659 |
| 166° | -0.9703 |
| 167° | -0.9744 |
| 168° | -0.9781 |
| 169° | -0.9816 |
| 170° | -0.9848 |
| 171° | -0.9877 |
| 172° | -0.9903 |
| 173° | -0.9925 |
| 174° | -0.9945 |
| 175° | -0.9962 |
| 176° | -0.9976 |
| 177° | -0.9986 |
| 178° | -0.9994 |
| 179° | -0.9998 |
| 180° | -1 |
…
| Угол | cos (косинус) |
|---|---|
| 181° | -0. 9998 9998 |
| 182° | -0.9994 |
| 183° | -0.9986 |
| 184° | -0.9976 |
| 185° | -0.9962 |
| 186° | -0.9945 |
| 187° | -0.9925 |
| 188° | -0.9903 |
| 189° | -0.9877 |
| 190° | -0.9848 |
| 191° | -0.9816 |
| 192° | -0.9781 |
| 193° | -0.9744 |
| 194° | -0.9703 |
| 195° | -0.9659 |
| 196° | -0.9613 |
| 197° | -0.9563 |
| 198° | -0.9511 |
| 199° | -0.9455 |
| 200° | -0.9397 |
| 201° | -0.9336 |
| 202° | -0.9272 |
| 203° | -0.9205 |
| 204° | -0.9135 |
| 205° | -0.9063 |
| 206° | -0.8988 |
| 207° | -0. 891 891 |
| 208° | -0.8829 |
| 209° | -0.8746 |
| 210° | -0.866 |
| 211° | -0.8572 |
| 212° | -0.848 |
| 213° | -0.8387 |
| 214° | -0.829 |
| 215° | -0.8192 |
| 216° | -0.809 |
| 217° | -0.7986 |
| 218° | -0.788 |
| 219° | -0.7771 |
| 220° | -0.766 |
| 221° | -0.7547 |
| 222° | -0.7431 |
| 223° | -0.7314 |
| 224° | -0.7193 |
| 225° | -0.7071 |
| 226° | -0.6947 |
| 227° | -0.682 |
| 228° | -0.6691 |
| 229° | -0.6561 |
| 230° | -0.6428 |
| 231° | -0.6293 |
| 232° | -0.6157 |
| 233° | -0. 6018 6018 |
| 234° | -0.5878 |
| 235° | -0.5736 |
| 236° | -0.5592 |
| 237° | -0.5446 |
| 238° | -0.5299 |
| 239° | -0.515 |
| 240° | -0.5 |
| 241° | -0.4848 |
| 242° | -0.4695 |
| 243° | -0.454 |
| 244° | -0.4384 |
| 245° | -0.4226 |
| 246° | -0.4067 |
| 247° | -0.3907 |
| 248° | -0.3746 |
| 249° | -0.3584 |
| 250° | -0.342 |
| 251° | -0.3256 |
| 252° | -0.309 |
| 253° | -0.2924 |
| 254° | -0.2756 |
| 255° | -0.2588 |
| 256° | -0.2419 |
| 257° | -0.225 |
| 258° | -0.2079 |
| 259° | -0. 1908 1908 |
| 260° | -0.1736 |
| 261° | -0.1564 |
| 262° | -0.1392 |
| 263° | -0.1219 |
| 264° | -0.1045 |
| 265° | -0.0872 |
| 266° | -0.0698 |
| 267° | -0.0523 |
| 268° | -0.0349 |
| 269° | -0.0175 |
| 270° | 0 |
…
| Угол | Cos (Косинус) |
|---|---|
| 271° | 0.0175 |
| 272° | 0.0349 |
| 273° | 0.0523 |
| 274° | 0.0698 |
| 275° | 0.0872 |
| 276° | 0.1045 |
| 277° | 0.1219 |
| 278° | 0.1392 |
| 279° | 0.1564 |
| 280° | 0.1736 |
| 281° | 0. 1908 1908 |
| 282° | 0.2079 |
| 283° | 0.225 |
| 284° | 0.2419 |
| 285° | 0.2588 |
| 286° | 0.2756 |
| 287° | 0.2924 |
| 288° | 0.309 |
| 289° | 0.3256 |
| 290° | 0.342 |
| 291° | 0.3584 |
| 292° | 0.3746 |
| 293° | 0.3907 |
| 294° | 0.4067 |
| 295° | 0.4226 |
| 296° | 0.4384 |
| 297° | 0.454 |
| 298° | 0.4695 |
| 299° | 0.4848 |
| 300° | 0.5 |
| 301° | 0.515 |
| 302° | 0.5299 |
| 303° | 0.5446 |
| 304° | 0.5592 |
| 305° | 0.5736 |
| 306° | 0.5878 |
| 307° | 0. 6018 6018 |
| 308° | 0.6157 |
| 309° | 0.6293 |
| 310° | 0.6428 |
| 311° | 0.6561 |
| 312° | 0.6691 |
| 313° | 0.682 |
| 314° | 0.6947 |
| 315° | 0.7071 |
| 316° | 0.7193 |
| 317° | 0.7314 |
| 318° | 0.7431 |
| 319° | 0.7547 |
| 320° | 0.766 |
| 321° | 0.7771 |
| 322° | 0.788 |
| 323° | 0.7986 |
| 324° | 0.809 |
| 325° | 0.8192 |
| 326° | 0.829 |
| 327° | 0.8387 |
| 328° | 0.848 |
| 329° | 0.8572 |
| 330° | 0.866 |
| 331° | 0.8746 |
| 332° | 0.8829 |
| 333° | 0. 891 891 |
| 334° | 0.8988 |
| 335° | 0.9063 |
| 336° | 0.9135 |
| 337° | 0.9205 |
| 338° | 0.9272 |
| 339° | 0.9336 |
| 340° | 0.9397 |
| 341° | 0.9455 |
| 342° | 0.9511 |
| 343° | 0.9563 |
| 344° | 0.9613 |
| 345° | 0.9659 |
| 346° | 0.9703 |
| 347° | 0.9744 |
| 348° | 0.9781 |
| 349° | 0.9816 |
| 350° | 0.9848 |
| 351° | 0.9877 |
| 352° | 0.9903 |
| 353° | 0.9925 |
| 354° | 0.9945 |
| 355° | 0.9962 |
| 356° | 0.9976 |
| 357° | 0.9986 |
| 358° | 0.9994 |
| 359° | 0. 9998 9998 |
| 360° | 1 |
…
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Пример
Чему равен косинус 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.866
Автор: Bill4iam
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град.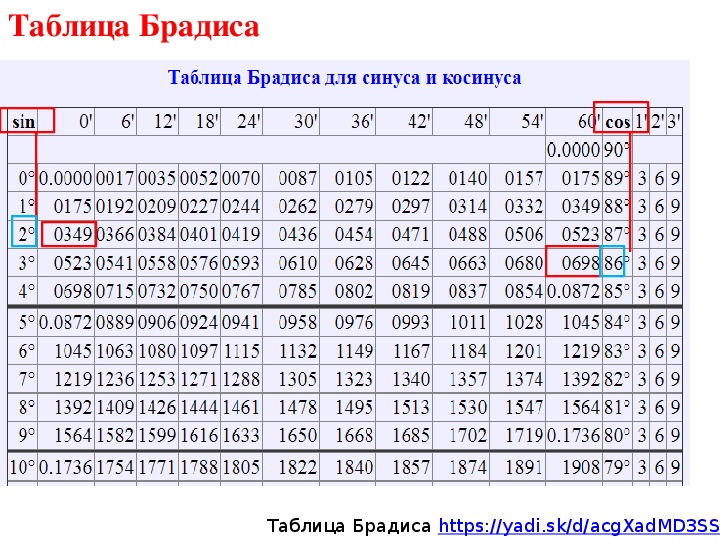 ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.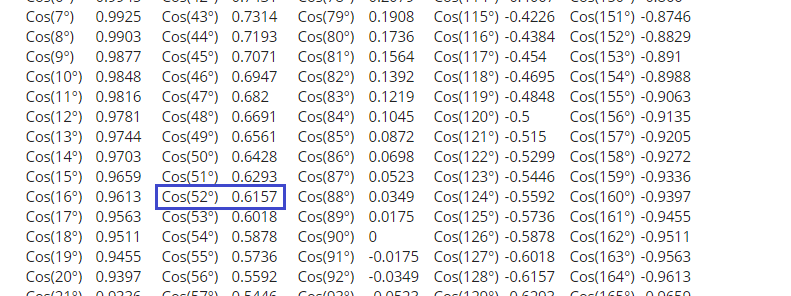 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.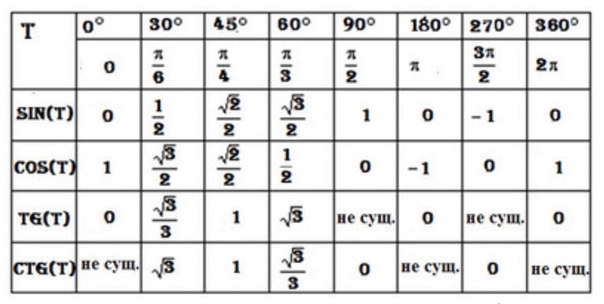 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.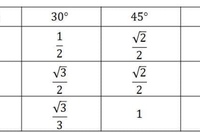 ) ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град.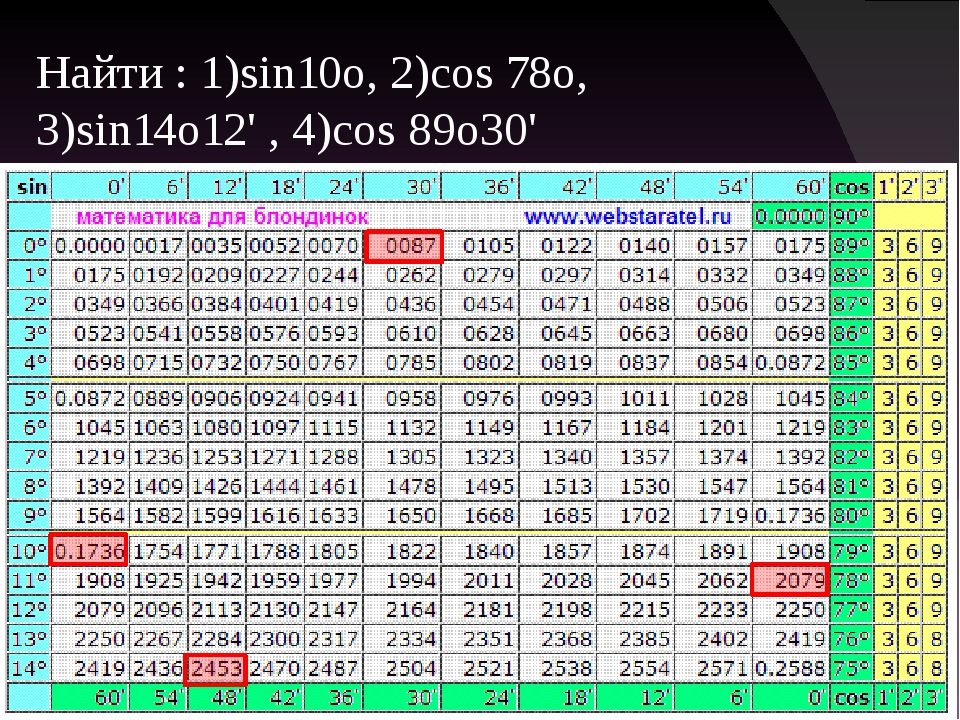 ) ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
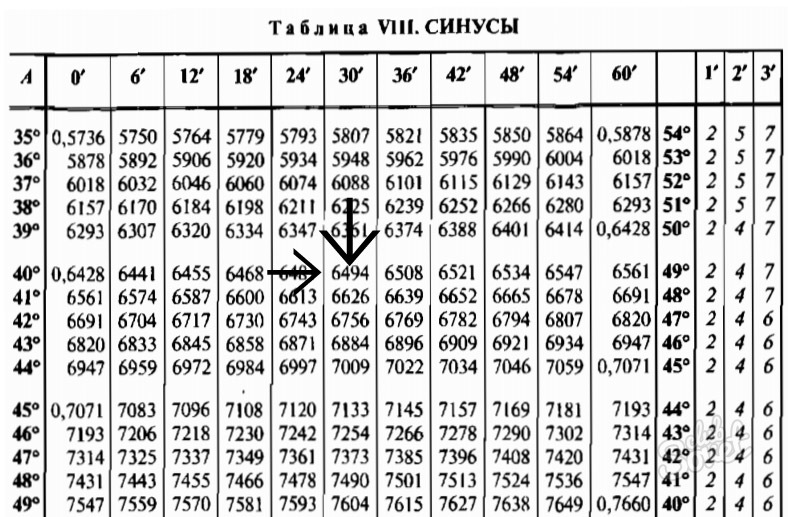
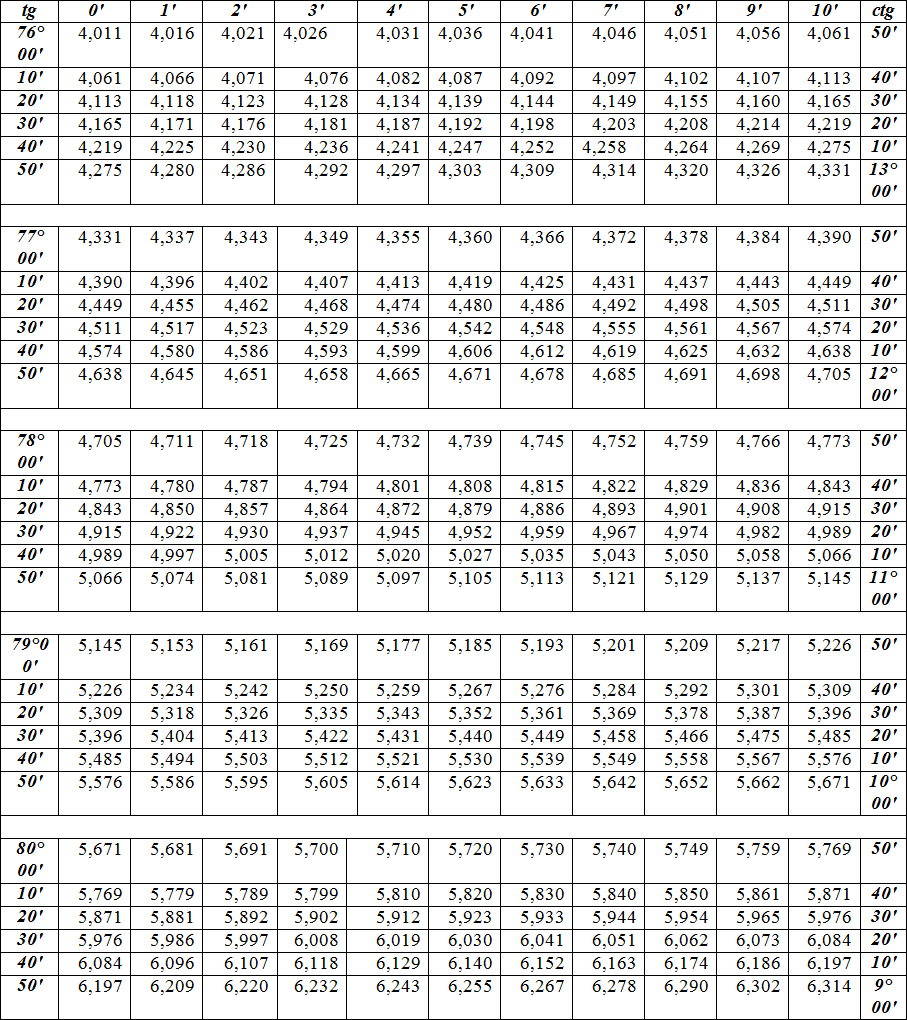
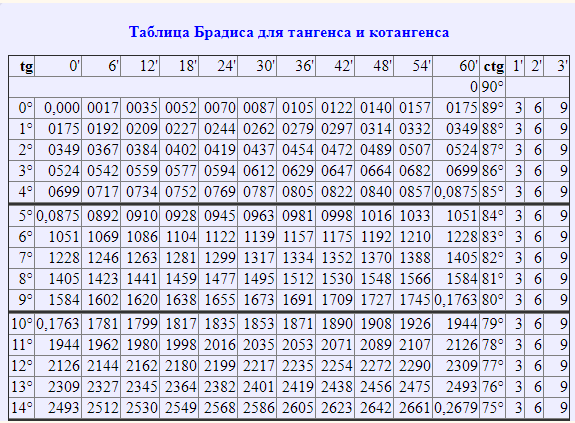
Таблица Брадиса sin cos tg ctg
Калькулятор поможет рассчитать точные значения тригонометрических функций sin, cos, tg и ctg для различных значений углов в градусах или радианах.
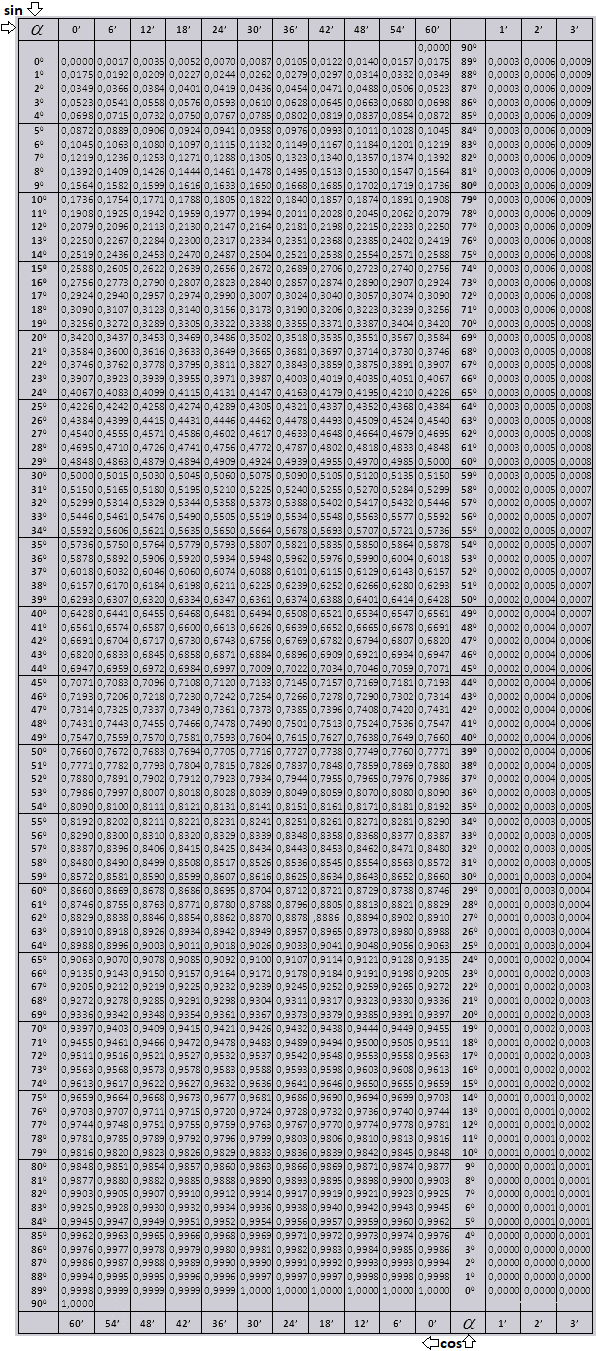
На данной странице таблица Брадиса, которая дает значение sin, cos, tg, ctg любого острого угла, содержащего целое число градусов и десятых долей градуса.
Для нахождения значения угла берется число на пересечении строки, которое соответствует числу градусов и столбца, которое соответствует числу минут. Например, sin 70°30′ = 0.9426.
Найти точное значение
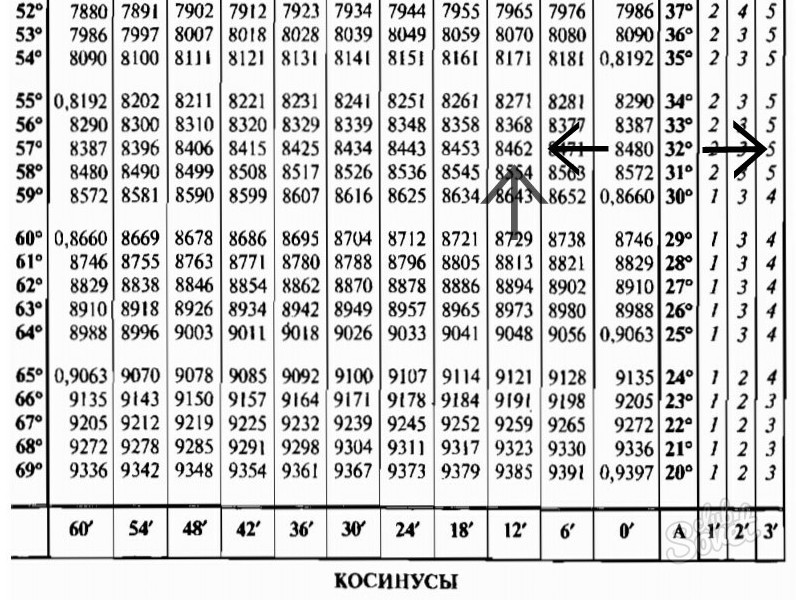
Таблица Брадиса sin, cos
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 0 | 90° | ||||||||||||||
| 0° | 0,0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0872 | 85° | 3 | 6 | 9 |
| 5° | 0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 1736 | 80° | 3 | 6 | 9 |
| 10° | 1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 2588 | 75° | 3 | 6 | 8 |
| 15° | 2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 3420 | 70° | 3 | 5 | 8 |
| 20° | 3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 4226 | 65° | 3 | 5 | 8 |
| 25° | 4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 5000 | 60° | 3 | 5 | 8 |
| 30° | 5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 5736 | 55° | 2 | 5 | 7 |
| 35° | 5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 6428 | 50° | 2 | 4 | 7 |
| 40° | 6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 6909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 7071 | 45° | 2 | 4 | 6 |
| 45° | 7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 7660 | 40° | 2 | 4 | 6 |
| 50° | 7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 8192 | 35° | 2 | 3 | 5 |
| 55° | 8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 8660 | 30° | 1 | 3 | 4 |
| 60° | 8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 9063 | 25° | 1 | 3 | 4 |
| 65° | 9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9265 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9385 | 9391 | 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | ||||
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 9848 | 10° | 1 | 1 | 2 |
| 80° | 9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.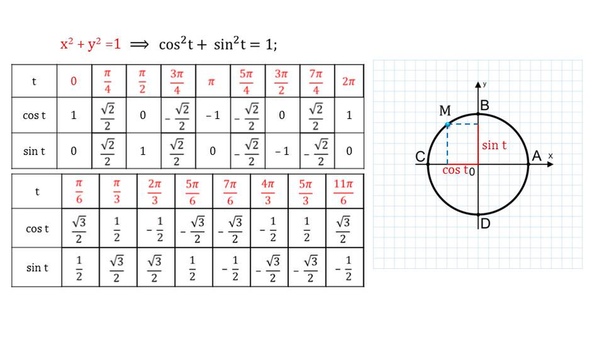 0 0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0° | 0 | 0 | 0 |
| 90° | 1 | ||||||||||||||
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos |
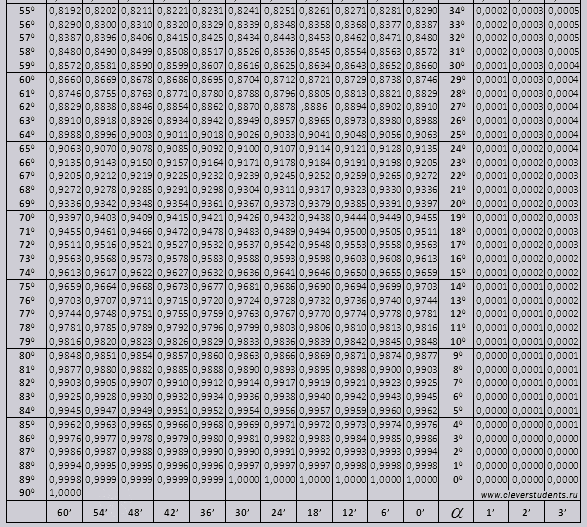
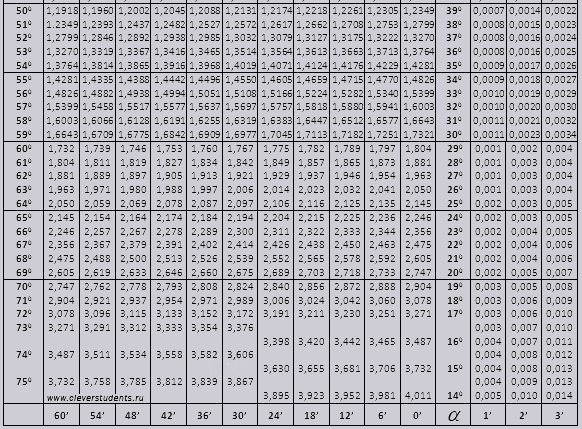
Таблица Брадиса tg, ctg
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | ||||
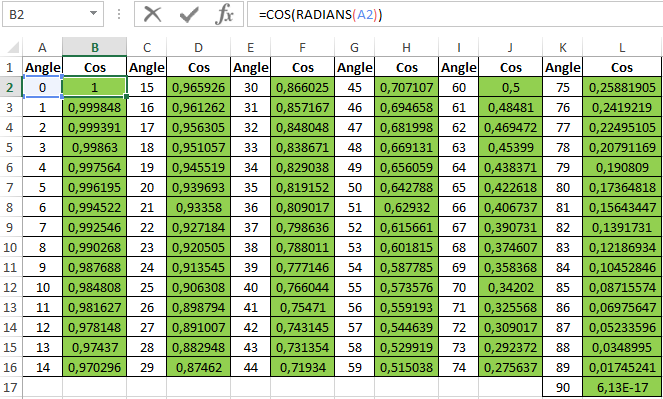
Функция COS
В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.
Описание
Возвращает косинус заданного угла.
Синтаксис
COS(число)
Аргументы функции COS описаны ниже.
Замечания
Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
|
|
|
|
=COS(1,047)
|
Косинус 1,047 радиан
|
0,5001711
|
|
=COS(60*ПИ()/180)
|
Косинус 60 градусов
|
0,5
|
|
=COS(РАДИАНЫ(60))
|
Косинус 60 градусов
|
0,5
|
Cos 0 — значение, объяснение и ответы на часто задаваемые вопросы
Cos 0 Значение градуса
Cos 0 равно 1 (Cos 0 = 1).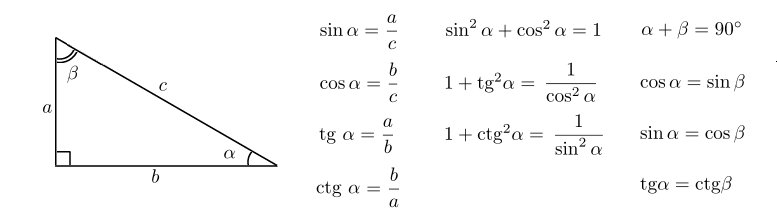 Другими словами, значение Cos 0 равно 1. Теперь вопрос в том, как было получено значение Cos 0. Значение может быть определено с помощью квадрантов единичного круга. Этот процесс обсуждается в следующем разделе.
Другими словами, значение Cos 0 равно 1. Теперь вопрос в том, как было получено значение Cos 0. Значение может быть определено с помощью квадрантов единичного круга. Этот процесс обсуждается в следующем разделе.
Как вы уже знаете, тригонометрические функции относятся к угловым функциям, которые связывают углы треугольника. Для изучения периодических явлений световых и звуковых волн использовались тригонометрические функции.Эти функции также важны для изучения гармонических колебаний и вариаций средней температуры.
Формула для нахождения косинуса
Функция косинуса угла подчиняется определенной формуле. Согласно этой формуле значение функции косинуса угла равно длине прилежащей стороны, деленной на длину стороны гипотенузы. Формула написана ниже.
Cos X = \[\frac{\text{Смежная сторона}}{\text{Сторона гипотенузы}}\]
Как найти значение Cos 0?
Существует три основных тригонометрических соотношения: функция синуса, функция косинуса и функция тангенса. С помощью функций sin, cos и tan можно вычислить углы треугольника.
С помощью функций sin, cos и tan можно вычислить углы треугольника.
Чтобы понять функцию косинуса острого угла, нужно нарисовать на листе бумаги прямоугольный треугольник. Треугольник, очевидно, имеет три стороны, и эти стороны можно определить следующим образом:
Выберите угол треугольника, и противоположная сторона выбранного угла будет называться «противоположная сторона».
Сторона треугольника, расположенная напротив прямого угла, называется стороной гипотенузы.Примечательно, что это самая длинная сторона прямоугольного треугольника.
Наконец, «прилежащая сторона» относится к оставшейся стороне треугольника.
Определение значения Cos 0 с помощью единичного круга
Используя единичный круг, можно получить значение «Cos 0».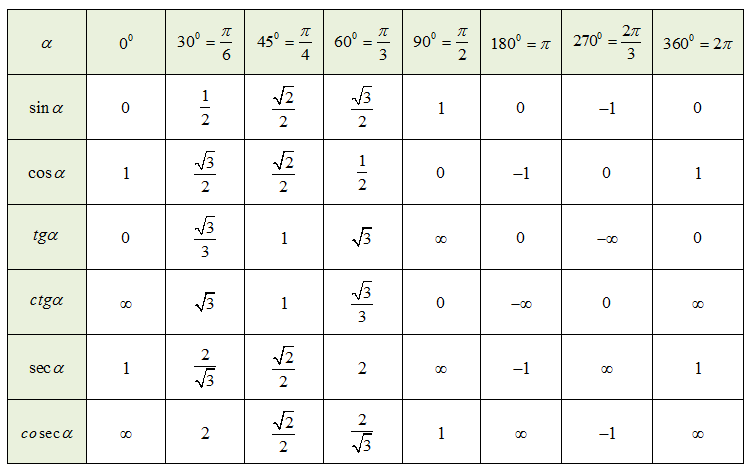 Процесс начинается с принятия единичной окружности, центр которой совпадает с началом осей координат.
Процесс начинается с принятия единичной окружности, центр которой совпадает с началом осей координат.
Что такое Cos 0 ?
Значение косинуса прямоугольного треугольника с углом 0° известно как косинус угла 0°.Косинус угла 0° — это величина, обозначающая остаток длины прилежащей стороны от длины гипотенузы, если угол прямоугольного треугольника равен 0°.
В шестидесятеричной системе косинус угла, равный нулю, математически выражается как косинус 0°, а точное значение косинуса угла 0° = 1 . Таким образом, математически это записывается в следующей форме в тригонометрии, т. е. cos 0 ° = 1
. Мы также можем выразить косинус угла ноль градусов в двух других формах в тригонометрической математике, т.е.круговая система и сотенная система.
Cos 0 в круговой системе
В круговой системе косинус нуля градусов математически представляется как косинус нуля радиан. Это записывается в следующей форме в круговой системе cos (0) = 1
Cos 0 в сотенной системе
Аналогично, в сотенной системе косинус нуля градусов математически представляется как косинус нулевого градуса степени. 9) = 1
9) = 1
Cos 9 градусов — Найдите значение Cos 9 градусов
Значение cos 9 градусов равно 0.9876883. . . . Cos 9 градусов в радианах записывается как cos (9° × π/180°), т. е. cos (π/20) или cos (0,157079…). В этой статье мы обсудим способы нахождения значения cos 9 градусов на примерах.
- Cos 9°: 0,9876883. . .
- Cos (-9 градусов): 0,9876883. . .
- Cos 9° в радианах: cos (π/20) или cos (0,1570796 . . .)
Каково значение Cos 9 градусов?
Значение cos 9 градусов в десятичной системе равно 0.987688340. . .. Cos 9 градусов также можно выразить с помощью эквивалента заданного угла (9 градусов) в радианах (0,15707 . . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/180°)
⇒ 9 градусов = 9° × (π/180°) рад = π/20 или 0,1570. . .
∴ cos 9 ° = cos (0,1570) = 0,9876883.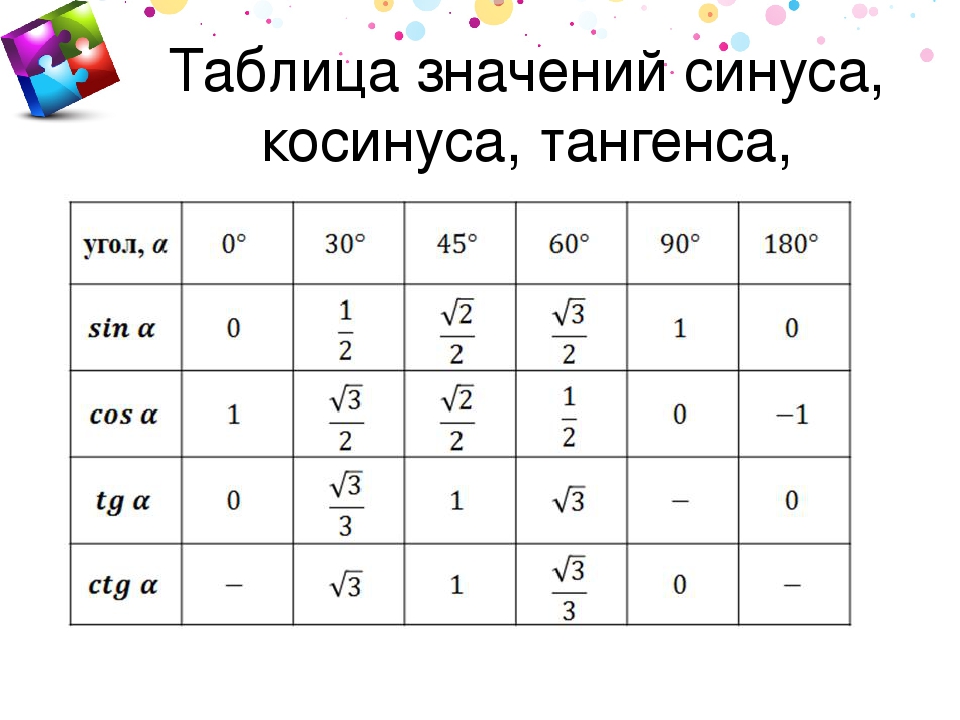 . .
. .
Объяснение:
Для cos 9 градусов угол 9° лежит между 0° и 90° (первый квадрант). Поскольку функция косинуса положительна в первом квадранте, значение cos 9° = 0.9876883. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 9° как cos 9 градусов = cos(9° + n × 360°), n ∈ Z.
⇒ cos 9° = cos 369° = cos 729° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-9°) = cos(9°).
Методы нахождения значения Cos 9 градусов
Функция косинуса положительна в 1-м квадранте. Значение cos 9° равно 0,98768. . .. Мы можем найти значение cos 9 градусов по:
- Использование единичного круга
- Использование тригонометрических функций
Cos 9 градусов с использованием единичной окружности
Чтобы найти значение cos 9 градусов, используя единичный круг:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 9° с положительной осью x.

- Cos 9 градусов равен x-координате (0,9877) точки пересечения (0,9877, 0,1564) единичной окружности и r.
Следовательно, значение cos 9° = x = 0,9877 (приблизительно)
Cos 9° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 9 градусов как:
- ± √(1-sin²(9°))
- ± 1/√(1 + tan²(9°))
- ± раскладушка 9°/√(1 + раскладушка²(9°))
- ±√(косек²(9°) — 1)/косек 9°
- 1/сек 9°
Примечание. Поскольку 9° лежит в 1-м квадранте, окончательное значение cos 9° будет положительным.
Мы можем использовать тригонометрические тождества для представления cos 9° как
- -cos(180° — 9°) = -cos 171°
- -cos(180° + 9°) = -cos 189°
- sin(90° + 9°) = sin 99°
- sin(90° — 9°) = sin 81°
☛ Также проверьте:
Часто задаваемые вопросы по Cos 9 градусов
Что такое Cos 9 градусов?
Cos 9 градусов — значение тригонометрической функции косинуса для угла, равного 9 градусам. Значение cos 9° равно 0.9877 (приблизительно)
Значение cos 9° равно 0.9877 (приблизительно)
Каково значение Cos 9 градусов относительно Sin 9°?
Используя тригонометрические тождества, мы можем записать cos 9° через sin 9° как cos(9°) = √(1 — sin²(9°)). Здесь значение sin 9° равно 0,1564.
Как найти Cos 9° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 9° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(9°))
- ± 1/√(1 + tan²(9°))
- ± раскладушка 9°/√(1 + раскладушка²(9°))
- ± √(косек²(9°) — 1)/косек 9°
- 1/сек 9°
☛ Также проверьте: тригонометрическую таблицу
Каково значение Cos 9° с точки зрения Sec 9°?
Поскольку функция секанса является обратной функцией косинуса, мы можем записать cos 9° как 1/сек(9°).Значение sec 9° равно 1,012465.
Как найти значение Cos 9 градусов?
Значение cos 9 градусов можно рассчитать, построив угол 9° с осью x и затем найдя координаты соответствующей точки (0,9877, 0,1564) на единичной окружности.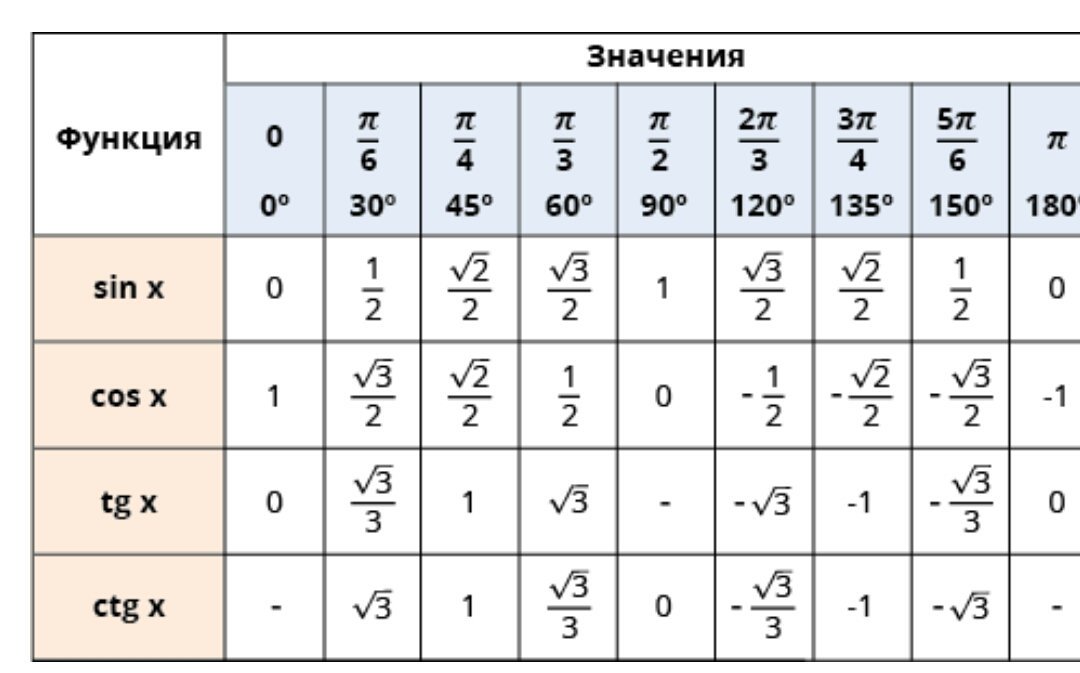 Значение cos 9° равно координате x (0,9877). ∴ cos 9° = 0,9877.
Значение cos 9° равно координате x (0,9877). ∴ cos 9° = 0,9877.
| cos(0°) = 1 cos(1°) = 0,999848 cos(2°) = 0,999391 cos(3°) = 0.99863 cos(4°) = 0,997564 cos(5°) = 0,996195 cos(6°) = 0,994522 cos(7°) = 0,9 cos(8°) = 0,9 7° 9 0 8 9 8 0 8 cos(10°) = 0,984808 cos(11°) = 0,981627 cos(12°) = 0,978148 cos(13°) = 0,97437 cos(14°) = 0,970296 cos(15°s) = 29690,90 16°) = 0,961262 cos(17°) = 0,956305 cos(18°) = 0,951057 cos(19°) = 0,945519 cos(20°) = 0,939693 °9 cos(21°) = 0,9033 ) = 0,4 cos(23°) = 0. | ||
| cos(46°) = 0,694658 cos(47°) = 0,681998 cos(48°)431 = 0,6°cos(48°)431 0.656059 COS (50 °) = 0.642788 COS (51 °) = 0.62932 COS (52 °) = 0.615661 COS (53 °) = 0,601815 COS (54 °) = 0.587785 COS (55 °) = 0.573576 cos(56°) = 0,559193 cos(57°) = 0,544639 cos(58°) = 0,529919 cos(59°) = 0,515038 cos(60°) = 0,5 cos(61°) = 0,48481 0,48481 0,48481 62°) = 0,469472 cos(63°) = 0.45399 COS (64 °) = 0.438371 COS (65 °) = 0,422618 COS (66 °) = 0,406737 COS (67 °) = 0.3 COS (68 °) = 0.374607 COS (69 °) = 0.358368 cos(70°) = 0,34202 cos(71°) = 0,325568 cos(72°) = 0,309017 cos(73°) = 0,2 cos(74°) = 0,275637 | cos(91°) = -0,017452 cos(92°) = -0,034899 cos(93°) = -0,052336 cos(94°) = -0,069756 cos(95° ) = -0,087156 cos(96°) = -0,104528 cos(97°) = -0,121869 cos(98°) = -0,139173 cos(99°) = -0,156434 cos(100°) = -0,1 9 cos(101°) = -0,1 cos(102°) = -0.207912 cos(103°) = -0,224951 cos(104°) = -0,241922 cos(105°) = -0,258819 cos(106°) = -0,275637 cos(107°) = -0,2 2 °) = -0,309017 cos(109°) = -0,325568 cos(110°) = -0,34202 cos(111°) = -0,358368 cos(112°) = -0,374607 cos(113°) = -0,37 cos(114°) = -0,406737 cos(115°) = -0,422618 cos(116°) = -0,438371 cos(117°) = -0,45399 cos(118°) = -0,469472
cos(120°) = -0.  5 5 cos(121°) = -0,515038 cos(122°) = -0,529919 cos(123°) = -0,544639 cos(124°) = -0,559193 cos(125°) = -0,573579 cos( ) °) = -0,587785 | cos(136°) = -0,779 137°) = -0,731354 cos(138°) = -0.743145 cos(139°) = -0,75471 cos(140°) = -0,766044 cos(141°) = -0,777146 cos(142°) = -0,788011 cos(143°) = -0,798636 °) = -0,809017 cos(145°) = -0,819152 cos(146°) = -0,829038 cos(147°) = -0,838671 cos(148°) = -0,848048 cos(149°) = -67. cos(150°) = -0,866025 cos(151°) = -0,87462 cos(152°) = -0,882948 cos(153°) = -0,8 cos(154°) = -0,898794 79° cos ) = -0,
|
6. Выразив в форме R sin(θ + α)
М. Борна
В электронике часто встречаются выражения
включая сумму синусов и косинусов. это удобнее
писать такие выражения, используя один термин.
Наша проблема:
Express a sin θ ± b cos θ в виде
R sin( θ ± α),
где a , b , R
и α – положительных констант.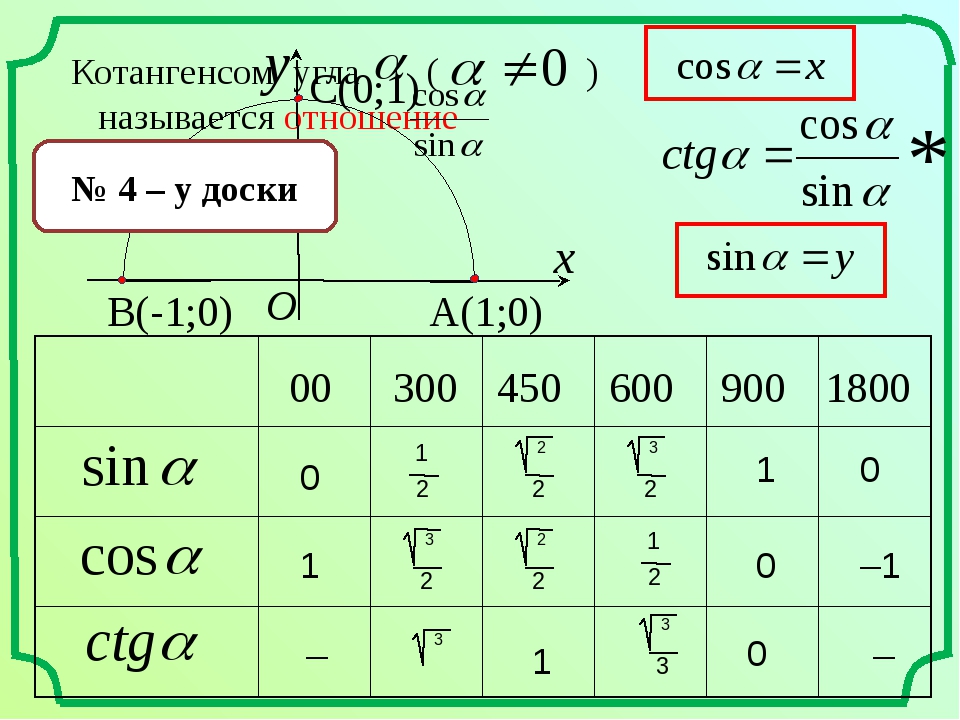
Решение:
Сначала возьмем случай «плюс» ( θ + α), чтобы упростить задачу.
Пусть
a sin θ + b cos θ ≡ R sin ( θ + α)
(Символ «≡» означает: «тождественно равно»)
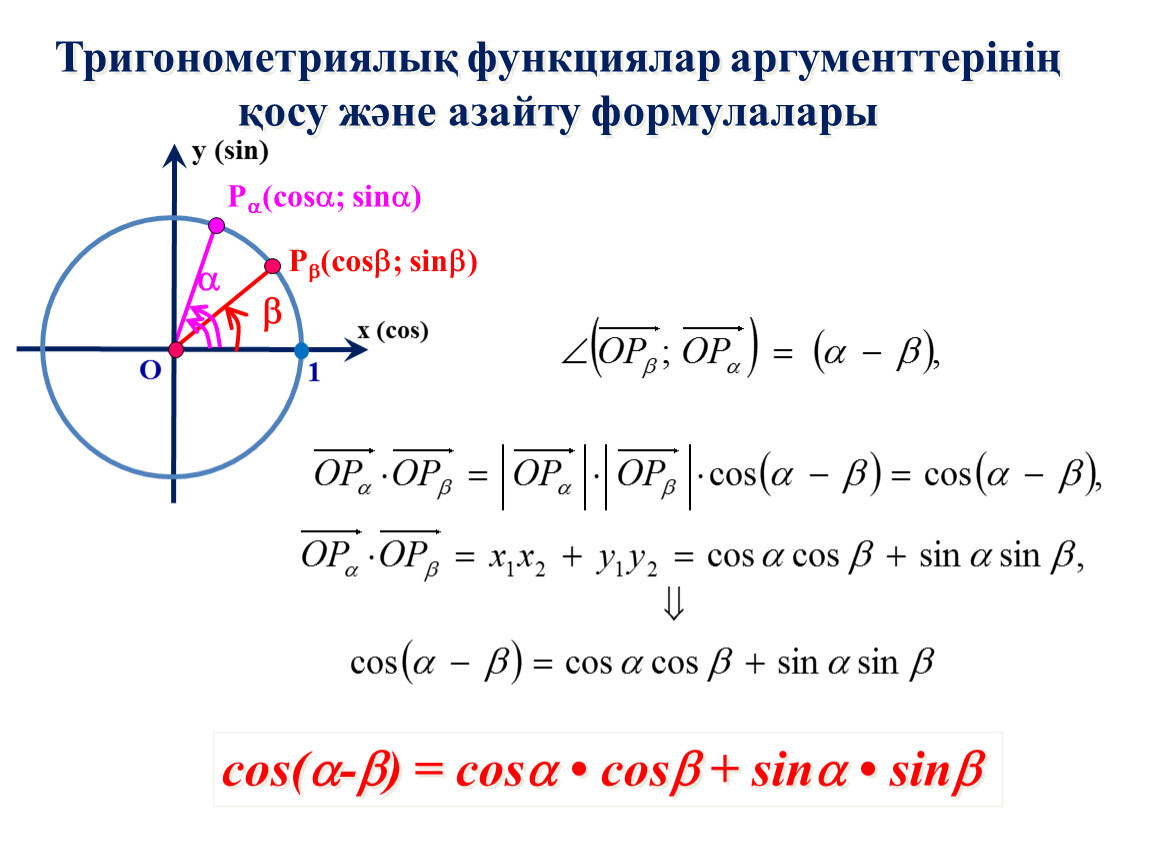
Используя приведенную выше формулу составного угла (Синус суммы углов),
sin(A + B) = sin A cos B + cos A sin B,
мы можем разложить R sin ( θ + α) следующим образом:
R sin ( θ + α)
≡ R (sin θ cos α + cos θ sin α)
≡ R sin θ cos α + R cos θ sin α
Так
a sin θ + b cos θ ≡ R cos α sin θ + R sin α cos
Приравнивая коэффициенты sin θ и cos θ в этом тождестве,
у нас есть:
Для sin θ :
a = R cos α . ………(1)
………(1)
(зеленый выше)
Для cos θ :
b = R sin α ……..(2)
(выделено красным выше)
Уравнение (2) ÷ уравнение (1):
`b/a=(R sin alpha)/(R cos alpha)=tan alpha`
Так
`альфа=арктан\ б/а`
(α — положительный острый угол и a и b
являются положительными .)
Теперь мы возводим в квадрат каждое уравнение. (1) и уравнение (2) и
добавьте их, чтобы найти выражение для R .
[Ур. (1)] 2 + [уравнение. (2)] 2 :
а 2 + б 2
= R 2 cos 2 α + R 2 sin 2 α
= R 2 (cos 2 α + sin 2 α)
= Р 2
(поскольку cos 2 A + sin 2 A = 1)
Так
`R=sqrt(a^2+b^2`
(Возьмем только положительный корень)
В итоге, если
`альфа=арктан\ б/а`
и
`R=sqrt(a^2+b^2)`
, то мы выразили a sin θ + b cos θ в требуемой форме:
a sin θ + b cos θ = R sin( θ + α )
Вы заметите, что это очень похоже на
преобразование прямоугольной формы в полярную форму в полярной форме комплекса
Числа. 2)`
2)`
Наше уравнение для отрицательного случая:
a sin θ − b cos θ = R sin( θ − α)
Уравнения типа
и
sin θ ± b cos θ = c
Чтобы решить уравнение в форме
и
sin θ ± b cos θ = c ,
выразить LHS в
форма R sin( θ ± α) и
затем решить
R sin( θ ± α) = c .
Упражнения — форма синуса
1. (a) Выразите 4 sin θ + 3 cos θ в форме R sin( θ + α).
(b) Используя ответ из пункта (а), решите
уравнение
4 sin θ + 3 cos θ = 2 для 0° ≤ θ < 360°.
Ответить
Часть (а)
Во-первых, пусть:
4 sin θ + 3 cos θ ≡ R sin( θ + α )
Тогда нам нужно:
`R=sqrt(4^2+3^2)=sqrt25=5`
`альфа=арктан(3/4)=36.
@`
Так
4 sin θ + 3 cos θ = 5 sin( θ + 36,87°)
Что мы сделали?
Компоненты оригинальной функции:
(i) 4 sin θ (черный)
(ii) 3 cos θ (синего цвета, с 4 sin θ )
Когда мы складываем эти 2 компонента, мы получаем синусоиду, которая была смещена влево на `36.@`:
4 sin θ + 3 cos θ = 5 sin( θ + 36,87°) (выделено красным)
Часть (б)
Из части (а),
4 sin θ + 3 cos θ = 5 sin( θ + 36,87°)
Итак,
5 sin( θ + 36,87°) = 2
sin( θ + 36,87°) = 0,4
Синус положителен в квадрантах I и II.
Решение sin α = 0.@`
Верны ли эти ответы?
Из графика видно, что в области 0° ≤ θ < 360° только два угла дают значение 2: 119,6° и 346,7°. 2)=13`
2)=13`
и `альфа=арктан(5/12)=0.39479`.
Итак, `12\ sin t+5\ cos t=` `13\ sin(t+0.39479)`
Итак, мы видим, что амплитуда 13 А и это максимум
ценность.
Чтобы найти первый случай, нам нужно решить
`13\ sin(t+0.39479)=13`
То есть
`sin(t+0,39479)=1`
Теперь sin θ = 1 в первый раз
когда `тета=пи/2`.
Итак, нам нужно решить:
`т+0,39479=пи/2`
`t=пи/2-0.39479=1,176`
Таким образом, максимальное значение 13 А впервые произойдет в момент времени t
= 1,176 с.
Из графика видно, что это верно:
`i=12\ sin t+5\ cos t`
4. Решите 7 sin 3 θ − 6 cos 3 θ = 3,8 для 0° ≤ θ < 360°.
Ответить
Сначала представим LHS в виде R sin(3 θ − α ).
(Обратите внимание на отрицательный знак и на `3θ`! Мы должны
увеличить домен в 3 раза.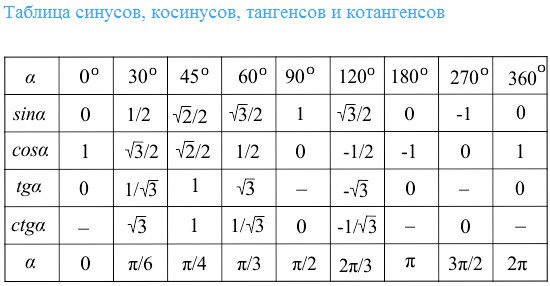 @`.
@`.
5. Сила тока и ампер
в определенной цепи через 90 155 t 90 156 секунд
предоставлено
`i=2\ sin(t-pi/3)-cos(t+pi/2)`
Найдите максимальный ток и самое раннее время его
имеет место.
(Примечание: t > 0)
Ответить
Нам нужно получить это в более простой форме. В этом
один, обратите внимание, что углы в скобках не совпадают с !
Мы должны сначала упростить их, чтобы углы в скобках были
такой же.2)=2,646`
`альфа=arctan(1.732/2)=` `0.714\ текст(радианы`
Так
`2\ sin t − 1,732\ cos t =` ` 2,646\
sin(t — 0,714)`
Таким образом, максимальное значение этого параметра равно `2,646\ «A»`.
Чтобы найти, когда это происходит, нам нужно решить:
`2,646\ sin(t − 0,714) = 2,646`
т. е. `sin(t − 0,714) = 1`
`t — 0,714 = π/2`
`t = 2,29`
Итак, `t = 2.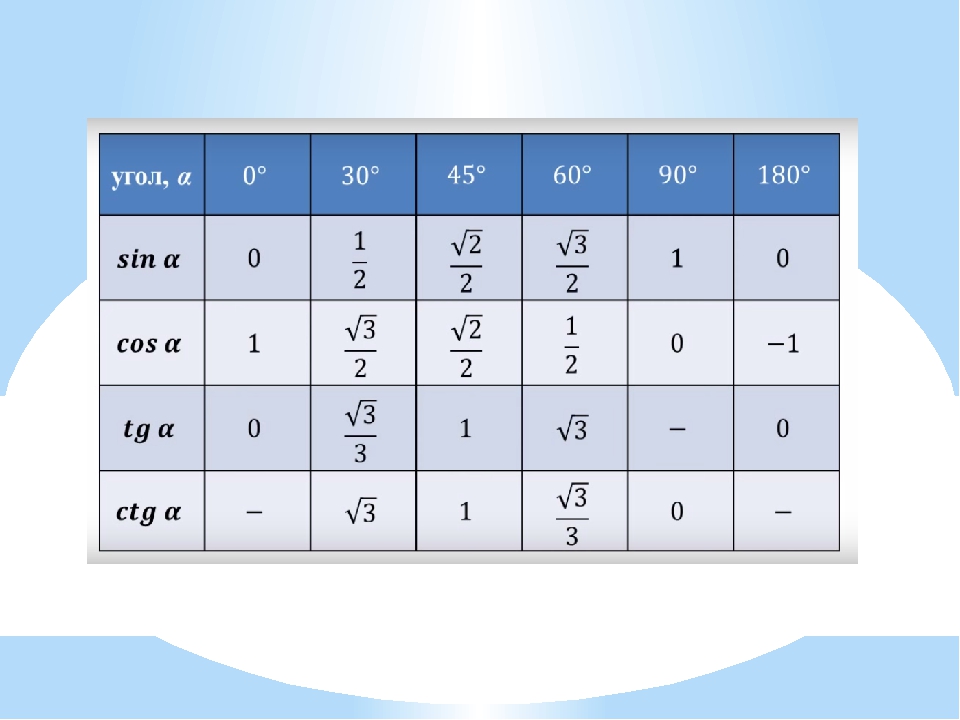 29\ «с»` — это время, когда
29\ «с»` — это время, когда
сначала достигается максимум.
Форма косинуса
Мы также можем выразить нашу сумму синуса и косинуса, используя косинус вместо синус . В некоторых ситуациях это может быть удобнее.
Полученные выражения аналогичны тем, которые мы получили для синусоидального случая, но обратите внимание на различия по ходу дела.
Для a , b и R положительного и острого α наше эквивалентное выражение дается следующим образом:
a sin θ + b cos θ ≡ R cos ( θ − α)
На этот раз способ получения α отличается от предыдущего.
Расширение R cos ( θ − α) с использованием нашего результата для расширения cos(A − B) дает нам:
R cos ( θ − α) = R cos θ cos α + R sin θ sin α
Перестановка и приравнивание коэффициентов дает нам
a sin θ + b cos θ ≡ R cos α cos θ + R sin α sin
Итак:
a = R sin α .
2)`
Итак, сумма синуса и косинуса объединена в один косинус:
a sin θ + b cos θ ≡ R cos( θ − α)
Еще раз, a , b , R и α положительны
константы, а α острая.
Футляр для косинуса минус
Если у нас есть a sin θ − b cos θ , и нам нужно выразить это в терминах одной функции косинуса, нам нужно использовать формулу:
a sin θ − b cos θ ≡ − R cos ( θ + α)
Еще раз, a , b и R положительны.2`
Упражнения на косинус
1. Выразить 7 sin θ + 12 cos θ в виде R cos ( θ − α), где 0 ≤ α < π/2.
Ответить
Находим α с помощью
`альфа=арктан\ а/б`
α должно быть в радианах для этого примера, так как нам говорят «0 ≤ α < π/2».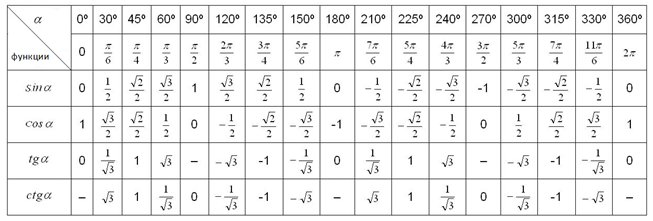
Так как `a = 7` и `b = 12`, мы имеем:
`α = арктангенс (7/12) = 0.2)=13,892`
Следовательно, мы можем написать:
7 sin θ + 12 cos θ = 13,892 cos ( θ − 0,528)
Чтобы проверить наш ответ, мы рисуем графики как y = 7 sin θ + 12 cos θ , так и y = 13,892 cos ( θ − 0,528). Мы видим, что они абсолютно одинаковы. (показан только один).
Мы видим, что наш график косинуса имеет амплитуду «13,892» и сдвинут вправо на «0».528` радиан, что согласуется с полученным выражением: 13,892 cos ( θ − 0,528)
2. Выразить 2,348 sin θ − 1,251 cos θ в виде −R cos ( θ + α), где 0 ≤ α < π/2.
Ответить
Мы находим α, используя
`a=текст(arctan)a/b`
Опять же, в этом примере `α` должно быть в радианах.
Так как `a = 2,348` и `b = 1,251`, мы имеем:
`α = арктангенс (2.2) = 2,660`
Итак, мы можем написать:
2,340 sin θ − 1,251 cos θ = -2,660 cos ( θ + 1,081)
Проверяя с помощью графика, получаем для каждой стороны нашего ответа следующее:
Мы видим, что наша кривая отрицательного косинуса имеет амплитуду 2,660 и смещена влево на 1,081 радиан, что согласуется с выражением −2,660 cos ( θ + 1,081).
Резюме
Вот сводка выражений и условий, которые мы нашли в этом разделе.
Исходное выражение Комбинированное выражение α a sin θ + b cos θ R sin ( θ + α ) `alpha=` арктан (б/а)` а sin θ − b cos θ R sin ( θ − α ) `alpha=` арктан (б/а)` a sin θ + b cos θ R потому что ( θ − α ) `альфа=` арктан (а/б)` а sin θ − b cos θ −R потому что ( θ + α ) `альфа=` арктан (а/б)` В каждом случае a , b и R положительные, а α острый угол.
2)`
Синус, косинус, тангенс, объяснение и примеры и практика определения противоположных, смежных сторон и гипотенузы
На этой странице объясняется соотношение синуса, косинуса и тангенса, дается обзор их диапазона значений и предлагаются практические задачи по определению сторон, противоположных и примыкающих к заданному углу.
Функции синуса, косинуса и тангенса выражают отношения сторон прямоугольного треугольника.
К какому(им) треугольнику(ам) ниже относится SOHCATOA?
Покажи ответ
Интерактивные уголки
SOHCATOA
Попробуйте активировать либо $$ \angle A $$, либо $$ \angle B$$, чтобы изучить, как меняются соседние и противоположные стороны в зависимости от угла.
Статус:
Угол активирован:
$$ \red{none} \text{, жду, пока вы выберете угол.}$$Ответ: синус угла всегда есть отношение $$\frac{противоположная сторона}{гипотенуза} $$.
$
синус(угол) = \frac{ \text{противоположная сторона}}{\text{гипотенуза}}
$Пример 1
$$
sin(\angle \red L) = \frac{противоположная} }{гипотенуза}
\\
грех (\ угол \ красный L) = \ гидроразрыва {9} {15}
$$Пример 2
$$
sin (\ угол \ красный K) = \ frac {напротив }{ гипотенуза}
\\
грех (\ угол \ красный K) = \ гидроразрыва {12} {15}
$$Помните: Когда мы используем слова «противоположный» и «смежный», мы всегда должны иметь в виду определенный угол.
Диапазон значений синуса
Для тех, кому удобно «Математический язык», домен и диапазон синуса следующие.
- Домен синуса = все действительные числа
- Диапазон синуса = {-1 ≤ y ≤ 1}
Синус угла имеет диапазон значений от -1 до 1 включительно.Ниже приведена таблица значений, иллюстрирующая некоторые ключевые значения синуса, которые охватывают весь диапазон значений.
Уголок Синус угла 270° sin (270°) = -1 (наименьшее значение, которое может иметь синус) 330° sin (330°) = -½ 0° sin(0°) = 0 30° sin(30°) = ½ 90° sin(90°) = 1 (наибольшее значение, которое может иметь синус) косинус угла всегда является отношением (прилежащей стороны к гипотенузе).
$
косинус (угол) = \frac{ \text{прилежащая сторона}}{\text{гипотенуза}}
$Пример 1
$$
cos(\angle \red L) = \frac{adjacent}{гипотенуза}
\\
потому что (\ угол \ красный L) = \ гидроразрыва {12} {15}$$
Пример 2
$$
потому что (\ угол \ красный K) = \ гидроразрыв {соседний }{гипотенуза}
\\
потому что (\ угол \ красный K) = \ гидроразрыва {9} {15}$$
Диапазон значений косинуса
Для тех, кто знаком с «Math Speak», домен и диапазон косинуса следующие.
- Область косинуса = все действительные числа
- Диапазон косинуса = {-1 ≤ y ≤ 1}
Косинус угла имеет диапазон значений от -1 до 1 включительно. Ниже приведена таблица значений, иллюстрирующая некоторые ключевые значения косинуса, которые охватывают весь диапазон значений.
Уголок Косинус угла 0° cos (0°) = 1 (наибольшее значение, которое может иметь косинус) 60° cos (60°) =½ 90° cos(90°) = 0 120° cos(120°) = -½ 180° cos(180°) = -1 (наименьшее значение, которое может иметь косинус) Тангенс угла всегда является отношением (противоположная сторона/прилежащая сторона).
$
касательная (угол) = \frac{ \text{противоположная сторона}}{\text{прилегающая сторона}}
$Пример 1
$$
загар (\ угол \ красный L) = \ гидроразрыв {напротив} {смежный}
\\
загар (\ угол \ красный L) = \ гидроразрыва {9} {12}$$
Пример 2
$$
загар (\ угол \ красный K) = \ гидроразрыв {напротив} {смежный}
\\
загар (\ угол \ красный K) = \ гидроразрыва {12} {9}$$
Выделенные проблемы
Проблема 1
В приведенных ниже треугольниках найдите гипотенузу и стороны, противоположные и примыкающие к заштрихованному углу.
Показать боковые метки
Гипотенуза = АВ
Противоположная сторона = ВС
Смежная сторона = АСПроблема 2
Показать боковые метки
Гипотенуза = АС
Противоположная сторона = ВС
Смежная сторона = АВПроблема 3
Показать боковые метки
Гипотенуза = YX
Противоположная сторона = ZX
Смежная сторона = ZYПроблема 4
Показать боковые метки
Гипотенуза = I
Сторона, противоположная A = H
Сторона, прилегающая к A = JНет выделения (сложнее)
Проблема 5
Определите гипотенузу, а также противолежащую и прилежащую стороны $$ \угла ACB $$.
Показать боковые метки
Сначала , помните, что средняя буква имени угла ($$ \angle A \red C B $$) — это расположение угла.
Второй: Ключ к решению такого рода задач состоит в том, чтобы помнить, что «противоположные» и «примыкающие» относятся к углу треугольника — в данном случае это красный угол на картинке.
Проблема 6
Определите гипотенузу, а также противолежащую и прилежащую стороны $$ \angle RPQ $$.
Показать боковые метки
Сначала , помните, что средняя буква имени угла ($$ \angle R \red P Q $$) — это расположение угла.
Второй: Ключ к решению такого рода задач состоит в том, чтобы помнить, что «противоположные» и «примыкающие» относятся к углу треугольника — в данном случае это красный угол на картинке.
Проблема 7
Определите гипотенузу, а также противолежащую и прилежащую стороны $$ \угла BAC $$.
Показать боковые метки
Сначала , помните, что средняя буква имени угла ($$ \angle B \red A C $$) — это расположение угла.
Второй: Ключ к решению такого рода задач состоит в том, чтобы помнить, что «противоположные» и «примыкающие» относятся к углу треугольника — в данном случае это красный угол на картинке.
Проблема 8
Определите сторону, противоположную $$\angle$$IHU, и сторону, примыкающую к $$\angle$$IHU.
Показать боковые метки
Сначала , помните, что средняя буква имени угла ($$ \angle I \red H U $$) — это местоположение угла.
Второй: Ключ к решению такого рода задач состоит в том, чтобы помнить, что «противоположные» и «примыкающие» относятся к углу треугольника — в данном случае это красный угол на картинке.
Синус, косинус, тангенс
Три функции, но одна и та же идея.

Прямоугольный треугольник
Синус, косинус и тангенс являются основными функциями, используемыми в тригонометрии и основаны на прямоугольном треугольнике.
Прежде чем углубляться в функции, полезно дать имя каждой стороне прямоугольного треугольника:
- «Противоположный» противоположен углу θ
- «Смежный» примыкает (рядом) к углу θ
- «Гипотенуза» самая длинная
Смежный всегда рядом с углом
И Противоположный угол находится напротив угла
Синус, косинус и тангенс
Синус , Косинус и Тангенс (часто сокращается до sin , cos и tan ) представляют собой отношение сторон прямоугольного треугольника
Для данного угла θ каждое отношение остается одним и тем же
независимо от того, насколько большой или маленький треугольникДля их расчета:
Разделить длину одной стороны на другую
Пример: чему равен синус 35°?
Используя этот треугольник (длина указана только до одного десятичного знака):
sin(35°) = Напротив Гипотенуза = 2. 8 4,9
= 0,57… кос(35°) = Смежный Гипотенуза = 4,0 4,9 = 0,82… желтовато-коричневый (35°) = напротив рядом = 2.8 4,0 = 0,70… Размер не имеет значения
Треугольник может быть большим или маленьким, а отношение сторон остается неизменным .
Только угол изменяет соотношение.
Попробуйте перетащить точку «А», чтобы изменить угол, и точку «В», чтобы изменить размер:
На хороших калькуляторах есть sin, cos и tan, чтобы вам было проще.Просто вставьте угол и нажмите кнопку.
Но вам все равно нужно помнить что они означают !
В виде изображения:
Тренируйтесь здесь:
Сохкахтоа
Как запомнить? Думаю «Сохкахтоа» !
Работает так:
Сох…
S ine = O pposite / H ypotenuse
…ка…
C осин = A djacent / H ypotenuse
… до
T угол = O точка / A точка
Вы можете прочитать больше о sohcahtoa .
.. пожалуйста, запомните это, это может помочь на экзамене!
Углы От 0° до 360°
Подвигайте мышью, чтобы увидеть, как различные углы (в радианах или градусах) влияют на синус, косинус и тангенс.
алгебра/изображения/круг-треугольник.js
В этой анимации гипотенуза равна 1, образуя единичный круг.
Обратите внимание, что соседняя сторона и противоположная сторона могут быть положительными или отрицательными, поэтому синус, косинус и тангенс также меняются между положительными и отрицательными значениями.
«Почему не грешил на , а загорел
на вечеринку?»
«… просто потому что !»Примеры
Пример: чему равны синус, косинус и тангенс угла 30°?
Классический треугольник с углом 30° имеет гипотенузу длины 2, противоположную сторону длины 1 и примыкающую сторону
√3:Теперь мы знаем длины, можем вычислить функции:
Синус
sin(30°) = 1 / 2 = 0. 5
Косинус
cos(30°) = 1,732 / 2 = 0,866… Касательная
тангенс(30°) = 1/1,732 = 0,577… (достаньте калькулятор и проверьте!)
Пример: чему равны синус, косинус и тангенс угла 45°?
Классический треугольник с углом 45° имеет две стороны, равные 1, и гипотенузу, равную √2:
Синус
sin(45°) = 1/1.414 = 0,707… Косинус
cos(45°) = 1 / 1,414 = 0,707… Касательная
тангенс (45°) = 1 / 1 = 1 Почему?
Почему важны эти функции?
- Потому что они позволяют нам вычислять углы, когда мы знаем стороны
- И они позволяют нам вычислять стороны, когда мы знаем углы
Пример: Используйте синусоидальную функцию
, чтобы найти «d»
Мы знаем:
- Трос образует угол 39° с морским дном
- Кабель имеет длину 30 метров .
И мы хотим знать «d» (расстояние вниз).
Начните с:sin 39° = напротив/гипотенуза
sin 39° = д/30
Поменять местами стороны:d/30 = sin 39°
Используйте калькулятор, чтобы найти sin 39°: d/30 = 0,6293…
Умножить обе стороны на 30:d = 0,6293… x 30
d = 18,88 с точностью до 2 знаков после запятой.
Глубина «d» 18,88 м
Упражнение
Попробуйте это бумажное упражнение, в котором вы можете вычислить синусоидальную функцию
для всех углов от 0° до 360°, а затем нанесите результат на график.Это поможет вам понять эти относительно
простые функции.Вы также можете увидеть графики синуса, косинуса и тангенса.
И поиграй с пружиной, которая создает синусоиду.
Менее распространенные функции
Для полноты картины есть еще 3 функции, где мы делим одну сторону на другую, но они не так часто используются.
Они равны 1 разделить на cos , 1 разделить на sin и 1 разделить на tan :
Функция секущей:
сек( θ ) = Гипотенуза Смежный (=1/cos) Функция косеканса:
csc( θ ) = Гипотенуза Напротив (=1/sin) Функция котангенса:
детская кроватка( θ ) = Смежный Напротив (=1/тангенс)
1494, 1495, 724, 725, 1492, 1493, 726, 727, 2362, 2363
косинусов
;point;vertex;ABC,2″/>Далее рассмотрим углы 30° и 60°.В прямоугольном треугольнике 30°-60°-90° отношения
сторон равны 1 : √3 : 2. Отсюда следует, что
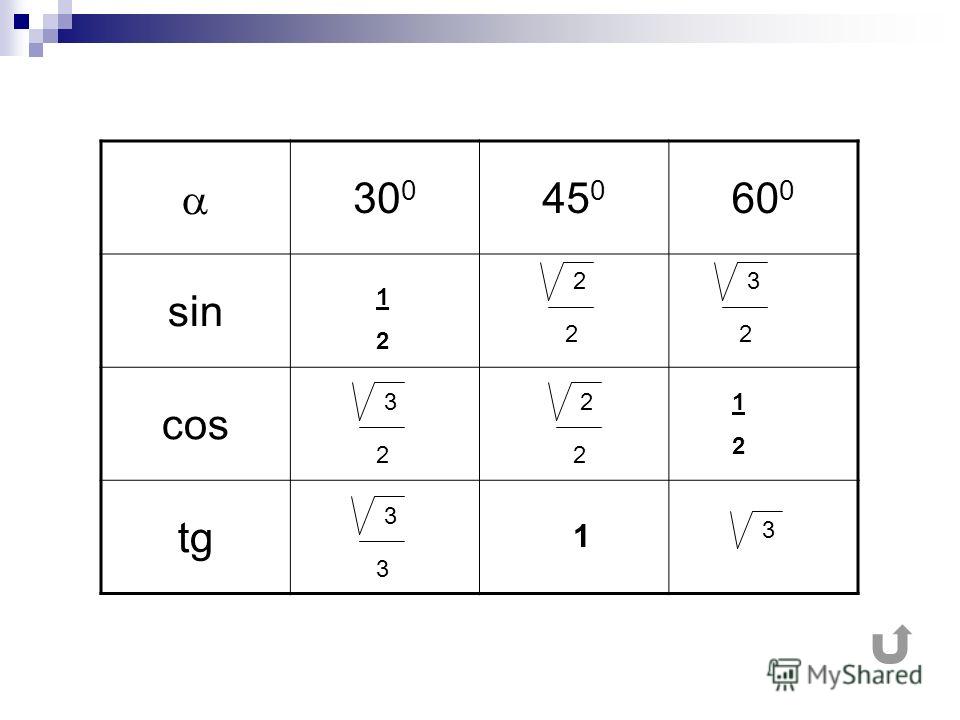
sin 30° = cos 60° = 1/2 и
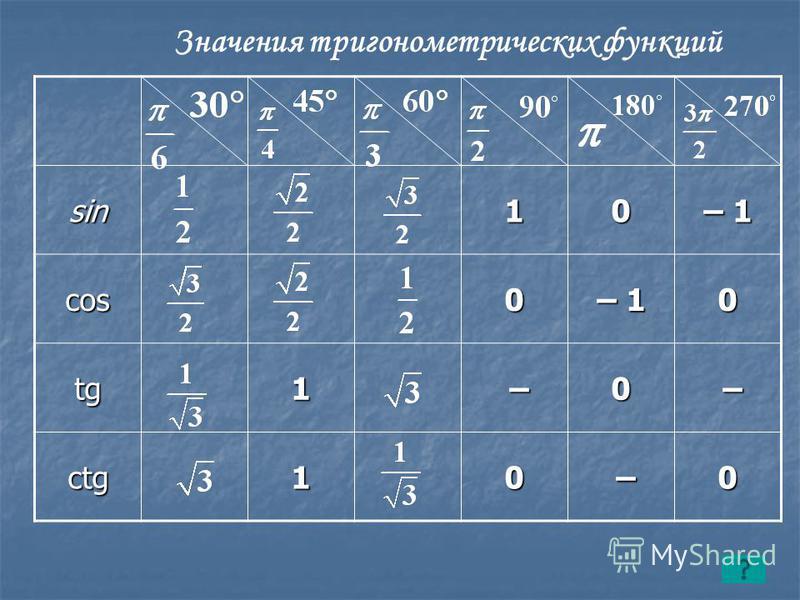
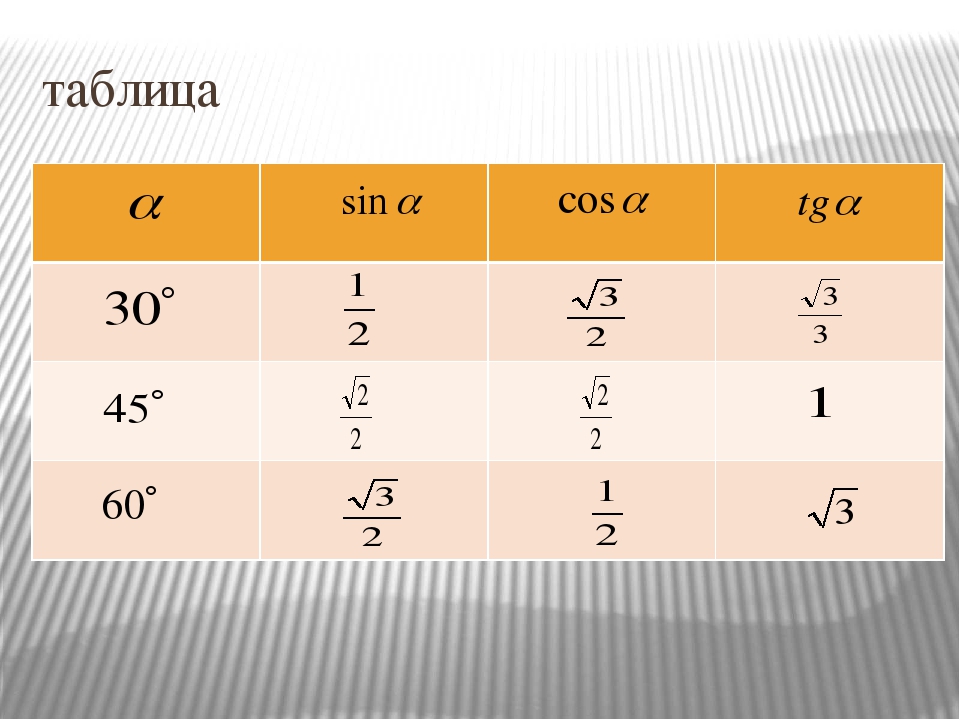
sin 60° = cos 30° = √3 / 2.Эти данные заносятся в эту таблицу.
Угол градусов Радианы косинус синусоидальной 90 ° π /2 0 1 60 ° π /3 1/2 1/2 √3 / 2 45 °39 π /4 √2 / 2 √2 / 2 30 ° 30 ° π /6 √3 / 2 1/2 0 ° 2 0 1 0 Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой.

30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. б = 6,4, в = 7,8. Найти А и А.
36. A = 23° 15′, c = 12.15. Найдите а и б.
Советы
30. Косинус A связывает b с гипотенузой c, , поэтому вы можете сначала вычислить c. Зная b и c, , вы можете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух неизвестных вам сторон, а именно a/c. Тем не менее, это дает вам уравнение для работы: 1/3 = a/c. Тогда c = 3 a. Из теоремы Пифагора следует, что a 2 + 144 = 9 a 2 .
Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
Ответы
30. c = b /cos A = 2,25/0,15 =
15 метров; a = 14,83 метра.33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24′, или 4’34’, или 4’34’, или 4’34’, или 4’34’,
c = 3 a , что равно 12.73 фута или 12 футов 9 дюймов.35. cos A = b/c = 6,4/7,8 = 0,82. Следовательно, A = 34,86° = 34°52′, или около 35°.
a 2 = 7,8 2 – 6,4 2 = 19,9, поэтому a равно примерно 4,5.36. a = c sin A = 12,15 sin 23°15′ = 4,796.

 731354
731354 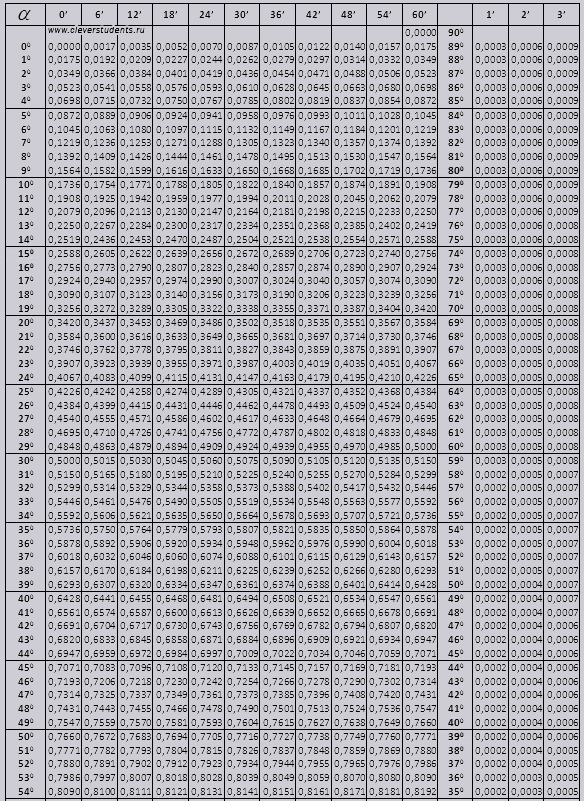 121869
121869  5
5  @`
@` 2)`
2)`
 2)`
2)`


 8 4,9
8 4,9 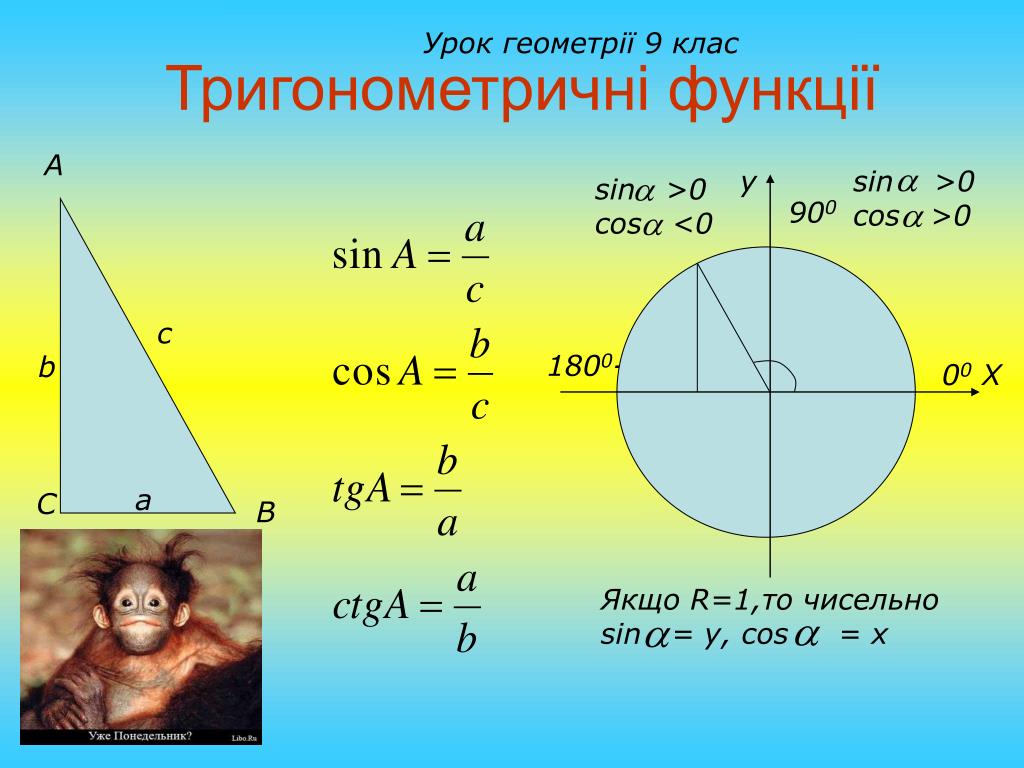
 .. пожалуйста, запомните это, это может помочь на экзамене!
.. пожалуйста, запомните это, это может помочь на экзамене!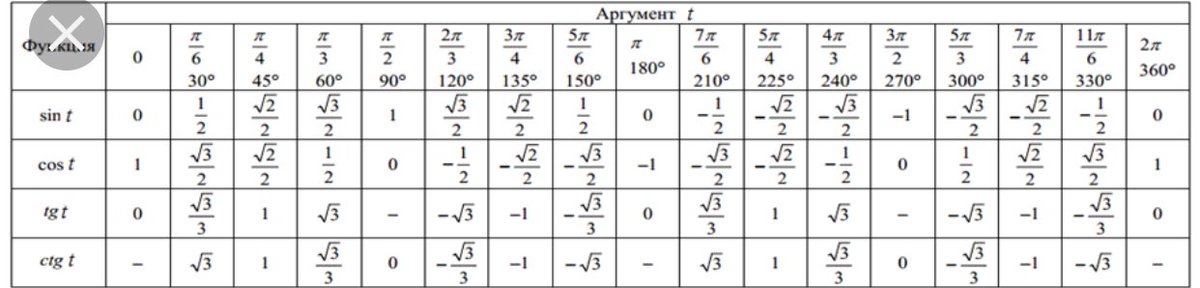 5
5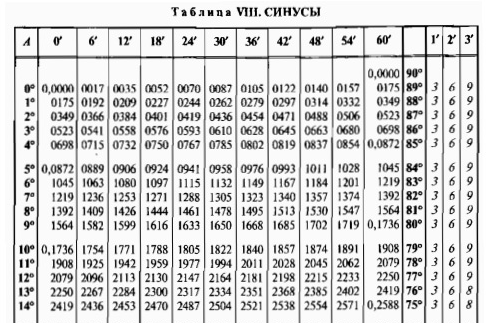
 Вы можете решить это последнее уравнение для a , а затем найти c.
Вы можете решить это последнее уравнение для a , а затем найти c.