Как обозначается давление в системе
Единицы измерения давления
Международная система единиц (СИ)
Давлением P называется физическая величина силы F, действующая на единицу поверхности площади S, направленная перпендикулярно этой поверхности.
т.е. P = F / S.
В международной системе единиц (СИ) давление измеряется в Паскалях:
Па — русское обозначение.
Pa — международное.
1 Па = 1 Ньютон / 1 кв. метр (1 Н/м²)
Для практических измерений в КИП и А, 1 Па часто оказывается слишком маленькой величиной давления, и для оперирования реальными данными применяются умножающие приставки — (кило, Мега), умножающие значения в 1тыс. и 1млн. раз соответственно.
1 МПа = 1000 кПа = 1000000 Па
Также, шкалы приборов для измерения давления могут быть непосредственно градуированы в величинах Ньютон / метр, или их производных:
Килоньютон, Меганьютон / м², см², мм².
Тогда получаем следующее соответствие:
1 МПа = 1 МН/м² = 1 Н/мм² = 100 Н/см² = 1000 кН/м² = 1000 кПа = 1000000 Н/м² = 1000000 Па
В России и Европе также широкое применение для измерения давления находят единицы бар (bar) и кгс/м² (kgf/m²), а также их производные (mbar, кгс/см²).
1 бар — это внесистемная единица, равная 100000 Па.
1 кгс/см² — это единица измерения давления в системе МКГСС, и широко применяется в промышленных измерениях давления.
1 кгс/см² = 10000 кгс/м² = 0.980665 бар = 98066.5 Па
Атмосфера
Атмосфера — это внесистемная единица измерения давления приблизительно равная атмосферному давлению Земли на уровне Мирового океана.
Существует два понятия атмосферы для измерения давления:
- Физическая (атм) — равна давлению столба ртути высотой 760 мм при температуре 0° C. 1 атм = 101325 Па
- Техническая (ат) — равна давлению, производимому силой в 1 кгс на площадь 1 см². 1 ат = 98066,5 Па = 1 кгс/см²
В России для использования в измерениях допущена только техническая атмосфера, и срок ее действия ограничен по некоторым данным 2016 годом.
Водяной столб
Метр водяного столба — внесистемная единица измерения давления, применяемая в ряде производств.
Физически он равен давлению столба воды высотой в 1 м при температуре около 4° C и стандартном для калибровки ускорении свободного падения — 9,80665 м/сек².
м вод. ст. — русское обозначение.
mH2O — международное.
Производными единицами являются см вод. ст. и мм вод. ст.
1 м вод. ст. = 100 см вод. ст. = 1000 мм вод. ст.
Соотносится к другим единицам измерения давления соответствующим образом:
1 м вод. ст. = 1000 кгс/м² = 0.0980665 бар = 9.80665 Па = 73.55592400691 мм рт. ст.
Ртутный столб
Миллиметр ртутного столба — внесистемная единица измерения давления, равная 133.3223684 Па. Синоним — Торр (Torr).
мм рт. ст. — русское обозначение.
mmHg. — международное.
Использование в России — не ограничено, но не рекомендовано. Применяется в ряде областей техники.
Соотношение к водному столбу: 1 мм рт. ст. = 13.595098063 мм вод. ст.
Единицы США и Британии
В США и Британии применяются также другие единицы измерения давления.
Это связано с тем, что длины выражаются в футах и дюймах, а вес в фунтах, британских и американских тоннах.
Примеры некоторых из них:
- Дюйм водного столба
Обозначение: inH2O = 249. 08891 Па.
08891 Па. - Фут водного столба
Обозначение: ftH2O = 2989.006692 Па. - Дюйм ртутного столба
Обозначение: inHg = 3386.38815789474 Па. - Фунт на квадратный дюйм
Обозначение: psi = 6894.757293178 Па. - 1000 фунтов на квадратный дюйм
Обозначение: ksi = 6894757.2931783 Па. - Фунт на квадратный фут
Обозначение: psf = 47.8802589803 Па. - Американская (короткая) тонна на квадратный дюйм
Обозначение: tsi = 13789514.58633672267344 Па. - Американская (короткая) тонна на квадратный фут
Обозначение: tsf = 95760.51796067168523226 Па. - Британская (длинная) тонна на квадратный дюйм
Обозначение: br.tsi = 15444256.3366971 Па. - Британская (длинная) тонна на квадратный фут
Обозначение: br. tsf = 107251.780115952 Па.
tsf = 107251.780115952 Па.
Приборы для измерения давления
Для измерения давления применяются манометры, дифманометры (разность давлений), вакуумметры (измерение разряжения).
Источник
Давление. В чем измеряется давление?
Давление — физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности. Для обозначения давления обычно используется символ p — от лат.pressūra (давление).
Давление на поверхность может иметь неравномерное распределение, поэтому различают давление на локальный фрагмент поверхности и среднее давление на всю поверхность.
Давление на локальной площади поверхности определяется как отношение нормальной составляющей силы dFn, действующей на этот фрагмент поверхности, к площади этого фрагмента dS:
Среднее давление по всей поверхности есть отношение нормальной составляющей силы Fn, действующей на данную поверхность, к её площади S:
Измерение давления газов и жидкостей выполняется с помощью манометров, дифманометров, вакуумметров, датчиков давления, атмосферного давления — барометрами.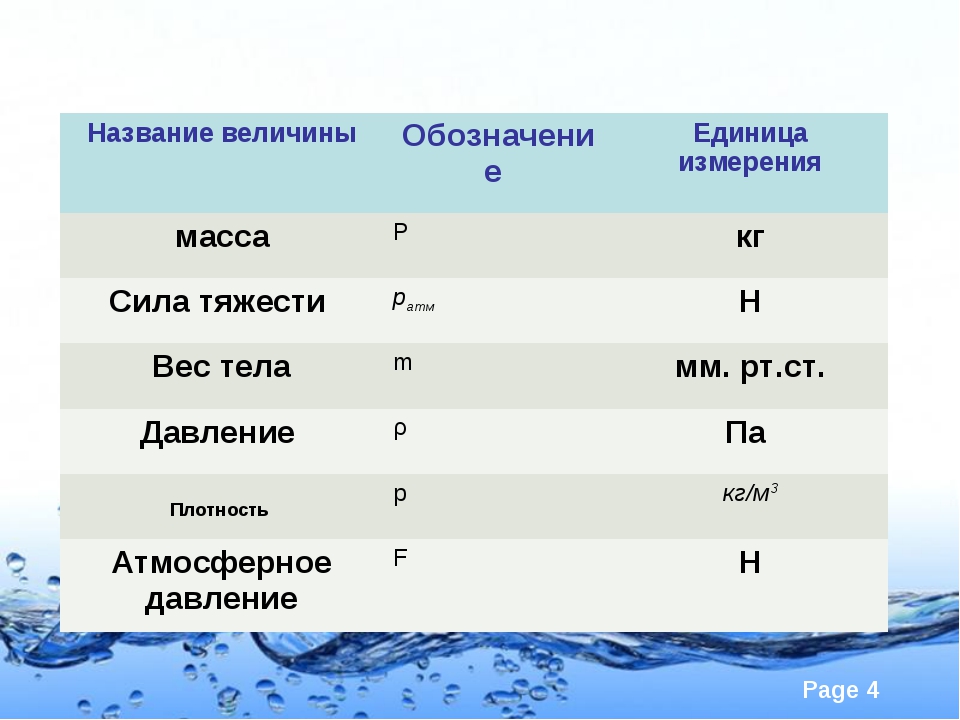
Единицы измерения давления имеют давнюю историю и с учетом разных сред (жидкость, газ, твердое тело) достаточно разнообразны. Приведем основные.
Паскаль
В Международной системе единиц (СИ) измеряется в паскалях (русское обозначение: Па; международное: Pa). Паскаль равен давлению, вызываемому силой, равной одному ньютону, равномерно распределённой по нормальной к ней поверхности площадью один квадратный метр.
Один паскаль — небольшое давление. Примерно такое давление создает лежащий на столе листок из школьной тетради. Поэтому очень часто используют кратные единицы давления:
| гектопаскаль (гПа) | 1 гПа = 100 Па = 10 2 Па |
| килопаскаль (кПа) | 1 кПа = 1′000 Па = 10 3 Па |
| мегапаскаль (МПа) | 1 МПа = 1′000′000 Па = 10 6 Па |
Тогда получаем следующее соответствие: 1 МПа = 1 МН/м² = 1 Н/мм² = 100 Н/см².
Также, шкалы приборов для измерения давления могут быть градуированы в величинах Н/м 2 или Н/мм 2 .
Соотношения величин к 1 Па:
| МПа | |
| Бар (bar, бар) | 0,1 |
| Техническая атмосфера (at, ат), кгс/см 2 | 10,197 |
| Физическая атмосфера (atm, атм) | 9,8692 |
| Миллиметр ртутного столба (мм рт.ст., mm Hg, Torr, торр) | 7500,6 |
| Метр водяного столба (м вод.ст., m H2O) | 10,197 |
| Фунт-сила на кв. дюйм (psi) | 145,04 |
Ди́на
Ди́на (русское обозначение: дин, международное обозначение: dyn) — единица силы в системе единиц СГС. Одна дина численно равна силе, которая сообщает телу массой в 1 грамм ускорение в один сантиметр в секунду за секунду.
1 дин = 1 г·см/с 2 = 10 -5 H = 1,0197·10 -6 кгс
СГС (сантиметр-грамм-секунда) — система единиц измерения, которая широко использовалась до принятия Международной системы единиц (СИ). Другое название — абсолютная физическая система единиц.
Другое название — абсолютная физическая система единиц.
Бар (bar, бар)
Бар (русское обозначение: бар; международное: bar😉 — внесистемная единица измерения давления, примерно равная одной атмосфере, используется для жидкостей и газов, находящихся под давлением.
Почему бар, а не паскаль? Для технических измерений, где присутствует высокое давление, паскаль — слишком мелкая единица. Поэтому ввели единицу более крупную — 1 бар. Приблизительно это давление земной атмосферы.
| 1 бар = | |
| Паскаль (Pa, Па) | 10 5 Па = 0,1 МПа |
| Физическая атмосфера (atm, атм) | 0,98692 атм |
| кгс/см 2 | 1,0197 кгс/см 2 |
| Миллиметр ртутного столба (мм рт.ст., mm Hg, Torr, торр) | 750,06 мм рт.ст. |
| дин/см 2 | 10 6 дин/см 2 |
Бар — внесистемная единица измерения давления.
| Российская Федерация | Без ограничения срока с областью применения «промышленность». |
| Международная организация законодательной метрологии (МОЗМ) | Могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться, если они не используются. |
Килограмм-сила
Килограмм-сила равен силе, которая сообщает покоящейся массе, равной массе международного прототипа килограмма, ускорение, равное нормальному ускорению свободного падения (9,80665 м/с 2 ).
1 кгс = 1 кг * 9,80665 м/с 2 = 9,80665 Н
Килограмм-сила примерно равна силе, с которой тело массой 1 килограмм давит на весы на поверхности Земли, поэтому удобна тем, что её величина равна весу тела массой в 1 кг, поэтому человеку легко представить, например, что такое сила 5 кгс.
| 1 кгс | = 9,80665 Н | ≈ 10 Н |
| 1 Н | ≈ 0,10197162 кгс | ≈ 0,1 кгс |
| 100 кгс/м 2 | ≈ 1 кПа | = 1 кН/м 2 |
| 1 лошадиная сила | 75 кгс·м/с |
Килограмм-сила (русское обозначение: кгс или кГ; международное: kgf или kgF) — единица силы в системе единиц МКГСС (Метр — КилоГрамм-Сила — Секунда).
| Международная организация законодательной метрологии (МОЗМ) | Должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются. |
| Российская Федерация | Килограмм-сила и грамм-сила допущены к использованию в качестве внесистемных единиц без ограничения срока действия с областью применения «все области»,, допускаемых к применению в Российской Федерации, используется только в тех случаях, когда количественные значения величин «невозможно или нецелесообразно» выражать в единицах СИ. |
Техническая атмосфера (at, ат), кгс/см 2
Техническая атмосфера (русское обозначение: ат; международное: at) — равна давлению, производимому силой в 1 кгс, равномерно распределённой по перпендикулярной к ней плоской поверхности площадью 1 см 2 . Таким образом,
1 ат = 98 066,5 Па
| Российская Федерация | — |
| Международная организация законодательной метрологии (МОЗМ) | Должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются. |
Физическая атмосфера (atm, атм)
Нормальная, стандартная или физическая атмосфера (русское обозначение: атм; международное: atm) — внесистемная единица, равна давлению столба ртути высотой 760 мм на его горизонтальное основание при плотности ртути 13 595,04 кг/м 3 , при температуре 0°C и при нормальном ускорении свободного падения 9,80665 м/с 2 .
1 атм = 760 мм.рт.ст.
В соответствии с определением:
| 1 атм | 101 325 Па |
| 1 атм | 1,033233 ат |
| Российская Федерация | Допущена к использованию в качестве внесистемной единицы с областью применения «все области». |
| Международная организация законодательной метрологии (МОЗМ) | Должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются. |
Миллиметр ртутного столба
Миллиметр ртутного столба (русское обозначение: мм рт. ст.; международное: mm Hg) — внесистемная единица измерения давления, иногда называется «торр» (русское обозначение — торр, международное — Torr) в честь Эванджелисты Торричелли.
ст.; международное: mm Hg) — внесистемная единица измерения давления, иногда называется «торр» (русское обозначение — торр, международное — Torr) в честь Эванджелисты Торричелли.
1 мм рт.ст. ≈ 133,3223684 Па
| Атмуровень моря | 760 мм рт.ст. |
| 760 мм рт.ст. | 101 325 Па |
| 1 мм рт.ст. | 101 325 / 760 ≈ 133,3223684 Па |
| 1 мм рт.ст. | 13,5951 мм вод.ст. |
Происхождение этой единицы связано со способом измерения атмосферного давления при помощи барометра, в котором давление уравновешивается столбиком жидкости. В качестве жидкости часто используется ртуть, поскольку у неё очень высокая плотность (≈13 600 кг/м 3 ) и низкое давление насыщенного пара при комнатной температуре.
| Российская Федерация | Допущен к использованию в качестве внесистемной единицы без ограничения срока с областью применения «медицина, метеорология, авиационная навигация» |
| Международная организация законодательной метрологии (МОЗМ) | Могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться, если они не используются. |
Миллиметры ртутного столба используются, например, в вакуумной технике, в метеорологических сводках и при измерении кровяного давления.
В США и Канаде также используется единица измерения «дюйм ртутного столба» (обозначение — inHg). 1 inHg = 3,386389 кПа при 0 °C.
Миллиметр водяного столба
Миллиметр водяного столба (русское обозначение: мм вод.ст., мм H2O; международное: mm H2O) — внесистемная единица измерения давления. Равен гидростатическому давлению столба воды высотой 1 мм, оказываемому на плоское основание при температуре воды 4 °С.
В Российской Федерации допущен к использованию в качестве внесистемной единицы измерения давления без ограничения срока с областью использования «все области».
В основном в теоретической физике жидкость рассматривают, как идеальную. Но на практике всё сложнее. Жидкость имеет и трение о стенки и внутреннее трение, вязкость и растворяет в себе газы и выделяет их, что создает определенные сложности. В этой статье рассмотрим основные физические свойства реальной жидкости.
В этой статье рассмотрим основные физические свойства реальной жидкости.
Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.
Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.
Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.
Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.
Источник
в физике, в чем измеряется, какой буквой обозначается, формула
Подготовили для вас краткую статью о том, что такое давление, чтобы помочь разобраться и структурировать свои знания по этой теме.
Что такое давление в физике
Давление — скалярная физическая величина, которая характеризует состояние сплошной среды. 2} ).\)
2} ).\)
Внесистемными единицами измерения данной величины являются мм рт.ст. (миллиметр ртутного столба), мм.в.ст. (миллиметр водяного столба), атмосфера, бар.
Общая формула
Значение давления находится по формуле:
\(p=\frac{F}{S} ,\)
где \(F\) — сила, которая действует на поверхность, \(S\) — площадь этой поверхности.
Основываясь на формуле, можно сделать вывод о том, что чем больше площадь опоры, тем меньше давление, которое воздействует одной и той же силой на эту опору. Это отлично демонстрируется, когда человек на лыжах меньше проваливается в снег, чем тот, который передвигается без них.
Давление, которое производится на жидкость или газ, передается на любую точку равнонаправленно, то есть одинаково в каждом из направлений. Данное утверждение получило название закона Паскаля.
Формула гидростатического давления
Гидростатическое давление — это воздействие столба жидкости в состоянии равновесия на дно, а также стенки сосуда.
Важно понимать:
- давление внутри жидкости на определенном уровне одинаково во всех направлениях. При увеличении глубины давление увеличивается;
- давление столба жидкости не зависит от формы сосуда.
Давление жидкости на дно сосуда обуславливается плотностью жидкости, а также ее высотой столба. Измерить можно по формуле:
\(p = gρh\)
При данном расчете плотность \(ρ\) следует считать в килограммах на кубический метр, а высоту столба жидкости \(h\) — в метрах, \(g = 9,8 \frac{Н}{кг}\), тогда итог будет выражен в паскалях.
Парциальное давление и его формула
Парциальное давление — то, которое имел бы газ, который входит в состав газовой смеси, если бы он один занимал весь объем, который занимает объем смеси при той же температуре.
Давление отдельного газа из смеси находится по формуле:
\(p1 = x1p,\)
где \(p1\) — парциональное давление конкретного газа в газовой смеси, \(x1\) — мольная доля этого газа, а \(p\) — общее давление газовой смеси.
Также его можно найти следующим образом:
\(p1=\frac{h2RT}{V}\)
Здесь \(V\) — объем смеси, \(T\) — температура смеси.
Общее давление газовой смеси равно сумме парциальных давлений каждого газа в смеси.
\(p = p1 + p2 + p3 … + p4\)
Формула давления идеального газа
Давление газа на стенки сосуда, а также на помещенное в него тело, возникает благодаря ударам молекул.
Для установления связи между объемом, давлением и температурой существует уравнение Клапейрона-Менделеева. Оно имеет вид:
\(pV=nRT\)
Здесь \(V\) — объем, \(R\) — газовая постоянная, равная \(8,31431 \frac{Дж}{моль\cdotК}\) , \(T\) — температура, \(n\) — количество молей газа.
Выводы на основе данного уравнения:
- при уменьшении объема газа его давление увеличивается, а при увеличении объема — уменьшается при условии того, что масса и температура газа остаются неизменными;
- давление газа в закрытом сосуде увеличивается при увеличении температуры газа.

Основное уравнение молекулярно-кинетической теории имеет вид:
\(p=\frac{2}{3}nEk\)
Сложно? Обращайтесь за помощью к нашим авторам. Для ФениксХелп нет ничего невозможного.
что это, единица измерения, от чего зависит, как вычислить, формулы МКТ
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.
Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
\(P=\frac{F}{S}\)
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
\(F*Δt = Δp\)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.
Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения.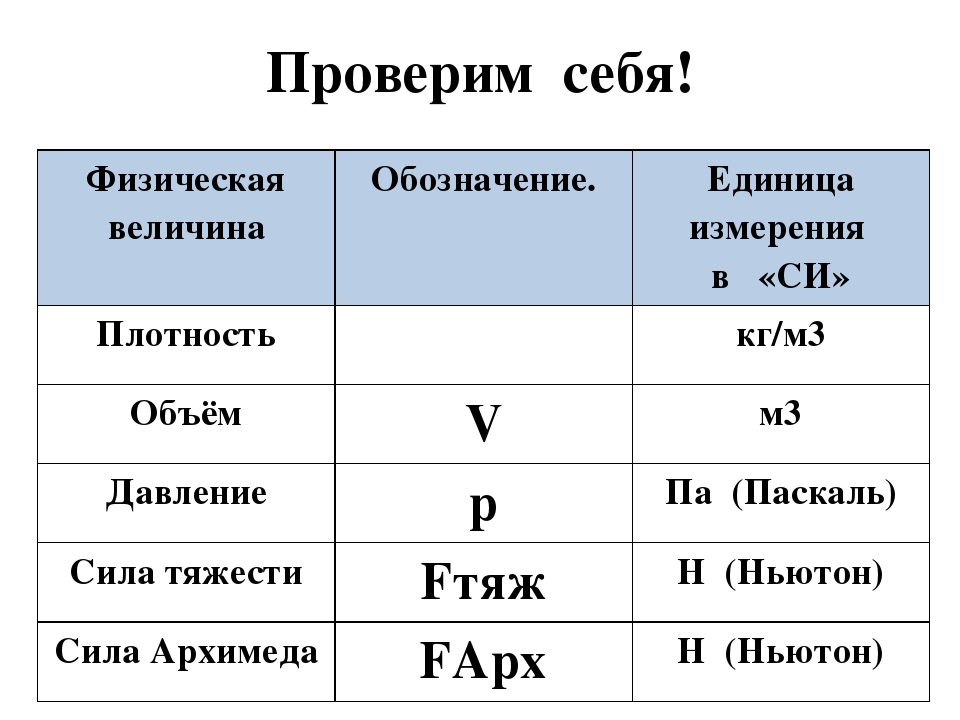 {2}}{3*V}\)
{2}}{3*V}\)
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
\(P*V = n*R*T \)
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
\(P=\frac{n*R*T}{V}\)
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.
Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.
Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
 {2}}{3*V}\)
{2}}{3*V}\)Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
определения и примеры по разделам
Формулы по физике 7 класс, все разделы
В 7 классе ученики, изучая физику, проходят следующий список разделов:
- Введение, в котором знакомятся с наукой, историей ее возникновения, мерами физических величин.
- Сведения о строении вещества. В этом разделе школьники узнают об атомах и молекулах.
- Взаимодействие тел, в котором изучают взаимодействие тел друг с другом под влиянием различных физических сил.
- Давление твердых тел, жидкостей и газов, в котором рассматриваются ключевые понятия и физические законы.
- Работа и мощность, энергия.
 В данном разделе учащиеся узнают об основных видах и законах превращения энергии.
В данном разделе учащиеся узнают об основных видах и законах превращения энергии.
Измерение физических величин
Людям часто приходится производить измерения при работе с техникой, в быту и при изучении различных явлений, которые можно объяснить с помощью науки. Например, чтобы узнать, сколько времени понадобится на то, чтобы дойти от дома до школы, нужно знать скорость движения и расстояние до учебного заведения от того места, где вы живете. Скорость, время и расстояние — это физические величины. Физическую величину всегда можно измерить.
Для того, чтобы это сделать, необходимо сравнить физическую величину с однородной величиной, которую принято считать единицей. Каждая физическая величина имеет свои единицы. Во всем мире приняты одинаковые единицы измерения физических величин. Для этого создана интернациональная система единиц — СИ. В ней за основную единицу длины принято считать 1 метр, единицу времени — 1 секунду, единицу массы — 1 килограмм.

Для измерения физических величин применяют измерительные приборы. К ним относятся:
- линейка;
- рулетка;
- секундомер;
- шагомер;
- термометр;
- весы;
- амперметр;
- вольтметр и т. п.
Механическое движение
Механическим движением называется изменение положения тела относительно других тел с течением времени.
Траектория движения — эта линия, по которой тело совершает свое движение.
Рассмотрим основные физические величины, которые характеризуют механическое движение.
Скорость, путь, время движения, средняя скорость
Длина траектории, по которой тело двигалось в течение какого-то времени, называется путем. Обозначается символом S и измеряется в метрах.
Время движения — это физическая величина, которая показывает, сколько времени понадобилось телу, чтобы совершить свой путь.
 Обозначается t, измеряется в секундах.
Обозначается t, измеряется в секундах.Скорость — это величина, которая характеризует быстроту движения тел. При равномерном движении эта величина остается постоянной и показывает, какой путь тело прошло за единицу времени. Обозначается V. В интернациональной системе единицей измерения скорости принято считать м/с.
Рассчитывается скорость по формуле:
\(V=\frac St\)
где S — путь, пройденный объектом за определенное время (t).
Скорость — векторная величина.
Физическая величина, которая помимо числового значения обладает направлением, называется векторной.
В физике существует понятие средней скорости, которая характеризует неравномерное движение.
Неравномерное движение — это движение тела, при котором его скорость меняется на отдельных участках пути.
Для того, чтобы определить среднюю скорость, нужно весь пройденный путь разделить на всё время движения.
Сила тяжести, вес, масса, плотность
В XVII веке Исаак Ньютон открыл закон всемирного тяготения, согласно которому:
- Силы притяжения между телами зависят от их массы.
 3\).
3\).Плотность определяется по формуле:
\(p=\frac mV\)
где m — масса, V — объем.
Весом называют силу, с которой тело действует на опору или растягивает подвес. Обозначается P, измеряется в ньютонах.
Рассчитать вес можно по той же формуле, что и силу тяжести.
Давление
Давлением называют физическую величину, которая равна отношению силы, перпендикулярно действующей на некоторую поверхность, к площади этой поверхности. Обозначается p, измеряется в паскалях.
Давление можно вычислить по формуле:
\(P=\frac FS\)
где F — сила, направленная перпендикулярно площади поверхности, S — площадь этой поверхности.
Сила давления
Силой давления называют силу, действующую перпендикулярно некоторой поверхности.
Примечание
В качестве силы давления может выступать сила упругости или вес тела.
Давление газов и жидкостей
Давление в жидкости или газе зависит от 2-х факторов:
- Уровня вещества в емкости.
 (Из-за того, что верхние слои «давят» на нижние слои жидкости).
(Из-за того, что верхние слои «давят» на нижние слои жидкости). - Плотности жидкости или газа. Чем больше плотность, тем больше давление.
В виде уравнения зависимость выглядит так:
\(P=p\times g\times h\)
где P — давление в жидкости / газе, p — плотность вещества, g — коэффициент силы тяжести, равный 9,8 м/с, h — уровень жидкости в емкости.
Давление в жидкости и газе также измеряется в паскалях.
Примечание
Согласно закону Паскаля, давление в жидкости и газах передается одинаково по всем направлениям.
Давление однородной жидкости
Источник: 900igr.netЗакон сообщающихся сосудов
Сообщающиеся сосуды — это два или несколько сосудов, соединенных между собой в нижней части таким образом, что жидкость может свободно перетекать из одного сосуда в другой.
Закон сообщающихся сосудов гласит: уровни однородной жидкости в сообщающихся сосудах устанавливаются на одной высоте.

Это правило верно для любого количества сообщающихся сосудов, независимо от их формы и расположения в пространстве. Главное условие — чтобы в сосудах находилась одна и та же жидкость.
Закон гидравлической машины
Источник: infourok.ruВ основе закона гидравлической машины лежит закон Паскаля, согласно которому давление, производимое на жидкость, передается в любую точку без изменения.
Описание этого закона уравнением выглядит так:
\(P=\frac FS\)
где F — сила, действующая на поршень, S — площадь поршня.
Закон Архимеда
Архимедова сила — это сила выталкивания, которая воздействует на тело, погруженное в жидкость или газ. Она всегда направлена вверх и равна по модулю весу жидкости, которое вытеснило тело. Обозначается \(F_a\), измеряется в ньютонах.
Сила Архимеда обладает следующими признаками:
- Зависит от плотности жидкости и объема погруженной части тела.

- Не зависит от плотности тела, его формы и высоты столба жидкости над телом.
Вычисляется по формуле:
\(F_a=p\times g\times V\)
где p — плотность жидкости или газа, g — коэффициент силы тяжести, V — объем погруженного в жидкость объекта.
Условие плавания тел
Тела, оказавшись в жидкости, ведут себя по-разному: одни тонут, другие плавают внутри жидкости, третьи всплывают на поверхность.
Такое поведение тел зависит:
- от взаимодействия силы тяжести и силы выталкивания;
- от плотности тела относительно плотности жидкости.
Примечание
Если сила тяжести больше силы Архимеда, тело будет тонуть.
Если сила тяжести приблизительно равна Архимедовой силе, тело будет плавать внутри жидкости.
Если сила тяжести меньше силы Архимеда, тело будет плавать на поверхности жидкости.
Примечание
Если плотность объекта больше плотности жидкости, он будет тонуть.

Если плотность объекта меньше плотности жидкости, он будет плавать на поверхности.
Если плотность объекта примерно равна плотности жидкости, он будет плавать внутри жидкости.
Работа, мощность
В физике термин «работа» употребляется в связи с действием силы и полученным в процессе этого действия перемещением тела.
Механическая работа силы — это физическая величина, которая прямо пропорциональна приложенной к телу силе и пройденному телом пути. Обозначается A, измеряется в джоулях.
Вычислить механическую работу можно по формуле:
\(A=F\times S\)
где F — значение силы, S — путь.
Работа может быть отрицательной при условии перемещения тела против направления действия силы.
В некоторых случаях механическая работа может равняться 0:
- На тело действует сила, но тело не перемещается. Например, сила тяжести на любой неподвижный объект.
- Тело перемещается по инерции, без воздействия на него каких-либо сил.

- На тело действует сила, направленная не по направлению движения тела, а перпендикулярно ему.
Мощность — это физическая величина, характеризующая быстроту работы и равная отношению работы ко времени ее выполнения. Обозначается N, выражается в ваттах.
Определить мощность можно двумя способами:
\(N=\frac At \)
где A — работа, t — время ее выполнения.
или
\(N=F\times V\)
где F — сила, приложенная к телу, v — скорость движения тела в направлении силы.
Механический рычаг
Механический рычаг — это простой механизм, с помощью которого можно совершать механическую работу. Рычаг представляет собой твердый предмет, у которого есть неподвижная ось вращения (точка опоры или подвеса) и на который действуют силы, стремящиеся повернуть его вокруг оси вращения.
Источник: infourok.ruУсловие равновесия рычага
Источник: infourok. ru
ruМомент силы
Источник: v.900igr.netКПД
Отношение полезной работы к затраченной называют коэффициентом полезного действия (КПД). Обозначается \eta и выражается в процентах.
Формула вычисления КПД выглядит так:
\( \eta=\frac{A_п}{A_з}\)
где \(А_п\) — полезная работа, \(A_з\) — затраченная работа.
Энергия
Механическая энергия — это способность тела или нескольких взаимодействующих тел совершать механическую работу. Обозначается Е, измеряется в джоулях.
Вычислить энергию можно по формуле:
\(E=A_{max}\)
где \(A_{max}\) — максимальная работа.
Механическая энергия может быть 2-х видов:
- Потенциальная.
- Кинетическая.
Потенциальная энергия
Потенциальная энергия — это энергия взаимодействия.
Она определяется по формулам:
\(E_п=A\)
где A — работа,
или
\(E=m\times g\times h\)
где m — масса, g — коэффициент силы тяжести, h — высота, на которое поднято тело.
 2}2\)
2}2\)где m — масса, V — скорость движения.
Сохранение и превращение механической энергии
Закон сохранения энергии гласит, что энергия в природе существует всегда, ее значение при этом остается постоянным, просто она видоизменяется при передаче от одного тела к другому и превращается из одного вида в другой.
Формула закона сохранения энергии выглядит так:
\(E_{k_1}+E_{p_1}=E_{k_2}+E_{p_2}\)
Уравнение означает, что полная механическая энергия тела, состоящая из кинетической и потенциальной, остается постоянной.
В данной формуле \(E_{k_1} и E_{k_2}\) — это кинетическая энергия тела, \(E_{p_1} и E_{p_2}\) — потенциальная.
Полную механическую энергию (E) можно рассчитать по формуле:
\(E=E_k+E_p\)
где \(E_k\) — кинетическая энергия, \(E_p\) — потенциальная.
Формулы меры длины и веса
Источник: infourok.ruПримеры задач
Рассмотрим самые распространенные задачи из каждого раздела.

Задачи на нахождение скорости, пути или времени движения
Задача
Дано: Поезд «Москва-Сочи» движется со скоростью 72 км/ч. Какой путь поезд преодолеет за 20 минут?
Решение
Сначала необходимо известные в задаче величины привести к одинаковым единицам измерения. 20 мин=1200 с. 72 км/ч=20 м/с.
\(S=V\times t=1200*20=24000м=24\) км.
Задача
Дано: Самолет «Нью-Йорк-Лондон» летит со скоростью 850 км/ч. За какое время он преодолеет расстояние в 3400 км?
Решение
По формуле \(t=\frac SV\) ищем время.
t=3400/850=4 часа.
Задача
Дано: Поезд, двигаясь с постоянной скоростью, за 2 часа прошел 108 км. Определите скорость движения поезда.
Решение
По формуле\( V=\frac St\) находим скорость.
V=108/2=54км/ч=15 м/с.
Задачи на вычисление силы тяжести, веса, массы, плотности
Задача
Дано: Льдина объемом 8 м^3 обладает массой в 7200 кг.
 2\) действует сила в 500 Н. Рассчитайте давление, производимое силой на поверхность.
2\) действует сила в 500 Н. Рассчитайте давление, производимое силой на поверхность.Решение
\(P=\frac FS=500/2=250\) Па.
Задача
Дано: Подводная лодка находится в Баренцевом море на глубине 300 метров. Определите давление воды на судно.
Решение
\(P=p\times g\times h=1030*9,8*300=3028200\) Па.
Задачи на вычисление работы, мощности, КПД
Задача
Дано: Тело массой 5 кг свободно перемещается с высоты в 5 метров. Определите работу силы тяжести.
Решение
\(A=F\times S\)
\(F=m\times g\)
\(A=m\times g\times S=5*5*9,8=245\) Дж.
Задача
Дано: Какую мощность развивает объект при движении с постоянной скоростью 3,6 км/ч, если его сила тяги равна 1 кН.
Решение
3,6 км/ч=1 м/с.
1 кН=1000 Н.
\(N=\frac At\)
\(A=F\times S\)
\(S=V\times t\)
\(N=F\times V=1*1000=1000 Вт=1\) кВт.

Задача
Дано: Машина мощностью 5 кВт поднимает 180 тонн песка на высоту 6 метров за один час. Определите КПД установки.
Решение
\( \eta=\frac{A_п}{A_з}\)
\(А_п=m\times g\times h\)
\(A_з=A=P\times t\)
\(\eta=\frac{m\times g\times h}{P\times t}=180000*9,8*6/(5000*3600)=0,59\)
0,59*100%=59%
Список обозначений в физике — Википедия. Что такое Список обозначений в физике
Материал из Википедии — свободной энциклопедии
Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин.
 Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.Шрифты
В печатном тексте математические обозначения, использующие латиницу, принято писать курсивом. Названия функций, а также цифры и греческие буквы оставляют прямыми. Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности, векторные величины принято обозначать жирным шрифтом, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Латинская азбука
В силу исторических причин, многие из обозначений используют латинские буквы — от первой буквы слова, обозначающего понятие на иностранном языке (преимущественно латинском, английском, французском и немецком).
 Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква O{\displaystyle O}.
Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква O{\displaystyle O}.Символ Значение и происхождение A{\displaystyle A} Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, Работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число a{\displaystyle a} Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора, натуральный показатель поглощения света B{\displaystyle B} Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ.  Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулыb{\displaystyle b} Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина распада (нем. Breite) C{\displaystyle C} Электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), очарование (чарм, шарм; англ. charm), коэффициенты Клебша — Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона — Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) c{\displaystyle c} Скорость света (лат. celeritas), скорость звука (лат. celeritas), Теплоёмкость (англ. heat capacity), очарованный кварк (англ.  charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная
charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постояннаяD{\displaystyle D} Вектор электрической индукции[1] (англ. electric displacement field), Коэффициент диффузии (англ. diffusion coefficient), Оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, D-мезон (англ. D meson), Диаметр (лат. diametros, др.-греч. διάμετρος) d{\displaystyle d} Расстояние (лат. distantia), Диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) E{\displaystyle E} Энергия (лат.  energīa), напряжённость электрического поля[1] (англ. electric field), Электродвижущая сила (англ. electromotive force), магнитодвижущая сила,
energīa), напряжённость электрического поля[1] (англ. electric field), Электродвижущая сила (англ. electromotive force), магнитодвижущая сила,Как обозначается давление воздуха. Чем его измеряют. Эксперименты — OneKu
Содержание статьи:
Давлением атмосферы называют силу, с которой воздух давит на Землю, человека и все, что его окружает. Статья расскажет, как в XVII в. с помощью эксперимента впервые была показана сила давления воздуха. Это очень интересно! Мы узнаем, как обозначается давление атмосферы и чем измеряется.
Опыт Отто фон Герике
Насколько велико атмосферное давление, мир узнал в 1654 году. Произошло это благодаря бургомистру города Магдебург (Германия) Отто фон Герике. Он продемонстрировал опыт с так называемыми магдебургскими полушариями. Тогда не шла речь о том, как обозначается давление воздуха, потому что измерять его еще не умели. Как выглядят полушария, видно на фотографии из магдебургского музея.

Вам будет интересно:Социальная модернизация общества: понятие, особенности, примеры
Это две бронзовых полусферы, одна из них сплошная, а во второй есть отверстие. Между полусферами для герметичности помещали промасленную кожаную прокладку и соединяли их. Через отверстие из полушарий выкачивали воздух. Интересно, что сам Герике за четыре года до этого, в 1650 г., изобрел вакуумный насос. Он тоже запечатлен на фото. Когда воздух был откачан, полусферы сдавливало атмосферное давление. Для того чтобы отсоединить их друг от друга, использовали тяговую силу лошадей.
Эксперимент с магдебургскими полушариями
Перед тем как узнать, как обозначается давление атмосферы, проведем опыт. Для него будем использовать модель магдебургских полушарий. Присоединим к отверстию полусферы при помощи резинового шланга вакуумный насос. Включим его, откроем кран на одном из полушарий. Давление в пространстве между ними понизится. Следовательно, сила, действующая на полушария изнутри, понижается, а действующая снаружи — увеличивается.

Во время откачивания воздуха разъединить полусферы оказывается невозможным, так как они плотно прилегают друг к другу. Выключим насос, отсоединим резиновый шланг. Воздух начнет заходить в пространство между полушариями. Тогда они легко разделятся.
Какой буквой обозначается давление воздуха
Попробуем рассчитать силу, которая сдавливала полусферы. Когда мы откачиваем воздух, на полушария действует только сила атмосферного давления. Она сдавливает полушария и направлена от внутренних стенок полых сфер к центру пространства между ними. Диаметр полушарий (d) у Герике был 35,5 см.
Исходя из того, что мы не смогли разъединить полусферы, становится понятно, что сила давления очень большая. Даже восемь лошадей с каждой стороны не смогли разорвать эти полушария. Вот гравюра, которая иллюстрирует опыт Отто фон Герике.
Какой буквой обозначается давление? Буквой Р. Нормальное атмосферное давление (Ратм) равно 100 килопаскалям (кПа). На каждый участок полушария действует такая сила.
 Сила давления F равна произведению атмосферного давления на площадь сечение полушарий S.
Сила давления F равна произведению атмосферного давления на площадь сечение полушарий S.S=π*d2/4. F=100*103 Па*3,14*(0,355 м)2/4≈10 кН (килоньютонов). Это вес груза массой одна тонна, поэтому лошади не смогли разорвать эти полушария.
Барометр
Как обозначается атмосферное давление, мы знаем, а чем его измеряют? Барометр, который изобрел итальянец Торричелли в первой половине XVII в., имел недостатки. Его легко можно было разбить, он был наполнен ядовитой ртутью, а ведь так хотелось возить его по разным местам, чтобы предсказывать погоду.
Нужно было придумать устройство без стеклянной трубки, т. е. безжидкостное. Такой барометр изобрели только через двести лет и назвали его анероид. Это слово в переводе на русский язык означает безжидкостный. Рассмотрим, что собой представляет барометр-анероид.
Это прибор небольшого размера. В отличие от ртутной трубки Торричелли высотой в один метр, его можно легко возить с собой куда угодно. Что же в нем внутри? Посмотрим на барометр в разобранном виде.

Как обозначается давление в нем? В устройстве есть шкала, похожая на циферблат часов. Давление в килопаскалях показывается стрелкой. Позади циферблата мы видим три уплощенные коробочки. Из них выкачан воздух, а внутри находится пружина. Если бы ее не было, атмосфера бы раздавила коробочки. Дальше от пружины отходит рычажок, он передает движения коробочек. Почему они двигаются? Коробочки могут менять свою толщину. Когда атмосферное давление больше, воздух сжимает коробочки, их толщина уменьшается. Когда давление меньше, пружина распрямляется и коробочки становятся толще. Через механизм рычажков движение передается стрелке.
Устройство безжидкостного барометра
Мы узнали, как обозначается давление в безжидкостном барометре, а теперь нарисуем его схему.
Три коробочки придают устройству большую точность, но в принципе достаточно и одной. Она специально сделана гофрированной для того, чтобы обладать способностью менять свою толщину. Вспомните гофрированные, а поэтому гибкие шланги пылесосов.
 Нижняя часть коробочки прикреплена к основанию. К верхней ее части прикреплена пружина, которая пытается расправить коробочку так же, как алюминиевая линейка, если ее согнуть, пытается распрямиться. Атмосферное давление, наоборот, пытается сжать коробочку.
Нижняя часть коробочки прикреплена к основанию. К верхней ее части прикреплена пружина, которая пытается расправить коробочку так же, как алюминиевая линейка, если ее согнуть, пытается распрямиться. Атмосферное давление, наоборот, пытается сжать коробочку.Когда давление увеличивается, толщина коробочки уменьшается, значит, рычаг поворачивает ось. Если к оси прикрепить стрелку, то она будет поворачиваться вправо, когда толщина уменьшается, и влево, когда толщина увеличивается.
Источник
Заставьте научную нотацию работать в физических задачах
- Образование
- Наука
- Физика
- Заставьте научную нотацию работать в физических задачах
Стивен Хольцнер
Физика имеет дело с очень большими и очень маленькими числами. Для работы с такими числами вы используете научную нотацию . Научная запись выражается числом от 1 до 10, умноженным на степень 10.
Например, предположим, что вы измеряете массу электрона в системе MKS.
 Вы кладете электрон на шкалу (на практике электроны слишком малы для измерения на шкале — вы должны видеть, как они реагируют на притяжение магнитных или электростатических сил, чтобы измерить их массу), и вы измеряете следующее:
Вы кладете электрон на шкалу (на практике электроны слишком малы для измерения на шкале — вы должны видеть, как они реагируют на притяжение магнитных или электростатических сил, чтобы измерить их массу), и вы измеряете следующее:0.00000000000000000000000000000091 кг
Что это за хрень? Здесь много нулей, и работать с этим числом очень неудобно. К счастью, вы знаете все о научных обозначениях, поэтому можете преобразовать число в следующее:
9.1 x 10 –31 кг
То есть 9,1, умноженное на степень 10, 10 –31 . Научная запись работает путем извлечения степени 10 и откладывания ее в сторону, где это удобно. Вы преобразуете число в научное представление, подсчитывая количество мест, на которое нужно переместить десятичную точку, чтобы получить первую цифру перед этой десятичной точкой.
Например, 0,050 равно 5,0 x 10 –2 , потому что вы переместите десятичную запятую на два разряда вправо, чтобы получить 5.
 0. Точно так же 500 равно 5,0 x 10 2 , потому что вы переместите десятичную запятую на два места влево, чтобы получить 5,0.
0. Точно так же 500 равно 5,0 x 10 2 , потому что вы переместите десятичную запятую на два места влево, чтобы получить 5,0.Пример вопроса
Что такое 0,000037 в экспоненциальном представлении?
Правильный ответ: 3,7 x 10 –5 . Вам нужно переместить десятичную запятую пять раз вправо, чтобы получить 3,7.
Практические вопросы
Что такое 0,0043 в экспоненциальном представлении?
Что такое 430 000.0 в научном обозначении?
Что такое 0,00000056 в экспоненциальном представлении?
Что такое 6700,0 в экспоненциальном представлении?
Ниже приведены ответы на вопросы практики:
4,3 x 10–3
Вам нужно переместить десятичную точку на три позиции вправо.
4,3 х 105
Вам нужно переместить десятичную запятую на пять позиций влево.

5.6 х 10–7
Вам нужно переместить десятичную запятую на семь разрядов вправо.
6,7 х 103
Вам нужно переместить десятичную запятую на три позиции влево.
Об авторе книги
Стивен Хольцнер, доктор философии, был преподавателем и ответственным редактором журнала PC Magazine .
14.3: Жидкости, плотность и давление (Часть 2)
Изменение давления с глубиной в жидкости постоянной плотности
Давление определено для всех состояний вещества, но особенно важно при обсуждении жидкостей.Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости. Молекулы жидкости просто текут, чтобы приспособиться к горизонтальной силе. Сила, приложенная перпендикулярно к поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что сила реакции развивается в каждой точке внутри жидкости во внешнем направлении, уравновешивая силу, приложенную к молекулам на границе.

Рассмотрим жидкость постоянной плотности, как показано на рисунке \ (\ PageIndex {1} \).Давление на дне контейнера возникает из-за давления атмосферы (стр. 0 ) плюс давление из-за веса жидкости. Давление, создаваемое жидкостью, равно весу жидкости, деленному на площадь. Вес жидкости равен ее массе, умноженной на ускорение свободного падения.
Рисунок \ (\ PageIndex {1} \): Дно этого контейнера поддерживает весь вес находящейся в нем жидкости. Вертикальные стороны не могут оказывать восходящее усилие на жидкость (поскольку она не может выдерживать силу сдвига), поэтому дно должно поддерживать все это.
Поскольку плотность постоянна, вес можно рассчитать, используя плотность:
\ [w = mg = \ rho Vg = \ rho Ahg \ ldotp \]
Таким образом, давление на дне контейнера равно атмосферному давлению, добавленному к весу жидкости, разделенному на площадь:
\ [p = p_ {0} + \ frac {\ rho Ahg} {A} = p_ {0} + \ rho hg \ ldotp \]
Это уравнение применимо только для давления на глубине для жидкости постоянной плотности
Давление на глубине для жидкости постоянной плотности
Давление на глубине в жидкости постоянной плотности равно давлению атмосферы плюс давление, обусловленное весом жидкости, или
\ [p = p_ {0} + \ rho hg, \ label {14.
 4} \]
4} \]Где p — давление на определенной глубине, p 0 — давление атмосферы, \ (\ rho \) — плотность жидкости, g — ускорение свободного падения, а h — глубина.
Рисунок \ (\ PageIndex {2} \): Плотина «Три ущелья», возведенная на реке Янцзы в центральном Китае в 2008 году, создала огромный водохранилище, в результате которого было перемещено более миллиона человек. (Источник: «Le Grand Portage» / Flickr)
Пример 14.1: Какую силу должна выдержать плотина?
Рассмотрим давление и силу, действующие на плотину, удерживающую резервуар с водой (Рисунок \ (\ PageIndex {2} \)).Предположим, что плотина имеет ширину 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Какое среднее давление на плотину из-за воды? (b) Рассчитайте силу, действующую на плотину.
Среднее давление p из-за веса воды — это давление на средней глубине h, равное 40,0 м, поскольку давление увеличивается линейно с глубиной. Сила, действующая на плотину со стороны воды, равна среднему давлению, умноженному на площадь контакта, F = pA.

Решение
- Среднее давление, обусловленное весом жидкости, составляет $$ p = h \ rho g \ ldotp \ label {14.{10} \; M \ ldotp \ end {split} $$
Значение
Хотя эта сила кажется большой, она мала по сравнению с массой воды в резервуаре 1,96 x 10 13 Н. На самом деле это всего 0,0800% от веса.
Упражнение 14.1
Если водохранилище в Примере \ (\ PageIndex {1} \) покрывает вдвое большую площадь, но сохраняется на той же глубине, потребуется ли реконструировать плотину?
Давление в статической жидкости в однородном гравитационном поле
Статическая жидкость — это жидкость, которая не движется.В любой точке внутри статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке отреагирует на результирующую силу и ускорится.
Давление в любой точке статической жидкости зависит только от глубины в этой точке.
 Как уже говорилось, давление в жидкости около Земли изменяется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности.Это разумное приближение для жидкостей, таких как вода, где для сжатия жидкости или изменения объема требуются большие силы. В плавательном бассейне, например, плотность примерно постоянна, и вода внизу очень слабо сжимается под весом воды наверху. Однако путешествие вверх в атмосфере — это совсем другая ситуация. Плотность воздуха начинает значительно меняться на небольшом расстоянии от поверхности Земли.
Как уже говорилось, давление в жидкости около Земли изменяется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности.Это разумное приближение для жидкостей, таких как вода, где для сжатия жидкости или изменения объема требуются большие силы. В плавательном бассейне, например, плотность примерно постоянна, и вода внизу очень слабо сжимается под весом воды наверху. Однако путешествие вверх в атмосфере — это совсем другая ситуация. Плотность воздуха начинает значительно меняться на небольшом расстоянии от поверхности Земли.Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость с плотностью \ (\ rho \) на поверхности Земли, мы должны начать с предположения, что плотность жидкости непостоянна.Жидкость, находящаяся на более глубоких уровнях, подвергается большей силе, чем жидкость, находящаяся ближе к поверхности, из-за веса жидкости над ней.
 Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.Представьте себе тонкий элемент жидкости на глубине h, как показано на рисунке \ (\ PageIndex {3} \). Пусть элемент имеет площадь поперечного сечения A и высоту \ (\ Delta \) y. Силы, действующие на элемент, возникают из-за давлений p (y) сверху и p (y + \ (\ Delta \) y) под ним.Вес самого элемента также показан на диаграмме свободного тела.
Рисунок \ (\ PageIndex {3} \): Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.
Поскольку элемент жидкости между y и y + \ (\ Delta \) y не ускоряется, силы уравновешены. Используя декартову ось y, ориентированную вверх, мы находим следующее уравнение для y-компоненты:
\ [p (y + \ Delta y) A — p (y) A — g \ Delta m = 0 (\ Delta y <0) \ ldotp \ label {14.6} \]
Обратите внимание, что если бы элемент имел ненулевую y-компоненту ускорения, правая часть не была бы равна нулю, а вместо этого была бы массой, умноженной на y-ускорение.
 Массу элемента можно записать через плотность жидкости и объем элементов:
Массу элемента можно записать через плотность жидкости и объем элементов:\ [\ Delta m = | \ rho A \ Delta y | = — \ rho A \ Delta y \ quad (\ Delta y <0) \ ldotp \]
Подставляя это выражение для \ (\ Delta \) m в уравнение \ ref {14.6}, а затем разделив обе части на A \ (\ Delta \) y, находим
\ [\ frac {p (y + \ Delta y) — p (y)} {\ Delta y} = — \ rho g \ ldotp \ label {14.7} \]
Переходя к пределу бесконечно тонкого элемента \ (\ Delta \) y → 0, мы получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:
\ [\ frac {dp} {dy} = — \ rho g \ ldotp \ label {14.8} \]
Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкости. Решение этого уравнения зависит от того, постоянна ли плотность \ (\ rho \) или изменяется с глубиной; то есть функция \ (\ rho \) (y).
Если диапазон анализируемой глубины не слишком велик, мы можем считать плотность постоянной.
 Но если диапазон глубин достаточно велик для того, чтобы плотность могла заметно меняться, как, например, в случае атмосферы, происходит значительное изменение плотности с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.
Но если диапазон глубин достаточно велик для того, чтобы плотность могла заметно меняться, как, например, в случае атмосферы, происходит значительное изменение плотности с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.Давление в жидкости постоянной плотности
Давайте воспользуемся уравнением \ ref {14.9}, чтобы найти формулу для давления на глубине h от поверхности в резервуаре с жидкостью, например с водой, где плотность жидкости можно считать постоянной.{-h} \ rho gdy \\ p — p_ {0} & = \ rho gh \\ p & = p_ {0} + \ rho gh \ ldotp \ end {split} \ label {14.9} \]
Следовательно, давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс \ (\ rho \) gh, если плотность жидкости постоянна по высоте, как мы обнаружили ранее.
Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы контейнера. Таким образом, в контейнере, где жидкость может свободно перемещаться в различных частях, жидкость остается на одном уровне во всех частях, независимо от формы, как показано на рисунке \ (\ PageIndex {4} \).

Рисунок \ (\ PageIndex {4} \): Если жидкость может свободно течь между частями контейнера, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление внизу каждой колонки одинаковое; если бы это было не так, жидкость текла бы до тех пор, пока давления не сравнялись бы.
Изменение атмосферного давления по высоте
Особый интерес представляет изменение атмосферного давления с высотой. Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна.(Мы обсудим закон идеального газа в следующей главе, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p (y) будет атмосферным давлением на высоте y. Плотность \ (\ rho \) в y, температура T в шкале Кельвина (K) и масса m молекулы воздуха связаны с абсолютным давлением по закону идеального газа в виде
\ [p = \ rho \ frac {k_ {B} T} {m} \; (атмосфера), \ label {14.
 10} \]
10} \], где k B — постоянная Больцмана, имеющая значение 1.38 x 10 −23 Дж / К.
Вы, возможно, встречали закон идеального газа в форме pV = nRT, где n — число молей, а R — газовая постоянная. Здесь тот же закон был записан в другой форме, используя плотность \ (\ rho \) вместо объема V. Следовательно, если давление p изменяется с высотой, то же самое происходит и с плотностью \ (\ rho \). Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как
\ [\ frac {dp} {dy} = -p \ left (\ dfrac {mg} {k_ {B} T} \ right), \]
, где в скобках указаны постоянные количества.{- \ alpha y} \ ldotp \]
Таким образом, атмосферное давление экспоненциально падает с высотой, поскольку ось y направлена вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря. Давление падает в \ (\ frac {1} {e} \) раз, когда высота равна \ (\ frac {1} {\ alpha} \), что дает нам физическую интерпретацию для \ (\ alpha \) : Константа \ (\ frac {1} {\ alpha} \) — это шкала длины, которая характеризует изменение давления с высотой и часто называется высотой шкалы давления.
 {-23} \; Дж / К) \ раз (300 \; К)} = \ гидроразрыва {1} {8800 \; m} \ ldotp \]
{-23} \; Дж / К) \ раз (300 \; К)} = \ гидроразрыва {1} {8800 \; m} \ ldotp \]Следовательно, на каждые 8800 метров давление воздуха падает в 1 / е, или примерно на одну треть своего значения. Это дает нам лишь приблизительную оценку реальной ситуации, поскольку мы предположили и постоянную температуру, и постоянный g на таких больших расстояниях от Земли, что в действительности не является правильным.
Направление давления в жидкости
Давление жидкости не имеет направления, будучи скалярной величиной, тогда как силы, возникающие под давлением, имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности.Причина в том, что жидкости не могут противостоять усилиям сдвига или проявлять их. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление действует перпендикулярно к поверхностям любого объекта в жидкости.
 На рисунке \ (\ PageIndex {5} \) показано давление воздуха на стенки покрышки и давление воды на тело пловца.
На рисунке \ (\ PageIndex {5} \) показано давление воздуха на стенки покрышки и давление воды на тело пловца.Рисунок \ (\ PageIndex {5} \): (a) Давление внутри этой шины оказывает силы, перпендикулярные всем поверхностям, с которыми она контактирует.Стрелки показывают направления и величины сил, действующих в различных точках. (b) Давление оказывается перпендикулярно всем сторонам этого пловца, так как вода текла бы в пространство, которое он занимает, если бы его там не было. Стрелками показаны направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы снизу больше из-за большей глубины, что дает чистую восходящую или подъемную силу. Чистая вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.
 0).
0).
Физический алфавит …
Нижний
регистр буквверхний
case Lettersгреческие буквы *
и их именаСокращенное обозначение уравнения
для физической величиныУсловное обозначение
С.I. Префикс и
его значение
NB оно всегда предшествует символу единицыa
А
a
А
альфа А
= площадьA = нуклон
число (атомная масса)a = ускорение
а =
Константа Вейнаa
= альфа-частицаа
= аттох
10 -18б
B
б
B
бета B
= плотность магнитного потокаб
= бета-частицаB
= звонок (сила звука)Бк = беккерель (активность)
c
С
c
С
чи С
= емкостьc = скорость света
c = удельная теплоемкость
o С
= градус Цельсия (температура)c
= сентих
10 -2d
D
d
D
дельта д
= диаметрd = расстояние
D = расстояние от экрана
в узор с бахромойD = поглощенная доза
D
= изменение вд
= небольшое изменение вD
= диоптрия (оптическая сила линзы)дБ = децибел (интенсивность звука)
д
= decida = дека (или дека)
х
10 –1x 10 1
e
E
e
E
эпсилон e
= заряд электронаE = энергия
E к
= кинетическая энергияE = электрический
напряженность поляE = Янга
Модуль упругостиe
= ЭДСe
= деформация растяженияe o
= диэлектрическая проницаемость свободного пространстваэВ
= электрон-вольт (энергия)E
= exaх
10 18f
F
f
F
фи ф
= силаf = частота
f = фокусное расстояние
f e = фокусное расстояние
линзы окуляраf o = фокусное расстояние
объективаF
= потокf
= работа выходаф
= фарад (емкость)f
= фемтох
10 -15г
G
г
G
гамма г
= напряженность гравитационного поляg = ускорение
под действием силы тяжестиG = гравитационный
постояннаяG = проводимость
г
= гамма-лучГр
= серый (поглощенная доза)г
= гигах
10 9ч
H
ч
H
эта ч
= высотаh = постоянная Планка
H = эквивалент дозы
H = постоянная Хаббла
h
= коэффициент вязкостиH
= Генри (индуктивность)Гц = герц (частота)
ч
= гектонх
10 2I
I
I
I
йота Я
= текущийI 0 = пиковый ток
I = интенсивность звука
I = момент инерции
Осторожно!
Всегда «верх» и «хвост» I, чтобы его можно было отличить от
1 или лj
Дж
j
Дж
тета Дж
= плотность токаДж = момент инерции
Дж
= уголДж
= джоуль (энергия)к
К
к
К
каппа к
= Постоянная Больцманаk = жесткость пружины
К
= кельвин (абсолютная температура)кг = килограмм (масса)
к
= килограммх
10 3л
L
л
L
Ламда л
= длинаl = удельная скрытая теплоемкость
л
= длина волныл
= константа распадаL = собственная индуктивность
L = угловой момент
ln = натуральный логарифм
лог = логарифм по основанию 10 из
л
= литр (= 1000 см 3 ) — измерение объемам
M
м
M
мю м
= массаM = увеличение
кв.
 м.
м.
= проницаемостьм
= коэффициент трениям
= метр (длина)м 2
= метр в квадрате (площадь)м 3
= кубический метр (объем)млн
= мегам = милли
м
= микрох
10 6x 10 -3
x 10 -6
n
N
n
N
nu N
= числоN O = оригинал
номерN A = Авогадро
постояннаяN = количество витков провода
n = количество молей
n = порядок дифракции
n = количество носителей заряда
на единицу объемаn = показатель преломления
N
= ньютон (сила или вес)n
= нанох
10 -9o
O
o
O
омикрон НЕ используется
для всего. его слишком легко спутать с числом
его слишком легко спутать с числом
нольп.
-П
п.
-П
пи П
= мощностьp = давление
p = импульс
p
= 3.14Па
= паскаль (давление)п
= picoP = пета
х
10 -12x 10 15
q
Q
Q
= зарядQ = тепло
энергияQ = качество
факторr
R
r
R
rho г
= радиусR = сопротивление
R = молярная газовая постоянная
R = реакционная сила
г
= плотностьг
= удельное сопротивлениерад = радиан
с
S
с
S
сигма с
= смещение (векторная версия расстояния)s = ширина щели
с
= проводимостьс
= растягивающее напряжениес
= Постоянная СтефанаS
= суммас
= секунда (время)Sv = зиверт (эквивалент дозы)
S = сименс (проводимость)
т
Т
т
Т
тау т
= времяT = температура
T = период формы волны
T 1/2 = период полураспада
T E = эффективный
период полураспадаT B = билогический
период полураспадаT P = физический
период полураспадат
= тесла (плотность магнитного потока)т
= терах
10 12u
U
u
U
ипсилон u
= начальная скорость вращенияu = изображение
расстояниеU = значение U
U = внутреннее
тепло системыu
= атомная единица массы (масса на атомных уровнях)v
В
v
= скоростьv = конечная скорость (когда
используется вместе с буквой u)v = расстояние изображения
V = объем
В = разность потенциалов
В 0 = пиковое напряжение
В
= вольт (электрический потенциал)Вт
Вт
Вт
Вт
омега Вт
= работа выполненаВт
= угловая скоростьw = ширина
бахромыВт
= Ом (электрическое сопротивление)Вт = ватт
(мощность)Вт = weber
(магнитный поток)х
Х
х
Х
дзета х
= ширинаX = реактивное сопротивление
y
Y
y
Y
xi г
= высотаz
Z
z
Z
дзета г
= глубинаZ = число протонов (атомное
число)В
Греческие буквы не в порядке греческого алфавита, а
поставьте рядом с их эквивалентной буквой, чтобы вы могли их найти
легко использовать шрифт ‘symbol’ в ‘MSWord’ ‘ПРИМЕЧАНИЕ
НАСКОЛЬКО ВАЖНЫЙ ПАНЕЛЬ БУКВЫ — УЗНАТЬ ПРИНЯТЫЕ СИМВОЛЫ
ВНИМАТЕЛЬНО!!!NB
А
кандидаты уровня должны:
(a) определять символы, используемые в уравнении
и
(b) условия , при которых
уравнения применяются !!!Физические символы — Список физических символов и названий
×
Извините !, эта страница сейчас недоступна для добавления в закладки.

Список физических символов и их названия
СМОТРЕТЬ БОЛЬШЕ
В физике есть большое количество физических величин, которые мы включаем при выполнении вычислений.
 Чтобы сделать его более удобным для пользователей и более простым в использовании и запоминании, мы часто используем обозначения / символы для представления этих физических величин. Эти обозначения / символы, которые мы используем для представления физических величин при решении связанных с ними проблем или для других целей, являются символами. Символы, используемые для физических величин, сильно отличаются. Иногда символ может быть первой буквой физических величин, которые они представляют, например, что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например c, которое означает скорость света.Они также могут быть в форме греческих символов, например λ, что означает длину волны.
Чтобы сделать его более удобным для пользователей и более простым в использовании и запоминании, мы часто используем обозначения / символы для представления этих физических величин. Эти обозначения / символы, которые мы используем для представления физических величин при решении связанных с ними проблем или для других целей, являются символами. Символы, используемые для физических величин, сильно отличаются. Иногда символ может быть первой буквой физических величин, которые они представляют, например, что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например c, которое означает скорость света.Они также могут быть в форме греческих символов, например λ, что означает длину волны.Ниже приведены некоторые символы, обычно используемые в физике, с их названиями, типами величин и их единицами СИ.
Символы, используемые для обозначения физических величин, связанных с пространством и временем:
Символ Количество / Коэффициенты Физическая величина Вектор) r Радиус, радиус кривизны Метр Работает как скаляр, так и вектор s Смещение Метр Вектор 9301 Расстояние
9301
9301 Расстояние
9301
Радиан Скаляр θ, φ Угловое смещение, угловое разделение, угол поворота Измеритель Работает как скалярная, так и как векторная x, y, z Декартовы координаты Декартовы координаты Скалярный î, ĵ, k̂ Декартовы единичные векторы Безразмерные Вектор r, θ, φ Сферические координаты Метр / радиан Скаляр r̂, θ̂, φ̂ Единичные векторы r̂, θ̂, φ̂ Сферические единичные векторы r, θ, z Цилиндрические координаты Метр / радиан Скалярный r̂, θ̂, ẑ Цилиндрические единичные векторы Без единиц Вектор без единиц
vector
Unitless Vector t̂ Тангенциальный единичный вектор Unitless Vector h Высота, глубина Метр 5 L
Длина Скаляр Измеритель Скаляр t Время Секунда 90 275 Скалярный D Диаметр Метр Скалярный C Окружность Метр 9055
9017 Площадь
975 975 Площадь 9179 скалярное и векторное
V Объем Кубический метр Скалярный t Время, длительность Секунда Скалярная Периодическая
5τ Постоянная времени Секунда Скалярная f Частота Герц Скалярная 9172 Угловая частота 9172 Угловая частота Символы, используемые для обозначения физических величин отн.  для Механиков :
для Механиков : Символ Количество / Коэффициенты S.I Единица Физическая величина (скалярная / векторная) v Скорость, скорость метр в секунду Функционирует как вектор a метр в секунду ускорение
метров на секунду Функции как и вектор
a c Центростремительное / центробежное ускорение метр в секунду в квадрате Функционирует как вектор g Вектор ускорения в секунду275 Вектор функций м Масса Килограмм Скалярный F Сила Ньютон Функционирует как вектор 955 955 W2 9017 Вес Вес 902 г Ньютон Функционирует как вектор F n 901 24, Н Нормальная сила, нормальная Ньютон Функционирует как вектор F f Сила трения Ньютон Функционирует как вектор µ Коэфф. Безразмерный
Скаляр p Импульс Килограмм-метр в секунду Функционирует как вектор Дж Импульс Ньютон-секунда 917 930 Функционирует как вектор Джоуль Скалярный K Кинетическая энергия Джоуль Скалярный U Потенциальная энергия Джоуль Гравитационная Гравитационная килограмм
Скаляр 9 1755 η КПД Безразмерный Скалярный P Мощность Ватт Скалярный ω Вектор скорости вращения, скорость вращения 75
Вектор скорости вращения, скорость вращения 9275 секунд
α Вращательное ускорение Радиан в квадрате секунды Функционирует как вектор τ Крутящий момент Ньютон-метр Функционирует как вектор I 917редтиа55 Момент
917aredtia 55
Скаляр L Угловой момент Килограмм-метр в секунду Функционирует как вектор H Угловой импульс 1 Ньютон-метр секунда 5
5 Функции как вектор постояннаяН ewton на метр Скаляр p Давление Паскаль Скаляр σ Напряжение Паскаль 2 Скаляр 9302
Скаляр 9302
ρ Плотность, объемная массовая плотность Килограмм на кубический метр Скалярная σ Поверхностная массовая плотность Килограмм на квадратный метр Скалярная Скалярная 9175
Килограмм на метр Скаляр F B , B Плавучесть Ньютон Функционирует как вектор q м 917 грамм Массовый расход q V Объемный расход Кубический метр в секунду Скаляр F D , R Сопротивление сопротивлению или сопротивлению воздуха Ньютон Функционирует как вектор C D Коэффициент сопротивления 5
902 Скаляр η Viscosi Паскаль-секунда Скаляр ν Кинематическая вязкость Квадратный метр в секунду Скалярное число Скалярное число Скалярный
Re Число Рейнольдса Безразмерный Скалярный Fr Число Фруда Безразмерный Скалярный 9055
9175 Эластичный
917 Модуль упругости 9017 917 917
G Модуль сдвига жесткость Паскаль Скаляр K Объемный модуль сжатия Паскаль Скаляр ε Линейная деформация Сдвиг Безразмерная деформация Сдвиг Безразмерный
Скалярный θ Объемная деформация Безразмерный Скалярный γ Поверхностное натяжение Ньютон на метр Скалярное обозначение , связанное с используемыми физическими величинами теплофизика:
Символ Количество / Коэффициенты S.I Единица Физическая величина (скалярная / векторная) COP Коэффициент полезного действия Безразмерный Скалярный w Ways Без скалярного 902 902 9175 способов, без скалярных микросостояний 902 917 917 S Энтропия Джоуль на кельвин Скаляр U Внутренняя энергия Джоуль Скалярная Активность
Единица Единица Теплопроводность Ватт на метр по Кельвину Скаляр P Тепловой поток Вт Скаляр N N Количество без частиц 9175
Количество вещества Моль Скаляр L Скрытая теплота / удельная скрытая теплота Джоуль на килограмм Скаляр c Удельная теплоемкость 75
75
75
75
75 К2 Теплота
Джоуль Скаляр Β Объемное расширение, коэффициент объемного теплового расширения Обратный кельвин Скалярный α Линейный коэффициент расширения 975 Коэффициент теплового расширения 917 T Температура Коэффициент Кельвина Скаляр Символы, используемые для обозначения физических величин, связанных с волнами и оптикой:
e
5 9175
С.I Единица Физическая величина (скалярная / векторная) M Увеличение Безразмерная Скалярная f Фокусное расстояние 5
Фокусное расстояние 5 Метр
Индекс преломления
Безразмерный Скалярный L Уровень Децибел, децибел Скаляр I Ватт Ватт Ватт 9175 Вт на квадрат Скорость волны Метр в секунду Скалярный λ Длина волны Метр Скалярный P Сила линзы Dioptre для обозначения физических величин, связанных с электричеством и магнетизмом: 901 12
Символ Количество / Коэффициенты S.I Единица Физическая величина (скалярная / векторная) S Вектор Пойнтинга, интенсивность Ватт на квадратный метр Функционирует как вектор η55 Плотность энергии метр Скалярный n Оборотов на единицу длины Обратный счетчик Скалярный N Число витков Безразмерный 9173 B1255
9175 Магнитный
9175
Weber Vector B Магнитное поле Tesla Функционирует как вектор F B Newton 9301 σ1 Электропроводность Сименс на метр Скаляр 9 0271
G Электропроводность Siemens Скалярный ρ Сопротивление Ом-метр Скалярный R, r Внутреннее сопротивление I Электрический ток Ампер Скалярный ϵ Диэлектрическая постоянная Безразмерный скалярный C сила (ЭДС) Вольт Скалярный В напряжение, электрический потенциал Вольт Скалярный U E Электрическая потенциальная энергия 9172 Φ E
Электрический эт. ux Ньютон-метр в квадрате на кулон Функционирует как вектор E Электрическое поле Ньютон на кулон / вольт на метр Функционирует как вектор F E Электроэнергия Ньютон
Функционирует как вектор λ Линейная плотность заряда Килограмм на метр Скаляр σ Плотность заряда площади Килограмм на квадратный метр 5
5
Объемная плотность заряда
Килограмм на кубический метр Скалярный q, Q Электрический заряд Кулонский Скалярный Символы, используемые в современной физике: 112917
Количество / коэффициенты С.I Единица Физическая величина (скалярная / векторная) D Доза / поглощенная доза серый Скалярная Период полураспада Второй (r, t), ψ (r) φ (t)
Волновая функция Безразмерный Функции как векторные Φ Работа выхода Джоуль Скалярная H Эффективная доза
Сиверт Скаляр Γ Фактор Лоренца / гамма Лоренца Безразмерный Скалярный Полное руководство по физике NEET: Советы по решению численных задач
Многие студенты-медики находят раздел NEET Physics трудным, поскольку он содержит широкий спектр теоретических концепций и числовых задач.
Большинство соискателей NEET выработали привычку все учить. Такой подход может помочь им в биологии NEET, но не в физике NEET. Когда вы пытаетесь изучать физику, не имея никакого практического преимущества в плане подготовки, вы чувствуете, что поняли все концепции, но во время их экзаменов вы не сможете применить то же самое.
Итак, чтобы преодолеть эту проблему, ниже мы предоставили идеальный план обучения и советы по подготовке к взлому NEET Physics.
Давайте проверим Как изучать физику для экзамена NEET 2021 ?
NEET Physics состоит из следующих тем:
Механика
Электродинамика
Современная физика
Тепло и термодинамика
Оптика
SHM и волны
Прежде чем вы познакомитесь с разделом «Советы по подготовке к взлому», давайте посмотрим на вес, который содержится в каждой теме:
Вес разделов по физике в NEET
Следующий вес глав по физике NEET для экзамена 2021 года.
S.No.
Название устройства
% Вес Возраст
1
Механика
35%
2
Электродинамика
27%
3
Современная физика и электроника
11%
4
Тепло и термодинамика
9%
5
Оптика
11%
6
SHM и волны
7%
Советы по подготовке к физике — Как подготовить физику к NEET?
Программа и схема экзаменов
Самый первый шаг к вашей подготовке к экзамену — это проверить программу NEET Physics Syllabus и шаблон экзамена.Вам также необходимо знать схему выставления оценок для раздела физики экзамена NEET.
Очистите свои концепции
Согласно отчетам предыдущего года, механика, тепло и термодинамика, электродинамика и современная физика являются наиболее важными темами в физике NEET. Итак, для вашей подготовки по физике вы должны сначала прояснить концепции, связанные с этими темами. Как только вы очистите все концепции, теперь вы готовы к следующему шагу.
Выучить формулы
Формулы — это основа физики. Изучение формул — самый важный шаг при подготовке к NEET Physics. Итак, старайтесь изучать эти формулы ежедневно. Сделайте небольшой дневник и запишите все физические формулы для NEET. Теперь вам просто нужно пересматривать эти формулы ежедневно, один или два раза в день.
Рекомендовать лучшие книги
Для подготовки вам необходимо обратиться к лучшим книгам по физике для экзамена NEET .
NCERT — лучшая книга для подготовки к экзамену NEET. Большинство вопросов задаются из книги NCERT. Но для отработки числовых задач вы можете также сослаться на другие книги. Эти книги включают:
Концепция конкурентной физики для CBSE PMT от
Аггарвала
NCERT- Физика, часть 1 и часть 2
Концепции физики Х.К. Верма
NCERT Physics: набор из 3 томов CBSE PMT, автор — Анил Аггарвал
Решите вопросы предыдущего года
Лучший способ подготовиться к NEET Physics — ответить на вопросы предыдущего года.Ответы на эти Вопросы по физике NEET помогут вам определить тип вопросов, задаваемых на экзамене NEET. Это также улучшает вашу скорость и точность. Итак, решите как можно больше вопросов и подготовьтесь к экзамену.
Сделать заметки
Во время подготовки к NEET Physics Preparation, вам необходимо записывать все важные формулы, теоремы и концепции. Physics Notes for NEET поможет вам быстрее изучить концепции, а также поможет в вашей последней подготовке.
Пройдите онлайн-пробные тесты
Пройдя пробные онлайн-тесты, вы сможете определить свой уровень подготовки и уровень подготовки к экзамену. Это также поможет вам определить свои слабые места.
Улучшите свои слабые места
Попытайтесь улучшить свои слабые места. Сосредоточьтесь больше на темах, в которых вы слабы. Составьте список этих тем и постарайтесь улучшить их.Вы должны начать с самых важных тем NEET Physics, а затем подготовиться к менее важным.
Ниже приведена таблица наиболее важных, важных и менее важных тем для физики NEET.
Важнейшие главы Важные главы Менее важные главы Электронные устройства Атомы и ядра переменного тока Электростатика Текущее электричество Поведение совершенного газа и кинетическая теория Тепло и термодинамика Двойная природа материи и излучения Электромагнитные волны Кинематика Электромагнитная индукция Гравитация Законы движения Движение системы частиц и твердого тела Физический мир и измерения Магнитное действие тока и магнетизма Оптика Свойства сыпучих материалов Колебания и волны Работа, энергия и сила – Итак, кандидаты, которые готовятся к экзамену NEET, должны начать с самых важных тем для подготовки по физике.Также важно знать нет. вопросов, заданных в каждой главе экзамена NEET 2020 в разделе физики.
Ниже приводится список глав, из которых были заданы вопросы на экзамене NEET Physics.
Анализ физики NEET: главы, задаваемые на экзамене NEET
Ниже приведен полный анализ физики NEET № вопросов, заданных в каждой главе, и оценок, которые они содержат на экзамене:
Название темы
No.Вопросов
Всего оценок
Емкость
1
4
Центр масс
1
4
Круговое движение
4
16
Текущее электричество
3
12
Электромагнитная индукция
2
8
Электростатика
3
12
Ошибка и анализ
1
4
Гидромеханика
1
4
Геометрическая оптика
4
16
Гравитация
2
8
KTG и термодинамика
2
8
Магнетизм
3
12
Современная физика
3
12
Законы движения Ньютона
1
4
Свойства вещества
1
4
Прямолинейное движение
1
4
Относительное движение
1
4
Динамика жесткого тела
2
8
Полупроводниковые приборы
2
8
Простое гармоническое движение
2
8
Поверхностное натяжение
1
4
Тепловое расширение
1
4
Единицы и размеры
1
4
Волновая оптика
1
4
Рабочая энергия и мощность
1
4
Итого
45
180
Как изучать физику для NEET: советы по тематической подготовке
Движение системы частиц и твердого тела
Вопросы для нахождения крутящего момента и момента инерции регулярных тел с использованием теоремы о параллельности и перпендикулярности осей считается важным разделом в NEET Physics.Практикуйтесь больше для таких вопросов.
Также практикуйте численные расчеты, основанные на сохранении углового момента и качении.
Вопросы по круговому движению могут быть легко решены кандидатами. Так что потренируйтесь над этими вопросами.
Кинематика
Кинематика — самый важный элемент NEET Physics. Большинство студентов находят эту главу легкой и интересной.
Задачи, основанные на определении дальности, максимальной высоты, времени полета, скорости в любой точке траектории, считаются важными в NEET Physics.
Записывайте все важные формулы, теоремы и выводы. Это поможет вам в подготовке в последнюю минуту.
Очистите все свои концепции перемещения, ускорения, средней скорости, относительной скорости.
Тепло и термодинамика
Очистите все ваши основы, связанные с этой главой NEET Physics.
Очистите все свои концепции Нулевого закона термодинамики, закона Джоуля и Первого закона термодинамики.
Попрактикуйтесь в некоторых модельных статьях о двигателе Карно — КПД и КПД.
Кинетическая теория газов — это легкая и простая тема и вопросы из этой темы, которые можно легко решить.
Современная физика
Современная физика — одна из самых важных и результативных тем NEET Physics. Начните с таких тем, как радиоактивный распад веществ, ядерное деление и синтез, двойственная природа материи, рентгеновские лучи и модель Бора.
Чтобы прояснить все ваши основные концепции, вам следует обратиться к книге NCERT.
Для теоретической части см. «Концепции физики Х. К. Вермы», а для численных задач см. «3000 решенных задач по физике» Шаума.
Как изучать физику для NEET: коучинг против самообучения
Большинство студентов, готовящихся к NEET Physics, не понимают, следует ли им идти на уроки коучинга или заниматься самообучением.Большинство кандидатов предпочитают ходить на уроки коучинга, потому что все в их группе тоже этим занимаются.
Коучинговые занятия сегодня очень дороги. Но чтобы прояснить все концепции, нужно правильное руководство.
Но самообучение экономит ваше время, деньги и силы. Итак, какой вариант подготовки к NEET Physics лучше всего?
Чтобы ответить на этот вопрос ниже, мы предоставили некоторые важные факторы для обучения физике NEET и самообучения.
Систематический и новейший учебный план
Институты коучинга
предоставляют новейшие книги, учебную программу, расписание подготовки, расписание серии тестов и все, что вам нужно во время подготовки к NEET Physics.
Но если вы пойдете на самостоятельное обучение, это сэкономит много денег и времени. Вы можете потерять много времени, чтобы выяснить, из какой книги лучше всего готовиться, какие темы являются важными в физике NEET и т. Д.
Сомнения
Готовясь к NEET Physics, нужно как можно скорее развеять все сомнения. Кандидаты, решившие пойти на занятия по коучингу, могут развеять все сомнения своих учителей. Нет лучших людей, чем ваши учителя, чтобы развеять ваши сомнения.
Стоимость
Тренерские уроки в наши дни стали очень дорогими. Вам нужно вкладывать много денег и времени на занятия по коучингу.Большинство кандидатов, готовящихся к NEET Physics, не могут посещать курсы коучинга, поскольку это требует огромных денег и времени.
Итак, выбирать вариант, который выбирают другие, — не лучшая идея. Вам следует выбрать тот вариант, который вам наиболее удобен.
Если вы готовы вложить огромное количество денег и времени, то отправляйтесь на занятия коучинга. Если вы думаете, что сможете взломать NEET Physics самостоятельно, сделайте это.
Горящие советы по подготовке к NEET Physics
По мере приближения экзамена NEET большинство кандидатов должны беспокоиться о своих результатах на экзамене.
Вместо того, чтобы беспокоиться о своем экзамене, вы должны следовать приведенным ниже советам по подготовке к экзамену по физике NEET в последнюю минуту:
Решите вопросы предыдущего года
Решение вопросов по NEET Physics за предыдущий год и образцы заданий — лучший способ подготовиться к экзамену. Это поможет вам определить схему экзамена и тип вопросов, заданных на экзаменах за последний год.
Избегайте изучения любой новой темы
Сейчас не время для подготовки к новым темам в NEET Physics.Вместо этого пересмотрите все темы, которые вы узнали ранее. Новые темы в последние дни подготовки могут повысить уровень стресса и привести к путанице.
Пересмотр и практика
Начните повторять и практиковаться по темам, которые вы уже выучили. Начните проходить серию онлайн-тестов и онлайн-пробные тесты. Это поможет вам повысить скорость и точность при решении вопросов.
Оставайтесь здоровыми
Соблюдайте здоровую диету и спите во время подготовки к экзамену по физике NEET.Экзамен проводится жарким летом, поэтому пейте много воды, чтобы поддерживать организм гидратированным. Избегайте нездоровой пищи, чтобы оставаться в форме к экзамену.
Исследование из NCERT Books
Поскольку большинство вопросов в NEET Physics задаются из книг NCERT, вам нужно больше изучать из своей книги NCERT. Не пропускайте ни одну из тем из NCERT Book.
Оставаться положительным
Держите свой ум ясным и позитивным при подготовке к экзамену по физике NEET.Отдохните и расслабьте свой разум. Занимайтесь йогой или медитацией, которые помогут вам расслабиться и хорошо подготовиться к экзамену.
Надеюсь, упомянутые выше советы по подготовке облегчат вашу подготовку по физике NEET, а также помогут вам преодолеть страх перед предметом «Физика».
Если вам нужна помощь или у вас есть вопросы, связанные с этой статьей, вы можете задать их в разделе комментариев ниже.Будьте в курсе последних обновлений и уведомлений на Eduncle.
Преобразование температуры из Цельсия в Фаренгейт
Быстрый Цельсий ( ° C ) / Фаренгейт ( ° F ) Преобразование:
Инструмент преобразования
Просто введите значение в любое поле:
Или воспользуйтесь интерактивным термометром,
Или этот метод:
° C до ° F Разделите на 5, затем умножьте на 9 и прибавьте 32 ° F до ° C Вычтите 32, затем умножьте на 5, затем разделите на 9 (объяснение ниже…)
Типичные температуры
° С ° F Описание 180 356 Духовка среднего размера 100 212 Вода закипает 40 104 Горячая ванна 37 98.6 Температура тела 30 86 Погода на пляже 21 70 Комнатная температура 10 50 Прохладный день 0 32 Температура замерзания воды −18 0 Очень холодный день −40 −40 Extremely Cold Day
(и столько же!)( полужирный точно) 16 примерно 61
28 примерно 82Пояснение
Существуют две основные температурные шкалы:
- ° C , шкала Цельсия (часть метрической
Система, используемая в большинстве стран) - ° F , шкала Фаренгейта (используется в США) и
Они оба измеряют одно и то же (температуру!), Но используют разные
номера:- Кипящая вода (при нормальном давлении) измеряет 100 ° по Цельсию, но 212 °
по Фаренгейту - А по мере замерзания воды он измеряет
0 ° по Цельсию, но 32 ° по Фаренгейту
Как это:
Обратите внимание на схему:
- Шкалы начинаются с другого числа (0 против 32), поэтому мы будем
нужно добавить или вычесть 32 - Шкала увеличивается с разной скоростью (100 против 180), поэтому мы
также нужно умножить
Итак, преобразовать:
от Цельсия до Фаренгейта:
сначала умножьте на 180 100 , затем добавьте 32от Фаренгейта до Цельсия: сначала вычтите 32, затем умножьте
по 100 180180 100 можно упростить до 9 5 , а 100 180 можно упростить до 5 9 , так что это самый простой способ:
от ° C до ° F: Разделите на 5, затем умножьте на 9 и прибавьте 32
от ° F до ° C: Вычтите 32, затем умножьте на 5, затем разделите на 9
Пример: преобразовать 25 ° Цельсия (хороший теплый день) в
Фаренгейта
Сначала: 25 ° / 5 = 5
Затем: 5 × 9 = 45
Затем: 45 + 32 = 77 ° FПример: преобразовать 98.6 ° Фаренгейта (нормальная температура тела) от до
Цельсия
Сначала: 98,6 ° — 32 = 66,6
Затем: 66,6 × 5 = 333
Затем: 333/9 = 37 ° CМы можем поменять местами порядок деления и умножения, если захотим, но не меняем сложение или вычитание. Так что это тоже нормально:
Пример: преобразование 98,6 ° Фаренгейта в Цельсий (снова)
Сначала: 98,6 ° — 32 = 66,6
Затем: 66.6/9 = 7,4
Тогда: 7,4 × 5 = 37 ° C(Тот же ответ, что и раньше, было легче или сложнее?)
Мы можем записать каждую формулу следующим образом:
Цельсия в Фаренгейта: (° C × 9 5 ) + 32 = ° F
Фаренгейта в Цельсию: (° F — 32) × 5 9 = ° CДругие эффективные методы
Используйте 1.8 вместо 9/5
9/5 равно 1.8, поэтому мы также можем использовать этот метод:
по Цельсию по Фаренгейту: ° C × 1,8 + 32 = ° F
по Фаренгейту по Цельсию: (° F — 32) / 1,8 = ° CЧтобы упростить «× 1,8», мы можем умножить на 2 и вычесть 10% , но это работает только от ° C до ° F:
Цельсия в Фаренгейта: (° C × 2) минус 10% + 32 = ° F
Пример: преобразовать 20 ° Цельсия (Хороший день) в
Фаренгейта
- 20 x2 = 40
- минус 10% равно 40-4 = 36
- 36 + 32 = 68 ° F
Сложить 40, умножить, вычесть 40
Поскольку обе шкалы пересекаются под углом −40 ° (−40 ° C равно −40 ° F), мы можем:
- доб 40,
- умножить на 5/9 (для ° F – ° C) или 9/5 (для ° C – ° F)
- вычесть 40
Как это:
градусов Цельсия в градусы Фаренгейта: прибавьте 40, умножьте на 9/5, затем вычтите 40
градусов по Фаренгейту в градусы Цельсия: прибавьте 40, умножьте на 5/9, затем вычтите 40Пример: преобразовать 10 ° Цельсия (прохладный день) в
Фаренгейта
- 10 +40 = 50
- 50 × 9/5 = 90
- 90-40 = 50 ° F
Чтобы запомнить 9/5 для ° C — ° F, подумайте, что «F больше, чем C, поэтому существует больше ° F, чем ° C»
Быстро, но Неточно
по Фаренгейту: удвоить, затем прибавить 30
по Фаренгейту к Цельсию: вычтите 30, затем уменьшите вдвоеПримеры ° C → ° F:
- 0 ° C → 0 + 30 → 30 ° F (низкий на 2 °)
- 10 ° C → 20 + 30 → 50 ° F (точно!)
- 30 ° C → 60 + 30 → 90 ° F (высокий на 4 °)
- 180 ° C → 360 + 30 → 390 ° F (высокий на 34 °, плохо)
Примеры ° F → ° C:
- 40 ° F → 10/2 → 5 ° C (почти справа )
- 80 ° F → 50/2 → 25 ° C (низкая примерно на 2 °)
- 120 ° F → 90/2 → 45 ° C (низкий примерно на 4 °)
- 450 ° F → 420/2 → 210 ° C (ниже примерно на 22 °, плохо)
Сноска: Температура — это мера того, насколько быстро движутся частицы объекта.
- Уровня вещества в емкости.

 08891 Па.
08891 Па. tsf = 107251.780115952 Па.
tsf = 107251.780115952 Па.
 {2}}{3*V}\)
{2}}{3*V}\) В данном разделе учащиеся узнают об основных видах и законах превращения энергии.
В данном разделе учащиеся узнают об основных видах и законах превращения энергии.
 Обозначается t, измеряется в секундах.
Обозначается t, измеряется в секундах. 3\).
3\). (Из-за того, что верхние слои «давят» на нижние слои жидкости).
(Из-за того, что верхние слои «давят» на нижние слои жидкости).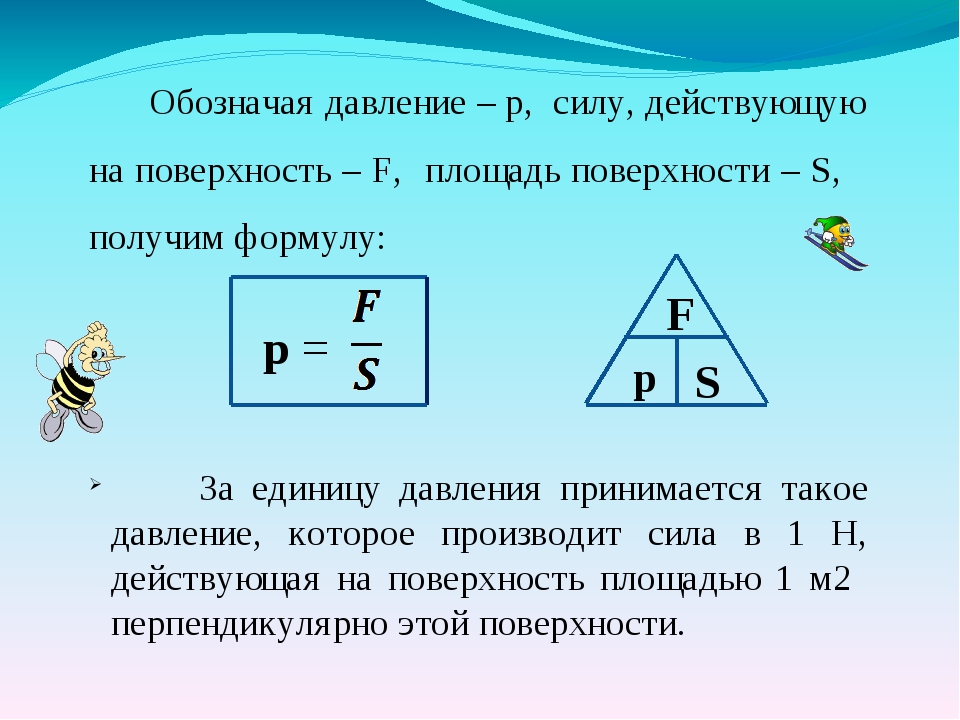



 ru
ru 2}2\)
2}2\)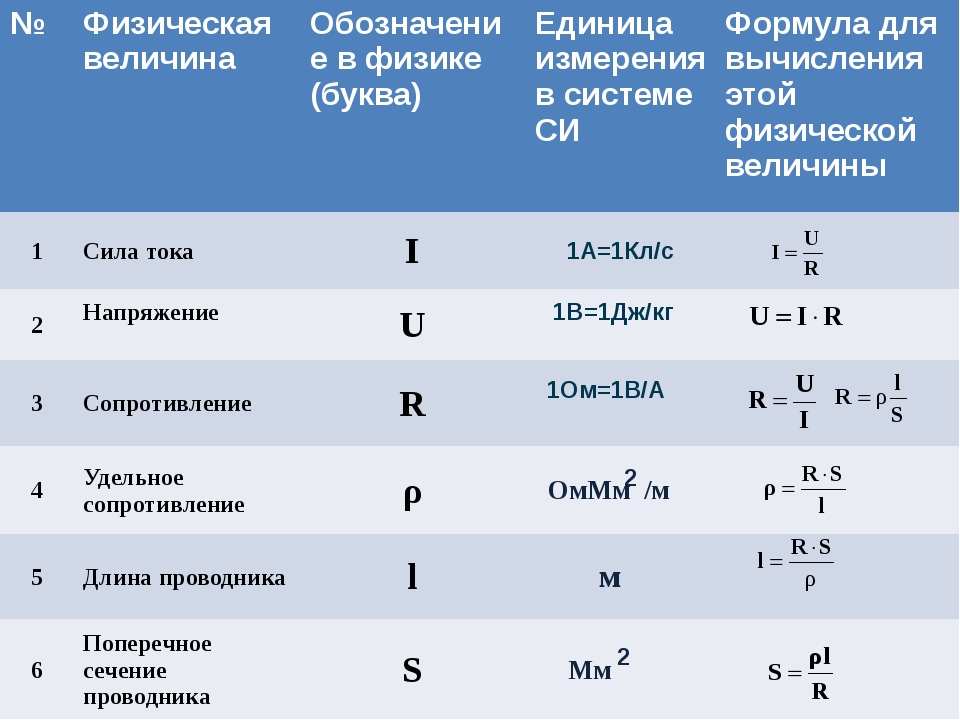
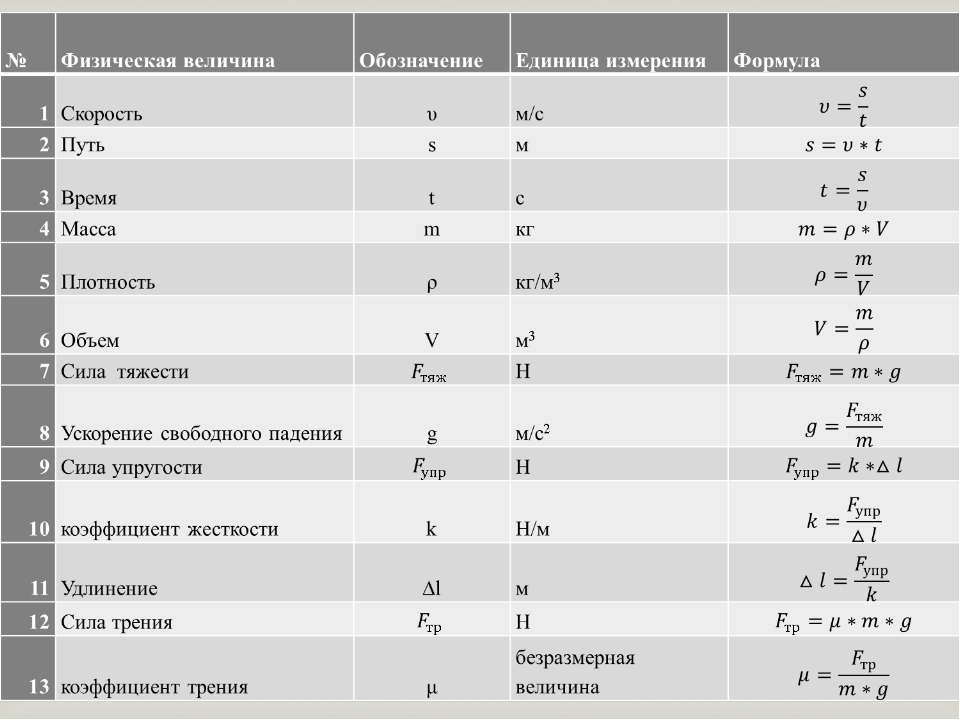 2\) действует сила в 500 Н. Рассчитайте давление, производимое силой на поверхность.
2\) действует сила в 500 Н. Рассчитайте давление, производимое силой на поверхность.
 Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики.
Для некоторых физических величин принято несколько обозначений (например для энергии, скорости, длины и других), чтобы предотвратить путаницу с другими величинами в данном разделе физики. Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква O{\displaystyle O}.
Когда такая связь существует, это обозначено в скобках. Среди латинских букв для обозначения физических величин практически не используется буква O{\displaystyle O}.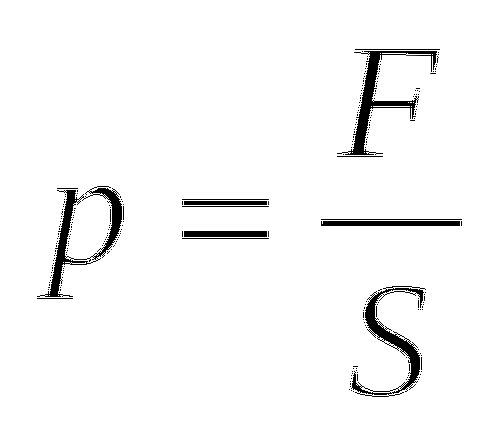 Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная
charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная energīa), напряжённость электрического поля[1] (англ. electric field), Электродвижущая сила (англ. electromotive force), магнитодвижущая сила,
energīa), напряжённость электрического поля[1] (англ. electric field), Электродвижущая сила (англ. electromotive force), магнитодвижущая сила,
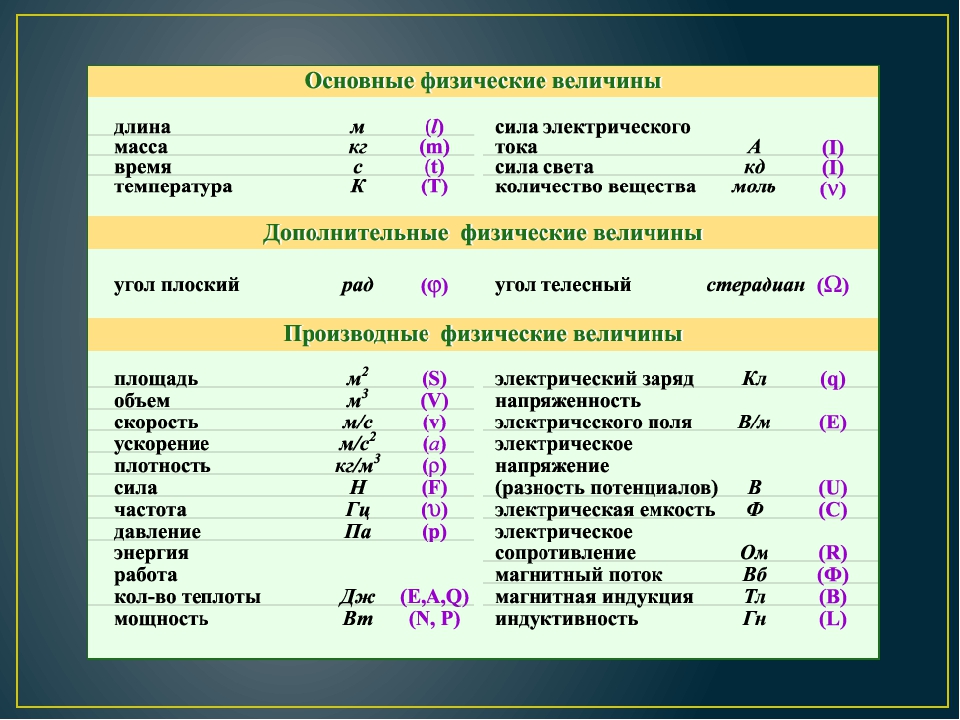 Сила давления F равна произведению атмосферного давления на площадь сечение полушарий S.
Сила давления F равна произведению атмосферного давления на площадь сечение полушарий S.
 Нижняя часть коробочки прикреплена к основанию. К верхней ее части прикреплена пружина, которая пытается расправить коробочку так же, как алюминиевая линейка, если ее согнуть, пытается распрямиться. Атмосферное давление, наоборот, пытается сжать коробочку.
Нижняя часть коробочки прикреплена к основанию. К верхней ее части прикреплена пружина, которая пытается расправить коробочку так же, как алюминиевая линейка, если ее согнуть, пытается распрямиться. Атмосферное давление, наоборот, пытается сжать коробочку. Вы кладете электрон на шкалу (на практике электроны слишком малы для измерения на шкале — вы должны видеть, как они реагируют на притяжение магнитных или электростатических сил, чтобы измерить их массу), и вы измеряете следующее:
Вы кладете электрон на шкалу (на практике электроны слишком малы для измерения на шкале — вы должны видеть, как они реагируют на притяжение магнитных или электростатических сил, чтобы измерить их массу), и вы измеряете следующее: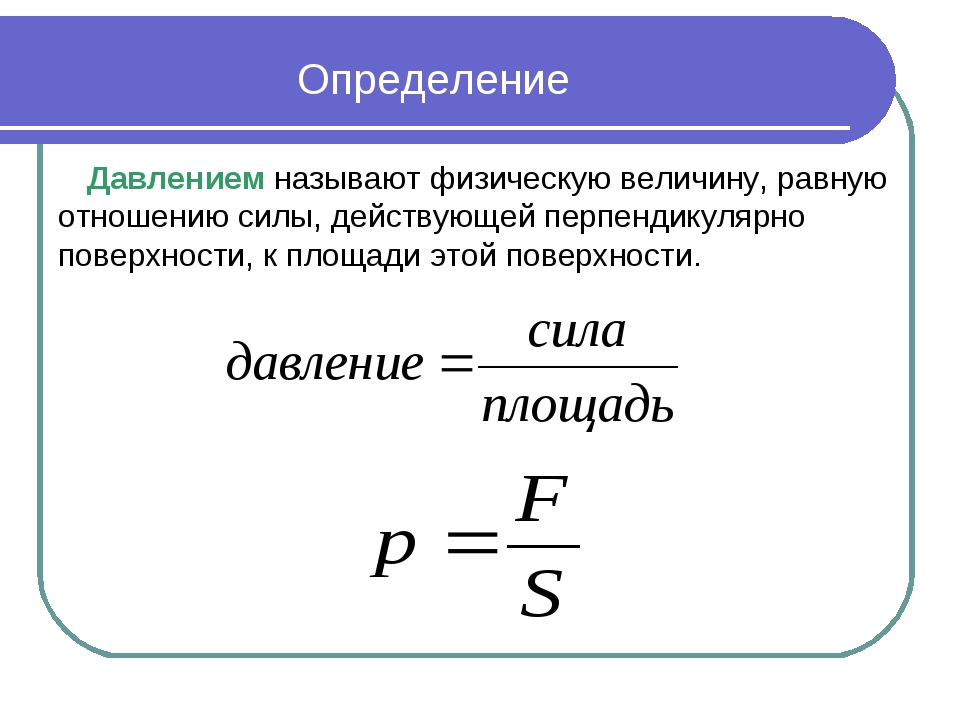 0. Точно так же 500 равно 5,0 x 10 2 , потому что вы переместите десятичную запятую на два места влево, чтобы получить 5,0.
0. Точно так же 500 равно 5,0 x 10 2 , потому что вы переместите десятичную запятую на два места влево, чтобы получить 5,0.

 4} \]
4} \]
 Как уже говорилось, давление в жидкости около Земли изменяется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности.Это разумное приближение для жидкостей, таких как вода, где для сжатия жидкости или изменения объема требуются большие силы. В плавательном бассейне, например, плотность примерно постоянна, и вода внизу очень слабо сжимается под весом воды наверху. Однако путешествие вверх в атмосфере — это совсем другая ситуация. Плотность воздуха начинает значительно меняться на небольшом расстоянии от поверхности Земли.
Как уже говорилось, давление в жидкости около Земли изменяется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности.Это разумное приближение для жидкостей, таких как вода, где для сжатия жидкости или изменения объема требуются большие силы. В плавательном бассейне, например, плотность примерно постоянна, и вода внизу очень слабо сжимается под весом воды наверху. Однако путешествие вверх в атмосфере — это совсем другая ситуация. Плотность воздуха начинает значительно меняться на небольшом расстоянии от поверхности Земли. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности. Массу элемента можно записать через плотность жидкости и объем элементов:
Массу элемента можно записать через плотность жидкости и объем элементов: Но если диапазон глубин достаточно велик для того, чтобы плотность могла заметно меняться, как, например, в случае атмосферы, происходит значительное изменение плотности с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.
Но если диапазон глубин достаточно велик для того, чтобы плотность могла заметно меняться, как, например, в случае атмосферы, происходит значительное изменение плотности с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.
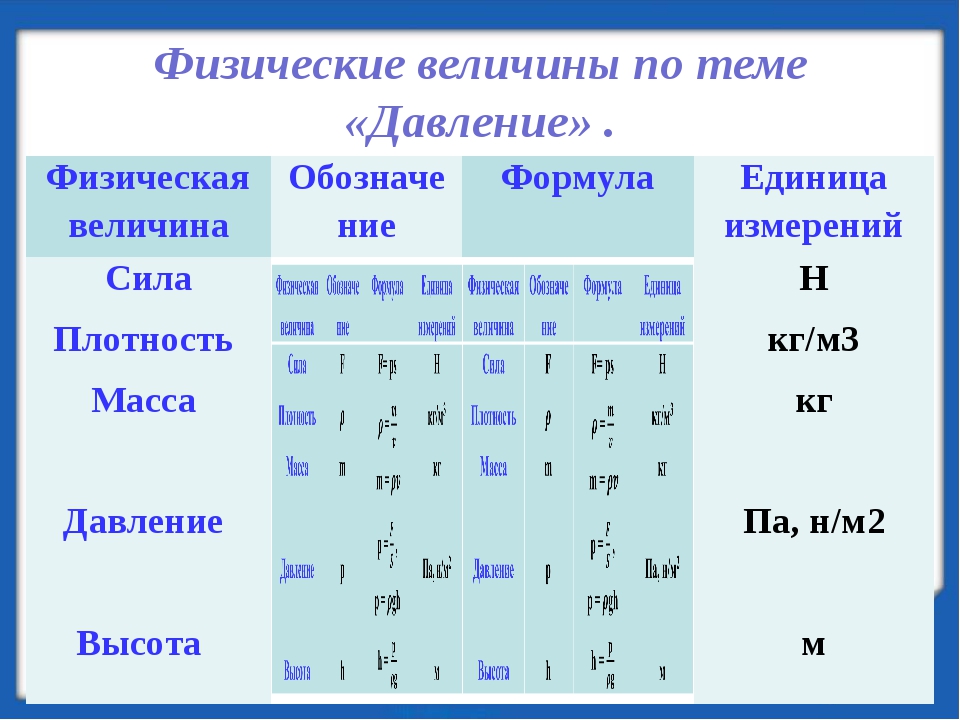 10} \]
10} \] {-23} \; Дж / К) \ раз (300 \; К)} = \ гидроразрыва {1} {8800 \; m} \ ldotp \]
{-23} \; Дж / К) \ раз (300 \; К)} = \ гидроразрыва {1} {8800 \; m} \ ldotp \] На рисунке \ (\ PageIndex {5} \) показано давление воздуха на стенки покрышки и давление воды на тело пловца.
На рисунке \ (\ PageIndex {5} \) показано давление воздуха на стенки покрышки и давление воды на тело пловца. 0).
0).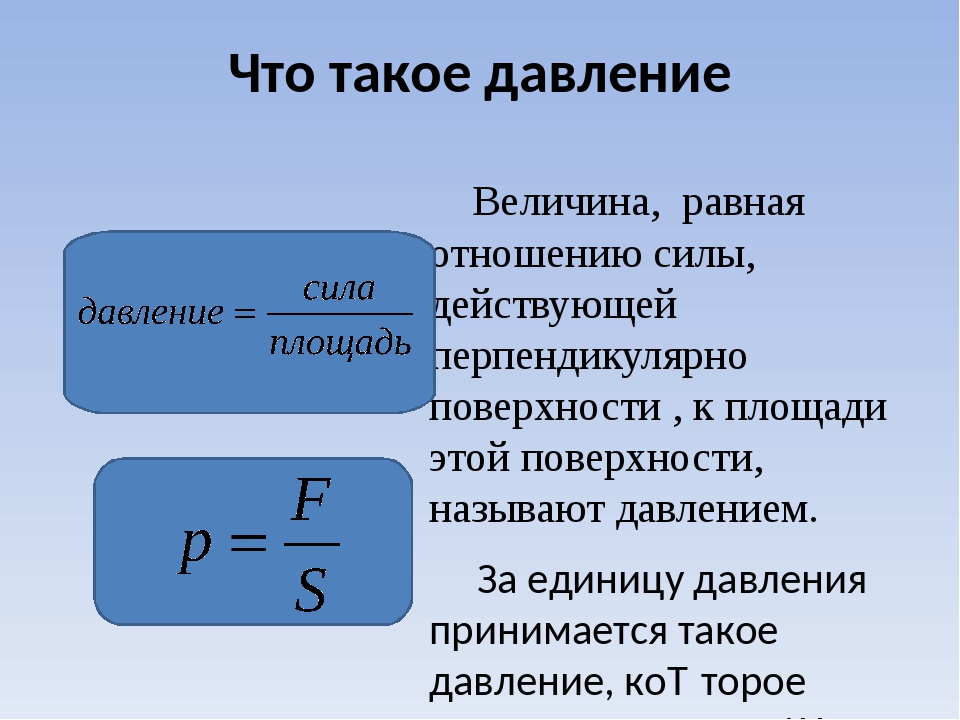 м.
м. его слишком легко спутать с числом
его слишком легко спутать с числом
 Чтобы сделать его более удобным для пользователей и более простым в использовании и запоминании, мы часто используем обозначения / символы для представления этих физических величин. Эти обозначения / символы, которые мы используем для представления физических величин при решении связанных с ними проблем или для других целей, являются символами. Символы, используемые для физических величин, сильно отличаются. Иногда символ может быть первой буквой физических величин, которые они представляют, например, что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например c, которое означает скорость света.Они также могут быть в форме греческих символов, например λ, что означает длину волны.
Чтобы сделать его более удобным для пользователей и более простым в использовании и запоминании, мы часто используем обозначения / символы для представления этих физических величин. Эти обозначения / символы, которые мы используем для представления физических величин при решении связанных с ними проблем или для других целей, являются символами. Символы, используемые для физических величин, сильно отличаются. Иногда символ может быть первой буквой физических величин, которые они представляют, например, что означает расстояние. В других случаях они могут быть совершенно не связаны с названием физических величин, например c, которое означает скорость света.Они также могут быть в форме греческих символов, например λ, что означает длину волны. для Механиков :
для Механиков :