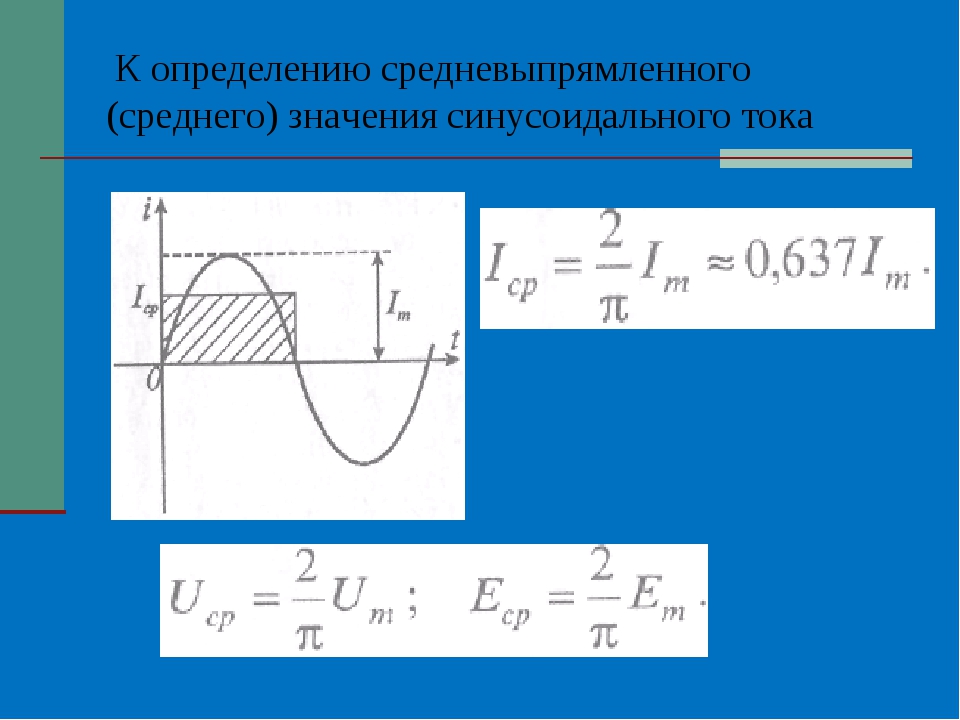
Действующие значения э. д. с., напряжения и силы переменного тока
При синусоидальном переменном токе средние значения напряжения и тока за период равны нулю и не могут служить его характеристиками. Однако среднее значение квадрата силы тока за период отлично от нуля. Следовательно, при включении в цепь переменного тока измерительного прибора, отклонение стрелки которого пропорционально квадрату силы тока, стрелка отклонится и установится на определенном делении шкалы. Каков смысл этого показания?
Вспомним, что количество выделенного в проводнике тепла изменяется пропорционально квадрату силы тока. Представим себе, что в цепь переменного тока включен тепловой амперметр, действие которого основано на выделении тепла электрическим током. Поскольку шкала такого амперметра градуируется на амперы для постоянного тока, можно заключить, что переменный ток по своему тепловому эффекту эквивалентен постоянному току, силу которого указывает на шкале прибора стрелка.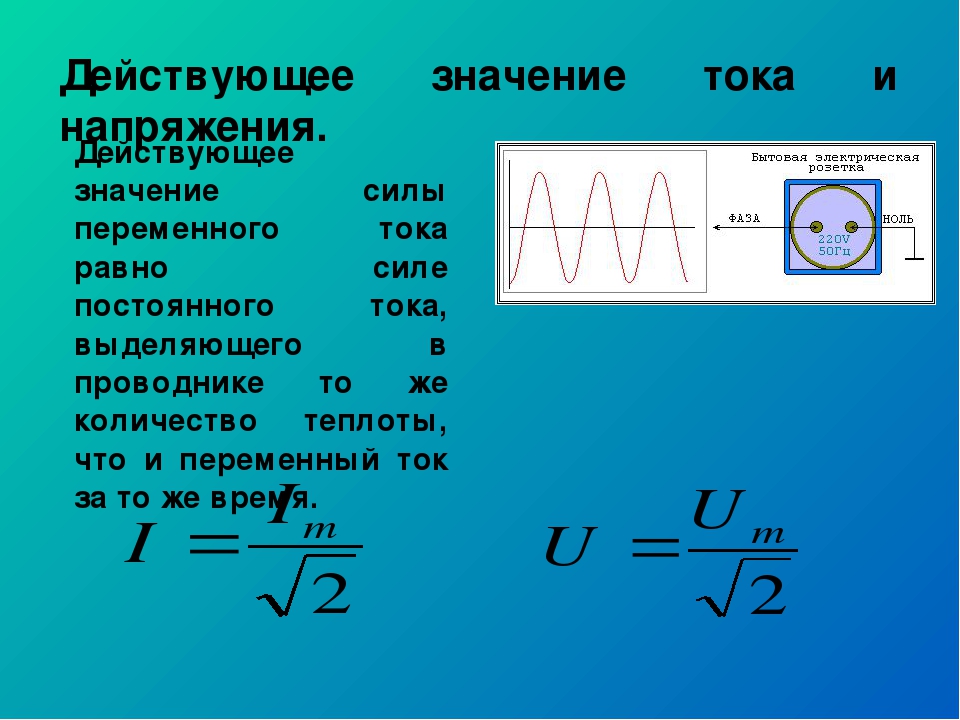 Это позволяет ввести понятие эффективного значения силы переменного тока. Эффективным (или действующим) значением силы переменного тока называют силу такого постоянного тока I, который за один период переменного тока выделяет столько же тепла, сколько последний за то же время.
Это позволяет ввести понятие эффективного значения силы переменного тока. Эффективным (или действующим) значением силы переменного тока называют силу такого постоянного тока I, который за один период переменного тока выделяет столько же тепла, сколько последний за то же время.
Все амперметры, предназначенные для переменного тока, показывают эффективное значение силы тока. В курсе электротехники доказывается, что оно в √2 раз меньше амплитудного значения силы тока Iм, т. е.
Iм = Iм/√2 ≈ 0,707Iм. (26.5)
Так как деления на шкале вольтметра соответствуют произведению Iвrв, где при переменном токе Iв — эффективное значение тока, протекающего через вольтметр, а rв — сопротивление вольтметра, то U=Iвrв называют эффективным напряжением переменного тока, которое в √2 раз меньше Uм, т. е.
U = Uм/√2 ≈ 0,7O7UM. (26.6)
Аналогично эффективное значение э. д. с. переменного тока Ɛ в √2 раз меньше его амплитудного значения Ɛм:
Ɛ = Ɛм/√2 ≈ 0,707Ɛм. (26.7)
(26.7)
Все вольтметры, предназначенные для переменного тока, показывают эффективные значения э. д. с. и напряжения.
Эффективная сила тока. Действующее значение переменного тока
>> Активное сопротивление. Действующие значения силы тока и напряжения
§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.
Сила тока в цени с резистором.
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством
Мощность в цепи с резистором.
В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.
Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
P = I 2 R. (4.18)
На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.
Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
P = i 2 R. (4.19)
(4.19)
Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение
График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
Средняя мощность равна, таким образом, первому члену в формуле (4.20):
Действующие значения силы тока и напряжения .
Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:
Действующее значение силы переменного тока
равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:
Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем
Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:
P = I 2 R = UI.
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков
Содержание урока
конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.
д. с.
Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .
На шкалах измерительных приборов и технической документации также указываются действующие значения величин.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени
а за период переменного тока Т
Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:
Сократив общий множитель , получим действующее значение тока
Рис. 5-8. График переменного тока и квадрата тока.
На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока
Если ток изменяется по закону синуса, т. е.
е.
Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.
Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.
Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.
Определение 1
Эффективным (действующим) называют значение переменного тока равное величине эквивалентного постоянного тока, который при прохождении через такое же сопротивление, что и переменный ток выделяет на нем то же количество тепла за одинаковые промежутки времени.
Количественная связь амплитуд силы и напряжения переменного тока и эффективных значений
Количество тепла, которое выделяется переменным током на сопротивлении $R$ за малый промежуток времени $dt$, равно:
Тогда за один период переменный ток выделяет тепла ($W$):
Обозначим через $I_{ef}$ силу постоянного тока, который на сопротивлении $R$ выделяет такое же количество тепла ($W$), как и переменный ток $I$ за время равное периоду колебаний переменного тока ($T$). Тогда выразим $W$ через постоянный ток и приравняем выражение к правой части уравнения (2), имеем:
Выразим из уравнения (3) силу эквивалентного постоянного тока, получим:
Если сила тока изменяется по синусоидальному закону:
подставим выражение (5) для переменного тока в формулу (4), тогда величина постоянного тока выразится как:
Следовательно, выражение (6) может быть преобразовано к виду:
где $I_{ef}$ называют эффективным значением силы тока. Аналогично записывают выражения для эффективных (действующих) значений напряжений:
Аналогично записывают выражения для эффективных (действующих) значений напряжений:
Применение действующих значений тока и напряжения
Когда в электротехнике говорят о силе переменного тока и напряжении, то имеют в виду их эффективные значения. В частности, вольтметры и амперметры градуируют обычно на эффективные значения. Следовательно, максимальное значение напряжения в цепи переменного тока примерно в 1,5 раза больше того, что показывает вольтметр. Этот факт следует учесть при расчете изоляторов, исследовании проблем безопасности.
Эффективные значения используют для характеристики формы сигнала переменного тока (напряжения). Так, вводят коэффициент амплитуды ($k_a$). равный:
и коэффициент формы ($k_f$):
где $I_{sr\ v}=\frac{2}{\pi }\cdot I_m$ —средневыпрямленное значение силы тока.
Для синусоидального тока $k_a=\sqrt{2},\ k_f=\frac{\pi }{2\sqrt{2}}=1,11.$
Пример 1
Задание:
Напряжение, которое показал вольтметр равно $U=220 В$. Какова амплитуда напряжения?
Какова амплитуда напряжения?
Решение:
Как было сказано, вольтметры и амперметры обычно градуируют на действующие значения напряжения (силу тока), следовательно, прибор показывает в наших обозначениях $U_{ef}=220\ В.$ В соответствии с известным соотношением:
найдем амплитудное значение напряжения, как:
Вычислим:
Ответ:
$U_m\approx 310,2\ В.$
Пример 2
Задание:
Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?
Решение:
Среднее значение мощности переменного тока в цепи равно
\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.1\right),\]
где $cos\varphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:
\[\left\langle P\right\rangle =\left\langle P_{tC}\right\rangle +\left\langle P_{tL}\right\rangle +\left\langle P_{tR}\right\rangle \left(2. 2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]
2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]
где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.
У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:
если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:
Следовательно, мощность тока можно записать как:
где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.
Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).
Ответ:
$P_{tR}=U_{ef}I_{ef}cos\varphi .$
Переменный
ток долгое время не находил практического
применения. Это было связано с тем,
Это было связано с тем,
что первые генераторы электрической
энергии вырабатывали постоянный ток,
который вполне удовлетворял технологическим
процессам электрохимии, а двигатели
постоянного тока обладают хорошими
регулировочными характеристиками.
Однако по мере развития производства
постоянный ток все менее стал удовлетворять
возрастающим требованиям экономичного
электроснабжения. Переменный ток дал
возможность эффективного дробления
электрической энергии и изменения
величины напряжения с помощью
трансформаторов. Появилась возможность
производства электроэнергии на крупных
электростанциях с последующим экономичным
ее распределением потребителям,
увеличился радиус электроснабжения.
В
настоящее время центральное производство
и распределение электрической энергии
осуществляется в основном на переменном
токе. Цепи с изменяющимися – переменными
– токами по сравнению с цепями постоянного
тока имеют ряд особенностей. Переменные
токи и напряжения вызывают переменные
электрические и магнитные поля. В
В
результате изменения этих полей в цепях
возникают явления самоиндукции и
взаимной индукции, которые оказывают
самое существенное влияние на процессы,
протекающие в цепях, усложняя их анализ.
Переменным
током (напряжением, ЭДС и т.д.)называется
ток (напряжение, ЭДС и т.д.), изменяющийся
во времени. Токи, значения которых
повторяются через равные промежутки
времени в одной и той же последовательности,
называются периодическими,
а
наименьший промежуток времени, через
который эти повторения наблюдаются, —
периодом
Т.
Для периодического тока имеем
Диапазон
частот, применяемых в технике: от
сверхнизких частот (0.01¸10 Гц – в системах
автоматического регулирования, в
аналоговой вычислительной технике) –
до сверхвысоких (3000 ¸ 300000 МГц –
миллиметровые волны: радиолокация,
радиоастрономия). В РФ промышленная
частота
f
= 50Гц
.
Мгновенное
значение переменной величины есть
функция времени. Ее принято обозначать
строчной буквой:
i
— мгновенное значение тока
;
u
–
мгновенное значение напряжения
;
е
—
мгновенное значение ЭДС
;
р
—
мгновенное значение мощности
.
Наибольшее
мгновенное значение переменной величины
за период называется амплитудой (ее
принято обозначать заглавной буквой с
индексом
m
).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение
периодического тока, равное такому
значению постоянного тока, который за
время одного периода произведет тот же
самый тепловой или электродинамический
эффект, что и периодический ток, называют
действующим
значением
периодического
тока:
Аналогично
определяются действующие значения ЭДС
и напряжения.
Синусоидально изменяющийся ток
Из
всех возможных форм периодических токов
наибольшее распространение получил
синусоидальный ток. По сравнению с
другими видами тока синусоидальный ток
имеет то преимущество, что позволяет в
общем случае наиболее экономично
осуществлять производство, передачу,
распределение и использование
электрической энергии. Только при
использовании синусоидального тока
удается сохранить неизменными формы
кривых напряжений и токов на всех
участках сложной линейной цепи. Теория
Теория
синусоидального тока является ключом
к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные
токи и напряжения можно изобразить
графически, записать при помощи уравнений
с тригонометрическими функциями,
представить в виде векторов на декартовой
плоскости или комплексными числами.
Приведенным
на рис. 1, 2 графикам двух синусоидальных
ЭДС е
1
и
е
2
соответствуют
уравнения:
Значения
аргументов синусоидальных функций
иназываютсяфазами
синусоид,
а значение фазы в начальный момент
времени (t
=0):
и
—начальной
фазой
(
).
Величину
,
характеризующую скорость изменения
фазового угла, называютугловой
частотой.
Так
как фазовый угол синусоиды за время
одного периода Т
изменяется на
рад.,
то угловая частота есть,
гдеf–
частота.
При
совместном рассмотрении двух синусоидальных
величин одной частоты разность их
фазовых углов, равную разности начальных
фаз, называют углом
сдвига фаз
.
Для
синусоидальных ЭДС е
1
и
е
2
угол
сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На
декартовой плоскости из начала координат
проводят векторы, равные по модулю
амплитудным значениям синусоидальных
величин, и вращают эти векторы против
часовой стрелки (в
ТОЭ данное направление принято за
положительное
)
с угловой частотой, равной w
.
Фазовый угол при вращении отсчитывается
от положительной полуоси абсцисс.
Проекции вращающихся векторов на ось
ординат равны мгновенным значениям ЭДС
е
1
и
е
2
(рис.
3). Совокупность векторов, изображающих
синусоидально изменяющиеся ЭДС,
напряжения и токи, называют векторными
диаграммами.
При
построении векторных диаграмм векторы
удобно располагать для начального
момента времени (t
=0),
что
вытекает из равенства угловых частот
синусоидальных величин и эквивалентно
тому, что система декартовых координат
сама вращается против часовой стрелки
со скоростью w
.
Таким образом, в этой системе координат
векторы неподвижны (рис. 4). Векторные
диаграммы нашли широкое применение при
анализе цепей синусоидального тока. Их
применение делает расчет цепи более
наглядным и простым. Это упрощение
заключается в том, что сложение и
вычитание мгновенных значений величин
можно заменить сложением и вычитанием
соответствующих векторов.
Пусть,
например, в точке разветвления цепи
(рис. 5) общий ток
равен
сумме токовидвух
ветвей:
Силу переменного тока (напряжения) можно
охарактеризовать при помощи амплитуды.
Однако амплитудное значение тока
непросто измерить экспериментально.
Силу переменного тока удобно связать
с каким-либо действием, производимым
током, не зависящим от его направления.
Таковым является, например, тепловое
действие тока. Поворот стрелки амперметра,
измеряющего переменный ток, вызывается
удлинением нити, которая нагревается
при прохождении по ней тока.
Действующим
илиэффективным
значением
переменного тока (напряжения) называется
такое значение постоянного тока, при
котором на активном сопротивлении
выделяется за период такое же количество
теплоты, как и при переменном токе.
Свяжем
эффективное значение тока с его
амплитудным значением. Для этого
рассчитаем количество теплоты, выделяемое
на активном сопротивлении переменным
током за время, равное периоду колебаний.
Напомним, что по закону Джоуля-Ленца
количество теплоты, выделяющееся на
участке цепи cсопротивлениемприпостоянном
токеза время,
определяется по формуле
.
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
.
Поделим период колебанийна очень большое число малых промежутков
времени
.
Количество теплоты
,
выделяемое на сопротивленииза время
:
.
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:
.
Сила тока в
цепи изменяется по синусоидальному
закону
,
.
Опуская
вычисления, связанные с интегрированием,
запишем окончательный результат
.
Если бы по
цепи шёл некоторый постоянный ток
,
то за время, равное,
выделилось бы тепло
.
По определению постоянный ток,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока
.
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов
(4.28)
Очевидно,
точно такое же соотношение связывает
эффективное и амплитудное значения
напряжения в цепи с синусоидальным
переменным током:
(4.29)
Например,
стандартное напряжение в сети 220 В –
это эффективное напряжение. По формуле
(4.29) легко посчитать, что амплитудное
значение напряжения в этом случае будет
равно 311 В.
4.4.5. Мощность в цепи переменного тока
Пусть на некотором участке цепи с
переменным током сдвиг фаз между током
и напряжением равен
,
т.е. сила тока и напряжение изменяются
по законам:
,
.
Тогда мгновенное
значение мощности, выделяемой на участке
цепи,
Мощность
изменяется со временем. Поэтому можно
говорить лишь о ее среднем значении.
Определим среднюю мощность, выделяемую
в течение достаточно длительного
промежутка времени (во много раз
превосходящего период колебаний):
С использованием
известной тригонометрической формулы
.
Величину
усреднять не нужно, так как она не зависит
от времени, следовательно:
.
За длительное
время значение косинуса много раз
успевает измениться, принимая как
отрицательные, так и положительные
значения в пределах от (1)
до 1. Понятно, что среднее во времени
значение косинуса равно нулю
,
поэтому
(4.30)
Выражая
амплитуды тока и напряжения через их
эффективные значения по формулам (4.28)
и (4.29), получим
. (4.31)
Мощность, выделяемая на участке цепи с
переменным током, зависит от эффективных
значений тока и напряжения и сдвига
фаз между током и напряжением
. Например,
если участок цепи состоит из одного
только активного сопротивления, то
и
.
Если участок цепи содержит только
индуктивность или только ёмкость, то
и
.
Объяснить среднее нулевое значение
мощности, выделяемой на индуктивности
и ёмкости можно следующим образом.
Индуктивность и ёмкость лишь заимствуют
энергию у генератора, а затем возвращают
её обратно. Конденсатор заряжается, а
затем разряжается. Сила тока в катушке
увеличивается, затем снова спадает до
нуля и т. д. Именно по той причине, что
на индуктивном и ёмкостном сопротивлениях
средняя расходуемая генератором энергия
равна нулю, их назвали реактивными. На
активном же сопротивлении средняя
мощность отлична от нуля. Другими словами
провод с сопротивлением
при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.
Если участок цепи содержит несколько
элементов, то сдвига фаз
может быть иным. Например, в случае
участка цепи, изображенного на рис. 4.5,
сдвиг фаз между током и напряжением
определяется по формуле (4.27).
Пример 4.7.
К генератору переменного
синусоидального тока подключён резистор
с сопротивлением.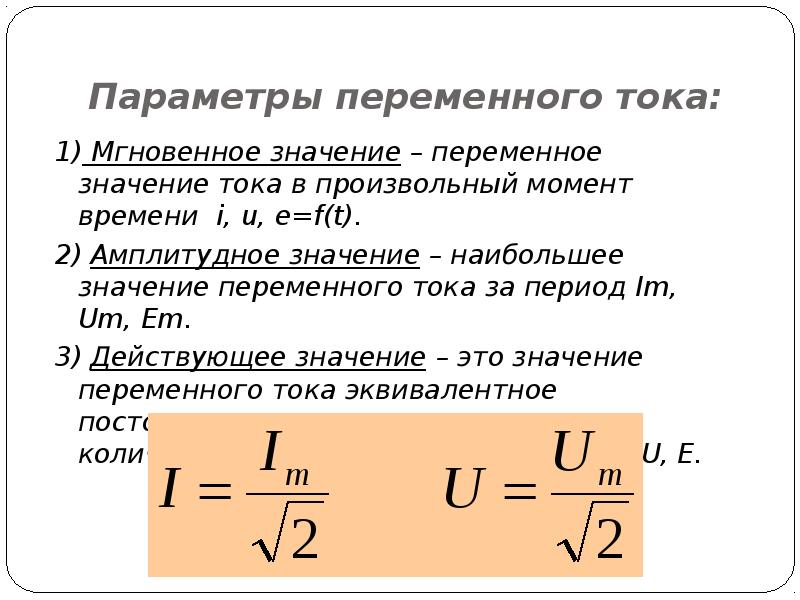
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлением
а) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.
Решение.
Когда к генератору подключено
одно только активное сопротивление,
расходуемая мощность
(см. формулу (4.30)).
Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:
.
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
.
В результате средняя расходуемая
генератором мощность
.
Ответ: при
последовательном включении в цепь
индуктивности средняя мощность,
расходуемая генератором, уменьшится в
2 раза.
Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора
.
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора
.
Тогда средняя
мощность, расходуемая генератором
Ответ: при
параллельном включении индуктивности
средняя мощность, расходуемая генератором,
не изменяется.
Ток переменный, действующее значени — Энциклопедия по машиностроению XXL
При подключении к концам катушки переменного напряжения с частотой 50 Гц в цепи при действующем значении напряжения 50 В течет переменный ток с действующим значением 0,2 А. Найдите индуктивность катушки. Активное сопротивление катуш-14и пренебрежимо мало.
[c.296]
В электротехнике для измерения полной мощности электрической цепи, определяемой произведением действующих значений напряжения и силы тока С/эф, /дф, не применяют единицу мощности ватт (которой измеряется только активная составляющая мощности), а пользуются единицей вольт-ампер (В А). Для измерения реактивной мощности применяют единицу вар, которую определяют как реактивную мощность цепи с синусоидальным переменным током при действующих значениях напряжения 1 В и тока 1 А, если сдвиг фазы между током и напряжением я/2. [c.260]
[c.260]
Чему было бы равно показание магнитоэлектрического прибора в этой цепи Ответ. Так как тепловой амперметр измеряет действующее значение тока, индукционный — действующее значение переменной составляющей тока, а магнитоэлектрический — постоянную составляющую, то его показания соответствовали бы 2,8 А.
[c.95]
При измерениях переменного напряжения нли силы тока определяют действующее значение электроизмерительными приборами электродинамической, электромагнитной, тепловой или термоэлектрической системы. [c.383]
Статические характеристики устойчивой и непрерывно горящей дуга переменного тока для действующих значений тока и напряжения подобны характеристикам дуги постоянного тока. [c.165]
ВОЛЬТАМПЕРНАЯ ХАРАКТЕРИСТИКА ДУГИ,статическая вольтам первая характеристика дуги — график зависимости между напряжением и силой тока сварочной дуги (для переменного тока — между действующими значениями этих величин) при постоянных
[c. 25]
25]
Если брать в а м у в омм А в л, то активная мощность будет определена в вт/м . В качестве примера рассчитаем активную мощность для двух параллельных шин (см. фиг. 6), по которым течет переменный ток с действующим значением I. [c.21]
Во всех случаях технологических расчетов ориентируются на действующее (эффективное) значение сварочного тока. Поэтому интегралы предыдущего параграфа упрощаются, так как вместо функциональной зависимости Р (t) можно оперировать с постоянной величиной эффективного тока. Эта величина весьма просто устанавливается при сварке переменным током длительностью не менее полупериода. Для некоторых особых форм кривых сварочного тока равенство действующих значений тока не обязательно обеспечивает одинаковую картину тепловыделения в контакте. Примером могут служить кривые рис. 48, а и б. Для таких кривых тока, а также для иных, еще более сложных, вполне рационально представлять изменение сварочного тока во времени в виде степенных функций.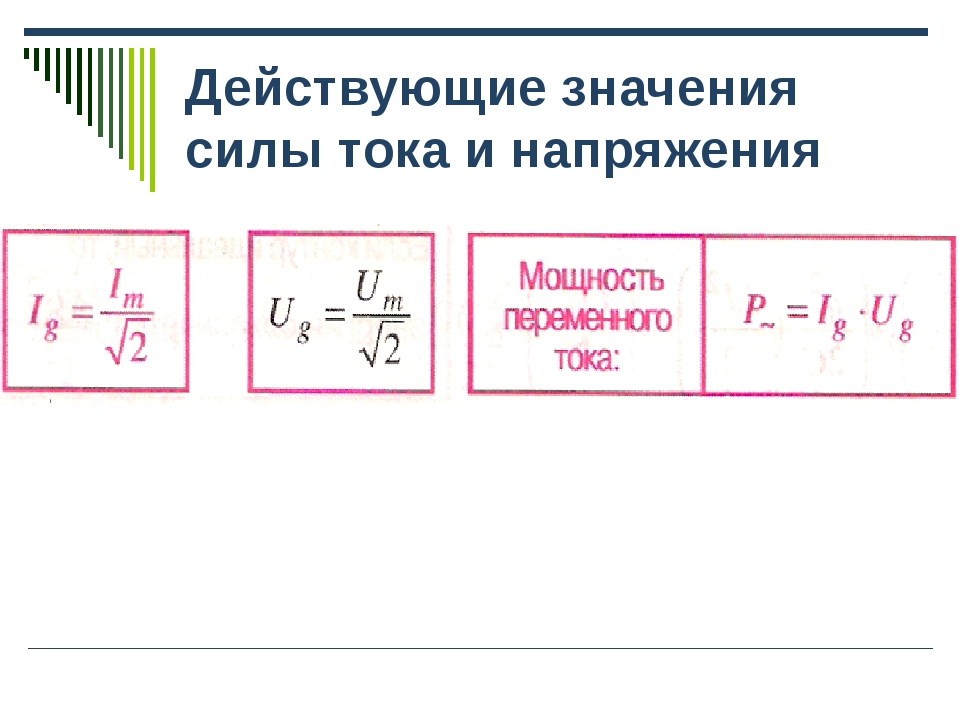 Обозначим пиковое (максимальное) значение тока через / , мгновенную величину через /j, i , координаты времени возрастания тока через ti и спада тока через /о. Тогда можно написать, например, для любой из кривых рнс. 48
[c.115]
Обозначим пиковое (максимальное) значение тока через / , мгновенную величину через /j, i , координаты времени возрастания тока через ti и спада тока через /о. Тогда можно написать, например, для любой из кривых рнс. 48
[c.115]
Для машин переменного тока параметры тока определяются действующим значением /св.д и длительностью 4в для основного тока (рис. 22,а) и соответственно /доп д и /доп и паузой / для дополнительного тока (рис. 22,6), применяемого, например, для термической обработки при ТС закаливающихся сталей. Дополнительный ток можно использовать для замедления охлаждения металла зоны сварки, тогда он следует за основным без паузы (рис. 22, в). [c.34]
Электродинамическая Сила тока 1 х 1 Постоянный переменный (действующее значение) 40 Гц — 20 кГц Амперметры Вольтметры Ваттметры Варметры Фазометры Частотомеры 0,001 А 0,045 В 0,75 Вт 75 вар 1Гц 10 А 600 В 0,05
[c.37]
Для расчета расхода электрической энергии электровоза и моторного вагона переменного тока определять действующее значение активного тока / а по токовым характеристикам (см. приложение 4, рис. 4.76—4.84 4.102—4.103).
[c.39]
приложение 4, рис. 4.76—4.84 4.102—4.103).
[c.39]
Средняя мощность переменного тока р или просто мощность переменного тока Р при совпадении фаз колебаний силы тока и напряжения определяется через действующее значение силы тока I и напряжения U выражением [c.241]
Отсюда средняя мощность на участь е цепи переменного тока равна произведению квадрата действующего значения силы тока lia активное сопротивление R участка цепи [c.241]
Какой. электроемкостью должен обладать конденсатор, для того чтобы при включении его в цепь переменного тока с частотой 1000 Гц при действующем напряжении 2 В действующее значение силы тока в цепи было равно 20 мА [c.296]
Наиболее высокое качество измерения достигается магнитоэлектрическими приборами, которые имеют достаточно широкий диапазон измерения для напряжения и силы постоянного тока. Для измерения действующих (средних или амплитудных) значений напряжения и силы переменного тока могут быть использованы приборы с любым ИМ (кроме магнитоэлектрического), но по качеству измерения следует отдать предпочтение электродинамическому ИМ. Обычно шкала прибора градуируется в действующих значениях напряжения или тока в случае градуирования шкалы в средних или амплитудных значениях делается соответствующее указание на шкале.
[c.145]
Обычно шкала прибора градуируется в действующих значениях напряжения или тока в случае градуирования шкалы в средних или амплитудных значениях делается соответствующее указание на шкале.
[c.145]
Действующее или эффективное значение переменного тока равно такому значению постоянного тока, который за тот же отрезок времени, равный одному или целому числу периодов переменного тока, выделит в некотором сопротивлении такое же количество тепла, как и данный переменный ток [c.519]
Эффективное, или действующее, значение синусоидального переменного тока численно равно такому постоянному току, который за промежуток времени, ранный одному периоду, выделяет в сопротивлении такое же количество тепла, как и переменный ток [c.340]
ПРОБОЙ магнитный — туннельный переход электрона, движущегося в металле при наличии магнитного поля, с одной орбиты на другую световой — переход вещества в состояние плазмы в результате сильной ионизации под действием мощного светового излучения электрический — общее название процессов, приводящих к резкому возрастанию электрического тока в среде, исходно не электропроводной) ПРОВОДИМОСТЬ ионная обусловлена движением свободных ионов комплексная определяется отношением действующего значения силы переменного тока в электрической цепи к действующему значению напряжения на ее зажимах магнитная измеряется отношением магнитного потока в каком-либо участке магнитной цепи к магнитодвижущей силе, действующей на этом участке полупроводника [примесная дырочная (/)-типа) обеспечивается движением дырок в направлении, противоположном движению электронов, перебрасываемых из валентной зоны в зону проводимости полупроводника электронная (я-типа) осуществляется электронами, перебрасываемыми с донорных уровней в зону
[c.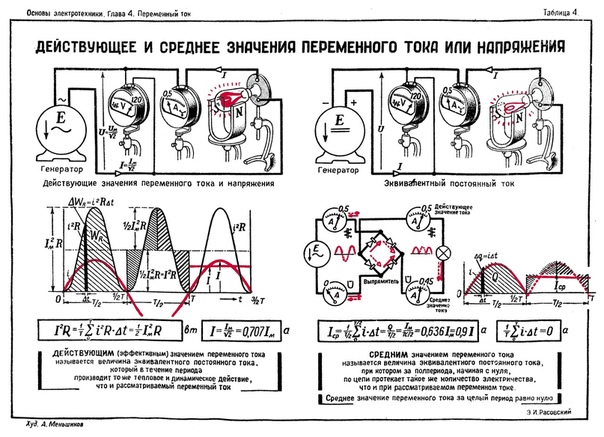 266]
266]
Действующее значение переменного тока равно такому постоянному току, который в равном сопротивлении за время одного периода выделяет одинаковое с переменным током количество тепла. Для синусоидального тока зависимость между действующим / и амплитудным / значениями имеет вид [c.298]
Приборы, применяемые для измерения переменных напряжений и токов, как правило, показывают действующие значения напряжения и тока. Действующими значениями обычно пользуются и при расчетах электрических цепей переменного тока. [c.299]
Полной мощностью 5 цепи переменного тока называется величина, равная произведению действующих значений напряжения U и силы тока I
[c.306]
Действующее значение э. д. с. Е синхронного генератора пропорционально частоте переменного тока f, числу витков W фазы, основному магнитному потоку полюсов Ф и обмоточному коэффициенту коъ [c.313]
Представителем усилителей дискретного действия является электромагнитное реле, в котором входной электрический ток, достигнув некоторого значения, преобразуется в перемещение якоря, механически замыкающего контакты более мошной электрической цепи управления. Различают нейтральное реле постоянного тока), реле переменного тока и поляризованное реле постоянного и переменного тока.
[c.104]
Различают нейтральное реле постоянного тока), реле переменного тока и поляризованное реле постоянного и переменного тока.
[c.104]
Наличие микроЭВМ позволяет сделать измерители тока универсальными (с широкими функциональными возможностями). По ординатам мгновенного значения измеряемого тока можно вычислить его действующее значение (для машин переменного тока) или максимальное (для импульсных машин). Причем в первом случае может быть измерено как действующее значение за определенный период тока, так и за весь импульс тока. Аналогично в импульсных машинах может быть определено среднее значение тока за импульс и т. д. Легко измеряются функционалы [c.229]
Для испытаний электроизоляционных масел и других жидких диэлектриков на электрическую прочность предназначена. установка типа АИМ-80. Эта установка позво,ряет получить в условиях лаборатории действующее значение напряжения переменного тока промышленной частоты до 80 кВ. Мощность установки 0,5 кВ-А, объем испытательного сосуда 400 см . [c.395]
[c.395]
Реактивная мощность электрической цепи ьтт- вар вар var Вар — реактивная мощность электрической цепи с синусоидальным переменным током при sin ф = = 1 и действующих значениях напряжения 1 В и силы тока I А [c.604]
С. При этом абсолютные значения равномерности при хромировании на токе переменной полярности на 10% выше, чем при хромировании на прямом токе это объясняется избирательным растворением в периоды анодной поляризации и изменением наклона поляризационных кривых вследствие периодической деполяризации электродов. Избирательное растворение выступов и неровностей в периоды анодной поляризации оказывает полирующее действие на поверхности деталей. [c.213]
НАПОР [массе жидкости в этом объеме температурный — разность температур двух различных смежных или разделенных стенкой сред, между которыми происходит теплообмен] НАПРЯЖЕНИЕ механическое [служит мерой внутренних сил, возникающих в деформированном теле и определяемой отношением выявленной силы к величине элементарной площадки, выбранной внутри или на поверхности тела в гидроаэростатике определяется как сила, отнесенная к единице площади поверхности, на которую она действует касательное возникает под действием сил, касательных к нормальное возникает под действием сил, нормальных к> поверхности тела трение численно равно силе внутреннего трения в газе, действующей на единицу площади поверхности слоя] электрическое (численно равно суммарной работе, совершаемой кулоновскими и сторонними силами при перемещении по участку цепи единичного положительного заряда анодное прилагается между анодом и катодом электронной лампы или гальванической ванны зажигания обеспечивает переход несамостоятельного газового разряда в самостоятельный переменное, действующее значение которого вычисляют (для периодического напряжения) как среднеквадратичное значение напряжения за период его изменения пробивное вызывает разряд через слой диэлектрика сеточное приложено между сеткой и катодом электронной лампы и служит для запирания лампы при определенном значении его на участке цепи равно произведению его сопротивления на силу тока) НАПРЯЖЕНИЯ механические (контактные возникают на площадках соприкосновения деформируемых тел температурные образуются в теле вследствие различия температур составных его частей и ограничения возможностей теплового расширения со стороны окружающих частей тела или других тел остаточные вызываются крупными дефектами материала, неоднородностью кристаллической структуры и дефектами атомно-кристаллических решеток)
[c. 253]
253]
Напряжение измеряют вольтметром (рис. 63). Зажимы этих приборов включают параллельно электроприбору. При таком включении вольтметра отклонение его стрелки будет пропорционально напряжению между теми точками цепи, к которым он подключен. Вольтметры переменного тока указывают действующее значение напряжения. Для расширения пределов измерения вольтметров при постоянном токе и переменном токе до 600 В включительно используют добавочные сопротивления, включаемые последовательно с катущкой прибора. [c.142]
В однофазной мостовой схеме (фиг. 43, а) вентили включены в четыре плеча, образующие так называемы мост В одну диагональ моста включается нагрузка Н, питаемая выпря.м-ленны.ч током действующее значение выпрямленного напряжения на выходе будет 7—, В другую д1 агональ моста включается однофазный источник переменного тока с действующим значением напряжения и [c.206]
Мы рассмотрели эффект близости для случая, когда радиусы сечений обоих проводников были одинаковы (ло). Но эффект близости имеет место и в том случае, если радиусы будут неодинаковы. Так, увеличивая до бесконечности радиус одного из проводников и уменьшая радиус другого до нуля, получим задачу протекания тока по линейному проводнику, параллельному плоской поверхности второго проводника [18]. Обратный ток возвращается по второму проводнику, имеющему радиус, равный бесконечности. При этом, если по проводникам протекает переменный ток с действующим значением / и если частота тока столь велика, что имеет мёсто ярко выраженный поверхностный эффект, то настил тока на поверхности проводника бесконечного радиуса в точке с координатой у будет определен соотношением
[c.12]
Но эффект близости имеет место и в том случае, если радиусы будут неодинаковы. Так, увеличивая до бесконечности радиус одного из проводников и уменьшая радиус другого до нуля, получим задачу протекания тока по линейному проводнику, параллельному плоской поверхности второго проводника [18]. Обратный ток возвращается по второму проводнику, имеющему радиус, равный бесконечности. При этом, если по проводникам протекает переменный ток с действующим значением / и если частота тока столь велика, что имеет мёсто ярко выраженный поверхностный эффект, то настил тока на поверхности проводника бесконечного радиуса в точке с координатой у будет определен соотношением
[c.12]
Элекгромагаитная 2 Сила тока I Постоянный переменный (действующее значение) 40 Гц — 8 кГц Амперметры Вольтметры 0,005 А 0,75 В ЗООА 600 В 0,2
[c.37]
Действующие значения нц-пряжевия в силы тока. Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток. При амплитуде 1т гармонических колебаний силы тока действующее значение 1 силы тока равно
[c.241]
При амплитуде 1т гармонических колебаний силы тока действующее значение 1 силы тока равно
[c.241]
Активное сопротивление. Активным сопротивлением R называется физическая величина, определяемая отношением мо1цно-сти Р переменного тока на участке электрической цепи к квадрату действующего значения силы тока I ка этом участке [c.241]
Действующие значения напряжения и тока. Соотношения между амплитудными и действующими значениями. Активное и реактивное сопротивления. Индуктивное и емкостное сопротивления. Примеры индуктивных и емкостных сопротивлений в электротехнике. Полное сопротивление цепи. Последовательное и параллельное соединение активных, индуктивных и емкостных сопротивлений. Закон Ома для цейи переменного тока. Мощность переменного тока. Активная и реактивная мощность. Полная мощность переменного тока. Коэффициент мощности. [c.318]
В диэлектрике, помещенном в переменное электрическое поле, часть энергии поля переходит в тепловую. Тепловые потери пропорциональны тангенсу угла диэлектрических потерь [4] = Uкруговая частота С — емкость участка изоляции tg 8 = /а / /реакт — отношение активного и реактивного токов на участке изоляции.
[c.320]
Тепловые потери пропорциональны тангенсу угла диэлектрических потерь [4] = Uкруговая частота С — емкость участка изоляции tg 8 = /а / /реакт — отношение активного и реактивного токов на участке изоляции.
[c.320]
Активная мощность электроэнергии Р — часть мощности переменного тока, характеризующая преобразование элекгромагюггной энергии в другие ее формы. Для синусоидального тока Р = IU os (р, где I— действующее значение тока U — напряжение угол между векторами напряжения и силы тока. [c.496]
Алюминиевые фольговые конденсаторы выпускаются и для цепей переменного тока (К50-19). В таких конденсаторах обе обкладки делаются на одинаково заформованных алюминиевых лент — анодов, разделенных бумагой, пропитанной электролитом, т. е. фактически мы имеем два электролитических конденсатора, включенных последовательно емкость такого неполярного конденсатора в 2 раза меньше обычного полярного. Неполярные конденсаторы выпускаются на напряжение до 320 В (действующее значение) и емкость до 750 мкФ. Они чаще всего применяются в пусковых цепях однофазных асинхронных двигателей малой мощности, в качестве фильтров в цепях низких и звуковых частот. Для длительного включения в цепи переменного тока такие конденсаторы целесообразно применять при низких рабочих напряжениях, когда сохраняются их габаритные преимущества по сравне-
[c.261]
Они чаще всего применяются в пусковых цепях однофазных асинхронных двигателей малой мощности, в качестве фильтров в цепях низких и звуковых частот. Для длительного включения в цепи переменного тока такие конденсаторы целесообразно применять при низких рабочих напряжениях, когда сохраняются их габаритные преимущества по сравне-
[c.261]
Действующее значение переменного синусоидального тока
Если в цепь переменного синусоидального тока включить прибор, который предназначен для измерения среднего значения тока в цепи, то этот прибор зафиксирует нулевое значение. Действительно, в каждый период ток протекает полпериода в одном направлении и полпериода — в другом.
В цепи такого тока не будет происходить электролиза, то есть осаждения металла на катоде в электролитической ванне. В то же время в сопротивлении, включенном в цепь переменного тока, идет непрерывный процесс выделения тепла независимо от направления тока: и в первый и во второй полупериоды. Поэтому, чтобы судить о силе переменного синусоидального тока, его сравнивают с постоянным током по одинаковому тепловому действию. Полученное путем такого сравнения значение силы переменного тока называют действующим.
Поэтому, чтобы судить о силе переменного синусоидального тока, его сравнивают с постоянным током по одинаковому тепловому действию. Полученное путем такого сравнения значение силы переменного тока называют действующим.
Таким образом, действующее (эффективное) значение переменного тока численно равно эквивалентной по тепловому действию силе постоянного тока, то есть такому току, который за то же время,
на том же сопротивлении выделит такое же количество тепла, что и переменный ток одинаковой силы.
В цепи постоянного тока на сопротивлении R за время Т при силе тока I выделяется количество теплоты
Q–= I2 RT. (6.6)
В подобном сопротивлении, включенном в цепь переменного тока, в каждый очень короткий отрезок времени ∆t, в течение которого мгновенное значение силы тока i можно считать практически неизменным, выделяется элементарное количество теплоты:
∆Q~ = i2R∆t,
то есть количество теплоты, пропорциональное произведению i2R.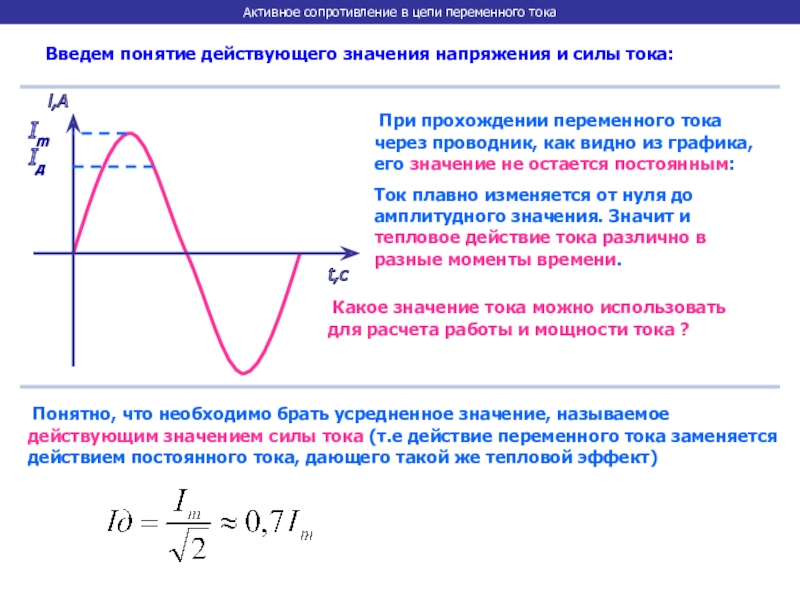 На рисунке 6.4 построены кривые i и i2 для синусоидального переменного тока. Как видно из графика, несмотря на то, что ток i в течение периода меняется по значению и направлению, i2 меняется только по значению и остается положительным независимо от направления тока i, то есть в первом полуперирде эта величина имеет положительное значение (+ i)•(+ i) = +i2, во втором полупериоде она также остается положительной: (—i)•(—i)= +i2.
На рисунке 6.4 построены кривые i и i2 для синусоидального переменного тока. Как видно из графика, несмотря на то, что ток i в течение периода меняется по значению и направлению, i2 меняется только по значению и остается положительным независимо от направления тока i, то есть в первом полуперирде эта величина имеет положительное значение (+ i)•(+ i) = +i2, во втором полупериоде она также остается положительной: (—i)•(—i)= +i2.
Разделив площадь, ограниченную кривой i2 и осью ωt, на время Т, получим среднюю ординату кривой i2 за период, которую обозначим i2ср. Тогда количество теплоты, которое выделится на сопротивлении в цепи переменного тока за время Т,
Q~= i2cр RT. (6.7)
Согласно приведенному выше определению действующего значения переменного тока, Q~= Q– , то есть из формул (6. 6) и (6.7) следует, что
6) и (6.7) следует, что
I2 RT=i2сp RT,
откуда действующее значение переменного тока
I = √i2сp. (6.8).
Действующее значение переменного тока есть среднеквадратичное за период значение переменного тока.
Величину i2, графически представленную на рисунке 6.4, можно определить аналитически через амплитудное значение Im2:
. 1-cos2ωt Im2 Im2
i2 = Im2 sin2ωt = Im2—————— = ——— — —— cos2ωt ,
. 2 2 2
где .
. 1-cos2ωt
sin2ωt = ————— ,
. 2
2
Среднее значение cos2ωt за период Т равно нулю (соответствует сумме площадей, помеченных на рисунке 6.4 знаками + и —). Тогда среднее за период значение квадрата силы синусоидального переменного тока
iср2 =Im2 /2
а действующее значение синусоидального переменного тока
I = √iср2 = √Im2/2 = Im/2 = Im/1.414 = 0,707 Im. (6.9)
Действующее значение переменного синусоидального напряжения может быть найдено из предыдущего как
. Im
IR = ——— R
. √2
или
. Um
U = —— = 0,707 Um.
. √2
Значит, если в сети напряжение U — 220 В, то его максимальное (амплитудное) значение
Um = 220•1,414 = 311 В.
Амплитуда напряжения 380 В равна 380•1,414 = 538 В. То обстоятельство, что амплитуда значительно превышает действующее значение, дает преимущество переменному току при использовании люминесцентных или дуговых ламп, которые легче зажигаются на переменном токе.
| < Предыдущая | Следующая > |
|---|
Переменный ток, генератор переменного тока. Действующее, амплитудное значения напряжения, силы тока в цепи. Тесты онлайн, куосы по физике, подготовка к ЦТ
Всего вопросов: 10
Вопрос 1. Вольтметр переменного тока, включенный в сеть, показывает напряжение 220 В. Найдите максимальное значение напряжения Umax в сети.
Вопрос 2. Напряжение в цепи переменного тока изменяется по закону . Чему равно амплитудное значение напряжения?
Вопрос 3. Зависимость силы тока от времени в цепи имеет вид . Чему равна частота колебаний тока в цепи?
Зависимость силы тока от времени в цепи имеет вид . Чему равна частота колебаний тока в цепи?
Вопрос 4. Плоский прямоугольный проводящий виток площадью вращается в однородном магнитном поле, совершая 5 об/с вокруг оси, перпендикулярной полю. Как изменяется ЭДС индукции в витке с течением времени, если индукция магнитного поля Тл и в начальный момент времени плоскость витка перпендикулярна магнитному полю? Рассчитайте амплитудное значение ЭДС в витке.
Вопрос 5. Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону . Определите время одного оборота рамки.
Вопрос 6. Прямоугольная рамка площадью 100 см2 имеет витки в количестве 200 и вращается в однородном магнитном поле, модуль индукции которого 0,02 Тл. Ось вращения рамки перпендикулярна силовым линиям магнитного поля. Амплитудное значение ЭДС индукции, возникающей в рамке, равно 0,5 В. Определите циклическую частоту вращения рамки.
Определите циклическую частоту вращения рамки.
Вопрос 7. Полагая, что напряжение в сети изменяется по закону синуса и начальная фаза , определите мгновенное значение напряжения в момент времени с. Действующее напряжение 220 В, частота 50 Гц.
Вопрос 8. В начальный момент времени напряжение на клеммах генератора переменного тока равно амплитудному, U0=100 В. Частота переменного тока 50 Гц. Определите напряжение на клеммах генератора через с.
Вопрос 9. Определите количество теплоты (кДж), которое выделяется за время 10 мин в кипятильнике сопротивлением 110 Ом, включенном в сеть переменного тока, напряжение в которой изменяется по закону
Вопрос 10. Квадратная рамка со стороной 10 см вращается в однородном магнитном поле с угловой скоростью 300 рад/с. Модуль индукции магнитного поля 20 мТл. Сопротивление рамки 10 Ом, ось вращения рамки перпендикулярна к линиям магнитной индукции. Определите максимальную силу тока (мА) в рамке.
Определите максимальную силу тока (мА) в рамке.
Так сколько вольт в Ваших розетках? Немного физики и много удивления | Электричество — просто!
Общеизвестно, что переменное напряжение в бытовой сети составляет 220 Вольт, но немногие из нас знают — какое в реальности напряжение приходит в нам в дом.
Обычно напряжение в бытовых розетках Вашего дома должно находиться в пределах 220 Вольт ±5%, то есть 209-231 Вольт. Иногда допускаются кратковременные отклонения напряжения до 10% — как правило, кратковременно, только на период устранения аварий и неисправностей в электросетях.
Итак, в бытовых сетях напряжение 220 Вольт — переменное, и физики электротехники называют его действующим (среднеквадратичным) значением.
А в реальности максимальное значение напряжения гораздо выше!
Все дело в том, что переменное напряжение изменяется по синусоиде, в которой пиковое (амплитудное) значение всегда 220*√2, то есть 220*1,41 = 310 Вольт!
То есть, напряжение сначала растет, затем достигает пикового значения в 310 Вольт, потом спадает и, меняя полярность, снова достигает значения максимума 310 Вольт.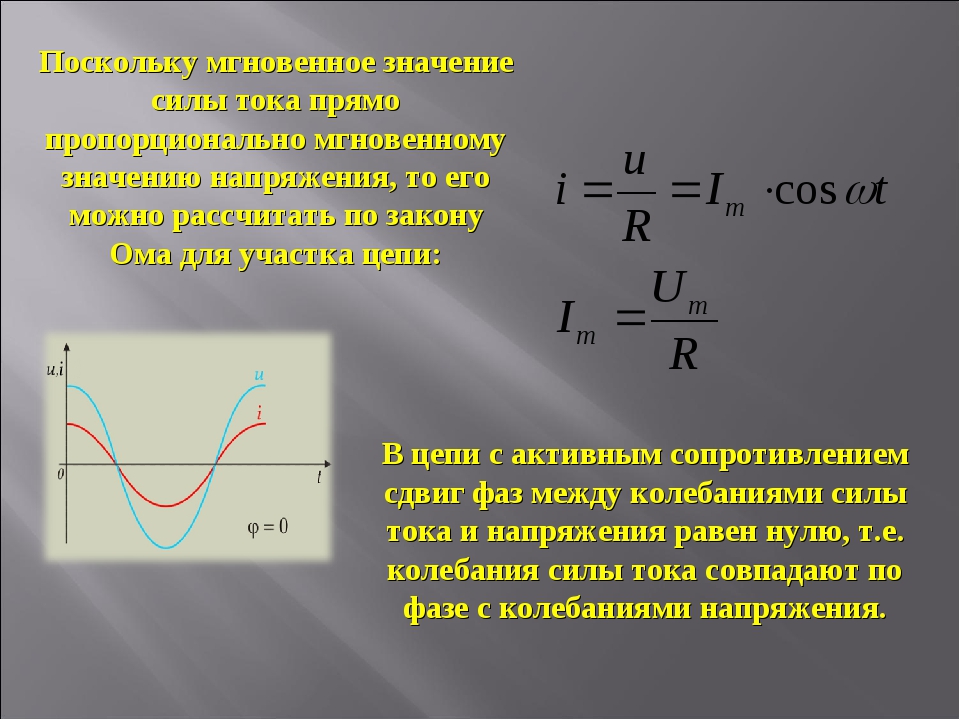
А то, что мы называем 220 Вольт – это действующее значение напряжения, при котором совершается такая же полезная работа, как если бы ток был постоянный с напряжением 220 Вольт. Можно представить, например, что постоянный ток с напряжением 220 Вольт за одно и тоже время кипятит чайник, что и переменный ток с амплитудой напряжения 310 Вольт.
Правда в электротехнике не совсем удобно использовать максимальное значение переменного напряжения 310 Вольт — поэтому при расчетах, например, за потребленную электроэнергию «как бы» считают, что это постоянное напряжение 220 Вольт. К слову сказать, практически все электротехнические приборы (вольтметры, тестеры и т.д.) измеряют именно действующее значение напряжения 220 Вольт.
А теперь снова представьте себе, что в действительности у Вас в розетках 310 Вольт! (можно похвастаться соседям).
Но переживать не стоит – теперь мы знаем, что это амплитуда или максимум, а усредненное действующее напряжение — как и обычно, 220 Вольт.
Желаем Вам электробезопасности!
Понравилась статья?
Для получения интересной и оригинальной информации из мира электричества самый простой способ — подписаться на канал и поставить лайк!
P.S. В следующих статьях как всегда много интересного.
Действующее напряжение переменного тока. Действующие значения тока и напряжения
Переменный синусоидальный ток имеет различные мгновенные значения в течение периода. Естественно задаться вопросом, какое значение тока будет измерять включенный в цепь амперметр? Действия тока не определяются ни амплитудой, ни мгновенными значениями. Для оценки действия переменного тока сравним его действие с тепловым действием постоянного тока.
Мощность P постоянный ток I прохождение через сопротивление r , будет
P = I 2 × r .
Мощность переменного тока выражается как среднее влияние мгновенной мощности i 2 × r за весь период или среднее значение из ( I m × sin ω t ) 2 × r за то же время .
Пусть среднее значение i 2 за период будет M … Приравнивая мощность постоянного и переменного тока, имеем:
I 2 × r = M × r ,
Величина I называется действующим значением переменного тока.
Среднее i 2 при переменном синусоидальном токе определяется следующим образом. Построим синусоидальную кривую тока (рисунок 1).
Рис. 1. Среднеквадратичное значение синусоидального тока
Возводя каждое мгновенное значение тока в квадрат, получаем кривую зависимости i 2 от времени.Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные токи (— i ) во второй половине периода при возведении в квадрат дают положительные значения. Постройте прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника M будет соответствовать среднему значению i 2 за период. Это значение за период, рассчитанное с помощью высшей математики, будет равно .
Это значение за период, рассчитанное с помощью высшей математики, будет равно .
Отсюда,
Так как действующее значение переменного тока I равно, то окончательно формула примет вид
Аналогично соотношение между действующим и амплитудным значениями для напряжения U и E имеет вид:
Действующие значения переменных, то есть действующие значения напряжения, тока и ЭДС, обозначаются прописными буквами без индексов ( U , I , E ).
На основании вышеизложенного можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, выделяет при этом такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующее значение тока и напряжения.
При построении векторных диаграмм удобнее откладывать не амплитуды, а действующие значения векторов. Для этого длины векторов уменьшаются в несколько раз. Это не изменит расположение векторов на диаграмме.
Для этого длины векторов уменьшаются в несколько раз. Это не изменит расположение векторов на диаграмме.
В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично, вынужденные электромагнитные колебания в электрической цепи возникают под действием внешней периодически изменяющейся ЭДС или внешнего переменного напряжения.
Вынужденные электромагнитные колебания в электрической цепи переменный электрический ток .
- Переменный электрический ток — это ток, сила и направление которого периодически меняются.
В дальнейшем будем изучать вынужденные электрические колебания, возникающие в цепях под действием напряжения, гармонически изменяющегося с частотой ω
по закону синусоиды или косинуса:
\(~u=U_m\cdot\sin\omega t\) или \(~u=U_m\cdot\cos\omega t\),
, где u — мгновенное значение напряжения, U м — амплитуда напряжения, ω — частота циклических колебаний. Если напряжение изменяется с частотой ω, то и ток в цепи будет изменяться с той же частотой, но колебания тока не обязательно должны быть синфазны с колебаниями напряжения. Поэтому в общем случае
Если напряжение изменяется с частотой ω, то и ток в цепи будет изменяться с той же частотой, но колебания тока не обязательно должны быть синфазны с колебаниями напряжения. Поэтому в общем случае
\(~i=I_m\cdot\sin(\omega t+\varphi_c)\),
где φc — разность фаз (сдвиг) между колебаниями тока и напряжения.
Исходя из этого, мы также можем дать следующее определение:
- Переменный ток Электрический ток, изменяющийся во времени по гармоническому закону.
Переменный ток обеспечивает работу электродвигателей станков на заводах и фабриках, привод осветительных приборов в наших квартирах и на улице, холодильников и пылесосов, отопительных приборов и т.д. Частота колебаний напряжения в сети 50 Гц . Переменный ток имеет такую же частоту колебаний. Это означает, что ток изменит направление 50 раз в течение 1 с. Частота 50 Гц принята для промышленного тока во многих странах мира.В США частота промышленного тока 60 Гц.
Генератор
Большая часть мировой электроэнергии в настоящее время вырабатывается гармоническими генераторами.
- Генератор переменного тока называется электрическим устройством, предназначенным для преобразования механической энергии в энергию переменного тока.
ЭДС индукции генератора изменяется по синусоидальному закону
\(е=(\rmE)_(m)\cdot\sin\omega\cdott,\)
где \((\rm E)_(m)=B\cdot S \cdot\omega\) — амплитудное (максимальное) значение ЭДС.При подключении к клеммам нагрузочной рамы с сопротивлением Ом Ом через нее будет проходить переменный ток. По закону Ома для участка цепи ток в нагрузке
\(i=\dfrac(e)(R)=\dfrac(B\cdot S\cdot\omega)(R)\cdot\sin\omega\cdot t=I_(m)\cdot\sin\omega\ кдот т, \)
где \(I_(m)=\dfrac(B\cdot S\cdot\omega)(R)\) — амплитудное значение тока.
Основными частями генератора являются (рис.1):
- индуктор — электромагнит или постоянный магнит, создающий магнитное поле;
- якорь — обмотка, в которой наводится переменная ЭДС;
- коллектор со щетками — устройство, с помощью которого ток снимается с вращающихся частей или подается через них.

Неподвижная часть генератора называется статор , а подвижная — ротор . В зависимости от конструкции генератора его якорь может быть как роторным, так и статорным.При приеме переменного тока большой мощности якорь обычно делают стационарным, чтобы упростить схему передачи тока в промышленную сеть.
В современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только один каркас (обмотку), то был бы получен переменный ток частотой 1-2 Гц. Поэтому для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту генерируемого тока.Для паровых турбин, ротор которых вращается очень быстро, применяют якорь с одной обмоткой. При этом частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Мощные генераторы выдают напряжение 15-20 кВ и имеют КПД 97-98%.
Из истории . .. Первоначально Фарадей обнаружил лишь едва заметный ток в катушке, когда возле нее двигался магнит. «Какая польза от этого?» спросили его.Фарадей ответил: «Какая польза от новорожденного?» Прошло чуть более полувека, и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-героя и изменил лик Земли так, как его гордый отец даже представить не мог».
.. Первоначально Фарадей обнаружил лишь едва заметный ток в катушке, когда возле нее двигался магнит. «Какая польза от этого?» спросили его.Фарадей ответил: «Какая польза от новорожденного?» Прошло чуть более полувека, и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-героя и изменил лик Земли так, как его гордый отец даже представить не мог».
*Принцип работы
Принцип работы генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости, перпендикулярной однородному магнитному полю, за счет индукции \ (\ vec (B) \) (см.1).
При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec(B)\) и нормалью к плоскости рамки \(\vec(n)\) изменяется с время по линейному закону. Если в момент времени t = 0 угол α 0 = 0 (см. рис. 1), то
\(\alpha=\omega\cdot t=2\pi\cdot\nu\cdot t,\)
, где ω — угловая скорость вращения рамки, ν — частота ее вращения.
В этом случае магнитный поток, пронизывающий рамку, будет изменяться следующим образом
\(\Phi\left(t\right)=B\cdot S\cdot\cos\alpha=B\cdot S\cdot\cos\omega\cdot t.\)
Тогда по закону Фарадея ЭДС индукции индуцируется
\(e=-\Phi»(t)=B\cdot S\cdot\omega\cdot\sin\omega\cdot t=(\rm E)_(m)\cdot\sin\omega\cdot t. \)
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
Действующие значения тока и напряжения
Пусть источник тока создает переменное гармоническое напряжение
\ (и = U_(m) \ cdot \ sin \ omega \ cdot t. \; \; \; (1) \)
По закону Ома ток на участке цепи, содержащем только резистор сопротивлением Ом , подключенный к этому источнику, изменяется во времени также по синусоидальному закону:
\ (i = \ dfrac (u) (R) = \ dfrac (U_ (m)) (R) \ cdot \ sin \ omega \ cdot t = I_ (m) \ cdot \ sin \ omega \ cdot t, \ ;\;\;(2)\)
, где \ (I_m = \ dfrac (U_ (m)) (R). \) Как видите, ток в такой цепи также изменяется во времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и тока . Зависящие от времени значения напряжения u и силы тока i называются мгновенными .
\) Как видите, ток в такой цепи также изменяется во времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и тока . Зависящие от времени значения напряжения u и силы тока i называются мгновенными .
Кроме этих значений используется еще одна характеристика переменного тока: действующие (действующие) значения тока и напряжения .
- Эффективной (действующей) величиной силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, как и этот переменный ток.
Обозначается буквой I .
- Действующее (действующее) значение напряжения переменный ток — это напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, как и этот переменный ток.
Обозначается буквой U . (2)) (R).\)
(2)) (R).\)
Следует отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R , выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и тока, в связи с тем, что их колебания совпадают в фазе.
Действующее (действующее) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, совершит такую же работу (тепловой или электродинамический эффект), как рассматриваемый переменный ток.(2) dt)).)
Для синусоидального тока:
I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m, (\ displaystyle I = (\ frac (1) (\ sqrt (2))) \ cdot I_(м)\приблизительно 0(,)707\cdot I_(м),)
I м(\displaystyle I_(м)) — пиковое значение тока.
Для треугольного и пилообразного тока:
I = 1 3 ⋅ I м ≈ 0,577 ⋅ I м. (\displaystyle I=(\frac(1)(\sqrt(3)))\cdot I_(m)\прибл 0(,)577\cdot I_(m).)
Действующие значения ЭДС и напряжение определяется аналогично.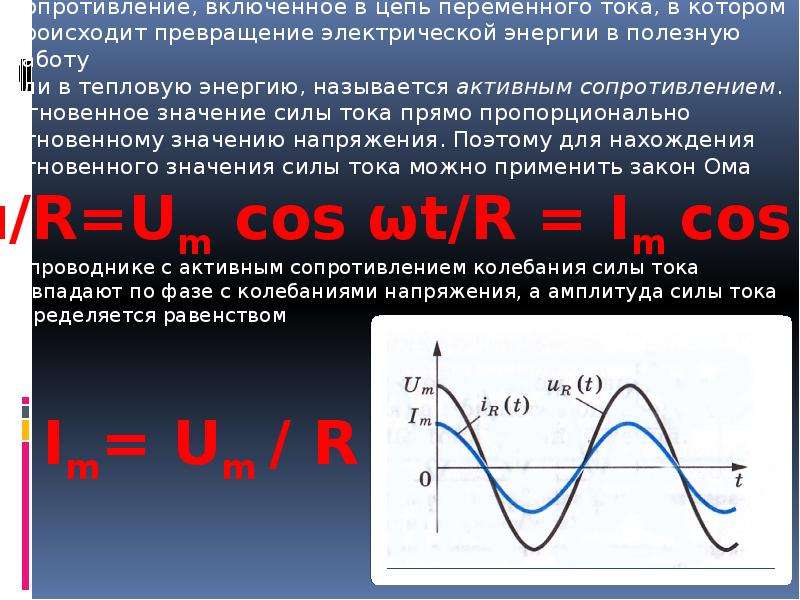
дополнительная информация
В англоязычной технической литературе этот термин используется для обозначения фактического значения. эффективное значение. — эффективное значение. Также применяется аббревиатура RMS (rms) — среднеквадратичное значение — среднеквадратичное значение (значение).
В электротехнике приборы электромагнитных, электродинамических и тепловых систем калибруют на действующее значение.
Источники
- «Справочник по физике», Яворский Б.М., Детлаф А.А., изд.«Наука», 1979 1
- Курс физики. Детлаф А. А., Яворский Б. М. М.: Высшее. шк., 1989. § 28.3, с. 5
- «Теоретические основы электротехники», Бессонов Л.А.: Высш. шк., 1996. § 7.8 — § 7.10
Звенья
- Действующие значения тока и напряжения
- Действующее значение
Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока
Мгновенные и максимальные значения. Величину переменной электродвижущей силы, тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают, соответственно, строчными буквами ( е, и, и, р ).
Величину переменной электродвижущей силы, тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают, соответственно, строчными буквами ( е, и, и, р ).
Максимальное значение (амплитуда) переменная e. и т.д. с. (или напряжение, или ток) — это максимальное значение, которого оно достигает за один период. Максимальное значение электродвижущей силы указано Е м, напряжения — U м, тока — I м.
Активный (или действующий) Значение переменного тока представляет собой постоянный ток, который, протекая через такое же сопротивление и в течение того же времени, что и переменный ток, выделяет такое же количество тепла.
Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раза, то есть на коэффициент.
Аналогично действующие значения переменной ЭДС и напряжения также в 1,41 раза меньше их максимальных значений.
По величине измеренных действующих значений переменного тока, напряжения или электродвижущей силы можно рассчитать их максимальные значения:
Е м = Е 1,41; U м = U 1,41; I м = I 1,41;
Среднее = отношение количества электрической энергии, прошедшей через поперечное сечение проводника за полупериод, к значению этого полупериода.
Под средним значением понимается его среднее арифметическое значение за половину периода.
/Средние и действующие значения синусоидальных токов и напряжений
Под средним значением синусоидально изменяющейся величины понимается ее среднее значение за полупериод. Средний ток
то есть среднее значение синусоидального тока получается из амплитудного. Аналогично,
Широко используется понятие эффективного значения синусоидально изменяющейся величины (его также называют эффективным или среднеквадратичным).Действующий ток
Таким образом, среднеквадратичное значение синусоидального тока в 0,707 раз больше пикового тока. Аналогично,
Можно сравнить тепловой эффект синусоидального тока с тепловым эффектом постоянного тока, протекающего в то же время при одном и том же сопротивлении.
Количество теплоты, выделяемое за один период синусоидальным током,
Теплота, выделяемая за это же время постоянным током равна Приравняем их:
Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество тепла, как и синусоидальный ток.
Для установления эквивалентности переменного тока по энергии и мощности, общности методов расчета, а также для сокращения вычислительной работы, непрерывно изменяющихся во времени токов. ЭДС и напряжения заменяются эквивалентными величинами, не меняющимися во времени. Эффективной или эквивалентной величиной является такой неизменный во времени ток, при котором в резистивном элементе с активным сопротивлением r за период выделяется такое же количество энергии, как и при реальном синусоидальном изменяющемся токе.
Энергия за период, выделяемая в резистивном элементе с синусоидальным током,
i 2 r dt = | I м 2 | |||
При постоянном во времени токе энергия
Вт = I 2 РТ
Приравнивание правых сторон
I м
0,707 I м .
Таким образом, действующее значение тока в √2 раза меньше амплитудного значения.
Аналогично определяются действующие значения ЭДС и напряжения:
Е = Е м /
√2 , U = U м /
√2 .
Действующее значение тока пропорционально силе, действующей на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д.Говоря о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока калибруются соответственно действующим значениям тока и напряжения. Например, если прибор показывает 10 А, то это означает, что амплитуда тока
I м
= √2 I = 1,41 10 = 14,1 А,
и мгновенное значение тока
i = I м
sin (ω t + ψ) = 14.1 sin (ω t + ψ).
При анализе и расчете выпрямительных устройств используют средние значения тока, ЭДС и напряжения, под которыми понимают среднее арифметическое соответствующего значения за полпериода (среднее значение за период, как известно, равно ноль):
Т 2 | ||||||||||
E Ср = | Е Т | sin ω t d ω t = | | cos ω t | π 0 = | 0,637 Е Т . | ||||||
Аналогично можно найти средние значения тока и напряжения:
I ср = 2 I T
/π; У Ср =
2 У Т
/π .
Отношение действующего значения к среднему значению любой периодически изменяющейся величины называется коэффициентом формы кривой.Для синусоидального тока
Переменный синусоидальный ток имеет различные мгновенные значения в течение периода. Естественно задаться вопросом, какое значение тока будет измерять включенный в цепь амперметр? При расчете цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Наиболее удобным было введение понятий о так называемых действующих значениях тока и напряжения … Эти понятия основаны на тепловом (или механическом) действии тока, не зависящем от его направление. Р.м.с. значение переменного тока — Это значение постоянного тока, при котором за период переменного тока в проводнике выделяется такое же количество тепла, как и при переменном токе. Для оценки действия переменного тока сравним его действие с тепловым действием постоянного тока. Мощность P постоянного тока I, проходящего через сопротивление r, будет равна P = P2r. Мощность переменного тока будет выражена как среднее влияние мгновенной мощности I2r за весь период или среднее значение (Im x sinωt) 2 x r за то же время. Пусть среднее значение t2 за период равно M. Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определяется следующим образом. Построим синусоидальную кривую тока. Возводя в квадрат каждое мгновенное значение тока, мы получаем кривую зависимости P от времени. Р.м.с. значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода при возведении в квадрат дают положительные значения. Построим прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью.Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, рассчитанное с помощью высшей математики, будет равно 1/2I2m. Следовательно, М = 1/2I2m Поскольку действующее значение переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями напряжения U и E имеет вид: U = Um / √2, E = Em / √2 Действующие значения переменных обозначаются прописными буквами без нижних индексов (I, U, E). Исходя из вышеизложенного, можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, выделяет за то же время такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), подключенные к цепи переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитуды, а действующие значения векторов.Для этого длины векторов уменьшаются в √2 раза. Это не меняет расположение векторов на диаграмме. |
Список параметров напряжения и тока
В связи с тем, что электрические сигналы являются величинами, изменяющимися во времени, в электротехнике и радиоэлектронике при необходимости применяют различные способы представления напряжения и силы электрического тока.
Значения переменного напряжения (тока)
Мгновенное значение
Мгновенное значение — это значение сигнала в конкретный момент времени, функцией которого является (u(t), i(t)(\displaystyle u(t)~,\quad i(t))). Мгновенные значения медленно меняющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или контурного осциллографа; для периодических быстропротекающих процессов применяют электронно-лучевой или цифровой осциллограф.
Значение амплитуды
- Амплитудное (пиковое) значение, иногда просто называемое «амплитуда» — наибольшее мгновенное значение напряжения или тока за период (без учета знака):
UM=max(|u(t)|),IM=max(|i(t)|)(\displaystyleU_(M)=\max(|u(t)|)~,\qquadI_(M) = \ max (| i (t) |))
Пиковое значение напряжения измеряется импульсным вольтметром или осциллографом.(2)(t)dt)))
Среднеквадратические значения являются наиболее распространенными, поскольку они наиболее удобны для практических расчетов, так как в чисто резистивных линейных цепях переменный ток со среднеквадратичными значениями I (\displaystyle I ) и U (\displaystyle U) выполняет ту же работу, что и постоянный ток. с одинаковыми значениями тока и напряжения. Например, лампа накаливания или котел, подключенные к сети переменного напряжения с действующим значением 220 В, работают (светят, нагреваются) так же, как и при подключении к источнику постоянного напряжения с таким же значением напряжения.
с одинаковыми значениями тока и напряжения. Например, лампа накаливания или котел, подключенные к сети переменного напряжения с действующим значением 220 В, работают (светят, нагреваются) так же, как и при подключении к источнику постоянного напряжения с таким же значением напряжения.
Если не указано иное, обычно имеются в виду среднеквадратичные значения напряжения или тока.
Показывающие устройства большинства вольтметров и амперметров переменного тока калибруются по среднеквадратичным значениям, за исключением специальных приборов, однако эти обычные приборы дают правильные среднеквадратичные показания только при синусоидальной форме волны. Устройства с термопреобразователем не критичны к форме сигнала, в которых измеряемый ток или напряжение преобразуются с помощью нагревателя, представляющего собой активное сопротивление, в дополнительно измеряемую температуру, характеризующую величину электрического сигнала.Нечувствительны к форме сигнала и специальные устройства, возводящие в квадрат мгновенное значение сигнала с последующим усреднением по времени (с квадратичным детектором), или АЦП, возводящие в квадрат входной сигнал тоже с усреднением по времени.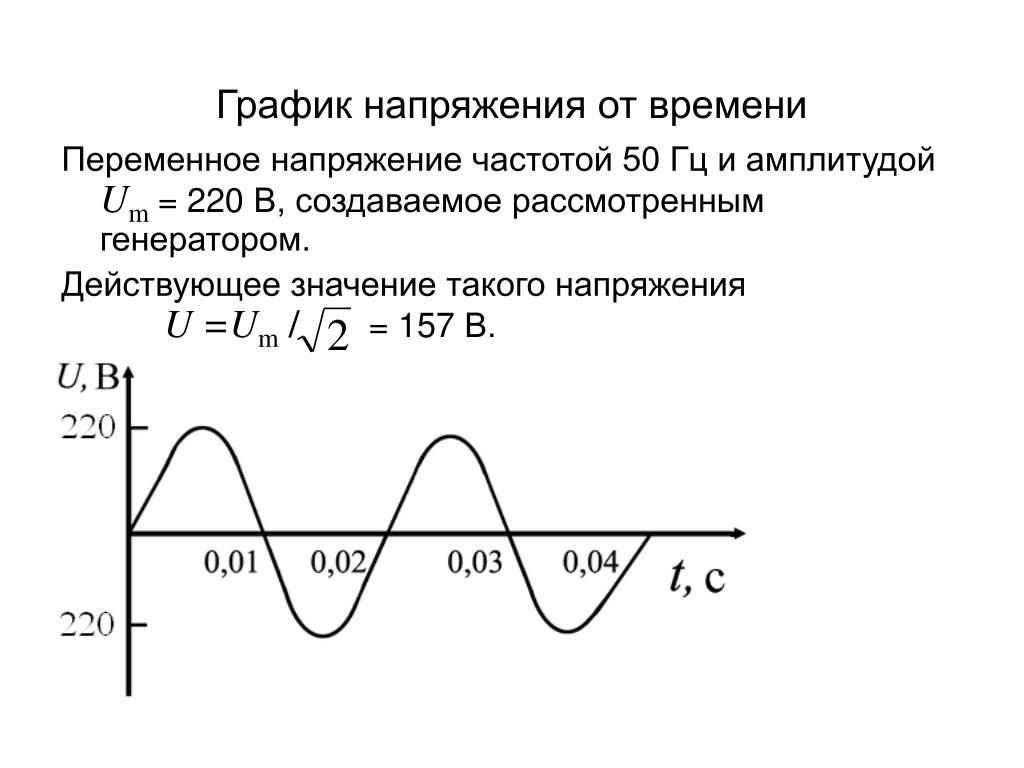 (T) i(t)dt)
(T) i(t)dt)
В электротехнике применяется редко, но в радиотехнике относительно часто (ток смещения и напряжение смещения).(T)\mid i (t)\mid dt)
На практике применяется редко, однако большинство средств измерений переменного тока — магнитоэлектрических систем (т.е. в которых перед измерением ток выпрямляется) реально измеряют именно это значение, хотя их шкала откалибрована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую погрешность. В отличие от приборов магнитоэлектрической системы приборы электромагнитных, электродинамических и тепловых измерительных систем всегда реагируют на действующее значение независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченных кривой выше и ниже оси времени во время измерения. При однополярном измеряемом напряжении среднее и среднее выпрямленное значения равны между собой.
Коэффициенты пересчета
- Коэффициент формы кривой переменного напряжения (тока) представляет собой величину, равную отношению действующего значения периодического напряжения (тока) к его среднему выпрямленному значению. Для синусоидального напряжения (тока) это π/2 2 ≈ 1.11(\displaystyle(\frac((\pi)/2)(\sqrt(2)))\ок 1,11).
- Амплитудный коэффициент кривой переменного напряжения (тока) представляет собой величину, равную отношению максимального абсолютного значения напряжения (тока) за период к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) это 2(\displaystyle(\sqrt(2))).
Параметры постоянного тока
- Размах пульсаций напряжения (тока) – величина, равная разнице между максимальным и наименьшим значениями пульсаций напряжения (тока) за определенный интервал времени
- Коэффициент пульсаций напряжения (тока) – величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.

- Среднеквадратичное значение коэффициента пульсаций напряжения (тока) — величина, равная отношению среднеквадратичного значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсаций напряжения (тока) по среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к ее постоянной составляющей
Параметры пульсаций определяют с помощью осциллографа или с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
- Справочник по радиоэлектронным устройствам : В 2-х томах; Эд.Д.П. Линде — М.: Энергия, 1978
- Шульц Ю.В. Электротехника: 1000 понятий для практиков: Справочник: Пер. с ним. М.: Энергоатомиздат, 1989.
.
Нормативно-техническая документация
- ГОСТ 16465-70 Сигналы радиоизмерительные. Термины и определения
- ГОСТ 23875-88 Качество электроэнергии.
 Термины и определения
Термины и определения - ГОСТ 13109-97 Энергия электрическая. Совместимость технических средств. Нормы качества электроэнергии в системах электроснабжения общего назначения
Звенья
- Электрические цепи постоянного тока
- Переменный ток.Отображение синусоидальных переменных
- Амплитуда, средняя, эффективная
- Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
- Системы тока и номинальные напряжения электроустановок
- Электричество
- Проблемы высших гармоник в современных системах электроснабжения
Каков физический смысл действующего значения напряжения и тока
Титов Александр
Действующее значение переменного тока – это значение постоянного тока, действие которого будет производить такую же работу (или тепловой эффект), как и действие переменного тока в течение одного периода его действия.2*Р*Т). На рисунке представлены графики силы тока и квадрат силы тока, отнесенный к максимальному значению. 2*R*T.2 = Im / 2, откуда I = Im / корень из 2. Это действующее значение тока.
2*R*T.2 = Im / 2, откуда I = Im / корень из 2. Это действующее значение тока.
То же с действующим значением напряжения и ЭДС.
Витас Латиш
грубо говоря
— напряжение — потенциальная энергия….гребень — волосы….напряжение = свечение, блестки, поднятие волос….
— ток это работа, действие, мощность…тепло, горение, движение кинетическое всплеск энергии
Физический смысл этих понятий примерно такой же, как физический смысл средней скорости или других величин, усредненных во времени.В разные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно только условно.
В то же время совершенно очевидно, что разные токи имеют разные энергетические характеристики — они производят разную работу за один и тот же промежуток времени. Работа, совершаемая током, принимается за основу для определения действующего значения силы тока.Они устанавливаются на определенный промежуток времени и рассчитывают работу, совершаемую переменным током за этот промежуток времени.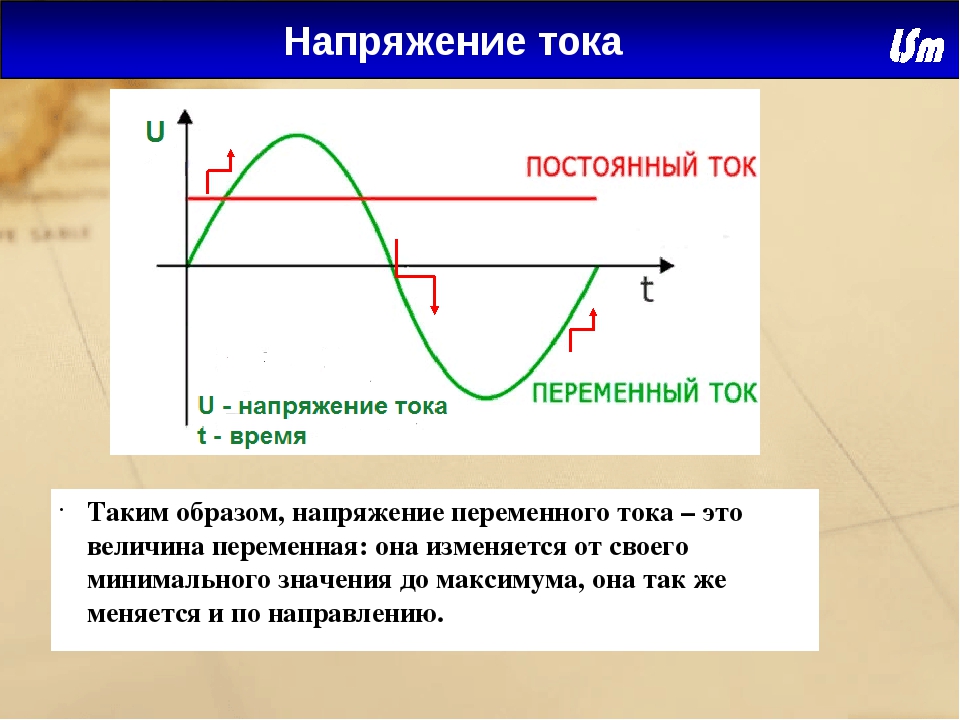 Затем, зная эту работу, производят обратный расчет: выясняют силу постоянного тока, которая произвела бы аналогичную работу за тот же промежуток времени. То есть выполняется усреднение мощности. Расчетная сила гипотетически протекающего по тому же проводнику постоянного тока, производящего ту же работу, есть действующее значение исходного переменного тока.Проделайте то же самое с напряжением. Этот расчет сводится к определению значения такого интеграла:
Затем, зная эту работу, производят обратный расчет: выясняют силу постоянного тока, которая произвела бы аналогичную работу за тот же промежуток времени. То есть выполняется усреднение мощности. Расчетная сила гипотетически протекающего по тому же проводнику постоянного тока, производящего ту же работу, есть действующее значение исходного переменного тока.Проделайте то же самое с напряжением. Этот расчет сводится к определению значения такого интеграла:
Откуда взялась эта формула? Из известной формулы мощности тока, выраженной через квадрат его силы.
Действующие значения периодических и синусоидальных токов
Вычисление действующего значения для произвольных токов — непродуктивное занятие. А вот для периодического сигнала этот параметр может оказаться очень полезным. Известно, что любой периодический сигнал можно разложить на спектр.То есть он представляется как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам необходимо знать, как рассчитать действующее значение простого синусоидального тока.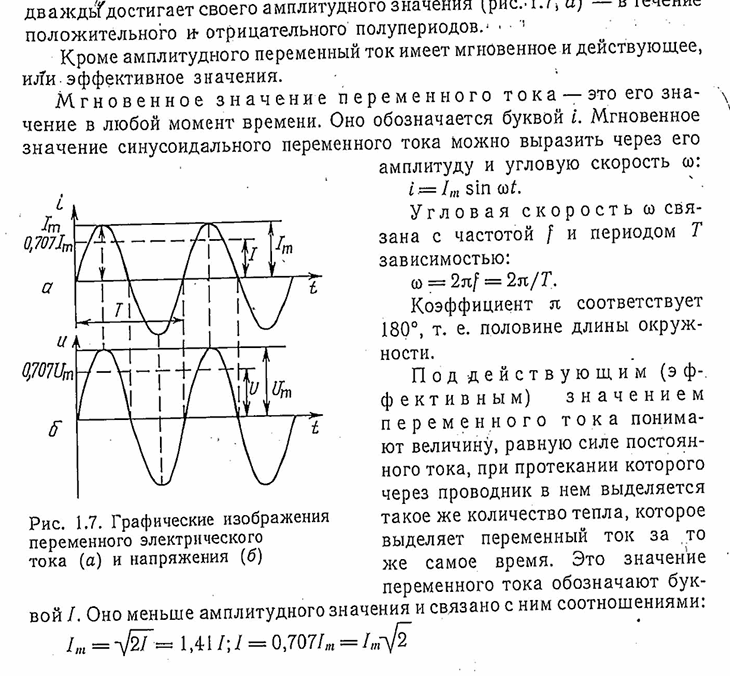 В результате, сложив среднеквадратичные значения первых нескольких гармоник с максимальной амплитудой, получим приближенное значение среднеквадратичного значения тока для произвольного периодического сигнала. Подставив выражение для гармонического колебания в приведенную выше формулу, получим следующую приближенную формулу.
В результате, сложив среднеквадратичные значения первых нескольких гармоник с максимальной амплитудой, получим приближенное значение среднеквадратичного значения тока для произвольного периодического сигнала. Подставив выражение для гармонического колебания в приведенную выше формулу, получим следующую приближенную формулу.
Силу переменного тока (напряжения) можно охарактеризовать с помощью амплитуды. Однако пиковое значение тока нелегко измерить экспериментально. Мощность переменного тока удобно связать с некоторым действием тока, не зависящим от его направления. Это, например, тепловое действие тока. Вращение стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити накала, нагревающейся при прохождении через нее тока.
Сила тока или действующая величина переменного тока (напряжения) – это такая величина постоянного тока, при которой на активном сопротивлении за период выделяется такое же количество тепла, как и при переменном токе.
Свяжем действующее значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделившееся на активном сопротивлении переменным током за время, равное периоду колебаний.Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи с сопротивлением постоянного тока в течение , определяется по формуле
Для этого рассчитаем количество теплоты, выделившееся на активном сопротивлении переменным током за время, равное периоду колебаний.Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи с сопротивлением постоянного тока в течение , определяется по формуле
. Переменный ток можно считать постоянным только в течение очень короткого времени периоды времени.
… Разделить период колебаний на очень большое число малых промежутков времени
… Количество теплоты
, выделившееся на сопротивлении в течение
:
… Общее количество теплоты, выделившееся за период, находится путем суммирования теплоты, выделяемой за отдельные небольшие промежутки времени, или, другими словами, путем интегрирования:
.
Ток в цепи изменяется по синусоидальному закону
,
.
Опустив вычисления, связанные с интегрированием, запишем окончательный результат
.
Если бы по цепи протекал некоторый постоянный ток , то за время равное , она нагрелась бы
. .. По определению постоянный ток , обладающий таким же тепловым действием, как и переменный, будет равен эффективное значение переменного тока
.. По определению постоянный ток , обладающий таким же тепловым действием, как и переменный, будет равен эффективное значение переменного тока
… Находим действующее значение силы тока, приравнивая тепловыделение за период, в случаях постоянного и переменного тока
(4.28)
Очевидно, точно такое же соотношение связывает действующее и пиковое значения напряжения в цепи с синусоидальным переменным током:
(4.29)
Например, действующим напряжением является стандартное напряжение 220 В. По формуле (4.29) легко подсчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.
4.4.5. Мощность переменного тока
Пусть на каком-то участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:
,
.
Тогда мгновенное значение мощности, выделенной на участке цепи, равно
Изменение мощности во времени. Поэтому можно говорить только о его среднем значении. Определим среднюю мощность, выделяемую за достаточно большой промежуток времени (многократно превышающий период колебаний):
Определим среднюю мощность, выделяемую за достаточно большой промежуток времени (многократно превышающий период колебаний):
Используя знаменитую тригонометрическую формулу
.
Значение
усреднять не надо, так как оно не зависит от времени, поэтому:
.
За долгое время значение косинуса успевает многократно изменяться, принимая как отрицательные, так и положительные значения в диапазоне от (1) до 1. Понятно, что среднее по времени значение косинуса равно нулю
, поэтому
(4.30)
Выражая амплитуды тока и напряжения через их действующие значения по формулам (4.28) и (4.29) получаем
. (4.31)
Мощность, выделяемая на участке цепи переменного тока, зависит от действующих значений тока и напряжения и фазового сдвига между током и напряжением … Например, если участок цепи состоит только из одно активное сопротивление, то
и
… Если участок цепи содержит только индуктивность или только емкость, то
и
.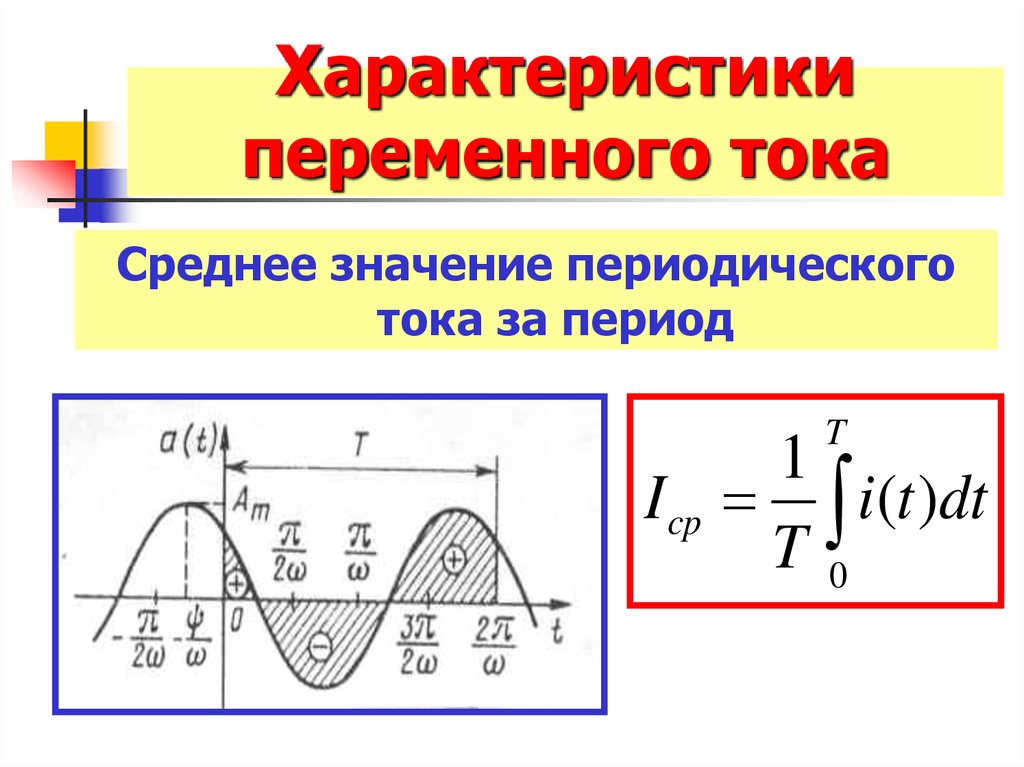
Среднее нулевое значение мощности, выделяемой на индуктивность и емкость, можно объяснить следующим образом.Индуктивность и емкость только заимствуют энергию у генератора и затем возвращают ее обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова падает до нуля и т. д. Именно по той причине, что средняя энергия, потребляемая генератором на индуктивном и емкостном сопротивлениях, равна нулю, их назвали реактивными. На активном сопротивлении средняя мощность отлична от нуля. Другими словами, провод с сопротивлением при протекании по нему тока нагревается.А энергия, выделяющаяся в виде тепла, обратно в генератор не возвращается.
Если участок цепи содержит несколько элементов, то фазовый сдвиг может быть другим. Например, для участка цепи, показанного на рис. 4.5, фазовый сдвиг между током и напряжением определяется по формуле (4.27).
Пример 4.7. К генератору переменного синусоидального тока подключен резистор с сопротивлением.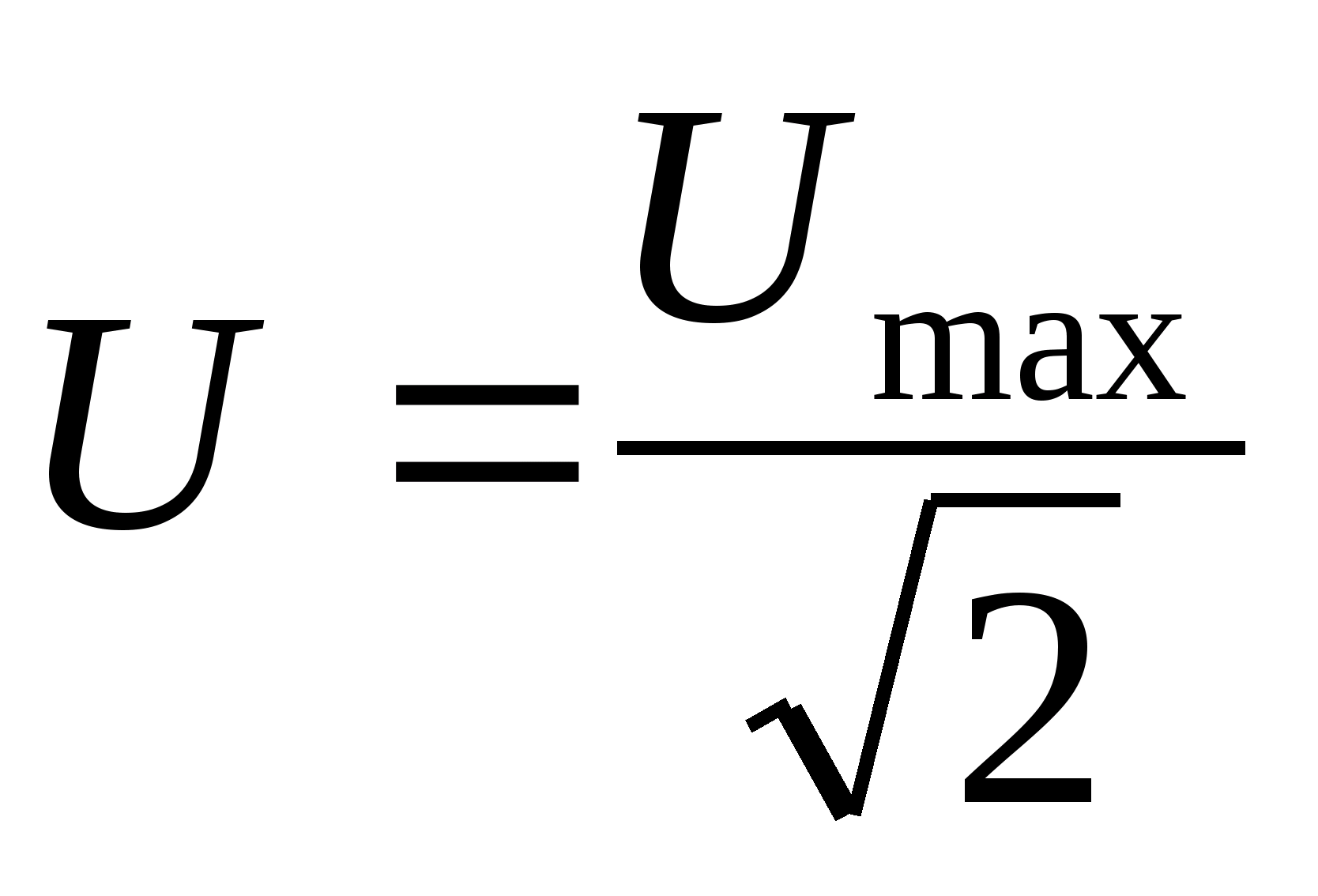 .. Во сколько раз изменится средняя мощность, потребляемая генератором, если к резистору
.. Во сколько раз изменится средняя мощность, потребляемая генератором, если к резистору
подключить катушку с индуктивным сопротивлением а) последовательно, б) параллельно ( Рисунок 4.10)? Активным сопротивлением катушки пренебречь.
Раствор. При подключении к генератору только одного сопротивления потребляемая мощность
(см. формулу (4.30)).
Рассмотрим схему на рис. 4.10, а. В примере 4.6 определялось амплитудное значение тока генератора:
… Из векторной диаграммы на рис. 4.11, и определяем фазовый сдвиг между током и напряжением генератора
.
В результате средняя мощность, потребляемая генератором, составляет
.
Ответ: при последовательном включении индуктивности в цепь средняя мощность, потребляемая генератором, уменьшится в 2 раза.
Рассмотрим схему на рис. 4.10, б. В примере 4.6 определялось амплитудное значение тока генератора
. Из векторной диаграммы на рис. 4.11, б определяем фазовый сдвиг между током и напряжением генератора
.
Тогда средняя мощность, потребляемая генератором
Ответ: при параллельном включении индуктивности средняя мощность, потребляемая генератором, не меняется.
обучения R.M.S. Значения переменного напряжения и тока
Обучение R.M.S. Значения переменного напряжения и тока
Почему 0,707?
Обучение R.M.S. Значения переменного напряжения и тока
Л. Б. Чебик, W4RNL
Знакомство учащихся с переменными напряжениями и токами неизбежно приводит к
обсуждение среднеквадратичных значений ценности. 1 вольт среднеквадратичное значение или 1 ампер среднеквадратичного значения равняется 0,707 от
Пиковое напряжение или ток 1 вольт или ампер. Когда студенты спрашивают: «Почему 0,707?» мы
обычно делаем то же, что и большинство наших текстов: мы приглашаем ученика к обсуждению
среднего квадрата всех бесконечно малых отрезков синуса
изгиб.Студент запоминает 1 единицу среднеквадратичного значения. = 0,707 единицы пика
отношения, но не связывает четко основные понятия в
переменный ток.
Конечно, некоторые ученики довольствуются тем, что запоминают отношения и
пусть дела идут. Тем не менее, некоторые хотят разобраться в отношениях
между пиковым и среднеквадратичным значением значения напряжения и силы тока. Когда я это чувствую,
вот как я поступаю. Я переворачиваю объяснение, начиная с мощности
и никогда не упоминайте r.РС. пока не потребуется назвать единицу измерения.
Задача не так проста, как кажется. Многие студенты радиолюбителей никогда не
освоил основные понятия математики и геометрии. Следовательно, процесс
сбор необходимых идей часто требует нескольких тайм-аутов для
повторение или обучение некоторым важным навыкам.
Однако результаты часто бывают поразительными: упражнение по завязыванию
совместные идеи по этой теме часто вызывают повторные выступления со стороны
студенты с более продвинутыми идеями в области электроники.Увидев студента
самостоятельно закреплять идеи вызывает чувство учителя
удовлетворение, которое оправдывает время и энергию, потраченные студентом на
подробное путешествие по основным идеям переменного тока.
Следующие примечания отражают то, как я обычно поступаю, в том числе то, как я
постарайтесь обвести учащихся вокруг ловушек и опасностей на этом пути.
Хотя в этой пошаговой процедуре нет ничего волшебного, кажется,
Работа. Методы могут быть с пользой адаптированы к другим учебным мероприятиям, как
по базовым предметам и по более сложным темам для обновления лицензии.
НАЧАТЬ С DC
Первым шагом к хорошему пониманию AC является
уверен, что студент полностью понимает как закон Ома, так и степенной закон
для постоянного тока. Для наших целей наиболее важной формой закона Ома является
R = E / I (1)
Если мы позволим R быть некоторым постоянным значением, таким как 1, то отношение E к I
должно быть 1:1 или любые другие парные значения, такие как 2:2, 3:3 или 4:4.
Чтобы учащийся понял это, используйте схему или
испытательная установка, сконфигурированная, как на рис.1. Так как трудно разработать
испытательное приспособление, позволяющее сравнять E и I без серьезной нагрузки
батареи, схема часто является лучшим учебным пособием, особенно если
дополнен многочисленными примерными расчетами.
Рис. 1 Основные цепи постоянного тока
Для урока постоянного тока по закону Ома можно использовать цифровые вольтметры и амперметры.
помогите понять, что отрицательные значения напряжения и тока
также подходят для отношения E к I.Комбинации значений -2:-2, -4:-4,
и -6:-6 все дают R 1 Ом, как и положительные числа. То
разница только в направлении движения электрона через измеритель и
резистор.
Также важно подчеркнуть, что показания счетчиков
— уровни напряжения и тока в момент считывания.
Если пренебречь реальными приборными задержками, каждое мгновенное показание представляет собой
одинаково мгновенный уровень напряжения и тока.
Мощность, конечно же, скорость использования энергии. При передаче постоянного тока
понимание AC, мы также должны быть уверены, что студент понимает
отношение мощности к работе или общему потреблению энергии. Работа – это скорость
потребление энергии, умноженное на время использования. Измеряем ли мы работу в
ватт-секунды, ватт-часы или киловатт-часы, общая электрическая энергия
используемой нашей схемой на рис. 1, отражает общее количество выделяемого тепла и
1, отражает общее количество выделяемого тепла и
рассеивается на резисторе.Чем дольше мы работаем с постоянной скоростью, тем
больше энергии мы используем. Игнорирование фактических средств, используемых для измерения мощности дома
использование, чем дольше мы используем электронагреватель, тем больше мы платим за мощность
компания, которая взимает с нас плату за всю энергию, которую мы используем. Если бы мы запустили то же самое
обогревателя от батарей, мы бы увидели такое же увеличение стоимости, если бы
периодически покупать сменные батареи.
Если фактор времени одинаков для всех расчетов, то мощность будет
быть прямо пропорциональна работе.Для постоянного постоянного тока через
резистор постоянного значения с постоянным напряжением, мощность будет пропорциональна
работать. Однако учащийся должен понимать важность
время до приближения к АС.
Во-первых, DC-эквиваленты переменного тока зависят от усреднения
определенные значения в течение как минимум одного цикла. Во-вторых, использование энергии и ее
Во-вторых, использование энергии и ее
ставки также являются средними по времени.
Формула мощности,
P = E x I (2)
будет иметь решающее значение для преобразования понимания DC в эквивалентное
понимание АС.На самом деле, сейчас самое время приступить к маркировке
элементы формул, чтобы учащийся мог легко разобраться в идеях. Так
давайте преобразуем форму наших формул постоянного тока в следующие:
R = Edc / Idc (3)
и
Pdc = Edc x Idc (4)
R, конечно, просто все, что преобразует электрическую энергию в тепло.
(или другая форма энергии) и, следовательно, не является должным образом ни переменным, ни постоянным током.
Обратите внимание, что в этих формулах я использую символы умножения и
подразделение, наиболее знакомое школьникам-любителям.С калькуляторами и компьютерами,
учащиеся понимают, что «/» означает деление, но при необходимости используют другой
символ деления.
ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
Если учащийся хорошо знаком с важными концепциями DC
дано на первом шаге, то он или она готовы ко второму шагу:
генерация стандартных форм переменного напряжения и тока. Конечно,
Конечно,
переменный ток – это любой ток, который периодически меняет направление.В виде
учителям, мы знаем о синусоидальных, прямоугольных, треугольных и
составные сигналы, которые невозможно передать одним словом. Тем не менее фундаментальные
к понятиям АС есть круговое движение, и ученику будет не комфортно
с АС без освоения его основных элементов.
Рис. 2 Генерация переменного тока
Чтобы ввести круговое движение, я обычно использую гипотетический генератор
который проходит через один электрический цикл для каждого механического цикла. Рис. 2
иллюстрирует, как я использую генератор.Когда генератор проходит через
момент времени T0, его положение по вертикали также равно 0. Напряжение и
ток, доступный для нагрузочного резистора, также равен 0. Когда генератор проходит
через Т30, указывающую 30-градусную точку движения по кругу,
его возвышение над 0 является определенной величиной. Здесь мы должны представить
просто количество тригонометрии, необходимое, чтобы узнать, насколько высока рука.
Независимо от того, изучал ли студент тригонометрию, несложно
передать идею о том, что отношение стороны, противоположной углу
процент, деленный на гипотенузу, является постоянной величиной для любого заданного угла.потом
мы можем назвать отношение синус угла. Далее мы можем вычислить
значения напряжения для каждого из указанных углов, выбивая
синус угла на недорогом «научном» калькуляторе. Если мы позволим
гипотенуза треугольника равна 1 для всех случаев, тогда
E(угол) или I(угол) = sin(угол) (5)
Если гипотенуза имеет значение, отличное от 1, то напряжение или ток
стать грехом угла, умноженным на действительное значение
гипотенуза.
Для этих вводных примеров удобно
гипотенуза треугольника равна 1, а сопротивление нагрузки равно 1 Ом. Числа
отличных от 1, будет затемнять связь синусов углов с
значениям напряжения и тока, а также к значению мощности. Когда
урок окончен, вы можете сообщить ученику, что он или она только что закончил
или ее первый опыт работы с якобы продвинутой концепцией «нормализованного
ценности. »
»
Вводя понятие мгновенного напряжения или тока, I
старайтесь использовать углы в 30 и 60 градусов, избегая 45 градусов как можно чаще.
возможный.Цель здесь состоит в том, чтобы убедиться, что учащийся чувствует себя комфортно.
круговое движение и синусы без преждевременного включения полуразвитого
понятие среднеквадратичного значения в объяснении.
Хотя на рис. 2 показан только первый квадрант движения, я обычно
брать примеры из всех четырех квадрантов. Это показывает, что значения
напряжение и ток (при чисто резистивной нагрузке) принимают как положительные, так и
отрицательные значения, и что они принимают их вместе. Здесь мы можем связать
эти расчеты мгновенных значений напряжения и тока для постоянного тока
измерения, которые мы сделали при изменении направления тока.
Фактически, теперь мы можем показать, что закон Ома применяется к мгновенному
измеренные или рассчитанные значения переменного тока. В любой точке пути
движение,
R = Einst / Iinst (6)
Кроме того,
Pinst = Einst x Iinst (7)
Одним из самых интересных наборов мгновенных значений является
получается, выполняя закон Ома при 90 градусах и снова при 270 градусах. С
С
пусть гипотенуза будет 1,
E90 = I90 = sin 90 = 1 (вольт или ампер),
и
P90 = E90 x I90 = 1 x 1 = 1 Вт.
Аналогично,
E270 = I270 = sin 270 = -1 (вольт или ампер),
и
P270 = E270 x I270 = -1 x -1 = 1 Вт.
Поскольку напряжение, ток и мощность никогда не достигают более высоких значений, мы можем
переименуйте эти специальные значения в пиковые значения. Таким образом, мы определили Epk,
Ипк и Ппк. В этот момент важно вернуть ученика к
диаграмма на рис. 2, чтобы связать значения особых точек в
круговой ход генератора.
Здесь мы можем открыть некоторые вопросы, на которые еще предстоит ответить.Поскольку
пиковое напряжение, ток и мощность возникают только в двух точках на всем протяжении
перемещаться внутри генератора, они не сами по себе определяют полную энергию
вырабатывается генератором и используется резистором в течение всего цикла.
Это значение должно быть меньше пикового значения. Но насколько меньше?
Существует ли систематическая связь между пиковым напряжением, током и
мощность и общее производство и использование энергии с течением времени? Эти вопросы
перейти к шагу 3.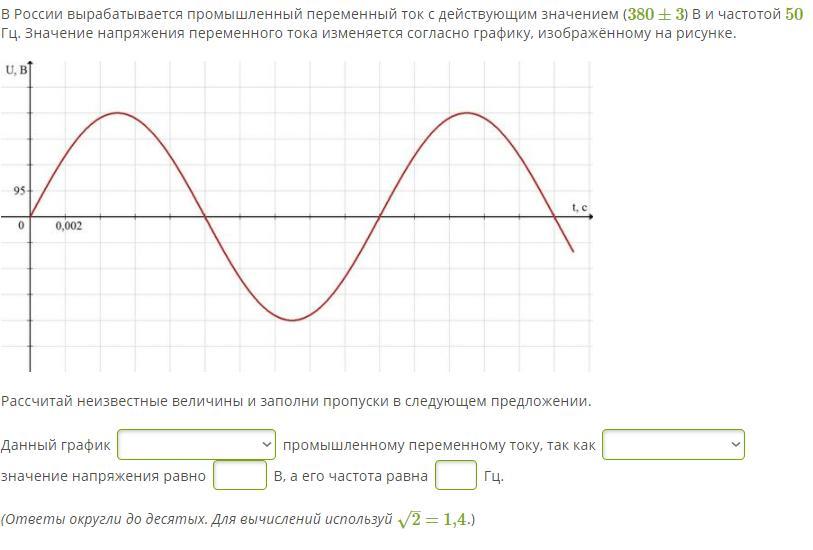
Каждый шаг урока целенаправленно заканчивается несколькими вопросами для обучения
на примере студентов способ обучения себя. Замечая детали
которые приводят к вопросам, а затем, задавая хороший вопрос, студент может
привести себя к хорошим ответам. Продолжайте медленно, чтобы метод
тонуть в.
Рис. 3. Кривая мощности переменного тока
ПИТАНИЕ ПЕРЕМЕННОГО ТОКА И РАБОТА
Одна из трудностей, с которыми я столкнулся при большинстве объяснений
Мощность переменного тока — это кривая этой мощности за полный цикл генератора.
показывается редко, если вообще когда-либо.Рис. 3 в верхней части этой страницы исправляет
ситуация. Некоторые опытные радиолюбители, которых я встречал, никогда не понимали, что кривая
был симметричен относительно его пиков и долин. Эта кривая может упростить
объяснение средней мощности переменного тока и ее отношение к среднеквадратичным значениям. напряжение и
Текущий.
Кривая, конечно, просто квадратичная синусоида с максимальным
значение 1. Если у вас есть доступ к программе для работы с электронными таблицами, вы можете создать
Если у вас есть доступ к программе для работы с электронными таблицами, вы можете создать
кривые на всю страницу, чтобы помочь учащимся в работе со следующим набором идей.Моя процедура началась с настройки столбцов электронной таблицы для каждых 5 градусов.
от 0 до 360 градусов. Следующая строка преобразует их в радианы. (Использовать
Формулу @RAD(X) в столбце A и скопируйте ее для остальных столбцов в виде
блок.) В третьей строке находится синус угла (@sin(X)) (используя
та же процедура «сделай это один раз и заблокируй копирование»). В четвертой строке используется формула «A3 *
A3″ (с блочной копией для остатка), чтобы получить значения для синусоидального
квадратная кривая. График результатов дает точную кривую, помеченную как
вкус.Кривые, показанные здесь, сглажены, чтобы занимать меньше места по вертикали.
но программы для работы с электронными таблицами с отличными графическими способностями (например, Quattro
Используемый здесь Pro 7.0) покажет полные графики 8,5 на 11 дюймов с прекрасным
разрешающая способность.
Кривая очень полезна. Во-первых, он показывает различия в
мгновенная мощность во времени. Учащийся теперь может видеть, что фактическое
генерируемая и используемая энергия будет зависеть от времени, как он или она себе представляет.
кривая повторяется снова и снова в течение многих циклов.Резистор
будет нагреваться и достигать довольно постоянной температуры с переменным током, так же, как
так было с DC.
Чтобы узнать, сколько энергии используется в единицу времени, потребуется больше
чем мгновенное считывание. Это потребует, чтобы мы усреднили мощность
цикла, что означает период времени в 360 градусов. Думая о степенях как
единицы измерения времени важны для понимания переменного тока, и многие учащиеся никогда не
уловить это фундаментальное понятие.Если это поможет, вы можете преобразовать каждый
градус (или пять градусов) в миллисекунды. Однако, чтобы сохранить
студент от мысли, что эти идеи применимы только к течению американского дома,
использовать несколько частот переменного тока в диапазоне мощностей. При частоте 60 Гц цикл занимает
При частоте 60 Гц цикл занимает
около 16,7 миллисекунд или около 46 микросекунд на градус. В Европе,
где 50 Гц является довольно стандартным, цикл занимает 20 миллисекунд примерно при 55
микросекунд на градус. Это быстро, но конечно.
Возвращаясь к рис.3, мы можем только с помощью визуального осмотра увидеть, что
Линия 0,5 представляет собой среднее значение всех значений на кривой. То
учащийся должен провести линию поперек страницы по этой пунктирной линии 0,5, чтобы
подчеркнуть это. Площадь внутри пиков над линией 0,5 равна площади
вне пиков и ниже линии 0,5: недостающая мощность и
нынешняя власть одинакова. Разрезание графика, чтобы показать это, может занять любое время.
недоверие к проверке ученика. Конечно, элементарно
методы интеграции подтвердят визуальные данные, но мы не будем
предположить студента любой математике, которую мы не можем легко преподавать по пути.
Результат этого упражнения является убедительным подтверждением факта
что средняя мощность составляет половину пиковой мощности.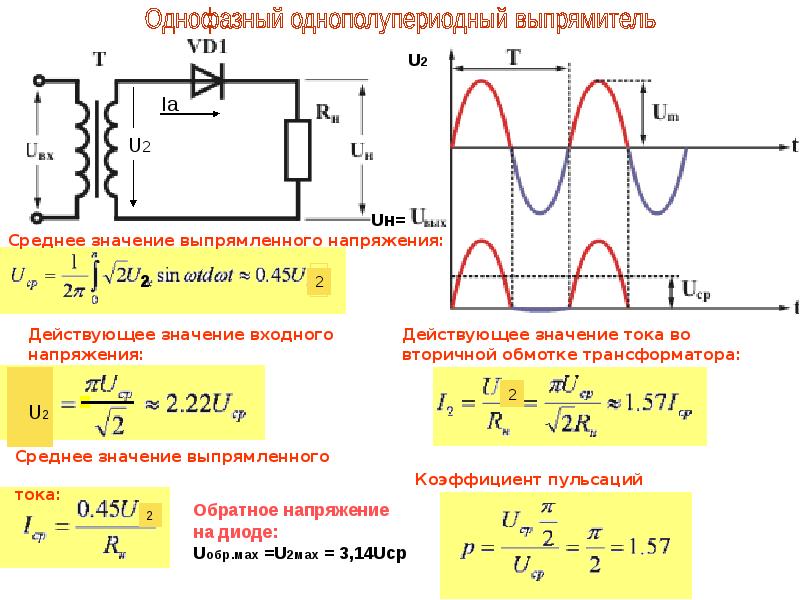 Иначе выражается.
Иначе выражается.
Паве = Ппк/2 (8)
Следовательно, если все циклы после первого одинаковы, то общее
генерируемая и используемая энергия является функцией средней мощности, умноженной на
время создания и использования.
PDC И ПАВЕ
Четвертый шаг в нашем процессе возвращает нас обратно в округ Колумбия.Предположим, мы хотим
нагревать резистор как в цепях постоянного, так и переменного тока до одинакового
температуры, что указывает на эквивалентное преобразование электрической энергии в
тепловая энергия. В этом случае среднее потребление энергии и, следовательно, среднее
мощность должна быть одинаковой в обоих случаях. Для постоянного тока эта скорость использования является
постоянное, одно и то же в каждое мгновение. Для переменного тока это средняя скорость использования
в течение по крайней мере полупериода из множества одинаковых циклов. В противном случае
выраженный,
Pave = Pdc (9)
Поскольку средняя мощность переменного тока равна постоянной мощности постоянного тока, пиковая мощность переменного тока
мощность должна быть в два раза больше мощности постоянного тока, или
Ppk = 2 x Pdc (10)
Прежде чем мы покинем рис. 3 позади, давайте еще раз взглянем на него. Там
3 позади, давайте еще раз взглянем на него. Там
четыре точки на графике, где мгновенная мощность переменного тока равна
средняя мощность переменного тока. Это точки, в которых график мгновенного
мощность пересекает горизонтальную линию 0,5. По времени или от 0 до 360 градусов
оси, эти точки составляют 45, 135, 225 и 315 градусов. Оглядываясь назад на рис.
2, мы видим, что эти точки являются точками на полпути вдоль дуги от
от 0 до 90 градусов, от 90 до 180 градусов и т. д. Смотрим ли мы на
круговую диаграмму или кривую мощности, мы можем сделать вывод, что мощность
ниже точки 45 градусов в половине случаев и выше ее в половине случаев.
Теперь у нас есть достаточно четкое представление о том, как электрическая энергия совершает работу.
является ли эта электрическая энергия переменным или постоянным током. Выполнение одной и той же работы указывает
эквивалентность двух форм электрической энергии.
Тем не менее, у нас еще остались один или два вопроса. Если мощность постоянного тока
эквивалент мощности переменного тока — это средняя мощность переменного тока или половина пиковой мощности переменного тока,
каковы будут значения переменного напряжения и тока по отношению к пиковому напряжению
и ток, который будет эквивалентен их аналогам постоянного тока?
EDC-ЭКВИВ И IDC-ЭКВИВ
Наш пятый шаг будет состоять в том, чтобы найти напряжение и ток, которые производят
средняя мощность переменного тока, которая составляет половину пиковой мощности. У нас есть несколько
У нас есть несколько
пути, по которым это можно сделать. Наилучший эффект на студентов происходит, когда мы используем
всех, ибо тогда мы можем показать взаимосвязь многочисленных основных
идеи переменного тока. Здесь мы покажем только два.
1. Помните, что пиковая мощность равна 1 ватту, произведенному пиковым
напряжение 1 вольт и пиковый ток 1 ампер, мы можем спросить, какое напряжение и
ток необходим для получения тока, равного половине пиковой мощности. Мы
специально ищут напряжение и ток с одинаковыми числовыми
ценность.Другие значения напряжения и тока, которые производят ту же мощность, могут быть
выводится с одной константой k, так что
(k x E) x (1/k x I) = P (11)
Следовательно, Edc-equiv = Idc-equiv для рассматриваемой задачи. Мы ищем
числовое значение, которое при умножении само на себя дает желаемую мощность
ценность. Это, конечно, просто квадратный корень из значения мощности.
Тем не менее, некоторые учащиеся, возможно, утратили представление о концепции квадрата.
корни и требуют объяснения этого порядка.
Напряжение и ток, эквивалентные постоянному току, представляют собой квадратный корень из
средней или эквивалентной мощности постоянного тока. Мы могли бы формализовать это как
Edc-экв x Idc-экв = 0,5 Ppk (12)
или
Edc-экв x Idc-экв = 0,5 x (Epk x Ipk) (13)
Чтобы найти множитель, применимый в равной степени к пиковому напряжению и к пику
ток, мы просто извлекаем квадратный корень из 0,5, то есть находим число
что при умножении само на себя равно 0.5. Результат можно обжать
любого калькулятора:
Edc-экв x Idc-экв = 0,707 Epk x 0,707 Ipk (14)
или
Edc-экв = 0,707 Epk (15)
и
Idc-экв = 0,707 Ipk (16)
Конечно, из нашего обсуждения базового генератора и резистора
цепи, как напряжение, так и ток могут быть отрицательными, но только при одном и том же
время.
Рис. 4 Синусоида циклически генерируемого переменного напряжения или тока.
2. График мгновенных значений напряжения и формы тока
синусоиды, как показано на рис. 4. Этот график можно сравнить с
4. Этот график можно сравнить с
рис. 3, чтобы получить некоторые ценные данные, но объединение графиков может сделать
сравнение проще. На рис. 5 объединена синусоида напряжение-ток с
график мгновенных значений мощности с использованием отдельных осей, одна на
слева, другой справа. На рис. 6 используется другой подход. Если
студент понимает, что отрицательное напряжение, умноженное на отрицательный ток, дает
положительная мощность, то мы можем построить график абсолютных значений напряжения или
ток, чтобы построить график на рис.6. Для построения графика абсолютных значений на
электронной таблицы, просто добавьте новую строку в столбец A, используя @ABS(X)
функция. Затем скопируйте новую строку в A для всех столбцов от 0 до 360.
градусов.
Рис. 5. Суммарный график переменного напряжения/тока и мощности переменного тока с отдельным Y
оси.
Рис. 6. Комбинированный график переменного напряжения/тока и мощности переменного тока с использованием абсолютного E
и я ценю.
Какую бы графическую систему вы ни использовали, обратите внимание на количество
градусов, при которых мощность пересекает 0.5 горизонтальная линия. Тогда спроси, что
напряжение и ток находятся в этих градусных точках. Ты можешь читать
приблизительные значения из графика для 45, 135, 225 и 315 градусов
баллы: чуть более 0,7.
Синус любой из этих точек дает значение 0,707 для
45 и 135 градусов и -0,707 для 225 и 315 градусов. Для мощности 0,5
Ppk, результирующие напряжение и ток составляют 0,707 Epk и 0,707 Ipk,
соответственно.
Рис.6 также демонстрирует, что за исключением точек 0 и 1 на
графике, как напряжение, так и ток должны иметь значения больше, чем
числовое значение мощности (при равенстве напряжения и тока, перед
умножив одно на k, а другое на 1/k).
Наконец, график показывает, что значение напряжения или тока
то есть в 0,707 раза больше пикового значения каждого из них представляет одно и то же время
линия деления как точка пиковой мощности 0,5. То есть за половину времени
То есть за половину времени
каждом цикле значение напряжения, тока или мощности меньше
указанное значение и для половины времени каждого цикла значение напряжения,
ток или мощность больше указанного значения.
Графические идеи совпадают с прямыми арифметическими идеями
отлично. В этом заключается цель преподавания одного и того же урока из более чем одного
точка зрения. Некоторые учащиеся лучше учатся, видя расчеты; другие
учиться лучше всего из изучения графиков. Некоторые даже объединят идеи из
две перспективы, прежде чем поймать. Не полагайтесь на простое повторение.
ОБРАТНАЯ ПРОЦЕДУРА
Какой бы маршрут мы ни использовали, результат один и тот же.Мы установили
что эквиваленты постоянного тока переменного напряжения и тока составляют 0,707 пикового значения.
значения переменного напряжения и тока. Теперь допустим, что 1 переменный вольт постоянного тока-экв = 1 вольт постоянного тока.
и 1 экв. переменного тока = 1 ампер постоянного тока. Эта процедура является правильной, поскольку эти значения
как в цепях переменного, так и постоянного тока производят одинаковое производство и использование энергии.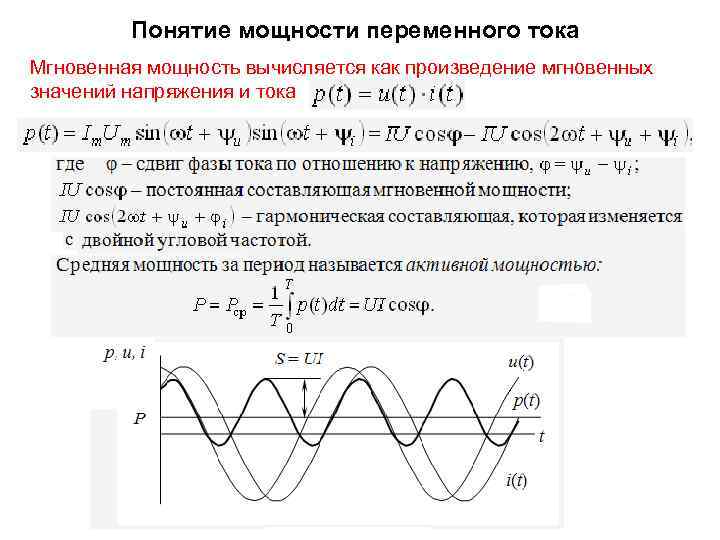
Каково тогда значение пикового напряжения и тока относительно
Эквивалентные значения постоянного тока. поскольку 1 эквивалентный вольт или ампер постоянного тока = 0,707 пикового значения
напряжения или тока, пиковое напряжение или ток должны равняться постоянному току.
эквивалентное напряжение или ток, деленное на 0.707 или
Epk = Edc-экв/0,707 (17)
и
Ipk = idc-экв/0,707 (18)
На этом этапе вы можете познакомить ученика с магией
квадратный корень из 2,1 разделить на 0,707 = 1,414 и наоборот. 0,707 равно
половина квадратного корня из 2 или 1,414/2. Если вашим ученикам интересно,
вы можете вернуться к основным идеям тригонометрии и геометрии, чтобы
проследите использование квадратного корня из 2 в связи со сторонами и
гипотенузы прямоугольных треугольников.Знакомство с этими отношениями
выплачивать дивиденды студенту в его или ее последующем изучении электроники.
Или вы можете просто дать в качестве упражнения на память обычные формулы:
Epk = Edc-экв x 1,414 (19)
и
Ipk = idc-экв x 1,414 (20)
ПЕРЕИМЕНОВАНИЕ DC-ЭКВИВАЛЕНТНОСТИ
Вернемся к рис. 4, который до сих пор очень мало работал в одиночку.
4, который до сих пор очень мало работал в одиночку.
Используя средний или «0.0″ в качестве нашего референта, мы можем спросить, какое значение
состоит из всех мгновенных значений напряжения или тока для
верхней или нижней части кривой. Так как напряжение и ток равны
постоянно меняясь, каждое мгновение бесконечно мало. Мы можем попробовать
процесс, взяв значения на каждом 5-градусном интервале, используя
калькулятор с триггерными функциями и накопительной памятью. (С помощью
первые 90 градусов кривой сокращают расчет до 19 точек данных.Тем не менее, компромисс заключается в несколько большем отклонении от правильного
полученное значение.) Результат составляет около 0,629 от пикового значения. Студент
не очень далеко, чтобы узнать, что среднее значение всех
мгновенные значения составляют 0,637 от пикового значения. Это «среднее» переменное напряжение
или текущее значение, конечно, полезно для понимания схем, где
переменный ток был выпрямлен, чтобы обеспечить импульсы только в одном
направление.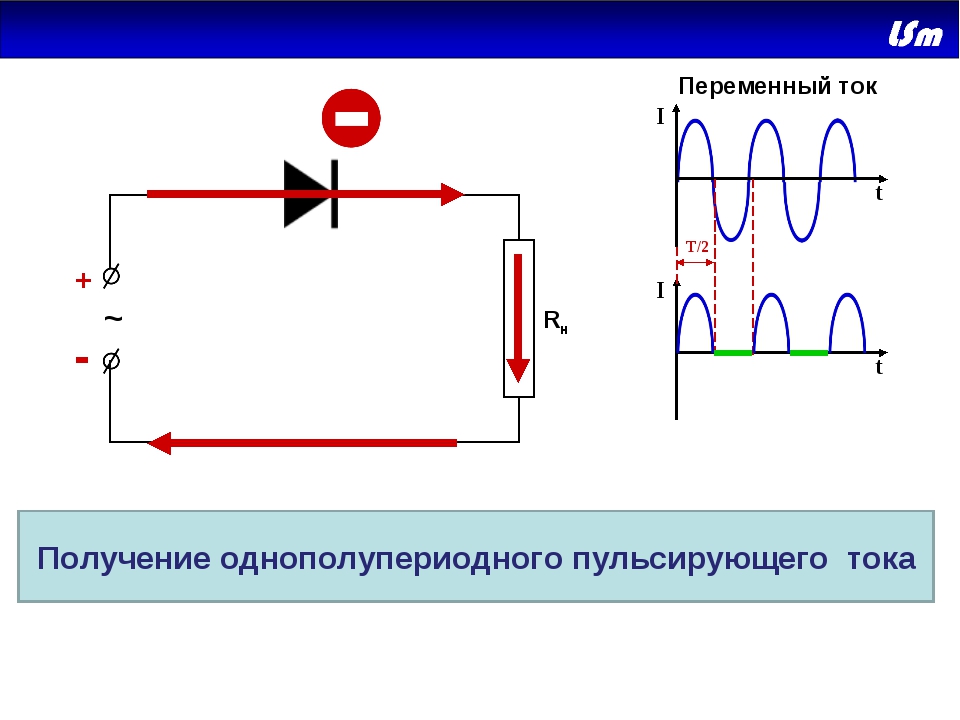
Попробуем другой метод «усреднения».«Сначала возьмем квадрат
каждое мгновенное значение. Затем сложите все квадраты. В-третьих, возьмите
среднее (или среднее) всех квадратов путем деления суммы
квадратов по количеству мгновенных значений. Наконец, возьмите квадрат
корень результата.
Этот метод «среднеквадратичного» (среднеквадратического) извлечения квадратного корня из
среднее квадратов всех значений напряжения или тока при
кривая в диапазоне от 0 до 1 дает значение, идентичное DC
эквивалентное значение напряжения и тока.Мы можем аппроксимировать процесс
проверка всех значений с интервалом в 5 градусов. Результат, используя 19 данных
точек (как результат использования всех возможных мгновенных значений), является
0,707 от пикового значения. Полное среднеквадратичное значение расчет просто расширяет наши
более ранний арифметический вывод эквивалентных значений постоянного тока.
Исходя из этого, Edc-equiv и Idc-equiv получили свои общие названия: Erms и
Irms, где «среднеквадратичное значение» означает «среднеквадратичное значение».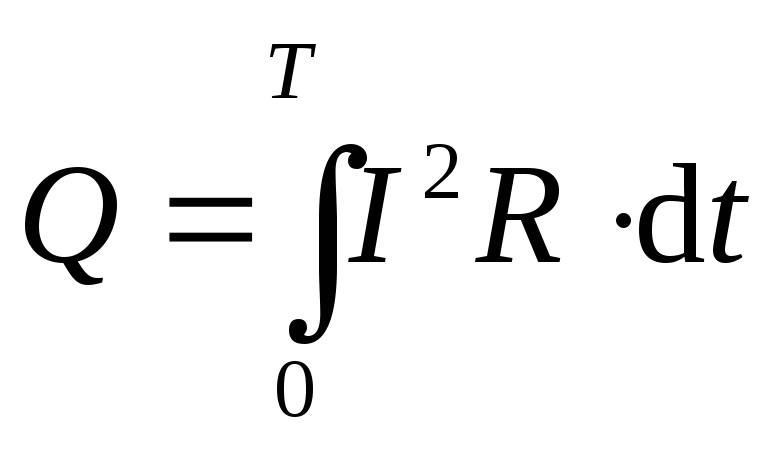 Следовательно, мы можем принять окончательный
Следовательно, мы можем принять окончательный
шаг перемаркировки предыдущих формул:
Erms = 0.707 x Epk (21)
Irms = 0,707 x Ipk (22)
И наоборот,
Epk = 1,414 x Erms (23)
Ipk = 1,414 x Irms (24)
Теперь учащийся имеет в своем распоряжении именно отношения
требуется на экзаменах. Кроме того, он или она также имеет представление о
взаимосвязь многих фундаментальных идей, касающихся переменного и постоянного тока
напряжение, ток и мощность. В долгосрочной перспективе последнее понимание
более важный.
Процесс тщательного обучения среднеквадратичным значениям. значения переменного тока требует
терпение. Это может быть не для каждого нового студента-любителя. Это требует
полезные аналогии и много личности учителя. Но, когда студент
действительно завоевывает популярность, эффект полезен как для учителя, так и для ученика.
Из Proceedings of the National ARRL Education Workshop 1995 г. (Ньюингтон: ARRL, 1995), стр. 33-40 L. B. Cebik, W4RNL. Данные могут быть использованы в личных целях, но не могут быть воспроизведены для публикации в печати или на любом другом носителе без разрешения автора.
B. Cebik, W4RNL. Данные могут быть использованы в личных целях, но не могут быть воспроизведены для публикации в печати или на любом другом носителе без разрешения автора.
Перейти к указателю образовательных заметок
Вернуться на страницу любительского радио
ПРИНЦИПЫ ПЕРЕМЕННОГО ТОКА
Щелкните или коснитесь приведенных ниже примеров цепей, чтобы вызвать TINACloud, и выберите интерактивный режим постоянного тока, чтобы проанализировать их онлайн.
Получите недорогой доступ к TINACloud, чтобы редактировать примеры или создавать свои собственные схемы. ПАССИВНЫЕ КОМПОНЕНТЫ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
Синусоидальное напряжение можно описать уравнением: v(t) = V M cos (ωt + Φ)
| где | v(t) | Мгновенное значение напряжения в вольтах (В). | |
| V M M | Максимальное или пиковое значение напряжения, в вольт (V) | ||
| T | Период: время, принятое для одного цикла, в секундах | ||
| f | Частота – количество периодов в 1 секунду, в Гц (Герцах) или 1/с.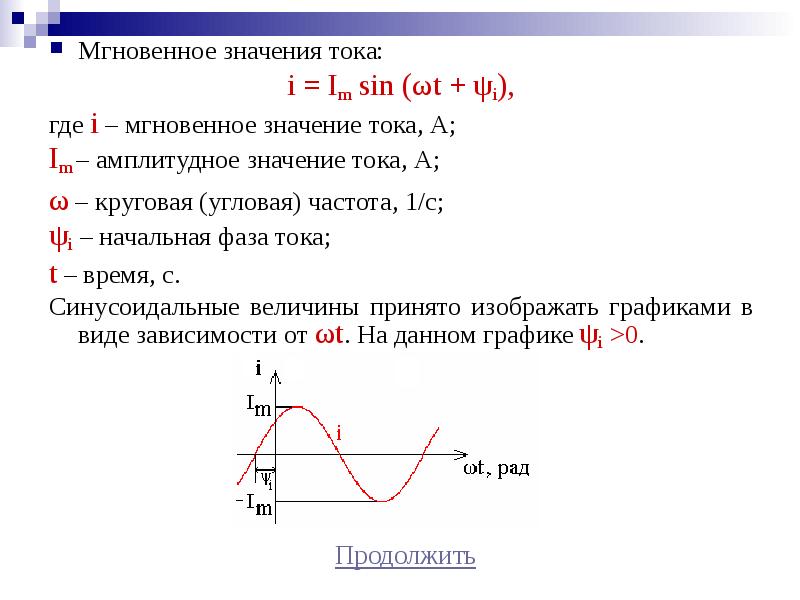 F = 1 / T F = 1 / T | ||
| Ω | ω | Угловая частота, экспрессированная в радианах / с ω = 2 * π * F или ω = 2 * π / T. | |
| Φ | Начальная фаза дается в радианах или градусах.Эта величина определяет значение синусоиды или косинуса att = 0, | ||
| Примечание. Амплитуда синусоидального напряжения иногда выражается как V Eff , эффективное или среднеквадратичное значение. Это связано с V M согласно соотношению V M =√2V Eff, или приблизительно V Eff = 0,707 V M |
.
Характеристики напряжения переменного тока 220 В в бытовых электрических розетках в Европе:
Действующее значение: В Eff = 220 В
Пиковое значение: В M = √2*220 В = 311 В
Частота: f = 50 1/с = 50 Гц
Угловая частота: ω = 2*π*f = 314 1/с = 314 рад/с
Период: T = 1/f = 20 мс
Функция времени: v(t)= 311 sin (314 t)
Давайте посмотрим на функцию времени с помощью команды TINA Analysis/AC Analysis/Time Function.
Щелкните/коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows
. Вы можете проверить, что период равен T = 20 м и что V M = 311 В.
Характеристики напряжения переменного тока 120 В в бытовой электросети в США:
Действующее значение: В Eff = 120 В
Пиковое значение: В M =√2 120 В = 169,68 В ≈ 170 В
Частота: f = 60 1/с = 60 Гц
Угловая частота: ω = 2*π*f= 376,8 рад/с ≈ 377 рад/с
Период: T = 1/f = 16,7 мс
Функция времени: v(t)=170 sin(377 t)
Обратите внимание, что в этом случае функция времени может быть задана как v(t)=311 sin(314 t+Φ) или v(t)=311 cos (314 t +Ф), так как в случае выходного напряжения мы не знаем начальную фазу.
Начальная фаза играет важную роль при одновременном наличии нескольких напряжений. Хорошим практическим примером является трехфазная система, в которой присутствуют три напряжения с одинаковым пиковым значением, формой и частотой, каждое из которых имеет фазовый сдвиг на 120° относительно других. В сети 60 Гц функции времени:
В сети 60 Гц функции времени:
v A (t)=170 sin (377 t)
v B (t)=170 sin (377 t – 120°)
v C (t)=170 sin (377 t + 120°)
На следующем рисунке, сделанном с помощью TINA, показана схема с этими временными функциями в качестве генераторов напряжения TINA.
Щелкните/коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows
Разность напряжений v AB = v A (t) – v B (t) показана как решение Команда TINA Analysis/AC Analysis/Time Function.
Обратите внимание, что пиковое напряжение v AB (t) составляет примерно 294 В, что больше, чем пиковое значение 170 В напряжений v A (t) или v B (t), но также не является простой суммой их пиковые напряжения. Это связано с разницей фаз.Мы обсудим, как рассчитать результирующее напряжение (которое в данном случае равно Ö3 * 170 @ 294) далее в этой главе, а также в отдельной главе Трехфазные системы .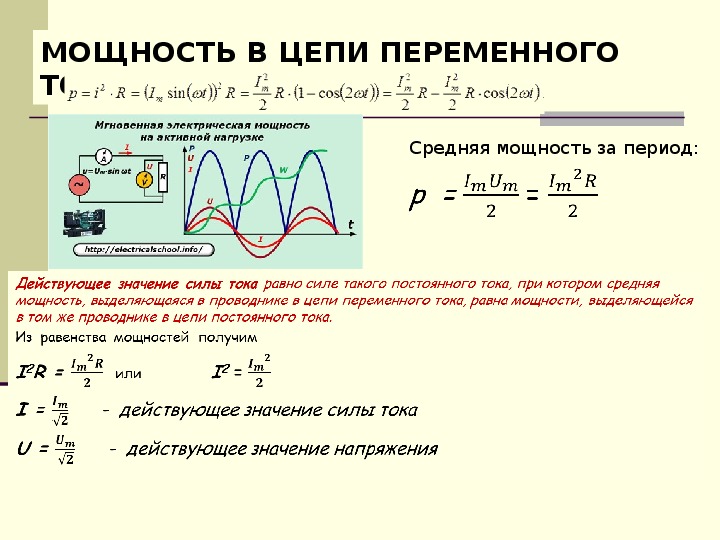
Характеристические значения синусоидальных сигналов
Хотя сигнал переменного тока непрерывно изменяется в течение своего периода, легко определить несколько характеристических значений для сравнения одной волны с другой: пиковое, среднее и среднеквадратичное ( среднеквадратичные значения.
Мы уже встречали пиковое значение V M , которое является просто максимальным значением временной функции, амплитуды синусоидальной волны.
Иногда используется значение размаха (размах). Для синусоидальных напряжений и токов значение размаха в два раза превышает пиковое значение.
Среднее значение синусоиды представляет собой среднее арифметическое значений положительного полупериода. Его также называют абсолютным средним значением , так как оно совпадает со средним значением абсолютного значения сигнала. На практике мы сталкиваемся с этой формой волны, когда выпрямляет синусоидальную волну с помощью схемы, называемой двухполупериодным выпрямителем.
Можно показать, что абсолютное среднее значение синусоидальной волны равно:
В AV = 2 / π V M ≅ 0,637 В M
Обратите внимание, что среднее значение всего цикла равно нулю.
Среднеквадратичное или эффективное значение синусоидального напряжения или тока соответствует эквивалентному значению постоянного тока, производящему ту же мощность нагрева. Например, напряжение с действующим значением 120 В обеспечивает такую же мощность нагрева и освещения в лампочке, как и 120 В от источника постоянного напряжения.Можно показать, что среднеквадратичное или эффективное значение синусоидальной волны составляет:
В среднеквадратичное значение = В M / √2 ≅ 0,707 В M
Эти значения могут быть рассчитаны одинаково для обоих напряжений и токи.
Среднеквадратичное значение очень важно на практике. Если не указано иное, напряжение переменного тока в сети электропитания (например, 110 В или 220 В) указано в среднеквадратичных значениях. Большинство измерителей переменного тока откалиброваны в среднеквадратичных значениях и показывают среднеквадратический уровень.
Большинство измерителей переменного тока откалиброваны в среднеквадратичных значениях и показывают среднеквадратический уровень.
Пример 1 Найдите пиковое значение синусоидального напряжения в электрической сети с действующим значением 220 В.Пример 2
V M
= 110 / 0,707 = 155,58 V
Пример 3 Найти (абсолютное) среднее значение синусоидального напряжения, если его среднеквадратичное значение 220 В.
V A = 0,637 * V M = 0,637*311,17 = 198,26 В
Пример 4 Найдите среднее абсолютное значение синусоидального напряжения, если его среднеквадратичное значение равно 110 В.
Пик напряжения из примера 2 IS155.58 V и следовательно:
A = 0,637 * V M = 0,637 * 155.58 = 99.13 V
Пример 5 Найдите отношение между абсолютным средним (V и ) и среднеквадратичным значением (V) для синусоидальной формы волны.
В/В a = 0,707/0,637 = 1,11
Обратите внимание, что нельзя складывать средние значения в цепи переменного тока, поскольку это приводит к неверным результатам.
ФАЗОРЫ
Как мы уже видели в предыдущем разделе, в цепях переменного тока часто необходимо добавлять синусоидальные напряжения и токи одной частоты. Хотя можно складывать сигналы численно с помощью TINA или с помощью тригонометрических соотношений, более удобно использовать так называемый векторный метод . Вектор представляет собой комплексное число, представляющее амплитуду и фазу синусоидального сигнала. Важно отметить, что вектор не представляет частоту, которая должна быть одинаковой для всех векторов.
Вектор можно обрабатывать как комплексное число или графически представлять в виде плоской стрелки на комплексной плоскости. Графическое представление называется векторной диаграммой. Используя векторные диаграммы, вы можете складывать или вычитать вектора на сложной плоскости по правилу треугольника или параллелограмма.
Существуют две формы комплексных чисел: прямоугольная и полярная .
Прямоугольное представление имеет форму + j b, где j = Ö-1 — мнимая единица.
Полярное представление имеет вид Ae j j , где A — абсолютное значение (амплитуда), а f — угол вектора относительно положительной действительной оси в направлении против часовой стрелки.
Мы будем использовать полужирных букв для комплексных величин.
Теперь давайте посмотрим, как получить соответствующий вектор из функции времени.
Сначала предположим, что все напряжения в цепи выражены в виде функций косинуса.(Все напряжения могут быть преобразованы в эту форму.) Тогда вектор , соответствующий напряжению v(t) = V M cos(w t+f): V M = V M e jf , которое также называют комплексным пиковым значением.
Например, рассмотрим напряжение: v(t) = 10 cos(w t+30°)
Соответствующий вектор: V
Таким же образом мы можем вычислить функцию времени из вектора. Сначала мы запишем фазовращатель в полярной форме e.г. V M = V M e j r и тогда соответствующая функция времени будет , рассмотрим вектор V M =10 – j 20 V
Сначала мы запишем фазовращатель в полярной форме e.г. V M = V M e j r и тогда соответствующая функция времени будет , рассмотрим вектор V M =10 – j 20 V
Приведя его к полярному виду:
Отсюда функция времени: v(t) = 22,36 °5 cos(wt – 9 52,4. ) V
Векторы часто используются для определения комплексного эффективного или среднеквадратичного значения напряжения и тока в цепях переменного тока.Дано v(t) = V M cos(wt+r)= 10cos(wt+30°)
Численно:
v(t) = 10*cos (wt-30°)
Комплекс Эффективно (RMS) Value: * 10289 = 0,707 * 10 * E — J 30 ° = 7.07 E — J 30 ° = 6.13 — J 3.535
наоборот: если комплексное действующее значение напряжения равно:
В = – 10 + Дж 20 = 22. 36 e j 116,5 °
36 e j 116,5 °
тогда значение комплексного пика:
и функция времени: v(t) = 31,63 cos (wt + 116,5° ) V 9163 как следует. Для заданной функции времени
V M (cos( w t+r) определим комплексную функцию времени как: E J J 9 WT = V M E J J WT 9 WT = V M (COS (R) + J SIN (R)) E J WT
где V м = V M E
2 E 8 J R T = V м (COS (R) + J SIN (R)) просто вектор, введенный выше.
Например, комплексная функция времени v(t)=10 cos(wt+30°) J 30288 J J j WT = 10e 8 j 8 J WT (COS (30) + J SIN (30)) = E J 9 WT 8. 66+ j 5)
66+ j 5)
Вводя комплексную функцию времени, мы получаем представление как с действительной, так и с мнимой частью.Мы всегда можем восстановить исходную действительную функцию времени, взяв действительную часть нашего результата: v(t) = Re { v (t)}
. функции времени в рассматриваемых цепях переменного тока имеют один и тот же множитель e j w t , мы можем вынести его и просто работать с векторами. Более того, на практике мы вообще не используем часть e j w t — только преобразования из функций времени в вектора и обратно.
Чтобы продемонстрировать преимущество использования векторов, рассмотрим следующий пример.
Пример 6 Найдите сумму и разность напряжений:
v 1 = 100 cos (314*t) и v 2 = 50 cos (314*t-45°)
Первая запись Фасоры обоих напряжений:
V 1M = 100 V 2M = 50 E — J 45 ° = 35,53 — j 35.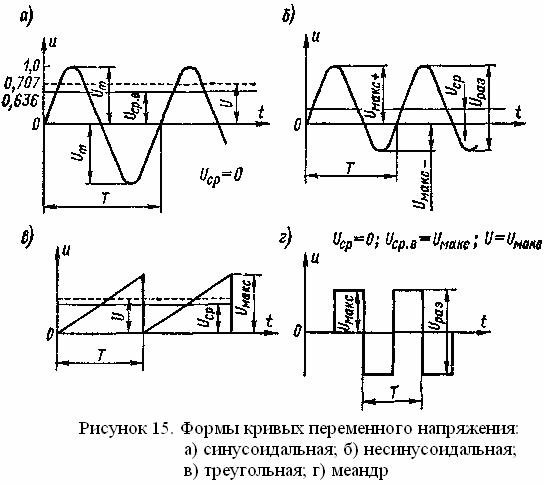 35
35
Отсюда:
V Добавить = V
2 = V
+ V
+ V
+ 2m = 135.35 — J 35.35 = 139.89 E — J 14.63 °
V Sub = V 1M — V 2m = 6421 2m = 64,65 + J 35.35 = 73,68 E J 28.67 °
, а затем Временные функции:
V добавить (т) = 139.89 * cos(wt – 14,63°)
v sub (t) = 73,68 * cos(wt + 28,67°)
Как показывает этот простой пример, метод фазоров является чрезвычайно мощным инструментом для решения задач переменного тока. .
Давайте решим задачу с помощью инструментов интерпретатора TINA.
| {расчет v1+v2} v1:=100 v2:=50*exp(-pi/4*j) v2=[35.3553-35.3553*j] v1add:=v1+v2 v1add=[135.  3553-35.3553*j] 3553-35.3553*j] абс(v1add)=[139.8966] radtodeg(дуга(v1add))=[-14.6388] {расчет v1-v2} 93 |
Результаты амплитуды и фазы подтверждают ручные вычисления.
Теперь давайте проверим результат с помощью анализа переменного тока TINA.
Перед выполнением анализа убедитесь, что функция Base для AC установлена на косинус в диалоговом окне Editor Options в меню View/Option.Мы объясним роль этого параметра в Пример 8 .
Схемы и результаты:
Щелкните/коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows
Опять же, результат тот же. Вот графики функции времени:
Пример 7 Найдите сумму и разность напряжений:
v 1 = 100 sin (314*t) и v 45°)
Этот пример поднимает новый вопрос. До сих пор мы требовали, чтобы все функции времени были заданы как функции косинуса. Что мы будем делать с функцией времени, заданной в виде синуса? Решение состоит в том, чтобы преобразовать функцию синуса в функцию косинуса. Используя тригонометрическое соотношение sin(x)=cos(xp/2)=cos(x-90°), наш пример можно перефразировать следующим образом:
До сих пор мы требовали, чтобы все функции времени были заданы как функции косинуса. Что мы будем делать с функцией времени, заданной в виде синуса? Решение состоит в том, чтобы преобразовать функцию синуса в функцию косинуса. Используя тригонометрическое соотношение sin(x)=cos(xp/2)=cos(x-90°), наш пример можно перефразировать следующим образом:
v 1 = 100 cos(314t – 90°) и v 2 = 50 COS (314 * T — 45 °)
Теперь фасорам напряжения:
V 1M = 100 E — J ° = -100 J В 2М = 50 е – j 45 ° = 35.53 — J 35288 J 35.35
, следовательно:
Добавить = V 1m + V 2m = 35.53 — J 135.35
V Sub = V 1M — V 2m = — 35. 53 — J 64,47
53 — J 64,47
, а затем функции времени:
V Добавить (T) = 139.8966 COS (WT-75.36 °)
v суб (т) = 73.68 cos(wt-118.68°)
Давайте решим задачу с помощью инструментов интерпретатора TINA.
{расчет v1+v2} {вычисление v1-v2} v1sub:=v1sub:=v1sub:=v1sub:=v1sub:=v1+v1add) v2 |
Давайте проверим результат с помощью анализа переменного тока TINA
Нажмите на схему выше, чтобы проанализировать в режиме онлайн, или нажмите на эту ссылку, чтобы сохранить под Windows
Пример 8
Найдите сумму напряжений:
В 1 = 100 sin (314*t) и v 2 = 50 sin (314*t-45°)
Этот пример поднимает еще одну проблему. Что, если все напряжения представлены в виде синусоид, и мы также хотим видеть результат в виде синусоид?Конечно, мы могли бы преобразовать оба напряжения в функции косинуса, вычислить ответ, а затем преобразовать результат обратно в функцию синуса, но в этом нет необходимости. Мы можем создавать векторы из синусоидальных волн так же, как мы делали из косинусоидальных волн, а затем просто использовать их амплитуду и фазу в качестве амплитуды и фазы синусоидальных волн в результате.
Что, если все напряжения представлены в виде синусоид, и мы также хотим видеть результат в виде синусоид?Конечно, мы могли бы преобразовать оба напряжения в функции косинуса, вычислить ответ, а затем преобразовать результат обратно в функцию синуса, но в этом нет необходимости. Мы можем создавать векторы из синусоидальных волн так же, как мы делали из косинусоидальных волн, а затем просто использовать их амплитуду и фазу в качестве амплитуды и фазы синусоидальных волн в результате.
Очевидно, что это даст тот же результат, что и преобразование синусоидальных волн в косинусоидальные. Как мы могли видеть в предыдущем примере, это эквивалентно умножению на – j и последующему использованию соотношения cos(x) = sin (x-90°) для преобразования его обратно в синусоиду.Это эквивалентно умножению на j . Другими словами, поскольку – j × j = 1, мы могли бы использовать векторы, полученные непосредственно из амплитуд и фаз синусоид, для представления функции, а затем вернуться к ним напрямую. Кроме того, рассуждая таким же образом о комплексных функциях времени, мы могли бы рассматривать синусоидальные волны как мнимые части комплексных функций времени и дополнять их функцией косинуса, чтобы создать полную комплексную функцию времени.
Кроме того, рассуждая таким же образом о комплексных функциях времени, мы могли бы рассматривать синусоидальные волны как мнимые части комплексных функций времени и дополнять их функцией косинуса, чтобы создать полную комплексную функцию времени.
Давайте посмотрим на решение этого примера, используя синусоидальные функции в качестве основы векторов (преобразование sin(w t) в действительный единичный вектор (1) ).
1m = 100 V 2m = 50 E — J 45 ° = 35.53 — J 35.35
Отсюда:
V Добавить = В 1М + В 2М = 135,53 – j 35.35
V Sub = V 1m — V 2m = 6421 2m = 64,47+ J 35.35
Обратите внимание, что фасоры точно такие же, как в примере 6, но не время функций:
v 3 (t) = 139,9sin(wt – 14,64°)
v 4 (t) = 73,68sin(wt + 28,68°)
получить результат, используя синусоидальные функции, особенно когда наши исходные данные представляют собой синусоидальные волны. Многие учебники предпочитают использовать синусоиду в качестве базовой функции векторов. На практике вы можете использовать любой метод, но не путайте их.
Многие учебники предпочитают использовать синусоиду в качестве базовой функции векторов. На практике вы можете использовать любой метод, но не путайте их.
При создании векторов очень важно, чтобы все временные функции сначала были преобразованы либо в синус, либо в косинус. Если вы начали с синусоидальных функций, ваши решения должны быть представлены синусоидальными функциями при возврате от фазоров к временным функциям. То же самое верно, если вы начинаете с функций косинуса.
Давайте решим ту же задачу, используя интерактивный режим TINA.Поскольку мы хотим использовать синусоидальные функции в качестве основы для создания векторов, убедитесь, что функция Base для AC установлена на sine в диалоговом окне Editor Options в меню View/Option.
Схемы для суммирования и разности форм сигналов и результата:
и временные функции:
ПАССИВНЫЕ КОМПОНЕНТЫ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
Среднеквадратичная мощность против средней мощности
51
Должен ли я использовать единицы среднеквадратичной (среднеквадратической) мощности для указания или описания мощности переменного тока, связанной с моим сигналом, системой или устройством?
Ответ:
Это зависит от того, как вы определяете среднеквадратичную мощность.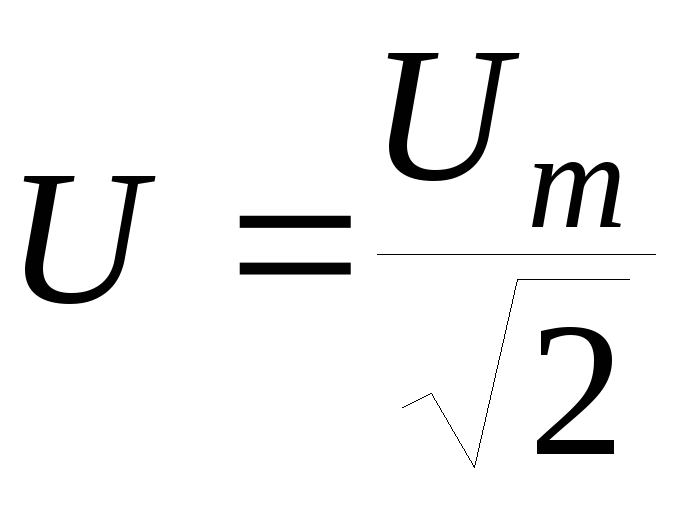
Вы не хотите вычислять среднеквадратичное значение сигнала мощности переменного тока. Это приводит к результату, который не имеет физического смысла.
Вы используете среднеквадратические значения напряжения и/или тока для расчета средней мощности, что дает значимые результаты.
Обсуждение:
Какая мощность рассеивается, когда среднеквадратичное синусоидальное напряжение 1 В подается на резистор сопротивлением 1 Ом?
Это хорошо понятно 1 и здесь нет спора.
Теперь давайте посмотрим, как это соотносится со значением, полученным при расчете среднеквадратичной мощности.
На рис. 1 показан график синусоиды 1 В (среднеквадратичное значение). Размах значения составляет 1 В (среднеквадратичное значение) × 2 √2 = 2,828 В с колебаниями от +1,414 В до –1,414 В. 2
Рисунок 1. График синусоиды 1 В среднеквадратичного значения.
Рисунок 2 представляет собой график мощности, рассеиваемой этой синусоидой 1 В (среднеквадратичное значение) на резисторе 1 Ом (P = V 2 /R), который показывает:
Рис. 2. График мощности, рассеиваемой синусоидой со среднеквадратичным значением 1 В на резисторе 1 Ом.
2. График мощности, рассеиваемой синусоидой со среднеквадратичным значением 1 В на резисторе 1 Ом.
- Кривая мгновенной мощности имеет смещение 1 Вт и колеблется от 0 Вт до 2 Вт.
- Среднеквадратичное значение этого сигнала мощности составляет 1,225 Вт.
- Одним из методов расчета этого числа является уравнение 2 3 :
- Это можно проверить, используя более подробную формулу 4 в MATLAB ® или Excel.
.
- Среднее значение этого сигнала мощности составляет 1 Вт. Это очевидно при осмотре; сигнал симметрично колеблется выше и ниже 1 Вт. То же значение получается при вычислении среднего численного значения точек данных сигнала.
- Среднее значение мощности соответствует мощности, рассчитанной с использованием среднеквадратичного значения напряжения.
Мощность, рассеиваемая синусоидальным среднеквадратичным значением 1 В на резисторе 1 Ом, составляет 1 Вт, а не 1,225 Вт. Таким образом, именно средняя мощность дает правильное значение, и, следовательно, именно средняя мощность имеет физическое значение. Среднеквадратическая мощность (как определено здесь) не имеет очевидного полезного значения (нет очевидного физического/электрического значения), кроме как величина, которую можно рассчитать в качестве упражнения.
Таким образом, именно средняя мощность дает правильное значение, и, следовательно, именно средняя мощность имеет физическое значение. Среднеквадратическая мощность (как определено здесь) не имеет очевидного полезного значения (нет очевидного физического/электрического значения), кроме как величина, которую можно рассчитать в качестве упражнения.
Выполнение того же анализа с использованием среднеквадратичного синусоидального тока 1 А через резистор сопротивлением 1 Ом является тривиальным упражнением.Результат тот же.
Источники питания для интегральных схем (ИС), как правило, работают от постоянного тока, поэтому среднеквадратическая мощность не является проблемой для питания ИС. Для постоянного тока среднее значение и среднеквадратичное значение равно значению постоянного тока. Важность использования средней мощности, в отличие от среднеквадратичной мощности, как определено в этом документе, относится к мощности, связанной с изменяющимися во времени напряжением и током, то есть шумом, ВЧ-сигналами и генераторами.
Используйте среднеквадратичное значение напряжения и/или среднеквадратичного значения тока для расчета средней мощности, в результате чего получаются значимые значения мощности.
1 Мощность, рассеиваемая напряжением на резисторе, представляет собой фундаментальное соотношение, которое легко вывести из закона Ома (V = IR) и основных определений напряжения (энергия/единица заряда) и тока (единица заряда/время). Напряжение × ток = энергия/время = мощность
2 Размах амплитуды синусоиды равен среднеквадратичному значению, умноженному на 2√2. Для синусоидального напряжения Vпик-пик = Vэфф. × 2√2, где Vпик-пик — размах напряжения, а Vэфф — среднеквадратичное напряжение.Это хорошо известное соотношение, описанное в бесчисленных учебниках, а также здесь: en.wikipedia.org/wiki/Root_mean_square.
3 Это адаптировано из среднеквадратичного значения, рассчитанного из постоянного значения смещения постоянного тока плюс отдельное среднеквадратичное значение переменного тока, а также из примечаний по применению «Улучшайте измерения среднеквадратичного значения переменного тока с помощью цифрового мультиметра» компании Keysight.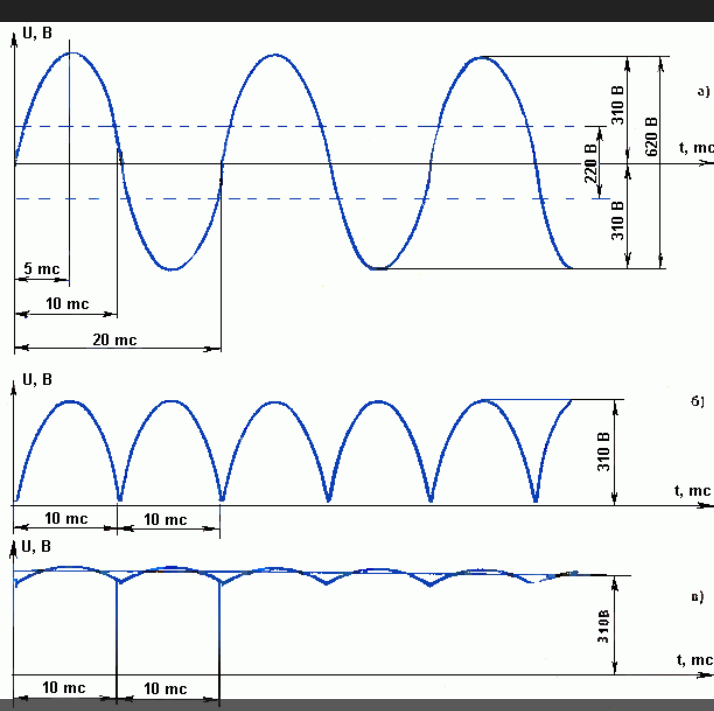
4 Стандартное определение из учебника является одним из примеров более подробной формулы.
среднеквадратичное значение переменного тока | Вывод
В системе постоянного тока напряжение и ток постоянны, поэтому нет проблем с определением их величины.Но в случае системы переменного тока переменное напряжение меняется от момента к моменту, и поэтому возникает проблема с определением величины.
Поэтому, чтобы выразить величины переменного тока в простой и понятной форме, было разработано понятие среднеквадратичного значения. Они также могут быть выражены в терминах пикового значения или среднего значения, но эти значения не отражают эффективность количества переменного тока.
Среднеквадратичное значение переменного тока равно той величине постоянного тока, которая вызывает такой же эффект нагрева, протекая через то же сопротивление в течение того же времени.
Термин RMS означает (квадратный) корень из среднего значения квадратов мгновенных значений тока.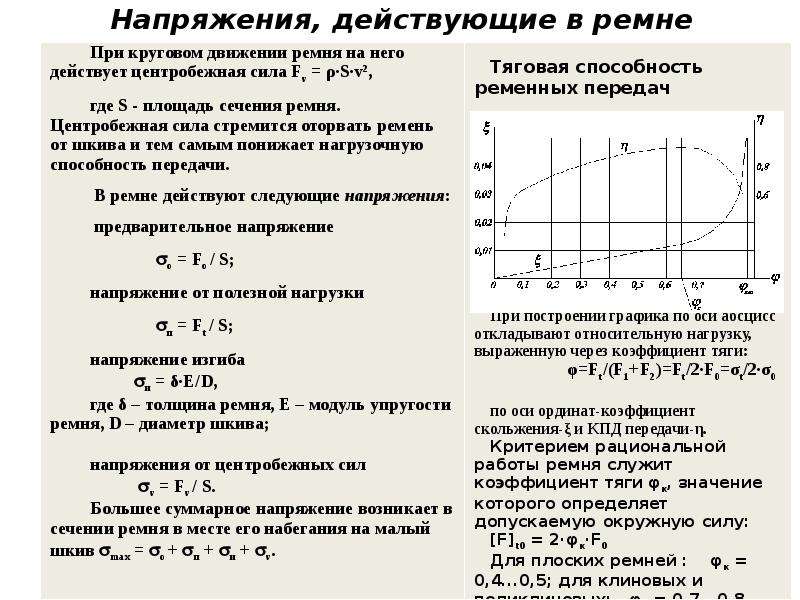 Среднеквадратичное значение переменного тока или напряжения можно рассчитать из следующего соотношения:
Среднеквадратичное значение переменного тока или напряжения можно рассчитать из следующего соотношения:
I СКЗ = 0,707 x пиковое значение тока
В СКЗ = 0,707 x пиковое значение напряжения
Фактическое значение переменной величины говорит нам о способности источника переменного тока передавать энергию. Например, если мы говорим, что через цепь протекает переменный ток 5 А, это означает, что среднеквадратичное значение переменного тока, протекающего через цепь, составляет 5 А.И он будет производить столько же тепла (энергии), сколько будет производить постоянный ток 5А.
Все амперметры и вольтметры переменного тока показывают среднеквадратичные значения переменного тока и напряжения соответственно . Все электроприборы оцениваются по среднеквадратичному значению. В Индии бытовая однофазная сеть переменного тока составляет 230 В, 50 Гц. Здесь 230 В — среднеквадратичное значение напряжения питания.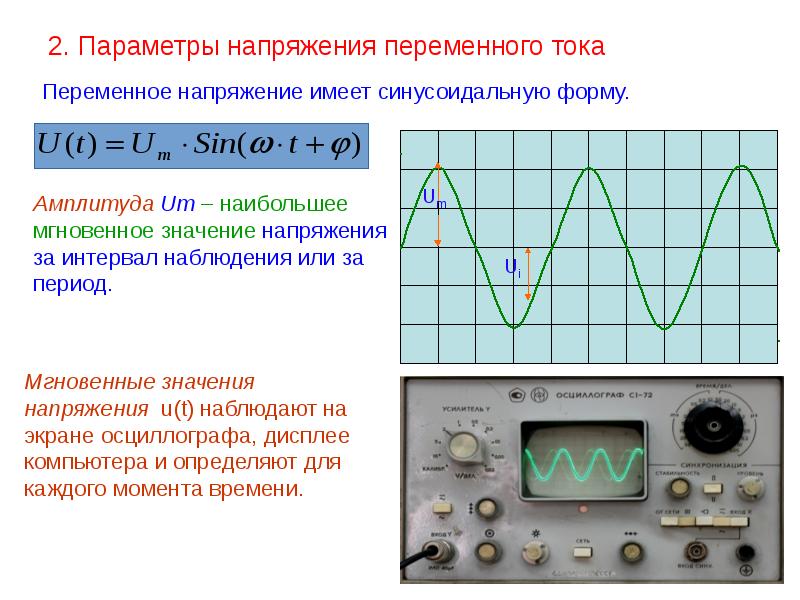
Среднеквадратичное значение AC всегда больше среднего значения, за исключением прямоугольной волны, когда они равны.Его значение никогда не может быть отрицательным.
Выполните выражение для среднеквадратичного значения переменного тока
Пусть i = I м sinωt — переменный ток, протекающий через сопротивление R Ом за время t секунд и производящий столько же тепла, сколько выделяет
I Текущий).
Основание полупериода разделено на n равных частей, как показано на рисунке, так что каждый интервал равен t/n секунд.
Пусть i 1 , i 2 , i 3 ……….i n — средние ординаты.
Тогда, тепло, произведенные в первом интервале = I 1 2 RT / N Joules
Второй интервал = I 2 2 RT / N Joules
Третий интервал = I 3 2 RT / N Joules
N Th Интервал = I N 2 RT / N Joules
Общее тепло, производимое во времени T
= RT [(I 1 2 + I 2 2 + I 3 2 + ……+ i n 2 )/n] …. .(1)
.(1)
Поскольку I эфф считается действующим значением этого тока.
Тогда тепла, произведенного этим током за время t = I эфф 2 Rt …….(2)
По определению уравнения (1) и (2) равны. Поэтому
I EFF 2 2 RT = RT [(I 1 2 + I 2 2 + I 3 2
+ …… + I N 2 ) / n]
или I EFF 2 = [(I 1 2 + I 2 2 + I 3 2 + …… + I N 2 ) / N]
или I EFF EFF = [(I 1 2 + I 2 2 + I 3 2 + …… + I n 2 )/n] 1/2
Или I eff = I RMS = квадратный корень из среднего квадрата мгновенного тока.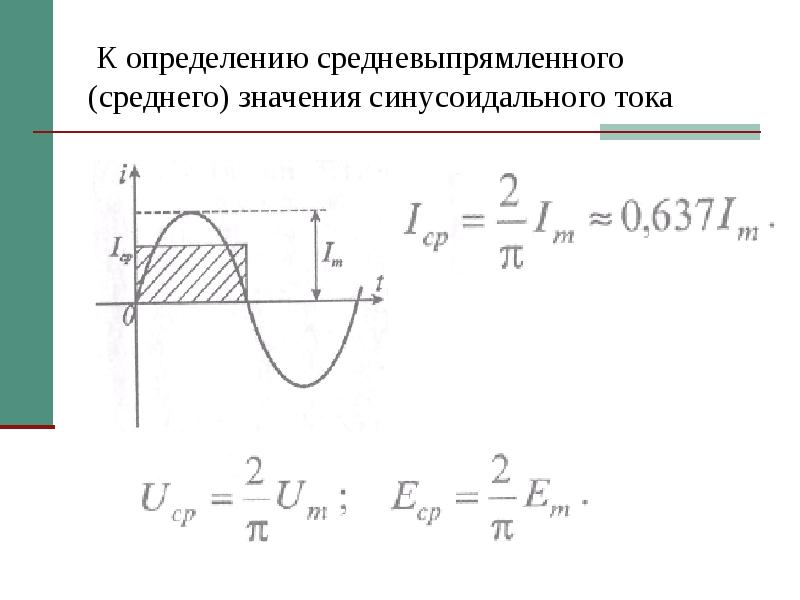
Теперь, используя интегральное исчисление, среднеквадратичное или эффективное значение переменного тока за период времени можно рассчитать следующим образом:
Важные термины, относящиеся к среднеквадратичному значению AC
Пиковое значение (I m ) : Максимальное значение, достигаемое переменным током в течение полного цикла, называется его пиковым значением. Синусоидальный переменный ток достигает максимального положительного значения при 90 o .
Форм-фактор (K f ) : Отношение среднеквадратичного значения к среднему значению переменной величины.
K f = среднеквадратичное значение/среднее значение
Для синусоидального сигнала это 1,11. Мы можем найти значение RMS из среднего значения и наоборот с помощью коэффициента формы.
Этот коэффициент показывает «пиковость» сигнала. Прямоугольная волна, которая более плоская, чем синусоида, имеет коэффициент формы 1,0. С другой стороны, треугольная волна более «остроконечная», чем синусоида, и имеет форм-фактор 1,15.
С другой стороны, треугольная волна более «остроконечная», чем синусоида, и имеет форм-фактор 1,15.
Пиковый коэффициент (Kp) : отношение пикового или максимального значения к среднеквадратичному значению переменной величины.
K p = пиковое значение / среднеквадратичное значение
Для синусоидального сигнала это 1,414. Это очень важно при испытании диэлектрической изоляции, поскольку диэлектрическая нагрузка на изоляционный материал зависит от пикового значения приложенного напряжения. Это также важно при измерении потерь в стали, поскольку эти потери зависят от значения максимального потока.
Среднее значение переменного тока
Среднее арифметическое всех мгновенных значений, рассматриваемых в переменной величине тока за один цикл, называется средним значением переменного тока (I av ).
Это постоянный ток (постоянный ток), который передает тот же заряд, что и переменный ток, за то же время по любой цепи.
В случае симметричных волн, таких как синусоидальный ток или волна напряжения, положительная половина точно равна отрицательной половине, поэтому среднее значение за полный цикл равно нулю.
Так как работа совершается током как в положительном, так и в отрицательном полупериоде, поэтому определяется среднее значение независимо от знаков, либо рассматривается только положительная половина.
Чтобы определить среднее значение переменного тока, рассмотрим только положительный полупериод и разделим его на n число равных частей. Пусть i 1 , i 2 , i 3 …… будут средними ординатами.
Теперь, среднее значение тока, I av = Среднее значение средних ординат
= (i 1 + i 2 + i 3 + …….+i n
= Площадь полупериода/длина основания полупериода
Теперь, используя интегральное исчисление, мы можем вычислить площадь полупериода и среднее значение переменного тока.После этого расчета мы получаем следующее выражение для синусоидального тока.
I av = 2I м /π = 0,637 I м
Основы переменного тока | Все сообщения
© http://www.yourelectricalguide.com/ Среднеквадратичное значение производной переменного тока.
Что такое среднеквадратичное значение напряжения переменного тока? – М.В.Организинг
Что такое среднеквадратичное значение напряжения переменного тока?
среднеквадратичных значений. Одним из основных применений среднеквадратичных значений являются переменные токи и напряжения.СРЕДНЕКВАДРАТИЧЕСКОЕ ЗНАЧЕНИЕ (RMS). Значение переменного напряжения непрерывно изменяется от нуля до положительного пика, от нуля до отрицательного пика и снова до нуля.
Как среднеквадратичное значение напряжения переменного тока связано с пиковым значением напряжения переменного тока?
Среднеквадратичное значение напряжения связано с пиковым напряжением соотношением Vrms=2 Vo.
Как рассчитать среднеквадратичное значение переменного тока?
Сначала вычислим среднее значение квадратов (I2mean) трех текущих значений. Для получения среднего значения квадратов вычислите сумму квадратов трех токов и разделите сумму на 3, поскольку токов три.Следовательно, среднеквадратичное значение трех заданных значений тока равно 2А.
Какая связь между среднеквадратичным значением и пиковым напряжением?
Пиковое значение — это максимальное напряжение, которого когда-либо достигает форма волны, подобно тому, как пик — это самая высокая точка горы. Значение RMS (среднеквадратичное значение) представляет собой действующее значение общей формы волны. Он равен уровню сигнала постоянного тока, который обеспечивает ту же среднюю мощность, что и периодический сигнал.
Что опаснее переменного или постоянного тока?
Переменный ток (А.C) в пять раз опаснее постоянного тока (D.C). Частота переменного тока является основной причиной такого тяжелого воздействия на организм человека. Частота 60 циклов находится в крайне вредном диапазоне. При такой частоте даже небольшое напряжение в 25 вольт может убить человека.
220 В среднеквадратичное или пиковое?
Пиковое значение 220 В переменного тока корень (2) * 220 = 1,414 * 220 В. Это потому, что 220 В — это среднеквадратичное значение.
Почему 220 В переменного тока опаснее, чем 220 В постоянного тока?
220 вольт а.в. означает эффективное или виртуальное значение a.c. составляет 220 вольт, т. е. Ev=220 вольт. Но 220 вольт постоянного тока. имеет такое же пиковое значение (т. е. только 220 вольт). Более того, шок переменного тока привлекательна, а d.c. отталкивает. Следовательно, 220 вольт переменного тока. опаснее, чем 220 вольт постоянного тока.
Среднеквадратичное значение напряжения переменного или постоянного тока?
«СКЗ» означает среднеквадратичное значение и представляет собой способ выражения величины переменного напряжения или тока в терминах, функционально эквивалентных постоянному току. Например, среднеквадратичное значение переменного тока 10 вольт — это величина напряжения, которая будет производить такое же количество тепла, рассеиваемое на резисторе заданного номинала, как источник питания постоянного тока 10 вольт.
Каково максимальное значение напряжения 240 вольт RMS?
В случае чисто синусоидального сигнала напряжение, которое обычно обсуждается, является среднеквадратичным напряжением, поскольку оно эквивалентно напряжению постоянного тока, которое производит такой же эффект нагрева для данного тока. Таким образом, среднеквадратичное значение 240 В эквивалентно пиковому напряжению 339 В или пиковому напряжению 679 В и может быть записано как среднеквадратичное значение 240 В.
Как рассчитать среднеквадратичное значение?
Тип среднего значения, иногда используемого в статистике и инженерии, часто сокращенно RMS.Чтобы найти средний квадрат набора чисел, возведите в квадрат все числа в наборе, а затем найдите среднее арифметическое квадратов. Возьмите квадратный корень из результата. Это среднеквадратичное значение.
Что такое среднеквадратичное напряжение сети?
Термин «RMS» означает «среднеквадратичный». При использовании для сравнения эквивалентного среднеквадратичного значения напряжения переменного синусоидального сигнала, который обеспечивает ту же электрическую мощность для данной нагрузки, что и эквивалентная цепь постоянного тока, среднеквадратичное значение называется «эффективным значением» и обычно представляется как: Veff или Ieff.
Что такое пиковое напряжение?
Пиковое напряжение — это самая высокая точка или самое высокое значение напряжения для любой формы волны напряжения. Это проблема качества электроэнергии, возникающая при добавлении в энергосистему устройств, использующих широтно-импульсную модуляцию, таких как частотно-регулируемый привод.
Может ли пиковое напряжение быть отрицательным?
Этот уровень напряжения также называется пиковым напряжением и может быть как положительным, так и отрицательным.
Какова формула пикового напряжения?
Для формы волны, показанной выше, пиковая амплитуда и пиковое значение совпадают, поскольку среднее значение функции равно нулю вольт.VP-P V P — P : Полное напряжение между положительными и отрицательными пиками сигнала, то есть сумма величин положительных и отрицательных пиков.
Что такое среднее напряжение?
Среднее напряжение (или ток) периодического сигнала, независимо от того, является ли он синусоидальным, прямоугольным или треугольным сигналом, определяется как «отношение площади под сигналом к времени». Другими словами, усреднение всех мгновенных значений по оси времени, когда время составляет один полный период (T).
Что такое эффективное напряжение?
«Эффективное напряжение» не является широко известным термином с универсальным значением. Это чаще называется «среднеквадратичное» или «среднеквадратичное» напряжение сигнала переменного тока. Его можно назвать «эффективным напряжением», потому что это напряжение постоянного тока, при котором такая же мощность будет подаваться на резистивную нагрузку.
Каково нормальное напряжение в доме?
110 вольт
Каково максимальное значение напряжения переменного тока 220 В?
311 В
Почему использование переменного напряжения предпочтительнее, чем постоянное, по двум причинам?
(i) Переменный ток может передаваться с гораздо меньшими потерями энергии по сравнению с постоянным током.(ii) Напряжение переменного тока можно отрегулировать (повысить или понизить) в соответствии с требованиями. (iii) переменным током в цепи можно управлять с помощью (почти) безваттных устройств, таких как дроссельная катушка.
Что такое сигналы переменного тока?
AC означает переменный ток, а DC означает постоянный ток. AC и DC также используются, когда речь идет о напряжениях и электрических сигналах, которые не являются токами! Например: источник питания переменного тока 12 В имеет переменное напряжение (которое создаст переменный ток).
Каково пиковое значение переменного тока при напряжении 220 Вольт?
Здесь 220 вольт является среднеквадратичным значением.Пиковое значение V0 = √2 Vrms = √2 x 220 = 311 вольт.
Каково пиковое значение переменного тока?
Пиковое значение переменного тока в √2 раза превышает среднеквадратичное значение переменного тока.
Напряжение переменного тока измеряется от пика к пику?
При большинстве напряжений переменного тока размах напряжения в два раза превышает пиковое напряжение. Например, когда мы говорим, что напряжение в бытовой электросети составляет 120 В переменного тока, на самом деле мы имеем в виду, что среднеквадратичное значение напряжения составляет 120 В. Если переменное напряжение соответствует истинной синусоиде, среднеквадратичное значение напряжения равно 0.707 раз больше пикового напряжения.
Что вы подразумеваете под пиковым значением переменного тока?
Определение: максимальное значение, достигаемое переменной величиной в течение одного цикла, называется пиковым значением. Он также известен как максимальное значение или амплитуда или пиковое значение. Синусоидальная переменная величина достигает своего пикового значения при 90 градусах, как показано на рисунке ниже.
Аккумуляторы заряжаются переменным или постоянным током?
В электромобилях можно использовать два вида «топлива».Они называются мощностью переменного тока (AC) и постоянного тока (DC). Энергия, поступающая из сети, всегда является переменным током. Однако батареи, такие как батарея вашего электромобиля, могут накапливать энергию только в виде постоянного тока.
Что такое эффективное значение переменного тока?
Эффективное значение переменного тока — это такой ток, который будет производить тот же эффект нагрева, что и эквивалентный постоянный ток. Эффективное значение называется среднеквадратичным значением (среднеквадратичное значение), и всякий раз, когда задается переменная величина, предполагается, что оно равно r.РС. ценность.
Каково значение среднеквадратичного значения?
Значение среднеквадратичного значения ► Среднеквадратичное значение напряжения/тока переменного тока эквивалентно напряжению/току постоянного тока, который дает такой же эффект нагрева при подаче на идентичный резистор. Следовательно, это также мера содержания энергии в данном сигнале.
Что означает среднеквадратичная мощность?
Среднеквадратичное значение
Что такое истинное среднеквадратичное значение?
Мультиметры
, реагирующие на истинное среднеквадратичное значение, измеряют потенциал «нагрева» приложенного напряжения.В отличие от измерения «усредненного отклика», измерение истинного среднеквадратичного значения используется для определения мощности, рассеиваемой в резисторе. Измеряется только «теплотворная способность» переменных составляющих входного сигнала (постоянный ток отбрасывается).
Какова среднеквадратичная скорость?
Среднеквадратическая скорость – это мера скорости частиц в газе, определяемая как квадратный корень из квадрата средней скорости молекул в газе. Среднеквадратическая скорость учитывает как молекулярную массу, так и температуру, два фактора, которые напрямую влияют на кинетическую энергию материала.
Напряжение переменного тока — HomoFaciens
Новости
Проект
Технологии
РобоСпатиум
Способствовать
Предметный указатель
Скачать
Ответы
Игры
Советы по покупкам
Контакт
<<< Вихревой ток Собственная индуктивность >>>
Напряжение постоянного тока
В главе о напряжении мы рассматривали его как неизменную во времени величину. В качестве причины возникновения напряжения мы упомянули разность потенциалов внутри электрического поля точечного заряда.
В последующих главах об электрическом токе, сопротивлении и мощности мы также считали напряжение постоянной величиной на отдельных компонентах электрических сетей.
В главе об индукции мы видели, что напряжение, создаваемое с помощью постоянного магнита и контура проводника, действительно непостоянно. В этом случае напряжение называют
Напряжение переменного тока
Напряжение, полярность которого меняется через равные промежутки времени и среднее значение которого в течение одного промежутка времени равно нулю, называется напряжением переменного тока.Точная прогрессия кривой не имеет значения.
Рисунок 1:
Прогресс трех кривых напряжения переменного тока с одинаковым периодом времени и пиковым напряжением:
Синяя кривая показывает синусоидальный ход, красная кривая образует треугольники с осью X (= треугольное напряжение), а зеленая кривая образует прямоугольники с осью X (= прямоугольное напряжение). Кроме того, кривые симметричны , что означает, что если вы перевернете кривую вокруг оси X и переместите ее в течение половины периодического времени, развитие кривой будет идентично исходной кривой.
Терминология
Период — Период — это наименьший интервал времени или длины, на котором повторяются значения функции.
Периодическое время — Периодическое время (T) отмечает наименьший возможный интервал времени, в течение которого значения функции повторяются.
[3.25]
Где находится:
T — периодическое время, n — целочисленное значение
Частота — Частота (f) описывает количество периодов в секунду.Единицей частоты является Герц (Гц), названный в честь немецкого физика Генриха Герца. Корреляция между частотой и периодическим временем определяется как:
[3.26]
Где находится:
f — Частота, T — периодическое время
Размах напряжения — Размах напряжения (U PP ) равен разнице между самым верхним положительным и отрицательным значением кривой.
Пиковое напряжение — Пиковое напряжение (U P ) — это максимальное значение напряжения, независимое от знака значения.
Эффективное среднеквадратичное напряжение (RMS) — Эффективное напряжение (U eff ) представляет собой квадратный корень из среднего арифметического (среднего) квадратов значений кривой. Использование «трюка» для вычисления квадратного корня из квадратов устраняет отрицательный знак (квадратный корень из -1 2 дает +1).
Выражение условия, при котором среднее значение за один период времени становится равным нулю:
[3.27]
Где находится:
T — периодическое время, t 1 — необязательный момент времени
Чтобы различать напряжение постоянного и переменного тока, для обозначения напряжения переменного тока используется символ U с тильдой в качестве индекса.U ˜ указывает напряжение переменного тока.
Рисунок 2:
Характерные параметры синусоидального переменного напряжения.
Для изменения напряжения (виртуального) эксперимента с катушкой индуктивности, движущейся вдоль постоянного магнита, мы получаем:
Рисунок 3:
Если бы мы возобновили эксперимент, как только он закончился, результатом тоже было бы переменное напряжение. Позже мы увидим, что подобная процедура выполняется внутри генератора.
В последующих главах мы увидим, как можно выпрямить переменное напряжение. В результате получается следующая кривая:
Рисунок 4:
Выпрямленное синусоидальное напряжение:
Согласно определению, это уже не переменное напряжение, хотя напряжение периодически изменяется. Ни одно значение не ниже нуля, что означает, что полярность не изменена. В главе о напряжении мы заметили, что напряжение — это энергия, используемая для перемещения заряженной частицы через две точки внутри электрического поля.



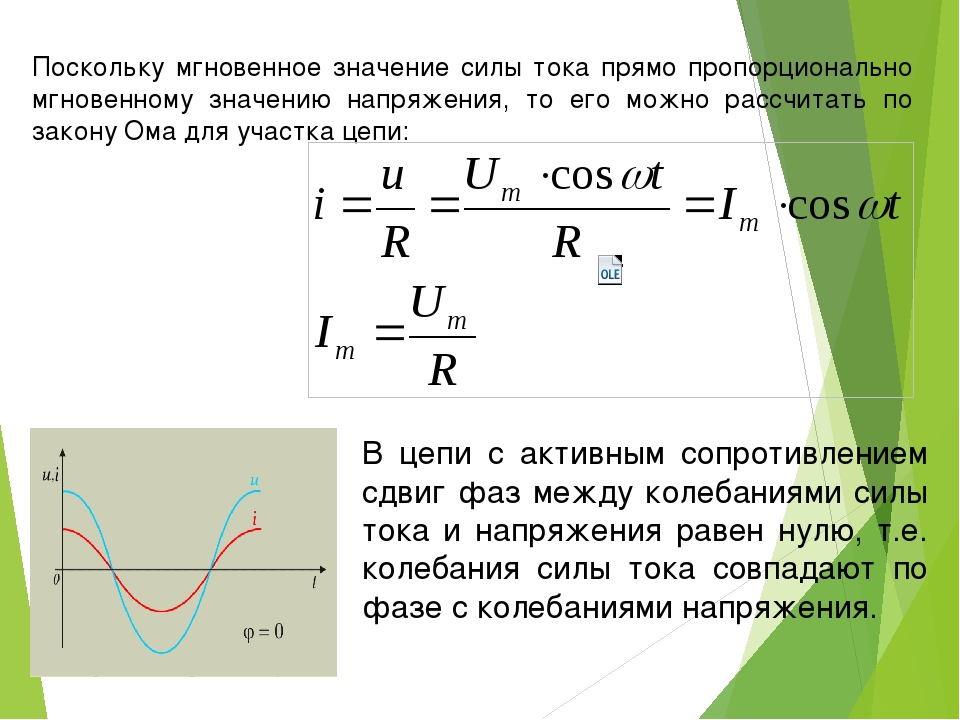 Кроме того, об электрическом действии периодически изменяющегося тока (количество выделяемого тепла, совершенная работа и т. д.) нельзя судить по амплитуде этого тока.
Кроме того, об электрическом действии периодически изменяющегося тока (количество выделяемого тепла, совершенная работа и т. д.) нельзя судить по амплитуде этого тока. Приравнивая мощность постоянного и переменного тока, имеем: I2r = Mr, откуда I = √M,
Приравнивая мощность постоянного и переменного тока, имеем: I2r = Mr, откуда I = √M,

 Термины и определения
Термины и определения