Размерности физических величин в системе СИ
В таблице приведены размерности различных физических величин в Международной системе единиц (СИ).
В столбцах «Показатели степени» указаны показатели степени в выражении единицы измерения через соответствующие единицы системы СИ. Например, для фарада указано ( −2 | −1 | 4 | 2 | | ), значит
- 1 фарад = м−2·кг−1·с4·A2.
| Название и обозначение величины | Единица измерения | Обозначение | Формула | Показатели степени | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| русское | международное | м | кг | с | А | К | кд | ||||
| Длина | L | метр | м | m | L | 1 | |||||
| Масса | m | килограмм | кг | kg | m | 1 | |||||
| Время | t | секунда | с | s | t | 1 | |||||
| Сила электрического тока | I | ампер | А | A | I | 1 | |||||
| Термодинамическая температура | T | кельвин | К | K | T | 1 | |||||
| Сила света | Iv | кандела | кд | cd | J | 1 | |||||
| Площадь | S | кв. метр метр | м2 | m2 | S | 2 | |||||
| Объём | V | куб. метр | м3 | m3 | V | 3 | |||||
| Частота | f | герц | Гц | Hz | f = 1/t | −1 | |||||
| Скорость | v | м/с | m/s | v = dL/dt | 1 | −1 | |||||
| Ускорение | a | м/с2 | m/s2 | ε = d2L/dt2 | 1 | −2 | |||||
| Плоский угол | φ | рад | rad | φ | |||||||
| Угловая скорость | ω | рад/с | rad/s | ω = dφ/dt | −1 | ||||||
| Угловое ускорение | ε | рад/с2 | rad/s2 | ε = d2φ/dt2 | −2 | ||||||
| Сила | F | ньютон | Н | N | F = ma | 1 | 1 | −2 | |||
| Давление | P | паскаль | Па | Pa | P = F/S | −1 | 1 | −2 | |||
| Работа, знергия | A | джоуль | Дж | J | A = F·L | 2 | 1 | −2 | |||
| Имульс | p | кг·м/с | kg·m/s | p = m·v | 1 | 1 | −1 | ||||
| Мощность | P | ватт | Вт | W | P = A/t | 2 | 1 | −3 | |||
| Электрический заряд | q | кулон | Кл | C | q = I·t | 1 | 1 | ||||
| Электрическое напряжение, электрический потенциал | U | вольт | В | V | U = A/q | 2 | 1 | −3 | −1 | ||
| Напряжённость электрического поля | E | В/м | V/m | E = U/L | 1 | 1 | −3 | −1 | |||
| Электрическое сопротивление | R | ом | Ом | Ω | R = U/I | 2 | 1 | −3 | −2 | ||
| Электрическая ёмкость | C | фарад | Ф | F | C = q/U | −2 | −1 | 4 | 2 | ||
| Магнитная индукция | B | тесла | Тл | T | B = F/I·L | 1 | −2 | −1 | |||
| Напряжённость магнитного поля | H | А/м | A/m | −1 | 1 | ||||||
| Магнитный поток | Ф | вебер | Вб | Wb | Ф = B·S | 2 | 1 | −2 | −1 | ||
| Индуктивность | L | генри | Гн | H | L = U·dt/dI | 2 | 1 | −2 | −2 | ||
См. также
также
Лекция Системы физических величин и их единиц. Единицы измерения системы СИ. Единицы измерения длины, времени.
Единство измерений подразумевает согласованность размеров единиц всех величин. Это становится очевидным, если рассмотреть измерения одной и той же величины прямыми и косвенными измерениями. Такая согласованность достигается созданием системы единиц.
Преимущества системы единиц по сравнению с набором разобщенных единиц были осознаны очень давно. Но первая система единиц появилась только в конце XVIII века. Это была знаменитая метрическая система (метр, килограмм, секунда), утвержденная 26 марта 1791 года Учредительным собранием Франции.
Первую научно обоснованную систему единиц, как совокупность произвольных единиц и зависимых от них производных единиц, предложил в 1832 году К. Гаусс. Он построил систему единиц, названную абсолютной, за основу которой были приняты три произвольные, независимые друг от друга единицы: миллиметр, миллиграмм и секунда.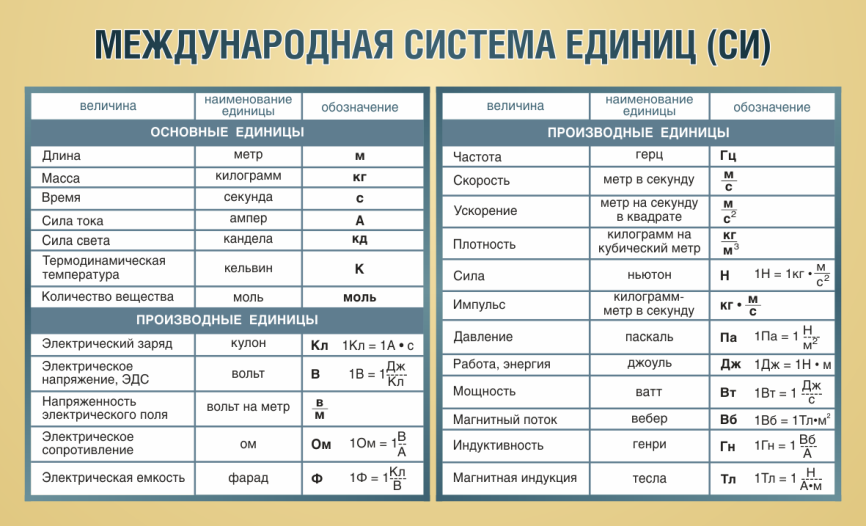 Развитием системы Гаусса были появившаяся в 1881 году система СГС (сантиметр, грамм, секунда), удобная для применения в электромагнитных измерениях, и различные ее модификации.
Развитием системы Гаусса были появившаяся в 1881 году система СГС (сантиметр, грамм, секунда), удобная для применения в электромагнитных измерениях, и различные ее модификации.
Развитие промышленности и торговли в эпоху первой промышленной революции потребовало унификации единиц в международном масштабе. Началом этому процессу было положено 20 мая 1875 года подписанием 17 странами (в том числе Россией, Германией, США, Францией и Англией) Метрической конвенции, к которой в дальнейшем присоединились многие другие страны.
Согласно этой конвенции было установлено международное сотрудничество в области метрологии. В Севре, расположенном в пригороде Парижа, было создано Международное бюро мер и весов (МБМВ) с целью проведения международных метрологических исследований и хранения международных эталонов. Для руководства МБМВ был учрежден Международных комитет мер и весов (МКМВ), включающий консультативные комитеты по единицам и ряду видов измерений. Для решения принципиальных вопросов международного сотрудничества стали регулярно проводить международные конференции, называемые Генеральными конференциями по мерам и весам (ГКМВ). Все страны, подписавшие Метрическую конвенцию, получили прототипы международных эталонов длины (метр) и массы (килограмм). Были также организованы периодические сличения этих национальных эталонов с международными эталонами, хранящимися в МБМВ. Тем самым метрическая система единиц впервые получила международное признание. Однако после подписания Метрической конвенции были разработаны системы единиц для различных областей измерений – СГС, СГСЭ, СГСМ, МТС, МКС, МКГСС. Вновь возникла проблема единства измерений, но уже между различными областями измерений.
Для решения принципиальных вопросов международного сотрудничества стали регулярно проводить международные конференции, называемые Генеральными конференциями по мерам и весам (ГКМВ). Все страны, подписавшие Метрическую конвенцию, получили прототипы международных эталонов длины (метр) и массы (килограмм). Были также организованы периодические сличения этих национальных эталонов с международными эталонами, хранящимися в МБМВ. Тем самым метрическая система единиц впервые получила международное признание. Однако после подписания Метрической конвенции были разработаны системы единиц для различных областей измерений – СГС, СГСЭ, СГСМ, МТС, МКС, МКГСС. Вновь возникла проблема единства измерений, но уже между различными областями измерений.
Поэтому в 1954 году X ГКМВ сначала предварительно, а в октябре 1960 года XI ГКМВ окончательно принимают Международную систему единиц SI, которая с незначительными изменениями действует по настоящее время.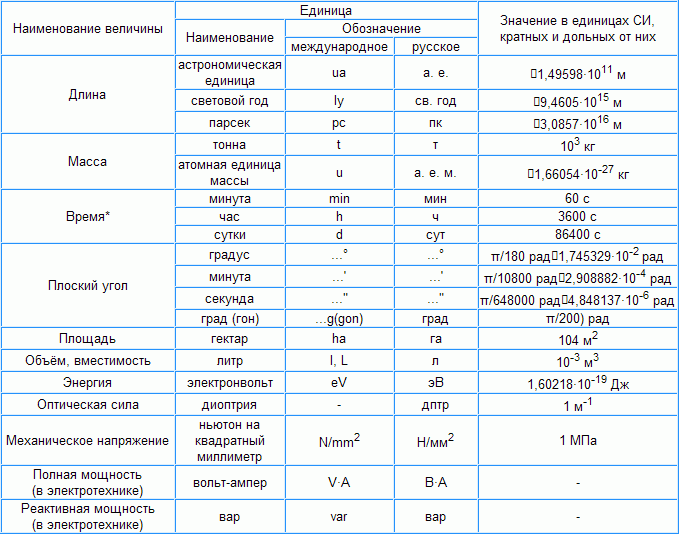 На следующих заседаниях ГКМВ в нее неоднократно вносились изменения и дополнения. В настоящее время система единиц SI регламентирована стандартом ISO 31 и по существу является международным регламентом, обязательным для применения.
На следующих заседаниях ГКМВ в нее неоднократно вносились изменения и дополнения. В настоящее время система единиц SI регламентирована стандартом ISO 31 и по существу является международным регламентом, обязательным для применения.
Система SI образована в соответствии с общим принципом образования системы единиц, который был предложен К.Гауссом в 1832 году.
В соответствии с ним все физические величины подразделяют на две группы:
- величины, принятые за независимые от других величин, которые называют основными величинами;
- все остальные величины, называемые производными, которые выражают через основные и уже определенные производные величины при помощи физических уравнений.
Из этого следует и классификация единиц: единицы основных величин являются основными единицами, а единицы производных величин – производными единицами.
Таким образом, сначала образуется система величин – совокупность величин, образованная в соответствии с принципом, когда одни величины принимаются за независимые, а другие являются функциями независимых величин.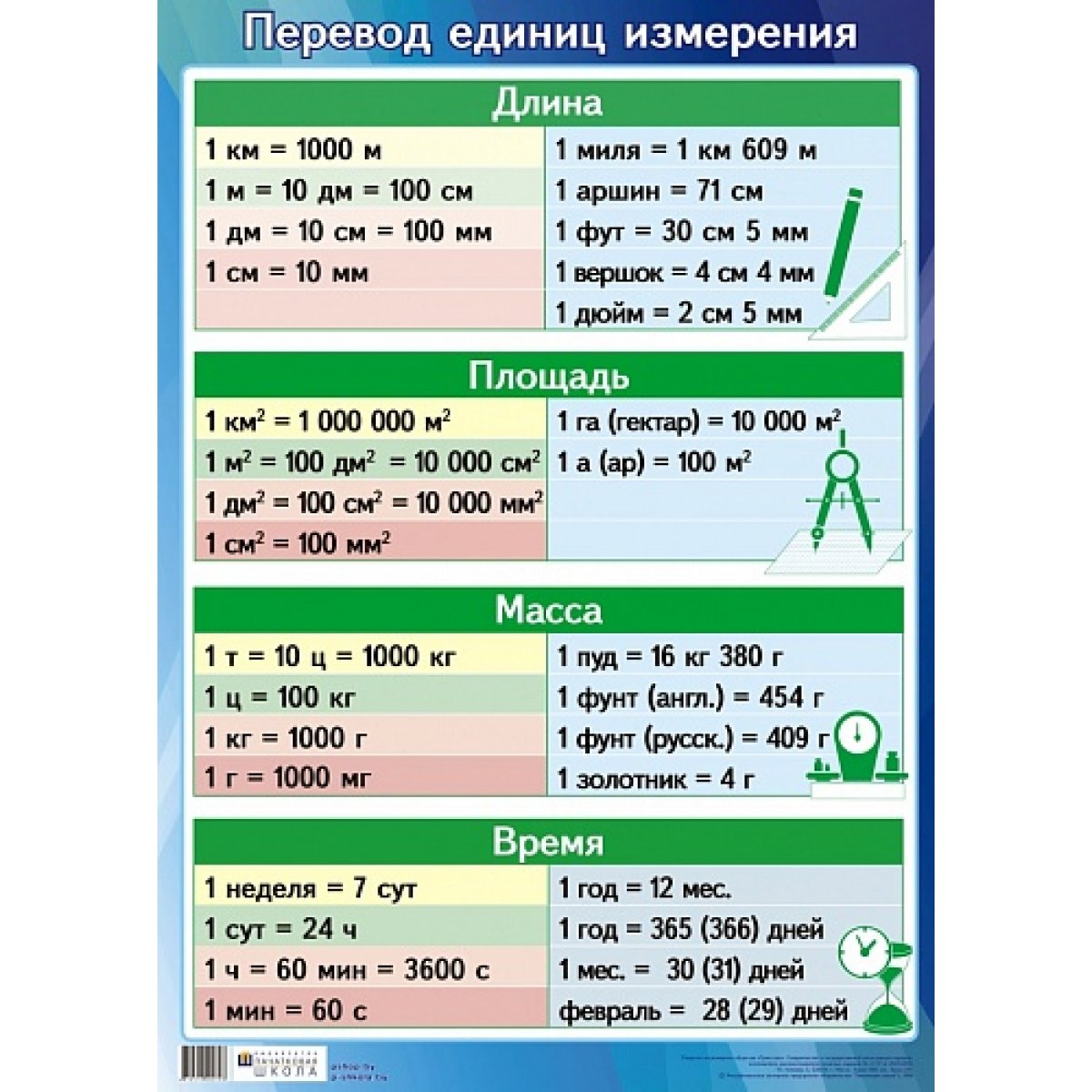
Величина, входящая в систему величин и условно принятая в качестве независимой от других величин этой системы, называется основной величиной.
Величина, входящая в систему величин и определяемая через основные и уже определенные производные величины, называется производной величиной.
Единица основной величины данной системы величин называется основной единицей. Производная единица – это единица производной величины данной системы величин, образованная в соответствии с уравнением, связывающим ее с основными единицами или же с основными и уже определенными производными единицами.
Примерами производных величин могут служить: плотность вещества, определяемая как масса вещества, заключенного в единице объема; ускорение — изменение скорости за единицу времени и др.
Таким путем образуется система единиц величин – совокупность основных и производных единиц заданной системы величин.
В названии системы физических величин применяют символы величин, принятых за основные. Например, система величин механики, в которой в качестве основных используется длина (), масса (), время (), называется системой . Действующая в настоящее время международная система СИ должна обозначаться символами , соответствующими символам основных величин: длине (), массе (), времени (),.току (), температуре (), количеству вещества () и силе света ().
Минимальное число основных единиц определяется следующим образом.
Пусть между числовыми значениями разнородных физических величин имеется уравнений связи, в качестве которых выступают известные физические закономерности. В каждом уравнении имеется свой коэффициент пропорциональности, которому можно придать любое значение и, в частности, приравнять его единице. Таким образом эти коэффициенты являются известными числами, а величины – неизвестными, искомыми. Число величин всегда больше числа уравнений связи, т.е. . Для того чтобы найти значения этих величин из имеющейся системы уравнений, необходимо добавить в эту систему еще уравнений, т. е. задать значения величин. Следовательно, эти величины должны иметь единицы, независимые от других величин.
е. задать значения величин. Следовательно, эти величины должны иметь единицы, независимые от других величин.
Таким образом, минимальное количество основных величин равно . Такая система величин считается теоретически оптимальной.
На практике число основных величин больше: . В этом случае в системе, состоящей из уравнений, число неизвестных меньше , т.к. равно . Следовательно, эта система уравнений переопределена и имеет бесконечное множество решений. Для того чтобы обеспечить единственное решение, необходимо добавить в эту систему уравнений. Поэтому приходится коэффициентов уравнений принимать равными не единице, а некоторым числам, определяемым в результате решения данной системы уравнений. Эти коэффициенты называются фундаментальными физическими константами. Примерами таких констант являются гравитационная постоянная, постоянные Больцмана и Планка.
Какие единицы из общей их совокупности следует выбрать в качестве основных единиц системы?
Однозначного ответа на это вопрос нет. При решении этой проблемы руководствуются практической целесообразностью, принимая во внимание различные аргументы, например, такие как:
При решении этой проблемы руководствуются практической целесообразностью, принимая во внимание различные аргументы, например, такие как:
— выбор в качестве основных минимального числа величин, отображающих наиболее общие свойства материи;
— наиболее ясное отражение взаимосвязи основных величин, принадлежащих различным разделам физики;
— высокая точность воспроизведения единиц и передачи их размеров;
— простота образования производных величин и единиц;
— преемственность единиц, т.е. сохранение их размеров и наименований при внесении изменений в систему единиц.
Эти критерии часто вступают в противоречие друг с другом. Поэтому выбор окончательного варианта является предметом соглашения.
Рассмотрим следующий пример.
В измерениях пространства и времени основным является уравнение движения
,
где — скорость, — длина, — время, — произвольно выбранный коэффициент, значение которого зависит от выбора единиц. Итак, и , следовательно, . Поэтому приняты две основные величины: длина и время и, соответственно, две основные единицы: метр и секунда. В 1983 году скорости света в вакууме, истинное значение которой неизвестно в принципе, по соглашению было придано точное значение — . При этом единица длины – метр была определена как расстояние, которое проходит свет в вакууме за долей секунды. При таком определении метра коэффициент пропорциональности в уравнении движения остался равным . Если бы было сохранено старое определение метра (криптоновое) и одновременно постулировалось постоянство скорости света, нельзя было бы принять равным , и он был бы фундаментальной физической константой.
Поэтому приняты две основные величины: длина и время и, соответственно, две основные единицы: метр и секунда. В 1983 году скорости света в вакууме, истинное значение которой неизвестно в принципе, по соглашению было придано точное значение — . При этом единица длины – метр была определена как расстояние, которое проходит свет в вакууме за долей секунды. При таком определении метра коэффициент пропорциональности в уравнении движения остался равным . Если бы было сохранено старое определение метра (криптоновое) и одновременно постулировалось постоянство скорости света, нельзя было бы принять равным , и он был бы фундаментальной физической константой.
Вся современная физика может быть построена на семи основных величинах, которые характеризуют фундаментальные свойства материального мира. К ним относятся семь физических величин, выбранных в системе СИ в качестве основных, и две дополнительные физические величины (таблица 1. 1). С помощью основных семи и двух дополнительных величин, введенных исключительно для удобства, образуется все многообразие производных физических величин и обеспечивается описание свойств физических объектов и явлений.
1). С помощью основных семи и двух дополнительных величин, введенных исключительно для удобства, образуется все многообразие производных физических величин и обеспечивается описание свойств физических объектов и явлений.
В Украине используется система единиц СИ, введенная ГОСТ 8.417-81.
В качестве основных единиц в системе СИ приняты метр, килограмм, секунда, ампер, кельвин, моль и кандела.
Таблица 1.1 Основные и дополнительные единицы измерения системы СИ
В качестве дополнительных единиц в системе СИ используются – радиан и стерадин.
Радиан (сокр. рад)– это единица измерения плоского угла — угла между двумя радиусами окружности, длина дуги которой равна радиусу. На практике, а в геодезии в обязательном порядке, часто используется другие единицы измерения плоского угла, такие как градус, минута, секунда.
— градус; ;
— минута; ;
— секунда; .
Соответственно:
Стерадиан – это единица измерения телесного (пространственного) угла – угла с вершиной в центре сферы, вырезающей на поверхности площадь, равную площади квадрата, со стороной равной радиусу сферы.
Во всех системах плоский и телесный углы вводятся с помощью уравнений:
, (5)
, (6)
где — длина дуги, вырезаемой центральным плоским углом на окружности, радиусом ; — площадь, вырезаемая центральным телесным углом на шаре с радиусом . В соответствии с этими определениями у этих единиц нет размерности в любой системе единиц:
, (7)
. (8)
Производные единицы системы СИ, имеющие собственные названия, приведены в табл. 1.2.
Таблица 1.2 Производные единицы измерения системы СИ, имеющие специальные названия
Для установления производных единиц необходимо:
1 – выбрать физические величины, единицы которых принимаются в качестве основных;
2 – установить размер этих единиц;
3 – выбрать определяющее уравнение, связывающее величины, измеряемые основными единицами, с величиной, для которой устанавливается производная единица.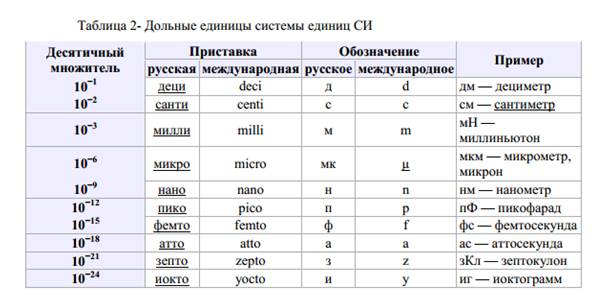 При этом символы всех величин, входящих в определяющее уравнение, должны рассматриваться не как сами величины, а как их именованные числовые значения;
При этом символы всех величин, входящих в определяющее уравнение, должны рассматриваться не как сами величины, а как их именованные числовые значения;
4 – приравнять единице (или другому постоянному числу) коэффициент пропорциональности , входящий в определяющее уравнение. Это уравнение следует записывать в виде явной функциональной зависимости производной величины от основных.
Установленные таким образом производные единицы могут быть использованы для введения новых производных величин. Поэтому в определяющее уравнение наряду с основными единицами могут входить и производные, единицы которых определены ранее.
Производные единицы могут быть когерентными и некогерентными.
Когерентной называется производная единица физической величины, связанная с другими единицами системы уравнением связи, в котором числовой множитель принят равным единице. Например, единицу скорости образуют с помощью уравнения, определяющего равномерное и прямолинейное движение точки:
,
где — длина пройденного пути, — время движения. Подстановка вместо и их единиц в системе СИ, дает . Следовательно, единица скорости является когерентной.
Подстановка вместо и их единиц в системе СИ, дает . Следовательно, единица скорости является когерентной.
Если уравнение связи содержит числовой коэффициент, отличный от единицы, то для образования когерентной единицы системы СИ в правую часть уравнения подставляют величины со значениями в единицах СИ, дающие после умножения на коэффициент общее числовое значение, равное единице. Например, если для образования когерентной единицы энергии используют уравнение
,
где — масса тела, — его скорость, то когерентную единицу энергии можно образовать двумя способами:
Следовательно, когерентной единицей СИ является джоуль, равный ньютону, умноженному на метр. В рассмотренных случаях он равен кинетической энергии тела массой , движущегося со скоростью , или тела массой , движущегося со скоростью .
Единицы физических величин делятся на системные и внесистемные.
Системная единица – это единица физической величины, входящая в одну из принятых систем. Все основные, производные, кратные и дольные единицы являются системными единицами.
Все основные, производные, кратные и дольные единицы являются системными единицами.
Внесистемная единица – это единица физической величины, не входящая ни в одну из принятых систем единиц. Внесистемные единицы по отношению к единицам системы СИ подразделяют на четыре вида:
1 – допускаемые наравне с единицами системы СИ. Например, единица массы – тонна, плоского угла – градус, минута, секунда, объема – литр и др. Внесистемные единицы, допускаемые к применению наравне с единицами СИ, приведены в табл. 1.3.
2 – допускаемые к применению в специальных областях. Например, единицы длины в астрономии – астрономическая единица, световой год, парсек; единица оптической силы в оптике – диоптрия; единица энергии в физике – электрон-вольт, и т.д.
3 – временно допускаемые к применению наравне с единицами СИ. Например, в морской навигации – морская миля; единица массы в ювелирном деле – карат и др. Эти единицы должны изыматься из употребления в соответствии с международными соглашениями.
4 – изъятые из употребления. Например, единица давления – миллиметры ртутного столба; единица мощности – лошадиная сила и некоторые другие.
Таблица 1.3 Внесистемные единицы, допускаемые к применению наравне с единицами СИ
Различают кратные и дольные единицы измерения физических величин.
Кратная единица – это единица физической величины в целое число раз превышающая системную или внесистемную единицу. Например, единица длины – километр – равна , т.е. кратна метру.
Дольная единица – это единица физической величины, значение которой в целое число раз меньше системной или внесистемной единицы. Например, единица длины – миллиметр – равна , т.е. является дольной.
Десятичные кратные и дольные единицы образуются с помощью стандартных приставок СИ, которые приведены в табл. 1.4.
Применительно к длине и времени кратные и дольные единицы измерения длины и времени приведены в табл. 1.5-1.6.
1.5-1.6.
Существуют также внесистемные единицы измерения длины:
— микрон, равный 1 мкм или 10-6 м;
— ангстрем ( Å), равный 0.1нм или 10-10 м,
но их применение не рекомендуется.
Таблица 1.4 Множители и приставки для образования десятичных кратных и дольных единиц и их наименований
Таблица 1.5 Кратные и дольные единицы измерения длины и их наименования
Таблица 1.6 Кратные и дольные единицы измерения времени и их наименования
Международная система единиц (СИ) (краткое изложение)
Международная система единиц (СИ)
(краткое изложение)
Метрология – это наука об измерениях, проводимых с |
Деятельность
Международного бюро мер и весов (МБМВ), основанного 20 мая 1875 года в
соответствии со статьей 1 Метрической Конвенции, направлена на обеспечение
основы единой когерентной системы измерений, использующейся во всем мире. В
основе десятичной метрической системы, заложенной во времена Французской
Революции, лежит метр и килограмм. По условиям Конвенции 1875 года были созданы
новые международные прототипы метра и килограмма, которые были официально
приняты 1-ой Генеральной конференцией по мерам и весам (ГКМВ) в 1889 году.
Дальнейшее развитие привело к тому, что в настоящее время в системе
насчитывается 7 основных единиц. Решением одиннадцатой ГКМВ в 1960 году она
получила название Международной Системы Единиц (СИ) (англ. – the International System of Units). СИ – не статическая система. Она развивается и
способна отвечать растущим мировым требованиям к измерениям всех уровней
точности и во всех областях науки, технологии и человеческой деятельности.
Данный документ – это краткое содержание опубликованной МБМВ брошюры “Международная
система единиц CИ” (далее именуемая “Брошюра СИ”), в
которой представлено современное состояние единиц СИ.
Семь основных единиц
СИ, приведенных в таблице 1, обеспечивают основу для определения всех единиц
измерения Международной системы единиц. В связи с развитием науки и
совершенствованием методов измерений определения основных единиц требуют
пересмотра. Чем точнее проводимые измерения, тем большая тщательность требуется
для реализации единицы измерения.
Единственный сохранившийся артефакт
Международного прототипа килограмма (К), используемый для определения
основной единицы СИ.
Таблица
1. Семь основных
единиц СИ
Наименование величины
Единица, обозначение: |
длина
метр, |
масса
килограмм, |
время
секунда, |
сила электрического тока
ампер, |
Системы физических величин и их единиц, система СИ — Мегаобучалка
Размер физической величины — это количественное содержание в данном объекте свойства, соответствующего понятию «физическая величина». Например, каждое тело обладает определенной массой, вследствие чего тела можно различать по их массе, т.е. по размеру интересующей нас ФВ.
Значение физической величины получают в результате ее измерения или вычисления в соответствии с основным уравнением измерения Q=q[Q], связывающим между собой значение ФВ Q, числовое значение q и выбранную для измерения единицу [Q]. В зависимости от размера единицы будет меняться числовое значение ФВ, тогда как размер ее будет оставаться неизменным.
Размерность единиц ФВ — dim Q — выражение в форме степенного многочлена, отражающее связь данной величины с основными ФВ. Коэффициент пропорциональности принят равным единице:
dim Q = LαMβTγIδ..,
где L, М, Т, I— условные обозначения основных величин данной системы; α, β, γ, δ — целые или дробные, положительные или отрицательные вещественные числа. Показатель степени, в которую возведена размерность основной величины, называют показателем размерности. Если все показатели размерности равны нулю, то такую величину называют безразмерной.
Над размерностями можно производить действия умножения, деления, возведения в степень и извлечение корня. Понятие размерности широко используется:
• для перевода единиц из одной системы в другую;
• для проверки правильности сложных расчетных формул, полученных в результате теоретического вывода;
• при выяснении зависимости между величинами;
• в теории физического подобия.
Совокупность ФВ, образованная в соответствии с принятыми принципами, когда одни величины принимаются за независимые, а другие являются их функциями, называется системой физических величин.
Обоснованно, но произвольным образом выбираются несколько ФВ, называемых основными. Остальные величины, называемые производными, выражаются через основные на основе известных уравнений связи между ними. Примерами производных величин могут служить: плотность вещества, определяемая как масса вещества, заключенного в единице объема; ускорение — изменение скорости за единицу времени и др.
Согласованная Международная система единиц физических величин была принята в 1960 г. XI Генеральной конференцией по мерам весам. Международная система — СИ (SI), SI — начальные буквы французского наименования Systeme International.
В Российской Федерации система СИ введена ГОСТ 8.417—81.
В названии системы ФВ применяют символы величин, принятых за основные. Например, система величин механики, в которой в качестве основных используются длина (L), масса (М) и время (T), называется системой LMT. Действующая в настоящее время международная система СИ должна обозначаться символами LMTIQNJ, соответствующими символам основных величин: длине (L), массе (М), времени (Т), силе электрического тока (I), температуре (Q), количеству вещества (N) и силе света (J) (таблица 1.1).
Например, система величин механики, в которой в качестве основных используются длина (L), масса (М) и время (T), называется системой LMT. Действующая в настоящее время международная система СИ должна обозначаться символами LMTIQNJ, соответствующими символам основных величин: длине (L), массе (М), времени (Т), силе электрического тока (I), температуре (Q), количеству вещества (N) и силе света (J) (таблица 1.1).
· Метр равен длине пути, проходимого светом в вакууме за 1/299.792.458 долю секунды.
· Килограмм равен массе международного прототипа килограмма.
· Секунда равна 9.192.631.770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
· Ампер равен силе не изменяющегося во времени электрического тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную 2•10 в минус 7-ой степени Н.
· Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды.
· Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0.012 кг.
· Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540•10 в 12-ой степени Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.
· Радиан равен углу между двумя радиусами окружности, дуга между которыми по длине равна радиусу.
· Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы.
Производные единицы системы СИ, имеющие собственное название, приведены в табл. 1.2.
1.2.
Таблица 1.1. Основные и дополнительные единицы системы СИ.
| Величина | Единица | ||||
|
Наименование |
Размерность | Рекомендуемое
обозначение |
Наименование | Обозначение | |
| русское | междуна-
родное | ||||
| Основные | |||||
| Длина | L | l | метр | м | m |
| Масса | M | m | килограмм | кг | kg |
| Время | T | t | секунда | с | s |
| Сила электри-
ческого тока | I | I | ампер | А | A |
| Теромодина-
мическая температура | Q | T | кельвин | К | K |
| Количество вещества | N | n, v | моль | моль | mol |
| Сила света | J | J | канделла | кд | cd |
| Дополнительные | |||||
| Плоский угол | - | - | радиан | рад | rad |
| Телесный угол | - | - | стерадиан | ср | sr |
Таблица 1. 2. Производные единицы системы СИ, имеющие специальное название.
2. Производные единицы системы СИ, имеющие специальное название.
| Величина | Единица | |||
| Наименование | Размер-ность | Наимено-вание | Обозна-чение | Выражение через единицы Си |
| Частота | Т-1 | герц | Гц | с-1 |
| Сила, вес | LMT-2 | ньютон | Н | м∙кг∙с-2 |
| Давление, механическое напряжение | L-1MT-2 | паскаль | Па | м-1∙кг∙с-2 |
| Энергия, работа, количество теплоты | L2MT-2 | джоуль | Дж | м2∙кг∙с-2 |
| Мощность | L2MT-3 | ватт | Вт | м2∙кг∙с-3 |
| Количество электричества | TI | кулон | Кл | с∙А |
| Электрический напряжение, потенциал, электродвижущая сила | L2MT-3I-1 | вольт | В | м2∙кг∙с-3∙А-1 |
| Электрическая емкость | L-2M-1T4I2 | фарад | Ф | м-2∙кг-1∙с4∙А2 |
| Электрическое сопротивление | L2MT-3I-2 | ом | Ом | м2∙кг∙с-3∙А-2 |
| Электрическая проводимость | L-2M-1T3I2 | сименс | См | м-2∙кг-1∙с3∙А2 |
| Поток магнитной индукции | L2MT-2I-1 | вебер | Вб | м2∙кг∙с-2∙А-1 |
| Магнитная индукция | MT-2I-1 | тесла | Тл | кг∙с-2∙А-1 |
| Индуктивность | L2MT-2I-2 | генри | Гн | м2∙кг∙с-2∙А-2 |
| Световой поток | J | люмен | лм | кд∙ср |
| Освещенность | L-2J | люкс | лк | м-2∙кд∙ср |
| Активность радионуклида | Т-1 | беккерель | Бк | с-1 |
| Поглощенная доза ионизирующего излучения | L2T-2 | грей | Гр | м2∙с-2 |
| Эквивалентная доза излучения | L2T-2 | зиверт | Зв | м2∙с-2 |
Производные единицы бывают когерентными и некогерентными. Когерентной называется производная единица ФВ, связанная с другими единицами системы уравнением, в котором числовой множитель принят равным единице. Например, единицу скорости образуют с помощью уравнения, определяющего скорость прямолинейного и равномерного движения точки: v = L/t, где L — Длина пройденного пути; t — время движения. Подстановка вместо L и t их единиц в системе СИ дает v = 1 м/с. Следовательно, единица скорости является когерентной.
Когерентной называется производная единица ФВ, связанная с другими единицами системы уравнением, в котором числовой множитель принят равным единице. Например, единицу скорости образуют с помощью уравнения, определяющего скорость прямолинейного и равномерного движения точки: v = L/t, где L — Длина пройденного пути; t — время движения. Подстановка вместо L и t их единиц в системе СИ дает v = 1 м/с. Следовательно, единица скорости является когерентной.
Единицы ФВ делятся на системные и внесистемные.
Системная единица — единица ФВ, входящая в одну из принятых систем. Все основные, производные, кратные и дольные единицы являются системными.
Внесистемная единица — это единица ФВ, не входящая ни в одну из принятых систем единиц. Внесистемные единицы по отношению к единицам СИ разделяют на четыре вида:
•-допускаемые наравне с единицами СИ, например: единицы массы — тонна; плоского угла — градус, минута, секунда; объема — литр и др. Внесистемные единицы, допускаемые к применению наравне с единицами СИ, приведены в табл. 1.3;
Внесистемные единицы, допускаемые к применению наравне с единицами СИ, приведены в табл. 1.3;
• допускаемые к применению в специальных областях, например: астрономическая единица, парсек, световой год — единицы длины в астрономии; диоптрия — единица оптической силы в оптике; электрон-вольт — единица энергии в физике и т.д.;
• временно допускаемые к применению наравне с единицами СИ, например: морская миля — в морской навигации; карат — единица массы в ювелирном деле и др. Эти единицы должны изыматься из употребления в соответствии с международными соглашениями;
• изъятые из употребления, например: миллиметр ртутного столба — единица давления; лошадиная сила — единица мощности и некоторые другие.
Таблица 1.3. Внесистемные единицы, допускаемые к применению наравне с единицами СИ
| Наименование величины | Единица | ||
| Наименование | Обозна-чение | Соотношение с единицей СИ | |
|
масса | тонна | т | 103 кг |
| атомная единица массы | а. е. м. е. м.
| 1.66057∙10-27 кг (приблизительно) | |
|
время | минута | мин | 60 с |
| час | ч | 3600 с | |
| сутки | сут | 86400 с | |
|
плоский угол | градус | ° | (π/180) рад=1.745329..∙10-2 рад |
| минута | …′ | (π/10800) рад=2.908882..∙10-4 рад | |
| секунда | …″ | (π/648000) рад=4.848137..∙10-6 рад | |
| град | град | (π/200) рад | |
| объем | литр | л | 10-3 м3 |
|
длина | астрономическая единица | а. е. | 1.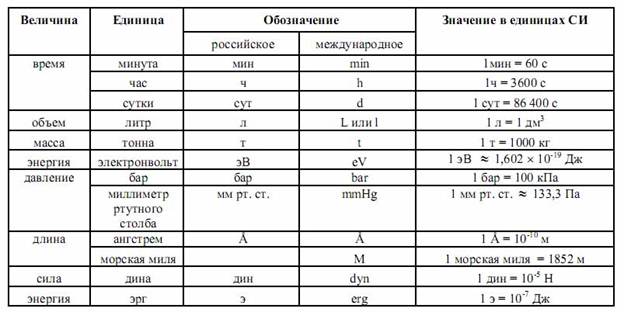 45598∙1011 м (приблизительно) 45598∙1011 м (приблизительно)
|
| световой год | св. год | 9.4605∙1015 м (приблизительно) | |
| парсек | пк | 3.0857∙1016 м (приблизительно) | |
| оптическая сила | диоптрия | дптр | 1 м-1 |
| площадь | гектар | га | 104 м2 |
| энергия | электрон-вольт | эВ | 1.60219∙10-19 Дж (приблизительно) |
| полная мощность | вольт-ампер | В∙А | - |
| реактивная мощность | вар | вар | - |
Различают кратные и дольные единицы ФВ.
Кратная единица— это единица ФВ, в целое число раз превышающая системную или внесистемную единицу. Например, единица длины — километр — равна 103 м, т.е. кратна метру.
Например, единица длины — километр — равна 103 м, т.е. кратна метру.
Дольная единица — единица ФВ, значение которой в целое число раз меньше системной или внесистемной единицы. Например, единица длины — миллиметр равна 10-3 м, т.е. является дольной. Приставки для образования кратных и дольных единиц приведены в табл. 1.4.
В системе СИ впервые введено понятие дополнительных единиц, к которым отнесены единицы плоского и телесного углов — радиан и стерадиан.
Таблица 1.4. Образование дольных и кратных единиц и их наименований
|
Множи-тель |
При-ставка | Обозначение приставки |
Множи-тель |
При-ставка | Обозначение приставки | ||
| Между-народное | Русское | Между-народное | Русское | ||||
| 1018 | экса | E | Э | 10-1 | деци | d | д |
| 1015 | пета | P | П | 10-2 | санти | c | с |
| 1012 | тера | T | Т | 10-3 | мили | m | м |
| 109 | гига | G | Г | 10-6 | микро | μ | мк |
| 106 | мега | M | М | 10-9 | нано | n | н |
| 103 | кило | k | к | 10-12 | пико | p | п |
| 102 | гекто | h | г | 10-15 | фемто | f | ф |
| 101 | дека | da | да | 10-18 | атто | a | а |
Вопросы и задания по материалу лекции 1.
1. Какой основной закон является юридическим основанием метрологии?
2. Дайте определение физической величины (ФВ) и приведите примеры.
3. Приведите примеры измеряемых и оцениваемых ФВ. В чем отличие между ними?
4. Чем измерения вещественных ФВ отличаются от измерений энергетических ФВ?
5. Какие из шкал физических величин (1-5) относятся к измеряемым ФВ, а какие – к оцениваемым?
6. Приведите отличия (минимум 2) шкалы интервалов от шкалы отношений.
7. Какова характерная особенность абсолютной шкалы? Для каких ФВ (размерных или безразмерных) она используется.
8. Для чего используется размерность ФВ?
9. *Знаете ли вы, что за система единиц была в СССР до 1981 года?
10. Можно ли получить одну основную единицу через комбинацию других основных единиц? Через комбинацию нескольких производных единиц?
11. *Как вы думаете, с какой целью принята категория внесистемных единиц «Временно допускаемые к применению наравне с единицами СИ»?
12. Дольные и кратные производные от системных единиц являются системными?
Дольные и кратные производные от системных единиц являются системными?
Вопросы со знаком * относятся к дополнительным (на общие знания и логику), т.к. ответов на них в лекции нет.
Лекция 2.
Калькулятор преобразования длины
Определение футов
Фут (сокращенно футов или ‘) — это единица измерения длины в британской / американской метрической системе. Это измерение также основано на человеческом теле, как следует из названия. Единица была стандартизирована в 1950-х годах, и с тех пор она равна точно 0,3048 метра:
1 фут = 0,3048 м = 304,8 мм
Ноги использовались с древних времен многими различными цивилизациями, но фактическая длина у них различалась.Нога использовалась, например в:
- Древний Рим: 1 фут = 11,6 дюйма (295,7 мм). Это стандартный фут, но в некоторых провинциях он может достигать 13,2 дюйма (334 мм)
- Греция: 1 фут = 10,6-13,8 дюйма (270-350 мм)
- города Инда в эпоху бронзы: 1 фут = 13,2 дюйма (333,5 мм)
- Египет , эквивалент в футах = 12 дюймов (304,8 мм)
Неофициальные государственные имперские стандарты измерения, Гринвич
В , Англия , размер стопы также менялся с течением времени — он начался с римских стандартов, затем с 13-го уровня у Бельгийских кельтов. 2 дюйма или валлийский фут приходили и уходили. Определение ступней менялось от региона к региону, от города к городу, позже даже короли изменили размер по своему желанию — например, Генрих I, как говорили, приказал новый стандарт, основанный на его руке. Затем Эдуард II Английский ввел некую стандартизацию, введя статутную ногу, которая составляла 10/11 старой ноги. Окончательное соглашение о длине фута было достигнуто намного позже, в 1959 году, когда было принято международное соглашение о ярдах и фунтах.С тех пор ярд в США и странах Британского Содружества равен ровно 0,9144 метра. Поскольку двор был определен, можно было рассчитать и фут. Таким образом, это равно:
2 дюйма или валлийский фут приходили и уходили. Определение ступней менялось от региона к региону, от города к городу, позже даже короли изменили размер по своему желанию — например, Генрих I, как говорили, приказал новый стандарт, основанный на его руке. Затем Эдуард II Английский ввел некую стандартизацию, введя статутную ногу, которая составляла 10/11 старой ноги. Окончательное соглашение о длине фута было достигнуто намного позже, в 1959 году, когда было принято международное соглашение о ярдах и фунтах.С тех пор ярд в США и странах Британского Содружества равен ровно 0,9144 метра. Поскольку двор был определен, можно было рассчитать и фут. Таким образом, это равно:
1 фут = (1/3) * ярд = (1/3) * 0,9144 м = 0,3048 м
В США ежедневно используются два типа опор: международная опора и опора для исследования:
Международный пеший
Также называется стандартной опорой; это тот, который был стандартизирован в 1950-х годах.
 Широко используется во многих приложениях, он равен 0,3048 м:
Широко используется во многих приложениях, он равен 0,3048 м:1 международный фут ≡ 0,3048 м, где мы использовали знак≡, чтобы подчеркнуть, что он равен ровно это значениеМеждународный размер стопы соответствует стопе человека с размером обуви 13 (Великобритания) или 14 (мужчина в США).
Обзорная стопа
Американская геодезическая стопа по размеру практически идентична международной. Но слово почти является ключевым — определение стопы точно составляет 1200/3937 метров:
.
1 фут съемки в США = 1200/3937 м ≈ 0,30480060960121920243840487680975... мКак видите, разница очень мала — что-то меняется на седьмом знаке после запятой! Разница составляет ≈0,609 мкм ≈ 609 нм, если сравнивать ступни одного типа с другими. Почему нас это вообще волнует?
Это важно, потому что разница незначительна, если мы измеряем относительно небольшие объекты, но она значительно возрастает, если мы начинаем измерять сотни тысяч футов, как при картировании или использовании системы координат плоскости состояния (SPCS).
 Кроме того, законодательство об обследовании варьируется в 50 штатах:
Кроме того, законодательство об обследовании варьируется в 50 штатах:В 24 штатах законодательно установлено, что геодезические меры должны основываться на обследовании US .
8 государств решили, что это должно быть сделано на основе международного пешего маршрута
18 состояний не указал коэффициент преобразования из метрических единиц
Но не беспокойтесь слишком сильно — если вам требуется преобразование для повседневной съемки земли или операций с недвижимостью, разница действительно незначительна для небольших расстояний (<1 мили), поэтому не имеет значения, какое определение вы выберете.
Есть еще одно измерение стопы — , индийский исследовательский фут . Это определено как , ровно 0,3047996 м:
1 Индийский геодезический фут = 0,3047996 м
футов — и вся имперская система — широко используются в США. И почти только там. США — единственная промышленно развитая страна в мире, которая официально не приняла Международную систему единиц, также называемую метрической системой. Две другие страны, использующие имперскую систему, — Либерия в Африке и Мьянма (также известная как Бирма) в Юго-Восточной Азии.Канадцы и британцы используют сочетание обеих систем — метрической и британской (например, рост мужчин обычно выражается в футах в сочетании с дюймами).
Feet широко не используется за пределами англоязычного мира. Единственный очевидный пример — измерение высоты в международной авиации.
Калькулятор преобразования
Используйте этот калькулятор преобразования для преобразования между обычно используемыми единицами. Выберите текущую единицу измерения в левом столбце, желаемую единицу измерения в правом столбце и введите значение в левом столбце для генерации результирующего преобразования.Полный список преобразований единиц доступен на unitconverters.net.
Различные системы единиц
Исторически использовалось много различных систем единиц, в которых система единиц определяется как совокупность единиц измерения с правилами, которые связывают их друг с другом. Единица измерения — это определенная величина величины, которую она использовала в качестве стандарта для измерения одного и того же типа величины, например длины, веса и объема.
В прошлом многие системы измерения определялись на местном уровне и могли основываться на таких произвольных факторах, как длина большого пальца короля.Хотя это может работать на местном уровне, при рассмотрении торговли, а также науки, наличие систем единиц, основанных на единицах, которые другие, возможно, не смогут связать или понять, затрудняет взаимодействие. Таким образом, с течением времени развивались более универсальные и последовательные системы. Сегодня некоторые из используемых систем единиц включают метрическую систему, имперскую систему и общепринятые единицы США.
Международная система единиц (СИ) — это стандартная метрическая система, которая используется в настоящее время, и состоит из семи основных единиц СИ: длины, массы, времени, температуры, электрического тока, силы света и количества вещества.Хотя СИ используется почти повсеместно в науке (в том числе в США), некоторые страны, такие как США, по-прежнему используют свою собственную систему единиц. Отчасти это связано со значительными финансовыми и культурными затратами, связанными с изменением системы измерения, по сравнению с потенциальной выгодой от использования стандартизированной системы. Поскольку общепринятые единицы измерения США (USC) так укоренились в Соединенных Штатах, а SI уже используется в большинстве приложений, где важна стандартизация, повседневное использование USC по-прежнему широко распространено в Соединенных Штатах и вряд ли изменится.Таким образом, существует множество конвертеров единиц, включая этот калькулятор преобразования, и они будут продолжать использовать их, чтобы люди во всем мире могли эффективно передавать различные измерения.
История фунта
В восьмом и девятом веках нашей эры (н.э.) арабская цивилизация процветала на Ближнем Востоке и в Испании. Арабы использовали монеты как единицы измерения веса, поскольку отчеканенную монету было нелегко разрезать или побрить, чтобы уменьшить ее вес, и, таким образом, обеспечивали измеримый стандарт.В качестве основной меры веса они использовали монету, называемую серебряным дирхемом, которая имела вес, примерно эквивалентный 45 взрослым зернам ячменя. Десять дирхемов составляли Wukryeh, что было переведено на латынь как «uncia» — происхождение слова «унция».
Со временем торговля распространилась из Средиземноморья в Европу, включая северные немецкие города-государства. В результате фунт, 16 унций серебра или 7200 гран стали широко используемой мерой во многих регионах.
В то время как Англия также приняла эту меру, нехватка серебра заставила короля Оффа уменьшить размер фунта до 5400 зерен, чтобы использовать более мелкие монеты.В конце концов, когда Вильгельм Завоеватель стал королем Англии, он сохранил фунт в 5400 г для чеканки монет, но вернулся к фунту в 7200 г для других целей.
Хотя с этого момента многие страны использовали фунт, включая Англию (британский фунт стерлингов, или GBP, был равен одному фунту серебра во времена короля Оффы), система веса энирдупуа была принята во время правления королевы Елизаветы в 16 век. Это была система, основанная на весе угля, и ее название произошло от французской фразы «Avoir de pois» (весовые товары или имущество).Экирдупуа эквивалентен 7000 гран, 256 драмам по 27,344 грана каждая, или 16 унциям по 437 ½ грана каждая. С 1959 года фунт экирдупуа был официально определен в большинстве англоязычных стран как 0,45359237 килограмма.
С течением времени в азиатских странах развивались различные системы измерения. Например, в древней Индии использовалась мера веса, называемая «сатамана», которая равнялась весу 100 ягод гунджи. В Китае первый император Ши Хуан Ди создал систему мер и весов в третьем веке до нашей эры (до нашей эры).Измерение веса основывалось на ши, что эквивалентно приблизительно 132 фунтам. Чи и чжан были единицами длины, эквивалентными примерно 25 сантиметрам (9,8 дюйма) и 3 метрам (9,8 фута) соответственно. Китайцы также разработали средство для обеспечения точности за счет использования чаши особого размера, используемой для измерений, которая также издавала определенный звук при ударе — если звук был невысоким, измерение было неточным.
Краткая история метрической системы
В 1668 году Джон Уилкинс предложил десятичную систему, в которой длина, площадь, объем и масса были связаны друг с другом на основе маятника, у которого в качестве базовой единицы длины был импульс в одну секунду.В 1670 году Габриэль Мутон предложил десятичную систему, основанную на длине окружности Земли. Эту идею поддержали другие выдающиеся ученые того времени, такие как Жан Пикар и Христиан Гюйгенс, но она не применялась еще примерно 100 лет.
К середине восемнадцатого века для стран, торгующих и обменивающихся научными идеями, стало ясно, что стандартизация мер и весов необходима. В 1790 году Чарльз Морис де Талейран-Перигор, принц Талейран, обратился к британцам (в лице Джона Риггса-Миллера) и американцам (в лице Томаса Джефферсона) с предложениями определить общий стандарт длины на основе длины маятник.В том же году Томас Джефферсон представил «План установления единообразия в чеканке, весах и единицах измерения Соединенных Штатов», в котором отстаивалась десятичная система, в которой единицы были связаны друг с другом степенями десяти. Комитет, который был сформирован во Франции, состоящий из некоторых из самых выдающихся ученых того времени, пришел к аналогичному выводу, а также предложил десятичную систему для всех мер и весов. Хотя Конгресс рассмотрел отчет Джефферсона, он не был принят.В Великобритании Джон Риггс-Миллер потерял свое место в британском парламенте на выборах 1790 года. Таким образом, система измерения была внедрена только во Франции, а в 1795 году метрическая система была официально определена во французском законодательстве. Однако только в 1799 году метрическая система была официально принята во Франции, хотя она не применялась повсеместно по всей стране.
Распространение метрической системы не произошло быстро, и области, которые были аннексированы Францией во время правления Наполеона, были первыми, кто принял метрическую систему.К 1875 году две трети населения Европы и почти половина населения мира приняли метрическую систему. К 1920 году процент населения мира, использующего имперскую систему или обычную систему США, составлял ~ 22%, при этом 25% использовали в основном метрическую систему, а 53% не использовали ни одну из них.
Международная система единиц, наиболее широко используемая в настоящее время система измерения, была опубликована в 1960 году. Она была принята во всех развитых странах, кроме США, хотя, как уже упоминалось ранее, она широко используется в науке. в армии, даже в США.
Количественные наблюдения / измерения данных. Базовые единицы в системе SI Длина: ________ Объем: _________ Масса: ________ Температура: __________ Метр (м)
Презентация на тему: «Количественные наблюдения / измерения данных. Базовые единицы в системе СИ Длина: ________ Объем: _________ Масса: ________ Температура: __________ Метр (м)» — стенограмма презентации:
1
Количественные наблюдения / измерения данных
2
Основные единицы в системе СИ Длина: ________ Объем: _________ Масса: ________ Температура: __________ Метр (м) Литр (Л) Грам (г) Цельсий (C)
3
Префиксы в системе СИ Кило: __________________ Пример: 1 километр = 1000 метров Деци: __________________ Пример: 1 дециметр = 0.1 метр Сенти: _________________ Пример: 1 сантиметр = 0,01 метра Милли: __________________ Пример: 1 миллиметр = 0,001 метра Микро: _________________ Пример: 1 микрометр = 0,000 001 метр Нано: _________________ Пример: 1 нанометр = 0,000 000 001 метр 10 3, (K ) 10-1, (г) 10-2, (в) 10-3, (м) 10-6, (µ) 10-9, (п)
4
Способы измерения длины: ____________________________ Масса: _____________________ ИЛИ ____________________ Температура: ________________ Объем жидкости: _______________________ — Не забудьте ВСЕГДА считывать с __________________________ сантиметровой линейки или измерительной ручки Трехлучевые весы Электрические весы Термометр Градуированный цилиндр Нижняя часть мениска
5
Способы измерения (продолжение)… Объем твердого тела неправильной формы: 1) Налейте жидкость в цилиндр и измерьте объем, запишите его как объем до _______ 2) ЗАТЕМ поместите объект в цилиндр и измерьте объем, запишите это как объем после _______ 3 ) Вычтите объем воды (до объема) ИЗ объема воды + объект (после объема).___________ — _____________ = ________________ 4) Теперь у вас есть объем неправильного объекта Объем твердого тела: Измерьте длину, ширину и высоту, а затем используйте формулу ниже Формула: _______________________________________________ Объем = Длина x Ширина x Высота
% PDF-1.6
%
1403 0 объект
>
endobj
xref
1403 98
0000000016 00000 н.
0000003075 00000 н.
0000003321 00000 п.
0000003358 00000 п.
0000003435 00000 н.
0000003468 00000 н.
0000003555 00000 н.
0000003774 00000 н.
0000003884 00000 н.
0000004096 00000 н.
0000004174 00000 п.
0000004253 00000 н.
0000004292 00000 н.
0000005529 00000 п.
0000006345 00000 п.
0000006908 00000 н.
0000007134 00000 н.
0000007366 00000 н.
0000007935 00000 п.
0000008828 00000 н.
0000008974 00000 н.
0000009167 00000 н.
0000009546 00000 н.
0000009792 00000 н.
0000010092 00000 п.
0000010335 00000 п.
0000011553 00000 п.
0000012650 00000 п.
0000013801 00000 п.
0000014571 00000 п.
0000015411 00000 п.
0000018104 00000 п.
0000018191 00000 п.
0000021496 00000 п.
0000021756 00000 п.
0000021975 00000 п.
0000025136 00000 п.
0000025177 00000 п.
0000025238 00000 п.
0000025346 00000 п.
0000025464 00000 п.
0000025629 00000 п.
0000025769 00000 п.
0000025983 00000 п.
0000026168 00000 п.
0000026322 00000 п.
0000026480 00000 п.
0000026665 00000 п.
0000026819 00000 п.
0000026995 00000 п.
0000027139 00000 п.
0000027335 00000 п.
0000027511 00000 п.
0000027681 00000 п.
0000027843 00000 п.
0000028015 00000 п.
0000028201 00000 п.
0000028389 00000 п.
0000028565 00000 п.
0000028739 00000 п.
0000028931 00000 п.
0000029099 00000 н.
0000029289 00000 п.
0000029469 00000 н.
0000029623 00000 п.
0000029807 00000 п.
0000029977 00000 н.
0000030175 00000 п.
0000030317 00000 п.
0000030507 00000 п.
0000030703 00000 п.
0000030899 00000 н.
0000031095 00000 п.
0000031257 00000 п.
0000031433 00000 п.
0000031619 00000 п.
0000031773 00000 п.
0000031961 00000 п.
0000032129 00000 п.
0000032319 00000 п.
0000032499 00000 н.
0000032687 00000 п.
0000032873 00000 п.
0000033053 00000 п.
0000033207 00000 п.
0000033391 00000 п.
0000033535 00000 п.
0000033721 00000 п.
0000033883 00000 п.
0000034081 00000 п.
0000034286 00000 п.
0000034476 00000 п.
0000034646 00000 п.
0000034898 00000 п.
0000035118 00000 п.
0000035302 00000 п.
0000035506 00000 п.
0000002256 00000 н.
трейлер
] / Назад 1307891 >>
startxref
0
%% EOF
1500 0 объект
> поток
hb«`e` «ū @ (M Ձ AIIE sxz» k !.ͬ @ Ɍa%; * (`pPx @ u + @ 0j ް &) ozNI`» @ «HnUj`: & g
S4,. [S8yThf> syȚ | SX` 骵 7u 岘 /] 2v} U’C # Mo! Mz9Po2EaN:
UaU. |} T`M% l
Длина строки в C | Упрощенное программирование
Программа на языке C для определения длины строки, например, длина строки «Программирование на языке C» составляет 13 (считается пробел). Нулевой символ не учитывается при его вычислении. Чтобы найти его, мы можем использовать функцию strlen для «string.h». Программа на C для определения длины строки без использования функции strlen, рекурсия.
Длина строки на языке C
#include
#include
int main ()
{
char a [100];
int length;
printf («Введите строку, чтобы вычислить ее длину \ n»);
получает (а);
длина = strlen (а);
printf («Длина строки =% d \ n», длина);
возврат 0;
}
Скачать программу длины строки.
Вывод программы:
Длина строки в C без strlen
Вы также можете найти длину строки без функции strlen.Мы создаем нашу функцию, чтобы ее найти. Мы просматриваем все символы в строке, если символ не является нулевым символом, а затем увеличиваем счетчик на единицу. Как только нулевой символ найден, счетчик равен длине строки.
#include
int main ()
{
char s [1000];
int c = 0;
printf («Введите строку \ n»);
товар (ов);
в то время как (s [c]! = ‘\ 0’)
c ++;
printf («Длина строки:% d \ n», c);
возврат 0;
}
Функция для поиска длины строки:
int string_length (char s []) {
int c = 0;
в то время как (s [c]! = ‘\ 0’)
c ++;
возврат c;
}
Программа на языке C для определения длины строки с помощью рекурсии
#include
int длина_строки (char *);
int main ()
{
символов [100];
получает (ов);
printf («Длина =% d \ n», длина_строки (s));
возврат 0;
}
int string_length (char * s) {
if (* s == ‘\ 0’) // Базовое условие
return 0;
return (1 + длина_строки (++ s));
}
Функция для определения длины строки с помощью указателей
int string_length (char * s) {
int c = 0;
в то время как (* s [c]! = ‘\ 0’)
c ++;
возврат c;
}
Лучшая длина si — Выгодные предложения на длину si от мировых продавцов длины si
Отличные новости !!! Вы находитесь в правильном месте для длины si.К настоящему времени вы уже знаете, что что бы вы ни искали, вы обязательно найдете это на AliExpress. У нас буквально тысячи отличных продуктов во всех товарных категориях. Ищете ли вы товары высокого класса или дешевые и недорогие оптовые закупки, мы гарантируем, что он есть на AliExpress.
Вы найдете официальные магазины торговых марок наряду с небольшими независимыми продавцами со скидками, каждый из которых предлагает быструю доставку и надежные, а также удобные и безопасные способы оплаты, независимо от того, сколько вы решите потратить.
AliExpress никогда не уступит по выбору, качеству и цене. Каждый день вы будете находить новые онлайн-предложения, скидки в магазинах и возможность сэкономить еще больше, собирая купоны. Но вам, возможно, придется действовать быстро, так как эта длина топа должна стать одним из самых популярных бестселлеров в кратчайшие сроки. Подумайте, как вам будут завидовать друзья, когда вы скажете им, что получили свою длину на AliExpress.Благодаря самым низким ценам в Интернете, дешевым тарифам на доставку и возможности получения на месте вы можете сэкономить еще больше.
Если вы все еще не уверены в длине товара и думаете о выборе аналогичного товара, AliExpress — отличное место для сравнения цен и продавцов. Мы поможем вам решить, стоит ли доплачивать за высококлассную версию или вы получаете столь же выгодную сделку, приобретая более дешевую вещь.А если вы просто хотите побаловать себя и потратиться на самую дорогую версию, AliExpress всегда позаботится о том, чтобы вы могли получить лучшую цену за свои деньги, даже сообщая вам, когда вам будет лучше дождаться начала рекламной акции. и ожидаемая экономия.AliExpress гордится тем, что у вас всегда есть осознанный выбор при покупке в одном из сотен магазинов и продавцов на нашей платформе. Реальные покупатели оценивают качество обслуживания, цену и качество каждого магазина и продавца.Кроме того, вы можете узнать рейтинги магазина или отдельных продавцов, а также сравнить цены, доставку и скидки на один и тот же продукт, прочитав комментарии и отзывы, оставленные пользователями. Каждая покупка имеет звездный рейтинг и часто имеет комментарии, оставленные предыдущими клиентами, описывающими их опыт транзакций, поэтому вы можете покупать с уверенностью каждый раз. Короче говоря, вам не нужно верить нам на слово — просто слушайте миллионы наших довольных клиентов.
А если вы новичок на AliExpress, мы откроем вам секрет.Непосредственно перед тем, как вы нажмете «купить сейчас» в процессе транзакции, найдите время, чтобы проверить купоны — и вы сэкономите еще больше. Вы можете найти купоны магазина, купоны AliExpress или собирать купоны каждый день, играя в игры в приложении AliExpress. Вместе с бесплатной доставкой, которую предлагают большинство продавцов на нашем сайте, вы сможете приобрести si length по самой выгодной цене.
У нас всегда есть новейшие технологии, новейшие тенденции и самые обсуждаемые лейблы.

 также
также


 Широко используется во многих приложениях, он равен 0,3048 м:
Широко используется во многих приложениях, он равен 0,3048 м: Кроме того, законодательство об обследовании варьируется в 50 штатах:
Кроме того, законодательство об обследовании варьируется в 50 штатах: