Репетитор-онлайн — подготовка к ЦТ
Пример 17. По грунтовой дороге прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии 60 см друг от друга. По этой дороге покатили детскую коляску массой 10 кг, имеющую две одинаковые рессоры. Известно, что груз массой 1,0 кг вызывает деформацию рессоры, равную 2,0 см. Найти скорость коляски, при которой она начнет сильно раскачиваться от толчков на углублениях дороги.
Решение. Коляска, движущаяся с определенной скоростью, проходит путь, равный расстоянию между углублениями на дороге, за время
t=Lv,
где L — расстояние между углублениями на дороге, L = 60 см; v — модуль скорости коляски (искомая величина).
Периодичность воздействия на коляску углублений, оставленных гусеницами трактора на дороге, позволяет считать это время периодом вынужденных колебаний:
T = t.
Коляска имеет период собственных колебаний, вызванных наличием рессор (пружин):
T0=2πMkобщ,
где M — масса коляски, M = 10 кг; k
oбщ — общий коэффициент жесткости рессор коляски (параллельное соединение), k
oбщ = 2k; k — жесткость одной рессоры.
Резонанс наступает при равенстве периодов внешнего воздействия и собственных колебаний коляски:
T = T
0.
Равенство
Lv=2πMkобщ=2πM2k
позволяет найти искомую величину скорости коляски:
v=L2π2kM=Lπk2M.
Определим жесткость одной рессоры с помощью равенства
mg = k∆x,
где m — масса груза, m = 1,0 кг; g — модуль ускорения свободного падения, g = 10 м/с2; Δx — деформация рессоры под действием указанного груза, Δx = 2,0 см.
Выразим из данного равенства жесткость одной рессоры:
k=mgΔx
и подставим ее в выражение для скорости коляски:
v=Lπmg2MΔx.
Вычислим:
v=60⋅10−23,141,0⋅102⋅10⋅2,0⋅10−2=96⋅10−2 м/с=96 см/с.
При скорости коляски, равной 96 см/с, наступает явление резонанса — коляска начинает сильно раскачиваться.
23.Резонанс в электрической цепи. Условие возникновения резонанса напряжений. Использование резонанса
Резонанс наблюдается в том случае, когда
собственная частота колебаний системы
совпадает с частотой изменения внешней
силы. Если трение мало, то амплитуда
Если трение мало, то амплитуда
установившихся вынужденных колебаний
при резонансе резко увеличивается.
Режим резонанса полностью
определяется параметрами электрической
цепи и не зависит от внешнего воздействия
на нее со стороны источников электрической
энергии. Если вы будете подталкивать
качели в соответствии с их резонансной
частотой, размах движения будет
увеличиваться, в противном случае
движения будут затухать.
Струны
таких инструментов, гитара, скрипка или
пианино, имеют основную резонансную
частоту, напрямую зависящую от длины,
массы и силы натяжения струны. Длина
волны первого резонанса струны равна
её удвоенной длине. При этом, его частота
зависит от скорости v, с которой волна
распространяется по струне.
24.Трансформаторы. Назначение трансформаторов. Устройство трансформатора. Определение коэффициента трансформации. Трансформатор на холостом ходу.
Измерительный
трансформа́тор то́ка — статическое
электромагнитное устройство предназначенная
для преобразования переменного тока
одного напряжения в переменный ток
другого напряжения той же частоты.
Первичная обмотка трансформатора тока
включается последовательно в цепь с
измеряемым переменным током, а во
вторичную включаются измерительные
приборы. Ток, протекающий по вторичной
обмотке трансформатора тока, пропорционален
току, протекающему в его первичной
обмотке.
Трансформаторы
тока широко используются для измерения
электрического тока и в устройствах
релейной
защиты электроэнергетических
систем, в связи с чем на них накладываются
высокие требования по точности.
Трансформаторы тока обеспечивают
безопасность измерений, изолируя
измерительные цепи от первичной цепи
с высоким напряжением, часто составляющим
сотни киловольт. Устройство: основа
трансформатора, сердечник из стальных
листов, вторичное напряжение, первичное
напряжение, нагрузка. Коэффициент
трансформации трансформатора —
это величина, выражающая масштабирующую
(преобразовательную) характеристику
трансформатора относительно какого-нибудь
параметра электрической цепи (напряжения,
тока, сопротивления) К=
=
,
где I – сила тока в первичной
и вторичной обмотке, U –
электрическое напряжение на концах
первичной и вторичной обмотки. Режим
Режим
холостого хода это режим, когда вторичная
обмотка разомкнута.
25.Трансформаторы. Принцип действия однофазного трансформатора. Коэффициент полезного действия трансформатора. Активная р и полная s мощности трансформатора.
Трансформа́тор — статическое
электромагнитное устройство предназначенная
для преобразования переменного тока
одного напряжения в переменный ток
другого напряжения той же частоты.
Принцип действия трансформатора основан
на явлении электромагнитной индукции.
Если в первичную обмотку с числом витков
N1, подавать переменный ток I1 напряжением
U1 от какого-либо источника (рис.3.2), то
под действием этого тока, намагничивающей
силе I1?N1, в магнитопроводе образуется
переменный магнитный поток, который
сцеплен с обеими обмотками и в них
индуктирует ЭДС. η = (Р1 —
ΔР)/Р1 = 1 — ΔР/(Р2
+ ΔР). Для расчета
тока в цепи используют условное понятие
полной мощности
.
Резонанс напряжений, условие возникновения — Ремонт220
Автор Фома Бахтин На чтение 3 мин. Просмотров 8.6k. Опубликовано
Обновлено
Явление резонанса электрических напряжений наблюдается в цепи последовательного колебательного контура, состоящего из емкости (конденсатора), индуктивности и резистора (сопротивления). Для обеспечения энергетической подпитки колебательного контура в последовательную цепь включается также источник электродвижущей силы Е. Источник вырабатывает переменное напряжение с частотой W. При резонансе ток, циркулирующий в последовательной цепи, должен совпадать по фазе с э.д.с. Е. Это обеспечивается, если общее сопротивление схемы Z = R+J(WL – 1/WС) будет лишь активным, т.е. Z=R. Равенство:
(L – 1/WС) = 0 (1),
является математическим условием резонанса в колебательном контуре.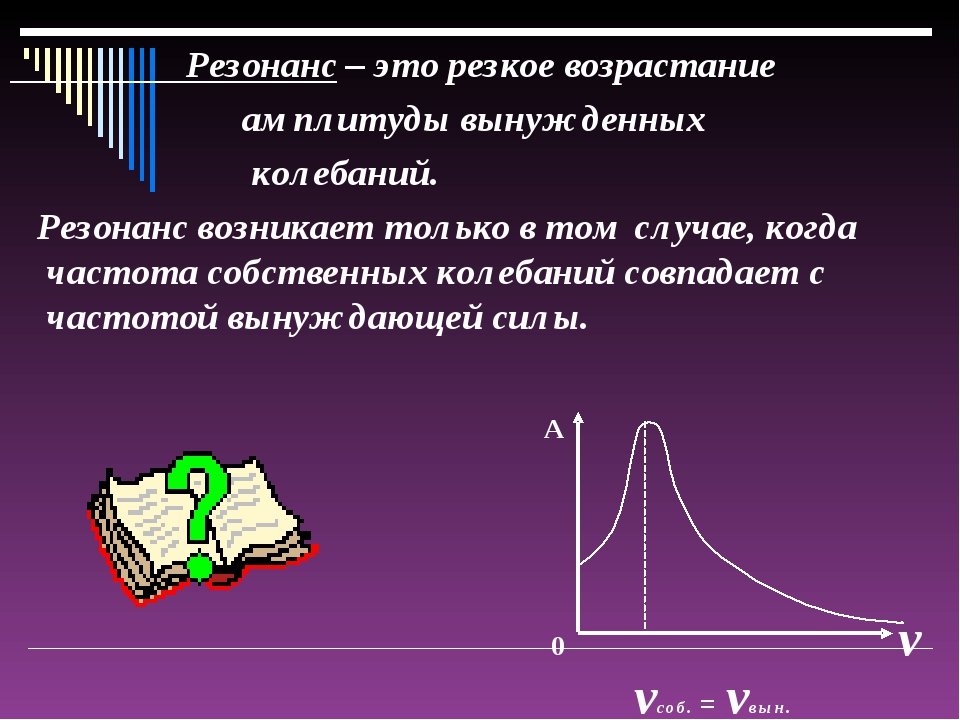 При этом величина тока в цепи составит I = E/R. Если преобразовать равенство (1), то получим:
При этом величина тока в цепи составит I = E/R. Если преобразовать равенство (1), то получим:
WL = 1/WС.
В этом выражении W – является резонансной частотой контура.
Важно то, что в процессе резонанса напряжение на индуктивности равно напряжению на конденсаторе и составляет:
UL = U = WL * I = WLE/R
Общая сумма энергий в индуктивности и емкости (магнитного и электрического полей) постоянна. Это объясняется тем, что между этими полями происходит колебательный обмен энергиями. Суммарное ее количество в любой момент неизменно. При этом обмена энергией между ее источником Е и цепью не происходит. Вместо этого имеет место непрерывное преобразование одного вида энергии в другой.
Для колебательных контуров применятся термин добротность, которая показывает, как соотносятся напряжение на реактивном элемента (емкость или индуктивность) и входное напряжение контура. Добротность вычисляется по формуле:
Q = WL/R
Для идеальной последовательной цепи с нулевым активным сопротивлением возникновение резонанса сопровождается незатухающими колебаниями. На практике затухание колебаний компенсируется подпиткой контура от генератора колебаний с частотой резонанса.
На практике затухание колебаний компенсируется подпиткой контура от генератора колебаний с частотой резонанса.
Применение резонанса напряжений
Явление колебательного резонанса широко используется в радиоэлектронике. В частности, входная цепь любого радиоприемника представляет собой регулируемый колебательный контур. Его резонансная частота, изменяемая с помощью регулировки емкости конденсатора, совпадает с частотой сигнала радиостанции, которую необходимо принять.
В электроэнергетике возникновение резонанса напряжений вследствие сопутствующих ему перенапряжений чревато нежелательными последствиями. Например, в случае подключения к генератору или промежуточному трансформатору длинной кабельной линии (являющейся колебательным контуром с распределенной емкостью и индуктивностью), не соединенной на приемном конце с нагрузкой (это называется режимом холостого хода), весь контур может оказаться в резонансом состоянии. В такой ситуации напряжения, возникающие на некоторых участках цепи, могут оказаться выше расчетных. Это может грозить пробоем изоляции кабеля и выходом его из строя. Такая ситуация предотвращается применением вспомогательной нагрузки.
Это может грозить пробоем изоляции кабеля и выходом его из строя. Такая ситуация предотвращается применением вспомогательной нагрузки.
Механизм возникновения электрического тока
Схема удивительного генератора СВЧ полей на разряднике Вина уникальное, в своём роде устройство
83046 Нагревание проводников электрическим током
примеры, польза и вред от его воздействия в жизни, методы борьбы с откликом
Определение понятия резонанса (отклика) в физике возлагается на специальных техников, которые обладают графиками статистики, часто сталкивающихся с этим явлением. На сегодняшний день резонанс представляет собой частотно-избирательный отклик, где вибрационная система или резкое возрастание внешней силы вынуждает другую систему осциллировать с большей амплитудой на определенных частотах.
Принцип действия
Это явление наблюдается, когда система способна хранить и легко переносить энергию между двумя или более разными режимами хранения, такими как кинетическая и потенциальная энергия. Однако есть некоторые потери от цикла к циклу, называемые затуханием. Когда затухание незначительно, резонансная частота приблизительно равна собственной частоте системы, которая представляет собой частоту невынужденных колебаний.
Эти явления происходят со всеми типами колебаний или волн: механические, акустические, электромагнитные, ядерные магнитные (ЯМР), электронные спиновые (ЭПР) и резонанс квантовых волновых функций. Такие системы могут использоваться для генерации вибраций определенной частоты (например, музыкальных инструментов).
Термин «резонанс» (от латинской resonantia, «эхо») происходит от поля акустики, особенно наблюдаемого в музыкальных инструментах, например, когда струны начинают вибрировать и воспроизводить звук без прямого воздействия игроком.
Примеры резонанса в жизни
Толчок человека на качелях является распространенным примером этого явления. Загруженные качели, маятник имеют собственную частоту колебаний и резонансную частоту, которая сопротивляется толканию быстрее или медленнее.
Примером является колебание снарядов на детской площадке, которое действует как маятник. Нажатие человека во время качания с естественным интервалом колебания приводит к тому, что качели идут все выше и выше (максимальная амплитуда), в то время как попытки делать качание с более быстрым или медленным темпом создают меньшие дуги. Это связано с тем, что энергия, поглощаемая колебаниями, увеличивается, когда толчки соответствуют естественным колебаниям.
Отклик широко встречается в природе и используется во многих искусственных устройствах. Это механизм, посредством которого генерируются практически все синусоидальные волны и вибрации. Многие звуки, которые мы слышим, например, когда ударяются жесткие предметы из металла, стекла или дерева, вызваны короткими колебаниями в объекте. Легкое и другое коротковолновое электромагнитное излучение создается резонансом в атомном масштабе, таким как электроны в атомах. Другие условия, в которых могут применяться полезные свойства этого явления:
Многие звуки, которые мы слышим, например, когда ударяются жесткие предметы из металла, стекла или дерева, вызваны короткими колебаниями в объекте. Легкое и другое коротковолновое электромагнитное излучение создается резонансом в атомном масштабе, таким как электроны в атомах. Другие условия, в которых могут применяться полезные свойства этого явления:
- Механизмы хронометража современных часов, колесо баланса в механических часах и кварцевый кристалл в часах.
- Приливной отклик залива Фанди.
- Акустические резонансы музыкальных инструментов и человеческого голосового тракта.
- Разрушение хрустального бокала под воздействием музыкального правого тона.
- Фрикционные идиофоны, такие как изготовление стеклянного предмета (стекла, бутылки, вазы), вибрируют, при потирании вокруг его края кончиком пальца.
- Электрический отклик настроенных схем в радиостанциях и телевизорах, которые позволяют избирательно принимать радиочастоты.
- Создание когерентного света оптическим резонансом в лазерной полости.

- Орбитальный отклик, примером которого являются некоторые луны газовых гигантов Солнечной системы.
Материальные резонансы в атомном масштабе являются основой нескольких спектроскопических методов, которые используются в физике конденсированных сред, например:
- Электронный спиновой.
- Эффект Мёссбауэра.
- Ядерный магнитный.
Типы явления
В описании резонанса Г. Галилей как раз обратил внимание на самое существенное — на способность механической колебательной системы (тяжелого маятника) накапливать энергию, которая подводится от внешнего источника с определенной частотой. Проявления резонанса имеют определенные особенности в различных системах и поэтому выделяют разные его типы.
Механический и акустический
Механический резонанс — это тенденция механической системы поглощать больше энергии, когда частота ее колебаний соответствует собственной частоте вибрации системы. Это может привести к сильным колебаниям движения и даже катастрофическому провалу в недостроенных конструкциях, включая мосты, здания, поезда и самолеты. При проектировании объектов инженеры должны обеспечить безопасность, чтобы механические резонансные частоты составных частей не соответствовали колебательным частотам двигателей или других осциллирующих частей во избежание явлений, известных как резонансное бедствие.
При проектировании объектов инженеры должны обеспечить безопасность, чтобы механические резонансные частоты составных частей не соответствовали колебательным частотам двигателей или других осциллирующих частей во избежание явлений, известных как резонансное бедствие.
Электрический резонанс
Возникает в электрической цепи на определенной резонансной частоте, когда импеданс схемы минимален в последовательной цепи или максимум в параллельном контуре. Резонанс в схемах используется для передачи и приема беспроводной связи, такой как телевидение, сотовая или радиосвязь.
Оптический резонанс
Оптическая полость, также называемая оптическим резонатором, представляет собой особое расположение зеркал, которое образует резонатор стоячей волны для световых волн. Оптические полости являются основным компонентом лазеров, окружающих среду усиления и обеспечивающих обратную связь лазерного излучения. Они также используются в оптических параметрических генераторах и некоторых интерферометрах.
Они также используются в оптических параметрических генераторах и некоторых интерферометрах.
Свет, ограниченный в полости, многократно воспроизводит стоячие волны для определенных резонансных частот. Полученные паттерны стоячей волны называются «режимами». Продольные моды отличаются только частотой, в то время как поперечные различаются для разных частот и имеют разные рисунки интенсивности поперек сечения пучка. Кольцевые резонаторы и шепчущие галереи являются примерами оптических резонаторов, которые не образуют стоячих волн.
Орбитальные колебания
В космической механике возникает орбитальный отклик, когда два орбитальных тела оказывают регулярное, периодическое гравитационное влияние друг на друга. Обычно это происходит из-за того, что их орбитальные периоды связаны отношением двух небольших целых чисел. Орбитальные резонансы значительно усиливают взаимное гравитационное влияние тел. В большинстве случаев это приводит к нестабильному взаимодействию, в котором тела обмениваются импульсом и смещением, пока резонанс больше не существует.
В большинстве случаев это приводит к нестабильному взаимодействию, в котором тела обмениваются импульсом и смещением, пока резонанс больше не существует.
При некоторых обстоятельствах резонансная система может быть устойчивой и самокорректирующей, чтобы тела оставались в резонансе. Примерами является резонанс 1: 2: 4 лун Юпитера Ганимед, Европа и Ио и резонанс 2: 3 между Плутоном и Нептуном. Неустойчивые резонансы с внутренними лунами Сатурна порождают щели в кольцах Сатурна. Частный случай резонанса 1: 1 (между телами с аналогичными орбитальными радиусами) заставляет крупные тела Солнечной системы очищать окрестности вокруг своих орбит, выталкивая почти все остальное вокруг них.
Атомный, частичный и молекулярный
Ядерный магнитный резонанс (ЯМР) — это имя, определяемое физическим резонансным явлением, связанным с наблюдением конкретных квантовомеханических магнитных свойств атомного ядра, если присутствует внешнее магнитное поле. Многие научные методы используют ЯМР-феномены для изучения молекулярной физики, кристаллов и некристаллических материалов. ЯМР также обычно используется в современных медицинских методах визуализации, таких как магнитно-резонансная томография (МРТ).
Многие научные методы используют ЯМР-феномены для изучения молекулярной физики, кристаллов и некристаллических материалов. ЯМР также обычно используется в современных медицинских методах визуализации, таких как магнитно-резонансная томография (МРТ).
Польза и вред резонанса
Для того чтобы сделать некий вывод о плюсах и минусах резонанса, необходимо рассмотреть, в каких случаях он может проявляться наиболее активно и заметно для человеческой деятельности.
Положительный эффект
Явление отклика широко используется в науке и технике. Например, работа многих радиотехнических схем и устройств основывается на этом явлении.
- Двухтактный двигатель. Глушитель двухтактного двигателя имеет особую форму, рассчитанную на создание резонансного явления. Оно улучшает работу двигателя засчет снижения потребления и загрязнения. Этот резонанс частично уменьшает несгоревшие газы и увеличивает сжатие в цилиндре.

- Музыкальные инструменты. В случае струнных и духовых инструментов звуковое производство происходит в основном при возбуждении колебательной системы (струны, колонны воздуха) до возникновения явления резонанса.
- Радиоприемники. Каждая радиостанция излучает электромагнитную волну с четко определенной частотой. Для его захвата цепь RLC принудительно подвергается вибрации с помощью антенны, которая захватывает все электромагнитные волны, достигающие ее. Для прослушивания одной станции собственная частота RLC-схемы должна быть настроена на частоту требуемого передатчика, изменяя емкость переменного конденсатора (операция выполняется при нажатии кнопки поиска станции). Все системы радиосвязи, будь то передатчики или приемники, используют резонаторы для «фильтрации» частот сигналов, которые они обрабатывают.
- Магнитно-резонансная томография (МРТ). В 1946 году два американца Феликс Блох и Эдвард Миллс Перселл самостоятельно обнаружили явление ядерного магнитного резонанса, также называемое ЯМР, которое принесло им Нобелевскую премию по физике.

Отрицательное воздействие
Однако не всегда явление полезно. Часто можно встретить ссылки на случаи, когда навесные мосты ломались при прохождении по ним солдат «в ногу». При этом ссылаются на проявление резонансного эффекта воздействия резонанса, и борьба с ним приобретает масштабный характер.
- Автотранспорт. Автомобилисты часто раздражаются шумом, который появляется при определенной скорости движения транспортного средства или в результате работы двигателя. Некоторые слабо закругленные части корпуса вступают в резонанс и излучают звуковые колебания. Сам автомобиль с его системой подвески представляет собой осциллятор, оснащенный эффективными амортизаторами, которые препятствуют возникновению острого резонанса.
- Мосты. Мост может выполнять вертикальные и поперечные колебания. Каждый из этих типов колебаний имеет свой период.
 Если стропы подвешены, система имеет очень разную резонансную частоту.
Если стропы подвешены, система имеет очень разную резонансную частоту. - Здания. Высокие здания чувствительны к землетрясениям. Некоторые пассивные устройства позволяют защитить их: они являются осцилляторами, чья собственная частота близка к частоте самого здания. Таким образом, энергия полностью поглощается маятником, препятствующим разрушению здания.
Борьба с резонансом
Но несмотря на иногда губительные последствия эффекта отклика с ним вполне можно и нужно бороться. Чтобы избежать нежелательного возникновения этого явления, обычно используют два способа одновременного применения резонанса и борьбы с ним:
- Производится «разобщение» частот, которые в случае совпадения приведут к нежелательным последствиям. Для этого повышают трение различных механизмов или меняют собственную частоту колебаний системы.
- Увеличивают затухание колебаний, например, ставят двигатель на резиновую подкладку или пружины.

последствия игнорирования резонансных колебаний оснастки
23 Октября 2019
Питер Авитабиле (Peter Avitabile), журнал «Sound and vibration»
Под ред. специалиста отдела проектов ИО Валентина Дубенского
[email protected]
Перевод: Артем Вахитов
Периодически в оснастке вибростендов возникают резонансные колебания, частота которых лежит в диапазоне, необходимом для проведения вибрационных испытаний. Такие резонансные частоты могут вызвать значительные проблемы во время проведения вибрационных тестов, особенно в диапазонах, которые могут включать данные резонансные частоты. Для контроля уровня входных вибраций на тестовом образце инженеры-испытатели используют акселерометры с обратной связью. Однако акселерометр может только контролировать уровень вибраций, но не способен изменить резонансное поведение оснастки. В статье описаны некоторые проблемы, а также рассмотрены основные причины возникновения подобного явления.
В статье описаны некоторые проблемы, а также рассмотрены основные причины возникновения подобного явления.
Очень часто вибрационные испытания проводятся для подтверждения допустимости применения определенных устройств и изделий в некоторых средах. Вибростенды используются в качестве генераторов усилий или ускорений с целью воспроизводства известных рабочих условий или источников входных сигналов широкого спектра для имитации реальной эксплуатации.
Сопряжение между вибростендом и тестируемым изделием — это оснастка вибростенда. В статье мы будем рассматривать оснастку как элемент, который включает арматуру вибростенда, расширительный стол (или стол скольжения), а также крепежное приспособление (например, для размещения тестируемого изделия). Поэтому, когда мы говорим «оснастка», то имеем в виду все, что находится между приводом вибростенда и тестируемым образцом (то, что мы не видим арматуру, не означает, будто она не является составляющей всей системы).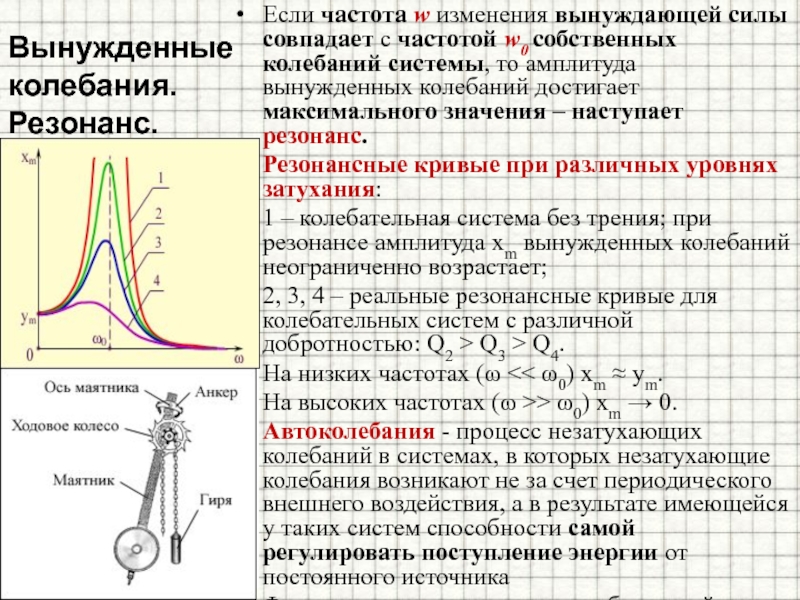 На рис. 1 схематически показана конструкция оснастки.
На рис. 1 схематически показана конструкция оснастки.
Рис. 1. Обычные компоненты оснастки
Наша основная цель — сделать оснастку очень жесткой и при этом безынерционной. Это подразумевает, что оснастка не будет испытывать резонансных колебаний, лежащих в рабочем диапазоне частот, и поверхность, на которую установлено тестируемое изделие, двигается как жесткое тело и имеет однородное смещение на границе с тестируемым образцом. Для крупных вибростендов этого добиться очень сложно, если не невозможно. В таких системах все равно будут появляться некоторые резонансные колебания из-за массы и жесткости оснастки, расширительного стола (или стола скольжения) и крепежных устройств для установки тестируемого изделия. Очень часто инженеры игнорируют эту проблему и предполагают, что контроллер, устанавливаемый на вибростенд, может компенсировать данные эффекты.
К сожалению, контроллер лишь удерживает уровень ускорения в том месте, где установлен управляющий акселерометр, и не может снизить резонансные колебания в оснастке. Наличие систем управления с обратной связью никак не влияет на резонансные колебания. Все, что делают данные системы, — регулируют (уменьшают или увеличивают) входные усилия, подаваемые на катушку привода вибростенда, для удержания необходимого уровня ускорений. Обычно на вибростенд устанавливается несколько акселерометров в разных точках на оснастке, а подаваемые ими сигналы усредняются в один контрольный. И опять же, это позволяет только удерживать среднее значение контрольного параметра — ускорения. Резонансные частоты и динамические характеристики не меняются. Усреднение сигналов с нескольких точек — прекрасный метод для получения «лучше выглядящего» спектра, но это не влияет на проблему резонансных колебаний, связанных с оснасткой.
Наличие систем управления с обратной связью никак не влияет на резонансные колебания. Все, что делают данные системы, — регулируют (уменьшают или увеличивают) входные усилия, подаваемые на катушку привода вибростенда, для удержания необходимого уровня ускорений. Обычно на вибростенд устанавливается несколько акселерометров в разных точках на оснастке, а подаваемые ими сигналы усредняются в один контрольный. И опять же, это позволяет только удерживать среднее значение контрольного параметра — ускорения. Резонансные частоты и динамические характеристики не меняются. Усреднение сигналов с нескольких точек — прекрасный метод для получения «лучше выглядящего» спектра, но это не влияет на проблему резонансных колебаний, связанных с оснасткой.
Управляющий акселерометр должен устанавливаться на поверхности, которая двигается как жесткое тело без резонансных колебаний в требуемом диапазоне частот. Это то, что контроллер ожидает увидеть в качестве обратной связи. Если поверхность упругая, обратная связь от управляющего акселерометра в большой степени зависит от места, где он установлен.
Если поверхность упругая, обратная связь от управляющего акселерометра в большой степени зависит от места, где он установлен.
Использование нескольких управляющих акселерометров, данные от которых усредняются, подразумевает, что будет контролироваться лишь некое среднее значение ускорения. Правильное применение нескольких акселерометров на упругой поверхности возможно только, если каждый акселерометр будет давать независимый ответ для отдельного вибростенда, которым он управляет. Конечно, это очень сложно практически воплотить, поскольку в таком случае понадобится несколько вибростендов и контроллеров типа MIMO (Multi-Input Multi-Output — многоканальные контроллеры входа/выхода).
Подобная ситуация может смутить многих инженеров-испытателей, так как они убеждены, что управляющие акселерометры — это все, на чем им нужно акцентировать свое внимание при проведении вибрационных испытаний. Но это ошибочное мнение.
Для того чтобы понять суть возникающих проблем, необходимо рассмотреть некоторые основные концепции теории вибраций, а также привести примеры и проиллюстрировать их. Динамическое взаимодействие между тестируемым изделием и оснасткой при переходе от собранных данных к лабораторным испытаниям уже неоднократно изучалось специалистами отрасли. Результаты исследований изложены в литературе, список которой представлен в конце этой статьи.
Динамическое взаимодействие между тестируемым изделием и оснасткой при переходе от собранных данных к лабораторным испытаниям уже неоднократно изучалось специалистами отрасли. Результаты исследований изложены в литературе, список которой представлен в конце этой статьи.
При опубликовании нашей концепции многие говорили: «это только научная теория», «это на самом деле не происходит», «убедитесь, что то, что должно быть описано, происходит на самом деле».
Что ж, давайте рассмотрим явление, а затем сделаем рациональные инженерные предположения и предложим решения, как лучше всего справиться с ситуацией.
Действительность заключается в том, что в некоторых случаях невозможно получить оснастку без резонансных колебаний. Однако инженерам-испытателям очень важно понимать и отслеживать динамику всей системы, чтобы проводить осмысленные вибрационные испытания. Например, если резонанс возник, то понимание типов и формы колебаний поможет или модифицировать конструкцию, поднимая частоту резонансных колебаний выше диапазона частот теста, или устанавливать тестируемое изделие так, чтобы минимизировать влияние этих нежелательных резонансных колебаний.
Теперь, иллюстрируя примерами, можно обсудить причины, почему это происходит (в следующем разделе читателя ждет информация не для слабонервных — возможно, вам не понравится изложенное).
Рис. 2. Система с одной степенью свободы (SDoF)
Основные теоретические выкладки
Демонстрируемые здесь формулы можно найти в любом учебнике по вибрациям (большинство формул взято из литературы [2]). Первое основное выражение приведем для систем с одной степенью свободы (SDoF) (рис. 2). Формула движения для таких систем выглядит следующимобразом:
Выражение, которое описывает систему SDoF с появлением синусоидального возбуждения, задается как:
Данное выражение записывается как соотношение динамического смещения к статическому смещению. Здесь ω — возбуждаемая синусоидальная частота, ωn — собственная частота, а ς — это критическое затухание, выраженное в процентах.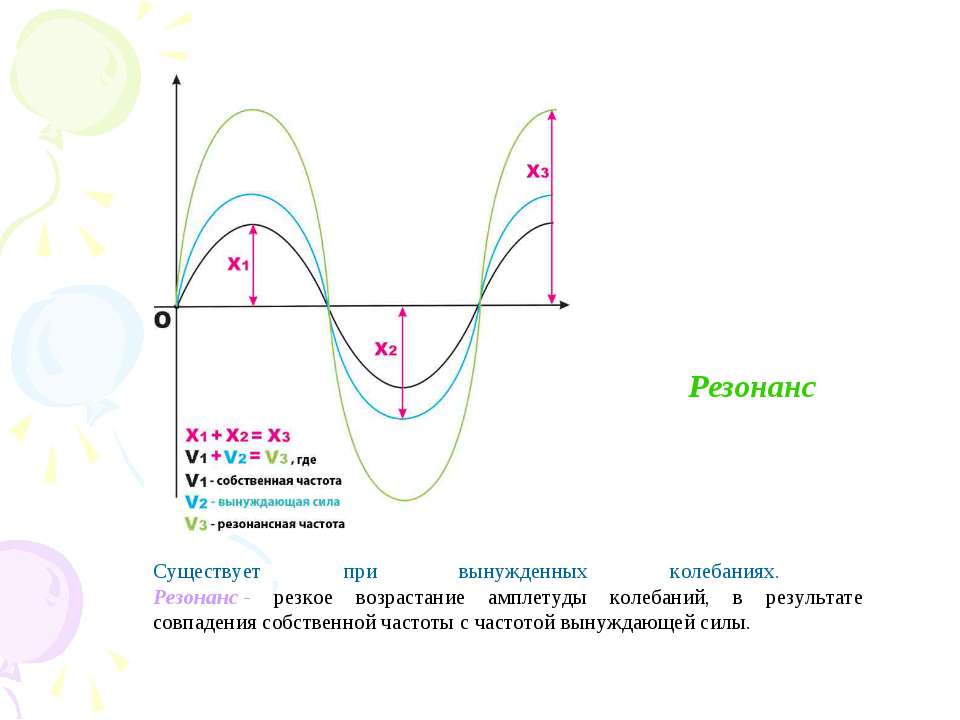 Величина данного соотношения сначала увеличивается, а затем уменьшается после того, как мы проходим собственную частоту системы (рис. 3).
Величина данного соотношения сначала увеличивается, а затем уменьшается после того, как мы проходим собственную частоту системы (рис. 3).
Рис. 3. Усиление системы с одной степенью свободы с помощью добавления синусоидального возбуждения
Теперь рассмотрим систему с двумя и более массами, соединенными между собой безынерционными пружинами, с несколькими степенями свободы (MDoF). Это следующий уровень аппроксимации. Для описания движения такой системы существует несколько выражений, так как в движении участвует большее количество масс, поэтому будем использовать матричную запись. Сначала рассмотрим системы с двумя степенями свободы, а затем обобщим на несколько систем DoF.
Рис. 4. Системы с несколькими (двумя) степенями свободы
Для системы с двумя массами (рис. 4) выражение, описывающее движение, выглядит следующим образом:
или в матричной форме:
или:
Используя такую форму представления, можно описать движение для систем с любым количеством масс. Теперь в данной форме выражение показывает связь между различными системами DoF. Мы используем математический метод, который называется «собственное решение», для того чтобы разбить эти более сложные связанные выражения в набор выражений для более простых систем SDoF. Затем получаем простые формулы:
Теперь в данной форме выражение показывает связь между различными системами DoF. Мы используем математический метод, который называется «собственное решение», для того чтобы разбить эти более сложные связанные выражения в набор выражений для более простых систем SDoF. Затем получаем простые формулы:
Каждое выражение отделено от каждого другого выражения, и каждое из них описывает отдельно системы SDoF в соответствии с каждой собственной частотой системы. Таким образом мы взяли сложную систему и разбили ее на гораздо более простые. Схематически это показано на рис. 5.
Рис. 5. Развязанная система с несколькими степенями свободы (MDoF)
Это подтверждает, что системы SDoF можно использовать для описания каждого вида вибраций систем MDoF. Посмотрим на частотные характеристики для системы, показанной на рис. 6, представляющей не что иное как сумму систем SDoF.
Рис.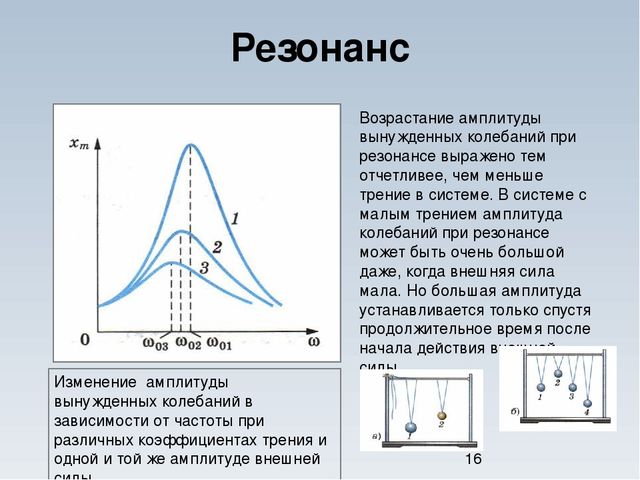 6. Совмещение каждой системы SDoF
6. Совмещение каждой системы SDoF
Если мы предположим, что взаимодействие между оснасткой и тестируемым образцом похоже на динамическое взаимодействие между каждым видом вибрации каждой системы, то для описания динамического взаимодействия между оснасткой и тестируемым изделием можно использовать несколько простых выражений. Давайте вспомним формулу для двух систем DoF, описывающих частотные характеристики резонансного поглотителя. Это очень знакомая формула, которую можно найти во всех учебниках по вибрациям:
Рис. 7. Характеристики поглощения колебаний
Данное выражение, взятое из [3], устанавливает связь между собственной частотой и коэффициентом жесткости для каждой отдельной системы DoF. Количество динамических взаимодействий сильно зависит от относительного соотношения данных характеристик. Для заданного соотношения масс с двумя отдельными системами DoF, имеющими одинаковую собственную частоту, типичный график конечных динамических характеристик показан на рис.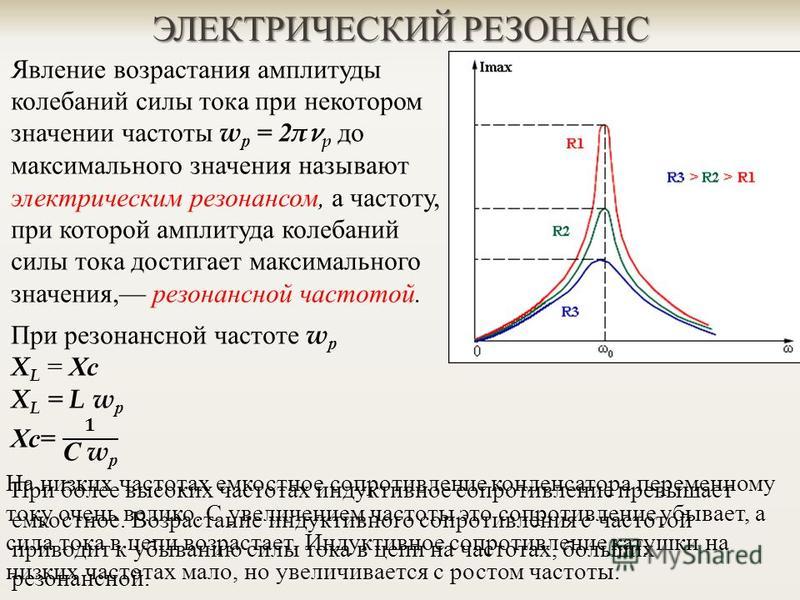 7. Количество затуханий между этими двумя пиками связанной системы зависит от соотношения масс.
7. Количество затуханий между этими двумя пиками связанной системы зависит от соотношения масс.
Теперь данное выражение можно применить для разработки поглотителя резонансных колебаний, изучения сейсмических масс и т. д. Кроме того, это выражение помогает описать динамическое взаимодействие между двумя любыми системами, если описать их как системы SDoF (вспомним, что любую сложную систему с несколькими степенями свободы всегда можно представить как набор простых систем с одной степенью свободы).
Простая модель для конструкции крепления
Для того чтобы продемонстрировать некоторые эффекты динамического взаимовлияния, упомянутые выше, давайте представим крепление и тестируемый образец с помощью простой модели и проиллюстрируем некоторые важные моменты.
Рассмотрим использование двух разных креплений для вибрационных испытаний. Для описания тестируемого образца возьмем простую систему из двух моделей, каждая из которых имеет две степени свободы DoF.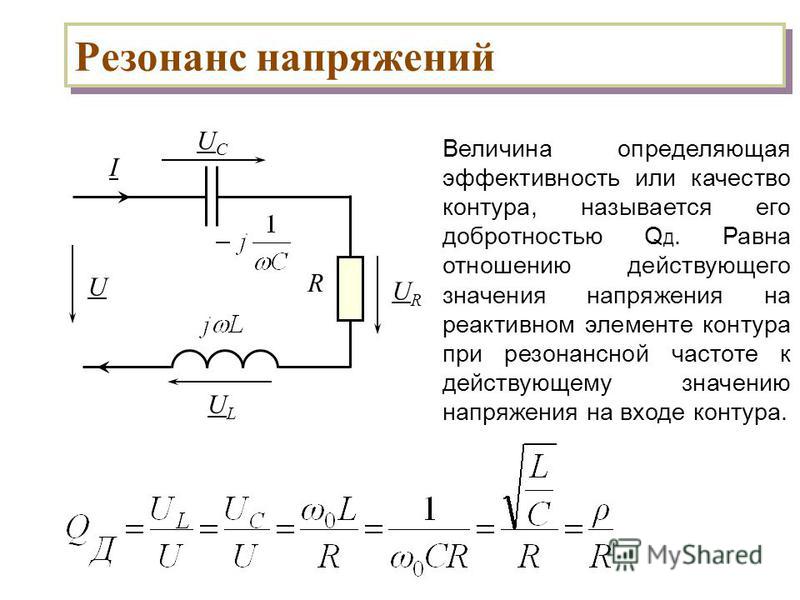 А для описания первой резонансной частоты для каждого крепления — простую модель с двумя степенями свободы. Схематически эта система показана на рис. 8.
А для описания первой резонансной частоты для каждого крепления — простую модель с двумя степенями свободы. Схематически эта система показана на рис. 8.
Рис. 8. Не связанные между собой крепление и тестируемый образец
В данном примере изделие нужно протестировать на максимальной частоте. Оба крепления имеют резонансные частоты за диапазоном рабочих тестовых частот, но крепление 1 имеет первую резонансную частоту, очень близкую к верхнему пределу диапазона рабочих частот.
Теперь рассмотрим связанные между собой элементы системы. На рис. 9 показана результирующая частота для обоих креплений.
Рис. 9. a) Несвязанные между собой крепление и тестируемые образцы; b) связанные между собой крепление и тестируемый образец
Первое, что необходимо отметить, — резонансные частоты тестируемого образца лишь немного отличаются друг от друга для двух различных креплений. Однако разница амплитуд колебаний значительная. Другими словами, интенсивность колебаний очень разная (не углубляясь в теорию, напомним, что амплитуды напрямую зависят от типа колебаний системы на каждой определенной частоте). Поэтому пока частоты меняются не сильно, формы колебаний (или, косвенно, интенсивность колебаний) очень отличаются. Это означает, что тестируемый образец будет подвергаться иным уровням ускорения, чем требуется из-за использования упругих креплений.
Однако разница амплитуд колебаний значительная. Другими словами, интенсивность колебаний очень разная (не углубляясь в теорию, напомним, что амплитуды напрямую зависят от типа колебаний системы на каждой определенной частоте). Поэтому пока частоты меняются не сильно, формы колебаний (или, косвенно, интенсивность колебаний) очень отличаются. Это означает, что тестируемый образец будет подвергаться иным уровням ускорения, чем требуется из-за использования упругих креплений.
Данный пример ясно показывает, что крепления должны быть как можно более жесткими, а их резонансная частота должна находиться далеко за пределами частот, при которых производится тестирование, иначе может произойти динамическое взаимовлияние между тестируемым образцом и креплением.
Пример расширительного стола
Последний пример показал, что даже если резонансная частота крепления находится далеко за пределами тестовой частоты, все равно наблюдается некоторое динамическое взаимодействие между тестируемым изделием и креплением. Но что, если крепление имеет резонансные частоты, лежащие в рабочем диапазоне частот тестирования?
Но что, если крепление имеет резонансные частоты, лежащие в рабочем диапазоне частот тестирования?
Изучим теоретическую модель расширительного стола с конструкцией из жестких ребер и простым креплением. Расширительная платформа теоретически смоделирована так, что имеет резонансные частоты в рабочем диапазоне частот теста. Если расширительная платформа бесконечно жесткая и не имеет резонансных частот, тогда неважно, где на расширительной платформе будет установлен тестируемый образец (но не там, где размещен акселерометр). Поэтому для такого случая были изучены две модели: одна — с тестируемым образцом, расположенным симметрично на расширительной платформе, а другая — с асимметрично расположенным на платформе образцом. Если расширительная платформа не имеет резонансных частот, тогда не имеет значения, где расположен тестируемый образец (или где расположен управляющий акселерометр).
Рис. 10. Форма колебаний для пустого расширительного стола
Для сравнения на рис. 10 показаны первые девять типов колебаний пустого расширительного стола. Заметьте, ни один тип колебаний относительно оси симметрии не будет возбуждаться однонаправленным входным воздействием.
10 показаны первые девять типов колебаний пустого расширительного стола. Заметьте, ни один тип колебаний относительно оси симметрии не будет возбуждаться однонаправленным входным воздействием.
Рис. 11. Формы колебаний для тестируемого образца, симметрично размещенного на расширительной платформе
На рис. 11 показаны первые девять типов колебаний расширительного стола с тестируемым образцом, расположенным на платформе симметрично. И снова, ни один тип колебаний относительно оси симметрии не будет возбуждаться однонаправленным входным воздействием. Заметьте, все формы колебаний в этом случае, когда крепление располагается симметрично относительно расширительного стола, также симметричны.
Рис. 12. Формы колебаний для тестируемых образцов, несимметрично размещенных на расширительной платформе
На рис. 12 показаны первые девять видов колебаний расширительного стола с тестируемым образцом, находящимся на платформе несимметрично.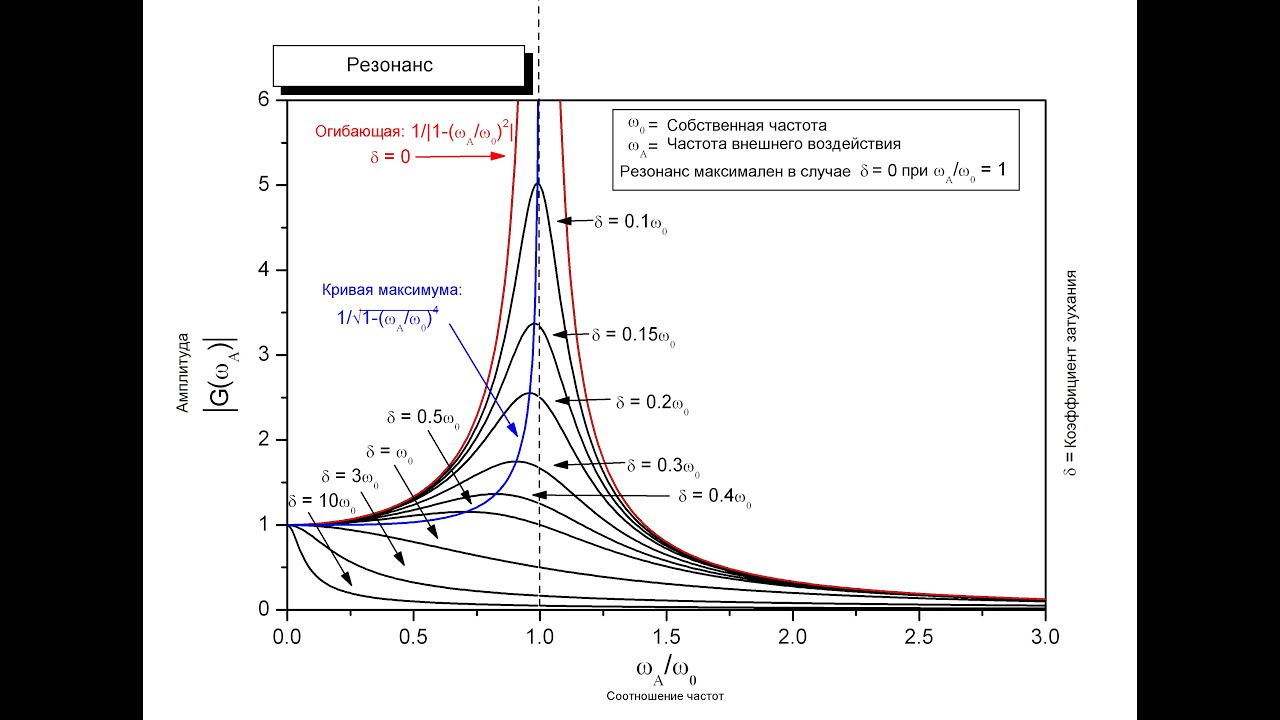 В этом случае, когда крепление расположено несимметрично относительно расширительного стола, все колебания также несимметричны. Важно отметить, что формы колебаний тестируемого образца значительно различаются для случаев симметричного и несимметричного расположения образца на расширительной платформе (рис. 11 и 12).
В этом случае, когда крепление расположено несимметрично относительно расширительного стола, все колебания также несимметричны. Важно отметить, что формы колебаний тестируемого образца значительно различаются для случаев симметричного и несимметричного расположения образца на расширительной платформе (рис. 11 и 12).
Рис. 13. Симметрично/несимметрично расположенные тестируемые образцы на резонирующей расширительной платформе
Если бы мы выполнили простые колебания и сравнили бы ответные колебания на одной из частот, то отметили бы большую разницу, как на рис. 13. Теперь, если посмотреть на ответные колебания на одной частоте, можно увидеть разницу, особенно вокруг верха испытуемого образца. При асимметричном расположении амплитуда колебаний заднего угла очень сильно отличается от амплитуд колебаний других частей. Очевидно, что и между двумя рассматриваемыми системами будет наблюдаться значительная разница.
Теперь нужно определить, где должен находиться управляющий акселерометр.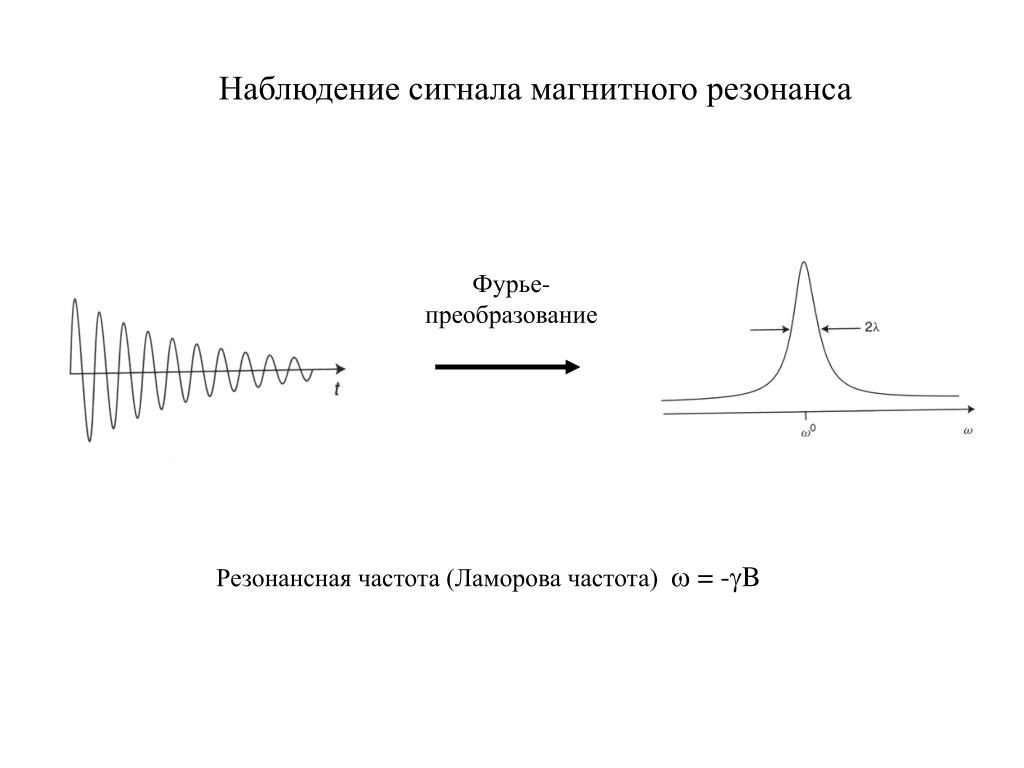 В нашем случае с этим будут сложности, поскольку расширительная платформа не является жесткой на всех частотах. При этом в зависимости от выбранного места может наблюдаться серьезная перегрузка или недогрузка тестируемого образца. Что если управляющий акселерометр расположить на самом образце? Но при асимметричном расположении наблюдается большая разница колебаний верха рамы. Поэтому обычно в таком месте управляющий акселерометр лучше не устанавливать.
В нашем случае с этим будут сложности, поскольку расширительная платформа не является жесткой на всех частотах. При этом в зависимости от выбранного места может наблюдаться серьезная перегрузка или недогрузка тестируемого образца. Что если управляющий акселерометр расположить на самом образце? Но при асимметричном расположении наблюдается большая разница колебаний верха рамы. Поэтому обычно в таком месте управляющий акселерометр лучше не устанавливать.
Но если корпус образца — это еще один промежуточный элемент на расширительной платформе, предназначенной для размещения тестируемых образов, будет ли динамический отклик корпуса/оснастки влиять на проводимый тест? Да, конечно!
Мы уже показали, как динамика движения крепления влияет на результаты проводимого теста. Управляющий акселерометр может только регулировать входной сигнал, меняя положение арматуры, и удерживать необходимый уровень. Управляющий акселерометр не может изменить динамику, основанную на взаимодействии расширительного стола и тестируемого образца.
Конечно, очень важно понять, что рассматриваемая оснастка — это не только крепление для размещения тестируемого образца, но и расширительная платформа (или стол скольжения), арматура вибростенда и промежуточное крепление для размещения тестируемого образца. При проведении вибрационных испытаний необходимо учитывать динамические характеристики всех этих элементов. Если любой из них будет иметь резонансные колебания с частотой, лежащей в диапазоне частот теста, могут возникнуть проблемы. Например, резонансная ситуация. Для изучения форм колебаний и определения данных потенциально проблемных частот полезно использовать модель конечных элементов или экспериментальный тест для определения формы колебаний.
Арматура в качестве крепления
До этого момента обсуждались только те части системы вибростенда, которые подвергаются воздействию. Однако даже пустая арматура вибростенда может иметь резонансные колебания ниже 2000 Гц. Это особенно верно для больших систем вибростендов с диаметром арматуры свыше 20 дюймов. В некоторых случаях арматура сама по себе может иметь более чем одно резонансное колебание с частотой ниже 2000 Гц.
Это особенно верно для больших систем вибростендов с диаметром арматуры свыше 20 дюймов. В некоторых случаях арматура сама по себе может иметь более чем одно резонансное колебание с частотой ниже 2000 Гц.
Такие резонансные колебания часто проявляются как трудности управления вибростендом. Поэтому инженеры, проводящие тест, немедленно начинают винить во всех проблемах систему управления, утверждая, что она «работает некорректно». Если в систему вибростенда включена расширительная платформа, то источником всех проблем видят ее. Очень редко, когда в качестве причины рассматривают механическую часть вибростенда. Но часто дело именно в ней, поскольку если арматура имеет резонансные колебания, они очень сильно влияют на тестируемый образец, расположенный на монтажной платформе вибростенда.
Рис. 14. Узел крепление/арматура
На рис. 14 проиллюстрированы возникающие проблемы с арматурой/креплением. Относительно жесткое, хорошо сконструированное крепление устанавливается на упругую арматуру, которая имеет резонансные колебания с частотами, лежащими в рабочем диапазоне частот испытания. Даже если крепление не имеет резонансных колебаний (с резонансными частотами, которые не лежат в рабочем диапазоне частот), система все равно должна рассматриваться как одно целое — ведь когда жесткое крепление устанавливается на упругую арматуру, оно все равно будет испытывать деформацию, так как связано со всей системой. Это значит, что на крепление влияет арматура, и разработать крепление, не учитывая значительную динамику присоединенной арматуры, очень сложно.
Относительно жесткое, хорошо сконструированное крепление устанавливается на упругую арматуру, которая имеет резонансные колебания с частотами, лежащими в рабочем диапазоне частот испытания. Даже если крепление не имеет резонансных колебаний (с резонансными частотами, которые не лежат в рабочем диапазоне частот), система все равно должна рассматриваться как одно целое — ведь когда жесткое крепление устанавливается на упругую арматуру, оно все равно будет испытывать деформацию, так как связано со всей системой. Это значит, что на крепление влияет арматура, и разработать крепление, не учитывая значительную динамику присоединенной арматуры, очень сложно.
Как уже обсуждалось, место размещения управляющего акселерометра вызывает проблему (например, как в случае на рис. 14). Место установки акселерометра — это деформированная гибкая поверхность, имеющая значительное влияние на проводимый тест.
Другое заблуждение состоит в том, что применение несколько управляющих акселерометров решае проблему. Но использование нескольких акселерометров для управления позволяет лишь откорректировать некое «среднее» значение ускорения согласно полученной обратной связи.
Но использование нескольких акселерометров для управления позволяет лишь откорректировать некое «среднее» значение ускорения согласно полученной обратной связи.
Решение задачи прежде всего связано с реконструкцией арматуры для снижения резонансных колебаний, вызывающих проблемы. Но в действительности никто не хочет вносить такие изменения в конструкции арматуры больших вибростендов из-за высокой стоимости и сложности. Кроме того, никто в лаборатории или на производстве не хочет стать «разоблачителем», обнаружившим, во-первых, что резонансные колебания существуют, а во-вторых, что они влияют на результаты теста.
Что же тогда делать?
Как было установлено, проблему решает разработка оснастки без резонансных колебаний для всех вибрационных испытаний. Следует помнить, что к оснастке относится арматура, расширительная платформа (или стол скольжения), промежуточные крепления и т. д.
Расчеты показали, что разработка бесконечно жесткой безынерционной оснастки без резонансных колебаний невозможна.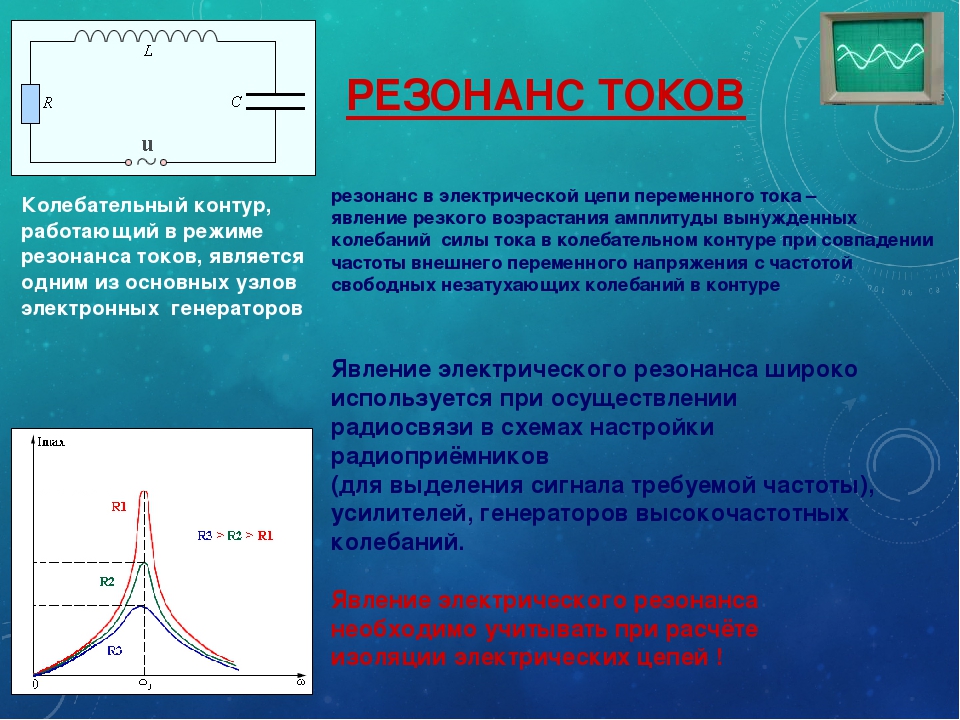 И инженерам нужно определить эффективную стратегию, а также аккуратно и полно все задокументировать.
И инженерам нужно определить эффективную стратегию, а также аккуратно и полно все задокументировать.
Арматура (или расширительная платформа) обычно имеют одно или два резонансных колебания, частоты которых необходимо определить, чтобы найти «обходной путь». На ранних стадиях разработки такой оснастки может использоваться модель конечных элементов для получения общего представления о слабых местах конструкции. Для уже существующих систем можно провести экспериментальное исследование колебаний, результаты которого помогут определить резонансные частоты и форму колебаний всего узла оснастки. Визуализация формы колебаний часто помогают наглядно выявить проблемные области. Все это позволит откорректировать возникающие проблемные частоты.
Основная задача — четко выявить проблемы, чтобы для их решения можно было применить именно инженерные решения и методы. Конечно, необходимо стремиться к получению конструкций без резонансных колебаний, а не прибегать к временным мерам, обходя проблемы.
Заключение
В статье обсуждались вопросы, связанные с выполнением динамических испытаний на вибростендах. Рассматривались резонансные и динамические воздействия и их влияние на проведение вибрационных испытаний. Данные воздействия могут иметь очень важное значение для общих характеристик теста.
Оснастка вибростендов — очень ответственная часть системы вибрационных испытаний, а потому необходимо учитывать все эти элементы (они не должны иметь резонансных колебаний в рабочем диапазоне частот испытания).
При появлении резонансных колебаний нельзя эффект от их влияния убрать только получением обратной связи от одного или нескольких акселерометров. Резонансные колебания необходимо полностью отслеживать и понять причину их возникновения. Затем необходимо получить инженерную оценку всей ситуации, чтобы проводить вибрационные тесты с лучшими возможными условиями.
Резонансные колебания имеют очень сильное влияние на проводимые вибрационные тесты. Они не исчезают при использовании системы виброконтроля и никуда не деваются, если кто-то не нашел времени для их изучения.
Они не исчезают при использовании системы виброконтроля и никуда не деваются, если кто-то не нашел времени для их изучения.
Условие ядерного магнитного резонанса — Справочник химика 21
Условие ядерного магнитного резонанса [c.253]
Основное условие ядерного магнитного резонанса выражается уравнением .. [c.272]
Метод ядерного магнитного резонанса (ЯМР), получивший широкое применение, в частности, для определения строения некоторых видов органических молекул, основан на исиользовании различия магнитных свойств атомных ядер. Так, спин ядра в атомах С, равен нулю, в атомах Н, ои равен половине, а в атомах Ы, — единице . Метод ЯМР дает возможность определять строение молекул некоторых органических соединений, подвижность частиц в кристаллах в разных условиях. Он все шире применяется при изучении кинетики и механизма химических реакций, состоятя веществ в растворах, процессов протонного обмена между молекулами в растворах, для анализа сложных смесей продуктов реакций и для других целей. [c.90]
[c.90]
Выражение (Х.З) отражает условия наблюдения ядерного магнитного резонанса. Так, в соответствии с табл. 23 и уравнениями (Х.З) — (Х.4) во внешнем постоянном магнитном поле напряженностью 1,4092 кГс резонансные частоты для ядер Н, и равны соответственно 60,54 56,446 24,4 МГц. [c.254]
В основе конструкции любого, спектрометра лежит осуществление условий ядерного магнитного резонанса (гл. 1) [c.117]
По спектру ядерного магнитного резонанса можно определить свойства ядер, строение молекул, подвижность частиц в кристаллах в разных условиях, ЯМР применяется при изучении кинетики и механизма химических реакций, состояния вещества в растворах, процессов протонного обмена меланализа сложных смесей продуктов реакции. [c.62]
Устройство спектрометров ЯМР имеет в своей основе возможность выполнения условий ядерного магнитного резонанса (1. 10), и при рассмотрении в гл. I (1.3) принципов реализации этих усло- [c.44]
10), и при рассмотрении в гл. I (1.3) принципов реализации этих усло- [c.44]
Ядерный магнитный резонанс (ЯМР). Много общего с ЭПР имеет явление резонансного поглощения электромагнитной энергии, обусловленное переориентацией магнитных моментов ядер, — ядерный магнитный резонанс. Явление это наблюдается на ядрах далеко не всех атомов. Ядра с четными числами протонов и нейтронов имеют спин / = О и, следовательно, не магнитны. Обычно ЯМР исследуют на ядрах Н , Р и спин которых / = /г. Магнитное квантовое число спина гП] в этом случае принимает два значения пц = Ч- /а и пц = —1/а. Этому отвечают в статическом магнитном поле две ориентации магнитного момента ядра— в направлении поля (т/ = = 1/2) и в противоположном (т/ — — /2), различающиеся по энергии на величину АЕ. При наложении слабого радиочастотного поля, перпендикулярного статическому, происходит резонансное поглощение, приводящее к переориентации спинов при частоте, определяемой условием резонанса V = АЕ/к. Обычно в поле порядка 10 ООО Э ([10 /4я]А/м) ЯМР наблюдается на частоте ч =42,57 мГц. Частота резонанса для ЯМР во столько же раз меньше частоты ЭПР (при одном и том же Н), во сколько раз масса ядра больше массы электрона. (Соответственно ядерный магнитный момент меньше электронного магнитного момента.) [c.149]
Частота резонанса для ЯМР во столько же раз меньше частоты ЭПР (при одном и том же Н), во сколько раз масса ядра больше массы электрона. (Соответственно ядерный магнитный момент меньше электронного магнитного момента.) [c.149]
Подставляя выражение АЕ из последней формулы в предшествующую, получаем условие ядерного магнитного резонанса, связывающего частоту Уо возбужденных переходов между двумя уровнями для атомов, имеющих гиромагнитное отношение у и находящихся в постоянном магнитном поле напряженности [c.280]
Физической величиной, измеряемой в условиях ядерного магнитного резонанса, является не магнитный момент одиночного атомного ядра, а так называемая ядерная намагниченность вещества, представляющая собой сумму средних значений магнитных моментов всех атомных ядер данного тина, заключенных в единице объема этого вещества [c.53]
Ядерный магнитный резонанс. Все рассмотренные нами до сих пор методы атомного и молекулярного спектрального анализа относились к оптическим областям спектра. Но оказалось, что и в радиоволновой области в определенных условиях можно получать ценные сведения о структуре химических, особенно органических, соединений. Метод ядерного магнитного резонанса, первые практические применения которого имеют всего 10 — 15-летнюю давность, стал в настоящее время одним из основных методов установления структуры органических соединений. Одновременно быстро увеличивается круг его применения для целей качественного и количественного анализа, особенно в случае сложных задач, когда применение других методов мало эффективно. Уже в настоящее время в ряде производств сложных органических соединений в химико-фармацевтической промышленности и производстве красителей для цветных фотоматериалов ход производства и качество готовой продукции контролируется методом ядерного магнитного резонанса. Несомненно, что и в ближайшем будущем применение этого метода в аналитических целях будет стремительно расти.
Все рассмотренные нами до сих пор методы атомного и молекулярного спектрального анализа относились к оптическим областям спектра. Но оказалось, что и в радиоволновой области в определенных условиях можно получать ценные сведения о структуре химических, особенно органических, соединений. Метод ядерного магнитного резонанса, первые практические применения которого имеют всего 10 — 15-летнюю давность, стал в настоящее время одним из основных методов установления структуры органических соединений. Одновременно быстро увеличивается круг его применения для целей качественного и количественного анализа, особенно в случае сложных задач, когда применение других методов мало эффективно. Уже в настоящее время в ряде производств сложных органических соединений в химико-фармацевтической промышленности и производстве красителей для цветных фотоматериалов ход производства и качество готовой продукции контролируется методом ядерного магнитного резонанса. Несомненно, что и в ближайшем будущем применение этого метода в аналитических целях будет стремительно расти. [c.342]
[c.342]
Величина магнитного момента всех ядер одного изотопа строго одинакова и поэтому на первый взгляд кажется, что в спектре должна присутствовать только одна линия поглощения. На самом деле это не так. Кроме внешнего магнитного поля, в любой молекуле имеются внутренние поля, обусловленные движением электронов. В зависимости от положения, которое занимает данный атом и его ядро в молекуле, оно окажется в определенном внутреннем поле. Поэтому для ядер, находящихся в молекуле в различных положениях, условие резонанса будет наступать при различных значениях внешнего поля в зависимости от того вклада, который вносит в данном месте внутреннее поле. Этот вклад очень мал обычно внутренние поля примерно в миллион раз слабее внешнего. Однако современные спектрометры ядерного магнитного резонанса имеют очень высокую разрешающую способность и дают отдельные линии поглощения для ядер, которым соответствует разница в напряженности внутренних полей, меньшее одной стомиллионной доли от напряженности внешнего поля. [c.343]
[c.343]
Дальнейшее развитие теории требует уточнения количественных оценок и рассмотрения кинетики самоорганизации. Экспериментальный подход к проблеме состоит в изучении кинетики ренатурации белков при постоянных внешних условиях. Сведения о термодинамически устойчивых стадиях ренатурации при изменяющихся внешних условиях можно получить с помощью ядерного магнитного резонанса (см. 5.10). [c.254]
Сущность ядерного магнитного резонанса заключается в резонансном поглощении электромагнитных волн веществом, находящимся в постоянном магнитном поле, при условии, что это поглощение обусловлено ядерным магнетизмом (этим ЯМР отличается от ЭПР). [c.213]
Спектроскопия магнитного резонанса отличается от других видов спектроскопии тем, что расщепление энергетических уровней существует только в присутствии магнитного поля. Для обычно достижимых в лабораторных условиях магнитных полей переходы между уровнями энергии ядер, являющихся магнитными диполями, наблюдаются в радиочастотной области, а переходы между уровнями энергии спинов неспаренных электронов —в микроволновой области. Эти новые спектроскопические методы — ядерный магнитный резонанс (ЯМР) и электронный парамагнитный резонанс (ЭПР) дают богатую структурную информацию, что делает их незаменимыми в химии. [c.495]
Эти новые спектроскопические методы — ядерный магнитный резонанс (ЯМР) и электронный парамагнитный резонанс (ЭПР) дают богатую структурную информацию, что делает их незаменимыми в химии. [c.495]
Измерение ядерного магнитного резонанса (ЯМР) — метод анализа, основанный на резонансном поглощении электромагнитных волн веществом, помещенным в постоянное магнитное поле. Ядерный магнитный резонанс использует явление ядерного магнетизма. Атомные ядра многих химических элементов имеют определенный момент количества движения, т. е. вращаются вокруг собственной оси (спин ядра). Спин ядра аналогичен спину электрона. Магнитный момент возникает потому, что каждое ядро имеет электрический заряд. Для наблюдения ЯМР ампулу, содержащую анализируемое вещество, помещают в катушку радиочастотного генератора. Образец может быть жидким, твердым или газообразным. Катушку с ампулой помещают в зазоре магнита перпендикулярно направлению магнитного поля Ни- Генератор создает на катушке слабое переменное магнитное поле Нх- Резонанс наступает при условии ф=фо= У о, где ф — скорость вращающегося поля Нх, фо — скорость прецессии ядер в поле На, 7 — гиромагнитное отношение у = т1Р (т — магнитный момент ядра атома, Р — момент количества движения ядра). При выполнении условия приемник регистрирует небольшое изменение напряжения на рабочем контуре в виде сигнала в форме гауссовой кривой. Кривая характеризуется высотой сигнала и шириной кривой (полосы), [c.452]
При выполнении условия приемник регистрирует небольшое изменение напряжения на рабочем контуре в виде сигнала в форме гауссовой кривой. Кривая характеризуется высотой сигнала и шириной кривой (полосы), [c.452]
Сущность метода ядерного магнитного резонанса (ЯМР) заключается в том, что, помещая вещество, содержащее атомы (водорода), ядра которых обладают магнитным моментом, в сильное постоянное магнитное поле и накладывая на эту систему значительно более слабое высокочастотное электромагнитное излучение, можно ири соблюдении определенных условий наблюдать резонансное поглощение энергии, происходящее на строго определенной частоте, зависящей от положения атома (водорода) в молекуле вещества. По спектрам ядерного магнитного резонанса в компонентах битума можно определить относительное количество протонов, находящихся в ароматических кольцах, в метиленовых и метильных группах, а также при насыщенных атомах углерода, непосредственно связанных с кольцом ( бензольный водород ). Используя эти данные и данные [c.25]
Используя эти данные и данные [c.25]
Спектры ядерного магнитного резонанса состоят из линий, каждая из которых отвечает переходу между определенной парой (т, п) уровней энергии ядерных спинов. Положение этих спектральных линий соответствует резонансному условию [c.77]
Оценим чувствительность метода СПЯ для регистрации спектров ЭПР короткоживущих РП. При комнатной температуре в полях порядка нескольких тесла, которые применяются в современных экспериментах по ядерному магнитному резонансу, равновесная поляризация спинов протонов порядка 10 В этих условиях удается регистрировать спектр ЯМР, если в образце находится порядка 10 протонов. Значит, спектрометры ЯМР позволяют измерить поляризацию порядка = 10 — 10 = 10 . Пусть г — время жизни РП, оно порядка наносекунд, а Т, — время релаксации поляризованных ядер — это время порядка секунд. Если стационарная концентрация РП равна N, то стационарная концентрация поляризованных ядер равна [c. 132]
132]
Таким образом, для наблюдения ядерного магнитного резонанса необходимо поместить образец в сильное однородное магнитное по ле Яо и подействовать на него излучением с частотой V, удовлетворяющей уравнению (1). При этих условиях будут происходить переходы с одного ядерного магнитного уровня на другой. Вероятность переходов на верхний и на нижний уровни одинаковы. Однако число магнитных ядер, находящихся на каждом из уровней, различно заселенность нижнего уровня выше, поскольку система всегда стремится перейти в состояние с более низкой энергией. При обычных температурах разность заселенности верхнего и нижнего уровней не превышает 10 от общего числа магнитных ядер. Именно эта незначительная разница обусловливает явление ядерного магнитного резонанса, т, е. поглощение радиочастотного излучения в соответствии с уравнением (1). Разность в заселенности уровней, обеспечивающая непрерывность поглощения, поддерживается за счет так называемой спин-решеточной релаксации. [c. 97]
97]
Следует обратить особое внимание на то, что простые правила, сформулированные выше для объяснения сверхтонкой структуры в спектрах ядерного магнитного резонанса, применимы только к группам магнитно эквивалентных ядер. Если ядра в группе магнитно неэквивалентны, то непосредственно из спектра уже нельзя получить отдельные константы спин-спинового взаимодействия, а химический сдвиг можно с достаточной точностью определить по центру мультиплета без анализа спек тра лишь при условии, что выполняется соотношение 7/уоб С 0,1 разд. 2.3.2 этой главы). Это легко видеть, сравнив спектры [c.56]
В то же время в периодической системе элементов имеется достаточное количество магнитных ядер, подходящих для экспериментов по ЯМР, н, таким образом, вещество как бы содержит различные датчики, позволяющие исследовать свойства составляющих его молекул и вещества как целого. В гл. X будут обсуждены некоторые из этих возможностей. Кроме того, в ЯМР всегда возможны разнообразные вариации экспериментальных условий, а физика спиновых систем остается и до сих пор столь же волнующей областью, какой она была в период становления спектроскопии ЯМР. Поэтому ядерный магнитный резонанс, несомненно, относится к числу наиболее универсальных спектроскопических методов. В настоящей главе читателю предстоит познакомиться с теми из специальных методик ЯМР, которые зарекомендовали себя как наиболее важные для химии. [c.300]
Поэтому ядерный магнитный резонанс, несомненно, относится к числу наиболее универсальных спектроскопических методов. В настоящей главе читателю предстоит познакомиться с теми из специальных методик ЯМР, которые зарекомендовали себя как наиболее важные для химии. [c.300]
Распространяя такой подход на все остальные колебательные полосы воды, можно получить еш е пятую характеристику структуры воды. На этот раз удается установить два ее кинетических свойства. Как было описано выше (см. гл. III, п. 5), достаточно интенсивная при 5° С полоса трансляционных колебаний воды vj, положение максимума которой не зависит от температуры, при 50° С практически полностью исчезает (см. рис. 61). Выше было показано, что положение V7-полосы не зависит от размера комплекса (см. гл. III, п. 5). Энергия и силовая постоянная водородной связи, последняя из которых определяет частоту vy, при повышении температуры от 5 до 50° С почти не меняются (см. гл. III, п. 2 и гл. V, п. 3). Таким образом, исчезновение vr-полосы жидкой воды при нагревании ее на 45° можно объяснить только тем, что в результате указанного повышения температуры число водородных связей со временем жизни больше 1,5-10 сек уменьшилось на порядок. Этот вывод полностью согласуется с данными, полученными методом ядерного магнитного резонанса, по которым это время при нормальных условиях оценивается lO ii — 10 сек. Кроме того, из температурного поведения vt-полосы следует, что при 50° С практически не остается молекул воды, живущих в связанном состоянии хотя бы 2-10 сек. [c.153]
Этот вывод полностью согласуется с данными, полученными методом ядерного магнитного резонанса, по которым это время при нормальных условиях оценивается lO ii — 10 сек. Кроме того, из температурного поведения vt-полосы следует, что при 50° С практически не остается молекул воды, живущих в связанном состоянии хотя бы 2-10 сек. [c.153]
Метод спектроскопии ядерного магнитного резонанса (метод ЯМР) в принципе применим для обнаружения, выяснения положения в молекуле и количественного определения Щ (и Н), и а также комбинированных меток типа — С, и т. п. Метод не требует никакой химической обработки меченого соединения и даже его выделения в особо чистом состоянии интерпретация основывается на результатах исследования немеченого соединения в тех же условиях тем же методом. Метод находит все более широкое применение, что связано с растущей доступностью соответствующих приборов, особенно для определения С. Метод ЯМР может не только заменить радиоизотопный метод, но и обеспечить информацией, не доступной при использовании других методов. Поэтому широкое внедрение метода ЯМР привело [c.475]
Поэтому широкое внедрение метода ЯМР привело [c.475]
В условиях ядерного магнитного резонанса эквивалентные ядра проявляют одинаковые химические сдвиги как в хиральн1з1Х, так и в ахиральных раство- [c.26]
Химический функциональный анализ далеко не всегда позволяет однозначно установить структуру органических соединений. Некоторые группы дают сходные реакции. Иногда вещества в условиях определения оказываются неустойчивыми. Функциональный анализ не нозволяет судить о составе смесей, числе тех или иных групп и о макроструктуре вещества (простраиствеином строении, структуре кристаллов или жидкости, межмолекулярных взаимодействиях и т, п.). Вследствие этого существенную роль в исследовании строения и свойств соединений играют физико-химические, или инструментальные, методы анализа спектральные, электрохимические, хроматографические, радиометрические и др. Для установления структуры вещества чаще всего используют методы, основанные на взаимодействии вещества или смеси веществ, их растворов с различного вида излучениями. К ним относятся ультрафиолетовая, видимая, инфракрасная спектроскопия, метод люми-иесценцин, оптический и рентгеновский спектральный анализ, рефрактометрия, поляриметрия, метод ядерного магнитного резонанса. На взаимодействии с магнитным полем основан метод электронного парамагнитного резонанса, а последовательно с электрическим и магнитным — масс-спектрометрия. Некоторые из этих методов рассмотрены в посебии. [c.82]
К ним относятся ультрафиолетовая, видимая, инфракрасная спектроскопия, метод люми-иесценцин, оптический и рентгеновский спектральный анализ, рефрактометрия, поляриметрия, метод ядерного магнитного резонанса. На взаимодействии с магнитным полем основан метод электронного парамагнитного резонанса, а последовательно с электрическим и магнитным — масс-спектрометрия. Некоторые из этих методов рассмотрены в посебии. [c.82]
В тридцатых — сороковых годах произошел резкий скачок в технических возможностях изучения химического состава сложных смесей. Для разделения тяжелых нефтяных фракций наряду с методами перегонки и ректификации начали использовать хроматографию на адсорбентах, комплексообразование с карбамидом, термическую диффузию. Получили широкое распространение многочисленные физические методы исследования УФ- и ИК-опектроскопия, ядерно-магнитный резонанс, масс-опектрометрия, дифференциально-термический анализ, электрофизические методы (определение диэлектрической проницаемости, удельного и объемного сопротивлений, диэлектрических потерь) и др. Большое применение нашли расчетные методы определения структурно-группового состава, позволившие в первом приближении получить представление о соста1ве масляных фракций. Новые методы разделения и анализа значительно углубили наши познания о составе и структуре тяжелых компонентов нефти и позволили более обоснованно решать технологические задачи производства масел и химмотологические проблемы рационального их использования в условиях эксплуатации. [c.8]
Большое применение нашли расчетные методы определения структурно-группового состава, позволившие в первом приближении получить представление о соста1ве масляных фракций. Новые методы разделения и анализа значительно углубили наши познания о составе и структуре тяжелых компонентов нефти и позволили более обоснованно решать технологические задачи производства масел и химмотологические проблемы рационального их использования в условиях эксплуатации. [c.8]
В методе ядерного магнитного резонанса минимальная естественная ширина пинии составляет 0,1 с (Гц). Следовательно, уширение снеггральных пиний, регистрируемое этим методом, позволяет, согласно (12.5), фиксировать обменные процессы с временами ХИ31Ш ниже 2 с или со скоростями, превышающими 0,5 с . Для слияния одиночных пиков сигналов, принадлежащих двум вза-имопревращающимся изомерам или топомерам и разделенных, например, на 200 Гц (обычный диапазон химических сдвигов в спектрах ЯМР- С), скорость процесса химического обмена должна быть равна 10 с Поскольку скорость реакции является функцией температуры (8.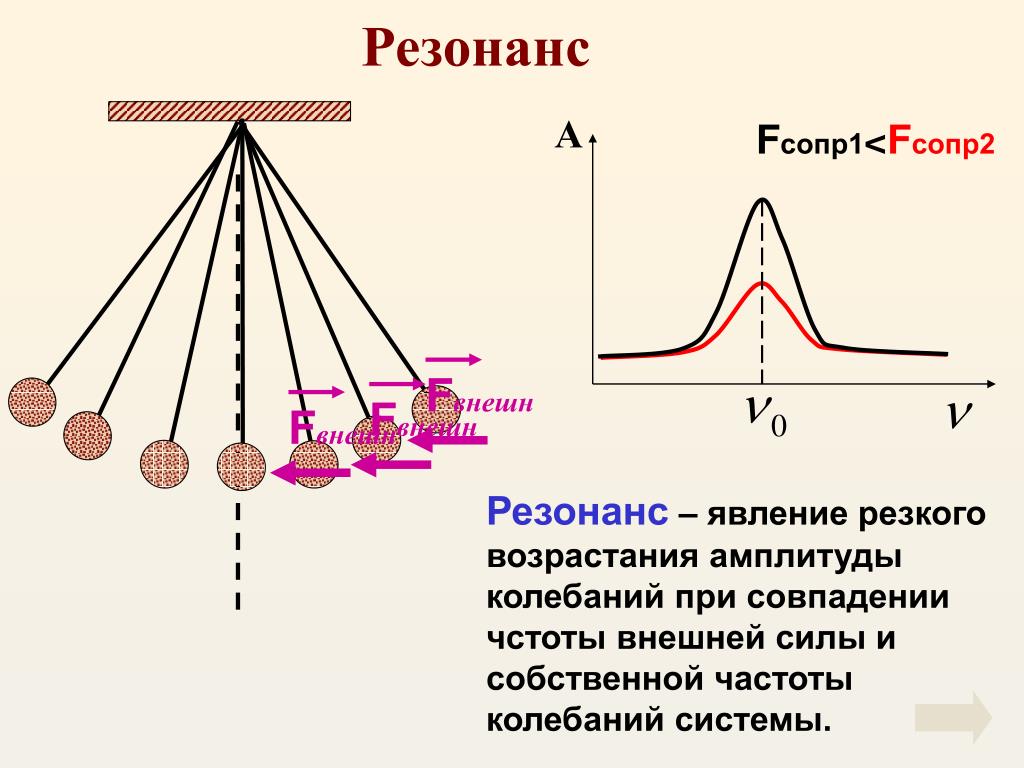 104), для одного и того же процесса при разных температурах можно выполнить условия как очень быстрого (г >Та), [c.462]
104), для одного и того же процесса при разных температурах можно выполнить условия как очень быстрого (г >Та), [c.462]
Если систему ядер, обладающих магнитными моментами, поместить во внешнее магнитное поле, то на них будет действовать сила, которая сориентирует их магнитные оси в направлении этого поля. В определенных условиях, характерных для данного ядра, магнитные моменты ядра будут резонансно поглощать энергию переменного. магнитного поля, частота изменения которого лежит в радиоднапазоне. Это поглощение приводит к возникновению ядерного магнитного резонанса (ЯМР). Первые успешные эксперименты по ядерному магнитному резонансу были проведены в конце 1945 г. независимо двумя группами исследователей под руководством Перселла и Блоха. [c.727]
Условие резонанса (652) по существу является одним и тем же и для электронных, и для ядерных магнитных переходов. Разница состоит лишь в том, что в случае ядерного магнитного резонанса (ЯМР) в уравнение (652) вместо магнетона Бера и gj — фактора Ланде — входят ядерный магнетон (ЯМ) (см.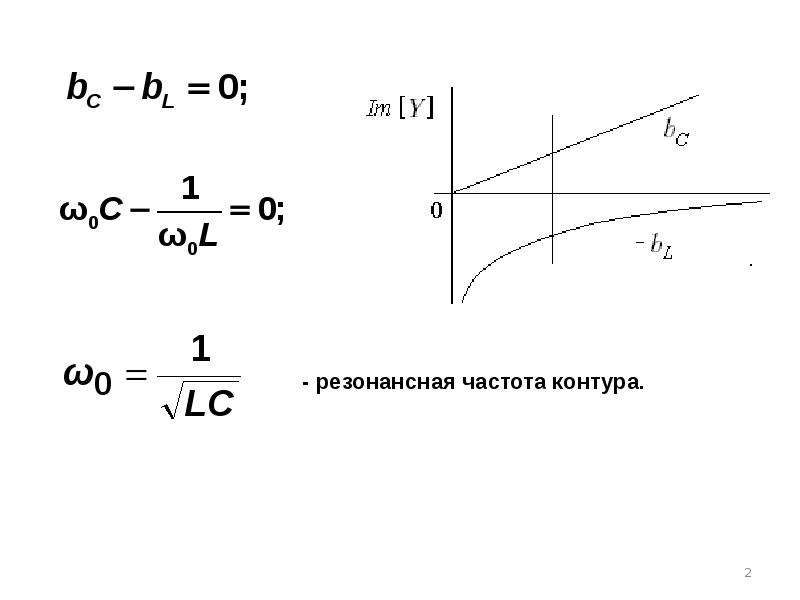 гл. VI, 1) и яд — фактор ядра, учитывающий сложную структуру ядра. В силу того, что М 1836m, резонансная частота ЯМР заметно меньше частоты электронного парамагнитного резонанса (ЭПР). Поэтому электронный резонанс наблюдается при микроволновых частотах в диапазоне 1 —10 Гц [8, 91, тогда как при исследовании ядерного магнитного резонанса обычно используют диапазон коротких радиоволн [10, 11]. [c.366]
гл. VI, 1) и яд — фактор ядра, учитывающий сложную структуру ядра. В силу того, что М 1836m, резонансная частота ЯМР заметно меньше частоты электронного парамагнитного резонанса (ЭПР). Поэтому электронный резонанс наблюдается при микроволновых частотах в диапазоне 1 —10 Гц [8, 91, тогда как при исследовании ядерного магнитного резонанса обычно используют диапазон коротких радиоволн [10, 11]. [c.366]
Баргон И., Фишер X. и Йонсен Ю., изучая спектры ядерного магнитного резонанса (ЯМР) диамагнитных продуктов сразу после их образования, впервые наблюдали химически индуцированную неравновесную поляризацию ядерных спинов [5] интенсивность линий в спектре существенно превосходила соответствующую величину в условиях термодинамического равновесия. Вскоре было показано, что химически индуцированная поляризация ядер может привести и к эмиссии на резонансных частотах ЯМР. В продуктах химических реакций спектры ЯМР обнаруживают два типа эффекта ХПЯ — интегральный и мультиплетный. Интегральный эффект характеризует суммарную интенсивность отдельных мультиплетов в спектре ЯМР, которые возникают благодаря спин-спиновому взаимодействию ядер. Мультиплетный эффект характеризует появление эмиссии и усиленного поглощения линий внутри мультиплетов. Для иллюстрации на рис. 2 приведены Фурье-образы спада сигнала свободной индукции, полученные после действия 7г/4 и 37г/4 импульсов (два верхних спектра, соответственно). Эти результаты получены для фотолиза ди-терт-бутил кетона. Их сумма дает интегральный эффект ХПЯ, в то время как их разность (нижний спектр на рис. 2) дает мультиплетный эффект ХПЯ. [c.6]
Интегральный эффект характеризует суммарную интенсивность отдельных мультиплетов в спектре ЯМР, которые возникают благодаря спин-спиновому взаимодействию ядер. Мультиплетный эффект характеризует появление эмиссии и усиленного поглощения линий внутри мультиплетов. Для иллюстрации на рис. 2 приведены Фурье-образы спада сигнала свободной индукции, полученные после действия 7г/4 и 37г/4 импульсов (два верхних спектра, соответственно). Эти результаты получены для фотолиза ди-терт-бутил кетона. Их сумма дает интегральный эффект ХПЯ, в то время как их разность (нижний спектр на рис. 2) дает мультиплетный эффект ХПЯ. [c.6]
После того как было изучено регулярное строение натурального каучука, исследователи неоднократно предпринимали попытки синтезировать полимеры, которые бы обладали сходными с ним структурой и свойствами. Многочисленные опыты полимеризации диенов дали интересные результаты, позволившие сделать теоретические выводы о влиянии температуры, инициаторов и роли поли-меризационной среды на способ соединения молекул мономера в цепи. Так, например, была высказана мысль о том, что более высокая температура способствует присоединению мономера по принципу А-Цис, а более низкая — по принципу , А-гранс это объяснялось различием в свободных энергиях активации этих типов реакций. И хотя долгое время не удавалось доказать справедливость этой гипотезы для полимеризации диенов, именно благодаря ее использованию был достигнут дальнейший прогресс в области получения полимеров с регулярной молекулярной структурой. Только недавно, с применением высокочувствительных физических методов, в особенности ядерного магнитного резонанса, было установлено, что при полимеризации виниловых мономеров с заместителями, имеющими большой объем, в условиях низких температур образуются соединения с повышенным содержанием фракций син-диотактической структуры. [c.8]
Так, например, была высказана мысль о том, что более высокая температура способствует присоединению мономера по принципу А-Цис, а более низкая — по принципу , А-гранс это объяснялось различием в свободных энергиях активации этих типов реакций. И хотя долгое время не удавалось доказать справедливость этой гипотезы для полимеризации диенов, именно благодаря ее использованию был достигнут дальнейший прогресс в области получения полимеров с регулярной молекулярной структурой. Только недавно, с применением высокочувствительных физических методов, в особенности ядерного магнитного резонанса, было установлено, что при полимеризации виниловых мономеров с заместителями, имеющими большой объем, в условиях низких температур образуются соединения с повышенным содержанием фракций син-диотактической структуры. [c.8]
Уравнение (I. 10) описывает так называемое условие резонанса, при котором частота излучения точно соответствует энергетической щели. Спектральная линия ядерного магнитного резонанса соответствует переходу, который обозначен стрелкой на рис. 1.2, 3 vo (ларморова частота) в соответствии с уравнением (I. 10) изменяется в зависимости от величины поля Во, испвйьэввАнж [c.19]
1.2, 3 vo (ларморова частота) в соответствии с уравнением (I. 10) изменяется в зависимости от величины поля Во, испвйьэввАнж [c.19]
Внимание, уделяемое изучению природы воды и ее роли в различных и особенно комплексных соединениях, непрерывно растет. Усиление интереса к природе воды вызвано не столько увеличением числа веществ, в составе которых она обнаружена, сколько тем, что эта миниатюрная, предельно простая молекула проявляет в этих веществах все новые и новые свойства. Наряду с хорошо известными аномалиями воды, такими как тепловое расширение, вязкость и теплопроводность, в последние годы обнаружен еще целый ряд совершенно новых, ранее никогда не предсказывавшихся и поэтому неожиданных свойств воды. Это, во-первых, очень высокая способность паров воды растворять при 400 С такие практически не растворимые при нормальных условиях вещества, как А12О3, Ре Оз, СаСОзИдр. 101, 156, 399], во-вторых, повышение предельных концентраций многих неорганических веществ в водных растворах, набухание клеток и протоплазмы и изменение объемов смешения водных растворов со спиртом под влиянием магнитного поля [165, 172] и, наконец, изменение во времени спектра ядерного магнитного резонанса воды, уже достигшей постоянной температуры [277]. [c.5]
[c.5]
Это обусловливает необходимость создания и внедрения методов контроля качества сырья, материалов и готовых изделий, что является важным условием развития производства полимеров. Качество полимерного материала характеризуется совокупностью его свойств, определяющих пригодно материала для использованм в тех или иных целях. Современный уровень экспериментальной техники позволяет описать свойства материгша на всех у ювнях атомномолекулярном (фотоэлектронная, рентгеновская, электронная и колебательная спектроскопия, ядерный магнитный резонанс, рассеяние нейтронов, эмиссионный анализ и т.д.) надмолекулярном (диэлектрическая и механическая релаксация, рентгенография, электронография, анш гиляция позитронов, рассеяние синхротронного излучения и т.д.) макроскопическом (вязкость, прочность, удлинение при разрыве, сопротивление изгибу, электрическому пробою и т.д.). [c.22]
Для измерения температуры стеклования каучуков может быть использован метод многоимпульсного спин-локинга [24]. Этот импульсный метод ядерного магнитного резонанса позволяет проводить релаксационные измерения на частотах порядка 10 Гц. Условия возникновения минимума на релаксационной кривой (см. рис. 14.4) определяются соотношением [c.385]
Этот импульсный метод ядерного магнитного резонанса позволяет проводить релаксационные измерения на частотах порядка 10 Гц. Условия возникновения минимума на релаксационной кривой (см. рис. 14.4) определяются соотношением [c.385]
Бермудец [69] использовал протонный ядерный магнитный резонанс для определения числа поверхностных силанольных групп даже прп условии покрытия поверхности адсорбированной водой толщиной вплоть до трех монослоев. Силикагель имел удельную поверхность 800 м /г, а найденная концентрация силанольных групп составила 7-10″ моль/м или 4,2 ОН-групп/нм . [c.875]
Спектроскопия поверхностного плазмонного резонанса
Дата публикации: 11.06.2020 00:00
Метод спектроскопии поверхностного плазмонного резонанса, также спектроскопия ППР – один из новых методов для изучения структуры и динамики молекулярных систем. Наряду со спектроскопией локального поверхностного плазмонного резонанса (ЛППР), спектроскопия ППР широко применяется в биохимии для наблюдения взаимодействия между антителами и антигенами.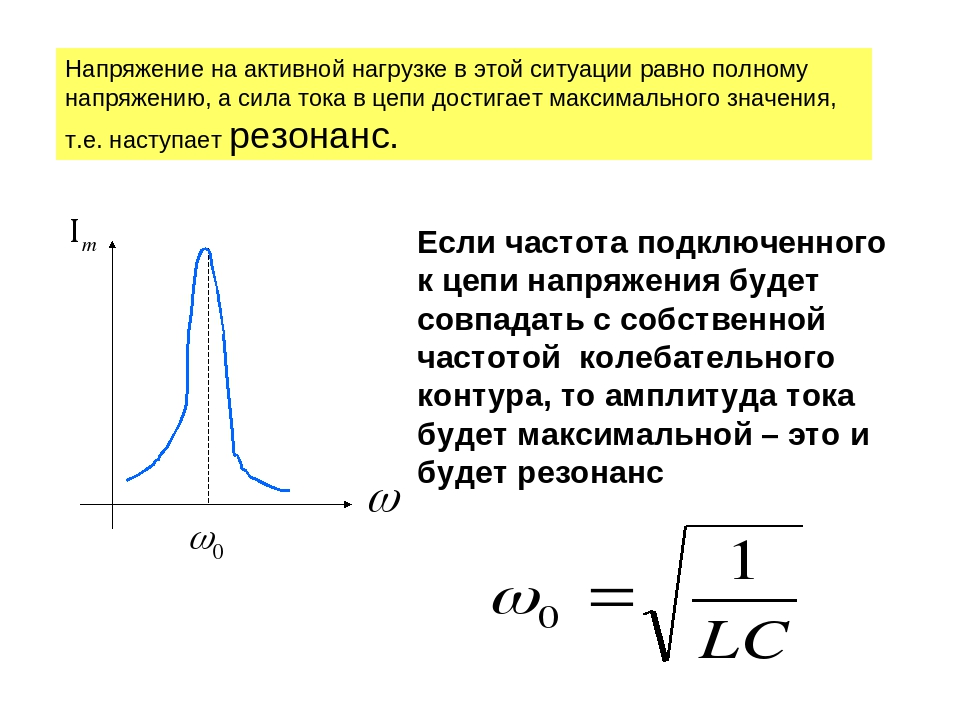 Изучение явления ППР стало ключом к созданию множества сенсорных систем для исследования образования и диссоциации как низкомолекулярных соединений, так и макромолекул. Примечательно, что в основе многих видов спектроскопии – рамановской, инфракрасной, флуоресцентной – лежит именно феномен ППР.
Изучение явления ППР стало ключом к созданию множества сенсорных систем для исследования образования и диссоциации как низкомолекулярных соединений, так и макромолекул. Примечательно, что в основе многих видов спектроскопии – рамановской, инфракрасной, флуоресцентной – лежит именно феномен ППР.
В этой статье кратко рассматриваются способы возбуждения поверхностного плазмонного резонанса, различия между ЛППР и ППР, примеры приложений.
Возбуждение поверхностных плазмонов
Плазмонами называют псевдочастицы, образованные квантами колебаний электронного газа в металле или диэлектрике. Подобно электромагнитной волне, поверхностные плазмоны задаются волновым вектором. Амплитуда волнового вектора зависит от относительной проводимости (диэлектрической постоянной) вещества. Если среда не имеет магнитных свойств, диэлектрическая постоянная приравнивается к квадратному корню из показателя преломления, следовательно, обладает зависимостью от длины волны.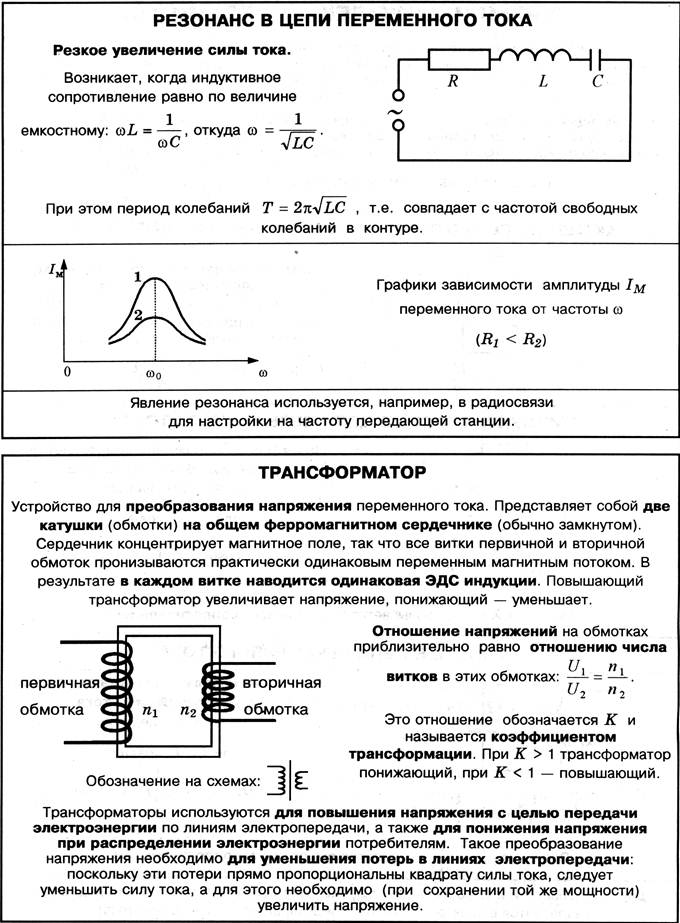 Любое изменение показателя преломления в приграничной области ведет к изменению условий ППР, еще одно условие эффективного возбуждения плазмона связано с поляризацией падающей волны. В ППР системах в основном используют плоскополяризованные волны, у которых вектор электрического поля параллелен плоскости падения: такие волны сильнее всего взаимодействуют с электронами в проводящей пленке.
Любое изменение показателя преломления в приграничной области ведет к изменению условий ППР, еще одно условие эффективного возбуждения плазмона связано с поляризацией падающей волны. В ППР системах в основном используют плоскополяризованные волны, у которых вектор электрического поля параллелен плоскости падения: такие волны сильнее всего взаимодействуют с электронами в проводящей пленке.
ППР-детекторы состоят из тонкой металлической пленки (чаще из золота или серебра из-за высокой химической устойчивости), нанесенной на диэлектрическую подложку (кварцевое стекло). Как в оптическом волокне, возникновение поверхностного плазмонного резонанса основано на явлении полного внутреннего отражения: при прохождении света из одной (оптически плотной) оптической среды в другую (оптически менее плотную) под углом падения, отвечающем углу преломления 90°, волна не сможет проникнуть вглубь оптически менее плотной среды. Однако электрическое поле фотонов все же проникает в среду с меньшим показателем преломления на расстояние порядка длины волны света.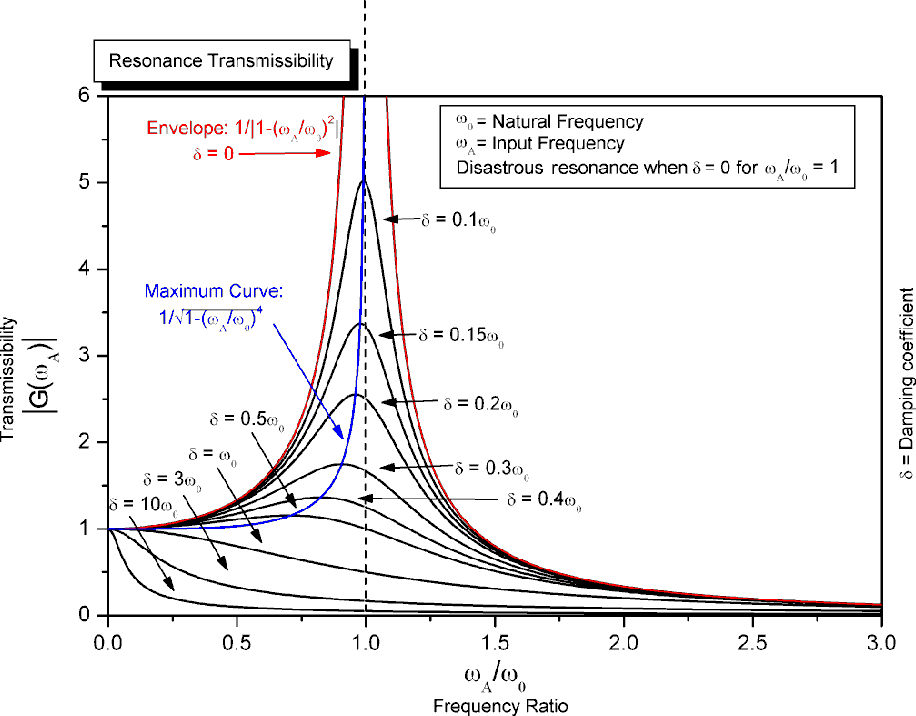 Для эффективного возбуждения ППР частота света должна быть ниже плазменной частоты (собственной частоты колебаний электронов) металла. Для большинства металлов плазменная частота принадлежит УФ диапазону, потому для возбуждения ППР применяется излучение видимой и ИК области.
Для эффективного возбуждения ППР частота света должна быть ниже плазменной частоты (собственной частоты колебаний электронов) металла. Для большинства металлов плазменная частота принадлежит УФ диапазону, потому для возбуждения ППР применяется излучение видимой и ИК области.
На практике импульс плазмонов оказывается больше импульса фотонов, поэтому для возникновения ППР используют согласующие устройства различных типов: призменные, волноводные, дифракционные, а также фотонные кристаллы. Механизм ППР в волноводах рассматривается далее.
Локальный поверхностный плазмонный резонанс
Локальный поверхностный плазмонный резонанс, в отличие от поверхностного плазмонного резонанса, в металлически наночастицах реализуется и без согласующих приспособлений. Механизм возникновения ЛППР в наночастицах в статье не рассматривается, однако для дальнейших рассуждений необходимо отметить следующее: чем выше поверхностная плотность заряда, тем сильнее усиливается импульс плазмонов. По этой причине в ЛППР и ППР основным материалом для пленок является серебро и золото: относительная проводимость этих металлов является самой высокой.
По этой причине в ЛППР и ППР основным материалом для пленок является серебро и золото: относительная проводимость этих металлов является самой высокой.
Оптические волноводные сенсоры на основе ППР
Метод поверхностного плазмонного резонанса используется при разработке оптоволоконных датчиков для эксплуатации в неблагоприятных условиях. Оптоволоконные зонды изготавливают путем снятия оболочки с участка волоконно-оптического кабеля, далее этот участок покрывается металлическим, а затем диалектическим слоем. Группа ученых в Индийском технологическом институте (Дели) недавно опубликовала результаты исследования эффективности обнаружения паров хлора с помощью оптоволоконного зонда на основе ППР. Сердцевина оптического волокна была покрыта слоем серебра, защитное покрытие было выполнено из оксида цинка. Эксперимент был поставлен с использованием оборудования Avantes: в качестве широкополосного источника излучения выбран AvaLight-HAL, спектр пропускания регистрировался с помощью оптоволоконного спектрометра AvaSpec-ULS3648-USB2. Молекулы газообразного хлора взаимодействовали с оксидом цинка, образуя хлорид цинка. Продукт реакции влияет на относительную диэлектрическую проницаемость и показатель преломления, изменяя длину волны возбуждения поверхностных плазмонов. На рисунке 1 приведены измеренные спектры как функции концентрации хлора, демонстрирующие диапазон обнаружения спектрометра Avantes от 10 до 100 частей на миллион.
Молекулы газообразного хлора взаимодействовали с оксидом цинка, образуя хлорид цинка. Продукт реакции влияет на относительную диэлектрическую проницаемость и показатель преломления, изменяя длину волны возбуждения поверхностных плазмонов. На рисунке 1 приведены измеренные спектры как функции концентрации хлора, демонстрирующие диапазон обнаружения спектрометра Avantes от 10 до 100 частей на миллион.
Рисунок 1. Энергетический спектр пропускания и график концентрации газообразного хлора
Изучение наноструктур методом ЛППР
Спектроскопия локального поверхностного плазмонного резонанса имеет ряд преимуществ перед классическими методами исследований межмолекулярных взаимодействий в биохимии и связывания антител к антигену. В ППР отсутствует необходимость в отметке реагентов, высокая чувствительность упрощает работу с небольшим объемом образцов.
Исследовательская группа из Венгрии изучила линии спектра поглощения при возбуждении локального поверхностного резонанса внутри наночастиц и пришла к выводу о спектральной зависимости от однородности наноматериала.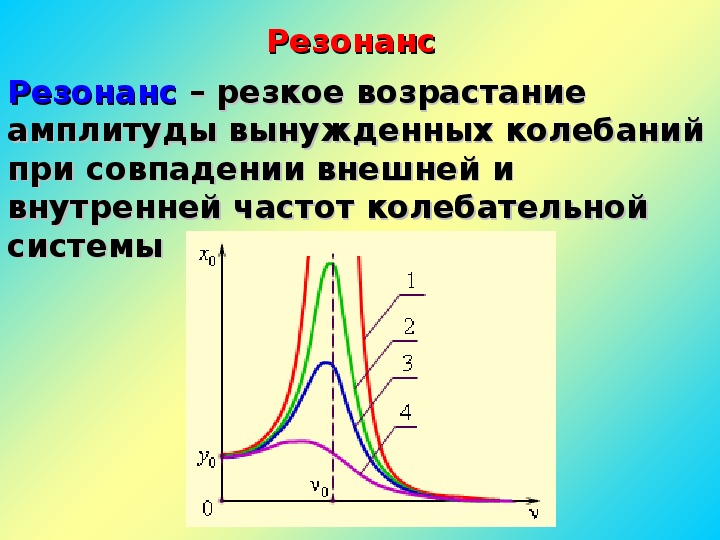 В своем эксперименте наночастицы золота распыляли слоем различной толщины. Предполагаемая толищна слоев: 7.5 нм, 12.5 нм, 15 нм и 30 нм.
В своем эксперименте наночастицы золота распыляли слоем различной толщины. Предполагаемая толищна слоев: 7.5 нм, 12.5 нм, 15 нм и 30 нм.
AvaSpec-ULS2048-4DT-USB2 – четырехканальный спектрометр высокого разрешения, и галогенный источник света AvaLight DHS использовались для измерения спектров поглощения четырех образцов в воздухе (n = 1), воде (n = 1.33) и масле (n = 1.616). Из этих данных, показанных на рисунке 2, венгерская группа вывела явную зависимость от соотношения между толщиной слоя и шириной на полувысоте поверхностного плазмонного резонанса, что указывает на более высокую степень изменчивости размера наночастиц при увеличении толщины слоя.
Рисунок 2. Ширина пика на полувысоте (FWHM) спектра поглощения четырех слоев различной толщины
Инструменты и приборы Avantes используются практически во всех OEM-приложениях и многих отраслях фотоники и лазерных технологий, микроскопии и спектроскопии. Физика наноструктур – одна из интереснейших и перспективных научных областей, в рамках которой регулярно приобретаются:
Физика наноструктур – одна из интереснейших и перспективных научных областей, в рамках которой регулярно приобретаются:
- Cпектрометры Avantes SensLine, StarLine, NIRLine
- Cпектрометры и наборы для спектроскопии комбинационного рассеяния AvaRaman
- Источники узкополосного и широкополосного излучения AvaLight
©Avantes
Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Avantes на территории РФ
14.4 Звуковые помехи и резонанс — Физика
Задачи обучения секции
К концу этого раздела вы сможете делать следующее:
- Опишите резонанс и биения
- Определить основную частоту и ряд гармоник
- Контрастность резонатора открытого и закрытого типа
- Решение проблем, связанных с гармоническими сериями и частотой биений
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (7) Научные концепции.
 Студент знает характеристики и поведение волн. Ожидается, что студент:
Студент знает характеристики и поведение волн. Ожидается, что студент:- (D)
исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.
- (D)
Кроме того, Руководство лаборатории по физике для старших классов рассматривает содержание этого раздела лаборатории под названием: Звуковые волны, а также следующие стандарты:
- (7) Научные концепции. Студент знает характеристики и поведение волн.Ожидается, что студент:
- (D)
исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.
- (D)
Раздел Ключевые термины
| удар | частота ударов | демпфирование | основной | гармоник |
| собственная частота | обертонов | резонанс | резонировать |
Teacher Support
Teacher Support
[BL] Перед началом этого раздела было бы полезно рассмотреть свойства звуковых волн и то, как они связаны друг с другом, стоячие волны, суперпозиция и интерференция волн.
Резонанс и удары
Сядьте как-нибудь перед пианино и спойте на нем короткую громкую ноту, нажимая на педаль сустейна. Он будет петь вам ту же ноту — струны, которые имеют те же частоты, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Это хороший пример того факта, что объекты — в данном случае струны фортепиано — можно заставить колебаться, но лучше всего они колеблются на своей собственной частоте.
Движущая сила (например, ваш голос в примере) вводит энергию в систему с определенной частотой, которая не обязательно совпадает с собственной частотой системы.Со временем энергия рассеивается, а амплитуда постепенно уменьшается до нуля — это называется затуханием. Собственная частота — это частота, с которой система будет колебаться, если бы не было движения и демпфирующей силы. Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
Большинство из нас играли с игрушками, в которых объект подпрыгивает на резинке, что-то вроде мяча, подвешенного на пальце на рисунке 14.18. Сначала вы держите палец неподвижно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе. Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете. По мере того, как частота возбуждения становится все выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.
Рисунок 14.18 Шарик на резиновой ленте перемещается в ответ на палец, поддерживающий его. Если палец движется с собственной частотой мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он отвечает колебаниями с меньшей амплитудой.
На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он отвечает колебаниями с меньшей амплитудой.
Другой пример: когда вы настраиваете радио, вы настраиваете его резонансную частоту так, чтобы оно колебалось только на частоте вещания (движения) желаемой станции.Кроме того, ребенок на качелях приводится в движение (толкается) родителем на собственной частоте качелей для достижения максимальной амплитуды (высоты). Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.
Рисунок 14.19 В некоторых типах наушников для подавления посторонних шумов используются явления конструктивных и деструктивных помех.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Камертоны и трубы могут использоваться для демонстрации концепции резонанса.Используйте любую трубу или трубку, закрытую с одного конца. Закрепите его так, чтобы он стоял вертикально открытым концом вверх.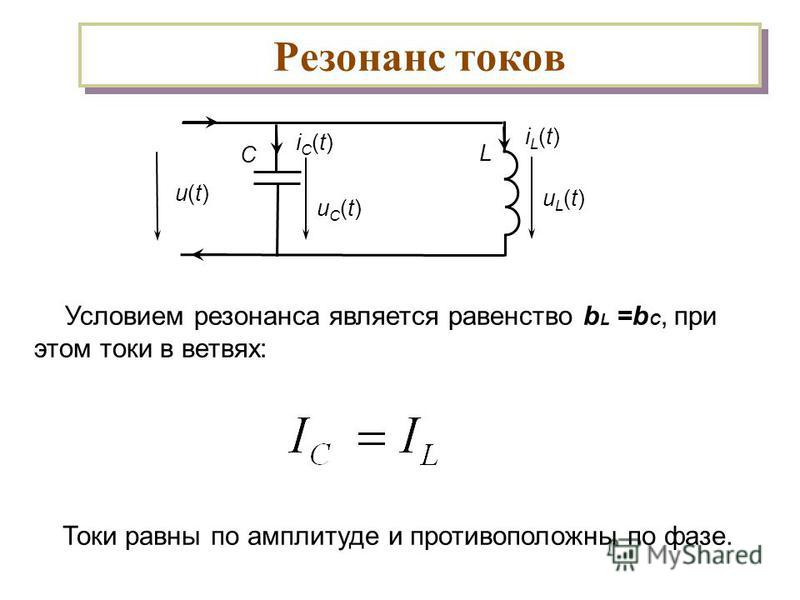 Выберите камертон и ударьте по нему, чтобы он завибрировал. Поднесите его к горлышку трубы и услышите звук. Теперь наполните трубу водой и повторите. При изменении уровня воды изменяется длина резонирующего столба воздуха. Продолжайте это делать. При достижении определенной длины звук камертона будет резонировать через колонку.
Выберите камертон и ударьте по нему, чтобы он завибрировал. Поднесите его к горлышку трубы и услышите звук. Теперь наполните трубу водой и повторите. При изменении уровня воды изменяется длина резонирующего столба воздуха. Продолжайте это делать. При достижении определенной длины звук камертона будет резонировать через колонку.
Все звуковые резонансы вызваны конструктивными и деструктивными помехами.Только резонансные частоты конструктивно интерферируют, образуя стоячие волны, в то время как другие мешают деструктивно и отсутствуют. От звука, издаваемого надуванием бутылки, до узнаваемости голоса великого певца, резонанс и стоячие волны играют жизненно важную роль в звуке.
Помехи случаются со всеми типами волн, включая звуковые волны. Фактически, один из способов подтвердить, что что-то является волной , — это наблюдать эффекты интерференции. На рис. 14.19 показан набор наушников, в которых для подавления шума используется разумное использование звуковых помех. Чтобы получить деструктивные помехи, выполняется быстрый электронный анализ, и вводится второй звук, максимумы и минимумы которого полностью противоположны входящему шуму.
Чтобы получить деструктивные помехи, выполняется быстрый электронный анализ, и вводится второй звук, максимумы и минимумы которого полностью противоположны входящему шуму.
Помимо резонанса, суперпозиция волн также может создавать биения. Биения производятся наложением двух волн с немного разными частотами, но одинаковой амплитудой. Волны чередуются во времени между конструктивной интерференцией и деструктивной интерференцией, придавая результирующей волне амплитуду, которая изменяется во времени.(См. Результирующую волну на рисунке 14.20).
Эта волна колеблется по амплитуде или биениям с частотой, называемой частотой биений. Уравнение для частоты биений
fB = | f1 − f2 |, fB = | f1 − f2 |,
14,13
, где f 1 и f 2 — частоты двух исходных волн. Если две частоты звуковых волн похожи, то мы слышим среднюю частоту, которая становится громче и тише с частотой биений.
Советы для успеха
Не путайте частоту биений с обычной частотой волны, возникающей в результате наложения. Хотя частота биений задается приведенной выше формулой и описывает частоту биений, фактическая частота волны, полученная в результате наложения, является средним значением частот двух исходных волн.
Хотя частота биений задается приведенной выше формулой и описывает частоту биений, фактическая частота волны, полученная в результате наложения, является средним значением частот двух исходных волн.
Рисунок 14.20 Биения возникают в результате наложения двух волн немного разных частот, но одинаковых амплитуд. Волны чередуются во времени между конструктивной интерференцией и деструктивной интерференцией, придавая результирующей волне изменяющуюся во времени амплитуду.
Виртуальная физика
Волновые помехи
Для этого упражнения перейдите на вкладку «Звук». Включите параметр «Звук» и поэкспериментируйте с изменением частоты и амплитуды, а также с добавлением второго динамика и барьера.
Проверка захвата
Согласно графику, что происходит с амплитудой давления с течением времени. Как называется это явление и что его вызывает?
- Амплитуда со временем уменьшается.
 Это явление называется затуханием.Это вызвано рассеянием энергии.
Это явление называется затуханием.Это вызвано рассеянием энергии. - Амплитуда со временем увеличивается. Это явление называется обратной связью. Это вызвано накоплением энергии.
- Амплитуда колеблется со временем. Это явление называется эхом. Это вызвано колебаниями энергии.
Основная частота и гармоники
Предположим, мы держим камертон возле конца трубки, которая закрыта другим концом, как показано на рисунке 14.21, Рис. 14.22 и Рис. 14.23. Если камертон имеет правильную частоту, столб воздуха в трубке громко резонирует, но на большинстве частот он очень мало вибрирует. Это означает, что столб воздуха имеет только определенные собственные частоты. На рисунках показано, как формируется резонанс на самой низкой из этих собственных частот. Возмущение движется по трубке со скоростью звука и отскакивает от закрытого конца. Если трубка как раз подходящей длины, отраженный звук возвращается на камертон ровно через полцикла и конструктивно мешает продолжающемуся звуку, производимому камертоном. Входящие и отраженные звуки образуют в трубке стоячую волну, как показано на рисунке.
Входящие и отраженные звуки образуют в трубке стоячую волну, как показано на рисунке.
Рисунок 14.21 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Возмущение движется по трубе.
Рисунок 14.22 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Возмущение отражается от закрытого конца трубки.
Рисунок 14.23 Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Если длина трубки L подходит, помеха возвращается на камертон через полцикла и конструктивно мешает продолжающемуся звуку камертона.Эта интерференция формирует стоячую волну, и столб воздуха резонирует.
Стоячая волна, сформированная в трубке, имеет максимальное смещение воздуха (пучность) на открытом конце и отсутствие смещения (узел) на закрытом конце. Вспомните из предыдущей главы, посвященной волнам, что движение неограничено в пучности и останавливается в узле. Расстояние от узла до пучности составляет одну четвертую длины волны, и это равно длине трубки; следовательно, λ = 4Lλ = 4L. Такой же резонанс может быть вызван вибрацией, возникающей на закрытом конце трубки или около него, как показано на рисунке 14.24.
Такой же резонанс может быть вызван вибрацией, возникающей на закрытом конце трубки или около него, как показано на рисунке 14.24.
Рис. 14.24 Такая же стоячая волна создается в трубке из-за вибрации, вносимой около ее закрытого конца.
Поскольку максимальное смещение воздуха возможно на открытом конце, а не на закрытом, существуют другие, более короткие длины волн, которые могут резонировать в трубке (см. Рис. 14.25). Здесь стоячая волна имеет в трубке три четверти своей длины волны, или L = (3/4) λ′L = (3/4) λ ′, так что λ ′ = 4L / 3λ ′ = 4L / 3. Есть целый ряд коротковолновых и высокочастотных звуков, резонирующих в трубке.
Мы используем специальные термины для обозначения резонансов в любой системе. Самая низкая резонансная частота называется основной, а все более высокие резонансные частоты — обертонами. Все резонансные частоты кратны основной и называются гармониками. Основная гармоника — это первая гармоника, первый обертон — это вторая гармоника и так далее. На рисунке 14.26 показаны основная гармоника и первые три обертона (первые четыре гармоники) в трубке, закрытой с одного конца.
На рисунке 14.26 показаны основная гармоника и первые три обертона (первые четыре гармоники) в трубке, закрытой с одного конца.
Рисунок 14.25 Еще один резонанс для трубки, закрытой с одного конца. У этого есть максимальные вытеснения воздуха на открытом конце и нет на закрытом конце. Длина волны короче: три четверти λ′λ ′ равны длине трубки, так что λ ′ = 4L / 3λ ′ = 4L / 3. Эта высокочастотная вибрация — первый обертон.
Рис. 14.26 Основной и три нижних обертона закрытой с одного конца трубки. У всех есть максимальное вытеснение воздуха на открытом конце и отсутствует на закрытом конце.
Основной тон и обертоны могут присутствовать одновременно в различных комбинациях.Например, средняя до ноты на трубе звучит очень иначе, чем средняя до на кларнете, хотя оба инструмента в основном представляют собой модифицированные версии закрытой с одного конца трубки. Основная частота такая же (и обычно самая интенсивная), но обертоны и их сочетание интенсивностей различны. Этот микс — это то, что придает музыкальным инструментам (и человеческим голосам) их отличительные характеристики, независимо от того, есть ли у них воздушные колонны, струны или барабанные пластинки. Фактически, большая часть нашей речи определяется формированием полости, образованной горлом и ртом, и расположением языка для настройки основных и сочетания обертонов.
Этот микс — это то, что придает музыкальным инструментам (и человеческим голосам) их отличительные характеристики, независимо от того, есть ли у них воздушные колонны, струны или барабанные пластинки. Фактически, большая часть нашей речи определяется формированием полости, образованной горлом и ртом, и расположением языка для настройки основных и сочетания обертонов.
Открытые и закрытые резонаторы
Резонансные частоты закрытой с одного конца трубки (известной как резонатор с закрытой трубкой): fn = nv4L, n = 1,3,5 …, fn = nv4L, n = 1,3,5 … ,
, где f 1 — основной тон, f 3 — первый обертон и т. Д. Обратите внимание, что резонансные частоты зависят от скорости звука v и длины трубки L .
Другой тип трубки — это трубка с открытыми трубками и с обоих концов (известная как резонатор с открытой трубкой). Примеры — органные трубы, флейты и гобои. Воздушные столбы в трубках, открытых с обоих концов, имеют максимальное вытеснение воздуха с обоих концов. (См. Рисунок 14.27). Стоячие волны формируются, как показано.
Примеры — органные трубы, флейты и гобои. Воздушные столбы в трубках, открытых с обоих концов, имеют максимальное вытеснение воздуха с обоих концов. (См. Рисунок 14.27). Стоячие волны формируются, как показано.
Рисунок 14.27 Показаны резонансные частоты трубки, открытой с обоих концов, включая основной тон и первые три обертона. Во всех случаях максимальные перемещения воздуха происходят на обоих концах трубы, что дает ей собственные частоты, отличные от собственных частот трубы, закрытой с одного конца.
Резонансные частоты открытого резонатора
fn = nv2L, n = 1,2,3…, fn = nv2L, n = 1,2,3 …,
, где f 1 — основной тон, f 2 — первый обертон, f 3 — второй обертон и т. Д. Обратите внимание, что трубка, открытая с обоих концов, имеет основную частоту в два раза больше, чем она была бы, если бы закрылась с одного конца. Он также имеет другой спектр обертонов, чем трубка, закрытая с одного конца. Итак, если у вас есть две лампы с одинаковой основной частотой, но одна из них открыта с обоих концов, а другая закрыта с одного конца, они будут звучать по-разному при игре, потому что у них разные обертоны.
Он также имеет другой спектр обертонов, чем трубка, закрытая с одного конца. Итак, если у вас есть две лампы с одинаковой основной частотой, но одна из них открыта с обоих концов, а другая закрыта с одного конца, они будут звучать по-разному при игре, потому что у них разные обертоны.
Например,
Middle C будет звучать богаче при игре на открытой трубе, так как в ней больше обертонов. Резонатор с открытой трубкой имеет больше обертонов, чем резонатор с закрытой трубой, потому что он имеет четные кратные основной и нечетной частоты, тогда как закрытая трубка имеет только нечетные кратные.
В этом разделе мы рассмотрели резонансные и стоячие волны для духовых инструментов, но вибрирующие струны на струнных инструментах также резонируют и имеют основы и обертоны, аналогичные таковым для духовых инструментов.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Другие инструменты также используют воздушный резонанс по-разному для усиления звука.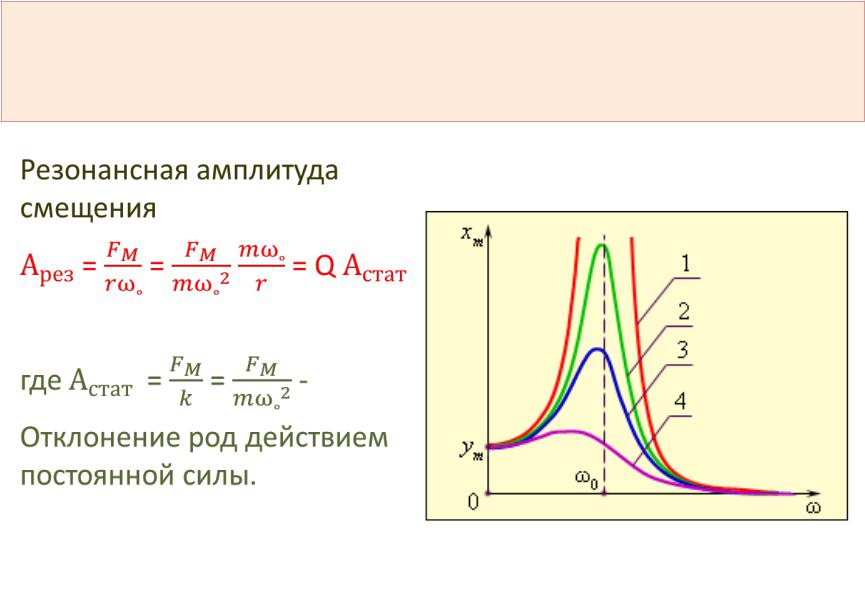 Например, и у скрипки, и у гитары есть звуковые коробки, но разной формы, что приводит к разным структурам обертонов. Вибрирующая струна создает звук, который резонирует в звуковой коробке, значительно усиливая звук и создавая обертоны, придающие инструменту его характерный аромат. Чем сложнее форма звукового блока, тем выше его способность резонировать в широком диапазоне частот.Тип и толщина дерева или других материалов, используемых для изготовления звуковой коробки, также влияют на качество звука. Попросите учащихся привести больше примеров того, как различные музыкальные инструменты используют явление резонанса.
Например, и у скрипки, и у гитары есть звуковые коробки, но разной формы, что приводит к разным структурам обертонов. Вибрирующая струна создает звук, который резонирует в звуковой коробке, значительно усиливая звук и создавая обертоны, придающие инструменту его характерный аромат. Чем сложнее форма звукового блока, тем выше его способность резонировать в широком диапазоне частот.Тип и толщина дерева или других материалов, используемых для изготовления звуковой коробки, также влияют на качество звука. Попросите учащихся привести больше примеров того, как различные музыкальные инструменты используют явление резонанса.
Решение проблем, связанных с рядом гармоник и частотой биений
Рабочий пример
Определение длины трубы для замкнутого трубного резонатора
Если звук распространяется по воздуху со скоростью 344 м / с, какой длины должна быть закрытая с одного конца трубка, чтобы основная частота составляла 128 Гц?
Стратегия
Длину L можно найти, переписав уравнение fn = nv4Lfn = nv4L
.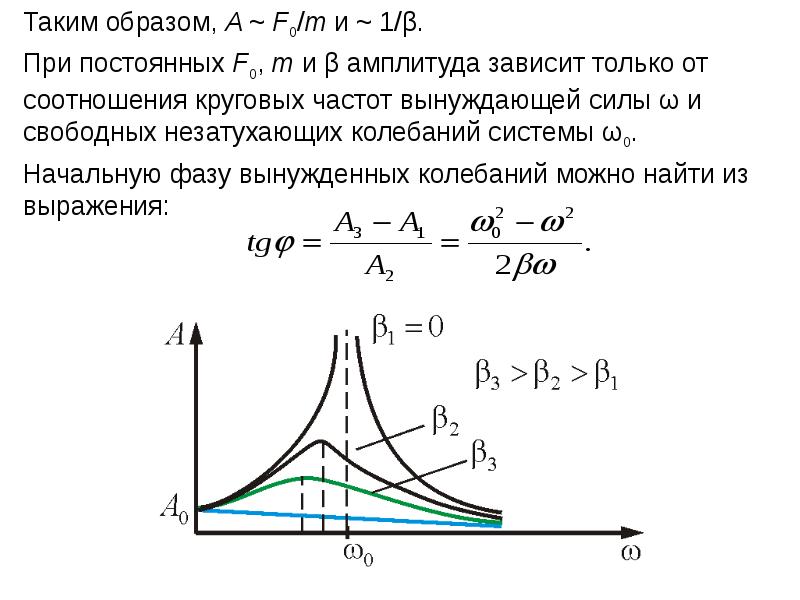
Решение
(1) Определите известных.
- Основная частота 128 Гц.
- Скорость звука 344 м / с.
(2) Используйте fn = nvw4Lfn = nvw4L, чтобы найти основную частоту ( n = 1).
(3) Решите это уравнение относительно длины.
(4) Введите значения скорости звука и частоты в выражение для L .
L = v4f1 = 344 м / с4 (128 Гц) = 0,672 мл = v4f1 = 344 м / с4 (128 Гц) = 0.672 м
14,16
Обсуждение
Многие духовые инструменты представляют собой модифицированные трубы с отверстиями для пальцев, клапанами и другими устройствами для изменения длины резонирующего столба воздуха и, следовательно, частоты проигрываемой ноты. Для рожков, воспроизводящих очень низкие частоты, таких как тубы, нужны лампы такой длины, чтобы они были скручены в петли.
Рабочий пример
Обнаружение третьего обертона в открытом резонаторе
Если лампа, открытая с обоих концов, имеет основную частоту 120 Гц, какова частота ее третьего обертона?
Стратегия
Так как нам уже известно значение основной частоты (n = 1), мы можем найти третий обертон (n = 4), используя уравнение fn = nv2Lfn = nv2L.
Решение
Так как основная частота (n = 1) равна
и
f4 = 4v2L, f4 = 4f1 = 4 (120 Гц) = 480 Гц. f4 = 4v2L, f4 = 4f1 = 4 (120 Гц) = 480 Гц.
14,18
Обсуждение
Чтобы решить эту проблему, не нужно было знать длину трубки или скорость воздуха из-за взаимосвязи между основным и третьим обертоном. В этом примере был резонатор с открытой трубой; обратите внимание, что для резонатора с закрытой трубой третий обертон имеет значение n = 7 (не n = 4).
Рабочий пример
Использование частоты ударов для настройки фортепиано
Настройщики фортепиано постоянно используют биты в своей работе. Сравнивая ноту с камертоном, они прислушиваются к ударам и регулируют струну, пока удары не исчезнут (до нулевой частоты). Если тюнер пианино слышит два удара в секунду, а камертон имеет частоту 256 Гц, каковы возможные частоты пианино?
Стратегия
Поскольку мы уже знаем, что частота биений f B равна 2, а одна из частот (скажем, f 2 ) равна 256 Гц, мы можем использовать уравнение fB = | f1 − f2 | fB = | f1 − f2 | решить для частоты фортепиано f 1 .
Решение
Так как fB = | f1 − f2 | fB = | f1 − f2 |,
мы знаем, что либо fB = f1 − f2fB = f1 − f2, либо −fB = f1 − f2 − fB = f1 − f2.
Решение для f 1 ,
f1 = fB + f2 или f1 = −fB + f2.f1 = fB + f2 или f1 = −fB + f2.
14,19
Подставляя значения,
f1 = 2 + 256 Гц или f1 = −2 + 256 Гц f1 = 2 + 256 Гц или f1 = −2 + 256 Гц
14,20
Итак,
f1 = 258 Гц или 254 Гц. f1 = 258 Гц или 254 Гц.
14,21
Обсуждение
Настройщик пианино может изначально не определить, просто слушая, является ли частота фортепиано слишком высокой или слишком низкой, и должен настроить ее методом проб и ошибок, сделав настройку, а затем снова протестировав.Если после настройки ударов еще больше, то тюнер знает, что пошел в неправильном направлении.
Практические задачи
21.
Две звуковые волны имеют частоты 250 Гц и 280 Гц. Какова частота биений при их наложении?
- 290 Гц
- 265 Гц
- 60 Гц
- 30 Гц
22.
Какова длина трубы, закрытой с одного конца с основной частотой 350 Гц? (Предположим, что скорость звука в воздухе составляет 331 м / с.)
- 26 см
- 26м
- 24 мес.
- 24 см
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти вопросы, чтобы оценить достижения учащихся по целям обучения раздела. Если учащиеся борются с определенной целью, эти вопросы помогут определить ее и направить студентов к соответствующему содержанию.
23.
Что такое демпфирование?
- Со временем энергия увеличивается, а амплитуда постепенно уменьшается до нуля. Это называется демпфированием.
- Со временем энергия рассеивается, а амплитуда постепенно увеличивается.
 Это называется демпфированием.
Это называется демпфированием. - Со временем энергия увеличивается, а амплитуда постепенно увеличивается. Это называется демпфированием.
- Со временем энергия рассеивается, и амплитуда постепенно уменьшается до нуля.Это называется демпфированием.
24.
Что такое резонанс? Когда можно сказать, что система резонирует?
- Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
- Явление возбуждения системы с частотой выше, чем ее собственная частота, называется резонансом, и система, работающая на собственной частоте, не резонирует.
- Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом, и система, работающая на собственной частоте, не резонирует.

- Явление возбуждения системы с частотой, превышающей ее собственную частоту, называется резонансом, а система, работающая на собственной частоте, называется резонансной.
25.
В эксперименте с камертоном и трубкой, в случае образования стоячей волны, в какой точке трубки наблюдается максимальное возмущение от камертона? Напомним, что трубка имеет один открытый конец и один закрытый конец.
- В середине трубки
- Оба конца трубки
- На закрытом конце трубки
- На открытом конце трубки
26.
В эксперименте с камертоном и лампой, когда столб воздуха будет издавать самый громкий звук?
- Если камертон вибрирует с частотой, вдвое превышающей собственную частоту столба воздуха.
- Если камертон вибрирует с частотой ниже собственной частоты столба воздуха.
- Если камертон вибрирует с частотой выше собственной частоты столба воздуха.

- Если камертон вибрирует с частотой, равной собственной частоте столба воздуха.
27.
Что такое резонатор с закрытой трубой?
- Труба или цилиндрическая воздушная колонна, закрытая с обоих концов
- Труба с пучностью на закрытом конце
- Труба с узлом на открытом конце
- Труба или цилиндрическая воздушная колонна, закрытая с одного конца
28.
Приведите два примера открытых резонаторов.
- фортепиано, скрипка
- барабан, таблица
- электрогитара, акустическая гитара
- флейта, гобой
вынужденных колебаний и резонанса | Физика
Цели обучения
К концу этого раздела вы сможете:
- Наблюдайте за резонансом ракетки на струне.
- Наблюдать за амплитудой затухающего гармонического осциллятора.
Рис. 1. Струны пианино могут вибрировать, просто создавая звуковые волны своим голосом. (Источник: Мэтт Биллингс, Flickr)
(Источник: Мэтт Биллингс, Flickr)
Сядьте как-нибудь перед пианино и спойте на нем короткую громкую ноту с отключенными демпферами. Он пропоет вам ту же ноту — струны, имеющие те же частоты, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Ваш голос и струны фортепиано — хороший пример того факта, что объекты — в данном случае струны пианино — можно заставить колебаться, но лучше всего колеблются на своей собственной частоте.В этом разделе мы кратко рассмотрим применение периодической движущей силы , действующей на простой гармонический осциллятор. Движущая сила вводит энергию в систему с определенной частотой, не обязательно такой же, как собственная частота системы. Собственная частота — это частота, на которой система будет колебаться, если бы не было движения и демпфирующей силы.
Большинство из нас играли с игрушками, в которых использовался предмет, поддерживаемый на резинке, что-то вроде шарика, подвешенного на пальце на рисунке 2. Представьте, что палец на рисунке — это ваш палец. Сначала вы держите палец ровно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе. Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете.Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом . Говорят, что система, работающая на собственной частоте, резонирует с . По мере того, как частота возбуждения становится все выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.
Представьте, что палец на рисунке — это ваш палец. Сначала вы держите палец ровно, а мяч подпрыгивает вверх и вниз с небольшим демпфированием. Если вы медленно двигаете пальцем вверх и вниз, мяч будет следовать за ним, не подпрыгивая сам по себе. Когда вы увеличиваете частоту, с которой вы двигаете пальцем вверх и вниз, мяч будет колебаться с возрастающей амплитудой. Когда вы ведете мяч с собственной частотой, колебания мяча увеличиваются по амплитуде с каждым колебанием, пока вы им управляете.Явление возбуждения системы с частотой, равной ее собственной частоте, называется резонансом . Говорят, что система, работающая на собственной частоте, резонирует с . По мере того, как частота возбуждения становится все выше, чем резонансная или собственная частота, амплитуда колебаний становится меньше, пока колебания почти не исчезнут, и ваш палец будет просто перемещаться вверх и вниз, практически не влияя на мяч.
Рис. 2. Шарик на резиновой ленте перемещается в ответ на палец, поддерживающий его. Если палец движется с собственной частотой f0 мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он отвечает колебаниями с меньшей амплитудой.
Если палец движется с собственной частотой f0 мяча на резиновой ленте, то достигается резонанс, и амплитуда колебаний мяча резко возрастает. На более высоких и более низких частотах движения энергия передается к шару менее эффективно, и он отвечает колебаниями с меньшей амплитудой.
На рис. 3 показан график зависимости амплитуды затухающего гармонического осциллятора от частоты движущей им периодической силы. На графике есть три кривые, каждая из которых представляет разную величину демпфирования.Все три кривые достигают максимума в точке, где частота движущей силы равна собственной частоте гармонического осциллятора. Самый высокий пик или самый высокий отклик — для наименьшего количества демпфирования, потому что демпфирующая сила снимает меньше энергии.
Рис. 3. Амплитуда гармонического осциллятора как функция частоты движущей силы. Кривые представляют один и тот же генератор с одинаковой собственной частотой, но с разной степенью демпфирования. Резонанс возникает, когда частота возбуждения равна собственной частоте, а наибольший отклик — при наименьшем затухании. Самый узкий отклик также соответствует наименьшему демпфированию.
Самый узкий отклик также соответствует наименьшему демпфированию.
Интересно, что ширина резонансных кривых, показанных на рисунке 3, зависит от затухания: чем меньше затухание, тем уже резонанс. Идея состоит в том, что если вы хотите, чтобы управляемый генератор резонировал на очень определенной частоте, вам нужно как можно меньше демпфирования. Небольшое демпфирование характерно для струн фортепиано и многих других музыкальных инструментов. И наоборот, если вам нужны колебания малой амплитуды, например, в системе подвески автомобиля, вам нужно сильное демпфирование.Сильное демпфирование снижает амплитуду, но компромисс заключается в том, что система реагирует на большем количестве частот.
Эти особенности управляемых гармонических генераторов применимы к огромному количеству систем. Например, когда вы настраиваете радио, вы настраиваете его резонансную частоту так, чтобы оно колебалось только на радиовещательной (движущей) частоте желаемой станции. Чем более избирательно радио различает станции, тем меньше его демпфирование. Магнитно-резонансная томография (МРТ) — широко используемый медицинский диагностический инструмент, в котором атомные ядра (в основном ядра водорода) заставляют резонировать входящими радиоволнами (порядка 100 МГц).Ребенок на качелях приводится в движение родителями на собственной частоте качелей для достижения максимальной амплитуды. Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.
Магнитно-резонансная томография (МРТ) — широко используемый медицинский диагностический инструмент, в котором атомные ядра (в основном ядра водорода) заставляют резонировать входящими радиоволнами (порядка 100 МГц).Ребенок на качелях приводится в движение родителями на собственной частоте качелей для достижения максимальной амплитуды. Во всех этих случаях эффективность передачи энергии от движущей силы к генератору лучше всего при резонансе.
Рис. 4. В 1940 году обрушился мост через Такома в штате Вашингтон. Сильный поперечный ветер приводил мост в колебания на его резонансной частоте. Демпфирование уменьшалось, когда опорные тросы разрывались и начинали скользить по опорам, что увеличивало амплитуду до разрушения конструкции (кредит: PRI’s Studio 360, через Flickr)
Неровности и гравийные дороги доказывают, что даже система подвески автомобиля не застрахована от резонанса.Несмотря на тонко спроектированные амортизаторы, которые обычно преобразуют механическую энергию в тепловую почти так же быстро, как она приходит, лежачие полицейские по-прежнему вызывают колебания большой амплитуды.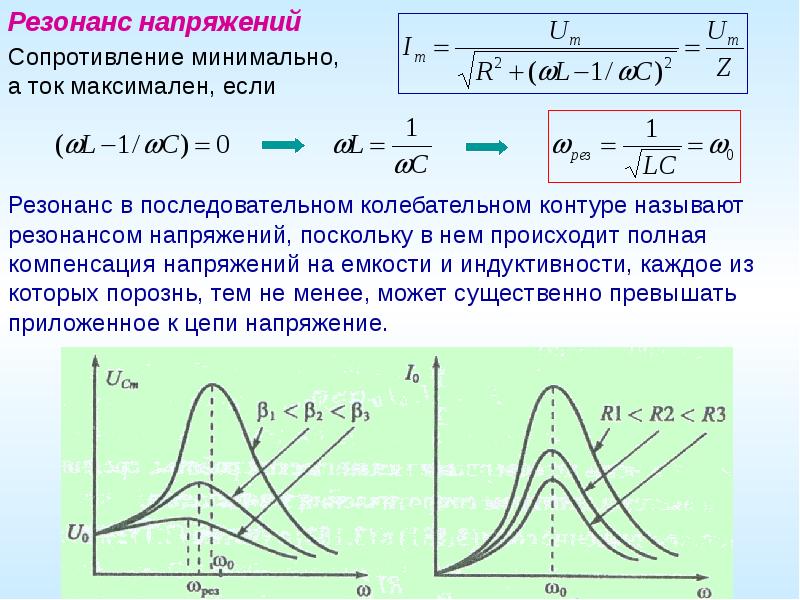 На гравийных дорогах с рифленым покрытием вы, возможно, заметили, что если вы едете с «неправильной» скоростью, неровности очень заметны, тогда как на других скоростях неровности вообще можно не почувствовать. На рисунке 4 показана фотография известного примера (моста Tacoma Narrows Bridge) деструктивного воздействия возбужденного гармонического колебания.Мост Миллениум в Лондоне был закрыт на короткое время по той же причине, пока проводились проверки.
На гравийных дорогах с рифленым покрытием вы, возможно, заметили, что если вы едете с «неправильной» скоростью, неровности очень заметны, тогда как на других скоростях неровности вообще можно не почувствовать. На рисунке 4 показана фотография известного примера (моста Tacoma Narrows Bridge) деструктивного воздействия возбужденного гармонического колебания.Мост Миллениум в Лондоне был закрыт на короткое время по той же причине, пока проводились проверки.
В нашем организме полость грудной клетки является ярким примером системы, находящейся в резонансе. Диафрагма и стенка грудной клетки вызывают колебания грудной полости, в результате чего легкие раздуваются и сдуваются. Система критически демпфирована, а мышечная диафрагма колеблется с резонансным значением для системы, что делает ее высокоэффективной.
Проверьте свое понимание
Известный магический трюк: исполнитель поет ноту в сторону хрустального стекла, пока стекло не разобьется.Объясните, почему этот трюк работает с точки зрения резонанса и собственной частоты.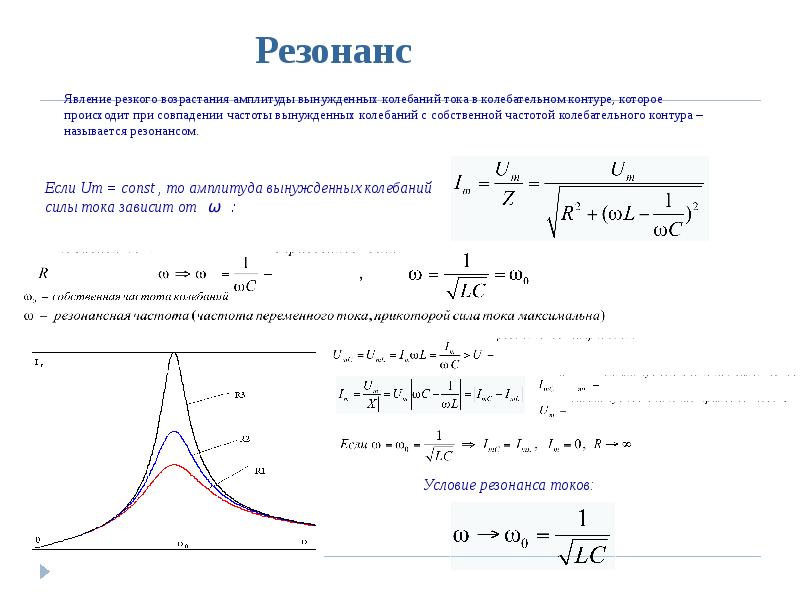
Решение
Исполнитель должен петь ноту, соответствующую собственной частоте стекла. Когда звуковая волна направлена на стекло, стекло резонирует с той же частотой, что и звуковая волна. Когда в систему поступает достаточно энергии, стекло начинает вибрировать и в конечном итоге разбивается.
Сводка раздела
- Собственная частота системы — это частота, с которой система будет колебаться, если на нее не действуют движущие или демпфирующие силы.
- Периодическая сила, управляющая гармоническим осциллятором на его собственной частоте, вызывает резонанс. Говорят, что система резонирует.
- Чем меньше демпфирование в системе, тем выше амплитуда вынужденных колебаний вблизи резонанса. Чем больше демпфирование у системы, тем более широкий отклик она имеет на изменение частот движения.
Концептуальные вопросы
- Почему солдатам обычно приказывают «идти шагом» (идти не в ногу) через мост?
Задачи и упражнения
- Сколько энергии должны рассеять амортизаторы автомобиля массой 1200 кг, чтобы погасить отскок, изначально имеющий скорость 0.
 800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение.
800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение. - Если у автомобиля есть система подвески с силовой константой 5,00 × 10 4 Н / м, сколько энергии должны отводить удары автомобиля, чтобы гасить колебания, начиная с максимального смещения 0,0750 м?
- (a) Насколько пружина с силовой постоянной 40,0 Н / м будет растянута объектом массой 0,500 кг, когда она неподвижно подвешена на пружине? (б) Рассчитайте уменьшение гравитационной потенциальной энергии 0.Объект весом 500 кг, когда он спускается на это расстояние. (c) Часть этой гравитационной энергии уходит в пружину. Вычислите энергию, запасенную в пружине на этом участке, и сравните ее с потенциальной энергией гравитации. Объясните, куда может уйти остальная энергия.
- Предположим, у вас есть объект весом 0,750 кг на горизонтальной поверхности, соединенный с пружиной, имеющей силовую постоянную 150 Н / м. Между объектом и поверхностью существует простое трение со статическим коэффициентом трения μ s = 0.
 100. а) Как далеко можно растянуть пружину, не перемещая массу? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения равен μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, он начинается с максимальной амплитуды.
100. а) Как далеко можно растянуть пружину, не перемещая массу? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения равен μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, он начинается с максимальной амплитуды. - Инженерное приложение. Подвесной мост колеблется с постоянной эффективной силы 1,00 × 10 8 Н / м. (а) Сколько энергии нужно, чтобы заставить его колебаться с амплитудой 0.100 м? (b) Если солдаты маршируют по мосту с частотой, равной собственной частоте моста, и каждую секунду передают 1,00 × 10 4 Дж энергии, сколько времени потребуется, чтобы колебания моста достигли амплитуды от 0,100 м до 0,500 м. .
Глоссарий
собственная частота: частота, при которой система будет колебаться, если бы не было движения и демпфирующих сил
резонанс: явление возбуждения системы с частотой, равной собственной частоте системы
резонирует: система работает на собственной частоте
Избранные решения проблем и упражнения
1.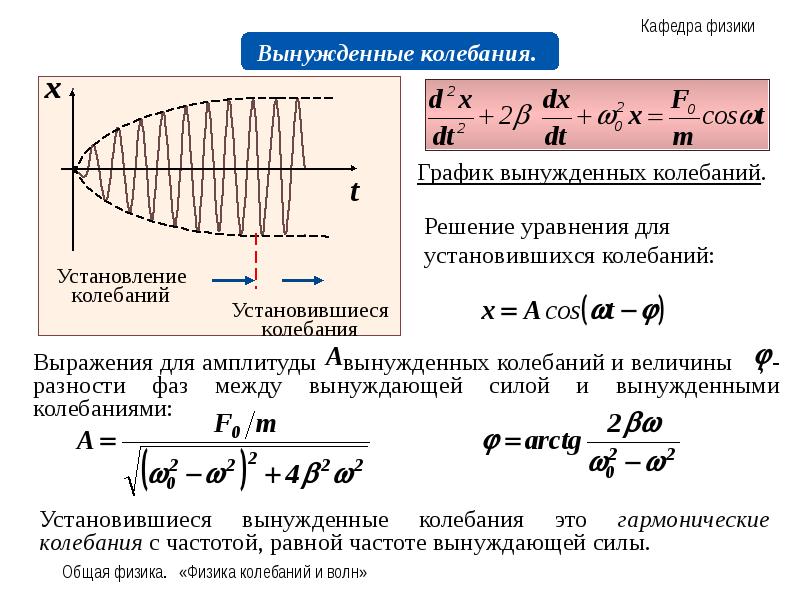 384 Дж
384 Дж
3. (а). 0,123 м; (б). -0,600 Дж; (с). 0,300 Дж. Остальная энергия может уйти в тепло из-за трения и других демпфирующих сил.
5. (а) 5.00 × 10 5 Дж; (б) 1,20 × 10 3 с
энергии — В общем, какие ключевые элементы необходимы для существования резонанса в физической системе?
Давайте сначала разберемся, что такое резонанс. Википедия говорит следующее:
В физике резонанс — это явление, состоящее в том, что данная система приводится в действие другой колебательной системой или внешними силами, чтобы колебаться с большей амплитудой на некоторых предпочтительных частотах.
По сути, некоторая амплитуда становится больше на определенной частоте.
ничто действительно не относится ко всем типам систем в целом
Это потому, что это не главная цель учебника физики.
Если вы хотите понять системы в целом, вы, вероятно, получите больше информации из книги по теории систем.
Они скорее дают примеры конкретных физических систем, таких как LC-цепи, в которых участвуют электрические и магнитные поля, или механические системы, в которых участвуют пружины и массы.
Это потому, что их можно описать одними и теми же дифференциальными уравнениями, просто используя разные символы. Вы можете заменить одно другим.
Очень важная вещь в теории систем — это передаточная функция, которая определяется как \ $ \ frac {output} {input} \ $. Если вы умножите эту функцию на вход, вы получите выход от системы. Эта функция обычно зависит от частоты.
Теперь это звучит подозрительно связанным с определением резонанса выше.Если передаточная функция имеет значение больше 1, выход (его значение или амплитуда) будет больше, чем вход. Часто бывает, что передаточная функция имеет максимум. В этом максимуме вход усиливается сильнее всего, что называется резонансом.
При наличии строковой цепи RLC как системы одной из возможных передаточных функций может быть функция полного напряжения на входе и напряжения на резисторе на выходе:
$$ \ frac {U_R} {U} = \ frac {R} {R + j \ omega L + \ frac {1} {j \ omega C}} $$
Другая передаточная функция может заключаться в том, что общее напряжение является входом, а ток — выходом:
$$ \ frac {I} {U} = \ frac {1} {R + j \ omega L + \ frac {1} {j \ omega C}} $$
Вы можете видеть, что оба зависят от $ \ omega = 2 \ pi f $.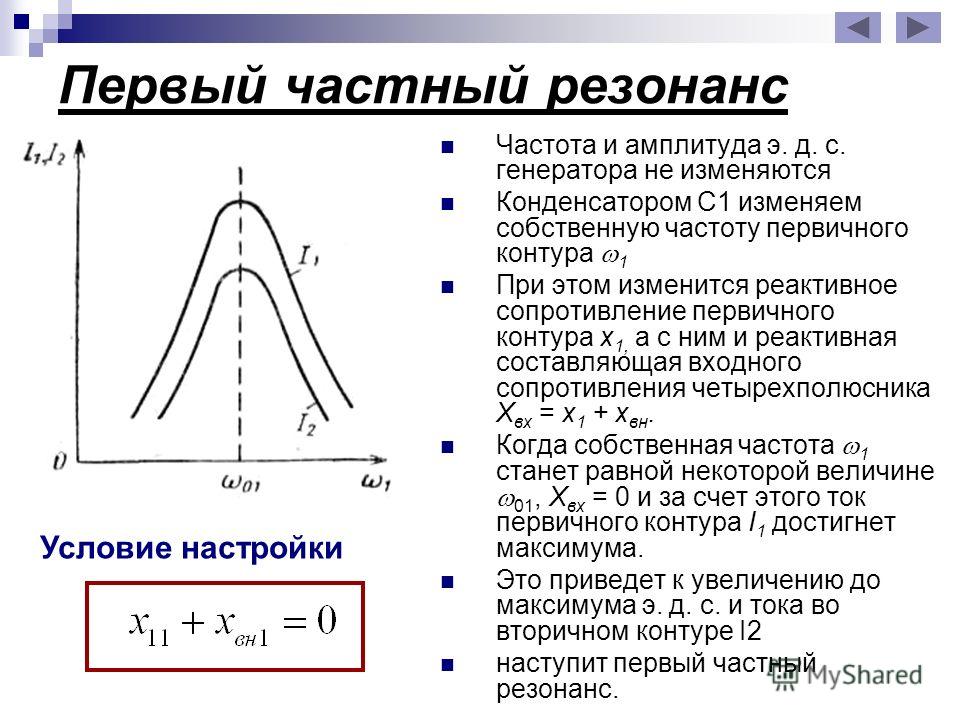 Чтобы показать резонанс, они должны иметь максимум, превышающий 1
Чтобы показать резонанс, они должны иметь максимум, превышающий 1
.
Я бы сказал, что резонанс — это не свойство системы как таковое, а свойство пары из двух ее свойств, одно из которых используется как вход, а другое — выход. Если передаточная функция, описывающая соотношение между входом и выходом, имеет максимум или пик на определенной частоте, то у вас есть резонанс.
Что такое резонанс?
Мы часто слышим это слово, но что такое резонанс? Во-первых, чтобы объяснить, мы должны объяснить термины, которые мы будем использовать.
- Период — это время, необходимое для завершения одного цикла
- Количество циклов в одной секунде — это частота колебаний.
- Частота измеряется в Герцах, названа в честь немецкого физика XIX века Генриха Рудольфа Герца
- Один герц равен одному циклу в секунду.
Что такое резонанс?
Резонанс возникает, когда конструкция или материал естественным образом колеблются с высокой амплитудой на определенной частоте. Эта частота известна как структурная резонансная частота. Обычно структура имеет много резонансных частот.
Эта частота известна как структурная резонансная частота. Обычно структура имеет много резонансных частот.
Словарное определение резонанса дает нам —
«состояние системы, в котором в ответ на внешний раздражитель возникает аномально сильная вибрация, возникающая, когда частота стимула такая же или почти такая же, как собственная частота колебаний системы».
Когда затухание в конструкции невелико, резонансные частоты приблизительно равны собственным частотам конструкции, которые являются частотами свободных колебаний молекул самого материала.
Кроме того, индивидуальный резонанс — это состояние, когда собственная частота конструкции или материала и частота, на которой она возбуждается, равны или почти равны. Это приводит к сильной вибрации конструкции или материала и является классическим резонансным состоянием. Это резонансное состояние часто может привести к неожиданному поведению конструкции или материала.
Самая низкая собственная частота, часто называемая основной частотой, связана с материалом, из которого сделана конструкция. Чем больше масса или плотность материала, тем ниже основная частота вибрации. Собственная частота также связана со скоростью, с которой форма волны может распространяться через конструкцию. Это во многом определяется молекулярным составом материала. Газ, например, имеет много свободных молекул с высокой кинетической энергией, поэтому форма волны может быстро перемещаться через материал. В твердом теле гораздо меньше свободных молекул и он намного плотнее, поэтому форма волны движется медленнее.
Чем больше масса или плотность материала, тем ниже основная частота вибрации. Собственная частота также связана со скоростью, с которой форма волны может распространяться через конструкцию. Это во многом определяется молекулярным составом материала. Газ, например, имеет много свободных молекул с высокой кинетической энергией, поэтому форма волны может быстро перемещаться через материал. В твердом теле гораздо меньше свободных молекул и он намного плотнее, поэтому форма волны движется медленнее.
Чтобы измерить резонанс конструкции или материала с помощью системы сбора данных Prosig P8000 и программного обеспечения для обработки сигналов DATS Professional, необходимо прикрепить к конструкции акселерометр.Затем требуется возбуждать или стимулировать структуру с частотами, которым она обычно подвергается в течение срока службы. Например, автомобильная шина должна подвергаться воздействию частот, с которыми она будет встречаться во время использования. Обычно это достигается с помощью встряхивателя или большого тяжелого молотка. Шину, например, необходимо тестировать изолированно и не подключать к чему-либо еще, например к подвеске транспортного средства или ободу колеса, поскольку эти другие части имеют свои собственные резонансные частоты и затрудняют захват и анализ резонансной частоты шины.
Шину, например, необходимо тестировать изолированно и не подключать к чему-либо еще, например к подвеске транспортного средства или ободу колеса, поскольку эти другие части имеют свои собственные резонансные частоты и затрудняют захват и анализ резонансной частоты шины.
Измеренный отклик акселерометра будет относиться к возбуждению и будет показывать только частоты, которые присутствуют в возбуждении. Возбуждение должно быть приемлемым представлением нормальных рабочих частот, применяемых к конструкции или материалу. Если структура имеет резонанс в этом диапазоне частот, в спектре отклика будет большой пик. Частота этого пика будет соответствовать одной из резонансных частот конструкции или материала.Если пик не обнаружен, то резонансные частоты лежат за пределами рабочего диапазона конструкции или материала. Чтобы найти резонансные частоты конструкции или материала, может потребоваться более широкий диапазон частот возбуждения.
Рисунок 1
Рисунок 1 показывает частотный спектр, этот спектр является реакцией структуры на ее возбуждение. Примерно на частоте 250 Гц отчетливо виден большой всплеск.
Примерно на частоте 250 Гц отчетливо виден большой всплеск.
Рисунок 2
Рисунок 2 показывает частотный спектр, этот спектр, как на рисунке 1, показывает частотную характеристику.Однако на рисунке 2 с помощью курсоров показана точная частота резонанса. В этом случае резонансная частота составляет 245 Гц.
Это означает, что эту структуру, вероятно, не следует использовать, если в течение срока службы она будет подвергаться воздействию этой частоты. На рисунке 2 также показано, что если бы эта структура использовалась и подвергалась воздействию только частот от 300 Гц до 400 Гц или, возможно, от 0 Гц до 200 Гц, эта конкретная резонансная частота не возбуждалась, и, следовательно, конструкция не вибрировала бы аномально.
Дополнительная литература
Что такое резонанс? (часть 2) (https: // blog.prosig.com/2012/08/20/what-is-resonance-part-2/)
Что такое резонанс? (часть 3) (https://blog.prosig.com/2013/07/17/what-is-resonance-part-3/)
5 видеороликов, объясняющих резонанс (https://blog. prosig.com/2011 / 09/20/5-видео-которые-объясняют-резонанс /)
prosig.com/2011 / 09/20/5-видео-которые-объясняют-резонанс /)
Следующие две вкладки изменяют содержимое ниже.
Джеймс Рен был менеджером по продажам и маркетингу в Prosig Ltd до 2019 года. Джеймс окончил Портсмутский университет в 2001 году со степенью магистра электронной техники.Он дипломированный инженер и зарегистрированный Eur Ing. Он был вовлечен в автоспорт с самого раннего возраста и особенно интересовался сбором данных. Джеймс является одним из основателей команды Dalmeny Racing.
Нравится:
Нравится Загрузка …
Связанные
2.6: Вынужденные колебания и резонанс
Рассмотрим на примере массы на пружине.Теперь рассмотрим случай вынужденных колебаний, с которым мы еще не работали. То есть мы рассматриваем уравнение
для некоторого ненулевого \ (F (t) \). Схема снова такова: \ (m \) — масса, \ (c \) — трение, \ (k \) — жесткость пружины, и \ (F (t) \) — внешняя сила, действующая на массу.
Нас интересует периодическое воздействие, например, нецентрированные вращающиеся части, или, возможно, громкие звуки, или другие источники периодической силы. Когда мы узнаем о рядах Фурье в главе 4, мы увидим, что охватываем все периодические функции, просто рассматривая \ (F (t) = F_0 \ cos (\ omega t) \) (или синус вместо косинуса, вычисления по сути одинаковый).
2.6.1 Незатухающее принудительное движение и резонанс
Сначала для простоты рассмотрим незатухающее \ (c = 0 \) движение. У нас есть уравнение
\ [mx » + kx = F_0 \ cos (\ omega t) \]
Это уравнение имеет дополнительное решение (решение связанного однородного уравнения)
\ [x_c = C_1 \ cos (\ omega_0t) + C_2 \ sin (\ omega_0t) \]
, где \ (\ omega_0 = \ sqrt {\ frac {k} {m}} \) — собственная частота , (угловая), то есть частота, на которой система «хочет колебаться» без внешних помех.2)} \ cos (\ omega t) \]
Следовательно, это суперпозиция двух косинусоидальных волн на разных частотах. 2} \ cos (\ pi t) \]
Решите для \ (C_1 \) и \ (C_2 \), используя начальные условия.2} (2 \ sin (\ frac {4 — \ pi} {2} t) \ sin (\ frac {4 + \ pi} {2} t)) \]
Обратите внимание, что \ (x \) — это высокочастотная волна, модулированная низкочастотной волной.
Теперь предположим, что \ (\ omega_0 = \ omega \). Очевидно, что мы не можем попробовать решение \ (A \ cos (\ omega t) \), а затем использовать метод неопределенных коэффициентов. Заметим, что \ (\ cos (\ omega t) \) решает соответствующее однородное уравнение. Следовательно, нам нужно попробовать \ (x_p = At \ cos (\ omega t) + Bt \ sin (\ omega t) \). На этот раз нам нужен синусоидальный член, так как вторая производная от \ (t \ cos (\ omega t) \) действительно содержит синусы.2 x = \ frac {F_0} {m} \ cos (\ omega t) \]
Вставляя \ (x_p \) в левую часть, получаем
\ [2B \ omega \ cos (\ omega t) — 2A \ omega \ sin (\ omega t) = \ frac {F_0} {m} \ cos (\ omega t) \]
Следовательно, \ (A = 0 \) и \ (B = \ frac {F_0} {2m \ omega} \). Наше частное решение — \ (\ frac {F_0} {2m \ omega} t \ sin (\ omega t) \), а общее решение —
\ [x = C_1 \ cos (\ omega t) + C_2 \ sin (\ omega t) + \ frac {F_0} {2m \ omega} t \ sin (\ omega t) \]
Рисунок 2.2_2} \), который становится все меньше и меньше пропорционально колебаниям последнего члена по мере увеличения \ (t \). На рисунке 2.6 мы видим график с \ (C_1 = C_2 = 0, F_0 = 2, m = 1, \ omega = \ pi \).
Настраивая систему на правильную частоту, мы производим очень дикие колебания. Такое поведение называется резонансом или, возможно, чистым резонансом. Иногда желателен резонанс. Например, помните, когда в детстве вы могли начать раскачиваться, просто двигаясь вперед и назад на сиденье качели с «правильной частотой»? Вы пытались добиться резонанса.Сила каждого вашего движения была небольшой, но через некоторое время она произвела большие колебания.
С другой стороны, резонанс может быть разрушительным. В результате землетрясения некоторые здания рушатся, а другие могут быть относительно неповрежденными. 2} \).2}} \ cos (\ omega t — \ gamma) \]
Если \ (\ omega = \ omega_0 \), мы видим, что \ (A = 0, B = C = \ frac {F_0} {2m \ omega p}, ~ \ rm {и} ~ \ gamma = \ frac {\ пи} {2} \).
Точная формула не так важна, как идея. Не запоминайте приведенную выше формулу, вместо этого запомните задействованные идеи. Для другой функции форсирования \ (F \) вы получите другую формулу для \ (x_p \). Так что нет смысла запоминать эту конкретную формулу. Вы всегда можете пересчитать его позже или посмотреть, если он вам действительно нужен.
По причинам, которые мы объясним позже, мы называем \ (x_c \) переходным решением и обозначаем его \ (x_ {tr} \). Мы называем \ (x_p \), найденное выше, стационарным периодическим решением и обозначаем его \ (x_ {sp} \). Общее решение нашей проблемы —
\ [x = x_c + x_p = x_ {tr} + x_ {sp} \]
Рисунок 2.7: Решения с разными начальными условиями для параметров \ (k = 1, m = 1, F_0 = 1, c = 0,7, \) и \ (\ omega = 1.1. \)
Отметим, что \ (x_c = x_ {tr} \) стремится к нулю как \ (t \ rightarrow \ infty \), поскольку все члены включают экспоненту с отрицательной экспонентой.Следовательно, для больших \ (t \) эффект \ (x_ {tr} \) незначителен, и мы, по сути, увидим только \ (x_ {sp} \). Отсюда и название преходящее. Обратите внимание, что \ (x_ {sp} \) не содержит произвольных констант, а начальные условия будут влиять только на \ (x_ {tr} \). Это означает, что влияние начальных условий будет незначительным по прошествии некоторого времени. Из-за такого поведения мы могли бы также сосредоточиться на стационарном периодическом решении и игнорировать переходное решение. На рис. 2.7 показан график различных начальных условий.
Обратите внимание, что скорость, с которой \ (x_ {tr} \) стремится к нулю, зависит от \ (P \) (и, следовательно, \ (c \)). Чем больше \ (P \) (чем больше \ (c \)), тем «быстрее» \ (x_ {tr} \) становится незначительным. Таким образом, чем меньше демпфирование, тем длиннее «переходная область». Это согласуется с наблюдением, что когда \ (c = 0 \), начальные условия влияют на поведение в течение всего времени (то есть бесконечная «переходная область»).
Опишем, что мы подразумеваем под резонансом при наличии затухания. Поскольку при решении с неопределенным коэффициентом конфликтов не было, нет члена, уходящего в бесконечность.Однако мы рассмотрим максимальное значение амплитуды стационарного периодического решения. Пусть \ (C \) будет амплитудой \ (x_ {sp} \). Если мы построим график \ (C \) как функцию от \ (\ omega \) (с фиксированными всеми другими параметрами), мы сможем найти его максимум. Мы называем \ (\ omega \), который достигает этого максимума, практической резонансной частотой. Мы называем максимальную амплитуду \ (C (\ omega) \) практической амплитудой резонанса. Таким образом, когда присутствует демпфирование, мы говорим скорее о практическом резонансе, чем о чистом резонансе.Примерный график для трех различных значений \ (c \) приведен на рисунке 2.8. Как вы можете видеть, практическая амплитуда резонанса растет по мере уменьшения демпфирования, и любой практический резонанс может исчезнуть, когда демпфирование велико.
Рисунок 2.8: График \ (C (\ omega) \), показывающий практический резонанс с параметрами \ (k = 1, m = 1, F_0 = 1 \). Верхняя строка содержит \ (c = 0,4 \), средняя строка — \ (c = 0,8 \), а нижняя строка — \ (c = 1,6 \).
Чтобы найти максимум, нам нужно найти производную \ (C ‘(\ omega) \).2} \) — практическая резонансная частота (то есть точка, в которой \ (C (\ omega) \) максимальна, обратите внимание, что в этом случае \ (C ‘(\ omega)> 0 \) для малых \ (\ omega \)). Если \ (\ omega = 0 \) является максимумом, то по существу практического резонанса нет, поскольку мы предполагаем, что \ (\ omega> 0 \) в нашей системе. В этом случае амплитуда увеличивается с уменьшением частоты воздействия.
Если возникает практический резонанс, частота меньше \ (\ omega_0 \). Когда демпфирование \ (c \) (и, следовательно, \ (P \)) становится меньше, практическая резонансная частота переходит в \ (\ omega_0 \).Поэтому, когда затухание очень мало, \ (\ omega_0 \) является хорошей оценкой резонансной частоты. Такое поведение согласуется с наблюдением, что когда \ (c = 0 \), то \ (\ omega_0 \) является резонансной частотой.
Поведение усложняется, если функция принуждения не является точной косинусоидальной волной, а, например, прямоугольной волной. Будет хорошо вернуться к этому разделу, когда мы узнаем о рядах Фурье.
Обработка низкочастотного резонанса | Конструкция машин
Механический резонанс — распространенная проблема в следящих системах.Большинство проблем с резонансом вызвано соответствием компонентов трансмиссии. Стандартные законы сервоконтроля разработаны для жестко связанных нагрузок. Однако в практических машинах всегда присутствует некоторая податливость. Такое соответствие часто снижает запас устойчивости, вынуждая сервоусилители снижаться и снижая производительность машины.
Механический резонанс делится на две категории: низкочастотный и высокочастотный. Низкочастотный резонанс распространен в промышленности. Он отличается от менее распространенной, но наиболее часто исследуемой проблемы высокочастотного резонанса.Высокочастотный резонанс вызывает нестабильность собственной частоты механической системы, обычно от 500 до 1200 Гц. Низкочастотный резонанс вызывает колебания в первой фазе кроссовера, обычно от 200 до 400 Гц.
Хорошо известно, что характеристики сервопривода улучшаются, когда усиление регулирующего закона велико. Однако нестабильность возникает, когда закон управления с высоким коэффициентом усиления применяется к согласованно соединенному двигателю и нагрузке. Конструкторы машин определяют компоненты трансмиссии, такие как муфты и редукторы, как жесткие, чтобы минимизировать механическую податливость.Однако некоторая уступчивость неизбежна. Кроме того, такие ограничения, как стоимость и вес, вынуждают разработчиков выбирать более легкие компоненты, чем было бы желательно. Результирующая жесткость трансмиссии настолько мала, что возникает нестабильность, когда усиление сервопривода повышается до уровней, необходимых для достижения желаемых характеристик.
Идеальным объектом для традиционных законов управления является масштабированный интегратор. Однако идеальное растение портится из-за соблюдения требований. Член податливости имеет пик усиления на резонансной частоте F R и минимум усиления на антирезонансной частоте F AR .Если бы нагрузка была жестко связана, установка была бы идеальным интегратором. Однако соответствие вызывает затухание на F AR и около него и усиление на F R , около и выше.
Ключевой проблемой низкочастотного резонанса является увеличение усиления на частотах выше F R . Ниже F AR система ведет себя как простой интегратор.Коэффициент усиления падает на 20 дБ / декаду, а фаза составляет приблизительно –90 ° . Он также ведет себя как интегратор выше F R , но со значительно увеличенным усилением по сравнению с коэффициентом усиления значительно ниже F AR . Выше F R нагрузка эффективно отключается от двигателя, так что усиление установки является инерцией двигателя.
Передаточная функция разомкнутого контура хорошо известна для прогнозирования проблем стабильности с использованием двух показателей: запаса по фазе (PM) и запаса по усилению (GM).PM — это разность –180 ° и фаза разомкнутого контура на частоте, где усиление составляет 0 дБ. GM — это отрицательное значение усиления разомкнутого контура на частоте, на которой фаза пересекает –180 ° .
Когда резонансная частота значительно ниже первого фазового кроссовера (270 Гц), эффект соответствующей нагрузки заключается в уменьшении GM. Если рассогласование по инерции равно 5, снижение GM составит 6 или около 16 дБ. Предполагая, что других средств защиты нет, усиление согласованно связанной системы должно быть уменьшено на 16 дБ по сравнению с жесткой системой, предполагая, что обе будут поддерживать один и тот же GM.Такое большое снижение усиления привело бы к системе с гораздо более плохим управлением и откликом на помехи.
Высокочастотный резонанс другой. Это происходит в механизмах с легким демпфированием, когда собственная частота механической системы ( F R ) намного выше кроссовера первой фазы. Здесь усиление около F R образует сильный пик. Хотя оба типа резонанса вызваны податливостью, соотношение F R и кроссовера первой фазы существенно меняет лекарство; Средства от высокочастотного резонанса могут усугубить проблемы с низкочастотным резонансом.Механические конструкции, вызывающие высокочастотный резонанс (жесткие компоненты передачи и низкое демпфирование), типичны для сервомашин высокого класса, таких как станки. Меньшие по размеру и более дорогостоящие машины общего назначения в таких отраслях, как упаковочная, текстильная, плоттерная и медицинская, обычно имеют менее жесткие трансмиссии и более высокое демпфирование, поэтому низкочастотный резонанс встречается чаще.
Лекарства от низкочастотного резонанса
Существует множество методов для устранения низкочастотного резонанса.Наиболее распространенным в промышленности и наиболее простым в реализации является фильтр нижних частот. Другой выбор — биквадратный фильтр. Биквадратный фильтр имеет два полюса и два нуля; его можно рассматривать как фильтр верхних частот, последовательно соединенный с фильтром нижних частот. Другой метод — это обратная связь по ускорению, при которой ускорение обеспечивает наблюдатель.
Обратная связь по ускорению, применяемая вместе с двухквадратным фильтром, обеспечивает значительное улучшение по сравнению со всеми другими методами за счет увеличения полосы пропускания (частота, при которой коэффициент усиления падает до –3 дБ).Кроме того, сохраняется запас устойчивости. Пиковое значение, нежелательное явление, когда усиление превышает 0 дБ на высокой частоте в замкнутом контуре, является надежным показателем стабильности. Пики всех четырех конфигураций примерно одинаковы, при этом базовая система показывает наибольший пик, что указывает на то, что средства устранения резонанса позволяют более высокое усиление при сохранении эквивалентных запасов стабильности.
Обратная связь по ускорению в сочетании с двухквадратным фильтром обеспечивает значительное улучшение для систем, страдающих от низкочастотного резонанса.По сравнению с традиционным решением однополюсного фильтра нижних частот, комбинация обратной связи по ускорению и двухквадратного фильтра позволяет сократить время установления в три раза и увеличить полосу пропускания в тот же коэффициент. При этом обратная связь по ускорению сохраняет запас устойчивости.
График Боде показывает ключевую проблему низкочастотного резонанса; увеличение усиления на частотах выше резонансной, F R .
Ниже F R система действует как простой интегратор с падением усиления на 20 дБ / декаду и фазой на –90 °.Выше F R , усиление контура значительно увеличивается, уменьшая запас устойчивости.
В типичном контуре управления скоростью ошибка скорости V E обрабатывается законом управления и фильтрами. Команда тока, I C , подключена к контроллеру тока, который производит ток, I F в двигателе. Установка двигатель / нагрузка подключена к энкодеру. Наблюдатель, питаемый током обратной связи и положением, производит наблюдаемое ускорение, A MO .
Увеличение эффективного усиления, которое является результатом соответствующей нагрузки, снижает запас усиления. Здесь запас по усилению составляет чуть более 10 дБ. Идеальный запас по усилению системы был бы около 30 дБ.
Наблюдатель Люенбергера принимает входные данные от тока двигателя и энкодера, складывает их и передает полученную сумму модели двигателя. Затем модель создает наблюдаемое положение и сравнивает его с фактическим положением. Компенсатор наблюдателя ПИД-регулятора вытесняет большую часть ошибки до полосы пропускания наблюдателя, которая обычно составляет от 200 до 500 Гц.Одним из побочных продуктов наблюдателя является сигнал ускорения, который представляет ускорение намного лучше, чем двойное дифференцирование сигнала обратной связи по положению. Переходная характеристика базовой системы показывает время установления около 60 мсек с некоторым выбросом и полосой пропускания системы 23 Гц.
Переходная характеристика системы с обратной связью по ускорению показывает время установления около 12 мсек с меньшим выбросом. Полоса пропускания системы увеличена до 77 Гц.
Джордж Элликс, старший научный сотрудник
Kollmorgen, Danaher Motion
Radford, VA.
16.6 Стоячие волны и резонанс — University Physics Volume 1
На протяжении всей этой главы мы изучали бегущие волны или волны, переносящие энергию из одного места в другое. При определенных условиях волны могут подпрыгивать взад и вперед через определенную область, фактически становясь стационарными. Они называются стоячими волнами .
Другой связанный эффект известен как резонанс. В книге «Колебания» мы определили резонанс как явление, при котором движущая сила малой амплитуды может вызывать движение большой амплитуды.Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки со стороны родителя относительно небольшой амплитуды могут вызывать колебания большой амплитуды. Иногда этот резонанс бывает хорошим — например, при создании музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения. В случае стоячих волн стоячие волны относительно большой амплитуды образуются в результате наложения составляющих волн меньшей амплитуды.
Стоячие волны
Иногда кажется, что волны не двигаются; скорее, они просто вибрируют на месте. Вы можете увидеть неподвижные волны, например, на поверхности стакана с молоком в холодильнике. Вибрация двигателя холодильника создает волны на молоке, которые колеблются вверх и вниз, но не движутся по поверхности. (Рисунок) показывает эксперимент, который вы можете попробовать дома. Возьмите миску с молоком и поставьте ее на обычный вентилятор. Вибрация вентилятора вызывает в молоке стоячие круглые волны.Волны на фото видны благодаря отражению от лампы. Эти волны образуются наложением двух или более бегущих волн, как показано на (Рисунок) для двух идентичных волн, движущихся в противоположных направлениях. Волны движутся друг сквозь друга, и их возмущения добавляются по мере прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией. Результирующая волна выглядит как стоячая волна и, следовательно, называется стоячей волной.
Рисунок 16.25 Стоячие волны образуются на поверхности миски с молоком, установленной на ящичном веере. Вибрация вентилятора заставляет поверхность молока колебаться. Волны видны из-за отражения света от лампы.
рисунок 16.26 Временные снимки двух синусоидальных волн. Красная волна движется в направлении -x, а синяя волна движется в направлении + x. Результирующая волна показана черным цветом. Рассмотрим результирующую волну в точках
и обратите внимание, что результирующая волна всегда равна нулю в этих точках, независимо от времени.Эти точки известны как фиксированные точки (узлы). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Рассмотрим две одинаковые волны, движущиеся в противоположных направлениях. Первая волна имеет волновую функцию
.
, а вторая волна имеет волновую функцию
. Волны интерферируют и образуют результирующую волну
Это можно упростить с помощью тригонометрического идентификатора
где
и
, что дает нам
, что упрощается до
Обратите внимание, что результирующая волна — это синусоида, которая является функцией только положения, умноженной на функцию косинуса, которая является функцией только времени.Графики y ( x , t ) в зависимости от x для различных моментов времени показаны на (Рисунок). Красная волна движется в отрицательном направлении x , синяя волна движется в положительном направлении x , а черная волна является суммой двух волн. По мере того как красная и синяя волны движутся друг через друга, они входят и выходят из-за конструктивной интерференции и деструктивной интерференции.
Первоначально, в момент времени
две волны находятся в фазе, и в результате получается волна, которая в два раза превышает амплитуду отдельных волн.Волны также находятся в фазе в момент
.
Фактически, волны находятся в фазе в любом целом кратном половине периода:
В другое время две волны равны
не в фазе, и результирующая волна равна нулю. Это происходит на
Обратите внимание, что некоторые положения результирующей волны x всегда равны нулю, независимо от фазового соотношения. Эти позиции называются узлами .Где встречаются узлы? Рассмотрим решение суммы двух волн
Нахождение позиций, в которых функция синуса равна нулю, обеспечивает положение узлов.
Есть также позиции, в которых y колеблется между
. Это пучности . Мы можем найти их, посчитав, какие значения x дают
.
В результате получается стоячая волна, как показано на (Рисунок), где показаны снимки результирующей волны двух идентичных волн, движущихся в противоположных направлениях.Результирующая волна выглядит как синусоидальная волна с узлами в целых кратных полуволнах. Пучности колеблются между
.
из-за члена косинуса,
, который колеблется между
.
Результирующая волна, кажется, стоит на месте, без видимого движения в направлении x , хотя она состоит из одной волновой функции, движущейся в положительном направлении, тогда как вторая волна движется в отрицательном направлении x .(Рисунок) показывает различные снимки получившейся волны. Узлы отмечены красными точками, а пучности отмечены синими точками.
Рисунок 16.27 Когда две одинаковые волны движутся в противоположных направлениях, результирующая волна является стоячей волной. Узлы появляются в целых числах, кратных половине длины волны. Пучности появляются с нечетными числами, кратными четверти длины волны, где они колеблются между
Узлы отмечены красными точками, а пучности отмечены синими точками.
Типичным примером стоячих волн являются волны, создаваемые струнными музыкальными инструментами. Когда струна защипывается, импульсы проходят по струне в противоположных направлениях. Концы струн фиксируются на месте, поэтому на концах струн появляются узлы — граничные условия системы, регулирующие резонансные частоты в струнах. Резонанс, создаваемый струнным инструментом, можно смоделировать в физической лаборатории с помощью устройства, показанного на (Рисунок).
Рисунок 16.28 Лабораторная установка для создания стоячих волн на струне. У струны есть узел на каждом конце и постоянная линейная плотность. Длина между фиксированными граничными условиями равна L. Подвешенная масса обеспечивает натяжение струны, а скорость волн на струне пропорциональна квадратному корню из натяжения, деленному на линейную плотность массы.
Лабораторная установка показывает струну, прикрепленную к струнному вибратору, который колеблет струну с регулируемой частотой f .Другой конец струны проходит через шкив без трения и привязан к подвешенной массе. Величина натяжения тетивы равна весу подвешенной массы. Струна имеет постоянную линейную плотность (масса на длину)
, а скорость, с которой волна распространяется по струне, равна
.
(рисунок). Симметричные граничные условия (узел на каждом конце) определяют возможные частоты, которые могут возбуждать стоячие волны.Начиная с нулевой частоты и медленно увеличивая частоту, первая мода
выглядит так, как показано на (Рисунок). Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами
. Основная частота или частота первой гармоники, которая управляет этим режимом, равна
, где скорость волны
Сохранение постоянного напряжения и увеличение частоты приводит ко второй гармонике или
режим.Этот режим — полная длина волны
, а частота в два раза больше основной частоты:
Рисунок 16.29 Стоячие волны, создаваемые на струне длиной L. Узлы возникают на каждом конце струны. Узлы — это граничные условия, ограничивающие возможные частоты, возбуждающие стоячие волны. (Обратите внимание, что амплитуды колебаний оставались постоянными для визуализации. Возможные модели стоячих волн на струне известны как нормальные моды.Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды при увеличении частоты.)
Следующие две моды или третья и четвертая гармоники имеют длины волн
и
на частотах
и
Все частоты выше частоты
известны как обертона . Уравнения для длины волны и частоты можно резюмировать как:
Модели стоячей волны, которые возможны для струны, первые четыре из которых показаны на (Рисунок), известны как нормальные моды с частотами, известными как нормальные частоты.Таким образом, первая частота, вызывающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота
нормальный режим струны — это первый обертон (или вторая гармоника). Частота
нормальный режим — это второй обертон (или третья гармоника) и так далее.
Решения, показанные как (Уравнение) и (Уравнение), предназначены для строки с граничным условием узла на каждом конце.Когда граничные условия с обеих сторон одинаковы, говорят, что система имеет симметричные граничные условия. (Уравнение) и (Уравнение) подходят для любых симметричных граничных условий, то есть узлов на обоих концах или пучностей на обоих концах.
Пример
Стоячие волны на струне
Рассмотрим строку
, прикрепленный к струнному вибратору с регулируемой частотой, как показано на (Рисунок). Волны, создаваемые вибратором, спускаются по струне и отражаются фиксированным граничным условием на шкиве.Струна, имеющая линейную массовую плотность
проходит через шкив без трения с незначительной массой, а натяжение обеспечивается подвешенной массой 2,00 кг. а) Какова скорость волн на струне? (b) Нарисуйте эскиз первых трех нормальных мод стоячих волн, которые могут возникать на струне, и пометьте каждой длиной волны. (c) Перечислите частоты, на которые должен быть настроен струнный вибратор, чтобы произвести первые три нормальные моды стоячих волн.
Рисунок 16.30 Струна, прикрепленная к струнному вибратору с регулируемой частотой.
Стратегия
- Скорость волны можно найти с помощью
Натяжение обеспечивается весом подвешенной массы.
- Стоячие волны будут зависеть от граничных условий. На каждом конце должен быть узел. Первая мода будет составлять половину волны. Второй можно найти, добавив половину длины волны. Это самая короткая длина, которая приведет к образованию узла на границах.Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на (Рисунок).
- Поскольку скорость волны равна длине волны, умноженной на частоту, частота равна скорости волны, деленной на длину волны.
Рис. 16.31 (a) На рисунке представлен второй режим строки, который удовлетворяет граничным условиям узла на каждом конце строки. (b) Этот рисунок не может быть нормальным режимом для струны, потому что он не удовлетворяет граничным условиям.На одном конце есть узел, а на другом — пучность.
Решение
- Начнем со скорости волны на струне. Натяжение равно весу подвешенной массы. Даны линейная массовая плотность и масса подвешенной массы:
- Первая нормальная мода с узлами на каждом конце — это половина длины волны. Следующие две моды находятся путем добавления половины длины волны.
- Частоты первых трех мод находятся с помощью
Значение
Три режима стоя в этом примере были получены путем поддержания натяжения струны и регулировки частоты возбуждения.Сохранение постоянного натяжения струны приводит к постоянной скорости. Те же самые режимы можно было бы получить, сохранив постоянную частоту и регулируя скорость волны в струне (изменяя висящую массу).
Проверьте свое понимание
Уравнения для длин волн и частот мод волны, создаваемой на струне:
были получены путем рассмотрения волны на струне, где были симметричные граничные условия узла на каждом конце.Эти режимы возникли в результате двух синусоидальных волн с идентичными характеристиками, за исключением того, что они движутся в противоположных направлениях, ограниченных областью L с узлами, необходимыми на обоих концах. Будут ли работать те же уравнения при наличии симметричных граничных условий с пучностями на каждом конце? Как бы выглядели нормальные режимы для среды, которая могла бы свободно колебаться на каждом конце? Если вы не можете себе представить такую среду, не беспокойтесь, просто рассмотрите две синусоидальные волновые функции в области длиной L с пучностями на каждом конце.
Да, уравнения будут одинаково хорошо работать для симметричных граничных условий среды, свободно колеблющейся на каждом конце, где на каждом конце есть пучности. Ниже показаны нормальные режимы первых трех режимов. Пунктирная линия показывает положение равновесия среды.
Обратите внимание, что первая мода составляет две четверти или половину длины волны. Вторая мода — это четверть длины волны, за которой следует половина длины волны, за которой следует четверть длины волны, или одна полная длина волны.Третья мода — полторы длины волны. Это тот же результат, что и у строки с узлами на каждом конце. Уравнения для симметричных граничных условий одинаково хорошо работают как для фиксированных граничных условий, так и для свободных граничных условий. Эти результаты будут рассмотрены в следующей главе при обсуждении звуковой волны в открытой трубке.
Свободные граничные условия, показанные в последней проверке понимания, могут показаться трудными для визуализации. Как может быть система, которая может свободно колебаться на каждом конце? На (Рисунок) показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим).В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия. При правильной частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце. В части (b) стержень поддерживается в положениях, составляющих одну четверть длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При правильной частоте этот стержень также можно привести в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности.Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длину волны можно измерить между любыми двумя ближайшими идентичными точками, и подумайте (рисунок).
Рисунок 16.32 (a) Металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на каждом конце. При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с узлом на каждом конце. (b) Тот же самый металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на расстоянии четверти длины стержня с каждого конца.При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с пучностями на каждом конце.
Рисунок 16.33 Длину волны можно измерить между ближайшими двумя повторяющимися точками. На волне на веревке это означает одинаковую высоту и наклон. (a) Длина волны измеряется между двумя ближайшими точками, где высота равна нулю, а наклон является максимальным и положительным. (b) Длина волны измеряется между двумя идентичными точками, где высота максимальна, а наклон равен нулю.
Обратите внимание, что изучение стоячих волн может стать довольно сложным. На (Рисунок) (а) модель
Показана мода стоячей волны
, которая дает длину волны, равную L . В этой конфигурации
Режим
также был бы возможен при стоячей волне, равной 2 L . Можно ли получить
для конфигурации, показанной в части (b)? Ответ — нет. В этой конфигурации помимо граничных условий устанавливаются дополнительные условия.Поскольку стержень установлен в точке, равной четверти длины с каждой стороны, там должен существовать узел, и это ограничивает возможные режимы стоячих волн, которые могут быть созданы. Мы оставляем читателю в качестве упражнения подумать, возможны ли другие режимы стоячих волн. Следует отметить, что когда система приводится в действие с частотой, которая не вызывает резонанс системы, вибрации все еще могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
Область машиностроения использует звук, издаваемый вибрирующими частями сложных механических систем, для устранения проблем с системами. Предположим, часть автомобиля резонирует с частотой двигателя автомобиля, вызывая нежелательные вибрации в автомобиле. Это может привести к преждевременной поломке двигателя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют метод, называемый анализом Фурье, для поиска частот звука, производимого с большими амплитудами, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте.Решение может быть таким простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Есть и другие многочисленные примеры резонанса стоячих волн в физическом мире. Воздух в трубке, например, в музыкальном инструменте, таком как флейта, может вызвать резонанс и произвести приятный звук, как мы обсуждаем в разделе «Звук».
В других случаях резонанс может вызвать серьезные проблемы. Более пристальный взгляд на землетрясения свидетельствует о наличии условий, подходящих для резонанса, стоячих волн, а также конструктивных и деструктивных помех.Здание может вибрировать в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственной вибрации здания, что вызывает резонанс, в результате которого одно здание рушится, а соседние — нет. Часто здания определенной высоты разрушаются, а другие более высокие здания остаются нетронутыми. Высота здания соответствует условию создания стоячей волны для данной высоты. Также важен пролет крыши. Часто можно увидеть, что спортзалы, супермаркеты и церкви страдают от повреждений, в то время как отдельные дома страдают гораздо меньше.Крыши с большой площадью поверхности, поддерживаемые только краями, резонируют с частотами землетрясений, вызывая их обрушение. Когда волны землетрясения распространяются по поверхности Земли и отражаются от более плотных горных пород, в определенных точках возникают конструктивные помехи. Часто участки, расположенные ближе к эпицентру, не повреждаются, а участки дальше — повреждены.
.



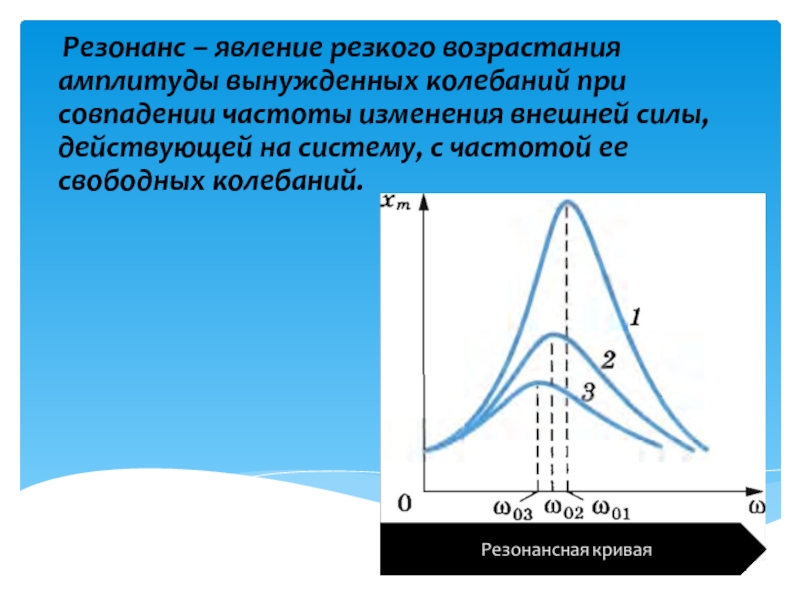
 Если стропы подвешены, система имеет очень разную резонансную частоту.
Если стропы подвешены, система имеет очень разную резонансную частоту.
 Студент знает характеристики и поведение волн. Ожидается, что студент:
Студент знает характеристики и поведение волн. Ожидается, что студент: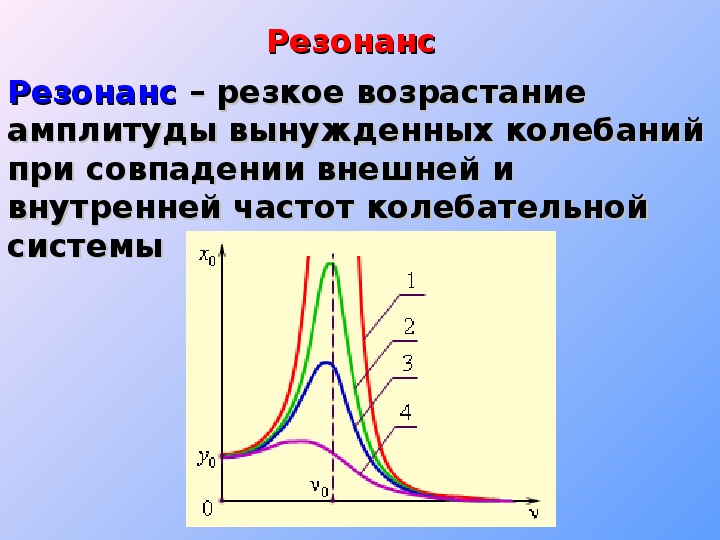 Это явление называется затуханием.Это вызвано рассеянием энергии.
Это явление называется затуханием.Это вызвано рассеянием энергии.
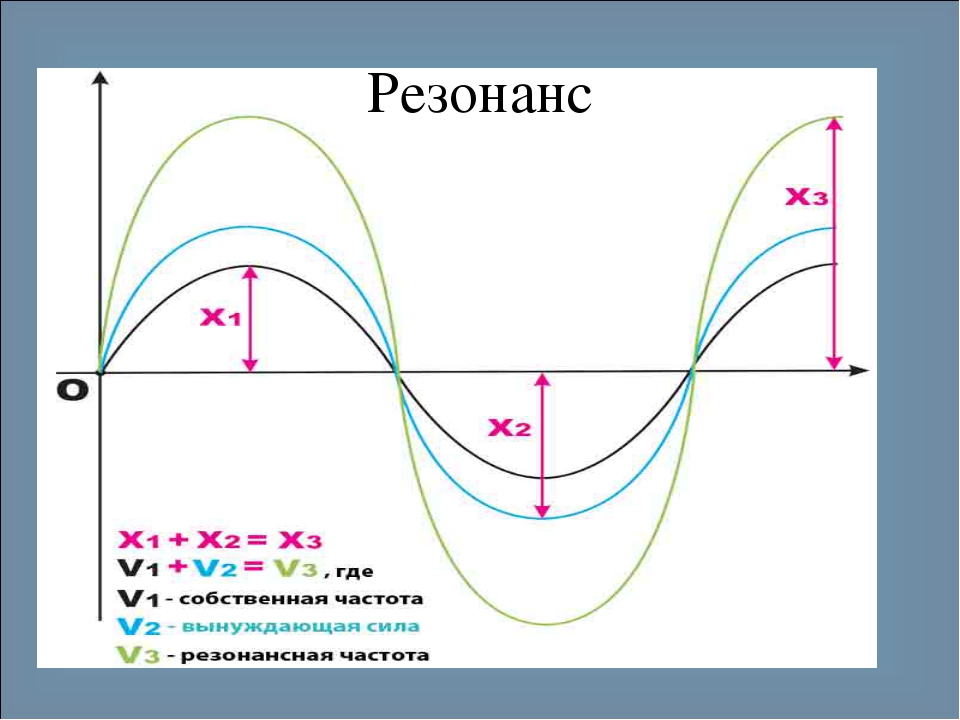
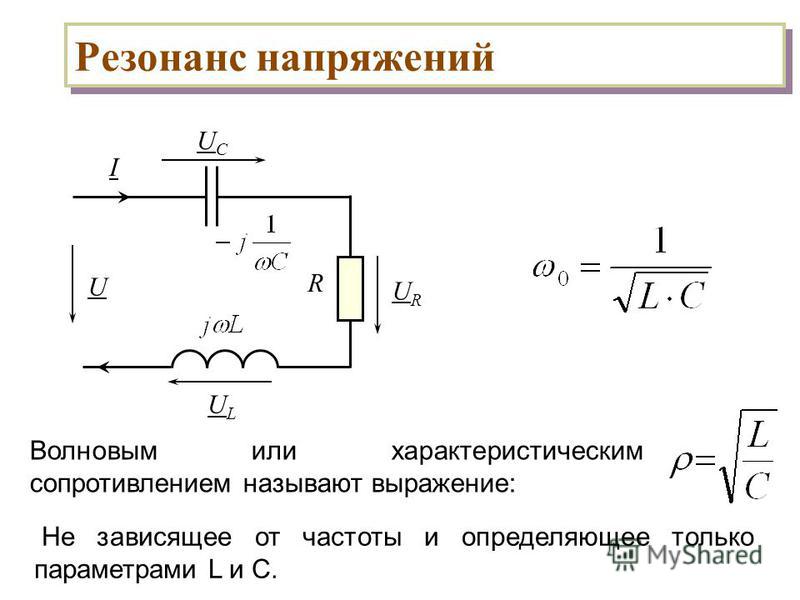 800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение.
800 м / с в положении равновесия? Предположим, автомобиль возвращается в исходное вертикальное положение.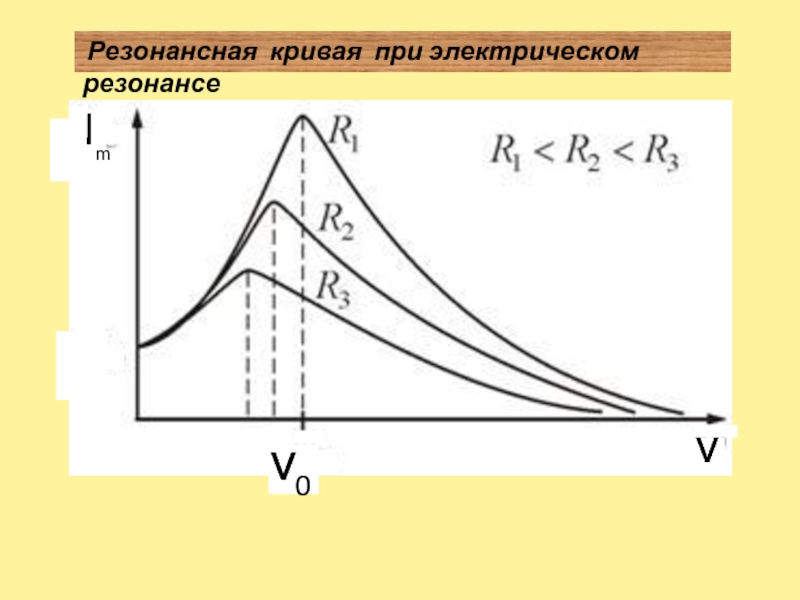 100. а) Как далеко можно растянуть пружину, не перемещая массу? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения равен μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, он начинается с максимальной амплитуды.
100. а) Как далеко можно растянуть пружину, не перемещая массу? (b) Если объект приводится в колебание с амплитудой, вдвое превышающей расстояние, указанное в части (a), и кинетический коэффициент трения равен μ k = 0,0850, какое общее расстояние он проходит до остановки? Предположим, он начинается с максимальной амплитуды.