Основные понятия и законы теории электрических цепей. Две электрические цепи содержат соответственно 3 и 4 элемента
Расчет электрических цепей | Физика
1. Смешанное соединение проводников
Рассмотрим электрическую схему на рисунке 61.1. Некоторые проводники в ней соединены последовательно друг с другом, а некоторые – параллельно.
? 1. Какие проводники в этой схеме соединены последовательно друг с другом? Какие – параллельно?
Соединение проводников, при котором часть проводников соединена последовательно друг с другом, а часть – параллельно, называют смешанным.При расчете сопротивления смешанного соединения проводников часто используют метод эквивалентного преобразования схем. При этом данную схему последовательно преобразуют в более простую, но имеющую такое же сопротивление.
Например, схему, изображенную на рисунке 61.1, можно преобразовать по следующему плану:1. Заменить участок цепи с резисторами 1 и 2 одним резистором с сопротивлением, которое мы обозначим R12.2. Заменить участок цепи, содержащий резисторы с сопротивлениями R12 и R3, одним резистором с сопротивлением, которое мы обозначим R123.3. Заменить участок цепи с резисторами 4 и 5 одним резистором с сопротивлением, которое мы обозначим R45.4. Заменить участок цепи с резисторами сопротивлением R123 и R45 одним резистором. Его сопротивление и будет равно сопротивлению всего участка цепи.
? 2. В цепи, схема которой изображена на рисунке 61.1, сопротивление каждого резистора, выраженное в омах, примите равным номеру этого резистора. Начертите схемы, соответствующие каждому пункту намеченного выше плана; найдите R12, R123, R45 и сопротивление всего участка.
Не всегда с первого взгляда на электрическую схему можно распознать вид соединения проводников.
В таком случае полезно найти точки с одинаковым потенциалом (например, соединенные проводами, сопротивление которых в таких задачах считают обычно пренебрежимо малым). Затем надо перечертить схему, объединив точки с одинаковым потенциалом.
Рассмотрим, например, схему участка цепи, изображенную на рисунке 61.2.
Точки А и С соединены проводом с пренебрежимо малым сопротивлением, поэтому потенциалы этих точек равны. То же можно сказать и о точках В и D.
Следовательно, схему можно перечертить, объединив точки А и С в одну точку (обозначим ее АС), а точки В и D объединив в точку ВD. При этом, согласно исходной схеме, один конец каждого из трех резистов соединен с точкой АС, а другой – с точкой BD (рис. 61.3).
Теперь мы видим, что резисторы соединены параллельно.
? 3. Перенесите в тетрадь рисунок 61.2 и отметьте на нем направление тока в каждом резисторе, считая, что потенциал точки А выше потенциала точки D.
? 4. На рисунке 61.4 изображена схема участка электрической цепи. Сопротивление каждого резистора, выраженное в омах, равно номеру резистора. Обратите внимание: потенциалы точек А и С различны.а) Перечертите схему, изображенную на рисунке 61.4, так, чтобы легко было распознать вид соединения резисторов.б) Найдите сопротивление всего участка цепи.
К сожалению, не всякую электрическую схему можно поэтапно упрощать, используя только формулы для последовательного и параллельного соединений. На рисунке 61.5 приведен пример схемы участка цепи, которую нельзя упростить таим образом.
Но для некоторых частных случав можно найти сопротивление и такого участка цепи уже известными нам способами. Чтобы догадаться, каковы эти случаи, заменим резистор 5 идеальным вольтметром (рис. 61.6). (Напомним, что идеальным считают вольтметр, сопротивление которого можно принять бесконечно большим.)
? 5. Разность потенциалов между точками А и В равна 21 В. Сопротивления резисторов, выраженные в омах, равны их номерам.а) Чему равна разность потенциалов между точками А и С?б) Чему равна разность потенциалов между точками А и D?в) Каковы показания вольтметра?г) Резистором с каким сопротивлением надо заменить резистор 4, чтобы показания вольтметра были равны нулю?
? 6. Объясните, почему показания вольтметра будут равны нулю независимо от напряжения между точками А и В, если сопротивления резисторов на схеме, изображенной на рисунке 61.6, удовлетворяют соотношению
R1/R2 = R3/R4. (1)
Схему, изображенную на рисунке 61.6, называют мостиком Уитстона. С ее помощью можно измерить сопротивление одного из четырех резисторов, подбирая сопротивления остальных трех так, чтобы выполнялось соотношение (1).
? 7. Для сопротивлений резисторов 1 – 4 в цепи, изображенной на рисунке 61.5, выполняется соотношение (1).а) Объясните, почему сопротивление данного участка цепи не зависит от сопротивления резистора 5.б) Сопротивления резисторов 1 и 3 равны соответственно 10 Ом и 15 Ом. Подберите такие значения сопротивлений резисторов 2 и 4, чтобы сопротивление всего участка было равно 24 Ом независимо от сопротивления резистора 5.
2. Максимальная мощность во внешней цепи
? 8. К источнику с ЭДС ξ и внутренним сопротивлением r подключено внешнее сопротивление R (рис. 61.7).а) Выразите мощность тока во внешней цепи через ξ, r и R.б) Используя производную, найдите, при каком R мощность тока во внешней цепи будет максимальной.
Эту задачу можно решить и без помощи производной. Для этого надо воспользоваться формулой для мощности тока во внешней цепи
P = UI,
где U – напряжение на внешнем сопротивлении (напомним, что оно равно напряжению на полюсах источника тока), I – сила тока в цепи.
? 9. Объясните, почему мощность тока во внешней цепи выражается формулой
P = (ξ – Ir)I. (2)
Подсказка. Выразите напряжение на полюсах источника через ξ, I, r, используя закон Ома для всей цепи.
Правая часть равенства (2) представляет собой квадратичную функцию от силы тока I. Графиком ее является парабола.
? 10. Начертите график зависимости P(I) при изменении силы тока I от нуля до максимального значения (равного силе тока при коротком замыкании).а) При каком значении I достигается максимум функции P(I)?б) Какому сопротивлению внешней цепи соответствует это значение I?Подсказка. Воспользуйтесь законом Ома для всей цепи.
Итак, максимальная мощность тока во внешней цепи достигается, когда сопротивление внешней цепи равно внутреннему сопротивлению источника тока.
? 11. Чему при этом равен КПД источника тока?
3. Конденсаторы в цепи постоянного тока
Постоянный ток не может идти через конденсатор, потому что между его обкладками находится диэлектрик. Однако между обкладками конденсатора, включенного в цепь постоянного тока, может существовать разность потенциалов, и тога конденсатор будет заряженным. Начнем с самых простых случаев, когда в цепи, помимо конденсатора, есть только один резистор.
? 12. На рисунке 61.8 изображена схема электрической цепи. ЭДС источника тока ξ = 12 В, его внутреннее сопротивление r = 2 Ом, сопротивление резистора R = 10 Ом, электроемкость конденсатора С = 2 мкФ.61.8а) Чему равна разность потенциалов между точками А и В?б) Чему равна разность потенциалов между точками А и D?в) Чему равен заряд конденсатора?г) Каков знак заряда обкладки конденсатора, соединенной с резистором?
? 13. На рисунке 61.9 изображена схема электрической цепи. ЭДС источника тока ξ, его внутреннее сопротивление r, сопротивление резистора R, электроемкость конденсатора C.а) Чему равна разность потенциалов между точками А и В?б) Чему равен заряд конденсатора?
Рассмотрим теперь более сложный случай, когда в цепи есть несколько резисторов, причем они по-разному подключены к конденсатору.
? 14. В цепи (рис. 61.10) ЭДС источника ξ = 6 В, его внутреннее сопротивление r = 1 Ом, сопротивления резисторов R1 = 3 Ом, R2 = 5 Ом, R3 = 12 Ом, электроемкость конденсатора C = 8 мкФ.а) Перенесите схему в тетрадь и обозначьте, через какие элементы цепи идет ток.б) Какова сила тока в резисторе 3?в) Чему равна разность потенциалов между точками А и D?г) Чему равна разность потенциалов между точками А и В?д) Чему равно напряжение на конденсаторе?е) Чему равен заряд конденсатора?ж) Каков знак заряда обкладки конденсатора, соединенной с резистором 2?
Дополнительные вопросы и задания
15. На рисунке 61.11 изображена схема участка электрической цепи. Сопротивление каждого резистора 1 Ом. Используя метод эквивалентного преобразования схем:а) начертите схемы последовательного упрощения данной схемы, содержащие меньше резисторов;б) для каждой схемы рассчитайте ее сопротивление и найдите общее сопротивление всего участка.
16. На схеме участка цепи, изображенной на рисунке 61.5, сопротивления резисторов R1 = 20 Ом, R2 = 100 Ом, R3 = 10 Ом, R4 = 50 Ом, R5 = 80 Ом. Каково общее сопротивление участка цепи?
17. Сопротивление внешней цепи в 4 раза больше того значения, при котором мощность тока во внешней цепи максимальна.а) Чему равен КПД источника тока?б) Во сколько раз при этом мощность тока во внешней цепи меньше максимально возможной?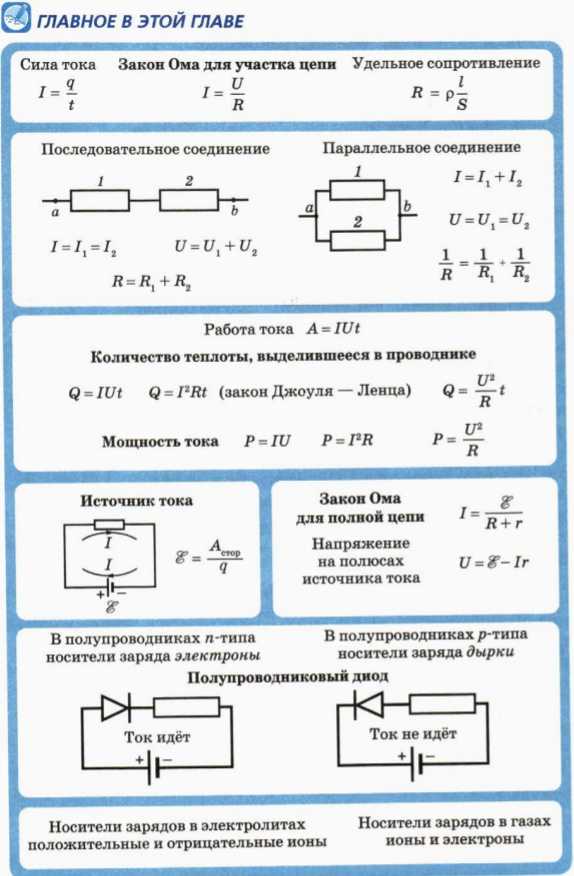
phscs.ru
Электрическая цепь и ее элементы
Электрической цепью называется совокупность электротехнических устройств, предназначенных для передачи, распределения и взаимного преобразования электрической и других видов энергии и информации.
Основными элементами электрической цепи являются источники электрической энергии и приемники электрической энергии.
В источниках механическая, химическая и другие виды энергии преобразуются в электрическую энергию. В приемниках электрическая энергия превращается в механическую, тепловую, световую и другие виды энергии.
В судовых электрических цепях в качестве источников могут использоваться дизель-генераторы, турбогенераторы, валогенераторы, аккумуляторные батареи (в режиме разрядки), гальванические элементы, статистические и машинные преобразователи. Основные приемники электрической энергии на судах – это электродвигатели, нагревательные элементы, светильники, устройства автоматики, аккумуляторные батареи (в режиме зарядки).
Электрические цепи содержат также вспомогательные элементы: соединительные провода (кабельные трассы, линии передачи), коммутационную аппаратуру (выключатели, переключатели), устройства измерения и контроля параметров.
Графическое изображение электрической цепи называется схемой. На рис. 1 приведен пример схемы электрической цепи постоянного тока, состоящей из источника, приемника и соединительных проводов.
Рис. 1. Схема простейшей электрической цепи постоянного тока
Процессы, происходящие в электрической цепи, описываются с помощью таких понятий как ток, напряжение, электродвижущая сила (ЭДС), мощность, энергия. В цепях постоянного тока ЭДС, напряжение, ток, мощность не зависят от времени. Символы этих величин для цепей, постоянного тока принято изображать прописными буквами E, U, I, P. В цепях переменного тока ЭДС, напряжение, ток, мощность являются функциями времени. Для обозначения мгновенных значений этих величин используются строчные буквы e, u, i, p.
Электрический ток (ток проводимости) как явление представляет собой упорядоченное движение носителей зарядов внутри проводника.
Количественно электрический ток (сила тока) определяется как скорость протекания зарядов q через любое поперечное сечение проводника:
Ток измеряется в амперах [А].
За истинное направление тока условно принято движение положительных зарядов. Поэтому во внешней по отношению к источнику цепи ток течет от точки схемы с большим потенциалом к точке схемы с меньшим потенциалом (от зажима «+» к зажиму «–» на рис. 1).
Напряжение на участке электрической цепи – это работа сил электрического поля по перемещению единичного положительного заряда между начальной и конечной точками этого участка. Напряжение равно разности электрических потенциалов начальной и конечной точек участка. Так, для участка ab на рис. 2
,
где φa, φb – потенциалы точек a и b соответственно.
Во внешней по отношению к источнику цепи направления напряжения и тока совпадают (см. рис. 1, 2).
Рис. 2. Участок электрической цепи
Перенос зарядов в электрических цепях в установившемся режиме работы осуществляется под воздействием ЭДС источников электрической энергии. ЭДС источника создается за счет затрат внешней по отношению к электрической цепи энергии: механической энергии приводного двигателя, вращающего генератор, электрохимической энергии аккумуляторной батареи или гальванического элемента, тепловой энергии в термопаре. ЭДС источника E численно равна разности потенциалов между положительным и отрицательным зажимами источника в режиме холостого хода (когда ток источника равен нулю).
Ток внутри источника ЭДС направлен от зажима «–» к зажиму «+», а стрелка внутри окружности, изображающей источник на схеме, направлена в сторону большего потенциала (см. рис. 1).
Напряжение и ЭДС измеряются в вольтах [В].
Электрическая энергия, выделяемая (потребляемая) на участке электрической цепи за время t, равна
Энергия измеряется в джоулях [Дж].
Электрическая мощность характеризует скорость изменения энергии
Мощность измеряется в ваттах [Вт].
Анализ работы электрической цепи значительно упрощается, если элементы считать идеальными. Поэтому на схемах реальные элементы цепи заменяются идеальными элементами схемы. Эти идеальные элементы схемы отражают какие-то определенные свойства реальных элементов цепи. Для отражения нескольких различных свойств реального элемента его схема может компоноваться из нескольких идеальных элементов с различными свойствами.
Для цепей постоянного тока используются понятия двух идеальных элементов: идеального источника и идеального приемника.
Идеальный приемник (см. рис. 1, 2) – это пассивный элемент цепи, в котором энергия электрического тока безвозвратно рассеивается в виде тепла. Свойствами идеального пассивного элемента практически обладает резистор, который характеризуется сопротивлением R или проводимостью g = 1/R. Единица измерения сопротивления называется ом [Ом], а проводимости – сименс [См], причем 1См = 1/Ом.
В соответствии с законом Джоуля-Ленца энергия, выделяющаяся в виде тепла в пассивном элементе, прямо пропорциональна сопротивлению, квадрату тока и времени. Этот закон выражается формулами:
Идеальный источник – это такой активный элемент цепи, который всю выработанную энергию отдает во внешнюю цепь. Коэффициент полезного действия (КПД) идеального источника h = 100 %. В природе такого источника не существует. По своим характеристикам к идеальному приближается источник, у которого потери энергии в виде тела внутри источника пренебрежимо малы по сравнению с энергией, отдаваемой приемнику.
Реальный источник в схеме электрической цепи можно представить, например, в виде совокупности двух идеальных элементов: идеального источника ЭДС Е и внутреннего сопротивления источника Ri (см. рис. 1). Введение в схему внутреннего сопротивления источника Ri позволяет учесть потери энергии в виде тепла внутри самого источника.
Элементы электрических цепей можно подразделить на линейные и нелинейные.
В пассивном линейном элементе отношение напряжения к току постоянно. В качестве пассивного линейного элемента можно рассматривать, например, резистор с постоянным сопротивлением R:
Графическую зависимость напряжения от тока (или тока от напряжения) для пассивных элементов принято называть вольт-амперной характеристикой. Вольт-амперная характеристика резистора приведена на рис. 3. Она представляет собой луч 1, выходящий из начала координат. У пассивного нелинейного элемента отношение напряжения к току непостоянно и вольт-амперная характеристика нелинейна (рис. 3, кривая 2).
Рис. 3. Вольт-амперные характеристики линейного 1
и нелинейного 2 пассивных элементов
Графическую зависимость напряжения от тока для источников электрической энергии принято называть внешней характеристикой. Внешняя характеристика реального линейного источника приведена на рис. 4. Она представляет собой отрезок прямой линии 1 между точкой холостого хода (U = E) и точкой короткого замыкания (U = 0). Пунктирной линией 2, параллельной оси абсцисс, на этом графике изображена внешняя характеристика идеального источника ЭДС. Внешняя характеристика реального нелинейного источника приведена на рис. 4, кривая 3. Цепь называется линейной, если все элементы цепи линейны. Если хотя бы один элемент цепи нелинеен, то цепь будет нелинейной. Практически все цепи нелинейные. Однако при рассмотрении изменений напряжений и токов в ограниченном диапазоне многие цепи можно считать линейными.
В настоящем учебном пособии рассматриваются линейные электрические цепи постоянного тока.
Рис. 4. Внешние характеристики линейного 1, идеального 2
и нелинейного 3 источников ЭДС
Похожие статьи:
poznayka.org
Электрическая цепь и ее элементы.
Электрическая цепь и ее элементы.
Реальная электрическая цепь - совокупность устройств, предназначенных для передачи, распределения и преобразования энергии. Содержит источники электрической энергии, приемники электрической энергии, измерительные приборы, коммутационную аппаратуру, соединительные линии и провода. Электрическая цепь представляет собойсовокупность связанных определенным образом источников, потребителей (или соответственно активных и пассивных элементов) и преобразователей электрической энергии. Цепь называют пассивной, если она состоит только из пассивных элементов, и активной, если в ней также содержатся активные элементы.
Источником электрической энергии называют элемент электрической цепи, осуществляющий преобразование энергии неэлектрического вида в электрическую. Потребителем электрической энергии называют элемент электрической цепи, преобразующий электрическую энергию в неэлектрическую. Преобразователем электрической энергии называют устройство, изменяющее величину и форму электрической энергии.
Для того чтобы выполнить расчет, необходимо каждое электротехническое устройство представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности идеализированных элементов(резистор, конденсатор, катушка индуктивности).
Напряжение:
Ток:
Зависимость между током и напряжением на элементе цепи называется вольт-амперной характеристикой (ВАХ) элемента, которая обычно изображается графически.
В качестве потребителя в теории электрических цепей постоянного тока выступает резистор, характеризующийся сопротивлением (R), для которого справедлив закон Ома:
Проводимость: измеряется в Сименсах (См).
Источники энергии моделируются с помощью источника ЭДС (Е), или источника напряжения, и источника тока (J). В большинстве случаев с увеличением тока напряжение источника уменьшается.
Идеализированный источник напряжения – это элемент цепи, напряжение которого не зависит от тока и является заданной постоянной величиной. В действительности мы имеем дело с реальными источниками напряжения, которые отличаются от идеальных источников тем, что их напряжение с ростом потребляемого тока уменьшается. Любой реальный источник при сопротивлении нагрузки R >> R0 может быть приведен к идеализированному следующим образом:
Идеализированный источник тока – это элемент цепи, ток которого не зависит от напряжения и является заданной постоянной величиной.
У реального источника тока с ростом напряжения вырабатываемый ток уменьшается.Любой реальный источник тока может быть приведен к идеализированному следующим образом :
,где J, G0 – постоянные параметры.
Обобщенный закон Ома.
Рассмотрим закон Ома для участка цепи, содержащего активные и пассивные элементы
.
Объединив эти две формулы, получаем:
Отсюда ток
Аналогияно:
)
Объединив эти две формулы в одну, получим:
, - обобщенный закон Ома.
Обобщенный закон Ома для ветви, содержащей источник тока:
Для содействующего источника тока
Для противодействующего источника тока
Объединенная форма обобщенного закона Ома для ветвей, содержащих источник тока:
(1.25)
где верхний знак соответствуют схеме, на которой UJ и J сонаправлены.
Законы Кирхгофа.
I закон Кирхгофа (для токов): алгебраическая сумма токов в узле равна нулю, или сумма притекающих и сумма истекающих токов одинаковы. Как правило, при суммировании притекающие токи берутся со знаком «+», а истекающие – со знаком «–».
II закон Кирхгофа (для напряжений): алгебраическая сумма ЭДС всех источников, встречающихся при обходе контура, равна алгебраической сумме напряжений на всех потребителях. В алгебраической форме
В сумму со знаком «+» входят ЭДС содействующих источников и со знаком «–» ЭДС противодействующих источников. При суммировании напряжений потребителей со знаком «+» берутся напряжения на всех потребителях, токи которых направлены согласно с обходом контура, и со знаком «–» берутся напряжения всех остальных потребителей.
8) Эквивалентные преобразования пассивных электрических цепей.
Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем.
При последовательном соединении роль эквивалентного сопротивления играет сумма сопротивлений всех потребителей (рис. 1.11.).
(II З. К.) =>
При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
Это следует из I закона Кирхгофа:
9-10) Эквивалентное преобразование «Звезда – треугольник»
В узлах a, b, c и треугольник , и звезда на рис. 1.14. соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены.
Выразим Uabтреугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.
Заменим в первом уравнении токи I3 и I2на соответствующие выражения:
Теперь получим выражение для этого же напряжения при соединении потребителей звездой:
=>
Аналогично
Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника.
Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений через проводимости:
или через сопротивления:
Баланс мощности.
Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию:
[Дж]
[Вт]
По обобщенному закону Ома.
Выражения, записанные для ветви с источником напряжения, справедливы и для ветви с источником тока, если произвести подстановку вместо и вместо .
Отсюда следует закон сохранения энергии, согласно которому алгебраическая сумма мощностей, подводимых ко всем ветвям разветвленной электрической цепи, равна нулю:
Существует еще одна форма записи баланса мощности:
.
В левой части суммируются мощности источников энергии, а в правой – мощности, преобразованные в потребителях в тепло. Мощности источников, отдающих энергию, берутся со знаком «+», а работающих в режиме потребителей – со знаком «–».
Метод уравнений Кирхгофа.
1. Обозначить токи ветвей и произвольно выбрать их положительное направление.
2. Произвольно выбрать опорный узел и совокупность p = m – n + 1 независимых контуров.
3. Для всех узлов, кроме опорного, составить уравнения по I закону Кирхгофа. Таких уравнений должно быть (n – 1).
4. Для каждого выбранного контура составить уравнения по II закону Кирхгофа. Таких уравнений должно быть p.
5. Система m уравнений Кирхгофа с m неизвестными токами решается совместно и определяются численные значения токов.
6. Если необходимо, рассчитать с помощью обобщенного закона Ома напряжения ветвей или разность потенциалов узлов.
7. Проверить правильность расчета с помощью баланса мощности.
Если в цепи есть q источников тока и контуры выбирать таким образом, чтобы каждый источник тока вошел только в один контур, то количество уравнений по II закону Кирхгофа можно уменьшить до m – n + 1 – q.
Метод Контурных Токов
За искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по II закону Кирхгофа, т.е. . Основан на II законе Кирхгофа
По найденным контурным токам при помощи I закона Кирхгофа определяются токи ветвей.
Таким образом, методика расчета цепи постоянного тока методом контурных токов следующая:
1. Обозначить все токи ветвей и их положительное направление.
2. Произвольно выбрать совокупность p независимых контуров, нанести на схему положительное направление контурных токов, протекающих в выбранных контурах.
3. Определить собственные, общие сопротивления и контурные ЭДС и подставить их в систему уравнений вида.
Общее сопротивление контура (Rij = Rji) представляет собой алгебраическую сумму сопротивлений потребителей ветви (нескольких ветвей), одновременно принадлежащих i-ому и j-ому контурам. В эту сумму сопротивление входит со знаком «+», если контурные токи протекают через данное сопротивление в одном направлении (согласно), и знак «–», если они протекают встречно.
Собственное сопротивление контура (Rii) представляет собой арифметическую сумму сопротивлений всех потребителей, находящихся в i-ом контуре.
Контурные ЭДС представляют собой алгебраическую сумму ЭДС источников, входящих в контур. Со знаком «+» в эту сумму входят ЭДС источников, действующих согласно с обходом контура, со знаком «–» входят ЭДС источников, действующих встречно.
4. Разрешить полученную систему уравнений относительно контурных токов, используя метод Крамера.
5. Определить токи ветвей через контурные токи по I закону Кирхгофа.
6. Проверить правильность расчетов при помощи баланса мощности.
Если в цепи содержится q источников тока, количество совместно рассматриваемых уравнений сокращается на q и становится равным р – q, поскольку токи в таких ветвях известны Необходимо, чтобы каждый источник тока входил только в один контур.
Метод узловых потенциалов.
В том случае, когда п-1 < p (n – количество узлов, p – количество независимых контуров), данный метод более экономичен, чем метод контурных токов. Выводится из первого закона Кирхгофа и обобщенному закону Ома(через потенциалы).
1. Обозначить все токи ветвей и их положительное направление.
2. Произвольно выбрать опорный узел (jn)и пронумеровать все остальные (n-1)-e узлы.
3. Определить собственные и общие проводимости узлов, а также узловые токи, т.е. рассчитать коэффициенты в системе уравнений.
Собственная проводимость узла (Gii) представляет собой арифметическую сумму проводимостей всех ветвей, соединенных в i-ом узле.
Общая проводимость i-ого и j-ого узлов (Gij = Gji) представляет собой взятую со знаком «–» сумму проводимостей ветвей, присоединенных одновременно к i-ому и j-ому узлам.
Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят!
Узловой ток (Jii) состоит из двух алгебраических сумм: первая содержит токи источников тока, содержащиеся в ветвях, соединенных в i -ом узле; вторая представляет собой произведение ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в i -ом узле. Со знаком «+» в эту сумму входят E и J источников, действие которых направлено к узлу, со знаком «–» остальные.
4. Записать систему уравнений в виде
В этой системе каждому узлу соответствует отдельное уравнение.
5. Полученную систему уравнений решить относительно неизвестных (n – 1) потенциалов при помощи метода Крамера.
6. С помощью обобщенного закона Ома рассчитать неизвестные токи.
7. Проверить правильность расчетов при помощи баланса мощности.
Порядок расчета не зависит от вида источников, действующих в цепи. Однако, расчет упрощается в случае, когда между одной или несколькими парами узлов включены идеализированные источники ЭДС. Тогда напряжения между этими парами узлов становятся известными величинами, определенными условиями задачи. Для успешного решения подобных задач необходимо правильно обозначить опорный узел, в качестве которого может быть выбран только один из узлов, к которым присоединена ветвь с идеализированным источником ЭДС.
Если таких ветвей q, то количество уравнений в системе сократится до k = n – 1 – q.
Метод двух узлов
Для разветвленной цепи, имеющей только два узла и произвольное количество ветвей, метод узловых потенциалов вырождается в метод двух узлов. Решение сводится к отысканию значения потенциала одного из узлов, т.к. потенциал другого узла может быть принятым равным нулю.
Система уравнений превращается в одно уравнение:
(2.15)
при условии, что
После определения U12 токи ветвей и напряжения источников тока находят при помощи обобщенного закона Ома.
Электрическая цепь и ее элементы.
Реальная электрическая цепь - совокупность устройств, предназначенных для передачи, распределения и преобразования энергии. Содержит источники электрической энергии, приемники электрической энергии, измерительные приборы, коммутационную аппаратуру, соединительные линии и провода. Электрическая цепь представляет собойсовокупность связанных определенным образом источников, потребителей (или соответственно активных и пассивных элементов) и преобразователей электрической энергии. Цепь называют пассивной, если она состоит только из пассивных элементов, и активной, если в ней также содержатся активные элементы.
Источником электрической энергии называют элемент электрической цепи, осуществляющий преобразование энергии неэлектрического вида в электрическую. Потребителем электрической энергии называют элемент электрической цепи, преобразующий электрическую энергию в неэлектрическую. Преобразователем электрической энергии называют устройство, изменяющее величину и форму электрической энергии.
Для того чтобы выполнить расчет, необходимо каждое электротехническое устройство представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности идеализированных элементов(резистор, конденсатор, катушка индуктивности).
Напряжение:
Ток:
Зависимость между током и напряжением на элементе цепи называется вольт-амперной характеристикой (ВАХ) элемента, которая обычно изображается графически.
В качестве потребителя в теории электрических цепей постоянного тока выступает резистор, характеризующийся сопротивлением (R), для которого справедлив закон Ома:
Проводимость: измеряется в Сименсах (См).
Источники энергии моделируются с помощью источника ЭДС (Е), или источника напряжения, и источника тока (J). В большинстве случаев с увеличением тока напряжение источника уменьшается.
Идеализированный источник напряжения – это элемент цепи, напряжение которого не зависит от тока и является заданной постоянной величиной. В действительности мы имеем дело с реальными источниками напряжения, которые отличаются от идеальных источников тем, что их напряжение с ростом потребляемого тока уменьшается. Любой реальный источник при сопротивлении нагрузки R >> R0 может быть приведен к идеализированному следующим образом:
Идеализированный источник тока – это элемент цепи, ток которого не зависит от напряжения и является заданной постоянной величиной.
У реального источника тока с ростом напряжения вырабатываемый ток уменьшается.Любой реальный источник тока может быть приведен к идеализированному следующим образом :
,где J, G0 – постоянные параметры.
Обобщенный закон Ома.
Рассмотрим закон Ома для участка цепи, содержащего активные и пассивные элементы
.
Объединив эти две формулы, получаем:
Отсюда ток
Аналогияно:
)
Объединив эти две формулы в одну, получим:
, - обобщенный закон Ома.
Обобщенный закон Ома для ветви, содержащей источник тока:
Для содействующего источника тока
Для противодействующего источника тока
Объединенная форма обобщенного закона Ома для ветвей, содержащих источник тока:
(1.25)
где верхний знак соответствуют схеме, на которой UJ и J сонаправлены.
infopedia.su
| Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. | ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Реальной электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и преобразования энергии. В общем случае электрическая цепь содержит источники электрической энергии, приемники электрической энергии, измерительные приборы, коммутационную аппаратуру, соединительные линии и провода. Электрическая цепь представляет собойсовокупность связанных определенным образом источников, потребителей (или соответственно активных и пассивных элементов) и преобразователей электрической энергии. Цепь называют пассивной, если она состоит только из пассивных элементов, и активной, если в ней также содержатся активные элементы. Источником электрической энергии называют элемент электрической цепи, осуществляющий преобразование энергии неэлектрического вида в электрическую. Например: гальванические элементы и аккумуляторы преобразуют химическую энергию, термоэлементы – тепловую, электромеханические генераторы – механическую. Потребителем электрической энергии называют элемент электрической цепи, преобразующий электрическую энергию в неэлектрическую. Например: лампы накаливания – в световую и тепловую, нагревательные приборы – в тепловую, электродвигатель – в механическую. Преобразователем электрической энергии называют устройство, изменяющее величину и форму электрической энергии. Например: трансформаторы, инверторы преобразуют постоянный ток в переменный, выпрямители – переменный ток в постоянный, устройства для преобразования частоты. Для того чтобы выполнить расчет, необходимо каждое электротехническое устройство представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности идеализированных элементов, отображающих отдельные свойства физически существующих устройств. Так, идеализированный резистор (сопротивление R) учитывает преобразование электромагнитной энергии в тепло, механическую работу или ее излучение. Идеализированный конденсатор (емкость С) и катушка индуктивности (индуктивность L) характеризуются способностью накапливать энергию соответственно электрического и магнитного поля. Объединение источников, потребителей и соединительных проводов образует электрическую цепь, на каждом участке которой может действовать электрическое напряжение и протекать электрический ток. Эти напряжения и токи в общем случае могут быть постоянными и переменными во времени и зависеть от свойств элементов цепи. В данном разделе будут рассматриваться постоянные токи и напряжения. Реальные электрические цепи изучаются на моделях, которые изображаются с помощью условных обозначение в виде электрических схем. Напряжение U на элементе электрической цепи обозначается на схеме (рис. 1.1.) знаками «+» и «–», имеющими смысл только при совместном рассмотрении, т.к. знак «+» указывает на точку с относительно более высоким потенциалом.
(1.1) Ток I в элементе электрической цепи обозначается стрелкой на схеме (рис. 1.2.) и указывает направление упорядоченного перемещения положительных электрических зарядов, если ток I выражается положительным числом. (1.2)
Зависимость между током и напряжением на элементе цепи называется вольт-амперной характеристикой (ВАХ) элемента, которая обычно изображается графически. На рис. 1.3. показаны ВАХ потребителей различного типа. Прямолинейные ВАХ (1) и (3) соответствуют линейным элементам, а криволинейная ВАХ (2) – нелинейным элементам. Мы изучаем в рамках этого пособия только линейные цепи, для которых отношение или его отклонение от постоянной величины невелико. В данном случае, когда ВАХ изображается линией, близкой к прямой, считают, что потребитель подчиняется закону Ома, согласно которому напряжение и ток пропорциональны друг другу. Этот коэффициент пропорциональности k называют электрическим сопротивлением элемента R, которое измеряется в Омах (Ом). В качестве потребителя в теории электрических цепей постоянного тока выступает резистор, характеризующийся сопротивлением (R), для которого справедлив закон Ома: или , (1.3) Обозначение резистора на электрических схемах изображено на рис. 1.4. Величину, обратную сопротивлению , называют проводимостью, которая измеряется в Сименсах (См). Закон Ома можно представить через проводимость: (1.4) В пассивных элементах ток течет от точек с относительно большим потенциалом к точкам, имеющим относительно меньший потенциал. Поэтому на рис. 1.5. стрелка тока направлена от «+» к «–», что соответствует закону Ома в форме: (1.5) Для обозначений, принятых на рис. 1.6., закон Ома должен быть записан в следующей форме: . Таким образом, в ТОЭ потребитель моделируется идеальным потребителем, свойства которого определяются значением единственного параметра (R или G). Источники энергии моделируются с помощью источника ЭДС (Е), или источника напряжения, и источника тока (J). ВАХ источников энергии – это внешние характеристики, обычно имеющие ниспадающий характер, т.к. в большинстве случаев с увеличением тока напряжение источника уменьшается. Идеализированный источник напряжения – это элемент цепи, напряжение которого не зависит от тока и является заданной постоянной величиной, ему соответствует на рис. 1.7. сплошная ВАХ. В действительности мы имеем дело с реальными источниками напряжения, которые отличаются от идеальных источников тем, что их напряжение с ростом потребляемого тока уменьшается. ВАХ реального источника напряжения представлена на рис. 1.7. пунктирной линией, тангенс угла наклона которой равен внутреннему сопротивлению источника напряжения R0. Любой реальный источник при сопротивлении нагрузки R >> R0 может быть приведен к идеализированному следующим образом (рис.1.8.): (1.6) Таким образом, свойства источника ЭДС или реального источника напряжения определяются двумя параметрами – вырабатываемойЭДС Е и внутреннимсопротивлением R0. Идеализированный источник тока – это элемент цепи, ток которого не зависит от напряжения и является заданной постоянной величиной, ему соответствует сплошная ВАХ на рис. 1.8. У реального источника тока с ростом напряжения вырабатываемый ток уменьшается. ВАХ реального источника напряжения представлена на рис. 1.8. пунктирной линией, тангенс угла наклона которой равен внутренней проводимости источника тока G0. Любой реальный источник тока может быть приведен к идеализированному следующим образом (рис. 1.9.): , (1.7) где J, G0 – постоянные параметры. Таким образом,свойства источника задающего тока определяются двумя параметрами: задающим током J и внутренней проводимостью G0. Чем меньше G0, тем ближе характеристика реального источника тока к идеализированному. Поскольку внутренние сопротивления реальных источников всегда можно отнести к потребителям цепи далее рассматриваются только идеализированные источники напряжения и тока. Провода, связывающие потребители и источники, по своей сущности также относятся к потребителям энергии. Однако, часто провода наделяют лишь соединительными функциями и считают, что они служат лишь для того, чтобы показать, как связаны между собой отдельные элементы цепи. Сопротивления проводов, если ими нельзя пренебречь, учитываются включением в соответствующих местах цепи дополнительных потребителей. Таким образом, в теории линейных электрических цепей объектом изучения является расчетная модель, состоящая из потребителей и идеализированных источников, конфигурация и свойства элементов которой определены условиями задачи. При решении задач большое значение придается структуре электрической цепи (топологии), определяемой характером связей между элементами. |
megapredmet.ru
Задание №1 - Расчет сложной электрической цепи постоянного тока
Оглавление
Задание №1 - Расчет сложной электрической цепи постоянного тока 3
1.1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа. 4
1.3 Расчёт токов во всех ветвях схемы методом узловых потенциалов 8
Задание № 2 - Расчет электрической цепи переменного синусоидального тока 17
Активная мощность. Единица измерения - ватт (W, Вт). 26
Реактивная мощность. Единица измерения - вольт-ампер реактивный (var, вар) 26
Указания к выбору варианта задания
Электрические схемы, предлагаемые для расчета, пронумерованы. Соответствие варианта и расчетной схемы обозначено в таблице №1 и одинаково для обеих групп. Значения сопротивлений резисторов для студентов групп, номера которых заканчиваются цифрой 1 и 2 приведены в таблицах №3 и №4 соответственно. Значения ЭДС, действующих в ветвях, приведены в таблице №2 (первая строка для всех студентов группы, номер которой заканчивается цифрой 1, вторая строка – для группы, номер которой заканчивается цифрой 2). Внутренними сопротивлениями источников ЭДС следует пренебречь.
Содержание работы
1. Рассчитать токи во всех ветвях электрической цепи
а) методом непосредственного применения правил Кирхгофа;
б) методом контурных токов;
в) методом узловых потенциалов.
Результаты расчетов свести в таблицу.
2. Составить и решить уравнение баланса мощностей.
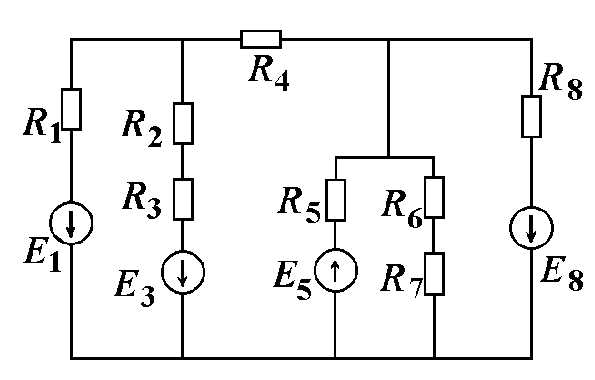
Рисунок 1.1
Таблица 1.1 – Значения параметров, вариант 10
| R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | R7, Ом | R8, Ом | Е1, В | Е3, В | Е5, В | Е8, В |
| 15 | 29 | 8 | 22 | 39 | 19 | 25 | 30 | 10 | 36 | 27 | 26 |
1.1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа.
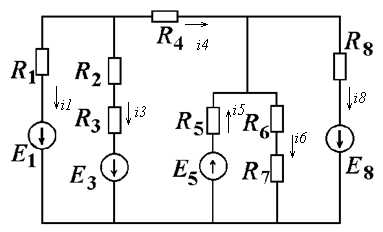
Рисунок 1.2 – Исследуемая схема цепи
Составим систему уравнений, согласно законам Кирхгофа для цепи (рисунок 1.2):
(1)
Решим систему матричным методом:
Находим токи в ветвях:
(2)
i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A), i8 = 0,656(A),
1.2 Расчёт токов в ветвях методом контурных токов.
Для схемы (1.2 обход по часовой стрелке) составим систему уравнений:
(3)
Решая систему, получаем:
Находим токи в контурах:
(4)
Рассчитаем токи в ветвях:
(5)
(6)
(7)
(8)
(9)
(10)
i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A), i8 = 0,656(A),
1.3 Расчёт токов во всех ветвях схемы методом узловых потенциалов
Найдём проводимости ветвей схемы.
g1 = 0,067(См), g23 = 0,027 (См), g4 = 0,045 (См),
g5 = 0,026(См), g67= 0,023 (См), g8 = 0,033 (См).
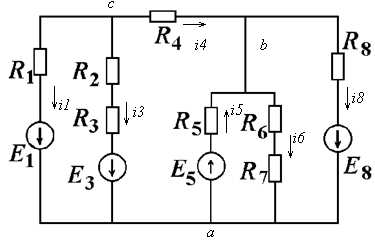
Рисунок 1.3
Запишем уравнения в матричной форме (φа=0):
(11)
Решая систему, получаем:
Находим токи в контурах:
(12)
Рассчитаем токи в ветвях:
(13)
(14)
(15)
(16)
(17)
(18)
i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A),
i8 = 0,656(A),
Таблица 1.2 – Результаты расчётов
| i1 | i3 | i4 | i5 | i6 | i8 | |
| Законы Кирхгофа | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
| Метод контурных токов | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
| Метод двух узлов | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
1.4 Баланс мощностей.
Уравнение баланса мощностей:
(19)
Суммарная мощность источников:
(20)
Суммарная мощность приёмников:
(21)
Контрольные вопросы по теме
«Расчет электрических цепей постоянного тока»
Дайте определение электрической цепи и ее схемы замещения.
Электрическая цепь — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитных процессов, в которых могут быть описаны с помощью понятий сила тока и напряжение.
Схема замещения — электрическая схема, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов.
Какими моделями пользуются при описании свойств идеальных и реальных источников электродвижущей силы (Э.Д.С.)?
Источник напряжения - идеализированный элемент ЭЦ, напряжение на зажимах которого не зависит от протекающего через него тока.
Какими моделями пользуются при описании свойств идеальных и реальных источников тока?
Источник тока – это идеализированный элемент ЭЦ, ток которого не зависит от напряжения на его зажимах.
Чем отличаются линейные и нелинейные элементы электрических цепей?
Элементы, ВАХ которых являются прямыми линиями, называются линейными. Электрические цепи, имеющие только линейные элементы, называются линейными электрическими цепями.
Элементы, ВАХ которых не являются прямыми линиями, называются нелинейными. Электрические цепи, имеющие хотя бы один нелинейный элемент, называются нелинейными.
Какие электрические цепи называются линейными электрическими цепями постоянного тока?
Элементы электрической цепи, ВАХ которых представляют собой прямые линии, называются линейными элементами, а цепи, состоящие из таких элементов, работающие от источника постоянного тока – линейными электрическими цепями постоянного тока.
Дайте определения ветви, узла и контура электрической цепи.
Ветвь – это участок электрической цепи от одного узла до другого узла. Ветвь обычно содержит один или несколько последовательно соединенных элементов цепи: сопротивления, источники ЭДС или источники тока.
Узел цепи в электронике — точка, в которой соединяются три (или более) проводника электрической цепи. Узел (наряду с контуром) является базовым понятием, необходимым при анализе электрических цепей.
Контур - это замкнутый участок электрической цепи. Любой замкнутый путь, проложенный через ветви цепи, и есть замкнутый контур.
Сформулируйте первое правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается в первом правиле Кирхгофа?
Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным.
Сформулируйте второе правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается во втором правиле Кирхгофа?
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю.
Докажите, что при последовательном соединении элементов в электрической цепи эквивалентное сопротивление равно сумме их сопротивлений.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: .
Так как ток в цепи один:
Докажите, что при параллельном соединении элементов в электрической цепи эквивалентная проводимость равна сумме их проводимостей.
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость складывается из проводимостей каждого резистора).
Для двух параллельно соединённых резисторов их общее сопротивление равно: .
Если , то общее сопротивление равно:, то естьэквивалентная проводимость равна сумме проводимостей.
Приведите пример расчета электрической цепи методом непосредственного применения правил Кирхгофа.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом контурных токов.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом узловых потенциалов.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом эквивалентного генератора.
Метод эквивалентного генератора используется при расчёте сложных схем, в которых одна ветвь выделяется в качестве сопротивления нагрузки, и требуется исследовать и получить зависимость токов в цепи от величины сопротивления нагрузки. В соответствии с данным методом неизменная часть схемы преобразовывается к одной ветви, содержащей ЭДС и внутреннее сопротивление эквивалентного генератора.
ЭДС эквивалентного генератора определяется по формуле:
где: —проводимость участка цепи, равная
Для определения эквивалентного сопротивления генератора применяется расчет последовательно и параллельно соединённых сопротивлений, а также, в случае более сложных схем, применяют преобразование треугольник-звезда.
После определения параметров эквивалентного генератора можно определить ток в нагрузке при любом значении сопротивления нагрузки по формуле:
Параметры иможно так же определить по исходной схеме из опытовхолостого хода икороткого замыкания .
По опыту холостого хода Для определенияв исходной схеме убирают сопротивление нагрузки и полученную схему рассчитываютметодом узловых потенциалов. Через полученные значения потенциалов определяют
Значение обычно определяется из опыта короткого замыкания, для этого в исходной схеме сопротивление нагрузки заменяют проводом и пометоду контурных токов определяют ток в проводе. После этого эквивалентное сопротивление генератора определяется по формуле:
Приведите пример расчета электрической цепи методом эквивалентных преобразований.
Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью. При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, каким они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.
Одним из наиболее часто встречающихся случаев смешанного соединения сопротивлений.
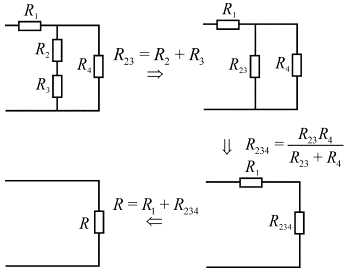
Исходная схема содержит параллельное соединение ветвей, содержащих и, т.е.. И этот участок с параллельным соединением включен последовательно с.
Поэтапным преобразованием эта цепь сводится к эквивалентному сопротивлению
.
Как и для чего составляется уравнение баланса мощностей при расчете электрической цепи? Приведите пример его составления.
Для проверки правильности расчёта электрической цепи. Пример приведён в работе.
studfiles.net
Основные понятия и законы теории электрических цепей
33
Электрическая цепь и ее элементы
Реальной электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и преобразования энергии. В общем случае электрическая цепь содержит источники электрической энергии, приемники электрической энергии, измерительные приборы, коммутационную аппаратуру, соединительные линии и провода.
Электрическая цепь представляет собой совокупность связанных определенным образом источников, потребителей (или соответственно активных и пассивных элементов) и преобразователей электрической энергии.
Цепь называют пассивной, если она состоит только из пассивных элементов, и активной, если в ней также содержатся активные элементы.
Источником электрической энергии называют элемент электрической цепи, осуществляющий преобразование энергии неэлектрического вида в электрическую. Например: гальванические элементы и аккумуляторы преобразуют химическую энергию, термоэлементы – тепловую, электромеханические генераторы – механическую.
Потребителем электрической энергии называют элемент электрической цепи, преобразующий электрическую энергию в неэлектрическую. Например: лампы накаливания – в световую и тепловую, нагревательные приборы – в тепловую, электродвигатель – в механическую.
Преобразователем электрической энергии называют устройство, изменяющее величину и форму электрической энергии. Например: трансформаторы, инверторы преобразуют постоянный ток в переменный, выпрямители – переменный ток в постоянный, устройства для преобразования частоты.
Для того чтобы выполнить расчет, необходимо каждое электротехническое устройство представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности идеализированных элементов, отображающих отдельные свойства физически существующих устройств. Так, идеализированный резистор (сопротивление R) учитывает преобразование электромагнитной энергии в тепло, механическую работу или ее излучение. Идеализированный конденсатор (емкость С) и катушка индуктивности (индуктивность L) характеризуются способностью накапливать энергию соответственно электрического и магнитного поля.
Объединение источников, потребителей и соединительных проводов образует электрическую цепь, на каждом участке которой может действовать электрическое напряжение и протекать электрический ток. Эти напряжения и токи в общем случае могут быть постоянными и переменными во времени и зависеть от свойств элементов цепи. В данном разделе будут рассматриваться постоянные токи и напряжения.
Реальные электрические цепи изучаются на моделях, которые изображаются с помощью условных обозначение в виде электрических схем.
Напряжение U на элементе электрической цепи обозначается на схеме (рис. 1.1.) знаками «+» и «–», имеющими смысл только при совместном рассмотрении, т.к. знак «+» указывает на точку с относительно более высоким потенциалом.
(1.1)
Ток I в элементе электрической цепи обозначается стрелкой на схеме (рис. 1.2.) и указывает направление упорядоченного перемещения положительных электрических зарядов, если ток I выражается положительным числом.
(1.2)
Зависимость между током и напряжением на элементе цепи называется вольт-амперной характеристикой (ВАХ) элемента, которая обычно изображается графически. На рис. 1.3. показаны ВАХ потребителей различного типа. Прямолинейные ВАХ (1) и (3) соответствуют линейным элементам, а криволинейная ВАХ (2) – нелинейным элементам. Мы изучаем в рамках этого пособия только линейные цепи, для которых отношение или его отклонение от постоянной величины невелико. В данном случае, когда ВАХ изображается линией, близкой к прямой, считают, что потребитель подчиняетсязакону Ома, согласно которому напряжение и ток пропорциональны друг другу.
Этот коэффициент пропорциональности k называют электрическим сопротивлением элемента R, которое измеряется в Омах (Ом).
В качестве потребителя в теории электрических цепей постоянного тока выступает резистор, характеризующийся сопротивлением (R), для которого справедлив закон Ома:
или ,(1.3)
Обозначение резистора на электрических схемах изображено на рис. 1.4.
Величину, обратную сопротивлению, называютпроводимостью, которая измеряется в Сименсах (См).
Закон Ома можно представить через проводимость:
(1.4)
В пассивных элементах ток течет от точек с относительно большим потенциалом к точкам, имеющим относительно меньший потенциал. Поэтому на рис. 1.5. стрелка тока направлена от «+» к «–», что соответствует закону Ома в форме:
(1.5)
Для обозначений, принятых на рис. 1.6., закон Ома должен быть записан в следующей форме: .
Таким образом, в ТОЭ потребитель моделируется идеальным потребителем, свойства которого определяются значением единственного параметра (R или G).
Источники энергии моделируются с помощью источника ЭДС (Е), или источника напряжения, и источника тока (J). ВАХ источников энергии – это внешние характеристики, обычно имеющие ниспадающий характер, т.к. в большинстве случаев с увеличением тока напряжение источника уменьшается.
Идеализированный источник напряжения – это элемент цепи, напряжение которого не зависит от тока и является заданной постоянной величиной, ему соответствует на рис. 1.7. сплошная ВАХ. В действительности мы имеем дело с реальными источниками напряжения, которые отличаются от идеальных источников тем, что их напряжение с ростом потребляемого тока уменьшается. ВАХ реального источника напряжения представлена на рис. 1.7. пунктирной линией, тангенс угла наклона которой равен внутреннему сопротивлению источника напряжения R0. Любой реальный источник при сопротивлении нагрузки R >> R0 может быть приведен к идеализированному следующим образом (рис.1.8.):
(1.6)
Таким образом, свойства источника ЭДС или реального источника напряжения определяются двумя параметрами – вырабатываемой ЭДС Е и внутренним сопротивлением R0.
Идеализированный источник тока – это элемент цепи, ток которого не зависит от напряжения и является заданной постоянной величиной, ему соответствует сплошная ВАХ на рис. 1.8.
У реального источника тока с ростом напряжения вырабатываемый ток уменьшается. ВАХ реального источника напряжения представлена на рис. 1.8. пунктирной линией, тангенс угла наклона которой равен внутренней проводимости источника тока G0. Любой реальный источник тока может быть приведен к идеализированному следующим образом (рис. 1.9.):
, (1.7)
где J, G0– постоянные параметры.
Таким образом, свойства источника задающего тока определяются двумя параметрами: задающим током J и внутренней проводимостью G0. Чем меньше G0, тем ближе характеристика реального источника тока к идеализированному.
Поскольку внутренние сопротивления реальных источников всегда можно отнести к потребителям цепи далее рассматриваются только идеализированные источники напряжения и тока.
Провода, связывающие потребители и источники, по своей сущности также относятся к потребителям энергии. Однако, часто провода наделяют лишь соединительными функциями и считают, что они служат лишь для того, чтобы показать, как связаны между собой отдельные элементы цепи. Сопротивления проводов, если ими нельзя пренебречь, учитываются включением в соответствующих местах цепи дополнительных потребителей.
Таким образом, в теории линейных электрических цепей объектом изучения является расчетная модель, состоящая из потребителей и идеализированных источников, конфигурация и свойства элементов которой определены условиями задачи.
При решении задач большое значение придается структуре электрической цепи (топологии), определяемой характером связей между элементами.
studfiles.net
Электрическая цепь и ее элементы
Электрическая цепь это совокупность устройств, соединенных определенным образом, которые обеспечивают путь для протекания электрического тока.
Элементами электрической цепи являются: источник тока, нагрузка и проводники. Простейшая электрическая цепь показана на рисунке 1.
Рисунок 1. Простейшая электрическая цепь.
В состав электрической цепи могут входить и другие элементы, таки как устройства коммутации, устройства защиты.
Как известно, для возникновения тока необходимо соединить две точки, одна из которых имеет избыток электронов в сравнении с другой. Другими словами необходимо создать разность потенциалов между этими двумя точками. Как раз для создания разности потенциалов в цепи применяется источник тока. Источником тока в электрической цепи могут быть такие устройства, как генераторы, батареи, химические элементы и т.д.
Нагрузкой в электрической цепи считается любой потребитель электрической энергии. Нагрузка оказывает сопротивление электрическому току и от величины сопротивления нагрузки зависит величина тока. Ток от источника тока к нагрузке течет по проводникам. В качестве проводников стараются использовать материалы с наименьшим сопротивлением (медь, серебро, золото).
Важно, что для протекания тока в цепи, цепь должна быть замкнута!
Типы электрических цепей
В электротехники по типу соединения элементов электрической цепи существуют следующие электрические цепи:
- последовательная электрическая цепь;
- параллельная электрическая цепь;
- последовательно-параллельная электрическая цепь.
Последовательная электрическая цепь.
В последовательной электрической цепи (рисунок 2.) все элементы цепи последовательно друг с другом, то есть конец первого с началом второго, конец второго с началом первого и т.д.
Рисунок 2. Последовательная электрическая цепь.
При таком соединении элементов цепи ток имеет только один путь протекания от источника тока к нагрузке.При этом общий ток цепи Iобщ будет равен току через каждый элемент цепи:
Iобщ=I1=I2=I3
Падение напряжения вдоль всей цепи, то есть на участке А-Б (Uа-б), будет равно приложенному к этому участку напряжению E и равно сумме падений напряжений на всех участках цепи (резисторах):
E=Uа-б=U1+U2+U3
Параллельная электрическая цепь.
В параллельной электрической цепи (рисунок 3.) все элементы соединены таким образом, что их начало соединены в одну общую точку, а концы в другую.
Рисунок 3. Параллельная электрическая цепь.
В этом случае у тока имеется несколько путей протекания от источника к нагрузкам, а общий ток цепи Iобщ будет равен сумме токов параллельных ветвей:
Iобщ=I1+I2+I3
Падение напряжения на всех резисторах будет равно приложенному напряжению к участку с параллельным соединением резисторов:
E=U1=U2=U3
Последовательно-параллельная электрическая цепь.
Последовательно-параллельная электрическая цепь является комбинацией последовательной и параллельной цепи, то есть ее элементы включаются и последовательно и параллельно (рисунок 4).
Рисунок 4. Последовательно-параллельная электрическая цепь.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.