Переводим числа между двоичной и десятичной системами «на лету», объяснение «на пальцах»
Здравствуйте, Хабровцы.
Пост можно было бы назвать: «Для любителей посчитать на пальцах», но это мы узнаем дальше.
Вступление: А что-же тянуть. Все что будет дальше, пойдет на тему подсчета в двоичной системе на пальцах. Кто еще не знает, постараюсь обьяснить, что это, как и зачем это осваивать.
Начну, пожалуй, с преимуществ:
1. Удобно переводить любое число с десятичной в двоичную системы и наоборот, не используя калькулятор.
2. Развивается моторика пальцев.
3. Развивается визуальное восприятие двоичных чисел.
Минусы:
1. Немного тренировки.
2. Нельзя в публичных местах показывать числа 26,27,352,378 и 891.
Суть:
Многим, наверняка, приходилось переводить между системами. И я думаю многие запомнили, что:
2-10
3-11
4-100
5-101
и т.д.
Логично, что исходя из того что каждая разрядность имеет два состояния, мы можем изобразить это дело на пальцах. n (на фото)
n (на фото)
То есть,
Теперь, представим, что нам нужно перевести число 25 в двоичную. Загибаем Мизинец — 16, Безымянный — 8 и большой — 1. т.к. 16+8+1=25.
Если не поняли, то вот еще пример, число 14, думаем: Мизинец — это много, средний нормально, но можно взять больше, поэтому — загибаем безымянный, это 8. Запомнили, далее средний — +4, єто уже 12 и указательный — +2, итог 14.
Так же поступаем с двоичными. Вот например видим где-то: 1011101. Представляем это на руках с разрядностями (уже две руки).
64+16+8+4+1=93
Имеем: 1011101(2) = 93(10)
Заключение: Таким образом мы можем использовать данный метод от 0 до 1023, используя пальцы и обладая элементарной арифметикой. Но при добавлении, хотя бы, одного разряда, можно будет считать до 2047, и далее до 4095, 8191 и т.д. А это могут быть руки, ноги, веки, либо что-то еще что может иметь два состояния 1 и 0.
Информатика. Выпуск 1. Системы счисления.
Главная
Видеотека
Естествознание
Физика
Математика
Химия
Биология
Экология
Обществознание
Обществознание — как наука
Иностранные языки
История
Психология и педагогика
Русский язык и литература
Культурология
Экономика
Менеджмент
Логистика
Статистика
Философия
Бухгалтерский учет
Технические науки
Черчение
Материаловедение
Сварка
Электротехника
АСУТП и КИПИА
Технологии
Теоретическая механика и сопромат
САПР
Метрология, стандартизация и сертификация
Геодезия и маркшейдерия
Программирование и сеть
Информатика
Языки программирования
Алгоритмы и структуры данных
СУБД
Web разработки и технологии
Архитектура ЭВМ и основы ОС
Системное администрирование
Создание программ и приложений
Создание сайтов
Тестирование ПО
Теория информации и кодирования
Функциональное и логическое программирование
Программы
Редакторы и компиляторы
Офисные программы
Работа с аудио видео
Работа с компьютерной графикой и анимацией
Автоматизация бизнеса
Прочие
Музыка
Природное земледелие
Рисование и живопись
Библиотека
Естествознание
Физика
Математика
Химия
Биология
Экология
Астрономия
Обществознание
Иностранные языки
Технические науки
Теоретическая механика и сопромат
Сварка
Двоичная/бинарная система счисления | Интересные истории
Все что-то слышали о двоичной системе счисления, все знают, что это некий «язык компьютеров». Но почему именно так? Почему не пользоваться привычной десятичной системой? В чем, собственно, смысл?
Но почему именно так? Почему не пользоваться привычной десятичной системой? В чем, собственно, смысл?
Что такое двоичная система? Это позиционная система счисления с основанием 2. Вот только цифры «два» в ней нет, есть только 0 и 1, и так как цифры две, система называется двоичной (бинарной). Современный цифровой язык, это ноли и единицы, а больше ничего и не нужно. Самое интересное, так называемый машинный код использовался людьми задолго до появления самих машин.
Чем удобна двоичная система
Двоичная, или бинарная система счисления удобна своей простотой. С помощью комбинации нолей и единиц можно записать любой число и любую букву, что угодно может быть закодировано таким образом. Но главное, что значения всего два. Это либо «ноль», либо «единица». Сигнал либо есть, либо его нет, свет горит или не горит, есть отверстие или нет (перфокарта), намагничен сектор или размагничен… Аналогии можно приводить бесконечно. Главное, что кодировать сигнал просто. Не нужно создавать сложные механизмы или устройства, достаточно только двух состояний.
В любой микросхеме транзистор может прибывать в двух положениях «закрыто» или «открыто» (0 или 1) ток пропускается или нет.
Кстати, азбука Морзе — это тоже двоичный код (точка или тире), так же, как и древнейшая сигнальная система — «оптический телеграф». Это это просто огонь костра, который можно закрыть и открыть (огонь есть, или огня нет) ночью, а днем так же использовать дым.
Двоичная система используется потому, что с ее помощью удобно кодировать информацию, нужны всего 2 значения. Но удобно ли считать?
Простое объяснение
Как использовать двоичную систему для записи чисел? Так же как и десятичную. Самым простым примером можно считать кодовый замок, такой как на чемоданах. Каждый диск которого, вращается и может принимать значение от 0 до 9. Достаточно представить, что вместо десяти цифр есть только 2, ноль и единица.
Так как система позиционная, это будет выглядит так:
000000 — ноль
Сейчас здесь записано число «ноль». Чтобы получилась единица, нужно провернуть крайний правый диск один раз.
Чтобы получилась единица, нужно провернуть крайний правый диск один раз.
000001 — один
Начинается самое интересное, как будет выглядеть число «два»? Крутим правое колесико… И снова получаем 0, ведь других значений нет. Нужно поступить так же, как и в десятичной системе, перенести разряд влево. Только в десятичной, это происходит когда значение превышает 9, а в двоичной сразу после 1.
000010 — два
000011 — три
000100 — четыре
| Двоичная система | Десятичная система |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
Сто в двоичной системе — это 1100100.
Очень интересно в бинарной системе выглядит таблица умножения:
Легко запомнить, неправда ли? 0*0=0, 0*1=0, 1*1=1… И все!
Все математические операции выполняются точно так же
2+2=4
10+10=100
Если сложит в столбик то получается нагляднее
Складываем ноли, получаем 0, складываем две единицы, получаем ноль (2 раза провернули диск) и единичку переносим вправо.
Как видите, математика та же, вот только запись чисел неудобная, слишком много нолей и единиц, для человека — неудобно, машине же все равно.
Так же как с цифрами можно поступить с буквами. Латинская буква «a» будет выглядеть как 01001010 кириллическая «а» — 000011100010111000011001, и даже пробел — 00010100.
История создания
Ясно, что человечество пользовалось двоичным кодом очень давно. И сигнальные системы и даже китайская Книга Перемен (700 лет до нашей эры) с ее гексаграммами известны очень давно. Но окончательно практический смысл бинарный код получил совсем недавно (если не считать азбуку Морзе).
Великий Лейбниц занимался двоичной системой в 17 веке, но применить бинарную систему счисления было особо негде. В том же Веке Паскаль создал свою счетную машину (суммирующую), использующую десятичную систему. Оказалось, что считать на таком «калькуляторе» не так уж и удобно.
Суммирующая машина Паскаля (десятичная)
И только в 40-х годах 20 веке, вместе с появлением первых электронный вычислительных машин двоичный код явил всю свою безусловную полезность и красоту. Именно как машинный язык. Записывать информацию в котором гораздо проще, чем привычными нам средствами, буквами и цифрами.
Именно как машинный язык. Записывать информацию в котором гораздо проще, чем привычными нам средствами, буквами и цифрами.
То же самое, в двоичном коде можно сделать проще
Сейчас, ноли и единицы используются намного чаще, чем десятичная система, даже если мы, люди, этого и не видим. Не удивительно, мы использовали двоичную систему на протяжении всей истории, но до эры машин даже не замечали этого.
Двоичная система счисления для младших школьников | Методическая разработка по информатике и икт (6 класс) на тему:
Двоичная система счисления для младших классов
Цифры десятичной системы: 0, 1,2,…9
В двоичной системе всего 2 цифры: 0, 1
Десятичная система | Двоичная система |
0 | 0 |
1 | 1 |
2 | 10 |
3 | 11 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
11 | 1011 |
Заполняем пока только первый столбец таблицы известными цифрами десятичной системы.
10 в десятичной системе (когда закончились цифры) записывается как комбинация 1 и 0.
Каждое следующее число получается прибавлением 1 к предыдущему числу, согласно закону сложения в позиционных системах, который дети уже хорошо знают.
Для записи количества 2 в двоичной системе поступают также, как в десятичной, когда цифры закончились – записывают 2 как комбинацию 1 и 0.
Арифметика двоичной системы выглядит так:
0+0=0; 0+1=1; 1+0=1; 1+1=10
Используя эти правила каждое следующее число двоичной системы, получаем прибавлением 1 к следующему числу:
10 11 100 101 110 111 1001 1010
+ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
—- —— —— ——- —— —— —— ———
11 100 101 110 111 1000 1010 1011
Записываем эти значения во второй столбец таблицы, по мере их получения.
Выясняем закономерность получения чисел 2,4,8,16: каждое число в двоичной системе получается добавлением нуля справа.
Выписываем эти строки в отдельную таблицу:
Десятичная система | Двоичная система |
0 | 0 |
1 | 1 |
2 | 10 |
4 | 100 |
8 | 1000 |
16 | 10000 |
32 | 100000 |
64 | 1000000 |
128 | 10000000 |
256 | 100000000 |
1024 | 10000000000 |
Теперь выясняем: какое десятичное число соответствует: 10000?
Дети сразу же отвечают: 16.
Далее следуют аналогичные вопросы про двоичные числа: 100000, 1000000, 10000000, 100000000?
И заполняем, по мере выяснения соответствующие строки таблицы.
Теперь, используем эту таблицу для перевода чисел из системы в систему: каждое предлагаемое число раскладываем на слагаемые соответствующего столбца, и, затем каждому слагаемому ставим аналог из соседнего столбца
Например:
25=16+8+1=10000+1000+1=11001
37=32+4+1=100000+100+1=100101
Двоичные числа лучше складывать столбиком, записывая разряд под разрядом, с этим дети легко справляются, т.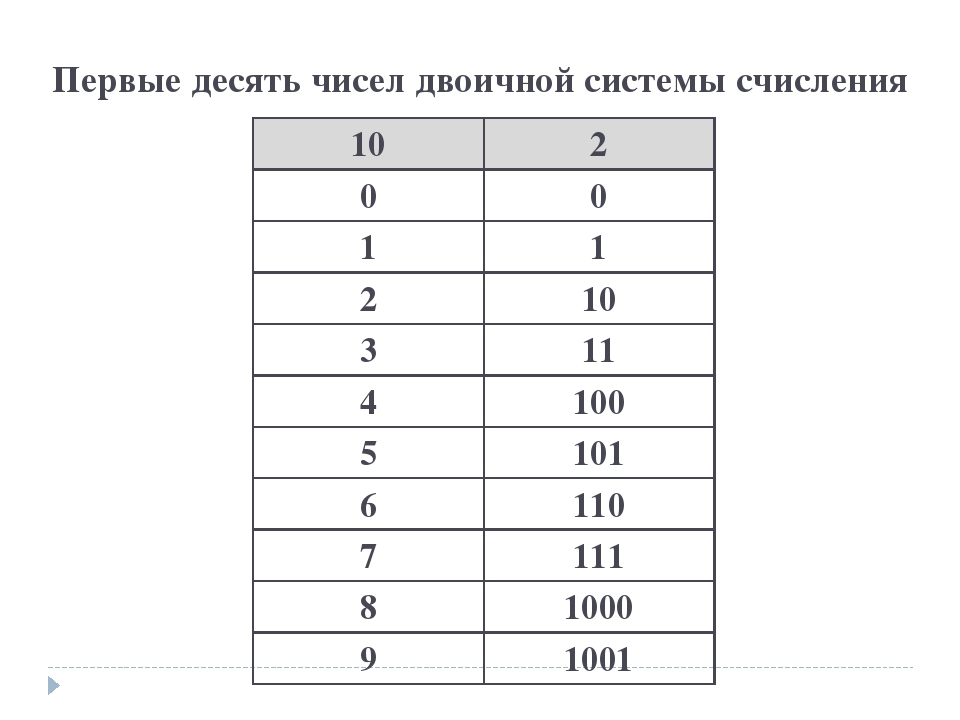 к. это все слагаемые вида: 1+0 или 0+1.
к. это все слагаемые вида: 1+0 или 0+1.
Перевод чисел из двоичной системы также легко осуществляется с помощью этой таблицы.
Например:
1011=1000+10+1=8+2+1=11
100101=100000+100+1=32+4+1=37
Системы счисления (Теория)
Сегодня разберём теоретический аспект работы с различными системами счисления. Основными системами счисления являются: двоичная, восьмеричная, десятичная (наша родная) и шестнадцатиричная.
Перевод чисел из двоичной системы в шестнадцатиричную систему счисления.
Для начала нужно написать себе в черновик следующую таблицу:
Давайте рассмотрим данную таблицу. В первом столбце идут числа от 0 до 15 в нашей родной десятичной системе счисления. Во втором столбце идут числа так же от 0 до 15, но уже в двоичной системе, а в третьем тоже от 0 до 15 в шестнадцатиричной системе счисления.
Написать числа от 0 до 15 в нашей родной десятичной системе не у кого затруднений не вызовет.
Числа в двоичной же системе лучше всего написать по следующему правилу: в младшем разряде чередуем ноль и единицу, в следующем разряде чередование нулей и единиц происходит в два раза медленнее (два нуля, две единицы, два нуля и т. д.), в следующем разряде ещё в два раза медленнее чередование (4 нуля, 4 единицы и т.д.) и наконец 8 нулей и 8 единиц — в самом старшем разряде.
д.), в следующем разряде ещё в два раза медленнее чередование (4 нуля, 4 единицы и т.д.) и наконец 8 нулей и 8 единиц — в самом старшем разряде.
В шестнадцатиричной системе счисления помимо наших привычных символов от 0 до 9 придуманы символы A, B, С, D, E, F, и из этих 16 символов (от 0 до 15) составляется любое число, так же как в нашей системе составляется любое число из десяти цифр (от 0 до 9).Соответственно, чтобы посчитать от 0 до 15 — нужно перебрать все символы, которые имеются в шестнадцатиричной системе (от 0 до F).
Теперь рассмотрим, как с помощью данной таблицы переводить из двоичной системы в шестнадцатиричную. Переведём число 100101000 из двоичной системы в шестнадцатиричную.
Чтобы выполнить данную задачу, необходимо разбить наше двоичное число по 4 цифры начиная с правого края, и каждую 4-ку цифр нужно найти в нашей таблице: 1000 — это будет 8, 0010 — 2, 0001 -это 1. В старшем разряде у нас осталась одна единица, мы её дополнили 3-мя нулями.
Значит число 1001010002 в двоичной системе счисления будет 12816 в шестнадцатиричной.
Перевод чисел из двоичной системы в восьмеричную
систему счисления.
Из двоичной системы в восьмеричную систему X2 -> X8 переводим точно так же, только теперь из таблицы берём не по четыре цифры, а по три цифры.
Таким образом, число 10011110012 в двоичной системе будет равно 11718 в восьмеричной системе.
Перевод чисел из шестнадцатиричной системы в двоичную
систему счисления.
Делаем точно так же, как и при переводе чисел из двоичной в шестнадцатиричную, но в обратном порядке. По таблице смотрим: D — 1101, F — 1111, 4 — 0100. Получается число 010011111101. Слева нули мы отбрасываем 10011111101.
4FD16 -> 100111111012.
Перевод чисел из восьмеричной системы в двоичную
систему счисления.
Поступаем, как мы поступали ранее. Разбиваем каждую цифру восьмеричной системы по 3 цифры двоичной системы, используя таблицу, которая приведена в начале статьи. Нули слева откидываем.
3478 -> 111001112.
Перевод чисел из двоичной системы в десятичную
систему счисления.
Переведём число:
Берём цифры двоичного числа, начиная с младшего разряда (т.е. справа), и начинаем умножать на двойку в соответствующей степени. Степень начинается с нуля и с каждым разом увеличивается на 1. Все эти произведения суммируем.
После вычисления получаем число в десятичной системе:
Результат 110100112 -> 21110
Перевод чисел из десятичной системы в двоичную
систему счисления.
Рассмотрим, как перевести из десятичной системы в двоичную. Возьмём число 213.
Перевод чисел из шестнадцатиричной системы в восьмеричную систему
счисления и обратно.
Переведём число A10 из шестнадцатиричной системы в восьмеричную A1016 -> X8.
Разбиваем каждую цифру шестнадцатиричного кода по 4-ри цифры двоичного кода из таблицы в начале статьи (Т.е. переводим число в двоичную систему). Полученное число разбиваем по три цифры — и собираем число уже в восьмеричной системе — как показано на рисунке. Обратно переводим аналогично, только в обратном порядке.
Перевод чисел из шестнадцатиричной системы в десятичную
систему счисления.
Переведём число 5B3 из шестнадцатиричной системы в десятичную систему счисления 5B316 -> X10.
Действуем точно также, как при переводе из двоичной системы в десятичную, только умножаем цифры на 16 в соответствующей степени. Буквы превращаем в десятичные числа из таблицы. Начинаем, как всегда, справа, т.е. с младшего разряда.
Перевод чисел из десятичной системы в шестнадцатиричную
систему счисления.
Переведём число 203 из десятичной системы в шестнадцатиричную систему счисления 20310 -> X16
Делим число на 16 до тех пор пока не получится число от 1 до 15. Записываем остатки в обратном порядке. Числа от 10 до 15 превращаем в буквы.
Перевод чисел из восьмеричной системы в десятичную
систему счисления.
Переведём число 347 из восьмеричной системы в десятичную систему счисления 3478 -> X10
Делаем аналогично предыдущим примерам, только теперь умножаем на 8 в соответствующей степени.
Перевод чисел из десятичной системы в восьмиричную
систему счисления.
Делаем аналогично предыдущим примерам.
Двоичная система счисления
Для каждой счетной системы можно составить таблицы сложения и других арифметических действий. В двенадцатеричной системе 5+8=11, а Зх4=10. В семеричной системе 3+6=12, а 5х3=21. Нам это может показаться странным, поскольку мы не используем подобные системы. Но если мы проводим все расчеты в рамках одной из таких систем, мы видим, что система также отвечает поставленным целям. Человечество остановилось на десятеричной системе по той простой причине, что на руках у человека десять пальцев, а вовсе не потому, что эта система более логична, чем любая другая.
В двенадцатеричной системе 5+8=11, а Зх4=10. В семеричной системе 3+6=12, а 5х3=21. Нам это может показаться странным, поскольку мы не используем подобные системы. Но если мы проводим все расчеты в рамках одной из таких систем, мы видим, что система также отвечает поставленным целям. Человечество остановилось на десятеричной системе по той простой причине, что на руках у человека десять пальцев, а вовсе не потому, что эта система более логична, чем любая другая.
Однако в отдельных случаях и для конкретных целей может оказаться, что какая-то система счета является гораздо более функциональной, нежели другие. Это справедливо в случае системы, основанной на 2, то есть двоичной системы.
Выражение 10 в двоичной системе равно 2 в десятеричной системе. Следовательно, в такой системе только две цифры, 0 и 1.
Перевод числа из двоичной системы в десятеричную не составляет труда. Рассмотрим, например, выражение 11001 в двоичной системе. Оно эквивалентно $(1\times2^4)+(1\times2^3)+(0\times2^2)+(0\times2^1)+(1\times2^0)$, или 16+8+0+0+1, или 25, что соответствует эквиваленту, приведенному в таблице.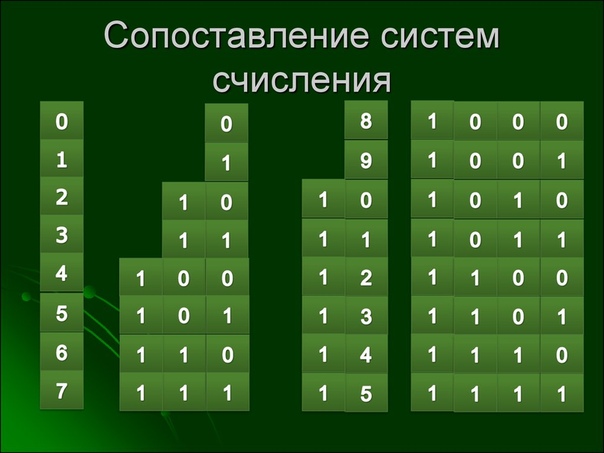 1$.
1$.
Теперь надо только правильно расставить по местам показатели степени справа налево. Единицы будут стоять на 1, 3, 4, 9 и 10-й позициях. На остальных позициях мы поставим нули. Таким образом, мы получаем число 11 000 011 010, двоичный эквивалент числа 1562 в десятеричной системе.
В двоичной системе очень простые таблицы сложения и умножения:
И это весь список.
Таким образом, в двоичной системе:
Правильность этих вычислений можно, при желании, проверить, учитывая, что числа 11, 110 и 1001 в двоичной системе равны соответственно 3, 6 и 9 в десятеричной системе.
Теперь представьте себе, что у вас есть счетная электронная машина с набором переключателей (например, полупроводниковых). Каждый переключатель может находиться в одной из двух позиций — «включено» (когда ток проходит через переключатель) или «выключено» (когда ток не проходит через переключатель).
Теперь предположим, что положение «включено» соответствует 1, а положение «выключено» соответствует 0. В этом случае счетную машину можно спроектировать таким образом, чтобы переключение электрического сигнала различными переключателями подчинялось правилам сложения, умножения и другим действиям с единицами и нулями в двоичной системе.
В этом случае счетную машину можно спроектировать таким образом, чтобы переключение электрического сигнала различными переключателями подчинялось правилам сложения, умножения и другим действиям с единицами и нулями в двоичной системе.
Такая машина будет так быстро производить переключение и производить вычисления с такой скоростью, что сможет выполнить за считанные секунды такой объем вычислений, на который человеку потребовалось бы не меньше месяца.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
Двоичные числа для начинающих
По моему опыту преподавания сетевых технологий, многие студенты борются с IP-адресами, потому что им не хватает базового понимания двоичных чисел.
Понимание двоичных чисел, двоичной системы и того, как преобразовывать двоичные числа в десятичные, важно для всех, кто занимается компьютерами, кодированием и сетями.
Binary 101 — Что вы узнаете
- Основы числовых баз — основание 10, основание 2 и основание 16
- Как преобразовать двоичное в десятичное и наоборот
- Как преобразовать двоичные числа в шестнадцатеричные и наоборот,
- Как преобразовать шестнадцатеричное в десятичное и наоборот,
Обзор десятичных и десятичных чисел с основанием 10
Прежде чем мы узнаем о двоичной системе счисления, мы более подробно рассмотрим нашу обычную десятичную систему счисления.
Принципы одинаковы для всех систем нумерации, и их легче освоить с помощью более знакомой вам системы.
Во-первых, наша десятичная система использует 10 в качестве основания , а числа находятся в диапазоне от 0 до 9
Давайте посмотрим на несколько примеров чисел
Начнем с трехзначного числа 129 (сто двадцать девять).
Это состоит из 100 +20 +9 = 129
Если мы посмотрим на диаграмму ниже, то увидим, что при движении справа налево столбцы увеличиваются в 10 раз.
2 во втором столбце не 2, а 2 * 10 = 20, а 1 в третьем столбце не 1, а 1 * 10 * 10 = 100.
означает 10 в степени 0. Это равно 1 и представляет наш столбец единиц.
В приведенной ниже короткой таблице показано еще несколько записей, использующих обозначение степени.
При записи десятичных чисел мы редко пишем значения столбцов над числами, так как мы уже знаем, что они собой представляют, поэтому просто пишем:
129 а не
Я ввел обозначение степени, потому что оно имеет фундаментальное значение для понимания двоичных чисел.
Минимальное возможное число из трех цифр — 000 , а максимальное — 999. Для чисел больше 999 нам нужен 4-й столбец, который будет столбцом 1000.
Двоичная система счисления
Двоичные числа являются числами с основанием 2 и имеют только два значения — 0 и 1.
Если мы посмотрим на двоичное число, такое как 101, то мы снова сможем присвоить значения столбцов, как мы это делали с нашим десятичным числом, но на этот раз мы используем 2, а не 10 в качестве основы.
Итак, двоичный код 101 имеет 1 в столбце единиц, 0 в столбце 2 и 1 в столбце 4.
Опять же, если работать справа налево, то:
1 — это 1, как в столбце единиц, но следующая 1 — это не 1, а 1 * 4 = 4
Двоичные числа используют базу 2, поэтому столбцы равны
Преобразование двоичного числа в десятичное
Давайте посмотрим на несколько двоичных чисел и преобразуем их в десятичные
Мы начинаем с трехзначного двоичного числа 101 (см. Изображение выше
Изображение выше
Число можно преобразовать в десятичное путем умножения следующим образом:
1 * 1 + 0 * 2 + 1 * 4 = 5
Максимальное значение, которое мы можем получить с тремя двоичными цифрами, составляет 111 = десятичное 7, рассчитанное следующим образом:
1 * 1 + 1 * 2 + 1 * 4
Другие примеры:
1011 двоичный = 1 * 1 + 1 * 2 + 0 * 4 + 1 * 8 = 11
1111 двоичный = 1 * 1 + 1 * 2 + 1 * 4 + 1 * 8 = 15
Попробуйте сами
1001 двоичный =?
1100 двоичный =?
Преобразование из десятичного в двоичное
Как преобразовать десятичное число в двоичное.
Пример того, что такое десятичное 10 двоичное.
Я использую следующий список из двух кратных.
128,64,32,16,8,4,2,1
Вот удобная диаграмма
Примечание: ошибка на диаграмме выше должна быть 2 7 = 128
Процедура заключается в вычитании числа с наибольшей степенью двойки из десятичного числа
.
наибольшая степень двойки числа r, которую мы можем вычесть, составляет 8 , что составляет 2 3 .
Итак, 10-8 = 2
, теперь мы делаем то же самое с остатком, поэтому наибольшее число, которое мы можем вычесть, равно 2, что равно 2 1
2-2 = 0
, так что у нас есть 1 восемь, без четверок, 1 два, без единиц = 1010 = 2 3 + 2 1 .
Пример 2 : десятичный 13 в двоичный код
1 восемь, 1 четыре, 0 два, 1 единица = 1101.
Пример 3 : из десятичного числа 7 в двоичный код
0 восемь, 1 четыре, 1 два, 1 единица = 0111.
Попробуйте сами вопросы
1001 двоичное = 9
1100 двоичный = 12
Байт, октеты и шестнадцатеричные числа
В компьютерах распространены 8-битные числа для кодирования и организации сети.
8-битное число известно как октет , а также чаще его называют байтом . См. Подробности в Wiki.
См. Подробности в Wiki.
Двоичное преобразование в десятичное и преобразование десятичного в двоичное 8-битные числа
8-битное двоичное число может представлять максимум десятичного числа 255 = двоичное 11111111 .
Рассчитывается следующим образом:
1 * 128 + 1 * 64 + 1 * 32 + 1 * 16 + 1 * 8 + 1 * 4 + 1 * 2 + 1 + 1 = в десятичном виде 255
Вот еще одно 8-битное двоичное число — 01101011.
Чтобы преобразовать его в десятичное, мы запишем число с номерами столбцов выше, как показано ниже:
, если мы преобразуем наши столбцы в десятичные эквиваленты, используя следующую таблицу.
, затем двоичное число 01101011 = 1 * 1 + 1 * 2 + 0 * 4 = 1 * 8 + 0 * 16 = 1 * 32 + 1 * 64 + 0 * 128
= 64 + 32 + 8 + 2 + 1 = 107
Уведомление состоит исключительно из единиц и нулей.
Чтобы преобразовать это число в десятичное, нам нужно понять, что представляет собой каждая единица.
Если мы напишем значение столбца с над числами, то станет легко преобразовать двоичное число в десятичное.
Пример преобразования десятичного числа в двоичное
Последний более крупный пример преобразования десятичного числа 200 в двоичный код
200 = 128 + 64 + 8 = 2 7 + 2 6 + 2 3 = 11001000
Если вы довольны процессом, вы можете использовать двоично-десятичный калькулятор , как в Windows.
Преобразует двоичные числа в десятичные
, и это преобразует десятичные числа в двоичные
Что такое шестнадцатеричные числа
Шестнадцатеричное число (основание 16) требует 4 бита и имеет максимальное значение 15 . Он использует символы 0-9, A, B, C, D, E, F .
Они представлены в двоичной форме следующим образом:
0000 = 0
0001 = 1
0010 = 2
0011 = 3
0100 = 4
..
1010 = A
1011 = B
1100 = C
1101 = D
1110 = E
1111 = F
Байт (8 бит) может быть представлен как два шестнадцатеричных числа.
т.
FF = двоичное 11111111 и десятичное 255
F0 = 11110000 двоичное и десятичное 240
Quick Quiz
Тест по основам двоичных чисел
Информация
Базовый тест на понимание студентами двоичных чисел.
Вы уже прошли тест раньше. Следовательно, вы не можете запустить его снова.
Вы должны войти в систему или зарегистрироваться, чтобы начать викторину.
Вы должны пройти следующую викторину, чтобы начать эту викторину:
Видео
Если вы предпочитаете видео, я подготовил видео, в котором описывается вышесказанное — Видео о двоичных числах
Ресурсы и статьи по теме:
Оцените? И используйте Комментарии, чтобы сообщить мне больше
[Всего: 79 Среднее: 4.5/5]
Двоичная система счисления
Двоичное число состоит только из 0 сек и 1 сек.
110100 |
| Пример двоичного числа |
В двоичном формате нет 2, 3, 4, 5, 6, 7, 8 или 9!
« bit » — это одинарная цифра b inary dig it . Число выше состоит из 6 бит.
Двоичные числа имеют множество применений в математике и не только.
Фактически в цифровом мире используются двоичные цифры.
Как считать с помощью двоичного кода?
Это похоже на десятичный счет, за исключением того, что мы достигаем 10 намного раньше.
| Двоичный | ||
| 0 | Начинаем с 0 | |
| 1 | Затем 1 | |
| ??? | Но тогда для 2 нет символа… что мы делаем? |
| ну как считать в десятичном формате? | |||
| 0 | Начать с 0 | ||
| … | Посчитайте 1,2,3,4,5,6,7,8, а затем … | ||
| 9 | Это последняя цифра в десятичном формате | ||
| 10 | Итак, мы снова начинаем с 0, но добавляем 1 слева | ||
То же самое делается в двоичном формате. ..
..
| двоичный | |||
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 10 | Теперь начните снова с 0, но добавьте 1 слева | |
| ••• | 11 | 1 еще | |
| •••• | ??? | Но СЕЙЧАС что…? |
| Что происходит в десятичной системе счисления? | |||
| 99 | Когда у нас заканчиваются цифры, мы … | ||
| 100 | … снова начать с 0, но добавить 1 слева | ||
И это то, что мы делаем в двоичном формате …
| двоичный | |||
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 10 | Начните снова с 0, но добавьте 1 слева | |
| ••• | 11 | ||
| •••• | 100 | снова начните с 0 и прибавьте единицу к числу слева. .. .. … но это число уже равно 1, поэтому оно также возвращается к 0 … … и 1 добавляется к следующей позиции слева | |
| ••••• | 101 | ||
| •••••• | 110 | ||
| ••••••• | 111 | ||
| •••••••• | 1000 | Снова начать с 0 (для всех трех цифр), прибавить 1 слева | |
| ••••••••• | 1001 | И так далее! |
Посмотрите, как это делается, на этой небольшой демонстрации (нажмите кнопку воспроизведения):
Десятичное и двоичное
Вот несколько эквивалентных значений:
| десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Двоичный: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Симметрия
Двоичные числа также имеют красивый и элегантный узор:
Вот несколько больших значений:
| десятичный: | 20 | 25 | 30 | 40 | 50 | 100 | 200 | 500 |
|---|---|---|---|---|---|---|---|---|
| Двоичный: | 10100 | 11001 | 11110 | 101000 | 110010 | 1100100 | 11001000 | 111110100 |
«Бинарный — это так же просто, как 1, 10, 11. «
«
Теперь посмотрим, как использовать двоичный код для подсчета на пальцах больше 1000:
Позиция
В десятичной системе есть единицы, десятки, сотни и т. Д.
В Binary есть единицы, двойки, четверки и т. Д., Например:
Это 1 × 8 + 1 × 4 + 0 × 2 + 1 + 1 × (1/2) + 0 × (1/4) + 1 × (1/8)
= 13,625 в десятичном виде
Цифры можно размещать слева
или справа от точки, чтобы отображать значения больше единицы
и меньше одного.
| 10,1 | |
| Число слева от точки целое число (например, 10) | |
| По мере продвижения влево каждое число получает 2 раз больше . | |
| Первая цифра справа означает половинки (1/2). | |
| По мере продвижения вправо каждое число становится в 2 раза меньше (вдвое меньше).  | |
Пример: 10.1
- «10» означает 2 в десятичной системе счисления,
- «.1» означает половину,
- Таким образом, «10,1» в двоичном формате равняется 2,5 в десятичном.
Вы можете преобразовывать двоичные числа в десятичные в шестнадцатеричные.
слов
Слово двоичное происходит от «Bi-», что означает два. Мы видим «би-» в таких словах, как «велосипед» (два колеса) или «бинокль» (два глаза).
| Когда вы произносите как двоичное число, произносите каждую цифру (например, двоичное число «101» произносится как «один ноль один» , или иногда «один ноль один» ). Так люди не запутаются с десятичным числом. |
Одна двоичная цифра (например, «0» или «1») называется «битом».
Например, 11010 — пять битов.
Слово бит состоит из слов « b inary dig it »
Как показать, что число двоичное
Чтобы показать, что число является двоичным числом , поставьте за ним маленькую двойку, например: 101 2
Таким образом, люди не подумают, что это десятичное число «101» (сто один).
Примеры
Пример: что такое 1111 2 в десятичном формате?
- «1» слева находится в позиции «2 × 2 × 2», то есть 1 × 2 × 2 × 2 (= 8)
- Следующая «1» находится в позиции «2 × 2», то есть 1 × 2 × 2 (= 4)
- Следующая цифра «1» находится в позиции «2», поэтому это означает 1 × 2 (= 2)
- Последняя «1» находится в позиции единиц, то есть 1
- Ответ: 1111 = 8 + 4 + 2 + 1 = 15 в десятичной системе счисления
Пример: что такое 1001 2 в десятичном формате?
- «1» слева находится в позиции «2 × 2 × 2», то есть 1 × 2 × 2 × 2 (= 8)
- «0» находится в позиции «2 × 2», то есть 0 × 2 × 2 (= 0)
- Следующий «0» находится в позиции «2», то есть 0 × 2 (= 0)
- Последняя «1» находится в позиции единиц, то есть 1
- Ответ: 1001 = 8 + 0 + 0 + 1 = 9 в десятичной системе счисления
Пример: Что такое 1.1 2 в десятичной системе счисления?
- «1» на левой стороне, как правило, в позиции единиц, так что это означает 1.

- 1 на правой стороне находится в положении «половинки», то есть 1 × (1/2)
- Итак, 1,1 — это «1 и 1 половина» = 1,5 в десятичном формате
Пример: что такое 10,11 2 в десятичном формате?
- «1» находится в позиции «2», это означает 1 × 2 (= 2)
- «0» находится в разряде единиц, то есть 0
- «1» справа от точки находится в положении «половинки», так что это означает 1 × (1/2)
- Последняя «1» справа находится в позиции «четверти», то есть 1 × (1/4)
- Итак, 10.11 равно 2 + 0 + 1/2 + 1/4 = 2,75 в десятичной системе счисления
«В мире есть 10 типов людей:
тех, кто понимает двоичные числа, и тех, кто не понимает».
двоичных цифр
| Двоичная цифра может быть только 0 или 1 |
В компьютерном мире « b inary dig it » часто сокращается до слова « bit »
Более одной цифры
Итак, есть только два способа получить двоичную цифру ( «0» и «1» , или «Вкл. » И «Выкл.» )… а как насчет 2 или более двоичных цифр?
» И «Выкл.» )… а как насчет 2 или более двоичных цифр?
Запишем их все, начиная с 1 цифры (можете сами проверить переключателями):
Вот последний список боком:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
И (без ведущих нулей) у нас есть первые 16 двоичных чисел:
| Двоичный: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Это пригодится! Чтобы запомнить последовательность двоичных чисел, просто подумайте:
- «0» и «1» {0,1}
- , затем повторите «0» и «1» еще раз, но с «1» впереди: {0,1,10,11}
- , затем повторите те с «1» впереди: {0,1,10,11,100,101,110,111}
- и так далее!
На каждом этапе мы повторяем все, что у нас есть до сих пор, но с 1 впереди.
Теперь узнайте, как использовать двоичный код, чтобы считать на пальцах больше 1000:
двоичных цифр … они удваиваются!
Также обратите внимание, что каждый раз, когда мы добавляем еще одну двоичную цифру, мы удваиваем возможных значений.
Почему двойной ? Потому что мы берем все предыдущие возможные значения и сопоставляем их с «0» и «1», как указано выше.
- Таким образом, только одна двоичная цифра имеет 2 возможных значения (0 и 1)
- Две двоичные цифры имеют 4 возможных значения (0, 1, 10, 11)
- Три имеют 8 возможных значений
- Четыре имеют 16 возможных значений
- Пять имеют 32 возможных значения
- Шесть имеют 64 возможных значения
- и др.
Используя экспоненты, это может быть показано как:
| Число цифр | Формула | Настройки |
|---|---|---|
| 1 | 2 1 | 2 |
| 2 | 2 2 | 4 |
| 3 | 2 3 | 8 |
| 4 | 2 4 | 16 |
| 5 | 2 5 | 32 |
| 6 | 2 6 | 64 |
и т. Д… Д… | и т. Д. .. | и т.д … |
Пример: когда у нас есть 50 двоичных цифр (или 50 элементов, каждая из которых может иметь только две позиции), сколько разных способов это?
Экспресс-двоичные числа в C ++
- Программирование
- C ++
- Экспресс-двоичные числа в C ++
Стивен Р. Дэвис
Переменные C ++ хранятся внутри как так называемые двоичные числа.Двоичные числа хранятся в виде последовательности значений 1 и 0, известной как бит. В большинстве случаев вам действительно не нужно иметь дело с конкретными битами, которые вы используете для представления чисел. Иногда, однако, практично и удобно возиться с числами на битовом уровне, поэтому C ++ предоставляет для этой цели набор операторов.
Так называемые побитовые логические операции оперируют своими аргументами на битовом уровне. Чтобы понять, как они работают, сначала изучите, как компьютеры хранят переменные.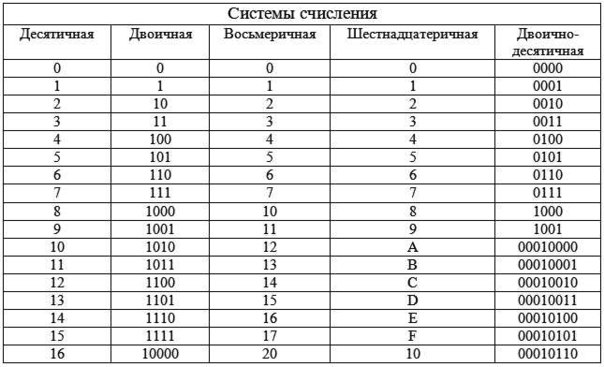
Десятичная система счисления
Числа, с которыми вы знакомы с того времени, когда вы впервые могли сосчитать на пальцах, известны как десятичные числа , , потому что они основаны на числе 10. Как правило, программист выражает переменные C ++ как десятичные числа. Таким образом, вы можете указать значение var как (скажем) 123, но примите во внимание последствия.
Число, такое как 123, относится к 1 * 100 + 2 * 10 + 3 * 1. Все эти основные числа — 100, 10 и 1 — являются степенями десяти.
123 = 1 * 100 + 2 * 10 + 3 * 1
Выраженное немного другим (но эквивалентным) способом, 123 выглядит так:
123 = 1 * 10 2 + 2 * 10 1 + 3 * 10 0
Помните, что любое число от до нулевой степени равно 1.
Другие системы счисления
Ну, хорошо, использование 10 в качестве основы (или база ) нашей системы счета, вероятно, происходит от тех 10 человеческих пальцев, первоначальных инструментов счета.Альтернативной базой для системы подсчета так же легко могло быть 20.
Если бы наша схема нумерации была изобретена собаками, она вполне могла бы быть основана на 8 (одна цифра каждой лапы находится вне поля зрения на задней части лапы). Математически такая восьмеричная система работала бы точно так же:
123 10 = 1 * 8 2 + 7 * 8 1 + 3 * 8 0 = 173 8
Маленькие 10 и 8 здесь относятся к системе счисления, 10 — для десятичной (основание 10) и 8 — для восьмеричной (основание 8).Система подсчета может использовать любую положительную базу.
Двоичная система счисления
У компьютеров по сути два пальца. Компьютеры предпочитают считать по основанию 2. Число 123 10 можно выразить так:
123 10 = 0 * 2 7 + 1 * 2 6 + 1 * 2 5 + 1 * 2 4 + 1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0
123 10 = 0 * 128 + 1 * 64 + 1 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1
= 01111011 2 Компьютерное соглашение выражает двоичные числа с использованием 4, 8, 16, 32 или даже 64 двоичных цифр, даже если ведущие цифры равны 0.Это также связано с тем, как компьютеры построены внутри.
Поскольку термин цифра относится к числу, кратному 10, двоичная цифра называется битом (сокращение от двоичной цифры ). Байт состоит из 8 бит. (Назвать двоичную цифру байтом — это не показалось хорошей идеей.) Память обычно измеряется в байтах (например, булочки измеряются в единицах пекарской дюжины).
С такой маленькой базой вы должны использовать большое количество битов для выражения чисел.Люди не хотят использовать такое выражение, как 011110112, для выражения такого обыденного значения, как 123 10 . Программисты предпочитают выражать числа с помощью четного числа битов.
Восьмеричная система, основанная на 3 битах, была двоичной системой по умолчанию в первые дни C. Мы видим следы этого даже сегодня — константа, начинающаяся с 0, считается восьмеричной в C ++. Таким образом, строка:
cout << "0173 =" << 0173 << endl;
дает следующий результат:
0173 = 123
Однако восьмеричная была почти полностью заменена шестнадцатеричной системой , которая основана на 4-битных цифрах.
В шестнадцатеричном формате используются те же цифры для чисел от 0 до 9. Для цифр от 9 до 16 в шестнадцатеричном формате используются первые шесть букв алфавита: A для 10, B для 11 и т. Д. Таким образом, 123 10 становится 7B 16 , вот так:
123 = 7 * 16 1 + B (т.е. 11) * 16 0 = 7B 16
Программисты предпочитают выражать шестнадцатеричные числа кратными 4 шестнадцатеричным цифрам, даже если ведущая цифра в каждом случае равна 0.
Наконец, кто хочет выразить шестнадцатеричное число, такое как 7B 16 , с помощью нижнего индекса? Терминалы даже не поддерживают индекса. Даже в текстовом процессоре сложно переключить шрифты в режим подстрочного индекса и обратно, просто чтобы ввести две паршивые цифры.
Следовательно, программисты (не дураки, они) используют соглашение о начале шестнадцатеричного числа с 0x. Таким образом, 7B становится 0x7B. Используя это соглашение, шестнадцатеричное число 0x7B равно 123 десятичному, а шестнадцатеричное 0x123 равно 291 десятичному.Фрагмент кода
cout << "0x7B =" << 0x7B << endl; cout << "0x123 =" << 0x123 << endl;
дает следующий результат:
0x7B = 123 0x123 = 291
Вы можете использовать все математические операторы с шестнадцатеричными числами так же, как вы их применяете к десятичным числам.
Если вы действительно хотите, вы можете записывать двоичные числа на C ++ ’14, используя префикс «0b». Таким образом, 123 становится 0b01111011.
Об авторе книги
Стивен Р.Дэвис - автор бестселлеров множества книг и статей, в том числе C # для чайников . Он занимается программированием более 30 лет и в настоящее время работает в Booz Allen Hamilton в области защиты родины.
Двоичная система счисления
Основное различие между двоичной системой счисления и нашей знакомой системой счисления по основанию 10 заключается в том, что группировка выполняется группами по 2 вместо 10.
Например, чтобы представить 24 в базе 10 с помощью палочек, вы можете использовать две группы по десять и четыре, как показано ниже.
Но нужно помнить кое-что важное, и это ключ к пониманию этого урока!
- Цифры 0,1,2,3,4,5,6,7,8,9 используются для представления всех возможных чисел. Обратите внимание, что основание 10 состоит из 10 цифр
- В зависимости от того, насколько велико число, мы составляем группы из десяти, сотен, тысяч, десяти тысяч и т. Д. (Это степень 10: 10 1 = 10, 10 2 = 100, 10 3 = 1000)
- Если число меньше 10, например 8 и 9, создавать группы не нужно.И это число будет занимать единичное значение
- Если число больше 9 и меньше 100, например 10, 55 и 98, необходимо создать группы из десяти. Группы по десять человек будут занимать десятичное значение.
- Если число больше 99 и меньше 1000, например 100, 255 и 999, необходимо создать группы по сотне. Группы сотен будут занимать разрядное значение сотен.
- И так далее ...
.
Например, внимательно изучите следующий номер, чтобы увидеть, как он был организован.
Так как число больше 99, пришлось сделать группы по сто десять. Обратите внимание также, как группы из сотен помещаются в разряд сотен, а группы из десяти помещаются в разряд десятков.
Аналогичным образом двоичная система счисления имеет собственное разрядное значение.
- Цифры 0,1 используются для представления всех возможных чисел в двоичной системе счисления.Обратите внимание, что основание 2 состоит из 2 цифр для представления всех возможных чисел.
- В зависимости от того, насколько велико число, мы составляем группы из 2, 4, 8, 16, 32 и т. Д. (Это степень 2: 2 1 = 2, 2 2 = 4, 2 3 = 8)
- Если число меньше 2, например 1, создавать группы не нужно. И это число будет занимать первое место со значением . Это значение позиции соответствует разряду единиц в базе 10
- Фактически, это 1 то же самое в двоичной системе счисления и системе с основанием 10.
- Если число больше 1 и меньше 4, например 2 и 3, необходимо создать группу из двух человек. Группа из двух человек займет второе место со значением . Вы также можете назвать это "двухзначным" значением
- Если число больше 3 и меньше 8, например 4 и 7, необходимо создать группу из четырех человек. Группа из четырех человек займет третье место со значением . Вы также можете назвать это "четырехзначным" значением
- Если число больше 7 и меньше 16, например 8, 11 и 14, необходимо создать группу из восьми.Группа из восьми займет четвертое место со значением . Вы также можете назвать это «восьмеркой».
- Если число больше 15 и меньше 32, например 16, 21 и 30, необходимо создать группу из шестнадцати. Группа из шестнадцати человек займет пятое место со значением . Вы также можете назвать это «шестнадцатиместным» значением.
- Если число больше 31 и меньше 64, например 32, 45 и 63, необходимо создать группу из тридцати двух.Группа из тридцати двух человек займет шестое место со значением . Вы также можете назвать это «тридцатью двумя» значениями.
- И так далее ...
Выше обратите внимание на многократное использование «A» в «A group of ...»
Ну, это означает, что мы можем создать только 1 группу, а не 2, не 3
Так как мы используем только 0 и 1 для представления чисел , записать двоичные числа с помощью числа 2 будет невозможно.
Теперь переведем 25 в двоичную систему счисления
Обратите внимание, что нет групп из двух и четырех.В результате поставьте нули на второе место и на третье место
Как выполняется группировка в двоичной системе счисления. Как преобразовать из базы 10 в базу 2
Группа с n-го места на первое. Это означает, что вы должны сначала создать группу с максимально возможной степенью 2
. Например, я пытаюсь преобразовать 45 в двоичную систему счисления.
Спросите себя. Какая наибольшая степень 2 меньше 45?
2 6 = 64,2 5 = 32.Таким образом, наибольшая степень 2 меньше 45 составляет 2 5 = 32
Поскольку 32 идет на шестом месте, поместите 1 на шестое место . Затем попытайтесь выяснить, что раньше входит в разряд.
45-32 = 13
Спросите себя. Какая наибольшая степень 2 меньше 13?
2 4 = 16. 2 3 = 8. Таким образом, наибольшая степень двойки меньше 13 равна 2 3 = 8
Поскольку 8 идет на четвертом месте, поместите 1 на четвертое место . .Затем попытайтесь выяснить, что раньше входит в разряд.
13-8 = 5
Спросите себя. Какая максимальная степень 2 меньше 5?
2 3 = 8. 2 2 = 4. Таким образом, наибольшая степень 2 меньше 5 равна 2 2 = 4
Поскольку 4 идет на третьем месте, поместите 1 на третье место . Затем попытайтесь выяснить, что раньше входит в разряд.
5-4 = 1 и 1 переходит на первое место .
Обратите внимание, что вы ничего не помещаете в пятое и второе места, поэтому в этих местах идут нули
Следовательно, 45, преобразованное в двоичную систему счисления, равно 101101
Вы также можете написать 45 десять или 101101 два
Будьте очень внимательны при чтении 101101 двух !
101101 2 читается один ноль один один ноль один основание 2
Введение в физику
18 ноя, 20 13:20
Первоклассное введение в физику.Универсальный ресурс для глубокого понимания важных концепций физики
Подробнее
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
Десятичная и двоичная системы счисления
Прежде чем мы начнем изучать более сложные вещи в разделе «Числовой анализ», мы должны сначала лучше понять десятичную и двоичную системы счисления.Сначала мы закрепим основы десятичной системы счисления, с которой мы все слишком хорошо знакомы.
Десятичная система счисления
Определение: Десятичная система счисления - это система счисления, в которой каждое действительное число $ x $ может быть записано в виде десяти цифр $ 0 $, 1 $, 2 $, 3 $, 4 $, 5 $. $, 6 $, 7 $, 8 $ и 9 $ как сумма степеней 10 $. Говорят, что число в десятичной системе счисления имеет основание $ 10 $, и чтобы указать это, мы добавляем индекс $ 10 $ к $ x $, записанный как $ (x) _ {10} $.{-n} \ right) + ... \ end {align}Двоичная система счисленияМы привыкли использовать десятичную систему счисления, описанную выше, и связанную с ней основную арифметику, однако двоичная система счисления также чрезвычайно важна, особенно в вычислениях. |





