Абсолютная диэлектрическая проницаемость. Единица измерения диэлектрическая проницаемость

Диэлектрическая проницаемость — Викизнание... Это Вам НЕ Википедия!

Диэлектрическая проницаемость — способность среды пропускать электрическое поле, физическая величина, связывающая электрическую индукцию с напряжённостью электрического поля. Является тензором, однако для изотропной среды может быть выражена скалярной величиной. Размерность и численное значение диэлектрической проницаемости зависит от выбор системы единиц измерения. В общем случае различают абсолютную и относительную диэлектрическую проницаемость.

Абсолютная диэлектрическая проницаемость является отношением вектора диэлектрической индукции и напряжённости электрического поля :

Относительная диэлектрическая проницаемость — отношение диэлектрической проницаемости среды к диэлектрической проницаемости вакуума, связанная с абсолютной посредством электрической постоянной :

Связь электрической индукцией и напряжённостью электрического поля имеет, таким образом, следующий вид:

Единицы измерения диэлектрической проницаемости[править]

Выбор единиц абсолютной диэлектрической проницаемости, как и величины электрической постоянной зависит от выбора единиц измерения. Например, в СГСЭ и гауссовой системе электрическая постоянная приравнена единице, и, таким образом, абсолютная и относительная электрические проницаемости не различаются. В других системах они могут различаться, а абсолютная диэлектрическая проницаемость может иметь размерность.

Единицы измерения диэлектрической проницаемости. Система единиц Единица измерения абсолютной диэлектрической проницаемости Величина электрической постоянной Единица измерения электрической индукции Единица измерения напряжённости электрического поля

СИ	фарада на метр	8,854 · 10−12 Ф / м	кулон на метр в квадрате	вольт на метр
СГСЭ, Гауссова	безразмерна	1

Диэлектрическая проницаемость некоторых материалов[править]

Диэлектрическая проницаемость некоторых материалов при нормальных условиях Материал Относительная диэлектрическая проницаемость

Вакуум	1 (точно)
Воздух	1,0006
Водяной пар	1,0126
Керосин	2,1
Трансформаторное масло	2,1—2,2
Парафин	2,2
Полиэтилен	2,2—2,3
Резина электроизоляционная	2,5—5
Лёд	3,2
Оргстекло	3,3
Антрацен	3,46
Эпоксидная смола	3,7
Поливинилхлорид	3—5
Кварц	4,3
Стекло	7,0
Слюда	7,0
Текстолит	8
Мрамор	8—10
Этанол	24
Вода	81

См. также: магнитная проницаемость.

www.wikiznanie.ru

Диэлектрическая проницаемость — Википедия

Диэлектри́ческая проница́емость среды абсолютная — коэффициент, входящий в математическую запись закона Кулона и уравнение связи векторов электрической индукции и напряженности электрического поля [1]. Абсолютную диэлектрическую проницаемость εa представляют[2] в виде произведения εa = εr ε0 относительной диэлектрической проницаемости среды εr (от англ. relative — относительный; εr для краткости часто называют просто диэлектрической проницаемостью и обозначают ε) и электрической постоянной ε0.

Диэлектри́ческая проница́емость среды относительная — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме. Относительная диэлектрическая проницаемость εr является безразмерной величиной, обусловлена эффектом поляризации диэлектриков под действием электрического поля и определяется характеризующей этот эффект величиной диэлектрической восприимчивости среды. Значение εr вакуума равно единице, для реальных сред εr > 1. Для воздуха и большинства других газов в нормальных условиях значение εr близко к единице в силу их низкой плотности. В статическом электрическом поле для большинства твёрдых или жидких диэлектриков значение εr лежит в интервале от 2 до 8, для воды значение εr достаточно высокое, около 80. Значение εr велико для веществ с молекулами, обладающими большим электрическим дипольным моментом. Значение εrсегнетоэлектриков составляет десятки и сотни тысяч.

Электрическая постоянная ε0 ≈ 8.85·10−12 Ф/м. Размерность ε0, как и размерность абсолютной диэлектрической проницаемости εa среды, в Международной системе величин составляет L−3M−1T4I². В СИ, основанной на Международной системе величин, единицей абсолютной диэлектрической постоянной является фарад, деленный на метр: []=Ф/м. Для вакуума значения εa и ε0 равны. В зарубежной литературе для электрической постоянной принято обозначение ε. Электрическая постоянная используется только в Международной системе единиц (СИ), в которой размерности электрической индукции и напряжённости электрического поля различны. В системе СГС необходимость во введении абсолютной диэлектрической проницаемости отсутствует.

Относительная диэлектрическая проницаемость εr среды наряду с относительной магнитной проницаемостью μr и удельной электропроводностью σ среды влияют на распределение напряженности компонент электромагнитного поля в пространстве и описывают среду в материальных уравнениях системы уравнений электродинамики (системы уравнений Максвелла), их называют электромагнитными параметрами среды. Среду со значениями μr = 1 и σ = 0 называют идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё εr определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды. Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых σ > 0) также влияет на значение тангенса угла диэлектрических потерь и погонное затухание электромагнитной волны в среде. Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение εr приводит к увеличению ёмкости. При изменении εr в пространстве (то есть если εr зависит от координат) говорят о неоднородной среде, зависимость εr от частоты электромагнитных колебаний — одна из возможных причин дисперсии электромагнитных волн, зависимость εr от напряженности электрического поля — одна из возможных причин нелинейности среды. Если в материальном уравнении εr является не скаляром, а тензором, то говорят об анизотропной среде. При использовании метода комплексных амплитуд в решении системы уравнений Максвелла и наличии потерь в среде (σ > 0) оперируют с комплексной диэлектрической проницаемостью.

Некоторые свойства[править]

Строго говоря, диэлектрическая проницаемость связывает электрическую индукцию и напряжённость электрического поля. В общем случае диэлектрическая проницаемость является тензором, определяемым из следующих соотношений (в записи использовано соглашение Эйнштейна):

или

здесь:

 — вектор напряжённости электрического поля,  — вектор электрической индукции,  — тензор абсолютной диэлектрической проницаемости.

Для среды с конечной проводимостью (поглощающая среда, среда с потерями) в тензор диэлектрической проницаемости часто включают мнимую компоненту, пропорциональную проводимости. Пусть напряженность электрического поля изменяется во времени по гармоническому закону (далее  — мнимая единица):

Тогда одно из уравнений Максвелла для непроводящей среды с постоянным во времени тензором :

С другой стороны, для проводящей среды с тензором проводимости :

Чтобы привести это уравнение к виду, формально совпадающему с видом уравнения для непроводящей среды, можно ввести тензор комплексной диэлектрической проницаемости :

Таким образом, становится возможным использование для проводящих сред формул, полученных для идеальных диэлектриков. Кроме того, даже в случаях, когда в постоянном электрическом поле среда обладает очень малой проводимостью, на высоких частотах могут проявиться существенные потери, которые при таком подходе также можно приписать некоторой «эффективной» диэлектрической проницаемости. В таком случае говорят о тангенсе угла δ диэлектрических потерь

Иногда при описании колебаний электрического поля в методом комплексных амплитуд используют "отрицательную временную зависимость": . В таких случаях следует везде перед заменить знак на противоположный.

Необходимо отметить, что:

Зависимость от частоты[править]

Следует отметить, что диэлектрическая проницаемость в значительной степени зависит от частоты электромагнитного поля. Это следует всегда учитывать, поскольку таблицы справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц без указания данного факта. В то же время существуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров. Полученное оптическим методом (частота 1014 Гц) значение будет значительно отличаться от данных в таблицах.

Рассмотрим, например, случай воды. В случае статического поля относительная диэлектрическая проницаемость воды приблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц εr начинает падать. В оптическом диапазоне εr составляет приблизительно 1,77, соответственно показатель преломления воды равен 1,33. О поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 1012 (инфракрасная область) можно прочитать на [1] (англ.)

Относительная диэлектрическая проницаемость вещества εr может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (Cx) и ёмкости того же конденсатора в вакууме (Co):

Практическое применение[править]

Диэлектрическая проницаемость изоляционных материалов является одним из основных параметров при разработке электрических конденсаторов. Применение материала с высокой диэлектрической проницаемостью позволяют существенно сократить габаритные размеры конденсатора. Например, ёмкость плоского конденсатора

где εr — относительная диэлектрическая проницаемость материала между обкладками, εо — электрическая постоянная, S — площадь обкладок конденсатора, d — расстояние между обкладками. Таким образом, требуемая площадь S обкладок обратно пропорциональна εr.

Значение диэлектрической проницаемости материала основания учитывается при разработке печатных плат, поскольку оно влияет на значение статической ёмкости проводящего рисунка слоев питания и волновое сопротивление проводников (линий передачи сигналов) на плате.

Значения диэлектрической проницаемости для некоторых веществ[править]

Вещество Химическая формула Условия измерения Характерное значение εr

Вакуум	-	-	1
Воздух	-	Нормальные условия, 0,9 МГц	1,00058986 ± 0,00000050
Углекислый газ	CO2	Нормальные условия	1,0009
Тефлон (политетрафторэтилен, фторопласт)	[-СF2-СF2-]n	-	2,1
Нейлон	-	-	3,2
Полиэтилен	[-СН2-СН2-]n	-	2,25
Полистирол	[-СН2-С(С6Н5)Н-]n	-	2,4-2,7
Каучук	-	-	2,4
Битум	-	-	2,5-3,0
Сероуглерод	CS2	-	2,6
Парафин	С18Н38 − С35Н72	-	2,0-3,0
Бумага	-	-	2,0-3,5
Электроактивные полимеры	−	−	2-12
Эбонит	(C6H9S)2	−	2,5-3,0
Плексиглас (оргстекло)	-	-	3,5
Кварц	SiO2	-	3,5-4,5
Диоксид кремния	SiO2	−	3,9
Бакелит	-	-	4,5
Бетон	−	−	4,5
Фарфор	−	−	4,5-4,7
Стекло	−	−	4,7 (3,7-10)
Стеклотекстолит FR-4	-	-	4,5-5,2
Гетинакс	-	-	5-6
Слюда	-	-	7,5
Резина	−	−	7
Поликор	98 % Al2O3	-	9,7
Алмаз	−	−	5,5-10
Поваренная соль	NaCl	−	3-15
Графит	C	−	10-15
Керамика	−	−	10-20
Кремний	Si	−	11.68
Бор	B	−	2.01
Аммиак	Nh4	20 °C	17
		0 °C	20
		−40 °C	22
		−80 °C	26
Спирт этиловый	C2H5OH или Ch4-Ch3-OH	−	27
Метанол	Ch4OH	−	30
Этиленгликоль	HO—Ch3—Ch3—OH	−	37
Фурфурол	C5h5O2	−	42
Глицерин	HOCh3CH(OH)-Ch3OH или C3H5(OH)3	0 °C	41,2
		20 °C	47
		25 °C	42,5
Вода	h3O	200 °C	34,5
		100 °C	55,3
		20 °C	81
		0 °C	88
Плавиковая кислота	HF	0 °C	83,6
Формамид	HCONh3	20 °C	84
Серная кислота	h3SO4	20-25 °C	84-100
Пероксид водорода	h3O2	−30 °C — +25 °C	128
Синильная кислота	HCN	(0-21 °C)	158
Двуокись титана	TiO2	-	86-173
Титанат кальция	CaTiO3	-	170
Титанат стронция	SrTiO3	-	310
Титанат бария-стронция	(Ba1−xSrx)TiO3, 0<x<1	-	500
Титанат бария	BaTiO3	(20-120 °C)	1250-10000
Цирконат-титанат свинца	(Pb[ZrxTi1-x]O3, 0<x<1)		500-6000
Сополимеры	-	-	до 100000
Сульфид кадмия	CdS		9,3

1. ↑ Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971. С. 11.
2. ↑ В. В. Никольский, Т. И. Никольская. Электродинамика и распространение радиоволн. М.: Наука, 1989. С. 35.

wp.wiki-wiki.ru

Новый документ в формате RTF (2)

Диэлектри́ческая проница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая зависимостьэлектрической индукции от напряжённости электрического поля.

Определяется эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды).

Различают относительную и абсолютную диэлектрические проницаемости.

Относительная диэлектрическая проницаемость ε является безразмерной и показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Эта величина для воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постояннаяводы в статическом поле достаточно высока — около 80. Велики её значения для веществ с молекулами, обладающими большим электрическим дипольным моментом. Относительная диэлектрическая проницаемость сегнетоэлектриков составляет десятки и сотни тысяч.

Абсолютная диэлектрическая проницаемость в зарубежной литературе обозначается буквой ε, в отечественной преимущественно используется сочетание , где  — электрическая постоянная. Абсолютная диэлектрическая проницаемость используется только в Международной системе единиц (СИ), в которой индукция и напряжённость электрического поля измеряются в различных единицах. В системе СГС необходимость в введении абсолютной диэлектрической проницаемости отсутствует. Абсолютная диэлектрическая постоянная (как и электрическая постоянная) имеет размерность L−3M−1T4I². В единицах Международной системы единиц (СИ): []=Ф/м.

Следует отметить, что диэлектрическая проницаемость в значительной степени зависит от частоты электромагнитного поля. Это следует всегда учитывать, поскольку таблицы справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц без указания данного факта. В то же время существуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров. Полученное оптическим методом (частота 1014 Гц) значение будет значительно отличаться от данных в таблицах.

Рассмотрим, например, случай воды. В случае статического поля (частота равна нулю), относительная диэлектрическая проницаемость при нормальных условияхприблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц εr начинает падать. В оптическом диапазоне εr составляет приблизительно 1,8. Это вполне соответствует факту, что в оптическом диапазоне показатель преломления воды равен 1,33.[1] В узком диапазоне частот, называемом оптическим, диэлектрическое поглощение падает до нуля, что собственно и обеспечивает человеку механизм зрения[источник не указан 1252 дня] в земной атмосфере, насыщенной водяным паром. С дальнейшим ростом частоты свойства среды вновь меняются. О поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 1012 (инфракрасная область) можно прочитать на [1] (англ.)

Диэлектрическая проницаемость диэлектриков является одним из основных параметров при разработке электрических конденсаторов. Использование материалов с высокой диэлектрической проницаемостью позволяют существенно снизить физические размеры конденсаторов.

Ёмкость конденсаторов определяется:

где εr — диэлектрическая проницаемость вещества между обкладками, εо — электрическая постоянная, S — площадь обкладок конденсатора, d — расстояние между обкладками.

Параметр диэлектрической проницаемости учитывается при разработке печатных плат. Значение диэлектрической проницаемости вещества между слоями в сочетании с его толщиной влияет на величину естественной статической ёмкости слоев питания, а также существенно влияет на волновое сопротивлениепроводников на плате.

УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ электрическое, физическая величина , равная электрическому сопротивлению (см.СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЕ) R цилиндрического проводника единичной длины (l = 1м) и единичной площади поперечного сечения (S =1 м2).. r = R S/l. В Си единицей удельного сопротивления является Ом.м. Удельное сопротивление могут выражать также в Ом.см. Удельное сопротивление является характеристикой материала, по которому протекает ток, и зависит от материала, из которого он изготовлен. Удельное сопротивление, равное r = 1 Ом.м означает, что цилиндрический проводник, изготовленный из данного материала, длиной l = 1м и с площадью поперечного сечения S = 1 м2 имеет сопротивление R = 1 Ом.м. Величина удельного сопротивления металлов (см. МЕТАЛЛЫ), являющихся хорошими проводниками (см. ПРОВОДНИКИ), может иметь значения порядка 10-8 – 10-6Ом.м (например, медь, серебро, железо и т. д.). Удельное сопротивление некоторых твердых диэлектриков (см. ДИЭЛЕКТРИКИ) может достигать значения 1016-1018Ом.м (например, кварцевое стекло, полиэтилен, электрофарфор и др.). Величина удельного сопротивления многих материалов (особенного полупроводниковых материалов (см.ПОЛУПРОВОДНИКОВЫЕ МАТЕРИАЛЫ)) существенно зависит от степени их очистки, наличия легирующих добавок, термических и механических обработок и т. д. Величина s, обратная удельному сопротивлению , называется удельной проводимостью: s = 1/r Удельная проводимость измеряется в сименсах (см. СИМЕНС (единица проводимости)) на метр См/м. Удельное электрическое сопротивление (проводимость) является скалярной величиной для изотропного вещества; и тензорной — для анизотропного вещества. В анизотропным монокристаллах анизотропия электропроводности является следствием анизотропии обратной эффективной массы (см. ЭФФЕКТИВНАЯ МАССА) электронов и дырок.

1-6. ЭЛЕКТРОПРОВОДНОСТЬ ИЗОЛЯЦИИ

При включении изоляции кабеля или провода на постоянное напряжение U через нее проходит ток i, изменяющийся во времени (рис. 1-3). Этот ток имеет постоянные составляющие - ток проводимости (i ∞ ) и ток абсорбции, гдеγ - проводимость, соответствующая току абсорбции; Т - время, в течение которого ток i абс спадает до 1/e своего первоначального значения. При бесконечно большом времени i абс →0 и i = i ∞ . Электропроводность диэлектриков объясняется наличием в них некоторого количества свободных заряженных частиц: ионов и электронов.

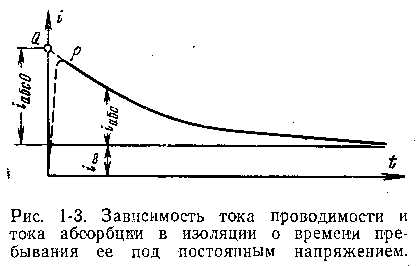
Наиболее характерна для большей части электроизоляционных материалов ионная электропроводность, которая возможна за счет неизбежно присутствующих в изоляции загрязнений (примеси влаги, солей, щелочей и т. п.). У диэлектрика с ионным характером электропроводности строго соблюдается закон Фарадея - пропорциональность между количеством прошедшего через изоляцию электричества и количеством выделившегося при электролизе вещества.

При повышении температуры удельное сопротивление электроизоляционных материалов уменьшается и характеризуется формулой

где_ρ о , А и В - постоянные для данного материала; Т- температура, °К.

Большая зависимость сопротивления изоляции от влаги имеет место у гигроскопичных изоляционных материалов, главным образом волокнистых (бумага, хлопчатобумажная пряжа и др.). Поэтому волокнистые материалы подвергаются сушке и пропитке, а также защите влагостойкими оболочками.

Сопротивление изоляции может уменьшаться с повышением напряжения за счет образования в изоляционных материалах объемных зарядов. Создающаяся при этом добавочная электронная проводимость приводит к увеличению электропроводности. Существует зависимость проводимости от напряжения в очень сильных полях (закон Я. И. Френкеля):

где γ о - проводимость в слабых полях; а - постоянная. Все электроизоляционные материалы характеризуются определенными значениями проводимости изоляции G. В идеале проводимость изоляционных материалов равна нулю. У реальных изоляционных материалов проводимость на единицу длины кабеля определяют по формуле

В кабелях, имеющих сопротивление изоляции более , 3-10 11 ом-м и кабелях связи, где потери на диэлектрическую поляризацию значительно больше тепловых потерь, проводимость определяют по формуле

Проводимость изоляции в технике связи является электрическим параметром линии, характеризующим потери энергии в изоляции жил кабелей. Зависимость величины проводимости от частоты приведена на рис. 1-1. Величина, обратная проводимости - сопротивление изоляции, представляет собой отношение приложенного к изоляции напряжения постоянного тока (в вольтах) к току утечки (в амперах), т. е.

где R V - объемное сопротивление изоляции, численно определяющее препятствие, создаваемое прохождению тока в толще изоляции; R S - поверхностное сопротивление, определяющее препятствие прохождению тока по поверхности изоляции.

Практической оценкой качества применяемых изоляционных материалов является удельное объемное сопротивление ρ V выражаемое в омо-сантиметрах (ом*см). Численно ρ V равно сопротивлению (в омах) куба с ребром 1 см из данного материала, если ток проходит через две противоположные грани куба. Удельное поверхностное сопротивление ρ S численно равно сопротивлению поверхности квадрата (в омах), если ток подводится к электродам, ограничивающим две противоположные стороны этого квадрата.

Сопротивление изоляции одножильного кабеля или провода определяют по формуле

Абсорбционными токами называются токи смещения различных видов замедленной поляризации. Абсорбционные токи при постоянном напряжении протекают в диэлектрике до момента установления равновесного состояния, изменяя свое направление при включении и выключении напряжения. При переменном напряжении абсорбционные токи протекают в течение всего времени нахождения диэлектрика в электрическом поле.

Влажностные свойства диэлектриков

Влагостойкость – это надежность эксплуатации изоляции при нахождении ее в атмосфере водяного пара близкого к насыщению. Влагостойкость оценивают по изменению электрических, механических и других физических свойств после нахождения материала в атмосфере с повышенной и высокой влажностью; по влаго- и водопроницаемости; по влаго- и водопоглощаемости.

 

Влагопроницаемость – способность материала пропускать пары влаги при наличии разности относительных влажностей воздуха с двух сторон материала.

Влагопоглощаемость – способность материала сорбировать воду при длительном нахождении во влажной атмосфере близкой к состоянию насыщения.

Водопоглощаемость – способность материала сорбировать воду при длительном погружении его в воду.

Тропикостойкость и тропикализация оборудования – защита электрооборудования от влаги, плесени, грызунов.

 

Тепловые свойства диэлектриков

Для характеристики тепловых свойств диэлектриков используются следующие величины.

Нагревостойкость – способность электроизоляционных материалов и изделий без вреда для них выдерживать воздействие высокой температуры и резких смен температуры. Определяют по температуре, при которой наблюдается существенное изменение механических и электрических свойств, например, в органических диэлектриках начинается деформация растяжения или изгиба под нагрузкой.

Теплопроводность – процесс передачи тепла в материале. Характеризуется экспериментально определяемым коэффициентом теплопроводности λт. λт – количество теплоты, переданной за одну секунду через слой материала толщиной в 1 м и площадью поверхности – 1 м2 при разности температур поверхностей слоя в 1 °К. Коэффициент теплопроводности диэлектриков изменяется в широких пределах. Самые низкие значения λт имеют газы, пористые диэлектрики и жидкости (для воздуха λт = 0,025 Вт/(м·К), для водыλт = 0,58 Вт/(м·К)), высокие значения имеют кристаллические диэлектрики (для кристаллического кварца λт = 12,5 Вт/(м·К)). Коэффициент теплопроводности диэлектриков зависит от их строения (для плавленого кварца λт = 1,25 Вт/(м·К)) и температуры.

Тепловое расширение диэлектриков оценивают температурным коэффициентом линейного расширения: . Материалы с малым тепловым расширением, имеют, как правило, более высокую нагревостойкость и наоборот. Тепловое расширение органических диэлектриков значительно (в десятки и сотни раз) превышает расширение неорганических диэлектриков. Поэтому стабильность размеров деталей из неорганических диэлектриков при колебаниях температуры значительно выше по сравнению с органическими.

1.      Абсорбционные токи

Абсорбционными токами называются токи смещения различных видов замедленной поляризации. Абсорбционные токи при постоянном напряжении протекают в диэлектрике до момента установления равновесного состояния, изменяя свое направление при включении и выключении напряжения. При переменном напряжении абсорбционные токи протекают в течение всего времени нахождения диэлектрика в электрическом поле.

В общем случае электрический ток j в диэлектрике представляет собой сумму сквозного тока jск и тока абсорбции jаб

j = jск + jаб.

Ток абсорбции можно определить через ток смещения jсм - скорость изменения вектора электрической индукции D

Сквозной ток определяется переносом (движением) в электрическом поле различных носителей заряда.

2.      Электронная электропроводность характеризуется перемещением электронов под действием поля. Кроме металлов она присутствует у углерода, оксидов металлов, сульфидов и др. веществ, а также у многих полупроводников.

3.      Ионная – обусловлена движением ионов. Наблюдается в растворах и расплавах электролитов – солей, кислот, щелочей, а также во многих диэлектриках. Она подразделяется на собственную и примесную проводимости. Собственная проводимость обусловлена движением ионов, получаемых при диссоциации[1] молекул. Движение ионов в электрическом поле сопровождается электролизом[2] – переносом вещества между электродами и выделением его на электродах. Полярные жидкости диссоциированы в большей степени и имеют большую электропроводность, чем неполярные.

В неполярных и слабополярных жидких диэлектриках (минеральные масла, кремнийорганические жидкости) электропроводность определяется примесями.

4.      Молионная электропроводность – обусловлена движением заряженных частиц, называемых молионами. Наблюдают ее в коллоидных системах, эмульсиях[3], суспензиях[4]. Движение молионов под действием электрического поля называют электрофорезом. При электрофорезе, в отличие от электролиза, новых веществ не образуется, меняется относительная концентрация дисперсной фазы в различных слоях жидкости. Электрофоретическая электропроводность наблюдается, например, в маслах, содержащихэмульгированную воду.

studfiles.net

Диэлектрическая проницаемость Википедия

Диэлектри́ческая проница́емость — коэффициент, входящий в математическую запись закона Кулона для силы взаимодействия точечных зарядов q1{\displaystyle q_{1}} и q2{\displaystyle q_{2}}, находящихся в однородной изолирующей (диэлектрической) среде на расстоянии r12{\displaystyle r_{12}} друг от друга:

F=14πεa⋅|q1q2|r122{\displaystyle F={\frac {1}{4\pi \varepsilon _{a}}}\cdot {\frac {|q_{1}q_{2}|}{r_{12}^{2}}}},

а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:

D=εaE{\displaystyle \mathbf {D} =\varepsilon _{a}\mathbf {E} }

в рассматриваемой среде[1]. Вводятся абсолютная (а) и относительная (r, от англ. relative — относительный) проницаемости:

εa=ε0εr{\displaystyle \varepsilon _{a}=\varepsilon _{0}\varepsilon _{r}},

где ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная[2]. Cам термин «диэлектрическая проницаемость» применяется и для εr{\displaystyle \varepsilon _{r}}, и для εa{\displaystyle \varepsilon _{a}}; ради краткости, одну из этих величин (в российской литературе чаще εr{\displaystyle \varepsilon _{r}}, в англоязычной εa{\displaystyle \varepsilon _{a}}) переобозначают как ε{\displaystyle \varepsilon } (из контекста всегда ясно, о чём идёт речь). Величина εr{\displaystyle \varepsilon _{r}} безразмерна, а εa{\displaystyle \varepsilon _{a}} по размерности совпадает с ε0{\displaystyle \varepsilon _{0}} (в Международной системе единиц (СИ): фарад на метр, Ф/м).

Проницаемость εr{\displaystyle \varepsilon _{r}}

ru-wiki.ru

Методика измерения диэлектрической проницаемости — Мегаобучалка

ОПРЕДЕЛЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПОЛУПРОВОДНИКОВ

 

ВИРТУАЛЬНАЯ ЛАБОРАТОРНАЯ РАБОТА №3 ПО

ФИЗИКЕ ТВЕРДОГО ТЕЛА

 

 

Методические указания к выполнению лабораторной работы №3 по разделу физики «Твердого тела» для студентов технических специальностей всех форм обучения

 

 

Красноярск 2012

УДК 539.194

Рецензент

Кандидат физико-математических наук, доцент О.Н. Бандурина

(Сибирский государственный аэрокосмический университет

имени академика М.Ф. Решетнева)

 

Печатается по решению методической комиссии ИКТ

 

Определение диэлектрической проницаемости полупроводников. Виртуальная лабораторная работа №3 по физике твердого тела: Методические указания к выполнению лабораторной работы №3 по разделу физики «Твердого тела» для студентов техн. спец. всех форм обучения / сост.: А.М. Харьков; Сиб. гос. аэрокосмич. ун-т. – Красноярск, 2012. – 21 с.

 

 

Сибирский государственный аэрокосмический

университет имени академика М.Ф. Решетнева, 2012

СОДЕРЖАНИЕ

 

Введение……………………………………………………………………………...4

Допуск к лабораторной работе……………………………………………………...4

Оформление лабораторной работы к защите……………………………………...4

Определение диэлектрической проницаемости полупроводников…………........5

Теория метода……………………………………………………………………......5

Методика измерения диэлектрической проницаемости…………………..……..11

Обработка результатов измерений………………………..………………………16

Контрольные вопросы…………..………………………………………………….17

Тест………………………………………………………………………………….17

Список литературы…………………………………………………………………20

Приложение…………………………………………………………………………21

 

 

ВВЕДЕНИЕ

 

Данные методические указания содержат описания к лабораторным работам, в которых используются виртуальные модели из курса «Физика твердого тела».

 

Допуск к лабораторной работе:

 

Проводится преподавателем по группам с персональным опросом каждого студента. Для допуска:

1) Каждый студент предварительно оформляет свой персональный конспект данной лабораторной работы;

2) Преподаватель индивидуально проверяет оформление конспекта и задает вопросы по теории, методике измерений, установке и обработке результатов;

3) Студент отвечает на заданные вопросы;

4) Преподаватель допускает студента к работе и ставит свою подпись в конспекте студента.

Оформление лабораторной работы к защите:

 

Полностью оформленная и подготовленная к защите работа должна соответствовать следующим требованиям:

Выполнение всех пунктов: все расчеты требуемых величин, заполнены чернилами все таблицы, построены все графики и т.д.

Графики должны удовлетворять всем требованиям преподавателя.

Для всех величин в таблицах должна быть записана соответствующая единица измерения.

Записаны выводы по каждому графику.

Выписан ответ по установленной форме.

Записаны выводы по ответу.

 

ОПРЕДЕЛЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПОЛУПРОВОДНИКОВ

Теория метода

Поляризация – это способность диэлектрика под действием электрического поля поляризоваться, т.е. изменять в пространстве расположение связанных заряженных частиц диэлектрика.

Важнейшим свойством диэлектриков является их способность к электрической поляризации, т.е. под влиянием электрического поля происходит направленное смещение заряженных частиц или молекул на ограниченное расстояние. Под действие электрического поля смещаются заряды, как в полярных, так и неполярных молекулах.

Существует более десятка различных видов поляризации. Рассмотрим некоторые из них:

1. Электронная поляризация – это смещение электронных орбит относительно положительно заряженного ядра. Оно происходит во всех атомах любого вещества, т.е. во всех диэлектриках. Электронная поляризация устанавливается за время 10-15–10-14с.

2. Ионная поляризация – смещение относительно друг друга разноименно заряженных ионов в веществах с ионными связями. Время ее установления 10-13 –10-12с. Электронная и ионная поляризация относятся к числу мгновенных или деформационных видов поляризации.

3. Дипольная или ориентационная поляризация обусловлена ориентацией диполей в направлении электрического поля. Дипольной поляризацией обладают полярные диэлектрики. Время ее установления 10-10–10-6с. Дипольная поляризация относится к числу медленных или релаксационных видов поляризации.

4. Миграционная поляризация наблюдается в неоднородных диэлектриках, в которых электрические заряды накапливаются на границе радела неоднородностей. Процессы установления миграционной поляризации очень медленны и могут протекать на протяжении минут и даже часов.

5. Ионно-релаксационная поляризация обусловлена избыточным перебросом слабо связанных ионов под действием электрического поля на расстояния, превышающие постоянную решетки. Ионно-релаксационная поляризация проявляется в некоторых кристаллических веществах при наличии в них примесей в виде ионов или неплотной упаковке кристаллической решетки. Время ее установления 10-8–10-4с.

6. Электронно-релаксационная поляризация возникает за счет возбужденных тепловой энергией избыточных «дефектных» электронов или «дырок». Этот вид поляризации, как правило, обуславливает высокое значение диэлектрической проницаемости.

7. Спонтанная поляризация – самопроизвольная поляризация, возникающая в некоторых веществах (например, сегнетовой соли) в определенной области температур.

8. Упруго-дипольная поляризация связана с упругим поворотом диполей на небольшие углы.

9. Остаточная поляризация – поляризация, которая остается в некоторых веществах (электретах) в течение продолжительного времени после снятия электрического поля.

10. Резонансная поляризация. Если частота электрического поля близка к собственной частоте колебаний диполей, то колебания молекул могут возрасти, что приведет к появлению резонансной поляризации в дипольном диэлектрике. Резонансная поляризация наблюдается при частотах лежащих в области инфракрасного света. Реальный диэлектрик может одновременно обладать несколькими видами поляризации. Возникновение того или иного вида поляризации определяется физико-химическими свойствами вещества и диапазоном используемых частот [5].

Основные параметры:

ε – диэлектрическая проницаемость – мера способности материала к поляризации; это величина, показывающая во сколько раз сила взаимодействия электрических зарядов в данном материале меньше, чем в вакууме. Внутри диэлектрика возникает поле, направленное противоположно внешнему.

Напряженность внешнего поля ослабевает по сравнению с полем тех же зарядов в вакууме в ε раз, где ε – относительная диэлектрическая проницаемость.

Если вакуум между обкладками конденсатора заменяется на диэлектрик, то в результате поляризации емкость возрастает. На этом основано простое определение диэлектрической проницаемости:

(1)

где C0 – емкость конденсатора, между обкладками которого – вакуум.

Cd – емкость того же конденсатора с диэлектриком.

Диэлектрическая проницаемость ε изотропной среды определяется отношением:

(2)

где χ – диэлектрическая восприимчивость.

D = tg δ – тангенс угла диэлектрических потерь

Диэлектрические потери – потери электрической энергии, обусловленные протеканием токов в диэлектриках. Различают ток сквозной проводимости Iск.пр, вызванный наличием в диэлектриках небольшого количества легкоподвижных ионов, и поляризационные токи. При электронной и ионной поляризации поляризационный ток называется током смещения Iсм, он очень кратковременный и не регистрируется приборами. Токи, связанные с замедленными (релаксационными) видами поляризации, называются токами абсорбции Iабс. В общем случае суммарный ток в диэлектрике определяется как: I=Iабс+Iск.пр. После установления поляризации суммарный ток будет равен: I=Iск.пр. Если в постоянном поле поляризационные токи возникают в момент включения и выключения напряжения, и суммарный ток определяется в соответствии с уравнением: I=Iск.пр, то в переменном поле поляризационные токи возникают в момент смены полярности напряжения. Вследствие этого потери в диэлектрике в переменном поле могут быть значительными, особенно если полупериод приложенного напряжения приближается к времени установления поляризации.

На рис. 1(a) приведена схема, эквивалентная конденсатору с диэлектриком, находящемуся в цепи переменного напряжения. В этой схеме конденсатор с реальным диэлектриком, который обладает потерями, заменен идеальным конденсатором C с параллельно включенным активным сопротивлением R. На рис. 1(б) приведена векторная диаграмма токов и напряжений для рассматриваемой схемы, где U – напряжения в цепи; Iак – активный ток; Iр – реактивный ток, который опережает по фазе на 90° активную составляющую; I∑ - суммарный ток. При этом: Iа=IR=U/R и Iр=IC=ωCU, где ω – круговая частота переменного поля.

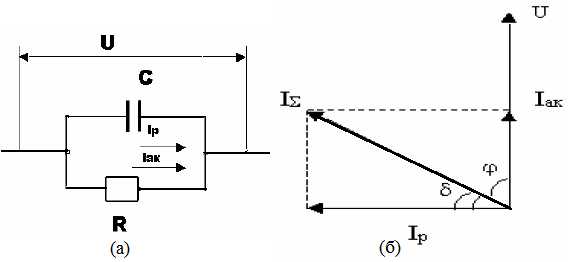
Рис. 1. (а) – схема; (б) – векторная диаграмма токов и напряжений

Углом диэлектрических потерь называется угол δ, дополняющий до 90° угол сдвига фаз φ между током I∑ и напряжением U в емкостной цепи. Потери в диэлектриках в переменном поле характеризуются тангенсом угла диэлектрических потерь: tg δ=Iа/Iр.

Предельные значения тангенса угла диэлектрических потерь для высокочастотных диэлектриков не должны превышать (0,0001 – 0,0004), а для низкочастотный – (0,01 – 0,02).

Зависимости ε и tg δ от температуры T и частоты ω

Диэлектрические параметры материалов в различной степени зависят от температуры и частоты. Большое количество диэлектрических материалов не позволяет охватить особенности всех зависимостей от указанных факторов.

Поэтому на рис. 2 (a, б) изображены общие тенденции, характерные для некоторых основных групп т.е. приведены типичные зависимости диэлектрической проницаемости ε от температуры T (а) и от частоты ω (б).

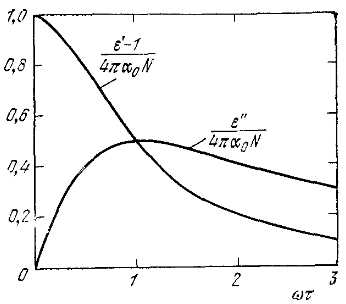
Рис. 2. Частотная зависимость действительной (εʹ) и мнимой (εʺ) частей диэлектрической проницаемости при наличии ориентационного механизма релаксации

 

Комплексная диэлектрическая проницаемость.При наличии процессов релаксации диэлектрическую проницаемость удобно записывать в комплексном виде. Если для поляризуемости справедлива формула Дебая:

(3)

где, τ – время релаксации, α0 – статистическая ориентационная поляризуемость. То, полагая локальное поле равным внешнему, получим (в СГС):

(4)

Графики зависимости εʹ и εʺ от произведения ωτ приведены на рис. 2. Заметим, что уменьшение εʹ (действительной части ε) имеет место вблизи максимума εʺ (мнимой части ε).

Такой ход изменения εʹ и εʺ с частотой служит частым примером более общего результата, согласно которому εʹ(ω) от частоты влечет за собой также и зависимость εʺ(ω) от частоты. В системе СИ следует заменить 4π на 1/ε0.

Под действием приложенного поля молекулы в неполярном диэлектрике поляризуются, становясь диполями с индуцированным дипольным моментом μи, пропорциональным напряженности поля:

(5)

 

В полярном диэлектрике дипольный момент полярной молекулы μ в общем случае равен векторной сумме собственного μ0 и индуцированного μи моментов:

(6)

 

Напряженности поля, создаваемого этими диполями, пропорциональны дипольному моменту и обратно пропорциональны кубу расстояния.

Для неполярных материалов обычно ε = 2 – 2,5 и не зависит от частоты до ω ≈1012Hz. Зависимость ε от температуры обусловлена у них тем, что при ее изменении изменяются линейные размеры твердых и объемы жидких и газообразных диэлектриков, что изменяет число молекул n в единице объема

и расстояния между ними. Используя известные из теории диэлектриков соотношения F=n\μии F=ε0(ε-1)Е, где F – поляризованность материала, для неполярных диэлектриков имеем:

(7)

При E=const также μи = const и температурное изменение ε обусловлено только изменением n, которое является линейной функцией температуры Θ, зависимость ε = ε(Θ) также является линейной. Для полярных диэлектриков аналитических зависимостей нет, и обычно пользуются эмпирическими.

1)С возрастанием температуры объем диэлектрика увеличивается и диэлектрическая проницаемость немного уменьшается. Особенно заметно уменьшение ε в период размягчения и плавления неполярных диэлектриков, когда их объем существенно возрастает. Ввиду высокой частоты обращения электронов на орбитах (порядка 1015–1016Hz) время установления равновесного состояния электронной поляризации очень мало и проницаемость ε неполярных диэлектриков не зависит от частоты поля в обычно используемом диапазоне частот (до 1012Hz).

2) При повышении температуры ослабевают связи между отдельными ионами, что облегчает их взаимодействие под действием внешнего поля и это приводит к увеличению ионной поляризации и диэлектрической проницаемости ε. Ввиду малости времени установления состояния ионной поляризации (порядка 1013Hz, что соответствует собственной частоте колебания ионов в кристаллической решетке) изменение частоты внешнего поля в обычных рабочих диапазонах практически не отражается на величине ε в ионных материалов.

3) Диэлектрическая проницаемость полярных диэлектриков сильно зависит от температуры и частоты внешнего поля. С возрастанием температуры увеличивается подвижность частиц и уменьшается энергия взаимодействия между ними, т.е. облегчается их ориентация под действием внешнего поля – возрастает дипольная поляризация и диэлектрическая проницаемость. Однако этот процесс продолжается лишь до определенной температуры. При дальнейшем возрастании температуры проницаемость ε уменьшается. Так как ориентация диполей по направлению поля осуществляется в процессе теплового движения и посредством теплового движения, то установление поляризации требует значительного времени. Это время настолько велико, что в переменных полях высокой частоты диполи не успевают ориентироваться по полю, и проницаемость ε падает [3].

Методика измерения диэлектрической проницаемости

Емкость конденсатора. Конденсатор – это система из двух проводников (обкладок), разделенных диэлектриком, толщина которого мала по сравнению с линейными размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные слоем диэлектрика, образуют конденсатор (рис. 3).

Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность электрического поля между пластинами будет в два раза больше, чем напряженность поля у одной пластины:

(8)

где ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Физическая величина, определяемая отношением заряда q одной из пластин конденсатора к разности потенциалов Δφ между обкладками конденсатора, называется электроемкостью конденсатора:

(9)

Единица электроемкости СИ – Фарад (Ф). Емкостью в 1 Ф обладает такой конденсатор, разность потенциалов между обкладками которого равна 1 В при сообщении обкладкам разноименных зарядов по 1 Кл: 1 Ф = 1 Кл/1 В.

Емкость плоского конденсатора. Формулу для вычисления электроемкости плоского конденсатора можно получить, используя выражение (8). В самом деле, напряженность поля: Е = φ/εε0 = q/εε0S, где S – площадь пластины. Поскольку поле однородное, то разность потенциалов между обкладками конденсатора равна: φ1 – φ2 = Еd = qd/εε0S, где d – расстояние между обкладками. Подставив в формулу (9), получим выражение для электроемкости плоского конденсатора:

(10)

где ε0 – диэлектрическая проницаемость воздуха; S – площадь пластины конденсатора, S=hl, где h – ширина пластины, l – ее длина; d – расстояние между пластинами конденсатора.

Выражение (10) показывает, что электроемкость конденсатора можно увеличить путем увеличения площади S его обкладок, уменьшения расстояния d между ними и применения диэлектриков с большими значениями диэлектрической проницаемости ε [4].

Рис. 3. Конденсатор с помещенным в него диэлектриком

Если между пластинами конденсатора поместить пластину из диэлектрика, емкость конденсатора изменится. Следует рассмотреть вариант расположения диэлектрической пластины между пластинами конденсатора.

Обозначим: dв – толщину воздушного промежутка, dм – толщину диэлектрической пластины, lВ – длину воздушной части конденсатора, lм – длину части конденсатора, заполненной диэлектриком, εм – диэлектрическую проницаемость материала. Если учесть, что l = lв+ lм, а d = dв + dм, то эти варианты можно рассмотреть для случаев:

В случае lв = 0, dв = 0 мы имеем конденсатор с твердым диэлектриком:

(11)

Из уравнений классической макроскопической электродинамики, основанной на уравнениях Максвелла следует, что при помещении диэлектрика в слабое переменное поле, изменяющееся по гармоническому закону с частотой ω, тензор комплексной диэлектрической проницаемости приобретает вид:

(12)

где σ – оптическая проводимость вещества, εʹ – диэлектрическая проницаемость вещества, связанная с поляризацией диэлектрика. Выражение (12) можно привести к следующему виду:

(13)

где мнимое слагаемое отвечает за диэлектрические потери [1].

На практике измеряют С – емкость образца, имеющего форму плоского конденсатора. Этот конденсатор характеризуется тангенсом угла диэлектрических потерь:

tgδ=ωCRc (14)

или добротностью:

Qc =1/ tgδ (15)

где Rc – сопротивление, зависящее, главным образом, от диэлектрических потерь. Для измерения этих характеристик существует ряд методов: различные мостовые методы, измерения с преобразованием измеряемого параметра во временной интервал и т.д. [2].

При измерениях емкости С и тангенса угла диэлектрических потерь D = tgδ в данной работе была использована методика, разработанная кампанией GOOD WILL INSTRUMENT Со Ltd. Измерения проведены на прецизионном измерителе иммитанса – LCR-819-RLC. Прибор позволяет измерять емкость в пределах 20 pF–2,083 mF, тангенс угла потерь в пределах 0,0001-9999 и подавать поле смещения. Внутреннее смещение до 2 В, внешнее смещение до 30 В. Точность измерений составляет 0,05 %. Частота тест-сигнала 12 Hz -100 kHz.

В этой работе измерения проведены на частоте 1 kHz в интервале температур 77 К < T < 270 К в нулевом магнитном поле и в поле 5 kOe. Образцы для измерений имели форму параллелепипеда с размерами 2*3*4 мм (х=0.1), где d = 2 мм – толщина образца, площадь грани S = 3*4 мм2.

С целью получений температурных зависимостей ячейка с образцом помещается в поток хладагента (азота) пропускаемый через теплообменник, температура которого задается нагревателем. Температура нагревателя контролируется терморегулятором. Обратная связь с измерителя температуры на терморегулятор позволяет задавать скорость измерения температуры, либо осуществлять ее стабилизацию. Для контроля температуры используется термопара. В данной работе температура изменялась со скоростью 1 град/мин. Указанный метод позволяет измерять температуру с погрешностью 0,1 град.

Измерительная ячейка с закрепленным на ней образцом помещается в проточный криостат. Связь ячейки с LCR-метром осуществляется экранированными проводами через разъем в капке криостата. Криостат размещен между полюсами электромагнита ФЛ-1. Блок питания магнита позволяет получать магнитные поля до 15 kOe. Для измерения величины напряженности магнитного поля Н используется термостабилизированный датчик Холла с блоком электроники. Для стабилизации магнитного поля между блоком питания и измерителем магнитного поля существует обратная связь.

Измеренные значения емкости С и тангенса угла потерь D = tg δ связаны со значениями искомых физических величин εʹ и εʺ следующими соотношениями:

(16)

(17)

 

 

№	C (pF)	Re (ε’)	T (°К)	tg δ	Qc	Im (ε”)	ω (Hz)	σ (ω)
	3,805	71,66		0,075	13,33	5,375	103
	3,838			0,093
	3,86			0,088
	3,849			0,094
	3,893			0,106
	3,917			0,092
	3,951			0,103
	3,824			0,088
	3,873			0,105
	3,907			0,108
	3,977			0,102
	4,031			0,105
	4,062			0,132
	4,144			0,109
	4,24			0,136
	4,435			0,175
	4,553			0,197
	4,698			0,233
	4,868			0,292
	4,973			0,361
	5,056			0,417
	5,164			0,491
	5,246			0,552
	5,362			0,624
	5,453			0,703
	5,556			0,783
	5,637			0,867
	5,738			0,955
	5,826			1,04
	5,902			1,136

Таблица №1. GdxMn1-xS, (x=0.1).

 

megaobuchalka.ru

Абсолютная диэлектрическая проницаемость | Virtual Laboratory Wiki

Абсолю́тная диэлектри́ческая проница́емость – величина, показывающая зависимость электрической индукции от напряжённости электрического поля. В зарубежной литературе обозначается буквой ε, в отечественной (где ε обычно обозначает относительную диэлектрическую проницаемость) преимущественно используется сочетание εε0, где ε0 – электрическая постоянная. В этой статье используется εa.

Из приведенных ниже формул следует, что абсолютная диэлектрическая постоянная (как и электрическая постоянная) имеет размерность L-3M-1T4I2. В единицах системы СИ: [εa]=Ф/м.

Вообще говоря, абсолютная диэлектрическая проницаемость является тензором, определяемым из следующих соотношений: (в записи использовано соглашение Эйнштейна)

$ ~(\epsilon_{a})_{ij} = \epsilon_{0}\epsilon_{ij} $

$ ~D_{i} = \epsilon_{0}\epsilon_{ij}E_{j} $

Или

$ ~\mathbf{D} = \boldsymbol{\epsilon}_{a}\mathbf{E} $

здесь: $ ~\mathbf{E} = E_{1}\mathbf{e}_1+E_{2}\mathbf{e}_2+E_{3}\mathbf{e}_3 $ – вектор электрического поля, $ ~\mathbf{D} = D_{1}\mathbf{e}_1+D_{2}\mathbf{e}_2+D_{3}\mathbf{e}_3 $ – вектор электрической индукции, $ ~\boldsymbol{\epsilon}_{a} = ((\epsilon_{a})_{ij}) $ – тензор абсолютной диэлектрической проницаемости. $ ~\boldsymbol{\epsilon} = (\epsilon_{ij}) $ – тензор относительной диэлектрической проницаемости.

Для среды с конечной проводимостью (поглощающая среда) в тензор диэлектрической проницаемости часто включают мнимую компоненту, пропорциональную проводимости. Пусть электрическое поле колеблется по гармоническому закону (здесь $ ~i $ – мнимая единица):

$ ~\mathbf{E} = \mathbf{E}_{0}e^{i\omega t} \ \Rightarrow\ \frac{\partial \mathbf{E}}{\partial t} = i\omega \mathbf{E} $

Тогда одно из уравнений Максвелла для непроводящей среды с постоянной во времени $ ~\boldsymbol{\epsilon}_{a} $:

$ ~\boldsymbol{\nabla}\times\mathbf{H} = \frac{\partial \mathbf{D}}{\partial t} = \boldsymbol{\epsilon}_{a} \frac{\partial \mathbf{E}}{\partial t} $

С другой стороны, для проводящей среды с тензором проводимости $ ~\boldsymbol{\sigma} $:

$ ~\boldsymbol{\nabla}\times\mathbf{H} = \mathbf{j} + \frac{\partial \mathbf{D}}{\partial t} = \boldsymbol{\sigma}\mathbf{E} + \boldsymbol{\epsilon}_{a} \frac{\partial \mathbf{E}}{\partial t} = \boldsymbol{\sigma}\frac{1}{i\omega}\frac{\partial \mathbf{E}}{\partial t} + \boldsymbol{\epsilon}_{a} \frac{\partial \mathbf{E}}{\partial t} = \left ( \frac{\boldsymbol{\sigma}}{i\omega} + \boldsymbol{\epsilon}_{a} \right ) \frac{\partial \mathbf{E}}{\partial t} $

Чтобы привести это уравнение в виду, формально совпадающему с видом уравнения для непроводящей среды, можно ввести комплексную диэлектрическую проницаемость $ ~\boldsymbol{\hat \epsilon}_{a} $:

$ ~\boldsymbol{\nabla}\times\mathbf{H} = \boldsymbol{\hat \epsilon}_{a} \frac{\partial \mathbf{E}}{\partial t}\ \Rightarrow\ \boldsymbol{\hat \epsilon}_{a} = \boldsymbol{\epsilon}_{a} + \frac{\boldsymbol{\sigma}}{i\omega} = \boldsymbol{\epsilon}_{a} - i\frac{\boldsymbol{\sigma}}{\omega} $

Таким образом, становится возможным использование для проводящих сред формул, полученных для идеальных диэлектриков. Кроме того, даже в случаях, когда в постоянном поле среда обладает очень малой проводимостью, на высоких частотах могут появиться потери, которые при таком подходе также можно приписать некоторой "эффективной" проводимости. В таком случае говорят о тангенсе угла диэлектрических потерь:

$ ~\operatorname{tg}(\delta) = - \frac{\mathrm{Im(\hat \epsilon_{a})}}{\mathrm{Re(\hat \epsilon_{a})}} = \frac{\sigma}{\epsilon_{a}\omega} $

В некоторых случаях колебания электрического поля изначально определяются как $ ~\mathbf{E} = \mathbf{E}_{0}e^{-i\omega t} $ ; тогда нужно везде обратить знак перед $ ~\boldsymbol{\omega} $.

Следует помнить, что:

• Приведенные выше формулы пригодны только для линейных (в электрическом отношении) сред. При небольших напряжённостях полей отклонения от линейности в подавляющем большинстве случаев пренебрежимо малы.
• В электрически изотропных (одинаковых во всех направлениях) средах $ ~\boldsymbol{\epsilon}_{ij} = ~\boldsymbol{\delta}_{ij}\epsilon $, где δij – символ Кронекера, поэтому уравнения Максвелла чаще всего записываются с использованием скалярных диэлектрических проницаемостей. В том числе, для вакуума εa считается равной ε0 (скаляр).
• Сами по себе $ ~\boldsymbol{\epsilon}_{a} $ и $ ~\boldsymbol{\sigma} $ обычно зависят от частоты электрического поля.
• На самом фундаментальном (с точки зрения классической электродинамики), микроскопическом уровне средой всегда является вакуум, а условие $ ~\epsilon_{a}\ne\epsilon_{0} $ является следствием электрической поляризации материалов.

ru.vlab.wikia.com

ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ - это... Что такое ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ?

        величина e, характеризующая поляризацию диэлектриков под действием электрич. поля Е. Д. п. входит в Кулона закон как величина, показывающая, во сколько раз сила вз-ствия двух свободных зарядов в диэлектрике меньше, чем в вакууме. Ослабление вз-ствия происходит из-за экранизации свободных зарядов связанными, образующимися в результате поляризации среды. Связанные заряды возникают вследствие микроскопич. перераспределения заряда в электрически нейтральной среде и, в отличие от свободных зарядов, не способны перемещаться под действием поля на макроскопич. расстояния, т. е. не участвуют в электропроводности в-в.

Связь между вектором поляризации P, вектором напряжённости электрич. поля Е в вакууме и в диэлектрике (вектором электрич. индукции D) в системе единиц СГСЭ имеет вид:

D=E+4pP=eE, (1)

в системе единиц СИ:

D=e0E+P=e0eE, (2)

где e0 — электрическая постоянная. Величина Д. п. e зависит от структуры и хим. состава в-ва, а также от давления, темп-ры и др. внешних условий (табл.).

Микроскопич. теория приводит к приближённому выражению для Д. п. неполярных диэлектриков:

где ni — концентрация i-того сорта атомов, ионов или молекул, ai — их поляризуемость, bi — т. н. фактор внутр. поля, учитывающий вз-ствие диполей друг с другом и обусловленный особенностями структуры кристалла. Для большинства диэлектриков с e=2—8, b»1/3 (в системе единиц СГСЭ b=4p/3), e практически не зависит от темп-ры, давления и электрич. поля вплоть до пробоя диэлектрика. Высокие значения e нек-рых окислов металлов и др. соединений обусловлены особенностями их структуры, приводящими к большим значениям b и к сильному уменьшению знаменателя дроби в формуле (3), Т. К. при Sniaibi ® 1, e ®?.

Рис. 1. а — изменение поляризации P во времени t при включении электрич. поля Е в случае ионного и электронного механизмов поляризации; б — частотные зависимости e' и tgd.

Рис. 2. а — изменение поляризации P во времени при включении поля Е при ориентац. механизме поляризации; б — частотные зависимости e' и tgd.

СТАТИЧ. ДИЭЛЕКТРИЧ. ПРОНИЦАЕМОСТЬ e НЕК-РЫХ ДИЭЛЕКТРИКОВ

Поляризация диэлектрика при наложении электрич. поля происходит не мгновенно, а в течение нек-рого времени t (время релаксации). В переменном поле E=E0sinwt; это приводит к отставанию поляризации P=P0•sin(wt-d) от поля Е. При описании колебаний P и Е методом комплексных амплитуд Д. п. представляют комплексной величиной:

e=e'-ie", (4)

причём e' и e" зависят от w и t (см. ДЕБАЯ ФОРМУЛЫ), а отношение e"/e'=tgd определяет диэлектрические потери в среде. Сдвиг фаз d зависит от соотношения времён т и T=2p/w. При tнизкие частоты) направление P изменяется практически одновременно с Е, т. е. d=0. Соответствующее значение e' обозначают e0. При t->Т (высокие частоты) поляризация не успевает за изменениями Е, d®p и e' в этом случае обозначают e?. Очевидно, что e0?e?, и в перем. полях Д. п. оказывается функцией со. Вблизи w=1/t происходит изменение e' от e0 до e? (область дисперсии), а зависимость tgd(w) проходит через максимум.

Характер зависимостей e'(w) и tgd (w) в области дисперсии определяется механизмом поляризации. В случае ионной и электронной поляризаций изменение R во времени t при включении поля Е имеет характер затухающих колебаний (рис. 1, а). Соответственно зависимости e' и tgd от w наз. резонансными (рис. 1,б). При ориентац. поляризации R(t) носит релаксац. характер (рис. 2, а), а зависимости e' и tgd от w наз. релаксационными (рис. 2, б). Времена т установления или исчезновения поляризации в этом случае зависят от интенсивности теплового движения атомов, молекул или ионов, т. е. от темп-ры. При ориентац. поляризации т определяется временем ориентации отд. молекул в направлении Е и зависит от величины дипольных моментов молекул, вязкости среды, энергии диполь-дипольного вз-ствия и т. д. При комнатной темп-ре t=10-4— 10-10 с, причём для газов и жидкостей, как правило, t меньше, чем для тв. тел.

В тв. диэлектриках поляризация часто обусловлена слабо связанными ионами, к-рые могут иметь неск. положений равновесия. Под действием поля Е и теплового движения они могут перемещаться из одного равновесного положения в другое, преодолевая потенциальный барьер U. В этом случае t=exp(U/kT) варьируется в широком интервале. В электрически неоднородных средах наблюдается межповерхностная поляризация, вызванная движением свободных носителей заряда, скапливающихся вблизи границ областей с повышенным уд. сопротивлением (межкристаллитная прослойка в керамике, приэлектродные запорные слои в кристаллах, микротрещины, флуктуации хим. состава и т. д.). При этом в системе единиц СГСЭ t=e/4ps (в СИ t=e0e/s), где e и s — Д. п. и проводимость высокопроводящих включений.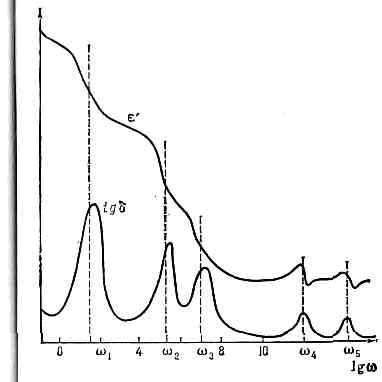

Рис. 3. Частотные зависимости e' и tgd в широком диапазоне частот для гипотетич. диэлектрика: частоты w1, w2 и w3 соответствуют ориентац. поляризации, w4 и w5 — электронной и ионной поляризациям.

В реальных диэлектриках нередко возможны одновременно неск. механизмов поляризации с различными т, что приводит к более сложному характеру зависимостей e(w) и tgd (w) (рис. 3).

Дифференциальная Д. п. в системе единиц СГСЭ:

eдиф=dD/dE, где D — электрич. индукция. В обычных диэлектриках e»eдиф вплоть до пробоя. В нелинейных диэлектриках (напр., сегнетоэлектриках) e?eдиф. Величину eдиф измеряют обычно в слабых перем. полях при одноврем. наложении сильного пост. поля и называют реверсивной Д. п.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

dic.academic.ru

---

• 
  Электричество тп
• 
  Структурная схема электропривода
• 
  Как узнать сколько должен за коммунальные услуги
• 
  Что изучает кибернетика
• 
  Епд личный кабинет московская область
• 
  Основные параметры резисторов
• 
  Для чего нужен амперметр
• 
  Формы квитанций по оплате коммунальных услуг
• 
  Обозначение на схеме катушка
• 
  Belregiongaz ru передать показания счетчика
• 
  Силовой кабель аввг