что это такое, единица измерения в СИ, формула ЭДС
Что такое электродвижущая сила — определение, физический смысл
Определение
Электродвижущая сила (ЭДС) — физическая величина, описывающая работу любых сил, которые действуют в квазистационарных цепях постоянного или переменного тока, за исключением диссипативных и электростатических сил.
Для определения силы тока Георг Симон Ом использовал принцип крутильных весов Кулона. На длинной тонкой нити подвешено горизонтальное коромысло с заряженным шариком на конце. Второй заряд закреплен на cпицe, пропущенной сквозь крышку весов. При их взаимодействии коромысло поворачивается. Вращение головки в верхней части весов закручивало нить, возвращая коромысло в исходное состояние. По углу закручивания можно рассчитать силу взаимодействия зарядов в зависимости от расстояния между ними.
Ом по величине угла закрутки судил о силе тока I в проводнике, т. е. количестве электричества, перенесенном через поперечное сечение проводника за единицу времени. В качестве основной характеристики источника тока Ом брал величину напряжения \varepsilon на электродах гальванического элемента при разомкнутой цепи. Эту величину \(\varepsilon\) он назвал электродвижущей силой, сокращенно ЭДС.
В качестве основной характеристики источника тока Ом брал величину напряжения \varepsilon на электродах гальванического элемента при разомкнутой цепи. Эту величину \(\varepsilon\) он назвал электродвижущей силой, сокращенно ЭДС.
В чем измеряется в системе СИ, как обозначается на схеме
Электродвижущая сила в системе СИ измеряется в вольтах.
На схеме обозначение источника тока с ЭДС — две линии с плюсом и минусом, иногда круг.
Природа ЭДС, какими причинами порождается
Определение
Термопара — проволоки из разнородных металлов, соединенные концами.
Изучая термопары, немецкий физик Томас Иоганн Зеебек обнаружил в 1821 году следующую закономерность: когда точки соединения имеют разную температуру, в цепи возникает электродвижущая сила. Это явление назвали термоэлектрическим эффектом Зеебека. Величина такой электродвижущей силы зависит от температуры и неодинакова для разных пар металлов. Наиболее точных измерений Ом добился в 1826 году, использовав термопару из меди и висмута.
Наиболее точных измерений Ом добился в 1826 году, использовав термопару из меди и висмута.
Внутри источника ЭДС электрический ток течет не от «плюса» к «минусу», а в противоположном направлении. Чтобы заставить ток двигаться в направлении, противоположном электростатической силе, которая воздействует на положительные заряды, необходимо приложить стороннюю силу: силу Лоренца, силу электрохимической природы, центробежную силу и т. п. Диссипативные силы не могут двигать электрические заряды против направления электростатической силы, поэтому к сторонним силам в данном случае не относятся.
По какой формуле определяется электродвижущая сила
В первых опытах Ом подключал к источнику тока проводники из разных материалов — серебра, меди, золота, — но одинакового сечения. Изменяя их длину l, Ом добивался, чтобы получалась одна и та же сила тока I. Обобщив результаты измерений, он вывел отношение:
\(I\;=\;\frac\varepsilon{R_i\;+\;R(l)}\)
Здесь \(R_i\) — некоторая постоянная, характеризующая внутреннее сопротивление гальванического элемента, а \(R(l)\) — величина, названная Омом сопротивлением проводника; она оказалась пропорциональна его длине, т. е. \(\;R(l)\;\sim\;l.\)
е. \(\;R(l)\;\sim\;l.\)
Из этой формулы следует, что найти электродвижущую силу можно, перемножив силу тока и полное сопротивление всей цепи:
\(\varepsilon\;=\;I\;\times\;R_i\;+\;I\;\times\;R(l)\)
Разность потенциалов на концах участка цепи равна падению напряжения на нем. Если в цепь включен источник тока, то ЭДС прибавляется к величине разности потенциалов или вычитается из нее в зависимости от полярности подключения. Когда на участке АВ имеется источник тока с ЭДС \(\varepsilon\), разность потенциалов изменяется на величину \(\triangle U\;=\;\pm\;\varepsilon.\)
Знак выбирается в зависимости от полярности включения источника: по току или против него. Закон Ома в этом случае принимает вид:
\(\varphi_А\;-\;\varphi_В\;\pm\;\varepsilon\;=\;IR\)
При последовательном соединении источников полная электродвижущая сила цепи будет равняться сумме ЭДС отдельных источников. При параллельном соединении только источник с самой большой ЭДС будет источником, остальные окажутся потребителями.
Чему равна электродвижущая сила источника тока
ЭДС источника тока — это работа сторонних сил, нужная для перемещения единичного положительного заряда внутри источника от одного полюса к другому. Эту работу нельзя выразить через разность потенциалов, так как сторонние силы не имеют потенциала, их работа зависит от траектории.
Пример
При перемещении заряда между клеммами источника вне самого источника работа сторонних сил окажется нулевой.
Формула коэффициента полезного действия в источниках электротока
Для работы электронных и электрических устройств необходимо подключать их к источникам питания. Источники питания могут быть как стационарные, так и автономные. В качестве питающих устройств используются гальванические элементы или преобразователи электроэнергии. И те, и другие являются источниками тока или напряжения.
Источники электрического тока и напряжения
Что такое источник тока
Это устройство или элемент, в общем понимании – двухполюсник, у которого проходящий через него ток не зависит от величины напряжения на полюсах.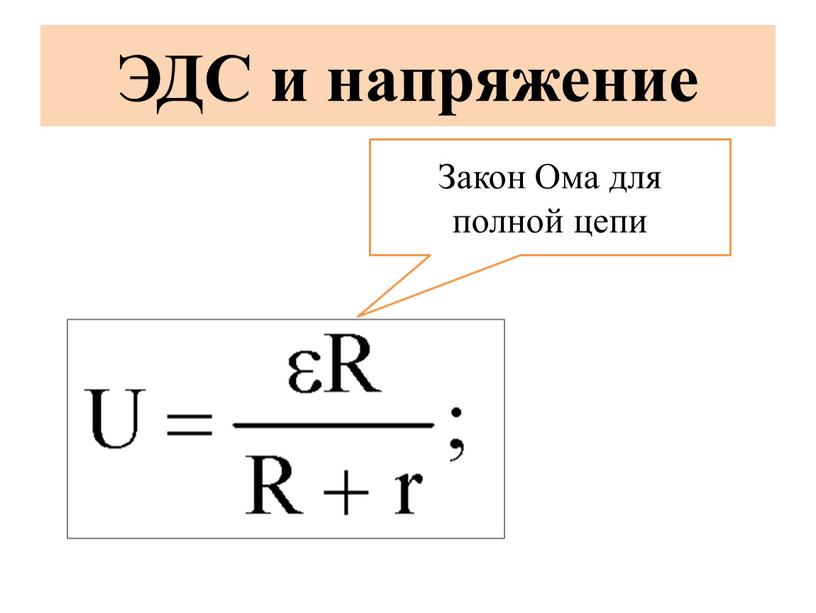 Основные характеристики источника тока (ИТ):
Основные характеристики источника тока (ИТ):
- величина;
- внутренняя проводимость (импеданс).
Внутреннее сопротивление такого двухполюсника очень мало. У идеального источника (ИИТ) оно приближается к нулю.
Графическое обозначение и вольт-амперная характеристика (ВАХ) ИТ
Генераторы движения электронов могут быть как независимыми, так и зависимыми.
Первые представляют собой идеальный двухполюсник, с двумя зажимами. У них ток, движущийся от одного зажима к другому, не зависит от формы и величины разности потенциалов на зажимах. Его изменения происходят по своим законам.
Второй тип ИТ – идеальный двухполюсник, с двумя зажимами, у которого движение зарядов от одного зажима к другому зависит от формы и величины напряжения на этих зажимах.
Существует управляемый зависимый ИТ. Он представляет собой идеальный двухполюсник, имеющий 2 зажима на входе и 2 зажима на выходе. Его особенность в том, что выходное значение тока на выходе зависит от его величины на входе. В таком ИТ происходит усиление мощности. Изменяя нулевое значение мощности на его входе, управляют величину мощности на выходных зажимах.
В таком ИТ происходит усиление мощности. Изменяя нулевое значение мощности на его входе, управляют величину мощности на выходных зажимах.
Информация. Управление производителем энергии может осуществляться напряжением (ИТУН) или током (ИТУТ). Одни находят применение для полевых триодов и электровакуумных ламп, вторые – для транзисторов биполярного типа.
В реальности генераторы тока имеют определённые ограничения по напряжению. Они далеки от идеальных ИТ и создают движение электричества в таком интервале напряжений, где их верхняя граница зависит от Uпит ИТ. Следовательно, у реального источника тока есть существенные пределы по нагрузке.
КПД электрической цепи
Выполняя продвижения зарядов через замкнутую цепь, двухполюсник проделывает некоторую работу. Когда генератор двигает заряды по внешнему контуру цепи, то это полезная работа. Когда ИТ продвигает электрические носители по всей цепи, говорят о полной работе.
Внимание! В этой цепочке перемещения зарядов особое значение имеет КПД (коэффициент полезного действия) источника. Он равен соотношению сопротивлений внешней цепи и полному сопротивлению цепи.
Он равен соотношению сопротивлений внешней цепи и полному сопротивлению цепи.
Обращая внимание на КПД электроцепи, нужно отметить, что он напрямую зависит от физических величин, определяющих скорость передачи или трансформации электрической энергии. Одной из таких величин является мощность Р (Вт).
Формулы мощности:
P = U * I = U2/R = I2 * R,
где:
- U – напряжение на нагрузке, В;
- I – ток, А;
- R – сопротивление нагрузки, Ом.
Для разных цепей значения напряжения и сила тока различаются, следовательно, производимая ими работа будет разной. Когда предстоит оценить скорость передачи и преобразования электрического тока, то обращают внимание на Р. Она соответствует работе, проделанной за единицу времени:
P = A/∆t,
где:
- P – мощность, Вт;
- A – работа, Дж;
- ∆t – временной интервал, с.
Исходя из этой формулы, чтобы найти работу А, нужно умножить Р на время:
A=P∙∆t
Чтобы найти КПД (η) электроцепи, нужно найти отношение полезно потраченной энергии к количеству всей энергии, поданной в цепь. Формула для расчёта:
Формула для расчёта:
η = A/Q *100%,
где:
- А – проделанная потребителем работа, Дж;
- Q – количество энергии, взятой от источника, Дж.
Важно! КПД не может быть выше единицы. В основном он или равен ей, или меньше её. Этому причина – Закон сохранения энергии. Согласно ему, полезная совершённая работа никогда не превысит затраты энергии, необходимые для её выполнения.
Наглядно это можно объяснить на примере электрической цепи, в которую включен проводник, имеющий определённое сопротивление. При прохождении электричества через цепь часть энергии будет рассеиваться на проводнике, превращаясь в тепло и нагревая его. Потери мощности будут зависеть от величины этого сопротивления.
КПД электрической цепи
Что такое КПД ИТ
Когда речь идёт о кпд источника тока, также рассматривают полезную и полную работу, совершаемую двухполюсником. Перемещая электроны во внешней цепи, он выполняет полезную работу, двигая их по всей цепи, включая и свою внутреннюю, он производит полную работу.
В виде формул это выглядит так:
- А полезн. = q*U = I*U*t = I2*R*t;
- А полн. = q*ε = I* ε*t = I2*(R+r)*t.
где:
- q – количество энергии, Дж;
- U – напряжение, В;
- ε – ЭДС, В;
- I – ток, А;
- R – сопротивление нагрузки, Ом;
- r – импеданс источника, Ом;
- t – время, за которое совершается работа, с.
С учётом этого можно выразить мощности двухполюсника:
- Р полезн. = А полезн./t = I*U = I2*R;
- P полн. = А полн./t = I*ε = I2*(R+r).
Формула кпд источников тока имеет вид:
η = Р полезн./P полн.= U/ε = R/ R+r.
Исследование мощности и КПД генератора тока
Максимальная полезная Pmax и максимальный КПДmax – несовместимые понятия. Нельзя добиться максимального КПД источника при максимальной мощности. Это обусловлено тем, что Р, отдаваемая двухполюсником, достигнет своего максимального значения только при условии согласования сопротивления нагрузки и внутреннего импеданса ИТ:
R = r.
В этом случае КПД источника будет:
η = R/ R+r = r/ r+r = 1/2, что составляет всего 50%.
Для согласования двухполюсника и нагрузки применяют электронные схемы или согласующие блоки, для того чтобы добиться максимального отбора мощности от источника.
Мощность ИТ и внутреннее сопротивление
Можно собрать последовательную схему, в которую войдут гальванический двухполюсник и сопротивление нагрузки. Двухполюсник, имеющий внутренний импеданс r и ЭДС – Е, отдаёт на внешнюю нагрузку R ток I. Задача цепи – питание электричеством активной нагрузки, выполняющей полезную работу. В качестве нагрузки может быть применена лампочка или обогреватель.
Простая схема для исследования зависимости Рполезн. от R
Рассматривая эту цепь, можно определиться с зависимостью полезной мощности от величины сопротивления. Для начала находят R-эквивалентное всей цепи.
Оно выглядит так:
Rэкв. = R + r.
Движение электричества в цепи находится по формуле:
I = E/(R + r).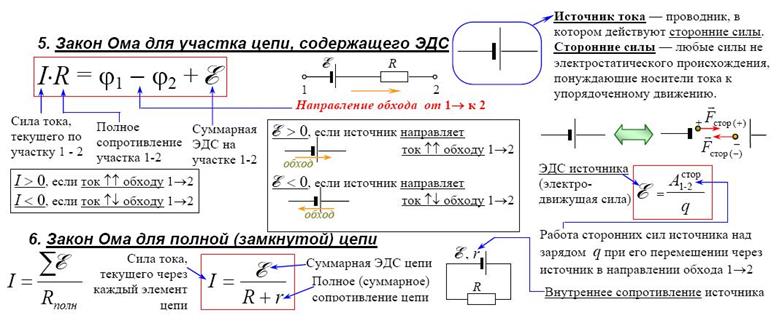
В таком случае Р ЭДС на выходе составит Рвых. = E*I = E²/(R + r).
Далее можно найти Р, рассеиваемую при нагреве генератора из-за внутреннего сопротивления:
Pr = I² * r = E² * r/(R + r)².
На следующем этапе определяются с мощностью, отбираемой нагрузкой:
PR = I² * R = E² * R/(R + r)².
Общая Р на выходе двухполюсника будет равна сумме:
Рвых. = Рr + PR.
Это значит, что потери энергии изначально происходят при рассеивании на импедансе (внутреннем сопротивлении) двухполюсника.
Далее, чтобы увидеть, при какой величине нагрузки достигается максимальная величина полезной мощности Рполезн., строят график.
При его рассмотрении видно, что самое большое значение мощности – в точке, где R и r сравнялись. Это точка согласования сопротивлений генератора и нагрузки.
Внимание! Когда R > r, то ток, возникающий в цепи, мал для передачи энергии нагрузке с достаточной скоростью. При R < r значительная доля энергии превращается в тепло в самом двухполюснике.
При R < r значительная доля энергии превращается в тепло в самом двухполюснике.
Наиболее наглядный пример согласования можно увидеть в радиотехнике при согласовании выходного сопротивления УНЧ (усилителя низкой частоты) и звуковых динамиков. На выходе усилителя сопротивление находится в пределах от 4 до 8 Ом, в то время как Rвх динамика составляет 8 Ом. Устройство позволяет подключить к своему выходному каскаду, как один динамик на 8 Ом, так и параллельно два по 4 Ома. И в том, и в другом случае УНЧ будет работать в заданном режиме, без потерь мощности.
В процессе разработок тех или иных реальных источников тока пользуются представлением его в виде эквивалентного блока. В его состав входят два компонента, с которыми ведётся работа: это идеальный источник и его импеданс.
Видео
ЭДС и напряжение в электрической цепи
Многие люди (в то числе и некоторые электрики) путают понятие электродвижущей силы (ЭДС) и напряжения. Хотя эти понятия имеют отличия. Несмотря на то, что они незначительные, не специалисту сложно в них разобраться. Не маловажную роль в этом играет единица измерения. Напряжение и ЭДС измеряются в одних единицах – Вольтах. На этом отличия не заканчиваются, подробно обо всем мы рассказали в статье!
Хотя эти понятия имеют отличия. Несмотря на то, что они незначительные, не специалисту сложно в них разобраться. Не маловажную роль в этом играет единица измерения. Напряжение и ЭДС измеряются в одних единицах – Вольтах. На этом отличия не заканчиваются, подробно обо всем мы рассказали в статье!
Что такое электродвижущая сила
Подробно этот вопрос мы рассмотрели в отдельной статье: https://samelectrik.ru/chto-takoe-eds-obyasnenie-prostymi-slovami.html
Под ЭДС понимается физическая величина, характеризующая работу каких-либо сторонних сил, находящихся в источниках питания постоянного или переменного тока. При этом, если имеется замкнутый контур, то можно сказать, что ЭДС равна работе сил по перемещению положительного заряда к отрицательному по замкнутой цепи. Или простыми словами, ЭДС источника тока представляет работу, необходимую для перемещения единичного заряда между полюсами.
При этом если источник тока имеющего бесконечную мощность, а внутреннее сопротивление будет отсутствовать (позиция А на рисунке), то ЭДС можно рассчитать по закону Ома для участка цепи, т.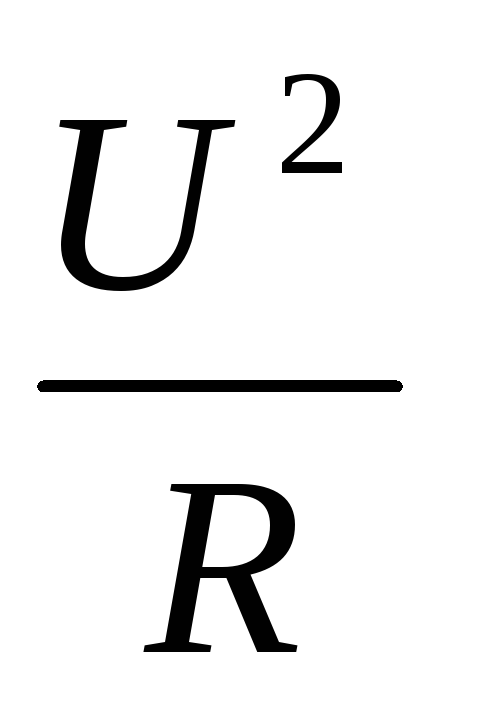 к. напряжение и электродвижущая сила в этом случае равны.
к. напряжение и электродвижущая сила в этом случае равны.
I=U/R,
где U – напряжение, а в рассмотренном примере — ЭДС.
Однако, реальный источник питания имеет конечное внутреннее сопротивление. Поэтому такой расчет нельзя применять на практике. В этом случае для определения ЭДС пользуются формулой для полной цепи.
I=E/(R+r),
где E (также обозначается как «ԑ») — ЭДС; R – сопротивление нагрузки, r – внутреннее сопротивление источника электропитания, I – ток в цепи.
Однако, эта формула не учитывает сопротивление проводников цепи. При этом необходимо понимать, что внутри источника постоянного тока и во внешней цепи, ток течет в разных направлениях. Разница заключается в том, что внутри элемента он течет от минуса к плюсу, то во внешней цепи от плюса к минусу.
Это наглядно представлено на ниже приведенном рисунке:
При этом электродвижущая сила измеряется вольтметром, в случае, когда нет нагрузки, т.е. источник питания работает в режиме холостого хода.
Чтобы найти ЭДС через напряжение и сопротивление нагрузки нужно найти внутреннее сопротивление источника питания, для этого измеряют напряжение дважды при разных токах нагрузки, после чего находят внутреннее сопротивление. Ниже приведен порядок вычисления по формулам, далее R1, R2 — сопротивление нагрузки для первого и второго измерения соответственно, остальные величины аналогично, U1, U2 – напряжения источника на его зажимах под нагрузкой.
Итак, нам известен ток, тогда он равен:
I1=E/(R1+r)
I2=E/(R2+r)
При этом:
R1=U1/I1
R2=U2/I2
Если подставить в первые уравнения, то:
I1=E/( (U1/I1)+r)
I2=E/( (U2/I2)+r)
Теперь разделим левые и правые части друг на друга:
(I1/I2)= [E/( (U1/I1)+r)]/[E/( (U2/I2)+r)]
После вычисления относительно сопротивления источника тока получим:
r=(U1-U2)/(I1-I2)
Внутреннее сопротивление r:
r= (U1+U2)/I,
где U1, U2 — напряжение на зажимах источника при разном токе нагрузки, I — ток в цепи.
Тогда ЭДС равно:
E=I*(R+r) или E=U1+I1*r
Что такое напряжение
Электрическое напряжение (обозначается как U) – это физическая величина, которая отражает количественную характеристику работы электрического поля по переносу заряда из точки А в точку В. Соответственно напряжение может быть между двумя точками цепи, но в отличии от ЭДС оно может быть между двумя выводами какого-то из элементов цепи. Напомним, что ЭДС характеризует работу, выполненную сторонними силами, то есть работу самого источника тока или ЭДС по переносу заряда через всю цепь, а не на конкретном элементе.
Это определение можно выразить простым языком. Напряжение источников постоянного тока – это сила, которая перемещает свободные электроны от одного атома к другому в определенном направлении.
Для переменного тока используют следующие понятия:
- мгновенное напряжение — это разность потенциалов между точками в данный промежуток времени;
- амплитудное значение – представляет максимальную величину по модулю мгновенного значения напряжения за промежуток времени;
- среднее значение – постоянная составляющая напряжения;
- среднеквадратичное и средневыпрямленное.

Напряжение участка цепи зависит от материала проводника, сопротивления нагрузки и температуры. Так же как и электродвижущая сила измеряется в Вольтах.
Часто для понимания физического смысла напряжения, его сравнивают с водонапорной башней. Столб воды отождествляют с напряжением, а поток с током.
При этом столб воды в башне постепенно уменьшается, что характеризует понижение напряжения и уменьшения силы тока.
Так в чем же отличие
Для лучшего понимания, в чем состоит разница электродвижущей силы от напряжения, рассмотрим пример. Имеется источник электрической энергии бесконечной мощности, в котором отсутствует внутреннее сопротивление. В электрической цепи смонтирована нагрузка. В этом случае будет справедливо утверждение, что ЭДС и напряжение тождественно равны, т.е между этими понятиями отсутствует разница.
Однако, это идеальные условия, которые в реальной жизни не встречаются. Эти условия используют исключительно при расчетах. В реальной жизни учитывается внутреннее сопротивление источника питания.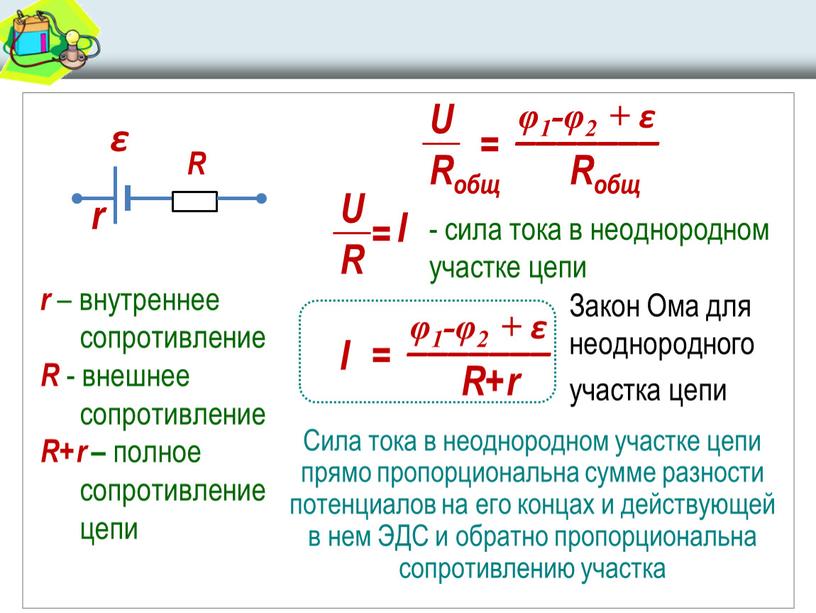 В этом случае ЭДС и напряжение имеют отличия.
В этом случае ЭДС и напряжение имеют отличия.
На рисунке представлено, какая разница будет в значениях электродвижущей силы и напряжении в реальных условиях. Вышеприведенная формула закона Ома для полной цепи описывает все процессы. При разомкнутой цепи на клеммах батарейки будет значение 1,5 Вольта. Это значение ЭДС. Подключив нагрузку, в данном случае это лампочка, на ней будет напряжение 1 вольт.
Разница от идеального источника заключается в наличии внутреннего сопротивления источника питания. На этом сопротивлении и происходит падение напряжения. Эти процессы описывает закон Ома для полной цепи.
Если измерительный прибор на зажимах источника электроэнергии показывает значение 1,5 Вольта, это будет электродвижущая сила, но повторим, при условии отсутствия нагрузки.
При подключении нагрузки на клеммах будет заведомо меньшее значение. Это и есть напряжение.
Вывод
Из вышесказанного можно сделать вывод, что основная разница между ЭДС и напряжением состоит:
- Электродвижущая сила зависит от источника питания, а напряжение зависит от подключенной нагрузки и тока, протекающего по цепи.

- Электродвижущая сила это физическая величина, характеризующая работу сторонних сил неэлектрического происхождения, происходящих в цепях постоянного и переменного тока.
- Напряжение и ЭДС имеет единую единицу измерения – Вольт.
- U -величина физическая, равная работе эффективного электрического поля, производимой при переносе единичного пробного заряда из точки А в точку В.
Таким образом, кратко, если представить U в виде столба воды, то ЭДС можно представить что это насос, поддерживающий уровень воды на постоянном уровне. Надеемся, после прочтения статьи Вам стало понятно основное отличие!
Материалы по теме:
Определение внутреннего сопротивления и ЭДС источника электрического тока
Приборы и принадлежности, используемые в работе:
- Источник электрической энергии.
- Амперметр.
- Вольтметр.
- Реостат.
- Ключ.
- Соединительные провода.
Цель работы:
1. Научится собирать, заданную электрическую схему.
Научится собирать, заданную электрическую схему.
2. Используя закон ОМА для всей цепи, определить опытным путём величину внутреннего сопротивления и ЭДС источника электрической цепи.
1.ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.
Формула закона Ома для всей цепи имеет вид:
, (1)
где:
Е — ЭДС источника электрической энергии
R — сопротивление внешней части цепи
r — внутреннее сопротивление источника
I — сила тока в цепи.
Перепишем формулу (I) в виде:
(2)
Величина является напряжением на внешней части цепи. Тогда формула (2) примет вид:
(3)
Если в полной цепи менять внешнее сопротивление, то будут меняться величины I и U (ток в цепи и напряжение на внешней её части). Пусть при силе тока в цепи , напряжение на внешней цепи равно , а при силе тока равно . Тогда дважды запишем формулу (3).
(4)
Левые части у уравнений одинаковые, поэтому приравняем правые части:
откуда:
и получим формулу для нахождения г внутреннего сопротивления источника:
(5)
Подставив (5) в одно из уравнений системы (4), получим формулу для нахождения Е ЭДС источника:
;
(6)
2. ХОД РАБОТЫ.
ХОД РАБОТЫ.
1. Определить цену деления амперметра и вольтметра.
2. Собрать следующую схему:
При сборке схемы соблюдать следующие требования:
— Собирать схему только при разомкнутом ключе К.
— Приступать к включению схемы и измерениям только после того, как преподаватель или лаборант проверят, правильно ли собрана Ваша схема.
— При замыкании ключа особое внимание обратить на показания амперметра — он не должен зашкаливать.
3. Изменяя величину внешнего сопротивления реостатом, получить 7 различных значений силы тока и напряжения во внешней цепи.
4. По формуле (5) вычислить 7 различных значений внутреннего сопротивления источника.
5. По формуле (6) вычислить 7 различных значений ЭДС источника электрической энергии.
6. Результаты измерений I и U, а также вычислений r и Е занести в таблицу.
В таблице n— число делений, на которое отклонилась стрелка амперметра или вольтметра при очередном измерении.
В следующую колонку после n записывается сила тока или напряжение в цепи, которые вычисляются по формуле:
(цена деления);
U = nV × (цена деления).
Таблица результатов измерений и вычислений
Цена одного деления амперметра = …
Цена одного деления вольтметра =…
7. Вычислить погрешности с которыми определены внутреннее сопротивление и ЭДС источника электрической энергии, по формулам:[13]
; sr = D rср/ rср × 100%
;
8. Значение погрешностей занести в таблицу и по результатам, полученным в лабораторной работе сделать вывод[14].
КОНТРОЛЬНЫЕ ВОПРОСЫ ПЕРВОГО УРОВНЯ.
1. Закон Ома для всей цепи (формула и формулировка).
2. Закон Ома при параллельном, последовательном и смешанном соединении одинаковых источников электрической энергии (формулы, схемы).
3. Определение цены деления многопредельного прибора.
КОНТРОЛЬНЫЕ ВОПРОСЫ ВТОРОГО И ТРЕТЬЕГО УРОВНЯ.
4. Закон Ома для участка цепи с ЭДС (3 случая и общий закон) и для всей цепи при нескольких ЭДС.
5. Что называется ЭДС источника электрической энергии? Единицы ЭДС.
6. Понятие внутреннего сопротивления источника.
7. Измерительные приборы вольтметр и амперметр[15].
Лабораторная работа № 8.
Закон Ома для участка цепи с источником ЭДС. (Лекция N 5)
Возьмем два участка цепи a—bи c—d (см.
рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на
рис. 1 положительных направлений напряжений
и токов.
Объединяя оба случая, получим
| (1) |
или для постоянного тока
.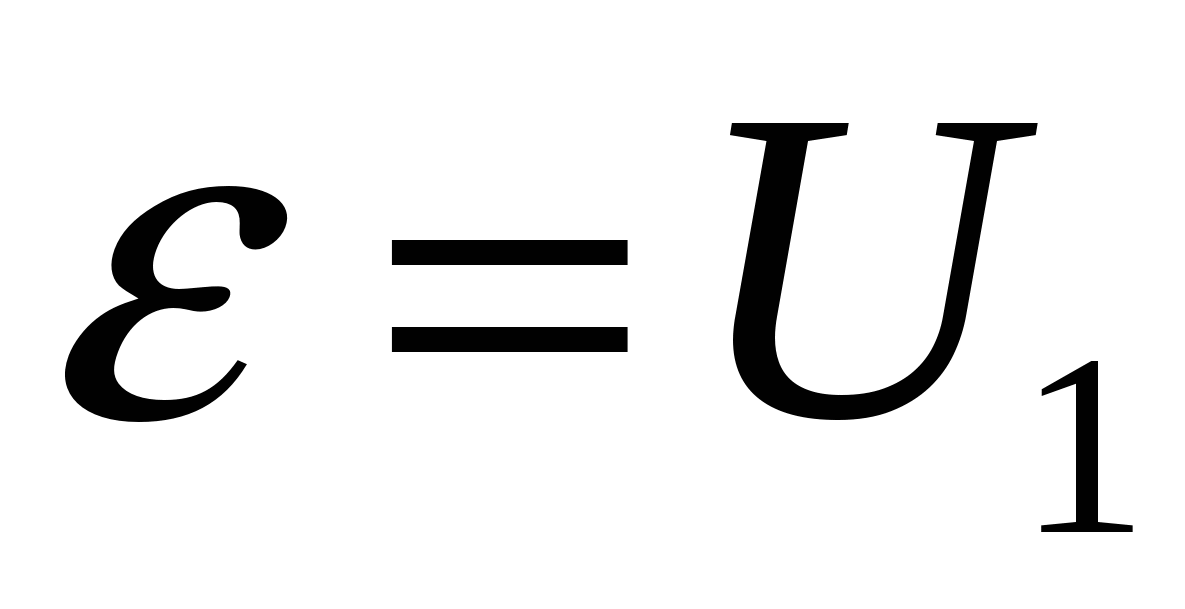 | (2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка
цепи с источником ЭДС, согласно которому ток на участке цепи с источником
ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной
на сопротивление участка. В случае переменного тока все указанные величины суть
комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление
совпадает с выбранным направлением тока, и со знаком “-”, если их направление
противоположно направлению тока.
Основы символического метода расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только
путем построения векторных диаграмм, но и аналитически – путем операций с комплексами,
символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством
векторных диаграмм является их наглядность, недостатком – малая точность графических
построений. Применение символического метода позволяет производить расчеты цепей
Применение символического метода позволяет производить расчеты цепей
с большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа
и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно
такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только
токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных
величин.
1.
Первый закон Кирхгофа в комплексной форме:
| . | (3) |
2.
Второй закон Кирхгофа в комплексной форме:
| (4) |
или применительно к схемам замещения с источниками
ЭДС
. | (5) |
3.
Соответственно матричная запись законов Кирхгофа в комплексной
форме имеет вид:
§
первый закон Кирхгофа:
| . ; | (6) |
§
второй закон Кирхгофа
| . | (7) |
Пример.
Дано:
Рис. 2
Решение:
1.
.
2.
.
3.
.
4.
Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда
.
5.
Поскольку ток распределяется обратно пропорционально сопротивлению
ветвей (это вытекает из закона Ома), то
6.
.
7.
Аналогичный результат можно получить, составив для данной схемы
уравнения по законам Кирхгофа в комплексной форме
или после подстановки численных значений параметров
схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными
на основании законов Кирхгофа. При этом необходимо составить и решить систему
с n неизвестными, что может оказаться
весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может
быть сокращено, если воспользоваться специальными методами расчета, к
которым относятся методы контурных токов и узловых потенциалов.
Метод контурных токов
Идея метода контурных токов: уравнения составляются только по второму закону
Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих
по замкнутым контурам, т. е. в случае выбора главных контуров равных токам ветвей
е. в случае выбора главных контуров равных токам ветвей
связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи
графа . Первый закон Кирхгофа выполняется автоматически.
Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя
бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.
Их выбор облегчает использование топологических понятий дерева и ветвей связи.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных
направлений перед началом расчета может не определять действительные направления
токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании
уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его
истинное направление противоположно.
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
; ;
; .
Обойдя контур aeda, по второму закону Кирхгофа
имеем
.
Поскольку ,
то
.
Таким образом, получили уравнение для первого контура относительно контурных
токов. Аналогично можно составить уравнения для второго, третьего и четвертого
контуров:
совместно с первым решить их относительно контурных токов и затем по уравнениям,
связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:
При составлении уравнений необходимо помнить следующее:
— сумма сопротивлений, входящих в
i-й контур;
— сумма сопротивлений, общих для i-го и k-го контуров, причем
;
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление
i-й и k-
й контурные токи проходят в одном направлении, в противном случае ставится знак
“-”;
если i-й и k- й контуры не имеют общих сопротивлений, то ;
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в
контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением
контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:
Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда
симметричны относительно главной диагонали.
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются
в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k-
м источником тока равен этому току .
Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа.
В качестве неизвестных принимаются потенциалы узлов, по найденным значениям
которых с помощью закона Ома для участка цепи с источником ЭДС затем находят
токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного
из узлов (любого) принимается равным нулю. Таким образом, число неизвестных
потенциалов, а следовательно, и число уравнений равно , т. е. числу ветвей дерева .
е. числу ветвей дерева .
Пусть имеем схему по рис. 4, в которой примем .
Допустим, что и известны. Тогда значения токов на основании
закона Ома для участка цепи с источником ЭДС
Запишем уравнение по первому закону Кирхгофа для
узла а:
и подставим значения входящих
в него токов, определенных выше:
.
Сгруппировав соответствующие члены, получим:
.
Аналогично можно записать для узла b:
.
Как и по методу контурных токов, система уравнений
по методу узловых потенциалов может быть составлена формальным путем. При этом
необходимо руководствоваться следующими правилами:
1. В
левой части i-го
уравнения записывается со знаком “+”потенциал i-го узла, для которого составляется данное
i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен
на сумму проводимостей ветвей, присоединенных к i-му
и k-му узлам.
Из сказанного следует, что все члены , стоящие на главной диагонали в левой части
системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”,
причем . Последнее равенство по аналогии с методом
контурных токов обеспечивает симметрию коэффициентов уравнений относительно
главной диагонали.
2. В
правой части i-го
уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих
к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается
со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих
к i-му узлу ветвях содержатся источники тока,
то знаки токов источников токов, входящих в узловой ток простыми слагаемыми,
определяются аналогично.
В заключение отметим,
что выбор того или иного из рассмотренных методов определяется тем, что следует
найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений.
При расчете токов при одинаковом числе уравнений предпочтительнее использовать
метод контурных токов, так как он не требует дополнительных вычислений с использованием
закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных
цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1.
Основы теории
цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е
изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2.
Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
Контрольные вопросы и задачи
1. В
ветви на рис. 1 . Определить ток .
Определить ток .
Ответ: .
2. В
чем заключается сущность символического метода расчета цепей синусоидального
тока?
3. В
чем состоит сущность метода контурных токов?
4. В
чем состоит сущность метода узловых потенциалов?
5.
В цепи на рис. 5 ; ;
; . Методом контурных токов определить комплексы
действующих значений токов ветвей.
Ответ: ; ; .
6. В
цепи на рис. 6 . Рассчитать токи в ветвях, используя метод
узловых потенциалов.
Ответ: ; ; ; ; ; ; .
5. 3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов
3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов
Физическая
величина, равная работе сторонних сил
по перемещению положительного единичного
заряда вдоль всей цепи, включая источник
тока, называется электродвижущей силой
источника тока (ЭДС)
:
. (5.15)
Работа сторонних
сил вдоль замкнутой цепи
,
(5.16)
где
E*
– напряженность поля сторонних сил.
Тогда
.
(5.17)
При
движении зарядов в проводнике кроме
сторонних сил на них действуют силы
электростатического поля ().
Следовательно, в любой точке цепи на
заряд q действует результирующая сила:
.
(5. 18)
18)
Работа, совершаемая
этой силой на участке 1 – 2,
(5.19)
Физическая
величина, численно равная работе
сторонних и электрических сил по
перемещению положительного единичного
заряда на данном участке цепи, называется
падением напряжения или напряжением
на данном участке цепи:
.
(5.20)
Если
на участке цепи отсутствует ЭДС (),
то
.
(5.21)
При
1
— 2
= 0,
. (5.22)
Измеряются
,
U, (1
— 2)
в системе СИ в вольтах (1 В).
Лекция 6. Классическая электронная теория проводимости металлов. Законы постоянного тока
Классическая
электронная теория электропроводности
металлов и ее опытные обоснования.
Закон Ома в дифференциальной и
интегральной формах. Электрическое
сопротивление проводников. Изменение
Изменение
сопротивления проводников от температуры
и давления. Сверхпроводимость. Соединения
сопротивлений: последовательное,
параллельное, смешанное. Шунтирование
электроизмерительных приборов.
Добавочные сопротивления к
электроизмерительным приборам. Правила
(законы) Кирхгофа и их применение к
расчету простейших электрических
цепей. Закон Джоуля-Ленца в дифференциальной
и интегральной формах. Энергия,
выделяющаяся в цепи постоянного тока.
Коэффициент полезного действия (КПД)
источника постоянного тока.
6.1. Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах
Классическая
электронная теория проводимости
металлов объясняет различные электрические
свойства веществ существованием и
движением в них так называемых
квазисвободных электронов проводимости.
Электроны проводимости при этом
рассматриваются как электронный газ,
подобный идеальному газу молекулярной
физики.
До
открытия электронов было экспериментально
показано, что прохождение тока в металлах
не связано, в отличие от тока в жидких
электролитах, с переносом вещества
металла. Опыт состоял в том, что через
контакт двух различных металлов,
например золота и серебра, в течение
времени, исчисляемого многими месяцами,
пропускали электрический ток. После
чего исследовался материал вблизи
контактов. Было показано, что никакого
переноса вещества через границу
различных металлов не наблюдается и
вещество по различные стороны границы
раздела имеет тот же состав, что и до
пропускания тока. Опыты доказали, что
атомы и молекулы металлов не принимают
участия в переносе электрического
тока, но они не ответили на вопрос о
природе носителей заряда в металлах.
Прямым
доказательством, что электрический
ток в металлах обусловливается движением
электронов, были опыты Толмена и Стюарда,
проведенные в 1916 г. Идея этих опытов
была высказана Мандельштамом и Папалекси
в 1913 г.
Представим
себе проводящую катушку, которая может
вращаться вокруг своей оси. Концы
катушки с помощью скользящих контактов
замкнуты на гальванометр. Если находящуюся
в быстром вращении катушку резко
затормозить, то свободные электроны в
проволоке продолжают движение по
инерции, в результате чего гальванометр
должен зарегистрировать импульс тока.
Обозначим
линейное ускорение катушки при торможении
– a.
Оно направлено по касательной к
поверхности катушки. При достаточно
плотной намотке и тонких проводах можно
считать, что ускорение направлено вдоль
проводов. При торможении катушки к
каждому свободному электрону приложена
сила инерции Fин
= mea,
направленная противоположно ускорению.
Под ее действием электрон ведет себя
в металле так, как если бы на него
действовало эффективное электрическое
поле с напряженностью
.
6.1)
Поэтому
эффективная электродвижущая сила в
катушке, обусловленная инерцией
свободных электронов,
,
(6.2)
где L – длина
провода на катушке.
Все
точки провода тормозятся с одинаковым
ускорением, и поэтому ускорение вынесено
за знак интеграла.
С учетом формулы
(6.2) запишем закон Ома для замкнутой
цепи в виде
,
(6.3)
где I – сила тока
в замкнутой цепи;
R
– сопротивление всей цепи, включая
сопротивление проводов катушки, проводов
внешней цепи и гальванометра.
Количество
электричества, протекшее через поперечное
сечение проводника в течение времени
dt при силе тока I,
.
(6.4)
Поэтому
в течение времени торможения катушки
от начальной линейной скорости vo
до полной остановки через гальванометр
пройдет количество электричества
.
(6.5)
Значение
q определяется по гальванометру, а
значения L, R, vo
известны. Поэтому можно найти как знак,
так и абсолютное значение e/me.
Эксперименты показали, что e/me
соответствует отношению заряда электрона
к его массе. Таким образом, было доказано,
что наблюдаемый с помощью гальванометра
ток обусловлен движением электронов.
В
отсутствие электрического поля в
проводниках электроны проводимости
движутся хаотично, в произвольных
направлениях со скоростями, обусловленными
температурой, т.е. с так называемой
тепловой скоростью u.
Через
определенный промежуток времени t = ,
двигаясь по прямой, электрон проводимости
может провзаимодействовать с ионом
кристаллической решетки или с другим
электроном проводимости. В результате
такого взаимодействия, а оно считается
в классической теории проводимости
абсолютно упругим, сохраняются полные
импульс и энергия, а величина и направление
скорости движения могут измениться.
Предельным является случай, когда через
время, равное
(время свободного пробега), направление
скорости теплового движения электрона
проводимости изменяется на противоположное.
Время свободного пробега зависит от
природы вещества и тем меньше, чем чаще
происходят взаимодействия. Между
соударениями (взаимодействиями) со
скоростью u
ничего не происходит.
При
наложении электричес-кого поля с
напряженностьюE
под действием силы F
= eE
эле-ктроны проводимости приобре-тают
некоторое ускорение a
и направленное движение с изме-няющейся
скоростью от vo
= 0 до v = vmax
за время t = .
Изменение
скорости направленного движения
электрона проводимости происходит до
его взаимодействия (рис. 6.1). В результате
взаимодействия эта скорость так же
может измениться как по величине, так
и по направлению.
Если
в единице объема проводника n электронов
проводимости, которые в некоторый
момент времени t обладают скоростью v,
то можно определить заряд, прошедший
через некоторую площадку S, расположенную
перпендикулярно направлению скорости
движения электронов проводимости:
,
(6.6)
где
<v> — средняя скорость упорядоченного
движения электронов проводимости.
Сила (величина)
тока в проводнике в этом случае
. (6.7)
Плотность тока
проводимости
.
(6.8)
В векторной форме
.
(6.9)
Согласно
(6.8) для определения плотности
электрического тока в проводнике
необходимо определить среднюю скорость
упорядоченного движения электронов
проводимости.
Средняя скорость
упорядоченного движения в данном случае
может быть определена по формуле
,
(6.10)
т.к.
в начальный момент времени t=0, когда
отсутствует электрическое поле, vo=0.
Максимальная
скорость упорядоченного движения,
которую приобретает электрон под
действием электрического поля за время
свободного пробега,
,
где
a – ускорение, приобретаемое электроном
проводимости под действием электрического
поля;
– время
пробега электрона проводимости от
взаимодействия до взаимодействия.
На
основании второго закона Ньютона F =
ma, где F — кулоновская сила,
F
= eE.
Имеем:
;
;
.
(6.11)
Для
средней скорости упорядоченного
движения электронов проводимости
получим
.
(6.12)
Зная
среднюю скорость теплового движения
электронов проводимости и среднее
расстояние, проходимое ими от
взаимодействия до взаимодействия,
можно определить время между двумя
последующими взаимодействиями:
. (6.13)
Сделав
подстановку и необходимые преобразования,
для плотности тока проводимости будем
иметь
, (6.14)
где
— удельная электропроводность металла
проводника.
В векторной форме
.
(6.15)
Выражения
(6.14) и (6.15) являются математической
формой записи закона Ома в дифференциальной
форме.
Закон
Ома в дифференциальной форме справедлив
для любых проводников, любых токов,
характеризует плотность тока проводимости
в любой точке проводника.
Из
закона Ома в дифференциальной форме
можно получить закон Ома в интегральной
форме для замкнутой (или полной) цепи.
Для чего выражение (6.15) умножим на
величину элементарного участка цепи
dl:
,
где
;;.
Таким образом,
имеем
или
;
.
(6.16)
Проинтегрировав
выражение (6.16) по замкнутому контуру
L, получим
,
(6.17)
где
– сопротивление внешнего и внутреннего
участков цепи;
–ЭДС,
действующая в замкнутой цепи, численно
равная циркуляции вектора напряженности
поля сторонних сил;
–разность
потенциалов между двумя рассматриваемыми
точками замкнутой цепи.
Для замкнутой
цепи
(1
— 2)
= 0;
.
Таким образом,
имеем
или
,
(6.18)
где
R1
– сопротивление внешнего участка цепи;
r – внутреннее
сопротивление источника тока.
Из формулы (6.18)
.
(6.19)
Следовательно,
ЭДС уравновешивает падение напряжения
во внешней и внутренней цепи и тем самым
обеспечивает непрерывное движение
электронов проводимости.
Если цепь не
замкнута и в ней отсутствует ЭДС, то
,
а
.
(6.20)
Выражения
(6.18) и (6.20) являются математической
формой записи закона Ома, соответственно,
для полной (замкнутой) цепи и участка
цепи, который был открыт им экспериментально.
Сила тока в цепи прямопропорциональна
ЭДС (напряжению на участке цепи) и
обратно пропорциональна сопротивлению
цепи.
Разница между ЭДС и напряжением (со сравнительной таблицей)
Одно из основных различий между ЭДС и напряжением состоит в том, что ЭДС — это энергия, подводимая к заряду, тогда как напряжение — это энергия, необходимая для перемещения единичного заряда из одной точки в другую. Другие различия между ними описаны ниже в сравнительной таблице.
Содержание: ЭДС против напряжения
- Таблица сравнения
- Определение
- Ключевые отличия
Сравнительная таблица
| Основа для сравнения | ЭДС | Напряжение |
|---|---|---|
| Определение | Количество энергии, подаваемой источником на каждый кулон заряда. | Энергия, потребляемая единицами заряда для перемещения из одной точки в другую |
| Формула | ||
| Символ | ε | V |
| Измерение | Измерьте расстояние между конечной точкой источника, когда через него не протекает ток. | Измерьте расстояние между любыми двумя точками. |
| Источник | Динамо, электрохимический элемент, трансформатор, солнечный элемент, фотодиоды и т. Д. | Электрическое и магнитное поле |
Определение напряжения
Напряжение определяется как энергия, необходимая для перемещения единичного заряда из одной точки в другую.Оно измеряется в вольтах и обозначается символом V. Напряжение вызывается электрическим и магнитным полями.
Напряжение возникает между концами (т. Е. Катодом и анодом) источника. Потенциал положительной конечной точки источника выше по сравнению с отрицательной точкой. Когда на пассивном элементе возникает напряжение, это называется падением напряжения. Сумма падений напряжения в цепи равна ЭДС согласно закону Кирхгофа.
Определение ЭМП
Подача энергии от источника к каждому кулону заряда называется ЭДС.Другими словами, это подача энергии некоторым активным источником, таким как аккумулятор, для единичного кулоновского заряда. ЭДС означает электродвижущую силу. Он измеряется в вольтах и обозначается символом ε.
Электродвижущая сила вышеуказанной цепи представлена формулой Где, r — внутреннее сопротивление цепи.
R — Внешний резистан цепи.
E — электродвижущая сила.
I — ток
Ключевые различия между ЭДС и напряжением
- ЭДС — это мера подачи энергии на каждый кулон заряда, тогда как напряжение — это энергия, используемая одним кулоном заряда для перемещения из одной точки в другую.
- ЭДС представлена буквой ε, тогда как символическое представление напряжения — V.
- ЭДС измеряется между конечной точкой источника, когда через него не течет ток, а напряжение измеряется между любыми двумя точками замкнутой цепи.
- ЭДС создается электрохимическим элементом, динамо-машиной, фотодиодами и т. Д., А напряжение создается электрическим и магнитным полями.
Вольт — это единица системы СИ как для ЭДС, так и для напряжения.
10.2: Электродвижущая сила — Physics LibreTexts
Цели обучения
К концу раздела вы сможете:
- Опишите электродвижущую силу (ЭДС) и внутреннее сопротивление батареи
- Объясните основную работу аккумулятора
Если вы забудете выключить автомобильные фары, они будут медленно тускнеть по мере разрядки аккумулятора. Почему они не мигают внезапно, когда разрядился аккумулятор? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи.Причина уменьшения выходного напряжения для разряженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электроэнергии и внутреннего сопротивления. В этом разделе мы исследуем источник энергии и внутреннее сопротивление.
Введение в электродвижущую силу
Voltage имеет множество источников, некоторые из которых показаны на рисунке \ (\ PageIndex {2} \). Все такие устройства создают разность потенциалов и могут подавать ток, если подключены к цепи.Особый тип разности потенциалов известен как электродвижущая сила (ЭДС) . ЭДС — это вовсе не сила, но термин «электродвижущая сила» используется по историческим причинам. Он был изобретен Алессандро Вольта в 1800-х годах, когда он изобрел первую батарею, также известную как вольтовую батарею . Поскольку электродвижущая сила не является силой, принято называть эти источники просто источниками ЭДС (произносится как «э-э-э-эфф»), а не источниками электродвижущей силы.
Рисунок \ (\ PageIndex {1} \): различные источники напряжения. а) ветряная электростанция Бразос в Флуванна, штат Техас; (б) Красноярская плотина в России; (c) солнечная ферма; (d) группа никель-металлогидридных батарей. Выходное напряжение каждого устройства зависит от его конструкции и нагрузки. Выходное напряжение равно ЭДС только при отсутствии нагрузки. (кредит a: модификация работы «Leaflet» / Wikimedia Commons; кредит b: модификация работы Алекса Полежаева; кредит c: модификация работы Министерства энергетики США; кредит d: модификация работы Тиаа Монто)
Если Электродвижущая сила — это вообще не сила, тогда что такое ЭДС и что является источником ЭДС? Чтобы ответить на эти вопросы, рассмотрим простую схему лампы 12 В, подключенной к батарее 12 В, как показано на рисунке \ (\ PageIndex {2} \).Батарея может быть смоделирована как устройство с двумя выводами, которое поддерживает один вывод с более высоким электрическим потенциалом, чем второй вывод. Более высокий электрический потенциал иногда называют положительной клеммой и обозначают знаком плюс. Клемму с более низким потенциалом иногда называют отрицательной клеммой и обозначают знаком минус. Это источник ЭДС.
Рисунок \ (\ PageIndex {2} \): Источник ЭДС поддерживает на одном выводе более высокий электрический потенциал, чем на другом выводе, действуя как источник тока в цепи.
Когда источник ЭДС не подключен к лампе, нет чистого потока заряда внутри источника ЭДС. Как только батарея подключена к лампе, заряды перетекают от одной клеммы батареи через лампу (в результате чего лампа загорается) и обратно к другой клемме батареи. Если мы рассмотрим положительный (обычный) ток, положительные заряды покидают положительный вывод, проходят через лампу и входят в отрицательный вывод.
Положительный ток полезен для большей части анализа схем в этой главе, но в металлических проводах и резисторах наибольший вклад в ток вносят электроны, протекающие в направлении, противоположном положительному потоку тока.Следовательно, более реалистично рассмотреть движение электронов для анализа схемы на рисунке \ (\ PageIndex {2} \). Электроны покидают отрицательную клемму, проходят через лампу и возвращаются к положительной клемме. Чтобы источник ЭДС поддерживал разность потенциалов между двумя выводами, отрицательные заряды (электроны) должны быть перемещены с положительного вывода на отрицательный. Источник ЭДС действует как зарядный насос, перемещая отрицательные заряды от положительного вывода к отрицательному, чтобы поддерживать разность потенциалов.Это увеличивает потенциальную энергию зарядов и, следовательно, электрический потенциал зарядов.
Сила, действующая на отрицательный заряд электрического поля, действует в направлении, противоположном электрическому полю, как показано на рисунке \ (\ PageIndex {2} \). Чтобы отрицательные заряды переместились на отрицательную клемму, необходимо провести работу с отрицательными зарядами. Для этого требуется энергия, которая возникает в результате химических реакций в батарее. Потенциал поддерживается высоким на положительной клемме и низким на отрицательной клемме, чтобы поддерживать разность потенциалов между двумя клеммами.ЭДС равна работе, выполняемой над зарядом на единицу заряда \ (\ left (\ epsilon = \ frac {dW} {dq} \ right) \) при отсутствии тока. Поскольку единицей измерения работы является джоуль, а единицей заряда — кулон, единицей измерения ЭДС является вольт \ ((1 \, V = 1 \, J / C) \).
Напряжение на клеммах \ (V_ {клемма} \) батареи — это напряжение, измеренное на клеммах батареи, когда к клемме не подключена нагрузка. Идеальная батарея — это источник ЭДС, который поддерживает постоянное напряжение на клеммах, независимо от тока между двумя клеммами.Идеальная батарея не имеет внутреннего сопротивления, а напряжение на клеммах равно ЭДС батареи. В следующем разделе мы покажем, что у реальной батареи действительно есть внутреннее сопротивление, а напряжение на клеммах всегда меньше, чем ЭДС батареи.
Источник потенциала батареи
ЭДС батареи определяется сочетанием химических веществ и составом выводов батареи. Свинцово-кислотный аккумулятор , используемый в автомобилях и других транспортных средствах, является одним из наиболее распространенных сочетаний химических веществ.На рисунке \ (\ PageIndex {3} \) показана одна ячейка (одна из шести) этой батареи. Катодная (положительная) клемма ячейки соединена с пластиной из оксида свинца, а анодная (отрицательная) клемма подключена к свинцовой пластине. Обе пластины погружены в серную кислоту, электролит для системы.
Рисунок \ (\ PageIndex {3} \): Химические реакции в свинцово-кислотном элементе разделяют заряд, отправляя отрицательный заряд на анод, который соединен со свинцовыми пластинами. Пластины из оксида свинца подключаются к положительному или катодному выводу ячейки.Серная кислота проводит заряд, а также участвует в химической реакции.
Небольшое знание того, как взаимодействуют химические вещества в свинцово-кислотной батарее, помогает понять потенциал, создаваемый батареей. На рисунке \ (\ PageIndex {4} \) показан результат одной химической реакции. Два электрона помещаются на анод , что делает его отрицательным, при условии, что катод подает два электрона. Это оставляет катод положительно заряженным, потому что он потерял два электрона.Короче говоря, разделение заряда происходит в результате химической реакции.
Обратите внимание, что реакция не происходит, если нет полной цепи, позволяющей подавать два электрона на катод. Во многих случаях эти электроны выходят из анода, проходят через сопротивление и возвращаются на катод. Также обратите внимание, что, поскольку в химических реакциях участвуют вещества, обладающие сопротивлением, невозможно создать ЭДС без внутреннего сопротивления.
Рисунок \ (\ PageIndex {4} \): В свинцово-кислотной батарее два электрона прижимаются к аноду элемента, а два электрона удаляются с катода элемента.В результате химической реакции в свинцово-кислотной батарее два электрона помещаются на анод и два электрона удаляются с катода. Для работы требуется замкнутая цепь, так как два электрона должны быть доставлены на катод.
Внутреннее сопротивление и напряжение на клеммах
Величина сопротивления протеканию тока внутри источника напряжения называется внутренним сопротивлением . Внутреннее сопротивление батареи r может вести себя сложным образом. Обычно она увеличивается по мере разряда батареи из-за окисления пластин или снижения кислотности электролита.Однако внутреннее сопротивление также может зависеть от величины и направления тока через источник напряжения, его температуры и даже его истории. Например, внутреннее сопротивление перезаряжаемых никель-кадмиевых элементов зависит от того, сколько раз и насколько глубоко они разряжались. Простая модель батареи состоит из идеализированного источника ЭДС \ (\ epsilon \) и внутреннего сопротивления r (рисунок \ (\ PageIndex {5} \)).
Рисунок \ (\ PageIndex {5} \): аккумулятор можно смоделировать как идеализированную ЭДС \ ((\ epsilon) \) с внутренним сопротивлением ( r ).Напряжение на клеммах аккумулятора равно \ (V_ {terminal} = \ epsilon — Ir \).
Предположим, что внешний резистор, известный как сопротивление нагрузки R , подключен к источнику напряжения, например батарее, как показано на рисунке \ (\ PageIndex {6} \). На рисунке показана модель батареи с ЭДС ε, внутренним сопротивлением R и нагрузочным резистором R , подключенным к ее клеммам. При обычном протекании тока положительные заряды покидают положительную клемму батареи, проходят через резистор и возвращаются к отрицательной клемме батареи.Напряжение на клеммах аккумулятора зависит от ЭДС, внутреннего сопротивления и силы тока и равно
.
Примечание
\ [V_ {терминал} = \ epsilon — Ir \]
При заданной ЭДС и внутреннем сопротивлении напряжение на клеммах уменьшается по мере увеличения тока из-за падения потенциала Ir внутреннего сопротивления.
Рисунок \ (\ PageIndex {6} \): Схема источника напряжения и его нагрузочного резистора R . Поскольку внутреннее сопротивление r включено последовательно с нагрузкой, оно может существенно повлиять на напряжение на клеммах и ток, подаваемый на нагрузку.
График разности потенциалов на каждом элементе цепи показан на рисунке \ (\ PageIndex {7} \). По цепи проходит ток I , а падение потенциала на внутреннем резисторе равно Ir . Напряжение на клеммах равно \ (\ epsilon — Ir \), что равно падению потенциала на нагрузочном резисторе \ (IR = \ epsilon — Ir \). Как и в случае с потенциальной энергией, важно изменение напряжения. Когда используется термин «напряжение», мы предполагаем, что это на самом деле изменение потенциала или \ (\ Delta V \).Однако \ (\ Delta \) часто для удобства опускается.
Рисунок \ (\ PageIndex {7} \): График напряжения в цепи батареи и сопротивления нагрузки. Электрический потенциал увеличивает ЭДС батареи из-за химических реакций, выполняющих работу с зарядами. В аккумуляторе происходит снижение электрического потенциала из-за внутреннего сопротивления. Потенциал уменьшается из-за внутреннего сопротивления \ (- Ir \), в результате чего напряжение на клеммах батареи равно \ ((\ epsilon — Ir) \).Затем напряжение уменьшается на ( IR ). Ток равен \ (I = \ frac {\ epsilon} {r + R} \).
Ток через нагрузочный резистор равен \ (I = \ frac {\ epsilon} {r + R} \). Из этого выражения видно, что чем меньше внутреннее сопротивление r , тем больший ток подает источник напряжения на свою нагрузку R . По мере разряда батарей r увеличивается. Если r становится значительной частью сопротивления нагрузки, то ток значительно снижается, как показано в следующем примере.
Пример \ (\ PageIndex {1} \): анализ цепи с батареей и нагрузкой
Данная батарея имеет ЭДС 12,00 В и внутреннее сопротивление \ (0,100 \, \ Omega \). (a) Рассчитайте напряжение на его клеммах при подключении к нагрузке с \ (10.00 \, \ Omega \). (b) Какое напряжение на клеммах при подключении к нагрузке \ (0.500 \, \ Omega \)? (c) Какая мощность рассеивается при нагрузке \ (0.500 \, \ Omega \)? (d) Если внутреннее сопротивление увеличивается до \ (0.500 \, \ Omega \), найдите ток, напряжение на клеммах и мощность, рассеиваемую \ (0.500 \, \ Омега \) загрузка.
Стратегия
Приведенный выше анализ дал выражение для тока с учетом внутреннего сопротивления. Как только ток будет найден, напряжение на клеммах можно рассчитать с помощью уравнения \ (V_ {terminal} = \ epsilon — Ir \). Как только ток будет определен, мы также сможем найти мощность, рассеиваемую резистором.
Решение
- Ввод данных значений ЭДС, сопротивления нагрузки и внутреннего сопротивления в выражение выше дает \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {10.10 \, \ Omega} = 1.188 \, A. \] Введите известные значения в уравнение \ (V_ {terminal} = \ epsilon — Ir \), чтобы получить напряжение на клеммах: \ [V_ { клемма} = \ epsilon — Ir = 12.00 \, V — (1.188 \, A) (0.100 \, \ Omega) = 11.90 \, V. \] Напряжение на клеммах здесь лишь немного ниже, чем ЭДС, что означает, что ток втягивается этой легкой нагрузкой не имеет значения.
- Аналогично, при \ (R_ {load} = 0.500 \, \ Omega \) ток равен \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {0.2} {R} \) или \ (IV \), где В — напряжение на клеммах (в данном случае 10,0 В).
- Здесь внутреннее сопротивление увеличилось, возможно, из-за разряда батареи, до точки, где оно равно сопротивлению нагрузки. Как и раньше, мы сначала находим ток, вводя известные значения в выражение, получая \ [I = \ frac {\ epsilon} {R + r} = \ frac {12.00 \, V} {1.00 \, \ Omega} = 12.00 \, A. \] Теперь напряжение на клеммах равно \ [V_ {terminal} = \ epsilon — Ir = 12.00 \, V — (12.2 (0.500 \, \ Omega) = 72.00 \, W. \] Мы видим, что увеличенное внутреннее сопротивление значительно снизило напряжение на клеммах, ток и мощность, подаваемую на нагрузку.
Значение
Внутреннее сопротивление батареи может увеличиваться по многим причинам. Например, внутреннее сопротивление перезаряжаемой батареи увеличивается с увеличением количества раз, когда батарея перезаряжается. Повышенное внутреннее сопротивление может иметь двоякое влияние на аккумулятор.Сначала снизится напряжение на клеммах. Во-вторых, аккумулятор может перегреться из-за повышенной мощности, рассеиваемой внутренним сопротивлением.
Упражнение \ (\ PageIndex {1} \)
Если вы поместите провод прямо между двумя выводами батареи, эффективно закоротив клеммы, батарея начнет нагреваться. Как вы думаете, почему это происходит?
- Решение
Если к клеммам подсоединен провод, сопротивление нагрузки близко к нулю или, по крайней мере, значительно меньше внутреннего сопротивления батареи.2р) \). Мощность рассеивается в виде тепла.
Тестеры батарей
Тестеры батарей, такие как те, что показаны на рисунке \ (\ PageIndex {8} \), используют малые нагрузочные резисторы, чтобы намеренно потреблять ток, чтобы определить, упадет ли потенциал клемм ниже допустимого уровня. Хотя трудно измерить внутреннее сопротивление батареи, тестеры батареи могут обеспечить измерение внутреннего сопротивления батареи. Если внутреннее сопротивление высокое, батарея разряжена, о чем свидетельствует низкое напряжение на клеммах.
Рисунок \ (\ PageIndex {8} \): Тестеры батарей измеряют напряжение на клеммах под нагрузкой, чтобы определить состояние батареи. (a) Техник-электронщик ВМС США использует тестер аккумуляторов для проверки больших аккумуляторов на борту авианосца USS Nimitz . Тестер батарей, который она использует, имеет небольшое сопротивление, которое может рассеивать большое количество энергии. (b) Показанное небольшое устройство используется на небольших батареях и имеет цифровой дисплей для индикации допустимого напряжения на клеммах. (кредит А: модификация работы Джейсона А.Джонстон; кредит б: модификация работы Кейта Уильямсона)
Некоторые батареи можно перезарядить, пропустив через них ток в направлении, противоположном току, который они подают в прибор. Это обычно делается в автомобилях и батареях для небольших электроприборов и электронных устройств (Рисунок \ (\ PageIndex {9} \)). Выходное напряжение зарядного устройства должно быть больше, чем ЭДС аккумулятора, чтобы ток через него реверсировал. Это приводит к тому, что напряжение на клеммах батареи превышает ЭДС, поскольку \ (V = \ epsilon — Ir \) и I теперь отрицательны.
Рисунок \ (\ PageIndex {9} \): автомобильное зарядное устройство меняет нормальное направление тока через батарею, обращая вспять его химическую реакцию и пополняя ее химический потенциал.
Важно понимать последствия внутреннего сопротивления источников ЭДС, таких как батареи и солнечные элементы, но часто анализ цепей выполняется с помощью напряжения на клеммах батареи, как мы это делали в предыдущих разделах. Напряжение на клеммах обозначается просто как В , без индекса «клемма».Это связано с тем, что внутреннее сопротивление батареи трудно измерить напрямую, и оно может со временем измениться.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Метод преобразования напряжения в температуру термопары
— Dataforth
Когда модули термопар SCM5B37 используются для измерения температуры,
измеренное выходное напряжение часто необходимо преобразовывать обратно в температуру.Этот
легко выполняется с серией SCM5B37, потому что компенсация холодного спая
встроен в модуль и задние панели SCMPB.
Метод проиллюстрирован здесь примером.
Термопара типа K должна использоваться с SCM5B37K.
Входные и выходные диапазоны SCM5B37K:
| Вход температуры | Выходное напряжение |
|---|---|
| -100 ° С | 0 В постоянного тока |
| + 1350 ° С | + 5 В постоянного тока |
- Из таблиц термопар типа K мы находим следующие напряжения:
-100 ° С = -3.554 мВ
+ 1350 ° C = 54,138 мВКоэффициент усиления модуля SCM5B37K (G) определяется по формуле:
G = V out полный диапазон шкалы / полный диапазон термопары в вольтах
Следовательно: G = 5 / [0,054138 — (-0,003554)] = 86,67 В / В.
- Рассчитайте эффективное входное напряжение термопары (V t ) на основе измеренного выходного напряжения (Vout) по следующей формуле:
В t = (В на выходе измерено / G) + Термопара отриц. полная шкала в вольтах
Следовательно: V t = (V out /86.67) + (-0,003554)
- Найти значение измеряемой температуры поля пересечением V t
к температуре термопары в вашем
таблица поиска термопар прикладной программы.
Коэффициенты усиления для других модулей термопар SCM5B37 показаны в следующей таблице.
| Тип модуля | Диапазон (° C) | Модуль усиления G (В / В) | Отрицательная термопара, полная шкала (мВ) |
|---|---|---|
| SCM5B37J | от -100 до 760 | -105. |



 3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов
3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов