Электродвижущая сила взаимной индукции — Электроэнергетическая группа
При изменении тока в одном из индуктивно связанных элементов цепи (см. рис. 6.1 и 6.2) в другом элементе возникает ЭДС взаимной индукции и между его разомкнутыми выводами появляется напряжение. Абсолютные значения ЭДС и напряжений, обусловленных взаимной индукцией (закон электромагнитной индукции),
Для облегчения решения вопроса о знаке этих величин прибегают к специальной разметке выводов индуктивно связанных элементов цепи.
Два вывода, принадлежащих двум разным индуктивно связанным элементам цепи, называют одноименными и обозначают одинаковыми значками, руководствуясь следующим правилом: при одинаковом направлении токов относительно одноименных выводов магнитные потоки самоиндукции и взаимной индукции в каждом элементе должны суммироваться.
Применим это правило для разметки выводов катушек, показанных на рис. 6.3, а. При направлении тока от вывода а к выводу b и тока от вывода с к выводу d магнитные потоки самоиндукции (или ) и взаимной индукции суммируются. Поэтому вывод а одноименен с выводом с и аналогично вывод b одноименен с выводом d. Для катушек, показанных на рис. 6.3,б, одноименными являются выводы и , а также и . Разница с предыдущим случаем обусловлена другим направлением намотки витков второй катушки.
Поэтому вывод а одноименен с выводом с и аналогично вывод b одноименен с выводом d. Для катушек, показанных на рис. 6.3,б, одноименными являются выводы и , а также и . Разница с предыдущим случаем обусловлена другим направлением намотки витков второй катушки.
Одну из двух пар одноименных выводов обозначают специальными значками, например точками, звездочками, треугольниками и т. п.
Рис. 6.3
Рис. 6.4
Рис. 6.5
Установить взаимное расположение катушек и направление намотки их витков так просто, как на рис. 6.3, не всегда представляется возможным. Но найти одноименные выводы можно на основании простого опыта, для которого требуются гальванический элемент (или аккумулятор) и гальванометр. Одна из катушек соединяется с гальванометром, другая подключается к гальваническому элементу (рис. 6.4). При замыкании ключа S кратковременно возникает ток , ослабляющий магнитное поле, созданное током . Следовательно, в момент включения источника питания токи , и направлены относительно одноименных выводов противоположно.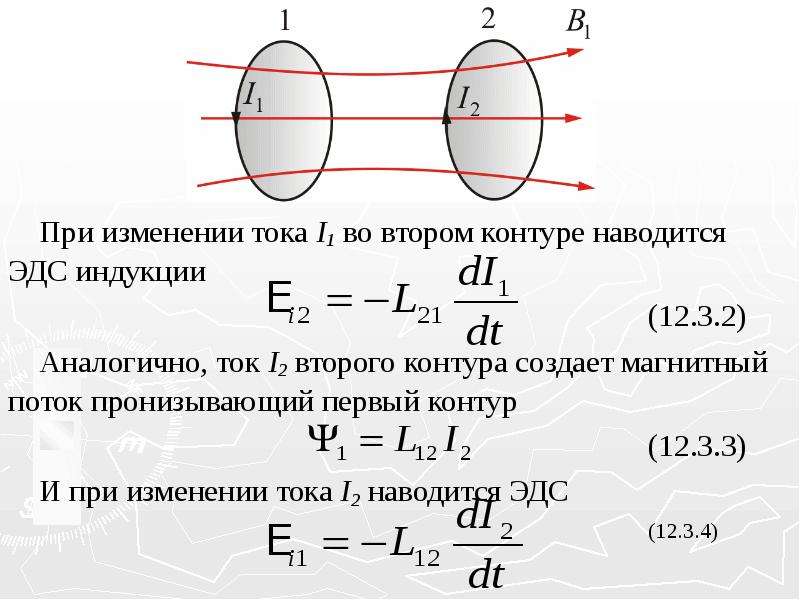 Направление тока определяется полярностью источника питания. О направлении тока судят по кратковременному отклонению стрелки гальванометра. Если стрелка отклоняется в сторону шкалы (имеется в виду гальванометр с односторонней шкалой), то ток направлен к положительному выводу гальванометра (рис. 6.4), при этом выводы катушек, присоединенные к положительным выводам гальванометра и источника питания, одноименны, точно так же одноименны и выводы катушек, присоединенные к отрицательным выводам гальванометра и источника питания; заметим, что в момент отключения источника питания стрелка гальванометра вновь отклоняется, но уже в обратном направлении, так как ток противодействует уменьшению магнитного поля.
Направление тока определяется полярностью источника питания. О направлении тока судят по кратковременному отклонению стрелки гальванометра. Если стрелка отклоняется в сторону шкалы (имеется в виду гальванометр с односторонней шкалой), то ток направлен к положительному выводу гальванометра (рис. 6.4), при этом выводы катушек, присоединенные к положительным выводам гальванометра и источника питания, одноименны, точно так же одноименны и выводы катушек, присоединенные к отрицательным выводам гальванометра и источника питания; заметим, что в момент отключения источника питания стрелка гальванометра вновь отклоняется, но уже в обратном направлении, так как ток противодействует уменьшению магнитного поля.
Перейдем теперь к решению вопроса о знаке в выражениях для ЭДС и напряжения, обусловленных взаимной индукцией.
Рассмотрим две катушки (рис. 6.5). Пусть катушка 1 разомкнута, а в катушке 2 протекает синусоидальный ток . Выберем положительные направления для ЭДС и напряжения в катушке 1 и для тока в катушке 2 относительно одноименных выводов одинаковыми, например от а к b и соответственно от с и d.
Прежде всего отметим, что при одинаковых положительных направлениях напряжения и ЭДС их значения численно равны, но противоположны по знаку: . Действительно, когда , потенциал вывода b больше потенциала вывода а, и, следовательно, .
Электродвижущая сила на основании закона Ленца должна иметь такое направление, при котором вызываемый ею ток препятствовал бы изменению магнитного потока взаимной индукции. Поэтому, если , то ЭДС должна иметь действительное направление от b к а, т. е. . Если , то ЭДС должна иметь действительное направление от а к b, т. е. .
Таким образом, при выбранных положительных направлениях (рис. 6.5) знаки и всегда противоположны, поэтому
Для комплексных величин получим
Если бы положительные направления для и в катушке 1 и тока в катушке 2 относительно одноименных выводов были выбраны различными, то аналогичные рассуждения показали бы, что знаки и всегда были бы одинаковы:
Из (6.2) и (6.3) видно, что напряжение , обусловленное взаимной индукцией, сдвинуто по фазе относительно тока на угол или . Знак этого угла зависит от выбора положительных направлений и относительно одноименных выводов.
Знак этого угла зависит от выбора положительных направлений и относительно одноименных выводов.
Величина имеет размерность сопротивления, называется сопротивлением взаимной индукции и обозначается . Величина называется комплексным сопротивлением взаимной индукции и обозначается . Таким образом,
Рис. 6.6
Если индуктивно связаны между собой не два, а несколько элементов цепи, надо у каждого из них отметить выводы, одноименные с выводами остальных элементов, при этом в общем случае приходится прибегать к разным условным обозначениям. Поясним это на примере трех катушек, расположенных, как указано на рис. 6.6.
Верхний вывод первой катушки одноименен с нижними выводами второй и третьей катушек, но эти последние не являются одноименными по отношению друг к другу, поэтому их нельзя обозначить одинаковыми значками. На рис. 6.6 одноименные выводы первой и второй катушек обозначены звездочками, первой и третьей — треугольниками, а второй и третьей — точками.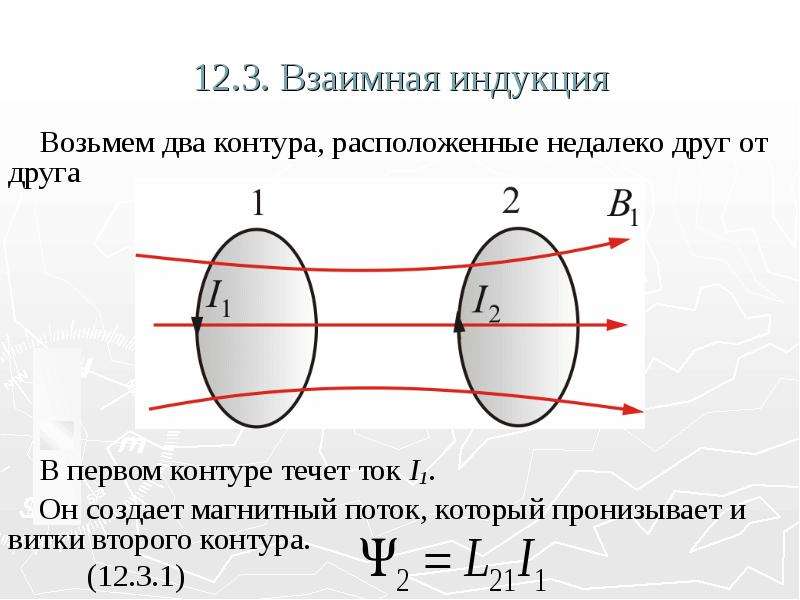 В частных случаях для разметки одноименных выводов нескольких катушек можно обойтись одним условным обозначением. Убедиться в этом можно на примере нескольких катушек, расположенных вдоль одной оси (аналогично рис. 6.3).
В частных случаях для разметки одноименных выводов нескольких катушек можно обойтись одним условным обозначением. Убедиться в этом можно на примере нескольких катушек, расположенных вдоль одной оси (аналогично рис. 6.3).
При большом числе индуктивно связанных элементов цепи указанная выше система разметки одноименных выводов получается недостаточно наглядной, так как приходится вводить много различных обозначений. В таких случаях удобнее другая система разметки, при которой взаимные индуктивности считают алгебраическими величинами.
Сначала совершенно произвольно указывают направления обхода каждого индуктивно связанного элемента цепи, например ставят букву н у вывода, от которого начинается обход, и букву к у другого вывода. Затем указывают знаки взаимных индуктивностей, руководствуясь следующим правилом. Если при совпадении направлений токов с выбранными направлениями обходов потоки взаимной индукции и потоки самоиндукции суммируются, то соответствующая взаимная индуктивность положительна, если же они вычитаются, то соответствующая взаимная индуктивность отрицательна.
Примем, например, для катушек, показанных на рис. 6.6, за начала обхода верхние выводы и за концы обхода — нижние выводы, при этом взаимные индуктивности будут отрицательны .
Знаки в выражениях для напряжений, обусловленных взаимной индуктивностью, получаются, конечно, такими же, как и при первой системе разметки выводов; при совпадении положительных направлений и с принятыми направлениями обходов получаем , при несовпадении получаем , при этом взаимная индуктивность считается величиной алгебраической и берется с тем знаком, который для нее указан при разметке выводов.
Вторая система разметки при наличии только двух индуктивно связанных элементов менее удобна, так как требует не только маркировки выводов, но и указания знака взаимной индуктивности. В дальнейшем применяется только первая система разметки.
HydroMuseum – Взаимная индукция
Взаимная индукция
Взаимная индукция — возникновение
электродвижущей силы (ЭДС) в одном проводнике вследствие изменения силы тока в
другом проводнике или вследствие изменения взаимного расположения проводников.
Взаимоиндукция — частный случай более общего явления —
электромагнитной индукции. При изменении тока в одном из проводников или при
изменении взаимного расположения проводников происходит изменение магнитного
потока, созданного током первого проводника и проходящего через контур второго,
что по закону электромагнитной индукции вызывает возникновение ЭДС во втором
проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции
в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи
вызовет появление ЭДС в первой. Направление тока, возникшего при
взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что
изменение тока в одной цепи (катушке) встречает противодействие со стороны
другой цепи (катушки).
Чем большая часть магнитного поля первой цепи
пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С
количественной стороны явление взаимоиндукции характеризуется взаимной
индуктивностью. Для изменения величины индуктивной связи между цепями, катушки
делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями,
Приборы, служащие для изменения взаимоиндукции между цепями,
называются вариометрами связи.
Явление взаимоиндукции широко используется
для передачи энергии из одной электрической цепи в другую, для преобразования
напряжения с помощью трансформатора.
Взаимная индукция — явление возбуждения ЭДС в одной электрической цепи при изменении
электрического потока в другой цепи или при изменении взаиморасположения этих
двух цепей.
Рис. 1 Тороидальный трансформатор
Взаимная
индукция с точки зрения физики:
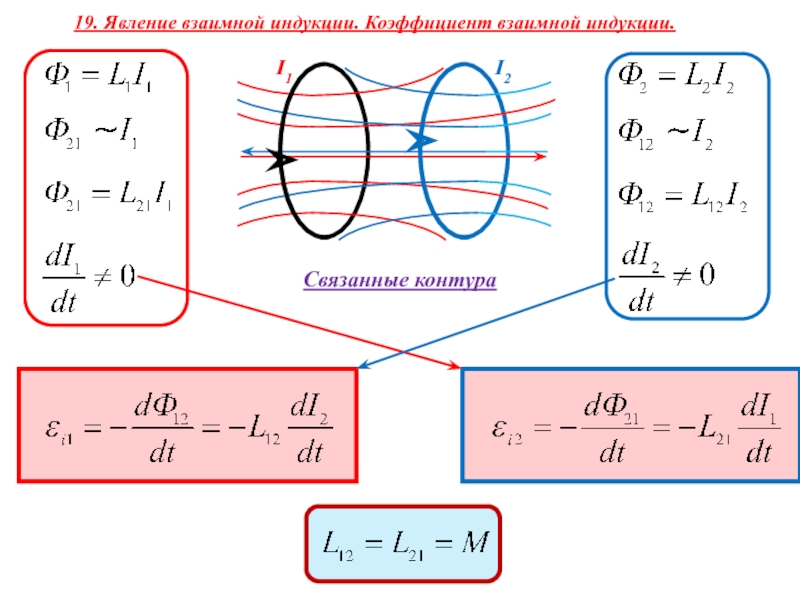
Рассмотрим два контура 1 и 2, расположенные
достаточно близко друг к другу, рис. 2. Пусть в контуре 1 течет ток
силы I1. Этот ток создаёт магнитное поле с индукцией B1, пронизывающее контур 2. Линии индукции этого поля
показаны на рисунке сплошными линиями. Полный
магнитный поток ψ2 через контур 2, как
показывает эксперимент, пропорционален силе тока I1, т. е. можно записать ψ2~ I1 или
е. можно записать ψ2~ I1 или
Рис. 2
ψ
2=L21· I1. (1)
Аналогично,
если в контуре 2 течёт ток силы I2, то возникающий полный
магнитный поток через контур 1 вычисляется по формуле
ψ
1=L12· I2. (2)
Линии индукции магнитного
поля, которое создаёт контур 2, показаны на рисунке пунктирными линиями.
Коэффициенты
пропорциональности L21 и L12 в формулах (1), (2)
называются взаимной индуктивностью контуров. Если вблизи контуров отсутствуют
ферромагнетики, то можно показать, что L21=L12.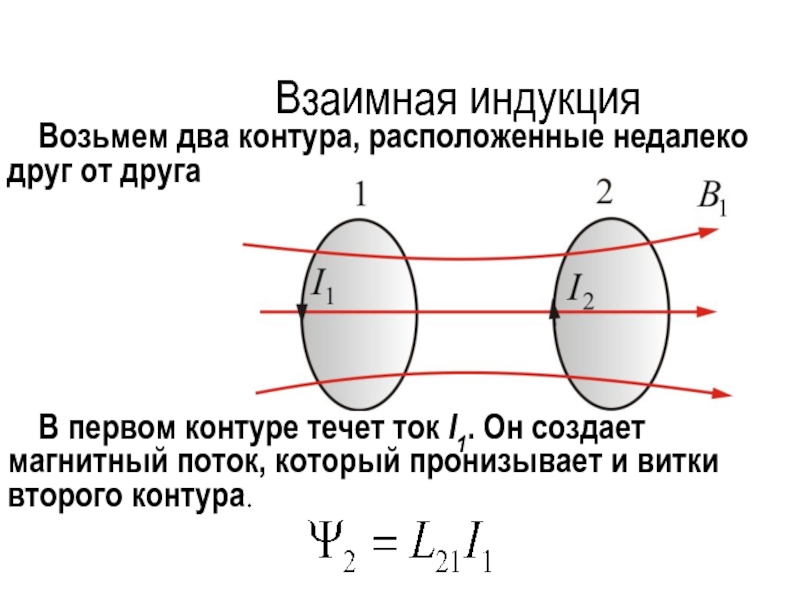 Коэффициенты L21 и L12 зависят от формы, размеров, расположения контуров и от
Коэффициенты L21 и L12 зависят от формы, размеров, расположения контуров и от
магнитной проницаемости среды.
Если в контуре 1 сила тока I1 изменяется, т.е. является
функцией времени t, то в контуре 2 индуцируется
электродвижущая сила εi2
εi2=− L21·d I1/dt ,
а при изменениях тока I2 в контуре 1 индуцируется электродвижущая сила εi1
εi1=− L12·d I2/dt .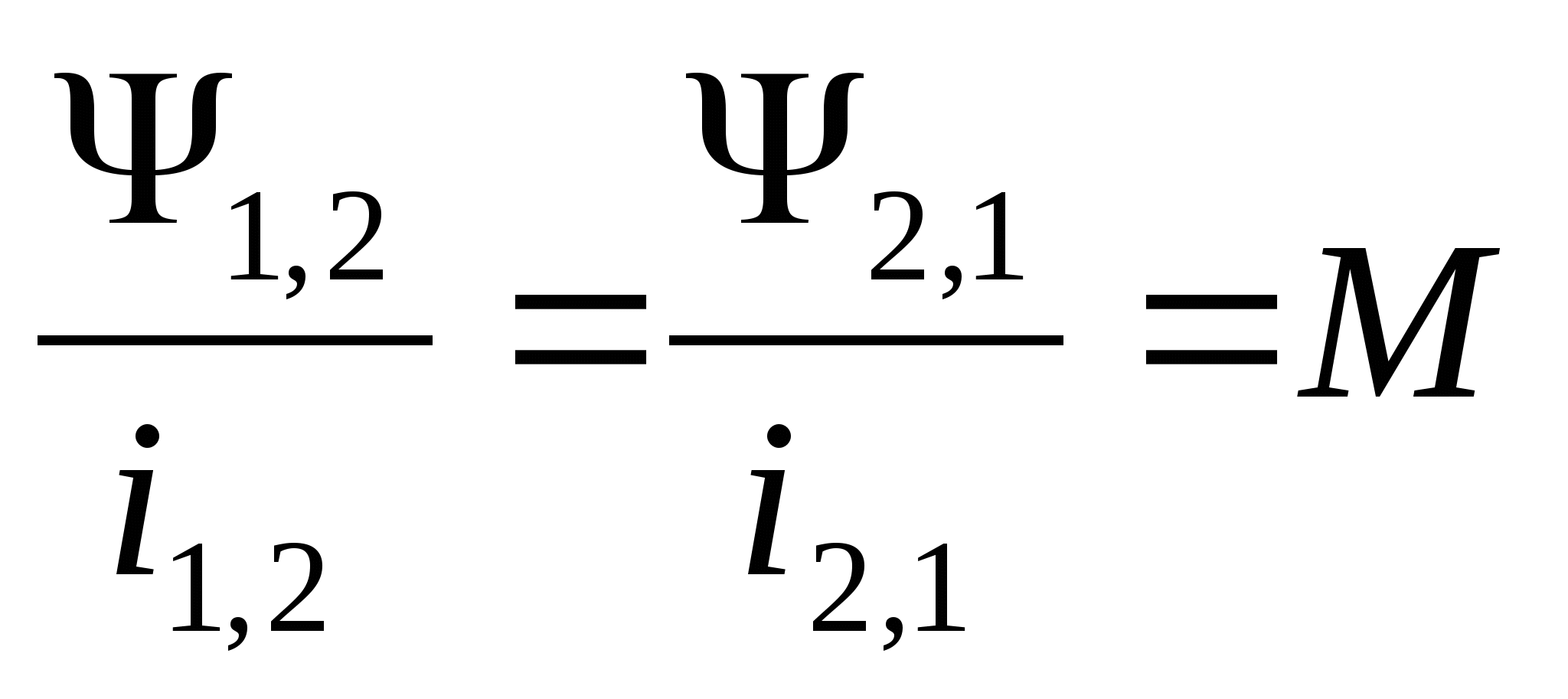
Явление возникновения ЭДС в
одном из контуров при изменении силы тока в другом называется взаимной индукцией, а сами контуры называются связанными.
Калькулятор взаимной индукции • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Этот калькулятор определяет взаимоиндукцию двух связанных катушек индуктивности.
Пример. Рассчитать взаимную индуктивность двух расположенных рядом катушек индуктивности 10 мкГн и 5 мкГн с коэффициентом связи 0,5.
Входные данные
Индуктивность первой катушки, L1
генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)
Индуктивность второй катушки, L2
миллигенри (мГн)
Коэффициент связи, k
0 ≤ k ≤ 1
Выходные данные
Взаимоиндукция
M миллигенри (мГн)
Введите величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать.
В токоизмерительных клещах с разъемным магнитопроводом для безопасного измерения тока без необходимости подключать прибор к схеме используется измерительный трансформатор. В приборе используется явление взаимной индукции. На разъемном магнитопроводе надета катушка, являющаяся вторичной обмоткой измерительного трансформатора. Первичной «обмоткой» является охватываемый магнитопроводом провод с током. Электродвижущая сила, возникающая в катушке на магнитопроводе, пропорциональна току, текущему в проводнике, охваченном клещами. Прибор измеряет напряжение на зажимах катушки и указывает на дисплее значение измеряемого тока.
Калькулятор определит взаимоиндукцию M двух связанных катушек индуктивности по формуле:
где k — коэффициент связи, L₁ — индуктивность первой катушки и L₂ — индуктивность второй катушки. Коэффициент связи определяется как отношение взаимоиндукции двух катушек к максимально возможному значению их взаимоиндукции. Коэффициент связи изменяется в пределах от 0 до 1 и зависит от близости катушек или обмоток, материала их сердечника, их взаимной ориентации, формы и количества витков. У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.
У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.
Тороидальные трансформатор и дроссель в импульсном блоке питания
Пример расчетов. Коэффициент связи двух катушек с индуктивностью 2 мкГн и 3 мкГн равен 0,5. Взаимоиндукция в микрогенри определяется как
Две катушки с взаимной индукцией на принципиальной схеме
При увеличении силы тока, протекающего через катушку индуктивности L₁ от внешней цепи, вокруг катушки создается увеличивающееся магнитное поле, в котором сохраняется энергия. При уменьшении тока магнитное поле также уменьшается. При этом на выводах катушки возникает напряжение (ЭДС самоиндукции) в направлении, противоположном направлению тока, и сохраняемая в магнитном поле энергия отдается обратно во внешнюю цепь.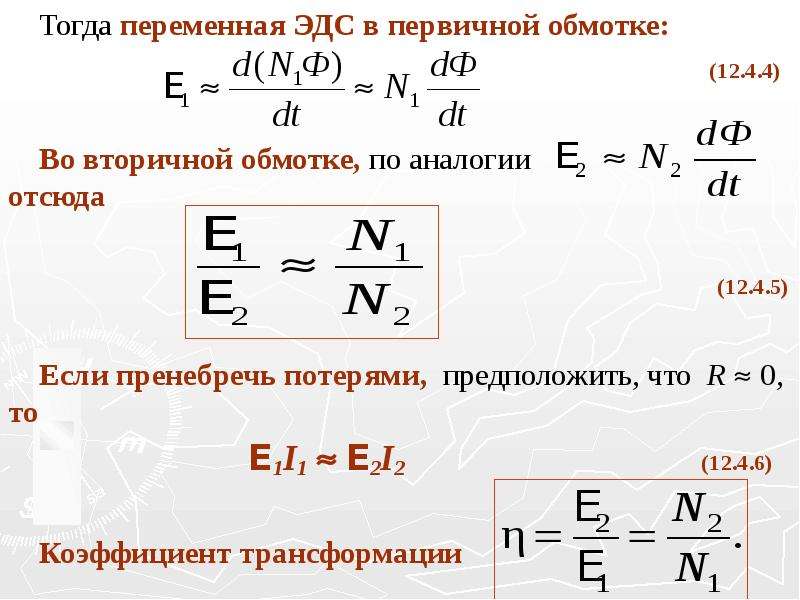 Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).
Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).
Взаимоиндукция в вашем автомобиле: для создания искры в свечах зажигания используется катушка зажигания, представляющая собой трансформатор с высоким коэффициентом трансформации. Когда ток через первичную обмотку с малым числом витков прерывается, очень большая ЭДС возникает во вторичной обмотке с большим числом витков, которая достаточна для создания искры в зазоре автомобильной свечи зажигания
В обратной ситуации, если ток течет в катушке L₂, а наводится ток в катушке L₁, взаимоиндукция будет той же. Отметим, что электродвижущая сила (ЭДС) возникает только при изменении тока, причем чем быстрее изменяется ток, тем больше будет ЭДС. То есть, ЭДС взаимной индукции прямо пропорциональна скорости изменения тока
Явление взаимной индукции используется в трансформаторах, электродвигателях, генераторах и других устройствах, в которых для функционирования необходимо взаимодействие с магнитным полем. В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.
В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.
Автор статьи: Анатолий Золотков
Определить скорость изменения силы тока в обмотке электромагнита. Open Library
Изменению силы тока в контуре препятствует ЭДС самоиндукции, равная произведению индуктивности контура и скорости изменения силы тока.
Электрический ток создаёт вокруг себя магнитное поле, и часть линий магнитной индукции этого поля всегда проходит через контур, по которому течет ток (рис.6а). В случае если ток через контур меняется во времени (переменный ток), то изменяется и магнитный поток через данный контур, а значит, возникает ЭДС индукции, препятствующая изменению магнитного потока (правило Ленца). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, при изменении тока в любом контуре возникает ЭДС индукции, препятствующая этим изменениям. Это явление называют самоиндукцией, а соответствующую ЭДС – ЭДС самоиндукции, Eis.
Это явление называют самоиндукцией, а соответствующую ЭДС – ЭДС самоиндукции, Eis.
Явление самоиндукции продемонстрировано на рис. 6б, где показано, как изменяется сила тока через катушку при подключении и отключении источника тока. Видно, что при замыкании цепи сила тока через катушку достигает величины, соответствующей сопротивлению катушки, не мгновенно, а постепенно. Причиной этого замедления роста силы тока является ЭДС самоиндукции, направленная против ЭДС источника тока. При размыкании цепи в катушке возникает ЭДС самоиндукции, стремящаяся удержать ту силу тока, которая была до размыкания ключа, в результате чего сила тока через катушку падает не мгновенно, а постепенно. Энергия, необходимая для протекания тока через катушку после того, как источник тока был отсоединён (рис. 6б) представляет собой энергию магнитного поля катушки.
Чтобы количественно описать явление самоиндукции, найдём зависимость магнитного потока Ф через контур от силы тока I в этом контуре. Очевидно, что магнитный поток через контур пропорционален магнитной индукции внутри контура, а магнитная индукция пропорциональна силе тока в проводнике.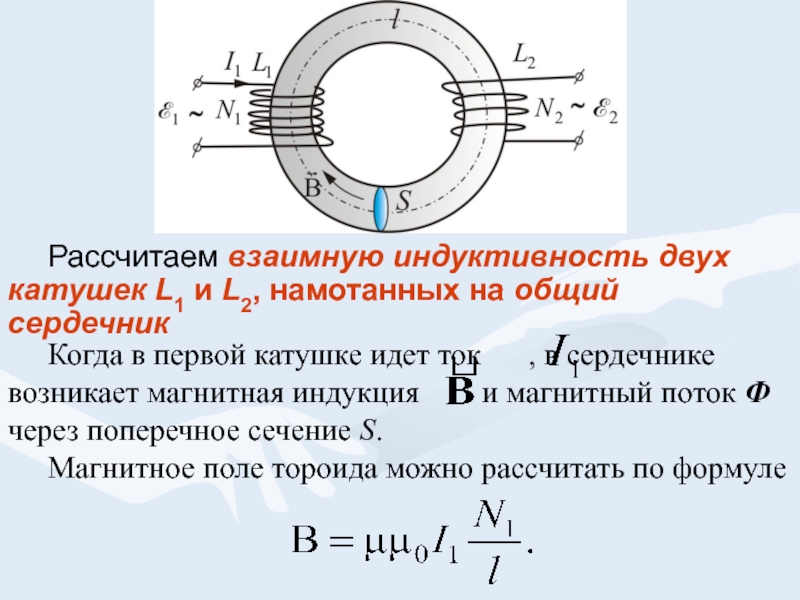 По этой причине магнитный поток должен быть пропорционален силе тока:
По этой причине магнитный поток должен быть пропорционален силе тока:
Ф = L.I , (6.1)
где L — коэффициент пропорциональности, называемый индуктивностью контура. Контур, обладающий индуктивностью, на схеме обозначают соответствующим значком (см. рис. 6б) Используя (6.1), закон электромагнитной индукции (5.2), а также считая, что индуктивность контура не изменяется при изменения силы тока в нём, можно найти ЭДС самоиндукции Eis:
Единицей индуктивности в СИ является генри (Гн). Из (6.2) следует, что Индуктивность контура зависит от формы и размеров этого контура. Так, индуктивность плоского контура тем больше, чем больше площадь его поверхности, а индуктивность катушки пропорциональна её диаметру и число витков в ней. Вместе с тем, индуктивность
катушки увеличивается, когда внутри неё находится сердечник из железа или сплава, способного намагничиваться.
Явление самоиндукции напоминает явление инерции в механике. Инерция тела, мерой которой служит его масса m, замедляет реакцию тела на приложенную к нему силу. То же происходит и в контуре, когда хотят изменить силу тока в нём. При этом, как следует из (6.2), мерой «инерции» контура является его индуктивность. Аналогия между электромагнитными и механическими явлениями позволяет считать, что ток в контуре играет туже роль, что и скорость тела v, а ЭДС аналогична силе, действующей на тело. Продолжая такую аналогию, можно вывести формулу для энергии магнитного поля катушки, исходя из того, что кинетическая энергия тела равна. Заменяя m на L, а v – на I, получаем следующее выражение для энергии WМ магнитного поля контура с индуктивностью L и силой тока I:
То же происходит и в контуре, когда хотят изменить силу тока в нём. При этом, как следует из (6.2), мерой «инерции» контура является его индуктивность. Аналогия между электромагнитными и механическими явлениями позволяет считать, что ток в контуре играет туже роль, что и скорость тела v, а ЭДС аналогична силе, действующей на тело. Продолжая такую аналогию, можно вывести формулу для энергии магнитного поля катушки, исходя из того, что кинетическая энергия тела равна. Заменяя m на L, а v – на I, получаем следующее выражение для энергии WМ магнитного поля контура с индуктивностью L и силой тока I:
Расчёты показывают, что выражение (6.3), действительно, верно, доказывая правоту аналогий между механическими и электромагнитными явлениями.
Вопросы для повторения:
· В чём состоит явление самоиндукции?
· Что называют индуктивностью, и в каких единицах её измеряют?
· Чему равна ЭДС самоиндукции?
· Чему равна энергия магнитного поля контура с током?
Рис. 6. (а) – линии магнитной индукции катушки с током; (б) – график изменения тока через катушку при включении и выключении источника тока.
6. (а) – линии магнитной индукции катушки с током; (б) – график изменения тока через катушку при включении и выключении источника тока.
Повтори теорию
:
1.Самоиндукция — это ________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________.
2.Индуктивность — ______________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
[L
] = ______.
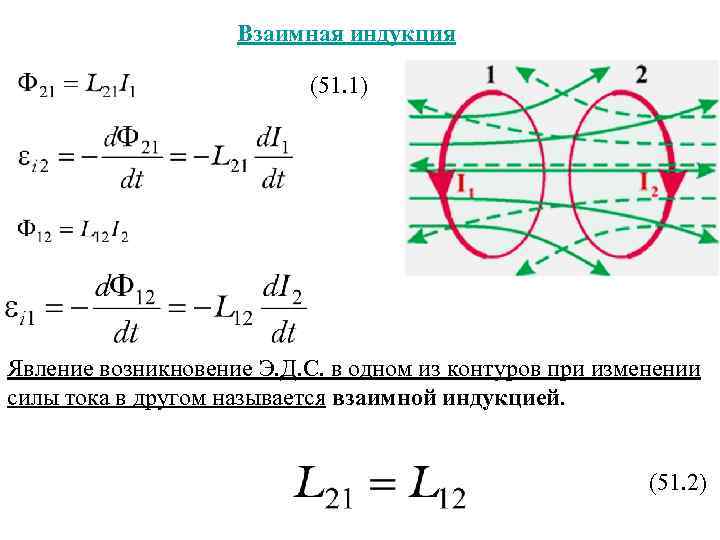
3.ЭДС самоиндукции:
______________, где L
— ______________________________, -_______________________ΔI
— _______________________________.
4.Правило Ленца: ______________________________________________________________________________
5.Правило Ленца: ______________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
6.Возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится __________________ изменение внешнего магнитного потока, вызвавшее данный ток.
7.Магнитный поток, пронизывающий соленоид Ф=________________.
8.Индукционный ток – это _______________________________________________________________________
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
9.Энергия магнитного поля W м =______________
10. Объёмная плотность энергии магнитного поля ω=_________________________.
Реши задачи
:
1. Какова индуктивность контура, если при силе тока 5А в нём возникает магнитный поток 0,5мВб?
Дано: СИ: Решение:
2. При равномерном уменьшении в течение 0,1с силы тока в катушке от 10 А до нуля в ней возникла ЭДС самоиндукции 60 В. Определите индуктивность катушки.
Дано: Решение:
3. При помощи реостата равномерно увеличивают силу тока в катушке со скоростью 2 А/с. Индуктивность катушки 200 мГн. Чему равна ЭДС самоиндукции в катушке?
Дано: СИ: Решение:
4. В катушке индуктивностью 0,6Гн сила тока равна 20А. Какова энергия магнитного поля катушки? Как изменится энергия поля, если сила тока уменьшается вдвое?
Дано: Решение:
Ответ: энергия магнитного поля _____________ в __________ раз при уменьшении силы тока вдвое.
5. Какой должна быть сила тока в обмотке дросселя индуктивностью 0,5Гн, чтобы энергия поля оказалась равной 1Дж?
Дано: Решение:
6. Чему равна энергия магнитного поля соленоида, в котором при силе тока 1А возникает магнитный поток 0,3Вб?
Чему равна энергия магнитного поля соленоида, в котором при силе тока 1А возникает магнитный поток 0,3Вб?
Дано: Решение:
Проверь себя
:
1. Какой магнитный поток возникает в контуре с индуктивностью 0,2мГн при силе тока 10А?
Дано: СИ: Решение:
2. Найти индуктивность проводника, в котором равномерное изменение силы тока на 2А в течение 0,25с возбуждает ЭДС самоиндукции 20мВ.
Дано: СИ: Решение:
3. Найти энергию магнитного поля соленоида, в котором при силе тока 10А возникает магнитный поток 0,5Вб.
Дано: Решение:
4. Индуктивность катушки 0,1мГн. При какой силе тока энергия магнитного поля будет равна 0,2мДж?
Дано: СИ: Решение:
Дата «___» _________20____г
Задание 35
Самостоятельная работа по теме
«Магнитное поле. Электромагнитная индукция»
ВАРИАНТ 1
1. Магнитное поле создается
1) электрическими зарядами 2) магнитными зарядами
3) движущимися электрическими зарядами 4) любым телом
2. Линии магнитной индукции вокруг проводника с током правильно показаны в случае.
Линии магнитной индукции вокруг проводника с током правильно показаны в случае.
1) А 2) Б 3)В 4) Г
3. Прямолинейный проводник с током / находится между полюсами магнита (проводник расположен перпендикулярно плоскости листа, ток течет к читателю). Сила Ампера, действующая на проводник, направлена
1) вправо → 2) влево ← 3) вверх 4) вниз ↓
4. Траектория полета электрона, влетевшего в однородное магнитное поле под углом 60°
5. Какой из ниже перечисленных процессов объясняется явлением электромагнитной индукцией?
1) взаимодействие проводников с током.
2) отклонение магнитной стрелки при прохождении по проводу электрического тока.
3) возникновение электрического тока в замкнутой катушке при увеличении силы тока в катушке, находящейся рядом с ней.
4) возникновение силы, действующей на прямой проводник с током.
6. Легкое проволочное кольцо подвешено на нити. При вдвигании в кольцо магнита северным полюсом оно будет:
1) отталкиваться от магнита 2) притягиваться к магниту 3) неподвижным 4) сначала отталкиваться, затем притягиваться
7.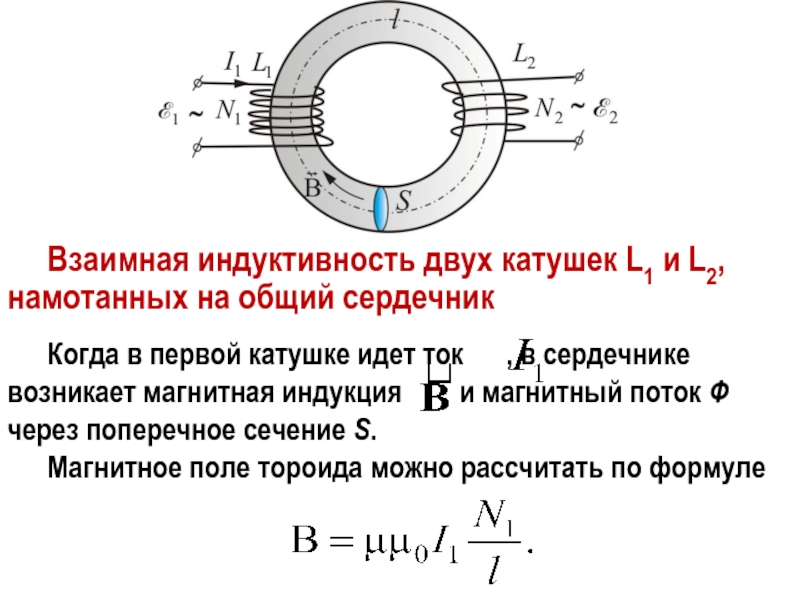 На рисунке приведен график зависимости силы тока в катушке индуктивности от времени. Модуль ЭДС самоиндукции принимает наибольшее значение в промежутке времени
На рисунке приведен график зависимости силы тока в катушке индуктивности от времени. Модуль ЭДС самоиндукции принимает наибольшее значение в промежутке времени
1) от 0 с до 1 с 2) от 1 с до 5 с 3) от 5 с до 6 с 4) от 6 с до 8 с
8. Установите соответствия технических устройств из левого столбца таблицы с физическими явлениями, используемыми в них, в правом столбце.
Устройства Явления
А.электродвигатель 1) действие магнитного поля на постоянный магнит
Б. компас 2) действие магнитного поля на движущийся электрический заряд
В. Гальванометр 3) действие магнитного поля на проводник с током
Г. МГД — генераторЧАСТЬ С
Решите задачу.
11. По горизонтальным рельсам, расположенным в вертикальном магнитном поле с индукцией 0,01 Тл, скользит проводник длиной 1 м с постоянной скоростью 10 м/с. Концы рельсов замкнуты на резистор сопротивлением 2 Ом. Найдите количество теплоты, которое выделится в резисторе за 4 с. Сопротивлением рельсов и проводника пренебречь.
Дано: СИ: Решение
Оценка _____ подпись преподавателя ________________/Л.С. Тишкина/
ВАРИАНТ 2
ЧАСТЬ А Выберите один верный ответ
1. Движущийся электрический заряд создает
1) только электрическое поле 2) только магнитное поле
3) как электрическое, так и магнитное поле 4) только гравитационное поле
2. На рисунке изображен цилиндрический проводник, по которому идет электрический ток. Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С?
1) в плоскости чертежа вверх
2) в плоскости чертежа вниз
3) от нас перпендикулярно плоскости чертежа
4) к нам перпендикулярно плоскости чертежа
3. На проводник с током, внесенный в магнитное поле, действует сила, направленная
«Скорость химической реакции» — Факторы, влияющие на скорость реакции. Механохимическая звуковая активация. Пример записи кинетического уравнения простой реакции. Скорость гетерогенных реакций. Химическая кинетика. Гетерогенный катализ. Гомогенный катализ. Предэкспонента и экспонента. Графическое определение n. Предэкспоненциальный множитель (А) дает некоторую характеристику полного числа столкновений.
Химическая кинетика. Гетерогенный катализ. Гомогенный катализ. Предэкспонента и экспонента. Графическое определение n. Предэкспоненциальный множитель (А) дает некоторую характеристику полного числа столкновений.
«Космическая скорость» — Движение тела в гравитационном поле. Гипербола. Восток. Траектория движения тел движущихся с малой скоростью. Первая космическая скорость. Изображение мужчины и женщины. Запущен в 1977году. Ю.А. Гагарин. Окружность. В 1989г аппарат Вояджер вышел за пределы Солнечной системы. Траектории движения тел.
«Скорость реакции» — Площадь соприкосновения реагирующих веществ. Определите тип реагирующих систем. Катализаторы и катализ. Влияние концентрации реагирующих веществ (для гомогенных систем) 3ряд. Гомогенные системы: Газ + газ Жидкость + жидкость. 2. Запишите кинетическое уравнение для реакции: 2Н2 +О2= 2Н2О. Факторы, влияющие на скорость.
«Скорость распространения звука» — Что называется чистым тоном? Именно поэтому гром сильно запаздывает после вспышки молнии. Скорость распространения звуковых волн в разных средах неодинакова. Чем определяется тембр звука? В жидкостях звук распространяется быстрее. Медленнее всего звук распространяется в газах. В твердых телах – еще быстрее.
Скорость распространения звуковых волн в разных средах неодинакова. Чем определяется тембр звука? В жидкостях звук распространяется быстрее. Медленнее всего звук распространяется в газах. В твердых телах – еще быстрее.
«Измерение скорости света» — Спутник опоздал появиться из тени на 22 минуты, по сравнению с раччётом. Оле Кристенсен Рёмер 25 сентября 1644 – 19 сентября 1710. С=214300 км/с. Арман Иполлит Луи Физо 23 сентября 1819 – 18 сентября 1896. Затем достигал зеркала, проходил между зубцами и попадал в глаз наблюдателя. Колесо вращалось медленно свет был виден.
«Урок Скорость время расстояние» — Скорость = Расстояние: время. Шел человек в город и по дороге догнал трех своих знакомых. Разминка. Пассажирский поезд прошёл 75 км за первый час, 60 км за второй час и 75 км за третий час. Товарный поезд прошёл 120 км за 3 ч, проходя за каждый час одинаковое расстояние. Задачи на движение. Однако обратный перелет занимает 80 мин.
ЭДС самоиндукции
При всяком изменении тока в катушке (или вообще в проводнике) в ней самой индуктируется ЭДС самоиндукции.
Чем больше скорость изменения тока, тем больше ЭДС самоиндукции.
Всякое уменьшение электрического тока сопровождается появлением э. д. с. самоиндукции, стремящейся, согласно правилу Ленца , поддержать убывающий ток. Вследствие этого могут значительно повыситься напряжения на катушках индуктивности при разрыве цепи тока. Иногда эти напряжения настолько большие, что обмотки могут сгореть, для предохранения обмоток параллельно им включают так называемые разрядные сопротивления.
Коэффициент пропорциональности
L
носит название индуктивности.
Индуктивность измеряется в
генри.
Индуктивностью в один генри обладает такая цепь, в которой при равномерном изменении тока со скоростью один ампер в секунду возникает э. д. с., равная одному вольту.
Индуктивность катушки есть величина, характеризующая свойство катушки индуктировать в себе ЭДС самоиндукции.
Индуктивность данной катушки есть величина постоянная, не зависящая как от силы проходящего по ней тока, так и от скорости его изменения.
Чем больше диаметр катушки, число ее витков и густота намотки, тем больше индуктивность и ЭДС самоиндукции.
Не следует забывать, что если ток в катушке не изменяется, то никакой ЭДС самоиндукции не возникает.
Явление самоиндукции особенно резко проявляется в цепи, содержащей в себе катушку с железным сердечником, так как железо значительно увеличивает магнитный поток катушки, а следовательно, и величину ЭДС самоиндукции при его изменении.На практике иногда нужна катушка (или обмотка), не обладающая индуктивностью. В этом случае провод наматывают на катушку, предварительно сложив его вдвойне. Такой способ намотки называется бифилярным.
ЭДС взаимоиндукции
Чтобы вызвать ЭДС индукции в одной катушке за счет изменения тока в другой, совершенно не обязательно вставлять одну из них внутрь другой, а можно расположить их рядом
И в этом случае при изменении тока в одной катушке возникающий переменный магнитный поток будет пронизывать (пересекать) витки другой катушки и вызовет в ней ЭДС.Взаимоиндукция дает возможность связывать между собой посредством магнитного поля различные электрические цепи. Такую связь принято называть индуктивной связью.
Величина ЭДС взаимоиндукции зависит прежде всего от того, с какой скоростью изменяется ток в первой катушке. Чем быстрее изменяется в ней ток, тем создается большая ЭДС взаимоиндукции.
Кроме того, величина ЭДС взаимоиндукции зависит от величины индуктивности обеих катушек и от их взаимного расположения, а также от магнитной проницаемости окружающей среды.Чтобы иметь возможность различать между собой различные пары катушек по их способности взаимно индуктировать ЭДС, введено понятие о взаимоиндуктивности или коэффициенте взаимоиндукции.
Обозначается сявзаимоиндуктивность буквой М. Единицей ее измерения, так же как и индуктивности, служит генри.
Генри — это такая взаимоиндуктивность двух катушек, при которой изменение тока в одной катушке на 1 ампер в 1 секунду вызывает в другой катушке ЭДС взаимоиндукции, равную 1 вольту.
На величину ЭДС взаимоиндукции влияет магнитная проницаемость окружающей среды. Чем больше магнитная проницаемость среды, по которой замыкается переменный магнитный поток, связывающий катушки, тем сильнее индуктивная связь катушек и больше величина ЭДС взаимоиндукции.
На явлении взаимоиндукции основана работа такого важного электротехнического устройства, как трансформатор.
14.2: Взаимная индуктивность — Физика LibreTexts
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Сопоставление двух близлежащих цепей, по которым текут переменные во времени токи, с ЭДС, индуцированной в каждой цепи
- Опишите примеры, в которых взаимная индуктивность может быть или не быть желательной
Индуктивность — это свойство устройства, которое говорит нам, насколько эффективно оно индуцирует ЭДС в другом устройстве.Другими словами, это физическая величина, выражающая эффективность данного устройства.
Когда две цепи, по которым текут изменяющиеся во времени токи, расположены близко друг к другу, магнитный поток в каждой цепи меняется из-за изменяющегося тока I в другой цепи. Следовательно, ЭДС индуцируется в каждой цепи изменением тока в другой. Поэтому этот тип ЭДС называется ЭДС взаимной индукции , а возникающее явление известно как взаимная индуктивность ( М ) .В качестве примера рассмотрим две плотно намотанные катушки (рис. \(\PageIndex{1}\)). Катушки 1 и 2 имеют \(N_1\) и \(N_2\) витков и пропускают токи \(I_1\) и \(I_2\) соответственно. Поток через один виток катушки 2, создаваемый магнитным полем тока в катушке 1, равен \(\Phi_{12}\), тогда как поток через один виток катушки 1 из-за магнитного поля \(I_2 \) равно \(\Phi_{12}\).
Рисунок \(\PageIndex{1}\): Некоторые силовые линии магнитного поля, создаваемые током в катушке 1, проходят через катушку 2.
Взаимная индуктивность \(M_{21}\) катушки 2 по отношению к катушке 1 равна отношению потока через \(N_2\) витков катушки 2, создаваемого магнитным полем тока в катушке 1, деленному по тому току, то есть
\[M_{21} = \dfrac{N_2\Phi_{21}}{I_1}.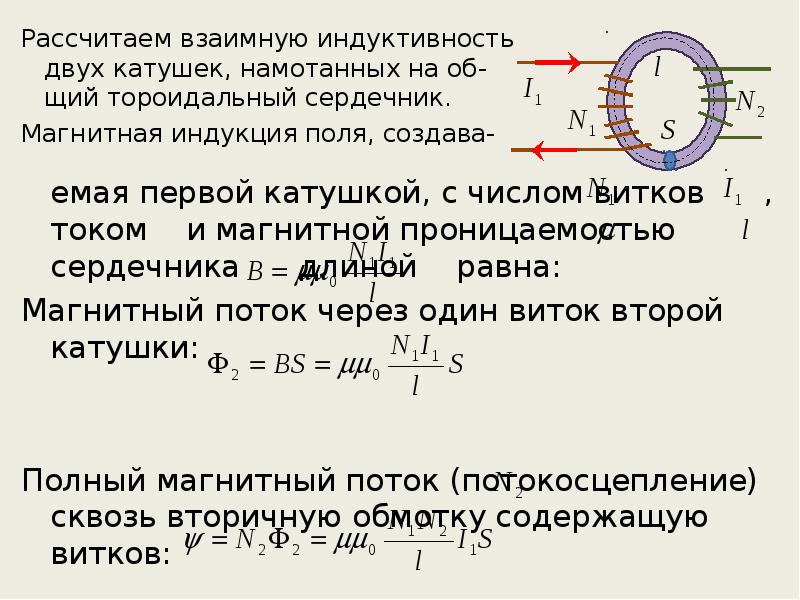 \метка{12.24}\]
\метка{12.24}\]
Аналогично, взаимная индуктивность катушки 1 по отношению к катушке 2 равна
.
\[M_{12} = \dfrac{N_1\Phi_{12}}{I_2}. \метка{12.25}\]
Как и емкость, взаимная индуктивность является геометрической величиной.Это зависит от формы и взаимного расположения двух катушек и не зависит от токов в катушках. Единица СИ для взаимной индуктивности М называется генри (Гн) в честь Джозефа Генри (1799–1878), американского ученого, открывшего ЭДС независимо от Фарадея. Таким образом, имеем \(1 \, H = 1 \, V \cdot s/A\). Из уравнений \ref{12.24} и \ref{12.25} мы можем показать, что \(M_{21} = M_{12}\), поэтому мы обычно опускаем индексы, связанные с взаимной индуктивностью, и пишем
\[M = \dfrac{N_2\Phi_{21}}{I_1} = \dfrac{N_1 \Phi_{12}}{I_2}.\метка{14.3}\]
ЭДС, развиваемая в каждой катушке, находится путем объединения закона Фарадея и определения взаимной индуктивности. Так как \(N_2\Phi_{21}\) — это полный поток через катушку 2 из-за \(I_1\), мы получаем
\[\begin{align} \epsilon_2 &= — \dfrac{d}{dt} (N_2 \Phi_{21}) \\[4pt] &= — \dfrac{d}{dt} (MI_1) \\ [4pt] & = — M\dfrac{dI_1}{dt} \label{14. 4} \end{align} \]
4} \end{align} \]
, где мы использовали тот факт, что \(M\) является постоянной, не зависящей от времени, потому что геометрия не зависит от времени.Точно так же у нас есть
\[\epsilon_1 = — M\dfrac{dI_2}{dt}. \метка{14.5}\]
В уравнении \ref{14.5} мы можем видеть значение более раннего описания взаимной индуктивности (\(M\)) как геометрической величины. Значение \(M\) точно отражает физические свойства элементов схемы и позволяет нам отделить физическую схему схемы от динамических величин, таких как ЭДС и ток. Уравнение \ref{14.5} определяет взаимную индуктивность с точки зрения свойств в цепи, тогда как предыдущее определение взаимной индуктивности в уравнении \ref{12.24} определяется с точки зрения испытанного магнитного потока, независимо от элементов цепи. Вы должны быть осторожны при использовании уравнений \ref{14.4} и \ref{14.4}, потому что \(\epsilon_1\) и \(\epsilon_2\) не обязательно представляют суммарные ЭДС в соответствующих катушках. В каждой катушке также может быть наведена ЭДС из-за ее собственной индуктивности (самоиндуктивность будет обсуждаться более подробно в следующем разделе).
Большая взаимная индуктивность M может быть или не быть желательной.Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать опасную ЭДС на своем металлическом корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность — встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле (рис. \(\PageIndex{2}\)).
Рисунок \(\PageIndex{2}\): Нагревательные спирали электрической сушилки для белья могут быть намотаны встречно, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.
Цифровая обработка сигналов — еще один пример, в котором взаимная индуктивность уменьшается за счет встречной обмотки катушек. ЭДС быстрого включения/выключения, представляющая 1 и 0 в цифровой схеме, создает сложное магнитное поле, зависящее от времени. ЭДС может генерироваться в соседних проводниках. Если этот проводник также несет цифровой сигнал, ЭДС индукции может быть достаточно большой, чтобы переключать 1 и 0 с последствиями от неудобных до катастрофических.
ЭДС может генерироваться в соседних проводниках. Если этот проводник также несет цифровой сигнал, ЭДС индукции может быть достаточно большой, чтобы переключать 1 и 0 с последствиями от неудобных до катастрофических.
Пример \(\PageIndex{1}\): взаимная индуктивность
На рисунке \(\PageIndex{3}\) показана катушка из \(N_2\) витков и радиуса \(R_2\), окружающая длинный соленоид длиной \(l_1\), радиусом \(R_1\) и \( N_1\) оборотов.
- Какова взаимная индуктивность двух катушек?
- Если \(N_1 = 500 \, витков, \, N_2 = 10 \, витков, \, R_1 = 3,10 \, см, \, l_1 = 75,0 \, см\), а ток в соленоиде изменяется в 200 А/с, какая ЭДС индуцируется в окружающей катушке?
Рисунок \(\PageIndex{3}\): соленоид, окруженный катушкой.
Стратегия
Магнитного поля снаружи соленоида нет, а поле внутри имеет величину \(B_1 = \mu_0(N_1/l_1)I_1\) и направлено параллельно оси соленоида.{-3}В. \end{выравнивание*} \]
Значение
Обратите внимание, что M в части (a) не зависит от радиуса \(R_2\) окружающей катушки, потому что магнитное поле соленоида ограничено его внутренней частью.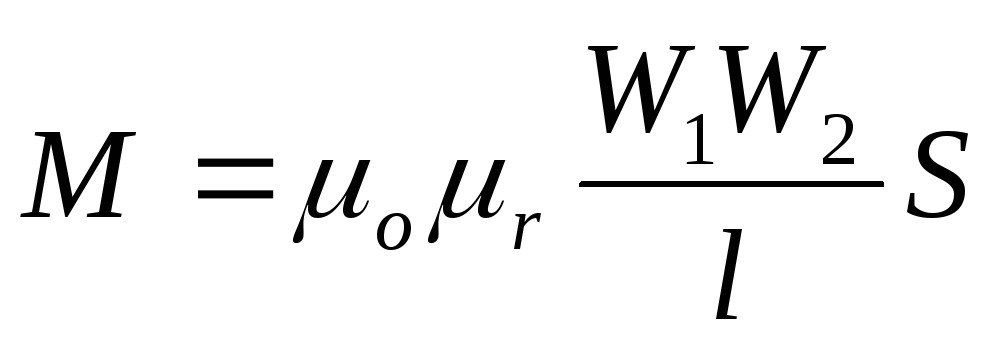 В принципе, мы также можем вычислить M , найдя магнитный поток через соленоид, создаваемый током в окружающей катушке. Этот подход намного сложнее, потому что \(\Phi_{12}\) очень сложен. Однако, поскольку \(M_{12} = M_{21}\), мы знаем результат этого вычисления.{-2} \, В\)
В принципе, мы также можем вычислить M , найдя магнитный поток через соленоид, создаваемый током в окружающей катушке. Этот подход намного сложнее, потому что \(\Phi_{12}\) очень сложен. Однако, поскольку \(M_{12} = M_{21}\), мы знаем результат этого вычисления.{-2} \, В\)
Авторы и авторство
Сэмюэля Дж. Линга (Государственный университет Трумэна), Джеффа Санни (Университет Лойолы Мэримаунт) и Билла Мёбса с многими соавторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Взаимная индуктивность
Взаимная индуктивность
Следующий: Магнитная энергия
Вверх: Магнитная индукция
Предыдущий: Самоиндукция
Рассмотрим теперь два длинных тонких соленоида, накрученных один поверх другого.Длина
каждого соленоида , а общий радиус . Предположим, что дно
катушка имеет витки на единицу длины и по ней течет ток . Магнитный
Магнитный
поток, проходящий через каждый виток верхней катушки, равен
, и
поэтому общий поток, связывающий верхнюю катушку, равен
, где — число витков на единицу длины в верхней
катушка. Отсюда следует, что взаимная индуктивность двух катушек, определяемая
, дан кем-то
| (916) |
Напомним, что собственная индуктивность нижней катушки равна
| (917) |
а верхняя катушка
| (918) |
Следовательно, взаимная индуктивность может быть записана
| (919) |
Заметим, что этот результат зависит от предположения, что всех произведенных потоков
одной катушкой проходит через другую катушку.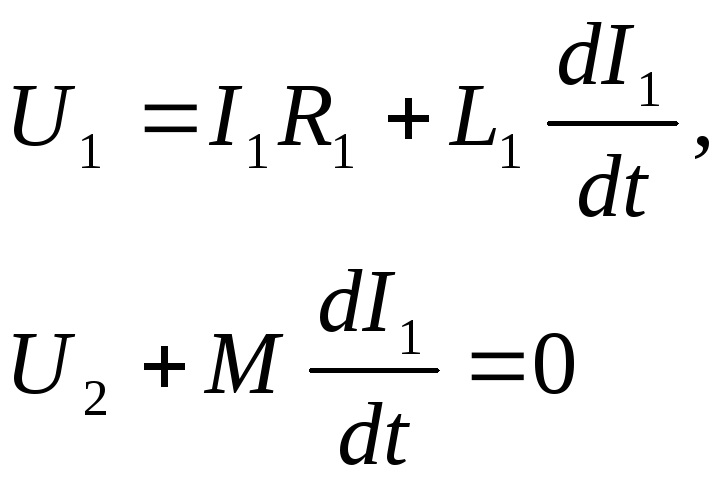 На самом деле часть потока
На самом деле часть потока
просачивается наружу, так что взаимная индуктивность оказывается несколько меньше указанной в
формула выше. Мы можем написать
| (920) |
где константа называется коэффициентом связи ,
и лежит в диапазоне
.
Предположим, что две катушки имеют сопротивление и . Если нижняя катушка
через него протекает мгновенный ток, а полное падение напряжения
, то падение напряжения на его сопротивлении равно .Падение напряжения
из-за противоэ.д.с. создается за счет собственной индуктивности катушки.
. Существует также обратная э.д.с. за счет индуктивной связи с
верхняя катушка. Мы знаем, что поток через нижний виток за счет мгновенного
ток в верхней катушке равен
| (921) |
Таким образом, по закону Фарадея и закону Ленца Э. Д.С. индуцированный в нижней части
Д.С. индуцированный в нижней части
катушка
| (922) |
Падение напряжения на нижней катушке из-за ее взаимной индуктивности с
верхняя катушка минус это выражение.Таким образом, уравнение цепи для нижней катушки имеет вид
| (923) |
Аналогично, уравнение цепи для верхней катушки:
| (924) |
Здесь – полное падение напряжения на верхней катушке.
Предположим, что мы внезапно подключаем батарею Э.Д.С.
до нижней катушки, в то время. Предполагается, что верхняя катушка
разомкнутая цепь или подключенная к вольтметру с очень высоким внутренним сопротивлением,
так что .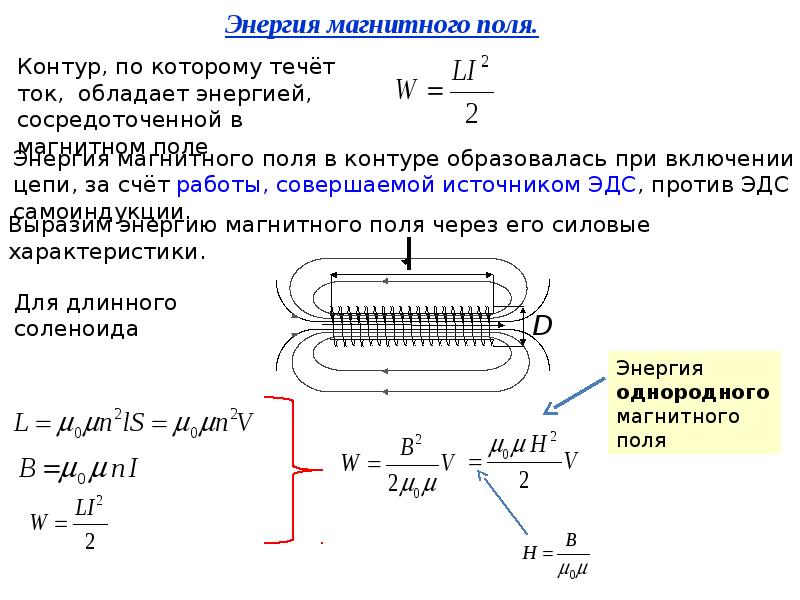 Что такое э.д.с. генерируется в верхней катушке?
Что такое э.д.с. генерируется в верхней катушке?
Поскольку уравнение цепи для нижней катушки имеет вид
| (925) |
где постоянная, а . Мы уже видели решение
это уравнение:
| (926) |
Уравнение цепи для верхней катушки:
| (927) |
давать
| (928) |
Это следует из уравнения(920) что
| (929) |
С
, мы получаем
| (930) |
Обратите внимание, что прерывистый в . Это не проблема, так как
Это не проблема, так как
сопротивление верхней цепи бесконечно, поэтому разрыва в цепи нет.
тока (а значит, и в магнитном поле). А как же ток смещения,
что пропорционально
? Конечно, это прерывисто
at (что явно нефизично)? Ключевой момент здесь,
что у нас конкретно
пренебрегали током смещения во всех наших предыдущих анализах, так что это не
имеет смысл начать беспокоиться об этом сейчас.Если бы мы сохранили смещение
тока в наших расчетах, то
мы бы обнаружили, что напряжение в верхней цепи подскакивает,
в , в масштабе времени, аналогичном времени прохождения света по цепи
( т.е. , прыжок мгновенный во всех смыслах и целях, но
ток смещения остается конечным).
Сейчас,
| (931) |
так что если то напряжение в нижней цепи значительно усиливается
в верхнем контуре.Этот эффект лежит в основе старомодного зажигания автомобиля.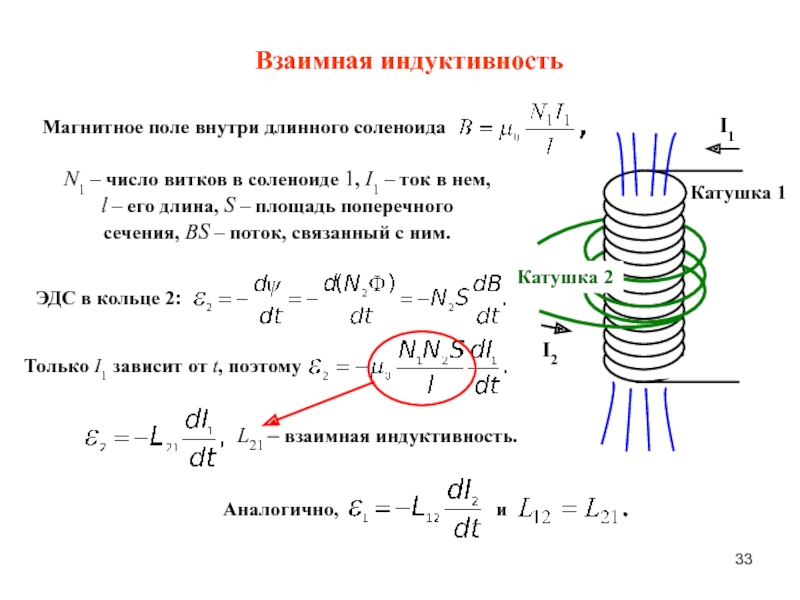
системы. Во вторичной цепи (подключенной к
катушка с очень большим количеством витков) всякий раз, когда ток в первичной цепи
(подключен к катушке с небольшим количеством витков) либо включен, либо выключен.
Первичная цепь подключена к автомобильному аккумулятору (ЭДС которого равна
обычно 12 вольт).
Переключение осуществляется набором точек, которые механически размыкаются и
закрывается при вращении двигателя. Большой скачок напряжения, индуцированный во вторичной цепи,
поскольку точки либо открыты, либо закрыты, искра прыгает через зазор
в этой цепи.Эта искра воспламеняет бензино-воздушную смесь в одном из цилиндров.
Мы могли бы подумать, что оптимальная конфигурация состоит в том, чтобы иметь только один виток в первичной обмотке.
цепи и много витков во вторичной цепи, так что отношение
делается максимально большим. Тем не менее, это не так. Большинство
силовые линии магнитного поля, создаваемые одновитковой первичной катушкой, вероятно,
пропустите вторичную катушку вообще. Это означает, что коэффициент связи
мала, что снижает наведенное во вторичной цепи напряжение. Таким образом, мы
Таким образом, мы
необходимо разумное количество витков в первичной обмотке, чтобы локализовать
индуцированное магнитное поле, так что оно эффективно связывается со вторичной катушкой.
Следующий: Магнитная энергия
Вверх: Магнитная индукция
Предыдущий: Самоиндукция
2006-02-02
11.1 Взаимная индуктивность – введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Сопоставление двух близлежащих цепей, по которым текут переменные во времени токи, с ЭДС, индуцированной в каждой цепи
- Опишите примеры, в которых взаимная индуктивность может быть или не быть желательной
Индуктивность это свойство устройства, которое говорит нам, насколько эффективно оно индуцирует ЭДС в другом устройстве.Другими словами, это физическая величина, выражающая эффективность данного устройства.
Когда две цепи, по которым текут изменяющиеся во времени токи, расположены близко друг к другу, магнитный поток в каждой цепи меняется из-за изменения тока в другой цепи. Следовательно, ЭДС индуцируется в каждой цепи изменением тока в другой. Поэтому этот тип ЭДС называется ЭДС взаимной индукции , а возникающее явление известно как взаимная индуктивность () .В качестве примера рассмотрим две плотно намотанные катушки (рис. 11.1.1). Катушки 1 и 2 имеют витки и и по ним текут токи и , соответственно. Поток через один виток катушки 2, создаваемый магнитным полем тока в катушке 1, равен , тогда как поток через один виток катушки 1 из-за магнитного поля равен .
(рис. 11.1.1)
Рисунок 11.1.1 Некоторые силовые линии магнитного поля, создаваемые током в катушке 1, проходят через катушку 2.
Взаимная индуктивность катушки 2 по отношению к катушке 1 равна отношению потока через витки катушки 2, создаваемого магнитным полем тока в катушке 1, к этому току, то есть
(11. 1.1)
1.1)
Аналогично, взаимная индуктивность катушки 1 по отношению к катушке 2 равна
.
(11.1.2)
Как и емкость, взаимная индуктивность является геометрической величиной. Это зависит от формы и взаимного расположения двух катушек и не зависит от токов в катушках.Единица взаимной индуктивности в системе СИ называется генри ( ) в честь Джозефа Генри (1799–1878), американского ученого, открывшего ЭДС независимо от Фарадея. Таким образом, мы имеем . Из уравнения 11.1.1 и уравнения 11.1.2 мы можем показать, что , поэтому мы обычно опускаем индексы, связанные с взаимной индуктивностью, и пишем
(11.1.3)
ЭДС, развиваемая в каждой катушке, находится путем объединения закона Фарадея и определения взаимной индуктивности.Так как это полный поток через катушку 2 из-за , мы получаем
(11.1.4)
, где мы использовали тот факт, что является постоянной, не зависящей от времени, поскольку геометрия не зависит от времени. Точно так же у нас есть
Точно так же у нас есть
(11.1.5)
В уравнении 11.1.5 мы можем видеть значение более раннего описания взаимной индуктивности () как геометрической величины. Значение аккуратно инкапсулирует физические свойства элементов схемы и позволяет нам отделить физическую схему схемы от динамических величин, таких как ЭДС и ток.Уравнение 11.1.5 определяет взаимную индуктивность с точки зрения свойств в цепи, тогда как предыдущее определение взаимной индуктивности в уравнении 11.1.1 определяется с точки зрения испытываемого магнитного потока, независимо от элементов цепи. Вы должны быть осторожны при использовании Уравнения 11.1.4 и Уравнения 11.1.5, потому что и не обязательно представляют суммарную ЭДС в соответствующих катушках. В каждой катушке также может быть наведена ЭДС из-за ее собственной индуктивности (самоиндуктивность будет обсуждаться более подробно в следующем разделе).
Большая взаимная индуктивность может быть желательной, а может и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать опасную ЭДС на своем металлическом корпусе, если взаимная индуктивность между его катушками и корпусом велика. Одним из способов уменьшить взаимную индуктивность является встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле (уравнение 11.1.3).
Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать опасную ЭДС на своем металлическом корпусе, если взаимная индуктивность между его катушками и корпусом велика. Одним из способов уменьшить взаимную индуктивность является встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле (уравнение 11.1.3).
(рис. 11.1.2)
Рисунок 11.1.2 Нагревательные спирали электрической сушилки для белья могут быть встречно намотаны, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.
Цифровая обработка сигналов является еще одним примером, в котором взаимная индуктивность уменьшается за счет встречной обмотки катушек. ЭДС быстрого включения / выключения, представляющая и в цифровой цепи, создает сложное магнитное поле, зависящее от времени. ЭДС может генерироваться в соседних проводниках. Если этот проводник также несет цифровой сигнал, ЭДС индукции может быть достаточно большой для переключения и с последствиями от неудобных до катастрофических.
Если этот проводник также несет цифровой сигнал, ЭДС индукции может быть достаточно большой для переключения и с последствиями от неудобных до катастрофических.
ПРИМЕР 11.1.1
Взаимная индуктивность
Рисунок 11.1.3 показана катушка из витков и радиуса, окружающая длинный соленоид длиной , радиусом и витками. а) Чему равна взаимная индуктивность двух катушек? (б) Если , , , и ток в соленоиде изменяется со скоростью , какова ЭДС, индуцируемая в окружающей катушке?
(рис. 11.1.3)
Рисунок 11.1.3 Соленоид, окруженный катушкой.
Стратегия
Снаружи соленоида магнитное поле отсутствует, а поле внутри имеет величину и направлено параллельно оси соленоида.Мы можем использовать это магнитное поле, чтобы найти магнитный поток через окружающую катушку, а затем использовать этот поток для расчета взаимной индуктивности для части (а), используя уравнение 11.1.3. Мы решаем часть (b), вычисляя взаимную индуктивность из заданных величин и используя уравнение 11.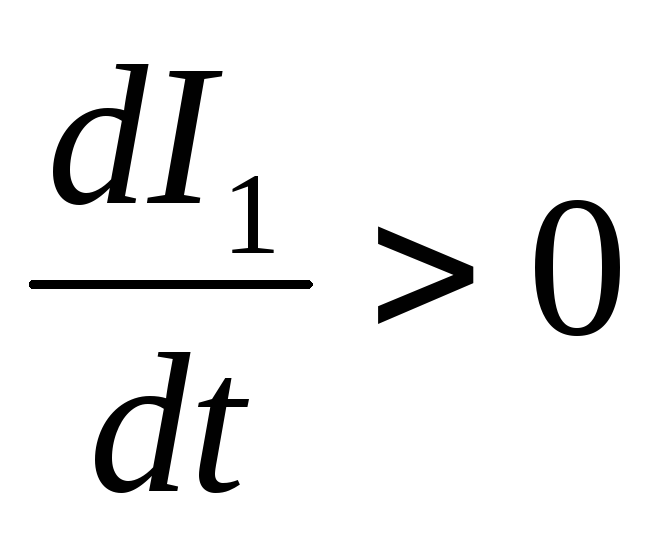 1.4 для расчета ЭДС индукции.
1.4 для расчета ЭДС индукции.
Решение
а. Магнитный поток через окружающую катушку равен
.
Теперь из уравнения 11.1.3 взаимная индуктивность равна
б.Используя предыдущее выражение и данные значения, взаимная индуктивность равна
.
Таким образом, из уравнения 11.1.4 ЭДС, индуцированная в окружающей катушке, равна
Значение
Обратите внимание, что в части (а) не зависит от радиуса окружающей катушки, потому что магнитное поле соленоида ограничено его внутренней частью. В принципе, мы также можем рассчитать, найдя магнитный поток через соленоид, создаваемый током в окружающей катушке.Этот подход намного сложнее, потому что он очень сложен. Однако, поскольку , мы знаем результат этого вычисления.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 11.1
Через соленоид части (b) примера 11.1.1 протекает ток. Какова максимальная ЭДС, индуцируемая в окружающей катушке?
Цитаты Кандела
Контент под лицензией CC, конкретное указание авторства
- Загрузите бесплатно по адресу http://cnx.
 org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
индуктивность
индуктивность
Взаимная и собственная индуктивность
Проблема:
Для запуска электропоезда нужно 12 В, а напряжение на выходе 120 В.
Каково отношение числа витков первичной обмотки к числу
включает вторичную обмотку трансформатора, который вы используете?
Решение:
- Концепты:
Взаимная индуктивность, собственная индуктивность, трансформатор - Рассуждение:
Прототип трансформатора имеет первичную и вторичную обмотки.
намотаны по обе стороны железного кольца.Если ток в первичной
меняется катушка, меняется поток через вторичную катушку и ЭДС
наводится во вторичной обмотке. ЭДС, индуцируемая во вторичной обмотке, равна
пропорциональна числу витков N 2 вторичной обмотки,
так как количество витков определяет общий магнитный поток, проходящий через
эта катушка. ЭДС индукции также пропорциональна напряжению В 1
ЭДС индукции также пропорциональна напряжению В 1
через первичную катушку, так как это определяет величину первичной
тока и связанного с ним магнитного поля.Индуцированное напряжение равно
обратно пропорциональна, однако, количеству витков N 1
первичная катушка. Отношения принимают формуВ 2 /Н 2 = В 1 /Н 1 .
Отношение количества витков на двух катушках определяет отношение
напряжения. Самоиндукция является причиной того, что ЭДС, индуцируемая в
вторичная обмотка обратно пропорциональна числу витков
первичная катушка.Если первичная обмотка имеет больше витков, ее труднее
производить быстрое изменение тока, протекающего через него, из-за обратного
ЭДС, создаваемая самоиндукцией. Этот эффект ограничивает ток и
поэтому величина магнитного поля, создаваемого первичной катушкой,
что, в свою очередь, ограничивает магнитный поток, проходящий через вторичную катушку.Предположим, что одно и то же поле B пронизывает обе катушки и поток на виток Φ B
одинаково для обеих катушек. Общий поток за виток обусловлен
Общий поток за виток обусловлен
токи в обеих катушках. В хорошо спроектированном трансформаторе сопротивление
катушек мало, и мы пренебрегаем здесь. Тогда ЭДС индукции в
первичная обмотка должна точно уравновешивать приложенное напряжение V p .
V p = N 1 dΦ B /dt.
Поскольку Φ B одинакова для вторичной обмотки, ЭДС индукции в
вторичная обмотка ε с
= N 2 dΦ B /dt.Пока нет нагрузки
подключены, измеряем выходное напряжение V s = N 2 dΦ B /dt.
V p /N p = V s /N s . - Детали расчета:
N 1 /N 2 = V 1 /V 2 . Ты нуждаешься в
трансформатор с в десять раз большим числом витков на первичной обмотке, чем на
вторичная катушка.
Проблема:
Большая катушка радиуса а лежит в плоскости х-у с центром в точке
Происхождение. Коаксиальная малая катушка радиуса b << a с
ось, параллельная оси z, лежит на расстоянии z выше большой
катушка. По маленькой катушке течет постоянный ток I.
Коаксиальная малая катушка радиуса b << a с
ось, параллельная оси z, лежит на расстоянии z выше большой
катушка. По маленькой катушке течет постоянный ток I.
а) Найдите магнитный поток, связанный с большой катушкой.
(b) Если маленькая катушка движется вдоль оси z с постоянной скоростью
против
= v 0 k , что
это ЭДС ε
индуцируется в большой катушке как
функция времени? Пусть z = 0 при t = 0,
Решение:
- Концепты:
Флюс
F = ∫ A B ∙ n дА, F = MI, M =
взаимная индуктивность, ε = -∂F/∂t
= ЭДС индукции - Рассуждение:
Найдя взаимную индуктивность катушек как функцию катушки
разделения, можно найти поток через большую катушку и ЭДС индукции. - Детали расчета:
(а) Поток через большую катушку из-за тока I в малой
катушка F = MI. Чтобы найти M, мы вычисляем поток через маленькую катушку
за счет тока I в большой катушке.
[При расчете взаимной индуктивности можно рассчитать поток через
цепи 1 из-за тока в цепи 2 или потока через цепь 2 из-за
ток в цепи 1. В данной задаче одним из этих расчетов является
часто намного проще, чем другие.]
То
поле на оси токовой петли радиуса a равно B =
к мк 0 Ia 2 /[2(a 2
+ z 2 ) 3/2 ] (единицы СИ), если ток течет в
ф
направление.
Поток через петлю радиуса b равен
F = ∫ А В ∙ н дА.
Ф =
πb 2 μ 0 Ia 2 /[2(a 2 + z 2 ) 3/2 ].
(Поскольку b << a, B почти постоянно по площади, если малый
петля.)
F = МИ, М =
πb 2 a 2 μ 0 /[2(a 2
+ z 2 ) 3/2 ].
(б) ε = -∂F/∂t
= -(πb 2 a 2 μ 0 I/2)(∂/∂t)(1/(a 2
+ z 2 ) 3/2 )
= (3πb 2 a 2 μ 0 I/4)(1/(a 2
+ з 2 ) 5/2 )2зв 0 .
ε =
(3πb 2 а 2 μ 0 I/2)(zv 0 /(а 2
+ z 2 ) 5/2 ).
Проблема:
Тороидальная катушка из N витков имеет квадратное поперечное сечение, каждая сторона
квадрат имеет длину a и внутренний радиус b.
а) Найдите индуктивность катушки.
б) Найти взаимную индуктивность системы, состоящей из катушки и
длинный прямой провод вдоль оси симметрии катушки.(Предположить, что
проводники, замыкающие цепь, частью которой является длинный прямой провод
расположены далеко от катушки, так что их влиянием можно пренебречь.)
в) Найти отношение собственной индуктивности катушки к взаимной
индуктивность системы.
Решение:
- Концепты:
Закон Ампера, магнитный поток, взаимная индуктивность, собственная индуктивность - Рассуждение
Закон Ампера можно использовать для нахождения магнитных полей, создаваемых катушкой и
к проводу. Найдя поток этих полей через катушку, мы можем
Найдя поток этих полей через катушку, мы можем
найти самоиндукцию и взаимную индуктивность. - Детали расчета:
(а) Закон Ампера дает магнитное поле внутри тора из-за тока
Я в обмотках. Симметрия диктует, что магнитное поле направлено в
в
( φ /φ)-направление.
Б =
( φ /φ) μ 0 NI/(2πr).
Здесь N — число витков обмоток.Поток этого поля через обмотки равен
F = ∫ В ∙d А
= [μ 0 N 2 I/(2π)]a∫ b b+a (1/r)dr
= [μ 0 N 2 I/(2π)]a
пер((б+а)/б).
F = LI, L = [μ 0 N 2 a/(2π)]
пер((б+а)/б).
(b) Закон Ампера дает магнитное поле внутри тора из-за
ток I в проводе.
Б =
( φ /φ)μ 0 I/(2πr).
Поток этого поля через обмотки равен
F = ∫ В ∙d А
= [μ 0 NI/(2π)]a∫ b b+a (1/r)dr
= [μ 0 NI/(2π)]a
пер((б+а)/б).
F = MI, M = [μ 0 Na/(2π)]
пер((б+а)/б).
(в) L/M = N,
Проблема:
По длинному кабелю течет ток в одном направлении, равномерно распределенный по всей его длине.
круглое сечение.Ток возвращается по поверхности (есть
очень тонкая изолирующая оболочка, разделяющая токи). Найдите себя
индуктивность на единицу длины.
Решение:
- Концепты:
Собственная индуктивность, Ампер
U = ½LI 2 = (1/(2µ 0 ))∫ B 2 dV. - Рассуждение:
Находим магнитное поле
произвести по току из закона Ампера и решить
½LI 2 = (1/(2μ 0 ))∫ B 2 дВ для собственной индуктивности L. - Детали расчета:
Предположим, что провод имеет радиус a и концентричен с осью z.
Предположим, что по ней течет ток I.
Для круговой петли Γ радиуса r,
концентрично оси z и лежащей в плоскости xy, мы имеем
2πrB = μ 0 I через
Г .
В = В ( φ / φ).
я через
Γ = Ir 2 /a 2 .
r < a: B = μ 0 Ir/(2πa 2 )
r > a: B = 0.
Для отрезка единичной длины имеем
(½μ 0 )∫ B 2 dV = (π/μ 0 )( μ 0 I/(2πa 2 8 )) 0 а р 3 др
= (π/μ 0 )(μ 0 I/(2πa 2 )) 2 (a 4 /4)
= (μ 0 I 2 8(19597 ) 2
знак равно
½LI 2 .
L = (μ 0 / (8π)).
Взаимная индуктивность — обзор
12.4.1.2.1 Катушка индуктивности
Ток, протекающий через катушку индуктивности, несет энергию, запасенную в магнитном поле. Напряжение на катушке индуктивности является результатом самоиндуцированной электродвижущей силы, которая противодействует этому напряжению и пропорционально производной тока по времени: «индуктивность» измеряется в генри (ч).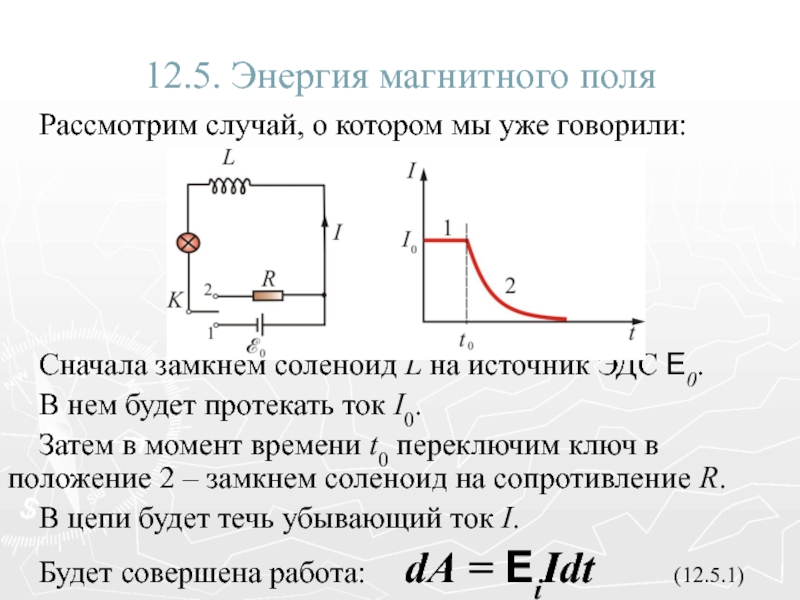 (Генри на самом деле представляет собой число оборотов Вебера на ампер или вольт на ампер/с и названо в честь американского физика Джозефа Генри (1797–1878 гг.).) Катушка индуктивности — это просто катушка проволоки, в которой используется взаимная магнитная связь (т. е. взаимная индуктивность) между катушками проволоки. Индуктивность связана с магнитным потоком Ф, переносимым катушкой индуктивности, а также с геометрией катушки и числом витков или «витков» не так полезно, как соответствующее уравнение резистора (уравнение 12.11) для определения значения индуктивности катушки, потому что фактический поток в катушке зависит от формы катушки.На практике индуктивность катушки определяется опытным путем.
(Генри на самом деле представляет собой число оборотов Вебера на ампер или вольт на ампер/с и названо в честь американского физика Джозефа Генри (1797–1878 гг.).) Катушка индуктивности — это просто катушка проволоки, в которой используется взаимная магнитная связь (т. е. взаимная индуктивность) между катушками проволоки. Индуктивность связана с магнитным потоком Ф, переносимым катушкой индуктивности, а также с геометрией катушки и числом витков или «витков» не так полезно, как соответствующее уравнение резистора (уравнение 12.11) для определения значения индуктивности катушки, потому что фактический поток в катушке зависит от формы катушки.На практике индуктивность катушки определяется опытным путем.
Запасенная энергия может быть определена из уравнения для мощности (уравнение 12.5) и соотношения напряжения и тока катушки индуктивности (уравнение 12.15): dt=Lidi
Суммарная энергия, хранящаяся в виде тока, увеличивается от 0 до значения I , определяемого как:
(12. 17)E=∫dE=L∫0Iidi=12LI2
17)E=∫dE=L∫0Iidi=12LI2
Позже в этой главе мы обнаружим сходство между уравнением кинетической энергии массы (уравнение 12.55) и энергия в индукторе. Уравнение 12.17 объясняет, почему индуктор считается инерционным элементом. Он ведет себя так, как если бы энергия хранилась в виде кинетической энергии, связанной с потоком движущихся электронов, и это хороший способ концептуализировать поведение индуктора, хотя на самом деле энергия хранится в электромагнитном поле. Катушки индуктивности следуют тем же правилам полярности, что и резисторы. На рисунке 12.6 показан символ индуктора, схематическое изображение катушки с соответствующими направлениями тока и напряжения.
Рисунок 12.6. Символ катушки индуктивности, показывающий полярность этого пассивного элемента.
Если ток через индуктор постоянный (т. е. «постоянный ток» или «постоянный ток»), то в индукторе не будет накапливаться энергия, и напряжение на индукторе будет равно нулю, независимо от величины установившегося тока течет через индуктор. 3 Состояние, когда напряжение на элементе равно нулю независимо от тока через элемент, известно как «короткое замыкание».Следовательно, индуктор появляется как короткое замыкание на постоянный ток, функция, которую можно использовать для решения определенных проблем с электрической цепью, возникающих позже.
3 Состояние, когда напряжение на элементе равно нулю независимо от тока через элемент, известно как «короткое замыкание».Следовательно, индуктор появляется как короткое замыкание на постоянный ток, функция, которую можно использовать для решения определенных проблем с электрической цепью, возникающих позже.
Зависимость v — i катушки индуктивности также может быть выражена через ток. Решение уравнения 12.15 для i :
(12.18)vL=LdiLdt;diL=1LvLdt;∫diL=∫1LvLdtiL=1L∫vLdt
Интеграл любой функции будет непрерывным, даже если эта функция содержит разрыв до тех пор, пока поскольку этот разрыв конечен.Непрерывная функция не изменяется мгновенно, т. е. для непрерывной функции:
(12.19)f(t−)=f(t+)foranyt
индуктора (уравнение 12.18), в реальных ситуациях ток будет непрерывным, потому что любые скачки напряжения, безусловно, будут конечными. Таким образом, ток через индуктор может изменяться медленно или быстро (в зависимости от тока), но он никогда не может изменяться прерывистым или ступенчатым образом.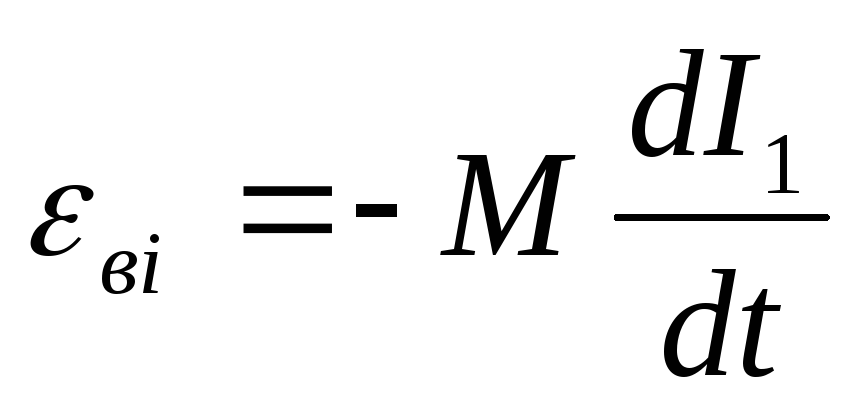 С математической точки зрения, для катушки индуктивности:
С математической точки зрения, для катушки индуктивности:
(12,20)iL(t−)=iL(t+)
Поскольку ток, проходящий через катушку индуктивности, всегда непрерывен, одним из популярных применений катушки индуктивности является снижение пиков тока ( то есть разрывы). У тока, проходящего через индуктор, любые пики будут «заглушены», поэтому индуктор, используемый для уменьшения пиков, иногда называют «дросселем».
Взаимная индуктивность и основные операции | Трансформеры
Поведение катушек индуктивности, намотанных на проводящий сердечник
Предположим, что нам необходимо намотать катушку изолированного провода на петлю из ферромагнитного материала и подать на эту катушку источник переменного напряжения: (рисунок ниже (a))
Изолированная обмотка на ферромагнитном контуре имеет индуктивное сопротивление, ограничивающее переменный ток
В качестве индуктора мы ожидаем, что эта катушка с железным сердечником будет противодействовать приложенному напряжению своим индуктивным сопротивлением, ограничивая ток через катушку, как предсказывается уравнениями:
X L = 2πfL и I=E/X (или I=E/Z)
Однако для целей этого примера нам необходимо более подробно рассмотреть взаимодействие напряжения, тока и магнитного потока в устройстве.
Закон напряжения Кирхгофа описывает, как алгебраическая сумма всех напряжений в контуре должна равняться нулю. В этом примере мы могли бы применить этот фундаментальный закон электричества для описания соответствующих напряжений источника и катушки индуктивности.
Здесь, как и в любой цепи с одним источником и одной нагрузкой, падение напряжения на нагрузке должно равняться напряжению, выдаваемому источником, при нулевом падении напряжения вместе с сопротивлением любых соединительных проводов.
Другими словами, нагрузка (катушка индуктивности) должна создавать противодействующее напряжение, равное по величине источнику, чтобы оно могло уравновесить напряжение источника и произвести алгебраическую сумму напряжений контура, равную нулю.
Откуда возникает это противоположное напряжение? Если бы нагрузкой был резистор (рисунок выше (б)), то падение напряжения возникает из-за потерь электроэнергии, «трения» носителей заряда, протекающих через сопротивление.
При идеальном индукторе (отсутствие сопротивления в проводе катушки) противодействующее напряжение возникает из-за другого механизма: реакции на изменение магнитного потока в железном сердечнике. При изменении переменного тока изменяется поток Φ. Изменение потока индуцирует противоЭДС.
Связь между напряжением, током и магнитным потоком
Майкл Фарадей открыл математическую связь между магнитным потоком (Φ) и наведенным напряжением с помощью этого уравнения:
Мгновенное напряжение (падение напряжения в любой момент времени) на проволочной катушке равно числу витков этой катушки вокруг сердечника (N), умноженному на мгновенную скорость изменения магнитного потока (dΦ/dt) соединение с катушкой.
На графике (рисунок ниже) это выглядит как набор синусоидальных волн (при условии, что источник синусоидального напряжения), волна магнитного потока отстает от волны напряжения на 90°:
Магнитный поток, как и ток, отстает от приложенного напряжения на 90°
Вот почему переменный ток через катушку индуктивности отстает от формы волны приложенного напряжения на 90°: потому что это то, что требуется для создания изменяющегося магнитного потока, скорость изменения которого создает противоположное напряжение, синфазное с приложенным напряжением.
Из-за его функции по обеспечению намагничивающей силы (ммс) для сердечника этот ток иногда называют током намагничивания .
Следует отметить, что ток через индуктор с железным сердечником не является идеально синусоидальным (синусоидальным) из-за нелинейной кривой намагничивания железа B/H.
На самом деле, если индуктор изготовлен дешево, с использованием как можно меньшего количества железа, плотность магнитного потока может достигать высоких уровней (приближаясь к насыщению), что приводит к форме волны намагничивающего тока, которая выглядит примерно так, как показано на рисунке ниже:
Когда плотность потока приближается к насыщению, форма волны тока намагничивания искажается
Когда ферромагнитный материал приближается к насыщению магнитного потока, требуются непропорционально большие уровни силы магнитного поля (mmf), чтобы обеспечить одинаковое увеличение потока магнитного поля (Φ).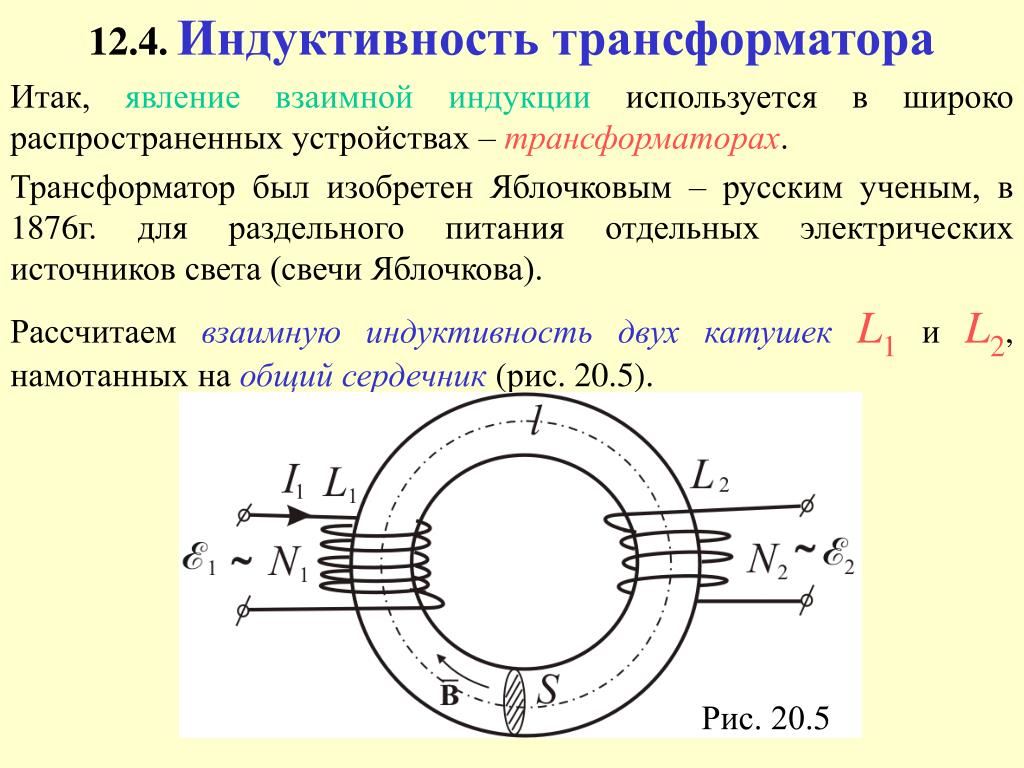
Поскольку ммс пропорциональна току через намагничивающую катушку (ммс = NI, где «N» — число витков провода в катушке, а «I» — ток через нее), большое увеличение ммс, необходимое для питания необходимое увеличение потока приводит к значительному увеличению тока катушки.
Таким образом, ток катушки резко увеличивается на пиках, чтобы поддерживать неискаженную форму волны потока, учитывая колоколообразные полупериоды формы волны тока на приведенном выше графике.
Возбуждающий ток и его эффекты
Ситуация еще больше осложняется потерями энергии в железном сердечнике. Эффекты гистерезиса и вихревых токов способствуют дальнейшему искажению и усложнению формы волны тока, делая ее еще менее синусоидальной и изменяя ее фазу так, чтобы она отставала от формы волны приложенного напряжения чуть менее чем на 90°.
Этот ток катушки, являющийся результатом суммы всех магнитных эффектов в сердечнике (намагничивание dΦ/dt плюс потери на гистерезис, потери на вихревые токи и т. д.) называется возбуждающим током .
д.) называется возбуждающим током .
Искажение тока возбуждения катушки индуктивности с железным сердечником можно свести к минимуму, если она спроектирована и работает при очень низкой плотности потока. Вообще говоря, для этого требуется сердечник с большой площадью поперечного сечения, что делает катушку индуктивности громоздкой и дорогой.
Однако для простоты предположим, что сердечник нашего примера далек от насыщения и свободен от всех потерь, что приводит к идеально синусоидальному току возбуждения.
Как мы уже видели в главе о катушках индуктивности, наличие кривой тока, сдвинутой по фазе на 90° с формой волны напряжения, создает условия, при которых мощность попеременно поглощается и возвращается в цепь катушкой индуктивности.
Если катушка индуктивности идеальна (нет сопротивления провода, нет потерь в магнитном сердечнике и т. д.), она будет рассеивать нулевую мощность.
Теперь рассмотрим тот же индуктор, но на этот раз со второй катушкой (рисунок ниже), намотанной на тот же железный сердечник. Первая катушка будет помечена как первичная катушка , а вторая будет помечена как вторичная катушка :
Первая катушка будет помечена как первичная катушка , а вторая будет помечена как вторичная катушка :
.
Ферромагнитный сердечник с первичной обмоткой (с приводом от переменного тока) и вторичной обмоткой.
Взаимная индукция
Если эта вторичная катушка претерпевает такое же изменение магнитного потока, как и первичная (что и должно происходить при условии идеального удерживания магнитного потока через общий сердечник), и имеет такое же число витков вокруг сердечника, напряжение равной величины и фазы к приложенному напряжению будет индуцироваться по всей его длине.
На следующем графике (рисунок ниже) форма сигнала наведенного напряжения немного меньше, чем форма сигнала напряжения источника, просто для того, чтобы отличить один от другого:
Вторичная цепь с разомкнутым контуром воспринимает тот же поток Φ, что и первичная. Следовательно, индуцированное вторичное напряжение e s имеет ту же величину и фазу, что и первичное напряжение e p .
Этот эффект называется взаимной индуктивностью : индукция напряжения в одной катушке в ответ на изменение тока в другой катушке.Как и нормальная (собственная) индуктивность, она измеряется в генри, но в отличие от нормальной индуктивности обозначается заглавной буквой «М», а не буквой «L»:
Во вторичной обмотке не будет тока, так как она разомкнута. Однако, если мы подключим к нему нагрузочный резистор, переменный ток будет проходить через катушку в фазе с наведенным напряжением (поскольку напряжение на резисторе и ток через него всегда синфазны друг с другом) .(Рисунок ниже)
Резистивная нагрузка на вторичной обмотке имеет синфазное напряжение и ток.
Во-первых, можно было бы ожидать, что этот ток вторичной обмотки вызовет дополнительный магнитный поток в сердечнике. На самом деле это не так. Если бы в сердечнике индуцировался больший поток, в первичной обмотке индуцировалось бы большее напряжение (помните, что e = dΦ/dt).
Этого не может быть, потому что индуцированное напряжение первичной обмотки должно оставаться с той же величиной и фазой, чтобы сбалансироваться с приложенным напряжением в соответствии с законом напряжения Кирхгофа.Следовательно, ток вторичной обмотки не может влиять на магнитный поток в сердечнике.
Однако то, что изменяет , так это количество ммс в магнитной цепи.
Магнитодвижущая сила
Магнитодвижущая сила возникает всякий раз, когда по проводу протекает ток. Обычно эта МДС сопровождается магнитным потоком в соответствии с уравнением МДС=ΦR «магнитного закона Ома».
Однако в этом случае дополнительный поток не допускается, поэтому МДС вторичной катушки может существовать только в том случае, если первичная катушка создает противодействующую МДС равной величины и с противоположной фазой.
Действительно, именно это и происходит: в первичной обмотке формируется переменный ток — на 180° в противофазе с током вторичной обмотки — для создания этой противодействующей МДС и предотвращения дополнительного потока в сердечнике.
На иллюстрацию добавлены метки полярности и стрелки направления тока для пояснения фазовых соотношений: (Рисунок ниже)
Поток остается постоянным при приложении нагрузки. Однако нагруженная вторичная обмотка создает противодействующую МДС.
Если этот процесс покажется вам немного запутанным, не волнуйтесь. Динамика трансформатора — сложная тема. Важно понимать следующее: когда переменное напряжение подается на первичную катушку, оно создает магнитный поток в сердечнике, который индуцирует переменное напряжение во вторичной катушке синфазно с напряжением источника.
Любой ток, проходящий через вторичную катушку для питания нагрузки, индуцирует соответствующий ток в первичной катушке, получая ток от источника.
Взаимная индуктивность и трансформаторы
Обратите внимание, что первичная обмотка ведет себя как нагрузка по отношению к источнику переменного напряжения, а вторичная обмотка ведет себя как источник по отношению к резистору.
Вместо того, чтобы просто поочередно поглощать и возвращать энергию в цепь первичной обмотки, теперь энергия передается во вторичную обмотку, где она подается на рассеивающую (потребляющую энергию) нагрузку. Насколько источник «знает», он напрямую питает резистор.
Конечно, имеется также дополнительный ток первичной обмотки, отстающий от приложенного напряжения на 90°, которого как раз достаточно, чтобы намагнитить сердечник и создать необходимое напряжение для уравновешивания с источником ( ток возбуждения ).
Мы называем этот тип устройства трансформатором , потому что он преобразует электрическую энергию в магнитную энергию, а затем снова в электрическую энергию. Поскольку его работа зависит от электромагнитной индукции между двумя стационарными катушками и магнитного потока изменяющейся величины и «полярности», трансформаторы обязательно являются устройствами переменного тока.
Его схематическое обозначение выглядит как две катушки индуктивности (катушки), имеющие общий магнитный сердечник: (рисунок ниже)
Схематическое обозначение трансформатора состоит из двух обозначений катушек индуктивности, разделенных линиями, обозначающими ферромагнитный сердечник.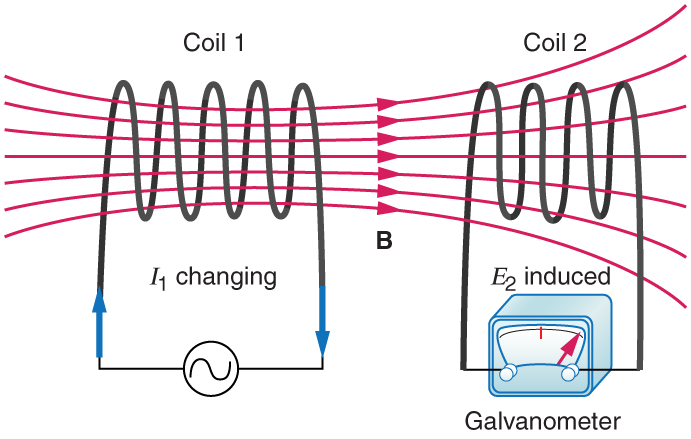
Две катушки индуктивности легко различимы по приведенному выше символу. Пара вертикальных линий представляет собой железный сердечник, общий для обоих индукторов. В то время как многие трансформаторы имеют ферромагнитные материалы сердечника, есть некоторые, у которых их нет, поскольку составляющие их катушки индуктивности магнитно связаны друг с другом через воздух.
На следующей фотографии показан силовой трансформатор того типа, который используется в газоразрядном освещении. Здесь хорошо видны две катушки индуктивности, намотанные на железный сердечник. В то время как в большинстве конструкций трансформаторов катушки и сердечник заключены в металлический каркас для защиты, этот конкретный трансформатор открыт для осмотра и поэтому хорошо служит для иллюстративных целей (рисунок ниже):
Пример газоразрядного трансформатора освещения.
Первичная и вторичная обмотки
Здесь видны обе катушки провода с изоляцией из лака медного цвета. Верхняя катушка больше, чем нижняя, и имеет большее количество «витков» вокруг сердечника. В трансформаторах катушки индуктивности часто называют обмотками в связи с производственным процессом, при котором провод наматывается вокруг материала сердечника.
Верхняя катушка больше, чем нижняя, и имеет большее количество «витков» вокруг сердечника. В трансформаторах катушки индуктивности часто называют обмотками в связи с производственным процессом, при котором провод наматывается вокруг материала сердечника.
Как смоделировано в нашем первоначальном примере, активная катушка индуктивности трансформатора называется первичной обмоткой , а катушка без питания называется вторичной обмоткой .
На следующей фотографии (рисунок ниже) трансформатор показан разрезанным пополам, обнажая поперечное сечение железного сердечника, а также обе обмотки.Как и в трансформаторе, показанном ранее, в этом устройстве также используются первичная и вторичная обмотки с разным числом витков.
Также видно, что сечение провода различается между первичной и вторичной обмотками. Причина этого несоответствия в калибре проволоки будет ясна в следующем разделе этой главы.
Кроме того, на этой фотографии видно, что железный сердечник состоит из множества тонких листов (слоев), а не из цельного куска.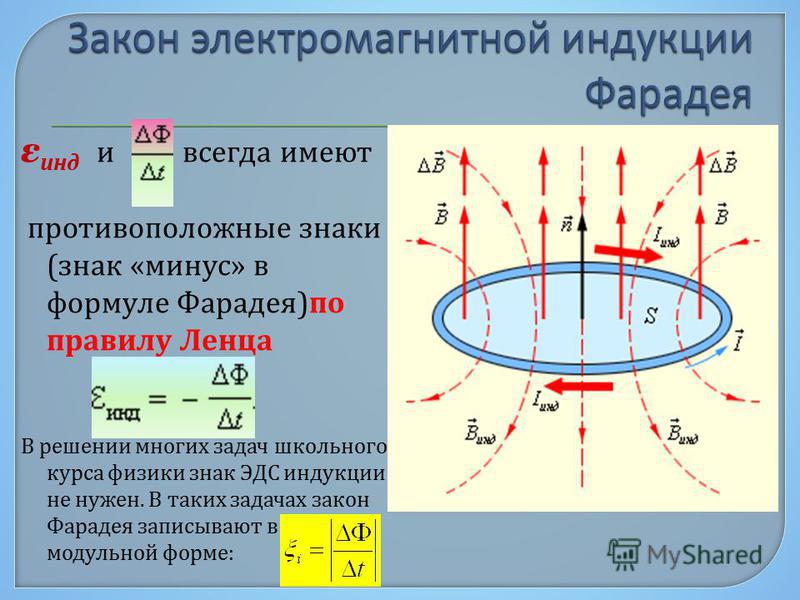 Причина этого также будет объяснена в следующем разделе этой главы.
Причина этого также будет объяснена в следующем разделе этой главы.
Поперечное сечение трансформатора показывает сердечник и обмотки.
Простое действие трансформатора с использованием SPICE
С помощью SPICE легко продемонстрировать действие простого трансформатора, установив первичную и вторичную обмотки имитируемого трансформатора в виде пары «взаимных» катушек индуктивности (рисунок ниже).
Коэффициент связи магнитного поля указан в конце строки «k» в описании схемы SPICE, этот пример приведен почти в совершенстве (1.000). Этот коэффициент описывает, насколько тесно «связаны» магнитные свойства двух катушек индуктивности. Чем лучше магнитно связаны эти два индуктора, тем эффективнее должна быть передача энергии между ними.
Цепь Spice для связанных катушек индуктивности.
трансформатор v1 1 0 ac 10 грех rbogus1 1 2 1e-12 rbogus2 5 0 9e12 л1 2 0 100 л2 3 5 100 ** Эта строка сообщает SPICE, что две катушки индуктивности ** l1 и l2 магнитно «связаны» друг с другом к л1 л2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac лин 1 60 60 .print переменный v (2,0) я (v1) .print ac v(3,5) i(vi1) .конец
Примечание: поддельные резисторы R необходимы для удовлетворения некоторых особенностей SPICE. Первый разрывает непрерывную петлю между источником напряжения и L 1 , что не разрешено SPICE. Второй обеспечивает путь к земле (узел 0) от вторичной цепи, что необходимо, поскольку SPICE не может работать ни с какими незаземленными цепями.
частота v(2) i(v1) 6.000Э+01 1.000Э+01 9.975Э-03 Первичная обмотка частота v(3,5) i(vi1) 6.000Э+01 9.962Э+00 9.962Э-03 Вторичная обмотка
Обратите внимание, что при одинаковой индуктивности обеих обмоток (по 100 генри каждая) переменные напряжения и токи для них почти равны. Разница между первичным и вторичным токами — это ток намагничивания, о котором говорилось ранее: ток отставания на 90 °, необходимый для намагничивания сердечника.
Как видно здесь, он обычно очень мал по сравнению с первичным током, индуцированным нагрузкой, поэтому первичный и вторичный токи почти равны.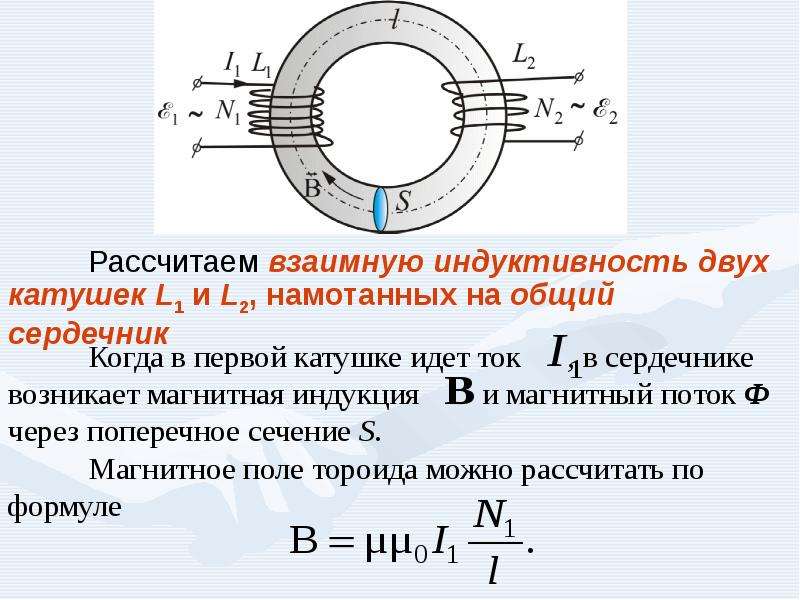 То, что вы видите здесь, вполне типично для КПД трансформатора.
То, что вы видите здесь, вполне типично для КПД трансформатора.
КПД менее 95% считается плохим для современных конструкций силовых трансформаторов, и эта передача мощности происходит без движущихся частей или других компонентов, подверженных износу.
Если мы уменьшим сопротивление нагрузки, чтобы потреблять больший ток при том же уровне напряжения, мы увидим, что ток через первичную обмотку в ответ увеличивается.
Несмотря на то, что источник питания переменного тока не подключен напрямую к сопротивлению нагрузки (скорее, он электромагнитно «связан»), величина тока, потребляемого от источника, будет почти такой же, как величина тока, который потреблялся бы, если бы нагрузка была напрямую подключена к источнику.
Внимательно посмотрите на следующие две симуляции SPICE, показывающие, что происходит с различными значениями нагрузочных резисторов:
трансформатор v1 1 0 ac 10 грех rbogus1 1 2 1e-12 rbogus2 5 0 9e12 л1 2 0 100 л2 3 5 100 к л1 л2 0.999 vi1 3 4 ac 0 ** Обратите внимание на сопротивление нагрузки 200 Ом. нагрузка 4 5 200 .ac лин 1 60 60 .print переменный v (2,0) я (v1) .print ac v(3,5) i(vi1) .конец
частота v(2) i(v1) 6.000E+01 1.000E+01 4.679E-02 частота v(3,5) i(vi1) 6.000E+01 9.348E+00 4.674E-02
Обратите внимание, как первичный ток близко следует за вторичным током. В нашем первом моделировании оба тока составляли приблизительно 10 мА, но теперь они оба составляют около 47 мА.В этом втором моделировании два тока ближе к равенству, потому что ток намагничивания остается таким же, как и раньше, в то время как ток нагрузки увеличился.
Обратите также внимание на то, как вторичное напряжение несколько уменьшилось при более тяжелой (большей токовой) нагрузке. Давайте попробуем другую симуляцию с еще меньшим значением сопротивления нагрузки (15 Ом):
.
трансформатор v1 1 0 ac 10 грех rbogus1 1 2 1e-12 rbogus2 5 0 9e12 л1 2 0 100 л2 3 5 100 к л1 л2 0.999 vi1 3 4 ac 0 4 5 15 .ac лин 1 60 60 .print переменный v (2,0) я (v1) .print ac v(3,5) i(vi1) .конец
частота v(2) i(v1) 6.000E+01 1.000E+01 1.301E-01 частота v(3,5) i(vi1) 6.000E+01 1.950E+00 1.300E-01
Наш ток нагрузки теперь составляет 0,13 А, или 130 мА, что значительно выше, чем в прошлый раз. Первичный ток очень близок к тому же самому, но обратите внимание, что вторичное напряжение упало значительно ниже первичного напряжения (1.95 вольт против 10 вольт на первичной обмотке).
Причиной этого является несовершенство конструкции нашего трансформатора: из-за того, что первичная и вторичная индуктивности не полностью связаны (коэффициент k 0,999 вместо 1,000), возникает «блуждающая» или « утечка » индуктивность. Другими словами, часть магнитного поля не связана со вторичной катушкой и, следовательно, не может передать ей энергию: (рисунок ниже)
Индуктивность рассеяния возникает из-за того, что магнитный поток не пересекает обе обмотки.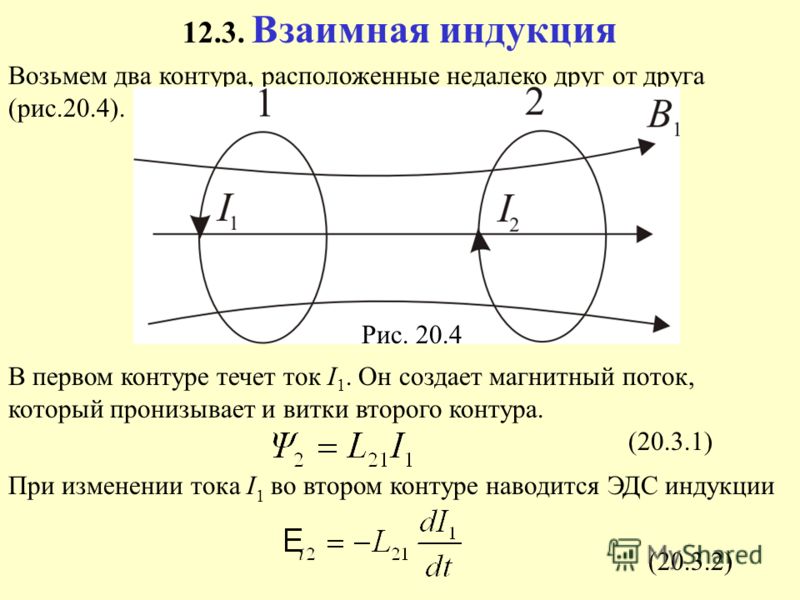
Следовательно, этот поток «утечки» просто накапливает и возвращает энергию в цепь источника через собственную индуктивность, эффективно действуя как последовательное сопротивление как в первичной, так и во вторичной цепях. Напряжение на этом последовательном импедансе падает, что приводит к снижению напряжения на нагрузке: напряжение на нагрузке «проседает» по мере увеличения тока нагрузки. (Рисунок ниже)
Эквивалентная схема моделирует индуктивность рассеяния как последовательные катушки индуктивности, не зависящие от «идеального трансформатора».
Если мы изменим конструкцию трансформатора, чтобы иметь лучшую магнитную связь между первичной и вторичной обмотками, значения напряжения между первичной и вторичной обмотками снова станут намного ближе к равенству:
трансформатор v1 1 0 ac 10 грех rbogus1 1 2 1e-12 rbogus2 5 0 9e12 л1 2 0 100 л2 3 5 100 ** Коэффициент связи = 0,99999 вместо 0,999.к л1 л2 0,99999 vi1 3 4 ac 0 4 5 15 .ac лин 1 60 60 .print переменный v (2,0) я (v1) .напечатать ac v(3,5) i(vi1) .конец
частота v(2) i(v1) 6.000E+01 1.000E+01 6.658E-01 частота v(3,5) i(vi1) 6.000E+01 9.987E+00 6.658E-01
Здесь мы видим, что наше вторичное напряжение снова стало равным первичному, а вторичный ток также равен первичному току. К сожалению, построить настоящий трансформатор с таким комплектом связи очень сложно.
Компромиссное решение состоит в том, чтобы спроектировать как первичную, так и вторичную катушки с меньшей индуктивностью, стратегия заключается в том, что меньшая индуктивность в целом приводит к меньшей индуктивности «утечек», вызывающей проблемы, для любой заданной степени неэффективности магнитной связи.Это приводит к напряжению нагрузки, которое ближе к идеальному при той же (сильноточной) нагрузке и том же коэффициенте связи:
трансформатор
v1 1 0 ac 10 грех
rbogus1 1 2 1e-12
rbogus2 5 0 9e12
** индуктивность = 1 генри вместо 100 генри
л1 2 0 1
л2 3 5 1
к л1 л2 0,999
vi1 3 4 ac 0
4 5 15
. ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
частота v(2) i(v1) 6.000E+01 1.000E+01 6.664E-01 частота v(3,5) i(vi1) 6.000E+01 9.977E+00 6.652E-01
Просто за счет использования первичной и вторичной катушек меньшей индуктивности напряжение нагрузки для этой большой нагрузки (высокий ток) было доведено почти до идеального уровня (9,977 вольт). В этот момент можно спросить: «Если меньшая индуктивность — это все, что нужно для достижения почти идеальной производительности при большой нагрузке, то зачем вообще беспокоиться об эффективности связи?
Если невозможно построить трансформатор с идеальной связью, но легко спроектировать катушки с низкой индуктивностью, то почему бы просто не построить все трансформаторы с катушками с низкой индуктивностью и иметь превосходный КПД даже при плохой магнитной связи?»
Ответ на этот вопрос можно найти в другом моделировании: тот же трансформатор с низкой индуктивностью, но на этот раз с более легкой нагрузкой (меньший ток) 1 кОм вместо 15 Ом:
трансформатор v1 1 0 ac 10 грех rbogus1 1 2 1e-12 rbogus2 5 0 9e12 л1 2 0 1 л2 3 5 1 к л1 л2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac лин 1 60 60 .print переменный v (2,0) я (v1) .print ac v(3,5) i(vi1) .конец
частота v(2) i(v1) 6.000E+01 1.000E+01 2.835E-02 частота v(3,5) i(vi1) 6.000E+01 9.990E+00 9.990E-03
При меньшей индуктивности обмотки первичное и вторичное напряжения почти равны, а первичный и вторичный токи — нет. В данном конкретном случае первичный ток равен 28.35 мА, в то время как вторичный ток составляет всего 9,990 мА: почти в три раза больше тока в первичной обмотке, чем во вторичной.
Почему это? Чем меньше индуктивность в первичной обмотке, тем меньше индуктивное реактивное сопротивление и, следовательно, гораздо больше ток намагничивания. Значительная часть тока через первичную обмотку просто работает на намагничивание сердечника, а не на передачу полезной энергии вторичной обмотке и нагрузке.
Идеальный трансформатор с идентичными первичной и вторичной обмотками будет иметь одинаковое напряжение и ток в обоих наборах обмоток при любых условиях нагрузки. В идеальном мире трансформаторы передавали бы электроэнергию от первичной обмотки к вторичной так же плавно, как если бы нагрузка была напрямую подключена к первичному источнику питания, а трансформатора там вообще не было.
В идеальном мире трансформаторы передавали бы электроэнергию от первичной обмотки к вторичной так же плавно, как если бы нагрузка была напрямую подключена к первичному источнику питания, а трансформатора там вообще не было.
Однако вы можете видеть, что эта идеальная цель может быть достигнута только при наличии идеальной связи магнитного потока между первичной и вторичной обмотками. Поскольку этого достичь невозможно, трансформаторы должны быть рассчитаны на работу в определенных ожидаемых диапазонах напряжений и нагрузок, чтобы работать как можно ближе к идеальным.
На данный момент самое важное, о чем следует помнить, это основной принцип работы трансформатора: передача мощности от первичной цепи к вторичной через электромагнитную связь.
ОБЗОР:
- Взаимная индуктивность — это когда магнитный поток двух или более катушек индуктивности «связан» таким образом, что в одной катушке индуцируется напряжение, пропорциональное скорости изменения тока в другой.

- Трансформатор представляет собой устройство, состоящее из двух или более катушек индуктивности, одна из которых питается от сети переменного тока, индуцируя переменное напряжение на второй катушке индуктивности.Если второй индуктор подключен к нагрузке, мощность будет электромагнитно связана с источником питания первого индуктора с этой нагрузкой.
- Катушка индуктивности в трансформаторе называется первичной обмоткой . Незапитанная катушка индуктивности в трансформаторе называется вторичной обмоткой .
- Магнитный поток в сердечнике (Φ) отстает на 90° от формы сигнала напряжения источника. Ток, потребляемый первичной катушкой от источника для создания этого потока, называется током намагничивания , и он также отстает от напряжения питания на 90°.
- Полный первичный ток в ненагруженном трансформаторе называется током возбуждения и состоит из тока намагничивания плюс любой дополнительный ток, необходимый для преодоления потерь в сердечнике.
 В реальном трансформаторе он никогда не бывает идеально синусоидальным, но его можно сделать более синусоидальным, если трансформатор сконструирован и эксплуатируется таким образом, чтобы плотность магнитного потока поддерживалась на минимальном уровне.
В реальном трансформаторе он никогда не бывает идеально синусоидальным, но его можно сделать более синусоидальным, если трансформатор сконструирован и эксплуатируется таким образом, чтобы плотность магнитного потока поддерживалась на минимальном уровне. - Поток сердечника индуцирует напряжение в любой катушке, обернутой вокруг сердечника. Индуцированное напряжение идеально совпадает по фазе с напряжением источника первичной обмотки и имеет одинаковую форму волны.
- Любой ток, проходящий через вторичную обмотку нагрузки, будет «отражаться» на первичную обмотку и отбираться от источника напряжения, как если бы источник напрямую питал аналогичную нагрузку.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Взаимная индуктивность
Из закона Фарадея мы узнаем, что изменение магнитного потока через поверхность, прикрепленную к петле, вызывает ЭДС в петле. Поэтому мы не удивимся, если обнаружим, что две отдельные цепи, по которым текут переменные во времени токи рядом друг с другом, будут индуцировать ЭДС друг в друге. Это должно произойти, поскольку ток каждой цепи будет создавать магнитное поле в месте расположения другой цепи. Изменяющийся ток будет производить изменяющееся магнитное поле, что приведет к изменению магнитного потока, тем самым индуцируя ЭДС.
Это должно произойти, поскольку ток каждой цепи будет создавать магнитное поле в месте расположения другой цепи. Изменяющийся ток будет производить изменяющееся магнитное поле, что приведет к изменению магнитного потока, тем самым индуцируя ЭДС.
Чтобы внимательно изучить этот эффект, давайте рассмотрим две цепи или петли \(C_1\) и \(C_2\), зафиксированные в своем положении относительно друг друга, как показано на рисунке 42.1.1.
Пусть ток \(I_1\) течет по цепи \(C_1\text{.}\) Этот ток создаст магнитное поле, зависящее от положения \(\vec B_1\text{.}\) Пусть \(\Phi_{21}\) — магнитный поток поля \(\vec B_1\) через площадь открытой поверхности \(S_2\), присоединенной к контуру \(C_2\text{.}\ )
Рисунок 42.1.1.
Поскольку \(\vec B_1\) пропорционален \(I_1\text{,}\), мы ожидаем, что поток \(\vec B_1\) также будет пропорционален \(I_1\text{.}\)
\begin{уравнение*}
\vec B_1\propto I_1\ \\Longrightarrow \\Phi_{21} \propto I_1.
\end{уравнение*}
Мы можем записать это как равенство, введя константу пропорциональности, которую мы запишем как \(\mathcal{M}\text{. }\)
}\)
\begin{уравнение}
\Phi_{21} = \mathcal{M} I_1. \label{eq-mutual-induct-1}\tag{42.1.1}
\end{уравнение}
Константой \(\mathcal{M}\) называется коэффициент взаимной индуктивности двух цепей. Взаимная индуктивность зависит только от геометрии двух цепей, их разделения и магнитных свойств среды. Единица СИ для \(\mathcal{M}\) известна как Генри (\(\text{H}\)).
\begin{уравнение*}
\text{Единица} \mathcal{M} : \frac{\text{T.2}{A} \text{ или } \Omega.\text{sec} \text{ или } \text{ Генри(H)}.
\end{уравнение*}
Используя уравнение (42.1.1) ЭДС, индуцированная в цепи 2 изменяющимся током в цепи 1, будет определяться правилом потока Фарадея.
\begin{уравнение}
\mathcal{E}_2 = — \frac{\Delta \Phi_{21}}{\Delta t} = — \mathcal{M} \frac{\Delta I_1}{\Delta t}. \тег{42.1.2}
\end{уравнение}
В пределе \(\Delta t\rightarrow 0\text{,}\) мы получим мгновенное уравнение.
\begin{уравнение}
\mathcal{E}_2 (t) = — \mathcal{M} \frac{d I_1}{d t},\label{eq-mutual-induct-2}\tag{42. 1.3}
1.3}
\end{уравнение}
, где я написал \(\mathcal{E}_2 (t)\), чтобы подчеркнуть, что это ЭДС в момент времени \(t\text{.}\)
Мы используем взаимную индуктивность в трансформаторах переменного тока, где мы изменяем ток в одной цепи, чтобы индуцировать ток в другой, даже если эти две цепи физически не связаны. Контролируя количество витков в каждой цепи, мы можем увеличивать или уменьшать индуцированный ток.
Подраздел 42.1.1 Симметрия взаимной индуктивности
Выше мы определили взаимную индуктивность двух цепей на основе магнитного потока через \(C_2\) по току в цепи \(C_1\text{.}\) Назовем полученную таким образом взаимную индуктивность \(\mathcal{M}_{21}\text{.}\) Схема для этой ситуации показана на рисунке 42.1.1.
Что произойдет, если мы обратим ситуацию, т.е. пропустим ток \(I_2\) по цепи \(C_2\) и изучим магнитный поток магнитного поля \(\vec B_2\) через цепь \(C_1\) как показано на рисунке 42.1.2? Обозначим здесь взаимную индуктивность через \(\mathcal{M}_{12}\text{. }\)
}\)
В этом случае мы будем иметь поток \(\Phi_{12}\) через поверхность, присоединенную к петле контура \(C_1\) относительно тока в контуре \(C_2\), как
\begin{уравнение}
\Phi_{12} = \mathcal{M}_{12} I_2, \label{eq-mutual-induct-3}\tag{42.1.4}
\end{уравнение}
Рисунок 42.1.2.
Мы не будем здесь доказывать, но вы можете попытаться доказать, что две взаимные индуктивности, \(\mathcal{M}_{21}\) и \(\mathcal{M}_{12}\text{,}\ ) должны быть равны, и мы представляем их одним и тем же символом \(\mathcal{M}\text{.}\)
\begin{уравнение}
\mathcal{M}_{12} = \mathcal{M}_{21} =\mathcal{M}. \label{eq-mutual-induct-4}\tag{42.1.5}
\end{уравнение}
Поскольку взаимная индуктивность не зависит от того, через какую цепь мы пропустим ток, мы используем эту симметрию для расчета взаимной индуктивности, как показано ниже.
Соленоидная петля \(C_1\) состоит из \(n\) круговых петель радиусом \(a\) на единицу длины, как показано на рисунке 42.1.4.
Другой контур \(C_2\) кругового контура радиуса \(R\) окружает соленоид так, что соленоид находится на оси второго контура. Предположим, что длина соленоида намного больше радиуса соленоида, так что мы можем использовать приближение бесконечного соленоида.
Предположим, что длина соленоида намного больше радиуса соленоида, так что мы можем использовать приближение бесконечного соленоида.
Рисунок 42.1.4.
(a) Найдите взаимную индуктивность двух контуров по потоку тока в \(C_1\) через площадь поверхности, присоединенной к контуру \(C_2\text{.}\) Предположим, что \(a\lt \lt R\text{.}\)
(b) (Исчисление) Найдите взаимную индуктивность двух контуров по потоку тока в \(C_2\) через площадь поверхности, присоединенной к контуру \(C_1\text{,}\) и продемонстрируйте два метода приводят к одной и той же формуле для взаимной индуктивности. Предположим, что \(a\lt \lt R\text{.}\)
Подсказка 1 (а)
Ввести ток \(I\) в одну цепь и найти магнитный поток этого тока через другую цепь.
Подсказка 2 (b)
Попробуйте настроить задачу для потока через петли в диапазоне \(z\) и \(z+dz\), а затем проинтегрировать.2\текст{.}\)
Решение 1 (а)
(a) Расчет взаимной индуктивности по току через длинный соленоид.
Нам нужен магнитный поток через одну цепь по току в других цепях.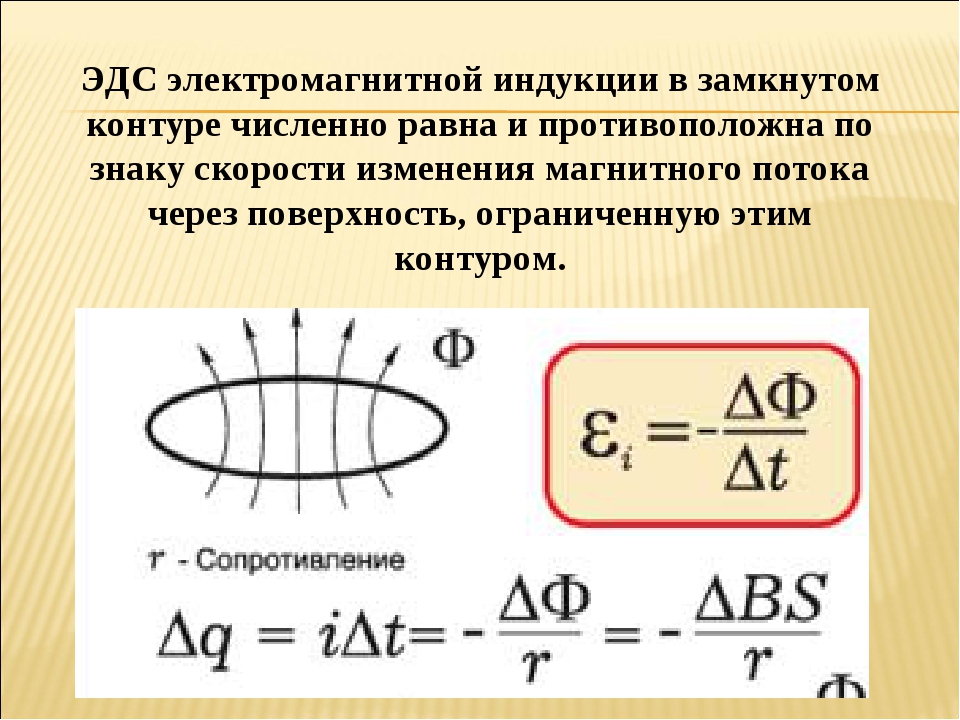 Поскольку с магнитным полем длинного соленоида легко работать, мы будем думать о произвольном токе \(I\) в соленоиде, как показано на рисунке 42.1.5. Это \(I\) в конце концов сократится, поэтому мы не беспокоимся о его значении.
Поскольку с магнитным полем длинного соленоида легко работать, мы будем думать о произвольном токе \(I\) в соленоиде, как показано на рисунке 42.1.5. Это \(I\) в конце концов сократится, поэтому мы не беспокоимся о его значении.
Рисунок 42.1.5.
Так как соленоид очень длинный, магнитное поле существенно только внутри пространства соленоида.Мы используем цилиндрическую координату с осью \(z\) вдоль оси соленоида и круговой петлей в плоскости \(xy\). Пусть \(s\) — расстояние точки от оси, т. е. радиальное расстояние в плоскости \(xy\).
Направление магнитного поля для направления тока, выбранного на рисунке, направлено к положительной оси \(z\) и имеет величину, определяемую следующей ступенчатой функцией.
\begin{уравнение*}
B _ {\ текст {соленоид}} =
\begin{случаи}
\mu_0 n I \amp\ \ s \lt a\\
0 \amp\ \ s \ge a
\end{случаи}
\end{уравнение*}
Прикрепим круглую поверхность к круглому проводу \(C_2\), чтобы найти поток через \(C_2\text{.2.
\end{уравнение*}
Хотя эта формула не выглядит симметричной в переключающих свойствах цепей 1 и 2.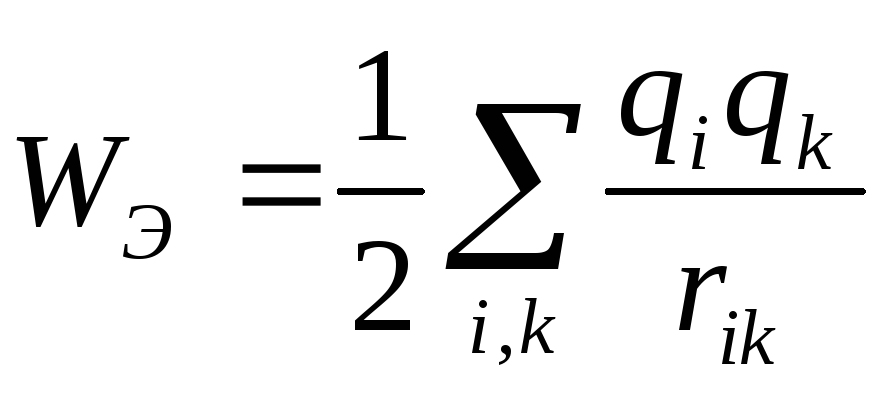 В (б) вы увидите, что вы получаете точно такое же выражение, когда вы включаете ток в петле и вычисляете поток в соленоид.
В (б) вы увидите, что вы получаете точно такое же выражение, когда вы включаете ток в петле и вычисляете поток в соленоид.
Решение 2 (б)
(b) Расчет взаимной индуктивности по току через кольцевой контур.
Теперь представьте, что ток \(I\) проходит через петлю вокруг соленоида, так что ток \(I\), как показано на рисунке 42.1.6. Магнитное поле этого тока будет проходить везде, и в частности, через поверхность, прикрепленную к проводам соленоида. Мы найдем формулу для этого потока, просуммировав поток через каждое кольцо соленоида.
Рисунок 42.1.6.
В приближении \(a\lt \lt R\text{,}\) магнитное поле в точке соленоида будет примерно таким же, как и в центре катушки соленоида. Так как магнитное поле тока во внешнем кольце зависит от расстояния \(|z|\) от центра кольца, можно установить магнитный поток \(d\Phi_1\) через петли соленоида между \( z\) и \(z+dz\text{.2,
\end{уравнение*}
, что совпадает с формулой взаимной индуктивности, полученной при пропускании тока через соленоид вместо внешнего круглого провода.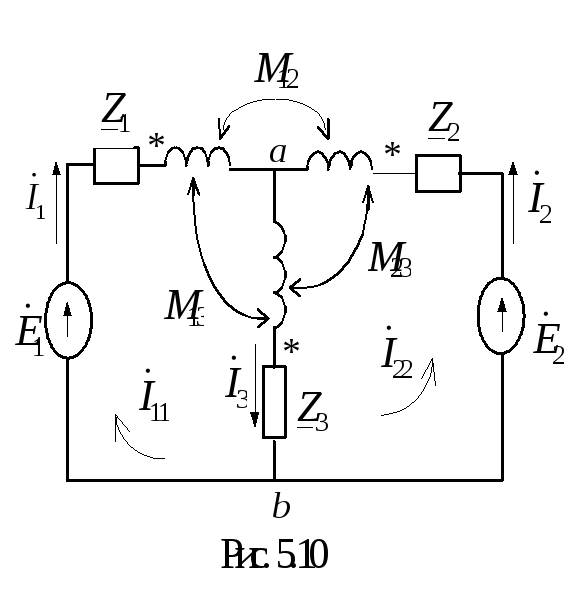
Небольшая петля соленоида \(C_1\) длиной \(L_1\text{,}\) \(N_1\) поворачивается, а круглое поперечное сечение радиуса \(R_1\) помещается внутрь очень длинной петли соленоида длины \(L_2\text{,}\) \(N_2\) витков и круглого поперечного сечения радиуса \(R_2\text{.}\) Рассчитайте взаимную индуктивность двух соленоидов, принимая \(L_1\ ll L_2\текст{.2}{L_2}\text{.}\)
Решение
Поскольку магнитное поле бесконечно длинного соленоида известно, мы будем использовать ток в более длинном соленоиде и вычислить магнитный поток этого тока через меньший соленоид, чтобы вычислить взаимную индуктивность двух соленоидов.
Введем ток \(I\) в большом соленоиде. Это создаст однородное магнитное поле \(\vec B_2\) внутри соленоида, которое имеет направление вдоль оси соленоида и величину, заданную как
\begin{уравнение*}
\text{Величина: } B_{2} = \mu_0 \frac{N_2}{L_2} I.2\текст{.}\)
Решение
Для целей расчета введем ток в одну из цепей, магнитное поле которого легко рассчитать и использовать в последующем расчете.



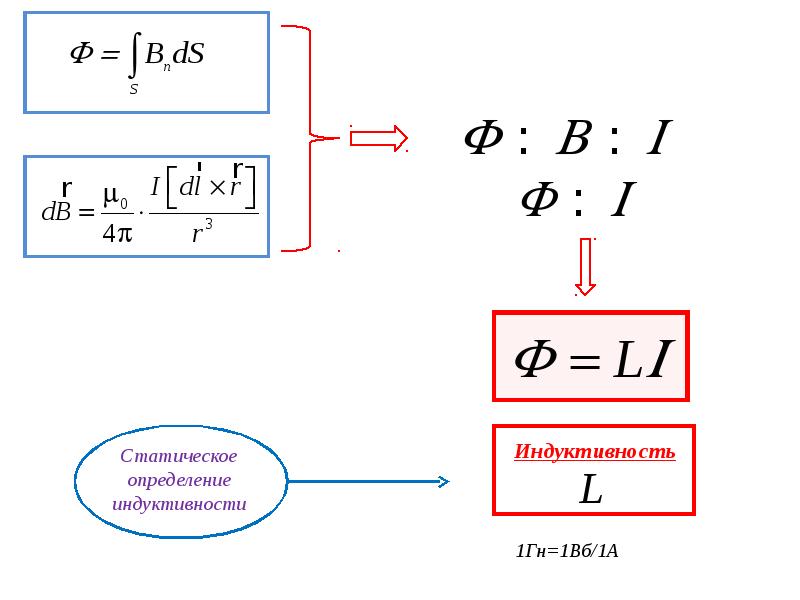
 org/contents/
org/contents/ ЭДС индукции также пропорциональна напряжению В 1
ЭДС индукции также пропорциональна напряжению В 1 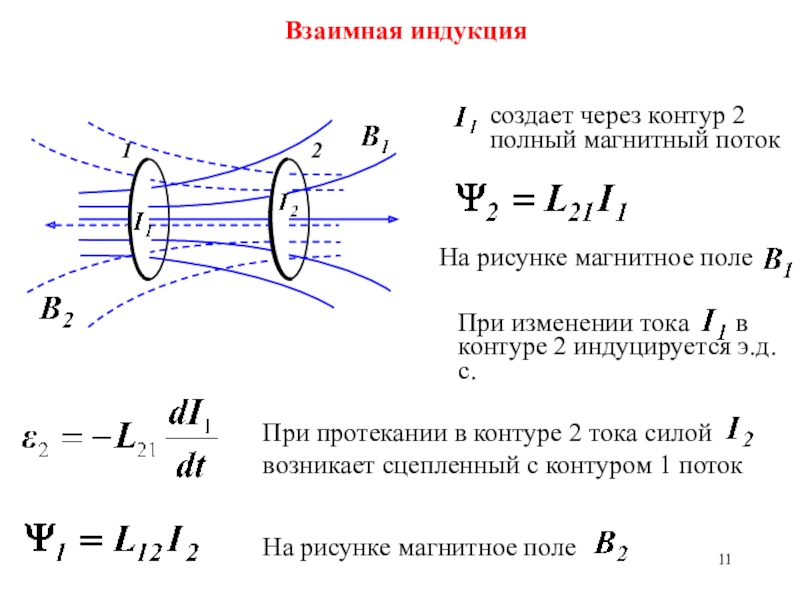 Общий поток за виток обусловлен
Общий поток за виток обусловлен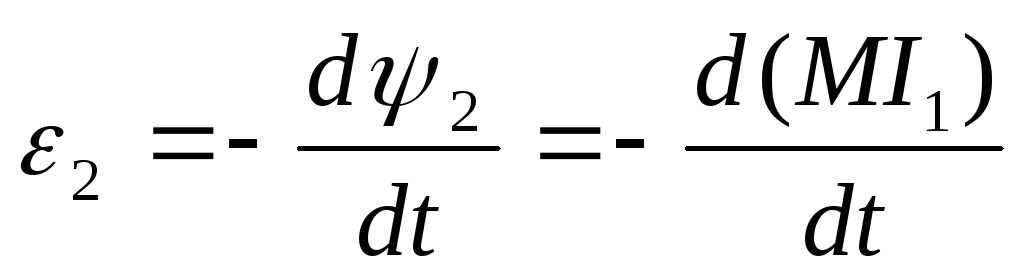

 Найдя поток этих полей через катушку, мы можем
Найдя поток этих полей через катушку, мы можем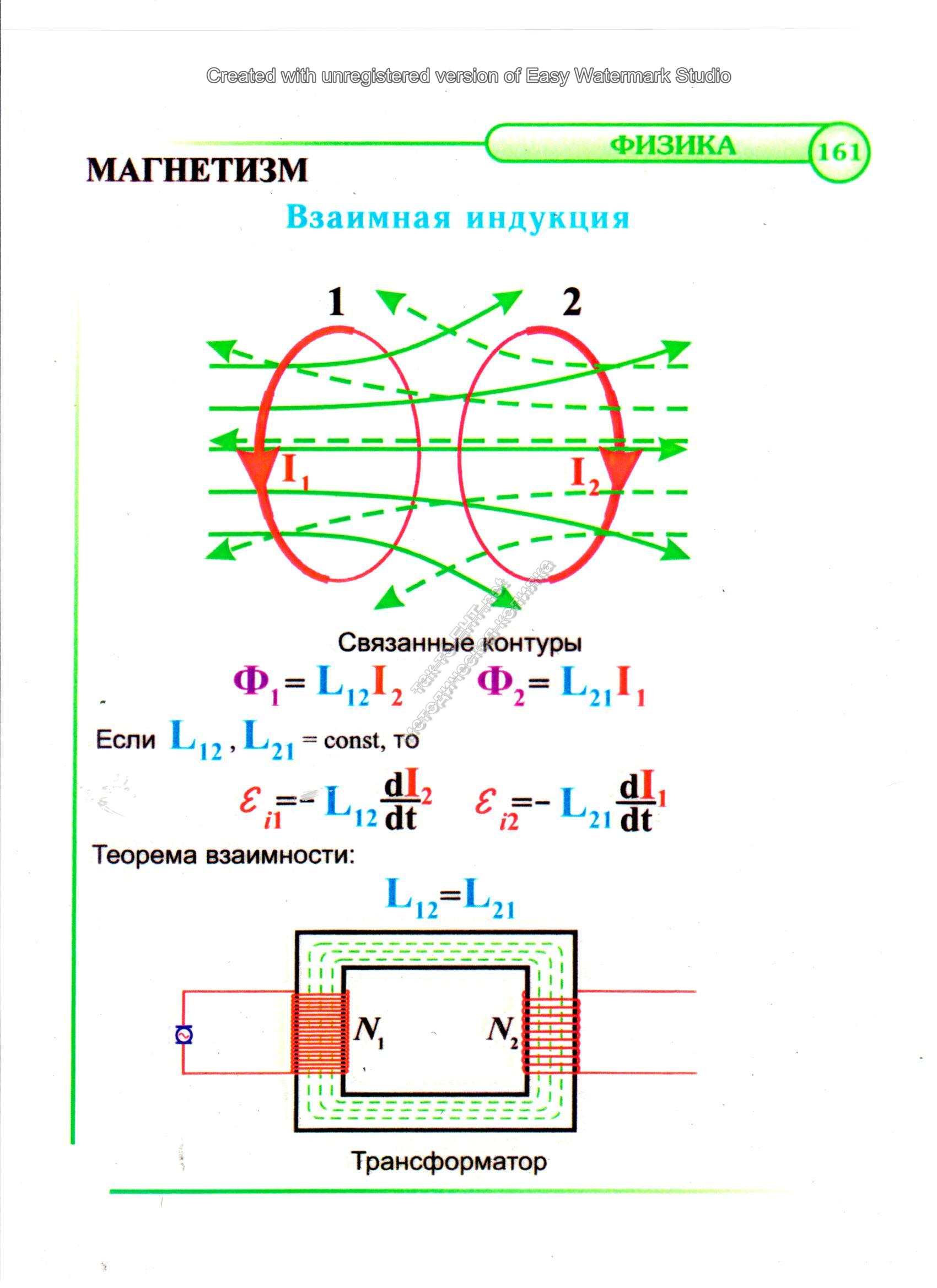

 999
vi1 3 4 ac 0
rload 4 5 1k
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
999
vi1 3 4 ac 0
rload 4 5 1k
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
 999
vi1 3 4 ac 0
** Обратите внимание на сопротивление нагрузки 200 Ом.
нагрузка 4 5 200
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
999
vi1 3 4 ac 0
** Обратите внимание на сопротивление нагрузки 200 Ом.
нагрузка 4 5 200
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
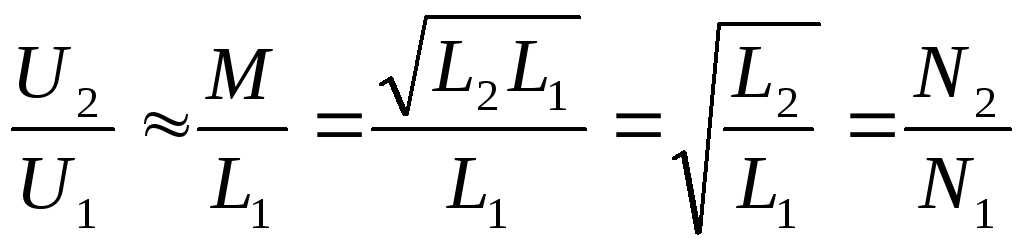 999
vi1 3 4 ac 0
4 5 15
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
999
vi1 3 4 ac 0
4 5 15
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
 к л1 л2 0,99999
vi1 3 4 ac 0
4 5 15
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.напечатать ac v(3,5) i(vi1)
.конец
к л1 л2 0,99999
vi1 3 4 ac 0
4 5 15
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.напечатать ac v(3,5) i(vi1)
.конец
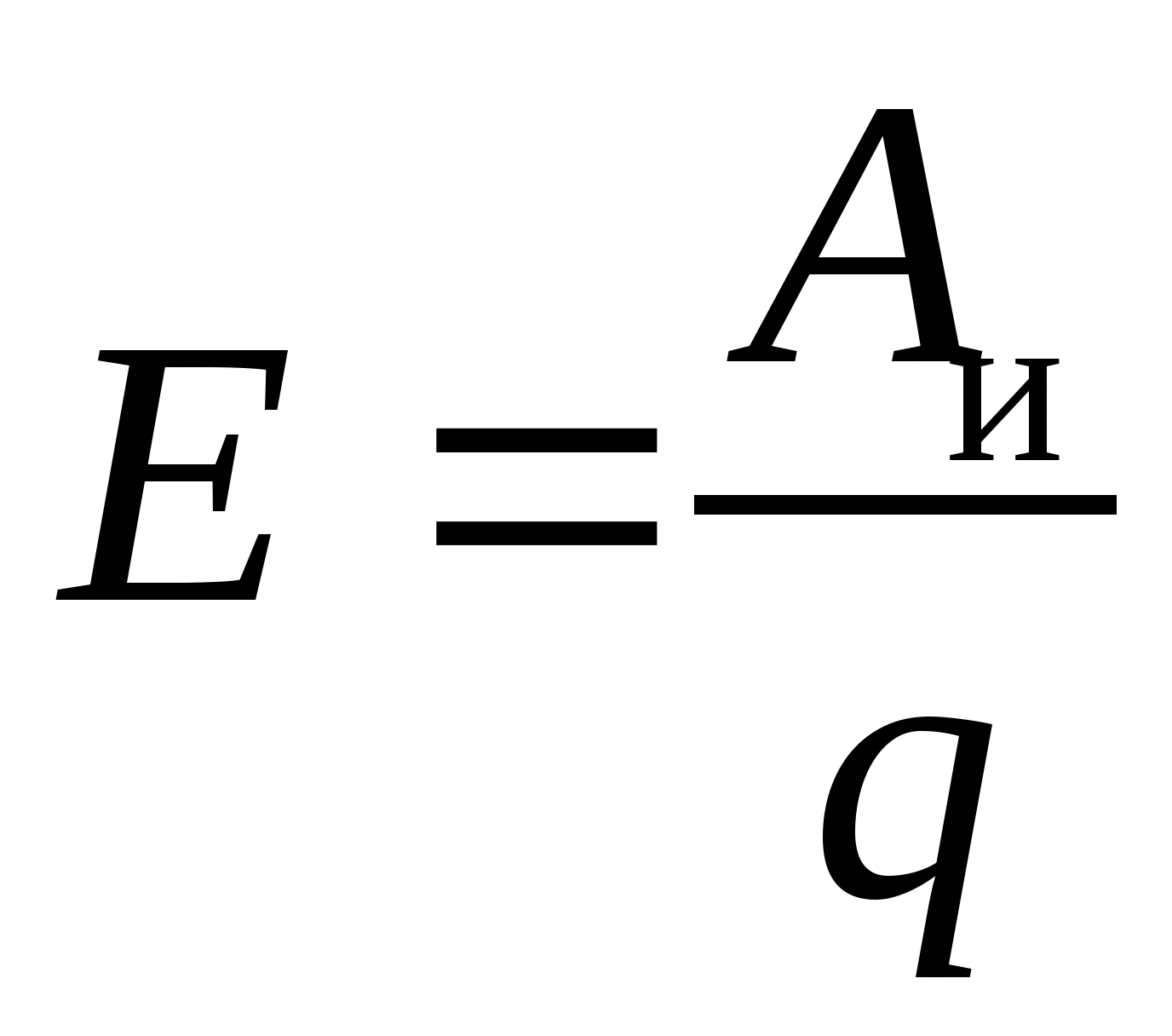 ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
 999
vi1 3 4 ac 0
rload 4 5 1k
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец
999
vi1 3 4 ac 0
rload 4 5 1k
.ac лин 1 60 60
.print переменный v (2,0) я (v1)
.print ac v(3,5) i(vi1)
.конец

 В реальном трансформаторе он никогда не бывает идеально синусоидальным, но его можно сделать более синусоидальным, если трансформатор сконструирован и эксплуатируется таким образом, чтобы плотность магнитного потока поддерживалась на минимальном уровне.
В реальном трансформаторе он никогда не бывает идеально синусоидальным, но его можно сделать более синусоидальным, если трансформатор сконструирован и эксплуатируется таким образом, чтобы плотность магнитного потока поддерживалась на минимальном уровне.