Электрическое поле в диэлектрике. Поле на границе диэлектрика. Электрическое поле в диэлектрике

Электрическое поле в диэлектрике. Поле на границе диэлектрика. — КиберПедия

Напряженность электростатического поля, согласно (88.5 ), зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле ещевектором электрического смещения, который для электрически изотропной среды, по определению, равен

(89.1)

Используя формулы (88.6 ) и (88.2 ), вектор электрического смещения можно выразить как

(89.2)

Единица электрического смещения — кулон на метр в квадрате (Кл/м2).

Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле свя­занных зарядов. Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, воз­никающие в диэлектрике, могут вызвать, однако, перераспределение свободных заря­дов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.

Аналогично, как и поле Е, поле D изображается с помощьюлиний электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности.

Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.

Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность

где Dn — проекция вектора D на нормаль n к площадке dS.

Теорема Гаусса дляэлектростатического поля в диэлектрике:

(89.3)

т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума Dn= e0En (e =1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность (ср. с (81.2)) равен

Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса (81.2) для поля Е в самом общем виде можно записать как

где — соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.

На границе двух диэлектриков с различными диэлектрическими проницаемостями , и при наличии внешнего поля возникают поляризационные заряды разного знака с различными поверхностными плотностями зарядов и (рис.14.7).

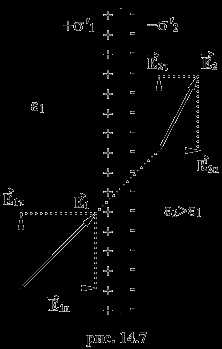
Дополнительное поле, создаваемое этими зарядами, перпендикулярно поверхности, поэтому нормальные составляющие полей , и в обеих средах у границы раздела различны, а касательный составляющие одинаковы, т.е.

(14.11)

и

(14.12)

Аналогично рассмотренному выше случаю границы диэлектрик - вакуум нормальная составляющая вектора на границе двух диэлектриков а отсюда следует, что

Из этого выражения следует, что в случае и линии вектора при переходе через границу раздела преломляются, отклоняясь от перпендикуляра к границе раздела. Из (14.11) и (14.12) следует, что

При и

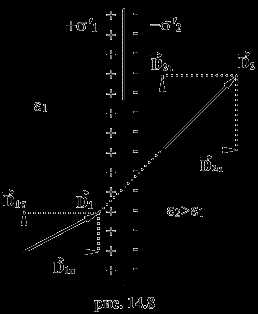
При переходе через границу раздела из диэлектрика с меньшим значением в диэлектрик с большим значением , нормальная составляющая вектора остается неизменной, а касательная увеличивается, так что линии вектора преломляются под таким же углом как и линии напряженности поля (рис. 14.8).

 

Таким образом, при переходе через границу раздела двух диэлектриков изменяется не только вектор напряженности электрического поля , но и вектор . Однако поток вектора через произвольную площадку на границе раздела, равный по определению , с обеих сторон поверхности на основании остается неизменным. Следовательно, число линий вектора электрического смещения, переходящих через границу, не меняется. Поэтому теорема Гаусса остается справедливой для вектора в самом общем случае при наличии в поле диэлектриков любой формы и размеров.

 

 

cyberpedia.su

06. Электрическое поле в диэлектриках

Электрическое поле в диэлектриках

Считается, что если сила взаимодействия между двумя зарядами в вакууме: 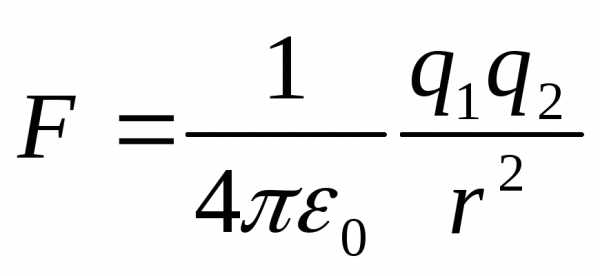,то в среде сила взаимодействия будет в раз меньше:

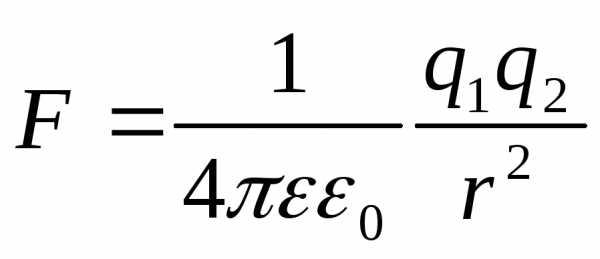. - диэлектрическая проницаемость, берётся из опыта. У разных веществ диэлектрическая проницаемость различная. Это чисто феноменологический подход, где константа определяется прямо из опыта.

В дальнейшем мы с вами будем рассматривать микроскопическую теорию, поскольку этот подход общий, удобный, практичный, но не всегда работает.

А микроскопическая теория позволяет на основе знания микроструктуры вещества и тех процессов, которые происходят в веществе, предсказать значение . Сейчас мы в это вдаваться не будем, но, по большому счёту,зависит и от температуры (для некоторых диэлектриков), и зависит от частоты, и ещё от целого ряда обстоятельств. Скажем сразу, что хоть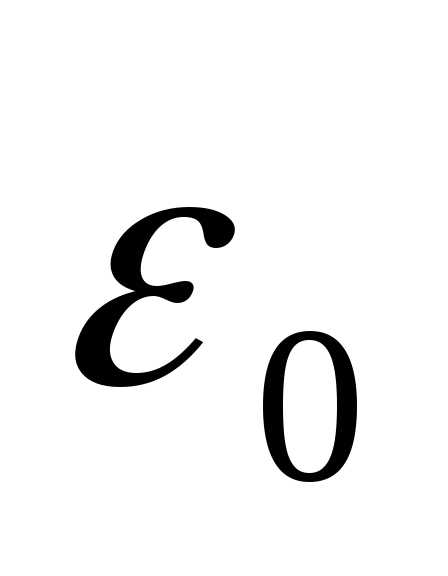и называется диэлектрической проницаемостью вакуума, но никакого отношения не имеет к диэлектрической проницаемости, оно необходимо для соблюдения размерности. Если переходить в Гауссовскую систему, как это сделано у И.Е. Тамма, то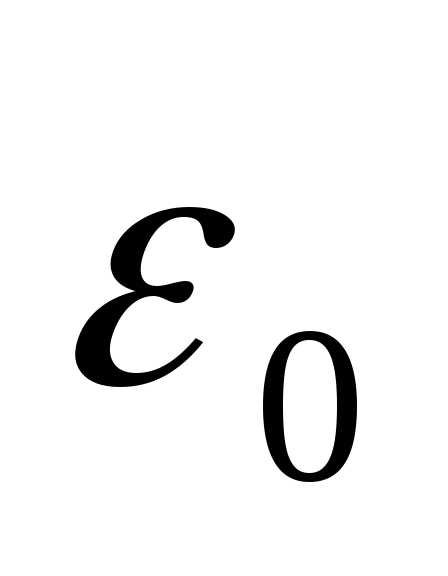вообще не существует.

Тогда система уравнений для электрических полей в диэлектрики примет вид:

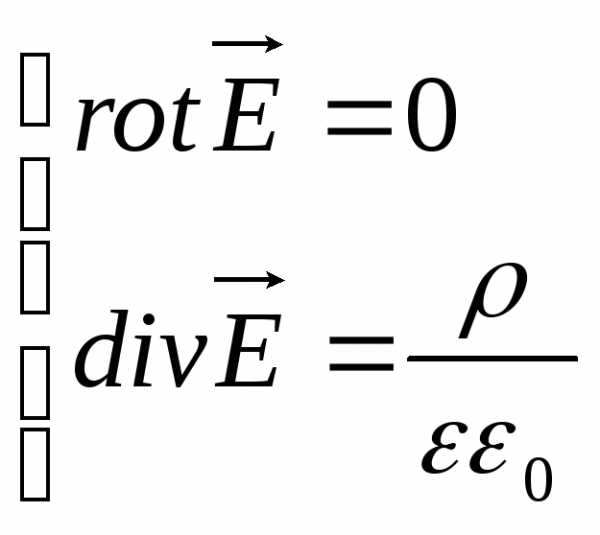
Если у нас однородный диэлектрик, то =const.

Введём - вектор электрической индукции:

.

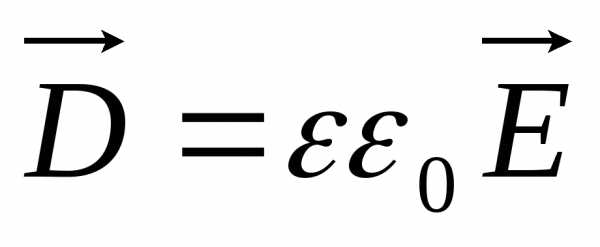Подставив данное уравнение в нашу систему, получаем

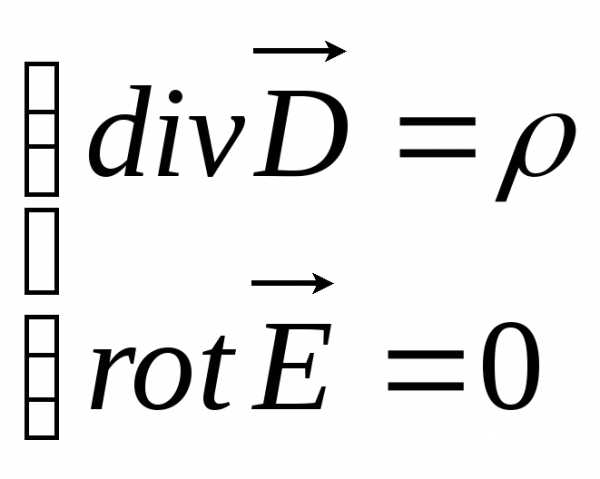
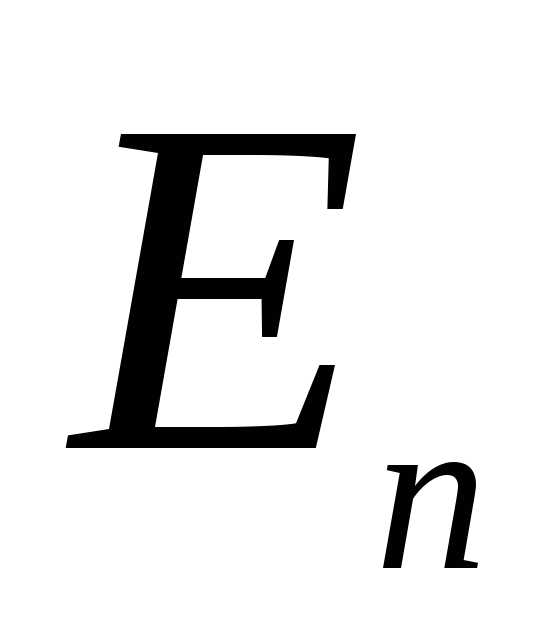
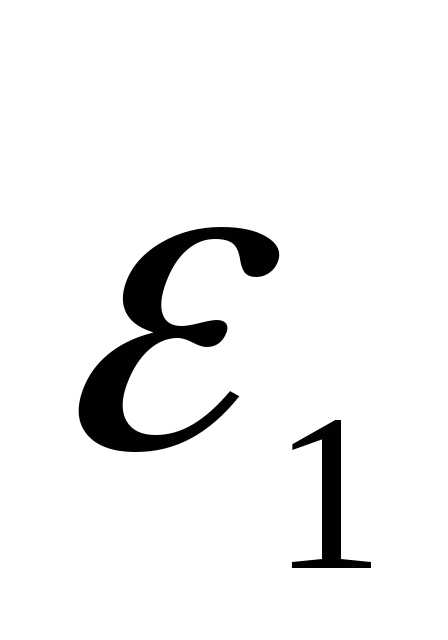
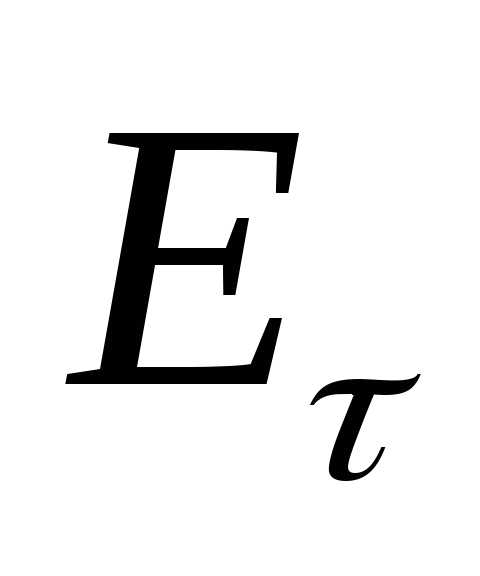
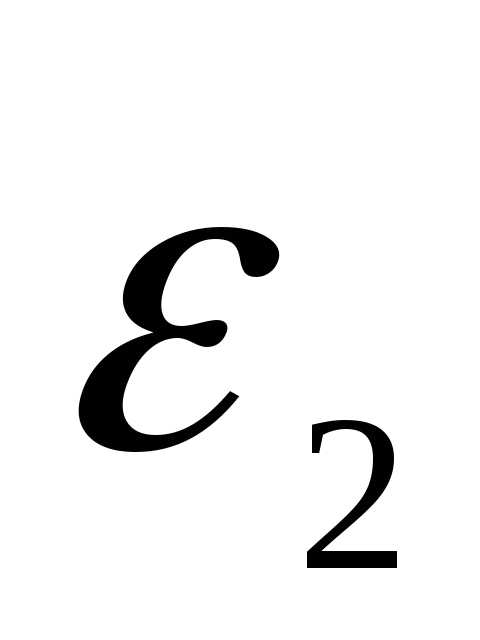
Рассмотрим поведение на границе раздела двух сред. В каждый из них разложим вектор напряжённости на нормальную и тангенсальную слагающую поверхности.

Воспользуемся уравнениями Максвелла для диэлектрика:

(по теореме Гаусса).

Вблизи раздела двух сред возьмём произвольную замкнутую поверхность с двух сторон так, чтобы граница раздела двух сред попадала в область 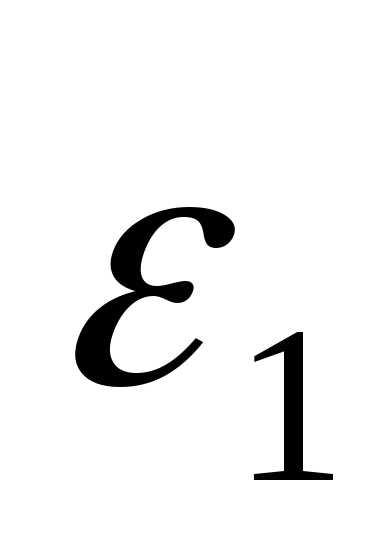S.

S

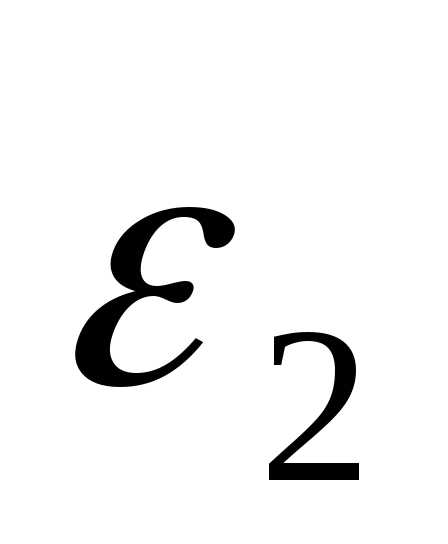
Для простоты поверхность сожмём так, чтобы она плотно прилегала к этой поверхности раздела с одной и другой стороны.

Тогда интеграл распадётся на два интеграла: по поверхности и поверхности: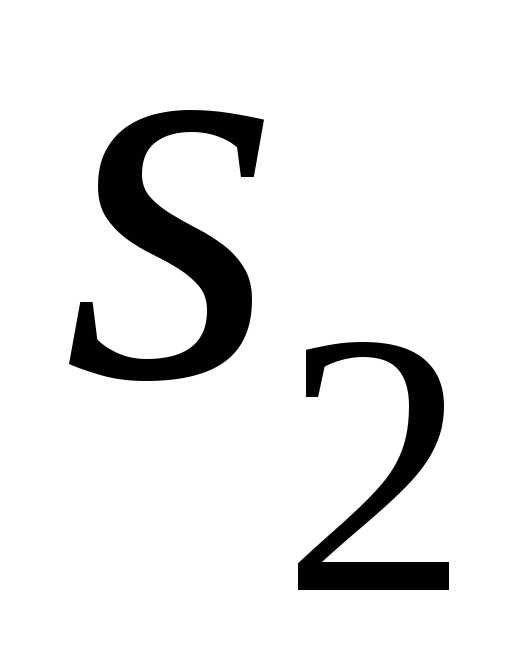

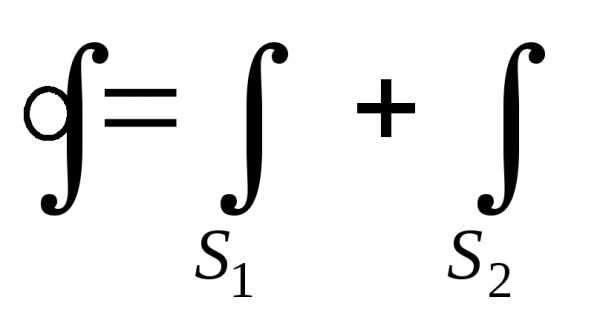
- поверхностная плотность свободных зарядов. Для простоты предположим, что D вдоль поверхности не меняется. Эти интегралы примут вид:

Пусть n нормаль к поверхности границы раздела.

В этом случае 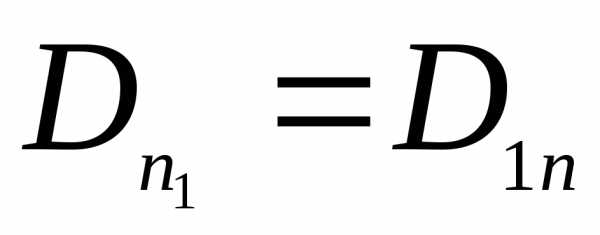- так как нормали совпадают по направлению.

- так как нормали противоположны по направлению.

Если нет поверхностных зарядов, то есть, если 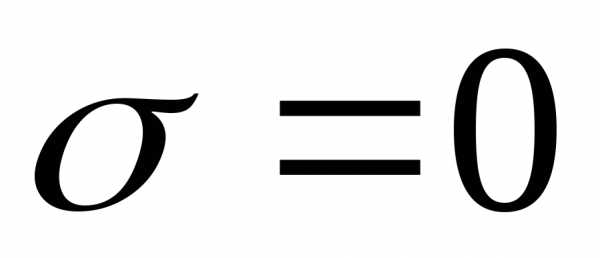, то

Нормальное слагаемое испытывает скачок, то есть .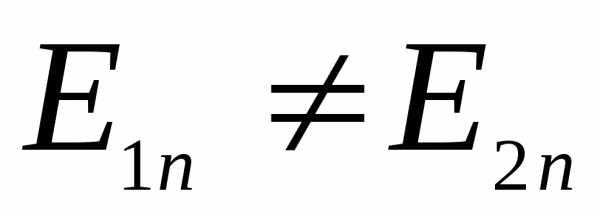

Если, например, 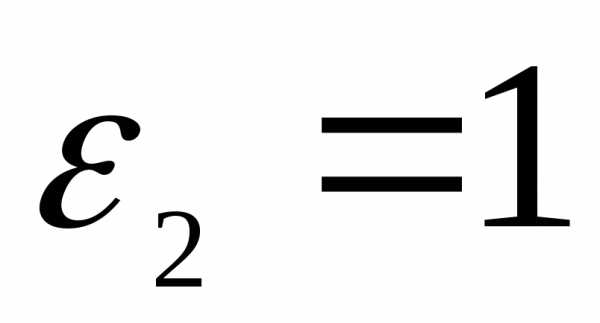, а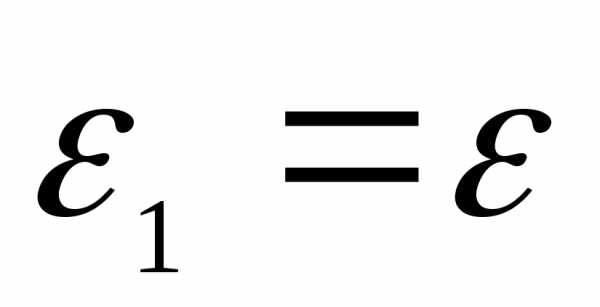, например, вода и воздух, стекло и воздух, то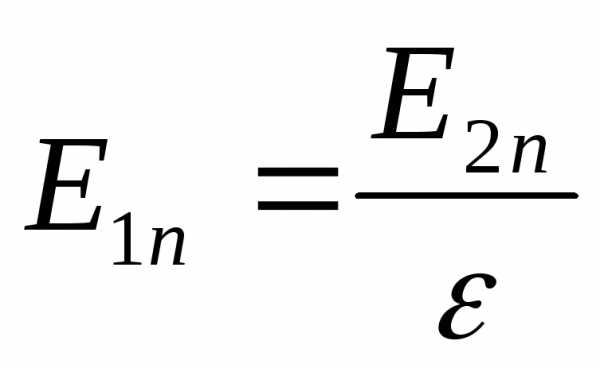, то есть нормальное слагаемое вектора напряжённости при переходе из вакуума в средуc будет уменьшаться враз.

А для тангенциальной слагающей воспользуемся витрорым уравнением для стационарным Эл. поля

Тогда из 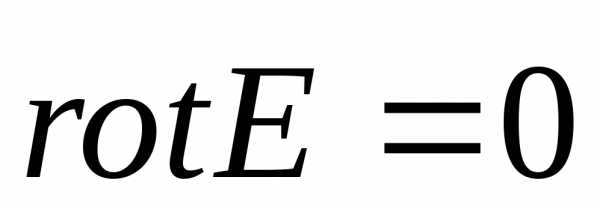следует

,

,

S- поверхность ограниченная

контуром

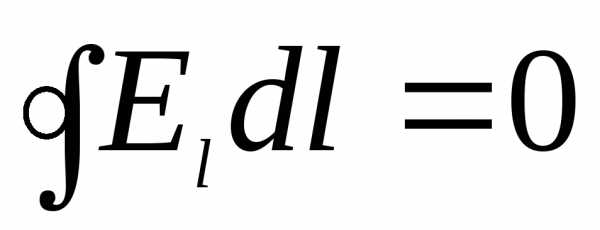
Если ввести dt вдоль поверхности, то для тангенсальных составляющих вектора E, получаем

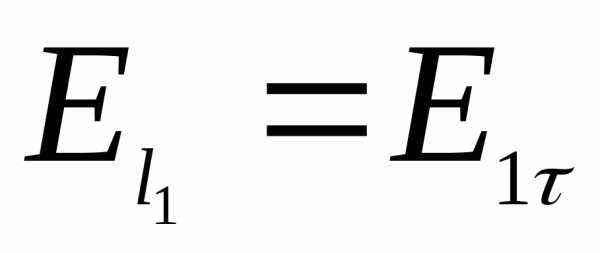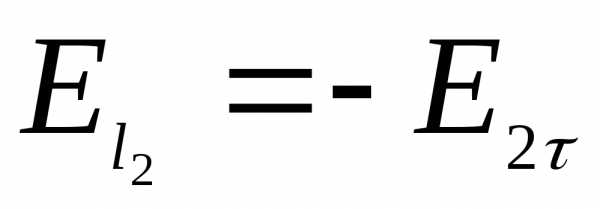; Откуда следует, что тангенсальная составляющая скачка не испытывает.

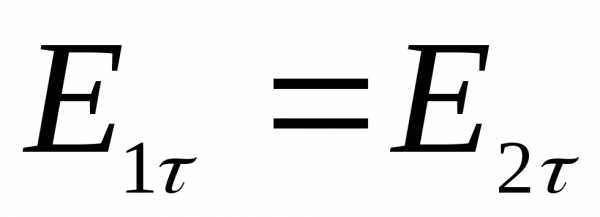
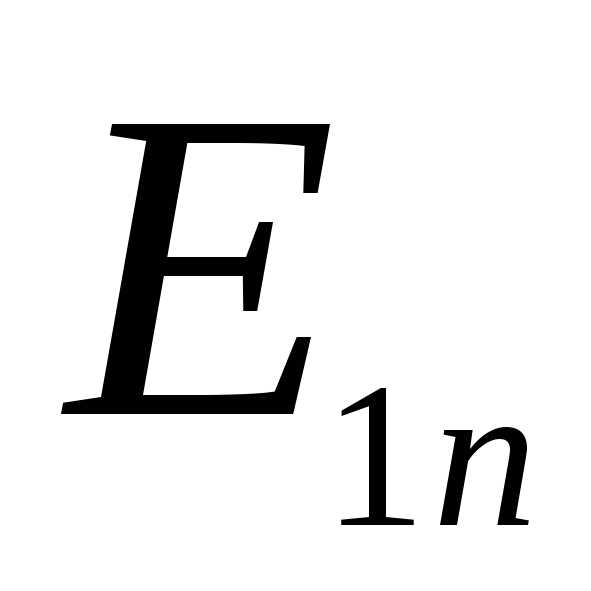
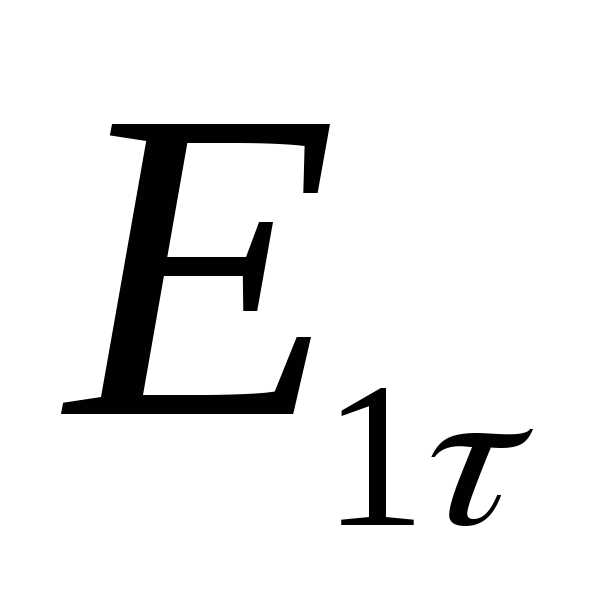
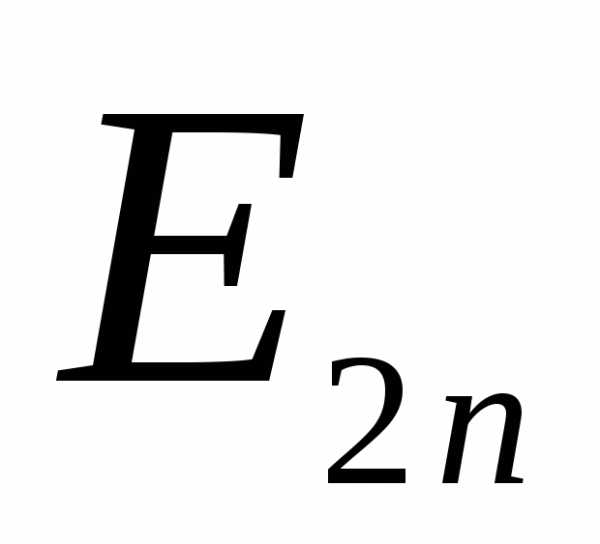
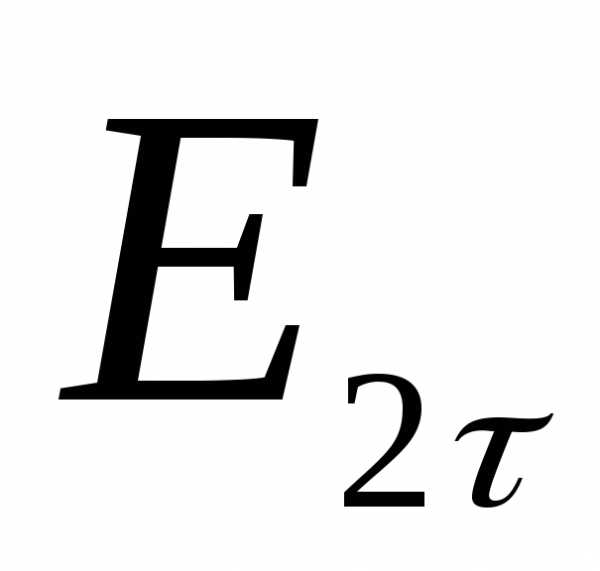
Силовая линия на границе двух сред испытывают преломление.

Энергия системы зарядов.

Мы знаем, что в электрическом поле объёмная плотность энергии равна:

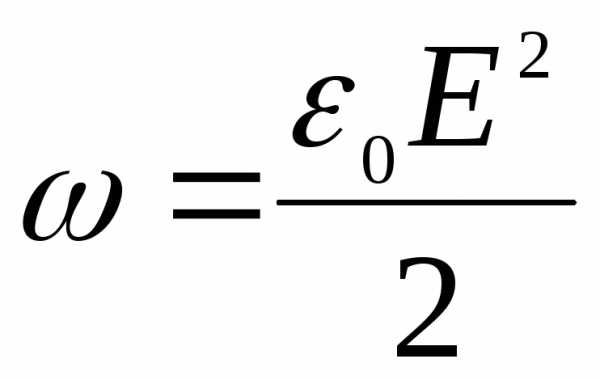
Преобразуем это выражение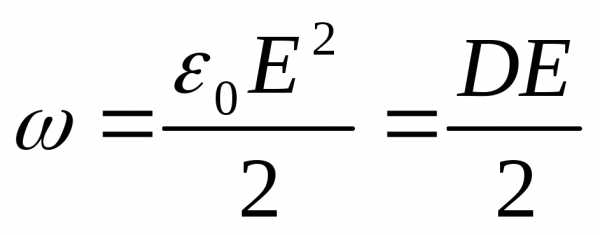

Преобразуем это выражение и подставим в выражение для напряжённости электрического поля:

А так как

Получаем

Возьмём интеграл по всему пространству(охватив всё) получаем:

Поскольку ~, 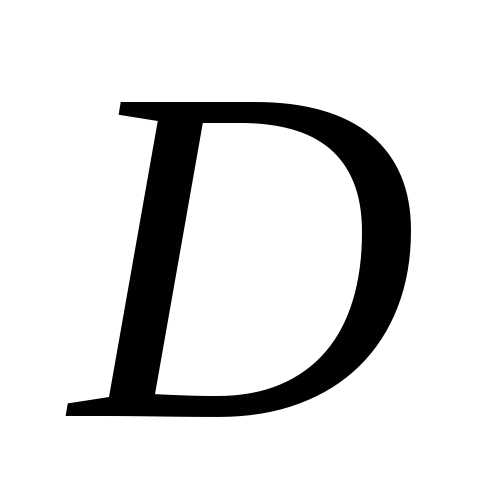~~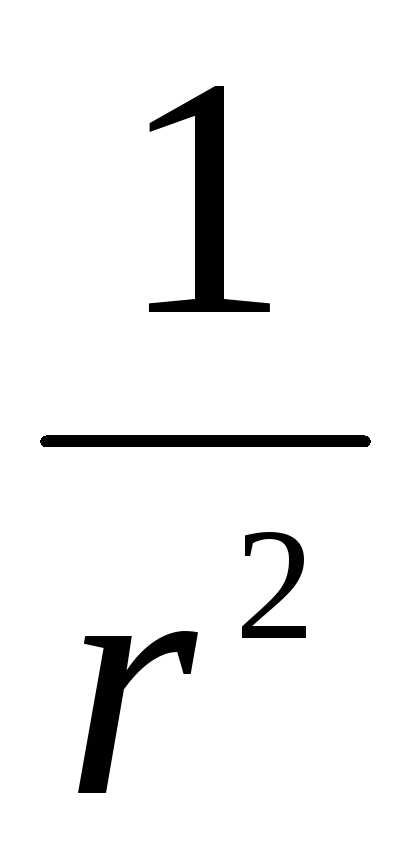, ~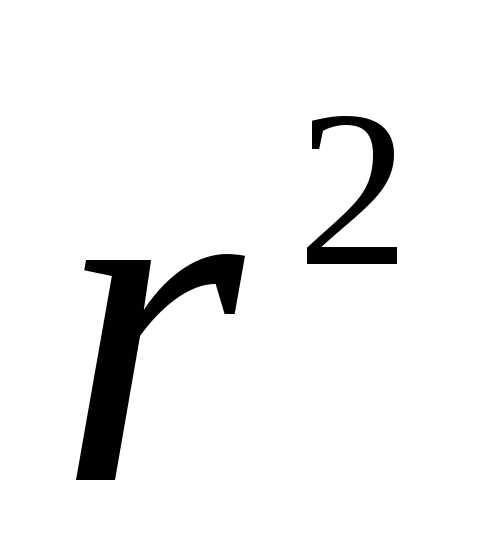, то на границе поверхности и выражение для энергии поля принимает вид

- это другое выражение для энергии, здесь уже входит заряд, то есть носителем энергии является заряд. Преобразуем правую часть: 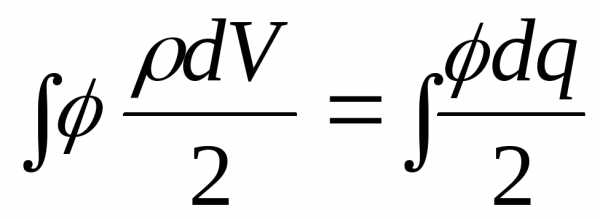. Для простоты перейдём от объёмного заряда к точечному.- потенциал создаваемый всеми зарядами кроме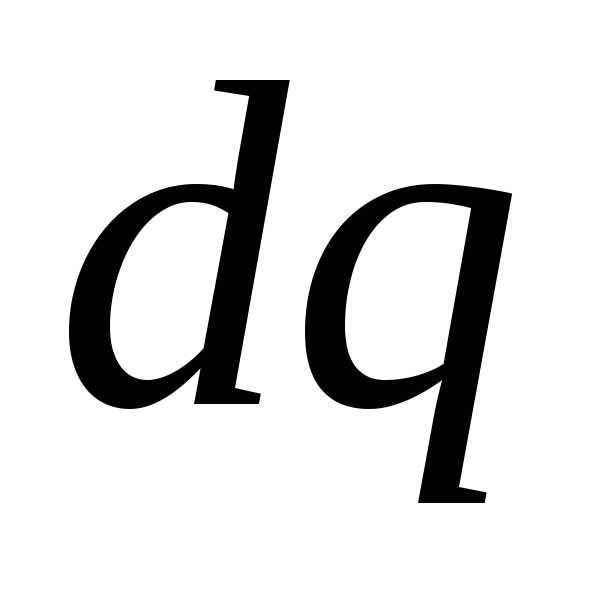в этой точке.

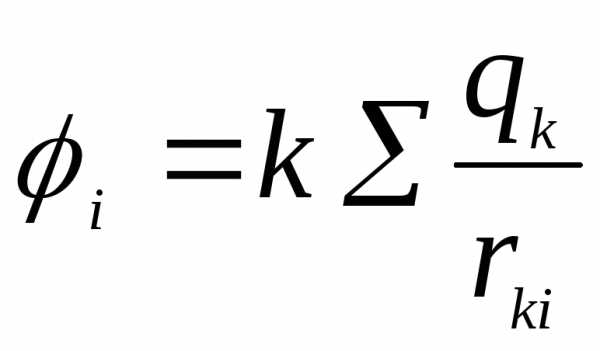- потенциал создаваемый k-тым зарядом в той точке, где находится i-тый заряд.

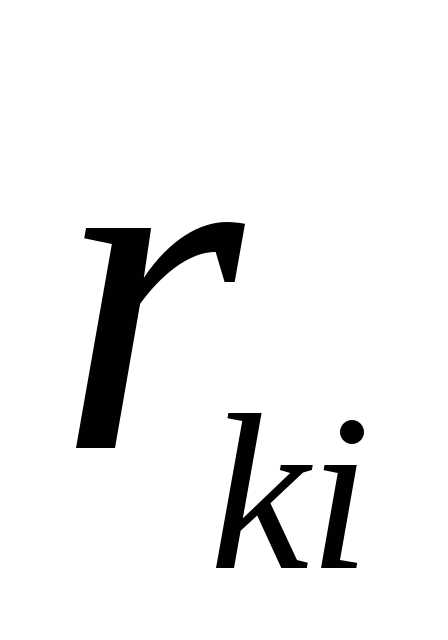- расстояние между зарядами i и k.

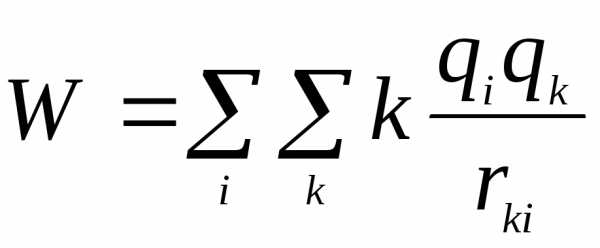- энергия всех зарядов системы.

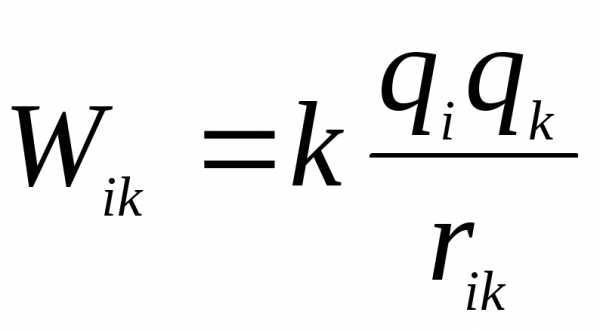- для одной пары зарядов.

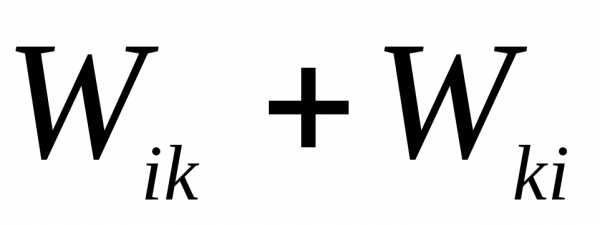- учитывает одну и туже величину дважды, отсюда

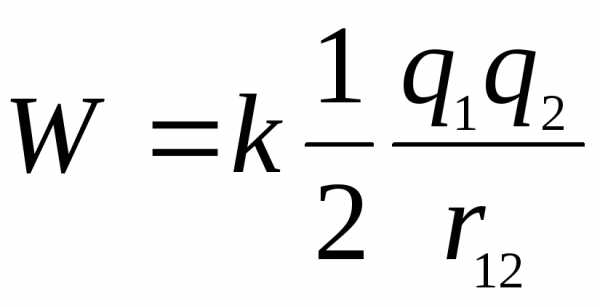-энергия взаимодействия двух зарядов.

Если у нас три заряда, энергию можно посчитать, как энергию взаимодействия первого со вторым, первого с третьим и второго с третьим.

r и k не ноль. Обратим внимание на энергию найденную тремя способами: через заряд, через и через. Если рассматривать точечный заряд в отдельности, то собственная его энергия, энергия взаимодействия элементов заряда между собой, то выражение для энергии двух зарядов не содержит собственные энергии самих зарядов, а лишь энергию их взаимодействия между собой. В отличии от формул содержащих выражение для полей и непрерывно распределённых зарядов. Последние уже содержат собственную энергию бесконечна. Выражение не содержит собственной энергии.

studfiles.net

2) Диэлектрики в электрическом поле

В отличие от проводников, в диэлектриках нет свободных зарядов. Все заряды являются

связанными : электроны принадлежат своим атомам, а ионы твёрдых диэлектриков колеблются

вблизи узлов кристаллической решётки.

Соответственно, при помещении диэлектрика в электрическое поле не возникает направлен-ного движения зарядов

1

. Поэтому для диэлектриков не проходят наши доказательства свойств

проводников — ведь все эти рассуждения опирались на возможность появления тока. И дей-ствительно, ни одно из четырёх свойств проводников, сформулированных в предыдущей статье,

не распростаняется на диэлектрики.

1. Напряжённость электрического поля внутри диэлектрика может быть не равна нулю.

2. Объёмная плотность заряда в диэлектрике может быть отличной от нуля.

3. Линии напряжённости могут быть не перпендикулярны поверхности диэлектрика.

4. Различные точки диэлектрика могут иметь разный потенциал. Стало быть, говорить о

«потенциале диэлектрика» не приходится.

Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.

Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.

Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков).

Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема.

Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры.

Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле c напряжённостью , направленное против внешнего поля с напряжённостью. В результате напряжённость поля внутри диэлектрика будет выражаться равенством:

В зависимости от механизма поляризации, поляризацию диэлектриков можно подразделить на следующие типы:

Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля. Самая быстрая поляризация (до 10−15 с). Не связана с потерями.

Ионная — смещение узлов кристаллической структуры под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки. Время протекания 10−13 с, без потерь.

Дипольная (Ориентационная) — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.

Электронно-релаксационная — ориентация дефектных электронов во внешнем электрическом поле.

Ионно-релаксационная — смещение ионов, слабо закрепленных в узлах кристаллической структуры, либо находящихся в междуузлие.

Структурная — ориентация примесей и неоднородных макроскопических включений в диэлектрике. Самый медленный тип.

Самопроизвольная (спонтанная) — благодаря этому типу поляризации у диэлектриков, у которых он наблюдается, поляризация проявляет существенно нелинейные свойства даже при малых значениях внешнего поля, наблюдается явление гистерезиса. Такие диэлектрики (сегнетоэлектрики) отличаются очень высокими значениямидиэлектрической проницаемости (от 900 до 7500 у некоторых видов конденсаторной керамики). Введение спонтанной поляризации, как правило, увеличивает тангенс угла потерь материала (до 10−2)

Резонансная — ориентация частиц, собственные частоты которых совпадают с частотами внешнего электрического поля.

Миграционная поляризация обусловлена наличием в материале слоев с различной проводимостью, образованию объемных зарядов, особенно при высоких градиентах напряжения, имеет большие потери и является поляризацией замедленного действия.

Поляризация диэлектриков (за исключением резонансной) максимальна в статических электрических полях. В переменных полях, в связи с наличием инерции электронов, ионов и электрических диполей, вектор электрической поляризации зависит от частоты.

studfiles.net

Напряженность электрического поля в диэлектрике.

В соответствии с принципом суперпозиции электрическое поле в диэлектрике векторно складывается из внешнего поля и поля поляризационных зарядов (рис.3.11).

или по абсолютной величине

Мы видим, что величина напряженности поля в диэлектрике меньше, чем вакууме. Другими словами, любой диэлектрик ослабляет внешнее электрическое поле.

Рис.3.11. Электрическое поле в диэлектрике.

Индукция электрического поля , где , , то есть . С другой стороны, , откуда находим, что ε0Е0= ε0εЕ и, следовательно, напряженность электрического поля в изотропном диэлектрике есть:

Эта формула раскрывает физический смысл диэлектрической проницаемости и показывает, что напряженность электрического поля в диэлектрике в раз меньше, чем в вакууме. Отсюда следует простое правило: чтобы написать формулы электростатики в диэлектрике, надо в соответствующих формулах электростатики вакуума рядом с приписать .

В частности, закон Кулона в скалярной форме запишется в виде:

14. Электрическая емкость. Конденсаторы (плоский, сферический, цилиндрический), их емкости.

Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создавается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.

 

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостьюконденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками:

(1)

Найдем емкость плоского конденсатора, который состоит из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если считать, что расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами на пластинах можно пренебречь и поле между обкладками считать однородным. Его можно найти используя формулу потенциала поля двух бесконечных параллельных разноименно заряженных плоскостей φ1-φ2=σd/ε0. Учитывая наличие диэлектрика между обкладками:

(2)

где ε — диэлектрическая проницаемость. Тогда из формулы (1), заменяя Q=σS, с учетом (2) найдем выражение для емкости плоского конденсатора:

(3)

Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2(r2 > r1), один вставлен в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l (l—длина обкладок). При наличии диэлектрика между обкладками разность потенциалов

(4)

Подставив (4) в (1), найдем выражение для емкости цилиндрического конденсатора:

(5)

Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов

(6)

Подставив (6) в (1), получим

Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид

где — заряд, — потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса Rравна (в системе СИ):

где ε0 — электрическая постоянная, ε — относительная диэлектрическая проницаемость.

Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком иливакуумом, — к конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:

где S — площадь одной обкладки (подразумевается, что они равны), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная.

 

Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

 

 

15. Соединение конденсаторов (параллельное и последовательное)

Помимо показанного на рис. 60 и 61, а также на рис. 62, а параллельного соединения конденсаторов, при котором соединены между собой все положительные и все отрицательные обкладки, иногда соединяют конденсаторы последовательно, т. е. так, чтобы отрицательная обкладкаРис. 62. Соединение конденсаторов: а) параллельное; б) последовательноепервого конденсатора была соединена с положительной обкладкой второго, отрицательная обкладка второго — с положительной обкладкой третьего и т. д. (рис. 62, б). В случае параллельного соединения все конденсаторы заряжаются до одной и той же разности потенциалов U, но заряды на них могут быть различными. Если емкости их равны С1, С2,..., Сn, то соответствующие заряды будутОбщий заряд на всех конденсаторахи, следовательно, емкость всей системы конденсаторов(35.1)Итак, емкость группы параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.

В случае последовательно соединенных конденсаторов (рис. 62, б) одинаковы заряды на всех конденсаторах. Действительно, если мы поместим, например, заряд +q на левую обкладку первого конденсатора, то вследствие индукции на правой его обкладке возникнет заряд —q, а на левой обкладке второго конденсатора — заряд +q. Наличие этого заряда на левой обкладке второго конденсатора опять-таки вследствие индукции создает на правой его обкладке заряд —q, а на левой обкладке третьего конденсатора — заряд +q и т. д. Таким образом, заряд каждого из последовательно соединенных конденсаторов равен q. Напряжение же на каждом из этих конденсаторов определяется емкостью соответствующего конденсатора:

где Сi — емкость одного конденсатора. Суммарное напряжение между крайними (свободными) обкладками всей группы конденсаторовСледовательно, емкость всей системы конденсаторовопределяется выражением (35.2)Из этой формулы видно, что емкость группы последовательно соединенных конденсаторов всегда меньше емкости каждого из этих конденсаторов в отдельности.

 

16. Энергия электрического поля и её объёмная плотность.

Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает

 

Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,

 

Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна

 

C учетом соотношения можно записать

 

В изотропном диэлектрике направления векторов D и E совпадают и Подставим выражение , получим

 

Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов qi на величину dri, составляет

 

Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно, .Вектор P связан с вектором E соотношением . Подставив это выражение в формулу для работы, получим

 

Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика

 

.

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:

 

17. Постоянный электрический ток, его характеристики и условия существования. Закон Ома для однородного участка цепи (интегральная и дифференциальная формы)

 

 

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

Источник тока - устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают при движении проводника в магнитном поле, в фотоэлементах - при действия света на электроны в металлах и полупроводниках.

Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.

 

Основные понятия.

 

Сила тока - скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

где I - сила тока, q - величина заряда (количество электричества), t - время прохождения заряда.

Плотность тока - векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

где j -плотность тока, S - площадь сечения проводника.

Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.

Напряжение - скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.

где A - полная работа сторонних и кулоновских сил, q - электрический заряд.

Электрическое сопротивление - физическая величина, характеризующая электрические свойства участка цепи.

где ρ - удельное сопротивление проводника,l - длина участка проводника, S - площадь поперечного сечения проводника.

 

Проводимостью называется величина, обратная сопротивлению

где G - проводимость.

 

 

Законы Ома.

 

Похожие статьи:

poznayka.org

ЛЕКЦИЯ №12 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ

Система, состоящая из двух одинаковых по величине и противоположных по знаку зарядов, разделенных некоторым промежутком, образуют диполь.Диполь является основным модельным представлением, которое используется для описания поля в диэлектриках. Электрический момент диполя, равный произведению величины заряда на расстояние между ними, направлен от – к + заряду.

 

ДИПОЛЬ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. Однородное поле. Силы, действующие на – и + заряды равны по величине и противоположны по направлению. Поэтому в однородном поле возможен лишь поворот диполя относительно своего центра. Момент сил, действующих на диполь .

Электрическое поле оказывает ориентирующее действие на диполь, стремясь повернуть его так, чтобы его электрический момент был … направлен по полю.

Неоднородное поле. Силы, действующие на + и – заряды, не равны по величине, поэтому электрическое поле оказывает не только ориентирующее воздействие на диполь, но и стремится переместить его в область больших полей.

Работа поворота диполя в электрическом поле: A=pE(cosa1-cosa2)

Энергия диполя в электрическом поле: W=-(pE)

 

Как и в случае проводников, диэлектрики существенно изменяют величину поля, создаваемого заряженными телами. По аналогии с металлами можно предположить, что в электрическом поле на поверхности диэлектриков возникают некомпенсированные заряды. Если под действием поля электрические заряды свободно перемещаются по проводникам, то в диэлектриках на очень малое перемещение возможно только в пределах отдельных молекул, составляющих диэлектрик.

ПОЛЯРНЫЕ И НЕПОЛЯРНЫЕ МОЛЕКУЛЫ

Если центры + и – зарядов совпадают, то такие молекулы называются неполярными. Если центры + и – зарядов не совпадают, то такие молекулы называются полярными.

НЕПОЛЯРНЫЕ МОЛЕКУЛЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ В электрическом поле + заряды смещаются по полю, а – против поля. Оказывается, что во многих случаях расстояние l между центрами + и – в неполярных молекулах увеличивается пропорционально величине электрического поля l~E

Поскольку под действием электрического поля изменяется состояние неполярного диэлектрика, этот процесс называется деформационной поляризацией. Говорят, что неполярные молекулы в электрическом поле ведут себя как упругий диполь.

ПОЛЯРНЫЕ МОЛЕКУЛЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ Газообразное состояние. В газообразном состоянии, как правило, молекулы находятся на достаточно большом расстоянии по сравнению с их размерами и участвуют в тепловом хаотическом движении. Каждая полярная молекула имеет дипольный момент рi. Однако из-за наличия теплового движения суммарный дипольный момент совокупности полярных молекул равен нулю.

Жидкое состояние. Для жидкого состояния вещества характерно наличие ближнего порядка. Из принципа минимума потенциальной энергии следует, что + одного диполя «прилипает» к – соседнего диполя. Каждая полярная молекула имеет дипольный момент рi .Однако из-за принципа min Wp суммарный дипольный момент совокупности полярных молекул равен нулю. Эти молекулы также участвуют в тепловом, хаотическом движении.

Полярные молекулы, попадая в электрическое поле, испытывают два противоположных воздействия: — ориентирующее воздействие электрического поля — и дезориентирующее воздействие теплового, хаотического движения. Оказывается, что во многих случаях из-за борьбы этих воздействий, суммарный дипольный момент совокупности полярных молекул пропорционален напряженности поля. В случае кристаллических диэлектриков, имеющих ионное строение, электрическое поле приводит к смещению положительных ионов в направлении Е и отрицательных – в противоположную сторону. В электрическом поле дипольный момент кристаллического диэлектрика направлен вдоль поля и пропорционален величине его напряженности. Говорят, что полярные молекулы в электрическом поле ведут себя как жесткий диполь.

ДИЭЛЕКТРИК В ЭЛЕКТРИЧЕСКОМ ПОЛЕ ВЕКТОР ПОЛЯРИЗАЦИИ

Поместим тело, состоящее из диэлектрика различного вида поляризации, в электрическое поле

Независимо от вида поляризации и объема тела суммарный электрический момент диэлектрика пропорционален напряженности поля. Поэтому величину суммарного электрического момента диэлектрика можно определить, зная электрический момент единицы объема и объем тела: где Р – вектор поляризации

Вектор поляризации пропорционален напряженности электрического поля

где β – диэлектрическая восприимчивость

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКЕ

 

Поместим между обкладками плоского конденсатора диэлектрик из неполярных молекул

При замыкании ключа К пластины заряжаются и диэлектрик, находящийся между ними, поляризуется. Поле, создаваемое поляризационными зарядами в диэлектрике, можно определить как поле, создаваемое в объеме поляризованного диэлектрика, и поля нескомпенсированных зарядов на поверхности

Несмотря на поляризацию, результирующее макроскопическое поле, создаваемое объемным зарядом, равно нулю.

Поле, создаваемое нескомпенсированными зарядами на поверхности, можно представить как поле двух параллельно заряженных плоскостей: где σ‘ – поверхностная плотность нескомпенсированного заряда. С другой стороны эти заряды можно рассматривать как гигантский диполь:

Из сравнения выражений, определяющич электрический момент диэлектрика следует: σ’=P

Таким образом, силовые линии напряженности электрического поля терпят разрыв на границе диэлектрика, что неудобно при расчетах электрических полей в среде, содержащей диэлектрик. Для ликвидации этого неудобства вводится вспомогательный вектор D – вектор электростатической индукции или электрического смещения D=ε0E+P

Трансформация основных соотношений электростатики Из факта уменьшения напряженности поля в диэлектрике по сравнению с ее значением в вакууме на величину ε следует, что во всех основных соотношениях электростатики, к величине ε0 необходимо добавить ε :

Теорема Гаусса при наличии диэлектрика. Трудности при вычислении этого интеграла состоят в том, что необходимо суммировать не только свободные, но и связанные заряды, возникающие на границе диэлектрика. Поэтому имеет смысл перейти от вектора Е к вектору D, поскольку его величина не зависит от поляризации диэлектрика (связанные заряды)

Появление вспомогательного вектора D, предназначенного для описания электрического поля в среде, обусловлено пропорциональностью между векторами Р и Е, что выполняется далеко не всегда. Это случаи анизотропных диэлектриков, сегнетоэлектриков, электретов, электрических полей высокой частоты.

 

 

	|	следующая страница ==>
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ПОТЕНЦИАЛ, РАЗНОСТЬ ПОТЕНЦИАЛОВ	|	ЭЛЕКТРИЧЕСКИЙ ТОК

Дата добавления: 2014-11-24; просмотров: 1.

Поделиться с ДРУЗЬЯМИ:

refac.ru

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ

Электротехника ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ

просмотров - 121

Диэлектрики — это вещества, не проводящие электрический ток. Диэлектрик (как и любое вещество) состоит из атомов или молекул, которые построены из ядер и электронов. Размеры атомных ядер и электронов примерно в 105 раз меньше размеров самих атомов. По этой причине объём заряженных частиц, находящихся в некотором телœе, ничтожно мал по сравнению с объёмом тела. Это позволяет представить тело как часть вакуумного пространства, в котором вкраплены заряженные частицы. При этом напряжённость поля в нём, согласно принципу суперпозиции полей, складывается из напряжённости внешнего поля и напряжённости электрических полей, создаваемых заряженными частицами тела в вакууме. Возникает вопрос, как можно рассчитать напряжённость поля внутри диэлектрика?

Для этого представим молекулы диэлектриков в виде диполей. Роль положительного заряда будут играть ядра, а отрицательного - электроны, входящие в состав молекулы. Будем считать, что располагаются заряды «диполя» в центре масс ядер и электронов соответственно. В расположении зарядов друг относительно друга возможны 2 случая. Первый, когда центры масс положительных и отрицательных зарядов совпадают, такие молекулы называются неполярными, а диэлектрики образованные этими молекулами – неполярными диэлектриками. Второй, когда центры масс не совпадают, молекулы при этом называются полярными, следовательно, и диэлектрики названы полярными.

Рассмотрим сначала поведение отдельной молекулы неполярного диэлектрика в электрическом поле. К таким диэлектрикам относятся вода, аммиак, эфир, кислоты, основания и другие вещества. В неполярных молекулах даже в отсутствии электрического поля заряды распределœены не симметрично, следовательно, они обладают дипольным моментом. При внесении полярного диэлектрика в электростатическое поле его молекулы стремятся ориентироваться так, чтобы их дипольные моменты были направлены вдоль поля. Это происходит под действием сил, приложенных к положительному и отрицательному зарядам диполя, которые приводят к его повороту (рис. 12.1).

Рис. 12.1

Предположим, что в однородное электростатическое поле помещен жесткий диполь так, что вектор его дипольного момента направлен под углом к вектору напряженности внешнего поля. Как видно из рисунка 12.1, на диполь действует пара сил: и . Момент этой пары сил численно равен

. (12.1)

Вектор момента равен векторному произведению векторов:

. (12.2)

Вектор направлен перпендикулярно плоскости, проходящей через векторы и (плоскость чертежа), причем из конца вращение от к по кратчайшему пути видно происходящим против часовой стрелки. В примере, изображенном на рис. 12.1, вектор направлен от нас за чертеж. Момент пары сил стремится повернуть диполь и установить его так, чтобы направления векторов и совпадали. В случае если пренебречь инœерцией диполя, то крайне важно считать, что после установления оси диполя вдоль поля он остановится. При этом силы, действующие на оба заряда жесткого диполя, равны по абсолютному значению и направлены по одной прямой в противоположные стороны. Οʜᴎ стремятся изменить расстояние между зарядами и . В случае если диполь жесткий, то действие этих сил должно быть компенсировано внутримолекулярными силами связи. При этом, как показывает опыт, действие внешнего поля всœегда приводит к некоторой деформации молекулы и появлению индуцированного дипольного момента (данный момент подробно рассмотрим для неполярных молекул).

При внесении диэлектрика в электрическое поле происходит так называемая поляризация диэлектрика. Для рассмотрения этого явления выясним, как ведет себя совокупность молекул-диполей, помещенных в электрическое поле.

В случае если диэлектрик с полярными молекулами не находится во внешнем электрическом поле, то вследствие беспорядочного теплового движения молекул векторы их дипольных моментов ориентированы хаотично (рис.12.2). По этой причине векторная сумма дипольных моментов всœех молекул, содержащихся в произвольном объеме диэлектрика, равна нулю.

Рис. 12.2

Иная картина наблюдается при внесении диэлектрика в электрическое поле. Под действием поля полярные молекулы диэлектрика (жесткие диполи) стремятся повернуться таким образом, чтобы векторы их дипольных моментов () совпали по направлению с . При этом тепловое движение молекул хаотически «разбрасывает» диполи и препятствует установлению их векторов вдоль поля. В результате совместного действия обеих причин в диэлектрике возникает преимущественная ориентация дипольных моментов молекул вдоль поля (рис. 12.3). Эта ориентация будет тем более полной, чем сильнее электрическое поле в диэлектрике и слабее тепловое движение молекул, ᴛ.ᴇ. чем ниже температура. Описанный процесс принято называть ориентационной поляризацией диэлектрика с полярными молекулами.

Рис. 12.3

Рассмотрим теперь диэлектрики с неполярными молекулами. К таким диэлектрикам относятся кислород, азот, углеводороды и т.д. Полярные молекулы симметричны и дипольный момент каждой молекулы, при отсутствии внешнего электрического поля, равен нулю.

В случае если неполярную молекулу диэлектрика поместить во внешнее электростатическое поле, то в ней индуцируется (наводится) дипольный момент . Рассмотрим, к примеру, что произойдет с атомом водорода, помещенным в электростатическое поле. Для простоты будем считать, что электрон в атоме водорода движется вокруг ядра по круговой орбите радиуса (рис. 12.4). В случае если отсутствует внешнее поле, то на электрон действует одна лишь электрическая сила его притяжения к ядру, численно равная, согласно формуле (1.2), . Эта сила сообщает электрону центростремительное ускорение, численно равное , в связи с этим

, (12.3)

где — масса электрона, — угловая скорость его движения по орбите. Из (12.3) легко определить радиус орбиты электрона.

Рис. 12.4

Пусть на атом водорода действует внешнее электрическое поле, вектор напряженности которого перпендикулярен плоскости орбиты электрона. Под влиянием поля орбита электрона деформируется. В первом приближении можно считать, что эта деформация заключается в смещении плоскости орбиты электрона на малое расстояние в направлении, противоположном направлению , причем радиус орбиты и угловая скорость электрона не изменяются (рис. 12.5). Теперь роль центростремительной силы будет играть равнодействующая сил, приложенных к электрону со стороны внешнего электрического поля и со стороны ядра : , где и . Из рис. 12.5 следует, что

, откуда

. 12.4

Рис. 12.5

Смещение орбиты электрона, а, следовательно, и центра тяжести заряда по отношению к ядру под влиянием внешнего электрического поля пропорционально напряженности этого поля. Смещение аналогично упругой деформации, в связи с этим диполь, возникший в атоме водорода, называют упругим диполем. Электрический момент упругого диполя с учетом выражения (12.4), численно равен

, (12.5)

или, если использовать формулу (12.3),

. (12.6)

Где — множитель, пропорциональный третьей степени радиуса орбиты, ᴛ.ᴇ. объему атома, и называемый поляризуемостью атома. Результат, полученный в этом примере, имеет общее значение. Индуцированный дипольный момент неполярной молекулы всœегда пропорционален напряженности внешнего электрического поля, причем поляризуемость этой молекулы зависит только от ее объема. Вектор совпадает по направлению с вектором напряженности внешнего электрического поля:

. (12.7)

Делаем вывод исходя из вышесказанного: под действием электрического поля неполярная молекула приобретает дипольный момент, направленный вдоль поля, который называют наведённым. Это обусловлено тем, что силы электрического поля деформируют электронные орбиты.

Рассмотрим диэлектрик с неполярными молекулами. Его дипольный момент при отсутствии внешнего электрического поля равен нулю, т.к. дипольный момент каждой молекулы неполярного диэлектрика, равен нулю. При помещении неполярного диэлектрика в электрическое поле, молекулы приобретают индуцированные дипольные моменты. Момент упругого диполя создается в каждой частице, причем в не очень сильных полях, и при не слишком большой плотности вещества формула (12.7) для момента изолированной молекулы остается справедливой для каждой молекулы, находящейся в некотором объеме диэлектрика. Очень существенно, что электрические дипольные моменты наводятся в таких молекулах всœегда в направлении действующего электрического поля независимо от температуры диэлектрика и связанного с нею теплового движения (рис. 12.6). Тепловое движение, хаотически разбрасывая упругие диполи, не влияет на смещение центров тяжести положительных и отрицательных зарядов в молекулах под действием электрического поля. В этом случае происходит так называемая электронная поляризация диэлектрика. Практически в жидких и газообразных диэлектриках наблюдается одновременно и ориентационная, и электронная поляризация.

Рис. 12.6

Выделяют еще одну группу диэлектриков – кристаллические диэлектрики с ионной решеткой. К ним относятся, к примеру, и т.д. У таких диэлектриков каждая пара сосœедних разноименных ионов подобна диполю (рис. 12.7). В электрическом поле эти диполи деформируются: удлиняются, если их оси направлены по полю, и укорачиваются, если оси направлены против поля (рис. 12.8). В результате диэлектрик поляризуется. Такого рода поляризация принято называть ионной. Степень ионной поляризации зависит от свойств диэлектрика и от напряженности поля .

рис. 12.7

рис.12.8

Читайте также

- Электрическое поле в диэлектриках.

Поляризационные заряды диэлектриков создают свое поле , противоположное внешнему . Результирующее поле при этом . рассмотрим для простоты частный случай поля между двумя плоскопараллельными пластинами, между которыми находится диэлектрик (рис.15.7). Результирующее поле... [читать подробенее]

- Электрическое поле в диэлектриках.

Поляризационные заряды диэлектриков создают свое поле , противоположное внешнему . Результирующее поле при этом . рассмотрим для простоты частный случай поля между двумя плоскопараллельными пластинами, между которыми находится диэлектрик (рис.15.7). Результирующее поле... [читать подробенее]

- Электрическое поле в диэлектриках и проводниках

Лекция 4 Все вещества по электрическим свойствам и, в первую очередь, по способности проводить электрический ток, разделяются на проводники и диэлектрики. Промежуточное положение между ними занимают полупроводники. Проводниками называют вещества, в которых имеются... [читать подробенее]

- Электрическое поле в диэлектриках.

Лекция 2.5. Теперь рассмотрим, как изменяются характеристики электрического поля в диэлектрике. Будем рассматривать идеальный диэлектрик, т.е. такой, в котором отсутствуют свободные заряды, все заряды связаны в микроскопические нейтральные комплексы (атомы, молекулы,... [читать подробенее]

- ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ

Диэлектрики — это вещества, не проводящие электрический ток. Диэлектрик (как и любое вещество) состоит из атомов или молекул, которые построены из ядер и электронов. Размеры атомных ядер и электронов примерно в 105 раз меньше размеров самих атомов. Поэтому объём заряженных... [читать подробенее]

- Лекция 4. Электрическое поле в диэлектриках

Все вещества по электропроводности разделяются на проводники и диэлектрики. Промежуточное положение между ними занимают полупроводники. Проводниками называют вещества, в которых имеются свободные носители зарядов, способные перемещаться под действием электрического... [читать подробенее]

oplib.ru

Описание электрического поля в диэлектриках

Рассмотрим диэлектрическую пластинку, заполняющую плоский конденсатор и находящуюся в однородном внешнем электрическом поле Е. В результате возникновения объемной поляризации на гранях диэлектрика, обращенных к пластинам конденсатора, концы молекулярных диполей окажутся нескомпенсированными соседними диполями, как это имеет место внутри диэлектрика. Поэтому грани диэлектрика окажутся заряженными с некоторой поверхностной плотностью . Эти возникшие заряды называются поляризационными или связанными. Они не могут быть переданы соприкосновением другому телу, т.к. они не могут покинуть пределы молекулы, в состав которой они входят. В остальном же их свойства такие же, как и свободных зарядов.

Образование поляризационных зарядов приводит к возникновению дополнительного поля Е’. Вне пластины это поле равно нулю (как в случае конденсатора). Внутри диэлектрика поле Е’ направлено против внешнего поля Е и ослабляет последнее. Результирующее поле внутри диэлектрика равно

Е= (1)

Поле Е можно рассчитать как поле между двумя плоскими бесконечными плоскостями заряженными с поверхностной плотностью , т.е. как поле конденсатора

,

где т.к. заряды сосредоточены на молекулах , и надо рассматривать среду между зарядами, т.е. между молекулами , следовательно вакуум.

(2)

 

Очевидно, что поверхностная плотность связанных зарядов связана с вектором поляризации Р. Найдем эту связь.

Обозначим через полный дипольный момент пластинки диэлектрика имеющей толщину d и площадь граней S. Тогда

(3)

C другой стороны можно написать так

 

(4)

Сравнивая (3) и (4) мы видим, что поверхностная плотность связанных зарядов численно равна величине вектора поляризации диэлектрика Р.

(5)

Подставляем (5) в (2) и получаем

(6)

Для Р мы раньше получили формулу

(7)

Здесь Е , как мы уже отмечали , есть результирующее поле в диэлектрике.

Подставляя (7) в (6) получим

(8)

отсюда

(9)

При рассмотрении закона Кулона , ослабление электрического поля в среде по сравнению с полем в вакууме мы характеризовали величиной диэлектрической проницаемости .

,

-сила взаимодействия в вакууме

F- сила взаимодействия в среде.

Отсюда напряженность поля в среде

(10)

Сравнивания (10) и (9) видим , что

Так как. вектор всегда направлен вдоль , то всегда положительно и следовательно > 1 .

Из (8) видно , что поле в диэлектрике Е и поле в вакууме различны и отличаются на величину , зависящую от свойств диэлектрика . Можно ввести некоторую вспомогательную величину , которая будет одинакова в вакууме и в диэлектрике и следовательно не будет зависеть от свойств среды. Из (8) видно , что такой величиной может быть , например,

обозначим

(11)

 

Величина D, определяемая соотношением (11) , называется электрическим смещением или электрической индукцией .

 

Используя выражение (7) для Р , можно записать D по другому:

 

(12)

Выражение (11) для D является более общим , чем (12) . Соотношение (11) справедливо при любом законе зависимости Р от Е , а соотношение (12) верно только для линейной зависимости Р от Е (ф.7) , которую мы использовали при получении выражения (12) .

При рассмотрении теоремы Гаусса мы записывали ее в виде :

(13)

Используя (12) и (13) можно переписать в виде

(14)

Вектор Е характеризует результирующее поле в диэлектрике, обусловленное свободными и связанными зарядами и поэтому зависит от свойств среды. Вектор электрического смещения D не зависит от свойств среды и следовательно не связан с полем связанных зарядов. Следовательно, вектор D характеризует то электрическое поле, которое создается в данном веществе одними лишь свободными зарядами. Поэтому теорему Гаусса следует записывать в форме

Поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов.

 

Сегнетоэлектрики

 

Существует группа веществ, которые могут обладать спонтанной (самопроизвольной) поляризацией в отсутствие внешнего поля..Подобные вещества называются сегнетоэлектриками. (Сегнетовая соль, титанат бария.)

Сегнетоэлектрики отличаются от остальных диэлектриков рядом характерных особенностей.

1. Диэлектрическая проницаемость сегнетоэлектриков достигает величины нескольких тысяч (у обычных диэлектриков ).
2. Зависимость D от Е не является линейной.

 

 

1. Как следствие 2) зависит от Е

До насыщения Р растет быстрее Е , возрастает . Затем Р=const , а Е растет и следовательно уменьшается .

1. D и Р зависят не только от Е в данный момент, но и от предшествующих значений Е. Гистерезис (запаздывание)

Dост – остаточная индукция

Ек- коэрцитивная сила

 

1. Температура Кюри –ТК .

При Т> ТК сегнетоэлектрик переходит в обычный диэлектрик , например , BaTiO3 TK=1250C

Все эти особенности сегнетоэлектриков связаны с их структурой. Взаимодействие частиц в кристалле сегнетоэлектрика приводит к тому, что их дипольные моменты спонтанно устанавливается параллельно друг другу. В исключительных случаях одинаковая ориентация дипольных моментов распространяется на весь кристалл. Обычно же дипольные моменты устанавливаются параллельно только в отдельных областях – доменах. Ориентация доменов различна.

В отсутствие поля результирующий момент равен 0. Под действием поля моменты доменов поворачиваются как целое, устанавливаясь вдоль поля.

Применяются при изготовлении малогабаритных конденсаторов большой емкости.

 

Пьезоэлектрический эффект

 

Некоторые кристаллы, не имеющие центра симметрии (в том числе все сегнетоэлектрики) при деформации поляризуются. Это явление называются пьезоэлектрическим эффектом. Величина поляризации пропорциональна деформации. При изменении знака деформации знак меняется также на обратный.Важнейшими пьезоэлектриками являются кварц, сегнетова соль, титанат бария.

Возьмем пластину из кварца, определенным образом вырезанную. Если сжимать ее по оси Y или растягивать по оси X, то на верхней и нижней гранях возникают связанные заряды. Если на грани пластинки наложить металлические обкладки и включить в замкнутую цепь, то при изменениях деформации кристалла в цепи будут возникать импульсы тока. Пьезоэлектрики широко используются в так называемых электроакустических приборах для преобразования механических (звуковых и ультразвуковых) колебаний в электрические и обратно. Пьезоэлектрические датчики позволяют регистрировать деформации, толчки, преобразовывая их в электрические импульсы.

Пьезоэлектрический эффект можно объяснить следующим образом. Решетку всякого кристалла можно представить в виде нескольких образованных разными атомами более простых решеток, вставленных друг в друга. Если кристалл не имеет центра симметрии, то при деформации происходит сдвиг простых решеток друг относительно друга, который может вызвать появление у кристалла электрического момента.

Наблюдается также обратный пьезоэлектрический эффект, заключающийся в том, что приложение внешней разности потенциалов к пластинке пьезоэлектрика приводит к механическим деформациям кристалла. Если прикладывать переменное напряжение, то в пластинке возбудятся механические колебания. Эти колебания станут особенно интенсивными, если частота переменного напряжения совпадает с собственной (резонансной) частотой пластинки. Такие настроенные в резонанс пьезоэлектрические пластинки используются для возбуждения ультразвуковых волн, для стабилизации частоты генераторов электрических колебаний в радиотехнике.

 

 

Постоянный электрический ток

Электрический ток. Сила и плотность тока.

 

Если в проводнике создать электрическое поле, то носители заряда придут в упорядоченное движение, положительные в направлении поля, отрицательные в противоположную сторону. Упорядоченное движение зарядов называется электрическим током.

Поле в проводнике может создаваться электронами и положительными ионами(поле кулоновских сил). Но кулоновские силы между зарядами всегда приводят к такому перераспределению зарядов, при котором электрическое поле в проводнике исчезает, а потенциалы во всех точках выравниваются. Например, при сообщении заряда проводнику, в нем в течение короткого времени заряды будут перемещаться , т.е. течь ток, но затем когда заряды перераспределяться так, что поле станет равным нулю, ток исчезнет. Или, например, если обкладки конденсатора соединить проводником, то тоже в течение некоторого времени будет протекать ток, пока потенциалы обкладок не выровняются. Таким образом,. поле кулоновских сил не может вызвать стационарный процесс упорядоченного движения зарядов, т.е. не может являться причиной возникновения тока. Очевидно, что для поддержания длительного тока в цепи на свободные заряды должны действовать помимо кулоновских сил еще какие-то иные, не электростатические силы.

Рассмотрим ,например, замкнутую цепь. Потенциал в точке А- , в точке В- .

Пусть , тогда под действием электростатических сил положительные заряды будут двигаться от А к В ,например, по пути C. Для существования тока нужно, чтобы заряды двигались по замкнутому пути, но под действием электростатических сил заряды по участку от В к А не пойдут (циркуляция ), т.к. . На участке D в направлении от В к А должен происходить перенос положительных зарядов в направлении возрастания потенциала, т.е. против сил электростатического поля. Перемещение носителей на этом участке возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами. Эти сторонние силы создаются в цепи источниками тока ( гальваническими элементами, электрическими генераторами). Природа сторонних сил различна в различных источниках тока( аналогия с циркуляцией воды в замкнутой цепи- насос- аналог сторонних сил, сила тяжести- аналог электростатических сил).

Таким образом для появления и существования электрического тока в проводнике необходимы 2 условия.

1. Наличие в данной среде электрических зарядов, которые могли бы в ней перемещаться ( металлы- электроны, электролиты - и + ионы, газы – и + ионы и электроны).

2. Наличие в данной среде электрического поля, энергия которого затрачивалась бы на перемещение электрических зарядов. Это поле должно создаваться источником тока ( источником электродвижущей силы).

Для характеристики электрического тока вводится понятие силы тока. Силой тока I называется скалярная физическая величина, численно равная электрическому заряду, проходящему через поперечное сечение проводника за единицу времени.

Если за время dt переносится заряд dq, то

Если сила тока не меняется с течением времени, то ток называют постоянным

Электрический ток может быть обусловлен движением как положительных, так и отрицательных зарядов. Если в проводнике движутся носители обоих знаков, то

За направление тока принимается направление, в котором перемещаются положительные заряды.

В отсутствии поля носители тока участвуют в хаотическом тепловом движении с некоторой скоростью . При включении поля на хаотическое движение носителей налагается упорядоченное движение со скоростью . Средняя скорость носителей .

Для характеристики распределения электрического тока по сечению проводника вводится вектор плотности тока . Вектор численно равен силе тока, который проходит через единицу площади сечения проводника, проведенного перпендикулярно к направлению тока

За направление принимается направление вектора скорости упорядоченного движения положительных носителей.

Зная вектор плотности тока в каждой точке проводника, можно найти силу тока через любую поверхность S

 

,где - проекция вектора на направление нормали к площадке dS.

В случае постоянного тока и однородного по сечению проводника

Единица силы тока ампер в СИ является основной, ее определение мы дадим дальше.

Единица заряда – кулон определяется как заряд переносимый за 1сек через поперечное сечение проводника при силе тока в 1А.

1Кл=1А*1сек.

 



infopedia.su

---

• 
  Какой вид топлива добывается на уренгойском месторождении
• 
  Стоимость автономной газификации частного дома
• 
  Как направлены линии магнитной индукции
• 
  Сила тока безопасная для человека
• 
  Чем отличается компрессорное масло от моторного
• 
  Алгебра логики схемы
• 
  Как пользоваться сварочным аппаратом ресанта 190
• 
  Постоянный электрический ток и его характеристики
• 
  Проект освещения производственного помещения
• 
  На что влияет мощность блока питания компьютера
• 
  Монтаж распределительного щита