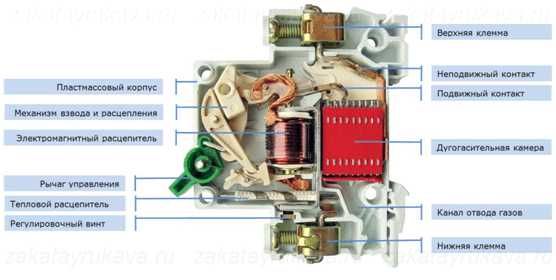
Расчет электромагнита (ЭМ). Электромагнит расчет

Расчёт электромагнита

Работа кольцевого электромагнита:

м = м sм  1,25 * Fпр * max = 1,25 * 230 * 0,4 = 115Нм

где Fм -тяговая сила магнита;

sм- ход якоря.

Площадь воздушного зазора между корпусом электромагнита и якорем:

Индукция электромагнитного поля в воздушном зазоре:

где 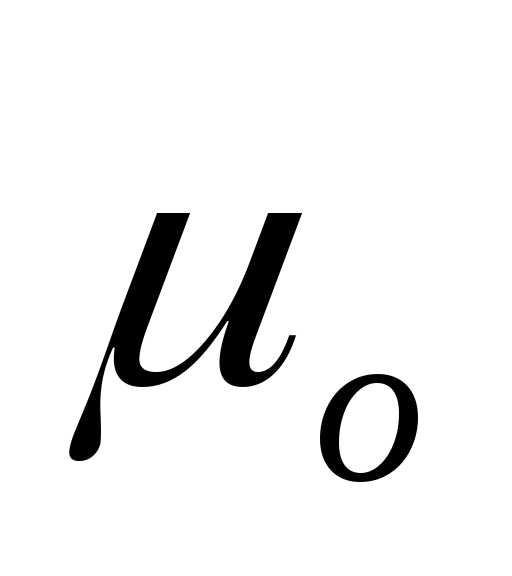= 410-7Гн/м- магнитная постоянная.

Напряжённость магнитного поля в воздушном зазоре:

Необходимое количество ампер-витков для создания индукционного потока, А,

Iw = 2 Ho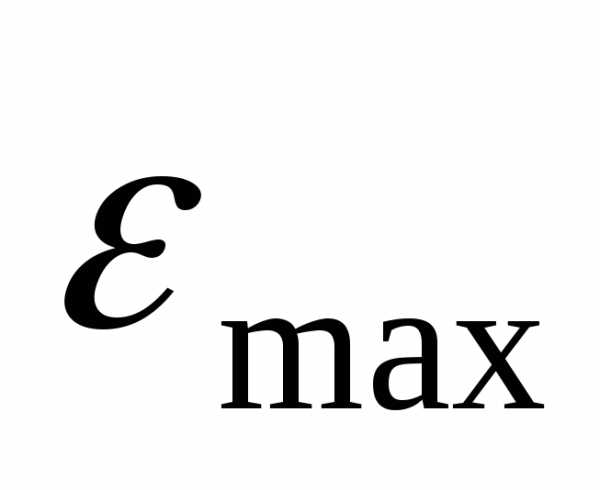= 20.950,0004 = 0,001A

где 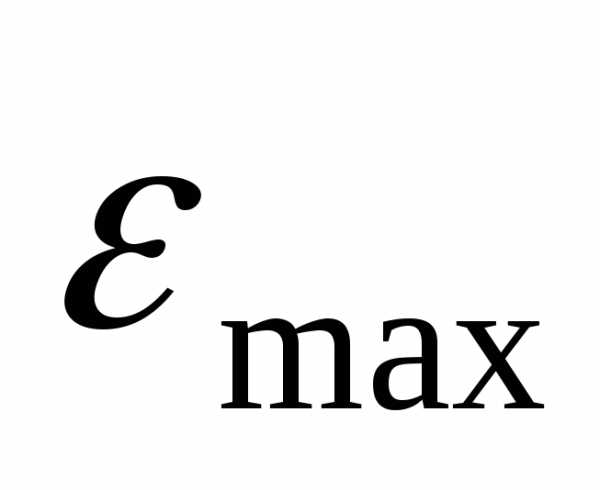- наибольшее значение воздушного зазора, м.

Площадь поперечного сечения катушки электромагнита

где 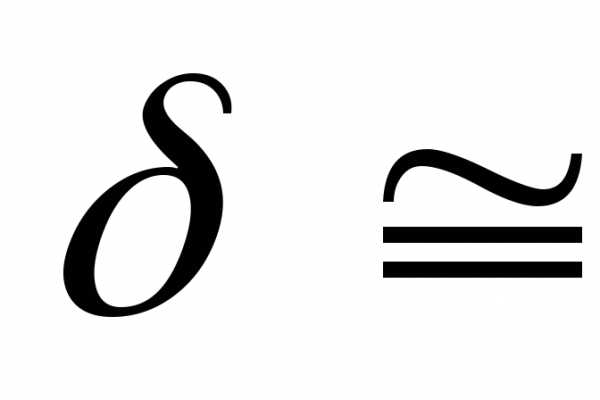2A/м2- плотность тока;

k 0,5- коэффициент, учитывающий заполнение проволокой сечения катушки.

Полученную площадь сравнивают с площадью поперечного сечения катушки по предварительному эскизу тормоза и электромагнита

Габаритные размеры электромагнита:

Dвн= 95мм

Dн= 160мм

В = 15мм

2. Расчет металлоконструкции.

Исходными данными для расчета является длина вылета L, грузоподъемностьQ.

Высота сечения стрелы

Принимаем

2.1 Определение основных размеров

Ширина сечения стрелы

Принимаем стандартную полосу с шириной

Толщина стенки:

Примем толщину стенки равной

Толщина верхнего пояса:

мм

Примем толщину равной 8 мм

Подвижная нагрузка от колеса:

, где

KQ=1,4 – коэффициент нагрузки

Kq=1,1 – коэффициент неравномерности

Толщина нижнего пояса:

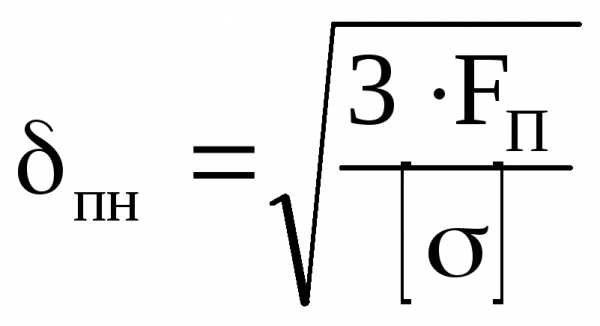, где

Принимаем толщину равной

Дальнейшие расчеты производят по эквивалентному сечению.

Высота эквивалентного сечения:

Расчетное сечение показано на рисунке 2.2.

Ширина нижнего сечения сделана больше

чем ширина верхнего, размещения колес электротали.

Расстояние между стенками принято стандартным, что позволяет выполнять диафрагмы

без обрезки по длине. Диафрагмы к верхнему растянутому поясу не приваривают.

Свес пояса над стенкой обеспечивает удобство автоматической сварки.

Координаты центра тяжести сечения.

Момент инерции определяем, пренебрегая собственными моментами инерции поясов.

2.2 Проверка статического прогиба.

Эпюра изгибающих моментов аналогична приведенной на рисунке.

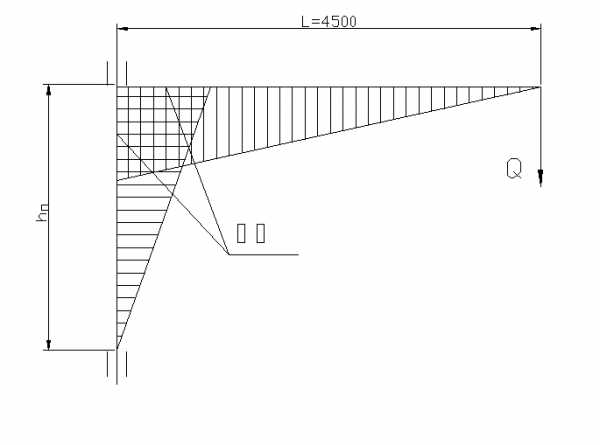
Расчетная длина стрелы:

Расстояние между подшипниками:

Принимаем

Диаметр колонны:

Dкол=0.5

Принимаем Dкол=300мм

Толщина стенки колонны:

кол=(0.05…0.08)Dкол=(0.05…0.08)*300=15…24мм

принимаем кол=20мм

Момент инерции колонны:

кол=0.32Dкол2*кол=0.32*3002*20=0.576*106мм4

Фактический прогиб:

Допустимый прогиб:

Как видно фактический прогиб не превышает допустимый.

2.3 Определение веса металлоконструкции.

Вес стрелы:

Координаты центра тяжести стрелы:

Вес подвижной колонны

2.4 Проверка времени затухания колебаний.

Приведенная масса, кг:

Жесткость:

Период собственных колебаний:

Логарифмический декремент затухания:

Начальная амплитуда:

Время затухания колебаний

2.5 Проверка прочности.

Допускаемое нормальное напряжение:

Допускаемое касательное напряжение, в том числе и для сварных швов:

Расчет в данном случае целесообразно начинать с подвижной колонны, так как в опасном сечении подвижной колонны действует наибольший момент в вертикальной плоскости.

Момент инерции в опасном сечении:

Момент сопротивления изгибу:

Напряжение изгиба:

Условие выполняется.

Расчет опорных узлов.

3.1. Расчет подшипников опорных узлов.

Определим силы действующие на корпуса опор:

Расчет подшипников производится на статическую грузоподъемность, т.к. частота вращения стрелы минимальна (n  10мин-1).

Для верхней опоры выбираем сферический радиально-упорный двухрядный шариковый подшипник.

Данный тип подшипников допускает большие углы перекосов во время работы крана.

Тип подшипника 1310, статическая радиальная грузоподъемность .

Условие пригодности подшипника:

Кне =0.63

Выбранный подшипник проходит по статической грузоподъемности.

Нижняя опора состоит из двух подшипников: упорного и сферического.

Сферический подшипник работает в тех же условиях, что и подшипник верхней опоры. Соответственно принимаем подшипник 1310.

Упорный подшипник выбирается так же из условий статической грузоподъемности. В данном случае также необходимо обеспечить геометрическую совместимость двух подшипников в одном опорном узле.

Тип 8204 Н .

15918Н  22400Н

studfiles.net

1.2 Расчёт ядра электромагнита. Расчёт электромагнита постоянного тока

Расчет электромагнита (ЭМ)

Поиск Лекций

Решается задача расчета электромагнита, вписанного в сектор, развивающего максимальный момент деформации сектора гибкого якоря торцевого волнового шагового двигателя (ТВШД) при заданных величинах постоянного напряжения питания и перегрева обмотки.

1.1. Определение основных размеров ЭМ

Тяговое усилие двухполюсного электромагнита

(1.1.1)

где , Тл – магнитная индукция в воздушном зазоре, Sc, м2 – площадь сечения магнитопровода, Гн/м – магнитная проницаемость воздуха.

Магнитный поток

Вб (1.1.2)

С учетом (1.1.2)

Н. (1.1.3)

Пренебрегая потоками рассеяния и падением магнитного напряжения в магни-топроводе можно записать, что

, Вб, (1.1.4)

где - сила тока в А и число витков обмотки;

Магнитное сопротивление воздушного зазора

, (1.1.5)

где , м – суммарный воздушный зазор.

С учетом (1.1.4), (1.1.5)

Н (1.1.6)

Сила тока в обмотке

А, (1.1.7)

где , - плотность тока, - сечение обмоточного привода без изоляции.

Число витков обмотки

, (1.1.8)

где , - площадь окна под обмотку; - коэффициент заполнения окна медью.

С учетом (1.1.7), (1.1.8)

Н (1.1.9)

и момент деформации (изгибающий момент)

, (1.1.10)

где , м – плечо приложения силы F.

Из (1.1.10) видно, что момент прямо пропорционален . Рассмотрим подробнее эту величину.

На рис. 1.1.1 показаны размеры электромагнита, вписанного в сектор, образованный наружным диаметром Dн, внутренним диаметром Dвн и углом α.

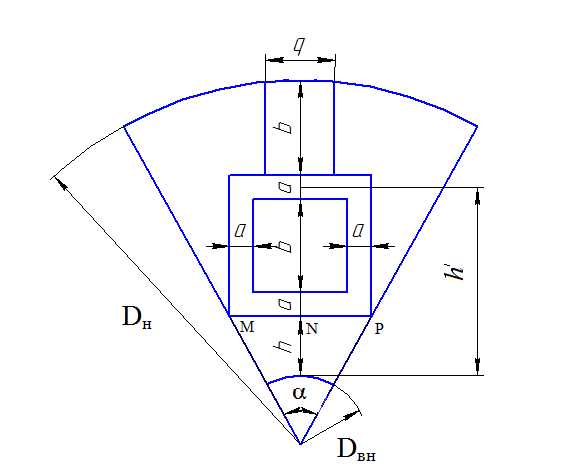
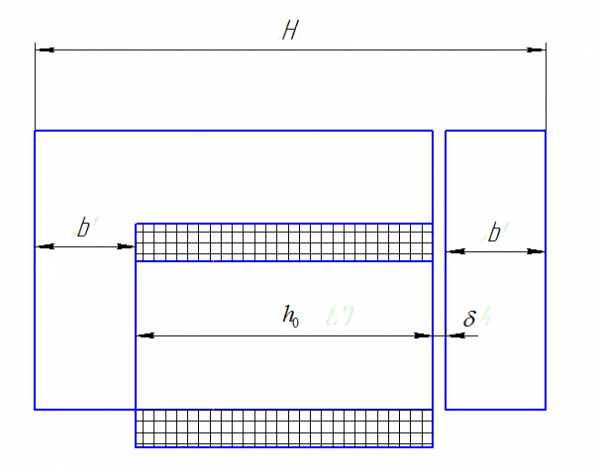Рис. 1.1.1 Размеры ЭМ

Из Рис. 1.1.1 можно записать, что:

Ширина полюса, м

, (1.1.11)где и , - наружный и внутренний диаметры сектора,

, и , - ширина окна под обмотку и расстояние от внутреннего диаметра сектора до обмотки;

толщина полюса,

, (1.1.12)

где - угол сектора;

высота окна под обмотку,

(1.1.13)

где ,

высота электромагнита,

, (1.1.14)

где , м – начальное значение немагнитного зазора между якорем ЭМ и сердечником.

Средний диаметр зубцовой зоны

, (1.1.15)

где - зазор по радиусу между наружным стержнем ЭМ и краем окна ГЯ, - выступ якоря, ЭМ для его крепления к ГЯ, - длина зубца (Рис. П3.2).

При перемещении зубца ГЯ на расстояние якорь ЭМ переместится на расстояние

, (1.1.16)

Где hз, м – высота зубца; δ0, м – начальное расстояние между вершинами зубцов.

Начальный немагнитный зазор якоря ЭМ

, (1.1.17)

где δк, м – конечный немагнитный зазор якоря ЭМ – толщина немагнитной прокладки между якорем и стержнями ЭМ.

Плечо приложения силы,

(1.1.18)

площадь окна под обмотку

, (1.1.19)

площадь полюса

, (1.1.20)

где - коэффициент заполнения сердечника сталью.

Поясним как зависит от и

С увеличением и произведение увеличивается. С увеличением , второй сомножитель в уменьшается, а третий – увеличивается, следовательно при изменении имеет максимум; при , имеет наибольшее значение, поэтому при изменении a и h, Sc имеет максимум. Координаты , максимума определяются из уравнений частных производных:

, (1.1.21)

; (1.1.22)

, (1.1.23)

. (1.1.24)

При изменении и , также будет иметь максимум, но его координаты , . C учетом проведенных расчетных исследований, координаты максимума можно приближенно определить по формуле:

, (1.1.25)

, (1.1.26)

где коэффициенты , .

С учетом найденных величин и , по вышеприведенным формулам определяют: (все размеры в системе СИ).

1.2. Электромагнитный расчет ЭМ

По найденным значениям и , заданным величинам напряжения питания , перегрева и изменении высоты окна под обмотку рассчитывают обмоточные данные, МДС обмотки, магнитную цепь с учетом падения МДС в магнитопроводе и потока рассеяния, магнитную индукцию , тяговое усилие и момент . Вы-брав максимальное значение определяют окончательно . Ниже приводятся и поясняются формулы, необходимые для вышеуказанной последовательности расчета.

Средний перегрев обмотки

(1.2.1)

где - коэффициент увеличения температуры внутри обмотки;

мощность потерь обмотки

, Вт (1.2.2)

где , А – сила тока обмотки;

коэффициент теплоотдачи при расчетной температуре

Вт/м2 ºС; (1.2.3)

боковая поверхность обмотки

, (1.2.4)

где - начальное значение высоты окна под обмотку по (1.1.13) при ;

- коэффициент теплоотдачи при 50ºС определяется по таблице 1.2.1

Таблица 1.2.1 коэффициенты теплоотдачи при 50ºС

, Вт/м2 оС
,	10-4	10-3	10-2	10-1

С учетом (1.2.1), (1.2.2) сила тока обмотки

, (1.2.5)

где перегрев обмоток при расчетной температуре θ и температуре окружаю-щего воздуха

, оС (1.2.6)

Сопротивление обмотки при расчетной температуре

Ом (1.2.7)

с другой стороны

Ом (1.2.8)

где удельное электрическое сопротивление провода при температуре

, (1.2.9)

средняя длина витка

м, (1.2.10)

W и Sпр, м2 – число витков и сечение провода обмотки по меди.

Из (1.2.8)

; (1.2.11)

с другой стороны

, (1.2.12)

где - коэффициент заполнения окна медью

С учетом (1.2.8), (1.2.12)

м2, (1.2.13)

где площадь окна

м2,(1.2.14)

Выбрав значение плотности тока A/м2 определяют сечение провода нулевого приближения

м2, (1.2.15)

округляют его до ближайшего большего стандартного значения и выбирают диаметры проводов без изоляции и с изоляцией по приложению 1.

Коэффициент заполнения окна медью при нулевом приближении

, (1.2.16)

где - коэффициент укладки

По (1.2.13) определяется сечение провода первого приближения , округляется до стандартного значения, выбираются и и по (1.2.16) . Если , то окончательно принимаются параметры провода первого приближения, по (1.2.12) – число витков и с учетом (1.2.5) – МДС обмотки .

Изгибающий момент ЭМ без учета магнитного насыщения стали и потока рассеяния

(1.2.17)

Начальное значение магнитной индукции в воздушном зазоре и якоре

Тл; (1.2.18)

С учетом насыщения и рассеяния выбирают на (5-10)% меньше . Магнитный поток в воздушном зазоре и якоря

Вб. (1.2.19)

Напряженность магнитного поля в воздушном зазоре

A/м. (1.2.20)

Напряженность магнитного поля в якоре при определяют по основной кривой намагничивания для выбранной марки стали по приложению 2.

Без учета падения МДС в магнитопроводе элементарный магнитный поток рассеяния через окно

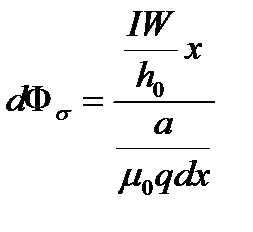(1.2.21)

Магнитный поток рассеяния

, Вб (1.2.22)

Магнитный поток в сердечнике

, Вб (1.2.23)

Магнитная индукция в сердечнике

, Тл (1.2.24)

По основной кривой намагничивания определяется напряженность магнитного поля в сердечнике , А/м.

По закону полного тока определяется МДС для создания выбранного значения .

А, (1.2.15)

где средние длины участков магнитопровода –сердечника и якоря:

м, (1.2.26)

м. (1.2.27)

Если , где - ранее найденная МДС при заданном перегреве обмотки , то корректируется выбранное значение и повторяется расчет магнитной цепи до совпадения обоих значений МДС.

Далее по (1.1.1) определяются тяговое усилие и изгибающий момент

(1.2.28)

Задавая другие значения в сторону увеличения проводят аналогичные расчеты, выбирают наибольший момент и соответствующее ему , , МДС и обмоточные данные.

Тяговое усилие и момент при конечном немагнитном зазоре определяются с учетом расчета магнитной цепи по найденному значению МДС при заданном перегреве обмотки.

Для начального немагнитного зазора и оптимального ЭМ рассчитывают:

индуктивность обмотки

Гн; (1.2.29)

электромагнитную постоянную времени

с; (1.2.30)

время такта

с; (1.2.31)

период следования импульсов напряжения (тока)

с, (1.2.32)

где - количество тактов коммутации фазы.

Для конечного немагнитного зазора аналогично рассчитывают , , .

poisk-ru.ru

Расчет электромагнита (ЭМ). Электромагнит расчет

Расчёт электромагнита

2. Расчет металлоконструкции.

1.2 Расчёт ядра электромагнита. Расчёт электромагнита постоянного тока

Похожие главы из других работ:

1.4 Расщепление ядра

2. Расчет времени трогания электромагнита постоянного тока

7. Расчет приводного электромагнита

1.2 Склад атомного ядра

1.2.1 Оболочечная модель ядра

1.2.2 Оптическая модель ядра

3. Расчет магнитных проводимостей, потоков и падений напряжения на участках электромагнита при начальном, среднем и конечном положениях якоря

4. Расчет обмотки электромагнита

6. Расчет тяговой характеристики электромагнита

1. Расчет электромагнита

1.3 Основные параметры ядра электромагнита

2. Разработка конструкции электромагнита

2.2 Уточнение размеров электромагнита

3. Проектный расчёт основных параметров электромагнита

3.1 Расчёт основных параметров электромагнита

Расчет электромагнита (ЭМ)

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30