формула, соотношение фазного и линейного напряжения
Электрические цепи характеризуются наличием различных типов напряжения. Линейное напряжение (ЛН) возникает между фазовыми проводами трёхфазной цепи. У всех частей (фаз) многофазной цепи характеристика тока идентична. Название цепей (шести-, трёх- или 2-фазные) обуславливаются числом фаз. Наибольшее распространение получили трёхфазные электроцепи, так как являются наиболее экономичными в сравнении с многофазными или 2-фазными. А также позволяют на одном агрегате получить ЛН и фазное напряжение (ФН).
Какое напряжение называется линейным, а какое фазным
Линейным называется напряженье между 2-мя фазами линии или когда определяется величина между 2-мя проводами различных фаз.
Напряжение между любой фазой и нулём — фазное. Оно меряется между начальной и конечной стадией фазы. Практически ФН от ЛН отличается на 58-60 процентов. То есть, величины ЛН в 1,73 раза больше величин ФН.
Трёхфазный ток
Трёхфазные цепи имеют 380В ЛН, что позволяет получить 220В фазного.
Отличия
Специфика ЛН — это показатель, по которому производится расчёт токов и остальных величин трёхфазной цепи. Подобная схема позволяет подключать одно- и трёхфазные контакты. Номинальное равно 380В и меняется при изменениях в ограниченной сети, к примеру, вследствие скачков.
Популярнейшей является цепь с нейтралью и заземлением. Подключение в такой системе производится по схеме:
- к фазным проводам подсоединяются однофазные провода;
- к 3-фазным — 3-фазные.
Типы соединений
Широта применения ЛН обуславливается его безопасностью и комфортностью разветвления цепи. Оборудование в таком случае подключается к фазному выводу, и лишь он не безопасен.
Расчёт системы несложен, при этом действуют стандартные физические формулы. Параметры ЛН сети замеряются мультиметром, а ФН — спецустройствами, например, вольтметром, датчиком тока, тестером.
Характеристики сети:
- Разводка подобной проводки не нуждается в применении профессионального оборудования.
 Достаточно отвёрток, которые имеют индикаторы.
Достаточно отвёрток, которые имеют индикаторы. - Вероятность удара током очень мала. Подобное объясняется присутствующей в цепи свободной нейтралью. Соединение проводников не требует подключения 0-вого вывода.
- Схема подходит для всех видов тока.
Важно! К 3-фазной цепи можно подключить 1-фазную. Наоборот сделать нельзя.
Включение в трёхфазную цепь приёмников электрической энергии
- Подобная схема подключения пригодна для многих устройств, которым необходима высокая мощность, чтобы работать. ЛН позволяет увеличить КПД двигателя на33%.
При переключении обмоток генератора к треугольнику со звезды обуславливает увеличение в 1,73 раза величины ЛН.
Соединения в трёхфазных цепях
Важно! Сложность обнаружения повреждений в линейном соединении является немаловажным недостатком цепи, так как вследствие этого может случиться пожар.
Отличие между ЛН и ФН состоит в различии соединяемых проводов обмоток. Чтобы проконтролировать параметры ЛН и ФН потребуется импульсный стабилизатор, по-другому — линейный стабилизатор. Этот прибор даёт возможность, сохраняя показатель на одном уровне, приводить в норму напряжение, если оно резко выросло. Прибор можно подключить к контактам электорооборудования, обычной розетке.
Чтобы проконтролировать параметры ЛН и ФН потребуется импульсный стабилизатор, по-другому — линейный стабилизатор. Этот прибор даёт возможность, сохраняя показатель на одном уровне, приводить в норму напряжение, если оно резко выросло. Прибор можно подключить к контактам электорооборудования, обычной розетке.
Соотношения фазного и линейного напряжения
Соотношение между напряжением линейным и фазным составляет 1,73. То есть при ста процентах мощности ЛН, напряжение фазы будет 58%. То есть, ЛН превышает ФН в 1,73 раза и при этом стабильно.
ФН и ЛН, отличие и соотношение
Напряжение в трёхфазной цепи оценивается по параметрам линейной составляющей. Обычно оно 380 вольт и тождественно 220 вольтам фазной компоненты сети трёхфазного электротока. В электрических сетях, где имеется четыре провода, напряжение 3-фазного тока обозначается 380/220В. Это позволяет подключить к подобной сети оборудование с 1-фазным потреблением электричества 220В и мощных приборов, которые могут работать от 380В.
Универсальной и приемлемой в большинстве случаев является трёхфазная цепь 380/220В 0-вым проводом. Электроприборы, которые функционируют от однофазного напряженья 220В, могут при подсоединении к паре проводов ФН питаться от ЛН.
Электрооборудование, которое запитывается от трёхфазной сети может работать, только если имеется подсоединение одновременно к 3-м выводам различных фаз. Тогда заземление не обязательно, но если изоляционный материал провода будет повреждён, то отсутствие 0-ого значительно увеличивает опасность удара электрическим током.
Важно! При понижении ЛН меняются величины ФН. При уже выясненном значении междуфазного напряжения определить величину ФН труда не составит.
Чему равно линейное напряжение
В большей части стран мира стандартное ЛН составляет примерно 380В.
В трёхфазных цепях фазное и линейное напряжение находятся в соотношении 220В/380В соответственно.
В чем измеряется
Согласно ГОСТ 13109 норма напряжения в электрической сети варьирует в диапазоне от 198В до 242В (то есть 220В плюс или минус 10 процентов). При частой поломке бытовой техники, ламп или их мигании потребуется измерение напряжения в электрической проводке. Подобная проверка делается мультиметром или вольтметром. Ночью, когда электроприборы используются по минимуму, полученные значения будут максимальными.
При частой поломке бытовой техники, ламп или их мигании потребуется измерение напряжения в электрической проводке. Подобная проверка делается мультиметром или вольтметром. Ночью, когда электроприборы используются по минимуму, полученные значения будут максимальными.
Мультиметром измеряется напряжение в трёхфазной сети так:
- Между рабочим 0 и каждой из фаз: А-N, В-N, С-N.
- Линейные напряжения: А-В, А-С, В-С.
Всего должно получиться шесть измерений. Иногда делается ещё один замер — между заземляющим и нулевым рабочим проводником: N-PE.
Как измерить
Измерить подобную систему можно мультиметром или применив физические формулы.
Измерение подключения к сети
ЛН рассчитывается по формуле Кирхгофа: ∑ Ik = 0. Здесь сила тока равняется нулю во всех частях электроцепи, то есть к=1. Используется также закон Ома: I=U/R. Применив обе формулы можно высчитать параметры клейма или электросети.
В системе из несколько линий, потребуется найти напряжение между 0 и фазой IL = IF. Значения IL и IF непостоянные и меняются при разных вариациях подключения. Потому линейные параметры точно такие же, как и фазные.
Значения IL и IF непостоянные и меняются при разных вариациях подключения. Потому линейные параметры точно такие же, как и фазные.
Фазное
Для того чтобы получить показания подключения фазного вида, потребуется специальное оборудование, например, мультиметр, вольтметр. Для того чтобы измерить токи и напряжения в трёхфазных цепях обычно достаточно знать данные одного линейного тока и одного ЛН.
Перекос фаз
ФН измеряется при проседании (падении) линейного. Из линейных величин извлекается Квадратный корень из трёх. Полученный показатель и есть параметры ФН.
Линейное
Для расчёта соотношения линейного проводника и фазы применяется формула: Uл=Uф∙√3, Uф — фазовое, Uл — линейное.
Важно! Формула справедлива, только если IL = IF. Когда в цепь добавлены другие отводящие элементы, то для них потребуется сделать персональный расчёт фазового напряжения. Тогда Uф нужно заменить цифровыми величинами самостоятельного клейма.
Реактивная трёхфазная мощность рассчитывается по формуле: Q = Qа + Qb + Qс. Значение активной мощности можно найти, используя аналогичную формулу: P = Pа + Pb + Pс. Необходимость в подобных расчётах возникает, если к электрической сети подключается промышленная система.
Значение активной мощности можно найти, используя аналогичную формулу: P = Pа + Pb + Pс. Необходимость в подобных расчётах возникает, если к электрической сети подключается промышленная система.
Распространённость сетей с линейным током объясняется их относительной безопасностью и несложностью разведения электропроводки. Электрооборудование присоединено исключительно к одному фазному проводу (по нему проходит ток) и только он может быть опасен, второй — это заземление. ЛН возникает в трёхфазной цепи и даёт увеличение приблизительно на 73%.
⚡ Фазное и линейное напряжение: определения, отличия, расчёт соотношения
С трёхфазными линиями электропередач сталкивались многие. И если в многоквартирных домах в основном используется напряжение 220 В, то в частном секторе в большинстве своём владельцы подключают 380 В. Такие трёхфазные линии позволяют использовать электродвигатели для станков и иное оборудование, которое в квартире не установить. Подавляющее большинство не знает, чем отличается фазное напряжение от линейного, а значит необходимо исправить это упущение. Именно об этом и пойдёт речь в сегодняшней статье.
Такие трёхфазные линии позволяют использовать электродвигатели для станков и иное оборудование, которое в квартире не установить. Подавляющее большинство не знает, чем отличается фазное напряжение от линейного, а значит необходимо исправить это упущение. Именно об этом и пойдёт речь в сегодняшней статье.
Содержание статьи
Что такое фазное и линейное напряжение
Для некоторых людей, далёких от электротехники, определяющим словом здесь является «напряжение», однако на самом деле всё не так. Рассмотрим основные определения этих терминов.
Фазным называется напряжение между любым из трёх токоведущих проводников и нулём. Оно равно 220 В.
ФОТО: prezentacii.infoФазное прикосновение – замыкание на нулевой и фазный провод
Линейным называют напряжение между двумя фазными проводниками. Оно равно 380 В, т.е. в 1.73 раза выше фазного. Что касается обозначений, то линейное напряжение можно определить по двум литерам (по наименованию фазы) после U (напряжение). Например UAB, UBC, или UCA, либо просто Uл.
ФОТО: prezentacii.infoЛинейное замыкание между двумя фазными проводниками
Использование трёхфазных линий в многоквартирных домах
Не все знают, что в многоквартирные дома также подведено 380 В. Именно это позволяет работать магазинам и различным мастерским на первых или цокольных этажах. В подъездных щитах трёхфазная цепь распределяется поквартирно, в результате чего на каждую из них приходится одна фаза и ноль. Именно они и обеспечивают фазное напряжение 220 В.
ФОТО: prezentacii.infoТак трёхфазная сеть разбивается на три однофазных
При необходимости подключения в квартире оборудования, требующего напряжения 380 В, владелец может обратиться с заявлением в управляющую компанию. Специалист определит возможность подобного подключения, после чего можно будет провести в квартиру трёхфазную линию, предварительно заменив прибор учёта электроэнергии на соответствующий.
ФОТО: vseinstrumenti.ruТрёхфазный прибор учёта электроэнергии значительно крупнее однофазного
Вычисление соотношения между фазным и линейным напряжением
Для расчёта соотношения следует знать линейные параметры. Все вычисления производятся по формуле: 1\2UAB=UA cos 30˚, либо UAB=2√3/2×UA=√3×UA. Таким образом, делаем вывод, что окончательная формула выглядит следующим образом – Uл=√3×UФ.
Все вычисления производятся по формуле: 1\2UAB=UA cos 30˚, либо UAB=2√3/2×UA=√3×UA. Таким образом, делаем вывод, что окончательная формула выглядит следующим образом – Uл=√3×UФ.
На первый взгляд может показаться, что формулы слишком сложны, однако это не так. С другой стороны, домашнему мастеру практически нет смысла заниматься подобными расчётами. Достаточно обычной проверки напряжения на каждой из фаз обычным мультиметром.
ФОТО: stanok.guruМультиметр незаменим при электромонтажных работах
Для чего требуется проверка напряжения фаз перед включением
При подключении оборудования, требующего напряжения 380 в (к примеру, асинхронного электродвигателя) следует проверить напряжение на каждой из трёх фаз и сравнить показатели. Особенно это касается частных секторов, где напряжение нестабильно или электромонтёры имеют недостаточную квалификацию. Дело в том, что в деревнях часто не обращают внимания на распределение нагрузки. В результате подобных действий одна из фаз может быть перегружена при минимальной нагрузке на остальные. Вкупе с устаревшими трансформаторами это приводит к перекосу фаз. Получается, что на одной из фаз напряжение значительно снижается. Это приводит к перегреву трёхфазных двигателей или иного оборудования и выходу его из строя.
Дело в том, что в деревнях часто не обращают внимания на распределение нагрузки. В результате подобных действий одна из фаз может быть перегружена при минимальной нагрузке на остальные. Вкупе с устаревшими трансформаторами это приводит к перекосу фаз. Получается, что на одной из фаз напряжение значительно снижается. Это приводит к перегреву трёхфазных двигателей или иного оборудования и выходу его из строя.
ФОТО: piccy.infoТакой перекос явно не пойдёт на пользу оборудованию, работающему от трёх фаз
Схемы подключения трёхфазных двигателей
Существует два способа подключения к трёхфазной сети, причём это касается не только электродвигателей. Нагревательные элементы также можно подключить «звездой» или «треугольником». Попробуем понять, в чём заключается различие между ними.
ФОТО: siemens-com.ruЭлектродвигатель можно подключить двумя способами
«Звезда» и её особенности
Соединение «звезда» представляет собой следующее: к началу каждой обмотки подключается фазный провод, а все концы соединяются между собой. При этом в месте соединения образуется «технический ноль». Он крайне нестабилен, а потому не используется в электрической цепи.
При этом в месте соединения образуется «технический ноль». Он крайне нестабилен, а потому не используется в электрической цепи.
Подобное соединение не позволяет двигателю выйти на полную мощность, однако это способствует увеличению срока службы оборудования. Также, в защиту подобного соединения можно сказать, что пуск двигателя будет очень плавным, оборудование сможет переносить кратковременные перегрузки и меньше нагреваться. Поэтому, если максимальная мощность электромотора не требуется, лучше всего выбрать именно способ подключения «звездой».
ФОТО: rusenergetics.ruСоединение «звезда» поможет увеличить срок службы электромотора
«Треугольник»: плюсы и минусы способа подключения
Здесь обмотки соединяются последовательно. Начало одной из них коммутируется с концом другой. Такой вариант имеет определённые недостатки, такие, как высокие пусковые токи и перегрев при длительной работе. Однако есть здесь и значительные преимущества перед соединением «звезда». Оборудование, при подобном подключении, выдаёт максимальную мощность, что зачастую становится решающим критерием при выборе способа монтажа. Электродвигатели, подключённые «треугольником» развивают максимальный крутящий момент. Чаще всего соединение «треугольник» используют для подключения агрегатов с большой мощностью, например, станков в промышленных цехах.
Электродвигатели, подключённые «треугольником» развивают максимальный крутящий момент. Чаще всего соединение «треугольник» используют для подключения агрегатов с большой мощностью, например, станков в промышленных цехах.
ФОТО: infourok.ruСоединение «треугольник» позволяет использовать максимальную мощность оборудования
Комбинированный вариант соединения
В некоторых случаях используется комбинированный вариант «звезда-треугольник». Электродвигатель мягко запускается на соединении «звезда», а после того, как набирает необходимые обороты, реле переключает его на «треугольник». Однако не все двигатели можно подключить подобным образом. К примеру, существуют электромоторы, имеющие всего 3 вывода в контактной группе. Они изначально изготовлены под соединение «звезда» и подключить их «треугольником» невозможно.
ФОТО: meganorm.ruКомбинированное соединение подойдёт не для всех типов двигателей
Если объединить распространённые типы включения в трёхфазную сеть, можно увидеть следующую картину.
ФОТО: birmaga.ruНаиболее распространённые типы включения в трёхфазную сеть
Подведём итог
Из всего изложенного можно сделать вывод, что фазное напряжение в сети 0.4 кВ всегда равно 220 В, в то время как линейное 380 В. Однако не стоит считать, что если значения фазного напряжения ниже, оно становится менее опасным. Редакция Homius со всей ответственностью заявляет, что поражение электрическим током может привести к летальному исходу независимо от того, линейное напряжение в цепи или фазное. Ведь поражение тканям и органам наносит не само напряжение, а сила тока. К примеру, 220 В трансформированные в 36 В становятся даже опаснее. Ведь человек практически не чувствует столь низкого напряжения, а в это время ток поражает органы. Поэтому при электромонтажных работах не следует забывать о технике безопасности.
ФОТО: metodist.siteПамятка начинающему электрику
Надеемся, что изложенная информация будет полезна начинающим электромонтажникам и домашним мастерам. При возникновении вопросов можете смело излагать их в обсуждениях ниже. Редакция Homius с удовольствием ответит на них как можно более развёрнуто и быстро. Там же Вы можете изложить своё мнение о статье, оставить комментарий или поделиться личным опытом в подключении трёхфазного оборудования. Если понравилась статья, не забываем её оценивать. А мы напоследок предлагаем Вашему вниманию короткий видеоролик, который позволит более полно раскрыть сегодняшнюю тему.
Редакция Homius с удовольствием ответит на них как можно более развёрнуто и быстро. Там же Вы можете изложить своё мнение о статье, оставить комментарий или поделиться личным опытом в подключении трёхфазного оборудования. Если понравилась статья, не забываем её оценивать. А мы напоследок предлагаем Вашему вниманию короткий видеоролик, который позволит более полно раскрыть сегодняшнюю тему.
Предыдущая
ИнженерияКак выбрать правильную печь для гаража: изучаем современные виды обогревательного оборудования
Следующая
ИнженерияМойка для кухни: как выбрать раковину, на что обратить внимание
Понравилась статья? Сохраните, чтобы не потерять!
ТОЖЕ ИНТЕРЕСНО:
ВОЗМОЖНО ВАМ ТАКЖЕ БУДЕТ ИНТЕРЕСНО:
Трёхфазный ток. Фазное и линейное напряжение. Перекос фаз. | Физик-шизик
В прошлой статье я обещал рассказать что такое трёхфазный ток и что такое фазное и линейное напряжение. Пожалуй, начнём.
Что такое полная фаза колебания? — это аргумент периодической функции, описывающей колебательный или волновой процесс.
Так же существует ещё и начальная фаза колебания. Это значение полной фазы в начальный момент времени, т. е. при t=0.
Математически это выражается так:
изображение автора
изображение автора
При однофазном токе пси=0. Когда же мы начинаем рассматривать трёхфазный ток, то тут появляется сразу три разные линии с пси равным 0, 120 и соответственно 240 гр., т.е. фазы повёрнуты друг относительно друга на 120 гр.
Теперь рассмотрим устройство трёхфазного генератора:
изображение из открытых источников.
изображение из открытых источников.
Следовательно в статоре генератора размещены 3 обмотки, сдвинутые относительно друг-друга на 120 гр.
Магнит, размещённый на роторе, обычно на роторе стоит отдельная обмотка, вращаясь создаёт вращающееся магнитное поле. При этом в обмотках статора наводится ЭДС, индуцирующее ток в соответствующих обмотках.
Обмотки соединяются либо по схеме «треугольник»:
изображение из открытых источников
изображение из открытых источников
Либо по схеме «звезда»
изображение из открытых источников
изображение из открытых источников
Схема «звезда» чаще всего применяется в низковольтных сетях 380/220В.
Фазное и линейное напряжение
Фазным напряжением называется напряжение, измеренное между любым из фазных проводников и нейтралью.
Линейным напряжением называется напряжение, измеренное между любыми парами фаз.
Так как в схеме «треугольник» нейтральный проводник отсутствует, следовательно напряжение там линейное.
Ниже приводятся функции фазного напряжения на каждой из фаз.
изображение автора
изображение автора
Линейное же напряжение выглядит так:
изображение автора
изображение автора
При этом линейное и фазное напряжение соотносятся между собой так:
изображение автора
изображение автора
Перекос фаз
А это вообще весьма распространённое явление. Его основная причина — не симметрия фазных нагрузок. Дело в том, что в случае, когда токи во всех фазах одинаковы в нулевом проводнике ток отсутствует. Он попросту говоря в такой ситуации не нужен. Но в условиях современных реалий добиться одинаковых токов во всех трёх фазах практически невозможно.
Его основная причина — не симметрия фазных нагрузок. Дело в том, что в случае, когда токи во всех фазах одинаковы в нулевом проводнике ток отсутствует. Он попросту говоря в такой ситуации не нужен. Но в условиях современных реалий добиться одинаковых токов во всех трёх фазах практически невозможно.
В результате, вследствие наличия тока в нулевом проводе на нём появляется некоторое напряжение, зависит оно ещё и от сопротивления самого провода. Это приводит к изменению фазных напряжений. При этом на наиболее загруженной фазе напряжение будет наименьшим, а на наименее загруженной — наибольшим.
На рисунке ниже приведена векторная диаграмма фазных и линейных напряжений при симметричной нагрузке:
изображение из открытых источников
изображение из открытых источников
А вот в случае не симметрии нагрузок картина может стать такой:
изображение из открытых источников
изображение из открытых источников
Из диаграммы выше видно, что линейные напряжения остались неизменными, а фазные — изменились.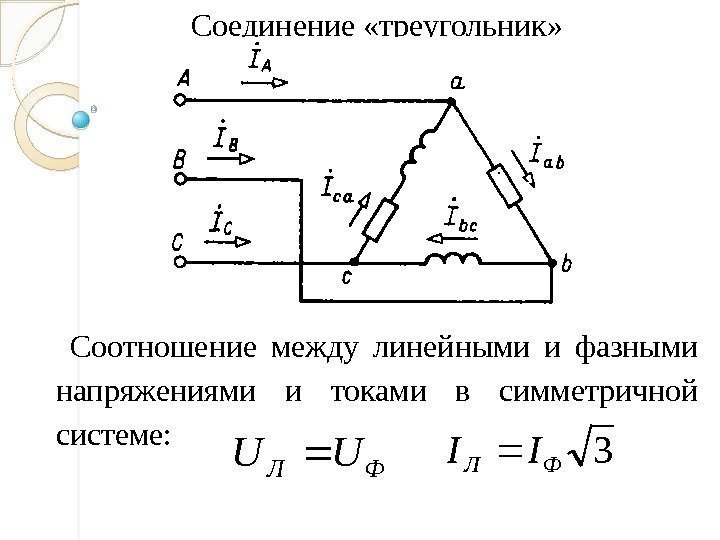
Появление тока в нулевом проводнике часто приводит к его отгоранию. Это особенно опасно в старых сетях, где сечение нулевой жилы намного меньше сечения фазных жил.
Для минимизации перекоса фаз следует выполнять заземление нейтрали, а так же эффективно распределять фазы по потребителям.
На мой взгляд, в условиях садоводческих товариществ и т.п., наиболее рациональным вариантом является трёхфазное подключение каждого участка, каждого частного дома.
Тема следующей статьи — «Отгорание нуля».
Анализ опасности поражения током в различных электрических сетях
Случаи поражения человека током возможны лишь при замыкании электрической цепи через тело человека или, иначе говоря, при прикосновении человека не менее чем к двум точкам цепи, между которыми существует некоторое напряжение.
Опасность такого прикосновения, оцениваемая величиной тока, проходящего через тело человека, или же напряжением прикосновения, зависит от ряда факторов: схемы включения человека в цепь, напряжения сети, схемы самой сети, режима ее нейтрали, степени изоляции токоведущих частей от земли, а также от величины емкости токоведущих частей относительно земли и т. п.
п.
Схемы включения человека в цепь могут быть различными. Однако наиболее характерными являются две схемы включения: между двумя проводами и между одним проводом и землей (рис. 68). Разумеется, во втором случае предполагается наличие электрической связи между сетью и землей.
Применительно к сетям переменного тока первую схему обычно называют двухфазным включением, а вторую — однофазным.
Двухфазное включение, т. е. прикосновение человека одновременно к двум фазам, как правило, более опасно, поскольку к телу человека прикладывается наибольшее в данной сети напряжение — линейное, и поэтому через человека пойдет больший ток:
где Ih — ток, проходящий через тело человека, А; UЛ = √3 Uф — линейное напряжение, т. е. напряжение между фазными проводами сети, В; Uф — фазное напряжение, т. е. напряжение между началом и концом одной обмотки (или между фазным и нулевым проводами), В.
Рис. 68. Случаи включения человека в цепь тока:
а — двухфазное включение; б, в — однофазные включения
Нетрудно представить, что двухфазное включение является одинаково опасным в сети как с изолированной, так и с заземленной нейтралями.
При двухфазном включении опасность поражения не уменьшится и в том случае, если человек надежно изолирован от земли, т. е. если он имеет на ногах резиновые галоши или боты либо стоит на изолирующем (деревянном) полу, или на диэлектрическом коврике.
Однофазное включение происходит значительно чаще, но является менее опасным, чем двухфазное включение, поскольку напряжение, под которым оказывается человек, не превышает фазного, т. е. меньше линейного в 1,73 раза. Соответственно меньше оказывается ток, проходящий через человека.
Кроме того, на величину этого тока влияют также режим нейтрали источника тока, сопротивление изоляции и емкость проводов относительно земли, сопротивление пола, на котором стоит человек, сопротивление его обуви и некоторые другие факторы.
В трехфазной трехпроводной сети с изолированной нейтралью ток, проходящий через человека, при прикосновении к одной из фаз сети в период ее нормальной работы (рис. 69, а) определяется следующим выражением в комплексной форме (А):
где Z — комплекс полного сопротивления одной фазы относительно земли (Ом):
здесь r и С — соответственно сопротивление изоляции провода (Ом) и емкость провода (Ф) относительно земли (приняты для упрощения одинаковыми для всех проводов сети).
Рис. 69. Прикосновение человека к проводу трехфазной трехпроводной сети с изолированной нейтралью: а — при нормальном режиме; б — при аварийном режиме
Ток в действительной форме равен (А):
, (35)
Если емкость проводов относительно земли мала, т. е. С = 0, что обычно имеет место в воздушных сетях небольшой протяженности, то уравнение (35) примет вид
, (36)
Если же емкость велика, а проводимость изоляции незначительна, т. е. r ≈ ∞, что обычно имеет место в кабельных сетях, то согласно выражению (35) ток через человека (А) будет:
, (37)
где хс = 1/wC — емкостное сопротивление, Ом.
Из выражения (36) следует, что в сетях с изолированной нейтралью, обладающих незначительной емкостью между проводами и землей, опасность для человека, прикоснувшегося к одной из фаз в период нормальной работы сети, зависит от сопротивления проводов относительно земли: с увеличением сопротивления опасность уменьшается.
Поэтому очень важно в таких сетях обеспечивать высокое сопротивление изоляции и контролировать ее состояние в целях своевременного выявления и устранения возникших неисправностей.
Однако в сетях с большой емкостью относительно земли роль изоляции проводов в обеспечении безопасности прикосновения утрачивается, что видно из уравнений (35) и (37).
При аварийном режиме работы сети, т. е. когда возникло замыкание одной из фаз на землю через малое сопротивление гзм ток через человека, прикоснувшегося к здоровой фазе (рис. 69, б), будет (А):
, (38)
а напряжение прикосновения (В):
, (39)
Если принять, что rзм = 0 или по крайней мере считать, что гзм < Rh (так обычно бывает на практике), то согласно выражению (39)
, (40)
т. е. человек окажется под линейным напряжением.
В действительных условиях гзм > 0, поэтому напряжение, под которым окажется человек, прикоснувшийся в аварийный период к исправной фазе трехфазной сети с изолированной нейтралью, будет значительно больше фазного и несколько меньше линейного напряжения сети. Таким образом, этот случай прикосновения во много раз опаснее прикосновения к той же фазе сети при нормальном режиме
работы [см. уравнения (36) и (39), имея в виду, что r/3>rзм].
уравнения (36) и (39), имея в виду, что r/3>rзм].
В трехфазной четырехпроводной сети с заземленной нейтралью проводимость изоляции и емкостная проводимость проводов относительно земли малы по сравнению с проводимостью заземления нейтрали, поэтому при определении тока через человека, касающегося фазы сети, ими можно пренебречь.
При нормальном режиме работы сети ток через человека будет (рис. 70, а):
, (41)
где г0 — сопротивление заземления нейтрали, Ом.
Рис. 70. Прикосновение человека к фазному проводу трехфазной четырехпроводной сети с заземленной нейтралью:
а — при нормальном режиме; б — при аварийном режиме
В обычных сетях r0 < 10 Ом, сопротивление тела человека Rh не опускается ниже нескольких сотен Ом. Следовательно, без большой ошибки в уравнении (41) можно пренебречь значением г0 и считать, что при прикосновении к одной из фаз трехфазной четырехпроводной сети с заземленной нейтралью человек оказывается практически под фазным напряжением Uф, а ток, проходящий через него, равен частному от деления Uф на Rh
Отсюда следует, что прикосновение к фазе трехфазной сети с заземленной нейтралью в период нормальной ее работы более опасно, чем прикосновение к фазе нормально работающей сети с изолированной нейтралью [ср. уравнения (36) и (41)], но менее опасно прикосновения к неповрежденной фазе сети с изолированной нейтралью в аварийный период [ср. уравнения (38) и (41)], так как rзм может в ряде случаев мало отличаться от г0.
уравнения (36) и (41)], но менее опасно прикосновения к неповрежденной фазе сети с изолированной нейтралью в аварийный период [ср. уравнения (38) и (41)], так как rзм может в ряде случаев мало отличаться от г0.
Полезная информация:
Трехфазные цепи (страница 1)
1. Линейное напряжение трехфазного генератора, соединенного звездой, равно 10500 В.
Определить напряжение между зажимами каждой фазы генератора. Какое напряжение было бы между зажимами генератора при соединении его обмоток треугольником?
Решение:
Фазное напряжение трехфазного генератора при схеме соединения звездой в раз меньше линейного напряжения:
В схеме соединения треугольником провода линии присоединяются к общим зажимам двух обмоток, и линейное напряжение между двумя проводами равно напряжению фазной обмотки:
2. Действующее значение э. д. с. в каждой обмотке симметричного трехфазного генератора равно 230 В.
Определить линейные напряжения при соединении обмоток неправильной звездой («веером») в режиме холостого хода.
Решение:
Неправильное присоединение одной из обмоток генератора к двум остальным при соединении звездой приводит к повороту вектора э. д. с. на 180° (рис. 35) по сравнению с нормальным расположением. Вместо симметричной трехлучевой звезды векторов получается так называемый веер векторов с углами по 60° между ними. Как видно из векторной диаграммы, напряжение
Следовательно, неправильное соединение обмоток звездой можно обнаружить путем измерения. При правильном соединении все линейные напряжения равны .
3. В каждой обмотке трехфазного генератора индуктируется э. д. с, равная 132 В.
Определить линейное напряжение генератора при холостом ходе в случае соединения обмоток треугольником.
Решение:
При правильном соединении обмоток трехфазного генератора треугольником результирующая э. д. с. в контуре обмоток равна нулю, так как сумма э. д. с. симметричной трехфазной системы равна нулю. Следовательно, при холостом ходе в контуре треугольника обмоток ток отсутствует и напряжение между концом и началом обмотки равно э. д. с. Это так называемое фазное напряжение. В схеме соединения генератора треугольником провода трехфазной линии присоединяют к точкам соединения обмоток. Каждый провод при этом присоединен к зажимам двух обмоток, а каждая пара проводов линии — к зажимам одной из трех обмоток. Поэтому линейное напряжение генератора, т. е. напряжение между двумя линейными проводами, оказывается равным при схеме соединения треугольником фазному напряжению, а при холостом ходе генератора — фазной э. д. с. генератора (132 В).
д. с. симметричной трехфазной системы равна нулю. Следовательно, при холостом ходе в контуре треугольника обмоток ток отсутствует и напряжение между концом и началом обмотки равно э. д. с. Это так называемое фазное напряжение. В схеме соединения генератора треугольником провода трехфазной линии присоединяют к точкам соединения обмоток. Каждый провод при этом присоединен к зажимам двух обмоток, а каждая пара проводов линии — к зажимам одной из трех обмоток. Поэтому линейное напряжение генератора, т. е. напряжение между двумя линейными проводами, оказывается равным при схеме соединения треугольником фазному напряжению, а при холостом ходе генератора — фазной э. д. с. генератора (132 В).
4. Фазная э, д. с. трехфазного генератора Е=247 В, частота сети f=50 Гц, активное сопротивление обмотки r=1,1 Ом, индуктивное сопротивление .
Определить величину тока в контуре треугольника при неправильном соединении обмоток генератора в режиме холостого хода.
Решение:
Переключение начала и конца обмотки трехфазного генератора поворачивает вектор э. д. с. этой обмотки на диаграмме на 180°. Дело в том, что после переключения положительное направление э. д. с. этой обмотки будет относительно зажимов остальных обмоток таким, каким было отрицательное направление э. д. с. в первоначальной схеме. Таким образом, при неправильном соединении, например, фазы В по отношению к остальным фазам получим векторную диаграмму, показанную на рис. 36.
д. с. этой обмотки на диаграмме на 180°. Дело в том, что после переключения положительное направление э. д. с. этой обмотки будет относительно зажимов остальных обмоток таким, каким было отрицательное направление э. д. с. в первоначальной схеме. Таким образом, при неправильном соединении, например, фазы В по отношению к остальным фазам получим векторную диаграмму, показанную на рис. 36.
Результирующая э. д. с. в контуре равна удвоенному значению фазной э. д. с, т. е. 494 В. Эта э. д. с. обусловливает ток в контуре, величина которого определяется по закону Ома:
где z — полное сопротивление фазной обмотки:
Следовательно,
Если оставить включенной схему неправильного соединения обмоток треугольником, то даже при холостом ходе генератора в контуре обмоток будет непроизводительно расходоваться энергия, переходящая в тепло. В рассматриваемой задаче потери мощности в контуре
Поэтому, прежде чем замыкать контур треугольника обмоток, следует проверить равнопотенциальность соединяемых точек при помощи вольтметра (рис. 37). При правильном соединении обмоток треугольником подвижная часть вольтметра не отклоняется.
37). При правильном соединении обмоток треугольником подвижная часть вольтметра не отклоняется.
5. К четырехпроводной трехфазной линии поочередно присоединяют три электрические лампы мощностью по 60 Вт каждая между линейным (соответственно А, В и С) и нейтральным проводами.
Определить изменение токов в проводах линии в каждом случае присоединения к ней ламп, если напряжение между каждым линейным проводом и нейтральным проводом 120 В.
Решение:
Пусть до присоединения к четырехпроводной трехфазной линии ламп в ее проводах не было токов. Тогда присоединение электрической лампы между линейным А и нейтральным N проводами вызовет ток в этих проводах, равный
Благодаря нейтральному проводу поддерживаются равными три фазных напряжения: и на векторной диаграмме узловой точке n цепи (рис. 38) соответствует точка того же наименования, расположенная в центре тяжести треугольника векторов линейных напряжений (рис. 39).
Электрическая лампа является однофазным приемником энергии, не вызывающим сдвига фаз тока относительно напряжения . Следовательно, вектор тока совпадает по фазе с вектором напряжения . Согласно первому закону Кирхгофа, примененному к точке n цепи (рис. 39), ток в нейтральном проводе изображается тем же вектором, что и ток в проводе А. Из этого рисунка видно, что при отсутствии нейтрального провода лампу нельзя было бы включить на фазное напряжение .
Следовательно, вектор тока совпадает по фазе с вектором напряжения . Согласно первому закону Кирхгофа, примененному к точке n цепи (рис. 39), ток в нейтральном проводе изображается тем же вектором, что и ток в проводе А. Из этого рисунка видно, что при отсутствии нейтрального провода лампу нельзя было бы включить на фазное напряжение .
Представим себе, что в дополнение к уже включенной лампе (см. рис. 38) присоединена вторая такая же лампа между линейным В и нейтральным N проводами (рис. 40).
Ток в проводе А при этом не изменился, но появился ток в проводе В. В нейтральном проводе N стал проходить ток , равный геометрической сумме токов .
Ток в линейном проводе В
Он совпадает по фазе с напряжением и тем самым отстает по фазе от тока на 1/3 периода (120°) (см. рис. 40).
Так как , то при определении тока в нейтральном проводе путем сложения векторов этих линейных токов получим ромб с углом в 120°. Диагональ ромба делит этот угол пополам, поэтому длина диагонали ромба равна его стороне, т. е.
е.
Таким образом, величина тока в нейтральном проводе осталась той же, что и при одной лампе в проводе А, только вектор этого тока на диаграмме повернулся на 60° по ходу часовой стрелки.
Наконец, допустим, что присоединена третья лампа (в дополнение к прежним двум) между линейным С и нейтральным N проводами (рис. 41). В этом случае ток
стал проходить в проводе С, причем ввиду отсутствия сдвига фаз этого тока относительно напряжения вектор тока на диаграмме начал совпадать по фазе с вектором напряжения .
Получилась симметричная трехлучевая звезда векторов токов. Геометрическое сложение этих векторов дает нуль: . Следовательно, при симметричном режиме нагрузки ток в нейтральном проводе равен нулю.
Таким образом, отсутствие тока в нейтральном проводе при однородной (например, активной) нагрузке свидетельствует о симметрии режима в трехфазной цепи.
6. Трехфазный асинхронный электродвигатель типа МАД-126/8 в схеме соединения обмоток статора звездой при номинальной нагрузке и номинальном напряжении 500 В имеет токи в обмотках статора по 220 А и развивает номинальную мощность на валу 130 кВт.
Определить и мощность на входе, если к. п. д. при номинальной нагрузке . Построить в масштабе векторную диаграмму.
Решение:
К. п. д. , откуда
Трехфазный электродвигатель — это симметричный приемник энергии, поэтому коэффициент мощности
Этому значению коэффициента мощности соответствует угол .
Строим векторную диаграмму в масштабе: (рис. 42). Так как трехфазный электродвигатель представляет собой симметричный приемник энергии, то геометрическая сумма его токов равна нулю и нейтральный провод становится Лишним. Поэтому при любой схеме соединения обмоток трехфазного двигателя к нему подводят только три провода.
7. Три одинаковые катушки включены звездой и присоединены к трехпроводной трехфазной цепи с линейным напряжением 220 В. Начало и конец одной из катушек (фаза А) замкнуты накоротко медной пластиной.
Определить токи при коротком замыкании в фазе А. Построить в масштабе векторную диаграмму.
Решение:
Замыкание накоротко точек A и n (рис.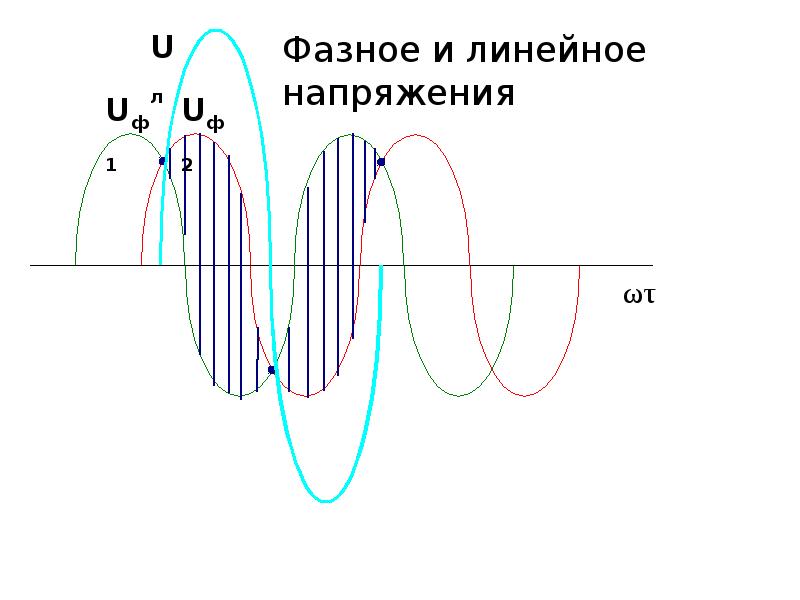 43) делает потенциал точки n равным потенциалу точки А.
43) делает потенциал точки n равным потенциалу точки А.
Катушки фаз В и С оказываются включенными на линейное напряжение. Токи в них равны по величине:
Они отстают по фазе соответственно от напряжений на угол, тангенс которого
Из таблиц тригонометрических величин . Ток в замкнутой накоротко фазе А определяют в этом случае по первому закону Кирхгофа:
Следовательно, вектор тока противоположен по направлению вектору, представляющему собой сумму векторов . Строим векторную диаграмму масштаба: .
Непосредственное измерение дает для величины тока замкнутой накоротко фазы А значение .
При нормальных условиях токи во всех линейных проводах были бы равны:
Поэтому в замкнутой накоротко фазе схемы «симметричная звезда» ток больше, чем при нормальной работе, в 3 раза, при этом в двух других фазах ток увеличивается в раз.
Ток замыкается через пластину, замкнувшую зажимы катушки. В этой катушке не может быть пробоя междувитковой изоляции, так как напряжение между зажимами катушки равно нулю. Опаснее для изоляции катушки внезапное прекращение тока, так как при этом в катушке индуктируется очень большая э. д. с. самоиндукции.
Опаснее для изоляции катушки внезапное прекращение тока, так как при этом в катушке индуктируется очень большая э. д. с. самоиндукции.
8. К трехпроводной трехфазной линии напряжением 122 В и частотой 50 Гц присоединены включенные звездой катушки . В проводе С линии расплавилась плавкая вставка предохранителя (рис. 44).
Определить токи. Построить в масштабе векторную диаграмму.
Решение:
Вследствие расплавления плавкой вставки предохранителя ток в линейном проводе С прекратился. Потенциалы точек и n стали равными.
В схеме под действием линейного напряжения продолжается прохождение тока в катушках фаз А и В, включенных теперь последовательно.
Так как катушки одинаковы, то напряжение делится между ними поровну.
Это означает, что точка n диаграммы находится посередине вектора линейного напряжения . Отрезок An означает напряжение , а отрезок Вn — напряжение .
Симметричная трехлучевая звезда векторов фазных напряжений, которая характеризовала симметричный режим при всех исправных предохранителях, искажается ввиду смещения точки n из центра тяжести треугольника линейных напряжений на середину стороны АВ (см.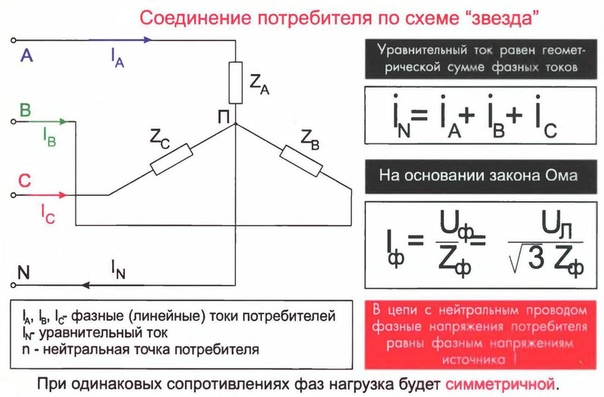 рис. 44). Токи равны по величине:
рис. 44). Токи равны по величине:
Они отстают по фазе соответственно от напряжений на угол, тангенс которого
Из таблиц тригонометрических величин .
Строим векторную диаграмму в масштабе: . Так как потенциал точки равен потенциалу точки n (в фазе С тока нет), то разность потенциалов между точками С и n такая же, как и между точками т.е. как между концами провода. Из векторной диаграммы следует, что это напряжение в 1,5 раза превышает номинальное фазное напряжение установки:
Если бы электромонтер стал сращивать концы провода (без отключения установки), он подвергся бы действию указанного напряжения.
9. Три активных сопротивления: — соединены звездой и присоединены к трехпроводной трехфазной линии с линейными напряжениями 120 В.
Определить напряжения на отдельных сопротивлениях и токи в них.
Решение:
Нагрузка фаз по условию задачи однородная (активная): . Однако симметричный режим в цепи невозможен, так как . В случае отсутствия нейтрального провода также невозможно обеспечить равенство напряжений на отдельных фазах при такой нагрузке.
Изменение фазных напряжений при изменении нагрузки в одной фазе можно связать со смещением точки n на векторной диаграмме. При симметричном режиме в цепи точка n находится в центре тяжести треугольника линейных напряжений.
Допустим, что в линейном проводе С произошел разрыв, прекративший ток в этой фазе . В других фазах проходит ток при действии линейного напряжения в неразветвленной цепи, состоящей из сопротивлений (рис. 45). Этот ток определяется по закону Ома:
При этом напряжение на сопротивлении
а напряжение на сопротивлении
Оба эти напряжения совпадают по фазе с током и, следовательно, с напряжением (так как ).
Напряжения являются частями напряжения , причем
Точка n, обозначенная в виде , в случае обрыва фазы С находится на стороне АВ треугольника векторов линейных напряжений и делит ее в отношении 1:2 (рис. 48). Этот треугольник построен в масштабе . Точку , нанесенную на стороне AB, соединяем отрезком прямой с вершиной С, в которой располагается точка n при коротком замыкании фазы С , когда потенциалы точек n и С равны.
Допустим, что разрыв произошел в линейном проводе В (рис. 47). В этом случае ток , а в фазах С и А проходит один и тот же ток, равный, по закону Ома,
Напряжения на участках неразветвленной цепи относятся, как сопротивления этих участков: ; кроме того, соблюдается равенство . Следовательно, сторону СА следует разбить на части, относящиеся друг к другу как 3:1 (точка на рис. 48).
Соединяем отрезком прямой точку с точкой В, в которой располагается точка n при коротком замыкании фазы В. Прямые, проведенные внутри треугольника АВС, пересекаются в точке n; она соответствует узловой точке n электрической схемы для случая всех трех исправных проводов, так как точка пересечения этих прямых удовлетворяет обоим условиям, положенным в основу проведения прямых, т. е.
Именно в таком соотношении находятся сопротивления фаз по условию задачи.
Теперь рассмотрим отрезки прямых, соединяющих точку n с точками А, В и С. На векторной диаграмме эти точки соответствуют потенциалам одноименных точек схемы, а отрезки прямых — напряжениям схемы. Отрезок An означает напряжение , отрезок Вn — соответственно напряжение , отрезок Сn — напряжение (в масштабе, принятом в начале построения ).
Отрезок An означает напряжение , отрезок Вn — соответственно напряжение , отрезок Сn — напряжение (в масштабе, принятом в начале построения ).
Путем измерения этих отрезков и применения масштаба устанавливаем, что .
Далее, зная сопротивления , определяем по закону Ома токи:
Эти токи совпадают по фазе соответственно с напряжениями , так как нагрузка активная.
Построим векторы токов в масштабе , направляя векторы токов вдоль векторов соответствующих напряжений. Сумма построенных векторов токов должна равняться нулю:
Несмотря на то что меньшее напряжение оказалось в фазе с меньшим сопротивлением (фаза А), ток в ней по сравнению с токами других фаз наибольший.
Особенности эксплуатации оборудования в трехфазных сетях
02.08.2021
Когда заходит речь об электрических сетях, большинство из нас, конечно, имеет в виду однофазные сети. Действительно, в многоквартирных домах используется однофазная цепь с напряжением 220В переменного тока. Да, и, практически все бытовые приборы рассчитаны на применение именно этого напряжения. Однако, использование однофазного тока целесообразно лишь для помещений, площадь которых не превышает 100м². Для обеспечения электроэнергией частных домов и производственных помещений оптимальным решением будет использование трехфазных сетей. Такая схема позволит равномерно перераспределять нагрузку по всем потребителям и избегать скачков напряжения.
Да, и, практически все бытовые приборы рассчитаны на применение именно этого напряжения. Однако, использование однофазного тока целесообразно лишь для помещений, площадь которых не превышает 100м². Для обеспечения электроэнергией частных домов и производственных помещений оптимальным решением будет использование трехфазных сетей. Такая схема позволит равномерно перераспределять нагрузку по всем потребителям и избегать скачков напряжения.
Не будем вдаваться в тонкости отличий однофазной сети от трехфазной. На данном этапе достаточно будет визуальных различий.
Однофазная сеть состоит из двух («фаза» и «ноль»), или трех («фаза», «ноль» и «земля») проводов:
Трехфазная же сеть имеет три фазных провода и один нулевой:
В данной структуре фазное напряжение составляет 220В (напряжение между любым фазным проводом и нулевым), а линейное — 380В (напряжение между двумя фазными проводами):
Причем ЭДС на фазных проводах совпадают по частоте и амплитуде, но имеют фазовый сдвиг на величину 1/3 периода, или 120°.
График трехфазного тока:
Использование трехфазной сети имеет довольно значительный ряд преимуществ, по отношению к однофазной сети, например:
- экономичность передачи электроэнергии на значительные расстояния;
- меньшая материалоемкость силовых кабелей;
- уравновешенность системы;
- возможность получения в одной установке двух напряжений – фазного и линейного, и двух уровней мощности при соединении «звездой», или «треугольником»;
- возможность резкого уменьшения стробоскопического эффекта (мерцания) светильников на люминесцентных лампах, путем размещения в светильнике трех групп ламп, питающихся от разных фаз.
Но, как известно, чем больше компонентов имеет система, тем более она становится уязвимой. Не является исключением и трехфазная сеть. Едва ли не единственными причинами выхода из строя электрооборудования, а также возникновение несчастных случаев в однофазных сетях являются, как правило, превышение значения максимального тока и снижение величины сопротивления изоляции проводов. Для трехфазных же сетей к этим параметрам добавляются обрыв нулевого провода, «перекос» фаз, отсутствие напряжения в одной, или двух фазах, асимметрия напряжений в фазах. В большинстве случаев, это приведет к «обгоранию», или даже обрыву нулевого провода. При этом фазное напряжение может подскочить с 220 до 380В, что может вывести из строя электрооборудование. Нарушение чередования фаз способно привести к дополнительному износу электрооборудования, повышенному потреблению электроэнергии и даже к возникновению короткого замыкания, в случае параллельного включения в работу нескольких устройств. А в случае нарушения правильной фазировки электродвигателя, не исключено изменение направления движения элементов, механически связанных с ротором. Кроме того, возможно присутствие потенциала на самом нулевом проводе, что может привести к поражению электрическим током человека, или животных.
Для трехфазных же сетей к этим параметрам добавляются обрыв нулевого провода, «перекос» фаз, отсутствие напряжения в одной, или двух фазах, асимметрия напряжений в фазах. В большинстве случаев, это приведет к «обгоранию», или даже обрыву нулевого провода. При этом фазное напряжение может подскочить с 220 до 380В, что может вывести из строя электрооборудование. Нарушение чередования фаз способно привести к дополнительному износу электрооборудования, повышенному потреблению электроэнергии и даже к возникновению короткого замыкания, в случае параллельного включения в работу нескольких устройств. А в случае нарушения правильной фазировки электродвигателя, не исключено изменение направления движения элементов, механически связанных с ротором. Кроме того, возможно присутствие потенциала на самом нулевом проводе, что может привести к поражению электрическим током человека, или животных.
Таким образом, основой безопасности эксплуатации трехфазных сетей необходимо считать:
- правильный проект энергоснабжения с учетом возможных нагрузок;
- изменение в существующей цепи схемы потребления энергии (для случаев, когда каждая фаза ранее не рассчитывалась на перегрузку;
- изменение мощности потребителей в критических ситуациях.

В таких условиях особое значение имеет установка специального оборудования, которое отключает сеть при обнаружении несоответствий требований, предъявляемых к безопасной эксплуатации трехфазных сетей — т.н. «Реле контроля фаз». Одним из таких приборов является реле контроля фаз CKF- BR производства компании «Евроавтоматика».
Прибор предназначен для отключения электродвигателей и электроустановок, подключенных к трехфазной сети в случаях:
- отсутствия хотя бы одной из фаз;
- асимметрии напряжения;
- обрыва нулевого провода;
- нарушения чередования фаз.
Кроме того, прибор имеет функцию регулировки асимметрии напряжения в пределах от 40 до 80В, что позволяет отключать электроустановки, не дожидаясь, пока «перекос» напряжений не достигнет критических значений. При превышении заданных величин асимметрии, прибор отключит электроустановку (электросеть) с задержкой от 0.5 до 15 сек. (выбирается пользователем). Во всех остальных случаях отключение происходит через 0.1 сек. Включение происходит автоматически после восстановления нормальных характеристик сетевого напряжения питания.
Во всех остальных случаях отключение происходит через 0.1 сек. Включение происходит автоматически после восстановления нормальных характеристик сетевого напряжения питания.
Подобные реле других производителей имеют сходные характеристики, и могут отличаться набором функций, способом монтажа и величинами регулировок. Так, например, аналогичный прибор того же производителя CKF-BT имеет дополнительную функцию отключения при падении напряжения ниже 160В и превышении 260В. А прибор производства ABB 1SVR730885R3300 имеет максимальное время задержки на выключение 30 сек. и диапазон отключения при падении напряжения ниже 180В и превышении напряжения 280В.
В целом, можно сказать, что безопасная эксплуатация трехфазных сетей достигается все-таки правильным проектированием и расчетом схемы потребления энергии. Использование же реле контроля фаз служит единственной цели — обеспечению безопасности в случае выхода параметров сети из допустимых норм.
Напряжение фазное — Энциклопедия по машиностроению XXL
Номинальное напряжение (фазное), в. . 49 Номинальная мощность, ква. …. 550 Пределы регулирования напряжения при номинальном напряжении сети, в. . . от 11,5 до 49
[c.152]
. 49 Номинальная мощность, ква. …. 550 Пределы регулирования напряжения при номинальном напряжении сети, в. . . от 11,5 до 49
[c.152]
Задача получения замкнутых систем уравнений в более сложных случаях, чем рассмотренные ранее (см. 3 гл. 1 и 5,6 гл.З), фактически сводится к определению тензоров напряжений или а,- в фазах, потоков энергий i, qi, Aj, интенсивностей меж-фазного взаимодействия /, /, работы внутренних сил в фа- [c.185]
Фазным (Уф) называется напряжение, создаваемое одной любой фазной обмоткой.
[c.113]
В системах с трехфазной сетью указывают линейное напряжение в системах с нулевым проводом (рис. 8, а) — линейное и фазное напряжения, например, 380/220 В. [c.113]
Однофазные потребители, рассчитанные на фазное напряжение в трехфазной системе с нулевым проводом, включают между нулевым проводом и любым из линейных проводов потребители, рассчитанные
[c. 113]
113]
Напряжения vi Uqу на преобразованных контурах статора w y и Wqi выражаются через напряжения Uqy и i, фазных обмоток Wgy и и>й1 как функции угла (см. рис. 5.1) или как проекции результирующего напряжения статора Wi в виде [c.104]
Силовые кабели с поясной изоляцией выпускаются трехжильного типа с секторными жилами из меди или алюминия в диапазоне сечений 6—240 мм . В качестве изоляции в них используется кабельная бумага, которая накладывается на жилу методом обмотки и пропитывается затем вязким маслоканифольным составом. Поверх скрученного из изолированных жил сердечника кабеля накладывается поясная изоляция, толщина которой меньше, чем толщина фазной (жильной) изоляции, так как жильная изоляция рассчитывается на линейное напряжение, которое в три раза больше фазного. [c.259]
При симметричной системе синусоидальных напряжений, приложенных к статору, для фазных напряжений, приведенных к осям d я q, имеем выражения
[c. 28]
28]
Для насоса первого и второго контуров были спроектированы и изготовлены регулируемые электроприводы по схеме АВК с электродвигателями на напряжение 6000 В и частоту 50 Гц с фазным ротором. Структурная схема системы управления станцией, АВК и ГЦН приведена на рис. 5.29. Регулируемый электропривод дает возможность [c.175]
Леонар- преобразователь муфта скольжения с фазным напряжения [c.305]
Фазным напряжением Up называется напряжение между началом и концом каждой фазной обмотки. Ток, протекающий по фазной [c.521]
В этом случае а) линейные напряжения равны фазным Ui == Up, б) линейные токи [c.522]
При правильном порядке следования фаз, равенстве напряжений ,[ = У, и небольшом неравенстве частот ф м лампы, включённые по схеме фиг. 54, а, будут одновременно загораться и потухать. Из фиг. 54, б видно, что при неравенстве частот звезда векторов сети А — S — С будет вращаться со скоростью, отличной от скорости вра-( щения векторов звезды А В — С, и напряжения на фазных лампах будут одновременно возрастать или уменьшаться.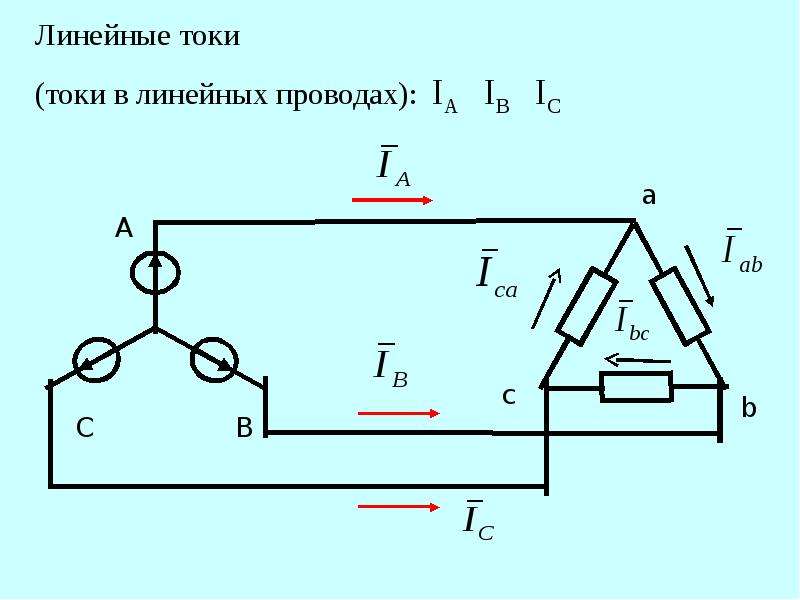 [c.535]
[c.535]
На фиг. 55 изображены кривая напряжения сети U и кривая э. д. с. приключаемого генератора Е и напряжение, приходящееся на каждую фазную лампу. Это напряжение будет возрастать от О до 2 6/, и поэтому лампы должны быть взяты на [c.535]
Сварочные посты включаются на фазное напряжение (порядка 65 в) через реакторы таким образом, чтобы создать равномерную нагрузку фаз (фиг. 35). [c.288]
В системах с нулевым проводом (фиг. 8, а) указываются линейное и фазное напряжения, например 380/220 в.
[c.225]
Включение однофазных потребителей (приемников) в трехфазной системе с нулевым проводом на фазное напряжение производится между нулевым и любым из линейных проводов потребители, рассчитанные на междуфазное напряжение, включаются между линейными проводами. [c.225]
Трехфазные потребители, например статоры асинхронных электродвигателей, включаются звездой, если напряжение сети соответствует линейному напряжению потребителя (фиг. 9, а), или треугольником, если напряжение сети соответствует фазному напряжению потребителя (фиг. 9, б). Например, двигатель, рассчитанный на 380/220 в, при напряжении сети 380 в включается звездой, при напряжении сети 220 в — треугольником. Номинальные напряжения установок см. в табл. 3.
[c.225]
9, а), или треугольником, если напряжение сети соответствует фазному напряжению потребителя (фиг. 9, б). Например, двигатель, рассчитанный на 380/220 в, при напряжении сети 380 в включается звездой, при напряжении сети 220 в — треугольником. Номинальные напряжения установок см. в табл. 3.
[c.225]
Фазным называется напряжение 11ф, создаваемое одной фазной обмоткой. [c.461]
Следуюн(ий метод регулирования основан на использовании индукционного регулятора (рис. 5-8, г). Простейшим индукционным регулятором может служить заторможенЕ1ый асинхронный двигатель с фазным ротором, устроенный таким образом, чтобы ротор можно было плавно поворачивать на 180°. К тре хфазной сети присоединяются три фазные обмотки либо ротора, либо статора, создающие вращающееся магнитное поле. Если к сети присоединен ротор, то в каждой фазной обмотке статора благодаря вращающемуся магнитному полю индуктируется переменное напряжение. При повороте ротора амплитуда этого напряжения остается одной и той же, а фаза будет изменяться. Первичная обмотка испытательного трансформатора присоединяется к сети последовательно с одной из указанных выше фазных обмоток. Вследствие этого к трансформатору прикладывается геометрическая сумма напряжения сети П] и напряжения фазной обмотки В зависимости от положения ротора сдвиг фаз между напряжениями П, и Пз имеет различное значение. Таким образом, напряжение на первичной обмотке трансформатора Пт при повороте ротора будет плавно и.зменяться от минимума (О1 — С/. ) до максимума (и214 >) Индукционные регуляторы обеспечивают плавное регулирование напряжения, по вызывают искажение кривой напряжения.
[c.106]
Первичная обмотка испытательного трансформатора присоединяется к сети последовательно с одной из указанных выше фазных обмоток. Вследствие этого к трансформатору прикладывается геометрическая сумма напряжения сети П] и напряжения фазной обмотки В зависимости от положения ротора сдвиг фаз между напряжениями П, и Пз имеет различное значение. Таким образом, напряжение на первичной обмотке трансформатора Пт при повороте ротора будет плавно и.зменяться от минимума (О1 — С/. ) до максимума (и214 >) Индукционные регуляторы обеспечивают плавное регулирование напряжения, по вызывают искажение кривой напряжения.
[c.106]
В общем случае при неформальной постановке задача оптимизации ЭМУ включает в себя выбор онтималыюго типа об1 СКта (например, электрические машины постоянного тока с электромагнитным возбуждением и возбуждением от постоянных магнитов, асинхронные с короткозамкнутым и фазным ротором, синхронные и пр ), его конструктивной схемы (нормальное и обращенное, цилиндрическое и торцевое исполнение, способы охлаждения и передачи электрической энергии на вращающиеся части устройства, тин опор вращающихся частей и пр. ), оптимизацию параметров объекта (геометрические размеры, обмоточные данные, характеристики электрических и магнитных материалов), а также поиск способов оптимального управления объектом (например, способов изменения напряжения и частоты питания) и, наконец, оптимизацию значений допусков па параметры.
[c.143]
), оптимизацию параметров объекта (геометрические размеры, обмоточные данные, характеристики электрических и магнитных материалов), а также поиск способов оптимального управления объектом (например, способов изменения напряжения и частоты питания) и, наконец, оптимизацию значений допусков па параметры.
[c.143]
Приведенные тензоры напряжений и векторы, характеризующие перенос импульса и энергии в дисперсной смеси. Рас-смотрпм более конкретные, нежели в 2, представления для осредненных тензоров напряжений и сил мея фазного взаимодействия в дисперсных смесях, учитывая структуру последних. [c.66]
Если пренебречь также работой вязких напряжений, то уравнение притока тепла на меж фазн,ой границе примет вид [c.82]
Если частота поля выбрана по условию (9-30) или (9-31), то электромагнитное поле в объеме нагреваемого тела син-фазно и, следовательно, квазистационарно. В квазистационарпом поле совпадают по фазе ток н напряженность магнитного поля, и поэтому (см. диаграмму на рис. 9-3) угол
[c.143]
диаграмму на рис. 9-3) угол
[c.143]
СУВ состоит из маломощного трансформатора TI с сетевой обмоткой и вторичными обмотками Wg, Wi. Обмотка нагружена на диодный мост (ДМ), к выходам которого подключены формирователи синхронизирующих импульсов (ФСИ), формируюшде синхроимпульсы из огибающих фазных напряжений в моменты естественной коммутации. Входы фазосдвигающих устройств (ФСУ) подключены к ФСИ, а выходы — к фор- [c.75]
Соотношения между линейным и фазным напряжениями и xoKaMt Соединение звездой [c.342]
Соединение обмоток источников трехфазного тока (генераторов, тран-сформатороа) производится либо звездой (фиг. 8, а), либо треугольником (фиг, 8, б). Фазным называется напряжение 11ф, создаваемое одной любой фазной обмоткой линейным, или междуфазным, называется напряжение иизмеренное между двумя любыми линейными проводами. [c.225]
Разница между линейным напряжением и фазным напряжением с решенными примерами
Линейное напряжение в трехфазной системе — это разность потенциалов между любыми двумя линиями или фазами, присутствующими в системе, обозначаемая как V line или V L-L . Присутствующие здесь фазы являются проводниками или обмотками катушки. Если R, Y и B являются тремя фазами (красная фаза, желтая фаза, синяя фаза), то разница напряжений между R и Y, Y и B или B и R образует линейное напряжение. Фазное напряжение, с другой стороны, представляет собой разность потенциалов между одной фазой (R, Y или B) и нейтральной точкой соединения, обозначаемую как V фаза = V R (напряжение в красной фазе) = V Y ( напряжение в желтой фазе) = V B (напряжение в синей фазе).
Присутствующие здесь фазы являются проводниками или обмотками катушки. Если R, Y и B являются тремя фазами (красная фаза, желтая фаза, синяя фаза), то разница напряжений между R и Y, Y и B или B и R образует линейное напряжение. Фазное напряжение, с другой стороны, представляет собой разность потенциалов между одной фазой (R, Y или B) и нейтральной точкой соединения, обозначаемую как V фаза = V R (напряжение в красной фазе) = V Y ( напряжение в желтой фазе) = V B (напряжение в синей фазе).
Точно так же линейный ток — это ток в одной фазе, а фазный ток — это ток внутри трехфазного соединения.
Чтобы понять отношение линейного и фазного напряжения, первое, что нам нужно понять, это различные типы трехфазных систем подключения.
Связь между линейным и фазным напряжением при соединении звездой
Рассмотрим три витка провода или обмотки трансформатора, соединенные общей точкой соединения. Три провода, идущие от каждой катушки к нагрузке, называются линейными проводами, а сами проводники — фазами. Эта система представляет собой типичную трехфазную трехпроводную систему соединения звездой. Если нейтральный провод подключен к общей средней точке, то это известно как трехфазная четырехпроводная система соединения звездой.
Три провода, идущие от каждой катушки к нагрузке, называются линейными проводами, а сами проводники — фазами. Эта система представляет собой типичную трехфазную трехпроводную систему соединения звездой. Если нейтральный провод подключен к общей средней точке, то это известно как трехфазная четырехпроводная система соединения звездой.
Термины линейное напряжение и фазное напряжение уже объяснялись ранее, и они связаны следующим образом:
Линейный ток = фазный ток.
Соотношение между линейным и фазным напряжением при соединении треугольником
При соединении треугольником все три конца фаз соединяются в замкнутый треугольный контур, и он не имеет общей нейтральной точки, как при соединении звездой. Здесь линейное и фазное напряжения связаны следующим образом:
В линия = В фаза
;
При этом линейный ток = √3 × фазный ток.
Разница между линейным и фазным напряжением
Sl No. | Линейное напряжение | Фазное напряжение |
1. | Линейное напряжение выше фазного напряжения при соединении звездой. | Фазное напряжение меньше линейного при соединении звездой. |
2. | Линейное напряжение – это разность потенциалов между двумя фазами или линиями. | Фазное напряжение – это разность потенциалов между фазой и нейтралью |
3. | При соединении звездой линейное напряжение в √3 раза превышает фазное. | При соединении звездой фазное напряжение в 1/√3 раза превышает линейное. |
Для соединения треугольником линейное напряжение и фазное напряжение равны.
Решаемые примеры
1. Рассчитайте фазное напряжение, если линейное напряжение составляет 460 вольт, учитывая, что система представляет собой трехфазную сбалансированную систему, соединенную звездой.
Ответ: Мы знаем,
В фаза = В линия / √3 = 460 / √3 = 265,59 вольт.
2. В какой из следующих цепей линейное и фазное напряжения равны? А как насчет отношения линейного напряжения и фазного напряжения в другой цепи?
Ответ: Как известно, при соединении треугольником (второй рисунок) линейное напряжение и фазное напряжение равны. В то время как при соединении звездой линейное напряжение выше фазного, которое определяется соотношением: В линия = √3 В фаза .
Забавные факты
В любой проблеме или вопросе обычно указывается линейное напряжение. В случае фазного напряжения это следует указать. Если не указано, считайте это линейным напряжением.
Наш отечественный трехфазный источник питания или 440 вольт является линейным напряжением.
Однофазное питание 230 В переменного тока представляет собой разность напряжений между фазой и нейтралью или, точнее, фазное напряжение.
Многофазная система, в которой все линейные напряжения и линейные токи равны, называется трехфазной сбалансированной системой. В случае несимметричных нагрузок система, как правило, является неуравновешенной.
Однофазная система
Однофазная система является одним из наиболее часто используемых типов систем, с которыми люди знакомы. Это также то, что большинство людей, как правило, имеют дома. Этот тип системы используется для обычных вилок и приборов.Однако, когда дело доходит до необходимости большего количества энергии, необходима трехфазная система. Электричество вырабатывается с помощью катушки с проволокой, которая продолжает двигаться через магнитные поля. Поскольку задействованы три катушки, система будет называться трехфазной. В то время как соединение между линией и нейтралью называется однофазной системой. Следовательно, необходимо понять разницу между линейным напряжением и фазным напряжением с помощью решенных примеров с помощью Vedantu, чтобы проверить мощность, которую обеспечивают обе системы.
Это также то, что большинство людей, как правило, имеют дома. Этот тип системы используется для обычных вилок и приборов.Однако, когда дело доходит до необходимости большего количества энергии, необходима трехфазная система. Электричество вырабатывается с помощью катушки с проволокой, которая продолжает двигаться через магнитные поля. Поскольку задействованы три катушки, система будет называться трехфазной. В то время как соединение между линией и нейтралью называется однофазной системой. Следовательно, необходимо понять разницу между линейным напряжением и фазным напряжением с помощью решенных примеров с помощью Vedantu, чтобы проверить мощность, которую обеспечивают обе системы.
Что означает связь со звездой?
Соединение звездой также известно как трехфазная четырехпроводная система, в которой участвуют 3 фазы, соединенные четырьмя проводами. Это одна из наиболее предпочтительных систем для распределения переменного тока, тогда как для передачи используется соединение треугольником. В звезде, которая также обозначается буквой Y, система взаимосвязи, начальная и конечная точки трех витков соединяются вместе, образуя нейтральную точку.
В звезде, которая также обозначается буквой Y, система взаимосвязи, начальная и конечная точки трех витков соединяются вместе, образуя нейтральную точку.
Соединение звездой получается путем соединения одинаковых концов трех катушек, два других конца которых соединены с линейными проводами. Общая точка также называется нейтральной или звездообразной точкой, которая представлена N.
Что означает соединение треугольником?
Соединение треугольником также называется соединением Mesh, где присутствуют три фазы, соединенные тремя проводами. Это также одна из наиболее предпочтительных систем переменного тока для передачи.
Проще говоря, можно также сказать, что три катушки, соединенные последовательно, образуют плотную сеть, и когда три провода выведены из трех соединений, все исходящие токи считаются положительными.Видно, что если система уравновешена, то значение алгебраической суммы всех напряжений в сетке останется равным нулю.
Преимущества использования трехфазной системы:
Трехфазные системы обладают определенными преимуществами и могут быть обеспечены следующим образом: сумма будет равна нулю, что делает его линейной сбалансированной нагрузкой. Следовательно, это позволяет уменьшить размер нейтрального проводника, поскольку по нему практически не проходит ток.
Передача мощности на линейную сбалансированную нагрузку является постоянной, что способствует снижению вибраций в двигателях или генераторах.
Трехфазная система также создает вращающееся магнитное поле, имеющее определенную величину и направление, что позволяет упростить конструкцию электродвигателей, поскольку не требуется пусковая цепь.
Теперь учащиеся могут узнать больше о разнице между линейным и фазным напряжением с помощью примеров решения с помощью Vedantu NCERT Solutions for Physics.
Взаимосвязь линейных и фазных напряжений и токов в системе, соединенной звездой
Чтобы вывести зависимости между линейными и фазными токами и напряжениями системы, соединенной звездой , мы должны сначала нарисовать сбалансированную систему, соединенную звездой.
Предположим, что из-за импеданса нагрузки ток отстает от приложенного напряжения в каждой фазе системы на угол ϕ. Поскольку мы считали, что система идеально сбалансирована, величина тока и напряжения каждой фазы одинаковы.Допустим, величина напряжения на красной фазе, то есть величина напряжения между нейтральной точкой (N) и клеммой красной фазы (R), составляет V R .
Аналогично, величина напряжения на желтой фазе равна V Y , а величина напряжения на синей фазе равна V B .
В сбалансированной звездной системе величина фазного напряжения в каждой фазе составляет V ph .
∴ V R = V Y = V B = V ph
Мы знаем, что при соединении звездой линейный ток такой же, как фазный ток. Величина этого тока одинакова во всех трех фазах и равна I L .
Величина этого тока одинакова во всех трех фазах и равна I L .
∴ I R = I Y = I B = I L , где I R — линейный ток фазы R, I Y — линейный ток фазы Y и I
3 B
4 линейный ток фазы B. Опять же, фазный ток I ph каждой фазы такой же, как линейный ток I L в системе, соединенной звездой.
∴ I R = I Y = I B = I L = I ph .
Допустим, теперь напряжение на клеммах R и Y цепи, соединенной звездой, равно V RY .
Напряжение на клеммах Y и B цепи, соединенной звездой, составляет В YB Напряжение на клеммах B и R цепи, соединенной звездой, составляет VBR .
Из диаграммы находим, что
В RY = V R + (− V Y )
Аналогично, V YB = V Y + (− V B
0 ) И V BR = V B + (− V R )
Теперь, поскольку угол между V R и V Y равен 120 o (электрический), угол между V и R –
3 V
Y равно 180 o – 120 o = 60 o (электрический).
Таким образом, для системы, соединенной звездой, линейное напряжение = √3 × фазное напряжение.
Линейный ток = фазный ток
Так как угол между напряжением и током на фазу равен φ, электрическая мощность на фазу равна
Таким образом, общая мощность трехфазной системы равна
9.3: Трехфазные соединения — Инженерные тексты
Возможна конфигурация систем с использованием источников, соединенных треугольником или звездой, с нагрузками, соединенными треугольником или звездой. Следует отметить, что системы, соединенные треугольником, всегда представляют собой трехпроводные системы, в то время как системы, соединенные звездой, могут использовать четвертый нейтральный провод (общая точка, к которой подключаются все три источника).
Гомогенные системы
Самые простые системы — это дельта-треугольник и Y-to-Y. Мы будем называть их однородными системами, поскольку структуры генератора и нагрузки аналогичны. Примеры показаны на рисунках \(\PageIndex{1}\) и \(\PageIndex{2}\) соответственно.
Рисунок \(\PageIndex{1}\): Генератор, соединенный треугольником, с нагрузкой, соединенной треугольником (треугольник-дельта). Рисунок \(\PageIndex{2}\): Генератор, соединенный звездой, с нагрузкой, соединенной треугольником. (ГГ). Показан дополнительный четвертый нейтральный провод от центра к центру.
В этих конфигурациях каждая ветвь нагрузки совпадает с соответствующей ветвью генератора. В конфигурации «треугольник-треугольник» на рисунке \(\PageIndex{1}\) уже при осмотре должно быть очевидно, что напряжение на любой ветви нагрузки должно равняться напряжению соответствующей ветви генератора. Например, импеданс нагрузки, подключенный между \(A’\) и \(B’\), должен видеть напряжение, представленное генератором, расположенным между \(A\) и \(B\), потому что \(A\) непосредственно связан с \(A’\), как \(B\) с \(B’\).Аналогично, для конфигурации YY на рисунке \(\PageIndex{2}\) ток через любую ветвь нагрузки должен быть равен току, протекающему через связанную ветвь генератора, поскольку нет других путей для тока между \(A\) и \ (А’\), \(В\) и \(В’\), а также \(С\) и \(С’\).
Поскольку нагрузка сбалансирована и ветви генератора идентичны, за исключением их фаз, должно быть так, что напряжения и токи (и, следовательно, мощности) для каждой ветви нагрузки должны быть одинаковыми, за исключением фаза.Это справедливо как для конфигурации Y-Y, так и для конфигурации дельта-треугольник. Сложность здесь заключается в разнице между током или напряжением источника (или нагрузки) и линейным током или напряжением.
\[\text{Линейное напряжение — это величина напряжения между любыми двумя проводниками, соединяющими источник с нагрузкой, за исключением земли или общего провода.} \nonumber\]
\[\text{Линейный ток — это величина тока, протекающего в любом проводнике, соединяющем источник с нагрузкой, за исключением заземления или общего.} \номер\]
Рассмотрим систему дельта-дельта на рисунке \(\PageIndex{1}\). Мы уже установили, что напряжение, развиваемое генератором \(A,B\), должно быть таким же, как и напряжение на нагрузке \(A’,B’\).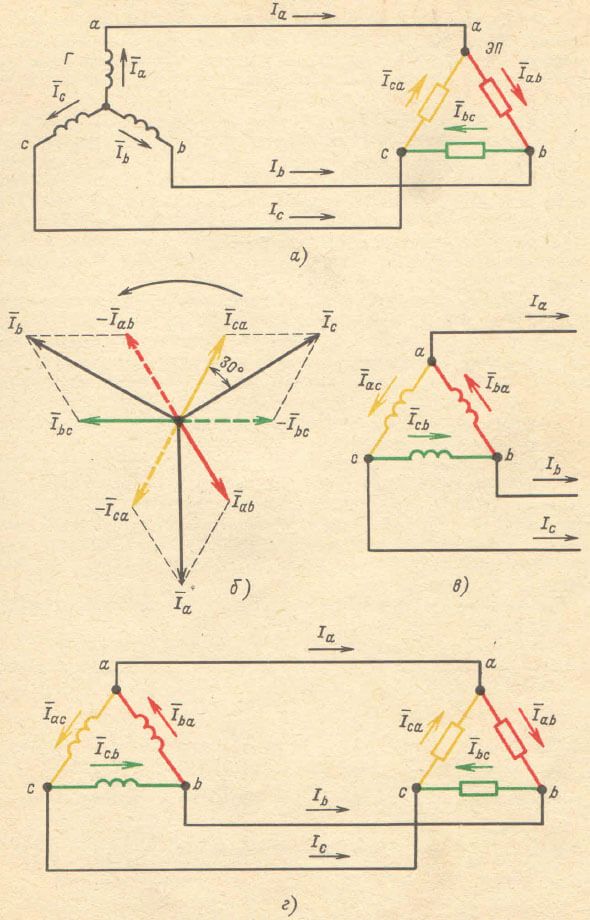 Таким образом, напряжение, измеренное от проводника A, A’ до проводника B, B’, должно быть таким же, как напряжение источника и нагрузки. Другими словами, в конфигурации «треугольник-треугольник» напряжения источника, нагрузки и сети одинаковы.
Таким образом, напряжение, измеренное от проводника A, A’ до проводника B, B’, должно быть таким же, как напряжение источника и нагрузки. Другими словами, в конфигурации «треугольник-треугольник» напряжения источника, нагрузки и сети одинаковы.
Мы также обнаружили, что токи источника и нагрузки должны быть одинаковыми для конфигурации треугольник-треугольник, однако это не означает, что ток, протекающий по проводу, соединяющему \(A\) с \(A’\), должен быть такой же, как ток, протекающий либо через генератор, либо через нагрузку.Ведь к \(A’\) подключаются два провода нагрузки, а не один. По определению, ток, протекающий по этому проводу, является линейным током, и, следовательно, в конфигурации треугольник-треугольник линейный ток не совпадает с током источника или нагрузки. Во избежание путаницы напряжение или ток, связанные с одной ветвью, называются фазным напряжением или током по отношению к линейному напряжению или току.
Обращаясь к конфигурации Y-Y на рисунке \(\PageIndex{2}\), мы видим противоположную ситуацию. Токи источника, нагрузки и линии будут одинаковыми. С другой стороны, линейное напряжение состоит из двух генераторов, а не одного (например, от \(A\) до \(B\) или от \(B\) до \(C\)). Таким образом, для конфигурации Y-Y напряжения источника и нагрузки одинаковы, но они не равны линейному напряжению (и не удваиваются благодаря фазовому сдвигу).
Токи источника, нагрузки и линии будут одинаковыми. С другой стороны, линейное напряжение состоит из двух генераторов, а не одного (например, от \(A\) до \(B\) или от \(B\) до \(C\)). Таким образом, для конфигурации Y-Y напряжения источника и нагрузки одинаковы, но они не равны линейному напряжению (и не удваиваются благодаря фазовому сдвигу).
Определение линейного напряжения и тока
Чтобы определить линейное напряжение для генератора, подключенного по схеме «звезда» (и, аналогично, линейный ток для генератора, подключенного по схеме «треугольник»), полезно изучить векторную диаграмму напряжений отдельных генераторов.Это показано на рисунке \(\PageIndex{3}\). У нас есть три напряжения одинаковой амплитуды, единственная разница между ними заключается в их фазе. Каждый вектор отделен от других на 120 градусов. Далее каждая отдельная образующая соединяется из общей точки с одной из внешних точек \(А\), \(В\) и \(С\). Линейное напряжение определяется как потенциал, существующий между любыми двумя или этими тремя точками.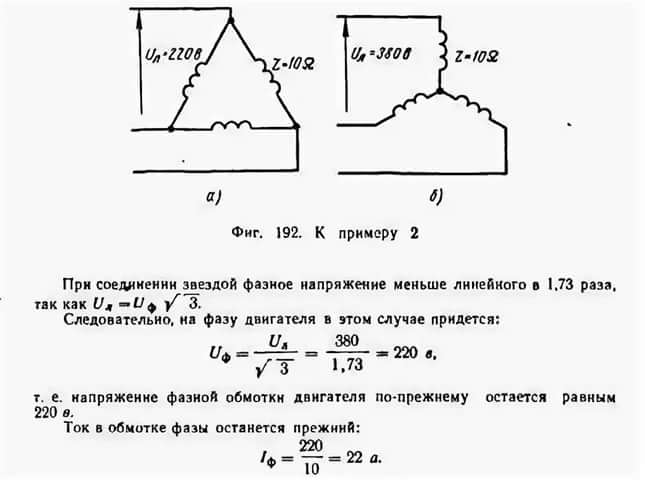 Хотя можно просто вычесть одно напряжение генератора из другого, чтобы получить разницу, существует хорошее графическое решение, из которого мы можем получить точную формулу для линейного напряжения, учитывая напряжение генератора.
Хотя можно просто вычесть одно напряжение генератора из другого, чтобы получить разницу, существует хорошее графическое решение, из которого мы можем получить точную формулу для линейного напряжения, учитывая напряжение генератора.
Рисунок \(\PageIndex{3}\): Векторная диаграмма Y-образного генератора
Начнем с того, что сосредоточимся на втором и третьем квадрантах векторной диаграммы. Этот раздел перерисован на рисунке \(\PageIndex{4}\). В действительности для следующего доказательства можно использовать любые два вектора, но эта пара оказывается особенно удобной по своей ориентации.
Рисунок \(\PageIndex{4}\): Решение линейного напряжения генератора, подключенного по схеме Y.
Для простоты использования нормируем величину напряжения генератора к единице.Мы видим, что векторы \(B\) и \(C\) идеально разделены горизонтальной осью; то, что находится над осью, идеально зеркально отражается под ней. В верхней части мы находим прямоугольный треугольник с гипотенузой, равной единице (темно-красный). Угол, который он образует с горизонтом, должен быть равен половине угла между ним и вектором \(C\). Это половина от 120 градусов или 60 градусов. Поскольку сумма внутренних углов треугольника должна быть 180 градусов, это означает, что третий угол должен быть равен 30 градусам. Горизонтальный катет треугольника (темно-желтый или, может быть, «пряно-горчичный») можно определить, потому что мы знаем и гипотенузу, и противолежащий угол.2} \номер\]
Угол, который он образует с горизонтом, должен быть равен половине угла между ним и вектором \(C\). Это половина от 120 градусов или 60 градусов. Поскольку сумма внутренних углов треугольника должна быть 180 градусов, это означает, что третий угол должен быть равен 30 градусам. Горизонтальный катет треугольника (темно-желтый или, может быть, «пряно-горчичный») можно определить, потому что мы знаем и гипотенузу, и противолежащий угол.2} \номер\]
\[\text{vertical} = \sqrt{\frac{3}{4}} \nonnumber\]
\[\text{vertical} = \frac{1}{2} \sqrt{3} \nonnumber\]
Вертикальная ножка идеально зеркально отражена под горизонтальной осью. Таким образом, диапазон от \(B\) до \(C\) должен быть в два раза больше этого значения или \(\sqrt{3}\). Поскольку напряжение, развиваемое на каждой ветви генератора, называется фазным напряжением генератора, мы можем указать:
\[\text{Напряжение сети для генератора, соединенного звездой, в } \sqrt{3} \text{ умножается на его фазное напряжение. } \метка{9.1}\]
} \метка{9.1}\]
Например, если фазное напряжение генератора, подключенного по схеме Y, составляет 120 вольт, линейное напряжение будет в \(\sqrt{3}\) раз больше, или примерно 208 вольт.
Для генератора, соединенного треугольником, то же верно для фазного и линейного токов, доказательство оставлено в качестве упражнения. То есть
\[\text{Сетевой ток для генератора, соединенного треугольником, в } \sqrt{3} \text{ умножен на его фазный ток.} \label{9.2}\]
Те же отношения справедливы как для нагрузок, так и для источников, т.е.г., ток в плече нагрузки, соединенной звездой, будет таким же, как линейный ток, а ее фазное напряжение будет в \(\sqrt{3}\) раз меньше, чем линейное напряжение.
\[\text{ Подводя итог: для конфигураций треугольника (генератор или нагрузка) фазное напряжение равно линейному напряжению, а линейный ток больше фазного тока на } \sqrt{3} \text{. Для конфигураций Y фазный ток равен линейному току, а линейное напряжение } \sqrt{3} \text{ больше, чем фазное напряжение. } \номер\]
} \номер\]
Для однородных систем, поскольку генератор и нагрузка имеют одинаковую конфигурацию, фазные напряжения и токи нагрузки должны быть идентичны таковым у генератора. Полезным помощником в запоминании является то, что мощность, рассеиваемая в системе, должна равняться генерируемой мощности.
Пример \(\PageIndex{1}\)
Трехфазный генератор, соединенный треугольником, питает трехфазную нагрузку, соединенную треугольником, как показано на рисунке \(\PageIndex{1}\). Предположим, что фазное напряжение генератора равно 120 В переменного тока (действующее значение).Груз состоит из трех одинаковых ветвей по 50 \(\Омега\) каждая. Определите линейное напряжение, фазное напряжение нагрузки, фазный ток генератора, линейный ток, фазный ток нагрузки и общую мощность, подаваемую на нагрузку.
Поскольку это однородная система (треугольник-треугольник), фазное напряжение и ток нагрузки такие же, как у генератора. Следовательно, фазное напряжение нагрузки также должно быть 120 вольт. Во-вторых, в конфигурации треугольника линейное напряжение равно фазному, опять же 120 вольт.Ток фазы нагрузки определяется по закону Ома и будет представлять собой среднеквадратичное значение, поскольку напряжение равно среднеквадратичному значению:
Во-вторых, в конфигурации треугольника линейное напряжение равно фазному, опять же 120 вольт.Ток фазы нагрузки определяется по закону Ома и будет представлять собой среднеквадратичное значение, поскольку напряжение равно среднеквадратичному значению:
.
\[i_{фаза} = \frac{v_{фаза}}{Z_{нагрузка}} \номер\]
\[i_{фаза} = \frac{120 В}{50 \Омега} \номер\]
\[i_{фаза} = 2,4 А \номер\]
Фазный ток генератора должен быть одинаковым, поскольку генератор и нагрузка имеют одинаковую конфигурацию. Для конфигураций треугольника линейный ток в \(\sqrt{3}\) раз больше, чем фазный ток, таким образом,
\[i_{строка} = \sqrt{3}\times i_{фаза} \nonnumber\]
\[i_{строка} = \sqrt{3}\times 2.2\умножить на 50 \Омега\номер\]
\[P_{всего} = 864 Вт \номер\]
Это эквивалентно примерно 1,2 л.с. Мы также могли бы вычислить мощность фазы нагрузки, используя квадрат фазного напряжения, деленный на сопротивление нагрузки, или умножив фазное напряжение на фазный ток. Поскольку это чисто резистивная нагрузка, здесь нет фазового угла и, следовательно, нет коэффициента мощности, на который следует обращать внимание.
Поскольку это чисто резистивная нагрузка, здесь нет фазового угла и, следовательно, нет коэффициента мощности, на который следует обращать внимание.
Пример \(\PageIndex{2}\)
Трехфазный генератор, соединенный звездой, питает трехфазную нагрузку, соединенную звездой, подобно системе, показанной на рисунке \(\PageIndex{2}\).Предположим, что фазное напряжение генератора составляет 220 В переменного тока (действующее значение). Груз состоит из трех одинаковых ветвей по 100 \(\Омега\) каждая. Определите линейное напряжение, фазное напряжение нагрузки, фазный ток генератора, линейный ток, фазный ток нагрузки и общую мощность, подаваемую на нагрузку.
Это однородная (Y-Y) система, поэтому фазное напряжение и ток нагрузки такие же, как у генератора. Следовательно, фазное напряжение нагрузки должно быть 220 вольт. В конфигурации Y линейное напряжение равно фазному напряжению, умноженному на \(\sqrt{3}\).
\[v_{строка} = \sqrt{3}\times v_{фаза} \номер\]
\[v_{line} = \sqrt{3}\times 220V \nonnumber\]
\[v_{линия} \приблизительно 381 В \номер\]
Ток фазы нагрузки находится по закону Ома и будет представлять собой среднеквадратичное значение, поскольку напряжение является среднеквадратичным. Это то же самое, что и фазный ток генератора, а также линейный ток.
Это то же самое, что и фазный ток генератора, а также линейный ток.
\[i_{фаза} = \frac{v_{фаза}}{Z_{нагрузка}} \номер\]
\[i_{фаза} = \frac{220 В}{100 \Омега} \номер\]
\[i_{фаза} = 2.2А \номер\]
Полную мощность можно найти с помощью основного степенного закона, поскольку нагрузка является чисто резистивной, и у нас есть среднеквадратичные значения. В этом случае мы будем использовать ток, умноженный на напряжение, для изменения темпа.
\[P_{всего} = 3\times i_{фаза} \times v_{фаза} \nonnumber\]
\[P_{общее} = 3\умножить на 2,2 А\умножить на 220 В \номер\]
\[P_{всего} = 1452 Вт \номер\]
Чуть меньше 2 л.с. Еще раз, это чисто резистивная нагрузка и фазового угла нет.Таким образом, коэффициент мощности равен единице, при этом реальная и кажущаяся мощности одинаковы.
Пример \(\PageIndex{3}\)
Для системы, показанной на рисунке \(\PageIndex{5}\), определите полную кажущуюся и реальную мощность, подаваемую на нагрузку. Также найдите напряжение в сети. Фазное напряжение источника составляет 240 вольт среднеквадратичного значения при частоте 60 Гц.
Также найдите напряжение в сети. Фазное напряжение источника составляет 240 вольт среднеквадратичного значения при частоте 60 Гц.
Рисунок \(\PageIndex{5}\): Схема для примера \(\PageIndex{3}\).
Учитывая тот факт, что все три опоры нагрузки находятся в одной общей точке (земля), это должна быть система Y-Y.Следовательно, мы знаем, что линейное напряжение должно быть в \(\sqrt{3}\) раз больше фазного напряжения генератора.
\[v_{строка} = \sqrt{3}\times v_{фаза} \номер\]
\[v_{линия} = \sqrt{3}\times 240 В \номер\]
\[v_{line} \приблизительно 416 В RMS \номер\]
Это однородная система (Y-Y), поэтому мы также знаем, что напряжение нагрузки равно напряжению генератора или 240 вольт RMS. Отсюда мы можем найти ток нагрузки (линейный ток должен быть таким же, потому что это Y-образная нагрузка).2\раз R_{нагрузка} \номер\]
\[P = 3\умножить на 4,8А 2\умножить на 40 \Омега \номер\]
\[P = 2765 Вт \без номера\]
Компьютерное моделирование
Схема примера \(\PageIndex{3}\) достойна моделирования. Первое, что нужно сделать, это определить подходящее значение индуктивности для достижения реактивного сопротивления \(j40 \Омега\). При частоте источника 60 Гц получается примерно 80 мГн. Схема построена, как показано на рисунке \(\PageIndex{6}\).Среднеквадратичное значение фазового напряжения источника 240 вольт эквивалентно примерно 340 вольтам пикового значения. Положения катушки индуктивности и резистора в каждом плече поменялись местами по причине, которая вскоре станет очевидной.
Первое, что нужно сделать, это определить подходящее значение индуктивности для достижения реактивного сопротивления \(j40 \Омега\). При частоте источника 60 Гц получается примерно 80 мГн. Схема построена, как показано на рисунке \(\PageIndex{6}\).Среднеквадратичное значение фазового напряжения источника 240 вольт эквивалентно примерно 340 вольтам пикового значения. Положения катушки индуктивности и резистора в каждом плече поменялись местами по причине, которая вскоре станет очевидной.
Рисунок \(\PageIndex{6}\): система, эквивалентная рис. \(\PageIndex{5}\) в симуляторе.
Непосредственный интерес представляет проверка временных сдвигов и амплитуд фазных напряжений. Они соответствуют узлам 1, 2 и 3. В этой конфигурации фазное напряжение нагрузки равно фазному напряжению генератора, поэтому они должны составлять 340 вольт пикового значения и быть разделены на 120 градусов или 1/3 цикла.
Выполняется анализ переходных процессов с нанесением интересующих узловых напряжений. Результат показан на рисунке \(\PageIndex{7}\). Напряжения в точности соответствуют ожидаемым, и график идеально соответствует теоретическому графику на рис. 9.2.4.
Результат показан на рисунке \(\PageIndex{7}\). Напряжения в точности соответствуют ожидаемым, и график идеально соответствует теоретическому графику на рис. 9.2.4.
Рисунок \(\PageIndex{7}\): Три напряжения нагрузки, смоделированные на рисунке \(\PageIndex{6}\).
Теперь проверяем напряжение в сети. Это было рассчитано как среднеквадратичное значение 416 вольт или пиковое значение примерно 588 вольт. Постпроцессор используется для отображения результата напряжения узла 1 минус напряжения узла 2.Это показано на рисунке \(\PageIndex{8}\). Опять же, результаты, как и ожидалось, с пиком чуть ниже 600 вольт.
Наконец, мы исследуем реальную мощность нагрузки. Возможно, самый простой способ сделать это — определить напряжение на резистивной части нагрузки. Из предыдущей работы мы знаем, что истинная мощность связана только с сопротивлением, а не реактивным сопротивлением. Таким образом, все, что нам нужно сделать, это измерить пиковое напряжение на резисторе. Оттуда мы находим его эквивалент RMS, возводим его в квадрат и делим на номинал резистора. Это дает нам реальную мощность нагрузки на одну ногу. Для общей мощности мы просто утраиваем результат. Получить напряжение на резисторе легко, если резистор подключен к земле. В этом случае это просто напряжение в узле, к которому подключен резистор. Вот почему при моделировании местами индуктор и резистор были поменяны местами. Поскольку они соединены последовательно, это не влияет на общее сопротивление нагрузки, однако новое расположение позволяет нам получать напряжение резистора напрямую, вместо того, чтобы полагаться на дифференциальное напряжение, полученное через постпроцессор.
Это дает нам реальную мощность нагрузки на одну ногу. Для общей мощности мы просто утраиваем результат. Получить напряжение на резисторе легко, если резистор подключен к земле. В этом случае это просто напряжение в узле, к которому подключен резистор. Вот почему при моделировании местами индуктор и резистор были поменяны местами. Поскольку они соединены последовательно, это не влияет на общее сопротивление нагрузки, однако новое расположение позволяет нам получать напряжение резистора напрямую, вместо того, чтобы полагаться на дифференциальное напряжение, полученное через постпроцессор.
Выполняется еще один анализ переходных процессов, на этот раз на графике отображается напряжение на одном из нагрузочных резисторов; а именно узел 4. Результат показан на рисунке \(\PageIndex{9}\). Измеренное пиковое значение этой формы волны составляет 271,5 вольта или около 192 вольт среднеквадратичного значения. Возведение этого числа в квадрат и деление на 40 \( \Omega \) дает чуть более 921 Вт на ногу, что в сумме составляет около 2765 Вт, как и ожидалось.
Рисунок \(\PageIndex{8}\): Одно из смоделированных линейных напряжений из рисунка \(\PageIndex{6}\). Рисунок \(\PageIndex{9}\): Смоделированное напряжение на одном из нагрузочных резисторов на рисунке \(\PageIndex{6}\).
Гетерогенные системы
Системы, сконфигурированные как треугольник-Y и Y-треугольник, кажутся немного более сложными, чем однородные системы. Мы будем называть их гетерогенными системами, поскольку структуры генератора и нагрузки противоположны. Примеры показаны на рисунках \(\PageIndex{10}\) и \(\PageIndex{11}\) соответственно.
Рисунок \(\PageIndex{10}\): Генератор, соединенный треугольником, с нагрузкой, соединенной треугольником (треугольник-Y). Рисунок \(\PageIndex{11}\): Генератор, соединенный треугольником, с нагрузкой, соединенной треугольником. (Идельта).
Эти системы не так сложны, как думают некоторые; все, что вам нужно сделать, это запомнить операторы \ref{9.1} и \ref{9.2}. Действительно, здесь стоит повторить итог:
\text{Для конфигураций треугольником (генератор или нагрузка) фазное напряжение равно линейному напряжению, а линейный ток больше фазного на } \sqrt{3} \text{. Для конфигураций Y фазный ток равен линейному току, а линейное напряжение } \sqrt{3} \text{ больше, чем фазное напряжение.} \номер\]
Для конфигураций Y фазный ток равен линейному току, а линейное напряжение } \sqrt{3} \text{ больше, чем фазное напряжение.} \номер\]
Анализ этих систем можно рассматривать как двухэтапный процесс. Сначала определите линейное напряжение и ток либо от генератора, либо от нагрузки; во-вторых, переход с линии на другую сторону (нагрузку или генератор). Если возникнет путаница, помните, что генерируемая мощность должна равняться рассеиваемой или отдаваемой мощности.
На рисунке \(\PageIndex{10}\) линейное напряжение равно фазному напряжению генератора. Нагрузка подключена по схеме Y, поэтому для каждой ветви линейное напряжение делится на \(\sqrt{3}\).На основании этого можно рассчитать каждую ветвь тока нагрузки. Обратите внимание, что линейный ток равен току нагрузки. Фазный ток генератора будет равен линейному току, деленному на \(\sqrt{3}\).
На рисунке \(\PageIndex{11}\) линейное напряжение равно \(\sqrt{3}\), умноженному на фазное напряжение генератора. Нагрузка соединена треугольником, поэтому на каждую ногу попадает линейное напряжение. Зная это, можно рассчитать каждую ветвь тока нагрузки. Кроме того, линейный ток равен фазному току генератора, а фазный ток нагрузки равен линейному току, деленному на \(\sqrt{3}\).{\circ}\) \( \Omega \), определите фазный ток генератора, линейное напряжение, фазное напряжение нагрузки, фазный ток нагрузки и общую мощность, отдаваемую в нагрузку.
Зная это, можно рассчитать каждую ветвь тока нагрузки. Кроме того, линейный ток равен фазному току генератора, а фазный ток нагрузки равен линейному току, деленному на \(\sqrt{3}\).{\circ}\) \( \Omega \), определите фазный ток генератора, линейное напряжение, фазное напряжение нагрузки, фазный ток нагрузки и общую мощность, отдаваемую в нагрузку.
Генератор соединен треугольником, поэтому линейное напряжение равно фазному напряжению генератора или 230 вольт. На нагрузке, подключенной по схеме Y, фазное напряжение будет уменьшено в \(\sqrt{3}\).
\[v_{load} = \frac{v_{line}}{\sqrt{3}} \nonnumber\]
\[v_{нагрузка} = \frac{230 В}{\sqrt{3}} \номер\]
\[v_{нагрузка} \ приблизительно 132.{\circ} \Omega} \nonumber\]
\[i_{нагрузка} \приблизительно 0,664 A RMS \номер\]
При соединении по схеме Y линейный ток должен быть таким же, как и фазный ток нагрузки, или 0,664 А. При соединении треугольником линейный ток в \(\sqrt{3}\) раз больше фазного тока, поэтому фазный ток генератора должен быть в \(\sqrt{3}\) раз меньше.
\[i_{gen} = \frac{i_{line}}{\sqrt{3}} \nonnumber\]
\[i_{gen} = \frac{0.664A}{\sqrt{3}} \nonnumber\]
\[i_{gen} \ приблизительно 0.2 \times 200 \Omega \nonnumber\]
\[P_{всего} = 264 Вт \номер\]
В качестве перекрестной проверки выработанная мощность составляет:
\[P_{всего} = 3\times i_{gen} \times v_{gen} \nonnumber\]
\[P_{общее} = 3\х 0,383А\х 230 В \без числа\]
\[P_{всего} = 264 Вт \номер\]
Генерируемая мощность равна рассеиваемой мощности.
Пример \(\PageIndex{5}\)
Система Y-треугольник, подобная той, что показана на рисунке \(\PageIndex{11}\), имеет фазное напряжение генератора, равное 100 вольт RMS при 60 Гц.Если нагрузка имеет величину 50 \( \Omega \) с отстающим коэффициентом мощности 0,8, определите фазный ток генератора, линейное напряжение, фазное напряжение нагрузки, фазный ток нагрузки и полную истинную мощность, подаваемую на нагрузку. .
Генератор, соединенный звездой, создает линейное напряжение, равное фазному напряжению генератора, умноженному на \(\sqrt{3}\). Это также фазное напряжение нагрузки, так как оно соединено треугольником.
Это также фазное напряжение нагрузки, так как оно соединено треугольником.
\[v_{строка} = \sqrt{3}\times v_{фаза} \номер\]
\[v_{line} = \sqrt{3}\times 100 V \nonnumber\]
\[v_{строка} \ приблизительно 173.2 В RMS \номер\]
На нагрузку, соединенную треугольником, будет приходиться фазное напряжение, такое же, как и линейное, или 173,2 вольта. Отсюда мы можем определить ток нагрузки.
\[i_{нагрузка} = \frac{v_{фаза}}{Z_{нагрузка}} \номер\]
\[i_{нагрузка} = \frac{173.2V}{50 \Omega} \nonnumber\]
\[i_{нагрузка} \приблизительно 3,464 A RMS \номер\]
Поскольку нагрузка соединена треугольником, линейный ток равен току нагрузки, умноженному на \(\sqrt{3}\). Фазный ток генератора будет таким же, как линейный ток.2\умножить на 40 \Омега\номер\]
\[P_{всего} = 1440 Вт \номер\]
Мы также можем найти полную мощность и использовать коэффициент мощности.
\[P_{total} = 3\times v_{load} \times i_{load} PF \nonumber\]
\[P_{total} = 3\times 173,2V\times 3,464 A\times 0,8 \nonnumber\]
\[P_{всего} = 1440 Вт \номер\]
В качестве перекрестной проверки сравните рассеиваемую мощность с генерируемой.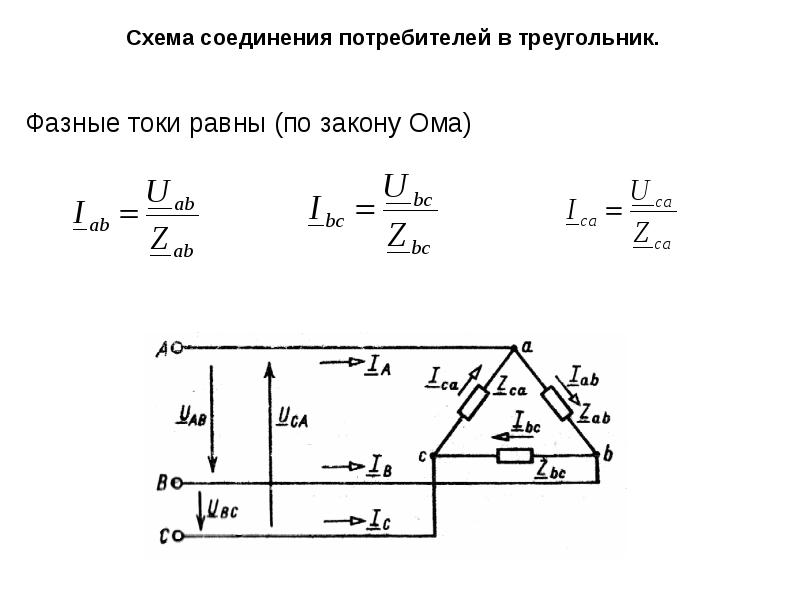
\[P_{всего} = 3\times v_{gen}\times i_{gen}\times PF \nonnumber\]
\[P_{всего} = 3\х 100В\х 6А\х0.8 \номер\]
\[P_{всего} = 1440 Вт \номер\]
Линейное и фазное напряжение в соединении треугольником
Рисунок 17.4. Напряжение отстает от тока на 90 градусов в чисто емкостной цепи.
fflt
Рисунок 17.4. Напряжение отстает от тока на 90 градусов в чисто емкостной цепи.
и амперы, используемые в формуле, измеряются на одной линии или фазе), чтобы учесть суммарный эффект трех фаз.Эта трехфазная мощность известна как активная мощность (см. рис. 17.5). Для более подробного анализа см. боковую панель 1.
Врезка 1: Трехфазные цепи
Чтобы проиллюстрировать трехфазное питание, представьте себе три катушки, расположенные на расстоянии 120 градусов друг от друга. Три напряжения, отстоящие друг от друга на 120 градусов, будут создаваться, когда магнитное поле проходит через катушки. Именно так генерируется трехфазная мощность. Есть два основных соединения для трехфазного питания: соединение звездой и соединение треугольником.
Именно так генерируется трехфазная мощность. Есть два основных соединения для трехфазного питания: соединение звездой и соединение треугольником.
Р Р
АПФ РЕАКТИВНЫЙ
НАСТОЯЩИЙ
Рисунок 17.5. Треугольник власти.
НАСТОЯЩИЙ
Рисунок 17.5. Треугольник власти.
Врезка 1: Трехфазные цепи (продолжение)
Соединение звездой состоит из трех катушек с одним общим соединением (см. рис. A). Напряжение, измеренное на одной катушке или обмотке, известно как фазное напряжение. Напряжение, измеренное от линии к линии, известно как линейное напряжение. В двигателе, соединенном звездой, линейное напряжение выше фазного на коэффициент квадратного корня из 3 или 1.732. Фазный ток и линейный ток одинаковы в двигателе, соединенном звездой.
Три катушки на рис. B расположены так, что образуют трехфазную цепь, соединенную треугольником. Фазное напряжение и линейное напряжение одинаковы в двигателе (или цепи), соединенном треугольником. Однако линейный ток и фазный ток различны. Линейный ток в двигателе, соединенном треугольником, выше фазного тока на коэффициент квадратного корня из 3, или 1,732.
Однако линейный ток и фазный ток различны. Линейный ток в двигателе, соединенном треугольником, выше фазного тока на коэффициент квадратного корня из 3, или 1,732.
- СЕТЕВОЕ НАПРЯЖЕНИЕ = ФАЗНОЕ НАПРЯЖЕНИЕ
- ЛИНЕЙНЫЙ ТОК (Ii) = 1.732 X ФАЗНЫЙ ТОК (IP)
- ЛИНЕЙНОЕ НАПРЯЖЕНИЕ = ФАЗНОЕ НАПРЯЖЕНИЕ
- ЛИНЕЙНЫЙ ТОК (Ii) = 1,732 X ФАЗНЫЙ ТОК (IP)
При расчете трехфазной мощности легко допустить ошибку. Путаница коренится в том факте, что на самом деле существует две формулы для расчета трехфазной мощности. Если используются линейное напряжение и линейный ток, мощность (Вт) в цепи двигателя выражается как
.
Если в расчетах используются фазное напряжение и фазный ток, определяется полная мощность, а не реальная мощность.Полная мощность в цепи двигателя (вольт-ампер [ВА]) составляет
Коэффициент мощности и полная мощность обсуждаются во врезке 2, посвященной треугольнику мощности и коэффициенту мощности.
На рис. 17.5 реактивная мощность показана как отстающая. Реактивная мощность может также легко быть ведущей, и в этом случае реактивная мощность будет показана отрицательной и направленной вниз. Треугольник мощности иллюстрирует тот факт, что формы сигналов напряжения и тока могут не совпадать по фазе.
17.5 реактивная мощность показана как отстающая. Реактивная мощность может также легко быть ведущей, и в этом случае реактивная мощность будет показана отрицательной и направленной вниз. Треугольник мощности иллюстрирует тот факт, что формы сигналов напряжения и тока могут не совпадать по фазе.
Реактивная мощность отображается перпендикулярно активной мощности, поскольку она не совпадает по фазе на 90 электрических градусов.Индуктивное сопротивление и емкостное сопротивление должны иметь разные знаки. Индуктивное сопротивление условно обозначается как положительное, а емкостное сопротивление условно обозначается как отрицательное.
Полная мощность в ВА является произведением измеренного напряжения и силы тока. В качестве альтернативы кажущаяся мощность может быть рассчитана путем умножения импеданса (Z) на квадрат тока. Импеданс можно рассчитать следующим образом:
Z = (R2 + (Х1 — ХС)2 )1/2
где
R = сопротивление, в Ом
XL = индуктивное сопротивление, в омах
XC = емкостное реактивное сопротивление, в омах
Косинус угла между реальной мощностью и кажущейся мощностью на рисунке 17. 5 известен как коэффициент мощности. Для более подробного анализа см. врезку 2.
5 известен как коэффициент мощности. Для более подробного анализа см. врезку 2.
Врезка 2: треугольник мощности и коэффициент мощности
В цепях переменного тока мощность не обязательно является произведением тока и напряжения, хотя она была бы в полностью резистивной цепи.
Существует три типа силы, как показано в треугольнике мощности
(рис. 17.5): полная мощность, активная мощность и реактивная мощность.
- Полная мощность является произведением линейного напряжения и линейного тока.Он получается путем измерения линейного напряжения и линейного тока и умножения двух измеренных значений.
- В индуктивной цепи, такой как цепь двигателя, существуют магнитные характеристики, которые приводят к потреблению большей полной мощности в ВА, чем реальной мощности в ваттах. Помните, что эта индукция заставляет напряжение опережать ток на 90 электрических градусов, как показано на рис. 17.5. Эта реактивная нагрузка эффективно отдает меньшую мощность нагрузке.
 Реактивная мощность измеряется в реактивных вольтамперах (ВАр).
Реактивная мощность измеряется в реактивных вольтамперах (ВАр). - Рисунок 17.5 представляет собой векторную диаграмму, показывающую компоненты мощности в цепи переменного тока. Компонент VAR представляет собой реактивную мощность, а компонент в ваттах представляет собой реальную мощность. Их комбинация представляет VA, полную мощность. Полная мощность представляет собой квадратный корень из суммы квадратов реактивной мощности и активной мощности.
- Коэффициент мощности равен реальной мощности, деленной на полную мощность. Коэффициент мощности также представляет собой косинус угла между реальной мощностью и кажущейся мощностью (угол обычно обозначается ‘).Косинус ‘ — это коэффициент мощности.
Электроэнергетические компании взимают плату за полную мощность, но рассеивается только реальная мощность. Можно уменьшить счета за электроэнергию, изменив коэффициент мощности (‘) без изменения реальной мощности. Это делается путем изменения реактивной мощности и широко известно как коррекция коэффициента мощности. Эту концепцию лучше всего объяснить на примере:
Эту концепцию лучше всего объяснить на примере:
Асинхронный двигатель мощностью 10 л.с., 460 вольт (В), 60 Гц потребляет 22 ампера (А) и имеет КПД 90 %. Найдите емкость, которую можно было бы соединить параллельно, чтобы повысить коэффициент мощности до 95 %.
Активная мощность =-nn „ ‘ v = 8289 Вт
, где Вт = Вт. Полная мощность определяется из измеренных значений:
Следовательно, реактивная мощность = (101202 — 82892)1/2 = 5805 Вт.
Угол степени, ‘, = arcos (8289/10120) = 35 градусов. При желаемом коэффициенте мощности = 0,95 новый угол мощности = arcos 0,95 = 18,2 градуса. Новая реактивная мощность будет равна (tan 18,2)(8289) = 2725 ВАР. Разница в реактивной мощности составляет (5805 — 2725) = 3080 ВАр.
Требуемая емкость, C (в микрофарадах [мФ]), равна изменению реактивной мощности, деленному на 2 пфВ 2:
В каждой из трех фаз будет установлен конденсатор емкостью 40 мкФ.
Следует отметить, что не рекомендуется повышать реактивную мощность холостого хода до точки, при которой может быть достигнут единичный коэффициент мощности (рекомендуется максимум 95%). Это вызовет перевозбуждение и может повредить двигатель или травмировать персонал. Перевозбуждение приводит к высоким переходным напряжениям, токам и крутящему моменту.
Это вызовет перевозбуждение и может повредить двигатель или травмировать персонал. Перевозбуждение приводит к высоким переходным напряжениям, токам и крутящему моменту.
Продолжить чтение здесь: Введение в электромагнитную теорию
Была ли эта статья полезной?
Новый взгляд на расчеты трехфазного переменного тока — Dataforth
Преамбула
Эти указания по применению являются продолжением рекомендаций Dataforth.
Примечание по применению AN109, которое содержит систему переменного тока
определения и основные правила расчетов с примерами.Читателю предлагается просмотреть AN109, ссылки 3,
4 и 5 в качестве фона для настоящих указаний по применению.
Трехфазная система напряжения
Системы трехфазного напряжения состоят из трех
синусоидальные напряжения одинаковой величины, одинаковой частоты
и разделены на 120 градусов.
На рис. 1 показаны функции косинуса в реальном времени и
1 показаны функции косинуса в реальном времени и
связанная векторная нотация для 3-фазной линейной линии
система напряжения с линейным напряжением V12 в качестве опорного.
Обзор свойств трехфазной системы напряжения
Трехфазные напряжения питания и системы нагрузки имеют два
базовые конфигурации; 4-проводная «звезда» и 3-проводная
«дельта». На рисунке 2 показана базовая 3-фазная 4-проводная схема «звезда».
настроенная система напряжения с V1N в качестве эталона и
На рис. 3 показана трехпроводная система напряжения, сконфигурированная по схеме «треугольник».
с V12 в качестве эталона соответственно.
Важные определения, соглашения и правила расчета
как для 3-фазного 4-проводного соединения «звезда», так и для 3-проводного соединения «треугольник»
сконфигурированные системы напряжения перечислены ниже
список с опущенной «грязной» векторной математикой.
Фазорная ориентация:
По определению, все синусоидальные векторы вращаются в
против часовой стрелки с {1-2-3} или {3-2-1}
последовательность и углы измеряются как положительные в
направление против часовой стрелки. 4-проводная 3-фазная система звезда
показан на рисунке 2, где V1N выбран в качестве эталона. То
междуфазные напряжения составляют V12, V23 и V32 с линейным
напряжения нейтрали показаны как V1N, V2N и V3N.Фигура
3 показаны надлежащие междуфазные фазовые напряжения для 3-фазного
фаза 3-проводная конфигурация треугольник с выбранным вектором V12
в качестве ссылки. Примечание. В качестве
ссылка, выбор совершенно произволен.
Последовательность фаз:
Последовательность фаз определяет последовательную синхронизацию, с которой
каждый вектор линейного напряжения отстает от линейного напряжения другого
вектор против часовой стрелки. Рисунки 1, 2 и
Рисунки 1, 2 и
3 показана последовательность фаз {1-2-3}. Последовательность {1-2-3}
означает, что V12 опережает V23 на 120 градусов, а V23 опережает
V31 на 120 градусов. Кроме того, V1N опережает V2N на 120
градусов, а V2N опережает V3N на 120 градусов. это
необходимо установить последовательность фаз перед выполнением
любые расчеты для того, чтобы вычисленный векторный вектор
углы могут быть правильно расположены относительно друг друга.
Имеется только две действительные последовательности фаз; {1-2-3}
последовательность и последовательность {3-2-1}. Обе эти фазы
последовательности определяются тем, как 3-фазный трансформатор
линии питания (L1, L2, L3) подключены и промаркированы.
Рисунок 4 иллюстрирует последовательность {3-2-1} относительно
Последовательность {1-2-3}. Примечание. Последовательность фаз может быть
изменить, просто поменяв местами соединения любых двух
из трех (L1, L2, L3) линий подачи; однако это
должно осуществляться только в соответствии со всеми надлежащими
кодексы, правила и утверждение проектирования завода
штат сотрудников.
Индексы:
Поддержание правильного порядка индексов для всех векторов
количество является одним из наиболее важных ключей к успешному
3-этапные расчеты. На рис. 4 показан правильный индекс
порядок для каждой из двух различных последовательностей фаз. За
последовательность {1-2-3}, правильный порядок индексов [12],
[23] и [31]; тогда как правильный порядок индекса для
последовательность {3-2-1} — это [32], [21] и [13].
Нижний индекс:
После определения последовательности фаз и правильного
индексы идентифицируются, расчеты с использованием этих
нижние индексы вместе с соглашениями, принятыми для
Версия закона Ома на переменном токе предотвратит угловые ошибки.
По соглашению, V12 представляет собой падение напряжения вектора плюс (1) до
минус (2) в направлении тока, протекающего из точки
(1) к точке (2) и равен этому току, умноженному на
импедансом переменного тока между точками (1) и (2). За
За
пример в векторной записи;
Фактор сложения/вычитания:
Правильное обозначение нижнего индекса устанавливает правильный метод
для векторного сложения/вычитания векторов. На рисунке 2
фазовращатели междуфазного напряжения в этой 3-фазной {1-2-3}
последовательность 4-х проводной системы «звезда» состоит из линейно-нейтральных
векторные напряжения следующим образом;
Если среднеквадратичное значение линейного напряжения равно
сбалансированная система), то приведенные выше уравнения показывают, что все
линейное напряжение питания фазора линейное к нейтрали
напряжения умножьте на 3 и соедините линию с нейтралью
вектора напряжения на 30 градусов .Например, стандарт
4-проводная 3-фазная система «звезда» с фазным напряжением
120 вольт и V1N, выбранный в качестве эталонного вектора при
ноль градусов имеет междуфазные напряжения;
V12 = 208∠ 30°; V23 = 208∠ -90°; V31 = 208∠ 150°.
Важная концепция: 3-фазная 3-проводная схема «треугольник»
система симметричных напряжений фактически не имеет линейного
нейтральные напряжения, такие как система звезда.Тем не менее
дельта междуфазных напряжений, как показано на рисунке 3, все еще может быть
построен из теоретического набора сбалансированных 3-фазных
фазное напряжение, как показано выше. То
отношения с этими теоретическими напряжениями чрезвычайно
полезно для определения углов дельта-фазора.
Процедуры расчета, рекомендации и формулы
Следующий список процедур, руководств и формул
проиллюстрировать схему того, как рассчитать трехфазный фазовращатель
количества, используя типичные данные паспортной таблички, взятые из
отдельные единицы нагрузки.
Вычисления выполняются следующим образом;
- Идентификация последовательности фаз; {1-2-3} или {3-2-1}
- Определить индексы; [12], [23], [31] или [32], [21], [13]
- Предположим, что линейные токи L1, L2, L3 текут к нагрузкам
и нейтральный (обратный) ток течет к источнику питания.
- Протекание тока нагрузки и падение напряжения должны соответствовать
нотации нижнего индекса, как определено ранее. - Используйте «Закон Ома для переменного тока» для расчета величин
и углы каждой отдельной однофазной нагрузки
Текущий. Обзор Dataforth AN109, ссылка 1. - Важные понятия: Линейные токи как для соединения по схеме «звезда», так и для
Трехфазные нагрузки, сбалансированные треугольником, рассчитываются с использованием
следующие отношения;- Входная мощность переменного тока = 3 x (Vline) x (Iline) x PF
- PF — косинус угла, на который прямая
токи опережают или отстают от фазного напряжения.Трехфазные линейные напряжения на самом деле
существуют в звездообразной конфигурации; тогда как они
теоретический в дельта-конфигурациях. Например,
Например,
допустим любой баланс 3-х фазной нагрузки на 10 ампер
линейного тока и PF 0,866 (30°) отставания. Если
системная последовательность {1-2-3} и V12 является эталоном,
тогда I1=10∠ -60°; I2=10∠ 180°; I3=10∠ 60° .
- Определить величины треугольника мощности; Вт «П»
и VAR «Q» для каждой нагрузки. Обзорный номер 1. - Суммируйте ранее рассчитанную индивидуальную нагрузку
токи с использованием надлежащего обозначения индекса для определения
ток каждой отдельной линии - Наконец, просуммируйте все треугольники мощности отдельных нагрузок.
количества (Ватт «P» и ВАР «Q»), чтобы установить
величины треугольника мощности системы; P, Q и PF.Это
этот последний шаг, который устанавливает, как загрузка системы
ведет себя население.
Примеры расчета
В следующих примерах предполагается типичное напряжение 208–120 вольт.
трехфазная конфигурация «4 звезды» с чередованием фаз
из {1 2 3}, и V12 выбран в качестве эталона. это вай
система; однако нагрузки, подключенные между каждым из
три отдельные линии подачи (L1, L2, L3) составляют
208-вольтовая 3-проводная схема треугольник.Три категории
однофазные нагрузки предполагаются для следующих
расчеты. Эти категории идентичны тем,
определено в примечаниях по применению AN109 (ссылка 1) и
перечисленных ниже с необходимыми данными паспортной таблички.
- Выходная мощность, киловатты; кВт, КПД (опционально), PF= 1
- Выходная мощность, л.с.; HP, Эффективность, P
- Вход кВА; КВА, ПФ, КПД 100%.
В таблице 1 показаны рассчитанные значения для предполагаемого
популяция этих нагрузок. Читатели должны убедиться в этом
Читатели должны убедиться в этом
расчеты. Dataforth предлагает интерактивный Excel
рабочая тетрадь, аналогичная Таблице 1, которая автоматически
рассчитывает все параметры трехфазной системы. Видеть
Ссылка 2 для загрузки этого файла Excel.
Пример расчетов для линейных нагрузок
Трехфазные системы «звезда» с нейтралью могут иметь равные или
неравные отдельные однофазные нагрузки, подключенные между
любая из линий питания (L1, L2, L3) и нейтраль.Системы
сбалансированы, если все нагрузки между фазой и нейтралью одинаковы.
На рис. 5 показаны три группы однофазных линейно-нейтральных
нагрузки, подключенные по трехфазной схеме «звезда».
Такая конфигурация однофазных нагрузок может быть
рассматривается как составная неуравновешенная нагрузка звездой
На рис. 6 показаны три группы однофазных
6 показаны три группы однофазных
нагрузки, подключенные по трехфазной схеме «звезда».Этот
конфигурация однофазных нагрузок может рассматриваться как
составная несбалансированная дельта-нагрузка
На рис. 7 показана группа сбалансированных нагрузок по схеме «звезда» и группа
сбалансированных дельта-нагрузок, обе из которых являются (могут быть)
подключены по трехфазной схеме «звезда».
Таблица 1 представляет собой составной набор результатов расчетов для
конфигурации, показанные на рисунках 5, 6 и 7.Эти
расчеты предполагают произвольную популяцию вида
загружает ранее определенные и использует все правила, процедуры и определения, как показано выше. То
система результаты расчетов таблицы 1 показаны ниже
в таблицах 2 и 3.
Линейное напряжение V12 (208 при нуле градусов) является эталонным для
указанные выше текущие углы.
Читателям рекомендуется проверить эти расчеты.
Как упоминалось выше, Dataforth предоставляет интерактивный
Файл Excel, предназначенный для помощи энтузиастам-исследователям.
при расчете системных токов и связанной с ними мощности
уровни. Этот файл позволяет следователю ввести табличку с именем
данные по всем нагрузкам системы; после чего все линейные токи
фазоры и величины мощности рассчитываются автоматически.
Интерактивная рабочая тетрадь Excel для трех-
Расчет фаз переменного тока» можно загрузить с
веб-сайт Dataforth, см. ссылку 2 .
На рис. 8 показана изолированная истина Dataforth.
Входной модуль RMS, SCM5B33. Эта функция также
доступен в упаковке на DIN-рейку; ДСКА33. Датафорт
имеет набор модулей формирования сигнала, разработанных
специально для измерения среднеквадратичного значения переменного тока высокого напряжения
параметры с использованием встроенного затухания. Читатель
Читатель
рекомендуется посетить ссылки 1, 6, 7 и 8.Ссылки на Dataforth
Читателю предлагается посетить веб-сайт Dataforth и
изучить их полную линейку изолированных преобразователей сигнала
модули и соответствующие указания по применению, см. ссылки
показано ниже.
- Dataforth Corp., http://www.dataforth.com
- Dataforth Corp., AN110 Excel
Интерактивная работа
Книга для расчета трехфазного переменного тока - Датафорт Корп., Примечание по применению AN109,
Измерения однофазного переменного тока - Dataforth Corp., AN109 Excel
Интерактивная работа
Книга для расчетов однофазного переменного тока - Национальный электротехнический кодекс, контролируемый Национальным пожарным управлением
Агентство защиты, NFPA - Датафорт Корп.
 , Система аттенюатора напряжения SCMVAS,
, Система аттенюатора напряжения SCMVAS, - Dataforth Corp., Серия SCM5B33 модульных формирователей сигналов истинного среднеквадратичного значения
- Dataforth Corp., серия формирователей сигналов истинного среднеквадратичного значения с креплением DIN DSCA33
Трехфазная терминология: фаза или линия?
«Фаза» и «линия» — как они определяются
© 2019 L A Waygood
Два основных термина, которые часто вызывают путаницу при изучении трехфазных систем переменного тока , это: « фаза » и « линия ».В этом нет ничего удивительного, ведь термины часто употребляются совершенно неправильно не только в полевых условиях, но очень часто, к сожалению, и в учебниках!
Часто, например, мы слышим, как кто-то называет три проводника, которые свисают с распределительной линии, « фазных проводников » или « фаз ».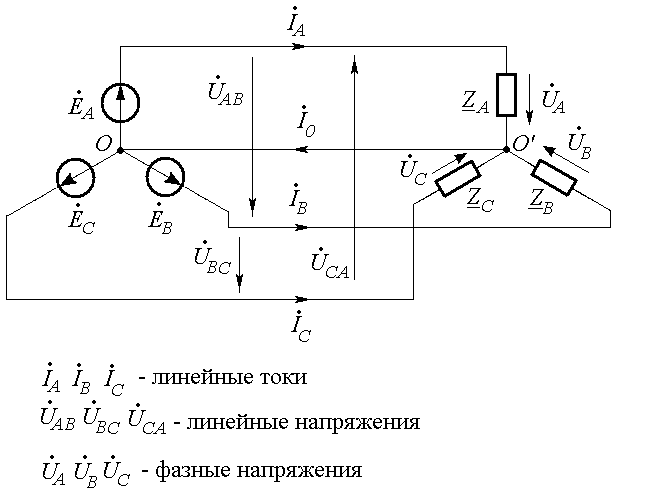 Это совершенно неверно . Правильная терминология — « линейных проводов » или « линий ».
Это совершенно неверно . Правильная терминология — « линейных проводов » или « линий ».
Три проводника под напряжением , которые соединяют трехфазную нагрузку с ее трехфазным питанием, называются линиями .Напряжение между любыми двумя линейными проводниками называется « линейное напряжение », а ток, который проходит по каждому линейному проводнику, называется « линейный ток ». Клеммы трехфазного источника (генератора или трансформатора) или трехфазной нагрузки, к которым присоединены линейные проводники, называются «линейными клеммами ».
‘ Фазы ‘, , с другой стороны, подключаются между любой парой линейных клемм (соединение «треугольником»), или между любой отдельной линейной клеммой и нейтралью («звезда» или «звезда» связь’). Независимо от того, соединены ли они по схеме «треугольник» или «звезда» («звезда»), три обмотки генератора переменного тока или трансформатора и три импеданса нагрузки являются « фазами ». Напряжение, возникающее на любой фазе, называется « фазное напряжение », а ток, проходящий через любую фазу, называется « фазный ток ».
Напряжение, возникающее на любой фазе, называется « фазное напряжение », а ток, проходящий через любую фазу, называется « фазный ток ».
В системе , соединенной треугольником , хотя линейное напряжение численно равно соответствующему фазному напряжению , мы должны всегда сохранять правильные термины в соответствии с ГДЕ измеряются эти напряжения.
В системе , соединенной звездой , несмотря на то, что линейный ток численно равен соответствующему фазному току , мы всегда должны сохранять правильные условия в соответствии с ГДЕ эти токи измеряются — как показано ниже:
Идентификация линий
Линейные провода и линейные клеммы (НЕ фазы) обозначены в соответствии с национальными стандартами. В Европе, например, цвета коричневый , черный и серый используются для обозначения линий и линейных терминалов. В других странах используются другие цвета. Однако на международном уровне принято использовать буквы A , B и C — например, на принципиальных схемах (как указано выше). Использование букв имеет дополнительное преимущество, заключающееся в том, что линии высокого напряжения (или клеммы ) могут быть идентифицированы с помощью прописных букв : A , B
В других странах используются другие цвета. Однако на международном уровне принято использовать буквы A , B и C — например, на принципиальных схемах (как указано выше). Использование букв имеет дополнительное преимущество, заключающееся в том, что линии высокого напряжения (или клеммы ) могут быть идентифицированы с помощью прописных букв : A , B
9 , и 8 9 низковольтные линии (или клеммы ) можно идентифицировать с помощью строчных букв : a , b и
c .
Британский стандарт, охватывающий трансформаторы, например, использует буквы A , B и C для обозначения клемм высоковольтного трансформатора, а также строчные буквы a , b и c , для идентификации низковольтных клемм.
Важно понимать, что эти цвета или буквы используются для обозначения линии ( проводников ) или клемм , НЕ фаз.
Идентификация фаз
Фазовые обмотки или сопротивления нагрузки сами по себе не идентифицируются. Вместо этого они идентифицируются с точки зрения линейных терминалов , между которыми они соединены. Например, в случае соединения треугольником , фазная обмотка, соединенная между линейными клеммами A и B , идентифицируется как ‘ Фаза A-B ’ ; фазная обмотка, подключенная между линейными клеммами B и C , обозначена как ‘ Phase B-C ’ ; фазная обмотка, подключенная между клеммами линии C и A , обозначена как ‘ Phase C-A ’ .То же самое применимо, если мы используем цвета вместо букв: например. «фаза коричнево-черная» и др.
«фаза коричнево-черная» и др.
В случае звездообразного соединения каждая фаза идентифицируется с точки зрения клеммы линии, к которой она подключена, и нейтральной точки, т.е. ‘ Фаза CN ‘ .
Нет никакого смысла ссылаться, например, на ‘ коричневую фазу ‘ или ‘ фазу А ‘ и т.д., поскольку эти цвета или буквы обозначают 90 228 линий 90 229 (или 90 228 клемм 90 229), 90 914, а не 90 915 фаз.
Полное руководство по извлечению квадратного корня из трех в расчетах мощности • Услуги Valence по обучению электрикам
Зак Стоун, ЧП связался со мной после того, как я (Крис Верстюк пишет прямо сейчас) опубликовал свой недавний пост «Понимание великих дебатов о лидирующей и отстающей силе», потому что я неправильно определил кажущуюся силу. Благодаря его острому глазу и знанию предмета, никто из тех, кто приобрел Руководство по тестированию реле: Тестирование защиты реле генератора, никогда не видел моей ошибки, и я все еще могу выглядеть экспертом 😃
После того, как он позвонил мне, я проверил его сайт и спросил себя: «Где был этот парень, когда я взял P.
Е. экзамен? Он любезно предложил написать гостевой пост о квадратном корне из трех, который, вероятно, является наиболее распространенным числом, используемым в тестировании реле, которое мало кто действительно понимает.
Надеюсь, вам понравится этот гостевой пост от Зака.
Крис Верстюк
Вы когда-нибудь задумывались, почему квадратный корень из трех фигурирует во многих расчетах трехфазной мощности?
Откуда этот номер и почему он такой особенный?
Хотя длинный ответ на эти вопросы исходит из тригонометрии, хорошая новость заключается в том, что мы можем использовать векторные диаграммы, чтобы сделать объяснение очень простым для понимания.
Понимание векторных диаграмм является важным навыком для тестирования реле, и работа с примерами в этой статье даст вам более глубокое понимание и понимание векторных величин в векторных диаграммах. Независимо от того, в какой отрасли вы работаете, это очень поможет вашей карьере в области электроэнергетики и тестирования реле.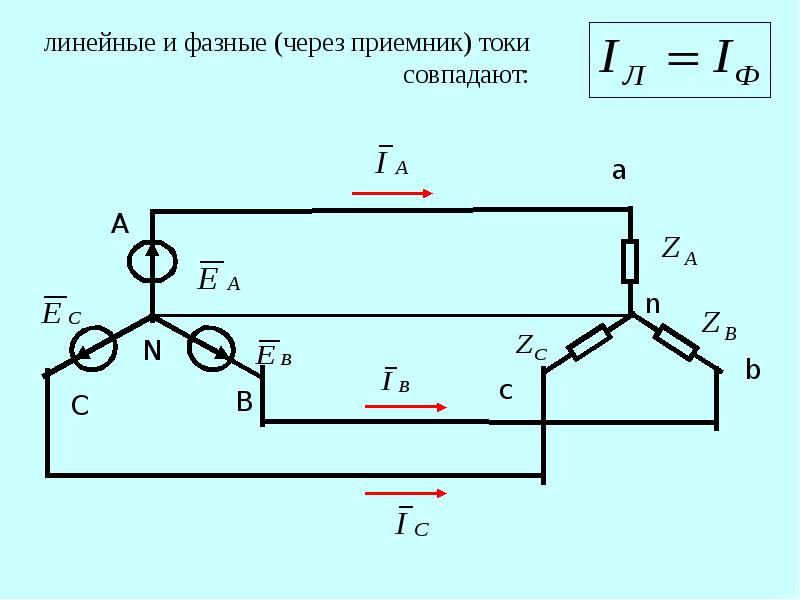
Поскольку некоторые математические расчеты, приведенные ниже, могут быть вам незнакомы, мы рассмотрим их шаг за шагом с четкими схемами и пояснениями, чтобы вам было легко их понять.
Меня зовут Зак Стоун, физкультурник, я ведущий инструктор популярной онлайн-программы обучения экзамену NCEES® по электроэнергетике на сайте www.electricalpereview.com, и в этой статье я собираюсь помочь вам понять, почему квадратный корень из трех так часто появляется в трехфазном питании.
Начнем со знакомого соединения звездой силового трансформатора.
1. Соединение звездой
Предположим, что у нас есть три отдельных вольтметра, подключенных поперек каждой линии к нейтрали на каждой фазе вторичных клемм трансформатора, соединенных звездой:
Рисунок 1: Вторичные клеммы трансформатора, соединенного звездой
Если мы используем опорный угол в ноль градусов для напряжения линии A-фазы к нейтрали (VAN), результирующая векторная диаграмма напряжения для системы прямой последовательности (ABC) будет выглядеть следующим образом:
Рис. 2: Векторная диаграмма напряжения фазы по схеме «звезда»
2: Векторная диаграмма напряжения фазы по схеме «звезда»
Взглянув на диаграмму трансформатора, мы можем использовать измерения напряжения между линией и нейтралью, чтобы рассчитать линейное напряжение на фазе А трансформатора (VAB) путем суммирования векторных величин напряжения последовательно от клеммы фазы А к терминал B-фазы:
Рис. 3. Линейное напряжение фазы А трансформатора (VAB)
Давайте сравним положительное опорное напряжение (+) на клемме фазы A и отрицательное опорное напряжение (-) на клемме фазы B для линейного напряжения фазы A (VAB) с фазой A и фазой B. напряжения линии к нейтрали (ВАН и ВБН):
- Полярность линии A-фазы к напряжению нейтрали (VAN) соответствует той же ориентации , что и полярность линейного напряжения A-фазы (VAB)
- Полярность линии B-фазы к напряжению нейтрали ( VBN) находится в противоположной ориентации полярности линейного напряжения фазы A (VAB)
Вот почему напряжение линии B-фазы к нейтрали (VBN) является отрицательным, когда мы суммируем напряжение от Клемма фазы A к клемме фазы B, когда мы вычисляем линейное напряжение фазы A (VAB) по формуле:
ВАБ = ВАН – ВБН.
Помните, что это не обычные числа, это векторные величины с амплитудой и фазовым углом. Чтобы использовать сложение фазоров ниже, будет проще думать об этой формуле как о сложении двух фазоров. За исключением того, что один из них был умножен на минус вот так:
ВАБ = ВАН + (-ВБН).
2. Соединение звездой — умножение вектора на отрицательную единицу
Умножение векторной (или векторной) величины на отрицательное равносильно повороту векторной диаграммы на плюс-минус 180 градусов без изменения величины.
Мы можем использовать эту связь, чтобы найти -VBN из VBN:
Рис. 4. Поворот VBN на 180 градусов
Так как линия B-фазы к напряжению нейтрали (VBN) имеет фазовый угол отрицательных 120 градусов, фазовый угол для -VBN будет положительным 60 градусов и равным по величине.
Поскольку мы будем добавлять VAN и -VBN для расчета линейного напряжения фазы A (VAB), давайте покажем только эти два вектора на векторной диаграмме:
Рисунок 5: Векторная диаграмма VAN и -VBN
Теперь мы готовы использовать векторное сложение, чтобы найти линейное напряжение фазы A (VAB).
3. Соединение звездой – добавление вектора
Чтобы сложить два вектора (или вектора) вместе, сложите их друг над другом от начала до конца, затем нарисуйте новый вектор, начиная с начала координат и заканчивая головой последнего вектора.
Поскольку у нас есть два разных вектора, мы можем сделать это двумя разными способами и все равно получить одно и то же количество векторов для линейного напряжения фазы A (VAB):
F рис. 6: VAN и -VBN Phasor Дополнение
Мы собираемся произвольно использовать первую диаграмму сложения векторов выше слева для расчета линейного напряжения фазы A (VAB), но любое из них приведет к тому же конечному значению.
Мы также собираемся предположить, что система сбалансирована, что означает, что величины напряжения каждой линии относительно нейтрали в каждой фазе равны. Чтобы упростить предстоящую математику, мы также будем произвольно использовать значение в один вольт для этих значений (VAN = VBN = VCN = 1V).
Чтобы рассчитать линейное напряжение фазы A (VAB) с помощью сложения векторов, мы собираемся использовать немного тригонометрии, но я обещаю, что это будет просто, поэтому не пугайтесь, если вам не слишком удобно работать с синусоидой. функции косинуса и тангенса.
Во-первых, мы вычислим действительную (a) и мнимую составляющие (b) -VBN, что является еще одним способом сказать, что мы собираемся вычислить длину двух других сторон прямоугольного треугольника, который составляет -VBN. по горизонтальной оси:
Рисунок 7: Действительные (а) и мнимые (б) компоненты -VBN
Действительный компонент (a) -VBN равен 0,5, который находится с помощью функции косинуса:
Помните, что когда мы поворачивали VBN, чтобы найти -VBN, величина не менялась.Это означает, что величина -VBN по-прежнему равна одному вольту, так как ранее мы произвольно установили величины напряжения линии на нейтраль для каждой фазы равными 1 вольту для упрощения математики (VAN = VBN = VCN = 1V).
Мнимая составляющая (b) -VBN приблизительно равна 0,866, что определяется с помощью функции синуса:
Мы можем использовать действительную (a) и мнимую составляющую (b) -VBN вместе с величиной VAN = 1 вольт при нуле градусов, чтобы заполнить недостающие значения векторной диаграммы линейного напряжения фазы A (VAB ):
Рис. 8: Векторная диаграмма линейного напряжения фазы А (VAB)
Обратите внимание, что на рисунке выше мнимая составляющая линейного напряжения фазы А (VAB) равна мнимой составляющей -VBN (0.866).
Чтобы найти действительную составляющую линейного напряжения фазы А (VAB), мы просто добавим величину VAN (1 вольт) к действительной составляющей -VBN (0,5), поскольку они оба находятся под углом ноль градусов. .
Действительная составляющая линейного напряжения фазы A (VAB) равна 1 + 0,5 = 1,5:
Рис. 9: Линейное напряжение фазы А (VAB), действительная и мнимая составляющие
Теперь мы готовы, наконец, рассчитать как амплитуду, так и фазовый угол линейного напряжения фазы А (VAB), откуда и берется квадратный корень из трех.
4. Соединение звездой – расчет величины линейного напряжения и фазового угла
Сначала мы рассчитаем величину линейного напряжения фазы A (VAB), используя теорему Пифагора, где C – величина VAB, A – действительная составляющая VAB (1.5), а B – мнимая составляющая VAB. (0,866):
Величина линейного напряжения фазы A (VAB) составляет 1,732 В.
Далее мы рассчитаем фазовый угол линейного напряжения фазы A (VAB) с помощью тангенса:
Фазовый угол (ɸ) линейного напряжения фазы А (VAB) составляет 30 градусов.
Завершенная векторная диаграмма линейного напряжения фазы A (VAB) выглядит следующим образом:
Рис. 10: Линейное напряжение фазы A (VAB), завершенная векторная диаграмма
Если вы знакомы с расчетами трехфазной мощности, то число 1,732 должно быть вам также знакомо.
Поскольку мы использовали значение 1 вольт для величины линейных напряжений фаз A, B и C к нейтрали (VAN = VBN = VCN = 1 В), линейное напряжение фазы A (VAB) ровно в 1,732 раза больше. чем линия А-фазы к напряжению нейтрали (VAN).
чем линия А-фазы к напряжению нейтрали (VAN).
1,732 на самом деле является квадратным корнем из трех:
5. Соединение звездой – линейные и фазовые отношения
Линейное напряжение сбалансированной трехфазной системы всегда будет больше, чем линейное напряжение к нейтрали, точно на квадратный корень из трех из-за сложения фазора.
В нашем случае мы добавили линию фазы A к напряжению нейтрали (VAN) с отрицательной линией фазы B к напряжению нейтрали (-VBN), чтобы найти линейное напряжение фазы A (VAB):
Рис. 11: Линейное напряжение фазы А трансформатора (VAB)
Поскольку мы использовали опорный угол, равный нулю градусов, для напряжения линии фазы A к напряжению нейтрали (VAN), напряжение линии фазы A (VAB) опережает линию фазы A к напряжению нейтрали (VAN) ровно на 30 градусов.
Это же отношение сложения фазора также является причиной того, что линейное напряжение всегда будет опережать линейное напряжение по отношению к нейтральному на 30 градусов для сбалансированной системы с прямой последовательностью (ABC).
Если бы мы завершили весь этот процесс для двух других оставшихся фаз B и C и нарисовали результирующую векторную диаграмму, то увидели бы, что это применимо к каждой фазе:
Рис. 12: Векторная диаграмма напряжения для всех трех фаз соединения звездой
Вы заметите, что приведенная выше векторная диаграмма представляет собой векторную диаграмму напряжения для сбалансированного соединения звездой прямой последовательности (ABC), с которым вы, скорее всего, уже знакомы.
6. Соединение звездой — использование калькулятора
Если у вас есть калькулятор, который может обрабатывать векторы как в полярной (величина и угол), так и в прямоугольной (действительная составляющая и мнимая составляющая), вы можете сделать все вышеперечисленное за один шаг в своем калькуляторе, хотя это действительно помогает знать что калькулятор делает в процессе, чтобы вы понимали, откуда берутся эти значения.
Здесь то же соединение трансформатора вторичной обмотки звездой, что и раньше, с линейным напряжением фазы A (VAB), показанным как разность между напряжением линии A-фазы и нейтрали (VAN) и напряжением фазы B-фазы-фазы-нейтрали (VBN).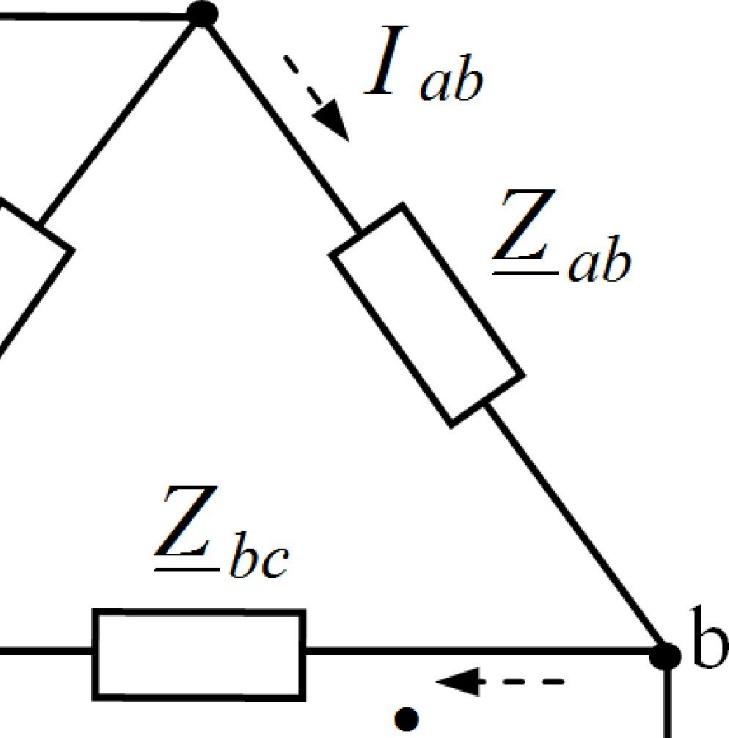 :
:
Рисунок 13: Линейное напряжение фазы А трансформатора (VAB)
Рассчитаем линейное напряжение фазы А (VAB) с помощью калькулятора.
Я использую Texas Instruments 36X Pro (TI 36X Pro), который мне больше всего нравится для электрических расчетов, поскольку он легко обрабатывает векторы как в полярной, так и в прямоугольной форме.
Мы будем использовать значение 1 В для величины напряжения между фазой A и нейтралью (VAN) и 1 В для величины напряжения между фазой B и нейтралью (VAB), как мы это делали вручную.
Мы также будем использовать 0 градусов для фазового угла между фазой A и напряжением нейтрали (VAN) и отрицательные 120 градусов для напряжения между фазой B и напряжением нейтрали (VAB):
Обратите внимание, что мы получаем то же значение 1.732 для величины линейного напряжения фазы А (VAB) и 30 градусов для фазового угла линейного напряжения фазы А (VAB).
Обратите внимание, что это идентично величине квадратного корня из трех под углом 30 градусов:
7.
 Дельта-соединение
Дельта-соединение
Теперь, когда мы понимаем, откуда берется квадратный корень из трех для соединения звездой, как насчет соединения треугольником?
Давайте посмотрим на клеммы вторичной обмотки трансформатора, соединенного треугольником, и покажем фазные токи внутри соединения треугольником:
Рисунок 14: Клеммы вторичной обмотки трансформатора Delta Connected
Используя амперметр в каждой фазе и опорный угол, равный нулю градусов, для фазного тока в фазе А соединения треугольником (IBA), результирующая векторная диаграмма токов фаз треугольника будет выглядеть следующим образом:
Рис. 15: Диаграмма вектора тока фазы «треугольник»
Глядя на схему трансформатора, мы можем рассчитать линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенной треугольником, используя закон Кирхгофа для тока:
Рис. 16. Линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенного треугольником
Текущий закон Кирхгофа гласит, что сумма токов, входящих в узел, должна равняться сумме токов, выходящих из того же узла.
Глядя на клемму фазы A выше, обратите внимание, что единственный входящий ток — это ток фазы треугольника A (IBA), в то время как ток, выходящий из узла, представляет собой ток фазы треугольника C (IAC) и ток фазы A. линейный ток (IA).
Мы воспользуемся законом тока Кирхгофа, чтобы установить их равными друг другу, а затем перегруппируем для определения линейного тока фазы А (IA):
Ток линии A (IA), выходящий из вторичной обмотки трансформатора, соединенного треугольником, равен разнице тока фазы треугольника A (IBA) и тока фазы треугольника C (IAC).
Или, если вместо этого мы хотим думать с точки зрения сложения, ток линии A (IA), выходящий из вторичной обмотки трансформатора, соединенного треугольником, равен сумме тока фазы треугольника A (IBA) и отрицательной единицы, умноженной на C -фазный дельта-фазный ток (IAC).
Выглядит знакомо? Это очень похоже на соотношение, с которым мы работали в предыдущем примере напряжения линии А для соединения звездой.
8. Дельта-соединение — умножение вектора на отрицательную единицу
Как и раньше, сначала найдем -ICA, повернув ICA на плюс-минус 180 градусов:
Рис. 17: Поворот IAC на 180 градусов
Поскольку дельта-фазный ток фазы С (IAC) имеет угол сдвига фаз 120 градусов, угол сдвига фаз для отрицательного IAC будет отрицательным 60 градусов.Помните, что это не влияет на величину.
Поскольку IA = IBA – ICA, давайте покажем только IBA и -ICA на векторной диаграмме:
Рисунок 18: Векторная диаграмма IBA и -IAC
Как и раньше, мы готовы использовать сложение векторов, складывая каждый вектор поверх другого и рисуя полученный вектор из начала координат.
9. Соединение треугольником – дополнение Phasor
Поскольку мы добавляем два вектора, мы выполняем добавление векторов двумя разными способами и по-прежнему получаем одно и то же количество векторов для линейного тока фазы A (IA):
Рисунок 19: Дополнение IBA и -IAC Phasor
Мы произвольно выберем диаграмму сложения первого вектора вверху слева для расчета линейного тока фазы A (IA).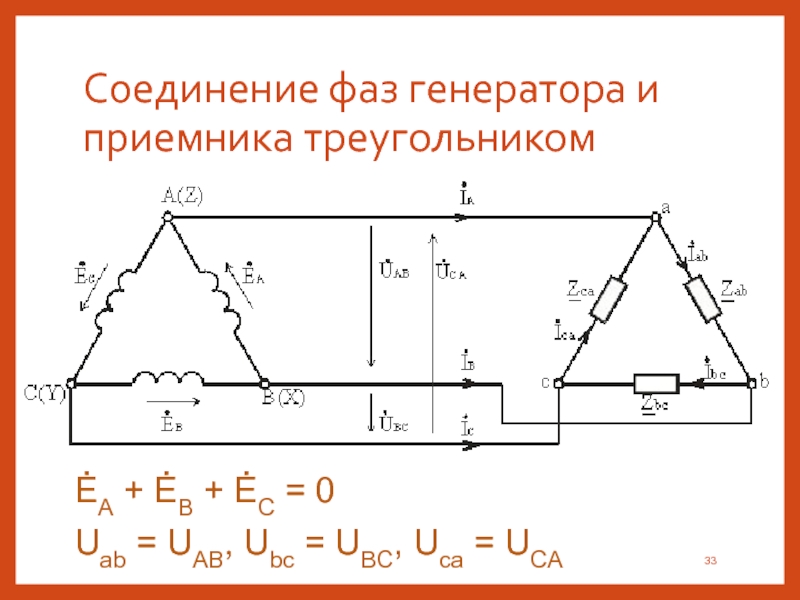
Как и прежде, мы также будем предполагать, что система сбалансирована, что означает, что величина дельта-фазного тока в каждой фазе одинакова. Чтобы упростить дальнейшую математику, мы также будем произвольно использовать значение в один ампер для этих значений (IBA = ICB = IAC = 1A).
Для расчета IA мы будем использовать те же тригонометрические отношения, что и раньше.
Во-первых, мы вычислим действительную (a) и мнимую составляющие (b) -IAC, что является еще одним способом сказать, что мы собираемся вычислить длину двух других сторон треугольника, который -IAC образует с горизонтальная ось:
Рисунок 20: Действительные (a) и мнимые (b) компоненты -IAC
Действительный компонент (a) -IAC равен 0.5, которое находится с помощью косинуса:
Помните, что когда мы поворачивали IAC, чтобы найти -IAC, величина не менялась. Это означает, что величина -IAC по-прежнему равна одному амперу, поскольку мы произвольно установили величины дельта-фазного тока в каждой фазе равными 1 амперу для упрощения математики (IBA = ICB = IAC = 1A).
Мнимая составляющая (b) -IAC приблизительно равна -0,866, что определяется с помощью синуса:
Мы можем использовать действительную (a) и мнимую составляющие (b) -IAC вместе с величиной IBA = 1 ампер при нуле градусов, чтобы заполнить значения для векторной диаграммы линейного тока фазы A (IA) :
Рис. 21. Векторная диаграмма линейного тока фазы А (IA)
Обратите внимание, что мнимая составляющая линейного тока фазы А (IA) равна мнимой составляющей -IAC (0.866).
Чтобы найти действительную составляющую линейного тока фазы А (IA), мы просто добавим величину IBA (1 ампер) к действительной составляющей -IAC (0,5), поскольку они оба находятся под одним и тем же углом нуля. градусов.
Действительная составляющая линейного тока фазы А (IA) равна 1 + 0,5 = 1,5:
Рис. 22: Действительная и мнимая составляющие линейного тока фазы A (IA)
Теперь мы готовы, наконец, рассчитать как величину, так и фазовый угол линейного тока фазы А (IA), откуда берется квадратный корень из трех.
10. Соединение треугольником – Расчет величины линейного напряжения и фазового угла
Сначала мы рассчитаем величину линейного тока фазы A (IA), используя Теорему Пифагора, где C – величина IA, A – действительная составляющая IA (1.5), а B – мнимая составляющая IA. (-0,866):
Величина линейного тока фазы A (IA) составляет 1,732 ампер.
Далее мы рассчитаем фазовый угол линейного тока фазы A (IA) с помощью тангенса:
Фазовый угол (ɸ) линейного тока фазы A (IA) составляет минус 30 градусов.
Завершенная векторная диаграмма линейного тока фазы A (IA) выглядит следующим образом:
Рис. 23. Линейный ток фазы А (IA), завершенная векторная диаграмма
Опять же, если вы знакомы с расчетами трехфазной мощности, то число 1,732 также должно быть вам знакомо.
Поскольку мы использовали значение 1 ампер для величины дельта-фазных токов фаз A, B и C (IBA = ICB = IAC = 1A), линейный ток фазы A (IA) точно в 1,732 раза больше, чем дельта-фазный ток фазы А (IBA).
1,732 на самом деле является квадратным корнем из трех:
11. Соединение по схеме «треугольник» — соотношение между линией и фазой
Линейный ток сбалансированной трехфазной системы всегда будет больше дельта-фазного тока ровно на квадратный корень из трех из-за сложения векторов.
В нашем случае мы добавили дельта-фазный ток фазы A (IBA) с отрицательным дельта-фазным током фазы C (-IAC), чтобы найти линейный ток фазы A (IA):
Рис. 24. Линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенного треугольником
Поскольку для дельта-фазного тока фазы A (IBA) мы использовали опорный угол, равный нулю, линейный ток фазы A (IA) отстает от дельта-фазного тока A-фазы (IBA) ровно на 30 градусов.
Это же отношение сложения векторов также является причиной того, что линейный ток системы всегда будет отставать от дельта-фазного тока на 30 градусов для сбалансированной системы с прямой последовательностью (ABC).
Если бы мы завершили весь этот процесс для двух других оставшихся фаз B и C и нарисовали результирующую векторную диаграмму, то увидели бы, что это применимо к каждой фазе:
Рисунок 25: Текущая векторная диаграмма для всех трех фаз соединения треугольником
Вы заметите, что приведенная выше векторная диаграмма представляет собой текущую векторную диаграмму для треугольного соединения со сбалансированной прямой последовательностью (ABC), с которым вы, скорее всего, уже знакомы.
12. Соединение треугольником — использование калькулятора
Как и раньше, давайте воспользуемся TI 36X Pro для расчета линейного тока фазы А (IA), выходящего из соединения треугольником, и сравним его со значением, полученным вручную.
Вот то же соединение вторичного трансформатора по схеме треугольника, где линейный ток фазы A (IA) показан как разница между током фазы треугольника A (IBA) и током фазы треугольником C (IAC):
Рис. 26: Линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенного треугольником
Мы будем использовать значение 1 А для величины дельта-фазного тока фазы А (IBA) и 1 А для величины дельта-фазного тока фазы С (IAC), как мы это делали вручную.
Мы также будем использовать 0 градусов для фазового угла дельта-фазы (IBA) фазы A и положительные 120 градусов для дельта-фазы тока C (IAC):
Обратите внимание, что мы получаем то же значение 1,732 для величины линейного тока фазы A (IA) и минус 30 градусов для фазового угла линейного тока фазы A (IA).
Обратите внимание, что это идентично величине квадратного корня из трех при отрицательном угле 30 градусов:
13. Трехфазная полная мощность и квадратный корень из трех
Мы выяснили, откуда берется квадратный корень из трех для соединения звездой и треугольником, но как насчет квадратного корня из трех в трехфазной формуле кажущейся мощности?
Формула трехфазной полной мощности представляет собой произведение квадратного корня из трех, величины линейного напряжения (VL) и величины линейного тока (IL):
Эти значения представляют собой величин только , поэтому избегайте распространенной ошибки использования векторных величин в этой формуле для расчета как кажущейся мощности, так и угла мощности.
Эта формула чаще всего используется для расчета тока полной нагрузки силового трансформатора путем подстановки номинальной трехфазной полной мощности трансформатора [вольт-ампер] и линейного напряжения первичного соединения для расчета полного тока первичной обмотки. ток нагрузки, потребляемый трансформатором, или линейное напряжение вторичного соединения для расчета тока полной вторичной нагрузки, выдаваемого трансформатором:
ток нагрузки, потребляемый трансформатором, или линейное напряжение вторичного соединения для расчета тока полной вторичной нагрузки, выдаваемого трансформатором:
Рис. 27. Первичный и вторичный номинальный ток
Чтобы понять, откуда в этой формуле берется квадратный корень из трех, давайте начнем с демонстрации того, как он получается из однофазной полной мощности (S1ø).
Для сбалансированной трехфазной системы величина полной мощности в каждой фазе всегда одинакова. Это означает, что трехфазная полная мощность (S3ø) на самом деле всего лишь в три раза больше полной мощности в любой заданной фазе (S1ø) сбалансированной трехфазной системы:
Однофазная полная мощность (S1ø) в любой заданной фазе сбалансированной трехфазной системы является произведением величины фазного напряжения (VP) и величины фазного тока (IP):
Подставим это обратно в формулу трехфазной полной мощности (S3ø):
Давайте воспользуемся этой версией формулы трехфазной кажущейся мощности (S3ø) и посмотрим, как она применима к соединению звездой или треугольником, чтобы выяснить, откуда берется квадратный корень из трех в исходной формуле.
Сначала начнем с соединения звездой.
14. Соединение звездой, трехфазная полная мощность и квадратный корень из трех
Для соединения звездой величина линейного напряжения фазы нейтрали (VP) меньше величины линейного напряжения системы (VL) на коэффициент квадратный корень из трех, как мы обнаружили в первой половине этой статьи. .
Однако величина фазного тока (IP) соединения звездой равна величине линейного тока (IL) системы.
Когда мы подставляем соотношения напряжения и тока фазы по схеме «звезда» в формулу трехфазной полной мощности (S3ø), она выглядит следующим образом:
Мы можем начать упрощение, отделив коэффициенты (3 и 1/√3) от переменных (VL и IL):
Теперь самое сложное. Мы собираемся умножить на квадратный корень из трех на квадратный корень из трех (√3/√3). Поскольку это то же самое, что умножение на 1, значение формулы не меняется (любое число, умноженное на 1, остается тем же числом, что и раньше):
Теперь два квадратных корня из трех в нижней части каждой дроби при умножении вместе будут равны трем (√3 X √3 = 3):
Наконец, три в верхней части дроби и три в нижней части дроби будут отменены (3/3 = 1):
Результатом является знакомая нам формула трехфазной кажущейся мощности (S3ø), которая включает квадратный корень из трех.
Квадратный корень из трех в этой формуле получается путем подстановки соотношений напряжения и тока фазы по схеме «звезда» в формулу трехфазной полной мощности (S3ø).
Справедливо ли то же самое для соединения треугольником?
15. Соединение треугольником, трехфазная полная мощность и квадратный корень из трех
При соединении треугольником величина фазного тока (IP) меньше величины линейного тока системы (IL) на коэффициент квадратный корень из трех, как мы обнаружили в первой половине этой статьи.
Однако величина фазного напряжения (VP) соединения треугольником равна величине линейного напряжения (VL) системы.
Когда мы подставляем отношения дельта-фазы тока и фазного напряжения в формулу трехфазной полной мощности (S3ø), она выглядит следующим образом:
Опять же, мы можем начать упрощение, отделив коэффициенты (3 и 1/√3) от переменных (VL и IL):
Давайте снова умножим на квадратный корень из трех из квадратного корня из трех (√3/√3), так как это то же самое, что умножить на 1, а затем продолжим упрощать выражение, используя те же методы, что и раньше:
В результате вновь получается та же знакомая нам трехфазная формула кажущейся мощности, которая включает квадратный корень из трех. Квадратный корень из трех в этой формуле получается из подстановки дельта-фазного напряжения и фазного тока в формулу трехфазной полной мощности (S3ø).
Квадратный корень из трех в этой формуле получается из подстановки дельта-фазного напряжения и фазного тока в формулу трехфазной полной мощности (S3ø).
Обратите внимание, что квадратный корень из трех в формуле трехфазной полной мощности (S3ø) существует независимо от того, присутствует ли соединение треугольником или звездой, пока мы используем линейные значения системы. Аккуратный!
16. Кто я и где меня найти
Надеюсь, вам понравилось исследовать, откуда берется квадратный корень из трех в большинстве расчетов трехфазной электроэнергии.
Меня зовут Зак Стоун, ЧП. и я являюсь ведущим инструктором популярной онлайн-программы обучения для экзамена NCEES® по электроэнергетике на сайте www.electricalpereview.com. Я создаю все их учебные материалы и провожу их живые занятия каждый семестр.
Зак Стоун, ЧП
Обзор электрического оборудования PE, INC
Вот моя 10-секундная биография:
- Я инженер с профессиональной лицензией в штате Флорида.

- В 2010 году я получил диплом инженера-электрика, аккредитованный ABET.
- Я сдал экзамены FE и PE с первой попытки.
- У меня богатый опыт работы в области промышленной автоматизации, управления двигателями, производства электроэнергии и подстанций среднего напряжения.
- Мне нравится заниматься математикой в области электротехники и учить других.
Если вы инженер-электрик и планируете когда-нибудь в будущем сдавать экзамен PE, или если вы хотите прочитать больше статей о нюансах математики, лежащих в основе электротехники, вы можете найти меня на www.www.electricpereview.com.
Если вы действительно хотите чему-то научиться, полезно посмотреть, как разные люди описывают тему. Я кратко освещаю эту тему в The Relay Testing Handbook: Principles and Practice/Глава 1, раздел D) Трехфазные соединения [страницы 14 и 15]. Вы можете просмотреть, если хотите сравнить два разных объяснения, чтобы копнуть глубже и по-настоящему понять, откуда берется квадратный корень из трех.

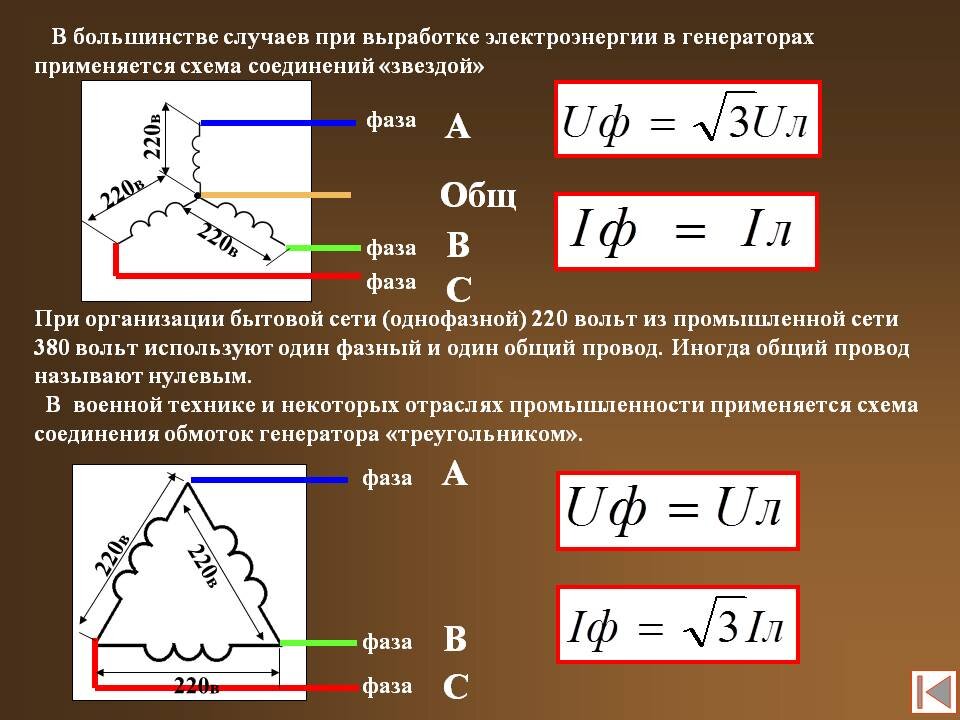 Достаточно отвёрток, которые имеют индикаторы.
Достаточно отвёрток, которые имеют индикаторы.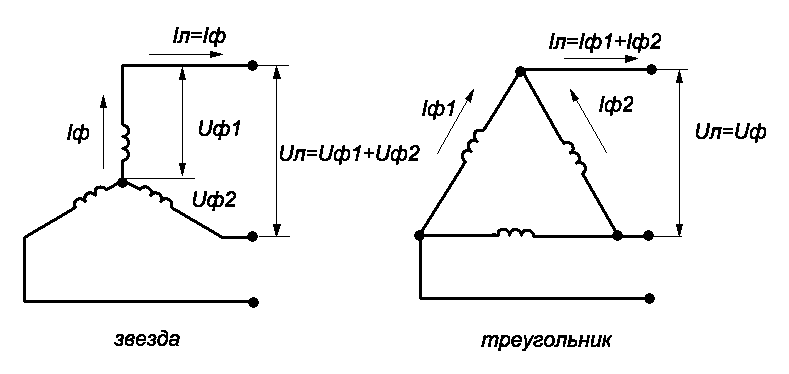

 Реактивная мощность измеряется в реактивных вольтамперах (ВАр).
Реактивная мощность измеряется в реактивных вольтамперах (ВАр).
 Например,
Например,
 , Система аттенюатора напряжения SCMVAS,
, Система аттенюатора напряжения SCMVAS, Е. экзамен? Он любезно предложил написать гостевой пост о квадратном корне из трех, который, вероятно, является наиболее распространенным числом, используемым в тестировании реле, которое мало кто действительно понимает.
Е. экзамен? Он любезно предложил написать гостевой пост о квадратном корне из трех, который, вероятно, является наиболее распространенным числом, используемым в тестировании реле, которое мало кто действительно понимает.
