Электрические цепи постоянного тока и методы их расчета (стр. 1 из 6). Формула для расчета напряжения на внешнем участке цепи

Формула напряжения тока. Как найти, вычислить электрическое напряжение, разность потенциалов. Формула для расчета напряжения на внешнем участке цепи

Формула напряжения тока. Как найти, вычислить электрическое напряжение.

 

 

 

Тема: как рассчитать величину напряжения зная ток, сопротивление, мощность.

 

Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.

 

Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).

 

 

Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.

 

 

Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.

 

 

Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт». Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.

 

Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».

 

 

В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.

 

P.S. Формула закона Ома является фундаментальной, и именно по ней всегда можно найти одну неизвестную величину из двух известных (ток, напряжение, сопротивление). На практике закон ома будет применяться очень часто, так что его просто необходимо знать наизусть каждому электрику и электронику.

 

electrohobby.ru

Расчет простых цепей постоянного тока

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.  

Пример 1

  Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов  R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

 

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи. 

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов. 

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. 

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. 

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2

  Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов. 

Токи в резисторах 

В данном случ

xn--90adflmiialse2m.xn--p1ai

Т. Работа и мощность тока — PhysBook

Работа и мощность тока

Электрическая энергия легко преобразуется в другие виды энергии — механическую, химическую, световую, внутреннюю энергию вещества, что широко применяется в промышленности и в быту.

Мерой изменения энергии электрического тока служит работа источника тока, создающего и поддерживающего электрическое поле в цепи.

Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения,

\(~A = qU ,\)

где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.

Учитывая, что q = It, где I — сила тока в проводнике, а t — время прохождения электрического тока, для работы тока получим

\(~A = IUt .\)

Если R — сопротивление однородного участка цепи, то, используя закон Ома для участка цепи, можно получить формулу для расчета работы тока:

\(~A = I^2Rt = \frac{U^2}{R} t .\)

Если участок цепи не является однородным, то работу совершает не только стационарное электрическое поле, но и сторонние силы, и полная работа определяется по формуле

\(~A = I(\varphi_1 - \varphi_2 \pm \varepsilon) t .\)

По вышеприведенным формулам можно рассчитать полную работу тока на данном участке цепи.

Если в цепи есть электродвигатель, то энергия электрического тока, во-первых, расходуется на совершение механической работы — полезная работа Ameh, во-вторых, затрачивается на нагревание обмоток электродвигателя и соединительных проводов — теряемая энергия. В этом случае коэффициент полезного действия можно рассчитать как

\(~A_0 = A_{meh} + Q ;\) \(~\eta = \frac{A_{meh}}{A_0} = \frac{A_{meh}}{A_{meh} + Q} .\)

Говоря о коэффициенте полезного действия источника тока, под полезной работой подразумевают работу, совершаемую во внешней цепи постоянного тока:

\(~A_p = IUt = I^2Rt .\)

Затраченная же работа источника тока равна работе сторонних сил:

\(~A_z = q \varepsilon = I \varepsilon t ,\)

где \(~\varepsilon = I (R + r)\).

Тогда \(~A_z = I^2 (R + r) t\) .

КПД источника \(~\eta = \frac{A_p}{A_z} = \frac{IUt}{I \varepsilon t} = \frac{U}{\varepsilon} = \frac{R}{R + r}\), где U — напряжение во внешней цепи (напряжение на полюсах источника тока). Графическая зависимость η = f(R) при r = const приведена на рис. 1.

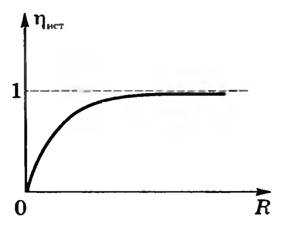
Рис. 1

Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж.

1 Дж = Кл·В = А·В·с.

Измеряют работу электрического тока счетчиками.

Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле \(~P = \frac At\) или P = IU.

Используя закон Ома для участка цепи, можно записать иначе формулу для мощности тока\[~P = I^2R = \frac{U^2}{R}\]. В этом случае речь идет о тепловой мощности.

Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.

Кроме того, применяют внесистемные единицы: киловатт-час или гектоватт-час: 1 кВт·ч = 3,6·106 Дж = 3,6 МДж; 1 гВт·ч = 3,6·105 Дж = 360 кДж.

Для измерения мощности тока существуют специальные приборы — ваттметры.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 267-270.

www.physbook.ru

Электрические цепи постоянного тока и методы их расчета

Электрические цепи постоянного тока и методы их расчета

1.1. Электрическая цепь и ее элементы

В электротехнике рассматривается устройство и принцип действия основных электротехнических устройств, используемых в быту и промышленности. Чтобы электротехническое устройство работало, должна быть создана электрическая цепь, задача которой передать электрическую энергию этому устройству и обеспечить ему требуемый режим работы.

Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении.

Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения. Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры, представлена на рис. 1.1.

Рис. 1.1

Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы:

1) Источники электрической энергии (питания).

Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками. Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства).

2) Потребители электрической энергии.

Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор). Иногда потребители называют нагрузкой.

3) Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает.

Все элементы цепи охвачены одним электромагнитным процессом.

В электрической схеме на рис. 1.1 электрическая энергия от источника ЭДС E, обладающего внутренним сопротивлением r0 , с помощью вспомогательных элементов цепи передаются через регулировочный реостат R к потребителям (нагрузке): электрическим лампочкам EL1 и EL2 .

1.2. Основные понятия и определения для электрической цепи

Для расчета и анализа реальная электрическая цепь представляется графически в виде расчетной электрической схемы (схемы замещения). В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают. Источник питания показывается как источник ЭДС E с внутренним сопротивлением r0 , реальные потребители электрической энергии постоянного тока заменяются их электрическими параметрами: активными сопротивлениями R1 , R2 , …, Rn . С помощью сопротивления R учитывают способность реального элемента цепи необратимо преобразовывать электроэнергию в другие виды, например, тепловую или лучистую.

При этих условиях схема на рис. 1.1 может быть представлена в виде расчетной электрической схемы (рис. 1.2), в которой есть источник питания с ЭДС E и внутренним сопротивлением r0 , а потребители электрической энергии: регулировочный реостат R, электрические лампочки EL1 и EL2 заменены активными сопротивлениями R, R1 и R2 .

Рис. 1.2

Источник ЭДС на электрической схеме (рис. 1.2) может быть заменен источником напряжения U, причем условное положительное направление напряжения U источника задается противоположным направлению ЭДС.

При расчете в схеме электрической цепи выделяют несколько основных элементов.

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Схема на рис. 1.2 имеет три ветви: ветвь bma, в которую включены элементы r0 , E, R и в которой возникает ток I; ветвь ab с элементом R1 и током I1 ; ветвь anb с элементом R2 и током I2 .

Узел электрической цепи (схемы) – место соединения трех и более ветвей. В схеме на рис. 1.2 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R1 и R2 (рис. 1.2) находятся в параллельных ветвях.

Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 1.2 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура.

Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах. На схеме (рис. 1.2) стрелками укажем положительные направления ЭДС, напряжений и токов:

а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу;

б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно;

в) для напряжений – совпадающими с направлением тока в ветви или элемента цепи.

Все электрические цепи делятся на линейные и нелинейные.

Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от тока в нем, называют линейным, например электропечь.

Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.

Следовательно, в линейной электрической цепи все элементы – линейные, а нелинейной называют электрическую цепь, содержащую хотя бы один нелинейный элемент.

1.3. Основные законы цепей постоянного тока

Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи.

Закон Ома для участка цепи

Соотношение между током I, напряжением UR и сопротивлением R участка аb электрической цепи (рис. 1.3) выражается законом Ома

Рис. 1.3

(1.1)

или UR = RI.

В этом случае UR = RI – называют напряжением или падением напряжения на резисторе R, а

– током в резисторе R.

При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:

.

В этом случае закон Ома для участка цепи запишется в виде:

I = Uq.

Закон Ома для всей цепи

Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 (рис. 1.3), током I электрической цепи и общим эквивалентным сопротивлением RЭ = r0 + R всей цепи:

(1.2)

.

Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.

Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

(1.3)

,

где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.2) I - I1 - I2 = 0.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

(1.4)

,

где n – число источников ЭДС в контуре;m – число элементов с сопротивлением Rк в контуре;Uк = Rк Iк – напряжение или падение напряжения на к-м элементе контура.

Для схемы (рис. 1.2) запишем уравнение по второму закону Кирхгофа:

E = UR + U1 .

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС равна нулю

(1.5)

.

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

mirznanii.com

Урок 8. Делим ток и роняем напряжение

Сегодня мы поговорим о нескольких видах простейших электрических цепей и узнаем, как же можно уронить напряжение и разделить ток на несколько частей. Урок будет длиииииинный, но содержательный, с разбором задачи в конце. Начнем с давно забытого всеми урока за номером четыре, где велся разговор о законе Ома для полной цепи. Было указано, что сила тока в цепи зависит от суммы сопротивлений: внешнего (нагрузки) и внутреннего сопротивления источника. Однако, а почему это мы так вдруг решили, что от суммы, а не, например, от разности или корня квадратного? Бездоказательно, однако! Рассмотрим схему этой цепи, немного отступив от правил прошлого урока… «Ну вот, учили-учили, а теперь забываем применять?! – скажете вы.» Нет, эти правила действительно нужны и мы их будем применять, но только когда нам нужно нарисовать именно принципиальную схему устройства, а сейчас мы будем рассматривать некую небольшую абстрактную схему и для наглядности и простоты некоторых (только некоторых!) правил не будем придерживаться. Но для начала посмотрим, как изображается и обозначается на принципиальной электрической схеме давно уже известное нам сопротивление.Как видите, это обычный прямоугольник, размерами 10мм*4мм.Итак, наша схема будет состоять из двух сопротивлений и идеального источника, нарисуем ее.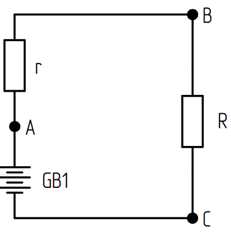

Рисунок 8.1 – Источник питания с внутренним сопротивлением

На этой схеме внутреннее сопротивление источника GB1 обозначено как r, а сопротивление внешней цепи (нагрузка) – как R. Причем, считаем, что R>>r. Здесь мы и отступаем от норм ГОСТ, поскольку для простоты понимания опускаем цифровые обозначения сопротивлений и добавляем на схему некоторые точки A, B и C. Такое включение сопротивлений называют последовательным, так как включены они как бы друг за другом – конец сопротивления r подключен к началу сопротивления R (точка B) и между ними нет больше каких-либо элементов или отводов. Закон Ома для полной цепи говорит, что ток, в электрической цепи зависит от сопротивления этой цепи и одинаков для всех элементов, то есть ток, протекающий через r, равен току, протекающему через R. Давайте рассмотрим этот момент с помощью метода доказательства «от противного». Предположим, что токи, протекающие через сопротивления различны. Ток через большее сопротивление R, исходя из закона Ома, должен быть меньше тока через r. В таком случае в точке B начал бы накапливаться заряд, поскольку ток, выходящий из точки B меньше тока, входящего в нее, а ток есть ни что иное, как отношение перенесенного полем заряда на время. Накапливаемый в точке B заряд создает в этой точке потенциал, который в некоторый момент времени сравняется с потенциалом положительной клеммы аккумулятора (точка A). В этом случае ток в цепи прекращается, поскольку при разности потенциалов двух точек равной нулю потенциальные энергии зарядов в этих точках равны, и работа поля равна нулю. Это умозаключение, кстати говоря, приводит нас к одному интересному выводу:

между точками одинакового потенциала протекание электрического тока невозможно.

Однако, электроны, образующие не скомпенсированный заряд в точке B постепенно будут поглощаться ионами материала, что приведет к снижению потенциала и возобновлению тока, который восстановит потенциал и опять прервёт сам себя. Но это бы противоречило закону Ома, который говорит, что ток в цепи всегда постоянен, а здесь имеет место прерывистый ток, значение которого зависит от времени. Соответственно, такой ситуации быть не может, мы пришли к противоречию.

Если же мы представим, что r>>R, тогда ток через большее сопротивление r исходя из закона Ома должен быть меньше тока через R. В этом случае ток, втекающий в точку B будет меньше, чем ток, вытекающий из нее, что приведет к уменьшению числа свободных электронов в материале до нуля и ток опять прекратится. Со временем за счет дрейфа и превращения атомов материала в ионы свободные электроны вновь образуются, и ток возобновиться, но истощение заряда продолжится, и ток опять прекратит сам себя. То есть мы видим такую же ситуацию, как в первом случае.

Остаётся только одно разумное решение:

ток в последовательной цепи одинаков для каждого элемента этой цепи.

В этом случае поддерживается постоянный баланс потенциалов всех точек цепи. Это не говорит о том, что потенциалы одинаковы! Это значит, что потенциал каждой точки строго определён протекающим в ней током.Теперь давайте разберемся, почему ток в цепи будет зависеть от суммы сопротивлений. Тут всё довольно просто. Последовательное соединение двух проводников приводит к увеличению длины эквивалентного проводника, а это в свою очередь – к росту сопротивления (формула из Урока 3). Отсюда запоминаем еще одно важное правило:

эквивалентное сопротивление участка цепи с последовательно включенными сопротивлениями равно сумме этих сопротивлений.

Наш вывод относительно протекания тока между точками одинакового потенциала приводит к тому, что точки A, B и C обладают различными потенциалами, раз ток в цепи существует. Причем потенциал точки C меньше потенциала точки B, а точки B меньше, чем точки A. Почему? А потому что уменьшение количества свободных электронов (за счет столкновения с узлами кристаллической решётки и прочих потерь в материале) происходит последовательно от «минуса» аккумулятора (он же является их источником!) через сопротивления R и r к «плюсу» аккумулятора (а он уже является источником положительных ионов). К тому же мы ведь считаем, что ток «течет» от «плюса» к «минусу», а электроны наоборот – от «минуса» к «плюсу», поэтому, исходя из формулы Урока 3 для потенциальной энергии заряда, видно, что наибольшим потенциалом обладает точка с наименьшим зарядом, – «плюс» аккумулятора.

А раз две точки имеют разный потенциал, то между ними есть напряжение, которое называют падением напряжения. Нетрудно догадаться, что падение напряжения на элементе пропорционально току, протекающему через него, так как величина тока регулирует количество заряда на концах элемента, т.е. разность потенциалов. По сути величина падения напряжения подчиняется закону Ома для участка цепи:

UR=IR∙R, где

IR – ток, протекающий через сопротивление,R – величина этого сопротивления.Для нашей схемы на Рисунке 8.1 справедливы следующие соотношения:

UAB=I∙r,UBC=I∙R,UAC=I∙(R+r)=εGB1

Из этих соотношений хорошо видно, что падение напряжения – часть эдс источника, доставшаяся участку цепи. Часто на схемах можно встретить такие обозначения падения напряжения: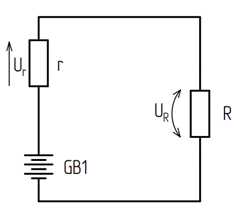

Рисунок 8.2 – Обозначение падения напряжения

Стрелку направляют в сторону уменьшения потенциала. Разумеется, на принципиальных электрических схемах падение напряжения указывать не допускается.Раз мы заговорили о последовательных цепях, наверное, существуют и параллельные? Да, действительно, такие соединения есть и выглядят они следующим образом:

Рисунок 8.3 – Параллельное соединение сопротивлений

Параллельным соединением называется такое соединение, при котором выходы элементов соединены в одних точках. На нашей схеме это точки A и B. Поскольку элементы имеют общие точки, разность потенциалов на этих элементах будет одинакова, как и падение напряжения. То есть, напряжение на параллельных ветвях электрической цепи одинаково.

Для удобства дальнейшего рассмотрения процессов в электрических цепях введем такие понятия как: узел, ветвь и контур. Ветвью называют любой двухполюсник, входящий в цепь, например, на Рисунке 8.3 отрезок AB есть ветвь. Узлом называют точку соединения трех и более ветвей (на Рисунке 8.3 обозначены жирными точками. На рисунке 8.1 точки A, B и C не являются узлами).

Контур – замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам. Например, контуром можно назвать параллельное соединение сопротивлений R1 и R2 на Рисунке 8.3Рассмотрим теперь, что происходит с токами ветвей I, I1 и I2:Эти соотношения получаются из довольно простого логического заключения: если источник включен параллельно сопротивлению, то падение напряжения на сопротивлении не может быть отличным от эдс источника, ведь потенциалы концов сопротивления R1 соответственно равны потенциалам концов сопротивления R2. Причем не играет роли, какое количество параллельных ветвей будет подключено – на каждой из них напряжение будет одно и то же. Как же получить выражение для тока I? Начнем рассуждать с того, что мощность, отдаваемая источником должна быть равна мощности, потребляемой нагрузкой, ведь закон сохранения энергии никто не отменял. Запишем выражения для мощностей, пренебрегая внутренним сопротивлением источника:Pист=I∙εPнагр=PR1+PR2=I1∙UR1+I2∙UR2=I1∙ε+I2∙ε=(I1+I2)∙εПриравнивая правые части уравнений, получим:

(I1+I2 )∙ε=I∙ε

Таким образом, сокращая на ε:

I=I1+I2

То есть, в параллельных ветвях происходит деление тока. Если перенести слагаемые I1 и I2 в левую часть уравнения, получим, что алгебраическая сумма токов в каждом узле электрической цепи равна нулю.Учитывается именно алгебраическая сумма (с учетом знака), потому что направление тока мы можем положить любым, ведь в сложной схеме можем заранее не знать, втекает ток в узел или вытекает из него (втекающий ток берётся со знаком «плюс», вытекающий – со знаком «минус»). То есть мы, например, могли бы перенести слагаемое I в правую часть и получили бы уравнение, в котором втекающие токи были бы со знаком «минус», а вытекающие со знаком «плюс», но ничего не мешает нам поделить обе части уравнения на -1. Это утверждение называется I правило Кирхгофа или правило токов Кирхгофа. Иногда его не совсем корректно называют законом Кирхгофа. Всё-таки это правило, потому что оно не является фундаментальным законом природы, а вытекает из других фундаментальных законов.

Кроме I правила Кирхгофа существует еще и II правило Кирхгофа:

алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме эдс ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю.

Закон Ома является частным случаем II правила Кирхгофа для цепи из одного контура. Здесь выражение «алгебраическая сумма» значит, ровно то же, что и для I правила, только для напряжений.Как использовать эти правила для расчета сложных электрических цепей мы рассмотрим на следующем уроке, который полностью будет посвящен практике.

Возвращаясь к схеме на рисунке 8.3 возникает логичный вопрос: как же нам рассчитать эквивалентное сопротивление параллельных ветвей? Ясно, что формула для последовательной цепи сюда не подойдет. Давайте заменим сопротивления R1 и R2 одним эквивалентным сопротивлением:

Рисунок 8.4 – Замена параллельных сопротивлений эквивалентным сопротивлением

Теперь ничто не мешает нам применить закон Ома, чтобы рассчитать Rэкв:При подобной замене мы будем пользоваться следующим вариантом записи:Пришло время запоминать еще одно важное правило: величина, обратная общему сопротивлению параллельных ветвей, равна сумме величин, обратных сопротивлениям каждой ветвиИли, иначе: эквивалентная проводимость параллельных ветвей равна сумме проводимостей этих ветвей.Немного тавтологии, пожалуй, не помешает…

Схема на рисунке 8.3 называется делитель тока и находит широкое применение. Более подробно применение делителя тока мы рассмотрим позже, а сейчас приведем такой пример, чтобы хоть немного убедить читателя в полезности этого схемного решения. Рассмотрим схему на рисунке 8.4. Допустим, эдс источника ε=5В, а сопротивление нагрузки Rэкв=1Ом, тогда мощность, выделяемая в нагрузке равна:Посмотрим, что произойдёт, если мы заменим эквивалентное сопротивление двумя одинаковыми параллельно включенными сопротивлениями (рисунок 8.3). Чтобы сохранить величину эквивалентного сопротивления равным 1Ом, рассчитаем величины сопротивлений R1 и R2:то есть каждое из сопротивлений должно быть больше эквивалентного в 2 раза.Рассчитаем мощность, выделяемую на каждом из этих сопротивлений:Суммарная мощность нагрузки осталась прежней, однако, как нам уже известно, мощность выделяемая на сопротивлении, полностью переходит в тепло, следовательно, при одной и той же рассеиваемой мощности, во втором случае мы получим более комфортный температурный режим для нагрузки (температура каждого сопротивления будет ниже, чем температура эквивалентного сопротивления) за счет увеличения в 2 раза площади рассеивания (ведь мы используем два проводника вместо одного). Соответственно, трата дополнительных денег на приобретение двух проводников позволяет нам сэкономить на охлаждении. Часто бывают такие ситуации, что слишком большой перегрев элемента может приводить к выходу его из строя (даже такой простой вещи как кусок проводника). Кроме того, многие полупроводниковые приборы (диод, транзистор, тиристор) рассчитаны на определенный номинальный ток, и, чтобы увеличить предел номинального тока, такие приборы включают параллельно. Можно, конечно, взять прибор с большим номинальным током, но чаще всего стоимость таких прибор намного больше. Экономия, однако…

Давайте немного изменим эту схему, пренебрегая внутренним сопротивлением и добавив еще одно сопротивление во внешнюю цепь: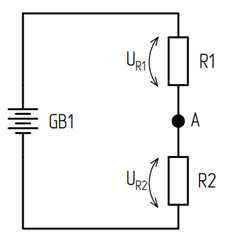

Рисунок 8.5 – Последовательное соединение сопротивлений

По сути, это та же схема последовательного соединения двух сопротивлений, только теперь оба эти сопротивления являются частью нагрузки. Из вышеприведенных соотношений видно, что напряжение на каждом сопротивлении определяется протекающим током и значением этого сопротивления. Используя закон Ома, выразим величину тока, протекающего через сопротивления:тогда, подставляя значение тока в выражение для падения напряжения, получим:Из полученных соотношений видно, что величина падения напряжения зависит от эдс источника и соотношения сопротивлений.При R1=R2 падение напряжения на каждом сопротивлении составит ровно половину эдс источника. Таким образом мы поделили напряжение пополам и теперь можем использовать отвод в точке А в качестве «плюса» своеобразного источника питания, но с пониженным напряжением. Такая схема называется делителем напряжения. Ее полезно применять, когда имеется источник с большим напряжением, чем требуется. Сопротивление R1 называется верхним плечом, а сопротивление R2 – нижним. Однако, резистивный делитель напряжения обладает существенными недостатками: во-первых, потери мощности на плечах делителя снижают кпд устройства, поскольку просто переходят в тепло, а, во-вторых, сопротивление выходного плеча (с которого снимается часть эдс) должно быть согласовано с сопротивлением нагрузки, чтобы сохранять требуемое напряжение. Рассмотрим эти два момента на примере общего случая включения сопротивлений так называемого смешанного соединения.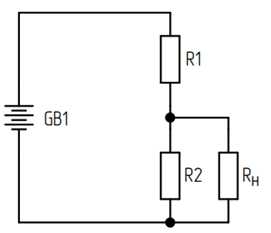

Рисунок 8.6 – Смешанное соединение сопротивлений

Как мы видим, сопротивления R2 и Rн включены параллельно, а их эквивалентное сопротивление включено последовательно с R1. Теперь сформулируем условия задачи: на нагрузке мощностьюPн=20 Вт необходимо получить напряжение Uн=5 В, если имеется аккумуляторная батарея номинальной эдс ε=12 В.Для начала обозначим направления протекания токов в каждой ветви.

Рисунок 8.7 – Направления протекания токов

Рассчитаем параметры нагрузки по известной мощности и напряжению:Однако, нам неизвестны токи I1 и I2, так же как и сопротивления R1 и R2. В таких случаях при разработке схемы необходимо самому задать необходимые недостающие условия, но так, чтобы задача имела решение. Например, мы могли бы задать R1=10 Ом, но ведь ток I1 не может быть менее 4А, а значит:UR1>I1∙R1=4А∙10Ом=40В,что заведомо больше, чем напряжение на аккумуляторе. Чтобы не угадывать значения сопротивлений, давайте для уменьшения потерь на сопротивлении R2 зададим ток I2 равным 10% от тока нагрузки, ведь ничто не мешает нам так сделать.

I2=0.1Iн=0.4 А

Напряжение Uн равно напряжению UR2, так как эти сопротивления включены параллельно, значит, сопротивление R2 из закона Ома равно:Ток I1 можно рассчитать двумя способами:

• Исходя из I правила Кирхгофа для узла А:

  I1=I2+Iн

• Используя закон Ома.

Для начала давайте рассчитаем его, используя второй способ, а потом сравним результаты.Поскольку нижним плечом делителя является эквивалентное сопротивление параллельно включенных сопротивлений R1 и Rн, рассчитаем его:Заметьте, что эквивалентное сопротивление всегда меньше меньшего сопротивления!Ток I1 соответствует току через последовательное соединение сопротивлений R1 и Rэкв. Его можно найти из закона Ома:Теперь рассчитаем этот же ток, используя первый способ:

I1=I2+Iн=0.4А + 4А = 4.4А

Результаты совпали, значит, расчет выполнен верно.Рассчитаем величину сопротивления R1, пользуясь опять же законом Ома:Итак, при помощи двух сопротивлений мы спроектировали (ого-го!) устройство понижения напряжения с 12 В до 5 В. Давайте оценим кпд этого устройства. Полезной мощностью у нас является мощность нагрузки Pн=20 Вт, а полной мощностью – мощность, отдаваемая аккумуляторной батареей, которая равна произведению потребляемого тока (I1) на эдс батареи:

PGB1=ε∙I1=12В ∙ 4.4А = 52.8Вт

Тогда кпд равен:Всего-то! Ужасно! Давайте подумаем, как можно увеличить этот показатель…Но сначала разберемся откуда берутся такие большие потери мощности… А браться им, кроме как на нагрев сопротивлений R1 и R2 неоткуда. Давайте рассчитаем мощность потерь для каждого из них:

PR1=I12∙R1=(4.4 А)2∙1.136 Ом=30.8 ВтPR2=I22∙R2=(0.4 А)2∙1.59 Ом=2 Вт

Сразу видно, что наибольшие потери рассеиваются на сопротивлении R_1. Величину тока мы значительно изменить не можем, так как она не может быть меньше величины тока нагрузки. Можно подкорректировать величину заданного нами тока I2… Стоп. А зачем нам вообще это сопротивление? Ведь делитель может быть собран с помощью самой нагрузки в качестве нижнего плеча! Смело убираем R2 из схемы.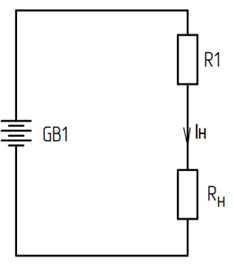

Рисунок 8.8 – Модернизированная схема

Теперь нам не нужен этот «паразитный» ток I2. Пересчитаем величину сопротивления R1:Потери мощности на нем:

PR1=Iн2∙R1=(4 А)2∙1.75 Ом=28 Вт

И кпд:Кпд вырос, но потери все равно огромные! Но больше мы сделать, к сожалению ничего не можем: такая схема попросту неэффективна… Мы впустую потратили больше энергии, чем получили полезной работы. Вот такой первый недостаток схемы делителя напряжения.

Теперь посмотрим, что будет, если мы изменим параметры нагрузки, например, вместо 20 Вт подключим 15 Вт. Изменится величина сопротивления нагрузки, ведь она определена номинальными значениями мощности и напряжения:Посмотрим, что произойдет с напряжением на нижнем плече делителя, то есть на нагрузке:В сумме напряжения на плечах делителя равны эдс источника, значит:Тогда нагрузке достанется часть эдс, равная:

Uн=ε-UR1=12 В-6.15 В=5.85 В

Получается, что мы превысили номинальное напряжение на ≈17%. И нельзя точно сказать, выдержит ли наша нагрузка такого превышения. А может она попросту выйдет из строя… Получается, что без изменения R1 подключать нагрузку, отличную от расчетной, нельзя. Это и есть второй недостаток схемы делителя. В основном эта схема применяется там, где мощность потерь невелика, например, в цепях с силой тока единицы – десятки миллиампер.

Теперь кратко опишем важные моменты урока, а на этом я с вами прощаюсь, ждем следующего урока, в котором подробно разберем задачу на расчет сложной электрической цепи.

• Между точками одинакового потенциала протекание электрического тока невозможно.
• Ветвью называют любой двухполюсник, входящий в цепь.
• Узлом называют точку соединения трех и более.
• Контуром называют замкнутый цикл из ветвей.
• При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.Ток в последовательной цепи одинаков для каждого элемента.Эквивалентное сопротивление цепи равно сумме входящих в нее сопротивлений:
• При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.Напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. Эквивалентное сопротивление цепи может быть рассчитано по формуле:
• I правило Кирхгофа: алгебраическая сумма токов в каждом узле электрической цепи равна нулю.
• II правило Кирхгофа: алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме эдс ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю.

← Урок 7. Основы составления электрических схем | Содержание | →

myblaze.ru

Постоянный ток. Электрические цепи постоянного тока: расчет

Постоянным током являются передвигающиеся в определенном направлении частицы с зарядом. По-другому ток можно назвать такими величинами, как сила тока или напряжение, которые являются постоянными и в направлении, и по значению.

Рассмотрим его характеристику, применение, а также электрические цепи постоянного тока. Ответим на вопросы, каким образом проводится исследование электрической цепи, как она рассчитывается и на некоторые другие.

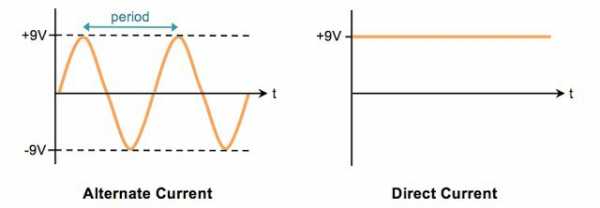
От плюса к минусу или наоборот?

В источнике электроны передвигаются от минусового значения к плюсовому. Несмотря на то что все об этом знают, принято считать направление от плюса к минусу. Интересно почему? Нам объясняют, что так исторически сложилось. Но так ли это на самом деле? Ведь эта «история» сложилась в какой-то совершенно незначительный промежуток времени.

В постоянном токе действуют главные законы электротехники: закон Ома и законы Кирхгофа. Ток называли раньше гальваническим, так как получили его в результате гальванической реакции. Когда электрический ток начали проводить в дома, велись жесткие споры о том, какой ток вводить: постоянный или переменный. «Войну» выиграл второй, так как он оказался менее затратным. Его гораздо проще передавать на большие расстояния благодаря легкой трансформации.

Как получается постоянный ток

Но и не исчез из использования постоянный ток. Электрические цепи постоянного тока встречаются, к примеру, в аккумуляторах.

Ток вырабатывается посредством электромагнитной индукции, после чего происходит выпрямление коллектором. Такую реакцию производит генератор, где тоже вырабатывается постоянный ток. Электрические цепи постоянного тока могут трансформироваться из переменного за счет преобразователей и выпрямителей.

Область применения

Применение этого вида достаточно широко. В большинстве бытовых приборов дома, к примеру, в компьютерном модеме, зарядке для мобильника, электрочайнике или кухонном комбайне работает именно постоянный ток. Электрические цепи постоянного тока вырабатываются и преобразуются на автомобильном генераторе и любом портативном приборе. На нем функционируют все промышленные двигатели, а в отдельных странах даже высоковольтные линии электрических передач. Даже в некоторых медицинских приборах он применяется.

Постоянный ток является более безопасным, так как смертельный исход может наступить при ударе током от 300 мА, а при переменном — уже при 50-100 мА.

Электрическая цепь

Связь обеспечивается всеми устройствами, благодаря которым осуществляется передача, распределение и преобразование тепловой, электромагнитной, световой и иных видов энергоинформации. Процессы описаны такими электродвижущими силами, как ток и напряжение.

Основные элементы электрических цепей постоянного тока

Основные элементы — это приемники и источники энергоинформации, соединяющиеся проводниками. В источниках различные виды энергии преобразуются в электрическую. А в приемниках, наоборот, электроэнергия переходит в иные виды.

Цепи, где преобразование, передача и получение электрической энергии происходит при постоянном значении напряжения и тока на протяжении всего времени, называются цепями постоянного тока. Там, где процесс происходит с переменным значением — цепями переменного тока.

Чтобы произвести расчет и исследование электрической цепи постоянного тока (лабораторная работа для этих целей обычно служит), применяется схема замещения, то есть идеализированная цепь для расчета реальной. Чтобы ее получить, заменить нужно все элементы схемы. Физические процессы должны быть выражены в каждом математическом описании.

Резистивные элементы

Резистор является одним из приемников электроцепи. Его характеризует активное сопротивление, которое измеряется в Омах. Резистивные сопротивления или, как их еще называют, активные вводятся в схемы замещения, чтобы учитывать преобразующуюся электромагнитную энергию в иные виды.

Расчет сложных электрических цепей постоянного тока производится, если задать положительное направление всех токов и напряжений. Выбирают направление их узла, имеющего большой потенциал к узлу с меньшим потенциалом.

При независящем сопротивлении от тока резистор называют линейным, а электрическую цепь — линейной резистивной. Вольт-амперная характеристика выражается через линейную функцию, проходящую через начало координат.

При анализе таких цепей часто применяют принцип упрощения, состоящий в замене сложных участков электрической цепи на простые. Но ток и напряжение меняться не должны. Тогда цепь свернется до самого простого вида. Соединенные резистивные элементы должны быть параллельно и последовательно преобразованы.

Последовательное и параллельное соединение

При последовательном соединении во всех элементах ток имеет одно и то же значение. Здесь напряжение определяется посредством суммы всех включенных сопротивлений, умноженной на I, то есть:

U=(R1+R2+RN)I=RI.

При параллельном соединении применяется постоянное напряжение, зато ток представляет собой сумму токов на каждом из элементов. Поэтому его можно представить как произведение напряжения на эквивалентную проводимость активных элементов. А она, в свою очередь, равна сумме проводимостей элементов. Вот из чего состоит постоянный ток.

Электрические цепи постоянного тока, помимо этого, содержат источники напряжения и тока.

Источники

Независимое напряжение (ЭДС, ток) от сопротивления внешней цепи называют его источником. Источник ЭДС (напряжения) измеряется на холостом ходу, то есть, где ток в источнике равен нулю. В схемах замещения резистор учитывает тепловые энергетические потери, которые выделяются из источника. Если он равен нулю, а источник тока — бесконечности, это — идеальный источник. Реальный всегда имеет конечное значение.

Внешние характеристики следующие: у источников ЭДС и напряжения зависимость возникает от протекающего тока, а у источника тока — от напряжения на зажимах.

Реальные источники имеют линейные и нелинейные участки. Рассмотрим методы расчета линейных электрических цепей постоянного тока. Они описаны в законе Ома для полной цепи, где I=E/(Rh+Rbh). Тогда U= E- RbhI. Из этих формул выводятся внутреннее сопротивление и внутренняя проводимость:

• Rbh=∆U/∆I;
• Gbh=∆I/∆U.

Расчет нелинейных электрических цепей постоянного тока производится на основе закона Кирхгофа. Методы расчета для линейных и нелинейных схем разные. Поэтому последние в рамках данной статьи не рассматриваются.

Приборы для измерения линейного участка

Электрическая емкость цепи постоянного тока содержит источники. А приборами, его измеряющие, являются: вольтметр для измерения напряжения на участке цепи и амперметр для последовательного включения в цепь. При нулевом значении внутреннего сопротивления и проводимости приборы являются идеальными.

Способы включения становятся более понятными при рассмотрении их с применением измерения сопротивления. По закону Ома R=U/I.

Мы знаем, что реальные приборы не имеют нулевого значения. Поэтому возможны лишь два варианта их включения:

• внутреннее сопротивление вольтметра в разы больше измеряемого амперметра — такое, чтобы снижение напряжения на нем не сокращало снижение на измеряемом сопротивлении, а напряжение, которое измеряется вольтметром должно соответствовать рабочему диапазону;
• внутреннее сопротивление вольтметра соизмеримо с измеряемым, а амперметра — существенно меньше измеряемого.

Эксперимент и задания для контрольной работы

Для измерения напряжения и тока применяются соответствующие генераторы. Внутреннее сопротивление у них измеряется посредством переключателей.

Вольтметр и амперметр входят в блок АВ1.

Для измерения сопротивления применяются специальные схемы. В источнике электродвижущей силы внутреннее сопротивление должно быть выключенным.

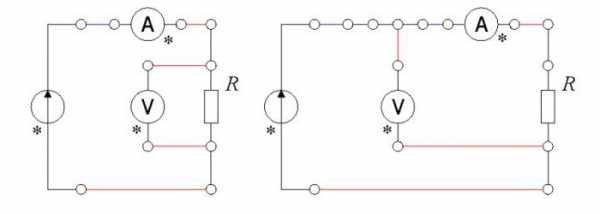
В рекомендуемом задании, которое должна иметь контрольная работа, электрические цепи постоянного тока изучаются посредством определения параметров источника электродвижущей силы, источника тока, измерения сопротивления, изучения включения параллельного и последовательного сопротивлений, ВАХ.

fb.ru

---

• 
  Бензогенератор устройство
• 
  Электрический привод линейный
• 
  Основы цифровой электроники
• 
  Проект освещения
• 
  Испытание кабельных силовых линий
• 
  Обозначение радиодеталей на схеме
• 
  Резистор реостат
• 
  Стабилизатор переменного тока схема
• 
  Работать здесь
• 
  Единица си давления
• 
  Виброускорение виброскорость и виброперемещение