Формула для расчета напряжения на внешнем участке цепи: запишите формулу для расчета напряжения на внешнем участке электрической цепи ?

ЭДС. Закон Ома для полной цепи

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.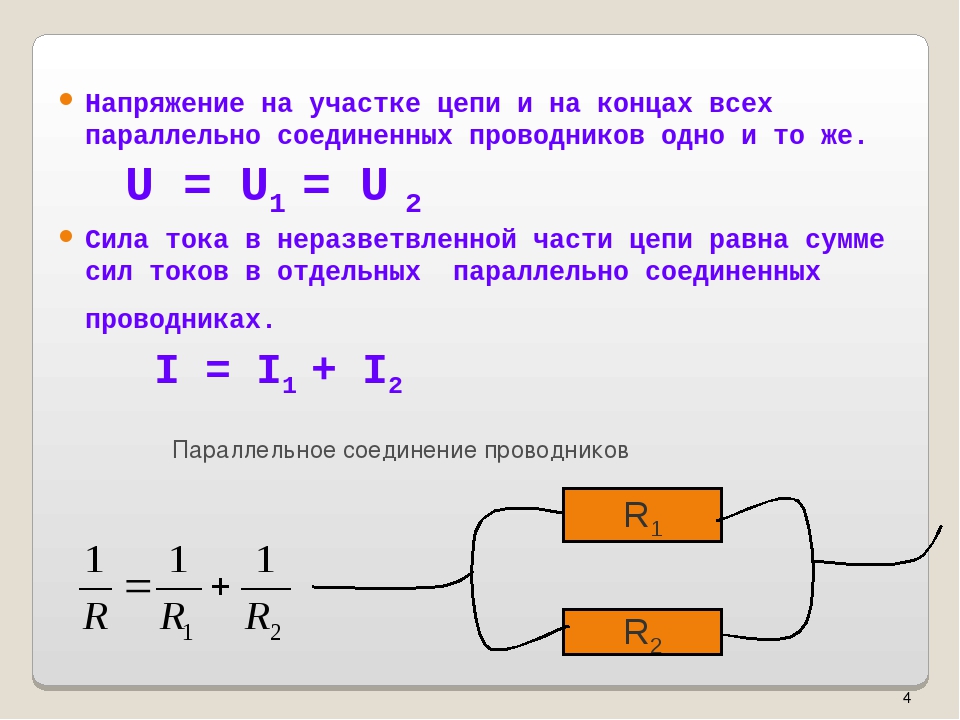

Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

(1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:

(2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

(4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

(5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .

Если сила тока в цепи равна , то

Некоторое количество теплоты выделяется также на источнике тока:

Полное количество теплоты, которое выделяется в цепи, равно:

КПД электрической цепи — это отношение полезного тепла к полному:

КПД цепи равен единице лишь в том случае, если источник тока идеальный .

Закон Ома для неоднородного участка

Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .

Подставляем сюда выражения для , и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца

Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.

Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени

Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.

Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то

Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид

Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).

Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения

где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.

Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников

Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников

Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления .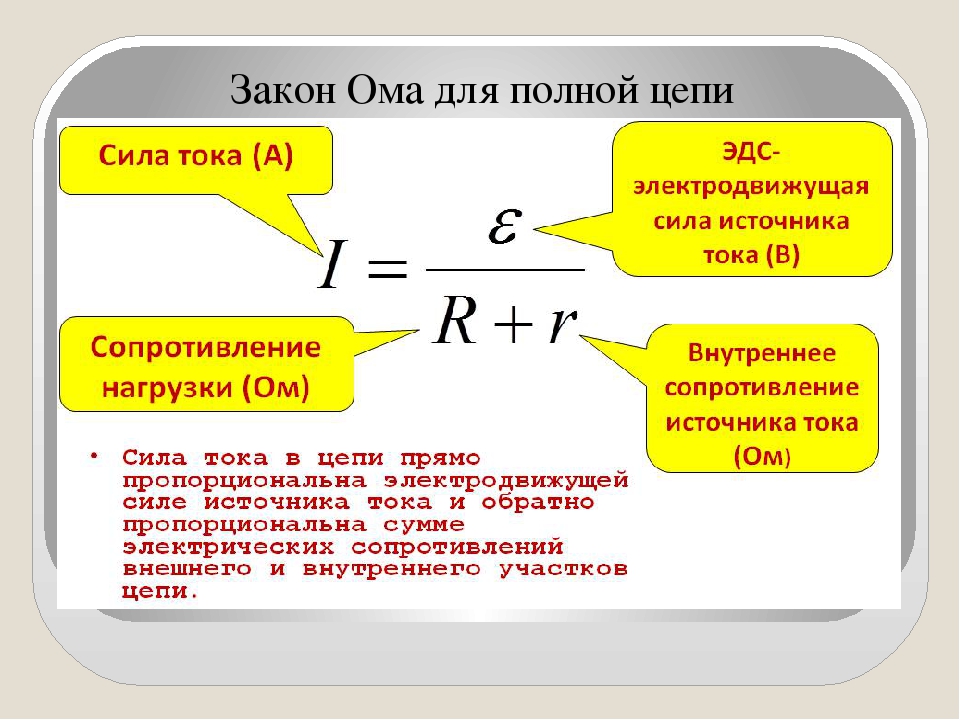 Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду

В этом случае сила тока в цепи равна

Формула (21.7) называется законом Ома для замкнутой электрической цепи.

При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно

(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение

которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.

Рассмотрим теперь задачи.

Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).

Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)

(ответ 2).

Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).

По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)

Таким образом, сила тока уменьшилась в 4 раза (ответ 3).

Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика

(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.

Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6

где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем

(ответ 3).

Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).

В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем

где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).

В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому

где — внутреннее сопротивление источника (ответ 3).

Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).

В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).

Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21. 2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.

Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.

Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно

(ответ 2).

Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что

(ответ 2).

При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что

(ответ 1).

Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка

а затем и эквивалентное сопротивление всей цепи

(ответ 3).

При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).

Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна

где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:

(ответ 2).

Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —

(ответ 1).

Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца

где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).

формулы и определения / Блог / Справочник :: Бингоскул

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

1. I — сила тока (в системе СИ измеряется — Ампер)
   • Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
   • Формула: I=\frac{U}{R}
2. U — напряжение (в системе СИ измеряется — Вольт)
   • Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
   • Формула: U=IR
3. R — электрическое сопротивление (в системе СИ измеряется — Ом).
   • Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
   • Формула R=\frac{U}{I}

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).

 

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

 

Формула I=\frac{\varepsilon}{R+r}

• \varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

 

Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

 

• U — электрическое напряжение;
• I — сила тока;
• P — электрическая мощность;
• R — электрическое сопротивление

---

 

Смотри также:

 

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

Формула мощности тока в физике

Содержание:

Электрический ток, на каком угодно участке цепи совершает некоторую работу (А). Допустим, что у нас есть произвольный участок
цепи (рис.1) между концами которого имеется напряжение U.

Работа, которая выполняется при перемещении заряда равного 1 Кл между точками A и B (рис.1) будет равна
U. В том случае, если через проводник протекает ток силой I за время равное
$\Delta t$ по указанному выше участку пройдет заряд (q) равный:

$$q=I \Delta t(1)$$

Следовательно, работа, которую совершает электрический ток на данном участке, равна:

$$A=U \cdot I \cdot \Delta t(2)$$

Надо отметить, что выражение (2) является справедливым при I=const для любого участка цепи
(в таком участке могут содержаться проводники 1–го и 2–го рода).{2}(6)$$

где j – плотность тока, $\rho$ – удельное сопротивление.

Единицы измерения мощности тока

Основной единицей измерения мощности тока (как и мощности вообще) в системе СИ является: [P]=Вт=Дж/с.

В СГС: [P]=эрг/с.

1 Вт=10⁷ эрг/( с).

Выражение (4) применяют в системе СИ для того, чтобы дать определение единицы напряжения.
Так, единицей напряжения (U) является вольт (В), который равен: 1 В= (1 Вт)/(1 А).

Вольтом называют электрическое напряжение, которое порождает в электроцепи постоянный ток силы 1 А при мощности 1 Вт.

Примеры решения задач

Пример

Задание. Какой должна быть сила тока, которая течет через обмотку электрического мотора для того,
чтобы полезная мощность двигателя (P_A) стала максимальной?Какова максимальная полезная мощность?
Если двигатель постоянного тока подключен к напряжению U, сопротивление обмотки якоря – R.

Решение. Мощность, которую потребляет электроприбор, идет на нагревание (P_Q) и совершение
работы (P_A):

$$P=P_{Q}+P_{A}(1.{2}}{P_{2}}}$$

Читать дальше: Формула напряжения электрического поля.

Часть ЭДС, затрачиваемая на перенос зарядов по внешнему участку цепи, называется падением напряжения во внешней цепи или просто напряжением и обозначается U.

Термин «падение напряжения» или «напряжение» обозначает часть ЭДС, затрачиваемую на преодоление сопротивления данного участка цепи.

ЭДС источника представляет собой сумму падений напряжения на внутреннем и внешнем участке цепи.

Е = U + U₀

Из этого равенства следует:

U = E – U_{0 ,}

т.е. напряжение на зажимах источника тока меньше его ЭДС на величину падения напряжения на внутреннем участке цепи.

Напряжение измеряется в Вольтах.

ЭДС и напряжения измеряется вольтметром (рис.1).

Рис.1

ЭДС измеряют вольтметром на зажимах источника при отключенном потребителе (ключ К разомкнут).

Напряжение измеряют там же, при включённом потребителе (ключ К разомкнут).

Для измерения напряжения на каком-либо участке электрической цепи вольтметр нужно включить к концам этого участка (Рис.2).

Внутреннее падение напряжения измерить нельзя! Его рассчитывают по формуле:

U₀ = E – U.

Закон Ома для полной цепи с источником ЭДС

 

Сила тока, протекающего в замкнутой цепи прямо пропорциональна ЭДС источника и обратно пропорциональна сумме сопротивлений внешнего R и внутреннего R_о участков цепи.

, где

 

I – сила тока;

Е — ЭДС источника;

R – сопротивление внешнего участка цепи;

R₀ – внутреннее сопротивление источника.

 

Закон Ома для участка цепи

 

Сила тока прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.

Основная формула:

Следствия:

—физический смысл данной формулы: сила тока тем больше, чем выше напряжение. В свою очередь напряжение больше там, где больше напряжение.

— данная формула физического смысла не имеет, т.е. сопротивление не зависит ни от силы тока ни от напряжения. Эта формула используется только для расчета сопротивления.

 

ТЕМЫ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ №1

ВТОРОЙ УРОВЕНЬ

Работа и мощность электрического тока

Работой электрического тока называется преобразование электрической энергии в другой вид энергии.

A = Е· q

Работа в системе СИ измеряется в джоулях [1 Дж = 1 В·А ·с]




Где: А [ Дж ] – работа электрического тока в замкнутой цепи

Е [ В ] — ЭДС источника

q [ Кл ] – заряд.

Имея в виду, что q = I · t, получаем

A = Е· I · t

Любая электрическая цепь состоит из двух участков – внутреннего и внешнего, следовательно: Е = U + U₀.Введем данное выражение a формулу работы:

 

A = (U + U₀)· I · t = U · I · t + U₀· I · t.

Из последней формулы видно, что ток совершает работу и на внутреннем, и на внешнем участках цепи. Разобьем данную формулу на две:

A = U · I · t –работа, совершаемая током на внешнем участке цепи;

А = U₀· I · t —работа, совершаемая током на внутреннем участке цепи (нагрев источника).

Величина, характеризующая скорость с которой происходит преобразование электрической энергии в другие виды энергии, или скорость с которой совершается работа, называется электрической мощность.

Где:

P [Вт] – электрическая мощность

А [Дж] — работа электрического тока

t [с ] – время, в течение которого совершается работа

 

1 МВт = 1 ·10⁶ Вт (мегаватт)

1 кВт = 1 ·10³ Вт (киловатт)

1 мВт = 1·10^-3 Вт (милливатт)

1 л.с. = 736 Вт.

Величина, характеризующая скорость, с которой другие виды энергии преобразуются в источнике питания в электрическую, называется мощностью генератора.

→ P_И = E· I

Величина, характеризующая скорость, с которой происходит преобразование электрической энергии в потребителе в другие виды энергии, называется мощностью потребителя

→ Р= U· I

Из этой формулы вытекают следующие:

А используя закон Ома можно вывести еще и такие формулы:

Мощность, характеризующая непроизводительный расход электрической энергии, например внутри генератора, называется мощностью потерь.

→ Р_о= U_о· I

По закону сохранения энергии мощность генератора равна сумме мощности потребителя и мощности потерь.

P_И = P + P₀

 

Соединение потребителей

Последовательное соединение

Соединение, при котором участки цепи включены один за другим без разветвлений и поэтому имеют одно значение тока, называется последовательным. (рис.4)

Рис.4

I_AB = I₁ = I₂ = I₃=…=I_n=const

При последовательномсоединении резисторов, их эквивалентное (общее) сопротивление равно сумме сопротивлений всех резисторов, входящих в цепочку

R_АВ = R₁+R₂+R₃+…+R_n

 

Если R₁ = R₂ = R₃ , то R_AB = n · R₁ , где

n – число сопротивлений.

U_AB = U₁ + U₂ + U₃

Параллельное соединение

 

Соединение, при котором несколько ветвей присоединены к одной паре узлов, называется параллельным (рис.5).

Электрический ток — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Электрический ток. Сила тока. Сопротивление

К оглавлению…

В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:

Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.

Средняя сила тока находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):

Если же ток равномерно меняется с течением времени от значения I₁ до значения I₂, то можно значение среднего тока можно найти как среднеарифметическое крайних значений:

Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:

При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:

где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.

Сопротивление проводника зависит и от его температуры:

где: R₀ – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.

Диод в цепи постоянного тока

Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:

Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.

 

Закон Ома. Последовательное и параллельное соединение проводников

К оглавлению…

Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.

1. Закономерности последовательного соединения:

Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R₀ находится по формуле:

2. Закономерности параллельного соединения:

Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R₀ находится по формуле:

Электроизмерительные приборы

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R_B. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R_A. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.

 

ЭДС. Закон Ома для полной цепи

К оглавлению…

Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы A_ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:

Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.

Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания:

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

Несколько источников ЭДС в цепи

Если в цепи присутствует несколько ЭДС подключенных последовательно, то:

1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:

Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.

2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:

В обоих случаях общее сопротивление источников увеличивается.

При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:

В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.

 

Работа и мощность тока. Закон Джоуля-Ленца

К оглавлению…

Работа A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в теплоту Q, выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока A к интервалу времени Δt, за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:

Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).

 

Энергобаланс замкнутой цепи

К оглавлению…

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. В этом случае полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R₁ и R₂ на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

 

Электролиз

К оглавлению…

Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.

Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза.

Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией.

Закон электролиза был экспериментально установлен английским физиком М.Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

где: n – валентность вещества, N_A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

 

Электрический ток в газах и в вакууме

К оглавлению…

Электрический ток в газах

В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов — электроны и положительные ионы. Этот процесс называется ионизацией газов.

Ионизировать молекулы газа можно внешним воздействием — ионизатором. Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α-частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов — электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).

Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.

Электрический ток в вакууме

Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.

Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.

Репетитор-онлайн — подготовка к ЦТ


Пример 11. Шесть одинаковых резисторов по 20 Ом каждый и два конденсатора с электроемкостями 15 и 25 мкФ соединены в цепь так, как показано на рисунке. К концам участка подключают источник с ЭДС, равной 0,23 кВ, и внутренним сопротивлением 3,5 Ом. Найти разность потенциалов между обкладками второго конденсатора.


Решение. Между точками A и Б ток не протекает, так как между этими точками в схему включены конденсаторы. Для определения разности потенциалов между указанными точками упростим схему, исключив из рассмотрения участок АБ.

На рис. а показана схема упрощенной цепи.

Ток течет через резисторы R
₁, R
₂, R
₃, R
₄ и R
₆, соединенные последовательно. Общее сопротивление такой цепи:


R
_общ = R
₁ + R
₂ + R
₃ + R
₄ + R
₆ = 5R,

где R
₁ = R
₂ = R
₃ = R
₄ = R
₆ = R.

Сила тока I определяется законом Ома для полной цепи:


I=ℰRобщ+r=ℰ5R+r,

где ℰ — ЭДС источника тока, ℰ = 0,23 кВ; r — внутреннее сопротивление источника тока, r = 3,5 Ом; R
_общ — общее сопротивление цепи, R
_общ = 5R.

Рассчитаем падение напряжения между точками А и Б.

Между точками А и Б находятся резисторы сопротивлениями R
₂, R
₃ и R
₄, соединенные между собой последовательно, как показано на рис. б.

Их общее сопротивление


R
_общ1 = R
₂ + R
₃ + R
₄ = 3R.

Падение напряжения на указанных резисторах определяется формулой


U
_АБ = IR
_общ1,

или в явном виде, —


UАБ=3ℰR5R+r.

Между точками А и Б включена батарея конденсаторов C
₁ и C
₂, соединенных между собой последовательно, как показано на рис. в.

Их общая электроемкость


Cобщ=C1C2C1+C2,

где C
₁ — электроемкость первого конденсатора, C
₁ = 15 мкФ; C
₂ — электроемкость второго конденсатора, C
₂ = 25 мкФ.

Разность потенциалов на обкладках батареи:


Uобщ=qCобщ,

где q — заряд на обкладках каждого из конденсаторов (совпадает с зарядом батареи при последовательном соединении конденсаторов), q = = C
₁U
₁ = C
₂U
₂; U
₁ — разность потенциалов между обкладками первого конденсатора; U
₂ — разность потенциалов между обкладками второго конденсатора (искомая величина).

В явном виде разность потенциалов между обкладками конденсаторов определяется формулой


Uобщ=C2U2Cобщ=(C1+C2)U2C1.

Падение напряжения на резисторах между точками А и Б совпадает с разностью потенциалов на батарее конденсаторов, подключенной к указанным точкам:


U
_АБ = U
_общ.

Данное равенство, записанное в явном виде


3ℰR5R+r=(C1+C2)U2C1,

позволяет получить выражение для искомой величины:


U2=3ℰRC1(5R+r)(C1+C2).

Произведем вычисление:


U2=3⋅0,23⋅103⋅20⋅15⋅10−6(5⋅20+3,5)(15+25)⋅10−6=50 В.

Между обкладками второго конденсатора разность потенциалов составляет 50 В.

Учебное пособие по физике: Комбинированные схемы

Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательного или параллельного соединения. Когда все устройства в цепи соединены последовательным соединением, эта схема называется последовательной схемой. Когда все устройства в цепи соединены параллельными соединениями, тогда схема называется параллельной цепью.Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной и той же цепи. В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .

При анализе комбинированных цепей критически важно иметь твердое представление о концепциях, которые относятся как к последовательным цепям, так и к параллельным цепям.Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.

Цепи серии Ток одинаков на всех резисторах; этот ток равен току в батарее. Сумма падений напряжения на отдельных резисторах равна номинальному напряжению батареи. Общее сопротивление набора резисторов равно сумме отдельных значений сопротивлений, R до = 1 + 2 R 3 + …

Параллельные схемы Падение напряжения одинаково на каждой параллельной ветви. Сумма тока в каждой отдельной ветви равна току вне ветвей. Эквивалентное или полное сопротивление набора резисторов определяется уравнением 1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 …

Каждое из приведенных выше понятий имеет математическое выражение. Комбинирование математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.

Анализ комбинированных схем

Основная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом. Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем полное или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.

Этот метод соответствует формуле

1 / R _экв. = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ + …

, где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, подключенных параллельно. Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, необходимо использовать приведенную выше формулу.Пример этого метода был представлен в предыдущем разделе Урока 4.

Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной схеме, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи. Рассмотрим следующие диаграммы ниже. Схема А представляет собой комбинированную схему с резисторами R ₂ и R ₃ , размещенными в параллельных ветвях.Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет

.

_{рандов до} = ₁ + ₂ рандов + ₃ + …

Итак, на схеме B полное сопротивление цепи составляет 10 Ом.

После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже на двух примерах.

Пример 1:

Первый пример — самый простой — резисторы, включенные параллельно, имеют одинаковое сопротивление. Цель анализа — определить ток и падение напряжения на каждом резисторе.

Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R ₂ и R ₃ ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор 4 Ом включен последовательно с R ₁ и R ₄ . Таким образом, общее сопротивление составляет

.

R _до = R ₁ + 4 Ом + R ₄ = 5 Ом + 4 Ом + 6 Ом

R _общ = 15 Ом

Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).

I _tot = ΔV _tot / R _tot = (60 В) / (15 Ом)

I _до = 4 А

Расчет тока 4 А представляет собой ток в месте расположения батареи. При этом резисторы R ₁ и R ₄ включены последовательно, а ток в последовательно соединенных резисторах везде одинаков.Таким образом,

I _до = I ₁ = I ₄ = 4 А

Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I ₂ + I ₃ должно равняться 4 ампер. Существует бесконечное количество возможных значений I ₂ и I ₃ , которые удовлетворяют этому уравнению. Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны.Следовательно, ток в резисторах 2 и 3 равен 2 А.

I ₂ = I ₃ = 2 А

Теперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.

ΔV ₁ = I ₁ • R ₁ = (4 А) • (5 Ом)

ΔV ₁ = 20 В

ΔV ₂ = I ₂ • R ₂ = (2 А) • (8 Ом)

ΔV ₂ = 16 В

ΔV ₃ = I ₃ • R ₃ = (2 А) • (8 Ом)

ΔV ₃ = 16 В

ΔV ₄ = I ₄ • R ₄ = (4 А) • (6 Ом)

ΔV ₄ = 24 В

На этом анализ завершен, и его результаты представлены на диаграмме ниже.

Пример 2:

Второй пример — более сложный случай — резисторы, включенные параллельно, имеют другое сопротивление. Цель анализа та же — определить ток и падение напряжения на каждом резисторе.

Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить, используя обычную формулу для эквивалентного сопротивления параллельных ветвей:

1 / R _экв = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ …

1 / R _экв = 1 / (4 Ом) + 1 / (12 Ом)

1 / R _экв. = 0,333 Ом ^-1

R _экв = 1 / (0,333 Ом ^-1 )

R _экв = 3.00 Ом

На основании этого расчета можно сказать, что два резистора ответвления (R ₂ и R ₃ ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор 3 Ом включен последовательно с R ₁ и R ₄ . Таким образом, общее сопротивление составляет

.

R _до = R ₁ + 3 Ом + R ₄ = 5 Ом + 3 Ом + 8 Ом

R _общ = 16 Ом

Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).

I _tot = ΔV _tot / R _tot = (24 В) / (16 Ом)

I _до = 1,5 А

Расчет тока 1,5 А представляет собой ток в месте расположения батареи. При этом резисторы R ₁ и R ₄ включены последовательно, а ток в последовательно соединенных резисторах везде одинаков.Таким образом,

I _до = I ₁ = I ₄ = 1,5 А

Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I ₂ + I ₃ должно равняться 1,5 А. Существует бесконечное множество значений I ₂ и I ₃ , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.

Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R ₁ и R ₄ ).Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.

ΔV ₁ = I ₁ • R ₁ = (1,5 А) • (5 Ом)

ΔV ₁ = 7,5 В

ΔV ₄ = I ₄ • R ₄ = (1,5 А) • (8 Ом)

ΔV ₄ = 12 В

Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R ₁ и R ₄ ). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R ₁ и R ₄ . Таким образом,

ΔV ₂ = V ₃ = 4,5 В

Зная падение напряжения на параллельно соединенных резисторах (R ₁ и R ₄ ), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.

I ₂ = ΔV ₂ / R ₂ = (4,5 В) / (4 Ом)

I ₂ = 1,125 А

I ₃ = ΔV ₃ / R ₃ = (4,5 В) / (12 Ом)

I ₃ = 0,375 A

На этом анализ завершен, и его результаты представлены на диаграмме ниже.

Разработка стратегии

Два приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче значения резистора могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.

Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:

• Если схематическая диаграмма не предоставлена, потратьте время на ее создание. Используйте условные обозначения, такие как те, что показаны в примере выше.
• При приближении к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например I _— , I ₁ , R ₃ , ΔV ₂ и т. Д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
• Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
• Преобразуйте комбинированную схему в строго последовательную, заменив (на ваш взгляд) параллельную секцию одним резистором, имеющим значение сопротивления, равное эквивалентному сопротивлению параллельной секции.
• Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при вычислении I ₂ важно подставить в уравнение значения ΔV ₂ и R ₂ .

Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.

Мы хотели бы предложить …

Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, расположить и подключить их так, как вам нужно. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).

Проверьте свое понимание

1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.

а. Ток в точке A равен _____ (больше, равен, меньше) току в точке B.

г. Ток в точке B равен _____ (больше, равен, меньше) ток в точке E.

г. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.

г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.

e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.

ф. Ток в точке A равен _____ (больше, равен, меньше) току в точке L.

г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.

2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)

а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.

г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.

г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.

ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.

3.Используйте концепцию эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.

4. Проанализируйте следующую схему и определите значения общего сопротивления, общего тока, а также тока и падения напряжения на каждом отдельном резисторе.

5. Обращаясь к диаграмме в вопросе №4, определите …

а. … номинальная мощность резистора 4.

г. … скорость, с которой энергия потребляется резистором 3.

Что такое закон Ома? | Fluke

Закон Ома — это формула, используемая для расчета взаимосвязи между напряжением, током и сопротивлением в электрической цепи.

Для изучающих электронику закон Ома (E = IR) столь же фундаментально важен, как уравнение относительности Эйнштейна (E = mc²) для физиков.

E = I x R

Когда прописано, это означает напряжение = ток x сопротивление , или вольт = амперы x ом , или В = A x Ω .

Названный в честь немецкого физика Георга Ома (1789-1854), закон Ома определяет ключевые величины, действующие в цепях:

Количество	Закон Ома символ	Единица измерения (сокращение)	Роль в схемы	Если вам интересно:
Напряжение	E	Вольт (В)	Давление, которое запускает поток электронов	E = электродвижущая сила (старый термин)
Ток	I	Ампер, ампер (A)	Скорость потока электронов	I = интенсивность
Сопротивление	R	Ом (Ом)	Ингибитор потока	Ω = греческая буква omega

Если известны два из этих значений, технические специалисты могут перенастроить закон Ома, чтобы вычислить третье.Просто измените пирамиду следующим образом:

Если вы знаете напряжение (E) и ток (I) и хотите узнать сопротивление (R), вытяните X-образную скобку из R в пирамиде и вычислите оставшееся уравнение (см. Первое или дальнее слева, пирамида вверху).

Примечание: Сопротивление нельзя измерить в рабочей цепи, поэтому закон Ома особенно полезен, когда его нужно вычислить. Вместо того, чтобы отключать цепь для измерения сопротивления, технический специалист может определить R, используя вышеуказанный вариант закона Ома.

Теперь, если вы знаете напряжение (E) и сопротивление (R) и хотите узнать ток (I), вытяните I и вычислите оставшиеся два символа (см. Среднюю пирамиду выше).

И если вы знаете ток (I) и сопротивление (R) и хотите знать напряжение (E), умножьте нижние половины пирамиды (см. Третью или крайнюю правую пирамиду выше).

Попробуйте несколько примеров расчетов на основе простой последовательной схемы, которая включает только один источник напряжения (аккумулятор) и сопротивление (свет).В каждом примере известны два значения. Используйте закон Ома, чтобы вычислить третье.

Пример 1: Напряжение (E) и сопротивление (R) известны.

Какой ток в цепи?

I = E / R = 12 В / 6 Ом = 2 А

Пример 2: Напряжение (E) и ток (I) известны.

Какое сопротивление создает лампа?

R = E / I = 24 В / 6 A = 4 Ом

Пример 3: Ток (I) и сопротивление (R) известны. Какое напряжение?

Какое напряжение в цепи?

E = I x R = (5A) (8Ω) = 40 В

Когда Ом опубликовал свою формулу в 1827 году, его ключевым выводом было то, что величина электрического тока, протекающего через проводник, прямо пропорциональна приложенному напряжению. в теме.Другими словами, требуется один вольт давления, чтобы протолкнуть один ампер тока через один ом сопротивления.

Что проверять с помощью закона Ома

Закон Ома можно использовать для проверки статических значений компонентов схемы, уровней тока, источников напряжения и падений напряжения. Если, например, измерительный прибор обнаруживает более высокое значение измерения тока, чем обычно, это может означать, что сопротивление уменьшилось или что напряжение увеличилось, вызывая ситуацию высокого напряжения. Это может указывать на проблему с питанием или цепью.

В цепях постоянного тока (dc) измерение тока ниже нормального может означать, что напряжение снизилось или сопротивление цепи увеличилось. Возможные причины повышенного сопротивления — плохие или неплотные соединения, коррозия и / или поврежденные компоненты.

Нагрузки в цепи потребляют электрический ток. Нагрузки могут быть любыми компонентами: небольшими электрическими устройствами, компьютерами, бытовой техникой или большим двигателем. На большинстве этих компонентов (нагрузок) есть паспортная табличка или информационная наклейка.На этих паспортных табличках указаны сертификаты безопасности и несколько ссылочных номеров.

Технические специалисты обращаются к заводским табличкам на компонентах, чтобы узнать стандартные значения напряжения и тока. Во время тестирования, если технические специалисты обнаруживают, что обычные значения не регистрируются на их цифровых мультиметрах или токоизмерительных клещах, они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и на основании этого определить, в чем может заключаться проблема.

Основы науки о схемах

Цепи, как и вся материя, состоят из атомов.Атомы состоят из субатомных частиц:

• Протонов (с положительным электрическим зарядом)
• Нейтронов (без заряда)
• Электронов (отрицательно заряженных)

Атомы остаются связанными силами притяжения между ядром атома и электронами в его внешняя оболочка. Под воздействием напряжения атомы в цепи начинают преобразовываться, и их компоненты проявляют потенциал притяжения, известный как разность потенциалов. Взаимно привлеченные свободные электроны движутся к протонам, создавая поток электронов (ток).Любой материал в цепи, ограничивающий этот поток, считается сопротивлением.

Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.

Статьи по теме

Делители напряжения — схемы, уравнения и приложения

Делитель напряжения, также известный как делитель потенциала, представляет собой очень распространенную простую схему, которая используется для преобразования большого напряжения в небольшое. Из этой статьи вы узнаете о:

• Что такое делитель напряжения?
• Цепи делителя напряжения
• Уравнение / формула делителя напряжения
• Применение делителей напряжения

Что такое делитель напряжения?

• Пассивная линейная цепь, вырабатывающая выходное напряжение, составляющее часть входного напряжения.
• Он уменьшает входное напряжение до меньшего напряжения в зависимости от соотношения двух резисторов путем распределения входного напряжения между компонентами делителя.
• Часто используется для подачи напряжения, отличного от имеющегося в наличии аккумулятора или источника питания.
• Выходное напряжение делителя напряжения зависит от сопротивления входящей нагрузки.

Схема делителя напряжения

Схема делителя напряжения обычно выглядит так в схеме с последовательностью из 2 резисторов.

• R1 = резистор, ближайший к входному напряжению (Vin)
• R2 = резистор, ближайший к земле
• В _вход = входное напряжение
• В _выход = выходное напряжение на R2, которое является разделенным напряжением (1/4 от входное напряжение)

Формула / уравнение делителя напряжения

Уравнение для определения выходного напряжения цепи делителя:

R2 / R1 + R2 = Ratio определяет масштабный коэффициент уменьшенного напряжения.

Например,
V _в = 100, ₁ = 20, ₂ = 10

С помощью калькулятора получите:

Правило делителя напряжения

• Правило деления напряжения гласит: Напряжение, разделенное между двумя последовательными резисторами, прямо пропорционально их сопротивлению
• Это означает, что ваша схема может иметь более 2 резисторов!
• Формула правила делителя напряжения:

Пример уравнения правила делителя напряжения:

Закон Ома

Теперь мы можем использовать закон Ома для расчета напряжения, протекающего через каждый резистор:

• Уравнение для закона Ома = E = IR
  • E = Ток на каждом резисторе
  • I = Ток цепи
  • R = Сопротивление

I

	R1	R2	R3	Итого
E (В)	5	10	15	30
2.5 м	2,5	2,5 м	2,5 м
R (Ом)	2K	4K	6K	12K

Таким образом, ток на каждом резисторе составляет 5 В, 10 В и 15 В. соответственно!

Упрощенные уравнения

• Если вы решаете для R1,
• Если вы решаете R2,

Применение делителей напряжения

Цепи делителей напряжения

очень распространены и используются во многих приложениях.Вот несколько примеров того, где находится схема делителя напряжения:

Потенциометр

• Потенциометр — это пассивный электронный компонент с функцией скольжения или вращения, который действует как регулируемый делитель напряжения.
• Входное напряжение подается на всю длину потенциометра, а выходное напряжение (падение напряжения) регулируется с помощью фиксированного и скользящего контакта потенциометра.
• Существует два типа потенциометров
  • Поворотные потенциометры (поворотная ручка)
  • Линейный потенциометр (ползунок)
• Компания Seeed предлагает оба типа!

Grove — Потенциометр скольжения

• Как это работает?
  • Ручной стеклоочиститель, который подвижен, касается резистивной полосы материала.Когда он перемещается ближе к клемме 1 и дальше от клеммы 2, сопротивление уменьшается до клеммы 1, в то время как сопротивление увеличивается на клемме 2, и наоборот.
• Потенциометр полезен для получения переменного напряжения от источника постоянного напряжения. Он может подключать внешние клеммы потенциометра к источнику напряжения и контролировать необходимое напряжение между потенциометром и одной из внешних клемм вашей цепи.
• Потенциометр Grove — Slide включает линейный переменный резистор с максимальным сопротивлением 10 кОм.При перемещении ползунка выходное напряжение будет варьироваться от 0 В до применяемого вами Vcc.
• Он подключается к другим модулям Grove через стандартный 4-контактный кабель Grove.
• Ниже приведено изображение принципиальной схемы потенциометра:
• У него много целей, например, в качестве регулируемого резистора, автономного делителя напряжения с Arduino или даже в качестве устройства интерфейса пользователя (HID), что означает, что его можно использовать для управления автомобилем!
• Некоторые проекты, которые вы можете выполнять с помощью потенциометра Grove — Slide, похожи на создание собственного битбокса или бумбокс на Arduino!

Grove — Датчик угла поворота (P)

• Датчик угла поворота Grove-Rotary (P) способен выдавать аналоговый выходной сигнал от 0 до Vcc (5 В постоянного тока с Seeeduino) на разъеме D1.
• Со значением сопротивления 10 кОм идеально подходит для использования с Arduino.
• Он поддерживается на всех платформах MCU, таких как Arduino, Raspberry Pi, BeagleBone, Wio, а также LinkIt ONE.
• Один из проектов, который вы можете сделать с этим потенциометром, — это использовать его для управления яркостью светодиодов.

Использование Arduino для управления яркостью светодиода с помощью датчика угла поворота Grove-Rotary (P)

Grove — Делитель напряжения

• Grove — делитель напряжения обеспечивает интерфейс для измерения внешнего напряжения, который устраняет необходимость подключения сопротивления к входному интерфейсу.
• С помощью дискового переключателя вы можете легко выбрать коэффициент усиления напряжения, что упрощает его использование.

Чтение резистивных датчиков

• Большинство датчиков представляют собой простые резистивные устройства, такие как наш Grove — инфракрасный датчик отражения. Однако большинство из них могут считывать только напряжение, но не сопротивление.
• Добавив в схему еще один резистор, мы можем создать делитель напряжения вместе с датчиком.
• Поскольку мы можем проверить выход делителя напряжения, теперь мы можем рассчитать величину сопротивления датчика.
• Пример схемы показан ниже, где R2 — резистивный датчик:
• Например, резистивный датчик — это датчик температуры Grove, который представляет собой термистор с сопротивлением комнатной температуры 350 Ом, где сопротивление R1 фиксировано на 350 Ом.
• Использование уравнения делителя напряжения:

Температура	Vin (фиксированный)	R2	R1	R2 / (R1 + R2)	Vout
Холодный	5V	300 Ом	350 Ом .46	2,3 В
Комнатная температура	5 В	350 Ом	350 Ом	0,5	2,5 В
Горячий	5 В	400 Ом	350 Ом	0,53	2,65 В

Переключатели уровня

• Что происходит, когда встречаются датчик и микроконтроллер с двумя разными напряжениями? Без выравнивания напряжения, например, напрямую связав микроконтроллер с логическим выходом 5 В с микроконтроллером 3.Входной датчик 3 В может вызвать повреждение цепи 3,3 В.
• Вот где главный герой: делитель напряжения спасает положение, действуя как переключатель уровня, соединяющий две цепи, использующие разные рабочие напряжения.
• Делитель напряжения может помочь выровнять напряжение с микроконтроллера (например, с 5 В до 3,3 В), чтобы избежать повреждения датчика, что делает его безопасным для обращения с датчиком.
• Обратите внимание, что делитель напряжения может работать только в одном направлении: понижать напряжение, но не повышать.
• Вот таблица комбинаций резисторов для понижения часто встречающихся напряжений:

Комбинация резисторов	Напряжения, которые необходимо выровнять
4,7 кОм и 3,9 кОм	9В до 5В
3,6 кОм и 9,1 кОм	от 12В до 3,3В
от 3,3 кОм и 5,7 кОм	от 9В до 3,3В

• Обратите внимание, что не рекомендуется использовать делитель напряжения для понижения уровня большой нагрузки, такой как 12В. до 5 В, поскольку они не предназначены для подачи такого питания на нагрузку, как с такой нагрузкой, это может расплавить резистор.(Вместо этого вы можете использовать регуляторы напряжения, такие как наш регулируемый преобразователь постоянного и постоянного тока (1,25 В — 35 В и 3 А)

Резюме

Обладая всеми знаниями делителя напряжения в ваших руках, вы можете превратить любое напряжение в меньшее, как фокусник! Хотите проверить свои навыки, создав свой собственный проект делителя напряжения? Вот несколько идей проектов, которые помогут вам начать использовать потенциометр и Arduino для создания битбокса или бумбокса на нашей вики-странице: Grove — Slide Potentiometer Wiki

Следите за нами и ставьте лайки:

Продолжить чтение

энергии в конденсаторах | Физика

Цели обучения

К концу этого раздела вы сможете:

• Перечислите некоторые варианты использования конденсаторов.
• Выразите в виде уравнения энергию, запасенную в конденсаторе.
• Объясните функцию дефибриллятора.

Большинство из нас видели инсценировки, в которых медицинский персонал использовал дефибриллятор , чтобы пропустить электрический ток через сердце пациента, чтобы заставить его нормально биться. (Просмотрите рис. 1.) Часто реалистичный в деталях, человек, применяющий электрошок, просит другого человека «сделать на этот раз 400 джоулей». Энергия, передаваемая дефибриллятором, накапливается в конденсаторе и может регулироваться в зависимости от ситуации.Часто используются единицы СИ — джоули. Менее драматично использование конденсаторов в микроэлектронике, например в некоторых портативных калькуляторах, для подачи энергии при зарядке аккумуляторов. (См. Рис. 1.) Конденсаторы также используются для питания ламп-вспышек на камерах.

Рис. 1. Энергия, накопленная в большом конденсаторе, используется для сохранения памяти электронного калькулятора, когда его батареи заряжены. (Источник: Kucharek, Wikimedia Commons)

Энергия, запасенная в конденсаторе, представляет собой электрическую потенциальную энергию, и, таким образом, она связана с зарядом Q и напряжением В на конденсаторе.Мы должны быть осторожны при применении уравнения для электрической потенциальной энергии ΔPE = q Δ V к конденсатору. Помните, что ΔPE — это потенциальная энергия заряда q , проходящего через напряжение Δ В . Но конденсатор начинает с нулевого напряжения и постепенно достигает своего полного напряжения по мере зарядки. Первый заряд, помещенный на конденсатор, испытывает изменение напряжения Δ В = 0, поскольку конденсатор имеет нулевое напряжение в незаряженном состоянии.Последний заряд, помещенный на конденсатор, испытывает Δ В = В , так как конденсатор теперь имеет на нем свое полное напряжение В . Среднее напряжение на конденсаторе во время процесса зарядки составляет [латекс] \ frac {V} {2} \\ [/ latex], поэтому среднее напряжение, испытываемое при полной зарядке q , составляет [латекс] \ frac {V} {2} \\ [/ латекс]. Таким образом, энергия, запасенная в конденсаторе, E _cap , равна [latex] E _ {\ text {cap}} = \ frac {QV} {2} \\ [/ latex], где Q — это заряд на конденсаторе приложено напряжение В .2} {2C} \\ [/ latex],

, где Q — заряд, В, — напряжение, а C — емкость конденсатора. Энергия выражается в джоулях для заряда в кулонах, напряжения в вольтах и ​​емкости в фарадах.

В дефибрилляторе доставка большого заряда коротким импульсом к набору лопастей на груди человека может быть спасением. Инфаркт у человека мог возникнуть в результате быстрого, нерегулярного сердцебиения — фибрилляции сердца или желудочков.Применение сильного разряда электрической энергии может прекратить аритмию и позволить кардиостимулятору тела вернуться к нормальному режиму. Сегодня в машинах скорой помощи обычно есть дефибриллятор, который также использует электрокардиограмму для анализа сердечного ритма пациента. Автоматические внешние дефибрилляторы (AED) можно найти во многих общественных местах (рис. 2). Они предназначены для использования непрофессионалами. Устройство автоматически диагностирует состояние сердца пациента, а затем применяет разряд с соответствующей энергией и формой волны.Во многих случаях перед использованием АВД рекомендуется СЛР.

Рис. 2. Автоматические внешние дефибрилляторы можно найти во многих общественных местах. Эти портативные устройства предоставляют устные инструкции по использованию в первые несколько важных минут для человека, страдающего сердечным приступом. (Источник: Оуайн Дэвис, Wikimedia Commons)

Пример 1. Емкость дефибриллятора сердца

Дефибриллятор сердца вырабатывает 4,00 × 10 ² Дж энергии за счет разряда конденсатора первоначально на 1.{-6} \ text {F} \\\ text {} & = & 8.00 \ mu \ text {F} \ end {array} \\ [/ latex]

Обсуждение

Это довольно большая, но управляемая емкость при 1,00 × 10 ⁴ В.

Сводка раздела

• Конденсаторы используются в различных устройствах, включая дефибрилляторы, микроэлектронику, такую ​​как калькуляторы, и лампы-вспышки, для подачи энергии.
• Энергия, запасенная в конденсаторе, может быть выражена тремя способами: [латекс] {E} _ {\ text {cap}} = \ frac {\ text {QV}} {2} = \ frac {{\ text {CV }} ^ {2}} {2} = \ frac {{Q} ^ {2}} {2C} \\ [/ latex], где Q — это заряд, В, — напряжение, а C — емкость конденсатора.Энергия выражается в джоулях, когда заряд — в кулонах, напряжение — в вольтах, а емкость — в фарадах.

Концептуальные вопросы

1. Как изменяется энергия, содержащаяся в заряженном конденсаторе, когда вставлен диэлектрик, если конденсатор изолирован и его заряд постоянен? Означает ли это, что работа была сделана?
2. Что происходит с энергией, накопленной в конденсаторе, подключенном к батарее, когда вставлен диэлектрик? Была ли проделана работа в процессе?

Задачи и упражнения

1. (a) Какая энергия хранится в 10.0 мкФ конденсатор дефибриллятора сердца заряжен до
   9,00 × 10 ³ В? (b) Найдите количество накопленного заряда.
2. При операции на открытом сердце гораздо меньшее количество энергии вызывает дефибрилляцию сердца. (a) Какое напряжение приложено к конденсатору 8,00 мкФ дефибриллятора сердца, который накапливает 40,0 Дж энергии? (b) Найдите количество накопленного заряда.
3. Конденсатор емкостью 165 мкФ используется вместе с двигателем. Сколько энергии в нем хранится при подаче 119 В?
4. Предположим, у вас есть 9.Батарея 00 В, конденсатор 2,00 мкФ и конденсатор 7,40 мкФ. (а) Найдите заряд и запасенную энергию, если конденсаторы подключены к батарее последовательно. (б) Сделайте то же самое для параллельного подключения.
5. Нервный физик опасается, что две металлические полки его книжного шкафа с деревянным каркасом могут получить высокое напряжение, если они заряжены статическим электричеством, возможно, вызванным трением. (а) Какова емкость пустых полок, если они имеют площадь 1,00 × 10 ² м ² и равны 0.200 м друг от друга? (б) Какое напряжение между ними, если на них помещены противоположные заряды величиной 2,00 нКл? (c) Чтобы показать, что это напряжение представляет небольшую опасность, рассчитайте запасенную энергию.
6. Покажите, что для данного диэлектрического материала максимальная энергия, которую может хранить конденсатор с параллельными пластинами, прямо пропорциональна объему диэлектрика (Объем = A · d ). Обратите внимание, что приложенное напряжение ограничено диэлектрической прочностью.
7. Создай свою задачу. Рассмотрим дефибриллятор сердца, аналогичный описанному в примере 1. Постройте задачу, в которой вы исследуете заряд, накопленный в конденсаторе дефибриллятора, как функцию накопленной энергии. Среди факторов, которые следует учитывать, — это приложенное напряжение и то, должно ли оно меняться в зависимости от подаваемой энергии, диапазон задействованных энергий и емкость дефибриллятора. Вы также можете рассмотреть гораздо меньшую энергию, необходимую для дефибрилляции во время операции на открытом сердце, как вариант решения этой проблемы.
8. Необоснованные результаты. (a) В определенный день для запуска двигателя грузовика требуется 9,60 × 10 ³ Дж электроэнергии. Вычислите емкость конденсатора, способного хранить такое количество энергии при напряжении 12,0 В. (б) Что неразумного в этом результате? (c) Какие допущения ответственны?

Глоссарий

дефибриллятор: устройство, используемое для электрического разряда сердца пострадавшего от сердечного приступа с целью восстановления нормального ритмического паттерна сердца

Избранные решения проблем и упражнения

1.(а) 405 Дж; (б) 90,0 мС

2. (а) 3,16 кВ; (б) 25,3 мС

4. (а) 1.42 × 10 ⁻⁵ C, 6.38 × 10 ⁻⁵ Дж; (б) 8.46 × 10 ⁻⁵ C, 3.81 × 10 ⁻⁴ J

5. (а) 4,43 × 10 ^–12 F; б) 452 В; (в) 4.52 × 10 ^–7 Дж

8. (а) 133 F; (б) Такой конденсатор будет слишком большим для перевозки в грузовике. Размер конденсатора был бы огромным; (c) Неразумно предполагать, что конденсатор может хранить необходимое количество энергии.

19,4 Электроэнергия | Texas Gateway

Цели обучения

К концу этого раздела вы сможете сделать следующее:

• Определить электрическую мощность и описать уравнение электрической мощности
• Расчет электрической мощности в цепях резисторов в последовательном, параллельном и сложном расположении

Раздел Ключевые термины

электроэнергия

Энергия для многих ассоциируется с электричеством.Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи — наглядные примеры электроэнергии, обеспечивающей мощность. Мы также используем электроэнергию для запуска автомобилей, работы компьютеров или освещения дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность — это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это означает, но и какие факторы определяют электрическую мощность.

Для начала представим себе лампочки, которые часто характеризуются номинальной мощностью в ваттах.Давайте сравним лампочку мощностью 25 Вт с лампой мощностью 60 Вт (см. Рисунок 19.23). Хотя обе работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходную мощность электрической цепи определяет нечто иное, чем напряжение.

Лампы накаливания, такие как две, показанные на рисунке 19.23, по сути являются резисторами, которые нагреваются, когда через них протекает ток, и становятся настолько горячими, что излучают видимый и невидимый свет. Таким образом, две лампочки на фото можно рассматривать как два разных резистора.В простой цепи, такой как электрическая лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, а также напряжение должны определять мощность.

Рисунок 19.23 Слева лампочка мощностью 25 Вт, а справа лампочка мощностью 60 Вт. Почему их выходная мощность различается, несмотря на то, что они работают при одинаковом напряжении?

Формулу мощности можно найти путем анализа размеров. Рассмотрим единицы мощности. В системе СИ мощность указывается в ваттах (Вт), которые представляют собой энергию в единицу времени, или Дж / с.

Напомним, что напряжение — это потенциальная энергия на единицу заряда, что означает, что напряжение имеет единицы Дж / Кл.

Мы можем переписать это уравнение как J = V × CJ = V × C и подставить его в уравнение для ватт, чтобы получить

W = Js = V × Cs = V × Cs.W = Js = V × Cs = V × Cs.

Но кулон в секунду (Кл / с) — это электрический ток, который мы можем видеть из определения электрического тока, I = ΔQΔtI = ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или

. Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .

Например, рассмотрим схему на рисунке 19.24. Согласно закону Ома, ток, протекающий по цепи, равен

19,49I = VR = 12 В 100 Ом = 0,12 AI = VR = 12 В 100 Ом = 0,12 А.

Таким образом, мощность, потребляемая цепью, составляет

19,50P = VI. = (12 В) (0,12 А) = 1,4 WP = VI = (12 В) (0,12 А) = 1,4 Вт.

Куда уходит эта мощность? В этой схеме мощность в основном идет на нагрев резистора в этой цепи.

Рисунок 19.24 Простая схема, потребляющая электроэнергию.

При вычислении мощности в цепи, показанной на рисунке 19.24, мы использовали сопротивление и закон Ома, чтобы найти ток.Закон Ома дает ток: I = V / RI = V / R, который мы можем вставить в уравнение для электроэнергии, чтобы получить

P = IV = (VR) V = V2R.P = IV = (VR) V = V2R.

Это дает мощность с точки зрения только напряжения и сопротивления.

Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электроэнергии и получить выражение для мощности, выраженное только через ток и сопротивление. Если мы запишем закон Ома как V = IRV = IR
и используя это, чтобы исключить V в уравнении P = IVP = IV, мы получим

P = IV = I (IR) = I2R.P = IV = I (IR) = I2R.

Это дает мощность с точки зрения только тока и сопротивления.

Таким образом, комбинируя закон Ома с уравнением P = IVP = IV для электроэнергии, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (не емкость или что-либо еще), ток и напряжение. Это означает, что физической характеристикой схемы, определяющей, сколько мощности она рассеивает, является ее сопротивление.Конденсаторы в цепи не рассеивают электроэнергию — напротив, конденсаторы либо накапливают электрическую энергию, либо отдают ее обратно в цепь.

Чтобы прояснить связь между напряжением, сопротивлением, током и мощностью, рассмотрим рисунок 19.25, на котором показано колесо формул . Количества в центральной четверти круга равны количествам в соответствующей внешней четверти круга. Например, чтобы выразить потенциал V через мощность и ток, мы видим из колеса формул, что V = P / IV = P / I.

Рисунок 19.25 Колесо формул показывает, как связаны между собой вольт, сопротивление, ток и мощность. Количества во внутренней четверти окружности равны количеству в соответствующей внешней четверти окружности.

Рабочий пример

Найдите сопротивление лампочки

Типичная старая лампа накаливания имела мощность 60 Вт. Если предположить, что к лампочке приложено 120 В, каков ток через лампочку?

СТРАТЕГИЯ

Нам даны напряжение и выходная мощность простой схемы, содержащей лампочку, поэтому мы можем использовать уравнение P = IVP = IV, чтобы найти ток I , который течет через лампочку.

Решение

Решение P = IVP = IV для тока и вставка данных значений для напряжения и мощности дает

19,51 P = IVI = PV = 60 Вт 120 V = 0,50 А. P = IVI = PV = 60 Вт 120 В = 0,50 А.

Таким образом, при подаче 120 В. через лампочку проходит половина ампера.

Обсуждение

Это значительное течение. Напомним, что в быту используется переменный, а не постоянный ток, поэтому 120 В, подаваемое от бытовых розеток, — это переменная, а не постоянная мощность. Фактически, 120 В — это усредненная по времени мощность, обеспечиваемая такими розетками.Таким образом, средний ток, протекающий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.

Рабочий пример

Подогреватели ботинок

Чтобы согреть ботинки в холодные дни, вы решили вшить цепь с некоторыми резисторами в стельку ботинок. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите, чтобы они работали от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление вы должны приложить к каждой стельке?

СТРАТЕГИЯ

Нам известны требуемая мощность и напряжение (18 В, потому что у нас есть две батареи на 9 В, соединенные последовательно), поэтому мы можем использовать уравнение P = V2 / RP = V2 / R, чтобы найти необходимое сопротивление.

Решение

Решая P = V2 / RP = V2 / R для сопротивления и вставляя заданные напряжение и мощность, получаем

19,52P = V2RR = V2P = (18 В) 210 Вт = 32 Ом. P = V2RR = V2P = (18 В) 210 Вт = 32 Ом.

Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.

Обсуждение

Давайте посмотрим, сколько тока пройдет через эту цепь. У нас есть 18 В, приложенное к сопротивлению 32 Ом, поэтому закон Ома дает

19,53 I = VR = 18 В 32 Ом = 0,56 А. I = VR = 18 В 32 Ом = 0,56 А.

На всех батареях есть этикетки, на которых указано, сколько заряда они могут доставить (в единицах силы тока, умноженного на время).Типичная щелочная батарея 9 В может обеспечить заряд 565 мА · ч · мА · ч.
(так две батареи 9 В обеспечивают 1130 мА · ч · мА · ч), поэтому эта система обогрева проработает в течение

часов.
19,54t = 1130 × 10−3 A⋅h0,56 A = 2,0 h.t = 1130 × 10−3 A⋅h0,56 A = 2,0 час.

Рабочий пример

Питание через ответвление цепи

Каждый резистор в приведенной ниже схеме имеет сопротивление 30 Ом. Какая мощность рассеивается средней ветвью схемы?

СТРАТЕГИЯ

Средняя ветвь схемы содержит последовательно включенные резисторы R3 и R5R3 и R5.Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем используем P = V2 / RP = V2 / R, чтобы найти мощность, рассеиваемую в ветви.

Решение

Эквивалентное сопротивление: R среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом R среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом. Мощность, рассеиваемая средней ветвью схемы, составляет

ед.
19,55P средний = V2R средний = (12 В) 260 Ом = 2,4 Вт. Средний = V2R средний = (12 В) 260 Ом = 2,4 Вт.

Обсуждение

Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, обеспечиваемой батареей.Во-первых, эквивалентное сопротивление левой ветви

19,56 Влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом + 30 Ом = 45 Ом. Влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом +30 Ом = 45 Ом.

Мощность через левую ветвь

19,57 Слева = V2R, слева = (12 В) 245 Ом = 3,2 Вт. Слева = V2R, слева = (12 В) 245 Ом = 3,2 Вт.

Правая ветвь содержит только R6R6, поэтому эквивалентное сопротивление Rright = R6 = 30 ΩRright = R6 = 30 Ω. Мощность через правую ветку

19,58 Правый = V2 Правый = (12 В) 230 Ом = 4,8 Вт. Правый = V2 Правый = (12 В) 230 Ом = 4,8 Вт.

Общая мощность, рассеиваемая схемой, представляет собой сумму мощностей, рассеиваемых в каждой ветви.

19,59P = складка + середина + прядь = 2,4 Вт + 3,2 Вт + 4,8 Вт = 10,4 WP = складка + середина + прядь = 2,4 Вт + 3,2 Вт + 4,8 Вт = 10,4 Вт

Мощность, обеспечиваемая аккумулятором, составляет

.

, где I — полный ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить I . Ветви вносят токи

19,61 слева = VR слева = 12 В 45 Ом = 0.2667 AIсредний = VR средний = 12 В 60 Ом = 0.20 AIright = VRright = 12 В 30 Ом = 0,40 A. Левый = VR Левый = 12 В 45 Ом = 0,2667 AI Средний = VR средний = 12 В 60 Ом = 0,20 AIright = VRright = 12 В 30 Ом = 0,40 А.

Суммарный ток

19,62 I = слева + Imiddle + I right = 0,2667 A + 0,20 A + 0,40 A = 0,87 A. I = I слева + Imiddle + I right = 0,2667 A + 0,20 A + 0,40 A = 0,87 A.

, а мощность, обеспечиваемая аккумулятором, составляет

19,63P = IV = (0,87 A) (12 В) = 10,4 Вт. P = IV = (0,87 A) (12 В) = 10,4 Вт.

Это та же мощность, которая рассеивается на резисторах схемы, что показывает, что в этой цепи сохраняется энергия.

7.2 Электрический потенциал и разность потенциалов — Университетская физика, Том 2

Цели обучения

К концу этого раздела вы сможете:

• Определение электрического потенциала, напряжения и разности потенциалов
• Определите электрон-вольт
• Вычислить электрический потенциал и разность потенциалов на основе потенциальной энергии и электрического поля
• Опишите системы, в которых электрон-вольт является полезной единицей.
• Применение энергосбережения в электрических системах

Напомним, что ранее мы определили электрическое поле как величину, не зависящую от тестового заряда в данной системе, что, тем не менее, позволило бы нам вычислить силу, которая возникнет при произвольном тестовом заряде.(При отсутствии другой информации по умолчанию предполагается, что тестовый заряд положительный.) Мы кратко определили поле для гравитации, но гравитация всегда притягивает, тогда как электрическая сила может быть либо притягивающей, либо отталкивающей. Следовательно, хотя потенциальная энергия вполне достаточна в гравитационной системе, удобно определить величину, которая позволяет нам вычислить работу над зарядом независимо от величины заряда. Непосредственный расчет работы может быть затруднен, поскольку W = F → · d → W = F → · d →, а направление и величина F → F → могут быть сложными для нескольких зарядов, для объектов нечетной формы и вдоль произвольных путей. .Но мы знаем, что, поскольку F → = qE → F → = qE →, работа и, следовательно, ΔU, ΔU, пропорциональны пробному заряду q . Чтобы получить физическую величину, не зависящую от испытательного заряда, мы определяем электрический потенциал В (или просто потенциал, поскольку понимается электрический) как потенциальную энергию на единицу заряда:

Электрический потенциал

Потенциальная электрическая энергия на единицу заряда составляет

Поскольку U пропорционально q , зависимость от q отменяется.Таким образом, V не зависит от q . Изменение потенциальной энергии ΔUΔU имеет решающее значение, поэтому нас беспокоит разность потенциалов или разность потенциалов ΔVΔV между двумя точками, где

ΔV = VB − VA = ΔUq.ΔV = VB − VA = ΔUq.

Разница электрических потенциалов

Разность электрических потенциалов между точками A и B , VB-VA, VB-VA, определяется как изменение потенциальной энергии заряда q , перемещенного с A на B , деленное на заряд.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

Знакомый термин «напряжение» — это общее название разности электрических потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками. Например, каждая батарея имеет две клеммы, а ее напряжение — это разность потенциалов между ними. По сути, точка, которую вы выбираете равным нулю вольт, произвольна. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например, на уровне моря или, возможно, на полу лекционного зала.Стоит подчеркнуть различие между разностью потенциалов и электрической потенциальной энергией.

Разность потенциалов и электрическая потенциальная энергия

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется формулой

.
ΔV = ΔUqorΔU = qΔV.ΔV = ΔUqorΔU = qΔV.

7,5

Напряжение — это не то же самое, что энергия. Напряжение — это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между выводами аккумулятора), но при этом один хранит гораздо больше энергии, чем другой, потому что ΔU = qΔV.ΔU = qΔV. Автомобильный аккумулятор может заряжать больше, чем аккумулятор мотоцикла, хотя оба аккумулятора — 12 В.

Пример 7,4

Расчет энергии

У вас есть мотоциклетный аккумулятор на 12,0 В, способный обеспечить заряд на 5000 C, и автомобильный аккумулятор на 12,0 В, способный обеспечить заряд на 60 000 C. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда имеет точность до трех значащих цифр.)

Стратегия

Сказать, что у нас есть батарея на 12,0 В, означает, что на ее выводах есть 12.Разность потенциалов 0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряд получает изменение потенциальной энергии, равное ΔU = qΔV.ΔU = qΔV. Чтобы найти выход энергии, мы умножаем перемещенный заряд на разность потенциалов.

Решение

Для аккумулятора мотоцикла q = 5000Cq = 5000C и ΔV = 12,0VΔV = 12,0V. Полная энергия, отдаваемая аккумулятором мотоцикла, составляет
ΔUцикл = (5000 ° C) (12,0 В) = (5000 ° C) (12,0 Дж / ° C) = 6,00 × 104 Дж. ΔUцикл = (5000 ° C) (12,0 В) = (5000 ° C) (12.0Дж / Кл) = 6,00 × 104Дж.

Аналогично для автомобильного аккумулятора q = 60,000 Cq = 60,000C и

ΔUcar = (60,000C) (12,0В) = 7,20 × 105Дж. ΔUcar = (60,000C) (12,0В) = 7,20 × 105Дж.

Значение

Напряжение и энергия связаны, но это не одно и то же. Напряжения батарей одинаковы, но энергия, подаваемая каждым из них, совершенно разная. Автомобильный аккумулятор требует запуска гораздо более мощного двигателя, чем мотоцикл. Также обратите внимание, что когда аккумулятор разряжается, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за разряда автомобильного аккумулятора.Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

Проверьте свое понимание 7.4

Сколько энергии у 1,5-В батареи AAA, которая может нагреться до 100 градусов Цельсия?

Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию. Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд — в частности, электроны.Батареи отталкивают электроны от своих отрицательных выводов ( A ) через любую задействованную схему и притягивают их к своим положительным выводам ( B ), как показано на рисунке 7.12. Изменение потенциала составляет ΔV = VB − VA = + 12 В ΔV = VB − VA = + 12 В, а заряд q отрицательный, так что ΔU = qΔVΔU = qΔV является отрицательным, что означает, что потенциальная энергия батареи уменьшилась, когда q переместился с A на B .

Рисунок 7.12 Аккумулятор перемещает отрицательный заряд от отрицательной клеммы через фару к ее положительной клемме.Соответствующие комбинации химикатов в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается к избыточному положительному заряду на другом выводе. С точки зрения потенциала положительный вывод находится под более высоким напряжением, чем отрицательный. Внутри аккумулятора движутся как положительные, так и отрицательные заряды.

Пример 7.5

Сколько электронов проходит через фару каждую секунду?

Когда автомобильный аккумулятор 12,0 В питает один аккумулятор 30.Фара 0-W, сколько электронов проходит через нее каждую секунду?

Стратегия

Чтобы узнать количество электронов, мы должны сначала найти заряд, который перемещается за 1,00 с. Перемещаемый заряд связан с напряжением и энергией посредством уравнений ΔU = qΔV.ΔU = qΔV. Лампа мощностью 30,0 Вт потребляет 30,0 джоулей в секунду. Поскольку батарея теряет энергию, мы имеем ΔU = -30JΔU = -30J, и, поскольку электроны переходят от отрицательной клеммы к положительной, мы видим, что ΔV = + 12.0V.ΔV = + 12.0V.

Решение

Чтобы найти заряд q перемещенного, решаем уравнение ΔU = qΔV: ΔU = qΔV:

Вводя значения ΔUΔU и ΔVΔV, получаем

q = -30.0J + 12,0V = -30,0J + 12,0J / C = -2,50C. Q = -30,0J + 12,0V = -30,0J + 12,0J / C = -2,50C.

Число электронов nene — это общий заряд, деленный на заряд одного электрона. То есть

ne = −2,50C − 1,60 · 10−19C / e− = 1,56 · 1019 электронов. ne = −2,50C − 1,60 · 10−19C / e− = 1,56 · 1019 электронов.

Значение

Это очень большое количество. Неудивительно, что мы обычно не наблюдаем отдельные электроны, так много которых присутствует в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих обстоятельствах были отрицательными.Положительный заряд, движущийся в направлении, противоположном отрицательному, часто производит идентичные эффекты; это затрудняет определение того, что движется или оба движутся.

Проверьте свое понимание 7,5

Сколько электронов прошло через лампу мощностью 24,0 Вт?

Электрон-вольт

Энергия, приходящаяся на один электрон, очень мала в макроскопических ситуациях, подобных тому, что было в предыдущем примере — крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на частицу (электрон, протон или ион), может иметь большое значение.Например, даже крошечной доли джоуля может быть достаточно, чтобы эти частицы разрушили органические молекулы и повредили живые ткани. Частица может нанести ущерб при прямом столкновении или может создать опасные рентгеновские лучи, которые также могут нанести ущерб. Полезно иметь единицу энергии, относящуюся к субмикроскопическим эффектам.

На рис. 7.13 показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как это могло бы быть в телевизионной лампе или осциллографе старой модели.Электрон приобретает кинетическую энергию, которая позже преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что с точки зрения энергии «спуск» для электрона означает «подъем» для положительного заряда.) Поскольку энергия связана с напряжением соотношением ΔU = qΔVΔU = qΔV, мы можем рассматривать джоуль как кулон-вольт.

Рис. 7.13 Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя отдельными металлическими пластинами. По закону сохранения энергии кинетическая энергия должна равняться изменению потенциальной энергии, поэтому KE = qVKE = qV.Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны с энергией 5000 эВ. Концептуальная конструкция, а именно две параллельные пластины с отверстием в одной, показана на (a), а реальная электронная пушка показана на (b).

электрон-вольт

В субмикроскопическом масштабе удобнее определять единицу энергии, называемую электрон-вольт (эВ), которая представляет собой энергию, передаваемую фундаментальному заряду, ускоренному через разность потенциалов в 1 В.В форме уравнения,

1эВ = (1,60 × 10−19C) (1V) = (1,60 × 10−19C) (1J / C) = 1,60 × 10−19J. 1эВ = (1,60 × 10−19C) (1V) = (1,60 × 10− 19C) (1Дж / Кл) = 1,60 × 10−19Дж.

Электрону, ускоренному через разность потенциалов 1 В, придается энергия 1 эВ. Отсюда следует, что электрон, ускоренный до 50 В, приобретает 50 эВ. Разность потенциалов 100 000 В (100 кВ) дает электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получает 200 эВ энергии.Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.

Электрон-вольт обычно используется в субмикроскопических процессах — химическая валентная энергия, молекулярная и ядерная энергия связи входят в число величин, часто выражаемых в электрон-вольтах. Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, он приобретает энергию 30 кэВ (30 000 эВ) и может разрушить до 6000 этих молекул (30 000 эВ ÷ 5 эВ на молекулу = 6000 молекул).(30,000 эВ ÷ 5 эВ на молекулу = 6000 молекул). Энергия ядерного распада составляет порядка 1 МэВ (1000000 эВ) на событие и, таким образом, может нанести значительный биологический ущерб.

Сохранение энергии

Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) из-за работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия постоянна.

Механическая энергия — это сумма кинетической энергии и потенциальной энергии системы; то есть K + U = константа.K + U = постоянная. Потеря U для заряженной частицы становится увеличением ее K . Сохранение энергии выражается в форме уравнения как

или

, где i и f обозначают начальные и конечные условия. Как мы уже много раз выясняли ранее, учет энергии может дать нам понимание и облегчить решение проблем.

Пример 7.6

Электрическая потенциальная энергия, преобразованная в кинетическую энергию

Вычислите конечную скорость свободного электрона, ускоренного из состояния покоя, через разность потенциалов 100 В.(Предположим, что это числовое значение имеет точность до трех значащих цифр.)

Стратегия

У нас есть система, в которой действуют только консервативные силы. Предполагая, что электрон ускоряется в вакууме, и пренебрегая гравитационной силой (мы проверим это предположение позже), вся электрическая потенциальная энергия преобразуется в кинетическую энергию. Мы можем идентифицировать начальную и конечную формы энергии как Ki = 0, Kf = 12mv2, Ui = qV, Uf = 0. Ki = 0, Kf = 12mv2, Ui = qV, Uf = 0.

Решение

Сохранение энергии утверждает, что

Вводя указанные выше формы, получаем

Решаем это для v :

Ввод значений для q , V и м дает

v = 2 (−1.60 × 10−19C) (- 100Дж / C) 9,11 × 10−31 кг = 5,93 × 106 м / зв = 2 (−1.60 × 10−19C) (- 100Дж / C) 9,11 × 10−31 кг = 5,93 × 106 м / с .

Значение

Обратите внимание, что и заряд, и начальное напряжение отрицательны, как показано на рисунке 7.13. Из обсуждения электрического заряда и электрического поля мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой тяжести. Большая конечная скорость подтверждает, что гравитационная сила здесь действительно незначительна. Большая скорость также указывает на то, насколько легко ускорить электроны с помощью малых напряжений из-за их очень малой массы.В электронных пушках обычно используются напряжения, намного превышающие 100 В. Эти более высокие напряжения вызывают настолько большие скорости электронов, что необходимо учитывать эффекты специальной теории относительности, и поэтому они оставлены для более поздней главы (Теория относительности). Вот почему в этом примере мы рассматриваем низкое напряжение (точно).

Проверьте свое понимание 7.6

Как этот пример изменится с позитроном? Позитрон идентичен электрону, за исключением того, что заряд положительный.

Напряжение и электрическое поле

До сих пор мы исследовали взаимосвязь между напряжением и энергией. Теперь мы хотим изучить взаимосвязь между напряжением и электрическим полем. Начнем с общего случая для неоднородного поля E → E →. Напомним, что наша общая формула для потенциальной энергии пробного заряда q в точке P относительно реперной точки R равна

UP = −RPF → · dl → ..доктор

, что упрощается до

Vr = −∫∞rkqr2dr = kqr − kq∞ = kqr.Vr = −∫∞rkqr2dr = kqr − kq∞ = kqr.

Этот результат,

— это стандартная форма потенциала точечного заряда. Это будет подробнее рассмотрено в следующем разделе.

Чтобы изучить еще один интересный частный случай, предположим, что однородное электрическое поле E → E → создается путем размещения разности потенциалов (или напряжения) ΔVΔV на двух параллельных металлических пластинах, обозначенных A и B (рис. 7.14). Изучение этой ситуации покажет нам, какое напряжение необходимо для создания определенного электрического поля.Это также покажет более фундаментальную взаимосвязь между электрическим потенциалом и электрическим полем.

Рисунок 7.14. Соотношение между V и E для параллельных проводящих пластин составляет E = V / dE = V / d. (Обратите внимание, что ΔV = VABΔV = VAB по величине. Для заряда, который перемещается от пластины A при более высоком потенциале к пластине B при более низком потенциале, необходимо включить знак минус следующим образом: −ΔV = VA − VB = VAB. − ΔV = VA − VB = VAB.)

С точки зрения физика, для описания любого взаимодействия между зарядами можно использовать ΔVΔV или E → E →.Однако ΔVΔV является скалярной величиной и не имеет направления, тогда как E → E → является векторной величиной, имеющей как величину, так и направление. (Обратите внимание, что величина электрического поля, скалярная величина, представлена ​​как E .) Связь между ΔVΔV и E → E → выявляется путем расчета работы, совершаемой электрической силой при перемещении заряда из точки A. к пункту B . Но, как отмечалось ранее, произвольное распределение заряда требует расчетов. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

Работа, совершаемая электрическим полем на рисунке 7.14 по перемещению положительного заряда q от A , положительная пластина, более высокий потенциал, к B , отрицательная пластина, более низкий потенциал, составляет

W = −ΔU = −qΔV.W = −ΔU = −qΔV.

Разница потенциалов между точками A и B составляет

−ΔV = — (VB − VA) = VA − VB = VAB. − ΔV = — (VB − VA) = VA − VB = VAB.

Если ввести это в выражение для работы, получится

Работа — это W = F → · d → = FdcosθW = F → · d → = Fdcosθ; здесь cosθ = 1cosθ = 1, так как путь параллелен полю.Таким образом, W = FdW = Fd. Поскольку F = qEF = qE, мы видим, что W = qEdW = qEd.

Подстановка этого выражения для работы в предыдущее уравнение дает

Заряд отменяется, поэтому для напряжения между точками A и B получаем

VAB = EdE = VABd} (только uniformE-field) VAB = EdE = VABd} (только uniformE-field)

, где d — это расстояние от A до B , или расстояние между пластинами на Рисунке 7.14. Обратите внимание, что это уравнение подразумевает, что единицы измерения электрического поля — вольт на метр.Мы уже знаем, что единицы измерения электрического поля — ньютоны на кулон; таким образом, верно следующее соотношение между единицами:

Кроме того, мы можем продолжить это до интегральной формы. Подставляя уравнение 7.5 в наше определение разности потенциалов между точками A и B , мы получаем

VBA = VB − VA = −∫RBE → · dl → + ∫RAE → · dl → VBA = VB − VA = −∫RBE → · dl → + ∫RAE → · dl →

, что упрощается до

VB − VA = −ABE → · dl → .VB − VA = −ABE → · dl →.

В качестве демонстрации из этого мы можем вычислить разность потенциалов между двумя точками ( A и B ), равноудаленными от точечного заряда q в начале координат, как показано на рисунке 7.= 0 и, следовательно,

Этот результат, заключающийся в отсутствии разницы в потенциале вдоль постоянного радиуса от точечного заряда, пригодится при отображении потенциалов.

Пример 7.7

Какое максимально возможное напряжение между двумя пластинами?

Сухой воздух может поддерживать максимальную напряженность электрического поля около 3,0 × 106 В / м. 3,0 × 106 В / м. Выше этого значения поле создает достаточную ионизацию в воздухе, чтобы сделать воздух проводником. Это допускает разряд или искру, которые уменьшают поле.Каково же максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

Стратегия

Нам дано максимальное электрическое поле E между пластинами и расстояние d между ними. Мы можем использовать уравнение VAB = EdVAB = Ed для расчета максимального напряжения.

Решение

Разность потенциалов или напряжение между пластинами составляет

Ввод заданных значений для E и d дает

VAB = (3,0 × 106 В / м) (0.025 м) = 7,5 × 104 VVAB = (3,0 × 106 В / м) (0,025 м) = 7,5 × 104 В

или

(Ответ состоит только из двух цифр, поскольку максимальная напряженность поля является приблизительной.)

Значение

Одним из следствий этого результата является то, что требуется около 75 кВ, чтобы совершить скачок искры через зазор размером 2,5 см (1 дюйм), или 150 кВ для искры 5 см. Это ограничивает напряжения, которые могут существовать между проводниками, возможно, на линии электропередачи. Меньшее напряжение может вызвать искру, если на поверхности есть шипы, поскольку острые точки имеют большую напряженность поля, чем гладкие поверхности.Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение заставит искру проскочить через влажный воздух. Наибольшие напряжения могут создаваться статическим электричеством в засушливые дни (рис. 7.16).

Рис. 7.16. Искровая камера используется для отслеживания траектории частиц высоких энергий. Ионизация, создаваемая частицами при прохождении через газ между пластинами, позволяет искре прыгнуть. Искры расположены перпендикулярно пластинам, следуя силовым линиям электрического поля между ними. Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, производимой частицами из экспериментов с ускорителем (или космическими лучами).Эта форма детектора сейчас устарела и больше не используется, кроме как в демонстрационных целях. (кредит b: модификация работы Джека Коллинза)

Пример 7.8

Поле и сила внутри электронной пушки

Электронная пушка (рис. 7.13) имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает электронам энергию 25,0 кэВ. а) Какова напряженность электрического поля между пластинами? (b) Какую силу это поле окажет на кусок пластика с зарядом 0,500 мкКл0,500 мкКл, который проходит между пластинами?

Стратегия

Поскольку напряжение и расстояние между пластинами указаны, напряженность электрического поля можно рассчитать непосредственно из выражения E = VABdE = VABd.Зная напряженность электрического поля, мы можем найти силу, действующую на заряд, используя F → = qE → .F → = qE →. Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин: F = qEF = qE.

Решение

1. Выражение для величины электрического поля между двумя однородными металлическими пластинами имеет следующий вид:

   Поскольку электрон является однозарядным и получает энергию 25,0 кэВ, разность потенциалов должна составлять 25,0 кВ. Ввод этого значения для VABVAB и разделения пластин 0.0400 м, получаем
   E = 25,0 кВ 0,0400 м = 6,25 × 105 В / м. E = 25,0 кВ 0,0400 м = 6,25 × 105 В / м.

2. Величина силы, действующей на заряд в электрическом поле, получается из уравнения

   Подстановка известных значений дает
   F = (0,500 × 10–6C) (6,25 × 105 В / м) = 0,313 Н. F = (0,500 × 10–6 ° C) (6,25 × 105 В / м) = 0,313 Н.

Значение

Обратите внимание, что единицы измерения — ньютоны, так как 1V / m = 1N / C1V / m = 1N / C. Поскольку электрическое поле между пластинами однородно, сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами.

Пример 7.9

Расчет потенциала точечного заряда

Учитывая точечный заряд q = + 2,0 нКл = + 2,0 нКл в начале координат, вычислите разность потенциалов между точкой P1P1 на расстоянии a = 4,0 см = 4,0 см от q и P2P2 на расстоянии b = 12,0 см = 12,0 см от q , где две точки имеют угол φ = 24 ° φ = 24 ° между собой (рисунок 7.17).

Рисунок 7.17. Найдите разность потенциалов между P1P1 и P2P2.

Стратегия

Сделайте это в два этапа. Первый шаг — использовать VB − VA = −ABE → · dl → VB − VA = −ABE → · dl → и пусть A = a = 4.= 0 и, следовательно, ΔV = 0. ΔV = 0. Складывая две части вместе, получаем 300 В.

Значение

Мы продемонстрировали использование интегральной формы разности потенциалов для получения численного результата. Обратите внимание, что в этой конкретной системе мы могли бы также использовать формулу для потенциала из-за точечного заряда в двух точках и просто взять разницу.

Проверьте свое понимание 7.7

Из приведенных примеров, как энергия удара молнии зависит от высоты облаков над землей? Считайте систему облако-земля двумя параллельными пластинами.

Прежде чем описывать проблемы, связанные с электростатикой, мы предлагаем стратегию решения проблем, которой следует придерживаться для этой темы.

Стратегия решения проблем

Электростатика

1. Изучите ситуацию, чтобы определить, присутствует ли статическое электричество; это может касаться отдельных стационарных зарядов, сил между ними и создаваемых ими электрических полей.
2. Определите интересующую систему. Это включает в себя указание количества, местоположения и типов взимаемых сборов.
3. Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен. Определите, следует ли рассматривать кулоновскую силу напрямую — если да, может быть полезно нарисовать диаграмму свободного тела, используя силовые линии электрического поля.
4. Составьте список того, что дано или может быть выведено из проблемы, как указано (указать известные). Например, важно отличать кулоновскую силу F от электрического поля E .
5. Решите соответствующее уравнение для количества, которое необходимо определить (неизвестное), или проведите линии поля, как требуется.
6. Изучите ответ, чтобы увидеть, разумен ли он: имеет ли он смысл? Правильны ли единицы и разумны ли числа?

Цепь делителя напряжения

| Разница потенциалов в резисторных цепях

Определение разницы потенциалов

Рассмотрим задачу перемещения заряда от A к B в однородном электрическом поле. Пусть это движение будет против электрического поля.Некоторая работа будет выполнена внешней силой с этим зарядом, и эта работа изменит потенциальную энергию на более высокое значение. Объем проделанной работы равен изменению потенциальной энергии. Это изменение потенциальной энергии приведет к разнице потенциалов между двумя точками A и B. Эта разность потенциалов называется разностью потенциалов и измеряется в вольтах (В).

Разность потенциалов обозначается ∆V и определяется как разность потенциалов или напряжений между двумя точками.
Если VA — это потенциал на A, а VB — это потенциал на B, тогда из определения разности потенциалов

∆VBA = VB — VA

Например, рассмотрим следующий резистор R1.

Потенциал, приложенный к одному концу резистора (точка A), равен 8 В, а потенциал на другом конце резистора (точка B) равен 5 В.

Разность потенциалов между двумя точками A и B равна

VAB = 8 — 5 = 3 В.

Это также называется потенциалом на резисторе.

Ток течет в электрической цепи в виде заряда, тогда как потенциал не течет и не движется. Возможная разница применяется между двумя точками.

Единица измерения разности потенциалов между двумя точками — Вольт. Вольт определяется как падение потенциала на резисторе 1 Ом (Ом) при протекании через него тока 1 Ампер.

Следовательно,

1 Вольт = 1 Ампер × 1 Ом

В = I × R

Согласно закону Ома ток, протекающий в линейной цепи, прямо пропорционален разности потенциалов в цепи.Следовательно, если разность потенциалов, приложенная к цепи, больше, то ток, протекающий в цепи, больше.

Например, если одна сторона резистора 1 Ом имеет потенциал 8 В, а другая сторона — 2 В, то разность потенциалов на резисторе составляет 5 В. Ток, протекающий в резисторе, равен

I = V / R = 5 В / 1 Ом = 5 Ампер.

Теперь для того же резистора 1 Ом, если потенциал, приложенный на одном конце, повышается с 8 В до 12 В, а на другом конце — с 2 В до 4 В.Тогда разность потенциалов на резисторе теперь составляет 8 В. Ток, протекающий в резисторе в этой ситуации, составляет 8 А.

I = V / R = 8 В / 1 Ом = 8 Ампер.

Обычно в электрических цепях более низкий потенциал — это земля или земля. Это значение обычно считается 0 В. Следовательно, разность потенциалов равна приложенному напряжению. Земля считается общей точкой в ​​цепи. Эта ссылка на землю или землю как общую точку в электрических цепях полезна для облегчения понимания схемы.Разность потенциалов также называется напряжением.

Напряжения, соединенные последовательно, складываются для получения общего напряжения в цепи. Это можно наблюдать в резисторах, включенных последовательно. Если V1, V2 и V3 соединены последовательно, то общее напряжение VT равно

В _T = V1 + V2 + V3.

При параллельном соединении элементов напряжение на них одинаковое. Это можно наблюдать в резисторах в параллельном руководстве.

В _T = V1 = V2 = V3.

Примеры разницы потенциалов

1. Если 1500 Джоулей потенциальной энергии передается для перемещения заряда 125 Кулонов между выводами батареи, то разность потенциалов составляет

∆E = 1500 Дж

Q = 125 C

Разность потенциалов V = ∆E / C

V = 1500/125 = 12 Дж / кулон = 12 В

2. Рассмотрим резистор сопротивлением 10 Ом. Пусть один конец резистора подключен к потенциалу 15 В. Пусть другой конец резистора подключен к потенциалу 5 В.Ток, протекающий через резистор, можно рассчитать следующим образом.

Две клеммы резистора имеют два разных потенциала, то есть 15 В и 5 В соответственно. Пусть двумя клеммами будут A и B. Следовательно, напряжение на A равно VA = 15 В, а напряжение на B равно VB = 5 В. Тогда разность потенциалов между A и B является напряжением на резисторе.

VAB = VA — VB = 15 — 5 = 10 В.

Тогда ток, протекающий через резистор, можно рассчитать по закону Ома как

I = VAB / R = 10/10 = 1 ампер.

Схема делителя напряжения

Резисторы, включенные последовательно, используются для создания схемы делителя напряжения. Делитель напряжения представляет собой линейную схему, выходное напряжение которой составляет часть входного напряжения.

Ниже показана простая схема делителя напряжения с 2 резисторами.

Потенциал на каждом резисторе при последовательном включении зависит от значения сопротивления. Принцип делителя напряжения заключается в создании напряжения, составляющего часть входного напряжения.

Следующая схема используется для демонстрации принципа делителя напряжения для нескольких выходных напряжений.

Здесь резисторы R1, R2, R3 и R4 включены последовательно. Выходное напряжение на каждом резисторе привязано к общей точке P. Пусть эквивалентное сопротивление последовательно соединенных резисторов равно RT. Тогда R _T = R1 + R2 + R3 + R4.

Пусть разность потенциалов на каждом резисторе равна V _R1 , V _R2 , V _R3 и V _R4 соответственно для R1, R2, R3 и R4.Тогда приведенная выше схема может производить 4 различных напряжения, составляющих доли напряжения питания V.

Формула делителя напряжения

Значение выходного напряжения в типовой схеме делителя напряжения рассчитывается следующим образом.

Здесь Vin — напряжение питания. I — это ток в цепи, протекающий через оба резистора.

Пусть VR1 будет падением напряжения на резисторе R1, а VR2 будет падением напряжения на резисторе R2. Тогда сумма этих отдельных падений напряжения равна общему напряжению в цепи, которое является напряжением питания Vin.

Vin = VR1 + VR2 — — — 1

Уравнения для отдельных падений напряжения на каждом резисторе могут быть рассчитаны по закону Ома.

VR1 = I × R1 — — — 2

И VR2 = I × R2 — — — 3

Но напряжение на резисторе R2 равно VOUT.

Следовательно, VOUT = I × R2 — — — 4

Следовательно, из уравнений 1, 2 и 3

Vin = I × R1 + I × R2 = I × (R1 + R2) — — — 5

Но значение тока I через выходное напряжение можно записать следующим образом, используя уравнение 4.

I = VOUT / R2 — — — 6

Используя уравнения 5 и 6

VOUT = Vin × (R¬2 / R1 + R2)

Следовательно, VOUT = VIN × R2 / (R1 + R2)

В случае схемы делителя напряжения, имеющей несколько выходов, выходное напряжение можно рассчитать по следующей формуле.

VX = V × (RX / REQ)

Где VX — напряжение, которое необходимо найти.

RX — полное сопротивление выходного напряжения.

Возможные значения RX:

R1 между P и P1

R1 + R2 между P и P2

R1 + R2 + R3 между P и P3

R1 + R2 + R3 + R4 между P и P4.

R _EQ — эквивалентное сопротивление резистора при последовательном включении.

R _EQ = R1 + R2 + R3 + R4

В — напряжение питания.

Следовательно, возможные выходные напряжения равны

V1 = V × R1 / R _EQ

V2 = V × (R1 + R2) / R _EQ

V3 = V × (R1 + R2 + R3) / R _EQ

V4 = V × (R1 + R2 + R3 + R4) / R _EQ = V

Пример делителя напряжения

Рассмотрим следующую схему делителя напряжения.

Он состоит из трех последовательно соединенных резисторов для создания двух выходных напряжений. Напряжение питания составляет 240 В.

Значения сопротивления: R1 = 10 Ом, R2 = 20 Ом и R3 = 30 Ом.

Следовательно, эквивалентное сопротивление цепи равно

R _EQ = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом.

Теперь два возможных выходных напряжения можно рассчитать следующим образом:

V _out1 = V × (R2 + R3) / REQ

V _out1 = 240 × (20 + 30) / 60

V _out1 = 200 В.

В _out2 = V × R3 / REQ

V _out2 = 240 × 30/60

V _out2 = 120 В.

Ток в цепи

I = V / R _EQ = 240/60 = 4 Ампер.

Следовательно, отдельные падения напряжения на каждом резисторе можно рассчитать следующим образом:

В _R1 = I × R1 = 4 × 10 = 40 В.

В _R2 = I × R2 = 4 × 20 = 80 В

В _R3 = I × R3 = 4 × 30 = 120 В.

Применение схем делителя напряжения

Последовательные резисторы образуют схемы делителя напряжения.