Формула емкости конденсатора, С
Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:
называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():
где – диэлектрическая проницаемость диэлектрика.
За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).
Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).
Формула электрической емкости плоского конденсатора
Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
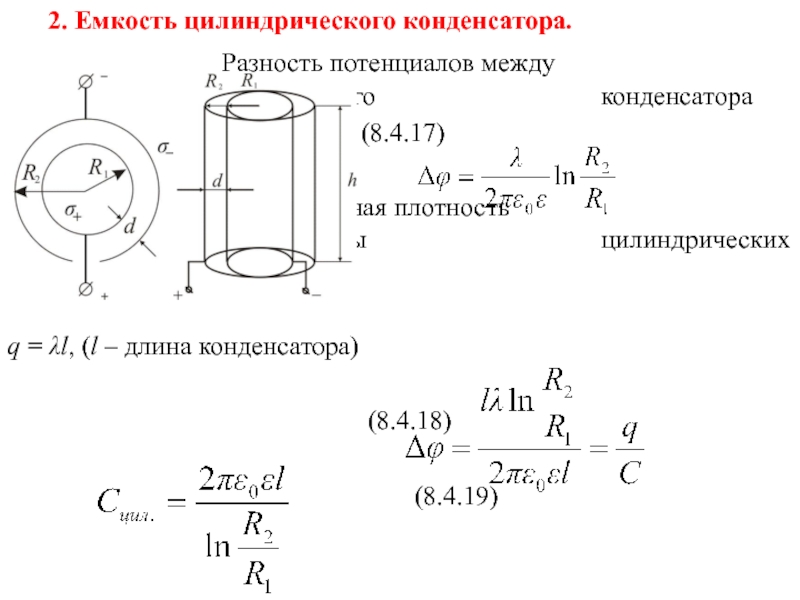
Формула электрической емкости цилиндрического конденсатора
Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик.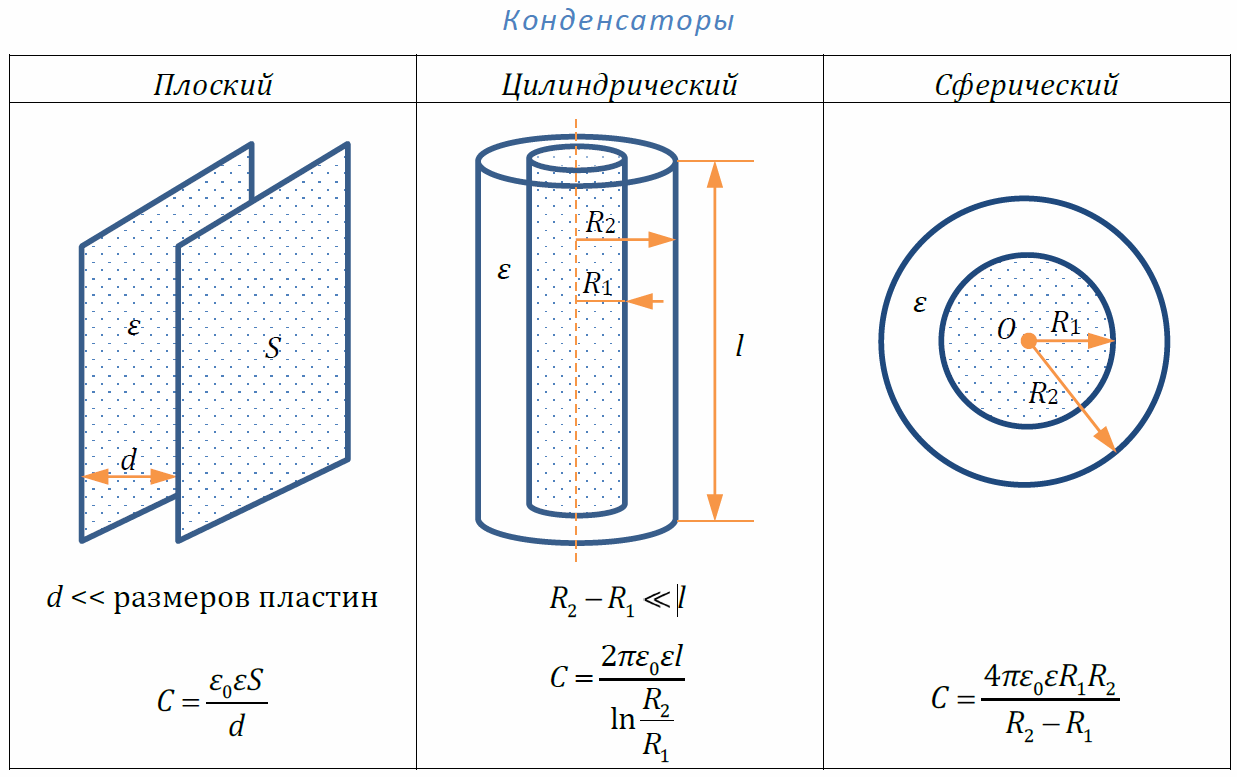 Электрическая емкость цилиндрического конденсатора вычисляется как:
Электрическая емкость цилиндрического конденсатора вычисляется как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Формула электрической емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач по теме «Емкость конденсатора»
формула для расчета электрической емкости
Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал. Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.
В чем измеряется емкость конденсатора
Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги. Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.
Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться. На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?
Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.). Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.
Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.
Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.
| В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах. |
Много это или мало — емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.
| Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн. |
Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.
Рассмотрим пример.
- В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.
Формула емкости плоского конденсатора
Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:
- где Q – заряд,
- φ – потенциал.
Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.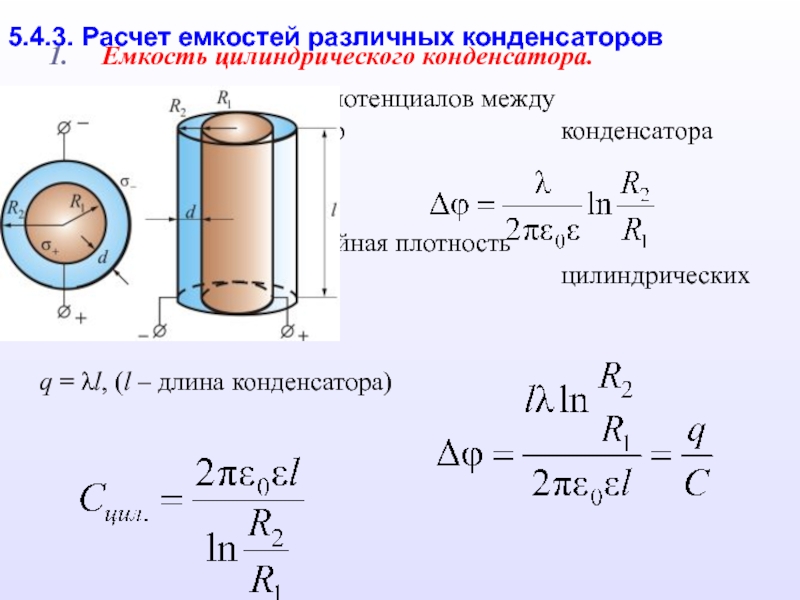
Для получения качественного конденсатора важны любые мелочи:
- ровная поверхность каждой обкладки;
- обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
- размеры обкладок должны быть строго идентичными;
- от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
- емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.
Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:
- где S – площадь одной обкладки,
- εr — диэлектрическая проницаемость диэлектрика,
- ε0 — электрическая постоянная,
- d – расстояние между обкладками.
Электрическая постоянная выражается числом 8,854187817×10-12.
Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади. |
Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.
В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.
Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?
Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.
Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.
При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.
Есть другая формула для плоского переменного конденсатора:
Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.
Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.
Формула емкости цилиндрического конденсатора
Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой. Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:
К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой. Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:
Здесь видим несколько новых переменных:
- l – высота цилиндра;
- R1 и R2 – радиус первого и второго (внешнего) цилиндров;
- ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.
Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).
Из нее видно, что все расстояния нужно приводить к метру.
Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.
Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.
Формула емкости сферического конденсатора
Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:
Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.
Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.
Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.
После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.
Рассмотрим, как найти емкость конденсатора каждого вида.
Примеры решения задач
Начнем с плоского конденсатора. Формула для этого вида:
Допустим, у нас есть следующие значения:
- в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
- конденсатор квадратный со сторонами в 7 мм.
Определяем площадь пластин: 7×7 = 49 мм2.
Приводим к единой системе: 4,9×10-5 = 0,000049 м2. Толщина диэлектрика 0,02×10-5 = 0,00002 м. Электрическая постоянная 8,854187817×10-12.
Подставляем в формулу и высчитываем числитель: 6×8,854187817×10-12 ×4,9×10-5, сокращаем и решаем 6×49×8,854187817×10-17 = 2,603131218198×10-14.
Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.
Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.
Важно понять сам метод вычисления.
Формула для цилиндрического конденсатора:
Выбираем значения:
- l = 1 см;
- R1 = 0,25 мм;
- R2 = 0,26 мм;
- ε = 2.
Подгоняем под единую систему: l — 1 см = 1×10-2 = 0,01 м; R1 – 0,25 мм = 0,0025 м; R2 – 0,26 мм = 0,0026 м.
Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10-12×2×0,01 1,11×10-12. Находим знаменатель: 0,26:0,25 = 1,04.
Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10-12/0,39 = 2,85×10-12.
Число с 12 нулями это приставка «пико», получаем 2,85 пФ.
Формула для сферического конденсатора:
Выбираем значения:
- ε= 4;
- r1= 5 см;
- r2= 5,01 см.
Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.
Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.
Похожие материалы на сайте:
Понравилась статья — поделись с друзьями!
Электричество и магнетизм
Повышения емкости проводника можно достигнуть не только увеличением его размеров, но и за счет приближения к нему другого проводника. Примерами могут служить плоский конденсатор, сферический конденсатор и др. Мы вычислим их емкости, исходя из данных определений и геометрии конденсатора.
Плоский конденсатор (рис. 2.11).
Рис. 2.12. Электрическое поле идеального плоского конденсатора
Идеальный плоский конденсатор представляет собой две металлические параллельные пластины, линейные размеры которых много больше расстояния между ними. Пусть площадь каждой из пластин равна (рис. 2.12). На одну пластину помещен заряд , на другую — Если пластины достаточно велики, то их можно считать «бесконечными» в том смысле, что допустимо пренебречь «краевыми» эффектами — распределениями зарядов и конфигурациями полей вблизи их краев.
Пусть площадь каждой из пластин равна (рис. 2.12). На одну пластину помещен заряд , на другую — Если пластины достаточно велики, то их можно считать «бесконечными» в том смысле, что допустимо пренебречь «краевыми» эффектами — распределениями зарядов и конфигурациями полей вблизи их краев.
Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью. Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними:
Рис. 2.12. Электрическое поле идеального плоского конденсатора
Видео 2.9. Геометрия реального плоского конденсатора и распределение заряда на его пластинах.
Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью . Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними:
|
|
(2. |
Поле, создаваемое двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями, является однородным, и его напряженность равна (см. (2.3)).
Напряженность поля в пространстве, окружающем пластины, можно считать равной нулю, если пренебречь краевыми эффектами. Интегрируя вдоль силовой линии (которые ортогональны пластинам), получаем
|
(2.11) |
Отсюда находим емкость плоского конденсатора:
|
(2.12) |
Цилиндрический конденсатор. Цилиндрический конденсатор представляет собой два коаксиальных длинных проводящих цилиндра радиусами и и длиной .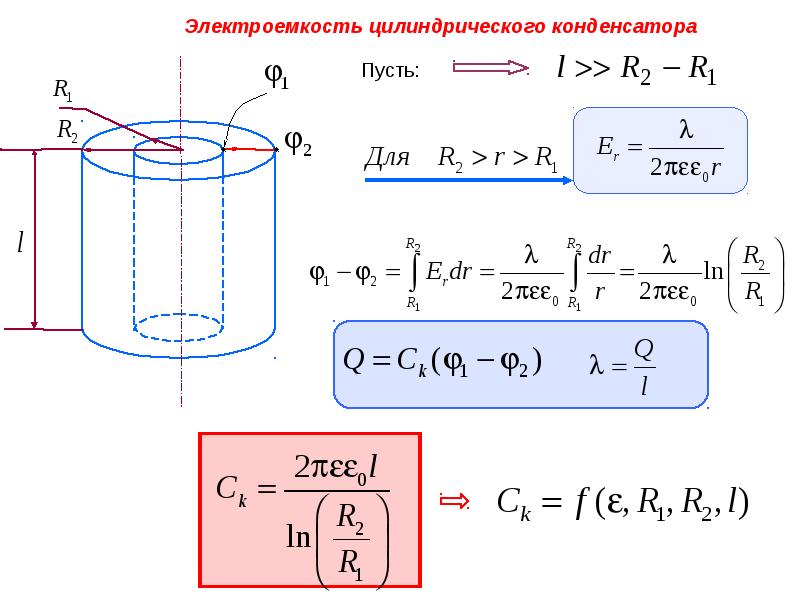 Предполагая, что , мы и в этом случае пренебрегаем краевыми эффектами. Линейная плотность заряда на цилиндрах равна . Мы уже вывели выражение для электрического поля длинного заряженного цилиндра (см. (1.17)):
Предполагая, что , мы и в этом случае пренебрегаем краевыми эффектами. Линейная плотность заряда на цилиндрах равна . Мы уже вывели выражение для электрического поля длинного заряженного цилиндра (см. (1.17)):
|
(2.13) |
Электрическое поле направлено по радиусу цилиндров. Интегрируя по этому пути от одной обкладки к другой, находим разность потенциалов между обкладками:
|
|
(2.14) |
Отсюда следует выражение для емкости цилиндрического конденсатора:
|
(2.15) |
В случае, когда зазор между обкладками , можно использовать первый член разложения логарифма в ряд Тейлора
что приводит к выражению
|
(2. |
В скобках стоит произведение длины окружности цилиндра на его высоту, что равно площади поверхности цилиндра (площади обкладок). Т. о. мы воспроизвели в этом пределе выражение (2.12) для емкости плоского конденсатора.
Сферический конденсатор. Сферический конденсатор образуется двумя концентрическими сферами радиусам и . Интегрируя вдоль радиуса уже хорошо знакомое выражение
получаем разность потенциалов между обкладками:
|
|
(2.17) |
откуда
|
(2.18) |
Если внешний радиус бесконечно велик (физически это значит, что ), то вычитаемым в знаменателе можно пренебречь, и мы приходим к формуле (2. 9) для емкости уединенной сферы. В обратном случае, когда зазор между обкладками можно положить в числителе Замечая, что есть площадь обкладок, мы снова приходим к формуле (2.12).
9) для емкости уединенной сферы. В обратном случае, когда зазор между обкладками можно положить в числителе Замечая, что есть площадь обкладок, мы снова приходим к формуле (2.12).
Видео 2.10. Влияние диэлектрика на распределение зарядов на проводнике и его емкость.
Задача. Конденсатор, используемый в чипе запоминающего устройства компьютера, имеет емкость и заряжается до разности потенциалов . Каково число избыточных электронов на его отрицательной обкладке? В какой массе воды полное число всех атомных электронов равно ?
Решение. Заряд конденсатора равен . Чтобы найти число избыточных электронов, надо разделить на заряд электрона: Почти два миллиона электронов, много это или мало? Для этого найдем массу воды с тем же числом электронов. Молекула воды содержит два атома и один атом , то есть всего 10 электронов. Стало быть, в интересующей нас массе воды должно содержаться молекул. Число молекул в одном моле равно то есть надо взять моля. Молярный вес воды равен кг/кмоль, так что искомая масса составляет кг, то есть крайне мала. Миллион частиц — много в мире электронов, но совсем мало в масштабах нашего мира.
Молярный вес воды равен кг/кмоль, так что искомая масса составляет кг, то есть крайне мала. Миллион частиц — много в мире электронов, но совсем мало в масштабах нашего мира.
Цилиндрический конденсатор — Энциклопедия по машиностроению XXL
Для цилиндра с внешним и внутренним диаметрами В и б соответственно и осевой длиной 1 (диэлектрик цилиндрического конденсатора изоляция коаксиального кабеля)
[c.87]
Емкость цилиндрического конденсатора (см. рис. 5,3, а) рассчитывают по формуле [c.150]
Емкость цилиндрического конденсатора [c.399]
С — емкость цилиндрического конденсатора в см. [c.113]
Осевое удлинение и угол закручивания измеряются механическими индикаторами. Измерение величины изменения диаметра образца этими приборами дает локальное значение деформации. Среднее значение радиальной деформации можно получить с помощью емкостного датчика, представляющего собой цилиндрический конденсатор, внутренней обкладкой которого является испытуемый образец, внешней — цилиндр из двух половин (рис. 1).
[c.238]
1).
[c.238]
Пользуясь формулой цилиндрического конденсатора
[c.239]
Емкость цилиндрического конденсатора (фиг. 4) [c.331]
Горизонтальный цилиндрический конденсатор встроен в сухопарник и отделен от основного парового пространства внутренним кожухом. Опреснители рассчитаны на повышенное солесодержа-ние дистиллята (50 лгг/л). [c.215]
Принцип действия измерительной части топливомера основан на изменении электрической емкости датчиков топливомера (представляющих собой цилиндрические конденсаторы) при изменении уровня топлива в баках.
[c.247]
Простота согласования цилиндрического конденсатор й электростатической фокусировки с отклоняющей [c.52]
Фиг. 78. Схема пластинчато о и цилиндрического конденсатора.
|
Напряженность поля в цилиндрическом конденсаторе [c.25]
Потенциал внутри цилиндрического конденсатора и r=Ui — Ег 1п Ri [c.26]
Емкость цилиндрического конденсатора 2-.e [c.26]
| Рис. 2.3. Участок изоляции между злектрода-мн в виде двух коаксиальных иилиндров (цилиндрический конденсатор) |
Для цилиндрического конденсатора (см. рис. 2.3) для точки в диэлектрике между электродами, находящейся на расстоянии х от оси конденсатора (/ 1[c.25]
Таким образом, в цилиндрическом конденсаторе (даже с однородным диэлектриком) поле неоднородно наибольшая напряженность имеет место в точках диэлектрика, непосредственно примыкающих к внутреннему электроду x = ri)
[c. 25]
25]
Если же диэлектрик цилиндрического конденсатора многослойный (п слоев), то напряженность в -м слое на расстоянии х от оси конденсатора ги х[c.25]
Емкостный метод контроля может быть как контактным, так и бесконтактным. При бесконтактном методе одной из пластин конденсатора служит само контролируемое изделие при контактном методе емкостный датчик представляет собой плоский или цилиндрический конденсатор, одна из пластин которого связана с измерительным стержнем. Бесконтактный метод находит ограниченное применение. [c.200]
Допустим, что необходимо произвести соединение колпачков с секцией цилиндрического конденсатора (рис. 3). Для выполнения этой работы прежде всего нужно определить сборочный состав изделия, необходимые детали и материалы, их количество, определить, базовую деталь или элемент. Анализ рабочего чертежа собираемого изделия показывает, что в качестве базовой детали можно использовать секцию конденсатора 1 в сборе с припаянными к ней выводами 2 колпачки 7 надевают на секцию с двух сторон, а затем вставляют в
[c.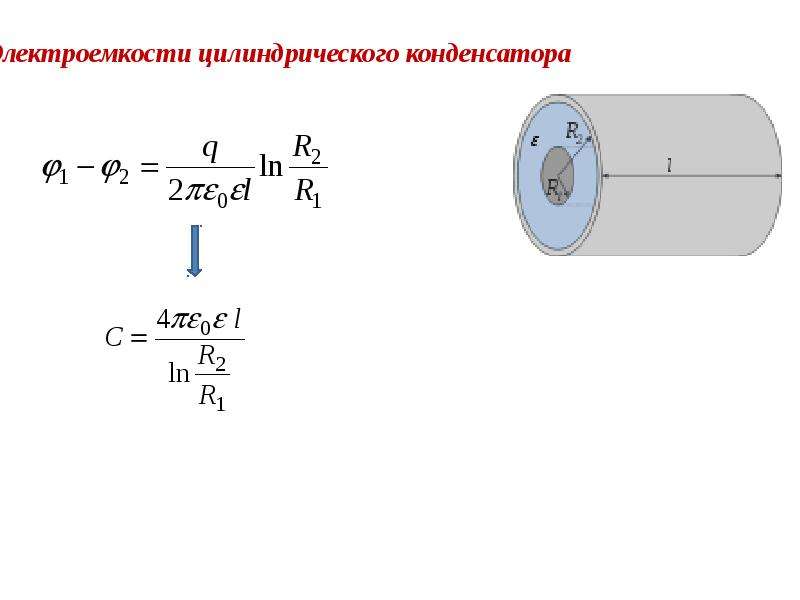 16]
16]
| Рис. 3. Общий вид двух вариантов цилиндрических конденсаторов |
Рассмотрим схему технологического процесса сборки секции цилиндрического конденсатора с двумя колпачками (рис. 4). За начало сборки (базовый элемент—
[c.18]
На основании полученных значений Qt можно сделать вывод, что с точки зрения осуществления автоматической сборки конструкция ламповой панели более технологична, чем конструкция цилиндрического конденсатора.
[c.29]
Кинематическая схема автоматической установки припайки выводов к секциям цилиндрических конденсаторов показана на рис. 74. В автомате совмещены операции изготовления двух выводов и припайки их к секциям. [c.212]
Рис. 74. Кинематическая схема автоматической установки припайки выводов к секциям цилиндрических конденсаторов.
|
Электрическая схема для управления работой автомата механической сборки цилиндрических конденсаторов представлена на рис. 121. [c.335]
Ионизационная камера обычно работает в режиме тока насыщения, где нет газового усиления. В этом случае число пар ионов, возникающих под действием попадающей в ионизационную камеру заряженной частицы, относительно невелико и регистрация отдельных. частиц с помощью ионизационной камеры при отсутствии газбвого усиления связана с большими трудностями. В режиме газового усиления ионизационная камера может работать в качестве счетчика отдельных заряженных частиц. Поэтому ионизационные камеры обычно подразделяются на два вида счетно-ионизационные камеры, предназначенные для регистрации прохождения через камеру одной какой-либо заряженной частицы, и интегрирующие ионизационные камеры, применяемые для измерения интенсивности потока частиц. В зависимости от условий задачи ионизационные камеры по форме электродов имеют вид плоского, сферического или цилиндрического конденсатора.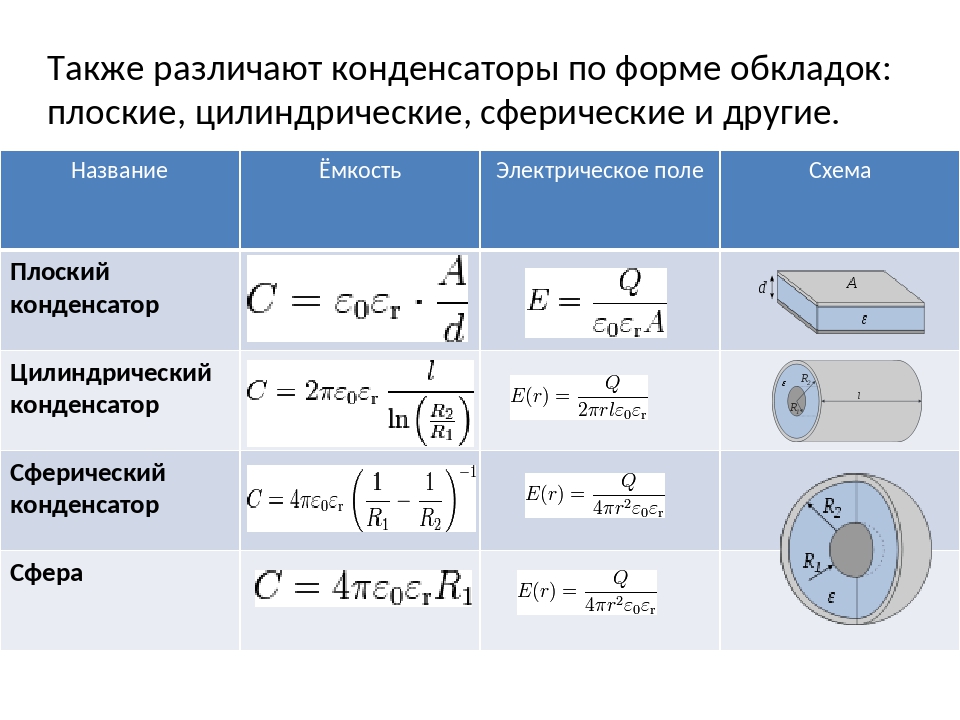 Размеры их могут быть весьма различными — от долей кубических миллиметров до сотен литров, в зависимости от их назначения.
[c.39]
Размеры их могут быть весьма различными — от долей кубических миллиметров до сотен литров, в зависимости от их назначения.
[c.39]
I — длина цилиндрического конденсатора в см, т. е. длина электрода для конкретной конструкции I = onst
[c.113]
С целью проверки полученных рекомендаций и выводов была проведена серия экспериментов по изучению газорегулируемой ТТ открытого типа. Исследуемая труба имела длину 1,5 м, внешний диаметр 10 м и состояла из испарителя и конденсатора. Испаритель был из меди, имел форму медного полого цилиндра длиной 500 мм, на внутренней поверхности которого было 16 аксиальных прямоугольных канавок шириной 0,4 мм и глубиной 0,6 мм. Выбирался он с малым термическим сопротивлением с целью получения высоких значений коэффициента температурной чувствительности, а также уменьшения пульсаций температуры и давления. Цилиндрический конденсатор был выполнен из термостойкого стекла длиной 1 м для уменьшения аксиальной составляющей теплового потока в зоне раздела пар—газ и визуализации процессов. Конденсатор имел гибкое соединение с испарителем и мог изменять угол наклона от —90 до +90°. На внешней поверхности испарителя имитировались граничные условия II рода (три секции омического нагревателя), а на внешней поверхности конденсатора— III рода (сб 10 Вт/(м -К)). Поля температур измерялись хромель-копелевыми термопарами, а также пленочным термонйдикатором на базе жидких кристаллов (в зоне раздела пар—газ). В качестве тепло-нос1 теля использовался этиловый спирт, а неконденси-рующегося газа — воздух или фреон-11. Отношения молекулярных весов имели значения /См= 1,324 и /См = 0,276 соответственно. Диаметр парового канала конденсатора намного превышал минимальное пороговое значение da для пары этанол—фреон-11. По результатам эксперимента были построены графики, показанные на рис. 9. Распределение температуры в области парогазового фронта соответствовало расчетам и рекомендациям. Протяженность зоны раздела этанол — воздух составила 0,004,а зоны этанол — фреон-11 —0,5 м, т. е. на два порядка больше.
Конденсатор имел гибкое соединение с испарителем и мог изменять угол наклона от —90 до +90°. На внешней поверхности испарителя имитировались граничные условия II рода (три секции омического нагревателя), а на внешней поверхности конденсатора— III рода (сб 10 Вт/(м -К)). Поля температур измерялись хромель-копелевыми термопарами, а также пленочным термонйдикатором на базе жидких кристаллов (в зоне раздела пар—газ). В качестве тепло-нос1 теля использовался этиловый спирт, а неконденси-рующегося газа — воздух или фреон-11. Отношения молекулярных весов имели значения /См= 1,324 и /См = 0,276 соответственно. Диаметр парового канала конденсатора намного превышал минимальное пороговое значение da для пары этанол—фреон-11. По результатам эксперимента были построены графики, показанные на рис. 9. Распределение температуры в области парогазового фронта соответствовало расчетам и рекомендациям. Протяженность зоны раздела этанол — воздух составила 0,004,а зоны этанол — фреон-11 —0,5 м, т. е. на два порядка больше. Аналогичные результаты были получены при отрицательных углах наклона конденсатора (испаритель над конденсатором).
[c.32]
Аналогичные результаты были получены при отрицательных углах наклона конденсатора (испаритель над конденсатором).
[c.32]
ЧТО теплопередающие характеристики гладкостемиых цилиндров значительно хуже характеристик усеченного конуса, что и следовало ожидать, так как в коническом конденсаторном участке центробежные силы ускоряют движение жидкости в направлении испарителя. Во вращающемся цилиндре течение конденсата вызывается градиентом гидростатического давления, который создается в конденсаторе за счет изменения толщины пленки вдоль его оси. При равных условиях стекания рабочей жидкости в конце конденсаторного участка результирующая толщина пленки жидкости в цилиндрическом конденсаторе больше, чем в коническом. [c.131]
Для изготовления конденсаторных втулок применяют те же материалы (намоточная бумага и лак), что и в производстве бумажнобакелитовых трубок. Технология лакировки бумаги, намотки изделия и его тепловой обработки также аналогичны с той лишь разницей, что в процессе намотки на заданных диаметрах в тело наматываемой втулки закладывают алюминиевые прокладки, служащие обкладками цилиндрического конденсатора. Количество обкладок обычно составляет 9—11. Медные трубки или стержни, на которые наматываются втулки, после термической обработки изделий не извлекаются из них и служат при эксплуатации
[c.341]
Количество обкладок обычно составляет 9—11. Медные трубки или стержни, на которые наматываются втулки, после термической обработки изделий не извлекаются из них и служат при эксплуатации
[c.341]
Рассмотрим конструкцию цилиндрического конденсатора (бумажного и металло-бумажного) с витой секцией, имеющего два тонких осевых вывода. Схема такого конденсатора была показана на рис. 3, а, вариант II. Конденсатор состоит из вигой секции 1, к торцам которой припаиваются выводы 2. Секция с выводами помещена в алюминиевый корпус 6 с колпачками 4, изготовляемыми из полимерных материалов. Колпачки служат для электроизоляции секции от корпуса и для компенсации погрешностей изготовления секции. Внутренняя полость конденсатора герметизируется заливкой компаундом на основе эпоксидных смол или уплотняется резиновыми шайбами (см. рис. 3, б). В подобны.к [c.171]
Электрическая емкость: определение, формулы, единицы измерения
В электротехнике часто встречается понятие ёмкости. При этом речь идёт не о ведре или другом сосуде, а об электрической ёмкости проводника, аккумулятора и конденсатора. Путать эти понятия нельзя. В этой статье мы разберемся, что такое электрическая ёмкость, от чего она зависит и в каких единицах измеряется.
При этом речь идёт не о ведре или другом сосуде, а об электрической ёмкости проводника, аккумулятора и конденсатора. Путать эти понятия нельзя. В этой статье мы разберемся, что такое электрическая ёмкость, от чего она зависит и в каких единицах измеряется.
Определение
Для проводников электрической ёмкостью называется величина, которая характеризует способность тела накапливать электрический заряд. Это и есть её физический смысл. Обозначается латинской буквой C. Она равна отношению заряда к потенциалу, если это записать в виде формулы, то получается следующее:
C=q/Ф
Электроемкость любого предмета зависит от его формы и геометрических размеров. Если рассмотреть проводник в форме шара, в качестве примера, то формула для расчета её величины будет иметь вид:
Эта формула справедлива для уединенного проводника. Если расположить рядом два проводника и разделить их диэлектриком, тогда получится конденсатор. Об этом немного позже, сейчас давайте разберемся, в чем измеряется электроемкость. (-12) Ф
(-12) Ф
Конденсаторы
Конденсатор — это две пластины из проводящего материала, расположенные друг напротив друга, между которым находится слой диэлектрика. В заряженном состоянии обкладки имеют разные потенциалы: одна из них будет положительной, а вторая отрицательной. Электроемкость конденсатора зависит от величины заряда на его обкладках и разности потенциалов, напряжения между ними. Между пластинами возникает электростатическое поле, которое удерживает заряды на обкладках. Формула электрической емкости конденсатора в общем случае:
C=q/U
Если сказать простыми словами, то емкость конденсатора зависит от площади пластин и расстояния между ними, а также относительной диэлектрической проницаемости материала, расположенного между ними. Их различают по используемому диэлектрику:
- керамические;
- плёночные;
- слюдяные;
- металлобумажные;
- электролитические;
- танталовые и пр.
По форме обкладок:
- плоские;
- цилиндрические;
- сферические и пр.

Так как формула площади фигуры зависит от её формы, то и формула ёмкости будет разной для каждого случая.
Для плоского конденсатора:
Для двух концентрических сфер с общим центром:
Для цилиндрического конденсатора:
Как и у других элементов электрической цепи и в этом случае есть два основных способа соединения конденсаторов: параллельное и последовательное.
От этого зависит итоговая электрическая емкость полученной цепи. Расчёты ёмкости нескольких конденсаторов напоминают расчёты сопротивления резисторов в разном включении, только формулы для способов соединения расположены наоборот, то есть:
- При параллельном соединении общая электроемкость цепи является суммой емкостей каждого из элементов. Каждый следующий подключенный увеличивает итоговую емкость
Cобщ=C1+C2+C3
- При последовательном подключении электроемкость цепи снижается, подобно снижение сопротивления в цепи параллельно включённых резисторов.
 То есть:
То есть:
Cобщ=(1/С1)+ (1/С2)+ (1/С3)
Важно! В параллельной схеме соединения напряжения на обкладках каждого элемента одинаковы. Это используют для получения больших значений электроемкости. В последовательном включении двух элементов напряжения на обкладках каждого из конденсаторов составляют по половине общего напряжения. Для трёх – трети и так далее.
Аккумуляторы и электроемкость
Основными характеристиками аккумуляторных батарей является:
- Номинальное напряжение.
- Емкость.
- Максимальный ток разряда.
В данном случае для определения количественной характеристики времени работы или, говоря простым языком, чтобы рассчитать, на какое время работы прибора хватит аккумулятора, используют величину ёмкости.
В аккумуляторных батареях для описания электрической ёмкости используют следующие размерности:
- А*ч — ампер-часы для больших аккумуляторов, например автомобильных.

- мА*ч — милиампер-часы, для аккумуляторов для носимых устройств, например смартфонов, квадрокопетров и электронных сигарет.
- Вт*часы — ватт-часы.
Эти характеристики позволяют определить, сколько времени работы выдержит аккумулятор при конкретной нагрузке. Для определения электрическую емкость аккумулятора измеряют в кулонах (Кл). В свою очередь кулон равен количеству электричества, переданному аккумулятору при силе тока 1А за 1с. Тогда если перевести в часы, то при токе в 1А за 1 час передается 3600 Кл.
Одним из способов измерения емкости аккумулятора является его разряд заведомо известным током, при этом вы должны замерить время разряда. Допустим, если аккумулятор разрядился до минимального уровня напряжения за 10 часов током в 5А – значит его емкость 50 А*ч
Электроемкость – это важная величина в электронике и электротехнике. На практике конденсаторы применяются практически в каждой схеме электронного устройства. Например, в блоках питания – для сглаживания пульсаций, уменьшения влияния высоковольтных всплесков на силовые ключи. Во времязадающих цепях различных схем, а также в ШИМ-контроллерах для того, чтобы задать рабочую частоту. Аккумуляторы также применяются повсеместно. Вообще задачи накапливания энергии и сдвига фаз встречаются очень часто.
Во времязадающих цепях различных схем, а также в ШИМ-контроллерах для того, чтобы задать рабочую частоту. Аккумуляторы также применяются повсеместно. Вообще задачи накапливания энергии и сдвига фаз встречаются очень часто.
Более подробно изучить вопрос поможет предоставленное видео:
Кратко объяснение изложено в этом видео уроке:
Теперь вы знаете, что такое электрическая емкость, в каких единицах происходит ее измерение и от чего зависит данная величина. Надеемся, предоставленная информация была для вас полезной и понятной!
Материалы по теме:
Вычисление емкости конденсатора. Наука техника технологии
Плоский конденсатор – это физическое упрощение, взявшее начало из ранних исследований электричества, представляющее собой конструкцию, где обкладки имеют форму плоскостей и в каждой точке параллельны.
Формулы
Многие ищут формулы, описывающие ёмкость плоского конденсатора. Если это так, то не читайте ниже любопытные и малоизвестные факты, потому что сухие математические знаки, конечно же, важнее.
Первым определил ёмкость плоского конденсатора Вольта. В его распоряжении ещё не было такой величины, как разница потенциалов, именуемая напряжением, но интуитивно он совершенно правильно объяснил суть явления. Что касается количества зарядов, то он трактовал её, как объем электрического флюида атмосферы – не совсем правильно, но в конечном итоге похоже на правду. Согласно этому мировоззрению ёмкость плоского конденсатора может быть найдена, как отношение объёма накопленного электрического флюида к разнице атмосферных потенциалов, то есть:
Эта формула применима к любому конденсатору, вне зависимости от его конструкции. То есть, является универсальной. Специально для плоских конденсаторов имеется формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры:
В этой формуле через S обозначена площадь обкладок, вычисляемая через произведение сторон, а d – показывает расстояние между обкладками. Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика, да простит Тот столь откровенные тавтологии. Электролитические конденсаторы обладают столь большой ёмкостью по той причине, что проводящий раствор отделен от металла очень тонким слоем оксида. Следовательно, d в этом случает будет минимальным. Единственный минус в том, что электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на каждом анод или катод обозначены значками плюса или минуса.
Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика, да простит Тот столь откровенные тавтологии. Электролитические конденсаторы обладают столь большой ёмкостью по той причине, что проводящий раствор отделен от металла очень тонким слоем оксида. Следовательно, d в этом случает будет минимальным. Единственный минус в том, что электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на каждом анод или катод обозначены значками плюса или минуса.
Плоские конденсаторы сегодня редко встречаются, и это преимущественно плёночные микроскопические технологии, где такой род поверхностей является доминирующим. Все пассивные и активные элементы образуются через трафарет. И, следовательно, имеют вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст.
От материала диэлектрика ёмкость зависит по той причине, что у каждого из них структура своя. Считается, что аморфное вещество состоит из неориентированных диполей, упруго укреплённых на своих местах. При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость. В результате заряд продолжает накапливаться, пока этот процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на свои места, делая возможным следующий рабочий цикл. Так функционирует плоский электрический конденсатор.
При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость. В результате заряд продолжает накапливаться, пока этот процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на свои места, делая возможным следующий рабочий цикл. Так функционирует плоский электрический конденсатор.
Из истории
Исторически первым начал исследовать накопление заряда великий Алессандро Вольта. В докладе Королевскому научному обществу за 1782 год он впервые озвучил слово конденсатор. В понимании Вольты электрофорус, представляющий собой две параллельные обкладки, выкачивал из эфира электрический флюид.
В то время все познания сводились к тому, что учёные думали, будто атмосфера Земли содержит в себе нечто, что не может быть определено приборами. Существовали только простейшие электроскопы, способные определить знак заряда и его наличие, но не дававшие представления о количестве. Учёные просто натирали мехом поверхность тела и подносили его для исследования в область влияния прибора. Ещё Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием. Поэтому учёные примерно знали, что нужно делать, но исследования не продвигались ни на йоту.
Ещё Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием. Поэтому учёные примерно знали, что нужно делать, но исследования не продвигались ни на йоту.
Гипотеза об атмосферном электричестве высказана Бенджамином Франклином. Он активно исследовал молнии и пришёл к выводу, что это проявления все той же единой силы. Запуская воздушного змея в небо, он соединял его шёлковой нитью с землёй и наблюдал дуговой разряд. Это были достаточно опасные опыты, и Бенджамин много раз рисковал своей жизнью ради развития науки. О том, что шёлковая нить проводит статический заряд, было известно от Стивена Грея, первым собравшего в 1732 году электрическую цепь.
Уже через 20 лет (1752 год) Бенджамин Франклин предложил конструкцию первого громоотвода, осуществлявшего молниезащиты близлежащих построек. Только вдуматься! – до этого всякий мог ожидать того, что его дом сгорит от случайного удара. Именно Бенджамин Франклин предложил один из видов заряда называть положительным (стеклянный), а другой отрицательным (смоляной).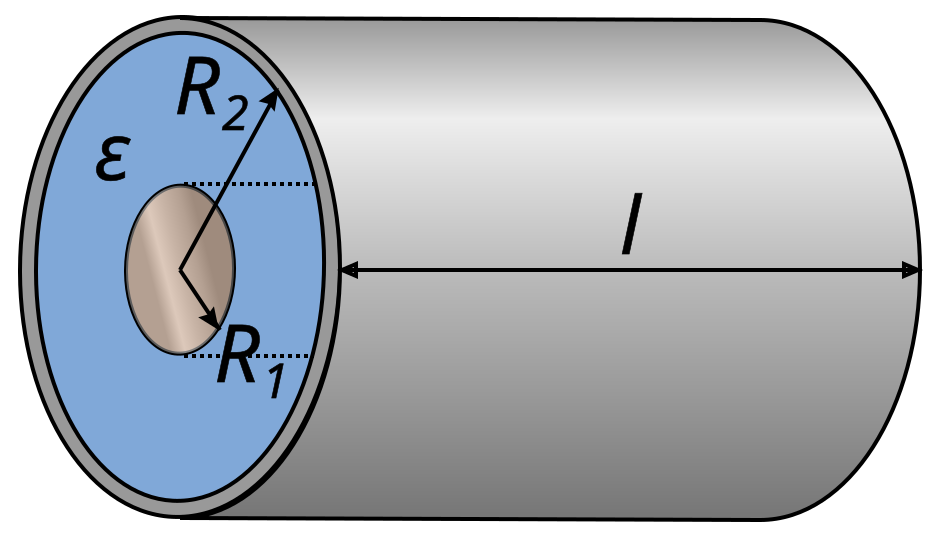 Так физики были введены в заблуждение относительно истинного направления движения электронов. Но как они могли думать иначе, когда в 1802 году на примере опытов нашего соотечественника Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, вот только это были ионы воздушной плазмы.
Так физики были введены в заблуждение относительно истинного направления движения электронов. Но как они могли думать иначе, когда в 1802 году на примере опытов нашего соотечественника Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, вот только это были ионы воздушной плазмы.
К началу исследования Вольтой электрических явлений, таким образом, были уже известны статические заряды и факт наличия у них двух знаков, кроме того люди упорно считали, что весь «флюид» берётся из воздуха. На эту мысль их натолкнули опыты с натиранием янтаря шерстью, которые не могли быть проведены под водой. Следовательно, логичным было предположить, что электричество может происходить только из атмосферы Земли, что, конечно же, совершенно неверно. В частности, многие растворы, исследованные Хампфри Дэви, могут проводить электрический ток.
Причина, следовательно, была в другом – при натирании янтаря под водой силы трения снижались в десятки и сотни раз, а заряд рассеивался по всему объёму жидкости. Следовательно, этот процесс был всего лишь неэффективным. Но сегодня каждый добытчик знает, что нефть прекрасно электризуется трением о трубы и без воздуха. Следовательно, атмосфера для «флюида» не является обязательным компонентом.
Следовательно, этот процесс был всего лишь неэффективным. Но сегодня каждый добытчик знает, что нефть прекрасно электризуется трением о трубы и без воздуха. Следовательно, атмосфера для «флюида» не является обязательным компонентом.
Самый большой в мире плоский конденсатор
Столь систематизированные, но в корне неверные толкования все-таки не смогли остановить Вольту на его исследовательском пути. Он упорно изучал электрофорус, как один из самых совершенных генераторов, существовавших в то время. Вторым был серный шар Отто фон Герике, изобретённый более чем за век до этого (1663 год). С тех самых пор его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. В частности, в для этого служат металлические гребёнки-нейтрализаторы.
Долгое время учёные ходили вокруг да около. Электрофорная машина 1880 года может считаться первым мощным генератором разряда, позволявшим получить дугу, но своей настоящей силы электроны достигли в генераторе Ван де Граафа (1929 год), где разница потенциалов составила единицы мегавольта.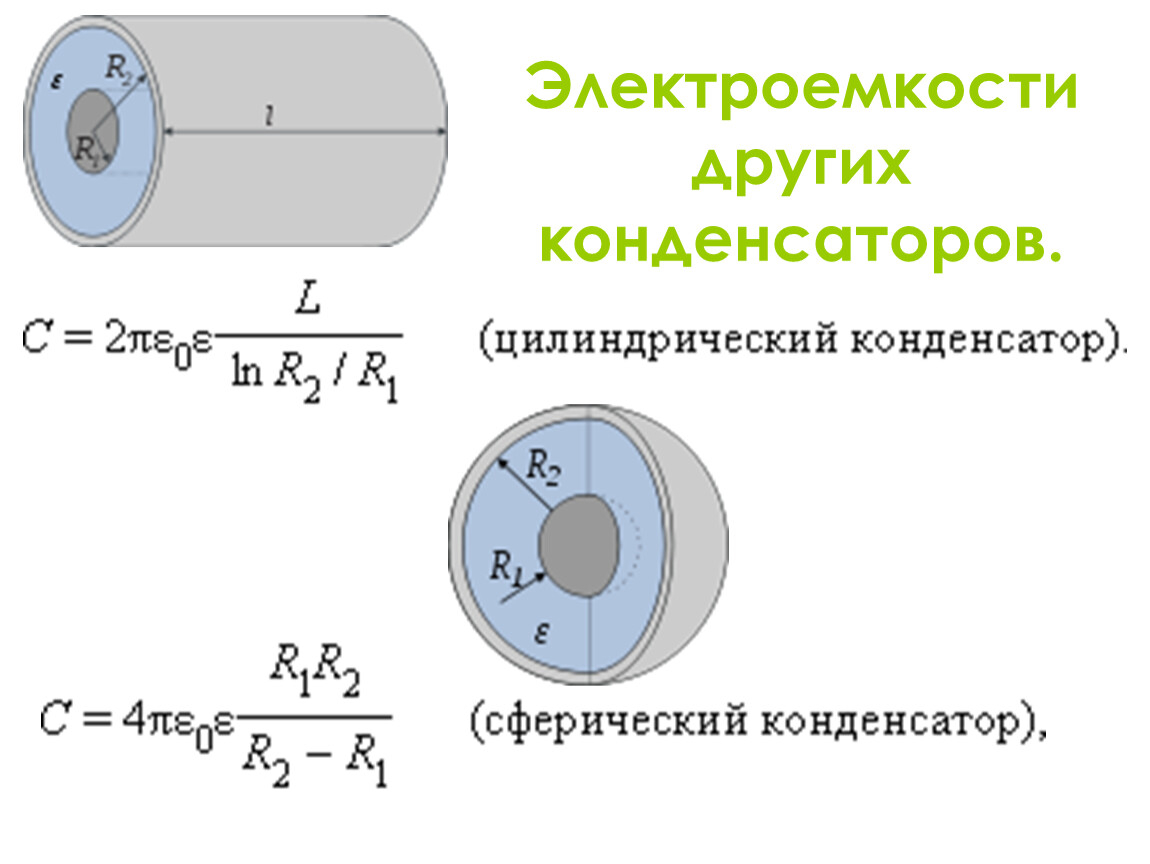 Для сравнения грозовое облако, согласно данным Википедии, может иметь потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Для сравнения грозовое облако, согласно данным Википедии, может иметь потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине).
Суммируя сказанное, можно с определённой долей уверенности сказать, что природные процессы используют в качестве принципа своего действия электризацию трением, влиянием и некоторые другие её виды, а мощный циклон является самым большим из известных нам плоских конденсаторов. Молния показывает, что бывает, когда диэлектрик (атмосфера) не выдерживает приложенной разницы потенциалов и пробивается. В точности то же самое происходит в любом плоском конденсаторе, созданном человеком, если вольтаж оказывается для него непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя.
Электрофорус
Итак, Вольта взялся за исследование модели природных процессов. Первый электрофорус появился в 1762 году сконструированный Йоханом Карлом Вильке. По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта же и дал прибору его нынешнее название.
По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта же и дал прибору его нынешнее название.
Электрофорус способен накапливать электростатический заряд, образованный трением резины куском шерсти. Он состоит из двух плоских, параллельных друг другу обкладок:
- Нижняя представляет собой тонкий кусок резины. Толщина его выбирается из соображений эффективности устройства. Если выбрать кусок более солидный, то значительная часть энергии будет накапливаться внутри диэлектрика на ориентацию его молекул. Что и наблюдается в современном плоском конденсаторе, куда диэлектрик помещается для увеличения электроёмкости.
- Верхняя пластина из тонкой стали кладётся сверху, когда заряд уже накоплен трением. За счёт влияния на верхней поверхности образуется избыток отрицательного заряда, и он должен быть снят на заземлитель, чтобы при расстыковке двух обкладок не произошло взаимной компенсации.

Принцип действия этого плоского конденсатора должен быть уже понятен. Оператор трёт резину шерстью, оставляя на ней отрицательный заряд. Затем сверху кладётся кусок металла. Из-за значительной шероховатости поверхностей они не соприкасаются, но находятся на некотором расстоянии друг от друга. В результате металл электризуется влиянием. Электроны отталкиваются поверхностным зарядом резины и уходят на внешнюю плоскость, где оператор их снимает через заземлитель лёгким кратковременным прикосновением.
Низ металлической обкладки остаётся заряженным положительно. При расстыковке двух поверхностей этот эффект сохраняется, потому что в материале наблюдается дефицит электронов. И можно наблюдать искру, если дотронуться до металлической обкладки. Этот опыт можно на одном и том же заряде резины проделывать сотни раз, поскольку её поверхностное статическое сопротивление весьма велико. Это не даёт заряду растекаться. Демонстрируя этот опыт, Вольта привлёк внимание всего научного мира, но исследования никак не двигались вперёд, если не считать открытий Шарля Кулона.
В 1800 году сам Алессандро даёт толчок развитию изысканий в области электричества, изобретя свой знаменитый гальванический источник питания.
Конструкция плоского конденсатора
Электрофорус по сути представляет собой первый из когда-либо сконструированных плоских конденсаторов. Его обкладки способны хранить только статический заряд, потому что иначе наэлектризовать резину невозможно. Поверхность очень долго хранит электроны. Вольта даже предлагал снимать их пламенем свечи через ионизированный воздух или ультрафиолетовым излучением Солнца. Сегодня каждый школьник знает, что то же самое можно проделать и водой. Правда, электрофорус нужно будет после этого высушить.
В современном мире нижней обкладкой может служить тефлоновое покрытие или пластик. Они тоже хорошо набирают статический заряд. Диэлектриком здесь служит воздух. Чтобы перейти к конструкции современного конденсатора, нужно обе обкладки сделать металлическими. Тогда при возникновении на одной из них заряда влиянием электризация распространится на вторую, и если другой контакт заземлён, накопленная энергия может храниться какое-то время.
Запас электронов напрямую зависит от материала диэлектриков. Так например, среди современных конденсаторов встречаются:
- Слюдяные.
- Воздушные.
- Электролитические (оксидные).
- Керамические.
В эти названия как раз и заложен материал диэлектрика. От его состава зависит напрямую ёмкость, которая может быть увеличена во много раз. Роль диэлектриков объяснялась выше, в частности их параметры определяются непосредственно строением вещества. Однако многие материалы, обладающие высокими характеристиками, использовать не удаётся по причине их непригодности. Так например, вода обладает высокой диэлектрической проницаемостью.
Характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.
Под зарядом конденсатора понимают заряд одной пластины.
Так же есть:
Энергия конденсатора:
Ёмкость цилиндрического конденсатора:
Емкость сферического конденсатора:
В формуле мы использовали:
Электрическая ёмкость (ёмкость конденсатора)
Относительная диэлектрическая проницаемость
Электрическая постоянная
Плоский конденсатор состоит из двух
параллельных пластин, разделённых
небольшим зазором шириной
,
заполненным однородным диэлектриком.
Нам известно, что поле между двумя
разноимённо заряженными пластинами с
одинаковой по величине поверхностной
плотностью
равно,
где,S– площадь каждой пластины.
Напряжение между обкладками:
Используя
определение емкости конденсатора,
получаем:
Отметим, что полученная формула является
приближенной, так как выведена без учета
искажения поля у краев пластин. Расчет
по этой формуле дает завышенное значение
ёмкости и тем точнее, чем меньше зазор
по сравнению с линейными размерами
пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет
собой систему двух концентрических
сфер с радиусами
и.
Электрическое поле между обкладками
сферического конденсатора согласно
теореме Гаусса определяется зарядом
внутренней сферы. Напряжение между
обкладками равно:
.
Для
ёмкости сферического конденсатора
получаем:
Это
формула точная.
Если
,
полученная формула переходит в выражение
для ёмкости плоского конденсатора.
Ёмкость
цилиндрического конденсатора.
Цилиндрический конденсатор составляет
систему двух коаксиальных цилиндров с
радиусами
и,
длиной.
Рассуждая
аналогично выводу ёмкости сферического
конденсатора, получаем:
..
Полученная формула является приближенной
и при малом зазоре
переходит в формулу емкости плоского
конденсатора.
Соединение
конденсаторов.
В практике для получения необходимых
значений емкости используют соединения
конденсаторов: а) последовательное, б)
параллельное, в) смешанное (см. рисунок).
Ёмкость
последовательного соединения
конденсаторов.
Заряды последовательно соединенных
конденсаторов равны
,
а напряжение на батарее.
Из определения емкости следует:
Если
,
то(ёмкость последовательного соединения
меньше наименьшей ёмкости в последовательном
соединении).
Для
последовательно соединенных конденсаторов
емкость вычисляется по формуле:
Ёмкость
параллельного соединения конденсаторов.
Заряд
батареи равен сумме зарядов:
а
напряжение
.
По определению емкости получаем:
Для
параллельно соединенных конденсаторов:.
В
случае одинаковых конденсаторов:
.
Оценить
емкость батареи (см. рисунок)
.
Используя
свойство бесконечности можно представить
цепь в виде соединения (см. рисунок).
Для
расчета ёмкости батареи получаем:
Откуда:
,
так как,
то.
Лекция 7.
Диэлектрики
в электрическом поле.
Диэлектриками (изоляторами) называют
вещества, не проводящие постоянного
электрического тока. Это означает, что
в диэлектриках отсутствуют «свободные»
заряды, способные перемещаться на
значительные расстояния.
Диэлектрики состоят либо из нейтральных
молекул, либо из ионов, находящихся в
узлах кристаллической решетки. Сами же
молекулы могут быть полярными
инеполярными.
Полярные молекулы
обладают дипольным моментом, у неполярных
молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики
поляризуются. Это явление связано с
появлением в объеме и на поверхности
диэлектрика «связанных
» зарядов.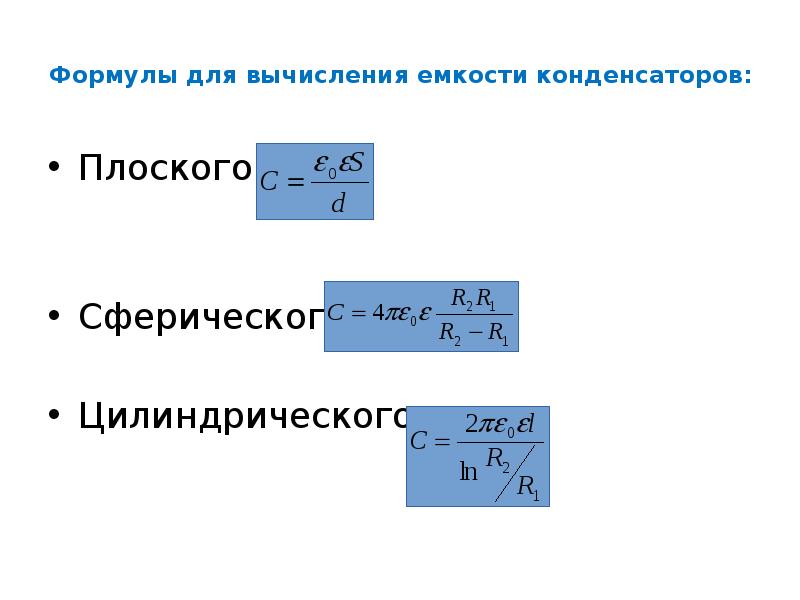
При этом конечный объем диэлектрика
приобретает дипольный момент. Механизм
поляризации связан с конкретным строением
диэлектрика. Если диэлектрик состоит
из неполярных молекул, то в пределах
каждой молекулы происходит смещение
зарядов – положительных по полю,
отрицательных против поля, т.е. молекулы,
приобретают дипольный момент. У
диэлектрика с полярными молекулами в
отсутствии внешнего электрического
поля их дипольные моменты ориентированы
хаотично.
Под действием электрического поля
диполи ориентируются преимущественно
в направлении поля. Рассмотрим подробнее
этот механизм (см. рисунок). Пара сил
исоздает
вращательный момент равный,
где-
дипольный момент молекулы. Этот момент
стремится ориентировать диполь вдоль
поля. В ионных кристаллах под действием
электрического поля все положительные
ионы смещаются по полю, отрицательные
– против поля. Отметим, что смещение
зарядов очень малы даже по сравнению с
размерами молекул. Это связано с тем,
что напряженность внешнего электрического
поля обычно много меньше напряженности
внутренних электрических полей в
молекулах.
Отметим, что существуют диэлектрики,
поляризованные даже при отсутствии
внешнего поля (электреты, сегнетоэлектрики).
Мы остановимся на рассмотрении только
однородных диэлектриков, в которых
отсутствует остаточная поляризация, а
объемный и «связанный» заряд всегда
равен нулю
.
КОНДЕНСАТОР
— означает накопитель. В радио и электронной
аппаратуре конденсатор является накопителем электрических
зарядов. Простейший конденсатор состоит из двух металлических
пластинок разделенных слоем диэлектрика. Диэлектрик — это
материал который не проводит электрического тока и обладает
определенными свойствами о которых поговорим чуть позже.
Так как конденсатор является накопителем, то он должен
обладать определенной емкостью (объемом для накопления
зарядов). На емкость конденсатора влияют площадь пластин
(еще их называют «обкладками»), расстояние между обкладками
и качество диэлектрика. К хорошим диэлектрикам
относятся вакуум, эбонит, фарфор, слюда, полиэтилен,
текстолит и много других синтетических материалов.
На рисунке изображен простейший конденсатор
с двумя параллельными обкладками площадью S
(S = m * n), которые находятся в вакууме на расстоянии d друг
от друга.
Если между верхней и нижней обкладками конденсатора
приложить напряжение Uab, то на верхней и нижней обкладках
конденсатора накопятся одинаковые положительный +q и
отрицательный -q заряды, которые называют свободными. Между
обкладками возникает электрическое поле обозначенное на рисунке
буквой Е.
Емкость нашего конденсатора (обозначается буквой С) будет:
С = Eo*S/d, где Ео — электрическая постоянная (для вакуума)
Ео=8,854 * 10 -12 Ф/м (Фарад на метр).
Если между обкладками поместить диэлектрик,
то ёмкость конденсатора
будет: С = Er * Eo *S / d. В формуле расчета ёмкости добавилась
величина Er — относительная диэлектрическая проницаемость
введённого диэлектрика.
Из формулы следует, что емкость конденсатора увеличивается на
величину Er проницаемости диэлектрика. Итак, чем больше площадь
S пластин конденсатора, больше значение Er и меньше расстояние
d между пластинами, тем больше емкость конденсатора.
Основной единицей емкости в системе единиц СИ является фарад
(Ф). Емкость 1Ф очень велика. В электротехнике обычно
используют дольные единицы емкости:
микрофарада (мкФ), 1мкФ = 1*10 -6 Ф,
нанофарада (нФ), 1нФ = 1*10 -9 Ф, и
пикофарада (пФ), 1пФ = 1*10 -12 Ф.
При выборе диэлектрика для конденсаторов, кроме относительной
диэлектрической проницаемости диэлектрика, учитывают еще два
важных параметра:
1) Электрическую прочность — прочность диэлектрика при подаче
на прокладки конденсатора высокого напряжения. При низкой
электрической прочности может произойти электрический пробой,
и диэлектрик станет проводником электрического тока;
2) Удельное объемное сопротивление — электрическое
сопротивление диэлектрика постоянному току. Чем больше удельное
сопротивление диэлектрика, тем меньше утечка накопленных
зарядов в конденсаторе.
КОНДЕНСАТОР В ЦЕПИ ПОСТОЯННОГО ТОКА.
На графике накопление заряда конденсатором выглядит как
показано на рисунке 1.
Время заряда конденсатора зависит от
ёмкости конденсатора (при одинаковом приложенном напряжении).
Чем больше ёмкость конденсатора, тем больше время заряда.
Аналогичная картина (Рис. 2) наблюдается при разрядке
конденсатора на сопротивление. При одинаковом сопротивлении
время разряда больше у конденсатора с большей ёмкостью.
КОНДЕНСАТОР В ЦЕПИ ПЕРЕМЕННОГО ТОКА.
Если напряжение приложенное к емкостному элементу, будет
изменяться по амплитуде (переменное напряжение),то будет
изменяться и заряд конденсатора, то есть в емкостном элементе
появится ток.
Ток Ic проходящий через конденсатор зависит от
частоты f приложенного переменного напряжения и ёмкости С
конденсатора. Если для постоянного тока сопротивление
конденсатора можно считать равным бесконечности, то для
переменного тока конденсатор обладает определённым
сопротивлением. Сопротивление конденсатора переменному току
Rc рассчитывается по формуле показанной на рисунке.
В формуле расчета емкостного сопротивления переменному току
частота выражается в герцах, а емкость конденсатора в
фарадах. Из формулы видно, что с увеличением частоты f при
Из формулы видно, что с увеличением частоты f при
неизменной емкости конденсатора сопротивление Rc снижается,
аналогично с увеличением емкости конденсатора при неизменной
частоте сопротивление Rc так же снижается.
Конденсаторы, так же как и резисторы, для получения заданной
емкости Со можно включать параллельно и последовательно.
Формулы расчета результирующей емкости показаны на рисунке.
КОНСТРУКЦИЯ, ПАРАМЕТРЫ И ТИПЫ КОНДЕНСАТОРОВ.
Предположим, что мы конструируем конденсатор и попробуем,
уже обладая определенными знаниями, рассчитать емкость
конденсатора. Как известно, емкость конденсатора зависит от
площади обкладок S, расстояния между обкладками d и
диэлектрической проницаемости применяемого диэлектрика Er.
Обкладки конденсатора изготавливаются из металлов с хорошей
электрической проводимостью — алюминий, медь, серебро, золото.
Емкость конденсатора не зависит от толщины обкладок, поэтому
чем тоньше обкладки конденсатора, тем лучше — экономим металл
и уменьшаем геометрический объём конденсатора.
Расстояние d не должно быть слишком малым, во избежание
электрического пробоя диэлектрика.
Выберем в качестве диэлектрика наиболее распространенный
материал — гетинакс с Er равной 6 … 8. Примем Er для
нашего конденсатора равной 7.
Площадь S вычисляется для одной обкладки конденсатора при условии,
что линейные размеры обкладок одинаковы.
Если одна из обкладок имеет меньшие длину или ширину то площадь
вычисляется для меньшей обкладки.
Все размеры — длина и ширина обкладок и расстояние между ними
должны быть выражены в метрах. Примем размеры такие, какие
показаны на рисунке. Подставим в формулу расчета емкости
конденсатора наши данные: C = Er * Eo * S / d;
C = 7 * 8.854*10 -12 * 0.0025 / 0.001= 0.000000000155Ф (фарады).
Возведем полученный результат в 12 степень чтобы получить
значение емкости в пикофарадах:
C = 0.000000000155 12 = 155пФ.
Полученная нами ёмкость конденсатора 155пф очень мала, обычно
такие ёмкости используются в аппаратуре работающей на высоких
частотах переменного тока порядка 1 — 600 МГц (мегагерц).
Представьте себе, что мы разрабатываем миниатюрный карманный
радиоприемник в котором требуется порядка 30 таких конденсаторов.
Если мы установим в схему 30 разработанных нами конденсаторов,
не считая других необходимых радиодеталей, то наш радиоприемник
никак не получится миниатюрным. Все дело в том, что объём
только наших конденсаторов получится таким, что его никак
нельзя будет назвать приемлемым.
Объем одного конденсатора Vc равен Vc = 5см * 5см * 0,1см
Vc = 2,5см в кубе. Тогда объем 30 конденсаторов будет равен:
V = 30 * 2,5 = 75см в кубе.
Что делать, как быть, как уменьшить геометрический объем
конденсатора для применения в миниатюрной радиоаппаратуре?
Для решения этой проблемы максимально уменьшают расстояние
между обкладками, тогда увеличивается емкость и уменьшается
геометрический объем конденсатора. Но расстояние уменьшают
до определенных пределов иначе конденсатор будет пробиваться
даже при низком напряжении подаваемом на конденсатор. В связи
с этим на каждом конденсаторе указывается напряжение которое
он может выдержать.
Для уменьшения площади обкладок конденсатор делают многослойным
состоящим как бы из нескольких параллельно включенных конденсаторов
(вспомните формулу параллельного включения конденсаторов).
В качестве диэлектрика в миниатюрных конденсаторах используют
тонкие пленки из синтетических материалов, а в качестве обкладок
металлическую фольгу, чаще всего из алюминия.
На корпусе конденсатора, обычно, указывается его тип, емкость и
рабочее напряжение. Остальные параметры конденсатора
определяются из справочников. Емкость конденсатора указывается
не так, как на электрических схемах. Например емкость 2,2пФ
обозначается 2П2, емкость 1500 пФ — 1Н5, емкость 0,1 мкФ — М1,
емкость 2,2 мкФ — 2М2, емкость 10 мкФ — 10М.
У обычных конденсаторов КМ, КД, МБМ и так далее трудно получить
большую ёмкость при малых габаритах поэтому были разработаны
так называемые электролитические конденсаторы у которых в
качестве диэлектрика используется специальная электролитическая
жидкость с очень большим Er.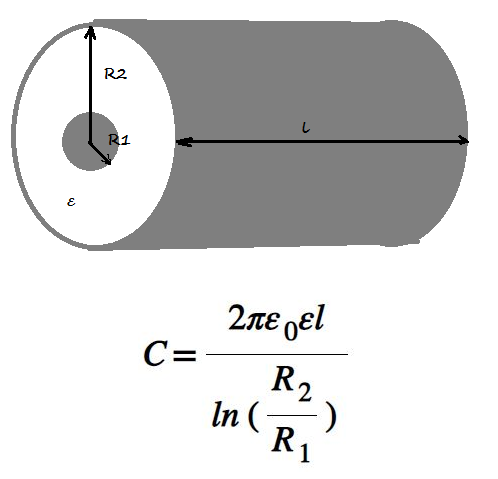 Ёмкость таких конденсаторов может
Ёмкость таких конденсаторов может
достигать сотен тысяч микрофарад. К недостатку таких конденсаторов
следует отнести низкое рабочее напряжение (до 500V) и обязательное
соблюдение полярности при включении в схему.
Для настройки и подстройки некоторых типов радиоаппаратуры,
например радиоприемник или телевизор, применяют специальные конденсаторы
с изменяемой ёмкостью.
В зависимости от назначения такие конденсаторы называют «подстроечные»
и «конденсаторы переменной емкости».
Емкость переменных и подстроечных конденсаторов изменяется
механическим способом, путем изменения расстояния между
обкладками или изменения площади пластин. В качестве
диэлектрика в таких конденсаторах используется воздух или
фарфор.
В заключение следует отметить, что в настоящее время, в связи
с бурным развитием радиоэлектроники подстроечные и переменные
конденсаторы практически не применяются. Их с успехом заменяют
специальные фильтры и полупроводниковые приборы которые не
требуют механического изменения параметров.
Формула емкости конденсатора через напряжение. Зарядка конденсатора от источника постоянной эдс
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины;
– расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки;
– радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов (рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
ru.solverbook.com
Формула емкости конденсатора, С
Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:
называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():
где – диэлектрическая проницаемость диэлектрика.
За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).
Формула электрической емкости плоского конденсатора
Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Формула электрической емкости цилиндрического конденсатора
Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:
Формула электрической емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком.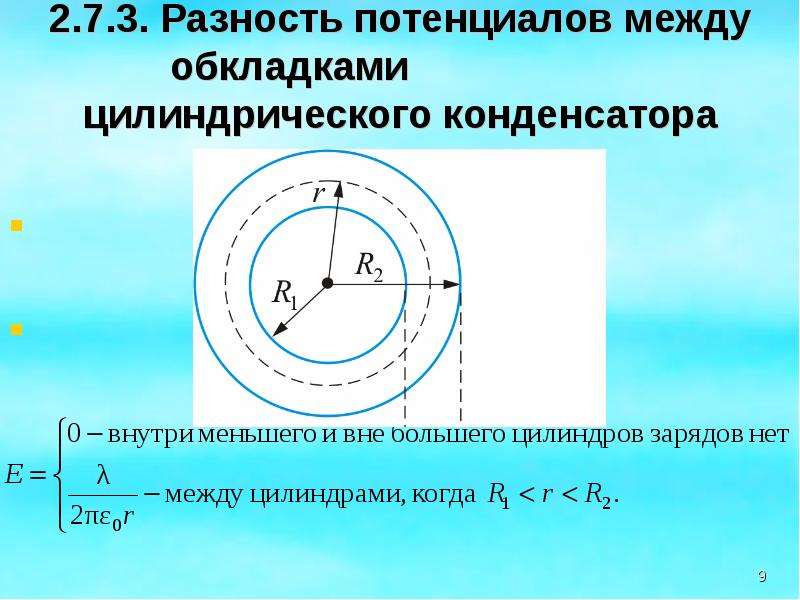 Емкость такого конденсатора находят как:
Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач по теме «Емкость конденсатора»
ru.solverbook.com
Ёмкость конденсатора — Все формулы
Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.
Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Конденсаторы можно классифицировать по следующим признакам и свойствам:
1) по назначению — конденсаторы постоянной и переменной емкости;
2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
3) по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.
Так же есть:
Энергия конденсатора:
Ёмкость цилиндрического конденсатора:
Ёмкость плоского конденсатора:
Емкость сферического конденсатора:
В формуле мы использовали:
Электрическая ёмкость (ёмкость конденсатора)
Потенциал проводника (Напряжение)
Потенциал
Относительная диэлектрическая проницаемость
Электрическая постоянная
Площадь одной обкладки
Расстояние между обкладками
xn--b1agsdjmeuf9e. xn--p1ai
xn--p1ai
Заряд конденсатора, теория и примеры задач
Определение и заряд конденсатора
Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).
По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.
Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.
При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.
Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.
Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
Примеры решения задач
ru.solverbook.com
Формула электроемкости конденсатора
Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.
Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.
Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:
q – величина заряда на обкладке; – разность потенциалов между обкладками.
Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в раз больше, чем емкость воздушного конденсатора ():
Формула электроемкости основных типов конденсаторов
При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок.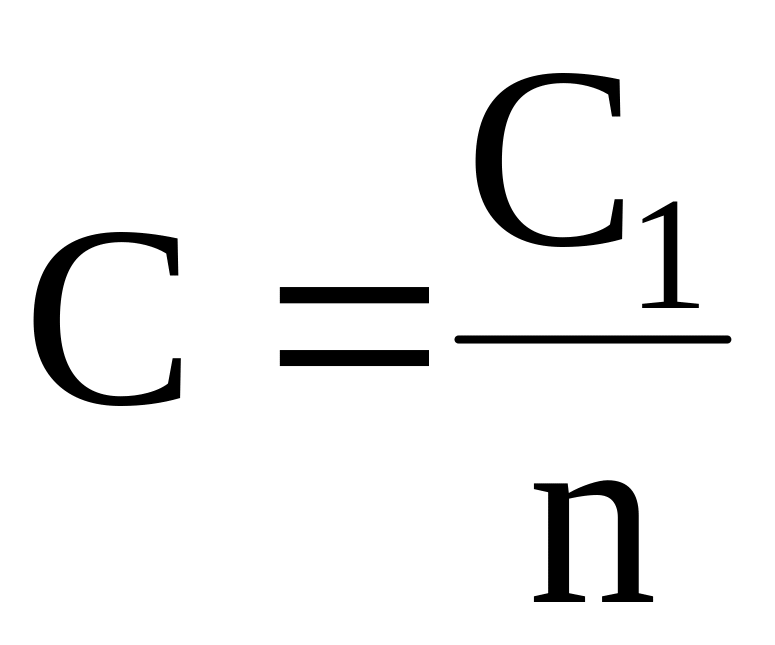 В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:
В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна , а диэлектрическая проницаемость , то его электрическую емкость рассчитывают при помощи формулы:
Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:
где – радиусы обкладок конденсатора.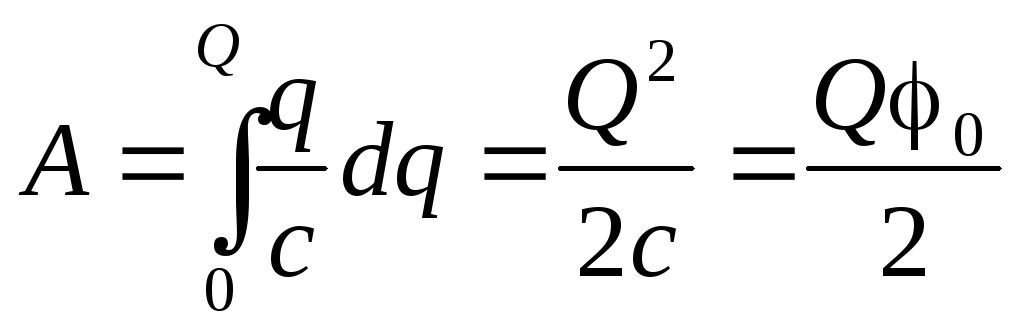 Если , то можно считать, что , тогда, мы имеем:
Если , то можно считать, что , тогда, мы имеем:
так как – площадь поверхности сферы, и если обозначить , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.
Электрическую емкость для линии из двух проводов находят как:
где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.
Формулы для вычисления электрической емкости соединений конденсаторов
Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов ():
При последовательном соединении конденсаторов емкость батареи вычисляют как:
Если последовательно соединены N конденсаторов, с емкостями то емкость батареи найдем как:
Сопротивление конденсатора
Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.
При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:
где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.
Энергия поля конденсатора
Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:
где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.
Энергия поля плоского конденсатора:
Примеры решения задач по теме «Электроемкость конденсатора»
ru.solverbook.com
Как найти заряд конденсатора 🚩 как определить величину заряда 🚩 Естественные науки
В обычном (без плагинов и модов) варианте Minecraft такого понятия, как конденсатор, не существует. Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое — компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.
Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.
Подобное устройство существует для проверки заполненности расположенных позади него контейнеров. Таковыми могут быть сундуки (в том числе в виде ловушек), варочные стойки, раздатчики, выбрасыватели, печи, загрузочные воронки и т.п.
Помимо этого, его часто используют для сравнения двух сигналов редстоуна между собою — он выдает результат в соответствии с тем, как было запрограммировано в данной цепи, и с тем, какой режим выбран для самого механизма. В частности, компаратор может разрешить зажигание факела, если первый сигнал больше либо равен другому.
Также порой конденсатор-компаратор устанавливают рядом с проигрывателем, подключая его входом к последнему. Когда в звуковоспроизводящем устройстве проигрывается какая-либо пластинка, вышеупомянутый прибор будет выдавать сигнал, равный по силе порядковому номеру диска.
Скрафтить такой компаратор несложно, если имеется достаточно трудно добываемый ресурс — адский кварц. Его надо поставить в центральный слот верстака, над ним и по бокам от него установить три красных факела, а в нижнем ряду — такое же количество каменных блоков.
В большом количестве модов попадаются конденсаторы, имеющие самое разное предназначение. К примеру, в Galacticraft, где у геймеров есть возможность слетать на многие планеты для ознакомления с тамошними реалиями, появляется рецепт крафта кислородного конденсатора. Он служит для создания механизмов вроде коллектора и накопителя газа для дыхания, а также рамки воздушного шлюза. Для его изготовления четыре стальных пластины размещаются по углам верстака, в центре — оловянная канистра, а под нею — воздуховод. Остальные три ячейки занимают пластины из олова.
В JurassiCraft существует конденсатор потока — некий телепорт, позволяющий переместиться в удивительный игровой мир, кишащий динозаврами. Для создания такого прибора нужно поместить в два крайних вертикальных ряда шесть железных слитков, а в средний — два алмаза и между ними единицу пыли редстоуна. Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.
Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.
С модом Industrial Craft2 у игрока появляется возможность создавать как минимум два вида тепловых конденсаторов — красный и лазуритовый. Они служат исключительно для охлаждения ядерного реактора и для накопления его энергии и хороши для циклических сооружений такого типа. Остужаются они сами, соответственно, красной пылью или лазуритом.
Красный теплоконденсатор делается из семи единиц пыли редстоуна — их надо установить в виде буквы П и расставить под ними теплоотвод и теплообменник. Крафтинг же лазуритового устройства чуть посложнее. Для его создания четыре единицы пыли редстоуна расставляются по углам станка, в центр пойдет блок лазурита, по бокам от него — два красных тепловых конденсатора, сверху — теплоотвод реактора, а снизу — его же теплообменник.
В ThaumCraft, где сделан акцент на настоящем чародействе, конденсаторы тоже используются. Например, один из них — кристаллический — существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея — исследования, проводимого за специальным столом и с определенными приборами.
Например, один из них — кристаллический — существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея — исследования, проводимого за специальным столом и с определенными приборами.
Делается такой конденсатор из восьми тусклых осколков, в центр которых на верстаке помещается мистический деревянный блок. К сожалению, подобный прибор — равно как и его составляющие — просуществовал лишь до ThaumCraft 3, а в четвертой версии мода был упразднен.
www.kakprosto.ru
Соединение конденсаторов: формулы
Содержание:
- Последовательное соединение
- Онлайн калькулятор
- Смешанное соединение
- Параллельное соединение
- Видео
В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.
Последовательное соединение
При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.
В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.
Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.
Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.
Смешанное соединение
Параллельное соединение конденсаторов
Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.
Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.
В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.
Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.
electric-220.ru
Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.
Расчёт конденсаторов
Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:
Рассчитать её можно по следующей формуле:
- C – ёмкость,
- q – заряд одной из обкладок элемента,
- U – разность потенциалов между обкладками.
В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».
Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:
С=Co*ε, где:
- С – реальная ёмкость,
- Со – идеальная, при условии, что между пластинами вакуум или воздух,
- ε – диэлектрическая проницаемость материала между ними.
Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.
Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).
Расчет плоской конструкции
- ε – диэлектрическая проницаемость изолирующего материала,
- d – расстояние между пластинами.
Расчет конструкции цилиндрической формы
Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.
Вычисляются параметры такого устройства по формуле:
C=(2π*l*R*ε)/d, где:
- l – длина устройства,
- R – радиус цилиндра,
- ε – диэлектрическая проницаемость изолятора,
- d – его толщина.
Расчёт сферической конструкции
Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:
Формула ёмкости такого прибора:
C=(4π*l*R1*R2*ε)/(R2-R1), где:
- R1 – радиус внутренней сферы,
- R2 – радиус внешней сферы,
- ε – диэлектрическая проницаемость.
Ёмкость одиночного проводника
Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:
- Q – заряд,
- φ – потенциал проводника.
Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.
Способы соединения элементов
Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.
Параллельное соединение
Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора.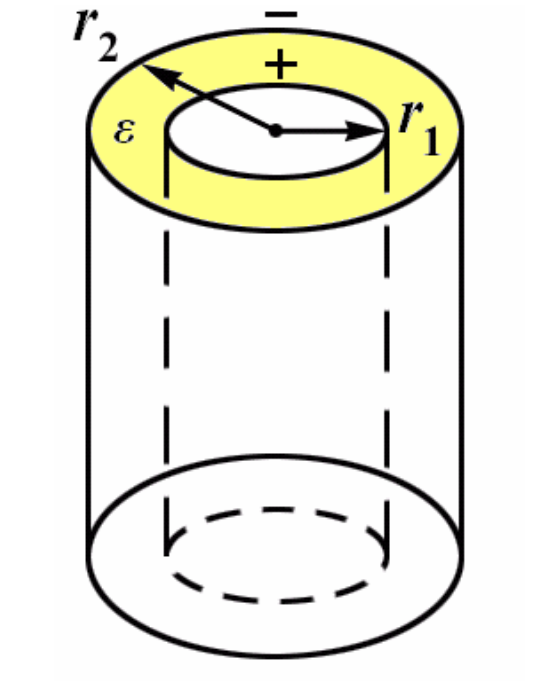 При этом вторые обкладки присоединяются к другой клемме.
При этом вторые обкладки присоединяются к другой клемме.
При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:
где C1-Cn – параметры деталей, участвующих в параллельном соединении.
Важно!
Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.
Последовательное соединение
Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.
При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.
Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.
Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.
Рассчитываются эти параметры следующим образом:
- Допустимое напряжение:
Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;
- Общая ёмкость:
1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.
Интересно.
Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).
Смешанное соединение
Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:
- определяются группы элементов, соединённые параллельно;
- для каждой группы в отдельности рассчитывается эквивалентные значения;
- рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
- получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.
Видео
Содержание:
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица — фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q — заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q — заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов используется формула:
в которой ε 0
= 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε — является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S — означает площадь обкладки, а d — зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как . После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде:W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W эл = CU 2 /2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U c = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I зар = Е/R i , поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора — способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: I ут = U/R d , где I ут, — это ток утечки, U — напряжение, прилагаемое к конденсатору, а R d — сопротивление изоляции.
§
6. Заряд и
разряд конденсатора
Чтобы зарядить
конденсатор, надо, чтобы свободные электроны перешли из одной обкладки на
другую. Переход электронов с одной обкладки конденсатора на другую происходит
Переход электронов с одной обкладки конденсатора на другую происходит
под действием напряжения источника по проводам, соединяющим этот источник с
обкладками конденсатора.
В момент
включения конденсатора зарядов на его обкладках нет и напряжение на нем равно
нулю μ
с =0.
Поэтому зарядный ток определяется внутренним сопротивлением источника r
в и имеет
наибольшую величину:
I З max =E/ r в.
По мере
накопления зарядов на обкладках конденсатора напряжение на нем увеличивается и
падение напряжения на внутреннем сопротивлении источника будет равно разности
ЭДС источника и напряжения на конденсаторе (Е- μ
с). следовательно, зарядный ток
i з =(Е- μ с)/ r в.
Таким образом, с
увеличением напряжения на конденсаторе ток заряда снизится и при μ
с =Е
становится равным нулю. Процесс изменения напряжения на конденсаторе и тока
заряда во времени изображен на рис. 1. В самом начале заряда напряжение на конденсаторе
резко возрастает, так как зарядный ток имеет наибольшее значение и накопление
зарядов на обкладках конденсатора происходит интенсивно. По мере повышения
По мере повышения
напряжения на конденсаторе зарядный ток уменьшается и накопление зарядов на
обкладках замедляется. Продолжительность заряда конденсатора зависит от его
емкости и сопротивления цепи, увеличение которых приводит к возрастанию
продолжительности заряда. С увеличением емкости конденсатора, возрастает
количество зарядов, накапливаемых на его пластинах, а если увеличить
сопротивление цепи уменьшится и зарядный ток, а это замедляет процесс
накопления зарядов на этих обкладках.
Если обкладки
заряженного конденсатора подключить к какому-либо сопротивлению R
, то за счет напряжения на
конденсаторе будет протекать разрядный ток конденсатора. При разряде
конденсатора электронысодной пластины (при их избытке) будут
переходить на другую (при их недостатке) и будет продолжается до тех пор, пока
потенциалы обкладок не выравняются, т. е. напряжение на конденсаторе станет
равным нулю. Изменение напряжения в процессе разряда конденсатора изображено на
рис. 2. Ток разряда конденсатора пропорционален напряжению на конденсаторе (i
р =μ
с /R
), и его изменение во
времени подобно изменению напряжения.
В начальный
момент разряда напряжение на конденсаторе наибольшее (μ
с =Е) и разрядный ток максимальный (I
р max
=E
/R
), так что разряд происходит быстро. При понижении напряжения, ток
разряда снижается и процесс перехода зарядов с одной обкладки на другую затормаживается.
Время процесса
разряда конденсатора зависит от сопротивления цепи и емкости конденсатора,
причем возрастание как сопротивления, так и емкости увеличивает
продолжительность разряда. С увеличением сопротивления разрядный ток снижается,
замедляется процесс переноски зарядов с одной на другую обкладок; с увеличением
емкости конденсатора повышается заряд на обкладках.
Таким образом, в цепи, содержащей конденсатор,
ток проходит только в процессе его заряда и разряда, т. е. когда напряжение на
обкладках претерпевает изменение во времени. При постоянстве напряжения ток
через конденсатор не проходит, т. е. конденсатор не пропускает постоянный ток,
так как между его обкладками помещен диэлектрик и в результате этого цепь
разомкнута.
При зарядке
конденсатора, последний способен накапливать электрическую энергию, потребляя
ее от энергоисточника. Накопленная энергия сохраняется определенное время. При
разряде конденсатора эта энергия переходит к разрядному резистору, нагревая
его, т. е. энергию электрического поля превращается в тепловую. Чем выше
емкость конденсатора и напряжение на его обкладках, тем будет больше энергии,
запасенной на нем. Энергия электрического поля конденсатора определяется
следующим выражением
W=CU 2 /2.
Если конденсатор
емкостью 100 мкФ заряжен до напряжения 200 В, то энергия, запасенная в
электрическом поле конденсатора, W
=100·
10 -6 ·
200 2 /2=2 Дж.
Вам понадобится
- — знание емкости или геометрических и физических параметров конденсатора;
- — знание энергии или заряда на конденсаторе.
Инструкция
Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C — емкость, а U — напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).
Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).
Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества ) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q — заряд). Следовательно, зная энергию и , можно вычислить напряжение между его пластинами по формуле: U=2∙W/q.
Поскольку заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C∙U), то, зная заряд и емкость, можно найти и напряжение. Соответственно, для проведения расчета используйте формулу: U=q/C.
Для получения значения напряжения на конденсаторе с известными геометрическими и параметрами, сначала рассчитайте его емкость. Для простого плоского конденсатора, состоящего из двух проводящих пластин, разделенных , расстояние между которыми пренебрежимо мало по сравнению с их размерами, емкость может быть вычислена по формуле: C=(ε∙ε0∙S)/d. -12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.
-12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.
Обратите внимание
Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ.
Для того чтобы знать, можно ли использовать в том или ином месте схемы конденсатор, следует определить его . Способ нахождения этого параметра зависит от того, каким образом он обозначен на конденсаторе и обозначен ли вообще.
Вам понадобится
- Измеритель емкости
Инструкция
На крупных конденсаторах
емкость
обычно обозначена открытым текстом: 0,25 мкФ или 15 uF. В этом случае, способ ее определения тривиален.
На менее крупных конденсаторах
(в том , SMD) емкость
двумя или тремя цифрами. В первом случае, она обозначена в пикофарадах. Во втором случае, первые две цифры емкость
Во втором случае, первые две цифры емкость
, а третья — в каких единицах она выражена:1 — десятки пикофарад;
2 — сотни пикофарад;
3 — нанофарады;
4 — десятки нанофарад;
5 — доли микрофарады.
Существует также система обозначения емкости, использующая сочетания латинских букв и цифр. Буквы обозначают следующие цифры:A — 10;
B — 11;
C — 12;
D — 13;
E — 15;
F — 16;
G — 18;
H — 20;
J — 22;
K — 24;
L — 27;
M — 30;
N — 33;
P — 36;
Q — 39;
R — 43;
S — 47;
T — 51;
U — 56;
V — 62;
W — 68;
X — 75;
Y — 82;
Z — 91.Полученное число следует умножить на число 10, предварительно возведенное в степень, равную цифре, следующей после . Результат будет выражен в пикофарадах.
Встречаются конденсаторы, емкость
на которых не обозначена вообще. Вы наверняка встречали их, в , в стартерах ламп дневного . В этом случае, измерить емкость
можно только специальным прибором. Они цифровыми и мостовыми.В любом случае, если конденсатор впаян в то или иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость
Они цифровыми и мостовыми.В любом случае, если конденсатор впаян в то или иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость
которого следует измерить, и лишь после этого выпаять его. Затем его необходимо подключить к прибору.На цифровом измерителе сначала выбирают самый грубый предел, затем переключают его до тех пор, пока он не покажет перегрузку. После этого переключатель переводят на один предел назад и читают показания, а по положению переключателя определяют, в каких единицах они выражены.На мостовом измерителе, последовательно переключая , на каждом из них прокручивают регулятор из одного конца шкалы в другой, пока звук из динамика не исчезнет. Добившись исчезновения , по шкале регулятора считывают результат, а единицы, в которых он выражен, также определяют по положению переключателя.Затем конденсатор устанавливают обратно в устройство.
Обратите внимание
Никогда не подключайте к измерителю заряженные конденсаторы.
Источники:
- Справочник по системам обозначения емкости
Найти значение электрического заряда
можно двумя способами. Первый – измерить силу взаимодействия неизвестного заряда
с известным и с помощью закона Кулона рассчитать его значение. Второй – внести заряд в известное электрическое поле и измерить силу, с которой оно действует на него. Для измерения заряда
протекающего через поперечное сечение проводника за определенное время измерьте силу тока и умножьте ее на значение времени.
Вам понадобится
- чувствительный динамометр, секундомер, амперметр, измеритель электростатического поля, воздушный конденсатор.
Инструкция
Измерение заряда
при его с известным зарядомЕсли известен одного тела, поднесите к нему неизвестный заряд и измерьте между ними в метрах. Заряды начнут взаимодействовать. С помощью динамометра измерьте силу их взаимодействия. Рассчитайте значение неизвестного заряда
— для этого квадрат измеренного расстояния умножьте на значение силы и поделите на известный заряд. 9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные.
9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные.
Измерение значения заряда
, внесенного в электрическое полеИзмерьте значение постоянного электрического поля специальным прибором (измеритель электрического поля). Если такого прибора нет, возьмите воздушный конденсатор, зарядите его, измерьте напряжение на его обкладках и поделите не расстояние между пластинами – это и будет значение электрического поля внутри конденсатора в вольтах на метр. Внесите в поле неизвестный заряд. С помощью чувствительного динамометра измерьте силу, которая на него действует. Измерение проводите в . Поделите значение силы на напряженность электрического поля. Результатом будет значение заряда
в Кулонах (q=F/Е).
Измерение заряда
, протекающего через поперечное проводникаСоберите электрическую цепь с проводниками и последовательно подключите к ней амперметр. Замкните ее на источник тока и измерьте силу тока с помощью амперметра в амперах. Одновременно секундомером засеките , в которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, через поперечное сечение каждого за это время (q=I t). При измерениях следите, чтобы проводники не перегревались и не произошло короткое замыкание.
Одновременно секундомером засеките , в которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, через поперечное сечение каждого за это время (q=I t). При измерениях следите, чтобы проводники не перегревались и не произошло короткое замыкание.
Конденсатором называется устройство, способное накапливать электрические заряды. Количество накапливаемой электрической энергии в конденсаторе характеризуется его емкостью
. Она измеряется в фарадах. Считается, что емкость в один фарад соответствует конденсатору, заряженному электрическим зарядом в один кулон при разности потенциалов на его обкладках в один вольт.
Инструкция
Определите емкость плоского конденсатора
по формуле С = S e e0/d, где S — площадь поверхности одной пластины, d — между пластинами, e — относительная диэлектрическая проницаемость , заполняющей пространство между пластинами (в вакууме она равна ), e0 — электрическая постоянная, равная 8,854187817 10(-12) Ф/м. Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, между ними и от материала диэлектрика. В качестве диэлектрика может применяться или слюда.
Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, между ними и от материала диэлектрика. В качестве диэлектрика может применяться или слюда.
Вычислите емкость сферического конденсатора
по формуле С = (4П e0 R²)/d, где П — число «пи», R — радиус сферы, d — величина зазора между его сферами.Величина емкости сферического конденсатора
прямо пропорциональна концентрической сферы и обратно пропорциональна расстоянию между сферами.
Рассчитайте емкость цилиндрического конденсатора
по формуле С = (2П e e0 L R1)/(R2-R1), где L — длина конденсатора
, П — число «пи», R1 и R2 — радиусы его цилиндрических обкладок.
Если конденсаторы в цепи соединены параллельно, рассчитайте их общую емкость по формуле С = С1+С2+…+Сn, где С1, С2,…Сn – емкости параллельно соединенных конденсаторов.
Вычислите общую емкость последовательно соединенных конденсаторов по формуле 1/С = 1/С1+1/С2+…+1/Сn, где С1, С2,…Сn — емкости последовательно соединенных конденсаторов.
Обратите внимание
На любом конденсаторе обязательно должна быть нанесена маркировка, которая может быть буквенно-цифровая или цветовая. Маркировка отражает его параметры.
Источники:
- Цветовая маркировка резисторов, конденсаторов и индуктивностей
Емкость – величина, в системе СИ выражаемая в фарадах. Хотя используются, фактически, лишь производные от нее – микрофарады, пикофарады и так далее. Что касается электроемкости плоского конденсатора, она зависит от зазора меж обкладок и их площади, от вида диэлектрика, в данном зазоре расположенного.
Инструкция
В том случае, если обкладки конденсатора имеют одинаковую площадь и имеют расположение строго одна над другой, рассчитайте площадь одной из обкладок – любой. Если же одна из них относительно другой смещена либо они разные , нужно рассчитывать площадь области, в которой обкладки друг дружку перекрывают.
При этом используются общепринятые формулы, рассчитывать площади таких геометрических фигур, как круг (S=π(R^2)), прямоугольника (S=ab), его частного случая – квадрата (S=a^2) – и других. (-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума.
(-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума.
8.1 Конденсаторы и емкость — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните понятие конденсатора и его емкости
- Опишите, как оценить емкость системы проводов
Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии. Конденсаторы обычно состоят из двух электрических проводников, разделенных расстоянием.(Обратите внимание, что такие электрические проводники иногда называют «электродами», но, точнее, они «обкладки конденсатора».) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор будет известен как «Вакуумный конденсатор». Однако пространство обычно заполняется изолирующим материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем накопителя в конденсаторе определяется свойством, называемым емкостью , , о котором вы узнаете больше чуть позже в этом разделе.
Конденсаторы
имеют различные применения: от фильтрации статического электричества, радиоприема до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как на рис. 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к первоначально незаряженному конденсатору, потенциал батареи перемещает небольшой заряд величиной Q с положительной пластины на отрицательную.Конденсатор в целом остается нейтральным, но с зарядами + Q + Q и −Q − Q, расположенными на противоположных пластинах.
Фигура
8,2
Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них на пластинах есть заряды + Q + Q и −Q − Q (соответственно). (a) Конденсатор с параллельными пластинами состоит из двух пластин противоположного заряда с площадью A, , разделенных расстоянием d . (b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).
(b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).
Система, состоящая из двух идентичных параллельно проводящих пластин, разделенных расстоянием, называется конденсатором с параллельными пластинами (рис. 8.3). Величина электрического поля в пространстве между параллельными пластинами составляет E = σ / ε0E = σ / ε0, где σσ обозначает поверхностную плотность заряда на одной пластине (напомним, что σσ — это заряд Q на площадь поверхности A ). Таким образом, величина поля прямо пропорциональна Q .
Фигура
8,3
Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора.Линии электрического поля в конденсаторе с параллельными пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.
Конденсаторы с разными физическими характеристиками (такими как форма и размер пластин) накапливают разное количество заряда для одного и того же приложенного напряжения В на своих пластинах. Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В, на его пластинах.Другими словами, емкость — это наибольшая величина заряда на вольт, которая может храниться на устройстве:
Единица измерения емкости в системе СИ — фарад (Ф), названная в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или
.
По определению, конденсатор емкостью 1,0 мкФ может сохранять заряд 1,0 К (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Следовательно, один фарад является очень большой емкостью.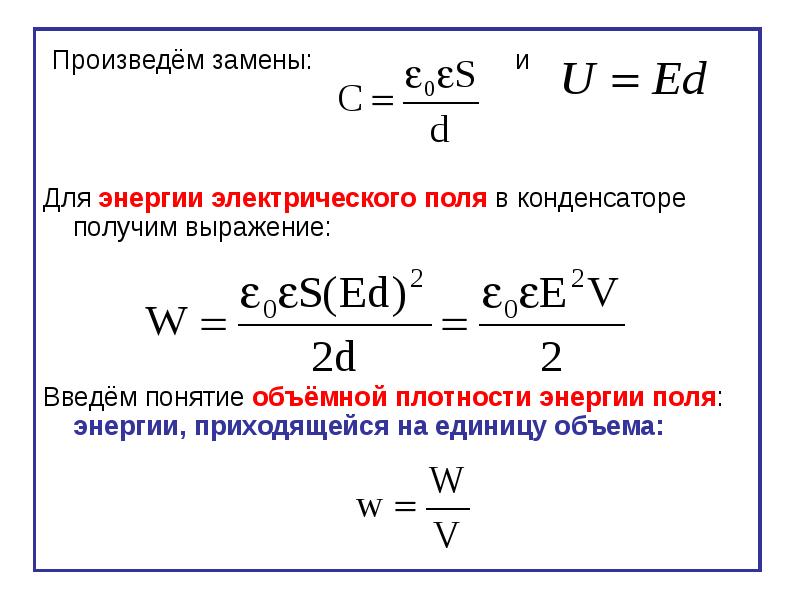 Типичные значения емкости варьируются от пикофарад (1 пФ = 10-12 Ф) (1 пФ = 10-12 Ф) до миллифарадов (1 мФ = 10-3 Ф) (1 мФ = 10-3 Ф), включая микрофарады (1 мкФ = 10-6 Ф 1 мкФ = 10- 6F). Конденсаторы могут быть разных форм и размеров (рис. 8.4).
Типичные значения емкости варьируются от пикофарад (1 пФ = 10-12 Ф) (1 пФ = 10-12 Ф) до миллифарадов (1 мФ = 10-3 Ф) (1 мФ = 10-3 Ф), включая микрофарады (1 мкФ = 10-6 Ф 1 мкФ = 10- 6F). Конденсаторы могут быть разных форм и размеров (рис. 8.4).
Фигура
8,4
Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно зависит от его емкости. (Источник: Windell Oskay)
Расчет емкости
Мы можем рассчитать емкость пары проводов с помощью следующего стандартного подхода.
Стратегия решения проблем
Расчет емкости
- Предположим, что конденсатор имеет заряд Q .
- Определить электрическое поле E → E → между проводниками. Если в расположении проводников присутствует симметрия, вы можете использовать закон Гаусса для этого расчета.
- Найдите разность потенциалов между проводниками из
VB − VA = −ABE → · dl →, VB − VA = −ABE → · dl →,8,2
где путь интегрирования ведет от одного проводника к другому.
 Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |.
Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |. - Зная В, , определите емкость непосредственно из уравнения 8.1.
Чтобы показать, как работает эта процедура, мы теперь вычисляем емкости параллельных пластин, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.
Конденсатор с параллельными пластинами
Конденсатор с параллельными пластинами (рисунок 8.5) имеет две идентичные токопроводящие пластины, каждая с площадью поверхности A, , разделенными расстоянием d . Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость может зависеть от A и d , рассмотрев характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить.Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины друг к другу, тем сильнее на них притяжение противоположных зарядов. Следовательно, C должно быть больше для меньшего d .
Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить.Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины друг к другу, тем сильнее на них притяжение противоположных зарядов. Следовательно, C должно быть больше для меньшего d .
Фигура
8,5
В конденсаторе с параллельными пластинами, разделенные пластинами на расстояние d , каждая пластина имеет одинаковую площадь поверхности A, .
Определим плотность поверхностного заряда σσ на пластинах как
Из предыдущих глав мы знаем, что когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и что его величина определяется как
.
где постоянная ε0ε0 — диэлектрическая проницаемость свободного пространства, ε0 = 8.85 × 10–12Ф / м. Ε0 = 8,85 × 10–12Ф / м. Единица СИ в Ф / м эквивалентна C2 / N · m2.C2 / N · m2. Поскольку электрическое поле E → E → между пластинами однородно, разность потенциалов между пластинами составляет
.
V = Ed = σdε0 = Qdε0A.V = Ed = σdε0 = Qdε0A.
Следовательно, уравнение 8.1 дает емкость конденсатора с параллельными пластинами как
C = QV = QQd / ε0A = ε0Ad.C = QV = QQd / ε0A = ε0Ad.
8,3
Обратите внимание на это уравнение, что емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора.Фактически, это верно не только для конденсатора с параллельными пластинами, но и для всех конденсаторов: емкость не зависит от Q или В . Если заряд изменяется, соответственно изменяется и потенциал, так что Q / V остается постоянным.
Пример
8.1
Емкость и заряд в конденсаторе с параллельными пластинами
(а) Какова емкость пустого конденсатора с параллельными пластинами с металлическими пластинами, каждая из которых имеет площадь 1?00м21.00м2, через 1,00 мм? (b) Сколько заряда хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 103 В3,00 × 103 В?
Стратегия
Определение емкости C представляет собой прямое применение уравнения 8.3. Найдя C , мы сможем найти накопленный заряд, используя уравнение 8.1.
Решение
- Ввод заданных значений в уравнение 8.3 дает
C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3м = 8,85 × 10−9F = 8,85nF.C = ε0Ad = (8,85 × 10−12Fm) 1,00м21.00 × 10−3m = 8,85 × 10−9F = 8,85 нФ.
Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью. - Обращение уравнения 8.
 1 и ввод известных значений в это уравнение дает
1 и ввод известных значений в это уравнение дает
Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл. Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл.
Значение
Этот заряд лишь немного больше, чем в типичных приложениях для статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3.0 МВ / м, на этом конденсаторе больше нельзя накапливать заряд при увеличении напряжения.
Пример
8,2
1-Ф конденсатор с параллельными пластинами
Предположим, вы хотите сконструировать конденсатор с параллельными пластинами емкостью 1,0 F. Какую площадь вы должны использовать для каждой пластины, если пластины разделены на 1,0 мм?
Решение
Преобразуя уравнение 8.3, получаем
A = Cdε0 = (1.0F) (1.0 × 10−3m) 8.85 × 10−12F / m = 1.1 × 108m2 A = Cdε0 = (1.0F) (1.0 × 10−3m) 8,85 × 10−12F / m = 1,1 × 108 м2.
Каждая квадратная пластина должна быть 10 км в поперечнике. Раньше было обычным розыгрышем — попросить студента пойти в склад лаборатории и попросить конденсатор с параллельными пластинами 1F, пока обслуживающий персонал не устанет от шуток.
Раньше было обычным розыгрышем — попросить студента пойти в склад лаборатории и попросить конденсатор с параллельными пластинами 1F, пока обслуживающий персонал не устанет от шуток.
Проверьте свое понимание
8.1
Проверьте свое понимание Емкость конденсатора с параллельными пластинами составляет 2,0 пФ. Если площадь каждой пластины составляет 2,4 см 22,4 см2, каково расстояние между пластинами?
Проверьте свое понимание
8,2
Проверьте свое понимание Убедитесь, что σ / Vσ / V и ε0 / dε0 / d имеют одинаковые физические единицы.
Сферический конденсатор
Сферический конденсатор — это еще один набор проводников, емкость которых можно легко определить (рис. 8.6). Он состоит из двух концентрических проводящих сферических оболочек радиусов R1R1 (внутренняя оболочка) и R2R2 (внешняя оболочка). Оболочкам приписываются равные и противоположные заряды + Q + Q и −Q − Q соответственно. Из-за симметрии электрическое поле между оболочками направлено радиально наружу. Мы можем получить величину поля, применив закон Гаусса к сферической гауссовой поверхности радиусом r , концентричной оболочкам.dr) = Q4πε0∫R1R2drr2 = Q4πε0 (1R1−1R2).
Из-за симметрии электрическое поле между оболочками направлено радиально наружу. Мы можем получить величину поля, применив закон Гаусса к сферической гауссовой поверхности радиусом r , концентричной оболочкам.dr) = Q4πε0∫R1R2drr2 = Q4πε0 (1R1−1R2).
В этом уравнении разность потенциалов между пластинами равна V = — (V2 − V1) = V1 − V2V = — (V2 − V1) = V1 − V2. Подставляем этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:
C = QV = 4πε0R1R2R2 − R1.C = QV = 4πε0R1R2R2 − R1.
8,4
Фигура
8,6
Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды на проводнике находятся на его поверхности.
Пример
8.3
Емкость изолированной сферы
Вычислите емкость одиночной изолированной проводящей сферы радиуса R1R1 и сравните ее с уравнением 8.4 в пределе R2 → ∞R2 → ∞.
Стратегия
Мы предполагаем, что заряд на сфере равен Q , и поэтому следуем четырем шагам, описанным ранее. Мы также предполагаем, что другой проводник представляет собой концентрическую полую сферу бесконечного радиуса.
Мы также предполагаем, что другой проводник представляет собой концентрическую полую сферу бесконечного радиуса.
Решение
На внешней стороне изолированной проводящей сферы электрическое поле задается уравнением 8.dr) = Q4πε0∫R1 + ∞drr2 = 14πε0QR1.
Таким образом, емкость изолированной сферы равна
.
C = QV = Q4πε0R1Q = 4πε0R1.C = QV = Q4πε0R1Q = 4πε0R1.
Значение
Тот же результат можно получить, взяв предел уравнения 8.4 при R2 → ∞R2 → ∞. Таким образом, одиночная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.
Проверьте свое понимание
8,3
Проверьте свое понимание Радиус внешней сферы сферического конденсатора в пять раз больше радиуса его внутренней оболочки.Каковы размеры этого конденсатора, если его емкость 5,00 пФ?
Цилиндрический конденсатор
Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рисунок 8. dA = E (2πrl) = Qε0.dr) = Q2πε0l∫R1R2drr = Q2πε0llnr | R1R2 = Q2πε0llnR2R1.
dA = E (2πrl) = Qε0.dr) = Q2πε0l∫R1R2drr = Q2πε0llnr | R1R2 = Q2πε0llnR2R1.
Таким образом, емкость цилиндрического конденсатора
C = QV = 2πε0lln (R2 / R1). C = QV = 2πε0lln (R2 / R1).
8,6
Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом.(Здесь мы предполагаем наличие вакуума между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком.) Эта конфигурация экранирует электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний провод обычно заземлен. Теперь из уравнения 8.6 емкость коаксиального кабеля на единицу длины равна
Теперь из уравнения 8.6 емкость коаксиального кабеля на единицу длины равна
.
Cl = 2πε0ln (R2 / R1).Cl = 2πε0ln (R2 / R1).
В практических приложениях важно выбирать конкретные значения C / l . Это может быть достигнуто за счет соответствующего выбора радиусов проводников и изоляционного материала между ними.
Проверьте свое понимание
8,4
Проверьте свое понимание Когда цилиндрический конденсатор получает заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Какова емкость этой системы? (b) Если цилиндры 1.Длина 0 м, каково соотношение их радиусов?
Несколько типов конденсаторов, которые можно использовать на практике, показаны на рис. 8.4. Обычные конденсаторы часто состоят из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. Рисунок 8.2 (b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторые распространенные изоляционные материалы — это слюда, керамика, бумага и антипригарное покрытие Teflon ™.
Некоторые распространенные изоляционные материалы — это слюда, керамика, бумага и антипригарное покрытие Teflon ™.
Другой популярный тип конденсатора — электролитический конденсатор.Он состоит из окисленного металла в проводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость одного типа алюминиевого электролитического конденсатора может достигать 1,0 F. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста. Когда возникает обратная поляризация, электролитическое действие разрушает оксидную пленку.Этот тип конденсатора не может быть подключен к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет свою полярность (см. Схемы переменного тока в цепях переменного тока).
Схемы переменного тока в цепях переменного тока).
Конденсатор переменного тока (рисунок 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначается как «ротор»). Поворачивая вал, можно изменять площадь поперечного сечения в перекрытии пластин; следовательно, емкость этой системы может быть настроена на желаемое значение.Настройка конденсатора находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильное радио на любимую станцию, думайте о емкости.
Фигура
8,8
В переменном воздушном конденсаторе емкость можно регулировать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спрула)
Символы, показанные на рисунке 8.9, представляют собой схемные изображения различных типов конденсаторов.Обычно мы используем символ, показанный на рис. 8.9 (а). Символ на Рисунке 8.9 (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор представлен символом на рис. 8.9 (b), где изогнутая пластина обозначает отрицательный вывод.
8.9 (а). Символ на Рисунке 8.9 (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор представлен символом на рис. 8.9 (b), где изогнутая пластина обозначает отрицательный вывод.
Фигура
8.9
Здесь показаны три различных схемных представления конденсаторов. Символ в (а) является наиболее часто используемым.Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет конденсатор переменной емкости.
Интересный прикладной пример модели конденсатора взят из клеточной биологии и имеет дело с электрическим потенциалом в плазматической мембране живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым отобранным ионам проходить внутрь или из клетки. Разность потенциалов на мембране составляет около 70 мВ. Клеточная мембрана может иметь толщину от 7 до 10 нм.Рассматривая клеточную мембрану как наноразмерный конденсатор, оценка наименьшей напряженности электрического поля на его « пластинах » дает значение E = Vd = 70 × 10−3V · 10 · 10−9m = 7 · 106V / m> 3MV / mE. = Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / m.
= Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / m.
Этой величины электрического поля достаточно, чтобы вызвать электрическую искру в воздухе.
Фигура
8.10
Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней.Диффузия перемещает ионы K + K + (калий) и Cl – Cl– (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Таким образом, внешняя часть мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая разность потенциалов на мембране. Мембрана обычно непроницаема для Na + (ионов натрия).
Физика для науки и техники II
5.5 Цилиндрический конденсатор от Office of Academic Technologies на Vimeo.
Для демонстраций см .:
http://maxwell.uncc.edu/aktas/PHYS2102nline/index2.html
5,05 Цилиндрический конденсатор
Теперь рассчитаем емкость цилиндрического конденсатора. Как следует из названия, теперь мы имеем дело с конденсатором, который состоит из двух концентрических проводящих цилиндрических поверхностей, скажем так, это большая поверхность или внешняя поверхность и меньшая концентрическая внутренняя поверхность. Хорошо. Поэтому наш цилиндрический конденсатор выглядит примерно так.И давайте также дадим некоторые размеры нашему конденсатору.
Предположим, что длина конденсатора равна h, а внутренний радиус равен a, другой радиус равен b. И мы заряжаем наш конденсатор так, чтобы мы подключали внутреннюю поверхность к положительной клемме источника питания, а внешнюю поверхность — к отрицательной клемме источника питания нашей батареи, скажем. Таким образом, внутренняя пластина будет заряжаться везде положительно, а внешняя пластина будет заряжаться отрицательно. Допустим, величина этого заряда равна плюс q, а внутренняя пластина, минус q, проходит вдоль внешней пластины.
Допустим, величина этого заряда равна плюс q, а внутренняя пластина, минус q, проходит вдоль внешней пластины.
Следовательно, заряжая конденсатор, мы уже выполнили первый шаг по вычислению емкости и говорим, что конденсатор заряжен до нескольких q кулонов. И в качестве второго шага мы рассчитаем электрическое поле между пластинами этого конденсатора, применив закон Гаусса, который был интегралом от E dot dA на замкнутой поверхности, равном чистому заряду внутри объема, окруженного этой замкнутой поверхностью, q, заключенный над Эпсилоном 0.
Опять же, изолирующая среда между этими двумя проводящими пластинами — воздух, поэтому это проводник, а это проводник, например, как алюминиевые пластины. Хорошо. Итак, теперь нас интересует электрическое поле между пластинами. Если мы посмотрим на геометрию пластин, мы увидим, что электрическое поле будет исходить от внутренней положительно заряженной пластины и войдет в отрицательно заряженную внешнюю пластину, в данном случае радиально наружу. Следовательно, электрическое поле будет заполнять пространство от положительной пластины до отрицательной в радиальном направлении наружу.
Следовательно, электрическое поле будет заполнять пространство от положительной пластины до отрицательной в радиальном направлении наружу.
Вся область между пластинами будет заполнена электрическим полем, создаваемым этими двумя заряженными пластинами. Итак, поскольку мы имеем дело с цилиндрической геометрией, мы собираемся выбрать нашу гауссову поверхность в форме цилиндра, так чтобы его боковая поверхность проходила через интересующую точку. Нашей точкой интереса в данном случае будет любая точка между пластинами. Давайте выберем эту точку как-нибудь подальше от концов этого цилиндра, где-нибудь примерно посередине в этой точке, стр.Это область между пластинами, и мы выбираем наш гауссовский цилиндр, гауссову поверхность в форме цилиндра, так чтобы его боковая поверхность проходила через интересующую точку. Следовательно, это будет поверхность, похожая на эту, цилиндрическую поверхность.
Теперь, когда мы применяем этот закон Гаусса, чтобы вычислить электрическое поле в этой точке между пластинами, мы собираемся сделать предположение, что мы далеко от конечных точек, и мы собираемся пренебречь конечные эффекты.Пренебрежение конечными эффектами означает, что, конечно, когда мы переходим к этой верхней границе, электрическое поле здесь не будет направлено радиально наружу, потому что у нас будет электрическое поле, направленное вверх, а результирующее поле будет векторной суммой те два. Но мы не будем обращать внимания на эти конечные эффекты. В противном случае мы не сможем применить закон Гаусса, потому что эта цилиндрическая поверхность в этом случае не будет удовлетворять условиям для применения закона Гаусса. Таким образом, мы должны сделать это предположение, и мы скажем, что пренебрегаем концевыми эффектами и предположим, что электрическое поле находится между этими двумя пластинами в радиальном направлении наружу.
Итак, учитывая это, мы можем разделить этот интеграл замкнутой поверхности на сумму открытых поверхностей, которая постепенно составляет весь этот цилиндр. И, как вы помните из цилиндрической геометрии, когда мы применяем закон Гаусса к задаче о бесконечном прямом маршруте, поскольку открытая форма этого цилиндра состоит из поверхности прямоугольного размера и круглых верхней и нижней поверхностей, которые эта прямоугольная поверхность охватывает, можно сказать, что этот интеграл можно выразить как интеграл по верхней поверхности цилиндра, которым является этот.И затем, то есть величина E dA величина.
И если мы посмотрим на угол между E и вектором dA для верхней поверхности, и где электрическое поле находится в этой области прямо здесь, так как для верхней поверхности dA перпендикулярно поверхности вот так, а электрическое поле радиально наружу угол между ними для верхней поверхности составляет 90 градусов.
Итак, у нас будет косинус 90. А поскольку косинус 90 равен нулю, этот интеграл не будет вносить никакого вклада. И плюс такой же для нижней поверхности; интегрируя по нижней поверхности, снова dA перпендикулярно поверхности, направлено вниз, а электрическое поле выходит радиально наружу, заполняя все это пространство.В этой части он будет указывать вот так, и снова угол между ними будет 90 градусов. Так что это тоже не поможет. У нас будет величина E dA, умноженная на косинус 90, что даст нам ноль.
И единственная оставшаяся поверхность — это интеграл боковой поверхности, для боковой поверхности, если мы посмотрим на нашу точку интереса, электрическое поле здесь радиально, и dA снова перпендикулярно поверхности. Следовательно, для этой точки и для всей боковой поверхности угол между вектором электрического поля и вектором увеличивающейся площади поверхности будет просто нулевым градусом.Таким образом, для интеграла боковой поверхности у нас будет EdA, умноженное на косинус 0,
.
Когда мы сложим все эти интегралы по открытой поверхности, то получится интеграл по всей замкнутой поверхности цилиндра. А в правой части у нас будет q, заключенное в эпсилон 0. Косинус 0, опять же, равен 1. И пока мы находимся на боковой поверхности этого гауссовского цилиндра, мы будем на таком же расстоянии от заряд, который он вмещает, который здесь является внутренним цилиндром. Таким образом, электрическое поле на боковой поверхности будет постоянным.Тогда мы можем вынести его за пределы интеграла.
Что ж, двигаясь дальше, у нас будет E-кратный интеграл по боковой поверхности цилиндра, где dA равно q, заключенному над эпсилоном 0. Что ж, если мы посмотрим на нашу форму открытой поверхности этого гауссовского цилиндра здесь, он имеет радиус r; это расположение точки относительно центра. Таким образом, эта сторона будет равна длине окружности либо верхнего круга, либо нижнего круга, что тогда будет равно 2 Pi r, поскольку оно оборачивается вокруг этих кругов.И мы дали размер h для высоты или длины цилиндра. Таким образом, интеграл dA по боковой поверхности, который даст нам площадь боковой поверхности, который будет равен e, умноженному на площадь боковой поверхности, что составляет 2 Pi r h. А в правой части у нас есть q, заключенное над Эпсилоном 0.
Опять же, q охватывает чистый заряд внутри области, окруженной гауссовой поверхностью, в данном случае это фиолетовый цилиндр. Когда мы смотрим на внутреннюю часть этой области, мы видим, что она охватывает всю внутреннюю поверхность и, следовательно, включает в себя любой заряд, распределенный по этой внутренней поверхности этого конденсатора, и который равен общему заряду вдоль этой поверхности, который это q.
Итак, вычисляя электрическое поле, величина электрического поля становится равной q в течение 2 Pi Epsilon 0 h, умноженных на r. Когда мы смотрим на это выражение как на отличное от конденсатора с параллельными пластинами, мы видим, что это не постоянная величина; он меняется на 1 по r. Другими словами, по мере того, как мы идем от внутренней поверхности к внешней поверхности, от внутренней поверхности к внешней поверхности, напряженность электрического поля уменьшается с 1 по r, с 1 по расстоянию относительно оси цилиндра.
Теперь, когда мы определим величину электрического поля, конечно, его направление радиально наружу от положительной пластины к отрицательной, теперь мы можем перейти к третьему этапу, который вычисляет разность потенциалов между пластинами путем взятия интеграла, интегральная линия, от положительной к отрицательной пластине e dot dl. Опять же, это интеграл по путям, и мы выберем простейший путь относительно нашего вектора электрического поля. И в этом случае простейший путь — это, по сути, путь, совпадающий с вектором электрического поля.
Ну, это будет радиальный путь, радиально наружу, и поэтому я собираюсь выбрать этот путь, вот так, и он будет совпадать с вектором электрического поля. При этом угол между этими двумя векторами становится равным нулю. И еще кое-что, если посмотреть на геометрию, это радиальное расстояние; электрическое поле направлено радиально наружу, и мы выбираем этот путь также в радиальном направлении. Тогда вектор приращения смещения вдоль этого пути будет dr, поэтому мы заменим dl на dr.
Хорошо. Выберите путь радиально наружу, тогда dl станет равным dr. Теперь рассчитаем разность потенциалов между пластинами цилиндрического конденсатора. V становится равным интегралу от величины E, которая равна q за 2 Pi Epsilon 0 hr, которую мы определили из шага или части два. q более 2 Pi Epsilon 0 ч умножить на r. И вместо dl мы заменим или воспользуемся dr, вектор приращения смещения в радиальном направлении. Итак, величина r, поскольку E и dr находятся в одном направлении, следовательно, угол между ними равен 0, косинусу 0.Косинус 0 равен 1, а наша переменная — r. И r меняется, когда мы вернемся к нашей диаграмме. Интеграл берется от положительной пластины к отрицательной пластине, поэтому r будет изменяться от внутреннего радиуса a до внешнего радиуса b.
Итак, границы интеграла пойдут от a к b. И здесь q 2 Pi Epsilon 0 и h постоянны. Мы можем вынести это за пределы интеграла, и это оставляет нас, разность потенциалов между пластинами равна q на 2 Pi Эпсилон 0 h, умноженный на интеграл dr по r, проинтегрированный от a до b.Интеграл от dr по r равен ln от r. Двигаясь дальше, у нас будет q больше 2 Pi Epsilon 0 h, умноженное на ln из r, вычисленное в a и d, что будет равно q для 2 Pi Epsilon 0 h, умноженное на ln из b минус ln из a, путем замены границы для r. И так как ln b минус ln a равно ln b над a, мы можем, наконец, выразить эту разность потенциалов как q на 2 Pi Epsilon 0 h умножить на ln b над a.
После того, как мы определим разность потенциалов между пластинами, в качестве последнего шага, мы можем вычислить емкость цилиндрического конденсатора по его определению, которое представляет собой отношение величины заряда, хранящегося в пластинах, деленного на, или к разности потенциалов. между пластинами, на котором стоит В.Таким образом, у нас будет q, разделенное на разность потенциалов, которая равна q на 2 Pi Epsilon 0 h, умноженное на ln b на a. Заряды сократятся в числителе и знаменателе, в результате чего емкость цилиндрического конденсатора будет равна 2 Pi Epsilon 0 h, умноженному на 1 на ln или b на a.
Это легко увидеть, как и в случае конденсатора с параллельными пластинами. В цилиндрическом конденсаторе емкость также зависит от физических свойств конденсатора. В данном случае длина равна высоте цилиндрического конденсатора, а также его внутренний и внешний радиус.
Физика для науки и техники II
5.11 Пример из отдела академических технологий на Vimeo.
5.11 Пример
Давайте рассмотрим пример, связанный с концепцией плотности энергии. Предположим, что у нас есть цилиндрический конденсатор радиусами a и b. Я хотел бы показать, что половина накопленной электрической потенциальной энергии находится внутри цилиндра, радиус r которого равен квадратному корню из внутреннего радиуса, умноженного на внешний радиус.
Таким образом, у нас есть цилиндрический конденсатор, и давайте посмотрим, это внешняя поверхность цилиндрического конденсатора, и это внутренняя поверхность цилиндрического конденсатора. И внутренний радиус этого конденсатора задан как a, а внешний радиус равен b. Вопрос заключается в том, чтобы найти цилиндрическую область внутри этого цилиндрического конденсатора, такую, чтобы количество хранимой электрической потенциальной энергии в этой области составляло половину общей энергии, хранящейся в электрическом поле этого конденсатора.
Теперь, как вы помните, плотность энергии задается как половина эпсилона, равная нулю, умноженная на квадрат электрического поля между пластинами конденсатора. Предположим, что интересующая нас цилиндрическая область — это область с радиусом r.
Теперь, когда мы заряжаем этот конденсатор, мы знаем, что если мы заряжаем внутренний положительно, а внешний отрицательно, путем подключения к клеммам источника питания, мы собираемся создать разность потенциалов между этими двумя пластинами, и мы также создадим электрическое поле, исходящее от положительной пластины и входящее в отрицательную пластину в радиальном направлении наружу, заполняя область между этими пластинами.
И мы можем вычислить напряженность этого электрического поля, что мы сделали ранее, применив закон Гаусса, и это было e dot da, интегрированное по этому гауссовскому цилиндру, который мы выбираем, используя симметрию задачи, так что его сторона Поверхность проходит через точку интереса, расположенную между пластинами, и мы выбираем это место подальше от концов конденсатора, вы знаете, чтобы иметь возможность применить закон Гаусса, пренебрегая концевыми эффектами, которые мы сделали это ранее. А правая часть закона Гаусса, как вы помните, будет равна q, заключенному в эпсилон-ноль, который представляет собой чистый заряд, заключенный в области, окруженной гауссовым цилиндром, деленный на эпсилон-ноль.
И снова, как вы помните, мы разделили это интегрирование замкнутой поверхности на сумму трех интегралов, взятых по верхней, нижней и боковым поверхностям цилиндра. И когда мы их сложили, мы получили интеграл по замкнутой поверхности. Таким образом, интегральная над верхней поверхностью EdA, как мы помним, здесь dA была перпендикулярна верхней поверхности, поэтому угол между ними, E и dA составлял 90 градусов, косинус 90 от этого продукта.
И интегрируя с нижней поверхностью EdA, мы снова имеем ситуацию аналогичного типа, когда dA направлен вниз, электрическое поле выходит радиально, без учета концевых эффектов.Следовательно, угол между ними снова составляет 90 градусов. Плюс интеграл по боковой поверхности, EdA, и для боковой поверхности, как мы снова видели ранее, e радиально выходит наружу, а dA также перпендикулярно поверхности. Следовательно, угол боковой поверхности между e и dA всегда равен нулю градусов, а правая часть снова равна q, заключенному над нулевым эпсилон. Поскольку косинус 90 равен нулю, не будет никакого вклада от интегрирования верхней и нижней поверхностей, кроме вклада, который будет исходить от боковой поверхности, поскольку косинус нуля равен 1, и пока мы находимся вдоль боковой поверхности цилиндра, электрическое поле постоянно, его можно вынести за пределы интеграла.А также мы можем легко увидеть, что, поскольку этот гауссов цилиндр полностью охватывал внутреннюю заряженную поверхность, и если общий заряд на этой поверхности равен q, то заключенный q просто равен q, и поэтому левая часть, выводящая E наружу, становится E, умноженным на интеграл dA по боковой поверхности, равен q над эпсилоном нуля для правой части.
Интеграл по боковой поверхности, как мы видели ранее, складывает все эти инкрементальные области друг с другом по боковой поверхности и дает нам площадь боковой поверхности цилиндра.Если мы скажем, что высота нашего цилиндрического конденсатора равна h, а радиус цилиндра равен r, то мы можем выразить площадь боковой поверхности как 2 pi r, умноженные на h. Если электрическое поле равно q над нулевым эпсилон, и отсюда электрическое поле оказывается равным q на 2 эпсилон ноль h, умноженное на r.
И, как мы видим, это электрическое поле меняется с радиальным расстоянием. И плотность энергии, по определению, равна половине эпсилон ноль E в квадрате, и поэтому плотность энергии, энергия на единицу объема этого цилиндрического конденсатора, становится равной половине эпсилон ноль E в квадрате, и это q в квадрате на 4 пи. в квадрате эпсилон ноль в квадрате h в квадрате и r в квадрате.
Итак, теперь мы видим, что плотность энергии меняется на единицу больше r в квадрате. Плотность энергии — это энергия на единицу объема, и эта плотность не постоянна. Если вы вспомните, например, задачу переменной плотности заряда, которую мы делали ранее, мы собираемся подойти к этой проблеме аналогичным образом. Сейчас нас интересует энергия. Итак, мы смотрим на количество энергии, хранящейся в этой области, хорошо? И мы говорим, что если общая энергия, накопленная между пластинами этого конденсатора, равна U, мы хотели бы вычислить радиус цилиндра, чтобы энергия, запасенная внутри этого цилиндра, который является областью внутри этого Гауссов цилиндр, будет составлять половину полной энергии.Это то, что нам нужно.
И поскольку наша плотность энергии изменяется с радиальным расстоянием, то, что мы собираемся сделать, в этом случае мы выберем инкрементную цилиндрическую оболочку с очень малой толщиной в радиальном направлении. Что-то вроде этого. И эта оболочка настолько тонка, что мы предположим, что количество энергии, запасенной вдоль этой сферической оболочки, и объем этой сферической оболочки, назовем этот объем db, объемом увеличивающейся цилиндрической оболочки. И предположим, что радиус этой оболочки равен s, а толщина, например, ds, и что это du настолько мало, что мы можем предположить, что эта плотность энергии, которая изменяется в зависимости от квадрата радиального расстояния, остается постоянной на этом расстоянии.Затем мы можем вычислить количество энергии, хранящейся внутри этой цилиндрической оболочки.
И как это вычислить? Энергия, назовем ее d sub u, энергия, запасенная в увеличивающейся цилиндрической оболочке. И это будет равно плотности энергии u, то есть энергии на единицу объема, как вы помните, по определению, умноженной на объем области, которая нас интересует, и это объем увеличивающейся цилиндрической оболочки. Таким образом, это выражение даст нам, сколько энергии находится внутри этой области.В явном виде это будет равняться половине эпсилон ноль q в квадрате на 4 пи в квадрате эпсилон ноль в квадрате h в квадрате r в квадрате. По сути, это плотность энергии u, и давайте определим ее как dv, объем увеличивающейся цилиндрической оболочки.
А давайте посчитаем этот объем. Это инкрементная цилиндрическая оболочка, что-то вроде этого, и нас интересует объем этого цилиндра. Он имеет радиус s и толщину ds. Конечно, поскольку его площадь поперечного сечения постоянна по всей длине, объем этой оболочки, dv, будет равен площади поверхности, и это будет площадь этого увеличивающегося кольца, которая равна 2 pi r dr , умноженное на высоту этого цилиндра, и это h.Поскольку здесь мы используем переменную s, давайте заменим эти «r» на ds, а также r в плотности энергии на s. Хорошо, тогда явная форма дополнительной потенциальной энергии, хранящейся внутри объема этой цилиндрической оболочки, будет равна единице на 2 эпсилон ноль q в квадрате на 4 пи в квадрате эпсилон в квадрате нуля h в квадрате s в квадрате, умноженном на dv, объем этого приращения цилиндрическая оболочка, которая равна 2 p s ds раз h.
Итак, у нас есть энергия на единицу объема, умноженная на объем, который нас интересует, поэтому объемы уравняются, и в итоге мы получим энергию внутри этой области, энергию, запасенную в этой области.И здесь мы можем отменить одно из этих s, числитель и знаменатель, и мы можем отменить одно из этих h в квадрате с h в числителе, и аналогично, эпсилон ноль отменяется с эпсилон ноль в квадрате, а квадрат пи отменяется этим pi, и мы можем отменить 2 с помощью этого 2. И мы собираемся получить инкрементную потенциальную энергию, хранящуюся внутри объема этой инкрементной цилиндрической оболочки, как q в квадрате, деленное на 4 пи-эпсилон ноль hs ds.
Хорошо. Что ж, это количество энергии, хранящейся в объеме этой увеличивающейся цилиндрической оболочки.Я могу просто пойти дальше и вычислить энергию, запасенную в следующей оболочке и в следующей оболочке, и так далее и так далее, по всей области, которая меня интересует. И эта область расширяется, радиус начинается от a до этого конкретного радиуса r, который я пытаюсь вычислить. Следовательно, если я проинтегрирую это du отсюда, от a до r, тогда я получу количество энергии, хранящейся внутри этого пурпурного цилиндра.
Что ж, я хочу, чтобы эта энергия составляла половину общей энергии, хранящейся в электрическом поле этого конденсатора, и общая энергия может быть получена путем сложения этих «du», дополнительных энергий, хранящихся в этих дополнительных цилиндрических оболочках, начиная с этого от внутреннего радиуса a до внешнего радиуса b.Другими словами, мы имеем здесь, что интеграл du, проинтегрированный от a до r, до радиуса, который нас интересует, мы хотим, чтобы эта энергия была равна половине полной энергии. И полная энергия является интегралом du, количества энергии, хранящейся в этих дополнительных цилиндрических оболочках, интегрированной от a до b, которая даст нам полную энергию, и я хочу, чтобы эта энергия составляла половину этой энергии. Поэтому я разделю это на 2.
Хорошо. Давайте теперь вычислим эти интегралы.Интеграл от a до r из q в квадрате на 4 пи-эпсилон ноль h, умноженный на s, умноженный на ds, будет равен половине интеграла от a до b из q, возведенного в квадрат 4 пи-эпсилон нуля h s, умноженного на ds. А здесь q в квадрате 4 пи эпсилон ноль h, эти члены постоянны, мы можем вынести их за пределы интеграла для обеих сторон. И после того, как мы вынесем их наружу, мы легко увидим, что, поскольку у нас есть одинаковые члены с обеих сторон, деля обе части уравнения на одни и те же члены, мы можем их исключить.
Итак, мы собираемся закончить тем, что интеграл от a до r от ds по s будет равен половинному интегралу от a до b от ds по s.Двигаясь дальше, интеграл ds по s равен ln от s, и он будет оцениваться в a и r, будет равен половине, снова ln от S, теперь он оценивается в a и b. Подставляя границы, мы получим ln из r минус ln из a, будет равно половине ln из b минус половина ln из a. Если мы оставим ln of r в покое на одной стороне уравнения, переместив ln of a на другую сторону, мы получим, что половина одной половины ln a будет положительной для другой стороны, а минус половина ln a даст нам одна половина ln плюс половина ln b.
Мы можем переписать это так, как ln of r равно ln a в половинных скобках плюс половина ln b, которая равна половине ln a, умноженному на b. ln числа r будет равно ln умноженного на b в степени половины, и если мы возьмем погруженный логарифм обеих сторон, то получим, что r равно квадратному корню из умножения на b. И это был тот случай, который мы должны были доказать. Действительно, если радиус цилиндра равен квадратному корню из внутреннего радиуса, умноженного на внешний радиус, то количество энергии для этого конденсатора, хранящейся в этой области, будет составлять половину потенциальной энергии, хранящейся между пластинами этого цилиндр.Другими словами, когда мы рассматриваем эту область с таким радиусом, что r равно квадратному корню из a, умноженному на b, внутри этого цилиндра количество запасенной энергии просто равно половине полной энергии, запасенной этим цилиндрическим конденсатором. .
Таким образом, этот пример демонстрирует использование плотности энергии, которую мы определяем как энергию на единицу объема. Это также показывает, как мы подходим к случаям переменной плотности. Это в некотором роде пример того же типа, что и проблема с переменной плотностью заряда.Но здесь вместо переменной плотности заряда мы имеем дело с переменной плотностью энергии. Но математический способ анализа таких проблем практически идентичен.
Формулы и калькуляторы емкости
На этой странице представлены формулы и калькуляторы емкостей
различные формы или типы конденсаторов. Это также полезно, если вы
собираетесь использовать свой конденсатор в
Танк LC резонансный
схема.
Емкость конденсаторов с параллельными пластинами
Конденсатор с параллельными пластинами состоит из двух плоских параллельных пластин, которые
электроды, разделенные
диэлектрик
или изолятор.Для формулы и калькулятора здесь пластины могут быть
любой формы, если они плоские, параллельные и вы знаете площадь
тарелки или что-то еще, что нужно, чтобы найти этот район.
Формула емкости конденсатора с параллельными пластинами:
Где:
- ε r = относительная диэлектрическая проницаемость диэлектрика
(реже К, диэлектрическая проницаемость) - ε 0 = 8.854×10 -12 Ф / м (фарад / метр) =
диэлектрическая проницаемость вакуума или диэлектрическая проницаемость свободного пространства
На схемах показаны конденсаторы с параллельными пластинами разной формы.
пластины, одна прямоугольная и одна круглая. Формула для расчета
площадь прямоугольника:
а формула для вычисления площади круга:
Где π — это число пи, равное 3,14159.
Емкость цилиндрических конденсаторов
Цилиндрический конденсатор состоит из двух цилиндров, также называемых
пластины, которые являются электродами, разделены
диэлектрик
или изолятор.
Формула емкости цилиндрического конденсатора:
Где:
- ε r = относительная диэлектрическая проницаемость диэлектрика
(реже К, диэлектрическая проницаемость) - ε 0 = 8,854×10 -12 Ф / м (фарад / метр) =
диэлектрическая проницаемость вакуума или диэлектрическая проницаемость свободного пространства
Видео — Как сделать конденсаторы — Низкое напряжение
В этом видео не только показано, как сделать конденсаторы, но и
формула емкости в более динамичном формате, чем указано выше.После всего,
если вы делаете конденсатор, вам сначала нужно знать, как
спроектировать конденсатор.
Видео — Как сделать конденсаторы — Высокое напряжение
В этом видео показано, как разработать конденсаторы для высокого напряжения, объясняя,
измерения и построения для напряжения пробоя / диэлектрической прочности, чтобы
что конденсатор может выдерживать желаемое высокое напряжение.
Калькулятор параллельных пластинчатых конденсаторов
— Емкость
Введите значения в поля ниже, чтобы рассчитать емкость между конденсаторами с параллельными пластинами с помощью калькулятора емкости.
Калькулятор конденсаторов — это онлайн-инструмент, который используется для расчета емкости, принимая в качестве входных данных диэлектрическую проницаемость, расстояние между пластинами и площадь пластин.
Что такое конденсатор?
Конденсатор — это устройство, которое может накапливать электрические заряды. Наиболее распространенный тип конденсатора, показанный ниже, — это параллельный конденсатор. В этом типе конденсатора пластины конденсатора разделены изолятором.
Емкость
Емкость — это количество электрического заряда, которое может накапливать конденсатор.
Формула емкости
Формула, используемая для определения емкости:
C = ε A / S
В этом уравнении:
A = площадь перекрытия пластин
S = расстояние между пластинами
ε = диэлектрическая проницаемость проводника
Значение диэлектрической проницаемости варьируется от проводника к проводнику. Чтобы найти емкость с учетом заряда и разности потенциалов, воспользуйтесь другим нашим калькулятором емкости.
Как рассчитать емкость?
Пример:
Рассчитайте емкость конденсатора, у которого 0,03 м 2 площадь пластин, разделенных свободным пространством, и расстояние между пластинами 0,7 м.
Решение :
Шаг 1: Определите значения.
A = 0,03 м 2
S = 0,7 м
Проницаемость свободного пространства = 8.85418782 × 10 -12 м -3 кг -1 с 4 A 2
Шаг 2: Введите значения в формулу емкости.
C = ε A / S
= 8,85418782 × 10 -12 × 0,03 / 0,7
= 0,38 F
4.1 Конденсаторы и емкость — Введение в электричество, магнетизм и схемы
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Объясните понятие конденсатора и его емкости
- Опишите, как оценить емкость системы проводов
Конденсатор — это устройство, используемое для хранения электрического заряда и электрической энергии.Он состоит как минимум из двух электрических проводников, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но, точнее, они «обкладки конденсатора».) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор будет известен как «Вакуумный конденсатор». Однако пространство обычно заполняется изолирующим материалом, известным как диэлектрик . (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем памяти в конденсаторе определяется свойством, называемым емкостью , , о котором вы узнаете больше чуть позже в этом разделе.
Конденсаторы
имеют различные применения: от фильтрации статического электричества, радиоприема до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 4.1.1. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к первоначально незаряженному конденсатору, потенциал батареи перемещает небольшой заряд величины от положительной пластины к отрицательной.Конденсатор в целом остается нейтральным, но заряжается и находится на противоположных пластинах.
(рисунок 4.1.1)
Рисунок 4.1.1 Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них есть заряды и (соответственно) на своих тарелках. (a) Конденсатор с параллельными пластинами состоит из двух пластин противоположного заряда с площадью A, разделенной расстоянием d. (b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).
Система, состоящая из двух идентичных параллельно проводящих пластин, разделенных расстоянием, называется конденсатором с параллельными пластинами (рисунок 4.1.2). Величина электрического поля в пространстве между параллельными пластинами равна, где обозначает поверхностную плотность заряда на одной пластине (напомним, что это заряд на площадь поверхности). Таким образом, величина поля прямо пропорциональна.
(рисунок 4.1.2)
Рисунок 4.1.2 Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора.Линии электрического поля в конденсаторе с параллельными пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.
Конденсаторы с разными физическими характеристиками (такими как форма и размер пластин) накапливают разное количество заряда для одного и того же приложенного напряжения на своих пластинах. Емкость конденсатора определяется как отношение максимального заряда, который может храниться в конденсаторе, к приложенному напряжению на его пластинах.Другими словами, емкость — это наибольшая величина заряда на вольт, которая может храниться на устройстве:
(4.1.1)
Единица измерения емкости в системе СИ — фарад (), названная в честь Майкла Фарадея (1791–1867). Поскольку емкость — это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или
.
По определению, конденсатор способен накапливать заряд (очень большой заряд), когда разность потенциалов между его пластинами равна всего.Следовательно, одна фарада — это очень большая емкость. Типичные значения емкости находятся в диапазоне от пикофарад () до миллифарад (), включая микрофарады (). Конденсаторы могут изготавливаться различных форм и размеров (рисунок 4.1.3).
(рисунок 4.1.3)
Рисунок 4.1.3 Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно зависит от его емкости.
Расчет емкости
Мы можем рассчитать емкость пары проводов с помощью следующего стандартного подхода.
Стратегия решения проблем: расчет емкости
Чтобы показать, как работает эта процедура, мы теперь вычисляем емкости параллельных пластин, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.
Конденсатор с параллельными пластинами
Конденсатор с параллельными пластинами (рисунок 4.1.4) имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности, разделенную расстоянием.Когда на конденсатор подается напряжение, он накапливает заряд, как показано на рисунке. Мы можем увидеть, как его емкость может зависеть от и , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить. Таким образом, должно быть больше для большего значения. Точно так же, чем ближе пластины друг к другу, тем сильнее на них притяжение противоположных зарядов.Следовательно, должно быть больше за меньшее.
(рисунок 4.1.4)
Рис. 4.1.4 В конденсаторе с параллельными пластинами, обкладки которых разнесены на расстояние, каждая пластина имеет одинаковую площадь поверхности.
Определим поверхностную плотность заряда на пластинах как
Из предыдущих глав мы знаем, что когда оно мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и что его величина определяется как
.
где константа — диэлектрическая проницаемость свободного пространства,.Единица СИ эквивалентна. Поскольку электрическое поле между пластинами однородно, разность потенциалов между пластинами составляет
.
Следовательно, уравнение 4.1.3 дает емкость конденсатора с параллельными пластинами как
(4.1.3)
Обратите внимание на это уравнение, что емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора. Фактически, это верно не только для конденсатора с параллельными пластинами, но и для всех конденсаторов: емкость не зависит от или.Если заряд изменяется, соответственно изменяется и потенциал, так что он остается постоянным.
ПРИМЕР 4.1.1
Емкость и заряд в конденсаторе с параллельными пластинами
(a) Какова емкость пустого конденсатора с параллельными пластинами с металлическими пластинами, каждая из которых имеет площадь, разделенную на? (б) Сколько заряда хранится в этом конденсаторе, если к нему приложено напряжение?
Стратегия
Определение емкости — это прямое приложение уравнения 4.1.3. Как только мы найдем, мы сможем найти накопленный заряд, используя уравнение 4.1.1.
Решение
а. Ввод данных значений в уравнение 4.1.3 дает
Это небольшое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью.
г. Обращение уравнения 4.1.1 и ввод известных значений в это уравнение дает
Значение
Этот заряд лишь немного больше, чем в типичных приложениях статического электричества.Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около, на этом конденсаторе больше не может храниться заряд при увеличении напряжения.
ПРОВЕРЬТЕ ПОНИМАНИЕ 4.1
Емкость конденсатора с параллельными пластинами составляет. Если площадь каждой пластины равна, каково расстояние между пластинами?
ПРОВЕРЬТЕ ПОНИМАНИЕ 4.2
Убедитесь, что у вас такие же физические единицы.
Конденсатор сферический
Сферический конденсатор — это еще один набор проводников, емкость которых можно легко определить (Рисунок 4.1.5). Он состоит из двух концентрических проводящих сферических оболочек радиусов (внутренняя оболочка) и (внешняя оболочка). Снарядам придаются равные и противоположные заряды и соответственно. Из-за симметрии электрическое поле между оболочками направлено радиально наружу. Мы можем получить величину поля, применив закон Гаусса к сферической гауссовой поверхности радиусом r , концентричной оболочкам. Вложенная плата есть; следовательно, у нас есть
Таким образом, электрическое поле между проводниками равно
Мы подставляем это в уравнение 4.1.2 и интегрировать по радиальному пути между оболочками:
В этом уравнении разность потенциалов между пластинами равна. Подставляем этот результат в уравнение 4.1.1, чтобы найти емкость сферического конденсатора:
(4.1.4)
(рисунок 4.1.5)
Рисунок 4.1.5 Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды на проводнике находятся на его поверхности.
ПРИМЕР 4.1,3
Емкость изолированной сферы
Рассчитайте емкость одиночной изолированной проводящей сферы радиуса и сравните ее с уравнением 4.1.4 в пределе как.
Стратегия
Мы предполагаем, что на сфере есть заряд, и поэтому выполняем четыре шага, описанные ранее. Мы также предполагаем, что другой проводник представляет собой концентрическую полую сферу бесконечного радиуса.
Решение
На внешней стороне изолированной проводящей сферы электрическое поле задается уравнением 4.1.2. Величина разности потенциалов между поверхностью изолированной сферы и бесконечностью составляет
.
Таким образом, емкость изолированной сферы равна
.
Значение
Тот же результат может быть получен, если взять предел уравнения 4.1.4 как. Таким образом, одиночная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.
ПРОВЕРЬТЕ ПОНИМАНИЕ 4.3
Радиус внешней сферы сферического конденсатора в пять раз больше радиуса его внутренней оболочки.Какие размеры у этого конденсатора, если его емкость?
Цилиндрический конденсатор
Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рисунок 4.1.6). Внутренний цилиндр радиуса может быть либо оболочкой, либо полностью твердым. Внешний цилиндр представляет собой оболочку внутреннего радиуса. Мы предполагаем, что длина каждого цилиндра равна и что избыточные заряды и находятся на внутреннем и внешнем цилиндрах соответственно.
(рисунок 4.1.6)
Рисунок 4.1.6 Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров. Здесь заряд на внешней поверхности внутреннего цилиндра положительный (обозначен значком), а заряд на внутренней поверхности внешнего цилиндра отрицательный (обозначен значком).
Без учета краевых эффектов электрическое поле между проводниками направлено радиально наружу от общей оси цилиндров. Используя гауссову поверхность, показанную на рисунке 4.1.6, мы имеем
Следовательно, электрическое поле между цилиндрами равно
(4.1,5)
Здесь \ hat {\ mathrm {r}} — единичный радиальный вектор по радиусу цилиндра. Мы можем подставить в уравнение 4.1.2 и найти разность потенциалов между цилиндрами:
Таким образом, емкость цилиндрического конденсатора
(4.1.6)
Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 4.1.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов.Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом. (Здесь мы предполагаем наличие вакуума между проводниками, но физика качественно почти такая же, когда пространство между проводниками заполнено диэлектриком.) Эта конфигурация экранирует электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний провод обычно заземлен.Теперь из уравнения 4.1.6 емкость коаксиального кабеля на единицу длины равна
.
В практических приложениях важно выбирать конкретные значения. Это может быть достигнуто за счет соответствующего выбора радиусов проводников и изоляционного материала между ними.
ПРОВЕРЬТЕ ПОНИМАНИЕ 4.4
Когда цилиндрический конденсатор заряжается, между цилиндрами измеряется разность потенциалов.а) Какова емкость этой системы? б) Если цилиндры длинные, каково отношение их радиусов?
Несколько типов конденсаторов, которые можно использовать на практике, показаны на рисунке 4.1.3. Обычные конденсаторы часто состоят из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. Рисунок 4.1.1 (b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторые распространенные изоляционные материалы — это слюда, керамика, бумага и антипригарное покрытие Teflon ™.
Другой популярный тип конденсатора — электролитический конденсатор . Он состоит из окисленного металла в проводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость одного типа алюминиевого электролитического конденсатора может достигать. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста.Когда возникает обратная поляризация, электролитическое действие разрушает оксидную пленку. Этот тип конденсатора не может быть подключен к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет свою полярность (см. Схемы переменного тока в цепях переменного тока).
Переменный воздушный конденсатор (рисунок 4.1.7) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначается как «ротор»).Поворачивая вал, можно изменять площадь поперечного сечения в перекрытии пластин; следовательно, емкость этой системы может быть настроена на желаемое значение. Настройка конденсатора находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильное радио на любимую станцию, думайте о емкости.
(рисунок 4.1.7)
Рисунок 4.1.7 В конденсаторе переменного тока емкость можно регулировать, изменяя эффективную площадь пластин.(кредит: модификация работы Робби Спрула)
Символы, показанные на рисунке 4.1.8, представляют собой схемные изображения различных типов конденсаторов. Обычно мы используем символ, показанный на рис. 4.1.8 (а). Символ на Рисунке 4.1.8 (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор представлен символом на рис. 4.1.8 (b), где изогнутая пластина обозначает отрицательный вывод.
(рисунок 4.1.8)
Рисунок 4.1.8 Здесь показаны три различных схемных представления конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет конденсатор переменной емкости.
Интересный прикладной пример модели конденсатора взят из клеточной биологии и имеет дело с электрическим потенциалом в плазматической мембране живой клетки (рис. 4.1.9). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым отобранным ионам проходить внутрь или из клетки.Разность потенциалов на мембране составляет около. Клеточная мембрана может быть слишком толстой. Рассматривая клеточную мембрану как конденсатор наноразмеров, оценка наименьшей напряженности электрического поля на его «пластинах» дает значение.
Этой величины электрического поля достаточно, чтобы вызвать электрическую искру в воздухе.
(рисунок 4.1.9)
Рис. 4.1.9 Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней.Диффузия перемещает ионы (калия) и (хлорида) в показанных направлениях, пока кулоновская сила не остановит дальнейшую передачу. Таким образом, внешняя часть мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая разность потенциалов на мембране. Мембрана обычно непроницаема для (ионов натрия).
Кандела Цитаты
Лицензионный контент CC, особая атрибуция
- Загрузите бесплатно по адресу http: // cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Конденсатор с параллельными пластинами
— обзор
Уменьшение межобмоточной емкости трансформатора
Емкость конденсатора с параллельными пластинами прямо пропорциональна площади пластин и обратно пропорциональна расстоянию, разделяющему их, поэтому, если бы мы могли уменьшить площадь между ними между первичной и вторичной обмотками и увеличив их разделение, мы уменьшим межобмоточную емкость.(Эффект от попытки отрегулировать диэлектрическую постоянную будет минимальным.)
В качестве примера, комплект трансформатора Maplin 100 VA EI имеет конструкцию раздельной катушки с первичной намоткой на одной половине катушки, а другая половина остается пустой на время пользователь для намотки вторичной обмотки. Площадь межобмоточного конденсатора на разделенном каркасном трансформаторе — это просто площадь разделителя между первичной и вторичной обмотками, за исключением углов, потому что медные обмотки имеют тенденцию изгибаться при изгибе вокруг каждого угла (см. Рисунок 5.56).
Рисунок 5.56. Межобмоточная емкость в разделенном катушечном трансформаторе.
Емкостная площадь делителя ≈1800 мм 2 . И наоборот, если бы разделитель был удален и бобина была заполнена многослойными обмотками, площадь между первичной и вторичной обмотками была бы ≈ 7200 мм 2 , увеличивая емкость в 7200/1800 = 4 раза.
Если посмотреть на толщину между пластинами, типичная полиэфирная изоляционная лента трансформатора может быть равна 0.055 мм, но хотя одна толщина теоретически может быть рассчитана на напряжение пробоя 3 кВ, производитель трансформатора должен знать, что на практике может потребоваться четыре слоя этой ленты между первичным и вторичным слоями, чтобы гарантировать соответствующую диэлектрическую прочность для адекватной изоляции сетевого напряжения. , давая общую толщину между обмотками 0,22 мм. Напротив, делитель в трансформаторе с разъемной катушкой имеет толщину 1,07 мм, поэтому он снижает емкость в 1,07 / 0,22 = 4 раза.9.
В совокупности уменьшенная площадь пластины и увеличенное разделение приведенного в качестве примера трансформатора с разделенной катушкой уменьшают межобмоточную емкость в 4 × 4,9≈19,5 раз, что означает уменьшение помех на ≈26 дБ.
Прежде чем сетевые помехи достигнут межобмоточной емкости, они должны пройти через индуктивность рассеяния трансформатора, так что эти два компонента образуют резонансную сеть. Если мы предположим (для целей сравнения), что результирующий ток развивает напряжение через сопротивление заземления 1 Ом между обмоткой нагревателя и шасси, мы можем смоделировать три основных конструкции трансформатора.

 10)
10) 16)
16)
 То есть:
То есть:


 Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |.
Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |. 1 и ввод известных значений в это уравнение дает
1 и ввод известных значений в это уравнение дает