Електричний потенціал: формула та рівняння, обчислення, приклади, вправи — Наука
Електричний потенціал: формула та рівняння, обчислення, приклади, вправи — Наука
Зміст:
електричний потенціал він визначається в будь-якій точці, де існує електричне поле, як потенційна енергія цього поля на одиницю заряду. Точкові заряди та розподіл точкових або безперервних зарядів створюють електричне поле і, отже, мають відповідний потенціал.
У Міжнародній системі одиниць (SI) електричний потенціал вимірюється у вольтах (V) і позначається як V. Математично це виражається як:
V = U / qабо
Де U — потенційна енергія, пов’язана із зарядом або розподілом, qабо це позитивний заряд тесту. Оскільки U — скаляр, то і потенціал.
З визначення, 1 вольт — це просто 1 джоуль / кулон (J / C), де Джоуль є одиницею енергії СІ, а Кулон (С) — одиницею електричного заряду.
Нехай точковий заряд q. Ми можемо перевірити природу поля, яке створює цей заряд, за допомогою невеликого позитивного випробувального заряду, який називається qабо, використовується як зонд.
Робота W необхідна для переміщення цього невеликого навантаження з точки до до моменту b, є мінусом різниці потенційна енергія ΔU між цими точками:
Wa → b = -ΔU = — (Ub — АБОдо)
Поділивши все на qабо:
Wa → b / qабо= — ΔU / qабо = — (Ub — АБОдо) / qабо = — (Vb — Vдо) = -ΔV
Тут Vb — потенціал в точках b і Vдо це точка а. Різниця потенціалів Vдо — Vb — це потенціал приблизно b і називається Vab. Порядок дії індексів важливий, якщо його змінити, то він представляв би потенціал b відносно a.
Різниця електричного потенціалу
З вищесказаного випливає, що:
-ΔV = Wa → b / qабо
Отже:
ΔV = -Wa → b / qабо
Тепер робота обчислюється як інтеграл скалярного добутку між електричною силою F між q і qабо і вектор переміщення dℓ між точками a і b. Оскільки електричне поле — це сила на одиницю заряду:
Оскільки електричне поле — це сила на одиницю заряду:
І = F/ qабо
Робота для перенесення випробувального навантаження від a до b:
Це рівняння пропонує спосіб безпосереднього обчислення різниці потенціалів, якщо електричне поле заряду або розподіл, який його створює, відомі раніше.
І також зазначається, що різниця потенціалів є скалярною величиною, на відміну від електричного поля, яке є вектором.
Ознаки та значення різниці потенціалів
З попереднього визначення ми спостерігаємо, що якщо І і dℓ перпендикулярні, різниця потенціалів ΔV дорівнює нулю. Це не означає, що потенціал у таких точках дорівнює нулю, а просто, що Vдо = Vb, тобто потенціал є постійним.
Викликаються лінії та поверхні, де це відбувається еквіпотенціал. Наприклад, еквіпотенціальні лінії поля точкового заряду є колами, концентричними до заряду. А еквіпотенціальні поверхні — це концентричні сфери.
А еквіпотенціальні поверхні — це концентричні сфери.
Якщо потенціал породжується позитивним зарядом, електричне поле якого складається з радіальних ліній, що проектують заряд, коли ми відходимо від поля, потенціал буде ставати все менше і менше. Як пробне навантаження qабо позитивне, він відчуває менше електростатичного відштовхування, чим далі від q.
Навпаки, якщо навантаження що від’ємне, тестовий заряд qабо (позитивний) буде мати менший потенціал у міру наближення до q.
Як розрахувати електричний потенціал?
Наведений вище інтеграл служить для знаходження різниці потенціалів, а отже, і потенціалу в даній точці b, якщо опорний потенціал відомий в іншій точці до.
Наприклад, є випадок точкового навантаження що, вектор електричного поля якого в точці, розташованій на відстані р навантаження становить:
І = kq / r2р
Де k — електростатична константа, значення якої в одиницях Міжнародної системи становить:
k = 9 x 10 9 Нм2 / C2.
І векторр— одиничний вектор уздовж лінії, що з’єднується що з точкою P.
Це замінено у визначенніΔV:
Вибираючи цю точку b бути на відстані р заряду і що при a → ∞ потенціал дорівнює 0, тоді Vдо = 0, а попереднє рівняння має вигляд:
V = kq / r
Виберіть Vдо = 0, коли a → ∞ має сенс, оскільки в точці, дуже далекій від навантаження, важко сприйняти, що вона існує.
Електричний потенціал для дискретного розподілу заряду
Коли в регіоні розподілено багато точкових зарядів, обчислюється електричний потенціал, який вони виробляють у будь-якій точці Р у просторі, додаючи індивідуальні потенціали, які кожен виробляє. Тому:
V = V1 + V2 + V3 +… VN = ∑ Vi
Підсумовування поширюється від i = до N, і потенціал кожного заряду обчислюється за допомогою рівняння, наведеного в попередньому розділі.
Електричний потенціал при безперервному розподілі навантаження
Починаючи з потенціалу точкового заряду, потенціал, що створюється зарядженим об’єктом вимірюваного розміру, можна знайти в будь-якій точці P.
Для цього тіло розділене на безліч невеликих нескінченно малих зарядів dq. Кожен з них вносить повний потенціал за допомогою дВ нескінченно малий.
Тоді всі ці внески додаються через інтеграл і таким чином отримується загальний потенціал:
Приклади електричного потенціалу
У різних пристроях є електричний потенціал, завдяки якому можна отримувати електричну енергію, наприклад, акумулятори, автомобільні акумулятори та електричні розетки. Електричні потенціали також встановлюються в природі під час електричних бур.
Батареї та батареї
У клітинах та батареях електрична енергія накопичується завдяки хімічним реакціям усередині них. Вони виникають, коли ланцюг замикається, дозволяючи протікати постійному струму і запалювати лампочку, або спрацьовувати стартерний двигун автомобіля.
Існують різні напруги: 1,5 В, 3 В, 9 В і 12 В є найбільш поширеними.
Розетка
Прилади та прилади, що працюють на комерційній електриці змінного струму, підключені до заглибленої розетки. Залежно від місця розташування напруга може становити 120 В або 240 В.
Залежно від місця розташування напруга може становити 120 В або 240 В.
Напруга між зарядженими хмарами та землею
Це той, який виникає під час електричних штормів, внаслідок руху електричного заряду через атмосферу. Це може бути порядку 108 В.
Генератор Van Der Graff
Завдяки гумовій конвеєрній стрічці створюється фрикційний заряд, який накопичується на провідній кулі, розміщеній зверху ізолюючого циліндра. Це породжує різницю потенціалів, яка може становити кілька мільйонів вольт.
Електрокардіограма та електроенцефалограма
У серці є спеціалізовані клітини, які поляризуються і деполяризуються, викликаючи різницю потенціалів. Їх можна виміряти як функцію часу за допомогою електрокардіограми.
Цей простий тест проводиться шляхом накладання електродів на груди людини, здатних вимірювати невеликі сигнали.
Оскільки вони мають дуже низьку напругу, вам доведеться їх зручно посилити, а потім записати на паперову стрічку або переглянути через комп’ютер. Лікар аналізує пульси на наявність відхилень і таким чином виявляє проблеми з серцем.
Лікар аналізує пульси на наявність відхилень і таким чином виявляє проблеми з серцем.
Електричну активність мозку також можна реєструвати за допомогою подібної процедури, яка називається електроенцефалограма.
Вправа вирішено
Навантаження Питання = — 50,0 нК знаходиться на відстані 0,30 м від точки ДО і 0,50 м від точки В, як показано на наступному малюнку. Дайте відповідь на наступні питання:
а) Який потенціал в А створюється цим зарядом?
б) А який потенціал у В?
в) Якщо заряд q рухається від A до B, яка різниця потенціалів, через яку він рухається?
г) Відповідно до попередньої відповіді, чи збільшується чи зменшується його потенціал?
д) Якщо q = — 1,0 нК, яка зміна його електростатичної потенціальної енергії при переміщенні від А до В?
е) Скільки роботи виконує електричне поле, яке створює Q, коли пробний заряд рухається від А до В?
Рішення для
Q — точковий заряд, тому його електричний потенціал в А обчислюється за формулою:
VДО = kQ / rДО = 9 х 109 х (-50 х 10-9) / 0,3 В = -1500 В
Рішення б
Так само
VB = kQ / rB = 9 х 109 х (-50 х 10-9) / 0,5 В = -900 В
Рішення c
ΔV = Vb — Vдо = -900 — (-1500) В = + 600 В
Рішення d
Якщо заряд q позитивний, його потенціал збільшується, а якщо він негативний, його потенціал зменшується.
Рішення e
ΔV = ΔU / qабо → ΔU = qабо ΔV = -1,0 х 10-9 x 600 Дж = -6,0 x 10-7 Дж.
Негативний знак вΔU вказує на те, що потенційна енергія в В менше енергії А.
Рішення f
Оскільки W = -ΔU, поле реалізується+6,0 х 10-7 J роботи.
Список літератури
- Фігероа, Д. (2005). Серія: Фізика для науки та техніки. Том 5. Електростатика. Під редакцією Дугласа Фігероа (USB).
- Джамбаттіста, А. 2010. Фізика. 2-й. Ред. Макгроу Хілл.
- Резнік, Р. (1999). Фізичний. Т. 2. 3-е видання Іспанською мовою. Compañía Editorial Continental S.A. де К.В.
- Тіплер, П. (2006) Фізика для науки і техніки. Видання 5-го випуску 2. Редакційне видання.
- Сервей Р. Фізика для науки та техніки. Том 2. 7-й. Ред. Cengage Learning.
Потенціал електростатичного поля. Різниця потенціалів
1-й семестр
ЕЛЕКТРОДИНАМІКА
1. Електричне поле
Електричне поле
УРОК 4/4
Тема. Потенціал електростатичного поля. Різниця потенціалів
Мета уроку: ознайомити учнів з енергетичною характеристикою електростатичного поля
Тип уроку: урок вивчення нового матеріалу.
ПЛАН УРОКУ
Контроль знань | 4 хв. | 1. Робота з переміщення заряду в однорідному електростатичному полі. 2. Робота з переміщення заряду в полі, створеному точковим зарядом. 3. Зв’язок роботи й потенціальної енергії заряду. |
Вивчення нового матеріалу | 29 хв. | 1. Потенціал електростатичного поля. 2. Різниця потенціалів. 3. Зв’язок напруженості електростатичного поля з різницею потенціалів. 4. Еквіпотенціальні поверхні |
Закріплення вивченого матеріалу | 12 хв. | 1. Якісні питання. 2. Навчаємося розв’язувати задачі. |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Потенціал електростатичного поля
Потенціал електростатичного поля
Для визначення роботи електростатичного поля необхідно ввести енергетичну характеристику поля. Скористаємося для цього тим, що кожній точці поля відповідає
певна потенціальна енергія Wp взаємодії заряду q з полем. Але ця енергія не є характеристикою поля – вона залежить від значення заряду q. Оскільки сила, з якою поле діє на заряд, прямо пропорційна q, потенціальна енергія Wp також прямо пропорційна q. Звідси випливає, що відношення Wp/q не залежить від заряду. Тому ця величина може служити характеристикою поля в певній точці. Її називають потенціалом і позначають?.
Потенціал електростатичного поля в певній точці – це скалярна величина, що характеризує енергетичні властивості поля й дорівнює відношенню потенціальної енергії Wn електричного заряду, розташованого в цій точці поля, до значення q цього заряду:
Якщо в полі, створеному у вакуумі точковим зарядом Q, на відстані r перебуває пробний заряд q, то потенціальна енергія Wn взаємодії цих зарядів
Використовуючи цю формулу, одержуємо вираз для обчислення потенціалу? поля, створеного точковим зарядом Q, у точках на відстані r від цього заряду:
Щоб однозначно визначити потенціал у будь-якій точці, спочатку необхідно вибрати нульову точку. За таку точку обрана “нескінченність”, тобто точка, віддалена на дуже велику відстань: ?
За таку точку обрана “нескінченність”, тобто точка, віддалена на дуже велику відстань: ?
0, якщо r ?.
Якщо Q > 0, то? > 0, а якщо Q < 0, то? < 0.
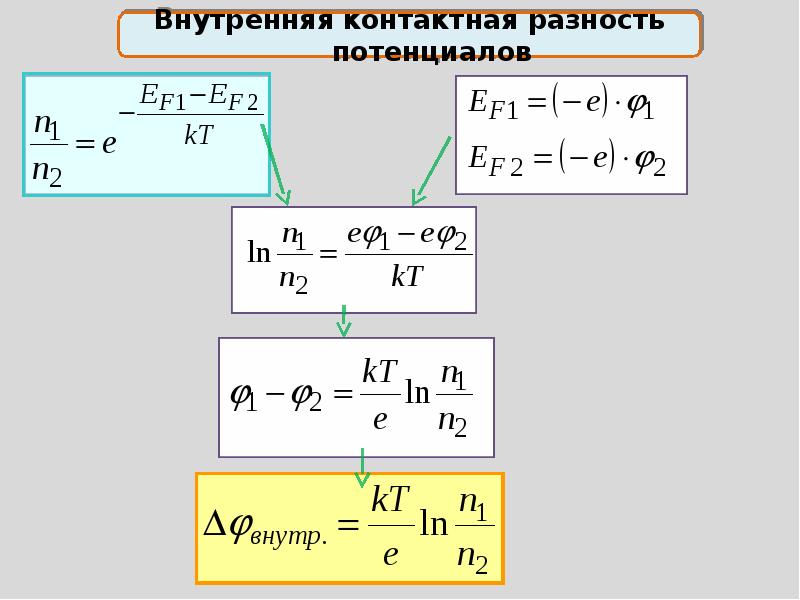
2. Різниця потенціалів
Потенціал у деякій точці може мати різні значення, пов’язані з вибором нульової точки, тому важливу роль тут відіграє не сам потенціал, а різниця потенціалів, що не залежить від вибору нульової точки.
Коли в електростатичному полі заряд рухається із точки 1 у точку 2, це поле виконує роботу, що дорівнює зміні потенціальної енергії заряду, узятої із протилежним знаком: A1-2 = – ?Wn. Таким чином A1-2 = – Wn1 – Wn2.
Скориставшись виразом Wn = q?, одержуємо:
Звідси:
Різниця потенціалів між двома точками дорівнює відношенню роботи поля під час переміщення заряду з початкової точки в кінцеву до цього заряду:
У СІ роботу виражають у джоулях, а заряд – у кулонах. Тому різниця потенціалів між двома точками поля дорівнює 1 В, якщо під час переміщення заряду в 1 Кл із однієї точки в іншу електричне поле виконує роботу в 1 Дж:
3. Зв’язок напруженості електростатичного поля з різницею потенціалів
Зв’язок напруженості електростатичного поля з різницею потенціалів
Нехай із точки 1 у точку 2 під дією поля переміщується заряд q.
Виконану при цьому роботу можна визначити двома способами:
– проекція вектора на вісь OX, проведену через точки 1 і 2. Порівнюючи обидва вирази для роботи, одержуємо: звідки або остаточно:
O напруженість електричного поля дорівнює різниці потенціалів, що припадає на одиницю довжини уздовж лінії напруженості:
Якщо d > 0 (тобто переміщення відбувається в напрямку силових ліній), ?1 – ?2 > 0, тобто потенціал зменшується.
Напруженість електричного поля напрямлена у бік убування потенціалу.
З останньої формули випливає, що одиниця напруженості може вимірюватися у В/м. Напруженість однорідного поля дорівнює 1 В/м, якщо різниця потенціалів між двома точками, з’єднаними вектором завдовжки 1 м і напрямленим уздовж напруженості поля, дорівнює 1 В.
4. Еквіпотенціальні поверхні
Для наочного подання електричного поля, крім силових ліній, використовують еквіпотенціальні поверхні.
O Еквіпотенціальна поверхня – це поверхня, у всіх точках якої потенціал електростатичного поля має однакове значення.
Еквіпотенціальні поверхні тісно пов’язані із силовими лініями електричного поля. Якщо електричний заряд переміщується по еквіпотенціальній поверхні, то робота поля дорівнює нулю, оскільки A = – q??, а на еквіпотенціальній поверхні?? = 0. Оскільки робота A = Fscos
, але A = 0, а F? 0 й s? 0, то cos = 0, отже, = 90°.
Силові лінії електростатичного поля перпендикулярні до еквіпотенціальних поверхонь.
Крім того, силові лінії вказують напрямок максимального зменшення потенціалу електростатичного поля.
ПИТАННЯ ДО УЧНІВ У ХОДІ ВИКЛАДУ НОВОГО МАТЕРІАЛУ
Перший рівень
1. Що таке потенціальна енергія?
2. Поблизу тіла, зарядженого позитивно, поміщають незаряджений ізольований провідник. Чи буде його потенціал позитивним або негативним?
3. Напруга між двома точками поля дорівнює 50 В. Що це означає?
4. Як різниця потенціалів між двома точками поля залежить від роботи електростатичного поля?
5. Наведіть приклади еквіпотенціальних поверхонь.
Наведіть приклади еквіпотенціальних поверхонь.
Другий рівень
1. Чи зміняться показання електрометра, установленого на ізоляційній підставці, якщо заряджений провідник з’єднати з його корпусом, а стрижень із землею?
2. Чи може бути еквіпотенціальним об’ємне тіло?
3. Чи можуть перетинатися різні еквіпотенціальні поверхні?
4. Чи можуть стикатися еквіпотенціальні поверхні, що відповідають різним потенціалам?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Якісні питання
1. Є два провідники. Один із них має заряд менший, але потенціал вищий, ніж в іншого. Як будуть переміщатися електричні заряди під час зіткнення провідників? (Відповідь: від провідника з меншим зарядом до провідника з більшим зарядом.)
2. Точки A і B розташовані на одній силовій лінії однорідного електричного поля. Куди напрямлена напруженість поля, якщо потенціал точки B більший, ніж потенціал точки A?
2). Навчаємося розв’язувати задачі
1. Порошина масою 10-8 г перебуває між горизонтальними пластинами з різницею потенціалів 5 кВ. Відстань між пластинами 5 см. Який заряд порошини, якщо вона висить у повітрі? (Відповідь: 10-15 Кл.)
Відстань між пластинами 5 см. Який заряд порошини, якщо вона висить у повітрі? (Відповідь: 10-15 Кл.)
2. Електрон пролетів прискорювальну різницю потенціалів -300 B. Визначте швидкість руху електрона, якщо початкова швидкість його руху дорівнює нулю. Маса електрона 9,1 – 10-31 кг, а заряд 1,6 – 10-19 Кл.
Розв’язання. Відповідно до теореми про кінетичну енергію маємо:
Де A – робота сил поля, що дорівнює A = e(?1 – ?2). Таким чином,
звідки одержуємо:
З’ясовуємо значення шуканої величини:
Відповідь: швидкість електрона, що пройшов прискорювальну різницю потенціалів, 107 м/с.
ЩО МИ ДІЗНАЛИСЯ НА УРОЦІ
– Потенціал електростатичного поля в певній точці – це скалярна величина, що характеризує енергетичні властивості поля й дорівнює відношенню потенціальної енергії Wп електричного заряду, розташованого в цій точці поля, до значення q цього заряду:
– Потенціал? поля, створеного точковим зарядом Q, у точках на відстані r від цього заряду:
– Різниця потенціалів між двома точками дорівнює відношенню роботи поля під час переміщення заряду з початкової точки в кінцеву до цього заряду:
– Різниця потенціалів між двома точками поля дорівнює 1 В, якщо під час переміщення заряду в 1 Кл із однієї точки в іншу електричне поле виконує роботу в 1 Дж.
– Напруженість електричного поля дорівнює різниці потенціалів, що припадає на одиницю довжини уздовж лінії напруженості:
– Еквіпотенціальна поверхня – це поверхня, у всіх точках якої потенціал електростатичного поля має однакове значення.
Домашнє завдання
1. Підр-1: § 4; підр-2: § 3 (п. 2, 3).
2. Зб.:
Рів1 № 2.7; 2.8; 2.9; 2.10.
Рів2 № 2.35; 2.36; 2.37, 2.38.
Рів3 № 2.47, 2.48; 2.49; 2.53.
Гальмує різниця потенціалів формула. Про різницю потенціалів, електрорушійну силу і напругу
Тема: що таке електрична напруга струму і різниця потенціалів.
Мабуть, одним з найбільш часто вживаних виразів у електриків, є поняття електрична напруга. Його так само називають різницю потенціалів і не зовсім вірне словосполучення, таке як напруга струму, ну сенс у назв по суті загальний. А що насправді означає це поняття? Мабуть, для початку наведу книжкову формулювання: електрична напруга
— це відношення роботи електричного поля зарядів при передачі пробного заряду з точки 1 в точку 2. Ну а простими словами кажучи, це пояснюється так.
Ну а простими словами кажучи, це пояснюється так.
Нагадаю Вам, що заряди бувають двох видів, це позитивні зі знаком «+» і негативні зі знаком «-». Більшість з нас в дитинстві гралися з магнітиками, які були чесно здобуті з черговою сломаной машинки з електромоторчиком, де вони і стояли. Так ось коли ми намагалися наблизити ці самі магніти один до одного, то в одному випадку вони притягувалися, а якщо розгорнути один з них навпаки, то відповідно відштовхувалися.
Це відбувалося, тому що у будь-якого магніту існує два полюси, це південний і північний. У тому випадку, коли полюса однакові, то магнітики будуть відштовхуватися, ну а коли різнойменні, притягатися. Те ж саме відбувається і з електричними зарядами, причому сила взаємодії залежить від кількості і різнойменний цих заряджених частинок. Простіше кажучи, чим на одному предметі більше «плюса», а на іншому відповідно «мінуса», тим сильніше вони будуть притягатися один до одного. Або навпаки, відштовхуватися при однаковому заряді (+ і + або — і -).
Тепер уявімо, що у нас є два невеликих залізних кульки. Якщо подумки зазирнути в них, можна побачити безліч маленьких частинок, які розташовані один від одного на не великому відстані і не здатні до вільного пересування, це ядра нашого речовини. Навколо цих частинок з неймовірно великою швидкістю обертаються більш дрібні частинки, під назвою електрони. Вони можуть відірватися від одних ядер і приєднаються до інших, тим самим подорожуючи по всьому залізному кульці. У разі, коли кількість електронів відповідає кількості протонів в ядрі, кульки електрично нейтральні.
А ось якщо якимось чином забрати деяку кількість, така кулька буде прагнути притягти до себе це саме, недостатня кількість електронів, тим самим утворюючи навколо себе позитивне поле зі знаком «+». Чим більше не вистачає електронів, тим сильніше буде це позитивне поле. У сусідньому кульці зробимо на оборот і додамо зайвих електронів. В результаті отримаємо надлишок і відповідно таке ж електричне поле, Але зі знаком «-».
В результаті отримаємо два потенціалу, один з яких жадає отримати електрони, ну а другий від них позбутися. У кулі з надлишком виникає тіснота і ці частинки, навколо яких існує поле, штовхаються і виштовхують один одного з кулі. А там де їх недолік, відповідно відбувається щось на зразок вакууму, який намагається втягнути в себе ці електрони. Це наочний приклад різниці потенціалів і нічим іншим як напруга між ними. Але, варто тільки ці залізні кулі з’єднати між собою, як відбудеться обмін і напруга пропаде, оскільки утворюється нейтральність.
Грубо кажучи, ця сила прагнення заряджених частинок, перейти від більш заряджених частин до менш зарядженим між двома точками і буде різницею потенціалів. Давайте подумки уявімо дроти, які підключені до батарейці від звичайного кишенькового ліхтарика. У самій батарейці відбувається хімічна реакція, в результаті якої виникає надлишок електронів ( «-»), всередині батареї вони виштовхуються на негативну клему. Ці електрони прагнуть, повернуться на своє місце, звідки їх до цього і виштовхали.
Усередині батареї у них не виходить, значить залишається чекати моменту, коли їм зроблять місток у вигляді електричного провідника і за яким вони швидко перейдуть на плюсову клему батареї, куди їх притягує. А поки містка немає, то і буде бажання перейти в вигляді цього самого електричної напруги або різниці потенціалів (Напруга струму).
Наведу деякий аналогічний приклад на іншому поданні. Є звичайний водопровідний кран з водою. Кран закритий і, отже, вода не піде з нього, але всередині вода все одно є і більш того, вона там знаходиться під деяким тиском, вона через це тиску прагне вирватися назовні, але їй заважає закритий кран. І як тільки Ви повернете ручку краника, вода тут же побіжить. Так ось цей тиск і можна приблизно порівняти з напругою, а воду з зарядженими частинками. Сам потік води буде в даному прикладі виступати як електричний струм в самих проводах, а закритий краник в ролі електричного вимикача. Цей приклад я навів тільки для наочності, і він не є повною аналогією!
Як не дивно, але люди не тісно пов’язані з професією електрика, досить часто називають електричну напругу ,
вираженіемнапряженіе струму і це є неправильним формулюванням, оскільки напруга, як ми з’ясували це різниця потенціалів електричних зарядів, а струм, це сам потік цих заряджених частинок. І виходить що, вимовляючи напруга струму в результаті невелике невідповідність самого поняття.
І виходить що, вимовляючи напруга струму в результаті невелике невідповідність самого поняття.
напруга, Так само як і всі інші величини, має свою одиницю виміру. Вона вимірюється в Вольтах. Це ті самі вольти, які пишуться на пристроях та джерела живлення. Наприклад, в звичайної домашньої розетки 220 В, або куплена вами батарейка з напругою 1.5 В. Загалом, думаю, ви зрозуміли в загальних рисах, що ж таке цей самий електричну напругу. У цій статті я грунтувався лише на простому розумінні цього терміна і не вдавався в глибини формулювань і формул, щоб не ускладнювати розуміння. Насправді цю тему можна набагато ширше вивчити, але це вже залежить від Вас і Вашого бажання.
P.S. Будьте уважні при роботі з електрикою, висока напруга небезпечно для життя.
Різниця потенціалів між двома точками в схемі є різницею їх напруг (щодо загальної точки, зазвичай землі). Наприклад, різниця потенціалів між точками А і В на рис. 1.8 VAВ = (VA — V ст), де VA — напруга в точці А і VВ — напруга в точці В. Напруження Уд і Уд вимірюються щодо проведення Е, що має нульовий потенціал. Напруга в будь-якій точці електричної схеми вимірюється щодо нульового проводу, Корпусу або землі.
Напруження Уд і Уд вимірюються щодо проведення Е, що має нульовий потенціал. Напруга в будь-якій точці електричної схеми вимірюється щодо нульового проводу, Корпусу або землі.
Наприклад, якщо VA = 5 В і V ст = 3 В, то VAВ = VA — V ст = 5 — 3 = 2 В (рис. 1.9 (а)).
Напруги можуть відрізнятися за знаком — бути негативними і позитивними. Різниця потенціалів між двома точками, що мають напруги з протилежними знаками, дорівнює сумі цих напруг.
Наприклад, якщо VС = 3 В, а VD = -2 В, то V = VС + VD = 3 + 2 = 5 В (рис. 1.9 (б)).
Отже, якщо два напруги мають однакову полярність, або однакові знаки, то різниця потенціалів між ними дорівнює їх різниці. Якщо ж напруги мають різні знаки, то різниця потенціалів між ними дорівнює їх сумі.
Мал. 1.9. Наочне уявлення напружень з різними знаками щодо лінії нульового потенціалу
Паралельне з’єднання резисторів
На рис. 1.10 зображені два резистора, R1 і R2 з’єднані паралельно. Струм I від батареї розгалужується в точці А на ток I1, що протікає через опір R1, і струм I2, що протікає через опір R2. У точці В ці струми складаються і утворюють повний струм I = I1 + I2.
У точці В ці струми складаються і утворюють повний струм I = I1 + I2.
Мал. 1.10.
З іншого боку, до кожного резистору докладено повне напруга V, т. Е.
Повна напруга V = напрузі на R1
Напрузі на R2.
загальний опір
Загальний опір (R) двох резисторів, з’єднаних паралельно, визначається формулою:
Зауважимо, що загальний опір двох паралельних резисторів завжди менше, ніж опір меншого з них. Загальний опір двох паралельно з’єднаних резисторів, що мають однаковий опір, дорівнює половині опору одного з них.
Паралельне з’єднання трьох і більше резисторів
У загальному випадку загальний опір довільного числа резисторів, з’єднаних паралельно, можна визначити за формулою вище.
приклад 4
Визначити загальний опір схеми, зображеної на рис. 1.11 (а).
Рішення
R1 і R2 з’єднані послідовно і їх загальний опір RТ1 = R1 + R2 = 6 + 8 = 14 Ом.
Тепер, після заміни резисторів R1 і R2 їхнім спільним опором RТ1, (схема на рис. 1.11 (б)), резистор R3 виявився включеним паралельно з RТ1, рівним йому за величиною. Отже, їх загальний опір RТ2 вполовину менше кожного з них. Тепер схема набуде вигляду, як показано на рис. 1.11 (в), де RТ2 = 7 Ом і з’єднане послідовно з R4. Звідси загальний опір схеми між точками А і В дорівнює RТ2 + R4 = 7 + 3 = 10 Ом
1.11 (б)), резистор R3 виявився включеним паралельно з RТ1, рівним йому за величиною. Отже, їх загальний опір RТ2 вполовину менше кожного з них. Тепер схема набуде вигляду, як показано на рис. 1.11 (в), де RТ2 = 7 Ом і з’єднане послідовно з R4. Звідси загальний опір схеми між точками А і В дорівнює RТ2 + R4 = 7 + 3 = 10 Ом
Мал. 1.11
Потенційні поля. Можна довести, що робота будь-якого електростатичного поля при переміщенні зарядженого тіла з однієї точки в іншу не залежить від форми траєкторії, гак само як і робота однорідного поля. На замкнутої траєкторії робота електростатичного поля завжди дорівнює нулю. Поля, що володіють такою властивістю, називають потенційними. Потенційний характер, зокрема, має електростатичне поле точкового заряду.
Роботу потенційного поля можна виразити через зміну потенційної енергії. Формула справедлива для довільного електростатичного поля. Але тільки в разі однорідного поля енергія виражається формулою (8.19)
Потенціал. Потенційна енергія заряду в електростатичному полі пропорціональназаряду. Це справедливо як для однорідного поля (див. Формулу 8.19), гак і для будь-якого іншого. Отже, ставлення потенційної енергії до заряду не залежить від вміщеного в поле заряду.
Потенційна енергія заряду в електростатичному полі пропорціональназаряду. Це справедливо як для однорідного поля (див. Формулу 8.19), гак і для будь-якого іншого. Отже, ставлення потенційної енергії до заряду не залежить від вміщеного в поле заряду.
Це дозволяє ввести нову кількісну характеристику поля — потенціал. Потенціалом електростатичного поля називають відношення потенційної енергії заряду в полі до цього заряду.
Згідно з цим визначенням потенціал дорівнює:
Напруженість поля є вектором і являє собою силову характеристику поля; вона визначає силу, що діє на заряд в даній точці поля. Потенціал — скаляр, це енергетична характеристика поля; він визначає потенційну енергію заряду в даній точці поля.
Якщо в якості нульового рівня потенційної енергії, а значить, і потенціалу прийняти негативно заряджену пластину (рис. 124), то відповідно до формул (8.19 і 8.20) потенціал однорідного поля дорівнює:
Різниця потенціалів. Подібно потенційної енергії, значення потенціалу в даній точці залежить від вибору нульового рівня для відліку потенціалу. Практичне значення має не сам потенціал в точці, а зміна потенціалу, яка не залежить від вибору нульового рівня відліку потенціалу.
Практичне значення має не сам потенціал в точці, а зміна потенціалу, яка не залежить від вибору нульового рівня відліку потенціалу.
Таким чином, різниця потенціалів (напруга) між двома точками дорівнює відношенню роботи поля по переміщенню заряду з початкової точки в кінцеву до цього заряду.
Знаючи напругу в освітлювальної мережі, Ми тим самим знаємо роботу, яку електричне поле може зробити при переміщенні одиничного заряду від одного контакту розетки до іншого по будь електричного кола. З поняттям різниці потенціалів ми будемо мати справу протягом усього курсу фізики.
Одиниця різниці потенціалів. Одиницю різниці потенціалів встановлюють за допомогою формули (8.24). У Міжнародній системі одиниць роботу висловлюють в джоулях, а заряд — в кулонах. Тому різниця потенціалів між двома точками дорівнює одиниці, якщо при переміщенні заряду в 1 Кл з однієї точки в іншу електричне поле здійснює роботу в 1 Дж. Цю одиницю називають вольт
1. Які поля називають потенційними? 2. Як пов’язана зміна потенційної енергії з роботою? 3. Чому дорівнює потенціальна енергія зарядженої частинки в однорідному електричному полі? 4. Дайте визначення потенціалу. Чому дорівнює різниця потенціалів між двома точками поля?
Як пов’язана зміна потенційної енергії з роботою? 3. Чому дорівнює потенціальна енергія зарядженої частинки в однорідному електричному полі? 4. Дайте визначення потенціалу. Чому дорівнює різниця потенціалів між двома точками поля?
У багатьох випадках для того, щоб правильно усвідомити суть питання, що стосується електротехніки, необхідно точно знати, що таке різниця потенціалів.
Визначення різниці потенціалів
Загальне поняття полягає в електричному напрузі, утвореному між двома точками, і представляє собою роботу електричного поля, яку необхідно здійснити для переміщення з однієї точки в іншу позитивного одиничного заряду.
Таким чином, в рівномірному і нескінченному електричному полі позитивний заряд під впливом цього поля буде переміщений на нескінченну відстань в напрямку, однаковим з електричним полем. Потенціал конкретної точки поля являє собою роботу, вироблену електричним полем при переміщенні з цієї точки позитивного заряду в точку, віддалену нескінченно. При переміщенні заряду в зворотному напрямку, зовнішніми силами проводиться робота, спрямована на подолання електричної сили поля.
При переміщенні заряду в зворотному напрямку, зовнішніми силами проводиться робота, спрямована на подолання електричної сили поля.
Різниця потенціалів на практиці
Різниця потенціалів, існуюча в двох різних точках поля, отримала поняття напруги, що вимірюється в вольтах. В однорідному електричному полі дуже добре проглядається залежність між електричною напругою і напруженістю електричного поля.
Точки з однаковим потенціалом, розташовані навколо зарядженої поверхні провідника, повністю залежать від форми цієї поверхні. При цьому різниця потенціалів для окремих точок, що лежать на одній і тій же поверхні має нульове значення. Така поверхня, де кожна точка має однаковим потенціалом називається еквіпотенційної поверхні.
Коли відбувається наближення до зарядженого тіла, відбувається швидке збільшення потенціалу, а розташування еквіпотенційних поверхонь стає більш тісним відносно один одного. При видаленні від заряджених тіл, розташування еквіпотенційних поверхонь стає більш рідкісним. Розташування електричних силових ліній завжди перпендикулярно з еквіпотенційної поверхнею в кожній точці.
Розташування електричних силових ліній завжди перпендикулярно з еквіпотенційної поверхнею в кожній точці.
У зарядженому провіднику всі крапки на його поверхні мають однаковий потенціал. Те ж значення є і у внутрішніх точках провідника.
Провідники, які мають різні потенціали, з’єднані між собою за допомогою металевого дроту. На її кінцях з’являється напруга або різниця потенціалів, тому уздовж всієї дроту спостерігається дію електричного поля. Вільні електрони починають рухатися в напрямку збільшення потенціалу, що викликає появу електричного струму.
Падіння потенціалу вздовж провідника
різниця потенціалів
Відомо, що одне тіло можна нагріти більше, а інше менше. Ступінь нагріву тіла називається його температурою. Подібно до цього, одне тіло можна наелектризована більше іншого. Ступінь електризації тіла характеризує величину, звану електричним потенціалом або просто потенціалом тіла.
Що значить наелектризована тіло? Це означає повідомити йому електричний заряд, Т. Е. Додати до нього кілька електронів, якщо ми тіло заряджаємо негативно, або відняти їх від нього, якщо ми тіло заряджаємо позитивно. В тому і іншому випадку тіло буде мати певний ступінь електризації, т. Е. Тих чи інших потенціалом, причому тіло, заряджене позитивно, має позитивним потенціалом, а тіло, заряджене негативно, — негативним потенціалом.
Е. Додати до нього кілька електронів, якщо ми тіло заряджаємо негативно, або відняти їх від нього, якщо ми тіло заряджаємо позитивно. В тому і іншому випадку тіло буде мати певний ступінь електризації, т. Е. Тих чи інших потенціалом, причому тіло, заряджене позитивно, має позитивним потенціалом, а тіло, заряджене негативно, — негативним потенціалом.
Різниця рівнів електричних зарядів двох тіл прийнято називати різницею електричних потенціалів або просто різницею потенціалів.
Слід мати на увазі, що якщо два однакових тіла заряджені однойменними зарядами, але одне більше, ніж інше, то між ними також буде існувати різниця потенціалів.
Крім того, різниця потенціалів існує між двома такими тілами, одне з яких заряджена, а інше не має заряду. Так, наприклад, якщо яке-небудь тіло, ізольоване від землі, має деякий потенціал, то різниця потенціалів між ним і землею (потенціал якої прийнято вважати рівним нулю) чисельно дорівнює потенціалу цього тіла.
Отже, якщо два тіла заряджені таким чином, що потенціали їх неоднакові, між ними неминуче існує різниця потенціалів.
всім відоме явище електризації гребінці при терті її про волосся є нічим іншим, як створення різниці потенціалів між гребінцем і волоссям людини.
Дійсно, при терті гребінця про волосся частина електронів переходить на гребінець, заряджаючи її негативно, волосся ж, втративши частину електронів, заряджаються в тій же мірі, що і гребінець, але позитивно. Створена таким чином різниця потенціалів може бути зведена до нуля дотиком гребінця до волосся. Цей зворотний перехід електронів легко виявляється на слух, якщо наелектризовану гребінець наблизити до вуха. Характерне потріскування буде свідчити про те, що відбувається розряді.
Говорячи вище про різниці потенціалів, ми мали на увазі два заряджених тіла, проте різницю потенціалів можна отримати і між різними частинами (точками) одного і того ж тіла.
Так, наприклад, розглянемо, що відбудеться в, якщо під дією будь-якої зовнішньої сили нам вдасться вільні електрони, що знаходяться в дроті, перемістити до одного кінця її. Очевидно, на іншому кінці дроту вийде недолік електронів, і тоді між кінцями дроту виникне різниця потенціалів.
Очевидно, на іншому кінці дроту вийде недолік електронів, і тоді між кінцями дроту виникне різниця потенціалів.
Варто нам припинити дію зовнішньої сили, як електрони відразу ж, в силу тяжіння різнойменних зарядів, кинуться до кінця дроту, зарядженого позитивно, т. Е. До місця, де їх бракує, і в дроті знову настане електричне рівновагу.
Електрорушійна сила і напруга
Д ля підтримки електричного струму в провіднику необхідний якийсь зовнішнє джерело енергії, який весь час підтримував би різницю потенціалів на кінцях цього провідника.
Такими джерелами енергії служать так звані джерела електричного струму, Що володіють певною електрорушійної силою, Яка створює і тривалий час підтримує різницю потенціалів на кінцях провідника.
Електрорушійна сила (скорочено ЕРС) позначається буквою Е. Одиницею вимірювання ЕРС служить вольт. У нас в країні вольт скорочено позначається буквою «В», а в міжнародному позначенні — буквою «V».
Отже, щоб отримати безперервний перебіг, потрібна електрорушійна сила, т. Е. Потрібен джерело електричного струму.
Е. Потрібен джерело електричного струму.
Першим таким джерелом струму був так званий «вольтів стовп», який складався з ряду мідних і цинкових гуртків, прокладених шкірою, змоченою в підкисленою воді. Таким чином, одним із способів отримання електрорушійної сили є хімічна взаємодія деяких речовин, в результаті чого хімічна енергія перетворюється в енергію електричну. Джерела струму, в яких таким шляхом створюється електрорушійна сила, називаються хімічними джерелами струму.
В даний час хімічні джерела струму — гальванічні елементи і акумулятори — широко застосовуються в електротехніці і електроенергетиці.
Іншим основним джерелом струму, який отримав широке поширення у всіх областях електротехніки та електроенергетики, є генератори.
Генератори встановлюються на електростанціях і служать єдиним джерелом струму для живлення електроенергією промислових підприємств, електричного освітлення міст, електричних залізниць, трамвая, метро, тролейбусів і т. Д.
Д.
Як у хімічних джерел електричного струму (елементів та акумуляторів), так і у генераторів дію електрорушійної сили абсолютно однаково. Воно полягає в тому, що ЕРС створює на затискачах джерела струму різниця потенціалів і підтримує її тривалий час.
Ці затиски називаються полюсами джерела струму. Один полюс джерела струму відчуває завжди недолік електронів і, отже, має позитивним зарядом, інший полюс відчуває надлишок електронів і, отже, має негативний заряд.
Відповідно до цього один полюс джерела струму називається позитивним (+), інший — негативним (-).
Джерела струму служать для харчування електричним струмом різних приладів -. Споживачі струму за допомогою провідників з’єднуються з полюсами джерела струму, утворюючи замкнутий електричний ланцюг. Різниця потенціалів, яка встановлюється між полюсами джерела струму при замкнутому електричному ланцюзі, називається напругою і позначається буквою U.
Одиницею вимірювання напруги, так само як і ЕРС, служить вольт.
Якщо, наприклад, треба записати, що напруга джерела струму дорівнює 12 вольт, то пишуть: U — 12 В.
Для вимірювання або напруги застосовується прилад, званий вольтметром.
Щоб виміряти ЕРС або напруга джерела струму, треба вольтметр підключити безпосередньо до його полюсів. При цьому, якщо розімкнути, то вольтметр покаже ЕРС джерела струму. Якщо ж замкнути ланцюг, то вольтметр вже покаже не ЕРС, а напруга на затискачах джерела струму.
ЕРС, що розвивається джерелом струму, завжди більше напруги на його затискачах.
Електричний потенціал: формула та рівняння, розрахунок, приклади, вправи — Наука
2022
Електричний потенціал: формула та рівняння, розрахунок, приклади, вправи — Наука
Зміст
The електричний потенціал він визначається в будь -якій точці, де існує електричне поле, як потенціальна енергія цього поля на одиницю заряду. Точкові заряди та розподіли точкових чи безперервних зарядів створюють електричне поле і тому мають пов’язаний потенціал.
У Міжнародній системі одиниць вимірювання (SI) електричний потенціал вимірюється у вольтах (V) і позначається як V. Математично це виражається як:
V = U / qабо
Малюнок 1. Додаткові кабелі, підключені до акумулятора. Джерело: Pixabay.
Де U — потенціальна енергія, пов’язана із зарядом або розподілом, і qабо це позитивний тест. Оскільки U — скаляр, то потенціал також.
З визначення, 1 вольт — це просто 1 Джоуль / Кулон (J / C), де Джоуль — одиниця енергоспоживання СІ, а Кулон (С) — одиниця електричного заряду.
Припустимо точковий заряд q. Ми можемо перевірити природу поля, яке створює цей заряд, за допомогою невеликого позитивного тестового заряду, званого qабо, використовується як зонд.
Робота W, необхідна для переміщення цього невеликого вантажу з точки до до моменту b, є від’ємним значенням різниці потенційна енергія ΔU між цими точками:
Wa → b = -ΔU = — (Ub — АБОдо)
Поділивши все між qабо:
Wa → b / qабо= — ΔU / qабо = — (Ub — АБОдо) / qабо = — (Vb — В. до) = -ΔV
до) = -ΔV
Тут В.b — потенціал у точках b і Vдо це пункт а. Різниця потенціалів Vдо — В.b є потенціал стосовно б і називається Vab. Порядок індексів важливий, якщо його змінити, він би представляв потенціал b щодо a.
Покажчик статей
- 1 Різниця електричних потенціалів
- 1.1 Ознаки та значення різниці потенціалів
- 2 Як розрахувати електричний потенціал?
- 2.1 Електричний потенціал для дискретних розподілів заряду
- 2.2 Електричний потенціал у безперервних розподілах навантаження
- 3 Приклади електричного потенціалу
- 3.1 Акумулятори та акумулятори
- 3.2 Розетка
- 3.3 Напруга між зарядженими хмарами та землею
- 3.4 Генератор Ван Дер Граффа
- 3.5 Електрокардіограма та електроенцефалограма
- 4 Вправа вирішена
- 4.1 Рішення а
- 4.2 Розв’язання b
- 4.3 Розв’язання c
- 4.
 4 Розв’язання d
4 Розв’язання d - 4.5 Розв’язання e
- 4.6 Рішення f
- 5 Посилання
Різниця електричних потенціалів
З вищесказаного випливає, що:
-ΔV = Wa → b / qабо
Тому:
ΔV = -Wa → b / qабо
Тепер робота обчислюється як інтеграл скалярного добутку між електричною силою F між q і qабо і вектор переміщення dℓ між точками a і b. Оскільки електричне поле є силою одиниці заряду:
І = F/ qабо
Робота по перенесенню тестового навантаження від a до b полягає в наступному:
Це рівняння пропонує спосіб прямого розрахунку різниці потенціалів, якщо електричне поле заряду або розподіл, що його виробляє, відомі раніше.
І також зазначається, що різниця потенціалів є скалярною величиною, на відміну від електричного поля, яке є вектором.
Ознаки та значення різниці потенціалів
З попереднього визначення ми спостерігаємо, що якщо І та dℓ є перпендикулярними, різниця потенціалів ΔV дорівнює нулю. Це не означає, що потенціал у таких точках дорівнює нулю, а просто, що Vдо = Vb, тобто потенціал постійний.
Лінії та поверхні, де це відбувається, називаються еквіпотенціальний. Наприклад, еквіпотенціальні лінії поля точкового заряду — це окружності, концентричні до заряду. А еквіпотенціальні поверхні — це концентричні сфери.
Якщо потенціал створюється позитивним зарядом, електричне поле якого складається з радіальних ліній, що випромінюють заряд, то у міру віддалення від поля потенціал стане все меншим. Як тестове навантаження qабо позитивний, він відчуває менше електростатичне відштовхування, чим далі від q.
Малюнок 2. Електричне поле, створене позитивним точковим зарядом та його еквіпотенціальними лініями (червоним кольором): джерело: Вікімедіа Спільнота. HyperPhysics/CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0).
HyperPhysics/CC BY-SA (https://creativecommons.org/licenses/by-sa/4.0).
Навпаки, якщо навантаження що є негативним, випробувальний заряд qабо (позитивний) буде мати менший потенціал у міру наближення q.
Як розрахувати електричний потенціал?
Інтеграл, наведений вище, служить для пошуку різниці потенціалів, а отже, потенціалу в даній точці b, якщо еталонний потенціал відомий в іншій точці до
Наприклад, є випадок точкового навантаження що, вектор електричного поля якого в точці, розташованій на відстані r навантаження становить:
І = kq / r2r
Де k — електростатична стала, значення якої в одиницях Міжнародної системи дорівнює:
k = 9 x 10 9 Нм2 / С2.
І векторr— одиничний вектор уздовж лінії з’єднання що з пунктом П.
Він замінений у визначенніΔV:
Вибір цієї точки b перебувати на відстані r заряду і що при a → ∞ потенціал дорівнює 0, то Vдо = 0, а попереднє рівняння виглядає так:
V = kq / r
Виберіть V. до = 0, коли a → ∞ має сенс, тому що в точці, дуже далекій від навантаження, важко уявити, що вона існує.
до = 0, коли a → ∞ має сенс, тому що в точці, дуже далекій від навантаження, важко уявити, що вона існує.
Електричний потенціал для дискретних розподілів заряду
Коли в певній області розподілено багато точкових зарядів, електричний потенціал, який вони виробляють у будь -якій точці P простору, обчислюється шляхом додавання окремих потенціалів, які виробляє кожен з них. А) Так:
V = V1 + V2 + V3 +… VN = ∑ Vi
Сума поширюється від i = до N, і потенціал кожного заряду обчислюється за допомогою рівняння, наведеного в попередньому розділі.
Електричний потенціал у безперервних розподілах навантаження
Починаючи з потенціалу точкового заряду, потенціал, вироблений зарядженим об’єктом вимірюваного розміру, можна знайти в будь -якій точці P.
Для цього тіло ділиться на безліч маленьких нескінченно малих зарядів кв. Кожен з них робить свій внесок у весь потенціал dV нескінченно малий.
Малюнок 3. Схема для знаходження електричного потенціалу безперервного розподілу в точці П. Джерело: Сервей, Р. Фізика для наук та техніки.
Тоді всі ці внески додаються через інтеграл і таким чином отримується загальний потенціал:
Приклади електричного потенціалу
У різних пристроях є електричний потенціал, завдяки якому можна отримувати електричну енергію, наприклад, акумулятори, акумулятори автомобіля та електричні розетки. Електричний потенціал також встановлюється в природі під час грози.
Акумулятори та батареї
В елементах і акумуляторах електрична енергія зберігається за допомогою хімічних реакцій всередині них. Вони виникають, коли ланцюг замикається, пропускаючи постійний струм і запалюючи лампочку, або запускається стартер двигуна автомобіля.
Існують різні напруги: 1,5 В, 3 В, 9 В і 12 В — найпоширеніші.
Розетка
Прилади та побутова техніка, що працюють від комерційного електричного струму, підключаються до вбудованої настінної розетки. Залежно від місця розташування напруга може становити 120 В або 240 В.
Залежно від місця розташування напруга може становити 120 В або 240 В.
Малюнок 4. У розетці є різниця потенціалів. Джерело: Pixabay.
Напруга між зарядженими хмарами і землею
Це той, який виникає під час грози, через рух електричного заряду через атмосферу. Він може бути порядку 108 В.
Малюнок 5. Гроза. Джерело: Wikimedia Commons. Себастьєн Д’АРКО, анімація від Koba-chan/CC BY-SA (https://creativecommons.org/licenses/by-sa/2.5)
Генератор Ван Дер Граффа
Завдяки гумовій конвеєрній стрічці утворюється фрикційний заряд, який накопичується на провідній кулі, розміщеній зверху ізоляційного циліндра. Це створює різницю потенціалів, яка може становити кілька мільйонів вольт.
Малюнок 6. Генератор Ван дер Граффа в Театрі електроенергії Бостонського наукового музею. Джерело: Вікімедіа. Бостонський музей науки/CC BY-SA (https://creativecommons.org/licenses/by-sa/3.0) Спільнота.
Електрокардіограма та електроенцефалограма
У серці є спеціалізовані клітини, які поляризують і деполяризують, викликаючи різницю потенціалів. Їх можна виміряти як функцію часу за допомогою електрокардіограми.
Їх можна виміряти як функцію часу за допомогою електрокардіограми.
Цей простий тест проводиться шляхом розміщення електродів на грудях людини, здатних вимірювати невеликі сигнали.
Оскільки це дуже низька напруга, їх потрібно зручно підсилити, а потім записати на паперову стрічку або переглянути через комп’ютер. Лікар аналізує пульс на наявність відхилень, щоб виявити проблеми з серцем.
Малюнок 7. Друкована електрокардіограма. Джерело: Pxfuel.
Електричну активність мозку також можна записати за допомогою подібної процедури, званої ЕЕГ.
Вправа вирішена
Навантаження Q = — 50,0 нС знаходиться в 0,30 м від точки ДО та 0,50 м від точки В, як показано на наступному малюнку. Дайте відповідь на наступні питання:
а) Який потенціал в А створює цей заряд?
б) А який потенціал у В?
в) Якщо заряд q рухається від А до В, яка різниця потенціалів, через яку він рухається?
г) Згідно з попередньою відповіддю, чи збільшується чи зменшується його потенціал?
д) Якщо q = — 1,0 нС, яка зміна його електростатичної потенціальної енергії при її переміщенні від А до В?
f) Скільки роботи виконує електричне поле, створене Q, коли випробувальний заряд рухається від A до B?
Малюнок 8. Схема розв’язаної вправи. Джерело: Джамбаттіста, А. Фізика.
Схема розв’язаної вправи. Джерело: Джамбаттіста, А. Фізика.
Рішення для
Q — точковий заряд, тому його електричний потенціал у A обчислюється:
В.ДО = kQ / rДО = 9 x 109 x (-50 x 10-9) / 0,3 В = -1500 В
Розв’язання б
Так само
В.B = kQ / rB = 9 x 109 x (-50 x 10-9) / 0,5 В = -900 В
Розв’язання c
ΔV = Vb — В.до = -900 -(-1500) V = + 600 В
Розв’язання d
Якщо заряд q позитивний, його потенціал зростає, але якщо він негативний, його потенціал зменшується.
Рішення д
ΔV = ΔU / qабо → ΔU = qабо ΔV = -1,0 х 10-9 х 600 Дж = -6,0 х 10-7 Дж.
Негативний знакΔU вказує на те, що потенціальна енергія в B менша за енергію A.
Розв’язання f
Оскільки W = -ΔU поле реалізується+6,0 х 10-7 Дж роботи.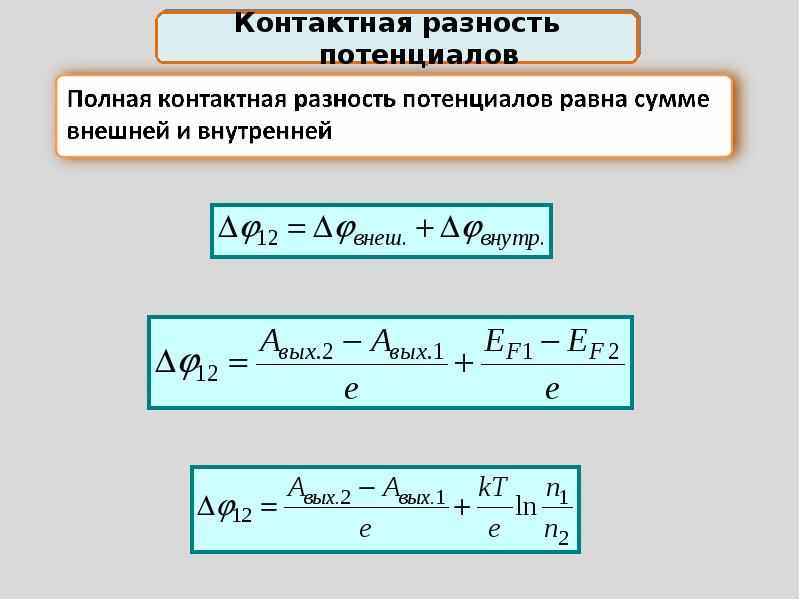
Посилання
- Фігероа, Д. (2005). Серія: Фізика для науки та техніки. Том 5. Електростатика. Під редакцією Дугласа Фігероа (USB).
- Джамбаттіста, А. 2010. Фізика. 2 -й. Ред. Макгроу Хілл.
- Резнік, Р. (1999). Фізичні. Т. 2. Третє видання іспанською мовою. Компанія Редакція Continental S.A. de C.V.
- Тіплер, П. (2006) Фізика для науки і техніки. 5 -е видання. Том 2. Редакційне повернення.
- Сервей, Р. Фізика для науки та техніки. Том 2. 7 -й. Ред. Cengage Learning.
ЕФЕКТ ХОЛЛА І ВИМІРЮВАННЯ ЕЛЕКТРОХІМІЧНИХ ПОТЕНЦІАЛІВ У КОНЦЕПЦІЇ «ЗНИЗУ – ВГОРУ»
Ю. О. Кругляк, М. В. Стріха Sensor Electronics and Мicrosystem Technologies 2014 — T. 11, № 1
8 9
Вже в 1982 році був експериментально
виявлено дробовий квантовий ефект Холла
[5, 6]. У феромагнетиках у холлівському опо-
рі був виявлений внесок, залежний безпосе-
редньо від намагніченості матеріалу, причому
цей внесок може бути набагато більшим від
нормального холлівського опору. Це явище
Це явище
отримало назву аномального ефекту Холла [7].
Відомі й інші, не менше цікаві, прояви ефек-
ту Холла: спіновий ефект Холла Дьяконова –
Переля [8, 9], квантовий спіновий ефект Хол-
ла в графені [10], ефект дії магнітного поля
на невзаємні електричні кола (non-reciprocity
circuits), які важко інтерпретувати в термінах
звичайних ефективних опорів [11]. Останній
ефект особливо цікавий, оскільки з’явився
новий клас матеріалів – топологічні діелек-
трики (topological insulators) [12]. Ці та інші
пов’язані питання ми розглянемо з різним сту-
пенем повноти в цій та подальших публікаціях
з позицій концепції «знизу – вгору» сучасної
наноелектроніки, використовуючи методоло-
гічну схему лекційного курсу [13], в якій ви-
конано наші попередні роботи [14, 15].
Ефект Холла: елементарний розгляд і
його обмеженість. Розгляньмо докладніше
звичайний класичний ефект Холла при низь-
ких магнітних полях. Однією з причин, що ви-
Однією з причин, що ви-
кликали підвищений інтерес до ефекту Холла,
було те, що холлівський опір має різний знак
для n- і p-провідників, що відкриває можли-
вість експериментально легко встановити
тип провідності. Цієї ж мети можна досяг-
ти, вимірюючи напрям струму в провіднику
між контактами, що перебувають при різних
температурах [14]. І в тому і в іншому випад-
ку звичайно користуються поняттям «дірок»
(«порожніх» станів, не зайнятих електронами
у «майже заповненій» валентній зоні) як но-
сіїв позитивного заряду в p-провідниках. Таке
трактування, вперше запроваджене Вернером
фон Гейзенбергом у 1931 р., добре описує ве-
ликі тривимірні напівпровідникові кристали,
але зустрічається з труднощами при переході
до нанорозмірів, де поняття трансляційної си-
метрії вже незастосовне, а носіями струму в
усіх випадках є тільки електрони.
Нагадаємо: при термоелектричних вимірю-
ваннях напрям струму визначається нахилом
функції густини станів D(E), яка або зростає
зі зростанням енергії (n-провідник), чи то спа-
дає (p-провідник) [14]. Натомість знак холлів-
ского ефекту визначається знаком ефективної
маси, введеної за формулою (75) з роботи [15]
як відношення імпульсу p до швидкості dE/dp.
Як наслідок, результуюча dv/dt має різний знак
для n- і p-провідників, відхиляючи електро-
ни, емітовані з витоку і зі стоку, до протилеж-
них граней пластини (рис.1), що і призводить
до зміни знаку холлівської різниці потенціалів
при зміні типу провідності від електронної до
«діркової».
Звернімося до звичайного «підручниково-
го» викладу елементарної теорії ефекту Хол-
ла (див., наприклад, [16]). Струм визначається
виразом
/d
I qN L
ν
=, (6)
де N/L є 2D густина електронів у площині,
перпендикулярній до напрямку струму, а їхня
дрейфова швидкість дорівнює добуткові рух-
ливості електронів на електричне поле уздовж
довжини провідника
/
d
νµ
=. (7)
(7)
В стані рівноваги поперечне поле компен-
сує силу Лоренца
/
ν
=, (8)
отже, використовуючи (6) і (7), для холлівсько-
го опору одержуємо:
( )
/
H
H
VB
RI q N LW
= = . (9)
Це співвідношення широко використо-
вується для визначення густини електронів
N/LW за нахилом залежності холлівського опо-
ру від магнітного поля.
Такий виклад елементарної теорії ефек-
ту Холла повторюється з тими або іншими
незначними нюансами в усіх підручниках.
І як причина виникнення струму як у поздо-
вжньому, так і в поперечному напрямі скрізь
фігурує електричне поле. Межі застосовності
такої інтерпретації для наносистем обговоре-
Однією з причин, що викликали підвищений інтерес до ефекту Холла, було те,
що холлівський опір має різний знак для n- і p-провідників, що відкриває
можливість експериментально легко встановити тип провідності. Цієї ж мети
Цієї ж мети
можна досягти, вимірюючи напрям струму в провіднику між контактами, що
перебувають при різних температурах [14]. І в тому і в іншому випадку
звичайно користуються поняттям «дірок» («порожніх» станів, не зайнятих
електронами у «майже заповненій» валентній зоні) як носіїв позитивного заряду
в p-провідниках. Таке трактування, вперше запроваджене Вернером фон
Гейзенбергом у 1931 р., добре описує великі тривимірні напівпровідникові
кристали, але зустрічається з труднощами при переході до нанорозмірів, де
поняття трансляційної симетрії вже незастосовне, а носіями струму в усіх
випадках є тільки електрони.
Нагадаємо: при термоелектричних вимірюваннях напрям струму
визначається нахилом функції густини станів D(E), яка або зростає зі
зростанням енергії (n-провідник),чи то спадає (p-провідник) [14]. Натомість
знак холлівского ефекту визначається знаком ефективної маси, введеної за
формулою (75) з роботи [15] як відношення імпульсу pдо швидкості dE/dp. Як
Як
наслідок, результуюча dv/dt має різний знак для n- і p-провідників, відхиляючи
електрони, емітовані з витоку і зі стоку, до протилежних граней пластини
(рис.1), що і призводить до зміни знаку холлівської різниці потенціалів при
зміні типу провідності від електронної до «діркової».
Звернімося до звичайного «підручникового» викладу елементарної теорії
ефекту Холла (див., наприклад, [16]). Струм визначається виразом
d
I qN L
ν
=
,
(6)
де N/L є 2Dгустина електронів у площині,перпендикулярній до напрямку
струму, а їхня дрейфова швидкість дорівнює добуткові рухливості електронів на
електричне поле уздовж довжини провідника
. (7)
В стані рівноваги поперечне поле компенсує силу Лоренца
, (8)
отже, використовуючи (6) і (7),для холлівського опору одержуємо:
. (9)
Це співвідношення широко використовується для визначення густини
електронів N/LW за нахилом залежності холлівського опору від магнітного
поля.
Такий виклад елементарної теорії ефекту Холла повторюється з тими або
іншими незначними нюансами в усіх підручниках. І як причина виникнення
струму як у поздовжньому, так і в поперечному напрямі скрізь фігурує
електричне поле. Межі застосовності такої інтерпретації для наносистем
Однією з причин, що викликали підвищений інтерес до ефекту Холла, було те,
що холлівський опір має різний знак для n- і p-провідників, що відкриває
можливість експериментально легко встановити тип провідності. Цієї ж мети
можна досягти, вимірюючи напрям струму в провіднику між контактами, що
перебувають при різних температурах [14]. І в тому і в іншому випадку
звичайно користуються поняттям «дірок» («порожніх» станів, не зайнятих
електронами у «майже заповненій» валентній зоні) як носіїв позитивного заряду
в p-провідниках. Таке трактування, вперше запроваджене Вернером фон
Гейзенбергом у 1931 р. , добре описує великі тривимірні напівпровідникові
, добре описує великі тривимірні напівпровідникові
кристали, але зустрічається з труднощами при переході до нанорозмірів, де
поняття трансляційної симетрії вже незастосовне, а носіями струму в усіх
випадках є тільки електрони.
Нагадаємо: при термоелектричних вимірюваннях напрям струму
визначається нахилом функції густини станів D(E), яка або зростає зі
зростанням енергії (n-провідник),чи то спадає (p-провідник) [14]. Натомість
знак холлівского ефекту визначається знаком ефективної маси, введеної за
формулою (75) з роботи [15] як відношення імпульсу pдо швидкості dE/dp. Як
наслідок, результуюча dv/dt має різний знак для n- і p-провідників, відхиляючи
електрони, емітовані з витоку і зі стоку, до протилежних граней пластини
(рис.1), що і призводить до зміни знаку холлівської різниці потенціалів при
зміні типу провідності від електронної до «діркової».
Звернімося до звичайного «підручникового» викладу елементарної теорії
ефекту Холла (див., наприклад, [16]). Струм визначається виразом
, (6)
де N/L є 2Dгустина електронів у площині,перпендикулярній до напрямку
струму, а їхня дрейфова швидкість дорівнює добуткові рухливості електронів на
електричне поле уздовж довжини провідника
d
νµ
=
.
(7)
В стані рівноваги поперечне поле компенсує силу Лоренца
, (8)
отже, використовуючи (6) і (7),для холлівського опору одержуємо:
. (9)
Це співвідношення широко використовується для визначення густини
електронів N/LW за нахилом залежності холлівського опору від магнітного
поля.
Такий виклад елементарної теорії ефекту Холла повторюється з тими або
іншими незначними нюансами в усіх підручниках. І як причина виникнення
струму як у поздовжньому, так і в поперечному напрямі скрізь фігурує
електричне поле. Межі застосовності такої інтерпретації для наносистем
Межі застосовності такої інтерпретації для наносистем
Однією з причин, що викликали підвищений інтерес до ефекту Холла, було те,
що холлівський опір має різний знак для n- і p-провідників, що відкриває
можливість експериментально легко встановити тип провідності. Цієї ж мети
можна досягти, вимірюючи напрям струму в провіднику між контактами, що
перебувають при різних температурах [14]. І в тому і в іншому випадку
звичайно користуються поняттям «дірок» («порожніх» станів, не зайнятих
електронами у «майже заповненій» валентній зоні) як носіїв позитивного заряду
в p-провідниках. Таке трактування, вперше запроваджене Вернером фон
Гейзенбергом у 1931 р., добре описує великі тривимірні напівпровідникові
кристали, але зустрічається з труднощами при переході до нанорозмірів, де
поняття трансляційної симетрії вже незастосовне, а носіями струму в усіх
випадках є тільки електрони.
Нагадаємо: при термоелектричних вимірюваннях напрям струму
визначається нахилом функції густини станів D(E), яка або зростає зі
зростанням енергії (n-провідник),чи то спадає (p-провідник) [14]. Натомість
знак холлівского ефекту визначається знаком ефективної маси, введеної за
формулою (75) з роботи [15] як відношення імпульсу pдо швидкості dE/dp. Як
наслідок, результуюча dv/dt має різний знак для n- і p-провідників, відхиляючи
електрони, емітовані з витоку і зі стоку, до протилежних граней пластини
(рис.1), що і призводить до зміни знаку холлівської різниці потенціалів при
зміні типу провідності від електронної до «діркової».
Звернімося до звичайного «підручникового» викладу елементарної теорії
ефекту Холла (див., наприклад, [16]). Струм визначається виразом
, (6)
де N/L є 2Dгустина електронів у площині,перпендикулярній до напрямку
струму, а їхня дрейфова швидкість дорівнює добуткові рухливості електронів на
електричне поле уздовж довжини провідника
. (7)
(7)
В стані рівноваги поперечне поле компенсує силу Лоренца
ν
=
, (8)
отже, використовуючи (6) і (7),для холлівського опору одержуємо:
. (9)
Це співвідношення широко використовується для визначення густини
електронів N/LW за нахилом залежності холлівського опору від магнітного
поля.
Такий виклад елементарної теорії ефекту Холла повторюється з тими або
іншими незначними нюансами в усіх підручниках. І як причина виникнення
струму як у поздовжньому, так і в поперечному напрямі скрізь фігурує
електричне поле. Межі застосовності такої інтерпретації для наносистем
Однією з причин, що викликали підвищений інтерес до ефекту Холла, було те,
що холлівський опір має різний знак для n- і p-провідників, що відкриває
можливість експериментально легко встановити тип провідності. Цієї ж мети
можна досягти, вимірюючи напрям струму в провіднику між контактами, що
перебувають при різних температурах [14]. І в тому і в іншому випадку
І в тому і в іншому випадку
звичайно користуються поняттям «дірок» («порожніх» станів, не зайнятих
електронами у «майже заповненій» валентній зоні) як носіїв позитивного заряду
в p-провідниках. Таке трактування, вперше запроваджене Вернером фон
Гейзенбергом у 1931 р., добре описує великі тривимірні напівпровідникові
кристали, але зустрічається з труднощами при переході до нанорозмірів, де
поняття трансляційної симетрії вже незастосовне, а носіями струму в усіх
випадках є тільки електрони.
Нагадаємо: при термоелектричних вимірюваннях напрям струму
визначається нахилом функції густини станів D(E), яка або зростає зі
зростанням енергії (n-провідник),чи то спадає (p-провідник) [14]. Натомість
знак холлівского ефекту визначається знаком ефективної маси, введеної за
формулою (75) з роботи [15] як відношення імпульсу pдо швидкості dE/dp. Як
Як
наслідок, результуюча dv/dt має різний знак для n- і p-провідників, відхиляючи
електрони, емітовані з витоку і зі стоку, до протилежних граней пластини
(рис.1), що і призводить до зміни знаку холлівської різниці потенціалів при
зміні типу провідності від електронної до «діркової».
Звернімося до звичайного «підручникового» викладу елементарної теорії
ефекту Холла (див., наприклад, [16]). Струм визначається виразом
, (6)
де N/L є 2Dгустина електронів у площині,перпендикулярній до напрямку
струму, а їхня дрейфова швидкість дорівнює добуткові рухливості електронів на
електричне поле уздовж довжини провідника
. (7)
В стані рівноваги поперечне поле компенсує силу Лоренца
, (8)
отже, використовуючи (6) і (7),для холлівського опору одержуємо:
( )
/
H
H
RI q N LW
= =
.
(9)
Це співвідношення широко використовується для визначення густини
електронів N/LW за нахилом залежності холлівського опору від магнітного
поля.
Такий виклад елементарної теорії ефекту Холла повторюється з тими або
іншими незначними нюансами в усіх підручниках. І як причина виникнення
струму як у поздовжньому, так і в поперечному напрямі скрізь фігурує
електричне поле. Межі застосовності такої інтерпретації для наносистем
Приклади разв’язування задач
1. Електростатичне
поле у вакуумі
1.
Фундаментальним
законом електростатичного поля є закон
Кулона (1.1), де і два точкових заряди,
які знаходяться на відстані r один від одного, — одиничний вектор, проведений в напрямку від заряду до заряду , = 8,85.10–12 Φ/м електрична стала
вакууму. Закон Кулона справедливий для точкових, нерухомих електричних зарядів.
2.
Основною характеристикою кожної точки поля є напруженість – векторна величина,
яка визначається із співвідношення (1. 2), де – сила Кулона, що діє
2), де – сила Кулона, що діє
на пробний заряд qпр в деякій точці поля, яке створене іншим
зарядом q. Якщо qпр = +1 Кл, то
напруженість поля чисельно дорівнює кулонівській силі. Графічно електричне поле
зображується силовими лініями. Силова лінія – це лінія, дотична до якої в
кожній точці співпадає з , а густота ліній пропорційна модулю . За напрямок силових ліній прийнято напрямок від позитивного
заряду до негативного заряду. Тобто вважається, що силові лінії електричного
поля починаються на позитивних зарядах і закінчуються на негативних зарядах.
Силові лінії між собою не перетинаються. Для точкового заряду q напруженість визначається за
формулою:(1.3), де одиничний вектор бере свій початок в
точці знаходження заряду q, r – відстань від заряду до точки А поля, в
якій визначається напруженість . Якщо q > 0, то
Якщо q > 0, то
вектор направлений по , якщо q < 0, то
вектор має протилежний
напрямок до (див. рис. а і б).
3.
На
взаємодію двох точкових зарядів не впливає наявність поряд інших зарядів. Тому
справедливий принцип суперпозиції
електричних полів: напруженість електричного поля, створеного декількома
точковими зарядами, в кожній точці поля дорівнює векторній (геометричній)
сумі напруженостей полів кожного заряду: (1.4), де n – кількість точкових зарядів, напруженість поля, яка
створена і – тим зарядом qі.
4. Властивості силових ліній електричного поля (
див. п. 2) дають можливість ввести поняття потоку вектора через поверхню S. Для однорідного поля ( = const) і плоскої поверхні S: =EScos(1. 5) або ==(1.6),де – кут між вектором і одиничною нормаллю до поверхні S, формально .Для неоднорідного
5) або ==(1.6),де – кут між вектором і одиничною нормаллю до поверхні S, формально .Для неоднорідного
електричного поля (const в кожній точці поля) і довільної поверхні S ==(1.7), де , dS – безмежно
мала ділянка поверхні S, в межах якої вектор = const, – нормаль до ділянки dS, інтегрування (сумування) малих
потоків = проводиться по
всій поверхні S.
5. Наслідком закону Кулона є теорема
Остроградського-Гаусса: потік вектора
напруженості через будь – яку замкнуту
поверхню S, що охоплює заряди q1, q2, …, qn,
дорівнює алгебраїчній сумі цих зарядів, поділеній на сталу вакууму :==(1. 8).
8).
6. Напруженість поля, створеного: а) безмежною тонкою рівномірно зарядженою
площиною E=(1.9), де ∆q/∆S – поверхнева
густина зарядів, яка чисельно дорівнює заряду одиничної (1 м2, 1 см2)
площі поверхні. Поле такої площини однорідне;
б) зарядженою сферою, радіус якої R: 1) всередині сфери (r
< R) E = 0; 2) зовні сфери (r > R) (1.10), 3) близько біля поверхні сфери (r = R) . в) нескінченно
довгою прямою рівномірно зарядженою ниткою (стержнем, циліндром) на відстані r від
нитки, осі стержня, осі циліндра (зовні стержня і циліндра):(1.11), де = ∆q/∆– лінійна густина заряду, яка чисельно дорівнює
заряду, що припадає на одиницю (1
м, 1 см)
довжини нитки (стержня, циліндра).
7. При переміщенні заряду qпр в електричному полі, яке створене іншим зарядом q, виконується робота А12 = (1.12), де цифри 1 і 2 позначають початкову і кінцеву
точки переміщення заряду qпр,
r1 і r2 – відстань точок 1 і 2 до
заряду q, – вектор елементарного
переміщення. Робота А12 не
залежить від форми траєкторії руху
заряду qпр, а
визначається його початковим і кінцевим пунктами. Ця властивість роботи А12 дає можливість ввести
поняття скалярної характеристики поля – різниці потенціалів: =(1.13) З точністю до константи можна ввести поняття
потенціалу в точці поля на відстані r від заряду q: . Якщо умовно прийняти, що потенціал на безмежності дорівнює нулеві, то (1.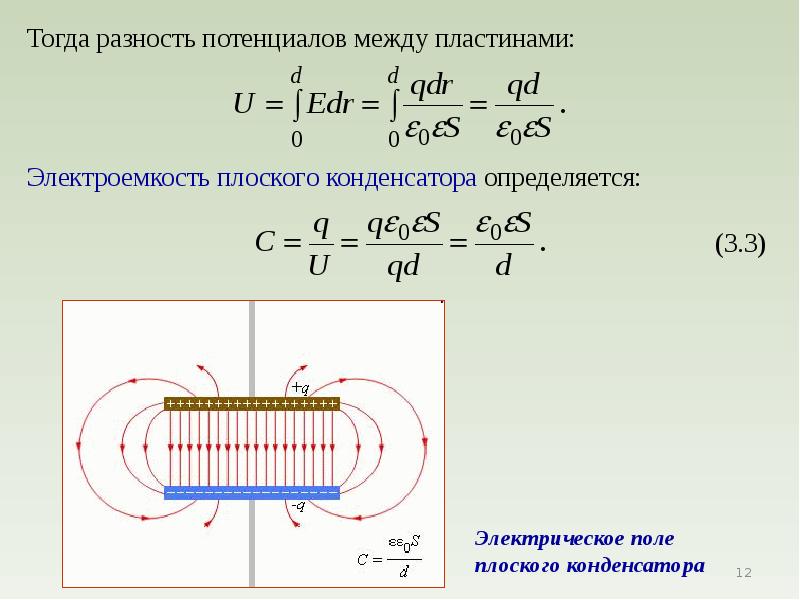 14). Потенціал електричного поля в
14). Потенціал електричного поля в
даній точці поля дорівнює алгебраїчній сумі потенціалів 1, 2,…,n, які відповідно створені в цій точці
кожним зарядом q1, q2,…, qn окремо (принцип суперпозиції):(1.15). Примітка.
Точки простору, які мають однаковий потенціал, називаються еквіпотенціальними.
Поверхня, на якій знаходяться еквіпотенціальні точки, називається
еквіпотенціальною поверхнею. Для точкового заряду такими поверхнями є
концентричні сфери, в центрі яких знаходиться заряд.
8.
Векторна характеристика електричного поля
напруженість і скалярна характеристика
цього поля потенціал в одній і тій же точці
поля зв’язані між собою співвідношенням: (1.16), де
grad = – математичний диференціальний векторний оператор, який
носить назву градієнт, – одиничні
вектори в напрямках координатних осей X, Y, Z. Проекції вектора на координатні осі X,
Проекції вектора на координатні осі X,
Y, Z дорівнюють: ;;(1.17), де , , – похідні по x, y, z, від потенціалу Проекція вектора на довільний
напрямок визначається як: (1.18) Примітка.
Формула (1.16) означає, що вектор направлений в сторону
максимального зменшення потенціалу. Це означає, що силові ліній вектора перпендикулярні до
еквіпотенціальних поверхонь (ліній на площині) потенціалу
9.
Якщо електричні заряди розподілені в просторі
неперервним чином, то можна ввести поняття об’ємної густини заряду ∆q/∆V,(1.19)
де ∆q заряд, що знаходиться в
об’ємі ∆V простору. Тобто це заряд, що
припадає на одиницю об’єму (1 м3, 1 см3) простору. Для такого випадку теорема
(1. 8) приймає вид рівняння Пуассона: div++ = (1.20), де div=++– математичний диференціальний скалярний оператор, який
8) приймає вид рівняння Пуассона: div++ = (1.20), де div=++– математичний диференціальний скалярний оператор, який
носить назву дивергенція.
10. Циркуляція
вектора напруженості електричного поля є фізична величина, яка чисельно
дорівнює роботі по переміщенні одиночного позитивного заряду вздовж замкнутого контуру Г:= =(1.21) де – проекція вектора
напруженості в даній точці контуру
на напрямок дотичний до контуру в цій же точці. Коло на значку інтеграла
означає, що інтеграл вираховується вздовж замкнутого онтуру. У випадку
електростатичного поля циркуляція вектора напруженості дорівнює нулю:= 0 (1.22).
2. Діелектрики
та провідники в електричному полі
1.
Основною характеристикою поляризації діелектрика в
електричному полі є вектор поляризації (2. 1), де – сумарний дипольний
1), де – сумарний дипольний
момент всіх молекул в об’ємі – фізично безмежно малий об’єм, тобто об’єм, достатньо малий,
щоб в його межах можна було вважати постійним макроскопічні величини (
наприклад: напруженість поля, густину, температуру та інше), а з другої сторони
повинен містити достатньо велику для усереднення кількість молекул.
2.
Потік вектора поляризації через замкнуту
поверхню : (2.2) , де – алгебраїчна сума
зв’язаних (поляризаційних) зарядів всередині цієї поверхні, а (2.3), де – об’ємна густина
зв’язаних зарядів.
3.Поверхнева густина
зв’язаних (поляризаційних зарядів) на межі діелектрик –
вакуум дорівнює проекції вектора на нормаль до поверхні діелектрика ( направлений назовні діелектрика): (2.4)
4.
Теорема Остроградського-Гаусса для електричного поля
в діелектриках (2. 5), де – вектор електричного
5), де – вектор електричного
зміщення (індукції), – напруженість електричного поля всередині діелектрика,
– алгебраїчна сума
сторонніх (вільних) зарядів всередині замкнутої поверхні S.
5.
Для ізотропного діелектрика , (2.6),де
– діелектрична
сприйнятливість, а – відносна діелектрична
проникність діелектрика.
6.
На границі розділу двох діелектриків у випадку
відсутності сторонніх (вільних) зарядів мають місце співвідношення:, D1n=D2n, E1=E2(2.7), де – поверхнева густина
зв’язаних зарядів, орт нормалі направлений із
середовища 1 в середовище 2, , – нормальна і тангенційна складові векторів і відповідно.
7.
Для випадку ізотропного однорідного діелектрика, який
заповнює весь простір між еквіпотенціальними поверхнями: (2.8) де – напруженість поля
всередині діелектрика, – напруженість поля зовні діелектрика, – відносна діелектрична проникність діелектрика.
8. Напруженість електричного поля біля поверхні
провідника у вакуумі: ,(2.9) де – густина зарядів
поверхні провідника.
9. При умові рівноваги надлишкові
заряди в провіднику розподіляються по поверхні таким чином, щоб потенціал
поверхні був однаковим, а напруженість поля всередині провідника дорівнювала
нулю.
10. Ємність
провідника ,(2.10) де q
– надлишковий заряд на провіднику, – потенціал
провідника.
11. Ємність
– а) провідної кулі: (2.11) де R
– радіус кулі, – діелектрична
проникність середовища, що оточує кулю; б) плоского конденсатора: (2. 12) де S – площа поверхні пластин, d – відстань між пластинами, – діелектрична
12) де S – площа поверхні пластин, d – відстань між пластинами, – діелектрична
проникність діелектрика, що повністю заповнює простір між пластинами; в) циліндричного конденсатора:(2.13) де – довжина циліндричних електродів, R1 –радіус
внутрішнього, а R2 радіус
зовнішнього циліндрів, – діелектрична
проникність діелектрика між циліндрами; г)
сферичного конденсатора: (2.14) де R1 – радіус
внутрішньої, R2 – радіус
зовнішньої сфери, – діелектрична
проникність діелектрика, що повністю заповнює простір між концентричними
сферами.
12.
Об’ємна густина енергії електричного поля (енергія
одиниці об’єму): (2.15)
13. Загальна
формула для енергії електричного поля:(2.16) де V
– об’єм, в якому існує електричне поле, – об’ємна густина
енергії поля.
14. Енергія
зарядженого конденсатора (2.17) де – різниця потенціалів
між обкладинками конденсатора, С –
ємність конденсатора, – заряд пластини конденсатора.
2.
Закони постійного струму
1. Сила струму – це кількість заряду,
що проходить через поперечний переріз провідника за одиницю часу: . (3.1) Сила струму вимірюється в Амперах (А). Сила
струму дорівнює 1А, якщо через
поперечний переріз провідника за одну секунду проходить заряд один Кулон.
Зауважимо, що одиниця сили струму один Ампер встановлюється із магнітної
взаємодії провідників зі струмом.
2.
Густина струму є векторна фізична
величина, яка чисельно дорівнює силі струму, що протікає через одиничну площу
поперечного перерізу провідника. Переріз вважається перпендикулярним до
напрямку протікання струму. (3.2). Густина
струму вимірюється в одиницях: А/м2
або в похідних одиницях, наприклад: мА/мм2.
3.
Опір однорідного провідника,
довжина якого , а площа поперечного перерізу S
розраховується за формулою: (3.3), де – питомий опір матеріалу провідника, тобто опір провідника,
для якого= 1 м,
а S = 1 м2. Питомий опір
залежить від якості кристалічної структури провідника, кількості домішок (інші
атоми хімічних речовин порівняно з атомами матеріалу провідника) в провіднику, температури провідника. Для
чистих (без домішок) провідників (металів) залежність питомого опору від
температури лінійна, тобто (3.4), де – питомий опір при , – температурний
коефіцієнт опору, значення якого для різних металів приводиться у справочних
таблицях. Питома електропровідність .(3.5).
4.
Електрорушійна сила (е.р.с.) – робота сторонніх сил,
які мають не електростатичну природу, по переміщенню одиночного позитивного
заряду в колі: . (3.6) Одиниця
(3.6) Одиниця
вимірювання е.р.с. – Вольт.
5.
Закон Ома для однорідної ділянки кола, яка не містить
електрорушійної сили (е.р.с.): , або , (3.7) де – сила струму пропорційна різниці потенціалів (або напрузі ) на кінцях ділянки (провідника) і обернено пропорційна опору
провідника.
6.
Закон Ома для
неоднорідної ділянки кола, яка містить е.р.с. (узагальнений закон Ома): (3.8), де = – спад напруги на даній ділянці кола 1–2, – різниця потенціалів на кінцях ділянки кола, – алгебраїчна сума* усіх
е.р.с на цій ділянці кола, – загальний опір ділянки кола.
7.
Закон Ома для замкнутого кола (кінці ділянки 1–2
з’єднані між собою і як наслідок =0):(3.9), де – алгебраїчна сума* усіх е.р.с., які діють у колі, – повний опір кола, який включає і внутрішні опори е. р.с.
р.с.
8. Закон Ома
у диференціальній формі (для точки провідника):(3.10) де – вектор напруженості кулонівського електричного поля, – вектор
напруженості сторонніх сил,
що діють на
носії заряду, – вектор густини струму, – електропровідність для даної точки провідника.
9.
Вектор густини струму для металів (3.11) де – заряд електрона, n – концентрація
електронів, – середня швидкість направленого руху електронів (або
дрейфова швидкість).
10. Перше правило Кірхгофа – алгебраїчна сума струмів,
які сходяться у вузлі, дорівнює нулю ( це правило є наслідком закону збереження
заряду): .(3.12)
11. Друге
правило Кірхгофа – алгебраїчна сума** спадів напруг для замкнутого контура
(кола) дорівнює алгебраїчній сумі**
е.р.с., що діють у контурі: (3.13)
12. Потужність
Потужність
струму на ділянці кола 1–2:.(3.14)
13. Теплова
потужність на даній ділянці кола
1 – 2: . (3.15)
14. Питома
потужність струму Рпит: ,(3.16)
* Знак е.р.с. на даній ділянці кола, або в замкненому колі визначається за
правилом, яке розглядається в методичних вказівках до даної теми.
** Правило
визначення знаків напруги і е.р.с. розглядається у методичних вказівках до
даної теми.
де –напруженість електростатичних кулонівських сил, – напруженість сторонніх сил. Питома теплова
потужність струму Qпит: (3.17) Питома потужність – це кількість енергії, що
виділяється в одиниці об’єму провідника
за одиницю часу. Питома потужність вимірюється таких одиницях: Дж/(м3.с)
або Вт/м3 .
4. Постійне магнітне поле
1. Джерелом
магнітного поля є електричнi заряди, що рухаються (тобто струми). Магнітне поле
Магнітне поле
точкового заряду, який рухається з нерелятивістською швидкістю : , (4.1) де =4Гн/м – магнітна стала вакууму, – радіус-вектор, який
визначає положення вибраної точки простору по відношенню до заряду.
2. Магнітне поле,
що створюється елементом струму –закон Біо-Савара-Лапласа: , (4.2)
де – радіус-вектор, який проведений від елемента струму до тієї точки, в якій
визначається індукція поля.
3.
Згідно принципу суперпозиції магнітних полів магнітна
індукція результуючого поля дорівнює векторній (геометричній ) сумі магнітних
індукцій , які створюються кожним елементом струму : ,(4.3) де інтеграл береться по всій довжині
провідника. Якщо магнітні поля
створюються струмами, то індукція результуючого поля , (4.4) де – індукція магнітного
поля, яка створюється – тим струмом. В конкретному випадку накладання двох полів: (4.5) а
В конкретному випадку накладання двох полів: (4.5) а
абсолютне значення вектора магнітної індукції , (4.6) де – кут між векторами і .
4.
Циркуляція вектора індукції магнітного поля по
замкнутому контуру дорівнює алгебраїчній сумі струмів, які охоплюються цим
контуром, помноженій на магнітну сталу вакууму (закон повного струму): (4.7) Примітка. Якщо напрямок
струму і обхід по контуру утворюють правогвинтову систему, то такий струм
береться із знаком „+”». Якщо
напрямок струму і обхід по контуру утворюють лівогвинтову систему, то такий
струм береться із знаком „–”.
5.
Теорема Остроградського-Гаусса для магнітного поля: , (4.8) де – потік вектора індукції магнітного поля через замкнуту
поверхню .
6. Індукція
магнітного поля в довільній точці А
(рис. 4.1), що створюється прямолінійним провідником зі струмом , (4. 9) де – відстань від точки А
9) де – відстань від точки А
до провідника , і – кути, що утворюються
радіус–векторами і , проведеними в точку А відповідно із початку і кінця
провідника, з напрямком струму. У випадку нескінченно довгого провідника ( = 0, = ) індукція магнітного поля в точці А . (4.10)
7.
Індукція магнитного поля на осі колового струму:, (4.11)
де – радіус колового
контуру зі струмом, х – відстань від
площини контуру до точки на осі, де визначається магнітна індукція. Індукція
магнітного поля в центрі колового струму (х
= 0): . (4.12) Індукція магнітного поля в центрі дуги кола, довжина
якої , якою протікає струм :,(4.13) де – радіус дуги кола.
8.
Індукція магнітного поля на осі соленоїда (4.14) де – густина намотки
соленоїда (число витків на одиницю довжини
соленоїда), і – кути між
радіус–векторами, проведеними в точку А
із початку і кінця соленоїда, і його віссю (рис.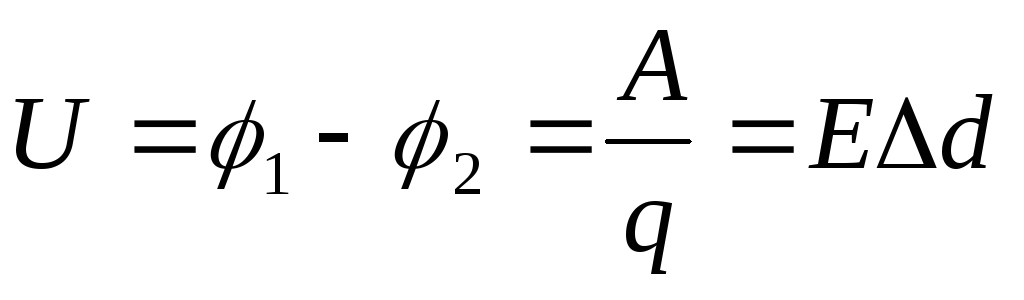 4.2). Якщо соленоїд
4.2). Якщо соленоїд
нескінченно довгий (, ), то магнітне поле всередині соленоїда: . (4.15)
9. Індукція магнітного поля тороїда на
відстані від центра О (рис. 4.3.):
(4.16) де – сила струму у витках тороїда, кількість витків. Примітка. Якщо тороїд тонкий, тобто його середній діаметр
, де – діаметр перерізу (рис. 4.3), то для розрахунку індукції
магнітного поля з високою точністю можна використовувати формулу (4.15).
10. Сила, яка діє
на елемент довжини провідника зі струмом , що знаходиться в магнітному полі (сила Ампера), . (4.17)
11. Сила
Лоренца – сила, яка діє на електричний заряд зі сторони електричного і
магнітного полів: ,(4.18) де – величина заряду, – напруженість електричного поля, – швидкість заряду, – індукція магнітного
поля.
12. Магнітний
момент замкнутого плоского контуру (магнітного диполя), по якому протікає струм
, , (4.19) де – площа контура, – позитивна нормаль до площини контуру, яка визначається
напрямком струму в контурі і правилом правого свердлика.
13. Механічний
момент, який діє на замкнутий контур зі струмом в однорідному магнітному полі,
індукція якого :. (4.20) Якщо
поле неоднорідне, то в цьому випадку на контур зі струмом крім обертального
моменту (4.20) діє сила , (4.21) де х
– напрямок найшвидшої зміни
величини , () – кут між векторами і .
14. Енергія взаємодії
магнітного диполя з магнітним полем : . (4.22)
15. Потік вектора магнітної індукції (магнітний потік)
через поверхню визначається
інтегралом , (4. 23) де , – нормаль до елементарної площадки поверхні S.
23) де , – нормаль до елементарної площадки поверхні S.
16. Робота сил магнітного поля по переміщенню
замкнутого контуру з постійним струмом І
дорівнює , (4.24), де – зміна магнітного потоку через поверхню, яка обмежена
контуром.
5. Магнітне поле в речовині
1. Намагніченість
(вектор намагнічування) визначається магнітним
моментом одиниці об’єму магнетика:, (5.1) де N – число частинок , які містяться у
фізично нескінченно малому об’ємі , – магнітний момент і – тої частинки.
2. Вектором
напруженості магнітного поля
називається лінійна комбінація векторів індукції магнітного поля і : (5.2)
3. Вектори і зв’язані
співвідношенням :, (5.3) де – магнітна проникність
середовища (для вакууму = 1).
4. Умови на межі
розділу двох магнетиків., (5.4)
5. Циркуляція
вектора напруженості вздовж замкнутого
контуру Г дорівнює алгебраїчній сумі струмів, які охоплюються цим контуром: (5.5)
де проекція вектора на напрямок елемента
контуру .
6.
Магнітна індукція в середині довгого соленоїда з
магнітним осердям (5.6) де n –
число витків, які приходяться на одиницю довжини соленоїда,
I – сила струму у
витках, – магнітна проникність речовини осердя.
7. Індуктивність
довгого соленоїда, об’єм якого V з магнітним осердям .(5.7)
8. Енергія W магнітного поля, яке створене
струмом І в соленоїді або тороїді з
індуктивністю L, визначається за формулою: (5.8)
9.
Об’ємна густина енергії магнітного поля : (5. 9) де В – магнітна індукція, Н – напруженість магнітного поля, – магнітна проникність
9) де В – магнітна індукція, Н – напруженість магнітного поля, – магнітна проникність
середовища.
Рис. 5.1.
Основна крива намагнічення технічно чистого заліза
6.
Електромагнітна індукція
1. Загальна
формула для визначення магнітного потоку, який пронизує поверхню S, зв’язану з
контуром: , (6.1) де – індукція
магнітного поля в точці знаходження елементарної поверхні dS, , – одиничний вектор
нормальний до площадки dS
2. Магнітний потік
Ф через поверхню, зв’язану з контуром, і сила струму I в контурі зв’язані співвідношенням: ,(6.2) де L – індуктивність контуру.
3. Основний
закон ЕМІ (закон Фарадея): при всякій зміні магнітного потоку, який пронизує
контур, в ньому виникає електрорушійна
сила індукції, яка пропорційна швидкості зміни магнітного потоку, тобто . (6.3) Знак
(6.3) Знак
«–» відображає правило Ленца.
4. Кількість
електрики, яка протікає по контуру, опір якого R, при зміні магнітного потоку через контур на величину Ф, .(6.4)
3.
Електрорушійна сила (е.р.с.) самоіндукції в контурі
яка виникає при зміні сили струму в ньому, визначається за законом (6.3). При
незмінній індуктивності контуру L е.р.с. самоіндукції визначається за формулою:.(6.5)
6. Власна
енергія струму і взаємна енергія двох струмів (6.6) де М12
– коефіцієнт взаємної індукції двох контурів, якими протікають струми І1 і І2, відповідно.
7. Миттєве
значення сили струму І в колі з
опором R та індуктивністю L: а) після замикання кола:(6.7),де – е.р.с. джерела
струму, t – час після
замикання кола. б) після розмикання кола: (6.8), де – початкове значення
б) після розмикання кола: (6.8), де – початкове значення
струму, t –
час після розмикання кола.
Формула ємності конденсатора через напругу. Заряджання конденсатора від джерела постійної ЕДС
За призначенням конденсатор можна порівняти з батареєю. Але є важлива відмінність у роботі цих елементів. Існують відмінності у граничній ємності та швидкості зарядки конденсатора та батарейки.
Формула заряду конденсатора
де q – величина заряду однієї з обкладок конденсатора, а – різницю потенціалів між його обкладками.
Електроємність конденсатора — це величина, яка залежить від розмірів і пристрою конденсатора.
Заряд на пластинах плоского конденсатора дорівнює:
де — Електрична постійна; — Площа кожної (або найменшої) пластини; — Відстань між пластинами; – діелектрична проникність діелектрика, що знаходиться між пластинами конденсатора.
Заряд на обкладках циліндричного конденсатора обчислюється за допомогою формули:
де l — Висота циліндрів; — Радіус зовнішньої обкладки; — Радіус внутрішньої обкладки.
Заряд на обкладинках сферичного конденсатора знайдемо як:
Заряд конденсатора пов’язаний з енергією поля (W) усередині нього:
З формули (6) випливає, що заряд можна виразити як:
Розглянемо послідовну сполуку з N конденсаторів (рис. 1).
Тут (рис.1) позитивне обкладання одного конденсатора з’єднується з негативною обкладкою наступного конденсатора. При такому з’єднанні обкладки сусідніх конденсаторів створюють єдиний провідник. У всіх конденсаторів, з’єднаних послідовно на обкладках, є рівні за величиною заряди.
При паралельному з’єднанні конденсаторів (рис.2) з’єднують обкладки, що мають заряди одного знака. Сумарний заряд з’єднання (q) дорівнює сумі зарядів конденсаторів.
Приклади розв’язання задач на тему «Заряд конденсатора»
ru.solverbook.com
Формула ємності конденсатора,
Якщо q – величина заряду однієї з обкладок конденсатора, а – різниця потенціалів між його обкладками, то величина C дорівнює:
називається ємністю конденсатора. Це постійна величина, яка залежить від розмірів і пристрою конденсатора.
Це постійна величина, яка залежить від розмірів і пристрою конденсатора.
Розглянемо два однакові конденсатори, різниця між яким полягає лише в тому, що між обкладками одного вакуум (або часто говорять повітря), між обкладками іншого знаходиться діелектрик. У такому разі при рівних зарядах на конденсаторах різниця потенціалів повітряного конденсатора буде в рази меншою, ніж між обкладками другого. Значить ємність конденсатора з діелектриком (C) у раз більше, ніж повітряного ():
де — Діелектрична проникність діелектрика.
За одиницю ємності конденсатора приймають ємність такого конденсатора, який одиничним зарядом (1 Кл) заряджається до різниці потенціалів, що дорівнює одному вольту (СІ). Одиницею ємності конденсатора (як будь-якої еклектичної ємності) у міжнародній системі одиниць (СІ) служить фарад (Ф).
Формула електричної ємності плоского конденсатора
Поле між обкладинками плоского конденсатора зазвичай вважають однорідним. Його однорідність порушується лише біля країв. При обчисленні ємності плоского конденсатора цими крайовими ефектами часто нехтують. Це слід робити, якщо відстань між пластинами мало в порівнянні з їх лінійними розмірами. Для розрахунку ємності плоского конденсатора застосовують формулу:
При обчисленні ємності плоского конденсатора цими крайовими ефектами часто нехтують. Це слід робити, якщо відстань між пластинами мало в порівнянні з їх лінійними розмірами. Для розрахунку ємності плоского конденсатора застосовують формулу:
Електрична ємність плоского конденсатора, який містить N шарів діелектрика товщина кожного , відповідна діелектрична проникність i-го шару дорівнює:
Формула електричної ємності циліндричного конденсатора
Циліндричний конденсатор є дві співвісні (коаксіальні) циліндричні провідні поверхні, різного радіусу, простір між якими заповнює діелектрик. Електрична ємність циліндричного конденсатора обчислюється як:
Формула електричної ємності сферичного конденсатора
Сферичним конденсатором називають конденсатор, обкладками якого є дві концентричні сферичні провідні поверхні, простір між ними заповнений діелектриком. Ємність такого конденсатора знаходять як:
де — Радіуси обкладок конденсатора.
Приклади розв’язання задач на тему «Ємність конденсатора»
ru.solverbook.com
Ємність конденсатора — Усі формули
Електрична ємність — характеристика провідника (конденсатора), міра його здатності накопичувати електричний заряд.
Конденсатор складається із двох провідників (обкладок), які розділені діелектриком. На ємність конденсатора не повинні впливати навколишні тіла, тому провідникам надають таку форму, щоб поле, яке створюється зарядами, що накопичуються, було зосереджено у вузькому зазорі між обкладками конденсатора. Цій умові задовольняють: 1) дві плоскі пластини; 2) дві концентричні сфери; 3) два коаксіальні циліндри. Тому залежно від форми обкладок конденсатори поділяються на плоскі, сферичні та циліндричні.
Так як поле зосереджено всередині конденсатора, то лінії напруженості починаються на одній обкладці та закінчуються на іншій, тому вільні заряди, що виникають на різних обкладках, рівні за модулем та протилежні за знаком. Під ємністю конденсатора розуміється фізична величина, що дорівнює відношенню заряду Q, накопиченого в конденсаторі, до різниці потенціалів (φ1 — φ2) між його обкладками
Для отримання більших ємностей конденсатори з’єднують паралельно. При цьому напруга між обкладинками всіх конденсаторів однакова. Загальна ємність батареї паралельно з’єднаних конденсаторів дорівнює сумі ємностей всіх конденсаторів, що входять до батареї.
При цьому напруга між обкладинками всіх конденсаторів однакова. Загальна ємність батареї паралельно з’єднаних конденсаторів дорівнює сумі ємностей всіх конденсаторів, що входять до батареї.
Конденсатори можна класифікувати за такими ознаками та властивостями:
1) за призначенням — конденсатори постійної та змінної ємності;
2) формою обкладок розрізняють конденсатори плоскі, сферичні, циліндричні та інших.;
3) на кшталт діелектрика — повітряні, паперові, слюдяні, керамічні, електролітичні тощо.
Також є:
Енергія конденсатора:
Ємність циліндричного конденсатора:
Ємність плоского конденсатора:
Ємність сферичного конденсатора:
У формулі ми використали:
Електрична ємність (ємність конденсатора)
Потенціал провідника (Напруга)
Потенціал
Відносна діелектрична проникність
Електрична постійна
Площа однієї обкладки
Відстань між обкладками
xn — b1agsdjmeuf9e.xn — p1ai
Заряд конденсатора, теорія та приклади задач
Визначення та заряд конденсатора
Можливість конденсатора накопичити електричний заряд залежить від основної характеристики конденсатора – ємності (C).
За своїм призначенням конденсатор можна уподібнити до батарейки. Однак існує принципова відмінність у принципах роботи цих елементів. Відрізняються також максимальні ємності і швидкості зарядки і розряду конденсатора і батарейки.
Якщо до конденсатора приєднати джерело напруги (рис.1), то на одній із пластин конденсатора стануть накопичуватися негативні заряди (електрони), на іншій позитивні частки (позитивні іони). Між обкладками конденсатора знаходиться діелектрик, внаслідок цього заряди не можуть перебратися на протилежну пластину. Однак зауважимо, що електрони рухаються від джерела струму до пластини конденсатора.
При початковому з’єднанні конденсатора та джерела струму на обкладинках конденсатора багато вільного місця. Це означає, що опір струму цей момент часу мінімальний, сам струм максимальний. У ході зарядки конденсатора сила струму в ланцюзі поступово падає, доти поки не закінчиться вільне місце на обкладках. При повній зарядці конденсатора струм у ланцюзі припиниться.
Час, який витрачається на зарядку конденсатора від нульового заряду (максимального струму) до повністю зарядженого конденсатора (мінімальна або нульова сила струму) називають перехідним періодом заряду конденсатора. Насправді процес зарядки конденсатора вважають закінченим, якщо сила струму зменшилася до 1% від початкової величини.
Величина заряду конденсатора (q) пов’язана з його ємністю (C) та різницею потенціалів (U) між його обкладками як:
Приклади розв’язання задач
ru.solverbook.com
Формула електроємності конденсатора
Обкладки повинні мати таку форму і бути розташовані відносно один одного, що поле, яке створюється даною системою, було максимально зосереджено в обмеженій області простору, між обкладками.
Призначення конденсатора в тому, щоб накопичувати та віддавати в електричному ланцюзі заряд.
Основною характеристикою конденсатора є електрична ємність (С). Електрична ємність конденсатора – це взаємна ємність обкладок, що належать йому:
q – величина заряду на обкладинці; — Різниця потенціалів між обкладками.
Електрична ємність конденсатора залежить від діелектричної проникності діелектрика, що заповнює простір між його обкладками. Якщо простір між обкладками одного конденсатора заповнено діелектриком з рівною проникністю , а у другого конденсатора повітря між пластинами, то ємність конденсатора з діелектриком (C) в раз більше, ніж ємність повітряного конденсатора ():
Формула електроємності основних типів конденсаторів
При розрахунку електроємності плоского конденсатора порушення однорідності поля біля країв обкладок зазвичай нехтують. Це стає можливим, якщо відстань між пластинами істотно менша, ніж лінійні розміри обкладок. У такому разі електричну ємність плоского конденсатора обчислюють за допомогою формули:
де — Електрична постійна; S – площа кожної (або найменшої) пластини; d – відстань між пластинами.
Якщо плоский конденсатор між обкладками має N шарів діелектрика, при цьому товщина кожного шару дорівнює а діелектрична проникність, то його електричну ємність розраховують за допомогою формули:
Циліндричний конденсатор складають дві співвісні (коаксіальні) циліндричні провідні поверхні, різного радіусу, простір між якими заповнено діелектриком. При цьому ємність циліндричного конденсатора знаходять як:
При цьому ємність циліндричного конденсатора знаходять як:
де l — Висота циліндрів; — Радіус зовнішньої обкладки; — Радіус внутрішньої обкладки.
У сферичного конденсатора обкладками є дві концентричні сферичні провідні поверхні, простір обкладками заповнює діелектрик. Ємність сферичного конденсатора обчислюють як:
де — Радіуси обкладок конденсатора. Якщо , то можна вважати, що , тоді ми маємо:
оскільки – площа поверхні сфери, і якщо позначити , то отримаємо формулу для ємності плоского конденсатора (3). Якщо відстань між обкладками сферичного та циліндричного конденсаторів малі (порівняно з їх радіусами), то у наближених розрахунках використовують формулу ємності для плоского конденсатора.
Електричну ємність для лінії з двох дротів знаходять як:
де d — Відстань між осями проводів; R – радіус дротів; l – довжина лінії.
Формули для обчислення електричної ємності з’єднань конденсаторів
Якщо конденсатори з’єднані паралельно, сумарна ємність батареї (C) знаходиться як сума ємностей окремих конденсаторів ():
При послідовному з’єднанні конденсаторів ємність батареї обчислюють як:
Якщо послідовно з’єднані N конденсаторів, з ємностями, то ємність батареї знайдемо як:
Опір конденсатора
Якщо конденсатор включений у ланцюг із постійного струму, то опір конденсатора можна вважати нескінченно більшим.
При включенні конденсатора в ланцюг змінного струму його опір носить назву ємнісного, і обчислюють його за допомогою формули:
де – частота змінного струму; — Кутова частота струму; C – ємність конденсатора.
Енергія поля конденсатора
Електричне поле локалізоване між пластинами конденсатора має енергію, яку можна обчислити за допомогою формули:
де — Енергія поля конденсатора; q – заряд конденсатора; C – ємність конденсатора; — Різниця потенціалів між обкладинками конденсатора.
Енергія поля плоского конденсатора:
Приклади розв’язання задач на тему «Електроємність конденсатора»
ru.solverbook.com
Як знайти заряд конденсатора 🚩 Як визначити величину заряду 🚩
У звичайному (без плагінів та модів) варіанті Minecraft такого поняття, як конденсатор, не існує. Вірніше, пристрій, що виконує його функції, є, але назва в нього зовсім інша — компаратор. Певна плутанина в цьому плані відбулася ще в період розробки такого приладу. Спочатку — у листопаді 2012-го — представники Mojang (компанії-творця гри) оголосили про швидку появу в геймплеї конденсатора. Однак через місяць вони висловилися вже про те, що як такого приладу не буде, а замість нього в грі буде компаратор.
Спочатку — у листопаді 2012-го — представники Mojang (компанії-творця гри) оголосили про швидку появу в геймплеї конденсатора. Однак через місяць вони висловилися вже про те, що як такого приладу не буде, а замість нього в грі буде компаратор.
Подібний пристрій існує для перевірки заповненості контейнерів, що розташовані за ним. Такими можуть бути скрині (у тому числі у вигляді пасток), варильні стійки, роздавачі, викидачі, печі, завантажувальні вирви тощо.
Крім цього, його часто використовують для порівняння двох сигналів редстоуна між собою — він видає результат відповідно до того, як було запрограмовано в даному ланцюгу, і з тим, який режим обрано самого механізму. Зокрема, компаратор може дозволити запалення факела, якщо перший сигнал більше або дорівнює іншому.
Також іноді конденсатор-компаратор встановлюють поруч із програвачем, підключаючи його входом до останнього. Коли у звуковідтворюючому пристрої програється будь-яка платівка, вищезгаданий прилад буде видавати сигнал, що дорівнює за силою порядковому номеру диска.
Скрафтить такий компаратор нескладно, якщо є досить складний ресурс — пекельний кварц. Його треба поставити в центральний слот верстата, над ним і з боків від нього встановити три червоні смолоскипи, а в нижньому ряду — таку ж кількість кам’яних блоків.
У великій кількості модів трапляються конденсатори, що мають різне призначення. Наприклад, в Galacticraft, де у геймерів є можливість злітати на багато планет для ознайомлення з тамтешніми реаліями, з’являється рецепт крафту кисневого конденсатора. Він служить для створення механізмів на кшталт колектора та накопичувача газу для дихання, а також рамки повітряного шлюзу. Для його виготовлення чотири сталеві пластини розміщуються по кутах верстата, у центрі – олов’яна каністра, а під нею – повітропровід. Інші три осередки займають пластини з олова.
У JurassiCraft існує конденсатор потоку — телепорт, який дозволяє переміститися в дивовижний ігровий світ, що кишить динозаврами. Для створення такого приладу потрібно помістити в два крайні вертикальні ряди шість залізних зливків, а в середній — два алмази і між ними одиницю пилу редстоуну. Щоб пристрій запрацював, треба поставити його на свиню або вагонетку, а потім клацнути по ньому правою кнопкою миші, швидко застрибнувши туди. При цьому потрібна підтримка високої швидкості пристрою.
Щоб пристрій запрацював, треба поставити його на свиню або вагонетку, а потім клацнути по ньому правою кнопкою миші, швидко застрибнувши туди. При цьому потрібна підтримка високої швидкості пристрою.
З модом Industrial Craft2 у гравця з’являється можливість створювати як мінімум два види теплових конденсаторів – червоний та лазуритовий. Вони служать виключно для охолодження ядерного реактора і для накопичення його енергії та хороші для циклічних споруд такого типу. Остуджуються вони самі, відповідно, червоним пилом чи лазуритом.
Червоний теплоконденсатор виготовляється з семи одиниць пилу редстоуна — їх треба встановити у вигляді букви П і розставити під ними тепловідведення та теплообмінник. Крафтинг лазуритового пристрою трохи складніше. Для його створення чотири одиниці пилу редстоуну розставляються по кутах верстата, в центр піде блок лазуриту, з боків від нього — два червоні теплові конденсатори, зверху — тепловідведення реактора, а знизу — його теплообмінник.
У ThaumCraft, де зроблено акцент на справжньому чарівництві, конденсатори теж використовуються. Наприклад, один з них – кристалічний – існує для акумуляції та віддачі магії. Причому, що цікаво, створювати його та багато інших речей дозволено лише після вивчення особливого елемента геймплею – дослідження, що проводиться за спеціальним столом та з певними приладами.
Наприклад, один з них – кристалічний – існує для акумуляції та віддачі магії. Причому, що цікаво, створювати його та багато інших речей дозволено лише після вивчення особливого елемента геймплею – дослідження, що проводиться за спеціальним столом та з певними приладами.
Робиться такий конденсатор із восьми тьмяних уламків, у центр яких на верстаті міститься містичний дерев’яний блок. На жаль, подібний прилад — так само, як і його складові — проіснував лише до ThaumCraft 3, а в четвертій версії мода була скасована.
www.kakprosto.ru
З’єднання конденсаторів: формули
Зміст:
- Послідовне з’єднання
- Онлайн калькулятор
- Змішане з’єднання
- Паралельне з’єднання
- Відео
В електронних та радіотехнічних схемах широкого поширення набуло паралельне та послідовне з’єднання конденсаторів. У першому випадку з’єднання здійснюється без будь-яких загальних вузлів, а в другому варіанті всі елементи об’єднуються у два вузли і не пов’язані з іншими вузлами, якщо це не передбачено схемою.
Послідовне з’єднання
При послідовному з’єднанні два і більше конденсаторів з’єднуються в загальний ланцюг таким чином, що кожен попередній конденсатор з’єднується з наступним лише в одній точці. Струм (i), що здійснює зарядку послідовного ланцюга конденсаторів буде мати однакове значення для кожного елемента, оскільки він проходить тільки єдиним можливим шляхом. Це положення підтверджується формулою: i = ic1 = ic2 = ic3 = ic4.
У зв’язку з однаковим значенням струму, що протікає через конденсатори з послідовним з’єднанням, величина заряду, накопиченого кожним з них, буде однаковою незалежно від ємності. Таке стає можливим, оскільки заряд, що надходить з обкладки попереднього конденсатора, накопичується на обкладинці наступного елемента ланцюга. Тому величина заряду у послідовно з’єднаних конденсаторів буде виглядати так: Qобщ = Q1 = Q2 = Q3.
Якщо розглянути три конденсатори С1, С2 і С3, з’єднані в послідовний ланцюг, то з’ясовується, що середній конденсатор С2 при постійному струмі є електрично ізольованим від загального ланцюга. Зрештою величина ефективної площі обкладок буде зменшена до площі обкладок конденсатора з мінімальними розмірами. Повне заповнення обкладок електричним зарядом, унеможливлює подальше проходження по ньому струму. В результаті, рух струму припиняється у всьому ланцюгу, відповідно припиняється і заряджання решти всіх конденсаторів.
Зрештою величина ефективної площі обкладок буде зменшена до площі обкладок конденсатора з мінімальними розмірами. Повне заповнення обкладок електричним зарядом, унеможливлює подальше проходження по ньому струму. В результаті, рух струму припиняється у всьому ланцюгу, відповідно припиняється і заряджання решти всіх конденсаторів.
Загальна відстань між обкладками при послідовному з’єднанні є сумою відстаней між обкладками кожного елемента. В результаті з’єднання в послідовний ланцюг формується єдиний великий конденсатор, площа обкладок якого відповідає обкладинкам елемента з мінімальною ємністю. Відстань між обкладками виявляється рівною сумі всіх відстаней, що є в ланцюзі.
Падіння напруги на кожен конденсатор буде різним, залежно від ємності. Це положення визначається формулою: С = Q/V, в якій ємність обернено пропорційна напрузі. Таким чином, зі зменшенням ємності конденсатора на нього падає більша напруга. Сумарна ємність всіх конденсаторів обчислюється за такою формулою: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Головна особливість такої схеми полягає у проходженні електричної енергії лише в одному напрямку. Тому в кожному конденсаторі значення струму буде однаковим. Кожен накопичувач у послідовному ланцюзі накопичує рівну кількість енергії, незалежно від ємності. Тобто ємність може відтворюватися за рахунок енергії, що є в сусідньому накопичувачі.
Онлайн калькулятор для розрахунку ємності конденсаторів з’єднаних послідовно в електричному ланцюзі.
Змішане з’єднання
Паралельне з’єднання конденсаторів
Паралельним вважається таке з’єднання, у якому конденсатори з’єднуються між собою двома контактами. Таким чином, в одній точці може з’єднуватися відразу кілька елементів.
Даний вид з’єднання дозволяє сформувати єдиний конденсатор з великими розмірами, площа обкладок якого дорівнюватиме сумі площ обкладок кожного, окремо взятого конденсатора. У зв’язку з тим, що ємність конденсаторів знаходиться в прямій пропорційній залежності з площею обкладок, загальна ємність складатиме сумарну кількість всіх ємностей конденсаторів, з’єднаних паралельно. Тобто, общ = С1 + С2 + С3.
Тобто, общ = С1 + С2 + С3.
Оскільки різниця потенціалів виникає лише у двох точках, то на всі конденсатори, з’єднані паралельно, падатиме однакова напруга. Сила струму в кожному з них відрізнятиметься, залежно від ємності та значення напруги. Таким чином, послідовне та паралельне з’єднання, що застосовується у різних схемах, дозволяє виконувати регулювання різних параметрів на тих чи інших ділянках. За рахунок цього виходять потрібні результати роботи всієї системи в цілому.
electric-220.ru
В усіх електронних пристроях використовуються конденсатори. При їх конструюванні або виготовленні власноруч параметри пристроїв розраховуються за спеціальними формулами.
Розрахунок конденсаторів
Один з основних параметрів таких пристроїв – ємність. Розрахувати її можна за такою формулою:
- C — ємність,
- q – заряд однієї з обкладок елемента,
- U – різниця потенціалів між обкладками.
У електротехніці замість поняття «різниця потенціалів між обкладками» використовується «напруга на конденсаторі».
Ємність елемента не залежить від конструкції та розмірів пристрою, а лише від напруги на ньому та заряду обкладок. Але ці параметри можуть змінюватись в залежності від відстані між ними та матеріалу діелектрика. Це враховується у формулі:
З=Co*ε, де:
- С – реальна ємність,
- З — ідеальна, за умови, що між пластинами вакуум або повітря,
- ε – діелектрична проникність матеріалу між ними.
Наприклад, якщо як діелектрик використовується слюда, «ε» якої 6, то ємність такого пристрою в 6 разів більше, ніж повітряного, а при зміні кількості діелектрика змінюються параметри конструкції. На цьому принципі заснована робота ємнісного датчика положення.
Одиницею ємності у системі СІ є 1 фарад (F). Це велика величина, тому найчастіше застосовуються мікрофаради (1000000mkF=1F) та пікофаради (1000000pF=1mkF).
Розрахунок плоскої конструкції
- ε – діелектрична проникність ізолюючого матеріалу,
- d – відстань між пластинами.

Розрахунок конструкції циліндричної форми
Циліндричний конденсатор – це дві співвісні трубки різного діаметра, вставлені одна в одну. Між ними є діелектрик. При радіусі циліндрів, близькому один до одного і набагато більшому, ніж відстань між ними, циліндричною формою можна знехтувати і звести розрахунок до формули, аналогічної до тієї, за якою розраховується плоский конденсатор.
Обчислюються параметри такого пристрою за такою формулою:
C=(2π*l*R*ε)/d, де:
- l – довжина пристрою,
- R – радіус циліндра,
- ε – діелектрична проникність ізолятора,
- d – його товщина .
Розрахунок сферичної конструкції
Є пристрої, обкладки яких є дві кулі, вкладені один в одного. Формула ємності такого приладу:
C=(4π*l*R1*R2*ε)/(R2-R1), де:
- R1 – радіус внутрішньої сфери,
- R2 — радіус зовнішньої сфери,
- ε – діелектрична проникність.
Ємність одиночного провідника
Крім конденсаторів, здатність накопичувати заряд мають окремі провідники. Поодиноким провідником вважається такий провідник, який нескінченно далекий від інших провідників. Параметри зарядженого елемента розраховується за такою формулою:
Поодиноким провідником вважається такий провідник, який нескінченно далекий від інших провідників. Параметри зарядженого елемента розраховується за такою формулою:
- Q – заряд,
- φ – потенціал провідника.
Обсяг заряду визначається розміром та формою пристрою, а також навколишнім середовищем. Матеріал приладу не має значення.
Способи з’єднання елементів
Не завжди є елементи з необхідними параметрами. Доводиться з’єднувати їх у різний спосіб.
Паралельне з’єднання
Це таке з’єднання деталей, коли до однієї клеми або контакту приєднуються перші обкладки кожного конденсатора. При цьому другі обкладки приєднуються до іншої клеми.
При такому з’єднанні напруга на контактах всіх елементів буде однаковою. Заряд кожного їх відбувається незалежно від інших, тому загальна ємність дорівнює сумі всіх величин. Її знаходять за такою формулою:
де C1-Cn – параметри деталей, що у паралельному соединении.
Важливо!Конденсатори мають граничну допустиму напругу, перевищення якої призведе до виходу з ладу. При паралельному з’єднанні пристроїв з різною допустимою напругою цей параметр збірки дорівнює елементу з найменшим значенням.
При паралельному з’єднанні пристроїв з різною допустимою напругою цей параметр збірки дорівнює елементу з найменшим значенням.
Послідовне з’єднання
Це таке з’єднання, при якому до клеми приєднується лише одна пластина першого елемента. Друга пластина приєднується до першої пластини другого елемента, друга пластина другого – першої пластини третього і так далі. До другої клеми приєднується лише друга обкладка останнього елемента.
При такому з’єднанні заряд на обкладках конденсатора в кожному приладі дорівнює іншим, проте напруга на них буде різним: для зарядки пристроїв більшої ємності тим же зарядом потрібна менша різниця потенціалів. Тому весь ланцюжок є однією конструкцією, різниця потенціалів якої дорівнює сумі напруг на всіх елементах, а заряд конденсатора дорівнює сумі зарядів.
Послідовне з’єднання збільшує допустиму напругу і зменшує загальну ємність, яка менша за найменший елемент.
Розраховуються ці параметри так:
- Допустима напруга:
Uобщ = U1 + U2 + U3 + . .. Un, де U1-Un — напруга на конденсаторі;
.. Un, де U1-Un — напруга на конденсаторі;
- Загальна ємність:
1/Сообщ=1/С1+1/С2+1/С3+…1/Сn, де С1-Сn – параметри кожного пристрою.
Цікаво.Якщо в ланцюзі лише два елементи, можна скористатися спрощеною формулою: Собщ=(С1*С2)/(С1+С2).
Змішане з’єднання
Це таке з’єднання, де є деталі, з’єднані послідовно, і є з’єднані паралельно. Параметри всього ланцюга розраховуються в наступній послідовності:
- визначаються групи елементів, з’єднані паралельно;
- для кожної групи окремо розраховується еквівалентні значення;
- поряд з кожною групою паралельно з’єднаних деталей пишуться величини, що вийшли;
- схема, що вийшла, еквівалентна послідовній схемі і розраховується за відповідними формулами.
Знання формул, якими можна знайти ємність під час виготовлення конденсаторів чи його з’єднанні необхідне під час конструювання електронних схем.
Відео
Зміст:
Одним з важливих елементів електричного ланцюга є конденсатор, формули для якого дозволяють розрахувати та підібрати найбільш підходящий варіант. Основна функція цього пристрою полягає у накопиченні певної кількості електроенергії. Найпростіша система включає два електроди або обкладки, розділені між собою діелектриком.
Основна функція цього пристрою полягає у накопиченні певної кількості електроенергії. Найпростіша система включає два електроди або обкладки, розділені між собою діелектриком.
У чому вимірюється ємність конденсатора
Однією з найважливіших параметрів конденсатора є його ємність. Цей параметр визначається кількістю електроенергії, що накопичується цим приладом. Нагромадження відбувається як електронів. Їхня кількість, що міститься в конденсаторі, визначає величину ємності конкретного пристрою.
Для вимірювання ємності застосовується одиниця – фарада. Ємність конденсатора в 1 фараду відповідає електричному заряду в 1 кулон, а на обкладинках різниця потенціалів дорівнює 1 вольту. Це класичне формулювання не підходить для практичних розрахунків, оскільки в конденсаторі збираються не заряди, а електрони. Місткість будь-якого конденсатора знаходиться в прямій залежності від обсягу електронів, здатних накопичуватися при нормальному робочому режимі. Для позначення ємності все одно використовується фарада, а кількісні параметри визначаються за формулою: С = Q/U, де означає ємність, Q — заряд в кулонах, а U є напругою. Таким чином, проглядається взаємний зв’язок заряду та напруги, що впливають на здатність конденсатора до накопичення та утримання певної кількості електрики.
Таким чином, проглядається взаємний зв’язок заряду та напруги, що впливають на здатність конденсатора до накопичення та утримання певної кількості електрики.
Для розрахунків використовується формула:
в якій ε 0
= 8,854187817 х 10 -12 ф/м є постійну величину. Інші величини: — є діелектричною проникністю діелектрика, що знаходиться між обкладками, S — означає площу обкладки, а d — зазор між обкладками.
Формула енергії конденсатора
З ємністю найтіснішим чином пов’язана інша величина, відома як . Після зарядки будь-якого конденсатора, у ньому утворюється певна кількість енергії, яка надалі виділяється у процесі розрядки. З цією потенційною енергією вступають у взаємодію обкладання конденсатора. Вони утворюються різноіменні заряди, які притягуються друг до друга.
У процесі зарядки відбувається витрачання енергії зовнішнього джерела для поділу зарядів з позитивним та негативним значенням, які потім розташовуються на обкладках конденсатора. Тому відповідно до закону збереження енергії вона не зникає безслідно, а залишається всередині конденсатора у вигляді електричного поля, зосередженого між пластинами. Різноіменні заряди утворюють взаємодію та подальше тяжіння обкладок між собою.
Тому відповідно до закону збереження енергії вона не зникає безслідно, а залишається всередині конденсатора у вигляді електричного поля, зосередженого між пластинами. Різноіменні заряди утворюють взаємодію та подальше тяжіння обкладок між собою.
Кожна пластина конденсатора під дією заряду створює напруженість електричного поля, що дорівнює Е/2. Загальне поле складатиметься з обох полів, що виникають у кожній обкладці з однаковими зарядами, що мають протилежні значення.
Отже, енергія конденсатора виражається формулою: W=q(E/2)d. У свою чергу, напруга виражається за допомогою понять напруженості та відстані та подається у вигляді формули U=Ed. Це значення, підставлене першу формулу, відображає енергію конденсатора у такому вигляді:W=qU/2. Для отримання остаточного результату необхідно використовувати визначення ємності: C=q/U, і зрештою енергія зарядженого конденсатора виглядатиме таким чином: W ел = CU 2 /2.
Формула заряду конденсатора
Для виконання зарядки конденсатор повинен бути підключений до ланцюга постійного струму. З цією метою можна використовувати генератор. Кожен генератор має внутрішній опір. При замиканні ланцюга відбувається заряджання конденсатора. Між його обкладками утворюється напруга, що дорівнює електрорушійній силі генератора: U c = E.
З цією метою можна використовувати генератор. Кожен генератор має внутрішній опір. При замиканні ланцюга відбувається заряджання конденсатора. Між його обкладками утворюється напруга, що дорівнює електрорушійній силі генератора: U c = E.
Обкладка, підключена до позитивного полюса генератора, позитивно заряджається (+q), а інша обкладка отримує рівнозначний заряд з негативною величиною (- q). Величина заряду q знаходиться у прямій пропорційній залежності з ємністю конденсатора і напругою на обкладках Uc. Ця залежність виражається такою формулою: q = C x Uc.
У процесі зарядки одна з обкладок конденсатора набуває, а інша втрачає певну кількість електронів. Вони переносяться зовнішнього ланцюга під впливом електрорушійної сили генератора. Таке переміщення є електричним струмом, відомим ще як зарядний ємнісний струм (Iзар).
Течія зарядного струму в ланцюзі відбувається практично за тисячні частки секунди, до того моменту, поки напруга конденсатора не стане рівною електрорушійній силі генератора. Напруга збільшується плавно, а потім поступово сповільнюється. Далі значення напруги конденсатора буде незмінним. Під час заряджання ланцюгом тече зарядний струм. На самому початку він досягає максимальної величини, тому що напруга конденсатора має нульове значення. Відповідно до закону Ома I зар = Е/R i, оскільки до опору Ri прикладена вся ЕРС генератора.
Напруга збільшується плавно, а потім поступово сповільнюється. Далі значення напруги конденсатора буде незмінним. Під час заряджання ланцюгом тече зарядний струм. На самому початку він досягає максимальної величини, тому що напруга конденсатора має нульове значення. Відповідно до закону Ома I зар = Е/R i, оскільки до опору Ri прикладена вся ЕРС генератора.
Формула струму витоку конденсатора
Струм витоку конденсатора цілком можна порівняти з впливом підключеного до нього резистора з будь-яким опором R. Струм витоку тісно пов’язаний з типом конденсатора і якістю використовуваного діелектрика. Крім того, важливим фактором стає конструкція корпусу та ступінь його забрудненості.
Деякі конденсатори мають негерметичний корпус, що призводить до проникнення вологи з повітря та зростання струму витоку. Насамперед це стосується пристроїв, де як діелектрик використаний промаслений папір. Значні струми витоку виникають через зниження електричного опору ізоляції. В результаті порушується основна функція конденсатора — здатність отримувати та зберігати заряд електричного струму.
В результаті порушується основна функція конденсатора — здатність отримувати та зберігати заряд електричного струму.
Основна формула для розрахунку виглядає наступним чином: I ут = U/R d , де I ут — це струм витоку, U — напруга, що додається до конденсатора, а R d — опір ізоляції.
§
6. Заряд та розряд конденсатора
Щоб зарядити конденсатор, треба щоб вільні електрони перейшли з однієї обкладки на іншу. Перехід електронів з однієї обкладки конденсатора на іншу відбувається під дією напруги джерела по дротах, що з’єднує джерело з обкладинками конденсатора.
У момент включення конденсатора зарядів на його обкладках немає і напруга на ньому дорівнює нулю μ =0. Тому зарядний струм визначається внутрішнім опором джерела r і має найбільшу величину:
I З max = E/r в.
У міру накопичення зарядів на обкладках конденсатора напруга на ньому збільшується і падіння напруги на внутрішньому опорі джерела дорівнює різниці ЕРС джерела і напруги на конденсаторі (Е — μ с). отже, зарядний струм
отже, зарядний струм
i з = (Е — μ с) / r в.
Таким чином, зі збільшенням напруги на конденсаторі струм заряду знизиться і при с = Е стає рівним нулю. Процес зміни напруги на конденсаторі та струму заряду у часі зображено на рис. 1. На самому початку заряду напруга на конденсаторі різко зростає, тому що зарядний струм має найбільше значення та накопичення зарядів на обкладках конденсатора відбувається інтенсивно. У міру підвищення напруги на конденсаторі зарядний струм зменшується та накопичення зарядів на обкладках уповільнюється. Тривалість заряду конденсатора залежить від його ємності та опору ланцюга, збільшення яких призводить до зростання тривалості заряду. Зі збільшенням ємності конденсатора зростає кількість зарядів, що накопичуються на його пластинах, а якщо збільшити опір ланцюга зменшиться і зарядний струм, а це уповільнює процес накопичення зарядів на цих обкладках.
Якщо обкладки зарядженого конденсатора підключити до будь-якого опору R, то за рахунок напруги на конденсаторі протікатиме розрядний струм конденсатора. При розряді конденсатора електронисодної пластини (при їх надлишку) переходитимуть на іншу (при їх нестачі) і буде продовжуватися доти, поки потенціали обкладок не вирівняються, тобто напруга на конденсаторі стане рівним нулю. Зміна напруги у процесі розряду конденсатора зображено на рис. 2. Струм розряду конденсатора пропорційний напрузі на конденсаторі (i р =μ з /R ), і його зміна в часі подібно до зміни напруги.
При розряді конденсатора електронисодної пластини (при їх надлишку) переходитимуть на іншу (при їх нестачі) і буде продовжуватися доти, поки потенціали обкладок не вирівняються, тобто напруга на конденсаторі стане рівним нулю. Зміна напруги у процесі розряду конденсатора зображено на рис. 2. Струм розряду конденсатора пропорційний напрузі на конденсаторі (i р =μ з /R ), і його зміна в часі подібно до зміни напруги.
У початковий момент розряду напруга на конденсаторі найбільша (μ = Е) і розрядний струм максимальний (I р max = E / R ), так що розряд відбувається швидко. При зниженні напруги струм розряду знижується і процес переходу зарядів з однієї обкладки на іншу загальмовується.
Час процесу розряду конденсатора залежить від опору ланцюга та ємності конденсатора, причому зростання як опору, так і ємності збільшує тривалість розряду. Зі збільшенням опору розрядний струм знижується, уповільнюється процес перенесення зарядів з одного на іншу обкладок; зі збільшенням ємності конденсатора збільшується заряд на обкладках.
Таким чином, в ланцюзі, що містить конденсатор, струм проходить тільки в процесі його заряду та розряду, тобто коли напруга на обкладках зазнає змін у часі. При сталості напруги струм через конденсатор не проходить, тобто конденсатор не пропускає постійний струм, так як між його обкладками вміщений діелектрик і в результаті ланцюг розімкнена.
При зарядці конденсатора останній здатний накопичувати електричну енергію, споживаючи її від енергоджерела. Накопичена енергія зберігається певний час. При розряді конденсатора ця енергія переходить до розрядного резистори, нагріваючи його, тобто енергію електричного поля перетворюється на теплову. Чим вище ємність конденсатора і напруга на його обкладках, тим більше енергії, запасеної на ньому. Енергія електричного поля конденсатора визначається наступним виразом
W=CU 2/2.
Якщо конденсатор ємністю 100 мкФ заряджений до напруги 200 В, то енергія, запасена в електричному полі конденсатора, W = 100 10 -6 200 2 /2 = 2 Дж.
Вам знадобиться
- — знання ємності або геометричних та фізичних параметрів конденсатора;
- — знання енергії чи заряду на конденсаторі.
Інструкція
Знайдіть напругу між пластинами конденсатора, якщо відома поточна величина накопиченої ним енергії, а також його ємність. Енергія, запасена конденсатором, може бути обчислена за формулою W=(C∙U²)/2, де C – ємність, а U – напруга між пластинами. Таким чином, значення напруги може бути отримано як корінь з подвоєного значення енергії, поділеного на ємність. Тобто, воно дорівнює: U=√(2∙W/C).
Енергія, запасена конденсатором, також може бути обчислена на підставі значення заряду (кількості ), що міститься в ньому, і напруги між обкладками. Формула, що визначає відповідність між цими параметрами, має вигляд: W=q∙U/2 (де q — заряд). Отже, знаючи енергію і можна обчислити напругу між його пластинами за формулою: U=2∙W/q.
Оскільки заряд на конденсаторі пропорційний як прикладеному до його пластин напруги, так і ємності пристрою (він визначається формулою q=C∙U), знаючи заряд і ємність, можна знайти і напругу. -12 Ф/м), ε – відносна діелектрична проникність простору між пластинами (її можна дізнатися з фізичних довідників). Обчисливши ємність, розрахуйте напругу одним із методів, наведених у кроках 1-3.
-12 Ф/м), ε – відносна діелектрична проникність простору між пластинами (її можна дізнатися з фізичних довідників). Обчисливши ємність, розрахуйте напругу одним із методів, наведених у кроках 1-3.
Зверніть увагу
Для отримання коректних результатів при обчисленні напруг між обкладками конденсаторів перед проведенням розрахунків наводьте значення всіх параметрів в систему СІ.
Щоб знати, чи можна використовувати у тому чи іншому місці схеми конденсатор, слід визначити його . Спосіб знаходження цього параметра залежить від того, як він позначений на конденсаторі і чи позначений взагалі.
Вам знадобиться
- Вимірник ємності
Інструкція
на великих конденсатори ємністьзазвичай позначена відкритим текстом: 0,25 мкФ або 15 uF. У цьому випадку спосіб її визначення тривіальний.
На менших конденсатори(у тому, SMD) ємністьдвома чи трьома цифрами. У першому випадку вона позначена в пикофарадах. У другому випадку, перші дві цифри ємність, А третя — у яких одиницях вона виражена: 1 — десятки пикофарад;
2 – сотні пікофарад;
3 – нанофаради;
4 – десятки нанофарад;
5 – частки мікрофаради.
Існує також система позначення ємності, що використовує поєднання латинських літер та цифр. Літери позначають такі цифри: A – 10;
B – 11;
C – 12;
D – 13;
E – 15;
F – 16;
G – 18;
H – 20;
J – 22;
K – 24;
L – 27;
M – 30;
N – 33;
P – 36;
Q – 39;
R — 43;
S – 47;
T – 51;
U – 56;
V – 62;
W – 68;
X – 75;
Y – 82;
Z — 91. Отримане число слід помножити на число 10, попередньо зведене в ступінь, що дорівнює цифрі, що настає після . Результат буде виражений у пикофарадах.
Зустрічаються конденсатори, ємністьна яких не зазначено взагалі. Ви напевно зустрічали їх, у стартерах ламп денного. У цьому випадку виміряти ємністьможна лише спеціальним приладом. Вони є цифровими та мостовими. У будь-якому випадку, якщо конденсатор впаяний у той чи інший пристрій, його слід знеструмити, розрядити в ньому конденсатори фільтра і сам конденсатор, ємністьякого слід виміряти, і лише після цього випаяти його. Потім його необхідно підключити до приладу. На цифровому вимірнику спочатку вибирають грубу межу, потім перемикають його до тих пір, поки він не покаже перевантаження. Після цього перемикач переводять на одну межу назад і читають показання, а за становищем перемикача визначають, в яких одиницях вони виражені. . Домогшись зникнення, за шкалою регулятора зчитують результат, а одиниці, в яких він виражений, також визначають за становищем перемикача. Потім конденсатор встановлюють назад у пристрій.
Потім його необхідно підключити до приладу. На цифровому вимірнику спочатку вибирають грубу межу, потім перемикають його до тих пір, поки він не покаже перевантаження. Після цього перемикач переводять на одну межу назад і читають показання, а за становищем перемикача визначають, в яких одиницях вони виражені. . Домогшись зникнення, за шкалою регулятора зчитують результат, а одиниці, в яких він виражений, також визначають за становищем перемикача. Потім конденсатор встановлюють назад у пристрій.
Зверніть увагу
Ніколи не підключайте до вимірювача заряджені конденсатори.
Джерела:
- Довідник з систем позначення ємності
Знайти значення електричного зарядуможна двома способами. Перший – виміряти силу взаємодії невідомого зарядуз відомим і за допомогою закону Кулона розрахувати його значення. Другий – внести заряд у відоме електричне поле та виміряти силу, з якою воно діє на нього. Для вимірювання зарядупровідника, що протікає через поперечний переріз, за певний час виміряйте силу струму і помножте її на значення часу. 9)). Якщо заряди відштовхуються, всі вони однойменні, якщо ж притягуються – різноіменні.
9)). Якщо заряди відштовхуються, всі вони однойменні, якщо ж притягуються – різноіменні.
Вимірювання значення заряду, внесеного в електричне полеВиміряйте значення постійного електричного поля спеціальним приладом (вимірювач електричного поля). Якщо такого приладу немає, візьміть повітряний конденсатор, зарядіть його, виміряйте напругу на його обкладках і поділіть не відстань між пластинами – це буде значення електричного поля всередині конденсатора у вольтах на метр. Внесіть у поле невідомий заряд. За допомогою чутливого динамометра виміряйте силу, яка діє. Вимірювання проводьте у . Розділіть значення сили на напруженість електричного поля. Результатом буде значення зарядуу Кулонах (q=F/Е).
Вимірювання заряду, що протікає через поперечний провідник Зберіть електричний ланцюг з провідниками і послідовно підключіть до нього амперметр. Замкніть її на джерело струму та виміряйте силу струму за допомогою амперметра в амперах. Одночасно заміряйте секундоміром , в якого в ланцюгу був електричний струм. Помноживши значення сили струму на отриманий час, дізнайтеся заряд через поперечний переріз кожного за цей час (q=I t). При вимірюваннях слідкуйте, щоб провідники не перегрівались і не відбулося коротке замикання.
Помноживши значення сили струму на отриманий час, дізнайтеся заряд через поперечний переріз кожного за цей час (q=I t). При вимірюваннях слідкуйте, щоб провідники не перегрівались і не відбулося коротке замикання.
Конденсатор називається пристрій, здатний накопичувати електричні заряди. Кількість накопичуваної електричної енергії в конденсаторі характеризується його ємністю. Вона вимірюється у фарадах. Вважається, що ємність на один фарад відповідає конденсатору, зарядженому електричним зарядом в один кулон при різниці потенціалів на його обкладках в один вольт.
Інструкція
Визначте ємність плоского конденсатораза формулою С = S e e0/d, де S — площа поверхні однієї пластини, d — між пластинами, e — відносна діелектрична проникність , що заповнює простір між пластинами (у вакуумі вона дорівнює), e0 — електрична постійна, рівна 8,854187817 10 (-12) Ф/м. Виходячи з наведеної формули, величина ємності залежатиме від площі провідників, між ними та від матеріалу діелектрика. Як діелектрик може застосовуватися або слюда.
Як діелектрик може застосовуватися або слюда.
Обчисліть ємність сферичного конденсатораза формулою С = (4П e0 R²)/d, де П – число «пі», R – радіус сфери, d – величина зазору між його сферами. Величина ємності сферичного конденсаторапрямо пропорційна концентричної сфери і обернено пропорційна відстані між сферами.
Розрахуйте ємність циліндричного конденсатораза формулою С = (2П e e0 L R1)/(R2-R1), де L — довжина конденсатора, П – число «пі», R1 і R2 – радіуси його циліндричних обкладок.
Якщо конденсатори в ланцюзі з’єднані паралельно, розрахуйте їхню загальну ємність за формулою С = С1+С2+…+Сn, де С1, С2,…Сn – ємності паралельно з’єднаних конденсаторів.
Обчисліть загальну ємність послідовно з’єднаних конденсаторів за формулою 1/С = 1/С1+1/С2+…+1/Сn, де С1, С2, Сn — ємності послідовно з’єднаних конденсаторів.
Зверніть увагу
На будь-якому конденсаторі обов’язково має бути нанесене маркування, яке може бути буквенно-цифрове або кольорове. (-12) Ф/м і є, власне, діелектричною проникністю вакууму.
(-12) Ф/м і є, власне, діелектричною проникністю вакууму.
Разность электрических потенциалов — Regents Physics
Напоминание: P1, 4, 7 Экзамен 2/11; Экзамен P9 2/10
Разность электрических потенциалов
Когда мы поднимали объект против силы тяжести, применяя силу на расстоянии, мы действительно работали, чтобы передать этому объекту гравитационную потенциальную энергию. Та же концепция применима и к электрическим полям. Если вы перемещаете заряд против электрического поля, вы должны приложить силу на некотором расстоянии, поэтому вы совершаете работу и сообщаете ему электрическую потенциальную энергию.Работа, совершаемая на единицу заряда при перемещении заряда между двумя точками в электрическом поле, известна как разность электрических потенциалов , (В) . Единицами электрического потенциала являются вольты, где вольт равен 1 джоулю на кулон. Следовательно, если вы совершили работу в 1 Дж, перемещая заряд в 1 кулон в электрическом поле, разность электрических потенциалов между этими точками составила бы 1 вольт. Это дается вам в справочной таблице как:
Это дается вам в справочной таблице как:
В в этой формуле — это разность потенциалов (в вольтах), Вт — это работа или электрическая энергия (в джоулях), а q — ваш заряд (в кулонах).Давайте рассмотрим пример задачи.
Вопрос: Между двумя точками А и В в электрическом поле существует разность потенциалов 10,0 вольт. Какова величина заряда, который требует работы 2,0 × 10–2 джоуля, чтобы переместить его из точки А в точку В?
Ответ:
Когда имеешь дело с электростатикой, часто количество электрической энергии или работы, совершаемой над зарядом, составляет очень маленькую долю джоуля. Работать с такими малыми числами обременительно, поэтому физики разработали альтернативную единицу измерения электрической энергии и работы, которая может быть более удобной, чем джоуль.Эта единица, известная как электрон-вольт (эВ), представляет собой количество работы, совершаемой при перемещении элементарного заряда через разность потенциалов в 1 В. Таким образом, один электрон-вольт эквивалентен одному вольту, умноженному на один элементарный заряд (в кулонах): 1 эВ = 1,6*10-19 джоулей.
Таким образом, один электрон-вольт эквивалентен одному вольту, умноженному на один элементарный заряд (в кулонах): 1 эВ = 1,6*10-19 джоулей.
Вопрос: Заряд 2*10-3 Кл проходит через разность потенциалов 10 вольт в электрическом поле. Какая работа в электрон-вольтах потребовалась для перемещения этого заряда?
Ответ:
Параллельные пластины
Если вы знаете разность потенциалов между двумя параллельными пластинами, вы можете легко рассчитать напряженность электрического поля между пластинами.Пока вы не находитесь рядом с краем пластин, электрическое поле между пластинами постоянно, а его напряженность определяется выражением:
Обратите внимание, что при разности потенциалов V в вольтах и расстоянии между пластинами в метрах единицами измерения напряженности электрического поля являются вольты на метр [В/м]. Ранее мы заявили, что единицами измерения напряженности электрического поля являются ньютоны на кулон [Н/Кл]. Легко показать, что эти единицы эквивалентны:
Легко показать, что эти единицы эквивалентны:
Вопрос: Какая электрическая единица эквивалентна одному джоулю?
- вольт/метр
- ампер * вольт
- вольт /
кулонов
- Кулон*вольт
Ответ: (4) Кулон*вольт
Давайте попробуем другую примерную задачу:
Вопрос: На схеме изображены два электрона e1 и e2, расположенные между двумя противоположно заряженными параллельными пластинами.Сравните величину силы, действующей со стороны электрического поля на e1, с величиной силы, действующей со стороны электрического поля на e2.
Ответ: Сила одинакова, потому что электрическое поле одинаково для обоих зарядов, так как электрическое поле постоянно между двумя параллельными пластинами.
Эквипотенциальные линии
Подобно топографической карте, на которой показаны линии одинаковой высоты или равной гравитационной потенциальной энергии, мы можем составить карту электрического поля и соединить точки с равным электрическим потенциалом. Эти линии, известные как эквипотенциальные линии, всегда пересекают линии электрического поля под прямым углом и показывают положения в пространстве с постоянным электрическим потенциалом. Если вы перемещаете заряженную частицу в пространстве, и она всегда остается на эквипотенциальной линии, никакой работы не будет.
Эти линии, известные как эквипотенциальные линии, всегда пересекают линии электрического поля под прямым углом и показывают положения в пространстве с постоянным электрическим потенциалом. Если вы перемещаете заряженную частицу в пространстве, и она всегда остается на эквипотенциальной линии, никакой работы не будет.
Разность потенциалов — объяснение того, что такое разность электрических потенциалов
Узнайте все о разнице электрических потенциалов, формуле для расчета разности потенциалов, о том, как рассчитать разность потенциалов между двумя точками.
Разность потенциалов можно просто определить как разность электрических потенциалов между двумя точками. Когда два положительных заряда приближаются друг к другу, они отталкиваются.
Когда два отрицательных заряда приближаются друг к другу, они также отталкиваются. Но когда положительный и отрицательный заряды сближены, они притягиваются друг к другу. Когда эти два противоположных заряда объединяются, их можно использовать для работы. Вот почему нам нужны положительный ( + ) и отрицательный ( – ) сигналы, чтобы зажечь лампочку или запустить любой электрический инструмент, оборудование, мобильный телефон или бытовую технику.Эта способность заряженных частиц совершать работу называется электрическим потенциалом .
Вот почему нам нужны положительный ( + ) и отрицательный ( – ) сигналы, чтобы зажечь лампочку или запустить любой электрический инструмент, оборудование, мобильный телефон или бытовую технику.Эта способность заряженных частиц совершать работу называется электрическим потенциалом .
Следовательно, два противоположных заряда имеют разность потенциалов или разность потенциалов . Единица разности потенциалов ( pd ) равна вольт .
Единица разности потенциалов
Единица измерения Разность потенциалов (Вольт) названа в честь Алессандро Вольта. Вольт является мерой электрического потенциала.Электрический потенциал является типом потенциальной энергии и относится к энергии, которая может быть высвобождена, если позволить протекать электрическому току.
Один вольт определяется как разность электрических потенциалов между двумя точками проводящего провода, когда электрический ток в один ампер рассеивает мощность в один ватт между этими точками. Он также равен разности потенциалов между двумя параллельными бесконечными плоскостями, отстоящими друг от друга на 1 метр, которые создают электрическое поле в 1 ньютон на кулон.
Он также равен разности потенциалов между двумя параллельными бесконечными плоскостями, отстоящими друг от друга на 1 метр, которые создают электрическое поле в 1 ньютон на кулон.
Единицей работы в системе СИ является джоулей ( Дж ). Единицей силы в СИ является ньютонов ( Н ). Единицей расстояния в СИ является метров ( м ).
Вт (джоули) = N (ньютоны) x m (метры)
Напряжение
В области электроники разность потенциалов обычно называют напряжением, и ее символом является В . В некоторых случаях также используется символ U или E для ЭДС ( электродвижущая сила ), но стандартный символ V обозначает любую разность потенциалов.Это относится к напряжению, генерируемому такими источниками, как батарея или солнечный элемент, а также к падению напряжения на пассивном электронном компоненте, таком как резистор.
Разность потенциалов, также называемая разностью потенциалов между двумя заданными точками, представляет собой работу в джоулях, необходимую для перемещения одного кулона заряда из одной точки в другую. Единицей напряжения в системе СИ является вольта .
Формула Вольта
Типы напряжения
Существует 2 типа напряжения – постоянный или постоянный ток и переменный или переменный ток.
DC – постоянное напряжение. Здесь электрический заряд ( ток ) течет только в одном направлении. Источники напряжения, такие как батарея мобильного телефона или солнечная батарея, обеспечивают напряжение постоянного тока. Пример – 12 В постоянного тока
AC – это переменный ток. Здесь электрический заряд (ток) периодически меняет направление. Источники напряжения, такие как генератор переменного тока, обеспечивают напряжение переменного тока. Пример – 240 В переменного тока.
Полярность напряжения
Предположим, есть 2 заряженные точки: точка A заряжена положительно (+), а точка B заряжена отрицательно (-). Теперь, если мы переместим замкнутую цепь A (+) из A в B или наоборот, это потребует работы. Разница между двумя точками заключается в полярности напряжения . Эта полярность напряжения обозначается положительным знаком (+) в точке A и отрицательным знаком (-) в точке B.
Теперь, если мы переместим замкнутую цепь A (+) из A в B или наоборот, это потребует работы. Разница между двумя точками заключается в полярности напряжения . Эта полярность напряжения обозначается положительным знаком (+) в точке A и отрицательным знаком (-) в точке B.
Как рассчитать разность электрических потенциалов по закону Ома
- Рассчитать силу тока, протекающего по цепи. Это мера в амперах ( I )
- Рассчитайте величину сопротивления в цепи.Сопротивление измеряется в Омах ( R ).
- Умножить величину тока в цепи на величину сопротивления в цепи – В = IR (закон Ома)
Что такое разность электрических потенциалов
Статьи по теме:
Нахождение разности электрических потенциалов между двумя точками — видео и стенограмма урока
Однородное электрическое поле
В однородном электрическом поле уравнение для расчета разности электрических потенциалов очень простое: В = Эд . В этом уравнении В представляет собой разность потенциалов в вольтах (или джоулях на кулон), E представляет собой напряженность электрического поля на площади (в ньютонах на кулон), а d представляет собой расстояние между двумя пластинами ( в метрах).
В этом уравнении В представляет собой разность потенциалов в вольтах (или джоулях на кулон), E представляет собой напряженность электрического поля на площади (в ньютонах на кулон), а d представляет собой расстояние между двумя пластинами ( в метрах).
Ситуация с параллельными пластинами, о которой я упоминал ранее, является примером однородного электрического поля. Между пластинами силовые линии расположены на одинаковом расстоянии друг от друга, поэтому напряженность поля везде одинакова — оно однородно. Если бы мы хотели вычислить разность потенциалов между пластинами, мы могли бы взять электрическое поле между пластинами, E , и просто умножить его на расстояние между пластинами.Строго говоря, это расстояние, d , всегда должно быть в направлении силовых линий (если вы двигаетесь влево и вправо на этой диаграмме, электрический потенциал на самом деле вообще не меняется).
Пример
Пришло время рассмотреть пример. Допустим, вы подключаете плоский конденсатор к 12-вольтовой батарее. Когда конденсатор полностью заряжен, между пластинами создается электрическое поле силой 10 ньютонов на кулон.Какое должно быть расстояние между пластинами?
Допустим, вы подключаете плоский конденсатор к 12-вольтовой батарее. Когда конденсатор полностью заряжен, между пластинами создается электрическое поле силой 10 ньютонов на кулон.Какое должно быть расстояние между пластинами?
Прежде всего, мы должны записать то, что мы знаем. Мы знаем, что напряжение В составляет 12 вольт. Мы знаем, что электрическое поле E составляет 10 ньютонов на кулон. И нас просят найти d , расстояние между пластинами. Мы знаем это, потому что если вы подключите 12-вольтовую батарею к параллельным пластинам, это создаст разность потенциалов 12 вольт между двумя пластинами.
Итак, все, что нам нужно сделать, это подставить наши числа, переставить d и решить.Когда мы это сделаем, мы получим 1,2 метра. И все — это наш ответ.
Резюме урока
Электрический потенциал в определенной точке пространства — это работа, совершаемая при перемещении положительного заряда из бесконечности в эту точку. Электрический потенциал на бесконечности определяется как ноль. Электрический потенциал связан с потенциальной электрической энергией в том смысле, что электрический потенциал представляет собой потенциальную электрическую энергию на единицу заряда.
Электрический потенциал на бесконечности определяется как ноль. Электрический потенциал связан с потенциальной электрической энергией в том смысле, что электрический потенциал представляет собой потенциальную электрическую энергию на единицу заряда.
В то время как электрическая потенциальная энергия специфична для конкретного заряда, электрический потенциал определяется только положением внутри поля. Разность электрических потенциалов — это разность электрических потенциалов между двумя точками в пространстве. Вот и все. Он также измеряется в джоулях на кулон, но обычно его сокращают до другой единицы: вольт.
Представим, что у нас есть две параллельные пластины: одна с положительным зарядом, другая с отрицательным зарядом. В электромагнетизме мы используем положительный заряд для определения электрических полей. Если вы отпустите положительный заряд на отрицательной пластине, он никуда не денется, потому что противоположности притягиваются.Но если вы отпустите его на положительной пластине, он будет следовать линиям поля и «упадет» на отрицательную пластину. Поэтому, когда мы говорим об электрических полях, мы можем сказать, что силовые линии указывают в направлении уменьшения электрического потенциала.
Поэтому, когда мы говорим об электрических полях, мы можем сказать, что силовые линии указывают в направлении уменьшения электрического потенциала.
В однородном электрическом поле уравнение для расчета разности электрических потенциалов очень простое: В = Эд . В этом уравнении В — это разность потенциалов в вольтах, E — это напряженность электрического поля (в ньютонах на кулон), а d — это расстояние между двумя точками (в метрах).
Результаты обучения
По окончании этого урока вы должны уметь:
- Описывать электрический потенциал и разность электрических потенциалов
- Расчет разности электрических потенциалов в однородном поле
Разница потенциалов: определение, формула и примеры — видео и расшифровка урока
Что такое электрический потенциал?
Чтобы понять разность электрических потенциалов, нам нужно сначала понять, что такое электрический потенциал.Лучший способ сделать это — провести аналогию с концепцией, с которой вы должны быть знакомы: гравитационная потенциальная энергия.
Электрический потенциал — это простой способ количественного определения потенциальной энергии, которой обладает электрическая частица в результате ее нахождения в электрическом поле. Это похоже на то, как мы говорим об объектах с массой и их потенциальной энергией в результате их нахождения в гравитационном поле.
Находясь в гравитационном поле Земли, объекты, обладающие массой, испытывают воздействие этого гравитационного энергетического поля. Эффект, который они ощущают, заключается в том, что их тянет вниз с некоторой силой, пропорциональной их массе и их положению в это поле.Означает ли это, что мы можем однозначно описать места в гравитационном поле Земли как места с изначально высокой потенциальной энергией? Нет, не обязательно. Почему нет? Потому что потенциальная энергия, которой обладает объект, зависит не только от его положения в гравитационном энергетическом поле, но и от его массы.
Например, космический шаттл на высоте 10 000 футов над поверхностью Земли обладает гораздо большей потенциальной энергией, чем молекула воздуха на той же высоте над поверхностью Земли. Они оба находятся в одном и том же месте в гравитационном поле, но их потенциальная энергия очень различна, потому что их масса очень различна. Что мы можем сделать, так это определить каждое местоположение как количество потенциальной энергии на единицу массы, необходимое для достижения этого местоположения. Это позволяет нам уравнять игровое поле и сравнить локации по энергии, необходимой для того, чтобы добраться до них. Это делает потенциальную энергию объекта исключительно функцией его местоположения. Мы называем это гравитационным потенциалом, и он определяется как количество потенциальной энергии объекта в гравитационном поле на единицу массы.
Они оба находятся в одном и том же месте в гравитационном поле, но их потенциальная энергия очень различна, потому что их масса очень различна. Что мы можем сделать, так это определить каждое местоположение как количество потенциальной энергии на единицу массы, необходимое для достижения этого местоположения. Это позволяет нам уравнять игровое поле и сравнить локации по энергии, необходимой для того, чтобы добраться до них. Это делает потенциальную энергию объекта исключительно функцией его местоположения. Мы называем это гравитационным потенциалом, и он определяется как количество потенциальной энергии объекта в гравитационном поле на единицу массы.
Электрический потенциал очень похож на гравитационный потенциал. Он описывает количество энергии, которой обладает частица, в зависимости от ее местоположения. Это способ количественной оценки того, сколько энергии было дано частице, чтобы заставить ее двигаться против электрического поля. В случае нашей электрической цепи это поле создается отталкиванием электрической частицы от других частиц. Итак, точно так же, как объект движется через наше гравитационное поле, мы описываем частицу, которая пробилась через электрическое поле, чтобы добраться туда, где она есть.И точно так же, как мы «уровняли игровое поле», описывая местоположения в гравитационном поле как количество энергии на единицу массы, чтобы добраться туда, мы описываем электрический потенциал как количество энергии, необходимое заряженной частице для достижения местоположения в этом месте. электрическое поле известной силы. Опять же, это делает электрический потенциал объекта исключительно функцией его местоположения.
Итак, точно так же, как объект движется через наше гравитационное поле, мы описываем частицу, которая пробилась через электрическое поле, чтобы добраться туда, где она есть.И точно так же, как мы «уровняли игровое поле», описывая местоположения в гравитационном поле как количество энергии на единицу массы, чтобы добраться туда, мы описываем электрический потенциал как количество энергии, необходимое заряженной частице для достижения местоположения в этом месте. электрическое поле известной силы. Опять же, это делает электрический потенциал объекта исключительно функцией его местоположения.
Разность потенциалов и емкость
Разность потенциалов и емкость
Следующий текст используется только для обучения, исследований, научных исследований, использования в образовательных и информационных целях в соответствии с принципами добросовестного использования.
Мы благодарим авторов текстов и исходный веб-сайт, которые дают нам возможность поделиться своими знаниями
Физика
Разность потенциалов (p.d.) между двумя точками есть работа, совершаемая при переносе заряда в 1 кулон из одной точки в другую*.
Единица разности потенциалов Вольт (обозначение В)
Вольт
Разность потенциалов между двумя точками равна одному вольту, если при переносе заряда в один кулон из одной точки в другую совершается работа в один джоуль.
Более распространенным (но менее правильным) словом для термина «разность потенциалов» является «Напряжение».
Обратите внимание, что разность потенциалов всегда находится между двумя точками.
Связь между работой, зарядом и напряжением
Работа = Напряжение × Заряд:
См. рабочие задачи 1–6, стр. 236.
рабочие задачи 1–6, стр. 236.
В частности, следует попробовать задачи 5 и 6, но, возможно, задачу № 5 следует оставить до 6-го класса. Затем попробуйте 1–8, стр. 237.
Потенциал в точке*
Потенциал в точке относится к работе, проделанной для переноса положительного заряда из этой точки на землю.
Выпускной сертификат Программа по физике: потенциальная разница
Содержание | Глубина обработки | Деятельность | СТС |
| Определение разности потенциалов: | Соответствующие расчеты. |
|
Емкость*
Обозначение емкости C
Пожалуйста, не путайте «Емкость» (символ C) с «Зарядкой» (символ Q).
Конденсатор — электрическое устройство, используемое для хранения заряда
Емкость проводника – это отношение заряда проводника к его потенциалу*.
Единицей измерения емкости является Фарад; символ F.
(Это похоже на определение Сопротивления, с которым мы встретимся в следующей главе.)
Конденсатор с параллельными пластинами*
Рассмотрим две противоположно заряженные параллельные пластины, как показано на рисунке*
Из диаграммы видно, что емкость увеличится, если увеличится общая площадь между пластинами (А) или если расстояние между пластинами (d) уменьшится.
Следовательно, C µ A и C µ Þ C µ Þ C = k
Пропорциональная константа оказывается равной e (помните, что мы встречались с ней в предыдущей главе как часть закона Кулона) и представляет собой диэлектрическую проницаемость среды между двумя пластинами.
Þ
См. рабочие примеры 11 и 12, стр. 241. Затем попробуйте ответить на вопросы 1–5, стр. 243
Для демонстрации факторов, влияющих на емкость плоскопараллельного конденсатора*
- Подсоедините две параллельные пластины к цифровому мультиметру (DMM), настроенному на измерение емкости.Обратите внимание на емкость.
- Увеличьте расстояние между ними — обратите внимание, что емкость уменьшается.
- Немного сдвиньте одну пластину в сторону (уменьшая площадь перекрытия) — обратите внимание, что емкость уменьшается.

- Поместите различные пластины изоляционного материала между пластинами – обратите внимание, что емкость минимальна, когда между пластинами ничего (воздуха) нет*.
Две формулы для энергии, запасенной в конденсаторе*
Вт =
Чтобы показать, что заряженный конденсатор накапливает энергию
- Установите, как показано на рисунке.
- Замкните переключатель, чтобы зарядить конденсатор.
- Извлеките аккумулятор и соедините клеммы вместе, чтобы «закоротить» цепь.
- Лампочка будет мигать, когда конденсатор разряжается, показывая, что он накапливает энергию.
Общее применение конденсаторов
- «Вспышка» на камеру
- Сглаживание колебаний постоянного тока
- Позволяет использовать переменный ток (a.
 c.) проходить через него, но блокирует постоянный ток (d.c.)*.
c.) проходить через него, но блокирует постоянный ток (d.c.)*. - Используется в цепях, пропускающих только переменный ток определенной частоты*
Выпускной сертификат Программа по физике: Емкость
Содержание | Глубина обработки | Деятельность | СТС |
|
|
|
|
Конденсаторы и | Определение: C = Q/V |
|
|
| Конденсатор с параллельными пластинами. | Демонстрация того, что емкость зависит от общей площади, расстояния между пластинами, и природы диэлектрика. | Обычное использование конденсаторов: |
| Энергия, хранящаяся в конденсаторе. Использование Вт = ½ CV 2 Конденсаторы – провод a. | Зарядный конденсатор – разряд через лампу или низковольтный источник постоянного тока. мотор. Соответствующие расчеты. |
|
Дополнительный кредит
*Определение потенциальной разницы
Примечание:
Если заряд +1 движется к положительной точке, то для его достижения необходимо совершить работу, но если он движется к отрицательной точке, то это (заряд +1) выполняет работу.
Это все равно, что сказать, что камень на вершине утеса имеет потенциальную энергию, скажем, 100 Дж.
Чтобы поднять камень туда, вы должны совершить 100 джоулей работы над камнем, или, альтернативно, если камень упадет на землю , он совершит 100 джоулей работы.
*W = В Q
Теперь, если вы знаете, сколько гравитационной энергии имеет камень (из формулы для потенциальной энергии гравитации E = mgh), вы можете рассчитать скорость, с которой он упадет на землю (из формулы для кинетической энергии E = ½ mv2).
От сохранения энергии; Потенциальная энергия = кинетическая энергия: MGH = ½ MV2
Точно так же, как камень будет ускоряться к земле, положительный заряд будет ускоряться к отрицательной точке.
На самом деле, если вы знаете, с какой потенциальной энергией заряд имел начальное состояние, то есть потенциал между двумя точками (из формулы W = QV), вы можете рассчитать его скорость, когда он достигнет второй точки (если вы знаете его массу). снова используя
Потенциальная энергия = кинетическая энергия, или QV = ½ mv2
*Потенциал в точке
Помните выше, что мы отметили разность потенциалов всегда между двумя точками?
Что ж, довольно часто нам нужно знать, насколько сложно передать положительный заряд от земли к положительному объекту.
Поскольку это происходит так часто, мы отказываемся от термина «разность потенциалов» и просто называем разность потенциалов между землей и объектом «потенциалом объекта» — это также известно как «потенциал в точке».
Отсюда должно быть очевидно, что чем больше положительный заряд имеет объект, тем больше работы придется совершить, чтобы донести до него другой положительный заряд, и поэтому потенциал в этой точке будет больше.
Теперь вы можете бросить вызов себе и объяснить, как электроскоп с золотым листом можно использовать для сравнения разности потенциалов между одним объектом и землей и другим объектом и землей (см. стр. 235 для большой подсказки).
*Емкость
Представьте емкость с водой.
Количество воды, которое может вместить контейнер (его вместимость), будет зависеть, среди прочего, от того, насколько быстро поднимается уровень воды при наливании воды; если уровень воды быстро поднимается, это говорит о том, что контейнер должен быть довольно узким и, следовательно, не может вместить много воды.
Мы бы сделали вывод, что контейнер имел небольшую «емкость».
Электрический конденсатор можно сравнить с этим контейнером для воды, и скорость, с которой увеличивается потенциал конденсатора, дает нам представление о том, сколько заряда конденсатор может удерживать; если наложение на него небольшого заряда значительно повышает его потенциал, то его емкость должна быть малой.
Помните, что «значительно повышает его потенциал» означает, что необходимо проделать гораздо больше работы, чтобы наполнить его дополнительным зарядом.
Так, например, если конденсатор имеет емкость 2 фарад, то при зарядке его 6 кулонов его потенциал увеличится на 3 вольта (из C = Q/V, поэтому V = Q/C).
Однако, если бы конденсатор имел емкость 200 фарад, заряд в 6 кулонов повысил бы его потенциал только на 0,03 вольта.
*Определение Емкость
Если на вопрос об определении емкости вы ответите, что « используется для хранения заряда» , вы получите нулевые баллы, потому что это не определение.
*К = К/В
Формулу C = Q/V легче запомнить, если переформулировать ее как Q = CV
.
*Конденсатор с параллельными пластинами
Потенциал положительно заряженного объекта показывает, какую работу необходимо совершить, чтобы приблизить к нему другой положительно заряженный объект.
Следовательно, чем больше положительного заряда находится на объекте, тем больше будет его потенциал.
Однако, если мы приблизим отрицательно заряженный объект к положительно заряженному объекту, их электрические поля будут иметь тенденцию компенсировать друг друга, и тогда станет легче донести больше положительного заряда до исходного — положительно заряженного — объекта.
Это означает, что потенциал исходного объекта уменьшается просто за счет приближения к нему противоположно заряженного проводника.
Это принцип, на котором основан конденсатор с плоскими пластинами.
*Рассмотрите две противоположно заряженные параллельные пластины, как показано на рисунке
Ключом к этому является помнить, что чем больше их электрические поля компенсируют друг друга, тем больше будет емкость системы.
*Две формулы для энергии, запасенной в конденсаторе
Вт = ½ CV2, Вт = Q2/2C
Вам не нужно знать, как вывести эти формулы, но на самом деле это очень просто, и, по крайней мере, для меня легче вывести их с нуля, чем запомнить.
Их вывод включает формулы W = QV и C = Q/V.
Я могу показать вам на доске через 5 минут, если вы спросите меня.
Обратите внимание, что если вы начнете с Q = CV и замените это на W = QV, вы получите W = CV без коэффициента ½!
Чтобы объяснить, откуда берется множитель ½, нужно пройтись по выводу, так что продолжайте — спросите меня!
Между прочим, учебники не объясняют эту очевидную аномалию.
*Допускает переменный ток (a. c.) проходить через него, но блокирует постоянный ток (d.c.)*.
c.) проходить через него, но блокирует постоянный ток (d.c.)*.
На первой диаграмме (постоянный ток) после замыкания цепи происходит внезапное движение электронов, но поскольку цепь не завершена, дальнейшего течения нет.
На второй диаграмме пластины непрерывно заряжаются и разряжаются; время, необходимое для этого (и, следовательно, частота) зависит от размера пластин (см. следующий пункт).
Строго говоря, ток не «проходит» через конденсатор, а просто действует так, как если бы он был.
*Используется в цепях, пропускающих только переменный ток определенной частоты
Это, в свою очередь, используется в радиоприемниках для приема только определенных частот , соответствующих радиоволнам, исходящим от определенной радиостанции.
Часть электронной схемы, ответственная за это, называется RC-цепью (сопротивление, емкость).
При переключении станций в радиоприемнике вы действительно меняете емкость этой части цепи.
Как это работает?
Что ж, чем больше размер конденсатора, тем дольше он разряжается (и заряжается). Теперь, если время, необходимое для зарядки и разрядки, соответствует частоте переменного тока, который, в свою очередь, несет звуковую информацию от радиостанции, тогда этот сигнал будет пропущен и в конечном итоге достигнет динамиков.
*Для демонстрации факторов, влияющих на емкость плоскопараллельного конденсатора
Примечание: альтернативная демонстрация приведена на странице 242, но понять, что происходит, смехотворно сложно — учебник не объясняет ее полностью.
Описанная демонстрация вполне адекватна и очень проста.
*Поместите различные пластины изоляционного материала между пластинами. Обратите внимание, что емкость минимальна, когда между пластинами ничего (или воздуха) нет.
Это может показаться запутанным, поэтому, если это вас беспокоит, попросите меня объяснить, почему.
Экзаменационные вопросы
- [2005] [2004] [2009] [2002 ПР]
Определение разности потенциалов.
Назовите прибор для измерения разности потенциалов.
- [2009][2008][2004] [2002 ПР]
Определение емкости.
Назовите электрический компонент, представленный на схеме.
- [ПР 2006] [ПР 2006] [ПР 2007] [ПР 2007]
Однократное использование конденсатора.
Какое из следующих устройств настраивается при настройке на радиостанцию?
Трансформатор, диод, конденсатор, реостат
Перечислите факторы, влияющие на емкость плоского конденсатора.
Как бы вы показали, что емкость плоского конденсатора зависит от расстояния между его пластинами?
Какой положительный заряд сохраняется на конденсаторе емкостью 5 мкФ при подключении к сети 120 В постоянного тока? поставка?
- [2006]
- Обкладки плоского конденсатора с воздушным наполнением имеют общую площадь 40 см2 и расстояние между ними 1 см.
 Конденсатор подключен к источнику питания 12 В постоянного тока. поставка. Вычислите емкость конденсатора.
Конденсатор подключен к источнику питания 12 В постоянного тока. поставка. Вычислите емкость конденсатора.
(Проницаемость свободного пространства = 8.85 × 10-12 Ф м-1)
- Рассчитайте величину заряда на каждой пластине.
- Каков суммарный заряд конденсатора?
Опишите эксперимент, демонстрирующий, что конденсатор может накапливать энергию.
- Конденсатор подключен к выключателю, батарее и лампочке, как показано на схеме. При переводе переключателя из положения А в положение В лампочка загорается на короткое время.
- Что происходит с конденсатором, когда переключатель находится в положении А?
- Почему лампочка горит, когда переключатель находится в положении B?
- Когда переключатель находится в положении А, заряд конденсатора равен 0.6 Кл, рассчитайте его емкость.
Рассчитайте энергию, запасенную в конденсаторе емкостью 5 мкФ, когда к нему приложена разность потенциалов 20 В.
Конденсатор емкостью 100 мкФ заряжен до разности потенциалов 20 В. Какая энергия запасена в конденсаторе?
Сколько энергии запасается в конденсаторе емкостью 100 мкФ, когда он заряжен до разности потенциалов 12 В?
Способность конденсатора накапливать энергию лежит в основе дефибриллятора.Во время сердечного приступа камеры сердца не могут перекачивать кровь, потому что их мышечные волокна сокращаются и расслабляются случайным образом. Чтобы спасти пострадавшего, сердечная мышца должна быть поражена током, чтобы восстановить нормальный ритм.
Дефибриллятор используется для разряда сердечной мышцы.
Конденсатор емкостью 64 мкФ в дефибрилляторе заряжается до разности потенциалов 2500 В.
Конденсатор разряжается за 10 миллисекунд через электроды, прикрепленные к груди пострадавшего от сердечного приступа.
- Рассчитайте заряд, накопленный на каждой пластине конденсатора.
- Рассчитайте энергию, запасенную в конденсаторе.
- Рассчитайте среднюю мощность, вырабатываемую при разрядке конденсатора.
- [2004]
- На принципиальной схеме показаны конденсатор емкостью 50 мкФ, соединенные последовательно с резистором, батареей на 6 В и переключателем.
Разность потенциалов на конденсаторе равна 2.24 В первоначально при токе 80 мкА.
Вычислите заряд конденсатора в этот момент.
- Рассчитайте энергию, запасенную в конденсаторе, когда он полностью заряжен.
- Опишите, что происходит в цепи, когда напряжение 6 В пост. источник питания заменен на 6 В переменного тока. поставка.
На схеме А показан конденсатор, подключенный к лампе накаливания, и источник питания 12 В переменного тока. поставка.
На диаграмме B показан тот же конденсатор, подключенный к лампе накаливания, но подключенный к источнику постоянного тока 12 В.в. поставка.
Что происходит в каждом случае, когда переключатель замкнут? Поясните свой ответ.
Решения для экзаменов
- Разность потенциалов между двумя точками — это работа, совершаемая при переносе заряда в 1 кулон из одной точки в другую.
- Вольтметр
- Емкость проводника – это отношение заряда проводника к его потенциалу.
- Конденсатор А
- Магазин зарядки/(радио)настройка/сглаживание/накопитель энергии/вспышки для фотоаппаратов, зарядка для телефона, блоки d.в.
- Конденсатор
- Общая площадь пластин, расстояние друг от друга, диэлектрическая проницаемость диэлектрика между пластинами.
- Подключите две параллельные пластины к цифровому мультиметру (DMM), настроенному на измерение емкости.
Обратите внимание на емкость.
Увеличивайте расстояние между ними — обратите внимание, что емкость уменьшается.
- Q = CV = (5 × 10–6)(120)
Q = 6,0 × 10–4 Кл
С = [(8.85 × 10-12)(40 × 10-4)] / (0,01)
С = 3,54 × 10-12 F
Q = (3,54 x 10-12)(12) = 4,2(5) x 10-11 C
- Ноль
- Установите, как показано.
- Замкните переключатель, чтобы зарядить конденсатор.
- Извлеките аккумулятор и соедините клеммы вместе, чтобы «закоротить» цепь.
- Лампочка будет мигать, когда конденсатор разряжается, показывая, что он накапливает энергию.
- Заряжается (на пластинах накапливается заряд).
- Конденсатор разряжается, и ток кратковременно проходит через лампу.
- Кл = Q/V = 0,6/6 = 0,1 фарад
- E = ½ CV2 = ½ (5 x 10–6)(20)2 = 1,0 x 10–3 Дж
- E = ½CV2 Þ E = ½(100 × 10-6)(20)2 = 0,02 Дж
- E = ½ CV2 = ½ (100 × 10-6)(12)2 = 7,2 × 10-3 Дж
- C = Q/v Þ q = CV Þ q = (64 × 10-6)(2500) Þ q = 0.16 С
- E = ½ CV2 = ½ (64 × 10-6)(2500)2 = 200 Дж
- P = Вт/т = (200)/(10 × 10-3) = 20000 Вт
- C = Q/V Þ Q = CV = (50 × 10–6) (2,24) = 1,12 × 10–4 C
- E = ½ CV2 = ½ (50 × 10–6)(6 )2 = 9 × 10–4 Дж
Обратите внимание, что здесь мы используем 6 Вольт в качестве разности потенциалов на конденсаторе, потому что, хотя разность потенциалов в начале составляет 2,24 В, когда конденсатор полностью заряжен, требуется максимальное количество энергии для дополнительного заряда.
- Ток будет течь постоянно.
- На схеме А лампочка горит, потому что конденсатор «проводит» переменный ток. (он постоянно заряжается и разряжается).
На схеме B лампочка не горит, потому что конденсатор не проводит постоянный ток.
Источник: http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/20.%20Potential%20Difference%20and%20Емкость.документ
Ссылка на веб-сайт: http://www.thephysicsteacher.ie
Автор: не указан в исходном документе вышеуказанного текста
Разность потенциалов и емкость
Разность потенциалов и емкость
Главная страница
Разность потенциалов и емкость
Это правильное место, где можно найти ответы на ваши вопросы, такие как:
Кто? Какие ? Когда ? Где ? Почему ? Который ? Как ? Что означает разность потенциалов и емкость? В чем смысл разности потенциалов и емкости?
Примечания по физике разности потенциалов и емкости
Аланпедия.com с 1998 год за годом новые сайты и инновации
Главная страница — Отказ от ответственности — Свяжитесь с нами
Electric Potential – Гиперучебник по физике
Обсуждение
введение
Вспомним историю развития электростатики.
- Плата взимается.
- Заряды воздействуют друг на друга.
- Эта сила действует на расстояниях любого размера.
Мы с вами не возражаем против последней идеи, но когда-то это называлось «действие на расстоянии» — довольно вежливо сформулированное оскорбление. Чтобы избежать концептуальных проблем, связанных с бестелесной силой, Майкл Фарадей изобрел электрическое поле, и мир остался доволен.
Что ж, пока доволен. Затем кто-то указал, что электрическое поле является векторной величиной, и вспомнили, что векторы громоздки и с ними трудно работать. Концептуальный комфорт был получен, но практическая реализация не изменилась.Будь прокляты эти ученые. Всегда ищет лучшее из всех возможных миров. Они хотели чего-то одновременно концептуально удовлетворительного и математически простого. Такая безрассудство!
Хотите верьте, хотите нет, но проблема уже была решена физиками и математиками, работавшими над темами, которые не имели ничего общего с электричеством. Вода, ветер, тепло и растворенные вещества — все течет. Некоторые концептуальные и математические приемы, используемые для понимания этих предметов, можно также использовать для понимания электричества, а затем магнетизма и гравитации.
Что такое линии поля, если не какая-то схема течения? Линии электрического поля «текут» от положительных зарядов к отрицательным. Положительный заряд подобен открытому крану, а отрицательный заряд подобен открытому водостоку. Любой, у кого есть работающая раковина, может сделать грубую модель электрического диполя на своей кухне или в ванной одним движением руки. Подобные аналогии существуют для ветра, тепла и растворенных веществ. (Технически тепло и растворенные вещества диффундируют, а не текут, поэтому аналогии здесь немного слабее.)
Задумайтесь на мгновение о других вещах, которые текут, и подумайте о том, что заставляет их течь. Это будет ответом на нашу следующую концептуальную проблему. Составим таблицу, сравнивающую подобные явления. Во всех случаях будет что-то, что течет, и что-то, что вызывает течение.
| поток… | вызвано |
|---|---|
| река (вода жидкая) | высота |
| ветер (атмосферные газы) | атмосферное давление |
| тепло (внутренняя энергия) | температура |
| растворенные вещества (растворенные вещества) | концентрация |
В каждом случае то, что течет, может быть описано векторным полем (количество, которое имеет величину и направление в любом месте), а то, что вызывает течение, может быть описано разностью скалярного поля (а величина, которая имеет величину только в любом месте).
| поток… | вызвано различием в… |
|---|---|
| векторное поле | скалярное поле |
Если мы сможем идентифицировать электрическое скалярное поле, которое вызывает электрическое векторное поле, мы математически упростим все электричество, поскольку скаляры математически проще, чем векторы. «Определить», наверное, не то слово. «Определить» больше похоже на это. Мы собираемся определить величину, которая выполняет ту же роль, что высота — для рек, давление — для ветра, температура — для тепла и концентрация — для растворенных веществ.
«Поток» электрического поля «вызван» разницей электрического потенциала .
| поток… | вызвано различием в… |
|---|---|
| электрическое поле (испытательные заряды) | электрический потенциал |
Теперь вы должны спросить себя, что такое «электрический потенциал».
Во-первых, вторая половина термина, потенциал, не подразумевает, что это может произойти или что-то, что может привести к будущей полезности.Электрический потенциал места в космосе буквально не «может стать электрическим». Это неверное представление основано на ином значении слова «потенциал».
Настоящее значение слова «потенциал» в этом контексте сейчас неясно и, таким образом, является источником потенциальной путаницы. В контексте данного обсуждения потенциал означает нечто более близкое к тому, что дает силу, могущество, могущество или способность. Для физика существительное потенциал более тесно связано с прилагательными мощный или потенция.В наши дни слово «потенциал» кажется скорее бессильным, чем могущественным. «У меня есть мощность » — фраза, которая вдохновляет. «У меня есть потенциал » — это фраза в поисках вдохновения.
Во-вторых, когда я писал термин «электрический потенциал», я не был отрезан на две трети от написания электрической потенциальной энергии. Это два отдельных (но связанных) понятия. Посмотрите, сможете ли вы проследить этот ход рассуждений. Обратите внимание, что я сказал рассуждение, а не логику. Это не доказательство.Математика покажет, как все связано.
Разность электрических потенциалов порождает электрическое поле. (Это концепция, которую я представляю вам в этой главе, которую вы сейчас читаете.) Электрическое поле — это сила, приходящаяся на заряд, действующая на воображаемый пробный заряд в любом месте пространства. (Эта концепция была введена в главе, предшествующей этой.) Работа, совершаемая по помещению фактического заряда в электрическое поле, дает заряду электрическую потенциальную энергию. (Эта концепция называется теоремой о работе и энергии и была введена давным-давно, в очень-далекой главе.) По переходному свойству (я думаю) электрический потенциал порождает электрическую потенциальную энергию; а в силу рефлексивного свойства (еще одно предположение) электрический потенциал — это энергия на один заряд, которую воображаемый пробный заряд имеет в любом месте пространства.
Это слова. Нам нужна математика. Мы можем сделать это трудным путем (без исчисления) или простым способом (с исчислением). Твой выбор.
В любом случае, вот правила для символов, характерных для этой темы…
- Символ электрического поля выделен жирным шрифтом в верхнем регистре E .Оно выделено жирным шрифтом, потому что это векторная величина. Это верхний регистр из-за произвольного выбора. Это E, потому что это просто имеет смысл. Если вы видите символ, написанный курсивом с перечеркнутой полосой вверху, например, E , это означает, что вы используете только среднее значение магнитуды. Иногда этого достаточно.
- Символ потенциальной электрической энергии выделен курсивом в верхнем регистре U . Он выделен курсивом, потому что это скалярная величина. Это заглавные буквы, потому что… никто не знает. Это U, потому что вы должны использовать какую-то букву.Думаю, теперь очередь У. Поскольку мы имеем дело с потенциальной электрической энергией, мы должны добавить нижний индекс, заглавную букву E. Это дает нам U E . Если я забыл добавить подстрочный E, это потому, что вы должны знать из контекста, что это электрическая потенциальная энергия, а не что-то еще.
- Символ электрического потенциала выделен курсивом в верхнем регистре V . Он выделен курсивом, потому что это скалярная величина. Это верхний регистр, чтобы соответствовать электрической потенциальной энергии (возможно).Это V, потому что V следует за U в алфавите… наверное. Возможно, это также связано с названием единицы измерения электрического потенциала — вольт. Вы можете подумать, что я должен добавить к этому символу букву E в верхнем регистре, например, V E , но я этого не сделаю. Никто не делает. Формы скалярного потенциала, не являющиеся электрическими, обсуждаются настолько редко, что добавление нижнего индекса делается только для исключений — например, гравитационный потенциал, 90 227 В 91 395 г 91 396 90 228 .
без исчисления
Начните с теоремы работы-энергии.Когда работа выполнена ( Вт ), энергия изменяется (∆ E ).
З = ∆ В
Более конкретно, когда работа совершается против действия электрической силы ( F E ), электрическая потенциальная энергия изменяется (∆ U E ). Напомним, что работа равна произведению силы на перемещение ( d ). Над символом силы есть полоса, указывающая, что мы будем использовать среднее значение. Это одно из ограничений выводов, сделанных без исчисления.
F E d = ∆ U E
Разделите обе части на заряд ( q ).
Немного переставить вещи.
Отношение силы к заряду слева называется электрическим полем ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Единственное, что изменилось, это то, что сейчас мы имеем дело со средними значениями. Отношение энергии к заряду справа называется электрического потенциала ( В ).Это новая идея, которая обсуждается прямо сейчас в этой книге.
Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в пространстве. Поскольку оно получено из силы, это векторное поле. Электрический потенциал представляет собой электрическую потенциальную энергию пробного заряда, деленную на его заряд для каждого места в пространстве. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.
Электрическое поле и электрический потенциал связаны смещением.Смещение времени поля потенциально…
Эд = ∆ В
или поле является потенциальным по смещению, если хотите.
На языке причудливого исчисления поле — это градиент потенциала, потому что реальный мир — причудливый, под которым я подразумеваю трехмерность. Градиент — это трехмерный эквивалент уклона. Обычный наклон одномерен, потому что линия одномерна (даже если она не прямая). При движении по кривой нужно принять только одно решение.Мне идти вперед или вернуться? В обычном евклидовом пространстве у нас есть три варианта. Вверх или вниз? Влево или вправо? Вперед или назад?
исчисление
Начните с теоремы работы-энергии. Когда работа выполнена ( Вт ), энергия изменяется (∆ E ).
З = ∆ В
Более конкретно, когда работа совершается против действия электрической силы ( F E ), электрическая потенциальная энергия изменяется (∆ U E ).Напомним, что работа есть интеграл силы-перемещения.
| − | ⌠ ⌡ | F E · d r = ∆ U E |
Разделите обе части на заряд ( q ).
| − | 1 | ⌠ ⌡ | F E · d r = | 1 | ∆ U E |
| к | q |
Немного переставить вещи.
| − | ⌠ ⌡ | Ф Е | · д г = | ∆ U E |
| к | q |
Отношение силы к заряду слева называется электрическим полем ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Отношение энергии к заряду справа называется электрического потенциала ( В ).Это новая идея, которая обсуждается прямо сейчас в этой книге.
Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в пространстве. Поскольку оно получено из силы, это векторное поле. Электрический потенциал представляет собой электрическую потенциальную энергию пробного заряда, деленную на его заряд для каждого места в пространстве. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.
Электрическое поле и электрический потенциал связаны континуальным интегралом, который работает во всех случаях.Мой совет при работе с интегралом по путям — всегда выбирать самый простой путь для работы. Электричество — консервативная сила, поэтому совершаемая им работа не зависит от выбранного пути. Это уравнение говорит нечто более поразительное. Интеграл слева настолько независим от пути, что его значение зависит только от электрического потенциала в начале и конце пути. Если вы можете найти эти два числа и вычесть их, вы сделали весь интеграл. Если бы таким образом работало больше интегралов, ученики не так зацикливались бы на вычислениях.
| − | ⌠ ⌡ | E · d r = ∆ В |
Электрическое поле и электрический потенциал также связаны производной, которая работает только для одномерных ситуаций — ситуаций со сферической, цилиндрической или плоской симметрией.
| E = — | д | В р̂ |
| др |
В более сложных терминах исчисления поле — это градиент потенциала, потому что реальный мир более причудлив, чем одномерная задача.Градиент является эквивалентом производной в более высоких измерениях (в этой книге двух и трех измерениях). Это соотношение работает для всех видов симметрии и несимметрии.
E = −∇ В
Греческая буква дельта выглядит как треугольник вершиной вверх (∆). Перевернутая дельта называется del (∇). Символы дельта и дельта являются примерами математических устройств, называемых операторами — символами, которые указывают, что над переменной необходимо выполнить операцию.Дельта-оператор неоднократно обсуждался в этой книге. Оператор del встречается немного реже.
Дельта-оператор используется всякий раз, когда требуется изменение или разность количества. Вернемся немного назад к уравнению, которое связывает электрическое поле с электрическим потенциалом через интеграл по путям.
| − | ⌠ ⌡ | E · d r = ∆ В |
Здесь ∆ В означает разность электрических потенциалов между двумя точками — обычно начальной или начальной точкой (обозначается в этой книге нижним индексом ноль) и конечной или конечной точкой (указывается в этой книге без нижнего индекса) .
| р | ||
| − | ⌠ ⌡ | E · d r = В − В 0 |
| р 0 |
В декартовых координатах оператор del представляет собой сумму частных производных по трем направлениям единичного вектора. (В недекартовых координатах del немного сложнее).
| ∇ = î | ∂ | + ĵ | ∂ | + к̂ | ∂ |
| ∂ х | ∂ у | ∂ с |
Когда оператор del применяется к скалярному полю, результирующая операция называется градиентом . Отпрыгните немного назад. Уравнение, в котором говорится, что электрическое поле есть градиент электрического потенциала…
E = −∇ В
выглядит так, когда оператор del расширяется…
| E = — î | ∂ | В — х | ∂ | В — к̂ | ∂ | В |
| ∂ х | ∂ у | ∂ с |
и тому подобное, когда члены переставлены так, что скаляры предшествуют векторам…
| E = — | ∂ | В î — | ∂ | В х — | ∂ | В к̂ |
| ∂ х | ∂ у | ∂ с |
Может быть, теперь вы понимаете, почему был изобретен символ del.В компактном уравнении 5 символов (не считая пробелов). Расширенное уравнение имеет 23 (считая «шляпы», но не считая пробелов).
Держи сейчас. Что за дела со всеми этими минусами? Позвольте мне объяснить… позже.
единиц
электрический потенциал
Что нового в этой главе этой книги? Полное понятие электрического потенциала. Я ввел электрический потенциал как способ решить проблемы векторной природы электрического поля, но электрический потенциал — это понятие, имеющее право на существование само по себе.Электрический потенциал – это потенциальная электрическая энергия пробного заряда, деленная на заряд этого пробного заряда.
Старые вещи. SI — это сокращение от le Système international d’unités на французском языке или International System of Units на английском языке. Единицей энергии в СИ является джоуль, названный в честь Джеймса Джоуля, английского пивовара, ставшего физиком, который определил, что тепло и электричество являются формами энергии, эквивалентными другим формам механической энергии, таким как гравитационная потенциальная энергия и кинетическая энергия.Единицей заряда в СИ является кулон, названный в честь Шарля-Огюстена Кулона, французского дворянина и солдата, ставшего физиком, открывшего правило обратных квадратов электростатической силы. Единицей перемещения (или расстояния) в СИ является метр — слово, названное в честь «никого» и в конечном счете происходящее от греческого слова «мера» (μετρον, метрон ).
Новые вещи. Единицей электрического потенциала в системе СИ является вольт, названный в честь итальянского дворянина, ставшего физиком Алессандро Вольта, чье полное имя — удивительно длинное имя графа Алессандро Джузеппе Антонио Анастасио Вольта.Шутка сегодня в том, что полное имя Вольты было настолько длинным, что когда его сократили до названия подразделения, то перегнули палку и отрубили последнюю «а». Единицу электрического потенциала по праву следует называть вольтой, а не вольтом (шутка, которую оценят только педанты среди нас). Граф Вольта наиболее известен как изобретатель гальванического элемента — того, что мы сейчас ошибочно называем батареей (еще одно отличие, которое ценят только педанты — батарея — это совокупность гальванических элементов).Для тех, кто заботится о важных вещах, вольта — это джоуль на кулон.
[В = Дж/Кл]
Разность электрических потенциалов между двумя точками равна одному вольту, если для перемещения заряда в один кулон из одной точки в другую требуется работа в один джоуль.
электрическое поле
Электрический потенциал — это способ объяснить «сложное» векторное поле с помощью «простого» скалярного поля. По определению, электрическое поле — это сила, приходящаяся на заряд воображаемого пробного заряда.
Посредством длинного объяснения, электрическое поле также является градиентом электрического потенциала (скоростью изменения электрического потенциала со смещением).
Установить две величины равными…
, а затем установите их единицы измерения равными.
[Н/З = В/м]
Ньютон на кулон и вольт на метр являются эквивалентными единицами измерения электрического поля. Вольт на метр чаще используется теми, кто действительно измеряет вещи, потому что вольт (который можно измерить вольтметром) и метр (который можно измерить линейкой любого размера, включая линейку с соответствующим названием) намного больше. легче измерить, чем силу (которую можно было бы измерить с помощью пружинной шкалы или тензодатчика, прикрепленного к заряженному объекту, я полагаю) и заряд (который можно было бы измерить без какого-либо устройства, о котором я знаю).
электрическая потенциальная энергия
Если вольт — это джоуль на кулон, то джоуль — это кулон-вольт. Когда один кулон заряда перемещается через разность электрических потенциалов в один вольт, его энергия изменяется на один джоуль.
[J = CV]
Для некоторых приложений джоуль слишком велик, в основном потому, что слишком велик кулон. Обычной малой единицей заряда является элементарный заряд [е]. Это самый маленький заряд из когда-либо наблюдавшихся. Некоторые частицы, например протон, имеют этот заряд со знаком плюс ( q протон = +1 е), а некоторые, например электрон, со знаком минус ( q электрон = -1 е ).Когда один элементарный заряд проходит через разность электрических потенциалов в один вольт, его энергия изменяется на один электронвольт [эВ] — плюс или минус один электронвольт в зависимости от знака заряда и знака разности потенциалов. Электронвольт используется для некоторых приложений в электромагнетизме; физика твердого тела, атома, ядра и элементарных частиц; и смежные науки, такие как биофизика, химия и астрономия. Это хороший небольшой блок для небольших физических систем, таких как атомы и молекулы.На самом деле это слишком мало для ядерной физики и физики элементарных частиц, но следующей по величине единицей СИ является джоуль, который на 19 порядков больше.
| кв = | кв |
| 1 электронвольт = | (1 элементарный заряд) (1 вольт) |
| 1 электронвольт = | (1,6 × 10 -19 Кулонов) (1 вольт) |
| 1 электронвольт = | 1,6 × 10 −19 джоулей |
| 1 EV = | 1.6 × 10 −19 Дж |
Электронвольт на самом деле не является единицей СИ, поскольку элементарный заряд не определяется как единица. Заряд электрона, протона или чего-либо еще с элементарным зарядом должен быть получен экспериментально и поэтому неизвестен. Электронвольт был «принят для использования» с SI МКМВ ( le Comité international des poids et mesures или Международный комитет мер и весов).
Эксперимент Миликана
Роберт Милликен (1865–1953) США
аппарат
выводы
Зарядка, разница тока и потенциала
Обозначения схем — вы встречали эти обозначения схем на выпускных экзаменах по физике.
Условный ток протекает по цепи от положительной (+) стороны элемента к отрицательной (-). Однако электрона текут по цепи в противоположном направлении от отрицательной (-) стороны ячейки к положительной (+).
Разница заряда, тока и потенциала
Заряд (Q) – заряд измеряется в кулонах (Кл).
- Один электрон несет заряд 1,6 x 10 -19 Кл.
Ток (I) – измеряется в амперах (А).
- Ток — скорость потока заряда . Ток в 1 А означает, что каждую секунду через точку цепи проходит заряд в 1 кулон. ( 1 A = 1 C s -1 ) Ток в цепи измеряется с помощью амперметра, который включается последовательно с интересующим компонентом в цепи.
- I = ток в амперах, А
- DQ = заряд в кулонах, Кл
- Dt = время в секундах, с
Разность потенциалов (В) — измеряется в вольтах (В).
- Потенциальная разница – это работа, выполненная на единицу заряда . Разность потенциалов в 1 В означает, что на один кулон заряда совершается работа в 1 джоуль. ( 1 В = 1 Дж C -1 ) Разность потенциалов в цепи измеряется с помощью вольтметра, который устанавливается параллельно интересующему компоненту в цепи.
- В = разность потенциалов в вольтах, В
- Вт = выполненная работа или переданная энергия в джоулях, Дж
- Q = заряд в кулонах, Кл

 4 Розв’язання d
4 Розв’язання d


 c.) проходить через него, но блокирует постоянный ток (d.c.)*.
c.) проходить через него, но блокирует постоянный ток (d.c.)*.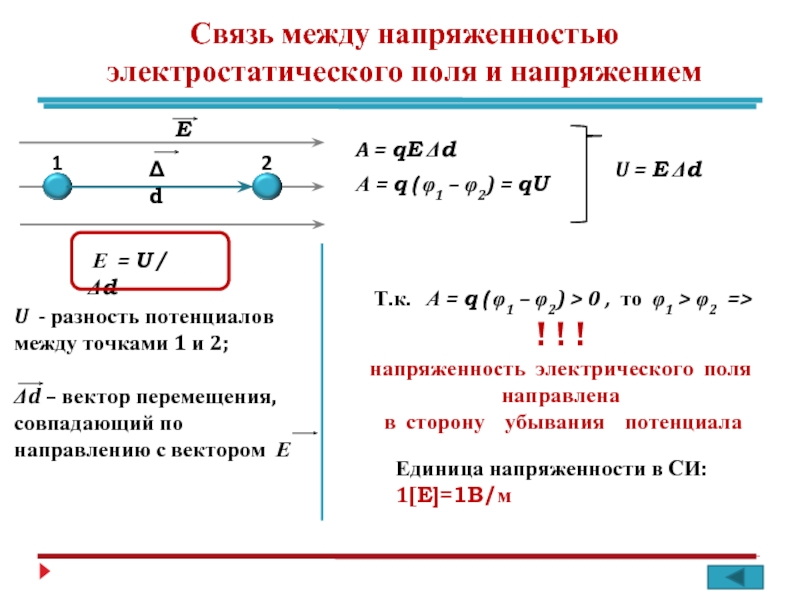
 в. но не
в. но не  Конденсатор подключен к источнику питания 12 В постоянного тока. поставка. Вычислите емкость конденсатора.
Конденсатор подключен к источнику питания 12 В постоянного тока. поставка. Вычислите емкость конденсатора.