Индуцированный заряд Вики. Индуцированные заряды

Индуцированный заряд

Физика > Индуцированный заряд

Электростатическая индукция – перераспределение зарядов внутри объекта, выступающее реакцией на присутствие близкого заряда.

Задача обучения

Сравните электростатические индукционные процессы в проводниках и диэлектриках.

Основные пункты

Если рядом с незаряженной частью вещества появилась заряженная, то она способна создать перераспределение заряда в нейтральном материале. Это один из типов индукции.
Если контактируют заряженный и незаряженный объекты, то они создают заряд, объединяющий промежуток между ними, а заряженный повышает свой заряд. Это еще один тип индукции.
Способные реагировать на индукторы субъекты включают проводники и диэлектрики. В первом варианте свободный поток зарядов приводит к сильной поляризации, а во втором – сила относительно слабая.

Термины

Диэлектрик – электрически изолирующий или непроводящий материал, рассматриваемый из-за его электрической восприимчивости.
Разряд – высвобождение накопленного заряда.
Индуктор – пассивное устройство, которое приводит индуктивность в электрическую цепь.

Электростатическая индукция – перераспределение заряда внутри объекта. Это реакция на соседний заряд. Единица материи обычно обладает равными частями положительного и отрицательного зарядов, распределенных равномерно по объему. Так что, можно говорить, что здесь нет чистого заряда.

Если заряженная часть вещества расположена близко к незаряженной, то приводит к перераспределению заряда в нейтральном материале. Тогда электроны в нейтральном перемещаются в соответствии с зарядом соседнего заряженного тела. При положительном знаке индуктора, электроны устремятся к нему, делая незаряженный объект еще более отрицательным.

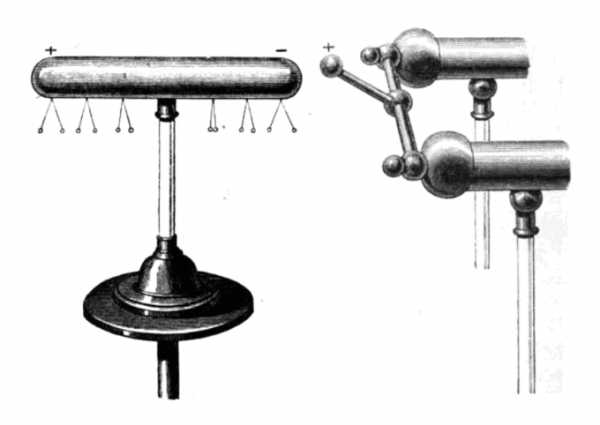
Положительный конец электростатического генератора движется рядом с незаряженным латунным цилиндром, заставляя его поляризоваться по мере того, как левый конец приобретает положительный заряд, а правый – отрицательный

Если заряженные и незаряженные тела контактируют, то создают разряд, объединяющий промежуток между ними. Основываясь на знаке заряда индуктора, электроны перейдут или уйдут из ранее незаряженного объекта. Общий заряд сберегается, а индуктор будет уменьшаться по мере передачи заряда объекту.

Субъекты, способные реагировать на индукторы, включают проводники и диэлектрики. В первом варианте поток зарядов создает сильную поляризацию. А во втором – сила относительно слабая.

Индуцированный заряд

Оцените нашу статью

v-kosmose.com

Индуцированный заряд - это... Что такое Индуцированный заряд?

Индуцированный заряд Эксперимент с электроскопом показывающий возникновение индуцированного заряда.

Генератор высокого напряжения на базе эффекта электростатической индукции.

Электростатическая индукция — явление наведения собственного электростатического поля, при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур[1] у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем.

Электростатическая индукция в проводниках

Перераспределение электронов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды практически полностью не скомпенсируют внешнее электрическое поле внутри тела. При этом на противоположных сторонах[2] проводящего тела появятся противоположные наведённые(индуцированные) заряды.

Электростатическая индукция в диэлектриках

Диэлектрики в электростатическом поле поляризуются.

Применение

Наиболее массовое применение находит основанная на данном явлении электростатическая защита приборов и соединительных цепей.

Данный эффект используется в ряде приборов, например в генераторе Ван де Граафа.

Ссылки

Примечания

↑ атомов, молекул, кристаллических решёток и т.п.
↑ относительно внешнего электрического поля

Wikimedia Foundation. 2010.

Индуцированное излучение
Индуцированное испускание

Смотреть что такое "Индуцированный заряд" в других словарях:

индуцированный заряд — наведённый заряд — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы наведённый заряд EN induced chargeinductive … Справочник технического переводчика
индуцированный заряд — indukuotasis krūvis statusas T sritis fizika atitikmenys: angl. induced charge vok. induzierte Ladung, f; Influenzladung, f rus. индуцированный заряд, m; наведенный заряд, m pranc. charge induite, f … Fizikos terminų žodynas
индуцированный электрический заряд — indukuotasis krūvis statusas T sritis Standartizacija ir metrologija apibrėžtis Dažniausiai tai tam tikroje terpės vietoje elektromagnetinio lauko ar kitokio poveikio sukurtas elektros krūvis. atitikmenys: angl. induced electric charge vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
индуцированный электрический заряд — indukuotasis elektros krūvis statusas T sritis fizika atitikmenys: angl. induced electric charge vok. induzierte elektrische Ladung, f rus. индуцированный электрический заряд, m; наведённый электрический заряд, m pranc. charge électrique induite … Fizikos terminų žodynas
наведенный заряд — indukuotasis krūvis statusas T sritis fizika atitikmenys: angl. induced charge vok. induzierte Ladung, f; Influenzladung, f rus. индуцированный заряд, m; наведенный заряд, m pranc. charge induite, f … Fizikos terminų žodynas
наведенный электрический заряд — indukuotasis krūvis statusas T sritis Standartizacija ir metrologija apibrėžtis Dažniausiai tai tam tikroje terpės vietoje elektromagnetinio lauko ar kitokio poveikio sukurtas elektros krūvis. atitikmenys: angl. induced electric charge vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
наведённый электрический заряд — indukuotasis elektros krūvis statusas T sritis fizika atitikmenys: angl. induced electric charge vok. induzierte elektrische Ladung, f rus. индуцированный электрический заряд, m; наведённый электрический заряд, m pranc. charge électrique induite … Fizikos terminų žodynas
Вольта Алессандро — (Volta) (1745 1827), итальянский физик и физиолог, один из основоположников учения об электричестве. Создал первый химический источник тока (1800, вольтов столб). Открыл контактную разность потенциалов. * * * ВОЛЬТА Алессандро ВОЛЬТА (Volta)… … Энциклопедический словарь
Influenzladung — indukuotasis krūvis statusas T sritis fizika atitikmenys: angl. induced charge vok. induzierte Ladung, f; Influenzladung, f rus. индуцированный заряд, m; наведенный заряд, m pranc. charge induite, f … Fizikos terminų žodynas
charge induite — indukuotasis krūvis statusas T sritis fizika atitikmenys: angl. induced charge vok. induzierte Ladung, f; Influenzladung, f rus. индуцированный заряд, m; наведенный заряд, m pranc. charge induite, f … Fizikos terminų žodynas

dic.academic.ru

Индуцированный заряд Википедия

Эксперимент с электроскопом показывающий возникновение индуцированного заряда.

Электростатическая индукция — явление наведения собственного электростатического поля при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур[1] у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем.

Электростатическая индукция в проводниках

Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах[2] проводящего тела появятся противоположные наведённые (индуцированные) заряды.

Электростатической индукцией в проводниках пользуются при их заряжении. Так, если проводник заземлить и поднести к нему заряженное отрицательно тело, не касаясь им проводника, то некоторое количество отрицательных зарядов перетечёт в землю, заместившись взамен положительными. Если теперь убрать заземление, а затем и заряженное тело, проводник останется положительно заряженным. Если же сделать то же самое, не заземляя проводник, то после убирания заряженного тела индуцированные на проводнике заряды перераспределятся, и все его части вновь станут нейтральными[3].

Электростатическая индукция в диэлектриках

Диэлектрики в электростатическом поле поляризуются.

Применение

Данный эффект используется в ряде приборов, например в генераторе Ван де Граафа.

Примечания

↑ атомов, молекул, кристаллических решёток и т.п.
↑ относительно внешнего электрического поля
↑ § 8. Электризация через влияние. // Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 2. Электричество и магнетизм. — С. 24—27.

Ссылки

wikiredia.ru

Fizika - Стр 3

где - длина конденсатора, R1 и R2 – радиусы внутренней и наружной цилиндрических обкладок. Емкость сферического конденсатора определяется формулой:

, (3.5.11)

где R1 и R2 – радиусы внутренней и наружной обкладок. Отметим, что формулы (3.5.10) и (3.5.11) при малом зазоре между обкладками переходят в формулу (3.5.9)

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу

Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4)

где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора. Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость Поэтому

где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.

Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладаетпотенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.

Рассмотрим сначала систему, состоящую из двух точечных зарядов. Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближаяq2кq1либоq1кq2. В обоих случаях совершается одинаковая работа:

В последней формуле - потенциал поля 1-го заряда в том месте, где находится второй заряд;- потенциал поля второго заряда в том месте, где находится первый заряд. С учетом сказанного, эту формулу можно записать также в виде:

Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов может быть представлена в виде:

В общем случае системы n неподвижных точечных зарядовэнергия системыопределяется по формуле:.

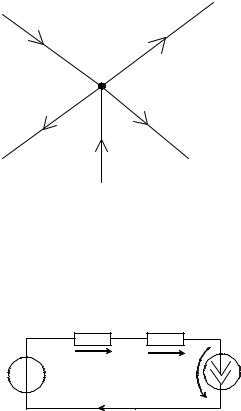
Если проводник поместить во внешнее электростатическое поле или зарядить его, то на заряды данного проводника будет действовать электростатическое поле, под действием которого они начнут двигаться. Движение зарядов (ток) будет длиться до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри данного проводника обращается в нуль. Это происходит в течение очень короткого времени. Действительно, если бы поле не было равно нулю, то в проводнике появилось бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что не согласуется с законом сохранения энергии. Значит, напряженность поля во всех точках внутри проводника равна нулю: Если внутри проводника электрического поле отсутствует, то потенциал во всех точках внутри проводника одинаков (φ = const), т. е.поверхность проводника в электростатическом поле является эквипотенциальной. Это означает, что вектор напряженности поля на внешней поверхности проводника направлен по перпендикуляру к каждой точке его поверхности. Если это было бы не так, то под действием касательной составляющейЕзаряды начали бы перемещаться по поверхности проводника, что, в свою очередь, противоречило бы равновесному распределению зарядов. Если проводнику дать некоторый дополнительный заряд Q, то нескомпенсированные заряды разместятьсятолько на поверхности проводника. Это вытекает непосредственно из теоремы Гаусса, согласно которой заряд Q, который находится внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равенпоскольку во всех точках внутри замкнутой поверхности D=0. Теперь мы будем искать взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью зарядов на его поверхности σ . Для этого используем теорему Гаусса для бесконечно малого цилиндра с основаниями ΔS, который пересекает границу проводник—диэлектрик. Ось цилиндра направлена вдоль вектораЕ(рис. 1). Поток вектора электрического смещения через внутреннюю часть цилиндрической поверхности равен нулю, так как внутри проводникаЕ1(а следовательно, иD1) есть нуль, поэтому поток вектораDсквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Используя теорему Гаусса, этот поток (DΔS) равен сумме зарядов (Q=σΔS), находящихся внутри поверхности: DΔS=σΔS т.е.(1) или(2) где ε — диэлектрическая проницаемость среды, находящаяся вокруг проводника. Значит, напряженность электростатического поля у поверхности проводника задается поверхностной плотностью зарядов. Можно показать, что формула (2) задает напряженность электростатического поля вблизи поверхности проводника абсолютно произвольной формы. Если во внешнее электростатическое поле поместить нейтральный проводник, то свободные заряды (электроны, ионы) будут совершать движение: положительные — по полю, отрицательные — против поля (рис. 2, а). На одном конце проводника будет собираться избыток положительного заряда, на другом — избыток отрицательного заряда. Эти заряды называютсяиндуцированными(наведенными). Процесс будет продолжаться до тех пор, пока внутри проводника напряженность поля не станет равной нулю, а линии напряженности вне проводника — перпендикулярными его поверхности (рис. 2, б). Значит, нейтральный проводник, который внесен в электростатическое поле, разрывает часть линий напряженности; эти линии напряженности заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности нашего проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называетсяэлектростатической индукцией. Из рис. 2, б мы видим, что индуцированные заряды образуются на проводнике вследствие смещения их под действием поля, т. е. σ есть поверхностной плотностью смещенных зарядов. Согласно (1), электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. По этой причине векторDполучил название вектора электрического смещения.

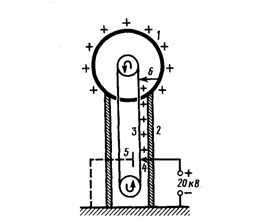
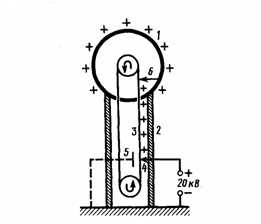
Поскольку в состоянии равновесия заряды отсутствуют внутри проводника, то создание внутри него полости не окажет влияния на конфигурацию расположения зарядов и тем самым на электростатическое поле. Значит, поле будет отсутствовать внутри полости. Если теперь заземлить данный проводник с полостью, то потенциал во всех точках полости будет равен нулю, т. е. полость полностью является изолированной от влияния внешних электростатических полей. На этом основана электростатическая защита— экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Для защиты вместо сплошного проводника может быть использована густая металлическая сетка, которая, также эффективна при наличии не только постоянных, но и переменных электрических полей. Свойство зарядов располагаться на внешней поверхности проводника на практике используется для устройстваэлектростатических генераторов, которые предназначены для накопления больших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, который изобретен американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 3), укрепленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, которые соединены с одним из полюсов источника, второй полюс которого заземлен. Заземленная пластина 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Значит, сфера постепенно получает большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы широко применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.

Индуцированные заряды- это заряды противоположного знака, появившиеся в результате разделения у концов проводника.

Результирующие поле определяется как суперпозиция внешнего поля и поля

индуцированных зарядов. Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах проводящего тела появятся противоположные индуцированные заряды.

Экранировка электростатического поля: Если внесенное во внешнее электрическое поле тело не было заряжено, то сумма наведенных на нем зарядов оказывается равной нулю. Эти заряды распределяются так, чтобы их поле внутри проводящего тела в точности скомпенсировало внешнее поле. Ничто не изменится, если проводящее тело будет полым – во всей полости тела поле также будет отсутствовать. Этим обстоятельством широко пользуются дляэлектростатического экранированияразличных приборов и аппаратов от внешних электрических полей. С этой целью приборы помещают в замкнутые металлические оболочки, называемые экранами. Как показывает опыт, экраны можно выполнять и из мелкой металлической сетки.

Если экран заземлить, то такой экран способен в равной мере защищать внешнее пространство от поля зарядов, помещенных внутри экрана.

studfiles.net

Распределение заряда по поверхности проводника

Задание: Бесконечно длинная нить, заряженная с линейной плотностью $\tau $, расположена перпендикулярно бесконечно большой проводящей плоскости. Расстояние от нити до плоскости $l$. Если продолжить нить до пересечения с плоскостью, то в месте пересечения получим некоторую точку А. Составьте формулу зависимости поверхностной плотности $\sigma \left(r\right)\ $индуцированных зарядов на плоскости от расстояния до точки А.

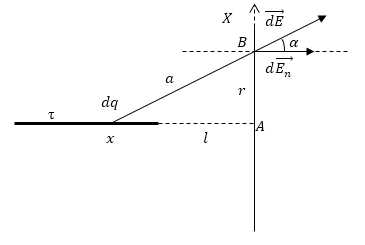
Рис. 1

Решение:

Рассмотрим некоторую точку В на плоскости. Бесконечно длинная заряженная нить в точке В создает электростатическое поле, в поле находится проводящая плоскость, на плоскости образуются индуцированные заряды, которые в свою очередь создают поле, которое ослабляет внешнее поле нити. Нормальная составляющая поля плоскости (индуцированных зарядов) в точке В будет равна нормальной составляющей поля нити в этой же точке, если система находится в равновесии. Выделим на нити элементарный заряд ($dq=\tau dx,\ где\ dx-элементарный\ кусочек\ нити\ $), найдем в точке В напряжённость, создаваемую этим зарядом ($dE$):

\[dE=\frac{\tau dx}{4\pi {\varepsilon }_0\varepsilon a^2}\left(1.1\right).\]

Найдем нормальную составляющую элемента напряженности поля нити в точке В:

\[dE_n=dEcos\alpha =\frac{\tau dxcos\alpha }{4\pi {\varepsilon }_0\varepsilon a^2}\left(1.2\right),\]

где $cos\alpha $ выразим как:

\[cos\alpha =\frac{x}{a}\left(1.3\right).\]

Выразим расстояние $a$ по теореме Пифагора как:

\[a=\sqrt{r^2+x^2}\ \left(1.4\right).\]

Подставим (1.3) и (1.4) в (1.2), получим:

\[dE_n=\frac{\tau dx}{4\pi {\varepsilon }_0\varepsilon a^2}\frac{x}{a}=\frac{\tau xdx}{4\pi {\varepsilon }_0\varepsilon {\left(r^2+x^2\right)}^{{3}/{2}}}\left(1.5\right).\]

Найдем интеграл от (1.5) где пределы интегрирования от $l\ (расстояние\ до\ ближайшего\ конца\ нити\ от\ плоскости)\ до\ \infty $:

\[E_n=\int\limits^{\infty }_l{\frac{\tau xdx}{4\pi {\varepsilon }_0\varepsilon {\left(r^2+x^2\right)}^{{3}/{2}}}}=\frac{\tau }{4\pi {\varepsilon }_0\varepsilon }\int\limits^{\infty }_l{\frac{xdx}{{\left(r^2+x^2\right)}^{{3}/{2}}}}=\frac{\tau }{4\pi {\varepsilon }_0\varepsilon }\cdot \frac{1}{{\left(r^2+x^2\right)}^{{1}/{2}}}\left(1.6\right).\]

С другой стороны, мы знаем, что поле равномерно заряженной плоскости равно:

\[E=\frac{\sigma}{2\varepsilon {\varepsilon }_0}\ \left(1.7\right).\]

Приравняем (1.6) и (1.7), выразим поверхностную плотность заряда:

\[\frac{1}{2}\cdot \frac{\sigma}{\varepsilon {\varepsilon }_0}=\frac{\tau }{4\pi {\varepsilon }_0\varepsilon }\cdot \frac{1}{{\left(r^2+x^2\right)}^{{1}/{2}}}\to \sigma=\frac{\tau }{2\cdot \pi {\left(r^2+x^2\right)}^{{1}/{2}}}.\]

Ответ: $\sigma=\frac{\tau }{2\cdot \pi {\left(r^2+x^2\right)}^{{1}/{2}}}.$

spravochnick.ru

Индуцированный заряд Википедия

Эксперимент с электроскопом показывающий возникновение индуцированного заряда.

Электростатическая индукция в проводниках[ | код]

Электростатическая индукция в диэлектриках[ | код]

Диэлектрики в электростатическом поле поляризуются.

Применение[ | код]

Данный эффект используется в ряде приборов, например в генераторе Ван де Граафа.

Примечания[ | код]

↑ атомов, молекул, кристаллических решёток и т.п.
↑ относительно внешнего электрического поля
↑ § 8. Электризация через влияние. // Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 2. Электричество и магнетизм. — С. 24—27.

Ссылки[ | код]

ru-wiki.ru