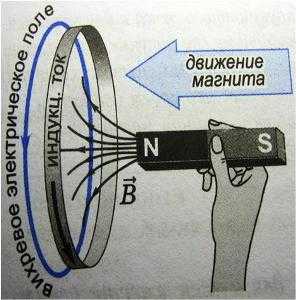
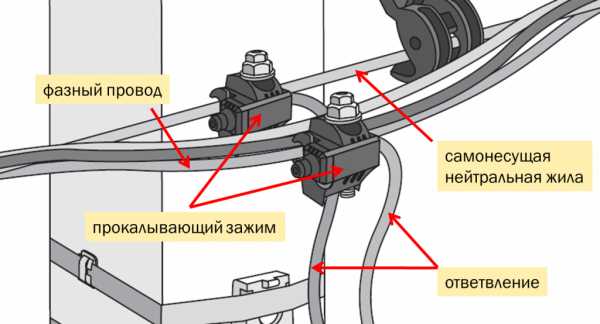
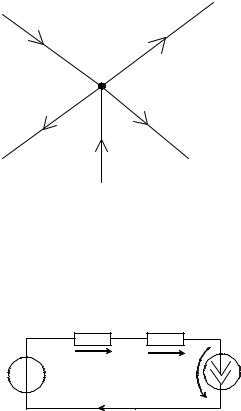
11. Расчёт сложных схем по уравнениям Кирхгофа. Для исследуемых электрических цепей запишите уравнения по законам кирхгофа

Уравнения Кирхгофа

89

ПРИЛОЖЕНИЕ Б

Примеры решения задач модуля 1

Задача 1 В узле электрической цепи сходятся ветви, направление токов в которых и их значения приведены на схеме.

Необходимо определить неизвестный ток I5.

Решение		I1
		5A
Запишем уравнение по первому за-
							I2
кону Кирхгофа для данного узла:							8A
I1− I2− I3+ I4− I5= 0 ,						I3
откуда	I5
					11A
I5= I1− I2− I3+ I4=				I4
=5−8−11+ 3= −11A.				3A

Проверка:

5 – 8 – 11 + 3 – (– 11) = 0, Рисунок 1.1 – Исследуемый узел

0 ≡ 0.

		Уравнения Кирхгофа
Задача	2 Дана электрическая цепь				R1	R2
(рис. 2.1): R1	= 10 Ом, R2	= 20 Ом, Е = 15 В,	E	+	u1
J = 1 A.						u2	uj	J
Определить uj.						I

Рисунок 2.1 – Исследуемая цепь

Решение

Направление тока I в данной схеме совпадает с направлением тока источника токаJ. Тогда напряженияU1 иU2 направлены как показано на рисунке и равны соответственно:

U1 = I R1 =1 10=10B;

U2 = I R2 =1 20= 20В.

Запишем уравнение по второму закону Кирхгофа для данного контура:

U1 +U2 +Uj − E= 0;

U j = E −U1 −U2 =10−10− 20= −10B.

Знак „минус” означает, что направление напряжения источника тока обратно указанному на схеме.

						90
	R1 I1		I2	R2		Задача 3 Определить токи в ветвях
	E1+ u1		I3		E2	методом уравнений Кирхгофа для цепи
		R3		u2		рис. 3.1.
			u3			Дано: R1 = 10 Ом,R2 = 20 Ом,
		К1		К2	+	R3 = 30 Ом,Е1 =20 В,Е2 =10 В.
						Для данной схемы можно записать
	Рисунок 3.1 – Исследуемая цепь
						одно независимое уравнение по первому

закону Кирхгофа и два – по второму закону. Для этого выберем произвольно направления токов I1,I2,I3. как показано на рис. 3.1 и направления обходов контуров, как показано на этом рисунке штриховыми стрелками. В результате, на основании первого и второго законов Кирхгофа, получим систему уравнений вида

Узел: I1− I 2− I3

= 0;

К1

U 1+ U 3− E1= 0;

К2

U 2− E2−U 3= 0.

Выразим напряжения U1,U2,U3 через токи и сопротивления:

I1− I2− I3= 0;

I1R1+ 0 + I3R3= E1;

0 + I2R2− I3R3= E2.

Теперь токи I1,I2,I3 можно определить с помощью определителей:

I1= ∆1 ; I2

= ∆2 ; I3

=

∆3

,

где

∆

∆

∆

−1

−1

−1

−1

1

1

∆ =

R1

0

R3

=

10

0

30

= −600−[10 (30+ 20)]= −1100;

0

R2

− R3

0

20

− 30

0

−1

−1

= −E1[R3 − R2 ]+ E2 [− R3 ]= −20 (50)+10 (−30)= −1000−300= −1300;

∆1 =

E1

0

R3

E2

R2

− R3

1

0

−1

= −E1[− R3 ]− E2 [R3 + R1 ]= 20(−30)−10(40)= −600− 400= −1000;

∆2 =

R1

E1

R3

0

E2

− R3

1

−1

0

∆3 =

R1

0

E1

=−E1 R2 +E2 R1 =−20 20+10 10=−400+100=−300;

0

R2

E2

										91
	I1	=	1300	=1,182A ,I2	=	1000	= 0,91A ,I3 =		300	= 0,273A .
			1100			1100		1100

Проверку найденных токов можно произвести с помощью баланса мощностей:

∑Pk=0 ,

или Рист= Рпотр.

− I1E1− I2E2+ I12 R1+ I22 R2+ I32 R3= 0.

После подстановки значений убеждаемся в правильности полученных значений токов. Эту операцию советуем проделать самостоятельно.

Анализ цепи с одним источником энергии

Задача 4 Определить токи ветвей и напряжения на элементах цепи, схема которой изображена на рис. 4.1. Параметры элементов следующие:

Е = 6 В,R1 = 5 Ом,R2 = 30 Ом,R3 = 10 Ом,R4 = 20 Ом.

I1	R1		I3	R3
	U1		I2	U3
					U4
E		R2	U2	R4
Рисунок 4.1 – Исследуемая цепь

				Решение
	1 Обозначим направления токов и					R1		I2
	напряжений, как показано на схеме					I1
								I3
	рис. 4.1.					U1
	2 Так как цепь содержит последо-								R34	U34
					E		R2	U2
	вательно-параллельные		соединения
	элементов, то воспользуемся методом
	эквивалентных преобразований. Со-
	противления R3 иR4 на схеме рис. 4.1					Рисунок 4.2 – Эквивалентное
	соединены последовательно; их можно					преобразование рис. 4.1
	заменить одним эквивалентным сопро-
	тивлением R34, величина которого
	R34 =R3 +R4 = 10 + 20 = 30 Ом.
	После преобразования схема приобретает вид рис. 4.2.
	В данной схеме сопротивления R2 и					R34 соединены параллельно. Заменим
	их одним эквивалентным сопротивлением R234:
	R		= R2 R34 = 30 30=15 Ом
	234			R2+ R34	30 + 30
	При этом U2 =U34 =U3 +U4 . Токи в ветвях определим по формуле „чужого”
	сопротивления: I2 = I1 R	R34		; I3= I1	R	R2
		+ R				+ R .
	2		34		2	34

92

I1

R1

Преобразованная схема приобретает вид

рис. 4.3.

+

Схема рис. 4.3 содержит последователь-

U1

ное соединение источника напряжения и двух

E

R234

U234

сопротивлений. Ток в цепи и напряжения на

элементах определим по закону Ома:

I

=

E

=

6

= 0,3A;

Рисунок 4.3 – Эквивалентное

1

R1

+ R234

5

+15

преобразование цепи 4.2

U1 = I1 R1 = 0,3 5=1,5B;

Определим токи I2 иI3 (см. выше)

U2 = I1 R234 = 0,3 15= 4,5B.

I2

= 0,3

30

= 0,15A;

30 +30

I

= 0,3

30

= 0,15A.

3

30 +30

По закону Ома определим напряжения

U3 =I 3 R3 = 0,15 10=1,5 B;

U4 =I 3 R4 = 0,15 20= 3 B.

3 Проверку расчетов можно выполнить, составив уравнение баланса мощностей для исходной цепи:

−E I1+ I1U1+ I2U2+ I3U3+ I4U4= 0.

Подставим значения и произведем расчеты:

−6 0,3 + 0,3 1,5+ 0,15 4,5+ 0,15 1,5+ 0,15 3= 0;

−1,8 + 0,45+ 0,675+ 0,225+ 0,45= 0;

−1,8 +1,8= 0;0≡ 0.

Проверка подтвердила правильность расчетов.

					Метод наложения
I1	R1	1 I	R3		2 I	Задача 5 Методом наложения
						определить токи ветвей цепи, схема
		I2	3		4
				J		которой изображена на рис. 5.1. Па-
E		R2			R4	раметры элементов следующие:
						Е = 6 В;I = 0,6 A;R1 =R2 = 20 Ом;
						R3 =R4 = 10 Ом.

3

Рисунок 5.1 – Исследуемая цепь

studfiles.net

1.7. Законы Кирхгофа

Законы Кирхгофа устанавливают соотношения между токами и напряже­ниями в разветвленных электрических цепях произвольного типа.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, чтоалгебраическая сумма токов, сходящихся в любом узле, равна нулю

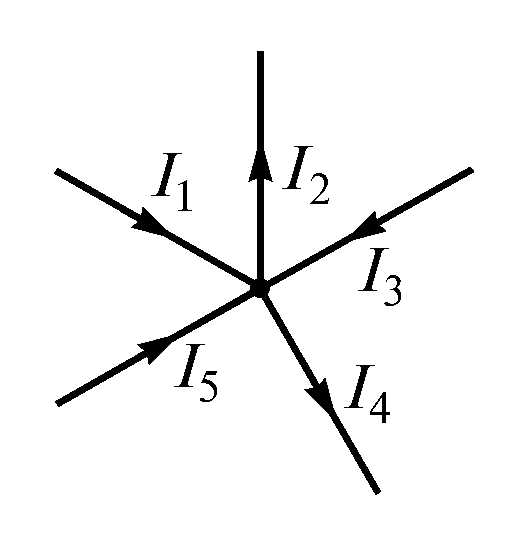
Рис. 1.15

, (1.29)

где – число токов, сходящихся в данном узле.

Например, для узла электрической цепи (рис. 1.15) уравне­ние по первому закону Кирхгофа можно записать в виде

.

В этом уравнении токи, направленные к узлу, приняты поло­жительными.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгеб­раической сумме ЭДС в этом контуре

, (1.30)

где k– число источников ЭДС;– число ветвей в замкнутом контуре;– ток и сопротивление-й ветви.

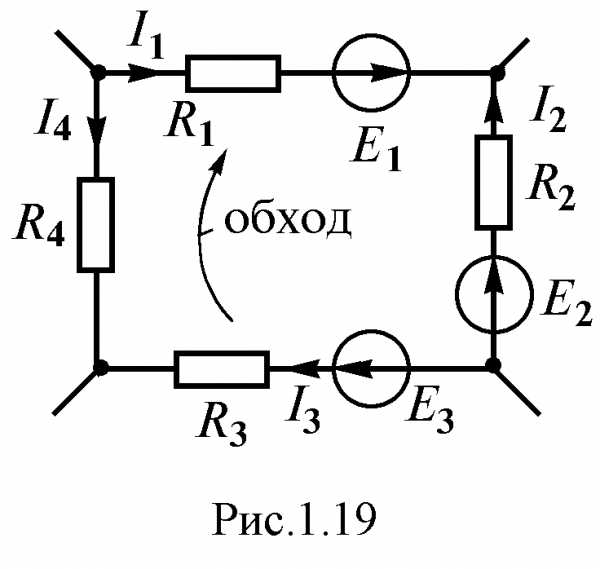
Рис. 1.16

Так, для замкнутого контура схемы (рис. 1.16)

.

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпа­дает с направлением произвольно выбранного об­хода контура;

2) падение напряжения на резисторе положи­тельно, если направление тока в нем совпадает с на­правлением обхода.

1.8. Преобразование линейных электрических схем

Расчет и исследование сложных электрических схем во многих случаях можно значительно облегчить за счет преобразования. Суть преобразования заключается в замене участков цепи эквивалентными, но более простыми, т.е. не вызывающими изменения напряжения и токов в остальной части цепи.

1.8.1. Последовательное соединение резисторов

Если несколько резисторов соединены один за другим без разветвлений и по ним протекает один и тот же ток, такое соединение называется последова­тельным(рис. 1.17 а). Обозначим сопротивления отдельных резисторов через, а напряжения на них соответственно.

По второму закону Кирхгофа имеем

. (1.31)

Разделим обе части формулы (1.31) на ток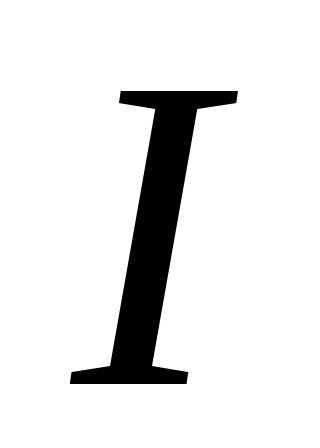

или

. (1.32)

Таким образом, при последовательном соединении эквивалентное или об­щее сопротивление равно сумме сопротивлений отдельных участков цепи (рис. 1.17 б). В общем случае

, (1.33)

где – число последовательно соединенных резисторов.

Ток в этой цепи

.

Напряжения на отдельных участках определяются по формулам

.

Последовательное соединение приемников энергии нашло широко применя­ется в различных областях техники. Оно используется обычно в тех слу­чаях, когда расчетное напряжение приемника меньше напряжения источника электрической энергии.

1.8.2. Параллельное соединение резисторов

Параллельнымсоединением приемников называется такое соединение, при котором к одним и тем же двум узлам электрической цепи присоединяется несколько ветвей (рис. 1.18).

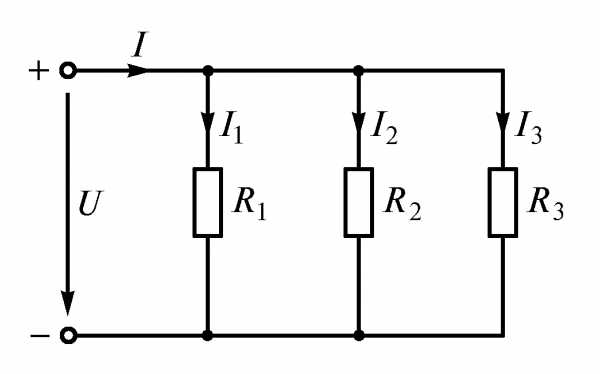
Рис. 1.18

В соответствии с законом Ома и пер­вым законом Кирхгофа

;

или

. (1.34)

Сократив обе части равенства на , получим

или

. (1.35)

Таким образом, общая (эквивалентная) проводимость при параллельном соединении приемников равна сумме проводимостей параллельных ветвей.

Из формулы (1.34) определяем общее сопротивление трех ветвей

. (1.36)

Если параллельно включены одинаковых резисторовRi, то эквивалент­ное сопротивление цепивраз меньше сопротивления одной ветви

. (1.37)

Во всех случаях параллельного соединения эквивалентное сопротивление меньше самого малого из параллельно включенных.

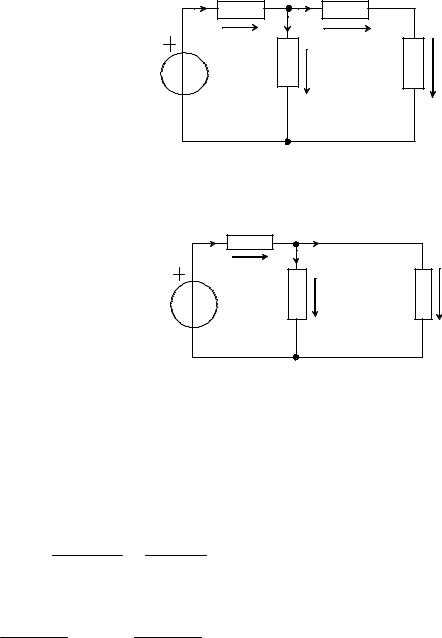
Практический интерес представляет цепь с двумя параллельными резисто­рами (рис. 1.19). Эквивалентное сопротивление ее рассчитывают по формуле

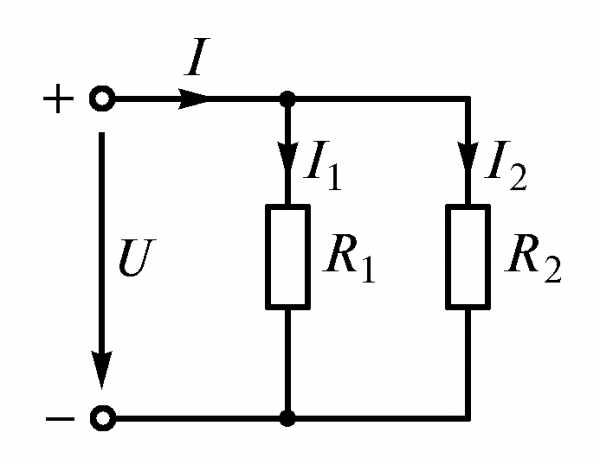
Рис. 1.19

. (1.38)

Токи в ветвях можно выразить через общий ток

;.

Параллельное соединение имеет свои особенности: все приемники находятся под одним напряжением; при неизменном напряжении отключение одного или не­скольких приемников энергии не нарушает режима работы оставшихся вклю­ченными приемников.

21

studfiles.net

Первый и второй законы Кирхгофа и их практическое применение

Уравнения, или правила, Кирхгофа относят к основным законам электрических цепей.

Они вытекают из таких фундаментальных законов как, закон сохранения заряда и безвихревости электростатического поля, в своё время описанных уравнениями Максвелла. Уравнения Кирхгофа довольно часто используются благодаря своей универсальности, пригодности для решения многих задач в теории электротехники, в том числе и связанных с расчётами сложных электрических цепей, практичности. Применяя правила Кирхгофа к линейной электрической цепи можно получить систему линейных уравнений, из которых в свою очередь, можно найти значения токов на всех ветвях цепи и все межузловые напряжения.

В правилах Кирхгофа применяют такие понятия электрической цепи, как: узел, ветвь, контур.  Участок электрической цепи с одним и тем же током называют ветвью, например отрезок 1-4, на рисунке 1, с протекающим по нему током i1 , есть ветвь. Точку, соединяющую три и более ветви называют узлом, например точки 1,2,3,4 на рисунке 1 есть узлы. Замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи называют контуром. Начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, и возвратившись в исходный узел, мы пройдём путь, который и называют замкнутым. Проходимые при таком обходе ветви и узлы принято называть принадлежащими данному контуру, при этом надо принимать во внимание, что ветвь и узел могут принадлежать одновременно нескольким контурам.

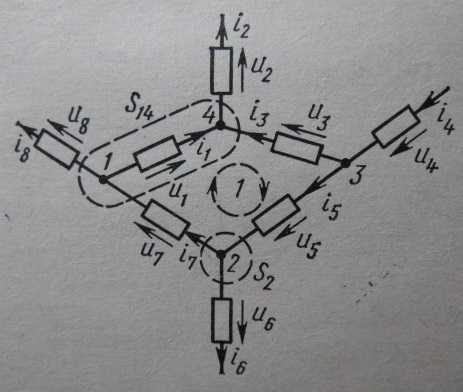Рисунок 1

Первое правило Кирхгофа построено на основании утверждения о непрерывности электрического тока для любого узла электрической цепи или замкнутого контура.

Первое правило Кирхгофа трактует, что алгебраическая сумма токов ветвей , для любого узла или замкнутого сечения электрической цепи, равна нулю:

Выше сказанное говорит о том, что электрические заряды в узле (например, S2 на рисунок 1) или сечении (например, S14  на рисунке 1) любой электрической цепи накапливаться не могут. Иными словами, сколько тока втекает в узел, столько из него и вытекает.

Второе правило Кирхгофа основано на утверждении, что любая электрическая цепь является потенциальной, а работа по перемещению электрических зарядов в замкнутом контуре равна нулю:

где U – работа(электрическое напряжение), k – число источников выполняющих работу;

Рассмотрим цепь, изображённую на рисунке1, образованную двухполюсными элементами, где ветви в местах соединений образуют узлы 1,2,3,4 и где направления напряжений и токов в ветвях совпадают. Для составления уравнений Кирхгофа выберем произвольно узел  S2 , замкнутое сечение S14 (”несколько узлов”) и замкнутый контур 1, направление обхода которого изображено на рисунке 1.

Если принять, что выходящие из сечений и узлов токи считать положительными, а входящие отрицательными, то тогда уравнения составленные по первому правилу Кирхгофа будут иметь вид:

Для составления уравнения по второму правилу Кирхгофа, напряжения совпадающие с направлением обхода контура считаем положительными, а не совпадающие отрицательными. При этом уравнение примет вид:

Рассмотрим второе правило Кирхгофа на более наглядном примере (рисунке 2, см. ниже) и с более понятной для практического применения трактовкой, утверждающей что: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.

Рисунок 2

Применяя второе правило Кирхгофа составляем уравнение для замкнутого контура схемы(рисунок 2) :

При составлении полученного уравнения знаки учитывались как:

— ЭДС (E) положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

— падение напряжения (IR) на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Мы рассмотрели применение правил Кирхгофа на простых примерах цепей постоянного тока и напряжений. На самом деле электрические цепи бывают значительно сложнее и состоять из различных элементов (источников ЭДС и тока , нелинейных и т.п.). Например, для второго правила Кирхгофа физическое представление уравнения для переменного тока уже будет иметь вид:

Следует отметить, что для цепей синусоидального(переменного) тока правила Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений. Чтобы решать уравнения Кирхгофа для цепей синусоидального тока их составляют в комплексной форме, в которой учитываются ”мгновенные” изменения значений токов и напряжений.

Но какие сложные уравнения не приходилось бы составлять и решать, следует помнить, что физически второе правило(закон) Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

elenergi.ru

11. Расчёт сложных схем по уравнениям Кирхгофа.

Предположим, перед нами стоит задача по расчету сложной электрической цепи, состоящей из k узлов, l ветвей и m идеальных источников тока (под идеальным источником тока подразумевается такой источник тока, для которого Rт равен бесконечности). Суть метода сводится к решению системы линейных уравнений c l неизвестными. В качестве неизвестных выступают токи ветвей. Решив такую систему мы получим значения токов во всех ветвях электрической цепи, зная которые очень просто рассчитать все другие параметры цепи (напряжения на отдельных элементах, мощность и т.д.)

Перед началом расчета будет нелишним, по возможности, упростить электрическую схему с целью уменьшения количества ветвей. Это может существенно упростить расчеты и уменьшить вероятность ошибки. Например, решение системы линейных уравнений с 4 неизвестными гораздо проще решения системы с 5 неизвестными.

Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий:

1. Выбирают положительные направления токов в ветвях электрической цепи.

2. Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.

3. Выбирают (l-k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.

4. Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа.

5. Решают систему из (l-m) линейных уравнений любым удобным способом.

Пример.

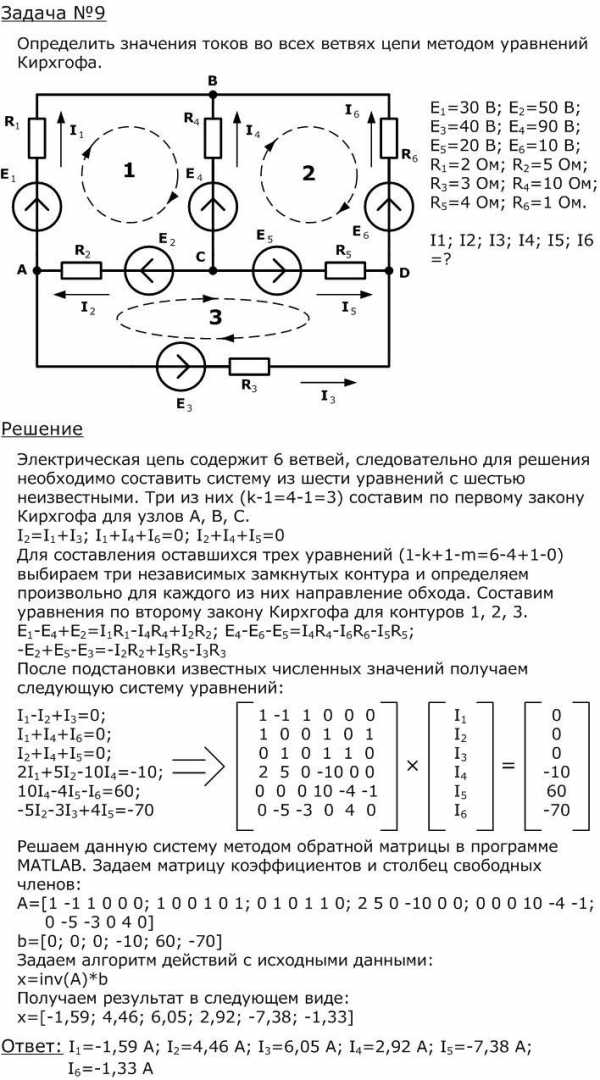
На рисунке изображена схема сложной электрической цепи, содержащей 4 узла и 6 ветвей (k=4, l=6). Для расчета цепи необходимо составить систему из 6 линейных уравнений. Предварительно выберем направления токов в каждой из ветвей. По первому закону Кирхгофа составляем 3 уравнения (k-1=4-1=3), например для узлов A, B и C. Вместо любого из этих узлов для составления уравнения можно взять узел D, на результат расчетов это не повлияет. Оставшиеся 3 уравнения (l-k+1-m=6-4+1-0=3) придется составлять по второму закону Кирхгофа ()

Подставляем известные значения

Решаем получившуюся систему.

Получаем ответы в матричном виде.

12. Метод контурных токов.

Теоретические сведения.

В данном методе расчета полагают, что в каждом контуре протекает свой контурный ток. Контурные токи и принимают за неизвестные, находят их, и уже затем через контурные токи определяют токи в ветвях. Чтобы сократить количество неизвестных, источник тока включают в контур, но только в один. Ток данного контура считают известным и равным току источника. Если в схеме несколько источников тока, количество неизвестных можно существенно сократить, включая источники в разные контура. В таких схемах применение этого метода наиболее рационально. Число неизвестных в данном методе равно количеству уравнений, которые необходимо было бы составить по второму закону Кирхгофа для данной схемы. Уравнения составляют только для контуров, не содержащих источников тока.

Алгоритм расчета цепи методом контурных токов.

1. Определяем общее число ветвей p*

2. Определяем число ветвей с источниками тока pит.

3. Определяем число ветвей с неизвестными токами p*-pит

4. Определяем число контуров, необходимое и достаточное для определения всех неизвестных токов m= p*-(q-1).

5. Произвольно наносим на схему номера и направления неизвестных токов.

6. Обозначаем на схеме контура и выбираем направления их обхода. Необходимо, чтобы каждая ветвь входила хотя бы в один из обозначаемых контуров. При этом ветви с источниками тока обязательно включаем, но каждую в свой контур. Токи данных контуров считаем известными и равными токам источников – таким образом, число неизвестных сокращается.

7. Записываем выражения для токов в ветвях через контурные токи. Контурные токи в ветвях, не являющихся смежными, и будут истинными токами. Для ветвей, входящих в несколько контуров (смежных ветвей) истинный ток будет являться суммой либо разностью контурных токов данных контуров. При этом те контурные токи, которые совпадают по направлению с током в ветви, берем со знаком плюс, а те, направления которых противоположны – со знаком минус. Определяем собственные сопротивления контуров как сумму всех сопротивлений, входящих в контур (только для контуров без источников тока). Эти сопротивления обозначаются двойным повторяющимся индексом: и т.д.

8. Определяем сопротивления смежных ветвей и их знаки: плюс – если контурные токи сонаправлены в данной ветви, и минус, если их направления встречны. Эти сопротивления обозначаются двойным индексом, цифры которого указывают номера смежных контуров и т.д.

9. Аналогично определяем сопротивления ветвей, являющихся смежными с контурами, содержащими источники тока.

10. Определяем суммарную ЭДС контура (также обозначается двойным повторяющимся индексом - и т.д.). Это алгебраическая сумма ЭДС, входящих в данный контур, причем со знаком плюс берут те ЭДС, направления которых совпадают с выбранным направлением обхода, и наоборот, со знаком минус те, что направлены встречно.

11. Записываем систему уравнений по форме, приведенной ниже:

12. Решаем данную систему относительно контурных токов.

13. Определяем токи в ветвях, подставляя контурные токи в выражения п. 7

Пример.

Найти токи в схеме рис. 35 с применением метода контурных токов.

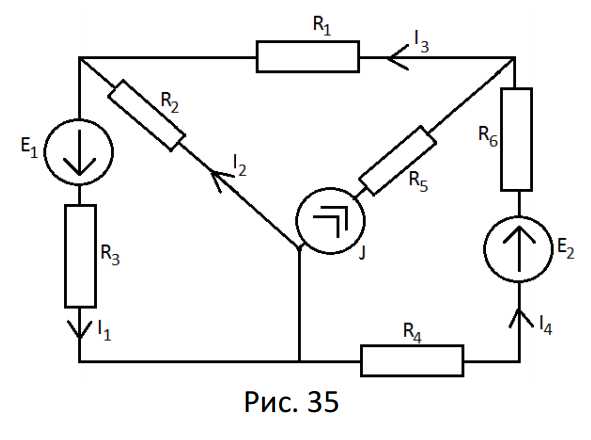
Дано:

1.2.1.1. Топология цепи.

1. Определяем общее число ветвей: p*=5

2. Определяем число ветвей с источниками тока: pит=1.

3. Определяем число ветвей с неизвестными токами: p*- pит=4.Количество узлов – 3

4. Определяем необходимое и достаточное число контуров: 3

5. Произвольно наносим на схему номера и направления неизвестных токов (рис. 36)

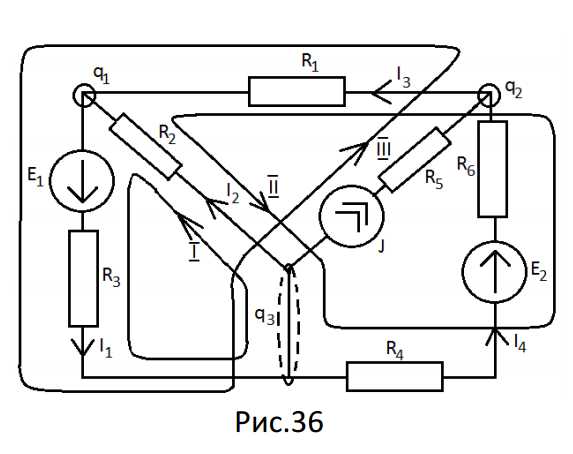
6. Определяем собственные сопротивления контуров (для контуров без источников тока):

7. Определяем сопротивления смежных ветвей и их знаки:

8. Аналогично определяем сопротивления ветвей, являющихся смежными с контуром, содержащим источник тока:

9. Определяем суммарную ЭДС контуров:

10. Записываем систему уравнений по форме:

Если произвести подстановку сопротивлений, то видно, что данная система полностью совпала с системой, полученной в п. 7:

11. Решаем данную систему относительно контурных токов:

12. Определяем токи в ветвях, подставляя контурные токи в выражения п. 7

studfiles.net

1 Исследование электрической цепи при помощи уравнений Кирхгофа

Транскрипт

1 Материалы для самостоятельной подготовки по дисциплине «Теория электрических цепей» для студентов специальностей: -6 4 з «Промышленная электроника» ( часть), -9 с «Моделирование и компьютерное проектирование РЭС» Исследование электрической цепи при помощи уравнений Кирхгофа Основными законами на базе которых разработаны методы исследования цепей являются закон Ома и законы Кирхгофа. Первый закон Кирхгофа вытекает из принципа непрерывности тока (рис..). Рис.. Графическое отображение принципа непрерывности тока. В узле электрической цепи А, где сходится проводов, не может быть накопления зарядов; следовательно сумма зарядов, протекающих в любой момент времени к узлу А равна сумме зарядов, уходящих из узла А. на основании этого формируется первый закон Кирхгофа. Алгебраическая сумма токов в проводах, сходящихся в любом узле электрической цепи, равна нулю: (.) При этом токи, текущие к узлу следует брать с одним знаком, а токи, текущие от узла, с другим знаком. Второй закон Кирхгофа устанавливает связь между ультирующей ЭДС, действующей в замкнутой электрической цепи, и произведениями токов в ветвях цепи на сопротивление ветвей. В рассматриваемой замкнутой электрической цепи ABСD (рис..) действуют три ЭДС: Е, Е, Е 4. две из них Е и Е действуют в одном направлении, а Е 4 навстречу, следовательно, выбирая направление обхода контура ABD и считая ЭДС, действующей в направлении обхода положительными, а ЭДС, действующей в обратном направлении, отрицательной, ультирующая ЭДС равна: E E. E E4

2 Рис.. Пример замкнутой электрической цепи. В соответствии с законом Ома: E E E E4 ( в ) ( в ) 4( 4 в 4) Обобщая данное выражение на любое число ветвей получаем второй закон Кирхгофа: Алгебраическая сумма ЭДС, действующих в любом замкнутом контуре, равна алгебраической сумме падений напряжений в ветвях этого контура. Для цепи с ветвями: E При последовательном соединении сопротивлений в цепи (рис..7) значение тока во всех исторах одинаково. (.) Рис.. Последовательное соединение в цепи постоянного тока. По второму закону Кирхгофа: E U U U U ( ) 4 4 4, Следовательно, при последовательном соединении исторов общее сопротивление цепи равно сумме сопротивлений этих исторов: (.) Напряжение на отдельных участках цепи по закону Ома: U ; U ; U ; U 4 4 ; P P 4...

3 Для параллельно соединенных исторов напряжение на зажимах всех параллельных участков одинаково (рис..): U 44 в соответствии с первым законом Кирхгофа U U U U ( ) 4 U 4 4 Рис..4 Параллельное соединение исторов. При параллельном соединении исторов (.4) общая проводимость цепи равна сумме проводимостей параллельных ветвей. или (.4) Токи параллельных ветвей по закону Ома: U ; U ; U ; U ; => ; ; ; (.5) (если дан общий ток, отдельные токи в ветвях распределены пропорционально проводимостям) P P Для простейшего смешанного соединения исторов в цепи постоянного тока (рис..5): / /. Общее сопротивление цепи U (.6)

4 Рис..5 Смешанное соединение исторов. Сначала находятся эквивалентные сопротивления параллельных участков, затем эквивалентное сопротивление цепи определяется как сумма найденных эквивалентных сопротивлений и сопротивлений других одиночных исторов, включенных последовательно. Метод составления и решения уравнений по законам Кирхгофа Общее число уравнений должно быть равно числу неизвестных токов, т.е. числу ветвей цепи. Число уравнений, составляемые по первому закону Кирхгофа, равно числу узлов цепи минус один (- уравнений). Остальные уравнения составляются по второму закону Кирхгофа (рис..6). Рис..6 Пример схемы. Считаем, что E, E, E известны; в, в, в известны;,, известны Необходимо определить токи:,,? Зададим направление токов. Если выбранные направления токов окажутся противоположны действительным, то при решении уравнений получим значения этих токов со знаком, следовательно, токи текут в обратном направлении. Цепь имеет два узла точку А и В. По первому закону Кирхгофа составляется одно уравнение, т.к. уравнение для точки А и В одинаковы. По второму закону Кирхгофа: Для первого контура, второго контура и контура АmBA, то уравнение для контура АmBA является следствием из уравнений для контура и уравнения для контура, следовательно, выбрав направление обхода имеем ( ) ( E E в в)

5 ( в ) ( в ) E E При совместном решении: ( E E )( в в ) ( E E)( ( )( ) ( )( ) ( )( в в в в в в ) в ) ПРИМЕР : Для цепи пользуясь законами Кирхгофа, найти токи и проверить баланс мощностей. Дано: Е= В, J=A, R=5 Ом, R =85 Ом. Решение: Выберем положительные направления токов и составим уравнения по законам Кирхгофа. Цепь содержит три ветви (Nв=), и два узла А и В (Nу=), один источник тока (N Т =). Число уравнений, составляемых по первому закону Кирхгофа, У= Nу-=, а по второму закону Кирхгофа: К=Nв- Nу+-N Т =-+-=. Уравнение для узла А J = Независимый контур выбираем так, чтобы он не содержал источника тока. Для него составляем уравнение второго закона Кирхгофа: R+ R =E Подставляя в уравнения цифровые значения и решив их, получим: =,5А: =,5А. Для расчета баланса мощностей необходимо знать напряжение на источнике тока, которое находим по ветвям, внешним по отношению к зажимам источника тока. Напряжение на нем U AB = R =4,5B. Составляем баланс мощностей: U AB J +Е= R+ R. Подставляя числовые значения, находим: 4,5 + (-,5)=(-,5) 5+,5 85. Получим тождество: 55=55. ПРИМЕР :

6 Для цепи схемы пользуясь законами Кирхгофа, найти токи и проверить баланс мощностей, если Е =5В, Е =7В, Е =5В, = =Ом, =Ом, сопротивления элементов в цепи: R =5Ом, R =4Ом, R =8Ом, R 4 =,5Ом, R 5 =5Ом. Решение: Всего на схеме цепи 5 ветвей (N В =5:bf, dc, b, bc, c), число узлов N у =(, b, c), источников тока нет (N т =), число неизвестных токов равно N В -N т =5. Число независимых уравнений составляемых по второму закону Кирхгофа равно (К= N В -N у +- N у =5-+=). Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, равно числу независимых токов в пяти ветвях схемы. Обозначим стрелками положительные направления токов и направления обхода трех независимых контуров:,,. Составим систему уравнений Кирхгофа: для узлов а =; b =; для контуров (R + ) -(R + ) =E +E (R + ) -R 4 4 R 5 5 =-E (R + ) +R 5 5 R 5 5 =E Уравнения после подстановки в них числовых значений имеют следующий вид: =, = 6 - =, -, =-5

7 =7 Решая эту систему уравнений, получим =5А; =8А; =А; 4 =-6А; 5 =А. Отрицательный знак для 4 означает, что истинное направление тока в R 4 противоположно принятому. Оно обозначено 4 и показано на схеме штриховой стрелкой. При проверке баланса мощностей надо иметь в виду, что в тех ветвях цепи, где направление тока совпадает с направлением ЭДС, соответствующая ЭДС является источником энергии, а в тех участках, где направления ЭДС и тока противоположны, ЭДС потребитель энергии. Все сопротивления, как внешние, так и источников энергии независимо от направления протекающего че них тока будут потребителями энергии. Баланc мощностей для рассматриваемой схемы: Е + Е Е = (R + )+ (R + )+ (R + )+ 4 R R 5 ; или = ,5 + 5; получено тождество 6=6 Резонанс в электрических цепях. Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз (угол сдвига фаз) напряжения и тока участка равны нулю. Резонанс напряжений возможен на участке цепи с последовательным соединением элементов, параметры которых R,,, т.е в последовательном контуре (рис..). Рис.. Последовательный R,, контур

8 Активное сопротивление R, показанное на схеме рис.. отдельно, может быть как сопротивление специально включенного истора, так и сопротивлением проводов катушки индуктивности. Из определения следует, что угол сдвига фаз при онансе равен нулю. Такой угол сдвига фаз можно получить тремя способами: При. изменением частоты ω напряжения питания;. изменением ;. изменением С. из выражения ct следует, что. Т.к, а, то при онансе, (.) где ω онансная частота. Сопротивление реактивного элемента при онансной частоте называется характеристическим сопротивлением последовательного контура. (.) Отношение характеристического сопротивления к активному сопротивлению контура называется добротностью последовательного контура Q / (.) Рассмотрим характерные особенности режима онанса напряжений:. Т.к, то cos и суммарное сопротивление участка цепи активное, т.е полное сопротивление при онансе равно активному сопротивлению Z сопротивлении R. и минимально при заданном

9 . Ток U / Z U / максимален. Это свойство позволяет обнаружить онанс напряжений при изменении,,. Однако, онансный ток при определенных условиях опасен он может привести к перегреву элементов цепи и выводу их из строя.. Напряжение на отдельных участках контура: U ; U ; U ; (.4) Т.к. при онансе реактивным сопротивлением равны U,то напряжения на участках контура с U, напряжение на участках с активным элементом U U на выводах контура и совпадает с ним по фазе. питания Если U * U j U U U (.5), то U U, т.е напряжение на участках с реактивными элементами больше, чем U питания. Это свойство усиление напряжения является важнейшей особенностью онанса и широко используется в технике, отсюда и название этого явления. Коэффициент усиления равен добротности контура U / U / / Q (.6) / Значительное повышение напряжения на реактивных элементах может привести к пробою изоляции и опасно для обслуживающего персонала. 4. Активная мощность при онансе максимальна, т.к максимален. Реактивные мощности равны, т.к P равны, но положительны по знаку мгновенной реактивной мощности., а ток P U si t; P U si t; (.7) Это значит, что в те интервалы времени, в течение которых энергия накапливается в магнитном поле индуктивного элемента, она поступает из электрического поля емкостного элемента. Происходит обмен энергией между реактивными элементами контура. Источник питания в этом обмене не участвует

10 Векторные диаграммы контура с R,, при онансе напряжений строится с учетом особенностей режима, * * U ; U * U * U (рис..). Рис.. Векторная диаграмма R,, контура Резонанс токов возможен в цепи с параллельным соединением двух ветвей с параметрами R, и R, в параллельном контуре (рис..). Рис.. Цепь с параллельным соединением двух ветвей с параметрами R, и R, Из определения онанса следует, что угол сдвига фаз равен нулю. Т.к b b ct, то при онансе B B. Учитывая, что b ; b ;, следует Z Z Z Z ' ' / или ' ', где / ' частота онанса тока, откуда после преобразований имеем: ' / / p p (.8) Из выражения (.8) следует: '. Резонансная частота при онансе токов зависит не только от параметров реактивных элементов, но и от активных сопротивлений и.

11 . Резонанс токов возможен, если сопротивления и или больше p, или меньше p '. Если p, онансная частота % имеет неопределенное значение, что означает существование онанса при любой частоте. 4. При и p, что справедливо для многих цепей, ' /, т.е онансная частота при онансе токов равна онансной частоте при онансе напряжений. Рассмотрим характерные особенности контура с малыми потерями при онансе токов с учетом того, активные сопротивления и не изменяются:. Т.к cos и общее сопротивление контура активное, то полная проводимость контура равна активной проводимости и практически минимальна: Y Сопротивление контура при этом активное и практически максимальное: b b Э (.9) Z экв Y экв R экв (.). Ток в неразветвленной части цепи практически минимален. U экв, что позволяет обнаружить онанс токов в контуре при изменении частоты, параметров и.. Активные и реактивные составляющие токов: ; ; b ; b U U p U p U; (.) Т.к b b, то. * p * p * p Векторная диаграмма цепи при онансе токов строится как для любой параллельной цепи, но с учетом ; p p;. Ток в общей части цепи равен активной составляющей тока p p (.)

12 Ток в ветвях Если, b bu (.) b U (.4) b, т.е,, то,,,,, т.е токи в ветвях значительно больше, p p чем ток в неразветвленной части цепи. Это свойство усиление тока широко используется, и дало название этому явлению., 4. Коэффициент усиления по току при, bu / / U / / / экв Q (.5) т.е равен добротности контура. 5. Реактивные мощности Q, т.к Q b U ; Q bu (.6) Q ; Это означает, что, как и при онансе напряжений, между катушкой и конденсатором происходит обмен энергией, но источник при этом обмене не участвует: источник только восполняет потери в активных сопротивлениях контура. Пример. Для реактивного двухполюсника, схема которого приведена на рис..4, требуется определить значения онансных частот и построить график зависимости х вх ( ). Параметры элементов схемы имеют следующие значения: = мгн; = мгн; = 4 мкф; С = мкф.

13 Рис..4 Схема цепи к примеру Решение. Найдем реактивную входную проводимость двухполюсника:, где реактивное сопротивление первой ветви; реактивное сопротивление второй ветви. Подставив значения сопротивлений ветвей, найдем реактивную проводимость двухполюсника ; отсюда находим:. Приравняв к нулю знаменатель этого выражения, найдем частоты онансов напряжений ;. Подставив значения параметров элементов, найдем частоты онансов напряжений: На этих частотах входная проводимость обращается в бесконечность (а соответственно, входное сопротивление обращается в нуль). ;.

14 Приравняв к нулю числитель входной проводимости, найдем частоту онанса токов. На этой частоте входная проводимость обращается в нуль, поэтому ток в цепи отсутствует. Выполненный расчет показывает, что частота онанса токов расположена между частотами онансов напряжений. График частотной характеристики входной проводимости начинается с нулевого значения b вх () =. Затем проводимость возрастает и на частоте первого онанса напряжений обращается в бесконечность. После этого входная проводимость изменяет знак и на частоте обращается в нуль, что соответствует онансу токов. Затем проводимость вновь возрастает и на частоте снова обращается в бесконечность. При дальнейшем повышении частоты проводимость изменяет знак и асимптотически стремится к нулевому значению.

docplayer.ru

Алгоритм составления уравнений по законом Кирхгофа

Алгоритм составления уравнений по законом Кирхгофа:

Составляем уравнения по первому закону Кирхгофа

Для составления уравнений по первому закону кирхгофа любой электрической цепи выполняем следующие действия.

1. Количество уравнений по 1 закону киргофа равно количеству узлов минус один. 
2. Произвольно задаемся направлением токов в каждой ветви электрической цепи.
3. Если в ветви присутствует источник тока, то считаем данный ток уже известным, равным величине источника тока.
4. Составляем уравнения по первому правилу Кирхгофа для любых узлов кроме одного.
5. Расставляем знаки. Токи, которые втекают в узел берем с одним знаком, например с плюсом. Токи, которые вытекают из узла берем с противоположным знаком, например с минусом.

Составляем уравнения по второму закону Кирхгофа

Для составления системы уравнения по 2 правилу Кирхгофа необходимо выполнить следующие пункты.

1. Количество уравнений по второму закону Киргофа равно количеству независимых контуров. По второму закону можно записать В-ВI-У+1 независимых уравнений. Где В - число ветвей в схеме. ВI- число ветвей в схеме с источником тока. У - число узлов в схеме.
2. Находим независимые контура в электрической цепи (чтобы отличались хотя бы одной ветвью).
3. Если в цепи присутствуют источники тока, то данные ветви не учитываем при нахождении независимых контуров. 
4. Задаемся произвольным направление обхода независимых контуров.
5. Составляем уравнения по второму правилу Кирхгофа для каждого выбранного контура.
6. Расставляем знаки на участках с нагрузкой. Если направление обхода контура совпадает с направлением протекающего тока, то падение напряжения на заданном участке берем со знаком "+". Если направление протекающего тока не совпадает с направлением обхода контура, то падение напряжения на данном участке берем со знаком "-".
7. Расставляем знаки на участках с источниками ЭДС. Если направление действия ЭДС (направление стрелочки) совпадает с направлением обхода независимого контура, то знак будет "плюс". Если не совпадает, то знак - "минус".

Расчет токов по правилам Кирхгофа 

Полученные уравнения объединяем в систему уравнений. Количество уравнений должно быть равно количеству неизвестных. Далее решаем систему уравнений любым известным способом.

Правильность расчета проверяется составлением уравнения баланса мощностей. 

p.s. Правила Кирхгофа необязательно использовать в виде систем уравнений. Они справедливы для любого узла и для любого замкнутого контура электрической цепи.

www.kurstoe.ru

Метод уравнений Кирхгофа - ТОЭ, РЗА

Уравнения Кирхгофа являются основными соотношениями, на которых базируются расчеты сложных электрических цепей.

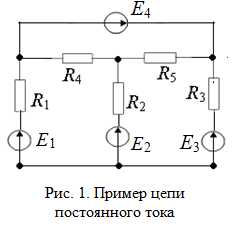Пусть имеется разветвленная сеть проводов, на различных участках которой находятся генераторы постоянного напряжения и резисторы с известными ЭДС Ek  и сопротивлениями Rk (k= 1, 2, 3,…).Такая сеть называется цепью постоянного тока (рис. 1). Ставится задача: рассчитать токи на каждом участке этой цепи. Такую задачу можно решить с помощью двух правил (уравнений) Кирхгофа.

Первое правило относится к узлам цепи и утверждает следующее: алгебраическая сумма токов, сходящихся в узле, равна нулю, т. е.

                                                (1)

При этом токам, «входящим в узел», условно приписывается знак «+», а «выходящим» − знак «−». Это правило означает то, что заряды в узле не накапливаются: «сколько входит, столько и выходит»; оно следует из закона сохранения электрического заряда.

Второе правило Кирхгофа относится к любому выделенному в цепи контуру и утверждает следующее: алгебраическая сумма напряжений на всех элементах произвольного контура (кроме генераторов) равна алгебраической сумме ЭДС генераторов, встречающихся в этом контуре, т. е.

                                                                   (2)

Напряжение иk= ikRk на элементе Rk считается положительным, если выбранное направление обхода данного контура совпадает с выбранной стрелкой тока через данный элемент; ЭДС Ek считается положительной, если выбранное направление обхода контура совпадает со стрелкой ЭДС данного генератора. Это правило следует из основного свойства электростатического поля: циркуляция электростатического поля по любому контуру равна нулю.

Правила Кирхгофа (1) и (2) позволяют написать полную систему линейных алгебраических уравнений, из которой можно однозначно определить токи на всех участках цепи. Практически последовательность составления таких уравнений следующая.

1. На всех участках цепи указать стрелками «направления» токов (стрелки токов наносятся прямо на линию провода). Вообще говоря, стрелки токов можно наносить как попало, их нет нужды угадывать. А вот знаки слагаемых в уравнениях Кирхгофа пишутся уже строго под выбранные стрелки. И если в результате вычислений окажется, что какой-либо ток ik< 0, то он и будет отрицательным по отношению к данной стрелке.

Замечание. Ток – это не вектор, а алгебраический скаляр. Стрелка же тока указывает лишь условно положительное направление его вычисления.

2. Выбрав контур, обходить его в определенном направлении, например, по часовой стрелке. Если очередная стрелка тока ik при обходе совпадает с этим направлением, то соответствующее слагаемое в левой сумме (2) пишется со знаком «+», т. е. «+ikRk», а иначе – «−ikRk». Аналогичное правило знаков применяется и для стрелок ЭДС Ekв правой части (2).

3. Если цепь содержит N узлов, то независимых уравнений типа (1) будет (N−1). Уравнения типа (2) должны учитывать все независимые контуры цепи, т. е. такие, которые нельзя образовать наложением друг на друга контуров, уже вошедших в уравнения (2). В качестве независимых удобно выбирать «простые» контуры, т. е. не содержащие в себе других контуров.

Пример. Найти токи через резисторы R1, R2 иR3 в цепи, показанной на рис.2, если все Ek и Rkизвестны.

Решение. Расставляем произвольно стрелки токов i1, i2 и i3 на всех участках. Так как независимый узел только один, то и уравнений типа (1) также будет одно:

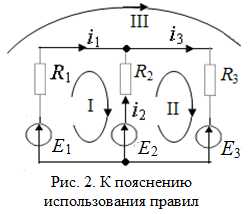i1 + i2 − i3 = 0.

Из трех возможных контуров (I, IIи III), берем, например, I и II; контур III зависим, так как он образуется наложением I и II. Задаем в этих контурах произвольные направления обходов, например, по часовой стрелке, и записываем для них уравнения типа (2) с учетом правила знаков:

i1R1 − i2R2 = E1 − E2,

i2R2 + i3R3 = E2 − E3.

Таким образом, имеем систему трех уравнений для трех искомых токов. Знаки полученных токов покажут, совпадают ли они с выбранными на рис. 2 стрелками, или противоположны им.

Для достаточно сложных цепей правила Кирхгофа приводят к слишком большим системам уравнений. В связи с этим, были разработаны более эффективные методы расчета цепей, которые хотя и базируются на правилах Кирхгофа, но дают значительно меньшее число уравнений. К таким методам относятся метод узловых потенциалов и метод контурных токов.

     Изначально мне показалось, что аналитического примера будет достаточно, но все же для полного понимания материала статьи давайте я выложу пример в полном виде, и так:

      Проставим все токи в ветвях в произвольном направлении и выберем направление обхода в независимых контурах I и II, например, против часовой стрелки.

Расчет:

         Составим для узла 1 уравнение по первому закону Кирхгофа и для контуров I и II уравнения по второму закону Кирхгофа:

                          Баланс мощности сошёлся, значит и расчеты верны.

 

        Возможно Вам будет полезна следующая статья по теме:

 

elekt.com.ua

---

• 
  Заявка на техприсоединение к электрическим сетям
• 
  Солнечные батареи в россии актуальность
• 
  Программы подготовки электротехнического персонала
• 
  Какой бесперебойник выбрать для телевизора
• 
  Электромагнитный тормоз для электродвигателя
• 
  Что служит индикатором вихревого электрического поля
• 
  Принцип работы индукционной печи
• 
  Зажим сип ответвительный
• 
  Система управления энергией
• 
  Программирование контроллера овен
• 
  Как подключить 380