Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца
Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
(21.1) |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
(21.2) |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
(21. |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).
Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
(21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
(21. |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников
(21.5) |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
(21. |
В этом случае сила тока в цепи равна
(21.7) |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
(21.8) |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения.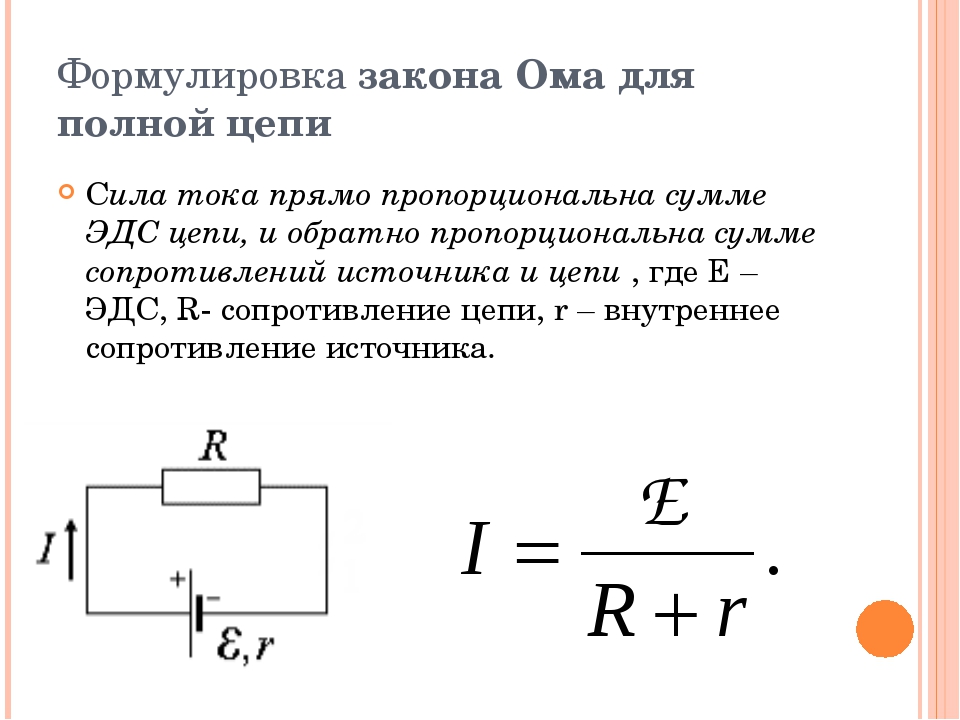 Поэтому отношение
Поэтому отношение
(21.9) |
которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ 3).
Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус.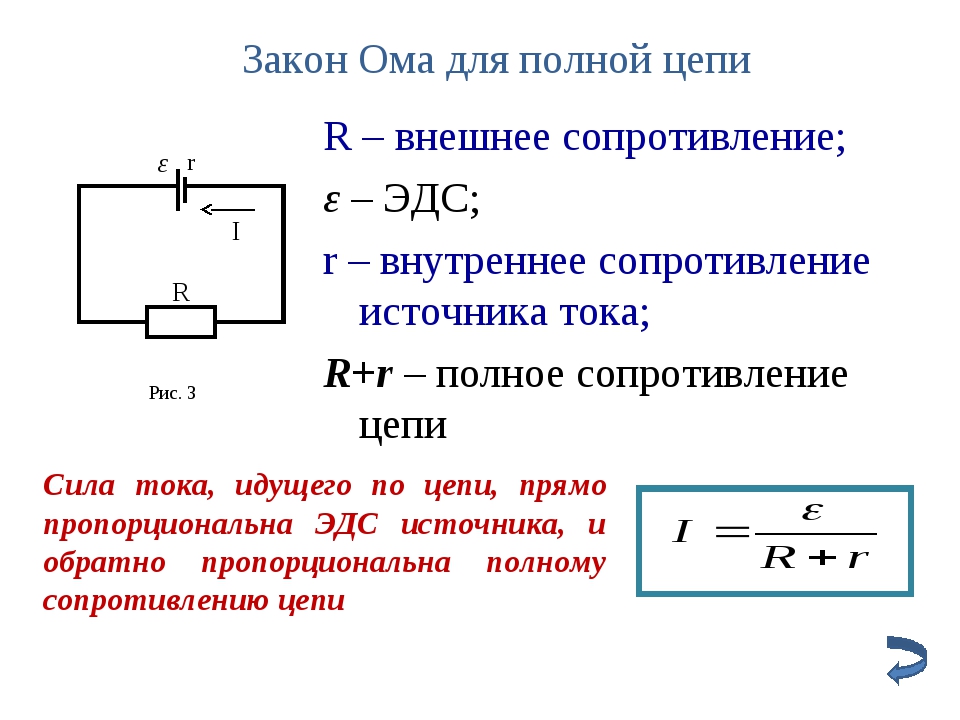 Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца.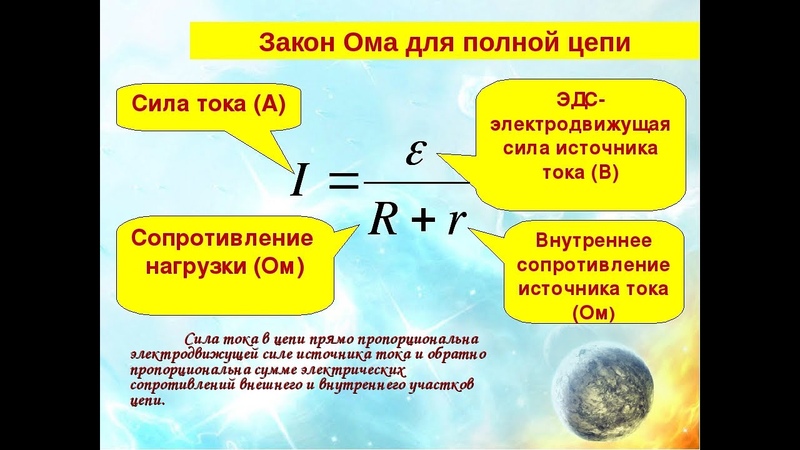 Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
Урок №6 Тема: «Законы постоянного тока»
Физика. Урок №6
Тема: «Законы постоянного
тока».
Задача 1.
Резистор и конденсатор соединены
последовательно с аккумулятором; при
этом заряд на обкладках конденсатора
q1
=
.
Если же резистор и конденсатор подключить
к аккумулятору параллельно, то заряд
на обкладках конденсатора q2
=
.
Найти внутреннее сопротивление
аккумулятора, если сопротивление
резистора R
= 45 Ом.
Дано: q1
=
,
q2
=
,
R
= 45 Ом.
Найти: r
— ?
Решение:
В первом случае (рис.1) тока в цепи
нет, напряжение на конденсаторе U1
равно ЭДС источника ε,
поэтому заряд на конденсаторе емкостью
С:
(1).![]()
Рис. 1
Рис.
2
Во втором случае (рис.2) отсутствует
ток в ветви АСВ, напряжение на конденсаторе
такое же , как и на подключенном к нему
параллельно резисторе, т.е.
,
где I
– сила тока. Ее мы найдем
по закону Ома для замкнутой цепи:
, где r
– внутреннее сопротивление аккумулятора.
Тогда:
, а заряд на конденсаторе:
. (2)
На основании выражений (1) и (2)
получим уравнение:
, решив которое относительно r
, найдем:
, r
= 23 Ом.
Ответ:
, r
= 23 Ом.
Рассмотрим более сложную схему, которая
приведена на рис. 3.
В цепи сопротивления резисторов
R1,
R2,
R3
– соответственно R1
= R2
= 2 Ом, R3
= 5Ом, ЭДС источника ε =
34 В, его внутреннее сопротивление r
= 1 Ом, емкость конденсатора С
= 20 мкФ.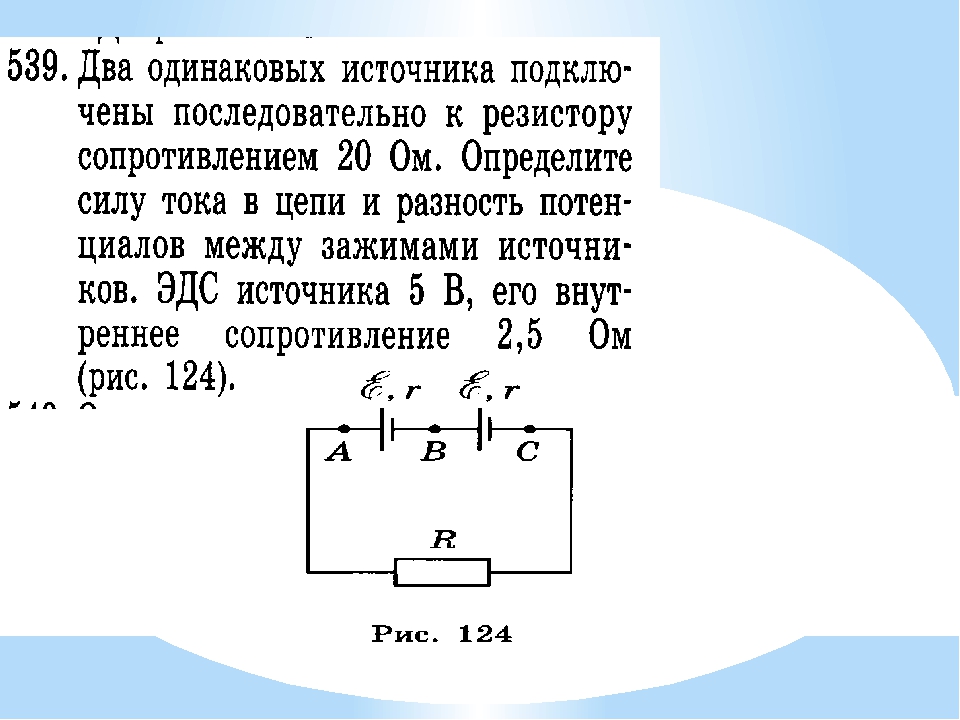 Определить, какой
Определить, какой
заряд q
пройдет через ключ К при
его замыкании.
Рис. 3
Дано: R1
= R2
= 2 Ом, R3
= 5Ом, ε = 34 В,
r
= 1 Ом, С = 20
мкФ.
Найти: q
— ?
Решение:
При замкнутом ключе конденсатор
зарядится до некоторого напряжения U,
после чего ток через резистор R2
проходить не будет. Напряжение U
на конденсаторе равно напряжению между
точками А и В. между этими точками
параллельно включены резисторы R1
и R3
(ток через R2
не идет). Поэтому:
.
Заряд на конденсаторе:
.
Силу тока найдем по закону Ома
для замкнутой цепи:
.
Подставив это значение в выражение
для заряда, получим:
, q
=
.
Ответ:
, q
=
.
Задача 2.
Два сопротивления R1=2
Ом и R2=8
Ом подключены в сеть один раз
последовательно, а второй раз параллельно.
Во сколько раз отличается сила тока во
второй цепи от силы тока в первой цепи?
В какой цепи выделится большая мощность
и во сколько раз?
Дано: R1
= 2 Ом, R2
= 8 Ом
—————————————
Найти:
Решение:
«По
умолчанию» можно считать, что: 1) напряжение
в сети постоянно, пусть оно равно U;
2) сопротивлением соединительных проводов
можно пренебречь; 3) под силой тока во
второй цепи подразумевается сила тока
в ее неразветвленной части
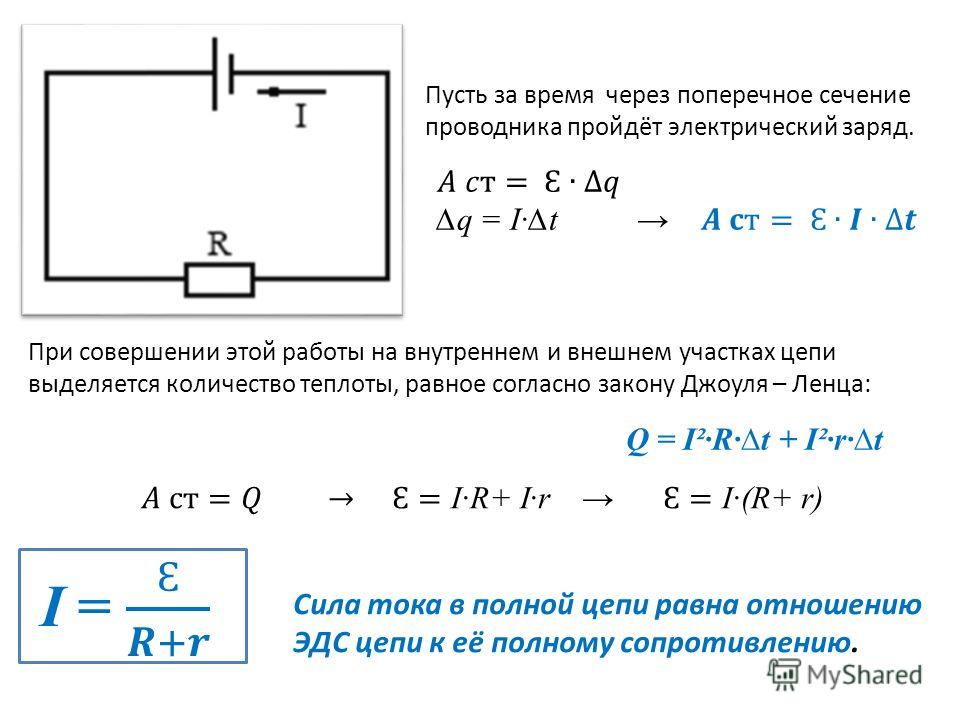
При последовательном cоединении
общее сопротивление Rn=R1+R2
и сила тока
.
При
параллельном подключении общее
сопротивление
и ток в неразветвленной части цепи
.
Отношение
токов
,
.
Выражаем
мощности через общее напряжение.
Мощность в первой цепи
,
мощность во второй цепи
.
Так как при последовательном соединении
общее сопротивление больше, то Р1
2
и
,
.
Ответ:
,
.
Задача 3.
Имеется источник тока с ЭДС,
равной ε, и
внутренним сопротивлением r,
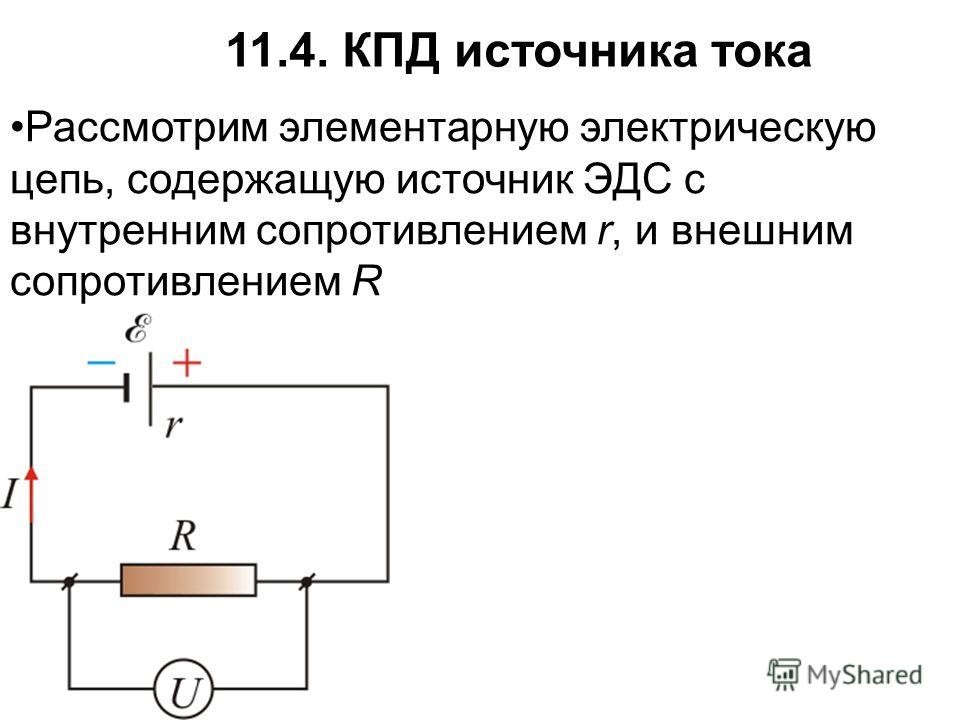
замкнутый на реостат (рис.4). Выразить
мощность P1,
выделяемую во внешней части цепи, как
функцию силы тока I.
Построить график этой функции. При какой
силе тока эта мощность будет максимальной?
Рис. 4
Дано: ε, r.
Найти: P1
(I)
— ? I
— ?
Решение:
Развиваемая источником полная
мощность
.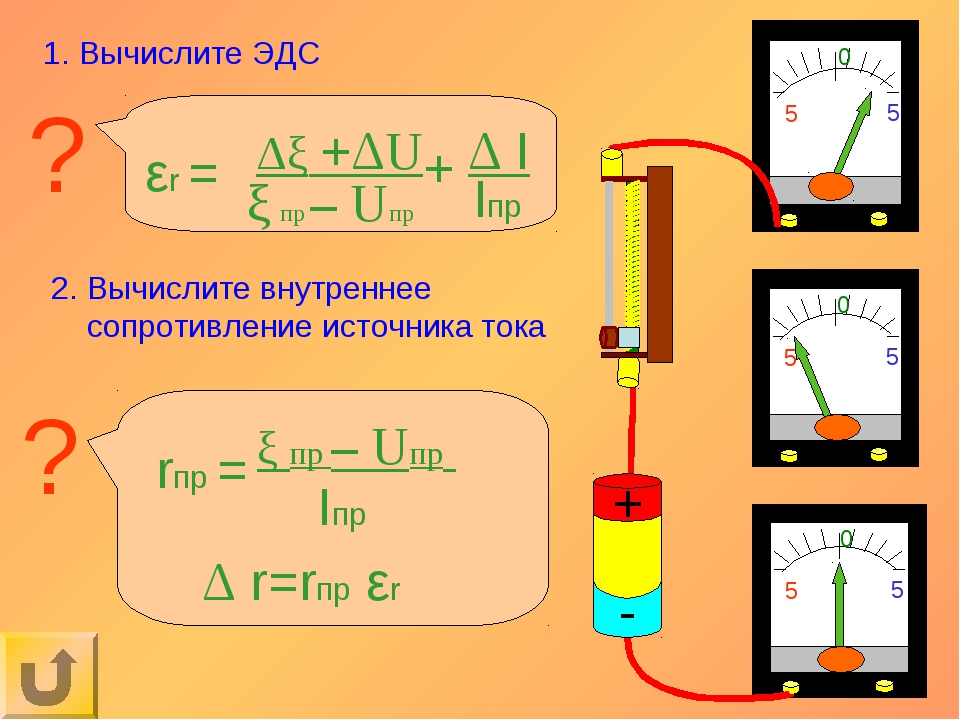
Часть этой мощности
выделяется внутри источника, остальная
– во внешней цепи:
(1)
Графиком этой функции (т.е. P1
(I))
является парабола, обращенная ветвями
вниз. Для построения графика преобразуем
выражение (1):
Отсюда видно, что координаты
вершины параболы соответствуют значениям
,
(рис. 5).
Рис. 5
Следовательно, при токе силой:
(2) мощность, выделяемая во
внешней части цепи, будет иметь
максимальное значение:
.
Пусть внешний участок цепи имеет
такое сопротивление R,
при котором сила тока равна
I1
. Тогда по закону Ома
для замкнутой цепи:
.
Сравнивая это выражение с формулой
(2), находим, что R
= r
.
Таким образом, мы приходим к
важному выводу: полезная мощность
(мощность выделяемая на внешнем участке
цепи) максимальна в том случае, когда
внутреннее сопротивление источника
равно сопротивлению внешнего участка
цепи. При этом КПД источника:
При этом КПД источника:
, или η =
50%.
Из графика, приведенного на
рис.5, также видно, что каждому значению
полезной мощности, кроме максимального,
соответствуют два значения сопротивления
внешнего участка цепи. При силе тока
короткого замыкания
полезная мощность равна нулю.
Получить условие,
что мощность, выделяемая на внешнем
участке цепи максимальна в том случае,
когда внутреннее сопротивление источника
равно сопротивлению внешнего участка
цепи (т.е. r
= R),
можно другим математическим
способом.
Выразим мощность P1,
выделяемую во внешней цепи, как функцию
сопротивления R
этого участка, т.е.
.
При некотором значении сопротивления
R,
значение функции максимально (экстремум
функции)! Поэтому первая производная
этой функции должна быть равна нулю,
т.е.
.
; =>
=>
.
При этом полученном условии
максимальная мощность
,
или
.
Ответ:
,
.
Задача 4.
Два вольтметра с внутренними
сопротивлениями R1
= 6,0 кОм и R2
= 4,0 кОм соединены, как показано на рисунке
6, сопротивление R3
= 10,0 кОм, напряжение U
= 180 В. Определить показания вольтметров
U1
и U2
при разомкнутом и при замкнутом ключе
К и установке движка D
на середине сопротивления R3.
На какие части R4
и R5
будет делить движок сопротивление R3
при одинаковых показаниях вольтметров?
Дано: R1
= 6,0 кОм , R2
= 4,0 кОм , R3
= 10,0 кОм, U
= 180 В.
Найти: U1
-? U2
— ?
-?
-?
R4
— ? R5
— ?
Решение:
При разомкнутом ключе К схема,
представленная на рис. 6 эквивалентна
схеме, указанной на рис. 7. Т.к. вольтметры
7. Т.к. вольтметры
присоединены к сопротивления R3
и к сети параллельно, то силу тока,
протекающего через вольтметры, можно
найти по формуле
.
Рис. 6 Рис. 7
Рис. 8
Следовательно, напряжение на
первом и втором вольтметрах соответственно
равны:
,
.
При замкнутом ключе К схема,
указанная на рис. 6 эквивалентна схеме,
представленной на рис. 8:
,
,
,
.
Ответ: U1=108
В, U2=72В,
,
,
,
Задача 5.
Во сколько раз изменится тепловая
мощность, выделяемая в цепи, при перемене
полярности на клеммах 1 и 2(рис.9)? Величину
напряжения на клеммах считать постоянной,
диоды идеальными, сопротивления
резисторов R1 = 10 Ом
, R2 = R3
= 5 Ом.
Дано: R1
= 10 Ом , R2 = R3
= 5 Ом.
Найти: P1
/P2
— ?
Рис. 9
Рис. 10
Решение:
На рисунке 10 (а и б) приведены
эквивалентные схемы, соответствующие
обоим случаям. В первом случае мощность:
, во втором –
, где U – напряжение на
клеммах.
Тогда
,
т.е. мощность уменьшится в 10 раз.
Ответ:
.
Задача 6.
Через двухэлектродную лампу
(диод) с плоскими электродами (рис. 11)
идет ток силой I = 10
мА. Напряжение на лампе U
= 100 В. С какой силой действуют на анод
лампы падающие на него электроны, если
скорость их вблизи катода равна нулю?
Отношение заряда электрона к его массе
e / me
=.
Рис. 11
Дано:
I = 10 мА , U
= 100 В, e / me
=.
Найти: F —
?
Решение:
Пусть
– скорость электрона в момент соударения
его с анодом. За время t
при силе тока I число
соударений:
,
(1)
где q – заряд,
переносимый N электронами;
e – заряд электрона.
По второму закону Ньютона импульс
силы, действующий со стороны анода на
электроны при соударениях, равен
изменению суммарного импульса электронов:
,
где me
– масса электрона;
– скорость электрона после соударения.
В проекциях на координатную ось,
направленную от анода к катоду, это
уравнение будет иметь вид:
,
или с учетом того, что
=
0,
,
(2)
где F – модуль
суммарной силы, с которой анод действует
на электроны. Согласно третьему закону
Согласно третьему закону
Ньютона, с такой же по модулю силой
действуют электроны на анод. Из соотношений
(1) и (2) получим:
.
(3)
Найдем модуль скорости
,
исходя из того, что изменение кинетической
энергии электрона в промежутке между
анодом и катодом равно работе электрического
поля:
.
Отсюда
. Подставив это значение скорости в
формулу (3), получим:
,
Н
.
Ответ:
Н.
Задачи для самостоятельного
решения
Задача 1.
Электрический нагреватель
работает от сети с напряжением U
= 120 В при силе тока I = 5,0
А. За время τ = 20 мин нагревает массу m
= 1,5 кг воды от начальной температуры 16
оС до температуры кипения t2
= 100 оС. Удельная теплоемкость воды
.
Определить коэффициент полезного
действия нагревателя (в %), определить
потери энергии в процессе нагревания
().
Задача 2.
Рис. 12
Зная все параметры указанной на
рисунке 12 схемы (значения ЭДС и внутреннего
сопротивления источника, сопротивления
резисторов и электроемкость конденсатора),
определить силу тока, протекающего в
неразветвленном участке цепи:
сразу
после замыкания ключа К;спустя
достаточно большой промежуток времени
после замыкания ключа К.
Задача 3.
При подключении резистора
сопротивлением R = 15 Ом к
источнику тока с ЭДС ε=10В, мощность,
выделяемая на этом резисторе, составляет
η = 75% полной мощности, которую развивает
источник. Какую максимальную мощность
может выделить данный источник во
внешней цепи?
Задача 4.
Какой заряд проходит через
раствор медного купороса за время t
= 10 с, если сила тока за это время равномерно
возрастает от I1 = 0
A до I2
= 4,0 А? Сколько меди выделяется при этом
на катоде? Электрохимический эквивалент
меди k =
.
Задача 5.
Рис. 13
Если вольтметр, имеющий конечное
сопротивление, подключен параллельно
к резистору с сопротивлением R1
в схеме, указанной на рис.13, то он
показывает напряжение U1
= 6В. Если этот вольтметр подключить
параллельно к резистору с сопротивлением
R2, то его показания
соответствуют напряжению U2
= 4 В. Каково будет напряжение на каждом
из этих резисторов, если подключать
идеальный вольтметр? ЭДС источника ε =
12 В, его внутреннее сопротивление
пренебрежимо мало.
Глава
1. Что на плате электронного устройства?
resistor
Резистор
Как
и собирался, я с помощью отвертки,
открутив винты, открыл испорченный
стрелочный прибор, который нашел в своей
«хламежке». Из него удалось извлечь
несколько
плат из стеклотекстолита с печатным
монтажом; на платах много резисторов,
есть конденсаторы, транзисторы, микросхемы
– почти все, что мне нужно для рассказа.
На
самой большой плате передо мной, следовало
бы посчитать, но не хочется, на первый
взгляд больше всего резисторов. Резистор
или сопротивление, наверное, простейший
для понимания компонент любого
электронного устройства…
Вот
так, не успев начать рассказ, я уже сделал
ошибку. Больше всего на плате не
резисторов, а проводников! И, пожалуй,
именно проводники самые простые
компоненты. Проводники соединяют все
остальные элементы устройства в сложные
или простые цепи, поэтому электрическую
схему я буду часто называть электрической
цепью. Как правило, проводники делают
из металла, вещества хорошо проводящего
электрический ток. Если под током
понимать любое направленное движение
электрических зарядов, то проводники
мало сопротивляются этому движению, то
есть, их сопротивление обычно невелико.
Свойства проводников хорошо понятны,
если рассматривать атомное строение
вещества, договорившись, что атомы
состоят из тяжелого электрически
заряженного ядра и легких электронов,
субатомных частиц противоположного
знака, расположенных вокруг ядра. У
У
разных веществ заряд ядра разный, но
количество электронов такое, что в целом
атом электрически нейтрален. У металлов,
уж так они устроены, электроны, далеко
расположенные от ядра, слабо связаны с
ним и могут «бродить» по металлу
от атома к атому (но не могут самопроизвольно
покинуть металл). Движутся они, конечно,
беспорядочно, но под действием внешнего
электрического поля, которое можно
создать с помощью источника питания,
его еще называют источником электродвижущей
силы (батарейка, аккумулятор, блок
питания), их движение упорядочивается
и можно говорить о протекании тока от
одного полюса источника питания к
другому; благодаря большому количеству
носителей зарядов в металлах
(электронов-бродяг) те оказываются
хорошими проводниками тока. За техническое
направление тока принято направление
от плюса источника ЭДС (электродвижущей
силы) к минусу, хотя реально в металле
под действием внешнего электрического
поля двигаться будут отрицательно
заряженные электроны от минуса источника,
поставляющего электроны в металл, к его
плюсу. Если можно посчитать количество
Если можно посчитать количество
зарядов, проходящих через поперечное
сечение проводника, то можно оценить
силу тока – чем больше зарядов проходит
через это сечение, тем больше ток.
Определяется сила тока отношением
количества зарядов, прошедших за
определенное время через поперечное
сечение, к этому времени. И еще о токе
можно сказать, что если его величина и
направление не меняется со временем,
то мы имеем дело с постоянным током,
иначе с переменным током. Батарейка –
источник постоянного тока, а силовая
сеть, куда мы подключаем пылесос или
телевизор, источник переменного тока.
Все
вещества по тому, как они проводят
электрический ток, можно разделить на
проводники, хорошо проводящие ток,
изоляторы, вещества не проводящие ток,
и полупроводники – «ни рыба, ни мясо»,
проводят ток много хуже проводников,
но лучше изоляторов. Их оценивают по
сопротивлению, маленькому у проводников
и огромному у изоляторов. Единица
сопротивления в электротехнике ом.
Теперь
можно перейти к тому, с чего я по ошибке
начал, к резисторам. Мы уже договорились,
Мы уже договорились,
что разные вещества по-разному проводят
электрический ток. Это касается и
металлов. Хотя они все проводники, но
одни металлы лучше проводят ток, другие
хуже. Очень хорошо, например, проводят
ток медь, серебро, золото. Хуже алюминий.
Еще хуже сплавы металлов, как нихром,
манганин, константан. Отчего зависит
сопротивление проводника? От вещества,
из которого он сделан, от толщины
проводника и от длины проводника.
Если
у вас есть мультиметр и медные провода
одинаковой длины, но разного диаметра,
вы можете измерить их сопротивление
(провода лучше взять достаточно длинные).
Если у вас найдется проводник из нихрома
(от перегоревшей спирали старого
нагревательного прибора) такой же длины,
вы непременно заметите разницу.
Есть
еще одно обстоятельство, влияющее на
сопротивление проводника, это температура.
При нагревании сопротивление проводника
увеличивается, потому что при нагревании
электроны бродяги становятся еще
энергичнее в своем хаотическом движении
и их труднее заставить двигаться
направленно. Убедиться в том, что при
Убедиться в том, что при
нагревании сопротивление увеличивается,
можно подключив к мультиметру в режиме
измерения сопротивления резистор, и
нагреть вывод резистора паяльником.
Если интересно, можете попробовать,
только аккуратно, чтобы не испортить
свой прибор. И не забывайте об этом,
когда, особенно в измерительных цепях,
пытаетесь получить нужную величину
сопротивления, подпаивая к одному
резистору другой. Обязательно дайте
остыть резисторам прежде, чем оценивать
результат.
Резисторы
для нужд электроники изготавливают по
разным технологиям и из разных материалов
так, что величина их сопротивления
колеблется от долей ома до десятков
миллионов ом (мегаом). Сопротивление в
электрической цепи может быть вредно,
так получается в силовых цепях, но может
быть полезно при разного рода манипуляциях
с электричеством. Самое простое полезное
действие электрического тока – нагрев.
При протекании электрического тока по
проводнику, оказывающему сопротивление,
проводник нагревается. В обогревателе,
В обогревателе,
где используется сопротивление,
изготовленное из нихрома, такой резистор
нагревается до красна. А в электрической
лампочке резистор (спираль лампочки
накаливания) раскаляется до бела. И в
том, и другом случае сопротивление мы
используем для превращения электрического
тока в полезные для нас тепло и свет.
Резисторы
широко используются в электронике. Есть
проволочные и непроволочные резисторы,
есть резисторы переменного сопротивления
(потенциометры), есть терморезисторы и
фоторезисторы. А такое свойство
резисторов, как изменение сопротивления
при механическом воздействии, находит
применение в тензодатчиках.
Я
сейчас отпаяю несколько резисторов с
платы прибора и перенесу их на макетную
плату, чтобы рассказать о нескольких
простых, но очень полезных правилах,
которые называют законами для электрических
цепей. Макетная плата у меня покупная.
Такие платы применяют при создании
прототипов электрических устройств.
На макетной плате можно спаять устройство,
проверить, наладить, а когда оно полностью
готово, можно перейти к изготовлению
образца. Очень часто макетная плата –
Очень часто макетная плата –
это набор контактных площадок из меди
с отверстиями для выводов компонентов
электрической схемы. Плату можно
изготовить самостоятельно из
фольгированного листового материала,
а при его отсутствии из любого жесткого
листового изолятора, желательно
термостойкого, чтобы плата не плавилась
при пайке. При механической обработке
стеклотекстолита — сверлении, распиливании,
обработке напильником – следует
соблюдать осторожность, поскольку пыль
стекловолокна травмирует дыхательные
пути. Можно использовать подходящий
кусок фанеры. Контактные площадки для
припаивания компонентов можно сделать
из кусочков медного электрического
провода без изоляции, продев из в два
просверленных рядом отверстия и загнув
с обратной стороны. Можно обойтись и
без контактных площадок, просверлив
отверстия, в которые продеваются выводы
элементов схемы, а к выводам с обратной
стороны припаиваются проводники. Если
макетную плату снабдить стойками в
1-1.5 см, то работать с ней будет еще
удобнее.
Для
пайки используется паяльник (еще один
пример полезного использования
сопротивления), у меня паяльник на 25
ватт 220 вольт, изготовленный в Подмосковье.
Сегодня можно купить хорошую паяльную
станцию – паяльник с регулировкой
температуры нагрева, с множеством
насадок для пайки и удобной подставкой.
Ручка моего паяльника сделана так, что
его можно положить на ровную поверхность
без подставки, но я привык использовать
подставку, которую сегодня, думаю, тоже
можно купить в магазине. Кроме паяльника
для пайки нужен припой, лучше ПОС-61 в
виде тонкого прутка, и паяльный флюс,
например, канифоль, хотя я использую
жидкий флюс ЛТИ-120, который держу в
пузырьке из-под лака для ногтей с
кисточкой, достаточно удобно. Флюс
растекается по месту пайки, помогая
припою лучше соединить детали, ведь
пайка – это один из способов соединения
деталей, кстати, не единственный, хотя
в электронных изделиях наиболее широко
применяемый. Кроме пайки можно использовать
скрутку, одно время монтаж с помощью
скрутки был очень популярен. При работе
При работе
с паяльником тоже следует соблюдать
осторожность и не только с тем, чтобы
не обжечься. Припой, испаряясь, не
принесет пользы при вдыхании. Не следует
паяльник постоянно держать включенным,
лучше лишний раз подождать, когда он
нагреется, или собрать одну из простых
схем, о которых мы поговорим позже.
Пока
я все это рассказывал, я успел включить
паяльник и выпаять резисторы из платы.
До
того, как продолжить рассказ об
электрических цепях, я хочу заметить,
что описать электрическую цепь и все,
что с ней связано, можно одними словами,
не прибегая ни к чему другому, но
получается длинно, и далеко не всегда
понятно. Поэтому для изображения
электрических схем используют графическое
представление – лучше один раз увидеть,
чем сто раз услышать. Каждый компонент
рисуют в виде небольшой простой картинки,
а провода, соединяющие элементы схемы,
изображают в виде линий. Собственно,
такое графическое представление и
называют схемой устройства. Простые
схемы можно нарисовать так, как они
будут нарисованы ниже, более сложные
схемы рисуются на многих листах бумаги,
а для объяснения их работы используют
еще один графический вид – функциональные
схемы: все устройство можно, и должно,
разбить на части, функциональные узлы,
как, скажем, выпрямитель, усилитель,
преобразователь и т. д., которые изображаются
д., которые изображаются
в виде прямоугольников, связанных
линиями или стрелками. К таким сложным
(очень полезно, если и к простым) схемам
прилагают их описание, которое может
занимать несколько томов.
Графическое
изображение элементов электрической
схемы в разных странах, в разные годы
выглядело несколько по-разному. Так для
изображения батарейки используют
изображение из двух черточек, одна из
которых длиннее другой, с перпендикулярными
к ним выводами, аккумулятор изображали
в виде нескольких таких батареек. Но,
порой, в схеме не делается различия
между этими двумя источниками ЭДС. В
последнее время, особенно в программах,
эти источники питания объединяют с
другими источниками тока в общий класс
источников (source) и изображают в виде
кружка со значками плюс и минус. Подобные
отличия есть в изображении резисторов
в виде прямоугольников, обозначенных
латинской буквой R с порядковым номером
однотипных элементов, и в виде ломаной
линии. Есть отличия в графическом
изображении других элементов, о которых
я буду рассказывать по мере их появления
в книге. Обычно это не вызывает больших
Обычно это не вызывает больших
затруднений, но если вы будете рисовать
свои схемы, лучше выбрать один стиль.
Для
черчения схем и пояснения их работы я
буду пользоваться компьютером, точнее
демонстрационной версией программы
PSIM, которую скачал с сайта производителя.
Программа предназначена для разработки
схем силовой электроники. Многие
программы имеют свою специализацию.
Если эта программа перестанет мне
помогать в рассказе, я использую другую.
Программа PSIM предназначена для работы
на платформе Windows, но работает у меня с
Linux, при этом я использую эмулятор Wine.
Как это все делается я расскажу позже,
а сейчас хочу заметить, что изображение
резистора в программе есть только в
виде ломаной линии. Второе изображение
мне пришлось пририсовать в графическом
редакторе.
Схема
(схемы) на рисунке ниже имеют один
графический элемент, о котором я еще не
говорил. Это земля или общий схемный
провод. Посмотрите
на изображение схемы (два изображения),
а потом я постараюсь ответить на вопрос
об общем проводе схемы.
Рис.
1.1. Графическое изображение проводника,
сопротивления и батарейки
Зачем
же нужно вводить обозначение для общего
провода схемы, который часто называют
земляным проводом, или, просто, землей?
Забегая
вперед, скажу, что в схеме удобно измерять
напряжения относительно одной точки
схемы, или одного общего проводника,
удобно смотреть сигналы относительно
этого проводника. Кроме того, если этот
общий провод схемы соединить с землей
– специально устраиваемым заземлением,
имеющим хороший контакт именно с землей
(грунтом, почвой) – схема меньше
подвержена вредным влияниям внешних
электрических полей, поэтому общий
провод схемы часто называют «землей».
Мы
пока познакомились только с тремя
компонентами электронного устройства:
батарейка, проводник, резистор. Можно
ли с их помощью построить что-либо
интересное?
Можно.
Во-первых, можно провести несколько
экспериментов для знакомства с тремя
законами: закон Ома и два закона Кирхгофа.
Все законы мы рассмотрим в простейшем
виде, а более сложный их вид при
необходимости можно найти в учебной
литературе. Этих трех законов
электротехники, я надеюсь, мне хватит
на протяжении всей книги, и не появится
необходимости в других. Как схемы удобнее
изображать в графическом виде, так
законы удобнее записывать в виде
математических соотношений. Для этого
используется латинская буква R для
сопротивления, латинская буква I для
тока, и латинские U или V для напряжения.
Закон
Ома (для участка цепи) звучит, приблизительно,
так:
Падение
напряжения (или напряжение) на участке
цепи равно произведению тока на
сопротивление: U=I*R.
Не
знаю, как вас, меня удивляет, вызывает
чувство уважения и восторга проницательность
и ум человека, который смог подметить
и определить столь простую и полезную
связь между этими тремя величинами.
Именно его именем названа единица
сопротивления.
Соотношение
между этими тремя величинами с точки
зрения математики можно записать в трех
видах: U=R*I, I=U/R и R=U/I. Все три вида записи
Все три вида записи
можно применять на практике, но не
следует забывать, что, например, последнее
соотношение позволяет вычислить
сопротивление, однако сопротивление
проводника или резистора определяется
свойствами материала и геометрией
проводника, а ток, вычисляемый по
напряжению и сопротивлению, как
упорядоченное движение носителей
заряда, вызвается источником электродвижущей
силы. Напряжение в этом смысле можно
рассматривать, как некоторое напряжение
в отношениях между током, протекающим
по проводнику, и материалом проводника,
оказывающим сопротивление протеканию
тока.
Для
экспериментальной проверки соотношения
между напряжением, током и сопротивлением
можно собрать схему, аналогичную
изображенной на рис. 1.1, в которую следует
добавить два измерительных прибора:
вольтметр и амперметр (или использовать
мультиметр, произведя два измерения).
Вольтметр – это прибор используемый
для измерения напряжения. Бывают
вольтметры для измерения постоянного
напряжения, которым воспользуемся мы,
а бывают вольтметры переменного
напряжения, о которых речь пойдет дальше.
Амперметр – это прибор для измерения
тока, который также бывает для измерений
в цепях постоянного и переменного тока.
Эти
приборы бывают очень разной конструкции.
Я говорил о мультиметре. В его основе
лежит работа специализированной и
достаточно сложной микросхемы, называемой
аналого-цифровой преобразователь (АЦП).
Многие мультиметры могут кроме этой
микросхемы не иметь других микросхем,
лишь вспомогательные резисторы,
переключатель и дисплей, отображающий
цифры. Возможно, к концу книги мы
рассмотрим работу такого прибора, а
сейчас, все-таки опять забегая вперед,
я немного расскажу о стрелочном измерителе
тока и стрелочном измерителе напряжения.
Правда и они бывают очень разных
конструкций, и их работа может быть
основана на разных принципах. Однако
достаточно часто в стрелочных измерительных
приборах используют следующую конструкцию:
рамку с намотанным на нее проводом
помещают в магнитное поле, создаваемое
постоянными магнитами, и крепят с помощью
спиральных пружинок на оси так, чтобы
стрелка, прикрепленная к этой рамке,
находилась в нулевом положении, отмеченном
на шкале. Когда по рамке протекает
Когда по рамке протекает
постоянный ток, то в магнитном поле на
рамку действует сила, заставляя ее
вращаться. Поворот происходит до тех
пор, пока сила, вызываемая током, не
уравновесит возвращающую силу пружинок.
Стрелка останавливается в положении,
которое пропорционально протекающему
току, значение которого считывается со
шкалы прибора. Если у вас есть тестер
со стрелочной измерительной головкой,
то она может быть устроена именно так
или похожим образом: часто оси вращения
и пружинки возврата стрелки в ноль
заменяют «растяжками». То есть, к
рамке с проводом прикрепляют очень
тонкую полоску из пружинящего материала.
Растянутая на двух таких полосках рамка
под их действием занимает «нулевое»
положение, а при протекании тока
поворачивается, отчего полоски упруго
скручиваются, образуя силу, возвращающую
рамку со стрелкой в первоначальное
положение, когда ток перестает протекать
по рамке. Но о механизме взаимодействия
провода с током и магнитного поля я
ничего вам не говорил, поэтому будем
считать, что ничего не говорил и о
стрелочных приборах. Хотя, пожалуй,
Хотя, пожалуй,
добавлю к тому, о чем не говорил, что
измеритель тока легко превратить в
измеритель напряжения, добавив к нему
резистор.
Итак,
посмотрим, на закон Ома, который я
постараюсь проиллюстрировать в программе
PSIM. Кроме того, я спаяю схему на макетной
плате, используя один из резисторов,
которые выпаял из платы, вдруг я что-то
напутал и ввел вас в заблуждение. Доверяй,
но проверяй.
Рис.
1.2. Эксперимент, иллюстрирующий закон
Ома в программе PSIM
Как
видно из рисунка, к источнику питания
10V (10 Вольт, на схеме обозначен VDC1)
подключен резистор 1 кОм (1000 Ом), параллельно
которому включен вольтметр VP1, и
последовательно с которым включен
амперметр I1. График измерения тока
показывает, что ток равен 10.00m (10 миллиампер)
или 0.01 А. Если умножить сопротивление
на ток, то есть, 1000 Ом умножить на 0.01 А,
то получится падение напряжения в 10
вольт, которые и показывает второй
график, отображающий показания вольтметра.
Для получения правильных значений при
расчетах следует пользоваться основными
единицами, в данном случае ампер, ом и
вольт.
А
вот, что получилось с макетом. На
батарейке, которую я использую, написано
9V, на резисторе 1к, ток должен получиться
9мА (миллиампер, 0.009А). Измеренный ток
8мА.
В
чем ошибка? Во-первых, я не измерил ЭДС
(напряжение на батарейке), во-вторых, не
измерил сопротивление. Реальное
сопротивление резистора, если его
измерить, не 1 кОм (килоом, 1000 Ом), а 910 Ом.
А ЭДС батарейки после подключения
резистора оказывается равной 7.31 вольт.
Отсюда и расхождение, скорее не в теории
и практике, а в моем представлении о
том, что я делаю, и тем, что делаю в
действительности. Доверяй, но проверяй!
От
закона Ома можно плавно перейти ко
второму закону Кирхгофа. Почему ко
второму, а не к первому? Мне так удобнее.
В
упрощенном виде закон Кирхгофа звучит
так:
ЭДС
в замкнутом контуре равна сумме падений
напряжений.
Действительно,
на рисунке выше ЭДС (источника питания
VDC1) 10 В, а напряжение на резисторе тоже
10 В. Можно изменить схему, включив
последовательно два резистора, например,
по 500 Ом, измерить на них напряжения и
убедиться, что на каждом из них будет
падение напряжения 5 В, а сумма этих
напряжений получится 10 В.
Здесь
уместно добавить, что более верно этот
закон звучал бы так: алгебраическая
сумма всех ЭДС в замкнутом контуре равна
алгебраической сумме падений напряжений.
Но об этом лучше почитать в учебнике.
Хотя
для разговора о первом законе Кирхгофа
следовало бы нарисовать другую схему
(другую цепь), я использую схему рис.
1.2. Выше я говорил о том, что часто
вольтметр – это тоже измеритель тока,
то есть, ток протекает не только через
резистор R1, но и через вольтметр. Таким
образом, в точке соединения вольтметра
и резистора ток разветвляется, одна его
часть протекает по резистору, другая
по вольтметру, а затем обе эти части
соединяются и протекают через амперметр.
Сумма
токов, вытекающих из узла электрической
цепи при ее ветвлении, равна току,
втекающему в этот узел.
Так
в упрощенном виде звучит первый закон
Кирхгофа. В реальной схеме это можно
было бы проверить, включив еще два
амперметра в ветвях схемы, одна из
которых относится к резистору, а вторая
к вольтметру.
На
практике, проводя измерения, всегда
следует помнить, что вольтметр имеет
некоторое внутреннее сопротивление,
которое может повлиять на результаты
измерения. Так достаточно хороший
вольтметр может иметь внутреннее
сопротивление в 100 кОм. Много это или
мало? Это не много и не мало, но ровно
столько, сколько есть. Как это может
повлиять на ваше понимание происходящего?
Положим, у вас есть вольтметр и амперметр,
и вы хотите провести измерения. Вольтметр
имеет внутреннее сопротивление равное
100 кОм. Вы хотите определить, используя
закон Ома, величину сопротивления,
маркировка которого стерлась от времени
(но это был резистор в 100 кОм, о чем ни
вы, ни я не знаем). В схеме рис. 1.2 я заменю
В схеме рис. 1.2 я заменю
вольтметр (напряжение на резисторе R1
при измерении будет равно 10 В) сопротивлением
в 100 кОм, и такое же сопротивление будет
иметь резистор R1. По результату измерения
тока в цепи определим величину
сопротивления.
Рис.
1.3. Ток в цепи при определении величины
сопротивления по закону Ома
Как
видно из рисунка, ток равен 200 мкА. При
падении напряжения в 10 В, величина
сопротивления определится делением
этого напряжения на ток и будет равна
50 кОм. Так мы измерили неизвестное
сопротивление без учета сопротивления
вольтметра. И ошиблись в два раза. А это
уже не мало. В данном конкретном случае
нам помогло бы проведение двух измерений
с помощью тестера или мультиметра.
Первый раз мы могли бы измерить напряжение,
а второй раз ток. Думаю, мы получили бы
правильный результат. Но… но только в
этом случае. Если немного усложнить
цепь, скажем, включив последовательно
с измеряемым сопротивлением еще одно
такой же величины, то и методика двух
измерений может дать неверный результат.
Рис.
1.4. Измерение величины сопротивления
без учета сопротивления вольтметра
По
графикам трудно определить точные
значения, но приблизительно это будет
напряжение 3.35 В и ток 66 мкА. В результате
деления получается значение около 51
кОм. Такое измерение в одних случаях
может только затруднить понимание
реального положения дел, но в других
может привести к неприятностям, которых
лучше избежать, если помнить, что каждый
прибор имеет определенные параметры,
и их следует учитывать при пользовании
прибором.
Можно
объединить все три закона в одно правило,
если кому-то удобно запомнить его.
Сумма
напряжений в электрической цепи, равных
произведению сопротивлений на ток,
протекающий через них, равна сумме ЭДС
в этой цепи, а сумма токов, вытекающих
из узла ко по всем ветвям цепи, равна
втекающему в узел току.
И
следует помнить, что на всех компонентах
электронных устройств проставляют
номинальное значение, которое, в
зависимости от изготовления, может
отличаться от реального на 5-10%, хотя
есть и компоненты, изготовленные с
большей точностью, 0.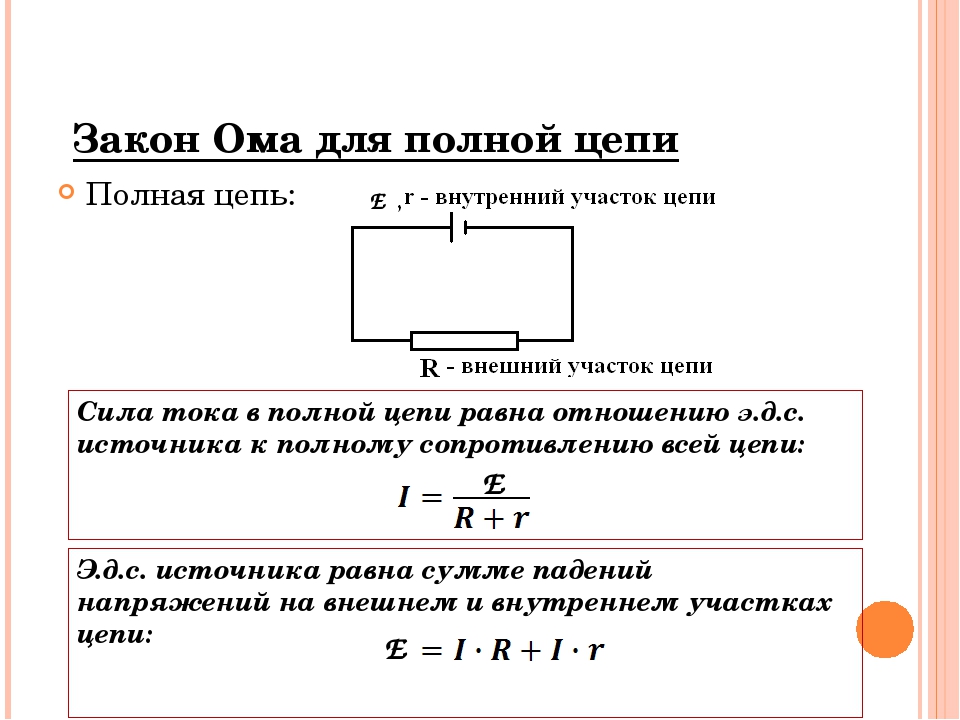 1-1%, но они применяются
1-1%, но они применяются
реже и стоят дороже.
Напомню,
что за техническое направление протекания
постоянного тока принято направление
от плюса к минусу. Цифровые мультиметры,
как правило, показывают знак измеряемого
напряжения и тока, и они не так чувствительны
к подключению с неверной полярностью,
как стрелочные приборы. Последние
зашкаливают «в обратную сторону»
и могут от этого пострадать. Всегда
следует проверять полярность подключения
стрелочных приборов. Минус у тестеров
при измерении напряжения и тока зачастую
помечают значком в виде звездочки. В
простых цепях, изображенных на рисунках,
все достаточно очевидно, но в сложных
цепях, когда есть много сопротивлений,
включенных сложным образом, когда есть
несколько источников питания, тогда
определение напряжений и токов
усложняется. Конечно, существуют
математические методы расчета подобных
цепей, описанные в учебниках, однако я
сомневаюсь в их популярности в любительских
кругах, поскольку удобнее измерить
интересующую величину, чем рассчитать
ее, но очень важно иметь ясное представление
об основных процессах в электрической
цепи.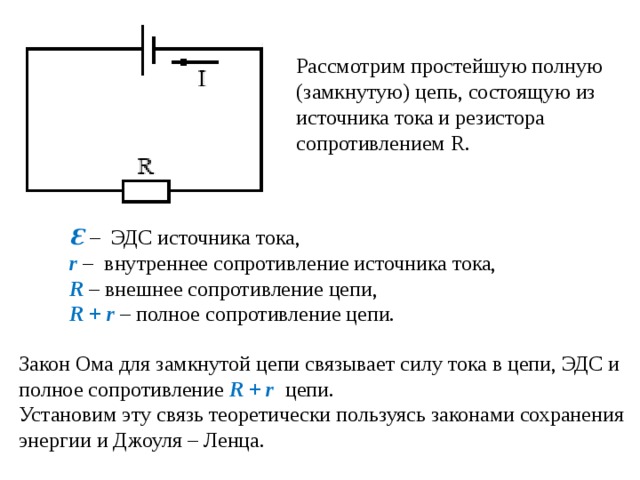 Подключая прибор, следует начинать
Подключая прибор, следует начинать
измерение с безопасного для прибора
предела измерения – самого большого
напряжения или тока, позже его можно
изменить.
Любой
справочник, любая реальная схема содержит
очень большое количество элементов
помимо тех, о которых шла речь выше, и
позже мы поговорим об этом, и я постараюсь
показать, что достаточно сложные с
теоретической точки зрения процессы
можно в любительской практике свести
к таким понятиям, как сопротивление,
напряжение и ток.
При
работе с электрическими цепями важно
учитывать мощность, определяемую
произведением напряжения на ток. Если
мы измеряем ток, уходящий от источника
питания, и умножаем его на ЭДС (напряжение)
источника питания, то мы можем говорить
о мощности, потребляемой схемой. Если
мы измеряем напряжение на сопротивлении
и ток, протекающий через него, то можем
говорить о мощности, потребляемой этим
сопротивлением и обычно выделяющейся
на нем в виде тепла. Естественно, что
резистор при этом нагревается, и если
неправильно выбрать его параметр,
допустимую мощность рассеяния, то
сопротивление перегреется и может
сгореть. Обычно на схеме указывается
Обычно на схеме указывается
мощность любого сопротивления, или она
указывается в спецификации – перечне
всех элементов схемы с их параметрами.
По параметру допустимой мощности
сопротивления делятся на ряд значений,
из которых наиболее часто употребляемые
в схемах – это резисторы в четверть и
половину ватта. Мощность, рассеиваемая
резистором, не должна превышать этой
величины. Вместе с тем, следует помнить,
что нагрев сопротивления приводит к
изменению его величины. Чем ближе
допустимая мощность рассеивания
резистора к мощности, выделяемой на
нем, тем сильнее он будет разогреваться.
Если вам важно сохранить величину
сопротивления, то следует выбрать более
мощное сопротивление. В измерительных
приборах, равно как любых цепях,
относящихся к измерению, там где значение
сопротивления очень важно, кроме
сопротивлений с более высокой допустимой
мощностью рассеяния применяют специальные
сопротивления, мало меняющие свое
значение при нагреве.
Есть
еще несколько интересных, и как мне
кажется, важных моментов, относящихся
к сопротивлению. Многие неисправности
Многие неисправности
в электронных устройствах связаны с
проблемами источников питания. Батарейки,
например, со временем «садятся».
Простейший способ проверить батарейку
– измерить ток, который она может
отдавать. Для этого достаточно включить
мультиметр (или тестер) в режим измерения
максимального для конкретного прибора
постоянного тока, мой мультиметр измеряет
токи до 10 А, и подключить амперметр к
батарейке. Свежая батарейка, в зависимости
от типа, покажет ток в несколько ампер,
тогда как разряженная сможет дать только
десятки миллиампер. Зная закон Ома, мы
можем определить ожидаемый ток до
проведения измерения. Положим батарейка
имеет напряжение 1.5 вольта. Амперметр
имеет сопротивление 0.1 Ом. Тогда мы
должны получить ток 15 А. Проверим это
утверждение сначала в программе PSIM.
Рис.
1.5. Проверка батарейки на пригодность
В
схеме на рисунке сопротивление R1 – это
сопротивление реального измерительного
прибора. Как мы и рассчитали, при измерении
протекает ток в 15 А. Но едва ли вы увидите
Но едва ли вы увидите
такой ток, если проведете реальное
измерение. И дело не в плохой батарейке.
Дело в том, что реальная батарейка, как
любой источник питания, это не идеальный
источник ЭДС. Любой реальный источник
питания имеет, как и реальный измерительный
прибор, внутреннее сопротивление.
Небольшое, зависящее от типа источника,
но это внутреннее сопротивление есть.
Оно-то и уменьшает ток через батарейку.
То есть, в схеме на рис. 1.5 следовало бы
нарисовать последовательно с источником
питания еще одно сопротивление, а при
расчете по закону Ома использовать
сумму двух резисторов. Однако внутреннее
сопротивление батарейки – это параметр,
который не увидишь на этикетке. Плохо
ли, что батарейка имеет внутреннее
сопротивление, да еще и меняющееся со
временем? С одной стороны плохо. А с
другой… современные мобильные телефоны
имеют аккумуляторы с очень низким
внутренним сопротивлением. Они могут
отдавать большой ток. По этой причине
многие из них приходится снабжать
специальным устройством, ограничивающим
этот ток. И проблема не в том, что если
И проблема не в том, что если
этого не сделать, и вы коснетесь выводов
аккумулятора, то вас «тряхнет»
током. Нет. Проблема в том, что если этого
не сделать, и вы решите почистить выводы
аккумулятора безопасной бритвой, бывает
такое, то при замыкании выводов бритвой
большой ток через нее может расплавить
бритву (вспомните про нагревание
резистора), а расплавленный металл
вызвать серьезные ожоги. При этом процесс
происходит настолько быстро, что
расплавленный металл разбрызгивается
в разные стороны. Что хорошо в одних
случаях, плохо в других. На практике,
если внутреннее сопротивление источника
на порядок меньше сопротивления цепи,
то им можно пренебречь.
Коль
скоро я упомянул внутреннее сопротивление
батареек, хочу немного рассказать о
граблях, на которые сам временами
наступаю. Схему на рисунке ниже я выберу
самую простую.
Вы
все знаете, что часто в пультах, плеерах
и т.п. ставят две батарейки, включая их
последовательно. Иногда две батарейки
включают параллельно, соединяя их
положительные и отрицательные выводы.
В этом случае они могут дать больший
ток, или служат вдвое дольше. Что будет,
если при параллельном включении соединить
их разнополярно, положительный вывод
одной батарейки соединить с отрицательным
другой, а отрицательный с положительным?
Согласно закону Кирхгофа сумма ЭДС
должна быть равна напряжению. Но сумма
ЭДС (алгебраическая, то есть, с учетом
знака) равна нулю. Значит напряжение
тоже будет равно нулю. А ток?
Если
я отвечаю не подумав, то готов сказать
– нет напряжения, нет и тока. Но это не
так. Нарисуем эту схему в программе
PSIM, добавив внутренние сопротивления
и приборы.
Рис.
1.6. Встречное включение батареек
Как
видно на рисунке напряжение (VP1) близко
к нулю и равно нескольким микровольтам,
тогда как ток (I1) равен 15 А. Действительно,
если убрать общий провод (землю) и
повернуть схему, то можно рассматривать
два источника питания, как включенные
последовательно и нагруженные на цепь,
состоящую из резисторов (внутренние
сопротивления батареек) R1 и R2. Тогда ЭДС
Тогда ЭДС
схемы будет 3 В, сопротивление цепи 0.2
Ома, ток по закону Ома 15 А, а сумма падений
напряжений U1=15A*0.1 Ом плюс такое же U2.
Падение напряжения происходит на
внутренних сопротивлениях источников
питания. Если бы внутреннее сопротивление
не было скрыто от глаз, было бы проще
ответить правильно, но, что глаз не
видит, того, вроде бы, и нет.
Две
батарейки по 1.5 вольта в реальном
эксперименте показали 0.2В. Отчего так
много? Попробуйте менять внутреннее
сопротивление R1 в схеме рис. 1.6.
Есть
еще один интересный эксперимент, который
легко провести, чтобы понять, что в
электротехнике называют источником
тока в отличие от источника напряжения.
Представим, что внутреннее сопротивление
батарейки очень велико. Скажем, 100 кОм.
Напряжение батарейки для определенности
пусть будет 10 В. Тогда максимальный ток,
который батарейка может отдавать во
внешнюю цепь будет не более, чем 10В/100кОм
= 0.0001А (или 100 мкА). Если мы к такой батарейке
подключим сопротивление в 1 кОм, то ток,
практически, не изменится. То есть, в
То есть, в
достаточно широком диапазоне изменений
сопротивления внешней цепи ток,
протекающий по этой цепи, не будет
зависеть от сопротивления цепи. Конечно,
напряжение такой батарейки будет
меняться очень сильно, но ток нет, что
и находит применение на практике.
Источник
питания, напряжение которого мало
зависит от сопротивления внешней цепи,
мы будем называть источником напряжения,
а тот, ток которого мало зависит от
сопротивления нагрузки, источником
тока.
Итак.
Всего несколько понятий: ЭДС, напряжение,
ток и сопротивление; всего три закона
электротехники: закон Ома и два закона
Кирхгофа, – дали нам возможность провести
ряд интересных экспериментов. И это
далеко не все интересные эксперименты,
которые можно было бы провести. Попробуйте
составлять цепи из многих батареек и
сопротивлений, включая их разными
способами, и попытайтесь ответить на
вопрос о падении напряжения на любом
из резисторов и токе через него! Уверен,
вы найдете много интереснейших вариантов.
Прежде,
чем продолжить рассказ, я хочу еще раз
обратить ваше внимание на то, что
электричество всегда несет с собой
некоторую опасность. Я уже говорил, что
некоторые источники питания при
неаккуратном обращении с ними могут
привести к травмам, как аккумулятор
сотового телефона, но речь шла об ожогах
при коротком замыкании. Теперь я хочу
сказать о других опасностях. Некоторые
аккумуляторы, источники питания
многократного применения, очень похожи
на батарейки. Если не обратить внимания
на предостерегающие надписи, если
попытаться заряжать батарейки, то это
может вызывать вытекание из них
электролита. А современные батарейки
в качестве электролита могут использовать
щелочи. Попадая на руки, электролит тоже
вызовет болезненный и долго не заживающий
ожог. Прежде, чем пытаться заряжать
что-либо, следует проверить, подлежит
ли оно заряду? И еще немного о поражении
электрическим током. Если через человека
проходит очень небольшой ток в несколько
десятков миллиампер, то это может
вызывать, если и не смертельное, то
весьма опасное поражение электрическим
током. Всего несколько десятков
Всего несколько десятков
миллиампер! А батарейка для фонарика
может дать ток в несколько ампер! Опасна
ли она? Здесь следует вспомнить закон
Ома. Если напряжение батарейки 1.5 В, а
сопротивление внешней цепи (то есть,
человека, который взялся одной рукой
за один вывод батарейки, а другой рукой
за другой вывод) несколько десятков
тысяч ом, то ток будет измерятся единицами
микроампер и вреда не принесет.
Сопротивление человека в основном
зависит от многих внешних и природных
факторов и составляет несколько тысяч
ом, поэтому при маленьких напряжениях
можно не слишком беспокоиться о поражении
электрическим током. Но такой подход
может сыграть злую шутку, если небольшое
напряжение, безопасное с точки зрения
расчетов, пройдет через человека
неудачным образом. Лучше сразу выработать привычку, даже работая с
батарейками
от карманного фонаря, никогда не касаться
двух полюсов одновременно, если есть
возможность, то не проводить измерений
под напряжением. Нужно измерить напряжение
в схеме, выключите питание, подключите
прибор и включите питание.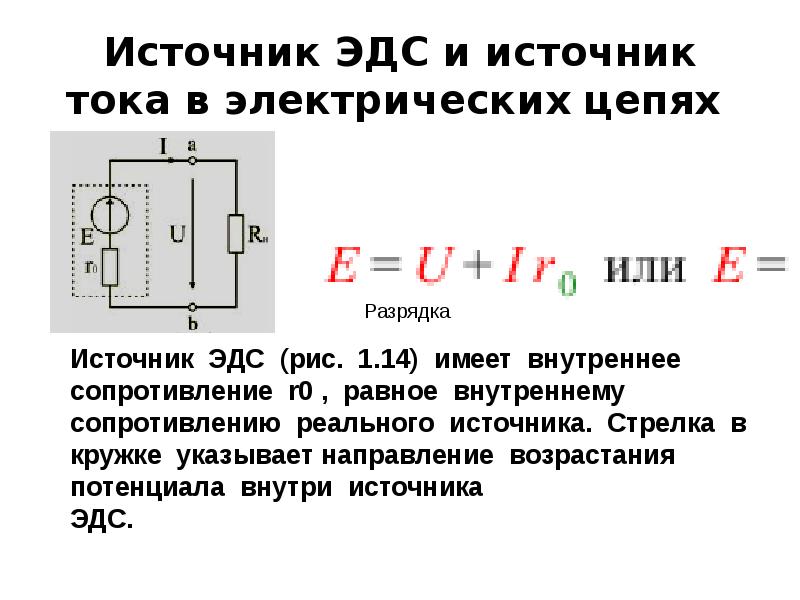 Небрежность,
Небрежность,
пренебрежение правилами безопасности
могут навсегда отбить охоту к работе
со схемами. Но небрежность, всегда
небрежность. Схема здесь ни в чем не
виновата.
Резюмируя
свои предостережения, я хочу посоветовать
начинающим использовать в экспериментах
либо простейшие батарейки, либо
качественные (с защитой) блоки питания,
а все сомнительные эксперименты вначале
проводить за компьютером, используя
программы САПР, такие как PSIM.
Насколько
они полезны станет понятно,
когда мы начнем говорить о переменном
токе.
Как пишется закон ома для участка цепи. Закон ома для полной цепи
Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.
При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).
Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).
Рис. 1. Изображение идеального и реального источников тока
Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.
Сформулируем закона Ома для полной цепи так (см. рис. 2): сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.
Рис. 2. Схема закона Ома для полной цепи.
- R – внешнее сопротивление [Ом];
- r – сопротивление источника ЭДС (внутреннее) [Ом];
- I – сила тока [А];
- ε– ЭДС источника тока [В].
Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.
I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.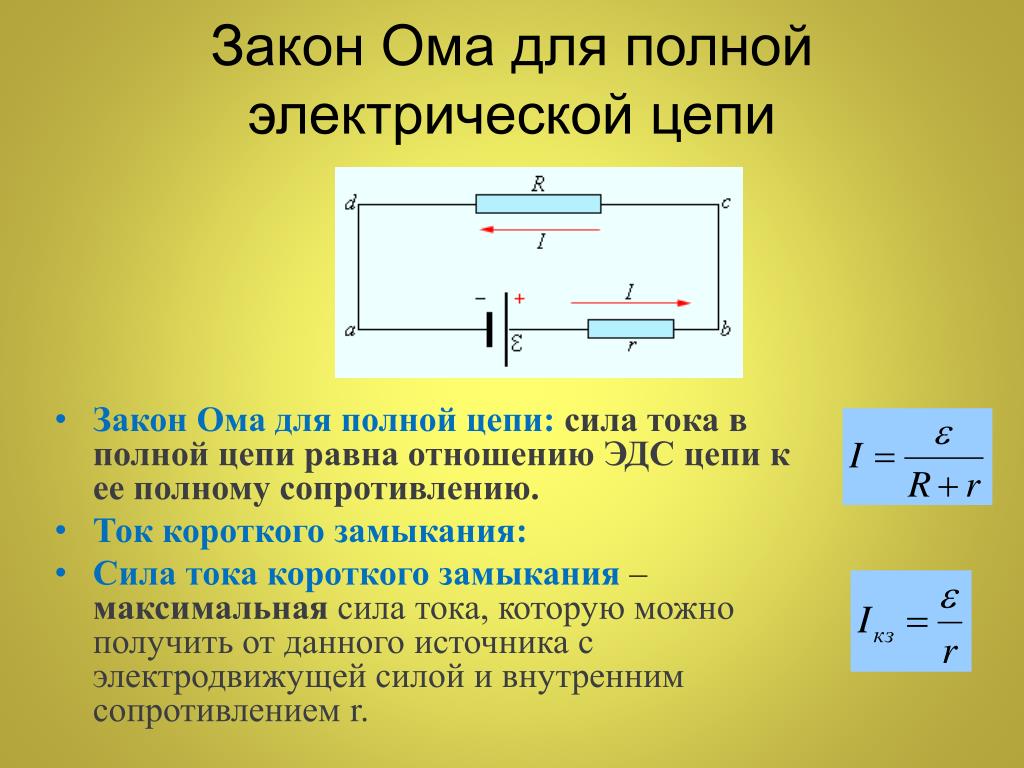
По определению закона Ома для полной цепи, сила тока равна:
II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.
Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:
III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?
Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:
следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления.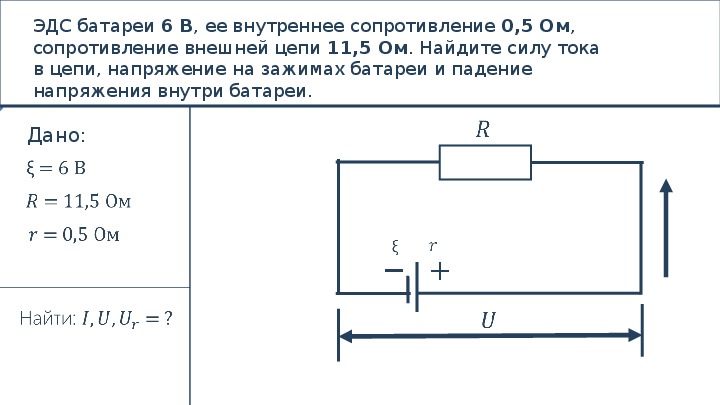 Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.
Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.
Закон
Ома для участка цепи: сила
тока
I
на участке электрической цепи прямо
пропорциональна напряжению
U
на концах участка и обратно пропорциональна
его сопротивлению
R.
Формула
закона:
I
=.
Отсюда запишем формулыU
=
IR
и R
=
.
Рис.1.
Участок
цепи
Рис.2.
Полная
цепь
Закон
Ома для полной цепи: сила
тока
I
полной электрической цепи
равнаЭДС
(электродвижущей силе) источника тока
Е
,
деленной на полное сопротивление цепи
(R
+ r).
Полное
сопротивление цепи равно сумме
сопротивлений внешней цепи R
и внутреннего r
источника тока.Формула
закона I
=
.
На
рис. 1 и 2 приведены схемы электрических
цепей.
3. Последовательное и параллельное соединение проводников
Проводники
в электрических цепях могут соединяться
последовательно
и параллельно
.
Смешанное соединение сочетает оба эти
соединения.
Сопротивление,при
включении которого
вместо всех других проводников,
находящихся между двумя точками цепи,
ток и напряжение остаются неизменными,
называют
эквивалентным
сопротивлением
этих
проводников.
Последовательное соединение
Последовательным
называется соединение, при котором
каждый
проводник соединяется только с одним
предыдущим и одним последующим
проводниками.
Как
следует из первого правила
Кирхгофа
,
при последовательном
соединении проводников сила электрического
тока, протекающего по всем проводникам,
одинакова (на основании закона сохранения
заряда).
1.
При последовательном соединении
проводников
(рис. 1)
сила
тока во всех проводниках одинакова:
I
1
=
I
2
=
I
3
=
I
Рис.
1.Последовательное
соединение двух проводников.
2.
Согласно закону Ома, напряженияU
1
иU
2
на
проводниках равны U
1
=
IR
1
,
U
2
=
IR
2
,
U
3
=
IR
3
.
Напряжение
при последовательном соединении
проводников равно сумме напряжений на
отдельных участках (проводниках)
электрической цепи.
U
=
U
1
+
U
2
+
U
3
Позакону
Ома, напряжения U
1,
U
2
на
проводниках равныU
1
=
IR
1
,
U
2
=
IR
2
,
В
соответствии вторым правилом Кирхгофа
напряжение на всем участке:
U
=
U
1
+
U
2
=
IR
1
+
IR
2
=
I(R
1
+
R
2
)=
I·R.
Получаем:
R
=
R
1
+
R
2
Общее
напряжение
U
на проводниках равно сумме напряжений
U
1
,
U
2
,
U
3
равно:
U
=
U
1
+
U
2
+
U
3
=
I
·
(R
1
+
R
2
+
R
3
)
=
IR
где
R
ЭКВ
–
эквивалентное
сопротивление всей цепи. Отсюда: R
ЭКВ
=
R
1
+
R
2
+
R
3
При
последовательном соединении эквивалентное
сопротивление цепи равно сумме
сопротивлений отдельных участков цепи:
R
ЭКВ
=
R
1
+
R
2
+
R
3
+…
Этот
результат справедлив для
любого числа
последовательно соединенных проводников.
Из
закона Омаследует:
при равенстве сил тока при последовательном
соединении:
I
=
,
I
=
.
Отсюда
=
или
=,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.
При
последовательном соединении n
одинаковых
проводников общее напряжение равно
произведению напряжению одного U 1
на
их количество n
:
U
ПОСЛЕД
=
n
·
U
1
.
Аналогично
для сопротивлений:
R
ПОСЛЕД
=
n
·
R
1
При размыкании
цепи одного из последовательно
соединенных потребителей ток исчезает
во всей цепи, поэтому последовательное
соединение на практике не всегда удобно.
Электрический ток и опасное напряжение невозможно услышать (за исключением гудящих высоковольтных линий и электроустановок).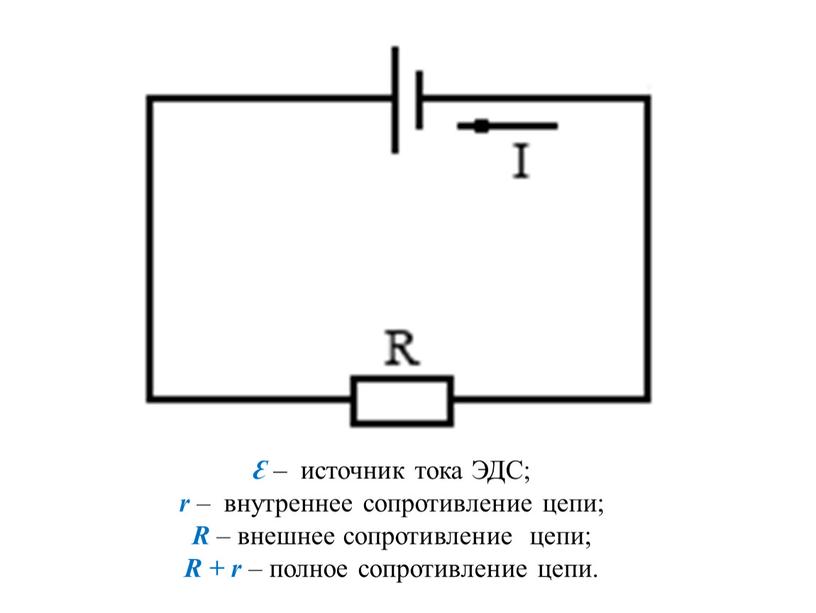 Токоведущие части, находящиеся под напряжением, ничем не отличаются по внешнему виду.
Токоведущие части, находящиеся под напряжением, ничем не отличаются по внешнему виду.
Невозможно узнать их и по запаху, и повышенной температурой в штатных режимах работы они не отличаются. Но включаем в безмолвную и тихую розетку пылесос, щелкаем выключателем — и энергия словно берется из ниоткуда, сама по себе, материализуясь в виде шума и компрессии внутри бытового прибора.
Опять же, если мы воткнем в разъемы розетки два гвоздя и возьмемся за них, то буквально всем своим телом ощутим реальность и объективность существования электрического тока. Делать это, конечно, настоятельно не рекомендуется. Но примеры с пылесосом и гвоздями наглядно демонстрируют нам, что изучение и понимание основных законов электротехники способствует безопасности при обращении с бытовым электричеством, а также устранению суеверных предубеждений, связанных с электрическим током и напряжением.
Итак, рассмотрим один, самый ценный закон электротехники, который полезно знать. И попытаемся сделать это в как можно более популярной форме.
Закон Ома
1. Дифференциальная форма записи закона Ома
Самый главный закон электротехники — это, конечно, закон Ома
. О его существовании знают даже люди, не имеющие отношения к электротехнике. Но между тем вопрос «А знаешь ли ты закон Ома?» в технических ВУЗах является ловушкой для зарвавшихся и самонадеянных школяров. Товарищ, разумеется, отвечает, что закон Ома знает отлично, и тогда к нему обращаются с просьбой привести этот закон в дифференциальной форме. Тут-то и выясняется, что школяру или первокурснику еще учиться и учиться.
Однако дифференциальная форма записи закона Ома на практике почти неприменима. Она отражает зависимость между плотностью тока и напряженностью поля:
где G — это проводимость цепи; Е — напряженность электрического тока.
Все это — попытки выразить электрический ток, принимая во внимание только физические свойства материала проводника, без учета его геометрических параметров (длина, диаметр и тому подобное). Дифференциальная форма записи закона Ома — это чистая теория, знание ее в быту совершенно не требуется.
Дифференциальная форма записи закона Ома — это чистая теория, знание ее в быту совершенно не требуется.
2. Интегральная форма записи закона Ома для участка цепи
Иное дело — интегральная форма записи. Она тоже имеет несколько разновидностей. Самой популярной из них является закон Ома для участка цепи: I=U/R
Говоря по-другому, ток в участке цепи всегда тем выше, чем больше приложенное к этому участку напряжение и чем меньше сопротивление этого участка.
Вот этот «вид» закона Ома просто обязателен к запоминанию для всех, кому хоть иногда приходится иметь дело с электричеством. Благо, и зависимость-то совсем простая. Ведь напряжение в сети можно считать неизменным. Для розетки оно равно 220 вольт. Поэтому получается, что ток в цепи зависит только от сопротивления цепи, подключаемой к розетке. Отсюда простая мораль: за этим сопротивлением надо следить.
Короткие замыкания, которые у всех на слуху, случаются именно по причине низкого сопротивления внешней цепи. Предположим, что из-за неправильного соединения проводов в ответвительной коробке фазный и нулевой провода оказались напрямую соединены между собой. Тогда сопротивление участка цепи резко снизится практически до нуля, а ток так же резко возрастет до очень большой величины. Если электропроводка выполнена правильно, то сработает автоматический выключатель, а если его нет, или он неисправен или подобран неправильно, то провод не справится с возросшим током, нагреется, расплавится и, возможно, вызовет пожар.
Предположим, что из-за неправильного соединения проводов в ответвительной коробке фазный и нулевой провода оказались напрямую соединены между собой. Тогда сопротивление участка цепи резко снизится практически до нуля, а ток так же резко возрастет до очень большой величины. Если электропроводка выполнена правильно, то сработает автоматический выключатель, а если его нет, или он неисправен или подобран неправильно, то провод не справится с возросшим током, нагреется, расплавится и, возможно, вызовет пожар.
Но бывает, что приборы, включенные в розетку и отработавшие уже далеко не один час, становятся причиной короткого замыкания. Типичный случай — вентилятор, обмотки двигателя которого подверглись перегреву из-за заклинивания лопастей. Изоляция обмоток двигателя не рассчитана на серьезный нагрев, она быстро приходит в негодность. В результате появляются межвитковые короткие замыкания, которые снижают сопротивление и, в соответствии с законом Ома, также ведут к увеличению тока.
Повышенный ток, в свою очередь, приводит изоляцию обмоток в полную негодность, и наступает уже не межвитковое, а самое настоящее, полноценное короткое замыкание. Ток идет помимо обмоток, сразу из фазного в нулевой провод. Правда, все сказанное может случиться только с совсем простым и дешевым вентилятором, не оборудованным тепловой защитой.
Ток идет помимо обмоток, сразу из фазного в нулевой провод. Правда, все сказанное может случиться только с совсем простым и дешевым вентилятором, не оборудованным тепловой защитой.
Закон Ома для переменного тока
Надо отметить, что приведенная запись закона Ома описывает участок цепи с постоянным напряжением. В сетях переменного напряжения существует дополнительное реактивное сопротивление, а полное сопротивление приобретает значение квадратного корня из суммы квадратов активного и реактивного сопротивления.
Закон Ома для участка цепи переменного тока принимает вид: I=U/Z
,
где Z — полное сопротивление цепи.
Но большое реактивное сопротивление свойственно, прежде всего, мощным электрическим машинам и силовой преобразовательной технике. Внутреннее электрическое сопротивление бытовых приборов и светильников практически полностью является активным. Поэтому в быту для расчетов можно пользоваться самой простой формой записи закона Ома: I=U/R.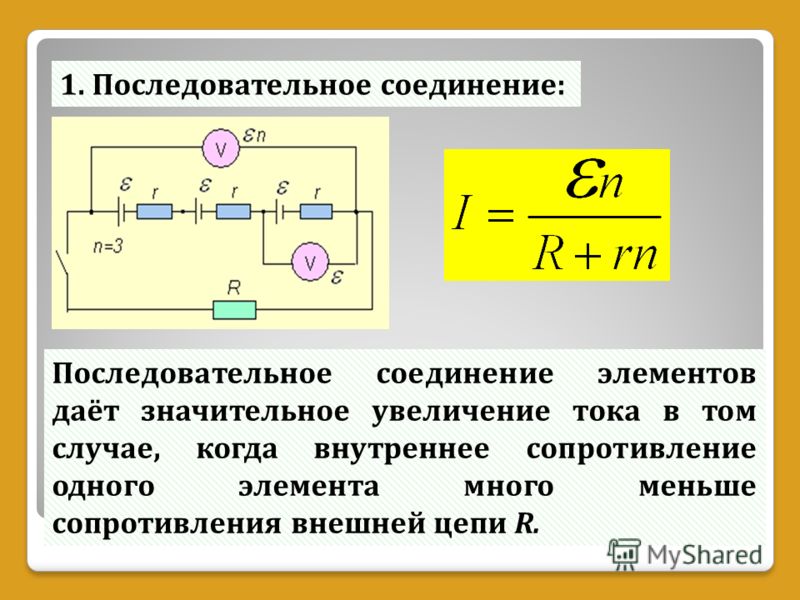
3. Интегральная форма записи для полной цепи
Раз есть форма записи закона для участка цепи, то существует и закон Ома для полной цепи: I=E/(r+R)
.
Здесь r — внутреннее сопротивление источника ЭДС сети, а R — полное сопротивление самой цепи.
За физической моделью для иллюстрации этого подвида закона Ома далеко ходить не надо — это бортовая электрическая сеть автомобиля, аккумулятор в которой является источником ЭДС. Нельзя считать, что сопротивление аккумулятора равно абсолютному нулю, поэтому даже при прямом замыкании между его клеммами (отсутствии сопротивления R) ток вырастет не до бесконечности, а просто до высокого значения. Однако этого высокого значения, конечно, хватит для того, чтобы вызвать расплавление проводов и возгорание обшивки авто. Поэтому электрические цепи автомобилей защищают от короткого замыкания при помощи предохранителей.
Такой защиты может оказаться недостаточно, если замыкание произойдет до блока предохранителей относительно аккумулятора, или если вовсе один из предохранителей заменен на кусок медной проволоки. Тогда спасение только в одном — необходимо как можно быстрее разорвать цепь полностью, откинув «массу», то есть минусовую клемму.
Тогда спасение только в одном — необходимо как можно быстрее разорвать цепь полностью, откинув «массу», то есть минусовую клемму.
4. Интегральная форма записи закона Ома для участка цепи, содержащего источник ЭДС
Следует упомянуть и о том, что есть и еще одна разновидность закона Ома — для участка цепи, содержащего источник ЭДС:
Здесь U — это разность потенциалов в начале и в окончании рассматриваемого участка цепи. Знак перед величиной ЭДС зависит от направленности ее относительно напряжения. Воспользоваться законом Ома для участка цепи нередко приходится при определении параметров цепи, когда часть схемы недоступна для детального изучения и не интересует нас. Допустим, она скрыта неразъемными деталями корпуса. В оставшейся схеме имеется источник ЭДС и элементы с известным сопротивлением. Тогда, замерив напряжение на входе неизвестной части схемы, можно вычислить ток, а после этого — и сопротивление неизвестного элемента.
Выводы
Таким образом, мы можем увидеть, что «простой» закон Ома далеко не так прост, как кому-то, возможно, казалось. Зная все формы интегральной записи законов Ома, можно понять и легко запомнить многие требования электробезопасности, а также приобрести уверенность в обращении с электричеством.
Зная все формы интегральной записи законов Ома, можно понять и легко запомнить многие требования электробезопасности, а также приобрести уверенность в обращении с электричеством.
Физический закон , определяющий связь (или электрического напряжения) с силой тока , протекающего в проводнике , и сопротивлением проводника. Установлен Георгом Омом в 1826 году и назван в его честь.
Закон Ома для переменного тока
Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига .
Если ток является синусоидальным с циклической частотой
ω
{\displaystyle \omega }
, а цепь содержит не только активные, но и реактивные компоненты (ёмкости , индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
U
=
I
⋅
Z
{\displaystyle \mathbb {U} =\mathbb {I} \cdot Z}
- U = U
0 e
i
ωt
— напряжение или разность потенциалов, - I
— сила тока, - Z = Re
−i
δ
— комплексное сопротивление (электрический импеданс), - R
= √ R a
2 + R r
2— полное сопротивление,
- R r
= ωL
− 1/(ωC
)
— реактивное сопротивление (разность индуктивного и емкостного), - R а
— активное (омическое) сопротивление, не зависящее от частоты, - δ = − arctg (R r
/R a
)
— сдвиг фаз между напряжением и силой тока. {i(\omega t+\varphi)},}
{i(\omega t+\varphi)},}
что
Im
U
=
U
.
{\displaystyle \operatorname {Im} \mathbb {U} =U.}
Тогда все значения токов и напряжений в схеме надо считать как
F
=
Im
F
{\displaystyle F=\operatorname {Im} \mathbb {F} }Здравствуйте, уважаемые читатели сайта «Заметки электрика»..
Сегодня открываю новый раздел на сайте под названием .
В этом разделе я постараюсь в наглядной и простой форме объяснить Вам вопросы электротехники. Скажу сразу, что далеко углубляться в теоретические знания мы не будем, но вот с основами познакомимся в достаточном порядке.
Первое, с чем я хочу Вас познакомить, это с законом Ома для участка цепи. Это самый основной закон, который должен знать каждый .
Знание этого закона позволит нам беспрепятственно и безошибочно определять значения силы тока, напряжения (разности потенциалов) и сопротивления на участке цепи.
Кто такой Ом? Немного истории
Закон Ома открыл всем известный немецкий физик Георг Симон Ом в 1826 году.
 Вот так он выглядел.
Вот так он выглядел.Всю биографию Георга Ома я рассказывать Вам не буду. Про это Вы можете узнать на других ресурсах более подробно.
Скажу только самое главное.
Его именем назван самый основной закон электротехники, который мы активно применяем в сложных расчетах при проектировании, на производстве и в быту.
Закон Ома для однородного участка цепи выглядит следующим образом:
I – значение тока, идущего через участок цепи (измеряется в амперах)
U – значение напряжения на участке цепи (измеряется в вольтах)
R – значение сопротивления участка цепи (измеряется в Омах)
Если формулу объяснить словами, то получится, что сила тока пропорциональная напряжению и обратно пропорциональна сопротивлению участка цепи.
Проведем эксперимент
Чтобы понять формулу не на словах, а на деле, необходимо собрать следующую схему:
Цель этой статьи — это показать наглядно, как использовать закон Ома для участка цепи.
 Поэтому я на своем рабочем стенде собрал эту схему. Смотрите ниже как она выглядит.
Поэтому я на своем рабочем стенде собрал эту схему. Смотрите ниже как она выглядит.С помощью ключа управления (избирания) можно выбрать, либо постоянное напряжение, либо переменное напряжение на выходе. В нашем случае используется постоянное напряжения. Уровень напряжения я меняю с помощью лабораторного автотрансформатора (ЛАТР).
В нашем эксперименте я буду использовать напряжение на участке цепи, равное 220 (В). Контроль напряжения на выходе смотрим по вольтметру.
Теперь мы полностью готовы провести самостоятельно эксперимент и проверить закон Ома в действительности.
Ниже я приведу 3 примера. В каждом примере мы будем определять искомую величину 2 методами: с помощью формулы и практическим путем.
Пример № 1
В первом примере нам нужно найти ток (I) в цепи, зная величину источника постоянного напряжения и величину сопротивления светодиодной лампочки.
Напряжение источника постоянного напряжения составляет U = 220 (В)
. Сопротивление светодиодной лампочки равно R = 40740 (Ом)
Сопротивление светодиодной лампочки равно R = 40740 (Ом)
.С помощью формулы найдем ток в цепи:
I = U/R = 220 / 40740 = 0,0054 (А)
Подключаем последовательно светодиодной лампочке , включенный в режиме амперметр, и замеряем ток в цепи.
На дисплее мультиметра показан ток цепи. Его значение равно 5,4 (мА) или 0,0054 (А), что соответствует току, найденному по формуле.
Пример № 2
Во втором примере нам нужно найти напряжение (U) участка цепи, зная величину тока в цепи и величину сопротивления светодиодной лампочки.
I = 0,0054 (А)
R = 40740 (Ом)
С помощью формулы найдем напряжение участка цепи:
U = I*R = 0,0054 *40740 = 219,9 (В) = 220 (В)
А теперь проверим полученный результат практическим путем.
Подключаем параллельно светодиодной лампочке мультиметр, включенный в режиме вольтметр, и замеряем напряжение.

На дисплее мультиметра показана величина измеренного напряжения. Его значение равно 220 (В), что соответствует напряжению, найденному по формуле закона Ома для участка цепи.
Пример № 3
В третьем примере нам нужно найти сопротивление (R) участка цепи, зная величину тока в цепи и величину напряжения участка цепи.
I = 0,0054 (А)
U = 220 (В)
Опять таки, воспользуемся формулой и найдем сопротивление участка цепи:
R = U/
I = 220/0,0054 = 40740,7 (Ом)
А теперь проверим полученный результат практическим путем.
Сопротивление светодиодной лампочки мы измеряем с помощью или мультиметра.
Полученное значение составило R = 40740 (Ом)
, что соответствует сопротивлению, найденному по формуле.Как легко запомнить Закон Ома для участка цепи!!!
Чтобы не путаться и легко запомнить формулу, можно воспользоваться небольшой подсказкой, которую Вы можете сделать самостоятельно.

Нарисуйте треугольник и впишите в него параметры электрической цепи, согласно рисунка ниже. У Вас должно получится вот так.
Как этим пользоваться?
Пользоваться треугольником-подсказкой очень легко и просто. Закрываете своим пальцем, тот параметр цепи, который необходимо найти.
Если оставшиеся на треугольнике параметры расположены на одном уровне, то значит их необходимо перемножить.
Если же оставшиеся на треугольнике параметры расположены на разном уровне, то тогда необходимо разделить верхний параметр на нижний.
С помощью треугольника-подсказки Вы не будете путаться в формуле. Но лучше все таки ее выучить, как таблицу умножения.
Выводы
В завершении статьи сделаю вывод.
Электрический ток — это направленный поток электронов от точки В с потенциалом минус к точке А с потенциалом плюс. И чем выше разность потенциалов между этими точками, тем больше электронов переместится из точки В в точку А, т.
 е. ток в цепи увеличится, при условии, что сопротивление цепи останется неизменным.
е. ток в цепи увеличится, при условии, что сопротивление цепи останется неизменным.Но сопротивление лампочки противодействует протеканию электрического тока. И чем больше сопротивление в цепи (последовательное соединение нескольких лампочек), тем меньше будет ток в цепи, при неизменном напряжении сети.
P.S. Тут в интернете нашел смешную, но поясняющую карикатуру на тему закона Ома для участка цепи.
Тест по теме «Закон Ома для полной цепи».
Тест по теме «Закон Ома для полной цепи».
тест
по физике 10 классЗакон Ома для полной цепи определяет значение тока в
реальной цепи, который зависит не только от сопротивления нагрузки, но и от
сопротивления самого источника тока. Другое название этого закона — закон Ома
для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно
пройдя тест.Вариант
1.1.
Аккумулятор с ЭДС 35 B и внутренним
сопротивлением 2 Ом замкнут на спираль с сопротивлением 5 Ом. Какой ток покажет
Какой ток покажет
амперметр, включённый в цепь. (внутренним сопротивлением
амперметра пренебречь).a.
5 А;b.
7 А;c.
9 А;d.
10,5 А;e.
2 А.2.
Аккумулятор с внутренним сопротивлением
0,4 Ом и ЭДС 4 B замкнут спиралью из проволокой сечением 1 мм2 и
удельным сопротивлением 0,0000008 Ом•м. Найдите длину спирали, если сила тока в
цепи 2 А.a.
2,3 м;b.
2 м;c.
1,5 м;d.
15 м;e.
13 м.3.
Если к гальваническому элементу с ЭДС 5
B и внутренним сопротивлением 1 Ом подключить амперметр, то он покажет силу
тока 1 A. Определите внутреннее сопротивление амперметра.a.
2 Ом;b.
1,5 Ом;c.
4 Ом;d.
3,1 Ом;e.
5,8 Ом;- Спираль
сопротивлением 4 Ом, подключили к гальваническому элементу с ЭДС 6 B.
Амперметр показал ток в спирали 0,6 A. Найдите ток короткого замыкания гальванического
Найдите ток короткого замыкания гальванического
элемента. (внутренним сопротивлением амперметра пренебречь).
a.
5,5 А;b.
6,5 А;c.
0,3 А;d.
2,4 А;e.
1 А.- При
подключении аккумулятора с ЭДС 10 B к резистору, напряжение на полюсах
источника вольтметр показал 8 B, а амперметр показал силу тока в цепи 4 А.
Найдите внутреннее сопротивление источника. (внутренним сопротивлением
амперметра пренебречь).
a.
5,7 Ом;b.
1,9 Ом;c.
3 Ом;d.
0,3 Ом;e.
0,5 Ом6.
Внутреннее сопротивление гальванического
элемента с ЭДС 3,6 B равно 0,4 Ом. К гальваническому элементу подключены
параллельно три спирали сопротивлением по 3 Ом каждая. Найдите разность
потенциалов на клеммах гальванического элемента?a.
2,6 В;b.
4,3 В;c.
3,9 В;d.

1,4 В;e.
0,9 В.7.
В цепи, состоящей из аккумулятора с ЭДС
8 В и внутренним сопротивлением 1 Ом. Подключили проволочный реостат, возник
ток в цепи 2 А. Какой будет сила тока в цепи, если сопротивление проволочного реостата
уменьшить в 2 раза?a.
5,1 А;b.
3,3 А;c.
1,4 А;d.
3,2 А;e.
2,7 А8.
Аккумулятор с ЭДС 12 B и внутренним
сопротивлением 2 Ом питает 4 параллельно соединенных лампочки по 8 Ом каждое.
Определите напряжение на каждой лампочке.a.
2,1 В;b.
6 В;c.
10,6 В;d.
8,5 В;e.
4,7 В.9.
К амперметру, с внутренним
сопротивлением 0,1 Ом, подключен шунт (проволочный резистор) сопротивлением
0,0111 Ом. Определите силу тока, протекающего через амперметр, если сила тока в
общей цепи 0,27 А.a.
2,7 А;b.
0,27 А;c.
0,027 А;d.

0,0027 А;e.
0,00027 А.10. В каких лампах нить накаливания тоньше: в более или менее
мощных?a.
В менее мощных нить накаливания тоньше,
больше сопротивление нити;b.
В более мощных нить накаливания тоньше,
меньше сила тока;c.
В менее мощных нить накаливания толще,
больше сила тока;d.
В более мощных нить накаливания тоньше,
меньше сопротивление нити;e.
Нет правильного ответа.Вариант 2.
1.
Определите силу тока в цепи, содержащей гальванический элемент с ЭДС,
равной 6 В, и внутренним сопротивлением 0,5 Ом при подключении во внешней цепи лампочки
с сопротивлением 2,5 Ом.a) 1 А;
b) 2 А;
c) 0,5 А;
d) 3 А;
e) 10 А;
2.
Электрический чайник, включенный в сеть напряжением 220 В, потребляет
ток 1,2 А. Определите сопротивление водонагревательного элемента чайника.
Определите сопротивление водонагревательного элемента чайника.a) 183,3 Ом;
b) 100 Ом;
c) 330 Ом;
d) 44,5 Ом;
e) 220,7 Ом;
3.
ЭДС гальванического элемента 3 В,
его внутреннее сопротивление равно1 Ом, сопротивления резисторов R1
= R2 = 1,75 Ом, R3 = 2 Ом, R4 = 6 Ом. Чему
равна сила тока, протекающего через резистор R4? (см. рис)a) 0,5
А;b) 0,045 А;
c) 2 А;
d) 0,35 А;
e) 0,125
А;4.
Определите сопротивление водонагревательного тэна, если при напряжении
110 В сила тока в нём 2 А.a) 60 Ом;
b) 35 Ом;
c) 55 Ом;
d) 100 Ом;
e) 135 Ом;
5.
Гальванический элемент имеет ЭДС, равный 2,2 В и внутреннее
сопротивление r =1 Ом. Он замкнут на лампочку сопротивление, которой равно R=9 Ом.
Какой будет при этом сила тока в цепи?a) 0,22 А;
b) 0,15 А;
c) 0,5 А;
d) 2 А;
e) 1 А;
6.

Две лампочки, сопротивления которых R1=10
Ом и R2=40 Ом, соединены последовательно и
подключены к аккумулятору с ЭДС равным 15 В. Определите внутреннее
сопротивление аккумулятора, если сила тока в цепи I=0,29
А.a) 1,25 А;
b) 0,34 А;
c) 2,15 А;
d) 1,72 А;
e) 3,3 А;
7.
Найти силу тока в электрической цепи, если известно, что сопротивление
цепи 11 Ом, а источник, подключенный к ней, имеет ЭДС 12 В и внутреннее
сопротивление 1 Ом.a) 1 А;
b) 2 А;
c) 3 А;
d) 4 А;
e) 5 А;
8.
Аккумулятор подключен к резистору сопротивлением 10 Ом с помощью медной спирали
длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока,
зная, что ЭДС аккумулятора равно 12 В, а внутреннее сопротивление 1,9825 Ом.a) 0,5 А;
b) 0,8 А;
c) 1 А;
d) 1,5 А;
e) 2 А;
9.

При внешнем сопротивлении 3,75 Ом в цепи идет ток 0,5 А. Когда в цепь
ввели еще сопротивление 1 Ом, сила тока стала равной 0,4 А. Найти ЭДС и
внутреннее сопротивление гальванического элемента.a) 1 В; 0,5
Ом;b) 2 В; 0,25
Ом;c) 1 В, 3 Ом;
d) 3 В; 1,5
Ом;e) 5 В; 4 Ом;
10.
Определить ток при коротком замыкании аккумулятора, если при внешнем
сопротивлении R1=50 Ом ток в цепи I1= 0,2 А, а при сопротивлении R2=
110 Ом ток I2= 0,1 А.a) 1400 мА;
b) 1000 мА;
c) 3000 мА;
d) 1600 мА;
e) 1200 мА;
Ответы: Вариант 1: 1 а; 2 b;
3 с; 4 е; 5 е; 6 а; 7 d; 8 b; 9 с; 10 a.Вариант 2: 1 b;
2 а; 3 е; 4 с; 5 а; 6 d; 7 а; 8 с; 9 b; 10 е.Скачано с www.znanio.ru
Задачи по физике и математике с решениями и ответами
Задача по физике — 9017
Зная, что показатель преломления $n$ водяных паров при нормальных условиях равен 1,000252 и что молекула воды обладает электрическим моментом $p = 6,1 \cdot 10^{-30} Кл \cdot м$, определить, какую долю от общей поляризуемости (электронной и ориентационной) составляет электронная поляризуемость молекулы.
 { \circ} С$. Найти сопротивление $R$ проводника, считая градиент температуры вдоль его оси постоянным.
{ \circ} С$. Найти сопротивление $R$ проводника, считая градиент температуры вдоль его оси постоянным.
Подробнее
Задача по физике — 9021
К источнику тока с ЭДС $\mathcal{E} = 1,5 В$ присоединили катушку с сопротивлением $R = 0,1 Ом$. Амперметр показал силу тока, равную $I_{1} = 0,5 А$. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока $I$ в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления $r_{1}$ и $r_{2}$ первого и второго источников тока.
Подробнее
Задача по физике — 9022
Имеется $N$ одинаковых гальванических элементов с ЭДС $\mathcal{E}$ и внутренним сопротивлением $r_{i}$ каждый. Из этих элементов требуется собрать батарею, состоящую из нескольких параллельно соединенных групп, содержащих по $n$ последовательно соединенных элементов.
 При таком значении $n$ сила тока $I$ во внешней цепи, имеющей сопротивление $R$, будет максимальной? Чему будет равно внутреннее сопротивление $R_{i}$ батареи при этом значении $n$?
При таком значении $n$ сила тока $I$ во внешней цепи, имеющей сопротивление $R$, будет максимальной? Чему будет равно внутреннее сопротивление $R_{i}$ батареи при этом значении $n$?
Подробнее
Задача по физике — 9023
Даны 12 элементов с ЭДС $\mathcal{E} = 1,5 В$ и внутреннем сопротивлением $r = 0,4 Ом$. Как нужно соединить эти элементы, чтобы получить от собранной из них батареи наибольшую силу тока во внешней цепи, имеющей сопротивление $R = 0,3 Ом$? Определить максимальную силу тока $I_{max}$.
Подробнее
Задача по физике — 9024
Два элемента ($\mathcal{E}_{1} =l,2 В, r_{1} = 0,1 Ом; \mathcal{E}_{2} = 0,9 В, r_{2} = 0,3 Ом$) соединены одноименными полюсами. Сопротивление $R$ соединительных проводов равно 0,2 Ом.
 Определить силу тока $I$ в цепи.
Определить силу тока $I$ в цепи.
Подробнее
Задача по физике — 9025
Две батареи аккумуляторов ($\mathcal{E}_{1} = 10 В, r_{1} = 1 Ом; \mathcal{E}_{2} =8 В, r_{2} = 2 Ом$) и реостат ($R = 6 Ом$) соединены, как показано на рис. Найти силу тока в батареях и реостате.
Подробнее
Задача по физике — 9026
Три батареис ЭДС $\mathcal{E}_{1} = 12 В, \mathcal{E}_{2} = 5 В$ и $\mathcal{E} = 10 В$ и одинаковыми внутренними сопротивлениями $r$, равными 1 Ом, соединены между собой одноименными полюсами. Сопротивление соединительных проводов ничтожно мало. Определить силы токов $I$, идущих через каждую батарею.
Подробнее
Задача по физике — 9027
ЭДС батареи аккумуляторов $\mathcal{E} = 12 В$, сила тока $I$ короткого замыкания равна 5 А.
 Какую наибольшую мощность $P_{max}$ можно получить во внешней цепи, соединенной с такой батареей?
Какую наибольшую мощность $P_{max}$ можно получить во внешней цепи, соединенной с такой батареей?
Подробнее
Задача по физике — 9028
ЭДС $\mathcal{E}$ батареи равна 20 В. Сопротивление $R$ внешней цепи равно 2 Ом, сила тока $I = 4 А$. Найти КПД батареи. При каком значении внешнего сопротивления $R$ КПД будет равен 99%?
Подробнее
Задача по физике — 9029
К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС $\mathcal{E}$ батареи равна 24 В, внутреннее сопротивление $r = 1 Ом$. Нагреватель, включенный в цепь, потребляет мощность $P = 80 Вт$. Вычислить силу тока $I$ в цепи и КПД $\eta$ нагревателя.
Подробнее
Задача по физике — 9030
Сила тока в проводнике сопротивлением $R = 12 Ом$ равномерно убывает от $I_{0} = 5 А$ до $I=0$ в течение времени $t= 10 с$.
 Какое количество теплоты $Q$ выделяется в этом проводнике за указанный промежуток времени?
Какое количество теплоты $Q$ выделяется в этом проводнике за указанный промежуток времени?
Подробнее
Задача по физике — 9031
По проводнику сопротивлением $R=3 Ом$ течет ток, сила которого возрастает. Количество теплоты $Q$, выделившееся в проводнике за время $\tau = 8 с$, равно 200 Дж. Определить количество электричества $q$, протекшее за это время по проводнику. В момент времени, принятый за начальный, сила тока в проводнике равна нулю.
Подробнее
Как рассчитать ЭДС | Sciencing
Обновлено 2 ноября 2020 г.
Ли Джонсон
Электродвижущая сила (ЭДС) — понятие незнакомое для большинства людей, но оно тесно связано с более знакомым понятием напряжения. Понимание разницы между ними и того, что означает ЭДС, дает вам инструменты, необходимые для решения многих проблем в физике и электронике, а также знакомит с концепцией внутреннего сопротивления батареи.
 ЭДС сообщает вам напряжение батареи без уменьшения внутреннего сопротивления, как при обычных измерениях разности потенциалов.Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть.
ЭДС сообщает вам напряжение батареи без уменьшения внутреннего сопротивления, как при обычных измерениях разности потенциалов.Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть.TL; DR (слишком долго; не читал)
Рассчитайте ЭДС по формуле:
ε = V + Ir
Здесь (В) означает напряжение элемента, (I) означает ток в цепи, а (r) означает внутреннее сопротивление ячейки.
Что такое ЭДС?
Электродвижущая сила — это разность потенциалов (т. Е. Напряжение) на клеммах батареи при отсутствии тока.Может показаться, что это не имеет значения, но каждая батарея имеет «внутреннее сопротивление». Это похоже на обычное сопротивление, которое снижает ток в цепи, но оно существует внутри самой батареи. Это связано с тем, что материалы, из которых состоят элементы в батарее, имеют собственное сопротивление (так как практически все материалы имеют).
Когда через элемент не течет ток, это внутреннее сопротивление ничего не меняет, потому что нет тока, который мог бы замедлить его.
 В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеальной ситуации, и на практике она всегда больше, чем напряжение аккумулятора.
В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеальной ситуации, и на практике она всегда больше, чем напряжение аккумулятора.Уравнения для расчета ЭДС
Есть два основных уравнения для расчета ЭДС. Наиболее фундаментальное определение — это количество джоулей энергии (E), которое каждый кулон заряда (Q) забирает при прохождении через ячейку:
Где (ε) — символ электродвижущей силы, (E) — энергия в цепи, а (Q) — заряд цепи.Если вы знаете результирующую энергию и количество заряда, проходящего через ячейку, это самый простой способ вычислить ЭДС, но в большинстве случаев у вас нет этой информации.
Вместо этого вы можете использовать определение, больше похожее на закон Ома (V = IR). Это может быть выражено как:
\ epsilon = I (R + r)
, где (I) означает ток, (R) — сопротивление рассматриваемой цепи, а (r) — внутреннее сопротивление ячейки. Расширение этого показывает тесную связь с законом Ома:
\ epsilon = IR + Ir = V + Ir
Это показывает, что вы можете рассчитать ЭДС, если вы знаете напряжение на клеммах (напряжение, используемое в реальных ситуациях) , протекающий ток и внутреннее сопротивление ячейки.

Как рассчитать ЭДС: пример
В качестве примера представьте, что у вас есть цепь с разностью потенциалов 3,2 В, протекающим током 0,6 А и внутренним сопротивлением батареи 0,5 Ом. Используя формулу выше:
\ epsilon = V + Ir = 3.2 \ text {V} + (0.6 \ text {A}) (0.5 \ text {} \ Omega) = 3.5 \ text {V}
Итак, ЭДС этой цепи составляет 3,5 В.
Движущая ЭДС | Физика
Цель обучения
К концу этого раздела вы сможете:
- Вычислить ЭДС, силу, магнитное поле и работу, обусловленную движением объекта в магнитном поле.
Как мы видели, любое изменение магнитного потока индуцирует противодействующую этому изменению ЭДС — процесс, известный как индукция. Движение — одна из основных причин индукции. Например, магнит, перемещенный к катушке, индуцирует ЭДС, а катушка, перемещенная к магниту, создает аналогичную ЭДС. В этом разделе мы сосредоточимся на движении в магнитном поле, которое является стационарным относительно Земли, производя то, что в общих чертах называется ЭДС движения .
 Одна ситуация, когда возникает двигательная ЭДС, известна как эффект Холла и уже была исследована.Заряды, движущиеся в магнитном поле, испытывают магнитную силу F = qvB sin θ , которая перемещает противоположные заряды в противоположных направлениях и создает em f = Bℓv . Мы видели, что у эффекта Холла есть приложения, включая измерения B и v . Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и мы обнаружим, что ЭДС движения может использоваться как источник энергии. Рассмотрим ситуацию, показанную на рисунке 1.Стержень перемещается со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ в однородном магнитном поле B . Рейки неподвижны относительно B и подключены к неподвижному резистору R . Резистором может быть что угодно, от лампочки до вольтметра. Рассмотрим площадь, ограниченную подвижным стержнем, направляющими и резистором.
Одна ситуация, когда возникает двигательная ЭДС, известна как эффект Холла и уже была исследована.Заряды, движущиеся в магнитном поле, испытывают магнитную силу F = qvB sin θ , которая перемещает противоположные заряды в противоположных направлениях и создает em f = Bℓv . Мы видели, что у эффекта Холла есть приложения, включая измерения B и v . Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и мы обнаружим, что ЭДС движения может использоваться как источник энергии. Рассмотрим ситуацию, показанную на рисунке 1.Стержень перемещается со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ в однородном магнитном поле B . Рейки неподвижны относительно B и подключены к неподвижному резистору R . Резистором может быть что угодно, от лампочки до вольтметра. Рассмотрим площадь, ограниченную подвижным стержнем, направляющими и резистором. B перпендикулярно этой области, и площадь увеличивается по мере перемещения стержня. Таким образом, увеличивается магнитный поток между рельсами, стержнем и резистором.Когда поток изменяется, возникает ЭДС согласно закону индукции Фарадея.
B перпендикулярно этой области, и площадь увеличивается по мере перемещения стержня. Таким образом, увеличивается магнитный поток между рельсами, стержнем и резистором.Когда поток изменяется, возникает ЭДС согласно закону индукции Фарадея.Рис. 1. (a) Между рельсами возникает ЭДС движения = B ℓ v , когда этот стержень перемещается вправо в однородном магнитном поле. Магнитное поле B, находится внутри страницы, перпендикулярно движущемуся стержню и рельсам и, следовательно, к области, окружающей их. (б) Закон Ленца определяет направления индуцированного поля и тока, а также полярность наведенной ЭДС.Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или за пределы страницы. RHR-2 дает указанное направление тока, и полярность стержня будет управлять таким током. RHR-1 также указывает на такую же полярность стержня. (Обратите внимание, что символ буквы E, используемый в эквивалентной схеме в нижней части части (b), представляет собой ЭДС.
 )
)Чтобы найти величину ЭДС, индуцированной вдоль движущегося стержня, воспользуемся законом индукции Фарадея без знака:
[латекс] \ text {emf} = \ text {N} \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].
Здесь и далее «ЭДС» означает величину ЭДС. В этом уравнении N = 1 и поток Φ = BA cos θ . У нас θ = 0º и cos θ = 1, так как B перпендикулярно A . Теперь Δ Φ = Δ ( BA ) = B Δ A , поскольку B является однородным. Обратите внимание, что площадь, заметаемая стержнем, составляет Δ A = ℓ Δ x .Ввод этих величин в выражение для ЭДС дает
[латекс] \ text {emf} = \ frac {B \ Delta A} {\ Delta t} = B \ frac {\ ell \ Delta x} {\ Delta t} \\ [/ latex].
Наконец, обратите внимание, что Δ x / Δ t = v , скорость стержня. Ввод этого в последнее выражение показывает, что
ЭДС = Bℓv ( B , ℓ и v перпендикулярно)
— ЭДС движения.
 Это то же выражение, что и для эффекта Холла ранее.
Это то же выражение, что и для эффекта Холла ранее.Соединения: объединение сил
Между электрической и магнитной силой существует множество связей. Тот факт, что движущееся электрическое поле создает магнитное поле, и, наоборот, движущееся магнитное поле создает электрическое поле, является частью того, почему электрические и магнитные силы теперь считаются различными проявлениями одной и той же силы. Это классическое объединение электрических и магнитных сил в так называемую электромагнитную силу является источником вдохновения для современных усилий по объединению других основных сил.
Чтобы найти направление индуцированного поля, направление тока и полярность наведенной ЭДС, мы применяем закон Ленца, как объяснено в Законе индукции Фарадея: Закон Ленца. (См. Рис. 1 (b).) Поток увеличивается, так как увеличивается площадь замкнутой области. Таким образом, индуцированное поле должно противостоять существующему и быть вне страницы. Таким образом, RHR-2 требует, чтобы I вращались против часовой стрелки, что, в свою очередь, означает, что верхняя часть стержня положительна, как показано.

ЭДС движения также возникает, если магнитное поле движется и стержень (или другой объект) неподвижен относительно Земли (или некоторого наблюдателя).Мы видели пример этого в ситуации, когда движущийся магнит индуцирует ЭДС в неподвижной катушке. Важно относительное движение. В этих наблюдениях обнаруживается связь между магнитным и электрическим полями. Движущееся магнитное поле создает электрическое поле за счет наведенной ЭДС. Мы уже видели, что движущееся электрическое поле создает магнитное поле: движущийся заряд подразумевает движущееся электрическое поле, а движущийся заряд создает магнитное поле.
ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы могли бы заметить напряжение вдоль металлических стержней, таких как отвертка, во время обычных движений.Например, простой расчет ЭДС движения стержня длиной 1 м, движущегося со скоростью 3,0 м / с перпендикулярно полю Земли, дает ЭДС = Bℓv = (5,0 × 10 −5 Тл) (1,0 м) (3,0 м / с) = 150 мкВ.
 Это небольшое значение согласуется с опытом. Однако есть впечатляющее исключение. В 1992 и 1996 годах с космическим шаттлом были предприняты попытки создать большие двигательные ЭДС. Привязанный спутник должен был быть выпущен на проводе длиной 20 км, как показано на рисунке 2, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли.Эту ЭДС можно было бы использовать для преобразования некоторой кинетической и потенциальной энергии шаттла в электрическую, если бы можно было создать полную схему. Чтобы замкнуть цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и неподвижные рельсы и соединительный резистор на рисунке 1, без которых не было бы полной цепи.) Затягивание тока в кабеле из-за магнитной силы F = IℓB sin θ выполняет работу, которая уменьшает кинетическую и потенциальную энергию шаттла и позволяет преобразовывать ее в электрическую.
Это небольшое значение согласуется с опытом. Однако есть впечатляющее исключение. В 1992 и 1996 годах с космическим шаттлом были предприняты попытки создать большие двигательные ЭДС. Привязанный спутник должен был быть выпущен на проводе длиной 20 км, как показано на рисунке 2, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли.Эту ЭДС можно было бы использовать для преобразования некоторой кинетической и потенциальной энергии шаттла в электрическую, если бы можно было создать полную схему. Чтобы замкнуть цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и неподвижные рельсы и соединительный резистор на рисунке 1, без которых не было бы полной цепи.) Затягивание тока в кабеле из-за магнитной силы F = IℓB sin θ выполняет работу, которая уменьшает кинетическую и потенциальную энергию шаттла и позволяет преобразовывать ее в электрическую. Оба теста были безуспешными. В первом случае кабель зависал, и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном растяжении. Следующий пример показывает принципиальную осуществимость.
Оба теста были безуспешными. В первом случае кабель зависал, и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном растяжении. Следующий пример показывает принципиальную осуществимость.Пример 1. Расчет большой ЭДС движения объекта на орбите
Рисунок 2.ЭДС движения как преобразование электроэнергии для космического челнока является мотивацией для эксперимента с привязанным спутником. Согласно прогнозам, ЭДС 5 кВ будет индуцироваться в тросе длиной 20 км при движении с орбитальной скоростью в магнитном поле Земли. Схема замыкается обратным трактом через неподвижную ионосферу.
Рассчитайте ЭДС движения, индуцированную вдоль проводника длиной 20,0 км, движущегося с орбитальной скоростью 7,80 км / с перпендикулярно магнитному полю Земли 5,00 × 10 −5 Тл.{3} \ text {V} \ end {array} \\ [/ latex].
Обсуждение
Полученное значение превышает измеренное напряжение 5 кВ для эксперимента с шаттлом, поскольку фактическое орбитальное движение троса не перпендикулярно полю Земли.
 Значение 7,80 кВ является максимальной ЭДС, полученной при θ = 90º и sin θ = 1.
Значение 7,80 кВ является максимальной ЭДС, полученной при θ = 90º и sin θ = 1.Сводка раздела
- ЭДС, индуцированная движением относительно магнитного поля B , называется ЭДС движения и определяется выражением
ЭДС = Bℓv ( B , ℓ и v перпендикулярно)
, где ℓ — длина объекта, движущегося со скоростью v относительно поля.
Концептуальные вопросы
- Почему часть схемы должна перемещаться относительно других частей, чтобы можно было использовать ЭДС движения? Рассмотрим, например, что рельсы на рисунке 1 неподвижны относительно магнитного поля, в то время как стержень движется.
- Мощную индукционную пушку можно сделать, поместив металлический цилиндр внутри катушки соленоида. Цилиндр принудительно выталкивается при быстром включении электромагнитного тока. Используйте законы Фарадея и Ленца, чтобы объяснить, как это работает.
 Почему цилиндр может стать активным / горячим при выстреле из пушки?
Почему цилиндр может стать активным / горячим при выстреле из пушки? - Индукционная плита нагревает кастрюлю с катушкой, по которой проходит переменный ток, расположенной под кастрюлей (и без горячей поверхности). Может ли поверхность печи быть проводником? Почему не работает катушка постоянного тока?
- Объясните, как можно разморозить замерзшую водопроводную трубу, намотав на нее катушку, по которой проходит переменный ток. Имеет ли значение, является ли труба проводником? Объясни.
Задачи и упражнения
1.Используйте закон Фарадея, закон Ленца и RHR-1, чтобы показать, что магнитная сила, действующая на ток в движущемся стержне на рисунке 1, направлена в противоположном направлении от его скорости.
2. Если в спутниковом тросе, показанном на рисунке 2, течет ток, используйте закон Фарадея, закон Ленца и RHR-1, чтобы показать, что на трос действует магнитная сила в направлении, противоположном его скорости.
3.
 (a) Реактивный самолет с размахом крыла 75,0 м летит со скоростью 280 м / с. Какая ЭДС возникает между законцовками крыльев, если вертикальная составляющая поля Земли равна 3?00 × 10 −5 Т? (б) Может ли ЭДС такой величины иметь какие-либо последствия? Объясни.
(a) Реактивный самолет с размахом крыла 75,0 м летит со скоростью 280 м / с. Какая ЭДС возникает между законцовками крыльев, если вертикальная составляющая поля Земли равна 3?00 × 10 −5 Т? (б) Может ли ЭДС такой величины иметь какие-либо последствия? Объясни.4. (a) Отвертка для цветных металлов используется в магнитном поле 2,00 Тл. Какая максимальная ЭДС может быть индуцирована на его длине 12,0 см, когда он движется со скоростью 6,00 м / с? б) Вероятно ли, что эта ЭДС будет иметь какие-либо последствия или даже будет замечена?
5. С какой скоростью должен двигаться скользящий стержень на Рисунке 1, чтобы создать ЭДС 1,00 В в поле 1,50 Тл, учитывая, что длина стержня равна 30.0 см?
6. Штанга длиной 12,0 см на Рисунке 1 движется со скоростью 4,00 м / с. Какова напряженность магнитного поля при наведении ЭДС 95,0 В.
7. Докажите, что когда B , ℓ и v не взаимно перпендикулярны, ЭДС движения определяется как ЭДС = Bℓv sin θ .
 Если v перпендикулярно B , тогда θ — это угол между ℓ и B . Если ℓ перпендикулярно B , тогда θ — это угол между v и B .
Если v перпендикулярно B , тогда θ — это угол между ℓ и B . Если ℓ перпендикулярно B , тогда θ — это угол между v и B .8. Во время полета космического челнока в августе 1992 г. удалось выпустить только 250 м проводящего троса, рассмотренного в Примере 1 (выше). ЭДС движения 40,0 В генерировалась в поле Земли 5,00 × 10 −5 Тл при движении со скоростью 7,80 × 10 3 м / с. Каков угол между скоростью шаттла и полем Земли, если предположить, что проводник перпендикулярен полю?
9. Integrated Concepts Выведите выражение для тока в системе, подобной показанной на рисунке 1, при следующих условиях.Сопротивление между рельсами составляет R , рельсы и подвижный стержень идентичны по сечению A, и имеют одинаковое удельное сопротивление ρ . Расстояние между рельсами l, а стержень движется с постоянной скоростью v перпендикулярно однородному полю B .
 В нулевой момент времени движущийся стержень находится рядом с сопротивлением R .
В нулевой момент времени движущийся стержень находится рядом с сопротивлением R .10. Integrated Concepts Привязанный спутник на Рисунке 2 имеет массу 525 кг и находится в конце 20-го.Кабель длиной 0 км, диаметром 2,50 мм с прочностью на разрыв, как сталь. (а) Насколько растягивается кабель, если приложить усилие 100 Н, чтобы втянуть спутник? (Предположим, что спутник и шаттл находятся на одной высоте над Землей.) (B) Какова эффективная силовая постоянная кабеля? (c) Сколько энергии хранится в нем при растяжении силой 100 Н.
11. Integrated Concepts Привязанный спутник, обсуждаемый в этом модуле, вырабатывает 5,00 кВ и ток 10.0 А течет. (а) Какую силу магнитного сопротивления это создает, если система движется со скоростью 7,80 км / с? (б) Сколько кинетической энергии уходит из системы за 1,00 ч, если не учитывать какие-либо изменения высоты или скорости за это время? (c) Каково изменение скорости, если масса системы составляет 100 000 кг? (d) Обсудите долгосрочные последствия (например, недельный полет) на орбите космического челнока, отметив, какой эффект имеет снижение скорости, и оценив величину этого эффекта.

Избранные решения проблем и упражнения
1.(а) 0,630 В (б) Нет, это очень малая ЭДС.
5. 2,22 м / с
11. (а) 10,0 Н (б) 2,81 × 10 8 Дж (в) 0,36 м / с (г) Для недельной миссии (168 часов) изменение скорости будет 60 м / с, или примерно 1%. В общем, уменьшение скорости приведет к тому, что орбита начнет вращаться по спирали внутрь, потому что скорости больше не будет достаточно для поддержания круговой орбиты. Долгосрочные последствия состоят в том, что шаттлу потребуется немного больше топлива для поддержания желаемой скорости, в противном случае орбита будет слегка закручиваться внутрь.В.
Данные можно ввести в любое из полей. Когда вы закончили ввод данных, щелкните количество, которое вы хотите вычислить, в активной формуле выше. Количество не будет принудительно согласованным, пока вы не нажмете на выбор. Для неопределенных параметров будут введены значения по умолчанию, но все значения могут быть изменены.
После того, как вы рассчитали генерируемое напряжение, разумным последующим вопросом будет «Какой ток и мощность я могу получить от генератора?».
 Несмотря на то, что это не будет практичной геометрией генератора, она может служить
Несмотря на то, что это не будет практичной геометрией генератора, она может служить
идеализация для обсуждения принципов генерации напряжения при взаимодействии с магнитным полем. Принимая это
простая геометрия, электрический ток в амперах, генерируемый при перемещении провода
через магнитное поле будет определяться сопротивлением цепи, к которой он подключен.
связаны по закону Ома I = V / R. Если вы генерировали 10 вольт и были подключены к цепи
сопротивление 1 Ом, результирующий ток будет 10 ампер, а передаваемая мощность P = VI = 10 вольт x 10
амперы = 100 Вт (см. соотношение мощности).Но бесплатного обеда не бывает, и вам придется усерднее двигаться.
провод через магнитное поле с такой скоростью — по сути, вы торгуете механической энергией толкания
для выработки электрической энергии, всегда ограничиваясь принципом сохранения энергии. Вам придется
приложите (по крайней мере) 100 Вт механической мощности нажатия, чтобы получить 100 Вт электроэнергии.
Практические генераторы почти всегда используют геометрию вращающейся катушки, а крупномасштабные генераторы энергии используют что-то вроде паровой турбины или водяной турбины для поворота катушки с проволокой в
магнитное поле, получающее напряжение, генерируемое с обеих сторон вращающейся катушки.
Если указанный выше генератор был подключен к цепи с сопротивлением R = Ом,
электрический ток будет I = V / R = амперы для скорости, перпендикулярной B.
Мощность, подаваемая в схему, будет P = VI = Вт.
В идеальном случае, когда не было потерь, механическая мощность P = Fv, необходимая для проталкивания провода через магнитное поле, была бы равна электрической мощности. Для указанной выше скорости требуемая сила равна
.
Идеальная минимально необходимая сила:
F = P / v = ньютоны = фунты.
Закон Ома и соотношение V-I-R
В физике есть определенные формулы, которые настолько сильны и распространены, что достигают уровня общеизвестных знаний. Студент, изучающий физику, записывал такие формулы столько раз, что запоминал их, даже не пытаясь. Безусловно, для профессионалов в этой области такие формулы настолько важны, что остаются в их сознании. В области современной физики E = m • c 2 . В области ньютоновской механики существует F net = m • a.
 В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.
В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.Преобладающим уравнением, которое пронизывает изучение электрических цепей, является уравнение
ΔV = I • R
Другими словами, разность электрических потенциалов между двумя точками в цепи ( ΔV ) эквивалентна произведению тока между этими двумя точками ( I ) и общего сопротивления всех электрических устройств, присутствующих между этими двумя точками ( R ).В остальной части этого раздела Физического класса это уравнение станет наиболее распространенным уравнением, которое мы видим. Это уравнение, часто называемое уравнением закона Ома , является мощным предсказателем взаимосвязи между разностью потенциалов, током и сопротивлением.
Закон Ома как предсказатель тока
Уравнение закона Ома можно переформулировать и выразить как
В качестве уравнения это служит алгебраическим рецептом для вычисления тока, если известны разность электрических потенциалов и сопротивление.
 Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает на две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение батареи (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение аккумулятора увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает на две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение батареи (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение аккумулятора увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.Приведенная ниже таблица иллюстрирует это соотношение как качественно, так и количественно для нескольких цепей с различными напряжениями и сопротивлением батарей.

Строки 1, 2 и 3 показывают, что удвоение и утроение напряжения батареи приводит к удвоению и утроению тока в цепи. Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления служит для уменьшения вдвое тока в цепи.
Поскольку на ток в цепи влияет сопротивление, в цепях электроприборов часто используются резисторы, чтобы влиять на величину тока, присутствующего в ее различных компонентах.Увеличивая или уменьшая величину сопротивления в конкретной ветви схемы, производитель может увеличивать или уменьшать величину тока в этой ветви . Кухонные приборы, такие как электрические миксеры и переключатели света, работают, изменяя ток нагрузки, увеличивая или уменьшая сопротивление цепи. Нажатие различных кнопок на электрическом микшере может изменить режим с микширования на взбивание, уменьшив сопротивление и позволив большему току присутствовать в миксере.Точно так же поворот ручки регулятора яркости может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.

На схеме ниже изображена пара цепей, содержащих источник напряжения (аккумуляторная батарея), резистор (лампочка) и амперметр (для измерения тока). В какой цепи у лампочки наибольшее сопротивление? Нажмите кнопку «Посмотреть ответ», чтобы убедиться, что вы правы.
Уравнение закона Ома часто исследуется в физических лабораториях с использованием резистора, аккумуляторной батареи, амперметра и вольтметра.Амперметр — это устройство, используемое для измерения силы тока в заданном месте. Вольтметр — это устройство, оснащенное датчиками, которых можно прикоснуться к двум точкам цепи, чтобы определить разность электрических потенциалов в этих местах. Изменяя количество ячеек в аккумуляторной батарее, можно изменять разность электрических потенциалов во внешней цепи. Вольтметр может использоваться для определения этой разности потенциалов, а амперметр может использоваться для определения тока, связанного с этим ΔV.К батарейному блоку можно добавить батарею, и процесс можно повторить несколько раз, чтобы получить набор данных I-ΔV.
 График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.
График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.Величины, символы, уравнения и единицы!
Тенденция уделять внимание единицам — неотъемлемая черта любого хорошего студента-физика.Многие трудности, связанные с решением проблем, могут быть связаны с тем, что не уделили внимание подразделениям. Поскольку все больше и больше электрических величин и их соответствующих метрических единиц вводится в этот раздел учебного пособия «Физический класс», становится все более важным организовать информацию в своей голове. В таблице ниже перечислены некоторые из введенных на данный момент количеств. Символ, уравнение и соответствующие метрические единицы также указаны для каждой величины.Было бы разумно часто обращаться к этому списку или даже делать свою копию и добавлять ее по мере развития модуля.
 Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.
Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.Кол-во Символ Уравнение (я) Стандартная метрическая единица Другие единицы Разность потенциалов (г.k.a. напряжение)
ΔV ΔV = ΔPE / Q ΔV = I • R
Вольт (В) J / C ток я I = Q / т I = ΔV / R
Амперы (А) Усилитель или К / с или В / Ом
Мощность п P = ΔPE / т (еще предстоит)
Ватт (Вт) Дж / с Сопротивление р R = ρ • L / A R = ΔV / I
Ом (Ом) В / А Энергия E или ΔPE ΔPE = ΔV • Q ΔPE = P • t
Джоуль (Дж) V • C или Вт • с
(Обратите внимание, что символ единицы C представляет собой кулоны.
 )
)В следующем разделе Урока 3 мы еще раз рассмотрим количественную мощность. Новое уравнение мощности будет введено путем объединения двух (или более) уравнений в приведенной выше таблице.
Мы хотели бы предложить …
Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. С легкостью перетащите источник напряжения, резисторы и провода на рабочее место. Соедините их, и у вас будет схема. Добавьте амперметр для измерения тока и используйте датчики напряжения для определения падения напряжения.
 Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).Проверьте свое понимание
1. Что из перечисленного ниже приведет к уменьшению тока в электрической цепи? Выберите все, что подходит.
а. уменьшить напряжение
г. уменьшить сопротивление
г. увеличить напряжение
г.увеличить сопротивление
2. Определенная электрическая цепь содержит аккумулятор из трех элементов, провода и лампочку. Из-за чего лампа будет светить менее ярко? Выберите все, что подходит.
а. увеличить напряжение батареи (добавить еще одну ячейку)
г. уменьшить напряжение аккумулятора (удалить элемент)
г.уменьшить сопротивление цепи
г. увеличить сопротивление цепи
3.
 Скорее всего, вас предупредили, чтобы вы не прикасались к электроприборам или даже к электрическим розеткам мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.
Скорее всего, вас предупредили, чтобы вы не прикасались к электроприборам или даже к электрическим розеткам мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.а.напряжение цепи должно быть выше
г. напряжение цепи должно быть ниже
г. ваше сопротивление будет выше
г. ваше сопротивление должно быть ниже
e. ток через тебя будет ниже
4. Если бы сопротивление цепи было утроено, то ток через цепь был бы ____.
а. треть от
г. втрое больше
г. без изменений
г. … ерунда! Сделать такой прогноз невозможно.
5. Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.
а.четверть от
г.
 в четыре раза больше
в четыре раза большег. без изменений
г. … ерунда! Сделать такой прогноз невозможно.
6. Схема соединена с блоком питания, резистором и амперметром (для измерения тока). Амперметр показывает значение тока 24 мА (миллиАмпер). Определите новый ток, если напряжение источника питания было…
а. … увеличился в 2 раза, а сопротивление осталось постоянным.
г. … увеличился в 3 раза, а сопротивление осталось постоянным.
г. … уменьшилось в 2 раза, а сопротивление осталось постоянным.
г. … оставалось постоянным, а сопротивление увеличивалось в 2 раза.
e. … оставалось постоянным, а сопротивление увеличивалось в 4 раза.
ф…. оставалось постоянным, а сопротивление уменьшалось в 2 раза.
г. … увеличилось в 2 раза, а сопротивление увеличилось в 2 раза.
ч. … увеличилось в 3 раза, а сопротивление уменьшилось в 2 раза.

и. … уменьшилось в 2 раза, а сопротивление увеличилось в 2 раза.
7.Используйте уравнение закона Ома, чтобы дать числовые ответы на следующие вопросы:
а. Электрическое устройство с сопротивлением 3,0 Ом позволит протекать через него току 4,0 А, если на устройстве наблюдается падение напряжения ________ Вольт.
г. Когда на электрический нагреватель подается напряжение 120 В, через нагреватель будет протекать ток 10,0 А, если сопротивление составляет ________ Ом.
г. Фонарик, который питается от 3 В и использует лампу с сопротивлением 60 Ом, будет иметь ток ________ ампер.
8. Используйте уравнение закона Ома для определения недостающих значений в следующих схемах.
9. См. Вопрос 8 выше. В схемах схем A и B какой метод использовался для управления током в схемах? А в схемах схем C и D какой метод использовался для контроля тока в схемах?
САМАЯ ПРОСТАЯ ЦЕПЬ:
САМАЯ ПРОСТАЯ ЦЕПЬ:
ЗАКОН ОМА
САМАЯ ПРОСТАЯ ЦЕПЬ:
Мы можем заставить ток течь по кругу (цепи)
путем соединения клемм аккумулятора вместе. Это растопит
Это растопит
провод, разжигай искры и, возможно, разжигай огонь, так что не делай этого.
Вместо этого подключите что-нибудь для управления током. Способность к
управляющий ток называется сопротивлением, и все материалы имеют его
в некоторой степени — на самом деле мы классифицируем материалы по их
сопротивление: с очень низким сопротивлением — проводники, с
много сопротивления — изоляторы. Есть устройства, называемые резисторами
которые используются в электронных гаджетах — они имеют сопротивление, которое
что-то среднее между проводимостью и изоляцией и предсказуемо.Так
вот безопасная цепь:Батарея имеет определенное нажатие,
называется электродвижущей силой или ЭДС. Это измеряется в единицах, называемых
вольт .
ЭДС (часто называемую напряжением) указываем в формулах буквой
E .
Напряжение должно быть измерено между двумя точками цепи в
таким же образом измеряется высота между двумя точками на
сторона горы. Нет такого понятия, как «0 вольт», кроме
напряжение между двумя точками равно 0, если они подключены
все вместе.
Резистор имеет определенную величину
Сопротивление, измеренное в единицах, называется Ом . Мы указываем
сопротивление в формулах с буквой R .Когда ток течет, мы измеряем его в
единицы обозначают ампер , и обозначают его буквой I .Эти три связаны простой формулой
называется законом Ома:I = E / R
Также написано E =
IR или R = E / I.Это говорит нам ток, если мы знаем
напряжение и сопротивление, или напряжение, если мы знаем ток и
сопротивление, или сопротивление, если мы знаем ток и напряжение. Если
это кажется вам немного замкнутым, вы правы. Мы можем измерить
ток силой магнитного поля, которое он будет генерировать, но там
не является критерием для измерения напряжения, кроме как увидеть, сколько тока течет
через известное сопротивление. А как узнать сопротивление? Мы применяем
известное напряжение и посмотрите, сколько тока течет.Определение единиц также круглое: 1
ампер — это количество тока, протекающего через резистор сопротивлением 1 Ом.
если приложено 1 вольт.Два резистора последовательно:
Будет немного сложнее, если есть
два резистора:Какой бы ни был ток, он такой же в A,
B и C. (Больше некуда течь ток).Напряжение между A и C равно этому
между A и B добавляется к тому, что между B и C.E AC =
E AB + E BCНапряжения складываются, как и высота
дом — это сумма высот его этажей.Напряжение на каждом резисторе равно
пропорционально сопротивлению каждого резистора.E AB /
R 1 = E BC /
R 2Видите ли, закон Ома верен для каждой части
схему, а также схему в целом.Какой бы ток ни тек,
он одинаков на каждом резисторе, поэтому напряжение будет регулироваться
самих себя.Суммарное сопротивление R 1
+
R 2Два параллельных резистора
Ток через А равен току
через B плюс ток через C. Ток разделяется и идет
Ток разделяется и идет
вместе, как вода, текущая вокруг острова.Напряжение на R 1 такое же, как на
напряжение на R 2.E AB = E AC,
так I B
R 1 =
I C R 2 и
I B /
R 2 =
I C / R 1Другими словами, ток через каждый
резистор обратно пропорционален номиналам резисторов.
Также важно помнить
резистор высокого номинала проходит через небольшой
текущий.Мы можем решить вышеуказанную проблему для полного тока
( I B +
I C) и получите эквивалент
сопротивление для двух резисторов:В частном случае, когда резисторы
То же, эквивалентное сопротивление — R 1 /2. Это появляется чаще, чем вы
можно было ожидать.В другом особом случае, когда R2 больше, чем
100-кратное значение R1, R2 составляет такую небольшую часть
ток, который мы не удосужились включать в расчеты.
Тогда мы говорим, что R2 не загружает цепи.Вот более сложный пример:
R1 — специальный тип резистора
с регулируемым краном посередине.Это действительно заставляет R1 вести себя
как два последовательно включенных резистора. Если мы скажем, что R2 в 100 раз больше R1, мы можем
оставьте это в расчетах и обнаружите, что напряжение E2 будет
напрямую зависит от положения крана.Если бы R2 был сопоставим по стоимости с R1, мы бы
нужно вычислить, сначала решив R2 и нижнюю часть R1 как
два резистора параллельно, и используя результат этого последовательно
расчет, чтобы найти напряжение E2 и полный ток. В
итоговая кривая напряжения (что вы получите, если построите E2 для различных
положения крана) довольно беспорядочно, поэтому мы действительно предпочитаем
R2, не нагружающий схему.Вернуться к темам Mu126
Страница не найдена | MIT
Перейти к содержанию ↓
- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!Что Вы ищете?
Увидеть больше результатов
Предложения или отзывы?
21.
 1 Последовательные и параллельные резисторы — College Physics: OpenStax
1 Последовательные и параллельные резисторы — College Physics: OpenStaxНа рисунке 3 показаны резисторы, подключенные параллельно и подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радиоприемник и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рис. 3 (b).)
Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс] \ boldsymbol {R _ {\ textbf {p}}} [/ latex], давайте рассмотрим протекающие токи и их связаны с сопротивлением.
 Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex].Сохранение заряда подразумевает, что общий ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов:
Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex].Сохранение заряда подразумевает, что общий ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов:[латекс] \ boldsymbol {I =} [/ latex] [latex] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {= V} [/ latex] [латекс] \ boldsymbol {(\ frac { 1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {R_3})}.[/ latex]
[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {= V} [/ латекс ] [latex] \ boldsymbol {(\ frac {1} {R_p})}.
 [/ latex]
[/ latex]Члены в скобках в последних двух уравнениях должны быть равны. Если обобщить на любое количество резисторов, общее сопротивление [латекс] \ boldsymbol {R_p} [/ latex] параллельного соединения связано с отдельными сопротивлениями соотношением
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_3}} [/ latex] [латекс] \ boldsymbol {+ \ cdots} [/ latex]
Это соотношение приводит к общему сопротивлению [латекс] \ boldsymbol {R_p} [/ latex], которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: [латекс] \ boldsymbol {V = 12.
 0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов определяется с помощью следующего уравнения. Ввод известных значений дает
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {R_3}} [/ latex] [latex] \ boldsymbol {=} [/ latex] [latex] \ boldsymbol {\ frac {1} {1.
 00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex]
00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex]Таким образом,
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.00} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.1667} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.07692} {\ Omega}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.2436} {\ Omega}} [/ латекс]
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны перевернуть это, чтобы найти полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {R_p =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.
 2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс]
2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс]Общее сопротивление с правильным количеством значащих цифр составляет [латекс] \ boldsymbol {R_p = 0.804 \; \ Omega} [/ latex]
Обсуждение для (а)
[латекс] \ boldsymbol {R_p} [/ latex], как и предполагалось, меньше минимального индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {0.8041 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 14.92 \; \ textbf {A}} [/ latex]
Обсуждение для (б)
Ток [latex] \ boldsymbol {I} [/ latex] для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см.
 Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, так как каждый резистор получает полное напряжение. Таким образом,
[латекс] \ boldsymbol {I_1 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {1.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 12.0 \; \ textbf {A}}. [/ Latex]
Аналогично
[латекс] \ boldsymbol {I_2 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {6.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 2.00 \; \ textbf {A}} [/ latex]
и
[латекс] \ boldsymbol {I_3 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.
 0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex]
0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex]Обсуждение для (c)
Полный ток складывается из отдельных токов:
[латекс] \ boldsymbol {I_1 + I_2 + I_3 = 14.92 \; \ textbf {A}}. [/ Latex]
Это соответствует сохранению заряда.
Стратегия и решение для (d)
Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.2} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 11.1 \; \ textbf {W}}. [/ Latex]
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором параллельно, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбирая [латекс] \ boldsymbol {P = IV} [/ latex] и вводя общий ток, получаем
[латекс] \ boldsymbol {P = IV = (14.
 92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]
92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]Обсуждение для (e)
Общая мощность, рассеиваемая резисторами, также 179 Вт:
[латекс] \ boldsymbol {P_1 + P_2 + P_3 = 144 \; \ textbf {W} + 24.0 \; \ textbf {W} + 11.1 \; \ textbf {W} = 179 \; \ textbf {W}}. [/ латекс]
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
.

- Спираль

 3)
3) 4)
4)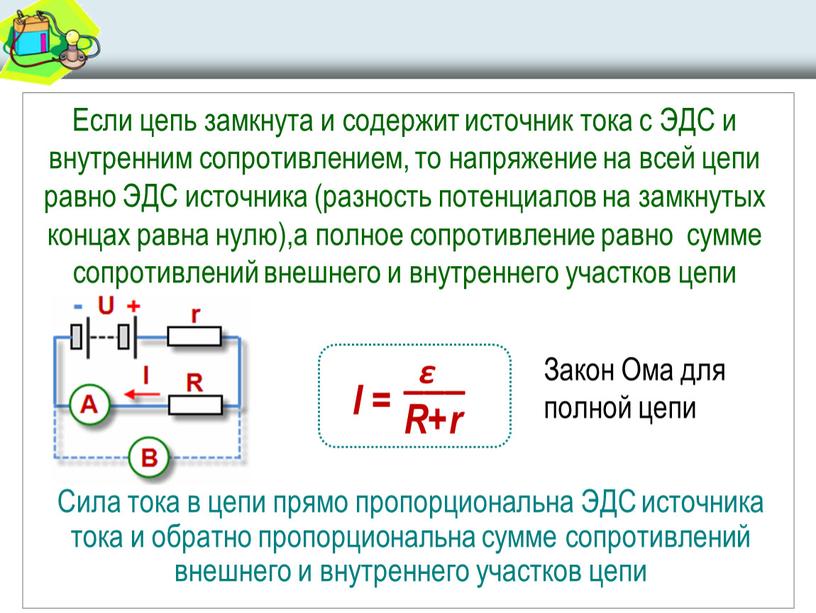 6)
6) {i(\omega t+\varphi)},}
{i(\omega t+\varphi)},}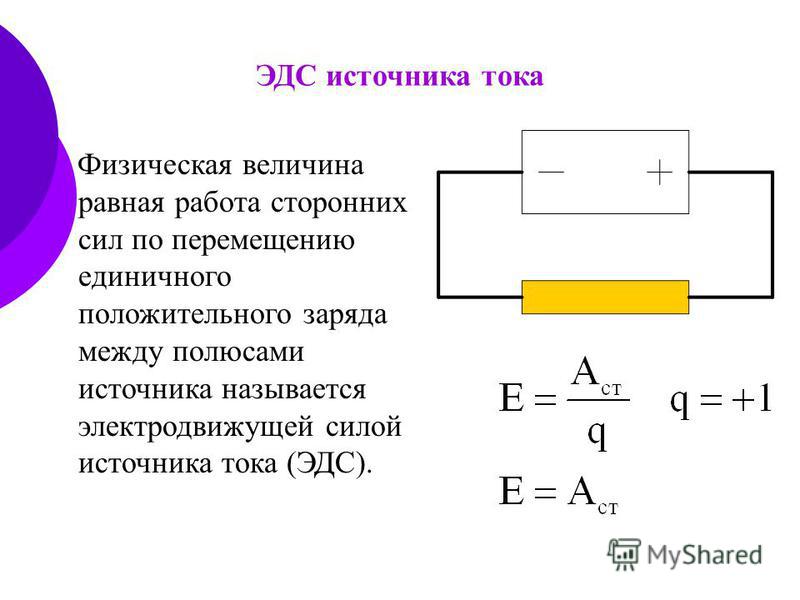 Вот так он выглядел.
Вот так он выглядел. Поэтому я на своем рабочем стенде собрал эту схему. Смотрите ниже как она выглядит.
Поэтому я на своем рабочем стенде собрал эту схему. Смотрите ниже как она выглядит. Сопротивление светодиодной лампочки равно R = 40740 (Ом)
Сопротивление светодиодной лампочки равно R = 40740 (Ом)
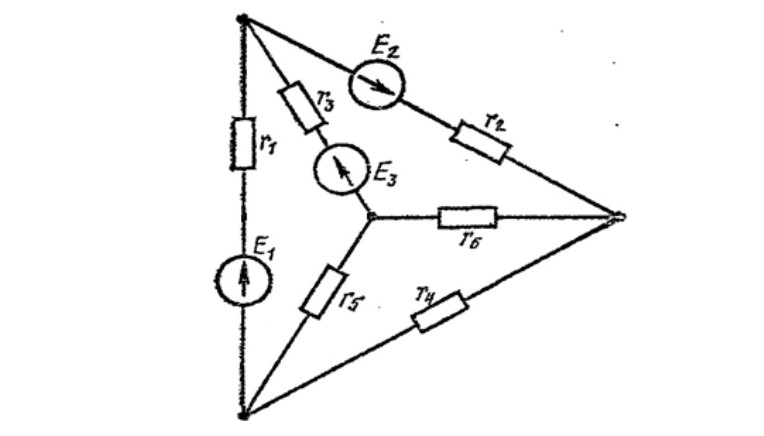
 е. ток в цепи увеличится, при условии, что сопротивление цепи останется неизменным.
е. ток в цепи увеличится, при условии, что сопротивление цепи останется неизменным. Какой ток покажет
Какой ток покажет Найдите ток короткого замыкания гальванического
Найдите ток короткого замыкания гальванического

 Определите сопротивление водонагревательного элемента чайника.
Определите сопротивление водонагревательного элемента чайника.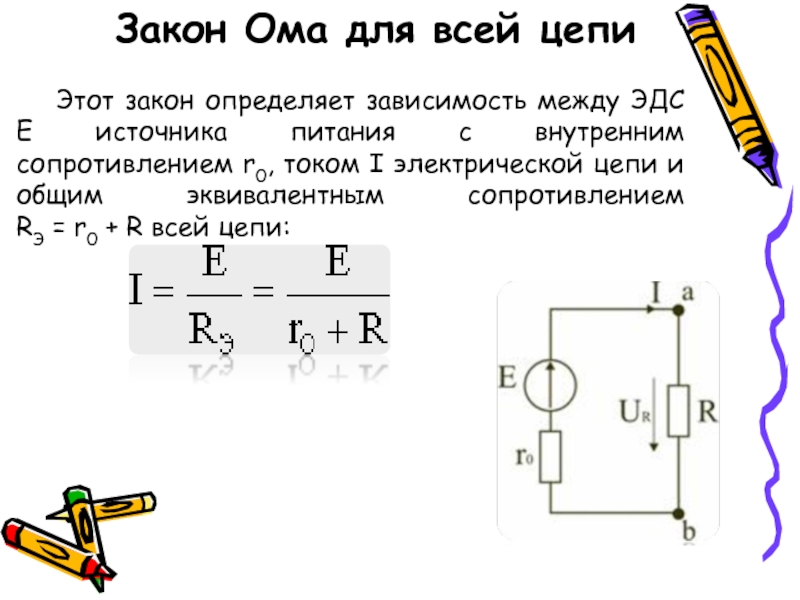

 { \circ} С$. Найти сопротивление $R$ проводника, считая градиент температуры вдоль его оси постоянным.
{ \circ} С$. Найти сопротивление $R$ проводника, считая градиент температуры вдоль его оси постоянным. При таком значении $n$ сила тока $I$ во внешней цепи, имеющей сопротивление $R$, будет максимальной? Чему будет равно внутреннее сопротивление $R_{i}$ батареи при этом значении $n$?
При таком значении $n$ сила тока $I$ во внешней цепи, имеющей сопротивление $R$, будет максимальной? Чему будет равно внутреннее сопротивление $R_{i}$ батареи при этом значении $n$? Определить силу тока $I$ в цепи.
Определить силу тока $I$ в цепи. Какую наибольшую мощность $P_{max}$ можно получить во внешней цепи, соединенной с такой батареей?
Какую наибольшую мощность $P_{max}$ можно получить во внешней цепи, соединенной с такой батареей? Какое количество теплоты $Q$ выделяется в этом проводнике за указанный промежуток времени?
Какое количество теплоты $Q$ выделяется в этом проводнике за указанный промежуток времени? ЭДС сообщает вам напряжение батареи без уменьшения внутреннего сопротивления, как при обычных измерениях разности потенциалов.Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть.
ЭДС сообщает вам напряжение батареи без уменьшения внутреннего сопротивления, как при обычных измерениях разности потенциалов.Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть. В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеальной ситуации, и на практике она всегда больше, чем напряжение аккумулятора.
В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеальной ситуации, и на практике она всегда больше, чем напряжение аккумулятора.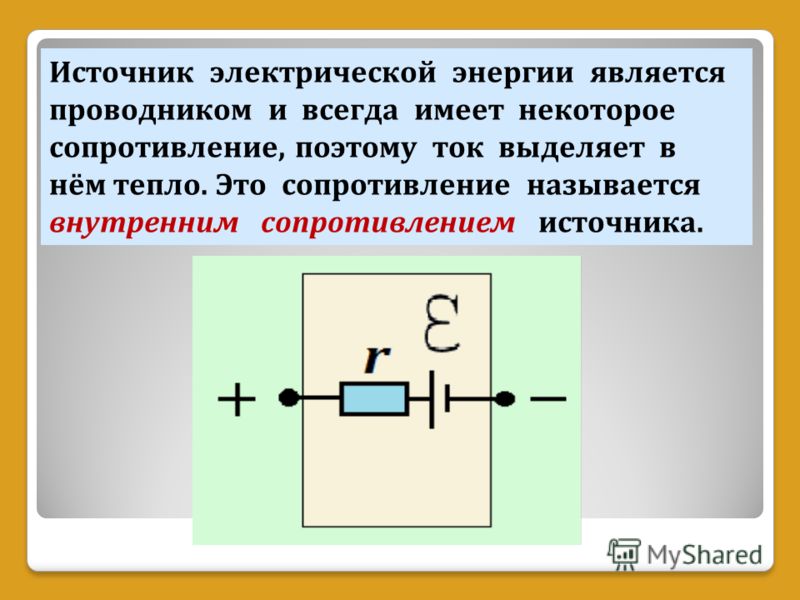
 Одна ситуация, когда возникает двигательная ЭДС, известна как эффект Холла и уже была исследована.Заряды, движущиеся в магнитном поле, испытывают магнитную силу F = qvB sin θ , которая перемещает противоположные заряды в противоположных направлениях и создает em f = Bℓv . Мы видели, что у эффекта Холла есть приложения, включая измерения B и v . Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и мы обнаружим, что ЭДС движения может использоваться как источник энергии. Рассмотрим ситуацию, показанную на рисунке 1.Стержень перемещается со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ в однородном магнитном поле B . Рейки неподвижны относительно B и подключены к неподвижному резистору R . Резистором может быть что угодно, от лампочки до вольтметра. Рассмотрим площадь, ограниченную подвижным стержнем, направляющими и резистором.
Одна ситуация, когда возникает двигательная ЭДС, известна как эффект Холла и уже была исследована.Заряды, движущиеся в магнитном поле, испытывают магнитную силу F = qvB sin θ , которая перемещает противоположные заряды в противоположных направлениях и создает em f = Bℓv . Мы видели, что у эффекта Холла есть приложения, включая измерения B и v . Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и мы обнаружим, что ЭДС движения может использоваться как источник энергии. Рассмотрим ситуацию, показанную на рисунке 1.Стержень перемещается со скоростью v по паре проводящих рельсов, разделенных расстоянием ℓ в однородном магнитном поле B . Рейки неподвижны относительно B и подключены к неподвижному резистору R . Резистором может быть что угодно, от лампочки до вольтметра. Рассмотрим площадь, ограниченную подвижным стержнем, направляющими и резистором. B перпендикулярно этой области, и площадь увеличивается по мере перемещения стержня. Таким образом, увеличивается магнитный поток между рельсами, стержнем и резистором.Когда поток изменяется, возникает ЭДС согласно закону индукции Фарадея.
B перпендикулярно этой области, и площадь увеличивается по мере перемещения стержня. Таким образом, увеличивается магнитный поток между рельсами, стержнем и резистором.Когда поток изменяется, возникает ЭДС согласно закону индукции Фарадея. )
)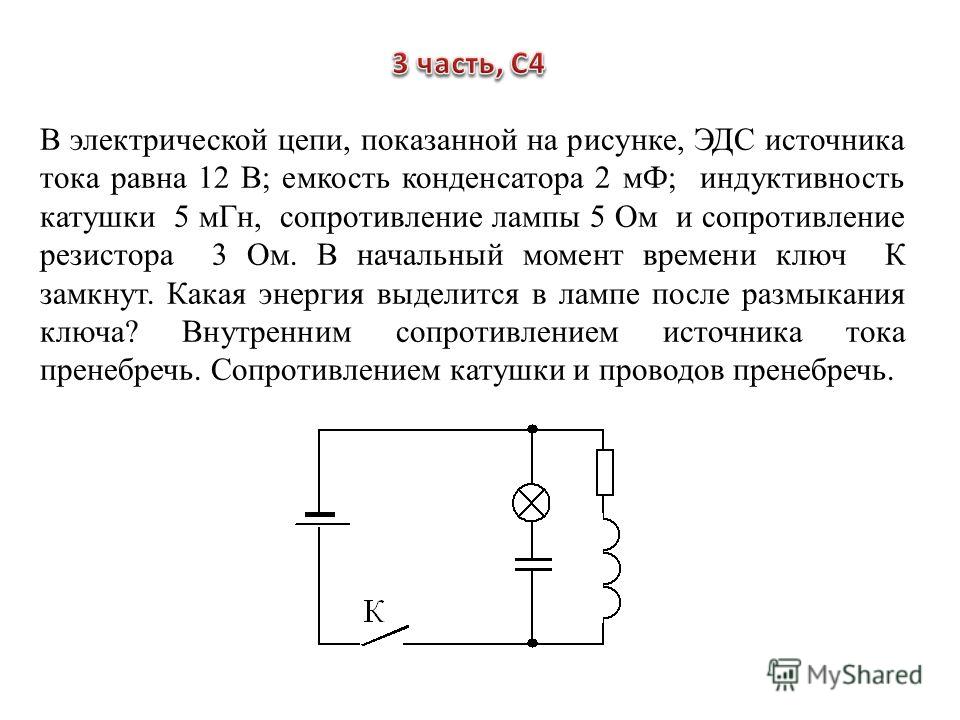 Это то же выражение, что и для эффекта Холла ранее.
Это то же выражение, что и для эффекта Холла ранее.
 Это небольшое значение согласуется с опытом. Однако есть впечатляющее исключение. В 1992 и 1996 годах с космическим шаттлом были предприняты попытки создать большие двигательные ЭДС. Привязанный спутник должен был быть выпущен на проводе длиной 20 км, как показано на рисунке 2, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли.Эту ЭДС можно было бы использовать для преобразования некоторой кинетической и потенциальной энергии шаттла в электрическую, если бы можно было создать полную схему. Чтобы замкнуть цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и неподвижные рельсы и соединительный резистор на рисунке 1, без которых не было бы полной цепи.) Затягивание тока в кабеле из-за магнитной силы F = IℓB sin θ выполняет работу, которая уменьшает кинетическую и потенциальную энергию шаттла и позволяет преобразовывать ее в электрическую.
Это небольшое значение согласуется с опытом. Однако есть впечатляющее исключение. В 1992 и 1996 годах с космическим шаттлом были предприняты попытки создать большие двигательные ЭДС. Привязанный спутник должен был быть выпущен на проводе длиной 20 км, как показано на рисунке 2, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли.Эту ЭДС можно было бы использовать для преобразования некоторой кинетической и потенциальной энергии шаттла в электрическую, если бы можно было создать полную схему. Чтобы замкнуть цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит из-за ионизации. Ионосфера выполняет ту же функцию, что и неподвижные рельсы и соединительный резистор на рисунке 1, без которых не было бы полной цепи.) Затягивание тока в кабеле из-за магнитной силы F = IℓB sin θ выполняет работу, которая уменьшает кинетическую и потенциальную энергию шаттла и позволяет преобразовывать ее в электрическую.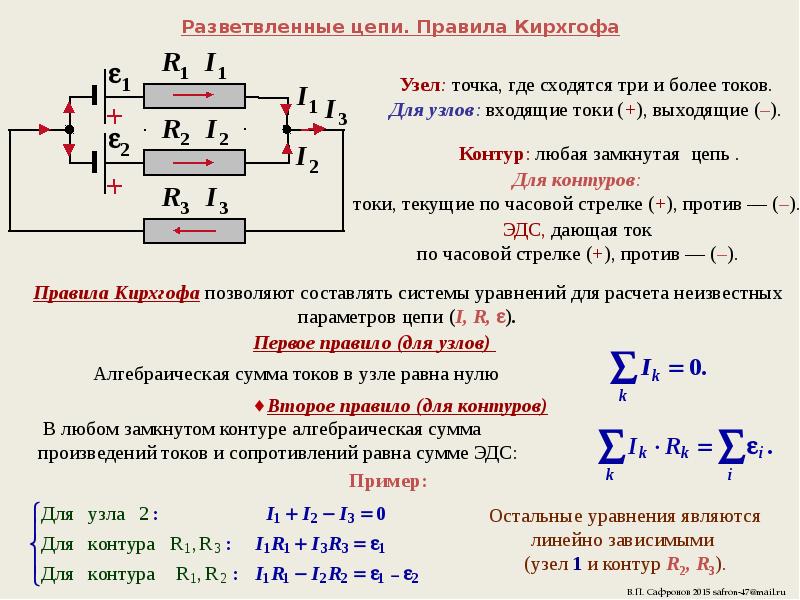 Оба теста были безуспешными. В первом случае кабель зависал, и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном растяжении. Следующий пример показывает принципиальную осуществимость.
Оба теста были безуспешными. В первом случае кабель зависал, и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном растяжении. Следующий пример показывает принципиальную осуществимость.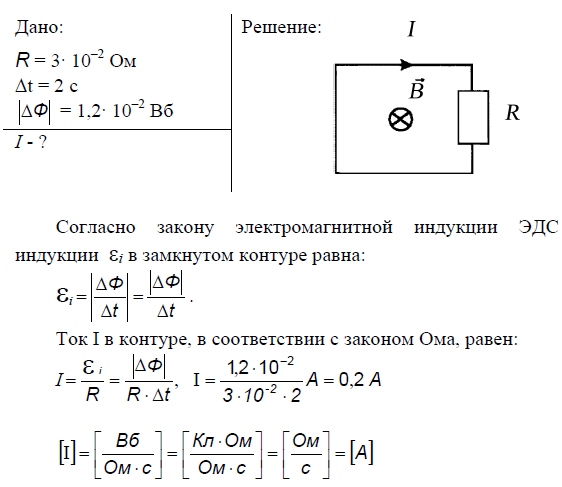 Значение 7,80 кВ является максимальной ЭДС, полученной при θ = 90º и sin θ = 1.
Значение 7,80 кВ является максимальной ЭДС, полученной при θ = 90º и sin θ = 1. Почему цилиндр может стать активным / горячим при выстреле из пушки?
Почему цилиндр может стать активным / горячим при выстреле из пушки? (a) Реактивный самолет с размахом крыла 75,0 м летит со скоростью 280 м / с. Какая ЭДС возникает между законцовками крыльев, если вертикальная составляющая поля Земли равна 3?00 × 10 −5 Т? (б) Может ли ЭДС такой величины иметь какие-либо последствия? Объясни.
(a) Реактивный самолет с размахом крыла 75,0 м летит со скоростью 280 м / с. Какая ЭДС возникает между законцовками крыльев, если вертикальная составляющая поля Земли равна 3?00 × 10 −5 Т? (б) Может ли ЭДС такой величины иметь какие-либо последствия? Объясни. Если v перпендикулярно B , тогда θ — это угол между ℓ и B . Если ℓ перпендикулярно B , тогда θ — это угол между v и B .
Если v перпендикулярно B , тогда θ — это угол между ℓ и B . Если ℓ перпендикулярно B , тогда θ — это угол между v и B . В нулевой момент времени движущийся стержень находится рядом с сопротивлением R .
В нулевой момент времени движущийся стержень находится рядом с сопротивлением R .
 Несмотря на то, что это не будет практичной геометрией генератора, она может служить
Несмотря на то, что это не будет практичной геометрией генератора, она может служить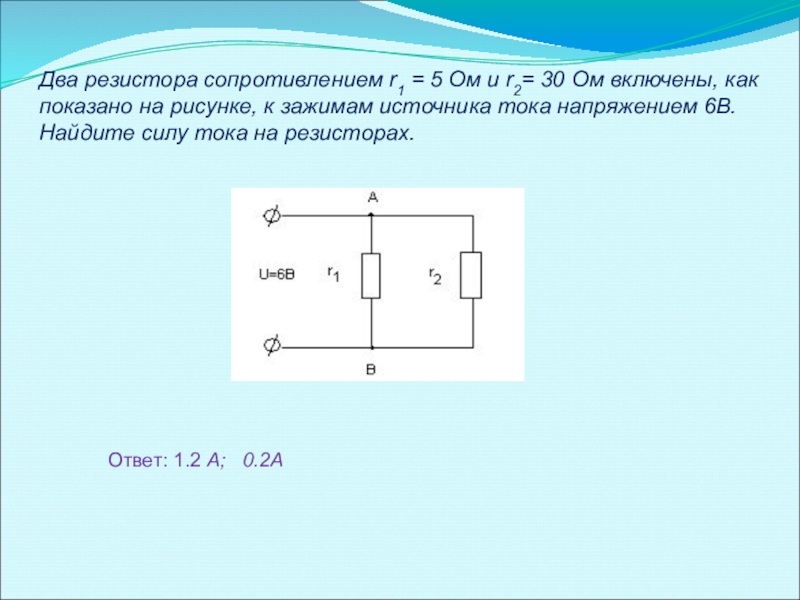
 В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.
В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R. Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает на две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение батареи (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение аккумулятора увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает на две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение батареи (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение аккумулятора увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.

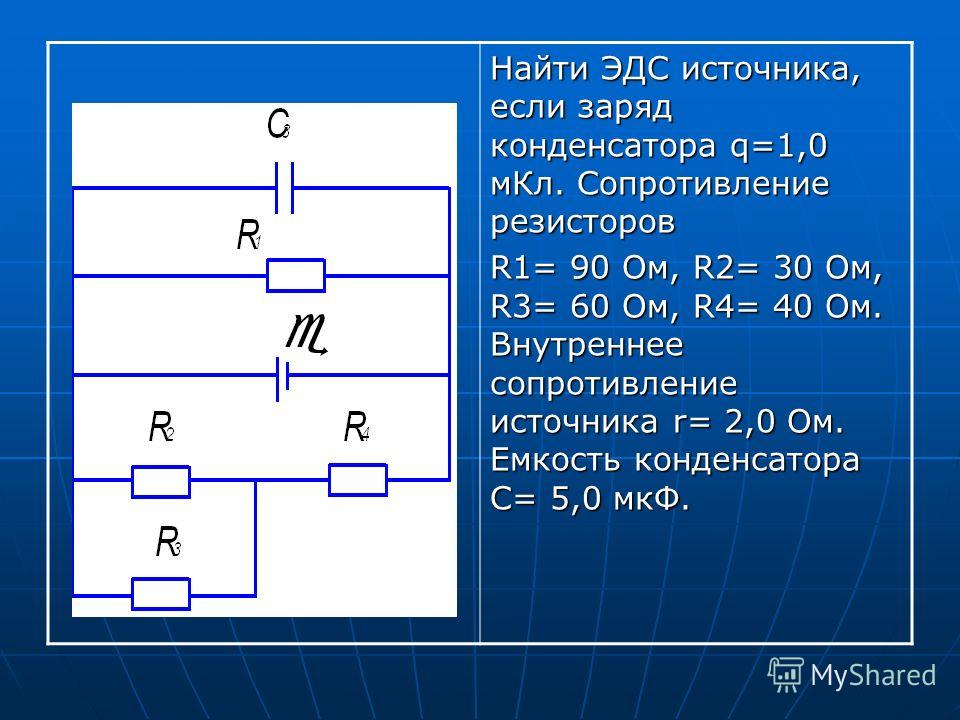 График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.
График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома. Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.
Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.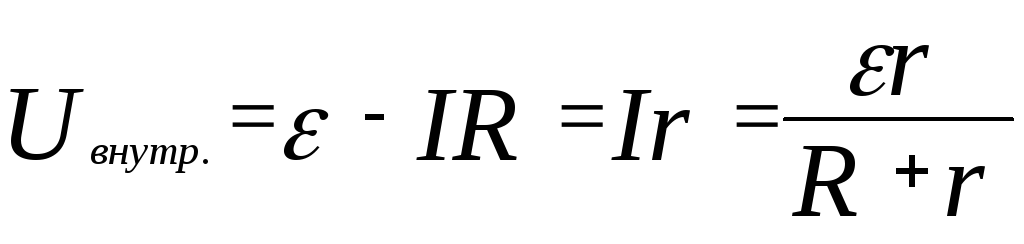 )
) Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной). Скорее всего, вас предупредили, чтобы вы не прикасались к электроприборам или даже к электрическим розеткам мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.
Скорее всего, вас предупредили, чтобы вы не прикасались к электроприборам или даже к электрическим розеткам мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____. в четыре раза больше
в четыре раза больше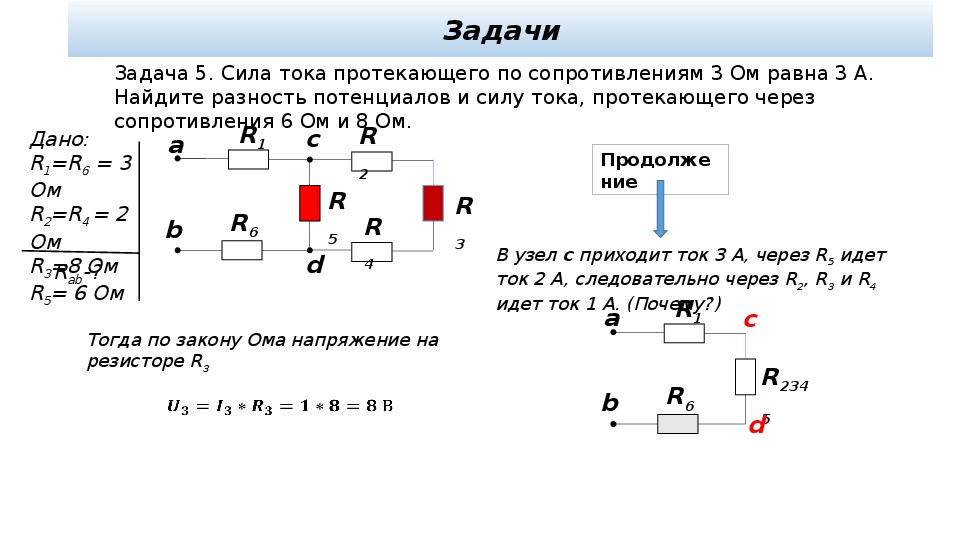
 Это растопит
Это растопит

 Ток разделяется и идет
Ток разделяется и идет
 1 Последовательные и параллельные резисторы — College Physics: OpenStax
1 Последовательные и параллельные резисторы — College Physics: OpenStax Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex].Сохранение заряда подразумевает, что общий ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов:
Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex].Сохранение заряда подразумевает, что общий ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов: [/ latex]
[/ latex] 0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами. 00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex]
00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex] 2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс]
2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс] Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.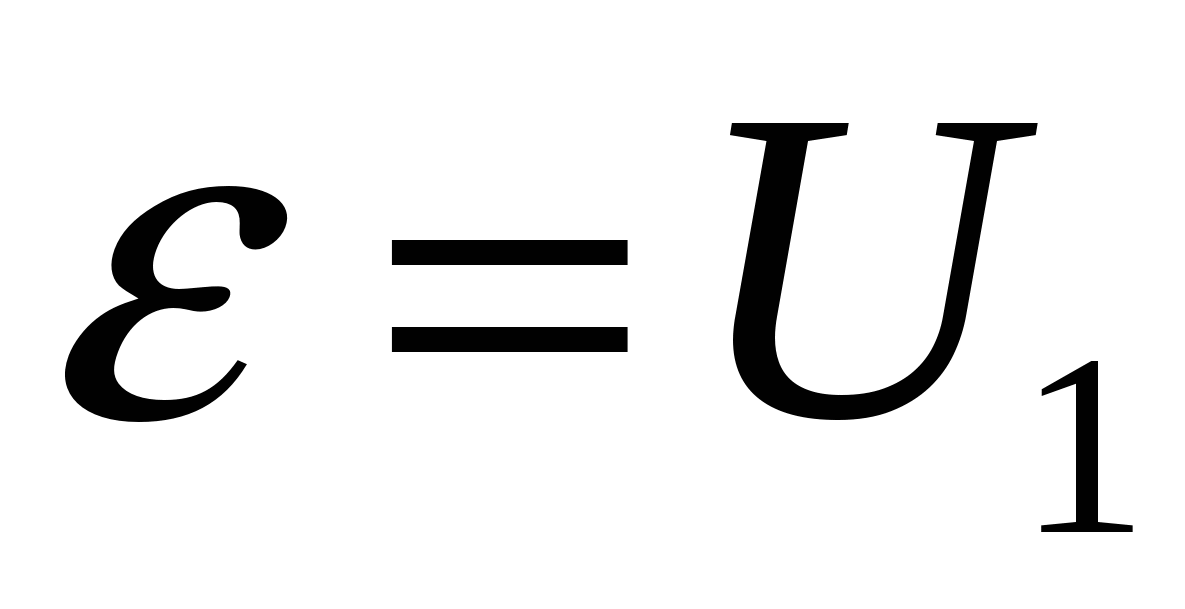 0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex]
0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex] 92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]
92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]