Расчет эквивалентного сопротивления электрической цепи. Как найти r эквивалентное

Физическая формула расчета (определения) эквивалентного сопротивления в цепи

Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.

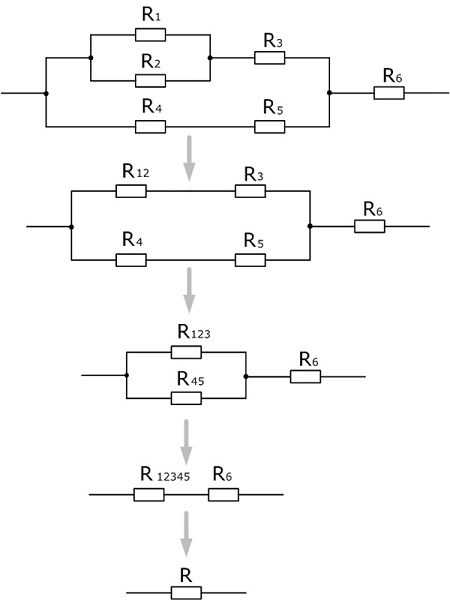
Метод свёртывания цепи

Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.

Последовательное соединение элементов

В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.

При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.

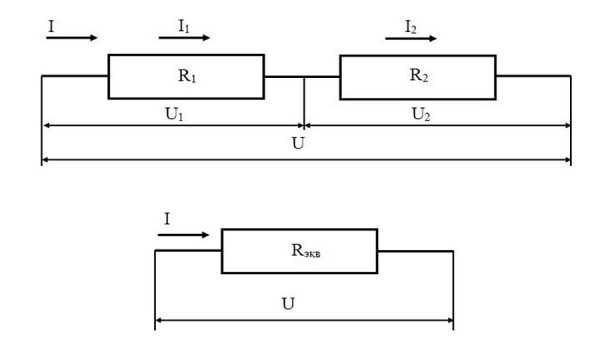
Последовательное подключение приборов

Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:

I = U/R.

Из вышестоящего выражения получаем значение R:

R = U/I (1).

Поскольку при последовательном соединении:

• I = I1 = I2 =…= IN (2),
• U = U1 + U2 +…+ UN (3),

формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:

• Rэкв = (U1 + U2 + …+ UN)/I,
• Rэкв = R1 + R2 + … + RN (4).

Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:

Rобщ = N·R (5).

Параллельное соединение

При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.

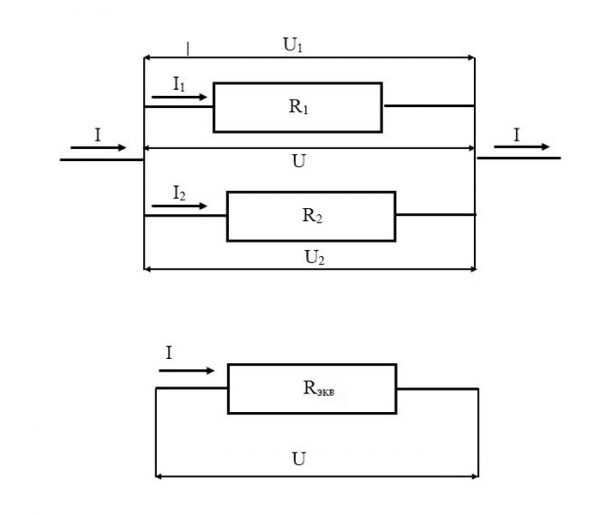
Параллельное соединение

Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.

В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.

Если имеются N резистивных устройств, подключенных таким образом, то:

I = I1 + I2  + … + IN (6),

U = U1 = U2 = … = UN (7).

Из выражений (1), (6) и (7) имеем:

• Rобщ = U/(I1 + I2 + …+ IN),
• 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).

Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:

Rобщ = R · R / N·R = R / N (9).

Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.

Расчёт при смешанном соединении устройств

В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.

При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.

Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:

• R1 = 1Ом,
• R2 = 2Ом,
• R3 = 3Ом,
• R4 = 6Ом,
• R5 = 9Ом,
• R6 = 18Ом,
• R7 = 2,8Ом,
• U = 32В.

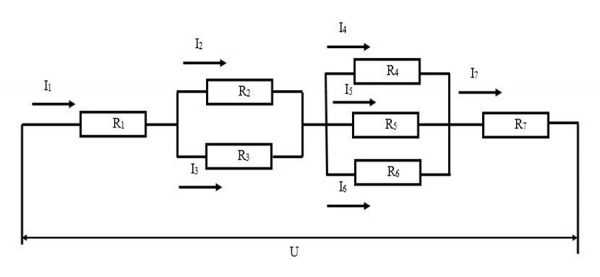
Электрическая схема

Из закона Ома имеем: 

I = U/R,

где R – суммарное сопротивление всех приборов.

Его будем находить, воспользовавшись методом сворачивания цепи.

Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:

R2,3= R2·R3 / (R2+R3).

R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:

1/R4,5,6 = 1/R4+1/R5+1/R6.

Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.

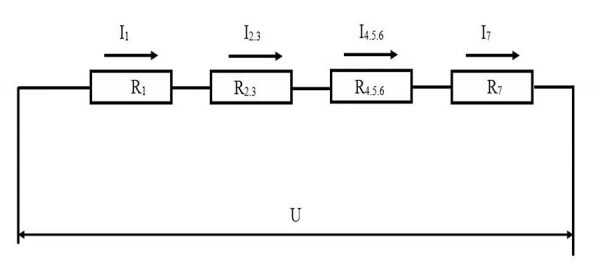
Эквивалентная схема

Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.

Rобщ может быть найдено по формуле:

Rобщ = R1 + R2,3 + R4,5,6 + R7.

Подставляем числовые значения и рассчитываем R для определённых участков:

• R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
• 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
• R4,5,6 = 3Ом,
• Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.

Теперь, после того, как нашли Rэкв, можно вычислять значение I:

I = 32В / 8Ом = 4А.

После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.

Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:

I1 = I2,3 = I4,5,6 = I7 = I = 4А.

На участке R2,3 напряжение находим по формуле:

• U2,3 = I2,3·R2,3,
• U2,3 = 4А·1,2Ом = 4,8В.

Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:

• I2 = U2 / R2,
• I2 = 4,8В / 2Ом = 2,4А,
• I3 = U3 / R3,
• I3 = 4,8В / 3Ом = 1,6А.

Проверяем правильность решения:

• I2,3 = I2 + I3,
• I2,3 = 2,4А + 1,6А = 4А.

На участке R4,5,б напряжение также находим, исходя из закона Ома:

• U4,5,6 = I4,5,6·R4,5,6,
• U4,5,6 = 4А·3Ом = 12В.

Так как R4, R5, Rб подключены параллельно друг к другу, то:

U4,5,6 = U4 = U5 = U6 = 12В.

Вычисляем I4, I5, I6:

• I4 = U4 / R4,
• I4 = 12В / 6Ом = 2А,
• I5 = U5 / R5,
• I5 = 12В / 9Ом » 1,3А,
• I6 = U6 / R6,
• I5 = 12В / 18Ом » 0,7А.

Проверяем правильность решения:

I4,5,6 = 2А + 1,3А + 0,7А = 4А.

Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.

Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.

Видео

Оцените статью:

elquanta.ru

Как определить величину эквивалентного сопротивления для исследуемой цепи?

Эквивалентное сопротивление м. б. найдено в несколько этапов. R3 и R4 соединены последовательно, поэтому R34 = R3 + R4 = 12Ом К сопротивлению R34 параллельно подсоединен резистор R2, поэтому R234 = R2*R34/(R2+R34) = 4*12/16 = 3Ом Сопротивление R234 соединено последовательно с резистором R1, поэтому R1234 = R1+ R234 = 7+3 = 10 Ом Наконец резистор R5 подсоединен параллельно R1234, поэтому общее (эквивалентное) сопротивление цепи Re = R5*R1234/(R5+R1234) = 10*10/20 = 5Ом Все остальное находится из закона Ома и правил для напряжений и токов при последовательном и параллельном соединении. U2 = I2*R2 = 2*4 = 8B U2 = U34 = I34*R34 => I34 = U2/R34 = 8/12 = 2/3 A = I3 = I4 U3 = I3*R3 = 10*2/3 = 20/3 B U4 = U34 - U3 = 8 - 20/3 = 4/3 B I1 = I2 + I34 = 2 + 2/3 = 8/3 A U1 = I1*R1 = 7*8/3 = 56/3 B U5 = U1+U2 = 8 + 56/3 = 80/3 B U5 - это общее напряжение в цепи I5 = U5 / R5 = (80/3)/10 = 8/3 A

<a href="/" rel="nofollow" title="15907216:##:1STErLe">[ссылка заблокирована по решению администрации проекта]</a>

Для постоянного тока - так.

touch.otvet.mail.ru

Определить эквивалентное сопротивление цепи - fiziku5.ru

Задача 3.12.

Определить эквивалентное сопротивление цепи, в которой XL=XC=R=10 Ом.

Задача 3.13.

Чему равно эквивалентное сопротивление цепи?

Задача 3.14.

При каком соотношении величин ток I на входе цепи опережает по фазе напряжение U?

3.6. Цепь синусоидального тока при смешанном соединении элементов.

Для цепей синусоидального тока справедливы все формулы расчета цепей постоянного тока, но в комплексной форме. Поэтому методика расчета цепей при смешанном соединении элементовсводится к постепенному упрощению схемы путем замены отдельных участков эквивалентными сопротивлениями, в результате чего определяется эквивалентное сопротивление всей цепи.

Решить задачи:

Задача 3.15.

Для электрической цепи, представленной на рисунке, найти полное сопротивление Z всей цепи при ХL=5 Ом, R=XC=10 Ом.

Задачи 3.16.

Найти комплексное сопротивление Z всей цепи при ХL=10 Ом, R=20 Ом, XC=5 Ом.

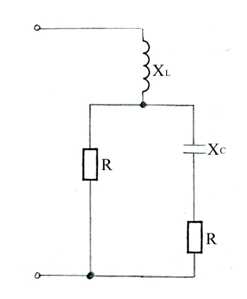
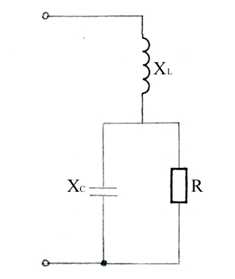
Задача 3.17.

Определить характер нагрузки цепи, если ХL=R=XC.

3.7. Мощность цепи синусоидального тока.

3.7.1. Мгновенная мощность – произведение мгновенных значений напряжения и тока, т. е. p=u*i.

Распишем её для отдельных элементов цепи, приняв начальную фазу для напряжения φu=0:

— цепь с резистивным (активным) элементом (см. рис. 3.5,а):

Рис. 3.10

Мгновенная мощность имеет две составляющие: постоянную и переменную , изменяющуюся по косинусоидальномузакону с удвоенной частотой.

В этой цепи мгновенная мощность всегда положительная, и энергия в цепи передается в одном направлении от источника к приемнику, где она полностью (необратимо) преобразуется в другие виды энергии (рис. 3.10).

— цепь с индуктивным элементом (см. рис. 3.6a )

Мгновенная мощность – переменная, изменяется по синусоидальному закону с удвоенной частотой. При возрастании тока i по абсолютной величине мгновенное значение мощности p>0, в это время происходит накопление энергии в магнитном поле индуктивности. При уменьшении тока i по абсолютной величине p<0 и в это время индуктивность становится источником электроэнергии (рис 3.11).

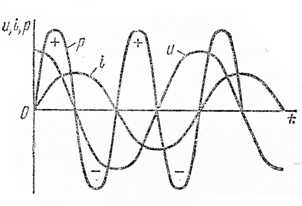
Рис 3.11

— цепь с емкостным элементом(см. рис. 3.7,а)

Мгновенная мощность – переменная, изменяющаяся по синусоидальному закону с удвоенной частотой. При возрастании тока по абсолютной величине мгновенное значение мощности p<0, в это время емкость становится источником электроэнергии. При уменьшении тока по абсолютной величине p>0, в это время происходит накопление энергии в электрическом поле емкости (рис 3.12).

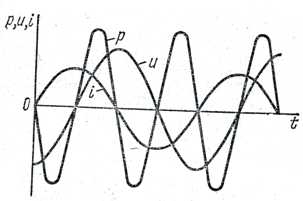
Рис 3.12

3.7.2. Активная мощность – мощность необратимых преобразований электрической энергии на участке цепи за период:

Из формулы следует, что средняя за период мощность не равна нулю, если участок цепи имеет активное сопротивление.

3.7.3. Реактивная мощность – мощность реактивных элементов полейpP=pL+pC в среднем за период равна нулю, но в течение четверти периода она положительна, что означает накопление энергии в магнитном поле катушки или электрическом поле конденсатора, а в течение следующей четверти периода – отрицательная, что соответствует обратному процессу.

Таким образом, имеет место процесс колебания энергии, но необратимых преобразований энергии (при отсутствии активной мощности) нет.

3.7.4. Полная мощность. Под полной мощностью участка цепи понимается максимально возможная мощность при заданных значениях тока I и напряжения U.

Необходимость введения понятия мощности заключается в том, что при конструировании любых электрических устройств их рассчитывают на определенное номинальное напряжение Uном и на определенный номинальный ток Iном, а их произведение Sном=UномIном дает максимально возможную мощность данного устройства (именно она указывается в паспорте большинства электрических устройств переменного тока).

Связь между различными мощностями:

Для облегчения запоминания этих формул можно обратить к так называемому треугольнику мощности (рис 3.13).

Рис 3.13

3.7.5. Коэффициент мощности.

Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии, в том числе используется для выполнения полезной работы.

Для повышения коэффициента мощности применяются меры, которые сводятся или к уменьшению реактивной мощности QL или к ее компенсации мощностью QC.

Решить задачу.

Задача 3.18.

Выбрать схему, которая является рациональной для увеличения cosφ, где Ском – компенсирующая емкость, Rпр, Lпр – активное и индуктивное сопротивление приемника соответственно.

fiziku5.ru

Эквивалентное сопротивление онлайн

Эквивалентное сопротивление при последовательном соединении

Альтернативное отображение

Эквивалентное сопротивление при паралельном соединении

Альтернативное отображение

Последовательное соединение

Что же такое эквивалентное сопротивление?

Все знаем что такое эквивалент. Это вещь или объект которое по своим характеристикам повторяет  оригинал.  В электротехнике эквивалент сопротивления это замена части схемы состоящей из нескольких резисторов - одним элементом(эквивалентом)

Сложные схемы соединений пока рассматривать не будем, а рассмотрим две самые простые схемы расчета эквивалентного сопротивления: последовательное и паралельное соединение

Вид последовательного соединения резисторов показан на рисунке ниже

 

И формула расчета эквивалентного сопротивления  выглядит так

 

Параллельное СОЕДИНЕНИЕ

Паралельное соединение нескольних резисторов (сопротивлений) выглядит так, как показано на рисунке

 

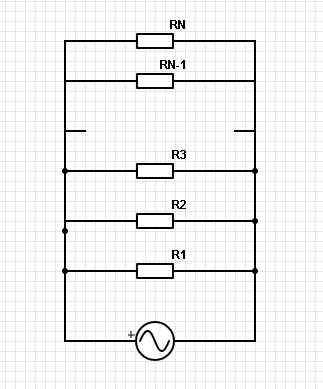
А формула превращается в такую

 

Стоит обратить внимание, что по таким же формулам считается эквивалентное сопротивление индуктивностей, но совершенно другой прицип будет при расчете эквивалентной ёмкости конденсаторов

 

Синтаксис

Он очень прост 

calc_e  список сопротивлений с размерностями через запятую.

В ответе мы получим эквививалентное значение  сопротивления  при последовательном и паралельных соединениях.

Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.

Примеры

Рассчитать эквивалентное сопротивление трех резисторов  следующих номиналов: 10 Ом, 0.2кОм и 344кОм

В запросе так и пишем calc_e 10 Ом, 0.2кОм, 344кОм

Ответ не заставит себя долго ждать и выглядит вот так

Эквивалентное сопротивление при последовательном соединении

344.21килоОм

Альтернативное отображение

Эквивалентное сопротивление при паралельном соединении

9.5235458597492Ом

Альтернативное отображение

Удачи в расчетах!

www.abakbot.ru

Расчет эквивалентного сопротивления электрической цепи — Мегаобучалка

Любое последовательное соединение можно преобразовать к последовательному соединению одного эквивалентного резистора и одного источника ЭДС. Причем, сопротивление эквивалентного резистора равно сумме всех сопротивлений входящих в соединение, а ЭДС эквивалентного источника равна алгебраической сумме ЭДС источников входящих в соединение.

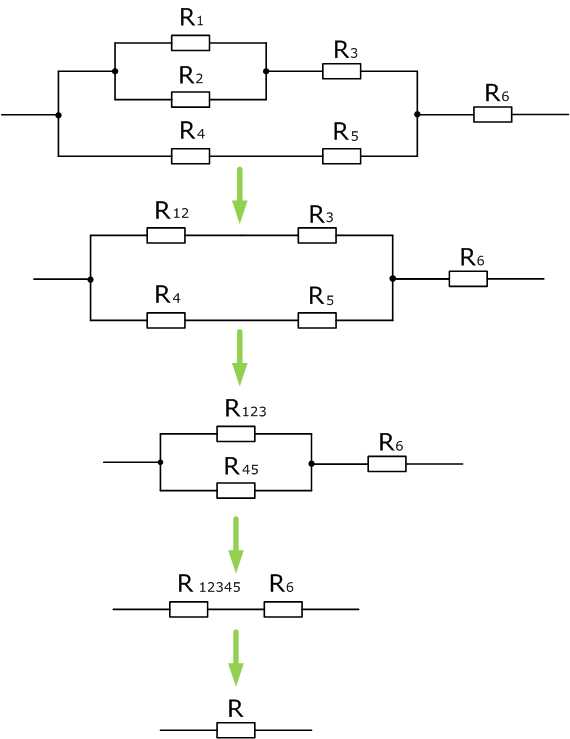
R4=20 Ом, R5=40 Ом, R6=15 Ом (пример)

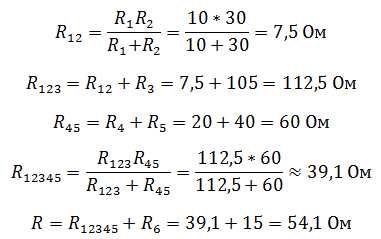
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.

 

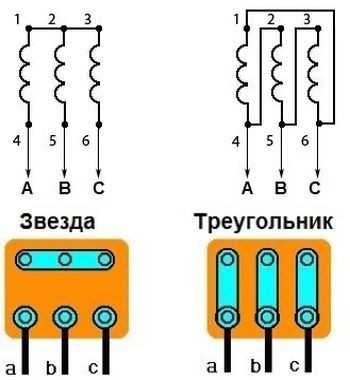
9. СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ

Схему еоедииения трех ветвей, образующих замкнутый контур с тремя узлами называют треугольником.

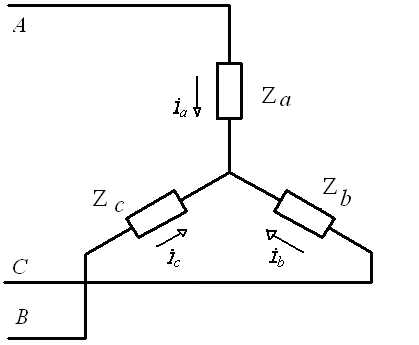
взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т. е. при соответственно равных напряжениях между вершинами А, Б и В треугольника и звезды токи IA, IБ, 1В в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.

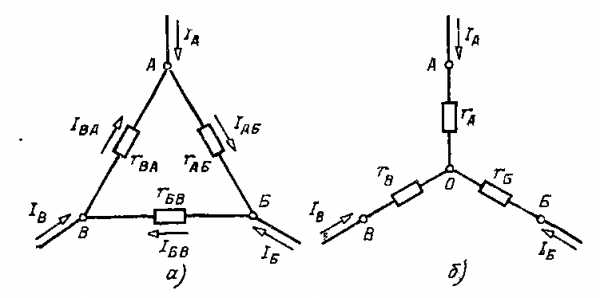
Рис 2.8 Соединение резисторов треугольником (а) и звездой (б)

Сопротивления эквивалентной звезды rа, rб, rв находятся в определенных соотношениях с сопротивлениями треугольника rаб, rбв, rва. Для выяснения этой зависимости допустим сначала, что в вершине А произошел обрыв подводящего провода и, следовательно, ток Iа=0. Сопротивления между двумя оставшимися присоединенными вершинами Б и В для обеих схем должны быть одинаковы, чтобы были соответственно равны токи IБ и Iв в обеих схемах.

 

Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника rаб,rбв, rва, требуется определить сопротивления лучей эквивалентной звезды rа, rб, rв . Для этого составим полусумму левых и правых частей уравнений (2.15) и (2.16):

 

и вычтем из полученного выражения уменьшенные вдвое левую и правую части (2.14). В результате получим

(2.17)

Аналогично получим

(2.18)

(2.19)

 

сли сопротивления треугольника равны друг другу: rаб = rбв=rва=rΔ, то будут равны друг другу и сопротив

ления звезды, т. е. rа = rб=rв=r λ, причем из формул (2.17)—(2.19) получается простое соотношение

(2.20)

При обратном преобразовании звезды в эквивалентный треугольник, т. е. при заданных сопротивленияхrа, rб, rв, надо решить три уравнения (2.17)—(2 19) относительно сопротивлений rаб, rбв:

 

 

Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды.

11. Режимы работы электрической цепи

· Режим короткого замыкания ( КЗ )

В режиме короткого замыкания источник питания замкнут накоротко. Режим является аварийным. Ток короткого замыкания КЗ во много раз превышает значение номинального тока.

Rн = 0 I = max

· Режим холостого хода ( ХХ )

В режиме холостого хода источник питания отсоединен от нагрузки и работает вхолостую. Сопротивление внешнего участка цепи и ток равен 0. Rн = ∞

· Режим согласованной нагрузки

Свойства электрической цепи – наибольшая мощность нагрузки развивается источником, когда сопротивление нагрузки ровно внутреннему сопротивлению источника.

Rн = I0

Из графика видно с ростом сопротивления нагрузки растёт мощность на нагрузке при Rн = I0 мощность нагрузки наибольшая при дальнейшем росте Rн – PRн уменьшается.

Мощность электрического тока

P = UI

 

 

megaobuchalka.ru

Эквивалентные преобразования схем

Стр 1 из 2Следующая ⇒

Применение законов Ома и Кирхгофа к расчету линейных электрических цепей постоянного тока

 

Законы Ома

 

Закон Ома для участка цепи (в пределах ветви) позволяет найти ток участка по известной разности потенциалов (напряжению) на зажимах участка.

 

̶ Закон Ома для участка цепи, не содержащего источник ЭДС (рисунок 1)

 

Рис.1

 

̶ Закон Ома для участка цепи, содержащего источник ЭДС (активная ветвь) (рисунок 2).

Рис.2

 

Если положительные направления напряжения и ЭДС

совпадают с произвольно выбранным положительным направлением тока ветви, то в приведенной формуле они учитываются со знаком плюс, и со знаком минус, если их направления не совпадают с направлением тока.

Задача 1.1.1.Найти ток ветви (рисунок 3), если: U=10 В, E=20 В, R =5 Ом.

 

а б в г

Рис. 3

Решение:

Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»:

а)

 

Аналогично определяются токи в схемах б, в, г рисунка 3:

б)

в)

г)

 

Задача 1.1.2.Найти напряжение между зажимами ветвей (рисунок 4).

 

а б в

Рис. 4

Решение:

Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:

 

 

откуда выразим напряжение на зажимах:

 

Uba= E – I·R = 150-2·50 = 50 В.

 

Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.

б)

или

Uab = IR + E1 – E2 = 1 50 + 150 – 50 = 150 B;

в)

или

Uab = I× (R1 + R2) + E = 2 (10 + 40) + 100 = 200 В;

 

Задача 1.1.3.Определить неизвестные потенциалы точек участка цепи (рисунок 5).

 

а б

Рис. 5

 

Решение:

Для схемы рисунка 5 а запишем обобщенный закон Ома:

 

 

откуда выразим напряжение на зажимах ветви:

 

Uab = I ⋅ R – E1+ E2

 

Если представить напряжение Uabкак разность потенциалов:

 

Uab = ja - jb

 

тогда при известных параметрах цепи, токе и потенциалеjb определим потенциал ja:

 

 

Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС, без учета внутреннего сопротивления источника, по величине равно E2 и направлено от точки с большим потенциалом (точка c) к точке с меньшим потенциалом (точка b):

 

и тогда, зная потенциал jb, определим потенциал точки c:

 

Потенциал точки d больше потенциала точки c на величину падения напряжения на сопротивлении R:

 

тогда

 

Потенциал точки a определяем с учетом направления напряжения на зажимах источника ЭДС E1. Напряжение Udaнаправлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка a):

 

откуда следует, что

или

.

 

Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки c параметрах элементов и токе, определим потенциалы крайних точек участка цепи jaи jb. Напряжение на участке b - c, выраженное через разность потенциалов, определим по закону Ома:

 

откуда следует

 

 

Напряжение на участке c−a, равное по величине E, направлено от точки с большим потенциалом к точке с меньшим потенциалом:

 

Задача 1.1.4.В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: R1 = 10 Ом, R2 = 20 Ом, входное напряжение U = 100 В и мощность, выделяемая на резистивном элементе с сопротивлением R1: Р1 = 40 Вт. Определить величину сопротивления резистора R3

 

Рис. 6

Решение:

Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется как P = U⋅I, или, согласно закону Ома:

P = I2⋅R.

 

По известному значению мощности на резистивном элементе и величине сопротивления этого элемента определим ток в ветви:

 

 

По закону Ома напряжение на зажимах определится:

 

 

тогда величина сопротивления резистивного элемента:

 

Задача 1.1.5.Определить показания вольтметров цепи (рисунок 7), если R1 = 50 Ом, R2 = 150 Ом, U = 150 В, E = 50 В.

 

Рис. 7

Решение:

Ток в цепи определим по закону Ома:

 

 

Вольтметр V1 показывает напряжение на источнике ЭДС E:

V1 = UE= E = 50 В.

 

Вольтметры V2 и V4 показывают величину падения напряжения на резистивных элементах R1 и R2:

 

 

Вольтметр V3, показывает напряжение на участке 2-1 U21, которое определим как алгебраическую сумма напряжений UE и UR1:

Задача 1.1.6.Ток симметричной цепи (рисунок 8) I = 2,5 А, R1 = 2,4 Ом, R2 = 4,8 Ом, R3 = 7,2 Ом, внутреннее сопротивлении источника ЭДС E = 0,6 Ом. Определить ЭДС E и мощность источника энергии.

 

Рис. 8

Решение:

Напряжение на зажимах 1-2 определим по закону Ома для пассивной ветви:

 

 

Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:

 

или

 

Мощность, развиваемая источником энергии, определится:

 

 

Законы Кирхгофа

 

П е р в ы й з а к о н К и р х г о ф а является следствием закона сохранения заряда, согласно которому в узле заряд одного знака не может ни накапливаться, ни убывать, и формулируется следующим образом:

Алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю: ΣIk= 0.

При этом токи, направленные к узлу, берут с одним произвольно выбранным знаком, а токи, направленные от узла – с противоположным.

В т о р о й з а к о н К и р х г о ф а является следствием закона сохранения энергии, в силу которого изменение потенциала в замкнутом контуре равно нулю.

При обходе замкнутого контура по отдельным участкам потенциал конечного узла этого участка повышается относительно потенциала его начального узла на величину напряжения, если направление обхода противоположно направлению напряжения, и понижается, когда направление обхода контура и направление напряжения совпадают. Поэтому изменения потенциала в замкнутом контуре можно определить суммированием напряжений с учетом их знаков. Согласно второму закону Кирхгофа алгебраическая сумма напряжений участков замкнутого контура равна нулю: ΣUk=0.

При этом напряжения, положительные направления которых совпадают с направлением обхода контура, берутся с положительными знаками, а напряжения, положительные направления которых противоположны направлению обхода – с отрицательными знаками.

Уравнение по второму закону Кирхгофа для замкнутого контура abcda (рисунок 9):

 

Рис. 9

 

Uba +Ubc +Ucd−Uad= 0

 

Существует другое определение второго закона Кирхгофа: алгебраическая сумма падений напряжений на элементах замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре

ΣIk⋅ Rk=ΣEk.

 

Падения напряжения входят в сумму со знаком «плюс», если направления тока и обхода контура совпадают, и со знаком «минус» – если не совпадают. Аналогично учитывают знаки, суммируя величины электродвижущих сил источников ЭДС:

 

Задача 1.2.1.В цепи (рисунок 10) известны значения токов I6 =2 А, I2=1,25 А, I5 =0,8 А; величины сопротивлений R1=2 Ом, R2 =3 Ом, R3=2 Ом, R4=2 Ом, R5=5 Ом. Определить напряжение U на входных зажимах цепи, сопротивление R6 и величину E источника ЭДС.

Рис. 10

Решение:

По закону Ома определим напряжение между узлами 3-2:

 

U32 = I5 ⋅ R5 = 0,8 ⋅ 5 = 4 В.

 

Из уравнения, составленного по первому закону Кирхгофа для узла 3:

I2 - I4- I5 = 0

определим ток I4:

 

 

Тогда, по закону Ома для ветви с сопротивлением R4:

 

 

откуда выражаем величину E источника ЭДС:

 

 

Напряжение U12можно выразить из уравнения, записанного по второму закону Кирхгофа для контура 1-3-2-1:

U13+U23–U12=0

U12 +U32 = I2×(R2 + R3) + U32 =1,25×(3 + 2) + 4 = 10,25 В.

 

Зная величины напряжения U12 и тока I6, определим величину сопротивления R6:

 

 

Напряжение на входных зажимах цепи определится:

 

 

Ток I1 определим из уравнения, записанного по первому закону Кирхгофа для 1 узла:

 

или

тогда

U =2,75⋅2+10,25 =15,75 В.

Задача 1.2.2.В цепи (рисунок 11) известны величины сопротивлений резистивных элементов R1 = 1 Ом, R2 = 12 Ом, R3 = 5 Ом, R4 = 1 Ом, мощность, изменяемая ваттметром P=320 Вт. Определить токи ветвей, напряжение на зажимах цепи.

 

Рис. 11

Решение:

Из формулы для расчета мощности выражаем ток I3:

 

 

Затем определяем напряжение на зажимах параллельных ветвей:

 

По закону Ома определяем ток в ветви с сопротивлением R2:

 

 

Значение тока в неразветвленной части цепи определим из уравнения, записанного по первому закону Кирхгофа для узла 1:

 

Напряжение на входных зажимах цепи можно представить как сумму падений напряжений на сопротивлениях R1 и R2:

где

тогда

U = 12 + 48 = 60 В.

Задача 1.2.3.На рисунке 12 показана часть сложной цепи. Задано: I1 = 3 А, I2 = 2,4 А, E1 = 70 В, E2 = 20 В, R1 = 3 Ом, R2 = 5 Ом. Найти напряжение Uab.

 

 

Рис. 12

Решение:

Уравнение по второму закону Кирхгофа для данного

контура, при выбранном направлении обхода контура, запишется следующим образом:

 

 

откуда выражаем напряжение Uab:

= 20 – 70 – 3·3 + 2,4·5 = –47 В.

Задача 1.2.4.В схеме (рисунок 13) известны: E1=10 В, E2=20 В, E3=30 В, R = 1 Ом, I1 =1 А, I2=2 А. Определить напряжения U12, U34, U13, U24. U14. U23.

 

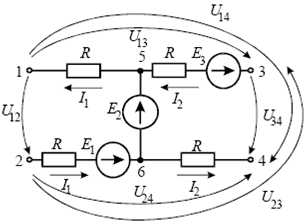
Рис. 13

 

Решение:

Считаем направления обходов контуров совпадающими с направлениями искомых напряжений. Запишем уравнения по второму закону Кирхгофа для каждого контура и выразим напряжения:

контур 1-2-6-5-1

контур 3-4-6-5-3

контур 1-3-5-1

контур 2-4-6-2

контур 1-4-6-5-1

контур 2-3-5-6-2

Задача 1.2.5.Определить показание амперметра (рисунок 14), если Uab= 107 В, Ubc= –60 В, R1 = 7 Ом, R2 = 8 Ом, E1 = 100 В, E2 = 70 В.

 

Рис. 14

Решение:

По закону Ома определим значения токов в ветвях:

 

 

Запишем уравнение по первому закону Кирхгофа для узла b:

I + I1 − I2 = 0

откуда

Задача 1.2.6.На рисунке 15 показана часть сложной цепи. Найти напряжение Uab, если Ucd =102 В, R1 = 8 Ом, R2 = 2 Ом, R3 = 6 Ом, E1 = 30 В, E2 = 100 В, E3 = 70 В, I1 = 10 А.

 

Риc. 15

Решение:

По закону Ома определим ток на участке b−d:

 

=1 А.

 

Запишем уравнение по второму закону Кирхгофа для контура a−b−c−d:

 

 

откуда выразим напряжение Uab:

Задача 1.2.7.В схеме электрической цепи, приведенной на рисунке 16, определить токи в ветвях пользуясь законами Кирхгофа. Параметры элементов цепи: R1 = 50 Ом, R2 = 20 Ом, R3 = 50 Ом, R4 = 80 Ом, E1 = 50 В, E2 = 400 В.

 

Рис. 16

Решение:

Выбираем произвольно положительные направления искомых токов ветвей и обозначаем их на схеме. Составляем уравнение по первому закону Кирхгофа для узла 1. Выбрав направления обходов контуров, составляем уравнения по второму закону Кирхгофа. Получаем систему из трех уравнений:

 

 

Решаем полученную систему уравнений с помощью определителей:

 

 

 

Находим значения токов:

 

Для проверки правильности расчета составим уравнение баланса мощностей:

 

Pист= Pпотр

Мощность источников:

 

 

Мощность потребителей:

 

 

Задача 1.2.8.Определить токи ветвей цепи (рисунок 17), если: R1 = 20 Ом, R2 = 40 Ом, E1 = 100 В, J = 1 А.

 

Рис. 17

Решение:

Произвольно задаемся положительными направлениями токов в ветвях с сопротивлениями R1 и R2. В ветви с источником тока направление тока уже определено полярностью источника. Составляем уравнение по первому закону Кирхгофа для узла 1. Количество контурных уравнений зависит от количества ветвей с неизвестными токами, т.е. ветвей, не содержащих источники тока. Для данной цепи количество контурных уравнений равно 1. Составим систему уравнений:

 

или

 

Решаем систему уравнений с помощью определителей:

 

 

 

 

Определяем значения токов:

 

 

Эквивалентные преобразования схем

 

Применяя законы Кирхгофа и Ома можно получить формулы для эквивалентных преобразований в электрических цепях. Эквивалентным считается преобразование, при котором напряжения и токи в оставшейся части схемы, не подвергшейся преобразованию, остаются прежними.

Последовательно соединенные сопротивления можно заменить эквивалентным, величина которого Rэ, на основании второго закона Кирхгофа, равна сумме последовательно включенных сопротивлений (см. рисунок 18).

.

 

Рис. 18

Параллельно соединенные сопротивления можно заменить эквивалентным сопротивлением, проводимость которого gэ = 1/Rэ, на основании первого закона Кирхгофа, она равна сумме проводимостей включенных параллельно сопротивлений (см. рисунок 19)

 

или

.

Рис. 19

 

Широко распространены схемы с двумя параллельно включенными сопротивлениями. Эквивалентное сопротивление в этом случае равно

 

.

Эквивалентное преобразование треугольника и звезды сопротивлений. Пусть требуется рассчитать цепь, показанную на рис. 20, а. Так как в цепи имеется только один источник питания, наиболее простым для расчета было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.

Треугольник и звезда сопротивлений имеют вид, показанный на рис. 21.

Рис. 20. Преобразования электрической цепи

 

Рис. 21. Треугольник и звезда сопротивлений

 

Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны. Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:

Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.

Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:

 

,

 

б) при преобразовании звезды в треугольник:

 

;

.

 

Структура приведенных формул проста и легко запоминается.

Пример 1.3.1.Рассчитать токи в цепи, изображенной на рис. 20, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.

 

а) Р е ш е н и е п р е о б р а з о в а н и е м т р е у –

г о л ь н и к а в з в е з д у.

После преобразования треугольника, образованного сопротивлениями R1, R2 и R5, в звезду, получаем схему, показанную на рис. 1.7, б. Обращаем внимание на то, что токи в непреобразованной части схемы (I, I3 и I4) остались теми же.

Сопротивления звезды определяем по сформулированному выше правилу:

 

,

 

Теперь общее сопротивление цепи легко находится:

 

 

Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен

 

 

Токи в параллельных ветвях:

 

 

Возвращаемся к исходной схеме (рис. 1.12, а):

 

.

 

Ток в пятой ветви находим из первого закона Кирхгофа:

 

I5 = I1 – I3 = 26 – 28 = –2 A.

 

Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.

 

б) Р е ш е н и е п р е о б р а з о в а н и е м з в е з д ы в

т р е у г о л ь н и к.

Преобразуем звезду, образуемую в схеме на рис. 1.7, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 1.7, в).

Определяем сопротивления треугольника:

 

;

;

.

 

Теперь рассчитываем преобразованную цепь.

Сначала находим эквивалентные сопротивления участков ac и cd:

; .

 

Затем определяем общее сопротивление и токи:

 

;

;

;

;

.

 

Возвращаемся к исходной схеме:

 

; ; .

 

Рекомендуется подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 20, а.

 

 

©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.

arhivinfo.ru

1.4. Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.

Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U1 + U2 + U3 или IRэкв = IR1 + IR2 + IR3,

откуда следует

(1.5)

Rэкв = R1 + R2 + R3.

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

,

и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

Рис. 1.6

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I1 + I2 + I3, т.е. ,

откуда следует, что

(1.6)

.

В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением

(1.7)

.

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

gэкв = g1 + g2 + g3.

По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

U = IRэкв = I1R1 = I2R2 = I3R3.

Отсюда следует, что

,

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Рис. 1.7

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:

.

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

Рис. 1.8

На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

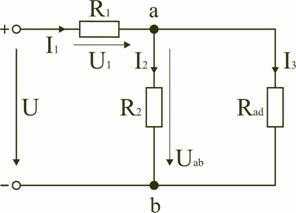
Рис. 1.9

На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно

.

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

Рис. 1.12

Рис. 1.13

В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

(1.8)

; ; .

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

(1.9)

; ; .

После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)

.

studfiles.net

---

• 
  В системе си масса в
• 
  Обслуживание счетчиков воды
• 
  Воровство электроэнергии
• 
  Сопротивления резисторов
• 
  Переход на автономное отопление в многоквартирном доме
• 
  Стабилизатор напряжения бытовой однофазный
• 
  Сколько на карте материков
• 
  Подключение электродвигателя асинхронного
• 
  Силовые трансформаторы технические характеристики
• 
  Месторождения нефти в россии на карте с названиями
• 
  Самонесущий изолированный провод сип технические характеристики