Потенциал. Разность потенциалов. Как определить разность потенциалов

Что такое разность потенциалов

Во многих случаях для того, чтобы правильно уяснить суть вопроса, касающегося электротехники, необходимо точно знать, что такое разность потенциалов.

Определение разности потенциалов

Общее понятие состоит в электрическом напряжении, образованном между двумя точками, и представляющем собой работу электрического поля, которую необходимо совершить для перемещения из одной точки в другую положительного единичного заряда.

Таким образом, в равномерном и бесконечном электрическом поле положительный заряд под воздействием этого поля будет перемещен на бесконечное расстояние в направлении, одинаковым с электрическим полем. Потенциал конкретной точки поля представляет собой работу, производимую электрическим полем при перемещении из этой точки положительного заряда в точку, удаленную бесконечно. При перемещении заряда в обратном направлении, внешними силами производится работа, направленная на преодоление электрической силы поля.

Разность потенциалов на практике

Разность потенциалов, существующая в двух различных точках поля, получила понятие напряжения, измеряемого в вольтах. В однородном электрическом поле очень хорошо просматривается зависимость между электрическим напряжением и напряженностью электрического поля.

Точки с одинаковым потенциалом, расположенные вокруг заряженной поверхности проводника, полностью зависят от формы этой поверхности. При этом разность потенциалов для отдельных точек, лежащих на одной и той же поверхности имеет нулевое значение. Такая поверхность проводника, где каждая точка обладает одинаковым потенциалом носит название эквипотенциальной поверхности.

Когда происходит приближение к заряженному телу, происходит быстрое увеличение потенциала, а расположение эквипотенциальных поверхностей становится более тесным относительно друг друга. При удалении от заряженных тел, расположение эквипотенциальных поверхностей становится более редким. Расположение электрических силовых линий всегда перпендикулярно с эквипотенциальной поверхностью в каждой точке.

В заряженном проводнике все точки на его поверхности обладают одинаковым потенциалом. То же значение имеется и во внутренних точках проводника.

Проводники, имеющие различные потенциалы, соединенные между собой с помощью металлической проволоки. На ее концах появляется напряжение или разность потенциалов, поэтому вдоль всей проволоки наблюдается действие электрического поля. Свободные электроны начинают двигаться в направлении увеличения потенциала, что вызывает появление электрического тока.

Падение потенциала вдоль проводника

electric-220.ru

12 Разность потенциалов

Разностью потенциалов между точками 1 и 2 называется работа, совершаемая силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2. для потенциальных полей эта работа не зависит от формы пути, а определяется только положениями начальной и конечной точек

потенциал определен с точностью до аддитивной постоянной. Работа сил электростатического поля при перемещении заряда q по произвольному пути из начальной точки 1 в конечную точку 2 определяется выражением

Практической единицей потенциала является вольт. Вольт есть разность потенциалов между такими точками, когда при перемещении одного кулона электричества из одной точки в другую электрическое поле совершает работу в один джоуль.

1 и 2 — бесконечно близкие точки, расположенные на оси х, так что Х2 — х1 = dx.

Работа при перемещении единицы заряда из точки 1 в точку 2 будет Ех dx. Та же работа равна . Приравнивая оба выражения, получим

- градиент скаляра

Градиент функцииесть вектор, направленный в сторону максимального возрастания этой функции, а его длина равна производной функциив том же направлении. Геометрический смысл градиента– эквипотенциальные поверхности ( поверхности равного потенциала) поверхность, на которой потенциал остается постоянным.

13 Потенциал зарядов

Потенциал поля точечного заряда q в однородном диэлектрике. - электрическое смещение точечного заряда в однородном диэлектрикеD –вектор электрической индукции или электрического смещения

В качестве постоянной интегрирования следует взять нуль, чтобы при потенциал обратился в ноль, тогда

Потенциал поля системы точечных зарядов в однородном диэлектрике.

Используя принцип суперпозии получаем:

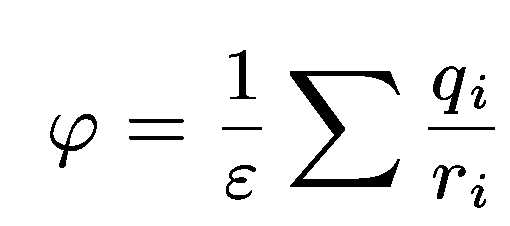
Потенциал непрерывно распределенных электрических зарядов.

- элементы объема и заряженных поверхностей с центрами в точке

- в случае если диэлектрик неоднороден, то интегрирование надо распространить и на поляризационные заряды. Включение таких

зарядов автоматически учитывает влияние среды, и величину вводить не надо

14 Электрическое поле в веществе

Электрическое поле в веществе. Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. При наличии внешнего поля происходит перераспределение заряженных частиц, и в веществе возникает собственное электрическое поле. Полное электрическое поле складывается в соответствии с принципом суперпозиции из внешнего поля и внутреннего поля , создаваемого заряженными частицами вещества. Вещество многообразно по своим электрическим свойствам. Наиболее широкие классы вещества составляют проводники и диэлектрики. Проводник - это тело или материал, в котором электрические заряды начинают перемещаться под действием сколь угодно малой силы. Поэтому эти заряды называют свободными. В металлах свободными зарядами являются электроны, в растворах и расплавах солей (кислот и щелочей) - ионы. Диэлектрик - это тело или материал, в котором под действием сколь угодно больших сил заряды смещаются лишь на малое, не превышающее размеров атома расстояние относительно своего положения равновесия. Такие заряды называются связанными. Свободные и связанные заряды. СВОБОДНЫЕ ЗАРЯДЫ 1) избыточные электрич. заряды, сообщённые проводящему или непроводящему телу и вызывающие нарушение его электронейтральности. 2) Электрич. заряды носителей тока. 3) положит. электрич. заряды атомных остатков в металлах. СВЯЗАННЫЕ ЗАРЯДЫ Электрич. заряды частиц, входящих в состав атомов и молекул диэлектрика, а также заряды ионов в кристаллич. диэлектриках с ионной решёткой.

studfiles.net

Потенциал. Разность потенциалов. Напряжение

К оглавлению...

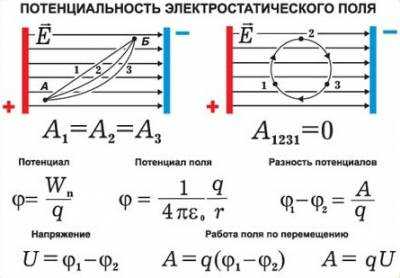
Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал - скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

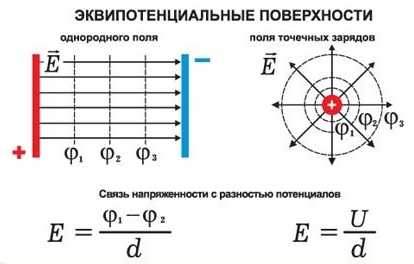
Для наглядного представления электрического поля наряду с силовыми линиями используютэквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

· φ – потенциал электрического поля.

· ∆φ – разность потенциалов.

· W – потенциальная энергия заряда во внешнем электрическом поле.

· A – работа электрического поля по перемещению заряда (зарядов).

· q – заряд, который перемещают во внешнем электрическом поле.

· U – напряжение.

· E – напряженность электрического поля.

· d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

pdnr.ru

Потенциал. Разность потенциалов — Мегаобучалка

Электростатическое поле является потенциальным полем, поэтому заряды, находящиеся в поле обладают энергией. Энергия единичного положительного заряда может служить энергетической характеристикой электрического поля.

Потенциал электростатического поля – скалярная физическая величина, являющаяся энергетической характеристикой поля в данной точке и равная энергии единичного положительного заряда, помещенного в данную точку поля:

.

Отсюда следует, что энергия любого точечного заряда, помещенного в точку с потенциалом , равна .

Если силы консервативны, то их работа равна убыли потенциальной энергии тела. Электростатические силы являются консервативными силами и поэтому их работа равна убыли потенциальной энергии перемещаемого заряда

или ;

Таким образом, работа сил электростатического поля по перемещению заряда, равна произведению величины этого заряда на разность потенциалов начальной и конечной точек пути.

Потенциал, как и потенциальная энергия, определяется с точностью до произвольной постоянной, зависящей от выбора нулевого потенциального уровня.

При перемещении положительного заряда из данной точки, с потенциалом в точку с нулевым потенциалом, силы поля совершат работу

откуда следует, что .

Можно дать еще одно определение потенциала:

Потенциал данной точки поля относительно некоторого нулевого уровня численно равен работе, совершаемой силами электростатического поля при перемещении единичного положительного заряда из данной точки поля на нулевой уровень.

Потенциал - величина алгебраическая. Знак потенциала определяется знаком заряда, создающего поле.

Для потенциала выполняется принцип суперпозиции: потенциал поля, создаваемого системой зарядов в данной точке равен алгебраической сумме потенциалов, создаваемых в этой точке отдельными зарядами.

Для системы точечных зарядов потенциал результирующего поля равен

Если поле создается непрерывным распределением заряда, то потенциал равен

Для наглядного представления о распределении электрического поля вокруг заряда используется не только линии вектора напряженности, но и эквипотенциальные поверхности. Эквипотенциальная поверхность - поверхность равного потенциала или поверхность, во всех точках которой потенциал имеет одинаковое значение. Сечение эквипотенциальных поверхностей на рисунках изображают штрих пунктирной линией.

Что надо помнить об эквипотенциальных поверхностях

1) Эквипотенциальная поверхность расположена перпендикулярно вектору напряженности поля в каждой точке.

2) Работа электростатических сил по перемещению заряда между любыми двумя точками поверхности всегда равна нулю.

Связь между напряженностью E и потенциалом j электрического поля.

Для количественной характеристики электрического поля имеется две величины: напряженность поля – это силовая характеристика поля и потенциал – энергетическая характеристика поля. Найдем связь между этими величинами.

Работа по перемещению точеного положительного заряда на бесконечно малое расстояние dх равна

С другой стороны та же работа равна

.

Приравняв правые части этих уравнений, получаем

.

Если перемещение заряда происходит в трехмерном пространстве, и имеются перемещения по всем трем пространственным осям, то получим следующие соотношения:

, , ,

тогда вектор напряженности поля можно выразить следующим образом

,

где , , - единичные векторы ( орты) координатных осей ОХ, ОУ, ОZ;

, , - частные производные от потенциала по координатам х, у, z.

Оператор называется градиентом и обозначается grad или .

Градиентом скалярной величины называется вектор, направленный в сторону наиболее быстрого возрастания величины и численно равный приращению величины на единицу длины данного направления.

Для напряженности получили , т.е. напряженность поля равна градиенту потенциала со знаком минус. Знак «минус» отражает тот факт, что вектор напряженности всегда направлен в сторону убыли потенциала.

 

 

Порядок решения задач

Задачи, в которых необходимо вычислить работу по перемещению электрического заряда в электрическом поле, созданном другими зарядами, можно решать двумя способами. Первый путь решения сводится к непосредственному вычислению работы сил поля по перемещению заряда из одной точки поля в другую. При таком способе решения необходимо знать зависимость величины напряженности от пространственных координат.

Второй подход к таким задачам использует тот факт, что работа сил потенциального поля всегда равна убыли потенциальной энергии заряда в поле: A = -DW = - q(j1 - j2).

где q - заряд, переносимый в поле,

j1 и j2 - потенциал точек поля, соответствующих начальному и конечному положениям заряда.

Если использовать этот способ, то решение задачи сводится к нахождению потенциала тех точек поля, в которых находился заряд в интересующие нас моменты времени.

Последовательность действий при решении таких задач:

1. Нарисовать силовые линии поля. Обозначить те точки, в которых находился заряд в начальный и конечный моменты времени, разобраться, какие скорости имел заряд в этих точках.

2. В этих выделенных точках рассмотреть характеристики поля и самого заряда, который движется в этом поле (Wк; Wn).

3. Для вычисления зависимости потенциала j от координат или от одного из расстояний использовать связь между напряженностью ипотенциалом электрического поля

или

, или ,

и получить j = f(x) или j = f(r)

4. Записать выражение для работы сил поля в виде или A12 = - q(j1 - j2).

В тех случаях, когда на заряд действуют только силы электрического поля, удобно воспользоваться законом сохранения энергии для заряда.

Wк1 + Wп1 = Wк2 + Wп2.

5. Решая систему полученных уравнений, найти аналитическое выражение для вычисления искомой величины. Подставить заданные численные значения и получить количественный ответ задачи.

Если по условию задачи необходимо построить графики зависимостей искомых величин от расстояния, то опять возможно два варианта:

а) При наличии численных надо вычислить численное значение искомой величины для нескольких расстояний, выбирать точки для расчета необходимо с учетом симметрии. Выбрать оси координат, задать разумный масштаб и нанести все точки, для которых выполнены расчеты. По полученным точкам провести график.

б) Если функция найдена только в аналитическом виде, то в произвольном масштабе показать график, соответствующий полученной зависимости.

 

Примеры решения задач

Пример 3.3.1

Шарик массой m = 40 мг, имеющий положительный заряд q =1 нКл, движется из беcконечности со скоростью V1 = 10 см/с. На какое минимальное расстояние r min может приблизиться шарик к положительному точечному заряду q0 = 1,33 нКл?

 

Дано:

m = 40 мг = 40×10-6 кг;

q = 1 нКл = 10-9 Кл;

V1 = 10 см/с = 0,1 м/с;

q = 1,33 нКл = 1,33×10-9Кл

______________________

rmin = ?

Анализ: На рисунке показана картина силовых линий поля, создаваемого зарядом q0 и показан выбор и направление оси координат. Заряд q движется в отрицательном направлении оси r, и сила электрического поля совершает при этом отрицательную работу, что приводит к превращению кинетической энергии этого заряда в потенциальную энергию заряда в поле. На заряд действует только электрическая сила поля точечного заряда q0, поэтому в этой задаче можно для решения использовать закон сохранения энергии.

Рассмотрим два положения заряда q.

Точка 1 - заряд q находится на достаточно далеком расстоянии от заряда , и потенциал j1 в этой точке поля можно считать равным нулю и Wр1 = 0. Скорость заряда в этом случае отлична от нуля, и кинетическая энергия равна ;

Точка 2 - потенциал j2 ¹ 0 и поэтому потенциальная энергия движущегося заряда в этой точке не равна нулю Wр2 = q×j2, а скорость движущегося заряда обращается в ноль, когда заряд q приблизится к заряду q0 на минимальное расстояние, V = 0 и Wк2 = 0.

Решение: Система двух зарядов замкнутая и консервативная, поэтому можно применить закон сохранения энергии

или

Потенциал поля точечного заряда можно вычислить по формуле для воздуха e =1.

Окончательно получим

Подставляем численные значения, получим

Ответ: заряд q приблизится к другому заряду на минимальное расстояние, равное 6 см.

 

Пример 3.3.2

Два шарика с зарядами q1 = 6,66 нКл и q2 = 13,33 нКл находятся на расстоянии r1 = 40 см друг от друга. Какую работу А надо совершить, чтобы сблизить их до расстояния r2 = 25 см?

Дано:

q 1 = 6,66 нКл;

q 2 = 13,33 нКл;

r1 = 40 см = 0,40 м;

r2 = 25 см = 0,25 м

_______________

А12 - ?

Анализ:

Для того чтобы сблизить одноименно заряженные шарики, необходимо совершить работу против сил электрического поля. Поэтому работа сил электрического поля при этом будет отрицательной, а работа внешней силы, перемещающей заряд, будет положительной.

Будем считать, что первый шарик неподвижен и создает поле, а второй перемещается в поле первого заряда.

Решение: 1 способ. Работа переменной силы находится через интеграл , где - величина перемещаемого заряда, - напряженность поля первого заряда, поскольку перемещение заряда происходит вдоль силовой линии, но в сторону обратную направлению напряженности поля, то угол будет равен .

Величина напряженности поля точечного заряда равна

,

Если в условии задачи не упоминается среда, в которой находятся заряды, то по умолчанию считается, что среда – воздух и .

Получили интеграл, взяв который, получим формулу для вычисления работы:

,

или окончательно получим

.

2 способ. При таком методе решения задачи мы воспользуемся теоремой о потенциальной энергии. Электростатические поля – потенциальные поля, поэтому работа сил поля по перемещению заряда равна убыли потенциальной энергии перемещаемого заряда. Тогда , где j1 и j2- - потенциалы электростатического поля, созданного первым шариком на расстояниях r1 и r2 от него. В этом случае мы воспользуемся уже выведенной формулой для вычисления потенциала. Потенциал поля точечного заряда q1 в точках на расстояниях r1 и r2 равен

 

и .

Тогда

Работа же внешних сил А = -Аэл = 1,2×10-6 Дж.

Ответ: для того чтобы сблизить указанные заряженные шарики, необходимо внешним силам совершить работу А = 1,2×10-6 Дж. Оба способа решения задачи дают одинаковый ответ.

Пример 3.3.3

Электрическое поле образовано положительно заряженной бесконечно длинной нитью с линейной плотностью заряда t = 0,2 мк Кл/м. Какую скорость V будет иметь покоящийся электрон, если он под действием сил поля, приблизится к нити с расстояния r1 = 1 см до расстояния r2 = 0,5 см.

 

Дано:

t = 0,2 мк Кл/м = 2×10-7 Кл/м ;

r1 = 1 см = 0,01 м;

r2 = 0,5 см = 5×10-3 м;

me = 9,1×10-31 кг;

V0 = 0

_е_=1,610-19Кл_

___________

V - ?

 

Анализ и решение: На рисунке показаны силовые линии поля нити в плоскости, перпендикулярной самой нити, и радиальная ось.

Для описания поведения заряженной частицы в электростатическом поле можно применить закон сохранения энергии, т.к. система замкнута и консервативна.

При движении отрицательной частицы силы поля будут совершать положительную работу, и это приведет к тому, что потенциальная энергия заряда будет убывать, а кинетическая возрастать.

В первой точке электрон имеет только потенциальную энергию, поскольку в начальный момент он покоился,

Wк1 = 0, W п1 = ej1.

Во второй точке у заряда будет и потенциальная и кинетическая энергия

W п2 = ej2.

По закону сохранения энергии

Wк1 + Wп1 = Wк2 + Wп2

или

;

Для нахождения (j2 - j1) воспользуемся формулой, связывающей E с потенциалом j. Для случая радиальной симметрии

или

Напряженность поля нити нам известна: , для воздуха e = 1, с учетом этого, получаем

Проинтегрируем это уравнение по координате r

вынесем постоянные множители из-под интеграла и получим

Используя табличные интегралы, получим

,

или

Подставляя полученное уравнение в выражение закона сохранения энергии, получим

-

отсюда

Подставляя численные значения, получаем

Ответ: электрон приобретет скорость, равную V = 2,97×107 м/с.

Пример 3.1 Две длинные одноимённо заряженные нити расположены на расстоянии r1= 10см друг от друга. Линейные плотности зарядов одинаковы и равны = =10мкКл/м.

Какую работу А на единицу длины нити надо совершить, чтобы раздвинуть нити до расстояния = 20см ?

 

Анализ :

Дано:
r	=10см =20см =10мкКл/м
r2
=
a	=10см
1) E-? 2) A-?

Электростатические поля, создаваемые различными распределениями зарядов, по принципу суперпозиции складываются в каждой точке пространства. Учитывая симметрию задачи, сделаем рисунок, расположив нити перпендикулярно плоскости чертежа. Точка А удалена от обеих нитей на расстояние а = r1.Получили равносторонний треугольник. Для того, чтобы найти направление вектора напряжённости поля, создаваемого в точке А зарядом каждой нити, поместим в эту точку пробный заряд «+1» и определим, как поля нитей действуют на этот заряд. Так как нити заряжены положительно, то они будут отталкивать пробный заряд и вектора и будут направлены так, как показано на рисунке. Вектор напряжённости суммарного поля, согласно принципу суперпозиции, находится по правилу параллелограмма.

Сила взаимодействия этих заряженных нитей зависит от расстояния между ними, поэтому работу сил электростатического поля при раздвижении нитей надо вычислять через интеграл.

Решение:

1) Из рисунка видно, что направлен вправо, и модуль его можно найти как:

т.к. и , где k= .

Окончательно получаем

.

2) Сила взаимодействия заряженных нитей зависит от расстояния между ними. Каждая нить создаёт поле, и это поле действует на заряд другой нити. - напряженность поля первой нити.

-сила, действующая на единицу длины второй нити равна:

Работу этой силы можно вычислить как:

.

Возьмём интеграл от этой функции. Все постоянные величины выносим за знак интеграла и получаем табличный интеграл, который равняется натуральному логарифму аргумента.

Подставим пределы интегрирования и окончательно получаем:

.

Используя данные задачи, получим численный ответ

 

Ответ: 1) 2)

 

Пример 3.3.4.

На отрезке прямого повода длиной распределен заряд с линейной плотностью

τ = 103 нКл/м. Определите работу сил поля А по перемещению заряда q = 1нКл из точки 1 в точку 2 (см. рис.).

Дано:

τ = 103 нКл/м

q = 1нКл

Найти:

А = ?

Анализ: Задачу можно, как рассматривалось выше, решать двумя способами. Мы выберем в этом случае второй способ решения,т.е. воспользуемся теоремой о потенциальной энергии. Работа сил электрического поля равна убылипотенциальной энергии переносимого заряда. Для того, чтобы воспользоваться этой теоремой, первым действием получим формулу для вычисления потенциала поля стержня в точках, лежащих на оси стержня, а затем вычислим работу сил поля по перемещению заряда. Поскольку в условии задачи не указана среда, в которой находятся заряды, то считается, что среда вакуум или воздух, т.е. .

Решение: На рисунке показан стержень; ось координат расположена вдоль стержня и начало координат связано с одним из концов стержня. Выделим на стержне бесконечно малый элемент длины dx, заряд на котором можно считать точечным dq = τ dx. Для определения потенциала создаваемого отрезком прямого тонкого стержня длинной , в точке с координатой , лежащей на продолжении оси этого стержня, воспользуемся принципом суперпозиции для потенциала. В случае непрерывного распределения заряда надо проинтегрировать уравнение

,

которое определяет потенциал поля, создаваемого зарядом dq, в точке с координатой х. Если перемещать элементарный заряд dq по всей длине стержня и суммировать потенциал в точке с координатой х, то придем к интегралу

.

Взяв его, получим формулу для вычисления потенциала поля заряженного стержня в токах, лежащих на оси стержня

.

Для определения работы сил поля по перемещению заряда q из положения 1 с координатой в положение 2 с координатой , воспользуемся теоремой о потенциальной энергии

.

В нашем случае , координата конечного положения заряда, равна , а , координата начального положения заряда, равна . С учетом этого, получаем выражение для вычисления разности потенциалов

.

Применим теорему о потенциальной энергии, подставив в нее полученное выражение для вычисления разности потенциалов,

Окончательно получаем

.

Подставим численные значения величин и получим численное значение искомой величины:

.

Ответ: Работа сил электростатического поля положительная и равная .

megaobuchalka.ru

Расчет потенциалов простейших электростатических полей

      Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.

Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями

      Мы показали, что напряженность связана с потенциалом

       тогда

,

(3.7.1)

где – напряженность электростатического поля между заряженными плоскостями, найденная в п. 2.5.2 с помощью теоремы Остроградского–Гаусса; σ = q/S– поверхностная плотность заряда.

      Теперь, чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение (3.7.1):

      

или .

(3.7.2)

При x1 = 0 и x2 = d .

(3.7.3)

Рис. 3.5

      На рисунке 3.5 изображена графическая зависимость напряженности E и потенциала φ от расстояния между плоскостями.

Разность потенциалов между точками поля,образованного бесконечно длинной цилиндрической поверхностью

      В п. 2.5 с помощью теоремы Остроградского-Гаусса мы показали, что, т.к. , то (см. рис. 3.6)

(3.7.4)

      Т.к. то , отсюда найдем разность потенциалов в произвольных точках 1 и 2:

      .

Рис. 3.6

(3.7.5)

      На рисунке 3.6 изображена зависимость напряженности E и потенциала от r. (Здесь и далее E – изображена сплошной линией, а – пунктирной).

Разность потенциалов между обкладками цилиндрического конденсатора

      В п. 2.5. мы нашли, что (рис. 3.7)

      Отсюда так же, как и в предыдущем случае, разность потенциалов будет равна:

.           

      Таким образом, внутри меньшего цилиндра имеем , Е = 0, между обкладками потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.

Рис. 3.7

(3.7.6)

      На рисунке 3.7 изображена зависимость напряженности E и потенциала от r.

Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)

      Напряженность поля сферы (рис. 3.8) определяется формулой: .

Рис. 3.8

      Т.к. , то

         

(3.7.7)

Разность потенциалов внутри диэлектрического заряженного шара

      Имеем диэлектрический шар (рис. 3.9), заряженный с объемной плотностью

      

      В п. 2.5 с помощью теоремы Остроградского–Гаусса мы нашли, что внутри шара .

Рис. 3.9

      Теперь найдем разность потенциалов внутри шара:

      или

      Отсюда находим потенциал шара:

                                         (3.7.9)

Из полученных соотношений можно сделать следующие выводы.

           С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.

           Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.

           Потенциал поля – всегда непрерывная функция координат.

ens.tpu.ru

Потенциал. Разность потенциалов.

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:

  - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.

Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.

- следствие принци­па суперпозиции полей (потенциалы складываются алгебраически).

Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.

В СИ потенциал измеряется в вольтах:

 Разность потенциалов

 

Напряжение — разность значений потенциала в начальной и конечной точках траектории.

Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.

Разность потенциалов (напряжение) не зависит от выбора

системы координат!

Единица разности потенциалов

напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).

Из этого соотношения видно:

1. Вектор напряженности направлен в сторону уменьшения потенциала.

2. Электрическое поле существует, если существует разность потенциалов.

3. Единица напряженности: -Напряженность поля равна

Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величи­на, равная

Поток вектора магнитной индук­ции Фв через произвольную поверхность S равен

Теорема Гаусса для поля В: поток век­тора магнитной индукции через любую замкнутую поверхность равен нулю:

полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,

Проводники в электростатическом поле. Электроемкость уединенного проводника.

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действо­вать электростатическое поле, в результа­те чего они начнут перемещаться. Переме­щение зарядов (ток) продолжается до тех пор, пока не установится равновесное рас­пределение зарядов, при котором электро­статическое поле внутри проводника обра­щается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напря­женность поля во всех точках внутри проводника равна нулю:

Е = 0.

По гауссу

Величину

С = Q/ф

называют электроемкостью (или просто емкостью) уединенного проводника. Ем­кость уединенного проводника определяет­ся зарядом, сообщение которого провод­нику изменяет его потенциал на единицу.

Емкость проводника зависит от его размеров и формы, но не зависит от мате­риала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциа­ла. Сказанное не противоречит формуле, так как она лишь показывает, что емкость уединенного проводника прямо пропорциональна его заряду и обратно пропорциональна потенциалу.

Единица электроемкости — фарад (Ф): 1Ф

studfiles.net

Формула нахождения потенциальной разницы между точками в электромагнитном поле

Важнейшим понятием, используемым в электрике, радиотехнике и в любой другой сфере, связанной с электричеством, выступает разность потенциалов между точками, или более привычное название – электрическое напряжение. С виду простое понятие включает в себя довольно много аспектов и тезисов.

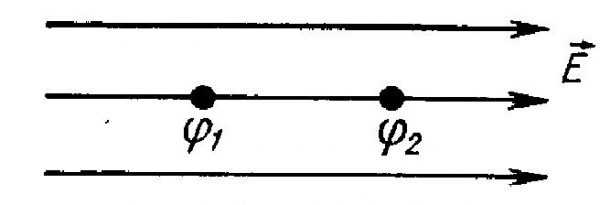
Энергопотенциалы в электрическом поле

Сущность понятия потенциальной разницы

Первоначально охарактеризуем сам термин, что такое разность потенциалов. Такая разница в потенциалах между двумя точками, находящимися на некотором расстоянии (А и Б), есть значение, прямо пропорциональное проведенному действию среды по переносу источника электромагнитного фона со знаком «+» из одной точки в другую и обратно пропорциональная величине самого источника электромагнитного поля.

Как найти разность потенциалов, отображено формулой:

φ1-φ2=А1-2/q, где:

• φ1 – заряженная частичка в исходном месте;
• φ2 – заряженная частичка в конечном месте;
• А1-2 – действие, потраченное на перенос частицы с первоначального местоположения до конечного размещения;
• q – заряд, находящийся в среде.

Потенциальная разница имеет свою единицу измерения – вольт. Итальянский физиолог, военный инженер и физик А.Вольт занимался этой проблематикой и явил миру ряд понятий: разность потенциалов и электрическое напряжение, назвав единицу измерения своей фамилией. По системе СИ характеристика 1 Вольт прямо пропорциональна параметру 1 Джоуль и обратно пропорциональна 1 Кулону.

Поведение заряженных частиц

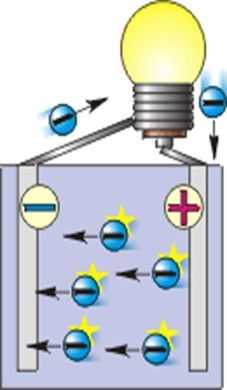
Токопроводящие материалы при более детальном рассмотрении состоят из плотно прилегающих друг к другу ядер вещества, не способных самостоятельно передвигаться. Вокруг этих ядер находятся мелкие частички, вращающиеся с огромной скоростью и называемые электронами. Их скорость настолько велика, что они способны отрываться от своих ядер и присоединяться к другим и таким образом беспрепятственно передвигаться по материалу. Молекула или частичка будет считаться электрически нейтральной при условии, что численность электронов в молекуле соответствует уровню протонов в ядре. Если же забрать некоторое число свободно вращающихся отрицательно заряженных частиц, то молекула будет всячески стремиться восстановить их количество. Образуя вокруг себя положительную область со знаком «+», молекула будет стремиться притянуть к себе недостающее число отрицательно заряженных частиц. От численности недостающих электронов и будет зависеть ускорение и сила тока, с которой они будут притягиваться, и, соответственно, сила положительного фона. Проведя обратную операцию, добавив в молекулу лишних электронов, получим силу, старающуюся вытолкнуть лишний их объем и, соответственно, образующую электрическое поле, но уже со знаком «-» – отрицательная среда. Эта ускоряющая разность потенциалов заставляет все электроны двигаться в одном направлении.

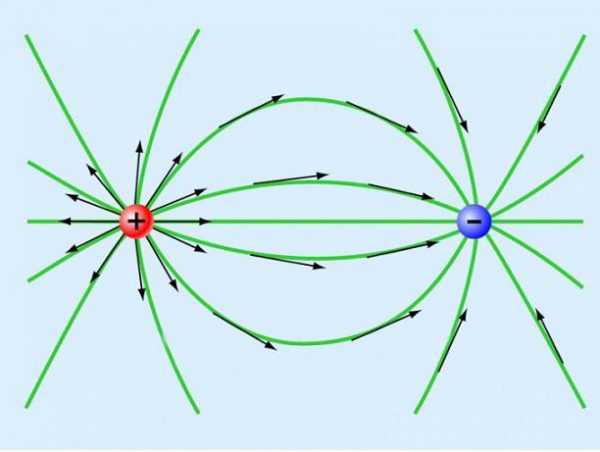
Силовые поля заряженных частиц

Изучив это явление, французский физик Шарль Огюстен Кулон ввел физическую величину, которая определяла способность тел быть источником ЭМ фона и принимать участие в электромагнитном взаимодействии. Такая величина получила название электрический заряд, с величиной измерения Кулон.

В итоге получены два источника ЭМ фона, один из которых стремится отдать излишек электронов, второй – притянуть электроны в достаточном количестве. Каждый такой заряд обладает своей «силой». Выражение, которое бы количественно характеризовало его сущность, представлено отношением:

φ= W/q

и пропорционально энергетике источника поля, размещенного в данной точке к этому заряду. Соответственно, этот показатель характеризует работу источника электромагнитного поля и является энергетической характеристикой области. В случае если имеется некоторое количество заряженных частиц, то, опираясь на принцип суперпозиции, суммарная энергия образовавшейся области равна сумме полей зарядов, сформированных каждым в отдельности:

φсумм.=φ1+φ2+…+ φі.

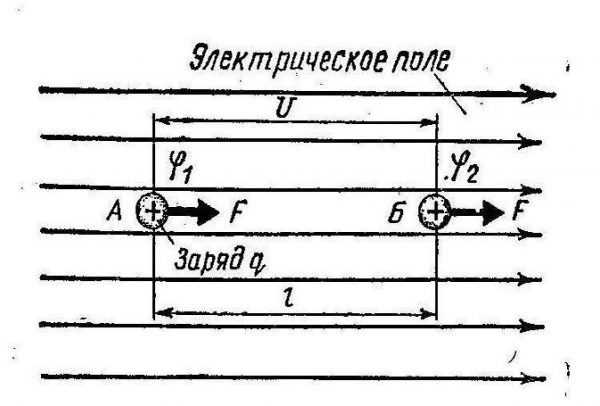
Поведение зарядов в электрическом поле

Неотъемлемой частью расчетов выступает работа по перемещению заряда в электрической среде. Опираясь на то, что на положительный точечный источник электромагнитного поля q в электрическом поле с напряженностью Е действует сила:

F=qE,

на отрезке L совершается действие, равное:

А=qElcos α.

Одно из свойств электростатического поля повествует о возможности пренебречь траекторией движения заряда при совершении работы по перемещению между двумя точками, а учитывать только первоначальную и конечную точку и величину источника электромагнитного поля. Соответственно косинусом можно пренебречь:

А=qEl=qE(l1-l2)=qEl1-qEl2,

поскольку действие А является мерой измерения энергии, и:

W=qEl.

В результате работу находить достаточно легко:

A=W1-W2=-(W2-W1).

Исходя из формулы, определяющей величину энергопотенциала:

φ= W/q

и воспринимая работу А как разницу энергий, доказана формула потенциальной разницы:

φ1-φ2=А1-2/q.

Изложенный материал подробно раскрывает такие термины, как разность потенциалов и потенциал. Детально рассмотрены порядок возникновения заряженных частиц, электростатического поля и их поведение по отношению друг к другу. Дополнительно рассмотрено ряд законов, касающихся основ электродинамики.

Видео

Оцените статью:

elquanta.ru

---

• 
  Ток какой
• 
  Перпендикулярно катушке с током расположен прямолинейный проводник с током
• 
  Отличие кабеля кг от кг
• 
  Установка точечных светильников в гипсокартон
• 
  Что такое сервопривод в автомобиле
• 
  Самый большой материк земли 4 класс
• 
  Что такое автоматическое управление
• 
  Добыча газа и нефти в западной сибири
• 
  Хвс кпу что такое
• 
  Тепловые лампы для кур
• 
  Ph метр своими руками