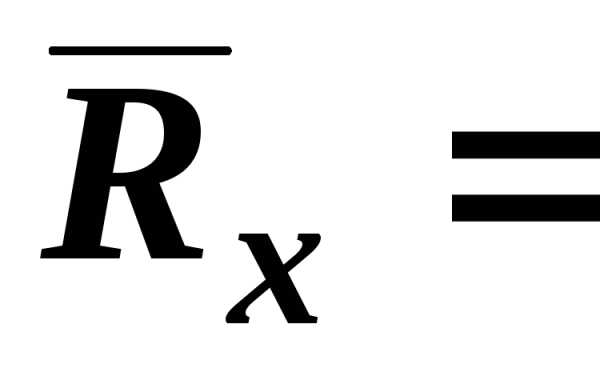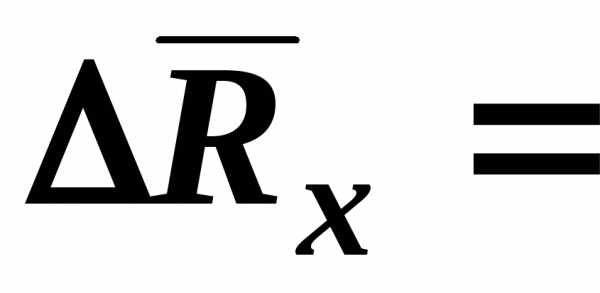Лабораторная работа 1. Определение сопротивлений мостиком уитстона. Каким образом можно измерять малые сопротивления мостиком уитстона

Измерительный мост Уинстона (Уитстона)

Измерительный мост, позволяющий определять величину неизвестного электрического сопротивления, был изобретён британским учёным Самуэлом Кристи в 1833 году, и позже модернизирован и популяризирован другим британским учёным, Чарьзом Витстоном в 1843 году.

Схема измерительного моста Уинстона.P1 - P3 - диагональ питания; P2 - P4 - измерительная диагональ моста;R1, R2 - левое плечо, R3, Rx - правое плечо моста.

Принцип работы

Принцип измерения неизвестного сопротивления основан на уравнивании отношений сопротивлений в обоих плечах моста, при этом гальванометр, включённый между этими плечами, будет показывать нулевое напряжение. На рисунке Rx - это неизвестное сопротивление, которое требуется измерить. R1, R2 и R3 - резисторы с известными значениями сопротивлений, причём резистор R2 переменный. Если отношение двух известных сопротивлений в плече R2/R1 равно отношению сопротивлений в плече Rx/R3, то в этом случае напряжение между точками схемы P2 и P4 будет равно нулю, и через гальванометр V ток не будет течь. Если же мост разбалансирован, то отклонение гальванометра будут указывать на то, что сопротивление резистора R2 слишком большое или слишком маленькое. Переменный резистор R2 регулируют до тех пор, пока гальванометр не укажет на ноль.

По гальванометру можно определять отсутствие тока в цепи с очень большой точностью. Следовательно, если резисторы R1, R2 и R3 - высокоточные, то неизвестное сопротивление Rx может быть измерено с большой точностью. Небольшие изменения сопротивления Rx разбалансируют измерительный мост, что обнаруживается по показанию гальванометра.

При сбалансированном мосте выполняется равенство R2/R1 = Rx/R3.

Отсюда Rx = R3*R2 / R1

В случае если сопротивления R1, R2 и R3 известны, а резистор R2 - постоянный, то неизвестное сопротивление Rx может быть рассчитано с помощью законов Кирхгофа. Этот метод измерения часто используется при применении измерительного моста в тензометрии, совместно с тензодатчиком, так как считать показания с гальванометра получится гораздо быстрее, чем балансировать мост переменным резистором.

Расчёт

Используя первый закон Кирхгофа, найдём токи, протекающие в узлах P2 и P4:

I3 - Ix + IG = 0I1 - I2 - IG = 0

Далее с помощью второго закона Кирхгофа найдём напряжения в контурах P1-P2-P4 и P2-P3-P4:

(I3 * R3) - (IG * RG) - (I1 * R1) = 0(Ix * Rx) - (I2 * R2) + (IG * RG) = 0

Мост сбалансирован, следовательно IG = 0, так что вторая система уравнений сократится:

I3 * R3 = I1 * R1Ix * Rx = I2 * R2

Решая эту систему уравнений, получим:

Rx = R2 * I2 * I3 * R3 / (R1 * I1 * Ix)

Из первого закона Кирхгофа следует, что I3 = Ix и I1 = I2. Следовательно величина неизвестного сопротивления Rx будет определятся по формуле:

Rx = R3*R2/R1

Если известны сопротивления всех четырёх резисторов и величина питающего напряжения Uпит, а сопротивление гальванометра достаточно высокое, так что током IG, протекающим через него можно пренебречь, то напряжение U между точками моста P2 и P4 может быть найдено путём расчёта каждого из делителей напряжения, вычтя затем напряжение на одном делителе из напряжения на другом делителе. В этом случае получится следующее уравнение:

U = Rx * Uпит / (R3 + Rx) - R2 * Uпит / (R1 + R2)

Напряжение питания Uпит можно вынести за скобки, в этом случае получится выражение:

U = (Rx / (R3 + Rx) - R2 / (R1 + R2)) * Uпит

Где U - напряжение в точке P2 относительно точки P4.

Измерительный мост Уинстона иллюстрирует концепцию дифференциальных измерений, результаты которых могут быть очень точными. Различные разновидности моста Уинстона используются для измерения ёмкости, индуктивности, импеданса и других величин. Одной из разновидностей моста является мост Кельвина, специально предназначенный для измерения малых сопротивлений. Во многих случаях измерение величины неизвестного сопротивления связано с измерением некоторых физических параметров, таких как сила, температура, давление и т.д., здесь в качестве измеряемого сопротивления используется соответствующий резистивный датчик.

В 1865 году Джеймс Максвелл применил измерительный мост Уинстона, питаемый переменным током, для измерения индуктивности, и в 1926 году Алан Блюмлейн подверг этот мост усовершенствованию.

Модификации основной схемы измерительного моста

Мост Уинстона является основной схемой измерительных мостов, но так же существуют различные его модификации, с помощью которых можно проводить измерения различных типов сопротивлений, когда основная схема моста для этого не подходит. Вот несколько разновидностей основной схемы измерительного моста:

BACK

zpostbox.ru

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА

Цель работы: измерить сопротивление резисторов при параллельном и последовательном соединении.

Приборы и принадлежности: магазин сопротивлений, нуль-гальванометр, реохорд с подвижным контактом, источник постоянного тока (аккумулятор), ключ, соединительные сопротивления, набор измеряемых сопротивлений.

Методика и техника эксперимента

Для точного измерения сопротивлений применяют электрическую схему, называемую мостом Уитстона. Эта схема представлена ниже.

R1, R2, R3, R4 – четыре сопротивления, образующих плечи моста, Г – чувствительный гальванометр, E– источник тока. Сопротивления плеч подбирают таким образом, чтобы ток через гальванометр был равен нулю. В этом случае говорят, что мост находится в равновесии. Условие равновесия моста можно получить, используя правила Кирхгофа. Так как ток через гальванометр равен 0, то применяя первое правило Кирхгофа к узлам В и D, можно записать:

I1 = I2, I3 = I4. (2.20)

Применяя второе правило Кирхгофа к контурам АВD и ВСD, получим:

I1R1 – I3R3 = 0,

I2R2 – I4R4 = 0,

или

I1R1 = I3R3, (2.21)

I2R2 = I4R4. (2.22)

Разделив почленно равенства (2.21) и (2.22) и используя (2.20), получим условие равновесия моста

. (2.23)

Из уравнения (2.23) можно определить любое из четырех сопротивлений, включенных в плечи, если известны три других сопротивления.

Вариант 1

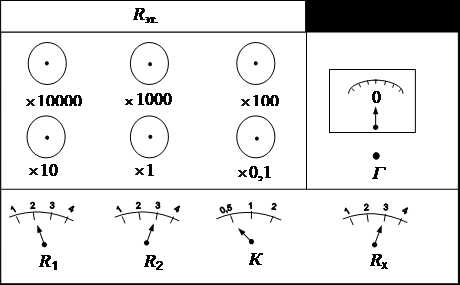Экспериментальная установка, используемая в данной работе содержит: R1, R2 – неизвестные сопротивления; Rэт – магазин сопротивлений; Г – гальванометр.

Сопротивления R3 и R4 подобраны таким образом, что их отношение равно: 0,5; 1; 2 Ом.

= k, где k = 0,5; 1 и 2.

Неизвестное сопротивление Rх может быть выражено через соответствующие сопротивления трех остальных плеч моста:

Rх = Rэт · , так как отношение = k, то

Rх = k·Rэт. (2.24)

Порядок выполнения работы

I. Определение сопротивления R1

1. Установить указатель неизвестного сопротивления Rх в положение 1. /позиция 1./ На короткий промежуток времени замкнуть электрическую цепь, нажав кнопку Г.

2. Изменяя сопротивление магазина Rэт, добейтесь равновесия моста. При достижении равновесия ток через гальванометр прекращается. (стрелка гальванометра устанавливается на нуль).

3. Произвести измерения для всех значений коэффициента К. (К = 0,5; 1; 2).

4. С помощью формулы (2.24) подсчитать значения сопротивления R1 для всех значений коэффициента k.

5. Найти среднее значение исследуемого сопротивления R1 ср.

6. Полученные результаты записать в таблицу 2.5.

Т а б л и ц а 2.5

Исследуемое сопротивление	№	k	Rэт	Rх	Rх ср
R1		0,5


R2		0,5


Rпосл.		0,5


Rпарал.		0,5

II. Определение сопротивления R2.

1. Установить переключатель сопротивления Rх в положение 2.

2. Замкнуть цепь и повторить измерения в том же порядке для всех значений коэффициента k.

3. По формуле (2.24) рассчитать значения сопротивления R2 и найти среднее значение.

III. Определение общего сопротивления при последовательном

соединении сопротивлений R1 и R2

1. Установить переключатель сопротивления Rх в положение 3, что соответствует последовательному соединению R1 и R2.

2. Произвести измерения для всех значений коэффициента k аналогично предыдущим.

3. По формуле (2.24) рассчитать значения Rпосл. Найти среднее значение Rпосл.ср.

IV. Определение общего сопротивления при параллельном соединении сопротивлений R1 и R2

1. Установить переключатель сопротивления Rх в позицию 4, что соответствует параллельному соединению R1 и R2.

2. Произвести измерения для всех значений коэффициента k аналогично предыдущим.

3. Полученные значения Rпар. записать в таблицу и найти среднее значение Rпар.ср.

4. Получив значения сопротивлений при последовательном и параллельном соединении экспериментально, сравнить их с результатами теоретических расчетов по соответствующим формулам:

Rпосл. = R1 + R2; Rпар. = .

5. Сопоставить расчетные и измеренные значения суммарных сопротивлений. Сравнения провести с учетом погрешности измерений.

Вариант 2

Для выполнения этого варианта используется рабочая схема, представленная ниже.

ИП – источник постоянного тока;

Rх – измеряемое сопротивление;

D – подвижный контакт;

R2 – магазин сопротивлений;

Р – нульгальванометр;

S – ключ;

RАВ – реохорд.

Поскольку для баланса моста не имеет значения абсолютные величины сопротивлений и , а важно их отношение, сопротивления и выполняют либо в виде высокоомного проводника, либо в виде реохорда (высокоомная проволока навита на тонкий стержень из изоляционного материала), по которым скользит подвижный контакт, являющийся вершиной моста D.

Так как сопротивления представляют собой реохорд, выполненный из однородного материала, то сопротивление между концом реохорда и подвижным контактом пропорционально длине участка реохорда от соответствующего конца до контакта и .

Поэтому отношение сопротивлений может быть с высокой точностью определено как отношение длин отрезков реохорда

и . (2.25)

Порядок выполнения работы

1. Установить подвижный контакт D на реохорде в среднее положение.

2. Тумблером подключить сопротивление .

3. Замкнуть цепь кнопкой S и, подбирая сопротивление магазином сопротивлений, добиться минимального отклонения стрелки нуль-гальванометра от нуля.

4. Перемещая контакт D, добиться точного баланса моста (стрелка нуль-гальванометра на нуле). Значение сопротивления и соотношение длин записать в таблицу 2.6.

Т а б л и ц а 2.6

5. Включить в плечо моста неизвестное сопротивление и повторить пункты 2-4.

6. Далее повторить пункты 2-4 для последовательно и параллельно соединенных сопротивлений и .

7. По формуле (2.25) вычислить неизвестные сопротивления и .

8. Определить общее сопротивление при последовательном и параллельном соединениях.

9. Сравнить полученные значения с соответствующими измеренными значениями.

10. Рассчитать абсолютные и относительные ε погрешности измерений и вычислений.

Примечание: Если стрелка нуль-гальванометра отклонится влево, уменьшить сопротивление; если вправо – увеличить сопротивление.

Контрольные вопросы

1. Дайте определение электрического тока. Чему равна сила и плотность тока?

2. Расскажите об устройстве и принципе работы моста постоянного тока.

3. Сформулировать правила Кирхгофа и условия их применения.

4. Что такое «баланс моста»? Вывести расчетную формулу для определения сопротивления с помощью моста Уитстона.

5. Выведите расчетную формулу для определения результирующего сопротивления при последовательном соединении трех сопротивлений.

6. Выведите расчетную формулу для определения результирующего сопротивления при параллельном соединении четырех сопротивлений.

Лабораторная работа

pdnr.ru

2. Мостик уитстона

ЛАБОРАТОРНАЯ РАБОТА № 2.05

ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ С ПОМОЩЬЮ МОСТА УИТСТОНА

Цель работы

Целью работы является изучение законов постоянного тока на примере классического метода измерения сопротивления проводников с помощью мостовой схемы и определение удельного сопротивления материала проводника.

Краткая теория

Электросопротивление проводника – это скалярная физическая величина, характеризующая его электропроводящие свойства. Сопротивление проводника зависит от его формы, размеров и электроповодящих свойств материала, из которого изготовлен проводник. В простейшем случае однородного проводника с постоянным поперечным сечением, сопротивление проводника определяется следующим образом:

, (2.05.1)

где – удельное сопротивление материала проводника, – длина проводника; S – площадь его поперечного сечения.

Из формулы (2.05.1) можно выразить удельное сопротивление:

, (2.05.2)

откуда видно, что удельное сопротивление численно равно сопротивлению проводника единичной длины, имеющего площадь поперечного сечения, равную единице площади. В системе СИ удельное сопротивление измеряют в омметрах (Ом·м).

Одним из методов измерения сопротивления является метод моста Уитстона.

Мост Уитстона состоит из четырех сопротивлений – плеч , которые соединены между собой так, что образуют замкнутый четырехугольник. К двум противоположным его угламА и В подключают полюса источника постоянного тока E, а к двум другим С и Д подсоединяют чувствительный гальванометр или измеритель разности потенциалов. Принципиальная схема моста Уитстона изображена на рис. 10.

Если мост подключен к источникуЕ, по участку моста СД вследствие неравенства потенциалов точек С и Д может протекать электрический ток и стрелка гальванометра отклонится. Для того, чтобы на участке СД ток отсутствовал, необходимо равенство потенциалов точек С и Д (условие равновесия моста).

Изменять разность потенциалов между точками С и Д можно таким способом: в качестве участка АДВ включается калиброванная проволока (реохорд) со скользящим контактом Д. Реохорд снабжен шкалой. Перемещая движок реохорда, можно добиться отсутствия тока на участке СД, что будет зарегистрировано гальванометром. Обозначим силу тока, текущего на участке АДВ через I1,а на участке АСВ – через I2. Для каждого из четырех плеч реохорда запишем уравнения по закону Ома:

(2.05.3)

где ,,,– потенциалы точек А, С, В, Д соответственно.

При отсутствии тока через гальванометр 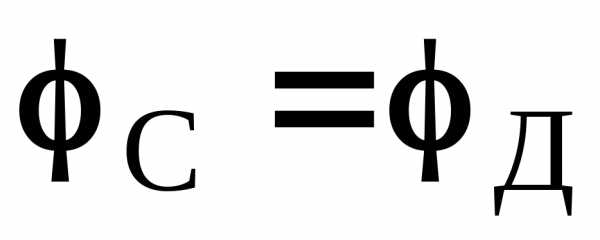. Следовательно, можно записать:

, , (2.05.4)

откуда

. (2.05.5)

Таким образом, условие равновесия моста определяется только соотношением плеч реохорда и не зависит от электродвижущей силы источника, питающего цепь.

Так как проволока, из которой изготовлен реохорд АДВ, однородна и имеет по всей длине одинаковое сечение, то сопротивления RАД и RДВ пропорциональны соответствующим длинам плеч 1 и 2 реохорда. Поэтому (2.05.5) можно переписать в виде:

, (2.05.6)

откуда неизвестное сопротивление:

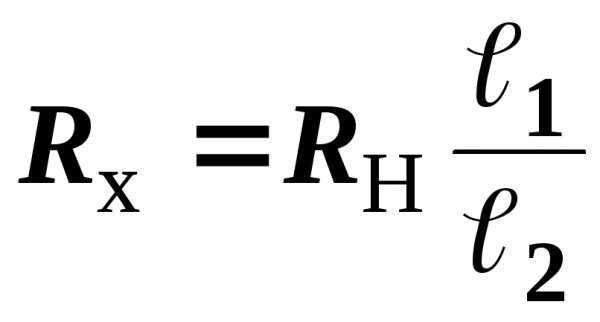. (2.05.7)

С другой стороны, сопротивление проводника можно выразить, зная его форму, размер и материал, из которого изготовлен проводник.

, (2.05.8)

где d – диаметр проводника.

Отсюда удельное сопротивление исследуемого проводника:

. (2.05.9)

В табл. 5.1 приведены значения удельного сопротивления некоторых проводников при комнатной температуре.

Таблица 5.1.

Удельное сопротивление проводников

Материал проводника
Серебро	0,016
Медь	0,017
Алюминий	0,028
Вольфрам	0,055
Цинк	0,060
Латунь	0,071
Свинец	0,120
Никелин	0,420
Манганин	0,459
Константан	0,500
Ртуть	0,958
Нихром	1,100

Удельное сопротивление горных пород изменяется в широких пределах. Наиболее низкое удельное сопротивление имеют самородные металлы: золото, платина, серебро, медь. Наиболее распространенные минералы (кварц, полевой шпат, слюда, каменная соль) имеют удельное сопротивление 1010  1014 Ом·м. Они являются хорошими изоляторами.

Выполнение работы

Н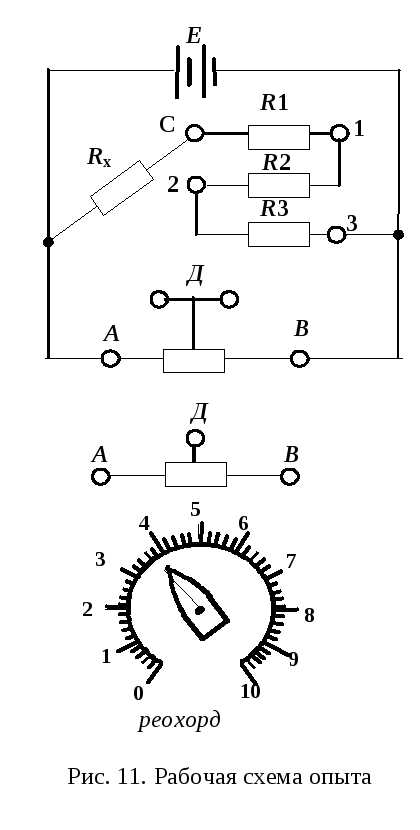еобходимые приборы: круговой реохорд, цифровой вольтметр, источник постоянного тока напряжением 4 В, проводник с известным сопротивлением Rx (длина проводника ,диаметр проводника , набор известных сопротивлений (R1 = 470 Ом, , ). Все элементы схемы, кроме цифрового вольтметра, смонтированы внутри лабораторного стенда. Рабочая схема опыта показана на рис. 11 и на панели лабораторного стенда.

Порядок выполнения работы

Подготовьте к работе цифровой вольтметр в соответствии с инструкцией по эксплуатации, находящейся на лабораторном столе.
Подключите цифровой вольтметр к клеммам С и Д.
Включите реохорд с помощью перемычек (соедините попарно клеммы А–А, Д–Д, В–В на реохорде и в измерительной цепи). Включите лабораторный стенд тумблером, расположенным в левой части передней стенки.
С помощью перемычки закоротите сопротивления R2 и R3, оставив включенным R1 (соединить клеммы 1 - 3).
Вращением ручки кругового реохорда добейтесь нулевого показания вольтметра и по шкале реохорда отсчитайте длину левого плеча 1 (слева от стрелки) и правого 2. Результаты запишите в табл. 5.2.
Опыт повторите еще два раза: при двух сопротивлениях: , для чего закоротите только сопротивлениеR3, (соединить клеммы 2 - 3) и , для чего перемычка убирается совсем.

По результатам измерений по формуле (2.05.7) три раза вычислите сопротивление исследуемого проводника, затем его среднее значение , среднюю абсолютную и среднюю относительную погрешности.

Таблица 5.2

Результаты измерений

Rн, Ом	1	2	Rx, Ом	Rx, Ом
	деления шкалы

Среднее значение

Вычислите среднее значение удельного сопротивления материала проводника по формуле (2.05.9). Сравнив результат с табличными значениями (см. табл. 5.1), определите материал, из которого изготовлен проводник.

Вычислите относительную и абсолютную погрешности удельного сопротивления по формулам:

. (2.05.10)

. (2.05.11)

Окончательный результат запишите в виде:

; (2.05.12)

. (2.05.13)

КОНТРОЛЬНЫЕ ВОПРОСЫ

Что такое электросопротивление проводника? Отчего оно зависит?
Что такое удельное сопротивление проводника, в каких единицах оно измеряется?
От чего зависит удельное сопротивление проводника?
Начертите схему моста Уитстона и опишите способ измерения сопротивления с его помощью.
Выведите расчетную формулу для определения сопротивления неизвестного проводника.
Как вычисляются относительная и абсолютная погрешности измерения сопротивления Rx и удельного сопротивления ?

studfiles.net

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА

⇐ ПредыдущаяСтр 9 из 23Следующая ⇒

Цель работы: Измерить сопротивление резисторов при параллельном и последовательном соединении.

Методика и техника эксперимента

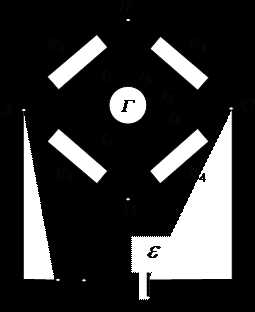R1, R2, R3, R4 – четыре сопротивления, образующих плечи моста, Г – чувствительный гальванометр, ε – источник тока. Сопротивления плеч подбирают таким образом, чтобы ток через гальванометр был равен нулю. В этом случае говорят, что мост находится в равновесии. Условие равновесия моста можно получить, используя правила Кирхгофа. Так как ток через гальванометр равен 0, то применяя первое правило Кирхгофа к узлам В и D, можно записать:

I1 = I2, I3 = I4. (2.20)

Применяя второе правило Кирхгофа к контурам АВD и ВСD, получим:

I1R1 – I3R3 = 0,

I2R2 – I4R4 = 0,

или I1R1 = I3R3 (2.21)

I2R2 = I4R4. (2.22)

Разделив почленно равенства (2.21) и (2.22) и используя (2.20), получим условие равновесия моста

. (2.23)

Вариант 1

Экспериментальная установка, используемая в данной работе содержит:

R1, R2 – неизвестные сопротивления; Rэт – магазин сопротивлений; Г – гальванометр.

Сопротивления R3 и R4 подобраны таким образом, что их отношение равно: 0,5; 1; 2 Ом.

= k, где k = 0,5; 1 и 2.

Rх = Rэт · , так как отношение = k, то

Rх = k·Rэт. (2.24)

Порядок выполнения работы

I. Определение сопротивления R1

3. Произвести измерения для всех значений коэффициента К. (К = 0,5; 1; 2).

4. С помощью формулы (2.24) подсчитать значения сопротивления R1 для всех значений коэффициента k.

5. Найти среднее значение исследуемого сопротивления R1 ср.

6. Полученные результаты записать в таблицу 2.5.

Т а б л и ц а 2.5

Исследуемое сопротивление	№	k	Rэт	Rх	Rх ср
R1		0,5


R2		0,5


Rпосл.		0,5


Rпарал.		0,5

II. Определение сопротивления R2.

1. Установить переключатель сопротивления Rх в положение 2.

2. Замкнуть цепь и повторить измерения в том же порядке для всех значений коэффициента k.

3. По формуле (2.24) рассчитать значения сопротивления R2 и найти среднее значение.

III. Определение общего сопротивления при последовательном

соединении сопротивлений R1 и R2

2. Произвести измерения для всех значений коэффициента k аналогично предыдущим.

3. По формуле (2.24) рассчитать значения Rпосл. Найти среднее значение Rпосл.ср.

IV. Определение общего сопротивления при параллельном соединении сопротивлений R1 и R2

1. Установить переключатель сопротивления Rх в позицию 4, что соответствует параллельному соединению R1 и R2.

2. Произвести измерения для всех значений коэффициента k аналогично предыдущим.

3. Полученные значения Rпар. записать в таблицу и найти среднее значение Rпар.ср.

Rпосл. = R1 + R2; Rпар. = .

Вариант 2

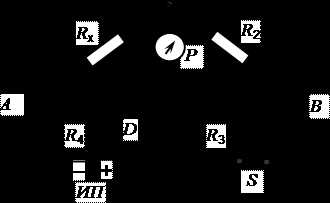Для выполнения этого варианта используется рабочая схема, представленная ниже.

ИП – источник постоянного тока;

Rх – измеряемое сопротивление;

D – подвижный контакт;

R2 – магазин сопротивлений;

Р – нульгальванометр;

S – ключ;

RАВ – реохорд.

и . (2.25)

Порядок выполнения работы

1. Установить подвижный контакт D на реохорде в среднее положение.

2. Тумблером подключить сопротивление .

Т а б л и ц а 2.6

5. Включить в плечо моста неизвестное сопротивление и повторить пункты 2-4.

6. Далее повторить пункты 2-4 для последовательно и параллельно соединенных сопротивлений и .

7. По формуле (2.25) вычислить неизвестные сопротивления и .

8. Определить общее сопротивление при последовательном и параллельном соединениях.

9. Сравнить полученные значения с соответствующими измеренными значениями.

10. Рассчитать абсолютные и относительные ε погрешности измерений и вычислений.

Контрольные вопросы

1. Дайте определение электрического тока. Чему равна сила и плотность тока?

2. Расскажите об устройстве и принципе работы моста постоянного тока.

3. Сформулировать правила Кирхгофа и условия их применения.

Лабораторная работа №7

Измерение сопротивления методом моста Уитстона

ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЯ

Цель работы: познакомиться с одним из методов измерения электрического сопротивления резисторов. Проверить правила сложения сопротивлений при различных способах соединения резисторов. Задача: собрать схему

Подробнее

Измерение сопротивления на постоянном токе

Федеральное агентство по образованию РФ Ухтинский государственный технический университет 4 Измерение сопротивления на постоянном токе Методические указания к лабораторной работе для студентов всех специальностей

Подробнее

R x R R2 R 1 R 2. R x = R. (2.4) l 2. l 1 B D

Методические указания к выполнению лабораторной работы.. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ МЕТОДОМ МОСТИКА УИТСТОНА Филимоненкова Л.В. Электростатика и постоянный ток: Методические указания к выполнению

Подробнее

МОСТОВЫЕ МЕТОДЫ ИЗМЕРЕНИЙ

КАЗАНСКАЯ ГОСУДАРСТВЕННАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ Кафедра физики МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ для студентов специальностей 2903, 2906, 2907, 2908, 2910 Лабораторная

Подробнее

МОСТИКОВАЯ СХЕМА В ПОЛНОЙ ЦЕПИ

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОСТИКОВАЯ СХЕМА В ПОЛНОЙ ЦЕПИ Мостиковая

Подробнее

E - нормальный элемент Вестона.

ЛАБОРАТОРНАЯ РАБОТА 3-7: ИЗМЕРЕНИЕ ЭЛЕКТРОДВИЖУЩИХ СИЛ ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ МЕТОДОМ КОМПЕНСАЦИИ Студент группа Допуск Выполнение Защита Цель работы: ознакомление с методами компенсации и применение

Подробнее

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ МОСТОВЫМ МЕТОДОМ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный

Подробнее

ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики

Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА - 2012 ЦЕЛЬ РАБОТЫ

Подробнее

Работа выхода электрона из металла

Московский государственный университет им. М.В.Ломоносова Физический факультет Кафедра общей физики Л а б о р а т о р н ы й п р а к т и к у м п о о б щ е й ф и з и к е (электричество и магнетизм) Козлов

Подробнее

Расширение пределов измерения амперметра

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ухтинский государственный технический университет» (УГТУ) 1 Расширение пределов

Подробнее

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ

На рисунке показана цепь постоянного тока. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (

Подробнее

Лабораторная работа «Мостовые измерения»

Лабораторная работа «Мостовые измерения» Измерительный мост Измерительным мостом называется электрический прибор для измерения сопротивлений, ёмкостей, индуктивностей и других электрических величин. Мост

Подробнее

Тема 3. Постоянный ток 1

Тема 3. Постоянный ток 1 Лабораторная работа 5 (2.4) Применение закона Ома для расчетов в цепях постоянного тока Введение Георг Ом в 1827 году экспериментально установил закон, согласно которому отношение

Подробнее

Тема 3. Постоянный ток

Тема 3. Постоянный ток Лабораторная работа 5 (2.4) Применение закона Ома для расчетов в цепях постоянного тока Введение Георг Ом в 1827 году экспериментально установил закон, согласно которому отношение

Подробнее

РЕОСТАТ И ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ

Лабораторная работа 306 РЕОСТАТ И ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ Приборы и принадлежности: источник тока, два вольтметра, два миллиамперметра, реостат, нагрузочные резисторы. Введение. Реостат устройство для регулирования

Подробнее

МГТУ им. Н.Э. Баумана

МГТУ им. Н.Э. Баумана 1 Л.И. Баландина, Т.В. Бородина, Ю.В. Герасимов, Н.В. Герасимов, М.Ю. Докукин ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ВЗАИМНАЯ ИНДУКЦИЯ Методические указания к лабораторной работе Э-1Б по курсу

Подробнее

шара не будет зависеть от заряда,

Лабораторная работа ОПРЕДЕЛЕНИЕ ЕМКОТИ КОНДЕНАТОРА ПРИ ПОМОЩИ МОТИКА ОТТИ. Оборудование: звуковой генератор, набор конденсаторов, реохорд, наушники, провода. Описание целей работы Конкретная цель Критерии

Подробнее

Лекция 2. АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ

4 Лекция АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ План Задача анализа электрических цепей Законы Кирхгофа Примеры анализа резистивных цепей 3 Эквивалентные преобразования участка цепи 4 Выводы Задача анализа электрических

Подробнее

docplayer.ru

Карпов В. А. Электрические измерительные приборы, 1927 год. 23. Мостик Витстона (Уитстона).

В. А. Карпов. Электрические измерительные приборы, 1927 год

ГЛАВА VI. Приборы для измерения сопротивлений.

23. Мостик Витстона (Уитстона).

Для измерения сопротивлений широко применяются на практике измерительные мостики. Из них основным и, вместе с тем, самым простым является мостик Уитстона, представленный на рис. 89. Питание мостика производится в точках А и В от источника тока, например, гальванического элемента или аккумулятора.

Если мы на одной ветви мостика возьмем, например, точку С, то и на другой ветви должна найтись точка, имеющая тот же потенциал. Пусть D будет такой точкой. В таком случае при соединении точек С и D проволокой ("мостиком"), по ней не будет протекать тока, так как оба ее конца обладают равными потенциалами и потому стрелка включенного в этот мостик гальванометра не даст отклонения. Благодаря гальванометру возможно отыскать эту точку D, если ветвь ADB представляет собою голую проволоку. Для этого нужно передвигать конец мостика вдоль проволоки ADB и наблюдать в то же время за уменьшениями отклонения стрелки гальванометра, приближаемся ли мы к искомой точке.

Если мы соединим две точки одинакового потенциала С и D между собою, то сила протекающего от точки А к точке С тока i1 должна быть равна силе вытекающего от точки С к точке В тока i2. Также и сила тока i3 между точками А и D должна равняться силе тока i4 — между точками D и В. А так как точки С и D обладают равными потенциалами, то и падение напряжения между точками А и С, а именно, e1, равно падению напряжения между точками А и D, обозначенному через e3. Равным образом и е2 = е4. Для тех обозначений, которые мы имеем на чертеже, можно написать:

Но i1 = i2 и i3 = i4; также e1 = e3 и е2 = е4.

Поэтому

Отсюда выводим уравнения

и, разделив эти уравнения одно на другое, получим:

или

Отсюда также следует:

то-есть, в мостике Витстона произведения противолежащих сопротивлений равны между собою.

Пропорция не нарушится, если мы переставим между собою ее крайние и средние члены. Не нарушится и последнее уравнение, если мы в произведениях переставим множители. Соответственно этому, мы можем также изменить устройство Витстонова мостика, присоединив гальваническую батарею к точкам С и D и перекинув мостик с гальванометром от точки A к точке В, как это и показано на рис. 90. Соответствующим подбором сопротивлений мы можем получить равенство потенциалов в точках А и В и тогда написать пропорцию

откуда

Если одно из этих сопротивлений неизвестно, то его из вышеприведенных уравнений легко определить. Так, например, для мостика, данного на рис. 89, определяя r1, как неизвестное, получим

На практике в качестве сопротивлений между узловыми точками мостика включаются магазины сопротивлений, наличие которых дает возможность, комбинируя величины сопротивлений в каждом из плеч мостика, подобрать такое их соотношение, при котором гальванометр не будет давать отклонения, что и требуется. При определении неизвестного сопротивления r1 (или х) можно облегчить себе подбор сопротивлений и последующее вычисление специальным подбором сопротивлений r3 и r4. Например:

Если возьмем r3 = r4, то r1 = r2.

Если r3 = 100 r4, то r1 = 100 r2.

Если r4 = 100 r3, то r1 = r2 / 100.

Ветви AD и DB, называемые балансными, обычно имеют магазины сопротивлений, дающими возможность получить соотношения 1 к 10, 1 к 100, 1 к 1000 или обратные соотношения (10 к 1 и т. д.).

В проволочных мостиках, впервые предложенных Кирхгофом (рис. 91), балансы r1 и r2 заменены одной полированной и калибрированной (имеющей строго одинаковое сечение) проволокой, натянутой вдоль масштаба или шкалы, так что отношение сопротивлений балансных плеч можно заменить отношением длин участков проволоки АС и СВ. Перемещая по проволоке АВ скользящий контакт С, можно получить какое угодно отношение балансов и при умело подобранном сопротивлении R достичь того, что тока в гальванометре G не будет. При этом отношение длин сопротивлений r1 и r2 дано готовым на той шкале, по которой натянута проволока АВ. Если это отношение равно а, то для рис. 91

Пример. Из сопротивлений четырех ветвей мостика Витстона (рис. 89) известны три сопротивления, а именно — r1 = 10, r2 = 100 и r3 12 омам. Определить неизвестное сопротивление четвертой ветви.

Так как

то

sergeyhry.narod.ru

Лабораторная работа 1. Определение сопротивлений мостиком уитстона

Цель работы: ознакомиться с мостиковым методом определения сопротивлений резисторов, найти неизвестные сопротивления нескольких резисторов, проверить формулы для их последовательного и параллельного соединения.

Приборы и принадлежности:источник тока, магазин сопротивлений, набор резисторов, реохорд, гальванометр, балластное сопротивление, кнопочный ключ, переключатель.

Изучите теоретический материал по одному из учебных пособий: [1, гл. V§ 34–36; 2, гл.IX§ 9.2, 9.4; 3, гл.IV§ 17; 4; гл.II§ 13].

В основе мостикового метода определения сопротивления лежат правила Кирхгофа для расчета параметров разветвленных электрических цепей.

Первое правило Кирхгофа применяется для узлов электрической цепи. Любая точка разветвления цепи, в которой соединены три и более проводников, называется узлом электрической цепи.

Первое правило Кирхгофа:алгебраическая сумма токов, сходящихся в узле, равна нулю:

. (1.1)

При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла, – отрицательным.

Это правило означает, что в случае установившегося тока ни в одной точке проводника не накапливаются заряды. В противном случае токи не могли бы оставаться постоянными.

Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Ii на сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС k, встречающихся в этом контуре:

k, (1.2)

где n1– число отдельных участков (ветвей) контура, на которые

контур разбивается узлами;

n2– число ЭДС в выбранном замкнутом контуре.

Для применения второго правила Кирхгофа выбирается определенное направление обхода контура (по часовой стрелке или против нее). Направления токов в ветвях контура выбираются произвольно.

Произведение IiRi записывается со знаком плюс, если направление тока совпадает с выбранным направлением обхода контура. ЭДС источников электрической энергии считаются положительными, если они создают токи, направления которых совпадают с направлением обхода контура (т.е. внутри источника ток направлен от отрицательного полюса к положительному).

Для выполнения работы нужно знать формулы параллельного и последовательного сопротивления проводников.

При последовательном соединении n проводников общее сопротивление определяется как сумма сопротивлений отдельных проводников:

. (1.3)

При параллельном соединении общее сопротивление определяется по формуле

. (1.4)

Описание лабораторной установки и вывод расчетной формулы

В данной работе для измерения сопротивления проводника используется мостик Уитстона, схема которого представлена на рис. 1.1. К точкам А иВподключен источник тока, к точкамСиD– индикатор тока.

Применяя мостовые схемы, можно электрическими методами измерять различные физические величины: сопротивление проводника, электроемкость, индуктивность, частоту, температуру, магнитные параметры и т.д.

В данной работе для определения неизвестного сопротивления его включают в плечо АСмостика, в плечоСВ– известное сопротивление (магазин сопротивлений).

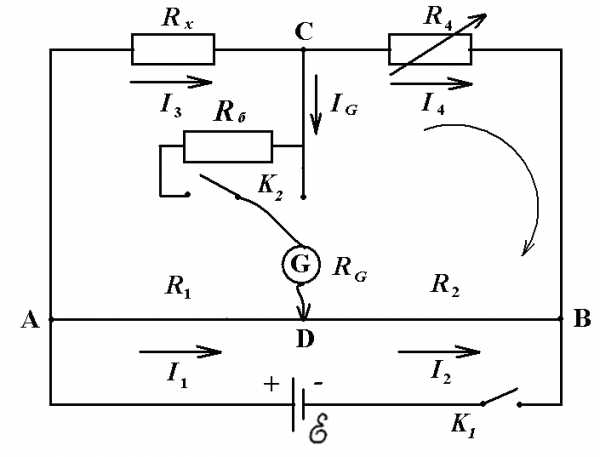
Рис. 1.1.

Плечи ADиDBпредставляют собой участки одной проволокиАВ, разделенной подвижным контактом на два отрезка. ПроволокаАВнатягивается на миллиметровую линейку, с помощью которой можно определить положение подвижного контакта. Это устройство называетсяреохордом.

На этой же схеме приняты обозначения:

Rx– неизвестное сопротивление;

R4– магазин сопротивлений, позволяющий устанавливать любое

сопротивление от 0 до 9999 Ом;

R1иR2– сопротивления частей проволоки АВ реохорда.

Между точками СиDвключен гальванометр. Последовательно с гальванометром можно включить балластное сопротивлениеRбс целью предотвращения порчи гальванометра при больших токах в мостике (при отсутствии равновесия).

При нажатии ключа К1по ветвям цепи потекут токиI1,I2, I3, I4(направления токов показаны на рис. 1.1). В ветви, содержащей гальванометр, пойдет токIG, направление которого зависит от того, какая из точек (СилиD) имеет более высокий потенциал. Направление токаIGтакже показано на рис.1.1.

Применив первое правило Кирхгофа к узловым точкам Си D, соответственно получим:

Применив второе правило Кирхгофа к контурам АСDА и СВDСс учетом указанного на рисунке направления обхода, получим:

Для определения неизвестного сопротивления Rxмостик приводится в равновесие при помощи магазина сопротивленийи подвижного контакта D. Равновесие наступает тогда, когда потенциалы точекСиDравны и ток в мостике отсутствует (IG = 0). Тогда приведенные выше уравнения примут следующий вид:

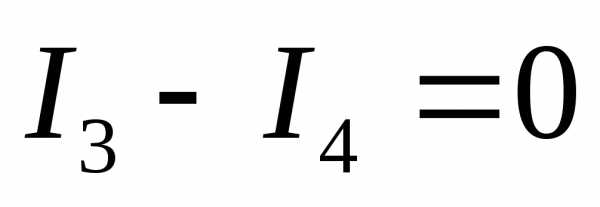, или 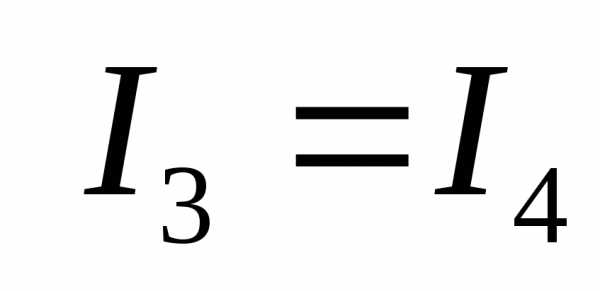; (1.5)

, или 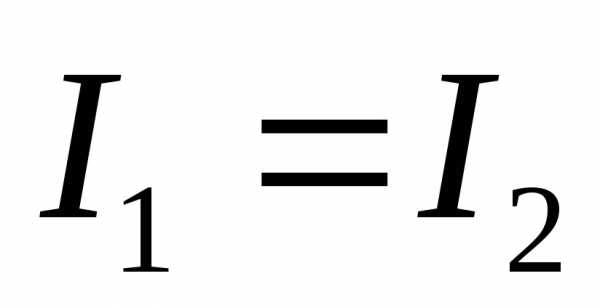; (1.6)

, или ; (1.7)

, или . (1.8)

Разделим равенство (1.7) на (1.8):

Учитывая, что , после сокращения получим:

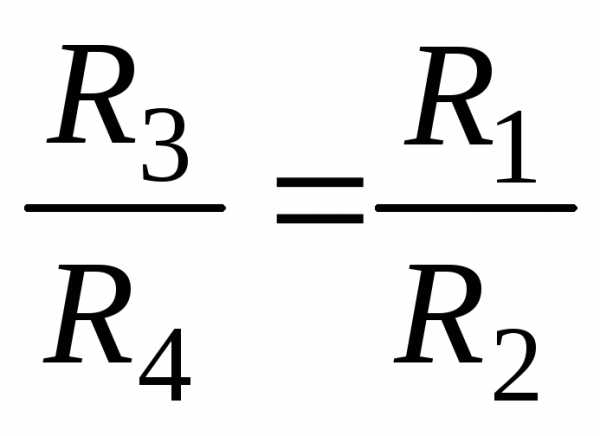откуда неизвестное сопротивление

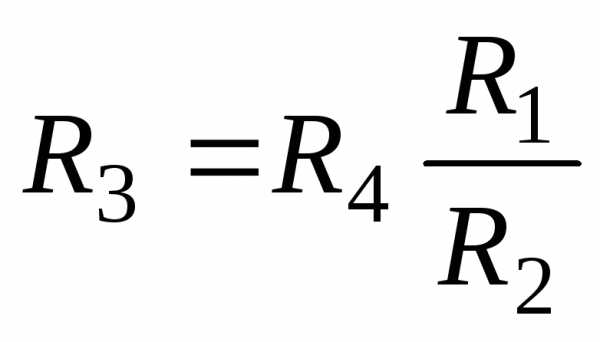. (1.9)

Сопротивление проводника определяется по зависимости , и поэтому в уравнении (1.9) отношениеможно заменить отношением длин плеч на реохорде:

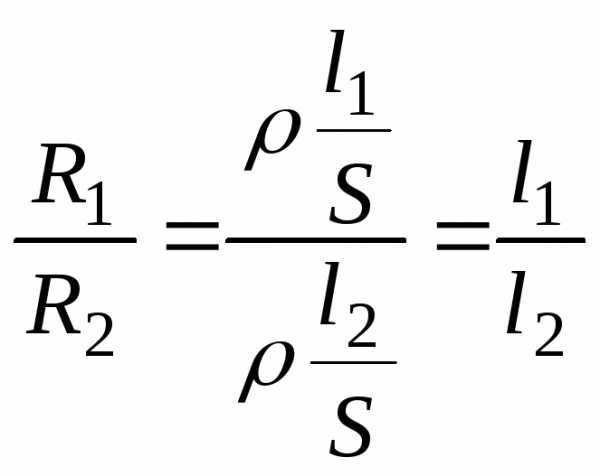Формула (1.9) примет следующий вид:

. (1.10)

Таким образом, для определения величины неизвестного сопротивления необходимо знать сопротивление, установленное на магазине сопротивлений, и длины левой и правой частей проволоки реохорда.

studfiles.net

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

Лабораторная работа 1. Определение сопротивлений мостиком уитстона. Каким образом можно измерять малые сопротивления мостиком уитстона

Измерительный мост Уинстона (Уитстона)

Принцип работы

Расчёт

Модификации основной схемы измерительного моста

BACK

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА

2. Мостик уитстона

ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ С ПОМОЩЬЮ МОСТА УИТСТОНА

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА

Измерение сопротивления методом моста Уитстона

ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЯ

Измерение сопротивления на постоянном токе

R x R R2 R 1 R 2. R x = R. (2.4) l 2. l 1 B D

МОСТОВЫЕ МЕТОДЫ ИЗМЕРЕНИЙ

МОСТИКОВАЯ СХЕМА В ПОЛНОЙ ЦЕПИ

E - нормальный элемент Вестона.

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ МОСТОВЫМ МЕТОДОМ

ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики

Работа выхода электрона из металла

Расширение пределов измерения амперметра

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ

Лабораторная работа «Мостовые измерения»

Тема 3. Постоянный ток 1

Тема 3. Постоянный ток

РЕОСТАТ И ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ

МГТУ им. Н.Э. Баумана

шара не будет зависеть от заряда,

Лекция 2. АНАЛИЗ РЕЗИСТИВНЫХ ЦЕПЕЙ

Карпов В. А. Электрические измерительные приборы, 1927 год. 23. Мостик Витстона (Уитстона).

ГЛАВА VI. Приборы для измерения сопротивлений.

Лабораторная работа 1. Определение сопротивлений мостиком уитстона

Описание лабораторной установки и вывод расчетной формулы

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация