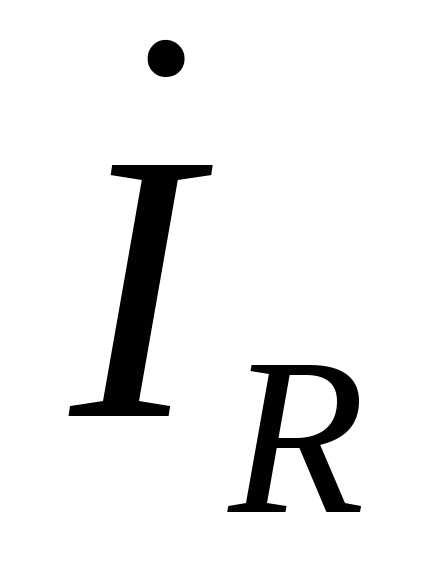Метод расчета линейных электрических цепей. Метод комплексных амплитуд. Комплексный метод расчета электрических цепей

Комплексный метод расчета цепей синусоидального тока

Широкое распространение на практике получил метод расчета цепей синусоидального тока, который принято называть комплексным. Сущность метода состоит в том, что синусоидальные токи, напряжения и ЭДС изображаются комплексными числами, а геометрические операции над векторами заменяются алгебраическими операциями над комплексными числами. Этот метод позволяет рассчитывать цепи синусоидального тока алгебраически аналогично цепям постоянного тока.

2.4.1. Векторное представление синусоидальных величин

Вращающийся вектор, который изображает синусоидальную функцию, можно поместить на комплексную плоскость, в систему перпендикулярных осей: – действительных чисел, – мнимых чисел. Положительные направления осей на комплексной плоскости обозначаются индексами: +1 – ось действительных чисел; + – ось мнимых чисел, где = – мнимая единица (рис. 2.17).

а) б) в)

Рис. 2.17

Известно, что координаты точки на комплексной плоскости определяются радиусом–вектором этой точки, т.е. вектором, начало которого совпадает с началом координат, а конец находится в точке, соответствующей заданному комплексному числу (рис. 2.17 а).

Показательная форма записи

где – модуль; – аргумент или фаза, отсчитываемая от оси +1 против часовой стрелки.

Применив формулу Эйлера, можно получить тригонометрическую и соответственно алгебраическую форму записи комплексного числа:

где ; .

Очевидно

; .

Заменим в уравнении для показательной формы записи на , а на . Получим комплекс тока

, (2.39)

который является символическим (комплексным) изображением функции и называется комплекс мгновенного значения тока.

Комплексы обозначаются теми же буквами, что и их действительные оригиналы, только с чертой внизу. Модуль комплекса мгновенного значения равен амплитуде синусоидального тока , а его переменный аргумент ( ) является аргументом изображаемой синусоиды (рис. 2.17 б). Из формулы (2.39) можно записать комплекс тока в тригонометрической форме

а также получить изображение функции (оригинала)

, (2.40)

т.е. мгновенное значение тока равно мнимой части комплекса мгновенного значения тока. Ток (2.39) можно представить в виде

где является другим символом, называемым комплексом амплитудного значения. Это аналитическое представление неподвижного вектора, длина которого равна амплитуде тока, а угол между направлениями вектора и осью «+1» на комплексной плоскости равен начальной фазе (рис. 2.17 в). Комплексом действующего значения называют изображение

Пример 2.2. Записать комплексы действующих значений напряжения и тока, если их мгновенные значения представлены уравнениями

, А.

Решение. Действующее значение напряжения =200 В, начальная фаза = –120°. В соответствии с определением комплекс действующего значения напряжения

В.

Аналогично для тока = 14,1 А, начальная фаза тока = –60°, а комплекс тока

А.

Пример 2.3. Для комплекса действующего значения напряжения

записать мгновенное значение.

Решение. От алгебраической формы переходим к показательной

где В; .

Комплекс находится во второй четверти комплексной плоскости.

Мгновенное значение напряжения

, B.

В заключение рассматриваемого вопроса рекомендуем усвоить следующие очевидные равенства

; ; и т.д.

;

Отметим, что умножение на оператор означает поворот вектора на 90° против часовой стрелки, а умножение на означает поворот вектора на 90° по часовой стрелке.

2.4.2. Комплекс полного сопротивления и комплекс полной проводимости. Законы Кирхгофа в комплексной форме

Отношение комплекса напряжения к комплексу тока называется комплексом полного сопротивления цепи

. (2.41)

Модуль комплексного сопротивления равен полному сопротивлению , его аргумент – углу сдвига фаз . Комплексное сопротивление в алгебраической форме выглядит следующим образом

. (2.42)

Следовательно, активное сопротивление есть вещественная часть, а реактивное – мнимая часть комплекса полного сопротивления цепи. Частные случаи формулы (2.42) приведены в таблице 2.1

Таблица 2.1

Величина, обратная комплексу полного сопротивления, называется комплексом полной проводимости

, (2.43)

где , , – полная, активная, реактивная проводимости цепи соответственно.

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений. Первый закон Кирхгофа: «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

. (2.44)

Второй закон Кирхгофа: «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура»

. (2.45)

Таким образом, при комплексном представлении всех параметров методы расчета сложных цепей постоянного тока, основанные на законах Ома и Кирхгофа (контурных токов, узловых потенциалов, эквивалентного генератора, преобразования и др.), можно применять для расчета цепей синусоидального тока.

Приложение 1. Комплексный метод расчета электрических цепей синусоидального тока

Все графические методы расчета цепей синусоидального тока не обеспечивают точного расчета электрических цепей, кроме того, они сложны и трудоемки.

Наиболее простым и точным методом расчета электрических цепей синусоидального тока является комплексный метод, основанный на теории комплексных чисел.

Синусоидальная величина изображается вращающимся вектором на комплексной плоскости с осями ±1 и ±j, где символ 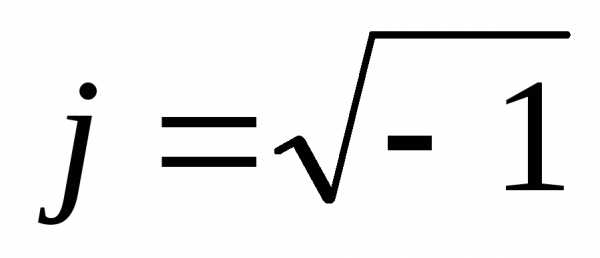- мнимая единица.

За положительное направление вращения вектора принято направление против часовой стрелки. За время, равное одному периоду, вектор совершает один оборот.

На рис.47 изображен вектор комплексного тока , которому соответствует комплексное число

Рис. 47. Составляющие комплексного числа на комплексной плоскости

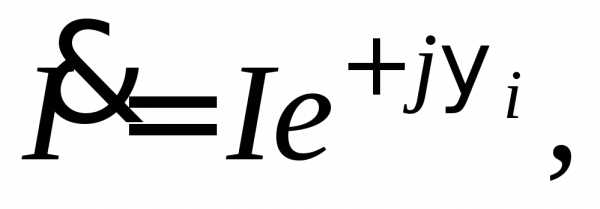
где I - модуль действующего значения тока, равный длине вектора;

где - действительная составляющая тока; - мнимая составляющая; yi= arctg (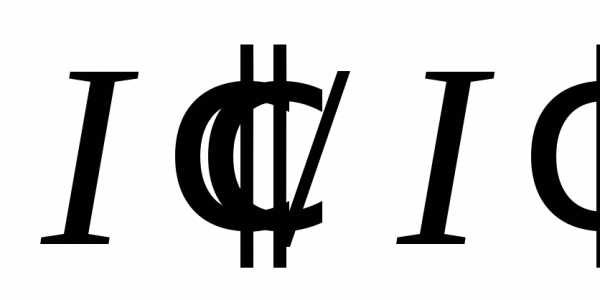) – аргумент тока, равный начальной фазе, т. е. угол между вектором и действительной полуосью +1 при t = 0. Аргумент положительный, если вектор отложен в направлении против движения часовой стрелки, и отрицательный, - если по часовой.

Комплексные значения синусоидальных величин обозначают 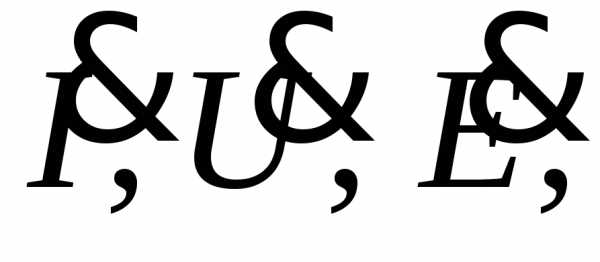несинусоидальных-z,S.

Над комплексными числами можно производить все алгебраические действия (при сложении и вычитании удобнее использовать алгебраическую форму, а при умножении, делении, возведении в степень, извлечении корня – показательную).

Алгебраическая форма записи:

Тригонометрическая форма записи:

İ = Icosyi + jsinyi .

Показательная форма записи:

İ = Iejyi .

Переход из одной формы записи в другую осуществляется по формуле Эйлера через тригонометрическую форму записи

e±jα= cosα ± j sinα.

Например:

İ = 10ej37º = 10cos37˚ + j10sin37º = 10 · 0,8 + j10 · 0,6 = 8 + j6

İ =8 + j6== 10e+j37º (А).

При работе с комплексными числами (İ) используют и сопряженные комплексные величины (I*), имеющие одинаковые модули и одинаковые по величине, но противоположные по знаку аргументы:

İ = 10e j37º, А; I* =10e–j37º, А.

Произведение İ· I* = 10e j37º· 10e–j37º = 100ej0°, À.

Приложение 2.

ОСНОВНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА

Таблица 22

Двухполюсник	Резистор (резистивное сопротивление	Катушка (индуктивное реактивное сопротивление	Конденсатор (емкостное реактивное сопротивление)
Обозначение
Связь между мгновенными значениями u и i	i= uR/R	uL = Ldi/dt	iС = CduC/dt
Если задано	uR = Umaxsinωt	uL = Umaxsinωt	uC = Umaxsinωt
То имеем	i = maxsinωt/R	i = Umaxsin(ωt – = Imax sin(ωt – π/2)	i= ωCUmaxcosωt= = Imax sin(ωt +π/2)
Действующее значение тока	I = UR/R	I = UL/ωL	I =ωCUC
Сопротивление (реактивное сопротивление)	R	XL = ωL	XC = 1/ωC
Сдвиг фаз	φ = ψU – ψi = 0	φ = ψU – ψi =+90	φ = ψU – ψi = –90 ͦ
Сдвиг по фазе
Комплексное сопротивление
Расчет комплексным методом
Зависимость сопротивления от частоты	R R ω	XL ωL ω	XC 1/ωC ω

studfiles.net

Комплексный метод расчета электрических цепей

Электротехника Комплексный метод расчета электрических цепей
просмотров - 247

Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, принято называть комплексным методом.

Существует несколько форм представления комплексного числа:

- алгебраическая форма: ;

- показательная (или экспоненциальная) форма: ;

- тригонометрическая форма: .

Эти формы связаны между собой соотношениями: - модуль комплексного числа; - главное значение аргумента комплексного числа.

Для геометрического изображения используют прямоугольную систему координат, в которой по горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые.

Для вещественной и мнимой частей комплексного числа употребляют также обозначения: , .

Полезно запомнить следующие соотношения:

; ; ; , и т.д.

Кроме того: ; .

Две комплексные величины, имеющие равные модули и равные, но противоположные по знаку аргументы, называются сопряженными.

В случае если , то сопряженное ему комплексное число запишется в форме . При этом соблюдается равенство: .

Пусть имеем синусоидально изменяющийся ток с начальной фазой ψi :

Комплексное изображение синусоидального тока, при заданной угловой частоте ω, определяется двумя величинами: амплитудой и начальной фазой.

где - комплексная амплитуда тока.

Тогда

Рассмотрим производную по времени от синусоидального тока:

Комплексное изображение производной будет иметь вид:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, операция дифференцирования действительной функции заменяется умножением ее комплексного изображения на .

Рассмотрим изображение интеграла от синусоидальной функции тока.

Комплексное изображение интеграла будет иметь вид:

Следовательно, операция интегрирования действительной функции сводится к делению ее комплексного изображения на .

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, комплексный метод позволяет заменить интегро-дифференциальное уравнение, содержащее функции времени, алгебраическим уравнением с их комплексными изображениями.

Алгоритм метода:

1. Замена заданных функций времени их комплексными изображениями.

2. Замена всех уравнений, составленных по закону Кирхгофа, алгебраическими уравнениями для комплексных изображений.

3. Отыскание комплексных изображений искомых функций.

4. Переход к оригиналам этих функций.

В качестве примера рассмотрим цепь с последовательно соединенными элементами R,L и C, к зажимам которой приложено напряжение, изменяющееся по синусоидальному закону . Требуется найти ток в цепи: .

1) Заменяем функции времени их изображениями: , .

2) Составляем уравнение по второму закону Кирхгофа:

Полученное уравнение является алгебраическим. Все слагаемые имеют общий множитель . Окончательно получаем уравнение в комплексных амплитудах:

3) Из последнего уравнения легко определяется комплексная амплитуда тока:

где – комплексное сопротивление цепи.

4) Зная выражение для комплексной амплитуды тока в виде , можем, используя обратный переход, записать выражение для мгновенного тока: .

Обычно рассматривают действующие значения токов и напряжений. Так как действующие синусоидальные токи и напряжения меньше их амплитуд в раз, то обычно вместо комплексных амплитуд рассматривают комплексные действующие величины: , .

Комплексный метод расчета электрических цепей

Электротехника Комплексный метод расчета электрических цепей
просмотров - 248

Существует несколько форм представления комплексного числа:

- алгебраическая форма: ;

- показательная (или экспоненциальная) форма: ;

- тригонометрическая форма: .

Для вещественной и мнимой частей комплексного числа употребляют также обозначения: , .

Полезно запомнить следующие соотношения:

; ; ; , и т.д.

Кроме того: ; .

В случае если , то сопряженное ему комплексное число запишется в форме . При этом соблюдается равенство: .

Пусть имеем синусоидально изменяющийся ток с начальной фазой ψi :

где - комплексная амплитуда тока.

Тогда

Рассмотрим производную по времени от синусоидального тока:

Комплексное изображение производной будет иметь вид:

Рассмотрим изображение интеграла от синусоидальной функции тока.

Комплексное изображение интеграла будет иметь вид:

Алгоритм метода:

1. Замена заданных функций времени их комплексными изображениями.

3. Отыскание комплексных изображений искомых функций.

4. Переход к оригиналам этих функций.

1) Заменяем функции времени их изображениями: , .

2) Составляем уравнение по второму закону Кирхгофа:

3) Из последнего уравнения легко определяется комплексная амплитуда тока:

где – комплексное сопротивление цепи.

Моделирование в электроэнергетике - Метод расчета линейных электрических цепей. Метод комплексных амплитуд.

Метод расчета линейных электрических цепей. Метод комплексных амплитуд.

Рассмотрим линейную электрическую цепь с сосредоточенными параметрами, находящуюся под гармоническим воздействием ЭДС (синусоидальная функция от времени). Определение значений токов и напряжений в рассматриваемой схеме сводится к составлению и решению системы дифференциальных уравнений с постоянными коэффициентами, которые могут быть записаны в следующем виде:

В общем виде решение данного дифференциального уравнения будет определяться суммой двух составляющих: свободной и вынужденной составляющей.

Свободная составляющая представляет собой общее решение системы однородных линейных дифференциальных уравнений, составленных для схемы цепи после коммутации. Свободная составляющая определяет процессы, которые возникают в электрической цепи, выведенной из состояния покоя некоторым воздействием. Свободная составляющая характеризует процесс обмена энергией между индуктивными и емкостными элементами электрической цепи, частота колебаний свободной составляющей определяется параметрами расчетной цепи. В линейных электрических цепях свободные составляющие затухают во времени по экспоненциальному закону.

Вынужденная составляющая представляет собой частное решение системы однородных линейных дифференциальных уравнений, составленных для схемы цепи после коммутации. Вынужденная составляющая определяет установившийся режим работы системы после окончания переходного процесса. Данная составляющая может также называться установившейся составляющей.

В большинстве решаемых задач рассматривают только квазистационарные режимы работы энергосистемы (установившийся режим работы), в связи с этим рассматривают только вынужденную составляющую, а свободной составляющей пренебрегают. В таком случае для расчёта сложной электрической цепи с гармоническими источниками ЭДС широко применяется метод комплексных амплитуд. Данный метод в технической литературе может встречаться под другими названиями: символический метод или комплексный метод, так как он основан на символическом изображении действительных синусоидальных функций времени комплексными числами. Данный метод разработан в конце XIX века американскими инженерами - электротехниками Ч.П.Штейнметцем и А.Е.Кеннели.

Метод комплексных амплитуд, основан на идее функционального преобразования, при котором гармоническая функция из временной области (оригинал функции) заменяется функцией, которая определена на комплексной области (изображение исходной функции). Переход от реальных гармонических токов и напряжений к комплексным амплитудам осуществляется с помощью формулы Эйлера, которая связывает комплексную экспоненту с тригонометрическими функциями.

Формула Эйлера позволяет определить тригонометрические функции через комплексные величины, которые записываются через экспоненты с мнимыми аргументами:

• Рассмотрим случай, когда гармонический сигнал представлен в виде косинусоидальной функции. В рассматриваемом случае в соответствии с представленными выражениями гармоническая функция, заданная во временной области, переписывается в виде двух экспонент в следующем виде:

Таким образом, оригинал косинусоидальной функции определяется проекцией комплексного числа на вещественную ось. В представленном выражении используются следующие обозначения:

- комплексная амплитуда, которая определяется по формуле:

- сопряженная комплексная амплитуда, которая определяется по формуле:

- оператор вращения, который имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью . Всякий неподвижный вектор, будучи умноженным на оператор вращения, начинает вращаться в комплексной плоскости против часовой стрелки с заданной угловой скоростью.

Рис.1.Разложение косинусоидальной функции в виде двух векторов

Таким образом, символическое изображение косинусоидальной функции (оригинала функции) определяется при заданной частоте ω вектором, который характеризуется двумя величинами - амплитудой и начальной фазой.

• Рассмотрим другой случай, когда гармонический сигнал представлен в виде синусоидальной функции. В рассматриваемом случае в соответствии с представленными выражениями гармоническая функция, заданная во временной области, переписывается в виде двух экспонент в следующем виде:

Таким образом, оригинал синусоидальной функции определяется проекцией комплексного числа на мнимую ось. В представленном выражении используются следующие обозначения:

- комплексная амплитуда, которая определяется по формуле:

- сопряженная комплексная амплитуда, которая определяется по формуле:

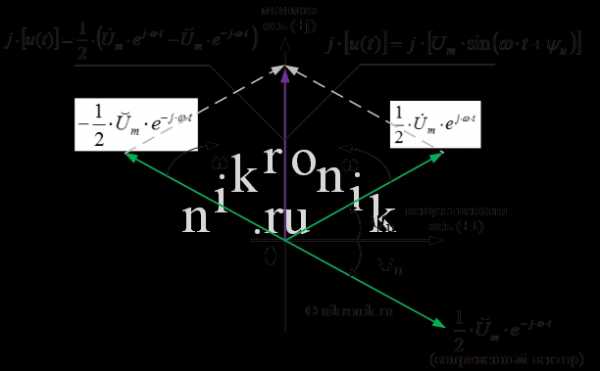
Рис.2.Разложение синусоидальной функции в виде двух векторов

Таким образом, символическое изображение синусоидальной функции (оригинала функции) определяется при заданной частоте ω вектором, который характеризуется двумя величинами - амплитудой и начальной фазой.

Использование метода комплексных амплитуд значительно упрощает расчет линейной электрической цепи, так как операции дифференцирования и интегрирования сводятся к задаче решения системы алгебраических уравнений: операция дифференцирование гармонической функции соответствует умножение комплексного числа на переменную «jω»,а операция интегрирование гармонической функции соответствует делению комплексного числа на «jω».

Объединяя полученные результаты можно сделать вывод, что любую гармоническую функцию с заданной частой ω можно представить в виде вектора на комплексной плоскости, который вращается с угловой скоростью ω. С целью единообразия выполнения расчетов в соответствии с методом комплексных амплитуд было принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для нулевого момента времени . Таким образом, символическое изображение синусоидальной функции определяется в следующем виде:

Для определения интенсивности действия электрических параметров (тока или напряжения) используют действующие комплексные значения, которые определяются следующим образом:

Расчет цепи синусоидального тока методом комплексных амплитуд проводится в следующем порядке:

- На первом этапе гармоническая функция, заданная во временной области, заменяется изображением данной функции на комплексной плоскости.

- На втором этапе составляется система уравнений, которая описывает рассматриваемую электрическую цепь, в соответствии с любым методом расчета электрических цепей. Далее выполняется расчет данной системы уравнений с определением комплексных значений искомых токов и напряжений.

- На третьем этапе выполняют обратное преобразование, с помощью которого переходят от изображения функции на комплексной плоскости к оригиналам функции во временной области. Чтобы восстановить исходное гармоническое колебание по известной комплексной амплитуде и частоте ω, необходимо комплексную амплитуду умножить на , а затем выделить мнимую часть (для синусоидальной функции).

Комплексное сопротивление электрической цепи

Определим комплексное сопротивление пассивных элементов электрической цепи, которые находятся под гармоническим воздействием. Для этого рассмотрим связь между током и напряжением на активном, индуктивном и емкостном элементах.

• Рассмотрим активное сопротивление, по которому протекает синусоидальный ток. Данный ток создает в активном напряжении падение напряжение на элементе, которое определяется в следующем виде:

Перепишем данную формулу для изображений синусоидальных функции в следующем виде:

Для нулевого момента времени данное выражение записывается в следующем виде:

Из полученного выражения видно, что ток на индуктивности совпадает по фазе с напряжением. Сопротивление на индуктивности носит активный характер и определяется в следующем виде:

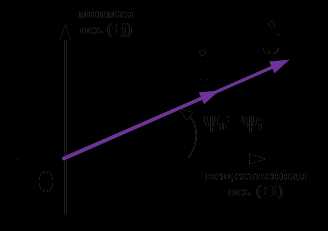
Рис.3. Векторная диаграмма токов и напряжений на резистивном элементе

• Рассмотрим индуктивный элемент, по которому протекает синусоидальный ток. Данный ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции. Таким образом, падение напряжение на элементе определяется в следующем виде:

Перепишем данную формулу для изображений синусоидальных функции в следующем виде:

Для нулевого момента времени данное выражение записывается в следующем виде:

Из полученного выражения видно, что ток на индуктивности отстает от напряжения на угол 90 градусов. Сопротивление на индуктивности носит реактивный характер и определяется в следующем виде:

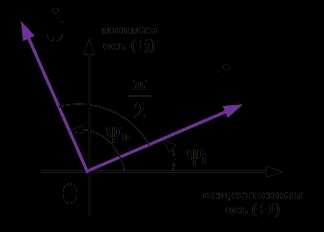
Рис.4. Векторная диаграмма токов и напряжений на индуктивном элементе

• Рассмотрим емкостной элемент, к которому приложено синусоидальное напряжение. Под действием синусоидального напряжения конденсатор будет периодически заряжаться и разряжаться. Периодическая перезарядка конденсатора будет сопровождаться протеканием тока. Таким образом, ток, протекающий между обкладками конденсатора, будет определяться следующим образом:

Перепишем данную формулу для изображений синусоидальных функции в следующем виде:

Для нулевого момента времени данное выражение записывается в следующем виде:

Из полученного выражения видно, что ток на емкости опережает напряжение на угол 90 градусов. Сопротивление на емкости носит реактивный характер и определяется в следующем виде:

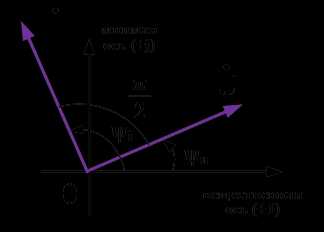
Рис.5. Векторная диаграмма токов и напряжений на емкостном элементе

Следует отметить, что для определения изображений синусоидальных функции (токов и напряжений) в электрической цепи необходимо составить систему уравнений любым доступным методом:

- с помощью первого и второго закона Кирхгофа, который записывается для изображений синусоидальных функции;

- с помощью метода контурных токов, который записывается для изображений синусоидальных функции;

- с помощью метода узловых потенциалов, который записывается для изображений синусоидальных функции.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

simenergy.ru

<<	<	Ноябрь 2013			>	>>
Пн	Вт	Ср	Чт	Пт	Сб	Вс
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

Метод расчета линейных электрических цепей. Метод комплексных амплитуд. Комплексный метод расчета электрических цепей

Комплексный метод расчета цепей синусоидального тока

Похожие статьи:

Приложение 1. Комплексный метод расчета электрических цепей синусоидального тока

Приложение 2.

Комплексный метод расчета электрических цепей

Электротехника Комплексный метод расчета электрических цепей
просмотров - 247

Читайте также

Комплексный метод расчета электрических цепей

Электротехника Комплексный метод расчета электрических цепей
просмотров - 248

Читайте также

Моделирование в электроэнергетике - Метод расчета линейных электрических цепей. Метод комплексных амплитуд.

Метод расчета линейных электрических цепей. Метод комплексных амплитуд.

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация

Метод расчета линейных электрических цепей. Метод комплексных амплитуд. Комплексный метод расчета электрических цепей

Комплексный метод расчета цепей синусоидального тока

Похожие статьи:

Приложение 1. Комплексный метод расчета электрических цепей синусоидального тока

Приложение 2.

Комплексный метод расчета электрических цепей

Электротехника Комплексный метод расчета электрических цепей просмотров - 247

Читайте также

Комплексный метод расчета электрических цепей

Электротехника Комплексный метод расчета электрических цепей просмотров - 248

Читайте также

Моделирование в электроэнергетике - Метод расчета линейных электрических цепей. Метод комплексных амплитуд.

Метод расчета линейных электрических цепей. Метод комплексных амплитуд.

Видеоматериалы

Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше

Соответствует ли вода и воздух установленным нормативам?

С начала года из ветхого и аварийного жилья в республике были переселены десятки семей

Столичный Водоканал готовится к зиме

Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе

Актуальные темы

Формирование энергосберегающего поведения граждан

Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год

НАУЧИМСЯ ЭКОНОМИТЬ В БЫТУ

Рубрикатор

Пользователю

Доп.информация

Электротехника Комплексный метод расчета электрических цепей
просмотров - 247

Электротехника Комплексный метод расчета электрических цепей
просмотров - 248