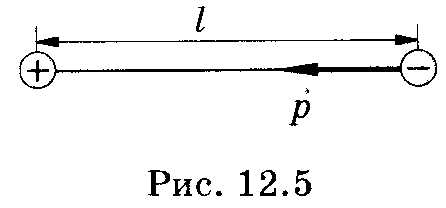Формула вычисления емкости конденсатора. Коэффициент электростатической емкости. Конденсаторы. Емкость конденсаторов различной геометрической конфигурации. Конденсатор формула емкости
Объем конденсатора формула. Коэффициент электростатической емкости. Конденсаторы. Емкость конденсаторов различной геометрической конфигурации
Рассмотрим уединенный проводник , т.е. проводник, который удален от других проводников, тел и зарядов. Его потенциал прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, принимают различные потенциалы. Поэтому для уединенного проводника можно записать
Величину (8.11.1.)
называют электроемкостью (или просто емкостью ) уединенного проводника.
Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.
Единица измерения электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл.
Согласно формуле , потенциал уединенного шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью , равен
Используя формулу (8.11.1.), получим, что емкость шара
Для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.
Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом q, т.е. понижают потенциал проводника, что приводит (см.(8.11.1.)) к повышению его электроемкости.
Конденсатор - устройство, состоящее из двух проводников (обкладок), разделенных диэлектриком.
На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.
Емкость конденсатора - это физическая величина, равная отношению заряда q одной из обкладок, к разности потенциалов () между его обкладками:
Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +q и -q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать, используя формулы (8.3.7) и (8.11.4.). При наличии диэлектрика между обкладками разность потенциалов между ними:
где - диэлектрическая проницаемость.
Тогда из формулы (8.11.4.), заменяя q= , с учетом (8.11.5.) получим выражение для емкости плоского конденсатора:
Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами и ( > ), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле для поля равномерно заряженного бесконечного цилиндра с линейной плотностью (l - длина обкладок). С учетом наличия диэлектрика между обкладкамиПодставив (8.11.9.) в (8.11.4.), получим
т.е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком.
Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками:
Используя определение емкости конденсатора, получаем:
Отметим, что полученная формула является приближенной, так как выведена без учета искажения поля у краев пластин. Расчет по этой формуле дает завышенное значение ёмкости и тем точнее, чем меньше зазор по сравнению с линейными размерами пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет собой систему двух концентрических сфер с радиусами и. Электрическое поле между обкладками сферического конденсатора согласно теореме Гаусса определяется зарядом внутренней сферы. Напряжение между обкладками равно:
.
Для ёмкости сферического конденсатора получаем:
Это формула точная.
Если , полученная формула переходит в выражение для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
..
Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора.
Соединение конденсаторов.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного соединения конденсаторов.
Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует:
Если , то(ёмкость последовательного соединения меньше наименьшей ёмкости в последовательном соединении).
Для последовательно соединенных конденсаторов емкость вычисляется по формуле:
Ёмкость параллельного соединения конденсаторов.
Заряд батареи равен сумме зарядов:
а напряжение . По определению емкости получаем:
Для параллельно соединенных конденсаторов:.
В случае одинаковых конденсаторов: .
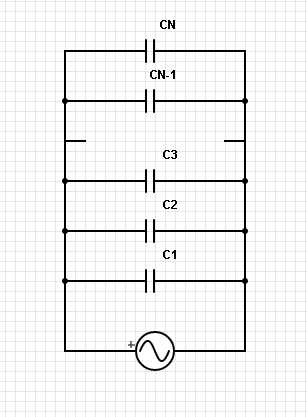
Оценить емкость батареи (см. рисунок) .
Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок).
Для расчета ёмкости батареи получаем:
Откуда: , так как, то.
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярными инеполярными. Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных » зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично.
Под действием электрического поля диполи ориентируются преимущественно в направлении п
stroygram.ru
Формула вычисления емкости конденсатора. Коэффициент электростатической емкости. Конденсаторы. Емкость конденсаторов различной геометрической конфигурации
Взаимная электроемкость. Конденсаторы. Пусть вблизи заряженного проводника А находятся незаряженные проводники или диэлектрики. Под действием поля проводника А в телах 1 и 2 возникают индуцированные (если 1 и 2 проводники) или связанные (если диэлектрики) заряды, причем ближе к А будут располагаться заряды противоположного знака (рис.1.25). Индуцированные (или связанные) заряды создают свое поле противоположного направления, чем ослабляют поле проводника А, уменьшая его потенциал и увеличивая его электроемкость.
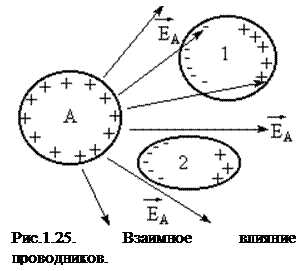На практике существует потребность в устройствах, которые при относительно небольшом потенциале накапливали (конденсировали) бы на себе заметные по величине заряды. В основу таких устройств, называемых конденсаторами, положен факт, что емкость проводника возрастает при приближении к нему других тел. Простейший плоский конденсатор состоит из двух близко расположенных проводников, заряженных равными по величине и противоположными по знаку зарядами. Образующие данную систему проводники называются обкладками.
Для того, чтобы поле, создаваемое заряженными обкладками, было полностью сосредоточено внутри конденсатора, обкладки должны быть в виде двух близко расположенных пластин, или коаксиальных цилиндров, или концентрических сфер. Соответственно конденсаторы называются плоскими, цилиндрическими или сферическими.
Разность потенциалов между обкладками пропорциональна абсолютной величине заряда обкладки. Поэтому отношение есть величина постоянная для конкретного конденсатора. Она обозначается С и называется взаимной электроемкостью проводников или емкостью конденсатора. Емкость конденсатора численно равна заряду, который нужно перенести с одной обкладки конденсатора на другую, чтобы изменить разность их потенциалов на единицу.
Разность потенциалов плоского конденсатора равна , где поверхностная плотность заряда обкладки.
S - площадь обкладки конденсатора.. Отсюда емкость плоского конденсатора . Из этой формулы следует, что С плоского конденсатора зависит от его геометрических размеров, т.е. от S и d, и диэлектрической проницаемости диэлектрика, заполняющего межплоскостное пространство. Применение в качестве прослойки сегнетоэлектриков значительно увеличивает емкость конденсатора, т.к. e у них достигает очень больших значений. В очень сильных полях (порядка Е пр »10 7 В/м) происходит разрушение диэлектрика или «пробой», он перестает быть изолятором и становится проводником. Это «пробивное напряжение» зависит от формы обкладок, свойств диэлектрика и его толщины..
Для получения устройств различной электроемкости конденсаторы соединяют параллельно и последовательно.
Конденса́тор (от лат. condensare - «уплотнять», «сгущать», или от от лат. condensatio - «накопление») - двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.
Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемыхобкладками ), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электр
wirin-expert.ru
Площадь конденсатора формула. Коэффициент электростатической емкости. Конденсаторы. Емкость конденсаторов различной геометрической конфигурации
Конденса́тор (от лат. condensare - «уплотнять», «сгущать», или от от лат. condensatio - «накопление») - двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.
Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемыхобкладками ), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).
Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончаниипереходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.
В методе гидравлических аналогийконденсатор - это гибкая мембрана, вставленная в трубу. Анимация демонстрирует мембрану, которая растягивается и сокращается под действием потока воды, что аналогично заряду и разряду конденсатора под действием электрического тока.
С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом
,
Где j - мнимая единица, ω - циклическая частота (рад/с ) протекающего синусоидального тока, f - частота в Гц , C - ёмкость конденсатора (фарад ). Отсюда также следует, что реактивное сопротивление конденсатора равно: . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
Резонансная частота конденсатора равна
При f > f p конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2-3 раза ниже резонансной.
Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
где U - напряжение (разность потенциалов), до которого заряжен конденсатор, а q - электрический заряд.
Обозначение конденсаторов на схемах. В России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ 2.728-74 ] либо международному стандарту IEEE 315-1975:
На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 1·10 6 пФ = 1·10 −6 Ф) и пикофарадах, но нередко и в нанофарадах (1 нФ = 1·10 −9 Ф). При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения. Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мкФ x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 - 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятично логарифмических рядов значений Е3, Е6, Е12, Е24, то есть на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.
Характеристики конденсаторов
Основные параметры Ёмкость Основной характеристикой конденсатора является его ёмкость , характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU ). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.
Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположена на расстоянии d друг от друга, в системе СИ выражается формулой: , где - диэлектрическая проницаемость среды, заполняющая пространство между пластинами (в вакууме равна единице), - электрическая постоянная, численно равная8,854187817·10 −12 Ф/м. Эта формула справедлива, лишь когда d намного меньше линейных размеров пластин.
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.
При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна
Или
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.
Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.
Удельная ёмкость Конденсаторы также характеризуются удельной ёмкостью - отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
Плотность энергии Плотность энергии электролитического конденсатора зависит от конструктивного исполнения. Максимальная плотность достигается у больших конденсаторов, где масса корпуса невелика по сравнению с массой обкладок и электролита. Например, у конденсатора EPCOS B4345 с ёмкостью 12 000 мкФ, максимально допустимым напряжением 450 В и массой 1,9 кг плотность энергии при максимальном напряжении составляет 639 Дж/кг или 845 Дж/л. Особенно важен этот параметр при использовании конденсатора в качестве накопителя энергии, с последующим мгновенным её высвобождением, например, в пушке Гаусса.
Рассмотрим уединенный проводник , т.е. проводник, который удален от других проводников, тел и зарядов. Его потенциал прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, принимают различные потенциалы. Поэтому для уединенного проводника можно записать
Величину (8.11.1.)
называют электроемкостью (или просто емкостью ) уединенного проводника.
Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.
Единица измерения электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл.
Согласно формуле , потенциал уединенного шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью , равен
Используя формулу (8.11.1.), получим, что емкость шара
Для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.
Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом q, т.е. понижают потенциал проводника, что приводит (см.(8.11.1.)) к повышению его электроемкости.
Конденсатор - устройство, состоящее из двух проводников (обкладок), разделенных диэлектриком.
На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.
Емкость конденсатора - это физическая величина, равная отношению заряда q одной из обкладок, к разности потенциалов () между его обкладками:
Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +q и -q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать, используя формулы (8.3.7) и (8.11.4.). При наличии диэлектрика между обкладками разность потенциалов между ними:
где - диэлектрическая проницаемость.
Тогда из формулы (8.11.4.), заменяя q= , с учетом (8.11.5.) получим выражение для емкости плоского конденсатора:
Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами и ( > ), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле для поля равномерно заряженного бесконечного цилиндра с линейной плотностью (l - длина обкладок). С учетом наличия диэлектрика между обкладкамиПодставив (8.11.9.) в (8.11.4.), получим
т.е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком.
Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками:
Используя определение емкости конденсатора, получаем:
Отметим, что полученная формула является приближенной, так как выведена без учета искажения поля у краев пластин. Расчет по этой формуле дает завышенное значение ёмкости и тем точнее, чем меньше зазор по сравнению с линейными размерами пластин.
Ёмкость сферического конденсатора.
Сферический конденсатор представляет собой систему двух концентрических сфер с радиусами и. Электрическое поле между обкладками сферического конденсатора согласно теореме Гаусса определяется зарядом внутренней сферы. Напряжение между обкладками равно:
.
Для ёмкости сферического конденсатора получаем:
Это формула точная.
Если , полученная формула переходит в выражение для ёмкости плоского конденсатора.
Ёмкость цилиндрического конденсатора.
Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной.
Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:
..
Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора.
Соединение конденсаторов.
В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).
Ёмкость последовательного соединения конденсаторов.
Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует:
Если , то(ёмкость последовательного соединения меньше наименьшей ёмкости в последовательном соединении).
Для последовательно соединенных конденсаторов емкость вычисляется по формуле:
Ёмкость параллельного соединения конденсаторов.
Заряд батареи равен сумме зарядов:
а напряжение . По определению емкости получаем:
Для параллельно соединенных конденсаторов:.
В случае одинаковых конденсаторов: .
Оценить емкость батареи (см. рисунок) .
Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок).
Для расчета ёмкости батареи получаем:
Откуда: , так как, то.
Лекция 7.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.
Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярными инеполярными. Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю.
Поляризация.
В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных » зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично.
Под действием электрического поля диполи ориентируются преимущественно в направлении поля. Рассмотрим подробнее этот механизм (см. рисунок). Пара сил исоздает вращательный момент равный, где- дипольный момент молекулы. Этот момент стремится ориентировать диполь вдоль поля. В ионных кристаллах под действием электрического поля все положительные ионы смещаются по полю, отрицательные – против поля. Отметим, что смещение зарядов очень малы даже по сравнению с размерами молекул. Это связано с тем, что напряженность внешнего электрического поля обычно много меньше напряженности внутренних электрических полей в молекулах.
Отметим, что существуют диэлектрики, поляризованные даже при отсутствии внешнего поля (электреты, сегнетоэлектрики). Мы остановимся на рассмотрении только однородных диэлектриков, в которых отсутствует остаточная поляризация, а объемный и «связанный» заряд всегда равен нулю .
stroykes.ru
По какой формуле определяется емкость конденсатора. Коэффициент электростатической емкости. Конденсаторы. Емкость конденсаторов различной геометрической конфигурации
Рассмотрим уединенный проводник , т.е. проводник, который удален от других проводников, тел и зарядов. Его потенциал прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, принимают различные потенциалы. Поэтому для уединенного проводника можно записать
Величину (8.11.1.)
называют электроемкостью (или просто емкостью ) уединенного проводника.
Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.
Единица измерения электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл.
Согласно формуле , потенциал уединенного шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью , равен
Используя формулу (8.11.1.), получим, что емкость шара
Для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.
Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом q, т.е. понижают потенциал проводника, что приводит (см.(8.11.1.)) к повышению его электроемкости.
Конденсатор - устройство, состоящее из двух проводников (обкладок), разделенных диэлектриком.
На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.
Емкость конденсатора - это физическая величина, равная отношению заряда q одной из обкладок, к разности потенциалов () между его обкладками:
Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +q и -q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать, используя формулы (8.3.7) и (8.11.4.). При наличии диэлектрика между обкладками разность потенциалов между ними:
где - диэлектрическая проницаемость.
Тогда из формулы (8.11.4.), заменяя q= , с учетом (8.11.5.) получим выражение для емкости плоского конденсатора:
Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами и ( > ), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле для поля равномерно заряженного бесконечного цилиндра с линейной плотностью (l - длина обкладок). С учетом наличия диэлектрика между обкладкамиПодставив (8.11.9.) в (8.11.4.), получим
т.е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.
Конденса́тор (от лат. condensare - «уплотнять», «сгущать», или от от лат. condensatio - «накопление») - двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.
Конденсатор является пассивным эле
ruscos.ru
Формулы Емкости Конденсатора / УКРПРОМТОРГ
Электрическая емкость. Конденсаторы. Емкость конденсатора. Апрель 12, 2014 08:23
|
Электрическая емкость. Конденсаторы. | |
|
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: , где e - диэлектрическая проницаемость окружающей среды. Следовательно: эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы. | |
|
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: . | |
|
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда. |
Емкость шара в СИ: - |
|
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. |
1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф |
|
Конденсаторы (condensare - сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы - лейденская банка (Мушенбрук, сер. XVII в.). | |
|
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. | |
|
На рисунке - плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального - все). Усферического - все поле сосредоточено между обкладками. | |
|
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: . | |
|
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды - конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними. | |
|
Емкость плоского конденсатора. , т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика. | |
|
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора. | |
|
Виды конденсаторов | |
|
При подключении электролитического конденсатора необходимо соблюдать полярность. | |
|
Назначение конденсаторов
| |
Источник: www.eduspb.com
Возможно, вам понравится:
Дой пак с дозатором для упаковки ...
На воронежском рынке жилья наметился спад — Российская ГазетаЕсли исходить из среднегодовой рождаемости и самой популярной площади квартиры (50 квадратных метров), то по простенькой формуле получаем цифру на уровне 1,2-1,3 миллиона "квадратов" в год на всю область. А минрегион призывает строить два ..
Похожие страницы:
ukrpromtorg.com.ua
Эквивалентная ёмкость конденсаторов
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
| Альтернативное отображение |
Последовательное соединение
Написав бот, расчета размерностей Система единиц измерения онлайн теперь начнем осваивать такую многогранную и сложную область как электротехника.
И первое, что нам пригодится, это расчет эквивалентных характеристик основных электрических элементов( ёмкость, индуктивность, сопротивление).
Хотелось бы напомнить, что ёмкости некоторых типовых конструкций мы уже умеем рассчитывать Ёмкость конденсатора онлайн
Сами по себе формулы очень просты, но нюанс состоит в том, как нам точно посчитать ёмкость двух последовательно соединенных конденсаторов если один из конденсаторов имеет ёмкость 10 пФ, а второй 250нФ. Размерность показывает что они различаются в 1000 раз. Можно конечно все перевести в абсолютные значения, но это при большом количестве конденсаторов способствует возникновению ошибок.
Итак, последовательное соединение конденсаторов имеет следующий вид
И формула расчета эквивалентной ёмкости выглядит так
Паралельное СОЕДИНЕНИЕ
Последовательное соединение нескольних конденсаторов выглядит так, как показано на рисунке
А формула становится до безобразия простой и наглядной
Синтаксис
Он очень прост
calc_e список емкостей с размерностями через запятую.
В ответе мы получим эквививалентное значение ёмкости при последовательном и паралельных соединениях.
Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.
Примеры
Рассчитать ёмкость трех конденсаторов следующих номиналов: 10 пФ, 0.2нФ и 344мФ
В запросе так и пишем calc_e 10пФ,0.2нФ,344мФ
Ответ не заставит себя долго ждать и выглядит вот так
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
|
9.5238095235459пикофарад |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
|
344.00000021милифарад |
| Альтернативное отображение |
Удачи в расчетах!
- Эквивалентное сопротивление онлайн >>
www.abakbot.ru
Ёмкость сферического конденсатора – Формулы по физике.рф
Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
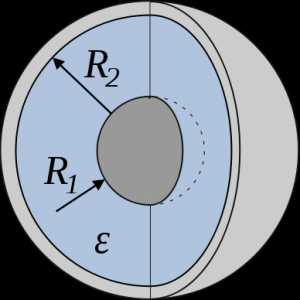
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
При малой величине зазора, то есть , а следовательно можно считать, что емкость сферического конденсатора будет равна . Площадь сферы следовательно формула будет совпадать с формулой емкости плоского конденсатора
Так же есть:
Энергия конденсатора:
Ёмкость конденсатора :
Ёмкость цилиндрического конденсатора :
Емкость плоского конденсатора : ;
В Формуле мы использовали :
— Электроемкость сферического конденсатора
— Относительная диэлектрическая проницаемость
— Электрическая постоянная
— Больший радиус (от центра, до края конденсатора)
— Малый радиус (Его может и не быть — это пустота)
xn--e1adcbkcgpcji1bjh6h.xn--p1ai
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
