Непосредственные и косвенные измерения — презентация онлайн
1. НЕПОСРЕДСТВЕННЫЕ И КОСВЕННЫЕ ИЗМЕРЕНИЯ
2. Виды измерений
• Однократные непосредственные
измерения
• Многократные непосредственные
измерения
• Косвенные измерения
3. НЕПОСРЕДСТВЕННЫЕ ИЗМЕРЕНИЯ
• Непосредственным называется измерение,
при котором численное значение физической
величины находят с помощью измерительного
прибора.
• Примеры непосредственных измерений:
измерение длины тела линейкой,
длительности промежутка времени –
секундомером, силы тока в проводнике –
амперметром, массы тела – при помощи
рычажных весов и гирь.
4. Однократные непосредственные измерения физических величин
ОДНОКРАТНЫЕ НЕПОСРЕДСТВЕННЫЕ
ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
5. АБСОЛЮТНАЯ ПОГРЕШНОСТЬ НЕПОСРЕДСТВЕННОГО ИЗМЕРЕНИЯ
• Абсолютная погрешность однократного
непосредственного измерения ∆Х
величины Х складывается из погрешности
измерительного прибора ∆пр
(инструментальной погрешности) и
погрешности отсчета ∆отс
∆Х = ∆пр + ∆отс
6.
 ПОГРЕШНОСТЬ ОТСЧЕТА
ПОГРЕШНОСТЬ ОТСЧЕТА
• Абсолютная погрешность отсчета ∆отс
берется равной половине цены деления
шкалы измерительного прибора
∆отс = ½ С
• Или равной цене деления шкалы прибора
со «скачущей» стрелкой (например, у
секундомера)
∆отс = С.
7. ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ
• Абсолютная погрешность прибора ∆пр
определяется на заводе-изготовителе и
указывается в паспорте прибора
8. Абсолютная погрешность некоторых приборов
№
Приборы
1 Линейка ученическая
2 Лента измерительная
3 Штангенциркуль
Пределы
измерения
Цена деления
0 – 50 см
0 – 150 см
0 – 150 мм
1 мм
0,5 см
0,1 мм
Абсолютная
погрешность
прибора
1 мм
0,5 см
0,05 мм
9. Алгоритм непосредственного измерения
1. Рассмотри шкалу прибора, найди цену
минимального деления С шкалы прибора.
2. Измерь физическую величину один раз,
найди ее измеренное значение Хи.
3. Найди абсолютную погрешность прибора,
используя справочные таблицы ∆пр.
4. Найди абсолютную погрешность отсчета
∆отс по цене деления прибора С.
5.Найди абсолютную погрешность измерения по
формуле
∆Х = ∆пр + ∆отс
Абсолютную погрешность округли до одной
значащей цифры
6. Запиши результат измерения в виде
Х = (Хи ± ∆Х)
Измеренное значение округли при этом до
разряда, оставшегося в абсолютной погрешности
7. Вычисли относительную погрешность
измерения
х =
11. Косвенные измерения
КОСВЕННЫЕ ИЗМЕРЕНИЯ
12. Косвенные измерения
• Косвенными называются измерения
физической величины, при которых
значение физической величины находится
по некоторой функциональной зависимости
(формуле)
.
• Измеренное
значение Хи подсчитывают по
,
,
измеренным значениям величин,
используя функциональную зависимость
.
• а, в, с — непосредственно измеренные
величины (в их числе могут быть и
величины известные заранее), причем
a (au a)
b (bu b)
c (cu c)
14.
 Относительная погрешность измерения
Относительная погрешность измерения
• По виду функциональной зависимости
величины Х от непосредственно
измеренных величин рассчитывают
относительную погрешность косвенного
измерения
Зависимость
величины Х от
других величин
Относительная
погрешность Х
косвенного
измерения
Зависимость
величины Х от
других величин
Относительная
погрешность Х
косвенного
измерения
а
аи
Х=а+в
Х
а в
аи ви
Х=n·а
Х
Х=а-в
Х
а в
аи ви
Х=аn
Х n
а в
аи ви
Х = n√а
Х
Х=а·в
Х = а/в
Х
Х
а в
аи ви
Х = sin а
а
аи
1 а
n аи
Х a ctga
16. Алгоритм косвенного измерения
1. Запиши формулу для расчета физической
величины
Х f (a, b, c)
2. Вычисли измеренное значение
физической величины, подставив в
формулу измеренные значения величин,
ранее известных
Хи f (aи , bи , cи )
3. Рассчитай относительную погрешность по виду
Рассчитай относительную погрешность по виду
функциональной зависимости
4. Рассчитай абсолютную погрешность измерения по
формуле
Абсолютную погрешность округли до одной значащей
цифры
х и
5. Результат измерения (истинное значение)
представляют в виде
( и )
при этом значение Хи округляют или уточняют до
разряда, оставшегося в значении после его
округления
18. Задача 1
• При помощи вольтметра и амперметра
надо измерить сопротивление проводника,
если при напряжении на концах
проводника U (4,8 0.1) B в нем возник ток,
сила которого I (1.10 0.05) A .
Проанализируем данные задачи.
U u = 4,8 В, U = 0,1В, Iu =1,10 А, I = 0,05А.
1. используя формулу закона Ома, выполняют косвенное измерение
сопротивления проводника:
Ru
Uu 4.8 B
= 4,4 Ом
Iu 1.10 A
2. По таблице находят формулу для расчета относительной погрешности
и вычисляют погрешность:
К
U I 0. 1 0.05
1 0.05
0.021 0.045 0.066 0.07
Uu Iu 4.8 1.10
3. Вычисляют абсолютную погрешность измерения:
R R Ru 0.07 4.36 0.29 0.3 (Ом).
4. Результат косвенного измерения записывают в виде интервала,
содержащего истинное значение величины:
R ( Ru R) (4.4 0.3) (Ом).
Относительные погрешности величин, входящих в функциональную
зависимость, по которой производят косвенное измерение, могут
значительно отличаться друг от друга. При этом погрешности одних величин
могут быть пренебрежимо малы по сравнению с погрешностями других.
Например, допустим, что величина измеряется косвенно по формуле
Х= а/в,
причем
а 0,05, в 0,003 .
Тогда имеем, что
Х а в 0,05 0,003 0,053 0,05 а .
Следовательно, в этом случае погрешность величины в пренебрежимо мала
по сравнению с погрешностью величины а. Поэтому погрешность величины
Х определяется только погрешностью величины а.
При выполнении лабораторных работ величины, у которых относительные
погрешность пренебрежимо малы, могут быть известны заранее (например,
табличные величины). В этих случаях вычисления погрешностей
В этих случаях вычисления погрешностей
выполняются по упрощенным формулам, без учета погрешностей таких
величин.
21. Задача 2
Определить длину окружности, если ее диаметр д (1,2 0,1) м , пренебрегая
погрешностью числа π.
Решение: 1) L d 3.768 м
2) L
d
du
, L
0.1
0.08( 3 ) 0.083
1.2
3) L L Lu 0 ,313 0 ,3 м
4) L ( Lu L ) ( 3.8 0.3 )м
Ответ: L ( 3.8 0.3 ) м.
22. Решите самостоятельно
Задача 3.
Определить массу сена в скирде, если ее объем V (450 3) м3, а средняя
плотность (92 1) кг/м3.
Ответ: m = (41±7)·103кг
Задача 4.
Определить скорость молокоотдачи, если за время дойки t (360 1)c
От коровы получено m (8,50 0,50) кг молока.
Справка: скорость молокоотдачи важная характеристика, позволяющая
определить пригодность коровы к доению доильным аппаратом.
Скорость молокоотдачи есть масса молока, получаемая от коровы в единицу
времени, она определяется по формуле с
m
.
t
Ответ: с=(2,36±0,02)·10-2кг/с
Задача 5.
Определить площадь круглой пластины, если известен ее диаметр:
д (1,2 0,1) м .
Ответ: S = (
? )м2
23. Измерительные приборы
ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
24. Штангенциркуль
Штангенциркуль применяется для измерений длин и
расстояний, не превышающих 25-30 см с точностью (в
зависимости от типа штангенциркуля) от 0,1 до 0,02 мм.
Измерения длин по линейным шкалам становятся более
точными за счет применения линейного нониуса.
2) Устройство штангенциркуля
Состоит штангенциркуль (см. рис.) из стальной линейки А,
несущей основную шкалу с ценой деления 1 мм; с левой
стороны линейки имеется неподвижная «щечка» Б.
Другая «щечка» В снабжена нониусом Г и может
перемещаться вдоль линейки А. Когда «щечки» Б и В
сдвинуты и соприкасаются, нуль основной шкалы и нуль
нониуса совпадают.
Линейный нониус представляет собой короткую
вспомогательную линейку с делениями, передвигаемую
вдоль основания шкалы; деления на нониусе нанесены
так, что 9 миллиметровых делений основной шкалы
равняются по длине 10 делениям нониуса; это означает,
что при цене деления основной шкалы Сш = 1 мм цена
деления нониуса Сн = 0,9 мм. .
.
Разность цен делений основной шкалы и нониуса
называется ценой точности нониуса:
Ст = Сш — Сн
Значение цены точности нониуса обычно указано на
подвижной части штангенциркуля.
25. Методика измерения линейных размеров объекта при помощи штангенциркуля
Для того, чтобы штангенциркулем
произвести измерение, измеряемый
предмет помещают между «щечками»,
которые сдвигают до соприкосновения
(без сильного нажима) с предметом и
закрепляют винтом Д. После этого
фиксируют показания штангенциркуля по
основной шкале и нониусу и находят
измеренное значение величины по
формуле линейного нониуса
L n = n и + С т · k.
Здесь n и – число целых делений основной
шкалы штангенциркуля, лежащих в
момент измерения левее нулевой метки
нониуса; k – значение метки нониуса,
совпавшей с какой-то меткой основной
шкалы; С т — цена точности нониуса
(значение обычно указано на подвижной
части штангенциркуля).
измерение диаметра d тела
штангенциркулем с ценой точности
нониуса С т = 0,1 мм. Число целых делений
основной шкалы, лежащих левее нуля
нониуса n и = 15; совпадает с некоторым
делением основной шкалы восьмое
деление нониуса, т.е. k = 8. Отсюда
следует, что
d и= 15 + 0,1 · 8 = 15,8 мм.
14 Метрологические основы технических измерений
Метрологические основы технических измерений
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств (ГОСТ 16263 -70).
Рассмотрим некоторые свойства измерений и средств измерений, характеризующие их основные качества.
По ГОСТ 16263-70 точность измерений – качество измерений, отражающее близость их результатов к истинному значению измеряемой величины.
Примечания: 1. Высокая точность измерений соответствует малым погрешностям всех видов, как систематических, так и случайных.
2. Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Например, при значении относительной погрешности 0,1 % точность измерений будет равна
Например, при значении относительной погрешности 0,1 % точность измерений будет равна
Т = 0,1/100 = 1000.
Поскольку любой результат измерений получают с некоторой погрешностью, возникает необходимость оценки ее характера и значения. Обобщенные характеристики погрешности используют для оценки точности измерения. Точность многократных измерений можно характеризовать такими их свойствами, как правильность, сходимость и воспроизводимость измерений (ГОСТ 16263-70).
Правильность измерений – качество измерений, отражающее близость к нулю систематических погрешностей в их результатах.
Рекомендуемые файлы
Сходимость измерений – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.
Здесь под условиями понимается весь комплекс обстоятельств, определяющий проведение измерений. Одинаковыми должны быть не только условия в узком смысле слова (влияющие величины, оказывающие нежелательное воздействие на измеряемый объект и средства измерений), но и средства измерений, и операторы, должно также соблюдаться единообразие измерительной процедуры.
Воспроизводимость измерений – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в различное время, в разных местах, разными методами и средствами).
Для обеспечения сопоставимости результатов измерений в рамках страны или в международном масштабе необходимо обеспечить единство измерений. Единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью.
Одним из необходимых условий обеспечения единства измерений является единообразие средств измерений – состояние средств измерений, характеризующееся тем, что они проградуированы в узаконенных единицах и их метрологические свойства соответствуют нормам.
Высокий уровень сходимости измерений соответствует малым значениям случайных погрешностей многократных измерений одной и той же физической величины с использованием одной методики выполнения измерений. В качестве упрощенной оценки сходимости может быть использован такой параметр, как размах результатов измерений
В качестве упрощенной оценки сходимости может быть использован такой параметр, как размах результатов измерений
R = Xmax – Xmin.
Геометрическое представление о размахе R результатов измерений можно получить на точечной диаграмме результатов многократных измерений одной и той же физической величины, которая строится в координатной системе «измеренные значения X – номер измерения N». Точечная диаграмма в определенных случаях позволяет высказать некоторые суждения и о правильности измерений. Например, устойчивая тенденция изменения результатов измерений свидетельствует о наличии в серии переменных систематических погрешностей. Выполнение нескольких серий многократных измерений одной и той же физической величины с использованием разных методик выполнения измерений позволяет оценить воспроизводимость измерений и получить предварительную оценку систематических постоянных погрешностей, присущих заведомо менее точным МВИ.
Для систематизации подхода к измерению, для выявления и оценки погрешностей необходимо классифицировать сами измерения.
В соответствии со стандартным определением, метод измерений – совокупность приемов использования принципов и средств измерений. Излишняя широта этого определения приводит к описаниям методов измерений с классификацией по разным признакам. В результате научно-техническая и учебная литература содержит множество наименований методов, не включенных в стандартную терминологию (например, абсолютный метод, косвенный метод, бесконтактный метод, интерференционный метод и ряд других).
Стандарт определяет значительное число методов измерений, но всех разновидностей измерений эти методы не покрывают. Для того, чтобы избавиться от путаницы предлагается укрупненное деление измерений на виды (с различными основаниями классификации), а также классификация методов измерений в зависимости от приемов использования мер в явном или опосредованном виде.
К видам измерений (если не разделять их по видам измеряемых физических величин на линейные, оптические, электрические и др.) можно отнести измерения:
— прямые и косвенные,
— совокупные и совместные,
— абсолютные и относительные,
— однократные и многократные,
— технические и метрологические,
— равноточные и неравноточные,
— равнорассеянные и неравнорассеянные,
— статические и динамические.
Прямые и косвенные измерения различают в зависимости от способа получения результата измерений.
Прямые измерения отличаются той особенностью, что искомое значение величины определяют непосредственно по устройству отображения измерительной информации применяемого средства измерений. Формально без учета погрешности измерения они могут быть описаны выражением
Q = X,
где Q – измеряемая величина,
X – результат измерения.
Косвенные измерения – измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Формальная запись такого измерения
Q = F (X, Y, Z,..),
где X, Y, Z,… – результаты прямых измерений.
Принципиальной особенностью косвенных измерений является необходимость обработки (преобразования) результатов вне прибора (на бумаге, с помощью калькулятора или компьютера), в противоположность прямым измерениям, при которых прибор выдает готовый результат. Классическими примерами косвенных измерений можно считать нахождение значения угла треугольника по измеренным длинам сторон, определение площади треугольника или другой геометрической фигуры и т.п.
Классическими примерами косвенных измерений можно считать нахождение значения угла треугольника по измеренным длинам сторон, определение площади треугольника или другой геометрической фигуры и т.п.
Прямые и косвенные измерения характеризуют измерения некоторой конкретной одиночной физической величины. Измерение любого множества физических величин классифицируется в соответствии с однородностью (или неоднородностью) измеряемых величин.
При совокупных измерениях осуществляется измерение нескольких одноименных величин, например, длин L1, L2, L3 и т.д. Подобные измерения выполняют на специальных устройствах для одновременного измерения ряда геометрических параметров валов.
Совместные измерения подразумевают измерение нескольких неодноименных величин (X, Y, Z и т.д.). Примерами таких измерений могут быть комплексные измерения электрических, силовых и термодинамических параметров электродвигателя или одновременные измерения длин и температур для нахождения температурного коэффициента линейного расширения.
Для отображения результатов, получаемых при измерениях, могут быть использованы разные шкалы, в том числе градуированные в единицах измеряемой физической величины, либо в некоторых относительных единицах, включая неименованные. В соответствии с этим принято различать абсолютные и относительные измерения.
По числу повторных измерений одной и той же величины различают однократные и многократные измерения, причем многократные измерения проводят или для страховки от грубых погрешностей или для математической обработки результатов (расчет средних значений, статистическая обработка и др.). В зависимости от поставленной цели число повторных измерений может колебаться в широких пределах (от двух измерений до нескольких десятков и даже сотен).
В зависимости от планируемой точности измерения делят на технические и метрологические, а от реализованной точности и от степени рассеяния результатов при многократном повторении измерений одной и той же величины – на равноточные и неравноточные, а также на равнорассеянные и неравнорассеянные.
Технические измерения выполняют с заранее установленной точностью, иными словами, при таких измерениях погрешность не должна превышать заранее заданного значения.
Метрологические измерения выполняют с максимально достижимой точностью, добиваясь минимальной (при имеющихся ограничениях) погрешности измерения.
В тех случаях, когда точность результата измерений не имеет принципиального значения, а цель измерений состоит в приблизительной оценке неизвестной физической величины прибегают к ориентировочным измерениям, погрешность которых может колебаться в достаточно широких пределах, поскольку любая реализуемая в процессе измерений погрешность принимается за допустимую.
Общность метрологического подхода ко всем этим видам измерений состоит в том, что при любых измерениях определяют значения реализуемых погрешностей, без чего невозможна достоверная оценка результатов.
Оценка равноточности и неравноточности, а также равнорассеянности и неравнорассеянности результатов измерений зависит от выбранных значений предельных мер расхождения точности или оценок рассеяния. Допустимые расхождения оценок устанавливают в зависимости от задачи измерения.
Допустимые расхождения оценок устанавливают в зависимости от задачи измерения.
Равноточными называют серии измерений для которых оценки погрешностей можно считать практически одинаковыми, а к неравноточным относят измерения с различающимися погрешностями. Измерения считают равнорассеянными или неравнорассеянными в зависимости от совпадения или различия оценок случайных составляющих погрешностей измерений сравниваемых серий.
Статические и динамические измерения наиболее логично рассматривать в зависимости от режима получения средством измерения входного сигнала измерительной информации. При измерении в статическом (квазистатическом) режиме скорость изменения входного сигнала несоизмеримо ниже скорости его преобразования в измерительной цепи и результаты фиксируются без динамических искажений.
При измерении в динамическом режиме появляются дополнительные динамические погрешности, связанные со слишком быстрым изменением либо самой измеряемой физической величины, либо входного сигнала измерительной информации, поступающего от постоянной измеряемой величины. Например, в подшипниковой промышленности при измерении диаметров тел качения (постоянных физических величин) с использованием контрольно-сортировочных автоматов скорость изменения измерительной информации на входе может оказаться соизмеримой со скоростью измерительных преобразований в цепи прибора.
Например, в подшипниковой промышленности при измерении диаметров тел качения (постоянных физических величин) с использованием контрольно-сортировочных автоматов скорость изменения измерительной информации на входе может оказаться соизмеримой со скоростью измерительных преобразований в цепи прибора.
Различают два основных метода измерений: метод непосредственной оценки и метод сравнения с мерой.
При использовании метода непосредственной оценки значение измеряемой физической величины определяют непосредственно по отсчетному устройству прибора прямого действия. Суть метода непосредственной оценки как и любого измерения состоит в сравнении измеряемой величины с мерой, принятой за единицу, но в этом случае мера «заложена» в измерительный прибор опосредовано. Прибор осуществляет преобразование входного сигнала измерительной информации, соответствующего всей измеряемой величине, после чего и происходит оценка ее значения.
Метод сравнения с мерой характеризуется тем, что измеряемая величина сравнивается с известной аналогичной величиной, которая воспроизводится мерой.
Принципиальные различия между двумя основными методами измерений заключаются в том, что метод непосредственной оценки реализуется с помощью приборов без применения мер в явном виде, а метод сравнения с мерой связан с обязательным использованием овеществленной меры. Меры воспроизводят с выбранной точностью физическую величину определенного (близкого к измеряемой) размера. Примерами мер являются гири, концевые меры длины или угла, резисторы и т.д.
Метод сравнения с мерой реализуется в нескольких разновидностях, среди которых различают:
— дифференциальный и нулевой методы,
— метод совпадений,
— методы замещения и противопоставления.
Дифференциальный и нулевой методы отличаются друг от друга в зависимости от степени приближения размера, воспроизводимого мерой, к измеряемой величине.
Дифференциальный метод измерений – метод сравнения с мерой, в котором на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой.
Нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия величин на прибор сравнения доводят до нуля.
Метод совпадений – метод сравнения с мерой, в котором значение измеряемой величины оценивают, используя совпадение ее с величиной, воспроизводимой мерой (т.е. с фиксированной отметкой на шкале физической величины). Для оценки совпадения используют прибор сравнения или органолептику, фиксируя появление определенного физического эффекта (стробоскопический эффект, совпадение резонансных частот, плавление или застывание индикаторного вещества при достижении определенной температуры и другие физические эффекты).
В зависимости от одновременности или неодновременности воздействия на прибор сравнения измеряемой величины и величины, воспроизводимой мерой, различают методы замещения и противопоставления.
Метод замещения – метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой, то есть эти величины воздействуют на прибор последовательно.
Метод противопоставления – метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами.
Примеры:
— измерение диаметра цилиндрической поверхности детали штангенциркулем в одном сечении – прямое абсолютное однократное (при повторении многократное) статическое измерение, выполняемое методом непосредственной оценки;
— нахождение значения угла прямоугольного треугольника по результатам измерений его сторон – косвенное измерение плоского угла, при котором осуществляются прямые абсолютные статические измерения линейных величин. Методы прямых измерений зависят от конкретной выбранной реализации;
— определение плотности материала по результатам измерений размеров (длин) образца и его массы – косвенное измерение искомой величины, требующее совместных измерений разноименных величин (длины и массы) и совокупных измерений нескольких одноименных физических величин (длин). Вычисляемый объем в этом случае также можно рассматривать как результат косвенного измерения.
Вычисляемый объем в этом случае также можно рассматривать как результат косвенного измерения.
В лекции «73 Понятие и стадии трудовой адаптации» также много полезной информации.
Для оценки метода измерений предлагается ответить на следующие вопросы:
а) применяется ли мера для воспроизведения физической величины в явном виде?
б) измеряются или сводятся к нулю значения отклонений физической величины от известного значения меры?
Отрицательный ответ на первый вопрос означает, что мы имеем дело с методом непосредственной оценки. Положительный ответ на этот вопрос позволяет утверждать, что применяется метод сравнения с мерой. Если при этом значение разности измеряемой величины и меры доводится до нуля, реализуется нулевой метод измерений (иногда его называют методом полного уравновешивания), а если разность этих значений алгебраически суммируется со значением меры – дифференциальный метод.
Если в ходе измерения мера и измеряемый объект последовательно воздействуют на вход средства измерений (СИ), «замещая» друг друга, реализуется метод замещения. Например, измерительная головка на стойке настраивается по плоскопараллельной концевой мере длины, после чего мера убирается и замещается контролируемой деталью.
Например, измерительная головка на стойке настраивается по плоскопараллельной концевой мере длины, после чего мера убирается и замещается контролируемой деталью.
Некоторые приборы (весы, измерительные мосты и др.) обеспечивают возможность одновременного воздействия на них меры и измеряемой физической величины. С помощью таких приборов реализуется метод противопоставления.
Методы измерений
Классификация измерений
МОДУЛЬ 4. КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ. ПОНЯТИЕ О КАЧЕСТВЕ ИЗМЕРЕНИЙ
В наиболее широком смысле к ʼʼизмерениямʼʼ относят последовательность действий, включающую констатацию наличия у объекта некоторого свойства, качественную оценку этого свойства как определенной величины (идентификацию свойства), сопоставление величины, воспроизводимой на объекте, с единицей этой величины, определение их количественного соотношения. Под измерением некоторого свойства можно понимать получение оценки этого свойства при сопоставлении измеряемой величины с единицей, воспроизводимой мерой (непосредственное воспроизведение) или прибором (опосредованное воспроизведение). Измерением свойства также часто называют помещение измеряемого свойства в определенную точку оценочной шкалы с использованием экспертных и/или аппаратурных методов. С этих позиций имеют право на существование как прямые, так и косвенные измерения. Косвенными измерениями называют расчет интересующей исследователя величины по известным зависимостям, в которые входят величины, полученные прямыми измерениями, к примеру, измерения площадей таких плоских фигур, как треугольник или параллелограмм.
Измерением свойства также часто называют помещение измеряемого свойства в определенную точку оценочной шкалы с использованием экспертных и/или аппаратурных методов. С этих позиций имеют право на существование как прямые, так и косвенные измерения. Косвенными измерениями называют расчет интересующей исследователя величины по известным зависимостям, в которые входят величины, полученные прямыми измерениями, к примеру, измерения площадей таких плоских фигур, как треугольник или параллелограмм.
В отличие от геометрии, социометрии, антропометрии, и квалиметрии (последняя имеет наиболее широкий набор объектов оценки), метрология занимается измерениями физических величин. Потому мы не будем рассматривать получение экспертных оценок, а сосредоточимся только на измерениях тех параметров, которые подлежат объективной оценке с использованием средств измерений. Такие параметры в большинстве представляют из себяфизические величины, а их экспериментальные оценки называют аппаратурными или инструментальными в отличие от экспертных (органолептических) оценок, при получении которых инструментарием являются чувства человека.
Измерение физической величины –совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины (РМГ 29 -99).
(Из отмененного ГОСТ 16263 –70: Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств).
Основное уравнение измерения физической величины можно записать в виде
Q = Nq,
где Q – измеряемая физическая величина;
q – единица физической величины;
N – числовое значение физической величины, которым определяется соотношение измеряемой физической величины и единицы, использованной при измерениях.
Из уравнения измерения следует, что в базе любого измерения лежит сравнение исследуемой физической величины с аналогичной величиной определенного размера, принятой за единицу, что обеспечивает нахождение соотношения только в явном виде. Суть измерения состоит в определении числового значения физической величины. Этот процесс называют измерительным преобразованием, подчеркивая связь измеряемой физической величины с полученным числом. Можно представить однократное преобразование или цепочку преобразований измеряемой физической величины в иную величину, но конечной целью преобразования является получение числа (рисунок 4.1).
Суть измерения состоит в определении числового значения физической величины. Этот процесс называют измерительным преобразованием, подчеркивая связь измеряемой физической величины с полученным числом. Можно представить однократное преобразование или цепочку преобразований измеряемой физической величины в иную величину, но конечной целью преобразования является получение числа (рисунок 4.1).
Более строго измерение можно представить как получение первичной информации о физической величине и такое ее преобразование, с помощью которого определяют соотношение измеряемой физической величины и единицы этой величины. Измерительное преобразование всегда осуществляется с использованием некоторого физического закона или эффекта͵ который рассматривают как принцип, положенный в основу измерения (измерительного преобразования).
Принцип измерений – физическое явление или эффект, положенное в основу измерений (РМГ 29 – 99).
(Из ГОСТ 16263 –70: Принцип измерений – совокупность физических явлений, на которых основаны измерения).
Как примеры можно рассмотреть измерение температуры с помощью термопары (использование термоэлектрического эффекта), измерение массы взвешиванием на пружинных весах (определение искомой массы по пропорциональной ей силы тяжести, основанное на принципе пропорционального упругого растяжения).
Из примеров видно, что фактически принципы измерений определяются принципами, заложенными в использованные средства измерений. Поскольку принципы измерений связаны с измерительными преобразованиями, то можно говорить о средствах измерений, построенных на определенных принципах преобразования измерительной информации с помощью механических, оптических, электрических, пневматических, гидравлических, магнитных и других устройств (преобразователей). В сложных средствах измерений используют комбинированные принципы, включающих два и более конкретных принципа преобразования, к примеру оптико-механические приборы, фотоэлектрические приборы, электромагнитные приборы и ряд других.
Важно заметить, что для систематизации подхода к измерению, для выявления и оценки погрешностей, прежде всего, крайне важно классифицировать сами измерения.
РМГ 29 – 99 вводит понятие область измерений – совокупность измерений физических величин, свойственных какой-либо области науки или техники и выделяющихся своей спецификой. В соответствии с определением выделяют ряд областей измерений: механические измерения, магнитные, акустические измерения, измерения ионизирующих излучений и др.
Видом измеренийназвана часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин. Как примеры видов измерений приведены измерения электрического сопротивления, электродвижущей силы, электрического напряжения, магнитной индукции, относящиеся к области электрических и магнитных измерений. Дополнительно выделены подвиды измерений – часть вида измерений, выделяющаяся особенностями измерений однородной величины (по диапазону, по размеру величины и др.) и приведены примеры подвидов (измерения больших длин, имеющих порядок десятков, сотен, тысяч километров или измерения сверхмалых длин — толщин пленок как подвиды измерений длины).
Такое истолкование видов и особенно подвидов измерений малоэффективно и не очень корректно – подвиды измерений фактически не определены, и неудачные примеры это подтверждают. Так толщины пленок бывают от десятых долей микрометра до десятых миллиметра, что соответствует различиям на три порядка, требующим существенно различающихся подходов к измерениям – объединение их в один подвид нерационально.
Более широкая трактовка видов измерений (с использованием различных оснований классификации) позволяет отнести к ним также приведенные в том же документе, но не сформированные в классификационные группы измерения, характеризуемые следующими альтернативными парами терминов:
· прямые и косвенные измерения,
· совокупные и совместные измерения,
· абсолютные и относительные измерения,
· однократные и многократные измерения,
· статические и динамические измерения,
· равноточные и неравноточные измерения.
Прямые и косвенные измерения различают исходя из способа получения результата измерений. Прямое измерение – измерение, при котором искомое значение физической величины получают непосредственно. В примечании к определению отмечено, что при строгом подходе существуют только прямые измерения и предлагается применять термин прямой метод измерений. Это предложение нельзя назвать удачным (см. далее классификацию методов измерений). Как примеры прямых измерений приведены: измерение длины детали микрометром, силы тока амперметром, массы на весах.
В ходе прямых измерений искомое значение величины определяют непосредственно по устройству отображения измерительной информации применяемого средства измерений. Формально без учета погрешности измерения они бывают описаны выражением
Q = х,
где Q – измеряемая величина,
х – результат измерения.
Косвенное измерение – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Далее в документе сказано, что вместо термина косвенное измерение часто применяют термин косвенный метод измерений. Этот вариант предпочтительно не использовать как явно неудачный.
Далее в документе сказано, что вместо термина косвенное измерение часто применяют термин косвенный метод измерений. Этот вариант предпочтительно не использовать как явно неудачный.
При косвенных измерениях искомое значение величины рассчитывают на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Формальная запись такого измерения
Q = F (X, Y, Z,…),
где X, Y, Z,… – результаты прямых измерений.
Принципиальной особенностью косвенных измерений является крайне важно сть обработки (преобразования) результатов вне прибора (на бумаге, с помощью калькулятора или компьютера), в противоположность прямым измерениям, при которых прибор выдает готовый результат. Классическими примерами косвенных измерений можно считать нахождение значения угла треугольника по измеренным длинам сторон, определение площади треугольника или другой геометрической фигуры и т. п. Один из наиболее часто встречающихся случаев применения косвенных измерений – определение плотности материала твердого тела. К примеру, плотность ρ тела цилиндрической формы определяют по результатам прямых измерений массы т, высоты h и диаметра цилиндра d, связанных с плотностью уравнением
п. Один из наиболее часто встречающихся случаев применения косвенных измерений – определение плотности материала твердого тела. К примеру, плотность ρ тела цилиндрической формы определяют по результатам прямых измерений массы т, высоты h и диаметра цилиндра d, связанных с плотностью уравнением
ρ = т/0,25π d2 h
С различением прямых и косвенных измерений связаны многочисленные дискуссии и ряд недоразумений. К примеру, споры о том, являются ли косвенными измерения радиального биения (b = Rmax – Rmin) или высоты детали при настройке прибора на отличное от нулевого деление. Некоторые метрологи отказываются от признания косвенных измерений как таковых (ʼʼсуществуют только прямые измерения, а все остальное – математическая обработка результатовʼʼ). Можно предложить компромиссное решение: признать за косвенными измерениями право на существование, поскольку специфика математической обработки результатов таких измерений и оценки их погрешностей никем не оспаривается.
Прямые и косвенные измерения характеризуют измерения некоторой конкретной одиночной физической величины. Измерение любого множества физических величин классифицируется в соответствии с однородностью (или неоднородностью) измеряемых величин. На этом и построено различение совокупных и совместных измерений.
Совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
Приведенный пример – определение значений массы отдельных гирь набора по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь подтверждает, что определению соответствуют не измерения, а специальные исследования, направленные на поиск погрешностей ряда мер массы.
Реально к совокупным измерениям следует отнести те, при которых осуществляется измерение нескольких одноименных величин, к примеру, длин L1, L2, L3 и т. д. Подобные измерения выполняют на специальных устройствах (измерительных установках) для одновременного измерения ряда геометрических параметров валов.
д. Подобные измерения выполняют на специальных устройствах (измерительных установках) для одновременного измерения ряда геометрических параметров валов.
Совместные измерения – проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними. В качестве примера можно рассмотреть одновременные измерения длин и температур для нахождения температурного коэффициента линейного расширения. В более узкой трактовке совместные измерения подразумевают измерение нескольких неодноименных величин (X, Y, Z и т.д.). Примерами таких измерений бывают комплексные измерения электрических, силовых и термодинамических параметров электродвигателя, а также измерения параметров движения и состояния транспортного средства (скорость, запас горючего, температура двигателя и др.).
Для отображения результатов, получаемых при измерениях, бывают использованы разные оценочные шкалы, в т.ч. градуированные в единицах измеряемой физической величины, либо в некоторых относительных единицах, в т. ч. и в неименованных. В соответствии с этим принято различать абсолютные иотносительные измерения.
ч. и в неименованных. В соответствии с этим принято различать абсолютные иотносительные измерения.
Абсолютное измерение – измерение, основанное на прямых измерениях одной или нескольких базовых величин и (или) использовании значений физических констант.
Это крайне неудачное определение сопровождается соответствующим примером (измерение силы F = mg основано на измерении основной величины – массы m и использовании физической постоянной g в точке измерения массы), который подтверждает нелепость предложенной трактовки. В примечании сказано, что понятие абсолютное измерение применяется как противоположное понятию относительное измерение и воспринимается как измерение величины в ее единицах, и что именно такое понимание находит все большее и большее применение в метрологии. Именно эту трактовку имеет смысл использовать для данных альтернативных видов измерений.
Относительное измерение – измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.
Пример — Измерение активности радионуклида в источнике по отношению к активности радионуклида в однотипном источнике, аттестованном в качестве эталонной меры активности.
По числу повторных измерений одной и той же величины различают однократные и многократные измерения. Однократное измерение – измерение, выполненное один раз.
Примечание — Во многих случаях на практике выполняются именно однократные измерения. К примеру, измерение конкретного момента времени по часам обычно производится один раз.
Пример не выдерживает критики, поскольку повторные измерения одного отрезка времени невозможны.
Многократное измерение – измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, ᴛ. ᴇ. состоящее из ряда однократных измерений.
ᴇ. состоящее из ряда однократных измерений.
Учитывая зависимость отпоставленной цели число повторных измерений может колебаться в широких пределах (от двух измерений до нескольких десятков и даже сотен). Многократные измерения проводят или для страховки от грубых погрешностей (в таком случае достаточно трех-пяти измерений) или для последующей математической обработки результатов (часто более пятнадцати измерений с последующими расчетами средних значений, статистической оценкой отклонений и др.). Многократные измерения называют также ʼʼизмерения с многократными наблюдениямиʼʼ.
Статическое измерение – измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
Приведенные примеры (измерение длины детали при нормальной температуре и измерение размеров земельного участка) скорее запутывают, чем проясняют ситуацию.
Динамическое измерение – измерение изменяющейся по размеру физической величины.
Примечания
1 Терминоэлемент ʼʼдинамическоеʼʼ относится к измеряемой величине.
2 Строго говоря, все физические величины подвержены тем или иным изменениям во времени. В этом убеждает применение все более и более чувствительных средств измерений, которые дают возможность обнаруживать изменение величин, ранее считавшихся постоянными, в связи с этим разделение измерений на динамические и статические является условным.
Трактовка статических и динамических измерений как измерений постоянной либо переменной физических величин примитивна и в философском плане всегда неоднозначна (ʼʼвсе течет, все меняетсяʼʼ). ʼʼНеизменныхʼʼ физических величин, кроме физических констант в практике измерений почти нет, все величины различаются только в соответствии со скоростью изменения.
Вместо абстрактных рассуждений желательны определения, обусловленные прагматическим подходом. Статические и динамические измерения наиболее логично рассматривать исходя из режима получения средством измерения входного сигнала измерительной информации. При измерении в статическом режиме (или квазистатическом режиме) скорость изменения входного сигнала несоизмеримо ниже скорости его преобразования в измерительной цепи, и результаты фиксируются без динамических искажений.
При измерении в статическом режиме (или квазистатическом режиме) скорость изменения входного сигнала несоизмеримо ниже скорости его преобразования в измерительной цепи, и результаты фиксируются без динамических искажений.
При измерении в динамическом режиме появляются дополнительные динамические погрешности, связанные со чересчур быстрым изменением либо самой измеряемой физической величины, либо входного сигнала измерительной информации, поступающего от постоянной измеряемой величины. К примеру, измерение диаметров тел качения (постоянных физических величин) в подшипниковой промышленности осуществляется с использованием контрольно-сортировочных автоматов. При этом скорость изменения измерительной информации на входе может оказаться соизмеримой со скоростью измерительных преобразований в цепи прибора. Измерение температуры с помощью ртутного термометра несоизмеримо медленнее измерений электронными термометрами, следовательно, применяемые средства измерений могут в значительной степени определить режим измерений.
По реализованной точности и по степени рассеяния результатов при многократном повторении измерений одной и той же величины различают равноточные и неравноточные, а также на равнорассеянные и неравнорассеянные измерения.
Равноточные измерения – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
В примечаниях к двум последним определениям предлагается до обработки ряда измерений, убедиться в том, что все измерения являются равноточными, а неравноточные измерения обрабатывать с учетом веса отдельных измерений, входящих в ряд.
Оценка равноточности и неравноточности, а также равнорассеянности и неравнорассеянности результатов измерений зависит от выбранных значений предельных мер расхождения точности или оценок рассеяния. Допустимые расхождения оценок устанавливают исходя из задачи измерения. Равноточными называют серии измерений 1 и 2, для которых оценки погрешностей Di и Dj можно считать практически одинаковыми
Допустимые расхождения оценок устанавливают исходя из задачи измерения. Равноточными называют серии измерений 1 и 2, для которых оценки погрешностей Di и Dj можно считать практически одинаковыми
(D1 ʼʼ D2),
а к неравноточным относят измерения с различающимися погрешностями
(D1 ¹ D2).
о о о о
Измерения в двух сериях считают равнорассеянными (D1 ʼʼ D2), или при (D1 ¹ D2) неравнорассеянными (в зависимости от совпадения или различия оценок случайных составляющих погрешностей измерений сравниваемых серий 1 и 2).
Учитывая зависимость отпланируемой точности измерения делят на технические и метрологические. К техническимследует относить те измерения, которые выполняют с заранее установленной точностью. Иными словами, при технических измерениях погрешность измерения D не должна превышать заранее заданного значения [D]:
Иными словами, при технических измерениях погрешность измерения D не должна превышать заранее заданного значения [D]:
D £ [D],
где [D] – допустимая погрешность измерения.
Именно такие измерения наиболее часто реализуются в производстве, откуда и взято их наименование.
Метрологические измерения выполняют с максимально достижимой точностью, добиваясь минимальной (при имеющихся ограничениях) погрешности измерения D, что можно записать как
D® 0.
Такие измерения имеют место при эталонировании единиц, при выполнении уникальных исследований.
В тех случаях, когда точность результата измерений не имеет принципиального значения, а цель измерений состоит в приблизительной оценке неизвестной физической величины прибегают кориентировочным измерениям, погрешность которых может колебаться в достаточно широких пределах, поскольку любая реализуемая в процессе измерений погрешность D, принимается за допустимую [D]
[D] = D.
Общность метрологического подхода ко всем этим видам измерений состоит в том, что при любых измерениях определяют значения D реализуемых погрешностей, без чего невозможна достоверная оценка результатов.
В соответствии с РМГ 29 – 99 метод измерений– прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений. В примечании сказано, что метод измерений обычно обусловлен устройством средств измерений.
(По ГОСТ 16263 –70: Метод измерений – совокупность приемов использования принципов и средств измерений).
Оба определения дают чересчур много возможностей для произвола, поскольку можно акцентировать принципы (ʼʼинтерференционный метод измерения длиныʼʼ, ʼʼфотоэлектрический метод угловых измеренийʼʼ), средства (ʼʼстробоскопический метод измерения частотыʼʼ), приемы использования средств измерений (ʼʼметод полного уравновешиванияʼʼ, ʼʼконтактный методʼʼ). Вместе с тем, если для конкретного случая достаточно подробно описать все входящие в определение операции, получим описание измерительной процедуры или методику выполнения измерений (МВИ), а метод измерений придется признать идентичным МВИ. В нормативном документе есть ряд частных понятий, определяющих разновидности метода измерений, но они не покрывают всех разновидностей методов. В частности НД содержит определения следующих терминов:
Вместе с тем, если для конкретного случая достаточно подробно описать все входящие в определение операции, получим описание измерительной процедуры или методику выполнения измерений (МВИ), а метод измерений придется признать идентичным МВИ. В нормативном документе есть ряд частных понятий, определяющих разновидности метода измерений, но они не покрывают всех разновидностей методов. В частности НД содержит определения следующих терминов:
— метод непосредственной оценки;
— метод сравнения с мерой;
— нулевой метод измерений;
— дифференциальный метод измерений;
— метод измерений замещением;
— метод измерений дополнением;
— контактный метод измерений;
— бесконтактный метод измерений.
Анализ приведенных терминов показывает, что классификация методов измерений осуществлялась по разным основаниям, к примеру, исходя из наличия или отсутствия в явном виде мер физической величины (гирь, концевых мер длины или др. ) или от ʼʼстепени уравновешиванияʼʼ объекта мерами. Методы измерений замещением и дополнением фиксируют особенности МВИ, рассматриваемые с позиций взаимодействия мер и прибора сравнения. Разделение методов измерений на контактные и бесконтактные связано с особенностями конструкции чувствительных элементов прибора. Поскольку набор терминов из РМГ 29 –99 отличается от терминов в отмененном с ГОСТ 16263 –70, а в литературе широко использовались именно включенные в старый стандарт термины, мы по крайне важно сти будем дополнять приведенный перечень.
) или от ʼʼстепени уравновешиванияʼʼ объекта мерами. Методы измерений замещением и дополнением фиксируют особенности МВИ, рассматриваемые с позиций взаимодействия мер и прибора сравнения. Разделение методов измерений на контактные и бесконтактные связано с особенностями конструкции чувствительных элементов прибора. Поскольку набор терминов из РМГ 29 –99 отличается от терминов в отмененном с ГОСТ 16263 –70, а в литературе широко использовались именно включенные в старый стандарт термины, мы по крайне важно сти будем дополнять приведенный перечень.
Анализ метода измерений следует начинать с выяснения базовых признаков: является он методом непосредственной оценки или методом сравнения с мерой.Фактически это единственное принципиальное деление, поскольку значительная часть терминов просто уточняет разновидности метода сравнения с мерой. Различия между двумя методами измерений заключаются в том, что метод непосредственной оценки реализуют с помощью приборов без дополнительного применения мер, а метод сравнения с мерой предусматривает обязательное использование овеществленной меры. Меры в явном виде воспроизводят с выбранной точностью физическую величину определенного (близкого к измеряемой) размера.
Меры в явном виде воспроизводят с выбранной точностью физическую величину определенного (близкого к измеряемой) размера.
Метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений
Метод сравнения с мерой (метод сравнения) – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
При использовании метода непосредственной оценки значение измеряемой физической величины определяют непосредственно по отсчетному устройству прибора прямого действия. Суть метода непосредственной оценки,как любого метода измерения состоит в сравнении измеряемой величины с мерой, принятой за единицу, но в данном случае мера ʼʼзаложенаʼʼ в измерительный прибор опосредованно. Прибор осуществляет преобразование входного сигнала измерительной информации, соответствующего всей измеряемой величине, после чего и происходит оценка ее значения.
Формальное выражение для описания метода непосредственной оценки должна быть представлено в следующей форме:
Q = х,
где Q – измеряемая величина,
х – показания средства измерения.
Метод сравнения с меройхарактеризуется тем, что прибор фактически используют для определения разности измеряемой величины и известной величины, воспроизводимой мерой. Для реализации этого метода можно использовать приборы с относительно небольшими диапазонами показаний, вплоть до вырожденной шкалы с одной нулевой отметкой. Примерами этого метода являются измерения массы на рычажных весах с уравновешиванием объекта гирями (мерами массы), измерения напряжения постоянного тока прибором-компенсатором путем сравнения с известной ЭДС нормального элемента.
Формально метод сравнения с мерой должна быть описан следующим выражением:
Q = х + Хм,
где Q – измеряемая величина,
х – показания средства измерения.
Хм – величина, воспроизводимая мерой.
Примерами используемых мер являются гири, концевые меры длины или угла, эталонные резисторы и т.д. В случае если использовать высокоточные меры, то инструментальные составляющие погрешности можно уменьшить не только за счёт точности меры, но и за счёт существенного уменьшения применяемого при измерении диапазона преобразований. При измерении методом непосредственной оценки измерительное преобразование полностью соответствует измеряемой величине, что при наличии у используемого прибора мультипликативной погрешности обычно приводит к существенному снижению точности. Метод сравнения с мерой позволяет свести работу прибора сравнения к измерительному преобразованию разности измеряемой величины и величины, воспроизводимой мерой, которая существенно меньше всей измеряемой величины.
Метод сравнения с мерой реализуется в нескольких разновидностях, среди которых различают:
— дифференциальный и нулевой методы измерений,
— метод совпадений,
— метод измерений замещением и метод противопоставления,
— метод измерений дополнением.
В данном перечислении курсивом выделены термины, включенные в РМГ 29 –99.
Дифференциальный и нулевой методы отличаются друг от друга исходя из степени приближения размера, воспроизводимого мерой, к измеряемой величине.
Дифференциальный метод измерений (дифференциальный метод) – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.
Пример – измерения длины, выполняемые на станковом приборе с измерительной головкой при настройке по блоку концевых мер.
Фактически дифференциальный метод измерений — ϶ᴛᴏ метод сравнения с мерой, в котором на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой, что формально соответствует х ≠ 0 в выражении
Q = х + Хм.
Нулевой метод измерений (нулевой метод) – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.
Формально это можно представить как х ≈ 0 в том же выражении Q = х + Хм из чего следует:
Q ≈ Хм.
Пример – измерения массы взвешиванием на равноплечих рычажных весах с полным уравновешиванием чашек.
Метод совпадений (по ГОСТ 16263 –70) – метод сравнения с мерой, в котором значение измеряемой величины оценивают, используя совпадение ее с величиной, воспроизводимой мерой (ᴛ.ᴇ. с фиксированной отметкой на шкале физической величины).
Для оценки совпадения можно использовать прибор сравнения или органолептику, фиксируя появление определенного физического эффекта (стробоскопический эффект, совпадение резонансных частот, плавление или застывание индикаторного вещества при достижении определенной температуры и другие физические эффекты).
Учитывая зависимость отодновременности или неодновременности воздействия на прибор сравнения измеряемой величины и величины, воспроизводимой мерой, различают метод измерений замещением и метод противопоставления.
Метод измерений замещением (метод замещения) – метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины. Пример — взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов (метод Борда).
Следует отметить, что РМГ 29 –99 представляет чересчур узкую трактовку метода замещения. В другой интерпретации, особенно характерной для линейно-угловых измерений, рассматривают альтернативную пару: методы замещения и противопоставления. В таком случае метод замещения – метод сравнения с мерой, в котором известную величину, воспроизводимую мерой, после настройки прибора замещают измеряемой величиной, то есть эти величины воздействуют на прибор последовательно. Метод противопоставления – метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливают соотношение между этими величинами.
Метод противопоставления – метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливают соотношение между этими величинами.
Кроме этих терминов в РМГ 29 –99 приведен термин метод измерений дополнением (метод дополнения) – метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению. Метод дополнения должна быть реализован как при замещении, так и при противопоставлении измеряемой величины и меры.
Для анализа МВИ использование классификации методов измерений по реализации измерительного преобразования имеет существенное практическое значение, поскольку они прямо связаны с поиском источников погрешностей и оценкой их характера. Так метод непосредственной оценки может характеризоваться прогрессирующей составляющей погрешности, которая увеличивается с увеличением измеряемой величины. У всех разновидностей методов сравнения с мерой обязательно присутствуют не только погрешности приборов, но и погрешности мер, причем механизмы их проявления несколько различаются в соответствии с разновидностью метода.
У всех разновидностей методов сравнения с мерой обязательно присутствуют не только погрешности приборов, но и погрешности мер, причем механизмы их проявления несколько различаются в соответствии с разновидностью метода.
|
Классификация методов измерений по наличию контакта сопровождается не вполне корректными определениями.
Контактный метод измерений (контактный метод) – метод измерений, основанный на том, что чувствительный элемент прибора приводится в контакт с объектом измерения. Примеры: измерение диаметра вала индикаторной скобой, измерение температуры тела термометром.
Бесконтактный метод измерений (бесконтактный метод) – метод измерений, основанный на том, что чувствительный элемент средства измерений не приводится в контакт с объектом измерения. Примерами бывают измерение температуры в доменной печи пирометром и измерение расстояния до объекта радиолокатором.
Примерами бывают измерение температуры в доменной печи пирометром и измерение расстояния до объекта радиолокатором.
В случае если под контактом подразумевать только механический контакт чувствительного элемента средства измерений с объектом, то деление методов на контактные и бесконтактные имеет определенный смысл. Это существенно для анализа погрешностей, которые возникают из-за взаимодействия прибора с объектом измерений. При механическом контакте крайне важно учитывать взаимодействия объекта и средства измерений (деформации из-за их недостаточной жесткости, контактные деформации, колебание переходных сопротивлений и др.). При отсутствии механического контакта следует учитывать особенности ʼʼбесконтактного съемаʼʼ измерительной информации – оптические искажения в воздухе, ослабление сигнала на расстоянии и т.д.
Для оценки метода измеренийпредлагается ответить на следующие вопросы:
– применяется ли для воспроизведения физической величины мера в явном виде?
– измеряются ли значения отклонений физической величины от известного значения меры?
Отрицательный ответ на первый вопрос означает, что мы имеем дело с методом непосредственной оценки. Положительный ответ на данный вопрос позволяет утверждать, что применяется метод сравнения с мерой, который подлежит дальнейшей уточняющей классификации. В случае если значение разности измеряемой величины и меры доводится до нуля, реализуется нулевой метод измерений (иногда называемый методом полного уравновешивания), а если разность этих значений алгебраически суммируется со значением меры – дифференциальный метод.
Положительный ответ на данный вопрос позволяет утверждать, что применяется метод сравнения с мерой, который подлежит дальнейшей уточняющей классификации. В случае если значение разности измеряемой величины и меры доводится до нуля, реализуется нулевой метод измерений (иногда называемый методом полного уравновешивания), а если разность этих значений алгебраически суммируется со значением меры – дифференциальный метод.
В случае если в ходе измерения мера и измеряемый объект последовательно воздействуют на вход средства измерений (СИ), заменяя друг друга, реализуется метод замещения. К примеру, измерительная головка на стойке настраивается по плоскопараллельной концевой мере длины, после чего мера убирается и замещается контролируемой деталью.
Некоторые приборы (весы, измерительные мосты и др.) обеспечивают возможность одновременного воздействия на них меры и измеряемой физической величины. С помощью таких приборов реализуется метод противопоставления.
Примеры кратких характеристик методик выполнения измерений:
· — измерение диаметра цилиндрической поверхности детали штангенциркулем в одном сечении – прямое абсолютное однократное (или многократное) статическое измерение, выполняемое методом непосредственной оценки;
· — нахождение значения угла прямоугольного треугольника по результатам измерений его сторон – косвенное измерение плоского угла, при котором реализуются прямые измерения длин. Методы прямых измерений зависят от конкретной выбранной реализации;
Методы прямых измерений зависят от конкретной выбранной реализации;
· — определение плотности материала по результатам измерений размеров (длин) образца и его массы – косвенное измерение искомой величины, требующее совместных измерений разноименных величин (длины и массы) и совокупных измерений нескольких одноименных физических величин (длин). Вычисляемый объём в данном случае также можно рассматривать как результат косвенного измерения.
| Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Поделиться:
Поиск в инженерном справочнике DPVA. Затем мы извлекаем квадратный корень из обеих частей, чтобы найти c , чтобы получить: c =? 925 = 30.414 Таким образом, похоже, что мы хотим, чтобы наш мост был около 30,414 футов в длину. Пропорции и подобные треугольникиВ математике пропорций — это два равных отношения. Пропорции записываются как a / b = c / d . Когда две величины пропорциональны, они удовлетворяют этому уравнению. Например, 1/2 = 4/8. Уменьшив это, мы получим 4/8 = 1/2. Следовательно, 1/2 пропорциональна 4/8. Теперь, когда мы рассмотрели, что такое пропорции, мы можем рассмотреть, что такое подобных треугольников .Подобные треугольники часто появляются при косвенных измерениях. Два треугольника называются подобными, если их соответствующие углы равны и их стороны пропорциональны. Они имеют одинаковую форму, но могут быть разных размеров. Мы видим, что похожие треугольники и пропорции идут рука об руку. Давайте посмотрим на пример. Предположим, вы находитесь на пляже и хотите узнать, насколько глубока вода в 70 метрах от берега.Вы знаете, что вода становится все глубже и глубже с постоянной скоростью, а когда вы находитесь в 10 метрах от берега, глубина воды составляет 2 метра. Обратите внимание, что два показанных треугольника похожи. Следовательно, мы можем представить нашу глубину на расстоянии 70 метров от берега как x и установить пропорцию сторон наших треугольников. У нас есть: x /2 = 70/10 Мы упрощаем это для решения x и получаем: x = 14 Следовательно, на расстоянии 70 метров от берега вода равна 14. метров глубиной. Теорема Фалеса о тени В VI веке до нашей эры греческий математик по имени Фалес Милетский обнаружил связь между своей собственной тенью и тенью пирамиды. Это соотношение часто используется при косвенном измерении. Например, предположим, что вы хотите определить высоту дерева.Он довольно высокий, поэтому вы не можете измерить его напрямую. Вы замечаете, что дерево отбрасывает тень высотой 50 футов. Вы также замечаете, что мужчина ростом 6 футов, который стоит возле дерева, отбрасывает тень высотой 10 футов. Поскольку эти измерения были сделаны в одно и то же время дня, мы можно применить теорему Фалеса. Допустим, что высота дерева будет x , и мы подставим все наши значения в теорему Фалеса, чтобы получить уравнение: 10/50 = 6/ x x = 30 Следовательно, наше дерево 30 футов.высокий. Краткое содержание урока Даже если мы не можем рассчитать расстояние между двумя точками напрямую, все равно можно получить точную цифру с помощью косвенного измерения . Косвенные измерения — Концепция — Геометрия Видео от BrightstormКосвенное измерение — это метод использования пропорций для нахождения неизвестной длины или расстояния на аналогичных фигурах.Два распространенных способа выполнения косвенного измерения включают (1) использование зеркала на земле и (2) использование длины тени и определение высоты объекта. Метод 1 измеряет рост человека и расстояние между ним, зеркалом и предметом. Метод 2 измеряет тени и рост человека. Вы можете использовать аналогичные треугольники для измерения чего-либо, не снимая рулетку и не растягивая ее. Выберите метод оценки — Университет Санта-КларыКосвенные измерения обучения учащихся оценивают мнения или мысли о знаниях, навыках, отношениях, опыте обучения и восприятии учащихся. Примерами косвенных мер являются: опросы студентов об обучении; фокус группы; опросы выпускников; опросы работодателей. Косвенные измерения могут помочь объяснить результаты, полученные в результате прямого оценивания, а также дать представление о том, как учащиеся воспринимают аспекты наших программ. Иногда косвенных мер может быть вполне достаточно для измерения некоторых результатов программы. Косвенные меры включают опросы, фокус-группы и другие мероприятия, которые собирают впечатления или мнения о программе и / или ее результатах обучения. Виды косвенных мер
Косвенные меры: обеспечение их эффективности
Какой косвенный метод измерения приведите на примере? — AnswersToAllКакой косвенный метод измерения приведите на примере? «Прямое измерение» означает измерение именно того, что вы хотите измерить, в то время как «косвенное измерение» означает, что вы измеряете что-то, измеряя что-то другое. Что такое косвенное измерение в науке?косвенное измерение: измерение, которое включает оценку неизвестного значения путем измерения чего-то известного. Что из следующего является примером косвенного измерения ABA?Косвенное измерение — это когда целевое поведение не наблюдается напрямую, выводы делаются на основании другого поведения или событий окружающей среды. К типам косвенного измерения относятся: постоянная регистрация продукта, самоконтроль, интервью, опросы и рейтинговые шкалы. Что такое косвенное измерение?метод, в котором исследователь собирает данные об одной переменной (или комбинации переменных) в качестве средства представления второй интересующей переменной, которую нельзя оценить более простым способом. Что такое косвенное измерение, объясните на двух примерах? Косвенное измерение — это метод использования пропорций для нахождения неизвестной длины или расстояния на аналогичных фигурах. Какой инструмент косвенного измерения?При косвенных измерениях размеры измеряются с помощью измерительных инструментов, таких как циферблатные индикаторы, которые определяют разницу между целями и эталонными устройствами, такими как калибровочные блоки и кольцевые калибры. Почему это называется косвенным измерением?Это ситуация, когда мы не можем измерить это расстояние с помощью линейки или другого измерительного устройства. Другими словами, мы не можем измерить это напрямую. Когда возникают подобные ситуации, мы используем то, что называется косвенным измерением. Что такое косвенные оценки в ABA? Косвенное оценивание — это сбор информации с помощью иных средств, нежели просмотр реальных образцов студенческой работы. К ним относятся опросы, интервью при выходе и фокус-группы (см. Является ли частота косвенным показателем?Прямое измерение Индивидуальное измерительное поведение берет данные, физически присутствуя и непосредственно наблюдая за поведением (Купер, Херон и Хьюард, 2007).Примеры: частота и продолжительность являются примерами прямого измерения. Какое определение и пример прямого измерения?«Прямое измерение» означает измерение именно того, что вы хотите измерить, в то время как «косвенное измерение» означает, что вы измеряете что-то, измеряя что-то другое. Например, при прямом измерении вес, расстояние и т. Д. Поэтому, если я хочу измерить длину куска дерева, я просто измеряю его. В чем разница между прямым и косвенным измерением? «Прямое измерение» означает измерение именно того, что вы хотите измерить, в то время как «косвенное измерение» означает, что вы измеряете что-то, измеряя что-то другое.Позвольте мне привести вам несколько примеров, которые могут помочь понять это. Что такое прямые и косвенные измерения?ПРЯМЫЕ И КОСВЕННЫЕ МЕРЫ ОБУЧЕНИЯ СТУДЕНТОВ. Учебу учащихся можно измерить с помощью ряда методов. Что такое косвенная мера?Косвенные меры.Косвенные меры — это меры, которые измеряют обучение учащихся путем оценки мнений или представлений о знаниях, навыках, отношениях и восприятии. Примеры косвенных показателей на уровне академической программы или курса включают: Опросы студентов, включая оценку курсов. Собеседования с выпускниками. Опросы выпускников или работодателей.
Прямые и косвенные меры — SMU (Южный методистский университет) ПРЯМЫЕ И КОСВЕННЫЕ ИЗМЕРЕНИЯ ОБУЧЕНИЯ УЧАЩИХСЯ ПРЯМЫЕ ИЗМЕРЕНИЯ ОБУЧЕНИЯ УЧАЩИХСЯ ПРЯМЫЕ МЕРЫ ДЛЯ АДМИНИСТРАТИВНОЙ, УЧЕБНОЙ ПОДДЕРЖКИ И УСЛУГ ПОДДЕРЖКИ СТУДЕНТОВ КОСВЕННЫЕ МЕРЫ ОБУЧЕНИЯ УЧАЩИХСЯ КОСВЕННЫЕ МЕРЫ ДЛЯ СЛУЖБ АДМИНИСТРАТИВНОЙ, УЧЕБНОЙ ПОДДЕРЖКИ И ПОДДЕРЖКИ СТУДЕНТОВ КОГДА И ГДЕ ИСПОЛЬЗОВАТЬ КОСВЕННЫЕ И ПРЯМЫЕ МЕРЫ
Косвенные меры могут быть расположены как на уровне курса, так и на уровне программы оценки обучения студентов. На уровне программы и кафедры косвенные меры могут использоваться для измерения эффективности услуг, процессов, программ, инициатив и т. Д. Если профессор заинтересован, он / она может использовать косвенные меры для оценки восприятия, ценностей, отношения и т. Д. .которые дают представление об успеваемости учащихся по прямым измерениям.
СОЧЕТАНИЕ ПРЯМЫХ И КОСВЕННЫХ МЕР ДЛЯ ЕДИНОГО ВЗГЛЯДА НА ОБУЧЕНИЕ И ДОСТИЖЕНИЕ Один из примеров того, как это может сработать, состоит в том, что факультет может обнаружить с помощью косвенного измерения, что студенты, получившие низкие баллы по определенному результату, могут не полностью осознавать ценность этого конкретного результата. Эти открытия могут быть очень полезны в том, чтобы дать направление преподаванию этого материала.Поскольку известно, что студенты стремятся овладеть теми навыками, которые они считают наиболее ценными, возможно, преподаватели могли бы подчеркнуть, как этот конкретный навык можно использовать в повседневной жизни или даже в рамках специальностей студентов. Косвенное измерение — Обмен уверенности на дивидендыОДНА ХОРОШАЯ ИДЕЯ Рэй Харкинс Непрямой маршрут часто бывает лучшим выходом. Прямое измерение применяет стандарт непосредственно к характеристика для его измерения.Косвенное измерение включает оценка некоторых других характеристик, которые оказываются статистически зависит от интересующей характеристики. Измерение других характеристик позволяет оценить первая характеристика — косвенно. Косвенные методы часто обеспечивают достаточное измерение надежность для приложения и стоимость намного меньше, чем прямые варианты измерения. Например, чтобы рассчитать площадь земельного участка, вы можно было использовать стальную ленту, чтобы напрямую измерить ее длину и ширину.Или косвенно, вы можете получить приблизительное приближение, просто подсчитывая ваши шаги по участку, чтобы измерить размеры в ярдах. Количество шагов пропорционально размеры участка — чем больше участок, тем больше шагов требуется, чтобы пересечь его. В этом примере вы, по сути, обмениваете надежность измерений для более быстрой и менее затратной оценки. Если ваша причина знать площадь земли — купить правильное количество удобрений для распределения по нему, добавленное в уверенности, полученной путем непосредственного измерения, нет необходимости. такой же обмен возможен во многих задачах измерения лицо инженеров. PEX ПримерКоманда инженеров Mercury Plastics в Мидлфилде, штат Огайо, недавно разработал метод косвенного измерения процент сшитого полиэтилена (PEX) в пластике трубки, которые он производит для сантехники и бытовой техники отрасли. Трубка PEX изготавливается путем сначала экструдирования полиэтилен, затем сшивая его, пропуская через электронно-лучевой ускоритель.Ускоритель сшивает материала, разрывая длинные молекулярные цепи в полиэтилен, заставляя их образовывать более стабильные, кристаллические структура. Полученный материал имеет множество преимуществ перед несшитый полиэтилен. Независимо от количества воздействия ускорителя, часть полиэтилена остается несшитой. Разные отраслевые стандарты требуют определенного минимального процента сшитых материал в трубке PEX, обычно определяемый с использованием растворителя метод экстракции. Следуя этому методу, образец сшитого пластика взвешивают, а затем погружают в ванну с кипящим растворителем на срок до 12 часов. Этот процесс растворяет несшитый полиэтилен. от образца, оставляя только сшитый материал. В Процент сшивки образца рассчитывается путем деления его вес после процесса с его весом до процесс. Хотя этот метод считается золотым стандартом для оценивая процент сшивки PEX, пора потребительно и дорого.Путем изучения ряда физических свойства при разной степени воздействия ускорителя, Команда Mercury Plastics обнаружила сильнейшую корреляцию между процент сшивки материала и его удлинение при повышенные температуры. В зависимости от процента сшивки это горячее тенденция к уменьшению удлинения с достаточно узкими вариациями (Рисунок 1). Формула регрессии, созданная на основе тестовых данных служит для оценки процента сшивки образца учитывая его горячее удлинение. Используя свои результаты в качестве основы, инженеры разработали испытательный прибор, который применяет стандартную нагрузку и температуру к Образец трубки PEX, а затем измеряет ее удлинение. удлиниться за пределы расстояния, связанного с минимумом сшитое процентное срабатывание концевого выключателя, уведомляющего инспектор отказа. Точно так же аппарат передает пробы которые остаются в пределах предела удлинения для заданного испытания время. Тест выполняется менее чем за пять минут — доля времени, необходимого для экстракции растворителем метод. Хотя потеря достоверности измерения очевидна недостаток, это в допустимых пределах для этого приложения. Использование косвенного измерения может быть оправдано с учетом значительные преимущества в области безопасности, стоимости и производительности. Похожий компромисс может быть возможен из-за ваших трудных или трудоемких проблема измерения. ССЫЛКА1. ASTM, D2765-01 Стандартные методы испытаний для определения Содержание геля и коэффициент набухания сшитых этиленовых пластиков, 2001 г. БИБЛИОГРАФИЯ Гриффит, Гэри К. четвертое издание, Prentice Hall, 2000. RAY HARKINS — менеджер по качеству Mercury. Plastics Inc. в Миддлфилде, штат Огайо. Он получил степень бакалавра степень в области инженерных технологий Университета Акрона. Харкинс является старшим членом ASQ и сертифицированным специалистом по калибровке. техник и техник по качеству. Что такое косвенное измерение? — Цвета-Нью-Йорк.comЧто такое косвенное измерение?Косвенное измерение — это метод использования пропорций для нахождения неизвестной длины или расстояния на аналогичных фигурах. Два распространенных способа выполнения косвенных измерений включают (1) использование зеркала на земле и (2) использование длины тени и определение высоты объекта. Что такое система прямого измерения? При прямых измерениях используются измерительные инструменты, такие как штангенциркуль, микрометры и координатно-измерительные машины, для непосредственного измерения размеров цели. Что такое косвенное измерение в химии?Косвенное измерение — это тип измерения, при котором вы не снимаете свое измерение напрямую с шкалы. Вместо этого обычно используется какая-то форма расчета. Например, вы можете косвенно измерить площадь прямоугольника, умножив длину прямоугольника на его ширину (A = l x w). Что из следующего является примером прямого измерения?Прямые меры — это меры, которые измеряют обучение студентов путем оценки реальных образцов студенческой работы.Примеры включают: экзамены / тесты, документы, проекты, презентации, портфолио, выступления и т. Д. Что такое прямая и косвенная оценка? Прямые оценки предусматривают прямую проверку или наблюдение знаний или навыков учащихся по сравнению с поддающимися измерению результатами обучения. Косвенная оценка обучения студентов позволяет установить предполагаемый объем или ценность учебного опыта. Они оценивают мнения или мысли о знаниях или навыках учащихся. Какой пример косвенного доказательства?Пример косвенного доказательства (по тому же делу) — свидетель, показывающий, что она видела, как подсудимый убегает с места преступления.Здесь присяжный заседатель мог использовать этот факт, чтобы сделать вывод о том, что обвиняемый совершил преступление. Прямые и косвенные доказательства используются как в: гражданских делах (например, дело о телесных повреждениях), так и. В чем разница между прямыми и косвенными доказательствами в науке?Прямое доказательство не требует каких-либо рассуждений или умозаключений для того, чтобы прийти к выводу, который следует сделать из доказательств. Косвенное свидетельство, также называемое косвенным свидетельством, требует, чтобы был сделан вывод между свидетельством и выводом, который следует из него сделать. Что такое метод косвенного интервью? Определение: Косвенные методы оценки требуют, чтобы преподаватели делали выводы о реальных способностях, знаниях и ценностях учащихся, а не наблюдали за прямыми доказательствами. Какие бывают косвенные методы?Косвенный метод — это один из двух методов подготовки отчета о движении денежных средств. При косвенном методе отчет о движении денежных средств начинается с чистой прибыли по методу начисления, а затем добавляются и вычитаются неденежные статьи для согласования с фактическими потоками денежных средств от операционной деятельности. В чем основное отличие прямого и косвенного методов качественного исследования?Качественные методы исследования могут быть прямыми и косвенными. Косвенные методы позволяют респондентам определить истинную цель исследования, тогда как косвенные методы скрывают цель исследования. Основные прямые методы — это фокус-группы и интервью по долгу. Что такое косвенные вопросы интервью?12 вопросов для косвенного собеседования и что они на самом деле раскрывают
Что такое прямое или косвенное интервью? Интервью могут быть как прямыми, так и косвенными. Какие бывают косвенные вопросы?Косвенный вопрос — это вопрос, заключенный в высказывание (т. Е. Повествовательное предложение) или другой вопрос (т. Е. Вопросительное предложение). Что такое метод прямого интервью?Автор.В рамках этого метода сбора данных с информаторами (лицами, от которых должна быть получена информация) устанавливается личный контакт. Интервьюер задает им вопросы, относящиеся к опросу, и собирает желаемую информацию. Как наиболее эффективно провести опрос?Настроить лучший онлайн-опрос легко, если вы воспользуетесь этими шестью шагами, которые помогут вам в этом процессе.
Какой вид исследования представляет собой опрос?Опросное исследование — это количественный подход, который предусматривает использование самоотчетов по тщательно отобранным выборкам. Это гибкий подход, который можно использовать для изучения широкого круга вопросов фундаментального и прикладного исследования. Какие методы обследования?Три основных типа — это поперечные сечения, последовательные независимые выборки и продольные исследования.
Какова основная цель опроса? Опросы используются для сбора или получения знаний в таких областях, как социальные исследования и демография. |

 Шпаргалки. Школа. / / Погрешности прямых и косвенных измерений. Абсолютная, относительная погрешность. Систематические и случайные погрешности. Среднее квадратическое отклонение (ошибка). Таблица определения погрешностей косвенных измерений различных функций.
Шпаргалки. Школа. / / Погрешности прямых и косвенных измерений. Абсолютная, относительная погрешность. Систематические и случайные погрешности. Среднее квадратическое отклонение (ошибка). Таблица определения погрешностей косвенных измерений различных функций. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах.
Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах. Свободные и вынужденные колебания. Гармонические колебания. Упругие колебания. Математический маятник. Превращения энергии при гармонических колебаниях
Свободные и вынужденные колебания. Гармонические колебания. Упругие колебания. Математический маятник. Превращения энергии при гармонических колебаниях Поляризация света
Поляризация света Понятие электромагнитной волны. Свойства электромагнитных волн. Волновые явления
Понятие электромагнитной волны. Свойства электромагнитных волн. Волновые явления 2
2 Оба они часто используются в косвенных измерениях.
Оба они часто используются в косвенных измерениях. Он обнаружил, что когда тени измерялись в одно и то же время дня, отношение его тени к тени пирамиды пропорционально отношению его высоты к высоте пирамиды.
Он обнаружил, что когда тени измерялись в одно и то же время дня, отношение его тени к тени пирамиды пропорционально отношению его высоты к высоте пирамиды. Этот метод включает в себя измерение других длин и расстояний, а затем использование таких стратегий, как теорема Пифагора , пропорций , подобных треугольников или теорема Фалеса .
Этот метод включает в себя измерение других длин и расстояний, а затем использование таких стратегий, как теорема Пифагора , пропорций , подобных треугольников или теорема Фалеса . Есть 2 метода.
Есть 2 метода.  Таким образом, это будет ваш прямой угол, и тогда этот угол будет соответствовать углу, образованному светом, отражающимся от этого зеркала. Таким образом, вы можете использовать мой рост, который вы можете измерить, вы можете измерить расстояние между мной и зеркалом, вы можете измерить расстояние между зеркалом и вашим объектом, и вы можете использовать эту пропорцию, чтобы найти ту недостающую сторону, высоту вашего тела. объект. Итак, это один из способов использования подобных треугольников для измерения чего-то высокого.
Таким образом, это будет ваш прямой угол, и тогда этот угол будет соответствовать углу, образованному светом, отражающимся от этого зеркала. Таким образом, вы можете использовать мой рост, который вы можете измерить, вы можете измерить расстояние между мной и зеркалом, вы можете измерить расстояние между зеркалом и вашим объектом, и вы можете использовать эту пропорцию, чтобы найти ту недостающую сторону, высоту вашего тела. объект. Итак, это один из способов использования подобных треугольников для измерения чего-то высокого.  В этом случае вы должны измерить длину тени и рост человека, а затем измерить длину тени. И вы можете использовать похожие треугольники, чтобы определить высоту вашего объекта.
В этом случае вы должны измерить длину тени и рост человека, а затем измерить длину тени. И вы можете использовать похожие треугольники, чтобы определить высоту вашего объекта. 
 Какой подход обеспечит наиболее значимые и контролируемые результаты?
Какой подход обеспечит наиболее значимые и контролируемые результаты? Например, при прямом измерении вес, расстояние и т. Д.
Например, при прямом измерении вес, расстояние и т. Д.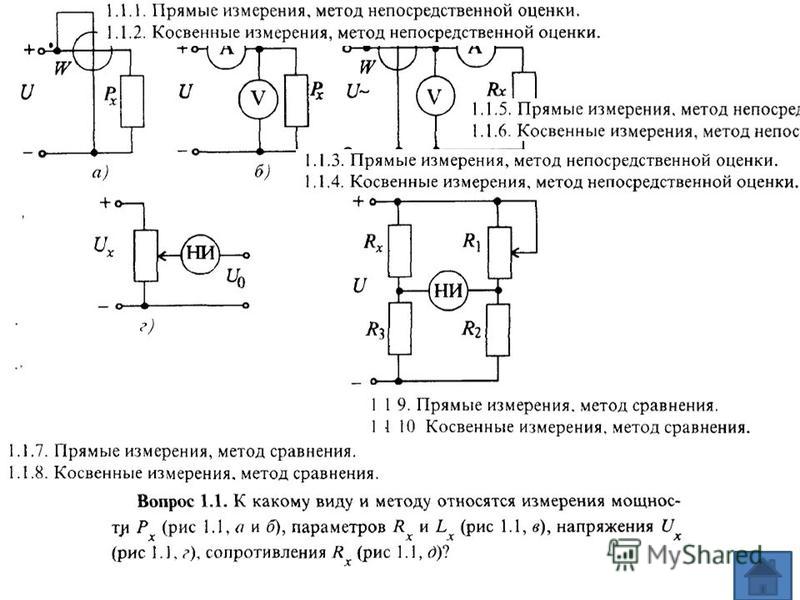 Два распространенных способа выполнения косвенных измерений включают (1) использование зеркала на земле и (2) использование длины тени и определение высоты объекта.
Два распространенных способа выполнения косвенных измерений включают (1) использование зеркала на земле и (2) использование длины тени и определение высоты объекта. Ниже). Каждый служит определенной цели.
Ниже). Каждый служит определенной цели.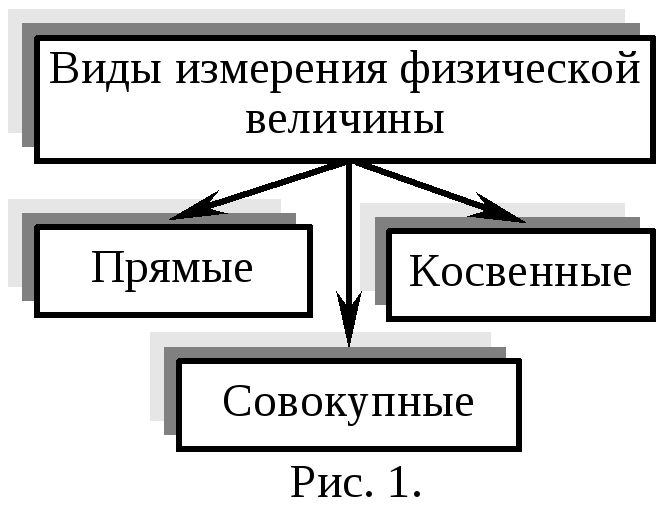
 Эти методы обычно делятся на две категории: прямые и косвенные меры. Лучшие практики рекомендуют использовать как прямые, так и косвенные меры при определении степени обучения студентов.
Эти методы обычно делятся на две категории: прямые и косвенные меры. Лучшие практики рекомендуют использовать как прямые, так и косвенные меры при определении степени обучения студентов. Результаты для этих областей могут относиться к эффективности процессов, результативности программ и т. Д.Бизнес и финансы, приемная комиссия и финансовая помощь — это лишь некоторые из отделов университетского городка, которые могут использовать такие результаты. Примеры прямых мер для административных, академических служб и служб поддержки студентов включают количественные отчеты о точности и своевременности финансовых отчетов, количестве и проценте участия заинтересованных сторон, выбытии заинтересованных сторон и множество других мер в зависимости от результатов и целей, установленных для отдела.
Результаты для этих областей могут относиться к эффективности процессов, результативности программ и т. Д.Бизнес и финансы, приемная комиссия и финансовая помощь — это лишь некоторые из отделов университетского городка, которые могут использовать такие результаты. Примеры прямых мер для административных, академических служб и служб поддержки студентов включают количественные отчеты о точности и своевременности финансовых отчетов, количестве и проценте участия заинтересованных сторон, выбытии заинтересованных сторон и множество других мер в зависимости от результатов и целей, установленных для отдела. Д. Косвенные меры лучше всего использовать на уровне программ или университетов. Эти меры обычно сочетаются с прямыми измерениями обучения студентов.
Д. Косвенные меры лучше всего использовать на уровне программ или университетов. Эти меры обычно сочетаются с прямыми измерениями обучения студентов. Профессор может точно оценить, насколько хорошо и на каком уровне студент изучает и использует терминологию, концепции и теории. В курсах и обучении более высокого уровня преподаватели имеют хорошие возможности для оценки когнитивного использования и расширения знаний на более высоком уровне.
Профессор может точно оценить, насколько хорошо и на каком уровне студент изучает и использует терминологию, концепции и теории. В курсах и обучении более высокого уровня преподаватели имеют хорошие возможности для оценки когнитивного использования и расширения знаний на более высоком уровне. Очень важно использовать рубрики, чтобы помочь в этом процессе оценки.Редко когда какое-либо задание или экзамен будут сосредоточены полностью на одном результате обучения учащегося, но, используя критерии, преподаватели могут быстрее оценивать уровни достижений по индивидуальным и конкретным результатам обучения.
Очень важно использовать рубрики, чтобы помочь в этом процессе оценки.Редко когда какое-либо задание или экзамен будут сосредоточены полностью на одном результате обучения учащегося, но, используя критерии, преподаватели могут быстрее оценивать уровни достижений по индивидуальным и конкретным результатам обучения. Тем самым информируя программу или отдел о том, что работает, а что нет в его деятельности.
Тем самым информируя программу или отдел о том, что работает, а что нет в его деятельности.

 Этот
Этот 1
1  Образцы, которые
Образцы, которые , Справочник специалиста по качеству,
, Справочник специалиста по качеству, Эти измерения также известны как абсолютные измерения.
Эти измерения также известны как абсолютные измерения.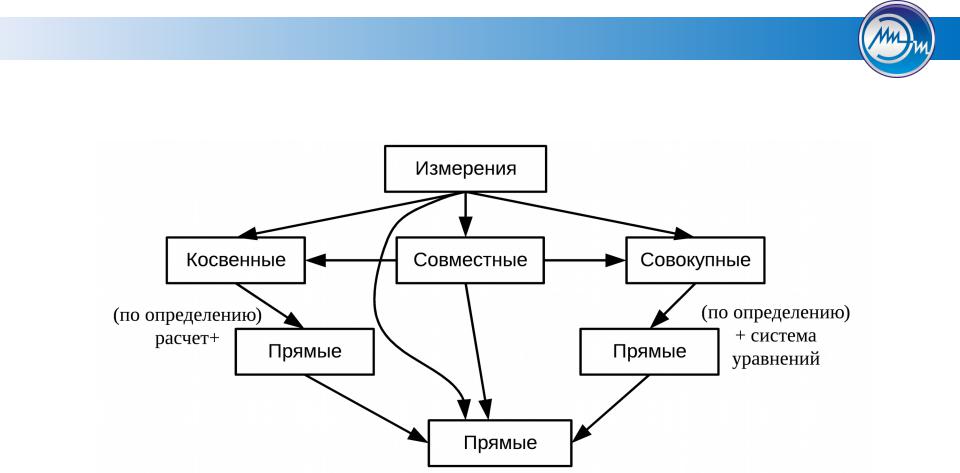
 К косвенным методам относятся опросы, интервью при выходе, фокус-группы и использование внешних рецензентов.
К косвенным методам относятся опросы, интервью при выходе, фокус-группы и использование внешних рецензентов.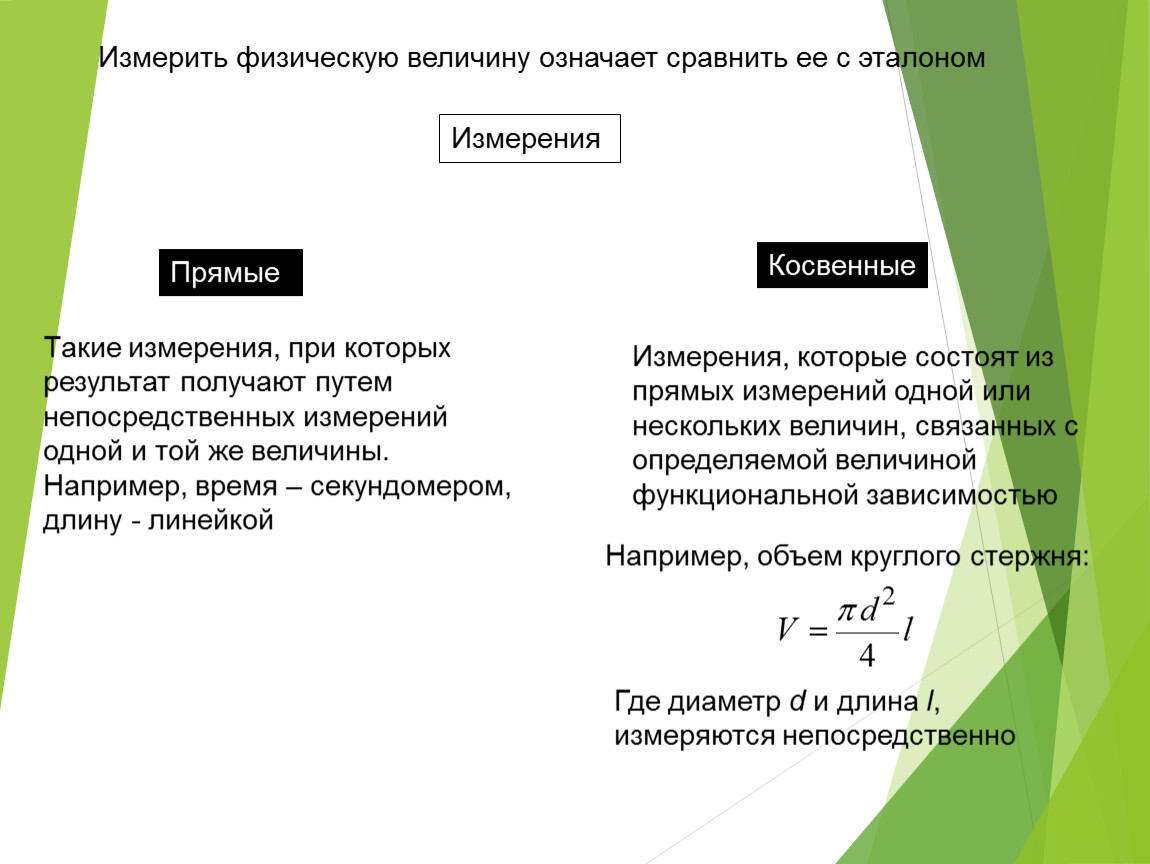 Прямое собеседование предполагает вопросы. вопросы таким образом, чтобы респондент понимал цель вопроса и предполагаемый ответ. Косвенные интервью включают в себя вопросы, когда респондент не знает цели или предполагаемого ответа.
Прямое собеседование предполагает вопросы. вопросы таким образом, чтобы респондент понимал цель вопроса и предполагаемый ответ. Косвенные интервью включают в себя вопросы, когда респондент не знает цели или предполагаемого ответа.
