Магнитное поле прямого тока — урок. Физика, 8 класс.
Обнаружить магнитное поле вокруг металлического проводника с током можно несколькими способами. Например, использовать мелкие железные опилки.
На плоскость, перпендикулярно которой расположен проводник, нужно насыпать железные опилки. Железо может намагничиваться, попадая в магнитное поле, и поэтому опилки станут маленькими магнитными стрелками. Магнитное поле развернет эти стрелки и выстроит в линии, по которым направлено действие магнитных сил.
Электрическое поле мы изображаем векторами электрической напряжённости. Для изображения магнитного поля используют линии магнитного поля.
За положительное направление линий магнитного поля принято направление, вдоль которого ориентируется магнитная стрелка — от южного полюса к северному.
Магнитные линии замкнуты вокруг проводника, непрерывны и не пересекаются между собой. Через любую точку около проводника с током можно провести магнитную линию.
Направление линий магнитного поля совпадает с направлением северного конца магнитной стрелки компаса.
Железные опилки намагничиваются в поле проводника с током и действуют как стрелки компаса, указывая направление линий магнитной индукции (рис. 1).
Рис. \(1\). Магнитные линии вокруг проводника
Для иллюстрации линий магнитного поля вокруг прямого проводника с током проводник продевают в отверстие подложки, на которую насыпаны железные опилки. При прохождении электрического тока по проводнику вокруг него возникает магнитное поле. Опилки выстраиваются в замкнутые линии, образующие концентрические окружности с центром в проводнике с током. Эти линии будут сгущаться ближе к проводнику (рис. 2).
Рис. \(2\). Положение магнитной стрелки
На рисунке показано расположение магнитных стрелок вокруг проводника с током, расположенного перпендикулярно плоскости чертежа, ток в нём направлен от нас, что условно обозначено кружком с крестиком. Магнитные стрелки располагаются вокруг проводника с током определенным образом (рис. 3, а). Если изменить направление тока в проводнике на противоположное, то все магнитные стрелки повернуться на \(180\)° (рис. 3, б).
Магнитные стрелки располагаются вокруг проводника с током определенным образом (рис. 3, а). Если изменить направление тока в проводнике на противоположное, то все магнитные стрелки повернуться на \(180\)° (рис. 3, б).
В этом случае направление тока условно обозначено кружком с точкой (это означает, что ток идет к нам).
Рис. \(3\). Расположение стрелки компаса в зависимости от направления тока
Изменение направления магнитных стрелок связано с изменением направления тока в проводнике, а значит, и с изменением направления магнитных линий магнитного поля.
Направление линий магнитного поля можно определить с помощью правила правой руки:
если обхватить проводник с током ладонью правой руки так, чтобы отставленный большой палец был сонаправлен с током (рис. 4), то согнутые четыре пальца укажут направление линий магнитного поля.
Рис. \(4\). Правило правой руки
Источники:
Рис. 1. Магнитные линии вокруг проводника. © ЯКласс.
© ЯКласс.
Рис. 2. Положение магнитной стрелки. © ЯКласс.
Рис. 3. Расположение стрелки компаса в зависимости от направления тока. © ЯКласс.
Рис. 4. Правило правой руки. https://www.shutterstock.com/ru/image-vector/physics-current-magnetic-field-flemings-right-1739151677. 2021-08-19.
Электричество и магнетизм
Вычислим поле, создаваемое током, текущим по тонкому прямолинейному проводу бесконечной длины.
Индукция магнитного поля в произвольной точке А (рис. 6.12), создаваемого элементом проводника dl, будет равна
Рис. 6.12. Магнитное поле прямолинейного проводника
Поля от различных элементов имеют одинаковое направление (по касательной к окружности радиусом R, лежащей в плоскости, ортогональной проводнику). Значит, мы можем складывать (интегрировать) абсолютные величины
|
(6. |
Выразим r и sin через переменную интегрирования l
|
(6.8) |
Тогда (6.7) переписывается в виде
Таким образом,
|
|
(6.9) |
Картина силовых линий магнитного поля бесконечно длинного прямолинейного проводника с током представлена на рис. 6.13.
Рис. 6.13. Магнитные силовые линии поля прямолинейного проводника с током:
1 — вид сбоку; 2, 3 — сечение проводника плоскостью, перпендикулярной проводнику
Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис.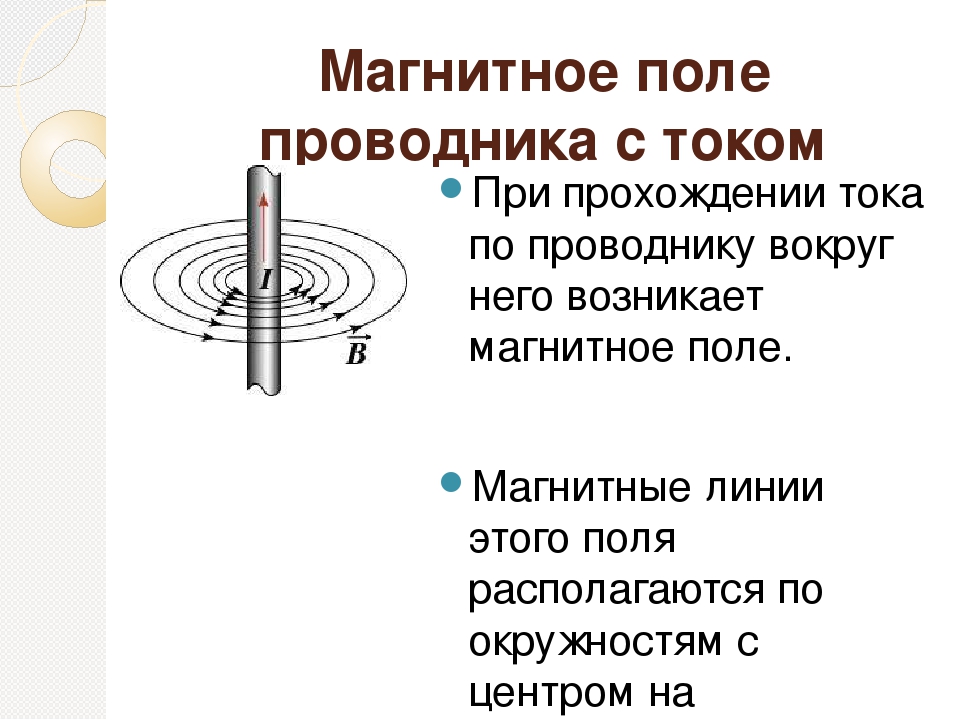 6.14):
6.14):
Рис. 6.14. Обозначения направления тока в проводнике
Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис. 6.14):
Напомним выражение для напряженности электрического поля тонкой нити, заряженной с линейной плотностью заряда
Сходство выражений очевидно: мы имеем ту же зависимость от расстояния до нити (тока), линейная плотность заряда заменилась на силу тока. Но направления полей различны. Для нити электрическое поле направлено по радиусам. Силовые линии магнитного поля бесконечного прямолинейного проводника с током образуют систему концентрических окружностей, охватывающих проводник. Направления силовых линий образуют с направлением тока правовинтовую систему.
На рис. 6.15 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг прямолинейного проводника с током. Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.
Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.
Вокруг прямого провода, перпендикулярного пластинке, наблюдаются кольцевые силовые линии, расположенные наиболее густо вблизи провода. При удалении от него поле убывает.
Рис. 6.15. Визуализация силовых линий магнитного поля вокруг прямолинейного проводника
На рис. 6.16 представлены опыты по исследованию распределения силовых линий магнитного поля вокруг проводов, пересекающих картонную пластинку. Железные опилки, насыпанные на пластинку, выстраиваются вдоль силовых линий магнитного поля.
Рис. 6.16. Распределение силовых линий магнитного поля
вблизи пересечения с пластинкой одного, двух и нескольких проводов
Магнитное поле прямого проводника с током.
 Все о магнитах :: Класс!ная физика
Все о магнитах :: Класс!ная физика
МАГНИТНОЕ ПОЛЕ ПРЯМОГО ПРОВОДНИКА С ТОКОМ
Если есть прямой проводник с током, то обнаружить наличие магнитного поля вокруг
этого проводника можно с помощью железных опилок …
… или магнитных стрелок.
Под действием магнитного поля тока магнитные стрелки или железные опилки
располагаются по концентрическим окружностям.
Магнитные линии.
Магнитное поле можно изобразить графически с помощью магнитных линий.
Магнитные линии магнитного поля тока – это линии, вдоль которых в магнитном поле располагаются оси маленьких магнитных стрелок.
Магнитные линии магнитного поля тока – это замкнутые кривые, охватывающие проводник.
У прямого проводника с током — это концентрические расширяющиеся окружности .
За направление магнитной линии принято направление, которое указывает северный полюс магнитной стрелки в каждой точке поля.
Графическое изображение магнитного поля прямого проводника с током.
Направление магнитных линий магнитного поля тока
связано с направлением тока в проводнике:
ЧИТАЕМ !
Магнитный вечный двигатель.
Магнитные фокусы.
Тайны магнита.
УДИВИСЬ !
Интересно видеть, как железные опилки, притянувшись к полюсу магнита образуют кисти, отталкивающиеся друг от друга. А ведь они всего-навсего располагаются вдоль силовых линий магнитного поля!
___
А можете ли вы нарисовать картину магнитные линии магнитного поля проводника с током, свернутого в виде восьмерки?
Этот рисунок похож на тот, что представил себе ты?
МОЖНО ЛИ УВИДЕТЬ МАГНИТНОЕ ПОЛЕ ?
Надо включить цветной телевизор на какой- нибудь неподвижный кадр и поднести к нему магнит.
Цвета изображения на экране вблизи магнита изменятся!
Картинка будет сиять радужными разводами. Цветные полосы сгущаются вблизи контура магнита
как бы визуализируя магнитное поле. Интересно при этом вращать магнит, сдвигать его
или приближать и удалять от экрана.
Картина магнитного поля будет куда интересней, чем в опытах с опилками!
ПОЧЕМУ ?
К небольшому латунному диску свободно подвесили несколько стальных иголок.
Если снизу к иголкам медленно подносить магнит (например, южным полюсом),
то сначала иголки разойдутся, а затем, когда магнит приблизится совсем вплотную,
снова вернутся в вертикальное положение.
Почему?
Устали? — Отдыхаем!
Магнитное поле прямого тока. Магнитные линии
Существование магнитного поля вокруг проводника с электрическим током можно обнаружить различными способами. Один из таких способов заключается в использовании мелких железных опилок.
В магнитном поле опилки — маленькие кусочки железа — намагничиваются и становятся магнитными стрелочками. Ось каждой из этих стрелочек в магнитном поле устанавливается вдоль направления действия сил магнитного поля.
На рисунке 278 изображена картина магнитного поля прямого проводника с током. Для получения такой картины прямой проводник пропускают сквозь лист картона. На картон насыпают тонкий слой железных опилок, включают ток, и опилки слегка встряхивают. Под действием магнитного поля тока железные опилки располагаются вокруг проводника не беспорядочно, а по концентрическим окружностям.
Линии, вдоль которых в магнитном поле располагаются оси маленьких магнитных стрелок, называют магнитными линиями магнитного поля. Цепочки, которые образуют в магнитном поле железные опилки, показывают форму магнитных линий магнитного поля. Магнитные линии магнитного поля тока представляют собой замкнутые кривые, охватывающие проводник.
С помощью магнитных линий удобно изображать магнитные поля графически. Так как магнитное поле существует во всех точках пространства, окружающего проводник с током, то через любую точку можно провести магнитную линию, но так, чтобы она охватывала проводник с током.
Так как магнитное поле существует во всех точках пространства, окружающего проводник с током, то через любую точку можно провести магнитную линию, но так, чтобы она охватывала проводник с током.
На рисунке 219, а показано расположение магнитных стрелок вокруг проводника с током. (Проводник расположен перпендикулярно плоскости чертежа, ток в нем направлен от нас, что условно обозначено кружком с крестиком.) Оси этих стрелок устанавливаются вдоль магнитных линий магнитного поля прямого тока. При изменении направления тока в проводнике все магнитные стрелки поворачиваются на 180° (рис. 279,6; в этом случае ток в проводнике направлен к нам, что условно обозначено кружком с точкой). Из этого опыта можно заключить, что направление магнитных линий магнитного поля тока связано с направлением тока в проводнике.
Вопросы. 1. Почему для изучения магнитного поля можно использовать железные опилки? 2. Как располагаются железные опилки в магнитном поле прямого тона? 3. Что называют магнитной линией магнитного поля? 4. Для чего вводят понятие магнитной линии поля? 5. Как на опыте показать, что направление магнитных линий связано с направлением тока?
Что называют магнитной линией магнитного поля? 4. Для чего вводят понятие магнитной линии поля? 5. Как на опыте показать, что направление магнитных линий связано с направлением тока?
Конспект урока по физике по теме «Магнитное поле прямого проводника и катушки с током. Электромагнит»
Конспект
урока по теме «Магнитное поле прямого проводника и катушки с током.
Электромагнит»
8
класс
Цель
обучения: формирование представления о природе
магнетизма, о связи между электрическим током и магнитным полем, о направлении
линий магнитных полей прямолинейного проводника с током и соленоидом.
Ход
урока
I.
Актуализация знаний (проводится
в ходе опроса учащихся)
1.
Чем подтверждается материальность
магнитного поля?
2.
С помощью каких тел можно изучить
магнитное поле?
3.
Почему полюса магнита называют северным и
южным?
4.
Что такое линии магнитного поля? Что
выбрано за направление этих линий?
5.
Из какого полюса постоянного магнита
выходят линии магнитного поля? В какой входят?
II.
Проблемный вопрос
Поднесем к магнитной стрелки
наэлектризованную стеклянную палочку. К палочке притянется ближний конец
стрелки независимо от того, северный он или южный. Так же будет вести себя и
полностью размагниченная стрелка. Объясните почему?
III.
Изучение нового материала
Размышляя над проблемным вопросом учащиеся
должны прийти к выводу: электризация через влияние.
Перераспределение заряда в теле, вызываемое |
Далее
учитель с учащимися рассматривает ряд опытов, на основании которых, учащиеся
делают выводы и записи в тетради.
Расположим Магнитное поле создается не только Гипотеза Ампера: В телах из Круговым током, создающим элементарное магнитное
| ||||||
Рассмотрим опыт. Насыплем Располагая около проводника магнитные стрелки, можно Для определения направления линий магнитного поля
Пример: на
Рассмотрим катушку с током – соленоид. Созданное катушкой |
Для
любознательных
Электромагниты, | |
Электросчетчик | |
Ваттметр- |
IV.
Закрепление знаний
1.
Как взаимодействует стрелка компаса с
наэлектризованными эбонитовой и стеклянной палочками? Какие выводы можно из
этого сделать?
2.
Чем, согласно гипотезе Ампера, различаются
намагниченное и ненамагниченное тело?
3.
Как взаимодействует стрелка компаса с
наэлектризованным железным телом (гвоздем)?
4.
Какими способами можно получить картину
линий магнитного поля различных проводников?
5.
Как можно определить направление линий
магнитного поля, создаваемого проводником с током?
6.
Как с помощью правой руки определить
направление линий магнитного поля: а) прямого проводника с током; б) катушки с
током?
7.
Как можно усилить магнитное поле
электромагнита?
8.
Где применяются катушки с током?
9.
Можно ли называть электромагнитом прямой
проводник с током? Почему?
V.
Рефлексия
VI.
Дом. Задание
VII.
Результат урока
Учащиеся
познакомится с природой магнетизма, связями между электрическим током и
магнитным полем, правилами нахождения линий магнитного поля (правило буравчика
или правого винта, правой руки).
Карта
урока (для учащихся)
I.
Актуализация знаний (проводится
в ходе опроса учащихся)
1.
Чем подтверждается материальность
магнитного поля?
2.
С помощью каких тел можно изучить
магнитное поле?
3.
Почему полюса магнита называют северным и
южным?
4.
Что такое линии магнитного поля? Что
выбрано за направление этих линий?
5.
Из какого полюса постоянного магнита
выходят линии магнитного поля? В какой входят?
II.
Проблемный вопрос
Поднесем к магнитной стрелки
наэлектризованную стеклянную палочку. К палочке притянется ближний конец
стрелки независимо от того, северный он или южный. Так же будет вести себя и
полностью размагниченная стрелка. Объясните почему?
III.
Изучение нового материала
Размышляя над проблемным вопросом учащиеся
должны прийти к выводу: электризация через влияние.
Перераспределение заряда в теле, вызываемое |
Далее
учитель с учащимися рассматривает ряд опытов, на основании которых, учащиеся
делают выводы и записи в тетради.
Расположим Магнитное поле создается не только постоянным Гипотеза Ампера: В телах из Круговым током, создающим элементарное магнитное поле,
| ||||||
Рассмотрим опыт. Насыплем Располагая около проводника магнитные стрелки, можно Для определения направления линий магнитного поля
Пример: на
Рассмотрим катушку с током – соленоид. Созданное |
Для
любознательных
Электромагниты, | |
Электросчетчик | |
Ваттметр- |
IV.
Закрепление знаний
1.
Как взаимодействует стрелка компаса с
наэлектризованными эбонитовой и стеклянной палочками? Какие выводы можно из
этого сделать?
2.
Чем, согласно гипотезе Ампера, различаются
намагниченное и ненамагниченное тело?
3.
Как взаимодействует стрелка компаса с
наэлектризованным железным телом (гвоздем)?
4.
Какими способами можно получить картину
линий магнитного поля различных проводников?
5.
Как можно определить направление линий
магнитного поля, создаваемого проводником с током?
6.
Как с помощью правой руки определить
направление линий магнитного поля: а) прямого проводника с током; б) катушки с
током?
7.
Как можно усилить магнитное поле
электромагнита?
8.
Где применяются катушки с током?
9.
Можно ли называть электромагнитом прямой
проводник с током? Почему?
V.
Рефлексия
VI.
Дом. Задание
Поле прямолинейного проводника — Энциклопедия по машиностроению XXL
Вначале следует составить уравнения связи для требуемой величины применительно к рассматриваемым системам единиц, а затем определить переводный коэффициент как отношение полученных выражений. Например, напряженность магнитного поля прямолинейного проводника с током / на расстоянии г от него определяется формулами
[c.89]
Поле прямолинейного проводника. Простейшим случаем является прямолинейный проводник с постоянным током/, протекающим в направлении оси z (рис. 31). Очевидно, что направление вектора dB перпендикулярно плоскости рисунка и вектор направлен от нас в соответствии с правилом правой руки независимо от расположения элемента тока Ids и точки Р. Таким образом, направление вектора В будет таким же после интегрирования вдоль проводника. Так как уже известно направление вектора В, можно вычислить его абсолютное значение. Из рис. 31 с очевидностью следует, что
[c.123]
Так как уже известно направление вектора В, можно вычислить его абсолютное значение. Из рис. 31 с очевидностью следует, что
[c.123]
Био (ВШ) Жан Батист (1774-1862) — французский физик и математик. Окончил Политехническую школу в Париже. Основные работы посвящены оптике (закон Био вращения плоскости поляризации света), электромагнетизму (закон Био — Савара о напряженности магнитного пола прямолинейного проводника). В области математики работал над теорией уравнений с частными производными, связанными с колебанием поверхностей, предложил классификацию дифференциально-разностных уравнений. Написал (1803 г.) Общую историю науки в годы Революции . [c.142]
При исследовании магнитного поля с помощью прямолинейного проводника с током магнитная индукция определяется следующим образом модуль магнитной индукции равен отношению максимального значения модуля силы Ампера F, действующей на проводник с током, к силе тока I в проводнике и его длине Z
[c. 177]
177]
Сила Ампера. Формулу (51.1) можно использовать для определения модуля максимального значения силы Ампера, действующей на прямолинейный проводник с током в магнитном поле с индукцией В [c.179]
Наиболее принятый в общем курсе физики путь состоит в том, что вся задача о взаимодействии токов разбивается на два этапа. Вначале рассматривается поведение прямолинейного проводника или контура с током /ц во внешнем магнитном поле, созданном другим контуром с током 2, параметры которого временно остаются в стороне. Удобно взять контур, о котором мы [c.229]
Согласно формуле Ампера сила, которую испытывает прямолинейный проводник длиной 1 с током I в магнитном поле с индукцией В (если угол между направлениями индукции и тока а), равна [c.238]
Напряженность магнитного поля бесконечно длинного прямолинейного проводника с током
[c.401]
Закон Фарадея. При движении прямолинейного проводника в равномерном магнитном поле под углом а к направлению поля в проводнике индуктируется э.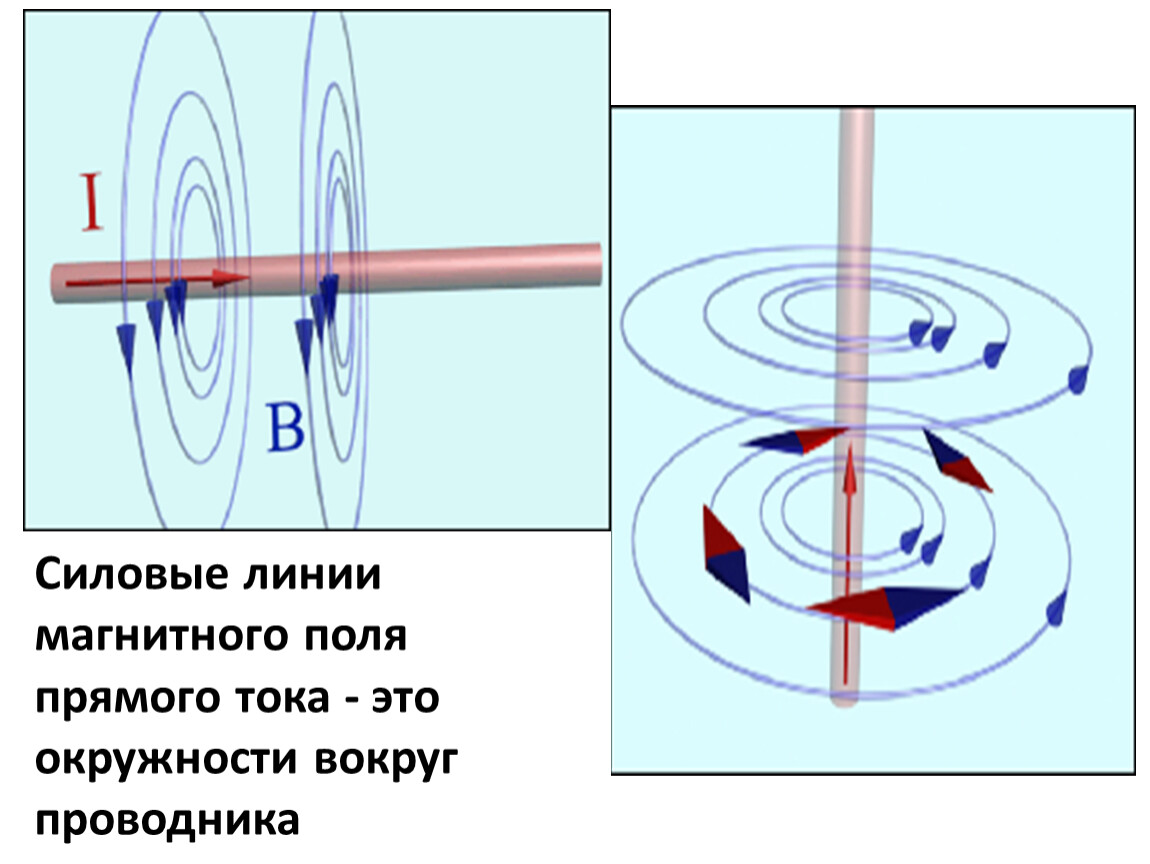 д. с., равная
[c.518]
д. с., равная
[c.518]
Индукция поля, создаваемого прямолинейным проводником, [c.216]
Кольцевой эффект. Если прямолинейный проводник свить в кольцо или спираль, то распределение тока по его сечению изменится. На внутренней стороне проводника ток будет иметь наибольшую плотность, а на его внешней стороне тока практически не будет. В связи с этим в проводнике и около него происходит неравномерное распределение магнитного потока. Силовые линии магнитного поля будут уплотнены у внутренней поверхности кольца. [c.51]
Наиболее принятый в общих курсах физики путь состоит в том, что вся задача о взаимодействии токов разбивается на два этапа. Вначале рассматривается поведение прямолинейного проводника или контура с током /1 во внешнем магнитном поле, созданном другим контуром с током 2, параметры которого временно остаются в стороне. Удобно взять контур, о котором мы уже знаем, что он обладает свойствами диполя. Опыт покажет, что в однородном поле он испытывает вращающий момент
[c. 188]
188]
Магнитная индукция. Основная характеристика магнитного поля — магнитная индукция В наиболее наглядно может быть определена по механическому действию, которое испытывает электрический ток в магнитном поле. Воспользуемся для этой цели формулой (7.12), в которой положим а = я/2, 5 = 1 см . Напомним, кроме Того, что коэффициент Же = 1/с. При этих условиях за единицу магнитной индукции можно принять индукцию такого поля, в котором максимальный момент, испытываемый контуром площадью 1 см и обтекаемым током, численная величина которого равна с (т. е. скорости света в вакууме, измеренной в см/с), составляет I дин-см. Эта единица индукции называется гаусс (Гс). Иначе можно определить гаусс как индукцию такого поля, в котором каждый сантиметр прямолинейного проводника, расположенного перпендикулярно полю и по которому протекает ток с единиц, испытывает силу в одну дину. Размерность индукции, согласно любому из определений, [c.204]
Действие магнитного поля на проводник с током. На прямолинейный проводник длиной /,,, по которому
[c.110]
На прямолинейный проводник длиной /,,, по которому
[c.110]
Эта единица называется гаусс (Гс). Гаусс равен индукции однородного магнитного поля, которое на отрезок длиной 1 см прямолинейного проводника с током силой 3- 10 Г /, действует с максимальной силой 1 дин. Размерность магнитной индукции [c.178]
В рассмотренном случае силовое поле все же называется потенциальным, но с многозначным потенциалом. Читателю может показаться, что мы привели весьма сложный и искусственный пример, интересный, может быть лишь с математической точки зрения это не так — пример взят из физики если по прямолинейному проводнику, ось которого совпадает с осью Oz, течет ток силы i, то в любой плоскости, перпендикулярной к оси Oz, он порождает магнитное поле, напряженность которого [c.203]
Примером безвихревого поля с многозначным потенциалом и замкнутыми векторными линиями может служить поле магнитной напряженности Н от прямолинейного проводника с током У, расположенного на оси Х3
[c.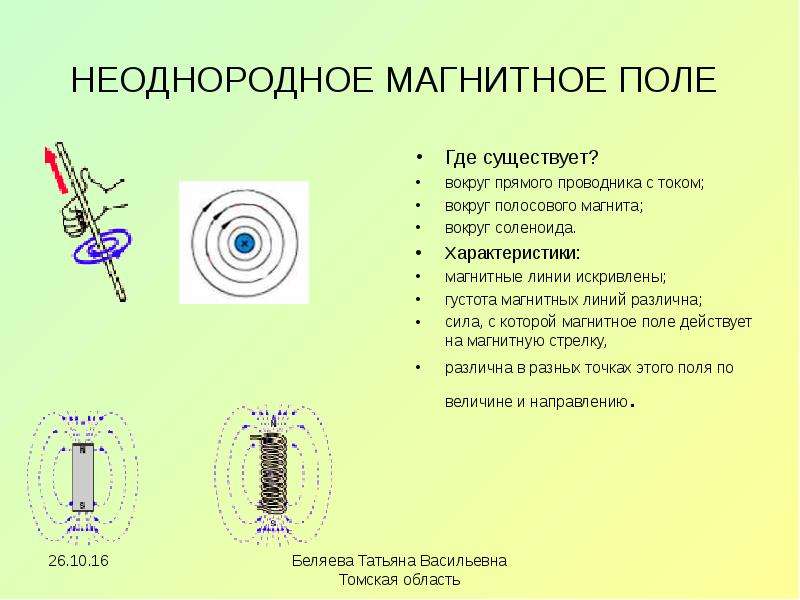 106]
106]
V.4.72. Напряженность магнитного поля на расстоянии г от бесконечного прямолинейного проводника с током [c.63]
V.4.79. Сила, действующая со стороны магнитного поля на прямолинейный проводник с током (формула Ампера) [c.64]
Пусть прямолинейный проводник с током /с, находящийся в первоначально однородном магнитном поле с составляющими Н , Ну и Нг, имеет сечение, симметричное относительно локальных координат X к у (рис. 3.1). Докажем, что мощность, выделяющаяся в проводнике, равна сумме мощностей от тока Л и от вихревых токов, вызванных составляющими Нх, Ну и Н . [c.114]
Ток, проходящий по прямолинейному проводнику, создает вокруг него очень слабое магнитное поле. Для получения более сильного поля наматывают на проводник большое количество витков катушки изолированного провода. Как видно из рис. 37, магнитные поля отдельных витков катушки складываются в общий магнитный поток. Сердечник из мягкой стали, помещенный внутрь катушки, по которой проходит ток, еще более усиливает ее магнитный поток.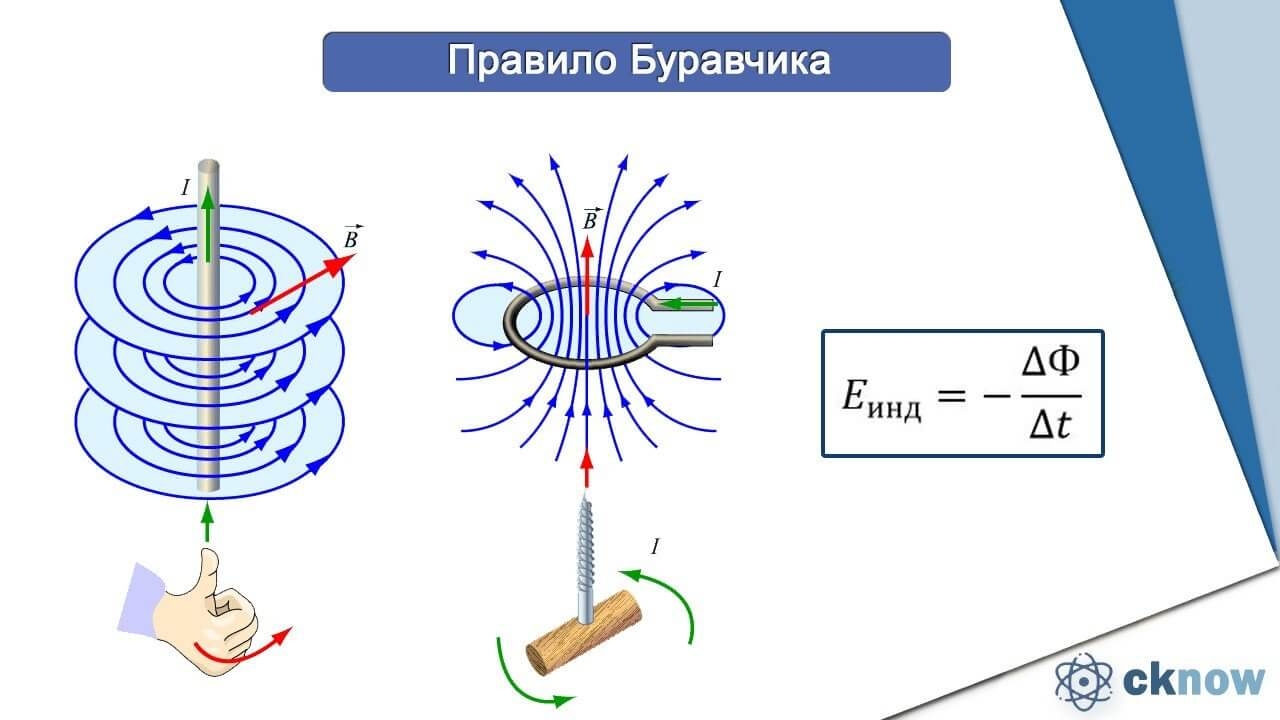 Такая катушка называется электромагнитом.
[c.90]
Такая катушка называется электромагнитом.
[c.90]
Индукция магнитного поля зависит от физических свойств среды, от величины и расположения электрических токов, создающих магнитное поле. Опыт показывает, что в однородной среде вокруг прямолинейного проводника с током образуется круговое магнитное поле, направление которого определяется правилом буравчика (фиг. 1).
[c.480]
При дви>кении прямолинейного проводника перпендикулярно силовым линиям магнитного поля в проводнике возникает также э. д. с. индукции, определяемая по формуле [c.483]
Если поле однородно, для прямолинейного проводника имеем [c.486]
Различные конфигурации магнитного поля. Простейшее (тороидальное) поле создается длинным прямолинейным проводником [c.386]
Возможны случаи, когда элементарная работа силы / есть полный дифференциал некоторой функции и х, у, г), но функция и (х, у, г) есть функция многозначная. В таких случаях поле силы Р также называется потенциальным, но говорят, что тала Р имеет многозначный потенциал. Примером потенциального поля с многозначным потенциалом может служить пространство, окружающее прямолинейный проводник электрического тока. В этом поле на магнитный полюс действует сила, имеющая многозначный потенциал
[c.63]
В таких случаях поле силы Р также называется потенциальным, но говорят, что тала Р имеет многозначный потенциал. Примером потенциального поля с многозначным потенциалом может служить пространство, окружающее прямолинейный проводник электрического тока. В этом поле на магнитный полюс действует сила, имеющая многозначный потенциал
[c.63]
Если конкретная задача магнитостатики обладает цилиндрической симметрией, то напряженность магнитного поля оказывается постоянной на круговом контуре, центр которого лежит на оси симметрии. Примером может служить задача о магнитном поле бесконечного прямолинейного проводника, для которой решение получается элементарными средствами на основании закона полного тока [c.27]
Практически прямолинейный проводник считается бесконечно длинным, если можно считать, что расстояние от его концов до точки, где отыскивается индукция магнитного поля, много больше, чем R. [c.256]
Направление напряженности стороннего электрического поля электромагнитной индукции в прямолинейном проводнике, движущемся в магнитном поле, определяется правилом правой руки если ладонь правой руки расположить так, чтобы вектор магнитной индукции В входил в ладонь, а отставленный на 90° большой палец совпадал с направлением перпендикулярной к проводнику составляющей его скорости, то вытянутые четыре пальца укажут направление напряженности стороннего электрического
[c. 267]
267]
Для магнитного поля прямолинейного проводника MN с током / (рис. 3-G) в про-тгзвольиой точке А [c.99]
Между тем не оправдано отсутствие коэффициента 4я в ряде формул, за-яисанных в нерационализованной форме, например, в формуле закона Кулона F=Q Qг гar , который характеризует действия одного точечного заряда на другой во все стороны, т. е. через сферу, в формуле, выражающей электроемкость шара, С=еог в выражении для напряженности магнитного поля прямолинейного проводника кругового сечения Н=211г в выражении для емкости цилиндрика Я [c.40]
Силопоо действие магнитного поля молсет обнарулсиваться по действию силы Ампера на прямолинейный проводник с током и по вращаю ц-зму действию на замкнутый контур. [c.177]
Для расчета шиммов прямоугольной конфигурации используется формула, описывающая 2-компоненту магнитного поля прямолинейного тонкого проводника с током /, расположенного параллельно оси х (рис. 1,а)
[c.207]
1,а)
[c.207]
Следует отметить, что электрические и магнитные единицы всех систем СГС образованы на основе нерационализованной формы уравнений электромагнитного поля, в которую в некоторые общие соотношения между величинами, используемые для установления размеров единиц, входит числовой множитель 4it. В то же время единицы СИ образованы по уравнениям электромагнитного поля в их рационализованной форме, исключающей множитель 4тс из всех соотношений, по которым устанавливают размеры единиц, и переводящей его в соотношения для частных случаев, характеризуемых осевой или сферической симметрией (например, в выражения для напряженности поля, создаваемого током, проходящим по прямолинейному проводнику кругового сечения, емкости уединенного шара, емкости цилиндрического или сферического конденсатора и т. д.). Этим и объясняется, что в переводные множители для единиц, подверженных рационализации, входит 4тг. [c.37]
Если к прямолинейному проводнику, по которому протекает электрический ток, поднести магнитную стрелку, то она будет стремиться стать перпендикулярно плоскости, проходящей через ось проводника и центр вращения стрелки.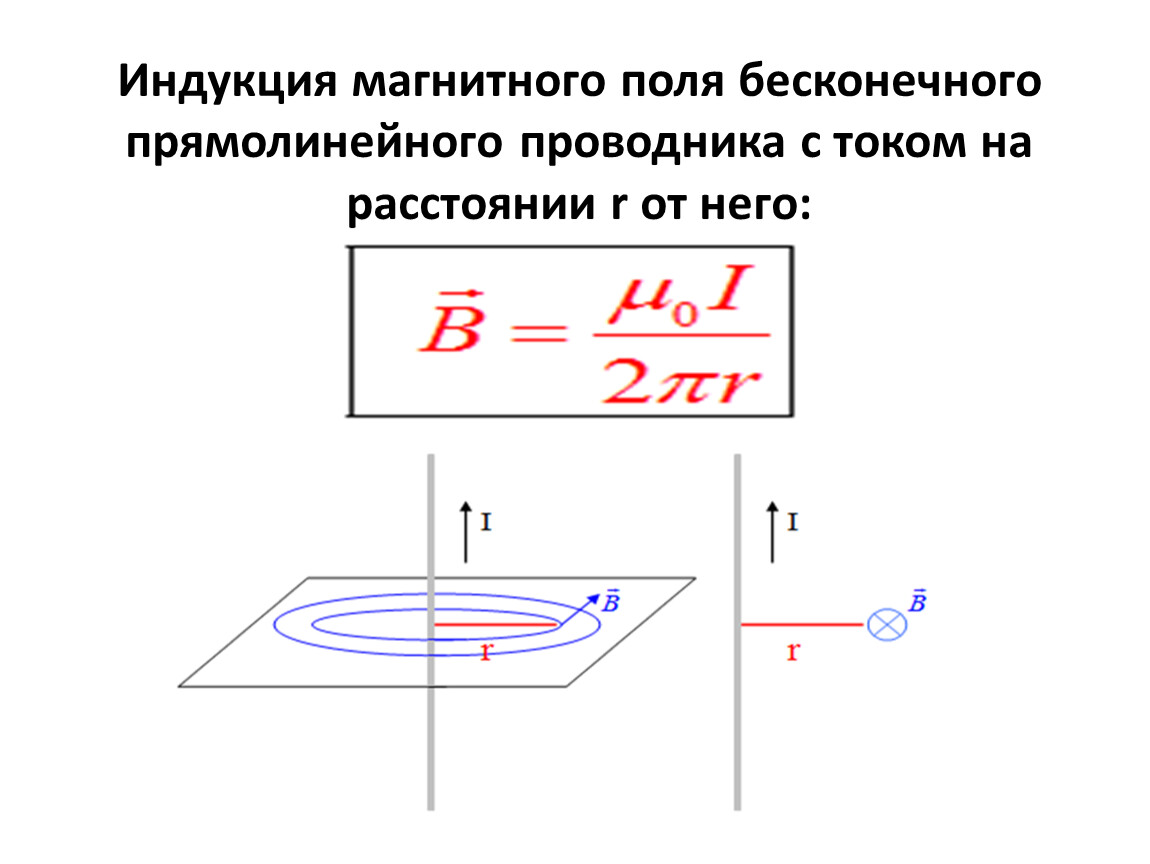 В данном случае на стрелку действуют так называемые магнитные силы, оказывающие также влияние на движущиеся заряженные частицы и на проводники с током. В проводниках, движущихся в магнитном поле, или в неподвижных, но находящихся в перемениом магнитном поле, возникает индуктированная ЭДС.
[c.26]
В данном случае на стрелку действуют так называемые магнитные силы, оказывающие также влияние на движущиеся заряженные частицы и на проводники с током. В проводниках, движущихся в магнитном поле, или в неподвижных, но находящихся в перемениом магнитном поле, возникает индуктированная ЭДС.
[c.26]
Графически магнитное поле изображают магнитными силовыми линиями. Вокруг прямолинейного проводника с током силовые линии располагаются в виде кон-центрргческих окружностей, густота которых увеличивается по мере приближения к проводнику. Магнитная индукция (интенсивность поля) зависит от силы тока в проводнике. Направление магнитных силовых линий зависит от направления тока в прово,днике. [c.26]
Постоянные магниты. Магнитное поле постоянных магнитов. Магнитное поле прямолинейного проводника с током. | Поурочные планы по физике 8 класс
Постоянные магниты. Магнитное поле постоянных магнитов. Магнитное поле прямолинейного проводника с током.
27.02.2014
5478
0
Цели: сформировать у учащихся
научные представления о магнитном поле и установить связь между электрическим
током и магнитным полем. Побуждать учащихся к
преодолению трудностей в процессе умственной деятельности, воспитать интерес к
физике.
Демонстрации: действие магнитного поля прямого проводника с током на магнитную стрелку;
магнитные спектры прямого и кругового проводников с током; усиление магнитного
поля катушки при введении железного сердечника.
Ход урока
I. Организационный момент
II. Изучение нового
материала
План изложения нового
материала:
1. Простейшие свойства магнитных материалов.
2. Связь электрических и магнитных явлений.
3. Магнитное поле. Определяющие свойства
магнитного поля.
4. Направление и линии магнитного поля.
1. Магнетизм, как явление,
известен, по крайней мере, с пятого, века до нашей эры, но изучение его
сущности продвигалось очень медленно. Еще древние греки знали, что существует
особый минерал — камень из Магнесии (область
в древнегреческой Фессалии), способный притягивать небольшие железные
предметы.
Однако впервые свойства магнита были описаны лишь в 1269 году. А: первой
крупной работой, посвященной исследованию магнитных явлений, является книга
Вильяма Гильберта «О магните», вышедшая в 1600 году.
На основании опытных исследований Гильберт установил простейшие свойства
магнитных материалов:
а) магнитное притяжение и
отталкивание присущи только некоторым телам: железной руде, железу, стали и
некоторым сплавам;
б) магнит имеет по крайней мере два полюса: северный и южный;
в) одноименные полюса магнитов
отталкиваются, а разноименные -притягиваются;
г) свободно подвешенный магнит ориентируется определенным образом
относительно стран света.
2.
Необходимо обратить внимание
учащихся на то, что магнитные взаимодействия рассматривались первоначально как
совершенно не связанные с электрическими. Хотя еще в далекие времена было
замечено, что молния перемагничивает
компасы на кораблях, намагничивает стальные предметы.
Прямое экспериментальное обнаружение связи между электрическими и
магнитными явлениями произошло благодаря счастливой случайности: когда Эрстед
читал лекцию о постоянных токах, он обратил внимание на То магнитная
стрелка, находившаяся вблизи проводника, повернулась включении тока.
После того, как были обнаружены взаимодействия магнита с магнитом и
электрического тока с магнитом, возник вопрос: будет ли иметь место магнитное
взаимодействие между электрическими токами?
Положительный ответ на этот вопрос был получен Ампером, который экспериментально
обнаружил, что параллельные проводники с токами взаимодействуют друг с другом.
3. Магнитное поле. На
На
основании опытов необходимо подвести учащихся к следующему выводу: в
пространстве вокруг проводника с током возникают силы, действующие на
движущиеся заряды и на магнитную стрелку.
Эти силы получили название магнитных. Таким образом,
магнитным полем мы будем называть то состояние пространства, которое дает себя
знать действием магнитных сил.
Определяющие свойства магнитного поля таковы:
а) магнитное поле порождается магнитами и токами;
б) магнитное поле обнаруживается по действию на магниты и
токи.
4. Из опытов видно, что
магнитная стрелка, которая может свободно вращаться вокруг своей оси, всегда
устанавливается, ориентируясь определенным образом, в данной области магнитного
поля. Исходя из этого, вводится понятие о направлении магнитного поля в
данной точке. Необходимо запомнить, что направление, на которое указывает
северный полюс магнитной стрелки, является направлением магнитного поля в
данной точке.
Используя железные опилки, следует показать учащимся спектр магнитного
поля прямого тока и ввести понятие о линиях магнитного поля.
Линиями магнитного поля являются линии, проведенные так, что касательные к
ним в каждой точке указывают направление поля в этой точке.
После введения понятия линий магнитного поля надо показать графическое
изображение магнитных полей и ввести правило для определения направления линий
магнитного поля. Например, правило «обхвата» правой рукой: если правой рукой
мысленно «обхватить» проводник так, чтобы большой палец был направлен по току,
то четыре пальца покажут направление линий магнитного поля.
При этом следует обратить особое внимание учащихся на отличие линий
магнитного поля от силовых линий электрического поля: линии магнитного поля
либо замкнуты, либо начинаются и заканчиваются на бесконечности.
Разумеется, необходимо объяснить, что линии магнитного поля реально не
существуют, они всего лишь удобный способ его описания.
III. Закрепление изученного
С целью закрепления материала в конце урока можно коллективно обсудить ряд
качественных вопросов и задач по изученной теме:
Какая связь существует между электрическим током и магнитным полем?
—
Как располагаются железные опилки в магнитном поле прямого тока? Почему?
—
Как на опыте показать, что направление магнитных линий связано с
направлением тока?
—
Каким образом можно узнать, есть ли ток в проводе, не пользуясь
амперметром?
—
Турист нашел в лесу стальное полотно ножовки. Как он может определить,
намагничено ли это полотно, если у него нет с собой предметов из магнитных
материалов?
Домашнее задание
1. § 52-54 учебника; вопросы к параграфам.
2. Сб. задач В. И. Лукашика,
Объяснение урока: Движение прямых проводников в однородных магнитных полях
Пример 3. Вращение проводников в однородных магнитных полях
Проводящий стержень вращается, один конец которого неподвижен. Стержень равномерно вращается в однородном магнитном поле, причем направление вращения стержня относительно магнитного поля изменяется, как показано на диаграммах I, II, III и IV. Стержень вращается с одинаковой скоростью на каждой диаграмме.
Стержень равномерно вращается в однородном магнитном поле, причем направление вращения стержня относительно магнитного поля изменяется, как показано на диаграммах I, II, III и IV. Стержень вращается с одинаковой скоростью на каждой диаграмме.
- На каком из рисунков величина разности потенциалов между закрепленным концом стержня и свободным концом стержня изменяется при вращении стержня?
- Является ли величина разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня на схеме I, равна величине разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня на схеме II?
- Является ли величина разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня на диаграмме III, равна величине разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня на схеме IV?
- Является ли величина разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня на схеме I, равна величине разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня на схеме III?
Ответ
Часть 1
Рассматривая четыре диаграммы, начнем с диаграммы I.
Диаграмма I показывает вращающийся стержень в четыре момента. Мы можем обозначить эти положения как 0∘, 90∘, 180∘ и 270∘, как показано на рисунке ниже.
В каждом положении стержень имеет ненулевую среднюю скорость и движется в однородном магнитном поле вправо.
На следующем рисунке показаны эти средние скорости с соответствующими векторами магнитного поля.
Чтобы определить, индуцируется ли и в каком направлении разность потенциалов в стержне в любом из этих положений, мы используем правило правой руки.
Это правило указывает, что направление действия магнитной силы на заряд 𝑞, движущийся со скоростью 𝑣 через магнитное поле 𝐵, можно определить следующим образом: пальцы правой руки указывают в направлении 𝑞𝑣, затем сгибаются в направление 𝐵. Направление, указанное большим пальцем правой руки, показывает направление магнитной силы, действующей на заряд.
Применяя это правило к четырем положениям стержня на рисунке выше, мы получаем результаты, показанные на следующем рисунке.
Обратите внимание, что во всех четырех положениях магнитная сила на положительном заряде никогда не действует по всей длине проводника. Положительные и отрицательные заряды по длине стержня не разделяются, поэтому разность потенциалов по длине стержня равна нулю.
Теперь рассмотрим стержень под некоторым произвольным углом поворота, отличным от углов, показанных выше. В таком произвольном положении вектор средней скорости стержня можно разделить на горизонтальную и вертикальную составляющие, как показано на рисунке ниже.
Для каждого компонента ЭДС индукции по длине стержня равна нулю. Поскольку угол тета на рисунке произвольный, ЭДС индукции по длине стержня на схеме I равна нулю во всех положениях.
Далее рассмотрим схему II. Обратите внимание, что единственная разница между диаграммой II и диаграммой I заключается в том, что диаграмма II повернута на 90° относительно диаграммы I против часовой стрелки.
Следовательно, на диаграмме II по длине стержня также не индуцируется разность потенциалов.
На диаграмме III магнитное поле указывает на экран. Следовательно, векторы скорости и соответствующие векторы магнитного поля выглядят так, как показано на следующем рисунке.
Опять же, используя правило правой руки для определения направления магнитной силы на положительном заряде в каждой позиции, мы находим результаты ниже, где красные стрелки указывают векторы силы на положительном заряде.
На диаграмме III положительный заряд отталкивается к оси вращения стержня, что означает, что отрицательный заряд отталкивается к свободному концу стержня.Поэтому разделение заряда происходит по длине стержня.
В результате по всей длине стержня индуцируется разность потенциалов.
Напомним, однако, что нас просят определить диаграммы, где наведенная разность потенциалов вдоль стержня изменяется.
Для сценария, показанного на диаграмме III, индуцированная разность потенциалов вдоль стержня отлична от нуля, но также постоянна — она не меняется при вращении стержня.
Наконец, рассмотрим ситуацию, изображенную на диаграмме IV.
Этот сценарий идентичен сценарию, показанному на диаграмме III, за исключением того, что магнитное поле теперь направлено за пределы экрана, а не внутрь него.
Результатом этой разницы является то, что в сценарии, показанном на диаграмме IV, положительный заряд выталкивается к свободному концу стержня, а отрицательный заряд выталкивается к его закрепленному концу.
По длине стержня индуцируется ненулевая разность потенциалов.
Однако, как и в ситуации, показанной на диаграмме III, эта разность потенциалов не меняется при вращении стержня.
Наш ответ на часть 1 вопроса заключается в том, что ни на одной из диаграмм не показаны сценарии, в которых разность потенциалов, индуцированная по длине стержня, изменяется.
Часть 2
Возвращаясь к нашему анализу в части 1, мы помним, что на диаграммах I и II наведенная разность потенциалов по длине стержня равна нулю. Следовательно, верно, что эти значения равны.
Следовательно, верно, что эти значения равны.
Часть 3
В сценарии, показанном на диаграмме III, положительный заряд накапливается в направлении фиксированного конца стержня, а отрицательный заряд накапливается в направлении его свободного конца, как показано на следующем рисунке.
Величина индуцированной разности потенциалов определяется уравнением
𝜖=𝑙𝑣𝐵(𝜃),грех
где 𝑙 — длина проводника, 𝑣 — его скорость, 𝐵 — напряженность магнитного поля, 𝜃 — угол между 𝐵 и 𝑣.
Мы должны сравнить эту величину с величиной ЭДС, индуцированной в сценарии, показанном на диаграмме IV. В этой ситуации положительные и отрицательные заряды накапливаются, как показано ниже.
Полярность индуцированной разности потенциалов противоположна сценарию на диаграмме III.Обратите внимание, однако, что ни одно из значений, влияющих на величину индуцированной разности потенциалов — 𝑙, 𝑣, 𝐵 и 𝜃 — не изменилось.
Таким образом, величина разности потенциалов, индуцированной по длине стержня, одинакова в сценариях, изображенных на диаграммах III и IV.
Часть 4
Мы видели, что на диаграмме I показана ситуация, когда наведенная разность потенциалов между концами стержня равна нулю.
Напротив, на стержне, показанном на диаграмме III, индуцируется ненулевая разность потенциалов.Следовательно, эти величины не равны.
22.7 Сила магнитного поля на проводнике с током – College Physics: OpenStax
Резюме
- Описать действие магнитной силы на проводник с током.
- Рассчитайте магнитную силу, действующую на проводник с током.
Поскольку заряды обычно не могут покинуть проводник, магнитная сила зарядов, движущихся в проводнике, передается самому проводнику.
Рис. 1. Магнитное поле действует на проводник с током в направлении, определяемом правилом правой руки 1 (то же направление, что и на отдельные движущиеся заряды). Эта сила легко может быть достаточно большой, чтобы сдвинуть провод, поскольку типичные токи состоят из очень большого количества движущихся зарядов.
Мы можем получить выражение для магнитной силы, действующей на ток, взяв сумму магнитных сил, действующих на отдельные заряды. (Силы складываются, потому что они действуют в одном направлении.) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа vdvd, определяется выражением [latex]\boldsymbol{F = qv_dB \;\textbf{sin} \;\theta}[/latex]. Принимая [латекс]\boldsymbol{B}[/латекс] равномерным по всей длине провода [латекс]\boldsymbol{l}[/латекс] и равным нулю в других местах, тогда общая магнитная сила на проводе равна [латекс]\ boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta)(N)}[/latex], где [latex]\boldsymbol{N}[/latex] – количество носителей заряда в сечении проволока длиной [латекс]\boldsymbol{l}[/латекс].Теперь [латекс]\boldsymbol{N=nV}[/latex], где [латекс]\boldsymbol{n}[/латекс] — количество носителей заряда в единице объема, а [латекс]\boldsymbol{V}[/ латекс] — объем проволоки в поле. Учитывая, что [латекс]\boldsymbol{V=Al}[/латекс], где [латекс]\жирный символ{А}[/латекс] — площадь поперечного сечения проволоки, сила, действующая на проволоку, равна [латекс] \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}[/latex]. Условия сбора,
Условия сбора,
[латекс]\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.[/латекс]
Поскольку [латекс]\boldsymbol{nqAv_d = I}[/латекс] (см. Главу 20.1 Текущая версия),
[латекс]\boldsymbol{F = IlB \;\textbf{sin} \;\theta}[/latex]
представляет собой уравнение для магнитной силы, действующей на отрезок [латекс]\boldsymbol{l}[/латекс] провода, по которому течет ток [латекс]\boldsymbol{I}[/латекс] в однородном магнитном поле [латекс]\boldsymbol {B}[/latex] , как показано на рисунке 2. Если мы разделим обе части этого выражения на [latex]\boldsymbol{l}[/latex], мы обнаружим, что магнитная сила на единицу длины провода в однородное поле равно [латекс]\boldsymbol{\frac{F}{l} = IB \;\textbf{sin} \;\theta}[/latex].Направление этой силы задается RHR-1, с большим пальцем в направлении текущего [латекс]\boldsymbol{I}[/латекс]. Затем, с пальцами в направлении [латекс]\boldsymbol{B}[/латекс], перпендикуляр к ладони указывает в направлении [латекс]\жирныйсимвол{F}[/латекс], как на рисунке 2.
Рис. 2. Сила, действующая на проводник с током в магнитном поле, равна F = IlB sin θ . Его направление задает RHR-1.
Расчет силы магнитного поля на проводе с током: сильное магнитное поле
Рассчитайте силу, действующую на проволоку, показанную на рисунке 1, при [латексе]\boldsymbol{B = 1.{\circ}}[/latex], так что [латекс]\boldsymbol{\textbf{sin} \;\theta = 1}[/latex].
Раствор
Ввод заданных значений в [latex]\boldsymbol{F = IlB \;\textbf{sin} \theta}[/latex] дает
[латекс]\boldsymbol{F = IlB \;\textbf{sin} \theta = (20.0 \;\textbf{A}) \; (0,0500 \;\textbf{м}) \; (1.50 \;\textbf{T}) \; (1)}.[/латекс]
Единицы тесла: [латекс]\жирныйсимвол{1 \;\textbf{T} = \frac{\textbf{N}}{\textbf{A} \cdot \; \textbf{м}}}[/латекс]; таким образом,
[латекс]\boldsymbol{F = 1.50 \;\textbf{N}}.[/latex]
Обсуждение
Это большое магнитное поле создает значительную силу на проводе небольшой длины.
Сила магнитного поля на проводниках с током используется для преобразования электрической энергии в работу. (Ярким примером являются двигатели — в них используются петли из проволоки, и они рассматриваются в следующем разделе.) Магнитогидродинамика (МГД) — это техническое название, данное умному приложению, в котором магнитная сила перекачивает жидкости без движущихся механических частей.(См. рис. 3.)
Рис. 3. Магнитогидродинамика. Магнитная сила тока, проходящего через эту жидкость, может быть использована в качестве немеханического насоса.
Сильное магнитное поле прикладывается к трубке, и ток проходит через жидкость под прямым углом к полю, в результате чего на жидкость действует сила, параллельная оси трубки, как показано на рисунке. Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах.Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар.По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
(Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар.По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводная ветвь будет выведена из эксплуатации последней из-за этой способности (см. рис. 4). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
Рис. 4. Двигательная установка МГД на атомной подводной лодке может создавать значительно меньшую турбулентность, чем гребные винты, и обеспечивать более тихую работу. Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ».
- Магнитная сила, действующая на проводники с током, определяется выражением
[латекс]\boldsymbol{F = IlB \;\textbf{sin} \;\theta},[/latex]
, где [латекс]\boldsymbol{I}[/латекс] – сила тока, [латекс]\boldsymbol{l}[/латекс] – длина прямого проводника в однородном магнитном поле [латекс]\boldsymbol{B} [/latex], а [latex]\boldsymbol{\theta}[/latex] — это угол между [latex]\boldsymbol{I}[/latex] и [latex]\boldsymbol{B}[/latex].
 Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Концептуальные вопросы
1: Нарисуйте схему ситуации на рисунке 1, показав направление электронов, несущих ток, и используйте RHR-1, чтобы проверить направление силы на проводе.
2: Убедитесь, что направление силы в МГД-приводе, таком как на рис. 3, не зависит от знака зарядов, переносящих ток через жидкость.
3: Почему магнитогидродинамический привод лучше работает в морской воде, чем в пресной? Кроме того, зачем нужны сверхпроводящие магниты?
4: Что больше мешает показаниям компаса, переменный ток в вашем холодильнике или постоянный ток, когда вы заводите машину? Объяснять.
Задачи и упражнения
1: Каково направление магнитной силы на ток в каждом из шести случаев на рис. 5?
Рисунок 5.
2: Каково направление тока, на который действует магнитная сила, показанная в каждом из трех случаев на рисунке 6, если предположить, что ток течет перпендикулярно [латексу]\boldsymbol{B}[/latex ]?
Рисунок 6
3: Каково направление магнитного поля, которое создает магнитную силу, показанную на токах в каждом из трех случаев на рисунке 7, при условии, что [латекс]\boldsymbol{B}[/латекс] перпендикулярно [латексу]\boldsymbol{I}[/латекс]?
Рис. 7.{-5}- \textbf{T}}[/latex]. Какая сила действует на отрезке этой линии длиной 100 м? (b) Обсудите практические проблемы, которые это вызывает, если таковые имеются.
6: Какая сила действует на воду в МГД-приводе с трубкой диаметром 25,0 см, если через трубку, перпендикулярную магнитному полю напряженностью 2,00 Тл, пропускают ток силой 100 А? (Относительно небольшой размер этой силы указывает на необходимость очень больших токов и магнитных полей для создания практических МГД-приводов.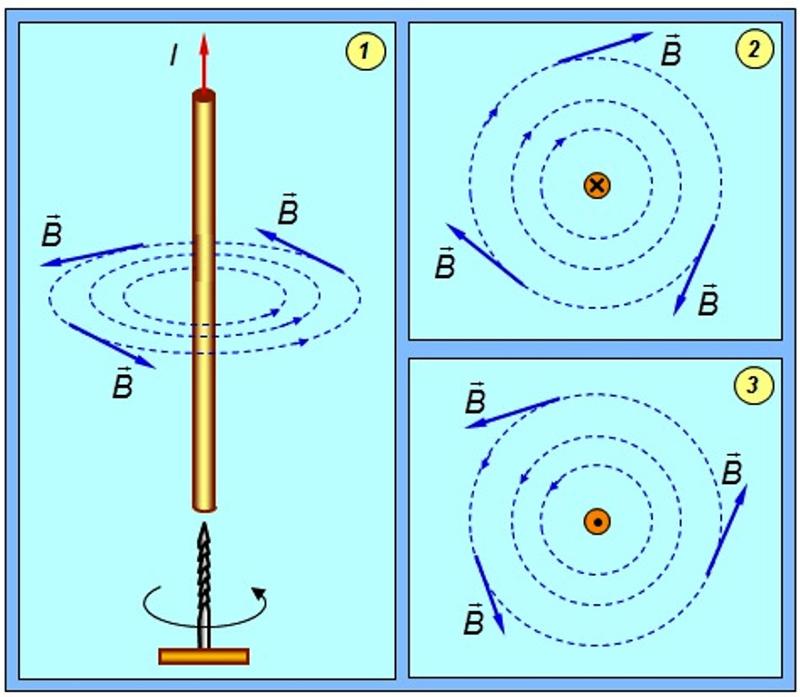 )
)
7: Провод, несущий 30.{\circ}}[/latex] с полем?
10: Сила, действующая на прямоугольную проволочную петлю в магнитном поле на рисунке 8, может использоваться для измерения напряженности поля. Поле однородно, и плоскость петли перпендикулярна полю. а) Как направлена магнитная сила, действующая на петлю? Обоснуйте утверждение, что силы на сторонах петли равны и противоположны, независимо от того, какая часть петли находится в поле, и не влияют на результирующую силу, действующую на петлю. б) если ток 5.00 А, какова сила на тесла на петле шириной 20,0 см?
Рисунок 8.
Решения
Задачи и упражнения
1: (а) запад (левый)
(б) на страницу
(с) север (вверх)
(г) без силы
(д) восток (право)
(ж) юг (вниз)
3: (а) на стр.
(б) запад (левый)
(c) со страницы
5: (а) 2. {\circ}}[/латекс]
{\circ}}[/латекс]
(б) 4,80 Н
Магнитное поле провода
Магнитный
поле длинной проволоки
Магнитный
поля возникают из зарядов, подобно электрическим полям,
но отличаются тем, что заряды должны двигаться. А
длинный прямой провод, по которому течет ток, является простейшим
пример движущегося заряда, который генерирует магнитное поле
поле. Мы упоминали, что сила, которую испытывает заряд, когда
движение через магнитное поле зависело от
правило правой руки.Направление магнитного поля из-за
к движущимся зарядам также будет зависеть от правой руки
правило. Для случая длинного прямого провода, несущего
ток I , линии магнитного поля закручиваются
вокруг провода. Направляя большой палец правой руки вдоль
направление тока, направление магнитного
поле можно найти, согнув пальцы вокруг
провод.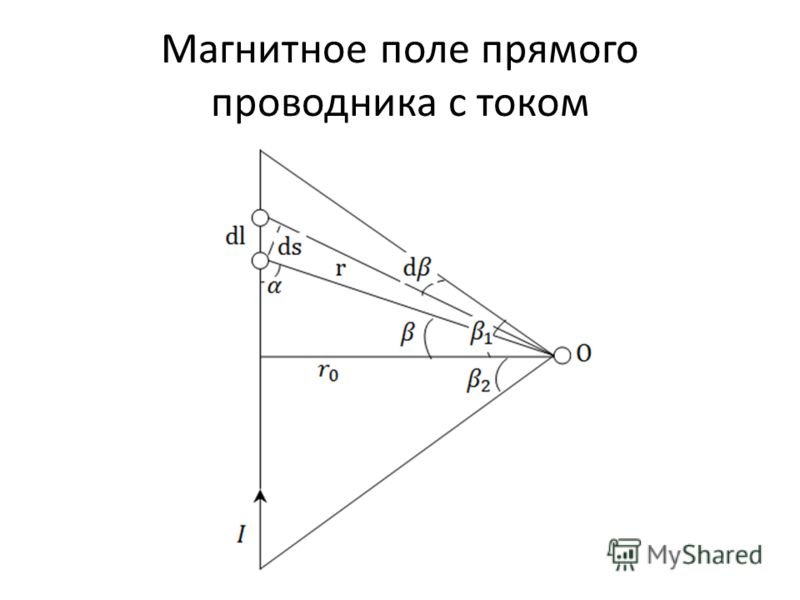
Сила
магнитного поля зависит от тока I в проводе и r ,
расстояние от провода.
Постоянная m 0 — это магнитная проницаемость.
Причина в том, что не отображается произвольное число
что единицы заряда и тока (кулоны и амперы)
были выбраны, чтобы дать простую форму для этой константы. Один
также можно заметить произведение m 0
и e 0 относятся к
скорость света. (подробнее об этом позже, фундаментальные константы)
Если один
вспоминается случай электрического поля однородного
заряженный провод, он же упал как 1/р .Нет реальной аналогии закону Кулона для магнетизма,
так как магнитное поле точечного заряда сложно
поскольку он не может стоять на месте, чтобы генерировать магнитное
поле.
Примеры Магнитный
индекс источника поля
Лаборатория 7. Магнитное поле длинного прямого провода
Введение
Магнитные поля создаются проводниками с током.Наличие этих магнитных полей можно обнаружить и измерить по силе, которую они оказывают на другие магнитные материалы и проводники с током. Например, когда компас подносят к проводнику с током, стрелка компаса отклоняется, что свидетельствует о наличии магнитного поля. Эту связь между электричеством и магнетизмом впервые заметил Ганс Христиан Эрстед.
Магнитное поле имеет как направление, так и величину. Направление магнитного поля, окружающего прямой проводник с током, задается правилом правой руки, а напряженность поля может быть получена из закона Ампера.
Обсуждение принципов
Магнитное поле длинного прямого провода определяется выражением
где
µ 0
— проницаемость свободного пространства, I — ток, текущий в прямом проводе, r — перпендикулярное (или радиальное) расстояние точки наблюдения от провода. Магнитное поле измеряется в единицах Тесла (Тл). Обратите внимание, что магнитное поле B обратно пропорционально расстоянию r .
Магнитное поле измеряется в единицах Тесла (Тл). Обратите внимание, что магнитное поле B обратно пропорционально расстоянию r .
Рисунок 1 : Токоведущий провод
На рис. 1 точка А находится на расстоянии r от провода, а величина магнитного поля в точке А определяется уравнением (1). Если рассмотреть окружность радиусом r , величина магнитного поля будет одинаковой во всех точках этой окружности. Точно так же точки на окружности другого радиуса будут иметь одинаковое магнитное поле. Другими словами, картина магнитного поля из-за провода с током представляет собой концентрические окружности с центром вокруг провода.
Рисунок 2 : Картина магнитного поля, обусловленная током в проводе
На рис. 2 показана картина магнитного поля, вызванного током в длинном прямом проводе. Чтобы найти направление поля в любом месте, воспользуемся правилом правой руки. Это отличается от правила правой руки для нахождения силы магнитного поля на проводе с током. Обведите провод правой рукой так, чтобы большой палец указывал в направлении тока.Пальцы указывают в направлении магнитного поля. На рис. 3 синими кружками показаны картины магнитного поля. В определенном месте на такой окружности направление магнитного поля задается касательной к окружности в этой точке. Глядя на провод сверху, мы говорим, что силовые линии идут против часовой стрелки.
Обведите провод правой рукой так, чтобы большой палец указывал в направлении тока.Пальцы указывают в направлении магнитного поля. На рис. 3 синими кружками показаны картины магнитного поля. В определенном месте на такой окружности направление магнитного поля задается касательной к окружности в этой точке. Глядя на провод сверху, мы говорим, что силовые линии идут против часовой стрелки.
Рисунок 3 : Использование правила правой руки
На компас, находящийся вблизи провода с током, будет воздействовать магнитное поле, создаваемое током.Рассмотрим следующую ситуацию. Длинный провод, по которому течет ток I , ориентирован на север, как показано на рис. 4. По правилу правой руки в местах над проводом поле будет направлено за пределы страницы, а в местах ниже провода поле будут направлены на страницу. Напомним, что X обозначает вектор, указывающий на страницу, а кружок с точкой обозначает вектор, указывающий за пределы страницы.
Рисунок 4 : Магнитное поле в двух местах из-за тока в проводе
Стрелка компаса всегда указывает в направлении общего магнитного поля.При отсутствии поблизости каких-либо ферромагнитных материалов или внешних магнитных полей это направление направлено к северному полюсу Земли. В точке А на рис. 4 магнитное поле из-за провода выходит за пределы страницы, что также является восточным направлением, поскольку на приведенной выше диаграмме север указывает вправо. На компас, расположенный в точке А, воздействуют два магнитных поля: одно из-за горизонтальной составляющей магнитного поля Земли, указывающей на север, а другое из-за тока в проводе.Стрелка компаса, таким образом, отклонится на угол
θ
и укажет направление чистого магнитного поля. Измерив угол отклонения и учитывая, что горизонтальная составляющая поля Земли составляет примерно 2,2 × 10 –5 Тл (см. Калькулятор магнитного поля), мы можем рассчитать величину поля, вызванного током в проводе.
Для любой ситуации, когда B провода и B E перпендикулярны, рис.5 дает направление чистого поля.
Рисунок 5 : Комбинация двух полей
Из диаграммы выше мы видим, что и, следовательно,
( 2 )
B проволока = B E желто-коричневый θ .
Объектив
Целью данного эксперимента является установление связи между полем, создаваемым проводом с током, и расстоянием точки наблюдения от провода и, исходя из этого, экспериментальное определение величины
μ 0 ,
свободного пространства.
Оборудование
Прямоугольная рама из ПВХ
Длинный провод
Компас
Источник питания
Кусочки пенопласта
метр палка
Мультиметр
Соединительные провода
Процедура
Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
Этот лист понадобится вам для записи ваших данных.
Для этого эксперимента постарайтесь держать металлические предметы как можно дальше от компаса.
Длинная проволока приклеивается к прямоугольной раме из ПВХ, чтобы получилась прямоугольная петля из проволоки.
1
Поместите рамку из ПВХ на угол лабораторного стола так, чтобы только одна секция прямоугольной петли из проволоки лежала на столе.
2
Выровняйте раму из ПВХ и проволоку так, чтобы и проволока, и компас были направлены на север (см.6 и 7).
3
Определите толщину одного куска пенопласта, сложив десять кусков, измерив высоту стопки и разделив на десять. Отсюда вы можете определить высоту компаса из проволоки в зависимости от количества кусков пенопласта, которые вы используете.
Рисунок 6 : Эскиз экспериментальной установки с торца
Рисунок 7 : Фотография экспериментальной установки
4
Компас должен опираться на красную точку на проводе, поддерживаемом с обеих сторон кусками пенопласта. См. рис. 8.
См. рис. 8.
Рисунок 8 : Вид сверху, показывающий ориентацию компаса и троса
5
Подключите блок питания, как показано на рис. 9, последовательно с проводом и мультиметром. Мультиметр будет использоваться как амперметр для измерения тока через провод.
Рисунок 9 : Соединения цепи
Контрольная точка 1:
Попросите вашего ТА проверить соединения вашей цепи.
6
Включите питание и поверните ручку «грубого» напряжения примерно наполовину.
7
Используйте известный «грубый» ток, чтобы отрегулировать ток таким образом, чтобы стрелка компаса отклонялась примерно на 40°.
8
Отрегулируйте ручку «точности» так, чтобы стрелка компаса отклонялась ровно на 40°.
9
Запишите ток и его погрешность в рабочий лист. Можно предположить, что погрешность тока составляет 1%.
Можно предположить, что погрешность тока составляет 1%.
10
Добавьте по одному куску пенопласта с каждой стороны. Запишите отклонение компаса, сохраняя ток таким же, как в шаге 9.
11
Повторите эту процедуру еще дважды, чтобы у вас было четыре расстояния и четыре отклонения.
Контрольная точка 2:
Попросите вашего ТА проверить ваши значения, прежде чем продолжить.
12
Предположим, что магнитное поле имеет форму
B = K r n ,
, где мы хотели бы найти значение n .Если мы возьмем натуральный логарифм обеих сторон, мы получим
( 3 )
ln B = ln(Kr n ) = ln K + n ln r.
Это имеет форму линейного уравнения:
y = mx + b,
, где
y = ln B, x = ln r,
, наклон равен n , а точка пересечения равна ln K .
13
Используйте Excel для построения графика зависимости ln B от ln r . См. Приложение G.
См. Приложение G.
14
Используйте линейную функцию в Excel, чтобы определить наклон, точку пересечения и их неопределенности.См. Приложение J.
Запишите эти значения в рабочий лист.
15
Рассчитайте n и его неопределенность по наклону графика.
16
Формула неопределенности в
μ 0
выглядит следующим образом:
Определим точку пересечения графика как b , тогда
K = e b
и
σ K
=
σ
- 2 K .0 b .
Используйте эту информацию, чтобы вычислить
μ 0
и его неопределенность от точки пересечения.
17
Рассчитайте процентную ошибку между экспериментальным и принятым значениями
μ 0 .
См. Приложение B.
Контрольная точка 3:
Попросите вашего ассистента проверить график и расчеты в Excel.
Copyright © 2012 Advanced Instructional Systems, Inc. и Университет штата Северная Каролина | Кредиты
Магнитное поле вокруг провода, I
Всякий раз, когда ток проходит через проводник, создается магнитное поле.
Всякий раз, когда ток проходит через проводник, создается магнитное поле, факт, на который наткнулся Ганс Кристиан Эрстед примерно в 1820 году. В зависимости от формы проводника контур магнитного поля будет меняться. Однако если проводник представляет собой провод, магнитное поле всегда принимает форму концентрических окружностей, расположенных под прямым углом к проводу. Магнитное поле сильнее всего в области, ближайшей к проводу, и его направление зависит от направления тока, создающего поле, как показано на этой интерактивной анимации.
В учебнике представлен прямой провод, по которому течет ток. Знаки плюс и минус указывают полюса батареи (не показана), к которым подключен провод. Обычное направление тока указано большой черной стрелкой. (Как диктует соглашение, ток течет против фактического направления электронов , показанных желтым цветом). Линии магнитного поля , генерируемые вокруг провода из-за наличия тока, показаны синим цветом.Чтобы увидеть направление поля в любой заданной точке по окружности провода, щелкните и перетащите стрелку компаса (ее северный полюс красный, южный полюс синий). Направление магнитного поля вокруг провода также указано маленькими стрелками на отдельных силовых линиях . Нажмите кнопку Reverse , чтобы изменить направление тока и посмотреть, как это изменение повлияет на магнитное поле провода.
Обычное направление тока указано большой черной стрелкой. (Как диктует соглашение, ток течет против фактического направления электронов , показанных желтым цветом). Линии магнитного поля , генерируемые вокруг провода из-за наличия тока, показаны синим цветом.Чтобы увидеть направление поля в любой заданной точке по окружности провода, щелкните и перетащите стрелку компаса (ее северный полюс красный, южный полюс синий). Направление магнитного поля вокруг провода также указано маленькими стрелками на отдельных силовых линиях . Нажмите кнопку Reverse , чтобы изменить направление тока и посмотреть, как это изменение повлияет на магнитное поле провода.
Существует простой метод определения направления магнитного поля, создаваемого вокруг провода с током, обычно называемый правилом правой руки.В соответствии с этим правилом, если большой палец правой руки направлен в направлении обычного тока, то направление, в котором остальные пальцы должны согнуться, чтобы сжать кулак (или обернуться вокруг рассматриваемого провода), равно направление магнитного поля.
Магнитное поле вокруг длинного прямого проводника
Контекст 1
… этих микроорганизмов для смещения молекул полупроводника или составных полупроводниковых материалов с целью селективного изготовления полупроводниковых компонентов на подложке.Наши предварительные результаты показывают, что такая технология соединений, включающая бактериальные носители и органические/неорганические молекулы полупроводников для изготовления блоков обработки и памяти информационных технологий, могла бы стать возможной альтернативой существующей технологии изготовления чипов на основе EUV. II. МИКРООРГАНИЗМЫ В НАПРАВЛЕННОМ ПРОИЗВОДСТВЕ В прошлом предпринимались попытки прикрепить виды бактерий к пластиковым подложкам, таким как полистирол, для изучения гидрофобности клеток [32]. Он продемонстрировал, что одной из сил, которая очень распространена на молекулярном уровне, является сила гидрофобного взаимодействия между атомами.Форма водорослей ( Clamydomonas Reinhardtii ) также использовалась в качестве носителя для полистироловых микрогранул (диаметром 1-6 мкм), которые переносились на расстояние до 20 см [33]. Микрогранулы были прикреплены к клетке водорослей с использованием химии поверхности, связывающей фрагменты метилкетона и первичного амида. Точно так же некоторые генно-инженерные вирусы также использовались для контролируемого упорядочения нанокристаллов ZnS (сульфида цинка) в наномасштабе вплоть до микро- и даже сантиметрового масштаба [34]. В работе [35] исследуется прикрепление полистироловых микрогранул для имитации скорости и направления прикрепленных бактерий.Однако один конкретный класс бактерий, называемый магнитотактическими бактериями, использовался относительно больше, чем любой другой класс, главным образом из-за их эффективного контроля с помощью магнитных полей. Одно из первых сообщений о таких видах было сделано еще в 1994 году, когда они использовались для поглощения металлов, показывая, что эти бактерии также могут действовать как сепараторы ориентации, обнаруживая концентрацию металлов до уровня 1 ppm в окружающей среде [36]. Как и любые другие микроорганизмы, МТБ также использовались для коллективных задач.
Микрогранулы были прикреплены к клетке водорослей с использованием химии поверхности, связывающей фрагменты метилкетона и первичного амида. Точно так же некоторые генно-инженерные вирусы также использовались для контролируемого упорядочения нанокристаллов ZnS (сульфида цинка) в наномасштабе вплоть до микро- и даже сантиметрового масштаба [34]. В работе [35] исследуется прикрепление полистироловых микрогранул для имитации скорости и направления прикрепленных бактерий.Однако один конкретный класс бактерий, называемый магнитотактическими бактериями, использовался относительно больше, чем любой другой класс, главным образом из-за их эффективного контроля с помощью магнитных полей. Одно из первых сообщений о таких видах было сделано еще в 1994 году, когда они использовались для поглощения металлов, показывая, что эти бактерии также могут действовать как сепараторы ориентации, обнаруживая концентрацию металлов до уровня 1 ppm в окружающей среде [36]. Как и любые другие микроорганизмы, МТБ также использовались для коллективных задач. Например, для управления направлением жгутиковых МТБ (вид МС-1, Морской кокк) используется компьютеризированный контроллер, посылающий рои МТБ, которые используют магнитное поле, генерируемое током, создаваемым фотогальваническими элементами, установленными на микро- робот [37]. В этом случае две V-образные структуры были сдвинуты МТБ достаточно близко друг к другу, образуя букву «М» в водном растворе. MC-1 также использовался при создании биосенсора для патогенных бактерий, где отдельные клетки сначала прикрепляются к полистироловым микрогранулам, которые затем используются для выделения патогенных бактерий из раствора [38].Как MC-1, так и MSR-1 (вид Magnetospirillum gryphiswaldense) были тщательно протестированы на предмет их прикрепления к полистироловым микрогранулам размером от 2 мкм до 5 мкм с точки зрения их скорости и силы тяги [39]. Как только бактерия прикрепляется к микрокомпоненту, микрокомпонент может перемещаться по поверхности, и это стратегия, на которой сосредоточена настоящая исследовательская работа, чтобы управлять сборкой полупроводникового компонента.
Например, для управления направлением жгутиковых МТБ (вид МС-1, Морской кокк) используется компьютеризированный контроллер, посылающий рои МТБ, которые используют магнитное поле, генерируемое током, создаваемым фотогальваническими элементами, установленными на микро- робот [37]. В этом случае две V-образные структуры были сдвинуты МТБ достаточно близко друг к другу, образуя букву «М» в водном растворе. MC-1 также использовался при создании биосенсора для патогенных бактерий, где отдельные клетки сначала прикрепляются к полистироловым микрогранулам, которые затем используются для выделения патогенных бактерий из раствора [38].Как MC-1, так и MSR-1 (вид Magnetospirillum gryphiswaldense) были тщательно протестированы на предмет их прикрепления к полистироловым микрогранулам размером от 2 мкм до 5 мкм с точки зрения их скорости и силы тяги [39]. Как только бактерия прикрепляется к микрокомпоненту, микрокомпонент может перемещаться по поверхности, и это стратегия, на которой сосредоточена настоящая исследовательская работа, чтобы управлять сборкой полупроводникового компонента. Некоторые из других применений, которые, как было показано, MTB управляют сборкой, включают штабелирование микрокубов для формирования структуры, подобной древним пирамидам [40], и перемещение микрокомпонентов на основе смолы размером 100x20x15 мкм 3 [41].III. КОНТРОЛЬ МАГНИТНОГО ПОЛЯ И ВЛИЯНИЕ ТЕПЛА НА СООБЩЕСТВА МТБ Хорошо известно, что проводник с током создает концентрическое магнитное поле, если проводник представляет собой прямой провод, как показано на рис. 1. Согласно закону Ампера , линейный интеграл магнитного поля B по отношению к изменению длины dl на замкнутом пути в μ 0 раз превышает ток, проходящий через …
Некоторые из других применений, которые, как было показано, MTB управляют сборкой, включают штабелирование микрокубов для формирования структуры, подобной древним пирамидам [40], и перемещение микрокомпонентов на основе смолы размером 100x20x15 мкм 3 [41].III. КОНТРОЛЬ МАГНИТНОГО ПОЛЯ И ВЛИЯНИЕ ТЕПЛА НА СООБЩЕСТВА МТБ Хорошо известно, что проводник с током создает концентрическое магнитное поле, если проводник представляет собой прямой провод, как показано на рис. 1. Согласно закону Ампера , линейный интеграл магнитного поля B по отношению к изменению длины dl на замкнутом пути в μ 0 раз превышает ток, проходящий через …
Контекст 2
… основных компонентов этого исследование представляет собой эффективный направленный контроль магнитного поля, чтобы предвидеть контролируемое движение видов бактерий через локально генерируемое магнитное поле.Как видно из рис. 1, длинный прямой проводник создает магнитное поле в виде концентрических кругов вокруг проводника, и, следовательно, требуемое перемещение видов не может эффективно контролироваться, поскольку переносчики бактерий будут двигаться либо к проводнику, либо от него.

 7)
7) В ненамагниченном теле
В ненамагниченном теле Направление вращения ручки буравчика укажет направление
Направление вращения ручки буравчика укажет направление Определим направление линий магнитного поля по правилу
Определим направление линий магнитного поля по правилу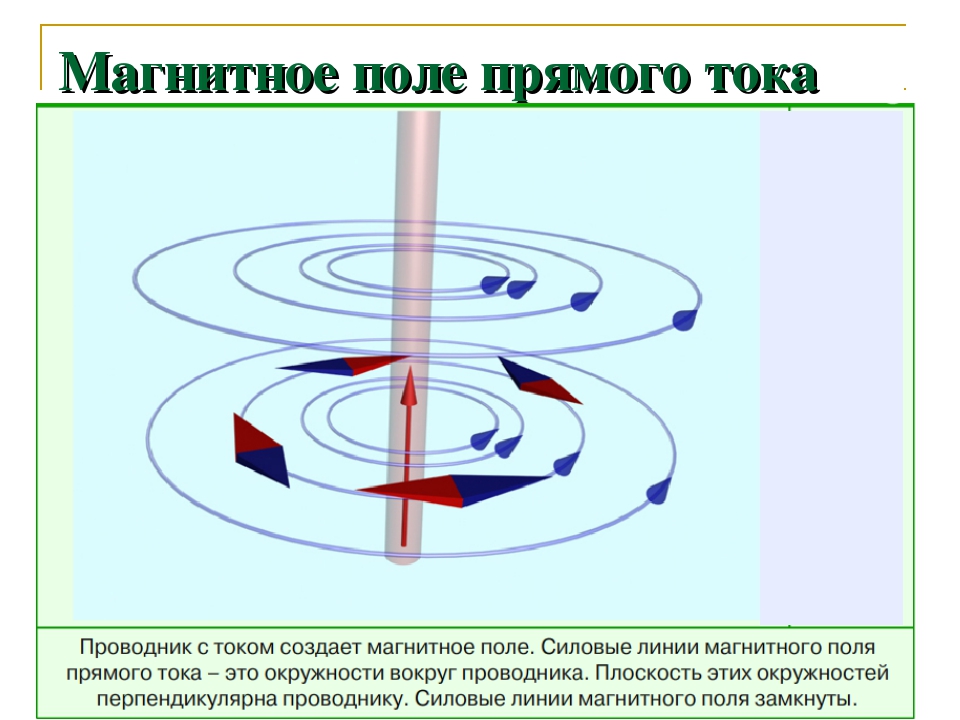 Включим ток. Стрелка поворачивается и устанавливается
Включим ток. Стрелка поворачивается и устанавливается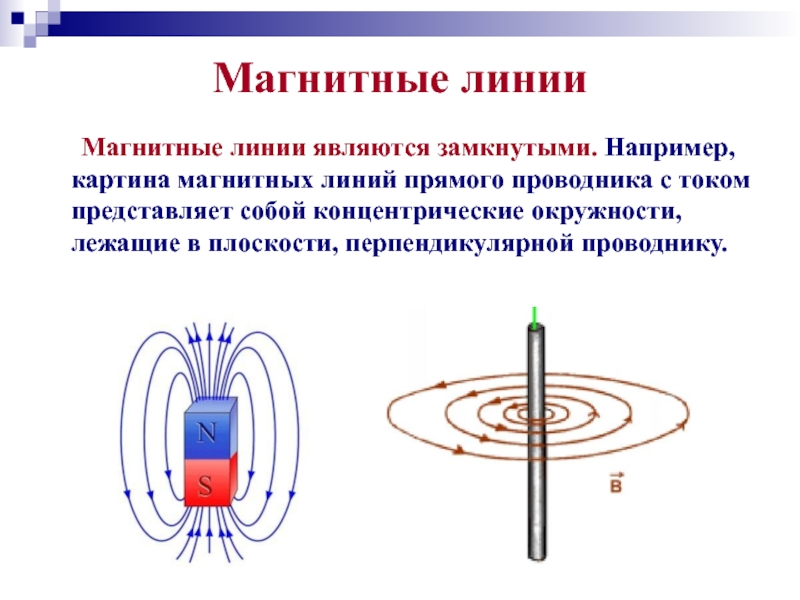 Подобные круговые токи протекают и внутри Земли.
Подобные круговые токи протекают и внутри Земли. Направление вращения ручки буравчика укажет направление
Направление вращения ручки буравчика укажет направление Определим направление линий магнитного поля по
Определим направление линий магнитного поля по Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].
Сила следует за RHR-1 большим пальцем в направлении [латекс]\boldsymbol{I}[/латекс].