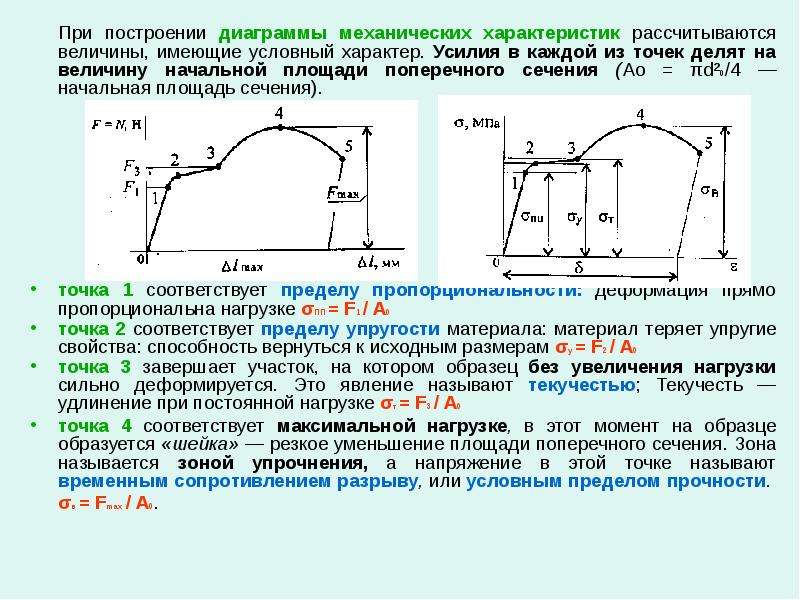
Механические характеристики двигателей и рабочих машин
Чаще всего механические характеристики двигателей и рабочих машин бывают заданы в виде соответствующих диаграмм, вследствие чего при решении задач о движении механизма приходится пользоваться не только численными, но и графическими методами.
[c.77]
Характер предельного режима движения машинного агрегата определяется, как известно, свойствами приведенного момента инерции, плотностью инерционных параметров системы и соотношением механических характеристик двигателя и рабочей машины. Приведенные момент инерции / и момент М всех действующих сил могут оказаться функциями одного или нескольких кинематических параметров tf, u), t в любой их комбинации [30]. [c.57]
Решению указанной задачи при различных предположениях относительно момента инерции 7 и механических характеристик двигателя и рабочей машины посвящены известные работы советских и зарубежных ученых [101. Интенсивные исследования, ведущиеся но этой проблеме, свидетельствуют о ее большой практической и теоретической значимости.
[c.57]
Интенсивные исследования, ведущиеся но этой проблеме, свидетельствуют о ее большой практической и теоретической значимости.
[c.57]
К настояш,ему времени предложено несколько графоаналитических способов решения этих задач при различных предположениях о механических характеристиках двигателя и рабочей машины и приведенном моменте инерции масс всех звеньев машинного [c.130]
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИГАТЕЛЕЙ И РАБОЧИХ МАШИН [c.19]
Механические характеристики двигателей и рабочих машин представляют собой большей частью сложные зависимости и изображаются в виде кривых линий. Динамическое исследование механизмов во многих случаях целесообразно производить аналитическими методами с тем, чтобы можно было установить закономерности изменения основных параметров машинного агрегата. Это возможно в тех случаях, когда удается решить дифференциальные уравнения движения механизма и представить их решения в конечном виде. Если механические характеристики двигателя и рабочей машины представляют собой сложные функции кинематических параметров, то сделать это оказывается невозможным, и тогда для решения дифференциальных уравнений приходится применять численные или графические методы. Путем их применения получаются результаты частного характера, по которым нельзя сделать обобщающих выводов.
[c.24]
Если механические характеристики двигателя и рабочей машины представляют собой сложные функции кинематических параметров, то сделать это оказывается невозможным, и тогда для решения дифференциальных уравнений приходится применять численные или графические методы. Путем их применения получаются результаты частного характера, по которым нельзя сделать обобщающих выводов.
[c.24]
По этим соображениям во многих случаях желательно представлять дифференциальное уравнение в таком виде, которое позволяло бы получить его решение в конечной форме. Для этой цели будем представлять механические характеристики двигателей и рабочих машин в виде несложных алгебраических выражений. Практически это вполне выполнимо, так как механические характеристики по большей части являются приблизительными зависимостями кинематических параметров. [c.24]
Работа машинного агрегата устойчива, если при установившемся движении при незначительных отклонениях приведенных моментов сил сопротивлений или движущих сил агрегат без участия регулятора восстанавливает режим установившегося движения.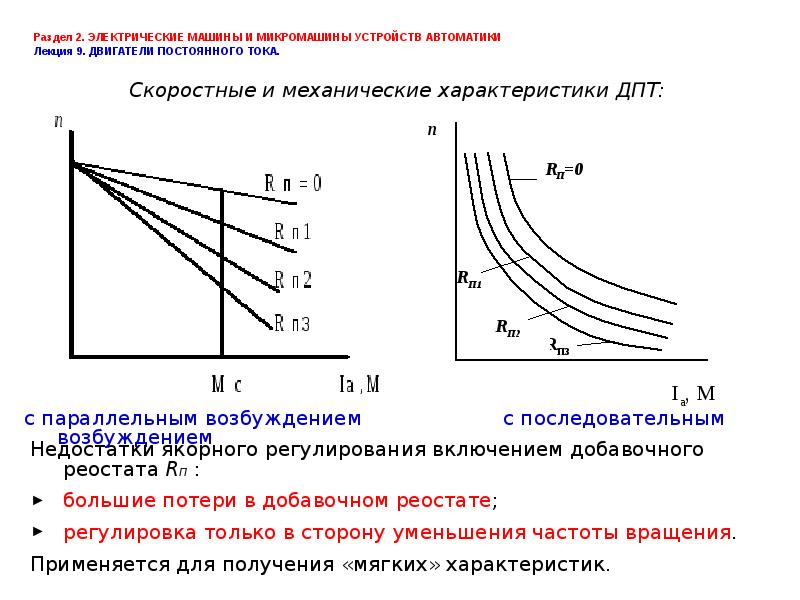 Это происходит при таком взаимном расположении совмещенных механических характеристик двигателя и рабочей машины, когда справа от точки их пересечения (в сторону увеличения скорости)
[c.205]
Это происходит при таком взаимном расположении совмещенных механических характеристик двигателя и рабочей машины, когда справа от точки их пересечения (в сторону увеличения скорости)
[c.205]
Механической характеристикой двигателя или рабочей машины называется зависимость силового параметра от одного или нескольких кинематических параметров (пути, скорости, ускорения времени). Механические характеристики определяются в результате теоретических или экспериментальных исследований, которыми занимаются энергетические и технологические дисциплины. [c.20]
Т. Рассмотрим типовые механические характеристики машин-двигателей и рабочих машин. [c.211]
Механические характеристики. Перейдем теперь к определению закона движения. Машинный агрегат — это комплекс, состоящий из машины-двигателя, передаточного механизма и рабочей машины. В двигателе создается движущий момент (или движущая сила). В рабочей машине образуется момент (или сила) полезных сопротивлений. Двигатель и рабочая машина имеют собственные кинематические цепи, но при изучении движения агрегата удобно рассматривать его общую кинематическую цепь, не разделяя ее на составные части, т. е. на цепь двигателя, передаточного механизма и рабочей машины. При этом действие внешней среды на механизм изображается внешними моментами (или силами), движущим моментом (силой) и моментом (силой) полезных сопротивлений, приложенными соответственно к ведущему и ведомому звеньям.
[c.58]
Двигатель и рабочая машина имеют собственные кинематические цепи, но при изучении движения агрегата удобно рассматривать его общую кинематическую цепь, не разделяя ее на составные части, т. е. на цепь двигателя, передаточного механизма и рабочей машины. При этом действие внешней среды на механизм изображается внешними моментами (или силами), движущим моментом (силой) и моментом (силой) полезных сопротивлений, приложенными соответственно к ведущему и ведомому звеньям.
[c.58]
Силы или моменты сил двигателей и рабочих машин в функции кинематических параметров (время, положения или скорости звена) называют механическими характеристиками (рис. 6.2.1). При решении задач динамики машин они считаются известными внешними силами и моментами.
[c.486]
При установившемся режиме движения необходимо в процессе исследования согласовать работу движущих сил и сил сопротивления, как это было показано вьппе.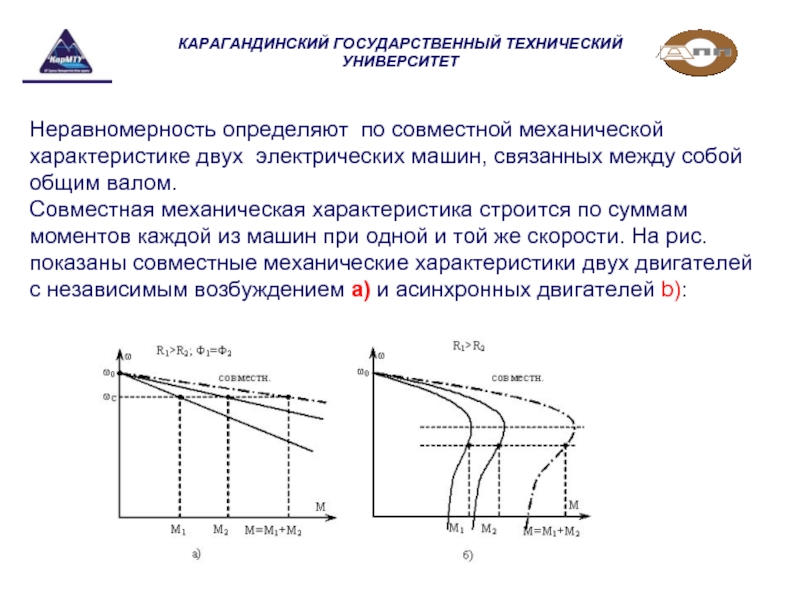 При переходном режиме разгона или торможения механические характеристики для двигателя и рабочей машины являются заданными. При переходном режиме пуск-останов требуется согласование параметров характеристик двигателя, рабочей машины или установки и тормозной системы, обеспечивающих безударное торможение.
[c.132]
При переходном режиме разгона или торможения механические характеристики для двигателя и рабочей машины являются заданными. При переходном режиме пуск-останов требуется согласование параметров характеристик двигателя, рабочей машины или установки и тормозной системы, обеспечивающих безударное торможение.
[c.132]
В подавляющем большинстве современных металлургических машин рабочий процесс протекает при повторно-кратковременных включениях двигателей. В таких условиях переходные процессы определяют движение машины и рабочие нагрузки, которые преимущественно являются динамическими. Для выявления картины переходных процессов с точки зрения фактических режимов движения и динамического нагружения разработана методика динамического расчета тяжелого металлургического привода при пусках, торможениях, переключениях скоростей и реверсах, учитывающая механическую характеристику двигателя и упругость деталей [191]. Эта методика была проверена экспериментальным путем в процессе натурных испытаний действующих кислородных конверторов на Нижне-Тагильском металлургическом комбинате по истечении различных сроков эксплуатации [25, 26]. Результаты эксперимента показали, что установленные аналитически законы движения агрегата весьма близки к экспериментальным, а замеренные в процессе эксперимента динамические нагрузки близки к вычисленным аналитически.
[c.252]
Результаты эксперимента показали, что установленные аналитически законы движения агрегата весьма близки к экспериментальным, а замеренные в процессе эксперимента динамические нагрузки близки к вычисленным аналитически.
[c.252]
При некоторых частных предположениях о характеристиках двигателя Afj и рабочей машины и законе изменения передаточного отношения в работах [95—103] были поставлены и решены различные задачи динамического анализа и синтеза механических систем с вариаторами. В общем же нелинейном случае уравнения движения (8.1) и (8.2) не интегрируются в квадратурах и решение подобных задач сопряжено с большими трудностями. В этой связи приходится прибегать к численным, графическим, графоаналитическим или иным качественным методам исследования. [c.268]
В дальнейшем мы рассмотрим три задачи расчета маховика для следующих машинных агрегатов 1) с поршневым двигателем, 2) с электродвигателем и рабочей машиной ударного действия и 3) с электродвигателем и рабочей машиной с механической характеристикой общего вида. [c.101]
[c.101]
При изучении этой системы необходимо принимать во внимание механическую характеристику двигателя, диссипативные свойства, характеризующие рассеяние энергии системы и взаимодействие обрабатываемого продукта с вибрирующим органом. Однако во многих вибрационных машинах силы взаимодействия продукта с рабочим органом малы, незначительны также диссипативные силы при возвратно-поступательном движении массы М. В таких вибраторах мощность двигателя расходуется только на преодоление трения в зубчатых передачах и во вращательных кинематических парах. Тогда обобщенные силы можно принять равными нулю. Рассмотрение движения указанной системы без внешних сил позволяет оценить влияние конструктивных параметров на характер движения системы. [c.125]
Электрический привод состоит из электродвигателя, аппаратуры управления и механической передачи от двигателя к рабочему органу машины. Тип двигателя выбирают в зависимости от рода тока и номинального напряжения, номинальной мощности и частоты вращения, вида естественной характеристики двигателя и его конструктивного исполнения.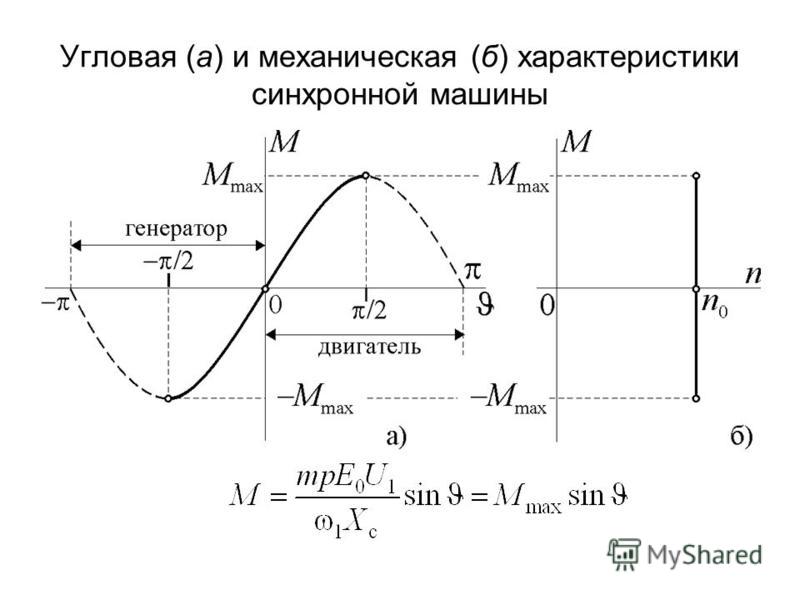 [c.281]
[c.281]
Привод состоит из двигателя, передачи, механизмов управления и вспомогательных устройств. В зависимости от основного вида передачи различают механический, гидравлический и пневматический приводы. Передачей называют устройство для преобразования энергии двигателя в движение рабочего органа машины. Применяя одну и ту же передачу, например гидродинамическую, с различными двигателями (например двигателем внутреннего сгорания или электродвигателем), получим различные свойства привода. Поэтому характеристика привода в целом складывается из взаимодействия характеристик двигателя и передачи. Это находит отражение и в названиях приводов дизель-электрический, электрогидравлический и др. [c.94]
Структура силовой передачи зависит от вида механической характеристики ротационного рабочего органа или исполнительного механизма рабочей машины и от механической характеристики двигателя. В технике встречаются следующие типовые случаи
[c.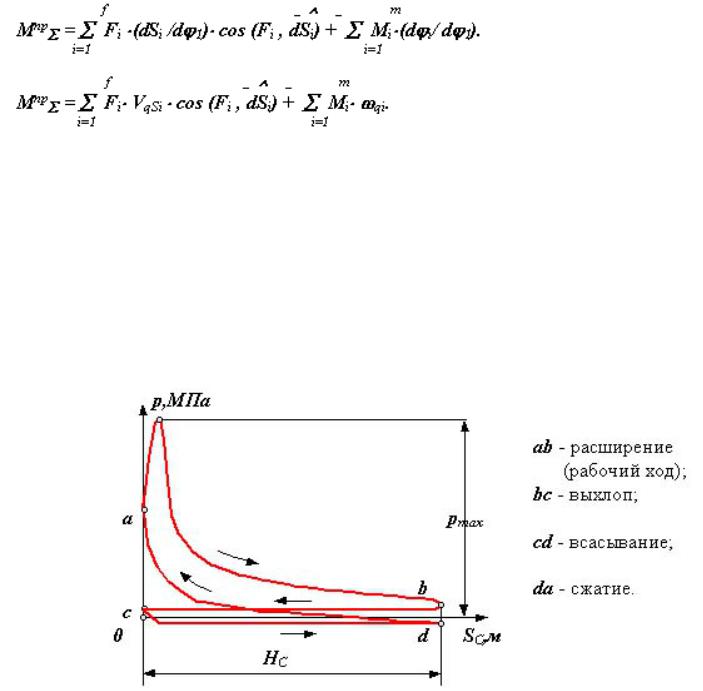 206]
206]
Для уменьшения влияния нагрева электрических машин и усилителей на механические характеристики главных приводов разработаны специальные устройства температурной компенсации, обеспечивающие стабильность механических характеристик двигателей (главным образом, их стопорных моментов) во всем диапазоне температур рабочего оборудования экскаваторов. Сущность таких устройств заключается в том, что потенциометры токовых узлов в схемах управления от силового магнитного усилителя подключаются к таким источникам питания, которые автоматически пропорционально увеличивают или уменьшают напряжение на участке подключения токовой обмотки управления главной цепи. [c.264]
Машинным агрегатом (рис. 1, 2) называется техническая система, состоящая из одной или нескольких соединенных последовательно или параллельно машин и предназначенная для выполнения каких-либо требуемых функций. Обычно в состав машинного агрегата входят двигатель, передаточный механизм и рабочая или энергетическая машина.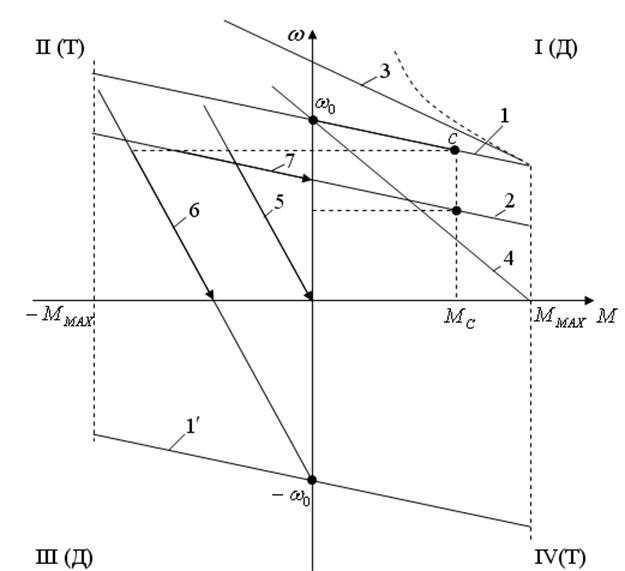 В настоящее время в состав машинного агрегата часто включается контрольно-управ-ляющая или кибернетическая машина. Передаточный механизм в машинном агрегате необходим для согласования механических характеристик двигателя с механическими характеристиками рабочей или энергетической машины.
[c.7]
В настоящее время в состав машинного агрегата часто включается контрольно-управ-ляющая или кибернетическая машина. Передаточный механизм в машинном агрегате необходим для согласования механических характеристик двигателя с механическими характеристиками рабочей или энергетической машины.
[c.7]
Основным назначением гидропривода, как упоминалось выше, является преобразование приведенной к выходному звену механической характеристики приводящего двигателя в соответствии с требованиями нагрузочной характеристики рабочей машины или механизма. При этом широкие возможности объемного гидропривода позволяют использовать в качестве привода почти любой машины или механизма наиболее простой и дешевый нерегулируемый трехфазный асинхронный двигатель с короткозамкнутым ротором. [c.217]
В нодавляюш ем большинстве практически важных случаев механические характеристики Мд, двигателя и рабочей машины являются нелинейными функциями соответствуюш,их кинематических параметров. Вследствие этого дифференциальное уравнение движения звена приведения машинного агрегата (1. 35)
[c.57]
Вследствие этого дифференциальное уравнение движения звена приведения машинного агрегата (1. 35)
[c.57]
Благодаря хорошим энергетическим показателям по коэффициенту мощности (созф), к. п. д., жесткости механических характеристик, высокой устойчивости, а также повышенной надежности вследствие значительного воздушного зазора между статором и ротором синхронный двигатель стал почти монопольным для поршневых компрессоров. Для поршневых компрессорных установок средней и большой мощности применяют обычно тихоходные синхронные приводы (частота вращения от 125 до 375 об/мин) с использованием многополюсных синхронных двигателей при непосредственном сочленении двигателя и рабочей машины (воздушные, аммиачные, фреоновые и газовые поршневые компрессоры). Для поршневых компрессорных установок малой и средней мощности (до 180 кВт) при частоте вращения п=500 об/мин используют фланцевые приводы. Статор двигателя крепят фланцем к станине компрессора, а ротор, выполняющий одновременно функцию маховика, устанавливают на удлиненном конце коленчатого вала.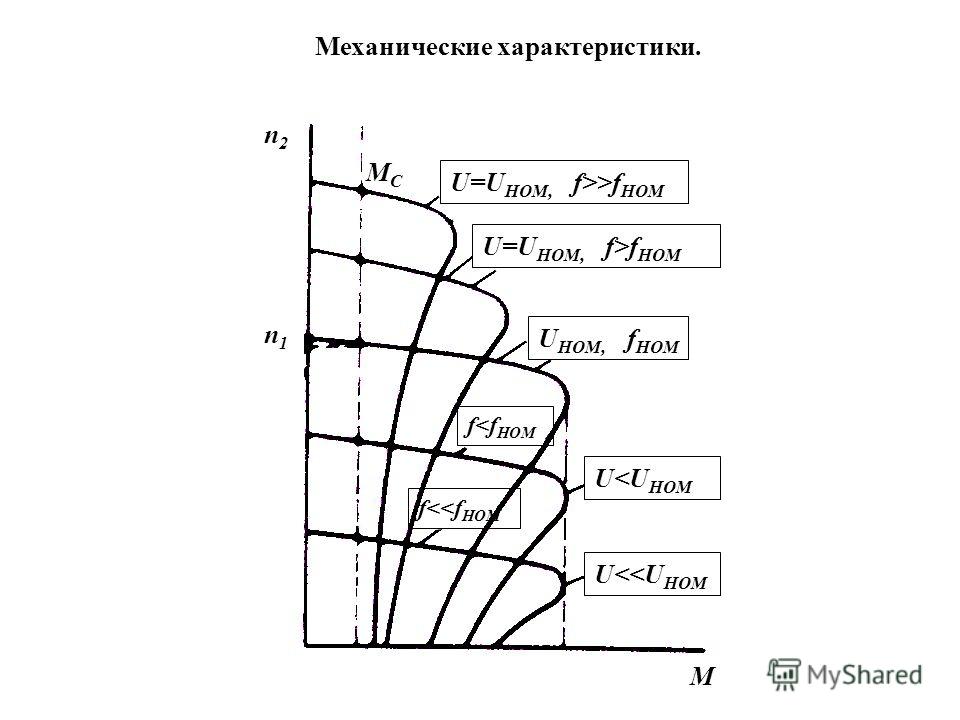 Таким приводом мощностью 178 кВт снабжают двухступенчатые вертикально-горизонтальные воздушные компрессоры производительностью 0,5 м /с при давлении сжатия 900 кН/м2.
[c.9]
Таким приводом мощностью 178 кВт снабжают двухступенчатые вертикально-горизонтальные воздушные компрессоры производительностью 0,5 м /с при давлении сжатия 900 кН/м2.
[c.9]
Двигатель служит источником механической энергии, необходимой для преодоления сопротивлений, возникающих при работе машины. Рабочий орган предназначен для выполнения технологических операций. Передаточный механизм (трансмиссия) предназначен для согласования характеристики двигателя и рабочего органа по угловой скорости и вращающему моменту. Для вращательного движения характерна зависимость Р 7со = onst (здесь Р — мощность Т — вращающий момент (О — угловая скорость), а для поступательного движения = onst F— сила v — скорость движения). Управляющее устройство служит для пуска и остановки машины, а также для поддержания заданного режима технологического процесса. [c.12]
Определить число Лу об1мин установившегося движения машинного агрегата, состоящего из двигателя, механическая характеристика которого задана равенством Мд = (100—0,1 п) нм, и рабочей машины, приведенный к валу двигателя момент сопротивления которой изменяется в соответствии с равенством Мс == = 0,000001 нм. [c.156]
[c.156]
В зависимости от типа двигателя или рабочей машины характеристики бывают более или менее сложными. Например, механическая характеристика гиревого привода представляет собой силу постоянной величины (рис. 47), пружинного привода — убывающую прямолинейную зависимость силы от деформации пружины, т. е. от пути (рис. 48). Механические характеристики электромагнитов и соленоидов бывают очень разнообразными и являюгся более сложными зависимостями силы от пути или момента пары сил от угла поворота. На рис. 49 показана одна из простых механических характеристик электромагнита. На рис. 50 изображена механическая [c.76]
На рис. 11.1 показана структурная схема объемного гидропривода. Входным элементом в этой структуре является приводящий двигатель (ПД). Гидропривод сам по себе не вырабатывает энергии. Он работает только тогда, когда в него вводится энергия. В качестве приводящего двигателя чаще всего применяется электродвигатель. Однако это может быть и двигатель внутреннего сгорания или дизель и т. п. Механическая энергия приводящего двигателя (МЭ) вводится в следующий структурный элемент привода (Н), который называется насосом. Однако функция этого элемента заключается не в перекачке жидкости, а в преобразовании механической энергии в энергию потока жидкости. Насосом он называется по принципу действия, а ктически является птеобразователем энергии. После насоса преобразованная энергия (ЭЖ) передается следующему структурному элементу — гидродвигателю (ГД), который преобразует энергию жидкости снова в механическую и в таком виде она подается в машину. На этапе преобразования, когда энергия передается жидкостью, на нее воздействуют регулирующие устройства (РУ), с помо1цью которых эне и придаются характеристики, необходимые для рабочей машины. При этом воздействие может осуществляться двумя путями непосредственно на поток жидкости между насосом и гидродвигателем (Л (дроссельное регулирование) и через геометрию гидромашин (2) (объемное регулирование). Преобразование происходит с частичной потерей энергии.
п. Механическая энергия приводящего двигателя (МЭ) вводится в следующий структурный элемент привода (Н), который называется насосом. Однако функция этого элемента заключается не в перекачке жидкости, а в преобразовании механической энергии в энергию потока жидкости. Насосом он называется по принципу действия, а ктически является птеобразователем энергии. После насоса преобразованная энергия (ЭЖ) передается следующему структурному элементу — гидродвигателю (ГД), который преобразует энергию жидкости снова в механическую и в таком виде она подается в машину. На этапе преобразования, когда энергия передается жидкостью, на нее воздействуют регулирующие устройства (РУ), с помо1цью которых эне и придаются характеристики, необходимые для рабочей машины. При этом воздействие может осуществляться двумя путями непосредственно на поток жидкости между насосом и гидродвигателем (Л (дроссельное регулирование) и через геометрию гидромашин (2) (объемное регулирование). Преобразование происходит с частичной потерей энергии.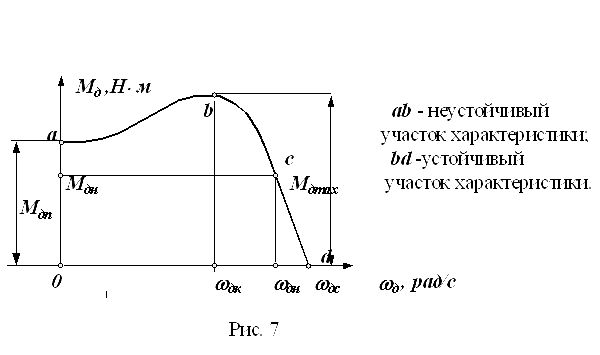 Механическая энергия после приводящего двигателя по величине больше, чем после гидродвигателя. Количественные потери энергии при применении гидропривода в горных машинах окупаются за счет эффективности использования основных его свойств.
[c.168]
Механическая энергия после приводящего двигателя по величине больше, чем после гидродвигателя. Количественные потери энергии при применении гидропривода в горных машинах окупаются за счет эффективности использования основных его свойств.
[c.168]
Однако существуют машины, в которых влияние скорости на силы и моменты ныражено очень резко. К ним относятся, например, асинхронные и шунтовые двигатели, получившие наиболее широкое распространение в промышленном электроприводе. Механические характеристики этих машин — в их рабочей части — представляют собой практически прямую линию, расположенную почти вертикально (например, рис. 4.1, 4.5, б). Это значит, что даже небольшие колебания угловой скорости вызывают заметные изменения движущего момента. Поэтому следует ожидать, что резко выраженная зависимость момента от скорости должна оказать свое влияние на результаты динамического анализа и синтеза. [c.173]
Отличительной особенностью машинных агрегатов с ДВС, управляемых по скорости посредством тахометрических обратных связей, являются обусловленные рабочим процессом ДВС весьма значительные циклические позиционные возмущения, действующие на коленчатый вал двигателя. Как отмечалось выше, важнейшими показателями эксплуатационной пригодности и качества машинных агрегатов, управляемых но скорости, являются устойчивость системы автоматического регулирования скорости (САРС), качество регулирования, достижимость расчетных регулируемых скоростных режимов. Расчетный анализ и экспериментальные исследования САРС машинных агрегатов с ДВС показали, что на динамические характеристики САРС, прежде всего на показатели устойчивости и качества регулирования, могут оказывать существенное влияние колебательные свойства механического объекта регулирования [21, 108].
[c.140]
Как отмечалось выше, важнейшими показателями эксплуатационной пригодности и качества машинных агрегатов, управляемых но скорости, являются устойчивость системы автоматического регулирования скорости (САРС), качество регулирования, достижимость расчетных регулируемых скоростных режимов. Расчетный анализ и экспериментальные исследования САРС машинных агрегатов с ДВС показали, что на динамические характеристики САРС, прежде всего на показатели устойчивости и качества регулирования, могут оказывать существенное влияние колебательные свойства механического объекта регулирования [21, 108].
[c.140]
Скоростные и механические характеристики электродвигателей постоянного тока с параллельным возбуждением
Выведенные в предыдущем параграфе уравнения скоростных и механических характеристик справедливы для любого электродвигателя постоянного тока.
Однако это не значит, что для всех электродвигателей характеристики одинаковы. Наоборот, как будет показано, между характеристиками различных электродвигателей постоянного тока имеются существенные различия.
Наоборот, как будет показано, между характеристиками различных электродвигателей постоянного тока имеются существенные различия.
Анализируя любое из полученных в статье особенности электродвигатели постоянного тока уравнений, нетрудно заметить, что все они являются уравнениями прямых линий, если U =соnst и Ф = соnst, т.е. механическая и скоростная характеристики электродвигателя постоянного тока с параллельным возбуждением прямолинейны и :при соответствующем выборе масштабов они могут быть представлены одной прямой (рис. 9).
Действительно, когда электродвигатель работает вхолостую, развиваемый им момент равен нулю, так как нулю равен момент сопротивления на валу двигателя. При этом, согласно выражению (28), нулю должен быть равен и ток в обмотке якоря. Таким образом, из уравнения (25) или (29) может быть получена скорость идеального холостого хода электродвигателя
Нужно иметь в виду, что фактическая скорость холостого хода электродвигателя всегда несколько ниже скорости идеального» холостого хода, так как в действительности момент сопротивления на валу электродвигателя не может быть равен нулю даже при отсутствии нагрузки на электродвигатель, а следовательно, и ток действительного холостого хода электродвигателя нулю не равен.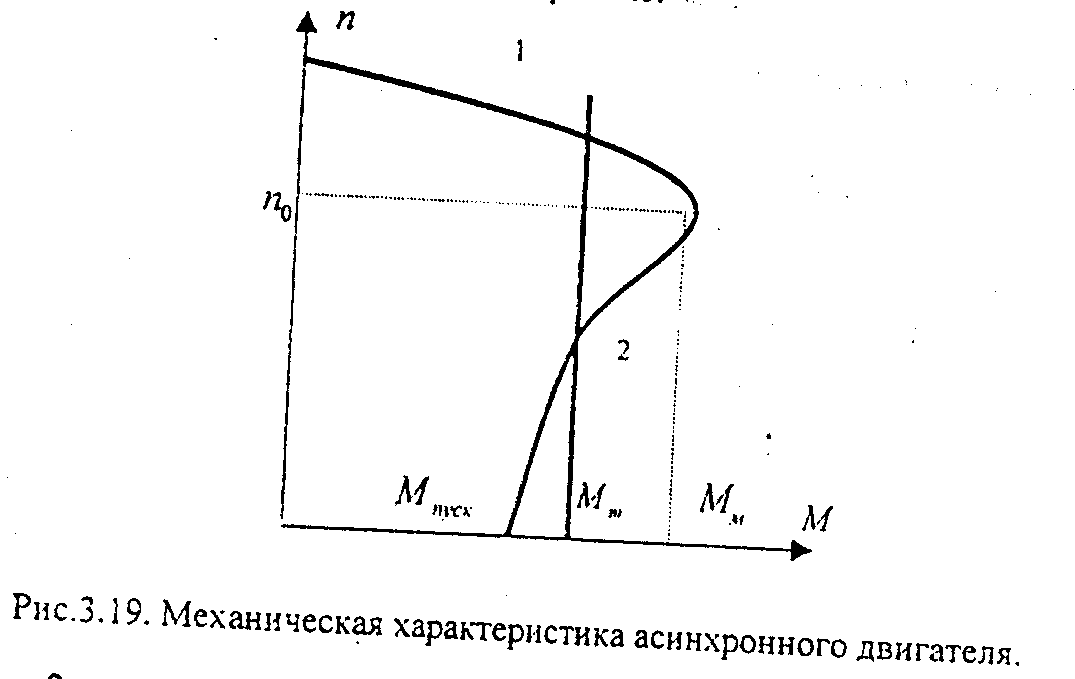
Если нагрузка на электродвигатель возрастает (т. е. возрастает момент сопротивления на его валу), то возрастает развиваемый электродвигателем вращающий момент и растет ток в его якорной обмотке. Это должно вызывать, согласно уравнениям (25) и (29), снижение скорости вращения электродвигателя. В режиме короткого замыкания электродвигателя (режим стоянки под током) n = 0, а ток короткого замыкания Аналогично, момент короткого замыкания Мк = кФІя.к. Таким образом, скоростная характеристика электродвигателя постоянного тока с параллельным возбуждением п = f(Ія) и механическая характеристика п = f(М) пересекают оси координат в совершенно определенных точках, соединив которые, можно получить указанные характеристики, представленные одной прямой (см. рис. 9). На рис. 9, помимо естественной характеристики, показан ряд искусственных характеристик двигателя при различных дополнительных сопротивлениях R в якорной цепи. Из уравнений (27) и (30) вытекает, что искусственные характеристики тоже прямолинейны, исходят из общей точки холостого хода и лежат ниже естественной характеристики, т. е. чем выше дополнительное сопротивление R в якорной цепи, тем круче (или мягче) характеристика электродвигателя. На рисунке обозначены: Мн (Iя.н) — номинальный момент и ток якоря; Мк (Iя.к) — момент и ток якоря при заторможенном якоре.
Из уравнений (27) и (30) вытекает, что искусственные характеристики тоже прямолинейны, исходят из общей точки холостого хода и лежат ниже естественной характеристики, т. е. чем выше дополнительное сопротивление R в якорной цепи, тем круче (или мягче) характеристика электродвигателя. На рисунке обозначены: Мн (Iя.н) — номинальный момент и ток якоря; Мк (Iя.к) — момент и ток якоря при заторможенном якоре.
Как видно из уравнений, скорость электродвигателя параллельного возбуждения меняется при различных нагрузках за счет изменения падения напряжения в сопротивлении якоря. Поскольку сопротивления якорей машин постоянного тока невелики, скорость электродвигателей параллельного возбуждения меняется незначительно, особенно при работе на естественной характеристике. Так, для электродвигателей мощностью от 5 до 100 квт перепад скорости пои номинальной нагрузке
где большие значения соответствуют электродвигателям меньшей мощности.
Ввиду прямолинейности, практическое построение характеристик электродвигателя с параллельным возбуждением выполнить нетрудно. Для этого достаточно иметь координаты двух точек. Обычно естественную характеристику электродвигателя строят по скорости идеального холостого хода, номинальной скорости вращения и номинальному моменту (или току). Скорость идеального холостого хода электродвигателя может быть вычислена следующим образом.
Против э. д. с. при работе электродвигателя в номинальном режиме на естественной характеристике
а на холостом ходу
Разделив второе выражение на первое, получим
В выражении (34) все величины, кроме Rя могут быть взяты из паспорта электродвигателя. Величина Rя может быть взята из формуляра на электродвигатель, определена измерением или приближенно из следующего выражения:
где Рн — номинальная мощность электродвигателя, квт;
?н — к. п.д. электродвигателя при номинальной нагрузке.
п.д. электродвигателя при номинальной нагрузке.
Выражение (35) составлено исходя из предположения, что при номинальной нагрузке электродвигателя потери мощности в сопротивлении якоря равны примерно половине общих потерь в электродвигателе. Если величина R определяется измерением, то нужно иметь в виду, что сопротивление якоря включает в себя сопротивления обмотки якоря, обмотки дополнительных полюсов, щеток и сопротивления компенсационной обмотки (если она имеется), соединенных последовательно.
Выше указывалось, что вращающий момент электродвигателя автоматически следует за моментом сопротивления механизма. Физическая сущность этого процесса состоит в следующем. Если электродвигатель работает с установившейся скоростью, то развиваемый им вращающий момент М1 равен моменту сопротивления на его валу Мс. Если же момент сопротивления возрастет до Mс2> M1, то скорость электродвигателя начнет уменьшаться.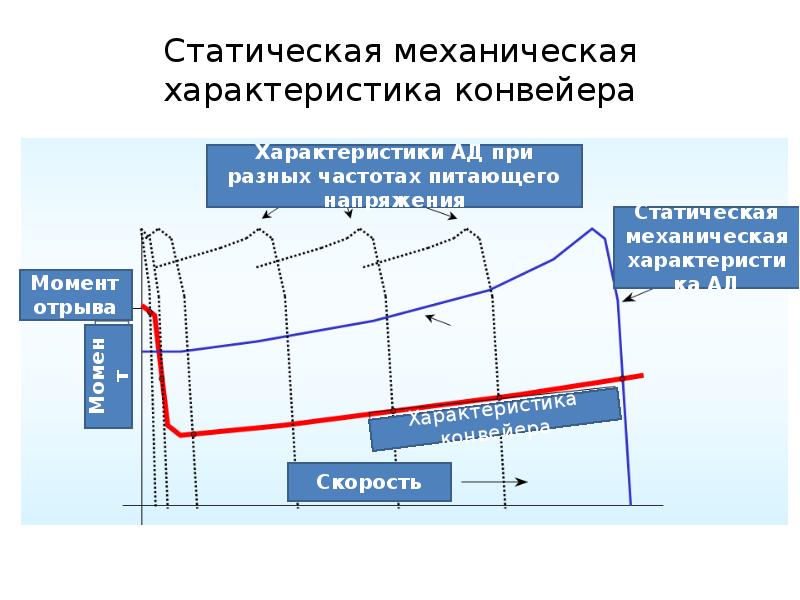 При этом уменьшается и против э. д. с., а ток в обмотке якоря, согласно выражению (22), будет возрастать, что вызовет возрастание вращающего момента. Уменьшение числа оборотов будет происходить до тех пор, пока вращающий момент не станет равным моменту сопротивления Мс2.
При этом уменьшается и против э. д. с., а ток в обмотке якоря, согласно выражению (22), будет возрастать, что вызовет возрастание вращающего момента. Уменьшение числа оборотов будет происходить до тех пор, пока вращающий момент не станет равным моменту сопротивления Мс2.
При уменьшении момента сопротивления происходит обратный процесс. Если момент сопротивления станет меньше вращающего момента, развиваемого электродвигателем, то скорость вращения последнего начнет возрастать. Это вызовет возрастание противо э. д. с., а значит, уменьшение тока и вращающего момента. Процесс прекратится, когда вращающий момент станет равным моменту сопротивления на валу электродвигателя.
Механические характеристики производственных механизмов и электродвигателей
из «Электрооборудование нефтяной и газовой промышленности Издание 2»
При выборе электродвигателей необходимо, чтобы их электромеханические свойства соответствовали характеристикам и технологическим требованиям нроизнодственпых механизмов. К электромеханическим свойствам относятся в первую очередь механические характеристики двигателей в различных режимах работы, а также пусковые и тормозные свойства двигателей. [c.128]
К электромеханическим свойствам относятся в первую очередь механические характеристики двигателей в различных режимах работы, а также пусковые и тормозные свойства двигателей. [c.128]
Механической характеристикой двигателя называется зависимость частоты вращения его нала от момента, который двигатель развивает. Механической характеристикой производственного механизма называется зависимость м омента сопротивления механизма от частоты его вращения. [c.128]
Основные типы механизмов имеют ==0 =1 и q==2. При д = 0 M = M = onst, т. е, момент сопротивления их не зависит от частоты вращения (рис. 3.3), Такую механическую характеристику имеют все машины, соверн1ающие работу подъема, формоизменения материала или преодолевающие трение (подъемные лебедки и краны, бумагоделательные машины, поршневые насосы при неизменной высоте подачи жидкости). Мощность таких машин растет линейно с частотой вращения. [c.128]
При =1 момент растет линейно с частотой вращения, а мощность — прямо пропорциональна юзадрату частоты вращения, Подобная характеристика имеется у генератора постоянного тока независимого возбуждения, работающего на постоянное сопротивление нагрузки.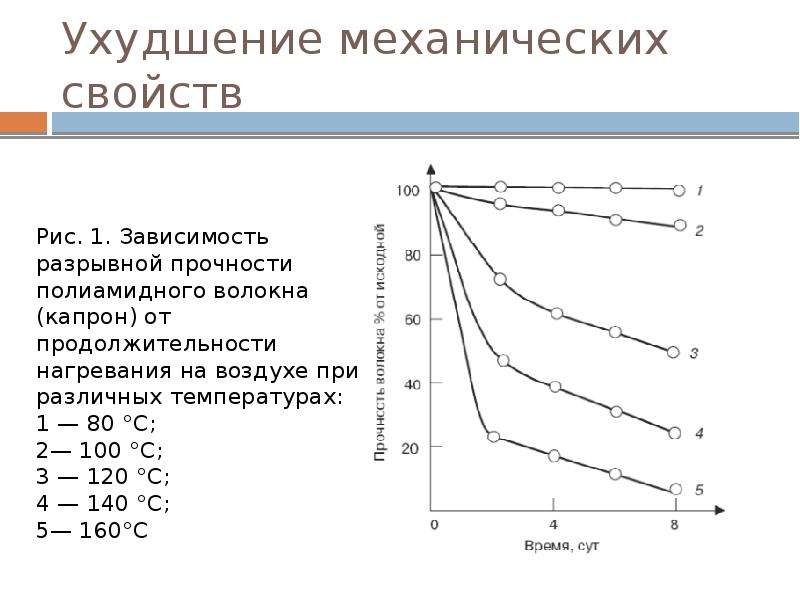 [c.128]
[c.128]
Во всех машинах с кривошипным механизмом (поршневые насосы и компрессоры, станки-качалки и т. п.) момент сопротивления зависит от положения кривошипа, т. е. от углового положения вала двигателя. Во всех подобных машинах момент сопротивления складывается из постоянной и переменной составляющих. Последняя периодически изменяется в зависимости от угла поворота вала. [c.129]
Такие кривые могут быть представлены в виде ряда Фурье, т. е. суммы гармонических колебаний различной частоты, что позволяет весьма упростить расчеты электропривода. [c.129]
В отличие от производственных механизмов практически все электродвигатели, за исключением синхронных, имеют падающую механическую характеристику, т. е. с увеличением момента на валу двигателя частота его вращения уменьшается. В зависимости от степени изменения частоты вращения двигателей их механические характеристики подразделяются на абсолютно жесткие, жесткие и мягкие (рис. 3, 4). [c.129]
3, 4). [c.129]
Абсолютно жесткую характеристику имеют синхронные двигатели (их частота вращения не зависит от момента сопротивления на валу). [c.129]
При жесткой характеристике изменению момента сопротивления от нуля до номинального значения соответствует незначительное (до 10%) изменение частоты вращения двигателя. Такие характеристики свойственны асинхронным двигателям и двигателям постоянного тока параллельного или независимого возбуждения. [c.129]
Мягкой характеристикой обладают двигатели постоянного тока последовательного возбуждения. У этих двигателей с увеличением момента частота вращения сильно падает. [c.129]
В зависимости от конфигурации механических характеристик производственного механизма и электродвигателя их совместная работа может быть устойчивой или неустойчивой. [c.129]
Предположим, что работа двигателя характеризовалась точкой 1 пересечения его механической характеристики II (см. рис. 3.4) с характеристикой механизма. При этом вращающий момент двигателя равен моменту сопротивления Ai i (установившийся режим). Если равновесие моментов нарушится и частота вращения будет уменьшаться. По мере снижения частоты вращения момент двигателя будет возрастать согласно его механической характеристике, пока не станет равным Мс2. Точке 2 (см. рис. 3.4) будет соответствовать новый установившийся режим. Если нагрузка уменьшится, например до величины Мез, частота вращения двигателя будет увеличиваться до тех пор, пока момент двигателя не станет равным Мез, чему соответствует точка 3 характеристики II. Таким образом, работа электропривода в данном случае будет устойчивой. [c.130]
рис. 3.4) с характеристикой механизма. При этом вращающий момент двигателя равен моменту сопротивления Ai i (установившийся режим). Если равновесие моментов нарушится и частота вращения будет уменьшаться. По мере снижения частоты вращения момент двигателя будет возрастать согласно его механической характеристике, пока не станет равным Мс2. Точке 2 (см. рис. 3.4) будет соответствовать новый установившийся режим. Если нагрузка уменьшится, например до величины Мез, частота вращения двигателя будет увеличиваться до тех пор, пока момент двигателя не станет равным Мез, чему соответствует точка 3 характеристики II. Таким образом, работа электропривода в данном случае будет устойчивой. [c.130]
Об устойчивости работы механизма с электроприводом можно судить по зависимости частоты вращения от динамического момента, которую иногда называют совместной механической характеристикой агрегата. Эту зависимость можно получить, если из значений момента двигателя при определенных частотах вращения вычесть значения момента сопротивления при тех же частотах вращения.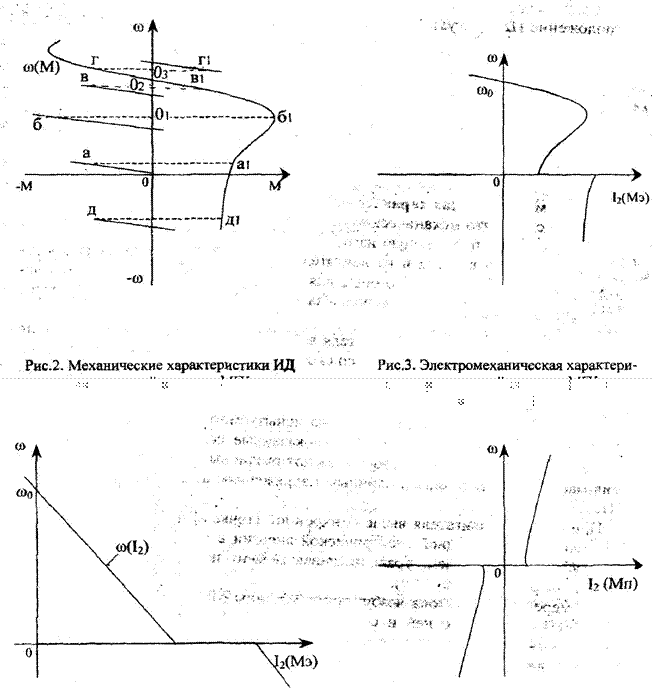 [c.130]
[c.130]
В установившемся режиме при некоторой частоте вращения динамический момент равен нулю. Работа агрегата при этой частоте вращения устойчива, если ее понижению соответствует положительное приращение динамического момента, а повышению — отрицательное приращение динамического момента. Под действием динамического момента частота вращения агрегата будет в первом случае повышаться, а во втором — понижаться до тех пор, пока не достигнет значения, при котором момент двигателя станет равным моменту сопротивления. [c.130]
Если бы при повышении частоты вращения приращение динамического момента было положительным, это приводило бы к дальнейшему увеличению частоты вращения, при понижении ее наблюдалось бы обратное явление следовательно, такой режим не был бы устойчивым. [c.130]
Работа в точке b будет неустойчивой, поскольку в этой точке dM ld(u = 0 и dMnJda 0. Это обстоятельство послужило основанием тому, что правую ветвь характеристики Рас асинхронного двигателя стали называть устойчивой, а левую Qb — неустойчивой. Последнее название не совсем отвечает действительности, так как работа электропривода и на левой ветви характеристики может быть вполне устойчивой. [c.131]
Последнее название не совсем отвечает действительности, так как работа электропривода и на левой ветви характеристики может быть вполне устойчивой. [c.131]
Рассмотрим привод центробежного вентилятора с механической характеристикой Aie — Точка пересечения характеристик является вполне устойчивой, поскольку для этой точки выполняется критерий [см. формулу (3.19)]. [c.131]
Следует заметить, что продолжительную работу асинхронного двигателя на левой ветви характеристики при питании его номинальным напряжением нельзя допускать вследствие большой силы тока и опасности перегрева обмоток. [c.131]
Если предположить, что момент сопротивления Мс равен максимальному моменту двигателя (рис. 3.5, точка с), то для бесконечно малого изменения частоты вращения dM ld( = = dMnBld(u и электропривод будет находиться в состоянии безразличного равновесия. Однако при больших отклонениях частоты вращения в сторону убывания электропривод полностью остановится. [c.131]
[c.131]
Электромагнитный момент [см. формулу (3.21)] больше момента на валу двигателя вследствие механических и вентиляционных потерь в двигателе. Однако обычно эти потери незначительны и момент на валу двигателя принимают равным его электромагнитному моменту. [c.132]
Вернуться к основной статье
Электродвигатели постоянного тока и области их применения | Полезные статьи
Электродвигатель постоянного тока (ДПТ) представляют собой механизм, преобразующий поступающую на него электрическую энергию в механическое вращение. Работа агрегата базируется на явлении электромагнитной индукции — на проводник, помещенный в магнитное поле, действует сила Ампера: F = B*I*L, где L — длина проводника, I — ток, протекающий по проводнику, B — индукция магнитного поля. Данная сила обуславливает возникновение крутящего момента, который может быть использован для неких практических целей.
Электродвигатели постоянного тока обладают следующими преимуществами:
- Практически линейные регулировочные и механические характеристики, благодаря чему обеспечивается удобство эксплуатации.

- Большая величина пускового момента.
- Компактные размеры (особенно сильно выражено у двигателей на постоянных магнитах).
- Возможность использования одного и того же механизма как в режиме двигателя, так и генератора.
- КПД при полной нагрузке, как правило, выше на 1–2 % чем у асинхронных и синхронных машин, а при неполной нагрузке преимущество может возрастать до 15 %.
Основным недостатком данных устройств является высокая цена их изготовления. Также стоит отметить необходимость регулярного обслуживания коллекторно-щеточного узла и определенное ограничение срока эксплуатации, вызванные его износом, однако на современных моделях эти недостатки практически полностью нивелированы.
Стоит отметить, что механическая характеристика, а значит, и все эксплуатационные показатели во многом зависят от схемы подключения обмотки возбуждения. Всего их четыре:
Способы возбуждения: а — независимое, б — параллельное, в — последовательное, г — смешанное.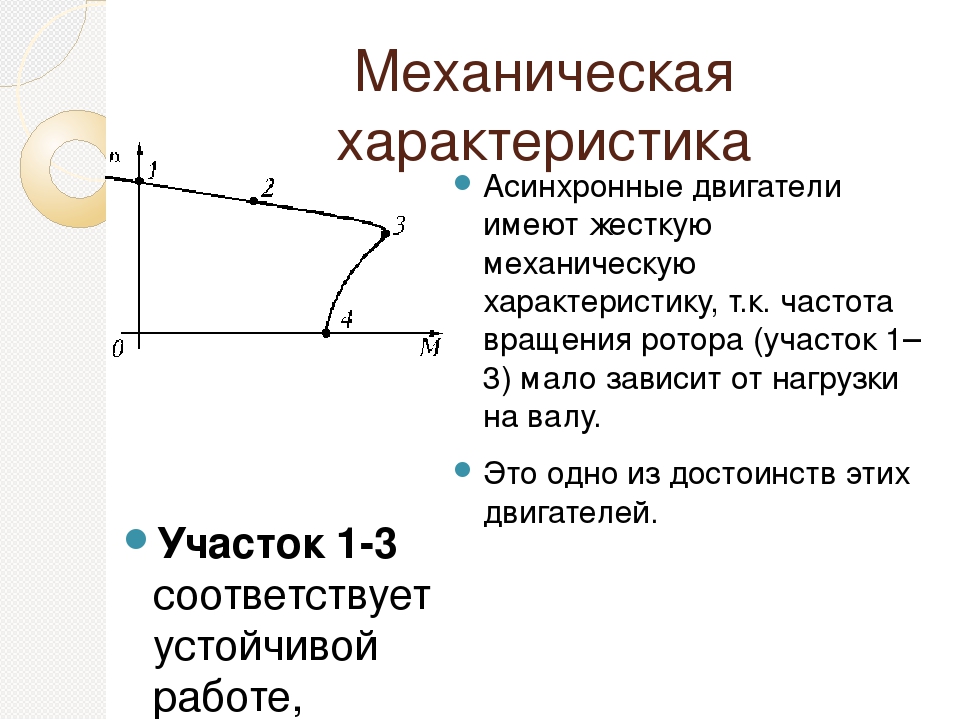
Области применения ДПТ
Несмотря на то, что подавляющее большинство электрических сетей обеспечивают переменное напряжение, электродвигатели постоянного тока используются весьма и весьма широко. Собственно говоря, все промышленные приводы, где требуется точная регулировка частоты вращения, реализованы именно на базе ДПТ. Кроме того, электрические машины на постоянных магнитах благодаря своей эффективности и большой плотности мощности широко используются в оборонительной отрасли.
Впрочем, не стоит думать, что вы не сталкивались вживую с данными механизмами. Отсутствие жестких ограничений по размерам приводит к тому, что мы зачастую их не замечаем. Например, в автомобилестроении используются только электродвигатели постоянного тока, причем, несмотря на различие в мощности, на всем грузовом транспорте и спецтехнике они запитаны от 24 вольт, в то время как на легковых автомобилях их рабочее напряжение составляет 12 вольт. Получая энергию от аккумуляторной батареи или генератора, они отвечают за позиционирование сидений, управление зеркалами, поднятие и опускание стекол, а также поддержание в салоне заданной температуры.
Впрочем, электродвигатели постоянного тока могут и сами приводить в движение транспортные средства, и это далеко не только игрушечные автомобили-аттракционы с 12-вольтным аккумулятором. Для того чтобы ощутить, насколько мощными могут быть эти устройства, достаточно оказаться вблизи проходящей мимо пригородной электрички, а мягкость и точность регулировки оборотов наглядно демонстрирует плавный разгон троллейбусов.
Данные электродвигатели широко применяются как в электрическом транспорте (метро, троллейбус, трамвай, пригородные электрические железные дороги, электровозы), так и в подъемных устройствах (электрические подъемные краны).
Для оформления заказа позвоните менеджерам компании Кабель.РФ® по телефону +7 (495) 646-08-58 или пришлите заявку на электронную почту [email protected] с указанием требуемой модели электродвигателя, целей и условий эксплуатации. Менеджер поможет Вам подобрать нужную марку с учетом Ваших пожеланий и потребностей.
Механическая характеристика двигателя постоянного тока последовательного возбуждения.
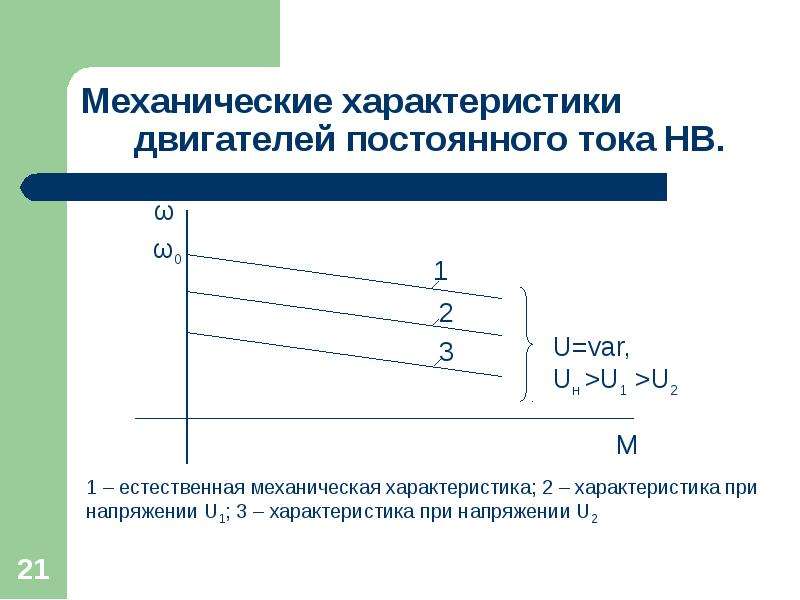 Характеристики двигателей последовательного возбуждения. Для поочередной подачи тока на обмотки якоря применяются специальные щетки из сплава графита и меди
Характеристики двигателей последовательного возбуждения. Для поочередной подачи тока на обмотки якоря применяются специальные щетки из сплава графита и меди
Электродвигатели, работающие на постоянном токе, используются не так часто, как двигатели переменного тока. Ниже приведем их достоинства и недостатки.
В быту двигатели постоянного тока нашли применение в детских игрушках, так как источниками для их питания служат батарейки. Используются они на транспорте: в метрополитене, трамваях и троллейбусах, автомобилях. На промышленных предприятиях электродвигатели постоянного тока применяются в приводах агрегатов, для бесперебойного электроснабжения которых используются аккумуляторные батареи.
Конструкция и обслуживание двигателя постоянного тока
Основной обмоткой двигателя постоянного тока является якорь
, подключающийся к источнику питания через щеточный аппарат
. Якорь вращается в магнитном поле, создаваемом полюсами статора (обмотками возбуждения)
. Торцевые части статора закрыты щитами с подшипниками, в которых вращается вал якоря двигателя. С одной стороны на этом же валу установлен вентилятор
Торцевые части статора закрыты щитами с подшипниками, в которых вращается вал якоря двигателя. С одной стороны на этом же валу установлен вентилятор
охлаждения, прогоняющий поток воздуха через внутренние полости двигателя при его работе.
Щеточный аппарат – уязвимый элемент в конструкции двигателя. Щетки притираются к коллектору, чтобы как можно точнее повторять его форму, прижимаются к нему с постоянным усилием. В процессе работы щетки истираются, токопроводящая пыль от них оседает на неподвижных частях, ее периодически нужно удалять. Сами щетки нужно иногда перемещать в пазах, иначе они застревают в них под действием той же пыли и «зависают» над коллектором. Характеристики двигателя зависит еще и от положения щеток в пространстве в плоскости вращения якоря.
Со временем щетки изнашиваются и заменяются. Коллектор в местах контакта со щетками тоже истирается. Периодически якорь демонтируют и протачивают коллектор на токарном станке. После протачивания изоляция между ламелями коллектора срезается на некоторую глубину, так как она прочнее материала коллектора и при дальнейшей выработке будет разрушать щетки.
Схемы включения двигателя постоянного тока
Наличие обмоток возбуждения – отличительная особенность машин постоянного тока. От способов их подключения к сети зависят электрические и механические свойства электродвигателя.
Независимое возбуждение
Обмотка возбуждения подключается к независимому источнику. Характеристики двигателя получаются такие же, как у двигателя с постоянными магнитами. Скорость вращения регулируется сопротивлением в цепи якоря. Регулируют ее и реостатом (регулировочным сопротивлением) в цепи обмотки возбуждения, но при чрезмерном уменьшении его величины или при обрыве ток якоря возрастает до опасных значений. Двигатели с независимым возбуждением нельзя запускать на холостом ходу или с малой нагрузкой на валу. Скорость вращения резко увеличится, и двигатель будет поврежден.
Остальные схемы называют схемами с самовозбуждением.
Параллельное возбуждение
Обмотки ротора и возбуждения подключаются параллельно к одному источнику питания. При таком включении ток через обмотку возбуждения в несколько раз меньше, чем через ротор. Характеристики электродвигателей получаются жесткими, позволяющие использовать их для привода станков, вентиляторов.
При таком включении ток через обмотку возбуждения в несколько раз меньше, чем через ротор. Характеристики электродвигателей получаются жесткими, позволяющие использовать их для привода станков, вентиляторов.
Регулировка скорости вращения обеспечивается включением реостатов в цепь ротора или последовательно с обмоткой возбуждения.
Последовательное возбуждение
Обмотка возбуждения включается последовательно с якорной, по ним течет один и тот же ток. Скорость такого двигателя зависит от его нагрузки, его нельзя включать на холостом ходу. Но он обладает хорошими пусковыми характеристиками, поэтому схема с последовательным возбуждением применяется на электрифицированном транспорте.
Смешанное возбуждение
При этой схеме используются две обмотки возбуждения, расположенные попарно на каждом из полюсов электродвигателя. Их можно подключить так, чтобы потоки их либо складывались, либо вычитались. В результате двигатель может иметь характеристики как у схемы последовательного или параллельного возбуждения.
Для изменения направления вращения
изменяют полярность одной из обмоток возбуждения. Для управления пуском электродвигателя и скоростью его вращения применяют ступенчатое переключение сопротивлений.
Естественные скоростная и механическая характеристики, область применения
В двигателях последовательного возбуждения ток якоря одновременно является также током возбуждения: i
в = I
а = I
. Поэтому поток Ф δ изменяется в широких пределах и можно написать, что
| (3) |
| (4) |
Скоростная характеристика двигателя [смотрите выражение (2)], представленная на рисунке 1, является мягкой и имеет гиперболический характер. При k
Ф = const вид кривой n
= f
(I
) показан штриховой линией. При малых I
скорость двигателя становится недопустимо большой.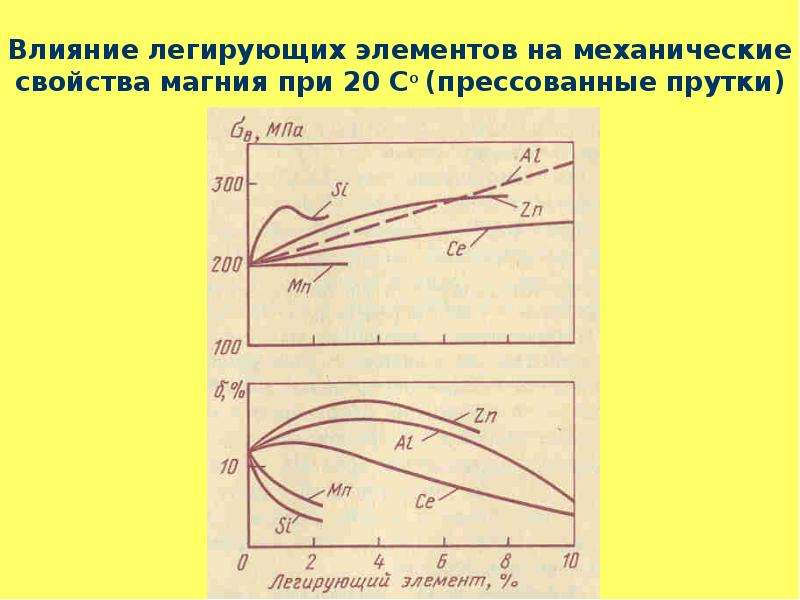 Поэтому работа двигателей последовательного возбуждения, за исключением самых маленьких, на холостом ходу не допускается, а использование ременной передачи неприемлемо. Обычно минимально допустимая нагрузка P
Поэтому работа двигателей последовательного возбуждения, за исключением самых маленьких, на холостом ходу не допускается, а использование ременной передачи неприемлемо. Обычно минимально допустимая нагрузка P
2 = (0,2 – 0,25) P
н.
Естественная характеристика двигателя последовательного возбуждения n
= f
(M
) в соответствии с соотношением (3) показана на рисунке 3 (кривая 1
).
Поскольку у двигателей параллельного возбуждения M
∼ I
, а у двигателей последовательного возбуждения приблизительно M
∼ I
² и при пуске допускается I
= (1,5 – 2,0) I
н, то двигатели последовательного возбуждения развивают значительно больший пусковой момент по сравнению с двигателями параллельного возбуждения. Кроме того, у двигателей параллельного возбуждения n
≈ const, а у двигателей последовательного возбуждения, согласно выражениям (2) и (3), приблизительно (при R
а = 0)
n
∼ U
/ I
∼ U
/ √M
.
Поэтому у двигателей параллельного возбуждения
P
2 = Ω × M
= 2π × n
× M
∼ M
,
а у двигателей последовательного возбуждения
P
2 = 2π × n
× M
∼ √M
.
Таким образом, у двигателей последовательного возбуждения при изменении момента нагрузки M
ст = M
в широких пределах мощность изменяется в меньших пределах, чем у двигателей параллельного возбуждения.
Поэтому для двигателей последовательного возбуждения менее опасны перегрузки по моменту. В связи с этим двигатели последовательного возбуждения имеют существенные преимущества в случае тяжелых условий пуска и изменения момента нагрузки в широких пределах. Они широко применяются для электрической тяги (трамваи, метро, троллейбусы, электровозы и тепловозы на железных дорогах) и в подъемно-транспортных установках.
| Рисунок 2. Схемы регулирования скорости вращения двигателя последовательного возбуждения посредством шунтирования обмотки возбуждения (а ), шунтирования якоря (б ) и включения сопротивления в цепь якоря (в ) |
Отметим, что при повышении скорости вращения двигатель последовательного возбуждения в режим генератора не переходит. На рисунке 1 это очевидно из того, что характеристика n
На рисунке 1 это очевидно из того, что характеристика n
= f
(I
) не пересекает оси ординат. Физически это объясняется тем, что при переходе в режим генератора, при заданном направлении вращения и заданной полярности напряжения, направление тока должно измениться на обратное, а направление электродвижущей силы (э. д. с.) E
а и полярность полюсов должны сохраняться неизменными, однако последнее при изменении направления тока в обмотке возбуждения невозможно. Поэтому для перевода двигателя последовательного возбуждения в режим генератора необходимо переключить концы обмотки возбуждения.
Регулирование скорости посредством ослабления поля
Регулирование n
посредством ослабления поля производится либо путем шунтирования обмотки возбуждения некоторым сопротивлением R
ш.в (рисунок 2, а
), либо уменьшением числа включенных в работу витков обмотки возбуждения. В последнем случае должны быть предусмотрены соответствующие выводы из обмотки возбуждения.
Так как сопротивление обмотки возбуждения R
в и падение напряжения на нем малы, то R
ш.в также должно быть мало. Потери в сопротивлении R
ш.в поэтому малы, а суммарные потери на возбуждение при шунтировании даже уменьшаются. Вследствие этого коэффициент полезного действия (к. п. д.) двигателя остается высоким, и такой способ регулирования широко применяется на практике.
При шунтировании обмотки возбуждения ток возбуждения со значения I
уменьшается до
и скорость n
соответственно увеличивается. Выражения для скоростной и механических характеристик при этом получим, если в равенствах (2) и (3) заменим k
Ф на k
Ф k
о.в, где
представляет собой коэффициент ослабления возбуждения. При регулировании скорости изменение числа витков обмотки возбуждения
k
о.в = w
в.раб / w
в.полн.
На рисунке 3 показаны (кривые 1
, 2
, 3
) характеристики n
= f
(M
) для этого случая регулирования скорости при нескольких значениях k
о. в (значению k
в (значению k
о.в = 1 соответствует естественная характеристика 1
, k
о.в = 0,6 – кривая 2
, k
о.в = 0,3 – кривая 3
). Характеристики даны в относительных единицах и соответствуют случаю, когда k
Ф = const и R
а* = 0,1.
| Рисунок 3. Механические характеристики двигателя последовательного возбуждения при разных способах регулирования скорости вращения |
Регулирование скорости путем шунтирования якоря
При шунтировании якоря (рисунок 2, б
) ток и поток возбуждения возрастают, а скорость уменьшается. Так как падение напряжения R
в × I
мало и поэтому можно принять R
в ≈ 0, то сопротивление R
ш.а практически находится под полным напряжением сети, его значение должно быть значительным, потери в нем будут велики и к. п. д. сильно уменьшится.
Кроме того, шунтирование якоря эффективно тогда, когда магнитная цепь не насыщена. В связи с этим шунтирование якоря на практике используется редко.
В связи с этим шунтирование якоря на практике используется редко.
На рисунке 3 кривая 4
n
= f
(M
) при
I
ш.а ≈ U
/ R
ш.а = 0,5 I
н.
Регулирование скорости включением сопротивления в цепь якоря
Регулирование скорости включением сопротивления в цепь якоря (рисунок 2, в
). Этот способ позволяет регулировать n
вниз от номинального значения. Так как одновременно при этом значительно уменьшается к. п. д., то такой способ регулирования находит ограниченное применение.
Выражения для скоростной и механической характеристик в этом случае получим, если в равенствах (2) и (3) заменим R
а на R
а + R
ра. Характеристика n
= f
(M) для такого способа регулирования скорости при R
ра* = 0,5 изображена на рисунке 3 в виде кривой 5
.
| Рисунок 4. Параллельное и последовательное включение двигателей последовательного возбуждения для изменения скорости вращения |
Регулирование скорости изменением напряжения
Этим способом можно регулировать n
вниз от номинального значения с сохранение высокого к. п. д. Рассматриваемый способ регулирования широко применяется в транспортных установках, где на каждой ведущей оси устанавливается отдельный двигатель и регулирование осуществляется путем переключения двигателей с параллельного включения в сеть на последовательное (рисунок 4). На рисунке 3 кривая 6
п. д. Рассматриваемый способ регулирования широко применяется в транспортных установках, где на каждой ведущей оси устанавливается отдельный двигатель и регулирование осуществляется путем переключения двигателей с параллельного включения в сеть на последовательное (рисунок 4). На рисунке 3 кривая 6
представляет собой характеристику n
= f
(M
) для этого случая при U
= 0,5U
н.
 Характеристики двигателя смешанного возбуждения.
Характеристики двигателя смешанного возбуждения.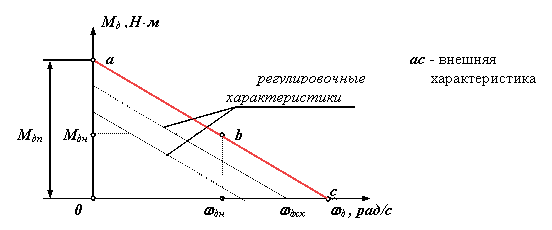
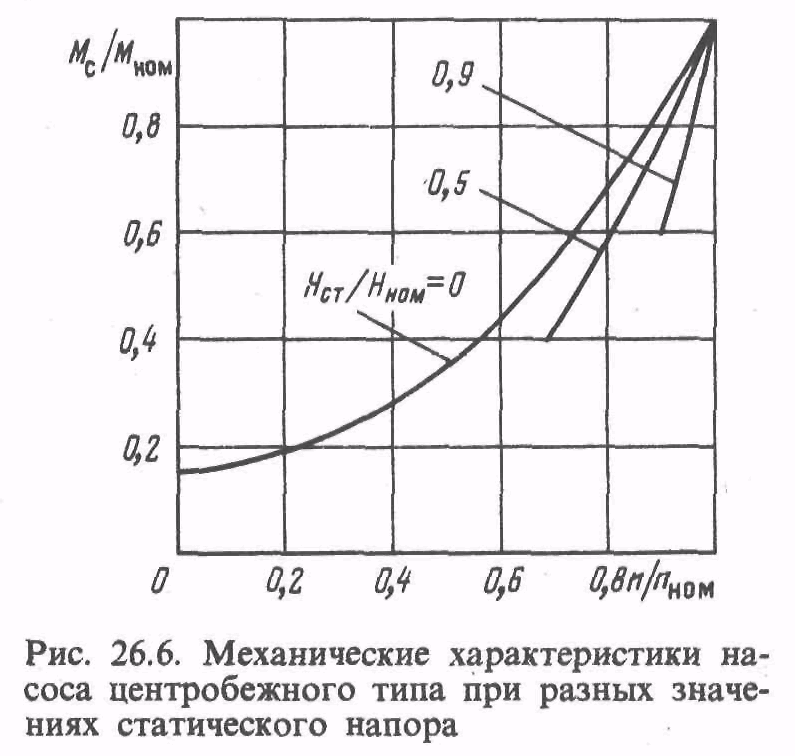

Принципиальная схема электродвигателя
смешанного возбуждения приведена на
рис. 1. В этом двигателе имеются две
обмотки возбуждения – параллельная
(шунтовая, ШО), подключенная параллельно
цепи якоря, и последовательная
(сериесная,СО), подключенная последовательно
цепи якоря. Эти обмотки по магнитному
потоку могут быть включены согласно
или встречно.
Рис.
1 — Схема электродвигателя смешанного
возбуждения.
При согласном включении обмоток
возбуждения их МДС складываются и
результирующий поток Ф примерно равен
сумме потоков, создаваемых обеими
обмотками. При встречном включении
результирующий поток равен разности
потоков параллельной и последовательной
обмоток. В соответствии с этим, свойства
и характеристики электродвигателя
смешанного возбуждения зависят от
способа включения обмоток и от соотношения
их МДС.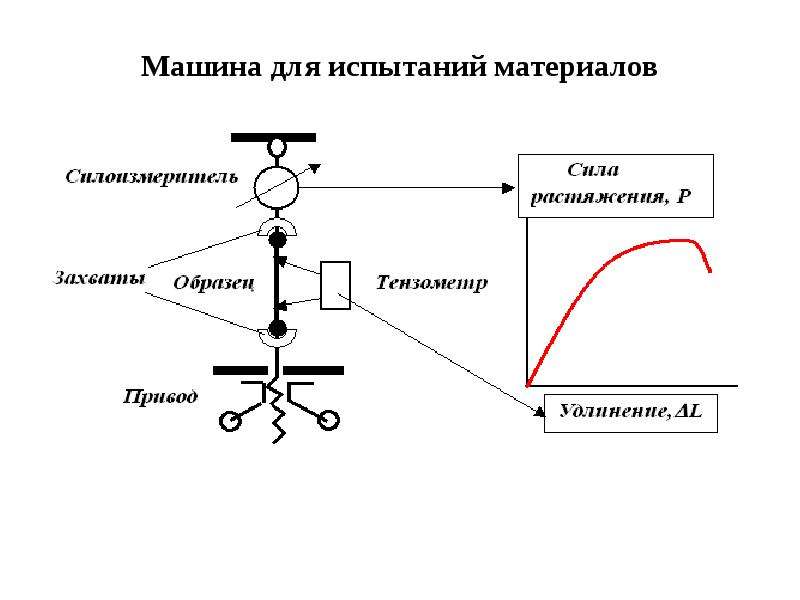
Скоростная характеристика
n=f (Ia) при U=Uн и Iв=const (здесь Iв — ток в
параллельной обмотке).
С увеличением нагрузки результирующий
магнитный поток при согласном включении
обмоток возрастает, но в меньшей степени,
чем у двигателя последовательного
возбуждения, поэтому скоростная
характеристика в этом случае оказывается
более мягкой, чем у двигателя параллельного
возбуждения, но более жесткой, чем у
двигателя последовательного возбуждения.
Соотношение между МДС обмоток может
меняться в широких пределах. Двигатели
со слабой последовательной обмоткой
имеют слабо падающую скоростную
характеристику (кривая 1, рис. 2).
Рис.
2 — Скоростные характеристики двигателя
смешанного возбуждения.
Чем больше доля последовательной
обмотки в создании МДС, тем ближе
скоростная характеристика приближается
к характеристике двигателя последовательного
возбуждения. На рис.2 линия 3 изображает
одну из промежуточных характеристик
двигателя смешанного возбуждения и для
сравнения дана характеристика двигателя
последовательного возбуждения (кривая
2).
При встречном включении последовательной
обмотки с увеличением нагрузки
результирующий магнитный поток
уменьшается, что приводит к увеличению
скорости двигателя (кривая 4). При такой
скоростной характеристике работа
двигателя может оказаться неустойчивой,
т.к. поток последовательной обмотки
может значительно уменьшить результирующий
магнитный поток. Поэтому двигатели со
встречным включением обмоток не
применяются.
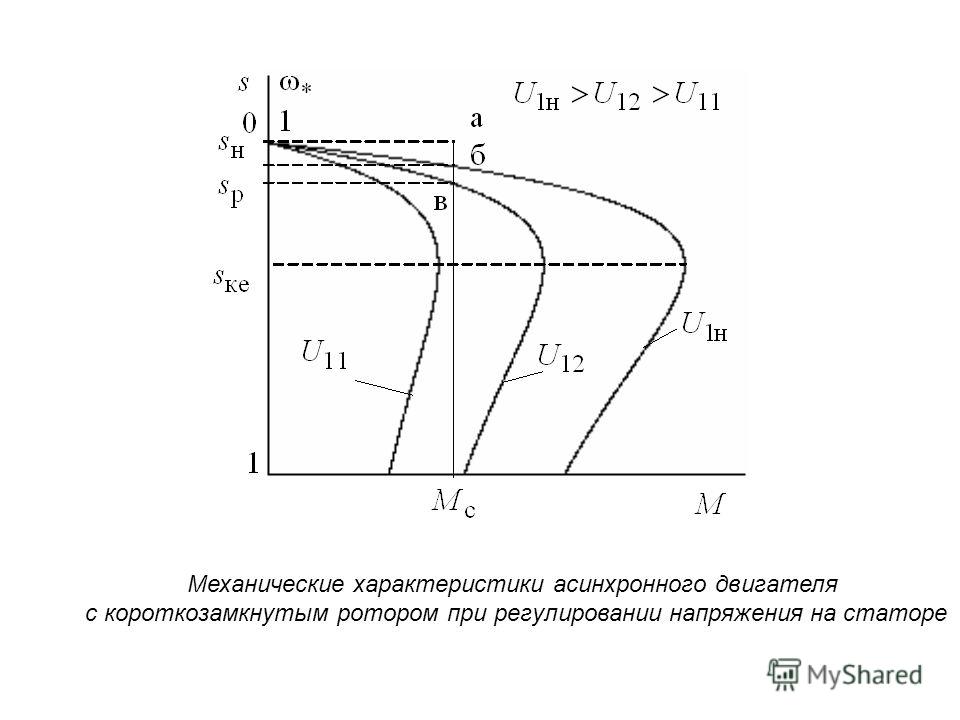
Механическая
характеристика
n=f (М) при U=Uн
и Iв=const. двигателя смешанного возбуждения
показана на рис.3 (линия 2).
Рис.
3 — Механические характеристики двигателя
смешанного возбуждения.
Она
располагается между механическими
характеристиками двигателей параллельного
(кривая 1) и последовательного (кривая
3) возбуждения. Подбирая соответствующим
образом МДС обеих обмоток, можно получить
электродвигатель с характеристикой,
близкой к характеристике двигателя
параллельного или последовательного
возбуждения.
Область
применения двигателей последовательного,
параллельного и смешанного возбуждения.
Поэтому
для двигателей последовательного
возбуждения менее опасны перегрузки
по моменту. В связи с этим двигатели
последовательного возбуждения имеют
существенные преимущества в случае
тяжелых условий пуска и изменения
момента нагрузки в широких пределах.
Они широко применяются для электрической
тяги (трамваи, метро, троллейбусы,
электровозы и тепловозы на железных
дорогах) и в подъемно-транспортных
установках.
Естественные
скоростная и механическая характеристики,
область применения в двигателях
параллельного возбуждения.
Естественные
скоростная и механическая характеристики,
область применения в двигателях
смешанного возбуждения.
Двигатель смешанного возбуждения
Двигатель смешанного возбуждения имеет две обмотки возбуждения: параллельную и последовательную (рис. 29.12, а). Частота вращения этого двигателя
, (29.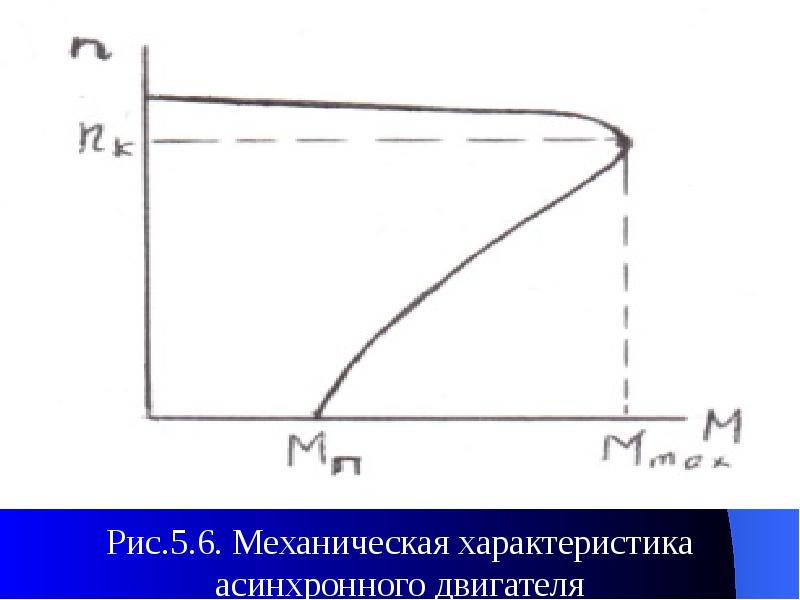 17)
17)
где и — потоки параллельной и последовательной обмоток возбуждения.
Знак плюс соответствует согласованному включению обмоток возбуждения (МДС обмоток складываются). В этом случае с увеличением нагрузки общий магнитный поток возрастает (за счет потока последовательной обмотки ), что ведет к уменьшению частоты вращения двигателя. При встречном включении обмоток поток при увеличении нагрузки размагничивает машину (знак минус), что, наоборот, повышает частоту вращения. Работа двигателя при этом становится неустойчивой, так как с увеличением нагрузки частота вращения неограниченно растет. Однако при небольшом числе витков последовательной обмотки с увеличением нагрузки частота вращения не возрастает и во всем диапазоне нагрузок остается практически неизменной.
На рис. 29.12, б показаны рабочие характеристики двигателя смешанного возбуждения при согласованном включении обмоток возбуждения, а на рис. 29.12, в — механические характеристики. В отличие от механических характеристик двигателя последовательного возбуждения последние имеют более пологий вид.
Рис. 29.12. Схема двигателя смешанного возбуждения (а), его рабочие (б) и механические (в) характеристики
Следует отметить, что по своей форме характеристики двигателя смешанного возбуждения занимают промежуточное положение между соответствующими характеристиками двигателей параллельного и последовательного возбуждения в зависимости от того, в какой из обмоток возбуждения (параллельной или последовательной) преобладает МДС.
Двигатель смешанного возбуждения имеет преимущества по сравнению с двигателем последовательного возбуждения. Этот двигатель может работать вхолостую, так как поток параллельной обмотки ограничивает частоту вращения двигателя в режиме х.х. и устраняет опасность «разноса». Регулировать частоту вращения этого двигателя можно реостатом в цепи параллельной обмотки возбуждения. Однако наличие двух обмоток возбуждения делает двигатель смешанного возбуждения более дорогостоящим по сравнению с двигателями рассмотренных выше типов, что несколько ограничивает его применение.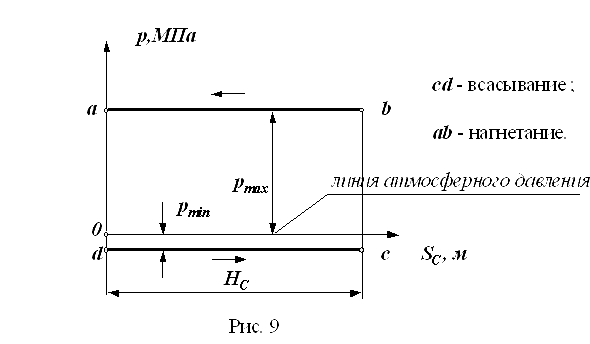 Двигатели смешанноговозбуждения применяют обычно там, где требуются значительные пусковые моменты, быстрое ускорение при разгоне, устойчивая работа и допустимо лишь небольшое снижение частоты вращения при увеличении нагрузки на вал (прокатные станы, грузовыеподъемники, насосы, компрессоры).
Двигатели смешанноговозбуждения применяют обычно там, где требуются значительные пусковые моменты, быстрое ускорение при разгоне, устойчивая работа и допустимо лишь небольшое снижение частоты вращения при увеличении нагрузки на вал (прокатные станы, грузовыеподъемники, насосы, компрессоры).
49. Пусковые и перегрузочные свойства двигателей постоянного тока.
Пуск двигателя постоянного тока прямым включением его на напряжение сети допустим только для двигателей небольшой мощности. При этом пик тока в начале пуска может быть порядка 4 — 6-кратного номинального. Прямой пуск двигателей постоянного тока значительной мощности совершенно недопустим, потому что начальный пик тока здесь будет равен 15 — 50-кратному номинальному. Поэтому пуск двигателей средних и больших мощностей производят при помощи пускового реостата, который ограничивает ток при пуске до допустимых по коммутации и механической прочности значений.
Пусковой реостат выполняется из провода или ленты с высоким удельным сопротивлением, разделенных на секции.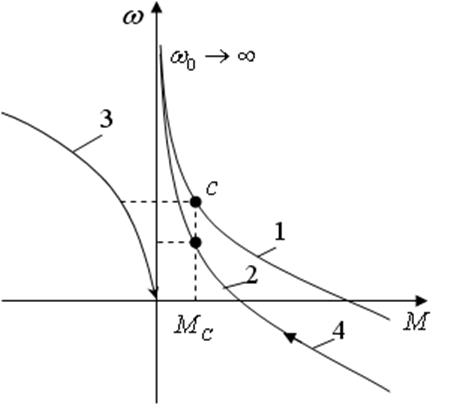 Провода присоединяются к медным кнопочным или плоским контактам в местах перехода от одной секции к другой. По контактам перемещается медная щетка поворотного рычага реостата. Реостаты могут иметь и другое выполнение. Ток возбуждения при пуске двигателя с параллельным возбуждением устанавливается соответствующим нормальной работе, цепь возбуждения включается прямо на напряжение сети, чтобы не было уменьшения напряжения, обусловленного падением напряжения в реостате (см. рис. 1).
Провода присоединяются к медным кнопочным или плоским контактам в местах перехода от одной секции к другой. По контактам перемещается медная щетка поворотного рычага реостата. Реостаты могут иметь и другое выполнение. Ток возбуждения при пуске двигателя с параллельным возбуждением устанавливается соответствующим нормальной работе, цепь возбуждения включается прямо на напряжение сети, чтобы не было уменьшения напряжения, обусловленного падением напряжения в реостате (см. рис. 1).
Необходимость иметь нормальный ток возбуждения связана с тем, что при пуске двигатель должен развивать возможно больший допустимый момент Мэм, необходимый для обеспечения быстрого разгона. Пуск двигателя постоянного тока производится при последовательном уменьшении сопротивления реостата, обычно — путем перевода рычага реостата с одного неподвижного контакта реостата на другой и выключения секций; уменьшение сопротивления может производиться и путем замыкания накоротко секций контакторами, срабатывающими по заданной программе.
При пуске вручную или автоматически ток изменяется от максимального значения, равного 1,8 -2,5-кратному номинальному в начале работы при данном сопротивлении реостата, до минимального значения, равного 1,1 — 1,5-кратному номинальному в конце работы и перед переключением на другое положение пускового реостата. Ток якоря после включения двигателя при сопротивлении реостата rп составляет
где Uс — напряжение сети.
После включения начинается разгон двигателя, при этом возникает противо-ЭДС Е и уменьшается ток якоря. Если учесть, что механические характеристики n = f1(Mн) и n = f2 (Iя) практически линейны, то при разгоне увеличение скорости вращения будет происходить по линейному закону в зависимости от тока якоря (рис. 1).
Рис. 1. Диаграмма пуска двигателя постоянного тока
Пусковая диаграмма (рис. 1) для различных сопротивлений в цепи якоря представляет собой отрезки линейных механических характеристик. При уменьшении тока якоря IЯ до значения Imin выключается секция реостата с сопротивлением r1 и ток возрастает до значения
где E1 — ЭДС в точке А характеристики; r1-сопротивление выключаемой секции.
Затем снова происходит разгон двигателя до точки В, и так далее вплоть до выхода на естественную характеристику, когда двигатель будет включен прямо на напряжение Uc. Пусковые реостаты рассчитаны по нагреву на 4 -6 пусков подряд, поэтому нужно следить, чтобы в конце пуска пусковой реостат был полностью выведен.
При остановке двигатель отключается от источника энергии, а пусковой реостат полностью включается — двигатель готов к следующему пуску. Для устранения возможности появления больших ЭДС самоиндукции при разрыве цепи возбуждения и при ее отключении цепь может замыкаться на разрядное сопротивление.
В регулируемых приводах пуск двигателей постоянного тока производится путем постепенного повышения напряжения источника питания так, чтобы ток при пуске поддерживался в требуемых пределах или сохранялся в течение большей части времени пуска примерно неизменным. Последнее можно осуществить путем автоматического управления процессом изменения напряжения источника питания в системах с обратными связями.
Пуск и Остановка МПТ
Прямым включением его на напряжение сети допустим только для двигателей небольшой мощности. При этом пик тока в начале пуска может быть порядка 4 — 6-кратного номинального. Прямой пуск двигателей постоянного тока значительной мощности совершенно недопустим, потому что начальный пик тока здесь будет равен 15 — 50-кратному номинальному. Поэтому пуск двигателей средних и больших мощностей производят при помощи пускового реостата, который ограничивает ток при пуске до допустимых по коммутации и механической прочности значений.
Пуск двигателя постоянного тока
производится при последовательном уменьшении сопротивления реостата, обычно — путем перевода рычага реостата с одного неподвижного контакта реостата на другой и выключения секций; уменьшение сопротивления может производиться и путем замыкания накоротко секций контакторами, срабатывающими по заданной программе.
При пуске вручную или автоматически ток изменяется от максимального значения, равного 1,8 -2,5-кратному номинальному в начале работы при данном сопротивлении реостата, до минимального значения, равного 1,1 — 1,5-кратному номинальному в конце работы и перед переключением на другое положение пускового реостата.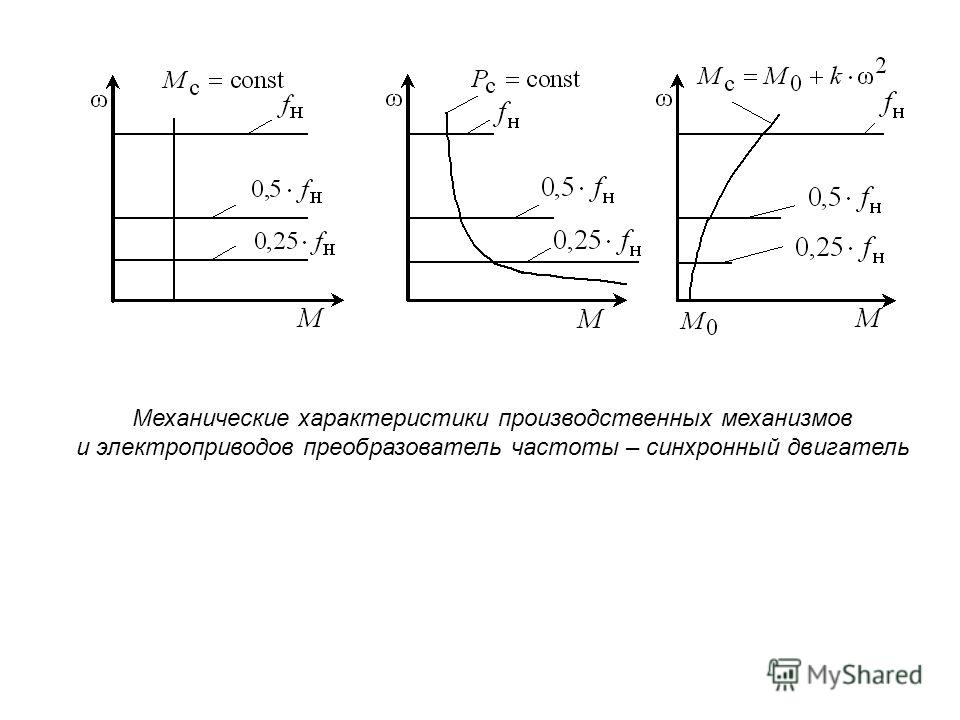
Торможение
необходимо для того, чтобы уменьшить время выбега двигателей, которое при отсутствии торможения может быть недопустимо велико, а также для фиксации приводимых механизмов в определенном положении. Механическое торможение
двигателей постоянного тока обычно производится при наложении тормозных колодок на тормозной шкив. Недостатком механических тормозов является то, что тормозной момент и время торможения зависят от случайных факторов: попадания масла или влаги на тормозной шкив и других. Поэтому такое торможение применяется, когда не ограничены время и тормозной путь.
В ряде случаев после предварительного электрического торможения при малой скорости можно достаточно точно произвести остановку механизма (например, подъемника) в заданном положении и зафиксировать его положение в определенном месте. Такое торможение применяется и в аварийных случаях.
Электрическое торможение
обеспечивает достаточно точное получение требуемого тормозящего момента, но не может обеспечить фиксацию механизма в заданном месте. Поэтому электрическое торможение при необходимости дополняется механическим, которое входит в действие после окончания электрического.
Поэтому электрическое торможение при необходимости дополняется механическим, которое входит в действие после окончания электрического.
Электрическое торможение происходит, когда ток протекает согласно с ЭДС двигателя. Возможны три способа торможения.
Торможение двигателей постоянного тока с возвратом энергии в сеть.
При этом ЭДС Е должна быть больше напряжения источника питания UС и ток будет протекать в направлении ЭДС, являясь током генераторного режима. Запасенная кинетическая энергия будет преобразовываться в электрическую и частично возвращаться в сеть. Схема включения показана на рис. 2, а.
Рис. 2. Схемы электрического торможения двигателей постоянного тока: я — с возвратом энергии в сеть; б — при противовключении; в — динамическое торможение
Торможение двигателя постоянного тока может быть выполнено, когда уменьшается напряжение источника питания так, что Uc
Торможение при противовключении
выполняется путем переключения вращающегося двигателя на обратное направление вращения. При этом ЭДС Е и напряжение Uc в якоре складываются, и для ограничения тока I следует включать резистор с начальным сопротивлением
При этом ЭДС Е и напряжение Uc в якоре складываются, и для ограничения тока I следует включать резистор с начальным сопротивлением
где Imах — наибольший допустимый ток.
Торможение связано с большими потерями энергии.
Динамическое торможение двигателей постоянного тока
выполняется при включении на зажимы вращающегося возбужденного двигателя резистора rт (рис. 2, в). Запасенная кинетическая энергия преобразуется в электрическую и рассеивается в цепи якоря как тепловая. Это наиболее распространенный способ торможения.
Схемы включения двигателя постоянного тока параллельного (независимого) возбуждения: а — схема включения двигателя, б — схема включения при динамическом торможении, в — схема для противовключения.
Переходные процессы в МПТ
В общем случае в электрической цепи переходные процессы могут возникать, если в цепи имеются индуктивные и емкостные элементы, обладающие способностью накапливать или отдавать энергию магнитного или электрического поля.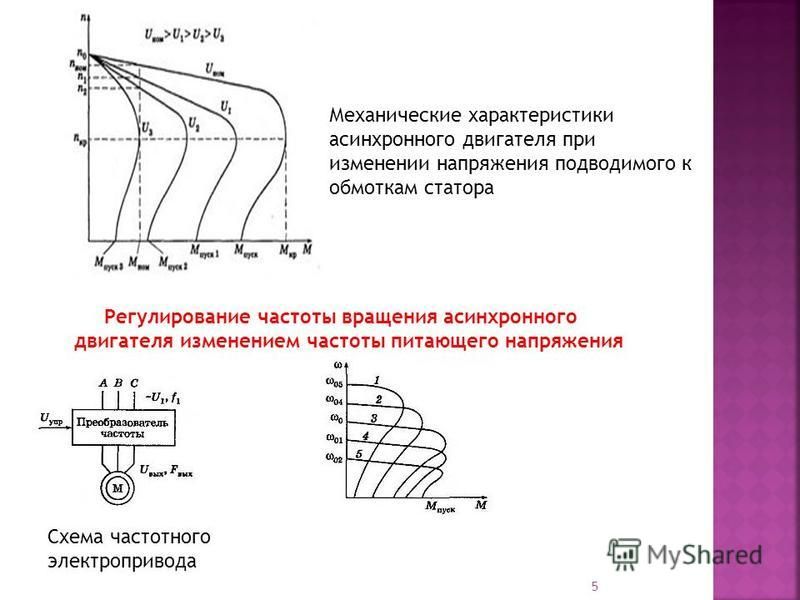 В момент коммутации, когда начинается переходный процесс, происходит перераспределение энергии между индуктивными, емкостными элементами цепи и внешними источниками энергии, подключенными к цепи. При этом часть энергия безвозвратно преобразуется в другие виды энергий (например, в тепловую на активном сопротивлении).
В момент коммутации, когда начинается переходный процесс, происходит перераспределение энергии между индуктивными, емкостными элементами цепи и внешними источниками энергии, подключенными к цепи. При этом часть энергия безвозвратно преобразуется в другие виды энергий (например, в тепловую на активном сопротивлении).
После окончания переходного процесса устанавливается новый установившийся режим, который определяется только внешними источниками энергии. При отключении внешних источников энергии переходный процесс может возникать за счет энергии электромагнитного поля, накопленной до начала переходного режима в индуктивных и емкостных элементах цепи.
Изменения энергии магнитного и электрического полей не могут происходить мгновенно, и, следовательно, не могут мгновенно протекать процессы в момент коммутации. В самом деле, скачкообразное (мгновенное) изменение энергии в индуктивном и емкостном элементе приводит к необходимости иметь бесконечно большие мощности p = dW/dt, что практически невозможно, ибо в реальных электрических цепях бесконечно большой мощности не существует.
Таким образом, переходные процессы не могут протекать мгновенно, так как невозможно в принципе мгновенно изменять энергию, накопленную в электромагнитном поле цепи. Теоретически переходные процессы заканчиваются за время t→∞. Практически же переходные процессы являются быстропротекающими, и их длительность обычно составляет доли секунды. Так как энергия магнитного W М и электрического полей W Э описывается выражениями
то ток в индуктивности и напряжение на емкости не могут изменяться мгновенно. На этом основаны законы коммутации.
Первый закон коммутации состоит в том, что ток в ветви с индуктивным элементом в начальный момент времени после коммутации имеет то же значение, какое он имел непосредственно перед коммутацией, а затем с этого значения он начинает плавно изменяться. Сказанное обычно записывают в виде i L (0 -) = i L (0 +), считая, что коммутация происходит мгновенно в момент t = 0.
Второй закон коммутации состоит в том, что напряжение на емкостном элементе в начальный момент после коммутации имеет то же значение, какое оно имело непосредственно перед коммутацией, а затем с этого значения оно начинает плавно изменяться: U C (0 -) = U C (0 +).
Следовательно, наличие ветви, содержащей индуктивность, в цепи, включаемой под напряжение, равносильно разрыву цепи в этом месте в момент коммутации, так как i L (0 -) = i L (0 +). Наличие в цепи, включаемой под напряжение, ветви, содержащей разряженный конденсатор, равносильно короткому замыканию в этом месте в момент коммутации, так как U C (0 -) = U C (0 +).
Однако в электрической цепи возможны скачки напряжений на индуктивностях и токов на емкостях.
В электрических цепях с резистивными элементами энергия электромагнитного поля не запасается, вследствие чего в них переходные процессы не возникают, т.е. в таких цепях стационарные режимы устанавливаются мгновенно, скачком.
В действительности любой элемент цепи обладает каким-то сопротивлением r, индуктивностью L и емкостью С, т.е. в реальных электротехнических устройствах существуют тепловые потери, обусловленные прохождением тока и наличием сопротивления r, а также магнитные и электрические поля.
Переходные процессы в реальных электротехнических устройствах можно ускорять или замедлять путем подбора соответствующих параметров элементов цепей, а также за счет применения специальных устройств
52. Магнитогидродинамические машины постоянного тока.
Магнитогидродинамические машины постоянного тока.
Магнитная гидродинамика (МГД) является областью науки, изучающей законы физических явлений в электропроводящих жидких и газовых средах при их движении в магнитном поле. На этих явлениях основан принцип действия различных магнитогидродинамических (МГД) машин постоянного и переменного тока. Некоторые МГД машины находят применение в различных областях техники, а другие имеют значительные перспективы применения в будущем. Ниже рассматриваются принципы устройства и действия МГД машин постоянного тока.
Электромагнитные насосы для жидких металлов
Рисунок 1. Принцип устройства электромагнитного насоса постоянного тока
В насосе постоянного тока (рисунок 1) канал 2 с жидким металлом помещается между полюсами электромагнита 1 и с помощью электродов 3, приваренных к стенкам канала, через жидкий металл пропускается постоянный ток от внешнего источника. Так как ток к жидкому металлу в данном случае подводится кондуктивным путем, то такие насосы называются также кондукционными.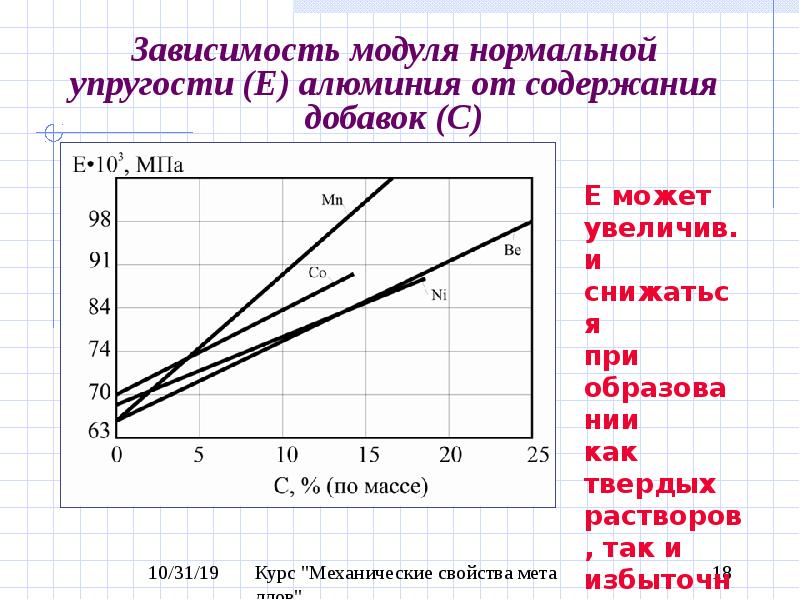
При взаимодействии поля полюсов с током в жидком металле на частицы металла действуют электромагнитные силы, развивается напор и жидкий металл приходит в движение. Токи в жидком металле искажают поле полюсов («реакция якоря»), что приводит к снижению эффективности насоса. Поэтому в мощных насосах между полюсными наконечниками и каналом помещаются шины («компенсационная обмотка»), которые включаются последовательно в цепь тока канала во встречном направлении. Обмотка возбуждения электромагнита (на рисунке 1 не показана) обычно включается последовательно в цепь тока канала и имеет при этом только 1 – 2 витка.
Применение кондукционных насосов возможно для малоагрессивных жидких металлов и при таких температурах, когда стенки канала можно изготовить из жаропрочных металлов (немагнитные нержавеющие стали и так далее). В противном случае более подходящими являются индукционные насосы переменного тока.
Насосы описанного типа стали находить применение около 1950 года в исследовактельских целях и в таких установках с ядерными реакторами, в которых для отвода тепла из реакторов используются жидкометаллические носители: натрий, калий, их сплавы, висмут и другие. Температура жидкого металла в насосах при этом составляет 200 – 600 °С, а в некоторых случаях до 800 °С. Один из выполненных насосов для натрия имеет следующие расчетные данные: температура 800 °С, напор 3,9 кгс/см², расход 3670 м³/ч, полезная гидравлическая мощность 390 кВт, потребляемый ток 250 кА, напряжение 2,5 В, потребляемая мощность 625 кВт, коэффициент полезного действия 62,5 %. Другие характерные данные этого насоса: сечение канала 53 × 15,2 см, скорость течения в канале 12,4 м/с, активная длина канала 76 см.
Температура жидкого металла в насосах при этом составляет 200 – 600 °С, а в некоторых случаях до 800 °С. Один из выполненных насосов для натрия имеет следующие расчетные данные: температура 800 °С, напор 3,9 кгс/см², расход 3670 м³/ч, полезная гидравлическая мощность 390 кВт, потребляемый ток 250 кА, напряжение 2,5 В, потребляемая мощность 625 кВт, коэффициент полезного действия 62,5 %. Другие характерные данные этого насоса: сечение канала 53 × 15,2 см, скорость течения в канале 12,4 м/с, активная длина канала 76 см.
Преимущество электромагнитных насосов состоит в том, что они не имеют движущихся частей и тракт жидкого металла может быть герметизирован.
Насосы постоянного тока требуют для питания источников с большой силой тока и малым напряжением. Для питания мощных насосов выпрямительные установки малопригодны, так как они получаются громоздкими и с малым коэффициентом полезного действия. Более подходящими в этом случае являются униполярные генераторы, смотрите статью «Специальные типы генераторов и преобразователей постоянного тока».
Плазменные ракетные двигатели
Рассмотренные электромагнитные насосы являются своеобразными двигателями постоянного тока. Подобные устройства в принципе пригодны также для разгона, ускорения или перемещения плазмы, то есть высокотемпературного (2000 – 4000 °С и больше) ионизированного и поэтому электропроводящего газа. В связи с этим производится разработка реактивных плазменных двигателей для космических ракет, причем ставится задача получения скоростей истечения плазмы до 100 км/с. Такие двигатели не будут обладать большой силой тяги и поэтому будут пригодны для работы вдали от планет, где поля тяготения слабы; однако они имеют то преимущество, что массовый расход вещества (плазмы) мал. Необходимую для их питания электрическую энергию предполагается получать с помощью ядерных реакторов. Для плазменных двигателей постоянного тока трудную проблему составляет создание надежных электродов для подвода тока к плазме.
Магнитогидродинамические генераторы
МГД машины, как и всякие электрические машины, обратимы. В частности, устройство, изображенное на рисунке 1, может работать также в режиме генератора, если через него прогонять проводящую жидкость или газ. При этом целесообразно иметь независимое возбуждение. Генерируемый ток снимается с электродов.
В частности, устройство, изображенное на рисунке 1, может работать также в режиме генератора, если через него прогонять проводящую жидкость или газ. При этом целесообразно иметь независимое возбуждение. Генерируемый ток снимается с электродов.
На таком принципе строятся электромагнитные расходомеры воды, растворов щелочей и кислот, жидких металлов и тому подобного. Электродвижущая сила на электродах при этом пропорциональна скорости движения или расходу жидкости.
МГД генераторы представляют интерес с точки зрения создания мощных электрических генераторов для непосредственного превращения тепловой энергии в электрическую. Для этого через устройство вида, изображенного на рисунке 1, необходимо пропускать со скоростью порядка 1000 м/с проводящую плазму. Такую плазму можно получить при сжигании обычного топлива, а также путем нагревания газа в ядерных реакторах. Для увеличения проводимости плазмы в нее можно вводить небольшие присадки легко ионизируемых щелочных металлов.
Электропроводность плазмы при температурах порядка 2000 – 4000 °С относительно мала (удельное сопротивление около 1 Ом × см = 0,01 Ом × м = 104 Ом × мм² / м, то есть примерно в 500 000 раз больше, чем у меди). Тем не менее в мощных генераторах (порядка 1 млн. кВт) возможно получение приемлемых технико-экономических показателей. Разрабатываются также МГД генераторы с жидкометаллическим рабочим телом.
Тем не менее в мощных генераторах (порядка 1 млн. кВт) возможно получение приемлемых технико-экономических показателей. Разрабатываются также МГД генераторы с жидкометаллическим рабочим телом.
При создании плазменных МГД генераторов постоянного тока возникают трудности с выбором материалов для электродов и с изготовлением надежных в работе стенок каналов. В промышленных установках также сложную задачу представляет собой преобразование постоянного тока относительно низкого напряжения (несколько тысяч вольт) и большой силы (сотни тысяч ампер) в переменный ток.
53. Униполярные машины.
Первыйлярный генератор изобрел Майкл Фарадей. Суть эффекта, открытого Фарадеем, заключается в том, что при вращении диска в поперечном магнитном поле, на электроны в диске действует сила Лоренца, которая смещает их к центру или к периферии, в зависимости от направления поля и вращения. Благодаря этому, возникает электродвижущая сила, и через токосъемные щетки, касающиеся оси и периферии диска, можно снимать значительный ток и мощность, хотя напряжение небольшое (обычно, доли Вольта). Позднее, было обнаружено, что относительное вращение диска и магнита не является необходимым условием. Два магнита и токопроводящий диск между ними, вращающиеся вместе, также показывают наличие эффекта униполярной индукции. Магнит, сделанный из электропроводящего материала, при вращении, также может работать, в качестве униполярного генератора: он сам является и диском с которого щетками снимаются электроны, и он же является источником магнитного поля. В связи с этим, принципы униполярной индукции развиваются в рамках концепции движения свободных заряженных частиц относительно магнитного поля, а не относительно магнитов. Магнитное поле, в таком случае, считается неподвижным.
Позднее, было обнаружено, что относительное вращение диска и магнита не является необходимым условием. Два магнита и токопроводящий диск между ними, вращающиеся вместе, также показывают наличие эффекта униполярной индукции. Магнит, сделанный из электропроводящего материала, при вращении, также может работать, в качестве униполярного генератора: он сам является и диском с которого щетками снимаются электроны, и он же является источником магнитного поля. В связи с этим, принципы униполярной индукции развиваются в рамках концепции движения свободных заряженных частиц относительно магнитного поля, а не относительно магнитов. Магнитное поле, в таком случае, считается неподвижным.
Споры о таких машинах шли долго. Понять, что поле есть свойство «пустого» пространства, физики, отрицающие существование эфира, не могли. Это правильно, поскольку «пространство не пустое», в нем есть эфир, и именно он обеспечивает среду существования магнитного поля, относительно которого вращаются и магниты, и диск. Магнитное поле можно понимать, как замкнутый поток эфира. Поэтому, относительное вращение диска и магнита не является обязательным условием.
Магнитное поле можно понимать, как замкнутый поток эфира. Поэтому, относительное вращение диска и магнита не является обязательным условием.
В работах Тесла, как мы уже отмечали, были сделаны усовершенствования схемы (увеличен размер магнитов, а диск сегментирован), что позволяет создавать самовращающиеся униполярные машины Тесла.
В рассматриваемых двигателях обмотка возбуждения выполняется с малым числом витков, но рассчитана на большие токи. Все особенности этих двигателей связаны с тем, что обмотка возбуждения включается (см. рис. 5.2,в)
последовательно с обмоткой якоря, в результате чего ток возбуждения равен току якоря и создаваемый поток Ф пропорционален току якоря:
где а
=/(/ я) — нелинейный коэффициент (рис. 5.12).
Нелинейность а
связана с формой кривой намагничивания двигателя и размагничивающим действием реакции якоря. Эти факторы проявляются при / я > , / ян (/ ян — номинальный ток якоря). При меньших токах а
можно считать величиной постоянной, а при / я > 2/ я н двигатель насыщается и поток мало зависит от тока якоря.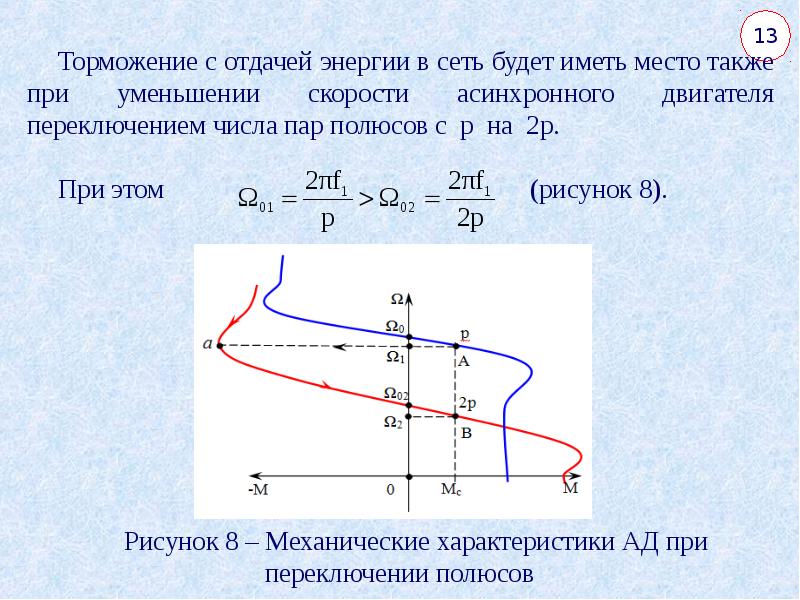
Рис. 5.12.
Основные уравнения двигателя последовательного возбуждения в отличие от уравнений двигателей независимого возбуждения нелинейны, что связано, в первую очередь, с произведением переменных:
При изменении тока в якорной цепи изменяется магнитный поток Ф, наводя в массивных частях магнитопровода машины вихревые токи. Влияние вихревых токов может быть учтено в модели двигателя в виде эквивалентного короткозамкнутого контура, описываемого уравнением
а уравнение для цепи якоря имеет вид:
где w B , w B т — число витков обмотки возбуждения и эквивалентное число витков вихревых токов.
В установившемся режиме
Из (5.22) и (5.26) получим выражения для механической и электромеханической характеристик двигателя постоянного тока последовательного возбуждения:
В первом приближении механическую характеристику двигателя последовательного возбуждения, без учета насыщения магнитной цепи, можно представить в виде гиперболы, не пересекающей ось ординат.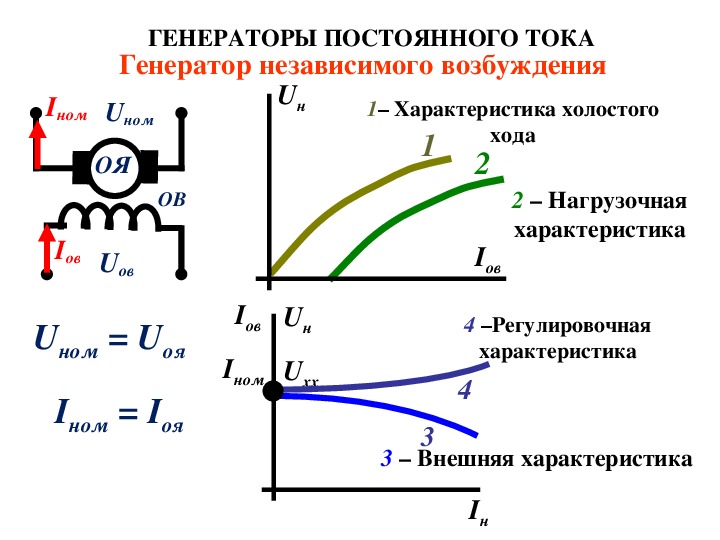 Если положить Л я
Если положить Л я
ц = /? я + /? в = 0, то характеристика не будет пересекать и ось абсцисс. Такую характеристику называют идеальной.
Реальная естественная характеристика двигателя пересекает ось абсцисс и вследствие насыщения магнитопровода при моментах больше М н
спрямляется (рис. 5.13).
Рис. 5.13.
Характерной особенностью характеристик двигателя последовательного возбуждения является отсутствие точки идеального холостого хода. При уменьшении нагрузки скорость возрастает, что может привести к неконтролируемому разгону двигателя. Оставлять такой двигатель без нагрузки нельзя.
Важным достоинством двигателей последовательного возбуждения является большая перегрузочная способность на низких скоростях. При перегрузке по току в 2-2,5 раза двигатель развивает момент 3,0…3,5М н.
Это обстоятельство определило широкое использование двигателей последовательного возбуждения в качестве привода электрических транспортных средств, для которых максимальные моменты необходимы при трогании с места.
Изменение направления вращения двигателей последовательного возбуждения не может быть достигнуто изменением полярности питания цепи якоря. В двигателях последовательного возбуждения при реверсировании нужно изменять направление тока в одной части якорной цепи: либо в обмотке якоря, либо в обмотке возбуждения (рис. 5.14).
Рис. 5.14.
Искусственные механические характеристики для регулирования скорости и момента могут быть получены тремя способами:
- введением добавочного сопротивления в цепь якоря двигателя;
- изменением питающего двигатель напряжения;
- шунтированием обмотки якоря добавочным сопротивлением. При введении добавочного сопротивления в цепь якоря жесткость механических характеристик уменьшается и уменьшается пусковой момент. Этот способ используют при пуске двигателей последовательного возбуждения, получающих питание от источников с нерегулируемым напряжением (от контактных проводов и др.) В этом случае (рис. 5.15) необходимое значение пускового момента достигается последовательным закорачиванием секций пускового резистора посредством контакторов К1-КЗ.

Рис. 5.15.
Реостатные механические характеристики двигателя последовательного возбуждения: /? 1до —R iao
-сопротивления ступеней добавочного резистора в цепи якоря
Наиболее экономичным способом регулирования скорости двигателя последовательного возбуждения является изменение питающего напряжения. Механические характеристики двигателя смещаются вниз параллельно естественной характеристике (рис. 5.16). По форме эти характеристики подобны реостатным механическим характеристикам (см. рис. 5.15), однако, существует принципиальная разница — при регулировании изменением напряжения отсутствуют потери в добавочных резисторах и регулирование производится плавно.
Рис. 5.1
Двигатели последовательного возбуждения при использовании в качестве привода мобильных агрегатов во многих случаях получают питание от контактной сети или других источников питания с постоянным значением напряжения, подаваемого на двигатель, в этом случае регулирование производится посредством широтно-импульсного регулятора напряжения (см.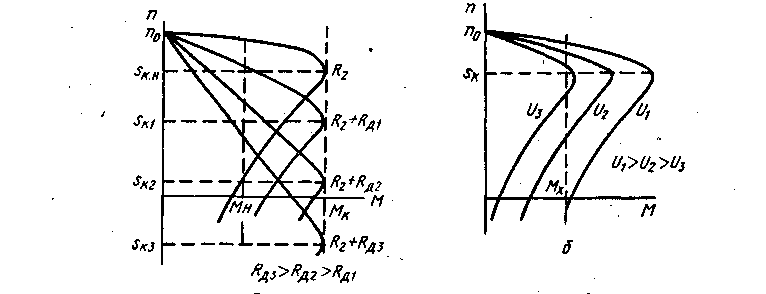 § 3.4). Такая схема показана на рис. 5.17.
§ 3.4). Такая схема показана на рис. 5.17.
Рис. 5.17.
Независимое регулирование потока возбуждения двигателя последовательного возбуждения возможно, если зашунтировать обмотку якоря сопротивлением (рис. 5.18,а). В этом случае ток возбуждения в = я + / ш, т.е. содержит постоянную составляющую, не зависящую от нагрузки двигателя. При этом двигатель приобретает свойства двигателя смешанного возбуждения. Механические характеристики (рис. 5.18,6) приобретают большую жесткость и пересекают ось ординат, что позволяет получить устойчивую пониженную скорость при малых нагрузках на валу двигателя. Существенный недостаток схемы — это большие потери энергии в шунтирующем сопротивлении.
Рис. 5.18.
Для двигателей постоянного тока с последовательным возбуждением характерны два тормозных режима: динамического торможения
и противовключения.
Режим динамического торможения возможен в двух случаях. В первом — якорная обмотка замыкается на сопротивление, а обмотка возбуждения питается от сети или другого источника через добавочное сопротивление.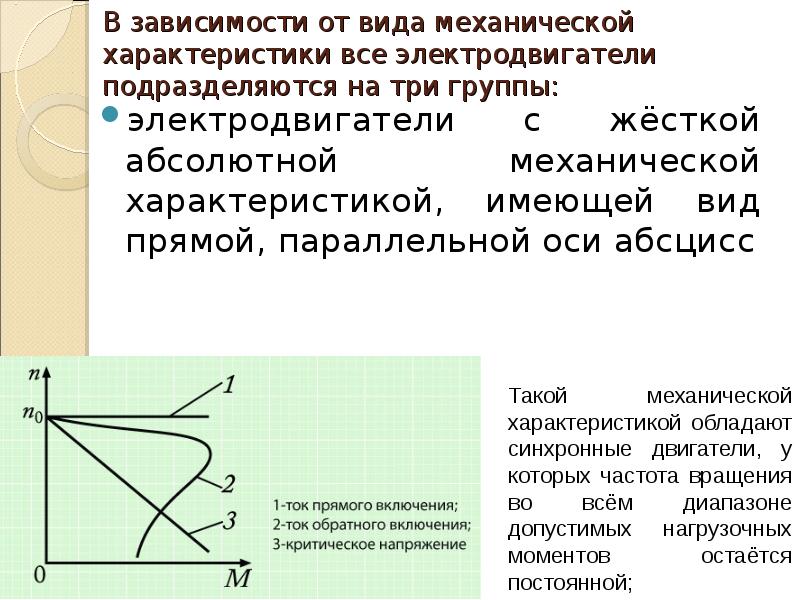 Характеристики двигателя в этом случае подобны характеристикам двигателя независимого возбуждения в режиме динамического торможения, (см. рис. 5.9).
Характеристики двигателя в этом случае подобны характеристикам двигателя независимого возбуждения в режиме динамического торможения, (см. рис. 5.9).
Во втором случае, схема которого показана на рис. 5.19, двигатель при отключении контактов КМ и замыкании контактов КВ работает как генератор с самовозбуждением. При переходе из двигательного режима в тормозной необходимо сохранить направление тока в обмотке возбуждения во избежание размагничивания машины, так как при этом машина переходит в режим самовозбуждения. Механические характеристики такого режима представлены на рис. 5.20. Существует граничная скорость со ф, ниже которой самовозбуждение машины не происходит.
Рис.5.19.
Рис. 5.20.
В режиме противовключения в цепь якоря включают добавочное сопротивление. На рис. 5.21 приведены механические характеристики двигателя для двух вариантов противовключения. Характеристика 1 получается, если при работе двигателя в направлении «вперед» В (точка с)
изменить направление тока в обмотке возбуждения и ввести в цепь якоря добавочное сопротивление. Двигатель переходит в режим противовключения (точка а)
Двигатель переходит в режим противовключения (точка а)
с тормозным моментом М торм.
Рис.5.21.
Если привод работает в режиме спуска груза,
когда задача привода подтормаживать механизм подъема при работе в направлении «назад» Н, то двигатель включают в направлении «вперед» В, но с большим добавочным сопротивлением в цепи якоря. Работе привода соответствует точка b
на механической характеристике 2. Работа в режиме противовключения сопряжена с большими потерями энергии.
Динамические характеристики двигателя постоянного тока последовательного возбуждения описывает система уравнений, вытекающих из (5.22), (5.23), (5.25) при переходе к операторной форме записи:
В структурной схеме (рис. 5.22) коэффициент а
= Д/ я) отражает кривую насыщения машины (см. рис. 5.12). Влиянием вихревых токов пренебрегаем.
Рис. 5.22.
Определить передаточные функции двигателя последовательного возбуждения аналитическим путем достаточно сложно, поэтому анализ переходных процессов производят методом компьютерного моделирования на основе схемы, приведенной на рис.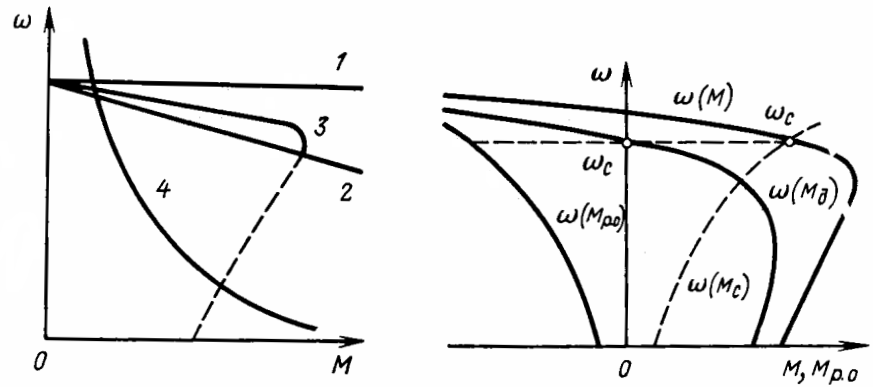 5.22.
5.22.
Двигатели постоянного тока смешанного возбуждения имеют две обмотки возбуждения: независимую
и последовательную.
Вследствие этого их статические и динамические характеристики сочетают характерные свойства двух рассматриваемых ранее видов двигателей постоянного тока. К какому из видов больше принадлежит тот или иной двигатель смешанного возбуждения зависит от соотношения намагничивающих сил, создаваемых каждой из обмоток: в/ п.в = в / п.в я> где в’ п. в — число витков обмотки независимого и последовательного возбуждения.
Исходные уравнения двигателя смешанного возбуждения:
где / в, R B ,
w b — ток, сопротивление и число витков обмотки независимого возбуждения; L m —
взаимная индуктивность обмоток возбуждения.
Уравнения установившегося режима:
Откуда уравнение электромеханической характеристики можно записать в виде:
В большинстве случаев обмотка последовательного возбуждения выполняется на 30.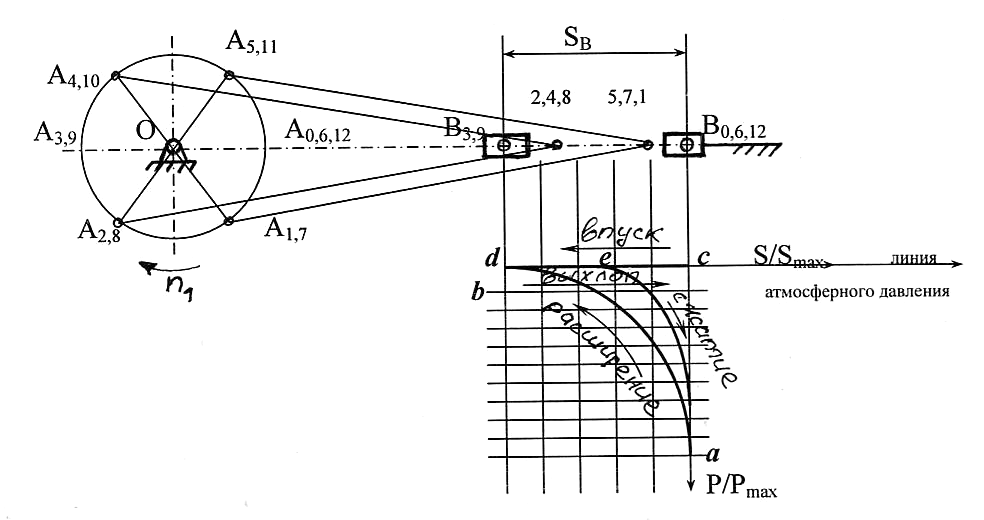 ..40% МД С, тогда скорость идеального холостого хода превышает номинальную скорость двигателя примерно в 1,5 раза.
..40% МД С, тогда скорость идеального холостого хода превышает номинальную скорость двигателя примерно в 1,5 раза.
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРОДВИГАТЕЛЕЙ ПЕРЕМЕННОГО ТОКА Механическая характеристика трехфазного асинхронного двигателя с короткозамкнутым ротор
Схема включения асинхронного электродвигателя с короткозамкнутым ротором показана на рис. 7.1, а. Механическая характеристика двигателя выражает зависимость между вращающим моментом и частотой вращения п, угловой скоростью или скольжением s.
Упрощенное уравнение механической характеристики асинхронного двигателя (формула Клосса) имеет вид
Зная величину Мн и si; и задаваясь значениями s, можно построить механическую характеристику асинхронного двигателя (рис. 7.1, б).
Участок 1, 2 представляет собой рабочую, устойчивую часть характеристики, на которой двигатель работает устойчиво. Потеря скорости при изменении нагрузки составляет 3—6% номинальной, поэтому эту часть характеристики относят к разряду жестких.
Участок характеристики 2, 3 — нерабочий. Двигатель работать под нагрузкой на этой части характеристики не может, поэтому эту часть характеристики называют неустойчивой.
Отношение критического момента Mti к номинальному /Ином называется перегрузочной способностью двигателя Л:
Отношение пускового момента Ма к номинальному Меом называется кратностью пускового момента
Такой частоты вращения ротор двигателя не может достичь самостоятельно, так как для этого необходимо, чтобы момент сопротивления был равен нулю.
Величина пускового тока в 3—8 раз больше номинального, поэтому недопустимо держать включенным двигатель, если он не развернулся после включения или если он опрокинулся (остановился) в результате перегрузки.
Трехфазный асинхронный электродвигатель с коротко- замкнутым ротором имеет следующие положительные качества: простота конструкции; отсутствие нормально искрящих частей; большая перегрузочная способность и жесткость характеристики; надежность в работе и дешевизна в изготовлении.
Наряду с положительными качествами электродвигатель с короткозамкнутым ротором имеет следующие недостатки: высокая чувствительность двигателя к колебаниям напряжения; большой пусковой ток; малый пусковой момент.
Учитывая особенности механической характеристики асинхронных электродвигателей с короткозамкутым ротором, применять их рекомендуется для установок с жесткой характеристикой, перегружаемых в процессе работы и запускаемых без нагрузки.
Трехфазные асинхронные двигатели с короткозамкнутым ротором общего назначения из-за малых пусковых моментов и больших пусковых токов мало пригодны для привода горных машин. Для них созданы специальные короткозамкнутые электродвигатели с уменьшенным пусковым током и увеличенным пусковым моментом, v В основу улучшения пусковых свойств короткозамкнутых двигателей положен принцип автоматического включения дополнительного активного сопротивления в обмотку ротора на период пуска при сохранении принципиального устройства короткозамкнутого ротора.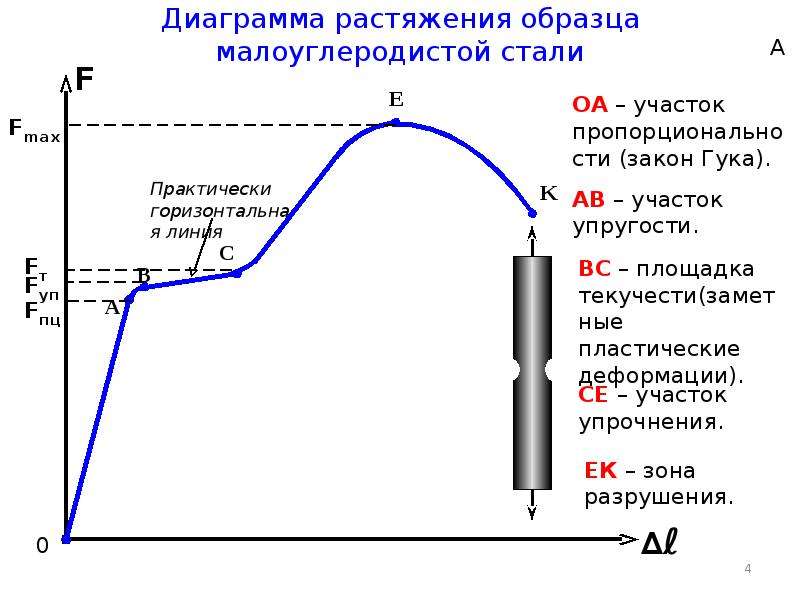 Осуществление этого принципа достигается за счет специальной конструкции обмоток ротора, активное сопротивление которых автоматически изменяется по мере изменения скольжения в двигателе. Для этого обмотки ротора выполняются либо с глубоким пазом (рис. 7.2, б), либо с двойной «беличьей клеткой» (рис. 7.2, а).
Осуществление этого принципа достигается за счет специальной конструкции обмоток ротора, активное сопротивление которых автоматически изменяется по мере изменения скольжения в двигателе. Для этого обмотки ротора выполняются либо с глубоким пазом (рис. 7.2, б), либо с двойной «беличьей клеткой» (рис. 7.2, а).
Механические характеристики двигателя с глубоким пазом 1 и двигателя с двойной «беличьей клеткой» 2 приведены на рис. 7.2 в.
Как видно из характеристик, пусковой момент двигателя с двойной «беличьей клеткой» больше критического, поэтому опрокидывание этого двигателя в результате перегрузки менее вероятно. Даже при вынужденной остановке двигатель сохранит большой пусковой момент п легко разгонится, как только будет устранена причина перегрузки.
(PDF) Анализ механических характеристик и определение зависимости мощности двигателя постоянного тока
534 Hao Hu / Procedia Engineering 15 (2011) 531 – 535
включает определение потерь мощности в зависимости от скорости и крутящего момента,
требуются следующие испытания:
1) Калибруемая машина механически соединена с другой машиной и приводится в движение ею. Предпочтительно, чтобы эта
Предпочтительно, чтобы эта
машина была откалибрована или имела известные характеристики, но при наличии точных приборов подойдет любой двигатель постоянного тока, способный
приводить в движение испытательную машину. Приводная машина должна иметь номинальную мощность, превышающую ожидаемые потери испытательной машины (обычно не менее 15 % от номинальной выходной мощности испытательной машины). Эта машина будет называться
как «приводная» машина в последующем обсуждении.
2) Приводная машина работает как двигатель, не соединенный с испытательной машиной, во всем диапазоне скоростей, который будет использоваться для
испытательной машины.Измеряется входная мощность в выбранной точке скорости.
3) Приводной двигатель и испытательная машина механически связаны. Испытательная машина приводится в движение во всем диапазоне скоростей, и
входная мощность приводного двигателя измеряется в каждой точке скорости. Разница между мощностью, подводимой к приводному двигателю в
каждой точке скорости, определенной в шагах (2) и (3), представляет собой механические потери испытательного двигателя.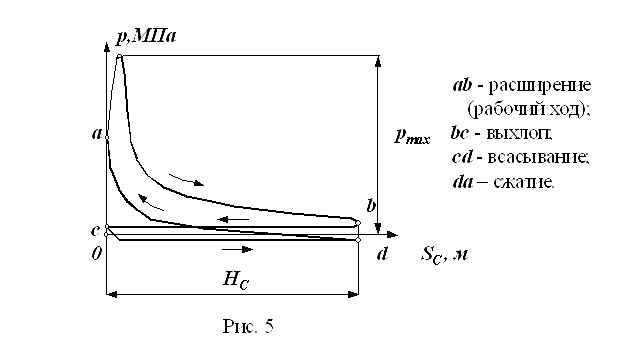 Нанесение этих точек на график в виде
Нанесение этих точек на график в виде
функции скорости дает механические потери испытательного двигателя как функцию скорости.
Механические потери можно разделить на составные части, если это желательно, путем проведения этого испытания дважды: во-первых, с поднятыми щетками испытательной машины
, что дает потери на сопротивление ветру и трение в подшипниках испытательной машины; и, во-вторых, с щетками, установленными на
коммутаторе, что дает полные механические потери. Разница между этими двумя тестами заключается в потере механического трения
щеток.
[4]
4) Тест, описанный в шаге (3) выше, повторяется с заданным значением тока возбуждения испытательной машины.
В дополнение к мощности, подводимой к приводному двигателю, теперь необходимо измерять ток возбуждения и напряжение якоря на испытательной машине
. Разница между мощностью, подводимой к приводному двигателю, измеренной на этом этапе, и мощностью, измеренной на этапе
(3), в каждой точке скорости, представляет собой магнитные потери испытательной машины для заданного значения тока возбуждения.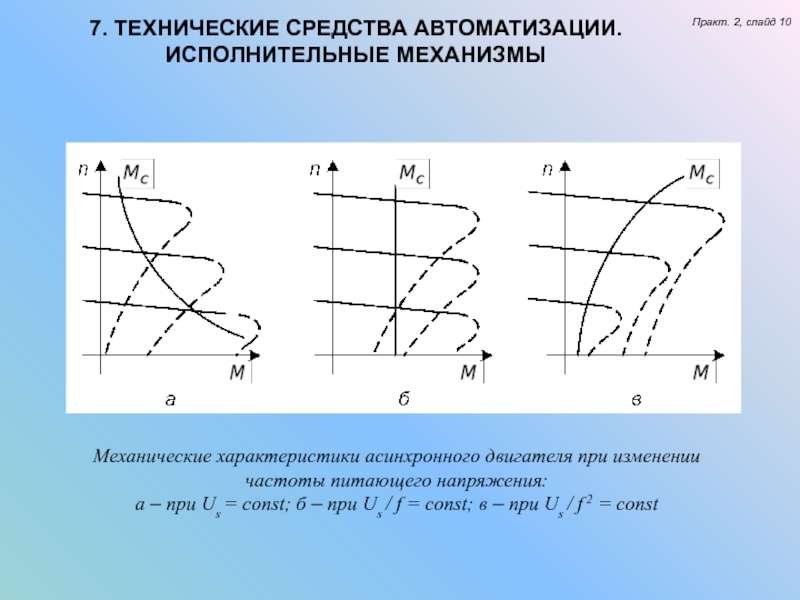 Этот шаг
Этот шаг
следует повторить для нескольких различных значений тока возбуждения — достаточных значений тока возбуждения, чтобы охватить диапазон
работы испытательной машины, поскольку она используется как «откалиброванная» машина.
5) Необходимо получить точное значение сопротивления якоря испытательной машины. Это может включать или не включать сопротивление контакта щетки, в зависимости от факторов, обсуждаемых в соответствующих ссылках. Должны быть известны сопротивление
температурных характеристик якоря и сопротивление щеточного контакта. Это довольно простой вопрос
для самой обмотки якоря, если известен материал проводника. Если электрические потери в щетках должны учитываться
независимо от потерь в обмотках якоря˄что часто делается для силовых машин с графитовыми щетками˅ ,
необходимо измерить падение напряжения на щеточном контакте в зависимости от тока якоря.В небольших машинах или в машинах
с металлическими графитовыми щетками сопротивление контакта щетки обычно может быть объединено с сопротивлением обмотки якоря
, а сопротивление, измеренное на клеммах якоря, может быть использовано для расчета электрических потерь якоря
. Сделаны температурные вариации сопротивления, в данном случае принимая во внимание характеристики материала проводника обмотки
Сделаны температурные вариации сопротивления, в данном случае принимая во внимание характеристики материала проводника обмотки
.
[4][5]
6) Заключительный этап включает измерение потерь от блуждающей нагрузки.Как отмечалось выше, в небольших машинах эти потери часто игнорируются. Чтобы определить, являются ли эти потери значительными, можно использовать следующий тест: Испытательная машина приводится в движение
с заданной скоростью приводным двигателем, как и в предыдущих шагах. При нулевом возбуждении цепь якоря
короткозамкнута. Небольшой ток якоря обычно появляется из-за остаточного магнетизма. Медленно и осторожно
увеличьте возбуждение поля от нуля до значения, при котором протекает номинальный ток якоря.Измерьте ток якоря, ток возбуждения
и входную мощность приводного двигателя. Рассчитайте потери в якоре
2
r и потери в щетках для номинального тока якоря
по значению сопротивления, определенному на шаге (5), с учетом повышения температуры якоря, как указано.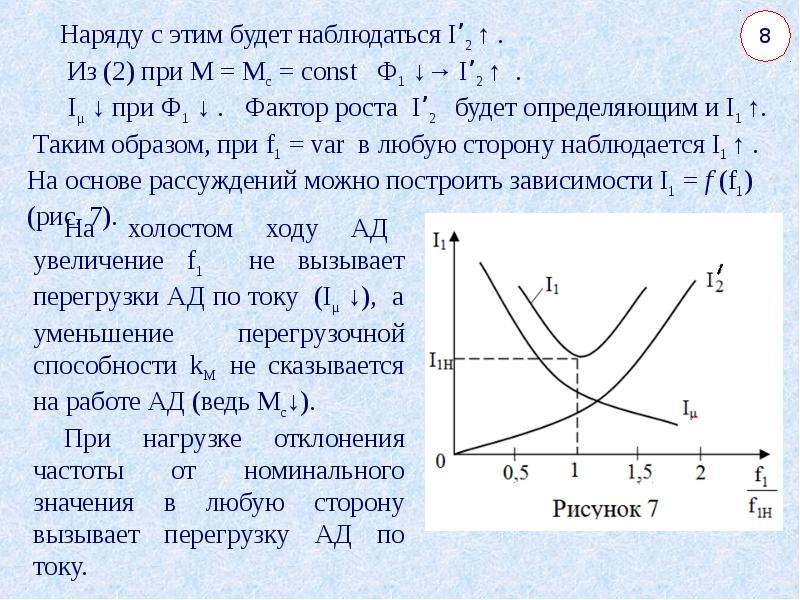
Определите механические потери и магнитные потери испытательного двигателя для скорости и тока возбуждения, используя данные
Механические характеристики машины и их влияние на качество контактной точечной сварки.
Abstract
Точечная сварка сопротивлением (RSW) представляет собой процесс соединения материалов, используемый преимущественно при сборке листового металла. RSW состоит из трех аспектов:  Характеристики и механизм изменения силы исследуются с учетом характеристик машины, таких как жесткость, трение и подвижная масса; параметры процесса, такие как заданное усилие, ток и время; и свойства заготовки, особенно предел текучести.(2)
Характеристики и механизм изменения силы исследуются с учетом характеристик машины, таких как жесткость, трение и подвижная масса; параметры процесса, такие как заданное усилие, ток и время; и свойства заготовки, особенно предел текучести.(2)  Влияние жесткости машины, трения и движущейся массы исследуется экспериментально. Жесткость машины положительно влияет на качество сварки; машинное трение неблагоприятно влияет на качество сварки, за исключением вдавливания алюминия; движущаяся масса не влияет на качество сварки.Разработана методология анализа характеристик процесса для исследования взаимосвязи между машиной RSW и качеством сварки. Научное понимание взаимосвязи достигается с помощью этого подхода. (4)
Влияние жесткости машины, трения и движущейся массы исследуется экспериментально. Жесткость машины положительно влияет на качество сварки; машинное трение неблагоприятно влияет на качество сварки, за исключением вдавливания алюминия; движущаяся масса не влияет на качество сварки.Разработана методология анализа характеристик процесса для исследования взаимосвязи между машиной RSW и качеством сварки. Научное понимание взаимосвязи достигается с помощью этого подхода. (4)
границ | Иерархическая модель машинного обучения для прогнозирования механических свойств полиуретановых эластомеров на основе небольших наборов данных
Введение
Полиуретаны повсеместно используются в покрытиях, пенопластах и твердых эластомерах (Oertel, 1994; Engels et al.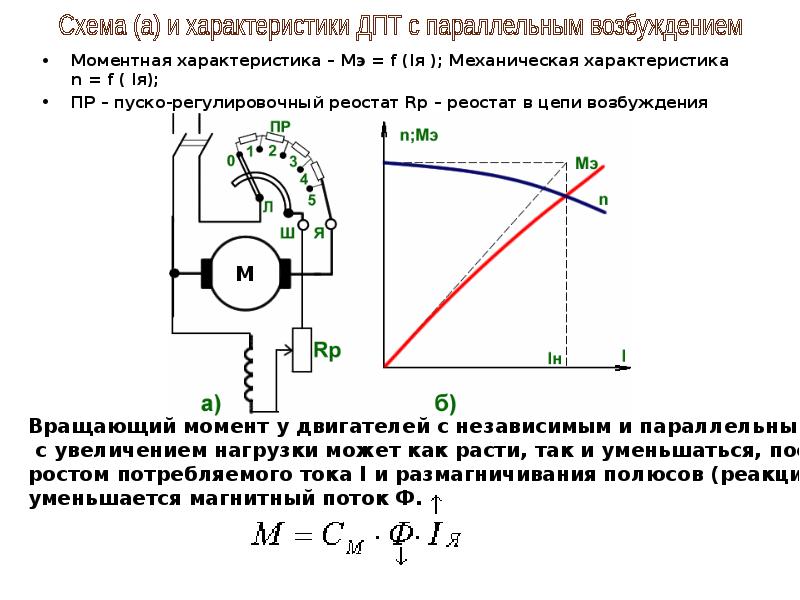 , 2013). Прототипы полиуретанов образуются в результате ступенчатой полимеризации ароматического диизоцианата и алифатического диола, что приводит к образованию материала, имеющего агрегированные ароматические твердые сегменты, соединенные каучукоподобными сегментами.Эта микроструктура лежит в основе замечательных механических свойств полиуретанов, характеризующихся прежде всего эластичностью и большими значениями предельного удлинения. Однако современные полиуретаны основаны на очень разнообразном семействе мономеров, которые обеспечивают контроль над количеством реакционноспособных изоцианатных или спиртовых групп, что позволяет получать линейные или разветвленные материалы с различным химическим составом мономеров, которые регулируют взаимодействие между жесткими сегментами и мягкими сегментами. , и контроль индекса NCO:OH, который контролирует степень полимеризации.Разработка модели для прогнозирования механических свойств этих материалов на основе всех этих композиционных переменных является нерешенной задачей.
, 2013). Прототипы полиуретанов образуются в результате ступенчатой полимеризации ароматического диизоцианата и алифатического диола, что приводит к образованию материала, имеющего агрегированные ароматические твердые сегменты, соединенные каучукоподобными сегментами.Эта микроструктура лежит в основе замечательных механических свойств полиуретанов, характеризующихся прежде всего эластичностью и большими значениями предельного удлинения. Однако современные полиуретаны основаны на очень разнообразном семействе мономеров, которые обеспечивают контроль над количеством реакционноспособных изоцианатных или спиртовых групп, что позволяет получать линейные или разветвленные материалы с различным химическим составом мономеров, которые регулируют взаимодействие между жесткими сегментами и мягкими сегментами. , и контроль индекса NCO:OH, который контролирует степень полимеризации.Разработка модели для прогнозирования механических свойств этих материалов на основе всех этих композиционных переменных является нерешенной задачей.
Существует множество аналитических подходов к прогнозированию свойств полимеров на основе их линейной или сшитой структуры. Вязкоупругие и реологические свойства линейных полимеров были предсказаны с помощью моделей труб (Milner and McLeish, 1998; Pattamaprom et al., 2000; van Ruymbeke et al., 2002, 2005), где теория рептации была расширена за счет колебаний длины контура и снятия ограничений. механизмы, ведущие к успешным предсказаниям, особенно для низкомолекулярных полимеров.Для сшитых полимеров механические свойства были предсказаны с использованием моделирования группового взаимодействия (GIM) (Foreman et al., 2008), где потенциал среднего поля рассчитывается на основе энергии когезии и других молярных констант, полученных с использованием подхода групповой аддитивности на основе каждого компонента. в повторяющемся блоке. Другая модель для прогнозирования термомеханического поведения использует подход молекулярного моделирования (Шеногина и др., 2012), тогда как Эом и др. показывают влияние нативной топологии на механическую прочность сшитых полимерных цепей (Эом и др., 2003).
показывают влияние нативной топологии на механическую прочность сшитых полимерных цепей (Эом и др., 2003).
С появлением машинного обучения во многих традиционных научных дисциплинах и инициативой Materials Genome Initiative появилось множество основанных на данных и машинном обучении подходов к прогнозированию свойств полимеров (de Pablo et al., 2014; Agrawal and Choudhary, 2016). ). Вязкоупругие свойства были смоделированы с использованием многомасштабной вычислительной основы обратного метода Больцмана (Li et al., 2012), а конкретные свойства (механические, тепловые, оптические и электрические) были обучены на микроскопических, мезоскопических и макроскопических структурах из полимерных баз данных. доступны онлайн с использованием искусственных нейронных сетей (Roy et al., 2006). Недавно Ким и др. (2018) разработали платформу полимерной информатики, которая обучает модели машинного обучения набора данных высокопроизводительных вычислений DFT и экспериментальных данных из литературы по полимерам.
Поскольку большинство подходов, основанных на машинном обучении, опираются на большие наборы данных, иерархическое машинное обучение (HML) было разработано на небольших наборах экспериментальных данных для прогнозирования свойств сложных материальных систем с использованием промежуточного слоя между желаемыми откликами и системными переменными (Menon et al., 2017). Эти промежуточные переменные основаны на скрытых физико-химических факторах из предметных знаний, относящихся к материальной системе. Эта методология была проверена на системе концентрированной суспензии MgO с дозированными диспергаторами, которая действовала как нетвердеющая модель цемента. Основываясь на предыдущей работе, HML был успешно использован для разработки суперпластификатора, специально предназначенного для смесей метакаолин-портландцемента (Menon et al., 2018).
В этой работе HML был применен к системе линейных и сшитых полиуретанов, моделирующих механические реакции: напряжение при разрыве, растяжение при разрыве и Tan δ с системными переменными, которые представляют собой структуру полимера, молекулярные массы и плотности реагентов. (диизоцианаты, полиолы), длина цепи полиола и изоцианат: спиртовой (NCO:OH) индекс.Промежуточные переменные, используемые для прогнозирования механических реакций, были выбраны для упрощенного представления межмолекулярного, межцепочечного и сшивающего поведения в системе. Входной набор данных из 18 синтезированных полимеров был разделен на обучающий набор из 14 и тестовый набор из 4 точек данных. Модель была разработана на обучающем наборе и проверена на тестовом наборе. Наконец, было выполнено сравнение алгоритма HML с моделью случайного леса (RF) (Breiman, 2001; Pedregosa et al., 2011), которая напрямую предсказывала механические свойства на основе состава с использованием того же обучающего набора.
Набор обучающих данных
Материалы
Олигомеры и мономеры, используемые для построения обучающего набора, поли(тетраметиленовый эфир)гликоль(ПТМЭГ) (M n = 1,000), поликапролактонтриол (PCL) (M n = 900), толуол-2,4- диизоцианат (TDI), гексаметилендиизоцианат (HDI), изофорондиизоцианат (IPDI) были приобретены у Sigma-Aldrich, а также катализатор, используемый для реакции полимеризации, дилаурат дибутилолова (DBDTL). Дихлорметан был приобретен у EMD Millipore.Все материалы использовались в том виде, в каком они были получены.
Синтез полимеров
Учебный набор состоял из 18 образцов, все из которых были приготовлены путем взаимодействия бифункционального диизоцианата с бифункциональным или трифункциональным полиолом при индексах NCO:OH 1,0, 1,2 или 1,5, как показано в дополнительной таблице 1. Реакции проводились при комнатной температуре в 8 мл дихлорметана в качестве растворителя в присутствии ДБТДЛ в качестве катализатора. Из синтезированных полимеров отливали пленки и оставляли сушиться при комнатной температуре на 24 ч, а затем повторно сушили в вакуумной печи в течение 24 ч при 60°С для удаления остатков растворителя.
Измерения
Прочность на разрыв и деформацию на разрыв измеряли для всех полимеров на универсальной испытательной машине (Instron). Ширина калибра, ширина параллельного сечения и толщина для каждого испытанного образца составляли 12 мм, 4 мм и 2 мм соответственно. Тангенс δ для всех полимеров измеряли с помощью развертки по частоте в реометре Discovery HR-2 (приборы TA), и значение при 1 Гц использовалось в качестве характеристического отклика системы в этом исследовании. ИК-Фурье анализ проводили на образцах пленок толщиной 2 мм на спектрометре Frontier (PerkinElmer) в стандартном диапазоне волновых чисел (4000–700 см -1 ).
Монте-Карло Моделирование
В R было выполнено
моделирования методом Монте-Карло ступенчатой полимеризации роста (R Core Team, 2018). Мы сосредоточились на параметрах, которые позволили бы понять склонность полимерных цепей к сшиванию из-за полифункциональности полиизоцианатов или полиольных реагентов. Эти параметры были определены путем моделирования методом Монте-Карло пространственно-однородного химического ансамбля мономеров; для этих симуляций мы использовали 200 000 мономеров. Алгоритм выполняет основанный на событиях стохастический процесс, аналогичный подходу, описанному Майкесом и Дусеком (1982), затем повторяет стохастический процесс до тех пор, пока не будет израсходована вся предельная реактивная группа, которая в нашем моделировании была группой ОН.Для рецептов с индексом NCO:OH, равным 1, моделирование на этом завершается. Для рецептов с индексом 1,2 и 1,5 мы дополнительно моделируем отверждение влагой. Отверждение влагой относится к реакции некоторых оставшихся непрореагировавших NCO с окружающей влагой с образованием NH 2 с последующими реакциями с NCO с образованием мочевинных связей. В этих случаях, когда весь -ОН израсходован, к ансамблю добавляется соответствующее количество воды, и стохастический процесс продолжается до тех пор, пока не перестанут образовываться связи.Моделирование обеспечивает параметры, которые описывают связность для всех мономеров в постгелевом термореактивном материале. Для нашего анализа мы идентифицируем и количественно оцениваем три типа молекулярных конфигураций, показанных на рисунке 1: золь — это олигомеры, которые не являются частью бесконечной сети, образующейся во время полимеризации, эластичная связь — это эффективные связи, образующиеся между реакционноспособными группами. и образуют часть сшитого сердцевинного гелевого компонента и оборванных элементов, которые представляют собой боковые группы, присоединенные к бесконечной сети и также известные как связанный пластификатор и неэффективные звенья.Важными параметрами являются эффективные поперечные связи на кг полимера (nEff), рассчитанные с использованием рекурсивного метода Миллера и Макоско (Miller and Macosko, 1976), средняя молекулярная масса эластичных связей, взвешенная в процентах от общей массы полимера (elastic_link_mtw). , средняя молекулярная масса гелевого компонента сердцевины, взвешенная в процентах от общей массы полимера (Mtw), процентная доля золя, присутствующего в синтезированном полимере (sol_pctWgt), и процентная доля гелевого компонента сердцевины в синтезированном полимере (Core_pctWgt).
Рис. 1. Схема золя, подвесок, эластичных звеньев и сердцевинных гелевых компонентов, смоделированных более чем для 300 мономеров с использованием моделирования методом Монте-Карло.
HML-моделирование
Моделирование HML было выполнено в Python (Rossum, 1995) с использованием библиотеки обучения Scikit (Pedregosa et al., 2011) для оценки машинного обучения. Моделирование HML теперь используется во многих системах; во всех этих системах верхний слой будет представлять сложную реакцию системы, которую необходимо либо предсказать, либо оптимизировать по отношению к нижнему слою, состоящему из простых экспериментально настраиваемых переменных.Однако существует промежуточный средний слой, который состоит из физических или химических факторов, параметризованных на основе переменных в нижнем слое посредством суррогатных физических измерений и существующих физико-химических взаимосвязей, относящихся к конкретной материальной системе. Алгоритм можно лучше понять со схемой, показанной на рисунке 2.
Рис. 2. Схема, изображающая три уровня подхода иерархического машинного обучения.
Нижний слой входных или экспериментальных переменных в модели для PU состоял из повторяющегося звена в синтезированном полимере, разделенного на химические структурные единицы на кг полимера, молекулярных масс и плотностей диизоцианатов и полиолов, индексов NCO:OH и предполагаемая длина цепи полиолов, предполагая, что PDI равен 1.Химическая структура диизоцианатов и полиолов, используемых в обучающем наборе, представлена на рисунке 3. Каждый из 18 полимеров, синтезированных из этих реагентов, был классифицирован по вектору структурных единиц на кг полимера (c, ch, ch3, ch4, c6h6, co, nh, o, nh3), рассчитанные по группам, входящим в состав реагентов – диизоцианатов и полиолов, индексу NCO:OH, длине цепи полиолов и общей массе синтезированного полимера.
Рис. 3. Химические структуры реагентов, использованных в учебном наборе (A) гексаметилендиизоцианат (B) изофорондиизоцианат (C) толуолдиизоцианат (D) ПТМЭГ
(D) ПТМЭГ
и 1 900.
Средний слой или промежуточные физические/химические переменные были сгруппированы в три категории: первая будет исследовать межмолекулярные взаимодействия и характеристики поглощения синтезированной полимерной молекулы с помощью ИК-Фурье-спектроскопии (Siesler, 1980). Наличие спектральных особенностей в определенных областях спектра указывает на определенные функциональные группы, которые имеют колебательные моды с большими смещениями и минимально подвержены влиянию присутствия других функциональных групп или атомов (Griffiths and de Haseth, 2007).Для нашего исследования полиуретанов волновые числа, демонстрируемые группами CO и NH, а также отношение значений поглощения групп NH к группам CO для каждого образца, имеют особое значение и обеспечат лучшую корреляцию с механическими реакциями. Ранее наблюдалось, что колебание растяжения CO и колебание растяжения NH демонстрируют разные волновые числа в зависимости от степени Н-связи, а также сшивки, происходящей из-за полиола с трифункциональной гидроксильной группой, что значительно влияет на механические свойства таких полиуретанов (Tsai et al., 1998). Ожидается, что определенное количество или степень этих факторов, Н-связей и сшивания, приводит к оптимальной механической реакции, подходящей для конкретного применения конечного пользователя. На степень водородной связи также влияет симметрия химической структуры реагентов и наличие четного/нечетного числа атомов (Caracciolo et al., 2009), что делает эти переменные очень важными для предсказания модели. Эти переменные были параметризованы по отношению ко всем переменным нижнего уровня с использованием фреймворка, основанного на регрессии Гаусса, с использованием библиотеки scikit-learning-ML в Python (Williams and Rasmussen, 1996; Pedregosa et al., 2011). Затем переменные FT-IR были пересчитаны с использованием функции прогнозирования из моделей гауссовых процессов для использования с переменными верхнего уровня.
Второй набор переменных среднего слоя состоит из межмолекулярных цепных взаимодействий и свойств, относящихся к полиуретановой полимерной системе. Жесткий сегмент (HS%) и мягкий сегмент (SS%) легко вычисляются по массе диизоцианата и полиолов по отношению к общей массе полимера. Аналогично, % ароматической и % циклической (неароматической) природы рассчитывали на основе массы соответствующих структурных единиц по отношению к общей массе полимера.Параметр растворимости и плотность энергии когезии (CED) рассчитывали с использованием молярной константы притяжения, молярного объема и энергии когезии повторяющегося звена полимера с использованием подхода, основанного на групповой аддитивности структурных единиц, присутствующих в нижнем слое. Значения группового вклада в молярную константу притяжения, молярный объем и энергию когезии легко доступны в литературе и широко использовались ранее для других полимерных систем.
Третьим набором переменных среднего уровня были прогнозы архитектуры цепи на основе моделирования методом Монте-Карло, как описано в разделе выше.Основываясь на существующей литературе, эти три категории переменных в достаточной степени моделируют основные силы и взаимодействия, определяющие механическое поведение полиуретанов — микроструктуру, состоящую из мягких и твердых доменов, которые контролируют остаточные деформации, высокий модуль и прочность на растяжение, водородные связи между соседними полимерными цепями. контролируют эластичность, а также деформационное поведение, тогда как моделирование химического сшивания направлено на механическое поведение из-за образования сети.
Наконец, верхний слой, который состоит из откликов системы (напряжение при разрыве, растяжение при разрыве и Tan δ), был смоделирован с переменными среднего уровня с использованием модели на основе регрессии случайного леса из журнала scikit- Библиотека машинного обучения на Python. Регрессия случайного леса — это метод ансамблевого обучения, основанный на нескольких деревьях решений, полученных из предоставленных переменных. Одним из преимуществ модели случайного леса является использование агрегации в мешках или начальной загрузки, когда каждое дерево решений моделируется на подмножестве входного набора, но путем составления выборок с заменой подмножество имеет тот же размер, что и исходный входной набор.Затем выполняется усреднение по всем деревьям решений для повышения точности прогноза и контроля переобучения. Количество деревьев решений, использованных в нашем обучающем наборе, равно 100, а максимальная глубина деревьев не ограничивалась, поскольку моделирование выполнялось на разреженном наборе данных и не касалось потребления памяти или вычислительной эффективности, что приводило к лучшей прогнозирующей способности модели. . Оценщик, используемый из библиотеки scikit-ML, представляет собой «RandomForestRegressor» со следующими атрибутами: bootstrap = True, критерий = «mse», max_depth = None, max_features = «auto», max_leaf_nodes = None, min_impurity_decrease = 0.0, min_impurity_split = None, min_samples_leaf = 1, min_samples_split = 2, min_weight_fraction_leaf = 0,0, n_estimators = 100, n_jobs = 4, oob_score = False, random_state = 0, verbose = 0, warm_start = False. Каждый из этих атрибутов хорошо описан на веб-сайте scikit learning для случайной регрессии леса:
.
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html
, и код доступен в дополнительных файлах.
Результаты и обсуждение
На рис. 4 показаны механические характеристики обучающего набора.В целом ожидается, что Tan δ и предел прочности при разрыве уменьшатся, а предел прочности при разрыве увеличится с увеличением индекса NCO:OH, связанного с переходом от резиноподобного состояния к стеклообразному (Petrovic et al., 2002; Levine). et al., 2012) из-за увеличения количества карбамидных связей в полимерной сетке в результате отверждения влагой избыточного содержания NCO. Кроме того, аналогичные тенденции ожидаются при общей замене бифункционального полиола полиолом с более высокой функциональностью благодаря сшиванию и образованию сети (Dušek and Dušková-Smrčková, 2000).Сшивание также происходит либо физически за счет водородных связей между твердыми уретановыми сегментами, либо химически за счет аллофанатных связей из-за избыточного содержания NCO во время реакции полимеризации (Kontou et al., 1990). Мы видим, что хотя некоторые из наших образцов показывают ожидаемое поведение, другие ведут себя по-разному либо в разных метриках отклика, либо во всех них. На рисунке 5 видно, что существует плохая корреляция между различными ответами в широком диапазоне полученных измерений.Диагональная сетка представляет собой одномерный разброс значений для отдельных ответов, тогда как верхняя правая часть представляет собой корреляцию графика рассеяния между парами ответов, а нижняя сетка представляет собой двумерный разброс, а также плотность значений для пар ответов. Это говорит о том, что существует множество факторов, контролирующих эти реакции, которые могут конкурировать друг с другом.
Рис. 4. Механические характеристики, измеренные для обучающего набора из 18 полимеров.
Рис. 5. Решетка, показывающая взаимосвязь между различными механическими свойствами.
Для деконволюции связи между этими механическими реакциями и переменными в нижнем слое модели переменные среднего слоя нашего алгоритма были параметризованы в терминах переменных нижнего слоя. Здесь волновое число CO, волновое число NH и отношение поглощения NH к поглощению CO были смоделированы с помощью регрессии гауссовского процесса с использованием разделения поезд/тест для обеспечения точности и возможности прогнозирования.Оценки обучения и теста для трех переменных показаны в таблице 1. Значения IR были регенерированы из изученной модели GP для дальнейшего использования на следующем этапе обучения.
Таблица 1. Результаты обучения и тестирования для модели GP между переменными FTIR и переменными нижнего слоя.
Параметр растворимости и плотность энергии когезии для полимеров были рассчитаны с использованием методов группового вклада (Van Krevelen and Te Nijenhuis, 2009) с использованием уравнения (1) для параметра растворимости
δ=∑Fi/∑Vm,i (1)
где F i – вклад молярного притяжения, а V m, i – вклад молярного объема для i-й структурной единицы в нижнем слое и уравнение (2) для плотности когезионной энергии
ecoh=∑Ecoh,i/∑Vm,i (2)
, где E coh, i – вклад когезионной энергии для i-й структурной единицы в нижнем слое.HS%, SS%, nEff, elastic_link_mtw, Mtw, sol_pctWgt и core_pctWgt были рассчитаны и смоделированы, как указано в предыдущем разделе.
После создания набора переменных среднего слоя регрессионная модель случайного леса была подобрана между последней и механическими реакциями (напряжение при разрыве, напряжение при разрыве и Tan δ), а также оценки поезда/теста для всех ответы показаны в таблице 2. Значения важности признаков из модели RF показаны на рисунке 6, прогнозируемые и тестовые значения показаны на рисунке 7, а деревья, усредненные по ансамблю, показаны на рисунке 8.
Таблица 2. Результаты обучения и тестирования для HML и моделирования механических свойств в зависимости от состава.
Рис. 6. Графики важности признаков из обученной модели случайного леса для каждого из измеренных механических откликов.
Рис. 7. Прогнозируемые и фактические значения для всех механических откликов по модели HML.
Рисунок 8. Усредненное по ансамблю дерево решений из модели Random Forest, обученное для прогнозирования (A) деформации при разрыве, (B) напряжения при разрыве и (C) Tan δ.
Интересно, что наиболее важными характеристиками для прогнозирования деформации при разрыве из обученной модели были волновое число CO, поглощение NH на поглощение CO, плотность когезионной энергии и волновое число NH. Это может быть связано с колебательным сдвигом в полосах CO и NH, которые относятся к химической среде, полученной с различными комбинациями реагентов (полиолы и диизоцианаты), тогда как отношение поглощения карбонильного пика к поглощению амидного пика может указывать на влияние NCO:OH. показатель.Сдвиг частот указывает на прочность водородных связей между полимерными цепями, в первую очередь из-за взаимодействий между группами CO и NH. Сильная водородная связь между группами сделает связь внутри карбонильной группы и группы NH более слабой, например, HDI и PTMEG 1000 демонстрируют сильную водородную связь, таким образом, более высокая деформация при разрыве, поскольку волновое число CO составляет ~ 1683 см -1 , а волновое число NH составляет ~3318 см -1 . Точно так же между HDI и PCL 900 более слабая водородная связь снижает деформацию при разрыве, где волновое число CO составляет ~ 1732 см -1 , а волновое число NH составляет ~ 3380 см -1 .Плотность когезионной энергии является показателем межмолекулярных сил внутри полимерных цепей и, как таковая, тесно связана с силами, необходимыми для механической деформации полимерного материала. CED также примечателен как инструмент прогнозирования свойств для расчета относительной деформации при разрушении для цепей с аналогичной сетью, т. Е. При наличии умеренного химического сшивания CED может повысить ударную вязкость цепей при большой деформации деформации (Safranski and Gall, 2008). Другие параметры в нашей модели, такие как % цикла и Mtw (средняя молярная масса гелевого компонента сердцевины в процентах от общей массы полимера), также имеют меньшее, но все же влияющее поведение на деформацию.
Помимо переменных, полученных с помощью ИК-Фурье, модель стресса зависит от % жесткого сегмента, core_pctWgt (процентное содержание гелевого компонента сердцевины) и % ароматического поведения. Это имеет смысл, поскольку твердый сегмент полиуретана является несущим компонентом при механической деформации и, как следствие, вызывает большую часть упругой реакции в системе. При более высоком % HS водородная связь уретан-уретан, в частности, также увеличивается. Гелевый компонент сердцевины представляет собой сшитую структуру в полиуретане, что опять-таки соответствует механической прочности и несущей способности полимера.Интересно, что модель определила % ароматического поведения как важную особенность: оно влияет на механическую прочность из-за гораздо более эффективной водородной связи и pi-укладки между ароматическими группами в соседних цепях. Ароматические группы в изоцианатах составляют более жесткие цепи и также приводят к более высокой температуре плавления полиуретана.
Tan δ представляет собой демпфирование механических характеристик вязкоупругого полимера, т. е. отношение пластического поведения к упругому поведению.Таким образом, неудивительно, что и % твердого сегмента, и % мягкого сегмента являются важными признаками, однако циклическое поведение % оказывает интересное значительное влияние на Tan δ. Несмотря на то, что циклические группы соответствуют жесткости и жесткости, они вносят меньший вклад, чем ароматические группы, из-за возможности конфигурационной изомерии, а также неплоских структур. Это может объяснить способность этих групп поглощать больше энергии при механическом воздействии и обеспечивать хороший баланс между эластичностью и пластичностью.Другими важными характеристиками, которые были идентифицированы в модели, были волновое число CO, плотность когезионной энергии и параметр мер-растворимости.
Каждая модель случайного леса, показанная на рис. 8, представляет усредненное дерево решений из ансамбля деревьев решений для каждого механического отклика. Классификатор случайного леса от Python scikit Learn использует агрегацию начальной загрузки, в которой несколько деревьев решений моделируются на подмножествах обучающих данных, выбранных случайным образом с заменой. Каждый предиктор или функция изучается и разделяется на значения на основе схемы уменьшения среднеквадратичной ошибки, которая продолжается до тех пор, пока все данные не будут разделены до последнего узла.Агрегация начальной загрузки — отличный стохастический метод, позволяющий избежать переобучения в обученной модели и уменьшающий дисперсию результата без увеличения смещения модели. В случайных лесах это позволяет использовать оценку ошибки вне пакета (OOB) для измерения ошибки прогнозирования обученного дерева решений на подмножестве данных, не используемых в этом дереве, что устраняет необходимость в независимом наборе данных проверки.
Чтобы оценить эффективность прогнозирования разреженности обучающей выборки, был применен стандартный подход к большим данным, в котором та же структура случайного леса была применена к обучающей выборке, содержащей механические реакции и наши настраиваемые переменные формулировки, а именно выбор полиола, диизоцианат выбор и показатель NCO:OH.Как и ожидалось, модель сошлась со значительно более низкими результатами тестов, как показано в таблице 2, а предсказанные ответы по сравнению с тестовыми данными можно увидеть на рисунке 9.
Рис. 9. Прогнозируемые и фактические значения для всех механических откликов из модели случайного леса с использованием подхода черного ящика.
По сравнению с другими подходами, эта методология в основном выигрывает от запланированных суррогатных физических и химических измерений и существующей научной литературы для включения знаний в предметной области со статистическим обучением для значительного улучшения прогностических возможностей.В традиционных отраслях промышленности трудно собрать данные о высокой пропускной способности для одного семейства продуктов с конкретным приложением конечного пользователя; это требует огромных затрат времени, усилий и затрат. Таким образом, вычислительные методы, основанные на больших данных, не будут способствовать сокращению цикла исследований и разработок в таких отраслях, как показано ранее. Аналитические подходы в некоторых отношениях лучше, поскольку они основаны на физических законах и химии в качестве основы для прогнозирования свойств, однако большинство подходов очень сложны для практического применения в промышленных условиях и очень чувствительны к отсутствию необходимых данных/измерений.План экспериментов предлагает общепринятый метод прогнозирования взаимосвязей структура-свойства для небольших наборов данных, но он не дает понимания того, как основные силы взаимодействуют друг с другом для достижения определенного отклика системы, поскольку он носит чисто статистический характер и не может точно предсказать синергии между переменными. HML стремится изучить недостатки, а также преимущества ранее упомянутых подходов, используя и опираясь на существующий опыт научной области с гораздо меньшими измерениями, предоставляя инструмент не только для прогнозирования свойств, но и для выяснения природы физических и химических явлений. взаимодействия, формирующие реакцию системы.
Заключение
Используя алгоритм HML, механические реакции обучающего набора полиуретанов были в зависимости от химии мономера, индекса и архитектуры цепи. Точность сравнивалась с моделью случайного леса, и было обнаружено, что HML дает значительно лучшие прогнозы тестовых данных. Это было связано с интеграцией промежуточного уровня переменных, включающих физико-химические факторы, основанные на знании предметной области, что значительно улучшило модель, связывающую экспериментальные переменные рецептуры и механические реакции отвержденных эластомеров.Некоторыми из преимуществ этого подхода являются (а) возможность моделирования категориальных и качественных реакций полиуретановых продуктов на состав и параметры обработки и (б) прогнозирование свойств новых мономеров, таких как материалы на биологической основе. В будущей работе мы намерены смоделировать такие реакции, а также протестировать нашу модель, заменив полиолы и диизоцианаты для дальнейшего изучения прогностического характера и возможностей алгоритма HML на полимерных системах.
Вклад авторов
AM (CMU) провел эксперименты, выполнил моделирование машинного обучения и написал части рукописи.Компания JT-C (Covestro, LLC) выполнила моделирование методом Монте-Карло и написала части рукописи. NW (CMU) курировал все аспекты исследования и написал части рукописи.
Заявление о конфликте интересов
JT-C работает в Covestro, LLC, и NW основал компанию для изучения коммерческих приложений описанного здесь алгоритма и заявляет о потенциальном конфликте интересов. NW владеет Ansatz AI, LLC. AM заявляет об отсутствии конкурирующих финансовых интересов.
Дополнительный материал
Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fmats.2019.00087/full#supplementary-material
Ссылки
Агравал, А., и Чоудхари, А. (2016). Перспектива: информатика материалов и большие данные: реализация «четвертой парадигмы» науки в материаловедении. АПЛ Матер. 4:053208. дои: 10.1063/1.4946894
Полнотекстовая перекрестная ссылка | Академия Google
Караччоло, П. К., Буффа, Ф., и Абрахам, Г. А. (2009). Влияние химии и структуры твердого сегмента на термические и механические свойства новых биомедицинских сегментированных полиэфируретанов. Дж. Матер. науч. Матер. Мед. 20, 145–155. doi: 10.1007/s10856-008-3561-8
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
де Пабло, Дж. Дж., Джонс, Б., Ковач, К. Л., Озолиньш, В., и Рамирес, А. П. (2014). Инициатива генома материалов, взаимодействие эксперимента, теории и вычислений. Курс. мнение Твердотельный материал. науч. 18, 99–117. doi: 10.1016/j.cossms.2014.02.003
Полнотекстовая перекрестная ссылка | Академия Google
Душек, К.и Душкова-Смрчкова, М. (2000). Формирование сетчатой структуры при сшивании систем органических покрытий. Прог. Полим. науч. 25, 1215–1260. doi: 10.1016/S0079-6700(00)00028-9
Полнотекстовая перекрестная ссылка | Академия Google
Engels, H.-W., Pirkl, H.-G., Albers, R., Albach, R.W., Krause, J., Hoffmann, A., et al. (2013). Полиуретаны: универсальные материалы и надежные решения для решения современных задач. Анжю. Чеми Инт. Эд . 52, 9422–9441.doi: 10.1002/anie.201302766
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Эом, К., Ли, П.-К., Макаров, Д.Е., и Родин, Г.Дж. (2003). Взаимосвязь между механическими свойствами и топологией сшитых полимерных молекул: параллельные нити максимизируют прочность модельных полимеров и белковых доменов. J. Phys. хим. В 107, 8730–8733. дои: 10.1021/jp035178x
Полнотекстовая перекрестная ссылка | Академия Google
Форман, Дж. П., Портер, Д., Бехзади, С., и Джонс, Ф. Р. (2008). Модель для прогнозирования отношений структура-свойство в сшитых полимерах. Полимер 49, 5588–5595. doi: 10.1016/j.polymer.2008.09.034
Полнотекстовая перекрестная ссылка | Академия Google
Гриффитс, П.Р., и де Хасет, Дж.А. (2007). Инфракрасная спектрометрия с преобразованием Фурье . Хобокен, Нью-Джерси: John Wiley & Sons, Inc.
Академия Google
Ким К., Чандрасекаран А., Хуан Т. Д., Дас Д. и Рампрасад Р.(2018). Полимерный геном: основанная на данных платформа полимерной информатики для прогнозирования свойств. J. Phys. Химия . С 122, 17575–17585. doi: 10.1021/acs.jpcc.8b02913
Полнотекстовая перекрестная ссылка | Академия Google
Конту Э., Спатис Г., Ниаунакис М. и Кефалас В. (1990). Физические и химические эффекты сшивки в полиуретановых эластомерах. Коллоидный полимер. науч. 268, 636–644. дои: 10.1007/BF01410405
Полнотекстовая перекрестная ссылка | Академия Google
Левин, Ф., Эскарсега, Дж., и Ла Скала, Дж. (2012). Влияние отношения изоцианата к гидроксильному индексу на свойства прозрачных полиуретановых пленок. Прог. Орг. Покрытия 74, 572–581. doi: 10.1016/j.porgcoat.2012.02.004
Полнотекстовая перекрестная ссылка | Академия Google
Li, Y., Tang, S., Abberton, B.C., Kröger, M., Burkhart, C., Jiang, B., et al. (2012). Прогностическая многомасштабная вычислительная структура для вязкоупругих свойств линейных полимеров. Полимер 53, 5935–5952. дои: 10.1016/ж.полимер.2012.09.055
Полнотекстовая перекрестная ссылка | Академия Google
Менон, А., Чайлдс, К.М., Почос, Б., Уошберн, Н.Р., и Куртис, К.Е. (2018). Молекулярная инженерия суперпластификаторов для смесей метакаолин-портландцемента с иерархическим машинным обучением. Доп. Теория Моделирование 2:1800164. doi: 10.1002/adts.201800164
Полнотекстовая перекрестная ссылка | Академия Google
Менон, А., Гупта, К., Перкинс, К.М., ДеКост, Б.Л., Будвал, Н., Риос, Р.Т. и др. (2017). Выяснение мультифизических взаимодействий в суспензиях для разработки полимерных диспергаторов: иерархический подход к машинному обучению. Мол. Сист. Дес. англ. 2, 263–273. дои: 10.1039/C7ME00027H
Полнотекстовая перекрестная ссылка | Академия Google
Майкс, Дж., и Дусек, К. (1982). Моделирование формирования полимерной сетки методом Монте-Карло. Макромолекулы 15, 93–99. дои: 10.1021/ma00229a018
Полнотекстовая перекрестная ссылка | Академия Google
Миллер, Д.Р. и Макоско, К.В. (1976). Новый вывод свойств сетчатых полимеров после геля. Макромолекулы 9, 206–211. дои: 10.1021/ma60050a004
Полнотекстовая перекрестная ссылка | Академия Google
Милнер С.Т. и Маклиш Т.С.Б. (1998). Рептация и флуктуации длины контура в расплавах линейных полимеров. Физ. Преподобный Летт. 81, 725–728. doi: 10.1103/PhysRevLett.81.725
Полнотекстовая перекрестная ссылка | Академия Google
Ортель, Г. (1994). Справочник по полиуретану: химия-сырье-обработка-применение-свойства. Второе издание . Нью-Йорк, штат Нью-Йорк: Hanser Publishers.
Паттамапром, К., Ларсон, Р. Г., и Ван Дайк, Т. Дж. (2000). Количественные прогнозы линейных вязкоупругих реологических свойств запутанных полимеров. Реол. Acta 39, 517–531. дои: 10.1007/s003970000104
Полнотекстовая перекрестная ссылка | Академия Google
Педрегоса, Ф., Вароко, Г., Грамфор, А., Мишель, В., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: машинное обучение в {p}ython. Дж. Маха. Учиться. Рез. 12, 2825–2830.
Академия Google
Петрович З.С., Чжан В., Златанич А., Лава С.С. и Илавский М. (2002). Влияние молярного соотношения OH/NCO на свойства полиуретановых сеток на основе сои. Дж. Полим. Окружающая среда. 10, 5–12. дои: 10.1023/A:1021009821007
Полнотекстовая перекрестная ссылка | Академия Google
Россум, Г. (1995). Справочное руководство Python .Амстердам: CWI (Центр математики и компьютерных наук).
Академия Google
Рой, Н.К., Поттер, В.Д., и Ландау, Д.П. (2006). Прогнозирование и оптимизация свойств полимеров с использованием нейронных сетей. IEEE Trans. Нейронная сеть. 17, 1001–1014. doi: 10.1109/TNN.2006.875981
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Сафрански Д.Л. и Галл К. (2008). Влияние химической структуры и плотности сшивания на термомеханические свойства и ударную вязкость (мет)акрилатных полимерных сетей с памятью формы. Полимер 49, 4446–4455. doi: 10.1016/j.polymer.2008.07.060
Полнотекстовая перекрестная ссылка | Академия Google
Шеногина Н.Б., Циге М., Патнаик С.С. и Мухопадхьяй С.М. (2012). Подход к молекулярному моделированию для предсказания термомеханического поведения термореактивных полимерных сеток. Макромолекулы 45, 5307–5315. дои: 10.1021/ma3007587
Полнотекстовая перекрестная ссылка | Академия Google
Siesler, HW (1980). Инфракрасная (FTIR) спектроскопия с преобразованием Фурье в исследованиях полимеров. Дж. Мол. Структура 59, 15–37. дои: 10.1016/0022-2860(80)85063-0
Полнотекстовая перекрестная ссылка | Академия Google
Цай, Ю.-М., Ю, Т.-Л., и Ценг, Ю.-Х. (1998). Физические свойства сшитого полиуретана. Полим. Междунар. 47, 445–450. doi: 10.1002/(SICI)1097-0126(199812)47:4 <445::AID-PI82>3.0.CO;2-B
Полнотекстовая перекрестная ссылка | Академия Google
Ван Кревелен, Д. В., и Те Нидженхуис, К. (2009). Свойства полимеров .Амстердам: Эльзевир. doi: 10.1016/B978-0-08-054819-7.X0001-5
Полнотекстовая перекрестная ссылка | Академия Google
van Ruymbeke, E., Keunings, R., and Bailly, C. (2005). Прогнозирование линейных вязкоупругих свойств полидисперсных смесей звездчатых и линейных полимеров: модифицированная трубчатая модель и сравнение с экспериментальными результатами. Дж. Нонньютон. Жидкостный мех. 128, 7–22. doi: 10.1016/j.jnnfm.2005.01.006
Полнотекстовая перекрестная ссылка | Академия Google
ван Руймбеке, Э., Кенингс Р., Стефан В., Хагенарс А. и Байи К. (2002). Оценка рептационных моделей для прогнозирования линейных вязкоупругих свойств запутанных линейных полимеров. Макромолекулы 35, 2689–2699. дои: 10.1021/ma011271c
Полнотекстовая перекрестная ссылка | Академия Google
Williams, C.K.I., и Rasmussen, CE (1996). Гауссовские процессы для регрессии. Доп. Нейронная инф. Процесс. Сист. 8, 515–520.
Академия Google
Влияние машинной податливости на механические характеристики материалов при испытаниях на статическое растяжение
C. Ullner, E. Reimann, H. Kohlhoff и A. Subaric-Leitis, «Эффект и измерение податливости машины в макродиапазоне инструментального теста на вдавливание», Measurement , 43 , № 2, 216–222 (2010).
Пашков П. О., Кириенко А. М. Особенности деформирования и разрушения стали в конструкциях различной жесткости // Прочность Матер.
Артикул
Google Scholar
Пресняков А.А., Мофа Н.Н., Аубакирова Р.К. и др. Влияние жесткости испытательной машины на механические свойства материалов // Прочность Матер. ).
Артикул
Google Scholar
Попов Н.Н. Влияние жесткости нагружения на предысторию деформирования при квазистатических испытаниях металлов // Прочность Матер. ., 22 .
Артикул
Google Scholar
Воробьев Е.В. О влиянии жесткости системы нагружения на сопротивление деформации и разрушение образцов сплавов при глубоком охлаждении // Прочность Матер. (2001).
Артикул
Google Scholar
ГОСТ 1497-84. Металлы. Метод испытаний на растяжение . Действителен с 1 января 1986 г.
ГОСТ 28840-90. Машины для испытаний на растяжение, сжатие и изгиб. Общие технические требования . Действительны с 1 января 1993 г.
Воробьев Е.В., Стрижало В.А., Анпилогова Т.В. Металлы в жидком гелии: прерывистая текучесть, скачки напряжений и прочность. в: Гелий: возникновение, применение и биологические эффекты , Nova Science Publishers, Inc., Нью-Йорк (2013), стр.1–38.
Воробьев Е.В., Анпилогова Т.В. Численный анализ деформационной неустойчивости металлов в жидком гелии // . Ж. вычисл. Матер. науч. , 68 , 66–72 (2013).
Артикул
Google Scholar
Иванченко Л.Г., Солдатов В.П. Влияние формы деформации на характер неустойчивого течения монокристаллов алюминия при низких температурах // Физ. Металл.Металлолюбивый. , № 1, 183–188 (1981).
ДСТУ 7305:2013. Металлы. Метод испытания металлов и сплавов на растяжение при низких и криогенных температурах , Действителен с 1 января 2014 г.
Обзор механических свойств металлов
В металлообрабатывающей промышленности механические свойства играют огромную роль при выборе подходящего сплава для каждой задачи. В процессе литья и механической обработки, а также в течение срока службы изделия выбранный материал будет подвергаться воздействию многих внешних сил.Производители должны создавать продукты, которые работают должным образом на каждом этапе пути. Зная механические свойства, специалисты-производители могут сделать правильный выбор материалов и процессов.
Механические свойства описывают, как материал реагирует на приложенные нагрузки или силы. Эти свойства непостоянны; они меняются в зависимости от температуры и других внешних факторов, поэтому производители должны иметь полное представление об условиях эксплуатации детали, прежде чем рекомендовать подходящий материал.Ключевые механические свойства металлов включают:
- Прочность
- Пластичность и пластичность
- Прочность
- Сопротивление усталости
- Твердость
Физические свойства — это еще один способ различения металлов. Вы можете узнать больше о физических свойствах в нашем блоге здесь.
Стресс против напряжения
Напряжение и деформация являются важными терминами при обсуждении механических свойств.Напряжение относится к силе, приложенной к объекту. Деформация относится к степени деформации объекта под действием этого напряжения.
Прочность металлов
Прочность можно измерить несколькими способами, но обычно она показывает, какую силу объект может выдержать, не согнувшись и не сломавшись. Отношение прочности к весу является ключевым свойством металлов, поскольку оно сообщает производителям, сколько материала необходимо использовать для удовлетворения конкретных требований прочности.
Прочность часто измеряется с точки зрения реакции материала на напряжения или приложенные силы в трех конфигурациях: сжатие , растяжение и сдвиг .Когда материал подвергается сжатию, на него действуют силы в направлении его центральной точки. Противоположное верно для напряжения, которое растягивает материал. Силы сдвига действуют параллельно друг другу в противоположных направлениях.
Пластичность и ковкость металлов
Несмотря на то, что прочность может быть хорошим предиктором реальной производительности, производителям необходимо продвигать материалы за пределы своих возможностей, чтобы формировать новые формы. Пластичность и ковкость показывают, насколько легко можно манипулировать материалом, не ломая его.Под пластичностью понимается реакция материала на растягивающее напряжение или его способность растягиваться, прокатываться или экструдироваться без разрушения. Ковкость относится к сжимающему напряжению, как и при сплющивании. Благодаря высокой пластичности алюминия он так широко используется для изготовления тонкой фольги.
Поскольку поведение материала меняется в зависимости от температуры, металл может иметь хорошую пластичность или ковкость при высоких температурах, но плохую пластичность или ковкость при комнатной температуре. Сотни лет назад кузнецы уже знали об этой переменной и нагревали изделия на основе железа до свечения, прежде чем придавать им форму.
Прочность: баланс между прочностью и пластичностью
Прочность представляет собой идеальный баланс между прочностью и пластичностью. Самые прочные металлы — это те, которые могут поглотить наибольшее количество энергии до разрушения. Проще говоря, самые прочные части труднее всего сломать.
Сопротивление усталости металлов
В реальных условиях металлические детали часто подвергаются повторяющимся нагрузкам в течение длительного периода времени. Хотя ни одно из этих напряжений, взятых по отдельности, не может повлиять на прочность, пластичность или ударную вязкость детали, само по себе повторение может привести к отказу.Фактически, по данным ASM International, усталость является причиной примерно 90% механических отказов.
Сопротивление усталости — это мера способности детали подвергаться повторяющимся циклическим нагрузкам без разрушения или необратимой деформации. Величина напряжения, близкая к предельной для материала, приведет к более раннему усталостному разрушению по сравнению с меньшим напряжением. Как и другие механические свойства, сопротивление усталости данного сплава зависит от температуры, при которой применяется напряжение, а также от других факторов окружающей среды.
Сопротивление усталости готовой детали зависит не только от ее материала, но и от наличия дефектов. Такие проблемы, как пористость, растрескивание или другие дефекты, возникшие во время производства, могут резко снизить сопротивление усталости детали. Чтобы узнать о распространенных дефектах литья и о том, как их предотвратить, прочитайте статью в нашем блоге.
Твердость
Твердость материалов может относиться к характеристикам по ряду параметров, включая устойчивость к деформации, устойчивость к царапинам или устойчивость к порезам.Металлы демонстрируют сильную корреляцию между пределом прочности при растяжении и твердостью, а твердость стали часто можно увеличить, увеличив процентное содержание углерода.
Твердость можно измерить разными способами, и тест на твердость по Бринеллю является одним из наиболее распространенных для металлических изделий. Тест, впервые предложенный в 1900 году, заключается в вдавливании сферы из карбида или закаленной стали в поверхность измеряемой детали. Образовавшуюся вмятину на поверхности затем измеряют с помощью микроскопа и определяют число твердости по Бринеллю (BHN) как нагрузку, деленную на площадь поверхности вмятины.
Более твердые сплавы часто хуже поддаются механической обработке, что может создавать трудности при изготовлении изделий. Принимая во внимание дизайн для технологичности, иногда в целом лучше использовать менее твердый сплав для отливки, особенно если изделие будет подвергаться интенсивной механической обработке на более позднем этапе.
Выбор подходящего сплава на основе механических свойств
В мире производства наиболее важные механические свойства зависят от предполагаемого использования продукта.Поскольку механические свойства зависят от окружающей среды, процесс проектирования продукта должен включать тщательный анализ среды, в которой продукт будет работать, включая требования к температуре, влажности и нагрузке. Производители также должны учитывать все процессы формирования материала, прежде чем он станет конечным продуктом. Часто перед инженерами и металлургами стоит задача найти баланс между показателями производительности, такими как прочность, и показателями процесса, такими как обрабатываемость.
Процесс APQP может гарантировать, что перед выбором сплава будут учтены все соответствующие переменные, и лучшие литейщики будут следовать процедурам APQP при разработке продукта.Чтобы узнать больше об оптимальных этапах проектирования изделий при литье металлов и обработке на станках с ЧПУ, прочитайте нашу серию блогов здесь.
Узнайте больше о производстве высококачественной продукции с помощью литья металлов и обработки на станках с ЧПУ из нашей бесплатной электронной книги:
Эффективные КЭ-модели для моделирования упруго-механических характеристик формовочных машин
Требования к КЭ-моделям
КЭ-модели должны отражать правильное упругое поведение упругих компонентов пресса независимо от того, какой формующий инструмент исследуется при моделировании. , включая его индивидуальное распределение нагрузки.Поскольку в этой статье основное внимание уделяется столу пресса и ползуну пресса как наиболее важным упругим компонентам, две отдельные модели должны быть подготовлены таким образом, чтобы их можно было комбинировать с формовочным инструментом при моделировании формования. Поскольку деформация упругого компонента сильно зависит от распределения индуцированной нагрузки, недостаточно создать эффективную модель КЭ на основе одного измеренного случая нагрузки. Вместо этого модель КЭ должна быть создана или оптимизирована с использованием набора различных загружений, которые идеально охватывают множество теоретически возможных распределений нагрузок, возникающих в процессе формования.
На практике это требование должно сводиться к наиболее типичным распределениям нагрузки. Как указывалось ранее, на этом этапе нельзя использовать формовочные инструменты, поскольку распределение давления не может быть в достаточной степени оцифровано. Приведение к единичным силам, измеренным тензодатчиками, является рекомендуемым подходом для воспроизведения экспериментального сценария нагрузки с помощью граничных условий в моделировании КЭ. Дополнительным преимуществом является доступность зажимных поверхностей. Измерение и оценка этих приведенных распределений нагрузки оправданы для упругого поведения в соответствии с принципом суперпозиции, который дается для аппроксимации двух рассматриваемых упругих компонентов.
Подход к моделированию, основанный на топологической оптимизации
Как правило, топологическая оптимизация используется для повышения эффективности материалов в процессе проектирования путем исключения областей с низкими нагрузками. Таким образом, можно оптимизировать соотношение жесткости к весу. Доступная структура для настройки модуля Юнга E j для каждого отдельного элемента КЭ j используется в этом подходе для моделирования упругого поведения прессового стола. Граничные условия включают измеренные нагрузки (через тензодатчики) совместно с неподвижной опорой в зоне фундамента пресса.Оптимизация f ( E j ), как показано в уравнении. 1 представляет собой минимизацию остатка между измеренной деформацией \(\hat {u}_{i}\) в точке измерения i и соответствующей смоделированной u i .
На этом этапе модель будет оптимизирована для одного измеренного случая нагрузки, что сильно отклоняется от требования получить универсальную модель, работающую для различных сценариев нагрузки p .{2} $$
(2)
Необходимо объединить все доступные загружения p в одну функцию оптимизации f ( E j ) с тем же набором оптимизированных модулей упругости элементов E
4 как видно из уравнения 2. После этого этапа модель в принципе способна эмулировать все требуемые загружения. При объединении нескольких измеренных загружений в одну процедуру оптимизации возникает необходимость взвешивания, чтобы определить, где допустима неизбежная неточность, вызванная более высоким сжатием информации в одной и той же модели.{2} $$
(3)
На рис. 5 а показан прямоугольный параллелепипед как наиболее универсальная отправная точка для итеративной топологической оптимизации прессового стола при усилиях прессования от F 1 до F 4 и с фиксированной опорой. Здесь опорная плита является отдельным элементом в сборке стола пресса, поэтому ее можно исключить из оптимизации, чтобы в дальнейшем обеспечить надежный контакт с инструментом и превратить отклонение зажимной поверхности в непрерывную функцию C 1 ( х , и ).Элементы, близкие к неподвижной опоре, также исключаются из оптимизации.
Рис. 5
Модель куба с областью оптимизации (синяя) и зонами взаимодействия (красная) ( a ). Результирующее распределение оптимизированного модуля Юнга ( b )
На рисунке 5b показана результирующая модель стола пресса с оптимизированными модулями Юнга для каждого элемента. Здесь модуль Юнга уменьшается от 100% (красный) до 0% (синий), а элементы с модулем, близким к нулю, маскируются.Из-за большой зависимости между соседними элементами оптимизация этой модели неэффективна. Из-за большого начального объема требуются многочисленные элементы, сильно зависящие от линейной зависимости, поэтому оптимизация занимает много времени даже при использовании более крупных элементов.
Используя приведенные выше сведения о базовой архитектуре обычного стола для пресса, начальную модель прямоугольного параллелепипеда можно определить в форме, которую легче оптимизировать. На рисунке 6 показан этот подход, объединяющий общую модель прессового стола с его зеркальным близнецом в качестве ползуна пресса вместе с формовочным инструментом.Геометрия двух моделей стола пресса и ползуна пресса состоит из оптимизированных разреженных корпусов (светлая часть) и зажимных пластин с неоптимизированными монтажными поверхностями (темная часть). Для оптимизируемых частей моделей предполагаемая сетка уже показана и иллюстрирует линейные независимые элементы, которые довольно велики по сравнению с размером конструкции.
Рис. 6
Комбинация формообразующего инструмента с топологически оптимизированными разреженными моделями ползуна пресса и стола пресса и на изгиб), и стропильный каркас из одноэлементных связей между ними.Таким образом, в дополнение к сильно уменьшенному количеству элементов значительно улучшается сходимость оптимизации, что в совокупности приводит к сокращению времени вычислений. Точность модели в воспроизведении измеренных прогибов для измеренных загружений по-прежнему высока, как показано для примера гидравлического пресса в [13]. Еще одним преимуществом модели, созданной с помощью этой стратегии, является снижение накладных расходов при моделировании в сочетании с геометрией формовочного инструмента и операциями формования.
Далее на рис. 6 показана простая взаимосвязь между моделью формовочного инструмента и установленными моделями ползуна пресса и стола пресса. Это обеспечивается непрерывными зажимными поверхностями пластин валика, которые не оптимизированы.
Подход к моделированию, основанный на оптимизации параметров
Хотя граничное условие для стола пресса достаточно надежное, относительно гибкая опора ползуна приводит к плохой сходимости и точности топологической оптимизации ползуна пресса.Это также основано на простой формулировке доступной целевой функции (уравнение). 3 в используемом программном обеспечении Simulia Tosca®;. Таким образом, на рис. 7а показан другой подход к моделированию упругого поведения ползуна пресса.
Рис. 7
Модель ползуна пресса из корпусов и дискретных вертикальных пружин для оптимизации параметров ( a ). Та же модель с сеткой КЭ вместе с моделью стола пресса вне топологической оптимизации ( b )
Чтобы преодолеть ограничительную целевую функцию в топологической оптимизации, касающуюся только перемещений, стратегия моделирования, основанная на оптимизации параметров, используется для ползуна пресса.Особенно при использовании метода наименьших квадратов возможно, что соседние точки оценки отклоняются в противоположных направлениях, что резко увеличивает ошибку наклона, как показано на рис. 8. Поскольку наклон имеет почти такое же значение, как и сам отклонение, но не может быть охвачены топологическим подходом, разработана новая стратегия оптимизации.
Рис. 8
Термины для прогибов и наклонов
Модель ползуна пресса создается из оболочек (прижимная поверхность, продольные и поперечные пластины стенки) и дискретных вертикальных пружин, как показано на рис.7а. Эта модель имеет значительно меньшее количество свободных параметров. Небольшое количество параметров, представляющих толщину оболочки и дискретную одноосную жесткость, позволяет в дополнение к сокращению времени моделирования передать оптимизацию в Matlab®; рутина. В этой процедуре целевая функция может быть определена свободно, и в текущем состоянии она включает три члена для отклонений и наклонов.{2} \\ && + b_{i,p}\left( \left.{2} \end{массив} $$
(4)
Уравнение 4 является адаптацией уравнения 3 с новыми параметрами оптимизации k , включающими дискретные пружины и толщину оболочки. Кроме того, он включает дополнительные условия для учета ошибок наклона, как показано на рис. 8.
Ошибка перемещения в точке оценки i при нагрузке p взвешивается с a i , p ; ошибка наклона в x -направлении в той же точке взвешивается с b i , p , а ошибка наклона в y -направлении взвешивается в соответствии с i c , р .Взвешивание, которое обычно не зависит от каких-либо физических свойств, является результатом важности отдельных точек оценки, где центральные точки более важны для взаимодействия с формовочным инструментом. Хорошая сходимость может быть обеспечена при использовании этого общего подхода к моделированию ползуна, где фиксированная опора пружин включает характеристику точек давления. Наклон можно настроить с помощью граничных условий.
При креплении одноосных пружин непосредственно к отдельным узлам поведение модели становится частично зависимым от размера сетки.Поскольку модель индивидуальна для каждой анализируемой формовочной машины, размер сетки может быть установлен в соответствии с требованиями моделирования, а также в зависимости от размера машины. Для моделирования измеряемых испытательных прессов с зажимными поверхностями размером 2500 мм × 4500 мм размер ячейки модели ползуна был определен равным 50 мм. Количество оптимизируемых параметров зависит от 45 одноосных пружин и 7 толщин корпуса.
Линеаризация и интегрирование нелинейностей в модели
В то время как представленные упрощенные модели демонстрируют линейное упругое поведение, измеренные прогибы нелинейны в зависимости от общей силы прессования, как показано на рис.4. При малых отношениях нелинейных частей к полным перемещениям ими можно пренебречь; в противном случае их необходимо учитывать в модели.
Одним из вариантов является добавление нелинейных частей к линейным, что не требует дополнительных усилий, но приводит к модели, которая является точной только для одной силы прессования, т. е. той, которая получена при измерении. Для меньших сил прессования смоделированные деформации будут слишком малы, так как нелинейное смещение занижено, а для больших сил прессования смещения будут слишком большими, так как фиксированные нелинейные части переоценены.
Другой вариант — исключить нелинейные части и рассматривать их отдельно в рабочем процессе моделирования. Это приводит к сокращенной модели, всегда приводящей к деформации, которая слишком мала по сравнению с измеренными полными перемещениями [13].
Наиболее точным вариантом является адаптация базовых моделей, созданных выше, таким образом, чтобы нелинейные смещения были возможны параллельно линейному поведению базовой модели, как показано на рис. 9.
Рис. 9
Адаптация базовой модели с интегрированными нелинейностями
Нелинейности могут быть включены в модель двумя различными способами.Одним из вариантов является сегментация опорной пластины таким образом, чтобы за зажимной поверхностью открывался зазор, равный нелинейному смещению, как показано на рис. 9а. Контакт между двумя пластинами вполне реально закроет зазор под нагрузкой, а благодаря плоской прижимной поверхности модель остается удобной в использовании.
Другой вариант является результатом перемещения узлов зажимной поверхности на величину нелинейного смещения и образования зазора между зажимной поверхностью и формующим инструментом, как показано на рис.9б. Этот параметр уменьшает размер модели, но повышает уязвимость к неуместным граничным условиям во время использования.
машина | Британика
машина , устройство, имеющее уникальное назначение, которое увеличивает или заменяет усилия человека или животного для выполнения физических задач. В эту широкую категорию входят такие простые устройства, как наклонная плоскость, рычаг, клин, колесо и ось, шкив и винт (так называемые простые машины), а также такие сложные механические системы, как современный автомобиль.
Работа машины может включать преобразование химической, тепловой, электрической или ядерной энергии в механическую или наоборот, или ее функция может заключаться просто в изменении и передаче сил и движений. Все машины имеют вход, выход и преобразующее или модифицирующее и передающее устройство.
Британская викторина
Машиностроение и производство
От сверления отверстий и перевозки грузов до автомобильных двигателей и их производства — поработайте над этими вопросами и проверьте свои знания в области машиностроения и производства в этой викторине.
Машины, которые получают входную энергию из природного источника, такого как воздушные потоки, движущаяся вода, уголь, нефть или уран, и преобразуют ее в механическую энергию, известны как первичные двигатели. Первичными двигателями являются ветряные мельницы, водяные колеса, турбины, паровые двигатели и двигатели внутреннего сгорания. В этих машинах входы различаются; выходы обычно представляют собой вращающиеся валы, которые можно использовать в качестве входов для других машин, таких как электрические генераторы, гидравлические насосы или воздушные компрессоры.Все три последних устройства можно отнести к генераторам; их выходы электрической, гидравлической и пневматической энергии могут использоваться в качестве входных данных для электрических, гидравлических или пневматических двигателей. Эти двигатели можно использовать для привода машин с различной мощностью, например машин для обработки материалов, упаковки или транспортировки, или таких устройств, как швейные и стиральные машины. Все машины последнего типа и все другие, которые не являются ни первичными двигателями, ни генераторами, ни двигателями, могут быть отнесены к операторам.В эту категорию также входят инструменты всех видов с ручным управлением, такие как счетные машины и пишущие машинки.
В некоторых случаях машины всех категорий объединяются в одну единицу. В дизель-электрическом локомотиве, например, дизельный двигатель является первичным двигателем, который приводит в действие электрогенератор, который, в свою очередь, подает электрический ток на двигатели, приводящие в движение колеса.
Компоненты машин в автомобиле
Как часть введения в компоненты машин, некоторые примеры, поставляемые с автомобилем, представляют ценность.В автомобиле основной проблемой является использование взрывного эффекта бензина для обеспечения мощности для вращения задних колес. Взрыв бензина в цилиндрах толкает поршни вниз, а передача и преобразование этого поступательного (линейного) движения во вращательное движение коленчатого вала осуществляется шатунами, которые соединяют каждый поршень с кривошипами, которые являются частью коленчатого вала. . Комбинация поршня, цилиндра, кривошипа и шатуна известна как кривошипно-ползунковый механизм; это широко используемый метод преобразования поступательного движения во вращение (как в двигателе) или вращения в поступательное движение (как в насосе).
Для подачи бензино-воздушной смеси в цилиндры и выпуска отработавших газов используются клапаны; они открываются и закрываются заклиниванием кулачков (выступов) на вращающемся распределительном валу, который приводится в движение от коленчатого вала шестернями или цепью.
В четырехтактном двигателе с восемью цилиндрами коленчатый вал получает импульс в какой-то точке по его длине каждую четверть оборота. Чтобы сгладить влияние этих прерывистых импульсов на частоту вращения коленчатого вала, используется маховик.Это тяжелое колесо, прикрепленное к коленчатому валу, своей инерцией противостоит и смягчает любые колебания скорости.
Поскольку развиваемый им крутящий момент (крутящая сила) зависит от его частоты вращения, двигатель внутреннего сгорания не может быть запущен под нагрузкой. Чтобы автомобильный двигатель можно было запустить в ненагруженном состоянии, а затем подключить к колесам без остановки, необходимы сцепление и трансмиссия. Первый устанавливает и разрывает связь между коленчатым валом и трансмиссией, а второй с конечными шагами изменяет соотношение между входной и выходной скоростями и крутящими моментами трансмиссии.На пониженной передаче выходная скорость низкая, а выходной крутящий момент выше, чем крутящий момент двигателя, поэтому автомобиль можно начать движение; на высокой передаче автомобиль движется со значительной скоростью, а крутящий момент и скорость равны.
Оси, к которым крепятся колеса, содержатся в картере заднего моста, который закреплен на задних рессорах, и приводятся в движение от трансмиссии приводным валом. Когда автомобиль движется и пружины изгибаются в ответ на неровности дороги, корпус перемещается относительно трансмиссии; чтобы обеспечить это движение, не мешая передаче крутящего момента, к каждому концу приводного вала прикреплен универсальный шарнир.
Приводной вал перпендикулярен задним мостам. Прямоугольное соединение обычно выполняется с помощью конических шестерен, имеющих такое передаточное число, что оси вращаются со скоростью от одной трети до одной четвертой скорости приводного вала. Корпус заднего моста также содержит дифференциальные шестерни, которые позволяют обоим задним колесам приводиться в движение от одного источника и вращаться с разными скоростями при повороте.
Как и все движущиеся механические устройства, автомобили не могут избежать воздействия трения.В двигателе, трансмиссии, картере заднего моста и всех подшипниках трение нежелательно, так как оно увеличивает мощность, требуемую от двигателя; смазка уменьшает, но не устраняет это трение. С другой стороны, трение между шинами и дорогой, а также в тормозных колодках делает возможным сцепление и торможение. Ремни, приводящие в движение вентилятор, генератор и другие аксессуары, зависят от трения. Трение также полезно при работе сцепления.
Некоторые из упомянутых выше устройств встречаются в машинах всех категорий, собранных множеством способов для выполнения всех видов физических задач.Функция большинства этих основных механических устройств заключается в передаче и изменении силы и движения. Другие устройства, такие как пружины, маховики, валы и крепежные детали, выполняют дополнительные функции.
Машина может быть дополнительно определена как устройство, состоящее из двух или более устойчивых, относительно ограниченных частей, которые могут служить для передачи и изменения силы и движения для выполнения работы. Требование, чтобы части машины были прочными, подразумевает, что они способны выдерживать приложенные нагрузки без отказа или потери функции.Хотя большинство деталей машин представляют собой твердые металлические тела подходящих пропорций, также используются неметаллические материалы, пружины, органы давления жидкости и натяжные органы, такие как ремни.
Ограниченное движение
Наиболее отличительной характеристикой машины является то, что части взаимосвязаны и направляются таким образом, что их движения относительно друг друга ограничены. По отношению к блоку, например, поршень поршневого двигателя вынужден двигаться цилиндром по прямой траектории; точки на коленчатом валу ограничены коренными подшипниками для перемещения по круговым траекториям; никакие другие формы относительного движения невозможны.
На некоторых машинах детали закреплены только частично. Если части соединены между собой пружинами или фрикционными элементами, траектории частей относительно друг друга могут быть фиксированными, но на движения частей может влиять жесткость пружин, трение и массы частей.